最新初中数学思维导图完整版
初中数学知识点思维导图

初中数学知识点思维导图1. 数与式1.1. 有理数- 定义:可以表示为两个整数的比的数。
- 性质:包括正有理数、负有理数和零。
- 运算:加法、减法、乘法、除法。
1.2. 无理数- 定义:不能表示为两个整数比的实数。
- 例子:π、√2等。
1.3. 代数式- 单项式:由数字和字母的乘积组成。
- 多项式:由多个单项式相加组成。
- 运算:合并同类项、分配律等。
2. 方程与不等式2.1. 一元一次方程- 形式:ax + b = 0。
- 解法:移项、合并同类项。
2.2. 二元一次方程组- 形式:ax + by = e, cx + dy = f。
- 解法:代入法、消元法。
2.3. 不等式- 性质:传递性、可加性、乘法性。
- 解法:移项、合并同类项、取交集。
3. 函数3.1. 一次函数- 形式:y = mx + b。
- 图像:直线。
3.2. 二次函数- 形式:y = ax^2 + bx + c。
- 图像:抛物线。
3.3. 反比例函数- 形式:y = k/x。
- 图像:双曲线。
4. 几何4.1. 点、线、面- 点:几何图形的基本元素。
- 线:由无数点组成。
- 面:由无数线组成。
4.2. 角- 锐角:小于90°。
- 直角:等于90°。
- 钝角:大于90°小于180°。
4.3. 三角形- 等边三角形:三边相等。
- 等腰三角形:两边相等。
- 直角三角形:一个角为90°。
4.4. 四边形- 正方形:四边相等且四个角都是直角。
- 矩形:对边相等且四个角都是直角。
- 平行四边形:对边平行。
4.5. 圆- 定义:所有点到中心点距离相等的点的集合。
- 性质:周长、面积、直径、半径。
5. 统计与概率5.1. 数据收集与处理- 收集:通过调查、实验等方式。
- 处理:数据整理、分类。
5.2. 统计图表- 条形图:表示数量的多少。
- 折线图:表示数量的变化趋势。
- 饼图:表示各部分占总体的比例。
七年级数学下册思维导图(超全)

七年级数学下册思维导图(超全)第一章:实数1. 实数的概念2. 实数的分类有理数整数正整数、负整数、零分数正分数、负分数无理数3. 实数的运算加法减法乘法除法乘方开方第二章:代数式1. 代数式的概念2. 代数式的分类单项式多项式3. 代数式的运算减法乘法除法乘方第三章:方程与不等式1. 方程的概念2. 一元一次方程求解方法3. 不等式的概念4. 一元一次不等式求解方法第四章:函数1. 函数的概念2. 函数的表示方法解析式法图象法3. 一次函数定义图象性质4. 二次函数定义图象第五章:几何图形1. 点、线、面2. 线段3. 角锐角、直角、钝角、平角、周角4. 三角形定义分类性质5. 四边形定义分类性质6. 圆定义性质第六章:概率与统计1. 概率的概念2. 概率的计算方法3. 统计的概念4. 数据的收集与整理5. 数据的表示方法表格法6. 数据的分析方法七年级数学下册思维导图(超全)第一章:实数1. 实数的概念实数是包括有理数和无理数在内的所有数的集合。
2. 实数的分类有理数整数正整数、负整数、零分数正分数、负分数无理数不能表示为两个整数比例的数,如根号2、π等。
3. 实数的运算加法将两个实数相加得到一个新的实数。
减法将一个实数减去另一个实数得到一个新的实数。
乘法将两个实数相乘得到一个新的实数。
除法将一个实数除以另一个非零实数得到一个新的实数。
乘方将一个实数乘以自身多次得到一个新的实数。
开方求一个实数的平方根或立方根等。
第二章:代数式1. 代数式的概念代数式是由数、字母和运算符号组成的表达式。
2. 代数式的分类单项式只有一个项的代数式。
多项式由多个项组成的代数式。
3. 代数式的运算加法将两个代数式相加得到一个新的代数式。
减法将一个代数式减去另一个代数式得到一个新的代数式。
乘法将两个代数式相乘得到一个新的代数式。
除法将一个代数式除以另一个非零代数式得到一个新的代数式。
乘方将一个代数式乘以自身多次得到一个新的代数式。
初中数学七年级上册思维导图

初中数学七年级上册思维导图一、数的认识1. 整数自然数:0, 1, 2, 3,正整数:1, 2, 3,负整数:1, 2, 3,整数:自然数和负整数的统称2. 分数真分数:分子小于分母的分数假分数:分子大于或等于分母的分数分数的基本性质:分子分母同时乘以或除以同一个非零整数,分数的值不变3. 小数小数的表示方法:整数部分和小数部分小数的性质:小数点向右移动一位,相当于乘以10;小数点向左移动一位,相当于除以10二、数的运算1. 整数的运算加法:将两个整数相加减法:将一个整数从另一个整数中减去乘法:将两个整数相乘除法:将一个整数除以另一个非零整数2. 分数的运算加法:将两个分数的分子相加,分母保持不变减法:将一个分数的分子从另一个分数的分子中减去,分母保持不变乘法:将两个分数的分子相乘,分母相乘除法:将一个分数的分子乘以另一个分数的分母,分母乘以另一个分数的分子3. 小数的运算加法:将两个小数的小数部分相加,整数部分相加减法:将一个小数的小数部分从另一个小数的小数部分中减去,整数部分相减乘法:将两个小数相乘除法:将一个小数除以另一个非零小数三、方程与不等式1. 方程一元一次方程:ax + b = 0(a, b为常数,x为未知数)方程的解:使方程成立的未知数的值2. 不等式一元一次不等式:ax + b > 0 或 ax + b < 0(a, b为常数,x 为未知数)不等式的解集:满足不等式的未知数的值的集合四、函数与图形1. 函数定义:函数是一种特殊的关系,每个输入值对应唯一的输出值表示方法:函数关系可以用函数表达式、函数图像、函数表格等方式表示2. 图形直线:一次函数的图像抛物线:二次函数的图像双曲线:反比例函数的图像五、统计与概率1. 统计数据的收集与整理:收集数据、整理数据、制作统计图表数据的分析与解释:分析数据、得出结论、解释结论2. 概率概率的定义:某个事件发生的可能性概率的计算:根据事件发生的次数和总次数计算概率初中数学七年级上册思维导图六、几何图形的认识1. 点、线、面点:没有长度、宽度和高度的几何元素线:只有长度没有宽度和高度的几何元素面:具有长度和宽度的几何元素2. 平面图形三角形:由三条线段组成的闭合图形四边形:由四条线段组成的闭合图形圆:由一个点到平面上所有点的距离相等的点的集合3. 空间图形立方体:由六个正方形面组成的立体图形圆柱:由两个平行圆面和一个侧面组成的立体图形圆锥:由一个圆面和一个侧面组成的立体图形七、几何图形的性质1. 三角形的性质内角和定理:三角形的内角和等于180度等腰三角形的性质:底角相等,底边上的高、中线、角平分线互相重合直角三角形的性质:直角边上的高、中线、角平分线互相重合2. 四边形的性质平行四边形的性质:对边平行且相等,对角相等,对角线互相平分矩形的性质:四个角都是直角,对边平行且相等,对角线互相平分且相等菱形的性质:四个角都是直角,对边平行且相等,对角线互相垂直平分3. 圆的性质圆的周长公式:C = 2πr(r为圆的半径)圆的面积公式:A = πr²圆的性质:圆心到圆上任意一点的距离都相等八、几何图形的计算1. 三角形的计算三角形的周长:三条边的长度之和三角形的面积:底乘以高除以22. 四边形的计算四边形的周长:四条边的长度之和四边形的面积:根据不同类型的四边形使用相应的公式计算3. 圆的计算圆的周长:2πr圆的面积:πr²九、综合应用1. 解决实际问题利用数学知识解决生活中的实际问题,如计算面积、周长、体积等运用几何知识解决空间布局问题,如设计家具布局、建筑平面图等2. 数学建模将实际问题抽象为数学模型,如建立函数模型、方程模型等利用数学模型解决问题,如预测趋势、优化资源配置等初中数学七年级上册思维导图十、数学思维与方法1. 逻辑推理演绎推理:从一般到特殊的推理过程归纳推理:从特殊到一般的推理过程类比推理:通过比较不同事物之间的相似性进行推理2. 数学建模实际问题抽象:将实际问题转化为数学问题建立模型:选择合适的数学模型来描述问题模型求解:利用数学方法求解模型,得到问题的解答3. 解决问题的策略分析问题:明确问题的目标和已知条件寻找规律:通过观察、实验、推理等方式寻找解决问题的规律制定计划:根据规律制定解决问题的步骤和方法执行计划:按照计划逐步解决问题检验结果:验证解答的正确性,对结果进行评估和反思十一、数学实验与探究1. 数学实验通过实际操作和观察,验证数学结论的正确性培养学生的动手能力和观察能力培养学生的探究精神和创新意识2. 数学探究提出问题:发现问题并提出有意义的数学问题收集信息:查阅资料、进行调查、进行实验等,获取解决问题的信息分析信息:对收集到的信息进行分析和整理提出假设:根据分析结果提出可能的解答或解决方案实验验证:通过实验或推理验证假设的正确性得出结论:根据实验结果或推理结果得出结论十二、数学交流与合作1. 数学交流表达观点:清晰地表达自己的数学观点和思考倾听他人:耐心倾听他人的数学观点和思考互相讨论:与他人进行数学问题的讨论和交流共享资源:分享自己的数学知识和经验,互相学习2. 数学合作分工合作:在解决问题或完成数学任务时,进行合理的分工和合作互相支持:在合作过程中互相支持和帮助共同解决问题:共同面对问题,共同寻找解决方案分享成果:分享合作成果,互相学习和借鉴初中数学七年级上册思维导图一、数与代数1. 实数(1)有理数:包括整数和分数,整数又分为正整数、0和负整数,分数分为正分数和负分数。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作+√a 和√a。
0的平方根是0,负数没有平方根。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
每个实数都有唯一的立方根。
3. 开方运算:开方运算是求一个数的平方根或立方根的运算。
对于正数a,开方运算可以表示为√a或³√a。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:实数可以分为正实数、负实数和0。
正实数是大于0的实数,负实数是小于0的实数,0既不是正实数也不是负实数。
3. 实数的运算:实数可以进行加法、减法、乘法和除法运算。
在运算过程中,需要遵循实数的运算规律,如交换律、结合律和分配律。
三、勾股定理1. 勾股定理的内容:勾股定理指出,在一个直角三角形中,直角边的平方和等于斜边的平方。
即a²+b²=c²,其中a、b是直角边,c是斜边。
2. 勾股定理的应用:勾股定理可以用来解决直角三角形中的边长问题,也可以用来解决一些与直角三角形相关的实际问题。
3. 勾股定理的证明:勾股定理的证明有多种方法,其中一种常见的证明方法是使用几何图形的面积关系。
四、一次函数1. 一次函数的概念:一次函数是指函数的图像是一条直线,其一般形式为y=kx+b,其中k是斜率,b是截距。
2. 一次函数的性质:一次函数的图像是一条直线,斜率k表示直线的倾斜程度,截距b表示直线与y轴的交点。
3. 一次函数的应用:一次函数可以用来描述一些线性关系,如物体的速度与时间的关系、正比例关系等。
五、不等式1. 不等式的概念:不等式是表示两个数之间大小关系的数学表达式,如a>b、a<b、a≥b、a≤b等。
2. 不等式的性质:不等式可以进行加减、乘除运算,但在乘除运算中需要注意符号的变化。
初中数学知识结构图思维导图

圆 上
圆 外
外心:是三边垂直平 分线的交点. 到三顶点的距离相等锐—形内;直—斜边上;钝—形外
相交
相切
相离
切线的 性质.判定
切线长 定理
内心:是三角平分线的交点. 到三边的距离相等在三角形内
外 离
内 含
外 切
内 切
相 交
等分圆周
正多边形
弧等
性质
平行线
相交线
对邻 顶补 角角
垂 直
性质
判定
相等
和 为1800
点到直线 的距离
性质
定义
画法
条件
平行公理.推论
一“放”二“靠” 三“推”四“画”
同位角相等
内错角相等
同旁内角互补
同位角相等
同旁内角互补
内错角相等
分类
结构
命题
关系
借助角研究平面内两条直线的位置关系
三角形
有关线段
多边形 及其 内角和
解决几何中的 极值问题
利用轴对称制作图案
对称轴
全等 三角形 与 相似 三角形
定义
性质
条件
角平分线
表示方法
完全重合 两个三角形
对应边、角、周长 面积、中线、高线、 角平分线相等
两个三角形 用符号≌连接
SSS
AAS
ASA
HL
SAS
适合判定所有三角形 全等
适用于 直角三角形
会画统计图
集中趋势
离散程度
平均数
中位数
众数
极 差
方 差
反映数据向其中心值聚集的程度
反映数据分布的离散程度
借助抽样做决策
比例线段
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作√a和√a。
0的平方根是0。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
立方根只有一个。
3. 算术平方根:正数a的正的平方根,记作√a,称为a的算术平方根。
4. 立方根的性质:①正数的立方根是正数;②负数的立方根是负数;③0的立方根是0。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:①正实数;②负实数;③零。
3. 实数的运算:实数的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
三、二次根式1. 二次根式的概念:形如√a的式子,其中a≥0,称为二次根式。
2. 二次根式的性质:①√a²=a(a≥0);②(√a)²=a(a≥0);③√ab=√a√b(a≥0,b≥0);④√a²+b²=√a²+√b²(a≥0,b≥0)。
3. 二次根式的运算:二次根式的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
四、一元二次方程1. 一元二次方程的概念:形如ax²+bx+c=0(a≠0)的方程,称为一元二次方程。
2. 一元二次方程的解法:①配方法;②求根公式法;③因式分解法。
3. 一元二次方程的根的判别式:判别式△=b²4ac,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根。
五、不等式1. 不等式的概念:表示不相等关系的式子称为不等式。
2. 不等式的性质:①两边同时加上或减去同一个数,不等号方向不变;②两边同时乘以或除以同一个正数,不等号方向不变;③两边同时乘以或除以同一个负数,不等号方向改变。
初中数学分章节知识图解思维导图省公开课获奖课件市赛课比赛一等奖课件
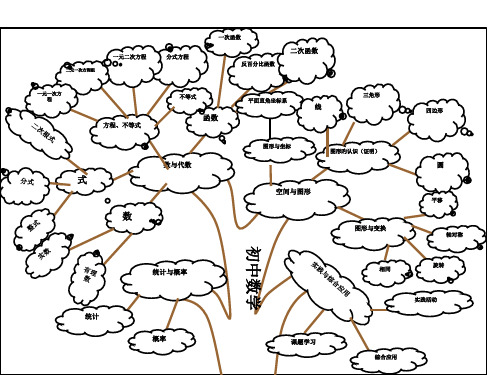
一元二次方程
分式方程
一次函数 反百分比函数
二次函数
一元一次方 程
方程、不等式
不等式
函数
数与代数
式
数
平面直角坐标系
线
三角形
图形与坐标
图形旳认识(证明)
空间与图形
图形与变换
四边形
圆
平移 轴对称
初中数学
统计
统计与概率 概率
课题学习
相同
旋转
实践活动
综合应用
逆用公式
平方 差、 完全 平方
多项式除以单项式
相应点与旋转中心所连线段旳夹角=
征
旋转角
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其本身 重叠
对称中心是对称点连线旳中 点
相应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 相应点坐标 旳变化规律
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
用平移.轴对称和旋转旳组合设计图 案
(3) a 2 a
Y随 x旳 增 大 而 增 大
b>0,图象在 一二三象限
y ox
y
b>0,图象在
o
x 一二四象限
b=0,图象在 一三象限
b<0,图象在 一三四象限
y
y
注意:过原点
o
x
o
b=0,图象在 二四象限
x
y
y
b<0,图象在
二三四象限
o
x 一条直线 o
x
Y随 x旳 增 大 而 减 小
Y随
x旳
②④
