约瑟夫环(C语言解答)
C语言用循环单链表实现约瑟夫环

C语⾔⽤循环单链表实现约瑟夫环⽤循环单链表实现约瑟夫环(c语⾔),供⼤家参考,具体内容如下源代码如下,采⽤Dev编译通过,成功运⾏,默认数到三出局。
主函数:main.c⽂件#include <stdio.h>#include "head.h"#include "1.h"int main(){Linklist L;int n;printf("请输⼊约瑟夫环中的⼈数:");scanf("%d",&n);Createlist(L,n);printf("创建的约瑟夫环为:\n");Listtrave(L,n);printf("依次出局的结果为:\n");Solution(L,n);return 0;}head.h⽂件:#include "1.h"#include <stdio.h>#include <stdlib.h>typedef int Elemtype;typedef struct LNode{Elemtype data;struct LNode *next;}LNode,*Linklist;void Createlist(Linklist &L,int n){Linklist p,tail;L = (Linklist)malloc(sizeof(LNode));L->next = L;//先使其循环p = L;p->data = 1;//创建⾸节点之后就先给⾸节点赋值,使得后⾯节点赋值的操作能够循环tail = L;for(int i = 2;i <= n;i++){p = (Linklist)malloc(sizeof(LNode));p->data = i;p->next = L;tail->next = p;tail = p;}printf("已⽣成⼀个长度为%d的约瑟夫环!\n",n);}void Listtrave(Linklist L,int n)//遍历函数{Linklist p;p = L;for(int i = 1;i <= n;i++){printf("%3d",p->data);p = p->next;}printf("\n");}int Solution(Linklist L,int n){Linklist p,s;p = L,s = L;int count = 1;while(L){if(count != 3){count++;p = p->next;//进⾏不等于3时的移位}else{Linklist q;q = p;//⽤q保存p所指的位置,⽅便进⾏节点的删除if(s->next->data == s->data)//当只有⼀个元素的时候{printf("%3d\n",s->data);free(s);return OK;}else//当有两个及两个以上的元素的时候{count = 1;//先将count重置为1printf("%3d",p->data);//再打印出出局的值while(s->next != p){s = s->next;//将s移位到p的前驱节点处}p = p->next;//使p指向⾃⼰的下⼀个节点s->next = p;//进⾏删除free(q);}}}}1.h⽂件:#define TRUE 1#define FALSE 0#define OK 1#define ERROR 0#define INFEASIBLE -1#define OVERFLOW -2运⾏结果:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
C实验报告约瑟夫斯环问题

约瑟夫斯(Josephus)问题的一种描述是:编号为1,2,…,n的n个人按顺时针方向围坐一圈,每人持有一个密码(正整数)。
一开始任选一个正整数作为报数上限值m,从第一个人开始按顺时针方向自1开始报数,报到m时停止报数。
报m的人出列,将他的密码作为新的m值,从他在顺时针方向下一个人开始重新从1报数,如此下去,直至所有的人全部出列为止。
试设计一个程序,按出列顺序印出各人编号。
2.基本要求:利用单向循环链表存储结构模拟此过程,按照出列的顺序印出各人的编号。
3.测试数据:m的初值为20;n=7,7个人的密码依次为:3,1,7,2,4,8,4。
m初值为6(正确的出列顺序应为6,1,4,7,2,3,5)。
4.简述每一部分的对象、目的和要求:(1)主函数部分:对象:链表;目的:创建新链表;要求:将该链表初始化。
(2)被调函数部分:对象:结构体;目的:创建循环链表并且模拟约瑟夫斯问题;要求:让链表首尾相接,并且释放原来单链表的头结点空间。
通过该函数的调用,依次输出各结点的编号,并且符合规则。
二.需求分析1.程序所能达到的基本可能:该程序用循环链表来模拟n个人顺时针围坐一圈,用链表中的每一个结点代表一个人,结点结构体中设置两个变量,分别存放其编号以及密码。
在输入初始密码后,对该链表进行遍历,直到遍历到第m个结点,释放其空间,使其出列。
然后用被释放空间结点的密码值作为新的密码值,重复上述过程,直至所有结点被释放空间出列,链表成为空链表。
2.输入输出形式及输入值范围:程序运行后显示提示信息:"Please input a data:",提示用户输入密码信息,在输入达预定次数后自动跳出该循环,同时循环链表创建成功,在主函数中有相应的输出给予检验。
然后程序显示提示信息:"Please input the number m:",提示用户输入初始密码,程序执行结束后会输出相应的出列结点的顺序,亦即其编号。
C++编写的 约瑟夫环问题 代码

程序源代码:#include <stdio.h>#include <malloc.h>#include<conio.h>#include <stdlib.h>#include<ctime>#define NULL 0typedef struct Node{int m;//密码int n;//序号struct Node *next;}Node,*Linklist;Linklist create(int z) //生成循环单链表并返回,z为总人数{int i,mm;Linklist H,r,s;H=NULL;printf("请按顺序依次为每个人添加密码:");for(i=1;i<=z;i++){printf("\ninput cipher=");scanf("%d",&mm);s=(Linklist)malloc(sizeof(Node));s->n=i;s->m=mm;printf("%d号的密码%d",i,s->m);if(H==NULL)//从链表的第一个节点插入{H=s;r=H;}else//链表的其余节点插入{r->next=s;r=s;//r后移}//for结束r->next=H;/*生成循环单链表*/return H;}void search(Linklist H,int m0,int z)//用循环链表实现报数问题{int count=1;//count为累计报数人数计数器int num=0;//num为标记出列人数计数器Linklist pre,p;p=H;printf("出列的顺序为:");while(num<z){do{count++;pre=p;p=p->next;}while(count<m0);{pre->next=p->next;printf("%d ",p->n);m0=p->m;free(p);p=pre->next;count=1;num++;}//while结束}void clean(){int system(const char *string);int inquiry;printf("请问需要清除上一次操作记录吗(1.清屏/2.不清屏)...?\n"); scanf("%d",&inquiry);if(inquiry ==1)system("cls");}void text(){int m0,z,i, choose,k=1; //k用来阻止第一次进入程序清屏操作Linklist H;bool chooseFlag=false;while(1){if(k!=1)clean();k++;while(!chooseFlag){printf(" ……………………欢迎进入约瑟夫环问题系统…………………… \n"); printf( "* 1.输入约瑟夫环数据 * \n"); printf(" * 2.什么是约瑟夫环 * \n"); printf(" * 3.退出系统 * \n"); printf("........................................................ \n"); printf("请输入相应的数字进行选择: ");scanf("%d",&choose);for(i=1;i<=4;i++){if(choose==i) { chooseFlag=true; break;}else chooseFlag=false;}if(!chooseFlag) printf("Error Input!\n");} //end while(!chooseFlag)if(choose==1) //if 开始{printf("Input how many people in it:");//z为总人数scanf("%d",&z);if(z<=30){H=create(z);//函数调用printf("\nInput the start code m0=");scanf("%d",&m0);search(H,m0,z);printf("\n\n\n");}else{printf("超过最大输入人数\n");break;}}else if(choose==2){printf("\n约瑟夫环问题:设有n个人,其编号分别为1,2,3,…,n,安装编号顺序顺时针围坐一圈。
约瑟夫环数据结构C语言版

{tail = tail->next;} } p = tail->next; printf("%d,", p->num); tail->next = p->next; code = p->code; free(p); p = NULL; --num; } } printf("%d.",tail->num); free(tail); tail = NULL; return; }
3. 程序执行的命令包括: (1)构造链表;(2)输入数据;(3)执行报数,储存出列人的序号,删除出列人 的信息以及把出列人的密码赋给 m;(4)结束。
4. 测试数据 n=7,7 个人的密码依次为:3,1,7,2,4,8,4,首先 m 值为 6,则这正确
的出列顺序为 6,1,4,7,2,3,5。
示范代码:(Tc 2.0 编译) #include "stdio.h" #include "alloc.h" #include "conio.h"
int num = 0,code = 0; scanf("%d%d",&num, &code); {
SeqList * tail = NULL; tail=Creat(num); OutQueue(tail, num, code); } } getch();
return(1); }
SeqList * Creat(int num) {
typedef struct Node {
int num; int code; struct Node * next; }SeqList;
C语言的循环链表和约瑟夫环

C语言的循环链表和约瑟夫环C语言的循环链表和约瑟夫环约瑟夫问题)是一个数学的应用问题,对于学习C语言四非常挺有帮助的,下面是店铺为大家搜集整理出来的有关于C语言的循环链表和约瑟夫环,一起了解下吧!循环链表的实现单链表只有向后结点,当单链表的尾链表不指向NULL,而是指向头结点时候,形成了一个环,成为单循环链表,简称循环链表。
当它是空表,向后结点就只想了自己,这也是它与单链表的主要差异,判断node->next是否等于head。
代码实现分为四部分:1. 初始化2. 插入3. 删除4. 定位寻找代码实现:1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1void ListInit(Node *pNode){int item;Node *temp,*target;cout<<"输入0完成初始化"<<endl; cin="">>item;if(!item)return ;if(!(pNode)){ //当空表的时候,head==NULLpNode = new Node ;if(!(pNode))exit(0);//未成功申请pNode->data = item;pNode->next = pNode;}else{//for(target = pNode;target->next!=pNode;target = target->next);4 15 16 17 18 19 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3temp = new Node;if(!(temp))exit(0);temp->data = item;temp->next = pNode;target->next = temp;}}}void ListInsert(Node *pNode,int i){ //参数是首节点和插入位置Node *temp;Node *target;int item;cout<<"输入您要插入的值:"<<endl; cin="">>item;if(i==1){temp = new Node;if(!temp)exit(0);temp->data = item;for(target=pNode;target->next != pNode;target = target->next);temp->next = pNode;target->next = temp;pNode = temp;}else{target = pNode;for (int j=1;j<i-1;++j) target="target-">next;temp = new Node;if(!temp)exit(0);temp->data = item;temp->next = target->next;target->next = temp;}}void ListDelete(Node *pNode,int i){Node *target,*temp;if(i==1){for(target=pNode;target->next!=pNode;target=target ->next);temp = pNode;//保存一下要删除的首节点 ,一会便于释放6 37 38 39 4 0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 5 1 5 2 5 3 5 4 5 5 5 6 5 7 5pNode = pNode->next;target->next = pNode;temp;}else{target = pNode;for(int j=1;j<i-1;++j) target="target-">next;temp = target->next;//要释放的nodetarget->next = target->next->next;temp;}}int ListSearch(Node *pNode,int elem){ //查询并返回结点所在的位置Node *target;int i=1;for(target = pNode;target->data!=elem && target->next!= pNode;++i)target = target->next;if(target->next == pNode && target->data!=elem)return 0;else return i;}</i-1;++j)></i-1;++j)></endl;></endl;>5 96 0 6 1 6 2 6 3 6 4 6 5 6 6 67 68 69 7 0 7 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 8约瑟夫问题约瑟夫环(约瑟夫问题)是一个数学的'应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。
c语言实现约瑟夫环问题解析

(一)基本问题1.问题描述设有编号为1,2,…,n的n(n>0)个人围成一个圈,每个人持有一个密码m。
从第一个人开始报数,报到m时停止报数,报m的人出圈,再从他的下一个人起重新报数,报到m 时停止报数,报m的出圈,……,如此下去,直到所有人全部出圈为止。
当任意给定n和m后,设计算法求n个人出圈的次序。
建立模型,确定存储结构。
对任意n个人,密码为m,实现约瑟夫环问题。
2.数据结构设计首先,设计实现约瑟夫环问题的存储结构。
由于约瑟夫环问题本身具有循环性质,考虑采用循环链表,为了统一对表中任意结点的操作,循环链表不带头结点。
将循环链表的结点定义为如下结构类型:struct Node{int data;Node *next;};其次,建立一个不带头结点的循环链表并由头指针first指示3.算法设计1、工作指针first,r,s,p,q初始化2、输入人数(n)和报数(m)3、循环n次,用尾插法创建链表Node *q;for(int i=1;i<=n;i++){Node *p;p=new Node;p-> data =i;p->next=NULL;if(i==1) L=q=p;else{q->next=p;q=q->next;}}q->next=L;if(L!=NULL){return(L);}4、输入报数的起始人号数k;5、Node *q = new Node;计数器初始化i=1;6、循环n次删除结点并报出位置(其中第一个人后移k个)当i<n时移动指针m-2次p=p->next;删除p结点的后一结点qq=p->next;p->next=q->next;*L = p->next;报出位置后Delete q;计数器i++;运行流程图代码和相关解释#include<iostream>using namespace std;struct Node//循环节点的定义{int data;//编号Node *next;};Node *CreateList(Node *L,int &n,int &m);//建立约瑟夫环函数void Joseph(Node *L,int n,int m);//输出每次出列号数函数Node *DeleteList(Node **L,int i,Node *q);//寻找每次出列人的号数int LengthList(Node *L);//计算环上所有人数函数void main()//主函数//在主函数中,完成人数(n)和报数(m)的输入和工作指针的初始化{Node *L;L=NULL;//初始化尾指针int n, m;cout<<"请输入人数N:";cin>>n;//环的长度if(n<1){cout<<"请输入正整数!";}//人数异常处理else{cout<<"请输入所报数M:";cin>>m;if(m<1){cout<<"请输入正整数!";}//号数异常处理else{L=CreateList(L,n,m);//重新给尾指针赋值Joseph(L,n,m);}}system("pause");}Node *CreateList(Node *L,int &n,int &m)//建立一个约瑟夫环(尾插法){Node *q;for(int i=1;i<=n;i++){Node *p;p=new Node;p->data=i;p->next=NULL;if(i==1) L=q=p;//工作指针的初始化else{q->next=p;q=q->next;}}q->next=L;if(L!=NULL){return(L);}//返回尾指针else cout<<"尾指针异常!"<<endl;//尾指针异常处理}void Joseph(Node *L,int n,int m)//输出每次出列的人{int k;cout<<"请输入第一个报数人:";cin>>k;if(k<1||k>n){cout<<"请输入1-"<<n<<"之间的数"<<endl;} else{cout<<"\n出列顺序:\n";for(int i=1;i<n;i++){Node *q = new Node;if(i==1) q=DeleteList(&L,k+m-1,q);//第一个出列人的号数else q=DeleteList(&L,m,q);cout<<"号数:"<<q->data<<endl;delete q;//释放出列人的存储空间}cout<<"最后一个出列号数是:"<<L->data<<endl;;//输出最后出列人的号数}}Node *DeleteList(Node **L,int i,Node *q) //寻找每次出列的人{if(i==1) i+=LengthList(*L);//顺序依次出列情况的处理方式Node *p;p=*L;int j=0;while(j<i-2) {p=p->next;j++;}q = p->next;p->next=p->next->next;*L = p->next;return(q);}int LengthList(Node *L)//计算环上的人数{if(L){cout<<"尾指针错误!"<<endl;}//异常处理else{int i=1;Node *p=L->next;while(p!=L){i++;p=p->next;}return(i);}}复杂度分析:for(int i=1;i<=n;i++){Node *p;p=new Node;p->number=i;p->next=NULL;if(i==1) L=q=p;else{q->next=p;q=q->next;}时间复杂度:O(n)if(i==1) i+=LengthList(*L);Node *p;p=*L;int j=0;while(j<i-2) {p=p->next;j++;}q = p->next;p->next=p->next->next;*L = p->next;return(q);时间复杂度:O(n2)算法的空间复杂度:O(n2)4.界面设计5. 运行、测试与分析(二)采用顺序存储结构如何实现约瑟夫环问题代码和解释#include <stdlib.h>#include<stdio.h>#include<malloc.h>#define MaxSize 50typedef char ElemType;typedef struct Seqlist{//线性表顺序存储结构定义ElemType *elem[MaxSize];//存放顺序表数据元素int length;//当前长度}*JSeqlist;//线性表存储结构类型名JSeqlist Int_SeqList(void){//顺序表初始化JSeqlist L;L=(JSeqlist)malloc(sizeof(struct Seqlist));if(L!=NULL)L->length=0;elseprintf("超出范围!!");return L;}ElemType *Locate_SeqList(JSeqlist L,int p){//查找线性表中下标为P的元素if(p>=0&&L->length)return(L->elem[p]);else{printf("顺序表中不存在相关元素");return NULL;}}int Insert_SeqList(JSeqlist L,int i,ElemType *x){//在顺序表中指定元素前插入Xint j;if(L->length==MaxSize)//L.length是最后一个元素的位置{printf("线性表已满,无法进行插入操作!!!!\n");return 0;}if(i<0||i>L->length){printf("插入位置不对,超出顺序表长度\n");return 0;}if(i==0){L->elem[i]=x;L->length=L->length+1;return 1;}for(j=L->length;j>=i;j--){L->elem[j]=x;}L->length++;return 1;}int Delete_JSeqlist(JSeqlist L,int i){//在顺序表中删除第i个元素int j;if(i<0||i>L->length-1){printf("删除位置不对,超出顺序表的长度啦\n");return 0;}for(j=i;j<L->length-1;j++)L->elem[j]=L->elem[j+1];L->length--;return 1;}void josephus(JSeqlist L,int start,int m){//josephus问题求解的非常牛逼的函数int s,i;ElemType *w;s=start-1;for(i=L->length;i>0;i--){s=(s+m-1)%i;w=Locate_SeqList(L,s);printf("出列人员为:%s\n",w);Delete_JSeqlist(L,s);}}int main (void){JSeqlist Josephus;int n,m,i,k,s;Josephus=Int_SeqList();//顺序表初始化printf(" 约瑟夫环问题顺序表求解_愚人节特别版\n\n");printf("请输入本问题中总人数m=");scanf("%d",&n);printf("请输入本问题开始人员的位置S=");scanf("%d",&s);printf("请输入本问题的计数值m=");scanf("%d",&m);printf("请输入本问题中这些人的名字\n");for(i=0;i<n;i++){printf("第%d位置的人员的名字为:",(i+1));Josephus->elem[i]=(ElemType *)calloc(10,sizeof(char));scanf("%s",Josephus->elem[i]);k=Insert_SeqList(Josephus,i,Josephus->elem[i]);if(k==0)exit(1);}josephus(Josephus,s,m);free(Josephus);getchar();return 0;}运行结果(三)密码不同#include <iostream.h>struct CList{int password;int number;struct CList *next;};typedef struct CList CNode;typedef CNode *CLink;CLink CreateList(int length){CLink head;CLink before;CLink new_node;int i;head=new CNode;if(head==NULL)return NULL;cout << "Please Input Password 1 :" << endl;cin >> head->password;head->number=1;head->next=NULL;before=head;for(i=1;i<length;i++){new_node=new CNode;if(new_node == NULL)return NULL;new_node->number = i+1;cout << "Please Input Password " << new_node->number << ":" <<endl;cin >> new_node->password;new_node->next = NULL;before->next=new_node;before=new_node;}new_node->next =head;return head;}int main(){CLink head;CLink ptr,back,last;int i,j,m,n;cout << "Please Input the Number of Persons: " << endl;cin >> n;cout << "Please Input the First Password M: " << endl;cin >> m;head=CreateList(n);ptr=head;for(i=0;i<n;i++){for(j=0;j<m-1;j++){back=ptr;//定位最后一个数的接点赋值给backptr=back->next;}cout <<"第"<<i+1<<"个出列的编号为:"<<ptr->number<<endl;m=ptr->password;if(ptr==head){last=head;while(last->next!=head)last=last->next;last->next=head->next;delete ptr;ptr=last->next;head=ptr;}else{back->next=ptr->next;delete ptr;ptr=back->next;}}return 0;}运行结果(三)心得体会:1.编程是个很细致的工作,尤其是在写顺序表的时候,涉及的函数很多,函数名中最初为了看在清晰,涉及成单词首字母是大写的,但是后来在函数调用的时候,就忘记了最初命名的时候是大写的了,导致编译的时候不能识别。
C语言程序设计漫谈之从“约瑟夫问题”谈起

从“约瑟夫问题”谈起约瑟夫问题是一个出现在计算机科学和数学中的问题。
在计算机编程的算法中,类似问题又称为约瑟夫环。
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。
然而Josephus 和他的朋友并不想自杀。
为避免与其他39个决定自杀的犹太人发生冲突,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行,直到仅余15个人为止。
问怎样的排法,才能使每次投入大海的都是非教徒。
【例1】约瑟夫问题。
N个人围成一圈,从某个人开始,按顺时针方向从1开始依次编号。
从编号为1的人开始顺时针“1,2,…M”报数,报到M的人退出圈子。
这样不断循环下去,圈子里的人将不断减少。
由于人的个数是有限的,因此最终会剩下一个人,该人就是优胜者。
输入N和M,输出出圈顺序。
例如,N=6、M=5,出圈的顺序是:5,4,6,2,3,1。
(1)编程思路。
为输出出圈顺序,采用一个数组来进行模拟。
定义int circle[N+1],并按circle[i]=i+1的方式赋予各元素初值。
该值代表两个含义:1)值为0,代表编号i+1的人不再圈中;2)值非0,代表圈中第i个位置的人编号为i+1。
定义变量i代表报数位置的流动,i的初值为0,代表编号为1的人的位置,i的变化方式为:i=(i+1)%(n),即0-->1-->2……->n-1 ->0-->1……。
C语言数组实现约瑟夫环问题,以及对其进行时间复杂度分析

C 语⾔数组实现约瑟夫环问题,以及对其进⾏时间复杂度分析尝试表达本⼈试着去表达约瑟夫环问题:⼀群⼈围成⼀个圈,作这样的⼀个游戏,选定⼀个⼈作起点以及数数的⽅向,这个⼈先数1,到下⼀个⼈数2,直到数到游戏规则约定那个数的⼈,⽐如是3,数到3的那个⼈就离开这个游戏;按这样的规则,剩下⼀个⼈,游戏就结束,这个⼈就为赢家。
(读者可以试着表达,不认同,直接忽略)抽象分析这个⼈就是⼀个数据个体,数据结点,数据元素。
上⾯产⽣的数据结构为:单⽅向循环的链。
可以⽤链表实现,也可以⽤数组来实现。
链表到数组的迁移⼈(数据元素、数据结点、数据个体)结点关系(结构关系结点移动)范型“指针”定义:能够定位到下⼀个结点(变)“指针“移到下⼀个结点拿到下⼀个结点的”指针“即可,⼀般都有作“移动”变量,移动变量变,就相当于移动。
删除结点数组连续的数组元素(基本数据类型,机构体)数组元素⾥⾯保存有下个结点元素的数组元素下标position 。
arrayname 固定的,只要给出position ,就可以算是定位到数组元素≈poisiton []move =array[move]元素内容 = -1(数组的⼤⼩固定)链表离散的链表结点(结构体)结构体⾥⾯保存有下⼀个结点的指针node* nextpoiter 直接定位到结点,在结合常员变量,就可以拿到数据=poiter ->move = move ->next销毁画图分析:代码实现:#include<stdio.h>#include<stdlib.h>/*Function:遍历数组实现的约瑟夫环。
traverse_joseph_circle_array*param:int[] array,int tail*return: void* 假设是⽤数组实现的约瑟夫环链⼀定存在。
* */void traverse_joseph_circle_array (int array[], int tail ){//数组保存的是下个结点的“指针”,只不过这个指针要通过array 才能够拿到结点的元素,因为array 是固定的,只要变换指针就能够变换结点。
约瑟夫环c语言代码指针函数,JavaScript使用指针操作实现约瑟夫问题实例

约瑟夫环c语⾔代码指针函数,JavaScript使⽤指针操作实现约瑟夫问题实例本⽂实例讲述了JavaScript使⽤指针操作实现约瑟夫问题的⽅法。
分享给⼤家供⼤家参考。
具体分析如下:实现之前当然要⾃⼰来编写⼀些 JS 数组内部指针的操作函数,就像:reset(), current(), next(), prev(), search(), end() 这些函数,我们都要来⾃⼰实现,因为 JS 没有内置这些神奇的操作函数Array.prototype.pointer = 0;//模拟数组内部指针//Reset 函数,将数组内部指针归位(指向第⼀个元素)var reset = function(arrayObj){if(!(arrayObj instanceof Array)){alert("Reset() 函数参数类型错误!请检查输⼊!");return;}arrayObj.pointer = 0;}//Current 函数,返回数组内部指针指向的当前元素var current = function(arrayObj){if(!(arrayObj instanceof Array)){alert("Current() 函数参数类型错误!请检查输⼊!");return;}return arrayObj[arrayObj.pointer];}//End 函数,将数组内部指针指向最后⼀个元素var end = function(arrayObj){if(!(arrayObj instanceof Array)){alert("End() 函数参数类型错误!请检查输⼊!");return;}arrayObj.pointer = arrayObj.length - 1;return arrayObj[arrayObj.pointer];}//Next 函数,将数组内部指针下移⼀位//如果已经指向最后⼀个元素则返回 FALSEvar next = function(arrayObj){if(!(arrayObj instanceof Array)){alert("Next() 函数参数类型错误!请检查输⼊!"); return;}arrayObj.pointer ++;if(typeof arrayObj[arrayObj.pointer] == 'undefined'){ arrayObj.pointer --;return false;}return true;}//Prev 函数,将数组内部指针上移⼀位//如果已经指向第⼀个元素则返回 FALSEvar prev = function(arrayObj){if(!(arrayObj instanceof Array)){alert("Prev() 函数参数类型错误!请检查输⼊!"); return;}arrayObj.pointer --;if(typeof arrayObj[arrayObj.pointer] == 'undefined'){ arrayObj.pointer ++;return false;}return arrayObj[arrayObj.pointer];}//Unset 函数,删除指定的数组元素var unset = function(index, arrayObj){if(!(arrayObj instanceof Array)){alert("Unset() 函数参数类型错误!请检查输⼊!"); return;}if(typeof arrayObj[index] == 'undefined'){alert("Unset() 函数参数 index 错误!不存在此元素!"); return false;}arrayObj.splice(index, 1);return true;}//Search 函数,通过数组键值返回数组的键名var search = function(value, arrayObj){if(!(arrayObj instanceof Array)){alert("Search() 函数参数类型错误!请检查输⼊!");return;}for(index in arrayObj){if(arrayObj[index] == value){return index;}}return false;}//getKingMonkey 函数,我们的约瑟夫主函数,n 只猴⼦,数到 m function getKingMonkey(n, m){a = new Array();for(i = 1; i <= n; i ++){a[i] = i;}a[0] = 0;unset(0, a);reset(a);while(a.length > 1){for(counter = 1; counter <= m; counter ++){if(next(a)){if(counter == m){unset(search(prev(a), a), a);}}else{reset(a);if(counter == m){unset(search(end(a), a), a);reset(a);}}}}return current(a);}alert("猴⼦⼤王的编号为:" + getKingMonkey(100, 17));希望本⽂所述对⼤家的javascript程序设计有所帮助。
c语言常考应用题

c语言常考应用题以下是一些C语言常考的应用题,可以帮助你提高编程能力和解决实际问题的能力:1. 斐波那契数列:给定一个整数n,计算第n个斐波那契数。
2. 约瑟夫环问题:有n个人围成一圈,从第一个人开始报数,每次数到m的人出圈,下一个人继续从1开始报数,直到所有的人都出圈。
求出出圈的顺序。
3. 冒泡排序:给定一个整数数组,将数组中的元素按照从小到大的顺序排列。
4. 选择排序:给定一个整数数组,将数组中的元素按照从小到大的顺序排列。
与冒泡排序不同的是,选择排序每次从未排序的元素中找到最小(或最大)的元素,将其放在已排序序列的末尾。
5. 插入排序:给定一个整数数组,将数组中的元素按照从小到大的顺序排列。
与选择排序不同的是,插入排序每次从未排序的元素中找到最小(或最大)的元素,将其插入到已排序序列的合适位置。
6. 快速排序:给定一个整数数组,将数组中的元素按照从小到大的顺序排列。
快速排序采用分治策略,将数组分成两个子数组,分别对子数组进行排序,然后合并两个已排序的子数组以产生最终的排序数组。
7. 二分查找:给定一个有序整数数组和一个目标值,在数组中查找目标值,并返回其索引。
如果目标值不存在于数组中,则返回-1。
8. 贪心算法:给定一个整数数组和一个目标值,要求在数组中找到若干个数字,使得它们的和最接近目标值。
9. 回溯算法:给定一个字符串和一组字符集,判断字符串是否为回文串。
如果是回文串,则返回true;否则返回false。
10. 动态规划:给定一个矩阵和一组值,判断是否能够从矩阵中选取一些数字,使得它们的和等于给定的值。
如果是可行的,则返回true;否则返回false。
约瑟夫环C++ 编程解析
【问题】
N个人围成一圈,从第一个人开始报数,报到m的人出圈,剩下的人继续从1开始报数,报到m的人出圈;如此往复,直到所有人出圈。(模拟此过程,输出出圈的人的序号)
【示例】
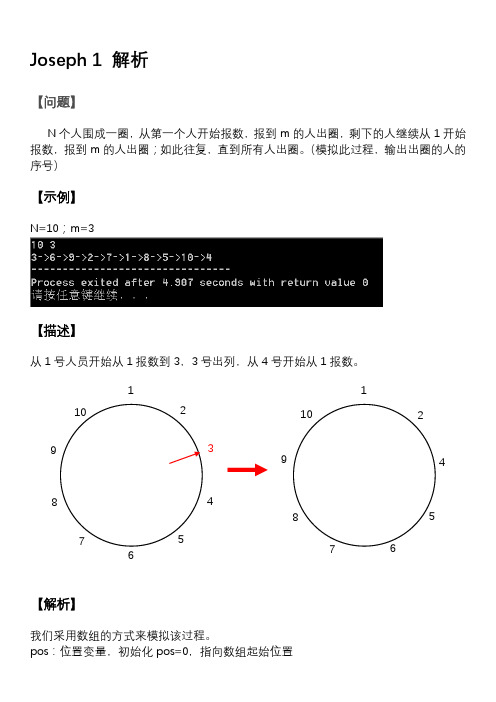
N=10;m=3
【描述】
从1号人员开始从1报数到3,3号出列,从4号开始从1报数。
【解析】
我们采用数组的方式来模拟该过程。
pos:位置变量,初始化pos=0,指向数组起始位置
len:长度变量,初始化pos=N,表示数组长度
原队列
1
2
3
4
5
6
7
8
9
10
10
3
位置
pos
pos
从pos当前位置开始报数,当报到m时,位置指向m-1;
该人员出列。
pos=(pos+m-1)%len;
新队列
1
2
4
5
6
7
8
9
10
9
6
pos
pos
pos=(pos+m-1)%len;
pos = (pos+m-1) % len;//指到出列人员位置
cout<<a[pos]<<"->";//输出出列人员
for(i=pos;i<len-1;i++){//删除出列人员
a[i]=a[i+1];
}
if(len)len--;//数组长度减一
}
cout<<a[0];//输出最后一位人员
return 0;
新队列
1
2
4
5
7
8
9
约瑟夫环问题(链式结构)

约瑟夫环问题(链式结构)#include <stdio.h>struct node{int v;struct node *next;}*p,*head,h; /*head是头指针,h是头结点*/main(){int n,m;int i;puts("请输入人数n和报数上限m :");scanf("%d%d",&n,&m);h.next=NULL; /*头结点的next为空*/head=&h; /*头指针指向头结点*/p=head; /*p也指向头结点*//*下面的循环用来建立循环链表*/for(i=1;i<=n;i++){p->next=(struct node*)malloc(sizeof(struct node));p=p->next;p->v=i;if(i!=n){p->next=NULL;}else{p->next=head->next;}}p=head;p=p->next; /*p指向第一个结点*/m%=n; /*当m>n时有用*/while(p!=p->next){for(i=1;i<=m-2;i++){p=p->next;}printf("%d ",p->next->v);p->next=p->next->next;p=p->next;}printf("%d",p->v);}2.约瑟夫环问题(顺序结构)#define N 6int yuesefu1(int data[],int sum,int k){int i=0,j=0,count=0;while(count<sum-1){if(data[i]!=0)/*当前人在圈子里*/j++;if(j==k)/*若该人应该退出圈子*/{ printf("\n%d",data[i]);data[i]=0;/*0表示不在圈子里*/count++;/*退出的人数加1*/j=0;/*重新数数*/}i++;/*判断下一个人*/if(i==sum)/*围成一圈*/i=0;}for(i=0;i<sum;i++)if(data[i]!=0)return data[i];/*返回最后一个人的编号*/}void main(){int data[N];int i,j,total,k;printf("\nPlease input the number of every people.\n"); for(i=0;i<N;)/*为圈子里的人安排编号*/{int input;scanf("%d",&input);if(input==0)break;/*0表示输入结束*/for(j=0;j<i;j++)/*检查编号是否有重复*/if(data[j]==input)break;if(j>=i&&input>0)/*无重复,记录编号,继续输入*/{data[i]=input;i++;}elseprintf("\nData error.Re-input:");}total=i;printf("\nYou have input:\n");for(i=0;i<total;i++){if(i%10==0)printf("\n");printf("%4d",data[i]);}printf("\nPlease input a number to count:");scanf("%d",&k);printf("\nThe last one''''s number is %d",yuesefu1(data,total,k)); }。
详解基于C++实现约瑟夫环问题的三种解法

详解基于C++实现约瑟夫环问题的三种解法⽬录⼀、前⾔⼆、循环链表模拟三、有序集合模拟四、递归公式解决五、结语⼀、前⾔什么是约瑟夫环问题?约瑟夫环问题在不同平台被"优化"描述的不⼀样,例如在⽜客剑指offer叫孩⼦们的游戏,还有叫杀⼈游戏,点名……最直接的感觉还是⼒扣上剑指offer62的描述:。
问题描述:0,1,···,n-1这n个数字排成⼀个圆圈,从数字0开始,每次从这个圆圈⾥删除第m个数字(删除后从下⼀个数字开始计数)。
求出这个圆圈⾥剩下的最后⼀个数字。
例如,0、1、2、3、4这5个数字组成⼀个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
当然,这⾥考虑m,n都是正常的数据范围,其中1 <= n <= 10^51 <= m <= 10^6对于这个问题,你可能脑海中有了印象,想着⼩时候村⾥⼀群孩⼦坐在⼀起,从某个开始报数然后数到⼏出列,下⼀个重新开始⼀直到最后⼀个。
⼆、循环链表模拟这个问题最本质其实就是循环链表的问题,围成⼀个圈之后,就没有结尾这就是⼀个典型的循环链表嘛!⼀个⼀个顺序报数,那不就是链表的遍历枚举嘛!数到对应数字的出列,这不就是循环链表的删除嘛!并且这⾥还有⾮常⽅便的地⽅:循环链表的向下枚举不需要考虑头尾问题,直接node=node.next向下循环聊表的删除也不需要考虑头尾问题,直接node.next=node.next.next删除当然也有⼀些需要注意的地⽅形成环形链表很简单,只需要将普通链表的最后⼀个节点的next指向第⼀个节点即可循环链表中只有⼀个节点的时候停⽌返回,即node.next=node的时候删除,需要找到待删除的前⾯节点,所以我们删除计数的时候要少即⼀位,利⽤前⾯的那个节点直接删除后⾯节点即可这样,思路明确,直接开撸代码:class Solution {class node//链表节点{int val;public node(int value) {this.val=value;}node next;public int lastRemaining(int n, int m) {if(m==1)return n-1;//⼀次⼀个直接返回最后⼀个即可node head=new node(0);node team=head;//创建⼀个链表for(int i=1;i<n;i++){team.next=new node(i);team=team.next;}team.next=head;//使形成环int index=0;//从0开始计数while (head.next!=head) {//当剩余节点不⽌⼀个的时候//如果index=m-2 那就说明下个节点(m-1)该删除了if(index==m-2){head.next=head.next.next;index=0;}else {index++;}head=head.next;}return head.val;}}当然,这种算法太复杂了,⼤部分的OJ你提交上去是⽆法AC的,因为超时太严重了,具体的我们可以下⾯分析。
C++约瑟夫环的实例代码

C++约瑟夫环的实例代码C++ 约瑟夫环的实例代码约瑟夫环是⼀个数学的应⽤问题:已知n个⼈(以编号1,2,3...n分别表⽰)围坐在⼀张圆桌周围。
从编号为k的⼈开始报数,数到m的那个⼈出列;他的下⼀个⼈⼜从1开始报数,数到m的那个⼈⼜出列;依此规律重复下去,直到圆桌周围的⼈全部出列。
分析:有n个⼈,要想所有的⼈都退出去,只有每个⼈喊到m,才可以退完,所以可以算出,n*m为所有⼈总共报数的总次数。
代码:/** 约瑟夫出圈*/#include <stdio.h>int main(){char peo[100] ;char *p_peo = peo;int i , n , skip , flag[100] = {0} , cnt;int *p_flag = NULL;printf("请输⼊⼈数:");scanf("%d", &n);printf("所有⼈如下:\n");for(p_peo , i = 0 ; p_peo < peo + n ; ++p_peo , ++i){*p_peo = 'a' + i;printf("%c ", *p_peo);}printf("\n");printf("请输⼊报数值:");scanf("%d", &skip);cnt = 0;while(cnt <= n * skip){for(p_peo = peo , p_flag = flag ; p_peo < peo + n ; ++p_peo , ++p_flag){if(*p_flag)continue;cnt++;if(!(cnt % skip)){*p_flag = 1;printf("%c ", *p_peo);}}}printf("\n");return 0;}如有疑问请留⾔或者到本站社区交流讨论,感谢阅读,希望能帮助到⼤家,谢谢⼤家对本站的⽀持!。
