苏教版七年级下期末模拟试卷3

合集下载

苏教版生物七年级下册期末综合检测 ( 三 )

期末测评卷(三)(第4单元)(60分钟100分)一、选择题(本题共25小题,每小题2分,共50分)1.(2020·昆明质检)某些药品说明书印制“孕妇禁用”,是因为胎儿与母体的血液相通,药品中的化学物质进入胎儿体内是通过下列哪个结构( C )A.卵巢B.输卵管C.胎盘D.子宫内膜2.关于胎儿获得营养物质的途径,下列正确的是( C )A.母体→脐带→胎盘→胎儿B.胎盘→脐带→母体→胎儿C.母体→胎盘→脐带→胎儿D.脐带→胎盘→母体→胎儿3.15岁的小峰身高已经1.7米,他觉得自己是个真正的男子汉了。

下列特征,小峰现阶段不该出现的是 ( C )A.声音变粗B.喉结突出C.体重迅速增加到98千克D.偶尔的遗精现象4.下列关于维生素的说法错误的是( C )A.医生给患佝偻病的儿童开钙片和鱼肝油是比较科学有效的处方B.食物“补铁”和“加碘”分别可以预防缺铁性贫血、地方性甲状腺肿C.长期不吃水果和蔬菜,导致牙龈出血,可能是因为体内缺乏维生素BD.小强同学由于体内缺乏维生素A造成夜晚看不清东西5.肝炎患者应少吃油腻食物,因为肝脏分泌的胆汁减少会影响( B )A.淀粉的消化B.脂肪的消化C.麦芽糖的消化D.蛋白质的消化6.(2020·滨州学业考)小丽在老师的指导下完成了“探究唾液对淀粉的消化作用”的实验,下列关于该实验的叙述错误的是 ( D )A.该实验的变量是唾液B.滴加碘液后的实验现象:①变蓝,②不变蓝C.37 ℃是唾液淀粉酶发挥消化作用的适宜温度D.该实验说明了唾液可以将淀粉分解为葡萄糖7.乐乐为妈妈设计了一份午餐食谱:红烧肉、米饭、排骨汤。

从“合理营养”的角度来分析,请你为乐乐同学再选一道菜( C )A.麻辣豆腐B.糖醋里脊C.炒青菜D.可乐鸡翅8.小胡老师从海南到西藏支教,他刚到高海拔地区时,红细胞的数量变化趋势是( D )9.魏莱学习了输血和血型的有关知识后,归纳了以下几点,不恰当的是 ( D )A.以输同型血为原则B.O型血的人是万能输血者C.AB型血的人是万能受血者D.初中生应积极参加无偿献血10.(2019·龙东学业考)如图,如果②是肺泡周围的毛细血管网,则①和③内的血液分别是( D )A.动脉血、动脉血B.静脉血、静脉血C.动脉血、静脉血D.静脉血、动脉血11.婴幼儿输液可选取头皮作为针刺部位,药物到达患病部位前可能不会流经 ( B )A.上腔静脉B.下腔静脉C.主动脉D.肺动脉12.人体每时每刻都进行着呼吸。

江苏省苏州市七年级数学第二学期期末模拟测试试卷3 苏科版

(时间：90分钟总分：100分)班级姓名一、选择题（）1．三角形的高线是A ．直线B ．线段C ．射线D ．三种情况都可能（）2.下列不等式变形正确的是A ．由a ＞b ，得a －2＜b －2B ．由a ＞b ，得－2a ＜－2bC ．由a ＞b ，得a ＞bD ．由a ＞b ，得a 2＞b2 （）3．下列能用平方差公式计算的式子是A ．(a －b )(b －a )B ．(－x ＋1)(x －1)C ．(－a －1)(a ＋1)D ．(－x —y )(－x ＋y )（）4. 关于x 的方程12mx x -=的解为正数，则m 的取值范围是A ．m ≥2B ．m ≤2C ．m ＞2D ．m ＜2（）5. 关于x 的不等式组1532223x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有4个整数解，则a 的取值范围是A ．-5≤a ≤-143B ．-5≤a<-143C ．-5<a ≤-143D ．-5<a<-143（）6．如图，已知AB ∥CD ，AB ＝CD ，AE ＝FD ，则图中的全等三角形有A ．1对B ．2对C ．3对D ．4对（）7．一个三角形的3个外角的度数之比为2：3：4，则与之相应的3个内角度数之比为A ． 4：3：2B ．3：2：4C ．5：3：1D ．2：3：4（）8．一个多边形截去一个角后，形成新多边形的内角和为2520°，则原多边形边数为A ．13B ．15C ．13或15D ．15或16或17 （）9．如图，在△ABC 中，AB ＝AC ，AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，则下列说法正确的有 ①DA 平分∠EDF ； ②AE ＝AF ，DE ＝DF ；③AD 上任意一点到B 、C 两点的距离相等；④图中共有3对全等三角形．A ．1个 B ．2个 C ．3个 D ．4个（）10．如图，ABC ∆中，8AB BC CA ===．一电子跳蚤开始时在BC 边的P 0处，BP 0＝3．跳蚤第一步从P 0跳到AC 边的P 1（第1次落点）处，且CP 1＝CP 0；第二步从P 1跳到AB 边的P 2（第2次落点）处，且AP 2＝AP 1；第三步从P 2跳到BC 边的P 3（第3次落点）处，且BP 3＝BP 2；…；跳蚤按照上述规则一直跳下去，第n 次落点为P n （n 为正整数），则点2012P 与点2013P 之间的距离为（）A ．2B ．3C ．4D ．5二、填空题11．若2x ＋y －3＝0，则4x ×2y ＝_______．12．若a ＋b ＝6，ab ＝4，则(a －b )2＝_______．13．若多项式x 2＋k x －6有一个因式是(x －2)，则k ＝_______14．若1222=+y x ，4=xy ，则=-y x ． 15．在日常生活中，如取款、上网等都需要密码．有一种“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x 4－y 4，因式分解的结果是(x －y )(x ＋y )(x 2＋y 2)，若取x ＝9，y ＝9时，则各个因式的值是：(x －y )＝0，(x ＋y )＝18，(x 2＋y 2)＝162，于是，就可以把“018162”作为—个六位数的密码，对于多项式4x 3－xy 2，取x ＝10，y ＝10时，用上述方法产生的密码是： ____ （写出一个即可）．16．如图，ABCDE 是封闭折线，则∠A 十∠B ＋∠C ＋∠D ＋∠E 为_________度．17．如图，△ABE 和△ACD 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠BAC ＝150°，则∠θ的度数是_______．18. 若等腰三角形的周长为16，腰长为x ，则x 得取值范围为．19．如图，小亮从A 点出发，沿直线前进了5米后向左转30°，再沿直线前进5米，又向左转30°，……照这样走下去，他第一次回到出发地A 点时，一共走了 _____ 米．20．如图，△ABC 的顶点都在小正方形的顶点上，在方格纸上画的格点三角形与△ABC 全等且仅有1条公共边，不同的三角形共有_______个．21．已知：在同一平面内，直线a ∥c ，且直线a 到直线c 的距离是3；直线b ∥c ，直线b到直线c 的距离为5，则直线a 到直线b 的距离为 _____ ．三、解答题 22．计算①()22011020111 3.142 2.2510π-⎛⎫-+---⨯ ⎪⎝⎭②203211()()(5)(5)39--++-÷-；③a ·a 2·a 3＋(－2a 3)2－a 8÷a 2． ④2(x 4)3＋x 4(x 2)4＋(x 3)3·x 3＋x 2·x 1023．先化简，再求值：(x ＋y )2－3x (x ＋3y )＋2(x ＋2y )(x －2y )，其中x ＝－13，y ＝13．24.解不等式（组）⑴ 215312+--x x ≤1 ⑵ 13212≤-<-x25．分解因式：(1)ax 3y ＋axy 3－2ax 2y2 (2)2182x y y - (3)32310a a a -- (4)81x 4－72x 2y 2＋16y426.若方程组⎩⎨⎧-=-+=+5222m y x m y x 的解是一对正数．则：⑴ 求m 的取值范围；⑵ 化简：24++-m m27．如图1和图2，∠ACB ＝90°，AC ＝BC ，BD ⊥DE ，AE ⊥DE ，垂足分别为D 、E ．(1)图1中，①证明：△ACE ≌△CBD ；②若AE ＝a ，BD ＝b ，计算△ACB 的面积．(2)图2中，若AE ＝a ，BD ＝b ，（b >a ）计算梯形ADBE 的面积．28.某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A 、B 两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元。

苏科版七年级数学下册期末模拟试卷(附参考答案).docx

七年级数学期末试卷一、选择题（每题3分，共30分）1.（-3） $的计算结果是（▲） 4•下列命题中是真命题的是C 、任何数的偶次幕都大于0D 、垂直于同一条直线的两条直线平行 5.下列运算正确的是（▲）A. - a 2 = 2a 2B. （^2）3 = a 5C. a 2 4-tz 3 = aD. a 2 - a 3 = a 6 6•三角形的两边长分别为4和9,则它的第三边长可以为（▲）A 、 4B 、 5 C. 9 D. 137.如图，有以下五个条件：①ZB+ZBCD 二180° ,②ZUZ2, ③Z3=Z4, @ZB=Z5,⑤ZB+ZBAD=180° ,其中能判定AB 〃CD 的条件有（▲）个A. 4B. 3—X W 1 &不等式组2的解集在数轴上表示正确的是（▲）2-x<3 9•方程3x+2y 二17的正整数解有（▲）对・10. 如果一个三角形的三条高的交点恰好是三角形的一个顶点，则这个三角形的形状一定是（▲）A.等腰三角形B.锐角三角形二、填空题（每题3分，共30分）11.（X - 2）°有意义，则x 的取值范围是 ▲ 12. 用科学记数法表示0. 000102为 ▲A. -6B. 6C. -9D. 9 2.如图直线若Zl = 70° ,则Z2 为(▲) A 、70° B 、 110° 3•八边形的内角和是（▲A 、 900°B 、 1080°C 、 1260°D 、 1440° A 、相等的角是对顶角B 、两条直线被笫三条直线所截，同位角相等D. 1C. 2 2C.钝角三角形D.直角三角形C 、70° 或 110°D 、120°B. D.13.若x2+kx + 25是一个完全平方式，则1<=―▲14.命题“两直线平行，内错角相等”的结论是▲15.如果 | / 一3 | +(y + I)2 = 0 ,贝ij x — y 二▲16.一个多边形每一个外角都等于30°,则这个多边形的边数是▲17.若a>0,且a—3,0二2,贝临-2y二▲.18.如图，将一张长方形纸片沿EF折叠后，点D、C分别落在D‘、C的位置，ED Z的延长线与BC交于点G.若Z EFG=50°,则Zl=▲ ° .19.若n为整数，代数式⑺+ 3）2-（刀-I）2一定能被_▲ 整除（填最大正整数）.20•计算（+寺|）・4X（p$*峙）寺存步的结果是厶_三、解答题：（本大题共9题，共90分.解答应写出文字说明、证明过程或演算步骤）21.（本题满分10分，每小题5分）计算或化简：（1）22-Q+ TT）°-32^33（2）（% - 2y）（x + y）—2y{x - 2y）22.（本题满分15分，每小题5分）因式分解:(1) 12xyz 一9 Ay2(2) 4a2 - 12ab + 9b2(3) x4-l23-"本题满分8分）解不等式组黑’并写出其整数解.24. （本题满分10分）解方程组P + 3 = 2KD严-尸5① 付+ 3尸=8② 山+2尸23②25. （本题满分8分）先化简，再求值：（无+ 3X —l ）+（x+2Xx —2）—2（兀—厅，其中x _丄226. （本题满分6分）如图，在正方形网格中有一个格点三角形ABC,（即AABC 的各顶点都在格点上），按要求进行下列作图：（1）画LBAABC 中AB 边上的高CD ；（提醉：别忘了标注字母！）27. （本题满分10分）如图，若AE 是AABC 边BC 上的咼，ZEAC 的平分线AD 交BC 于D,若 ZDAC=25° ,求ZC 的度数.28. （本题满分10分）学校准备购进一批办公桌和椅子,若购进2张办公桌和3张椅子,（2）画出将AABC 向右平移4格后的△ A1TC ；厂:（3）边AC 扫过的封闭图形的面积是 ▲笔26題则需要费用880元；若购进5张办公桌和6张椅子，共需费用2080元・(1)求：办公桌和椅子每张分别多少元？(用方程组解)；(2)若购进办公桌和椅子共30张，且总费用不超过5000元，则最多可以购进办公桌多少张？29.(本题满分13分)已知如图，ZMBC和ZNDC是四边形ABCD的外角,若ZBAD二a, ZBCD二P ・(1)如图1①若«=50° , 0=100° ,则ZMBC+ZNDO ▲度；②若Q+0=200° ,则ZMBC+ZNDC二▲度;(2)ZMBC的平分线BE与ZNDC的平分线DF交于点G.①如图2,求ZEBC+ZCDF的度数(用含Q , 0的代数式表示)；②如图3,若BE〃DF，请探求Q与0Z间的大小关系•参考答案及评分标准一、选择题（每题3分，共30分）1 ------ 5 D B B D A 6—10 C B C C D二、填空题（每题3分，共30分）11、x H 2；12、1.02x 10「4 ；13、±10；14、内错角相等；15、4；16、12;3 1317、一. 18、100；19、8；20、——4，9三、解答题（共60分）21、（1）原式二4— 1 — | = |；（2）原式二兀2+小一2厂，一2歹2 一2小+4尸（去括号都正确3分，只对1个2分）二兀2一3小+ 2于（4分）22^ （1）原式=3xy（4z-3y）（3 分）；（2）原式=（2a-3b）2（3 分）（3）原式二（送 + i）（x + 1）（x — 1）（3 分）23、由①得X〉—2；由②得兀S3 （两个不等式只解对一个2分，两个都对3分），・••该不等式组的解集为：・2<x<3 （4分）.其整数解为：-1, 0, 1, 2, 3 （5分）24、由①得x = 2y — 3③，将③代入②得y = 2,将y = 2代入③得x = l（兀,）；的值求对一个2分，结论1分，共5分）所以原方程组的解为25、（1）如图（2分）（2）如图（4分）（3） 8 （6 分）笔26題26、TAD 平分ZEAC, ZDAC=ZEAD=25° , A ZEAC=50° , （2 分）•・・AE是\ABC的高,・・・ZAEC二90°（4 分）/. ZC=180° -ZAEC-ZEAC=180° -90° -50°二40°（7 分）.5x + 6y = 2080 27 （1）设办公桌和椅子每张分别x元和y元，则2x + 3y = 880 叫::80°（4分）②a ；如图3,延长BC交DF与H,因为BE〃DF,所以ZEBC二ZDHC,所以ZBCD二ZCDH+ZCHD二ZCDF+ ZEBC二仅 + "二｛3,所以 a 二B （12 分）（2）设购买办公桌m张，则有32血+8。

江苏省苏州市2022学年七年级数学第二学期期末模拟测试试卷3 苏科版

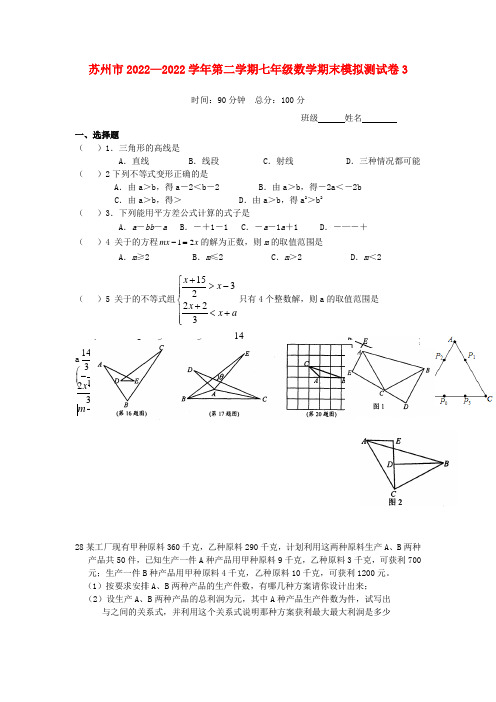
苏州市2022—2022学年第二学期七年级数学期末模拟测试卷3时间：90分钟总分：100分班级姓名一、选择题（）1．三角形的高线是 A ．直线 B ．线段 C ．射线 D ．三种情况都可能（）2下列不等式变形正确的是A ．由a ＞b ，得a －2＜b －2B ．由a ＞b ，得－2a ＜－2bC ．由a ＞b ，得＞D ．由a ＞b ，得a 2＞b2 （）3．下列能用平方差公式计算的式子是A ．a －bb －aB ．－＋1－1C ．－a －1a ＋1D ．－—－＋（）4 关于的方程12mx x -=的解为正数，则m 的取值范围是A ．m ≥2B ．m ≤2C ．m ＞2D ．m ＜2（）5 关于的不等式组1532223x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有4个整数解，则a 的取值范围是 A ．-5≤a ≤-143 B ．-5≤a 143143143ABC ∆8AB BC CA ===1222=+y x 4=xy =-y x 018162”5米5米()22011020111 3.142 2.2510π-⎛⎫-+---⨯ ⎪⎝⎭203211()()(5)(5)39--++-÷-2a 1313215312+--x x 13212≤-<-x 2182x y y -32310a a a --⎩⎨⎧-=-+=+5222m y x m y x 24++-m m a ）计算梯形ADBE 的面积．28某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A 、B 两种产品共50件，已知生产一件A 种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B 种产品用甲种原料4千克，乙种原料10千克，可获利1200元。

（1）按要求安排A 、B 两种产品的生产件数，有哪几种方案请你设计出来；（2）设生产A 、B 两种产品的总利润为元，其中A 种产品生产件数为件，试写出与之间的关系式，并利用这个关系式说明那种方案获利最大最大利润是多少29．如图，直线CB//OA，∠C＝∠A＝120°，E、F在CB上，且满足∠FOB＝∠AOB，OE平分∠COF．1求∠EOB的度数；2若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化若变化，找出变化规律或求出变化范围：若不变，求出这个比值；3在平行移动AB的过程中，是否存在某种情况，使∠OEC＝∠OBA若存在，求出其度数；若不存在，说明理由．30．如图，△ABC中，∠ACB＝90°，AC＝6，BC＝8．点P从A点出发沿A－C－B路径向终点运动，终点为B点；点Q从B点出发沿B－C－A路径向终点运动，终点为A点．点P 和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥于E，QF⊥于F．问：点P运动多少时间时，△PEC与QFC全等请说明理由．参考答案一、选择题BBDCC CCDDD二、填空题8；20；1；；103010；180；60；48x <<；60；4；2或8三、简答题22题①100；②-1；③；④23题277y xy --；024题⑴1x ≥-；⑵712x -≤≤25题⑴2()axy x y -；⑵1(4)(4)2y x x +-；⑶(2)(5)a a a +-；⑷22(32)(32)x y x y +-26题（1）14m <<；（2）627题28题（1） A B30 2031 1932 18（2）50060000y x =-+ 当X=30时最大利润为4500030题（1）0＜t ＜8/3时，P 在AC 上，Q 在BC 上，此时∠CPEPCE=90°，∠QCF ∠CQF=90° ∵∠ACB ＝90°，∠ACE ∠QCF=90°∴∠QCF=∠CPE ，又是直角三角形∴△PCE ∽△CQF此时要得△PCE ≌△CQF ，则PC=CQ 即6-t=8-3t ，t=1，满足（2）8/3＜t＜14/3时，P,Q都在AC上,此时两个三角形如果全等，则它们必须是重合的，PC=CQ即6-t=3t-8，t=7/2，满足（3）t＞14/3时，Q已经在A点停止运动，此时P在AC上不可能,即t＞6，和（1）一样的原因可知，此时PC=CQ即满足PC=AC=6∴t=66=12综上t=1或t=7/2或t=12。

(完整版)苏教版七年级下册期末数学模拟试卷优质及答案解析

（完整版）苏教版七年级下册期末数学模拟试卷优质及答案解析一、选择题1．下列各式中，计算正确的是（）A．(a3)2＝a5B．a2+a3＝a5C．( ab2)3＝ab6D．a2•a3＝a5答案：D解析：D【分析】直接利用积的乘方运算法则，合并同类项的法则，幂的乘方运算法则、同底数幂的乘法运算法则分别计算即可答案．【详解】解：A、(a3)2＝a6，故此选项错误,不合题意；B、a2+a3，无法合并，故此选项错误，不合题意；C、(ab2)3＝a3b6，故此选项错误，不合题意；D、a2•a3＝a5，故此选项正确，符合题意．故选：D．【点睛】本题考查幂的乘方与积的乘方，合并同类项法则，同底数幂的乘法，解题关键是掌握相关运算法则．2．如图，下列结论中错误的是（）A．∠1与∠2是同旁内角B．∠1与∠4是内错角C．∠5与∠6是内错角D．∠3与∠5是同位角答案：B解析：B【分析】根据同位角、内错角、同旁内角的定义结合图形进行判断即可．【详解】解：如图，∠1与∠2是直线a与直线b被直线c所截的同旁内角，因此选项A不符合题意；∠1与∠6是直线a与直线b被直线c所截的内错角，而∠6与∠4是邻补角，所以∠1与∠4不是内错角，因此选项B符合题意；∠5与∠6是直线c与直线d被直线b所截的内错角，因此选项C不符合题意；∠3与∠5是直线c与直线d被直线b所截的同位角，因此选项D不符合题意；故选：B．【点睛】本题主要考查同位角、内错角、同旁内角，掌握同位角、内错角、同旁内角的定义是关键．3．若方程组31433x y k x y +=-⎧⎨+=⎩的解满足2x y -=，则k 的值为（） A ．32- B ．﹣1 C ．12- D ．1答案：A解析：A【分析】根据等式的性质，可得关于k 的方程，根据解方程，可得答案．【详解】31433x y k x y +=-⎧⎨+=⎩①②， ①-②得：2242x y k -=--可得：21x y k -=--，因为2x y -=，所以212k --=，解得：32k =-，故选A ．【点睛】本题考查了二元一次方程组的解，整体代入的出关于k 的方程是解题关键．4．若a b <，则下列不等式中正确的是（）A ．33a b -<-B ．0a b ->C ．1133a b >D ．22a b -<- 答案：A解析：A【分析】根据不等式的性质逐项判断即得答案．【详解】解：A 、若a b <，则33a b -<-，故本选项变形正确，符合题意；B 、若a b <，则0a b -<，故本选项变形错误，不符合题意；C 、若a b <，则1133a b <，故本选项变形错误，不符合题意；D 、若a b <，则22a b ->-，故本选项变形错误，不符合题意．故选：A ．【点睛】本题考查了不等式的性质，属于基础题型，熟练掌握不等式的性质是解题关键．5．若关于x 的不等式组2242332x x x x a--⎧>⎪⎨⎪->--⎩的解集是2x <，则a 的取值范围是（） A ．2a ≥ B ．2a <- C ．2a > D ．2a ≤答案：A解析：A【分析】分别求出每个不等式的解集，根据不等式组的解集为2x <可得关于a 的不等式，解之可得．【详解】解：解不等式22x -＞243x -，得：2x <，解不等式-3x ＞-2x-a ，得：x ＜a ，∵不等式组的解集为2x <，∴2a ≥，故选：A ．【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．6．下列命题中，属于假命题的是（）A ．如果三角形三个内角的度数比是1:2:3，那么这个三角形是直角三角形B ．平行于同一直线的两条直线平行C ．内错角不一定相等D ．若a 的绝对值等于a ，则a 一定是正数答案：D解析：D【分析】根据所学知识对命题依次判断真假．【详解】解：A 、如果三角形三个内角的度数比是1:2:3，则三个角的度数分别是：30,60,90︒︒︒，所以这个三角形是直角三角形，为真命题，不符合题意；B 、平行于同一直线的两条直线平行，为真命题，不符合题意；C 、内错角不一定相等，为真命题，不符合题意；D 、若a 的绝对值等于a ，当0a =时成立，0不是正数，故为假命题，符合题意；故选：D ．【点睛】本题考查了命题的判断真假，解题的关键是：结合所学知识对命题依次判断，正确的为真命题，错误的为假命题．7．一列数123,,n a a a a ⋅⋅⋅，其中1231211111,,111n n a a ,a a a a a -=-==⋅⋅⋅⋅⋅⋅=---，则2020a =（）A ．1-B ．1C ．2020D ．2020- 答案：A解析：A【分析】根据题意，可以写出这列数的前几项，从而可以发现数字的变化特点，然后即可得到a 2020的值．【详解】解：由题意可得，a 1=-1，a 2=11112a =-， a 3=2121a =-， a 4=3111a =--， …，由上可得，这列数依次以-1，12，2循环出现，∵2020÷3=673…1，∴a 2020=-1，故选A ．【点睛】本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，写出相应的数据．8．如图，CD 是ABC 的一条中线，E 为BC 边上一点且2,BE CE AE CD =、相交于,F 四边形BDFE 的面积为6，则ABC 的面积是（）A．14B．14.4C．13.6D．13.2答案：B解析：B【分析】连结BF，设S△BDF＝x，则S△BEF＝6－x，由CD是中线可以得到S△ADF＝S△BDF，S△BDC＝S△ADC，由BE＝2CE可以得到S△CEF＝12S△BEF，S△ABE＝23S△ABC，进而可用两种方法表示△ABC的面积，由此可得方程，进而得解．【详解】解：如图，连接BF，设S△BDF＝x，则S△BEF＝6－x，∵CD是中线，∴S△ADF＝S△BDF＝x，S△BDC＝ S△ADC＝12△ABC，∵BE＝2CE，∴S△CEF＝12S△BEF＝12(6－x)，S△ABE＝23S△ABC，∵S△BDC＝ S△ADC＝12△ABC，∴S△ABC＝2S△BDC＝2[x＋32(6－x)]＝18－x，∵S△ABE＝23S△ABC，∴S△ABC＝32S△ABE＝32[2x＋ (6－x)]＝1.5x＋9，∴18－x ＝1.5x＋9，解得：x＝3.6，∴S△ABC＝18－x，＝18－3.6＝14.4，故选：B ．【点睛】本题考查了三角形的中线能把三角形的面积平分，等高三角形的面积比等于底的比，熟练掌握这个结论记以及方程思想是解题的关键．二、填空题9．计算：()23223a b a b ⋅-=______．解析：536a b -【分析】根据单项式乘单项式的运算法则进行计算．【详解】解：原式()231253236ab a b ++=⨯-⋅⋅=-．故答案是：536a b -．【点睛】本题考查单项式乘单项式，解题的关键是掌握单项式乘单项式的运算法则．10．命题“若11a b =，则a b =”，这个命题是_____命题．（填“真”或“假”）解析：真【分析】根据题意判断正误即可确定是真、假命题．【详解】解：命题“若11a b=，则a=b”，这个命题是真命题，故答案为：真．【点睛】本题考查了命题与定理的知识，解题的关键是当判断一个命题为假命题时可以举出反例，难度不大．11．如图，正五边形和正六边形有一条公共边AB ，并且正五边形在正六边形内部，连接AC 并延长，交正六边形于点D ，则ADE ∠=______.答案：A解析：84【分析】据正多边形的内角，可得∠ABE、∠E、∠CAB，根据四边形的内角和，可得答案．【详解】解：正五边形的内角是(52)1801085ABC︒︒-⨯∠==∵AB=BC，∴∠CAB=36°，正六边形的内角是(62)1801206ABE E︒︒-⨯∠=∠==∵∠ADE+∠E+∠ABE+∠CAB=360°，∴∠ADE=360°-120°-120°-36°=84°，故答案为84．【点睛】本题考查了多边形的内角与外角，利用求多边形的内角得出正五边形的内角、正六边形的内角是解题关键．12．已知：a+b＝3，则代数式a2+2ab+b2的值为_____．解析：9【分析】根据完全平分公式：（a+b）2＝a2+2ab+b2，即可解答．【详解】解：因为a+b＝3，所以a2+2ab+b2＝（a+b）2＝32＝9．故答案为：9．【点睛】此题主要考查了因式分解的应用，熟练掌握完全平方公式是解答此题的关键．13．如果关于x，y的二元一次方程组25232x yx y k+=⎧⎨+=-⎩的解满足4x y+>，则k的取值范围为_______________．解析：k＞3【分析】先把方程组的两个方程相加求出x+y=k+1，再解不等式即可解答．【详解】解：由方程组解得：x+y=k+1，由x+y＞4，得：k+1＞4，解得：k＞3．则k的取值范围为k＞3；故答案为：k＞3．【点睛】本题考查了二元一次方程组的解和一元一次不等式，解决本题的关键是解二元一次方程组．14．如图，大矩形长是10厘米，宽是8厘米，阴影部分宽为2厘米，则空白部分面积__________．解析：48cm2【分析】把两个矩形形状的阴影部分分别向上和向左平移，这样空白部分就变成了了一个矩形，然后利用矩形面积公式计算即可.【详解】解：把阴影部分平移后如图：S空白部分=(10-2)×(8-2)=48（cm2）故答案为48 cm2.【点睛】本题考查了平移. 通过平移，把不规则的几何图形转化为规则的几何图形，然后根据面积公式进行计算.15．三角形中，其中两条边长分别为4cm和7cm，则第三边c的长度的取值范围是_______．答案：3＜c＜11【分析】直接运用三角形的三边关系判断即可．【详解】根据三角形的三边关系得：，故答案为：．【点睛】本题考查三角形的三边关系，熟记基本定理是解题关键．解析：3＜c＜11【分析】直接运用三角形的三边关系判断即可．【详解】根据三角形的三边关系得：7474c -<<+，故答案为：311c <<．【点睛】本题考查三角形的三边关系，熟记基本定理是解题关键．16．如图，在ABC 中E 是BC 上的一点，EC ＝2BE ，点D 是AC 的中点，设ABC ，ADF ，BEF 的面积分别为ABC S，ADF S △，BEF S ，且18ABC S =，则ADF S △﹣BEF S ＝_____．答案：3【分析】利用三角形面积公式，等高的三角形的面积比等于底边的比，则＝＝12，＝＝9，然后利用＝3即可得到答案．【详解】解：∵EC ＝2BE ，∴＝＝×18＝12，∵点D 是AC 的中点，∴＝＝解析：3【分析】利用三角形面积公式，等高的三角形的面积比等于底边的比，则AEC S ＝23ABC S ＝12，BCD S △＝12ABC S ＝9，然后利用AEC BCD S S -△△＝3即可得到答案．【详解】解：∵EC ＝2BE ，∴AEC S ＝23ABC S ＝23×18＝12， ∵点D 是AC 的中点， ∴BCD S △＝12ABC S ＝12×18＝9，∴AEC S ﹣BCD S △＝3，即ADF S △+S 四边形CEFD ﹣（BEF S﹣S 四边形CEFD ）＝3， ∴ADF S △﹣BEF S ＝3．故答案为：3．【点睛】本题考查了三角形面积：三角形的面积等于底边长与高线乘积的一半，即S △＝12×底×高；三角形的中线将三角形分成面积相等的两部分．17．计算：（1（﹣2013）0﹣（12）﹣2．（2）a （3a ﹣b ）﹣3a 4b ÷a 2b ．答案：（1）-1；（2）﹣ab【分析】（1）根据算术平方根，零指数次幂，负整数指数幂的性质求解各项的值，再相加减（2）根据单项式乘多项式及单项式除以单项式的运算法则计算，再合并即可求解．【详解】解析：（1）-1；（2）﹣ab【分析】（1）根据算术平方根，零指数次幂，负整数指数幂的性质求解各项的值，再相加减（2）根据单项式乘多项式及单项式除以单项式的运算法则计算，再合并即可求解．【详解】解：（1）原式＝2+1﹣4＝﹣1；（2）原式＝3a 2﹣ab ﹣3a 2＝﹣ab ．【点睛】本题主要考查了算术平方根，零指数次幂，负整数指数幂和整式的混合运算，解题的关键在于能够熟练掌握相关计算法则．18．因式分解：（1）3312x x -（2）()()223a b b a b --- 答案：（1）；（2）【分析】（1）原式提取公因式，然后利用平方差公式分解即可；（2）原式利用完全平方公式和单项式乘以多项式的计算法则展开合并，然后再运用完全平方公式分解即可．【详解】（1）解：解析：（1）()()31212x x x +-；（2）()22a b - 【分析】（1）原式提取公因式3x ，然后利用平方差公式分解即可；（2）原式利用完全平方公式和单项式乘以多项式的计算法则展开合并，然后再运用完全平方公式分解即可．【详解】（1）3312x x -解：原式()2314x x =-()()31212x x x =+-（2）()()223a b b a b ---解：原式222223a ab b ab b =-+-+2244a ab b =-+ ()22a b =-．【点睛】本题主要考查了因式分解，整式的混合运算，解题的关键在于能够熟练掌握相关知识进行求解．19．解方程组：（1）528x y x y =+⎧⎨-=⎩；（2）3410435x y x y +=⎧⎨-=⎩．答案：（1）；（2）【分析】（1）应用代入消元法，求出方程组的解是多少即可．（2）应用加减消元法，求出方程组的解是多少即可．【详解】解：（1），①代入②，可得：，解得，把代入①，解得，原解析：（1）32x y =⎧⎨=-⎩；（2）21x y =⎧⎨=⎩ 【分析】（1）应用代入消元法，求出方程组的解是多少即可．（2）应用加减消元法，求出方程组的解是多少即可．【详解】解：（1）528x y x y =+⎧⎨-=⎩①②， ①代入②，可得：2(5)8y y +-=，解得2y =-，把2y =-代入①，解得3x =，∴原方程组的解是32x y =⎧⎨=-⎩．（2）3410435x y x y +=⎧⎨-=⎩①②， ①3⨯+②4⨯，可得2550x =，解得2x =，把2x =代入①，解得1y =，∴原方程组的解是21x y =⎧⎨=⎩．【点睛】此题主要考查了解二元一次方程组的方法，要熟练掌握，注意代入消元法和加减消元法的应用．20．请你根据下框内所给的内容，完成下列各小题．n 的值；（2）若m 满足40m <※，且()380m ->※，求m 的取值范围．答案：（1）；（2）【分析】（1）根据新定义的运算，列出关于m 、n 的方程求解即可；（2）根据新定义的运算，列出关于m 的不等式组求解即可【详解】解：（1）依题意列方程组，把① -②得：，解得，解析：（1）11m n =⎧⎨=⎩；（2）2 3m -<< 【分析】（1）根据新定义的运算，列出关于m 、n 的方程求解即可；（2）根据新定义的运算，列出关于m 的不等式组求解即可【详解】解：（1）依题意列方程组431462m n m n -=⎧⎨-=-⎩①②，把① -②得：33n =，解得1n =，把1n =代入① 解得1m =∴方程组的解为：11m n =⎧⎨=⎩；（2）依题意，列不等式组得412012240m m -<⎧⎨+>⎩①②，解不等式①得3m <，解不等式②得2m >-∴不等式组的解集为2 3m -<<．【点睛】本题主要考查了解一元一次不等式组，解二元一次方程组，新定义下的运算，解题的关键在于能够熟练掌握相关知识进行求解．三、解答题21．（1）已知：如图1，B C BEC ∠+∠=∠．求证：//AB CD（2）如图2，已知//AB CD ，在BCD ∠的平分线上取两个点M 、N ，使得BMN BNM ∠=∠，求证：CBM ABN ∠=∠．答案：（1）见解析；（2）见解析【分析】（1）过点E 作，则由平行线的性质可得，再由即可推出，即可判断，即可得到；（2）过点N 作，交于点G ，则由平行线的性质可得，，再由三角形外角的性质可得，即可推出，解析：（1）见解析；（2）见解析【分析】（1）过点E 作//EF AB ，则由平行线的性质可得B BEF ∠=∠，再由B C BEC ∠+∠=∠即可推出C CEF ∠=∠，即可判断//EF CD ，即可得到//AB CD ；（2）过点N 作//NG AB ，交BM 于点G ，则由平行线的性质可得ABN BNG ∠=∠，GNC NCD ∠=∠，再由三角形外角的性质可得BMN BCM CBM ∠=∠+，即可推出BCM CBM ABN NCD ∠+∠=∠+∠，再由角平分线的定义BCM NCD ∠=∠，由此即可证明．【详解】解：（1）证明：如图1，过点E 作//EF AB ．∴B BEF ∠=∠，∵B C BEC ∠+∠=∠，BEF FEC BEC ∠+∠=∠（已知），∴B C BEF FEC ∠+∠=∠+∠（等量代换），∴C CEF ∠=∠（等式性质），∴//EF CD ，∵//EF AB ，∴//AB CD （平行于同一条直线的两条直线互相平行）；（2）证明：过点N 作//NG AB ，交BM 于点G ，如图2所示：则////NG AB CD ，∴ABN BNG ∠=∠，GNC NCD ∠=∠，∵BMN ∠是BCM 的一个外角，∴BMN BCM CBM ∠=∠+，又∵BMN BNM ∠=∠，BNM BNG GNC ∠=∠+∠，∴BCM CBM BNG GNC ∠+∠=∠+∠，∴BCM CBM ABN NCD ∠+∠=∠+∠，∵CN 平分BCD ∠，∴BCM NCD ∠=∠，∴CBM ABN ∠=∠．【点睛】本题主要考查了平行线的性质与判定，三角形外角的性质，角平分线的定义，解题的关键在于能够准确作出辅助线进行求解．22．某工厂准备用图甲所示的A 型正方形板材和B 型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．（1）若现有A 型板材150张，B 型板材300张，可制作竖式和横式两种无盖箱子各多少个？（2）若该工厂准备用不超过24000元资金去购买A 、B 两种型号板材，制作竖式、横式箱子共100个，已知A 型板材每张20元，B 型板材每张60元，问最多可以制作竖式箱子多少个？（3）若该工厂新购得65张规格为3m 3m ⨯的C 型正方形板材，将其全部切割成A 型或B 型板材（不计损耗），用切割的板材制作两种类型的箱子，要求竖式箱子不少于10个，且材料恰好用完，则最多可以制作竖式箱子多少个？答案：（1）可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）最多可以制作竖式箱子50个；（3）最多可以制作竖式箱子45个【分析】（1）根据题意可以列出相应的二元一次方程组，再解方程组即可解答解析：（1）可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）最多可以制作竖式箱子50个；（3）最多可以制作竖式箱子45个【分析】（1）根据题意可以列出相应的二元一次方程组，再解方程组即可解答本题；（2）根据题意可以列出相应的不等式，从而可以求得最多可以制作竖式箱子多少个；（3）根据题意可以列出相应的二元一次方程，再根据a 为整数和a≥10，即可解答本题．【详解】解：（1）设可制作竖式无盖箱子m 个，可制作横式无盖箱子n 个，依题意有215043300m n m n +=⎧⎨+=⎩，解得3060m n =⎧⎨=⎩，故可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）由题意可得，1个竖式箱子需要1个A 型和4个B 型，1个横式箱子需要2个A 型和3个B 型，设竖式箱子x 个，则横式箱子（100-x ）个，（20+4×60）x+（2×20+3×60）（100-x ）≤24000，故x 的最大值是50，答：最多可以制作竖式箱子50个；（3）C 型可以看成三列，每一列可以做成3个A 型或1个B 型，65个C 型就有65×3=195列，∵材料恰好用完，∴最后A 型的数量一定是3的倍数，设竖式a 个，横式b 个，∵1个竖式箱子需要1个A 型和4个B 型，1个横式箱子需要2个A 型和3个B 型，1个B 型相当于3个A 型，∴（1+4×3）a+（2+3×3）b=195×3，∴13a+11b=585，∵a 、b 均为整数，a≥10，∴450a b =⎧⎨=⎩或3413a b =⎧⎨=⎩或2326a b =⎧⎨=⎩或1239a b =⎧⎨=⎩，故最多可以制作竖式箱子45个．【点睛】本题考查一元一次不等式的应用、二元一次方程（组）的应用，解答本题的关键是明确题意，利用方程和不等式的性质解答．23．阅读材料：形如2213x <+<的不等式，我们就称之为双连不等式.求解双连不等式的方法一，转化为不等式组求解，如221213x x <+⎧⎨+<⎩；方法二，利用不等式的性质直接求解，双连不等式的左、中、右同时减去1，得122x <<，然后同时除以2，得1112x <<．解决下列问题：（1）请你写一个双连不等式并将它转化为不等式组；（2）利用不等式的性质解双连不等式2235x ≥-+>-；（3）已知532x -≤<-，求35x +的整数值．答案：（1）见解析；（2）；（3）或【分析】（1），转化为不等式组；（2）根据方法二的步骤解答即可；（3）根据方法二的步骤解答，得出，即可得到结论．解：（1），转化为不等式组；（2解析：（1）见解析；（2）142x <；（3）4-或3- 【分析】（1）325x <-<，转化为不等式组3225x x <-⎧⎨-<⎩；（2）根据方法二的步骤解答即可；（3）根据方法二的步骤解答，得出54352x -+<-，即可得到结论．【详解】解：（1）325x <-<，转化为不等式组3225x x <-⎧⎨-<⎩；（2）2235x -+>-，不等式的左、中、右同时减去3，得128x -->-，同时除以2-，得142x <；（3）532x -<-，不等式的左、中、右同时乘以3，得15932x -<-，同时加5，得54352x -+<-，35x ∴+的整数值4-或3-．【点睛】本题考查了解一元一次不等式组，参照方法二解不等式组是解题的关键，应用的是不等式的性质．24．如图，直线m 与直线n 互相垂直，垂足为O 、A 、B 两点同时从点O 出发，点A 沿直线m 向左运动，点B 沿直线n 向上运动．(1)若∠BAO 和∠ABO 的平分线相交于点Q ，在点A ，B 的运动过程中，∠AQB 的大小是否会发生变化？若不发生变化，请求出其值，若发生变化，请说明理由．(2)若AP 是∠BAO 的邻补角的平分线，BP 是∠ABO 的邻补角的平分线，AP 、BP 相交于点P ，AQ 的延长线交PB 的延长线于点C ，在点A ，B 的运动过程中，∠P 和∠C 的大小是否会发生变化？若不发生变化，请求出∠P 和∠C 的度数；若发生变化，请说明理由．答案：(1)∠AQB的大小不发生变化，∠AQB＝135°；(2)∠P和∠C的大小不变，∠P=45°，∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和，由角平分线和角的和差可求出∠BA 解析：(1)∠AQB的大小不发生变化，∠AQB＝135°；(2)∠P和∠C的大小不变，∠P=45°，∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和，由角平分线和角的和差可求出∠BAQ与∠ABQ 的和，最后在△ABQ中，根据三角形的内角各定理可求∠AQB的大小．第(2)题求∠P的大小，用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解．【详解】解：(1)∠AQB的大小不发生变化，如图1所示，其原因如下：∵m⊥n，∴∠AOB＝90°，∵在△ABO中，∠AOB+∠ABO+∠BAO＝180°，∴∠ABO+∠BAO＝90°，又∵AQ、BQ分别是∠BAO和∠ABO的角平分线，∴∠BAQ＝12∠BAC，∠ABQ＝12∠ABO,∴∠BAQ+∠ABQ＝12 (∠ABO+∠BAO)＝190452⨯=又∵在△ABQ中，∠BAQ+∠ABQ+∠AQB＝180°，∴∠AQB＝180°﹣45°＝135°．(2)如图2所示：①∠P 的大小不发生变化，其原因如下：∵∠ABF+∠ABO ＝180°，∠EAB+∠BAO ＝180°∠BAQ+∠ABQ ＝90°，∴∠ABF+∠EAB ＝360°﹣90°＝270°，又∵AP 、BP 分别是∠BAE 和∠ABP 的角平分线，∴∠PAB ＝12∠EAB ，∠PBA ＝12∠ABF ， ∴∠PAB+∠PBA ＝12 (∠EAB+∠ABF)＝12×270°＝135°，又∵在△PAB 中，∠P+∠PAB+∠PBA ＝180°，∴∠P ＝180°﹣135°＝45°．②∠C 的大小不变，其原因如下：∵∠AQB ＝135°，∠AQB+∠BQC ＝180°，∴∠BQC ＝180°﹣135°，又∵∠FBO ＝∠OBQ+∠QBA+∠ABP+∠PBF ＝180°∠ABQ ＝∠QBO ＝12∠ABO ，∠PBA ＝∠PBF ＝∠ABF ， ∴∠PBQ ＝∠ABQ+∠PBA ＝90°，又∵∠PBC ＝∠PBQ+∠CBQ ＝180°，∴∠QBC ＝180°﹣90°＝90°．又∵∠QBC+∠C+∠BQC ＝180°，∴∠C ＝180°﹣90°﹣45°＝45°【点睛】本题考查三角形内角和定理，垂直，角平分线，平角，直角和角的和差等知识点，同时，也是一个以静求动的一个点型题目，有益于培养学生的思维几何综合题．25．阅读材料：如图1，点A 是直线MN 上一点，MN 上方的四边形ABCD 中，140ABC ∠=︒，延长BC ，2DCE MAD ADC ∠=∠+∠，探究DCE ∠与MAB ∠的数量关系，并证明.小白的想法是：“作ECF ECD ∠=∠（如图2），通过推理可以得到CF MN ，从而得出结论”.请按照小白的想法．．．．．完成解答：拓展延伸：保留原题条件不变，CG 平分ECD ∠，反向延长CG ，交MAB ∠的平分线于点H （如图3），设MAB α∠=，请直接写出H ∠的度数（用含α的式子表示）.答案：阅读材料：，见解析；拓展延伸：.【分析】（1）作，，，由平行线性质可得，结合已知，可证，进而得到，从而，，将代入可得.（2）过H 点作HP ∥MN ，可得∠CHA=∠PHA+∠PHC ，结合（1）的结解析：阅读材料：40∠=︒+∠ECD MAB ，见解析；拓展延伸：120CHA α=∠︒-.【分析】（1）作ECF ECD ∠=∠，DG MN ，BH MN ，由平行线性质可得180MAD ADG ∠+∠=︒，结合已知2DCE MAD ADC ∠=∠+∠，可证180CDG DCF ∠+∠=︒，进而得到DG CF ，从而CF BH ，140BCF MAB ABC ∠+∠=∠=︒，将180180BCF ECF ECD ∠=︒-∠=︒-∠代入可得40∠=︒+∠ECD MAB .（2）过H 点作HP ∥MN ，可得∠CHA=∠PHA+∠PHC ，结合（1）的结论和CG 平分∠ECD 可得∠PHC =∠FCH =120°-3MAB 2∠，即可得120CHA α=∠︒-.【详解】解：【阅读材料】作ECF ECD ∠=∠，DG MN ，BH MN （如图1）.∵DG MN ，∴180MAD ADG ∠+∠=︒.∴()180CDG MAD ADC ∠+∠+∠=︒.∵2DCE MAD ADC ∠=∠+∠，∴2180CDG DCE ∠+∠=︒.∴180CDG DCF ∠+∠=︒.∴DG CF . ∵DG MN ， ∴MN CF . ∵BH MN ， ∴CF BH .∴BCF CBH ∠=∠，MAB ABH ∠=∠.∴140BCF MAB ABC ∠+∠=∠=︒.∵180180BCF ECF ECD ∠=︒-∠=︒-∠，∴40∠=︒+∠ECD MAB .【拓展延伸】结论：120CHA α=∠︒-.理由：如图，作ECF ECD ∠=∠，过H 点作HP ∥MN ，∴∠PHA=∠MAH=1BAM 2∠，由（1）得FC ∥MN ，∴FC ∥HP ，∴∠PHC=∠FCH ，∵40∠=︒+∠ECD MAB ,CG 平分∠ECD ，∴∠ECG=20°+1MAB 2∠，∴∠FCH=180ECG ECF ︒-∠-∠=180°-(40MAB ︒+∠)-(20°+1MAB 2∠)=120°-3MAB 2∠∴∠CHA=∠PHA+∠PHC=1MAB 2∠∠+（120°-3MAB 2∠）=120°-MAB ∠即：120CHA α=∠︒-.【点评】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．。

（完整版）苏教版七年级下册期末数学测试模拟试卷经典答案

（完整版）苏教版七年级下册期末数学测试模拟试卷经典答案一、选择题1．下列各式计算正确的是（）A ．5a ﹣3a ＝3B ．a 2·a 5＝a 10C ．a 6÷a 3＝a 2D ．（a 2）3＝a 6 答案：D解析：D【分析】由合并同类项判断,A 由同底数幂的乘法判断,B 由同底数幂的除法判断,C 由幂的乘方判断,D 从而可得答案.【详解】解：532,a a a -= 故A 不符合题意；257,a a a = 故B 不符合题意；633,a a a ÷= 故C 不符合题意；()632,a a = 故D 符合题意；故选：.D【点睛】本题考查的是合并同类项，同底数幂的乘法，同底数幂的除法，幂的乘方，掌握以上运算的运算法则是解题的关键.2．如图，图中的内错角的对数是（）A ．3对B ．4对C ．5对D ．6对答案：C解析：C【分析】利用内错角的定义分析得出答案．【详解】解：如图所示：内错角有：∠FOP 与∠OPE ，∠GOP 与∠OPD ，∠CPA 与∠HOP ，∠FOP 与∠OPD ，∠EPO 与∠GOP 都是内错角，故内错角一共有5对．故选：C ．【点睛】此题主要考查了内错角的定义，正确把握内错角的定义是解题关键．x+≥的解集在数轴上表示为（）3．不等式237A．B．C．D．答案：C解析：C【分析】两边都减3除以2即可求得不等式的解集【详解】x+≥解：不等式两边同时减3得：23-37-3整理得：2x4≥x≥解得：2在数轴上表示为：故选C.【点睛】本题主要考查对解一元一次不等式，在数轴上表示不等式的解集，不等式的性质等知识点的理解和掌握，能根据不等式的性质正确解不等式是解此题的关键．4．若a＞b．则依据不等式的基本性质下列变形不正确的是（）A．3﹣2a＞3﹣2b B．4+a＞4+bC．ac2＞bc2（c≠0）D．﹣a＜﹣b答案：A解析：A【分析】利用不等式的性质对各选项进行判断．【详解】∵a＞b，∴a不等式两边同时乘以-2再加上3得，3﹣2a＜3﹣2b，A选项错误；不等式两边同时加上4，不变号，4+a＞4+b，B选项正确；不等式两边同时乘以一个c2，不变号，ac2＞bc2（c≠0），C选项正确；不等式两边同时乘以-1，变号，﹣a ＜﹣b ，D 选项正确．故选：A ．【点睛】本题考查不等式的性质，需要特别注意不等式两边同时乘以一个负数，不等式变号.5．不等式组9511x x x m +<+⎧⎨>+⎩的解集是x ＞2，则m 的取值范围是（） A ．m ≤2 B ．m ≥2 C ．m ≤1 D ．m ＞1答案：C解析：C【分析】分别解出不等式，进而利用不等式的解得出m+1的取值范围，进而求出即可；【详解】解：∵不等式组1951x m x x +⎧⎨++⎩＞＜①② 的解集是x ＞2，解不等式①得x ＞2，解不等式②得x ＞m+1，不等式组的解集是x ＞2，∴不等式①解集是不等式组的解集，∴m+1≤2，解得：m≤1，故选：C ．【点睛】本题考查了解一元一次方程组，根据不等式组的解得出m+1的取值范围是解题的关键； 6．下列命题：①如果a b >，那么a b >；②如果22ac bc >，那么a b >；③同旁内角互补；④若α∠与β∠互余，β∠与γ∠互余，则α∠与γ∠互余．真命题的个数为（） A ．0 B ．1 C ．2 D ．3答案：B解析：B【分析】根据绝对值、不等式的性质、平行线的性质、同角的余角相等分别对各小题进行判断后即可求解．【详解】①当a ＝1，b ＝−2时，|a|＝1，|b|＝2，|a|＜|b|，故此命题假命题；②如果22ac bc >，那么a ＞b ；真命题；③同旁内角互补；假命题；④若α∠与β∠互余，β∠与γ∠互余，则α∠与γ∠相等，故此命题是假命题；真命题的个数为1个；故选：B ．【点睛】本题考查了命题与定理，熟记概念与性质是解题的关键．7．如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为1n，每个数是它下一行左右相邻两数的和，则第8行第3个数（从左往右数）为（）A．160B．1168C．1252D．1280答案：B 解析：B 【分析】根据给出的数据可得：第n行的第三个数等于112n n--的结果再乘11n-，再把n的值代入即可得出答案．【详解】解：根据给出的数据可得：第n行的第三个数等于112n n--的结果再乘11n-，则第8行第3个数（从左往右数）为1111 82881168⎛⎫-⨯=⎪--⎝⎭；故选：B．【点睛】本题考查与实数运算相关的规律题，通过阅读题意归纳总结有关规律再运算是解题关键．8．如图，小明从一张三角形纸片ABC的AC边上选取一点N，将纸片沿着BN对折一次使得点A落在A′处后，再将纸片沿着BA′对折一次，使得点C落在BN上的C′处，已知∠CMB ＝68°，∠A＝18°，则原三角形的∠C的度数为（）A ．87°B ．84°C ．75°D ．72°答案：A解析：A【分析】根据折叠的性质可知ABN A BN A BC ''∠=∠=∠，根据三角形内角和定理可得180,3180A BC C CMB A A BC C ''∠+∠+∠=︒∠+∠+∠=︒,进而可得原三角形的∠C 的度数．【详解】由折叠的性质可知ABN A BN A BC ''∠=∠=∠，则3ABC A BC '∠=∠,180,3180A BC C CMB A A BC C ''∠+∠+∠=︒∠+∠+∠=︒,∠CMB ＝68°，∠A ＝18°,即68180183180A BC C A BC C ∠+∠+︒=︒⎧⎨︒+∠+'∠=︒'⎩解得87C ∠=︒故选A【点睛】本题考查了折叠的性质，三角形内角和定理，二元一次方程组的应用，掌握折叠的性质是解题的关键．二、填空题9．计算：3x 3•（﹣2x ）2＝_______．解析：12x 5【分析】根据积的乘方运算，同底数幂相乘，单项式乘单项式，把系数和相同字母分别相乘．【详解】解：原式＝3x 3•4x 2＝12x 5，故答案为：12x 5．【点睛】本题考查了积的乘方运算，同底数幂相乘，单项式乘单项式，把系数和相同字母分别相乘是解题的关键．10．命题“对顶角相等”的逆命题是一个__________命题（填“真”或“假”）．解析：假【分析】先交换原命题的题设与结论得到逆命题，然后根据对顶角的定义进行判断．【详解】解：命题“对顶角相等”的逆命题是相等的角为对顶角，此逆命题为假命题．故答案为：假．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．11．一个多边形的每一个外角都等于30°，则这个多边形的边数是__．解析：12【分析】多边形的外角和为360°，而多边形的每一个外角都等于30°，由此做除法得出多边形的边数．【详解】∵360°÷30°=12，∴这个多边形为十二边形，故答案为：12．【点睛】本题考查了多边形的内角与外角．关键是明确多边形的外角和为360°．12．如图是一个长和宽分别为a、b的长方形，它的周长为14、面积为10，则a2b+ab2的值为___．解析：70【分析】根据已知条件长方形的长与宽之和即a+b=7，长与宽的积为ab=10，再将所给的代数式分解因式，将a+b与ab代入计算即可．【详解】解：根据长方形的周长为14，面积为10，可得a+b=12×14=7，ab=10，a2b+ab2=ab(a+b)=10×7=70．故答案为：70．【点睛】本题考查了因式分解的应用，由已知可得到a与b的和，a与b的积；求所给代数式的值，关键先分解因式，用已知式子的值整体代入．13．已知关于x ，y 的二元一次方程组3233235x y k x y k ++=⎧⎨++=⎩的解满足8x y +=，则k 的值为________．解析：-8【分析】直接利用已知方程组得出5（x +y ）=8-4k ，进而得出k 的值．【详解】解：∵关于x ，y 的二元一次方程组3233235x y k x y k ++=⎧⎨++=⎩的解满足x +y =8， ∴5（x +y ）=8-4k ，则40=8-4k ，解得：k =-8．故答案为：-8．【点睛】此题主要考查了二元一次方程组的解，正确利用已知分析是解题关键．14．如图，在一块长为a 米、宽为b 米的长方形地上，有一条弯曲的柏油马路，马路的任何地方的水平宽度都是2米，其他部分都是草地，则草地的面积为__________平方米．解析：（ab ﹣2b ）【分析】根据图形的特点，可以把小路的面积看作是一个底是2米，高是b 米的平行四边形，根据平行四边形的面积＝底×高，长方形的面积＝长×宽，用长方形的面积减去小路的面积即可．【详解】解：由题可得，草地的面积是(ab ﹣2b )平方米．故答案为：(ab ﹣2b )．【点睛】本题考查了平移的实际应用．化曲为直是解题的关键．15．已知a ，b ，c 为△ABC 的三边长，b ，c 满足2(2)|3|0b c -+-=，且a 为方程42a -= 的解，则△ABC 的周长为___________．答案：7【分析】利用绝对值的性质以及偶次方的性质得出b ，c 的值，进而利用三角形三边关系得出a 的值，进而求出△ABC 的周长即可．【详解】解：∵，∴，∴，即，∵，∴或，∵，∴，∴△ABC解析：7【分析】利用绝对值的性质以及偶次方的性质得出b ，c 的值，进而利用三角形三边关系得出a 的值，进而求出△ABC 的周长即可．【详解】解：∵2(2)|3|0b c -+-=，∴2,3b c ==，∴3232a -<<+，即15a <<， ∵42a -=，∴6a =或2a =，∵15a <<，∴2a =，∴△ABC 的周长为2237++=，故答案为：7．【点睛】本题主要考查三角形三边关系及绝对值和偶次方的性质，解题关键是熟练掌握三角形三边关系．16．如图，在△ABC 中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且△ABC 的面积等于4cm 2，则阴影部分图形面积等于_____cm 2答案：1【分析】由点为的中点，可得的面积是面积的一半；同理可得和的面积之比，利用三角形的等积变换可解答．【详解】解：如图，点是的中点，的底是，的底是，即，而高相等，，是的中点，，，，解析：1【分析】由点E 为AD 的中点，可得EBC ∆的面积是ABC ∆面积的一半；同理可得BCE ∆和EFB ∆的面积之比，利用三角形的等积变换可解答．【详解】解：如图，点F 是CE 的中点，BEF 的底是EF ，BEC ∆的底是EC ，即12EF EC =，而高相等， 12BEF BEC S S ∆∆∴=， E 是AD 的中点，12BDE ABD S S ∆∆∴=，12CDE ACD S S ∆∆=， 12EBC ABC S S ∆∆∴=， 14BEF ABC S S ∆∆∴=，且24ABC S cm ∆=， 21BEF S cm ∆∴=，即阴影部分的面积为21cm ．故答案为1．【点睛】本题主要考查了三角形面积的等积变换：若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍．17．计算：（1）3021232-⎛⎫-+-- ⎪⎝⎭ （2）()232372()x x x x x --⋅+÷- （3）(3)(3)x y x y -++- （4）22(23)(23)x x +-答案：（1）-18；（2）；（3）；（4）【解析】【分析】（1）原式第一项利用零指数幂法则计算，第二项利用负指数幂法则计算，第三项利用平方计算，即可得到结果；（2）原式第一项利用幂的乘方计算法则计解析：（1）-18；（2）6x ；（3）2296x y y --+；（4）42168172x x +-【解析】【分析】（1）原式第一项利用零指数幂法则计算，第二项利用负指数幂法则计算，第三项利用平方计算，即可得到结果；（2）原式第一项利用幂的乘方计算法则计算，第二项利用同底数幂的乘法法则计算，最后一项利用同底数幂的除法运算法则计算，合并后即可得到结果；（3）原式利用平方差公式化简，再利用完全平方公式展开，即可得到结果；（4）原式利用积的乘方的逆运算，平方差公式，完全平方公式，即可得到结果．【详解】解：（1）原式18918=---=-；（2）原式6556x x x x =-+=；（3）原式()()33x y x y ⎡⎤⎡⎤=--+-⎣⎦⎣⎦()223x y =--， ()2296x y y =-+-，2296x y y =--+；（4）原式()()22323x x ⎡⎤=+-⎣⎦()2249x =-，42168172x x =+-．故答案为（1）-18；（2）6x ；（3）2296x y y --+；（4）42168172x x +-．【点睛】本题考查整式的混合运算，以及实数的运算，涉及的知识有：完全平方公式，平方差公式，零指数幂，负整数指数幂，以及合并同类项法则，熟练掌握公式及法则是解题的关键．18．把下列各式分解因式（1）236mx nx -（2）()22214a a +-答案：（1）；（2）【分析】（1）用提公因式法因式分解；（2）用公式法因式分解即可【详解】（1）解：原式．（2）解：原式【点睛】本题考查了因式分解，用提公因式法因式分解，公式法因式分解，解析：（1）3(2)x m nx -；（2）22(1)(1)a a +- 【分析】（1）用提公因式法因式分解；（2）用公式法因式分解即可【详解】（1）解：原式3(2)x m nx =-．（2）解：原式()()221212a a a a =+++-22(1)(1)=+-a a【点睛】本题考查了因式分解，用提公因式法因式分解，公式法因式分解，熟练以上方法是解题的关键． 19．解方程组：（1）232y x y x y =-⎧⎨=-⎩ （2）34332(1)20x y x y ⎧+=⎪⎨⎪--=⎩答案：（1）；（2）【分析】（1）利用代入消元法解方程组即可；（2）整理后，利用加减消元法求解．【详解】解：（1），把②代入①，得，解得：，代入②中，解得：，∴方程组的解为：；（2）方解析：（1）11x y =⎧⎨=⎩；（2）83x y =⎧⎨=⎩【分析】（1）利用代入消元法解方程组即可；（2）整理后，利用加减消元法求解．【详解】解：（1）232y x y x y =-⎧⎨=-⎩①②，把②代入①，得()232y y y =--，解得：1y =，代入②中，解得：1x =，∴方程组的解为：11x y =⎧⎨=⎩；（2）方程组整理得34363218x y x y +=⎧⎨-=⎩①②，①-②得：618y =，解得：3y =，代入②中，解得：8x =，∴方程组的解为：83x y =⎧⎨=⎩．【点睛】本题考查的是二元一次方程组的解法，掌握代入消元法和加减消元法的一般步骤是解题的关键．20．解不等式组：2042(25)3(42)x x x -⎧<⎪⎨⎪-≤+⎩①②，并写出该不等式组的整数解．答案：，整数解为-2，-1，0，1 【分析】分别求出不等式组中两不等式的解集，找出解集的公共部分，确定出不等式组的整数解即可．【详解】解：由①得．由②得，不等式组的解集为，则不等式组的整数解为解析：22x -≤<，整数解为-2，-1，0，1 【分析】分别求出不等式组中两不等式的解集，找出解集的公共部分，确定出不等式组的整数解即可．【详解】解：由①得2x <．由②得2x ≥-，∴不等式组的解集为22x -≤<，则不等式组的整数解为-2，-1，0，1．【点睛】此题考查了解一元一次不等式组，以及一元一次不等式组的整数解，熟练掌握运算法则是解本题的关键．三、解答题21．如图，已知点E 、F 在直线AB 上，点G 在线段CD 上，ED 与FG 交于点H ，C EFG ∠=∠，CED GHD ∠=∠．（1）求证：//AB CD ；（2）若80,30EHF D ∠=︒∠=︒，求BEM ∠的度数．答案：（1）见解析；（2）70° 【分析】（1）根据同位角相等，两直线平行可得CE ∥GF ，再根据平行线的性质可得∠C ＝∠DGF ，再等量代换可得∠DGF ＝∠EFG ，进而证明AB ∥CD ；（2）结合（1）根解析：（1）见解析；（2）70° 【分析】（1）根据同位角相等，两直线平行可得CE ∥GF ，再根据平行线的性质可得∠C ＝∠DGF ，再等量代换可得∠DGF ＝∠EFG ，进而证明AB ∥CD ；（2）结合（1）根据∠EHF ＝70°，∠D ＝30°，利用三角形内角和定理和平行线的性质即可求∠BEM 的度数．【详解】（1）证明：∵∠CED ＝∠GHD ， ∴CE //GF ， ∴∠C ＝∠DGF ，又∵∠C ＝∠EFG ，∴∠DGF＝∠EFG，∴//AB CD；（2）解：∵∠CED＝∠GHD，∠GHD＝∠EHF＝80°，∴∠CED＝80°，在CDE中，∠CED＝80°，∠D＝30°，∴∠C＝180°﹣80°﹣30°＝70°，∵AB∥CD，∴∠BEM＝∠C＝70°，答：∠BEM的度数为70°．【点睛】本题考查了平行线的判定与性质以及三角形的内角和，解决本题的关键是准确区分平行线的判定与性质，并熟练运用．22．某县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：（进价、售价均保持不变，利润＝销售收入﹣进货成本）（1）求A、B两种型号的电风扇的销售单价；（2）若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？（3）在（2）的条件下，商场销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．答案：（1）A型电风扇单价为200元，B型单价150元；（2）37台；（3）方案一：采购A型36台B型14台；方案二：采购A型37台B型13台．【解析】（1）设A、B两种型号电风扇的销售单价分别为x元解析：（1）A型电风扇单价为200元，B型单价150元；（2）37台；（3）方案一：采购A型36台B型14台；方案二：采购A型37台B型13台．【解析】（1）设A、B两种型号电风扇的销售单价分别为x元、y元，依题意得：341200, 561900. x yx y+=⎧⎨+=⎩解得：200,150. xy=⎧⎨=⎩答：A、B两种型号电风扇的销售单价分别为200元、150元.（2）设采购A种型号电风扇a台，则采购B种型号电风扇（50﹣a）台．依题意得：160a+120（30﹣a）≤7500，解得：a≤1 372．答：超市最多采购A种型号电风扇37台时，采购金额不多于7500元.（3）依题意有：（200﹣160）a+（150﹣120）（50﹣a）＞1850解得：a＞35，∵a≤1372，且a应为整数∴a=36，37∴在（2）的条件下超市能实现利润超过1850元的目标．相应方案有两种：当a=36时，采购A种型号的电风扇36台，B种型号的电风扇14台；当a=37时，采购A种型号的电风扇37台，B种型号的电风扇13台．23．我市某包装生产企业承接了一批上海世博会的礼品盒制作业务，为了确保质量，该企业进行试生产．他们购得规格是170cm40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材．如图甲，（单位：cm）（1）列出方程（组），求出图甲中a与b的值；（2）在试生产阶段，若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图乙的竖式与横式两种礼品盒．①两种裁法共产生A型板材________张，B型板材_______张；②已知①中的A型板材和B型板材恰好做成竖式有盖礼品盒x个，横式无盖礼品盒的y 个，求x、y的值．答案：（1）a=60，b=40；（2）①64，38；②x=7，y=12【分析】（1）由图示利用板材的长列出关于a、b的二元一次方程组求解；（2）①根据已知和图示计算出两种裁法共产生A 型板材和B 型板材解析：（1）a =60，b =40；（2）①64，38；②x =7，y =12 【分析】（1）由图示利用板材的长列出关于a 、b 的二元一次方程组求解；（2）①根据已知和图示计算出两种裁法共产生A 型板材和B 型板材的张数；②根据竖式与横式礼品盒所需要的A 、B 两种型号板材的张数列出关于x 、y 的二元一次方程组，然后求解即可．【详解】解：（1）由题意得：210170230170a b a b ++=⎧⎨++=⎩，解得：6040a b =⎧⎨=⎩，答：图甲中a 与b 的值分别为：60、40；（2）①由图示裁法一产生A 型板材为：23060⨯=，裁法二产生A 型板材为：144⨯=，所以两种裁法共产生A 型板材为60464+=（张)，由图示裁法一产生B 型板材为：13030⨯=，裁法二产生A 型板材为，248⨯=，所以两种裁法共产生B 型板材为30838+=（张)，故答案为：64，38；②根据题意竖式有盖礼品盒的x 个，横式无盖礼品盒的y 个，则A 型板材需要(43)x y +个，B 型板材需要(22)x y +个，所以43642238x y x y +=⎧⎨+=⎩，解得712x y =⎧⎨=⎩．【点睛】本题考查的知识点是二元一次方程组的应用，关键是根据已知先列出二元一次方程组求出a 、b 的值，根据图示列出算式以及关于x 、y 的二元一次方程组． 24．如图①所示，在三角形纸片中，，，将纸片的一角折叠，使点落在ABC 内的点处. （1）若，________.（2）如图①，若各个角度不确定，试猜想，2∠，A ∠之间的数量关系，直接写出结论.②当点落在四边形外部时（如图②），（1）中的猜想是否仍然成立？若成立，请说明理由，若不成立，A ∠，，2∠之间又存在什么关系？请说明．（3）应用：如图③：把一个三角形的三个角向内折叠之后，且三个顶点不重合，那么图中的和是________.答案：(1)50°；(2)①见解析;②见解析;(3)360°.【分析】（1）根据题意，已知，，可结合三角形内角和定理和折叠变换的性质求解；（2）①先根据折叠得：∠ADE=∠A′DE，∠AED=∠A′解析：(1)50°；(2)①见解析;②见解析;(3)360°.【分析】（1）根据题意，已知，，可结合三角形内角和定理和折叠变换的性质求解；（2）①先根据折叠得：∠ADE=∠A′DE，∠AED=∠A′ED，由两个平角∠AEB和∠ADC得：∠1+∠2等于360°与四个折叠角的差，化简得结果；②利用两次外角定理得出结论；（3）由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去（∠B'GF+∠B'FG）以及（∠C'DE+∠C'ED）和（∠A'HL+∠A'LH），再利用三角形的内角和定理即可求解．【详解】解：（1）∵，，∴∠A′=∠A=180°-（65°+70°）=45°，∴∠A′ED+∠A′DE =180°-∠A′=135°，∴∠2=360°-（∠C+∠B+∠1+∠A′ED+∠A′DE）=360°-310°=50°；（2）①,理由如下由折叠得：∠ADE=∠A′DE，∠AED=∠A′ED，∵∠AEB+∠ADC=360°，∴∠1+∠2=360°-∠ADE-∠A′DE-∠AED-∠A′ED=360°-2∠ADE-2∠AED，∴∠1+∠2=2（180°-∠ADE-∠AED）=2∠A；②，理由如下：∵2∠是的一个外角∴.∵AFD∠是的一个外角∴又∵∴（3）如图由题意知，∠1+∠2+∠3+∠4+∠5+∠6=720°-（∠B'GF+∠B'FG ）-（∠C'DE+∠C'ED ）-（∠A'HL+∠A'LH ）=720°-（180°-∠B'）-（180°-C'）-（180°-A'）=180°+（∠B'+∠C'+∠A'）又∵∠B=∠B'，∠C=∠C'，∠A=∠A'， ∠A+∠B+∠C=180°，∴∠1+∠2+∠3+∠4+∠5+∠6=360°．【点睛】题主要考查了折叠变换、三角形、四边形内角和定理．注意折叠前后图形全等；三角形内角和为180°；四边形内角和等于360度．25．[原题]（1）已知直线 //AB CD ，点P 为平行线AB ，CD 之间的一点，如图①，若52,64ABP CDP ∠∠=︒=︒，BE 平分ABP ∠，DE 平分CDP ∠，则BED ∠=__________．[探究]（2）如图②， //AB CD ，当点P 在直线AB 的上方时．若,ABP CDP αβ∠=∠=，ABP ∠和CDP ∠的平分线相交于点1E ，1ABE ∠与1CDE ∠的平分线相交于点2E ，2ABE ∠与2CDE ∠的平分线相交于点3E ……以此类推，求n E ∠的度数．[变式]（3）如图③， //AB CD ，ABP ∠的平分线的反向延长线和CDP ∠的补角的平分线相交于点E ，试猜想P ∠与E ∠的数量关系，并说明理由．答案：（1）；（2）；（3），理由见解析【分析】（1）过作，依据平行线的性质，即可得到，依据角平分线即可得出的度数；（2）依据平行线的性质以及三角形外角性质，求得，，，以此类推的度数为；（3）过作解析：（1）58︒；（2）1()2n βα-；（3）1902DEB P ∠=︒-∠，理由见解析【分析】（1）过E 作//EF AB ，依据平行线的性质，即可得到BED BEF DEF ABE CDE ∠=∠+∠=∠+∠，依据角平分线即可得出BED ∠的度数；（2）依据平行线的性质以及三角形外角性质，求得11()2E βα∠=-，21()4E βα∠=-，31()8E βα∠=-，以此类推n E ∠的度数为1()2n βα-；（3）过E 作//EG AB ，进而得出DEB BEG DEG MBE FDE ABQ FDE ∠=∠+∠=∠+∠=∠+∠，再根据平行线的性质以及三角形外角性质，即可得到11190()90()90222DEB CDP ABP AHP ABP P ∠=︒-∠-∠=︒-∠-∠=︒-∠【详解】解：（1）如图1，过E 作//EF AB ，而//AB CD ，////AB CD EF ∴，ABE FEB ∴∠=∠，CDE FED ∠=∠， BED BEF DEF ABE CDE ∴∠=∠+∠=∠+∠，又52ABP ∠=︒，64CDP ∠=︒，BE 平分ABP ∠，DE 平分CDP ∠， 1262ABE ABP ∴∠=∠=︒，1322CDE CDP ∠=∠=︒， 263258BED ∴∠=︒+︒=︒，故答案为：58︒；（2）如图2，ABP ∠和CDP ∠的平分线交于点1E ，11122ABE ABP α∴∠=∠=，11122CDE CDP β∠=∠=，//AB CD ，112CDF AFE β∴∠=∠=，111111()222E AFE ABE βαβα∴∠=∠-∠=-=-，1ABE ∠与1CDE ∠的角平分线交于点2E ，211124ABE ABE α∴∠=∠=，211124CDE CDE β∠=∠=，//AB CD ，214CDG AGE β∴∠=∠=，2221()4E AGE ABE βα∴∠=∠-∠=-，同理可得，31()8E βα∠=-，以此类推，n E ∠的度数为1()2nβα-．（3）1902DEB P ∠=︒-∠．理由如下：如图3，过E 作//EG AB ，而//AB CD ，////AB CD EG ∴，MBE BEG ∴∠=∠，FDE GED ∠=∠，DEB BEG DEG MBE FDE ABQ FDE ∴∠=∠+∠=∠+∠=∠+∠，又ABP ∠的角平分线的反向延长线和CDP ∠的补角的角平分线交于点E ，11(180)22FDE PDF CDP ∴∠=∠=︒-∠，12ABQ ABP ∠=∠，111(180)90()222DEB ABP CDP CDP ABP ∴∠=∠+︒-∠=︒-∠-∠，//AB CD ，CDP AHP ∴∠=∠，11190()90()90222DEB CDP ABP AHP ABP P ∴∠=︒-∠-∠=︒-∠-∠=︒-∠．【点睛】本题考查了平行线性质以及三角形外角性质的应用，在解答此题时要注意作出辅助线，构造出平行线求解．。

(完整版)苏教版七年级下册期末数学模拟试卷经典套题答案

（完整版）苏教版七年级下册期末数学模拟试卷经典套题答案一、选择题1．下列计算正确的是（）A ．a 8 ÷ a 2=a 4B ．a 3·a 4=a 7C ．（2a 2）3=6a 6D ．（1? 2?）-2=14 答案：B解析：B【分析】分别根据同底数幂的乘除法法则，幂的乘方与积的乘方运算法则以及负整数指数幂的运算法则逐一判断即可．【详解】解：A ．a 8÷a 2=a 6，故本选项不合题意；B ．a 3·a 4=a 7，正确；C ．（2a 2）3=8a 6，故本选项不合题意；D ，（12）-2=4，故本选项不合题意．故选：B ．【点睛】本题主要考查了同底数幂的乘除法，幂的乘方与积的乘方以及负整数指数幂，熟记幂的运算法则是解答本题的关键．2．如图，下列说法正确的是（）A ．2∠与1∠是同位角B ．C ∠与1∠是内错角 C ．2∠与3∠是同旁内角D ．B 与3∠是同位角答案：B解析：B【分析】根据内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角可得答案．【详解】解：∵∠3与∠1是同位角，∠C 与∠1是内错角，∠2与∠3是邻补角，∠B 与∠3是同旁内角，∴B 选项正确，故选：B ．【点睛】此题主要考查了三线八角，在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F “形，内错角的边构成“Z “形，同旁内角的边构成“U ”形．3．已知方程组135x y a x y a +=-⎧⎨-=+⎩的解x 为正数，y 为非负数，给出下列结论：①－1＜a≤1；②当a ＝－53时，x ＝y ；③当a ＝－2时，方程组的解也是方程x ＋y ＝5＋a 的解．其中正确的是( )A ．①②B ．②③C ．①③D ．①②③ 答案：B解析：B【解析】解：解方程组得：x =3+a ，y =－2－2a ．∵x 为正数，y 为非负数，∴3+a ＞0，－2－2a ≥0，解得：－3＜a ≤－1，故①错误；当a =53-时，x =54333-=，y =542233-+⨯=，∴x =y ，故②正确；当a =－2时，x =3+(－2)=1，y =－2+4=2，x +y =3=5+(－2)=3，故③正确．故选B ．点睛：本题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．4．下列式子中，能用平方差公式运算的是（）A ．()()a b a c ++B ．()()a b a b +--C ．()()a b a b +-D ．()()a b a b -+- 答案：C解析：C【分析】根据平方差公式（a+b ）（a-b ）=a 2-b 2对各选项分别进行判断．【详解】解：A 、（a+b ）（a+c ）中存在相同项，没有相反项，不能用平方差公式计算，故本选项不符合题意；B 、（a+b ）（-a-b ）=-（a+b ）（a+b ）两项都是相同，不能用平方差公式计算，故本选项不符合题意；C 、（a+b ）（a-b ）存在相同的项与互为相反数的项，能用平方差公式计算，故本选项符合题意；D 、（-a+b ）（a-b ）中两项都是相反项，没有相同项，不能用平方差公式计算，故本选项不符合题意；故选：C ．【点睛】本题考查了平方差公式．运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．5．若关于x的一元一次不等式组20xx a+>⎧⎨-<⎩无解，则a的取值范围是（）A．a＞2 B．a≥2C．a＜﹣2 D．a≤﹣2答案：D解析：D【分析】先把a当作已知条件表示出不等式的解集，再由不等式组无解即可得出结论．【详解】解：20?0?xx a+>⎧⎨-<⎩①②，由①得，x＞﹣2；由②得，x＜a，∵不等式组无解，∴a≤﹣2．故选：D．【点睛】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．6．下列四个命题中，真命题有（）①两条直线被第三条直线所截，内错角相等；②如果∠1和∠2是对顶角，那么∠1＝∠2；③平方等于4的数是2；④如果a＝b，那么a＝b或a＋b＝0．A．1个B．2个C．3个D．4个答案：B解析：B【分析】根据平行线的性质、对顶角、平方和绝对值判断即可．【详解】解：①两条平行线被第三条直线所截，内错角相等，原命题是假命题；②如果∠1和∠2是对顶角，那么∠1=∠2，是真命题；③平方等于4的数是2或-2，原命题是假命题．④如果|a|=|b|，那么a=b或a+b=0，是真命题；故选：B．【点睛】本题考查了命题的真假，熟练掌握真假命题的定义及几何图形的性质是解答本题的关键，当命题的条件成立时，结论也一定成立的命题叫做真命题；当命题的条件成立时，不能保证命题的结论总是成立的命题叫做假命题．也考查了平行线的性质，对顶角的性质，乘方的意义，以及绝对值的意义．7．（阅读理解）计算：2511275⨯=，1311143⨯=，4811528⨯=，7411814⨯=，观察算式，我们发现两位数乘11的速算方法：头尾一拉，中间相加，满十进一．（拓展应用）已知一个两位数，十位上的数字是a ，个位上的数字是b ，这个两位数乘11，计算结果中十位上的数字可表示为（）A ．a 或1a +B ．a b +或abC ．10a b +-D ．a b +或10a b +- 答案：D解析：D【分析】根据题目中的速算法可以解答本题.【详解】由题意可得，某一个两位数十位数字是a ，个位数字是b ，将这个两位数乘11，得到一个三位数，则根据上述的方法可得：当a +b < 10时，该三位数百位数字是a ，十位数字是a + b ，个位数字是b ，当a +b ≥10时，结果的百位数字是a + 1，十位数字是a +b - 10，个位数字是b .所以计算结果中十位上的数字可表示为：a +b 或a +b −10.故选D.【点睛】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式.8．将一张长方形纸条折成如图所示的形状，BC 为折痕，若80,DBA ∠=︒则ABC ∠等于（）A ．40B ．50︒C ．60D ．70答案：B解析：B【分析】根据折痕旁边的两个角相等，所以∠ABC 等于180°减去80°除以2，即可得到本题答案．【详解】解：∵80DBA ∠=︒∴由折叠性质可得：∠ABC=180-802︒︒=50° 故选B ．【点睛】本题主要考查了折叠的性质，熟悉折痕旁边两个角度相等是解决本题的关键．二、填空题9．计算：()223x y xy ⋅-=__________．解析：433x y【分析】根据整式的运算直接进行求解即可．【详解】解：()2222243333x y xy x y x y x y ⋅-=⋅=；故答案为433x y ．【点睛】本题主要考查整式的运算，熟练掌握整式的运算是解题的关键．10．下列命题中，①对顶角相等；②两条直线被第三条直线所截，同旁内角互补；③在同一平面内，垂直于同一条直线的两条直线互相平行；④经过一点，有且只有一条直线与这条直线平行；⑤若一个角的两边分别与另一个角的两边平行，那么这两个角相等或互补，其中假命题是_________．解析：②④【分析】根据对顶角的性质、直线的性质、平行线的判定和性质进行判断，即可得出答案．【详解】解：①对顶角相等；真命题；②两条平行直线被第三条直线所截，同旁内角互补，故原命题为假命题；③在同一平面内，垂直于同一条直线的两条直线互相平行；真命题；④过直线外一点有且只有一条直线与已知直线平行，故原命题为假命题；⑤若一个角的两边分别与另一个角的两边平行，那么这两个角相等或互补，真命题；故答案为：②④．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．正确的命题叫做真命题，错误的命题叫做假命题．11．若一个正多边形的每一个外角都是30，则这个正多边形的边数为__________．解析：12【分析】根据正多边形的每一个外角都相等以及多边形的外角和为360°，多边形的边数=360°÷30°，计算即可求解．【详解】解：这个正多边形的边数：360°÷30°=12，故答案为：12．【点睛】本题考查了多边形的内角与外角的关系，熟记正多边形的边数与外角的关系是解题的关键．12．已知2x y -=，3xy =，则22x y xy -的值为__________．解析：6【分析】直接提取公因式xy ，进而分解因式，再整体代入数据即可得出答案．【详解】∵2x y -=，3xy =，∴()22x y xy xy x y -=-=3×2=6．故答案为：6．【点睛】本题主要考查了分解因式的应用以及代数式的求值，正确找出公因式是解题关键．13．已知关于x 、y 的方程组3522323x y m x y m +=+⎧⎨+=-⎩的解满足不等式23x y +≥，则m 的取值范围为___．解析：2m ≤【分析】先利用加减消元法解二元一次方程组，求得用m 表示的x 、y ，根据方程组的解满足不等式x +2y ≥3可得关于m 的不等式，解不等式即可．【详解】解：3522323x y m x y m +=+⎧⎨+=-⎩①②， ①×2-②×3，得：134y m =-，将134y m =-代入②，得：721x m =-，∴方程组的解为721134x m y m =-⎧⎨=-⎩， ∵方程组的解满足不等式x +2y ≥3，∴()72121343m m -+-≥，解得：2m ≤，故答案为：2m ≤．【点睛】本题主要考查了解二元一次方程组和一元一次不等式，熟练掌握解二元一次方程组的基本方法和解不等式的基本步骤是解题的关键．14．如图，想在河堤两岸搭建一座桥，在如图所示的几种搭建方式中，最短的是PB ，理由是______．答案：B解析：垂线段最短【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．【详解】解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∵PB⊥AD，∴PB最短．故答案为：垂线段最短．【点睛】本题考查了垂线段最短，利用垂线段的性质是解题的关键．15．正多边形的一个内角等于144°，则这个多边形的边数是 _________ ．答案：10【分析】先根据已知条件设出正多边形的边数，再根据正多边形的计算公式得出结果即可．【详解】解：设这个正多边形是正n边形，根据题意得：（n-2）×180°=144°n，解得：n=10．解析：10【分析】先根据已知条件设出正多边形的边数，再根据正多边形的计算公式得出结果即可．【详解】解：设这个正多边形是正n边形，根据题意得：（n-2）×180°=144°n，解得：n=10．故答案为：10．【点睛】本题考查了正多边形的内角，在解题时要根据正多边形的内角和公式列出式子是本题的关键．16．如图，在ABC 中，点D E F 、、分别为AC BD CE 、、的中点，若212ABC S cm =△，则AEF 的面积为________2cm ．答案：3【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答即可．【详解】解：为中点，，为中点，，，故答案为：3．【点睛】本题考查了三角形的面积计算，主要利用了三角形的中线把解析：3【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答即可．【详解】解：F 为CE 中点， 12AEF AEC S S ∴=， E 为BD 中点， 111222AEC CDE ADE BCD ABD ABC S S S S S S ∴=+==+，2134AEF ABC S S cm ∴==，故答案为：3．【点睛】本题考查了三角形的面积计算，主要利用了三角形的中线把三角形分成两个面积相等的三角形，原理为等底等高的三角形的面积相等．17．计算：（1）2x -3y 2.9x 2 ÷6x 4 y（2）021( 3.14)()3π----．答案：（1）-3xy ；（2）-8．【分析】（1）原式从左到右依次进行计算即可得到答案；（2）分别根据零指数幂和负整数指数幂的运算法则化简各项后再进行加减运算即可．【详解】解：（1）3y2.9x2解析：（1）-3xy ；（2）-8．【分析】（1）原式从左到右依次进行计算即可得到答案；（2）分别根据零指数幂和负整数指数幂的运算法则化简各项后再进行加减运算即可．【详解】解：（1）2x -3y 2.9x 2 ÷6x 4 y= -18x 5y 2 ÷6x 4 y=-3xy（2）021( 3.14)()3π---- =1-9= -8【点睛】此题主要考查了整式的运算以及零指数幂和负整数指数幂的运算，熟练掌握它们的运算法则是解答此题的关键．18．因式分解：（1） a 3b ﹣9ab ；（2） x 4﹣8x 2y 2+16y 4；答案：（1）ab(a+3)(a-3)；（2）(x+2y)2(x-2y)2．【分析】（1）综合利用提取公因式法和平方差公式法进行因式分解即可得；（2）先利用完全平方公式，再利用平方差公式进行因式分解即解析：（1）ab (a+3)(a-3)；（2）(x+2y )2(x-2y )2．【分析】（1）综合利用提取公因式法和平方差公式法进行因式分解即可得；（2）先利用完全平方公式，再利用平方差公式进行因式分解即可．【详解】（1）原式29)(a ab =-223()b a a =-(3)(3)ab a a -=+；（2）原式222222()8(4)x x y y =+-222(4)x y =-222(2)x y ⎡⎤=-⎣⎦ []2(2)(2)x y x y =+-22(2)(2)x y x y =+-．【点睛】本题考查了综合利用提取公因式法和公式法进行因式分解，熟练掌握因式分解的方法是解题关键．19．解方程组（1）2325y x x y =-⎧⎨+=⎩；（2）3455217x y x y +=⎧⎨-=⎩．答案：（1）；（2）【分析】（1）把①代入②得出2x+2x-3=5，求出x=2，再把x=2代入①求出y 即可；（2）①+②×2得出13x=39，求出x ，再把x=3代入①求出y 即可．【详解】解：（1解析：（1）21x y =⎧⎨=⎩；（2）31x y =⎧⎨=-⎩ 【分析】（1）把①代入②得出2x +2x -3=5，求出x =2，再把x =2代入①求出y 即可；（2）①+②×2得出13x =39，求出x ，再把x =3代入①求出y 即可．【详解】解：（1）2325y x x y =-⎧⎨+=⎩①②，把①代入②，得2x +2x -3=5，解得：x =2，把x =2代入①，得y =2×2-3=1，所以方程组的解是21x y =⎧⎨=⎩；（2）3455217x y x y +=⎧⎨-=⎩①②， ①+②×2，得13x =39，解得：x =3，把x=3代入①，得9+4y=5，解得：y=-1，所以方程组的解是31xy=⎧⎨=-⎩．【点睛】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．20．解不等式组：221113x xx-<+⎧⎪-⎨⎪⎩，并在数轴上表示解集．答案：x<3，图见解析【分析】先求得每个不等式的解集，后确定不等式组的解集．【详解】解：由①得，由②得，则不等式的解集是，原不等式组的解集在数轴上表示如图．【点睛】本题考查了一元一解析：x<3，图见解析【分析】先求得每个不等式的解集，后确定不等式组的解集．【详解】解：221113x xx-<+⎧⎪⎨-⎪⎩①②由①得3x<，由②得4x，则不等式的解集是3x<，原不等式组的解集在数轴上表示如图．【点睛】本题考查了一元一次不等式组的解法，熟练掌握不等式的解题步骤是解题的关键．三、解答题21．已知：如图，CD⊥AB，FG⊥AB，垂足分别为D、G，点E在AC上，且∠1＝∠2．（1）那么DE与BC平行吗？为什么？（2）如果∠B＝40°，且∠A比∠ACB小10°，求∠DEC的度数．答案：（1）DE∥BC，理由见解析；（2）∠DEC＝105°．【分析】（1）根据CD⊥AB，FG⊥AB，可判定CD∥FG，利用平行线的性质可知∠2=∠BCD，已知∠1=∠2，等量代换得∠1=∠BCD，解析：（1）DE∥BC，理由见解析；（2）∠DEC＝105°．【分析】（1）根据CD⊥AB，FG⊥AB，可判定CD∥FG，利用平行线的性质可知∠2=∠BCD，已知∠1=∠2，等量代换得∠1=∠BCD，故可证DE与BC平行；（2）根据三角形内角和求出∠ACB=75°，再根据平行线的性质即可求解．【详解】（1）DE∥BC，理由如下：∵CD⊥AB，FG⊥AB，∴CD∥FG．∴∠2＝∠BCD，又∵∠1＝∠2，∴∠1＝∠BCD，∴DE∥BC；（2）∵∠B＝40°，∠ACB﹣10°＝∠A，∴∠ACB+（∠ACB﹣10°）+40°＝180°，∴∠ACB＝75°，由（1）知，DE∥BC，∴∠DEC+∠ACB＝180°，∴∠DEC＝105°．【点睛】此题考查了平行线的判定与性质，熟记“内错角相等，两直线平行”、“两直线平行，同旁内角互补”是解题的关键．22．某工厂准备用图甲所示的A 型正方形板材和B 型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．（1）若现有A 型板材150张，B 型板材300张，可制作竖式和横式两种无盖箱子各多少个？（2）若该工厂准备用不超过24000元资金去购买A 、B 两种型号板材，制作竖式、横式箱子共100个，已知A 型板材每张20元，B 型板材每张60元，问最多可以制作竖式箱子多少个？（3）若该工厂新购得65张规格为3m 3m ⨯的C 型正方形板材，将其全部切割成A 型或B 型板材（不计损耗），用切割的板材制作两种类型的箱子，要求竖式箱子不少于10个，且材料恰好用完，则最多可以制作竖式箱子多少个？答案：（1）可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）最多可以制作竖式箱子50个；（3）最多可以制作竖式箱子45个【分析】（1）根据题意可以列出相应的二元一次方程组，再解方程组即可解答解析：（1）可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）最多可以制作竖式箱子50个；（3）最多可以制作竖式箱子45个【分析】（1）根据题意可以列出相应的二元一次方程组，再解方程组即可解答本题；（2）根据题意可以列出相应的不等式，从而可以求得最多可以制作竖式箱子多少个；（3）根据题意可以列出相应的二元一次方程，再根据a 为整数和a≥10，即可解答本题．【详解】解：（1）设可制作竖式无盖箱子m 个，可制作横式无盖箱子n 个，依题意有215043300m n m n +=⎧⎨+=⎩，解得3060m n =⎧⎨=⎩，故可制作竖式无盖箱子30个，可制作横式无盖箱子60个；（2）由题意可得，1个竖式箱子需要1个A 型和4个B 型，1个横式箱子需要2个A 型和3个B 型，设竖式箱子x 个，则横式箱子（100-x ）个，（20+4×60）x+（2×20+3×60）（100-x ）≤24000，解得x≤50，故x 的最大值是50，答：最多可以制作竖式箱子50个；（3）C 型可以看成三列，每一列可以做成3个A 型或1个B 型，65个C 型就有65×3=195列，∵材料恰好用完，∴最后A 型的数量一定是3的倍数，设竖式a 个，横式b 个，∵1个竖式箱子需要1个A 型和4个B 型，1个横式箱子需要2个A 型和3个B 型，1个B 型相当于3个A 型，∴（1+4×3）a+（2+3×3）b=195×3，∴13a+11b=585，∵a 、b 均为整数，a≥10，∴450a b =⎧⎨=⎩或3413a b =⎧⎨=⎩或2326a b =⎧⎨=⎩或1239a b =⎧⎨=⎩，故最多可以制作竖式箱子45个．【点睛】本题考查一元一次不等式的应用、二元一次方程（组）的应用，解答本题的关键是明确题意，利用方程和不等式的性质解答．23．阅读理解：定义：A ，B ，C 为数轴上三点，若点C 到点A 的距离是它到点B 的时距离的n （n 为大于1的常数）倍，则称点C 是(),A B 的n 倍点，且当C 是(),A B 的n 倍点或(),B A 的n 倍点时，我们也称C 是A 和B 两点的n 倍点．例如，在图1中，点C 是(),A B 的2倍点，但点C 不是(),B A 的2倍点．（1）特值尝试．①若2n =，图1中，点______是(),D C 的2倍点．（填A 或B ）②若3n =，如图2，M ，N 为数轴上两个点，点M 表示的数是2-，点N 表示的数是4，数______表示的点是(),M N 的3倍点．（2）周密思考：图2中，一动点P 从N 出发，以每秒2个单位的速度沿数轴向左运动t 秒，若P 恰好是M 和N 两点的n 倍点，求所有符合条件的t 的值．（用含n 的式子表示）（3）拓展应用数轴上两点间的距离不超过30个单位长度时，称这两点处于“可视距离”．若（2）中满足条件的M 和N 两点的所有n 倍点P 均处于点N 的“可视距离”内，请直接写出n 的取值范围．（不必写出解答过程）答案：（1）①B ；②7或；（2）或或；（3）n≥．【分析】（1）①直接根据新定义的概念即可求出答案；②根据新定义的概念列出绝对值方程即可求解；（2）设P 点所表示的数为4-2t ，再根据新定义的概念列解析：（1）①B ；②7或52；（2）31t n =+或31n t n =+或31n t n =-；（3）n ≥54．【分析】（1）①直接根据新定义的概念即可求出答案；②根据新定义的概念列出绝对值方程即可求解；（2）设P 点所表示的数为4-2t ，再根据新定义的概念列出方程即可求解；（3）分31t n =+，31n t n =+，31n t n =-三种情况分别表示出PN 的值，再根据PN 的范围列出不等式组即可求解．【详解】（1）①由数轴可知，点A 表示的数为-1，点B 表示的数为2，点C 表示的数为1，点D 表示的数为0，∴AD =1，AC =2∴AD =12AC∴点A 不是(),D C 的2倍点∴BD =2，BC =1∴BD =2BC∴点B 是(),D C 的2倍点故答案为：B ；②若点C 是点(),M N 的3倍点∴CM =3CN设点C 表示的数为x∴CM =2x +，CN =4x - ∴2x + =34x -即()234x x +=-或()234x x +=--解得x =7或x =52∴数7或52表示的点是(),M N 的3倍点．故答案为：7或52；（2）设点P 表示的数为4-2t ，∴PM =422t -+，PN =2t∵若P 恰好是M 和N 两点的n 倍点，∴当点P 是(),M N 的n 倍点∴PM =nPN ∴422t -+=n ×2t即6-2t =2nt 或6-2t =-2nt 解得31t n =+或31t n=- ∵n ＞1 ∴31t n =+ ∴当点P 是(),N M 的n 倍点∴PN =nPM∴2t =n ×422t -+即2t = n ×()62t -或-2t = n ×()62t - 解得31n t n =+或31n t n =- ∴符合条件的t 值有31t n =+或31n t n =+或31n t n =-；（3）∵PN =2t∴当31t n =+时，PN =61n + 当31n t n =+时，PN =61n n +，当31n t n =-时，PN =61n n - ∵点P 均在点N 的可视距离之内∴PN ≤30 ∴6301630163011n n n n n n ⎧≤⎪+⎪⎪≤⎪+⎨⎪≤⎪-⎪⎪⎩＞解得n ≥54∴n 的取值范围为n ≥54．【点睛】此题主要考查主要方程与不等式组的应用，解题的关键是根据新定义概念列出方程或不等式求解．24．如图，直线m与直线n互相垂直，垂足为O、A、B两点同时从点O出发，点A沿直线m向左运动，点B沿直线n向上运动．(1)若∠BAO和∠ABO的平分线相交于点Q，在点A，B的运动过程中，∠AQB的大小是否会发生变化？若不发生变化，请求出其值，若发生变化，请说明理由．(2)若AP是∠BAO的邻补角的平分线，BP是∠ABO的邻补角的平分线，AP、BP相交于点P，AQ的延长线交PB的延长线于点C，在点A，B的运动过程中，∠P和∠C的大小是否会发生变化？若不发生变化，请求出∠P和∠C的度数；若发生变化，请说明理由．答案：(1)∠AQB的大小不发生变化，∠AQB＝135°；(2)∠P和∠C的大小不变，∠P=45°，∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和，由角平分线和角的和差可求出∠BA 解析：(1)∠AQB的大小不发生变化，∠AQB＝135°；(2)∠P和∠C的大小不变，∠P=45°，∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和，由角平分线和角的和差可求出∠BAQ与∠ABQ 的和，最后在△ABQ中，根据三角形的内角各定理可求∠AQB的大小．第(2)题求∠P的大小，用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解．【详解】解：(1)∠AQB的大小不发生变化，如图1所示，其原因如下：∵m⊥n，∴∠AOB＝90°，∵在△ABO中，∠AOB+∠ABO+∠BAO＝180°，∴∠ABO+∠BAO＝90°，又∵AQ、BQ分别是∠BAO和∠ABO的角平分线，∴∠BAQ＝12∠BAC，∠ABQ＝12∠ABO,∴∠BAQ+∠ABQ＝12 (∠ABO+∠BAO)＝190452⨯=又∵在△ABQ中，∠BAQ+∠ABQ+∠AQB＝180°，∴∠AQB＝180°﹣45°＝135°．(2)如图2所示：①∠P的大小不发生变化，其原因如下：∵∠ABF+∠ABO＝180°，∠EAB+∠BAO＝180°∠BAQ+∠ABQ＝90°，∴∠ABF+∠EAB＝360°﹣90°＝270°，又∵AP、BP分别是∠BAE和∠ABP的角平分线，∴∠PAB＝12∠EAB，∠PBA＝12∠ABF，∴∠PAB+∠PBA＝12 (∠EAB+∠ABF)＝12×270°＝135°，又∵在△PAB中，∠P+∠PAB+∠PBA＝180°，∴∠P＝180°﹣135°＝45°．②∠C的大小不变，其原因如下：∵∠AQB＝135°，∠AQB+∠BQC＝180°，∴∠BQC＝180°﹣135°，又∵∠FBO＝∠OBQ+∠QBA+∠ABP+∠PBF＝180°∠ABQ＝∠QBO＝12∠ABO，∠PBA＝∠PBF＝∠ABF，∴∠PBQ＝∠ABQ+∠PBA＝90°，又∵∠PBC＝∠PBQ+∠CBQ＝180°，∴∠QBC＝180°﹣90°＝90°．又∵∠QBC+∠C+∠BQC＝180°，∴∠C＝180°﹣90°﹣45°＝45°【点睛】本题考查三角形内角和定理，垂直，角平分线，平角，直角和角的和差等知识点，同时，也是一个以静求动的一个点型题目，有益于培养学生的思维几何综合题．25．（问题情境）苏科版义务教育教科书数学七下第42页有这样的一个问题：（1）探究1：如图1，在ABC 中，P 是ABC ∠与ACB ∠的平分线BP 和CP 的交点，通过分析发现1902BPC A ∠=︒+∠，理由如下： ∵BP 和CP 分别是ABC ∠和ACB ∠的角平分线，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠． ∴()12PBC PCB ABC ACB ∠+∠=∠+∠．又∵在ABC 中，180ABC ACB A ∠+∠+∠=︒， ∴()111809022PBC PCB A A ∠+∠=︒-∠=︒-∠ ∴()11180180909022BPC PBC PCB A A ︒⎛⎫∠=︒-∠+∠=︒--∠=+∠ ⎪⎝⎭︒（2）探究2：如图2中，H 是外角MBC ∠与外角NCB ∠的平分线BH 和CH 的交点，若80A ∠=︒，则BHC ∠=______．若A n =︒，则BHC ∠与A ∠有怎样的关系？请说明理由．（3）探究3：如图3中，在ABC 中，P 是ABC ∠与ACB ∠的平分线BP 和CP 的交点，过点P 作DP PC ⊥，交AC 于点D ．ABC 外角ACF ∠的平分线CE 与BP 的延长线交于点E ，则根据探究1的结论，下列角中与ADP 相等的角是______；A ．APC ∠B ．APB ∠C ．BPC ∠（4）探究4：如图4中，H 是外角MBC ∠与外角NCB ∠的平分线BH 和CH 的交点，在探究3条件的基础上，①试判断DP 与CE 的位置关系，并说明理由；②在BHE 中，存在一个内角等于DPE ∠的3倍，则BAC ∠的度数为______答案：（2）；；理由见解析；（3）B ；（4）①，理由见解析；②45°或60°【分析】（2）由（1）中结论可得，依据角平分线的定义，即可得出和均为直角；再根据四边形内角和进行计算，即可得到的度数以及与的解析：（2）50BHC ∠=︒；1902BHC n ∠=-︒︒；理由见解析；（3）B ；（4）①//DP CE ，理由见解析；②45°或60°【分析】（2）由（1）中结论可得130P ∠=︒，依据角平分线的定义，即可得出PBH ∠和PCH ∠均为直角；再根据四边形内角和进行计算，即可得到H ∠的度数以及BHC ∠与A ∠的关系；（3）由（1）中结论可得1902APB ACB ∠=︒+∠，再根据垂线的定义以及三角形外角性质，即可得出1902ADP ACB ∠=︒+∠，进而得到APB ADP ∠=∠；（4）①根据DP PC ⊥，即可得到90DPC ∠=︒，再根据角平分线的定义，即可得到()1902PCE ACB ACF ∠=∠+∠=︒，依据180DPC PCE ∠+∠=︒，即可判定DP EC ∥； ②由①可得//DP EC ，即可得出DPE E ∠=∠，再根据在BHE 中一个内角等于DPE ∠的3倍，分三种情况讨论，即可得出BAC ∠的度数．【详解】解：（2）由（1）可得，19090401302P A ∠=︒+∠=︒+︒=︒， ∵H 是外角MBC ∠与外角NCB ∠的平分线BH 和CH 的交点，P 是ABC ∠与ACB ∠的平分线BP 和CP 的交点， ∴()11190222PBH PBC HBC ABC MBC ABC MBC ∠=∠+∠=∠+∠=∠+∠=︒，同理可得90PCH ∠=︒，∴四边形PBHC 中，360360*********BHC P PBH PCH ∠=︒-∠-∠-∠=︒-︒-︒-︒=︒，故答案为：50︒；若A n ∠=︒，则BHC ∠与A ∠关系为：1902BHC n ∠=-︒︒．理由：由（1）可得，11909022P A n ∠=︒+∠=︒+︒， ∵H 是外角MBC ∠与外角NCB ∠的平分线BH 和CH 的交点，P 是ABC ∠与ACB ∠的平分线BP 和CP 的交点， ∴()11190222PBH PBC HBC ABC MBC ABC MBC ∠=∠+∠=∠+∠=∠+∠=︒，同理可得90PCH ∠=︒，∴四边形PBHC 中，113603609090909022BHC P PBH PCH n n ⎛⎫∠=︒-∠-∠-∠=︒-︒+︒-︒-︒=︒-︒ ⎪⎝⎭．（3）由（1）可得，1902APB ACB ∠=︒+∠， ∵DP PC ⊥，PC 平分ACB ∠，∴90DPC ∠=︒，12DCP ACB ∠=∠， ∵ADP 是CDP 的外角， ∴1902ADP DPC DCP ACB ∠=∠+∠=︒+∠， ∴APB ADP ∠=∠，故答案为：B ；（4）①//DP EC ．理由：∵DP PC ⊥，∴90DPC ∠=︒，∵PC ，EC 分别平分ACB ∠，ACF ∠， ∴12DCP ACB ∠=∠，12DCE ACF ∠=∠， ∴()111809022PCE DCP DCE ACB ACF ∠=∠+∠=∠+∠=⨯︒=︒， ∴180DPC PCE ∠+∠=︒，∴//DP EC ；②由①可得//DP EC ，∴DPE E ∠=∠， ∵BP 平分ABC ∠，BH 平分MBC ∠， ∴()1902PBH PBC HBC ABC MBC ∠=∠+∠=∠+∠=︒， ∴90H E ∠=︒-∠，分三种情况：①若3E DPE ∠=∠，则3E E ∠=∠，解得0E ∠=︒（不合题意），②若3H DPE ∠=∠，则3H E ∠=∠，∴903E E ︒-∠=∠，解得22.5E ∠=︒，∴67.5H ∠=︒，由（2）可得，1902H A ∠=︒-∠，即167.5902A ︒=︒-∠， ∴45A ∠=︒；③若3EBH DPE ∠=∠，则3EBH E ∠=∠，∴903E ︒=∠，解得30E ∠=︒，∴60H ∠=︒，由（2）可得，1902H A ∠=︒-∠，即160902A ︒=︒-∠， ∴60A ∠=︒；综上所述，BAC ∠的度数为45︒或60︒．故答案为：45︒或60︒．【点睛】本题属于三角形综合题，主要考查的是角平分线的定义，三角形外角性质，三角形内角和定理以及平行线的判定的综合运用，熟记基本图形中的结论，准确识图并灵活运用基本结论是解题的关键．。

苏教版七年级下册期末数学模拟试卷优质及答案解析

苏教版七年级下册期末数学模拟试卷优质及答案解析一、选择题1．下列计算中，正确的是（）．A ．()33xy xy =B ．2a a a +=C ．()336y y =D ．222b b b ⋅=答案：D解析：D【分析】根据单项式乘单项式、合并同类项、幂的乘方进行计算，积的乘方判断即可．【详解】A. ()333xy x y =，故该选项不正确，不符合题意；B. 2a a a +=，故该选项不正确，不符合题意；C. ()933y y =，故该选项不正确，不符合题意；D. 222b b b ⋅=，故该选项正确，符合题意；故选D【点睛】本题考查了单项式乘单项式、合并同类项、幂的乘方进行计算，积的乘方，掌握以上运算法则是解题的关键．2．如图，∠B 的同位角是（）A ．∠1B ．∠2C ．∠3D ．∠4答案：C解析：C【分析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．【详解】解：∠B 与∠3是DE 、BC 被AB 所截而成的同位角，故选：C ．【点睛】本题主要考查了同位角，解答此类题确定三线八角是关键，可直接从截线入手．同位角的边构成F 形，内错角的边构成Z 形，同旁内角的边构成U 形．3．观察下列式子：4×6-2×4=4×4；6×8-4×6=6×4；8×10-6×8=8×4；…若第n 个等式的右边的值大于 180，则n的最小值是（）A．20 B．21 C．22 D．23答案：C解析：C【分析】根据规律确定第n个等式：2（n+1）（2n+4）-2n（2n+2）=2（n+1）×4，根据第n个等式的右边的值大于180，列不等式可得结论．【详解】解：第1个式子：4×6-2×4=4×4；第2个式子：6×8-4×6=6×4；第3个式子：8×10-6×8=8×4；…∴第n个等式：2（n+1）（2n+4）-2n（2n+2）=2（n+1）×4；∵第n个等式的右边的值大于180，即2（n+1）×4＞180，n＞21.5，∴n的最小值是22．故选：C．【点睛】本题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键，注意n的值为正整数，在解得n＞21.5时，要注意向上取整．4．下列各式可以用完全平方公式进行因式分解的是（）A．a2+2a+14B．a2+a+14C．x2﹣2x+4 D．x2﹣xy+y2答案：B解析：B【分析】直接利用公式法分解因式进而判断得出答案．【详解】解：A、a2+2a+14，无法运用公式法分解因式，不合题意；B、a2+a+14＝(a+12)2，可以用完全平方公式进行因式分解，符合题意；C、x2﹣2x+4，无法运用公式法分解因式，不合题意；D、x2﹣xy+y2，无法运用公式法分解因式，不合题意；故选：B．【点睛】本题考查了完全平方公式进行因式分解，熟练掌握a 2±2ab +b 2=(a ±b )2是解答本题的关键．两个平方项的符号需相同；有一项是两底数积的2倍，是易错点．5．如果点(), 21P m m -在第三象限，那么m 的取值范围是（）A ．12m >B ．102m <<C ．0m <D ．102m -<< 答案：C解析：C【分析】第三象限的符号特征为（－，－），据此列不等式组解答．【详解】∵ P （m ，2m －1）在第三象限，∴ m 02m-10⎧⎨⎩＜＜，解得：m 0＜，故选C ．【点睛】本题考查象限的符号特征和不等式组的应用，熟练掌握第三象限符号为（－，－）是关键．6．下列四个命题：①两直线平行，内错角相等；②若a ＞0，则a+3＞0；③两个角相等，它们一定是对顶角；④二元一次方程23x y -=的解为21x y =⎧⎨=⎩其中为真命题的个数是( )A ．1B ．2C ．3D ．4答案：B解析：B【分析】根据平行线的性质，不等式的性质，对顶角的定义及方程解得定义分别判断即可得解．【详解】解：两直线平行，内错角相等，故①正确；若a ＞0，则a+3＞0，故②正确；两个角相等，它们不一定是对顶角，故③不正确；21x y =⎧⎨=⎩是二元一次方程23x y -=的一个解，二元一次方程23x y -=的解由无数种，不唯一，故④不正确．因此真命题有①②，共2个，故选：B【点睛】本题主要考查了平行线的性质，不等式的性质，对顶角的定义及方程解得定义及命题真假的．正确的掌握有关的性质和定义是解题的关键．7．观察下列式子：4×6-2×4=4×4；6×8-4×6=6×4；8×10-6×8=8×4；…若第n 个等式的右边的值大于 180，则 n 的最小值是（）A ．20B ．21C ．22D ．23答案：C解析：C【分析】根据规律确定第n 个等式：2（n +1）（2n +4）-2n （2n +2）=2（n +1）×4，根据第n 个等式的右边的值大于180，列不等式可得结论．【详解】解：第1个式子：4×6-2×4=4×4；第2个式子：6×8-4×6=6×4；第3个式子：8×10-6×8=8×4；…∴第n 个等式：2（n +1）（2n +4）-2n （2n +2）=2（n +1）×4；∵第n 个等式的右边的值大于180，即2（n +1）×4＞180，n ＞21.5，∴n 的最小值是22．故选：C ．【点睛】本题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键，注意n 的值为正整数，在解得n ＞21.5时，要注意向上取整．8．如图，ABC 中，90,30,,B A E F ∠=︒∠=︒分别是边,AB AC 上的点，连接EF ，将AEF 沿着者EF 折叠，得到A EF '△，当A EF '△的三边与ABC 的三边有一组边平行时，AEF ∠的度数不可能是（）A ．120︒B ．105︒C ．75︒D ．45︒答案：B解析：B【分析】分三种情况讨论，利用翻折变换和平行线的性质可求∠AEF 的度数，再利用排除法可求解．解：如图1，若A'E∥BC时，∴∠AEA'=∠CBA=90°，∵将△AEF沿着者EF折叠，∴∠AEF=∠A'EF=45°；如图2，设A'F与AB交于点H，若A'F∥BC时，∴∠CBA=∠FHA=90°，∴∠AFH=180°-∠AHF-∠A=180°-90°-30°=60°，∵将△AEF沿着者EF折叠，∴∠AFE=∠A'FE=30°；∴∠AEF=180°-∠A-∠AFE=120°；如图3，若A'E∥AF时，∴∠A'EB=∠A=30°，∴∠A'EA=150°，∵将△AEF沿着者EF折叠，∴∠AEF=∠A'EF=75°；∴∠AEF的度数不可能是105°，故选：B．本题是翻折变换，平行线的性质，利用分类讨论思想解决问题是本题的关键．二、填空题9．计算：2x •（﹣3xy ）＝___．解析：-6x 2y【分析】根据单项式乘单项式法则，即可求解．【详解】解：2x •（﹣3xy ）=-6x 2y ，故答案是：-6x 2y ．【点睛】本题主要考查单项式乘单项式，掌握单项式乘单项式法则是解题的关键．10．以下四个命题：①-8 27的立方根是23；②要调查一批灯泡的使用寿命适宜用抽样调查；③两条直线被第三条直线所截，同旁内角互补；④已知∠ABC 与其内部一点D ，过点D 作DE ∥BA ，作DF ∥BC ，则∠EDF=∠B ．其中假命题的序号______．答案：A解析：①③④【分析】利用立方根的定义对①进行判断；根据普查和抽样调查的特点对②进行判断；根据平行线的性质对③进行判断．画好符合题意的图形，利用推理的方法判断④．【详解】解：827-的立方根是23-，所以①为假命题；要调查一批灯泡的使用寿命适宜用抽样调查，所以②为真命题；两条平行直线被第三条直线所截，同旁内角互补，所以③为假命题；已知∠ABC 与其内部一点D ，过D 点作DE ∥BA ，作DF ∥BC ，则1B EDF ∠=∠或2180.B EDF ∠+∠=︒ 所以④为假命题．理由如下：1//,//,DE AB DF BC1,,B DEC EDF DEC ∴∠=∠∠=∠1B EDF ∴∠=∠．1//,//,DE AB DF BC2,180,B DEC EDF DEC ∴∠=∠∠+∠=︒2180.B EDF ∴∠+∠=︒故答案为①③④．【点睛】本题考查了命题的“真”“假”判断．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可，掌握以上知识是解题的关键．11．一个正多边形的每一个外角都等于36︒，那么这个正多边形的内角和是______．解析：1440°【分析】利用多边形的外角和为360°计算出这个正多边形的边数，然后再根据内角和公式进行求解即可．【详解】解：∵正多边形的每一个外角都等于36︒，∴正多边形的边数为360°÷60°=10，所有这个正多边形的内角和为（10-2）×180°=1440°．故答案为：1440°【点睛】本题考查了多边形内角与外角等知识，熟知多边形内角和定理（n ﹣2）•180 （n≥3）和多边形的外角和等于360°是解题关键．12．已知4m n +=，5mn =，则多项式22m n mn +的值是________.解析：20【分析】将所求代数式因式分解成含已知式子的形式，再整体代入求值即可得解．【详解】解：∵4m n +=，5mn =∴()225420m n mn mn m n +=+=⨯=．故答案是：20【点睛】本题考查了因式分解中的提取公因式法、整体代入求值法，比较简单，熟练掌握相关知识点是解决问题的关键．13．已知关于x ，y 的方程组322(1)tx y x t y t +=⎧⎨+-=⎩，当正整数t =_____时，方程组有整数解．解析：4【分析】将t 看做未知数，求出x 与y ，再求出有整数解时，正整数t 的值．【详解】解：由方程组322(1)tx y x t y t +=⎧⎨+-=⎩得t ≠2，解方程组322(1)tx y x t y t +=⎧⎨+-=⎩得： 13x t =--，23t y t -=-， ∵方程组有整数解，当t =4时，1x =-，2y =，故答案为：4．【点睛】此题考查了二元一次方程组的解，解答本题的关键是用t 表示出x 和y 的值，此题难度不大．14．如图，要在河岸l 上建一个水泵房D ，修建引水渠到村庄C 处．施工人员的做法是：过点C 作CD l ⊥于点D ，将水泵房建在了D 处．这样修建引水渠CD 最短，既省人力又省物力，这样做蕴含的数学原理是________．解析：垂线段最短【分析】根据垂线段最短原理解题．【详解】过点C 作CD l ⊥于点D ，将水泵房建在了D 处，这样做既省人力又省物力，其数学原理是：垂线段最短，故答案为：垂线段最短．【点睛】本题考查垂线段最短的实际应用，是重要考点，难度较易，掌握相关知识是解题关键． 15．如图，将透明直尺叠放在正五边形之上，若正五边形有两个顶点在直尺的边上，且有一边与直尺的边垂直．则α∠=_______ °．答案：54°【分析】如图，标注字母，先求解正五边形的内角的大小，再利用平行线的性质及角的和差求解再利用三角形的内角和求解从而利用平行线的性质可得答案．【详解】解：如图，标注字母，由题意得：解析：54°【分析】如图，标注字母，先求解正五边形的内角,D DCB ∠∠的大小，再利用平行线的性质及角的和差求解,DCE ∠ 再利用三角形的内角和求解,DEC ∠ 从而利用平行线的性质可得答案．【详解】解：如图，标注字母，由题意得：540//,108,90,5AB EC D DCB ABC ︒∠=∠==︒∠=︒1809090,1089018,ECB DCE ∴∠=︒-︒=︒∠=︒-︒=︒18054,DEC D DCE ∴∠=︒-∠-∠=︒//,AB EC54.DEC α∴∠=∠=︒故答案为：54.︒【点睛】本题考查的是平行线的性质，正多边形的内角和，三角形的内角和，掌握利用平行线结合内角和定理进行计算是解题的关键．16．如图，在△ABC 中，AD 是BC 上的中线，点E 在线段AC 上且EC=2AE ，线段AD 与线段BE 交于点F ，若△ABC 对面积为3，则四边形EFDC 的面积为__________.答案：【解析】【分析】连接CF，根据CE=2AE，△ABC的面积为3可知S△ABE=×3=1，S△CEF=×3=2，S△AEF：S△CEF=1：2，设S△AEF=S，则S△CEF=2S故S△ABF=解析：5 4【解析】【分析】连接CF，根据CE=2AE，△ABC的面积为3可知S△ABE=13×3=1，S△CEF=23×3=2，S△AEF：S△CEF=1：2，设S△AEF=S，则S△CEF=2S故S△ABF=1-S，则S△BCF=2-2S，设S△ABF=x=1-S，则S△BCF=2x=2-2S，由AD是BC边上的中线可知S△BDF=S△CDF=x，2x=x+3S，即x=3S，所以S△ABC=12S，S四边形EFDC=5S，由此可得出结论．【详解】连接CF，∵CE=2AE，△ABC的面积为3，∴S△ABE=13×3=1，S△BCE=23×3=2，S△AEF：S△CEF=1：2，设S△AEF=S，则S△CEF=2S，∴S△AFB=1-S，则S△BCF=2-2S，设S△ABF=x=1-S，则S△BCF=2x=2-2S，∵AD是BC边上的中线，∴S△BDF=S△CDF=x，2x=x+3S，即x=3S，∴S△ABC=12S，S四边形EFDC=5S，∴121255ABC EFDC S S S S ==四边形． ∴S 四边形EFDC =1512= 54．故答案为：54．【点睛】本题考查的是三角形的面积，熟知三角形的面积公式是解答此题的关键．17．计算：（1）101()(5)|3|22π-----+；（2）（﹣2x 2）3+x 2•x 4+（﹣3x 3）2．答案：（1）0；（2）2x6．【分析】（1）根据负指数幂，零指数幂，绝对值的运算法则进行化简运算即可；（2）根据积的乘方，同底数幂的乘法法则进行运算即可．【详解】（1）原式＝＝0；（2）原式解析：（1）0；（2）2x 6．【分析】（1）根据负指数幂，零指数幂，绝对值的运算法则进行化简运算即可；（2）根据积的乘方，同底数幂的乘法法则进行运算即可．【详解】（1）原式＝2132--+＝0；（2）原式＝﹣8x 6+x 6+9x 6＝2x 6．【点睛】本题主要考查了实数的混合运算，其中涉及到了零指数幂，负指数幂，绝对值，积的乘方，同底数幂的乘法等知识点，熟悉掌握运算的法则是解题的关键．18．因式分解（1）2a ab a +-；（2）22222()4a b a b +-答案：（1）；（2）．【分析】（1）利用提公因式法分解即可；（2）利用平方差公式以及完全平方公式分解．【详解】解：（1）；（2）==．【点睛】本题考查了因式分解，解题的关键是要掌握分式解析：（1）(1)a a b +-；（2）22()()a b a b +-．【分析】（1）利用提公因式法分解即可；（2）利用平方差公式以及完全平方公式分解．【详解】解：（1）2a ab a +-=(1)a a b +-；（2）22222()4a b a b +-=2222(2)(2)a b ab a b ab +++-=22()()a b a b +-．【点睛】本题考查了因式分解，解题的关键是要掌握分式分解的基本方法．19．解方程组（1）20328x y x y -=⎧⎨+=⎩（2）12333(1)1x y x y ⎧-=⎪⎨⎪-=+⎩ 答案：（1）；（2）【分析】（1）根据加减消元法，即可求解；（2）先化简二元一次方程组，再利用加减消元法，即可求解．【详解】解：（1），①+②得：4x=8，解得：x=2，把x=2代入①得：2解析：（1）21x y =⎧⎨=⎩；（2）22x y =⎧⎨=⎩ 【分析】（1）根据加减消元法，即可求解；（2）先化简二元一次方程组，再利用加减消元法，即可求解．【详解】解：（1）20328x y x y -=⎧⎨+=⎩①②， ①+②得：4x =8，解得：x =2，把x =2代入①得：2-2y =0，解得：y =1，∴方程组的解为：21x y =⎧⎨=⎩；（2）12333(1)1x y x y ⎧-=⎪⎨⎪-=+⎩，化简得：32234x y x y -=⎧⎨-=⎩①②， ①-②得：-y =-2，解得：y =2，把y =2代入②得：3x -2=4，解得：x =2，∴方程组的解为：22x y =⎧⎨=⎩．【点睛】本题主要考查解二元一次方程组，熟练掌握加减消元法是解题的关键．20．解不等式组（要求：借助数轴求解集）：()412,253x x x x ⎧-≥+⎪⎨+<⎪⎩①② 答案：【分析】分别求出每一个不等式的解集，再在数轴上表示出每个不等式的解集，找到其公共部分即可确定不等式组的解集．【详解】解：解不等式①，得．解不等式②，得．在同一条数轴上表示不等式①②的解集解析：3x >【分析】分别求出每一个不等式的解集，再在数轴上表示出每个不等式的解集，找到其公共部分即可确定不等式组的解集．【详解】解：解不等式①，得2x ≥．解不等式②，得3x >．在同一条数轴上表示不等式①②的解集，如下图：x ．所以，原不等式组的解集是3【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．三、解答题21．已知2x﹣y＝3．（1）用含x的代数式表示y；（2）若2＜y＜3，求x的取值范围；（3）若﹣1≤x≤2，求y的最小值．答案：（1）y＝2x﹣3；（2）2.5＜x＜3；（3）﹣5【分析】（1）移项即可得出答案；（2）由2＜y＜3得出关于x的不等式组，分别求解即可；（3）由-1≤x≤2得-2≤2x≤4，可得-5≤2x解析：（1）y＝2x﹣3；（2）2.5＜x＜3；（3）﹣5【分析】（1）移项即可得出答案；（2）由2＜y＜3得出关于x的不等式组，分别求解即可；（3）由-1≤x≤2得-2≤2x≤4，可得-5≤2x-3≤1，据此知-5≤y≤1，继而得出答案．【详解】解：（1）由2x﹣y＝3可得y＝2x﹣3；（2）由2＜y＜3得2＜2x﹣3＜3，解2x﹣3＞2，得：x＞2.5，解2x﹣3＜3，得：x＜3，∴2.5＜x＜3；（3）由﹣1≤x≤2得-2≤2x≤4，则﹣5≤2x﹣3≤1，∴﹣5≤y≤1，∴y的最小值为﹣5．【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．22．9岁的小芳身高1.36米，她的表姐明年想报考北京的大学．表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟，对北京有所了解．他们四人7月31日下午从苏州出发，1日到4日在北京旅游，8月5日上午返回苏州．苏州与北京之间的火车票和飞机票价如下：火车（高铁二等座）全票524元，身高1.1～1.5米的儿童享受半价票；飞机（普通舱）全票1240元，已满2周岁未满12周岁的儿童享受半价票．他们往北京的开支预计如下：假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和，7月31日和8月5日合计按一天计算，不参观景点，但产生住宿、伙食、市内交通三项费用．（1）他们往返都坐火车，结算下来本次旅游总共开支了13668元，求x ，y 的值；（2）他们往返都坐飞机（成人票五五折），其他开支不变，至少要准备多少元？（3）他们去时坐火车，回来坐飞机（成人票五五折），其他开支不变，准备了14000元，是否够用？如果不够，他们准备不再增加开支，而是压缩住宿的费用，请问他们预定的标准间房价每天不能超过多少元？答案：（1）；（2）至少要准备15332元；（3）不够，标准间房价每日每间不能超过450元.【解析】（1）结合本次旅游总共开支了13668元，以及他们四人在北京的住宿费刚好等于上表所示其他三项费用之和分解析：（1）500{54x y ==；（2）至少要准备15332元；（3）不够，标准间房价每日每间不能超过450元.【解析】（1）结合本次旅游总共开支了13668元，以及他们四人在北京的住宿费刚好等于上表所示其他三项费用之和分别得出等式求出答案；（2）结合他们往返都坐飞机（成人票五五折），表示出总费用，进而求出答案；（3）利用已知求出总费用进而去掉住宿费得出住宿费的最大值，即可得出答案．解：（1）往返高铁费：(524×3+262)×2=1834×2=3668（元），根据题意可列方程组，25100545444120{36682510054544412013668x y x y ⨯=⨯⨯+⨯+⨯⨯+⨯+⨯⨯+⨯+⨯⨯= 解得： 500{54x y ==；答：x 的值是500，y 的值是54.（2）根据题意可得，飞机票的费用为：(1240×3×0.55+1240×0.5)×2=2666×2=5332（元）总的费用：5332+5000+20×100+54×20+120×16=15332（元），答：至少要准备15332元；（3）根据题意可得：1834+2666+5000+2000+1080+1920=14500＞14000，不够；14000-（1834+2666+2000+1080+1920）=4500，即10x ≤4500，则x ≤450，答：标准间房价每日每间不能超过450元．点睛：本题主要考查了实际问题与二元一次方程组、一元一次不等式．理解题意，并根据题意建立解决实际问题的方程组及不等式的模型，即是本题解题的关键，也是体现学生应用数学知识解决实际问题的表现.23．小语爸爸开了一家茶叶专卖店，包装设计专业毕业的小语为爸爸设计了一款纸质长方体茶叶包包装盒（纸片厚度不计）．如图，阴影部分是裁剪掉的部分，沿图中实线折叠做成的长方体纸盒的上下底面是正方形，有三处长方形形状的“接口”用来折叠后粘贴或封盖．（1）若小语用长40cm ，宽34cm 的长方形纸片，恰好能做成一个符合要求的包装盒，盒高是盒底边长的2.5倍，三处“接口”的宽度相等．则该茶叶盒的容积是多少？（2）小语爸爸的茶叶专卖店以每盒200元购进一批茶叶，按进价增加18%作为售价，第一个月由于包装粗糙，只售出不到一半但超过三分之一的量；第二个月采用了小语的包装后，马上售完了余下的茶叶，但每盒成本增加了6元，售价仍不变，已知在整个买卖过程中共盈利1800元，求这批茶叶共进了多少盒？答案：（1）；（2）【分析】（1）根据题意设盒底边长，接口的宽度，分别为，,根据题意列方程组，再根据长宽高求得体积；（2）分别设第一个月和第二个月的销售量为盒，根据题意列出方程和不等式组，根据不等式解析：（1）12803()cm ；（2）【分析】（1）根据题意设盒底边长，接口的宽度，分别为acm ，bcm ,根据题意列方程组，再根据长宽高求得体积；（2）分别设第一个月和第二个月的销售量为,x y 盒，根据题意列出方程和不等式组，根据不等式确定二元一次方程的解，两个月的销售总量为()x y 盒【详解】（1）设设盒底边长为acm ，接口的宽度为bcm ，则盒高是2.5acm ，根据题意得： 2.52240434a a b a b ++=⎧⎨+=⎩解得：82a b =⎧⎨=⎩茶叶盒的容积是：332.5 2.5 2.581280a a a a ⨯⨯=⨯=⨯=3()cm答：该茶叶盒的容积是12803()cm（2）设第一个月销售了x 盒，第二个月销售了y 盒，根据题意得：20018%(20018%6)1800x y ⨯⨯+⨯-⨯=化简得：65300x y +=①第一个月只售出不到一半但超过三分之一的量32x y x y x ++∴<< 即2x y x <<由①得：6605y x =- ∴660566025x x x x ⎧->⎪⎪⎨⎪-<⎪⎩解得：231627311x <<,x y 是整数，所以x 为5的倍数2036x y =⎧∴⎨=⎩或者2530x y =⎧⎨=⎩ x y ∴+56=或者55答：这批茶叶共进了56或者55盒．【点睛】本题考查了二元一次方程组的应用，一元一次不等式组的求解，理解题意列出方程组和不等式组是解题的关键．24．如图，直线//PQ MN ，一副直角三角板,ABC DEF ∆∆中，90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=．（1）若DEF ∆如图1摆放，当ED 平分PEF ∠时，证明：FD 平分EFM ∠．（2）若,ABC DEF ∆∆如图2摆放时，则PDE ∠=（3）若图2中ABC ∆固定，将DEF ∆沿着AC 方向平移，边DF 与直线PQ 相交于点G ，作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H （如图3），求GHF ∠的度数．（4）若图2中DEF ∆的周长35,5cm AF cm =，现将ABC ∆固定，将DEF ∆沿着CA 方向平移至点F 与A 重合，平移后的得到''D E A ∆，点D E 、的对应点分别是''D E 、，请直接写出四边形'DEAD 的周长．（5）若图2中DEF ∆固定，（如图4）将ABC ∆绕点A 顺时针旋转，1分钟转半圈，旋转至AC 与直线AN 首次重合的过程中，当线段BC 与DEF ∆的一条边平行时，请直接写出旋转的时间．答案：（1）见详解；（2）15°；（3）67.5°；（4）45cm；（5）10s或30s或40s【分析】（1）运用角平分线定义及平行线性质即可证得结论；（2）如图2，过点E作EK∥MN，利用平行线性解析：（1）见详解；（2）15°；（3）67.5°；（4）45cm；（5）10s或30s或40s【分析】（1）运用角平分线定义及平行线性质即可证得结论；（2）如图2，过点E作EK∥MN，利用平行线性质即可求得答案；（3）如图3，分别过点F、H作FL∥MN，HR∥PQ，运用平行线性质和角平分线定义即可得出答案；（4）根据平移性质可得D′A＝DF，DD′＝EE′＝AF＝5cm，再结合DE＋EF＋DF＝35cm，可得出答案；（5）设旋转时间为t秒，由题意旋转速度为1分钟转半圈，即每秒转3°，分三种情况：①当BC∥DE时，②当BC∥EF时，③当BC∥DF时，分别求出旋转角度后，列方程求解即可．【详解】（1）如图1，在△DEF中，∠EDF＝90°，∠DFE＝30°，∠DEF＝60°，∵ED平分∠PEF，∴∠PEF＝2∠PED＝2∠DEF＝2×60°＝120°，∵PQ∥MN，∴∠MFE＝180°−∠PEF＝180°−120°＝60°，∴∠MFD＝∠MFE−∠DFE＝60°−30°＝30°，∴∠MFD＝∠DFE，∴FD平分∠EFM；（2）如图2，过点E作EK∥MN，∵∠BAC＝45°，∴∠KEA＝∠BAC＝45°，∵PQ∥MN，EK∥MN，∴PQ∥EK，∴∠PDE＝∠DEK＝∠DEF−∠KEA，又∵∠DEF＝60°．∴∠PDE＝60°−45°＝15°，故答案为：15°；（3）如图3，分别过点F、H作FL∥MN，HR∥PQ，∴∠LFA＝∠BAC＝45°，∠RHG＝∠QGH，∵FL∥MN，HR∥PQ，PQ∥MN，∴FL∥PQ∥HR，∴∠QGF＋∠GFL＝180°，∠RHF＝∠HFL＝∠HFA−∠LFA，∵∠FGQ和∠GFA的角平分线GH、FH相交于点H，∴∠QGH＝12∠FGQ，∠HFA＝12∠GFA，∵∠DFE＝30°，∴∠GFA＝180°−∠DFE＝150°，∴∠HFA＝12∠GFA＝75°，∴∠RHF＝∠HFL＝∠HFA−∠LFA＝75°−45°＝30°，∴∠GFL＝∠GFA−∠LFA＝150°−45°＝105°，∴∠RHG＝∠QGH＝12∠FGQ＝12（180°−105°）＝37.5°，∴∠GHF＝∠RHG＋∠RHF＝37.5°＋30°＝67.5°；（4）如图4，∵将△DEF沿着CA方向平移至点F与A重合，平移后的得到△D′E′A，∴D′A＝DF，DD′＝EE′＝AF＝5cm，∵DE＋EF＋DF＝35cm，∴DE＋EF＋D′A＋AF＋DD′＝35＋10＝45（cm），即四边形DEAD′的周长为45cm；（5）设旋转时间为t秒，由题意旋转速度为1分钟转半圈，即每秒转3°，分三种情况：BC∥DE时，如图5，此时AC∥DF，∴∠CAE＝∠DFE＝30°，∴3t＝30，解得：t＝10；BC∥EF时，如图6，∵BC∥EF，∴∠BAE＝∠B＝45°，∴∠BAM＝∠BAE＋∠EAM＝45°＋45°＝90°，∴3t＝90，解得：t ＝30；BC ∥DF 时，如图7，延长BC 交MN 于K ，延长DF 交MN 于R ，∵∠DRM ＝∠EAM ＋∠DFE ＝45°＋30°＝75°，∴∠BKA ＝∠DRM ＝75°，∵∠ACK ＝180°−∠ACB ＝90°，∴∠CAK ＝90°−∠BKA ＝15°，∴∠CAE ＝180°−∠EAM −∠CAK ＝180°−45°−15°＝120°，∴3t ＝120，解得：t ＝40，综上所述，△ABC 绕点A 顺时针旋转的时间为10s 或30s 或40s 时，线段BC 与△DEF 的一条边平行．【点睛】本题主要考查了平行线性质及判定，角平分线定义，平移的性质等，添加辅助线，利用平行线性质是解题关键．25．如图1，已知//AB CD ，P 是直线AB ，CD 外的一点，PF CD ⊥于点F ，PE 交AB 于点E ，满足60FPE ∠=︒．（1）求AEP ∠的度数；（2）如图2，射线PN 从PE 出发，以每秒10︒的速度绕P 点按逆时针方向匀速旋转，当PN 到达PF 时立刻返回至PE ，然后继续按上述方式旋转；射线EM 从EA 出发，以相同的速度绕E 点按顺时针方向旋转至EP 后停止运动，此时射线PN 也停止运动．若射线PN 、射线EM 同时开始运动，设运动时间为t 秒．①当射线PN 平分EPF ∠时，求MEP ∠的度数()0180MEP ︒<∠<︒；②当直线EM 与直线PN 相交所成的锐角是60︒时，则t =________．答案：（1）；（2）①；②．【分析】（1）根据，，可以得到，即，再根据三角形外角定理求解即可．（2）①射线平分时，可知此时，根据题意可以确定运动时间t=3s 或t=9s ，从而计算的度数即可；②用含t 的解析：（1）150AEP ∠=；（2）①60120MEP ∠=或；②3922t s s =或．【分析】（1）根据//AB CD ，PF CD ⊥，可以得到PF AB ⊥，即90AMP ∠=，再根据三角形外角定理求解即可．（2）①射线PN 平分EPF ∠时，可知此时30EPN ∠=，根据题意可以确定运动时间t =3s 或t =9s ，从而计算MEP ∠的度数即可；②用含t 的代数式表示出所成的角度，然后进行动态分析求解即可．【详解】解（1）∵//AB CD ，PF CD ⊥∴PF AB ⊥∴90AHP ∠=又∵60FPE ∠=∴150AEP PHE FPE ∠=∠+∠=（2）①∵射线PN 平分EPF ∠∴==30EPN FPN ∠∠∵射线EM 从EA 出发，以相同的速度绕E 点按顺时针方向旋转至EP 后停止运动，此时射线PN 也停止运动，150AEP ∠=∴运动的总时间1501015t s =÷=总∵射线PN 从PE 出发，以每秒10︒的速度绕P 点按逆时针方向匀速旋转，当PN 到达PF 时立刻返回至PE ，然后继续按上述方式旋转 ∴第一次=60EPN ∠，130103t s =÷=，第二次=60EPN ∠时，190109t s =÷=，第三次=60EPN ∠时，31501015t s =÷=以此类推故当第一次=60EPN ∠，130103t s =÷=∴150103120MEP AEP AEM ∠=∠-∠=-⨯=故第二次=60EPN ∠时，190109t s =÷=∴15010960MEP AEP AEM ∠=∠-∠=-⨯=故第三次=60EPN ∠时，31501015t s =÷=∴15010150MEP AEP AEM ∠=∠-∠=-⨯= ∵0180MEP ︒<∠<︒∴60120MEP ∠=或②如图所示直线EM 与直线PN 相交所成的锐角是60︒ ∴600MOP ∠=或12∵EGO PEB EPN ∠=∠+∠，GEO MEA ∠=∠，18030PEB AEP ∠=-∠= ∴180MOP MEA EPN PEB ∠=-∠-∠-∠ ∴150MOP MEA EPN ∠=-∠-∠ 又∵10MEA t ∠=∴15010MOP t EPN ∠=--∠第一种情况，当06t ≤≤时=10EPN t ∠∴1501015020MOP t EPN t ∠=--∠=- 当150101502060MOP t EPN t ∠=--∠=-=时解得192t s = 当1501015020120MOP t EPN t ∠=--∠=-= 解得232t s = 第二种情况，当612t <≤=12010EPN t ∠︒-∴1501060MOP t EPN ∠=--∠= 此时t 无解，第三种情况当1215t <≤ 同理可以计算出()3212t s =舍去，()4152t s =舍去综上所述：3922t s s =或【点睛】本题主要考查了三角形内角和定理，解题的关键在于能够正确的分析动态过程．。

（完整版）数学初中苏教七年级下册期末测试模拟试卷答案

（完整版）数学初中苏教七年级下册期末测试模拟试卷答案一、选择题1．下列计算正确的是（）A ．3332a a a ⋅=B ．632a a a ÷=C ．()236a a =D ．235a a a += 2．如图所示，下列说法正确的是（）A ．1∠和2∠是内错角B ．1∠和2∠是同旁内角C ．1∠和5∠是同位角D ．1∠和4∠是内错角3．已知二元一次方程组63x y x y +=⎧⎨-=⎩，则22x y -的值是（） A ．27 B ．18 C ．9D ．3 4．若a ＜b ，则下列不等式中成立的是（） A ．a +3＞b +3 B ．a ﹣3＞b ﹣3 C ．12a ＞12b D ．﹣2a ＞﹣2b5．若不等式210x m --<的解为1x ＜，则m 的值是（） A ．m =-1 B ．m =0C ．m =1D ．m =3 6．给出下列4个命题：①相等的角是对顶角；②互补的两个角中一定是一个为锐角，另一个为钝角；③平行于同一条直线的两条直线平行；④同位角相等．其中真命题的个数为（）A ．1B ．2C ．3D ．47．有依次排列的三个数：6，2，8，先将任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新的数串：6，-4，2，6，8，这称为第一次操作，第二次操作后同样可以产生一个新数串：6，-10，-4，6，2，4，6，2，8，继续操作下去，问：第2021次操作后所产生的新数串的所有数之和是（）A ．4054B ．4056C ．4058D ．4060 8．将一张长方形纸条折成如图所示的形状，BC 为折痕，若80,DBA ∠=︒则ABC ∠等于（）A ．40B ．50︒C ．60D ．70二、填空题9．计算：﹣3x •2xy ＝．10．“若a b =，则22a b =”的逆命题是_____________命题．（填“真”或“假”）11．如图，正五边形和正六边形有一条公共边AB ，并且正五边形在正六边形内部，连接AC 并延长，交正六边形于点D ，则ADE ∠=______.12．若a 2-b 2=8，a-b=2，则a+b 的值为_________．13．如果二元一次方程组216x y x y +=⎧⎨+=⎩☆的解为6x y =⎧⎨=∆⎩，则“☆”表示的数为__________． 14．如图，三角形ABC 中，AC ⊥BC ，则边AC 与边AB 的大小关系是________，依据是________．15．将正三角形、正方形、正五边形，按如图所示的位置摆放，且每一个图形的一个顶点都在另一个图形的一条边上，则123∠+∠+∠=__________度．16．ABC 中，BAC B ∠>∠，50C ∠=︒，将B 折叠，使得点B 与点A 重合，折痕PD 分别交AB 、BC 于点D 、P ，当APC △中有两个角相等时，B 的度数为______．17．计算：（1）()020201113π---++（）（2）242()a a ÷18．因式分解：（1）2242x x -+（2）481x -19．解方程组（1）4541x y y x -=⎧⎨=-+⎩（2）14332(1)20x y x y ⎧+=⎪⎨⎪--=⎩ 20．利用数轴解不等式组3(2)41213x x x x --≤-⎧⎪+⎨-≤⎪⎩，并判断32是否是该不等式组的解．三、解答题21．（1）如图1，在三角形ABC 中，CD 平分ACB ∠，点E 在边AC 上，12∠=∠，试说明DE 与BC 的位置关系，并予以证明；（2）如图2，在（1）的条件下，若CBD CDB ∠=∠，CDE ∠的平分线交AC 于点F ，连接BF ．求证：90DBF DFB ∠+∠=︒；（3）如图3，在前面的条件下，若ACD ∠的平分线与AB 、DF 分别交于G 、H 两点，且54BGC ∠=︒，求ACB ∠的度数．22．如图，某工厂与A 、B 两地有公路、铁路相连．这家工厂近期从A 地购买一批原料运回工厂，制成的产品再全部运到B 地．已知公路的运价为2元/（吨⋅千米），铁路的运价为1.5元/（吨⋅千米），且这两次运输共支出公路运费48000元，铁路运费207000元．（1）求从A 地购买的原料和运到B 地的产品各多少吨？（2）如果购买这批原料的价格为每吨1千元，且这家工厂希望这批产品全部售出后获得不低于20万元的利润（利润=销售额-原料费-运输费），那么每吨产品的最低售价应定为多少元（结果取整数）？23．若点(),P x y 的坐标满足244x y a b x y b +=--⎧⎨-=-⎩．（1）当1a =，1b =时，求点P 的坐标；（2）若点P 在第二象限，且符合要求的整数a 只有三个，求b 的取值范围；（3）若点P 为不在x 轴上的点，且关于z 的不等式40yz x ++>的解集为23z <，求关于t 的不等式at b >的解集．24．在ABC 中，射线AG 平分BAC ∠交BC 于点G ，点D 在BC 边上运动（不与点G 重合），过点D 作//DE AC 交AB 于点E .（1）如图1，点D 在线段CG 上运动时，DF 平分EDB ∠.①若100BAC ︒∠=，30C ︒∠=，则AFD ∠=_____；若40B ︒∠=，则AFD ∠=_____； ②试探究AFD ∠与B 之间的数量关系？请说明理由；（2）点D 在线段BG 上运动时，BDE ∠的角平分线所在直线与射线AG 交于点F .试探究AFD ∠与B 之间的数量关系，并说明理由.25．已如在四边形ABCD 中，90A C ∠=∠=︒．（1）如图1，若70ABC ∠=︒，则NDC ∠=________．（2）如图2，若BF 、DE 分别平分CBM ∠、CDN ∠，判断DE 与BF 位置关系并证明理由．（3）如图3，若BP 、DP 分别五等分CBM ∠、CDN ∠（即15CBP CBM ∠=∠，15CDP CDN ∠=∠），则P ∠=_______．【参考答案】一、选择题1．C解析：C【分析】根据幂的运算法则逐项计算即可．【详解】解：A . 336a a a ⋅=，原选项不正确，不符合题意；B . 633a a a ÷=，原选项不正确，不符合题意；C . ()236a a =，原选项正确，符合题意； D . 23a a 、不是同类项，原选项不正确，不符合题意；故选：C ．【点睛】本题考查了幂的运算，解题关键是熟记幂的运算法则，准确进行计算．2．B解析：B【分析】利用“三线八角”的定义分别判断后即可确定正确的选项．【详解】解：A 、∠1和∠2是同旁内角，故错误；B 、∠1和∠2是同旁内角，正确；C 、∠1和∠5不是同位角，故错误；D 、∠1和∠4不是同旁内角，故错误，故选：B ．【点睛】本题考查了同位角、内错角及同旁内角的定义，解题的关键是了解三类角的定义，难度不大．3．B解析：B【分析】根据加减消元法，可得方程组的解，根据代数式求值，可得答案．【详解】解：63x y x y +=⎧⎨-=⎩①②， ①+②，得29x =，解得：92x =， ①-②，得23y =，解得：32y =， ∴原方程组的解为9232x y ⎧=⎪⎪⎨⎪=⎪⎩，∴22x y-=229322⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭=18，故选B．【点睛】本题考查了解二元一次方程组，利用加减法是解题关键，又利用了代数式求值．4．D解析：D【分析】根据不等式的性质逐个判断即可．【详解】解：A、∵a＜b，∴a+3＜b+3，故本选项不符合题意；B、∵a＜b，∴a﹣3＜b﹣3，故本选项不符合题意；C、∵a＜b，∴12a12<b，故本选项不符合题意；D、∵a＜b，∴﹣2a＞﹣2b，故本选项符合题意；故选：D．【点睛】本题考查了不等式的问题，掌握不等式的性质是解题的关键．5．C解析：C【分析】根据不等式的运算法则可得12mx+＜，因为1x＜，所以可得m112+=，进而求解即可．【详解】210x m--<∴12mx+＜原不等式的解为1x＜∴m11 2+=解得m=1故选C．【点睛】本题主要考查含参数不等式的运算，关键是根据不等式的性质来得到12mx+＜，再根据题意建立含参数的方程，进而求解问题的答案．6．A解析：A【分析】根据平行线的性质和角的性质逐一判定即可.【详解】解：①相等的角是对顶角；是假命题；②互补的两个角中一定是一个为锐角，另一个为钝角；是假命题；③平行于同一条直线的两条直线平行；是真命题命题；④同位角相等，是假命题；故答案为A;【点睛】本题考查了命题真假的判断，但解题的关键在于对平行线的性质、对顶角、补角概念的掌握.7．C解析：C【分析】首先根据题意，分别求出前三次操作得到的数分别是多少，再求出它们的和各是多少；然后总结出第n 次操作：求和结果是16+2n ，再把n =2021代入，求出算式的值是多少即可．【详解】解：第一次操作：6，-4，2，6，8，求和结果：18，第二次操作：6，-10，-4，6，2，4，6，2，8，求和结果：20，第三次操作：6，-16，-10，6，-4，10，6，-4，2，2，4，2，6，-4，2，6，8，求和结果：22，……第n 次操作：求和结果：16+2n ，∴第2021次结果为：16+2×2021=4058．故选：C ．【点睛】此题主要考查了有理数加减法的运算方法，以及数字的变化规律，要熟练掌握． 8．B解析：B【分析】根据折痕旁边的两个角相等，所以∠ABC 等于180°减去80°除以2，即可得到本题答案．【详解】解：∵80DBA ∠=︒∴由折叠性质可得：∠ABC=180-802︒︒=50° 故选B ．【点睛】本题主要考查了折叠的性质，熟悉折痕旁边两个角度相等是解决本题的关键．二、填空题9．﹣6x2y【分析】根据单项式乘以单项式的法则即可求出答案．【详解】解：﹣3x•2xy＝﹣3×2•（x•x）y＝﹣6x2y．故答案为：﹣6x2y．【点睛】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．10．假【分析】把一个命题的条件和结论互换就得到它的逆命题，再判断命题的真假即可．【详解】解：根据题意得：命题“如果a=b，那么a2=b2”的条件是如果a=b，结论是a2=b2”，故逆命题是如果a2=b2，那么a=b，我们知道如果a2=b2，那么a=±b，所以该命题是假命题．故答案为：假．【点睛】本题考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．11．A解析：84【分析】据正多边形的内角，可得∠ABE、∠E、∠CAB，根据四边形的内角和，可得答案．【详解】解：正五边形的内角是(52)1801085ABC︒︒-⨯∠==∵AB=BC，∴∠CAB=36°，正六边形的内角是(62)1801206ABE E︒︒-⨯∠=∠==∵∠ADE+∠E+∠ABE+∠CAB=360°，∴∠ADE=360°-120°-120°-36°=84°，故答案为84．【点睛】本题考查了多边形的内角与外角，利用求多边形的内角得出正五边形的内角、正六边形的内角是解题关键．12．4【分析】先对a2-b2=8左侧因式分解，然后将a-b=2代入求解即可．【详解】解：∵a2-b2=8∴（a-b）（a+b）=8∴2（a+b）=8∴a+b=4．故答案为4．【点睛】本题考查了代数式求值和因式分解，灵活运用因式分解是正确解答本题的关键．13．10【分析】把x=6代入2x+y=16求出y，然后把x，y的值代入x+y=☆求解．【详解】解：把x=6代入2x+y=16得2×6+y=16，解得y=4，把64xy=⎧⎨=⎩代入x+y=☆得☆=6+10=10．故答案为：10．【点睛】本题考查二元一次方程组的解，解题关键是熟练掌握解二元一次方程组的方法．14．A解析：AC＜AB垂线段最短【分析】点到直线的距离也是点到直线的垂线段，是最短的；据此解答【详解】AC小于AB，因为垂线段最短故答案为①AC<AB②垂线段最短【点睛】本题考查两点之间垂线段最短，掌握这一点就能正确解题．15．102°【分析】根据领补角的定义、正多边形的内角和及三角形内角和进行求解即可．【详解】解：由题意得，如图所示，正五边形的每个内角为108°，正方形的每个内角为90°，正三角形的每个内角为6解析：102°【分析】根据领补角的定义、正多边形的内角和及三角形内角和进行求解即可．【详解】解：由题意得，如图所示，正五边形的每个内角为108°，正方形的每个内角为90°，正三角形的每个内角为60°，所以2418010872∠+∠=︒-︒=︒，3618060120∠+∠=︒-︒=︒，151809090∠+∠=︒-︒=︒，因为54+6180∠+∠∠=︒，所以可得1+2372+120+90180102∠∠+∠=︒︒︒-︒=︒．故答案为102°．【点睛】本题主要考查三角形内角和、正多边形的内角，关键是根据图形得到角之间的等量关系，然后利用三角形内角和进行求解即可．16．40°或25°或32.5°【分析】由对折可得：设则再分三种情况讨论即可得到答案.【详解】解：由对折可得：设则当时，当时，则当时，则故解析：40°或25°或32.5°【分析】由对折可得：,B PAB ∠=∠ 设,B x ∠=︒ 则,2,PAB x APC x ∠=︒∠=︒ 1302,PAC x ∠=︒-︒再分三种情况讨论即可得到答案.【详解】解：由对折可得：,B PAB ∠=∠设,B x ∠=︒ 则,2,PAB x APC x ∠=︒∠=︒50,C ∠=︒1805021302,PAC x x ∴∠=︒-︒-︒=︒-︒当APC C ∠=∠时，250,x =25,x ∴=25,B x ∴∠=︒=︒当PAC C =∠∠时，则130250,x -=40,x ∴=40,B ∴∠=︒当PAC APC ∠=∠时，则13022,x x -=32.5,x ∴=︒32.5.B ∴∠=︒故答案为：40°或25°或32.5°【点睛】本题考查的是轴对称的性质，三角形的内角和定理，分类讨论的数学思想，做到清晰的分类讨论是解题的关键.17．（1）；（2）a6【分析】（1）利用乘方、零指数幂、负指数幂法则计算，即可得到结果；（2）原式利用幂的乘方和同底数幂的除法法则计算，即可得到结果．【详解】解：（1）==；（2）=解析：（1）13；（2）a 6 【分析】（1）利用乘方、零指数幂、负指数幂法则计算，即可得到结果；（2）原式利用幂的乘方和同底数幂的除法法则计算，即可得到结果．【详解】解：（1）()020201113π---++（） =1113-+ =13；（2）242()a a ÷=28a a ÷= a 6．【点睛】本题考查幂的乘方和同底数幂的除法，以及实数的运算，熟练掌握运算法则是解题的关键．18．（1）；（2）【分析】（1）先提取公因式2，然后运用完全平方公式分解因式即可；（2）运用平方差公式因式分解即可．【详解】解：（1）；（2）．【点睛】本题主要考查提公因式法与公解析：（1）22(1)x -；（2）2(9)(3)(3)x x x ++-【分析】（1）先提取公因式2，然后运用完全平方公式分解因式即可；（2）运用平方差公式因式分解即可．【详解】解：（1）2242x x -+22(21)x x =-+22(1)x =-；（2）481x -22(9)(9)x x =+-2(9)(3)(3)x x x =++-．【点睛】本题主要考查提公因式法与公式法因式分解，熟知完全平方公式与平方差公式的结构特点时解题的关键，注意结果要分解完全．19．（1）；（2）【分析】（1）方程组利用代入消元法求解即可；（2）方程组利用加减消元法求解即可．【详解】解：（1），将②代入①得：，解得：，代入②中，解得：，∴方程组的解为：；（2解析：（1）10x y =⎧⎨=⎩；（2）1631x y ⎧=⎪⎨⎪=-⎩ 【分析】（1）方程组利用代入消元法求解即可；（2）方程组利用加减消元法求解即可．【详解】解：（1）4541x y y x -=⎧⎨=-+⎩①②，将②代入①得：()4514x x --+=，解得：1x =，代入②中，解得：0y =，∴方程组的解为：10x y =⎧⎨=⎩；（2）方程组化简为：34123218x y x y +=⎧⎨-=⎩①②， ①-②得：66y =-，解得：1y =-，代入②中，解得：163x =， ∴方程组的解为：1631x y ⎧=⎪⎨⎪=-⎩．【点睛】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．20．1≤x≤4，不是【分析】分别求出每一个不等式的解集，在数轴上表示出不等式的解集，从而得到不等式组的解集，再进一步判断是否在此范围即可．【详解】解：，解不等式①，得：x≥1，解不等式②，得解析：1≤x≤4，不是【分析】分别求出每一个不等式的解集，在数轴上表示出不等式的解集，从而得到不等式组的解集，再进一步判断32是否在此范围即可．【详解】解：3(2)41213x xxx--≤-⎧⎪⎨+-≤⎪⎩①②，解不等式①，得：x≥1，解不等式②，得：x≤4，将不等式的解集表示在数轴上如下：∴不等式组的解集为1≤x≤4，∵324，∴32【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是解答此题的关键．三、解答题21．（1）DE∥BC，证明见解析；（2）证明见解析；（3）72°【分析】（1）证明∠2=∠BCD，可得结论．（2）根据DE∥BC，得到∠EDB+∠DBC=180°，再利用角平分线的性质，即可解答；解析：（1）DE∥BC，证明见解析；（2）证明见解析；（3）72°【分析】（1）证明∠2=∠BCD，可得结论．（2）根据DE∥BC，得到∠EDB+∠DBC=180°，再利用角平分线的性质，即可解答；（3）根据FD⊥AB，∠BGC=54°，得到∠DHG=36°，利用外角的性质得到∠FDC+∠HCD=36°，再根据DF平分∠EDC，CG平分∠ACD，得到∠EDC=2∠FDC，∠ACD=2∠HCD，得到∠EDC+∠ACD=2（∠FDC+∠HCD）=108°，利用三角形内角和为180°，∠DEC=180°-（∠EDC+∠ACD）=180°-108°=72°，再利用平行线的性质求出∠AC B．【详解】解：（1）结论：DE∥B C．理由：如图1中，∵CD平分∠ACB，∴∠1=∠BCD，∵∠1=∠2，∴∠2=∠BCD，∴DE∥B C．（2）证明：如图2中，∵DE∥BC，∴∠EDB+∠DBC=180°，∴∠EDF+∠FDC+∠CDB+∠DBC=180°，∵∠CDB=∠DBC，∠EDF=∠FDC，∴2∠FDC+2∠CDB=180°，∴∠FDC+∠CDB=90°，∴FD⊥BD，∴∠DBF+DFB=90°．（3）如图3中，∵∠BGC=54°，FD⊥BD，∴∠DHG=36°，∴∠FDC+∠HCD=36°，∵DF平分∠EDC，CG平分∠ACD，∴∠EDC=2∠FDC，∠ACD=2∠HCD，∴∠EDC+∠ACD=2（∠FDC+∠HCD）=72°，∴∠DEC=180°-（∠EDC+∠ACD）=180°-72°=108°，∵DE∥BC，∴∠ACB+∠DEC=180°，∴∠ACB=72°．【点睛】本题属于三角形综合题，考查了平行线的性质、三角形角平分线、外角的性质、三角形内角和定理，解决本题的关键是利用三角形的角平分线、外角得到角之间的关系．22．（1）从地购买的原料为600吨和运到地的产品为400吨；（2）每吨产品的最低售价应定2638元．【分析】（1）根据公路的运价为2元（吨千米），铁路的运价为1.5元（吨千米），且这两次运输共支出公解析：（1）从A地购买的原料为600吨和运到B地的产品为400吨；（2）每吨产品的最低售价应定2638元．【分析】（1）根据公路的运价为2元/（吨⋅千米），铁路的运价为1.5元/（吨⋅千米），且这两次运输共支出公路运费48000元，铁路运费207000元和图中的数据，可以列出相应的二元一次方程组，然后求解即可；（2）根据购买这批原料的价格为每吨1千元，且这家工厂希望这批产品全部售出后获得不低于20万元的利润，可以列出相应的不等式，从而可以求得每吨产品的售价的取值范围，从而可以求得每吨产品的最低售价应定为多少元．【详解】解：（1）设从A地购买的原料为a吨和运到B地的产品为b吨，由题意可得，220230480001.5150 1.5120207000a ba b⨯+⨯=⎧⎨⨯+⨯=⎩，解得600400ab=⎧⎨=⎩，答：从A地购买的原料为600吨和运到B地的产品为400吨；（2）设每吨产品的售价为x元，由题意可得，400600100048000207000200000x-⨯--，解得2637.5x，x为整数，x 的最小值是2638，答：每吨产品的最低售价应定2638元．【点睛】本题考查一元一次不等式的应用、二元一次方程组的应用，解题的关键是明确题意，找出等量关系和不等关系，列出相应的方程组和不等式．23．（1）（-3，0）；（2）0≤b＜1；（3）t＞【分析】（1）解方程组得，当a=1，b=1时，，即可得出答案；（2）解方程组得，由点P在第二象限，得x=a-4＜0，a-b＞0，则a＜4，a＞b解析：（1）（-3，0）；（2）0≤b＜1；（3）t＞5 2【分析】（1）解方程组得4x ay a b=-⎧⎨=-⎩，当a=1，b=1时，3xy=-⎧⎨=⎩，即可得出答案；（2）解方程组得4x ay a b=-⎧⎨=-⎩，由点P在第二象限，得x=a-4＜0，a-b＞0，则a＜4，a＞b，由题意得出a=1，2，3，得出0≤b＜1即可；（3）由（1）得x=a-4，y=a-b，P（a-4，a-b），由题意得出y=a-b≠0，a≠b，由不等式的解集得关于z的方程yz+x+4=0的解为z=23，得出b=52a，求出a＞0，解不等式即可．【详解】解：（1）解方程组244x y a bx y b+=--⎧⎨-=-⎩得：4x ay a b=-⎧⎨=-⎩，当a=1，b=1时，3xy=-⎧⎨=⎩，∴点P的坐标为（-3，0）；（2）若点P在第二象限，则x=a-4＜0，a-b＞0，∴a＜4，a＞b，∵符合要求的整数a只有三个，∴a=1，2，3，∴0≤b＜1，即b的取值范围为0≤b＜1；（3）由（1）得：x=a-4，y=a-b ，P （a-4，a-b ），∵点P 为不在x 轴上的点，∴y=a-b≠0，∴a≠b ，∵关于z 的不等式yz+x+4＞0的解集为z ＜23， yz ＞-（x+4），∴y ＜0，则z ＜()4x y-+， ∴()423x y -+=，代入4x a y a b =-⎧⎨=-⎩得：5a=2b ，且a ＜b ， ∴a ＜52a ， ∴a ＞0，∵at ＞b ，∴at ＞52a ， ∴t ＞52．【点睛】本题是综合题，考查了二元一次方程组的解法、点的坐标特征、一元一次不等式的解法等知识；本题综合性强，熟练掌握二元一次方程组的解法和一元一次不等式的解法是解题的关键．24．（1）①115°，110°；②，证明见解析；（2），证明见解析.【解析】【分析】（1）①根据角平分线的定义求得∠CAG=∠BAC=50°；再由平行线的性质可得∠EDG=∠C=30°，∠FMD=解析：（1）①115°，110°；②1902AFD B ︒∠=+∠，证明见解析；（2）1902AFD B ︒∠=-∠，证明见解析. 【解析】【分析】（1）①根据角平分线的定义求得∠CAG=12∠BAC=50°；再由平行线的性质可得∠EDG=∠C=30°，∠FMD=∠GAC=50°；由三角形的内角和定理求得∠AFD 的度数即可；已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=12∠BAC，∠FDM=12∠EDG；由DE//AC，根据平行线的性质可得∠EDG=∠C，∠FMD=∠GAC；即可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12（∠BAC+∠C）=12×140°=70°；再由三角形的内角和定理可求得∠AFD=110°；②∠AFD=90°+12∠B，已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=12∠BAC，∠FDM=12∠EDG；由DE//AC，根据平行线的性质可得∠EDG=∠C，∠FMD=∠GAC；由此可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12（∠BAC+∠C）=12×（180°-∠B）=90°-12∠B；再由三角形的内角和定理可得∠AFD=90°+12∠B；（2）∠AFD=90°-12∠B，已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=12∠BAC，∠NDE=12∠EDB，即可得∠FDM=∠NDE=12∠EDB；由DE//AC，根据平行线的性质可得∠EDB=∠C，∠FMD=∠GAC；即可得到∠FDM=∠NDE=12∠C，所以∠FDM+∠FMD =12∠C+12∠BAC=12（∠BAC+∠C）=12×（180°-∠B）=90°-12∠B；再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-12∠B.【详解】（1）①∵AG平分∠BAC，∠BAC=100°，∴∠CAG=12∠BAC=50°；∵//DE AC，∠C=30°，∴∠EDG=∠C=30°，∠FMD=∠GAC=50°；∵DF平分∠EDB，∴∠FDM=12∠EDG=15°；∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°；∵∠B=40°，∴∠BAC+∠C=180°-∠B=140°；∵AG平分∠BAC，DF平分∠EDB，∴∠CAG=12∠BAC，∠FDM=12∠EDG，∵DE//AC，∴∠EDG=∠C，∠FMD=∠GAC；∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12（∠BAC+∠C）=12×140°=70°；∴∠AFD=180°-（∠FDM +∠FMD）=180°-70°=110°；故答案为115°，110°；②∠AFD=90°+12∠B，理由如下：∵AG平分∠BAC，DF平分∠EDB，∴∠CAG=12∠BAC，∠FDM=12∠EDG，∵DE//AC，∴∠EDG=∠C，∠FMD=∠GAC；∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12（∠BAC+∠C）=12×（180°-∠B）=90°-12∠B；∴∠AFD=180°-（∠FDM +∠FMD）=180°-（90°-12∠B）=90°+12∠B；（2）∠AFD=90°-12∠B，理由如下：如图，射线ED交AG于点M，∵AG平分∠BAC，DF平分∠EDB，∴∠CAG=12∠BAC，∠NDE=12∠EDB，∴∠FDM=∠NDE=12∠EDB，∵DE//AC，∴∠EDB=∠C，∠FMD=∠GAC；∴∠FDM=∠NDE=12∠C，∴∠FDM +∠FMD =12∠C+12∠BAC=12（∠BAC+∠C）=12×（180°-∠B）=90°-12∠B；∴∠AFD=∠FDM +∠FMD=90°-12∠B.【点睛】本题考查了角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质，根据角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质确定各角之间的关系是解决问题的关键.25．（1）70°；（2）DE∥BF，证明见解析；（3）54°【分析】（1）根据四边形内角和计算即可；（2）根据平角的定义和等量代换可得∠MBC+∠CDN=180°，再根据角平分线的定义得到∠CBF解析：（1）70°；（2）DE∥BF，证明见解析；（3）54°【分析】（1）根据四边形内角和计算即可；（2）根据平角的定义和等量代换可得∠MBC+∠CDN=180°，再根据角平分线的定义得到∠CBF+∠CDE=90°，从而推出∠EDB+∠FBD=180°，可得结论；（3）根据五等分得到∠CDP+∠CBP=36°，连接PC并延长，证明∠DCB=∠DPB+∠CBP+∠CDP，即可计算．【详解】解：（1）∵∠A=∠C=90°，∠ABC=70°，∴∠ADC=360°-90°-90°-70°=110°，∴∠NDC=180°-110°=70°；（2）DE∥BF，如图，连接BD，∵∠ABC+∠ADC=180°，且∠MBC+∠ABC=180°，∠CDN+∠ADC=180°，∴∠MBC+∠CDN=180°，∵∠CBF=12∠MBC，∠CDE=12∠CDN，∴∠CBF+∠CDE=90°，∵∠C=90°，∴∠CBD+∠CDB=90°，∴∠EDB+∠FBD=∠CBF+∠CDE+∠CBD+∠CDB=180°，∴DE∥BF；（3）∵∠MBC+∠CDN=180°，∴∠CDP+∠CBP=1（∠MBC+∠CDN）=36°，5连接PC并延长，∵∠DCE=∠CDP+∠CPD，∠BCE=∠CPB+∠CBP，∴∠DCB=∠DCE+∠BCE=∠DPB+∠CBP+∠CDP，∴∠DPB=90°-36°=54°．【点睛】本题考查多边形内角和与外角，三角形内角和定理，平行线的判定等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．。

(完整版)苏教七年级下册期末数学模拟试卷经典答案

（完整版）苏教七年级下册期末数学模拟试卷经典答案一、选择题1．下列运算正确的是（）A ．()325a a =B ．623a a a ÷=C ．235a a a ⋅=D ．55102a a a += 2．在下列图形中，1∠与2∠是内错角的是（）A ．B ．C ．D ．3．已知方程组135x y a x y a +=-⎧⎨-=+⎩的解x 为正数，y 为非负数，给出下列结论：①－1＜a≤1；②当a ＝－53时，x ＝y ；③当a ＝－2时，方程组的解也是方程x ＋y ＝5＋a 的解．其中正确的是( )A ．①②B ．②③C ．①③D ．①②③ 4．下列式子中，能用平方差公式运算的是（）A ．()()a b a c ++B ．()()a b a b +--C ．()()a b a b +-D ．()()a b a b -+- 5．如果关于x 的不等式组2243(2)x m x x -⎧⎪⎨⎪-≤-⎩的解集为1≥x ，且关于x 的方程1233m x x --=-有正整数解，则所有符合条件的整数m 的值有几个（）A ．0个B ．1个C ．2个D ．3个6．下列命题中：①长为5cm 的线段AB 沿某一方向平移10cm 后，平移后线段AB 的长为10cm ；②三角形的高在三角形内部；③六边形的内角和是外角和的两倍；④在同一平面内，平行于同一直线的两直线平行：⑤两个角的两边分别平行，则这两个角相等．假命题个数有（） A ．1个 B ．2个 C ．3个 D ．4个7．古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”．从图7中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（）A ．13310=+B ．25916=+C ．361521=+D ．491831=+8．如图，△ABC 中，∠B ＝40°，∠C ＝30°，点D 为边BC 上一点，将△ADC 沿直线AD 折叠后，点C 落到点E 处，若DE ∥AB ，则∠ADE 的度数为（）A ．100°B ．110°C ．120°D ．130°二、填空题9．计算（﹣2x 3y 2）3•4xy 2=_____．10．“若两条直线不相交，则这两条直线平行”是_____命题．（填“真”或“假”） 11．如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F =_______°．12．已知30++=a b ，且40a b --=，则22a b -=______．13．如果二元一次方程组13223ax by ax by -=⎧⎨+=⎩的解是54x y =⎧⎨=⎩，则a ﹣b ＝___ 14．在高3米，水平距离为4米的楼梯表面铺地毯，地毯的长度至少需要______米．15．在ABC 中，AB=6，AC=9，则第三边BC 的值可以是_________ ．16．如图，若AD 是△ABC 的BC 边上的高，AE 是∠BAC 的角平分线，∠C ＝42°，∠BAE ＝15°，则∠DAB ＝_______°17．计算、化简：（1）()()22019014153π-⎛⎫-+⨯--- ⎪⎝⎭．（2）()2741023a a a a a ⨯--+÷．（3）()()2323a b c a b c +--+．（4）用简便方法计算：2212964244⨯-⨯． 18．因式分解（1）﹣3a 3+6a 2b ﹣3ab 2；（2）4a 2（x ﹣y ）+9b 2（y ﹣x ）；（3）a 4﹣8a 2b 2+16b 4．19．解方程组：（1）1227y x y +=⎧⎨+=⎩；（2）3524x y y x -=⎧⎨+=⎩． 20．解不等式组593(1)133722x x x x ->-⎧⎪⎨-≤-⎪⎩，并写出它的整数解．三、解答题21．如图，已知1BDC ∠=∠，23180∠+∠=(1)求证://AD CE(2)若DA 平分BDC ∠，CE AE ⊥于点E ，164∠=，试求FAB ∠的度数22．小宇骑自行车从家出发前往地铁2号线的B 站，与此同时，一列地铁从A 站开往B 站．3分钟后，地铁到达B 站，此时小宇离B 站还有2400米．已知A 、B 两站间的距离和小宇家到B 站的距离恰好相等，这列地铁的平均速度是小宇骑车的平均速度的5倍．（1）求小宇骑车的平均速度（2）如果此时另有一列地铁需10分钟到达B 站，且小宇骑车到达B 站后还需2分钟才能走到地铁站台候车，那么他要想乘上这趟地铁，骑车的平均速度至少应提高多少？（假定这两列地铁的平均速度相同）23．阅读材料：关于x ，y 的二元一次方程ax+by=c 有一组整数解00x x y y =⎧⎨=⎩，则方程ax+by=c 的全部整数解可表示为00x x bt y y at=-⎧⎨=+⎩（t 为整数）．问题：求方程7x+19y=213的所有正整数解．小明参考阅读材料，解决该问题如下：解：该方程一组整数解为0069x y =⎧⎨=⎩，则全部整数解可表示为61997x t y t =-⎧⎨=+⎩（t 为整数）．因为61909+70.t t ->⎧⎨>⎩，解得96719t -<<．因为t 为整数，所以t =0或-1．所以该方程的正整数解为69xy=⎧⎨=⎩和252xy=⎧⎨=⎩．（1）方程3x-5y=11的全部整数解表示为：253x ty tθ=+⎧⎨=+⎩（t为整数），则θ= ；（2）请你参考小明的解题方法，求方程2x+3y=24的全部正整数解；（3）方程19x+8y=1908的正整数解有多少组? 请直接写出答案．24．【问题探究】如图1，DF∥CE，∠PCE=∠α，∠PDF=∠β，猜想∠DPC与α、β之间有何数量关系？并说明理由；【问题迁移】如图2，DF∥CE，点P在三角板AB边上滑动，∠PCE=∠α，∠PDF=∠β.（1）当点P在E、F两点之间运动时，如果α=30°，β=40°，则∠DPC= °.（2）如果点P在E、F两点外侧运动时（点P与点A、B、E、F四点不重合），写出∠DPC 与α、β之间的数量关系，并说明理由．（图1）（图2）25．（数学经验）三角形的中线，角平分线，高是三角形的重要线段，我们知道，三角形的3条高所在直线交于同一点．（1）①如图1，△ABC 中，∠A ＝90°，则△ABC 的三条高所在的直线交于点； ②如图2，△ABC 中，∠BAC ＞90°，已知两条高BE ，AD ，请你仅用一把无刻度的直尺（仅用于过任意两点作直线、连接任意两点、延长任意线段）画出△ABC 的第三条高．（不写画法，保留作图痕迹）．（综合应用）（2）如图3，在△ABC 中，∠ABC ＞∠C ，AD 平分∠BAC ，过点B 作BE ⊥AD 于点E ． ①若∠ABC ＝80°，∠C ＝30°，则∠EBD ＝；②请写出∠EBD 与∠ABC ，∠C 之间的数量关系，并说明理由．（拓展延伸）（3）三角形的中线将三角形分成面积相等的两部分，如果两个三角形的高相同，则他们的面积比等于对应底边的比．如图4，M 是BC 上一点，则有=ABM BM ACM CM∆∆的面积的面积．如图5，△ABC 中，M 是BC 上一点BM =14BC ，N 是AC 的中点，若三角形ABC 的面积是m 请直接写出四边形CMDN 的面积．（用含m 的代数式表示）【参考答案】一、选择题1．C解析：C【分析】利用幂的乘方的性质、同底数幂的除法的计算法则、同底数幂的乘法运算法则、以及合并同类项计算法则进行计算即可．【详解】解：A 、（a 2）3=a 6，故原题计算错误；B 、a 6÷a 2=a 4，故原题计算错误；C 、a 2•a 3=a 5，故原题计算正确；D 、a 5+a 5=2a 5，故原题计算错误；故选：C．【点睛】此题主要考查了幂的乘方、同底数幂的除法和乘法、以及合并同类项，关键是熟练掌握各运算法则．2．C解析：C【分析】根据内错角定义进行解答即可．【详解】解：A、∠1与∠2是同位角，故此选项不合题意；B、∠1与∠2是同旁内角，故此选项不合题意；C、∠1与∠2是内错角，故此选项符合题意；D、∠1与∠2不是内错角，此选项不合题意；故选：C．【点睛】此题主要考查了内错角，关键是掌握内错角的边构成“Z“形．3．B解析：B【解析】解：解方程组得：x=3+a，y=－2－2a．∵x为正数，y为非负数，∴3+a＞0，－2－2a≥0，解得：－3＜a≤－1，故①错误；当a=53-时，x=54333-=，y=542233-+⨯=，∴x=y，故②正确；当a=－2时，x=3+(－2)=1，y=－2+4=2，x+y=3=5+(－2)=3，故③正确．故选B．点睛：本题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．4．C解析：C【分析】根据平方差公式（a+b）（a-b）=a2-b2对各选项分别进行判断．【详解】解：A、（a+b）（a+c）中存在相同项，没有相反项，不能用平方差公式计算，故本选项不符合题意；B、（a+b）（-a-b）=-（a+b）（a+b）两项都是相同，不能用平方差公式计算，故本选项不符合题意；C、（a+b）（a-b）存在相同的项与互为相反数的项，能用平方差公式计算，故本选项符合题意；D、（-a+b）（a-b）中两项都是相反项，没有相同项，不能用平方差公式计算，故本选项不符合题意；故选：C ．【点睛】本题考查了平方差公式．运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．5．B解析：B【分析】表示出不等式组的解集，由已知解集确定出m 的范围，表示出方程的解，由方程的解为正整数，确定出整数m 的值即可．【详解】解：不等式组整理得：41≥+⎧⎨≥⎩x m x ，由不等式组的解集为x ≥1，得到m +4≤1，即m ≤-3，方程去分母得：m -1+x =3x -6，解得：5+2=m x ，由方程有正整数解，故50+>m ，且5+m 能被2整除，∴m =-3，则符合条件的整数m 的值有1个．故选：B ．【点睛】此题考查了一元一次不等式组的整数解，熟练掌握不等式组的解法是解本题的关键． 6．B解析：B【分析】根据平移的性质、三角形的高、多边形的内角和和外角和，平行线的判定进行判断即可．【详解】解：①长为5cm 的线段AB 沿某一方向平移10cm 后，平移后线段AB 的长为5cm ，原命题是假命题；②锐角三角形的高在三角形内部，原命题是假命题；③六边形的内角和是外角和的两倍，是真命题；④在同一平面内，平行于同一直线的两直线平行，是真命题：⑤两个角的两边分别平行，则这两个角相等或互补，原命题是假命题；故选：B ．【点睛】考查了命题与定理的知识，解题的关键是了解平移的性质、三角形的高、多边形的内角和和外角和，平行线的判定，难度较小．7．C解析：C【分析】根据给定的部分“三角形数”和“正方形数”找出“三角形数”可看成从1开始几个连续自然数的和以及“正方形数”可看成某个自然数的平方，依此规律逐一分析四个选项中的三个数是否符合该规律，由此即可得出结论．【详解】解：A、13不是正方形数，不合题意；B、9和16不是三角形数，不合题意；C、36=62=（5+1）2，n=5；两个三角形的数分别是：1+2+3+4+5=15；1+2+3+4+5+6=21；故C符合题意；D、18和31不是三角形数，不合题意；故选：C．【点睛】本题考查了规律型中数字的变化类，根据给定的部分“三角形数”和“正方形数”找出“三角形数”和“正方形数”的特点是解题的关键．8．B解析：B【分析】根据三角形的内角和得到∠BAC＝110°，由折叠的性质得到∠E＝∠C＝30°，∠EAD＝∠CAD，∠ADC＝∠ADE，根据平行线的性质得到∠BAE＝∠E＝30°，根据三角形的内角和即可得到结论．【详解】解：∵∠B＝40°，∠C＝30°，∴∠BAC＝110°，由折叠的性质得，∠E＝∠C＝30°，∠EAD＝∠CAD，∠ADE＝∠ADC，∵DE∥AB，∴∠BAE＝∠E＝30°，∴∠CAD＝40°，∴∠ADE＝∠ADC＝180°﹣∠CAD﹣∠C＝110°，故选：B．【点睛】本题考查了三角形的内角和，折叠的性质，平行线的性质，熟练掌握折叠的性质是解题的关键．二、填空题9．﹣32x10y8【详解】试题分析：分析：先算乘方，再算乘法（﹣2x3y2）3=（﹣2）3（x3）3（y2）3=﹣8x9y6，所以（﹣2x3y2）3•4xy2=（﹣8x9y6）•4xy2=﹣32x10y8．解：（﹣2x 3y 2）3•4xy 2=（﹣8x 9y 6）•4xy 2=﹣32x 10y 8点评：本题考查整式的乘法混合运算，按照运算顺序先算乘方再算乘法．10．假【分析】若空间中两条直线不相交，则这两条直线平行，也有可能异面．【详解】解：若空间中两条直线不相交，则这两条直线平行，也有可能异面，故是假命题．故答案为：假．【点睛】本题考查命题真假的判断，考查学生的推理能力，属于基础题．11．D解析：360【分析】根据多边形内角与外角、三角形内角和定理、三角形外角性质进行推理计算即可．【详解】解：如图，延长DE 交AB 于点G ，由三角形外角性质可知：∠1=∠F +∠DEF ，∠2=∠1+∠A ，∴∠2=∠F +∠DEF +∠A ，∴在四边形BCDG 中，由四边形内角和可知：∠2+∠B +∠C +∠D =360°，∴∠A +∠F +∠DEF +∠B +∠C +∠D =360°．故答案为：360．【点睛】本题考查了多边形内角与外角、三角形外角性质，解决本题的关键是掌握多边形内角和定理、三角形外角性质．12．12-【分析】将题中已知条件变形，根据平方差公式因式分解直接代入计算即可．【详解】解：0403a a b b +==--+，，34a b a b ∴+=--=，，22()()3412a b a b a b ∴-=+-=-⨯=-，故答案为：12-．【点睛】本题主要考查平方差公式因式分解，熟记平方差公式的结构特点是解题的关键． 13．0【分析】将x 和y 的值代入二元一次方程组，再解方程组即可得出答案.【详解】解：将54x y =⎧⎨=⎩代入方程组得：54115823a b a b -=⎧⎨+=⎩①②，把②+①×2得2525a =，解得1a =把1a =代入① 解得1b =∴110a b -=-=故答案为：0.【点睛】本题考查的是二元一次方程组的解，将解代入方程组解方程组即可得出答案.14．7【解析】【分析】把楼梯的水平线段向下平移，竖直线段向右平移可得地毯长度为水平距离与高的和．【详解】解：把楼梯的水平线段向下平移，竖直线段向右平移可得地毯长度为水平距离与高的和．所以地毯长度至少需3+4=7米．故答案为：7．【点睛】此题主要考查了生活中的平移及平移的性质，根据已知得出地毯的长度应等于水平距离与高的和是解题关键．15．10（答案不唯一）【分析】先根据三角形的三边关系定理求出第三边的取值范围，再选一个合适的值即可．【详解】由三角形的三边关系定理得：，即则第三边BC 的值可以是10故答案为：10（答案不解析：10（答案不唯一）先根据三角形的三边关系定理求出第三边的取值范围，再选一个合适的值即可．【详解】-<<+由三角形的三边关系定理得：AC AB BC AC AB==6,9AB ACBC∴-<<+，即315<<9696BC则第三边BC的值可以是10故答案为：10（答案不唯一）．【点睛】本题考查了三角形的三边关系定理，熟记三角形的三边关系定理是解题关键．16．18【分析】先由三角形的高和内角和求出∠DAC，然后由角平分线得出∠BAC，从而计算即可得到答案．【详解】解：∵AD是△ABC的BC边上的高，∠C＝42°，∴∠DAC=180°-90°-4解析：18【分析】先由三角形的高和内角和求出∠DAC，然后由角平分线得出∠BAC，从而计算即可得到答案．【详解】解：∵AD是△ABC的BC边上的高，∠C＝42°，∴∠DAC=180°-90°-42°=48°，∵AE是∠BAC的角平分线，∴∠BAC=2∠BAE=15°×2=30°，∴∠DAB=∠DAC-∠BAC=48°-30°=18°，故答案为：18．【点睛】本题主要考查了三角形的高和角平分线的内容，注意三角形的内角和是180°，以及三角形的高和角平分线的性质即可解答．17．（1）4；（2）；（3）；（4）19600【分析】（1）先算负指数幂，乘方和零指数幂，再算加减法；（2）先计算同底数幂的乘除法，幂的乘方和积的乘方，再合并；（3）利用平方差公式变形，再将括号解析：（1）4；（2）8--+；（4）19600a b c bc-；（3）2227a496（1）先算负指数幂，乘方和零指数幂，再算加减法；（2）先计算同底数幂的乘除法，幂的乘方和积的乘方，再合并；（3）利用平方差公式变形，再将括号展开；（4）先变形为()2212962242⎛⎫⨯-⨯ ⎪⎝⎭，再利用平方差公式计算．【详解】解：（1）()()22019014153π-⎛⎫-+⨯--- ⎪⎝⎭ =941--=4；（2）()2741023a a a a a ⨯--+÷ =8889a a a -+=87a -；（3）()()2323a b c a b c +--+=()()2323a b c a b c +---⎡⎤⎡⎤⎣⎦⎣⎦=()2243a b c --=222496a b c bc --+；（4）2212964244⨯-⨯ =222212962242⎛⎫⨯-⨯ ⎪⎝⎭=()2212962242⎛⎫⨯-⨯ ⎪⎝⎭ =2214848-=()()1484814848+-=196100⨯=19600【点睛】本题考查了整式的混合运算，实数的混合运算，解题的关键是掌握幂的运算法则和乘法公式的应用．18．（1）﹣3a （a ﹣b ）2；（2）（x ﹣y ）（2a+3b ）（2a ﹣3b ）；（3）（a+2b ）2（a ﹣2b ）2【分析】（1）直接提取公因式﹣3a ，再利用完全平方公式分解因式得出答案；（2）直接提取解析：（1）﹣3a （a ﹣b ）2；（2）（x ﹣y ）（2a +3b ）（2a ﹣3b ）；（3）（a +2b ）2（a ﹣2b）2【分析】（1）直接提取公因式﹣3a，再利用完全平方公式分解因式得出答案；（2）直接提取公因式x﹣y，再利用平方差公式分解因式即可；（3）直接利用完全平方公式分解因式，再利用平方差公式分解因式得出答案．【详解】解：（1）原式＝﹣3a（a2﹣2ab+b2）＝﹣3a（a﹣b）2；（2）原式＝（x﹣y）（4a2﹣9b2）＝（x﹣y）（2a+3b）（2a﹣3b）；（3）原式＝（a2﹣4b2）2＝[（a+2b）（a﹣2b）]2＝（a+2b）2（a﹣2b）2．【点睛】本题主要考查提公因式法因式分解以及公式法因式分解，积的乘方的逆运算，熟知平方差公式以及完全平方公式的结构特点是解题的关键．19．（1）；（2）【分析】（1）先解出y的值，再代入求出x；（2）方程组利用加减消元法求解即可．【详解】解：（1），由①得：y=1，代入②中，解得：x=3，则原方程组的解为：；（2），解析：（1）31xy=⎧⎨=⎩；（2）21xy=⎧⎨=⎩【分析】（1）先解出y的值，再代入求出x；（2）方程组利用加减消元法求解即可．【详解】解：（1）1227yx y+=⎧⎨+=⎩①②，由①得：y=1，代入②中，解得：x=3，则原方程组的解为：31xy=⎧⎨=⎩；（2）3524x y y x -=⎧⎨+=⎩①②， ①×2+②得：7x =14，解得：x =2，代入②中，解得：y =1，则原方程组的解为：21x y =⎧⎨=⎩．【点睛】此题考查了消元法解二元一次方程组，用到的知识点是加减法和代入法，关键是掌握两种方法的步骤．20．，整数解为4，5【分析】先求出每个不等式的解集，然后求出不等式组的解集，再找出整数解即可．【详解】解：解不等式①，得解不等式②，得∴原不等式组的解集为原不等式组的整数解为解析：35x <≤，整数解为4，5【分析】先求出每个不等式的解集，然后求出不等式组的解集，再找出整数解即可．【详解】解：()5931133722x x x x ⎧->-⎪⎨-≤-⎪⎩①② 解不等式①，得3x >解不等式②，得5x ≤∴原不等式组的解集为35x <≤原不等式组的整数解为：4，5．【点睛】本题考查了解一元一次不等式组，一元一次不等式组的整数解的应用，关键是能根据不等式的解集找出不等式组的解集．三、解答题21．（1）详见解析；（2）58°【分析】（1）由平行线的判定定理进行证明，即可得到结论成立；（2）由角平分线性质和平行线的性质，求出∠2的度数，然后即可求出的度数．【详解】（1）证明：∵∠1=解析：（1）详见解析；（2）58°【分析】（1）由平行线的判定定理进行证明，即可得到结论成立；（2）由角平分线性质和平行线的性质，求出∠2的度数，然后即可求出FAB∠的度数．【详解】（1）证明：∵∠1=∠BDC∴AB//CD（同位角相等，两直线平行）∴∠2=∠ADC（两直线平行，内错角相等）∵∠2+∠3=180°∴∠ADC+∠3=180°（等量代换）∴AD//CE（同旁内角互补，两直线平行）（2）解：∵∠1=∠BDC，∠1=64°∴∠BDC=64°∵DA平分∠BDC∠BDC= 32°（角平分线定义）∴∠ADC=12∴∠2=∠ADC=32°(已证)又∵CE⊥AE∴∠AEC=90°（垂直定义）∵AD//CE(已证)∴∠DAF=∠AEC=90°（两直线平行，同位角相等）∴∠FAB=∠DAF-∠2=90°-32°=58°．【点睛】本题考查了平行线的判定和性质，角平分线的定义，以及余角的计算，解题的关键是熟练掌握所学的知识进行解题．22．（1）小宇骑车的平均速度是米/分；（2）至少应提高米/分【分析】（1）设小明骑车的平均速度是x米/分，、两站间的距离和小宇家到站的距离恰好相等，列出方程 3x+2400=3×5 x，解方程即可得解析：（1）小宇骑车的平均速度是200米/分；（2）至少应提高100米/分【分析】（1）设小明骑车的平均速度是x米/分，A、B两站间的距离和小宇家到B站的距离恰好相等，列出方程 3x+2400=3×5 x，解方程即可得解；（2）设小明的速度提高y米/分，根据题意列出一元一次不等式-⨯+≥，即可得出答案；(102)(200)2400y【详解】解：（1）设小宇骑车的平均速度是x 米/分．根据题意，得3240035x x +=⨯解得200x =答：小宇骑车的平均速度是200米/分．（2）设小宇骑车的平均速度提高y 米/分．根据题意，得(102)(200)2400y -⨯+≥解得100y ≥．答：小宇骑车的平均速度至少应提高100米/分．【点睛】本题考查了一元一次方程的应用及一元一次不等式的应用，弄清题中的不等及相等关系是解本题的关键．23．（1）-1；（2）t=-2，-1，0，1；（3）13组【分析】（1）把x=2代入方程3x-5y=11得，求得y 的值，即可求得θ的值；（2）参考小明的解题方法求解即可；（3）参考小明的解题方法解析：（1）-1；（2）t=-2，-1，0，1；（3）13组【分析】（1）把x=2代入方程3x-5y=11得，求得y 的值，即可求得θ的值；（2）参考小明的解题方法求解即可；（3）参考小明的解题方法求解后，即可得到结论．【详解】解：（1）把x=2代入方程3x-5y=11得，6-6y=11，解得y=-1，∵方程3x-5y=11的全部整数解表示为：253x t y tθ=+⎧⎨=+⎩（t 为整数），则θ=-1，故答案为-1；（2）方程2x+3y=24一组整数解为0066x y =⎧⎨=⎩，则全部整数解可表示为6362x t y t =-⎧⎨=+⎩（t 为整数）．因为630620t t ->⎧⎨+>⎩，解得-3＜t ＜2．因为t 为整数，所以t=-2，-1，0，1．（3）方程19x+8y=1908一组整数解为1001x y =⎧⎨=⎩，则全部整数解可表示为1008119x t y t=-⎧⎨=+⎩（t 为整数）． ∵100801190t t ->⎧⎨+>⎩，解得119-＜t ＜12.5．因为t 为整数，所以t=0，1，2，3，4，5，67，8，9，10，11，12，∴方程19x+8y=1908的正整数解有13组．【点睛】本题考查了二元一次方程的解，一元一次不等式的整数解，理解题意、掌握解题方法是本题的关键．24．∠DPC=α+β，理由见解析；（1）70 ；(2) ∠DPC=α – β，理由见解析.【解析】（1）过P 作PE ∥AD 交CD 于E ，推出AD ∥PE ∥BC ，根据平行线的性质得出∠α=∠DPE ，∠β=∠C解析：∠DPC=α+β，理由见解析；（1）70 ；(2) ∠DPC=α – β，理由见解析.【解析】（1）过P 作PE ∥AD 交CD 于E ，推出AD ∥PE ∥BC ，根据平行线的性质得出∠α=∠DPE ，∠β=∠CPE ，即可得出答案；（2）化成图形，根据平行线的性质得出∠α=∠DPE ，∠β=∠CPE ，即可得出答案．【问题探究】解：∠DPC=α+β如图，过P 作PH ∥DF∵DF ∥CE ,∴∠PCE =∠1=α， ∠PDF =∠2∵∠DPC =∠2+∠1=α+β【问题迁移】（1）70（图1）（图2）(2) 如图1，∠DPC=β -α∵DF∥CE,∴∠PCE=∠1=β，∵∠DPC=∠1-∠FDP=∠1-α．∴∠DPC=β -α如图2，∠DPC= α -β∵DF∥CE,∴∠PDF=∠1=α∵∠DPC=∠1-∠ACE=∠1-β．∴∠DPC=α - β25．（1）①A；②见解析；（2）①25°；②2∠EBD＝∠ABC﹣∠ACB；（3）m．【分析】（1）①由直角三角形三条高的定义即可得出结论；②分别延长BE，DA，两者交于F，连接CF交BA的延长线解析：（1）①A；②见解析；（2）①25°；②2∠EBD＝∠ABC﹣∠ACB；（3）920m．【分析】（1）①由直角三角形三条高的定义即可得出结论；②分别延长BE，DA，两者交于F，连接CF交BA的延长线于H，CH即为所求；（2）①由三角形内角和定理和角平分线的性质可以得出∠BAE＝12∠BAC＝35°，再由直角三角形的性质得∠ABE＝55°，即可求解；②由三角形内角和定理和角平分线的性质求解即可；（3）连接CD，由中线的性质得S△ADN＝S△CDN，同理：S△ABN＝S△CBN，设S△ADN＝S△CDN＝a，S△ABN＝S△CBN＝12m，再求出S△CDM＝34S△BCD＝3384m a，S△ACM＝34S△ABC＝34m，利用面积关系求解即可.【详解】解：（1）①∵直角三角形三条高的交点为直角顶点，∠A＝90°，∴△ABC的三条高所在直线交于点A，故答案为：A；②如图，分别延长BE，DA，两者交于F，连接CF交BA的延长线于H，CH即为所求；（2）①∵∠ABC＝80°，∠ACB＝30°，∴∠BAC＝70°，∵AD平分∠BAC，∴∠BAE＝12∠BAC＝35°，∵BE⊥AD，∴∠AEB＝90°，∴∠ABE＝90°﹣35°＝55°，∴∠EBD＝∠ABC﹣∠ABE＝80°﹣55°＝25°，故答案为：25°；②∠EBD与∠ABC，∠C之间的数量关系为：2∠EBD＝∠ABC﹣∠ACB∵BE⊥AD，∴∠AEB＝90°，∴∠ABE＝90°﹣∠BAD，∴∠EBD＝∠ABC﹣∠ABE＝∠ABC+∠BAD﹣90°，∵AD平分∠BAC，∴∠BAD＝∠CAD＝12∠BAC，∵∠BAC＝180°﹣∠ABC﹣∠ACB，∴∠BAD＝90°﹣12∠ABC﹣12∠ACB，∴∠EBD＝∠ABC+∠BAD﹣90°＝∠ABC+90°﹣12∠ABC﹣12∠C﹣90°=12∠ABC﹣12∠C，∴2∠EBD＝∠ABC﹣∠ACB，故答案为：2∠EBD＝∠ABC﹣∠ACB；（3）连接CD，如图所示：∵N是AC的中点，∴1ADN CDN S AN S CN ==△△， ∴S △ADN ＝S △CDN ，同理：S △ABN＝S △CBN ，设S △ADN ＝S △CDN ＝a ，∵△ABC 的面积是m ，∴S △ABN ＝S △CBN ＝12m ，∴S △BCD ＝S △ABD ＝12m ﹣a ，∵BM ＝14BC ， ∴13BM CM =， ∴13BDMCDM SBM S CM ==，13ABMACM S BM S CM ==， ∴S △CDM ＝3S △BDM ，S △ACM ＝3S △ABM ，∴S △CDM ＝34S △BCD ＝34×（12m ﹣a ）＝3384m a -，S △ACM ＝34S △ABC ＝34m ， ∵S △ACM ＝S 四边形CMDN +S △ADN ＝S △CDM +S △CDN +S △ADN ，即：333484m m a a a =-++，解得：a ＝310m ， ∴S 四边形CMDN ＝S △CDM +S △CDN ＝3333984101020m m m m -⨯+=，【点睛】本题主要考查了三角形的高，三角形的中线，三角形内角和，三角形面积，解题的关键在于能够熟练掌握相关知识进行求解.。

苏科版七年级下期末模拟试卷(三)及答案

七下数学期终复习练习三姓名1．已知空气的单位体积质量为1.24×10－3克／厘米3，将1.24×10－3用小数表示为( )A．0.000124 B．0.0124 C．－0.00124 D．0.001242．下列各组数可能是一个三角形的边长的是( )A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，113．下列命题是假命题的是( )A．三角形的内角和是180°B．多边形的外角和都等于360°C．五边形的内角和是900°D．三角形的一个外角等于和它不相邻的两个内角的和4．在6×6方格中，将图①中的图形Ⅳ平移后位置如图②所示，则图形N的平移方法中，正确的是( ) A．向下移动1格B．向上移动1格C．向上移动2格D．向下移动2格5．如图，下列条件中能判断直线l1//l2的是( )A．∠1＝∠2 B．∠1＝∠5 C．∠1＋∠3＝180°D．∠3＝∠56．下列运算正确的是( ) A．(a＋b)2＝a2＋b2B．x3＋x3＝x6C．(a3)2＝a5D．（2x2）（－3x3)＝－6x57．分解因式a3－a的结果是( ) A．a（a2－1）B．a(a－1)2C．a（a＋1）（a－1）D．(a2＋a)（a－1）8．在一年一度的“安仁春分药王节”市场上，小明的妈妈用280元买了甲、乙两种药材，甲种药材每斤20元，乙种药材每斤60元，且甲种药材比乙种药材多买了2斤，设买了甲种药材x斤，乙种药材y斤，你认为小明应该列出的方程组为( )A．20602802x yx y+=⎧⎨-=⎩B．60202802x yx y+=⎧⎨-=⎩C．20602802x yy x+=⎧⎨-=⎩D．60202802x yy x+=⎧⎨-=⎩9．不等式组()3112323x xx⎧+>-⎪⎨-+≥⎪⎩的整数解( )A．－1，0，1 、B．0，1 、C．－2，0，1 、D．－1，110．把一块直尺与一块三角板如图放置．若∠1＝40°，则∠2的度数为()A．125°B．120°C．140°D．130°11．计算：3a·a2＋a3＝_______．12．六边形的外角和等于_______． 13．不等式（a －3）x >1的解集是x <13a -，则a 的取值范围_______． 14．在△ABC 中，∠A ＝60°，∠B ＝2∠C ，则∠B ＝_______°．15．把多项式x 2＋mx ＋5因式分解得(x ＋5)（x ＋n ），则m ＝_______，n ＝_______．16．某班组织20名同学去春游，同时租用两种型号的车辆，一种车每辆有8个座位，另一种车每辆有4个座位，要求租用的车辆不留空座，也不能超载，有_______种租车方案．17．计算：(1)（－2ab 2）2·（3a 2b －2ab －1）； (2)4（a －b )2－（2a ＋b ）(－b ＋2a )；(3)(1＋x －y )(x ＋y －1)；(4)22122a b ⎛⎫- ⎪⎝⎭．18．用代入消元法解方程组23514x y x y -=⎧⎨+=⎩19．分解因式：(1)(a －3)2＋(3－a )； (2)a n ＋2＋a n ＋1－3a n ； (3)(a 2＋4)2－16a 2．①②20．解不等式组：()321931x x x -≥⎧⎪⎨+<+⎪⎩21．甲、乙二人在一环形场地上从A 点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长．（列方程（组）求解）22．如图，∠AED ＝∠ACB ，∠DEB ＝∠GFC ，BE ⊥AC ，求证：FG ⊥AC ．23．同庆中学为丰富学生的校园生活，准备从军跃体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格也相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．(1)购买一个足球、一个篮球各需多少元？(2)根据同庆中学的实际情况，需从军跃体育用品商店一次性购买足球和篮球共96个．要求购买足球和篮球的总费用不超过5 720元，则同庆中学最多可以购买多少个篮球？①②24．平面内的两条直线有相交和平行两种位置关系．(1)AB平行于CD，如图①，点P在AB、CD外部时，由AB∥CD，有∠B＝∠BOD，又∠BOD是△POD 的外角，故∠BOD＝∠BPD＋∠D，得∠BPD＝∠B－∠D．如图②，将点P移到AB、CD内部，以上结论是否成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；(2)在图②中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图③，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）(3)根据(2)的结论求图④中∠4＋∠B＋∠C＋∠D＋∠E＋∠F的度数．复习练习三参考答案1.D2.C3.C4.D5.C6.D7.C8.A9.A10.D11．4a312．360°13．a<3 14．80 15．6 1 1 6．217．(1)原式＝12a4b5－8a3b5－4a2b4．(2)原式＝5b2－8ab．(3)原式＝x2－y2＋2y－1．(4)原式＝4a2－2ab2＋14b4．18．31 xy=⎧⎨=⎩19．(1)原式＝（a－3）（a－4）．(2)原式＝a n（a2＋a－3）．(3)原式＝(a－2)2(a＋2)2．20．x>321．375米／分、150米／分，环形场地周长为900米．22．略23．(1)50元，80元．(2)30个24．(1)不成立，结论是∠BPD＝∠B＋∠D．(2)结论：∠BPD＝∠BQD＋∠B＋∠D．(3)360°．。

苏教版七年级下册期末模拟测试含答案

苏教版七年级下册期末模拟测试（考试时间：150分钟满分：150分）第一部分选择题（12分）1.下列各组中加点字注音没有错误的一组是A.遴选(1 m)伫立（zh驯良(sh in)深邃(su 1)B.蛰伏(zh e)翌日(y i)粗犷（g u di c濒危(b in g)C.参天(c 01)要塞（s①步履(l G)牌坊(f ang)D.分娩(w di)摒弃(b in c)镶嵌(qi m)翩跹(xi ai)2. 下列标点符号使用没.有错误的一项是（2分）（）A. 柳叶儿能够吃的日子，只有那么七、八天，至多十几天。

B. 我不知道为什么家里的人要将我送进书塾里去？C. 我又一次瞻仰了人民英雄永垂不朽几个大字和碑文。

D. 他的口头禅是：“猪羊怕杀，人怕打！”3. 下列句子没有语病的一项是（）A. 通过这次主题班会，使同学们认识到了端正学习态度的重要性。

B. 最近部分企业安全保卫工作出现了纰漏，有关部门及时分析并解决了问题。

C. 伊拉克局势能不能稳定下来，是联合国工作人员返回巴格达工作的基本条件。

D. 虽然我进初中快一年了，但小学时代同学们愉快的笑容，至今还在我耳际萦绕。

4. 下列各句中加点的成语使用正确的一项是（）（2分）A、听到湖中有人喊救命，正在散步的老张忘乎所以..地跳入水中去营救。

B、黄山的石、雾、松是大自然的创造，无不巧夺天工，令人赞叹不已。

C、这类经济节目办得栩栩如生.，显现出编导很有水平。

D沉迷于玩游戏机的王刚面对同学善意的批评反唇相讥...，不理不睬，结果成绩一落千丈。

5. 下列加点词语解释全部正确的一组是（）A.亭亭净植（种植）太祖常劝以读书（拿）陶后鲜有闻（很少）B.卒用其人（终于）普少习吏事（学习）及为相（等到）C.虽多忌克（虽然）太祖乃悟（才）但闻黄河流水鸣溅溅（只）D.复奏如初（又，再）上依河汉（银河）尝奏荐某人为某官（品尝）6. 从上下文连贯的要求看，依次填入下面横线上的语句，最恰当的一项是（）有人说，宽容是一种润滑剂，__________________ ，宽容是一幅镇静剂， ________________ ，宽容是一束阳光，，宽容是一座桥梁，__________________ 。