【精品】课件---偏心距增大系数
合集下载
同济大学混凝土结构基本原理第6章答案
其中 当 当
为混凝土极限压应变。 时，截面属于大偏心受压； 时，截面属于小偏心受压。
6-6.长细比对偏心受压构件的承载力有直接影响， 请说明基本计算公式中是如何来考虑这一 问题的。 答：当 ，即短柱情况下，取弯矩增大系数 ；否则，取
28
其中，
。
6-7 请根据 N cu − M u 相关曲线说明大偏心受压及小偏心受压时轴向力与弯矩的关系，偏压 构件在什么情况下的抗弯承载力最大？ 答：在小偏心受压破坏时候，随着轴向力 N c 的增大，构件的抗弯能力 M 逐渐减少；在大偏 心受压构件破坏的时候，随着轴向力 N c 的增大,会提高构件的抗弯承载力。在偏心构件的破 坏处于破坏时,构件的抗弯承载力达到最大值。 6-8 N cu − M u 相关曲线有哪些用途？ 答：Ncu-Mu 相关曲线是由具有相同的截面尺寸,相同高度,相同配筋,相同材料强度但偏心距 e0 不同的构件进行系列偏心受压实验得到破坏时每个构件所承受的不同轴力 Ncu 和弯矩 Mu 所 绘制而成的,在此曲线中,我们可以轻松查阅到此构件在小偏心受压或者大偏心受压时候构 件的破坏荷载,了解构件性能.
思考题
6-1.偏心受力构件截面上同时作用有轴向力和弯矩， 除教材上列出的外， 再举出实际工程中 的偏心受压构件和偏心受拉构件各五种。 答：偏心受压构件有屋架的上弦杆、框架结构柱，砖墙及砖垛等。偏心受拉构件有矩形水池 的池壁、矩形剖面料仓或煤斗的壁板、受地震作用的框架边柱，以及双肢柱的受拉肢等。 6-2.对比偏心受压构件与受弯构件正截面的应力及应变分布，说明其相同之处与不同之处。 答： 受弯构件在混凝土出现裂缝前， 混凝土分为受压区和受拉区， 分别承受压应力和拉应力， 受拉区混凝土开裂后， 退出工作， 钢筋单独承担拉应力， 受压区混凝土受压区高度逐渐变小， 压应力不断增大，最终压碎破坏。应变一开始钢筋与混凝土应变相同，慢慢达到混凝土开裂 应变，钢筋屈服应变。而偏心受压构件则因偏心距不同其应力分布亦有不同。当 较大 中时，出现大偏心受压破坏，形式接近受弯。而当 较大 较大或 较小 适
结构设计原理-叶见曙版-课后习题第7-9(附答案)
第七章7-2试简述钢筋混凝土偏心受压构件的破坏形态和破坏类型。
答：破坏形态：（1）受拉破坏—大偏心受压破坏，当偏心距较大时，且受拉钢筋配筋率不高时，偏心受压构件的破坏是受拉钢筋先达到屈服强度，然后受压混凝土压坏，临近破坏时有明显的预兆，裂缝显著开展，构件的承载能力取决于受拉钢筋的强度和数量。
（2）受压破坏—小偏心受压破坏，小偏心受压构件的破坏一般是受压区边缘混凝土的应变达到极限压应变，受压区混凝土被压碎；同一侧的钢筋压应力达到屈服强度，破坏前钢筋的横向变形无明显急剧增长，正截面承载力取决于受压区混凝土的抗压强度和受拉钢筋强度。
破坏类型：1）短柱破坏；2）长柱破坏；3）细长柱破坏7-3由式（7-2）偏心距增大系数与哪些因素有关？由公式212000)/e 140011ζζη⎪⎭⎫⎝⎛+=h l h （可知，偏心距增大系数与构件的计算长度，偏心距，截面的有效高度，截面高度，荷载偏心率对截面曲率的影响系数，构件长细比对截面曲率的影响系数。
7-4钢筋混凝土矩形截面偏心受压构件的截面设计和截面复核中，如何判断是大偏心受压还是小偏心受压？答：截面设计时，当003.0h e ≤η时，按小偏心受压构件设计，003.0h e >η时，按大偏心受压构件设计。
截面复核时，当b ξξ≤时，为大偏心受压，b ξξ>时，为小偏心受压.7-5写出矩形截面偏心受压构件非对称配筋的计算流程图和截面复核的计算流程图注意是流程图7-6解： 查表得：.1,280',5.110====γMPa f f MPa f sd sd cd m kN M M kN N N d d •=⨯=•==⨯=•=6.3260.16.326,8.5420.18.54200γγ偏心距mm N M e 6028.5426.3260===，弯矩作用平面内的长细比51060060000>==h l ，故应考虑偏心距增大系数。
设mm a a s s 40'==，则mm a h h s 5600=-=0.1,15606027.22.07.22.01001=>⨯+=+=ζζ取h e 0.1,105.1600600001.015.101.015.1202=>=⨯-=-=ζζ取h l 所以偏心距增大系数07.11110560/602140011)(140011221200=⨯⨯⨯⨯+=+=ζζηh l h e （1）大小偏心受压的初步判断003.064460207.1h mm e >=⨯=η，故可先按照大偏心受压来进行配筋计算。
《建筑结构》第12讲
第三节 偏心受压构件的受力性能
教学目标： 1.了解大小偏心受压构件破坏特征 ; 2. 掌握大小偏心受压构件的承载力计算公式 及其适用条件。 —————————————————————— 1，偏心受压构件受的内力有：弯矩、剪力和轴力。 2，当弯矩和剪力等于0时，为轴心受压构件，而当轴力等于0 时，为梁构件。
(2) 矩形对称配筋的计算方法
将对称配筋条件As=As′，fy= fy′代入上式得 ： N=α1fcbx
e= ηe0+ho/2-as
x Ne 1 f c bx h0 Ne 1 f c bh0 2 1 0.5 2 ' As As h a f f h a
其中ξ可近似按下式计算：
N b f cbh0 b 2 Ne 0.431 f cbh0 1 f cbh0 1 b h0 as
三、矩形对称配筋的计算方法 1，计算初始偏心距 2，计算偏心距增大系数 3，大小偏心的判断 4，大偏心受压构件的计算 1）计算公式 2）适用条件 5，小偏心受压构件的计算 （1）ξ的计算 （2）钢筋的计算
2，大偏心受压破坏——受拉边的钢筋达到受拉 屈服后，而混凝土受压破坏，破坏经历三个阶 段。 破坏特征：受拉钢筋首先达到屈服强度，最后 受压区混凝土达到界限压应变而被压碎，构件 破坏。此时，受压区钢筋也达到屈服强度。 破坏性质：延性破坏
图6.7 大偏心受压破坏形态
3，小偏心受压破坏——受拉（或受压）钢筋没达到屈 服，混凝土就达到了受压破坏，破坏表现为脆性性质。 破坏特征：临近破坏时，构件截面压应力较大一侧混 凝土达到极限压应变而被压碎。构件截面压应力较大 一侧的纵向钢筋应力也达到了屈服强度；而另一侧混 凝土及纵向钢筋可能受拉，也可能受压，但应力较小， 均未达到屈服强度。 破坏性质：脆性破坏
教学目标： 1.了解大小偏心受压构件破坏特征 ; 2. 掌握大小偏心受压构件的承载力计算公式 及其适用条件。 —————————————————————— 1，偏心受压构件受的内力有：弯矩、剪力和轴力。 2，当弯矩和剪力等于0时，为轴心受压构件，而当轴力等于0 时，为梁构件。
(2) 矩形对称配筋的计算方法
将对称配筋条件As=As′，fy= fy′代入上式得 ： N=α1fcbx
e= ηe0+ho/2-as
x Ne 1 f c bx h0 Ne 1 f c bh0 2 1 0.5 2 ' As As h a f f h a
其中ξ可近似按下式计算：
N b f cbh0 b 2 Ne 0.431 f cbh0 1 f cbh0 1 b h0 as
三、矩形对称配筋的计算方法 1，计算初始偏心距 2，计算偏心距增大系数 3，大小偏心的判断 4，大偏心受压构件的计算 1）计算公式 2）适用条件 5，小偏心受压构件的计算 （1）ξ的计算 （2）钢筋的计算
2，大偏心受压破坏——受拉边的钢筋达到受拉 屈服后，而混凝土受压破坏，破坏经历三个阶 段。 破坏特征：受拉钢筋首先达到屈服强度，最后 受压区混凝土达到界限压应变而被压碎，构件 破坏。此时，受压区钢筋也达到屈服强度。 破坏性质：延性破坏
图6.7 大偏心受压破坏形态
3，小偏心受压破坏——受拉（或受压）钢筋没达到屈 服，混凝土就达到了受压破坏，破坏表现为脆性性质。 破坏特征：临近破坏时，构件截面压应力较大一侧混 凝土达到极限压应变而被压碎。构件截面压应力较大 一侧的纵向钢筋应力也达到了屈服强度；而另一侧混 凝土及纵向钢筋可能受拉，也可能受压，但应力较小， 均未达到屈服强度。 破坏性质：脆性破坏
偏心受压构件课件
si
cu
Es
(
x
/ h0i
1)
得一元三次方程
Ax3 Bx2 Cx D 0
7-20
1.当 h / h0 z b 时,取 x / h0
由7-10可钢筋应力 s
s
cu
E
s
(
h0
x
1)
求得钢
筋中的应力 。s 再将钢筋面积 、As 钢筋应力 以及s 值代x
入式（7-4）中，
0 Nd fcdbx fsd As s As
即可得所需钢筋面积 As且应满足 。 As' m inbh
当 时h / h，0 取 则钢x 筋h面积 计算式为As ：
As'
Nes
)]
➢当 2as x 时bh，0
As
fcdbx
f
' sd
As'
0 Nd
f sd
➢当 x ，bh且0
时x ， 2as
令 x ,2则a可s 求得
As
0 Nd es
fsd (ho as )
2）当 e0 0时.3h0
已知：b h N d M d
f cd
f sd
f sd
l0
求： As 、As'
N
2．受压破坏——小偏心受压破坏
N
产生条件： （1）偏心距很小。 （2）偏心距 (e0 较/ h小) ，或偏心距较大而受拉钢
筋较多。 （3）偏心距 (e0很/ h小) ，但离纵向压力较远一侧
钢筋数量少，而靠近纵向力N一侧钢筋较多时。 破坏特征：
一般是靠近纵向力一侧的混凝土首先达到极限 压应变而压碎，该侧的钢筋达到屈服强度，远离 纵向力一侧的钢筋不论受拉还是受压，一般达不 到屈服强度。构件的承载力取决于受压区混凝土 强度和受压钢筋强度。 破坏性质：脆性破坏。
附加偏心距和偏心距增大系数
8.3 附加偏心距和偏心距增大系数
N
对于长细比l0/h≤5的短柱
◆ 侧向挠度
f 与初始偏心距ei
N0 Nus Num Nul Nusei Numei Nul ei Num fm Nul fl
相比很小,
◆ 柱跨中弯矩M=N(ei+f
) 随轴 力N的增加基本呈线性增 长，
◆ 直至达到截面承载力极限状
态产生破坏。
8.3 附加偏心距和偏心距增大系数
按有侧移考虑的框架结构，当竖向荷载较小，水平荷载较 大，或竖向荷载大部分作用在框架节点及其附近时，柱的计 算长度可取，
⎧[1 + 0.15(ψ u + ψ l )]H l0 = min ⎨ ⎩(2 + 0.2ψ min ) H
∑ ( EI ψ= ∑ ( EI
c b
◆ The moment in the middle M=N(ei+f ) is increasing with the increase of the N
M0
M
◆ Until the section reaches ultimate limit states and occurs failure. ◆ For a short column ,the deformation f is negligible.
f
l0le
l02 f = ⋅φ 10
φb =
，
φ=
εc + εs
h0
x ei
N
1 1 0.0033 × 1.25 + 0.0017 = ⋅ h0 171.7 h0 l0 ζ 1 = 0.5 f c A / N ζ 2 = 1.15 − 0.01 h
N
对于长细比l0/h≤5的短柱
◆ 侧向挠度
f 与初始偏心距ei
N0 Nus Num Nul Nusei Numei Nul ei Num fm Nul fl
相比很小,
◆ 柱跨中弯矩M=N(ei+f
) 随轴 力N的增加基本呈线性增 长，
◆ 直至达到截面承载力极限状
态产生破坏。
8.3 附加偏心距和偏心距增大系数
按有侧移考虑的框架结构，当竖向荷载较小，水平荷载较 大，或竖向荷载大部分作用在框架节点及其附近时，柱的计 算长度可取，
⎧[1 + 0.15(ψ u + ψ l )]H l0 = min ⎨ ⎩(2 + 0.2ψ min ) H
∑ ( EI ψ= ∑ ( EI
c b
◆ The moment in the middle M=N(ei+f ) is increasing with the increase of the N
M0
M
◆ Until the section reaches ultimate limit states and occurs failure. ◆ For a short column ,the deformation f is negligible.
f
l0le
l02 f = ⋅φ 10
φb =
，
φ=
εc + εs
h0
x ei
N
1 1 0.0033 × 1.25 + 0.0017 = ⋅ h0 171.7 h0 l0 ζ 1 = 0.5 f c A / N ζ 2 = 1.15 − 0.01 h
4.3 偏心受压构件承载力计算
4.2轴心受压构件承载力计算一、偏心受压构件破坏特征偏心受压构件在承受轴向力N和弯矩M的共同作用时，等效于承受一个偏心距为的偏心力N的作用，当弯矩M相对较小时，气就很小，构件接近于轴心受压，相反当N相对较小时，气就很大，构件接近于受弯，因此，随着气的改变，偏心受压构件的受力性能和破坏形态介于轴心受压和受弯之间。
按照轴向力的偏心距和配筋情况的不同，偏心受压构件的破坏可分为受拉破坏和受压破坏两种情况。
1.受拉破坏当轴向压力偏心距分较大，且受拉钢筋配置不太多时，构件发生受拉破坏。
在这种情况下，构件受轴向压力N后，离N较远一侧的截面受拉，另一侧截面受压。
当N增加到一定程度，首先在受拉区出现横向裂缝，随着荷载的增加，裂缝不断发展和加宽，裂缝截面处的拉力全部由钢筋承担。
荷载继续加大，受拉钢筋首先达到屈服，并形成一条明显的主裂缝，随后主裂缝明显加宽并向受压一侧延伸，受压区高度迅速减小。
最后，受压区边缘出现纵向裂缝，受压区混凝土被压碎而导致构件破坏（图4.3.1）。
此时，受压钢筋一般也能屈服。
由于受拉破坏通常在轴向压力偏心距分较大发生，故习惯上也称为大偏心受压破坏。
受拉破坏有明显预兆，属于延性破坏。
2.受压破坏当构件的轴向压力的偏心距分较小，或偏心距分虽然较大但配置的受拉钢筋过多时，就发生这种类型的破坏。
加荷后整个截面全部受压或大部份受压，靠近轴向压力M 一侧的混凝土压应力较高，远离轴向压力一侧压应力较小甚至受拉。
随着荷载逐渐增加，靠近轴一侧混凝土出现纵向裂缝，进而混凝土达到极限应变先被压碎,受压钢筋的应力也达到远离一侧的钢筋可能受压，也可能受拉，但因本身截面应力太小，或因配筋过多，都达不到屈服强度（图4.3.2）。
由于受压破坏通常在轴向压力偏心距％较小时发生，故习惯上也称为小偏心受压破坏。
受压破坏无明显预兆，属脆性破坏。
3.受拉破坏与受压破坏的界限综上可知，受拉破坏和受压破坏都属于“材料破坏”。
其相同之处是，截面的最终破坏都是受压区边缘混凝土达到极限压应变而被压碎。
《偏心距增大系数》课件
THANKS
感谢观看
单位
偏心距增大系数的单位是1，没有特 定的物理单位。
在应用中，需要根据具体问题确定偏 心距增大系数的取值范围和计算方法 。
它是一个无量纲的系数，用于描述结 构偏心距的变化程度。
02
偏心距增大系数的影响因素
结构形式
框架结构
由于框架结构的刚度较小，对偏 心距的增大系数影响较小。
剪力墙结构
由于剪力墙结构的刚度较大，对 偏心距的增大系数影响较大。
监测结构位移
通过监测结构在不同荷载下的位移变化，可以判断结构的稳定性，并采取相应的措施。
设计结构的支撑系统
确定支撑位置
根据偏心距增大系数，可以确定支撑系 统的位置，以提高结构的整体稳定性。
VS
选择支撑类型
根据工程需求和偏心距增大系数，可以选 择合适的支撑类型，如钢支撑、混凝土支 撑等。
05
偏心距增大系数的实际案例分析
加强实验验证
为了进一步验证理论模型的准确性，未来研究应 加强实验验证工作，通过实际测试数据与模拟结 果的对比分析，提高研究结论的可信度。
推广应用范围
目前研究成果主要应用于土木工程领域，未来可 以尝试将其拓展至其他工程领域，如航空航天、 机械等。
关注绿色建筑与可持续发展
在未来的研究中，应注重绿色建筑和可持续发展 理念的应用，通过优化结构设计，降低能耗和资 源消耗，实现建筑行业的可持续发展。
总结词
详细说明计算偏心距增大系数的步骤 ，帮助用户理解和操作。
详细描述
首先，用户需要确定偏心距e和参考 直径d的具体数值。然后，将这些数 值代入公式K = e / d中进行计算。最 后，得出偏心距增大系数的值。
注意事项
总结词
第八章 偏心受力构件
ea=h/30≥20mm 则 ei= ea+ e0 e0=M/N ei----为偏心受压柱的初始偏心距 由于附加偏心距的存在，柱的弯矩增加量为 取 ∆M = Nea
第
钢筋混凝土结构设计原理
章
八
8.3.6. 偏心距增大系数 纵向弯曲 • 钢筋混凝土受压构件在承受偏心荷载后，将产 生纵向弯曲变形即会产生侧向挠度，对长细比 小的短柱，计算时一般忽略不计；对于长细比 较大的长柱，由于侧向挠度的影响，各个截面 的弯矩都有所增加，而弯矩的增加势必造成侧 向挠度的增加 ——“细长效应”或“压弯效用” Ne——为初始弯矩或一阶弯矩 增加弯矩——附加弯矩或二阶弯矩
2、什么情况下使用复合式箍筋？复合式箍筋 有什么具体要求？
第
钢筋混凝土结构设计原理
章
八
§8.3 偏心受压构件的受力性能 8.3.1 试验研究分析 偏心受压构件是介于轴压构件和受弯构件之间 的受力状态。 e0 → 0 e0 → ∝ 轴压构件 受弯构件
大量试验表明：构件截面中的符合 平截面假定 ，偏压 构件的最终破坏是由于混凝土压碎而造成的。其影响因 素主要与 偏心距 的大小和所配 钢筋数量 有关。
8.2.2 截面形式 截面形式应考虑到受力合理和模板制作方便。 矩形 b ≥250mm
( ) 工字型(截面尺寸较大时) h′f ≥ 100mm d ≥ 80mm 且 为避免长细比过大降低构件承载力 l0/h≤25， l0/d≤25。
第
l0/b ≤ 30
八 章
钢筋混凝土结构设计原理
8.2.3 配筋形式 • 纵筋布置于弯矩作用方向两侧面 d≥12mm 纵筋间距>50mm 中距≤ 350mm
(a)
N
(b)
(c)
6第6章6.3-8
可取x=bh0得
6.5 矩形截面正截面承载力计算
第六章 受压构件
▲求解：利用两个基本公式可得
2 Ne a1 f cbh0 b (1 0.5b ) As f y (h0 a)
As
a1 f cbh0b f y As N fy
▲验算最小配筋率 ★若A's<0.002bh? 则取A’s=0.002bh（此时宜先选配好压筋），然后按 A’s为已知情况计算（即转类型二）。 ★若As<rminbh ? 应取As=rminbh
第六章 受压构件
（8）类型二：已知b×h；fc、fy，fy’； l0/h；N、M， A’s， 求As
▲分析： 两个公式，两个未知数，As和 x， 故有唯一解。 链接简图、计算公式 ▲求解：先由第二式求出x（解x的一元二次方程）：
第六章 受压构件
若2a’ x bh0，则可将x代入第一式求得As
（1）界限破坏的特征：受拉钢筋屈服与受压区混凝土边缘达到 极限压应变 cu 同时发生。 （2）相对界限受压区高度b （与适筋梁和超筋梁界限的b计算公式相同）
y
AS
AS’
有屈服点钢筋 b
1
1 fy Es cu
cu
（3）大小偏心的分界: b > b
为大偏心受压 为小偏心受压
第六章 受压构件
（3）计算公式的条件 x bh0
x2a'
（4） As 、A’s应满足最小配筋率：
As 0.002bh； A's 0.002bh
As + A's 0.006bh （5） As 、A’s应满足最大配筋率： As + A's 0.05bh
6.5 矩形截面正截面承载力计算
第六章 受压构件
▲求解：利用两个基本公式可得
2 Ne a1 f cbh0 b (1 0.5b ) As f y (h0 a)
As
a1 f cbh0b f y As N fy
▲验算最小配筋率 ★若A's<0.002bh? 则取A’s=0.002bh（此时宜先选配好压筋），然后按 A’s为已知情况计算（即转类型二）。 ★若As<rminbh ? 应取As=rminbh
第六章 受压构件
（8）类型二：已知b×h；fc、fy，fy’； l0/h；N、M， A’s， 求As
▲分析： 两个公式，两个未知数，As和 x， 故有唯一解。 链接简图、计算公式 ▲求解：先由第二式求出x（解x的一元二次方程）：
第六章 受压构件
若2a’ x bh0，则可将x代入第一式求得As
（1）界限破坏的特征：受拉钢筋屈服与受压区混凝土边缘达到 极限压应变 cu 同时发生。 （2）相对界限受压区高度b （与适筋梁和超筋梁界限的b计算公式相同）
y
AS
AS’
有屈服点钢筋 b
1
1 fy Es cu
cu
（3）大小偏心的分界: b > b
为大偏心受压 为小偏心受压
第六章 受压构件
（3）计算公式的条件 x bh0
x2a'
（4） As 、A’s应满足最小配筋率：
As 0.002bh； A's 0.002bh
As + A's 0.006bh （5） As 、A’s应满足最大配筋率： As + A's 0.05bh
结构设计原理偏心受压构件PPT学习教案
偏心距增大系数η:当偏心受压构件较长时，会引起较大挠度，为计入挠
度影响而引入的系数。
1
11400 (e0来自h0)(
l0 h
)2
1
2
1
0.2
2.7
e0 h0
≤1.0
2
1.15
0.01 l0 h
≤1.0
《公路桥规》规定下面情况需考虑偏心距增大 系数对构件承载力的影响：
矩形截面 l0/h > 5 圆形截面 l0/h > 4.4 其他截面 l0/r > 4.4（r为构件截面回转半径）
e0 ≤ 0.3h0 时：假设按小偏心受压构件进行设计计算
第22页/共56页
N 0 d ≤
Nu
fcdbx
f
' sd
As'
s As
➢ 假设为大偏心受压构件
As和As′均未知
Ne ≤ 0 ds
Mu
fcd bx(h0
x) 2
f
' sd
As'
(h0
as' )
★两个基本方程中
取补充条件 b ，即 x bh0
如 （N，M ）在曲 线外侧 ，则表 明截面 承载力 不足。
(2) 截面受 弯承载 力在b 点达到 最大， 该点近 似为界 限破坏 。
ab 段为大 偏心受 压，受 拉破坏 ；
bc 段为小 偏心受 压，受 压破坏 。
(3) 截面受 弯承载 力Mu与 作用的 轴压力 N大小 有关。
在 大偏心 受压段 ，当轴 压力较 小时，M u随N的 增加而 增加（ ab段） ；
N
fyAs
f'yA's
第6页/共56页
矩形截面偏心受压构件计算PPT课件
第23页/共73页
三、钢筋的应力ss 可由平截面假定求得
cu 0.0033
xc
s h0 xc
cu
xc
s
cu
h0
xc
xc
cu
h0
x
x
1
1
cu
(
1h0
x
-1)
h0 xc
s
ss
cu
Es
(
1h0
x
-1)
ss
cu
Es
(
0.8h0 x
-1)
混凝土强度等级C50 时，1=0.8。
6-27~33a连立求x，三次方程。？？ 第24页/共73页
N 1 fcbx f yAs f y As
0.9
1
=x/h0
1.1 1.2
ss
fy
1 b 1
f
' y
ss
fy
当 h h0 时，中和轴在外面，此时，取x h, 但计算s s时，仍按 a h0 计算。
h a
第26页/共73页
6.4.5 大小偏心分界限
b即x bh0属于大偏心破坏形态 ＞ b即x > bh0属于小偏心破坏形态
0
Nf有两种可能的分布。
e0 N
M2=N e0 M2 Nf
N
M0
M2
M2
N e1
N M1 = -N e1 M1
第13页/共73页
Mmax= M0+ Nf
情形1最大弯矩M2，二阶弯矩不引起最大弯矩 的增加
情形2最大弯矩Mmax ，距离端部某距离，Nf只能使Mmax比 M2稍大。
e0 N
M2=N e0 M2 Nf
N (ei
三、钢筋的应力ss 可由平截面假定求得
cu 0.0033
xc
s h0 xc
cu
xc
s
cu
h0
xc
xc
cu
h0
x
x
1
1
cu
(
1h0
x
-1)
h0 xc
s
ss
cu
Es
(
1h0
x
-1)
ss
cu
Es
(
0.8h0 x
-1)
混凝土强度等级C50 时，1=0.8。
6-27~33a连立求x，三次方程。？？ 第24页/共73页
N 1 fcbx f yAs f y As
0.9
1
=x/h0
1.1 1.2
ss
fy
1 b 1
f
' y
ss
fy
当 h h0 时，中和轴在外面，此时，取x h, 但计算s s时，仍按 a h0 计算。
h a
第26页/共73页
6.4.5 大小偏心分界限
b即x bh0属于大偏心破坏形态 ＞ b即x > bh0属于小偏心破坏形态
0
Nf有两种可能的分布。
e0 N
M2=N e0 M2 Nf
N
M0
M2
M2
N e1
N M1 = -N e1 M1
第13页/共73页
Mmax= M0+ Nf
情形1最大弯矩M2，二阶弯矩不引起最大弯矩 的增加
情形2最大弯矩Mmax ，距离端部某距离，Nf只能使Mmax比 M2稍大。
e0 N
M2=N e0 M2 Nf
N (ei
轴向受力构件2—偏心受压柱参考幻灯片
6.3.7.1 对称配筋的截面配筋设计
建筑工程中，柱截面常用对称配筋。对称配筋情况下， fy= fy/、As=As/ ，as=as/ 。
对称配筋通常用于控制截面在不同荷载组合下可能承受 正、负弯矩作用，如承受不同方向风荷载、地震荷载的框架 柱，以及为避免安装可能出现错误的预制排架柱等，都应采 用对称配筋。
6.3.5 矩形截面偏心受压构件正截面承载力计算
6.3.3.4 小偏心受压构件承载力计算 小偏压（ξ>ξb）
6.3.5 矩形截面偏心受压构件正截面承载力计算
6.3.3.5 垂直弯矩作用平面的承载力计算
混凝土结构设计规范7.3.13条：偏心受压构件除应计算 弯矩作用平面的受压承载力外，尚应按轴心受压构件验算垂 直于弯矩作用平面的受压承载力，此时，可不计入弯矩的作 用，但应考虑稳定系数 的影响。
6.3.6 矩形截面非对称配筋的计算方法
计算分为截面设计和承载力复核两类。 6.3.6.1 截面设计—大偏心受压 (1) As和As/均未知，三个未知数两个方程。此时，为使 (As+As/)的总用钢量最小，应取ξ= ξb（使压区混凝土充分 发挥，并保证受拉钢筋屈服）， 求得As/，最后求As 。 若求得的As/<0，则取As/=ρminbh，然后按As/已知，求As的 问题。 (2) 已知As/，求As。两个未知数，两个方程，可求解唯一 解，计算过程与双筋矩形截面受弯构件类似，计算过程 中注意验算适用条件。 例题参见教材。
6.3.4 偏心受压长柱的纵向弯曲影响
6.3.4.1 偏心距增大系数—二阶效应 N
N0
NusHale Waihona Puke NumNusei Numei
Nul Nul ei
Num fm Nul fl
建筑工程中，柱截面常用对称配筋。对称配筋情况下， fy= fy/、As=As/ ，as=as/ 。
对称配筋通常用于控制截面在不同荷载组合下可能承受 正、负弯矩作用，如承受不同方向风荷载、地震荷载的框架 柱，以及为避免安装可能出现错误的预制排架柱等，都应采 用对称配筋。
6.3.5 矩形截面偏心受压构件正截面承载力计算
6.3.3.4 小偏心受压构件承载力计算 小偏压（ξ>ξb）
6.3.5 矩形截面偏心受压构件正截面承载力计算
6.3.3.5 垂直弯矩作用平面的承载力计算
混凝土结构设计规范7.3.13条：偏心受压构件除应计算 弯矩作用平面的受压承载力外，尚应按轴心受压构件验算垂 直于弯矩作用平面的受压承载力，此时，可不计入弯矩的作 用，但应考虑稳定系数 的影响。
6.3.6 矩形截面非对称配筋的计算方法
计算分为截面设计和承载力复核两类。 6.3.6.1 截面设计—大偏心受压 (1) As和As/均未知，三个未知数两个方程。此时，为使 (As+As/)的总用钢量最小，应取ξ= ξb（使压区混凝土充分 发挥，并保证受拉钢筋屈服）， 求得As/，最后求As 。 若求得的As/<0，则取As/=ρminbh，然后按As/已知，求As的 问题。 (2) 已知As/，求As。两个未知数，两个方程，可求解唯一 解，计算过程与双筋矩形截面受弯构件类似，计算过程 中注意验算适用条件。 例题参见教材。
6.3.4 偏心受压长柱的纵向弯曲影响
6.3.4.1 偏心距增大系数—二阶效应 N
N0
NusHale Waihona Puke NumNusei Numei
Nul Nul ei
Num fm Nul fl
考虑二阶效应的钢筋混凝土L形截面柱偏心距增大系数的研究
N / mm2 ； 箍筋取 HPB235 ， 12 @ 100 ， 屈服强度 f yk =
5 2 235 N / mm2 ， 弹性模量 E s = 2. 1 × 10 N / mm 。
图3 Fig． 3
模型 Model
图 2 钢筋应力应变关系曲线 Fig． 2 Stressstrain curve of reinforcing bar
σc = fc 2
c
c
c
当 ε c ≤ ε0 时（ 1 ） 当 ε0 ＜ ε c ≤ ε cu 时 （ 2）
0
0
3
结构模型
c
0
cu
0
选取截面为 L800 mm × 500 mm × 200 mm （ 图 3 ） 两端铰支的柱进行全过程分析。 混凝土取 C40 ， 2 轴心抗压 f ck = 26. 8 N / mm ， 强度设计 值 f c = 19. 1
表 1 L 形柱 η 的计算值 shaped column η counting data of Lf / mm 长肢 A 点 2． 412 06 1． 467 21 3． 887 83 1． 081 85 短肢 B 点 2． 281 85 1． 737 89 2． 478 70 2． 357 81 转角 C 点 3． 442 65 2． 402 82 2． 601 61 1． 214 03 长肢 A 点 1． 007 26 1． 008 15 1． 011 70 1． 006 05 η 短肢 B 点 1． 006 86 1． 009 66 1． 007 46 1． 013 10 转角 C 点 1． 010 36 1． 013 35 1． 007 83 1． 006 75
— —为当截面作用一偏心 荷载角（ 即荷载角 α — ， 力时 荷载作用点与形心的连线与形心轴 X 轴正向 90° 、 的夹角， 规定逆时针为正 （ 图 4 ） ） 分 别 为 0° 、 180° 和 270° ， 取长细比 l0 / r α = 17. 500 （ 相当于矩形
06-2偏心受压构件
适用条件：
对矩形截面受压构件，其截面应符合：
V Vu
1 . 75
1 .0
f t bh 0 0 . 07 N )
对矩形截面受压构件，截面剪力如果符合：
V 0 . 25 c f c bh 0
则可不进行承载力计算，直接按构造要求配箍。
偏心受压构件的构造要求
轴心受压柱的纵向受力钢筋、箍筋以及混凝土保护层的各项 构造措施均适用于偏心受压柱，此外，在值心受压拄中还应 满足下列构造要求： (一)截面形式及尺寸 偏心受压柱多采用矩形截面，且将长边布置在弯矩作用方 向。长短边的比值一般在1.0~2.0范围内变化，当偏心距较大 时，可适当加大，但最大不宜超过3.0。 正方形柱网无梁顶盖中的支柱，由于弯矩可能作用在两个 相互垂直方向中的任意一方，故可采用正方形截面，并在两 个相互垂直的方向均采用对称配筋。
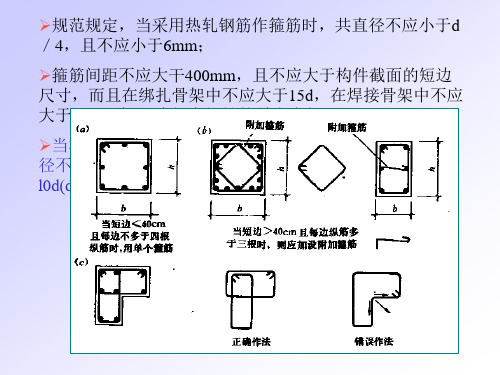
规范规定，当采用热轧钢筋作箍筋时，共直径不应小于d ／4，且不应小于6mm； 箍筋间距不应大干400mm，且不应大于构件截面的短边 尺寸，而且在绑扎骨架中不应大于15d，在焊接骨架中不应 大于20d，此处d为纵向钢筋的最小直径。 当柱中全部纵向受力钢筋的配筋率超过3%时，则箍筋直 径不宜小于8mm，且应焊成封闭式环，其间距不应大干 l0d(d为纵向钢筋的最小直径)．且不应大于100mm。
二、大、小偏心受压构件的界限
受拉破坏，受拉侧钢筋先屈服，而后压区混凝土 压坏。 ☆界限破坏———受拉钢筋屈服的同时，受压区混 凝土刚好达到极限压应变εcu。 受压破坏，受压区混凝土先压坏，而另一侧钢筋 可能受拉，也可能受压，但未屈服。
界限破坏——当纵向受拉钢筋屈服的同时，受压 区边缘混凝土达到极限压应变。它与正截面界限破 坏的概念是相同的。
' ' '
相关主题