复旦大学2015~2016学年《高等数学B上》第一学期期末考试试卷及答案
2015-2016高等数学(上)期末试题A卷解答与评分标准

2x 3 x 1 x 1
2
x 1 x 1 2! 2 2! 1 2 因为 f x 2 , f x 2 2 3 x 1 x 1 x 1 x 13 1 2 n 所以 f n x 1 n ! n 2 , 3 , n 1 n 1 x 1 x 1 10 因此 f 0 10!
1 x 2 x 1 arctan x x ln 1 x 2 C 2
(4 分) (6 分)
2、
x2
1 x
3 2 2
dx
(1 分) (2 分)
解 设 x tan x x2 tan2 t sin 2 t 2 dx sec tdt dt 3 cost sec3 t 2 2 1 x
共6页 西北工业大学命题专用纸
第3页
四、计算题(每小题 6 分,共 18 分) 1、 2 x 1 arctan x dx 解 原式 x 2 x arctanx
x2 x 1 x2
dx
(3 分)
1 x xx 1 arctanx 1 dx 2 1 x2 1 x
由条件知 lima cos x b a b 0
x 0
(2 分)
所以 lim
x 0
a cos x b a sin x a sin x a lim lim 1 x2 3 2 x 0 x 0 2x 2 x 2 ln 1 x 2 1 x
(7 分)
所以,向量 c 是向量 a 和向量 b 的角平分向量。
(8 分)
高数期末考试题及答案复旦

停车场停车券活动方案一. 活动目标本次停车场停车券活动的目标是吸引更多的用户使用停车场服务,增加停车场的收入。
通过发行停车券,提供优惠价位的停车服务,提高用户的体验及满意度,同时提升停车场的知名度和竞争力。
二. 活动时间活动时间为2022年1月1日至2022年3月31日,共计三个月。
三. 活动内容1. 停车券发行在活动期间,停车场将发行特定面额的停车券,用户可以在购买时获得相应的折扣或免费停车时间。
停车券的发行方式包括:•定期会员赠送:停车场会定期向会员赠送停车券,以奖励他们的忠诚度和支持。
•社交媒体活动:通过停车场的社交媒体平台,开展相关活动,让用户有机会赢得免费停车券。
•合作伙伴赞助:与合作伙伴合作,通过赞助方式提供免费或折扣停车券,吸引更多用户关注和使用停车场服务。
2. 会员特权为增加用户粘性和提高会员参与度,停车场将为定期会员提供特殊服务和特权,例如:•优先停车位:为会员提供专门的VIP停车区域或优先选择的停车位,方便会员快速进出停车场。
•免费车辆清洗:定期会员在停车期间,停车场将提供免费的车辆清洗服务,提升会员的停车体验。
3. 推荐奖励通过推荐活动,停车场将为用户提供额外的停车券作为奖励。
当用户成功推荐朋友或家人使用停车场服务时,推荐者将获得相应面额的停车券作为奖励。
4. 良性竞争在活动期间,停车场将与周边的其他停车场进行良性竞争。
通过提供更好的服务和更有竞争力的价格,吸引更多用户选择停车场停车券,并增加停车场的使用率。
四. 活动宣传为确保活动的成功,停车场将进行全方位的宣传推广。
宣传渠道和方式包括但不限于:•广告投放:通过户外广告牌、公交车身广告等方式进行线下宣传;•线上宣传:通过停车场官方网站、社交媒体平台、电子邮件等进行线上宣传;•合作推广:与相关合作伙伴进行合作推广,如APP推广、OTA平台推广等。
五. 活动效果评估活动结束后,停车场将根据以下指标对活动的效果进行评估:•停车场的总收入增长情况;•会员数量的增加情况;•用户对停车场服务的评价及满意度提升情况。
复旦大学2011 ~2012学年《高等数学C上》第一学期期末考试试真题及答案

3. 设 y f x由方程 xy2 sin x3 y 3x 确定,求 dy 。
4. y arctan 3ex ,求 dy 。 d sin x 1, x 0
5. 设 f x x 1,0 x 1 ,求 f xdx 。
2x, x 1
1 1 2x
6. 2
dx
0 1 2x
xf
x
0
,则
lim
x 0
6
f x2
x
1 0 0 0 0
0 2 0 0 0
3.
A
0
0
2
1
0
,则
A
1
=
0 0 3 2 0
0
0
0
0
3
。 。 。
4. lim n 2n 3n
。
n
5.
x cos x
2
2
1
sin
2
x
dx
。
二、单选题( 3 5 )
1. lim xx0
f x 是
f x 在 x0 的某空心邻域内无界的(
1 x ln
x
dx
5. x ,有 f x f x,且 f x0 k 0 ,则 f x0 ( )。
A.
1 k
B.
1 k
C. k
D. k
三、计算题( 68 )
x 1 t 2 1 t 2 dt
1. lim 0 x0
x2 sin x
2.
cos2 x sin x dx
cos x 1 cos xesin x
A.
1 k
B.
1 k
答案:C
C. k
D. k
三、计算题( 68 )
复旦大学16年高数C(上)(A)期末考试试题
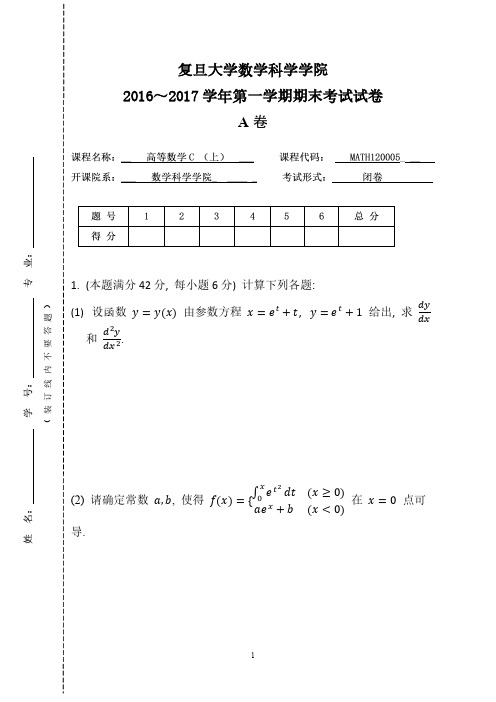
复旦大学数学科学学院
2016~2017学年第一学期期末考试试卷
A卷
1.(本题满分42分, 每小题6分) 计算下列各题:
(1)设函数由参数方程, 给出, 求
和.
(2) 请确定常数, 使得在点可
导.
(
装
订
线
内
不
要
答
题
)
(3) 计算积分
(4) 计算由() 绕轴一周所得的旋转体的体积.
(5) 设过原点的直线同曲线相切, 求此直线的斜率。
(6) 设, 求.
(7) 设, 问在什么范围内时积分收敛.
2. (本题满分10分) 证明当时.
3.(本题满分12分) (1) 求函数的极值点(需指
出是极大值点还是极小值点); (2) 求曲线的渐近线.
4. (本题满分12分) 设.
(1) 证明存在使得; (2) 计算
5.(本题满分12分) (1) 计算;
(2) 计算.
6.(本题满分12分) (1) 设是正整数, 计算;
(2) 证明对任何正实数, 函数极限存在.。
复旦大学2009~2010学年《高等数学C下》第二学期期末考试试卷及答案

七、(8
分)求幂级数
n1
n xn 的和函数,并计算数项级数 (n 1)
n1
(1)n1 n (n 1)2n
的和。
八、(8 分)设函数 f (x) 在 (0, ) 上连续,并满足
f (t) 2
(x2 y2 ) f ( x2 y2 )dxdy t4 ,
x2 y2 t2
求 f (t) 。
使面积最大。
四、(8
分)计算 I
D
x (1 x2
dxdy ,其中 D 由 y2 )2
y
x2 2
,x
0 及 y 1所围。
五、(8 分)试证:[ n f (x)dx]2 (n m) n f 2 (x)dx ( m 、 n 均为常数)。
m
m
六、(6 分)判别级数
an
的敛散性( a 0 )。
n1 an n2
C
(
x)
x
2
0
x 4000 其它
(1)求常数 C ;
(2)计算 P(X 4800 4500 X 5000) ;
(3)已知一设备装有 3 个这样的 LED 灯,每个 LED 灯能否正常工作相互独立, 求在使用的最初 4500 天只有一个损坏的概率。
复旦大学数学科学学院 2009~2010 学年第二学期期末考试试卷
A 卷答案
一、(15 分)1、0; 2、 1 ; 3、0。
2
二、(8
分) dz
z xF1
yF2 (F1dx
F2dy) 。
三、(8 分)当三角形的三个顶点为 (0, 2),(3, 1),(3, 1) ; (0, 2),(3,1),(3,1) 时,
三角形面积一定存在最大值,且为 Smax 9 。
第一学期《高等数学B》期末考试试题及答案

武汉大学数学与统计学院2007—2008第一学期《高等数学B 》期末考试试题(180学时)一、(87'⨯)试解下列各题:1、计算n →∞2、计算0ln(1)lim cos 1x x xx →+--3、计算arctan d x x x ⎰4、 计算4x ⎰5、计算d x xe x +∞-⎰6、设曲线方程为sin cos 2x t y t=⎧⎨=⎩,求此曲线在点4t π=处的切线方程。
7、已知2200d cos d y x te t t t =⎰⎰,求x y d d8、设11x y x-=+,求()n y二、(15分)已知函数32(1)x y x =-求: 1、函数)(x f 的单调增加、单调减少区间,极大、极小值;2、函数图形的凸性区间、拐点、渐近线 。
三、(10分)设()g x 是[1,2]上的连续函数,0()()d x f x g t t =⎰1、用定义证明()f x 在(1,2)内可导;2、证明()f x 在1x =处右连续;四、(10分)1、设平面图形A 由抛物线2y x = ,直线8x =及x 轴所围成,求平面图形A 绕x轴旋转一周所形成的立体体积; 2、在抛物线2(08)y x x =≤≤上求一点,使得过此点所作切线与直线8x =及x 轴所围图形面积最大。
五、(9分)当0x ≥,对()f x 在[0,]b 上应用拉格朗日中值定理有: ()(0)()(0,)f b f f bb ξξ'-=∈对于函数()arcsin f x x =,求极限0lim b bξ→武汉大学数学与统计学院 B 卷2007—2008第一学期《高等数学B 》期末考试试题一、(86'⨯)试解下列各题:1、计算30arctan lim ln(12)x x x x →-+2、计算120ln(1)d (2)x x x +-⎰ 3、计算积分:21arctanxd x x +∞⎰ 4、已知两曲线()y f x =与1x yxy e++=所确定,在点(0,0)处的切线相同,写出此切线方程,并求极限2lim ()n nf n→∞5、设,2221cos cos t x t udu y t t ⎧=⎪⎨=-⎪⎩,试求:d d y x,22d |d t y x 的值。
复旦数学分析期末试题.

注:式中a的取值范围可结合分析判定
(
装订
线
内不要答题3.
计算:
1
11
1
1
lim1
n
n
n
n n
+
→+∞
⎡⎤
⎛⎫⎛⎫
+-+
⎢⎥
⎪ ⎪
+
⎝⎭⎝⎭
⎢⎥
⎣⎦
4.
推导:反双曲正旋函数(
sinh ln
ar x x
=+在零点的高阶多项式逼近。注:获得一般阶数的表达式
0lim x x f x l g x →∈∃=∈。②证明:设{}n x为无穷小量且单调趋于零,{}n y为无穷小量,如有11lim n n n n
n y y l x x →∞++-∃=∈- ,则有:lim n n n
y l x →∞∃=∈
(装
订线内不
要答题五(12分定性研究函数图像
研究函数y=
①设定0
四(10分Bernoulli-L’Hospital法则与Stolez定理的内在相似性①证明:设(f x ,g(x在(0B x λ上可导,0x ∈ ,设有((00lim li 00m x x x x f x g x →∈→∈⎧∃=⎪⎨∃=⎪⎩ ,且
((0'lim 'x x f x l g x →∈∃=∈ ,则有:((
一、严格表述题(每题3分,共3题,共9分注:需给出具体内容,但无需证明
1.叙述:函数连续性的Cauchy收敛原理/振幅刻画与区间上一致连续性的定义。
高等数学试卷及答案

《高等数学》试卷及答案填空题(本大题共10小题, 每小题2分, 共20分)1. ;2. ;3. ;4. ;5. ;6. 已知 , 则 ;7. 函数 的单调增区间为 ;8. ; 9. (-5) ;10. 微分方. 的通解. y=C1ex+C.......... ...单项选择题(本大题共8小题, 每小题3分, 共24分)1. 函数 的定义域是( A )。
A. (-1 , 1 ]B. [ -1 , 1 ]C. (-1 , 2 ]D. [-1 , 2 ]2.当 时, 是 的( D )。
A. 低阶无穷小B. 等阶无穷小C. 同阶但不等阶无穷小D. 高阶无穷小3.设 在 上连续, 则 的值为( )。
A. -1B. 0C. 1D. 24. 函数 在 点( D )。
A. 连续且可导B. 连续但不可导C. 不连续但可导D. 不连续且不可导5. 下列论述正确的是( C )。
A. 驻点必是极值点B. 极值点必是最值点C. 可导的极值点必是驻点D. 极值点必是拐点6. 下列凑微分正确的是( )。
A. B.C. D.7.设 是 的一个原函数, 则有下面成立的是( C )。
A. B.C. D.8. 下列那一项不是常微分方程( A )。
A. B.一. C . D.1.计算题(本大题共5小题, 每小题6分, 共30分)2.011lim cot sin x x x x →⎛⎫- ⎪⎝⎭2. 设 , 求3.4.40d x e x ⎰5.求微分方程)(e d d 3x x xy y +=-的通解。
应用题(本大题共3小题, 每小题7分, 共21分)已知曲线 满足方程 , 试求曲线在点(0, 0)处的切线方程。
2. 计算抛物线与所围成的图形的面积。
要制作一个容积为V的圆柱形带盖铁罐, 问圆柱的高h和底半径r各为多少时, 可使所用材料最少?二.证明题(本大题共5分)当时, .。
同济大学2015-2016学年高等数学(B)上期末考试试卷(word文档良心出品)

本资料仅供参考复习练手之用,无论是重修只求及格,还是为了拿优保研,复习课本上的基础知识点和例题、课后习题才是重中之重,作为一个重修过高数的学长,望大家不要舍本求末,记住这样一句话,只有当你付出了,你才可能有收获。
同济大学2015-2016学年第一学期高等数学B(上)期终试卷一. 填空选择题(3'824'⨯=)1. 极限1202lim()23h h h e h-→-=+.2. 积分(12sin )cos '(12sin )2f x x f x dx C--⋅-=+⎰.3. 函数220()sin(1)x F x t dt =+⎰的导函数4'()2sin(1)F x x x =+.4. 曲线322(1)1(12)3y x x =++-≤≤的弧长143s =.5. 极限0lim ()x x f x -→=+∞的定义是 【D 】()0,0A εδ∀>∃>, 当00x x δ<-<时, 有()f x A ε-<;()0,0B εδ∀>∃>, 当x δ>时, 有()f x ε>; ()0,0C M X ∀>∃>, 当x X >时, 有()f x M >; ()0,0D M δ∀>∃>, 当00x x x δ-≤<时, 有()f x M >.6. 若123(),(),()y x y x y x 是二阶微分方程"()'()()y a x y b x y c x =++的三个线性无关的解, 则该方程的通解为 【D 】112233()()()()A C y x C y x C y x ++, 其中123,,C C C 是任意常数; 11223()()()()B C y x C y x y x ++, 其中12,C C 是任意常数; 11223()()[()()]C C y x C y x y x ++, 其中12,C C 是任意常数; 112233()()()()D C y xC y x C y x ++, 其中任意常数1231C C C ++=.7. 若()f x 是连续函数, 则极限121lim()2nn k n k f n n→∞=+∑等于 【A 】 3212()()A f x d x ⎰; 2()()B f x dx ⎰; ()C 12()f x dx ⎰; 10()()2xD f dx ⎰.8. 若对于积分0(2)af a x dx -⎰作换元2a x u -=, 则该定积分化为 【C 】()()aaA f u d u -⎰; 0()2()a B f u du ⎰; ()C 1()2aa f u du -⎰; 0()()a D f u du ⎰.二. 计算下列各题(6'424'⨯=)1. 试求曲线2sin y x y x ++=在点(1,0)处的切线方程. [21x y +=] 2. 求不定积分2ln(1)x dx +⎰. [2ln(1)22arctan x x x x c +-++]3. 求微分方程3'xy x y =-的通解. [411()4y x c x =+] 4. 求微分方程"2'15153y y y x --=-的通解. [531213x xy C e C e x -=+-+]三. (8')计算由22y x x =+与直线2y x =+所围图形的面积. [1229(2)2x x dx ---=⎰]四. (8')计算反常积分31arctan xdx x +∞⎰. [211111arctan arctan 2222I x x x x +∞=---=]五. (8')已知'()y f x =的函数图像如图,(1)求函数()y f x =的单调区间、极大值与极小值; (2)求曲线()y f x =的凹凸区间与拐点. [35353(,],[,);[,];()x x x x f x -∞+∞极大,5()f x 极小124124[,],[,);(,],[,];x x x x x x +∞⋃-∞⋂拐点112244(,()),(,()),(,())x f x x f x x f x ] 六. (10')在半径为R 的半球内内接一圆锥体, 使得该锥体的锥顶位于半球的球心上, 锥体的底面平行于半球的底面, 求这样的内接圆锥体体积的最大值.[322max 1(3),3V R h h V π=-=七. (10')一椭球形容器由长半轴为2m , 短半轴为1m 的半支椭圆曲线绕其短半轴旋转而成,若容器内盛满了水, 试求要把该容器内的水全部吸出需作的功.[2221(10),4(1)(),4x y y dW y dy g y W g πρπ+=-≤≤=--=]八. (8')已知()f x 具有二阶导数, 且"()f x ≥判断lim ()x f x →∞的情况, 并给出判断的理由. [21"()()(0)'(0)"()2f x f x f f x f x ξ≥=++→+∞]。
复旦大学高数考试题及答案

复旦大学高数考试题及答案一、选择题(每题3分,共30分)1. 下列函数中,在x=0处不可导的是()。
A. y = x^2B. y = |x|C. y = sin(x)D. y = e^x答案:B2. 二次方程x^2 + ax + b = 0有一个根为0,那么b的值是()。
A. 0B. aC. -aD. 1答案:A3. 函数f(x) = 1/x在区间(-∞,0)∪(0,+∞)上是()。
A. 单调递增B. 单调递减C. 有界D. 无界答案:D4. 定积分∫₀^(π/2) sin(x)dx的值是()。
A. 1B. 2C. π/2D. π答案:A5. 微分方程y'' - y' - 6y = 0的特征方程是()。
A. r^2 - r - 6 = 0B. r^2 - r - 6 = rC. r^2 - 6 = 0D. r^2 - r - 6 = r^2答案:A6. 利用洛必达法则求解极限lim (x->0) [sin(x)/x]的正确步骤是()。
A. 直接代入x=0B. 计算分子的导数C. 计算分母的导数D. 计算分子和分母的导数答案:D7. 函数序列fn(x) = x^n在[0, 1]上一致收敛的n的取值范围是()。
A. n > 1B. n ≥ 1C. n = 1D. n < 1答案:C8. 曲线y = x^3在点(1,1)处的切线斜率是()。
A. 0B. 1C. 2D. 3答案:D9. 函数f(x) = ln(x)的泰勒展开式在x=1处的余项是()。
A. R_2(x) = (x-1)^2/2B. R_3(x) = (x-1)^3/3C. R_2(x) = (x-1)^3/3D. R_3(x) = (x-1)^2/2答案:C10. 利用分部积分法计算定积分∫₀^(π/2) x sin(x)dx,得到的结果是()。
A. π/2B. πC. 2D. 1答案:B二、填空题(每题4分,共20分)11. 若函数f(x)在点x=a处的导数为3,则lim (x->a) [f(x) -f(a)]/(x-a) = ____。
大学数学2015-2016(1) 微积分B(1) 练习题参考答案

而 f (0) a, 故要使 lim f ( x) lim f ( x) f (0) ,须且只须 a 1 .
x 0 x 0
所以当且仅当 a 1 时,函数 f ( x) 在 x 0 处连续. (2)因为 lim f ( x) lim
5 t
1 t lim 1 t t
5
e 5 . e
1 2x
(13)因为 (1 2 x)
(1 2 x) lim e
x 0
x 1 6 2 x sin x
e
1
x 1 6 ln(1 2 x ) 2 x sin x
3 2
所以方程 x 4 x 1 0 在 (0,1) 内至少有一个根.
3 2
(2)设 f ( x ) e 3 x ,则 f ( x ) 在 [0,1] 上连续,
x
且 f ( 0) 1 0, f (1) e 3 0 ,故由零点定理知方程在 (0,1) 内至少有一个根.
x 0
所以, lim f ( x) 0 ,且 f (0) 0 ,因此,函数在 x 0 处连续.
x 0
f ( x) f (0) f ( x) f (0) 1 , f ' (0) lim 1 , x 0 x 0 x0 x0 所以函数在 x 0 处可导. f ' (0) lim
18、 y
1 2 1 x ,所以 y ( 4 ) x 2 2 2
1
1
x4
1 , 4
所以切线方程为 y 2
1 ( x 4) ,法线方程为 y 2 4( x 4) . 4
复旦大学2017~2018学年《高等数学C上》第一学期期末考试试卷及答案

复旦大学数学科学学院 2017~2018学年第一学期期末考试试卷 A 卷一、选择题()43⨯' 1. 已知()x f 的导数是x sin ,则()x f 的原函数是( )。
()A x sin 1+ ()B 1s i n x - ()C 1c o s x + ()D 1c o s x - 2. 设()x f 可导,()()()x x f x F sin 1+=,则()00=f 是()x F 在0=x 可导的( )。
()A 充要条件 ()B 充分非必要条件 ()C 必要非充分条件 ()D 即不充分又不必要条件 3.设()x f 在()+∞∞-,上有定义,且a x =∞→lim ,()⎪⎩⎪⎨⎧=≠⎪⎭⎫ ⎝⎛=0,00,1x x x f x g ,则( )。
()A 0=x 是()x g 的第一类间断点 ()B 0=x 是()x g 的第二类间断点 ()C ()x g 在0=x 的连续性与a 相关 ()D ()x g 在0=x 的连续 4. 设A 、B 为n 阶方阵,2=A ,3-=B ,则12-*B A =( )。
()A 12- ()B 34- ()C 3212--n ()D 321+-n 二、填充题()43⨯' 1. ⎰20sin ln πxdx = 。
:我已知悉学校对于考试纪律的严肃规定,将秉持诚实守信宗旨,严守考试纪律,不作弊,不剽窃;若有违反学校考试纪律的行为,自愿接受学校严肃处理。
签名: 年 月 日 )2. ⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-12111ln 1dx x x x = 。
3. 设⎪⎪⎪⎭⎫ ⎝⎛-----=1471481510A ,则1-A = 。
4. 已知()x f 在0=x 连续,()[]1sin 2ln lim 0=-+→x x x f x ,则()='0f 。
三、计算题()88⨯' 1. 22011lim x x x +-→2. ()[]x x dtt x x x 22030sin 1211ln lim 2-++⎰+→3. 设()x e x f x cos =,求()()x f n 。
16级高数B(上)(A)试题解答

3.
首先,转化为求自然对数的极限
lim
x
ln
e
1
x3
1
1
x3
2
x3
1 2
。
所以,原极限
1
e2
。
4. ln y 1 1 ln x 1 ln cos x , 2x 4 8
y y
1 2x2
1 4x
1 8 cos
x
( sin
x)
,
1
y
y
1 2x2
1 4x
1 8
tan
x
。
5.
原式
sin2 x cos2 x dx
A=
A* 2
1
3 1 1
2 1 0
1 1 。 1
若| A|=2,
3 2 1
A
1
1
1
。
1 0 1
六.
1.
0 x , 0 tan x 1,所以
4 x tan xdx
4
xdx
2
。
4
0
0
32
2.
4
(x tan
x
tan
x)dx
8
(
x) tan xdx
0
8
08
0
n!
(2n 1)! n
0
1 ! 1! n!
n! n! 。
(2n 1)!
(依次消去对角线下方元素)
0!
n
D k! k 0
0
1 ! 1!
n!
n!
n
(k !)2 。
k 0
n!
2. xi , 0 i k 1,
m0,0
【精品】2015-2016年上海市复旦大学附中高一(上)期末数学试卷带解析

2015-2016学年上海市复旦大学附中高一(上)期末数学试卷一、填空题(每题4分,共48分)1.(4.00分)函数的定义域为.2.(4.00分)设f(x)=,若f(x)=3,则x=.3.(4.00分)已知幂函数f(x)=xα是偶函数,在[0,+∞)上递增的,且满足.请写出一个满足条件的α的值,α=.4.(4.00分)函数的反函数为f﹣1(x)=.5.(4.00分)函数f(x)=(x2﹣2x﹣3)的单调递增区间为.6.(4.00分)函数的图象与函数y=﹣log3x的图象关于直线对称.7.(4.00分)已知log53=a,5b=7,则用a,b的代数式表示log63105=.8.(4.00分)方程:的解为.9.(4.00分)若函数的值域是R,则实数a的取值范围是.10.(4.00分)若函数的值域为[﹣2,+∞),则实数a的取值范围为.11.(4.00分)已知函数,若方程f(x)=a有四个不同的实根x1,x2,x3,x4.则x1+x2+x3+x4的取值范围为.12.(4.00分)已知函数(1)f(x)=3lnx;(2)f(x)=3x2+1;(3)f(x)=3e x;(4).其中满足对于任意x1∈D(其中D为函数的定义域),相应地存在唯一的x∈D,使的函数的序号为.二、选择题(每题4分,共16分)13.(4.00分)下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的是()A.B.y=2|x|C.D.y=x314.(4.00分)若0<a<1,b<﹣1,则函数f(x)=a x+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限15.(4.00分)已知a,b,c均大于1,且log a c•log b c=4,则下列各式中,一定正确的是()A.ac≥b B.ab≥c C.bc≥a D.ab≤c16.(4.00分)定义在实数集R上函数y=f(x)的反函数为y=f﹣1(x).若函数y=f (﹣x)的反函数是y=f﹣1(﹣x),则y=f(﹣x)是()A.是奇函数,不是偶函数B.是偶函数,不是奇函数C.既是奇函数数,又是偶函数D.既不是奇函数,也不是偶函数三、解答题17.(8.00分)已知函数f(x)=lg(x+1),解关于x的不等式0<f(1﹣2x)﹣f (x)<1.18.(10.00分)已知实数a>0,且函数为奇函数.判断函数f(x)的单调性,并用单调性的定义证明.19.(12.00分)已知函数f(x)=,其中a∈R.(1)若a=0,解不等式f(x)≥;(2)已知函数y=f(x)存在反函数,其反函数记为y=f﹣1(x).若关于x的不等式:f﹣1(4﹣a)≤f(x)在x∈[0,+∞)上恒成立,求实数a的取值范围.20.(12.00分)若函数f(x)满足:对于其定义域D内的任何一个自变量x0,都有函数值f(x0)∈D,则称函数f(x)在D上封闭.(1)若下列函数的定义域为D=(0,1),试判断其中哪些在D上封闭,并说明理由.f1(x)=2x﹣1,f2(x)=2x﹣1.(2)若函数g(x)=的定义域为(1,2),是否存在实数a,使得g(x)在其定义域(1,2)上封闭?若存在,求出所有a的值,并给出证明:若不存在,请说明理由.(3)已知函数f(x)在其定义域D上封闭,且单调递增.若x0∈D且f(f(x0))=x0,求证:f(x0)=x0.21.(14.00分)设定义在R上的函数f(x)、f1(x)和f2(x),满足f(x)=f1(x)+f2(x),且对任意实数x1、x2(x1≠x2),恒有|f1(x1)﹣f1(x2)|>|f2(x1)﹣f2(x2)|成立.(1)试写出一组满足条件的具体的f1(x)和f2(x),使f1(x)为增函数,f2(x)为减函数,但f(x)为增函数.(2)判断下列两个命题的真假,并说明理由.命题1):若f1(x)为增函数,则f(x)为增函数;命题2):若f2(x)为增函数,则f(x)为增函数.(3)已知f(x)=x3+x2+x+1,写出一组满足条件的具体的f1(x)和f2(x),且f2(x)为非常值函数,并说明理由.2015-2016学年上海市复旦大学附中高一(上)期末数学试卷参考答案与试题解析一、填空题(每题4分,共48分)1.(4.00分)函数的定义域为{x|x>﹣1且x≠2} .【解答】解:由,解得:x>﹣1且x≠2.∴函数的定义域为{x|x>﹣1且x≠2}.故答案为:{x|x>﹣1且x≠2}.2.(4.00分)设f(x)=,若f(x)=3,则x=.【解答】解:当x≤﹣1时,即x+2=3,解得x=1(舍去)当﹣1<x<2时,即x2=3,解得x=,或x=﹣(舍去)当x≥2时,即2x=3,解得x=(舍去)故当f(x)=3,则x=故答案为:3.(4.00分)已知幂函数f(x)=xα是偶函数,在[0,+∞)上递增的,且满足.请写出一个满足条件的α的值,α=.【解答】解:根据幂函数f(x)=xα是偶函数,在[0,+∞)上递增的,知α>0,且α为偶数;又满足.所以α<1;写出一个满足条件的α值,则α=即可.故答案为:.4.(4.00分)函数的反函数为f﹣1(x)=,(x∈(0,1)).【解答】解:由y=,解得x=>0,解得0<y<1,因此f(x)的反函数为f﹣1(x)=,(x∈(0,1)).故答案为:,(x∈(0,1)).5.(4.00分)函数f(x)=(x2﹣2x﹣3)的单调递增区间为(﹣∞,﹣1).【解答】解:函数的定义域为{x|x>3或x<﹣1}令t=x2﹣2x﹣3,则y=因为y=在(0,+∞)单调递减t=x2﹣2x﹣3在(﹣∞,﹣1)单调递减,在(3,+∞)单调递增由复合函数的单调性可知函数的单调增区间为(﹣∞,﹣1)故答案为:(﹣∞,﹣1)6.(4.00分)函数的图象与函数y=﹣log3x的图象关于直线y=x对称.【解答】解:∵y=﹣log 3x=log x,∴同底的指数函数和对数函数互为反函数,则图象关于y=x对称,故答案为:y=x7.(4.00分)已知log53=a,5b=7,则用a,b的代数式表示log63105=.【解答】解:∵log53=a,5b=7,∴=a,b=log57=,∴lg3=alg5,lg7=blg5,∴log63105===.故答案为:.8.(4.00分)方程:的解为{log23} .【解答】解:由22x+1﹣6>0,得2×4x>6,即4x>3,则方程等价为=log22x+log2(2x+1)=log22x(2x+1),即22x+1﹣6=2x(2x+1),即2(2x)2﹣6=(2x)2+2x,即(2x)2﹣2x﹣6=0,则(2x+2)(2x﹣3)=0,则2x﹣3=即2x=3,满足4x>3,则x=log23,即方程的解为x=log23,故答案为:{log23}9.(4.00分)若函数的值域是R,则实数a的取值范围是(﹣∞,﹣4]∪[0,+∞).【解答】解:∵函数的值域是R,∴其真数函数g(x)=x2+ax﹣a的函数值应该能够取遍所有正数,∴函数y=g(x)的图象应该与x轴相交即△=a2+4a≥0解得a≤﹣4或a≥0.∴实数a的取值范围是(﹣∞,﹣4]∪[0,+∞).故答案为:(﹣∞,﹣4]∪[0,+∞).10.(4.00分)若函数的值域为[﹣2,+∞),则实数a的取值范围为[﹣2,] .【解答】解:∵函数的值域为[﹣2,+∞),当x≥2时,f(x)=﹣6+2x≥﹣2.当x<2,f(x)=x2﹣ax+3=(x﹣)2+3﹣,当=2时,f(x)=(x﹣)2+3﹣≥3﹣≥﹣2,解得﹣2≤a≤2,a=4∈[﹣2,2],故a=4成立;当<2时,f(x)=(x﹣)2+3﹣≥3﹣≥﹣2,解得﹣2≤a<4.当>2时,f(x)=(x﹣)2+3﹣≥(2﹣)2+3﹣≥﹣2,解得4<a.综上所述,实数a的取值范围是[﹣2,].故答案为:[﹣2,].11.(4.00分)已知函数,若方程f(x)=a有四个不同的实根x1,x2,x3,x4.则x1+x2+x3+x4的取值范围为(,9).【解答】解:作函数的图象如下,方程f(x)=a有四个不同的实根x1,x2,x3,x4,结合图象,A,B,C,D的横坐标分别为x1,x2,x3,x4,故x1+x2=﹣2,x3∈(,1),x4∈(1,10),故x3+x4∈(,11),∴x1+x2+x3+x4∈(,9),故答案为:(,9).12.(4.00分)已知函数(1)f(x)=3lnx;(2)f(x)=3x2+1;(3)f(x)=3e x;(4).其中满足对于任意x1∈D(其中D为函数的定义域),相应地存在唯一的x∈D,使的函数的序号为(3)、(4).【解答】解:根据题意可知:对于(1),函数f(x)=3lnx,x=1时,lnx没有倒数,不成立;对于(2),函数f(x)=3x2+1,当x 1=0时,存在x2=±使得使,故不符合题意;对于(3),函数f(x)=3e x,对任意一个自变量x,函数f(x)都有倒数,且使成立;对于(4),函数f(x)=,对定义域内的任意一个自变量x,函数f(x)都有倒数,且使成立;所以成立的函数序号为(3)、(4).故答案为:(3)、(4).二、选择题(每题4分,共16分)13.(4.00分)下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的是()A.B.y=2|x|C.D.y=x3【解答】解:对于A,函数是奇函数,不满足;对于B,是偶函数,又是在区间(0,+∞)上单调递增,不满足;对于C,既是偶函数,又是在区间(0,+∞)上单调递减,满足;对于D,函数是奇函数,不满足,故选:C.14.(4.00分)若0<a<1,b<﹣1,则函数f(x)=a x+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:函数f(x)=a x(0<a<1)的是减函数,图象过定点(0,1),在x 轴上方,过一、二象限,函数f(x)=a x+b的图象由函数f(x)=a x的图象向下平移|b|个单位得到,∵b<﹣1,∴|b|>1,∴函数f(x)=a x+b的图象与y轴交于负半轴,如图,函数f(x)=a x+b的图象过二、三、四象限.故选:A.15.(4.00分)已知a,b,c均大于1,且log a c•log b c=4,则下列各式中,一定正确的是()A.ac≥b B.ab≥c C.bc≥a D.ab≤c【解答】解:∵a、b、c均大于1,log a c•log b c=4,∴log c a•log c b=,∴log c a、log c b大于零,则log c a•log c b≤(log c a+log c b)2,即≤(log c a+log c b)2,∴(log c a+log c b)2≥1,∴(log c ab)2≥1,∴log c ab≥1或log c ab≤﹣1,当且仅当log c a=log c b,即a=b时取等号,∵a、b、c均大于1,∴log c ab>1,解得ab≥c,故选:B.16.(4.00分)定义在实数集R上函数y=f(x)的反函数为y=f﹣1(x).若函数y=f (﹣x)的反函数是y=f﹣1(﹣x),则y=f(﹣x)是()A.是奇函数,不是偶函数B.是偶函数,不是奇函数C.既是奇函数数,又是偶函数D.既不是奇函数,也不是偶函数【解答】解:函数y=f(﹣x)的反函数是y=f﹣1(﹣x)=﹣f﹣1(x),关于原点对称,∴y=f(﹣x)是奇函数,故选:A.三、解答题17.(8.00分)已知函数f(x)=lg(x+1),解关于x的不等式0<f(1﹣2x)﹣f (x)<1.【解答】解:∵函数f(x)=lg(x+1),∴不等式0<f(1﹣2x)﹣f(x)<1可化为0<lg(1﹣2x+1)﹣lg(x+1)<1,即;化简得,即,解得即﹣<x<;∴原不等式的解集为{x|﹣<x<}.18.(10.00分)已知实数a>0,且函数为奇函数.判断函数f(x)的单调性,并用单调性的定义证明.【解答】解:∵函数为奇函数,实数a>0,∴有f(0)=0,即=0,解可得a=1,∴f(x)=;f(x)=1﹣理由:设x1<x2,则f(x1)﹣f(x2)=,∵x1<x2,∴f(x1)﹣f(x2)<0,∴f(x)是增函数.19.(12.00分)已知函数f(x)=,其中a∈R.(1)若a=0,解不等式f(x)≥;(2)已知函数y=f(x)存在反函数,其反函数记为y=f﹣1(x).若关于x的不等式:f﹣1(4﹣a)≤f(x)在x∈[0,+∞)上恒成立,求实数a的取值范围.【解答】解:(1)a=0时,,∵,∴当x≥0时,f(x)=x2,解得x≥;当x<0时,f(x)=,解得﹣2≤x<0;综上,不等式的解集为{x|﹣2≤x<0或x≥};(2)若函数y=f(x)存在反函数,则函数f(x)在R为单调函数,则a≥1,此时函数f(x)在R为单调递增函数,x∈[0,+∞)时,f(x)≥f(0)=a;此时f﹣1(x)=在(0,+∞)上也为增函数,若关于x的不等式:f﹣1(4﹣a)≤f(x)在x∈[0,+∞)上恒成立,则,当0<4﹣a<1,即3<a<4时,log2(4﹣a)≤a恒成立,当4﹣a≥1,即1≤a≤3时,解:得:﹣1+≤a≤2综上可得:a∈[﹣1+,2]∪(3,4).20.(12.00分)若函数f(x)满足:对于其定义域D内的任何一个自变量x0,都有函数值f(x0)∈D,则称函数f(x)在D上封闭.(1)若下列函数的定义域为D=(0,1),试判断其中哪些在D上封闭,并说明理由.f1(x)=2x﹣1,f2(x)=2x﹣1.(2)若函数g(x)=的定义域为(1,2),是否存在实数a,使得g(x)在其定义域(1,2)上封闭?若存在,求出所有a的值,并给出证明:若不存在,请说明理由.(3)已知函数f(x)在其定义域D上封闭,且单调递增.若x0∈D且f(f(x0))=x0,求证:f(x0)=x0.【解答】解:(1)在f1(x)=2x﹣1中,对于定义域D内的任意一个自变量x0,都有函数值f1(x0)∈(﹣1,1)∉D1,故函数f1(x)=2x﹣1在D1上不封闭;在f2(x)=2x﹣1中,2x﹣1∈(0,1),在D1上封闭.(2)g(x)=的定义域为(1,2),对称中心为(﹣2,5),当a+10>0时,函数g(x)=在D2上为增函数,只需,解得a=2当a+10<0时,函数g(x)=在D2上为减函数,只需,解得a∈∅综上,所求a的值等于2.证明:(3)∵函数f(x)在其定义域D上封闭,且单调递增.x0∈D且f(f(x0))=x0,∴根据单调函数性质f(x0)∈D,则有唯一的x0∈D,∴f(x0)=x0.21.(14.00分)设定义在R上的函数f(x)、f1(x)和f2(x),满足f(x)=f1(x)+f2(x),且对任意实数x1、x2(x1≠x2),恒有|f1(x1)﹣f1(x2)|>|f2(x1)﹣f2(x2)|成立.(1)试写出一组满足条件的具体的f1(x)和f2(x),使f1(x)为增函数,f2(x)为减函数,但f(x)为增函数.(2)判断下列两个命题的真假,并说明理由.命题1):若f1(x)为增函数,则f(x)为增函数;命题2):若f2(x)为增函数,则f(x)为增函数.(3)已知f(x)=x3+x2+x+1,写出一组满足条件的具体的f1(x)和f2(x),且f2(x)为非常值函数,并说明理由.【解答】解:(1)根据题意,设函数f1(x)=3x为(0,+∞)上的增函数,f2(x)=﹣2x为(0,+∞)减函数,则f(x)=3x﹣2x是(0,+∞)上的单调增函数;(2)命题1):若f1(x)为增函数,则f(x)为增函数,是真命题;理由是:设x1<x2由y=f1(x)是区间D上的增函数可得f1(x1)<f1(x2)①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数②若函数f2(x1)>f2(x2),则由|f1(x1)﹣f1(x2)|>|f2(x1)﹣f2(x2)|可得,﹣f1(x1)+f1(x2)>f2(x1)﹣f2(x2)∴f1(x1)+f2(x1)<f1(x2)+f2(x2),即f(x1)<f(x2);综上,函数f(x)为单调递增函数;命题2):若f2(x)为增函数,则f(x)为增函数,是假命题;如函数f1(x)=﹣3x为减函数,f2(x)=2x为增函数,但f(x)=2x﹣3x不是单调递增函数;(3)由f(x)=x3+x2+x+1,令f1(x)=x3,为定义域R上的增函数,f2(x)=x2+x+1,且f2(x)为非常值函数,则f′(x)=3x2+2x+1=3+>0,所以f(x)是定义域R上的增函数.赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC.(1)如图,当∠APB=90°时,若AC=5,PC=,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD 中,AB=AD ,∠DAB=∠BCD=90°, (1)若AB =3,BC +CD =5,求四边形ABCD 的面积(2)若p = BC +CD ,四边形ABCD 的面积为S ,试探究S 与p 之间的关系。
复旦大学《高等数学A(I)》试题(2016.1)

方程,其中 t 为常数;
(3)求由曲面 ,平面 z 0和 z 1所围立体的体积。
7
复旦大学数学科学学院 2015~2016 学年第一学期期末考试试卷
A卷
数学科学学院
(
1.(本题满分 40 分,每小题 5 分)计算下列各题:
装
(1)确定常数 b,使得直线 y 9x b 为曲线 y x3 3x 的切线;
订
线
内
不
要
答
题
)
(2)求极限
lim
x
ln( ln(
x2 x3
5
5.(本题满分 10 分)若 lim x4 3 [ A B(x 1) C(x 1)2 ] 0 ,求常数 A ,B ,C 。
x1
(x 1) sin(x 1)
6.(本题满分 10 分)证明:
1 0
1
sin
π 2
n
x
dx
2n1 1 ( n 1
n
1,
2,
);
1
(2)求极限 lim n
1 0
1
sin
π 2
x
n
dx
n。Fra bibliotek67.(本题满分
10
分)设过点
(1,
c,
c)
的直线
L
的方程为
cx y x cy
z c, cz 1,
其中 c 为实
数。
(1)求直线 L 的对称式方程;
(2)当 c 连续变化时,L 随之移动而生成曲面 ,求曲面 与平面 z t 的交线的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.(本题满分 10 分)证明:当 x 0 时成立
ln 1 x x 1 x2 1 x3 1 x4 。
234
6.(本题满分 10 分)证明:
1 0
1
sin
π 2
x
n
dx
2n1 1 ( n 1
n
1,
2,
);
1
(2)求极限
lim
n
1 0
1
sin
π 2
x
n
dx
n
。
6
7.(本题满分
7.(本题满分 10 分)(1) L 的方向向量可取为
i jk c 1 1 2cj (1 c2 ) j (1 c2 )k ,
1 c c
因此 L 的对称式方程为
x 1 2c
yc 1 c2
zc 1 c2
。
(2)在以上方程中令 z t ,得
x
2ct (c2 1 c2
1)
A
Bt,
y
2c (c2 1)t 1 c2
7
复旦大学数学科学学院 2015~2016 学年第一学期期末考试试卷
《高等数学 B(I)》试题答案
1.(本题满分 40 分,每小题 5 分)(1) 16 ;(2) 2 ;(3)在 ( 1, e1 1] 上单 3
调减少,在[e1 1, ) 上单调增加; f (e1 1) e1 为极小值;
(4)
1 2
arcsin
x2 2
C
;(5) e2
1
1 e
2
;
(6)收敛;(7)
14 8
8 5
3 2
;(8)
x
2
y
z
0
。
(
3 2 1
装
2.(本题满分 10 分)3 个。
订 线
3.(本题满分 10 分)底面半径和高均为 3 V 。 π
内
不
4.(本题满分 10 分)(1) f (x) 28x6 cx ( c 为任意常数);(2)无拐点;(3)
和 z 1所围立体的截面均为圆,其面积为
A(z) π(1 z2 ) ,
因此该立体的体积为
V
1
A(z)dx π
1 1 z2 dz = 4π 。
0
0
3
At
B,
其中
A
c2 1 1 c2
,B
2c 1 c2
。
显然 A2 B2 1,于是
x2 y2 A2 (1 t2 ) B2 (1 t2 ) 1 t2 , 因此曲面 与平面 z t 的交线的方程为
x2 y2 1 t2, z t.
(3)由(2)知,过 (0, 0, z) 点且与 Oxy 平面平行的平面截由曲面 ,平面 z 0
10
分)设过点
(1,
c,
c)
的直线
L
的方程为
cx y x cy
z c, cz 1,
其中 c 为实
数。
(1)求直线 L 的对称式方程;
(2)当 c 连续变化时,L 随之移动而生成曲面 ,求曲面 与平面 z t 的交线的
方程,其中 t 为常数;
(3)求由曲面 ,平面 z 0和 z 1所围立体的体积。
(7)求矩阵
1 2
2 5
1 4的逆矩阵;来自1 4 6 (8)求经过原点,且与两平面 x 2 y 3z 13 0 和 3x y z 1 0 都垂直的平面的 方程。
3
2.(本题满分 10 分)问方程 2x3 3x2 1 0 有几个实根?请说明理由。 2
3.(本题满分 10 分)要制作一个体积为V 的圆柱形无盖铁桶,问如何确定其底面半 径和高才能用料最省?
复旦大学数学科学学院 2015~2016 学年第一学期期末考试试卷
A卷
数学科学学院
(
1.(本题满分 40 分,每小题 5 分)计算下列各题:
装
(1)确定常数 b,使得直线 y 9x b 为曲线 y x3 3x 的切线;
订
线
内
不
要
答
题
)
(2)求极限
lim
x
ln( ln(
x2 x3
3x 2x
要
答
不存在。
题
5.(本题满分 10 分)证: 作函数
)
f
(
x)
ln(1
x)
x
1 2
x2
1 3
x3
1 4
x4
,
x
1
,
则当 x (1, ) 时,
f (x) 1 1 x x2 x3 1 x
1 (1 x)(1 x2 ) 1 (1 x2 )(1 x2 )
1 x
1 x
x4 0 . 1 x
4
4.(本题满分 10 分)设函数 f 在 (, ) 上有连续二阶导数,且满足方程 x f (x) f (x) 140x6 。
(1)求 f (x) 的表达式; (2)问曲线 y f (x) 是否有拐点?请说明理由。 (3)是否存在函数 f ,它在开区间 (0, 1) 上大于零,并满足上面的方程,且曲线 y f (x) ( x [0, 1] )与直线 x 1和 y 0 所围的图形 D 的面积为 2?请说明理由。
这说明函数 f 在[0, ) 上严格单调增加,从而当 x 0 时,
f (x) f (0) 0 ,
即
ln 1 x x 1 x2 1 x3 1 x4 。
234
6.(本题满分 10 分)(1)证;由 sin x 2 x( 0 x π )知 sin π x x( 0 x 1),
π
2
1) 1)
;
1
(3)求函数 f (x) (x 1) ln(x 1) 的单调区间和极值;
(4)求不定积分
x dx ; 4 x4
(5)设
f
(x)
x, 2
x,
0 x 1, 求 4 f (x 2) ex dx ;
1 x,
2
2
(6)问反常积分
cos3 x
dx 是否收敛?请说明理由;
1 (x 2e3x ) 1 x
2
所以
1 0
1
sin
π 2
x
n
dx
11 xn dx = 1 1 x n1 1 2n1 1 。
0
n 1
0 n 1
(2)由于
2n 2n1 1
n1 n1
1 0
1
sin
π 2
x
n
dx
111n dx 2n ,
0
利用极限的夹逼性可得
1
lim n
1 0
1
sin
π 2
n
x
dx
n
=2
。
