【三维设计】2014届高考数学一轮复习 (基础知识+高频考点+解题训练)数系的扩充与复数的引入教学案

合集下载

数学三维设计答案及解析

第一部分专题复习培植新的增分点专题一集合与常用逻辑用语、函数与导数、不等式第一讲集合与常用逻辑用语基础·单纯考点[例1] 解析：(1)∵A ＝{x >2或x <0}，B ＝{x |－5<x <5}， ∴A ∩B ＝{x |－5<x <0或2<x <5}， A ∪B ＝R .(2)依题意，P ∩Q ＝Q ，Q ⊆P ，于是⎩⎪⎨⎪⎧2a ＋1<3a －5，2a ＋1>3，3a －5≤22，解得6<a ≤9，即实数a 的取值范围为(6，9]．答案：(1)B (2)D[预测押题1] (1)选A 本题逆向运用元素与集合的关系求参数的取值范围，抓住1∉A作为解题的突破口，1∉A 即1不满足集合A 中不等式，所以12－2×1＋a ≤0⇒a ≤1.(2)选B 对于2x (x －2)<1，等价于x (x －2)<0，解得0<x <2，所以A ＝{x |0<x <2}；集合B 表示函数y ＝ln(1－x )的定义域，由1－x >0，得x <1，故B ＝{x |x <1}，∁R B ＝{x |x ≥1}，则阴影部分表示A ∩(∁R B )＝{x|1≤x<2}．[例2] 解析：(1)命题p 是全称命题：∀x ∈A ，2x ∈B ，则┐p 是特称命题：∃x ∈A ，2x ∉B .(2)①中不等式可表示为(x －1)2＋2>0，恒成立；②中不等式可变为log 2x ＋1log 2x≥2，得x >1；③中由a >b >0，得1a <1b，而c <0，所以原命题是真命题，则它的逆否命题也为真；④由p 且q 为假只能得出p ，q 中至少有一为假，④不正确．答案：(1)D (2)A[预测押题2] (1)选A 因为x 2－3x ＋6＝⎝ ⎛⎭⎪⎫x －322＋154>0，所以①为假命题；若ab ＝0，则a 、b 中至少一个为零即可，②为假命题；x ＝k π＋π4(k ∈R )是tan x ＝1的充要条件，③为假命题．(2)解析：“∃x ∈R ，2x 2－3ax ＋9<0”为假命题，则“∀x ∈R ，2x 2－3ax ＋9≥0”为真命题，因此Δ＝9a 2－4×2×9≤0，故－22≤a ≤2 2.答案：[－22，22][例3] 解析：(1)当x ＝2且y ＝－1时，满足方程x ＋y －1＝0，即点P (2，－1)在直线l 上．点P ′(0，1)在直线l 上，但不满足x ＝2且y ＝－1，∴“x ＝2且y ＝－1”是“点P (x ，y )在直线l 上”的充分而不必要条件．(2)因为y ＝－m n x ＋1n 经过第一、三、四象限，所以－m n >0，1n<0，即m >0，n <0，但此为充要条件，因此，其必要不充分条件为mn <0.答案：(1)A (2)B[预测押题3] (1)选B 由10a >10b 得a >b ，由lg a >lg b 得a >b >0，所以“10a >10b”是“lg a >lg b ”的必要不充分条件．(2)解析：由|x －m |<2，得－2<x －m <2，即m －2<x <m ＋2.依题意有集合{x |2≤x ≤3}是{x |m－2<x <m ＋2}的真子集，于是有⎩⎪⎨⎪⎧m －2<2，m ＋2>3，由此解得1<m <4，即实数m 的取值范围是(1，4)．答案：(1，4)交汇·创新考点 [例1] 选A 在同一坐标系下画出椭圆x 2＋y 24＝1及函数y ＝2x的图象，结合图形不难得知它们的图像有两个公共点，因此A ∩B 中的元素有2个，其子集共有22＝4个．[预测押题1] 选B A ＝{x |x 2＋2x －3>0}＝{x |x >1或x <－3}，函数y ＝f (x )＝x 2－2ax －1的对称轴为x ＝a >0，f (－3)＝6a ＋8>0，根据对称性可知，要使A ∩B 中恰含有一个整数，则这个整数解为2，所以有f (2)≤0且f (3)>0，即⎩⎪⎨⎪⎧4－4a －1≤09－6a －1>0，所以⎩⎪⎨⎪⎧a ≥34，a <43，即34≤a <43，选B.[例2] 解析：对①：取f (x )＝x －1，x ∈N *，所以B ＝N *，A ＝N 是“保序同构”；对②：取f (x )＝92x －72(－1≤x ≤3)，所以A ＝{x |－1≤x ≤3}，B ＝{x |－8≤x ≤10}是“保序同构”；对③：取f (x )＝tan ⎝⎛⎭⎪⎫πx －π2(0<x <1)，所以A ＝{x |0<x <1}，B ＝R 是“保序同构”，故应填①②③.答案：①②③[预测押题2] 解析：∵A ⊆M ，且集合M 的子集有24＝16个，其中“累计值”为奇数的子集为{1}，{3}，{1，3}，共3个，故“累积值”为奇数的集合有3个．答案：3[例3] 解析：对于①，命题p 为真命题，命题q 为真命题，所以p ∧綈q 为假命题，故①正确；对于②当b ＝a ＝0时，l 1⊥l 2，故②不正确，易知③正确．所以正确结论的序号为①③.答案：①③[预测押题3] 选D 由y ＝tan x 的对称中心为⎝ ⎛⎭⎪⎫k π2，0(k ∈Z )，知A 正确；由回归直线方程知B 正确；在△ABC 中，若sin A ＝sin B ，则A ＝B ，C 正确．第二讲函数的图像与性质基础·单纯考点[例1] 解析：(1)由题意，自变量x应满足{x ＋3>0，1－2x≥0，解得⎩⎪⎨⎪⎧x ≤0，x >－3，∴－3<x ≤0.(2)设t ＝1＋sin x ，易知t ∈[0，2]，所求问题等价于求g (t )在区间[0，2]上的值域．由g (t )＝13t 3－52t 2＋4t ，得g ′(t )＝t 2－5t ＋4＝(t －1)(t －4)．由g ′(t )＝0，可得t＝1或t ＝4.又因为t ∈[0，2]，所以t ＝1是g (t )的极大值点．由g (0)＝0，g (1)＝13－52＋4＝116，g (2)＝13×23－52×22＋4×2＝23，得当t ∈[0，2]时，g (t )∈⎣⎢⎡⎦⎥⎤0，116，即g (1＋sin x )的值域是⎣⎢⎡⎦⎥⎤0，116.答案：(1)A (2)⎣⎢⎡⎦⎥⎤0，116[预测押题1] (1)解析：∵f (π4)＝－tan π4＝－1，∴f (f (π4))＝f (－1)＝2×(－1)3＝－2.答案：－2(2)由题意知：a ≠0，f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2是偶函数，则其图像关于y 轴对称，所以2a ＋ab ＝0，b ＝－2.所以f (x )＝－2x 2＋2a 2，因为它的的值域为(－∞，2]，所以2a 2＝2.所以f (x )＝－2x 2＋2.答案：－2x 2＋2[例2] 解析：(1)曲线y ＝e x 关于y 轴对称的曲线为y ＝e －x ，将y ＝e －x向左平移1个单位长度得到y ＝e －(x ＋1)，即f (x )＝e －x －1.(2)由题图可知直线OA 的方程是y ＝2x ；而k AB ＝0－23－1＝－1，所以直线AB 的方程为y ＝－(x －3)＝－x ＋3.由题意，知f (x )＝⎩⎪⎨⎪⎧2x ，0≤x ≤1，－x ＋3，1<x ≤3，所以g (x )＝xf (x )＝⎩⎪⎨⎪⎧2x 2，0≤x ≤1，－x 2＋3x ，1<x ≤3.当0≤x ≤1时，故g (x )＝2x 2∈[0，2]；当1<x ≤3时，g (x )＝－x 2＋3＝－⎝ ⎛⎭⎪⎫x －32＋94，显然，当x ＝32时，取得最大值94；当x ＝3时，取得最小值0. 综上所述，g (x )的值域为⎣⎢⎡⎦⎥⎤0，94. 答案：(1)D (2)B[预测押题2] (1)选C 因为函数的定义域是非零实数集，所以A 错；当x <0时，y >0，所以B 错；当x →＋∞时，y →0，所以D 错．(2)选B 因为f (x )＝f (－x )，所以函数f (x )是偶函数．因为f (x ＋2)＝f (x )，所以函数f (x )的周期是2，再结合选项中的图像得出正确选项为B.[例3] 解析：(1)函数y ＝－3|x |为偶函数，在(－∞，0)上为增函数．选项A ，D 是奇函数，不符合；选项B 是偶函数但单调性不符合；只有选项C 符合要求．(2)∵f (x )＝ax 3＋b sin x ＋4， ①∴f (－x )＝a (－x )3＋b sin(－x )＋4，即f (－x )＝－ax 3－b sin x ＋4， ② ①＋②得f (x )＋f (－x )＝8. ③又∵lg(log 210)＝lg ⎝ ⎛⎭⎪⎫1lg 2＝lg(lg 2)－1＝－lg(lg 2)，∴f (lg(lg 210))＝f (－lg(lg 2))＝5.又由③式知f (－lg(lg 2))＋f (lg(lg 2))＝8， ∴5＋f (lg(lg 2))＝8， ∴f (lg(lg 2))＝3. 答案：(1)C (2)C[预测押题3] (1)选A 依题意得，函数f (x )在[0，＋∞)上是增函数，且f (x )＝f (|x |)，不等式f (1－2x )<f (3)⇔f (|1－2x |)<f (3)⇔|1－2x |<3⇔－3<1－2x <3⇔－1<x <2.(2)解析：∵f (x )＝－f ⎝ ⎛⎭⎪⎫x ＋32， ∴f ⎝ ⎛⎭⎪⎫x ＋32＝－f (x ＋3)＝－f (x )， ∴f (x )＝f (x ＋3)，∴f (x )是以3为周期的周期函数．则f (2014)＝f (671×3＋1)＝f (1)＝3. 答案：3(3)解析：因为函数f (x )的图像关于y 轴对称，所以该函数是偶函数，又f (1)＝0，所以f (－1)＝0.又已知f (x )在(0，＋∞)上为减函数，所以f (x )在(－∞，0)上为增函数.f （－x ）＋f （x ）x<0，可化为xf (x )<0，所以当x >0时，解集为{x |x >1}；当x <0时，解集为{x |－1<x <0}．综上可知，不等式的解集为(－1，0)∪(1，＋∞)．答案：(－1，0)∪(1，＋∞)交汇·创新考点[例1] 解析：设x <0，则－x >0.∵当x ≥0时，f (x )＝x 2－4x ，∴f (－x )＝(－x )2－4(－x )．∵f (x )是定义在R 上的偶函数，∴f (－x )＝f (x )，∴f (x )＝x 2＋4x (x <0)，∴f (x )＝⎩⎪⎨⎪⎧x 2－4x ，x ≥0，x 2＋4x ，x <0.由f (x )＝5得⎩⎪⎨⎪⎧x 2－4x ＝5，x ≥0，或⎩⎪⎨⎪⎧x 2＋4x ＝5，x <0，∴x ＝5或x ＝－5.观察图像可知由f (x )<5，得－5<x <5.∴由f (x ＋2)<5，得－5<x ＋2<5，∴－7<x <3.∴不等式f (x ＋2)<5的解集是{x |－7<x <3}．答案：{x |－7<x <3}[预测押题1] 解析：根据已知条件画出f (x )图像如图所示．因为对称轴为x ＝－1，所以(0，1)关于x ＝－1的对称点为(－2，1)．因f (m )<1，所以应有－2<m <0，m ＋2>0.因f (x )在(－1，＋∞)上递增，所以f (m ＋2)>f (0)＝1.答案：>[例2] 解析：因为A ，B 是R 的两个非空真子集，且A ∩B ＝∅，画出韦恩图如图所示，则实数x 与集合A ，B 的关系可分为x ∈A ，x ∈B ，x ∉A 且x ∉B 三种．(1)当x ∈A 时，根据定义，得f A (x )＝1.因为A ∩B ＝∅，所以x ∉B ，故f B (x )＝0.又因为A ⊆(A ∪B )，则必有x ∈A ∪B ，所以f A ∪B (x )＝1.所以F (x )＝f A ∪B （x ）＋1f A （x ）＋f B （x ）＋1＝1＋11＋0＋1＝1.(2)当x ∈B 时，根据定义，得f B (x )＝1.因为A ∩B ＝∅，所以x ∉A ，故f A (x )＝0.又因为B ⊆(A ∪B )，则必有x ∈A ∪B ，所以f A ∪B (x )＝1.所以F (x )＝f A ∪B （x ）＋1f A （x ）＋f B （x ）＋1＝1＋11＋0＋1＝1.(3)当x ∉A 且x ∉B ，根据定义，得f A (x )＝0，f B (x )＝0.由图可知，显然x ∉(A ∪B )，故f A ∪B (x )＝0，所以F (x )＝f A ∪B （x ）＋1f A （x ）＋f B （x ）＋1＝0＋10＋0＋1＝1.综上，函数的值域中只有一个元素1，即函数的值域为{1}．答案：{1}[预测押题2] 解：当x ∈A ∩B 时，因为(A ∩B )⊆(A ∪B )，所以必有x ∈A ∪B .由定义，可知f A (x )＝1，f B (x )＝1，f A ∪B (x )＝1，所以F (x )＝f A ∪B （x ）＋1f A （x ）＋f B （x ）＋1＝1＋11＋1＋1＝23. 故函数F (x )的值域为{23}．第三讲基本初等函数、函数与方程及函数的应用基础·单纯考点[例1] 解析：(1)当x ＝－1，y ＝1a －1a ＝0，所以函数y ＝a x－1a的图像必过定点(－1，0)，结合选项可知选D.(2)a ＝log 36＝log 33＋log 32＝1＋log 32，b ＝log 510＝log 55＋log 52＝1＋log 52，c ＝log 714＝log 77＋log 72＝1＋log 72，∵log 32>log 52>log 72，∴a >b >c .答案：(1)D (2)D[预测押题1] (1)选A 函数y ＝x －x 13为奇函数．当x >0时，由x －x 13>0，即x 3>x ，可得x 2>1，故x >1，结合选项，选A.(2)选B 依题意的a ＝ln x ∈(－1，0)，b ＝⎝ ⎛⎭⎪⎫12ln x ∈(1，2)，c ＝e ln x ∈(e －1，1)，因此b >c >a .[例2] 解析：(1)由f (－1)＝12－3<0，f (0)＝1>0及零点定理，知f (x )的零点在区间(－1，0)上．(2)当f (x )＝0时，x ＝－1或x ＝1，故f [f (x )＋1]＝0时，f (x )＋1＝－1或1.当f (x )＋1＝－1，即f (x )＝－2时，解得x ＝－3或x ＝14；当f (x )＋1＝1即f (x )＝0时，解得x ＝－1或x ＝1.故函数y ＝f [f (x )＋1]有四个不同的零点．答案：(1)B (2)C[预测押题2] 解析：当x >0时，由f (x )＝ln x ＝0，得x ＝1.因为函数f (x )有两个不同的零点，则当x ≤0时，函数f (x )＝2x －a 有一个零点，令f (x )＝0得a ＝2x ，因为0<2x ≤20＝1，所以0<a ≤1，所以实数a 的取值范围是0<a ≤1.答案：(0，1][例3] 解：(1)由年销售量为x 件，按利润的计算公式，有生产A ，B 两产品的年利润y 1，y 2分别为y 1＝10x －(20＋mx )＝(10－m )x －20(x ∈n ，0≤x ≤200)，y ＝18x －(8x ＋40)－0.05x 2＝－0.05x 2＋10x －40(x ∈n ，0≤x ≤120)．(2)因为6≤m ≤8，所以10－m >0，函数y 1＝(10－m )x －20在[0，200]上是增函数，所以当x ＝200时，生产A 产品有最大利润，且y 1max ＝(10－m )×200－20＝1980－200m (万美元)．又y 2＝－0.05(x －100)2＋460(x ∈N ，0≤x ≤120)，所以当x ＝100时，生产B 产品有最大利润，且y 2max ＝460(万美元)．因为y 1max －y 2max ＝1980－200m －460＝1520－200m ⎩⎪⎨⎪⎧>0，6≤m <7.6，＝0，m ＝7.6，<0，7.6<m ≤8.所以当6≤m <7.6时，可投资生产A 产品200件；当m ＝7.6时，生产A 产品或生产B 产品均可(投资生产A 产品200件或生产B 产品100件)；当7.6<m ≤8时，可投资生产B 产品100件．[预测押题3] 解：(1)设投入广告费t (百万元)后由此增加的收益为f (t )(百万元)，则f (t )＝(－t 2＋5t )－t ＝－t 2＋4t ＝－(t －2)2＋4(0≤t ≤3)．所以当t ＝2时，f (t )max ＝4，即当集团投入两百万广告费时，才能使集团由广告费而产生的收益最大．(2)设用于技术改造的资金为x (百万元)，则用于广告费的费用为(3－x )(百万元)，则由此两项所增加的收益为g (x )＝⎝ ⎛⎭⎪⎫－13x 3＋x 2＋3x ＋[－(3－x )2＋5(3－x )]－3＝－13x 3＋4x ＋3(0≤x ≤3)．对g (x )求导，得g ′(x )＝－x 2＋4，令g ′(x )＝－x 2＋4＝0，得x ＝2或x ＝－2(舍去)．当0≤x <2时，g ′(x )>0，即g (x )在[0，2)上单调递增；当2<x ≤3时，g ′(x )<0，即g (x )在(2，3]上单调递减．∴当x ＝2时，g (x )max ＝g (2)＝253.故在三百万资金中，两百万元用于技术改造，一百万元用于广告促销，这样集团由此所增加的受益最大，最大收益为253百万元．交汇·创新考点[例1] 选B ∵⎝⎛⎭⎪⎫x －π2f ′(x )>0，x ∈(0，π)且x ≠π2，∴当0<x <π2时，f ′(x )<0，f (x )在(0，π2)上单调递减．当π2<x <π时，f ′(x )>0，f (x )在⎝ ⎛⎭⎪⎫π2，π上单调递增． ∵当x ∈[0，π]时，0<f (x )<1.∴当x ∈[π，2π]，则0≤2π－x ≤π.又f (x )是以2π为最小正周期的偶函数，知f (2π－x )＝f (x )．∴x ∈[π，2π]时，仍有0<f (x )<1.依题意及y ＝f (x )与y ＝sin x 的性质，在同一坐标系内作y ＝f (x )与y ＝sin x 的简图．则y ＝f (x )与y ＝sin x 在x ∈[－2π，2π]有4个交点．故函数y ＝f (x )－sin x 在[－2π，2π]上有4个零点．[预测押题] 选D 根据f ⎝ ⎛⎭⎪⎫x ＋54＝－f ⎝ ⎛⎭⎪⎫x －54，可得f ⎝ ⎛⎭⎪⎫x ＋52＝－f (x )，进而得f (x ＋5)＝f (x )，即函数y ＝f (x )是以5为周期的周期函数．当x ∈[－1，4]时，f (x )＝x 2－2x，在[－1，0]内有一个零点，在(0，4]内有x 1＝2，x 2＝4两个零点，故在一个周期内函数有三个零点．又因为2012＝402×5＋2，故函数在区间[0，2010]内有402×3＝1206个零点，在区间(2010，2012]内的零点个数与在区间(0，2]内零点的个数相同，即只有一个零点，所以函数f (x )在[0，2012]上零点的个数为1207.第四讲不等式基础·单纯考点[例1] 解析：(1)原不等式等价于(x －1)(2x ＋1)<0或x －1＝0，即－12<x <1或x ＝1，所以原不等式的解集为⎝ ⎛⎦⎥⎤－12，1. (2)由题意知，一元二次不等式f (x )>0的解集为⎩⎨⎧⎭⎬⎫x |－1<x <12.而f (10x )>0，∴－1<10x <12，解得x <lg 12，即x <－lg 2.答案：(1)A (2)D[预测押题1] (1)选B 当x >0时，f (x )＝－2x ＋1x2>－1，∴－2x ＋1>－x 2，即x 2－2x＋1>0，解得x >0且x ≠1.当x <0时，f (x )＝1x>－1，即－x >1，解得x <－1.故x ∈(－∞，－1)∪(0，1)∪(1，＋∞)．(2)解析：∵f (x )＝x 2＋ax ＋b 的值域为[0，＋∞)，∴Δ＝0，∴b －a 24＝0，∴f (x )＝x2＋ax ＋14a 2＝⎝ ⎛⎭⎪⎫x ＋12a 2.又∵f (x )<c 的解集为(m ，m ＋6)，∴m ，m ＋6是方程x 2＋ax ＋a 24－c ＝0的两根．由一元二次方程根与系数的关系得⎩⎪⎨⎪⎧2m ＋6＝－a ，m （m ＋6）＝a 24－c ，解得c ＝9. 答案：9[例2] 解析：(1)曲线y ＝|x |与y ＝2所围成的封闭区域如图阴影部分所示，当直线l ：y ＝2x 向左平移时，(2x －y )的值在逐渐变小，当l 通过点A (－2，2)时，(2x －y )min ＝－6.(2)设租用A 型车x 辆，B 型车y 辆，目标函数为z ＝1600x ＋2400y ，则约束条件为⎩⎪⎨⎪⎧36x ＋60y ≥900，x ＋y ≤21，y －x ≤7，x ，y ∈n ，作出可行域，如图中阴影部分所示，可知目标函数过点(5，12)时，有最小值z min ＝36800(元)．答案：(1)A (2)C[预测押题2] (1)选C 题中的不等式组表示的平面区域如图阴影部分所示，平移直线x －y ＝0，当平移经过该平面区域内的点(0，1)时，相应直线在x 轴上的截距达到最小，此时x －y 取得最小值，最小值是x －y ＝0－1＝－1；当平移到经过该平面内区域内的点(2，0)时，相应直线在x 轴上的截距达到最大，此时x －y 取得最大值，最大值是x －y ＝2－0＝2.因此x －y 的取值范围是[－1，2]．(2)解析：作出可行域，如图中阴影部分所示，区域面积S ＝12×⎝ ⎛⎭⎪⎫2a ＋2×2＝3，解得a＝2.答案：2[例3] 解析：(1)因－6≤a ≤3，所以3－a ≥0，a ＋6≥0，∴（3－a ）（a ＋6）≤3－a ＋a ＋62＝92，当且仅当a ＝－32时等号成立．(2)f (x )＝4x ＋a x≥24x ·ax ＝4a (x >0，a >0)，当且仅当4x ＝a x，即x ＝a2时等号成立，此时f (x )取得最小值4a .又由已知x ＝3时，f (x )min ＝4a ，∴a2＝3，即a ＝36.答案：(1)B (2)36[预测押题3] (1)选D 依题意，点A (－2，－1)，则－2m －n ＋1＝0，即2m ＋n ＝1(m >0，n >0)，∴1m ＋2n ＝⎝ ⎛⎭⎪⎫1m ＋2n (2m ＋n )＝4＋⎝ ⎛⎭⎪⎫n m ＋4m n ≥4＋2n m ×4m n ＝8，当且仅当n m ＝4m n，即n ＝2m＝12时取等号，即1m ＋2n的最小值是8. (2)选A 由已知得a ＋2b ＝2.又∵a >0，b >0，∴2＝a ＋2b ≥22ab ，∴ab ≤12，当且仅当a ＝2b ＝1时取等号．交汇·创新考点[例1] 选C 作出可行域，如图中阴影部分所示，三个顶点到圆心(0，1)的距离分别是1，1，2，由A ⊆B 得三角形所有点都在圆的内部，故m ≥2，解得：m ≥2.[预测押题1] 选C 如图，若使以(4，1)为圆心的圆与阴影部分区域至少有两个交点，结合图形，当圆与直线x －y －2＝0相切时，恰有一个公共点，此时a ＝⎝ ⎛⎭⎪⎫122＝12，当圆的半径增大到恰好过点A (2，2)时，圆与阴影部分至少有两个公共点，此时a ＝5，故a 的取值范围是12<a ≤5，故选C.[例2] 选 C z ＝x 2－3xy ＋4y 2(x ，y ，z ∈R ＋)，∴z xy ＝x 2－3xy ＋4y 2xy ＝x y ＋4yx－3≥2x y ·4y x －3＝1.当且仅当x y ＝4y x ，即x ＝2y 时“＝”成立，此时z ＝x 2－3xy ＋4y 2＝4y2－6y 2＋4y 2＝2y 2，∴x ＋2y －z ＝2y ＋2y －2y 2＝－2y 2＋4y ＝－2(y －1)2＋2.∴当y ＝1时，x ＋2y －z 取得最大值2.[预测押题2] 解析：4x 2＋y 2＋xy ＝1，∴(2x ＋y )2＝3xy ＋1＝32×2xy ＋1≤32×⎝ ⎛⎭⎪⎫2x ＋y 22＋1，∴(2x ＋y )2≤85，∴(2x ＋y )max ＝2105.答案：2105第五讲导数及其应用基础·单纯考点[例1] 解析：(1)∵点(1，1)在曲线y ＝x 2x －1上，y ′＝－1（2x －1）2，∴在点(1，1)处的切线斜率为y ′|x ＝1＝－1（2－1）2＝－1，所求切线方程为y －1＝－(x －1)，即x ＋y －2＝0.(2)因为y ′＝2ax －1x，所以y ′|x ＝1＝2a －1.因为曲线在点(1，a )处的切线平行于x 轴，故其斜率为0，故2a －1＝0，a ＝12.答案：(1)x ＋y －2＝0 (2)12[预测押题1] 选D 由f (x ＋2)＝f (x －2)，得f (x ＋4)＝f (x )，可知函数为周期函数，且周期为4.又函数f (x )为偶函数，所以f (x ＋2)＝f (x －2)＝f (2－x )，即函数的对称轴是x ＝2，所以f ′(－5)＝f ′(3)＝－f ′(1)，所以函数在x ＝－5处的切线的斜率k ＝f ′(－5)＝－f ′(1)＝－1.[例2] 解：(1)f ′(x )＝e x(ax ＋a ＋b )－2x －4.由已知得f (0)＝4，f ′(0)＝4.故b ＝4，a ＋b ＝8.从而a ＝4，b ＝4.(2)由(1)知，f (x )＝4e x (x ＋1)－x 2－4x ，f ′(x )＝4e x(x ＋2)－2x －4＝4(x ＋2)⎝⎛⎭⎪⎫e x －12.令f ′(x )＝0，得x ＝－ln2或x ＝－2.从而当x ∈(－∞，－2)∪(－ln2，＋∞)时，f ′(x )>0；当x ∈(－2，－ln2)时，f ′(x )<0.故f (x )在(－∞，－2)，(－ln2，＋∞)上单调递增，在(－2，－ln2)上单调递减．[预测押题2] 解：(1)当m ＝1时，f (x )＝13x 3＋x 2－3x ＋1，又f ′(x )＝x 2＋2x －3，所以f ′(2)＝5.又f (2)＝53，所以所求切线方程为y －53＝5(x －2)，即15x －3y －25＝0.所以曲线y ＝f (x )在点(2，f (2))处的切线方程为15x －3y －25＝0.(2)因为f ′(x )＝x 2＋2mx －3m 2，令f ′(x )＝0，得x ＝－3m 或x ＝m .当m ＝0时，f ′(x )＝x 2≥0恒成立，不符合题意；当m >0时，f (x )的单调递减区间是(－3m ，m )，若f (x )在区间(－2，3)上是减函数，则⎩⎪⎨⎪⎧－3m ≤－2，m ≥3，解得m ≥3；当m <0时，f (x )的单调递减区间是(m ，－3m )，若f (x )在区间(－2，3)上是减函数，则⎩⎪⎨⎪⎧m ≤－2，－3m ≥3，解得m ≤－2.综上所述，实数m 的取值范围是(－∞，－2]∪[3，＋∞)．[例3] 解：(1)f ′(x )＝1－aex ，①当a ≤0时，f ′(x )>0，f (x )为(－∞，＋∞)上的增函数，所以函数f (x )无极值．②当a >0时，令f ′(x )＝0，得e x＝a ，即x ＝ln a . 当x ∈(－∞，ln a )时，f ′(x )<0；当x ∈(ln a ，＋∞)时，f ′(x )>0，所以f (x )在(－∞，ln a )上单调递减，在(ln a ，＋∞)上单调递增，故f (x )在x ＝ln a 处取得最小值，且极小值为f (ln a )＝ln a ，无极大值．综上，当a ≤0时，函数f (x )无极值；当a >0时，函数f (x )在x ＝ln a 处取得极小值ln a ，无极大值．(2)当a ＝1时，f (x )＝x －1＋1e x .直线l ：y ＝kx －1与曲线y ＝f (x )没有公共点，等价于关于x 的方程kx －1＝x －1＋1e x 在R 上没有实数解，即关于x 的方程：(k －1)x ＝1ex (*)在R 上没有实数解．①当k ＝1时，方程(*)可化为1e x ＝0，在R 上没有实数解．②当k ≠1时，方程(*)可化为1k －1＝x e x.令g (x )＝x e x ，则有g ′(x )＝(1＋x )e x.令g ′(x当x ＝－1时，g (x )min ＝－e，同时当x 趋于＋∞时，g (x )趋于＋∞，从而g (x )的取值范围为⎣⎢⎡⎭⎪⎫－1e ，＋∞.所以当1k ＋1∈⎝ ⎛⎭⎪⎫－∞，－1e 时，方程(*)无实数解，解得k 的取值范围是(1－e ，1)．综合①②，得k 的最大值为1.[预测押题3] 解：(1)f ′(x )＝a ＋2x 2－3x ，由题意可知f ′(23)＝1，解得a ＝1.故f (x )＝x －2x －3ln x ，∴f ′(x )＝（x －1）（x －2）x2，由f ′(x )＝0，得x ＝2.∴f min (2)f ′(x )＝a ＋2x －3x ＝ax 2－3x ＋2x(x >0)，由题意可得方程ax 2－3x ＋2＝0有两个不等的正实根，不妨设这两个根为x 1，x 2，并令h (x )＝ax 2－3x ＋2，则⎩⎪⎨⎪⎧Δ＝9－8a >0，x 1＋x 2＝3a >0，x 1x 2＝2a >0.也可以为⎩⎪⎨⎪⎧Δ＝9－8a >0，－－32a >0，h （0）>0.解得0<a <98.交汇·创新考点[例1] 解：(1)证明：设φ(x )＝f (x )－1－a ⎝⎛⎭⎪⎫1－1x ＝a ln x －a ⎝ ⎛⎭⎪⎫1－1x (x >0)，则φ′(x )＝a x －ax2.令φ′(x )＝0，则x ＝1，易知φ(x )在x ＝1处取到最小值，故φ(x )≥φ(1)＝0，即f (x )－1≥a ⎝ ⎛⎭⎪⎫1－1x .(2)由f (x )>x 得a ln x ＋1>x ，即a >x －1ln x .令g (x )＝x －1ln x (1<x <e)，则g ′(x )＝ln x －x －1x （ln x ）2.令h (x )＝ln x －x －1x (1<x <e)，则h ′(x )＝1x －1x2>0，故h (x )在定义域上单调递增，所以h (x )>h (1)＝0.因为h (x )>0，所以g ′(x )>0，即g (x )在定义域上单调递增，则g (x )<g (e)＝e －1，即x －1ln x<e －1，所以a 的取值范围为[e －1，＋∞)．[预测押题1] 解：(1)由f (x )＝e x (x 2＋ax －a )可得，f ′(x )＝e x [x 2＋(a ＋2)x ]．当a ＝1时，f (1)＝e ，f ′(1)＝4e.所以曲线y ＝f (x )在点(1，f (1))处的切线方程为y －e ＝4e(x －1)，即y ＝4e x －3e.(2)令f ′(x )＝e x [x 2＋(a ＋2)x ]＝0，解得x ＝－(a ＋2)或x ＝0.当－(a ＋2)≤0，即a ≥－2时，在区间[0，＋∞)上，f ′(x )≥0，所以f (x )在[0，＋∞)上是增函数，所以方程f (x )＝k 在[0，＋∞)上不可能有两个不相等的实数根．当－(a ＋2)>0，即a <－2时，f ′(x )，f (x )随由上表可知函数f (x )在[0，＋∞)上的最小值为f (－(a ＋2))＝ea ＋2.因为函数f (x )在(0，－(a ＋2))上是减函数，在(－(a ＋2)，＋∞)上是增函数，且当x ≥－a 时，有f (x )≥f (－a )＝e －a(－a )>－a ，又f (0)＝－a ，所以要使方程f (x )＝k 在[0，＋∞)上有两个不相等的实数根，k 的取值范围是⎝ ⎛⎦⎥⎤a ＋4e a ＋2，－a .[例2] 选C 法一：曲线y ＝x 与直线x ＝1及x 轴所围成的曲边图形的面积S ＝⎠⎛01xd x ＝⎪⎪⎪23x 3210＝23，又∵S △AOB ＝12，∴阴影部分的面积为S ′＝23－12＝16，由几何概型可知，点P 取自阴影部分的概率为P ＝16.法二：S 阴影＝⎠⎛01(x －x )d x ＝16，S 正方形OABC ＝1，∴点P 取自阴影部分的概率为P ＝16.[预测押题2] 解析：画出草图，可知所求概率P ＝S 阴影S △AOB ＝⎠⎛04x d x18＝⎪⎪⎪23x 324018＝16318＝827.答案：827[例3] 解：(1)因为方程ax －(1＋a 2)x 2＝0(a >0)有两个实根x 1＝0，x 2＝a1＋a 2，故f (x )>0的解集为{x |x 1<x <x 2}．因此区间I ＝⎝ ⎛⎭⎪⎫0，a 1＋a 2，故I 的长度为a1＋a 2.(2)设d (a )＝a 1＋a 2，则d ′(a )＝1－a2（1＋a 2）2(a >0)．令d ′(a )＝0，得a ＝1.由于0<k <1，故当1－k ≤a <1时，d ′(a )>0，d (a )单调递增；当1<a ≤1＋k 时，d ′(a )<0，d (a )单调递减．所以当1－k ≤a ≤1＋k 时，d (a )的最小值必定在a ＝1－k 或a ＝1＋k 处取得．而d （1－k ）d （1＋k ）＝1－k1＋（1－k ）21＋k 1＋（1＋k ）2＝2－k 2－k 32－k 2＋k3<1，故d (1－k )<d (1＋k )．因此当a ＝1－k 时，d (a )在区间[1－k ，1＋k ]上取得最小值1－k2－2k ＋k2.[预测押题3] 解：(1)f (x )的定义域为(－∞，－1)∪(－1，＋∞)，f ′(x )＝a （x ＋1）－（ax ＋b ）（x ＋1）2＝a －b（x ＋1）2.当a >b 时，f ′(x )>0，函数f (x )在(－∞，－1)，(－1，＋∞)上单调递增；当a 0，f (b a )＝2ab a ＋b >0，f (b a )＝ab >0.因为f (1)f (ba)＝a ＋b2·2ab a ＋b ＝ab ＝⎣⎢⎡⎦⎥⎤f （b a ）2，即f (1)f (b a )＝⎣⎢⎡⎦⎥⎤f （b a ）2. (*)所以f (1)，f (b a)，f (b a )成等比数列．因为a ＋b 2≥ab ，所以f (1)≥f (b a )．由(*)得f (b a )≤f (b a)． ②由①知f (b a )＝H ，f (b a )＝G .故由H ≤f (x )≤G ，得f (b a )≤f (x )≤f (ba )． (**)当a ＝b 时，(b a )＝f (x )＝f (b a )＝a .这时，x 的取值范围为(0，＋∞)；当a >b 时，0<ba<1，从而b a 1，从而b a >b a ，由f (x )在(0，＋∞)上单调递减与(**)式，得b a≤x ≤b a ，即x 的取值范围为⎣⎢⎡⎦⎥⎤b a ，b a .综上，当a ＝b 时，x 的取值范围为(0，＋∞)；当a >b时，x 的取值范围为⎣⎢⎡⎦⎥⎤b a ，b a ；当a 0，故原式＝sin θ－cos θ.(2)由已知得|OP |＝2，由三角函数定义可知sin α＝12，cos α＝32，即α＝2k π＋π6(k ∈Z )．所以2sin2α－3tan α＝2sin ⎝ ⎛⎭⎪⎫4k π＋π3－3tan ⎝ ⎛⎭⎪⎫2k π＋π6＝2sin π3－3tan π6＝2×32－3×33＝0. 答案：(1)A (2)D[预测押题1] (1)选C 由已知可得－2tan α＋3sin β＋5＝0，tan α－6sin β＝1，解得tan α＝3，故sin α＝31010.(2)解析：由A 点的纵坐标为35及点A 在第二象限，得点A 的横坐标为－45，所以sin α＝35，cos α＝－45，tan α＝－34.故tan2α＝2tan α1－tan 2α＝－247. 答案：35 －247[例2] 解析：(1)∵34T ＝512π－⎝ ⎛⎭⎪⎫－π3＝34π，∴T ＝π，∴2πω＝π(ω>0)，∴ω＝2.由图像知当x ＝512π时，2×512π＋φ＝2k π＋π2(k ∈Z )，即φ＝2k π－π3(k∈Z )．∵－π2<φ<π2，∴φ＝－π3.(2)y ＝cos(2x ＋φ)的图像向右平移π2个单位后得到y ＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π2＋φ的图像，整理得y ＝cos(2x －π＋φ)．∵其图像与y ＝sin ⎝⎛⎭⎪⎫2x ＋π3的图像重合，∴φ－π＝π3－π2＋2k π，∴φ＝π3＋π－π2＋2k π，即φ＝5π6＋2k π.又∵－π≤φ<π∴φ＝5π6.答案：(1)A (2)5π6[预测押题2] (1)选C 将y ＝sin ⎝⎛⎭⎪⎫2x ＋π4的图像向左平移π4个单位，再向上平移2个单位得y ＝sin ⎝⎛⎭⎪⎫2x ＋3π4＋2的图像，其对称中心的横坐标满足2x ＋3π4＝k π，即x ＝k π2－3π8，k ∈Z ，取k ＝1，得x ＝π8. (2)选C 根据已知可得，f (x )＝2sin π4x ，若f (x )在[m ，n ]上单调，则n －m 取最小值．又当x ＝2时，y ＝2；当x ＝－1时，y ＝－2，故(n －m )min ＝2－(－1)＝3.[例3] 解：(1)f (x )4cos ωx ·sin ⎝ ⎛⎭⎪⎫ωx ＋π4＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin2ωx ·cos2ωx )＋2＝2sin ⎝⎛⎭⎪⎫2ωx ＋π4＋ 2.因为f (x )的最小正周期为π，且ω>0，从而由2π2ω＝π，故ω＝1.(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋ 2.若0≤x ≤π2，则π4≤2x ＋π4≤5π4.当π4≤2x ＋π4≤π2，即0≤x ≤π8时，f (x )单调递增；当π2≤2x ＋π4≤5π5，即π8≤x ≤π2时，f (x )单调递减；综上可知，f (x )在区间[0，π8]上单调递增，在区间[π8，π2]上单调递减．[预测押题3] 解：(1)因为f (x )＝32sin 2x ＋1＋cos 2x 2＋a ＝sin(2x ＋π6)＋a ＋12，所以T ＝π.由π2＋2k π≤2x ＋π6≤3π2＋2k π，k ∈Z ，得π6＋k π≤x≤2π3＋k π，k∈Z .故函数f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤π6＋k π，2π3＋k π(k ∈Z )． (2)因为－π6≤x ≤π3，所以－π6≤2x ＋π6≤5π6，－12≤sin ⎝⎛⎭⎪⎫2x ＋π6≤1.因为函数f (x )在⎣⎢⎡⎦⎥⎤－π6，π3上的最大值与最小值的和为⎝⎛⎭⎪⎫1＋a ＋12＋⎝ ⎛⎭⎪⎫－12＋a ＋12＝32，所以a ＝0.交汇·创新考点[例1] 解：(1)f (x )＝1＋cos （2ωx －π3）2－1－cos2ωx 2＝12⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫2ωx －π3＋cos2ωx ＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12cos2ωx ＋32sin2ωx ＋cos2ωx ＝12⎝ ⎛⎭⎪⎫32sin2ωx ＋32cos2ωx ＝32⎝ ⎛⎭⎪⎫12sin2ωx ＋32cos2ωx ＝32sin ⎝ ⎛⎭⎪⎫2ωx ＋π3.由题意可知，f (x )的最小正周期T ＝π，∴2π|2ω|＝π.又∵ω>0，∴ω＝1，∴f (π12)＝32sin ⎝ ⎛⎭⎪⎫2×π12＋π3＝32sin π2＝32.(2)|f (x )－m |≤1，即f (x )－1≤m ≤f (x )＋1.∵对∀x ∈⎣⎢⎡⎦⎥⎤－7π12，0，都有|f (x )－m |≤1，∴m ≥f (x )max －1且m ≤f (x )min ＋1.∵－7π12≤x ≤0，∴－5π6≤2x ＋π3≤π3，∴－1≤sin ⎝ ⎛⎭⎪⎫2x ＋π3≤32，∴－32≤32sin ⎝ ⎛⎭⎪⎫2x ＋π3≤34，即f (x )max ＝34，f (x )min ＝－32，∴－14≤m ≤1－32.故m 的取值范围为⎣⎢⎡⎦⎥⎤－14，1－32.[预测押题1] 解：(1)f (2π3)＝cos 2π3·cos π3＝－cos π3·cos π3＝－⎝ ⎛⎭⎪⎫122＝－14.(2)f (x )＝cos x ·cos ⎝ ⎛⎭⎪⎫x －π3＝cos x ·⎝ ⎛⎭⎪⎫12cos x ＋ 32sin x ＝12cos 2x ＋32sin x cos x ＝14(1＋cos2x )＋34sin2x ＝12cos ⎝ ⎛⎭⎪⎫2x －π3＋14.f (x )<14等价于12cos ⎝ ⎛⎭⎪⎫2x －π3＋14<14，即cos ⎝⎛⎭⎪⎫2x －π3<0.于是2k π＋π2<2x －π3<2k π＋3π2，k ∈Z .解得k π＋5π12<x <k π＋11π12，k ∈Z .故使f (x )<14成立的x 的取值集合为⎩⎨⎧⎭⎬⎫x |k π＋5π12<x <k π＋11π12，k ∈Z .[例2] 解析：因为圆心由(0，1)平移到了(2，1，)，所以在此过程中P 点所经过的弧长为2，其所对圆心角为2.如图所示，过P 点作x 轴的垂线，垂足为A ，圆心为C ，与x 轴相切与点B ，过C 作PA 的垂线，垂足为D ，则∠PCD ＝2－π2，|PD |＝sin ⎝⎛⎭⎪⎫2－π2＝－cos2，|CD |＝cos ⎝⎛⎭⎪⎫2－π2＝sin2，所以P 点坐标为(2－sin2，1－cos2)，即OP →的坐标为(2－sin2，1－cos2)．答案：(2－sin2，1－cos2)[预测押题2] 选A 画出草图，可知点Q 点落在第三象限，则可排除B 、D ；代入A ，cos∠QOP ＝6×（－72）＋8×（－2）62＋82＝－502100＝－22，所以∠QOP ＝3π4.代入C ，cos ∠QOP ＝6×（－46）＋8×（－2）62＋82＝－246－16100≠－22.第二讲三角恒等变换与解三角形基础·单纯考点[例1] 解：(1)因为f (x )＝2cos ⎝ ⎛⎭⎪⎫x －π12，所以f (－π6)＝2cos ⎝ ⎛⎭⎪⎫－π6－π12＝2cos ⎝ ⎛⎭⎪⎫－π4＝2cos π4＝2×22＝1. (2)因为θ∈⎝ ⎛⎭⎪⎫3π2，2π，cos θ＝35，所以sin θ＝1－cos 2θ＝－1－⎝ ⎛⎭⎪⎫352＝－45，cos2θ＝2cos 2θ－1＝2×(35)2－1＝－275，sin 2θ＝2sin θcos θ ＝2×35×⎝ ⎛⎭⎪⎫－45＝－2425.所以f (2θ＋π3)＝2cos ⎝ ⎛⎭⎪⎫2θ＋π3－π12＝2cos ⎝ ⎛⎭⎪⎫2θ＋π4＝2×⎝ ⎛⎭⎪⎫22cos2θ－22sin2θ＝cos2θ－sin2θ＝－725－⎝ ⎛⎭⎪⎫－2425＝1725.[预测押题1] 解：(1)由已知可得f (x )＝3cos ωx ＋3sin ωx ＝23sin ⎝ ⎛⎭⎪⎫ωx ＋π3.所以函数f (x )的值域为[－23，23]．又由于正三角形ABC 的高为23，则BC ＝4，所以函数f (x )的周期T ＝4×2＝8，即2πω＝8，解得ω＝π4.(2)因为f (x 0)＝835，由(1)得f (x 0)＝23sin ⎝ ⎛⎭⎪⎫πx 04＋π3＝835，即sin ⎝⎛⎭⎪⎫πx 04＋π3＝45.由x 0∈⎝ ⎛⎭⎪⎫－103，23得πx 04＋π3∈⎝ ⎛⎭⎪⎫－π2，π2.所以cos ⎝ ⎛⎭⎪⎫πx 04＋π3＝1－⎝ ⎛⎭⎪⎫452＝35，故f (x 0＋1)＝23sin ⎝ ⎛⎭⎪⎫πx 04＋π4＋π3＝23sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫πx 04＋π3＋π4 ＝23⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫πx 04＋π3cos π4＋cos ⎝ ⎛⎭⎪⎫πx 04＋π3sin π4＝23⎝ ⎛⎭⎪⎫45×22＋35×22＝765.[例2] 解：(1)由已知得，∠PBC ＝60°，所以∠PBA ＝30°.在△PBA 中，由余弦定理得PA 2＝3＋14－2×3×12cos30°＝74.故PA ＝72. (2)设∠PBA ＝α，由已知得PB ＝sin α.在△PBA 中，由正弦定理得3sin150°＝sin αsin （30°－α），化简得3sin α＝4sin α.则tan α＝34，即tan ∠PBA ＝34.[预测押题2] 解：(1)由正弦定理得2sin B cos C ＝2sin A －sin C .∵在△ABC 中，sin A ＝sin(B ＋C )＝sin B cos C ＋sin C cos B ，∴sin C (2cos B －1)＝0.又0<C <π，sin C >0，∴cos B ＝12，注意到0<B <π，∴B ＝π3.(2)∵S △ABC ＝12ac sin B ＝3，∴ac ＝4，由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝a 2＋c 2－ac ≥ac ＝4，当且仅当a ＝c ＝2时，等号成立，∴b 的取值范围为[2，＋∞)．交汇·创新考点[例1] 解：(1)∵f (x )＝cos ⎝ ⎛⎭⎪⎫2x －4π3＋2cos 2x ＝cos ⎝⎛⎭⎪⎫2x ＋π3＋1，∴f (x )的最大值为2.f (x )取最大值时，cos ⎝⎛⎭⎪⎫2x ＋π3＝1，2x ＋π3＝2k π(k ∈Z )，故x 的集合为{x |x ＝k π－π6，k ∈Z }．(2)由f (B ＋C )＝cos ⎣⎢⎡⎦⎥⎤2（B ＋C ）＋π3＋1＝32，可得cos ⎝⎛⎭⎪⎫2A －π3＝12，由A ∈(0，π)，可得A ＝π3.在△ABC 中，由余弦定理，得a 2＝b 2＋c 2－2bc cos π3＝(b ＋c )2－3bc ，由b ＋c ＝2，知bc ≤⎝ ⎛⎭⎪⎫b ＋c 22＝1，当b ＝c ＝1时，bc 取最大值，此时a 取最小值1.[预测押题1] 解：(1)由已知得AB →·AC →＝bc cos θ＝8，b 2＋c 2－2bc cos θ＝42，故b 2＋c 2＝32.又b 2＋c 2≥2bc ，所以bc ≤16，(当且仅当b ＝c ＝4时等号成立)，即bc 的最大值为16.即8cos θ≤16，所以cos θ≥12.又0<θ<π，所以0<θ≤π3，即θ的取值范围是(0，π3]．(2)f (θ)＝3sin2θ＋cos2θ＋1＝2sin ⎝⎛⎭⎪⎫2θ＋π6＋1.因为0<θ≤π3，所以π6<2θ＋π6≤5π6，12≤sin ⎝⎛⎭⎪⎫2θ＋π6≤1.当2θ＋π6＝5π6，即θ＝π3时，f (θ)min ＝2×12＋1＝2；当2θ＋π6＝π2，即θ＝π3时，f (θ)max ＝2×1＋1＝3.[例2] 解：(1)在△ABC 中，因为cos A ＝1213，cos C ＝35，所以sin A ＝513，sin C ＝45.从而sin B ＝sin[π－(A ＋C )]＝sin(A ＋C )＝sin A cos C ＋cos A sin C ＝513×35＋1213×45＝6365.由正弦定理AB sin C ＝AC sin B ，得AB ＝ACsin B ×sin C ＝12606365×45＝1040(m)．所以索道AB 的长为1040m. (2)假设乙出发t 分钟后，甲、乙两游客距离为d ，此时，甲行走了(100＋50t )m ，乙距离A 处130t m ，所以由余弦定理得d 2＝(100＋5t )2＋(130t )2－2×130t ×(100＋50t )×1213＝200(37t 2－70t ＋50)，因0≤t ≤1040130，即0≤t ≤8，故当t ＝3537(min)时，甲、乙两游客距离最短．(3)由正弦定理BC sin A ＝AC sin B ，得BC ＝AC sin B ×sin A ＝12606365×513＝500(m)．乙从B 出发时，甲已经走了50×(2＋8＋1)＝550(m)，还需要走710m 才能到达C .设乙步行的速度为v m/min ，由题意得－3≤500v －71050≤3，解得125043≤v ≤62514，所以使两位游客在C 处互相等待的时间不超过3min ，乙步行的速度控制在⎣⎢⎡⎦⎥⎤125043，62514(单位：m/min)范围内．[预测押题2] 解：(1)因为点C 的坐标为⎝ ⎛⎭⎪⎫35，45，根据三角函数的定义，得sin ∠COA ＝45，cos ∠COA ＝35.因为△AOB 为正三角形，所以∠AOB ＝60°.所以cos ∠BOC ＝cos (∠COA ＋60°)＝cos ∠COA cos60°－sin ∠COA sin60°＝35×12－45×32＝3－4310.(2)因为∠AOC ＝θ⎝⎛⎭⎪⎫0<θ<π2，所以∠BOC ＝π3＋θ.在△BOC 中，|OB |＝|OC |＝1，由余弦定理，可得f (θ)＝|BC |2＝|OC |2＋|OB |2－2|OC |·|OB |·cos ∠COB ＝12＋12－2×1×1×cos ⎝ ⎛⎭⎪⎫θ＋π3＝2－2cos ⎝⎛⎭⎪⎫θ＋π3.因为0<θ<π2，所以π3<θ＋π3<5π6.所以－32<cos ⎝ ⎛⎭⎪⎫θ＋π3<12.所以1<2－2cos ⎝ ⎛⎭⎪⎫θ＋π3<2＋ 3.所以函数f (θ)的值域为(1，2＋3)．第三讲平面向量基础·单纯考点[例1] 解析：以向量：a 的终点为原点，过该点的水平和竖直的网格线所在直线为x 轴、y 轴建立平面直角坐标系，设一个小正方形网格的边长为1，则a ＝(－1，1)，b ＝(6，2)，c ＝(－1，－3)．由c ＝λa ＋μb ，即(－1，－3)＝λ(－1，1)＋μ(6，2)，得－λ＋6μ＝－1，λ＋2μ＝－3，故λ＝－2，μ＝－12，则λμ＝4.答案：4[预测押题1] (1)选A 由已知，得AB →＝(3，－4)，所以|AB →|＝5，因此与AB →同方向的单位向量是15AB →＝⎝ ⎛⎭⎪⎫35，－45.(2)选C 如图，连接BP ，则AP →＝AC →＋CP →＝b ＋PR →，① AP →＝AB →＋BP →＝a ＋RP →－RB →，②①＋②，得2AP →＝a ＋b －RB →.③ 又RB →＝12QB →＝12(AB →－AQ →)＝12⎝ ⎛⎭⎪⎫a －12AP →，④将④代入③，得2AP →＝a ＋b －12⎝⎛⎭⎪⎫a －12AP →，解得AP →＝27a ＋47b .[例2] 解析：(1)由已知得AB →＝(2，1)，CD →＝(5，5)，因此AB →在CD →方向上的投影为AB →·CD →|CD →|＝1552＝322.(2)设AB 的长为a (a >0)，又因为AC →＝AB →＋AD →，BE →＝BC →＋CE →＝AD →－12AB →，于是AC →·BE →＝(AB→＋AD →)·(AD →－12AB →)＝12AB →·AD →－12AB →2＋AD →2＝－12a 2＋14a ＋1，由已知可得－12a 2＋14a ＋1＝1.又a >0，∴a ＝12，即AB 的长为12.答案：(1)A (2)12[预测押题2] (1)选D a ⊥(a ＋b)⇒a ·(a ＋b )＝a 2＋a·b ＝|a |2＋|a ||b |cos<a ，b >＝0，故cos<a ，b >＝－963＝－32，故所求夹角为5π6.(2)选C 设BC 的中点为M ，则AG →＝23AM →.又M 为BC 中点，∴AM →＝12(AB →＋AC →)，∴AG →＝23AM →＝13(AB →＋AC →)，∴|AG →|＝13AB →2＋AC →2＋2AB →·AC →＝13AB →2＋AC →2－4.又∵AB →·AC →＝－2，∠A ＝120°，∴|AB →||AC →|＝4.∵|AG →|＝13AB →2＋AC →2－4≥132|AB →||AC →|－4＝23，当且仅当|AB →|＝|AC→|时取等号，∴|AG →|的最小值为23.交汇·创新考点[例1] 解析：设P (x ，y )，则AP →＝(x －1，y ＋1)．由题意知AB →＝(2，1)，AC →＝(1，2)．由AP →＝λAB →＋μAC →知(x －1，y ＋1)＝λ(2，1)＋μ(1，2)，即⎩⎪⎨⎪⎧2λ＋μ＝x －1，λ＋2μ＝y ＋1.∴⎩⎪⎨⎪⎧λ＝2x －y －33，μ＝2y －x ＋33，∵1≤λ≤2，0≤μ≤1，∴⎩⎪⎨⎪⎧3≤2x －y －3≤6，0≤2y －x ＋3≤3.作出不等式组表示的平面区域(如图阴影部分)，由图可知平面区域D 为平行四边形，可求出M (4，2)，N (6，3)，故|MN |＝ 5.又x －2y ＝0，x －2y －3＝0之间的距离d ＝35，故平面区域D 的面积为S ＝5×25＝3.答案：3[预测押题1] 选D 如图作可行域，z ＝OA →·OP →＝x ＋2y ，显然在B (0，1)处z max ＝2.故选D.[例2] 解：(1)∵g (x )＝sin(π2＋x )＋2cos(π2－x )＝2sin x ＋cos x ，∴OM →＝(2，1)，∴|OM →|＝22＋12＝ 5.(2)由已知可得h (x )＝sin x ＋3cos x ＝2sin(x ＋π3)，∵0≤x ≤π2，∴π3≤x ＋π3≤5π6，∴h (x )∈[1，2]．∵当x ＋π3∈[π3，π2]时，即x ∈[0，π6]时，函数h (x )单调递增，且h (x )∈[3，2]；当x ＋π3∈(π2，5π6]时，即x ∈(π6，π2]时，函数h (x )单调递减，且h (x )∈[1，2)．∴使得关于x 的方程h (x )－t ＝0在[0，π2]内恒有两个不相等实数解的实数t 的取值范围为[3，2)．[预测押题2] 解：(1)由题设，可得(a ＋b )·(a －b )＝0，即|a |2－|b |2＝0.代入a ，b的坐标，可得cos 2α＋(λ－1)2sin 2α－cos 2β－sin 2β＝0，所以(λ－1)2sin 2α－sin 2α＝0.因为0<α<π2，故sin 2α≠0，所以(λ－1)2－1＝0，解得λ＝2或λ＝0(舍去，因为λ>0)．故λ＝2.(2)由(1)及题设条件，知a·b ＝cos αcos β＋sin αsin β＝cos(α－β)＝45.因为0<α<β<π2，所以－π2<α<β<0.所以sin(α－β)＝－35，tan(α－β)＝－34.所以tan α＝tan[(α－β)＋β]＝tan （α－β）＋tan β1－tan （α－β）tan β＝－34＋431－（－34）×43＝724.所以tan α＝724.[例3] 选D a ∘b ＝a·b b 2＝|a||b||b|2cos θ＝|a||b|cos θ，b ∘a ＝|a||b|cos θ，因为|a |>0，|b |>0，0<cos θ<22，且a ∘b 、b ∘a ∈⎩⎨⎧⎭⎬⎫n 2|n ∈Z ，所以|a||b|cos θ＝n 2，|a||b|cos θ＝m 2，其中m ，n ∈N *，两式相乘，得m ·n 2＝cos 2θ.因为0<cos θ<22，所以0<cos 2θ<12，得0<m ·n <2，故m＝n ＝1，即a ∘b ＝12.[预测押题3] 选D 依题意，MF 1→＝(－1－x ，－y )＝(－1－x )e 1－y e 2，MF 2→＝(1－x ，－y )＝(1－x )e 1－y e 2，由|MF 1→|＝|MF 2→|，得MF 1→2＝MF 2→2，∴[(－1－x )e 1－y e 2]2＝[(1－x )e 1－y e 2]2，∴4x ＋4y e 1·e 2＝0.∵∠xOy ＝45°，∴e 1·e 2＝22，故2x ＋2y ＝0，即2x ＋y ＝0.专题三数列第一讲等差数列、等比数列基础·单纯考点[例1] 解析：(1)∵{a n }是等差数列，S m －1＝－2，S m ＝0，∴a m ＝S m －S m －1＝2.∵S m ＋1＝3，∴a m ＋1＝S m ＋1－S m ＝3，∴d ＝a m ＋1－a m ＝1.又S m ＝m （a 1＋a m ）2＝m （a 1＋2）2＝0，∴a 1＝－2，∴a m＝－2＋(m －1)·1＝2，∴m ＝5.(2)设等比数列{a n }的首项为a 1，公比为q ，则：由a 2＋a 4＝20得a 1q (1＋q 2)＝20，①，由a 3＋a 5＝40得a 1q 2(1＋q 2)＝40.②由①②解得q ＝2，a 1＝2.故S n ＝a 1（1－q n ）1－q ＝2（1－2n ）1－2＝2n ＋1－2.答案：(1)C (2)2 2n ＋1－2[预测押题1] 解：(1)设等差数列的公差为d ，d >0.由题意得，(2＋d )2＝2＋3d ＋8，d 2＋d －6＝(d ＋3)(d －2)＝0，得d ＝2.故a n ＝a 1＋(n －1)·d ＝2＋(n －1)·2＝2n ，故a n ＝2n .(2)b n ＝a n ＋2a n ＝2n ＋22n .S n ＝b 1＋b 2＋…＋b n ＝(2＋22)＋(4＋24)＋…＋(2n ＋22n)＝(2＋4＋6＋...＋2n )＋(22＋24＋ (22))＝（2＋2n ）·n 2＋4·（1－4n ）1－4＝n 2＋n ＋4n ＋1－43.[例2] 解：(1)设数列{a n }的公比为q (q ≠0，q ≠1)，由a 5，a 3，a 4成等差数列，得2a 3＝a 5＋a 4，即2a 1q 2＝a 1q 4＋a 1q 3.由a 1≠0，q ≠0得q 2＋q －2＝0，解得q 1＝－2，q 2＝1(舍去)，。

数学三维设计一轮复习资料

数学三维设计一轮复习资料数学三维设计是高考数学难度较大的一项，要求考生在三维几何空间中进行计算和分析，并能够进行图形的设计与实现。

由于数学三维设计的考察范围涉及的知识点较多且难度较大，因此对于考生来说复习备考不可掉以轻心。

在这篇文章中，我将会为大家整理一些数学三维设计的复习资料，以帮助大家更好地备考。

一、知识点整理要备考数学三维设计，首先需要掌握相关的知识点和概念。

数学三维设计的考察范围包括了三维几何空间的基本概念、向量的应用、直线和平面的方程、球面的方程、圆锥曲线的方程和参数方程等等。

在备考的过程中，我们需要将这些内容进行分类整理，进行深入的理解和掌握。

二、例题练习例题练习是备考数学三维设计时必不可少的环节。

通过高质量的例题练习，我们能够切实提高自己的解题能力和应试经验。

在备考过程中，我们可以通过参考历年高考数学试题中的数学三维设计部分来进行例题练习。

同时，我们也可以通过参考教辅材料中的例题进行深入的训练。

三、模拟测试模拟测试是检测备考成果的重要环节，有效的模拟测试练习可以帮助我们全面地了解自己的备考成果和复习情况，并及时发现和解决存在的问题。

在备考过程中，我们可以通过模拟考试来检测自己的备考水平并提高应试能力。

此外，备考时还可以参加各类模拟考试，学习不同的解题方法和策略。

四、思维拓展数学三维设计不仅考验了考生的计算能力和操作水平，同时也考察了考生的思维能力和逻辑思维能力。

因此，在备考过程中，我们需要注意深入理解和扩展思维。

从历史的数学思想到现代的科技应用，我们需要通过多方面的学习和了解来扩展自己的思维。

五、课程辅导针对某些难点和需要进一步澄清的知识，我们可以参加数学相关的培训或课程辅导。

这些课程辅导不仅可以为我们解答疑惑，更可以帮助我们系统性地学习和掌握数学三维设计的相关内容。

以上就是关于数学三维设计一轮复习资料的整理总结。

备考数学三维设计需要我们掌握基本的知识点和概念，通过例题练习和模拟测试来巩固和提高应试经验，同时还需要拓展思维，吸收多方面的思考和理解。

《三维设计》高考数学

解答題増分TT系列讲座〔六〕QJJ I EDATI ZENC I FEN XILIE IIANCIZUO“概率与统计〞类题目的审题技巧与解题标准［审题技巧］宙图表’明目标［技法概述］在高考的实际综合应用问题中，题目中的图表、数据包含着问题的根本信息，也往往暗示着解决问题的目标和方向，在审题时，要认真观察分析图表、数据的特征和规律，为问题解决提供有助的方法.［适用题型］在高考中以下几种题型常用到此审题方法：(1) 概率与统计局部；(2) 回归分析与统计案例；(3) 算法与程序框图•［解题标准］［典例］(2021湖•南高考)(此题总分值12分)某人在如下图的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物•根据历年的种植经验，一株该种作物的年收获量Y(单位：kg)与它的“相近〞作物株数X之间的关系如下表所示：X1234Y51484542这里，两株作物“相近〞是指它们之间的直线距离不超过1米.(1)从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近〞的概率;⑵从所种作物中随机选取一株，求它的年收获量的分布列与数学期望.［解题步步标准1［解题流程］第一步由图表确定总株数及内部株数，边界株数. 第二步计算事件根本数及所求事件数.第三步解：1所种作物总株数N = 1 + 2+ 3 ? +4 + 5= 15,其中三角形地块内部的作物株数为3,边界上的作物株数为12.从三角形地块的内部和边界上分别随机选取一株的不同结果有c 3C i2 = 36种, ?选取的两株作物恰好“相近〞的不同结果有3 + 3 + 2 = 8种.［失分警示］ ——结合图形准确计算“相近〞的结果易无视某一类导致结果计算出错求円戶51)数晨m1的值h^J期卑第2问求概率.第四步故从三角形地块的内部和边界上分别随机选取一株作物，它们恰好“相近〞的概率为36=9.2先求从所种作物中随机选取的一株作物的年收获量丫的分布列.因为 P Y = 51 = P X = 1 , P Y = 48 = PP Y = 45 = P X = 3 , P Y = 42 = P•转化变量间关系如 P Y = 51 = PX = 1 是关键.对Y 的每个取值相对应的概率求法易失误量Y 取值：所以只需求出PX = k k = 1 , 2, 3, 4即可. 记九为其“相近〞作物恰有k 株的作物株数 k = 1, 2, 3, 4，那么 n 1 = 2,匕=4,出=6,加=3.得 PX = 1 = £4 6 2 31PX =2 = 15，PX = 3 = 15= 5，PX =4 = 15= 5. 9分的概率.■故所求的分布列为1 34+ 64+9°+ 化 46. 12分第五步井析泊FI 峙踪论，佛紀所求-4#. M 相.程两•嗽值诵宜隧机戏啟用所样町噩収慎・值的戦抓条门弋KM ：査醱.朮肾"bi 町能〔M 对川的W 〔卓话哉如辿韦I乏 H 伯廿斎列.利用井布网豹性朋世订检验是杳准射1. 〔2021武昌模拟〕某市准备从7名报名者〔其中男4人，女3人〕中选3人参加三个副局长职务竞选.为女副局长的概率.解：〔1〕依题意，X 可取0,1,2,3 ,故X 的分布列为3X 5 1⑵记D = “A 局是男副局长〞，E = “B 局是女副局长〞，贝U P 〔E|D 〕 = 6X5 = 2-第五步写出Y 的分布列.？第六步求期望.〔7分〕所求的数学期望为E Y = 51 X 15 + 48 X 15 + 45 X | +42 15 15 5•计算期望法由于不细心、易算错，导致丢2分模板形成［解答题观范专练］概率与统计第二加利用匚他和H<瓷进点、闔钿点〔1〕设所选3人中女副局长人数为 X , 求X 的分布列;〔2〕假设选派三个副局长依次到 A , B , C 三个局上任，求 A 局是男副局长的情况下,P (X =0)=C 7= 35, P (X = 1)=曲_ 18 C 7= 35，C® 12P (x =2) = CCT = 32, C 3丄 P (x =3)=C 7= 35，2•某单位举行一次全体职工的象棋比赛〔实行三局两胜制〕，甲、乙两人进入决赛.甲、乙两人平时进行过屡次对弈，其中记录了30局的对弈结果如右表:根据表中的信息，预测在以下条件下的比赛结果:〔1〕在比赛时由掷硬币的方式决定谁先，试求甲在第一局获胜的概率;⑵假设第一局由乙先，以后每局由负者先.①求甲以二比一获胜的概率；②假设胜一局得2分，负一局得0分，用E表示甲在这场比赛中所得的分数，试求布列与数学期望E〔8.解：根据题中表格的信息可知，假设甲先，那么甲获胜的概率是2 12，乙获胜的概率是1假设乙3 2先，那么甲获胜的概率是？乙获胜的概率是~.5 51 2 1 3 19〔1〕甲在第一局获胜的概率是P1 =尹3 +寸5 =五.⑵①假设甲以二比一获胜，那么甲胜第一局和第三局，或甲胜第二局和第三局.所以，甲以二比一获胜的概率是P2= 3x 2x 2+ 2x 2x 3=色P2 5 5 3^ 5 3 5 25.②由题意知，E的所有可能取值为0,2,4，那么2「2 P(E=0)=5X1= 15；P(三=2) = 2x 打-x-P(' 2) 5 5 3十5 3x5=玮；P&4) = 3X 3+血=立P(' 4) 5 5 25 25.所以E的分布列为2 14 17 232E(8=0 x-+2X 74+4x27=石.3 . 〔2021成都模拟〕某校高三〔1〕班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见局部如下：试根据图表中的信息解答以下问题:〔1〕求全班的学生人数及分数在［70,80〕之间的频数；〔2〕为快速了解学生的答题情况，老师按分层抽样的方法从位于［70,80〕，［80,90〕和［90,100］分数段的试卷中抽取8份进行分析，再从中任选3人进行交流，求交流的学生中成绩位于［70,80〕分数段的人数X的分布列和数学期望.解：〔1〕由茎叶图可知，分数在［50,60〕上的频数为4,频率为0.008X 10= 0.08，故全班的4学生人数为0-4〕8= 50.分数在［70,80〕之间的频数等于50 —〔4 + 14+ 8 + 4〕= 20.〔2〕按分层抽样原理，三个分数段抽样数之比等于相应人数之比.又［70,80〕, ［80,90〕和［90,100］分数段人数之比等于5 ：2 ：1，由此可得抽出的样本中分数在［70,80〕之间的有5人，分数在［80,90〕之间的有2人，分数在［90,100］之间的有1人.从中任取3人，共有C8= 56种不同的结果.被抽中的成绩位于［70,80〕分数段的学生人数X的所有取值为0,1,2,3.它们的概率分别是：C3 1 C s C3 15 c5c3 30 15 C3 10 5 P〔x =0〕=56= 56, P〔x=1〕=w=56，P〔x=2〕=石=辰=28, P〔X=3〕=56=56=云•••X的分布列为X0123P1r 1515:5 56562828卑叶=<3668~013334J5077889了L334454T1 15 15 5 105 15 •••x 的数学期望为E〔x〕= o x 56+仆15+2X云+3X28=105= 8。

《三维动画设计》试题与答案

《三维动画设计》试题与答案单选题[1]、将下面工作视图中图1用户视图的显示内容调整成图2的显示内容，应进行的最准确操作是（）。

图1 图2【答案】D【分数】1分【选项】A、直接打开渲染工具，进行渲染B、调整冰激凌机模型的材质高光和背景颜色C、在该视图显示模式中打开Active Shade显示模式D、在图1红色箭头所示的位置单击鼠标右键，在弹出菜单的视图项中选择Active Shade视图[2]、移动物体有多种坐标轴模式，如果要将图1中红线框选物体的轴向模式改变成图2中红线框选物体的轴向模式，应执行的正确操作是（）。

图1 图2图3【答案】B【分数】1分【选项】A、移动它的坐标轴方向B、选择图3中的【局部】坐标系统C、选择图3中的【视图】坐标系统D、选择图3中的【世界】坐标系统[3]、如下图所示，在建立一些尺寸精度较高的工业造型时，需要对某个造型细节进行精确变换。

可以打开【移动变换输入】对话框，准确地输入该造型移动的方向和距离的操作是（）。

【答案】C【分数】1分【选项】A、将光标移动到主工具栏中的任意工具按钮上，单击鼠标右键B、将光标移动到主工具栏中的【移动】按钮上，单击鼠标中键C、将光标移动到主工具栏中的【移动】按钮上，单击鼠标右键D、将光标移动到主工具栏中的任意工具按钮上，单击鼠标左键[4]、三维动画渲染的图像尺寸取决于最终播出平台的标准，下列渲染输出尺寸设置中，中国大陆的电视模拟信号标准是（）。

【答案】D【分数】1分【选项】A、NTSC D-1B、PAL D-1，尺寸是720×480C、HDTV，1920×1080D、PAL D-1，尺寸是720×576[5]、当制作复杂的max项目时，经常会在不同的场景中创建项目所需的模型，然后将所有模型整合到一个场景中。

现在要将一个名为“汽船”的模型文件引入到当前的户外场景中，下列操作正确的是（）。

【答案】B【分数】1分【选项】A、选择【文件】->【替换】命令，将“汽船.max”输入进来B、选择【文件】->【合并】命令，将“汽船.max”合并进来C、选择【文件】->【合并动画】命令，将“汽船.max”合并进来D、选择【文件】->【保存副本为】命令，将“汽船.max”输入进来[6]、有效的使用捕捉工具能让操作更准确和快速，如下图1所示。

高中数学立体几何 10.三视图技巧

高中数学 | 三视图还原——七字真言闯天下解决三视图问题，尤其是一些比较复杂的三视图还原问题，需要极强的空间想象能力．这给好多同学（包括一些空间想象能力挺强的同学）造成了一定的压力，如果在高考中碰到一个稍有些不常规的三视图，绝对会给在高考中以数学成绩为倚傍的同学设置了一道拦路虎，要是稍微一心慌，那我们与这一道分题就失之交臂了，也会给后面的答题造成心理影响．比如2014年全国1卷第12题，当时就将相当大一部分同学斩于马下．今天小编就带领大家为曾经在类似这样的三视图还原问题上折戟沉沙的同学报仇雪恨．我们的口号是“七字真言扫天下，不破胡虏誓不归．”就从这道高考题入手吧．2014年高考全国 I 卷理科第12题（选择压轴题）：如图，网格纸上小正方形的边长为，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度是（）A ．26B ．6C ．24D ．4正确答案是 B ．解由三视图可知，原几何体的长、宽、高均为，所以我们可用一个正方体作为载体对三视图进行还原．先画出一个正方体，如图（1）：第一步，根据正视图，在正方体中画出正视图上的四个顶点的原象所在的线段，这里我们用红线表示．如图（2），即正视图的四个顶点必定是由图中红线上的点投影而成的．第二步，左视图有三个顶点，画出它们的原象所在的线段，用蓝线表示，如图（3）．第三步，俯视图有三个顶点，画出它们的原象所在的线段，用绿线表示，如图（4）．最后一步，三种颜色线的公共点（只有两种颜色线的交点不行）即为原几何体的顶点，连接各顶点即为原几何体，如图（5）．至此，易知哪条棱是最长棱，求出即可．大家是不是体会到了用这种方法还原三视图的妙处呢？这种方法的核心其实就是七个字：“三线交汇得顶点”．这样是不是比我们以前那种天马行空的遐想接地气一些呢？由此，我们在三视图还原上就可以七字真言扫天下了．注一此方法更适用于解决三棱锥的问题，画直观图后需要验证一下是否符合．注二参考文章：下面给出一道练习．如图，网格纸上的小正方形的边长为，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为______．答案是．提示如图．。

2014年高考数学真题汇编(含答案)：数列

2014年全国高考理科数学试题分类汇编(纯word 解析版) 十一、数列（逐题详解）第I 部分1.【2014年重庆卷（理02）】对任意等比数列{}n a ,下列说法一定正确的是（）139.,,A a a a 成等比数列 236.,,B a a a 成等比数列 248.,,C a a a 成等比数列 369.,,D a a a 成等比数列【答案】D【解析】设{}n a 公比为q ，因为336936,a aq q a a ==，所以369,,a a a 成等比数列，选择D2.【2014年福建卷（理03）】等差数列{a n }的前n 项和为S n ，若a 1=2，S 3=12，则a 6等于（） A ．8 B ．10 C ．12 D ．14【答案】C【解析】由题意可得S 3=a 1+a 2+a 3=3a 2=12，解得a 2=4，∴公差d=a 2﹣a 1=4﹣2=2，∴a 6=a 1+5d=2+5×2=12，故选：C ．3.【2014年辽宁卷（理08）】设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（）A ．0d C ．10a d <D ．10a d >【答案】C【解析】∵等差数列{a n }的公差为d ，∴a n+1﹣a n =d ，又数列{2}为递减数列，∴=＜1，∴a 1d ＜0．故选：C4.【2014年全国大纲卷（10）】等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于（）A ．6B ．5C ．4D ．3【答案】C【解析】∵等比数列{a n }中a 4=2，a 5=5，∴a 4•a 5=2×5=10，∴数列{lga n }的前8项和S=lga 1+lga 2+…+lga 8=lg （a 1•a 2…a 8）=lg （a 4•a 5）4=4lg （a 4•a 5）=4lg10=4故选：C第II 部分5.【2014年上海卷（理08）】设无穷等比数列{}n a 的公比为q ，若()134lim n n a a a a →∞=+++，则q = .【答案】q =【解析】：22311110112a a q a q q q q q -±==⇒+-=⇒=--，∵01q <<，∴q =6.【2014年广东卷（理13）】若等比数列{}n a 的各项均为正数，且512911102e a a a a =+，则1220ln ln ln a a a +++= 。

【三维设计】高考数学一轮复习第5节函数的图像课件

A．(－1,1]∪(2，＋∞)
B．(－2，－1]∪(1,2]
C．(－∞，－2)∪(1,2]
D．[－2，－1]
依题意可得
[巧妙运用]
f(x)＝xx2－－12，，x－＜1－≤1x或≤x2＞，2，作出其示意图如图所示．由数形结合知，实数c需有1＜c≤2或－2＜c≤－1.
答案：B
[题后悟道] 解答本题利用了数形结合思想，属于“以形助数”，是指把某些抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，揭示数学问题的本质．本题首先作出f(x) 的图象，观察图象上、下平移后与x轴交点情况确定c的范围，应注意c的端点值．
答案： D
[冲关锦囊] “看图说话”常用的方法有 (1)定性分析法：通过对问题进行定性的分析，从而得出图像的上升(或下降)的趋势，利用这一特征分析解决问题． (2)定量计算法：通过定量的计算来分析解决问题． (3)函数模型法：由所提供的图像特征，联想相关函数模型，利用这一函数模型来分析解决问题.
[精析考题]
[例3] (2011·新课标全国卷)已知函数y＝f(x)的周期为2，
当x∈[－1,1]时f(x)＝x2，那么函数y＝f(x)的图像与函数y
＝|lg x|的图像的交点共有
()
A．10个
Bபைடு நூலகம்9个
C．8个
D．1个
[自主解答] 根据f(x)的性质及f(x)在[－1,1]上的解析式可作图如下：
答案： B
4．(教材习题改编)为了得到函数y＝2x－3的图像，只需把函数y＝2x的图像上所有的点向______平移______ 个单位长度．答案：右 3
5．若关于x的方程|x|＝a－x只有一个解，则实数a的取值范围是________．

立体几何高考题_模拟试题带答案解析

WORP文档下载可编辑2014 高考及模拟立体几何带答案一．解答题（共17小题）1．(2014•山东）如图，四棱锥P﹣ABCD中，AP⊥平面PCD,AD∥BC，AB=BC=AD,E，F分别为线段AD，PC的中点．（Ⅰ)求证：AP∥平面BEF；(Ⅱ）求证：BE⊥平面PAC．2．（2014•四川）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明:直线BC⊥平面ACC1A1;（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M,使直线DE∥平面A1MC？请证明你的结论．3．（2014•湖北）在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．（Ⅰ）求证：BE∥平面PAD;（Ⅱ)求证：BC⊥平面PBD；（Ⅲ）设Q为侧棱PC上一点,，试确定λ的值，使得二面角Q﹣BD﹣P为45°．4．（2014•江苏）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：(1)直线PA∥平面DEF;（2）平面BDE⊥平面ABC．5．（2014•黄山一模）如图，PA垂直于矩形ABCD所在的平面，AD=PA=2，CD=2,E、F分别是AB、PD的中点．(1)求证：AF∥平面PCE；(2)求证：平面PCE⊥平面PCD;(3）求四面体PEFC的体积．6．（2014•南海区模拟）如图，四棱锥P﹣ABCD的底面是直角梯形，AB∥CD,AB⊥AD，△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点，E为PA的中点．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ)求证:OE∥平面PDC；(Ⅲ)求直线CB与平面PDC所成角的正弦值．7．（2014•天津模拟)如图，在四棱台ABCD﹣A1B1C1D1中，下底ABCD是边长为2的正方形，上底A1B1C1D1是边长为1的正方形，侧棱DD1⊥平面ABCD，DD1=2．(1）求证：B1B∥平面D1AC；（2)求证：平面D1AC⊥平面B1BDD1．8．（2013•北京）如图,在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB,平面PAD⊥底面ABCD，PA⊥AD．E和F分别是CD和PC的中点，求证:(Ⅰ）PA⊥底面ABCD；（Ⅱ）BE∥平面PAD;（Ⅲ）平面BEF⊥平面PCD．9．(2013•天津）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．（Ⅰ）证明：EF∥平面A1CD；（Ⅱ)证明:平面A1CD⊥平面A1ABB1;（Ⅲ）求直线BC与平面A1CD所成角的正弦值．10．(2013•浙江）如图，在四棱锥P﹣ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=,PA=,∠ABC=120°，G为线段PC上的点．(Ⅰ）证明：BD⊥平面PAC；(Ⅱ）若G是PC的中点,求DG与PAC所成的角的正切值；(Ⅲ）若G满足PC⊥面BGD，求的值．11．（2013•湖南）如图．在直棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=,AA1=3，D是BC的中点，点E在棱BB1上运动．（1)证明：AD⊥C1E；(2)当异面直线AC，C1E 所成的角为60°时,求三棱锥C1﹣A1B1E的体积．12．（2012•山东）如图,几何体E﹣ABCD是四棱锥，△ABD为正三角形,CB=CD，EC⊥BD．（Ⅰ）求证:BE=DE;（Ⅱ)若∠BCD=120°，M为线段AE的中点，求证：DM∥平面BEC．13．（2012•江苏)如图,在直三棱柱ABC﹣A1B1C1中，A1B1=A1C1，D，E分别是棱BC，CC1上的点（点D 不同于点C），且AD⊥DE，F为B1C1的中点．求证：（1)平面ADE⊥平面BCC1B1；(2）直线A1F∥平面ADE．14．（2011•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点．（Ⅰ）证明：PB∥平面ACM；（Ⅱ）证明：AD⊥平面PAC；(Ⅲ）求直线AM与平面ABCD所成角的正切值．15．(2011•北京)如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；(Ⅱ）若PA=AB，求PB与AC所成角的余弦值;（Ⅲ)当平面PBC与平面PDC垂直时，求PA的长．16．（2010•深圳模拟）如图，在四棱锥S﹣ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD，E、F分别是AB、SC 的中点（1）求证:EF∥平面SAD（2)设SD=2CD，求二面角A﹣EF﹣D的大小．17．（2010•重庆）如图，三棱锥P﹣ABC中,PC⊥平面ABC，PC=AC=2,AB=BC，D是PB上一点，且CD⊥平面PAB．（1）求证:AB⊥平面PCB；（2)求二面角C﹣PA﹣B的大小的余弦值．2014年12月05日180********的高中数学组卷参考答案与试题解析一．解答题（共17小题）1．（2014•山东）如图，四棱锥P﹣ABCD中,AP⊥平面PCD，AD∥BC，AB=BC=AD，E，F分别为线段AD，PC的中点．（Ⅰ）求证：AP∥平面BEF；(Ⅱ)求证：BE⊥平面PAC．考点：直线与平面垂直的判定；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（Ⅰ)证明四边形ABCE是平行四边形,可得O是AC的中点，利用F为线段PC的中点，可得PA∥OF,从而可证AP∥平面BEF；（Ⅱ）证明BE⊥AP、BE⊥AC,即可证明BE⊥平面PAC．解答:证明：（Ⅰ）连接CE,则∵AD∥BC，BC=AD，E为线段AD的中点，∴四边形ABCE是平行四边形,BCDE是平行四边形，设AC∩BE=O，连接OF，则O是AC的中点，∵F为线段PC的中点，∴PA∥OF，∵PA⊄平面BEF，OF⊂平面BEF,∴AP∥平面BEF；（Ⅱ）∵BCDE是平行四边形，∴BE∥CD，∵AP⊥平面PCD，CD⊂平面PCD，∴AP⊥CD，∴BE⊥AP，∵AB=BC，四边形ABCE是平行四边形,∴四边形ABCE是菱形,∴BE⊥AC，∵AP∩AC=A，∴BE⊥平面PAC．点评：本题考查直线与平面平行、垂直的判定，考查学生分析解决问题的能力，正确运用直线与平面平行、垂直的判定是关键2．(2014•四川）在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ)设D、E分别是线段BC、CC1的中点,在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．考点: 直线与平面垂直的判定；直线与平面平行的判定．专题: 综合题；空间位置关系与距离．分析：（Ⅰ）先证明AA1⊥平面ABC，可得AA1⊥BC，利用AC⊥BC，可以证明直线BC⊥平面ACC1A1；(Ⅱ)取AB的中点M，连接A1M，MC,A1C,AC1,证明四边形MDEO为平行四边形即可．解答：(Ⅰ）证明：∵四边形ABB1A1和ACC1A1都为矩形,∴AA1⊥AB，AA1⊥AC，∵AB∩AC=A，∴AA1⊥平面ABC，∵BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AA1∩AC=A，∴直线BC⊥平面ACC1A1；（Ⅱ）解:取AB的中点M，连接A1M，MC，A1C，AC1,设O为A1C,AC1的交点，则O为AC1的中点．连接MD,OE，则MD∥AC,MD=AC,OE∥AC,OE=AC，∴MD∥OE,MD=OE，连接OM,则四边形MDEO为平行四边形，∴DE∥MO，∵DE⊄平面A1MC，MO⊂平面A1MC,∴DE∥平面A1MC,∴线段AB上存在一点M（线段AB的中点），使直线DE∥平面A1MC．点评：本题考查线面垂直的判定与性质的运用,考查存在性问题，考查学生分析解决问题的能力,属于中档题．3．(2014•湖北）在四棱锥P﹣ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1，CD=2．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）求证：BC⊥平面PBD；（Ⅲ）设Q为侧棱PC上一点，，试确定λ的值，使得二面角Q﹣BD﹣P为45°．考点：直线与平面平行的判定；直线与平面垂直的判定；与二面角有关的立体几何综合题．专题: 证明题．分析:（Ⅰ）取PD的中点F，连接EF、AF，由中位线得性质和AB∥CD及AB=1证出四边形ABEF为平行四边形，则BE∥AF，根据线面平行的判定得BE∥平面PAD；(Ⅱ）由平面PCD⊥底面ABCD,PD⊥CD证出PD⊥AD，利用三条线相互垂直关系,建立直角坐标系，求出,即BC⊥DB，再由PD⊥平面ABCD,可得PD⊥BC，即证BC⊥平面PBD;（Ⅲ）利用(Ⅱ）建立的坐标系和结论，求出平面PBD的法向量，利用求出Q的坐标，再利用垂直关系求平面QBD的法向量的坐标，由两个法向量的数量积运算表示二面角的余弦值,化简后求出λ∈（0，1）的值．解答:解：（Ⅰ）取PD的中点F，连接EF，AF，∵E为PC中点，∴EF∥CD，且，在梯形ABCD中,AB∥CD,AB=1，∴EF∥AB，EF=AB,∴四边形ABEF为平行四边形,∴BE∥AF，∵BE⊄平面PAD，AF⊂平面PAD，∴BE∥平面PAD．（4分）（Ⅱ）∵平面PCD⊥底面ABCD，PD⊥CD，∴PD⊥平面ABCD，∴PD⊥AD．(5分）如图，以D为原点建立空间直角坐标系D﹣xyz．则A（1，0，0)，B（1,1,0），C（0，2，0）,P（0，0，1）．（6分），，∴,BC⊥DB，（8分)又由PD⊥平面ABCD,可得PD⊥BC，∴BC⊥平面PBD．（9分）（Ⅲ)由（Ⅱ)知,平面PBD的法向量为，（10分）∵，,且λ∈（0，1）∴Q(0，2λ，1﹣λ），（11分）设平面QBD的法向量为=（a，b，c）,，,由,，得,∴,（12分)∴，（13分)因λ∈(0，1），解得．（14分）点评：本题用了几何法和向量法进行证明平行及垂直关系、求值,有中点时通常构造中位线证明线线平行，根据线面平行的判定定理转化到线面平行;向量法主要利用数量积为零证明垂直,对待二面角、线面角问题用向量法要简单些，建立坐标系要利用几何体中的垂直条件．4．（2014•江苏）如图,在三棱锥P﹣ABC中，D，E，F分别为棱PC,AC，AB的中点，已知PA⊥AC,PA=6，BC=8，DF=5．求证：（1)直线PA∥平面DEF；(2）平面BDE⊥平面ABC．考点：平面与平面垂直的判定；直线与平面垂直的判定．专题: 证明题；空间位置关系与距离．分析:（1）由D、E为PC、AC的中点，得出DE∥PA，从而得出PA∥平面DEF；（2）要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF，且DE⊥AC即可．解答:证明：（1）∵D、E为PC、AC的中点，∴DE∥PA,又∵PA⊄平面DEF，DE⊂平面DEF，∴PA∥平面DEF；（2)∵D、E为PC、AC的中点，∴DE=PA=3;又∵E、F为AC、AB的中点,∴EF=BC=4;∴DE2+EF2=DF2，∴∠DEF=90°，∴DE⊥EF;∵DE∥PA,PA⊥AC,∴DE⊥AC;∵AC∩EF=E，∴DE⊥平面ABC；∵DE⊂平面BDE，∴平面BDE⊥平面ABC．点评：本题考查了空间中的平行与垂直问题，解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系，是基础题目．5．(2014•黄山一模）如图,PA垂直于矩形ABCD所在的平面，AD=PA=2，CD=2,E、F分别是AB、PD的中点．（1）求证：AF∥平面PCE；（2）求证：平面PCE⊥平面PCD；(3）求四面体PEFC的体积．考点：直线与平面平行的判定；棱锥的结构特征；平面与平面垂直的判定．专题：计算题；证明题．分析：（1）设G为PC的中点，连接FG，EG，根据中位线定理得到FG CD，AE CD，进而可得到AF∥GE，再由线面平行的判定定理可证明AF∥平面PCE，得证．（2）根据PA=AD=2可得到AF⊥PD,再由线面垂直的性质定理可得到PA⊥CD，然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD,同样得到GE⊥平面PCD，再由面面垂直的判定定理可得证．（3）先由（2）可得知EG为四面体PEFC的高,进而求出S△PCF，根据棱锥的体积公式可得到答案．解答：解：（1)证明：设G为PC的中点，连接FG，EG，∵F为PD的中点,E为AB的中点，∴FG CD，AE CD∴FG AE，∴AF∥GE∵GE⊂平面PEC,∴AF∥平面PCE;（2）证明:∵PA=AD=2，∴AF⊥PD又∵PA⊥平面ABCD,CD⊂平面ABCD，∴PA⊥CD，∵AD⊥CD，PA∩AD=A,∴CD⊥平面PAD，∵AF⊂平面PAD，∴AF⊥CD．∵PD∩CD=D，∴AF⊥平面PCD，∴GE⊥平面PCD，∵GE⊂平面PEC，∴平面PCE⊥平面PCD；（3）由(2）知，GE⊥平面PCD，所以EG为四面体PEFC的高，又GF∥CD,所以GF⊥PD,EG=AF=，GF=CD=，S△PCF=PD•GF=2．得四面体PEFC的体积V=S△PCF•EG=．点评：本题主要考查线面垂直的判定定理和性质定理、面面垂直的判定定理．考查对立体几何中基本定理的掌握程度和灵活运用能力．6．（2014•南海区模拟)如图，四棱锥P﹣ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点,E为PA的中点．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求证:OE∥平面PDC；(Ⅲ）求直线CB与平面PDC所成角的正弦值．考点：直线与平面平行的判定；直线与平面垂直的判定；直线与平面所成的角．专题：证明题．分析：（Ⅰ）由条件先证明四边形ABFD为正方形，由等腰三角形的性质证明PO⊥BD,由勾股定理求得PO⊥AO，从而证得PO⊥平面ABCD．（Ⅱ)过O分别做AD，AB的平行线，以它们做x,y轴，以OP为z轴建立如图所示的空间直角坐标系，求出和的坐标，由可得OE∥PF，从而证得OE∥平面PDC．（Ⅲ) 设平面PDC的法向量为，直线CB与平面PDC所成角θ，求出一个法向量为，又,可得和夹角的余弦值，即为直线CB与平面PDC所成角的正弦值．解答：解：(Ⅰ)证明:设F为DC的中点，连接BF，则DF=AB．∵AB⊥AD,AB=AD,AB∥DC,∴四边形ABFD为正方形．∵O为BD的中点，∴O为AF，BD的交点，∵PD=PB=2,∴PO⊥BD，…。

【三维设计】高考数学大一轮复习(夯基保分卷+提能增分卷)导数与函数极值、最值课时训练理(含14

课时跟踪检测(十五) 导数与函数极值、最值(分Ⅰ、Ⅱ卷，共2页) 第Ⅰ卷：夯基保分卷1．当函数y ＝x ·2x取极小值时，x ＝________.2．设函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R )．若x ＝－1为函数f (x )e x的一个极值点，则下列图像不可能为y ＝f (x )图像的是________．(填写序号)3．(2013·南通三模)定义在[1，＋∞)上的函数f (x )满足：①f (2x )＝cf (x )(c 为正常数)；②当2≤x ≤4时，f (x )＝1－|x －3|.若函数的所有极大值点均落在同一条直线上，则c ＝________.4．已知函数f (x )＝－x 3＋ax 2－4在x ＝2处取得极值，若m ，n ∈[－1,1]，则f (m )＋f ′(n )的最小值是________．5．(2013·盐城三调)设a >0，函数f (x )＝x ＋a 2x，g (x )＝x －ln x ，若对任意的x 1，x 2∈[1，e]，都有f (x 1)≥g (x 2)成立，则实数a 的取值范围为________．6．已知函数f (x )＝x 3＋mx 2＋(m ＋6)x ＋1既存在极大值又存在极小值，则实数m 的取值范围是________．7．已知函数y ＝f (x )＝x 3＋3ax 2＋3bx ＋c 在x ＝2处有极值，其图像在x ＝1处的切线平行于直线6x ＋2y ＋5＝0，则f (x )极大值与极小值之差为________．8．已知f (x )＝x 3－6x 2＋9x －abc ，a 0； ②f (0)f (1)<0； ③f (0)f (3)>0；④f (0)f (3)<0.其中正确结论的序号是________．9．(2013·江苏高考节选)设函数f (x )＝ln x －ax ，g (x )＝e x－ax ，其中a 为实数．若f (x )在(1，＋∞)上是单调减函数，且g (x )在(1，＋∞)上有最小值，求a 的取值范围．10．已知函数f (x )＝x 2－1与函数g (x )＝a ln x (a ≠0)．(1)若f (x )，g (x )的图像在点(1,0)处有公共的切线，求实数a 的值； (2)设F (x )＝f (x )－2g (x )，求函数F (x )的极值．第Ⅱ卷：提能增分卷1．(2014·常州调研)已知函数f (x )＝ax －ln x ，g (x )＝ln xx，它们的定义域都是(0，e]，其中e 是自然对数的底e≈2.7，a ∈R .(1)当a ＝1时，求函数f (x )的最小值；(2)当a ＝1时，求证：f (m )>g (n )＋1727对一切m ，n ∈(0，e]恒成立；(3)是否存在实数a ，使得f (x )的最小值是3？如果存在，求出a 的值；如果不存在，说明理由．2．(2014·苏州期末)设函数f (x )＝ln x －kx －aax－ln a (x >0，a >0且为常数)． (1)当k ＝1时，判断函数f (x )的单调性，并加以证明； (2)当k ＝0时，求证：f (x )>0对一切x >0恒成立；(3)若k <0，且k 为常数，求证：f (x )的极小值是一个与a 无关的常数．3．(2014·泰州质检)已知函数f (x )＝(x －a )(x －b )2，a ，b 是常数． (1)若a ≠b ，求证：函数f (x )存在极大值和极小值；(2)设(1)中f (x )取得极大值、极小值时自变量的值分别为x 1，x 2，设点A (x 1，f (x 1))，B (x 2，f (x 2))．如果直线AB 的斜率为－12，求函数f (x )和f ′(x )的公共递减区间的长度；(3)若f (x )≥mxf ′(x )对于一切x ∈R 恒成立，求实数m ，a ，b 满足的条件．答案第Ⅰ卷：夯基保分卷1．解析：y ′＝2x ＋x ·2xln 2＝0，∴x ＝－1ln 2. 答案：－1ln 22．解析：因为[f (x )e x ]′＝f ′(x )e x ＋f (x )(e x )′＝[f (x )＋f ′(x )]e x，且x ＝－1为函数f (x )e x的一个极值点，所以f (－1)＋f ′(－1)＝0；④中，f (－1)>0，f ′(－1)>0，不满足f ′(－1)＋f (－1)＝0.答案：④3．解析：易知当2≤x ≤4时，其极大值点为(3,1)；当1≤x ≤2时，2≤2x ≤4，从而由条件得f (x )＝1c f (2x )＝1c (1－|2x －3|)．因为c >0，故极大值点为⎝ ⎛⎭⎪⎫32，1c ；当2≤x ≤4时，4≤2x ≤8，从上述步骤得f (2x )＝cf (x )＝c (1－|4x －3|)．因为c >0，故极大值点为(6，c )；上述三点在同一直线上，所以1－1c 3－32＝c －16－3，解得c ＝2或1.答案：1或24．解析：求导得f ′(x )＝－3x 2＋2ax ，由函数f (x )在x ＝2处取得极值知f ′(2)＝0，即－3×4＋2a ×2＝0，∴a ＝3. 由此可得f (x )＝－x 3＋3x 2－4，f ′(x )＝－3x 2＋6x ，易知f (x )在[－1,0)上单调递减，在(0,1]上单调递增， ∴当m ∈[－1,1]时，f (m )min ＝f (0)＝－4.又f ′(x )＝－3x 2＋6x 的图像开口向下，且对称轴为x ＝1， ∴当n ∈[－1,1]时，f ′(n )min ＝f ′(－1)＝－9.故f (m )＋f ′(n )的最小值为－13. 答案：－135．解析：问题可转化为f (x )min ≥g (x )max ，当x ∈[1，e]时，g ′(x )＝1－1x≥0，故g (x )单调递增，则g (x )max ＝g (e)＝e －1.又f ′(x )＝1－a 2x 2＝x 2－a 2x2，令f ′(x )＝0，得x ＝a ，易知，x ＝a 是函数f (x )的极小值，当0<a ≤1时，f (x )min ＝f (1)＝1＋a 2，则1＋a 2≥e－1，所以e －2≤a ≤1；当1<a ≤e 时，f (x )min ＝f (a )＝2a ，则2a ≥e－1，显然成立，所以1<a ≤e；当a >e 时，f (x )min ＝f (e)＝e ＋a 2e ，则e ＋a 2e≥e－1，显然成立，所以a >e.综上，a ≥e －2.答案：[e －2，＋∞)6．解析：f ′(x )＝3x 2＋2mx ＋m ＋6＝0有两个不等实根，即Δ＝4m 2－12×(m ＋6)>0.所以m >6或m <－3.答案：(－∞，－3)∪(6，＋∞) 7．解析：∵y ′＝3x 2＋6ax ＋3b ，⎩⎪⎨⎪⎧3×22＋6a ×2＋3b ＝03×12＋6a ＋3b ＝－3⇒⎩⎪⎨⎪⎧a ＝－1，b ＝0.∴y ′＝3x 2－6x ，令3x 2－6x ＝0，得x ＝0或x ＝2. ∴f (x )极大值－f (x )极小值＝f (0)－f (2)＝4. 答案：48.解析：∵f ′(x )＝3x 2－12x ＋9＝3(x －1)(x －3)，由f ′(x )<0，得1<x <3，由f ′(x )>0，得x <1或x >3，∴f (x )在区间(1,3)上是减函数，在区间(－∞，1)，(3，＋∞)上是增函数．又a 0，y 极小值＝f (3)＝－abc <0.∴0<abc <4.∴a ，b ，c 均大于零，或者a <0，b <0，c >0.又x ＝1，x ＝3为函数f (x )的极值点，后一种情况不可能成立，如图．∴f (0)<0.∴f (0)f (1)<0，f (0)f (3)>0.∴正确结论的序号是②③. 答案：②③9．解：令f ′(x )＝1x －a ＝1－ax x<0，考虑到f (x )的定义域为(0，＋∞)，故a >0，进而解得x >a －1，即f (x )在(a －1，＋∞)上是单调减函数．同理，f (x )在(0，a －1)上是单调增函数．由于f (x )在(1，＋∞)上是单调减函数，故(1，＋∞)⊆(a －1，＋∞)，从而a －1≤1，即a ≥1.令g ′(x )＝e x－a ＝0，得x ＝ln a ．当x <ln a 时，g ′(x )<0；当x >ln a 时，g ′(x )>0.又g (x )在(1，＋∞)上有最小值，所以ln a >1，即a >e.综上，a 的取值范围为(e ，＋∞)． 10．解：(1)因为f (1)＝0，g (1)＝0，所以点(1,0)同时在函数f (x )，g (x )的图像上，因为f (x )＝x 2－1，g (x )＝a ln x ，所以f ′(x )＝2x ，g ′(x )＝a x，由已知，得f ′(1)＝g ′(1)，所以2＝a1，即a ＝2.(2)因为F (x )＝f (x )－2g (x )＝x 2－1－2a ln x (x >0)，所以F ′(x )＝2x －2ax＝x 2－ax，当a <0时，因为x >0，且x 2－a >0，所以F ′(x )>0对x >0恒成立，所以F (x )在(0，＋∞)上单调递增，F (x )无极值；当a >0时，令F ′(x )＝0，解得x 1＝a ，x 2＝－a (舍去)，所以当x >0时，F ′(x )，F (x )的变化情况如下表：所以当x 1－a ln a . 综上，当a <0时，函数F (x )在(0，＋∞)上无极值；当a >0时，函数F (x )在x ＝a 处取得极小值a －1－a ln a . 第Ⅱ卷：提能增分卷1．解：(1)当a ＝1时，f (x )＝x －ln x . 所以f ′(x )＝1－1x.令f ′(x )＝0，得x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如下表：所以当x ＝1时，min (2)证明：由(1)知，当m ∈(0，e]时，有f (m )≥1.因为0<x ≤e，所以g ′(x )＝1－ln xx2≥0，即g (x )在区间(0，e]上为增函数，所以g (x )≤g (e)＝ln e e ＝1e <12.7＝1027，所以g (x )＋1727<1027＋1727＝1，所以当m ，n ∈(0，e]时，g (n )＋1727<1≤f (m )．所以f (m )>g (n )＋1727对一切m ，n ∈(0，e]恒成立．(3)假设存在实数a ，使f (x )的最小值是3，则 f ′(x )＝a －1x ＝ax －1x.①当a ≤1e 时，因为0<x ≤e，所以ax ≤1，所以f ′(x )≤0，所以f (x )在(0，e]上为减函数．所以当x ＝e 时，f min (x )＝a e －1＝3，解得a ＝4e (舍去)；②当a >1e时，若0<x <1a时，f ′(x )<0，f (x )在⎝ ⎛⎦⎥⎤0，1a 上为减函数；若1a<x ≤e 时，f ′(x )>0，f (x )在⎝ ⎛⎦⎥⎤1a ，e 上为增函数．所以当x ＝1a 时，f min (x )＝1－ln 1a＝3，解得a ＝e 2.所以假设成立，存在实数a ＝e 2，使得f (x )的最小值是3. 2．解：(1)当k ＝1时，f (x )＝ln x －1a ·x 12＋ax －12－ln a ，因为f ′(x )＝1x －12a ·x －12－a 2x －32＝－x －a 22x ax≤0，所以函数f (x )在(0，＋∞)上是单调减函数． (2)证明：当k ＝0时，f (x )＝ln x ＋ax －12－ln a ，故f ′(x )＝1x －a 2x x ＝2x －a2x x .令f ′(x )＝0，解得x ＝a4.当0<x <a4时，f ′(x )<0，f (x )在⎝ ⎛⎭⎪⎫0，a 4上是单调减函数；当x >a 4时，f ′(x )>0，f (x )在⎝ ⎛⎭⎪⎫a4，＋∞上是单调增函数．所以当x ＝a4时，f ′(x )有极小值，为f ⎝ ⎛⎭⎪⎫a 4＝2－2ln 2.因为e>2，所以f (x )的极小值，为f ⎝ ⎛⎭⎪⎫a 4＝2(1－ln 2)＝2ln e 2>0. 所以当k ＝0时，f (x )>0对一切x >0恒成立． (3)证明：f (x )＝ln x －k a ·x 12＋ax －12－ln a ，所以f ′(x )＝－kx ＋2ax －a2x ax .令f ′(x 0)＝0，得kx 0－2ax 0＋a ＝0. 所以x 0＝a －1－kk⎝⎛⎭⎪⎫x 0＝a ＋1－kk舍去.所以x 0＝a＋1－k2.当0<x <x 0时，f ′(x )<0，f (x )在(0，x 0)上是单调减函数；当x >x 0时，f ′(x )>0，f (x )在(x 0，＋∞)上是单调增函数．因此，当x ＝x 0时，f (x )有极小值f (x 0)．又f (x 0)＝ln x 0a －k x 0a ＋ a x 0，而x 0a＝1＋1－k2是与a 无关的常数，所以ln x 0a，－k x 0a， ax 0均与a 无关．所以f (x 0)是与a 无关的常数．故f (x )的极小值是一个与a 无关的常数． 3．解：(1)证明：f ′(x )＝(x －b )[3x －(2a ＋b )]，因为a ≠b ，所以b ≠2a ＋b3，所以f ′(x )＝0有两个不等实根b 和2a ＋b3，所以f (x )存在极大值和极小值． (2)①当a ＝b 时，f (x )不存在减区间； ②当a >b 时，由(1)知x 1＝b ，x 2＝2a ＋b3，所以A (b,0)，B ⎝⎛⎭⎪⎫2a ＋b 3，－a －b327，所以－a －b3272a ＋b 3－b ＝－12，即4(a －b )3＝9(a －b )，所以a －b ＝32或a －b ＝－32(舍去)；③当a b 且a －b ＝32或a <b 且a －b ＝－32.所以f (x )的减区间为⎝ ⎛⎭⎪⎫b ，2a ＋b 3，即(b ，b ＋1)或f (x )的减区间为⎝ ⎛⎭⎪⎫2a ＋b 3，b ，即(b －1，b )；f ′(x )的减区间为⎝⎛⎭⎪⎫－∞，b ＋12或⎝⎛⎭⎪⎫－∞.b －12. 所以公共减区间为⎝ ⎛⎭⎪⎫b ，b ＋12或⎝ ⎛⎭⎪⎫b －1，b －12，长度均为12.(3)由题意f (x )≥mxf ′(x )，所以(x －a )(x －b )2≥mx (x －b )[3x －(2a ＋b )]，所以(x －b ){(1－3m )x 2＋[m (2a ＋b )－(a ＋b )]x ＋ab }≥0.若m ≠13，则左边是一个一次因式乘一个恒正(或恒负)的二次三项式，或者是三个一次因式的积，无论哪种情况，总有一个一次因式的指数是奇次的，这个因式的零点左右的符号不同，因此不可能恒非负．所以m ＝13，所以(x －b )[(a ＋2b )x －3ab ]≤0.若a ＋2b ＝0，则a ＝－2b ，所以a ＝b ＝0；若a ＋2b ≠0，则x 1＝b ，x 2＝3aba ＋2b，所以⎩⎪⎨⎪⎧a ＋2b <0，b ＝3aba ＋2b，①若b ＝0，则a <0； ②若b ≠0，则3aa ＋2b＝1，所以a ＝b 且b <0. 综上，m ＝13，a ＝b ≤0.。

【聚焦典型题】(苏教版)2014届高考一轮数学(理)：《抛物线》

考向一抛物线定义及其应用
【训练 1】设 P 是曲线 y ＝4x 上的一个动点，则点 P 到点 B(－1,1)的距离与点 P 到直线 x＝－1 的距离之和的最小值为 ________．
2
【审题视点】
由定义知，抛物线上点 P 到焦点 F 的距离等于点 P 到准线 l 的距离 d，利用梯形中位线定理即得
考点自测
答案显示单击图标显示详解
C
C
B
y2＝4x
6
考向一抛物线定义及其应用
【例 1】►已知抛物线 y ＝2x 的焦点是 F，点 P 是抛物线上的动点，又有点 A(3,2)，求|PA|＋|PF|的最小值，并求出取最小值时 P 点的坐标． 2 解将 x＝3 代入抛物线方程 y ＝2x，得 y＝± 6.
助学微博
一个重要转化
一次项的变量与焦点所在的坐标轴的名称相同，一次项系数的符号决定抛物线的开口方向，即 “对称轴看一次项，符号决定开口方向”．
交抛物线于 A(x1， 1)， y 六个常见结论直线 AB 过抛物线的焦点， B(x2，y2)两点，如图． p2 ①y1y2＝－p2，x1x2＝ . 4 ②|AB|＝x1＋x2＋p，x1＋x2≥2 x1 x2 ＝p，即当 x1＝x2 时，弦长最短为 2p. 1 1 2 ③ ＋为定值 . |AF| |BF| 2p p ④弦长 AB＝ 2 (α 为 AB 的倾斜角)． sin α ⑤以 AB 为直径的圆与准线相切． ⑥焦点 F 对 A，B 在准线上射影的张角为 90° .
助学微博
考点自测
抛物线的标准方程和几何性质考向一抛物线定义及其应用
【例1】【训练1】【例2】【训练2】【例3】【训练3】
突破3个考向

2014-2019年高考数学真题分类汇编专题10：立体几何3(空间线面关系)带详细答案

2014-2019年高考数学真题分类汇编专题10：立体几何（空间线面关系）（一）空间线面的平行与垂直选择题1．（2014•广东文）若空间中四条两两不同的直线1l ，2l ，3l ，4l ，满足12l l ⊥，23//l l ，34l l ⊥，则下列结论一定正确的是( ) A ．14l l ⊥B ．14//l lC ．1l 与4l 既不垂直也不平行D ．1l 与4l 的位置关系不确定【考点】空间中直线与直线之间的位置关系【分析】根据空间直线平行或垂直的性质即可得到结论．【解答】解：在正方体中，若AB 所在的直线为2l ，CD 所在的直线为3l ，AE 所在的直线为1l ，若GD 所在的直线为4l ，此时14//l l ，若BD 所在的直线为4l ，此时14l l ⊥，故1l 与4l 的位置关系不确定，故选：D ．【点评】本题主要考查空间直线平行或垂直的位置关系的判断，比较基础．2．（2014•广东理）若空间中四条两两不同的直线1l ，2l ，3l ，4l ，满足12l l ⊥，23l l ⊥，34l l ⊥，则下列结论一定正确的是( ) A ．14l l ⊥B ．14//l lC ．1l 与4l 既不垂直也不平行D ．1l 与4l 的位置关系不确定【考点】空间中直线与直线之间的位置关系【分析】根据在空间中垂直于同一直线的二直线的位置关系是平行、相交或异面可得，1l ∴与4l 的位置关系不确定．【解答】解：12l l ⊥，23l l ⊥，1l ∴与3l 的位置关系不确定，又43l l ⊥，1l ∴与4l 的位置关系不确定．故A 、B 、C 错误．故选：D ．【点评】本题考查了空间直线的垂直关系的判定，考查了学生的空间想象能力，在空间中垂直于同一直线的二直线的位置关系是平行、相交或异面．3．（2014•辽宁文理）已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是( ) A ．若//m α，//n α，则//m n B ．若m α⊥，n α⊂，则m n ⊥ C ．若m α⊥，m n ⊥，则//n α D ．若//m α，m n ⊥，则n α⊥【考点】空间中直线与平面之间的位置关系【分析】A ．运用线面平行的性质，结合线线的位置关系，即可判断；B ．运用线面垂直的性质，即可判断；C ．运用线面垂直的性质，结合线线垂直和线面平行的位置即可判断；D ．运用线面平行的性质和线面垂直的判定，即可判断．【解答】解：A ．若//m α，//n α，则m ，n 相交或平行或异面，故A 错；B ．若m α⊥，n α⊂，则m n ⊥，故B 正确；C ．若m α⊥，m n ⊥，则//n α或n α⊂，故C 错；D ．若//m α，m n ⊥，则//n α或n α⊂或n α⊥，故D 错．故选：B ．【点评】本题考查空间直线与平面的位置关系，考查直线与平面的平行、垂直的判断与性质，记熟这些定理是迅速解题的关键，注意观察空间的直线与平面的模型．4．（2014•浙江文）设m 、n 是两条不同的直线，α，β是两个不同的平面，则( ) A ．若m n ⊥，//n α，则m α⊥ B ．若//m β，βα⊥，则m α⊥ C ．若m β⊥，n β⊥，n α⊥，则m α⊥ D ．若m n ⊥，n β⊥，βα⊥，则m α⊥【考点】空间中直线与平面之间的位置关系【分析】根据空间线线，线面，面面之间的位置关系分别进行判定即可得到结论．【解答】解：A ．若m n ⊥，//n α，则m α⊥或m α⊂或//m α，故A 错误．B ．若//m β，βα⊥，则m α⊥或m α⊂或//m α，故B 错误．C ．若m β⊥，n β⊥，n α⊥，则m α⊥，正确．D ．若m n ⊥，n β⊥，βα⊥，则m α⊥或m α⊂或//m α，故D 错误．故选：C ．【点评】本题主要考查空间直线，平面之间的位置关系的判定，要求熟练掌握相应的判定定理和性质定理． 5．（2015•北京理）设α，β是两个不同的平面，m 是直线且m α⊂，“//m β “是“//αβ”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【考点】充分条件、必要条件、充要条件；面面平行的判定定理【分析】//m β并得不到//αβ，根据面面平行的判定定理，只有α内的两相交直线都平行于β，而//αβ，并且m α⊂，显然能得到//m β，这样即可找出正确选项．【解答】解：m α⊂，//m β得不到//αβ，因为α，β可能相交，只要m 和α，β的交线平行即可得到//m β；//αβ，m α⊂，m ∴和β没有公共点，//m β∴，即//αβ能得到//m β；∴ “//m β”是“//αβ”的必要不充分条件．故选：B ．【点评】考查线面平行的定义，线面平行的判定定理，面面平行的定义，面面平行的判定定理，以及充分条件、必要条件，及必要不充分条件的概念．6．（2015•福建理）若l ，m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”是“//l α”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【考点】充分条件、必要条件、充要条件；直线与平面平行与垂直关系【分析】利用直线与平面平行与垂直关系，判断两个命题的充要条件关系即可．【解答】解：l ，m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”可能“//l α”也可能l α⊂，反之，“//l α”一定有“l m ⊥”，所以l ，m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”是“//l α”的必要而不充分条件．故选：B ．【点评】本题考查空间直线与平面垂直与平行关系的应用，充要条件的判断，基本知识的考查． 7．（2015•广东理）若空间中n 个不同的点两两距离都相等，则正整数n 的取值( ) A ．至多等于3B ．至多等于4C ．等于5D ．大于5【考点】棱锥的结构特征【分析】先考虑平面上的情况：只有三个点的情况成立；再考虑空间里，只有四个点的情况成立，注意运用外接球和三角形三边的关系，即可判断．【解答】解：考虑平面上，3个点两两距离相等，构成等边三角形，成立；4个点两两距离相等，三个点在圆上，一个点是圆心，圆上的点到圆心的距离都相等，则不成立；n 大于4，也不成立；在空间中，4个点两两距离相等，构成一个正四面体，成立；若4n >，由于任三点不共线，当5n =时，考虑四个点构成的正四面体，第五个点，与它们距离相等，必为正四面体的外接球的球心，且球的半径不等于边长，即有球心与正四面体的底面的中心重合，但显然球的半径不等于棱长，故不成立；同理5n >，不成立．故选：B ．【点评】本题考查空间几何体的特征，主要考查空间两点的距离相等的情况，注意结合外接球和三角形的两边与第三边的关系，属于中档题和易错题．8．（2015•广东文）若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是( ) A ．l 与1l ，2l 都不相交 B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 至少与1l ，2l 中的一条相交【考点】空间中直线与平面之间的位置关系【分析】可以画出图形来说明l 与1l ，2l 的位置关系，从而可判断出A ，B ，C 是错误的，而对于D ，可假设不正确，这样l 便和1l ，2l 都不相交，这样可推出和1l ，2l 异面矛盾，这样便说明D 正确．【解答】解：A ．l 与1l ，2l 可以相交，如图：∴该选项错误；B ．l 可以和1l ，2l 中的一个平行，如上图，∴该选项错误；C ．l 可以和1l ，2l 都相交，如下图：，∴该选项错误；D ．“l 至少与1l ，2l 中的一条相交”正确，假如l 和1l ，2l 都不相交； l 和1l ，2l 都共面； l ∴和1l ，2l 都平行；12//l l ∴，1l 和2l 共面，这样便不符合已知的1l 和2l 异面；∴该选项正确．故选：D ．【点评】考查异面直线的概念，在直接说明一个命题正确困难的时候，可说明它的反面不正确． 9．（2015•湖北文）1l ，2l 表示空间中的两条直线，若1:p l ，2l 是异面直线，1:q l ，2l 不相交，则( ) A ．p 是q 的充分条件，但不是q 的必要条件 B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件【考点】空间直线的位置关系【分析】根据充分条件和必要条件的定义结婚空间直线的位置关系，进行判断即可．【解答】解：若1l ，2l 是异面直线，则1l ，2l 不相交，即充分性成立，若1l ，2l 不相交，则1l ，2l 可能是平行或异面直线，即必要性不成立，故p 是q 的充分条件，但不是q 的必要条件，故选：A ．【点评】本题主要考查充分条件和必要条件的判断，根据空间直线的位置关系是解决本题的关键． 10．（2015•浙江文）设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂，( ) A ．若l β⊥，则αβ⊥ B ．若αβ⊥，则l m ⊥ C ．若//l β，则//αβD ．若//αβ，则//l m【考点】空间中直线与平面之间的位置关系【分析】A 根据线面垂直的判定定理得出A 正确；B 根据面面垂直的性质判断B 错误；C 根据面面平行的判断定理得出C 错误；D 根据面面平行的性质判断D 错误．【解答】解：对于A ，l β⊥，且l α⊂，根据线面垂直的判定定理，得αβ⊥，A ∴正确；对于B ，当αβ⊥，l α⊂，m β⊂时，l 与m 可能平行，也可能垂直，B ∴错误；对于C ，当//l β，且l α⊂时，α与β可能平行，也可能相交，C ∴错误；对于D ，当//αβ，且l α⊂，m β⊂时，l 与m 可能平行，也可能异面，D ∴错误．故选：A ．【点评】本题考查了空间中的平行与垂直关系的应用问题，也考查了数学符号语言的应用问题，是基础题目．11．（2015•安徽理）已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是( ) A ．若α，β垂直于同一平面，则α与β平行 B ．若m ，n 平行于同一平面，则m 与n 平行 C ．若α，β不平行，则在α内不存在与β平行的直线 D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面【考点】空间中直线与直线之间的位置关系；空间中直线与平面之间的位置关系；平面与平面之间的位置关系【分析】利用面面垂直、线面平行的性质定理和判定定理对选项分别分析解答．【解答】解：对于A ，若α，β垂直于同一平面，则α与β不一定平行，例如墙角的三个平面；故A 错误；对于B ，若m ，n 平行于同一平面，则m 与n 平行．相交或者异面；故B 错误；对于C ，若α，β不平行，则在α内存在无数条与β平行的直线；故C 错误；对于D ，若m ，n 不平行，则m 与n 不可能垂直于同一平面；假设两条直线同时垂直同一个平面，则这两条在平行；故D 正确；故选：D ．【点评】本题考查了空间线面关系的判断；用到了面面垂直、线面平行的性质定理和判定定理．12．（2016•浙江文理）已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足//m α，n β⊥，则() A ．//m lB ．//m nC ．n l ⊥D ．m n ⊥【考点】直线与平面垂直【分析】由已知条件推导出l β⊂，再由n β⊥，推导出n l ⊥．【解答】解：互相垂直的平面α，β交于直线l ，直线m ，n 满足//m α， //m β∴或m β⊂或m 与β相交，l β⊂， n β⊥， n l ∴⊥．故选：C ．【点评】本题考查两直线关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养． 13．（2016•上海文）如图，在正方体1111ABCD A B C D -中，E 、F 分别为BC 、1BB 的中点，则下列直线中与直线EF 相交的是( )A ．直线1AAB ．直线11A BC ．直线11A DD ．直线11B C【考点】空间中直线与平面之间的位置关系【分析】根据异面直线的定义便可判断选项A ，B ，C 的直线都和直线EF 异面，而由图形即可看出直线11B C 和直线相交，从而便可得出正确选项．【解答】解：根据异面直线的概念可看出直线1AA ，11A B ，11A D 都和直线EF 为异面直线； 11B C 和EF 在同一平面内，且这两直线不平行；∴直线11B C 和直线EF 相交，即选项D 正确．故选：D ．【点评】考查异面直线的概念及判断，平行直线和相交直线的概念及判断，并熟悉正方体的图形形状． 14．（2016•山东文理）已知直线a ，b 分别在两个不同的平面α，β内．则“直线a 和直线b 相交”是“平面α和平面β相交”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【考点】充分条件、必要条件、充要条件; 空间位置关系【分析】直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交” ⇒ “平面α和平面β相交”，反之不成立．【解答】解：直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交” ⇒ “平面α和平面β相交”，反之不成立．∴ “直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件．故选：A ．【点评】本题考查了空间位置关系、简易逻辑的判定方法，考查了推理能力，属于基础题．15．（2017•新课标Ⅰ文）如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是( )A ．B ．C ．D ．【考点】直线与平面平行【分析】利用线面平行判定定理可知B 、C 、D 均不满足题意，从而可得答案．【解答】解：对于选项B ，由于//AB MQ ，结合线面平行判定定理可知B 不满足题意；对于选项C ，由于//AB MQ ，结合线面平行判定定理可知C 不满足题意；对于选项D ，由于//AB NQ ，结合线面平行判定定理可知D 不满足题意；所以选项A 满足题意，故选：A ．【点评】本题考查空间中线面平行的判定定理，利用三角形中位线定理是解决本题的关键，注意解题方法的积累，属于中档题．16．（2017•新课标Ⅲ文）在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则( ) A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥【考点】空间中直线与直线之间的位置关系【分析】法一：连1B C ，推导出11BC B C ⊥，111A B BC ⊥，从而1BC ⊥平面11A ECB ，由此得到11A E BC ⊥．法二：以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，利用向量法能求出结果．【解答】解：法一：连1B C ，由题意得11BC B C ⊥， 11A B ⊥平面11B BCC ，且1BC ⊂平面11B BCC ，111A B BC ∴⊥， 1111A B B C B =，1BC ∴⊥平面11A ECB ， 1A E ⊂平面11A ECB ， 11A E BC ∴⊥．故选：C ．法二：以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，设正方体1111ABCD A B C D -中棱长为2，则1(2A ，0，2)，(0E ，1，0)，(2B ，2，0)，(0D ，0，0)，1(0C ，2，2)，(2A ，0，0)，(0C ，2，0)， 1(2A E =-，1，2)-，1(0DC =，2，2)，(2BD =-，2-，0)， 1(2BC =-，0，2)，(2AC =-，2，0)，112A E DC =-，12A E BD =，110A E BC =，16A E AC =， 11A E BC ∴⊥．故选：C ．【点评】本题考查线线垂直的判断，是中档题，解题时要认真审题，注意向量法的合理运用． 17．（2018•浙江）已知平面α，直线m ，n 满足m α⊂/，n α⊂，则“//m n ”是“//m α”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件【考点】充分条件、必要条件、充要条件【分析】根据线面平行的定义和性质以及充分条件和必要条件的定义进行判断即可．【解答】解：m α⊂/，n α⊂，∴当//m n 时，//m α成立，即充分性成立，当//m n不一定成立，即必要性不成立，mα时，//则“//mα”的充分不必要条件．m n”是“//故选：A．【点评】本题主要考查充分条件和必要条件的判断，根据线面平行的定义和性质是解决本题的关键，是基础题．αβ的充要条件是()18．（2019新课标Ⅱ文理）设α，β为两个平面，则//A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．α，β平行于同一条直线D．α，β垂直于同一平面【考点】；充分条件、必要条件、充要条件；空间位置关系【分析】充要条件的定义结合面面平行的判定定理可得结论αβ；【解答】解：对于A，α内有无数条直线与β平行，αβ或//αβ；对于B，α内有两条相交直线与β平行，//αβ；对于C，α，β平行于同一条直线，αβ或//αβ．对于D，α，β垂直于同一平面，αβ或//故选：B．【点评】本题考查了充要条件的定义和面面平行的判定定理，考查了推理能力，属于基础题．19．（2019•新课标Ⅲ文理）如图，点N为正方形ABCD的中心，ECD∆为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则()A．BM EN=，且直线BM，EN是相交直线B．BM EN≠，且直线BM，EN是相交直线C．BM EN=，且直线BM，EN是异面直线D．BM EN≠，且直线BM，EN是异面直线【考点】空间中直线与直线之间的位置关系【分析】推导出BM是BDE∆中BD边上的中线，从而直线BM，EN是∆中DE边上的中线，EN是BDE相交直线，设DE a≠．=，则BD，BE=，从而BM EN【解答】解：点N为正方形ABCD的中心，ECD∆为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，BM ∴⊂平面BDE ，EN ⊂平面BDE ，BM 是BDE ∆中DE 边上的中线，EN 是BDE ∆中BD 边上的中线，∴直线BM ，EN 是相交直线，设DE a =，则BD =，BE =，BM ∴=，EN a =， BM EN ∴≠，故选：B ．【点评】本题考查两直线的位置关系的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理能力与计算能力，是中档题．20．（2019•上海）已知平面α、β、γ两两垂直，直线a 、b 、c 满足：a α⊆，b β⊆，c γ⊆，则直线a 、b 、c 不可能满足以下哪种关系( )A ．两两垂直B ．两两平行C ．两两相交D ．两两异面【考点】空间中直线与直线之间的位置关系；空间中直线与平面之间的位置关系【分析】利用面面垂直的性质．画图判定【解答】解：如图1，可得a 、b 、c 可能两两垂直；如图2，可得a 、b 、c 可能两两相交；如图3，可得a 、b 、c 可能两两异面；故选：B ．【点评】本题考查面面垂直的性质，属于基础题．填空题1．（2016•新课标Ⅱ理）α，β是两个平面，m ，n 是两条直线，有下列四个命题： ①如果m n ⊥，m α⊥，//n β，那么αβ⊥． ②如果m α⊥，//n α，那么m n ⊥． ③如果//αβ，m α⊂，那么//m β．④如果//m n ，//αβ，那么m 与α所成的角和n 与β所成的角相等．其中正确的命题是 ②③④ （填序号）【考点】命题的真假判断与应用；空间中直线与直线之间的位置关系；空间中直线与平面之间的位置关系【分析】根据空间直线与平面的位置关系的判定方法及几何特征，分析判断各个结论的真假，可得答案．【解答】解：①如果m n ⊥，m α⊥，//n β，不能得出αβ⊥，故错误；②如果//n α，则存在直线l α⊂，使//n l ，由m α⊥，可得m l ⊥，那么m n ⊥．故正确； ③如果//αβ，m α⊂，那么m 与β无公共点，则//m β．故正确④如果//m n ，//αβ，那么m ，n 与α所成的角和m ，n 与β所成的角均相等．故正确；故答案为：②③④【点评】本题以命题的真假判断与应用为载体，考查了空间直线与平面的位置关系，难度中档． 2．（2019北京文理科12）已知l ，m 是平面α外的两条不同直线．给出下列三个论断： ①l m ⊥；②//m α；③l α⊥．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：若l α⊥，l m ⊥，则//m α ．【考点】空间中直线与平面之间的位置关系【分析】由l ，m 是平面α外的两条不同直线，利用线面平行的判定定理得若l α⊥，l m ⊥，则//m α．【解答】解：由l ，m 是平面α外的两条不同直线，知：由线面平行的判定定理得：若l α⊥，l m ⊥，则//m α．故答案为：若l α⊥，l m ⊥，则//m α．【点评】本题考查满足条件的真命题的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理能力与计算能力，属于中档题．（二）空间线面所成的角1．（2014•新课标Ⅱ理）直三棱柱111ABC A B C -中，90BCA ∠=︒，M ，N 分别是11A B ，11A C 的中点，1BC CA CC ==，则BM 与AN 所成角的余弦值为( )A ．110B ．25C D 【考点】异面直线及其所成的角【分析】画出图形，找出BM 与AN 所成角的平面角，利用解三角形求出BM 与AN 所成角的余弦值．【解答】解：直三棱柱111ABC A B C -中，90BCA ∠=︒，M ，N 分别是11A B ，11A C 的中点，如图：BC 的中点为O ，连结ON ，//1112MN B C OB ==，则0MN B 是平行四边形，BM 与AN 所成角就是ANO ∠，1BC CA CC ==，设12BC CA CC ===，1CO ∴=，AO =AN MB ==在ANO ∆中，由余弦定理可得：222cos2AN NO AO ANO AN NO +-∠===故选：C ．【点评】本题考查异面直线对称角的求法，作出异面直线所成角的平面角是解题的关键，同时考查余弦定理的应用．2．（2014•大纲版文）已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为()A ．16B C ．13D 【考点】异面直线及其所成的角【分析】由E 为AB 的中点，可取AD 中点F ，连接EF ，则CEF ∠为异面直线CE 与BD 所成角，设出正四面体的棱长，求出CEF ∆的三边长，然后利用余弦定理求解异面直线CE 与BD 所成角的余弦值．【解答】解：如图，取AD 中点F ，连接EF ，CF ，E 为AB 的中点，//EF DB ∴，则CEF ∠为异面直线BD 与CE 所成的角，ABCD 为正四面体，E ，F 分别为AB ，AD 的中点， CE CF ∴=．设正四面体的棱长为2a ，则EF a =，CE CF =．在CEF ∆中，由余弦定理得：2222cos 2CE EF CF CEF CE EF +-∠===故选：B ．【点评】本题考查异面直线及其所成的角，关键是找角，考查了余弦定理的应用，是中档题．3．（2014•大纲版理）已知二面角l αβ--为60︒，AB α⊂，AB l ⊥，A 为垂足，CD β⊂，C l ∈，135ACD ∠=︒，则异面直线AB 与CD 所成角的余弦值为( )A ．14B C D ．12【考点】异面直线及其所成的角【分析】首先作出二面角的平面角，然后再构造出异面直线AB 与CD 所成角，利用解直角三角形和余弦定理，求出问题的答案．【解答】解：如图，过A 点做AE l ⊥，使BE β⊥，垂足为E ，过点A 做//AF CD ，过点E 做EF AE ⊥，连接BF ， AE l ⊥ 90EAC ∴∠=︒ //CD AF又135ACD ∠=︒ 45FAC ∴∠=︒ 45EAF ∴∠=︒在Rt BEA ∆中，设AE a =，则2AB a =，BE =，在Rt AEF ∆中，则EF a =，AF =，在Rt BEF ∆中，则2BF a =，∴异面直线AB 与CD 所成的角即是BAF ∠，222cos 2AB AF BF BAF AB AF +-∴∠===．故选：B ．【点评】本题主要考查了二面角和异面直线所成的角，关键是构造二面角的平面角和异面直线所成的角，考查了学生的空间想象能力和作图能力，属于难题．4．（2014•四川理）如图，在正方体1111ABCD A B C D -中，点O 为线段BD 的中点，设点P 在线段1CC 上，直线OP 与平面1A BD 所成的角为α，则sin α的取值范围是( )A．，1] B．1] C．]3D．[3，1] 【考点】直线与平面所成的角【分析】由题意可得：直线OP 于平面1A BD 所成的角α的取值范围是111[,][,]22AOA C OA ππ∠∠．再利用正方体的性质和直角三角形的边角关系即可得出．【解答】解：由题意可得：直线OP 于平面1A BD 所成的角α的取值范围是111[,][,]22AOA C OA ππ∠∠．不妨取2AB =．在1Rt AOA ∆中，111sin AA AOA AO ∠===111111sin sin(2)sin 22sin cos 2C OA AOA AOA AOA AOA π∠=-∠=∠=∠∠==>， sin12π=．sin α∴的取值范围是．故选：B ．【点评】本题考查了正方体的性质和直角三角形的边角关系、线面角的求法，考查了推理能力，属于中档题．5．（2015•浙江理）如图，已知ABC ∆，D 是AB 的中点，沿直线CD 将ACD ∆折成△A CD '，所成二面角A CDB '--的平面角为α，则( )A ．A DB α∠'…B ．A DB α∠'…C ．ACB α∠'…D ．ACB α∠'…【考点】二面角的平面角及求法【分析】解：画出图形，分AC BC =，AC BC ≠两种情况讨论即可．【解答】解：①当AC BC =时，A DB α∠'=； ②当AC BC ≠时，如图，点A '投影在AE 上，AOE α=∠'，连结AA '，易得ADA AOA ∠'<∠'，A DB AOE ∴∠'>∠'，即A DB α∠'>综上所述，A DB α∠'…，故选：B ．【点评】本题考查空间角的大小比较，注意解题方法的积累，属于中档题．6．（2016•新课标Ⅰ文理）平面α过正方体1111ABCD A B C D -的顶点A ，//α平面11CB D ，α⋂平面ABCD m =，α⋂平面11ABB A n =，则m 、n 所成角的正弦值为( )A B C D ．13【考点】异面直线及其所成的角【分析】画出图形，判断出m 、n 所成角，求解即可．【解答】解：如图：//α平面11CB D ，α⋂平面ABCD m =，α⋂平面11ABA B n =，可知：1//n CD ，11//m B D ，△11CB D 是正三角形．m 、n 所成角就是1160CD B ∠=︒．则m 、n ．故选：A ．【点评】本题考查异面直线所成角的求法，考查空间想象能力以及计算能力．7．（2017•新课标Ⅱ理）已知直三棱柱111ABC A B C -中，120ABC ∠=︒，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为( )ABCD【考点】异面直线及其所成的角【分析】【解法一】设M 、N 、P 分别为AB ，1BB 和11B C 的中点，得出1AB 、1BC 夹角为MN 和NP 夹角或其补角；根据中位线定理，结合余弦定理求出AC 、MQ ，MP 和MNP ∠的余弦值即可．【解法二】通过补形的办法，把原来的直三棱柱变成直四棱柱，解法更简洁．【解答】解：【解法一】如图所示，设M 、N 、P 分别为AB ，1BB 和11B C 的中点，则1AB 、1BC 夹角为MN 和NP 夹角或其补角（因异面直线所成角为(0,])2π，可知112MN AB ==，112NP BC ==；作BC 中点Q ，则PQM ∆为直角三角形； 1PQ =，12MQ AC =， ABC ∆中，由余弦定理得2222cos AC AB BC AB BC ABC =+-∠ 141221()2=+-⨯⨯⨯-7=，AC ∴=MQ ∴=在MQP ∆中，2MP =；在PMN ∆中，由余弦定理得222222cos 2MN NP PMMNP MN NP+-+-∠===；又异面直线所成角的范围是(0，]2π，1AB ∴与1BC．【解法二】如图所示，补成四棱柱1111ABCD A B C D -，求1BC D ∠即可；1BC =，BD =1C D =∴22211BC BD C D +=，190DBC ∴∠=︒，1cos BC D ∴∠==故选：C ．【点评】本题考查了空间中的两条异面直线所成角的计算问题，也考查了空间中的平行关系应用问题，是中档题．8．（2017•浙江）如图，已知正四面体D ABC -（所有棱长均相等的三棱锥），P 、Q 、R 分别为AB 、BC 、CA 上的点，AP PB =，2BQ CRQC RA==，分别记二面角D PR Q --，D PQ R --，D QR P --的平面角为α、β、γ，则( )A ．γαβ<<B ．αγβ<<C ．αβγ<<D ．βγα<<【考点】二面角的平面角及求法【分析】解法一：如图所示，建立空间直角坐标系．设底面ABC ∆的中心为O ．不妨设3OP =．则(0O ，0，0)，(0P ，3-，0)，(0C ，6，0)，(0D ，0，，Q ，(R -，利用法向量的夹角公式即可得出二面角．解法二：如图所示，连接OP ，OQ ，OR ，过点O 分别作垂线：OE PR ⊥，OF PQ ⊥，OG QR ⊥，垂足分别为E ，F ，G ，连接DE ，DF ，DG ．．可得tan OD OE α=．tan OD OF β=，tan ODOGγ=．由已知可得：OE OG OF >>．即可得出．【解答】解法一：如图所示，建立空间直角坐标系．设底面ABC ∆的中心为O ．不妨设3OP =．则(0O ，0，0)，(0P ，3-，0)，(0C ，6，0)，(0D ，0，，B 3-，0)．Q ，(R -，(PR =-，(0PD =，3，，(3PQ =6，0)，(3,0)QR =--，(QD =-．设平面PDR 的法向量为(n x =，y ，)z ，则00n PR n PD ⎧=⎪⎨=⎪⎩，可得3030y y ⎧-+=⎪⎨+=⎪⎩，可得(6,21)n =-，取平面ABC 的法向量(0m =，0，1)．则cos ,||||15m n m n m n <>==，取α=同理可得：β=γ=>>．αγβ∴<<．解法二：如图所示，连接OP ，OQ ，OR ，过点O 分别作垂线：OE PR ⊥，OF PQ ⊥，OG QR ⊥，垂足分别为E ，F ，G ，连接DE ，DF ，DG ．设OD h =．则tan ODOEα=．同理可得：tan OD OF β=，tan ODOGγ=．由已知可得：OE OG OF >>．tan tan tan αγβ∴<<，α，β，γ为锐角． αγβ∴<<．故选：B ．【点评】本题考查了空间角、空间位置关系、正四面体的性质、法向量的夹角公式，考查了推理能力与计算能力，属于难题．9．（2018•浙江）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点）．设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则()A ．123θθθ剟B ．321θθθ剟C ．132θθθ剟D ．231θθθ剟【考点】棱锥的结构特征；异面直线及其所成的角；直线与平面所成的角；二面角的平面角及求法【分析】作出三个角，表示出三个角的正弦或正切值，根据三角函数的单调性即可得出三个角的大小．【解答】解：由题意可知S 在底面ABCD 的射影为正方形ABCD 的中心．过E 作//EF BC ，交CD 于F ，过底面ABCD 的中心O 作ON EF ⊥交EF 于N ，连接SN ，取AB 中点M ，连接SM ，OM ，OE ，则EN OM =，则1SEN θ=∠，2SEO θ=∠，3SMO θ=∠．显然，1θ，2θ，3θ均为锐角． 1tan SN SN NE OM θ==，3tan SOOMθ=，SN SO …， 13θθ∴…，又3sin SO SM θ=，2sin SOSEθ=，SE SM …， 32θθ∴…．故选：D ．【点评】本题考查了空间角的计算，三角函数的应用，属于中档题．10．（2018•新课标Ⅰ理）已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( )A B C D 【考点】直线与平面所成的角【分析】利用正方体棱的关系，判断平面α所成的角都相等的位置，然后求解α截此正方体所得截面面积的最大值．【解答】解：正方体的所有棱中，实际上是3组平行的棱，每条棱所在直线与平面α所成的角都相等，如图：所示的正六边形平行的平面，并且正六边形时，α截此正方体所得截面面积的最大，，α截此正方体所得截面最大值为：26．故选：A ．【点评】本题考查直线与平面所成角的大小关系，考查空间想象能力以及计算能力，有一定的难度． 11．（2018•新课标Ⅰ文）在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30︒，则该长方体的体积为( )A ．8B ．C ．D ．【考点】直线与平面所成的角【分析】画出图形，利用已知条件求出长方体的高，然后求解长方体的体积即可．【解答】解：长方体1111ABCD A B C D -中，2AB BC ==， 1AC 与平面11BB C C 所成的角为30︒，即130AC B ∠=︒，可得1tan30ABBC ==︒可得1BB ==．所以该长方体的体积为：22⨯⨯= 故选：C ．【点评】本题考查长方体的体积的求法，直线与平面所成角的求法，考查计算能力．12．（2018•新课标Ⅱ文）在正方体1111ABCD A B C D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为( )A B C D 【考点】异面直线及其所成的角。

2024年高考总复习优化设计一轮用书数学配人教A版(适用于新教材)课时规范练40

课时规范练40《素养分级练》P374基础巩固组1.(2023·山东青岛模拟)设集合A={(x ,y )|y=2x-3},B={(x ,y )|4x-2y+5=0},则A ∩B= ( )A.⌀B.{(118,14)} C.{(18,-114)} D.{(-18,-134)} 答案:A解析:由直线4x-2y+5=0,得y=2x+52.因为直线y=2x+52与直线y=2x-3的斜率相等,截距不相等,所以两直线相互平行,故A ∩B=⌀. 2.(2023·江苏无锡高三检测)在平面直角坐标系xOy 中,点(0,4)关于直线x-y+1=0的对称点为( ) A.(-1,2) B.(2,-1) C.(1,3) D.(3,1)答案:D解析:设点(0,4)关于直线x-y+1=0的对称点是(a ,b ),则{a 2-b+42+1=0,b -4a=-1,解得{a =3,b =1.3.(多选)(2023·山东青岛高三开学考试)已知直线l 1:4x-3y+4=0,l 2:(m+2)x-(m+1)y+2m+5=0(m ∈R ),则( )A.直线l 2过定点(-3,-1)B.当m=1时,l 1⊥l 2C.当m=2时,l 1∥l 2D.当l 1∥l 2时,两直线l 1,l 2之间的距离为1 答案:ACD解析:对于A,l 2:(m+2)x-(m+1)y+2m+5=0(m ∈R )变形为m (x-y+2)+2x-y+5=0,令{x -y +2=0,2x -y +5=0,则{x =-3,y =-1,因此直线l 2过定点(-3,-1),故A 正确;对于B,当m=1时,l 1:4x-3y+4=0,l 2:3x-2y+7=0,4×3+(-3)×(-2)≠0,故两直线不垂直,故B 错误;对于C,当m=2时,l 1:4x-3y+4=0,l 2:4x-3y+9=0,44=-3-3≠94,故两直线平行,故C 正确;对于D,当l 1∥l 2时,则满足m+24=-(m+1)-3≠2m+54⇒m=2,此时l 1:4x-3y+4=0,l 2:4x-3y+9=0,则两直线间的距离为√42+(-3)=1,故D 正确.故选ACD .4.已知A (4,0),B (0,4),从点P (2,0)射出的光线经直线AB 反射后,再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是( ) A.3√3 B.6 C.2√10 D.2√5答案:C解析:由题意直线AB 的方程为x+y=4,设P 关于直线AB 的对称点Q (a ,b ),则{ba -2=1,a+22+b2=4,解得{a =4,b =2,即Q (4,2).又P 关于y 轴的对称点为T (-2,0),所以光线所经过的路程为|QT|=√(-2-4)2+(0-2)2=2√10.5.(2023·福建福州高三检测)若直线ax+2y+1=0与直线x cos 2π3+y-1=0互相垂直,则a= . 答案:4解析:由题意得a2·cos 2π3=-1,解得a=4.6.已知直线l 过点P (-1,2),且点A (2,3),B (-4,5)到直线l 的距离相等,则直线l 的方程为 . 答案:x+3y-5=0或x=-1解析:(方法1)当直线l 的斜率存在时,设直线l 的方程为y-2=k (x+1),即kx-y+k+2=0.由题意知√k 2+1=√k 2+1,即|3k-1|=|-3k-3|,解得k=-13,所以直线l 的方程为y-2=-13(x+1),即x+3y-5=0.当直线l 的斜率不存在时,直线l 的方程为x=-1,符合题意.故所求直线l 的方程为x+3y-5=0或x=-1.(方法2)当AB ∥l 时,直线l 的斜率k=k AB =-13,则直线l 的方程为y-2=-13(x+1),即x+3y-5=0.当直线l 过AB 的中点(-1,4)时,直线l 的方程为x=-1.故所求直线l 的方程为x+3y-5=0或x=-1.综合提升组7.(2023·湖北武汉模拟)某菱形的一组对边所在的直线方程分别为x+2y+1=0和x+2y+3=0,另一组对边所在的直线方程分别为3x-4y+c 1=0和3x-4y+c 2=0,则|c 1-c 2|=( ) A.2√3 B.2√5 C.2 D.4答案:B解析:设直线x+2y+1=0与直线3x-4y+c 2=0的交点为A ,联立{x +2y +1=0,3x -4y +c 2=0,解得{x =-c 2+25,y =c 2-310,故A -c 2+25,c 2-310.同理,设直线x+2y+1=0与直线3x-4y+c 1=0的交点为B ,则B -c 1+25,c 1-310,设直线x+2y+3=0与直线3x-4y+c 1=0的交点为C ,则C -c 1+65,c 1-910,设直线x+2y+3=0与直线3x-4y+c 2=0的交点为D ,则D -c 2+65,c 2-910.由菱形的性质可知AC ⊥BD ,且AC ,BD 的斜率均存在,所以k AC ·k BD =-1,则c 2-310-c 1-910-c 2+25+c 1+65·c 1-310-c 2-910-c 1+25+c 2+65=-1,即36-(c 2-c 1)24[16-(c 2-c 1)2]=-1,解得|c 1-c 2|=2√5.8.(2023·河北大名高三检测)已知点P (-2,2),直线l :(λ+2)x-(λ+1)y-4λ-6=0,则点P 到直线l 的距离的取值范围为 . 答案:[0,4√2)解析:把直线l :(λ+2)x-(λ+1)y-4λ-6=0化为(2x-y-6)+λ(x-y-4)=0,联立{2x -y -6=0,x -y -4=0,解得{x =2,y =-2,即直线l 过定点M (2,-2).又k PM =-2-22-(-2)=-1,且λ+2λ+1×(-1)≠-1,所以直线PM 与l 不垂直,所以点P 到直线l 的距离的最大值小于|PM|=√(2+2)2+(-2-2)2=4√2,即点P 到直线l 的距离的取值范围为[0,4√2).9.(2023·四川成都七中高三检测)已知△ABC 的顶点B (5,1),AB 边上的高所在的直线方程为x-2y-5=0.(1)求直线AB 的方程.(2)在①②两个条件中任选一个,补充在下面问题中,并解答. ①角A 的平分线所在直线方程为x+2y-13=0; ②BC 边上的中线所在的直线方程为2x-y-5=0.,求直线AC 的方程.解:(1)因为AB 边上的高所在的直线方程为x-2y-5=0,所以直线AB 的斜率为k=-2. 又因为△ABC 的顶点B (5,1),所以直线AB 的方程为y-1=-2(x-5),即2x+y-11=0.(2)若选①:角A 的平分线所在直线方程为x+2y-13=0, 由{2x +y -11=0,x +2y -13=0,解得{x =3,y =5,所以点A (3,5).设点B 关于x+2y-13=0的对称点B'(x 0,y 0),则{y 0-1x 0-5×(-12)=-1,x 0+52+2×y 0+12-13=0,解得{x 0=375,y 0=295,所以B'375,295.又点B'375,295在直线AC 上,所以k AC =5-2953-375=211.所以直线AC 的方程为y-5=211(x-3),即2x-11y+49=0. 若选②:BC 边上的中线所在的直线方程为2x-y-5=0, 由{2x +y -11=0,2x -y -5=0,解得{x =4,y =3,所以点A (4,3).设点C (x 1,y 1),则BC 的中点在直线2x-y-5=0上,所以2×5+x 12−1+y 12-5=0,即2x 1-y 1-1=0,所以点C 在直线2x-y-1=0上.又点C 在直线x-2y-5=0上,由{x -2y -5=0,2x -y -1=0,解得{x =-1,y =-3,即C (-1,-3),所以k AC =-3-3-1-4=65.所以直线AC 的方程为y-3=65(x-4),即6x-5y-9=0.创新应用组10.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,这条直线被后人称之为三角形的欧拉线.已知△ABC 的顶点A (2,0),B (0,4),C (-4,0),则其欧拉线方程为 . 答案:x-y+2=0解析:设△ABC 的重心为G ,垂心为H ,由重心坐标公式得x=2+0+(-4)3=-23,y=0+4+03=43,所以G -23,43.由题,△ABC 的边AC 上的高线所在直线方程为x=0,直线BC :y=x+4,A (2,0),所以△ABC 的边BC上的高线所在直线方程为y=-x+2,联立{x =0,y =-x +2⇒H (0,2).所以欧拉线GH 的方程为y-2=2-430-(-23)x ,即x-y+2=0.。

【三维设计】2014届高考数学一轮复习 (基础知识+高频考点+解题训练)数列求和教学案

第四节数_列_求_和[知识能否忆起]一、公式法1．如果一个数列是等差数列或等比数列，则求和时直接利用等差、等比数列的前n 项和公式，注意等比数列公比q 的取值情况要分q ＝1或q ≠1.2．一些常见数列的前n 项和公式： (1)1＋2＋3＋4＋…＋n ＝n n ＋12；(2)1＋3＋5＋7＋…＋2n －1＝n 2； (3)2＋4＋6＋8＋…＋2n ＝n 2＋n . 二、非等差、等比数列求和的常用方法 1．倒序相加法如果一个数列{a n }，首末两端等“距离”的两项的和相等或等于同一常数，那么求这个数列的前n 项和即可用倒序相加法，等差数列的前n 项和即是用此法推导的．2．分组转化求和法若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转化法，分别求和而后相加减．3．错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可用此法来求，等比数列的前n 项和就是用此法推导的．4．裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．[小题能否全取]1．(2012·某某六校联考)设数列{(－1)n}的前n 项和为S n ，则对任意正整数n ，S n ＝( )A.n [－1n－1]2B.－1n －1＋12C.－1n＋12 D.－1n－12解析：选 D 因为数列{(－1)n}是首项与公比均为－1的等比数列，所以S n ＝－1－－1n×－11－－1＝－1n－12. 2．等差数列{a n }的通项公式为a n ＝2n ＋1，其前n 项的和为S n ，则数列⎩⎨⎧⎭⎬⎫S n n 的前10项的和为( )A ．120B ．70C ．75D ．100 解析：选C ∵S n ＝n a 1＋a n2＝n (n ＋2)，∴S n n ＝n ＋2.故S 11＋S 22＋…＋S 1010＝75. 3．数列a 1＋2，…，a k ＋2k ，…，a 10＋20共有十项，且其和为240，则a 1＋…＋a k ＋…＋a 10的值为( )A ．31B ．120C ．130D ．185解析：选C a 1＋…＋a k ＋…＋a 10＝240－(2＋…＋2k ＋…＋20)＝240－2＋20×102＝240－110＝130.4．若数列{a n }的通项公式为a n ＝2n＋2n －1，则数列{a n }的前n 项和为________．解析：S n ＝21－2n1－2＋n 1＋2n －12＝2n ＋1－2＋n 2.答案：2n ＋1＋n 2－25．数列12×4，14×6，16×8，…，12n 2n ＋2，…的前n 项和为________．解析：因a n ＝12n2n ＋2＝14⎝ ⎛⎭⎪⎫1n －1n ＋1则S n ＝14⎝ ⎛⎭⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝14⎝ ⎛⎭⎪⎫1－1n ＋1＝n4n ＋1. 答案：n4n ＋1数列求和的方法(1)一般的数列求和，应从通项入手，若无通项，先求通项，然后通过对通项变形，转化为与特殊数列有关或具备某种方法适用特点的形式，从而选择合适的方法求和．(2)解决非等差、等比数列的求和，主要有两种思路：①转化的思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解或错位相减来完成．②不能转化为等差或等比数列的数列，往往通过裂项相消法、错位相减法、倒序相加法等来求和．分组转化法求和典题导入[例1] (2011·某某高考)等比数列{a n }中，a 1，a 2，a 3分别是下表第一、二、三行中的某一个数，且a 1，a 2，a 3中的任何两个数不在下表的同一列.第一列第二列第三列第一行 3 2 10 第二行 6 4 14 第三行9818(1)求数列{a n }的通项公式；(2)若数列{b n }满足：b n ＝a n ＋(－1)nln a n ，求数列{b n }的前2n 项和S 2n . [自主解答] (1)当a 1＝3时，不合题意；当a 1＝2时，当且仅当a 2＝6，a 3＝18时，符合题意；当a 1＝10时，不合题意．因此a 1＝2，a 2＝6，a 3＝18.所以公比q ＝3，故a n ＝2·3n －1.(2)因为b n ＝a n ＋(－1)n ln a n ＝2·3n －1＋(－1)n ln(2·3n －1)＝2·3n －1＋(－1)n(ln 2－ln3)＋(－1)nn ln 3，所以S 2n ＝b 1＋b 2＋…＋b 2n ＝2(1＋3＋…＋32n －1)＋[－1＋1－1＋…＋(－1)2n](ln 2－ln 3)＋[－1＋2－3＋…＋(－1)2n2n ]ln 3＝2×1－32n1－3＋n ln 3＝32n＋n ln 3－1.由题悟法分组转化法求和的常见类型(1)若a n ＝b n ±，且{b n }，{}为等差或等比数列，可采用分组求和法求{a n }的前n 项和．(2)通项公式为a n ＝⎩⎪⎨⎪⎧b n ，n 为奇数，，n 为偶数的数列，其中数列{b n }，{}是等比数列或等差数列，可采用分组求和法求和.以题试法1．已知数列{x n }的首项x 1＝3，通项x n ＝2n p ＋nq (n ∈N *，p ，q 为常数)，且x 1，x 4，x 5成等差数列．求：(1)p ，q 的值；(2)数列{x n }前n 项和S n 的公式．解：(1)由x 1＝3，得2p ＋q ＝3，又因为x 4＝24p ＋4q ，x 5＝25p ＋5q ，且x 1＋x 5＝2x 4，得3＋25p ＋5q ＝25p ＋8q ，解得p ＝1，q ＝1.(2)由(1)，知x n ＝2n＋n ，所以S n ＝(2＋22＋…＋2n )＋(1＋2＋…＋n )＝2n ＋1－2＋n n ＋12.错位相减法求和典题导入[例2] (2012·某某高考)已知数列{a n }的前n 项和S n ＝k －k (其中c ，k 为常数)，且a 2＝4，a 6＝8a 3.(1)求a n ；(2)求数列{na n }的前n 项和T n .[自主解答] (1)由S n ＝k －k ，得a n ＝S n －S n －1＝k －k －1(n ≥2)．由a 2＝4，a 6＝8a 3 ，得kc (c －1)＝4，kc 5(c －1)＝8kc 2(c －1)，解得⎩⎪⎨⎪⎧c ＝2，k ＝2，所以a 1＝S 1＝2，a n ＝k －k －1＝2n(n ≥2)，于是a n ＝2n.(2)T n ＝∑i ＝1nia i ＝∑i ＝1ni ·2i，即T n ＝2＋2·22＋3·23＋4·24＋…＋n ·2n.T n ＝2T n －T n ＝－2－22－23－24－…－2n ＋n ·2n ＋1＝－2n ＋1＋2＋n ·2n ＋1＝(n －1)2n ＋1＋2.由题悟法用错位相减法求和应注意：(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n －qS n ”的表达式．(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解．以题试法2．(2012·某某模拟)已知等比数列{a n }的前n 项和为S n ，且满足S n ＝3n＋k . (1)求k 的值及数列{a n }的通项公式； (2)若数列{b n }满足a n ＋12＝(4＋k )a n b n ，求数列{b n }的前n 项和T n .解：(1)当n ≥2时，由a n ＝S n －S n －1＝3n＋k －3n －1－k ＝2·3n －1，得等比数列{a n }的公比q ＝3，首项为2.∴a 1＝S 1＝3＋k ＝2，∴k ＝－1，∴数列{a n }的通项公式为a n ＝2·3n －1.(2)由a n ＋12＝(4＋k )a n b n ，可得b n ＝n2·3n －1，即b n ＝32·n 3n .∵T n ＝32⎝ ⎛⎭⎪⎫13＋232＋333＋…＋n 3n ，∴13T n ＝32⎝ ⎛⎭⎪⎫132＋233＋334＋…＋n 3n ＋1，∴23T n ＝32⎝ ⎛⎭⎪⎫13＋132＋133＋…＋13n －n 3n ＋1，∴T n ＝94⎝ ⎛⎭⎪⎫12－12·3n －n 3n ＋1.裂项相消法求和典题导入[例3] 已知数列{a n }的前n 项和为S n ，a 1＝1，S n ＝na n －n (n －1)(n ∈N *)． (1)求数列{a n }的通项公式； (2)设b n ＝2a n a n ＋1，求数列{b n }的前n 项和T n .[自主解答] (1)∵S n ＝na n －n (n －1)，当n ≥2时，S n －1＝(n －1)·a n －1－(n －1)(n －2)，∴a n ＝S n －S n －1＝na n －n (n －1)－(n －1)a n －1＋(n －1)·(n －2)，即a n －a n －1＝2.∴数列{a n }是首项a 1＝1，公差d ＝2的等差数列，故a n ＝1＋(n －1)·2＝2n －1，n ∈N *.(2)由(1)知b n ＝2a n a n ＋1＝22n －12n ＋1＝12n －1－12n ＋1，故T n ＝b 1＋b 2＋…＋b n ＝⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1＝1－12n ＋1＝2n 2n ＋1.本例条件不变，若数列{b n }满足b n ＝1S n ＋n，求数列{b n }的前n 项和T n . 解：S n ＝na n －n (n －1)＝n (2n －1)－n (n －1)＝n 2.b n ＝1S n ＋n ＝1n 2＋n ＝1n n ＋1＝1n －1n ＋1，T n ＝⎝⎛⎭⎪⎫11－12＋⎝⎛⎭⎪⎫12－13＋⎝⎛⎭⎪⎫13－14＋…＋⎝⎛⎭⎪⎫1n －1n ＋1＝1－1n ＋1＝nn ＋1.由题悟法利用裂项相消法求和应注意(1)抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项； (2)将通项裂项后，有时需要调整前面的系数，使裂开的两项之差和系数之积与原通项相等．如：若{a n }是等差数列，则1a n a n ＋1＝1d ⎝ ⎛⎭⎪⎫1a n －1a n ＋1，1a n a n ＋2＝12d ⎝ ⎛⎭⎪⎫1a n －1a n ＋2. 以题试法3．(2012·“江南十校”联考)在等比数列{a n }中，a 1>0，n ∈N *，且a 3－a 2＝8，又a 1、a 5的等比中项为16.(1)求数列{a n }的通项公式；(2)设b n ＝log 4a n ，数列{b n }的前n 项和为S n ，是否存在正整数k ，使得1S 1＋1S 2＋1S 3＋…＋1S n<k 对任意n ∈N *恒成立．若存在，求出正整数k 的最小值；不存在，请说明理由．解：(1)设数列{a n }的公比为q ，由题意可得a 3＝16， ∵a 3－a 2＝8，则a 2＝8，∴q ＝2. ∴a n ＝2n ＋1.(2)∵b n ＝log 42n ＋1＝n ＋12，∴S n ＝b 1＋b 2＋…＋b n ＝n n ＋34.∵1S n ＝4nn ＋3＝43⎝ ⎛⎭⎪⎫1n －1n ＋3， ∴1S 1＋1S 2＋1S 3＋…＋1S n＝43⎝ ⎛⎭⎪⎫11－14＋12－15＋13－16＋…＋1n －1n ＋3＝43⎝⎛⎭⎪⎫1＋12＋13－1n ＋1－1n ＋2－1n ＋3<229，∴存在正整数k 的最小值为3.1．已知{a n }是首项为1的等比数列，S n 是{a n }的前n 项和，且9S 3＝S 6，则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为( )A.158或5B.3116或5 C.3116D.158解析：选C 设数列{a n }的公比为q .由题意可知q ≠1，且91－q 31－q＝1－q 61－q，解得q ＝2，所以数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项，12为公比的等比数列，由求和公式可得S 5＝3116.2．已知数列{a n }的前n 项和S n ＝an 2＋bn (a 、b ∈R )，且S 25＝100，则a 12＋a 14等于( ) A ．16 B ．8 C ．4 D ．不确定解析：选B 由数列{a n }的前n 项和S n ＝an 2＋bn (a 、b ∈R )，可知数列{a n }是等差数列，由S 25＝a 1＋a 25×252＝100，解得a 1＋a 25＝8，所以a 1＋a 25＝a 12＋a 14＝8.3．数列112，314，518，7116，…，(2n －1)＋12n ，…的前n 项和S n 的值等于( )A ．n 2＋1－12nB ．2n 2－n ＋1－12nC ．n 2＋1－12n －1D ．n 2－n ＋1－12n解析：选A 该数列的通项公式为a n ＝(2n －1)＋12n ，则S n ＝[1＋3＋5＋…＋(2n －1)]＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n ＝n 2＋1－12n .4．(2012·“江南十校”联考)若数列{a n }为等比数列，且a 1＝1，q ＝2，则T n ＝1a 1a 2＋1a 2a 3＋…＋1a n a n ＋1的结果可化为( )A ．1－14nB ．1－12nC.23⎝⎛⎭⎪⎫1－14n D.23⎝ ⎛⎭⎪⎫1－12n解析：选C a n ＝2n －1，设b n ＝1a n a n ＋1＝⎝ ⎛⎭⎪⎫122n －1，则T n ＝b 1＋b 2＋…＋b n ＝12＋⎝ ⎛⎭⎪⎫123＋…＋⎝ ⎛⎭⎪⎫122n －1＝12⎝ ⎛⎭⎪⎫1－14n 1－14＝23⎝ ⎛⎭⎪⎫1－14n .5．已知等差数列{a n }的前n 项和为S n ，a 5＝5，S 5＝15，则数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前100项和为( )A.100101B.99101C.99100D.101100解析：选A 设等差数列{a n }的首项为a 1，公差为d .∵a 5＝5，S 5＝15，∴⎩⎪⎨⎪⎧a 1＋4d ＝5，5a 1＋5×5－12d ＝15，∴⎩⎪⎨⎪⎧a 1＝1，d ＝1，∴a n ＝a 1＋(n －1)d ＝n .∴1a n a n ＋1＝1nn ＋1＝1n －1n ＋1，∴数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前100项和为1－12＋12－13＋…＋1100－1101＝1－1101＝100101.6．已知函数f (n )＝⎩⎪⎨⎪⎧n 2当n 为奇数时，－n 2当n 为偶数时，且a n ＝f (n )＋f (n ＋1)，则a 1＋a 2＋a 3＋…＋a 100等于( )A ．0B ．100C ．－100D ．10 200解析：选B 由题意，a 1＋a 2＋a 3＋…＋a 100＝12－22－22＋32＋32－42－42＋52＋…＋992－1002－1002＋1012＝－(1＋2)＋(3＋2)＋…－(99＋100)＋(101＋100)＝－(1＋2＋…＋99＋100)＋(2＋3＋…＋100＋101)＝－1＋101＝100.7．在等差数列{a n }中，S n 表示前n 项和，a 2＋a 8＝18－a 5，则S 9＝________. 解析：由等差数列的性质及a 2＋a 8＝18－a 5，得2a 5＝18－a 5，则a 5＝6，故S 9＝a 1＋a 9×92＝9a 5＝54.答案：548．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项公式为2n，则数列{a n }的前n 项和S n ＝________.解析：∵a n ＋1－a n ＝2n ，∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1 ＝2n －1＋2n －2＋…＋22＋2＋2＝2－2n1－2＋2＝2n －2＋2＝2n.∴S n ＝2－2n ＋11－2＝2n ＋1－2.答案：2n ＋1－29．已知等比数列{a n }中，a 1＝3，a 4＝81，若数列{b n }满足b n ＝log 3a n ，则数列⎩⎨⎧⎭⎬⎫1b n b n ＋1的前n 项和S n ＝________.解析：设等比数列{a n }的公比为q ，则a 4a 1＝q 3＝27，解得q ＝3.所以a n ＝a 1q n －1＝3×3n －1＝3n，故b n ＝log 3a n ＝n ，所以1b n b n ＋1＝1nn ＋1＝1n －1n ＋1. 则数列⎩⎨⎧⎭⎬⎫1b n b n ＋1的前n 项和为1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1.答案：nn ＋110．(2013·某某统考)在等比数列{a n }中，a 2a 3＝32，a 5＝32.(1)求数列{a n }的通项公式；(2)设数列{a n }的前n 项和为S n ，求S 1＋2S 2＋…＋nS n . 解：(1)设等比数列{a n }的公比为q ，依题意得⎩⎪⎨⎪⎧a 1q ·a 1q 2＝32，a 1q 4＝32，解得a 1＝2，q ＝2，故a n ＝2·2n －1＝2n.(2)∵S n 表示数列{a n }的前n 项和， ∴S n ＝21－2n1－2＝2(2n－1)，∴S 1＋2S 2＋…＋nS n ＝2[(2＋2·22＋…＋n ·2n )－(1＋2＋…＋n )]＝2(2＋2·22＋…＋n ·2n )－n (n ＋1)，设T n ＝2＋2·22＋…＋n ·2n，① 则2T n ＝22＋2·23＋…＋n ·2n ＋1，②①－②，得－T n ＝2＋22＋…＋2n －n ·2n ＋1＝21－2n1－2－n ·2n ＋1＝(1－n )2n ＋1－2，∴T n ＝(n －1)2n ＋1＋2，∴S 1＋2S 2＋…＋nS n ＝2[(n －1)2n ＋1＋2]－n (n ＋1)＝(n －1)2n ＋2＋4－n (n ＋1)．11．(2012·某某调研)已知等差数列{a n }满足：a 5＝9，a 2＋a 6＝14. (1)求{a n }的通项公式；(2)若b n ＝a n ＋qa n (q >0)，求数列{b n }的前n 项和S n .解：(1)设数列{a n }的首项为a 1，公差为d ，则由a 5＝9，a 2＋a 6＝14，得⎩⎪⎨⎪⎧a 1＋4d ＝9，2a 1＋6d ＝14，解得⎩⎪⎨⎪⎧a 1＝1，d ＝2，所以{a n }的通项a n ＝2n －1.(2)由a n ＝2n －1得b n ＝2n －1＋q 2n －1.当q >0且q ≠1时，S n ＝[1＋3＋5＋…＋(2n －1)]＋(q 1＋q 3＋q 5＋…＋q 2n －1)＝n 2＋q 1－q 2n1－q2；当q ＝1时，b n ＝2n ，则S n ＝n (n ＋1)．所以数列{b n }的前n 项和S n ＝⎩⎪⎨⎪⎧n n ＋1，q ＝1，n 2＋q 1－q 2n1－q 2，q >0，q ≠1.12．(2012·“江南十校”联考)若数列{a n }满足：a 1＝23，a 2＝2,3(a n ＋1－2a n ＋a n －1)＝2.(1)证明：数列{a n ＋1－a n }是等差数列；(2)求使1a 1＋1a 2＋1a 3＋…＋1a n >52成立的最小的正整数n .解：(1)由3(a n ＋1－2a n ＋a n －1)＝2可得：a n ＋1－2a n ＋a n －1＝23，即(a n ＋1－a n )－(a n －a n －1)＝23，故数列{a n ＋1－a n }是以a 2－a 1＝43为首项，23为公差的等差数列．(2)由(1)知a n ＋1－a n ＝43＋23(n －1)＝23(n ＋1)，于是累加求和得a n ＝a 1＋23(2＋3＋…＋n )＝13n (n ＋1)，∴1a n ＝3⎝ ⎛⎭⎪⎫1n －1n ＋1， ∴1a 1＋1a 2＋1a 3＋…＋1a n ＝3－3n ＋1>52，∴n >5， ∴最小的正整数n 为6.1．已知数列{a n }的前n 项和S n ＝n 2－6n ，则{|a n |}的前n 项和T n ＝( ) A ．6n －n 2B ．n 2－6n ＋18C.⎩⎪⎨⎪⎧6n －n 21≤n ≤3n 2－6n ＋18n >3 D.⎩⎪⎨⎪⎧6n －n 21≤n ≤3n 2－6n n >3解析：选C ∵由S n ＝n 2－6n 得{a n }是等差数列，且首项为－5，公差为2. ∴a n ＝－5＋(n －1)×2＝2n －7， ∴n ≤3时，a n <0，n >3时，a n >0，∴T n ＝⎩⎪⎨⎪⎧6n －n 21≤n ≤3，n 2－6n ＋18n >3.2．(2012·某某二模)若数列{a n }满足a 1＝2且a n ＋a n －1＝2n＋2n －1，S n 为数列{a n }的前n项和，则log 2(S 2 012＋2)＝________.解析：因为a 1＋a 2＝22＋2，a 3＋a 4＝24＋23，a 5＋a 6＝26＋25，….所以S 2 012＝a 1＋a 2＋a 3＋a 4＋…＋a 2 011＋a 2 012＝21＋22＋23＋24＋…＋22 011＋22 012＝21－22 0121－2＝22 013－2.故log 2(S 2 012＋2)＝log 222 013＝2 013.答案：2 0133．已知递增的等比数列{a n }满足：a 2＋a 3＋a 4＝28，且a 3＋2是a 2，a 4的等差中项． (1)求数列{a n }的通项公式；(2)若b n ＝a n log 12a n ，S n ＝b 1＋b 2＋…＋b n ，求S n .解：(1)设等比数列{a n }的首项为a 1，公比为q . 依题意，有2(a 3＋2)＝a 2＋a 4，代入a 2＋a 3＋a 4＝28，得a 3＝8. ∴a 2＋a 4＝20.∴⎩⎪⎨⎪⎧a 1q ＋a 1q 3＝20，a 3＝a 1q 2＝8，解得⎩⎪⎨⎪⎧q ＝2，a 1＝2，或⎩⎪⎨⎪⎧q ＝12，a 1＝32.又{a n }为递增数列， ∴⎩⎪⎨⎪⎧q ＝2，a 1＝2.∴a n ＝2n.(2)∵b n ＝2n ·log 122n ＝－n ·2n，∴－S n ＝1×2＋2×22＋3×23＋…＋n ×2n.①∴－2S n ＝1×22＋2×23＋3×24＋…＋(n －1)×2n ＋n ×2n ＋1.②①－②得S n ＝2＋22＋23＋…＋2n －n ·2n ＋1＝21－2n1－2－n ·2n ＋1＝2n ＋1－n ·2n ＋1－2.∴S n ＝2n ＋1－n ·2n ＋1－2.1．已知{a n }是公差不为零的等差数列，a 1＝1，且a 1，a 3，a 9成等比数列． (1)求数列{a n }的通项； (2)求数列{2a n }的前n 项和S n .解：(1)由题设知公差d ≠0，由a 1＝1，a 1，a 3，a 9成等比数列得1＋2d 1＝1＋8d1＋2d ，解得d ＝1或d ＝0(舍去)，故{a n }的通项a n ＝1＋(n －1)×1＝n . (2)由(1)知2a n ＝2n，由等比数列前n 项和公式得S n ＝2＋22＋23＋ (2)＝21－2n1－2＝2n ＋1－2.2．设函数f (x )＝x 3，在等差数列{a n }中，a 3＝7，a 1＋a 2＋a 3＝12，记S n ＝f (3a n ＋1)，令b n ＝a n S n ，数列⎩⎨⎧⎭⎬⎫1b n 的前n 项和为T n .(1)求{a n }的通项公式和S n ； (2)求证：T n <13.解：(1)设数列{a n }的公差为d ，由a 3＝a 1＋2d ＝7，a 1＋a 2＋a 3＝3a 1＋3d ＝12，解得a 1＝1，d ＝3，则a n ＝3n －2.∵f (x )＝x 3，∴S n ＝f (3a n ＋1)＝a n ＋1＝3n ＋1. (2)证明：∵b n ＝a n S n ＝(3n －2)(3n ＋1)， ∴1b n＝13n －23n ＋1＝13⎝ ⎛⎭⎪⎫13n －2－13n ＋1.∴T n ＝1b 1＋1b 2＋…＋1b n＝13⎝ ⎛⎭⎪⎫1－14＋14－17＋…＋13n －2－13n ＋1＝13⎝ ⎛⎭⎪⎫1－13n ＋1.∴T n <13. 3．已知二次函数f (x )＝x 2－5x ＋10，当x ∈(n ，n ＋1](n ∈N *)时，把f (x )在此区间内的整数值的个数表示为a n .(1)求a 1和a 2的值； (2)求n ≥3时a n 的表达式； (3)令b n ＝4a n a n ＋1，求数列{b n }的前n 项和S n (n ≥3)．解：(1)f (x )＝x 2－5x ＋10，又x ∈(n ，n ＋1](n ∈N *)时，f (x )的整数个数为a n ，所以f (x )在(1,2]上的值域为[4,6)⇒a 1＝2；f (x )在(2,3]上的值域为⎣⎢⎡⎦⎥⎤154，4⇒a 2＝1.(2)当n ≥3时，f (x )是增函数，故a n ＝f (n ＋1)－f (n )＝2n －4.(3)由(1)和(2)可知，b 1＝42×1＝2，b 2＝41×2＝2.而当n ≥3时，b n ＝42n －42n －2＝2⎝⎛⎭⎪⎫12n －4－12n －2.所以当n ≥3时，S n ＝b 1＋b 2＋b 3＋b 4＋…＋b n＝2＋2＋2⎝ ⎛⎭⎪⎫12－14＋14－16＋…＋12n －4－12n －2 ＝4＋2⎝ ⎛⎭⎪⎫12－12n －2＝5－1n －1.。

2014届高考数学一轮复习教学案(基础知识+高频考点+解题训练)两直线的位置关系(含解析)2014届

两直线的位置关系[知识能否忆起]一、两条直线的位置关系斜截式一般式方程 y ＝k 1x ＋b 1 y ＝k 2x ＋b 2 A 1x ＋B 1y ＋C 1＝0(A 21＋B 21≠0) A 2x ＋B 2y ＋C 2＝0(A 22＋B 22≠0)相交 k 1≠k 2 A 1B 2－A 2B 1≠0⎝⎛⎭⎫当A 2B 2≠0时，记为A 1A 2≠B 1B 2垂直k 1＝－1k 2或k 1k 2＝－1A 1A 2＋B 1B 2＝0⎝⎛⎭⎫当B 1B 2≠0时，记为A 1B 1·A 2B 2＝－1平行k 1＝k 2 且b 1≠b 2{ A 1B 2－A 2B 1＝0，B 2C 1－B 1C 2≠0或{ A 1B 2－A 2B 1＝0，A 1C 2－A 2C 1≠0⎝⎛⎭⎫当A 2B 2C 2≠0时，记为A 1A 2＝B 1B 2≠C 1C 2 重合 k 1＝k 2 且b 1＝b 2A 1＝λA 2，B 1＝λB 2，C 1＝λC 2(λ≠0)⎝⎛⎭⎫当A 2B 2C 2≠0时，记为A 1A 2＝B 1B 2＝C 1C 2二、两条直线的交点设两条直线的方程是l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，两条直线的交点坐标就是方程组{ A 1x ＋B 1y ＋C 1＝0，A 2x ＋B 2y ＋C 2＝0的解，若方程组有唯一解，则两条直线相交，此解就是交点坐标；若方程组无解，则两条直线无公共点，此时两条直线平行；反之，亦成立．三、几种距离 1．两点间的距离平面上的两点A (x 1，y 1)，B (x 2，y 2)间的距离公式：d (A ，B )＝|AB |＝(x 1－x 2)2＋(y 1－y 2)2.2．点到直线的距离点P (x 1，y 1)到直线l ：Ax ＋By ＋C ＝0的距离d ＝|Ax 1＋By 1＋C |A 2＋B 2.3．两条平行线间的距离两条平行线Ax ＋By ＋C 1＝0与Ax ＋By ＋C 2＝0间的距离d ＝|C 1－C 2|A 2＋B 2.(4)[小题能否全取]1．(教材习题改编)已知l 1的倾斜角为45°，l 2经过点P (－2，－1)，Q (3，m )．若l 1⊥l 2，则实数m 为( )A ．6 B ．－6 C ．5D ．－5解析：选B 由已知得k 1＝1，k 2＝m ＋15.暑期报名海外游学的人数增长达到∵l 1⊥l 2，∴k 1k 2＝－1， ∴1×m ＋15＝－1，即m ＝－6.2．(教材习题改编)点(0，－1)到直线x ＋2y ＝3的距离为( )A.55B.5教案目的是用更严格的监管、更严厉的处罚、更严肃的问责化学教案切实保障“舌尖上的安全C ．5D.15解析：选B d ＝|0＋2×(－1)－3|5＝ 5.3．点(a ，b )关于直线x ＋y ＋1＝0的对称点是( ) A ．(－a －1，－b －1)B ．(－b －1，－a －1)C ．(－a ，－b )D ．(－b ，－a )解析：选B 设对称点为(x ′，y ′)，则⎩⎨⎧y ′－b x ′－a×(－1)＝－1，x ′＋a 2＋y ′＋b2＋1＝0，解得x ′＝－b －1，y ′＝－a －1.4．l 1：x －y ＝0与l 2：2x －3y ＋1＝0的交点在直线mx ＋3y ＋5＝0上，则m 的值为( )A ．3B ．5C ．－5D ．－8解析：选D 由{x －y ＝0，2x －3y ＋1＝0，得l 1与l 2的交点坐标为(1,1)．所以m＋3＋5＝0，m＝－8.5．与直线4x＋3y－5＝0平行，并且到它的距离等于3的直线方程是______________________．|m＋5|，得m＝10或－20.解析：设所求直线方程为4x＋3y＋m＝0，由3＝42＋32答案：4x＋3y＋10＝0或4x＋3y－20＝01.在判断两条直线的位置关系时，首先应分析直线的斜率是否存在，两条直线都有斜率时，可根据斜率的关系作出判断，无斜率时，要单独考虑．2．在使用点到直线的距离公式或两平行线间的距离公式时，直线方程必须先化为Ax ＋By＋C＝0的形式，否则会出错．两直线的平行与垂直典题导入[例1](2012·浙江高考)设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x ＋(a＋1)y＋4＝0平行”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件[自主解答]由a＝1，可得l1∥l2；反之，由l1∥l2，可得a＝1或a＝－2.[答案] A在本例中若l1⊥l2，试求a.解：∵l1⊥l2，∴a×1＋2×(a＋1)＝0，∴a＝－23.由题悟法1．充分掌握两直线平行与垂直的条件是解决本题的关键，对于斜率都存在且不重合的两条直线l 1和l 2，l 1∥l 2⇔k 1＝k 2，l 1⊥l 2⇔k 1·k 2＝－1.若有一条直线的斜率不存在，那么另一条直线的斜率是多少一定要特别注意．2．(1)若直线l 1和l 2有斜截式方程l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则直线l 1⊥l 2的充要条件是k 1·k 2＝－1.(2)设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0.则l 1⊥l 2⇔A 1A 2＋B 1B 2＝0.以题试法1．(2012·大同模拟)设a ，b ，c 分别是△ABC 中角A ，B ，C 所对的边，则直线x sin A ＋ay ＋c ＝0与bx －y sin B ＋sin C ＝0的位置关系是( )A ．平行 B ．重合C ．垂直D ．相交但不垂直解析：选C 由已知得a ≠0，sin B ≠0，所以两直线的斜率分别为k 1＝－sin A a ，k 2＝bsin B ，由正弦定理得k 1·k 2＝－sin A a ·bsin B＝－1，所以两条直线垂直．两直线的交点与距离问题典题导入[例2] (2012·浙江高考)定义：曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l 的距离．已知曲线C 1：y ＝x 2＋a 到直线l ：y ＝x 的距离等于曲线C 2：x 2＋(y ＋4)2＝2到直线l ：y ＝x 的距离，则实数a ＝________.[自主解答] 因曲线C 2：x 2＋(y ＋4)2＝2到直线l ：y ＝x 的距离为0－(－4)2－2＝22－2＝2，所以曲线C 1与直线l 不能相交，故x 2＋a ＞x ，即x 2＋a －x ＞0.设C 1：y ＝x 2＋a上一点为(x 0，y 0)，则点(x 0，y 0)到直线l 的距离d ＝|x 0－y 0|2＝－x 0＋x 20＋a2＝⎝⎛⎭⎫x 0－122＋a －142≥4a －142＝2，所以a ＝94.”化学教案结合全文化学教案概述作者这样认为的依据试卷试题[答案] 94由题悟法1．点到直线的距离问题可直接代入距离公式去求．注意直线方程为一般式．2．点到与坐标轴垂直的直线的距离，可用距离公式求解．也可用如下方法去求解：(1)点P (x 0，y 0)到与y 轴垂直的直线y ＝a 的距离d ＝|y 0－a |.(2)点P (x 0，y 0)到与x 轴垂直的直线x ＝b 的距离d ＝|x 0－b |.以题试法2．(2012·通化模拟)若两平行直线3x －2y －1＝0,6x ＋ay ＋c ＝0之间的距离为21313，则c的值是________．解析：由题意得63＝a －2≠c－1，得a ＝－4，c ≠－2，则6x ＋ay ＋c ＝0可化为3x －2y ＋c2＝0，则⎪⎪⎪⎪c 2＋113＝21313，解得c ＝2或－6.答案：2或－6对称问题典题导入[例3] (2012·成都模拟)在直角坐标系中，A (4,0)，B (0，4)，从点P (2,0)射出的光线经直线AB 反射后，再射到直线OB 上，最后经直线OB 反射后又回到P 点，则光线所经过的路程是( )A ．210 B ．6C ．3 3D ．25②________试卷试题它们使用着同样的文字化学教案③__________________化学[自主解答] 如图，设点P 关于直线AB ，y 轴的对称点分别为D ，C ，易求得D (4,2)，C (－2,0)，由对称性知，D ，M ，N ，C 共线，则△PMN 的周长＝|PM |＋|MN |＋|PN |＝|DM |＋|MN |＋|NC |＝|CD |＝40＝210即为光线所经过的路程．[答案] A由题悟法对称问题主要包括中心对称和轴对称 (1)中心对称①点P (x ，y )关于O (a ，b )的对称点P ′(x ′，y ′)满足{ x ′＝2a －x ，y ′＝2b －y .②直线关于点的对称可转化为点关于点的对称问题来解决． (2)轴对称①点A (a ，b )关于直线Ax ＋By ＋C ＝0(B ≠0)的对称点A ′(m ，n )，则有⎩⎨⎧n －b m －a ×⎝⎛⎭⎫－A B ＝－1，A ·a ＋m 2＋B ·b ＋n 2＋C ＝0.②直线关于直线的对称可转化为点关于直线的对称问题来解决．以题试法3．(2012·南京调研)与直线3x －4y ＋5＝0关于x 轴对称的直线方程为( )A ．3x ＋4y ＋5＝0 B ．3x ＋4y －5＝0 C ．－3x ＋4y －5＝0 D ．－3x ＋4y ＋5＝0解析：选A 与直线3x －4y ＋5＝0关于x 轴对称的直线方程是3x －4(－y )＋5＝0，即3x ＋4y ＋5＝0.1．(2012·海淀区期末)已知直线l 1：k 1x ＋y ＋1＝0与直线l 2：k 2x ＋y －1＝0，那么“k 1＝k 2”是“l 1∥l 2”的( )A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：选C 由k 1＝k 2,1≠－1，得l 1∥l 2；由l 1∥l 2知k 1×1－k 2×1＝0，所以k 1＝k 2.故“k 1＝k 2”是“l 1∥l 2”的充要条件．2．当0＜k ＜12时，直线l 1：kx －y ＝k －1与直线l 2：ky －x ＝2k 的交点在( )A ．第一象限 B ．第二象限C ．第三象限D ．第四象限解析：选B 解方程组{ kx －y ＝k －1，ky －x ＝2k ，得两直线的交点坐标为⎝ ⎛⎭⎪⎫k k －1，2k －1k －1，因为0＜k ＜12，所以k k －1＜0，2k －1k －1＞0，故交点在第二象限．3．(2012·长沙检测)已知直线l 1的方程为3x ＋4y －7＝0，直线l 2的方程为6x ＋8y ＋1＝0，则直线l 1与l 2的距离为( )A.85B.32（C ．4D ．8解析：选B ∵直线l 1的方程为3x ＋4y －7＝0，直线l 2的方程为6x ＋8y ＋1＝0，即为3x ＋4y ＋12＝0，∴直线l 1与直线l 2的距离为⎪⎪⎪⎪12＋732＋42＝32.4．若直线l 1：y ＝k (x －4)与直线l 2关于点(2,1)对称，则直线l 2恒过定点( )A ．(0,4) B ．(0,2) C ．(－2,4)D ．(4，－2)解析：选B 由于直线l 1：y ＝k (x －4)恒过定点(4,0)，其关于点(2,1)对称的点为(0,2)．又由于直线l 1：y ＝k (x －4)与直线l 2关于点(2,1)对称，故直线l 2恒过定点(0,2)．5．已知直线l 1：y ＝2x ＋3，若直线l 2与l 1关于直线x ＋y ＝0对称，又直线l 3⊥l 2，则l 3的斜率为( )A ．－2 B ．－12C.12D ．2解析：选A 依题意得，直线l 2的方程是－x ＝2(－y )＋3，即y ＝12x ＋32，其斜率是12，由l 3⊥l 2，得l 3的斜率等于－2.6．(2012·岳阳模拟)直线l 经过两直线7x ＋5y －24＝0和x －y ＝0的交点，且过点(5,1)．则l 的方程是( )A ．3x ＋y ＋4＝0 B ．3x －y ＋4＝0 C ．x ＋3y －8＝0D ．x －3y －4＝0解析：选C 设l 的方程为7x ＋5y －24＋λ(x －y )＝0，即(7＋λ)x ＋(5－λ)y －24＝0，则(7＋λ)×5＋5－λ－24＝0.解得λ＝－4.l 的方程为x ＋3y －8＝0.7．(2012·郑州模拟)若直线l 1：ax ＋2y ＝0和直线l 2：2x ＋(a ＋1)y ＋1＝0垂直，则实数a 的值为________．解析：由2a ＋2(a ＋1)＝0得a ＝－12.答案：－128．已知平面上三条直线x ＋2y －1＝0，x ＋1＝0，x ＋ky ＝0，如果这三条直线将平面划分为六部分，则实数k 的所有取值为________．解析：若三条直线有两条平行，另外一条与这两条直线相交，则符合要求，此时k ＝0或2；若三条直线交于一点，也符合要求，此时k ＝1，故实数k 的所有取值为0,1,2.答案：0,1,29．(2013·临沂模拟)已知点P (4，a )到直线4x －3y －1＝0的距离不大于3，则a 的取值范围是________．解析：由题意得，点到直线的距离为|4×4－3×a －1|5＝|15－3a |5.又|15－3a |5≤3，即|15－3a |≤15，解得，0≤a ≤10，所以a ∈[0,10]．答案：[0,10]10．(2013·舟山模拟)已知1a ＋1b ＝1(a ＞0，b ＞0)，求点(0，b )到直线x －2y －a ＝0的距离的最小值．解：点(0，b )到直线x －2y －a ＝0的距离为d ＝a ＋2b 5＝15(a ＋2b )⎝⎛⎭⎫1a ＋1b ＝15⎝⎛⎭⎫3＋2b a ＋a b ≥15(3＋22)＝35＋2105，当且仅当a 2＝2b 2，a ＋b ＝ab ，即a ＝1＋2，b ＝2＋22时取等号．所以点(0，b )到直线x －2y －a ＝0的距离的最小值为35＋2105.11．(2012·荆州二检)过点P (1,2)的直线l 被两平行线l 1：4x ＋3y ＋1＝0与l 2：4x ＋3y ＋6＝0截得的线段长|AB |＝2，求直线l 的方程．解：设直线l 的方程为y －2＝k (x －1)，由{y ＝kx ＋2－k ，4x ＋3y ＋1＝0，解得A ⎝ ⎛⎭⎪⎫3k －73k ＋4，－5k ＋83k ＋4；由{y ＝kx ＋2－k ，4x ＋3y ＋6＝0，解得B ⎝⎛⎭⎪⎫3k －123k ＋4，8－10k 3k ＋4.∵|AB |＝2， ∴⎝ ⎛⎭⎪⎫53k ＋42＋⎝ ⎛⎭⎪⎫5k 3k ＋42＝2，整理，得7k 2－48k －7＝0，解得k 1＝7或k 2＝－17.因此，所求直线l 的方程为x ＋7y －15＝0或7x －y －5＝0.12．已知直线l ：3x －y ＋3＝0，求： (1)点P (4,5)关于l 的对称点；(2)直线x －y －2＝0关于直线l 对称的直线方程．解：设P (x ，y )关于直线l ：3x －y ＋3＝0的对称点为P ′(x ′，y ′)．∵k PP ′·k l ＝－1，即y ′－yx ′－x ×3＝－1.①又PP ′的中点在直线3x －y ＋3＝0上，∴3×x ′＋x 2－y ′＋y 2＋3＝0.②由①②得⎩⎪⎨⎪⎧x ′＝－4x ＋3y －95， ③ y ′＝3x ＋4y ＋35. ④ (1)把x ＝4，y ＝5代入③④得x ′＝－2，y ′＝7， ∴P (4,5)关于直线l 的对称点P ′的坐标为(－2,7)．(2)用③④分别代换x －y －2＝0中的x ，y ，得关于l 的对称直线方程为－4x ＋3y －95－3x ＋4y ＋35－2＝0，化简得7x ＋y ＋22＝0.1．点P 到点A (1,0)和直线x ＝－1的距离相等，且点P 到直线y ＝x 的距离为22，这样的点P 的个数是( )A ．1 B ．2 C ．3D ．4解析：选C ∵点P 到点A 和定直线距离相等， ∴P 点轨迹为抛物线，方程为y 2＝4x . 设P (t 2,2t )，则22＝|t 2－2t |2，解得t 1＝1，t 2＝1＋2，t 3＝1－2，故P 点有三个．2．(2012·福建模拟)若点(m ，n )在直线4x ＋3y －10＝0上，则m 2＋n 2的最小值是( )A ．2B ．2 2C ．4D ．2 3解析：选C 设原点到点(m ，n )的距离为d ，所以d 2＝m 2＋n 2，又因为(m ，n )在直线4x ＋3y －10＝0上，所以原点到直线4x ＋3y －10＝0的距离为d 的最小值，此时d ＝|－10|42＋32＝2，所以m 2＋n 2的最小值为4.3．在直线l ：3x －y －1＝0上求一点P ，使得P 到A (4,1)和B (0，4)的距离之差最大．解：如图所示，设点B 关于l 的对称点为B ′，连接AB ′并延长交l 于P ，此时的P 满足|P A |－|PB |的值最大．设B ′的坐标为(a ，b )，则k BB ′·k l ＝－1，即3·b －4a ＝－1. 则a ＋3b －12＝0.①又由于线段BB ′的中点坐标为⎝ ⎛⎭⎪⎫a 2，b ＋42，且在直线l 上，则3×a 2－b ＋42－1＝0，即3a －b －6＝0.②解①②，得a ＝3，b ＝3，即B ′(3,3)．于是AB ′的方程为y －13－1＝x －43－4，即2x ＋y －9＝0.解{ 3x －y －1＝0，2x ＋y －9＝0，得{ x ＝2，y ＝5，即l 与AB ′的交点坐标为P (2,5)．1．点(1，cos θ)(其中0≤θ≤π)到直线x sin θ＋y cos θ－1＝0的距离是14，那么θ等于( )A.5π6B.π6或5π6mLC.π6D.π6或7π6图①可判断可逆反应“A2(g)+3B2(g)2AB3(g)”的解析：选B 由已知得|sin θ＋cos 2θ－1|sin 2θ＋cos 2θ＝14，即|sin θ－sin 2θ|＝14， ∴4sin 2θ－4sin θ－1＝0或4sin 2θ－4sin θ＋1＝0，∴sin θ＝1±22或sin θ＝12.∵0≤θ≤π，∴0≤sin θ≤1，∴sin θ＝12，即θ＝π6或5π6.2．已知直线l ：x －y －1＝0，l 1：2x －y －2＝0.若直线l 2与l 1关于l 对称，则l 2的方程是( )A ．x －2y ＋1＝0B ．x －2y －1＝0C ．x ＋y －1＝0D ．x ＋2y －1＝0解析：选B l 1与l 2关于l 对称，则l 1上任一点关于l 的对称点都在l 2上，故l 与l 1的交点(1,0)在l 2上．又易知(0，－2)为l 1上一点，设其关于l 的对称点(x ，y )，则⎩⎨⎧ x ＋02－y －22－1＝0，y ＋2x ×1＝－1，得{ x ＝－1，y ＝－1.即(1,0)，(－1，－1)为l 2上两点，可得l 2方程为x －2y －1＝0.3．光线沿直线l 1：x －2y ＋5＝0射入，遇直线l ：3x －2y ＋7＝0后反射，求反射光线所在的直线方程．解：法一：由{ x －2y ＋5＝0，3x －2y ＋7＝0，得{ x ＝－1，y ＝2.即反射点M 的坐标为(－1,2)．又取直线x －2y ＋5＝0上一点P (－5,0)，设P 关于直线l 的对称点P ′(x 0，y 0)，由PP ′⊥l 可知，k PP ′＝－23＝y 0x 0＋5.充其量只算得小河沟罢了试卷试题然而毕竟有水化学教案便是理直气壮的河了试卷试题有水化而PP ′的中点Q 的坐标为⎝ ⎛⎭⎪⎫x 0－52，y 02，Q 点在l 上，即3·x 0－52－2·y 02＋7＝0.由⎩⎪⎨⎪⎧ y 0x 0＋5＝－23，32(x 0－5)－y 0＋7＝0.得⎩⎨⎧ x 0＝－1713，y 0＝－3213.根据直线的两点式方程可得所求反射光线所在直线的方程为29x －2y ＋33＝0.法二：设直线x －2y ＋5＝0上任意一点P (x 0，y 0)关于直线l 的对称点为P ′(x ，y )，则y 0－y x 0－x ＝－23，又PP ′的中点Q ⎝ ⎛⎭⎪⎫x ＋x 02，y ＋y 02在l 上，即3×x ＋x 02－2×y ＋y 02＋7＝0，由⎩⎨⎧ y 0－y x 0－x ＝－23，3×x ＋x 02－(y ＋y 0)＋7＝0.可得P 点的坐标为x 0＝－5x ＋12y －4213，y 0＝12x ＋5y ＋2813，代入方程x －2y ＋5＝0中，化简得29x －2y ＋33＝0，故所求反射光线所在的直线方程为29x －2y ＋33＝0.。

2014届高考数学一轮复习教学案空间向量与空间角(含解析)

空间向量与空间角[知识能否忆起]利用向量求空间角1．两条异面直线所成的角的求法设两条异面直线a ，b 的方向向量为a ，b ，其夹角为θ，则cos φ＝|cos θ|＝|a ·b ||a||b |(其中φ为异面直线a ，b 所成的角)．2．直线和平面所成角的求法如图所示，设直线l 的方向向量为e ，平面α的法向量为n ，直线l 与平面α所成的角为φ，两向量e 与n 的夹角为θ，则有sin φ＝|cos θ|＝|e ·n ||e ||n |.3．求二面角的大小(1)如图1，AB 、CD 是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝〈AB ，CD〉．(2)如图2、3，n 1，n 2分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ＝〈n 1，n 2〉(或π－〈n 1，n 2〉)．[小题能否全取]1．(教材习题改编)已知向量m ，n 分别是直线l 和平面α的方向向量、法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°解析：选A 由于cos 〈m ，n 〉＝－12，∴〈m ，n 〉＝120°.所以直线l 与α所成的角为30°.2．(教材习题改编)已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角的大小为( )A ．45°B ．135°C ．45°或135°D ．90°解析：选C cos 〈m ，n 〉＝m ·n |m ||n |＝11×2＝22，即〈m ，n 〉＝45°，其补角为135°， ∴两平面所成的二面角为45°或135°.3.在如图所示的正方体A1B 1C 1D 1－ABCD 中，E 是C 1D 1的中点，则异面直线DE 与AC 夹角的余弦值为( )A ．－1010B ．－120C.120D.1010解析：选D 如图建立直角坐标系D －xyz ，设DA ＝1，A (1,0,0)，C (0,1,0)，E ⎝⎛⎭⎫0，12，1.则AC ＝(－1,1,0)，DE ＝⎝⎛⎭⎫0，12，1，若异面直线DE 与AC 所成的角为θ，cos θ＝|cos 〈AC ，DE 〉|＝1010.4．已知点E 、F 分别在正方体ABCD －A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则平面AEF 与平面ABC 所成的二面角的正切值为________．解析：如图，建立直角坐标系D －xyz ，设DA ＝1由已知条件A (1,0,0)， E ⎝⎛⎭⎫1，1，13，F ⎝⎛⎭⎫0，1，23， AE ＝⎝⎛⎭⎫0，1，13，AF ＝⎝⎛⎭⎫－1，1，23，设平面AEF 的法向量为n ＝(x ，y ，z )，面AEF 与面ABC 所成的二面角为θ，由⎩⎨⎧n ·AE ＝0，n ·AF ＝0，得⎩⎨⎧y ＋13z ＝0，－x ＋y ＋23z ＝0.令y ＝1，z ＝－3，x ＝－1，则n ＝(－1,1，－3)．设平面ABC 的法向量为m ＝(0,0，－1)，则cos θ＝cos 〈n ，m 〉＝311，tan θ＝23.答案：235．(教材习题改编)如图，在长方体ABCD －A 1B 1C 1D 1中，已知DA ＝DC ＝4，DD 1＝3，则异面直线A 1B 与B 1C 所成角的余弦值________．解析：建立如图所示直角坐标系，则A 1(4,0,3)，B (4,4,0)，B 1(4,4,3)，C (0,4,0)，1A B ＝(0,4，－3)，1B C＝(－4,0，－3)．设异面直线A 1B 与B 1C 所成角为θ，则cos θ＝|cos 〈1A B ，1B C 〉|＝925.答案：925(1)利用向量求空间角，一定要注意将向量夹角与所求角区别开来，在将向量夹角转化为各空间角时注意空间各角的取值范围，异面直线所成角的范围是⎝⎛⎦⎤0，π2，直线与平面所成角的范围是⎣⎡⎦⎤0，π2，二面角的范围是[0，π]． (2)利用平面的法向量求二面角的大小时，当求出两半平面α、β的法向量n 1，n 2时，要根据向量坐标在图形中观察法向量的方向，从而确定二面角与向量n 1，n 2的夹角是相等，还是互补，这是利用向量求二面角的难点、易错点．典题导入[例1] (2012·陕西高考)如图，在空间直角坐标系中有直三棱柱ABC －A 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1夹角的余弦值为( )A.55B.53C.255D.35[自主解答] 不妨令CB ＝1，则CA ＝CC 1＝2.可得 O (0,0,0)，B (0,0,1)，C 1(0,2,0)，A (2,0,0)，B 1(0,2,1)，∴1BC ＝(0,2，－1)，1AB＝(－2,2,1)，∴cos 〈1BC ，1AB 〉＝1BC ·1AB|1BC ||1AB |＝4－15×9＝15＝55>0.∴1BC 与1AB的夹角即为直线BC 1与直线AB 1的夹角，∴直线BC 1与直线AB 1夹角的余弦值为55. [答案] A本例条件下，在线段OB 上，是否存在一点M ，使C 1M 与AB 1所成角的余弦为13？若存在，求出M 点；不存在，说明理由．解：不妨令CB ＝1，CA ＝CC 1＝2，建系如本例题图，假设存在符合条件的点M ，设M (0,0，a )，则1C M ＝(0，－2，a )，又1AB＝(－2,2,1)， ∴|cos 〈1C M ，1AB 〉|＝|a －4|4＋a 2·9＝13. ∴|a －4|＝4＋a 2，∴a 2－8a ＋16＝a 2＋4. ∴8a ＝12，∴a ＝32.又CB ＝1，∴a ＝32>1.故不存在符合条件的点M .由题悟法利用直线的方向向量的夹角求异面直线的夹角时，注意区别：当异面直线的方向向量的夹角为锐角或直角时，就是此异面直线所成的角；当异面直线的方向向量的夹角为钝角时，其补角才是异面直线所成的角．以题试法1．(2012·安徽模拟)如图所示，在多面体ABCD －A 1B 1C 1D 1中，上、下两个底面A 1B 1C 1D 1和ABCD 互相平行，且都是正方形，DD 1⊥底面ABCD ，AB ＝2A 1B 1＝2DD 1＝2a .(1)求异面直线AB 1与DD 1所成角的余弦值； (2)已知F 是AD 的中点，求证：FB 1⊥平面BCC 1B 1.解：以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则A (2a,0,0)，B (2a,2a,0)，C (0,2a,0)，D 1(0,0，a )，F (a,0,0)，B 1(a ，a ，a )，C 1(0，a ，a )．(1)∵1AB ＝(－a ，a ，a )，1DD＝(0,0，a )，∴cos 〈1AB ，1DD 〉＝1AB ·1DD|1AB |·|1DD |＝33，所以异面直线AB 1与DD 1所成角的余弦值为33. (2)证明：∵1BB＝(－a ，－a ，a )，BC ＝(－2a,0,0)， 1FB＝(0，a ，a )，∴⎩⎪⎨⎪⎧1FB ·1BB ＝0， 1FB ·BC＝0，∴FB 1⊥BB 1，FB 1⊥BC . ∵BB 1∩BC ＝B ，∴FB 1⊥平面BCC 1B 1.典题导入[例2] (2012·大纲全国卷)如图，四棱锥P －ABCD 中，底面ABCD 为菱形，P A ⊥底面ABCD ，AC ＝22，P A ＝2，E 是PC 上的一点，PE ＝2EC .(1)证明：PC ⊥平面BED ；(2)设二面角A -PB -C 为90°，求PD 与平面PBC 所成角的大小．[自主解答] (1)证明：以A 为坐标原点，射线AC 为x 轴的正半轴，建立如图所示的空间直角坐标系A －xyz ，则C (22，0,0)．设D (2，b,0)，其中b >0，则 P (0,0,2)，E ⎝⎛⎭⎫423，0，23，B (2，－b,0)．于是PC＝(22，0，－2)， BE ＝⎝⎛⎭⎫23，b ，23，DE ＝⎝⎛⎭⎫23，－b ，23，从而PC ·BE＝0，PC ·DE ＝0，故PC ⊥BE ，PC ⊥DE . 又BE ∩DE ＝E ，所以PC ⊥平面BED .(2) AP ＝(0,0,2)，AB＝(2，－b,0)．设m ＝(x ，y ，z )为平面P AB 的法向量，则m ·AP ＝0，m ·AB＝0，即2z ＝0且2x －by ＝0，令x ＝b ，则m ＝(b ，2，0)．设n ＝(p ，q ，r )为平面PBC 的法向量，则n ·PC ＝0，n ·BE＝0，即22p －2r ＝0且2p 3＋bq ＋23r ＝0，令p ＝1，则r ＝2，q ＝－2b ，n ＝⎝⎛⎭⎫1，－2b ，2. 因为二面角A －PB －C 为90°，所以面P AB ⊥面PBC ，故m ·n ＝0，即b －2b＝0，故b ＝2，于是n ＝(1，－1，2)，DP＝(－2，－2，2)，所以cos 〈n ，DP 〉＝n ·DP|n ||DP |＝12，所以〈n ，DP〉＝60°.因为PD 与平面PBC 所成角和〈n ，DP〉互余，故PD 与平面PBC 所成的角为30°.由题悟法利用向量法求线面角的方法(1)分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)，取其余角就是斜线和平面所成的角(如例2)．以题试法2.(2012·宝鸡模拟)如图，已知P A ⊥平面ABC ，且P A ＝2，等腰直角三角形ABC 中，AB ＝BC ＝1，AB ⊥BC ，AD ⊥PB 于D ，AE ⊥PC 于E .(1)求证：PC ⊥平面ADE ；(2)求直线AB 与平面ADE 所成角的大小．解：(1)证明：因为P A ⊥平面ABC ，所以P A ⊥BC ，又AB ⊥BC ，且P A ∩AB ＝A ，所以BC ⊥平面P AB ，从而BC ⊥AD . 又AD ⊥PB ，BC ∩PB ＝B ，所以AD ⊥平面PBC ，得PC ⊥AD ，又PC ⊥AE ，AE ∩AD ＝A ，所以PC ⊥平面ADE .(2)如图所示，建立空间直角坐标系B －xyz . 则A (1,0,0)，C (0,1,0)， P (1,0，2)，因为PC ⊥平面ADE ，所以PC＝(－1,1，－2)是平面ADE 的一个法向量．设直线AB 与平面ADE 所成的角为θ，则sin θ＝|PC ·AB||PC||AB |＝(－1，1，－2)·(－1，0，0)2＝12，则直线AB 与平面ADE 所成的角为30°.典题导入[例3] (2012·江西高考)在三棱柱ABC －A 1B 1C 1中，已知AB＝AC ＝AA 1＝5，BC ＝4，点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ，使得OE ⊥平面BB 1C 1C ，并求出AE 的长；(2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值．[自主解答] (1)证明：连接AO ，在△AOA 1中，作OE ⊥AA 1于点E ，因为AA 1∥BB 1，得OE ⊥BB 1，因为A 1O ⊥平面ABC ，所以A 1O ⊥BC .因为AB ＝AC ，OB ＝OC ，得AO ⊥BC ，所以BC ⊥平面AA 1O ，所以BC ⊥OE ，所以OE ⊥平面BB 1C 1C .又AO ＝AB 2－BO 2＝1，AA 1＝5，得AE ＝AO 2AA 1＝55.(2)如图，分别以OA ，OB ，OA 1所在直线为x ，y ，z 轴，建立空间直角坐标系，则A (1,0,0)，B (0,2,0)，C (0，－2,0)，A 1(0,0,2)，B 1(－1,2,2)，由AE ＝151AA 得点E 的坐标是⎝⎛⎭⎫45，0，25，由(1)得平面BB 1C 1C 的法向量是OE ＝⎝⎛⎭⎫45，0，25，设平面A 1B 1C 的法向量n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·11A B＝0，n ·1A C＝0，得⎩⎪⎨⎪⎧－x ＋2y ＝0，y ＋z ＝0. 令y ＝1，得x ＝2，z ＝－1，即n ＝(2,1，－1)，所以cos 〈OE ，n 〉＝OE·n| OE |·|n |＝3010，即平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值是3010.由题悟法求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．以题试法3．(2012·山西模拟)如图，四棱锥S －ABCD 的底面是正方形，SD ⊥平面ABCD ，SD ＝AD ＝a ，点E 是SD 上的点，且DE ＝λa (0<λ≤1)．(1)求证：对任意的λ∈(0,1]，都有AC ⊥BE ； (2)若二面角C －AE －D 的大小为60°，求λ的值．解：(1)证明：如图，建立空间直角坐标系D －xyz ，则A (a,0,0，)，B (a ，a,0)，C (0，a,0)，D (0,0,0)，E (0,0，λa )，∴AC ＝(－a ，a,0)，BE＝(－a ，－a ，λa )， ∴AC ·BE＝0对任意λ∈(0,1]都成立，即对任意的λ∈(0,1]，都有AC ⊥BE . (2)显然n ＝(0,1,0)是平面ADE 的一个法向量，设平面ACE 的法向量为m ＝(x ，y ，z )，∵AC ＝(－a ，a,0)，AE＝(－a,0，λa )，∴⎩⎨⎧m ·AC＝0，m ·AE＝0.即⎩⎪⎨⎪⎧ －ax ＋ay ＝0，－ax ＋λaz ＝0，∴⎩⎪⎨⎪⎧x －y ＝0，x －λz ＝0. 取z ＝1，则x ＝y ＝λ，∴m ＝(λ，λ，1)， ∵二面角C －AE －D 的大小为60°， ∴|cos 〈n ，m 〉|＝|n ·m ||n ||m |＝λ1＋2λ2＝12， ∵λ∈(0,1]， ∴λ＝22.1.如图所示，在三棱柱ABC －A 1B 1C 1中，AA 1⊥底面ABC ，AB ＝BC＝AA 1，∠ABC ＝90°，点E 、F 分别是棱AB 、BB 1的中点，则直线EF 和BC 1所成的角为________．解析：建立如图所示的空间直角坐标系．设AB ＝BC ＝AA 1＝2，则C1(2,0,2)，E (0,1,0)，F (0,0,1)，则EF＝(0，－1,1)，1BC ＝(2,0,2)，∴EF ·1BC＝2， ∴cos 〈EF ，1BC〉＝22×22＝12，∴EF 和BC 1所成角为60°. 答案：60°2．如图，在直三棱柱ABC －A 1B 1C 1中，∠ACB ＝90°，2AC ＝AA 1＝BC ＝2.若二面角B 1－DC －C 1的大小为60°，则AD 的长为________．解析：如图，以C 为坐标原点，CA ，CB ，CC 1所在的直线分别为x轴，y 轴，z 轴建立空间直角坐标系，则C (0,0,0)，A (1,0,0)，B 1(0,2,2)，C 1(0,0,2)．设AD ＝a ，则D 点坐标为(1,0，a )，CD ＝(1,0，a )，1CB＝(0,2,2)，设平面B 1CD 的一个法向量为m ＝(x ，y ，z )．则⎩⎪⎨⎪⎧m ·1CB ＝0m ·CD ＝0⇒⎩⎪⎨⎪⎧2y ＋2z ＝0x ＋az ＝0，令z ＝－1，得m ＝(a,1，－1)，又平面C 1DC 的一个法向量为n ＝(0,1,0)，则由cos 60°＝|m·n ||m ||n |，得1a 2＋2＝12，即a ＝2，故AD ＝ 2. 答案： 23.如图，在正四棱锥S －ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，则直线BC 与平面P AC 所成角为________．解析：如图所示，以O 为原点建立空间直角坐标系O －xyz .设OD ＝SO ＝OA ＝OB ＝OC ＝a ，则A (a,0,0)，B (0，a,0)，C (－a,0,0)，P ⎝⎛⎭⎫0，－a 2，a2. 则CA ＝(2a,0,0)，AP ＝⎝⎛⎭⎫－a ，－a 2，a 2，CB ＝(a ，a,0)．设平面P AC 的法向量为n ，可求得n ＝(0,1,1)，则cos 〈CB ，n 〉＝CB·n | CB ||n |＝a 2a 2·2＝12. ∴〈CB，n 〉＝60°，∴直线BC 与平面P AC 的夹角为90°－60°＝30°. 答案：30°4．(2012·山西模拟)如图，在底面为直角梯形的四棱锥P －ABCD 中，AD ∥BC ，∠ABC ＝90°，P A ⊥平面ABCD ，P A ＝3，AD ＝2，AB ＝23，BC ＝6.(1)求证：BD ⊥平面P AC ； (2)求二面角P －BD －A 的大小．解：(1)证明：由题可知，AP 、AD 、AB 两两垂直，则分别以AB 、AD 、AP 所在直线为x 、y 、z 轴建立如图所示的空间直角坐标系，则A (0,0,0)，B (23，0,0)，C (23，6,0)，D (0,2,0)，P (0,0,3)，∴AP ＝(0,0,3)，AC ＝(23，6,0)，BD＝(－23，2,0)，∴BD ·AP ＝0，BD ·AC＝0.∴BD ⊥AP ，BD ⊥AC .又P A ∩AC ＝A ，∴BD ⊥平面P AC .(2)显然平面ABD 的一个法向量为m ＝(0,0,1)，设平面PBD 的法向量为n ＝(x ，y ，z )，则n ·BD ＝0，n ·BP ＝0. 由(1)知，BP＝(－23，0,3)，∴⎩⎨⎧－23x ＋2y ＝0，－23x ＋3z ＝0，整理得⎩⎪⎨⎪⎧y ＝3x ，z ＝233x .令x ＝3，则n ＝(3，3,2)， ∴cos 〈m ，n 〉＝m ·n |m ||n |＝12.∴结合图形可知二面角P －BD －A 的大小为60°.5．(2012·辽宁高考)如图，直三棱柱ABC －A ′B ′C ′，∠BAC＝90°，AB ＝AC ＝λAA ′，点M ，N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面A ′ACC ′；(2)若二面角A ′－MN －C 为直二面角，求λ的值．解：(1)法一：证明：如图，连接AB ′，AC ′，由已知∠BAC ＝90°，AB ＝AC ，三棱柱ABC －A ′B ′C ′为直三棱柱，所以M 为AB ′中点．又因为N 为B ′C ′的中点，所以MN ∥AC ′. 又MN ⊄平面A ′ACC ′， A ′C ⊂平面A ′ACC ′，所以MN ∥平面A ′ACC ′.法二：证明：取A ′B ′ 中点P ，连接MP ，NP ，而M ，N 分别为AB ′与B ′C ′的中点，所以MP ∥AA ′，PN ∥A ′C ′，所以MP ∥平面A ′ACC ′，PN ∥平面A ′ACC ′. 又MP ∩NP ＝P ，因此平面MPN ∥平面A ′ACC ′.而MN ⊂平面MPN ，因此MN ∥平面A ′ACC ′.(2)以A 为坐标原点，分别以直线AB ，AC ，AA ′为x 轴，y 轴，z 轴建立空间直角坐标系O －xyz ，如图所示．设AA ′＝1，则AB ＝AC ＝λ，于是A (0,0,0)，B (λ，0,0)，C (0，λ，0)，A ′(0,0,1)， B ′(λ，0,1)，C ′(0，λ，1)，所以M ⎝⎛⎭⎫λ2，0，12，N ⎝⎛⎭⎫λ2，λ2，1. 设m ＝(x 1，y 1，z 1)是平面A ′MN 的法向量，由⎩⎨⎧m ·A M ' ＝0，m ·MN＝0，得⎩⎨⎧λ2x 1－12z 1＝0，λ2y 1＋12z 1＝0，可取m ＝(1，－1，λ)．设n ＝(x 2，y 2，z 2)是平面MNC 的法向量，由⎩⎨⎧n ·NC ＝0，n ·MN＝0，得⎩⎨⎧－λ2x 2＋λ2y 2－z 2＝0，λ2y 2＋12z 2＝0，可取n ＝(－3，－1，λ)．因为A ′－MN －C 为直二面角，所以m·n ＝0，即－3＋(－1)×(－1)＋λ2＝0，解得λ＝2(负值舍去)．6．如图1，在Rt △ABC 中，∠C ＝90°，BC ＝3，AC ＝6，D ，E 分别是AC ，AB 上的点，且DE ∥BC ，DE ＝2.将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2.(1)求证：A 1C ⊥平面BCDE ；(2)若M 是A 1D 的中点，求CM 与平面A 1BE 所成角的大小；(3)线段BC 上是否存在点P ，使平面A 1DP 与平面A 1BE 垂直？说明理由．解：(1)证明：因为AC ⊥BC ，DE ∥BC ，所以DE ⊥AC .所以ED ⊥A 1D ，DE ⊥CD ，所以DE ⊥平面A 1DC . 所以DE ⊥A 1C . 又因为A 1C ⊥CD . 所以A 1C ⊥平面BCDE .(2)如图，以C 为坐标原点，建立空间直角坐标系C －xyz ，则A 1(0,0,23)，D (0,2,0)，M (0,1, 3)，B (3,0,0)，E (2,2,0)．设平面A 1BE 的法向量为n ＝(x ，y ，z )，则n ·1A B ＝0，n ·BE =0.又1A B(3,0－＝ (－1,2，0)，所以⎩⎨⎧3x －23z ＝0，－x ＋2y ＝0.令y ＝1，则x ＝2，z ＝ 3. 所以n ＝(2,1，3)．设CM 与平面A 1BE 所成的角为θ.因为CM＝所以sin θ＝|cos 〈n , CM 〉|＝|n ·CM|n ||CM ||＝48×4＝22. 所以CM 与平面A 1BE 所成角的大小为π4.(3)线段BC 上不存在点P ，使平面A 1DP 与平面A 1BE 垂直，理由如下：假设这样的点P 存在，设其坐标为(p,0,0)，其中p ∈[0,3]．设平面A 1DP 的法向量为m ＝(x ，y ，z )，则m ·1A D ＝0，m ·DP ＝0. 又1A D ＝(0，2，－23),DP＝(p ，－2,0)，所以⎩⎨⎧2y －2 3z ＝0，px －2y ＝0.令x ＝2，则y ＝p ，z ＝p 3. 所以m ＝(2，p ，p 3)．平面A 1DP ⊥平面A 1BE ，当且仅当m ·n ＝0，即4＋p ＋p ＝0.解得p ＝－2，与p ∈[0,3]矛盾．所以线段BC 上不存在点P ，使平面A 1DP 与平面A 1BE 垂直．1．(2013·湖北模拟)如图所示，四棱锥P －ABCD 中，底面ABCD为正方形，PD ⊥平面ABCD ，PD ＝AB ＝2，E 、F 、G 分别为PC 、PD 、BC 的中点．(1)求证：P A ⊥EF ；(2)求二面角D －FG －E 的余弦值．解：以D 为坐标原点，建立如图所示的空间直角坐标系D －xyz ，则D (0,0,0)，A (0,2,0)，C (－2,0,0)，P (0,0,2)，E (－1,0,1)，F (0,0,1)，G (－2,1,0)．(1)证明：由于PA ＝(0,2，－2)，EF ＝(1,0,0)，则PA ·EF＝1×0＋0×2＋(－2)×0＝0，∴P A ⊥EF .(2)易知DF ＝(0,0,1)，EF＝(1,0,0)，FG ＝(－2,1，－1)，设平面DFG 的法向量m ＝(x 1，y 1，z 1)，则⎩⎨⎧m ·DF ＝0，m ·FG＝0，解得⎩⎪⎨⎪⎧z 1＝0，－2x 1＋y 1－z 1＝0. 令x 1＝1，得m ＝(1,2,0)是平面DFG 的一个法向量．设平面EFG 的法向量n ＝(x 2，y 2，z 2)，同理可得n ＝(0,1,1)是平面EFG 的一个法向量． ∵cos 〈m ，n 〉＝m ·n |m |·|n |＝25·2＝210＝105，设二面角D －FG －E 的平面角为θ，由图可知θ＝π－〈m ，n 〉， ∴cos θ＝－105， ∴二面角D －FG －E 的余弦值为－105. 2．(2012·北京西城模拟)如图，在直三棱柱ABC －A1B 1C 1中，AB ＝BC ＝2AA 1，∠ABC ＝90°，D 是BC 的中点．(1)求证：A 1B ∥平面ADC 1； (2)求二面角C 1－AD －C 的余弦值；(3)试问线段A 1B 1上是否存在点E ，使AE 与DC 1成60°角？若存在，确定E 点位置；若不存在，说明理由．解：(1)证明：连接A 1C ，交AC 1于点O ，连接OD .由ABC －A 1B 1C 1是直三棱柱，得四边形ACC 1A 1为矩形，O 为A 1C 的中点．又D 为BC 的中点，所以OD 为△A 1BC 的中位线，所以A 1B ∥OD ，因为OD ⊂平面ADC 1，A 1B ⊄平面ADC 1，所以A 1B ∥平面ADC 1.(2)由ABC －A 1B 1C 1是直三棱柱，且∠ABC ＝90°，得BA ，BC ，BB 1两两垂直．以BC ，BA ，BB 1所在直线分别为x ，y ，z 轴，建立如图所示的空间直角坐标系B －xyz . 设BA ＝2，则B (0,0,0)，C (2,0,0)，A (0,2,0)，C 1(2,0,1)，D (1,0,0)，所以AD＝(1，－2,0)，1AC ＝(2，－2,1)．设平面ADC 1的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧n ·AD ＝0，n ·1AC ＝0.所以⎩⎪⎨⎪⎧x －2y ＝0，2x －2y ＋z ＝0.取y ＝1，得n ＝(2,1，－2)．易知平面ADC 的一个法向量为v ＝(0,0,1)．所以cos 〈n ，v 〉＝n ·v |n |·|v |＝－23.因为二面角C 1－AD －C 是锐二面角，所以二面角C 1－AD －C 的余弦值为23.(3)假设存在满足条件的点E .因为点E 在线段A 1B 1上，A 1(0,2,1)，B 1(0,0,1)，故可设E (0，λ，1)，其中0≤λ≤2.所以AE＝(0，λ－2,1)，1DC ＝(1,0,1)．因为AE 与DC 1成60°角，所以|cos 〈AE ，1DC 〉|＝⎪⎪⎪⎪⎪⎪⎪⎪AE ·1DC|AE |·|1DC |＝12. 即⎪⎪⎪⎪⎪⎪1(λ－2)2＋1·2＝12，解得λ＝1或λ＝3(舍去)．所以当点E 为线段A 1B 1的中点时，AE 与DC 1成60°角．1．(2012·北京东城模拟)如图，四边形ABCD 为正方形，PD⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD .(1)证明：平面PQC ⊥平面DCQ ； (2)求二面角Q －BP －C 的余弦值．解：(1)证明：如图，以D 为坐标原点，DA 、DP 、DC 所在的直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系D －xyz .设DA ＝1，则有D (0,0,0)，Q (1,1,0)，C (0,0,1)，P (0,2,0)，所以DQ ＝(1,1,0)，DC ＝(0,0,1)，PQ＝(1，－1,0)，所以PQ ·DQ ＝0，PQ ·DC ＝0，即PQ ⊥DQ ，PQ ⊥DC .又DQ ⊂平面DCQ ，DC ⊂平面DCQ ，且DQ ∩DC ＝D ，所以PQ ⊥平面DCQ .又PQ ⊂平面PQC ，所以平面PQC ⊥平面DCQ .(2)由(1)易知B (1,0,1)，CB ＝(1,0,0)，BP＝(－1,2，－1)．设n ＝(x ，y ，z )是平面PBC 的法向量，则⎩⎨⎧n ·CB ＝0，n ·BP＝0，即⎩⎪⎨⎪⎧x ＝0，－x ＋2y －z ＝0，可取n ＝(0，－1，－2)．设m ＝(x 1，y 1，z 1)是平面PBQ 的法向量，则⎩⎪⎨⎪⎧m ·BP＝0，m ·PQ ＝0，即⎩⎪⎨⎪⎧－x 1＋2y 1－z 1＝0，x 1－y 1＝0，可取m ＝(1,1,1)．所以cos 〈m ，n 〉＝－155，故二面角Q －BP －C 的余弦值为－155. 2．(2012·天津高考)如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，AC ⊥AD ，AB ⊥BC ，∠BAC ＝45°，P A ＝AD ＝2，AC ＝1.(1)证明PC ⊥AD ；(2)求二面角A －PC －D 的正弦值；(3)设E 为棱P A 上的点，满足异面直线BE 与CD 所成的角为30°，求AE 的长．解：如图，以点A 为原点建立空间直角坐标系，依题意得A (0,0,0)，D (2,0,0)，C (0,1,0)，B ⎝⎛－12，⎭⎫12，0，P (0,0,2)．(1)证明：易得PC＝(0,1，－2)， AD＝(2,0,0)，于是PC ·AD＝0，所以PC ⊥AD .(2) PC ＝(0,1，－2)，CD＝(2，－1,0)．设平面PCD 的法向量n ＝(x ，y ，z )，则⎩⎨⎧n ·PC＝0，n ·CD＝0，即⎩⎪⎨⎪⎧y －2z ＝0，2x －y ＝0.不妨令z ＝1，可得n ＝(1,2,1)．可取平面P AC 的法向量m ＝(1,0,0)．于是cos 〈m ，n 〉＝m·n|m |·|n |＝16＝66，从而sin 〈m ，n 〉＝306. 所以二面角A －PC －D 的正弦值为306. (3)设点E 的坐标为(0,0，h )，其中h ∈[0,2]．由此得BE ＝⎝⎛⎭⎫12，－12，h .由CD ＝(2，－1,0)，故cos 〈BE ，CD 〉＝BE ·CD|BE|·|CD |＝3212＋h 2×5＝310＋20h 2，所以310＋20h 2＝cos 30°＝32，解得h ＝1010，即AE ＝1010. 3.如图，在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝1，AB ＝2.(1)证明：当点E 在棱AB 上移动时，D 1E ⊥A 1D ； (2)在棱AB 上是否存在点E ，使二面角D 1－EC －D 的平面角为π6？若存在，求出AE 的长；若不存在，请说明理由．解：以D 为原点，DA 、DC 、DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系，则D (0,0,0)，C (0,2,0)，A 1(1,0,1)，D 1(0,0,1)．设E (1，y 0,0)(0≤y 0≤2)．(1)证明：∵1D E ＝(1，y 0，－1)，1A D＝(－1,0，－1)，则1D E ·1A D＝(1，y 0，－1)·(－1,0，－1)＝0， ∴1D E⊥1A D，即D 1E ⊥A 1D .(2)当AE ＝2－33时，二面角D 1－EC －D 的平面角为π6. ∵EC ＝(－1,2－y 0,0)，1D C＝(0,2，－1)，设平面D 1EC 的一个法向量为n 1＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 1·EC ＝0，n 1·1D C ＝0⇒⎩⎪⎨⎪⎧－x ＋y (2－y 0)＝0，2y －z ＝0.取y ＝1，则n 1＝(2－y 0,1,2)是平面D 1EC 的一个法向量．而平面ECD 的一个法向量为n 2＝1DD ＝(0,0,1)，要使二面角D 1－EC －D 的平面角为π6，则cos π6＝|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1|·|n 2|＝2(2－y 0)2＋12＋22＝32，解得y 0＝2－33(0≤y 0≤2)． ∴当AE ＝2－33时，二面角D 1－EC －D 的平面角为π6. 4．(2012·湖北模拟)在直三棱柱ABC －A 1B 1C 1中，AB ＝AC ＝1，∠BAC ＝90°.(1)若异面直线A 1B 与B 1C 1所成的角为60°，求棱柱的高； (2)设D 是BB 1的中点，DC 1与平面A 1BC 1所成的角为θ，当棱柱的高变化时，求sin θ的最大值．解：建立如图所示的空间直角坐标系A －xyz ，设AA 1＝h (h >0)，则有B (1,0,0)，B 1(1,0，h )，C 1(0,1，h )，A 1(0,0，h )，11B C ＝(－1,1,0)，11A C ＝(0,1,0)，1A B＝(1,0，－h )． (1)因为异面直线A 1B 与B 1C 1所成的角为60°，所以cos60°＝|11B C ·1A B ||11B C |·|1A B |，即12·h 2＋1＝12，得1＋h 2＝2，解得h ＝1. (2)由D 是BB 1的中点，得D ⎝⎛⎭⎫1，0，h 2，于是1DC ＝⎝⎛⎭⎫－1，1，h2. 设平面A 1BC 1的法向量为n ＝(x ，y ，z )，于是由n ⊥1A B ，n ⊥11A C可得⎩⎪⎨⎪⎧n ·1A B ＝0，n ·11A C＝0，即⎩⎪⎨⎪⎧x －hz ＝0，y ＝0，可取n ＝(h,0,1)，故sin θ＝|cos 〈1DC，n 〉|，而|cos 〈1DC ，n 〉|＝|1DC·n ||1DC |·|n |＝⎪⎪⎪⎪－h ＋h 214h 2＋2·h 2＋1＝hh 4＋9h 2＋8.令f (h )＝hh 4＋9h 2＋8＝1h 2＋8h2＋9，因为h 2＋8h 2＋9≥28＋9，当且仅当h 2＝8h 2，即h ＝48时，等号成立．所以f (h )≤19＋28＝18＋1＝22－17，故当h ＝48时，sin θ的最大值为22－17.立体几何(时间：120分钟，满分150分)一、选择题(本题共12小题，每小题5分，共60分)1．(2012·重庆模拟)若两条直线和一个平面相交成等角，则这两条直线的位置关系是( )A ．平行B ．异面C ．相交D ．平行、异面或相交解析：选D 经验证，当平行、异面或相交时，均有两条直线和一个平面相交成等角的情况出现．2．(2012·福建高考)一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( )A ．球B ．三棱锥C ．正方体D ．圆柱解析：选D 球、正方体的三视图形状都相同，大小均相等，首先排除选项A 和C.对于如图所示三棱锥O －ABC ，当OA 、OB 、OC 两两垂直且OA ＝OB ＝OC 时，其三视图的形状都相同，大小均相等，故排除选项B.不论圆柱如何放置，其三视图的形状都不会完全相同． 3．(2012·安徽模拟)在空间，下列命题正确的是( ) A ．若三条直线两两相交，则这三条直线确定一个平面 B ．若直线m 与平面α内的一条直线平行，则m ∥αC ．若平面α⊥β，且α∩β＝l ，则过α内一点P 与l 垂直的直线垂直于平面βD ．若直线a ∥b ，且直线l ⊥a ，则l ⊥b解析：选D 三条直线两两相交，可确定一个平面或三个平面，故A 错；m 与平面α内一条直线平行，m 也可在α内，故B 错；若平面α⊥β，且α∩β＝l ，当P ∈l 时，过P 点与l 垂直的直线可在β外，也可在β内，故C 错．由等角定理知D 正确．4．(2012·新课标全国卷)平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( )A.6πB ．43πC ．46πD ．63π解析：选B 设球的半径为R ，由球的截面性质得R ＝(2)2＋12＝3，所以球的体积V ＝43πR 3＝43π.5．(2012·北京海淀二模)某几何体的正视图与俯视图如图所示，侧视图与正视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是( )A.203 B.43 C ．6D ．4解析：选A 由三视图知，该几何体是正方体挖去一个以正方体的中心为顶点、以正方体的上底面为底面的四棱锥后的剩余部分，其体积是23－13×22×1＝203.6．(2013·安徽模拟)沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的侧视图为( )解析：选B 由三视图的相关知识易知选B.7．正方体ABCD －A 1B 1C 1D 1中，与体对角线AC 1异面的棱有( ) A ．3条 B ．4条 C ．6条D ．8条解析：选C 从定义出发，同时考虑到正方体的体对角线AC 1与正方体的6条棱有公共点A 和C 1，而正方体有12条棱，所以与AC 1异面的棱有6条．8.(2012·衡阳模拟)如图，一个空间几何体的正视图和侧视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的侧面积为( )A.π4B.π2C.2π2D.2π4 解析：选B 此几何体是底面半径为12，母线长为1的圆锥，其侧面积S ＝πrl ＝π×12×1＝π2. 9．如图，在正方体ABCD －A1B 1C 1D 1中，M ，N 分别是BC 1，CD 1的中点，则下列判断错误的是( )A ．MN 与CC 1垂直B ．MN 与AC 垂直C ．MN 与BD 平行D ．MN 与A 1B 1平行解析：选D 由于C 1D 1与A 1B 1平行，MN 与C 1D 1是异面直线，所以MN 与A 1B 1是异面直线，故选项D 错误．10．(2012·皖南八校三联)某几何体的三视图如图所示(单位：cm)，则此几何体的体积为( )A ．18 cm 3B ．15 cm 3C ．12 cm 3D ．9 cm 3解析：选B 由三视图可知，该几何体是一个上下均为长方体的组合体．如图所示，由图中数据可得该几何体体积为3×3×1＋1×2×3＝15(cm 3)．11．在正四面体A －BCD 中，棱长为4，M 是BC 的中点，P 在线段AM 上运动(P 不与A 、M 重合)，过点P 作直线l ⊥平面ABC ，l 与平面BCD 交于点Q ，给出下列命题：①BC ⊥面AMD ；②Q 点一定在直线DM 上；③V C －AMD ＝4 2.其中正确的是( )A ．①②B ．①③C ．②③D ．①②③解析：选A ∵A －BCD 是正四面体，M 为BC 中点，∴AM ⊥BC ，DM ⊥BC ，且AM ∩DM ＝M ，∴BC ⊥面AMD .∴①正确．V C －AMD ＝13S △AMD ·CM (∵BC ⊥面AMD ，∴CM 为四面体C －AMD 的高)．如图，在△AMD 中，AM ＝DM ＝AB 2－BM 2＝42－22＝23，MN ＝AM 2－AN 2＝12－22＝22，∴S △AMD ＝12AD ·MN ＝12×4×22＝42， ∴V C －AMD ＝13×42×2＝823，故③不正确．由排除法知选A. 12．(2012·浙江高考)已知矩形ABCD ，AB ＝1，BC ＝ 2.将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中，( )A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直解析：选B 对于AB ⊥CD ，因为BC ⊥CD ，可得CD ⊥平面ACB ，因此有CD ⊥AC .因为AB ＝1，BC ＝2，CD ＝1，所以AC ＝1，所以存在某个位置，使得AB ⊥CD .二、填空题(本题共4小题，每小题5分，共20分)13．(2012·肇庆二模)已知某几何体的三视图如图所示，则该几何体的表面积和体积分别为________，________.解析：由三视图可知，该几何体的下部是一底边长为2，高为4的长方体，上部为一球，球的直径等于正方形的边长．所以长方体的表面积为S 1＝2×2×2＋4×2×4＝40，长方体的体积为V 1＝2×2×4＝16，球的表面积和体积分别为S 2＝4×π×12＝4π，V 2＝43×π×13＝4π3，故该几何体的表面积为S ＝S 1＋S 2＝40＋4π，该几何体的体积为V ＝V 1＋V 2＝16＋4π3.答案：40＋4π 16＋4π314． (2012·北京怀柔模拟)P 为△ABC 所在平面外一点，且P A 、PB 、PC 两两垂直，则下列命题：①P A ⊥BC ；②PB ⊥AC ；③PC ⊥AB ；④AB ⊥BC .其中正确的个数是________．解析：如图所示．∵P A ⊥PC ，P A ⊥PB ，PC ∩PB ＝P ，∴P A ⊥平面PBC .又∵BC ⊂平面PBC ，∴P A ⊥BC .同理PB ⊥AC ，PC ⊥AB .但AB 不一定垂直于BC .共3个．答案：315.已知正三棱柱ABC －A 1B 1C 1的所有棱长都等于6，且各顶点都在同一球面上，则此球的表面积等于________．解析：如图，三棱柱的外接球球心为O ，其中D 为上底面三角形外接圆的圆心，其中AD ＝33×6＝23，又OD ＝3，故在Rt △OAD 中可得R ＝|OA |＝(23)2＋32＝21，故球的表面积为4π(21)2＝84π.答案：84π16．(2012·长春名校联考)如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，点M ∈AB 1，N ∈BC 1，且AM ＝BN ≠2，有以下四个命题：①AA 1⊥MN ；②A 1C 1∥MN ；③MN ∥平面A 1B 1C 1D 1；④MN 与A 1C 1是异面直线．其中正确命题的序号是________．(注：把你认为正确命题的序号都填上)解析：过N 作NP ⊥BB 1于点P ，连接MP ，可证AA 1⊥平面MNP ，∴AA 1⊥MN ，①正确；过M 、N 分别作MR ⊥A 1B 1、NS ⊥B 1C 1于点R 、S ，则当M 不是AB 1的中点，N 不是BC 1的中点时，直线A 1C 1与直线RS 相交；当M 、N 分别是AB 1、BC 1的中点时，A 1C 1∥RS ，∴A 1C 1与MN 可以异面，也可以平行，故②④错误．由①正确知，AA 1⊥平面MNP ，而AA 1⊥平面A 1B 1C 1D 1，∴平面MNP ∥平面A 1B 1C 1D 1，故③对．综上所述，其中正确命题的序号是①③.答案：①③三、解答题(本大题有6小题，共70分)17．(本小题满分10分)(2012·陕西高考)在直三棱柱ABC －A 1B 1C 1中，AB ＝AA 1，∠CAB ＝π2. (1)证明：CB 1⊥BA 1；(2)已知AB ＝2，BC ＝5，求三棱锥C 1－ABA 1的体积．解：(1)证明：如图所示，连接AB 1，∵ABC －A 1B 1C 1是直三棱柱，∠CAB ＝π2， ∴AC ⊥平面ABB 1A 1，故AC ⊥BA 1.又∵AB ＝AA 1，∴四边形ABB 1A 1是正方形，∴BA 1⊥AB 1，又CA ∩AB 1＝A ，∴BA 1⊥平面CAB 1，故CB 1⊥BA 1.(2)∵AB ＝AA 1＝2，BC ＝5，∴AC ＝A 1C 1＝1，由(1)知，A 1C 1⊥平面ABA 1，∴VC 1－ABA 1＝13S △ABA 1·A 1C 1＝13×2×1＝23. 18．(本小题满分12分) (12分)如图所示，四棱锥P －ABCD 的底面是边长为a 的正方形，侧棱P A ⊥底面ABCD ，侧面PBC 内有BE ⊥PC于E ，且BE ＝63a ，试在AB 上找一点F ，使EF ∥平面P AD . 解：在平面PCD 内，过E 作EG ∥CD 交PD 于G ，连接AG ，在AB 上取点F ，使AF ＝EG ，则F 即为所求作的点．∵EG ∥CD ∥AF ，EG ＝AF ，∴四边形FEGA 为平行四边形，∴FE ∥AG .又AG ⊂平面P AD ，FE ⊄平面P AD ，∴EF ∥平面P AD .又在Rt △BCE 中， CE ＝BC 2－BE 2＝ a 2－23a 2＝33a . 在Rt △PBC 中，BC 2＝CE ·CP ，∴CP ＝a 23a3＝3a ，又EG CD ＝PE PC， ∴EG ＝PE PC ·CD ＝23a ，∴AF ＝EG ＝23a . ∴点F 为AB 靠近点B 的一个三等分点．19．(本小题满分12分) (12分)(2012·新课标全国卷)如图，在三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点．(1)证明：平面BDC 1⊥平面BDC ；(2)平面BDC 1分此棱柱为两部分，求这两部分体积的比．解：(1)证明：由题设知BC ⊥CC 1，BC ⊥AC ，CC 1∩AC ＝C ，所以BC ⊥平面ACC 1A 1.又DC 1⊂平面ACC 1A 1，所以DC 1⊥BC .由题设知∠A 1DC 1＝∠ADC ＝45°，所以∠CDC 1＝90°，即DC 1⊥DC .又DC ∩BC ＝C ，所以DC 1⊥平面BDC .又DC 1⊂平面BDC 1，故平面BDC 1⊥平面BDC .(2)设棱锥B －DACC 1的体积为V 1，AC ＝1.由题意得V 1＝13×1＋22×1×1＝12. 又三棱柱ABC －A 1B 1C 1的体积V ＝1，所以(V －V 1)∶V 1＝1∶1.故平面BDC 1分此棱柱所得两部分体积的比为1∶1.20．(本小题满分12分) (12分)(2012·安徽高考)如图，长方体ABCD －A 1B 1C 1D 1中，底面A 1B 1C 1D 1是正方形，O 是BD 的中点，E 是棱AA 1上任意一点．(1)证明：BD ⊥EC 1；(2)如果AB ＝2，AE ＝2，OE ⊥EC 1，求AA 1的长．解：(1)证明：连接AC ，A 1C 1.由底面是正方形知，BD ⊥AC .因为AA 1⊥平面ABCD ，BD ⊂平面ABCD ，所以AA 1⊥BD .又AA 1∩AC ＝A ，所以BD ⊥平面AA 1C 1C .由EC 1⊂平面AA 1C 1C 知，BD ⊥EC 1.(2)法一：设AA 1的长为h ，连接OC 1.在Rt △OAE 中，AE ＝2，AO ＝2，故OE 2＝(2)2＋(2)2＝4.故Rt△EA1C1中，A1E＝h－2，A1C1＝22，故EC21＝(h－2)2＋(22)2.在Rt△OCC1中，OC＝2，CC1＝h，OC21＝h2＋(2)2. 因为OE⊥EC1，所以OE2＋EC21＝OC21，即4＋(h－2)2＋(22)2＝h2＋(2)2，解得h＝32，所以AA1的长为3 2.法二：∵OE⊥EC1，∴∠AEO＋∠A1EC1＝90°.又∵∠A1C1E＋∠A1EC1＝90°，∴∠AEO＝∠A1C1E.又∵∠OAE＝∠C1A1E＝90°，∴△OAE∽△EA1C1，∴AEA1C1＝AOA1E，即222＝2A1E，∴A1E＝22，∴AA1＝AE＋A1E＝3 2.21．(本小题满分12分) (12分)(2012·郑州一模)如图，在四棱锥S－ABCD中，AB⊥AD，AB∥CD，CD＝3AB＝3，平面SAD⊥平面ABCD，E是线段AD上一点，AE＝ED＝3，SE⊥AD.(1)证明：平面SBE⊥平面SEC；(2)若SE＝1，求三棱锥E－SBC的高．解：(1)证明：∵平面SAD⊥平面ABCD且平面SAD∩平面ABCD＝AD，SE⊂平面SAD，SE⊥AD，∴SE⊥平面ABCD.∵BE⊂平面ABCD，∴SE⊥BE.∵AB⊥AD，AB∥CD，CD＝3AB＝3，AE＝ED＝3，∴∠AEB＝30°，∠CED＝60°.∴∠BEC＝90°，即BE⊥CE.又SE∩CE＝E，，∴BE⊥平面SEC，∵BE⊂平面SBE，∴平面SBE⊥平面SEC.(2)如图，过点E作EF⊥BC于点F，连接SF.由(1)知SE⊥平面ABCD，而BC ⊂平面ABCD ，∴BC ⊥SE ，又SE ∩EF ＝E ，∴BC ⊥平面SEF ，∵BC ⊂平面SBC ，∴平面SEF ⊥平面SBC .过点E 作EG ⊥SF 于点G ，则EG ⊥平面SBC ，即线段EG 的长即为三棱锥E －SBC 的高．由(1)易知，BE ＝2，CE ＝23，则BC ＝4，EF ＝ 3.在Rt △SEF 中，SE ＝1，SF ＝SE 2＋EF 2＝2，则EG ＝ES ·EF SF ＝32，∴三棱锥E －SBC 的高为32.22．(本小题满分12分) (14分)(2012·北京昌平二模)在正四棱柱ABCD －A 1B 1C 1D 1中，E 为AD 的中点，F 为B 1C 1的中点．(1)求证：A 1F ∥平面ECC 1；(2)在CD 上是否存在一点G ，使BG ⊥平面ECC 1？若存在，请确定点G 的位置，并证明你的结论；若不存在，请说明理由．解：(1)证明：在正四棱柱ABCD －A 1B 1C 1D 1中，取BC 的中点M ，连接AM ，FM .∴B 1F ∥BM 且B 1F ＝BM .∴四边形B 1FMB 是平行四边形．∴FM ∥B 1B 且FM ＝B 1B .∴FM ∥A 1A 且FM ＝A 1A ，∴四边形AA 1FM 是平行四边形．∴F A 1∥AM .∵E 为AD 的中点，∴AE ∥MC 且AE ＝MC .∴四边形AMCE 是平行四边形．∴CE ∥AM .∴CE ∥A 1F .∵A 1F ⊄平面ECC 1，EC ⊂平面ECC 1，∴A 1F ∥平面ECC 1.(2)在CD上存在一点G，使BG⊥平面ECC1.取CD的中点G，连接BG.在正方形ABCD中，DE＝GC，CD＝BC，∠ADC＝∠BCD，∴△CDE≌△BCG.∴∠ECD＝∠GBC.∵∠CGB＋∠GBC＝90°，∴∠CGB＋∠DCE＝90°.∴BG⊥EC.∵CC1⊥平面ABCD，BG⊂平面ABCD，∴CC1⊥BG，又EC∩CC1＝C，∴BG⊥平面ECC1.故在CD上存在中点G，使得BG⊥平面ECC1.。

2014年江苏高考数学试题及详细答案(含附加题)

2014年江苏高考数学试题数学Ⅰ试题参考公式:圆柱的侧面积公式:S 圆柱=cl , 其中c 是圆柱底面的周长，l 为母线长. 圆柱的体积公式:V 圆柱=Sh ,其中S 是圆柱的底面积，h 为高.一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上．．．．．．．．.1．已知集合{2134}A =--，，，，{123}B =-，，，则A B =．【答案】{13}-，2．已知复数2(52)z i =+(i 为虚数单位)，则z 的实部为．【答案】213．右图是一个算法流程图，则输出的n 的值是．【答案】54．从1236，，，这4个数中一次随机地取2个数，则所取2个数的乘积为6的概率是．【答案】135．已知函数cos y x =与sin(2)(0)y x ϕϕ=+<π≤，它们的图象有一个横坐标为 3π的交点，则ϕ的值是．【答案】6π6．为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：cm ），所得数据均在区间[80130]，上，其频率分布直方图如图所示，则在抽测的60株树木中，有株树木的底部周长小于100 cm ．【答案】247．在各项均为正数的等比数列{}n a 中，若21a =，8642a a a =+，则6a 的值是．【答案】48．设甲、乙两个圆柱的底面积分别为12S S ，，体积分别为12V V ，，若它们的侧面积相等，且1294S S =，则12V V 的值是．【答案】329．在平面直角坐标系xOy 中，直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为．【答案】255510．已知函数2()1f x x mx =+-，若对任意[1]x m m ∈+，，都有()0f x <成立，则实数m 的取值范围是．【答案】202⎛⎫- ⎪⎝⎭，11．在平面直角坐标系xOy 中，若曲线2b y ax x =+(a b ，为常数)过点(25)P -，，且该曲线在点P 处的切线与直线7230x y ++=平行，则a b +的值是．【答案】3-12．如图，在平行四边形ABCD 中，已知，85AB AD ==，，32CP PD AP BP =⋅=，，则AB AD ⋅的值是．【答案】2213．已知()f x 是定义在R 上且周期为3的函数，当[03)x ∈，时，21()22f x x x =-+．若函数()y f x a =-在区间[34]-，上有10个零点(互不相同)，则实数a 的取值范围是．【答案】()102，14．若ABC ∆的内角满足sin 2sin 2sin A B C +=，则cos C 的最小值是．【答案】624- 二、解答题：本大题共6小题, 共计90 分. 请在答题卡指定区域内．．．．．．．．作答, 解答时应写出文字说明、证明过程或演算步骤.15．(本小题满分14 分)已知()2απ∈π，，5sin 5α=．（1）求()sin 4απ+的值；（2）求()cos 26α5π-的值．【答案】本小题主要考查三角函数的基本关系式、两角和与差及二倍角的公式，考查运算求解能力. 满分14分.（1）∵()5sin 25ααπ∈π=，，，∴225cos 1sin 5αα=--=-()210sin sin cos cos sin (cos sin )444210αααααπππ+=+=+=-；（2）∵2243sin 22sin cos cos 2cos sin 55αααααα==-=-=，∴()()3314334cos 2cos cos2sin sin 2666252510ααα5π5π5π+-=+=-⨯+⨯-=-．16．(本小题满分14 分)如图，在三棱锥P ABC -中，D E F ，，分别为棱PC AC AB ，，的中点．已知6PA AC PA ⊥=，，8BC =，5DF =．（1）求证：直线P A ∥平面DEF ；（2）平面BDE ⊥平面ABC ．【答案】本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系，考查空间想象能力和推理论证能力.满分14分. （1）∵D E ，为PC AC ，中点 ∴DE ∥P A ∵PA ⊄平面DEF ，DE ⊂平面DEF ∴P A ∥平面DEF （2）∵D E ，为PC AC ，中点 ∴132DE PA ==∵E F ，为AC AB ，中点 ∴142EF BC ==∴222DE EF DF +=∴90DEF ∠=°，∴DE ⊥EF ∵//DE PA PA AC ⊥，，∴DE AC ⊥ ∵ACEF E =∴DE ⊥平面ABC∵DE ⊂平面BDE ， ∴平面BDE ⊥平面ABC ．17．(本小题满分14 分)如图，在平面直角坐标系xOy 中，12F F ，分别是椭圆22221(0)y x a b a b +=>>的左、右焦点，顶点B 的坐标为(0)b ，，连结2BF 并延长交椭圆于点A ，过点A 作x 轴的垂线交椭圆于另一点C ，连结1FC ．（1）若点C 的坐标为()4133，，且22BF =，求椭圆的方程；（2）若1FC AB ⊥，求椭圆离心率e 的值．【答案】本小题主要考查椭圆的标准方程与几何性质、直线与直线的位置关系等基础知识，考查运算求解能力. 满分14分.（1）∵()4133C ，，∴22161999a b+=∵22222BF b c a =+=，∴22(2)2a ==，∴21b =∴椭圆方程为2212x y += （2）设焦点12(0)(0)()F c F c C x y -，，，，，∵A C ，关于x 轴对称，∴()A x y -，∵2B F A ，，三点共线，∴b y b c x +=--，即0bx cy bc --=① ∵1FC AB ⊥，∴1yb xc c ⋅=-+-，即20xc by c -+=② ①②联立方程组，解得2222222ca x b c bc y b c ⎧=⎪-⎨⎪=-⎩∴()2222222a c bc C b c b c --， ∵C 在椭圆上，∴()()222222222221a cbc b c b c a b --+=，化简得225c a =，∴55c a =, 故离心率为5518．(本小题满分16分)如图，为保护河上古桥OA ，规划建一座新桥BC ，同时设立一个圆形保护区．规划要求：新桥BC 与河岸AB 垂直；保护区的边界为圆心M 在线段OA 上并与BC 相切的圆，且古桥两端O 和A 到该圆上任意一点的距离均不少于80m ．经测量，点A 位于点O 正北方向60m 处，点C 位于点O 正东方向170m 处(OC 为河岸)，4tan 3BCO ∠=．（1）求新桥BC 的长；（2）当OM 多长时，圆形保护区的面积最大？解：本小题主要考查直线方程、直线与圆的位置关系和解三角形等基础知识，考查建立数学模型及运用数学知识解决实际问题的能力.满分16分. 解法一：(1) 如图，以O 为坐标原点，OC 所在直线为x 轴，建立平面直角坐标系xOy .由条件知A (0, 60)，C (170, 0)，直线BC 的斜率k BC =－tan ∠BCO =－43.又因为AB ⊥BC ，所以直线AB 的斜率k AB =34. 设点B 的坐标为(a ,b )，则k BC =04,1703b a -=--k AB =603,04b a -=- 解得a =80，b=120. 所以BC =22(17080)(0120)150-+-=. 因此新桥BC 的长是150 m.(2)设保护区的边界圆M 的半径为r m,OM =d m,(0≤d ≤60). 由条件知，直线BC 的方程为4(170)3y x =--，即436800x y +-= 由于圆M 与直线BC 相切，故点M (0，d )到直线BC 的距离是r ，即|3680|680355d dr --==. 因为O 和A 到圆M 上任意一点的距离均不少于80 m,所以80(60)80r d r d -⎧⎨--⎩≥≥即68038056803(60)805dd d d -⎧-⎪⎪⎨-⎪--⎪⎩≥≥解得1035d ≤≤故当d =10时,68035dr -=最大，即圆面积最大. 所以当OM = 10 m 时，圆形保护区的面积最大. 解法二:(1)如图，延长OA , CB 交于点F . 因为tan ∠BCO =43.所以sin ∠FCO =45，cos ∠FCO =35.因为OA =60,OC =170，所以OF =OC tan ∠FCO =6803. CF =850cos 3OC FCO =∠,从而5003AF OF OA =-=. 因为OA ⊥OC ，所以cos ∠AFB =sin ∠FCO ==45，又因为AB ⊥BC ，所以BF =AF cos ∠AFB ==4003，从而BC =CF －BF =150. 因此新桥BC 的长是150 m.(2)设保护区的边界圆M 与BC 的切点为D ，连接MD ，则MD ⊥BC ，且MD 是圆M 的半径，并设MD =r m ，OM =d m(0≤d ≤60).因为OA ⊥OC ，所以sin ∠CFO =cos ∠FCO ，故由(1)知，sin ∠CFO =3,68053MD MD r MF OF OM d ===--所以68035d r -=. 因为O 和A 到圆M 上任意一点的距离均不少于80 m,所以80(60)80r d r d -⎧⎨--⎩≥≥即68038056803(60)805dd d d -⎧-⎪⎪⎨-⎪--⎪⎩≥≥解得1035d ≤≤故当d =10时,68035dr -=最大，即圆面积最大. 所以当OM = 10 m 时，圆形保护区的面积最大.19．(本小题满分16分)已知函数()e e x x f x -=+其中e 是自然对数的底数．（1）证明：()f x 是R 上的偶函数；（2）若关于x 的不等式()e 1x mf x m -+-≤在(0)+∞，上恒成立，求实数m 的取值范围；（3）已知正数a 满足：存在0[1)x ∈+∞，，使得3000()(3)f x a x x <-+成立．试比较1e a -与e 1a -的大小，并证明你的结论．【答案】本小题主要考查初等函数的基本性质、导数的应用等基础知识，考查综合运用数学思想方法分析与解决问题的能力.满分16分.（1）x ∀∈R ，()e e ()x x f x f x --=+=，∴()f x 是R 上的偶函数（2）由题意，(e e )e 1x x x m m --++-≤，即(e e 1)e 1x x x m --+--≤ ∵(0)x ∈+∞，，∴e e 10x x -+->，即e 1e e 1x x x m ---+-≤对(0)x ∈+∞，恒成立令e (1)x t t =>，则211t m t t --+≤对任意(1)t ∈+∞，恒成立∵2211111(1)(1)113111t t t t t t t t --=-=---+-+-+-++-≥，当且仅当2t =时等号成立 ∴13m -≤（3）'()e e x x f x -=-，当1x >时'()0f x >，∴()f x 在(1)+∞，上单调增令3()(3)h x a x x =-+，'()3(1)h x ax x =--∵01a x >>，，∴'()0h x <，即()h x 在(1)x ∈+∞，上单调减∵存在0[1)x ∈+∞，，使得3000()(3)f x a x x <-+，∴1(1)e 2e f a =+<，即()11e 2ea >+ ∵e-1e 111ln ln ln e (e 1)ln 1ea a aa a a ---=-=--+设()(e 1)ln 1m a a a =--+，则()e 1e 111'()1e 2ea m a a a a ---=-=>+，当()11e e 12e a +<<-时，'()0m a >，()m a 单调增；当e 1a >-时，'()0m a <，()m a 单调减因此()m a 至多有两个零点，而(1)(e)0m m == ∴当e a >时，()0m a <，e 11e a a --<；当()11e e 2e a +<<时，()0m a <，e 11e a a -->；当e a =时，()0m a =，e 11e a a --=．20．(本小题满分16分)设数列{}n a 的前n 项和为n S ．若对任意的正整数n ，总存在正整数m ，使得n m S a =，则称{}n a 是“H 数列”．（1）若数列{}n a 的前n 项和2()n n S n *=∈N ，证明：{}n a 是“H 数列”；（2）设{}n a 是等差数列，其首项11a =，公差0d <．若{}n a 是“H 数列”，求d 的值；（3）证明：对任意的等差数列{}n a ，总存在两个“H 数列”{}n b 和{}n c ，使得()n n n a b c n *=+∈N 成立．【答案】本小题主要考查数列的概念、等差数列等基础知识，考查探究能力及推理论证能力, 满分16分.（1）当2n ≥时，111222n n n n n n a S S ---=-=-=当1n =时，112a S ==∴1n =时，11S a =，当2n ≥时，1n n S a += ∴{}n a 是“H 数列” （2）1(1)(1)22n n n n n S na d n d --=+=+ 对n *∀∈N ，m *∃∈N 使n m S a =，即(1)1(1)2n n n d m d -+=+- 取2n =得1(1)d m d +=-，12m d=+∵0d <，∴2m <，又m *∈N ，∴1m =，∴1d =-（3）设{}n a 的公差为d令111(1)(2)n b a n a n a =--=-，对n *∀∈N ，11n n b b a +-=- 1(1)()n c n a d =-+，对n *∀∈N ，11n n c c a d +-=+则1(1)n n n b c a n d a +=+-=，且{}{}n n b c ，为等差数列 {}n b 的前n 项和11(1)()2n n n T na a -=+-，令1(2)n T m a =-，则(3)22n n m -=+ 当1n =时1m =；当2n =时1m =；当3n ≥时，由于n 与3n -奇偶性不同，即(3)n n -非负偶数，m *∈N 因此对n ∀，都可找到m *∈N ，使n m T b =成立，即{}n b 为“H 数列”． {}n c 的前ｎ项和1(1)()2n n n R a d -=+，令1(1)()n m c m a d R =-+=，则(1)12n n m -=+ ∵对n *∀∈N ，(1)n n -是非负偶数，∴m *∈N即对n *∀∈N ，都可找到m *∈N ，使得n m R c =成立，即{}n c 为“H 数列” 因此命题得证.数学Ⅱ(附加题)21.【选做题】本题包括A, B,C,D 四小题，请选定其中两小题，并在相应的答题区域内作答.若多做，则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. A.【选修4-1:几何证明选讲】(本小题满分10分)如图，AB 是圆O 的直径，C 、 D 是圆O 上位于AB 异侧的两点证明:∠OCB =∠D .本小题主要考查圆的基本性质，考查推理论证能力.满分10分. 证明：因为B , C 是圆O 上的两点，所以OB =OC . 故∠OCB =∠B .又因为C , D 是圆O 上位于AB 异侧的两点，故∠B ，∠D 为同弧所对的两个圆周角，所以∠B =∠D . 因此∠OCB =∠D .B.【选修4-2:矩阵与变换】(本小题满分10分)已知矩阵121x -⎡⎤=⎢⎥⎣⎦A ，1121⎡⎤=⎢⎥-⎣⎦B ，向量2y ⎡⎤=⎢⎥⎣⎦α，x y ，为实数，若A α=B α，求x y ，的值．【答案】本小题主要考查矩阵的乘法等基础知识，考查运算求解能力.满分10分. 222y xy -⎡⎤=⎢⎥+⎣⎦A α，24y y +⎡⎤=⎢⎥-⎣⎦B α，由A α=B α得22224y y xy y -=+⎧⎨+=-⎩，，解得142x y =-=， C.【选修4-4:坐标系与参数方程】(本小题满分10分) 在平面直角坐标系xOy 中，已知直线l 的参数方程为212222x t y t ⎧=-⎪⎨⎪=+⎩，(t 为参数)，直线l 与抛物线24y x =交于A B ，两点，求线段AB 的长．【答案】本小题主要考查直线的参数方程、抛物线的标准方程等基础知识，考查运算求解能力.满分10分.直线l ：3x y +=代入抛物线方程24y x =并整理得21090x x -+= ∴交点(12)A ，，(96)B -，，故||82AB = D.【选修4-5:不等式选讲】(本小题满分10分) 已知x >0, y >0,证明：(1+x +y 2)( 1+x 2+y )≥9xy.本小题主要考查算术一几何平均不等式.考查推理论证能力.满分10分. 证明：因为x >0, y >0, 所以1+x +y 2≥2330xy >，1+x 2+y ≥2330x y >，所以(1+x +y 2)( 1+x 2+y )≥223333xy x y ⋅=9xy.【必做题】第22题、第23题，每题10分，共计20分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤. 22．(本小题满分10分)盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同．（1）从盒中一次随机取出2个球，求取出的2个球颜色相同的概率P ；（2）从盒中一次随机取出4个球，其中红球、黄球、绿球的个数分别记为123x x x ，，，随机变量X 表示123x x x ，，中的最大数，求X 的概率分布和数学期望()E X ．22.【必做题】本小题主要考查排列与组合、离散型随机变量的均值等基础知识，考查运算求解能力.满分10分.（1）一次取2个球共有29C 36=种可能情况，2个球颜色相同共有222432C C C 10++=种可能情况∴取出的2个球颜色相同的概率1053618P ==（2）X 的所有可能取值为432，，，则4449C 1(4)C 126P X === 3131453639C C C C 13(3)C 63P X +=== 11(2)1(3)(4)14P X P X P X ==-=-==∴X 的概率分布列为X 2 3 4 P111413631126故X 的数学期望1113120()23414631269E X =⨯+⨯+⨯=23．(本小题满分10分)已知函数0sin ()(0)x f x x x=>，设()n f x 为1()n f x -的导数，n *∈N ．（1）求()()122222f f πππ+的值；（2）证明：对任意的n *∈N ，等式()()124442n n nf f -πππ+=成立．23.【必做题】本题主要考查简单的复合函数的导数，考查探究能力及运用数学归纳法的推理论证能力.满分10分.(1)解：由已知，得102sin cos sin ()(),x x x f x f x x x x '⎛⎫'===- ⎪⎝⎭于是21223cos sin sin 2cos 2sin ()(),x x x x x f x f x x x x x x ''⎛⎫⎛⎫'==-=--+ ⎪ ⎪⎝⎭⎝⎭所以12234216(),(),22f f πππππ=-=-+ 故122()() 1.222f f πππ+=- (2)证明：由已知，得0()sin ,xf x x =等式两边分别对x 求导，得00()()cos f x xf x x '+=，即01()()cos sin()2f x xf x x x π+==+，类似可得 122()()sin sin()f x xf x x x π+=-=+，2333()()cos sin()2f x xf x x x π+=-=+， 344()()sin sin(2)f x xf x x x π+==+. 下面用数学归纳法证明等式1()()sin()2n n n nf x xf x x π-+=+对所有的n ∈*N 都成立. (i)当n =1时，由上可知等式成立.(ii)假设当n =k 时等式成立, 即1()()sin()2k k k kf x xf x x π-+=+. 因为111[()()]()()()(1)()(),k k k k k k k kf x xf x kf x f x xf x k f x f x --+'''+=++=++(1)[sin()]cos()()sin[]2222k k k k x x x x ππππ+''+=+⋅+=+，所以1(1)()()k k k f x f x +++(1)sin[]2k x π+=+. 所以当n=k +1时,等式也成立.综合(i),(ii)可知等式1()()sin()2n n n nf x xf x x π-+=+对所有的n ∈*N 都成立. 令4x π=，可得1()()sin()44442n n n nf f πππππ-+=+(n ∈*N ). 所以12()()4442n n nf f πππ-+=(n ∈*N ).。

专题17：三视图高考真题集锦(解析版)

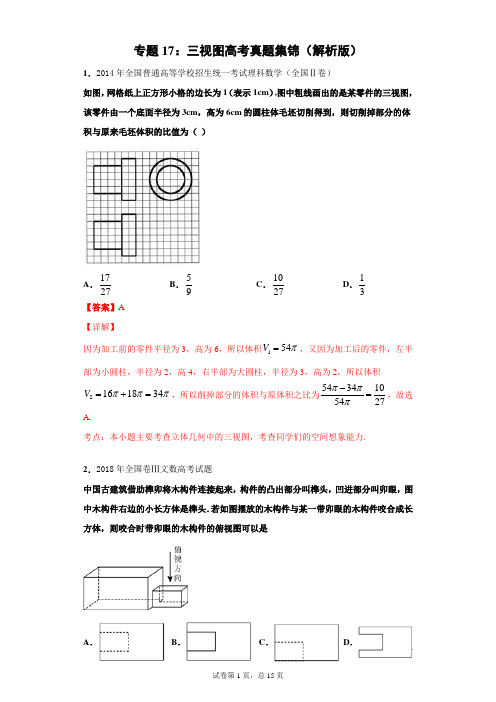
专题17：三视图高考真题集锦（解析版）1．2014年全国普通高等学校招生统一考试理科数学（全国Ⅱ卷）如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A ．1727B ．59C ．1027D ．13【答案】A 【详解】因为加工前的零件半径为3，高为6，所以体积154V π=，又因为加工后的零件，左半部为小圆柱，半径为2，高4，右半部为大圆柱，半径为3，高为2，所以体积2161834V πππ=+=，所以削掉部分的体积与原体积之比为5434105427πππ-=，故选A.考点：本小题主要考查立体几何中的三视图，考查同学们的空间想象能力.2．2018年全国卷Ⅲ文数高考试题中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是A ．B ．C ．D ．【答案】A【详解】详解：由题意知，题干中所给的是榫头，是凸出的几何体，求得是卯眼的俯视图，卯眼是凹进去的，即俯视图中应有一不可见的长方形，且俯视图应为对称图形故俯视图为故选A.点睛：本题主要考查空间几何体的三视图，考查学生的空间想象能力，属于基础题．3．2017年全国普通高等学校招生统一考试文科数学（新课标1卷）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是A．B．C．D．【答案】A【解析】对于B，易知AB∥MQ，则直线AB∥平面MNQ；对于C，易知AB∥MQ，则直线AB∥平面MNQ；对于D，易知AB∥NQ，则直线AB∥平面MNQ．故排除B，C，D，选A．点睛:本题主要考查线面平行的判定定理以及空间想象能力，属容易题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．4．2017年全国普通高等学校招生统一考试文科数学（新课标2卷）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A ．90πB ．63πC ．42πD ．36π【答案】B 【解析】由题意，该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱，故其体积为2213634632V πππ=⋅⋅⋅+⋅⋅=，故选B.点睛:（1）解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．（2）三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．5．2014年全国普通高等学校招生统一考试理科数学如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A ．63B ．6C ．2D ．4【答案】B 【详解】由正视图、侧视图、俯视图形状，可判断该几何体为四面体，且四面体的长、宽、高均为4个单位，故可考虑置于棱长为4个单位的正方体中研究，如图所示，该四面体为D ABC -，且4AB BC ==,42AC =,25DB DC ==,2(42)46DA =+=，故最长的棱长为6，选B ．6．2016年全国普通高等学校招生统一考试理科数学（全国2卷）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）A ．20πB ．24πC ．28πD ．32π【答案】C 【解析】试题分析：由三视图分析可知，该几何体的表面积为圆锥的表面积与圆柱的侧面积之和．，，所以几何体的表面积为．考点：三视图与表面积．7．2016年全国普通高等学校招生统一考试文科数学（新课标3卷）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（）A．B．C．90D．81【答案】B【解析】【详解】试题分析：解：由已知中的三视图可得：该几何体是一个以俯视图为底面的斜四棱柱，其底面面积为：3×6=18，前后侧面的面积为：3×6×2=36，左右侧面的面积为：，故棱柱的表面积为：．故选：B．点睛：本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键，由三视图判断空间几何体（包括多面体、旋转体和组合体）的结构特征是高考中的热点问题.8．2015年全国普通高等学校招生统一考试文科数学（新课标Ⅰ）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体的三视图+，则r=( )中的正视图和俯视图如图所示，若该几何体的表面积为1620πA ．1B ．2C ．4D ．8 【答案】B【解析】试题分析：由正视图和俯视图知，该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r ，圆柱的高为2r ，其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+="16" + 20π，解得r=2，故选B. 考点：简单几何体的三视图；球的表面积公式；圆柱的测面积公式9．2015年全国普通高等学校招生统一考试文科数学（新课标Ⅱ）一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（）A ．18B ．17C ．16D ．15【答案】D 【详解】试题分析：如图所示，截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为,故选D. 考点：本题主要考查三视图及几何体体积的计算.10．2014年全国普通高等学校招生统一考试文科数学（新课标Ⅰ）如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（）A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱【答案】B 【解析】试题分析：由三视图中的正视图可知，由一个面为直角三角形，左视图和俯视图可知其它的面为长方形．综合可判断为三棱柱．考点：由三视图还原几何体.11．2014年全国普通高等学校招生统一考试文科数学（全国Ⅱ卷）如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削的部分的体积与原来毛坯体积的比值为（） A ．2717 B ．95 C ．2710 D ．31【答案】C 【解析】试题分析：由三视图还原几何体为一个小圆柱和大圆柱组成的简单组合体．其中小圆柱底面半径为2、高为4，大圆柱底面半径为3、高为2，则其体积和为22243234πππ⨯⨯+⨯⨯=，而圆柱形毛坯体积为23654ππ⨯⨯=，故切削部分体积为20π，从而切削的部分的体积与原来毛坯体积的比值为20105427ππ=．考点：三视图．12．2020年全国统一高考数学试卷（理科）（新课标Ⅱ）如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A ．EB ．FC ．GD ．H【答案】A 【分析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点. 【详解】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E . 故选：A 【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题. 13．2020年全国统一高考数学试卷（理科）（新课标Ⅲ）下图为某几何体的三视图，则该几何体的表面积是（）A ．2B ．2C ．3D ．3【答案】C 【分析】根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积. 【详解】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△ 根据勾股定理可得：22AB AD DB ===∴ADB △是边长为22的等边三角形根据三角形面积公式可得：2113sin 60(22)23222ADB S AB AD =⋅⋅︒=⋅=△ ∴该几何体的表面积是：2362332=⨯++.故选：C. 【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.14．2017年全国普通高等学校招生统一考试理科数学（新课标1卷）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A ．10B ．12C ．14D ．16【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)2122⨯+⨯⨯=，故选B.点睛:三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15．2015年全国普通高等学校招生统一考试理科数学（新课标Ⅱ）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（）A．B．C．D．【答案】D【解析】试题分析：设正方体的棱长为1，由三视图判断，正方体被切掉的部分为三棱锥，∴正方体切掉部分的体积为111111326⨯⨯⨯⨯=，∴剩余部分体积为15166-=，∴截去部分体积与剩余部分体积的比值为15．故选D．考点：由三视图求体积16．2016年全国普通高等学校招生统一考试理科数学（新课标1卷）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是A．17πB．18πC．20πD．28π【答案】A【解析】试题分析：由三视图知，该几何体的直观图如图所示：是一个球被切掉左上角的,即该几何体是个球，设球的半径为，则，解得，所以它的表面积是的球面面积和三个扇形面积之和,即，故选A．【考点】三视图及球的表面积与体积【名师点睛】由于三视图能有效地考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般与几何体的表面积与体积相结合.由三视图还原出原几何体是解决此类问题的关键.17．2016年全国普通高等学校招生统一考试理科数学（新课标2卷）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）A．B．C．D．【答案】C【解析】试题分析：由三视图分析可知，该几何体的表面积为圆锥的表面积与圆柱的侧面积之和。