第7讲图型结构

合集下载

一年级下册美术教案-第7课童话城堡 ▏人美版

学前准备
教师
课件，示范画
学生
绘图工具，课本
流程及时间
教学活动
二次备课
导入新课
1、视频导入
师：教师播放一段动画视频（《白雪公主》节选）
提问：你们看到了什么？
学：城堡
2、欣赏图片
师：你们看到城堡会想到什么呢？
学：灰姑娘、白雪公主……
师：无论灰姑娘、白雪公主还是睡美人，都是来自童话王国，今天童话王国国王，需要你们帮忙，为他设计一个新的童话城堡。（板书课题）
艺术实践
用各种图形，为你自己建筑一座漂亮的童话城堡。
要求：1、明确自己的城堡修建地点
2、构图饱满色彩鲜艳
播放音乐，教师巡视
欣赏评价
1、同学们上台展示作品，请学生们自己上台介绍自己的城堡。2、教师评价学生作品
知识拓展
板书设计
童话城堡
各种各样的图形组成
城堡有高有矮，有大有小
漂亮的颜色和花纹
教学后记
3.情意目标
通过对童话城堡的创作表现，引导学生感受城堡建筑的形式美，以及它与生活的密切关系，体验图形组合、创新表现城堡造型的乐趣，丰富学生的想象，寄托他们对生活的美好愿望。
学习重点
运用各种图形组合出具有高低、大小等变化的城堡造型，根据想象，适当添加有趣的情景，使画面富有童话色彩。
学习难点
表现的城堡造型新颖富有创意，注意细节的添加与描绘。
学：不是，有很多层。
师，总结：所以，漂亮的城堡是有高有矮，有前有后，有大有小的变化。
3、观察细节—装饰
出示细节图，师：仔细看一看，是什么使城堡变得更加漂亮？
学：有漂亮的颜色，花纹……
师：所以，漂亮的童话城堡不仅仅需要各种各样的图形组成，还需要有高的房间，矮一点的房间，和漂亮的颜色与花纹。

离散数学7-1图论

图7-1.9 不同构的图
作业
P279 (1) (4)
如图7-1.6中的(a)和(b)互为补图。
[定义] 子图(subgraph) 设图G=<V,E>，如果有图G’= <V’,E’>，若有 V’ V ，E’ E，则称图G’是图G的子图。 [定义] 生成子图(spanning subgraph) 如果图G的子图G’包含G的所有结点,则称该图 G’为G的生成子图。如图7-1.8中G'和G"都是 G的生成子图。
[定义] 相对于图G的补图设图G'＝〈V',E'〉是图G＝〈V,E〉的子图,若给定另外一个图G"＝〈V",E"〉使得E"＝EE', 且 V" 中仅包含 E"的边所关联的结点。则称G"是子图G'的相对于图G的补图。
图7-1.7 (c )为(b)相对于(a)的补图
如图 7-1.7 中的图 (c) 是图 (b) 相对于图 (a) 的补图。而图 (b) 不是图 (c) 相对于图 (a) 的补图 , 因为图(b)中有结点c。在上面的一些基本概念中,一个图由一个图形表示,由于图形的结点的位置和连线长度都可任意选择 , 故一个图的图形表示并不是唯一的。下面我们讨论图的同构的概念。
表7-1.1
结点出度入度
a 2 0
b 1 1
c 0 2
d 1 1
结点出度
入度
v1 1 1
v2 0 2
v3 2 0
v4 1 1
分析本例还可以知道 , 此两图结点的度数也分别对应相等,如表7-1.1所示。
两图同构的一些必要条件: 1.结点数目相等; 3.边数相等; 3.度数相等的结点数目相等。需要指出的是这几个条件不是两个图同构的充分条件,例如图7-1.9中的(a)和(b)满足上述的三个条件,但此两个图并不同构。

7图版的编排构成

在页与页之间，页与整体之间．如图片比例均大小相似，整体结构无强弱节奏的变化关系，设计就会显得平淡．难给人留下深刻印象。
这对于刚接触设计的学生掌握有一定难度，常容易出现问题。
Bucknall画册设计欣赏
超有趣小册子欣赏
7
图版的编排构成
图版率 /角版、挖版、出血版/视觉度 /图形面积与张力 /延续页面的整体设计版心/页码、页眉、页脚/开本尺寸/封面设计/装订形式
1.
纸张大小 a. 正度纸——787x1092mm b. 大度纸——889x1194mm 2. 折叠次数（开数） a. 全开——未经裁切的纸张 b. 对开或半开——将全开纸对折裁开后的幅面 c. 四开——将对开纸对折裁开后的幅面 d. 八开——将对四纸对折裁开后的幅面 e. 十六开——将八开纸对折裁开后的幅面 f. 以此类推三十二开，六十四开注意：由于纸张有正度和大度之分，所以开数也有正度对开和大度对开等称谓
7
图版的编排构成
图版率 /角版、挖版、出血版/视觉度 /图形面积与张力 /延续页面的整体设计版心/页码、页眉、页脚/开本尺寸/封面设计/装订形式
2．小图形精密而沉静将小图形插入字群中，显得简洁而精致，有点缀和呼应版面的作用。但同时也给人拘谨、静止、趣味弱的感觉。
7
图版的编排构成
图版率 /角版、挖版、出血版/视觉度 /图形面积与张力 /延续页面的整体设计版心/页码、页眉、页脚/开本尺寸/封面设计/装订形式
。
7
图版的编排构成
图版率 /角版、挖版、出血版/视觉度 /图形面积与张力 /延续页面的整体设计版心/页码、页眉、页脚/开本尺寸/封面设计/装订形式
1．图版率低，减少阅读兴趣
图版率是指图所占版面的比例，用％作表示，如版面全是文字版．图版率为0％，相反全是图形画面图版率为100％。光有文字无图画或者小画面、少画面的版面，阅读的兴趣会降低。像小说、诗集等以文字为主的版面，图版率为10％则更能增进阅读性，假如一本小说无插图．版面则显得沉闷。插图会给人真实的联想，透过插图，我们从中可感知此书的内容，这就是图画传达的魅力与价值。

新北师大版小学数学图形与几何模块知识结构讲解(课堂PPT)

图（参见例 32 ）。
9．通过观察、操作，认识长方体、正方体、圆柱和圆锥，认识
长方体、正方体和圆柱的展开图。
12
（一）图形的认识
3、教学要领（1）图形的认识的教学要明确两点：
一是这部分内容属于图形认识的哪个水平，前后继知识各是什么；二是多数学生现在的形象思维处于一个什么阶段，要通过教学达到什么阶段或水平。
26
（一）图形与位置
1.教学内容
主要内容
二上
三下
五上
六下
认识上下、前后、辨认东、南、西、在方格纸上用数
左右。
北四个方向；了对确定位置；描
解东南、东北、述简单的路线图
西南、西北。
根据方向和距离确定位置；自建参照物系确定位置。
27
（四）图形与位置
2．教学目标
辨认方向和使用路线图
19
（二）测量
（3）．重视在测量过程中，培养学生的估测意识和能力
20
（二）测量
2、教学要领：
( 1 )使学生体会建立统一度量单位的重要性； ( 2 ) 使学生理解与把握度量单位的实际意义，对测量结果有很好的感悟； ( 3 ) 在具体的问题情境中恰当地选择度量单位、工具和方法进行测量； ( 4 )重视估测及其简单应用； ( 5 ) 帮助学生在测量活动中感悟数学思想，掌握测量的基本方法，积累数学活动经验，培养空间观念。
15
（二）测量
1.教学内容
第一学段主要内容
一上
二上
二下
三上
三下
大小、多少、统一测量单分米、毫长短、轻重位的必要性；米、千米的比较。厘米、米的的认识。
认识

专题7几何图形—7.11之中点结构-2021年鲁教版(五四制)九年级数学专题复习训练

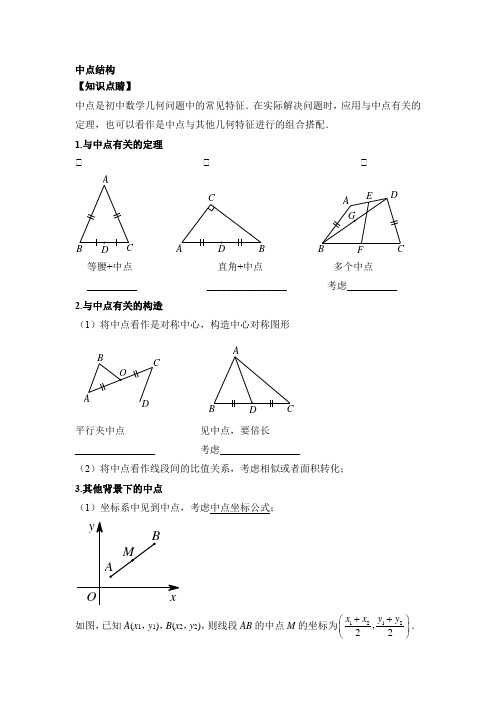
中点结构【知识点睛】中点是初中数学几何问题中的常见特征．在实际解决问题时，应用与中点有关的定理，也可以看作是中点与其他几何特征进行的组合搭配．1.与中点有关的定理① ① ①等腰+中点直角+中点多个中点__________ ________________ 考虑__________2.与中点有关的构造（1）将中点看作是对称中心，构造中心对称图形平行夹中点见中点，要倍长________________ 考虑________________（2）将中点看作线段间的比值关系，考虑相似或者面积转化；3.其他背景下的中点（1）坐标系中见到中点，考虑中点坐标公式；如图，已知A (x 1，y 1)，B (x 2，y 2)，则线段AB 的中点M 的坐标为1212,22x x y y ++⎛⎫ ⎪⎝⎭．（2）圆背景下的中点，考虑圆中的相关定理；如：①圆中四组量关系定理；②垂径定理；③圆周角定理等；倍长中线（1）【条件】：在矩形ABCD中，BD=BE，DF=EF；【结论】：AF⊥CF；模型思路：存在平行线AD平行BE；平行线间线段有中点DF=EF；可以构造“8”字全等△ADF≌△HEF；（2）【条件】在平行四边形ABCD中，BC=2AB，AM=DM，CE⊥AB；【结论】∠EMD=3∠MEA辅助线：有平行AB①CD，有中点AM=DM，延长EM，构造①AME①①DMF，连接CM构造等腰①EMC，等腰①MCF。

（通过构造8字全等线段数量及位置关系，角的大小转化）【经典例题1】已知，点P是直角三角形ABC斜边AB上一动点（不与A，B 重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是，QE与QF的数量关系式；（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；（3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．【解析】（1）AE①BF，QE=QF，理由是：如图1，①Q为AB中点，①AQ=BQ，①BF①CP，AE①CP，①BF①AE，①BFQ=①AEQ，在①BFQ和①AEQ中①①BFQ①①AEQ（AAS），①QE=QF，故答案为：AE①BF，QE=QF．（2）QE=QF，证明：如图2，延长FQ交AE于D，①AE①BF，①①QAD=①FBQ，在①FBQ和①DAQ中①①FBQ①①DAQ（A SA），①QF=QD，①AE①CP，①EQ是直角三角形DEF斜边上的中线，①QE=QF=QD，即QE=QF．（3）（2）中的结论仍然成立，证明：如图3，延长EQ、FB交于D，①AE①BF，①①1=①D，在①AQE和①BQD中，①①AQE①①BQD（AAS），①QE=QD，①BF①CP，①FQ是斜边DE上的中线，①QE=QF．练习1-1已知正方形ABCD，以CE为边在正方形ABCD外部作正方形CEFG，连AF，H是AF的中点，连接BH，HE．（1）如图1所示，点E在边CB上时，则BH，HE的关系为；（2）如图2所示，点E在BC延长线上，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请给出新的结论并证明．（3）如图3，点B，E，F在一条直线上，若AB＝13，CE＝5，直接写出BH的长．【解析】（1）BH⊥HE，BH＝HE；理由如下：延长EH交AB于M，如图1所示：∵四边形ABCD和四边形CEFG是正方形，∴AB∥CD∥EF，AB＝BC，CE＝FE，∠ABC＝90°，∴∠AMH＝∠FEH，∵H是AF的中点，∴AH＝FH，∴△AMH≌△FEH（AAS），∴AM＝FE＝CE，MH＝EH，∴BM＝BE，∵∠ABC＝90°，ME＝HE；∴BH⊥HE，BH＝12（2）结论仍然成立．BH⊥HE，BH＝HE．理由如下：延长EH交BA的延长线于点M，如图2所示：∵四边形ABCD是正方形，四边形EFGC是正方形，∴∠ABE＝∠BEF＝90°，AB＝BC，AB∥CD∥EF，CE＝FE，∴∠HAM＝∠HFE，∴△AHM≌△FHE（ASA），∴HM＝HE，AM＝EF＝CE，∴BM＝BE，∵∠ABE＝90°，EM＝EH；∴BH⊥EH，BH＝12（3）延长EH到M，使得MH＝EH，连接AH、BH，如图3所示：同（2）得：△AMH≌△FEH（SAS），∴AM＝FE＝CE，∠MAH＝∠EFH，∴AM∥BF，∴∠BAM+∠ABE＝180°，∴∠BAM+∠CBE＝90°，∵∠BCE+∠CBE＝90°∴∠BAM＝∠BCE，∴△ABM≌△CBE（SAS），∴BM＝BE，∠ABM＝∠CBE，∴∠MBE＝∠ABC＝90°，EM＝MH＝EH，∵MH＝EH，∴BH⊥EH，BH＝12在Rt△CBE中，BE＝2−CE2＝12，∵BH＝EH，BH⊥EH，BE＝6√2．∴BH＝√22练习1-2（1）如图1，在线段AB上取一点C（BC＞AC），分别以AC、BC为边在同一侧作等边①ACD与等边①BCE，连结AE、BD，则ACE经过怎样的变换（平移、轴对称、旋转）能得到①DCB？请写出具体的变换过程；（不必写理由）【A】（2）如图2，在线段AB上取一点C（BC＞AC），如果以AC、BC为边在同一侧作正方形ACDG与正方形CBEF，连结EG，取EG的中点M，设DM的延长线交EF于N，并且DG=NE；请探究DM与FM的关系，并加以证明；【B】（3）在图2的基础上，将正方形CBEF绕点C顺时针旋转（如图3），使得A、C、E在同一条直线上，请你继续探究线段MD、MF的关系，并加以证明．【解析】（1）将①ACE绕点C顺时针旋转60°后能得到①DCB；理由如下：①①ACD和①BCE是等边三角形，①AC＝CD，CE＝CA，①ACD＝①BCE＝60°，①①ACE＝①DCB，在①ACE和①DCB中，，①①ACE①①DCB（SAS），①将①ACE绕点C顺时针旋转60°后能得到①DCB；（2）如图，相等且垂直．理由如下：①EF①GD，①①NEM＝①DGM，在①MGD和①MEN中，，①①MGD①①MEN（SAS），①DM＝NM，在Rt①DNF中，FM＝DN＝DM，①NE＝GD，GD＝CD，①NE＝CD，①FN＝FD，即FM①DM，①DM与FM相等且垂直．（3）MD与MF相等且垂直．理由如下：延长DM交CE于N，连接DF、FN，如图所示：根据（2）可以得到①MGD①①MNE，①DM＝NM，NE＝DG，①①DCF＝①FEN＝45°，DC＝DG＝NE，FC＝FE，①在①DCF和①NEF中，，①①DCF①①NEF（SAS），①DF＝FN，①DFC＝①NFE，①①DFN＝90°，即①FDN为等腰直角三角形，①DM＝NM，即FM为斜边DN的中线，①FM＝DM＝NM＝DN，且FM①DN，则FM＝DM，FM①DM．练习1-3如图，已知①BAD和①BCE均为等腰直角三角形，①BAD=①BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）当A ，B ，C 三点在同一直线上时（如图1），求证：M 为AN 的中点；（2）将图1中的①BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时（如图2），求证：①ACN 为等腰直角三角形；（3）将图1中①BCE 绕点B 旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．【解析】（1）证明：如图1，①EN①AD ，①①MAD=①MNE ，①ADM=①NEM ．①点M 为DE 的中点，①DM=EM ．在①ADM 和①NEM 中，①MAD MNE ADM NEM DM EM ∠=∠⎧⎪∠=∠⎨⎪=⎩．①①ADM①①NEM ．①AM=MN ．①M 为AN 的中点．（2）证明：如图2，①①BAD 和①BCE 均为等腰直角三角形， ①AB=AD ，CB=CE ，①CBE=①CEB=45°． ①AD①NE ，①①DAE+①NEA=180°．①①DAE=90°，①①NEA=90°．①①NEC=135°．①A ，B ，E 三点在同一直线上， ①①ABC=180°-①CBE=135°．①①ABC=①NEC ．①①ADM①①NEM （已证），①AD=NE ．①AD=AB ，①AB=NE ．在①ABC 和①NEC 中，AB NE ABC NEC BC EC =⎧⎪∠=∠⎨⎪=⎩①①ABC①①NEC ．①AC=NC ，①ACB=①NCE ．①①ACN=①BCE=90°．①①ACN 为等腰直角三角形．（3）①ACN 仍为等腰直角三角形．证明：如图3，延长AB 交NE 于点F ，①AD①NE ，M 为中点，①易得①ADM①①NEM ，①AD=NE ．①AD=AB ，①AB=NE ．①AD①NE ，①AF①NE ，在四边形BCEF 中，①①ACN=①BFE=90°①①FBC+①FEC=360°-180°=180°①①FBC+①ABC=180°①①ABC=①FEC在①ABC 和①NEC 中，AB NE ABC NEC BC EC =⎧⎪∠=∠⎨⎪=⎩①①ABC①①NEC ．①AC=NC ，①ACB=①NCE ．①①ACN=①BCE=90°．①①ACN 为等腰直角三角形．练习1-4图1，在①ABC中，①ACB=90①，点D、点E分别在AC、AB边上，连结DE、DB，使得①DEA=90①，若点O是线段BD的中点，连结OC、OE，则易得OC=OE；操作：现将①ADE绕A点逆时针旋转得到①AFG(点D. 点E分别与点F. 点G对应)，连结FB，若点O是线段FB的中点，连结OC、OG，探究线段OC、OG 之间的数量关系；(1)如图2，当点G在线段CA的延长线上时，OC=OG是否成立；若成立，请证明；若不成立，请说明理由；(2)如图3，当点G在线段CA上时，线段OC=OG是否成立；若成立，请证明；若不成立，请说明理由；(3)如图4，在①ADE的旋转过程中，线段OC、OG之间的数量关系是否发生了变化?请直接写出结论，不用说明理由.【解析】（1）当点G在线段CA的延长线上时，OC=OG成立理由：如图2，延长GF，CO相较于点D，①①ACB=①FGA=90°，①GD①BC，①①BCO=①D ，①点O 是线段BD 的中点，①OB=OF ，在①BOC 和①FOD 中，①BCO=①D ①BOC=①FOD OB=OF ，①①BOC①①FOD ，①OC=OD ，在Rt①CDG 中，OG=21CD=OC ，（2）当点G 在线段CA 上时，线段OC=OG 是成立，理由：如图3，延长GF ，CO 相较于点D ，①①ACB=①FGA=90°，①GD①BC ，①①BCO=①D ，①点O 是线段BD 的中点，①OB=OF ，在①BOC 和①FOD 中，①BCO=①D ①BOC=①FOD OB=OF ，①OC=OD ，在Rt①CDG 中，OG=21CD=OC ，（3）在①ADE 的旋转过程中，线段OC 、OG 之间的数量关系不发生了变化，理由：如图4，连接CG ，延长GF 交BC 于M ，过点F 作FD①BC ，连接DG ，①①BCO=①FDO ，①点O 是线段BD 的中点，①OB=OF ，在①BOC 和①FOD 中，①BCO=①D ①BOC=①FOD OB=OF ，①①BOC①①FOD ，①OC=OD ，BC=DF由题意知，①AFG①①ABC ，①AF/AB=FG/BC ，①AF/AB=FG/DF ，①①ACB=①AGF=90°，①点A ，C ，M ，G 四点共圆，①①CAG=①BMG ，①FD①BC ，①①GFD=①BMG ，①①CAG=①GFD ，①AF/AB=FG/DF ，①①GAC①①GFD ，①①CGD=①ACF=90°，①OC=OD ， ①OG=21CD=OC ．点评此题是几何变换综合题，主要考查了全等三角形的性质和判定，相似三角形的性质和判定，直角三角形的性质，解本题的关键是判断出①BOC①①FOD ，难点是（3）中判断出①CGD=90°．练习1-5已知：点P 是平行四边形ABCD 的对角线AC 所在直线上的一个动点（点P 不与点A 、C 重合），分别过点A 、C 向直线BP 作垂线，垂足分别为点E 、F ．点O 为AC 的中点．（1）如图1，当点P 与点O 重合时，线段OE 和OF 的关系是__________；（2）当点P 运动到如图2所示的位置时，请在图中补全图形并通过证明判断（1）中的结论是否仍然成立？（3）如图3，点P 在线段OA 的延长线上运动，当∠OEF=30°时，试探究线段CF 、AE 、OE 之间的关系．【解析】（1）①AE①PB ，CF①BP ，①①AEO=①CFO=90°，在①AEO 和①CFO 中，①AEO=①CFO①AOE=①COFAO=OC ，①①AOE①①COF ，①OE=OF．（2）图2中的结论为：CF=OE+AE．图3中的结论为：CF=OE-AE．选图2中的结论证明如下：延长EO交CF于点G，①AE①BP，CF①BP，①AE①CF，①①EAO=①GCO，在①EOA和①GOC中，①EAO=①GCOAO=OC①AOE=①COG，①①EOA①①GOC，①EO=GO，AE=CG，在Rt①EFG中，①EO=OG，①OE=OF=GO，①①OFE=30°，①①OFG=90°-30°=60°，①①OFG是等边三角形，①OF=GF，①OE=OF，①OE=FG，①CF=FG+CG，①CF=OE+AE．选图3的结论证明如下：延长EO交FC的延长线于点G，①AE①BP，CF①BP，①AE①CF，①①AEO=①G，在①AOE和①COG中，①AEO=①G①AOE=①GOCAO=OC，①①AOE①①COG，①OE=OG，AE=CG，在Rt①EFG中，①OE=OG，①OE=OF=OG，①①OFE=30°，①①OFG=90°-30°=60°，①①OFG是等边三角形，①OF=FG，①OE=OF，①OE=FG，①CF=FG-CG，①CF=OE-AE．练习1-6如图1，在Rt①ABC中，①BAC＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，BE，点P为DC的中点，【观察猜想】图1中，线段AP与BE的数量关系是，位置关系是．（1）（2）【探究证明】把①ADE 绕点A 逆时针旋转到图2的位置，（1）中的猜想是否仍然成立？若成立请证明，否请说明理由；（3）【拓展延伸】把①ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出线段AP 长度的最大值和最小值．图1 图2【答案】（1）AP ＝BE ，P A ①BE ；（2）（3）见解析．【解析】（1）设P A 交BE 于点O ．①AD ＝AE ，AC ＝AB ，①DAC ＝①EAB ，①①DAC ①①EAB ，①BE ＝CD ，①ACD ＝①ABE ，①①DAC ＝90°，DP ＝PC ，①P A ＝CD ＝PC ＝PD ， ①P A ＝BE ，①C ＝①P AE ， ①①CAP +①BAO ＝90°，①①ABO +①BAO ＝90°，①①AOB ＝90°，①P A ①BE ，（2）结论成立．121212理由：延长AP 至M ，使PM ＝P A ，连接MC ，延长P A 交BE 于O ．①P A ＝PM ，PD ＝PC ，①APD ＝①CPM ，①①APD ①①MPC ，①AD ＝CM ，①ADP ＝①MCP ，①AD ①CM ，①①DAC +①ACM ＝180°，①①BAC ＝①EAD ＝90°，①①EAB ＝①ACM ，①AB ＝AC ，AE ＝CM ，①①EAB ①①MCA ，①BE ＝BM ，①CAM ＝①ABE ，①P A ＝AM ，P A ＝BE ， ①①CAM +①BAO ＝90°，①①ABE +①BAO ＝90°，①①AOB ＝90°，①P A ①BE ．（3）①AC ＝10，CM ＝4，①10﹣4≤AM ≤10+4，①6≤AM ≤14，①AM ＝2AP ，①3≤P A ≤7．①P A 的最大值为7，最小值为3．1212练习1如图，在矩形ABCD 中，①BAD 的平分线交BC 于点E ，交DC 的延长线于点F .（1）若AB =2，AD =3，求EF 的长；（2）若G 是EF 的中点，连接BG 和DG ，求证：DG =BG .【解析】（1）EC=CF=1 EF=2（2）连接CG ，易证△CGD ≌△CGB ，∴DG=BG练习小题1.如图所示，在①ABC 中，AD 是①BAC 的平分线，M 是BC 的中点，ME①AD 且交AC 的延长线于E ，CE=21CD ，求证：①ACB=2①B ．【解析】延长EM 交AB 于F ，过B 作BG①EF 交AD 的延长线于K ，交AE 的延长线于G ，设AK ，EF 交于H ，连接DG ，①AD 是①BAC 的平分线，①①BAH=①EAH ，①ME①AD ，①①AHF=①AHE ，在①AFH 与①AEH 中，①FAH=①EAH AH=AH ①AHF=①AHE ，①①AFH①①AEH ，①FH=EH ，①AH 垂直平分EF ，①AK 垂直平分BG ，①AB=AG ，①EF①BG ，BM=CM ， ①CE=21CG ， ①CE=21CD ，①CD=CG ，①①CDG=①CGD ，①①ACB=①CDG+①CGD=2①CGD ，在①ABD 与①AGD 中，AB=AG ①BAD=①GAD AD=AD ，①①ABD①①AGD ，①①ABC=①AGD ，①①ACB=2①B ．点评本题考查了全等三角形的判定和性质，线段垂直平分线的性质，角平分线的定义，平行线的性质，正确的作出辅助线是解题的关键．2.如图，在ABC ∆中，90ACB ∠=︒，90ABD CBE ∠=∠=︒，BA BD =，BC BE =，延长CB 交DE 于F .求证：EF DF =.【解析】3.已知：如图，AD 为ABC ∆的中线，AG HG =.求证：BH AC =.【解析】4.已知：如图，AD 是△ABC 的中线，求证：AB+AC ＞2AD ．【解析】证明：延长AD 到M ，使AD=DM ，连接BM ，CM ，∵AD 是△ABC 的中线，∴BD=DC ，∵AD=DM ，∴四边形ABMC 是平行四边形，∴BM=AC ，在△ABM 中，AB+BM>AM ，即AB+AC>2AD ．5.如图所示，BCD ∆和BCE ∆中，90BDC BEC ∠=∠=︒，O 为BC 的中点，BD ，CE 交于A ，120BAC ∠=︒，求证：DE OE =.【解析】法一：连接OD.∵∠BDC=∠BEC=90°，O 为BC 的中点∴B ，C ，D ，E 四点共圆，且圆心为O∴OD=OE ，∠COD=2∠CBD ，∠BOE=2∠BCE∵∠BAC=120°∴∠CBD+∠BCE=60°∠COD+∠BOE=120°∴∠DOE=60°∴△DOE 是等边三角形∴DE=OE法二：如图，连接OD ，∵∠BDC=∠BEC=90°，O 为BC 的中点，∴OD=OE=OB=OC ，∴∠CBA=∠BDO ，∠BCA=∠CEO ，由三角形的外角性质得，∠BOE=∠BCA+∠CEO=2∠BCA ，∠COD=∠CBA+∠BDO=2∠CBA ，∵∠BAC=120°，∴∠CBA+∠BCA=180°-120°=60°，∴∠DOE=60°，∴△DOE 是等边三角形，∴DE=OE ．6.如图所示，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交AB 于点G ，若BG CF =，求证：2BAC BAD ∠=∠.【解析】延长FE ，截取EH=EG ，连接CH①E 是BC 中点，那么BE=CE①BEG=①CEH①①BEG①①CEH(SAS)①①BGE=①H ，那么①BGE=①FGA=①HBG=CH①CF=BG①CH=CF①①F=①H=①FGA①EF①AD①①F=①CAD ，①BAD=①FGA①①CAD=①BAD那么AD 平分①BAC7.如图，在四边形ABCD 中，①ABC =90°，AC =AD ，M ，N 分别为AC ，CD 的中点，连接BM ，MN ，BN ．若∠BAD =60°，AC 平分∠BAD ，AC =2，则BN 的长为____________．【解析】28.如图，在□ABCD 中，AD =2AB ，CE ⊥AB 于点E ，F 为AD 的中点，连接CF ，NMDC B A则下列结论：△BEC =2S △CEF ；④∠DFE =3∠AEF ．其中一定正确的是_________．【解析】①∵F 是AD 的中点，∴AF=FD ，∵在▱ABCD 中，AD=2AB ，∴AF=FD=CD ，∴∠DFC=∠DCF ，∵AD ∥BC ，∴∠DFC=∠FCB ，∴∠DCF=∠BCF ，∴∠BCD=2∠DCF ，故①正确； ②延长EF ，交CD 延长线于M ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠A=∠MDF ，∵F 为AD 中点，∴AF=FD ，在△AEF 和△DFM 中，∠A=∠FDMAF=DF∠AFE=∠DFM ，∴△AEF ≌△DMF （ASA ）， AB C DE F∴FE=MF，∠AEF=∠M，∵CE⊥AB，∴∠AEC=90°，∴∠AEC=∠ECD=90°，∵FM=EF，∴FC=FE，∴∠ECF=∠CEF，故②正确；③∵EF=FM，∴S△EFC=S△CFM，∵MC>BE，∴S△BEC<2S△EFC，故S△BEC=2S△CEF错误；④设∠FEC=x，则∠FCE=x，∴∠DCF=∠DFC=90°-x，∴∠EFC=180°-2x，∴∠EFD=90°-x+180°-2x=270°-3x，∵∠AEF=90°-x，∴∠DFE=3∠AEF，故此选项正确．故答案为：①②④．9.如图，在①ABC中，点D是BC的中点，若AB=5，AC=13，AD=6，则BC的长为____________．【解析】延长AD 到E ，使DE=AD=6，连接BE ，CE ．①CD=BD ，①四边形ABEC 是平行四边形，①AB①CE ，EB=CA=13；①52+122=132，①①CEA=90°，①①EAB=90°，=．10.如图，在①ABC 中，①ACB =60°，AC =1，D 是边AB 的中点，E 是边BC 上一点．若DE 平分①ABC 的周长，则DE 的长是___________．【解析】23 ECB A11.如图，在四边形ABCD 中，AD ①BC ，①D =90°，AD =4，BC =3，分别以点A ，C 为圆心，大于12AC 长为半径作弧，两弧交于点E ．作射线BE 交AD 于点F ，交AC 于点O ．若点O 是AC 的中点，则CD 的长为（）A． B ．4 C ．3 D【解析】10F EDC B A O。

图形结构与知识点总结

图形结构与知识点总结一、引言图形结构是计算机科学中一种重要的数据结构，它是一种通过连接各种数据项来表示抽象实体之间关系的数据结构。

图形结构广泛应用于计算机网络、社交网络、路由算法、图像处理、计算机图形学、人工智能等领域。

在本次总结中，我们将深入探讨图形结构的基本概念、存储表示、图的遍历、最短路径算法、最小生成树算法等知识点，并对相关知识进行系统总结。

二、基本概念1.图形结构的定义图形是一个由结点和边组成的数学模型，它表示了一些对象之间的二元关系。

其中，结点表示对象，边表示对象之间的关系。

图形结构可以分为有向图和无向图。

2.图的术语图的术语包括结点、边、度、路径、环、连通图等。

结点是图形中的基本单位，边表示结点之间的关系，度是结点所连接的边的数量，路径是从一个结点到另一个结点的边的序列，环是起点和终点相同的路径，连通图是图中任意两个结点之间都存在路径的图。

三、存储表示1.邻接矩阵邻接矩阵是一种常用的图形结构存储表示方法。

它使用一个二维数组来表示结点之间的边的关系，其中数组的值表示边的权重或是否存在边。

邻接矩阵适合表示稠密图，但对于稀疏图来说，它会浪费大量的空间。

2.邻接表邻接表是另一种常用的图形结构存储表示方法。

它使用一个数组和一个链表来表示结点之间的边的关系，数组中的元素表示结点，链表中的元素表示结点的邻接结点。

邻接表适合表示稀疏图，但对于稠密图来说，查找邻接结点会消耗较多的时间。

3.其他存储表示方法除了邻接矩阵和邻接表之外，还有其他存储表示方法，如邻接多重表、十字链表等。

这些方法适用于特定类型的图，可以根据具体情况选择合适的存储表示方法。

四、图的遍历1.深度优先搜索（DFS）深度优先搜索是一种图的遍历算法，它从起始结点开始，沿着一条路径一直向下搜索，直到遇到已访问过的结点或者死路为止，然后回溯到最近的一个分支结点继续搜索。

DFS可以用递归或者栈来实现。

2.广度优先搜索（BFS）广度优先搜索是另一种图的遍历算法，它从起始结点开始，一层一层地往外扩展，直到遍历完所有结点。

数学图形的结构知识点总结

数学图形的结构知识点总结1. 二维图形的结构：1.1 线段与射线的结构：线段是由两点之间的所有点组成的，而射线是一个起点和一个方向的无限延伸线段。

1.2 直线的结构：直线是由无数个点的集合组成的，这些点满足直线上的任意两个点之间的距离为常数。

1.3 多边形的结构：多边形是一个由直线段组成的封闭几何图形，其边界上的所有角都是直角。

1.4 正多边形的结构：正多边形是一个所有边和角相等的多边形。

1.5 圆的结构：圆是一个由平面上距离一个固定点的距离相等的所有点组成的图形。

2. 三维图形的结构：2.1 直线和射线的结构：在三维空间中，直线是由无穷个平行的点组成的，而射线是在一个端点的方向上无限延伸的直线段。

2.2 平面的结构：平面是一个无限延伸的二维图形，可以由三个非共线的点来唯一确定。

2.3 空间图形的结构：空间图形是一个由平面和直线组成的三维几何图形。

3. 图形的性质和特点：3.1 对称性：图形的对称性是指图形在某个轴或中心点上的镜像重合。

3.2 等边性：当一个图形的各边长度相等时，我们称之为等边图形。

3.3 等腰性：当一个图形的两条边长度相等时，我们称之为等腰图形。

3.4 直角性：当一个图形中的所有角都为直角时，我们称之为直角图形。

3.5 全等性：当一个图形的形状和大小都相同时，我们称之为全等图形。

4. 图形的相互关系：4.1 直线与平面的关系：直线可以在平面内或平面外相交，也可以平行于平面。

4.2 直线与直线的关系：两条直线可以相交、平行或重合。

4.3 点与直线的关系：一个点可以在直线上、在直线外或在直线上延伸成射线。

4.4 点与平面的关系：一个点可以在平面内、在平面外或在平面上。

4.5 线段与直线的关系：线段可以在直线上、在直线外或在直线上延伸成射线。

5. 图形的运动和变换：5.1 平移：平移是指图形在平面上沿着一定方向和距离移动的过程。

5.2 旋转：旋转是指图形以某个点为中心按一定角度转动的过程。

小学美术图形结构绘制讲解

小学美术图形结构绘制讲解美术是小学生们学习的一门重要课程，其中图形结构绘制是基础中的基础。

通过学习图形结构绘制，孩子们可以培养观察力、想象力和创造力，提高他们的审美能力和艺术表现力。

在本文中，我将为大家详细讲解小学美术图形结构绘制的相关知识和技巧。

一、直线和曲线的运用在绘制图形结构时，直线和曲线是非常常见的基本元素。

直线可以用来勾勒出图形的边框，而曲线则可以用来表现图形的柔和和曲折。

在使用直线和曲线时，需要注意线条的流畅性和连续性，使图形看起来更加协调和自然。

二、图形的基本形状图形的基本形状是构成各种复杂图形的基础。

常见的基本形状包括：圆形、矩形、三角形等。

绘制图形时，可以先确定基本形状，再进行细化和修饰。

例如，可以通过绘制几个相交的圆形勾勒出一个花朵的形状，再在花朵的基础上添加花瓣等细节，使图形更加丰富和生动。

三、图形的对称性和比例对称性和比例是绘制图形时需要考虑的重要因素。

通过对称性可以使图形更加平衡和和谐，而比例则是绘制真实、立体图形的关键。

在绘制图形时，可以利用镜像法来实现对称性，通过简单的测量和比较来达到正确的比例。

例如，在绘制一个人物头像时，眼睛、鼻子和嘴巴的位置和大小都需要按照比例来确定，以确保整个头像看起来更加真实和逼真。

四、颜色的运用颜色是美术创作中不可或缺的因素，它可以增加图形的差异和表现力。

在选择颜色时，可以根据图形的主题和表达的情感来进行搭配。

例如，可以选用鲜艳的颜色来绘制欢乐的场景，而选择柔和的颜色来表达安静和平和的氛围。

此外，还可以利用颜色的明暗变化来增强图形的层次感和立体感。

五、综合练习为了巩固和应用所学的知识和技巧，可以进行一些综合练习。

例如，可以给小朋友们提供一个简单的素描，要求他们根据素描来绘制一个完整的图形。

通过综合练习，可以让小朋友们更好地掌握图形结构的绘制方法，并提高他们的艺术创作能力。

小学美术图形结构绘制是培养孩子们艺术能力的基础，通过学习和练习，孩子们可以逐渐掌握绘制各种图形的技巧，提高他们的艺术表现力和创造力。

图形的结构原理

图形的结构原理图形的结构原理是指图形设计中各种元素之间的组织关系和相互作用的原则和规律。

在图形设计中，图形的结构起着非常重要的作用，它决定了图形的整体形象和视觉效果。

图形的结构原理是图形设计师必须要掌握的基本知识之一。

以下将从构图、平衡、对比、重复、节奏和动态性等方面，详细介绍图形的结构原理。

首先是构图原理。

构图是指将各个元素有机地组合在一起，形成整体形象的过程。

在构图时，要注意元素的位置、大小、形状和数量等因素。

构图原理主要包括对称、平衡和层次等。

对称是指图形中重要元素在空间上对称分布的情况。

对称的构图能够给人带来安定、平和的感觉，常用于正式、庄重的场合。

但过分追求对称容易造成图形的单调、缺乏张力。

平衡是指图形中各种元素在视觉上的均衡分布。

平衡可以分为对称平衡和不对称平衡两种。

对称平衡是指图形中的元素按照相同的比例、间距和形状等布局，使整个图形呈现出稳定和谐的感觉。

不对称平衡是指图形中的元素按照不同的比例、间距和形状等布局，使整个图形呈现出活泼、生动的感觉。

平衡既能给人带来稳定感，又能给人带来活力感，能够吸引人的注意力。

层次是指图形中各个元素之间的前后关系。

通过不同元素的大小、形状、颜色和明暗等差异来表现空间的远近和深浅。

层次可以使图形更加丰富和立体感，增强视觉效果。

其次是对比原理。

对比是指图形中各种元素之间的明显差异。

对比可以通过元素的大小、形状、颜色、纹理、明暗等来实现。

对比能够在视觉上产生冲突、张力和互动，吸引人的注意力。

但对比过分繁杂也容易造成视觉的紊乱和混乱，所以要适度地运用对比。

重复是指图形中某个元素或多个元素按照一定的规律、次序和间隔进行重复出现的情况。

重复可以给人带来稳定感和统一感，使图形看起来更加有序和整齐。

节奏是指图形中元素之间的有规律的变化和重复，形成一种有节奏感的运动。

节奏能够使图形更具活力和动感，吸引人的眼球。

但过分强调节奏会使图形变得刺眼、紊乱和混乱。

动态性是指图形中元素的运动形式和感觉。

小学美术图形结构布局讲解

小学美术图形结构布局讲解美术是一门通过图形和颜色来表达思想和情感的艺术形式。

图形结构布局是美术创作中非常重要的一环，它决定了作品的整体效果和观感。

在小学阶段，教导学生掌握正确的图形结构布局技巧是培养艺术素养的关键一步。

本文将重点讲解小学美术图形结构布局的基本要点和技巧。

一、线条的运用线条在图形结构布局中起着基础性的作用。

通过合理运用线条，可以使作品具有鲜明的层次感和动态感。

小学生在绘画过程中，可通过以下几个方面运用线条：1. 线条的方向：线条的方向对整个作品的表现形式有很大的影响。

直线、曲线、斜线等不同的线条方向可以表达出不同的情感和意境。

例如，画一条上升的直线可以表现出向上的力量和追求；而下降的弧线则能表达出平静和舒适的感觉。

2. 线条的粗细：线条的粗细也可以对作品产生很大的影响。

较粗的线条通常显示出较强烈的表现力，适合用来描绘大型物体或突出某个区域；而较细的线条则可以用来描绘细节或柔和的部分。

3. 线条的连接：将线条相互连接，可以在画面中形成不同的图形结构。

直线连接通常表现出刚硬和稳定的感觉，适合描绘建筑物等；而曲线的连接则更能表现出柔和和流畅的感觉，适用于描绘自然界的景物。

二、构图的原则构图是指将不同的元素有机地组织在一起，形成整体结构。

在小学美术教育中，培养学生正确的构图能力是非常重要的。

以下是几个常用的构图原则：1. 对称构图：对称构图是指将图形元素以中心对称的方式排列。

对称构图能够给人一种平衡和稳定的感觉。

例如，在画布的中心位置画一个形状对称的图案，可以使整个作品更加和谐。

2. 边缘构图：边缘构图是将重要的元素集中在画面的一侧或边缘，以突出主题。

这种构图方式可以使作品更加动感和有层次感。

例如，将一个花朵绘制在画布的边缘，可以使花朵成为整个作品的焦点。

3. 黄金分割构图：黄金分割构图是指将画面分割成按照一定比例排列的不同部分。

这种构图方式能够给人一种和谐和美感。

例如，将画布分为三等分，将主题放在其中一段的黄金分割点上，可以使作品更加吸引人。

二年级数学教材详解认识形状和结构

二年级数学教材详解认识形状和结构二年级数学教材详解：认识形状和结构数学是一门重要的学科，它帮助我们认识和探索世界。

在二年级的数学教材中，我们将了解形状和结构的概念。

本文将对二年级数学教材中的形状和结构做详细的解析。

第一章：认识形状形状是固定空间中物体的外形特征。

在认识形状这一章节中，主要包括以下几个方面的内容：1. 点、线和面的认识在几何中，点是最基本的要素，没有大小和方向。

线是由无数个点连成的，没有宽度，只有长度和方向。

面是由无数个线连接成的，有两个维度，有长度和宽度。

通过学习点、线和面的概念，我们可以更好地理解形状。

2. 常见的二维形状二维形状是只有长度和宽度，没有高度的形状。

其中包括圆形、三角形、正方形、长方形等。

我们需要学会认识并能够正确命名这些二维形状。

3. 认识和分类多边形多边形是一种有固定边数的封闭图形，包括三角形、四边形、五边形等。

我们可以通过边数将多边形进行分类，并能够正确识别和描述各个多边形的特征。

4. 认识和分辨立体形状立体形状是具有三个维度的形状，包括长方体、正方体、圆柱体、圆锥体等。

我们需要学会认识这些立体形状，并能够正确命名、描述它们的特征。

第二章：结构和变换结构是指事物的内部或外部构成方式。

在结构和变换这一章节中，主要包括以下几个方面的内容：1. 母线和轴线母线和轴线是指物体中确定位置的线。

通过学习母线和轴线，我们可以更好地理解物体的构成方式以及变换规律。

2. 对称和轴对称对称是指一个物体在某条轴线上的两侧部分关于该轴线相互呈镜像关系。

轴对称是具有轴线对称的特点。

通过学习对称和轴对称的概念，我们可以更好地认识物体的结构特征。

3. 平移、旋转和翻折平移是指物体在平面上沿着固定方向移动一定的距离。

旋转是指物体围绕某一点旋转一定角度。

翻折是指物体相对于某一条线呈对称关系。

通过学习这些变换方式，我们可以更好地认识和描述物体的结构特征。

4. 结构的认知和拼装通过拼装积木、拼图等活动，我们可以培养孩子的观察力、动手能力和逻辑思维能力。

图形层次结构

第11页/共33页
第10页/共33页
块的实例
一般把块的中心放在坐标原点，通过局部变换产生放在不同位置及不同大小方向的实例
在类Instance中我们分别用dx, dy, rax,ray, sx, sy表示变换的参数，用于描述实例实际的位置、大小和旋转角度。
第12页/共33页
第11页/共33页
块的实例
这里并不要求专门建立局部坐标系的变换，我们还是可以用世界坐标中的变换来实现。在OpenGL中世界坐标系的二维变换为： glScale（sx，sy,0,0）在x、y方向分别放缩sx及sy倍 glRotate（rax,ray,0,0）旋转ra角 gltranslate（dx，dy,0,0）在x、y方向分别平移dx、dy
第9页/共33页
第8页/共33页
图形结构块
2. 图形结构块 class Block public Element{ char * name; CElement **eList； Block *next; void draw(){….} }
1
setInteriorStyle(solid)
2
setInteriorColourIndex(4)
3
fillArea(n,verts1)
元素指针
第27页/共33页
第26页/共33页
5.3.3 结构编辑
setElementPointer（k）改变指针所指向的位置，指针指向第k个元素。
元素：一个结构中，介于openStructure及closeStructure二命令中的属性设置及图形输出命令称为元素。元素以先后次序从1开始有个编号。
1
SetLinetype(lt)
2
SetPolylineColourIndex(lc);

高中数学人教A版必修《空间几何体的结构》课件

1、两个互相平行的面叫棱柱的底面。
2、其余各面叫棱柱的侧面。
3、相邻侧面的公共边叫侧棱。
4、侧面与底面的公共顶点叫
棱柱的顶点。
E’ F’A’
D’ B’ C’
2.棱柱的结构特征：
①底面互相平行且全等；
侧棱
②侧面都是平行四边形；
③侧棱都相等且互相平行。
E
F A
侧面
底面
D C
B
顶点
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
4、棱柱的表示法:

A1
D1 B1
C1 A1
D A
C BA
C1
A1
B1 B1
E1 D1 C1
C
B
A B
E D
C
用平行的两底面多边形的字母表示棱柱, 如：棱柱ABCDE- A1B1C1D1E1 。
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
练习：观察下面的几何体，哪些是棱柱？
√
√
√
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）
高中数学人教A版必修2第1章第1节《1 .1空间几何体的结构》课件（共39 张PPT ）

形体结构 PPT

圆锥体——直角三角形以夹角的任意一边为轴旋转一周所形成的立体。
作业
在作业纸上,分析出家里某一只水杯的结构线。
星期一下午第一节课后课代表交至初一级组。
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档（部分VIP专享文档由于上传者设置不可下载只能阅读全文），每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权，一次发放，全年内有效。
VIP专享文档下载特权自VIP生效起每月发放一次，每次发放的特权有效期为1个月，发放数量由您购买的VIP类型决定。
每月专享9次VIP专享文档下载特权，自VIP生效起每月发放一次，持续有效不清零。自动续费，前往我的账号 -我的设置随时取消。
阅读页去广告
VIP有效期内享有搜索结果页以及文档阅读页免广告特权，清爽阅读没有阻碍。
多端互通
抽奖特权福利特权
其他特 VIP专享精彩活动
权
VIP专属身份标识
VIP有效期内可以无限制将选中的文档内容一键发送到手机，轻松实现多端同步。开通VIP后可以在VIP福利专区不定期抽奖，千万奖池送不停！开通VIP后可在VIP福利专区定期领取多种福利礼券。开通VIP后可以享受不定期的VIP优惠活动，活动多多，优惠多多。
0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能：一键搜索0下载券文档，下载券不够用不再有压力！
内容特无限次复制特权权文档格式转换
VIP有效期内可以无限次复制文档内容，不用下载即可获取文档内容 VIP有效期内可以将PDF文档转换成word或ppt格式，一键转换，轻松编辑！

图形结构知识点总结

图形结构知识点总结一、基本图形的性质和特点1. 直线、线段、射线直线、线段和射线是几何中最基本的图形，它们都由无数个点组成。

直线是由连续的点组成的，没有起始点和终止点，可以延伸到无限远；线段是由直线上的有限个点组成的，有一个起始点和一个终止点；射线有一个起始点，但是没有终止点，可以延伸到无限远。

2. 角在几何中，两条线段的交点就构成了一个角。

角的度量是用角度来表示的，一个完整的圆周角是360度，一个直角是90度，一个平角是180度。

角可以根据其大小和性质进行分类，常见的角有锐角、直角、钝角、对顶角等。

3. 多边形多边形是由若干条线段组成的封闭图形，它是平面几何中最基本的图形之一。

根据边的数量和长度，多边形可以分为三角形、四边形、五边形、六边形等不同种类。

常见的多边形有三角形、正方形、矩形、菱形、梯形等。

4. 圆圆是一个特殊的几何图形，它由一个固定点到平面上距离相等的所有点构成。

圆的性质包括半径、直径、周长和面积等，它在生活中有着广泛的应用，例如轮胎、钟表等都是圆形的。

二、图形的计算1. 长度的计算在几何中，我们经常需要计算线段、周长等图形的长度。

计算线段的长度可以通过勾股定理、平移、旋转等方法进行，计算多边形的周长则是将各边的长度相加。

对于曲线或者不规则图形，可以采用逼近法来计算其长度。

2. 面积的计算面积是图形的一个重要属性，它表示了图形所围成的平面的大小。

计算面积的方法各种各样，例如矩形的面积可以直接通过长和宽相乘得到，三角形的面积可以通过底边和高相乘再除以2得到。

对于曲线或者不规则图形，可以采用分割成小部分再累加的方法来计算其面积。

3. 体积的计算体积是三维立体图形的一个重要属性，它表示了图形所占用的空间大小。

计算体积的方法也有很多种，例如长方体的体积可以通过长、宽、高相乘得到，圆柱体的体积可以通过底面积乘以高得到。

对于不规则的立体图形，计算体积可以采用积分法或者近似法等方法。

三、图形的问题解决1. 直角三角形的问题在几何中，直角三角形的性质和计算是一个重要的知识点。

图形结构知识点

图形结构是计算机科学中一种重要的数据结构，它通过节点和边的组合来描述对象之间的关系。

在计算机科学中，图形结构被广泛应用于各种领域，例如社交网络分析、路由算法、信息检索和图像处理等。

本文将介绍图形结构的基本概念和常见算法，以加深读者对图形结构的理解。

一、图形结构的定义和基本概念图形结构由节点和边组成，节点表示对象，边表示节点之间的关系。

图形结构可以用来描述许多实际问题，例如社交网络中的用户和关注关系，地图中的城市和道路连接关系等。

在图形结构中，节点和边可以有不同的属性，例如节点可以表示人的姓名、年龄等，边可以表示两个人之间的关系类型。

图形结构可以分为有向图和无向图两种类型。

有向图中的边有方向，表示节点之间的单向关系；而无向图中的边没有方向，表示节点之间的双向关系。

有向图和无向图都可以用邻接矩阵或邻接表来表示。

在邻接矩阵中，使用一个二维数组来表示节点之间的连接关系；而在邻接表中，使用链表来表示。

二、图形结构的常见算法 1. 广度优先搜索(BFS) 广度优先搜索是一种用于遍历图形结构的算法，它从起始节点开始，逐层遍历图形结构，直到找到目标节点或遍历完所有节点。

广度优先搜索使用队列数据结构来存储遍历的节点，每次从队列中取出一个节点，并将与之相邻的未访问节点加入队列。

广度优先搜索可以用于查找最短路径、寻找连通分量等问题。

2.深度优先搜索(DFS) 深度优先搜索是一种用于遍历图形结构的算法，它从起始节点开始，沿着一个路径一直遍历到无法再继续下去为止，然后回溯到上一个节点，继续遍历其他路径。

深度优先搜索使用栈数据结构来存储遍历的节点，每次从栈中取出一个节点，并将与之相邻的未访问节点加入栈。

深度优先搜索可以用于拓扑排序、生成迷宫等问题。

3.最小生成树最小生成树是指一个连通图的一棵生成树，它的所有边的权值之和最小。

最小生成树算法可以用于解决网络设计、电路布线等问题。

常见的最小生成树算法有Prim算法和Kruskal算法。