储油罐的变位识别与罐容表标定模型
(整理)储油罐的变位识别与罐容表标定模型.

储油罐的变位识别与罐容表标定模型摘要 本文研究的是储油罐变位识别与罐容表标定的数学关系模型。
对于问题一, 罐体没有纵向变位时, 在储油罐本身几何分析的基础上,建立无变位的油量体积V 与标定表读数h 的关系模型。
计算出理论值,通过误差分析和线性拟合,求出系统误差和随机误差,修正了罐容表。
在罐体有纵向变位时,将储油罐的纵向变位划分为三种不同情况,利用积分思想求解不同变位情况下的油量的理论体积。
根据纵向倾斜参数︒=1.4α建立有纵向变位的油量体积V 与标定表读数h 的关系模型。
利用MATLAB 软件和excel 工具的解出油量体积V 的理论值。
然后,充分考虑模型中系统误差和偶然误差的影响,重新标定了罐容表,给出间隔为1cm 的罐容表标定表,解决了加油站罐容表无法准确反映储油量的问题。
对问题二罐体,我们建立了纵向α和横向β同时发生时,标定表读数h 与油量V 的数学模型。
我们不仅考虑了纵向变位的三种情况、横向变位的两种情况,而且考虑了纵向和横向变位同时发生的情况。
利用积分思想建立模型,运用MATLAB 软件对模型的不同情况进行了详细、精确的计算。
然后充分结合误差分析,以平方误差最小原则对α、β采取搜索算法,得出实际变化值2.0524, 4.0αβ==,并给出罐容表间隔为10cm 的标定表。
最后结合题目所给数据对所求数据进行检验。
通过模型分析,结合系统误差与读数h 的函数关系。
在多次误差分析的基础上再对模型进行了检验,得到了理想结果。
本文通过以上各模型的深入分析和研究,解决了储油罐变位时储油量与罐容表刻度不一致的问题,具有广泛的运用价值。
在运用方法上,我们采用了系统误差和观察误差双重误差分析,线性回归、拟合相结合的误差分析法以及搜索法等方法的运用,提高了罐容表标定的精确度,大大增添了本文的的科学性和结构的严谨性。
关键词:线性回归、拟合、MATLAB 、误差分析、搜索法一、 问题的重述大部分加油站储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
储油罐的变位识别与罐容表标定模型1

储油罐的变位识别 与罐容表标定模型 1
孙 纯 兴 ’ 于 小 龙 郭昊 陈 六 新 2 李 敏
( . 邮 电 大 学 自动化 学院 重庆 4 06 ; 2重庆 邮 电 大 学数 理 学 院 重庆 40 6 ) 1重庆 ( 05 ) . 00 5
摘要 : k 旨在 对储 油罐 的 变位 识 别 与罐 容表 标 定 问题进 行 深入 探讨 , 用数 值积 分 、 值 法以及 解析 几何 等理 论 建 立 了罐体 变位对罐 a r 运 插 容表 影 响模型 以及 变位 后罐 容表标 定模 型 , 结合 相 关算法并 应用MA L B 学软件 进行 随机模 拟求得 了变位 参数 的数值 , TA 数 最终 完整地 解决 了储 油 罐 的 变位 识 别 与罐 容表 标 定 的有 关 问题 实践 证 明 , 文提 出的模 型具 有较 高的 实 用性 , 以为罐 客 表 的 准确标 定 奠 定理 论 基 础 。 . 本 可 关 键词 : 数值 积分 插值 法 解析 几何 随机模 拟 辛 森公 式 中图 分类 号 . E 7 T 92 文献标识 码 : A 文章 编号 :0 79 1 ( 0 10 — 1 40 1 0 4 62 1 ) 90 9 .5
Ta e bl
SUN Ch n i g u -x n ,YU Xi o— on a l g ,G UO o , Ha aAdvs :CHEN u x n i or Li — i , L i 。 IM n
(.c o l f tmain,bS h o f ah maia,Ch n qn iesyo P s n l o a h o Auo t S o o .c o l M te t l o c o g igUnvri f ot a dTe c mmu iain , C o g ig t s e nct s h n qn o 4 0 6 ,Chn ) 005 ia
储油罐的变位标识与罐容表的标定

摘要为解决加油站的地下储油罐在使用一段时间后,由于地基的变形会导致无法根据预先标定的罐容表计算储油罐内油量容积的问题,研究如何识别储油罐变位以及对罐容表的重新标定的问题.得到储油罐的总油量与油标高度、纵向偏转角、横向偏转角之间的关系模型.利用该模型可根据加油站的出油量以及对应的油标高度来识别储油罐的变位,通过建立优化模型, 搜索算法和MATLAB软件求解出了所识别的变位的变位角度, 并利用实验数据对求解结果进行了检验; 最后利用得到的油量表达式给出了两个储油罐的罐容表.为了得到变位参数的有效估计,对进出油实测数据建立非线性的最小二乘回归模型,在数值求解中,采用截面积的微元方法,有效减少了复杂的体积积分计算,从而完成罐容表的修正标定。
关键词:MATLAB 变位标识罐容表标定储油罐ABSTRACTIn order to solve the problem that the calculation of oil tank volume must be calibrated periodically because an oil tank shift for the foundation deformation,the fuction relation between oil volume,altitude,direction deflection angle,transverse direction deflection angle is given out.The shift parameter Can be found with the model and data of oil volume.The new calculation of oil tank volume can be finned after tank shift.a1.Further more,we have gained the displacement angle by developing a optimization model, gradually decrease interval search algorithm and Matlab software, and then apply the experimental data to verify our solved results.We develop the non—linear of least squared regression model to estimate the parameters of position change.In particular,the differential element method of the sectional area is proposed to effectively reduce the complex numerical computation of integral.Therefore,the volume table is readjusted by the estimation of parameters of position change.Keywords:MATLAB;shift confirm ;calibration calculation of volume;oil tank第一章绪论1.1 储油罐问题的背景由来储油罐是储存油品的容器,在我们周边加油站是普遍存在的,一般加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,先通过流量计和油位计来测量进/出油量与罐内油位高度等数据,再通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,使地面上的人很容易了解罐内油位高度和储油量的变化情况。
储油罐的变位识别与罐容表标定模型

2. 对问题二的分析:因为两个变位参数都是未知的,要直接求得油量与油位高度及两
个参数的总的关系式是较困难的。故我们可以求出油量分别随两个参数的变化关系式 y(h, α)和 y(h, β ),并且这两个函数是建立在问题一的基础上,然后研究两个关系式的关 系,求出油量与油位高度及两个参变量的综合关系式 y(h, α, β),这样问题二便能求解出 来。这当中较难部分是如何把两个函数关系式综合到一起。
2
8、假设储油罐的管壁所占的体积忽略不计; 9、假设注油口,检查口的的严谨性是很强的;
§4 名词解释与符号说明
4.1 名词解释 1、罐容表——罐容表是在油罐制作安装完成后由专业部门通过实测标定的油高与
体积的关系表,油高以厘米为单位,体积以立方分米为单位。由于罐容标定一般是每间 隔 1cm 确定一个容积值,这样罐容表中只有整厘米数油高具有对应的容积值。
§3 模型的假设
1.假设罐体位置横向不发生变位(对于问题一); 2.假设罐内油的体积不会随温度的变化而变化(即忽略热胀冷缩对油体积的影响); 3.假设油罐在检测过程中完好无损,不会出现漏油、汽化等现象; 4.纵向偏转角度 a 不大,可近似认为两端球缺中含油量相同;
5 假设题目所给的数据真实可靠; 6、假设固定油浮子的油位探针始终垂直于油罐底部; 7、假设深入油罐内的管子体积忽略不计;
+
储油罐的变为识别与罐容表的标定

储油罐的变位识别与罐容表标定摘要罐容表是用于实时精确测定罐存油品的重要依照之一,地基的变化造成储油罐位使得罐内的油位探测装置无法正确的测量出油量所对应的油位高度。
为了掌握实际罐体变位后对罐容表的影响,本文先分析无变位和纵向倾斜α=4.10时,小椭圆型储油罐油位高度与部分容积的关系,由于储油罐在发生纵向和横向变位后,计算罐容表的方法已经发生变化,建立实际储油罐体变位后标定罐容表的数学模型。
首先,对于理想的小椭圆型油罐,根据已知的示意图,建立油罐无变位模型和油罐纵向倾斜模型,用二重积分思想,求得任意油位高度时油平面的面积,将此面积对高度积分,得到储油量计算值与油位高度的对应关系,计算出无变位以及纵向倾角为α时罐容表,比较储油量计算值与真实值的大小,无变位时得到平均相对误差为0.0337,纵向发生倾斜时为0.0223。
分析变位前后的罐容表,发现在相同高度下,变位后的储油量总是小于变位前的储油量,对罐容表进行重新标定具有实际意义。
接着,由小椭圆型油罐数学模型推广到实际储油罐的数学模型,同样用二重积分的数学思想。
由于实际的储油罐的两端是球冠体,所求的油量体积是两端的球冠体内油量体积与中间柱体的油量体积之和。
变位分为纵向倾斜和横向倾斜,而横向倾斜不改变油在储油罐中的形状,只改变了测量高度。
但纵向倾斜会改变油在储油罐中的形状,使测量高度不能再真实的反应储油量。
根据不同的油位高度,本文分析了5种可能的情况,得出不同情况下的油位高度与油量,变位参数α的关系式。
再考虑横向偏转对模型的影响,利用几何关系,得到考虑横向偏转前后油位高度之间的转化关系,将只存在纵向倾斜变位时的油位高度代换为考虑横向偏转后的油位高度,得到综合得到油位高度与油量,变位参数α、β的关系式。
代入实测数据,借助MATLAB,得到该模型的变位参数纵向倾斜角1.442度和横向倾斜角5.8643度。
然后得出罐体变位后油位高度间隔为10cm的罐容表标定值。
储油罐的变位识别与罐容表标定

储油罐的变位识别与罐容表标定摘要许多储油罐在使用一段时间后,由于地基变形等原因,使油罐发生纵向倾斜或者横向偏转,从而导致罐容表发生改变。
据此,我们用微积分与数据拟合的方法建立储油罐的变位识别与罐容表标定的模型。
通过对问题的分析,将问题化成若干个小问题,从而建立了五个数学模型。
其中模型一、二主要针对的是一问提出的,模型三、四、五针对的是二问提出的。
模型一通过用微积分知识确定了无变位时罐内油量与油位高度的关系式,并通过编写MATLAB程序对模型进行了求解。
模型二考虑变位时罐内油量与油位高度的关系,通过附件1中给的数据,拟合出了罐内油量的理论值与实验值之差v∆与油位高度h的关系式,通过v∆与h的关系式可以将倾斜角度α拟合进去,从而得到v∆与h、α的函数关系式,再根据v v v=-∆理实确定出v实的表达式。
模型三考虑的是无变位时储油量与油位高度的关系,与模型一不同的是储油罐的形状不同,通过二重积分求得储油量与油位高度的关系式,最后通过编写MATLAB程序对模型进行了求解。
模型四考虑的也是无变位时储油量与油位高度的关系,只是研究方法与模型三不同,即模型三和模型四是研究同一问题的不同方法。
模型四是将罐子看成一个卧式的圆柱体,求其体积,进而分析误差,并求出误差,最后也可得到较为精确的罐内油量与油位高度的关系式,最后通过编写MATLAB程序对模型进行了求解。
模型五考虑了横向和纵向的倾斜角度的变化,通过对附件2显示油高和显示油量容积两列数据的拟合确定油位高度为0时的罐内油量,即常数L,然后根据新建立的关系式和模型四来确定纵向倾斜角α和横向偏转角β,最终得到了存在倾斜角α和横向偏转角β罐内油量与油位高度的关系式。
应用以上五个模型可以很好的解决题中的两个问题,即模型一、二解决一问,模型三、四、五解决二问。
关键词:微积分数据拟合储油罐油位高度罐容表1 基本假设1)储油罐的形状是规则的2)油位高度为0时,罐内油量为常数L2 符号说明1) h ——油位高度2) l ——小椭圆形储油罐的长度3) a ——小椭圆形储油罐横截面椭圆的长半轴长 4) b ——小椭圆形储油罐横截面椭圆的短半轴长3 模型的建立、求解与应用3.1模型一3.1.1模型的建立对于(1)问,首先考虑储油罐无变位的情况,其横截面积如图:其阴影部分的面积2hs xdy =⎰ ,其中x =则 2v sl =理,其中v 理表示无变位罐内的油量。
最新储油罐的变位识别与罐容表标定的数学模型

储油罐的变位识别与罐容表标定的数学模型储油罐的变位识别与罐容表标定的数学模型摘要本文解决了储油罐罐容表变位后标定的问题。
通过把实际的储油罐抽象成直角坐标系下的几何柱体,然后从区分不同的油面高度入手建立了几何柱体体积的积分模型。
再通过合理运用所给数据进行数据拟合,得出了油量体积与油面高度之间的函数关系,进而进行理论与实际体积之间的误差分析和模型可行性分析。
针对问题一,首先对于无变位的小椭圆柱体建立了直角坐标系下的容积积分模型(见第4页)。
通过Minitab15软件对实验数据进行曲线拟合,得出一个油量作为高度的函数关系。
利用这个函数关系计算出相应罐容表高度的实际油量容积,对比理论积分模型的容积值,计算出误差值(见表3和表5)。
观察知误差属于正常范围内,则得出通过理论模型来标定的标准罐容表(见第7页表6)。
然后当只有纵向倾斜的变位时,根据柱体内的倾斜油面将柱体容积分为三个部分,分段计算出相对应部分中的容积积分,建立了变位后的分段容积积分模型,通过Matlab7.0编程得出容积积分函数(见第9页)。
而这个模型是与纵向倾斜角度和油高两个因素有关的。
当倾斜角一定时,代入条件数据进行拟合对比,得出模型是合理有效的,从而得出变位后的罐容表(见第12页表7)。
最后将每变化0.01m的油量变化量与标准罐容表作比,得出比例系数。
针对问题二,将储油罐分割成两个球冠和一个圆柱三部分,并将其截面放入平面直角坐标系下建立容积积分模型,分别求出各个部分的油量容积,再相加求总容积(见第15页)。
而当纵向倾斜和横向偏转都存在时,考虑将空间直角坐标系作一个相应变换,即把轴乘以相应的三角函数得到新的坐标系,此时积分模型得出的是关于两个倾斜角度和高度的函数。
然后根据所给数据作拟合计算出实际油量,且分别选取两个倾斜角度的合理范围,固定高度后代入容积积分函数,将得到的油量与拟合出的实际油量作比较,利用最小二乘的方法从两边逐步逼近,最终得出最优的倾斜角度(见第17页)和倾斜后的罐容表(见第17页表8)。
(推荐)数学建模A题--储油罐的变位识别与罐容表标定的论

储油罐的变位识别与罐容表标定摘要本文主要探讨了储油罐的变位识别与罐容表标定的问题。
本文通过建立合适的坐标系,使用二重积分的方法和近似积分、坐标变换等技巧,求解了小椭圆储油罐和实际储油罐在发生变位时储油量与油高变化的函数关系,从而分析了罐体变位后对罐容表的影响,并对数据结果和误差进行了详实的分析。
本文在模型的建立与求解的过程中始终遵循化繁为简的原则,最先考虑简化的基本模型,再通过变换推导出实际的模型。
在第一问中,我们首先假设油罐壁的厚度为零,并通过二重积分的计算了小椭圆储油罐在无变位情况下的理论储油量。
其次我们通过运用几何原理通过坐标变换利用现有模型计算了小椭圆储油罐在纵向倾斜后的理论储油量。
在进行误差分析时,我们发现误差非线性,且误差数量级较大,得出油罐壁的厚度应不为零的结论,且经过理论分析油量3()V O d =,故我们用三次多项式拟合误差曲线()f H ,并通过'()()()V H V H f H =-修正了油量的计算公式。
经检验,修正后模型的计算值与实际值十分吻合,模型准确度很高。
并且,我们用修正后的模型V'(H)对油罐进行了标定。
在第二问中,我们利用了问题一中的模型求解罐身中的油量体积,并通过二重积分给出了油罐凸头部分油量的计算公式,其中,在油罐发生纵向倾斜时,我们队凸头部分的油量进行了合理的近似计算。
并且,我们通过坐标变换,给出了211()((,,((),))V H f f H f H αββα==))的变位参数修正形式。
在求解变为参数α、β时,我们通过最小二乘法拟合()V H ,求出了 2.1258, 4.6814αβ︒︒==。
将此变位参数代入模型中进行检验,得出理论计算值与实际值的相对误差限为5.006%,平均相对误差为0.029%,模型准确可靠。
最后我们用所得模型对油罐进行了标定。
关键词:储油罐 油量 倾斜 标定问题的重述与分析1、问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
数学建模储油罐的变位识别与罐容表的标定

储油罐的变位识别与罐容表的标定摘要本文运用定积分、重积分,数理统计等知识研究储油罐变位后对罐容表的影响。
观测油罐探针的变化,分情况讨论变位油罐进/出油的罐内油液体积。
采用图形结合建立数学模型。
用定积分求解椭圆面积,进而求出油位高对应储油罐(无变位)的油容量的对应关系,利用数理统计与Excel 2003对数据分析并绘制图形,建立当前最优的实验储油罐无变位模型(模型一)。
模型二即是实验储油罐纵向倾斜(固定角)的数学模型。
对模型一、二两组数据进行对比,估算出油位高度相同时不变位以及变位后储油罐内油容量,再将两部分的油容量相减可算出油位高度和油容量的函数,得出罐体变位后油位高度间隔为1厘米的罐容表的标度。
模型四采用大量图形分析和数学知识,建立空间直角坐标系,将问题分出四种情况讨论。
建立当前最优的实际储油罐无变位模型(模型三),并与模型四进行对比可得关于油位高度和油容量的函数,那么将相隔10cm油位高的油容量代入模型即求得。
关键词:定积分重积分数理统计图形结合一、问题重述加油站的储油罐是大家非常熟悉的一种储油罐,就目前世界各地来看,它不能脱离我们的现实生活。
所以我们有必要对储油罐进行彻底的了解。
根据我们所学的知识,用数学模型方法研究解决储油罐的变位识别与罐容表标定的问题。
通常加油站的储油罐都有与之配套的“油位计量管理系统”,采用专业的测量仪器测出罐内的储油体积与罐内油位高度,通过预先标定的罐容表(罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
但是,许多储油罐在使用一段时间后,罐体的位置会地基变形发生纵向倾斜和横向偏转等变化(称为变位),从而导致罐容表发生改变。
根据以上的情况,为了掌握罐体变位后对罐容体的影响,利用小椭圆型储油罐(两端平头的圆柱体)做了罐体无变位和倾斜角为一定角的纵向变位两种情况的实验,且得到了实验数据。
在实验图形的基础上,我们深入了实际油罐的变位分析。
储油罐的变位识别与罐容表标定模型

储油罐的变位识别与罐容表标定模型摘要本文针对储油罐的油位计量问题,采用机理分析法,以积分求体积法建立数学模型,求解得到了罐体变位后对罐容表的影响,并重新标定了罐容表;同时利用附件提供的实际检测数据,根据所建数学模型,采用最小二乘法拟合[1]相应的变位参数,完整地解决了问题。
最后以误差分析法分析检验了所建模型的正确性和可靠性。
对于问题(1),为了研究罐体变位后对罐容表的影响,分别建立了罐体区变位和纵向变位两种情况的罐容表模型。
建立罐体变位后罐容表模型时,以探针所测油面高度处横截面面积为基准,利用几何关系确定任一油面高度处横截面的面积,利用变面积的线积分求体积方法,对罐内油面可能存在的三种位置情况进行分段积分,确立了罐容表模型。
根据所建模型,重新标定了罐容表(见表 4.1)。
将其与无变位罐容表相比较,在同一测量油面高度,如题目所示的纵向变位后的小椭圆油罐储油量低于无变位时储油量。
最后根据小椭圆储油罐的实验数据对罐容表模型进行了误差分析,无变位模型最大误差为0.14%,纵向变位后最大误差误差为0.5879%。
对于问题(2),罐体实际储油罐为一个两端为球冠形封头的圆柱体,与问题(1)相比,罐体形状有所改变,但仍可利用问题(1)所建模型思想,只是要增加两端冠形封头中油体积的计算。
实际储油罐除需要考虑纵向变位外,还需要考虑横向变位。
在建模过程中,首先假定横向变位为零,只考虑纵向变位产生的影响,建立罐容表模型,然后再引入横向变位对纵向油位探针测量油位高度的影响,最后得到基于测量油面高度和α、β变位参数的罐容表模型。
根据所建立模型,利用实际检测数据,采用最小二乘法拟合出变位参数α为4.1151°,β为2.2078°,并重新标定了罐容表(见表4.2)。
通过对上述模型分析及检验可知,在实际运营过程中,罐体产生的某一倾斜状态,会对储油量的计量造成误差,罐容表必须进行修正。
储油罐的变位识别与罐容表标定模型有重要的工种应用价值。
储油罐的变位识别与罐容表标定

(5)
(3)当 2R l1 tan H 2R 时, 类似于 (1)中的方法, 在 O yz 坐标面上:平面 与 卧 式 容 器 在 平 面 z l2 d 的 交 点 为 (0, y(l2 d ), l2 d ) , 其 中
V2 *
y
y ( l1 d )
R2 y 2
R2 y 2
[( H R y ) tan r 2 x 2 y 2 d l1 r ]dxdy
3
y(l1 d ) y 2 (l1 d ) 3 2 H R y* 2 R3 R ( d l1 r ) { f [ ] f ( )} {[1 ] tan R R 3tan R2
{[(d l2 r ) s sign( )
d l2 r r ( H R) 2
2
] tan }
其中 sign() 为符号函数。 利用微积分学的基本近似公式进行计算,其中注意 f (t ) 2 1 t 2 ,定积分用 简单的矩形近似,可从 (10)推得:
V ( H ) V ( H , ) R2 ( H R)2 [(l2 l1 ) (l2 l1 2d r ) ( H R)2 ] tan
R 2 ( H R) 2 [r ( H R) ] [l2 l1 r sign( ) r ( H R) ] f ( 2 ) tan (11) r ( H R) 2
A题储油罐的变位识别与罐容表标定
A题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
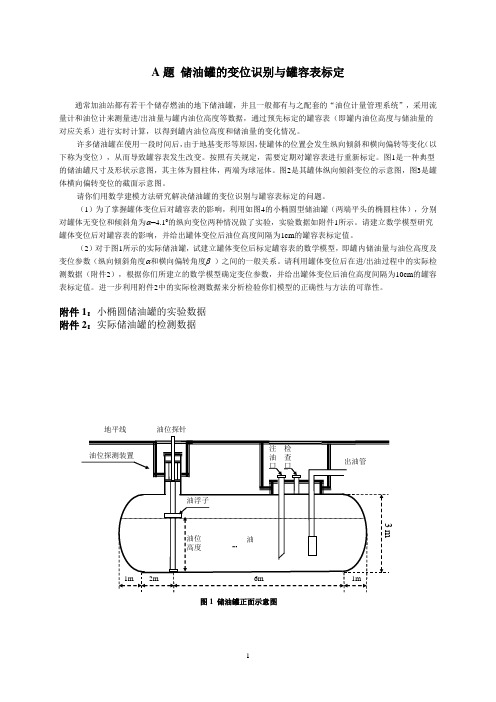
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据油位探针地平线油位探针地平线图2 储油罐纵向倾斜变位后示意图图3 储油罐截面示意图(b)横向偏转倾斜后正截面图地平线地平线垂直线油位探针(a)无偏转倾斜的正截面图油位探针变位储油罐的罐容表标定模型摘要:加油站的地下储油罐会出现变位的情况,计量储油罐油量的罐容表需要重新标定。
储油罐的变位识别与罐容表标定

油量(L )
3000
2000
1000
200
400
600 800 油 位 高 度 ( mm)
1000
1200
图 3 无变位时油量高度与储油量的关系
第二步: 问题一我们先考虑建立小椭圆油罐无变位时罐内油位高度与储油量的函数关系式. 下面我们通过小椭圆油罐截面示意图推导小椭圆油罐无变位时罐内油位高度与储油量 的函数关系式. 油罐的一个端面是椭圆面,所以现在要计算的是任意液面高度对应的储 油量,如图 4:
二、问题假设
假设实验采集到的数据准确无误,油罐始终不变形,且不考虑油罐罐体厚度. 不考虑温度、气压等因素对测量值的影响. 油罐的变位只考虑纵向倾斜(靠近油位探针单侧地质塌陷)和横向偏转,不考虑其 他复杂变化. 假设罐体发生变位的纵向倾斜角度 和横向偏转角度 都有一个安全限度,并且在 安全限度内油位计量系统正常工作. 不考虑油罐体中部分油管对油容积的影响.
储油罐的变位识别与罐容表标定
摘要
加油站卧式储油罐都有配套的预先标定罐容表来反映罐内油位高度和储油量的变 化情况. 但是由于地基变形等原因,会使显示油位高度与真实储油量的关系发生改变. 本文就储油罐的变位识别与罐容表标定问题展开探讨与研究. 对于问题一,我们首先综合分析在无变位情况下的出油量和进油量,通过出油量对 进油量进行修正,得到高度间隔为 1cm 的预先标定罐容表. 然后,在显示油位高度一定 的情况下, 我们用积分求解得出罐体无变位储油量 v1 与 h 的关系式 v1 h 和变位储油量 v2 与 h 的关系式 v2 h ,从而建立差值模型即 v v1 h v2 h . 在 4.1 时,将通过模型求得的油量差值与实测数据进行对比,并借助 MATLAB 画出 v 和 v 的相对误差曲线, 发现相对误差控制在允许范围内, 验证了模型的准确性, 从而给出罐体纵向倾斜 4.1 后新的罐容表. 对于问题二, 在考虑纵向偏转对罐容表的影响时, 我们直接套用差值模型进行分析. 而在考虑横向偏转对罐容表的影响时, 我们假定罐体在发生纵向倾斜后再发生横向偏移. 我们根据所提供的数据给出了实际储油罐高度间隔为 10cm 的预先标定罐容表,并 得出横向倾斜角度 、纵向倾斜角度 、油面高度与储油量差值之间的关系式. 同时, 将实际检测数据代入新建立的一般化差值模型得出 4.15 , 1 .9 2 . 借助 MATLAB 画出实际值与模型求解值的相对误差曲线,发现相对误差控制在允 许范围内,验证了模型的正确性. 最后根据模型结果给出罐体变位后对应的新罐容表. 最后, 我们对所建的模型进行了综合评价. 同时又对模型进行了改进, 在问题一中, 为了使构建的模型更加的完善和合理,在从实际角度出发论证方案的可行性时,可以考 虑更多的因素,使可行性分析更加符合真实情况. 在模型的推广中,我们将模型推广到 池塘蓄水量、潜水艇排水量等领域.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):A甲1112所属学校(请填写完整的全名):中国海洋大学参赛队员(打印并签名) :1. 刘光鹏2. 刘红阳3. 孙迪指导教师或指导教师组负责人(打印并签名):指导教师组日期: 2010 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定模型摘要针对两种卧式储油罐变位后的标定问题,本文利用微分思想、数值逼近、拟合的原理,建立了卧式罐不变位和变位时的油量随油高模型。
针对小椭圆油罐,首先,根据几何特征写成体积的积分式。
然后,将积分变量离散化,用MATLAB的编程计算实现了规定1cm的等间距油高时精确的罐内油量。
给出了间隔1cm的变位后的标定表(见附录一)。
针对实际储油罐,首先在未发生变位时,同样利用积分知识通过组合形式写出积分表达式。
然后将变量离散化求的很小的间隔内油量值,并用3次多项式逼近作为表达式,通过MATLAB画图发现拟合较好。
当发生变位时,利用近似的体积等价法,将变位油高等价一个未变位高度。
利用积分表达式计算,并通过相邻的油位高度与实际体积之间的关系,求得α的平均值为0.033弧度,β平均值为0.035弧度,但考虑到具体情况不能简单的认为β就是0.035。
并通过求出的α,β值,利用积分运算给出间隔为10cm的变位后标定表(见附录二)。
模型的建立数学原理可靠,求解方法精度较高,可以作为非严格要求精度下的实际应用模型。
关键词:卧式罐,灌容表标定,几何积分,matlab,离散拟合,多项式逼近一、问题的引入、描述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
将常见的主体为圆柱体,两端为球冠体的油罐为例,标定变位后的灌容表。
用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题:(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
二、问题的分析问题给出的两个油罐都是标准的几何体的组合,可以进行积分求解体积,并要充分利用椭圆,圆的性质。
体积的表达式复杂,进行积分计算时既不能保证一定可积又耗时费力,所以应考虑数值计算的方法。
模型的建立以实际的利用为主要目的,所以忽略一定的范围是必须的,而且变位的情况有很多种,可以等价成水平的液高简化求解。
三、模型假设1.假设地形的改变不引起油罐的形变。
2.油罐的形状规则。
3.油罐发生变位时,油位探针相对于油罐的位置不发生变化。
4.出于现实考虑,出油管进油管不能完全触及底部。
出于安全考虑油罐也不能完全装满,标定值范围在可应用范围内即可。
5.国家有关标准规定:在装卸温差不超过30℃时,最大充装量为总容积的85%,所以下模型求解中液面变化在高位时,可省略一部分标定【1】。
23四、模型建立与求解、结果4.1小椭圆形油罐体积的求解4.1.1小椭圆型油罐未发生变位的体积计算 (1)模型建立对于未发生变位的小椭圆油罐,利用积分求油的体积。
首先,先求出油面的截面积,截面积与长度的积即为所求的体积。
具体步骤如下:图1:小椭圆油罐侧面示意图如图1,坐标原点为O 点,此坐标系下建立椭圆函数2222()1x y b a b-+= (1)A 点坐标为(x,h ),h 为油面的高度,由函数求得x = (2)当00.6h ≤≤时油面积是:S(h)=1002()2(12()xb h h b dx h b x a s =-=-+⎰⎰ (3)将(2)式的值代入(3)积分求得:4S(h)=1()(12()*arcsinb h a h ab b bs --=+ (4) 当0.6 1.2h <≤时由对称性得:S(h)=21()(2)h ab b h s s π=-- (5)又油桶长度L,所以油面的体积为:()v s h L = (6)(2)模型求解小椭圆的a=0.89m,b=0.6m 将数值代入(6) 由此公式即可求解油罐未变位的精确解,与附表1的未变位进油量数据比较如图2图2 小椭圆油罐函数数据与实测数据对比图 (3)评价或结论理论值与实测值基本一致,存在一定误差,可能是由测量方法引起。
由图像看出,油面高度较低时误差较大,随着高度的升高误差先减少后增大。
4.1.2 小椭圆油罐纵向倾斜α求体积方法一:利用积分准确求体积以罐底和垂直方向建立坐标系,在倾角为α时随着油面不断升高油面将由三角形到梯形再到三角形过度(如下两图所示),α=4.1°时最后一个阶段可以忽略不计,油面为三角形和梯形的情况下计算体积的公式:图3 油面较低的示意图如图所示为油罐的正面示意图,从0B段到A点,将油面切割积分,每一部分从侧面看都如图1所示,由图示几何关系有0.4/tanOA hα=+,'()(0.4)tanH x h xα=+-,所以每个切面的油面面积可由公式(4)(5)求得体积:0('())OAV S H x dx=⎰ (7) 同理如油面继续升高变位梯形时如下图:图4 油面升高后的示意图5此时积分上限不变是定值2.05m, '()(0.4)tanH x h xα=+-所以油的体积是2.050('())V S H x dx=⎰(8)通过表达式可以看出,由于(')S H表达式很复杂造成积分的求解理论上可行,但是实际中费时且难度较大,这时充分利用计算工具的计算优势,应题目要求每1cm标定一次,所以h离散化即可得到相应的理论值(编程代码见附录三),并且是很精确的与附表2的变位进油量数据比较如图图5 小椭圆形储油罐变位后理论计算值与实验值比较如图说明实际测量中,加油,减油,测量总会不可避免的存在误差。
由上述公式将h离散化可以确定标定表,见附录一。
67方法二【2】:利用体积近似等价求体积图6:体积近似等价示意图如图6,AB 为油罐内油页面的高度,O 为AB 的中点,做KE ,KE 经过O 点且平行于油罐的底OH 。
考虑到α角很小,可近似的认为OKB 和OAE 的体积相等。
故将BA 面转化到KE 面,即把液高H 转化成了h 。
如图*tan 2tan h IG GF H OF H αα=+=+=+此时,该问题转化成了油罐未发生变位的情况,利用公式(6)求解。
()(2tan )L v s h L s H α==+⋅4.2实际储油罐体积的求解4.2.1实际储油罐未发生位变情况(1).实际油罐的形状由原题图像给出,中间是圆柱形的,对于中间部分的体积计算有:8已知油面高度,圆柱油罐的横切面油面的截面积公式[3]:如图7-1:装少半罐油:即油深1h 2D <油。
油罐界面圆心为o ,圆心角为θ,圆的直径为D 。
则截面积为22D 2h D arccos D 2h D D sin arccos 7208D s π--⎛⎫=- ⎪⎝⎭油油油2 (9)如图7-2 装大半罐:即油深1h 2D >油。
截面积为: 222D180arccos 2h D D sin arccos 7208D h D s D π---⎛⎫=+ ⎪⎝⎭油油油2(10) (2).对于两头球冠球体积,计算过程如下:M 图7-2M 图7-19图8:球冠处示意图如图8:有几何关系2220R r E =+ 得 R=1.625m;先求油罐两端的油的体积,建立图示坐标系,当0 1.5h ≤≤时取油面的横切面,沿y 轴积分,所以先求任意截面的油面面积:图9:CD 切面的俯视圆油面示意图如图9: OH=R-1=0.625; OF r == (11)2 1.58.5a r c c o s ()-(1.5)1.523h V -=圆柱(1 =8(2.25arccos(1- (12)()22OFH S y S =*r sin()*r S r OH θθθ∆=--=-扇形 (13)所以顶端部分的油的体积为:22100.625()()(*r (arccos()hhhy S y dy r rv θ==-=-⎰⎰⎰(14)再计算圆柱部分体积,油面的面积可直接由公式(9)代入本题具体数据整理化简2 1.5()8.5arccos(1.523hV h -=圆柱(1 =8(2.25arccos(1- (15)OrFGHθ101()2()V V y v y =+圆柱 (16)当1.5<h 3≤时,可根据对称性得油桶一端头的体积为:2211(3)(31)()(3)(3)33r BC BC r v y v y v y ππ--=--=-- (17)圆柱部分为: 28(*1.5)h h V V ππ-圆柱圆柱(3-)=9-(3-) (18) 化简得: 总体积22v ()9h V y V π=+-总圆柱(3-) (19) 对于(14)式的单纯积分问题相当复杂,总体积几乎难以求解。
所以同样利用实验中椭圆模型的处理方法,将油高离散化得出相应的数值(代码见附录四)。
