2015-2016年四川省遂宁市高一下学期数学期末试卷与解析PDF
四川省遂宁市高一下学期数学期末考试试卷

四川省遂宁市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2012·重庆理) 设平面点集,则A∩B 所表示的平面图形的面积为()A .B .C .D .2. (2分)已知两条直线l1:x+2ay﹣1=0,l2:x﹣4y=0,且l1⊥l2 ,则满足条件a的值为()A . ﹣B .C .D . 23. (2分)求值:sin(﹣)=()A . -B .C .D . -4. (2分)函数的图象大致是()A .B .C .D .5. (2分) (2017高三上·甘肃开学考) 公差不为0的等差数列{an}中,3a2005﹣a20072+3a2009=0,数列{bn}是等比数列,且b2007=a2007 ,则b2006b2008=()A . 4B . 8C . 16D . 366. (2分)若锐角△ABC中,C=2B,则的取值范围是()A . (0,2)B . (, 2)C . (,)D . (, 2)7. (2分)(2017·桂林模拟) 若实数x,y满足不等式组且x+y的最大值为9,则实数m=()A . ﹣2B . ﹣1C . 1D . 28. (2分)已知等比数列{an}的公比q=2,且成等差数列,则{an}的前8项和为()A . 127B . 255C . 511D . 10239. (2分)已知正数满足:三数的倒数成等差数列,则的最小值为()A . 1B . 2C .D . 410. (2分)在平行四边形ABCD中,AC为一条对角线,=(2,4),=(1,3),则=()A . (2,4)B . (3,5)C . (1,1)D . (﹣1,﹣1)二、填空题 (共7题;共9分)11. (1分) (2016高一上·六安期中) 下列四个命题中正确的有________①函数y= 的定义域是{x|x≠0};②lg =lg(x﹣2)的解集为{3};②31﹣x﹣2=0的解集为{x|x=1﹣log32};④lg(x﹣1)<1的解集是{x|x<11}.12. (1分)不论k为何实数,直线(2k﹣1)x﹣(k+3)y﹣(k﹣11)=0恒通过一个定点,这个定点的坐标是________13. (1分) (2018高二下·双鸭山月考) 已知点在椭圆上,则的最大值是________。
四川省遂宁市高一下学期期末数学考试试卷(理科)

四川省遂宁市高一下学期期末数学考试试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2018高一下·南阳期中) 某工厂生产了 60个零件,现将所有零件随机编号,用系统抽样方法,抽取一个容量为5的样本.已知4号、16号、40号、52号零件在样本中,则样本中还有一个零件的编号是()A . 26B . 28C . 30D . 322. (2分)甲、乙两人参加一次射击游戏,规则规定,每射击一次,命中目标得2分,未命中目标得0分.已知甲、乙两人射击的命中率分别为和p,且甲、乙两人各射击一次所得分数之和为2的概率是.假设甲、乙两人射击是相互独立的,则p的值为()A .B .C .D .3. (2分)已知函数是定义在R上的奇函数,当时则()A .B .C .D .4. (2分)设等差数列满足:,公差. 若当且仅当时,数列的前项和取得最大值,则首项的取值范围是()A .B .C .D .5. (2分)设cos(﹣80°)=m那么tan100° 等于()A .B . ﹣C .D . ﹣6. (2分)如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为()A . 10 13B . 12.5 12C . 12.5 13D . 10 157. (2分)如下图是函数图像的一部分,则()A .B .C .D .8. (2分) (2015高二上·葫芦岛期末) 在空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,N为BC的中点,则等于()A . ﹣ +B . ﹣ + +C .D .9. (2分)(2017·陆川模拟) 已知α,β为锐角,且,,则cos2β=()A .B .C .D .10. (2分) (2016高二上·郑州开学考) 已知△ABC内一点O满足 = ,若△ABC内任意投一个点,则该点△OAC内的概率为()A .B .C .D .11. (2分)执行右面的程序框图,若输入N=2013,则输出S等于()A . 1B .C .D .12. (2分) (2019高三上·洛阳期中) 已知函数若有三个不等实数根,则的取值范围是()A . (2,+∞)B . [2,+∞)C . (,)D . [ , ]二、填空题 (共4题;共4分)13. (1分)计算11011(2)﹣101(2)=________ (用二进制表示)14. (1分)一支田径队有男运动员 56 人,女运动员 42 人,若用分层抽样的方法从全体运动员中抽出一个容量为28的样本,则样本中女运动员的人数为________ 人.15. (1分) (2017高一下·湖北期中) 已知,为单位向量且夹角为,设 = + , = ,在方向上的投影为________.16. (1分) (2016高一上·嘉峪关期中) 下列说法中,正确的是________①任取x>0,均有3x>2x .②当a>0,且a≠1时,有a3>a2 .③y=()﹣x是增函数.④y=2|x|的最小值为1.⑤在同一坐标系中,y=2x与y=2﹣x的图象关于y轴对称.三、解答题 (共6题;共70分)17. (5分)四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.(1)试求,表示;(2)求2+2的值;(3)求•的最大值.18. (10分) (2016高一下·郑州期末) 某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表x3456789y66697381899091(1)求纯利y与每天销售件数x之间的回归方程;(2)若该周内某天销售服装20件,估计可获纯利多少元?已知: x =280, y =45309, xiyi=3487, = , = ﹣.19. (10分) (2018高一下·商丘期末) 已知角的终边经过点 .(1)求的值;(2)求的值.20. (15分)已知函数f(x)= sin(ωx+φ)(ω>0,﹣≤φ<)图象的一个对称中心为(,0),且图象上相邻两条对称轴间的距离为.(1)求函数f(x)的解析式;(2)求函数f(x)的单调减区间;(3)若f()= (<α<),求cos(α+ )的值.21. (20分)某校高二年级的600名学生参加一次科普知识竞赛,然后随机抽取50名学生的成绩进行统计分析.分组频数频率[50,60)5[60,70)10[70,80)15[80,90)15[90,100)5合计50(1)完成频率分布表;(2)根据上述数据画出频率分布直方图;(3)估计这次竞赛成绩在80分以上的学生人数是多少?(4)估计这次竞赛中成绩的众数,中位数,平均数分别是多少?22. (10分) (2017高一下·衡水期末) 已知向量 = , = ,且(1)求及| |(2)若f(x)= ﹣2λ| |的最小值为,求正实数λ的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共70分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、21-3、21-4、22-1、22-2、第11 页共11 页。
四川省遂宁市高中高一下学期期末教学水平监测数学试题(解析版)

四川省遂宁市高中高一下学期期末教学水平监测数学试题一、选择题1.计算sin 43cos13cos 43sin13- 的结果等于( )A.122.下列各组平面向量中,可以作为基底的是( )A. B. C. D.3.n S 为等差数列{}n a 的前n 项和, 286a a +=,则9S =( ) A.272B. 54C. 27D. 1084.设,,则下列不等式成立的是( )A. B. C. D.5.在中,已知D 是AB 边上一点,若,,则=( )A. B. C. D.6.在中,则B 等于( ) A.B.C.D.7.某几何体的三视图如图所示,则该几何体的表面积为( )A. 180B. 200C. 220D. 2408.设1e 、2e 是夹角为60的两个单位向量, 12122,32a e e b e e =+=-+ ,则向量a 与b 的夹角为( )A. 30B. 60C. 120D. 1509.如图,设A,B两点在涪江的两岸,一测量者在A的同侧所在的江岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°. 则A,B两点间的距离为()A. mB. mC. mD. m10.已知等差数列{a n}的前n项和为,,,则使得取最大值时n的值为()A. 11或12B. 12C. 13D. 12或1311.若,,,则的最小值是()A. B. C. D.12.中,角的对边分别为,且满足,,,则的取值范围是A. B. C. D.二、填空题13._____14.一个蜂巢里有1只蜜蜂.第1天,它飞出去找回了2个伙伴;第2天,3只蜜蜂飞出去,各自找回了2个伙伴……如果这个找伙伴的过程继续下去,第5天所有的蜜蜂都归巢后,蜂巢中一共有_____只蜜蜂.15.若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的体积为_____.16.有下列命题:①等比数列中,前n项和为,公比为,则,,仍然是等比数列,其公比为;②一个正方体的顶点都在球面上,它的棱长为2cm,则球的体积是cm3;③若数列是正项数列,且,则;④在中,D是边BC上的一点(包括端点),则的取值范围是.其中正确命题的序号是_____(填番号)三、解答题17.已知(1)求;(2)当为何实数时,与平行, 平行时它们是同向还是反向?18.已知不等式的解集为(1)求a、b的值;(2)若不等式恒成立,则求出c的取值范围.19.已知锐角中,角所对的边分别为,向量,,且. (1)求角的大小;(2)若,求的面积的最大值.20.已知函数的最小值为(1)求常数的值;(2)若,,求的值.21.已知数列中,,(1)求证:数列是等差数列;(2)求数列的通项公式;(3)设数列满足:,求的前项和.22.已知二次函数同时满足:①在定义域内存在,使得成立;②不等式的解集有且只有一个元素;数列的前项和为,,,。
2015-2016年四川省遂宁市高一(下)期末数学试卷(解析版)

2015-2016学年四川省遂宁市高一(下)期末数学试卷一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.(5分)对于数列a,a,a,…a下列说法正确的是()A.一定为等差数列B.一定为等比数列C.既是等差数列,又是等比数列D.以上都不正确2.(5分)下列结论正确的是()A.若a>b,则ac>bc B.若a>b,则a2>b2C.若a<b<0,则a2>ab>b2D.若a<b<0,则<3.(5分)计算cos18°cos42°﹣cos72°cos48°=()A.B.C.D.4.(5分)二次不等式ax2+bx+c<0的解集是空集的条件是()A.B.C.D.5.(5分)在△ABC中,若a cos A=b cos B,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形6.(5分)下列结论正确的是()A.两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱B.若△ABC中,•<0,则△ABC是钝角三角形C.函数f(x)=x+(x>1)的最小值为5D.若G2=ab,则G是a,b的等比中项7.(5分)我国古代数学名著《算法统宗》中有如下问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏8.(5分)已知x,y满足约束条件,则z=﹣2x+y的最大值是()A.﹣1B.﹣2C.﹣5D.19.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2﹣b2)tan B=ac,则角B的值为()A.B.C.或D.或10.(5分)已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣11.(5分)已知O是△ABC内部一点,++=,•=2且∠BAC=60°,则△OBC的面积为()A.B.C.D.12.(5分)存在正实数b使得关于x的方程sin x+cos x=b的正根从小到大排成一个等差数列,若点P(6,b)在直线nx+my﹣2mn=0上(m,n均为正常数),则m+4n的最小值为()A.5+2B.4C.8D.7+4二、填空题(本题共4小题,每小题5分,共20分)13.(5分)正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=.14.(5分)如图是一个空间几何体的三视图,则该几何体的体积大小为.15.(5分)在等腰△ABC中,∠BAC=90°,AB=AC=2,=2,=3,则在方向上的投影.16.(5分)已知数列{a n}满足a1=﹣1,a2>a1,|a n+1﹣a n|=2n(n∈N*),若数列{a2n﹣1}单调递减,数列{a2n}单调递增,则数列{a n}的通项公式为a n=.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)已知向量=(1,2),向量=(x,﹣2),且⊥(﹣)(Ⅰ)求|3+|;(Ⅱ)若向量﹣λ与2+平行,求λ的值.18.(12分)已知公差不为零的等差数列{a n}中,a3=7,且a1,a4,a13成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.19.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(Ⅰ)求实数a,b的值;(Ⅱ)解关于x的不等式(ax﹣b)(x﹣c)>0(c为常数).20.(12分)已知=(2sin x,cos2x),=(cos x,2),函数f(x)=•﹣.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f(﹣)=,且sin B+sin C=,求△ABC的面积.21.(12分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB =θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.22.(12分)已知数列{a n}的前n项和是S n,且S n=2a n﹣n(Ⅰ)求证:数列{a n+1}为等比数列;并求数列{a n}的通项公式a n;(Ⅱ)数列{b n}满足b n=,求数列{b n}的前n项和T n;(Ⅲ)若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.2015-2016学年四川省遂宁市高一(下)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.(5分)对于数列a,a,a,…a下列说法正确的是()A.一定为等差数列B.一定为等比数列C.既是等差数列,又是等比数列D.以上都不正确【考点】81:数列的概念及简单表示法.【解答】解:对于数列a,a,a,…a,一定是公差为0等差数列,当a≠0时,此数列也是等比数列.故只有A正确.故选:A.2.(5分)下列结论正确的是()A.若a>b,则ac>bc B.若a>b,则a2>b2C.若a<b<0,则a2>ab>b2D.若a<b<0,则<【考点】R3:不等式的基本性质.【解答】解:对于A,c=0时,不成立,对于B,令a=﹣1,b=﹣2,显然不成立,对于C,根据不等式的性质,显然成立,对于D,令a=﹣2,b=﹣1,显然不成立,故选:C.3.(5分)计算cos18°cos42°﹣cos72°cos48°=()A.B.C.D.【考点】GP:两角和与差的三角函数.【解答】解:原式=.故选:B.4.(5分)二次不等式ax2+bx+c<0的解集是空集的条件是()A.B.C.D.【考点】3V:二次函数的性质与图象.【解答】解:若二次不等式ax2+bx+c<0的解集是空集,即二次不等式ax2+bx+c≥0在R恒成立,故,故选:A.5.(5分)在△ABC中,若a cos A=b cos B,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形【考点】GZ:三角形的形状判断.【解答】解:由正弦定理a sin A=b sin B化简已知的等式得:sin A cos A=sin B cos B,∴sin2A=sin2B,∴sin2A=sin2B,又A和B都为三角形的内角,∴2A=2B或2A+2B=π,即A=B或A+B=,则△ABC为等腰或直角三角形.故选:D.6.(5分)下列结论正确的是()A.两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱B.若△ABC中,•<0,则△ABC是钝角三角形C.函数f(x)=x+(x>1)的最小值为5D.若G2=ab,则G是a,b的等比中项【考点】2K:命题的真假判断与应用.【解答】解:对于A,有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故A错;对于B,若△ABC中,•<0,即为||•||cos(π﹣B)<0,则cos B>0,B为锐角,不能确定三角形的形状,故B错;对于C,函数f(x)=x+(x>1)=(x﹣1)++1≥2+1=5,当且仅当x﹣1=,即x=3,取得等号,则f(x)的最小值为5,故C正确;对于D,若G=a=b=0,满足G2=ab,则G不为a,b的等比中项,故D错.故选:C.7.(5分)我国古代数学名著《算法统宗》中有如下问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏【考点】89:等比数列的前n项和.【解答】解:设塔顶的a1盏灯,由题意{a n}是公比为2的等比数列,∴S7==381,解得a1=3.故选:B.8.(5分)已知x,y满足约束条件,则z=﹣2x+y的最大值是()A.﹣1B.﹣2C.﹣5D.1【考点】7C:简单线性规划.【解答】解:由已知不等式组表示的平面区域如图阴影部分,当直线y=2x+z经过A时使得z最大,由得到A(1,1),所以z的最大值为﹣2×1+1=﹣1;故选:A.9.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2﹣b2)tan B=ac,则角B的值为()A.B.C.或D.或【考点】HR:余弦定理.【解答】解:由∴,即∴,又在△中所以B为或故选:D.10.(5分)已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣【考点】GG:同角三角函数间的基本关系;GP:两角和与差的三角函数.【解答】解:∵α∈(0,),β∈(﹣,0),∴α﹣β∈(0,π),又cos(α﹣β)=,sinβ=﹣,∴sin(α﹣β)==,cosβ==,则sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ=×+×(﹣)=.故选:A.11.(5分)已知O是△ABC内部一点,++=,•=2且∠BAC=60°,则△OBC的面积为()A.B.C.D.【考点】9O:平面向量数量积的性质及其运算;9S:数量积表示两个向量的夹角.【解答】解:∵∴∴O为三角形的重心∴△OBC的面积为△ABC面积的∵∴∵∠BAC=60°∴△ABC面积为=∴△OBC的面积为故选:A.12.(5分)存在正实数b使得关于x的方程sin x+cos x=b的正根从小到大排成一个等差数列,若点P(6,b)在直线nx+my﹣2mn=0上(m,n均为正常数),则m+4n的最小值为()A.5+2B.4C.8D.7+4【考点】84:等差数列的通项公式.【解答】解:由sin x+cos x=b,可得:2=b存在正数b,使得方程sin x+cos x=b的正根从小到大排成一个等差数列,即有0<b≤2.若0<b<2,由y=sin(x+)的图象可得:直线y=b与函数y=2sin(x+)的图象的交点的横坐标不成等差数列,若b=2,即有x+=2kπ+,即为x=2kπ+,k∈Z,可得所有正根从小到大排成一个等差数列,公差为2π.由点P(6,2)在直线直线nx+my﹣2mn=0上(m,n均为正常数),∴6n+2m﹣2mn=0,化为:=1.则m+4n=(m+4n)=7+≥7+2=7+4,当且仅当m=2n =3+2时取等号.故选:D.二、填空题(本题共4小题,每小题5分,共20分)13.(5分)正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=4.【考点】88:等比数列的通项公式.【解答】解:由正项等比数列{a n}中,可得a2a98=16=a3a97,∴正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=log216=4.故答案为:4.14.(5分)如图是一个空间几何体的三视图,则该几何体的体积大小为.【考点】L!:由三视图求面积、体积.【解答】由三视图可知,该几何体时一个边长为2,2,1的长方体挖去一个半径为1的半球.所以长方体的体积为2×2×1=4,半球的体积为,所以该几何体的体积为.故答案为:.15.(5分)在等腰△ABC中,∠BAC=90°,AB=AC=2,=2,=3,则在方向上的投影.【考点】9O:平面向量数量积的性质及其运算.【解答】解:如图,以A为坐标原点建立如图所示的平面直角坐标系,∵AB=AC=2,=2,=3,∴A(0,0),B(2,0),C(0,2),则D(1,1),E(0,),∴.则,||=.∴在方向上的投影为.故答案为:.16.(5分)已知数列{a n}满足a1=﹣1,a2>a1,|a n+1﹣a n|=2n(n∈N*),若数列{a2n﹣1}单调递减,数列{a2n}单调递增,则数列{a n}的通项公式为a n=.【考点】82:数列的函数特性;8E:数列的求和.【解答】解:方法一:先采用列举法得a1=﹣1,a2=1,a3=﹣3,a4=5,a5=﹣11,a6=21,…,然后从数字的变化上找规律,得,∴a n=(a n﹣a n﹣1)+(a n﹣1﹣a n﹣2)+…+(a2﹣a1)+a1=(﹣1)n•2n﹣1+(﹣1)n﹣1•2n﹣2+…﹣22+2﹣1==.方法二:∵,,∴,而{a2n﹣1}递减,∴a2n+1﹣a2n﹣1<0,故;同理,由{a2n}递增,得;又a2>a1,∴,以下同上.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)已知向量=(1,2),向量=(x,﹣2),且⊥(﹣)(Ⅰ)求|3+|;(Ⅱ)若向量﹣λ与2+平行,求λ的值.【考点】9O:平面向量数量积的性质及其运算.【解答】解:(Ⅰ)∵=(1,2),=(x,﹣2),∴=(1﹣x,4),由⊥(﹣),得(1,2)•(1﹣x,4)=1﹣x+8=0,∴x=9.则=(12,4),∴;(Ⅱ)∵=(1,2),=(9,﹣2),∴=(1﹣9λ,2+2λ),=(11,2).∵向量﹣λ与2+平行,∴(1﹣9λ)×2﹣11×(2+2λ)=0.解得:.18.(12分)已知公差不为零的等差数列{a n}中,a3=7,且a1,a4,a13成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.【考点】84:等差数列的通项公式;8E:数列的求和.【解答】解:(Ⅰ)设数列{a n}的公差为d.∵,∴,解得:d=2或d=0(舍),∴a1=3,∴a n=2n+1(n∈N*);(Ⅱ)∵a n=2n+1,∴,∴=(n∈N*).19.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(Ⅰ)求实数a,b的值;(Ⅱ)解关于x的不等式(ax﹣b)(x﹣c)>0(c为常数).【考点】73:一元二次不等式及其应用.【解答】解:(1)由题意知1,b是关于x的方程ax2﹣3x+2=0的两根…(2分)将x=1代入方程得a﹣3+2=0,解得a=1,…(4分)从而原方程变为x2﹣3x+2=0,即(x﹣1)(x﹣2)=0,∴方程的另一个根为b=2;…(6分)(2)不等式为(x﹣2)(x﹣c)>0,当c>2时,不等式的解集为{x|x<2或x>c};当c=2时,不等式的解集为{x|x≠2,x∈R};当c<2时,不等式的解集为{x|x<c或x>2}.…(12分)20.(12分)已知=(2sin x,cos2x),=(cos x,2),函数f(x)=•﹣.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f(﹣)=,且sin B+sin C=,求△ABC的面积.【考点】GL:三角函数中的恒等变换应用;H1:三角函数的周期性.【解答】解:(Ⅰ)由题意,函数f(x)=•﹣.可得f(x)=2sin x cos x+2cos2x﹣=sin2x+cos2x=2sin(2x+)∴f(x)的最小正周期为T=.(Ⅱ)已知锐角A满足f(﹣)=,可得2sin[2(﹣)+]=,即2sin A=又∵A为锐角,∴A=.又∵a=7,sin B+sin C=,由正弦定理可得:sin B=,sin C=,∴+=,可得:b+c=13由余弦定理可知,cos A===.可求得:bc=40.故得S△ABC=bc sin A=.21.(12分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB =θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.【考点】HU:解三角形.【解答】解:(1)如图,作CD⊥AF于D,则CD=EF,设∠ACD=α,∠BCD=β,CD=x,则θ=α﹣β,在Rt△ACD和Rt△BCD中,tanα=,tanβ=,则tanθ=tan(α﹣β)==(x>0),令u=,则ux2﹣2x+1.25u=0,∵上述方程有大于0的实数根,∴△≥0,即4﹣4×1.25u2≥0,∴u≤,即(tanθ)max=,∵正切函数y=tan x在(0,)上是增函数,∴视角θ同时取得最大值,此时,x==,∴观察者离墙米远时,视角θ最大;(2)由(1)可知,tanθ===,即x2﹣4x+4=﹣a2+6a﹣4,∴(x﹣2)2=﹣(a﹣3)2+5,∵1≤a≤2,∴1≤(x﹣2)2≤4,化简得:0≤x≤1或3≤x≤4,又∵x>1,∴3≤x≤4.22.(12分)已知数列{a n}的前n项和是S n,且S n=2a n﹣n(Ⅰ)求证:数列{a n+1}为等比数列;并求数列{a n}的通项公式a n;(Ⅱ)数列{b n}满足b n=,求数列{b n}的前n项和T n;(Ⅲ)若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.【考点】8E:数列的求和;8K:数列与不等式的综合.【解答】解:(Ⅰ)证明:当n=1时,s1=2a1﹣1=a1,∴a1+1=2≠0 …(1分)当n≥2时,∵S n=2a n﹣n,∴s n﹣1=2a n﹣1﹣(n﹣1),两式相减∴a n=2a n﹣2a n﹣1﹣1,∴a n=2a n﹣1+1,∴a n+1=2(a n﹣1+1)…(3分)∴数列{a n+1}是首项和公比都是2的等比数列,得a n+1=2n⇒a n=2n﹣1…(4分)(Ⅱ)可得b n==,T n=+n×=1×+…+(n﹣2)+(n﹣1)+n×,两式相减得=2﹣∴…(8分)(Ⅲ)不等式(﹣1)nλ<T n+对一切n∈N*恒成立⇔不等式(﹣1)nλ<4﹣对一切n∈N*恒成立由为递增函数.…(9分)若n为偶数,则λ<f(2)=3,∴λ<3 …(10分)若n为奇数,则﹣λ<f(1)=2,∴﹣λ<2,λ>﹣2 …(11分)∴﹣2<λ<3 …(12分)。
四川省遂宁市高一下学期期末数学考试试卷
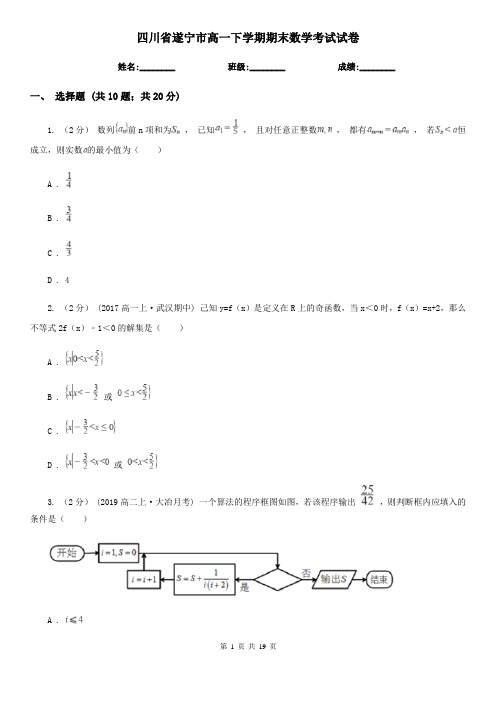
四川省遂宁市高一下学期期末数学考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)数列前n项和为,已知,且对任意正整数,都有,若恒成立,则实数的最小值为()A .B .C .D . 42. (2分) (2017高一上·武汉期中) 己知y=f(x)是定义在R上的奇函数,当x<0时,f(x)=x+2,那么不等式2f(x)﹣1<0的解集是()A .B . 或C .D . 或3. (2分) (2019高二上·大冶月考) 一个算法的程序框图如图,若该程序输出,则判断框内应填入的条件是()A .B .C .D .4. (2分)(2019·福建模拟) 已知变量,满足约束条件,则目标函数的最大值为()A . 9B . 8C . 7D . 65. (2分)已知正方形ABCD的边长为2,H是边DA的中点.在正方形ABCD内部随机取一点P,则满足|PH|<的概率为()A .B . +C .D . +6. (2分) (2016高二上·临川期中) 某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为()A . 45,75,15B . 45,45,45C . 30,90,15D . 45,60,307. (2分) (2019高一下·惠州期末) 已知三个内角A、B、C的对边分别是,若,则b等于()A . 3B .C .D .8. (2分)甲、乙两同学5次综合测评的成绩如茎叶图所示.甲乙9883372109●9老师在计算甲、乙两人平均分时,发现乙同学成绩的一个数字无法看清.若从{0,1,2,…,9}随机取一个数字代替,则乙的平均成绩超过甲的平均成绩的概率为()A .B .C .D .9. (2分) (2020高二下·铜陵期中) 已知函数,若对任意两个不等的正数,,都有恒成立,则a的取值范围为()A .B .C .D .10. (2分) (2018高一下·柳州期末) 在中,角的对边分别为,若,则的面积为()A .B .C .D .二、填空题 (共6题;共6分)11. (1分) (2020高三上·新疆月考) 函数的定义域是________ .12. (1分) (2019高一下·安徽期中) 在等差数列中,已知,,,则________.13. (1分)已知2,4,2x,4y四个数的平均数是5而5,7,4x,6y四个数的平均数是9,则xy的值是________14. (1分) (2017高二下·如皋期末) 已知x,y满足约束条件,则z=x2+y2+2y+1的最小值为________.15. (1分)(2013·上海理) 盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是________(结果用最简分数表示).16. (1分) (2019高三上·涟水月考) 对于数列,定义数列为数列的“ 倍差数列”,若的“ 倍差数列”的通项公式为,则数列的前项和 ________.三、解答题 (共6题;共60分)17. (10分)(2020·山东模拟) 已知各项均不相等的等差数列的前项和为 , 且成等比数列.(1)求数列的通项公式;(2)求数列的前项和 .18. (15分)(2020·日照模拟) 某公司准备投产一种新产品,经测算,已知每年生产万件的该种产品所需要的总成本(万元),依据产品尺寸,产品的品质可能出现优、中、差三种情况,随机抽取了1000件产品测量尺寸,尺寸分别在,,,,,,(单位:)中,经统计得到的频率分布直方图如图所示.产品的品质情况和相应的价格(元/件)与年产量之间的函数关系如下表所示.产品品质立品尺寸的范围价格与产量的函数关系式优中差以频率作为概率解决如下问题:(1)求实数的值;(2)当产量确定时,设不同品质的产品价格为随机变量,求随机变量的分布列;(3)估计当年产量为何值时,该公司年利润最大,并求出最大值.19. (5分) (2017高一下·双鸭山期末) 在中,求的值。
2015年四川省遂宁市高一下学期人教A版数学期末考试试题

2015年四川省遂宁市高一下学期人教A版数学期末考试试题一、选择题(共10小题;共50分)1. 数列23,−39,427,−581,⋯的一个通项公式是 A. −1n n+13n B. −1n+1n+13nC. −1n n3nD. −1n+1n3n2. sin75∘的值等于 A. 6+24B. 6−24C. 3+24D. 3−243. 已知a = 4,2,b = 6,y,若a∥b,则y等于 A. −12B. −3C. 3D. 124. 在等差数列a n中,已知a4+a8=16,则该数列前11项和S11= A. 58B. 88C. 143D. 1765. 已知x∈ −π2,0,cos x=45,则tan2x= A. 724B. −724C. 247D. −2476. 已知a<0,−1<b<0,则有 A. ab>ab2>aB. ab2>ab>aC. ab>a>ab2D. a>ab>ab27. 函数y=3x2+6x+1的最小值是 A. 3−3B. −3C. 6D. 6−38. 在△ABC中,cos2B+C+2sin A sin B<0,则△ABC的形状为 A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不确定9. 如图所示,P,Q为△ABC内的两点,且AP=25AB+15AC,AQ=23AB+14AC,则△ABP的面积与△ABQ的面积的比值为 A. 15B. 45C. 14D. 1310. 已知数列a n满足a1=1,a n+1⋅1a n2+4=1,令b n=a n2⋅a n+12,Sn是数列b n的前n项和,若S n>m16对任意n∈N∗恒成立,则整数m的最大值为 A. 1B. 2C. 3D. 4二、填空题(共5小题;共25分)11. 不等式x−2x+1≤0的解集是.12. 不等式组4x+3y+8>0,x<0,y<0,表示的平面区域内的整点坐标是.13. 在△ABC中,若∠A=120∘,AB=5,BC=7,则△ABC的面积S=.14. 已知数列a n是等差数列,若它的前n项和S n有最小值,且a11a10<−1,则使S n>0成立的最小自然数n的值为.15. △ABC中,角A,B,C所对的边分别为a,b,c,①若sin A>sin B,则B>A;②若△ABC最小内角为α,则cosα≥12;③存在某钝角△ABC,有tan A+tan B+tan C>0;④若2aBC+bCA+cAB=0,则△ABC的最小角小于π6;其中正确的命题是.(写出所有正确命题的序号)三、解答题(共6小题;共78分)16. 已知a n为等差数列,且a3=−6,a6=0.(1)求a n的通项公式;(2)若等比数列b n满足b1=−8,b2=a1+a2+a3,求b n的前n项和S n.17. 已知向量p1=3,2,向量p2=−1,2.(1)若p1+kp2∥2p2−p1,求实数k的值;(2)求p1在p2方向上的投影.18. 已知cosα+β=15,cosα−β=35.(1)求tanαtanβ的值;(2)若α+β∈0,π,α−β∈ −3π2,0,求cos2β的值.19. 2015年6月1日约21时28分,一艘从南京驶往重庆的客船“东方之星”在长江中游湖北监利水域遭遇龙卷风翻沉.如图所示,A,B是江面上位于东西方向相距53+3千米的两个观测点.现位于A点北偏东45∘,B点北偏西60∘的客船东方之星(D点)发出求救信号,位于B 点南偏西60∘且与B点相距203千米的C点的救援船立即前往营救,其航行速度为30千米每小时,该救援船到达D点需要多长时间?20. 已知二次函数f x的二次项系数为a,且不等式f x>−2x的解集是1,3.(1)若方程f x+6a=0有两个相等的根,求f x的解析式;(2)若f x的最大值为正实数,求a的取值范围.21. 已知数列a n的前n项和S n=2a n−3⋅2n+4n∈N∗.(1)求证:数列a n2n是等差数列;(2)设T n为数列S n−4的前n项和,求T n.(3)设C n=3n+52n−1a n a n+1,数列c n的前n项和为Q n,求证:Q n≥25.答案第一部分1. B2. A3. C4. B5. D6. A7. D 【解析】y=3 x2+2x+1=3 x2+1+2x+1−1≥322−1=62−3.当且仅当x2+1=2x+1,即x2=2−1时取得等号.8. B 9. B 【解析】如图,设AM=25AB,AN=15AC,则AP=AM+AN,由平行四边形法则知NP∥AB,所以S△ABPS△ABC=ANAC=15,同理得S△ABQS△ABC =14,故S△ABPS△ABQ=45.10. C第二部分11. −1,212. −1,−113. 153414. 20【解析】由已知得,a1<0,d>0,a10<0,a11>0,所以a1+a19<0,a10+a11>0,所以a1+a20>0,则S19<0,S20>0,故所求n=20.15. ②④第三部分16. (1)a3=a1+2d=−6,a6=a1+5d=0⇒a1=−10,d=2,所以a n=2n−12n∈N∗;(2)b2=a1+a2+a3=−24,设等比数列b n的公比为q,q=b2b1=3,S n=b11−q n1−q =−81−3n1−3=4−4⋅3n.17. (1)p1+kp2=3−k,2k+2,2p2−p1=−5,2,又因为p1+kp2∥2p2−p1,则3−k⋅2−2k+2⋅−5=0,(2)p1在p2方向上的投影为p1⋅cos⟨p1,p2 ⟩=p1 ⋅p2p2=55.18. (1)cosα+β=cosαcosβ−sinαsinβ=15, ⋯⋯①cosα−β=cosαcosβ+sinαsinβ=3, ⋯⋯②由①+②得cosαcosβ=25, ⋯⋯③由①−②得sinαsinβ=15, ⋯⋯④由④/③得tanαtanβ=12.(2)因为cosα+β=15且0<α+β<π得sinα+β=265,又因为cosα−β=35且−3π2<α−β<0得sinα−β=−45,cos2β=cosα+β−α−β=cosα+βcosα−β+sinα+βsinα−β=3−86.19. 由题意知AB=53+3km,∠DBA=90∘−60∘=30∘,∠DAB=90∘−45∘=45∘,所以∠ADB=180∘−45∘+30∘=105∘.在△DAB中,由正弦定理得DBsin∠DAB =ABsin∠ADB,所以DB=AB sin∠DAB=53+3⋅sin45∘sin105∘=103km.又∠DBC=∠DBA+∠ABC=30∘+90∘−60∘=60∘,在△DBC中,由余弦定理得:CD2=BD2+BC2−2BD⋅BC⋅cos∠DBC=300+1200−2×103×203×1=900,所以CD=30km.则需要的时间t=1(小时).答:该救援船到达D点需要1小时.20. (1)因为f x+2x>0的解集为1,3,设f x+2x=a x−1x−3且a<0,由f x+6a=0得ax2−2+4a x+9a=0,有两个相等的根:Δ=−2+4a2−4a⋅9a=0,解得a=1或a=−15,由a<0舍去a=1,所以f x=−15x2−65x−35.f x=ax2−21+2a x+3a=a x−1+2a2−a2+4a+1,a<0f x max=−a2+4a+1a,−a2+4a+1a >0,a<0⇒a<−2−3或0>a>−2+3,故当f x的最大值为正实数时,a的取值范围是 −∞,−2−3∪ −2+3,0.21. (1)当n=1时,S1=2a1−3⋅21+4,a1=2,S n=2a n−3⋅2n+4, ⋯⋯1S n−1=2a n−1−3⋅2n−1+4n≥2, ⋯⋯2.由1−2两边同除以2n得a n2−a n−12=32n≥2,所以a n2是以1为首项,32为公差的等差数列.(2)由(Ⅰ)知a n=3n−12n−1n∈N∗,S n=2⋅3n−1⋅2n−1−3⋅2n+4=3n−4⋅2n+4,S n−4=3n−4⋅2n,T n=−1⋅21+2⋅22+5⋅23+⋯+3n−4⋅2n, ⋯⋯①2T n=−1⋅22+2⋅23+5⋅24+⋯+3n−4⋅2n+1. ⋯⋯②由①−②错位相减得:−T n=−1⋅21+3⋅22+23+24+⋯+2n−3n−4⋅2n+1=−2+3⋅221−2n−11−2−3n−4⋅2n+1.T n=14+3n−7⋅2n+1n∈N∗.(3)C n=3n+53n−13n+2⋅12=23n+2−3n−13n−13n+2⋅12n=23n−1−13n+2⋅12=13n−1⋅12−13n+2⋅12.Q n=12⋅120−15⋅121+15⋅121−18⋅122+18⋅122+⋯+13n−1⋅12n−1−13n+2⋅12n =1−1⋅1n∈N∗.令f n=13n+2⋅12,则f n+1=13n+5⋅12,f n+1f n=123n+23n+5=121−33n+5<1,f n+1<f n,f n对n∈N∗递减,f1=110,Q n min=12−110=410=25,则Q n≥25.。
四川省遂宁市高一下学期数学期末联考试卷

四川省遂宁市高一下学期数学期末联考试卷姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) 已知 α 是第三象限角,且的值为( )A.B.C.D.2. (2 分) 已知 O 为坐标原点,向量,且, 则点 P 的坐标为( )A.B. C. D. 3. (2 分) 已知 cos θ=- ,θ∈(-π,0),则 sin +cos =( ) A. B. C. D.第 1 页 共 12 页4. (2 分) (2016 高一下·滁州期中) 已知等比数列{an}的公比为正数,且 a3a9=2a52 , a2=2,则 a1=( ) A.B. C. D.2 5. (2 分) (2018 高二上·宁夏月考),该三角形的面积为 ,则的内角 、 、 的对边分别为 、 、 ,已知 的值为( )A. B. C. D.6. (2 分) (2019 高一下·安徽月考) 设变量 , 满足约束条件的最小值为 1,则的最小值为( )A.,若目标函数B.C.D.7. (2 分) (2016 高三上·沙市模拟) 已知函数 f(x)=sin(ωx+φ)(ω>0,|φ|< )的最小正周期 为 π,且其图象向左平移 个单位后得到函数 g(x)=cosωx 的图象,则函数 f(x)的图象( )第 2 页 共 12 页A . 关于直线 x= 对称 B . 关于直线 x= 对称 C . 关于点( ,0)对称 D . 关于点( ,0)对称 8. (2 分) (2017·抚顺模拟) 已知菱形 ABCD 的边长为 2,E 为 AB 的中点,∠ABC=120°,则 为( ) A.3 B . ﹣3 C. D.﹣ 9. (2 分) (2020·甘肃模拟) 被誉为“中国现代数学之父”的著名数学家华罗庚先生倡导的“的值 优选法”在生产和科研实践中得到了非常广泛的应用,就是黄金分割比的近似值,黄金分割比还可以表示成 A.,则()B. C.D.10. (2 分) 设等差数列 的前 n 项和为 ,若,则 的值等于( )A . 54B . 45第 3 页 共 12 页C . 36 D . 2711. (2 分) M 是△ABC 所在平面内一点, A. B. C.1 D.2,D 为 AC 中点,则的值为( )12. (2 分) (2016·普兰店模拟) 已知实数 x,y 满足: 是( ),z=|2x﹣2y﹣1|,则 z 的取值范围A . [ ,5] B . [0,5] C . [0,5)D . [ ,5)二、 填空题 (共 4 题;共 4 分)13. (1 分) (2019 高一下·哈尔滨月考) 已知向量,________.,若,则14. (1 分) (2018 高一上·海安月考) 在 大边长为________.中,,,,则此三角形的最15. (1 分) (2016 高一下·苏州期末) 函数 f(x)=2sin(ωx+φ)(ω>0,且|φ|< )的部分图象如 图所示,则 f( ) 的值为________.第 4 页 共 12 页16. (1 分) 已知| |=| |=| |=1,且 ⊥ , 则( + ﹣ )• 的最大值是________三、 解答题 (共 6 题;共 60 分)17. (15 分) 已知 tanx=2,求下列各式的值:(1);(2) sin2x+ cos2x; (3) sinxcosx.18. (10 分) (2020·东莞模拟) 已知等差数列 的前 n 项和为 ,,.(1) 求 的通项公式;(2) 设,求 的前 2n 项的和 .19. (10 分) (2019 高一下·涟水月考) 在中, , , 分别是角 , , 的对边,且(1) 求的值;(2) 若,且,求的面积.20. (10 分) (2016 高二上·惠城期中) 等比数列{an}中,已知 a1=1,a4=8,若 a3 , a5 分别为等差数列{bn} 的第 4 项和第 16 项.(1) 求数列{an}﹑{bn}的通项公式;第 5 页 共 12 页(2) 令 cn=an•bn , 求数列{cn}的前 n 项和 Sn .21. (10 分) 定义非零向量=(a,b)的“相伴函数”为 f(x)=asinx+bcosx(x∈R),向量=(a,b)称为 f(x)=asinx+bcosx,(x∈R)的“相伴向量”(其中 O 为坐标原点).记平面内所有向量的“相伴函数”构成的集合为 S(1) 设 h(x)= cos(x+ )﹣3cos( ﹣x)(x∈R) ①求证:h(x)∈S ②求函数 h(x)的“相伴向量”的模;(2) 已知点 M(a,b)满足: 求 tan2x0 的取值范围.∈(0,],向量“相伴函数”f(x)在 x=x0 处取得最大值,22. (5 分) (2020·浙江) 已知数列{an},{bn},{cn}中,a1=b1=c1=1,cn+1=an+1﹣an , cn+1= •cn(n∈N*).(Ⅰ)若数列{bn}为等比数列,且公比 q>0,且 b1+b2=6b3 , 求 q 与 an 的通项公式;(Ⅱ)若数列{bn}为等差数列,且公差 d>0,证明:c1+c2+…+cn<1+ .第 6 页 共 12 页一、 选择题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 12 页16-1、三、 解答题 (共 6 题;共 60 分)17-1、 17-2、 17-3、18-1、18-2、19-1、第 8 页 共 12 页19-2、 20-1、20-2、第 9 页 共 12 页21-1、 21-2、第 10 页 共 12 页。
四川省遂宁市数学高一下学期理数期末联考试卷

四川省遂宁市数学高一下学期理数期末联考试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题;共 24 分)1. (2 分) 平面向量 与 的夹角为 60°,,则等于()A.B. C.4 D . 122. (2 分) 已知点 P 在曲线 y=上, 为曲线在点 处的切线的倾斜角,则 的取值范围是( )A.B.C.D.3. (2 分) 已知 p:“x2+ y2 +2x=F 为一圆的方程(F∈R)”,q:“F>0”,则 p 是 q 的( )A . 充要条件B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件4. ( 2 分 ) (2019 高 一 下 · 辽 源 期 末 ) 在,那么()中,内角的对边分别为,若第 1 页 共 11 页A.B.C.D.5. (2 分) (2019 高一下·辽源期末) 圆的圆心坐标和半径分别为( )A.,2B.,2C.,4D.,46. (2 分) 在中,已知 a=6,b=8,C=45°,则的面积为( )A.B.C.D. 7. (2 分) (2019 高一下·辽源期末) 已知 {an} 为等差数列, Sn 为其前 n 项和.若 a1+a9=18,a4=7, 则 S10=( ) A . 55 B . 81 C . 90 D . 100 8. (2 分) (2019 高一下·辽源期末) 过点 A(4,1) 且在两坐标轴上截距相等的直线方程是( )第 2 页 共 11 页A.B.C.或D.或9. (2 分) (2012·广东) 某几何体的三视图如图所示,它的体积为( )A . 12π B . 45π C . 57π D . 81π 10. (2 分) (2019 高一下·辽源期末) 设 m、n 是两条不同的直线, α 、β 是两个不同的平面,则下列 叙述正确的是( )①若 ④若A . ①② B . ③④ C . ①③ D . ②④,则 ,则;②若 .,则;③若第 3 页 共 11 页,则;11. (2 分) (2019 高一下·辽源期末) 点 M(4,m)关于点 N(n, - 3)的对称点为 P(6,-9)则( ) A . m=-3,n=10 B . m=3,n=10 C . m=-3, n=5 D . m =3, n = 512. (2 分) (2019 高一下·辽源期末) 数列{an}的通项公式 an= 为( ).,若{an}前 n 项和为 24,则 nA . 25B . 576C . 624D . 625二、 填空题 (共 4 题;共 5 分)13. (1 分) (2016 高一上·无锡期末) 若函数 f(x)=x2﹣ax+2a﹣4 的一个零点在区间(﹣2,0)内,另一 个零点在区间(1,3)内,则实数 a 的取值范围是________.14. (1 分) (2018·广元模拟) 设变量 ________.满足约束条件:,则目标函数的最小值为15. (2 分) (2018 高一上·兰州期末) 如图,在四面体 A-BCD 中,已知棱 AC 的长为 1,则二面角 A-CD-B 的平面角的余弦值为________.,其余各棱长都为16. (1 分) (2019 高一下·辽源期末) 公比为 2 的等比数列 的各项都是正数,且第 4 页 共 11 页,则 的值为________三、 解答题 (共 6 题;共 50 分)17. (10 分) 已知抛物线 (1) 求抛物线 的方程;在第一象限内的点到焦点 F 的距离为 .(2) 若直线 与抛物线 C 相交于 A,B 两点,与圆相交于 D,E 两点,O 为坐标原点,,试问:是否存在实数 a,使得|DE|的长为定值?若存在,求出 a 的值;若不存在,请说明理由.18. (10 分)(1) 设直线 方程;的方程为.若直线 在两坐标轴上的截距相等,求直线 的(2) 过直线 : 直线 的方程.上的点作直线 ,若直线 , 与 轴围成的三角形的面积为 2,则19. (10 分) (2020·海南模拟) 已知椭圆 :的左、右焦点分别为 , ,左顶点为 ,满足,其中 为坐标原点, 为椭圆 的离心率.(1) 求椭圆 的标准方程;(2) 过 的直线 与椭圆 交于 , 两点,求面积的最大值.20. (10 分) (2019 高二下·上海月考) 已知椭圆的焦点为圆上一点,且是,的等差中项.(1) 求椭圆方程;(2) 如果点 在第二象限且,求,,( ) , 为椭的值.21. (5 分) (2020 高二下·北京期中) 已知是曲线上动点以及定点,(1) 当时,求曲线在点 处的切线方程;第 5 页 共 11 页(2) 求面积的最小值,并求出相应的点的坐标.22. (5 分) (2019 高一下·辽源期末) 在如图所示的几何体中,D 是 AC 的中点,EF∥DB.(Ⅰ)已知 AB=BC,AE=EC.求证:AC⊥FB; (Ⅱ)已知 G,H 分别是 EC 和 FB 的中点.求证:GH∥平面 ABC.第 6 页 共 11 页一、 单选题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 5 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 6 题;共 50 分)17-1、17-2、 18-1、18-2、第 8 页 共 11 页19-1、19-2、 20-1、第 9 页 共 11 页20-2、21-1、21-2、第 10 页 共 11 页22-1、第11 页共11 页。
最新版四川省遂宁市高一下学期6月月考试卷 数学 Word版含答案

射洪中学2015级高一第三学月考试数 学本试卷分选择题和非选择题两部分,满分150分,考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名,考籍号填写在答题卡规定的位置上;2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦拭干净后,再选涂其他答案标号;3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上;4.所有题目必须在答题卡上做答,在试题卷上答题无效;5.考试结束后,只将答题卡交回.第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.1.若a =(2,3),b =(4,-1+y ),且a ∥b ,则y =( )A.6B.5C.7D.8211两数的等比中项是 ( )A .1B .1-C .12D .1± 3.若a 、b 、c ∈R ,a >b ,则下列不等式成立的是 ( )A.1a <1bB.a 2>b 2C.ac 2+1>b c 2+1 D.| a |>| b |4.已知等差数列}{n a 中,12497,1,16a a a a 则==+的值是( )A.15B.30C.31D.645.平面区域⎩⎪⎨⎪⎧ x +y ≥2,x ≤1,y ≤2的面积是( ) A .14B .12C .1 D .26.在△ABC 中,tan A +tan B +3=3tan A tan B ,则C 等于( )A.π3B.2π3C.π6D.π47.在ABC ∆中, ∠A,∠B,∠C 所对的边分别为a , b , c .若 30,8,5=∠==A b a ,则∠B的 解的个数是 ( )A.0个B.1个C.2个D.不确定的8.函数()()()sin 10sin 70f x x x =+++的最大值是 ( )9.某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为( )A .2sin α-2cos α+2B .sin α-3cos α+3C .3sin α-3cos α+1D .2sin α-cos α+110.若O 是△ABC 所在平面内一点,且满足|OB →-OC →|=|OB →+OC →-2OA →|,则△ABC 一定是( )A .等边三角形B .直角三角形C .等腰三角形D .等腰直角三角形11.已知等比数列{}n a 的首项11a =,公比2q =,等差数列{}n b 的首项13b =,公差3d =,在{}n a 中插入{}n b 中的项后从小到大构成新数列{}n c ,则{}n c 的第100项为( )A.270B.273C.276D.27912.对于一个有限数列12(,,,)n p p p p =⋅⋅⋅,p 的蔡查罗和(蔡查罗是一位数学家)定义为121()n S S S n++⋅⋅⋅+,其中12(1,)k k S p p p k n k N =++⋅⋅⋅+∈≤≤.若一个99项的数列(1299,,,)p p p ⋅⋅⋅的蔡查罗和为1000,那么100项数列1299(9,,,,)p p p ⋅⋅⋅的蔡查罗和为( )A.991B.992C.993D.999第II 卷(非选择题,共90分)二、填空题:本大题共4小题,每小题4分,共16分。
遂宁市高中2015-2016学年高一下学期教学水平监测(期末)数学试题含答案

遂宁市高中2018级第二学期教学水平监测数 学 试 题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
总分150分。
考试时间120分钟.第Ⅰ卷(选择题,满分60分)注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上.并检查条形码粘贴是否正确。
2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.对于数列,,,,a a a a 下列说法正确的是A .一定为等差数列B .一定为等比数列C .既是等差数列,又是等比数列D .以上都不正确 2.下列结论正确的是A .若a b >,则ac bc >B .若a b >,则22a b >C .若0a b <<,则22aab b >>D .若0a b <<,则11a b <3.计算cos18°cos42°-cos72°cos48°等于A.12- B .12C . D4.二次不等式20ax bx c ++<的解集是空集的条件是A.20,40.a b ac >⎧⎨-≤⎩B 。
20,40.a b ac >⎧⎨-<⎩C 。
20,40.a b ac <⎧⎨-≥⎩D.20,40.a b ac <⎧⎨-<⎩ 5.在ABC ∆中,若cos cos a A b B =,则ABC ∆的形状为A 。
等腰三角形B 。
直角三角形C 。
等腰直角三角形 D. 等腰或直角三角形6.下列结论正确的是A. 两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱B 。
四川省遂宁市高一数学下学期期末统考试题-人教版高一全册数学试题

某某省某某市2014-2015学年高一数学下学期期末统考试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
总分150分。
考试时间120分钟。
第Ⅰ卷(选择题,满分50分)注意事项:1.答题前,考生务必将自己的某某、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。
并检查条形码粘贴是否正确。
2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题(本大题共10小题,每题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求) 1. 数列23、39-、427、581-,…的一个通项公式是 A. (1)n -13n n + B. 11(1)3n nn ++- C. (1)3nnn-D. 1(1)3n nn +- 2. 0sin 75的值等于A.4 B. 43. 已知(2,1)a =,(,2)b x =-,若a b ⊥,则x =A. -4B. -1C. 1D.4 4. 在等差数列{}n a 中,已知4816a a +=,则该数列前11项和11S =A. 58B. 88C. 143D. 176 5. 已知4(,0),cos 25x x π∈-=,则tan 2x =A.724 B. 724- C. 247 D. 247- 6. 已知0,10,a b <-<<则有A. 2ab ab a >> B. 2ab ab a >> C. 2ab a ab >> D. 2a ab ab >> 7. 函数22631y x x =++的最小值是 A .32-3 B .-3 C .6 2 D .62-38. 在ABC ∆中,cos(2)2sin sin 0B C A B ++<,则ABC ∆的形状为A.锐角三角形B.钝角三角形C.直角三角形D.不确定 9. 如图设,P Q 为ABC ∆内的两点,且21,55AP AB AC =+ 2134AQ AB AC =+, 则ABP ∆的面积与ABQ ∆的面积之比为 A. 45 B. 15C. 14D. 1310. 已知数列{}n a 满足11211,41n na a a +=+=,令221n n n b a a +=,n S 是数列{}n b 的前n 项和,若16n m S >对任意n N *∈恒成立,则整数m 的最大值为 A. 1B. 2 C . 3D. 4第Ⅱ卷(非选择题,满分100分)注意事项:1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
四川省遂宁市高一下学期期末数学试卷

四川省遂宁市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共16分)1. (1分) (2018高三上·云南月考) 已知,则 =________;2. (1分) (2018高二上·嘉兴月考) 已知点A(2,1),B(-2,3),C(0,1),则△ABC中,BC边上中线所在的直线方程为________.3. (1分)(2018·商丘模拟) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲,1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2018这2017个整数中能被2除余1且被3除余1的数按由小到大的顺序排成一列,构成数列,则此数列的项数为________.4. (1分)过点(5,2),且在x轴上截距是在y轴上截距的2倍的直线方程是________.5. (1分)(2017·浦东模拟) 不等式≥2的解集是:________.6. (1分) (2015高一下·南阳开学考) 如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是________.7. (2分) (2016高二上·温州期中) 一个几何体的三视图如图所示(单位:cm),则该几何体的体积是________ cm3 ,该几何体的表面积是________ cm2 .8. (1分)(2014·天津理) 在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b﹣c= a,2sinB=3sinC,则cosA的值为________.9. (1分) (2016高一下·惠阳期中) 已知数列{an}的前n项和Sn=n2+n+1,那么它的通项公式为an=________10. (2分) (2018高二下·温州期中) 如下图,正方体棱长为 ,分别为的中点,则在底面上投影的面积是________;四棱锥的体积是________.11. (1分) (2016高一下·扬州期末) 已知l,m,n为两两不重合的直线,α,β,γ为两两不重合的平面,给出下列四个命题:①若α∥β,l⊂α,则l∥β;②若α⊥γ,β⊥γ,则α⊥β;③若m⊄α,n⊂α,m∥n,则m∥α;④若m⊂α,n⊂α,m∥β,n∥β,则α∥β.其中命题正确的是________.(写出所有正确结论的序号)12. (1分) (2017高一上·泰州月考) 函数在上是增函数,则实数的取值范围是________.13. (1分) (2020高一上·石景山期末) 已知,且,则的最大值为________.14. (1分) (2016高一下·长春期中) 在等差数列{an}中,a5+a10+a15+a20=20,则S24=________.二、解答题 (共6题;共50分)15. (5分) (2016高二下·浦东期末) 已知直线l平行于直线3x+4y﹣7=0,并且与两坐标轴围成的三角形的面积为24,求直线l的方程.16. (5分)已知sinα=,sinβ=,且α、β为锐角,求α+β的值.17. (10分) (2017高三上·连城开学考) 如图,己知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且=λ(0<λ<1)(1)求证:不论λ为何值,总有EF⊥平面ABC:(2)若λ= ,求三棱锥A﹣BEF的体积.18. (10分) (2019高三上·上海月考) 问题:正数、满足,求的最小值.其中一种解法是:,当且仅当且时,即且时取等号.学习上述解法并解决下列问题:(1)若实数、、、满足,试比较和的大小,并指明等号成立的条件;(2)利用(1)的结论,求函数的值域.19. (10分) (2016高二上·商丘期中) 如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点,∠BPC=90°.(1)若PB= ,求PA;(2)若∠APB=150°,求tan∠PBA.20. (10分) (2016高二上·宜昌期中) 已知{an}是等差数列,{bn}是等比数列,Sn为数列{an}的前n项和,a1=b1=1,且b3S3=36,b2S2=8(n∈N+).(1)求an和bn;(2)若an<an+1,求数列的前n项和Tn.参考答案一、填空题 (共14题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共50分) 15-1、16-1、17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、。
四川省遂宁市高一下学期数学期末考试试卷

四川省遂宁市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高一下·黄冈期末) 函数y=asinx﹣bcosx的一条对称轴为x= ,则直线l:ax﹣by+c=0的倾斜角为()A . 45°B . 60°C . 120°D . 135°2. (2分) (2016高二上·自贡期中) 直线ax+y﹣1=0与直线2x+3y﹣2=0垂直,则实数a的值为()A .B . ﹣1C . ﹣2D . ﹣3. (2分)某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。
为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为A . 9B . 18C . 27D . 364. (2分)执行下面的框图,若输出结果为1,则可输入的实数x值的个数为()A . 1B . 2C . 3D . 45. (2分)(2017·漳州模拟) 已知点P的坐标(x,y)满足过点P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为()A .B .C .D .6. (2分)为了解某大学的学生是否爱好体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:男女总计爱好a b73不爱好c25总计74则a﹣b﹣c等于()A . 6B . 7C . 8D . 97. (2分) (2017高二上·大庆期末) 从装有黑球和白球各2个的口袋内任取2个球,那么互斥而不对立的两个事件是()A . 至少有1个黑球,至少有1个白球B . 恰有一个黑球,恰有2个白球C . 至少有一个黑球,都是黑球D . 至少有1个黑球,都是白球8. (2分)已知三点,则外接圆的圆心到原点的距离为()A .B .C .D .9. (2分)设随机变量,且则P等于()A . 0.1B . 0.2C . 0.3D . 0.410. (2分)某程序框图如图1所示,该程序运行后输出的值是()A . 63B . 31C . 27D . 1511. (2分)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()A .B .C .D .12. (2分) (2016高二上·射洪期中) 已知直线l1:x+y+1=0,l2:x+y﹣1=0,则l1 , l2之间的距离为()A . 1B .C .D . 2二、填空题 (共5题;共5分)13. (1分)将十进制数34化为二进制数,结果为________14. (1分)袋子中装有分别标注数字为1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出两个小球,则取出的小球上标注的数字之和为5或7的概率是________.15. (1分)(2016·浦城模拟) 如果实数x,y满足条件,则z= 的最小值为________.16. (1分)入射光线沿直线x﹣2y+3=0射向直线l:y=x被直线反射后的光线所在的方程是________.17. (1分) (2018高二下·泰州月考) 若的方差为3,则的方差为________.三、解答题 (共5题;共50分)18. (5分)已知直线l1:mx+8y+n=0与l2:2x+my﹣1=0互相平行,且l1 , l2之间的距离为,求直线l1的方程.19. (10分)设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:(1) 1个孩子显露显性特征的概率是多少?(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?20. (5分)关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料x1234y0.51 1.53试用最小二乘法求出y关于x的线性回归方程参考公式:用最小二乘法求线性回归方程系数公式:.21. (15分) (2016高二上·河北期中) 甲、乙两位学生参加数学竞赛培训,他们在培训期间8次模拟考试的成绩如下:甲:82 81 79 78 95 88 93 84乙:92 95 80 75 83 80 90 85(1)画出甲、乙两位学生成绩的茎叶图,并求学生乙成绩的平均数和方差;(2)从甲同学超过80分的6个成绩中任取两个,求这两个成绩中至少有一个超过90分的概率.(3)甲同学超过80(分)的成绩有82 81 95 88 93 84,22. (15分) (2017高一下·赣州期末) 已知直线l的方程为(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.(1)求证:直线l恒过定点;(2)当m变化时,求点P(3,1)到直线l的距离的最大值;(3)若直线l分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题;共5分)13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共50分)18-1、19-1、19-2、20-1、21-1、21-2、21-3、22-1、22-2、22-3、。
四川省遂宁高一下学期期末考试数学试题

高中部2016年上期期末校考高2015级数学试题一、选择题:本大题共12小题,每小题5分,共60分.1.一几何体的直观图如图,下列给出的四个俯视图中正确的是()2.已知()()1,2,,1a b x ==-,且a 与b 是共线向量,则x =( )A .1B .2C .12- D .123.化简cos 15°cos 30°-cos 75°sin 30°的值为( ) A.32 C ..- 32 4.设a b <<0,0<<c d ,则下列各不等式中恒成立的是 ( ) A. bd ac > B. db c a> C.d b c a +>+ D. d b c a ->-5.已知等比数列{a n }的前n 项和为S n ,若S 2n =4(a 1+a 3+a 5+…+a 2n -1),a 1a 2a 3=27,则a 6=( )A .27B .81C .243D .7296.已知实数x ,y 满足110220x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩,则2t x y =+的最小值是 ( )A. 1B.2C. 4D. 107.已知正方形ABCD 的边长为1, 点P 满足AP AC λ=,[0,1]λ∈则()AP PB PD ∙+的最大值是( )A. 1B. 12C.14D. 28.在C ∆AB 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若3πB =,且a ,b ,c 成等比数列,则C ∆AB 一定是( )A .不等边三角形B .钝角三角形C .等腰直角三角形D .等边三角形 9.{}n a 中,若()783sin 5a a =,则()215cos a a 的值是( )A .725- B .725C .45-D .45 10.一船向正北航行,看见正西方向相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( ).A .5海里B .10海里C .53海里D .103海里11.古希腊人常用小石子在沙滩上摆成各种形状来研究数, 例如:他们研究过图①中的1,3,6,10,...,由于这些数能表示成三角形,将其称为三角形数;类似地,将图②中的1,4,9,16,...,这样的数称为正方形数.下列数中既是三角形数又是正方形数的是. . .941. . .10631A .1225B .1024C .289D .1378 12.设a >b >0,则)(112b a a ab a -++的最小值是( ) A.1 B.2 C.3 D.4二、填空题:本大题共4小题,每小题5分,共20分. 13,在ABC ∆中,角,,A B C 对边分别为,,a b c .若6A π=,3,4a b ==,则sin sin a bA B+=+.14.已知数列{}na 的前n 项和12n n S =+,则n a = . 15.若一元二次方程2(1)0mx m x m --+=有两个不等实根,则m 的取值范围应是 . 16.在钝角△ABC 中,∠A 为钝角,令AB AC ==,a b ,若()AD x y x y =+∈R ,a b .现给出下面结论:① 当1133x y ==,时,点D 是△ABC 的重心; ② 记△ABD ,△ACD 的面积分别为ABDS ∆,ACDS∆,当4355x y ==,时,34ABD ACD S S ∆∆=;③ 若点D 在△ABC 内部(不含边界),则12y x ++的取值范围是1(1)3,; ④ 若AD AE λ=,其中点E 在直线BC 上,则当43x y ==,时,5λ=. 其中正确的有 (写出所有正确结论的序号).三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图.右边两个是其正(主)视图和侧(左)视图.(1)请在正(主)视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程).(2)求该多面体的体积(尺寸如图).18.(本小题满分12)在∆ABC中,222+=+a c b . (1)求B ∠ 的大小;(2)cos cos A C + 的最大值.19.(本小题满分12分)在平面直角坐标系xOy 中,已知)1,2(=a ,25||=b .(I)若b ∥a ,求b 的坐标;(II)若b a +与b a 52-垂直,求a 与b 的夹角θ的大小.20.(本小题满分12分)已知函数22()cos(2)2cos 3f x x x kπ=-++最小值为3- (1)求常数k 的值(2)若07()5f x =-,00,4x π⎡⎤∈⎢⎥⎣⎦求0cos 2x 的值21.设数列{}n a 的前n 项和为n S ,已知2112121,,*33n n S a a n n n N n +==---∈. (1)求2a 的值;(2)求数列{}n a 的通项公式;22.(本小题满分12分)(本小题满分12分)已知函数2()(1)1()f x ax a x b a b =-++-∈R ,. (1) 若1a =,关于x 的不等式()6f x x ≥在区间[13],上恒成立,求b 的取值范围;(2) 若0b =,解关于x 的不等式()0f x <;(3) 若(1)(1)0f f ⋅->,且22a b --<,求22(2)a b a b +-+的取值范围.遂宁市卓同教育高中部2016年上期期末校考高2015级文科数学答案1*3,12,2,n n n a n n N -=⎧=⎨≥∈⎩17.【解】(1)(4分)作出俯视图如图所示.(2)(6分)依题意,V E -A 1B 1D 1 =13·S △A 1B 1D 1 ·A 1E =13×()12×2×2×1=23, 正方体体积V正方体AC 1 =23=8,所以所求多面体的体积V =8-23=223.18【答案】(1)4π;(2)1.cos()4A A A π==-,因为304A π<∠<,所以当4A π∠=时,cos A C +取得最大值1. 19.解:(1)5||= ,5||b =,1||||2b a =,又//b a 11(1,)22b a ∴=±=±,1(1,)2b ∴=或1(1,)2b =--. --------------6分(2)a b +与25a b -垂直, ()(25)0a b a b ∴+⋅-=2252||35||0,4a a b b a b ∴-⋅-=∴⋅=1cos 2||||a b a b θ⋅∴==--------------10分[0]θπ∈,3πθ∴=--------------------12分20.解:(1)11cos2()2cos22222xf x x x k+=-+⨯+12cos212x x k+++ =sin(2x +6π)+1+k ,∴ f (x )min =-1+1+k =-3,解得k =-3.……………………………………………………5分 (2)∵ f (x )= sin(2x +6π)-2.∴ f (x 0)= sin(2x 0+6π)-2=57-,即sin(2x 0+6π)=53.…………………………………6分 ∵0x ∈]40[π,,∴ 2x 0+6π∈]326[ππ,. ∵ 若2x 0+6π∈]26[ππ,,则sin(2x 0+6π)∈[21, 1], 若2x 0+6π∈]322[ππ,,则sin(2x 0+6π)∈[23,1],显然53∈[21,1],且53∉[23,1],∴ 2x 0+6π∈]26[ππ,.∴ cos(2x 0+6π)=)62(sin 102π+-x =54,…………………………………………10分∴ cos2x 0= cos[(2x 0+6π)-6π]= cos(2x 0+6π) cos6π+ sin(2x 0+6π) sin6π=54×23+53×21 =10334+. ……12分21试题分析(1)令1n =,得1121222133S a a ==---把11a =代入,解得24a =…………4分 (2)由2121233n n S a n n n +=---,得32112233n n S na n n n+=---………………①……6分 3212122(1)(1)(1)33n n S na n n n ++=-+-+-+……………② ②-①化得211,(*)21n n a a n N n n ++-=∈++。
四川省遂宁市高一下学期数学期末统一考试试卷

四川省遂宁市高一下学期数学期末统一考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共12分)1. (1分)设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则=A . {4,5}B . {2,3}C . {1}D . {3}2. (1分)(2017·赣州模拟) sin15°+cos165°的值为()A .B .C .D .3. (1分)下列函数中,满足“对任意的当时,都有”的是()A .B .C .D .4. (1分) (2016高一上·温州期末) 已知平面向量,且,则可能是()A . (2,1)B . (﹣2,﹣1)C . (4,﹣2)D . (﹣1,﹣2)5. (1分)已知定义在R上的函数f(x)满足且, ,则()A . -2B . -1C . 0D . 16. (1分)则=()A . 1B . 4C . 2D . 87. (1分)(2018·河北模拟) 已知等比数列中,,,则()A .B . -2C . 2D . 48. (1分)设m,n是两条不同的直线,是两个不同的平面,则下列命题正确的是()A . 若m⊥n,m⊥α,n∥β,则α∥βB . 若m∥α,n∥β,α∥β则m∥nC . 若m∥n,m∥α,n∥β则α∥βD . 若m⊥α,n∥β,α∥β,则m⊥n9. (1分) (2018高一下·宁夏期末) 已知,则()A .B .C .D .10. (1分) (2018高三上·泸州模拟) 如图,网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为()A . 16B . 8C . 4D . 2011. (1分) (2019高三上·郑州期中) 已知中,,延长交于,则()A .B .C .D .12. (1分) (2017高一下·正定期末) 已知定义在上的函数满足,当时,,其中,若方程恰有3个不同的实数根,则的取值范围为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高三上·苏州期中) 已知tanα=﹣,则tan(α﹣)=________.14. (1分) (2019高二上·上海月考) 在数列-1,0,,…中,0.08是它的第________项.15. (1分)(2017·鞍山模拟) 已知四面体ABCD,AB=4,AC=AD=6,∠BAC=∠BAD=60°,∠CAD=90°,则该四面体外接球半径为________.16. (1分) (2018高一下·定远期末) 已知数列与满足,,,若,对一切恒成立,则实数的取值范围是________.三、解答题 (共6题;共13分)17. (1分) (2019高一上·武功月考) 已知集合,集合 ,求:(1) ;(2)(3).18. (2分)(2017高二上·汕头月考) 在中,角所对的三边分别为,(1)求;(2)求的面积19. (2分) (2016高一下·黄冈期末) 设数列{an}满足a1+3a2+32a3+…+3n﹣1an= ,n∈N* .(1)求数列{an}的通项;(2)设,求数列{bn}的前n项和Sn.20. (3分) (2016高二上·武邑期中) 如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D 是BC的中点.(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与ABA1所成二面角的正弦值.21. (2分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示(1)求函数f(x)的解析式并写出其对称中心;(2)若g(x)的图象与f(x)的图象关于直线x=4对称,当x∈[2,8],求g(x)的最大值和最小值.22. (3分) (2015高一上·雅安期末) 已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.(1)判断f(x)的单调性,并加以证明;(2)解不等式;(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.参考答案一、单选题 (共12题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共13分) 17-1、17-2、17-3、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年四川省遂宁市高一(下)期末数学试卷一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.(5分)对于数列a,a,a,…a下列说法正确的是()A.一定为等差数列B.一定为等比数列C.既是等差数列,又是等比数列D.以上都不正确2.(5分)下列结论正确的是()A.若a>b,则ac>bc B.若a>b,则a2>b2C.若a<b<0,则a2>ab>b2D.若a<b<0,则<3.(5分)计算cos18°cos42°﹣cos72°cos48°=()A.B.C.D.4.(5分)二次不等式ax2+bx+c<0的解集是空集的条件是()A.B.C.D.5.(5分)在△ABC中,若acosA=bcosB,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形 D.等腰或直角三角形6.(5分)下列结论正确的是()A.两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱B.若△ABC中,•<0,则△ABC是钝角三角形C.函数f(x)=x+(x>1)的最小值为5D.若G2=ab,则G是a,b的等比中项7.(5分)在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔(古称浮屠),本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯?你算出的结果是()A.6 B.5 C.4 D.38.(5分)已知x,y满足约束条件,则z=﹣2x+y的最大值是()A.﹣1 B.﹣2 C.﹣5 D.19.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2﹣b2)tanB=ac,则角B的值为()A.B.C.或D.或10.(5分)已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣11.(5分)已知O是△ABC内部一点,++=,•=2且∠BAC=60°,则△OBC的面积为()A.B.C.D.12.(5分)存在正实数b使得关于x的方程sinx+cosx=b的正根从小到大排成一个等差数列,若点P(6,b)在直线nx+my﹣2mn=0上(m,n均为正常数),则m+4n的最小值为()A.5+2B.4 C.8 D.7+4二、填空题(本题共4小题,每小题5分,共20分)13.(5分)正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=.14.(5分)如图是一个空间几何体的三视图,则该几何体的体积大小为.15.(5分)在等腰△ABC中,∠BAC=90°,AB=AC=2,=2,=3,则在方向上的投影.16.(5分)已知数列{a n}满足a1=﹣1,a2>a1,|a n+1﹣a n|=2n(n∈N*),若数列{a2n}单调递减,数列{a2n}单调递增,则数列{a n}的通项公式为a n=.﹣1三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)已知向量=(1,2),向量=(x,﹣2),且⊥(﹣)(Ⅰ)求|3+|;(Ⅱ)若向量﹣λ与2+平行,求λ的值.18.(12分)已知公差不为零的等差数列{a n}中,a3=7,且a1,a4,a13成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.19.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(Ⅰ)求实数a,b的值;(Ⅱ)解关于x的不等式(ax﹣b)(x﹣c)>0(c为常数).20.(12分)已知=(2sinx,cos2x),=(cosx,2),函数f(x)=•﹣.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f(﹣)=,且sinB+sinC=,求△ABC的面积.21.(12分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.22.(12分)已知数列{a n}的前n项和是S n,且S n=2a n﹣n(Ⅰ)求证:数列{a n+1}为等比数列;并求数列{a n}的通项公式a n;(Ⅱ)数列{b n}满足b n=,求数列{b n}的前n项和T n;(Ⅲ)若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.2015-2016学年四川省遂宁市高一(下)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.(5分)对于数列a,a,a,…a下列说法正确的是()A.一定为等差数列B.一定为等比数列C.既是等差数列,又是等比数列D.以上都不正确【解答】解:对于数列a,a,a,…a,一定是公差为0等差数列,当a≠0时,此数列也是等比数列.故只有A正确.故选:A.2.(5分)下列结论正确的是()A.若a>b,则ac>bc B.若a>b,则a2>b2C.若a<b<0,则a2>ab>b2D.若a<b<0,则<【解答】解:对于A,c=0时,不成立,对于B,令a=﹣1,b=﹣2,显然不成立,对于C,根据不等式的性质,显然成立,对于D,令a=﹣2,b=﹣1,显然不成立,故选:C.3.(5分)计算cos18°cos42°﹣cos72°cos48°=()A.B.C.D.【解答】解:原式=.故选:B.4.(5分)二次不等式ax2+bx+c<0的解集是空集的条件是()A.B.C.D.【解答】解:若二次不等式ax2+bx+c<0的解集是空集,即二次不等式ax2+bx+c≥0在R恒成立,故,故选:A.5.(5分)在△ABC中,若acosA=bcosB,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形 D.等腰或直角三角形【解答】解:由正弦定理asinA=bsinB化简已知的等式得:sinAcosA=sinBcosB,∴sin2A=sin2B,∴sin2A=sin2B,又A和B都为三角形的内角,∴2A=2B或2A+2B=π,即A=B或A+B=,则△ABC为等腰或直角三角形.故选:D.6.(5分)下列结论正确的是()A.两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱B.若△ABC中,•<0,则△ABC是钝角三角形C.函数f(x)=x+(x>1)的最小值为5D.若G2=ab,则G是a,b的等比中项【解答】解:对于A,有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故A错;对于B,若△ABC中,•<0,即为||•||cos(π﹣B)<0,则cosB>0,B为锐角,不能确定三角形的形状,故B错;对于C,函数f(x)=x+(x>1)=(x﹣1)++1≥2+1=5,当且仅当x﹣1=,即x=3,取得等号,则f(x)的最小值为5,故C正确;对于D,若G=a=b=0,满足G2=ab,则G不为a,b的等比中项,故D错.故选:C.7.(5分)在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔(古称浮屠),本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯?你算出的结果是()A.6 B.5 C.4 D.3【解答】解:设塔顶的a1盏灯,由题意{a n}是公比为2的等比数列,∴S7==381,解得a1=3.故选:D.8.(5分)已知x,y满足约束条件,则z=﹣2x+y的最大值是()A.﹣1 B.﹣2 C.﹣5 D.1【解答】解:由已知不等式组表示的平面区域如图阴影部分,当直线y=2x+z经过A时使得z最大,由得到A(1,1),所以z的最大值为﹣2×1+1=﹣1;故选:A.9.(5分)在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2﹣b2)tanB=ac,则角B的值为()A.B.C.或D.或【解答】解:由∴,即∴,又在△中所以B为或故选:D.10.(5分)已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣【解答】解:∵α∈(0,),β∈(﹣,0),∴α﹣β∈(0,π),又cos(α﹣β)=,sinβ=﹣,∴sin(α﹣β)==,cosβ==,则sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ=×+×(﹣)=.故选:A.11.(5分)已知O是△ABC内部一点,++=,•=2且∠BAC=60°,则△OBC的面积为()A.B.C.D.【解答】解:∵∴∴O为三角形的重心∴△OBC的面积为△ABC面积的∵∴∵∠BAC=60°∴△ABC面积为=∴△OBC的面积为故选:A.12.(5分)存在正实数b使得关于x的方程sinx+cosx=b的正根从小到大排成一个等差数列,若点P(6,b)在直线nx+my﹣2mn=0上(m,n均为正常数),则m+4n的最小值为()A.5+2B.4 C.8 D.7+4【解答】解:由sinx+cosx=b,可得:2=b存在正数b,使得方程sinx+cosx=b的正根从小到大排成一个等差数列,即有0<b≤2.若0<b<2,由y=sin(x+)的图象可得:直线y=b与函数y=2sin(x+)的图象的交点的横坐标不成等差数列,若b=2,即有x+=2kπ+,即为x=2kπ+,k∈Z,可得所有正根从小到大排成一个等差数列,公差为2π.由点P(6,2)在直线直线nx+my﹣2mn=0上(m,n均为正常数),∴6n+2m﹣2mn=0,化为:=1.则m+4n=(m+4n)=7+≥7+2=7+4,当且仅当m=2n=3+2时取等号.故选:D.二、填空题(本题共4小题,每小题5分,共20分)13.(5分)正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=4.【解答】解:由正项等比数列{a n}中,可得a2a98=16=a3a97,∴正项等比数列{a n}中,若a2a98=16,则log2(a3a97)=log216=4.故答案为:4.14.(5分)如图是一个空间几何体的三视图,则该几何体的体积大小为.【解答】由三视图可知,该几何体时一个边长为2,2,1的长方体挖去一个半径为1的半球.所以长方体的体积为2×2×1=4,半球的体积为,所以该几何体的体积为.故答案为:.15.(5分)在等腰△ABC中,∠BAC=90°,AB=AC=2,=2,=3,则在方向上的投影.【解答】解:如图,以A为坐标原点建立如图所示的平面直角坐标系,∵AB=AC=2,=2,=3,∴A(0,0),B(2,0),C(0,2),则D(1,1),E(0,),∴.则,||=.∴在方向上的投影为.故答案为:.16.(5分)已知数列{a n}满足a1=﹣1,a2>a1,|a n+1﹣a n|=2n(n∈N*),若数列{a2n﹣1}单调递减,数列{a2n}单调递增,则数列{a n}的通项公式为a n=.【解答】解:方法一:先采用列举法得a1=﹣1,a2=1,a3=﹣3,a4=5,a5=﹣11,a6=21,…,然后从数字的变化上找规律,得,∴a n=(a n﹣a n﹣1)+(a n﹣1﹣a n﹣2)+…+(a2﹣a1)+a1=(﹣1)n•2n﹣1+(﹣1)n﹣1•2n﹣2+…﹣22+2﹣1==.方法二:∵,,∴,而{a2n﹣1}递减,∴a2n+1﹣a2n﹣1<0,故;同理,由{a2n}递增,得;又a2>a1,∴,以下同上.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)已知向量=(1,2),向量=(x,﹣2),且⊥(﹣)(Ⅰ)求|3+|;(Ⅱ)若向量﹣λ与2+平行,求λ的值.【解答】解:(Ⅰ)∵=(1,2),=(x,﹣2),∴=(1﹣x,4),由⊥(﹣),得(1,2)•(1﹣x,4)=1﹣x+8=0,∴x=9.则=(12,4),∴;(Ⅱ)∵=(1,2),=(9,﹣2),∴=(1﹣9λ,2+2λ),=(11,2).∵向量﹣λ与2+平行,∴(1﹣9λ)×2﹣11×(2+2λ)=0.解得:.18.(12分)已知公差不为零的等差数列{a n}中,a3=7,且a1,a4,a13成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.【解答】解:(Ⅰ)设数列{a n}的公差为d.∵,∴,解得:d=2或d=0(舍),∴a1=3,∴a n=2n+1(n∈N*);(Ⅱ)∵a n=2n+1,∴,∴=(n∈N*).19.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(Ⅰ)求实数a,b的值;(Ⅱ)解关于x的不等式(ax﹣b)(x﹣c)>0(c为常数).【解答】解:(1)由题意知1,b是关于x的方程ax2﹣3x+2=0的两根…(2分)将x=1代入方程得a﹣3+2=0,解得a=1,…(4分)从而原方程变为x2﹣3x+2=0,即(x﹣1)(x﹣2)=0,∴方程的另一个根为b=2;…(6分)(2)不等式为(x﹣2)(x﹣c)>0,当c>2时,不等式的解集为{x|x<2或x>c};当c=2时,不等式的解集为{x|x≠2,x∈R};当c<2时,不等式的解集为{x|x<c或x>2}.…(12分)20.(12分)已知=(2sinx,cos2x),=(cosx,2),函数f(x)=•﹣.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f(﹣)=,且sinB+sinC=,求△ABC的面积.【解答】解:(Ⅰ)由题意,函数f(x)=•﹣.可得f(x)=2sinxcosx+2cos2x﹣=sin2x+cos2x=2sin(2x+)∴f(x)的最小正周期为T=.(Ⅱ)已知锐角A满足f(﹣)=,可得2sin[2(﹣)+]=,即2sinA=又∵A为锐角,∴A=.又∵a=7,sinB+sinC=,由正弦定理可得:sinB=,sinC=,∴+=,可得:b+c=13由余弦定理可知,cosA===.可求得:bc=40.=bcsinA=.故得S△ABC21.(12分)如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.(1)若a=1.5,问:观察者离墙多远时,视角θ最大?(2)若tanθ=,当a变化时,求x的取值范围.【解答】解:(1)如图,作CD⊥AF于D,则CD=EF,设∠ACD=α,∠BCD=β,CD=x,则θ=α﹣β,在Rt△ACD和Rt△BCD中,tanα=,tanβ=,则tanθ=tan(α﹣β)==(x>0),令u=,则ux2﹣2x+1.25u=0,∵上述方程有大于0的实数根,∴△≥0,即4﹣4×1.25u2≥0,∴u≤,即(tanθ)max=,∵正切函数y=tanx在(0,)上是增函数,∴视角θ同时取得最大值,此时,x==,∴观察者离墙米远时,视角θ最大;(2)由(1)可知,tanθ===,即x2﹣4x+4=﹣a2+6a﹣4,∴(x﹣2)2=﹣(a﹣3)2+5,∵1≤a≤2,∴1≤(x﹣2)2≤4,化简得:0≤x≤1或3≤x≤4,又∵x>1,∴3≤x≤4.22.(12分)已知数列{a n}的前n项和是S n,且S n=2a n﹣n(Ⅰ)求证:数列{a n+1}为等比数列;并求数列{a n}的通项公式a n;(Ⅱ)数列{b n}满足b n=,求数列{b n}的前n项和T n;(Ⅲ)若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.【解答】解:(Ⅰ)证明:当n=1时,s1=2a1﹣1=a1,∴a1+1=2≠0 …(1分)当n≥2时,∵S n=2a n﹣n,∴s n﹣1=2a n﹣1﹣(n﹣1),两式相减∴a n=2a n﹣2a n﹣1﹣1,∴a n=2a n﹣1+1,∴a n+1=2(a n﹣1+1)…(3分)∴数列{a n+1}是首项和公比都是2的等比数列,得a n+1=2n⇒a n=2n﹣1…(4分)(Ⅱ)可得b n==,T n=+n×=1×+…+(n﹣2)+(n﹣1)+n×,两式相减得=2﹣∴…(8分)(Ⅲ)不等式(﹣1)nλ<T n+对一切n∈N*恒成立⇔不等式(﹣1)nλ<4﹣对一切n∈N*恒成立由为递增函数.…(9分)若n为偶数,则λ<f(2)=3,∴λ<3 …(10分)若n为奇数,则﹣λ<f(1)=2,∴﹣λ<2,λ>﹣2 …(11分)∴﹣2<λ<3 …(12分)赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
