实数复习框架图(新人教版八年级上)
实数学习的的学习的知识结构图.doc

实数知识结构图实数的概念及分类1、实数的分类实数有理数正有理数零负有理数正无理数有限小数和无限循环小数无理数无限不循环小数负无理数2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一实质,归纳起来有四类:( 1)开方开不尽的数,如7, 3 2 等;π( 2)有特定意义的数,如圆周率π,或化简后含有π的数,如+8 等;3(3)有特定结构的数,如 0.1010010001 等;(4)某些三角函数值,如 sin60o等。
实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果 a 与 b 互为相反数,则有a+b=0, a=-b,反之亦成立。
2、绝对值在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值。
可看成它的相反数,若|a|=a,则 a≥0;若 |a|=-a,则 a≤0。
( |a|≥0)。
零的绝对值是它本身,也3、倒数如果 a 与 b 互为倒数,则有ab=1,反之亦成立。
1 和 -1 的倒数等于本身。
零没有倒数。
4、数轴规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)实数与数轴的点是一一对应的。
平方根、算数平方根和立方根。
1、算术平方根:一般地,如果一个正数方根。
特别地,0 的算术平方根是0。
x 的平方等于a,即x2=a,那么这个正数x 就叫做 a 的算术平表示方法:记作“ a ”,读作根号a。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数 x 的平方等于 a,即 x2=a,那么这个数 x 就叫做 a 的平方根(或二次方根)。
表示方法:正数 a 的平方根记做“ a ”,读作“正、负根号a”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
3、开平方:求一个数 a 的平方根的运算,叫做开平方。
人教版八年级各章知识结构图
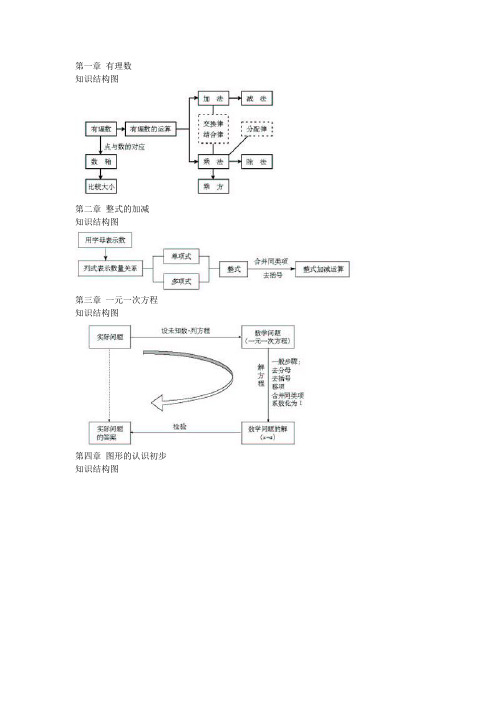
第一章有理数
知识结构图
第二章整式的加减
知识结构图
第三章一元一次方程知识结构图
第四章图形的认识初步知识结构图
第五章相交线与平行线知识结构图
第六章平面直角坐标系知识结构图
第七章三角形
知识结构图
第八章二元一次方程组
知识结构图
第九章不等式与不等式组
知识结构图
第十章数据的收集、描述与整理知识结构图
第十一章全等三角形知识结构图
第十二章轴对称
知识结构图
等十三章实数
知识结构图
第十四章一次函数知识结构图
第十五章整式的乘除与因式分解知识结构图
第十六章分式
知识结构图
第十七章反比例函数
知识结构图
第十八章勾股定理知识结构图
第十九章四边形
知识结构图
第二十章数据的分析知识结构图
第二十一章二次根式
知识结构图
第二十二章一元二次方程知识结构图
第二十三章旋转
知识结构图
第二十四章圆
知识结构图
第二十五章概率初步知识结构图
第二十六章二次函数知识结构图
第二十七章相似
知识结构图
第二十八章锐角三角函数知识结构图
第二十九章投影与视图知识结构图。
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
人教版八年级各章知识结构图

第一章有理数学问构造图
第二章整式的加减
学问构造图
第三章一元一次方程
学问构造图
第四章图形的相识初步
学问构造图
第五章相交线与平行线
学问构造图
第六章平面直角坐标系
学问构造图
第七章三角形
学问构造图
第八章二元一次方程组
学问构造图
第九章不等式与不等式组
学问构造图
第十章数据的搜集、描绘与整理
学问构造图
第十一章全等三角形
学问构造图
学问构造图
等十三章实数
学问构造图
第十四章一次函数
学问构造图
第十五章整式的乘除与因式分解学问构造图
第十六章分式
学问构造图
第十七章反比例函数
学问构造图
第十八章勾股定理
学问构造图
第十九章四边形
学问构造图
第二十章数据的分析
学问构造图
第二十一章二次根式
学问构造图
第二十二章一元二次方程
学问构造图
学问构造图
第二十四章圆
学问构造图
第二十五章概率初步
学问构造图
第二十六章二次函数
学问构造图
第二十七章相像
学问构造图
第二十八章锐角三角函数学问构造图
第二十九章投影与视图学问构造图。
2020人教版八上数学思维导图(史上最新最全)

整章内容预览,梳理知识脉络,学习记忆好帮手,复习补漏好工具 目录
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十一章 三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十二章 全等三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十三章 轴对称
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十四章 整式的公众号“数学资料库”,更多优质内容免费领。
第十五章 分式
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
人教版八年级数学上册知识点汇总(框架图)

人教版八年级数学上册知识点汇总(框架图)人民教育版,八年级,第一册,数学知识点总结第11章全等三角形同构:两个完全重合的图形称为同构全等三角形:两个完全重合的三角形称为全等三角形基本上定义相应的顶点:在全等三角形中互相重合的顶点称为相应的顶点对应边:全等三角形中的重叠边称为对应边对应角:在全等三角形中彼此重合的角称为对应角三角形的稳定性:当三角形的三条边的长度被确定时,三角形的形状和大小都被确定在。
这个性质叫做三角形的稳定性。
全等三角形的性质:全等三角形的对应边相等,对应角相等边和边:三条边对应于两个三角形的等价角边:两条边和夹角相等的三角形是全等的判断定理转角(ASA):两个三角形,其两个角和它们的夹紧边对应于相等的同余角边:两个角的对边相等的两个三角形,其中一个角是全等的斜边和直角边:斜边和直角边对应于两个相等的直角三角形的同余。
绘画:教科书第19页角平分线的性质定理:角平分线上的点到角两边的距离相等性质定理的逆定理:从角的内侧到角的两侧距离相等的点在角的平分线上1、明确已知命题并验证基本方法2,根据问题的含义画一个图形,并用数字符号来表示已知的和经过验证的3、经过分析,从已知中找出证明的方法,写出证明过程全等三角形第12章轴对称轴对称图形:如果一个图形是沿直线折叠的,则直线两侧的部分相互之间的重量为,该图形称为轴对称图形两个图形形成轴对称:一个图形沿某一条直线折叠,如果它能与另一个图形重合,那么这两个图形就称为关于直线对称基本概念线段的垂直平分线:穿过线段中点并垂直于线段的直线称为线段的垂直平分线等腰三角形:两条边相等的三角形称为等腰三角形两条相等的边叫做腰,另一边叫做底边,两条腰之间的角叫做顶角,底边和腰之间的角叫做底角等边三角形:三条边相等的三角形称为等边三角形1.无论是轴对称图形还是两个图形关于一条直线对称,的对称性质是轴是由任何一对对应点连接的线段的垂直平分线轴对2的基本性质,对称图相等轴对称1。
人教版初二数学上册重点高清思维导图
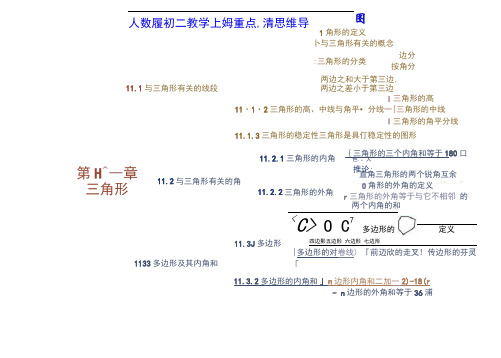
1角形的定义卜与三角形有关的概念I 三角形的高11・1・2三角形的高、中线与角平•分线一|三角形的中线I 三角形的角平分线 11.1.3三角形的稳定性三角形是具仃稳定性的图形<C> O C 7多边形的定义四边影五边形 六边形 七边形|多边形的对卷线) 『前迈欣的走叉! 传边形的芬灵「11.3.2多边形的内角和j n 边形内角和二加一2)-18(r- n 边形的外角和等于36浦人数履初二教学上姆重点,清思维导第H ^一章三角形11.2与三角形有关的角11.2.1三角形的内角色,、人推论;11.2.2三角形的外角{三角形的三个内角和等于180口直角三角形的两个锐角互余< __________________ u L ____________________________ __ 2_2 ________JO 角形的外角的定义r 三角形的外角等于与它不相邻 的两个内角的和:三角形的分类边分 按角分两边之和大于第三边, 11.1与三角形有关的线段两边之差小于第三边11.3J 多边形1133多边形及其内角和fl、11 J.1三角形的边不等边一:角形(三边都不相等)顶点用个大写字母来表示.如A、B、C等腰三角形(底边和腰不相等c的等腹三角形)按边分与三角形有关概念边AB.边BC、边AC角<rtA) /A, ZB,^2C三角形记作5等边三角形«(三边都相等)三角形分类△ ABC对角BC边的对角是/A百箱三角形锐角三角形L及詹金钝角三角形•对边NC的对边是BA.通常简记为c; 从三角形的一个顶点向它的对边所在直线 /X 做垂线,顶点和垂足之间的线段叫做三角 ,学一"形的高线,筒称三角形的高锐角三角形的高 锐角三角形的三条高交于同一点, ------ ---------- 「且在三角形的内部 Pi 在三角形中,一个内角的角平分线与它的Ax 对边相交,这个角的顶点与交点之间的线•7 3段,叫做三角形的角平分线/K !三角形的三条角平分线相交于一点,交点 八”、在三角形的内部,三角形三条角平分线的 LW 交点叫做三角形的内心三角形的高 三角形的高直角三角形的三条高直角顶点钝角三角形的高六;落钝角三角形的三条高不相交于一点, 厂钝角三角形的三条高所在直线相交 于一点11 J.2三角形的高、 中线与角平分线三角形 的中线连结三角形ABC 的顶点A 和它所 对的边BC 的中点D,线段AD 叫 做二角形ABC 的边BC 上的中线 三角形的三条中线相交于一 点,交点在三角形的内部, 三角形三条中线的交点叫做 三角形的重心[ 一.角形的先平分线二角形的稳定性三角形木架的形状不会改变,而四边形木架的形状会改变. [这就是说,三角形是具有稳定的图形,而四边形没有稳定性. &11J.3三角形的稳定性I,三角形的稳定性实例三角形的三个内角的和等于180。
八年级数学实数知识点总结归纳图

八年级数学实数知识点总结归纳图实数是数学中重要的一个概念,它包括有理数和无理数。
八年级数学中的实数知识点较多,从整数、分数到根号、无理数等,掌握好这些知识点对于学习数学非常重要。
本文将对八年级数学中的实数知识点进行总结归纳,并通过图表的方式呈现,以便读者更好地理解和记忆。
一、实数的分类实数分为有理数和无理数两大类。
其中,有理数包括整数、分数和循环小数,可以表示为两个整数的比值,可以用分数形式表示,还可以表示为循环小数形式;而无理数是指不能表示为两个整数的比值的数,它的小数部分是无线不循环的。
二、整数整数包括正整数、负整数和0。
它们可以用图表的方式表示如下:```… -3 -2 -1 0 1 2 3 …```三、分数分数是指两个整数的比值,其中分子为整数,分母为非零整数。
分数可以用图表的方式表示如下:```… -2/3 -1/2 -1/3 -1/4 0 1/4 1/3 …```四、循环小数循环小数是指小数部分有限个或无限个数字循环出现的小数,其中循环节用括号表示。
循环小数可以用图表的方式表示如下:```… -0.75 -0.6666… -0.6 -0.25 0 0.25 0.6 …```五、根号根号是指数学运算中的符号,表示求一个数的平方根、立方根等。
在数轴上,根号表示的数在原点附近。
根号可以用图表的方式表示如下:```… √2 √3 √5 √6 0 √6 √5 √3 √2 …```六、无理数无理数是指不能表示为两个整数的比值的数,它的小数部分是无线不循环的。
无理数可以用图表的方式表示如下:```… -√2 -√3 -√5 -√6 0 √6 √5 √3 √2 …```七、实数的运算实数的运算包括加法、减法、乘法和除法。
通过实数的运算,可以得到一个新的实数。
实数的运算可以用图表的方式表示如下:```… -2 -1 0 1 2 …```八、实数的大小关系实数之间可以进行大小的比较。
对于两个实数a和b,a<b表示a小于b,a>b表示a大于b。
第二章:实数知识结构图

第二章:实数知识结构图一、实数的概念及分类1、实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一实质,归纳起来有四类:(1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数值,如sin60o等。
二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a 与b 互为相反数,则有a+b=0,a=-b ,反之亦成立。
2、绝对值在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值。
(|a|≥0)。
零的绝对值是它本身,也可看成它的相反数,若|a|=a ,则a ≥0;若|a|=-a ,则a ≤0。
3、倒数如果a 与b 互为倒数,则有ab=1,反之亦成立。
1和-1的倒数等于本身。
零没有倒数。
4、数轴规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
实数与数轴的点是一一对应的。
三、平方根、算数平方根和立方根1、算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 就叫做a 的算术平方根。
特别地,0的算术平方根是0。
表示方法:记作“a ”,读作根号a 。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数x 的平方等于a ,即x 2=a ,那么这个数x 就叫做a 的平方根(或二次方根)。
表示方法:正数a 的平方根记做“a ”,读作“正、负根号a ”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
3、开平方:求一个数a 的平方根的运算,叫做开平方。
人教版八年级数学上册知识点汇总(框架图)
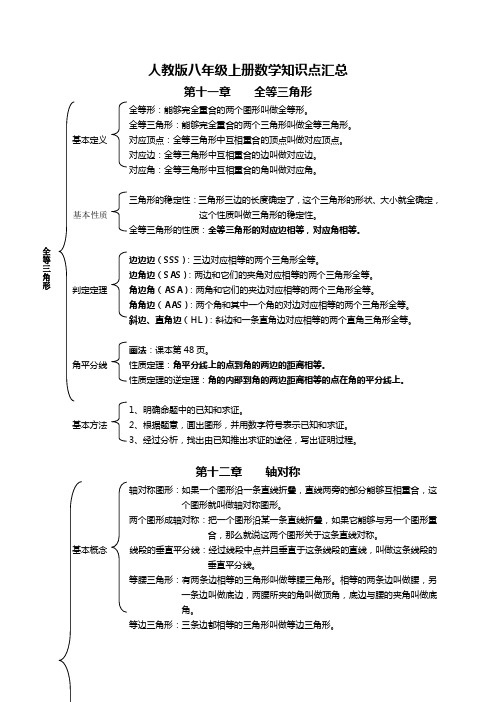
公式: = ; = ( ≥0)
定义:若 ,那么 为 的立方根。(记作 )。
性质:正数的立方根是正数,负数的立方根是负数,0的立方根循环小数)统称为实数。
分类:有理数和无理数或正实数、0、负实数。
人教版八年级上册数学知识点汇总
第十一章 全等三角形
全等形:能够完全重合的两个图形叫做全等形。
全等三角形:能够完全重合的两个三角形叫做全等三角形。
基本定义 对应顶点:全等三角形中互相重合的顶点叫做对应顶点。
对应边:全等三角形中互相重合的边叫做对应边。
对应角:全等三角形中互相重合的角叫做对应角。
三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性。
基本判定
1、三条边都相等的三角形是等边三角形。
2、三个角都相等的三角形是等边三角形。
3、有一个角是60°的等腰三角形是等边三角形。
1、做已知线段的垂直平分线:书本第63页。
2、作对称轴:连接两个对应点,作所连线段的垂直平分线。
基本方法 3、作已知点关于直线的对称点的方法:书本第67页。
4、作已知图形关于某直线的对称图形:书本第67页。
垂直平分线上。
1、点P(x,y)关于x轴对称的点的坐标为
关于坐标轴对称的P′(x,-y)。
点的坐标性质 2、点P(x,y)关于y轴对称的点的坐标为
P〞(-x,y)。
基本性质 1、等腰三角形两腰相等。
2、等腰三角形两底角相等(等边对等角)。
3、等腰三角形的顶角角平分线、底边上的中线,底边上的
高相互重合(三线合一)。
等边三角形:三条边都相等的三角形叫做等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算: 计算:
(1) ( ) 1、 、 3 + 4 − 3 、
(2)、 2 −3(1−3 2) 2 要 2 2 3 3 学 (3)、 (-2) − (−3) + ( −2) × 4 会 2、(结果保留 个有效数字) 、(结果保留 个有效数字) 、(结果保留3个有效数字 计 (1)、5 −π 算 (2)、 3 − 2 2) × 2 ( 哟! (3)、× 9 + 2 ( 5 − 2 ) 2
注意:计算过程中要多保留一位 注意:计算过程中要多保留一位!
(1)a是一个实数,它的相反数为 ) 是一个实数 是一个实数, 绝对值为
−a
,
a
;
(2)如果 )如果a
≠
0,那么它的倒数为 ,
1 a
.
2
特殊:0的算术平方根是0。
记作: 0 记作: = 0
平方根、 平方根、立方根 概念及性质
2. 平方根的定义: 平方根的定义:
这就是说,如果x = a ,那么 x 就是说, 的平方根. 的平方根记为± 就叫做 a 的平方根.a的平方根记为±
3.平方根的性质: 平方根的性质: 平方根的性质 正数有2个平方根,它们互为相反数 互为相反数; 正数有 个平方根,它们互为相反数; 0的平方根是 ; 的平方根是0; 的平方根是 负数没有平方根 没有平方根。 负数没有平方根。
是负数 等于它的相反数 是正数 等于它本身 是负数 等于它的相反数
− (3.14 − π ) = π − 3.14
3− 2
−
(
2− 3
)
= 3− 2
原式 = π − 3.14 + 3 − 2 − 3 − 2) ( = π − 3.14 + 3 − 2 − 3 + 2 = π − 3.14 + 3 − 3 + 2 − 2
算术平方根 表示方法
平方根
立方根
3
a
≠
0
a 的取值
性 质
正数 0 负数
a≥
0 没有
± a
a≥
0 没有
a
0
a 是任何数
0 负数(一个) 负数(一个)
正数(一个) 互为相反数(两个) 正数(一个) 正数(一个) 互为相反数(两个) 正数(一个)
开 方 是本身
0,1
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方 0 0,1,-1
25 (4) (3) ± 9
3
−1
求根也好,求值也好 关键要弄清它是什么意 求根也好 求值也好,关键要弄清它是什么意 求值也好 然后可以选择定义和性质来求. 思,然后可以选择定义和性质来求 然后可以选择定义和性质来求
− 8是
64的平方根是
64的值是
8
64
的平方根
±8
不 要 − 64的立方根是 -4 搞 错 -4,-3,-2,-1, ___ 了 大于 − 17小于 11的所有整数为 ___ 0,1,2,3 ___.
一般地,如果一个数的平方等于 一般地,如果一个数的平方等于a ,那 的平方根( 么这个数就叫做a 的平方根(或二次方 根). a 2
4.立方根的定义: 立方根的定义: 立方根的定义
一般地,如果一个数的立方等于a 一般地,如果一个数的立方等于a,那 么这个数就叫做a 立方根,也叫做a 么这个数就叫做a的立方根,也叫做a的 三次方根. 三次方根.记作 3 . 其中a是被开方数, 是根指数, 其中 是被开方数,3是根指数,符号 是被开方数 3 ”读做“三次根号”. 读做“三次根号” “
9的平方根是
± 3
解下列方程: 解下列方程:
1.
9(3 − y ) = 4
2
2.
解: (3 − y ) 2 = 4 9
解:
5 3 27 − ) + 8 = 0 (x 3 53
27( x − ) = −8 3 5 3 8 (x − ) = − 3 27
5 3 8 x− = − 3 27
不 要 遗 漏 哦!
有限小数及无限循环小数
整数 分数
有理数 实 数 无理数
无限不循环小数
一般有三种情况
正整数 0 负整数 正分数 负分数
自然数
正无理数 负无理数
(1)、 π
(2)、“
”, “
3
”开不尽的数
(3)、 类似于0.01001000100001L
3.14 − π + 3 − 2 − 2 − 3
化 简 绝 对 值 要 看 它 里 面 的 数 的 符 号
5.立方根的性质: 立方根的性质: 立方根的性质
a
一个正数有一个正的立方根; 一个正数有一个正的立方根; 一个负数有一个负的立方根, 一个负数有一个负的立方根, 零的立方根是零。 零的立方根是零。
平方根、 平方根、立方根 概念及性质
你知道算术平方根、平方根、 你知道算术平方根、平方根、立方根联 系和区别吗? 系和区别吗?
(1) 0.16 ( 2 ) −
9 16
(1) 0.04;(2) 1; (3) 56 ; (4) (-3)2 ; (5) 64 (1) 121;(2) 16; (3) 0 ; (4) (-3)2 ; (5) 9
49
4 78
(5 )3 125 27
(1) -0.008;(2) 43; (3) -64; (4) (-3)3; (5) 2
八年级实数复习结构框架
本章知识结 构图
乘 方
开 方
平方根、 平方根、立方根 概念及性质
1.算术平方根的定义: 算术平方根的定义: 算术平方根的定义
一般地,如果一个正数x的平方等于 a,即 x =a,那么这个正数x叫做a的 算术平方根。a的算术平方根记为 , 算术平方根 读作“根号a”,a叫做被开方数。
4 3− y = ± 9
1 2 y = 2 或y = 3 3 3
2 y = 3± 3
5 2 x= − 3 3
x =1
当方程中出现平方时,若有解,一般都有 两个解
当方程中出现立方时, 当方程中出现立方时,一般都有一个解
实数的有关 概念和性质 1、无限不循环的小数 叫做无理数. 叫做无理数. 有理数和无理数统称实数 实数. 有理数和无理数统称实数. 2、实数与数轴上的点是一一对应的. 、实数与数轴上的点是一一对应的 3、同样的,平面直角坐标系中的点与有序实数对是一一对应的 、同样的 平面直角坐标系中的点与有序实数对是一一对应的 平面直角坐标系中的点与有序实数对是一一对应的. 4、在实数范围内,相反数、倒数、绝对值的意义和有理 在实数范围内,相反数、倒数、 数范围内的相反数、倒数、 数范围内的相反数、倒数、绝对值的意义完全一样 5、实数的大小比较方法有:利用数轴比较、利 、实数的大小比较方法有:利用数轴比较、 用绝对值比较、求平方比较、求差比较、 用绝对值比较、求平方比较、求差比较、求商比 较和计算近似值比较等方法。 较和计算近似值比较等方法。 6、在进行实数的运算时,有理数的运算法则及运算性 、在进行实数的运算时, 实数的运算时 质同样适用。 质同样适用。
− a (a < 0) 2 ( a ) = a (a ≥ 0) 3 = a (a为任何数 ) a 3 ( a ) = a (a为任何数) 3 3 − a = − a (a为任何数 )
3
3
a =a=
2
a
0
(a > 0) (a = 0)
1.求下列各数的算术平方根: 1.求下列各数的算术平方根: 求下列各数的算术平方根 2.求下列各数的平方根: 2.求下列各数的平方根: 求下列各数的平方根 3.求下列各数的立方 3.求下列各数的立方根: 4.求下列各式的值: 4.求下列各式的值: 求下列各式的值
