山东省济宁市2016届高三数学下学期第二次模拟考试试题 文
山东省济宁市2013届高三第二次模拟考试数学文试题(WORD解析版)

2013年山东省济宁市高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.(5分)(2013•济宁二模)已知全集U=R,集合A={x||x|<2},B={x|x>1},则∁U(A∩B)等于()A.{x|1<x<2} B.{x|x≤﹣2} C.{x|x≤1或x≥2} D.{x|x<1或x>2}考点:交、并、补集的混合运算.专题:计算题.分析:求解绝对值得不等式化简集合B,求出A与B的交集后直接取补集运算.解答:解由全集U=R,集合A={x||x|<2}={x|﹣2<x<2},B={x|x>1},所以A∩B={x|﹣2<x<2}∩{x|x>1}={x|1<x<2},所以∁U(A∩B)={x|x≤1或x≥2}.故选C.点评:本题考查了交、并、补集的混合运算,考查了绝对值不等式的解法,是基础题.2.(5分)(2013•济宁二模)复数z=(i是虚数单位)的共扼复数是()A.1+i B.﹣1+i C.1﹣i D.﹣1﹣i考点:复数代数形式的混合运算;复数的基本概念.专题:计算题.分析:把给出的复数的分子展开平方运算,然后利用复数的除法运算进行化简,化为a+bi(a,b∈R)的形式后可求其共轭复数.解答:解:z==.所以.故选B.点评:本题考查了复数的概念,考查了复数的代数形式的乘除运算,解答的关键是掌握复数的除法运算法则,是基础题.3.(5分)(2013•济宁二模)平面向量与的夹角为,=(2,0),||=1,则|+|等于()A.B.3C.7D.79考点:平面向量数量积的坐标表示、模、夹角.专题:平面向量及应用.分析:利用向量数量积得性质可得|+|==,把已知代入即可.解答:解:∵向量与的夹角为,=(2,0),||=1,∴|+|====.故选A.点评:熟练掌握向量数量积得性质是解题的关键.4.(5分)(2013•济宁二模)已知曲线y=﹣x2的切线方程为y=﹣x+b,则b的值是()A.﹣B.C.D.﹣考点:利用导数研究曲线上某点切线方程.分析:求导函数,求出切线方程,结合条件,即可求b的值.解答:解:求导函数可得y′=x2﹣2x令y′=x2﹣2x=﹣1,则x=1∴切点坐标为(1,﹣)∴切线方程为y+=﹣x+1,即y=﹣x+∴b=故选B.点评:本题考查导数的几何意义,考查切线方程,考查学生的计算能力,属于基础题.5.(5分)(2013•济宁二模)已知圆(x﹣a)2+(y﹣b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为()A.B.C.(x﹣1)2+y2=1 D.x2+(y﹣1)2=1考点:圆与圆锥曲线的综合;直线与圆的位置关系.专题:计算题.分析:抛物线y2=4x的焦点坐标为(1,0),即为圆心坐标,利用圆与直线3x+4y+2=0相切,可求半径,即可得到圆的方程.解答:解:由题意,抛物线y2=4x的焦点坐标为(1,0),即为圆心坐标∵圆与直线3x+4y+2=0相切,∴∴圆的方程为(x﹣1)2+y2=1故选C.点评:本题考查圆与抛物线的综合,考查直线与圆相切,解题的关键是确定圆的圆心与半径.6.(5分)(2013•济宁二模)对于平面α和共面的直线m,n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n考点:命题的真假判断与应用;空间中直线与直线之间的位置关系;空间中直线与平面之间的位置关系.专题:空间位置关系与距离.分析:利用直线和平面平行、垂直的判定和性质,判断命题A、B、C都不正确,只有D正确,从而得到结论.解答:解:由于平面α和共面的直线m,n,若m,n与α所成的角相等,则直线m,n平行或相交,故A不正确.若m∥α,n∥α,则,直线m,n平行或相交,故B不正确.若m⊥α,m⊥n,则n与平面α平行或n在平面α内,故C不正确.若m⊂α,n∥α,根据直线m,n是共面的直线,则一定有m∥n,故D正确,故选D.点评:本题主要考查空间直线和平面的位置关系的判定,命题的真假的判断,属于基础题.7.(5分)(2013•济宁二模)已知命题p:“存在正实数a,b,使得lg(a+b)=lga+lgb”;命题q:“异面直线是不同在任何一个平面内的两条直线”.则下列命题为真命题的是()A.p∧(¬q)B.(¬p)∧q C.(¬p)v(¬q)D.p∧q考点:复合命题的真假.专题:计算题.分析:根据对数的运算性质可知,当a=b=2时,lg(a+b)=lga+lgb成立,命题p为真,根据异面直线的定义可知,命题q为真,根据复合命题的真假关系可判断解答:解:根据对数的运算性质可知,当a=b=2时,lg(a+b)=lga+lgb成立,故命题p为真,根据异面直线的定义可知,命题q为真,根据复合命题的真假关系可知,p∧q为真故选D点评:本题主要考查了对数的运算性质及异面直线的定义的简单应用及复合命题的真假关系的应用,属于基础试题8.(5分)(2013•济宁二模)设二次函数f(x)=ax2﹣4x+c(x∈R)的值域为[0,+∞),则的最小值为()A.3B.C.5D.7考点:基本不等式.专题:不等式的解法及应用.分析:先判断a、c是正数,且ac=4,把所求的式子变形使用基本不等式求最小值.解答:解:由题意知,a>0,△=1﹣4ac=0,∴ac=4,c>0,则则≥2×=3,当且仅当时取等号,则的最小值是3.故选A.点评:本题考查函数的值域及基本不等式的应用,求解的关键就是拆项,属于基础题.。
2016届高三上学期第一次月考数学(文)试题Word版含答案

2016届高三上学期第一次月考数学(文)试题Word版含答案2016届高三上学期第一次月考数学文试卷考试时间120分钟,满分150分一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M ={x |x ≥0,x ∈R },N ={x |x 2<1,x ∈R },则M ∩N 等于( ) A .[0,1] B .[0,1) C .(0,1]D .(0,1)2.已知集合A ={1,2},B ={1,a ,b },则“a =2”是“A ?B ”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知命题p :所有有理数都是实数;命题q :正数的对数都是负数,则下列命题中为真命题的是( ) A .﹁p 或q B .p 且q C .﹁p 且﹁qD .﹁p 或﹁q4.设函数f (x )=x 2+1,x ≤1,2x ,x >1,则f (f (3))等于( )A.15B .3C.23D.1395.函数f (x )=log 12(x 2-4)的单调递增区间是( )A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)6.已知函数f (x )为奇函数,且当x >0时,f (x )=x 2+1x ,则f (-1)等于( )A .-2B .0C .1D .27. 如果函数f (x )=x 2-ax -3在区间(-∞,4]上单调递减,则实数a 满足的条件是( ) A .a ≥8 B .a ≤8 C .a ≥4D .a ≥-48. 函数f (x )=a x -2+1(a >0且a ≠1)的图像必经过点( ) A .(0,1) B .(1,1) C .(2,0)D .(2,2)9. 函数f (x )=lg(|x |-1)的大致图像是( )10. 函数f (x )=2x +3x 的零点所在的一个区间是( ) A .(-2,-1) B .(-1,0) C .(0,1)D .(1,2)11. 设f (x )=x ln x ,若f ′(x 0)=2,则x 0的值为( ) A .e 2B .eC.ln22D .ln212. 函数f (x )的定义域是R ,f (0)=2,对任意x ∈R ,f (x )+f ′(x )>1,则不等式e x ·f (x )>e x +1的解集为( ).A .{x |x >0}B .{x |x <0}C .{x |x <-1或x >1}D .{x |x <-1或0<1}<="" p="">二、填空题:本大题共4小题,每题5分.13. 已知函数y =f (x )及其导函数y =f ′(x )的图像如图所示,则曲线y =f (x )在点P 处的切线方程是__________.14. 若函数f (x )=x 2+ax +b 的两个零点是-2和3,则不等式af (-2x )>0的解集是________. 15. 函数y =12x 2-ln x 的单调递减区间为________.16. 若方程4-x 2=k (x -2)+3有两个不等的实根,则k 的取值范围是________.三、解答题:解答应写出文字说明、证明过程或演算步骤17.(10分) 化简:(1)3131421413223b a b a ab b a -(a >0,b >0);(2)(-278)23-+(0.002)12--10(5-2)-1+(2-3)0.18.(12分)已知函数f (x )=1a -1(a >0,x >0),(1)求证(用单调性的定义证明):f (x )在(0,+∞)上是增函数; (2)若f (x )在[12,2]上的值域是[12,2],求a 的值.19.(12分)已知定义在R 上的奇函数f (x )有最小正周期2,且当x ∈(0,1)时,f (x )=2x4x +1.(1)求f (1)和f (-1)的值; (2)求f (x )在[-1,1]上的解析式.20.(12分)已知函数f (x )=x 2+2ax +3,x ∈[-4,6]. (1)当a =-2时,求f (x )的最值;(2)求实数a 的取值范围,使y =f (x )在区间[-4,6]上是单调函数;(3)当a =1时,求f (|x |)的单调区间. 21.(12分)已知函数f (x )=x 3+x -16. (1)求曲线y =f (x )在点(2,-6)处的切线的方程;(2)直线l 为曲线y =f (x )的切线,且经过原点,求直线l 的方程及切点坐标; 22.(12分)已知函数f (x )=x 3-3ax -1,a ≠0. (1)求f (x )的单调区间;(2)若f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图像有三个不同的交点,求m 的取值范围.2016届高三上学期第一次月考数学答题卡一、选择题(共12小题,每小题5分,共60分,每小题有一个正确答案)13、 14、15、 16、三、解答题17.(10分) 化简:(1)131421413223b a b a ab b a -(a >0,b >0);(2)(-278)23-+(0.002)12--10(5-2)-1+(2-3)0.18.(10分)已知函数f (x )=1a -1x(a >0,x >0),(1)求证(用单调性的定义证明):f (x )在(0,+∞)上是增函数; (2)若f (x )在[12,2]上的值域是[12,2],求a 的值.19.(12分)已知定义在R 上的奇函数f (x )有最小正周期2,且当x ∈(0,1)时,f (x )=2x4x +1.(1)求f (1)和f (-1)的值; (2)求f (x )在[-1,1]上的解析式.20.(12分)已知函数f(x)=x3+x-16.(1)求曲线y=f(x)在点(2,-6)处的切线的方程;(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;21.(13分)已知函数f(x)=x2+2ax+3,x∈[-4,6].(1)当a=-2时,求f(x)的最值;(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;(3)当a=1时,求f(|x|)的单调区间.22.(13分)已知函数f(x)=x3-3ax-1,a≠0.(1)求f(x)的单调区间;(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图像有三个不同的交点,求m的取值范围.2016届高三上学期第一次月考数学文试卷参考答案1.B2.A3.D4.D5.D6.A7.A8.D9.B10.B11.B12.A13. x -y -2=0 14. {x |-32<1}<="" p="">15. (0,1] 16. (512,34]17. 解 (1)原式=121311113233211212633311233().a b a b abab ab a b+-++----==(2)原式=(-278)23-+(1500)12--105-2+1=(-827)23+50012-10(5+2)+1=49+105-105-20+1=-1679. 18. (1)证明设x 2>x 1>0,则x 2-x 1>0,x 1x 2>0,∵f (x 2)-f (x 1)=(1a -1x 2)-(1a -1x 1)=1x 1-1x 2=x 2-x 1x 1x 2>0,∴f (x 2)>f (x 1),∴f (x )在(0,+∞)上是增函数. (2)解∵f (x )在[12,2]上的值域是[12,2],又f (x )在[12,2]上单调递增,∴f (12)=12,f (2)=2.易得a =25.19. 解(1)∵f (x )是周期为2的奇函数,∴f (1)=f (1-2)=f (-1)=-f (1),∴f (1)=0,f (-1)=0. (2)由题意知,f (0)=0. 当x ∈(-1,0)时,-x ∈(0,1).由f (x )是奇函数,∴f (x )=-f (-x )=-2-x4-x +1=-2x4x +1,综上,在[-1, 1]上,f (x )=2x4x +1,x ∈(0,1),-2x 4x+1,x ∈(-1,0),0,x ∈{-1,0,1}.20.解 (1)当a =-2时,f (x )=x 2-4x +3=(x -2)2-1,∵x ∈[-4,6],∴f (x )在[-4,2]上单调递减,在[2,6]上单调递增,∴f (x )的最小值是f (2)=-1,又f (-4)=35,f (6)=15,故f (x )的最大值是35. (2)∵函数f (x )的图像开口向上,对称轴是x =-a ,∴要使f (x )在[-4,6]上是单调函数,应有-a ≤-4或-a ≥6,即a ≤-6或a ≥4. (3)当a =1时,f (x )=x 2+2x +3,∴f (|x |)=x 2+2|x |+3,此时定义域为x ∈[-6,6],且f (x )=?x 2+2x +3,x ∈(0,6],x 2-2x +3,x ∈[-6,0],∴f (|x |)的单调递增区间是(0, 6],单调递减区间是[-6,0].21.解 (1)可判定点(2,-6)在曲线y =f (x )上.∵f ′(x )=(x 3+x -16)′=3x 2+1.∴f ′(x )在点(2,-6)处的切线的斜率为k =f ′(2)=13. ∴切线的方程为y =13(x -2)+(-6),即y =13x -32.(2)法一设切点为(x 0,y 0),则直线l 的斜率为f ′(x 0)=3x 20+1,∴直线l 的方程为y =(3x 20+1)(x -x 0)+x 30+x 0-16,又∵直线l 过点(0,0),∴0=(3x 20+1)(-x 0)+x 30+x 0-16,整理得,x 30=-8,∴x 0=-2,∴y 0=(-2)3+(-2)-16=-26,k =3×(-2)2+1=13. ∴直线l 的方程为y =13x ,切点坐标为(-2,-26.) 法二设直线l 的方程为y =kx ,切点为(x 0,y 0),则k=y0-0x0-0=x30+x0-16x0又∵k=f′(x0)=3x20+1,∴x30+x0-16x0=3x2+1,解之得x0=-2,∴y0=(-2) 3+(-2)-16=-26,k=3×(-2)2+1=13.∴直线l的方程为y=13x,切点坐标为(-2,-26).22.解(1)f′(x)=3x2-3a=3(x2-a),当a<0时,对x∈R,有f′(x)>0,∴当a<0时,f(x)的单调增区间为(-∞,+∞).当a>0时,由f′(x)>0,解得x<-a或x>a.由f′(x)<0,解得-a<x<a,< p="">∴当a>0时,f(x)的单调增区间为(-∞,-a),(a,+∞),单调减区间为(-a,a).(2)∵f(x)在x=-1处取得极值,∴f′(-1)=3×(-1)2-3a=0,∴a=1.∴f(x)=x3-3x-1,f′(x)=3x2-3,由f′(x)=0,解得x1=-1,x2=1.由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.∵直线y=m与函数y=f(x)的图像有三个不同的交点,结合如图所示f(x)的图像可知:实数m的取值范围是(-3,1).</x<a,<>。
2024学年山东省新泰市第二中学高三下学期第二次模拟考试数学试题理试卷

2024学年山东省新泰市第二中学高三下学期第二次模拟考试数学试题理试卷 注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足2(13)(1)i z i +=+,则||z =( ) A .54 B .55 C .102 D .1052.若复数()()31z i i =-+,则z =( )A .22B .25C .10D .203.已知向量()()1,2,2,2a b λ==-,且a b ⊥,则λ等于( )A .4B .3C .2D .14.已知12,F F 是双曲线222:1(0)x C y a a-=>的两个焦点,过点1F 且垂直于x 轴的直线与C 相交于,A B 两点,若2AB =,则2ABF ∆的内切圆半径为( )A .23B .33C .323D .2335.已知数列满足:.若正整数使得成立,则( )A .16B .17C .18D .196.已知复数z 满足(3)1i z i +=+,则z 的虚部为( )A .i -B .iC .–1D .17.第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )A .110B .15C .140D .9408.设i 为数单位,z 为z 的共轭复数,若13z i =+,则z z ⋅=( ) A .110 B .110i C .1100 D .1100i 9.命题“20,(1)(1)∀>+>-x x x x ”的否定为( )A .20,(1)(1)∀>+>-x x x xB .20,(1)(1)∀+>-x x x xC .20,(1)(1)∃>+-x x x xD .20,(1)(1)∃+>-x x x x10.已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域的面积为9,若点, 则的最大值为( )A .3B .6C .9D .12 11.若函数()3cos 4sin f x x x =+在x θ=时取得最小值,则cos θ=( )A .35B .45-C .45D .3512.如图,正方体1111ABCD A B C D -的棱长为1,动点E 在线段11A C 上,F 、M 分别是AD 、CD 的中点,则下列结论中错误的是( )A .11//FM AC ,B .存在点E ,使得平面//BEF 平面11CCD D C .BM ⊥平面1CC F D .三棱锥B CEF -的体积为定值二、填空题:本题共4小题,每小题5分,共20分。
2016届新课标高三数学(文)一轮复习习题 §6.4数列求和、数列的综合应用 2年模拟

§ 6。
4 数列求和、数列的综合应用A 组 2014-2015年模拟·基础题组限时:35分钟1。
(2014河南安阳二模,6)已知数列{a n }中,a n =—4n+5,等比数列{b n }的公比q 满足q=a n —a n —1(n≥2)且b 1=a 2,则|b 1|+|b 2|+|b 3|+…+|b n |=( )A.1-4n B 。
4n —1 C.1-4n3 D.4n-132。
(2014辽宁五校协作体联考,15)已知数列{a n }满足a n =1+2+3+…+nn,则数列{1a n a n+1}的前n 项和为 。
3.(2014广东揭阳3月模拟,13)对于每一个正整数n,设曲线y=x n+1在点(1,1)处的切线与x 轴的交点的横坐标为x n ,令a n =lg x n ,则a 1+a 2+…+a 99= 。
4。
(2015河北石家庄调研)在数列{a n }中,已知a 1=14,a n+1a n=14,b n +2=3lo g 14a n (n∈N *). (1)求数列{a n }的通项公式; (2)求证:数列{b n }是等差数列;(3)设数列{c n }满足c n =a n +b n ,求{c n }的前n 项和S n .5.(2014广东湛江二模,19)已知等差数列{a n}的首项a1=1,公差d>0,且a2,a5,a14分别是等比数列{b n}的b2,b3,b4。
(1)求数列{a n}和{b n}的通项公式;(2)设数列{c n}对任意正整数n均有c1b1+c2b2+…+c nb n=a n+1成立,求c1+c2+…+c2 014的值。
B组2014—2015年模拟·提升题组限时:50分钟1.(2015长春外国语学校期中)若数列{a n}满足1a n+1—pa n=0,n∈N*,p为非零常数,则称数列{a n}为“梦想数列”.已知正项数列{1b n}为“梦想数列”,且b1b2b3…b99=299,则b8+b92的最小值是()A。
山东省济宁市第一中学2024届高三上学期12月月考数学试题(解析版)

济宁一中高三12月份定时检测数学试题一、单选题(本大题共8小题,共40分.在每小题列出的选项中,选出符合题目的一项.)1. 已知1i22i z -=+,则z z -=( )A. i -B. iC. 0D. 1【答案】A 【解析】【分析】根据复数的除法运算求出z ,再由共轭复数的概念得到z ,从而解出.【详解】因为()()()()1i 1i 1i 2i 1i 22i 21i 1i 42z ----====-++-,所以1i 2z =,即i z z -=-.故选:A .2. 若集合{}2230A x x x =--≤,(){}lg 10B x x =+≤,则A B ⋃=( )A. {}10x x -≤≤ B. {}10x x -<≤C. {}13x x -≤≤ D. {}13x x -<≤【答案】C 【解析】【分析】由一元二次不等式的解法求A ,再根据对数函数的定义域及单调性求B ,最后求并集即可.【详解】由()()[]2231301,3x x x x x --=+-≤⇒∈-,即{}13A x x =-≤≤,由()(](]lg 10lg110,11,0x x x +≤=⇒+∈⇒∈-,即{}10B x x =-<≤,故A B ⋃={}13x x -≤≤.故选:C3. 已知()2,3AB = ,()3,AC t = ,1BC = ,则AB BC ⋅=( )A 8B. 5C. 2D. 7【答案】C 【解析】.【分析】由()1,3BC AC AB t =-=-及1BC = ,可得3t =,从而根据向量数量积的坐标表示即可求解.【详解】解:因为()2,3AB = ,()3,AC t = ,所以()1,3BC AC AB t =-=-,因为1BC = ,所以()22131t +-=,解得3t =,所以()1,0BC =u u u r,所以21302AB BC ⋅=⨯+⨯=,故选:C.4. 函数()3e e x xf x x-+=的图像可能是( )A. B.C. D.【答案】B 【解析】【分析】先判断函数奇偶性,以图像的对称性排除错误选项CD ;再以图像的切线情况去排除错误选项A ,即可得到函数()3e e x xf x x -+=的正确图像.【详解】()3e e x xf x x -+=的定义域为{}0x x ≠()()()()33e e e e x x x xf x f x x x ----++-===---,则()f x 为奇函数,其图像关于原点中心对称,排除选项CD ;()()()()()3264e e 3e e e 3e e xx x x xx x x x x e x f x x x ------+--+'==的则()()()1010101010104410e e 3e e 7e 13e 1001010f -----+-'==>即函数()f x 在点()()10,10f 的切线斜率为正值,选项A 的图像在第一象限内每一点的切线斜率均为负值,故排除选项A.选项B 的图像在第一象限内存在切线斜率为正值的点.故选:B 5. 已知1sin ,123πθ⎛⎫-= ⎪⎝⎭则sin 23πθ⎛⎫+= ⎪⎝⎭( )A. 29-B.29C. 79-D.79【答案】D 【解析】【分析】设12παθ=-,则1,sin 123πθαα=+=,则sin 2sin 3223[1πππθα⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭化简,由余弦的二倍角公式可得答案.【详解】设12παθ=-,则1,sin 123πθαα=+=,从而2[7sin 2sin 2sin 2cos 212sin 3329πππθαααα⎛⎫⎛⎛⎫+=+=+==-= ⎪ ⎪⎝⎭⎝⎝⎭.故选:D【点睛】关键点睛:本题考查三角函数中知值求值的问题,解答本题的关键是设12παθ=-,然后可得sin 2sin 32]23[1πππθα⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭,属于中档题.6. 已知等比数列{}n a 的前n 项和为n S ,2532a a a =,47245a a +=,则5S =( )A. 29 B. 31C. 33D. 36【答案】B 【解析】【分析】根据2532a a a =,47245a a +=可求出首项1a ,公比q ,然后利用等比数列求和公式即可求解.【详解】因为数列{}n a 是等比数列,2532a a a =,所以3252222a a a a q a q =⨯=,即222a q =,则42a =.又因为47245a a +=,故有714a =.所以37418a q a ==,则12q =,所有41316a a q ==,所有551161231112S ⎡⎤⎛⎫-⎢⎥⎪⎝⎭⎢⎥⎣⎦==-,故B 项正确.故选:B.7. 已知抛物线()220x py p =>上一点(),1M m 到焦点的距离为32,则其焦点坐标为( )A. 10,2⎛⎫ ⎪⎝⎭B. 1,02⎛⎫⎪⎝⎭C. 1,04⎛⎫⎪⎝⎭D. 10,4⎛⎫ ⎪⎝⎭【答案】A 【解析】【分析】由抛物线的定义可求p 的值,进而可求焦点坐标.【详解】解: 抛物线()220x py p =>上一点(),1M m 到焦点的距离为32,∴由抛物线的定义知322M p y +=,即3122p +=,所以1p =,所以122p =,∴抛物线的焦点坐标为10,2⎛⎫ ⎪⎝⎭,故选:A .8. 如图1,某广场上放置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的正三棱锥得到的,它的所有棱长均相同,数学上我们称之为半正多面体(semiregular solid ),亦称为阿基米德多面体,如图2,设1AB =,则平面BCG 与平面EMQ 之间的距离是()A.B.C.D.【答案】D 【解析】【分析】不妨记正方体为22221111A B C D A B C D -,设对角线21A C 分别交平面EMQ 和平面BCG 于点1M ,1N ,可推出11M N 即为平面EMQ 与平面BCG 的距离,结合等体积法求得21A M ,结合对称性求得11M N 即可.【详解】如图,不妨记正方体为22221111A B C D A B C D -,1122//A D B C ,1122A D B C =,故四边形1122A D C B 是平行四边形,所以1221//A B C D ,又E ,Q 分别为12A A ,22A B 的中点,所以12//EQ A B ,同理21//BG C D ,所以//EQ BG ,又EQ ⊄平面BCG ,BG ⊂平面BCG ,所以//EQ 平面BCG ,同理//EM 平面BCG ,又EM EQ E ⋂=,EM ,EQ ⊂平面EMQ ,所以平面//EMQ 平面BCG ,设对角线21A C 分别交平面EMQ 和平面BCG 于点1M ,1N ,因为12C C ⊥平面2222A B C D ,MQ Ì平面2222A B C D ,所以12C C MQ ⊥,连接2211,A C A C ,因为,M Q 分别为2222,D A B A 的中点,故22A C MQ ⊥,又12C C ,22A C ⊂平面1221A A C C ,12222C C A C C = ,所以MQ ⊥平面1221A A C C ,又21A C ⊂平面1221A A C C ,所以21A C MQ ⊥,同理21A C EQ ⊥,又MQ EQ Q ⋂=,MQ ,EQ ⊂平面EMQ ,所以21A C ⊥平面EMQ ,又平面//EMQ 平面BCG ,所以21A C ⊥平面BCG ,11M N 即为平面EMQ 与平面BCG 的距离,则11212111M N A C A M N C =--,得21A C ==,由题意得222EA MA QA ===EMQ 为等边三角形,故21EMQ S ==,根据22E A MQ A EMQ V V --=,得1111323M ⨯=,解得21A M =根据对称性知2111A M N C =,所以112121112M N A C A M N C =--=-=,则平面EMQ 与平面BCG .故选:D【点睛】方法点睛:求点到平面的距离方法,一是建立空间直角坐标系,利用空间向量求解;二是利用等体积法求解;三是作出辅助线,在三角形中结合余弦定理等方法进行求解.二、多选题(本大题共4小题,共20分.在每小题有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9. 下列表述正确的是( ).A. 如果0a b >>,c d >,那么ac bd >B. 如果0a b >>>C. 如果0a b >>,0c d >>,那么11ac bd<D. 如果0a b ≥>,那么2a bb a +≤≤【答案】BCD 【解析】【分析】根据函数的单调性、不等式的性质等知识逐个验证选项即可.【详解】A .如果0a b >>,c d >,取2a =,1b =,1c =-,2d =-,则2ac bd =-=,故A 错误;B .由于12y x ==在[0,)+∞为单调增函数,从而若0a b >>>B 正确;C .如果0a b >>,0c d >>,则0ac bc bd >>>,而1()f x x =在(0,)+∞上单调递减,从而11ac bd<,故C 正确;D .如果0a b ≥>,则22a a b b ≥+≥,故2a bb a +≤≤,故D 正确.故选:BCD .10. 已知直线:210l x my ++=,圆22:3E x y +=,则下列说法正确的是( )A. 直线l 必过点(1,0)B. 直线l 与圆E 必相交C. 圆心E 到直线l 的距离的最大值为1D. 当12m =时,直线l 被圆E 【答案】BC 【解析】【分析】利用直线和圆的相关性质求解即可.【详解】易知直线l 必过点(1,0)-,故A 错误;点(1,0)-在圆E 内,所以直线l 与圆E 必相交,故B 正确;圆心(0,0)E 到直线l 的距离d =,当0m =时距离取最大值1,故C 正确;当12m =时,直线:10l x y ++=,则直线l 被圆E 截得的弦长为=,故D 错误.故选:BC11. 把函数sin y x =图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向左平移π6个单位长度,得到函数()y g x =的图象,则( )A. ()g x 在π5π,36⎛⎫⎪⎝⎭上单调递减B. ()g x 在[]0,π上有2个零点C. ()y g x =的图象关于直线π12x =对称D. ()g x 在π,02⎡⎤-⎢⎥⎣⎦上的值域为⎡⎢⎣【答案】BC 【解析】【分析】由题意,由函数sin(+)y A x ωϕ=的图象变换规律,求得()y g x =的解析式,再根据正弦函数的图象和性质,逐一判断各选项得出结论.【详解】把函数sin y x =图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,可得到sin 2y x =的图象;再把所得曲线向左平移π6个单位长度,得到函数()πsin(2)3y g x x ==+的图象,π5π(,36x ∈时,π2(π,2π)3x +∈,则()g x 在π7π(,)312单调递减,在7π5π(,)126单调递增,故A 错误;令()0g x =,得π2π(Z)3x k k +=∈,即ππ26k x =-,因为[0,π]x ∈,所以ππ0π26k ≤-≤,解得1733k ≤≤,因为Z k ∈,所以1k =或2k =,所以()g x 在[]0,π上有2个零点,故B 正确;因为ππππ()sin(2)sin 1121232g =⨯+==,为()g x 的最大值,所以直线π12x =是()y g x =的图象的一条对称轴,故C 正确;当π,02x ⎡⎤∈-⎢⎥⎣⎦时,π2ππ2,333x ⎡⎤+∈-⎢⎥⎣⎦,()g x ⎡∈-⎢⎣,故D 错误.故选:BC12. 如图,1P 是一块半径为1的圆形纸板,在1P 的左下端前去一个半径为12的半圆后得到图形2P ,然后依次剪去一个更小半圆(其直径为前一个前掉半圆的半径)得图形3P ,4,,,n P P ,记纸板n P 的周长为n L ,面积为n S ,则下列说法正确的是( )A. 37142L π=+ B. 31132S π=C. 1111222n n n L π-+⎡⎤⎛⎫⎛⎫=-+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ D. 1212n n n S S π++=-【答案】ABD 【解析】【分析】观察图形,分析剪掉的半圆的变化,纸板n P 相较于纸板1n P -()2n ≥剪掉了半径为112n -的半圆,再分别写出n L 和n S 的递推公式,从而累加得到通项公式再逐个判断即可【详解】根据题意可得纸板n P 相较于纸板1n P -()2n ≥剪掉了半径为112n -的半圆,故1111122222n n n n L L π---=-⨯+⨯,即112122n n n n L L π----=-,故12L π=+,2110122L L π-=-,3221122L L π-=-,4332122L L π-=- (1121)22n n n n L L π----=-,累加可得1210121112......222222n n n L ππππ--⎛⎫⎛⎫=+++++-++ ⎪ ⎪⎝⎭⎝⎭1111112222111122n n ππ--⎛⎫-- ⎪⎝⎭=++---1211222n n π--⎛⎫=-+ ⎪⎝⎭,所以132171421222L ππ⎛⎫=-+ ⎪⎝⎭=+,故A 正确,C 错误;又1211122n n n S S π--⎛⎫=- ⎪⎝⎭,故1212n n n S S π---=-,即1212n n n S S π++=-,故D 正确;又12S π=,2132S S π-=-,3252S S π-=- (121)2n n n S S π---=-,累加可得3521...2222n n S ππππ-=----111841214n ππ-⎛⎫- ⎪⎝⎭=--211132n π-⎛⎫=+ ⎪⎝⎭,故31132S π=正确,故B 正确;故选:ABD三、填空题(本大题共4小题,共20分)13. 设等差数列{a n }的前n 项和为S n ,a 1≠0,a 1+a 5=3a 2,则1020S a =_____.【答案】114##2.75【解析】【分析】由1523a a a +=,得到1a 与d 的关系,再利用等差数列的前n 项和公式和通项公式求解.【详解】解:1523a a a += ,∴112433a d a d +=+,∴1a d =,1012011045551119204S a d d a a d d +===+.故答案为:11414. 已知双曲线2222:1x y M a b-=的左焦点为F 1,A ,B 为双曲线M 上的两点,O 为坐标原点若四边形1F ABO 为菱形,则双曲线M 的离心率为___________.1+【解析】【分析】利用双曲线的对称性,连结1BF ,2BF ,根据图形分析可得12BF F △是直角三角形,且260BF O ∠= ,在结合双曲线的定义,即可得到双曲线的离心率.【详解】如图,设双曲线的右焦点2F ,连结1BF ,2BF ,四边形1F ABO 是菱形,1212BO F F ∴=,12BF BF ∴⊥,并且根据对称性可知2OBF △是等边三角形,260BF O ∴∠=,1BF ∴=,根据双曲线定义可知,122B F B F a -=,2c a -=,即1c a ==1题型,一般求双曲线离心率的方法是1.直接法:直接求出,a c ,然后利用公式ce a=求解;2.公式法:c e a ===,3.构造法:根据条件,可构造出,a c 的齐次方程,通过等式两边同时除以2a ,进而得到关于e 的方程.15. 如图,已知正四棱台的两底面均为正方形,且边长分别为20cm 和10cm ,侧面积为2780cm ,则其体积为________.【答案】32800cm 【解析】【分析】利用四棱台的结构特征,作出辅助线,根据侧面积列出方程,求出正四棱台的高,结合棱台的体积公式计算得结论【详解】如图,取11A B 的中点1E 、AB 的中点E ,上、下底面的中心1O 、O ,则1E E 为斜高,四边形11EOO E 为直角梯形.正四棱台的侧面积1114(1020)7802S EE =⨯⨯+⨯=,113cm EE ∴=,在直角梯形11EOO E 中,过点1E 作1M ⊥OE 于点M ,则115cm O E OM ==,11O O E M =,因为111115cm 2O E A B ==,110cm 2OE AB ==,所以5EM OE OM =-=cm ,1112O O E M ∴====cm ,∴该四棱台的体积为()()223112102010202800cm 3V =⨯⨯++⨯=故答案为:32800cm 16. 已知函数()()1f x x sinx cosx =++,若对于任意的()1212,0,2x x x x π⎡⎤∈≠⎢⎥⎣⎦,均有()()1212|x x f x f x a e e --成立,则实数a 的取值范围为______.【答案】[)1,+∞【解析】【分析】求导可知函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上为增函数,进而原问题等价于对于任意的()1212,0,2x x x x π⎡⎤∈≠⎢⎥⎣⎦,均有()()1212x x f x ae f x ae ->-,构造函数()()x h x f x ae =-,则函数()h x 在0,2π⎡⎤⎢⎥⎣⎦上为减函数,求导后转化为最值问题求解即可.【详解】解:()()()sin 1cos sin 1cos f x x x x x x x =++-=+',任意的()1212,0,2x x x x π⎡⎤∈≠⎢⎥⎣⎦,()0f x '>恒成立,所以()f x 单调递增,不妨设12x x <,则()()12f x f x <,又12x x e e <,故()()1212|xxf x f x a e e --等价于()()2121x xf x f x ae ae -<-,即()()1212xxf x ae f x ae ->-,设()()()1,0,2x xh x f x ae x sinx cosx ae x π⎡⎤=-=++-∈⎢⎥⎣⎦,易知函数()h x 在0,2π⎡⎤⎢⎥⎣⎦上为减函数,故()()'10xh x x cosx ae =+-≤在0,2π⎡⎤⎢⎥⎣⎦上恒成立,即()1xx cosx a e +≥在0,2π⎡⎤⎢⎥⎣⎦上恒成立,设()()1,0,2xx cosx g x x eπ+⎡⎤=∈⎢⎥⎣⎦,则()()()211'0()x xx xcosx x sinx e x cosx e xsinx sinx xcosx g x e e ⎡⎤-+-+⋅---⎣⎦==≤,故函数()g x 在0,2π⎡⎤⎢⎥⎣⎦上为减函数,则()()01max g x g ==,故1a ≥.故答案为:[)1,+∞.【点睛】本题考查利用导数研究函数的单调性,最值及不等式的恒成立问题,考查转化思想,属于中档题.四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17. 已知函数()sin()14f x x x π=+-.(1)求()4f π的值及()f x 的单调递增区间;(2)求()f x 在区间[0,2π上的最大值和最小值.【答案】(1)(14f π=;单调递增区间为3[,]88k k ππ-+π+π,Z k ∈(2;最小值1-【解析】【分析】(1)由()sin()14f x x x π=+-,直接求()4f π;将函数转化为())4f x x π=+,利用正弦函数的性质求解;(2)根据函数())4f x x π=+,利用正弦函数的性质求解.【小问1详解】解:()sin 1442f πππ=-,11=-,1=;()sin(14f x x x π=+-,)1x x x =⋅-, 22sin cos 2cos 1x x x =+-,sin 2cos 2x x =+,4x π=+,令222,242k x k k Z πππππ-+≤+≤+∈,322244k x k ππππ-+≤≤+,k Z ∈,388k x k ππππ-+≤≤+,k Z ∈, 所以()f x 的单调递增区间为3[,]88k k ππ-+π+π,Z k ∈;【小问2详解】因02x π≤≤,所以52444x πππ≤+≤,所以sin 214x π⎛⎫≤+≤ ⎪⎝⎭, 故124x π⎛⎫-≤+≤ ⎪⎝⎭,当2,42x ππ+=即8x π=时,()f x;当2,44x π5π+=即2x π=时,()f x 有最小值1-.18. 已知等差数列{}n a 满足1235n n a a n ++=+.(1)求数列{}n a 的通项公式;(2)设()22nn n b a =+,求数列{}n b 的前n 项和n T .【答案】(1)1n a n =+ (2)()1422n n T n +=-++【解析】【分析】(1)利用赋值法可得数列的首项及公差;(2)利用错位相减法求数列的前n 项和.【小问1详解】当1n =时,1228a a +=①,当2n =时,23211a a +=②,②-①得,33d =,解得1d =,所以12112228a a a a +=++=,12a =,所以()2111n a n n =+-⨯=+;【小问2详解】由(1)得1n a n =+,为则()()2232nn n nn b a =++=,()()12314252622232n n n T n n -=⨯+⨯+⨯+++++ ,()()234124252622232n n n T n n +=⨯+⨯+⨯+++++ ,()12314222232n n n T n +∴-=⨯++++-+ ()()21121283212n n n -+-=+-+-()1422n n +=-+,()1422n n T n +∴=-++.19. 如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 是菱形,E 是BC 的中点.(1)求证:1//BD 平面1C DE ;(2)已知120ABC ∠=︒,1AA =,求直线1A D 与平面1C DE 所成角的正弦值.【答案】(1)证明见解析. (2【解析】【分析】(1)连接1CD 交1DC 于O ,连接OE ,易得1//OE BD ,再根据线面平行的判定即可证结论.(2)F 为AB 中点,结合已知可构建以D 为原点,,DF DC ,1DD为x 、y 、z 轴正方向的空间直角坐标系,设1AA ==,写出对应点坐标,并求出直线1A D 的方向向量和平面1C DE 的法向量,由空间向量夹角的坐标表示求直线1A D 与平面1C DE 所成角的正弦值.【小问1详解】由题设,连接1CD 交1DC 于O ,易知:O 是1CD 的中点,连接OE ,∵E 是BC 的中点,∴1//OE BD ,又OE ⊂面1C DE ,1BD ⊄面1C DE ,∴1//BD 面1C DE .【小问2详解】底面ABCD 是菱形,120ABC ∠=︒,即60DAB ∠=︒,若F 为AB 中点,则DF AB ⊥,∴30ADF ∠=︒,故在直四棱柱1111ABCD A B C D -中有DF DC ⊥、1DD DC ⊥、1DD DF ⊥,∴可构建以D 为原点,,DF DC ,1DD为x 、y 、z轴正方向的空间直角坐标系,设1AA ==,∴1131(0,0,0),,0),42D E C A -,则1131,0),42DE DC DA ===- ,若(,,)m x y z = 是面1C DE的一个法向量,则13040DE m x y DC m y ⎧⋅=+=⎪⎨⎪⋅=+=⎩,令x =m=-,∴111|cos,|||||||m DAm DAm DA⋅<>===,故直线1A D与平面1C DE.20. 已知等比数列{}n a的前n项和为n S,且11a=,6328SS=,数列{}nb满足()33log1n nb a=+.(1)求数列{}n a和{}n b的通项公式;(2)若对任意的*n∈N,3n nb aλ<恒成立,求实数λ的取值范围.【答案】(1)13nna-=,*n∈N;32nb n=-,*n∈N(2)9,4⎛⎫-∞⎪⎝⎭.【解析】【分析】(1)设等比数列{}n a的公比为q,由6328SS=求得公比,再由11a=求解;进而由()33log1n nb a=+求解.(2)由332nnλ<-对于任意的*n∈N恒成立,令()332nf nn=-,*n∈N,求得其最小值即可.【小问1详解】解:设等比数列{}n a的公比为q,由6328SS=,显然1q≠,所以631281qq-=-,解得3q=,由于11a=,所以{}n a的通项公式为13nna-=,*n∈N;所以()1333log13log3132nn nb a n-=+=+=-,*n∈N,所以{}n b的通项公式为32nb n=-,*n∈N.【小问2详解】因为3n nb aλ<恒成立,即332nnλ<-对于任意*n∈N恒成立.的令()332nf n n =-,*n ∈N ,则()()()()()136733131323132n n nn f n f n n n n n +⋅-+-=-=+-+-,当1n >时()()1f n f n +>,,所以()()()()1234f f f f ><<<⋅⋅⋅,即()f n 的最小值为()924f =,所以实数λ的取值范围为9,4⎛⎫-∞ ⎪⎝⎭.21. 已知椭圆()2222:10x y C a b a b +=>>过点⎛ ⎝,且C(1)求椭圆C 的方程;(2)过点()1,0P 的直线l 交椭圆C 于A 、B 两点,求PA PB ⋅的取值范围.【答案】(121y +=;(2)3,34⎡⎤⎢⎥⎣⎦.【解析】【分析】(1)根据已知条件可得出关于a 、、c 的方程组,解出a 、b 的值,进而可求得椭圆C 的方程;(2)对直线l 分两种情况讨论,直线l 与x 轴重合时,直接求出PA PB ⋅的值,在直线l 不与x 轴重合,设直线l 的方程为1x my =+,设点()11,A x y 、()22,B x y ,将直线l 的方程与椭圆C 的方程联立,列出韦达定理,利用弦长公式可得出PA PB ⋅关于m 的代数式,综合可得出PA PB ⋅的取值范围.【详解】(1)由题意得222221314c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得21a b =⎧⎨=⎩.所以椭圆C 的方程为2214x y +=;(2)分以下两种情况讨论:①若直线l 与x 轴重合,则()()21113PA PB a a a ⋅=-⋅+=-=;②若直线l 不与x 轴重合,设直线l 的方程为1x my =+,设点()11,A x y 、()22,B x y ,联立22114x my x y =+⎧⎪⎨+=⎪⎩,消去x 可得()224230m y my ++-=,则()()22241241630m m m ∆=++=+>恒成立,由韦达定理可得12224m y y m +=-+,12234y y m =-+,由弦长公式可得()()221223114m PA PB m y y m +⋅=+⋅=+()2223499344m m m +-==-++,244m +≥ ,则299044m <≤+,所以,2393344m ≤-<+.综上所述,PA PB ⋅的取值范围是3,34⎡⎤⎢⎥⎣⎦.【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()11,x y 、()22,x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,必要时计算∆;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x 的形式;(5)代入韦达定理求解.22. 已知函数()21)xf x e ax a =-->(,(1)证明:函数()y f x =在(),0∞-内存在唯一零点;(2)若函数()y f x =有两个不同零点12,x x 且12x x >,当12x x -最小时,求此时a 的值.【答案】(1)证明见解析;(2)2.【解析】【分析】(1)求出导数,可判断()f x 在(,0)-∞单调递减,再根据零点存在性定理即可判断;(2)令120t x x =->,则由题可得()22212x t x e e ea tx --==,利用导数可得1()(0)t e g t t t -=>在(0,)+∞单调递增,判断出要求t 的最小值即求()g t 最小值,构造函数()22222x x e v x x e -=,利用导数判断单调性求出其最小值即可.【详解】(1)()x f x e a '=-, 0x <,1x e ∴<,又1a >,∴()0f x '<,∴()f x 在(,0)-∞单调递减,(0)10f =-<,220a f e a -⎛⎫-=> ⎪⎝⎭,存在唯一02,0x a ⎛⎫∈- ⎪⎝⎭使得0()0f x =,所以函数()y f x =在(),0∞-内存在唯一零点;(2)由条件知12122020x x e ax e ax ⎧--=⎨--=⎩,1212121222x x x x e e e e a x x x x ---∴===-,令()22122120,x t x e e e t x x a t x --=->∴==,则有22212x t x e e t x e --=,令1()(0)t e g t t t -=>,2(1)1()t t e g t t -+=',令()(1)1t h t t e =-+,()0th t te =>',()h t ∴(0,)+∞单调递增,()(0)0h t h ∴>=,()g t ∴在(0,)+∞单调递增,要求t 的最小值即求()g t 最小值,令()22222x x e v x x e -=,()()()22222222222222,12220x x x x x x e x e x e v x x x e x e'-+-+-==<,在令()22222x m x x e =+-,()2220x m x e =->',()2m x ∴在(,0)-∞单调递增,又1(0)10,(1)0m m e -=>-=-<,∴存在唯一0(1,0)x ∈-使得()00m x =.此时0022x e x =+,2x ()0,x -∞0x ()0,x +∞()2v x '-0+()2v x 极小 当02x x =时,()2v x 有最小值故12x x -取最小值时000022222x x e a x x +--===.【点睛】关键点睛:解决本题得关键是得出()22212x t x e e e a t x --==,利用导数判断出要求t 的最小值即求()g t 最小值,构造函数()22222x x e v x x e -=,利用导数判断单调性求出其最小值.。
高三数学模拟试卷(八)文(含解析)-人教版高三全册数学试题

2016年某某省某某市东北育才学校高考数学模拟试卷(文科)(八)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为()A.50 B.45 C.40 D.202.若命题p:∃x0∈R,x02+1>3x0,则¬p是()A.∃x0∈R,x02+1≤3x0B.∀x∈R,x2+1≤3xC.∀x∈R,x2+1<3x D.∀x∈R,x2+1>3x3.设z=1+i(是虚数单位),则+=()A.1 B.﹣1 C.i D.﹣i4.已知集合A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N},则A∩B=()A.{0,2} B.{0,1,2} C.{﹣2,0,1,2} D.{﹣2,﹣1,0,1,2}5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡瑽(圆柱体)的体积为:V=×(底面的圆周长的平方×高).则由此可推得圆周率π的取值为()A.3 B.3.14 C.3.2 D.3.36.执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6 B.k≤7 C.k≤8 D.k≤97.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数 D.f(x)的值域为[﹣1,+∞)8.如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为()A.4πB.5πC.6πD.7π9.已知不等式组的解集记为D,则对∀(x,y)∈D使得2x﹣y取最大值时的最优解是()A.(2,1)B.(2,2)C.3 D.410.若等比数列的各项均为正数,前4项的和为9,积为,则前4项倒数的和为()A.B.C.1 D.211.tan20°+4sin20°的值为()A.B.C.D.12.已知A,B分别为椭圆的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当取最小值时,椭圆C的离心率为()A.B.C.D.二.填空题:本大题共4小题,每小题5分.13.过原点作曲线y=e x的切线,则切线方程为.14.某一简单几何体的三视图如图,则该几何体的外接球的表面积为.15.在△ABC中,内角A、B、C的对边分别为a、b、c,且a=4,b=3,c=2,若点D为线段BC上靠近B的一个三等分点,则AD=.16.已知函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,则实数a的取值X 围是.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程和演算步骤17.设数列{a n}的前n项和为S n,且2a n=S n+2.(Ⅰ)求{a n}的通项公式;(Ⅱ)设数列b n=,其前n项和为T n,求T n.18.在某学校一次考试的语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;语文成绩的频数分布表:语文成绩分组[50,60)[60,70)[70,80)[80,90)[90,100)[100,110)[110,120]频数(Ⅲ)设上述样本中第i位考生的语文、历史成绩分别为x i,y i(i=1,2,…,25).通过对样本数据进行初步处理发现:语文、历史成绩具有线性相关关系,得到:=x i=86, =y i =64,(x i﹣)(y i ﹣)=4698,(x i﹣)2=5524,≈0.85.①求y关于x的线性回归方程;②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:==, =﹣.19.如图,在四棱锥P ﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;(Ⅱ)当点A到平面PDE的距离为时,求三棱锥A﹣PDE的侧面积.20.已知椭圆C: =1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2﹣1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.(1)求椭圆C的方程;(2)设点B,C,D是椭圆上不同于椭圆顶点的三点,点B与点D关于原点O对称,设直线CD,CB,OB,OC的斜率分别为k1,k2,k3,k4,且k1k2=k3k4.(i)求k1k2的值;(ii)求OB2+OC2的值.21.设函数f(x)=lnx+,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;(Ⅱ)讨论函数g(x)=f′(x)﹣零点的个数;(Ⅲ)若对任意b>a>0,<1恒成立,求m的取值X围.请从下面所给的22、23、24三题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多涂均按所答第一题评分;多答按所答第一题评分.[选修4-1:几何证明选讲]22.如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.(1)求△ABP的面积;(2)求弦AC的长.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,圆C的参数方程(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;(Ⅱ)直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.[选修4-5:不等式选讲]24.已知函数f(x)=|x+2|﹣|x﹣1|.(Ⅰ)试求f(x)的值域;(Ⅱ)设若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,试某某数a的取值X围.2016年某某省某某市东北育才学校高考数学模拟试卷(文科)(八)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为()A.50 B.45 C.40 D.20【考点】分层抽样方法.【分析】利用分层抽样性质求解.【解答】解:∵高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,∴由分层抽样性质,得:,解得n=45.故选:B.2.若命题p:∃x0∈R,x02+1>3x0,则¬p是()A.∃x0∈R,x02+1≤3x0B.∀x∈R,x2+1≤3xC.∀x∈R,x2+1<3x D.∀x∈R,x2+1>3x【考点】命题的否定.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题.所以,命题p:∃x0∈R,x02+1>3x0,则¬p 是∀x∈R,x2+1≤3x,故选B.3.设z=1+i(是虚数单位),则+=()A.1 B.﹣1 C.i D.﹣i【考点】复数代数形式的乘除运算.【分析】利用复数的除法运算法则化简复数为a+bi的形式即可.【解答】解:z=1+i(是虚数单位),则+===1.故选:A.4.已知集合A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N},则A∩B=()A.{0,2} B.{0,1,2} C.{﹣2,0,1,2} D.{﹣2,﹣1,0,1,2}【考点】交集及其运算.【分析】求出B中x的值确定出B,找出A与B的交集即可.【解答】解:∵A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N}={0,1,2,…},∴A∩B={0,1,2},故选:B.5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡瑽(圆柱体)的体积为:V=×(底面的圆周长的平方×高).则由此可推得圆周率π的取值为()A.3 B.3.14 C.3.2 D.3.3【考点】排序问题与算法的多样性.【分析】由题意,圆柱体底面的圆周长20尺,高4尺,利用圆堡瑽(圆柱体)的体积V=×(底面的圆周长的平方×高),求出V,再建立方程组,即可求出圆周率π的取值.【解答】解:由题意,圆柱体底面的圆周长20尺,高4尺,∵圆堡瑽(圆柱体)的体积V=×(底面的圆周长的平方×高),∴V=×=,∴∴π=3,R=,故选:A.6.执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6 B.k≤7 C.k≤8 D.k≤9【考点】程序框图.【分析】根据程序框图,写出运行结果,根据程序输出的结果是S=3,可得判断框内应填入的条件.【解答】解:根据程序框图,运行结果如下:S k第一次循环 log23 3第二次循环 log23•log34 4第三次循环 log23•log34•log45 5第四次循环 log23•log34•log45•log56 6第五次循环 log23•log34•log45•log56•log67 7第六次循环 log23•log34•log45•log56•log67•log78=log28=3 8故如果输出S=3,那么只能进行六次循环,故判断框内应填入的条件是k≤7.故选B.7.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数 D.f(x)的值域为[﹣1,+∞)【考点】函数的值域;函数单调性的判断与证明;函数奇偶性的判断.【分析】根据函数的性质分别进行判断即可.【解答】解:当x≤0时,f(x)=cos2x不是单调函数,此时﹣1≤cos2x≤1,当x>0时,f(x)=x4+1>1,综上f(x)≥﹣1,即函数的值域为[﹣1,+∞),故选:D8.如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为()A.4πB.5πC.6πD.7π【考点】几何概型.【分析】由几何概型概率计算公式,以面积为测度,可求该阴影部分的面积.【解答】解:设该多边形的面积为S,则,∴S=5π,故选B.9.已知不等式组的解集记为D,则对∀(x,y)∈D使得2x﹣y取最大值时的最优解是()A.(2,1)B.(2,2)C.3 D.4【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).设z=2x﹣y,则y=2x﹣z,平移直线y=2x﹣z,由图象可知当直线y=2x﹣z经过点C时,直线y=2x﹣z的截距最小,此时z最大.即,即C(2,1),故使得2x﹣y取最大值时的最优解是(2,1),故选:A.10.若等比数列的各项均为正数,前4项的和为9,积为,则前4项倒数的和为()A.B.C.1 D.2【考点】等比数列的前n项和.【分析】设此等比数列的首项为a1,公比为q,前4项之和为S,前4项之积为P,前4项倒数之和为M,由等比数列性质推导出P2=()4,由此能求出前4项倒数的和.【解答】解:∵等比数列的各项均为正数,前4项的和为9,积为,∴设此等比数列的首项为a1,公比为q前4项之和为S,前4项之积为P,前4项倒数之和为M,若q=1,则,无解;若q≠1,则S=,M==,P=a14q6,∴()4=(a12q3)4=a18q12,P2=a18q12,∴P2=()4,∵,∴前4项倒数的和M===2.故选:D.11.tan20°+4sin20°的值为()A.B.C.D.【考点】三角函数的化简求值.【分析】首先利用弦切互化公式及正弦的倍角公式对原式进行变形,再两次运用和差化积公式,同时结合正余弦互化公式,转化为特殊角的三角函数值,则问题解决.【解答】解:tan20°+4sin20°========2sin60°=.故选B.12.已知A,B分别为椭圆的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当取最小值时,椭圆C的离心率为()A.B.C.D.【考点】椭圆的简单性质.【分析】设P(x0,y0),则Q(x0,﹣y0),=.A(﹣a,0),B(a,0),利用斜率计算公式肯定:mn=,=++=,令=t>1,则f(t)=+﹣2lnt.利用导数研究其单调性即可得出.【解答】解:设P(x0,y0),则Q(x0,﹣y0),=.A(﹣a,0),B(a,0),则m=,n=,∴mn==,∴=++=,令=t>1,则f(t)=+﹣2lnt.f′(t)=+1+t﹣=,可知:当t=时,函数f(t)取得最小值=++﹣2ln=2+1﹣ln2.∴=.∴=.故选:D.二.填空题:本大题共4小题,每小题5分.13.过原点作曲线y=e x的切线,则切线方程为y=ex .【考点】利用导数研究曲线上某点切线方程.【分析】欲求切点的坐标,先设切点的坐标为( x0,e x0),再求出在点切点( x0,e x0)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=x0处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用切线过原点即可解决问题.【解答】解:y′=e x设切点的坐标为(x0,e x0),切线的斜率为k,则k=e x0,故切线方程为y﹣e x0=e x0(x﹣x0)又切线过原点,∴﹣e x0=e x0(﹣x0),∴x0=1,y0=e,k=e.则切线方程为y=ex故答案为y=ex.14.某一简单几何体的三视图如图,则该几何体的外接球的表面积为25π.【考点】由三视图求面积、体积.【分析】几何体为底面为正方形的长方体,底面对角线为4,高为3.则长方体的对角线为外接球的直径.【解答】解:几何体为底面为正方形的长方体,底面对角线为4,高为3,∴长方体底面边长为2.则长方体外接球半径为r,则2r==5.∴r=.∴长方体外接球的表面积S=4πr2=25π.故答案为:25π.15.在△ABC中,内角A、B、C的对边分别为a、b、c,且a=4,b=3,c=2,若点D为线段BC上靠近B的一个三等分点,则AD=.【考点】解三角形.【分析】利用余弦定理求出cosB,再利用余弦定理解出AD.【解答】解:在△ABC中,由余弦定理得cosB==.在△ABD中,BD==.由余弦定理得:AD2=BD2+AB2﹣2BD•AB•cosB=.∴AD=.故答案为:.16.已知函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,则实数a的取值X 围是.【考点】函数奇偶性的性质.【分析】根据函数的奇偶性求出g(x),h(x)的表达式,然后将不等式恒成立进行参数分离,利用基本不等式进行求解即可得到结论.【解答】解:∵函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,∴e x=g(x)+h(x),e﹣x=g(x)﹣h(x),∴g(x)=,h(x)=.∵∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,即﹣a•≥0恒成立,∴a≤==(e x﹣e﹣x)+,设t=e x﹣e﹣x,则函数t=e x﹣e﹣x在(0,2]上单调递增,∴0<t≤e2﹣e﹣2,此时不等式t+≥2,当且仅当t=,即t=时,取等号,∴a≤2,故答案为:.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程和演算步骤17.设数列{a n}的前n项和为S n,且2a n=S n+2.(Ⅰ)求{a n}的通项公式;(Ⅱ)设数列b n=,其前n项和为T n,求T n.【考点】数列的求和;数列递推式.【分析】(Ⅰ)运用n=1时,a1=S1,当n≥2时,a n=S n﹣S n﹣1,结合等比数列的通项公式,计算即可得到所求;(Ⅱ)求得b n=﹣,运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.【解答】解:(Ⅰ)当n=1时,由2a1=S1+2=a1+2,得a1=2.当n≥2时,由,以及a n=S n﹣S n﹣1,两式相减可得,则数列{a n}是首项为2,公比为2的等比数列,故;(Ⅱ)由(Ⅰ)可得,故其前n项和化简可得T n =﹣.18.在某学校一次考试的语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;语文成绩的频数分布表:语文成绩分组[50,60)[60,70)[70,80)[80,90)[90,100)[100,110)[110,120]频数(Ⅲ)设上述样本中第i位考生的语文、历史成绩分别为x i,y i(i=1,2,…,25).通过对样本数据进行初步处理发现:语文、历史成绩具有线性相关关系,得到:=x i=86, =y i=64,(x i ﹣)(y i ﹣)=4698,(x i ﹣)2=5524,≈0.85.①求y关于x的线性回归方程;②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:==, =﹣.【考点】线性回归方程;茎叶图.【分析】(Ⅰ)根据所给数据,可得历史成绩的茎叶图;(Ⅱ)根据所给数据,可得语文成绩的频数分布表及语文成绩的频率分布直方图;(Ⅲ)求出a,b,可得y关于x的线性回归方程,并据此预测当某考生的语文成绩为100分时,该考生的历史成绩.【解答】解:(Ⅰ)根据题意,在茎叶图中完成历史成绩统计,如图所示;(Ⅱ)语文成绩的频数分布表;语文成绩分组[50,60﹚[60,70﹚[70,80﹚[80,90﹚[90,100﹚[100,110﹚[110,120]频数 1 2 3 7 6 5 1 语文成绩的频率分布直方图:;(Ⅲ)由已知得b=0.85,a=64﹣0.85×86=﹣9.1,∴y=0.85x﹣9.1,∴x=100时,y=75.9≈76,预测当某考生的语文成绩为100分时,该考生的历史成绩为76分.19.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;(Ⅱ)当点A到平面PDE的距离为时,求三棱锥A﹣PDE的侧面积.【考点】直线与平面垂直的判定;棱柱、棱锥、棱台的体积.【分析】(Ⅰ)在Rt△DAE中,求出BE=3.在Rt△EBC中,求出∠CEB=.证明CE⊥DE.PD ⊥CE.即可证明CE⊥平面PDE.(Ⅱ)证明平面PDE⊥平面ABCD.过A作AF⊥DE于F,求出AF.证明BA⊥平面PAD,BA⊥PA.然后求出三棱锥A﹣PDE的侧面积S侧=++.【解答】(本小题满分12分)解:(Ⅰ)在Rt△DAE中,AD=,∠ADE=,∴AE=AD•tan∠ADE=•=1.又AB=CD=4,∴BE=3.在Rt△EBC中,BC=AD=,∴tan∠CEB==,∴∠CEB=.又∠AED=,∴∠DEC=,即CE⊥DE.∵PD⊥底面ABCD,CE⊂底面ABCD,∴PD⊥CE.∴CE⊥平面PDE.…(Ⅱ)∵PD⊥底面ABCD,PD⊂平面PDE,∴平面PDE⊥平面ABCD.如图,过A作AF⊥DE于F,∴AF⊥平面PDE,∴AF就是点A到平面PDE的距离,即AF=.在Rt△DAE中,由AD•AE=AF•DE,得AE=•,解得AE=2.∴S△APD=PD•AD=××=,S△ADE=AD•AE=××2=,∵BA⊥AD,BA⊥PD,∴BA⊥平面PAD,∵PA⊂平面PAD,∴BA⊥PA.在Rt△PAE中,AE=2,PA===,∴S△APE=PA•AE=××2=.∴三棱锥A﹣PDE的侧面积S侧=++.…20.已知椭圆C: =1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2﹣1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.(1)求椭圆C的方程;(2)设点B,C,D是椭圆上不同于椭圆顶点的三点,点B与点D关于原点O对称,设直线CD,CB,OB,OC的斜率分别为k1,k2,k3,k4,且k1k2=k3k4.(i)求k1k2的值;(ii)求OB2+OC2的值.【考点】直线与圆锥曲线的综合问题.【分析】(1)设出椭圆右焦点坐标,由题意可知,椭圆右焦点F2到直线x+y+2﹣1=0的距离为a,再由椭圆C的两焦点与短轴的一个端点的连线构成等边三角形得到a,b,c的关系,结合焦点F2到直线x+y+2﹣1=0的距离为a可解得a,b,c的值,则椭圆方程可求;(2)(i)由题意设B(x1,y1),C(x2,y2),则D(﹣x1,﹣y1),由两点求斜率公式可得是,把纵坐标用横坐标替换可得答案;(ii)由k1k2=k3k4.得到.两边平方后用x替换y可得.结合点B,C在椭圆上得到.则OB2+OC2的值可求.【解答】解:(1)设椭圆C的右焦点F2(c,0),则c2=a2﹣b2(c>0),由题意,以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为(x﹣c)2+y2=a2,∴圆心到直线x+y+2﹣1=0的距离①,∵椭圆C的两焦点与短轴的一个端点的连线构成等边三角形,∴,a=2c,代入①式得,,故所求椭圆方程为;(2)(i)设B(x1,y1),C(x2,y2),则D(﹣x1,﹣y1),于是=;(ii)由(i)知,,故.∴,即,∴.又=,故.∴OB2+OC2=.21.设函数f(x)=lnx+,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;(Ⅱ)讨论函数g(x)=f′(x)﹣零点的个数;(Ⅲ)若对任意b>a>0,<1恒成立,求m的取值X围.【考点】利用导数研究函数的极值;函数恒成立问题;函数的零点.【分析】(Ⅰ)m=e时,f(x)=lnx+,利用f′(x)判定f(x)的增减性并求出f(x)的极小值;(Ⅱ)由函数g(x)=f′(x)﹣,令g(x)=0,求出m;设φ(x)=m,求出φ(x)的值域,讨论m的取值,对应g(x)的零点情况;(Ⅲ)由b>a>0,<1恒成立,等价于f(b)﹣b<f(a)﹣a恒成立;即h (x)=f(x)﹣x在(0,+∞)上单调递减;h′(x)≤0,求出m的取值X围.【解答】解:(Ⅰ)当m=e时,f(x)=lnx+,∴f′(x)=;∴当x∈(0,e)时,f′(x)<0,f(x)在(0,e)上是减函数;当x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上是增函数;∴x=e时,f(x)取得极小值为f(e)=lne+=2;(Ⅱ)∵函数g(x)=f′(x)﹣=﹣﹣(x>0),令g(x)=0,得m=﹣x3+x(x>0);设φ(x)=﹣x3+x(x>0),∴φ′(x)=﹣x2+1=﹣(x﹣1)(x+1);当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;∴x=1是φ(x)的极值点,且是极大值点,∴x=1是φ(x)的最大值点,∴φ(x)的最大值为φ(1)=;又φ(0)=0,结合y=φ(x)的图象,如图;可知:①当m>时,函数g(x)无零点;②当m=时,函数g(x)有且只有一个零点;③当0<m<时,函数g(x)有两个零点;④当m≤0时,函数g(x)有且只有一个零点;综上,当m>时,函数g(x)无零点;当m=或m≤0时,函数g(x)有且只有一个零点;当0<m<时,函数g(x)有两个零点;(Ⅲ)对任意b>a>0,<1恒成立,等价于f(b)﹣b<f(a)﹣a恒成立;设h(x)=f(x)﹣x=lnx+﹣x(x>0),则h(b)<h(a).∴h(x)在(0,+∞)上单调递减;∵h′(x)=﹣﹣1≤0在(0,+∞)上恒成立,∴m≥﹣x2+x=﹣+(x>0),∴m≥;对于m=,h′(x)=0仅在x=时成立;∴m的取值X围是[,+∞).请从下面所给的22、23、24三题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多涂均按所答第一题评分;多答按所答第一题评分.[选修4-1:几何证明选讲]22.如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.(1)求△ABP的面积;(2)求弦AC的长.【考点】与圆有关的比例线段.【分析】(1)利用圆的切线的性质,结合切割线定理,求出PA,即可求△ABP的面积;(2)由勾股定理得AE,由相交弦定理得EC,即可求弦AC的长.【解答】解:(1)因为PA是⊙O的切线,切点为A,所以∠PAE=∠ABC=45°,…又PA=PE,所以∠PEA=45°,∠APE=90°…因为PD=1,DB=8,所以由切割线定理有PA2=PD•PB=9,所以EP=PA=3,…所以△ABP的面积为BP•PA=…(2)在Rt△APE中,由勾股定理得AE=3…又ED=EP﹣PD=2,EB=DB﹣DE=8﹣2=6,所以由相交弦定理得EC•EA=EB•ED=12 …所以EC==2,故AC=5…[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,圆C的参数方程(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;(Ⅱ)直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.【考点】简单曲线的极坐标方程;直线与圆的位置关系.【分析】(I)圆C的参数方程(φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简即可得到此圆的极坐标方程.(II)由直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=.可得普通方程:直线l,射线OM.分别与圆的方程联立解得交点,再利用两点间的距离公式即可得出.【解答】解:(I)圆C的参数方程(φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简得:ρ=2cosθ,即为此圆的极坐标方程.(II)如图所示,由直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=.可得普通方程:直线l,射线OM.联立,解得,即Q.联立,解得或.∴P.∴|PQ|==2.[选修4-5:不等式选讲]24.已知函数f(x)=|x+2|﹣|x﹣1|.(Ⅰ)试求f(x)的值域;(Ⅱ)设若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,试某某数a的取值X围.【考点】函数恒成立问题;函数的值域.【分析】(1)将含有绝对值的函数转化为分段函数,再求分段函数的值域;(2)恒成立问题转化成最小值最大值问题,即g(x)min≥f(x)max.【解答】解:(Ⅰ)函数可化为,∴f(x)∈[﹣3,3](Ⅱ)若x>0,则,即当ax2=3时,,又由(Ⅰ)知∴f(x)max=3若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,即g(x)min≥f(x)max,∴,∴a≥3,即a的取值X围是[3,+∞).。
高三数学上学期第二次月考试卷 理(含解析)-人教版高三全册数学试题

2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>04.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣26.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.278.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.49.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.2011.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=__________.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是__________.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=__________.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是__________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}【考点】Venn图表达集合的关系及运算.【专题】应用题;集合思想;定义法;集合.【分析】由图知,阴影部分表示的集合中的元素是在集合N中的元素但不在集合M中的元素组成的,即N∩C U M.【解答】解:由韦恩图知阴影部分表示的集合为N∩(C U M)M={x|y=ln(x2﹣2x) }∴x2﹣2x>0,解得x<0,或x>2,∴M={x|x<0,或x>2},∴C U M={x|0≤x≤2}=[0,2],N={y|y=}={y|y≥1}=[1,+∞),∴N∩(C U M)=[1,2],故选:C【点评】本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识,属于基础题2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣【考点】分段函数的应用;函数的零点.【专题】函数的性质及应用.【分析】由f(a)=﹣3,结合指数和对数的运算性质,求得a=7,再由分段函数求得f(6﹣a)的值.【解答】解:函数f(x)=且f(a)=﹣3,若a≤1,则2a﹣1﹣2=﹣3,即有2a﹣1=﹣1<0,方程无解;若a>1,则﹣log2(a+1)=﹣3,解得a=7,则f(6﹣a)=f(﹣1)=2﹣1﹣1﹣2=﹣.故选:A.【点评】本题考查分段函数的运用:求函数值,主要考查指数和对数的运算性质,属于中档题.3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0【考点】命题的真假判断与应用.【专题】计算题;规律型;简易逻辑.【分析】利用命题的否定判断A的正误;四种命题的逆否关系判断B的正误;充要条件判断C 的正误;命题的真假判断D的正误;【解答】解:对于A,命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠x0,不满足命题的否定形式,所以不正确;对于B,命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5,不满足否命题的形式,所以不正确;对于C,若ω=1是函数f(x)=cosx在区间[0,π]上单调递减的,而函数f(x)=cosωx在区间[0,π]上单调递减的,ω≤1,所以ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件,正确.对于D,命题:∃x0∈R,x02+a<0为假命题,则命题:a≥0,∀x∈R,x2+a≥0是真命题;所以,命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0,不正确;故选:C.【点评】本题考查命题的真假的判断与应用,基本知识的考查.4.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.【考点】由三视图求面积、体积.【专题】图表型.【分析】先由三视图还原成原来的几何体,再根据三视图中的长度关系,找到几何体中的长度关系,进而可以求几何体的体积.【解答】解:由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得:V=××=,故选C.【点评】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,一般组合体的体积要分部分来求.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣2【考点】椭圆的简单性质.【专题】计算题.【分析】通过题意可推断出当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.进而可根据椭圆的方程求得焦点的坐标和P的坐标,进而求得和,则•的值可求得.【解答】解:根据题意可知当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.这时,F1(﹣,0),F2(,0),P(0,1),∴=(﹣,﹣1),=(,﹣1),∴•=﹣2.故选D【点评】本题主要考查了椭圆的简单性质.考查了学生数形结合的思想和分析问题的能力.6.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b【考点】对数值大小的比较.【专题】函数的性质及应用.【分析】分别讨论a,b,c的取值X围,即可比较大小.【解答】解:1<log37<2,b=21.1>2,c=0.83.1<1,则c<a<b,故选:B.【点评】本题主要考查函数值的大小比较,根据指数和对数的性质即可得到结论.7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.27【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行程序,依次写出每次循环得到的R,P,Q的值,当Q=0时,满足条件Q=0,退出循环,输出P的值为3.【解答】解:模拟执行程序,可得P=153,Q=63不满足条件Q=0,R=27,P=63,Q=27不满足条件Q=0,R=9,P=27,Q=9不满足条件Q=0,R=0,P=9,Q=0满足条件Q=0,退出循环,输出P的值为9.故选:C.【点评】本题主要考查了程序框图和算法,依次写出每次循环得到的R,P,Q的值是解题的关键,属于基本知识的考查.8.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.4【考点】三角函数的化简求值.【专题】计算题;转化思想;转化法;三角函数的求值.【分析】先根据对数的运算性质求出tanθ,再化简代值计算即可.【解答】解:点(16,tanθ)在函数y=log2x的图象上,∴tanθ=log216=4,∴====,故选:B.【点评】本题考查了二倍角公式,函数值的求法,以及对数的运算性质,属于基础题.9.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零【考点】函数的零点与方程根的关系.【专题】函数的性质及应用.【分析】由函数的性质可知,f(x)=()x﹣log3x在(0,+∞)上是减函数,且可得f(x0)=0,由0<x0<x1,可得f(x1)<f(x0)=0,即可判断【解答】解:∵实数x0是方程f(x)=0的解,∴f(x0)=0.∵函数y()x,y=log3x在(0,+∞)上分别具有单调递减、单调递增,∴函数f(x)在(0,+∞)上是减函数.又∵0<x0<x1,∴f(x1)<f(x0)=0.∴f(x1)的值恒为负.故选A.【点评】本题主要考查了函数的单调性的简单应用,解题的关键是准确判断函数f(x)的单调性并能灵活应用.10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.20【考点】数列的求和.【专题】等差数列与等比数列.【分析】首先根据题中的已知条件已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,进一步求出数列的通项公式,然后根据通项公式求出各项的值,最后确定结果.【解答】解:已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2则:∴a n=3n﹣5a2+a4+a5+a9=40故选:B【点评】本题考查的知识点:根据点的斜率求出数列的通项公式,由通项公式求数列的项.11.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.【考点】对数的运算性质;函数的图象与图象变化.【分析】根据函数y=e|lnx|﹣|x﹣1|知必过点(1,1),再对函数进行求导观察其导数的符号进而知原函数的单调性,得到答案.【解答】解:由y=e|lnx|﹣|x﹣1|可知:函数过点(1,1),当0<x<1时,y=e﹣lnx﹣1+x=+x﹣1,y′=﹣+1<0.∴y=e﹣lnx﹣1+x为减函数;若当x>1时,y=e lnx﹣x+1=1,故选D.【点评】本题主要考查函数的求导与函数单调性的关系.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)【考点】函数奇偶性的性质.【专题】转化思想;数学模型法;函数的性质及应用;导数的综合应用.【分析】f(x)是定义在R上的奇函数,可得:f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),可得:xf′(x)+2f(x)>0,由g(x)=x2f(x),可得g′(x)>0.可得函数g(x)在(0,+∞)上单调递增.即可得出.【解答】解:∵f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),∴xf′(x)+2f(x)>0,∵g(x)=x2f(x),∴g′(x)=2xf(x)+x2f′(x)>0.∴函数g(x)在(0,+∞)上单调递增.又g(0)=0,g(﹣x)=x2f(﹣x)=﹣g(x),∴函数g(x)是R上的奇函数,∴g(x)是R上的增函数.由不等式g(x)<g(1﹣3x),∴x<1﹣3x,解得.∴不等式g(x)<g(1﹣3x)的解集为:.故选:B.【点评】本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=.【考点】对数的运算性质;有理数指数幂的化简求值.【专题】计算题;函数思想;定义法;函数的性质及应用.【分析】根据对数和幂的运算性质计算即可.【解答】解:()+lg+lg70+=+lg()+1﹣lg3=+lg+1=+1+1=,故答案为:.【点评】本题考查了对数和幂的运算性质,关键是掌握性质,属于基础题.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是﹣8.【考点】简单线性规划.【专题】不等式的解法及应用.【分析】将z=x﹣3y变形为,此式可看作是斜率为,纵截距为的一系列平行直线,当最大时,z最小.作出原不等式组表示的平面区域,让直线向此平面区域平移,可探求纵截距的最大值.【解答】解:由z=x﹣3y,得,此式可看作是斜率为,纵截距为的直线,当最大时,z最小.画出直线y=x,x+2y=2,x=﹣2,从而可标出不等式组表示的平面区域,如右图所示.由图知,当动直线经过点P时,z最小,此时由,得P(﹣2,2),从而z min=﹣2﹣3×2=﹣8,即z=x﹣3y的最小值是﹣8.故答案为:﹣8.【点评】本题考查了线性规划的应用,为高考常考的题型,求解此类问题的一般步骤是:(1)作出已知不等式组表示的平面区域;(2)运用化归思想及数形结合思想,将目标函数的最值问题转化为平面中几何量的最值问题处理.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=﹣8.【考点】奇偶性与单调性的综合;函数的周期性.【专题】数形结合.【分析】由条件“f(x﹣4)=﹣f(x)”得f(x+8)=f(x),说明此函数是周期函数,又是奇函数,且在[0,2]上为增函数,由这些画出示意图,由图可解决问题.【解答】解:此函数是周期函数,又是奇函数,且在[0,2]上为增函数,综合条件得函数的示意图,由图看出,四个交点中两个交点的横坐标之和为2×(﹣6),另两个交点的横坐标之和为2×2,所以x1+x2+x3+x4=﹣8.故答案为﹣8.【点评】数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是①②④.【考点】命题的真假判断与应用;奇偶性与单调性的综合.【专题】函数思想;定义法;函数的性质及应用.【分析】是结合复合函数单调性的关系进行判断.②根据基本由函数奇偶性的定义判断函数为偶函数判断;③利用对勾函数的单调性判断;④由对勾函数的最值及函数奇偶性的性质进行判断即可.【解答】解:①函数f(x)=lg,(x∈R且x≠0).∵=2,∴f(x)=lg≥2,即f(x)的最小值是lg2,故①正确,②∵f(﹣x)==f(x),∴函数f(x)为偶函数,图象关于y轴对称,故②正确;③当x>0时,t(x)=,在(0,1)上单调递减,在(1,+∞)上得到递增,∴f(x)=lg在(0,1)上单调递减,在(1,+∞)上得到递增,故③错误;④∵函数f(x)是偶函数,由③知f(x)在(0,1)上单调递减,在(1,+∞)上得到递增,∴在(﹣1,0)上单调递增,在(﹣∞,﹣1)上得到递减,故④正确,故答案为:①②④【点评】本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,考查了复合函数的单调性,是中档题.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.【考点】必要条件;绝对值不等式的解法.【专题】规律型.【分析】先求出命题p,q的等价条件,利用¬p是¬q的必要不充分条件转化为q是p的必要不充分条件,建立条件关系即可求出m的取值X围.【解答】解:由||=,得|x﹣4|≤6,即﹣6≤x﹣4≤6,∴﹣2≤x≤10,即p:﹣2≤x≤10,由x2+2x+1﹣m2≤0得[x+(1﹣m)][x+(1+m)]≤0,即1﹣m≤x≤1+m,(m>0),∴q:1﹣m≤x≤1+m,(m>0),∵¬p是¬q的必要不充分条件,∴q是p的必要不充分条件.即,且等号不能同时取,∴,解得m≥9.【点评】本题主要考查充分条件和必要条件的应用,将¬p是¬q的必要不充分条件转化为q 是p的必要不充分条件是解决本题的关键.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.【考点】函数零点的判定定理;根的存在性及根的个数判断.【专题】计算题;函数的性质及应用;导数的综合应用;不等式的解法及应用.【分析】(1)由基本不等式可得g(x)=x+≥2=2e,从而求m的取值X围;(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,求导F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);从而判断函数的单调性及最值,从而确定m的取值X围.【解答】解:(1)∵g(x)=x+≥2=2e;(当且仅当x=,即x=e时,等号成立)∴若使函数y=g(x)﹣m有零点,则m≥2e;故m的取值X围为[2e,+∞);(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);故当x∈(0,e)时,F′(x)<0,x∈(e,+∞)时,F′(x)>0;故F(x)在(0,e)上是减函数,在(e,+∞)上是增函数,故只需使F(e)<0,即e+e+e2﹣2e2﹣m+1<0;故m>2e﹣e2+1.【点评】本题考查了基本不等式的应用及导数的综合应用,同时考查了函数零点的判断与应用,属于中档题.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.【考点】求对数函数解析式;函数解析式的求解及常用方法;函数最值的应用.【专题】计算题;转化思想.【分析】(1)由已知条件可知函数g(x)的图象上的任意一点P(x,y)关于原点对称的点Q (﹣x,﹣y)在函数f(x)图象上,把Q(﹣x,﹣y)代入f(x),整理可得g(x)(2)由(1)可令h(x)=f(x)+g(x),先判断函数h(x)在[0,1)的单调性,进而求得函数的最小值h(x)min,使得m≤h(x)min【解答】解:(1)设点P(x,y)是g(x)的图象上的任意一点,则Q(﹣x,﹣y)在函数f (x)的图象上,即﹣y=log a(﹣x+1),则∴(2)f(x)+g(x)≥m 即,也就是在[0,1)上恒成立.设,则由函数的单调性易知,h(x)在[0,1)上递增,若使f(x)+g(x)≥m在[0,1)上恒成立,只需h(x)min≥m在[0,1)上成立,即m≤0.m的取值X围是(﹣∞,0]【点评】本题(1)主要考查了函数的中心对称问题:若函数y=f(x)与y=g(x)关于点M (a,b)对称,则y=f(x)上的任意一点(x,y)关于M(a,b)对称的点(2a﹣x,2b﹣y)在函数y=g(x)的图象上.(2)主要考查了函数的恒成立问题,往往转化为求最值问题:m≥h(x)恒成立,则m≥h(x)m≤h(x)恒成立,max则m≤h(x)min20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.【考点】基本不等式在最值问题中的应用.【专题】计算题.【分析】(1)赢利总额y元即x年中的收入50x减去购进机床的成本与这x年中维修、保养的费用,维修、保养的费用历年成等差数增长,,(2)由(1)的结论解出结果进行判断得出何年开始赢利.(3)算出每一种方案的总盈利,比较大小选择方案.【解答】解:(1)y=﹣2x2+40x﹣98,x∈N*.(2)由﹣2x2+40x﹣98>0解得,,且x∈N*,所以x=3,4,,17,故从第三年开始盈利.(3)由,当且仅当x=7时“=”号成立,所以按第一方案处理总利润为﹣2×72+40×7﹣98+30=114(万元).由y=﹣2x2+40x﹣98=﹣2(x﹣10)2+102≤102,所以按第二方案处理总利润为102+12=114(万元).∴由于第一方案使用时间短,则选第一方案较合理.【点评】考查审题及将题中关系转化为数学符号的能力,其中第二问中考查了一元二次不等式的解法,第三问中考查到了基本不等式求最值,本题是一个函数基本不等式相结合的题.属应用题中盈利最大化的问题.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【专题】综合题;导数的综合应用.【分析】(1)求导数,利用导数的正负,即可讨论函数h(x)=的单调性;(2)求出g(x)max=g(2)=1,当x∈[,2]时,f(x)=+xlnx恒成立,等价于a≥x﹣x2lnx 恒成立,然后利用导数求函数u(x)=x﹣x2lnx在区间[,2]上取得最大值,则实数a的取值X围可求.【解答】解:(1)h(x)==+lnx,h′(x)=,①a≤0,h′(x)≥0,函数h(x)在(0,+∞)上单调递增②a>0时,h'(x)>0,则x∈(,+∞),函数h(x)的单调递增区间为(,+∞),h'(x)<0,则x∈(0,),函数h(x)的单调递减区间为(0,),.(2)g(x)=x3﹣x2﹣3,g′(x)=3x(x﹣),x 2g′(x)0 ﹣0 +g(x)﹣递减极小值递增 13由上表可知,g(x)在x=2处取得最大值,即g(x)max=g(2)=1所以当x∈[,2]时,f(x)=+xlnx≥1恒成立,等价于a≥x﹣x 2lnx恒成立,记u(x)=x﹣x2lnx,所以a≥u(x)max,u′(x)=1﹣x﹣2xlnx,可知u′(1)=0,当x∈(,1)时,1﹣x>0,2xlnx<0,则u′(x)>0,∴u(x)在x∈(,2)上单调递增;当x∈(1,2)时,1﹣x<0,2xlnx>0,则u′(x)<0,∴u(x)在(1,2)上单调递减;故当x=1时,函数u(x)在区间[,2],上取得最大值u(1)=1,所以a≥1,故实数a的取值X围是[1,+∞).【点评】本题考查了利用导数研究函数的单调性,考查了导数在最大值、最小值问题中的应用,考查了数学转化思想方法和函数构造法,训练了利用分离变量法求参数的取值X围,属于中档题.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).【考点】参数的意义;简单曲线的极坐标方程.【专题】选作题;转化思想;综合法;坐标系和参数方程.【分析】(1)把参数方程和极坐标方程化为直角坐标方程,联立方程组求出交点的坐标,再把交点的直角坐标化为极坐标;(2)画出图象,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.【解答】解:(1)由(θ为参数),消去参数得:x2+(y﹣2)2=4,即x2+y2﹣4y=0;由ρ=﹣4cosθ,得ρ2=﹣4ρcosθ,即x2+y2=﹣4x.两式作差得:x+y=0,代入C1得交点为(0,0),(﹣2,2).其极坐标为(0,0),(2,);(2)如图,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.此时|AB|=2+4,O到AB的距离为.∴△OAB的面积为S=×(2+4)×=2+2.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程,考查了推理能力与计算能力,属于基础题.23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.【考点】绝对值不等式的解法.【专题】不等式的解法及应用.【分析】(1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)求得f(x)=|2x+2|﹣|x﹣1|=在区间[﹣4,2]内的值域,结合|2x+2|﹣|x﹣1|>a无解,求得a的X围.【解答】解:(1)当a=0时,不等式即|2x+2|﹣|x﹣1|>0,可得①,或②,或③.解①求得 x<﹣3,解②求得﹣<x<1,解③求得x≥1.综上可得,原不等式的解集为{x|x<﹣3,或x>﹣}.(2)当x∈[﹣4,2],f(x)=|2x+2|﹣|x﹣1|=的值域为[﹣2,3],而不等式|2x+2|﹣|x﹣1|>a无解,故有a≤3.【点评】本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想;还考查了分段函数的应用,求函数的值域,属于中档题.。
【推荐】山东省2016届高三数学(文)优题精练:圆锥曲线 Word版含答案[ 高考]
![【推荐】山东省2016届高三数学(文)优题精练:圆锥曲线 Word版含答案[ 高考]](https://img.taocdn.com/s3/m/99b0e313eefdc8d376ee32be.png)
半轴相交于两点M,N(点M必在点N的右侧),且
已知椭圆D: 的焦距等于 ,且过点
( I )求圆C和椭圆D的方程;
(Ⅱ)若过点M斜率不为零的直线与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
15、已知椭圆 : 的焦距为 ,离心率为 ,其右焦点为 ,过点 作直线交椭圆于另一点 .
山东省2016届高三数学文优题精练
圆锥曲线
一、选择、填空题
1、(2015年高考)过双曲线 的右焦点作一条与其渐近线平行的直线,交 于点 .若点 的横坐标为 ,则 的离心率为.
2、(2014年高考)已知双曲线 的焦距为 ,右顶点为 ,抛物线 的焦点为 ,若双曲线截抛物线的准线所得线段长为 ,且 ,则双曲线的渐近线方程为 。
(1)求椭圆C的方程;
(2)A,B为椭圆C上满足△AOB的面积为 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设 =t ,求实数t的值.
4、(滨州市2015届高三一模)已知椭圆 的左右焦点分别是 ,且 的坐标为 ,离心率为 。
直线 与椭圆 交于 两点,当 时,M是椭圆C的上顶点,且 的周长为6.
(I)求椭圆C的标准方程;
(II)点P(2, ),Q(2,- )在椭圆上,A,B是椭圆上位于直线PQ两侧的动点。当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由。
6、(菏泽市2015届高三一模)椭圆 过点 ,离心率为 ,左右焦点分别为 ,过点 的直线交椭圆于 两点。
(1)求椭圆 的方程;
(Ⅰ)求椭圆 的方程;
(Ⅱ)过原点的直线与椭圆 交于 两点( 不是椭圆 的顶点),点 在椭圆 上,且 ,直线 与 轴、 轴分别交于 两点.
三年高考两年模拟高考数学专题汇编 第三章 导数及其应用2 文-人教版高三全册数学试题

第二节导数的应用A组三年高考真题(2016~2014年)1.(2016·某某,6)已知a是函数f(x)=x3-12x的极小值点,则a=( )A.-4B.-2C.4D.22.(2015·某某,9)设f(x)=x-sin x,则f(x)( )A.既是奇函数又是减函数B.既是奇函数又是增函数C.是有零点的减函数D.是没有零点的奇函数3.(2015·某某,10)函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )A.a>0,b<0,c>0,d>0B.a>0,b<0,c<0,d>0C.a<0,b<0,c>0,d>0D.a>0,b>0,c>0,d<04.(2014·新课标全国Ⅱ,11)若函数f(x)=kx-ln x在区间(1,+∞)单调递增,则k的取值X围是( )A.(-∞,-2] B.(-∞,-1]C.[2,+∞) D.[1,+∞)5.(2014·某某,9)若0<x1<x2<1,则( )A.e2x-e1x>ln x2-ln x1B.e2x-e1x<ln x2-ln x1C.x2e1x>x1e2x D.x2e1x<x1e2x6.(2014·新课标全国Ⅰ,12)已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值X围是( )A.(2,+∞) B.(1,+∞)C.(-∞,-2) D.(-∞,-1)7.(2016·新课标全国卷Ⅱ,20)已知函数f(x)=(x+1)ln x-a(x-1).(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;(2)若当x∈(1,+∞)时,f(x)>0,求a的取值X围.8.(2016·新课标全国Ⅲ,21)设函数f(x)=ln x-x+1.(1)讨论f (x )的单调性;(2)证明:当x ∈(1,+∞)时,1<x -1ln x<x ;(3)设c >1,证明:当x ∈(0,1)时,1+(c -1)x >c x. 9.(2016·某某,20)设f (x )=x ln x -ax 2+(2a -1)x ,a ∈R . (1)令g (x )=f ′(x ),求g (x )的单调区间;(2)已知f (x )在x =1处取得极大值.某某数a 的取值X 围.10.(2016·某某,21)设函数f (x )=ax 2-a -ln x ,g (x )=1x -e e x ,其中a ∈R ,e =2.718…为自然对数的底数. (1)讨论f (x )的单调性; (2)证明:当x >1时,g (x )>0;(3)确定a 的所有可能取值,使得f (x )>g (x )在区间(1,+∞)内恒成立. 11.(2016·,20)设函数f (x )=x 3+ax 2+bx +c . (1)求曲线y =f (x )在点(0,f (0))处的切线方程;(2)设a =b =4,若函数f (x )有三个不同零点,求c 的取值X 围; (3)求证:a 2-3b >0是f (x )有三个不同零点的必要而不充分条件. 12.(2015·新课标全国Ⅱ,21)已知f (x )=ln x +a (1-x ). (1)讨论f (x )的单调性;(2)当f (x )有最大值,且最大值大于2a -2时,求a 的取值X 围. 13.(2015·新课标全国Ⅰ,21)设函数f (x )=e 2x-a ln x . (1)讨论f (x )的导函数f ′(x )零点的个数; (2)证明:当a >0时,f (x )≥2a +a ln 2a.14.(2015·某某,22)已知函数f (x )=ln x -(x -1)22.(1)求函数f (x )的单调递增区间; (2)证明:当x >1时,f (x )<x -1;(3)确定实数k 的所有可能取值,使得存在x 0>1,当x ∈(1,x 0)时,恒有f (x )>k (x -1). 15.(2015·某某,17)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l 1,l 2,山区边界曲线为C ,计划修建的公路为l ,如图所示,M ,N 为C 的两个端点,测得点M 到l 1,l 2的距离分别为5千米和40千米,点N 到l 1,l 2的距离分别为20千米和2.5千米,以l 2,l 1所在的直线分别为x ,y 轴,建立平面直角坐标系xOy ,假设曲线C 符合函数y =ax 2+b(其中a ,b 为常数)模型. (1)求a ,b 的值;(2)设公路l 与曲线C 相切于P 点,P 的横坐标为t . ①请写出公路l 长度的函数解析式f (t ),并写出其定义域; ②当t 为何值时,公路l 的长度最短?求出最短长度.16.(2015·某某,21)已知a >0,函数f (x )=a e xcos x (x ∈[0,+∞)).记x n 为f (x )的从小到大的第n (n ∈N *)个极值点. (1)证明:数列{f (x n )}是等比数列;(2)若对一切n ∈N *,x n ≤|f (x n )|恒成立,求a 的取值X 围.17.(2015·某某,20)设函数f (x )=(x +a )ln x ,g (x )=x 2e x . 已知曲线y =f (x ) 在点(1,f (1))处的切线与直线2x -y =0平行. (1)求a 的值;(2)是否存在自然数k ,使得方程f (x )=g (x )在(k ,k +1)内存在唯一的根?如果存在,求出k ;如果不存在,请说明理由;(3)设函数m (x )=min{f (x ),g (x )}(min{p ,q }表示p ,q 中的较小值),求m (x )的最大值. 18.(2015·某某,20)设函数f (x )=x 2+ax +b (a ,b ∈R ).(1)当b =a 24+1时,求函数f (x )在[-1,1]上的最小值g (a )的表达式;(2)已知函数f (x )在[-1,1]上存在零点,0≤b -2a ≤1,求b 的取值X 围. 19.(2015·某某,20)已知函数f (x )=4x -x 4,x ∈R . (1)求f (x )的单调区间;(2)设曲线y =f (x )与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为y =g (x ), 求证:对于任意的实数x ,都有f (x )≤g (x );(3)若方程f (x )=a (a 为实数)有两个实数根x 1,x 2,且x 1<x 2,求证:x 2-x 1≤-a3+134.20.(2015·某某,21)设a 为实数,函数f (x )=(x -a )2+|x -a |-a (a -1). (1)若f (0)≤1,求a 的取值X 围; (2)讨论f (x )的单调性;(3)当a ≥2时,讨论f (x )+4x在区间(0,+∞)内的零点个数.21.(2014·某某,20)设函数f (x )=1+(1+a )x -x 2-x 3,其中a >0. (1)讨论f (x )在其定义域上的单调性;(2)当x ∈[0,1]时,求f (x )取得最大值和最小值时的x 的值. 22.(2014·某某,21)已知函数f (x )=13x 3+x 2+ax +1(a ∈R ).(1)求函数f (x )的单调区间;(2)当a <0时,试讨论是否存在x 0∈⎝ ⎛⎭⎪⎫0,12∪⎝ ⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12. 23.(2014·某某,19)已知函数f (x )=x 2-23ax 3(a >0),x ∈R .(1)求f (x )的单调区间和极值;(2)若对于任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)·f (x 2)=1.求a 的取值X 围.24.(2014·某某,21)设函数f (x )=ln x +m x,m ∈R . (1)当m =e(e 为自然对数的底数)时,求f (x )的极小值; (2)讨论函数g (x )=f ′(x )-x3零点的个数;(3)若对任意b >a >0,f (b)-f (a )b -a<1恒成立,求m 的取值X 围.25.(2014·新课标全国Ⅰ,21)设函数f (x )=a ln x +1-a 2x 2-bx (a ≠1),曲线y =f (x )在点(1, f (1))处的切线斜率为0. (1) 求b ;(2)若存在x 0≥1,使得f (x 0)<aa -1,求a 的取值X 围.B 组 两年模拟精选(2016~2015年)1.(2016·某某某某第二次模拟)已知函数f (x )=x 2-2cos x ,则f (0),f ⎝ ⎛⎭⎪⎫-13,f ⎝ ⎛⎭⎪⎫25的大小关系是( )A.f (0)<f ⎝ ⎛⎭⎪⎫-13<f ⎝ ⎛⎭⎪⎫25B.f ⎝ ⎛⎭⎪⎫-13<f (0)<f ⎝ ⎛⎭⎪⎫25C.f ⎝ ⎛⎭⎪⎫25<f ⎝ ⎛⎭⎪⎫-13<f (0) D.f (0)<f ⎝ ⎛⎭⎪⎫25<f ⎝ ⎛⎭⎪⎫-13 2.(2016·某某师大附中检测)若函数f (x )=x 3-tx 2+3x 在区间[1,4]上单调递减,则实数t 的取值X 围是( )A.⎝ ⎛⎦⎥⎤-∞,518B.(-∞,3]C.⎣⎢⎡⎭⎪⎫518,+∞ D.[3,+∞)3.(2016·某某某某第三次诊断模拟)设函数f (x )的导函数为f ′(x ),对任意x ∈R ,都有xf ′(x )<f (x )成立,则( )A.3f (2)>2f (3)B.3f (2)=2f (3)C.3f (2)<2f (3)D.3f (2)与2f (3)大小不确定4.(2016·某某某某诊断)若函数f (x )=⎩⎪⎨⎪⎧2x 3+3x 2+1 (x ≤0),e ax (x >0)在[-2,2]上的最大值为2,则a 的取值X 围是( )A.⎣⎢⎡⎭⎪⎫12ln 2,+∞B.⎣⎢⎡⎦⎥⎤0,12ln 2C.(-∞,0]D.⎝ ⎛⎦⎥⎤-∞,12ln 25.(2015·某某省实验中学二诊)已知函数f (x )(x ∈R )满足f (1)=1,且f (x )的导函数f ′(x )<13,则f (x )<x 3+23的解集是( )A.{x |-1<x <1}B.{x |x <-1}C.{x |x <-1或x >1}D.{x |x >1}6.(2015·某某某某调研)若函数f (x )=x 3-3x 在(a ,6-a 2]上有极小值,则实数a 的取值X 围是( ) A.(-5,1)B.[-5,1)C.[-2,1)D.(-2,1)7.(2015·某某市十二县联考)若函数f (x )=13x 3-a 2x 2+(3-a )x +b 有三个不同的单调区间,则实数a 的取值X 围是________.8.(2015·某某某某三模)已知函数f (x )=x 3+x ,对任意的m ∈[-2,2],f (mx -2)+f (x )<0恒成立,则x 的取值X 围为________.9.(2015·某某某某中学模拟)已知函数f (x )=x ln x ,g (x )=-x 2+ax -3,其中 a 为实数. (1)求函数f (x )在[t ,t +2]上的最小值;(2)对一切x ∈(0,+∞),2f (x )≥g (x )恒成立,某某数a 的取值X 围.答案精析A 组 三年高考真题(2016~2014年)1.解析 ∵f (x )=x 3-12x ,∴f ′(x )=3x 2-12, 令f ′(x )=0,则x 1=-2,x 2=2.当x ∈(-∞,-2),(2,+∞)时,f ′(x )>0,则f (x )单调递增; 当x ∈(-2,2)时,f ′(x )<0,则f (x )单调递减, ∴f (x )的极小值点为a =2. 答案 D2.解析 f (x )=x -sin x 的定义域为R ,关于原点对称, 且f (-x )=-x -sin(-x )=-x +sin x =-f (x ), 故f (x )为奇函数.又f ′(x )=1-sin x ≥0恒成立,所以f (x )在其定义域内为增函数,故选B. 答案 B3.解析 由已知f (0)=d >0,可排除D ;其导函数f ′(x )=3ax 2+2bx +c 且f ′(0)=c >0,可排除B ;又f ′(x )=0有两不等实根,且x 1x 2=c a>0,所以a >0.故选A. 答案 A4.解析 因为f (x )=kx -ln x ,所以f ′(x )=k -1x.因为f (x )在区间(1,+∞)上单调递增, 所以当x >1时,f ′(x )=k -1x≥0恒成立,即k ≥1x在区间(1,+∞)上恒成立.因为x >1,所以0<1x<1,所以k ≥1.故选D.答案 D5.解析 构造函数f (x )=e x -ln x ,则f ′(x )=e x -1x,故f (x )=e x-ln x 在(0,1)上有一个极值点,即f (x )=e x-ln x 在(0,1)上不是单调函数,无法判断f (x 1)与f (x 2)的大小,故A 、B 错;构造函数g (x )=e xx ,则g ′(x )=x e x-e xx 2=e x(x -1)x 2,故函数g (x )=exx在(0,1)上单调递减,故g (x 1)>g (x 2),x 2e x 1>x 1e x 2,故选C. 答案 C6. 解析 由题意知f ′(x )=3ax 2-6x =3x (ax -2),当a =0时,不满足题意. 当a ≠0时,令f ′(x )=0,解得x =0或x =2a,当a >0时,f (x )在(-∞,0),⎝ ⎛⎭⎪⎫2a,+∞上单调递增,在 ⎝⎛⎭⎪⎫0,2a 上单调递减.又f (0)=1,此时f (x )在(-∞,0)上存在零点,不满足题意;当a <0时,f (x )在⎝ ⎛⎭⎪⎫-∞,2a ,(0,+∞)上单调递减,在⎝ ⎛⎭⎪⎫2a ,0上单调递增,要使f (x )存在唯一的零点x 0,且x 0>0,则需f ⎝ ⎛⎭⎪⎫2a>0,即a ×⎝ ⎛⎭⎪⎫2a 3-3×⎝ ⎛⎭⎪⎫2a 2+1>0,解得a <-2,故选C. 答案 C7.解 (1)f (x )的定义域为(0,+∞),当a =4时,f (x )=(x +1)ln x -4(x -1),f ′(x )=ln x +1x-3,f ′(1)=-2,f (1)=0,曲线y =f (x )在(1,f (1))处的切线方程为2x +y-2=0.(2)当x ∈(1,+∞)时,f (x )>0等价于ln x -a (x -1)x +1>0,设g (x )=ln x -a (x -1)x +1,则g ′(x )=1x -2a (x +1)2=x 2+2(1-a )x +1x (x +1)2,g (1)=0.(ⅰ)当a ≤2,x ∈(1,+∞)时,x 2+2(1-a )x +1≥x 2-2x +1>0,故g ′(x )>0,g (x )在(1,+∞)单调递增,因此g (x )>0;(ⅱ)当a >2时,令g ′(x )=0得,x 1=a -1-(a -1)2-1,x 2=a -1+(a -1)2-1. 由x 2>1和x 1x 2=1得x 1<1,故当x ∈(1,x 2)时,g ′(x )<0,g (x )在(1,x 2)单调递减,因此g (x )<0, 综上,a 的取值X 围是(-∞,2].8.(1)解 由题设,f (x )的定义域为(0,+∞),f ′(x )=1x-1,令f ′(x )=0解得x =1.当0<x <1时,f ′(x )>0,f (x )单调递增;当x >1时,f ′(x )<0,f (x )单调递减. (2)证明 由(1)知f (x )在x =1处取得最大值,最大值为f (1)=0. 所以当x ≠1时,ln x <x -1.故当x ∈(1,+∞)时,ln x <x -1,ln 1x <1x -1,即1<x -1ln x <x .(3)证明 由题设c >1,设g (x )=1+(c -1)x -c x,则g ′(x )=c -1-c xln c ,令g ′(x )=0,解得x 0=lnc -1ln cln c.当x <x 0时,g ′(x )>0,g (x )单调递增;当x >x 0时,g ′(x )<0,g (x )单调递减.由(2)知1<c -1ln c<c ,故0<x 0<1.又g (0)=g (1)=0,故当0<x <1时,g (x )>0. 所以当x ∈(0,1)时,1+(c -1)x >c x. 9.解 (1)由f ′(x )=ln x -2ax +2a .可得g (x )=ln x -2ax +2a ,x ∈(0,+∞), 则g ′(x )=1x -2a =1-2axx.当a ≤0时,x ∈(0,+∞)时,g ′(x )>0,函数g (x )单调递增; 当a >0时,x ∈⎝ ⎛⎭⎪⎫0,12a 时,g ′(x )>0时,函数g (x )单调递增,x ∈⎝ ⎛⎭⎪⎫12a ,+∞时,g ′(x )<0,函数g (x )单调递减. 所以当a ≤0时,g (x )的单调递增区间为(0,+∞);当a >0时,g (x )的单调增区间为⎝ ⎛⎭⎪⎫0,12a ,单调减区间为⎝ ⎛⎭⎪⎫12a ,+∞.(2)由(1)知,f ′(1)=0. ①当a ≤0时,f ′(x )单调递增,所以当x ∈(0,1)时,f ′(x )<0,f (x )单调递减, 当x ∈(1,+∞)时,f ′(x )>0,f (x )单调递增, 所以f (x )在x =1处取得极小值,不合题意.②当0<a <12时,12a >1,由(1)知f ′(x )在⎝ ⎛⎭⎪⎫0,12a 内单调递增.可得当x ∈(0,1)时,f ′(x )<0,x ∈⎝ ⎛⎭⎪⎫1,12a 时,f ′(x )>0.所以f (x )在(0,1)内单调递减,在⎝ ⎛⎭⎪⎫1,12a 内单调递增. 所以f (x )在x =1处取得极小值,不合题意. ③当a =12时,12a =1,f ′(x )在(0,1)内单调递增,在(1,+∞)内单调递减.所以当x ∈(0,+∞)时,f ′(x )≤0,f (x )单调递减,不合题意. ④当a >12时,0<12a <1,当x ∈⎝ ⎛⎭⎪⎫12a ,1时,f ′(x )>0,f (x )单调递增, 当x ∈(1,+∞)时,f ′(x )<0,f (x )单调递减. 所以f (x )在x =1处取极大值,合题意 .综上可知,实数a 的取值X 围为⎝ ⎛⎭⎪⎫12,+∞.10.(1)解 f ′(x )=2ax -1x =2ax 2-1x(x >0).当a ≤0时,f ′(x )<0,f (x )在(0,+∞)内单调递减. 当a >0时,由f ′(x )=0有x =12a .当x ∈⎝⎛⎭⎪⎫0,12a 时,f ′(x )<0,f (x )单调递减;当x ∈⎝ ⎛⎭⎪⎫12a ,+∞时,f ′(x )>0,f (x )单调递增.(2)证明 令s (x )=ex -1-x ,则s ′(x )=ex -1-1.当x >1时,s ′(x )>0,所以e x -1>x ,从而g (x )=1x -1ex -1>0.(3)解 由(2)知,当x >1时,g (x )>0. 当a ≤0,x >1时,f (x )=a (x 2-1)-ln x <0,故当f (x )>g (x )在区间(1,+∞)内恒成立时,必有a >0. 当0<a <12时,12a >1,由(1)有f ⎝ ⎛⎭⎪⎫12a <f (1)=0,而g ⎝ ⎛⎭⎪⎫12a >0.所以f (x )>g (x )在区间(1,+∞)内不恒成立; 当a ≥12时,令h (x )=f (x )-g (x )(x ≥1),当x >1时,h ′(x )=2ax -1x +1x 2-e 1-x>x -1x +1x 2-1x =x 3-2x +1x 2>x 2-2x +1x2>0. 因此,h (x )在区间(1,+∞)单调递增.又因为h (1)=0,所以当x >1时,h (x )=f (x )-g (x )>0,即f (x )>g (x )恒成立.综上,a ∈⎣⎢⎡⎭⎪⎫12,+∞.11.(1)解 由f (x )=x 3+ax 2+bx +c ,得f ′(x )=3x 2+2ax +b ,切线斜率k =f ′(0)=b . 又f (0)=c ,所以切点坐标为(0,c ).所以所求切线方程为y -c =b (x -0),即bx -y +c =0. (2)解 由a =b =4得f (x )=x 3+4x 2+4x +c ∴f ′(x )=3x 2+8x +4=(3x +2)(x +2) 令f ′(x )=0,得(3x +2)(x +2)=0,解得x =-2或x =-23,f ′(x ),f (x )随x 的变化情况如下:所以,当c >0且c -3227<0时,存在x 1∈(-∞,-2),x 2∈⎝ ⎛⎭⎪⎫-2,-23,x 3∈⎝ ⎛⎭⎪⎫-23,+∞,使得f (x 1)=f (x 2)=f (x 3)=0.由f (x )的单调性知,当且仅当c ∈⎝ ⎛⎭⎪⎫0,3227时,函数f (x )=x 3+4x 2+4x +c 有三个不同零点.(3)证明 当Δ=4a 2-12b <0时,即a 2-3b <0,f ′(x )=3x 2+2ax +b >0,x ∈(-∞,+∞),此时函数f (x )在区间(-∞,+∞)上单调递增, 所以f (x )不可能有三个不同零点.当Δ=4a 2-12b =0时,f ′(x )=3x 2+2ax +b 只有一个零点,记作x 0. 当x ∈(-∞,x 0)时,f ′(x )>0,f (x )在区间(-∞,x 0)上单调递增; 当x ∈(x 0,+∞)时,f ′(x )>0,f (x )在区间(x 0,+∞)上单调递增. 所以f (x )不可能有三个不同零点.综上所述,若函数f (x )有三个不同零点,则必有Δ=4a 2-12b >0, 故a 2-3b >0是f (x )有三个不同零点的必要条件.当a =b =4,c =0时,a 2-3b >0,f (x )=x 3+4x 2+4x =x (x +2)2只有两个不同零点, 所以a 2-3b >0不是f (x )有三个不同零点的充分条件. 因此a 2-3b >0是f (x )有三个不同零点的必要而不充分条件. 12.解 (1)f (x )的定义域为(0,+∞),f ′(x )=1x-a .若a ≤0,则f ′(x )>0,所以f (x )在(0,+∞)上单调递增.若a >0,则当x ∈⎝⎛⎭⎪⎫0,1a 时,f ′(x )>0;当x ∈⎝ ⎛⎭⎪⎫1a ,+∞时,f ′(x )<0.所以f (x )在⎝⎛⎭⎪⎫0,1a 上单调递增,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递减.(2)由(1)知,当a ≤0时,f (x )在(0,+∞)无最大值;当a >0时,f (x )在x =1a取得最大值,最大值为f ⎝ ⎛⎭⎪⎫1a =ln ⎝ ⎛⎭⎪⎫1a +a ⎝ ⎛⎭⎪⎫1-1a =-ln a +a -1.因此f ⎝ ⎛⎭⎪⎫1a>2a -2等价于ln a +a -1<0. 令g (a )=ln a +a -1,则g (a )在(0,+∞)上单调递增,g (1)=0. 于是,当0<a <1时,g (a )<0;当a >1时,g (a )>0. 因此,a 的取值X 围是(0,1).13.(1)解 f (x )的定义域为(0,+∞),f ′(x )=2e 2x-a x(x >0). 当a ≤0时,f ′(x )>0,f ′(x )没有零点. 当a >0时,因为e 2x单调递增,-a x单调递增, 所以f ′(x )在(0,+∞)上单调递增.又f ′(a )>0,当b 满足0<b <a 4且b <14时,f ′(b )<0,故当a >0时,f ′(x )存在唯一零点.(2)证明 由(1)可设f ′(x )在(0,+∞)的唯一零点为x 0, 当x ∈(0,x 0)时,f ′(x )<0;当x ∈(x 0,+∞)时,f ′(x )>0. 故f (x )在(0,x 0)上单调递减,在(x 0,+∞)上单调递增, 所以当x =x 0时,f (x )取得最小值,最小值为f (x 0).由于2e2x 0-a x 0=0,所以f (x 0)=a 2x 0+2ax 0+a ln 2a ≥2a +a ln 2a.故当a >0时,f (x )≥2a +a ln 2a.14.解 (1)f ′(x )=1x -x +1=-x 2+x +1x,x ∈(0,+∞).由f ′(x )>0得⎩⎪⎨⎪⎧x >0,-x 2+x +1>0.解得0<x <1+52. 故f (x )的单调递增区间是⎝⎛⎭⎪⎫0,1+52.(2)令F (x )=f (x )-(x -1),x ∈(0,+∞).则有F ′(x )=1-x2x.当x ∈(1,+∞)时,F ′(x )<0,所以F (x )在[1,+∞)上单调递减, 故当x >1时,F (x )<F (1)=0, 即当x >1时,f (x )<x -1.(3)由(2)知,当k =1时,不存在x 0>1满足题意. 当k >1时,对于x >1,有f (x )<x -1<k (x -1), 则f (x )<k (x -1),从而不存在x 0>1满足题意. 当k <1时,令G (x )=f (x )-k (x -1),x ∈(0,+∞), 则有G ′(x )=1x -x +1-k =-x 2+(1-k )x +1x.由G ′(x )=0得,-x 2+(1-k )x +1=0.解得x 1=1-k -(1-k )2+42<0,x 2=1-k +(1-k )2+42>1.当x ∈(1,x 2)时,G ′(x )>0,故G (x )在[1,x 2)内单调递增. 从而当x ∈(1,x 2)时,G (x )>G (1)=0, 即f (x )>k (x -1).综上,k 的取值X 围是(-∞,1).15.解 (1)由题意知,点M ,N 的坐标分别为(5,40),(20,2.5).将其分别代入y =ax 2+b,得⎩⎪⎨⎪⎧a25+b =40,a 400+b =2.5,解得⎩⎪⎨⎪⎧a =1 000,b =0.(2)①由(1)知,y =1 000x2(5≤x ≤20),则点P 的坐标为⎝⎛⎭⎪⎫t ,1 000t2,设在点P 处的切线l 交x ,y 轴分别于A ,B 点,y ′=-2 000x3,则l 的方程为y -1 000t 2=-2 000t3(x -t ),由此得A ⎝ ⎛⎭⎪⎫3t 2,0,B ⎝⎛⎭⎪⎫0,3 000t 2.故f (t )=⎝ ⎛⎭⎪⎫3t 22+⎝ ⎛⎭⎪⎫3 000t 22=32t 2+4×106t4,t ∈[5,20].②设g (t )=t 2+4×106t 4,则g ′(t )=2t -16×106t5. 令g ′(t )=0,解得t =10 2.当t ∈(5,102)时,g ′(t )<0,g (t )是减函数; 当t ∈(102,20)时,g ′(t )>0,g (t )是增函数. 从而,当t =102时,函数g (t )有极小值,也是最小值, 所以g (t )min =300,此时f (t )min =15 3.答:当t =102时,公路l 的长度最短,最短长度为153千米.16.解 (1)f ′(x )=a e x cos x -a e x sin x =2a e xcos ⎝⎛⎭⎪⎫x +π4.令f ′(x )=0,由x ≥0, 得x +π4=m π-π2,即x =m π-3π4,m ∈N *.而对于cos ⎝⎛⎭⎪⎫x +π4,当k ∈Z 时,若2k π-π2<x +π4<2k π+π2,即2k π-3π4<x <2k π+π4,则cos ⎝⎛⎭⎪⎫x +π4>0. 若2k π+π2<x +π4<2k π+3π2,即2k π+π4<x <2k π+5π4,则cos ⎝⎛⎭⎪⎫x +π4<0.因此,在区间⎝ ⎛⎭⎪⎫(m -1)π,m π-3π4与⎝ ⎛⎭⎪⎫m π-3π4,m π+π4上,f ′(x )的符号总相反.于是当x =m π-3π4(m ∈N *)时,f (x )取得极值,所以x n =n π-34π(n ∈N *).此时,f (x n )=a e n π-3π4cos ⎝⎛⎭⎪⎫n π-3π4=(-1)n +12a 2e n π-3π4.易知f (x n )≠0,而f (x n +1)f (x n )=(-1)n +22a 2e (n +1)π-3π4(-1)n +12a 2e n π-3π4=-e π是常数,故数列{f (x n )}是首项为f (x 1)=2a 2e π4,公比为-e π的等比数列. (2)对一切n ∈N *,x n ≤|f (x n )|恒成立,即n π-3π4≤2a 2e n π-3π4恒成立,亦即2a ≤e n π-3π4n π-3π4恒成立(因为a >0).设g (t )=e tt (t >0),则g ′(t )=e t(t -1)t2. 令g ′(t )=0得t =1.当0<t <1时,g ′(t )<0,所以g (t )在区间(0,1)上单调递减; 当t >1时,g ′(t )>0,所以g (t )在区间(1,+∞)上单调递增. 因为x 1∈(0,1),且当n ≥2时,x n ∈(1,+∞),x n <x n +1, 所以[g (x n )]min =min{g (x 1),g (x 2)}=min ⎩⎨⎧⎭⎬⎫g ⎝ ⎛⎭⎪⎫π4,g ⎝ ⎛⎭⎪⎫5π4=g ⎝ ⎛⎭⎪⎫π4=4πe π4. 因此,x n ≤|f (x n )|恒成立,当且仅当2a ≤4πe π4,解得a ≥2π4e -π4. 故a 的取值X 围是⎣⎢⎡⎭⎪⎫2π4e -π4,+∞.17.解 (1)由题意知,曲线y =f (x )在点(1,f (1))处的切线斜率为2,所以f ′(1)=2,又f ′(x )=ln x +a x+1,所以a =1. (2)k =1时,方程f (x )=g (x )在(1,2)内存在唯一的根. 设h (x )=f (x )-g (x )=(x +1)ln x -x 2e x ,当x ∈(0,1]时,h (x )<0.又h (2)=3ln 2-4e 2=ln 8-4e 2>1-1=0,所以存在x 0∈(1,2),使得h (x 0)=0. 因为h ′(x )=ln x +1x +1+x (x -2)e x, 所以当x ∈(1,2)时,h ′(x )>1-1e >0,当x ∈(2,+∞)时,h ′(x )>0, 所以当x ∈(1,+∞)时,h (x )单调递增,所以k =1时,方程f (x )=g (x )在(k ,k +1)内存在唯一的根. (3)由(2)知方程f (x )=g (x )在(1,2)内存在唯一的根x 0. 且x ∈(0,x 0)时,f (x )<g (x ),x ∈(x 0,+∞)时,f (x )>g (x ), 所以m (x )=⎩⎪⎨⎪⎧(x +1)ln x ,x ∈(0,x 0],x 2e x ,x ∈(x 0,+∞).当x ∈(0,x 0)时,若x ∈(0,1],m (x )≤0; 若x ∈(1,x 0),由m ′(x )=ln x +1x+1>0,可知0<m (x )≤m (x 0); 故m (x )≤m (x 0).当x ∈(x 0,+∞)时,由m ′(x )=x (2-x )ex,可得x ∈(x 0,2)时,m ′(x )>0,m (x )单调递增;x ∈(2,+∞)时,m ′(x )<0,m (x )单调递减;可知m (x )≤m (2)=4e 2,且m (x 0)<m (2).综上可得,函数m (x )的最大值为4e2.18.解 (1)当b =a 24+1时,f (x )=⎝ ⎛⎭⎪⎫x +a 22+1,故对称轴为直线x =-a2.当a ≤-2时,g (a )=f (1)=a 24+a +2.当-2<a ≤2时,g (a )=f ⎝ ⎛⎭⎪⎫-a 2=1.当a >2时,g (a )=f (-1)=a 24-a +2.综上,g (a )=⎩⎪⎨⎪⎧a 24+a +2,a ≤-2,1,-2<a ≤2,a 24-a +2,a >2.(2)设s ,t 为方程f (x )=0的解,且-1≤t ≤1,则⎩⎪⎨⎪⎧s +t =-a ,st =b ,由于0≤b -2a ≤1,因此-2t t +2≤s ≤1-2tt +2(-1≤t ≤1).当0≤t ≤1时,-2t 2t +2≤st ≤t -2t2t +2,由于-23≤-2t 2t +2≤0和-13≤t -2t 2t +2≤9-45,所以-32≤b ≤9-4 5.当-1≤t <0时,t -2t 2t +2≤st ≤-2t2t +2,由于-2≤-2t 2t +2<0和-3≤t -2t2t +2<0,所以-3≤b <0.故b 的取值X 围是[-3,9-45].19.(1)解 由f (x )=4x -x 4,可得f ′(x )=4-4x 3. 当f ′(x )>0,即x <1时,函数f (x )单调递增; 当f ′(x )<0,即x >1时,函数f (x )单调递减.所以,f (x )的单调递增区间为(-∞,1),单调递减区间为(1,+∞). (2)证明 设点P 的坐标为(x 0,0),则x 0=413,f ′(x 0)=-12.曲线y =f (x )在点P 处的切线方程为y =f ′(x 0)(x -x 0),即g (x )=f ′(x 0)(x -x 0). 令函数F (x )=f (x )-g (x ),即F (x )=f (x )-f ′(x 0)(x -x 0), 则F ′(x )=f ′(x )-f ′(x 0).由于f ′(x )=-4x 3+4在(-∞,+∞)上单调递减, 故F ′(x )在(-∞,+∞)上单调递减,又因为F ′(x 0)=0,所以当x ∈(-∞,x 0)时,F ′(x )>0,当x ∈(x 0,+∞)时,F ′(x )<0, 所以F (x )在(-∞,x 0)上单调递增,在(x 0,+∞)上单调递减, 所以对于任意的实数x ,F (x )≤F (x 0)=0, 即对于任意的实数x ,都有f (x )≤g (x ). (3)证明 由(2)知g (x )=-12(x -413).设方程g (x )=a 的根为x 2′,可得x 2′=-a 12+413.因为g (x )在(-∞,+∞)上单调递减, 又由(2)知g (x 2)≥f (x 2)=a =g (x 2′), 因此x 2≤x 2′.类似地,设曲线y =f (x )在原点处的切线方程为y =h (x ), 可得h (x )=4x .对于任意的x ∈(-∞,+∞),有f (x )-h (x )=-x 4≤0,即f (x )≤h (x ). 设方程h (x )=a 的根为x 1′,可得x 1′=a4.因为h (x )=4x 在(-∞,+∞)上单调递增,且h (x 1′)=a =f (x 1)≤h (x 1),因此x 1′≤x 1,由此可得x 2-x 1≤x 2′-x 1′=-a 3+413.20.解 (1)f (0)=a 2+|a |-a 2+a =|a |+a ,因为f (0)≤1,所以|a |+a ≤1, 当a ≤0时,|a |+a =-a +a =0≤1,显然成立; 当a >0,则有|a |+a =2a ≤1,所以a ≤12,所以0<a ≤12,综上所述,a 的取值X 围是a ≤12.(2)f (x )=⎩⎪⎨⎪⎧x 2-(2a -1)x ,x ≥a ,x 2-(2a +1)x +2a ,x <a .对于u 1=x 2-(2a -1)x ,其对称轴为x =2a -12=a -12<a ,开口向上,所以f (x )在(a ,+∞)上单调递增;对于u 1=x 2-(2a +1)x +2a ,其对称轴为x =2a +12=a +12>a ,开口向上,所以f (x )在(-∞,a )上单调递减.综上,f (x )在(a ,+∞)上单调递增,在(-∞,a )上单调递减,(3)由(2)得f (x )在(a ,+∞)上单调递增,在(0,a )上单调递减,所以f (x )min =f (a )=a -a 2.(ⅰ)当a =2时,f (x )min =f (2)=-2,f (x )=⎩⎪⎨⎪⎧x 2-3x ,x ≥2,x 2-5x +4,x <2,令f (x )+4x =0,即f (x )=-4x(x >0),因为f (x )在(0,2)上单调递减,所以f (x )>f (2)=-2,而y =-4x 在(0,2)上单调递增,y <f (2)=2,所以y =f (x )与y =-4x在(0,2)无交点.当x ≥2时,f (x )=x 2-3x =-4x,即x 3-3x 2+4=0,所以x 3-2x 2-x 2+4=0,所以(x -2)2(x +1)=0, 因为x ≥2,所以x =2,即当a =2时,f (x )+4x有一个零点x =2.(ⅱ)当a >2时,f (x )min =f (a )=a -a 2, 当x ∈(0,a )时,f (0)=2a >4,f (a )=a -a 2,而y =-4x 在x ∈(0,a )上单调递增,当x =a 时,y =-4a,下面比较f (a )=a -a 2与-4a的大小,因为a -a 2-⎝ ⎛⎭⎪⎫-4a =-(a 3-a 2-4)a =-(a -2)(a 2+a +2)a <0所以f (a )=a -a 2<-4a.结合图象不难得当a >2,y =f (x )与y =-4x有两个交点,综上,当a =2时,f (x )+4x 有一个零点x =2;当a >2,y =f (x )与y =-4x有两个零点.21.解 (1)f (x )的定义域为(-∞,+∞),f ′(x )=1+a -2x -3x 2. 令f ′(x )=0,得x 1=-1-4+3a 3,x 2=-1+4+3a3,x 1<x 2,所以f ′(x )=-3(x -x 1)(x -x 2).当x <x 1或x >x 2时,f ′(x )<0;当x 1<x <x 2时,f ′(x )>0.故f (x )在(-∞,x 1)和(x 2,+∞)内单调递减,在(x 1,x 2)内单调递增. (2)因为a >0,所以x 1<0,x 2>0.①当a ≥4时,x 2≥1,由(1)知,f (x )在[0,1]上单调递增, 所以f (x )在x =0和x =1处分别取得最小值和最大值. ②当0<a <4时,x 2<1.由(1)知,f (x )在[0,x 2]上单调递增,在[x 2,1]上单调递减, 因此f (x )在x =x 2=-1+4+3a3处取得最大值.又f (0)=1,f (1)=a ,所以当0<a <1时,f (x )在x =1处取得最小值; 当a =1时,f (x )在x =0和x =1处同时取得最小值; 当1<a <4时,f (x )在x =0处取得最小值. 22.解 (1)f ′(x )=x 2+2x +a 开口向上, 方程x 2+2x +a =0的判别式Δ=4-4a =4(1-a ),若a ≥1,则Δ≤0,f ′(x )=x 2+2x +a ≥0恒成立,∴f (x )在R 上单调递增.若a <1,则Δ>0,方程x 2+2x +a =0有两个不同的实数根,x 1=-1-1-a ,x 2=-1+1-a ,当x <x 1或x >x 2时,f ′(x )>0;当x 1<x <x 2时,f ′(x )<0, ∴f (x )的单调递增区间为(-∞,-1-1-a )和(-1+1-a ,+∞), 单调递减区间为(-1-1-a ,-1+1-a ).综上所述,当a ≥1时,f (x )在R 上单调递增;当a <1时,f (x )的单调递增区间为(-∞,-1-1-a )和(-1+1-a ,+∞),f (x )的单调递减区间为(-1-1-a ,-1+1-a ).(2)当a <0时,Δ>0,且f (0)=1,f ⎝ ⎛⎭⎪⎫12=3124+a2,f (1)=73+a ,此时x 1<0,x 2>0, 令x 2=12得a =-54.①当-54<a <0时,x 1<0<x 2<12,f (x )在(0,x 2)上单调递减,在⎝⎛⎭⎪⎫x 2,12上单调递增,在⎝⎛⎭⎪⎫12,1上单调递增.(ⅰ)若-54<a <-712,则f (0)=1>f ⎝ ⎛⎭⎪⎫12, ∴存在x 0∈(0,x 2),使得f (x 0)=f ⎝ ⎛⎭⎪⎫12;(ⅱ)当-712≤a <0时,f (0)≤f ⎝ ⎛⎭⎪⎫12, ∴不存在x 0∈⎝ ⎛⎭⎪⎫0,12∪⎝ ⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12.②当a =-54时,f (x )在⎝ ⎛⎭⎪⎫0,12上单调递减,在⎝ ⎛⎭⎪⎫12,1上单调递增. ∴不存在x 0,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12.③当-2512<a <-54时,f ⎝ ⎛⎭⎪⎫12<f (1), ∴存在x 0∈⎝ ⎛⎭⎪⎫0,12∪⎝ ⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12.④当a ≤-2512时,f ⎝ ⎛⎭⎪⎫12≥f (1), ∴不存在x 0∈⎝ ⎛⎭⎪⎫0,12∪⎝ ⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12. 综上,当a ∈⎣⎢⎡⎭⎪⎫-712,0∪{-54}∪⎝ ⎛⎦⎥⎤-∞,-2512时,不存在x 0∈⎝ ⎛⎭⎪⎫0,12∪⎝ ⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12;当a ∈⎝⎛⎭⎪⎫-2512,-54∪⎝⎛⎭⎪⎫-54,-712时,存在x 0∈⎝⎛⎭⎪⎫0,12∪⎝⎛⎭⎪⎫12,1,使得f (x 0)=f ⎝ ⎛⎭⎪⎫12. 23.解 (1)由已知,有f ′(x )=2x -2ax 2(a >0). 令f ′(x )=0,解得x =0或x =1a.当x 变化时,f ′(x ),f (x )的变化情况如下表:所以,f (x )的单调递增区间是⎝⎛⎭⎪⎫0,a ;单调递减区间是(-∞,0),⎝ ⎛⎭⎪⎫a ,+∞.当x =0时,f (x )有极小值,且极小值f (0)=0;当x =1a时,f (x )有极大值,且极大值f ⎝ ⎛⎭⎪⎫1a =13a2. (2)由f (0)=f ⎝ ⎛⎭⎪⎫32a =0及(1)知,当x ∈⎝ ⎛⎭⎪⎫0,32a 时,f (x )>0;当x ∈⎝ ⎛⎭⎪⎫32a ,+∞时,f (x )<0.设集合A ={f (x )|x ∈(2,+∞)},集合B =⎩⎨⎧⎭⎬⎫1f (x )|x ∈(1,+∞),f (x )≠0,则“对于任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)·f (x 2)=1”等价于A ⊆B . 显然,0∉B .下面分三种情况讨论:(1)当32a >2,即0<a <34时,由f ⎝ ⎛⎭⎪⎫32a =0可知,0∈A ,而0∉B ,所以A 不是B 的子集.(2)当1≤32a ≤2,即34≤a ≤32时,有f (2)≤0,且此时f (x )在(2,+∞)上单调递减,故A =(-∞,f (2)),因而A ⊆(-∞,0);由f (1)≥0,有f (x )在(1,+∞)上的取值X 围包含(-∞,0),则(-∞,0)⊆B .所以A ⊆B . (3)当32a <1,即a >32时,有f (1)<0,且此时f (x )在(1,+∞)上单调递减,故B =⎝⎛⎭⎪⎫1f (1),0,A =(-∞,f (2)),所以A 不是B 的子集.综上,a 的取值X 围是⎣⎢⎡⎦⎥⎤34,32. 24.解 (1)由题设,当m =e 时,f (x )=ln x +e x ,则f ′(x )=x -ex2,∴当x ∈(0,e),f ′(x )<0,f (x )在(0,e)上单调递减, 当x ∈(e ,+∞),f ′(x )>0,f (x )在(e ,+∞)上单调递增, ∴x =e 时,f (x )取得极小值f (e)=ln e +ee =2,∴f (x )的极小值为2.(2)由题设g (x )=f ′(x )-x 3=1x -m x 2-x3(x >0),令g (x )=0,得m =-13x 3+x (x >0).设φ(x )=-13x 3+x (x ≥0),则φ′(x )=-x 2+1=-(x -1)(x +1),当x ∈(0,1)时,φ′(x )>0,φ(x )在(0,1)上单调递增; 当x ∈(1,+∞)时,φ′(x )<0,φ(x )在(1,+∞)上单调递减. ∴x =1是φ(x )的唯一极值点,且是极大值点, 因此x =1也是φ(x )的最大值点. ∴φ(x )的最大值为φ(1)=23.又φ(0)=0,结合y =φ(x )的图象(如图),可知①当m >23时,函数g (x )无零点;②当m =23时,函数g (x )有且只有一个零点;③当0<m <23时,函数g (x )有两个零点;④当m ≤0时,函数g (x )有且只有一个零点. 综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且只有一个零点;当0<m <23时,函数g (x )有两个零点.(3)对任意的b >a >0,f (b )-f (a )b -a<1恒成立,等价于f (b )-b <f (a )-a 恒成立.(*) 设h (x )=f (x )-x =ln x +m x-x (x >0), ∴(*)式等价于h (x )在(0,+∞)上单调递减. 由h ′(x )=1x -mx2-1≤0在(0,+∞)上恒成立,得m ≥-x 2+x =-⎝ ⎛⎭⎪⎫x -122+14(x >0)恒成立,∴m ≥14(对m =14,h ′(x )=0仅在x =12时成立),∴m 的取值X 围是⎣⎢⎡⎭⎪⎫14,+∞.25.解 (1)f ′(x )=a x+(1-a )x -b . 由题设知f ′(1)=0,解得b =1. (2)f (x )的定义域为(0,+∞). 由(1)知,f (x )=a ln x +1-a 2x 2-x ,f ′(x )=a x +(1-a )x -1=1-a x (x -a1-a)(x -1).①若a ≤12,则a1-a ≤1,故当x ∈(1,+∞)时,f ′(x )>0,f (x )在(1,+∞)单调递增.所以,存在x 0≥1,使得f (x 0)<aa -1的充要条件为f (1)<a a -1,即1-a 2-1<aa -1, 解得-2-1<a <2-1. ②若12<a <1,则a1-a>1,故当x ∈⎝ ⎛⎭⎪⎫1,a 1-a 时,f ′(x )<0;当x ∈⎝ ⎛⎭⎪⎫a1-a ,+∞时,f ′(x )>0. f (x )在⎝⎛⎭⎪⎫1,a 1-a 单调递减,在⎝ ⎛⎭⎪⎫a 1-a ,+∞单调递增.所以,存在x 0≥1,使得f (x 0)<aa -1的充要条件为f ⎝ ⎛⎭⎪⎫a 1-a <aa -1. 而f ⎝ ⎛⎭⎪⎫a 1-a =a ln a 1-a +a 22(1-a )+a a -1>a a -1,所以不合题意. ③若a >1,则f (1)=1-a 2-1=-a -12<a a -1.综上,a 的取值X 围是(-2-1,2-1)∪(1,+∞).B 组 两年模拟精选(2016~2015年)1.解析 f ′(x )=2x +2sin x ,当x ∈[0,1]时f ′(x )>0.∴f (x )为增函数,所以f (0)<f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫25,又f (x )为偶函数,所以f ⎝ ⎛⎭⎪⎫-13=f ⎝ ⎛⎭⎪⎫13, 则f (0)<f ⎝ ⎛⎭⎪⎫-13<f ⎝ ⎛⎭⎪⎫25. 答案 A2.解析 f ′(x )=3x 2-2tx +3,由于f (x )在区间[1,4]上单调递减,则有f ′(x )≤0在[1,4]上恒成立,即3x 2-2tx +3≤0,即t ≥32⎝ ⎛⎭⎪⎫x +1x 在[1,4]上恒成立,因为y =32⎝ ⎛⎭⎪⎫x +1x 在[1,4]上单调递增,所以t ≥32⎝ ⎛⎭⎪⎫4+14=518,故选C.答案 C3.解析 令F (x )=f (x )x ,则F ′(x )=xf ′(x )-f (x )x 2<0, 所以F (x )为减函数,f (2)2>f (3)3,所以3f (2)>2f (3).答案 A4.解析 当x ≤0时,f ′(x )=6x 2+6x ,易知函数f (x )在(-∞,0]上的极大值点是x =-1,且f (-1)=2,故只要在(0,2]上,e ax≤2即可,即ax ≤ln 2在(0,2]上恒成立,即a ≤ln 2x在(0,2]上恒成立,故a ≤12ln 2.答案 D5.解析 构造函数F (x )=f (x )-⎝ ⎛⎭⎪⎫x 3+23,F (1)=f (1)-1=0, ∵f ′(x )<13,∴F ′(x )=f ′(x )-13<0,∴F (x )在R 上单调递减,f (x )<x 3+23的解集即F (x )<0=F (1)的解集,得x >1.答案 D6.解析 f (x )=x 3-3x ,f ′(x )=3x 2-3, 令f ′(x )=0,解得x =±1, 可以判断当x =1时函数有极小值,∴⎩⎪⎨⎪⎧a <1,6-a 2≥1,6-a 2>a ,解得a ∈[-5,1), ∴选B. 答案 B7.解析 f ′(x )=x 2-ax +3-a ,要使f (x )有三个不同单调区间,需Δ=(-a )2-4(3-a )>0,即a ∈(-∞,-6)∪(2,+∞). 答案 (-∞,-6)∪(2,+∞)8.解析 ∵f ′(x )=3x 2+1>0恒成立,∴f (x )在R 上是增函数. 又f (-x )=-f (x ),∴y =f (x )为奇函数.由f (mx -2)+f (x )<0得f (mx -2)<-f (x )=f (-x ), ∴mx -2<-x ,即mx -2+x <0在m ∈[-2,2]上恒成立. 记g (m )=xm -2+x ,则⎩⎪⎨⎪⎧g (-2)<0,g (2)<0,即⎩⎪⎨⎪⎧-2x -2+x <0,2x -2+x <0, 解得-2<x <23.答案 ⎝⎛⎭⎪⎫-2,23 9.解 (1)由题知函数f (x )的定义域为(0,+∞),f ′(x )=ln x +1,当x ∈⎝ ⎛⎭⎪⎫0,1e 时,f ′(x )<0,故f (x )在⎝ ⎛⎭⎪⎫0,1e 上单调递减,当x ∈⎝ ⎛⎭⎪⎫1e ,+∞时,f ′(x )>0.故f (x )在⎝ ⎛⎭⎪⎫1e ,+∞上单调递增. ①当0<t <t +2<1e 时,无解;②当0<t <1e <t +2,即0<t <1e时,函数f (x )在[t ,t +2]上的最小值f (x )min =f ⎝ ⎛⎭⎪⎫1e =-1e ;③当1e ≤t <t +2,即t ≥1e 时,f (x )在[t ,t +2]上单调递增,故函数f (x )在[t ,t +2]上的最小值f (x )min =f (t )=t ln t .综上可知f (x )min=⎩⎪⎨⎪⎧-1e ,0<t <1e ,t ln t ,t ≥1e .(2)由题知2x ln x ≥-x 2+ax -3,即a ≤2ln x +x +3x对一切x ∈(0,+∞)恒成立.设h (x )=2ln x +x +3x(x >0),则h ′(x )=(x +3)(x -1)x2, 当x ∈(0,1)时,h ′(x )<0,故h (x )在(0,1)上单调递减, 当x ∈(1,+∞)时,h ′(x )>0, 故h (x )在(1,+∞)上单调递增.所以h (x )在(0,+∞)上有唯一极小值h (1),即为最小值, 所以h (x )min =h (1)=4,因为对一切x ∈(0,+∞),a ≤h (x )恒成立,所以a ≤4.。
山东省各地市2023届高三二模文言文阅读汇编

山东省各地市2023届高三二模文言文阅读汇编(一)文言文阅读(本题共5小题,20分)阅读下面的文言文,完成完成10~14题。
贞观八年,太宗将发诸道黜陟使,畿内道未有其人,太宗亲定,问于房玄龄等曰:"此道事最重,谁可充使?"右仆射李靖曰:"畿内事大,非魏征莫可。
"太宗作色曰:“朕今欲向九成宫,亦非小,宁可遣魏征出使?朕每行不欲与其相离者,适为其见朕是非得失。
公等能正朕不?何因辄有所言,大非道理。
”乃即令李靖充使。
贞观十一年,太宗谓侍臣曰:“朕昨往怀州,有上封事者云:‘何为恒差山东众丁于苑内营造?即日征役,似不下隋时。
怀、洛以东,残人不堪其命,而田猎犹数,骄逸之主也。
今者复来怀州田猎,忠谏不复至洛阳矣。
'四时范田,既是帝王常礼,今日怀州,秋毫不干于百姓。
凡上书谏正自有常准臣贵有词主肯能改如斯诋毁,有似咒诅。
"侍中魏征奏称:"国家开直言之路,所以上封事者尤多。
陛下亲自披阅,或冀臣言可取,所以侥幸之士得肆其丑。
臣谏其君,甚须折衷,从容讽谏。
汉元帝尝以酎祭宗庙,出便门,御楼船。
御史大夫薛广德当乘舆免冠曰:'宜从桥,陛下不听臣言,臣自刎,以颈血污车轮,陛下不入庙矣。
’元帝不悦。
光禄卿张猛进曰:‘臣闻主圣臣直,乘船危,就桥安。
圣主不乘危,广德言可听。
’元帝曰:‘晓人不当如是耶!’乃从桥。
以此而言,张猛可谓直臣谏君也。
”太宗大悦。
贞观十五年,太宗谓侍臣曰:“守天下难易?”侍中魏征对曰:“甚难。
”太宗曰:“任贤能,受谏诤,即可。
何谓为难?”征曰:“观自古帝王,在于忧危之间,则任贤受谏。
及至安乐,必怀宽怠,言事者惟令荒惧,日陵月替,以至危亡。
圣人所以居安思危,正为此也。
安而能惧,岂不为难?”(节选自《贞观政要》)10.文中画波浪线的部分有三处需加句读,请将加句读处的字母填写在答题卡的横线上。
(3分)凡A上B书C谏D正E自F有G常H准I臣J贵K有L词M主N肯O能P改11.下列对文中加点的词语及相关内容的解说,不正确的一项是(3分)A.畿内,古时称王都及其周围千里以内的地区,也指京城管辖之地。
山东省济宁市2014届高三上学期期末考试数学(文)答案解析

2013——2014学年度高三复习阶段性检测数学(文史类)试题2014.01本试卷共5页,分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟.第I 卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再改涂其它答案标号.一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合()(){}{}2340,log 1,A x R x x B x R x A B =∈+-≤=∈≥⋂=则A.[)2,4B.[]2,4C.()4,+∞D.[)4,+∞ 2.直线12,l l 平行的一个充分条件是A.12,l l 都平行于同一个平面B.12,l l 与同一个平面所成的角相等C.12l l 平行与所在的平面D.12,l l 都垂直于同一个平面3.若(),0ln ,0x e x g x g x x ⎧≤=⎨>⎩,则(g (12))= A.ln 2- B.1 C.12 D.24.已知实数2,a ,8构成一个等比数列,则圆锥曲线221x y a+=的离心率为5.等差数列{}n a 满足1234345661525=a a a a a a a a S +++=+++=,,则A.12B.30C.40D.256.已知不等式组51,0x y x y y +≤⎧⎪-≥⎨⎪≥⎩则目标函数2z y x =-的最大值是A.1B.1-C.5-D.47. 函数[]sin y x x ππ=-在,上的图象是8.M 是抛物线24y x =上一点,且在x 轴上方,F 是抛物线的焦点,若直线FM 的倾斜角为60 ,则FM =A.2B.3C.4D.69.某三棱锥的三视图如图所示,则该三棱锥的体积是 A.83B.4C.2D.4310.已知()()()1f x x x x m =--,满足()()01f f ''=,则函数()f x 的图象在点()(),m f m 处的切线方程为A.2810x y +-=B.2810x y --=C.2810x y -+=D.2810x y ++= 11.函数()()sin f x A x ωϕ=+(0,2A πϕ><其中)的部分图象如图所示,为了得到函数()cos2g x x =的图象,则只需将()f x 的图象A.向右平移6π个长度单位 B.向右平移12π个长度单位 C.向左平移6π个长度单位 D.向左平移12π个长度单位 12.已知定义在R 上的函数()f x ,满足()()()(),3f x f x f x f x -=--=,当30,2x ⎛⎫∈ ⎪⎝⎭时,()()2ln 1f x x x =-+,则函数()f x 在区间[]0,6上的零点个数是A.3B.5C.7D.9第II 卷(非选择题 共90分)注意事项:1.将第II 卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共4小题,每小题4分,共16分.13.已知向量()()1,1,2,,a b a b λλ==⊥且则的值为__▲__.14.以双曲线221916x y -=的左焦点为圆心,并与其渐近线相切的圆的标准方程是__▲__. 15.已知()35cos ,sin 0051322ππαββαβ⎛⎫⎛⎫-==-∈∈- ⎪ ⎪⎝⎭⎝⎭,且,,,,则sin α=_▲_. 16.观察下列等式: ()2331212+=+,()2333123123,++=++()2333312341234+++=+++,… … … … … …根据以上规律,3333333312345678+++++++=___▲___.(结果用具体数字作答)三、解答题:本大题共6小题,共74分.解答应写文字说明,证明过程或演算步骤.17.(本小题满分12分)已知等比数列{}13232423,2,n a a a a a a a +=+满足且是的等差中项.(I )求数列{}n a 的通项公式;(II )若212l ,,n n n n n n b a og a S b b b S =+=++⋅⋅⋅+求.18.(本小题满分12分)已知函数()2cos 2cos ,f x x x x x R =-∈.(I )求函数()f x 的最小正周期和最小值;(II )ABC ∆中,A,B,C 的对边分别为a,b,c ,已知()1,sin 2sin c f C B A ===,求a,b 的值.19.(本小题满分12分)如图,在四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA PD ⊥,底面ABCD 是直角梯形,其中BC//AD ,90,3,BAD AD BC O ∠== 是AD 上一点.(I )若AD=3OD ,求证:CD//平面PBO ;(II )求证:平面PAB ⊥平面PCD.20.(本小题满分12分)如图,两个工厂A,B (视为两个点)相距2km ,现要在以A,B 为焦点,长轴长为4km 的椭圆上某一点P 处建一幢办公楼.据测算此办公楼受工厂A 的“噪音影响度”与距离AP 成反比,办公楼受工厂B 的“噪音影响度”与距离BP 也成反比,且比例系数都为1.办公楼受A ,B 两厂的“总噪音影响度”y 是受A,B 两厂“噪音影响度”的和,设AP=.xkm(I )求“总噪音影响度”y 关于x 的函数关系式;(II )当AP 为多少时,“总噪音影响度”最小?21.(本小题满分13分)已知椭圆()222210x y C a b a b +=>>:的离心率为2,且经过点A (0,1-). (I )求椭圆的方程;(II )若过点30,5⎛⎫ ⎪⎝⎭的直线与椭圆交于M,N 两点(M,N 点与A 点不重合),求证:以MN 为直径的圆恒过A 点;22.(本小题满分13分)已知函数()()(),ln ,a f x x g x f x x a R x=+=+∈. (I )当a=2时,求函数()g x 的单调区间;(II )当()()()()21002a h x g x x x b R b h x b==--∈≠时,记且,求在定义域内的极值点; (III )[)()()12121221,1,ln ln x x x x f x f x x x ∀∈+∞<-<-且,都有成立,求实数a 的取值范围.。
高考数学模拟复习试卷试题模拟卷第01节 算法与程序框图002 5
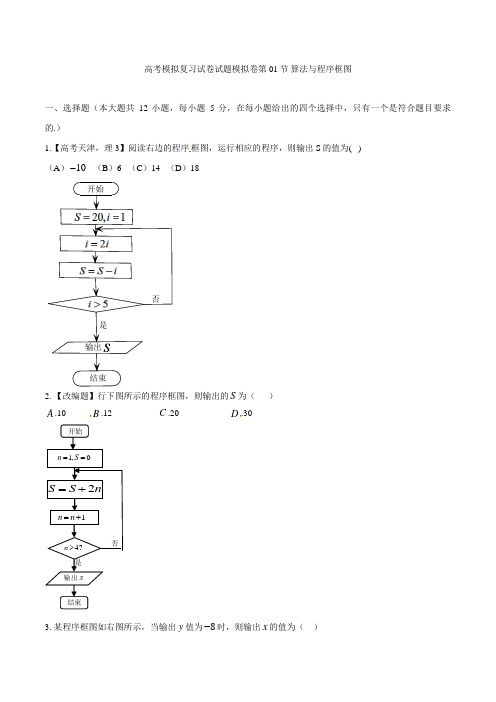
高考模拟复习试卷试题模拟卷第01节 算法与程序框图一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.【高考天津,理3】阅读右边的程序框图,运行相应的程序,则输出S 的值为( )(A )10- (B )6 (C )14 (D )18 否是开始结束输出2. 【改编题】行下图所示的程序框图,则输出的S 为( )A .10B .12C .20D .30 3. 某程序框图如右图所示,当输出y 值为8-时,则输出x 的值为( )开始4?n >否是1,0n S ==结束S输出2S S n=+1n n =+A. 64B. 32C. 16D.84.【改编题】如图所示的程序框图,输出S 的值是20161,则判断框内应填()A. 2015?n <B. 2014?n ≤C.2016?n ≤D. 2015?n ≤5. 【高考湖南卷第6题】执行如图1所示的程序框图,如果输入的]2,2[-∈t ,则输出的S 属于( )A.]2,6[--B.]1,5[--C.]5,4[-D.]6,3[-6.【改编题】执行如图所示的程序框图,输出结果是i =1209x dx ⎰.若{}01,2,3a ∈,则0a 所有可能的取值为( )A .1,2,3B .1C .2D .2,3是否 开始结束1S =1n =1n S S n =⨯+ 1n n =+输出S7.【山东高考理第11题改编】执行右面的程序框图,若输入的x的值为1,则输出的n的值为().A. 1B. 2C. 3D. 48.一个算法的程序框图如下图所示,若该程序输出的结果为56,则判断框中应填入的条件是()A.4i <B.5i <C. 5i ≥D. 6i <9. 【郑州市高中毕业年级第一次质量预测试题】执行如图的程序框图,若输出的78S =,则输入的整数P 的值为( ).A. 1B. 2C. 3D. 410. 【原创题】如图是一个算法的流程图.若输入x 的值为3,则输出y 的值是( )A.12B.12-C.32-D.3-11.【高考湖北卷第13题】设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为()I a,按从大到小排成的三位数记为()D a(例如815a=,则()158I a=,()851D a=).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=( ).A.495B.594C.693D.81512. 【原创题】执行如图所示的程序框图,输出的a值为______.输入x112y x=-||1y x-<2x y=否是结束开始输出yA .12B .3C .2-D .13- 二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中的横线上.)13. 如图,是一程序框图,则输出结果为K =,S =.(说明,M N =是赋值语句,也可以写成M N ←,或:M N =14. 下图是一个算法的程序框图,最后输出的W =_______.开始a =3,i =1i >511a a a +=- i =i +1结束输出a是否,则输出的S的最大值为15. 【高考四川卷文第6题】执行如图1所示的程序框图,如果输入的,x y R_________16. 【高考山东卷第11题】执行右面的程序框图,若输入的x的值为1,则输出的n的值为.17. 【黄冈市重点中学第二学期高三三月月考】若下框图所给的程序运行结果为S=20,那么判断框中应填入的关于整数k 的条件是 _______________18. 【湖北八校高三第二次联考数学试题】定义某种运算⊗,b a S ⊗=的运算原理如图所示.设)3()0()(x x x x f ⊗-⊗=.则=)3(f ______;()f x 在区间[]3,3-上的最小值为______高考模拟复习试卷试题模拟卷高考模拟复习试卷试题模拟卷第03节 几何概型A 基础巩固训练1.在区间[0,π]上随机取一个数x ,则事件“sin x≥cos x”发生的概率为( ) A.14 B.12 C.34D .1 【答案】 C【解析】 ∵sin x≥cos x ,x ∈[0,π],∴π4≤x≤π, ∴事件“sin x≥cos x”发生的概率为π-π4π-0=34. 2.(·西城模拟)在区间[0,2]上任取两个实数a ,b ,则函数f(x)=x3+ax -b 在区间[-1,1]上有且只有一个零点的概率是( )A.18B.14C.34D.78【答案】D3.如图10-6-8所示,墙上挂有一边长为a 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,a 2为半径的扇形,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )A .1-π4B.π4C .1-π8D.与a 的取值有关【解析】 由题意知,阴影部分的面积为a2-4×14×π⎝⎛⎭⎫a 22=⎝⎛⎭⎫1-π4a2,故概率为1-π4. 【答案】 A4. (·阜阳模拟)一艘轮船从O 点的正东方向10 km 处出发,沿直线向O 点的正北方向10 km 处的港口航行,某台风中心在点O ,距中心不超过r km 的位置都会受其影响,且r 是区间[5,10]内的一个随机数,则轮船在航行途中会遭受台风影响的概率是( ) A.2-12B.1-22C.2-1D.2- 2【答案】 D【解析】 以O 为圆心,r 为半径作圆,易知当r >52时,轮船会遭受台风影响,所以P =10-5210-5=10-525=2- 2. 5.在棱长为2的正方体ABCD -A1B1C1D1中,点O 为底面ABCD 的中心,在正方体ABCD -A1B1C1D1内随机取一点P ,则点P 到点O 的距离大于1的概率为________. 【答案】1-π12B 能力提升训练1. 【高考辽宁卷第6题】若将一个质点随机投入如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( ) A .2π B .4π C .6π D .8π【答案】B2. 在区间(0,1)内任取两个实数,则这两个实数的和大于13的概率为()A.1718B.79C.29D.118【答案】A3.【湖北八校高三第二次联考数学试题】记集合{}22(,)|4A x y x y=+≤和集合{}(,)|20,0,0B x y x y x y=+-≤≥≥表示的平面区域分别为1Ω和2Ω,若在区域1Ω内任取一点(,)M x y,则点M落在区域2Ω的概率为.【答案】12πBAyxO4.一只小蜜蜂在一个棱长为4的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )A .18B .116C .127D .2764【答案】A【解析】根据几何概型知识,概率为体积之比,即P =4-2343=18. 5. (·福建三明质量检测)已知集合M ={x|-2≤x ≤8},N ={x|x2-3x +2≤0},在集合M 中任取一个元素x ,则“x ∈(M ∩N)”的概率是( )A .110B .16C .310D .12【答案】A【解析】因为N ={x|x2-3x +2≤0}=[1,2],所以M ∩N =[1,2],所以所求的概率为2-18+2=110.C 思维扩展训练1. 【东莞市高三模拟考试一】已知(2,1)A ,(1,2)B -,31,55C ⎛⎫- ⎪⎝⎭,动点(,)P a b 满足02OP OA ≤⋅≤且02OP OB ≤⋅≤,则点P 到点C 的距离大于14的概率为( )A .5164π-B .564πC .116π- D .16π 【答案】A2. 【高考重庆卷第15题】某校早上8:00开始上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为_____(用数字作答)【答案】932【解析】用x表示小张到校的时间,3050x≤≤,用y表示小王到校的时间,3050y≤≤则所有可能的结果对应直角坐标平面内的正方形区域ABCD记“小张比小王至少早到5分钟”为事件M,则M所对区域为图中的阴影部分DEF∆所以()1151592202032DEFABCDSP AS∆⨯⨯===⨯正方形,所以答案应填:932.3. (济南市高三3月考模拟考试)如图,长方体ABCD—A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A—A1BD内的概率为.【答案】164. 【北京市丰台区高三一模】设不等式组2210x yy⎧+-≤⎨≥⎩,表示的平面区域为M,不等式组201t x ty t-≤≤⎧⎪⎨≤≤-⎪⎩,表示的平面区域为N.在M内随机取一个点,这个点在N内的概率的最大值是_________.【答案】2π5. 若k∈[-3,3],则k的值使得过A(1,1)可以作两条直线与圆(x-k)2+y2=2相切的概率等于( )A .12B .13C .23D .34【答案】C【解析】点在圆外,过该点可做两条直线与圆相切.故使圆心与点A 的距离大于半径即可,即(1-k)2+1>2,解得k <0或k >2,所以所求k ∈[-3,0)∪(2,3],所求概率P =46=23.高考模拟复习试卷试题模拟卷第八章 直线与圆一.基础题组1.(重庆市巴蜀中学高三月考数学、文、1)若直线210ax y ++=与直线20x y +-=互相垂直,那么a 的值等于( )A .1B .13-C .23-D .2- 2.(文昌中学高三模拟考试、文、15)圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________________.3.(重庆市巴蜀中学高三月考数学、文、15)在平面直角坐标系xOy 中,以点)0,1(为圆心且与直线)(012R m m y mx ∈=---相切的所有圆中,半径最大的圆的标准方程为.4.(重庆市部分区县高三上学期入学考试、文、16)若实数c b a ,,成等差数列,点)0,1(-P 在动直线0:==+c by ax l 上的射影为M ,点)3,0(N ,则线段MN 长度的最小值是.二.能力题组1.(五校协作体高三上学期期初考试数学、文、9)曲线21y x =+在点(1,2)处的切线为l ,则直线l 上的任意点P 与圆22430x y x +++=上的任意点Q 之间的最近距离是( )A.4515- B.2515- C.51- D.2 2.(示范高中高三第一次联考、文、14)已知圆的方程为()2214x y +-=。
山东省济宁市2024届高三下学期4月二模试题语文word版含答案

济宁市2024届高考模拟考试语文试题2024.04注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答案卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成1~5题。
荀子以主张“人性恶”而著名,这与孟子所主张的“人性本善”正好相反。
表面上看,荀子对人性的评价很低,而事实上恰好相反,荀子的理论可以称之为一种文化哲学。
他的理论主旨是认为,一切良善和有价值的事物都是人所创造的。
价值来自文化,而文化则是人的创造性成就。
因此,在宇宙中,人和天地同等重要。
荀子认为,天、地、人构成宇宙的三个力量,它们又各有自己的作用。
“列星随旋,日月递照,四时代御,阴阳大化,风雨博施,万物各得其和以生”,这是天、地的作用。
至于人的作用,则是运用天时地利以创造自身的文化。
按照荀子的看法,人性也应当受到教养,没有经过教养就不可能成善。
在《性恶》篇中,荀子说:“人之性恶,其善者伪也。
”伪,就是人为。
荀子的人性论虽然与孟子的正好相反,但是他也同意孟子所说,人皆可以为尧舜。
他自己也说过“涂(途)之人可以为禹”,即路上的普通人也可以成为禹。
这种一致,让有些人认为这两位儒家并无根本的不同,这是一个很大的误解。
在孟子看来,人生来就有仁、义、礼、智“四善端”,人只要充分发展这四善端,就能成为圣人。
而荀子的看法是:人生来不仅没有善端,相反地倒是具有恶端。
在《性恶》篇中,荀子一方面认定人生来就有贪图利益和感官享受的欲望,另一方面也肯定人生来又有智性,可以使人成善:“涂之人也,皆有可以知仁、义、法、正之质,皆有可以能仁、义、法、正之具,然则其可以为禹,明矣。
”也就是说,孟子认为人皆可以为尧舜,是因为人的本性是善的;而荀子认为涂之人皆可以为禹,是因为人有智性。
山东省济宁市2024届高三第一次高考模拟 基本能力试题Word版(2024济宁一模)

山东省济宁市2024届高三第一次模拟考试基本实力试题本试卷分第一部分和其次部分,两部分均为选择题,满分100分。
以考生得分的60%计入总分。
答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置,并仔细核准条形码上的信息。
考试结束后,将本试卷和答题卡—并交回。
第一部分留意事项:1.第一部分70题,每题1分,共70分。
在每题给出的四个选项中,只有一个选项最符合题目要求。
2.每小题选出答案后,用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂答题卡,只答在试卷上不得分。
1.由乔羽作词、刘炽作曲的混声合唱《我的祖国》和斯美塔那创作的交响诗套曲《我的祖国》都分别以他们的母亲河( )为背景,这两部音乐作品都从时代背景、体裁、题材、音乐的叙述性及主题各方面阐述了它们的异曲同工之妙。
A.长江、尼罗河B.黄河、多瑙河C.长江、莱茵河D.黄河、沃尔塔瓦河2.我国的民族民间音乐既有悠久的历史,又有无限的生命力,是中华传统文化的重要组成部分,以下有关中国民族民间音乐叙述完全正确的是①民歌是经过广泛的群众性的即兴编作、口头传唱而渐渐形成和发展起来的,它是多数人才智的结晶。
②中国民间器乐的历史悠久,演奏形式丰富多样,有各种乐器的独奏、重奏和合奏。
③江南丝竹的音乐风格以轻愉快泼为主,有时也表现的较为粗犷。
主奏乐器是二胡、唢呐。
④“打溜子”是流行于湖南土家族的一种民间器乐合奏,通常用马锣、大锣、头钹、二钹四件乐器演奏,乐曲内容多描绘动物形象及劳动生活场景。
⑤藏族人民创建了绚丽的民族文化,对中华民族有着重要的贡献。
藏族音乐可分为长调音乐、宗教音乐和宫廷音乐三大类。
A.①②⑤B.①④⑤C.②③④D.①②④3.选修乐器演奏模块的同学们在新年音乐会上演奏了乐曲《金蛇狂舞》,乐队中不应当出现的乐器是①扬琴②长笛③小号④琵琶⑤风笛⑥架子鼓⑦木鱼⑧二胡A.①②③④B.②③④⑤C.②③⑥⑦D.②③⑤⑥4.漂亮的奥地利诞生过很多闻名的音乐家,“艺术歌曲之王”舒伯特就是其中之一。
山东省济宁市2024届高三一模考试语文试题【含答案】

山东省济宁市2024届高三一模考试语文试题济宁市2024届高考模拟考试语文试题2024.03注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答案卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成1~5题。
材料一:公共艺术泛指公共空间中具有公共性质的艺术形态及艺术活动,是创造性解决社会公共问题的独特艺术形式,是一种地方公众共同参与并享有的具有在地性的文化艺术。
随着社会不断进步,国家对乡村建设愈加重视,因其满足艺术的公共性和促进文化发展的双重特点,人们对公共艺术应用于乡村文化建设的需求更加强烈。
公共艺术以自由开放的空间来设计和制作具有文化意义的艺术作品,将公共艺术引入乡村建设中,有利于传承乡村传统文化,为乡村振兴提供文化基础。
同时,公共艺术建设也是农村公共文化的重要体现,以这种全新的方式来展示新时代农村面貌,不仅能丰富村民的精神世界,还能增强全村居民的凝聚力,使乡村文化更加多元化,从而使农民的精神面貌得到不断提升。
加强乡村文化建设不仅是乡村经济建设的有效助推力,更是增强乡村文化自信的必然要求。
以文化自信为本,突出艺术赋予乡村空间的特色。
在对乡村公共空间进行规划时,重视本土地域特色,应选择部分与当地人文环境相关的设计理念,加入乡村文化建设中,利用艺术的优势,用符号、图画、文字等艺术手法展示和推广乡村本土文化,真正反映当地居民的心声,引起村民与观赏者的共鸣,产生乡土认同感和文化参与感,进一步形成乡村文化自信。
当代乡村社会尽管经历过很多挑战和失败,却依然保留了很多具有鲜明人文特质的古老村落,这给“艺术乡建”创造了必不可少的社会文化空间。
山东省各地市2023届高三二模语言文字运用题汇编

山东省各地市2023届高三二模语言文字运用题汇编语言文字运用Ⅰ2023年山东省潍坊市高考语文二模试卷(一)语言文字运用I(本题共2小题,8分)阅读下面的文字,完成18~19题。
2023年2月3日,我国首条跨海高铁——福厦高铁进入静态验收阶段,为后续线路开通运营创造条件。
验收完成后,预计4月进入联调联试阶段,年内具备开通运营条件。
静态验收是高速铁路竣工验收的重要环节,也是对工程建设、系统设备等的第一次全面“体检”。
铁路部门在这一过程中将检查确认工程按设计完成且质量合格,设备安装调试完毕且质量合格。
福厦高铁于2017年9月全线开工,正线全长277.42公里,设计最高行车时速350 公里。
建成通车后,福厦高铁将推动福州、厦门形成“一小时生活圈”,串联起一条“黄金旅游带”,加速经济贸易,让城市更繁荣。
福厦高铁的修建,将成为我国高速铁路网中沿海大通道的重要组成部分,有利于长三角与大湾区的南北贯通带来益处。
18.文中画横线的句子有语病,请修改。
可以改变语序,少量增删词语,但不得改变原意。
(4分)19.根据文中信息,给"静态验收"下定义。
不超过50个字。
(4分)静态验收是_________________。
18.福厦高铁将成为我国高速铁路网中沿海大通道的重要组成部分,有利于长三角与大湾区的南北贯通。
(原句有两处语病,一是结构混乱,去掉“带来益处”;二是搭配不当,把“的修建”去掉。
4分。
每处2分)19.(静态验收是)对铁路建设项目工程按设计完成且质量合格、设备安装调试完毕且质量合格进行全面检查确认的过程。
(4 分。
单句1分,“按设计完成且质量合格”1分,“设备安装调试完毕且质量合格”1分,“全面检查确认”1分)2023届山东省泰安市高三下学期二模考试语文试题阅读下面的文字,完成18~20题。
《红楼梦》中多次用到"岔话"方式,在叙写某事时停住而转向其他事。
岔话不仅使人物心理微妙丰富,也自然转换了情节。
2016年高考+联考模拟生物试题分项版解析——专题03 物质进出细胞的方式-(学生版) 缺答案

专题03 物质进出细胞的方式1。
(2016上海卷.3)将紫色洋葱鳞叶外表皮细胞置于30%蔗糖溶液数分钟后,结果如图1所示,紫色分部的区域和影响色素分布的结构分别是A。
①和细胞膜B。
①和细胞膜、液泡膜C.②和细胞膜、液泡膜D。
②和细胞膜、液泡膜、细胞壁2。
(2016海南卷。
1)下列关于膜蛋白和物质跨膜运输的叙述,错误的是A。
膜蛋白在细胞膜上的分布是不对称的B。
膜蛋白不参与物质跨膜运输的被动运输过程C。
主动运输可以使被运输离子在细胞内外浓度不同D.物质通过脂质双分子层的扩散速率与脂溶性有关3。
(2016海南卷.5)下列属于主动运输的是A。
动物肺泡细胞释放CO2B。
蔗糖通过植物细胞的细胞壁C。
苯分子进入人的皮肤细胞D.丽藻细胞吸收SO42-的过程4.(2016课标1卷.2)离子泵是一张具有ATP水解酶活性的载体蛋白,能利用水解ATP释放的能量跨膜运输离子。
下列叙述正确的是A。
离子通过离子泵的跨膜运输属于协助扩散B。
离子通过离子泵的跨膜运输是顺着浓度阶梯进行的C. 动物一氧化碳中毒会降低离子泵跨膜运输离子的速率D. 加入蛋白质变性剂会提高离子泵跨膜运输离子的速率5.(2016江苏卷。
2)下列关于生物膜透性的叙述,正确的是A.核糖体合成的分泌蛋白能够自由透过高尔基体膜B。
细胞质中合成的光合作用相关蛋白须通过内质网输入叶绿体C。
子叶细胞中包被脂肪颗粒的膜对葡萄糖具有选择透性D.细胞外高浓度的超氧化物歧化酶可以自由扩散进入细胞6.(2016江苏卷。
6)右图为一种溶质分子跨膜运输的示意图。
下列相关叙述错误的是A。
载体①逆浓度运输溶质分子B。
载体②具有ATP酶活性C.载体①和②转运方式不同D。
载体②转运溶质分子的速率比自由扩散快7。
(2016浙江卷。
1)当人体血糖浓度偏高时,质膜中的某种葡萄糖载体可将葡萄糖转运至肝细胞内,血糖浓度偏低时则转运方向相反。
下列叙述正确的是A。
该载体在血糖浓度偏低时的转运需要消耗ATP B.转运速率随血糖浓度升高不断增大C.转运方向不是由该载体决定的D.胰岛素促进葡萄糖运出肝细胞8。
山东省各地市2024年高考数学(文科)最新试题分类大汇编24:复数-推理与证明

【山东省济宁市邹城二中2024届高三其次次月考文】1.已知i 是虚数单位,=-+i i21( )A .i 5151+ B .i 5351+C .i 5153+D .i 5353-【答案】B【山东省济宁市邹城二中2024届高三其次次月考文】13.给出下列命题:命题1:点(1,1)是直线y = x 与双曲线y = x1的一个交点; 命题2:点(2,4)是直线y = 2x 与双曲线y = x8的一个交点; 命题3:点(3,9)是直线y = 3x 与双曲线y = x27的一个交点; … … .请视察上面命题,猜想出命题n (n 是正整数)为: .【答案】),(2n n ) 是直线y=nx 与双曲线yn y 3=的一个交点【山东省济宁市鱼台二中2024届高三11月月考文】6.设i z -=1(为虚数单位),则=+zz 22( )A .i --1B .i +-1C .i +1D . i -1【答案】D【山东省济宁市汶上一中2024届高三11月月考文】7、计算=+-i i13( )A 、i 21+B 、i 21-C 、i +2D 、 i -2【答案】B【山东省济南市2024届高三12月考】6.复数z 满意(12)7i z i -=+,则复数z 的共轭复数z =A.i 31+B. i 31-C. i +3D. i -3【答案】B【山东省济南市2024届高三12月考】16. )(x f 是定义在R 上恒不为0的函数,对随意x 、R ∈y 都有)()()(y x f y f x f +=,若))((,21*1N n n f a a n ∈==,则数列{}n a 的前n 项和n S 为A .12121+-=n n SB .1211+-=n n S C.n n S 211-= D .n n S 2121-=【答案】C【山东省济宁市重点中学2024届高三上学期期中文】11. 若复数3(R,12a iz a i i+=∈-是虚数单位),且z 是纯虚数,则|2|a i +等于( )A .5B .210C .25D .40 【答案】B【山东省济宁一中2024届高三第三次定时检测文】2.复数123,1z i z i =+=-,则复数12z z 在复平面内对应的点位于 ( ) A .第一象限 B .其次象限 C .第三象限 D .第四象限 【答案】A【山东省莱州一中2024届高三其次次质量检测】对于连续函数)(x f 和)(x g ,函数|)()(|x g x f -在闭区间[b a ,]上的最大值为)(x f 与)(x g 在闭区间[b a ,]上的“肯定差”,记为b x a x g x f ≤≤∆)).(),((则322221331≤≤-+∆x x)x ,x (= 【答案】103【山东省青州市2024届高三2月月考数学(文)】13.若复数312a ii-+(,a R i ∈为虚数单位)是纯虚数,则实数a 的值为 . 【答案】6【山东省青州市2024届高三2月月考数学(文)】15.在一次演讲竞赛中,10位评委对一名选手打分的茎叶图如下所示,若去掉一个最高分和一个最低分,得到一组数据(18)i x i ≤≤,在如图所示的程序框图中,x 是这8个数据中的平均数,则输出的2S 的值为_ ____【答案】15【山东省青州市2024届高三上学期期中文16.已知数列{}n a 中,11211,241n n a a a n +==+-,则n a = 。
高三数学一轮专题突破训练:《统计与概率》(文)及答案

山东省2016届高三数学文一轮复习专题突破训练统计与概率一、选择、填空题1、(2015年高考)为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:①甲地该月14时的平均气温低于乙地该月14时的平均气温;②甲地该月14时的平均气温高于乙地该月14时的平均气温;③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.其中根据茎叶图能得到的统计结论的标号为( )(A)①③ (B) ①④ (C) ②③ (D) ②④2、(2015年高考)在区间[0,2]上随机地取一个数x,则事件“121-1log2x≤+≤()1”发生的概率为( )(A)34(B)23(C)13(D)143、(2014年高考)为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为舒张压/kPa频率 / 组距0.360.240.160.08171615141312(A)6(B)8(C)12(D)184、(2013年高考)将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示.则7个剩余分数的方差为( )8 7 79 4 0 1 0 x 9 1图1-4A.1169B.367C.36 D.6 775、(滨州市2015届高三一模)根据如下样本数据得到的回归方程为1212ˆ55y x=+,则m的值为()A.1 B.32C.4 D.56、(德州市2015届高三一模)某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是____人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年济宁市高考模拟考试
高三数学(文)试题
2016.5
本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分.考试时间120分钟.考试结束后,将本试卷和答题卡一并收回. 注意事项:
1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上. 2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上.
第I 卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设i 是虚数单位,则复数341i
i +-的共轭复数为 A .17
22
i -
+ B .1722i -- C .1722i - D .1722
i +
2.已知全集{}1,2,3,4,5,6U =,集合{}2,4,6A =,集合{}3,5,6B =,则()U A C B ⋂= A .{}2,4,6
B .{}2,4
C .{}2,6
D .{}6
3.设30.22
0.22log 3,log ,3a b c ===,则这三个数的大小关系是 A .c b a >> B .a c b >> C .a b c >>
D .b c a >>
4.从编号为001,002,003,…,300的300个产品中用系统抽样的方法抽取一个样本,已知样本编号从小到大依次为006,018,030,…,则样本中编号排在第11位的是 A .102
B .114
C .126
D .138
5.设2:log 0,:22x p x q <≥,则p 是q ⌝的
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
6.某三棱锥的三视图如图所示,则该三棱锥的体积为
A .2
3 B .16
C .1
D .
13
7.将函数()2sin 23f x x π⎛⎫
=+ ⎪⎝
⎭
的图象向右平移
4
π
个单位后,再将得到的图象上各点的横坐标缩短为原来的
1
2
,纵坐标不变,所得到图象对应的函数解析式为 A .2sin 6y x π⎛⎫
=-
⎪⎝
⎭
B .2sin 412y x π⎛⎫
=+
⎪⎝
⎭
C .52sin 46
y x π⎛⎫=+
⎪⎝
⎭
D .2sin 46y x π⎛⎫
=-
⎪⎝
⎭
8.已知0,0x y >>,且12
1x y
+=,若2x y m +>恒成立,则实数m 的取值范围是 A .()8,+∞ B .[)8,+∞ C .(),8-∞
D .(],8-∞
9.已知,x y 满足约束条件24020,0x y x y y -+≥⎧⎪
+-≤⎨⎪≥⎩
若目标函数z ax y =-仅在点()0,2处取得最
小值,则a 的取值范围是 A .1,12⎛⎫- ⎪⎝⎭
B .()1,1,2⎛⎫-∞-⋃+∞ ⎪⎝⎭
C .11,2⎛⎫- ⎪⎝
⎭
D .()1,1,2⎛⎫
-∞-
⋃+∞ ⎪⎝⎭
10.已知双曲线()22
2210,0x y a b a b
-=>>的右焦点与抛物线()220y px p =>的焦点重
合,若抛物线的准线交双曲线于A 、B 两点,当4AB a =时,此双曲线的离心率为 A
B
C .2
D .3
第Ⅱ卷(非选择题共100分)
注意事项:
1.第Ⅱ卷共2页,必须使用0.5毫米的黑色墨水签字笔书写,要字体工整,笔迹清晰,严格在题号所指示的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共5小题。
每小题5分。
共25分. 11.执行如图所示的程序框图,输出S 的值是 ▲
12.已知函数()(
)321,1
log 1,1x x f x x x ⎧+≤⎪=⎨+>⎪⎩,则
()2f f =⎡⎤⎣⎦ ▲ .
13.如图,在△ABC 中,60BAC ∠=
,AB=2,
AC=1,D 是BC 边上一点,BD=2DC ,则AD BC
⋅
等于 ▲ .
14.已知点(),P x y 是直线():20l y k x k =
+>上一动点,过P 作圆
()
()2
2
221x y -+-=的切线,
此时直线l 的斜率k= ▲ .
15.如图()f x 是定义在R 上的偶函数,当0x ≥时,()()2
1,02
1,2
x x f x f x x ⎧-≤≤⎪=⎨->⎪⎩,若方程
()f x kx =恰有4个不同的根,则实数k 的取值范围是 ▲ .
三、解答题:本大题共6小题。
共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)
在某校统考中,甲、乙两班数学学科前10名的成绩如右表:
(I)若已知甲班l0位同学数学成绩的中位数为125,乙班10位同学数学成绩的平均分为130,求x ,y 的值; (II)设定分数在135分之上的学生为数学尖优生,从甲、乙两班的所有数学尖优生中任两人,求两人在同一班的概率.
17.(小题满分12分)
已知向
量(),cos ,cos ,cos 022m x x n x x ωωωωω⎫⎛=-=+>⎪ ⎪ ⎭⎝⎭
,若()f
x m n =⋅,且()f x 的图象上两相邻对称轴间的距离为
2
π
. (I)求()f x 的单调递减区间;
(II)设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,
且满足()1
,22
c f C b a ===,求,a b 的值.
18.(本小题满分12分)
如图,已知四边形ADEF 为矩形,四边形ABCD 为直角梯形且AB ⊥AD ,AB //CD ,M 、N 、P 分别为EC 、FC 、FB 的中点.
(I)求证:MP //平面ABCD ; (II)求证:平面MNP ⊥平面EDC .
19.(本小题满分12分)
已知公比不为1的等比数列{}n a 的前n 项和为1,1n S a =且1234,3,2a a a 成等差数列. (I)求数列{}n a 的通项公式; (II)设数列{}n b 满足()
21
log 1n n b S =+,求满足方程1223120152016n n b b b b b b -++⋅⋅⋅+=的
正整数n 的值.
20.(本小题满分13分)
已知椭圆()2222:1x y C a b a b +=>>0的右焦点为(1,0),离心率为2
.
(I)求椭圆C 的方程;
(II)过椭圆C 的左焦点且斜率为k 的直线l 与椭圆C 交于M 、N 两点. (i)若以MN 为直径的圆过坐标原点O ,求k 的值; (ii)若P(-1,2),求△MNP 面积的最大值.
21.(本小题满分14分)
已知函数()()()1ln f x a x x a R =+-∈
(I)若函数f (x )在点P(1,f (1))处的切线与直线y =2x +1垂直,求实数a 的值; (II)若函数f (x )在(]0,x e ∈上的最小值为3,求实数a 的值; (III)当(]0,x e ∈时,证明:2
2
5
ln ln 2
e x x x x x ->+
.。
