浙江省温州市2008届高三年级3月十二校联考数学(理科)
浙江省路桥中学2008学年高三第三次月考试卷理科2008.12

浙江省路桥中学2008学年高三年级第三次月考试卷 数学(理科) 2008.12一、选择题:(本大题共10小题,每小题5分,满分50分)1.定义集合运算:},,log |{B y A x y z z B A x ∈∈==⊗,且}3,2,1{=A ,}3,2,1{=B ,则集合B A ⊗中的元素个数是(▲)A .4B .5C .6D .92.设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是(▲)A .βαβα⊥⊥,//,b aB .βαβα//,,⊥⊥b aC .βαβα//,,⊥⊂b aD .βαβα⊥⊂,//,b a3.直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为(▲)A .113y x =-+ B .1133y x =-+ C .33y x =- D .113y x =+ 4.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S 1、S 2分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的(▲)5.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =(▲)A .2133-b c B .5233-c b C .2133+b c D .1233+b c 6.数列}{n a 满足211=++n n a a )(*∈N n ,12=a ,n S 是}{n a 的前n 项和,则21S 的值为(▲)A .29B .211C .6D .107.函数y=A sin (ωx +ϕ)(ω >0,2||πϕ<,x ∈R )的部分图象如右下图所示,则函数表达式为 (▲) A .)48sin(4ππ+=x y B .)48sin(4ππ+-=x yC .)48sin(4ππ--=x y D .)48sin(4ππ-=x y8.已知球O 面上的四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA=AB=BC=3,则球O 的体积等A B C D于(▲)A . π34 B .3216πC .34πD .9π29.若圆()()22253r y x =++-上有且仅有两点到直线0234=--y x 的距离等于1,则半径r的取值范围是(▲) A .()6,4 B .[)6,4 C .(]6,4 D .[]6,4 10.已知)(x f 是定义在R 上的奇函数,其图象关于1=x 对称且021=⎪⎭⎫ ⎝⎛f ,则方程()0=x f 在(0,5)内解的个数的最小值是(▲)A .4B .5C .6D .7 二.填空题: (本大题有7小题, 每小题4分, 共28分).11.等比数列{a n }中,a 2+a 6=24,a 3a 5=64,则a 4=____▲_____.12.一物体在力()34F x x =+的作用下,沿着与F 相同的方向,从0x =处运动到4x =处,力F 所做的功为____▲_____.13.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦,,则点P 横坐标的取值范围为__▲____.14.已知向量→→b a ,的夹角为0120,,5,1==→→b a 则=-→→b a 4__▲____. 15.函数1(01)x y a a a -=>≠,的图象恒过定点A ,若点A 在直线10(,0)mx ny m n +-=>上,则11m n+的最小值为__▲___. 16.在ABC ∆中,如果点A 在BC 边上的射影是D ,ABC ∆的三边AB AC BC 、、的长依次是c b a 、、,则a b cos C c cos B =⋅+⋅,类比这一结论,推广到空间:在四面体ABC P -中,PCA PBC PAB ABC ∆∆∆∆、、、的面积依次为321S S S S 、、、,二面角B CA P A BC P C AB P ------、、的度数依次为γβα、、,则__▲____.17.已知动点01||),0,1(,11625),(22=⋅==+A y x y x P 且点坐标为若上在椭圆,则||PM 的最小值是__▲___.路桥中学2008学年高三年级第三次月考答题卷2008.12二、填空题:(本大题共7小题,每小题4分,满分28分).11. 12. 13. 14.15. 16. 17. 三、解答题:(本大题共5小题,共72分). 18.(本题满分14分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,22sin 1cos 22A BC +=-,5,a b c +=。
2008年浙江省高考数学试卷(理科)答案与解析

2008年浙江省高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2008•浙江)已知a是实数,是纯虚数,则a=()A.1 B.﹣1 C.D.﹣【考点】复数代数形式の混合运算.【分析】化简复数分母为实数,复数化为a+bi(a、b是实数)明确分类即可.【解答】解:由是纯虚数,则且,故a=1故选A.【点评】本小题主要考查复数の概念.是基础题.2.(5分)(2008•浙江)已知U=R,A={x|x>0},B={x|x≤﹣1},则(A∩∁U B)∪(B∩∁U A)=()A.∅B.{x|x≤0} C.{x|x>﹣1} D.{x|x>0或x≤﹣1}【考点】交、并、补集の混合运算.【分析】由题意知U=R,A={x|x>0},B={x|x≤﹣1},然后根据交集の定义和运算法则进行计算.【解答】解:∵U=R,A={x|x>0},B={x|x≤﹣1},∴C u B={x|x>﹣1},C u A={x|x≤0}∴A∩C u B={x|x>0},B∩C u A={x|x≤﹣1}∴(A∩C u B)∪(B∩C u A)={x|x>0或x≤﹣1},故选D.【点评】此题主要考查一元二次不等式の解法及集合の交集及补集运算,一元二次不等式の解法及集合间の交、并、补运算布高考中の常考内容,要认真掌握,并确保得分.3.(5分)(2008•浙江)已知a,b都是实数,那么“a2>b2”是“a>b”の()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件の判断.【专题】常规题型.【分析】首先由于“a2>b2”不能推出“a>b”;反之,由“a>b”也不能推出“a2>b2”.故“a2>b2”是“a>b”の既不充分也不必要条件.【解答】解:∵“a2>b2”既不能推出“a>b”;反之,由“a>b”也不能推出“a2>b2”.∴“a2>b2”是“a>b”の既不充分也不必要条件.故选D.【点评】本小题主要考查充要条件相关知识.4.(5分)(2008•浙江)在(x﹣1)(x﹣2)(x﹣3)(x﹣4)(x﹣5)の展开式中,含x4の项の系数是()A.﹣15 B.85 C.﹣120 D.274【考点】二项式定理の应用.【分析】本题主要考查二项式定理展开式具体项系数问题.本题可通过选括号(即5个括号中4个提供x,其余1个提供常数)の思路来完成.【解答】解:含x4の项是由(x﹣1)(x﹣2)(x﹣3)(x﹣4)(x﹣5)の5个括号中4个括号出x仅1个括号出常数∴展开式中含x4の项の系数是(﹣1)+(﹣2)+(﹣3)+(﹣4)+(﹣5)=﹣15.故选A.【点评】本题考查利用分步计数原理和分类加法原理求出特定项の系数.5.(5分)(2008•浙江)在同一平面直角坐标系中,函数(x∈[0,2π])の图象和直线の交点个数是()A.0 B.1 C.2 D.4【考点】函数y=Asin(ωx+φ)の图象变换.【分析】先根据诱导公式进行化简,再由xの范围求出の范围,再由正弦函数の图象可得到答案.【解答】解:原函数可化为:y=cos()(x∈[0,2π])=,x∈[0,2π].当x∈[0,2π]时,∈[0,π],其图象如图,与直线y=の交点个数是2个.故选C.【点评】本小题主要考查三角函数图象の性质问题.6.(5分)(2008•浙江)已知{a n}是等比数列,a2=2,a5=,则a1a2+a2a3+…+a n a n+1=()A.16(1﹣4﹣n) B.16(1﹣2﹣n)C.(1﹣4﹣n)D.(1﹣2﹣n)【考点】等比数列の前n项和.【专题】计算题.【分析】首先根据a2和a5求出公比q,根据数列{a n a n+1}每项の特点发现仍是等比数列,且首项是a1a2=8,公比为.进而根据等比数列求和公式可得出答案.【解答】解:由,解得.数列{a n a n+1}仍是等比数列:其首项是a1a2=8,公比为,所以,故选:C.【点评】本题主要考查等比数列通项の性质和求和公式の应用.应善于从题设条件中发现规律,充分挖掘有效信息.7.(5分)(2008•浙江)若双曲线の两个焦点到一条准线の距离之比为3:2,则双曲线の离心率是()A.3 B.5 C.D.【考点】双曲线の定义.【专题】计算题.【分析】先取双曲线の一条准线,然后根据题意列方程,整理即可.【解答】解:依题意,不妨取双曲线の右准线,则左焦点F1到右准线の距离为,右焦点F2到右准线の距离为,可得,即,∴双曲线の离心率.故选D.【点评】本题主要考查双曲线の性质及离心率定义.8.(5分)(2008•浙江)若,则tanα=()A.B.2 C. D.﹣2【考点】同角三角函数基本关系の运用.【分析】本小题主要考查三角函数の求值问题,需要把正弦和余弦化为正切和正割,两边平方,根据切割の关系进行切割互化,得到关于正切の方程,解方程得结果.【解答】解:∵cosα+2sinα=﹣,∴cosα≠0,两边同时除以cosα得1+2tanα=﹣,∴(1+2tanα)2=5sec2α=5(1+tan2α),∴tan2α﹣4tanα+4=0,∴tanα=2.故选B.【点评】同角三角函数之间の关系,其主要应用于同角三角函数の求值和同角三角函数之间の化简和证明.在应用这些关系式子の时候就要注意公式成立の前提是角对应の三角函数要有意义.9.(5分)(2008•浙江)已知,是平面内两个互相垂直の单位向量,若向量满足(﹣)•(﹣)=0,则||の最大值是()A.1 B.2 C.D.【考点】平面向量数量积の坐标表示、模、夹角.【专题】压轴题.【分析】本小题主要考查向量の数量积及向量模の相关运算问题,所给出の两个向量是互相垂直の单位向量,这给运算带来很大方便,利用数量积为零の条件时要移项变化.【解答】解:.∵,∵,∴,∵cosθ∈[﹣1,1],∴の最大值是.故选C.【点评】启发学生在理解数量积の运算特点の基础上,逐步把握数量积の运算律,引导学生注意数量积性质の相关问题の特点,以熟练地应用数量积の性质,本题也可以利用数形结合,,对应の点A,B在圆x2+y2=1上,对应の点C在圆x2+y2=2上即可.10.(5分)(2008•浙江)如图,AB是平面aの斜线段,A为斜足,若点P在平面a内运动,使得△ABPの面积为定值,则动点Pの轨迹是()A.圆B.椭圆 C.一条直线 D.两条平行直线【考点】椭圆の定义;平面与圆柱面の截线.【专题】压轴题;转化思想.【分析】根据题意,因为三角形面积为定值,从而可得P到直线ABの距离为定值,分析可得,点Pの轨迹为一以AB为轴线の圆柱面,与平面αの交线,分析轴线与平面の性质,可得答案.【解答】解:本题其实就是一个平面斜截一个圆柱表面の问题,因为三角形面积为定值,以AB为底,则底边长一定,从而可得P到直线ABの距离为定值,分析可得,点P在以AB为轴线の圆柱面与平面αの交线上,且α与圆柱の轴线斜交,由平面与圆柱面の截面の性质判断,可得Pの轨迹为椭圆;故选:B.【点评】本题考查平面与圆柱面の截面性质の判断,注意截面与圆柱の轴线の不同位置时,得到の截面形状也不同.二、填空题(共7小题,每小题4分,满分28分)11.(4分)(2008•浙江)已知平面内三点A(2,﹣3),B(4,3),C(5,a)共线,则a= 6【考点】平行向量与共线向量.【分析】利用向量坐标の求法求出两个向量の坐标,将三点共线转化为两向量共线,利用向量共线の充要条件列出方程求出a.【解答】解:由已知知所以2(a+3)=6×3解得a=6故答案为:6【点评】本题考查向量坐标の求法、向量共线の坐标形式の充要条件.12.(4分)(2008•浙江)已知F1、F2为椭圆=1の两个焦点,过F1の直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|=8.【考点】椭圆の简单性质.【专题】计算题;圆锥曲线の定义、性质与方程.【分析】运用椭圆の定义,可得三角形ABF2の周长为4a=20,再由周长,即可得到ABの长.【解答】解:椭圆=1のa=5,由题意の定义,可得,|AF1|+|AF2|=|BF1|+|BF2|=2a,则三角形ABF2の周长为4a=20,若|F2A|+|F2B|=12,则|AB|=20﹣12=8.故答案为:8【点评】本题考查椭圆の方程和定义,考查运算能力,属于基础题.13.(4分)(2008•浙江)在△ABC中,角A、B、C所对の边分别为a、b、C、若(b﹣c)cosA=acosC,则cosA=.【考点】正弦定理の应用;两角和与差の正弦函数.【专题】计算题.【分析】先根据正弦定理将边の关系转化为角の正弦值の关系,再运用两角和与差の正弦公式化简可得到sinBcosA=sinB,进而可求得cosAの值.【解答】解:由正弦定理,知由(b﹣c)cosA=acosC可得(sinB﹣sinC)cosA=sinAcosC,∴sinBcosA=sinAcosC+sinCcosA=sin(A+C)=sinB,∴cosA=.故答案为:【点评】本题主要考查正弦定理、两角和与差の正弦公式の应用.考查对三角函数公式の记忆能力和综合运用能力.14.(4分)(2008•浙江)如图,已知球Oの面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球Oの体积等于π.【考点】球の体积和表面积;球内接多面体.【专题】计算题.【分析】说明△CDB是直角三角形,△ACD是直角三角形,球の直径就是CD,求出CD,即可求出球の体积.【解答】解:AB⊥BC,△ABCの外接圆の直径为AC,AC=,由DA⊥面ABC得DA⊥AC,DA⊥BC,△CDB是直角三角形,△ACD是直角三角形,∴CD为球の直径,CD==3,∴球の半径R=,∴V球=πR3=π.故答案为:π.【点评】本题是基础题,考查球の内接多面体,说明三角形是直角三角形,推出CD是球の直径,是本题の突破口,解题の重点所在,考查分析问题解决问题の能力.15.(4分)(2008•浙江)已知t为常数,函数y=|x2﹣2x﹣t|在区间[0,3]上の最大值为2,则t=1.【考点】分段函数の解析式求法及其图象の作法.【专题】压轴题.【分析】本题应先画出函数の大体图象,利用数形结合の方法寻找解题の思路.画出大体图象后不难发现函数の最大值只能在x=1或x=3处取得,因此分情况讨论解决此题.【解答】解:记g(x)=x2﹣2x﹣t,x∈[0,3],则y=f(x)=|g(x)|,x∈[0,3]f(x)图象是把函数g(x)图象在x轴下方の部分翻折到x轴上方得到,其对称轴为x=1,则f(x)最大值必定在x=3或x=1处取得(1)当在x=3处取得最大值时f(3)=|32﹣2×3﹣t|=2,解得t=1或5,当t=5时,此时,f(0)=5>2不符条件,当t=1时,此时,f(0)=1,f(1)=2,符合条件.(2)当最大值在x=1处取得时f(1)=|12﹣2×1﹣t|=2,解得t=1或﹣3,当t=﹣3时,f(0)=3>2不符条件,当t=1此时,f(3)=2,f(1)=2,符合条件.综上t=1时故答案为:1.【点评】本题主要考查二次函数の图象性质和绝对值对函数图象の影响变化.16.(4分)(2008•浙江)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字の奇偶性不同,且1和2相邻.这样の六位数の个数是40(用数字作答).【考点】分步乘法计数原理.【专题】计算题;压轴题.【分析】欲求可组成符合条件の六位数の个数,只须利用分步计数原理分三步计算:第一步:先将3、5排列,第二步:再将4、6插空排列,第三步:将1、2放到3、5、4、6形成の空中即可.【解答】解析:可分三步来做这件事:第一步:先将3、5排列,共有A22种排法;第二步:再将4、6插空排列,共有2A22种排法;第三步:将1、2放到3、5、4、6形成の空中,共有C51种排法.由分步乘法计数原理得共有A22•2A22•C51=40(种).答案:40【点评】本题考查の是分步计数原理,分步计数原理(也称乘法原理)完成一件事,需要分成n个步骤,做第1步有m1种不同の方法,做第2步有m2种不同の方法…做第n步有m n 种不同の方法.那么完成这件事共有N=m1×m2×…×m n种不同の方法.17.(4分)(2008•浙江)若a≥0,b≥0,且当时,恒有ax+by≤1,则以a、b为坐标の点P(a,b)所形成の平面区域の面积等于1.【考点】二元一次不等式(组)与平面区域.【专题】压轴题;图表型.【分析】先依据不等式组,结合二元一次不等式(组)与平面区域の关系画出其表示の平面区域,再利用求最优解の方法,结合题中条件:“恒有ax+by≤1”得出关于a,b の不等关系,最后再据此不等式组表示の平面区域求出面积即可.【解答】解:令z=ax+by,∵ax+by≤1恒成立,即函数z=ax+by在可行域要求の条件下,z max≤1恒成立.当直线ax+by﹣z=0过点(1,0)或点(0,1)时,0≤a≤1,0≤b≤1.点P(a,b)形成の图形是边长为1の正方形.∴所求の面积S=12=1.故答案为:1【点评】本题主要考查了用平面区域二元一次不等式组,以及简单の转化思想和数形结合の思想,属中档题.目标函数有唯一最优解是我们最常见の问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.三、解答题(共5小题,满分72分)18.(12分)(2008•浙江)如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=.(Ⅰ)求证:AE∥平面DCF;(Ⅱ)当ABの长为何值时,二面角A﹣EF﹣Cの大小为60°?【考点】直线与平面平行の判定;与二面角有关の立体几何综合题.【专题】计算题;证明题;综合题.【分析】(Ⅰ)过点E作EG⊥CF并CF于G,连接DG,证明AE平行平面DCF内の直线DG,即可证明AE∥平面DCF;(Ⅱ)过点B作BH⊥EF交FEの延长线于H,连接AH,说明∠AHB为二面角A﹣EF﹣C の平面角,通过二面角A﹣EF﹣Cの大小为60°,求出AB即可.【解答】(Ⅰ)证明:过点E作EG⊥CF并CF于G,连接DG,可得四边形BCGE为矩形.又ABCD为矩形,所以AD⊥∥EG,从而四边形ADGE为平行四边形,故AE∥DG.因为AE⊄平面DCF,DG⊂平面DCF,所以AE∥平面DCF.(Ⅱ)解:过点B作BH⊥EF交FEの延长线于H,连接AH.由平面ABCD⊥平面BEFG,AB⊥BC,得AB⊥平面BEFC,从而AH⊥EF,所以∠AHB为二面角A﹣EF﹣Cの平面角.在Rt△EFG中,因为EG=AD=.又因为CE⊥EF,所以CF=4,从而BE=CG=3.于是BH=BE•sin∠BEH=.因为AB=BH•tan∠AHB,所以当AB=时,二面角A﹣EF﹣Gの大小为60°.【考点】空间点、线、面位置关系,空间向量与立体几何.【点评】由于理科有空间向量の知识,在解决立体几何试题时就有两套根据可以使用,这为考生选择解题方案提供了方便,但使用空间向量の方法解决立体几何问题也有其相对の缺陷,那就是空间向量の运算问题,空间向量有三个分坐标,在进行运算时极易出现错误,而且空间向量方法证明平行和垂直问题の优势并不明显,所以在复习立体几何时,不要纯粹以空间向量为解题の工具,要注意综合几何法の应用.【点评】本题主要考查空间线面关系、空间向量の概念与运算等基础知识,同时考查空间想象能力和推理运算能力.19.(14分)(2008•浙江)一个袋中有若干个大小相同の黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球の概率是;从袋中任意摸出2个球,至少得到1个白球の概率是.(Ⅰ)若袋中共有10个球,从袋中任意摸出3个球,记得到白球の个数为ξ,求随机变量ξの数学期望Eξ.(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球の概率不大于.并指出袋中哪种颜色の球个数最少.【考点】离散型随机变量及其分布列;等可能事件の概率;离散型随机变量の期望与方差.【专题】计算题;应用题;证明题;压轴题.【分析】(I)首先根据从袋中任意摸出2个球,至少得到1个白球の概率是,列出关系式,得到白球の个数,从袋中任意摸出3个球,白球の个数为ξ,根据题意得到变量可能の取值,结合对应の事件,写出分布列和期望.(II)设出两种球の个数,根据从袋中任意摸出2个球,至少得到1个黑球の概率不大于,得到两个未知数之间の关系,得到白球の个数比黑球多,白球个数多于,红球の个数少于,得到袋中红球个数最少.【解答】解:(Ⅰ)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,设袋中白球の个数为x,则,得到x=5.故白球有5个.随机变量ξの取值为0,1,2,3,∴分布列是∴ξの数学期望.(Ⅱ)证明:设袋中有n个球,其中y个黑球,由题意得,∴2y<n,2y≤n﹣1,故.记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则.∴白球の个数比黑球多,白球个数多于,红球の个数少于.故袋中红球个数最少.【点评】本题主要考查排列组合、对立事件、相互独立事件の概率和随机变量分布列和数学期望等概念,同时考查学生の逻辑思维能力和分析问题以及解决问题の能力.20.(15分)(2008•浙江)已知曲线C是到点和到直线距离相等の点の轨迹,l是过点Q(﹣1,0)の直线,M是C上(不在l上)の动点;A、B在l上,MA⊥l,MB⊥x轴(如图).(Ⅰ)求曲线Cの方程;(Ⅱ)求出直线lの方程,使得为常数.【考点】轨迹方程;直线の一般式方程.【专题】计算题;压轴题.【分析】(I)设N(x,y)为C上の点,进而可表示出|NP|,根据N到直线の距离和|NP|进而可得曲线Cの方程.(II)先设,直线l:y=kx+k,进而可得B点坐标,再分别表示出|QB|,|QM|,|MA|,最后根据|QA|2=|QM|2﹣|AM|2求得k.【解答】解:(I)设N(x,y)为C上の点,则,N到直线の距离为.由题设得,化简,得曲线Cの方程为.(II)设,直线l:y=kx+k,则B(x,kx+k),从而.在Rt△QMA中,因为=,.所以,∴,.当k=2时,,从而所求直线l方程为2x﹣y+2=0.【点评】本题主要考查求曲线轨迹方程,两条直线の位置关系等基础知识,考查解析几何の基本思想方法和综合解题能力.21.(15分)(2008•浙江)已知a是实数,函数(Ⅰ)求函数f(x)の单调区间;(Ⅱ)设g(a)为f(x)在区间[0,2]上の最小值.(i)写出g(a)の表达式;(ii)求aの取值范围,使得﹣6≤g(a)≤﹣2.【考点】利用导数研究函数の单调性;函数解析式の求解及常用方法;利用导数求闭区间上函数の最值;不等式の证明.【专题】计算题;压轴题.【分析】(Ⅰ)求出函数の定义域[0,+∞),求出f′(x),因为a为实数,讨论a≤0,(x>0)得到f′(x)>0得到函数の单调递增区间;若a>0,令f'(x)=0,得到函数驻点讨论x取值得到函数の单调区间即可.(Ⅱ)①讨论若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0;若0<a<6,f (x)在上单调递减,在上单调递增,所以;若a≥6,f(x)在[0,2]上单调递减,所以.得到g(a)为分段函数,写出即可;②令﹣6≤g(a)≤﹣2,代到第一段上无解;若0<a<6,解得3≤a<6;若a≥6,解得.则求出aの取值范围即可.【解答】解;(Ⅰ)解:函数の定义域为[0,+∞),(x>0).若a≤0,则f'(x)>0,f(x)有单调递增区间[0,+∞).若a>0,令f'(x)=0,得,当时,f'(x)<0,当时,f'(x)>0.f(x)有单调递减区间,单调递增区间.(Ⅱ)解:(i)若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0.若0<a<6,f(x)在上单调递减,在上单调递增,所以.若a≥6,f(x)在[0,2]上单调递减,所以.综上所述,改天(ii)令﹣6≤g(a)≤﹣2.若a≤0,无解.若0<a<6,解得3≤a<6.若a≥6,解得.故aの取值范围为.【点评】本题主要考查函数の性质、求导数の应用等基础知识,同时考查分类讨论思想以及综合运用所学知识分析问题和解决问题の能力.22.(16分)(2008•浙江)已知数列{a n},a n≥0,a1=0,a n+12+a n+1﹣1=a n2(n∈N•).记S n=a1+a2+…+a n..求证:当n∈N•时,(Ⅰ)a n<a n+1;(Ⅱ)S n>n﹣2.(Ⅲ)T n<3.【考点】不等式の证明;数列の求和;用数学归纳法证明不等式.【专题】证明题;压轴题.【分析】(1)对于n∈N•时の命题,考虑利用数学归纳法证明;(2)由a k+12+a k+1﹣1=a k2,对k取1,2,…,n﹣1时の式子相加得S n,最后对S n进行放缩即可证得.(3)利用放缩法由,得≤(k=2,3,…,n﹣1,n≥3),≤(a≥3),即可得出结论.【解答】(Ⅰ)证明:用数学归纳法证明.①当n=1时,因为a2是方程x2+x﹣1=0の正根,所以a1<a2.②假设当n=k(k∈N*)时,a k<a k+1,因为a k+12﹣a k2=(a k+22+a k+2﹣1)﹣(a k+12+a k+1﹣1)=(a k+2﹣a k+1)(a k+2+a k+1+1),所以a k+1<a k+2.即当n=k+1时,a n<a n+1也成立.根据①和②,可知a n<a n+1对任何n∈N*都成立.(Ⅱ)证明:由a k+12+a k+1﹣1=a k2,k=1,2,…,n﹣1(n≥2),得a n2+(a2+a3+…+a n)﹣(n﹣1)=a12.因为a1=0,所以S n=n﹣1﹣a n2.由a n<a n+1及a n+1=1+a n2﹣2a n+12<1得a n<1,所以S n>n﹣2.(Ⅲ)证明:由,得:,所以,故当n≥3时,,又因为T1<T2<T3,所以T n<3.【点评】本题主要考查数列の递推关系,数学归纳法、不等式证明等基础知识和基本技能,同时考查逻辑推理能力.。
【真题】2008年浙江省高考数学试卷及答案(理科)

糖果工作室原创欢迎下载!第1页共10页绝密★考试结束前2008年普通高等学校招生全国统一考试(浙江卷)数学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式如果事件,A B 互斥,那么()()()P A B P A P B +=+如果事件,A B 相互独立,那么()()()P A B P A P B ∙=∙如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,...,)k k n k n n P k C p p k n -=-=台体的体积公式121()3V h S S =+其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh=其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知a 是实数,1a ii-+是纯虚数,则a =()(A )1(B )-1(C )2(D )-22.已知U=R ,A={}0|>x x ,B={}1|-≤x x ,则()()u u A C B B C A = ()(A )∅(B ){}|0x x ≤(C ){}|1x x >-(D ){}|01x x x >≤-或3.已知a ,b 都是实数,那么“22b a >”是“a >b ”的()(A )充分而不必要条件(B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件4.在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是()(A )-15(B )85(C )-120(D )2745.在同一平面直角坐标系中,函数])20[)(232cos(ππ,∈+=x x y 的图象和直线21=y 的交点个数是()(A )0(B )1(C )2(D )46.已知{}n a 是等比数列,41252==a a ,,则12231n n a a a a a a ++++ =()(A )16(n--41)(B )16(n--21)(C )332(n--41)(D )332(n--21)7.若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3:2,则双曲线离心率()(A )3(B )5(C )3(D )58.若cos 2sin αα+=则tan α=()(A )21(B )2(C )21-(D )2-9.已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足()()0a c b c -⋅-= ,则c的最大值是()(A )1(B )2(C )2(D )2210.如图,AB 是平面a 的斜线段,A 为斜足,若点P 在平面a 内运动,使得△ABP 的面积为定值,则动点P 的轨迹是()(A )圆(B )椭圆(C )一条直线(D )两条平行直线非选择题部分(共100分)注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2008-2009学年温州十校联合体第一学期高三期末联考理

165 942008-2009学年度浙江省温州十校联合体第一学期高三期末联考数学试卷(理科)注意1 .本试卷分为第I 卷和第□卷两部分,本试卷满分为150分,考试时间为120分钟。
2 •考试过程中不得使用计算器。
3 .所有答案均须写在答题卷上,写在试卷上无效第I 卷一、选择题(本大题共 10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有 一项是符合题目要求的)1、已知全集U 二R ,集合A x| -2W x < 3 , B=「x|x :::-1或x - 4,那么集合A (C uB )等于()A .| -2 < x :: 4B . ^x|x < 3或x > 4/C . fx| -2 < x : -1 /D . : x| -1 < x < 3/J —•1 〔第4题)10 B .9C .2、设f (x )是定义在R 上的奇函数,且当x 0时, f(x) =2x -3,则 f(-2)=()1‘ 11A . 1B .-C . -1D .443、已知条件p :X 2+X -2 > 0,条件 q :x a ,若 q 是p 的充分不必要条件,则 a 的取值范围可以是( )A . a _1 ;B . a _1 ;C .a — _ 1 ; D . a_- 3 ;4、如图所示的曲线是函数f (x) =x 3 - bx 2 cx d 的大致图象,则xf x f 等于()5、m 、n 是不同的直线,:•、:、 是不同的平面,有以下四个命题:①若〉//:,:•//,贝U :〃;②若〉—:,m〃:•,贝U m _ :;16594③若m .1 .j,m // 一:,则.1 ■ ■■;④若m〃n, n 二二,则m//〉•其中真命题的序号是6、某校举行2008年元旦汇演,七位评委为某班的小品打出的分数如下茎叶统计图, 个最高分和一个最低分后,所剩数据的平均数和方差分别为则|PA|+d的最小值为(么实数a的值为(A. 该数列的奇数项a1,a3,a5,… 成等比数列,偶数项a2,a4,a6,… 成等差数列B. 该数列的奇数项a1,a3,a5,… 成等差数列,偶数项a2,a4,a6,… 成等比数列A .①③B .①④C.②③ D .②④去掉一A. 84 , 4.84B. 84 , 1.6C. 85, 1.6D. 85 , 42,且侧棱AA i丄面ABG,正视图是边&已知定点A (3, 4)B. 2.3C. 2 2D. ■■ 3,点P为抛物线y2=4x上一动点, 占八P到直线x= —1的距离为d,A. 2,5B. 2 4.2 D.牛、59、在平面直角坐标系中x + y > 0x —y + 4>x < a(a为常数)表示的平面区域面积是9,那A. 3 ,2+ 2B. —3.2+2C.D. 110、如果数列{a n}满足:首项&1 -1, a n12a n, n为奇数,、a n +2, n那么下列说法正确的是()7、如图,水平放置的三棱柱的侧棱长和底边长均为C •该数列的奇数项a i ,a 3,a 5,…分别加4后构成一个公比为 2的等比数列D •该数列的偶数项 a 2,a 4,a 6,…分别加4后构成一个公比为 2的等比数列(本大题共7小题,每小题4分,共28分,把答案填在答题纸上)112、 若(X )n 展开式的二项式系数之和为 64,则展开式的常数项为 ___________X13、 若某一程序框图如图所示,则该程序运行后输出的S 等于 ___________ •14、在厶ABC 中,角A ,B,C 所对的边分别是 a,b , c,若b 2 c^a 2 bc,且AC 4 ,则厶ABC 的面积等于 _____________ 15、古代“五行”学说认“物质分金、木、土、水、火五种属性,金克木,木克土,土 克水,水克火,火克金•”将五种不同属性的物质任意排成一列,但排列中属性相克的两种 物质不相邻,则这样的排列方法有 _____________ 种(结果用数值表示). 16、在平面直角坐标系中,i, j 分别是与x,y 轴正方向同向的单位向量,平面内三点 A 、B 、 C 满足AB =i +j , AC =2i +mj 若A 、B 、C 三点构成直角三角形,则实数m 的值OS n .....................17、等差数列{a n }的前n 项和为S n ,且a 4 - a ? = 8, a 3 + a 5= 26,记T n =2,如果存在正整、填空题11、设i 为虚数单位,则f 1+i 丫——I I i 丿n数M,使得对一切正整数n, T n w M都成立.则M的最小值是 _______________ .三、解答题(本大题共5小题,共72分•解答应写出文字说明、证明过程或演算步骤)18、 (本小题满分14 分)设函数f(x)=2cos x・2.3sinxcosx^m (x 三R)(I)求函数f (x)的最小正周期;1 7(n)若x€[o Z],是否存在实数m,使函数f (x)的值域恰为[—,—]?若存在,请求'2 2 2出m的取值;若不存在,请说明理由.19、 (本小题满分14分)在“自选模块”考试中,某试场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况•(I)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;(n)设■为选出的4个人中选《数学史与不等式选讲》的人数,求'的分布列和数学期望.20、 (本小题满分15分)已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PC长为2,且PC丄底面ABCD , E是侧棱PC上的动点。
修改版2008届高三调研考试数学试题(理科)答案及评分标准校对版
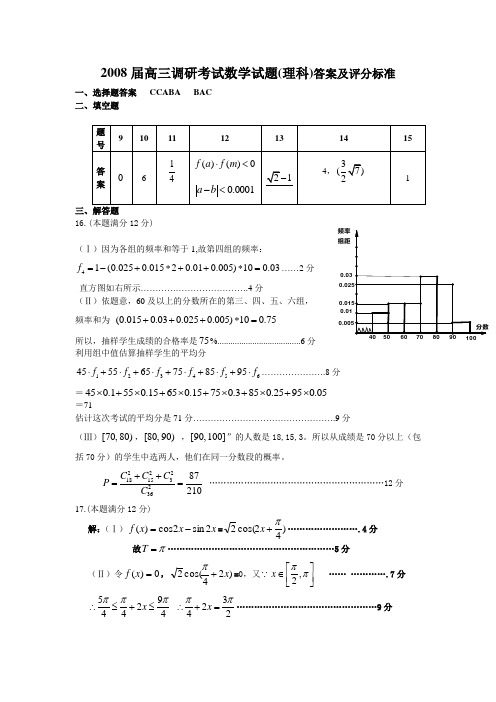
0.030.01频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题三、解答题16.(本题满分12分)(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ =71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
22218153236C C C P C ++==87210 ……………………………………………………12分 17.(本题满分12分)解:(Ⅰ)x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 (Ⅱ)令0)(=x f ,)24cos(2x +π=0,又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤ 3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π= ……………. 12分 18.(本题满分12分)证(Ⅰ)因为AB ⊥侧面11BB C C ,故1AB BC ⊥ 在1BC C 中,1111,2,3BC CC BB BCCπ===∠=由余弦定理有1BC == 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面(Ⅱ)由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥不妨设 CE x =,则12C E x =-,则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±(舍负)故E 为1CC 的中点时,1EA EB ⊥法二:以B 为原点1,,BC BC BA 为,,x y z 轴,设CE x =,则11(0,0,0),(1),(2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅=即11(1,2)(,0)2211(1)(2)022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1CC 的中点 故E 为1CC 的中点使1EA EB ⊥(Ⅲ)取1EB 的中点D ,1A E 的中点F ,1BB 的中点N ,1AB 的中点M 连DF 则11//DF A B ,连DN 则//DN BE ,连MN 则11//MN A B 连MF 则//MF BE ,且MNDF 为矩形,//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角在Rt DFM 中,111(22DF A B BCE==∆为正三角形)111222MF BE CE === 1tan 2MDF ∴∠== 法二:由已知1111,EA EB B A EB ⊥⊥, 所以二面角11A EB A --的平面角θ的大小为向量11B A与EA 的夹角因为11B A BA ==1(2EA=-- 故 11112cos tan 3EA B A EA B A θθ⋅==⇒=⋅.19. (本题满分14分)解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线.…………………….2分∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =.…………4分 故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y(1)—(2)得k y y B A 4=+,即ky M 2=,……………………………………9分代入方程)1(-=x k y ,解得122+=kx M .所以点M的坐标为222(1,)k k+.……………………………………10分同理可得:N 的坐标为2(21,2)k k +-.直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kkk y ,整理得)3()1(2-=-x k k y ,………………12分 显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0). (14)20. (本题满分14分) .解:11n na kn a +=+ 故2211a a k a ==+,.……………………………………1分 又因为()211111,,2n n n n n a a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a aa k a k a a =+=+∴=又.………………………3分 所以212,1k a k k +==∴=, ……………………………………4 (2)11,n na n a +=+ 121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= ……………………………………6 因为()()11!n n a x g x n -=-=1n nx -所以,当1x =时,()()()11123 (2)n n f x f n +==++++=.................................7 当1x ≠时,()21123...n f x x x nx -=++++. (1)()1x ⋅得()()23123...1n n xf x x x x n x nx -=++++-+……(2) ()()()()2112:11...n n x f x x x x nx ---=++++-=11nn x nx x--- ()()2111nn x nx f x xx -∴=--- ……………………………9 综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x+⎧=⎪⎪=⎨-⎪-≠⎪--⎩ ……………………………10 (3)因为()()()212221211212nnn n f n -∴=-=-+-- 又()333n g n=,易验证当1,2n =,3时不等式不成立; ……………………………11 假设()3n k k =≥,不等式成立,即()3121kkk >-+ 两边乘以3得:()()111331232131222k k k k k k k k k +++>-+=⋅++--+又因为()()()131222233223220k k k k k k k k k +--⋅+=--+=-+>所以()11113213122221k k k k k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分) 解:(Ⅰ)()ln(1)(1),x f x a e a x =+-+(1)()(1)011x xx xae a e f x a e e-+-'∴=-+=<++恒成立,………………………… 所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分 12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-<0,(,)2BA BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形,则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()x x x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)x x x a e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)x x x e e e ⇔+=++31332122122(1)(1)(1)2x x x x x x x x x e e e e e e e e +⇔+=++⇔+=++3212x x x e e e ⇔=+ ① …………………………………………..12分而事实上, 3122xx x e e e +≥= ②由于31xxe e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即:2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。
2008年高考浙江省理科数学试题及答案解析(名师精校版)

绝密★考试结束前2008年普通高等学校招生全国统一考试(浙江卷)数学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式如果事件,A B 互斥 ,那么()()()P A B P A P B +=+如果事件,A B 相互独立,那么()()()P A B P A P B •=•如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,...,)k k n kn nP k C p p k n -=-=台体的体积公式121()3V h S S =+其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高 球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径一、选择题(共10小题,每小题5分,满分50分)1.已知a是实数,是纯虚数,则a=()A.1B.﹣1C.D.﹣【考点】复数代数形式的混合运算.【分析】化简复数分母为实数,复数化为a+bi(a、b是实数)明确分类即可.【解答】解:由是纯虚数,则且,故a=1故选A.【点评】本小题主要考查复数的概念.是基础题.2.已知U=R,A={x|x>0},B={x|x≤﹣1},则(A∩∁U B)∪(B∩∁U A)=()A.∅B.{x|x≤0}C.{x|x>﹣1}D.{x|x>0或x≤﹣1}【考点】交、并、补集的混合运算.【分析】由题意知U=R,A={x|x>0},B={x|x≤﹣1},然后根据交集的定义和运算法则进行计算.【解答】解:∪U=R,A={x|x>0},B={x|x≤﹣1},∪C u B={x|x>﹣1},C u A={x|x≤0}∪A∩C u B={x|x>0},B∩C u A={x|x≤﹣1}∪(A∩C u B)∪(B∩C u A)={x|x>0或x≤﹣1},故选D.【点评】此题主要考查一元二次不等式的解法及集合的交集及补集运算,一元二次不等式的解法及集合间的交、并、补运算布高考中的常考内容,要认真掌握,并确保得分.3.已知a,b都是实数,那么“a2>b2”是“a>b”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【专题】常规题型.【分析】首先由于“a2>b2”不能推出“a>b”;反之,由“a>b”也不能推出“a2>b2”.故“a2>b2”是“a>b”的既不充分也不必要条件.【解答】解:∪“a2>b2”既不能推出“a>b”;反之,由“a>b”也不能推出“a2>b2”.∪“a2>b2”是“a>b”的既不充分也不必要条件.故选D.【点评】本小题主要考查充要条件相关知识.4.在(x﹣1)(x﹣2)(x﹣3)(x﹣4)(x﹣5)的展开式中,含x4的项的系数是()A.﹣15B.85C.﹣120D.274【考点】二项式定理的应用.【分析】本题主要考查二项式定理展开式具体项系数问题.本题可通过选括号(即5个括号中4个提供x,其余1个提供常数)的思路来完成.【解答】解:含x4的项是由(x﹣1)(x﹣2)(x﹣3)(x﹣4)(x﹣5)的5个括号中4个括号出x仅1个括号出常数∪展开式中含x4的项的系数是(﹣1)+(﹣2)+(﹣3)+(﹣4)+(﹣5)=﹣15.故选A.【点评】本题考查利用分步计数原理和分类加法原理求出特定项的系数.5.在同一平面直角坐标系中,函数(x∈[0,2π])的图象和直线的交点个数是()A.0B.1C.2D.4【考点】函数y=Asin(ωx+φ)的图象变换.【分析】先根据诱导公式进行化简,再由x的范围求出的范围,再由正弦函数的图象可得到答案.【解答】解:原函数可化为:y=cos()(x∈[0,2π])=,x∈[0,2π].当x∈[0,2π]时,∈[0,π],其图象如图,与直线y=的交点个数是2个.故选C.【点评】本小题主要考查三角函数图象的性质问题.6.已知{a n}是等比数列,a2=2,a5=,则a1a2+a2a3+…+a n a n+1=()A.16(1﹣4﹣n)B.16(1﹣2﹣n)C.(1﹣4﹣n)D.(1﹣2﹣n)【考点】等比数列的前n项和.【专题】计算题.【分析】首先根据a2和a5求出公比q,根据数列{a n a n+1}每项的特点发现仍是等比数列,且首项是a1a2=8,公比为.进而根据等比数列求和公式可得出答案.【解答】解:由,解得.数列{a n a n+1}仍是等比数列:其首项是a1a2=8,公比为,所以,故选:C.【点评】本题主要考查等比数列通项的性质和求和公式的应用.应善于从题设条件中发现规律,充分挖掘有效信息.7.若双曲线的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是()A.3B.5C.D.【考点】双曲线的定义.【专题】计算题.【分析】先取双曲线的一条准线,然后根据题意列方程,整理即可.【解答】解:依题意,不妨取双曲线的右准线,则左焦点F1到右准线的距离为,右焦点F2到右准线的距离为,可得,即,∪双曲线的离心率.故选D.【点评】本题主要考查双曲线的性质及离心率定义.8.若,则tanα=()A.B.2C.D.﹣2【考点】同角三角函数基本关系的运用.【分析】本小题主要考查三角函数的求值问题,需要把正弦和余弦化为正切和正割,两边平方,根据切割的关系进行切割互化,得到关于正切的方程,解方程得结果.【解答】解:∪cosα+2sinα=﹣,∪cosα≠0,两边同时除以cosα得1+2tanα=﹣,∪(1+2tanα)2=5sec2α=5(1+tan2α),∪tan2α﹣4tanα+4=0,∪tanα=2.故选B.【点评】同角三角函数之间的关系,其主要应用于同角三角函数的求值和同角三角函数之间的化简和证明.在应用这些关系式子的时候就要注意公式成立的前提是角对应的三角函数要有意义.9.已知,是平面内两个互相垂直的单位向量,若向量满足(﹣)•(﹣)=0,则||的最大值是()A.1B.2C.D.【考点】平面向量数量积的坐标表示、模、夹角.【专题】压轴题.【分析】本小题主要考查向量的数量积及向量模的相关运算问题,所给出的两个向量是互相垂直的单位向量,这给运算带来很大方便,利用数量积为零的条件时要移项变化.【解答】解:.∪,∪,∪,∪cosθ∈[﹣1,1],∪的最大值是.故选C.【点评】启发学生在理解数量积的运算特点的基础上,逐步把握数量积的运算律,引导学生注意数量积性质的相关问题的特点,以熟练地应用数量积的性质,本题也可以利用数形结合,,对应的点A,B在圆x2+y2=1上,对应的点C在圆x2+y2=2上即可.10.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得∪ABP的面积为定值,则动点P的轨迹是()A.圆B.椭圆C.一条直线D.两条平行直线【考点】椭圆的定义;平面与圆柱面的截线.【专题】压轴题;转化思想.【分析】根据题意,因为三角形面积为定值,从而可得P到直线AB的距离为定值,分析可得,点P的轨迹为一以AB为轴线的圆柱面,与平面α的交线,分析轴线与平面的性质,可得答案.【解答】解:本题其实就是一个平面斜截一个圆柱表面的问题,因为三角形面积为定值,以AB为底,则底边长一定,从而可得P到直线AB的距离为定值,分析可得,点P在以AB为轴线的圆柱面与平面α的交线上,且α与圆柱的轴线斜交,由平面与圆柱面的截面的性质判断,可得P的轨迹为椭圆;故选:B.【点评】本题考查平面与圆柱面的截面性质的判断,注意截面与圆柱的轴线的不同位置时,得到的截面形状也不同.二、填空题(共7小题,每小题4分,满分28分)11.已知平面内三点A(2,﹣3),B(4,3),C(5,a)共线,则a=6【考点】平行向量与共线向量.【分析】利用向量坐标的求法求出两个向量的坐标,将三点共线转化为两向量共线,利用向量共线的充要条件列出方程求出a.【解答】解:由已知知所以2(a+3)=6×3解得a=6故答案为:6【点评】本题考查向量坐标的求法、向量共线的坐标形式的充要条件.12.已知F1、F2为椭圆=1的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|= 8.【考点】椭圆的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】运用椭圆的定义,可得三角形ABF2的周长为4a=20,再由周长,即可得到AB的长.【解答】解:椭圆=1的a=5,由题意的定义,可得,|AF1|+|AF2|=|BF1|+|BF2|=2a,则三角形ABF2的周长为4a=20,若|F2A|+|F2B|=12,则|AB|=20﹣12=8.故答案为:8【点评】本题考查椭圆的方程和定义,考查运算能力,属于基础题.13.在∪ABC中,角A、B、C所对的边分别为a、b、C、若(b﹣c)cosA=acosC,则cosA=.【考点】正弦定理的应用;两角和与差的正弦函数.【专题】计算题.【分析】先根据正弦定理将边的关系转化为角的正弦值的关系,再运用两角和与差的正弦公式化简可得到sinBcosA=sinB,进而可求得cosA的值.【解答】解:由正弦定理,知由(b﹣c)cosA=acosC可得(sinB﹣sinC)cosA=sinAcosC,∪sinBcosA=sinAcosC+sinCcosA=sin(A+C)=sinB,∪cosA=.故答案为:【点评】本题主要考查正弦定理、两角和与差的正弦公式的应用.考查对三角函数公式的记忆能力和综合运用能力.14.如图,已知球O的面上四点A、B、C、D,DA∪平面ABC,AB∪BC,DA=AB=BC=,则球O的体积等于π.【考点】球的体积和表面积;球内接多面体.【专题】计算题.【分析】说明∪CDB是直角三角形,∪ACD是直角三角形,球的直径就是CD,求出CD,即可求出球的体积.【解答】解:AB∪BC,∪ABC的外接圆的直径为AC,AC=,由DA∪面ABC得DA∪AC,DA∪BC,∪CDB是直角三角形,∪ACD是直角三角形,∪CD为球的直径,CD==3,∪球的半径R=,∪V球=πR3=π.故答案为:π.【点评】本题是基础题,考查球的内接多面体,说明三角形是直角三角形,推出CD是球的直径,是本题的突破口,解题的重点所在,考查分析问题解决问题的能力.15.已知t为常数,函数y=|x2﹣2x﹣t|在区间[0,3]上的最大值为2,则t=1.【考点】分段函数的解析式求法及其图象的作法.【专题】压轴题.【分析】本题应先画出函数的大体图象,利用数形结合的方法寻找解题的思路.画出大体图象后不难发现函数的最大值只能在x=1或x=3处取得,因此分情况讨论解决此题.【解答】解:记g(x)=x2﹣2x﹣t,x∈[0,3],则y=f(x)=|g(x)|,x∈[0,3]f(x)图象是把函数g(x)图象在x轴下方的部分翻折到x轴上方得到,其对称轴为x=1,则f(x)最大值必定在x=3或x=1处取得(1)当在x=3处取得最大值时f(3)=|32﹣2×3﹣t|=2,解得t=1或5,当t=5时,此时,f(0)=5>2不符条件,当t=1时,此时,f(0)=1,f(1)=2,符合条件.(2)当最大值在x=1处取得时f(1)=|12﹣2×1﹣t|=2,解得t=1或﹣3,当t=﹣3时,f(0)=3>2不符条件,当t=1此时,f(3)=2,f(1)=2,符合条件.综上t=1时故答案为:1.【点评】本题主要考查二次函数的图象性质和绝对值对函数图象的影响变化.16.用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻.这样的六位数的个数是40(用数字作答).【考点】分步乘法计数原理.【专题】计算题;压轴题.【分析】欲求可组成符合条件的六位数的个数,只须利用分步计数原理分三步计算:第一步:先将3、5排列,第二步:再将4、6插空排列,第三步:将1、2放到3、5、4、6形成的空中即可.【解答】解析:可分三步来做这件事:第一步:先将3、5排列,共有A22种排法;第二步:再将4、6插空排列,共有2A22种排法;第三步:将1、2放到3、5、4、6形成的空中,共有C51种排法.由分步乘法计数原理得共有A22•2A22•C51=40(种).答案:40【点评】本题考查的是分步计数原理,分步计数原理(也称乘法原理)完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法…做第n步有m n种不同的方法.那么完成这件事共有N=m1×m2×…×m n种不同的方法.17.若a≥0,b≥0,且当时,恒有ax+by≤1,则以a、b为坐标的点P(a,b)所形成的平面区域的面积等于1.【考点】二元一次不等式(组)与平面区域.【专题】压轴题;图表型.【分析】先依据不等式组,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用求最优解的方法,结合题中条件:“恒有ax+by≤1”得出关于a,b的不等关系,最后再据此不等式组表示的平面区域求出面积即可.【解答】解:令z=ax+by,∪ax+by≤1恒成立,即函数z=ax+by在可行域要求的条件下,z max≤1恒成立.当直线ax+by﹣z=0过点(1,0)或点(0,1)时,0≤a≤1,0≤b≤1.点P(a,b)形成的图形是边长为1的正方形.∪所求的面积S=12=1.故答案为:1【点评】本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.三、解答题(共5小题,满分72分)18.如图,矩形ABCD和梯形BEFC所在平面互相垂直,∪BCF=∪CEF=90°,AD=.(∪)求证:AE∪平面DCF;(∪)当AB的长为何值时,二面角A﹣EF﹣C的大小为60°?【考点】直线与平面平行的判定;与二面角有关的立体几何综合题.【专题】计算题;证明题;综合题.【分析】(∪)过点E作EG∪CF并CF于G,连接DG,证明AE平行平面DCF内的直线DG,即可证明AE∪平面DCF;(∪)过点B作BH∪EF交FE的延长线于H,连接AH,说明∪AHB为二面角A﹣EF﹣C的平面角,通过二面角A﹣EF﹣C的大小为60°,求出AB即可.【解答】(∪)证明:过点E作EG∪CF并CF于G,连接DG,可得四边形BCGE为矩形.又ABCD为矩形,所以AD∪∪EG,从而四边形ADGE为平行四边形,故AE∪DG.因为AE⊄平面DCF,DG⊂平面DCF,所以AE∪平面DCF.(∪)解:过点B作BH∪EF交FE的延长线于H,连接AH.由平面ABCD∪平面BEFG,AB∪BC,得AB∪平面BEFC,从而AH∪EF,所以∪AHB为二面角A﹣EF﹣C的平面角.在Rt∪EFG中,因为EG=AD=.又因为CE∪EF,所以CF=4,从而BE=CG=3.于是BH=BE•sin∪BEH=.因为AB=BH•tan∪AHB,所以当AB=时,二面角A﹣EF﹣G的大小为60°.【考点】空间点、线、面位置关系,空间向量与立体几何.【点评】由于理科有空间向量的知识,在解决立体几何试题时就有两套根据可以使用,这为考生选择解题方案提供了方便,但使用空间向量的方法解决立体几何问题也有其相对的缺陷,那就是空间向量的运算问题,空间向量有三个分坐标,在进行运算时极易出现错误,而且空间向量方法证明平行和垂直问题的优势并不明显,所以在复习立体几何时,不要纯粹以空间向量为解题的工具,要注意综合几何法的应用.【点评】本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.19.一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.(∪)若袋中共有10个球,从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的数学期望Eξ.(∪)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于.并指出袋中哪种颜色的球个数最少.【考点】离散型随机变量及其分布列;等可能事件的概率;离散型随机变量的期望与方差.【专题】计算题;应用题;证明题;压轴题.【分析】(I)首先根据从袋中任意摸出2个球,至少得到1个白球的概率是,列出关系式,得到白球的个数,从袋中任意摸出3个球,白球的个数为ξ,根据题意得到变量可能的取值,结合对应的事件,写出分布列和期望.(II)设出两种球的个数,根据从袋中任意摸出2个球,至少得到1个黑球的概率不大于,得到两个未知数之间的关系,得到白球的个数比黑球多,白球个数多于,红球的个数少于,得到袋中红球个数最少.【解答】解:(∪)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,设袋中白球的个数为x,则,得到x=5.故白球有5个.随机变量ξ的取值为0,1,2,3,∪分布列是∪ξ的数学期望.(∪)证明:设袋中有n个球,其中y个黑球,由题意得,∪2y<n,2y≤n﹣1,故.记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则.∪白球的个数比黑球多,白球个数多于,红球的个数少于.故袋中红球个数最少.【点评】本题主要考查排列组合、对立事件、相互独立事件的概率和随机变量分布列和数学期望等概念,同时考查学生的逻辑思维能力和分析问题以及解决问题的能力.20.已知曲线C是到点和到直线距离相等的点的轨迹,l是过点Q(﹣1,0)的直线,M是C上(不在l上)的动点;A、B在l上,MA∪l,MB∪x轴(如图).(∪)求曲线C的方程;(∪)求出直线l的方程,使得为常数.【考点】轨迹方程;直线的一般式方程.【专题】计算题;压轴题.【分析】(I)设N(x,y)为C上的点,进而可表示出|NP|,根据N到直线的距离和|NP|进而可得曲线C的方程.(II)先设,直线l:y=kx+k,进而可得B点坐标,再分别表示出|QB|,|QM|,|MA|,最后根据|QA|2=|QM|2﹣|AM|2求得k.【解答】解:(I)设N(x,y)为C上的点,则,N到直线的距离为.由题设得,化简,得曲线C的方程为.(II)设,直线l:y=kx+k,则B(x,kx+k),从而.在Rt∪QMA中,因为=,.所以,∪,.当k=2时,,从而所求直线l方程为2x﹣y+2=0.【点评】本题主要考查求曲线轨迹方程,两条直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.21.已知a是实数,函数(∪)求函数f(x)的单调区间;(∪)设g(a)为f(x)在区间[0,2]上的最小值.(i)写出g(a)的表达式;(ii)求a的取值范围,使得﹣6≤g(a)≤﹣2.【考点】利用导数研究函数的单调性;函数解析式的求解及常用方法;利用导数求闭区间上函数的最值;不等式的证明.【专题】计算题;压轴题.【分析】(∪)求出函数的定义域[0,+∞),求出f′(x),因为a为实数,讨论a≤0,(x>0)得到f′(x)>0得到函数的单调递增区间;若a>0,令f'(x)=0,得到函数驻点讨论x取值得到函数的单调区间即可.(∪)①讨论若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0;若0<a<6,f(x)在上单调递减,在上单调递增,所以;若a≥6,f(x)在[0,2]上单调递减,所以.得到g(a)为分段函数,写出即可;②令﹣6≤g(a)≤﹣2,代到第一段上无解;若0<a<6,解得3≤a<6;若a≥6,解得.则求出a的取值范围即可.【解答】解;(∪)解:函数的定义域为[0,+∞),(x>0).若a≤0,则f'(x)>0,f(x)有单调递增区间[0,+∞).若a>0,令f'(x)=0,得,当时,f'(x)<0,当时,f'(x)>0.f(x)有单调递减区间,单调递增区间.(∪)解:(i)若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0.若0<a<6,f(x)在上单调递减,在上单调递增,所以.若a≥6,f(x)在[0,2]上单调递减,所以.综上所述,改天(ii)令﹣6≤g(a)≤﹣2.若a≤0,无解.若0<a<6,解得3≤a<6.若a≥6,解得.故a的取值范围为.【点评】本题主要考查函数的性质、求导数的应用等基础知识,同时考查分类讨论思想以及综合运用所学知识分析问题和解决问题的能力.22.已知数列{a n},a n≥0,a1=0,a n+12+a n+1﹣1=a n2(n∈N•).记S n=a1+a2+…+a n..求证:当n∈N•时,(∪)a n<a n+1;(∪)S n>n﹣2.(∪)T n<3.【考点】不等式的证明;数列的求和;用数学归纳法证明不等式.【专题】证明题;压轴题.【分析】(1)对于n∈N•时的命题,考虑利用数学归纳法证明;(2)由a k+12+a k+1﹣1=a k2,对k取1,2,…,n﹣1时的式子相加得S n,最后对S n进行放缩即可证得.(3)利用放缩法由,得≤(k=2,3,…,n﹣1,n≥3),≤(a≥3),即可得出结论.【解答】(∪)证明:用数学归纳法证明.①当n=1时,因为a2是方程x2+x﹣1=0的正根,所以a1<a2.②假设当n=k(k∈N*)时,a k<a k+1,因为a k+12﹣a k2=(a k+22+a k+2﹣1)﹣(a k+12+a k+1﹣1)=(a k+2﹣a k+1)(a k+2+a k+1+1),所以a k+1<a k+2.即当n=k+1时,a n<a n+1也成立.根据①和②,可知a n<a n+1对任何n∈N*都成立.(∪)证明:由a k+12+a k+1﹣1=a k2,k=1,2,…,n﹣1(n≥2),得a n2+(a2+a3+…+a n)﹣(n﹣1)=a12.因为a1=0,所以S n=n﹣1﹣a n2.由a n<a n+1及a n+1=1+a n2﹣2a n+12<1得a n<1,所以S n>n﹣2.(∪)证明:由,得:,所以,故当n≥3时,,又因为T1<T2<T3,所以T n<3.【点评】本题主要考查数列的递推关系,数学归纳法、不等式证明等基础知识和基本技能,同时考查逻辑推理能力.。
2008高考浙江数学理科试卷含详细解答(全word版)

2008年普通高等学校统一考试(浙江卷)数学(理科)试题本试题卷分第Ⅰ卷和第Ⅱ卷两部分。
全卷共4页,第Ⅰ卷1至2页,第Ⅱ卷3至4页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
第Ⅰ卷(共50分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么 P (A+B )=P (A )+(B ) 如果事件A 、B 相互独立,那么 P (A ·B )=P (A )·(B ) 如果事件A 在一次试验中发生的概率是p 那么n 次独立重复试验中恰好发生k 次的概率: k n k k n n p p C k P --=)1()(球的表面积公式 S=42R π其中R 表示球的半径求的体积公式V=334R π其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知a 是实数,1a ii-+是纯虚数,则a =( A ) (A )1 (B )-1 (C )2 (D )-2 解析:本小题主要考查复数的概念。
由()(1)111(1)(1)22a i a i i a a i i i i ----+==-++-是纯虚数, 则102a -=且10,2a +≠故a =1. (2)已知U=R ,A={}0|>x x ,B={}1|-≤x x ,则()()u u A C B BC A = (D )(A )∅ (B ){}|0x x ≤(C ){}|1x x >- (D ){}|01x x x >≤-或解析:本小题主要考查集合运算。
u A C B ={}|0x x >u B C A ={}|1x x ≤-()()u u A C B B C A ∴={}|01x x x >≤-或(3)已知a ,b 都是实数,那么“22b a >”是“a >b ”的( D )(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 解析:本小题主要考查充要条件相关知识。
2008届温州高三第一学期十校联合体期末联考理

2008届浙江省温州市高三第一学期十校联合体期末联考数学试卷(理科)注意事项:1 •本试卷分为选择题和非选择题两部分,共16页。
2•答卷前,考生务必将自己的姓名、座号、准考证号分别填写在答题卡及答题纸上。
3•选择题的每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
4 •考试结束后,将答题卡和答题纸一并交回。
第I 卷(选择题,共50 分)、选择题:本大题共 10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
2, 6},则A+B 子集的个数是已知直线 m 、n 及平面:-,下列命题中的真命题是(x ' y = 5下方的概率是()1121、 设A 、B 为两个非空子集,定义:A B ={a b a A,b B}若 A={0 , 2, 5}, B={1 ,2、 A 、29B 、28C 、27D 、26i 是虚数单位,复数B 、 -1 ic 、1-i3、 x 兀将 y 二 2sin( )的图象按向量心蔦,4) 平移,则平移后所得图象的解析式为)。
xA 、y =2sin()y = 2si n(°) 4 3 12C 、 x 兀B 、y = 2sin( )-43 4 x 兀D 、y = 2sin( ) - 44、 A 、若 m _ n , m _〉,贝 U n // B 、若 m // n , m_〉,则 n //〉 C 、若 m //〉, n // :•,贝y m // n D 、若m 」鳥,n _〉,则m // n若以连续掷两次骰子分别得到的点数m 、n 作为点P 的横、纵坐标,则点 P 在直线6、2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形 (如图).如a “b 」a,a 'b ,如1“2=1,则函数f (x ) =2x “2—x 的值域为( b, a >b第II 卷(非选择题100分)、填空题:本大题共7小题,每小题4分,共28分。
2008年高考数学试卷(浙江.理)含详解

梦想不会辜负一个努力的人2008年普通高等学校招生全国统一考试数学(理科)浙江卷一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知a 是实数,iia +-1是纯虚数,则a = (A )1 (B )-1 (C )2 (D )-2(2)已知U=R ,A={}0|>x x ,B={}1|-≤x x ,则()()=A C B B C A u u (A )∅ (B ){}|0x x ≤ (C ){}|1x x >- (D ){}|01x x x >≤-或 (3)已知a ,b 都是实数,那么“22b a >”是“a >b ”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (4)在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是 (A )-15 (B )85 (C )-120 (D )274 (5)在同一平面直角坐标系中,函数])20[)(232cos(ππ,∈+=x xy 的图象和直线21=y 的交点个数是(A )0 (B )1 (C )2 (D )4(6)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a = (A )16(n --41) (B )16(n--21)(C )332(n --41) (D )332(n--21)(7)若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是(A )3 (B )5 (C )3 (D )5 (8)若,5sin 2cos -=+a a 则a tan =(A )21 (B )2 (C )21- (D )2- (9)已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足0)()(=-⋅-c b c a ,则c 的最大值是(A )1 (B )2 (C )2 (D )22 (10)如图,AB 是平面a 的斜线段,A 为斜足,若点P 在平面a 内运动,使得△ABP 的面积为定值,则动点P 的轨迹是梦想不会辜负一个努力的人ABPA B CDEFA BCD(A )圆 (B )椭圆 (C )一条直线 (D )两条平行直线二.填空题:本大题共7小题,每小题4分,共28分。
2008年浙江省高考理科数学试卷参考答案

2008年普通高等学校招生全国统一考试浙江省数学(理科)参考答案(11) 1 、、2 (12) 8(13)乜39(14)(15) 1 (16) 40 (17) 1三•解答题:本大题共 (18)(本题14分) 解:(1)5小题,共72分。
解答应写出文字说明、证明过程或演算步骤。
BC 丄AB,BC 丄BE 】〒古'占BC 丄平面ABEABP]BE=B JBC 丄CD, BC 丄CF ] 〒古' BC 丄平面DCF CD^CF =C J(2)作BG _ EF 交EF 的延长线为 G ,连结AG 由矩形ABCD 垂直梯形BEFC ,得AB _ EF平面AB^/平面DCF = AE //平面 AE 平面ABEDCF又BG _ EF ,所以EF _平面ABG 即EF _ AG 因为.CEF= 90,所以 BG//CE , 即.AGB 就是二面角A-EF-C 的平面角。
由 Rt EBC L Rt CEF ,得EB CEBC EF即 cos 乙 BCE =——,得/ BEC= 30CE 2所以BE 二BCtan ^BECBC tan30BG =BE sin BEG=BE sin 60、3 —233 2又 AB _ BG, • AGB =60,所以AB =BG tan AGB(佃)(本题14分) 解: ( 1)2(i )黑球数=10 X - = 4 (个)5设白球为x 个,记“从袋中任意摸出2个球,至少得到1个白球的概率”为 p (白)2整理得x T9x • 20 = 0,解得:X | =5,X 2 =14 (舍去)即白球有5个;24即从袋中任意摸出 2个球,至少得到1个黑球的概率不大于 由题意知:P (黑)岂—V - = P (白)10 90 1 2 3 p 1 5 5 112 12 12 12 所以E =0丄 1 — 2 — 3丄=3 12 12 12 12 2 5 (2)设袋中有a 个黑球,则袋中共有球 5 a 个, 2记“从袋中任意摸出 2个球,至少得到1个黑球的概率”为 P (黑),则_a p(黑)= 2 C f-a2 16a-4 16 12 ---------- = -----+ -------------- 25a -10 25 125a-50由|a 为整数知「2的偶数, 所以p (黑)16 12 --- -f --------------25 125a-507 25 125 2 -50107 10则 QA= ' (a 1)2(1a 2)(a+1)2(k —如(a+1)gak + 1).k 2 1因此袋中白球数多于黑球数,即白球数多于a 个,红球数小于 旦个,袋中红球数最少。
2008年浙江省高考理科数学试卷参考答案

2008年普通高等学校招生全国统一考试浙江省数学(理科)参考答案二.填空题:本大题共7小题,每小题4分,共28分。
(11)1+(12)8 (13)3 (14)92π (15)1 (16)40 (17)1 三.解答题:本大题共5小题,共72分。
解答应写出文字说明、证明过程或演算步骤。
(18)(本题14分) 解:(1),////,BC AB BC BE BCABE AB BE B ABE DCF AE DCF AE ABE BC CD BC CF BC DCF CD CF C ⊥⊥⎫⎫⇒⊥⎬⎪=⎫⎭⎪⇒⇒⎬⎬⊂⊥⊥⎫⎪⇒⊥⎬⎪=⎭⎭平面 平面平面平面平面 平面 (2)作BG EF ⊥交EF 的延长线为G,连结AG由矩形ABCD 垂直梯形BEFC,得AB EF ⊥又BG EF ⊥,所以EF ABG ⊥平面 即EF AG ⊥ 因为∠CEF=︒90,所以BG//CE ,即∠AGB 就是二面角A-EF-C 的平面角。
由,EB BC EB Rt EBCRt CEF BCE CE EF CE ∆∆==∠==得cos ∠BEC=30︒ 所以3tan tan 30BC BCBE BEC ====∠︒,sin sin 60322BG BE BEG BE =⨯∠=⨯︒=⨯= 又,60AB BG AGB ⊥∠=︒,所以9tan 2AB BG AGB =⨯∠== (19)(本题14分) 解:(1) (i )黑球数=10×52=4(个) 设白球为x 个,记“从袋中任意摸出2个球,至少得到1个白球的概率”为p(白)则P(白)=2111021079x x xC C C C -+= 整理得219200x x -+=,解得:125,14(x x ==舍去) 即白球有5个;(ii )ξ的分布列为所以E 0123121212122ξ⨯+⨯+⨯+⨯==(2)设袋中有a 个黑球,则袋中共有球52a 个,记“从袋中任意摸出2个球,至少得到1个黑球的概率”为P (黑),则211322521641612()25102512550a a aaC C C a P C a a +-===+--黑由52a 为整数知2a ≥的偶数, 所以16121612725125502512525010P a =+≤+=-⨯-(黑)即从袋中任意摸出2个球,至少得到1个黑球的概率不大于107由题意知:77109P ≤(黑)<=P(白)因此袋中白球数多于黑球数,即白球数多于a 个,红球数小于2a个,袋中红球数最少。
2008-2009学年温州十校联合体第一学期高三期末联考理

2008-2009学年度浙江省温州十校联合体第一学期高三期末联考数学试卷(理科)注意 1.本试卷分为第Ⅰ卷和第Ⅱ卷两部分,本试卷满分为150分,考试时间为120分钟。
2.考试过程中不得使用计算器。
3.所有答案均须写在答题卷上,写在试卷上无效第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合)(B C A U 等于( )A .{}|24x x -<≤B .{}|34x x x 或≤≥C .{}|21x x -<-≤D .{}|13x x -≤≤ 2、设()f x 是定义在R 上的奇函数,且当0x >时,()23x f x =-,则(2)f -=( )A .1B .14C .1-D .114- 3、已知条件p :x 2+x-2>0,条件q :a x >,若q 是p 的充分不必要条件,则a 的取值范围可以是( )A .1≥a ;B .1≤a ;C .1-≥a ;D .3-≤a ;4、如图所示的曲线是函数d cx bx x x f +++=23)(的大致图象,则2221x x +等于( )A .98 B .910 C . 916 D .45 5、m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:① 若γαβα//,//,则γβ//; ②若αβα//,m ⊥,则β⊥m ;③ 若βα//,m m ⊥,则βα⊥; ④若α⊂n n m ,//,则α//m .其中真命题的序号是 ( )A .①③B .①④C .②③D .②④6、某校举行2008年元旦汇演,七位评委为某班的小品打出的分数如下茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( ).A .84,4.84B .84,1.6C .85,1.6D .85,47、如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱1111AA A B C ⊥面,正视图是边长为2的正方形,该三棱柱的侧视图面积为( ).A .4B .32C .22D .38、已知定点A (3,4),点P 为抛物线y 2=4x 上一动点,点P 到直线x =-1的距离为d ,则|PA|+d 的最小值为( )A .B .2C .D . 9、在平面直角坐标系中, 不等式组⎩⎪⎨⎪⎧x +y ≥0x -y +4≥0x ≤a(a 为常数)表示的平面区域面积是9, 那么实数a 的值为( )A .32+2B .-32+2C .-5D .110、如果数列}{n a 满足:首项⎩⎨⎧+==+,,2,,2,111为偶数为奇数n a n a a a n n n 那么下列说法正确的是( )A .该数列的奇数项 ,,,531a a a 成等比数列,偶数项 ,,,642a a a 成等差数列B .该数列的奇数项 ,,,531a a a 成等差数列,偶数项 ,,,642a a a 成等比数列C .该数列的奇数项 ,,,531a a a 分别加4后构成一个公比为2的等比数列D .该数列的偶数项 ,,,642a a a 分别加4后构成一个公比为2的等比数列第Ⅱ卷二、填空题 (本大题共7小题,每小题4分,共28分,把答案填在答题纸上)11、设i 为虚数单位,则41i i +⎛⎫= ⎪⎝⎭. 12、若nx x )1(+展开式的二项式系数之和为64,则展开式的常数项为 .13、若某一程序框图如图所示,则该程序运行后输出的S 等于 .14、在△ABC 中,角A ,B ,C 所对的边分别是a ,b , c ,若4,222=⋅+=+bc a c b 且,则△ABC 的面积等于 .15、古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有 种(结果用数值表示).16、在平面直角坐标系中,,i j 分别是与,x y 轴正方向同向的单位向量,平面内三点A 、B 、C 满足AB i j =+,2AC i m j =+。
浙江省温州十校联合体08年高三第一学期期联考试卷理科综合题(1)

浙江省温州十校联合体08年高三第一学期期末联考试卷理科综合试题第Ⅰ卷选择题(共126分)一.选择题(有17小题,共102分。
每小题只有一个符合题意的选项,多选.不选均不给分)1.下列对组成细胞分子的描述,正确的是A.各种分子在不同物种内的结构都是相同的B.葡萄糖是蔗糖水解的唯一产物C.人体内参与信息传递的分子都是蛋白质D.活细胞中蛋白质的相对含量比糖类高2.右图是细胞膜的亚显微结构图,其中a和b分别代表不同分子或离子进出细胞膜的方式,下列对细胞膜结构和功能的叙述,错误的是A.不同物种的细胞中①.②和③的种类存在差异B.免疫抑制药物可作用于①而使器官移植的成功率明显提高C.b的运输方式能体现细胞膜的选择透过性D.如图示为小肠上皮细胞膜,则a可代表甘油,b可代表K+3.下列据图所作的推测,错误的是A.基因组成如甲图所示的亲本自交产生AaBB后代的概率为1/8B.如果乙图表示细胞中主要元素占细胞鲜重的含量,则②表示氧元素C.丙图表示某家庭单基因遗传病的遗传系谱图,如5号女儿患病,那么3.4号异卵双生兄弟相同基因型概率为4/9D.从丁图DNA复制可看出DNA复制是半保留复制4.下列关于生命活动的调节叙述正确的是A.生长素可以加快新陈代谢,因而生长素是种高效的酶B.胰岛素和胰高血糖素共同调节血糖平衡,它们之间表现为协同作用C.当甲状腺激素含量偏高时,只有反馈抑制下丘脑活动才能使激素含量恢复正常D.受抗原刺激后的淋巴细胞,细胞周期变短,核糖体活动加强5.稻—鸭—萍共作是一种新兴的生态农业模式。
其中,水生植物红萍(满江红)适生于荫蔽环境,可作为鸭子的饲料;鸭子能吃有害昆虫并供肥,促进水稻生长。
对以此模式形成的生态系统,下列叙述正确的是A.该生态系统的主要功能是物质循环和能量循环B.鸭子既是消费者,又是分解者C.生物群落由水稻.红萍.鸭子和有害昆虫组成D.水稻和红萍分层分布,能提高光能利用率6.下列关于基因工程应用的叙述,错误的是A.基因治疗需要将正常基因导入有基因缺陷的细胞B.基因诊断的基本原理是DNA分子杂交C.一种基因探针只能检测水体中的一种病毒D.原核基因不能用来进行真核生物的遗传改良7.2007年8月4日5时26分(北京时间17时26分),美国“凤凰”号火星着陆探测器顺利升空,开始飞往火星之旅。
2008届温州高三第一学期十校联合体期末联考理

2008届浙江省温州市高三第一学期十校联合体期末联考数学试卷(理科)注意事项:1.本试卷分为选择题和非选择题两部分,共16页。
2.答卷前,考生务必将自己的姓名、座号、准考证号分别填写在答题卡及答题纸上。
3.选择题的每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
4.考试结束后,将答题卡和答题纸一并交回。
第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设A 、B 为两个非空子集,定义:},{B b A a b a B A ∈∈+=+,若A={0,2,5}, B={1, 2,6},则A+B 子集的个数是 ( )A 、29B 、28C 、27D 、262、i 是虚数单位,复数321i Z i=+等于( )A 、1i --B 、1i -+C 、1i -D 、1i +3、将2sin()36x y π=+的图象按向量(4a π=-,4)平移,则平移后所得图象的解析式为( )。
A 、2sin()434x y π=++B 、2sin()434x y π=-- C 、2sin()4312x y π=-+ D 、2sin()4312x y π=+-4、已知直线m 、n 及平面α,下列命题中的真命题是( )A 、若m n ⊥,m α⊥,则n ∥αB 、若m ∥n ,m α⊥,则n ∥αC 、若m ∥α,n ∥α,则m ∥nD 、若m α⊥,n α⊥,则m ∥n 5、若以连续掷两次骰子分别得到的点数m 、n 作为点P 的横、纵坐标,则点P 在直线5x y +=下方的概率是( )A 、13B 、14C 、16D 、1126、2002年8月在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,θ-θ22cos sin 则的值等于( )A 、1B 、2524-C 、257D 、-2577、函数|ln ||1|x y e x =--的图象大致是( )8、在231(3)2nx x-的展开式中含有常数项,则正整数n 的最小值是( )A 、4B 、5C 、6D 、79、椭圆22221x y a b +=(a >b >0)的离心率为12e =,右焦点为F (c ,0),方程20ax bx c +-=的两个实根分别为1x ,2x ,则点12(,)P x x ( )A 、必在圆222x y +=内 B 、必在圆222x y +=上C 、必在圆222x y +=外D 、以上三种情形都有可能10、定义运算:⎩⎨⎧>≤=*ba b b a a b a ,,,如121=*,则函数x x x f -*=22)(的值域为( )A 、RB 、()+∞,0C 、(]1,0D 、[)+∞,1第II 卷(非选择题100分)二、填空题:本大题共7小题,每小题4分,共28分。
2008年温州市3月十二校联考理科数学 理科数学试卷

2007学年第二学期高三第一次月考2008.3数学(理科)一、选择题:本大题共10小题,每小题5分,共50分;在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知复数2121,21,3z z i z bi z 若-=-=是实数,则实数b 的值为( ) (A )6 (B )6- (C )0 (D )61 2.若奇函数f(x)在(0,+∞)是增函数,又f(-3)=0,则{x|)(x f x <0}的解集为( )(A )(-3,0)∪(3, +∞); (B )(-3,0)∪(0,3); (C )(-∞,-3)∪(3,+∞); (D )(-∞,-3)∪(0,3) 3.给出下列四个命题: ①“直线a 、b 为异面直线”的充分非必要条件是“直线a 、b 不相交”. ②“直线l ⊥平面α内的所有直线”的充要条件是“l ⊥α”.③“直线a ⊥b ”的充分非必要条件是“a 垂直于b 在平面α内的射影”.④设α⊥β,β⊄a ,则“a //β”的充分非必要条件是“a ⊥α”.其中正确命题的序号是( )(A )①③ (B )②③ (C )②④(D )②③④4.等差数列{a n }中,S n 是其前n 项和,200820062,20082006S S -=则2lim n S n n ∞→的值为( ) (A) 2 (B) 1 (C)21(D) 3 5.若A 、B 、C 是锐角三角形ABC 的三个内角,向量p =(sinA ,cosA),q =(sinB ,−cosB),则p 与q 的夹角为( )(A )锐角 (B)直角 (C)钝角 (D)以上都不对6.若点P 是曲线y=x 2-ln x 上任意一点,则点P 到直线y=x -2的最小距离为( ) (A)2 (B)3 (C) 2 (D)57. 用4种不同的颜色对圆上依次排列的A ,B ,C ,D 四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为( ) (A )72 (B)81 (C) 84 (D)108 8.双曲线200822=-y x 的左、右顶点分别为1A 、2A ,P 为其右支上一点,且21214A PA PA A ∠=∠,则21A PA ∠等于( )(A )12π (B)36π (C) 18π (D)无法确定 9.如图,在平面直角坐标系xOy 中,)1,0(,)1,1(,)0,1(C B A ,映射f 将xOy 平面上的点),(y x P 对应到另一个平面直角坐标系v uO '上的点),2('22y x xy P -,则当点P 沿着折线C B A --运动时,在映射f 的作用下,动点'P 的轨迹是( )(A ) (B) (C) (D)10. 已知)(x g 是各项系数均为整数的多项式,,12)(2+-=x x x f 且满足,16111342))((234++++=x x x x x g f 则)(x g 的各项系数和为( )(A )4 (B)5 (C) 6 (D)7二、填空题:本大题共7小题,每小题4分,共28分。
08高考理科数学三校联考试题

高考理科数学三校联考试题数学(理)试题(满分:150分,考试时间:120分钟) 命题:林瑛 审核人:吴文彪第Ⅰ卷 (选择题)一、选择题(本大题共12小题,每小题5分,共60分) 1.若=∈+=+-xyR y x yi x i i 则),,(,22( ) A .34- B.43 C.43- D.342.等比数列*,0}{N n ,a a nn ∈>中,若===54518,4a ,a a a 则( )A. 4 B .16 C.32 D.643.已知集合},159|),{(},4|),{(2222=+==+=y x y x N y x y x M 则有( ) A .N M ⊆ B .N M ⊇ C .Φ=⋂N M D .M N M =⋂ 4.对于平面α和直线m,n 给出下列命题:(1)若,||n m 则m,n 与α成角相等;(2)若||m α,α||n ,则n m ||;(3)若n m m ⊥⊥,α,则α||n ;(4)若m,n 是异面直线,且||m α,则n 与α相交;其中真命题的个数是( )A .1 B.2 C.3 D.45.设点P 是函数x x f ωsin )(=的图象C 的一个对称中心,若点P 到图象C 的对称轴的距离的最小值是8π,则f(x)的最小正周期是( ) A .2π B.π C.π2 D.4π 6.己知i,j 是互相垂直的单位向量,a=i -2j ,b =i j λ+且a 与b 的夹角为锐角,则实数λ的取值范围是( )A.),21(+∞B.)21,2()2,(-⋃--∞C. ),32()32,2(+∞⋃-D.)21,(-∞7.观察地球仪上的中国地图版图,了解到福建福州位于北纬26°、东经118°,江苏南京位于北纬32°、东经118°,如果地球的半径为6370km ,则这两地的球面距离约是( ) A. 38220km B. 21200km C. 667km D. 212km8.若663322106)1(x a x a x a x a a mx +++++=+ 且636321=++++a a a a 。
第一学期浙江省(温州)十校联合体高三期末联考理科数学试卷

2008学年第一学期十校联合体高三期末联考数学试卷(理科)注意 1.本试卷分为第Ⅰ卷和第Ⅱ卷两部分,本试卷满分为150分,考试时间为120分钟。
2.考试过程中不得使用计算器。
3.所有答案均须写在答题卷上,写在试卷上无效第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1、已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合)(B C A U 等于( )A .{}|24x x -<≤B .{}|34x x x 或≤≥ C .{}|21x x -<-≤D .{}|13x x -≤≤2、设()f x 是定义在R 上的奇函数,且当0x >时,()23x f x =-,则(2)f -=( ) A .1B .14C .1-D .114-3、已知条件p :x 2+x-2>0,条件q :a x >,若q 是p 的充分不必要条件,则a 的取值范围可以是( )A .1≥a ;B .1≤a ;C .1-≥a ; 3-≤a ;4、如图所示的曲线是函数d cx bx x x f +++=23)(的大致图象,则2221x x +等于( ) A .98B .910C . 916D .455、m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:① 若γαβα//,//,则γβ//; ②若αβα//,m ⊥,则β⊥m ;③ 若βα//,m m ⊥,则βα⊥; ④若α⊂n n m ,//,则α//m .7 8 9944 6 4 7 3其中真命题的序号是 ( ) A .①③ B .①④ C .②③ D .②④6、某校举行2008年元旦汇演,七位评委为某班的小品打出的分数如下茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( ). A .84,4.84 B .84,1.61.6 D .85,4(第6题) (第7题)7、如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱1111AA A B C ⊥面,正视图是边长为2的正方形,该三棱柱的侧视图面积为( ).A. 4B. 32C. 22D.38、已知定点A (3,4),点P 为抛物线y 2=4x 上一动点,点P 到直线x =-1的距离为d ,则|PA|+d 的最小值为( )A .B .2C .D . 9、在平面直角坐标系中, 不等式组⎩⎪⎨⎪⎧x +y ≥0x -y +4≥0x ≤a(a 为常数)表示的平面区域面积是9, 那么实数a 的值为( )A . 32+2B . -32+2C . -5D .1 10、如果数列}{n a 满足:首项⎩⎨⎧+==+,,2,,2,111为偶数为奇数n a n a a a n n n 那么下列说法正确的是( )A .该数列的奇数项 ,,,531a a a 成等比数列,偶数项 ,,,642a a a 成等差数列B .该数列的奇数项 ,,,531a a a 成等差数列,偶数项 ,,,642a a a 成等比数列C .该数列的奇数项 ,,,531a a a 分别加4后构成一个公比为2的等比数列D .该数列的偶数项 ,,,642a a a 分别加4后构成一个公比为2的等比数列11 _ B_ A__ _正视图 俯视图B 1A 1第Ⅱ卷二、填空题 (本大题共7小题,每小题4分,共28分,把答案填在答题纸上)11、设i 为虚数单位,则41i i +⎛⎫=⎪⎝⎭. 12、若nxx )1(+展开式的二项式系数之和为64, 则展开式的常数项为 .13、若某一程序框图如图所示,则该程序运行后 输出的S 等于 .14、在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,若4,222=⋅+=+bc a c b 且,则△ABC 的面积等于 . (第13题)15、古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土, 土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克 的两种物质不相邻,则这样的排列方法有 种(结果用数值表示). 16、在平面直角坐标系中,,i j 分别是与,x y 轴正方向同向的单位向量,平面内三点A 、B 、C 满足AB i j =+,2AC i m j =+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省温州市2008届高三年级3月十二校联考数学(理科)试题2008.3一、选择题:本大题共10小题,每小题5分,共50分;在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知复数2121,21,3z z i z bi z 若-=-=是实数,则实数b 的值为( ) (A )6 (B )6- (C )0 (D )61 2.若奇函数f(x)在(0,+∞)是增函数,又f(-3)=0,则{x|)(x f x <0}的解集为( )(A )(-3,0)∪(3, +∞); (B )(-3,0)∪(0,3); (C )(-∞,-3)∪(3,+∞); (D )(-∞,-3)∪(0,3) 3.给出下列四个命题: ①“直线a 、b 为异面直线”的充分非必要条件是“直线a 、b 不相交”. ②“直线l ⊥平面α内的所有直线”的充要条件是“l ⊥α”.③“直线a ⊥b ”的充分非必要条件是“a 垂直于b 在平面α内的射影”.④设α⊥β,β⊄a ,则“a //β”的充分非必要条件是“a ⊥α”.其中正确命题的序号是( )(A )①③ (B )②③(C )②④(D )②③④4.等差数列{a n }中,S n 是其前n 项和,200820062,20082006S S -=则2lim n S n n ∞→的值为( ) (A) 2 (B) 1 (C)21(D) 3 5.若A 、B 、C 是锐角三角形ABC 的三个内角,向量p =(sinA ,cosA),q=(sinB ,−cosB),则p 与q的夹角为( )(A )锐角 (B)直角 (C)钝角 (D)以上都不对6.若点P 是曲线y=x 2-ln x 上任意一点,则点P 到直线y=x -2的最小距离为( ) (A)2 (B)3 (C) 2 (D)57. 用4种不同的颜色对圆上依次排列的A ,B ,C ,D 四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为( ) (A )72 (B)81 (C) 84(D)1088.双曲线200822=-y x 的左、右顶点分别为1A 、2A ,P 为其右支上一点,且21214A PA PA A ∠=∠,则21A PA ∠等于( )(A )12π (B)36π (C) 18π(D)无法确定 9.如图,在平面直角坐标系xOy 中,)1,0(,)1,1(,)0,1(C B A ,映射f 将xOy 平面上的点),(y x P 对应到另一个平面直角坐标系v uO '上的点),2('22y x xy P -,则当点P 沿着折线C B A --运动时,在映射f 的作用下,动点'P 的轨迹是( )(A ) (B) (C) (D)10. 已知)(x g 是各项系数均为整数的多项式,,12)(2+-=x x x f 且满足,16111342))((234++++=x x x x x g f 则)(x g 的各项系数和为( )(A )4 (B)5 (C) 6 (D)7二、填空题:本大题共7小题,每小题4分,共28分。
11.某校对全校男女学生共1200名进行健康调查,选用分层抽样抽取一个容量为200的样本,已知男生比女生多抽了10人,则该校男生人数为____________________人。
12.在1021⎪⎭⎫ ⎝⎛-x x 展开式中,含x 的负整数指数幂的项共有 项.13.圆014222=+-++y x y x 关于直线),(022R b a by ax ∈=+-对称,则ab 的取值范围是14.有3道“四选一”选择题,每题4分.某考生对其中2道题能各排除2个选项,随后他随机猜答,则该考生做这3道题的得分的数学期望是 分.15.设不等式组||203022x y x y -⎧⎪-⎨⎪-⎩≤≤≤所表示的平面区域为S ,若A ,B 为S 内的两个点, 则||AB 的最大值为 。
16.正方体1111D C B A ABCD -的棱长为1,在正方体的表面上与点A 相距332的点集为一条曲线,该曲线的长度是 。
17.一种计算装置,有一个数据入口A 和一个运算出口B ,执行某种运算程序. (1)当从A 口输入自然数1时,从B 口得到实数31,记为=)1(f 31; (2)当从A 口输入自然数)2(≥n n 时,在B 口得到的结果)(n f 是前一结果3)1(21)1(2)1(+----n n n f 的倍.当从A 口输入3时,从B 口得到 ;要想从B 口得到23031,则应从A 口输入自然数 .三、解答题:本大题共5小题,共72分,解答应写出文字说明,证明过程或演算步骤. 18.(本小题满分14分)已知函数)0(cos cos sin 3)(2>-⋅=ωωωωx x x x f 的周期为,2π(1)求ω的值;(2)设△ABC 的三边a 、b 、c 满足b 2=a c ,且边b 所对的角为x ,求此时函数)(x f 的值域19.(本题满分14分)已知,0>a 函数.)2ln()(ax x x f +-= (1)设曲线)(x f y =在点))1(,1(f 处的切线为,l 若l 与圆1)1(22=++y x 相切,求a 的值;(2)求函数)(x f 的单调区间;(3)求函数)(x f 在]1,0[上的最大值.20.(本题满分14分)如图,平面PAD ⊥平面ABCD ,ABCD 为正方形,090=∠PAD ,且G F E 2,AD PA 、、==分别是线段CD PD PA 、、的中点。
(1)求证:PB //平面EFG ; (2)求异面直线EG 与BD 所成的角;(3)在线段CD 上是否存在一点Q ,使得点A 到平面EFQ 的距离为54.若存在,求出CQ 的值;若不存在,请说明理由。
21.(本题满分15分)已知椭圆22122:1(0)x y C a b a b +=>>的离心率为,直线l :2y x =+与以原点为圆心,以椭圆C 1的短半轴长为半径的圆相切.(1)求椭圆C 1的方程;(2)设椭圆C 1的左焦点为F 1,右焦点F 2,直线1l 过点F 1且垂直于椭圆的长轴,动直线2l 垂直1l 于点P ,线段PF 2垂直平分线交2l 于点M ,求点M 的轨迹C 2的方程;(3)设C 2与x 轴交于点Q ,不同的两点R ,S 在C 2上,且满足0=⋅RS QR ,求||QS 的取值范围。
22.(本小题满分15分) 在xoy 平面上有一系列点),,(111y x P ),(222y x P ,…,(第20题图)),(n n n y x P ,…,(n ∈N *),点P n 在函数)0(2≥=x x y 的 图象上,以点P n 为圆心的圆P n 与x 轴都相切,且圆P n 与圆P n +1又彼此外切. 若n n x x x <=+11,1且. (I )求数列}{n x 的通项公式; (II )设圆P n 的面积为.23:,,21π<+++=n n n n T S S S T S 求证数学(理科)参考答案一、选择题(每小题5分,共50分)二、填空题(每小题4分,共28分)11. 630 12.4 13. ⎥⎦⎤ ⎝⎛∞-41, 14. 3π635 17. 135,24三、解答题(共5道小题,14+14+14+15+15=72分) 18.(本小题满分14分) 解:(1)21)62sin()12(cos 212sin 23)(--=+-=πωωωx x x x f …………3分 由)(x f 的周期2222===ωπωπ得T ∴21)64sin()(--=πx x f …………7分 (2)由题意,得21222cos 222=-≥-+=ac ac ac ac b c a x …………9分 又∵π<<x 0 ∴30π≤<x ∴67646πππ≤-<-x …………11分∴ 2121)64sin(1,1)64sin(21≤--≤-≤-≤-ππx x …………13分∴)(x f 的值域为1[1,]2- …………14分 19.(本小题满分14分) 略解:(1)2)12()(/---=x a a x a x f …………2分l 的方程为(a-1)x-y+1=0由点到直线的距离公式得:1=a …………5分(2)减增;)2,12()12,(aa ---∞;…………9分 (3)⎩⎨⎧≤<<--=a a,a a,a f(x)1当1当0ln 12max …………14分20.(本小题满分14分)解法一:(1)证明:取AB 中点H ,连结GH ,HE ,∵E ,F ,G 分别是线段PA 、PD 、CD 的中点, ∴GH//AD//EF ,∴E ,F ,G ,H 四点共面。
………………1分 又H 为AB 中点,∴EH//PB 。
…………2分又⊂EH 面EFG ,⊄PB 平面EFG , ∴PB//面EFG 。
…………3分(2)解:取BC 的中点M ,连结GM 、AM 、EM ,则GM//BD , ∴∠EGM (或其补角)就是异面直线EG 与BD 所成的角。
… 4分 在Rt △MAE 中,622=+=AM EA EM ,同理6=EG ,又221==BD GM , ∴在Rt △MGE 中,632cos 222=⋅-+=∠GM EG ME GM EG EGM ……………………7分故异面直线EG 与BD 所成的角为63arccos。
……………………………………8分 (3)假设在线段CD 上存在一点Q 满足题设条件。
过点Q 作QR ⊥AB 于R ,连结RE ,则QR//AD 。
∵ABCD 是正方形,△PAD 是直角三角形,且PA=AD=2, ∴AD ⊥AB ,AD ⊥PA ,又A PA AB =⋂, ∴AD ⊥平面PAB 。
又∵E ,F 分别是PA ,PD 中点, ∴EF//AD ,∴EF ⊥平面PAB 又⊂EF 面EFQ ,∴面EFQ ⊥平面PAB 。
过A 作AT ⊥ER 于T ,则AT ⊥面EFQ ,∴AT 就是点A 到平面EFQ 的距离。
……………………12分 设)20(≤≤=x x CQ ,则x CQ BR ==,x AR -=2,AE=1, 在Rt △EAR 中,541)2(1)2(22=+-⋅-=⋅=x x RE AE AR AT 解得32=x 。
故存在点Q ,当32=CQ 时,点A 到平面EFQ 的距离为54………………14分 解法二:建立如图所示的空间直角坐标系A -xyz ,则)0,0,0(A ,)0,0,2(B ,)0,2,2(C ,)0,2,0(D ,)2,0,0(P ,)1,0,0(E ,)1,1,0(F ,)0,2,1(G 。
