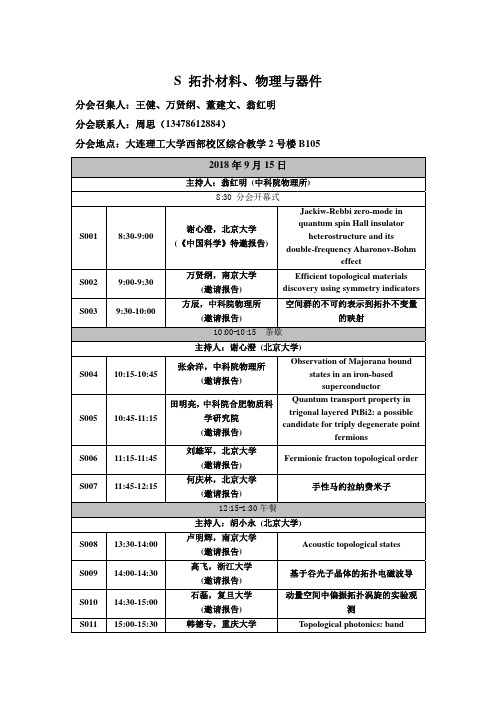
S拓扑材料、物理与器件
凝聚态物理中的拓扑结构及其物理效应

凝聚态物理中的拓扑结构及其物理效应拓扑结构一直是凝聚态物理研究中的一个重要话题。
它指的是物理体系中的空间结构,这种结构决定了物体的导电性、磁性、热性等性质。
拓扑结构在凝聚态物理中的应用包括了半导体器件、聚合物材料、超导体等方面的研究。
拓扑结构的一个独特的特性是拓扑不变性。
这种不变性是指拓扑结构的变化并不会改变物体的某些物理性质。
拓扑不变性在凝聚态物理中的应用主要有两个方面:导电性和带隙性。
导电性是指物体内部的电子会发生对流,从而产生导电现象。
在许多材料中是通过费米能级来实现的。
拓扑结构可以影响费米能级的位置,从而影响材料的导电性。
另一个方面是带隙性,即材料中的电子在运动过程中的能量将呈现为带隙状的能谱结构。
通常来说,这种能谱的结构会随着材料的性质而改变。
但是,在许多情况下,即使材料的其他性质发生了变化,带隙仍然保持着不变。
这种不变性是由于拓扑性质所引起的。
凝聚态物理中最引人注目的是拓扑效应的物理效应。
这种效应可以带来新颖的物理现象,例如量子霍尔效应、拓扑绝缘体等。
量子霍尔效应是指材料在特定条件下呈现出特定的电导率。
这种电导率的变化是由于材料内部的拓扑结构的影响。
拓扑绝缘体同样具有特殊的导电性质。
它们的导电性质在绝缘态和导电态之间切换,这种切换是由于材料的内部拓扑结构所引起的。
拓扑效应在凝聚态物理中的应用,不仅仅是理论上的研究,实际上还有很多实际的应用。
例如,在量子计算机中,拓扑绝缘体可以帮助人们实现非常快速的计算速度。
此外,这种结构可以在制造没有细小电子颗粒的超导体时提供更多帮助。
除此之外,拓扑效应在新型能源材料的研究中也发挥了重要作用。
通过研究能够保持能量不耗散的拓扑物质,科学家们可以为新型能源系统的开发做出积极的贡献。
总之,拓扑效应在凝聚态物理中是一个极为重要和富有潜力的领域。
它不仅能为新型材料和新型能源系统的开发提供支持,也为人们对于材料性质和电子行为的研究提供了新的思路和方法。
在未来的研究中,拓扑效应的研究势必会更加深入和广泛,从而推动物理学和其他领域的发展。
S拓扑材料物理与器件
输运与量子霍尔效应
12:15-13:30 午餐
主持人:冯济 (北京大学)
何珂,清华大学 (邀请报告)
寻找本征磁性拓扑绝缘体
S025 S026 S027
S028 S029 S030 S031 S032
14:00-14:30 14:30-15:00 15:00-15:30
15:45-16:15 16:15-16:45 16:45-17:15 17:15-17:45 17:45-18:15
万贤纲,南京大学 (邀请报告)
方辰,中科院物理所
Jackiw-Rebbi zero-mode in quantum spin Hall insulator
heterosnov-Bohm
effect
Efficient topological materials discovery using symmetry indicators 空间群的不可约表示到拓扑不变量
赵宇心,南京大学
K 理论下拓扑绝缘体和超导的体和
(邀请报告)
边界的对应
秦维,中国科学技术大学 (邀请报告)
Chiral topological superconductivity induced by the constructive
interplay of geometric phase and electron correlation
高飞,浙江大学 (邀请报告)
基于谷光子晶体的拓扑电磁波导
石磊,复旦大学
动量空间中偏振拓扑涡旋的实验观
(邀请报告)
测
韩德专,重庆大学
Topological photonics: band
S012 15:45-16:15 S013 16:15-16:45 S014 16:45-17:15 S015 17:15-17:45 S016 17:45-18:15
自旋轨道耦合和拓扑材料的物理性质

自旋轨道耦合和拓扑材料的物理性质引言:自旋轨道耦合(spin-orbit coupling,SOC)是一种重要的凝聚态物理现象,发挥着在自旋电子学和量子计算等领域重要作用。
而拓扑材料则是一类具有特殊的能带结构和非平凡拓扑性质的材料,被广泛研究和关注。
在本文中,我们将讨论自旋轨道耦合和拓扑材料的物理性质以及它们的相互关系。
一、自旋轨道耦合自旋轨道耦合是自旋和轨道运动之间的相互作用。
它的本质是电子的自旋与它们的运动轨道之间的相互作用。
在自旋轨道耦合存在的情况下,电子的自旋和动量变得不再是守恒的量,这对于研究自旋电子学尤为重要。
自旋轨道耦合可以分为强耦合和弱耦合两种情况。
强耦合指自旋和轨道之间的相互作用非常强烈,而弱耦合则表示自旋和轨道之间的相互作用较小。
由于自旋轨道耦合的存在,电子能带的结构和物质的物理性质都会发生改变,这对于实现新的器件和技术具有重要意义。
二、拓扑材料拓扑材料是一类具有特殊的能带结构和非平凡拓扑性质的材料。
它们的拓扑性质体现在能带的拓扑不变量上,这使得它们具有一些令人惊奇的性质,如稳定的边界态、量子振荡等。
拓扑材料可以分为三类:绝缘体、拓扑绝缘体和拓扑绝缘体。
绝缘体是指带隙中不存在能级,而正常的绝缘体带隙中是没有边界态的。
而拓扑绝缘体和拓扑半金属则具有特殊的边界态,这些态是由拓扑性质保护的。
三、自旋轨道耦合与拓扑材料的相互关系自旋轨道耦合和拓扑材料之间存在着密切的联系和相互作用。
自旋轨道耦合可以改变材料的能带结构,从而使其成为拓扑材料。
同时,拓扑材料的拓扑性质也可以增强自旋轨道耦合效应的作用。
自旋轨道耦合能够产生拓扑绝缘体的边界态,并且这些边界态是由于自旋轨道耦合产生的。
拓扑绝缘体的边界态在应用中具有重要意义,如用于量子计算、拓扑量子比特等。
此外,自旋轨道耦合还可以引起一些其他的物理现象,如自旋霍尔效应、自旋电流等。
这些现象也与拓扑材料的研究有着密切联系。
总结:自旋轨道耦合和拓扑材料都是当前凝聚态物理研究的热点。
拓扑学在物理学研究中的应用

拓扑学在物理学研究中的应用在物理学研究中,拓扑学扮演着重要的角色。
拓扑学是研究空间性质不随形状的变化而改变的数学分支,它的应用不仅局限于数学领域,而且在物理学领域也有广泛的应用。
本文将探讨拓扑学在物理学研究中的应用,并详细介绍其中的两个重要领域:拓扑材料和拓扑光学。
一、拓扑材料拓扑材料是指具有特殊拓扑性质的材料,其电子行为在一些方面与传统材料不同。
拓扑绝缘体是其中一种重要类型的拓扑材料。
在拓扑绝缘体中,电子束缚在材料的边缘或表面上,不受杂质或缺陷的影响。
这种特殊的束缚态使拓扑绝缘体具有高度的输运稳定性,这对于开发新的电子器件和实现量子计算具有潜在的应用前景。
除了拓扑绝缘体,拓扑超导体也是拓扑材料研究的重要领域。
拓扑超导体是指在超导体中存在特殊的拓扑性质,如Majorana费米子。
Majorana费米子是一种具有非阿贝尔任意子交换统计的粒子,其在量子计算和量子信息处理中具有重要的应用潜力。
通过研究拓扑超导体,科学家们希望能够实现更稳定和可控的量子计算体系,并为量子信息领域的发展做出贡献。
二、拓扑光学拓扑光学是近年来发展起来的一门新兴领域,它研究的是光在特殊拓扑结构中的传播行为。
通过设计和制造具有特定拓扑结构的光学材料,科学家们可以实现光的流动被限制在材料表面或边缘的状态,这种边界态被称为拓扑边界态。
拓扑边界态具有良好的传输性能,并且不受杂质和缺陷的影响。
这使得拓扑光学在光电子学和光学器件的设计中具有潜在的应用价值。
拓扑光学的一个重要研究方向是拓扑激光器。
传统的激光器是通过在材料中不断增加折射率来实现光的反射和放大,而拓扑激光器则通过特殊的拓扑结构来实现光的传输和放大。
这种新型设计可以有效地避免传统激光器中存在的光损耗和散射问题,提高激光器的性能指标,并为新一代光学通信和光纤传输系统提供更高的可靠性和稳定性。
总结起来,拓扑学在物理学研究中发挥着重要作用。
从拓扑材料到拓扑光学,这些新兴领域的发展潜力巨大。
拓扑绝缘体物理学在新型电子器件中的应用

拓扑绝缘体物理学在新型电子器件中的应用随着科技的快速发展,人们对电子器件的需求日益增长。
拓扑绝缘体物理学作为一种新兴的研究领域,引起了人们的广泛关注。
它具有独特的电学性质和应用潜力,被认为是未来电子器件领域的重要突破口。
本文将探讨拓扑绝缘体物理学在新型电子器件中的应用,并分析其前景和挑战。
一、拓扑绝缘体物理学概述拓扑绝缘体是一种新型材料,其具有特殊的能带结构和边缘态特性。
与传统绝缘体不同的是,拓扑绝缘体在材料的体内是绝缘的,但在边缘却存在导电态。
这种特殊的电子结构使得拓扑绝缘体具有一系列非常有趣的物理性质,如存在自旋-轨道耦合效应、存在拓扑保护的表面态等。
二、拓扑绝缘体在电子器件中的应用1. 量子计算拓扑绝缘体中的拓扑保护态具有很好的抗噪声特性,适合用于量子计算中的存储和操作。
利用拓扑绝缘体的特殊性质,可以实现更加稳定和可靠的量子比特存储,为量子计算的实现提供了新的思路和方法。
2. 量子通信拓扑绝缘体的边缘态具有特殊的高度导电性,可以实现高速、低耗能的量子信息传输。
利用拓扑绝缘体作为导线,可以实现高效的量子通信网络,提高信息传输的速度和安全性。
3. 自旋电子学器件拓扑绝缘体中存在自旋-轨道耦合效应,可以实现自旋的控制和操纵。
这为自旋电子学器件的发展提供了新的途径和可能性。
利用拓扑绝缘体的特性,可以实现高效的自旋输运和自旋操控,提高自旋电子器件的性能和稳定性。
三、拓扑绝缘体在新型电子器件中的前景和挑战拓扑绝缘体物理学在新型电子器件中有着广阔的应用前景,可以实现高速、低耗能、稳定可靠的电子器件。
然而,实际应用中还存在许多挑战和困难。
首先,拓扑绝缘体的制备和加工过程仍然面临技术瓶颈,需要发展出高效、可控的制备方法。
其次,理论和实验研究仍然不够深入,对于拓扑绝缘体的物理机制和性质还需要更加深入的理解和研究。
此外,拓扑绝缘体的集成和封装技术也需要进一步发展,以实现其在实际应用中的可靠性和稳定性。
结论拓扑绝缘体物理学作为一种前沿的研究领域,具有巨大的应用潜力。
现代无机化学中的拓扑结构材料研究

现代无机化学中的拓扑结构材料研究随着科技的不断发展,无机化学作为一门重要的学科,正逐渐展现出其在材料科学领域的重要性。
其中,拓扑结构材料的研究成为了无机化学领域的热点之一。
本文将探讨现代无机化学中的拓扑结构材料研究。
一、拓扑结构材料的概念拓扑结构材料是指具有特殊的电子结构和拓扑性质的材料。
拓扑性质是指材料的电子结构在不同的拓扑相之间发生显著变化,而不受材料的微观细节影响。
这种特殊的电子结构使得拓扑结构材料具有许多独特的物理性质,如量子霍尔效应、拓扑绝缘体、拓扑超导体等。
二、无机化学中的拓扑结构材料研究方法无机化学中的拓扑结构材料研究方法主要包括合成方法和表征方法。
1. 合成方法合成方法是指通过化学合成的方式来制备拓扑结构材料。
无机化学家通过合成不同元素和化合物的化学反应,制备出具有特殊拓扑结构的材料。
例如,通过气相沉积、溶液法、热解法等方法,可以合成出二维拓扑绝缘体、三维拓扑绝缘体等材料。
2. 表征方法表征方法是指通过实验手段来研究拓扑结构材料的结构和性质。
无机化学家利用各种表征技术,如X射线衍射、扫描电子显微镜、透射电子显微镜等,对拓扑结构材料进行结构表征和性质测试。
这些表征方法可以帮助无机化学家深入了解拓扑结构材料的微观结构和宏观性质。
三、拓扑结构材料的应用拓扑结构材料由于其特殊的电子结构和物理性质,在许多领域具有广泛的应用前景。
1. 电子器件拓扑结构材料在电子器件领域有着广泛的应用。
例如,拓扑绝缘体的量子霍尔效应可以用于制造高速电子器件,拓扑超导体的超导性质可以用于制造高效能的超导电子器件。
2. 光电器件拓扑结构材料在光电器件领域也有着重要的应用。
例如,拓扑绝缘体的表面态可以用于制造高效的光电转换器件,拓扑光学材料可以用于制造高效的光学器件。
3. 能源领域拓扑结构材料在能源领域的应用也备受关注。
例如,拓扑绝缘体的独特电子结构可以用于制造高效的太阳能电池,拓扑超导体的超导性质可以用于制造高效的能源传输材料。
拓扑绝缘体材料的制备与性质研究

拓扑绝缘体材料的制备与性质研究拓扑绝缘体(Topological Insulator)作为一种新兴的材料,具有特殊的电子结构和丰富的物理性质,引起了广泛的研究兴趣。
本文将介绍拓扑绝缘体材料的制备方法以及其独特的性质。
一、拓扑绝缘体的制备方法1.外延生长法外延生长法是制备拓扑绝缘体的一种常用方法。
一般采用分子束外延(MBE)或金属有机化学气相沉积(MOCVD)等技术,通过在晶体衬底上沉积原子层薄膜,使得晶体结构具有特殊的拓扑性质。
2.化学合成法化学合成法是另一种常见的拓扑绝缘体制备方法。
通过合成特定化学组成和结构的化合物,如硒化铋(Bi2Se3)、硒化锡(SnSe2)等,可以得到拓扑绝缘体材料。
3.离子液体法离子液体法是一种新兴的制备拓扑绝缘体的方法。
通过在离子液体中溶解特定的化合物或金属离子,并通过电化学反应或热解反应,可以制备出具有拓扑绝缘体性质的材料。
二、拓扑绝缘体的性质研究1.拓扑保护的表面态拓扑绝缘体具有在体态能带中存在的拓扑保护的表面态。
这些表面态能够在晶体中存在杂质或缺陷的情况下保持不变,具有非常高的稳定性。
2.强狄拉克费米子拓扑绝缘体表面的电子结构呈现狄拉克锥状能带,其中的狄拉克费米子质量接近零,速度非常高。
这种特殊的电子结构使得拓扑绝缘体具有优异的电子传输性质。
3.自旋-轨道耦合效应拓扑绝缘体中的自旋-轨道耦合效应是其特殊性质之一。
自旋-轨道耦合可以在表面态和体态之间实现耦合,使得拓扑绝缘体具有自旋流输送的特性。
4.量子霍尔效应由于其特殊的电子结构,拓扑绝缘体表面的载流子在外加磁场作用下可以呈现量子霍尔效应,即洛伦兹力将电流限制在材料的边界上,形成电流的分立通道。
三、应用前景与展望拓扑绝缘体材料的研究与应用具有广泛的前景。
其在信息存储、量子计算和低功耗电子器件等领域具有重要的应用潜力。
例如,拓扑绝缘体的表面态可以用于实现更稳定的量子比特,从而提高量子计算的可靠性和稳定性。
此外,还可以利用拓扑绝缘体中特殊的自旋-轨道耦合效应,实现自旋操控和自旋电子学器件的制备。
基于拓扑绝缘体的低功耗电子器件设计与制备

基于拓扑绝缘体的低功耗电子器件设计与制备摘要随着电子器件向着小型化、高性能、低功耗方向发展,传统硅基材料已难以满足未来需求。
拓扑绝缘体作为一种新型材料,具有独特的能带结构和表面态,展现出优异的电学性质,为低功耗电子器件设计提供了新的思路。
本文将深入探讨拓扑绝缘体的物理性质及其在低功耗电子器件中的应用前景,重点介绍基于拓扑绝缘体的器件设计与制备技术,包括基于拓扑绝缘体的场效应晶体管、忆阻器、自旋电子器件等,并展望其在未来电子技术中的应用趋势。
关键词:拓扑绝缘体,低功耗电子器件,场效应晶体管,忆阻器,自旋电子学1. 绪论随着摩尔定律的逐渐失效,传统的硅基半导体材料正面临着越来越大的挑战。
为了满足不断增长的电子设备小型化、高性能、低功耗等需求,探索新型材料和器件结构成为未来电子技术发展的重要方向。
拓扑绝缘体作为一种具有独特能带结构的新型量子材料,展现出优异的电学性质,为低功耗电子器件设计提供了新的思路。
拓扑绝缘体在内部是绝缘体,但在表面却具有导电的金属态,而且这种表面态具有拓扑保护特性,不受杂质和缺陷的影响,能够在高温下保持稳定。
这意味着拓扑绝缘体可以在不牺牲器件性能的前提下,实现低功耗、高速度、高效率的电子器件设计。
2. 拓扑绝缘体的物理性质2.1 拓扑绝缘体的能带结构拓扑绝缘体的能带结构与普通绝缘体截然不同,其最大的特点是存在着拓扑保护的表面态。
简单来说,拓扑绝缘体的能带结构具有以下特点:*体能带结构为绝缘体:类似于普通绝缘体,拓扑绝缘体的体能带结构中存在着能带隙,没有自由电子可以进行导电。
*表面态为金属态:与体能带结构不同,拓扑绝缘体表面存在着金属态的表面态,这些表面态具有特殊的拓扑性质,不受杂质和缺陷的影响,能够在高温下保持稳定。
*自旋动量锁定:拓扑绝缘体的表面态具有自旋动量锁定的特性,即电子自旋方向与动量方向严格锁定,这使得拓扑绝缘体成为自旋电子学应用的理想材料。
2.2 拓扑绝缘体的性质特点*高导电性:拓扑绝缘体表面的金属态能够实现高导电性,这为制作高性能电子器件提供了可能性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10:30-10:55 10:55-11:20 11:20-11:45 11:45-12:10
姚裕贵,北京理工大学 (邀请报告)
廖志敏,北京大学 (邀请报告)
Recent progress in the study of topological materials Bi4X4 (X = I,
Br)
拓扑半金属-超导体异质结
齐静波,电子科技大学 (邀请报告)
Chiral broadband terahertz wave emission from the Weyl semimetals
16:40-17:05
BALOGUN(唐杰),湖南大 学 (邀请报告)
Topological Understanding on the Lithium Storage Properties at the Interfaces of Transition Metal Oxide
江华,苏州大学 (邀请报告)
Topological Quantum Chemistry and its applications in materials
search
石墨烯拓扑界面态的研究
14:20-14:45
陆久阳,华南理工大学 (邀请报告)
Weyl points and nodal rings in phononic semimetals
17:05-17:30
袁璐琦,上海交通大学 (邀请报告)
在合成空间中探索拓扑光子效应
17:30-17:55
孙家涛,北京理工大学 (邀请报告)
First-principles Studies of Periodically Driven Quantum
Materials
17:55-18:20
刘伟,国防科技大学 (邀请报告) 18:20 晚餐
The Geometry of Electromagnetic Multipoles
S020 8:30-8:55 S021 8:55-9:20 S022 9:20-9:45
2019 年 9 月 22 日
主持人:万贤纲 ,南京大学
方辰,中科院物理所 (邀请报告)
杭志宏,苏州大学 (邀请报告)
The evolving understanding of insulators in solids
徐煌,中国科学院上 基于II类狄拉克半金属PtTe2的太赫
海技术物理研究所
兹探测器
谢筱意,复旦大学 刘彦昭,北京大学
基于新型拓扑绝缘体碲化银的宽波
段光电探测器
Log-periodic Quantum Oscillations and Discrete Scale Invariance in Topological Materials
16:15-16:40
刘海文,北京师范大学 (邀请报告)
16:40-17:05
张铮,北京科技大学 (邀请报告)
Microscopic theory of in-plane critical field in two-dimensional Ising superconducting systems
Defect Engineering on Monolayer MoS2 for 2D Electronics and Optoelectronics
宋道红,南开大学 (邀请报告)
Pseudospin and topological phenomena in Dirac-like photonic
lattices
12:05-13:30 午餐&午休
主持人:宋凤麒 ,南京大学
13:30-13:55 13:55-14:20
王志俊 ,中科院物理所 (邀请报告)
数学研究所
injection
张博文,中国科学院 Pressure-tuned colossal
合肥物质科学研究院
magnetoresistance CdCr2Se4
effect
in
n-type
李永恺,北京理工大
学
拓扑材料的单晶生长和物性研究
张建丰,中国人民大 新型拓扑超导体预测:beta-RhPb2 学
surface states in topological insulator BiSbTeSe2
郑浩,上海交通大学 (邀请报告)
拓扑节线半金属ZrSiSe中的“半缺 失”Umklapp散射
18:20-晚餐
墙报 墙报张贴时间:9 月 20 日 12:00-14:30 优秀墙报评选:9 月 20 日 14:30-18:00 地点:郑州大学新校区钟楼广场/主会场
14:45-15:10
卢明辉, 南京大学 (邀请报告)
高阶光子拓扑绝缘体
15:10-15:35
15:50-16:15 16:15-16:40
王锐,重庆大学 (邀请报告)
铁磁拓扑材料的理论设计
15:35-15:50 茶歇
主持人:王志俊,中科院物理所
宋凤麒,南京大学 (邀请报告)
Optimization of the intrinsic magnetic topological insulator MnBi2Te4 and transport study
王欢,中国人民大学 de Haas-van Alphen oscillation in topological semimetal BaGa4
王思思,中国科学院
The variation of the orbital
半导体研究所 magnetization during the localization
devices
米振宇,中国科学 Torque Magnetometry Based on a
院物理所
Commercial Membrane-Type Surface Stress Sensor
S-P004
学
magnetic Weyl semimetal Co3Sn2S2
S-P005 S-P006 S-P007
S-P008 S-P009 S-P010 S-P011 S-P012 S-P013 S-P014 S-P015 S-P016 S-P017
陈诚,南京大学
应力状态下碲化汞中多种拓扑相的 非线性霍尔效应
multilayer graphene systems
张立源,南方科技大学 Three-dimensional Quantum Hall
(邀请报告)
Effect in ZrTe5
15:35-15:50 茶歇
主持人:翁红明,中科院物理所
雷和畅,中国人民大学 (邀请报告)
Magnetic Topological Semimetals with Kagome Lattices
是否评优
S-P018 S-P019 S-P020 S-P021 S-P022 S-P023 S-P024 S-P025 S-P026
Single crystal growth and
李延杰,中国科学院 magnetoresistivity study of topological
物理所
semimetal SrAs3 on micro fabricated
Nonlinear Hall effect
9:50-10:05 茶歇
主持人:谢心澄 (北京大学)
10:05-10:30
王健,北京大学 (邀请报告)
High-Chern-Number and HighTemperature Quantum Hall Effect
without Landau Levels
Visualization of topological kink states and corner states in two dimensional photonic crystals
陈晓东,中山大学 (邀请报告)
光子晶体平板中拐角模式的实验观测
9:45-10:00 茶歇
主持人:方辰 ,中科院物理所
S023 S024 S025 S026 S027
S028 S029 S030 S031 S032
S033 S034 S035
10:00-10:25
修发贤,复旦大学 (邀请报告)
拓扑狄拉克半金属中的三维量子霍尔 效应
10:25-10:50
温锦生,南京大学 (邀请报告)
中子散射对拓扑磁振子与拓扑材料声 子的研究
route for quantum anomalous Effect.
王小艳,中国人民大 Extremely large magnetoresistance
学
and Shubnikov-de Haas oscillations
in DyBi
热导率降低一个数量级的纳米结构 张燕燕,南京大学 Zr/HfTe5单晶
吴丹丹,安徽大学
The Novel Thermal Spin Transport Properties based on Low-dimensional Nanoscale Materials
李 源 远 , 裴 森 Dynamic properties of terahertz
北京应用物理与计算 quantum cascade lasers under optical
主持人:孙庆丰,北京大学
13:30-13:55
翁红明,中科院物理所 (邀请报告)
Topological Crystalline Insulators with C2 Rot学 (邀请报告)
Static and dynamical axion states in magnetic topological materials
编号 S-P001 S-P002 S-P003
姓名、单位
