最新人教版《勾股定理》PPT课件
合集下载
勾股定理数学优秀ppt课件

实际应用
在建筑、工程等领域,经常需要利用勾股定理求解直角三角形的边长问题,如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式,则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中,斜边是最长的一边,通过勾股定理可以判断
哪条边是斜边,哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中,直角边的平方和等于斜边的平方,即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形(如正方形、梯形等)的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用,如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础,通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中,勾股定理可以表示 为两个向量的点积等于它们模长的 平方和,这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用,如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一, 也是几何学中的基础概念,对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期,但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国,商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用, 如求解三角形边长、角度、面积等问题,以及力学、光学等领 域的计算。
在建筑、工程等领域,经常需要利用勾股定理求解直角三角形的边长问题,如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式,则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中,斜边是最长的一边,通过勾股定理可以判断
哪条边是斜边,哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中,直角边的平方和等于斜边的平方,即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形(如正方形、梯形等)的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用,如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础,通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中,勾股定理可以表示 为两个向量的点积等于它们模长的 平方和,这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用,如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一, 也是几何学中的基础概念,对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期,但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国,商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用, 如求解三角形边长、角度、面积等问题,以及力学、光学等领 域的计算。
勾股定理课件(共19张PPT)人教版初中数学八年级下册

1
+2·
2
ab =
即:在Rt△ABC 中,∠C=90 °
c2 = a2 + b2
1 2
c +ab
2
伽
菲
尔
德
证
法
归纳小结
“赵爽弦图”通过图形的切割、拼接,巧妙地利用面积关系证实
了命题的正确性,命题与直角三角形的边有关,我国把它称为
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
即a2+b2=c2.
勾股定理: 直角三角形两直角边a、b的平
方和,等于斜边c的平方。
即:a2+b2 =c2
谢谢观看
哲学家、数学家、天文学家
新知探究
思考
图17.1-2中三个正方形的面积有什么关系?等腰
直角三角形的三边之间有什么关系?
A
B
a
b
c
C
图17.1-2
三个正方形A、
B、C的面积有
什么关系?
新知探究
探究
等腰直角三角形有上述性质,其他
直角三角形是否也有这个性质?
C
A
B
C'
图1
A'
B'
图17.1-3
图2
(图中每个小方格代表一个单位面积)
教 学 目 标 / Te a c h i n g a i m s
1
2
了解勾股定理文化背景,体验勾股定理的探究过
程。
理解不同勾股定理的证明方法,能够分析
它们的异同。
能够用勾股定理解决直角三角形的相关学习
3
和解决生活中的实际问题。
情景导入
图17.1-1
毕达哥拉斯(Pythagoras,约前
《勾股定理》PPT优质课件(第1课时)

A. 3
B.3
C. 5
D.5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12,则斜边的
长为( C)
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17,一条直角边长为15,则
另一直角边长为( A )
A.8
B.40
C.50
D.36
3.在Rt△ABC中,∠C=90°,若a︰b=3︰4,c=100,则 a= _6_0___,b = __8_0___.
课堂检测
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角 形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面 积之和为_____4_9_____cm2 .
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,BC 42 32 7;
形,拼成一个新的正方形.
探究新知 剪、拼过程展示:
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
探究新知
毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图 示进行拼图,然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152,
人教版八年级下册课件 17.1.3 勾股定理 (共19张PPT)

C D
B A
C+D
A+B A+B+C+D
E
古代笑话
截竿进城
某人拿一根竹竿想进城,可是竹竿太长了,横竖都进不 了城。这时,一位老人给他出了个主意,把竹竿截成两 半……
探究1:
一个门框尺寸如图所示,一块长3m,宽 2.2m的薄木板能否从门框内穿过?为什么?
5 2.236 2.2 D
C
3m
2m
A 2.2m 1m
B
实际问题
数学问题
木板能否进门? 求AC? 比较木板宽与斜边AC长度的大小
勾股定理
AC≥2.2能进,AC<2.2不能进
探究2:
一个3m长的梯子AB,斜靠在一竖直的墙AO 上, 这时AO的距离为2.5m, 如果梯子的顶端A沿 墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:DB=OD-OB,求
1.如图,分别以Rt △ABC三边为边向 外作三个正方形,其面积分别用S1、 S2、S3表示,容易得出S1、S2、S3之 间有的关系式为
S1 S2 S3
C
S3
A
S2
B
S1
2.如图,所有的四边形都是正方形,所有 的三角形都是直角三角形,其中最大的正 方形E的边长为7cm,求正方形A,B,C, D的面积的和.
C
2 3
2
3
B 3 D 1 A
拓展提高
4.一个圆柱状的杯子,由内部测得其底面直径为 4cm,高为10cm,现有一支12cm的吸管任意斜放 于杯中,则吸管 露出杯口外. (填“能”或 能 “不能”)
4 10 116 10.78 12
2 2
10
4
《九章算术》:有一个水池, 水面是一个边长为10尺的正方 形,在水池正中央有一根芦苇, 它高出水面1尺,如果把这根 芦苇拉向水池一边的中点,它 的顶端恰好到达池边的水面, 请问这个水的深度与这根芦苇 的长度各是多少?
B A
C+D
A+B A+B+C+D
E
古代笑话
截竿进城
某人拿一根竹竿想进城,可是竹竿太长了,横竖都进不 了城。这时,一位老人给他出了个主意,把竹竿截成两 半……
探究1:
一个门框尺寸如图所示,一块长3m,宽 2.2m的薄木板能否从门框内穿过?为什么?
5 2.236 2.2 D
C
3m
2m
A 2.2m 1m
B
实际问题
数学问题
木板能否进门? 求AC? 比较木板宽与斜边AC长度的大小
勾股定理
AC≥2.2能进,AC<2.2不能进
探究2:
一个3m长的梯子AB,斜靠在一竖直的墙AO 上, 这时AO的距离为2.5m, 如果梯子的顶端A沿 墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:DB=OD-OB,求
1.如图,分别以Rt △ABC三边为边向 外作三个正方形,其面积分别用S1、 S2、S3表示,容易得出S1、S2、S3之 间有的关系式为
S1 S2 S3
C
S3
A
S2
B
S1
2.如图,所有的四边形都是正方形,所有 的三角形都是直角三角形,其中最大的正 方形E的边长为7cm,求正方形A,B,C, D的面积的和.
C
2 3
2
3
B 3 D 1 A
拓展提高
4.一个圆柱状的杯子,由内部测得其底面直径为 4cm,高为10cm,现有一支12cm的吸管任意斜放 于杯中,则吸管 露出杯口外. (填“能”或 能 “不能”)
4 10 116 10.78 12
2 2
10
4
《九章算术》:有一个水池, 水面是一个边长为10尺的正方 形,在水池正中央有一根芦苇, 它高出水面1尺,如果把这根 芦苇拉向水池一边的中点,它 的顶端恰好到达池边的水面, 请问这个水的深度与这根芦苇 的长度各是多少?
勾股定理ppt课件

创设情境 数学是科技发展中最重要的学科,2002年全球最顶级数学家大 会在北京召开,大会会徽是:
赵爽弦图
数学文化 赵爽,名婴,字君卿,是我国三国时期杰出的数学家, 他在注解《周髀算经》时给出的这个图.
创设情境 请你观察这个图中有哪些基本几何图形?2002年的数学家大会为 什么用这个图作为会徽呢?
继续探究
1.如图,表格中左、右各有一组图,每组图中的三个正方形的面积分 别是多少,它们之间有什么关系?(设表格中每个小正方形面积为1)
C A
B
C A
B
继续探究 2.观察图形,请完成下面表格:
两个图中正 方形C的面积 如何求呢?
项目
左图 右图 A、B、C 面积关系
A的面积 4 16
B的面积 9 9
A
8
B 6
C
应用新知
例2 如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形 B,D的边长分别是16,12,SE=625,S1=400,求正方形A、C的边长. 解:依题意,得SB=162=256,SD=122=144, ∵S1=SA+SB且S1=400, ∴SA=S1-SB=400-256=144, ∴正方形A的边长为 144 12, ∵SE=S1+S2且SE=625,S1=400, ∴S2=SE-S1=625-400=225, ∵S2=SC+SD,∴SC=S2-SD=225-144=81, ∴正方形C的边长 81 9 .
证明2: 如图,四个全等直角三角形拼成
如图所示的正方形,直角边为a、
b,斜边为c. S四个直角三角形面积和= 4 1 ab 2ab,
2
S四个直角三角形面积和=(a+b)2-c2
《勾股定理》PPT课件精选全文

化简得: a2 b2 c2
方法三:
c
b b-a c
a c
c
S正
c2
4
1 2
ab
(b
a)2
,
化简得: a2 b2 c2
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
2.求下列直角三角形中未知边的长:
比
5
一
比8
17
看
x
16
x 12
看
x
谁
20
算
得
4 个单位面积.
C
正方形C的面积是
A
8 个单位面积.
B
(图中每个小方格代表图一2个单位面积)
SA+SB=SC在图3中还成立吗?
2.观察右边两个图 并填写下表:
A
A的面积 B的面积 C的面积
图3
16 9
25
即:两条直 角边上的正
C B
图3
方法
(1)式子SA+SB=SC能用直角三角形 的三边a、b、c来表示吗?
17.1勾股定理
复习提问
1、任意三角形三边满足怎样的关系?
2、对于等腰三角形,三边之间存在 怎样的特殊关系?等边三角形呢?
3、对于直角三角形,三边之间存在 怎样的特殊关系?
2002年在北京召开了第24届国际数学家大 会,它是最高水平的全球性数学科学学术 会议,被誉为数学界的“奥运会”,这就 是本届大会会徽的图案。
C A
B
C A
B
SA SB SC
a2 b2 c2
(2)你能发现直角三角形三边长度之间存在什么 关系吗?
人教版八年级数学下册17.1 勾股定理课件 (共84张PPT)

3 . AC=___ 6.在一个直角三角形中, 两边长分别为3,4,则
5 或 7 第三边的长为________.
7.蚂蚁沿图中的折线从A点爬到D点,一共爬了____厘米.(小方 格的边长为1厘米)
A
3
G
4
B
12
E 5 C 6
8
F
答案:28
D
· ·
· ·
· ·
·
·
3.如图所示,一棵大树在一 次强台风中离地面5米处折 断倒下,倒下部分与地面 成30°角,则这棵大树在 折断前的高度和AB的长分 别为( ) B.15米, 125米 D.15米, 75 米 A.10米, 75 米 C.10米, 125米
第十七章 勾股定理
17.1 勾股定理(第1课时)
1.掌握勾股定理的内容. 2.理解勾股定理的证明.
3.应用勾股定理进行有关计算与证明.
星期日老师带领初二全体学生去凌峰山风景区游 玩,同学们看到山势险峻,查看景区示意图得知:凌峰 山主峰高约为900米,如图:为了方便游人,此景区从主 峰A处向地面B处架了一条缆车路线,已知山底端C处与 地面B处相距1200米, ACB 90 ,请问缆车路线AB长 应为多少?
2ab+(b² -2ab+a² )=c²
赵爽弦图
∴a² +b²=c²
结论: 直角三角形中,两条直角边的平方和等于斜边 的平方. B
在Rt△ABC中,∠C=90°, 边BC,AC,AB所对应的边 勾 分别为a,b,c,则存在下 C 列关系 a2+b2=c2 b
勾股定理
如果直角三角形的两条直角边长分别为a,b, a 2 + b 2 = c 2. 斜边长为c,那么 即直角三角形两直角边长的平方和等于斜边长的平方. ∵ ∠C=90°
5 或 7 第三边的长为________.
7.蚂蚁沿图中的折线从A点爬到D点,一共爬了____厘米.(小方 格的边长为1厘米)
A
3
G
4
B
12
E 5 C 6
8
F
答案:28
D
· ·
· ·
· ·
·
·
3.如图所示,一棵大树在一 次强台风中离地面5米处折 断倒下,倒下部分与地面 成30°角,则这棵大树在 折断前的高度和AB的长分 别为( ) B.15米, 125米 D.15米, 75 米 A.10米, 75 米 C.10米, 125米
第十七章 勾股定理
17.1 勾股定理(第1课时)
1.掌握勾股定理的内容. 2.理解勾股定理的证明.
3.应用勾股定理进行有关计算与证明.
星期日老师带领初二全体学生去凌峰山风景区游 玩,同学们看到山势险峻,查看景区示意图得知:凌峰 山主峰高约为900米,如图:为了方便游人,此景区从主 峰A处向地面B处架了一条缆车路线,已知山底端C处与 地面B处相距1200米, ACB 90 ,请问缆车路线AB长 应为多少?
2ab+(b² -2ab+a² )=c²
赵爽弦图
∴a² +b²=c²
结论: 直角三角形中,两条直角边的平方和等于斜边 的平方. B
在Rt△ABC中,∠C=90°, 边BC,AC,AB所对应的边 勾 分别为a,b,c,则存在下 C 列关系 a2+b2=c2 b
勾股定理
如果直角三角形的两条直角边长分别为a,b, a 2 + b 2 = c 2. 斜边长为c,那么 即直角三角形两直角边长的平方和等于斜边长的平方. ∵ ∠C=90°
《勾股定理》PPT课件

AC 2 6
1.在△ABC中,∠C=90°.
练 习
(1)若a=6,c=10,则b=
;
(2)若a=12,b=9,则c= (3)若c=25,b=15,则a=
; ;
2.等边三角形边长为10,求它的高及面积。 C 3.如图,在△ABC中,C=90°,
CD为斜边AB上的高,你可以得 b 出哪些与边有关的结论? A m h
c2
;
a c
c a
b a
∵ c2= 4•ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2 ∴a2+b2=c2
a
b
b c
b c
2 (a+b) 大正方形的面积可以表示为 ;
也可以表示为 c2 +4•ab/2
a b
a
b
c
c
a
b
c
∵ (a+b)2 = c2 + 4•ab/2 a2+2ab+b2 = c2 +2ab ∴a2+b2=c2
a
B D n
如图,在△ABC中,AB=AC,D点在CB延长线上, A 求证:AD2-AB2=BD· CD
证明:过A作AE⊥BC于E ∵AB=AC,∴BE=CE D 在Rt △ADE中, AD2=AE2+DE2 在Rt △ABE中, AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2) B E C
a b
c
勾股定理的证明
证明方法3:赵爽弦图,动手拼图
勾股定理的证明
证明方法4:美国总统加菲尔德的证明方法
a b
人教版数学八年级下册:17.1 勾股定理 课件(共35张PPT)

探究 如图,以Rt△ 的三边为边向外作正方形,
其面积分别为 S1 、S2、S3,请同学们想一想
S1 、S2、S3 之间有何关系呢?
S2 + S3 =a2+b2
S1=c2
B
S1c a S2
b
A S3 C
∵a2+b2=c2
S2 + S3 = S1
探究S1、S2、S3之间的关系
S2
S3
1 2
a 2
2
1 2
b 2
2
1 a2 1 b2
8
8
S1
1 2
c 2
2
1
8
c2
由勾股定理得 a2+b2=c2
∴S2+S3=S1
S2
c
SS3 2
A
S1
S1
动手操作:例2如图,Rt△ABC中
,AC=8,BC=6,∠C=90°,分别 以AB、BC、AC为直径作三个半圆 ,那么阴影部分的面积为__24_ .
A
E
D
B
F
C
A
A =625
225
400
81
B =144
225
2、如图所示的图形中,所 有的四边形都是正方形,所 有的三角形都是直角三角形 ,其中最大的正方形的边长 是8厘米,则正方形A,B, C,D的面积之和是 __6_4_____平方厘米
利用勾股定理解决平面几何问题3——折叠中的计算问题
能算好算直接算,不能算不好算,设未知数,列方程(勾股定理、全等、相似等)
利用勾股定理解决平面几何问题1— —最短路径问题
勾股定理ppt课件
2 2 22
“总统证法”. 比较上面二式得 c2=a2+b2
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
做一做:
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
AC=__1_5_______
面积 面积 面积
图1
C
9A
图1 2B5
每个小方格的面积均为1 图18.1-2
图2
A、B、 C面积 关系
直角三 角形三 边关系
补全
分割
探究
顶顶点点在在格格点点上上的的直直角角三三角角形形两两 直直角角边边的的平平方方和和等等于于斜斜边边的的平平方方吗。?
B
A C
正方形A 正方形B 正方形C 的单位 的单位 的单位
┏
勾a
a2+b2=c2
证明2:
大正方形的面积可以表示为 (a+b)2 ;
也可以表示为
ab 4 C2
2
c a
b
c a
b
c a
b
c a
b
∵ (a+b)2 = 4 ab C2 2
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
证明3:
C
你能只用这两个 D
直角三角形说明 a c
b c
a2+b2=c2吗?
3
s1 s2 s3
返 拼回 图
合作 & 交S流1+☞S2=S3
“总统证法”. 比较上面二式得 c2=a2+b2
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
做一做:
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
AC=__1_5_______
面积 面积 面积
图1
C
9A
图1 2B5
每个小方格的面积均为1 图18.1-2
图2
A、B、 C面积 关系
直角三 角形三 边关系
补全
分割
探究
顶顶点点在在格格点点上上的的直直角角三三角角形形两两 直直角角边边的的平平方方和和等等于于斜斜边边的的平平方方吗。?
B
A C
正方形A 正方形B 正方形C 的单位 的单位 的单位
┏
勾a
a2+b2=c2
证明2:
大正方形的面积可以表示为 (a+b)2 ;
也可以表示为
ab 4 C2
2
c a
b
c a
b
c a
b
c a
b
∵ (a+b)2 = 4 ab C2 2
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
证明3:
C
你能只用这两个 D
直角三角形说明 a c
b c
a2+b2=c2吗?
3
s1 s2 s3
返 拼回 图
合作 & 交S流1+☞S2=S3
初二数学《勾股定理》PPT课件

如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
勾
弦
b
股
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
勾股定理的各种表达式:
c2=a2+b2 a2=c2-b2 b2=c2-a2
5米
B
A
C
12米
解:∵BC⊥AC, ∴在Rt△ABC中, AC=12,BC=5, 根据勾股定理,
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )
B
A
勾 股 定 理
C
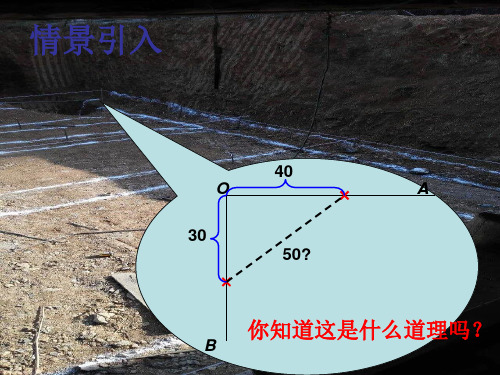
一、情景引入
如图,一根电线杆在离地面5米处断裂,电线杆顶部落在离电线杆底部12米处,电线杆折断之前有多高?
5米
B
A
C
12米
电线杆折断之前的高度=BC+AB=5米+AB的长
SA+SB=SC
图甲
图乙
A的面积
B的面积
C的面积
4
4
A
B
C
C
图甲
1.观察图甲,小方格 的边长为1. ⑴正方形A、B、C的 面积各为多少?
A.3米 B.4米 C.5米 D.6米
C
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
勾
弦
b
股
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
勾股定理的各种表达式:
c2=a2+b2 a2=c2-b2 b2=c2-a2
5米
B
A
C
12米
解:∵BC⊥AC, ∴在Rt△ABC中, AC=12,BC=5, 根据勾股定理,
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )
B
A
勾 股 定 理
C
一、情景引入
如图,一根电线杆在离地面5米处断裂,电线杆顶部落在离电线杆底部12米处,电线杆折断之前有多高?
5米
B
A
C
12米
电线杆折断之前的高度=BC+AB=5米+AB的长
SA+SB=SC
图甲
图乙
A的面积
B的面积
C的面积
4
4
A
B
C
C
图甲
1.观察图甲,小方格 的边长为1. ⑴正方形A、B、C的 面积各为多少?
A.3米 B.4米 C.5米 D.6米
C
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
人教版勾股定理 PPT

B A
C D
勾股树
E
10
H
E
公知道DA 元道许C前和多P 应约 勾大中的载用3股约总高的0B勾0数公结低第0股组年元出差一大高载I 定,,前了.位约就在理古如勾可与2在提《0,巴3股以勾0公出周,0公欧给他比4术说股年“元髀,元几出们伦5,,定,勾前算.前里一还人用禹理大1三经13德个知就来是有禹0、》世0巨勾确世关在股年中纪著股定界的治四,.,《定两上人水、周古几理处有.的弦朝希何的水史实五数腊公 汉明原证位记践学”数元时了本明家,学2期勾》.世商记家,股中纪刘定的徽理东证.
则是“半文圆明A人,”B,,也C必的定面认积识关这系种图为形.
根据勾股定理, a2 + b2=c2,
C c
b B
aA
C
圆的面积公式c:
S=πr2
aA
,
b
得到半圆A,B,C的面积关系 B
为SA+SB=SC.
数形结合
13
从直角三角形的各边向外作正方形能否推广到从 各边向外作等边三角形(正n边形)吗?
C c aA b
后的土地时,也应规作用律出过的了勾证详股明为细定.大注理会释.会和徽证的明图.案.
11
在探索勾股定理的过程中,你有什么感悟和欣赏.
C B
A
H
D C
E
A
P
I B
c
a
b
a bc
ac b
b
c
a
cb a
GQ
F
12
如放眼图未,来以,直华角罗庚三曾角设形想各:边向为太空直发径射向一外种作图半形,圆因,为
这种图形在几千年前就已经被人类所认识,如果外星人
c a2 b2 12 22 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弦 勾
勾股
股
考一考:
1.求下列图中字母所代表的正方形的面积:
A
81
144
B
144
169
①
②
2. 直角三角形的两直角边为5、12,则三角形的
周长为30 .
1、如图,一个高3米,宽4米的大门,需在相对 角的顶点间加一个加固木条,则木条的长为
(C )
A.3 米 B.4 米 C.5米 D.6米
B
3
C
4
A
②
①?
Rt△ABC中,已知AC=8,BC=6,
能否求出AB的长?
A C D
四、归纳小结
1、勾股定理:如果直角三角形的两条直角边长分 别为a,b,斜边长为c,那么 a2+b2=c.2 2、赵爽弦图利用了__面_积____关系进行勾股定理的
证明.
3、学习反思:
_____________________________
____________________
_______
_______________________________________.
教师寄语
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现 在我们的身边,我们的眼前, 还有 很多象 “勾股定理”那样的知识 等待我们去探索,等待我们去发 现……
SUCCESS
THANK YOU
2019/6/26
有什么关系?
如果直角三角形两直角边
分别为a,b,斜边为c
ab
c
思考:直角三角形三 边之间有什么关系?
A
a B bc
C
图中每个小方格的 面积均为1,请分别
算出正方形A,B,C 的面积,利用面积 关系验证三边关系.
A
a B bc
C
图1
SA
SB
SC
9 16 25
A
a B bc
C
SA SB SC 4 9 13
从A地到B地 哪条路近?
②
①?
Rt△ABC中,已知AC=8,BC=6,
能否求出AB的长?
2500年前,古希腊著名数 学家毕达哥拉斯非常善于 观察和思考,经常能从平 淡的生活现象中发现数学 问题.
有一次他在朋友家做客 时,发现朋友家用砖铺成的 地面中隐藏着深刻的道理
观察:图中两个 小正方形与大正 方形的面积之间
b
a
证
A
c
B
明
又∵S大正方形=C2
∴____a__2+___b___2=_____c__2
勾股定理
如果直角三角形两直角边长分 别为a,b,斜边为c,那么a²+b²=c²
弦c 股b
┏
勾a
在西方又称毕达 哥拉斯定理!
a2+b2=c2
人类最伟大的十个科学发现之一 .
辉煌发现
我国早在三千多年就知道了这个定理,人们 把弯曲成直角的手臂的上半部分称为“勾”,下 半部分称为“股”,我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为 “股”,斜边称为“弦”.因此就把这一定理称 为勾股定理.
识
的边长为_b_-_a_____,利用面积证明勾股定理.
点
二
∵ S大正方形
D
C
勾 股
=4S直角三角形+S小正方形
定
=4×_______+ (_b_-_a_ )2
理 的
=__2_a_b_+__b_2_-2_a_b__+_a_2________ =__a_2_+_b_2_________________
cC Aa
b
B
C
图2
A
B图2赵爽弦图用4个全等的直角三角形,拼成一个 正方形,利用所拼的正方形的面积证明.
a
a
a
a
b
cb
cb
cb
c
SUCCESS
THANK YOU
2019/6/26
1、赵爽弦图利用了_面__积____关系进行勾股定理的证明.
知
2、剪4个全等的直角三角形,拼成如图图形,其中直 角三角形的两直角边分别是a、b,则中间的小正方形
