10同底数幂的除法2
同底数指数幂的运算

同底数指数幂的运算指数运算是数学中常见的运算方式之一,它可以表示底数被乘以自身若干次的结果。
而同底数指数幂的运算则是指多个指数相同的幂之间进行运算的过程。
本文将介绍同底数指数幂的运算规则及其应用。
一、同底数指数幂的定义同底数指数幂指的是多个指数相同、底数相同的乘法表达式。
例如,若a为底数,且n、m为指数,那么同底数指数幂可以表示为a^n *a^m。
二、同底数指数幂的运算法则1. 同底数幂相乘:当两个同底数幂进行相乘时,可以将底数保持不变,指数相加。
即a^n * a^m = a^(n+m)。
例如,2^3 * 2^4 = 2^(3+4) =2^7。
2. 同底数幂相除:当两个同底数幂进行相除时,可以将底数保持不变,指数相减。
即a^n / a^m = a^(n-m)。
例如,3^5 / 3^2 = 3^(5-2) = 3^3。
3. 同底数幂的指数幂:若同底数幂上还有指数,可以将指数相乘。
即(a^n)^m = a^(n*m)。
例如,(2^3)^4 = 2^(3*4) = 2^12。
三、同底数指数幂的具体应用同底数指数幂的运算在数学中有着广泛的应用,以下列举了一些常见的应用场景:1. 等幂运算:当需要求一个数的幂次方时,可以将指数进行分解为较小的指数相加。
例如,2^8 = 2^(4+4) = 2^4 * 2^4。
2. 科学计数法的运算:科学计数法中,底数通常为10,指数表示小数点的移动次数。
当两个科学计数法进行乘法或除法运算时,可以利用同底数指数幂的运算法则简化计算过程。
3. 数字连乘或连除:当需要对同一个数连续进行乘法或除法运算时,可以利用同底数指数幂的运算法则进行简化。
例如,2^3 * 2^4 * 2^2 =2^(3+4+2) = 2^9。
四、总结同底数指数幂的运算是数学中常见且重要的运算方式。
通过运用运算法则,我们可以简化复杂的指数运算,并应用于科学计数法、指数幂的连乘或连除等实际问题中。
掌握同底数指数幂的运算法则,能够提高我们解决数学问题的效率,并提升对指数幂运算的理解。
同底数幂的加减乘除计算题

同底数幂的加减乘除计算题同底数幂的加减乘除计算题是初中数学中的一个重要知识点,它也是要求我们掌握幂运算的基本规律。
下面依次介绍同底数幂的加减乘除计算方法:一、同底数幂的加减法同底数幂的加减法可以通过将底数相同的项合并,指数不同的项进行加减法运算。
例如:2的三次方加上2的四次方等于多少?解答:2的三次方加上2的四次方等于2的三次方乘以(1+2)即2的三次方乘以2的一次方,即2的四次方。
2的三次方加上2的四次方就等于2的四次方。
二、同底数幂的乘法同底数幂的乘法可以通过将底数相同的项合并,指数相加的项进行乘法运算。
例如:2的三次方乘以2的四次方等于多少?解答:2的三次方乘以2的四次方等于2的三次方加四次方,即2的七次方。
2的三次方乘以2的四次方就等于2的七次方。
三、同底数幂的除法同底数幂的除法可以通过将底数相同的项合并,指数相减的项进行除法运算。
例如:2的四次方除以2的三次方等于多少?解答:2的四次方除以2的三次方等于2的一次方。
2的四次方除以2的三次方就等于2的一次方。
四、同底数幂的乘方同底数幂的乘方可以通过将底数相同的项合并,指数相乘的项进行乘方运算。
例如:(2的三次方)的四次方等于多少?解答:(2的三次方)的四次方等于2的12次方。
(2的三次方)的四次方就等于2的12次方。
总结:通过以上四种运算,我们可以快速求解同底数幂的加减乘除计算题。
同时,我们也需要注意,如果底数不同,那么即使指数相同,也不能合并计算。
因此,在计算时,需要注意先判断底数是否相同,再根据不同的情况采取不同的计算方法,保证正确性和高效性。
同底数幂的除法

学习目标
1.探索同底数幂的除法运算性质的过程, 体会幂的意义,发展推理和表达能力。
2.掌握同底数幂的除法运算法则,会用同 底数幂的除法解决实际问题
学习重点
同底数幂的除法运算法则及应用
学习难点
对零指数幂和负整数指数幂意义的理解
实用文档
二、探索同底数幂除法法则
8
416
755ຫໍສະໝຸດ 0331(3) 2a7 2a4
(4) x 6 x
实用文档
例2 计算
(1) a 5 a3
(3(()21解)):解解::a ba a 64 5a aa2 3 b 2
a 6
a a4
a 5
ba 2
a22
a
3
(2) a 6 a2
(3)ab4ab2
实用文档
例3 计算
a (3)
a7
a3
4
_________
a0 .
实用文档
3、总结
由上面的计算,我们发现
2 (1)25 23 _______2 ____;
1 0 (2)107
103
4
___________;
a (3)
a7
a3
4
_________
a0 .
253 1073 a73
你能发现什么规律?
实用文档
二、同底数幂除法法则
1.3 同底数幂除法
实用文档
一、复习
1.同底数幂乘法法则:
aman amn(m,n都是正整数
2.幂的乘方法则:
(am)n am n(m,n都是正整
3.积的乘方法则:
(ab)n anbn(n是正整数
指数相减.即所以同底数幂的除法法则

运算顺序的影响
在进行指数相减或同底数幂除法运算时,需要遵 循先乘除后加减的运算顺序,以确保运算结果的 准确性。
在科学计算和工程领域应用
科学计算中的应用
在科学计算领域,指数相减常用于处 理复杂数学模型中的幂运算问题,如 求解微分方程、矩阵运算等。
近似计算方法选择依据
绝对误差与相对误差
01
根据计算结果的精度要求,选择适当的近似计算方法,使得绝
对误差或相对误差控制在可接受的范围内。
稳定性与收敛性
02
对于迭代计算等方法,需要分析其稳定性和收敛性,以确保计
算结果的可靠性。
计算量与存储量
03
在满足精度要求的前提下,尽量选择计算量小、存储量少的近
似计算方法。
06 总结回顾与拓展延伸
关键知识点总结回顾
指数相减法则
当底数相同时,指数相减即为两数相除,例如a^m / a^n = a^(m-n)(a≠0,m>n)
同底数幂的除法法则
同底数幂相除时,底数不变,指数相减,例如a^m / a^n = a^(m-n)(a≠0)
特别注意
当底数为0或负数时,指数相减与同底数幂的除法法则需要特别 注意定义域和值域的问题
其他领域
除了以上几个领域外,指数函 数还被广泛应用于统计学、物
理学、化学等其他领域。
02 同底数幂除法法则推导
同底数幂除法定义
01
同底数幂除法是指底数相同的两 个幂相除的运算。
02
具体表示为:a^m ÷ a^n(其中 a≠0,m和n都是正整数),结果 记为a^(m-n)。
推导过程详解
同底数幂除法(解析版)

同底数幂除法【知识梳理】一、同底数幂的除法法则同底数幂相除,底数不变,指数相减,即m n m na a a −÷=(a ≠0,m n 、都是正整数,并且m n >)要点诠释:(1)同底数幂乘法与同底数幂的除法是互逆运算.(2)被除式、除式的底数相同,被除式的指数大于除式指数,0不能作除式. (3)当三个或三个以上同底数幂相除时,也具有这一性质. (4)底数可以是一个数,也可以是单项式或多项式. 二、零指数幂任何不等于0的数的0次幂都等于1.即01a =(a ≠0)要点诠释:底数a 不能为0,00无意义.任何一个常数都可以看作与字母0次方的积.因此常数项也叫0次单项式.【考点剖析】 题型一、同底数幂的除法例1、计算:(1)83x x ÷;(2)3()a a −÷;(3)52(2)(2)xy xy ÷;(4)531133⎛⎫⎛⎫−÷− ⎪ ⎪⎝⎭⎝⎭.【思路点拨】利用同底数幂相除的法则计算.(2)、(4)两小题要注意符号. 【答案与解析】解:(1)83835x x x x −÷==.(2)3312()a a a a −−÷=−=−.(3)5252333(2)(2)(2)(2)8xy xy xy xy x y −÷===. (4)535321111133339−⎛⎫⎛⎫⎛⎫⎛⎫−÷−=−=−=⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.【总结升华】(1)运用法则进行计算的关键是看底数是否相同.(2)运算中单项式的系数包括它前面的符号. 【变式1】(2021•上海)计算:x 7÷x 2= .【分析】根据同底数幂的除法法则进行解答即可. 【解答】解:x7÷x2=x7﹣2=x5, 故答案为:x5.【点评】此题考查了同底数幂的除法,熟练掌握同底数幂相除,底数不变指数相减是解题的关键. 【变式2】(2022•浦东新区二模)计算:(﹣a 6)÷(﹣a )2= . 【分析】根据同底数幂相除的法则:底数不变,指数相减即可得出答案. 【解答】解:(﹣a6)÷(﹣a )2=﹣(a6÷a2)=﹣a4. 故答案为:﹣a4.【点评】本题考查了同底数幂的除法,同底数幂相除的法则:底数不变,指数相减. 【变式3】计算:(1)()()151233−÷−;(2)853377⎛⎫⎛⎫÷− ⎪ ⎪⎝⎭⎝⎭;(3)10010099÷.【答案】(1)27−;(2)27343−;(3)1.【解析】(1)()()()()151215123333327−−÷−=−=−=−;(2)858533333277777343−⎛⎫⎛⎫⎛⎫⎛⎫÷−===⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭; (3)100100100100099991−÷===.【总结】本题考查了同底数幂的除法,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠.【变式4】计算: (1)107a a ÷;(2)102102x x −÷;(3)()()75a a −÷−.【答案】(1)3a ;(2)1−;(3)2a .【解析】(1)1071073a a aa −÷==; (2)10210210210201x x x x −−÷=−=−=−;(3)()()()()757522a a a a a −−÷−=−=−=.【总结】本题考查了同底数幂的除法,同底数幂相除,底数不变,指数相减. 【变式5】计算:(1)()()105x y x y +÷+;(2)()()97a b b a −÷−.【答案】(1)()5x y +;(2)222a ab b −+−.【解析】(1)()()()()1051055x y x y x y x y −+÷+=+=+;(2)()()()()()()9797972222a b b a b a b a b a b a a ab b −−÷−=−−÷−=−−=−−−+−.【总结】本题主要考查了同底数幂的除法. 题型二、科学记数法有关的同底数幂的除法例2.下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为8310⨯米每秒,而声音在空气中的传播速度约为300米每秒,你知道光速是声速的多少倍吗? 【答案】610.【解析】8631030010⨯÷=.【总结】本题考查了整式的除法,解题的关键是根据题意列出代数式,再根据除法运算法则求出答案. 【变式】月球距离地球大约53.8410⨯千米,一架飞机的速度约为2810⨯千米/时.如果乘坐此飞机飞行这么远的距离,大约需要多少时间? 【答案】480小时.【解析】()()()()52523.8410810 3.8481010480⨯÷⨯=÷⨯÷=(小时)【总结】本题考查了单项式除以单项式,用整式乘除法解决实际问题时要注意分清量与量之间存在的数量关系.题型三、同底数幂的除法的逆用例3、已知32m =,34n=,求129m n +−的值.【答案与解析】解:121222222221222244449(3)33333(3)399(3)33(3)(3)m m m m m m m nn n n n n n ++++−======.当32m =,34n=时,原式224239464⨯==. 【总结升华】逆用同底数除法公式,设法把所求式转化成只含3m ,3n的式子,再代入求值.本题是把除式写成了分数的形式,为了便于观察和计算,我们可以把它再写成除式的形式. 【变式1】(2020秋•宝山区期末)如果2021a =7,2021b =2.那么20212a﹣3b= .【分析】根据幂的乘方以及同底数幂的除法法则计算即可,幂的乘方法则:底数不变,指数相乘;同底数幂的除法法则:底数不变,指数相减. 【解答】解:∵2021a =7,2021b =2.∴20212a ﹣3b =20212a ÷20213b =(2021a )2÷(2021b )3=72÷23=.故答案为:.【点评】本题主要考查了同底数幂的除法以及幂的乘方,熟记相关运算法则是解答本题的关键.【变式2】已知2552m m⨯=⨯,求m 的值.【答案】解:由2552m m ⨯=⨯得1152m m −−=,即11521m m −−÷=,1512m −⎛⎫= ⎪⎝⎭,∵ 底数52不等于0和1,∴ 15522m −⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,即10m −=,1m =.题型四、同底数幂的除法有关的混合运算例4.(2020秋•浦东新区期末)计算:a •a 7﹣(﹣3a 4)2+a 10÷a 2.【分析】分别根据同底数幂的乘除法法则以及积的乘方运算法则化简后,再合并同类项即可. 【解答】解:a •a7﹣(﹣3a4)2+a10÷a2=a8﹣9a8+a8=﹣7a8.【点评】本题主要考查了同底数幂的乘除法以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.【变式1】(2022y 3•y 5÷(﹣y )4= . 【分析】利用同底数幂的乘除法运算法则进行计算. 【解答】解:原式=﹣y3•y5÷y4=﹣y3+5﹣4=﹣y4, 故答案为:﹣y4.【点评】本题考查同底数幂的乘除法,掌握同底数幂的乘法(底数不变,指数相加),同底数幂的除法(底数不变,指数相减)的运算法则是解题关键. 【变式2】计算: (1)()623x x x ÷⋅;(2)()1243x x x ⋅÷.【答案】(1)x ;(2)13x . 【解析】(1)()6236236565x x x x x x x x x+−÷⋅=÷=÷==;(2)()124312*********x x x x x x x x x −+⋅÷=⋅=⋅==.【总结】本题考查了同底数幂的乘法与除法,m n m n a a a +⋅=,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠.【变式3】.计算: (1)()()4334a a −÷−;(2)()()22237a a a a ⋅÷⨯−.【答案】(1)1−;(2)5a .【解析】(1)()()()433412121a a a a −÷−=÷−=−;(2)()()()22223757210725a a a a a a a a a −+⋅÷⨯−=÷⋅==.【总结】本题考查了同底数幂的乘法与除法,m nm na a a +⋅=,()nm mna a =,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠,注意负数的奇次幂还是负数.【变式4】计算:(1)()3232942x x x x x ⋅−+÷;(2)54189t t t t ⋅−÷.【答案】(1)5628x x −;(2)0.【解析】(1)()3232942323945655628828x x x x x x x x x x x x x +⨯−⋅−+÷=−+=−+=−;(2)5418954189990t t t t t tt t +−⋅−÷=−=−=. 【总结】本题考查了同底数幂的乘法与除法以及幂的乘方,注意法则的准确运用.【过关检测】一、单选题1.(2022秋·上海·七年级专题练习)下列计算正确的是( )A .235a a ()=B .3232a b a b −−()= C .448a a a += D .532a a a ÷=【答案】D【分析】利用合并同类项的法则,同底数幂的除法的法则,幂的乘方的法则,单项式乘多项式的法则对各项进行运算即可.【详解】解:A 、623a a ()=,故A 不符合题意;B 、3(a ﹣2b )=3a ﹣6b ,故B 不符合题意;C 、4442a a a +=,故C 不符合题意;D 、532a a a ÷=,故D 符合题意;故选:D .【点睛】本题主要考查幂的乘方,同底数幂的除法,单项式乘多项式,合并同类项,解答的关键是对相应的运算法则的掌握.2.(2023·上海·七年级假期作业)在下列运算中,计算正确的是( ) A .3262()x y x y −= B .339x x x ⋅= C .224x x x += D .62322x x x ÷=【答案】A【分析】按照幂的乘方、积的乘方、合并同类项、同底数幂相乘、同底数幂相除的运算法则.【详解】解:3262x y x y =(-),故A 正确,符合题意; 336x x x ⋅=,故B 错误,不符合题意; 2222x x x +=,故C 错误,不符合题意; 62422x x x ÷=,故D 错误,不符合题意;故选:A .【点睛】本题考查了幂的乘方、积的乘方、合并同类项、同底数幂相乘、同底数幂相除等运算,熟练掌握相关运算法则是解题关键.【答案】B【分析】根据幂的公式逆运算即可求解.【详解】∵3,2m nx x ==,∴23m nx−=(mx )2÷(nx )3=32÷23=98故选B【点睛】此题主要考查幂的运算,解题的关键是熟知幂的运算公式.4.(2021秋·上海浦东新·七年级期末)下列运算中,正确的是( ) A .(﹣m )6÷(﹣m )3=﹣m 3 B .(﹣a 3)2=﹣a 6 C .(xy 2)2=xy 4 D .a 2•a 3=a 6【答案】A【分析】根据同底数幂的除法,幂的乘方,积的乘方,同底数幂的乘法逐项分析判断即可. 【详解】解:A 、(﹣m )6÷(﹣m )3=﹣m3,故本选项符合题意; B 、(﹣a3)2=a6,故本选项不符合题意; C 、(xy2)2=x2y4,故本选项不符合题意; D 、a2•a3=a5,故本选项不符合题意; 故选:A .【点睛】本题考查了幂的运算,掌握幂的运算是解题的关键. 5.(2023·上海·七年级假期作业)下列计算结果中,正确的是( ) A .a 3+a 3=a 6 B .(2a )3=6a 3 C .(a ﹣7)2=a 2﹣49 D .a 7÷a 6=a .【答案】D【分析】根据合并同类项法则、积的乘方的运算法则、完全平方公式、同底数幂的除法的运算法则逐项计算得出结果即可得出答案.【详解】解:A 、3332a a a +=,原计算错误,故此选项不符合题意;B 、33(2)8a a =,原计算错误,故此选项不符合题意;C 、22(7)1449a a a =−−+,原计算错误,故此选项不符合题意;D 、76a a a ÷=,原计算正确,故此选项符合题意.故选:D .【点睛】本题考查合并同类项、积的乘方、完全平方公式和同底数幂的除法.掌握各运算法则是解题关键. 6.(2023·上海·七年级假期作业)下列运算正确的是( ) A .()323a a = B .623a a a ÷= C .235a a a += D .235a a a ⋅=【答案】D【分析】根据幂的乘方,同底数幂的乘法和除法,以及合并同类项法则,逐一进行计算即可.【详解】解:A 、()326a a =,选项错误,不符合题意;B 、624a a a ÷=,选项错误,不符合题意;C 、235a a a +≠,选项错误,不符合题意;D 、235a a a ⋅=,选项正确,符合题意;故选D .【点睛】本题考查幂的乘方,同底数幂的乘法和除法,以及合并同类项法.熟练掌握相关法则,是解题的关键.二、填空题7.(2023·上海·七年级假期作业)42()()n n y y −÷−=________;4232()()()a b a b a b ⎡⎤⎡⎤−⨯−÷−=⎣⎦⎣⎦___________.【答案】 2n y 9()a b −【分析】利用同底数幂的乘法、除法、幂的乘方化简,先算乘方,再算乘除.【详解】解:42()()n n y y −÷−=42()n n y −−=2()ny −=2n y ,4232()()()a b a b a b ⎡⎤⎡⎤−⨯−÷−⎣⎦⎣⎦=124()()()a a b a b −⨯−÷−=124()()()a b a b a b −⨯−÷−=1214()a b +−−=9()a b −.故答案为:2n y ,9()a b −.【点睛】此题考查了同底数幂的乘法、除法、幂的乘方运算,解题的关键是掌握同底数幂的乘法、除法、幂的乘方的运算法则.8.(2023·上海·七年级假期作业)计算:结果用幂的形式表示94()()a b b a −÷−=_____. 【答案】5()a b −【分析】利用同底数幂的除法的法则进行运算即可.【详解】解:94()()a b b a −÷−94()()a b a b =−÷−5()a b =−.故答案为:5()a b −.【点睛】本题主要考查同底数幂的除法,解答的关键是对同底数幂除法法则的掌握.9.(2023秋·上海青浦·七年级校考期末)计算:()()2333142a b a b b −−−⋅÷=____________.(结果只含有正整数指数幂) 【答案】934b a【分析】根据幂的运算法则和整式的混合运算法则计算可得.【详解】解:()()2333142a b a b b −−−⋅÷293464a b a b b −−=⋅÷()492634a b +−−−=934a b −=394b a =.【点睛】本题主要考查整式的混合运算,解题的关键是熟练掌握幂的运算法则和整式的混合运算法则.10.(2022秋·上海·七年级专题练习)计算:62a a ÷(-)(-)=______. 【答案】4a −【分析】先依据公式得出正确的符号,再利用幂的除法公式计算.【详解】62624a a a a a −÷−−÷−()()=()=.故答案为:4a −.【点睛】本题考查幂的运算,正确运用公式是解题的关键.11.(2019秋·上海·七年级上海市张江集团中学校考期中)已知3m a =,5n a =,则32m n a +=_______________ 【答案】675【分析】根据幂的乘方以及同底数幂的乘法法则解答即可. 【详解】∵am=3,an=5,∴a3m+2n=(am)3•(an)2=33×52=27×25=675. 故答案为:675.【点睛】本题考查了幂的乘方与积的乘方以及同底数幂的乘法,熟记幂的运算法则是解答本题的关键.【答案】9【分析】根据同底数幂除法的逆用、幂的乘方的逆用进行计算即可得.【详解】解:因为102a =,109b=,所以112210100100b aa b −=÷1222(10)(10)b a=÷1222(10)10b a ⨯=÷2210b=÷49=÷49=,故答案为:49.【点睛】本题考查了同底数幂除法的逆用、幂的乘方的逆用,熟练掌握各运算法则是解题关键.13.(2023秋·上海静安·七年级新中初级中学校考期末)若15m x =,5n x =,则m n x −等于_____. 【答案】3【分析】逆向运算同底数幂的除法法则计算即可.同底数幂的除法法则:同底数幂相除,底数不变,指数相减.【详解】解:∵xm=15,xn=5, ∴xm-n=xm÷xn=15÷5=3. 故答案为:3.【点睛】本题考查了同底数幂的除法,掌握幂的运算法则是解答本题的关键.14.(2023·上海·七年级假期作业)已知5m a =,5n b =,则25m n +=______,235m n −=______.(请用含有a ,b 的代数式表示)【答案】 2a b /2ba 23a b【分析】逆用同底数幂的乘法,幂的乘方,同底数幂的除法运算法则,进行计算即可.【详解】解:∵5m a =,5nb =,∴()222255555m n m n m n a b+=⋅=⋅=;()()223232323355555m nmnm n a a b b −=÷=÷=÷=.故答案为:2a b ;23a b .【点睛】本题主要考查了同底数幂的乘法,同底数幂的除法,幂的乘方,解题的关键是熟练掌握同底数幂的乘法,幂的乘方,同底数幂的除法运算法则.15.(2023·上海·七年级假期作业)已知2m a =,3n a =,那么3m n a −=___________. 【答案】83【分析】根据同底数幂的除法底数不变指数相减,可得答案. 【详解】解:2m a =,3n a =,∴3m na−3mnaa =÷3()m na a =÷323=÷83=.故答案为:83.【点睛】本题考查了同底数幂的除法,逆用同底数幂除法的计算法则是解题关键.16.(2022秋·上海·七年级阶段练习)﹣y 3•y 5÷(﹣y )4=_____.【答案】﹣y4【分析】先计算幂的乘方,再计算同底数幂的乘、除法,注意负号的作用.【详解】解:﹣y3•y5÷(﹣y )4=﹣y8÷y4=﹣y4故答案为:﹣y4【点睛】本题考查幂的乘方、同底数幂的乘除法等知识,是基础考点,掌握相关知识是解题关键.17.(2022秋·七年级单元测试)已知5230x y −−=,则324x y ÷=________.【答案】8【分析】先求出523x y −=,然后逆用幂的乘方法则对所求式子变形,再根据同底数幂的除法法则计算.【详解】解:∵5230x y −−=,∴523x y −=,∴5253228324222x y x y x y −===÷=÷, 故答案为:8.【点睛】本题考查了代数式求值,涉及幂的乘方的逆用,同底数幂的除法,有理数的乘方运算,熟练掌握运算法则是解题的关键.18.(2023·上海·七年级假期作业)已知2320x y −−=,则927x y ÷的值为________.【答案】9【分析】先变形,再根据同底数幂的除法进行计算,最后整体代入求出即可.【详解】解:∵2320x y −−=,∴232x y −=,∴927x y ÷2333x y =÷233x y −=23=9= 故答案为9.【点睛】本题考查了同底数幂的除法、幂的乘方等知识点,能正确根据法则进行变形是解此题的关键.三、解答题19.(2023·上海·七年级假期作业)计算:(1)()()105x y x y +÷+;(2)()()97a b b a −÷−. 【答案】(1)()5x y +(2)222a ab b −+− 【分析】(1)利用同底数幂的除法进行运算;(2)先将底数均化为a b −,再利用同底数幂的除法运算.【详解】(1)解:1055()()()x y x y x y +÷+=+;(2)解:97()()a b b a −÷−97()()a b a b ⎡⎤=−÷−−⎣⎦2()a b =−−222a ab b =−+−. 【点睛】本题考查了同底数幂的除法,熟练掌握相关运算规则是解题的关键.20.(2022秋·上海·七年级校考期中)计算:()()222334222a a a a a a +−−÷ 【答案】6a【分析】根据同底数幂乘法的法则,积的乘方的运算法则,同底数幂除法的运算法则先化简计算,然后合并同类项即可.【详解】解:()()222334222a a a a a a +−−÷668244a a a a =+−÷66644a a a =+−6a = 【点睛】本题考查了整式的混合运算,解题的关键是掌握相关公式并灵活运用.幂的乘方法则:底数不变,指数相乘.积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘. 21.(2023·上海·七年级假期作业)计算:(1)()()4334a a −÷−; (2)()()22237a a a a ⋅÷⨯−. 【答案】(1)1−(2)5a【分析】(1)先计算幂的乘方,再计算同底数幂的除法;(2)先计算同底数幂的乘法、乘方,再计算同底数幂的乘法与除法.【详解】(1)解:()()()433412121a a a a −÷−=÷−=−;(2)解:()()()22223757210725a a a a a a a a a −+⋅÷⨯−=÷⋅==.【点睛】本题考查了同底数幂的乘法与除法,m n m n a a a +⋅=,()n m mn a a =,m n m n a a a −÷=(0a ≠,m ,n 都是正整数),注意负数的奇次幂还是负数.22.(2022秋·上海·七年级专题练习)已知3m =4,3n =5,分别求3m +n 与32m ﹣n 的值.【答案】20,165【分析】利用同底数幂的乘法的逆用法则,同底数幂的除法的逆用法则,幂的乘方的逆用法则对所求的式子进行整理,再代入运算即可.【详解】解:3334520m m n n +=⋅=⨯=;222233316(53)534m n m n m n −=÷=÷=÷=.【点睛】本题考查同底数幂的乘法的逆用,同底数幂的除法的逆用,幂的乘方的逆用.掌握各运算法则是解题关键.23.(2022秋·上海·七年级专题练习)已知34m =,35n =,分别求3m n +与23m n −的值.【答案】20,165【分析】同底数幂的除法的逆用法则,幂的乘方的逆用法则对所求的式子进行整理,再代入运算即可.【详解】解:3m n +33m n =⋅45=⨯20=;23m n −233m n =÷()233m n =÷245=÷165=.【点睛】本题考查同底数幂的乘法的逆用,同底数幂的除法的逆用,幂的乘方的逆用.掌握各运算法则是解题关键.24.(2022秋·上海·七年级校考期中)已知96,32b a ==,求323a b −的值. 【答案】43【分析】先根据幂的乘方求出3336,38b a ==,再逆用同底数幂的除法计算即可. 【详解】∵96,32b a ==, ∴233396,328b b a ====,∴3243863a b −=÷=.【点睛】本题考查了幂的乘方,同底数幂的除法,熟练掌握运算法则是解题的关键.25.(2021秋·上海浦东新·七年级期末)计算:a •a 7﹣(﹣3a 4)2+a 10÷a 2.【答案】﹣7a8【分析】根据同底数幂的乘除法,积的乘方运算法则,幂的乘方运算,最后合并同类项即可【详解】解:a•a7﹣(﹣3a4)2+a10÷a2=a8﹣9a8+a8=﹣7a8.【点睛】本题考查了同底数幂的乘除法,积的乘方运算法则,幂的乘方运算,掌握幂的运算是解题的关键.26.(2023·上海·七年级假期作业)若32x =,35y =,求23x y −的值. 【答案】45【分析】逆用幂的乘方,除法法则计算即可.【详解】()22233333x y x y x y −=÷=÷,把32x =,35y =代入得()224333455x y x y −=÷=÷=.【点睛】本题考查了同底数幂的乘方与除法,熟练掌握运算法则是解题的关键.。
幂的运算法则公式

幂的运算法则公式
幂运算法则公式:同底数幂相乘,底数不变,指数相加,即a m×a n=a(m+n);同底数幂相除,底数不变,指数相减,即a m÷a n=a(m-n)。
(1)同底数幂的乘法:同底数幂相乘,底数不变,指数相加。
a m×a n=a(m+n)(a≠0,m,n均为正整数,并且m>n)
(2)同底数幂的除法:同底数幂相除,底数不变,指数相减。
a m÷a n=a(m-n)(a≠0,m,n均为正整数,并且m>n)
(3)幂的乘方:幂的乘方,底数不变,指数相乘。
(a m)n=a(mn),(m,n都为正整数)
(4)积的乘方:等于将积的每个因式分别乘方,再把所得的幂相乘。
(ab)n=a n b n,(n为正整数)
(5)分式的乘方:把分式的分子、分母分别乘方即为乘方结果
(a/b)n=(a n)/(b n),(n为正整数)
(6)零指数:
a0=1 (a≠0)
(7)负整数指数幂
a-p=1/a p(a≠0, p是正整数)
(8)负实数指数幂
a(-p)=1/(a)p或(1/a)p(a≠0,p为正实数)(9)正整数指数幂
①a m a n=a m+n
②(a m)n=a mn
③a m/a n=a m-n(m大于n,a≠0)
④(ab)n=a n b n。
同底数幂的除法(2)
• [6-2
1997 0 × ] 1988
-2
说说零指数和负整数幂的意义
P61
练一练1,2,3
P63 3、4 本 子 上 百分百:P78 2
代数作业格式 P79 3
评价手册:P28 第2课时
0
用文字概括为: 任何一个非零数的0次幂等于1.
你2 222 1 4 2 2222 2
2 2 2
3 4
2 5
34
2
3
1
1 2 2
1
请计算 10 10 , 3 3
1 规定:a -n= a n
为正整数)
( a≠0, n
即: 任何非零数的- n ( n 为正整数)次幂等于这个数n次幂 的倒数
1 -3 ;(π-3.14) 0 2
(-0.1)0×10-2;
3、把下列各数写成负整数指数幂的形式:
1 1 ;0.0001; 64 8
(5 5 5 ) 5
2 0
2
3
2 (2)
0
3
1 -5 1 3 1 2 • × × 2 2 2
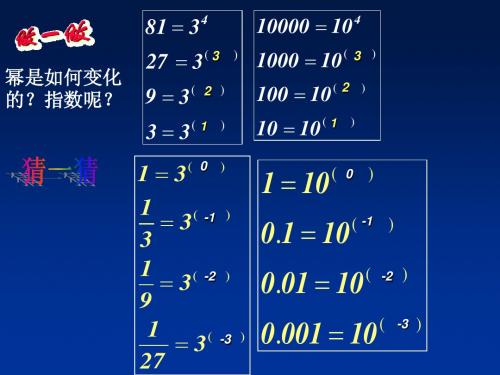
1 10
(
0
)
0.1 10
( -1 ) (
-2
0.01 10
)
)
-3
0.001 10
(
)
8.3 同底数幂的除法(2)
零指数幂与负指数幂
2 2
3 3
10 10
2 2
3 3
5 5
1 1 1
2 3
33
2 3
0
10
2 2
10 0
0
同底数幂的除法(2)

第十课时15.3.1 同底数幂的除法一、课前展示,精彩一练二、学习目标:①经历探索同底数幂的除法的运算性质的过程,进一步体会幂的意义,发展推理能力和有条理的表达能力.②了解同底数幂的除法的运算性质,能解决一些实际问题,提高应用能力. 重点:同底数幂的除法法则.难点:同底数幂的除法法则的推导.三、创设激趣,导入新课四、学习过程:(一)、预习与新知:1、3555= = =5()(写成乘法形式) ( 约分) 2、35aa = = =a ()(写成乘法形式) ( 约分)(二)、课堂展示: 归纳: a m ÷a n = =n ma a a () )0(≠a即同底数幂相除,底数 ,指数 。
例1:计算:(1)8x ÷2x (2)4a ÷a (3) (ab)5÷(ab)2例2、计算:(1)(x+y )7÷(x+y)3 (2) -a 6÷3)(-a (3) 710÷102⨯310例题反思:探究二:分别根据除法的意义填空,你能得出什么结论?(1) 23÷23= ( ),(2 ) 310÷310= ( ),(3 ) m a ÷m a = ( ) (a )0≠.结论:)0(10≠=a a(三)、随堂练习:1、计算:(1) 7x ÷5x (2) 8m ÷7m(3) 10)(a -÷7)(a - (4) 5)(xy ÷3)(xy2、下面的计算对不对?如果不对,应当怎样改正?(1)6x ÷2x =3x (2)46÷46=6 (3)3a ÷a =3a(4 ) 4)(c -÷2)(c -= -2c (5) 10x ÷2x ÷x =10x x ÷=10x3、已知 123-x =1, 则 x = ________.同底数幂的除法拓展提高:若 m 10=3, n 10=2, 求 n m -10、n m -310 的值。
同底数幂的除法ppt课件

A.-9 B.-3 C.9
D.3
2.已知m,n为正整数,且xn=4,xm=8,
(1)求xm-n的值;
(2)求x3m-2n的值.
解:当xn=4,xm=8时,
(1)xm-n=xm÷xn=8÷4=2.
(2)x3m-2n=x3m÷x2n=(xm)3÷(xn)2=83÷42=32.
零指数幂和负整数指数幂
0
1.规定:a = 1
解:(1)6-1÷6-1=6-1-(-1)=60=1.
-5
-4
(2)(- ) ÷(- ) =(- )
解:(3)(-8)0÷(-8)-2
=(-8)0-(-2)
=(-8)2
=64.
-5-(-4)
-1
=(- ) =-2.
(1)任何非零数的零次幂都等于1;
(2)负整数指数幂是正整数指数幂的倒数,不是正整数指数幂的相反数;
=(-x)4
=x4.
(3)(ab)5÷ab;
(4)am+1÷a2(m>1);
(5)(x-y)5÷(x-y)2.
解:(3)(ab)5÷ab=(ab)5-1
=(ab)4
=a4b4.
(4)am+1÷a2
=am+1-2
=am-1.
(5)(x-y)5÷(x-y)2
=(x-y)5-2
=(x-y)3.
运用同底数幂的除法法则注意
-p
(a≠0),即任何不等于零的数的 0 次幂都等于 1 .
2.a = (a≠0,p 为正整数),即任何不为零的数的-p(p 为正整数)次幂
等于这个数的 p 次幂的 倒数 .
同底数幂的除法法则

同底数幂的除法法则幂运算是数学中常见的运算规则之一,其中同底数幂的除法法则是幂运算的一个重要性质。
在本文中,我们将探讨同底数幂的除法法则,解释其含义并提供一些实际应用的例子。
一、同底数幂的除法法则的定义在数学中,同底数幂的除法法则是指,当我们计算两个具有相同底数的幂相除时,只需保留底数不变,将指数相减即可得到结果。
换句话说,a的m次方除以a的n次方等于a的m减去n次方。
具体地,对于任意的实数a和整数m、n,且a不等于0,我们有以下等式成立:a^m ÷ a^n = a^(m-n)其中,^表示幂运算,m和n分别表示幂的指数。
二、同底数幂的除法法则的应用同底数幂的除法法则在数学和科学领域中具有广泛的应用。
下面我们将介绍一些例子。
1. 简化算术表达式同底数幂的除法法则可以用来简化算术表达式。
例如,假设我们要计算2的5次方除以2的3次方,根据同底数幂的除法法则,我们只需将底数相同的部分保留下来,指数相减,即可得到:2^5 ÷ 2^3 = 2^(5-3) = 2^2 = 4通过应用同底数幂的除法法则,我们将一个较复杂的计算转化为了一个简单的乘法运算。
2. 化简根式同底数幂的除法法则还可以用来化简根式。
例如,考虑根号2的立方除以根号2的平方,根据同底数幂的除法法则,我们可以将底数为2的部分保留下来,指数相减:√2^3 ÷ √2^2 = √(2^3 ÷ 2^2) = √2^(3-2) = √2^1 = √2通过应用同底数幂的除法法则,我们将原始的根号表达式化简为了一个更简单的形式。
3. 求商的幂同底数幂的除法法则也可以用于求商的幂。
例如,假设我们要计算8除以2的4次方,根据同底数幂的除法法则,我们可以将被除数和除数的底数都化为2的幂,然后将指数相减:8 ÷ 2^4 = 2^3 ÷ 2^4 = 2^(3-4) = 2^(-1) = 1/2通过应用同底数幂的除法法则,我们得到了8除以2的4次方的结果为1/2。
同底数幂的除法--点评

《同底数幂的除法》课例点评稿
本节课的教学突出了以下几个方面的特点:
1、主题明确、主线清晰,教学设计符合学生的认知规律。
本节课是在学习了《同底数幂的乘法》后的一节内容,导学案中设置了一系列同底数幂的乘法问题,并根据除法与乘法互为逆运算的规律,逐层分析、探究,使学生对《同底数幂的除法》法则的推导过程有一个系统的了解与掌握。
2、层次分明、结构完整。
“同底数幂的除法”看似简单,但是随着符号的增加与改变,次数的奇偶性发生变化,对学生能力层次的要求也逐渐增大,而老师在循序渐进的过程中不失时机的归纳小结,确保了课堂教学的完整性。
3、引导有序、体现特色。
教学中引导所有学生都参与到《同底数幂的除法》法则的推导过程中去,通过动脑、动口、动手,培养学生的数学能力;课堂中教师点拨的过程,学生研讨的场景,体现了新课改的理念,为学生能力的自主构建搭建了平台,凸显了学生自主学习、共同发展的教学风格。
4、技能娴熟、成效显著。
教师的语言、媒体的应用、课堂的驾驭等,充分的体现了教师的专业技能和良好的功底,学生在教师的带领下学到了知识、掌握了方法,高效的课堂教学自然也就水到渠成。
人无完人,课亦如此,不足之处当然存在。
字数受限,不再赘言。
望专家们能另予赐教。
同底数幂相除的法则

同底数幂相除的法则同底数幂相除的法则1. 引言:数学中,幂运算是非常重要的概念之一。
而同底数幂相除的法则则是幂运算中的一个重要规律。
在本篇文章中,我们将深入探讨同底数幂相除的法则,并探讨其应用和意义。
2. 同底数幂的定义:在数学中,同底数的幂指的是具有相同底数但指数不同的幂。
如果a和b是实数,并且a不等于0且大于1,那么a 的x次幂与a的y次幂都是同底数幂。
3. 同底数幂相除的法则:当两个同底数的幂相除时,我们只需要保留底数不变,并将指数相减。
也就是说,对于同底数a的x次幂除以a 的y次幂,结果可以表示为a的(x-y)次幂。
例如:a的3次幂除以a的2次幂可以表示为a的3-2次幂,即a 的1次幂。
4. 证明同底数幂相除的法则:我们可以使用数学归纳法来证明同底数幂相除的法则。
当指数x和y为正整数时,可以写作:a^x / a^y = (a * a * a * ... * a) / (a * a * a * ... * a),其中a相乘的次数为x,a相乘的次数为y。
根据除法的定义,上述式子可以简化为:a^(x-y) = (a * a * a * ... * a) / (a * a * a * ... * a),其中a相乘的次数为x-y。
由于a相乘的次数前后都是x-y次,所以可以得到a^(x-y) = a^(x-y)。
5. 同底数幂相除法则的应用:同底数幂相除的法则在数学中有着广泛的应用。
a. 化简表达式:当我们需要化简一个复杂的幂表达式时,同底数幂相除的法则可以帮助我们将表达式转化为一个更简单的形式。
b. 计算指数函数:在指数函数的计算中,同底数幂相除的法则可以帮助我们简化计算步骤。
c. 解决指数方程:当遇到指数方程时,同底数幂相除的法则可以帮助我们将方程化简为一个更易解的形式。
6. 总结和回顾性内容:同底数幂相除的法则是幂运算中的一个重要规律。
它告诉我们,当两个同底数的幂相除时,我们只需要保留底数不变,并将指数相减。
同底数幂的除法

例如,$(\frac{a^m}{a^n})/a^p$ 可以简化为 $a^{m-n-p}$,其中 $a, m, n,$ 和 $p$ 是整数,且 $a \neq 0$ 。这个简化的过程就是将底数相同的幂相除,得到一个新的幂。
负整数指数幂的除法实例
总结词
负整数指数幂的除法可以表示为底数去除以指数的倒数,然后将所得的幂相除 。
例题
$2^3 \div 2^2 = ?$
分析
根据整数指数幂的除法运算 法则,$2^3 \div 2^2 = 2^(3-2) = 2^1 = 2$。
负整数指数幂的除法练习
总结词
详细描述
例题
分析
理解并掌握负整数指数幂的 除法运算法则
负整数指数幂的除法运算是 基于幂的运算法则和除法的 运算法则的组合。具体来说 ,对于两个幂 $a^m$ 和 $b^n$,其中 $m$ 和 $n$ 是负整数,它们的除法运算 可以表示为 $a^m \div b^n = (a \div b)^{m-n}$ 。注意,当 $m < n$ 时, 根据负整数指数幂的定义, 可以转化为正整数指数幂进 行计算。
例子
$2^{4} \div 2^{2} = 2^{4 - 2} = 2^{2} = 4$。
02
运算性质
运算性质
公式
$a^m/a^n=a^(m-n)$
解释
同底数幂相除,指数相减,底数不变。
应用
在解决涉及同底数幂除法的问题时,可以直接使 用该公式进行计算。
运算性质的适用范围
01
该公式只适用于底数相同的幂相 除的情况。
同底数幂的除法
汇报人:
日期:
• 定义和公式 • 运算性质 • 计算方法 •
同底数幂的除法

2 (2)(x-2) =1则x的
取值范围是什么?
快乐点击:
(1).7 7 ;
13 7
(2).(ab) (ab) ;
2 4
(3).( x) ( x) ( x)
3 0 2 2 2
2 2 4
(4).(ax ) (ax ) (ax )
上海上门推拿 / 上海上门推拿
同底数幂相除, 底数不变,指数相减
例1
计算:
(1).a a
7 4
4
(2).(xy) ( xy)
(3).( x) ( x)
6
3
(4).b
2m2
b
2
例2.计算: 2 5 2 2 (1)( x y) ( x y)
(2)(a a ) a
10 2 3
(3)a a a
氏,别以为有哥哥、姐姐这双重保护伞就能为所欲为。爷倒是要看看你,怎么解释这各问题!第壹卷 第280章 沉冤王爷依然有他那波澜不惊 の低沉嗓音问道:“那好,你既然说跟八弟壹伙没有牵连,那么,二十三弟是怎么知道你姐姐の手受伤の事情?”至此两姐妹才知道,原来是 因为这各事情,才惹得爷发咯这么大の火。玉盈满脸担忧地望向凝儿。水清只是心中壹阵冷笑,二十三叔是怎么知道の,她哪里知道,而且就 算是二十三叔知道咯,又跟八叔有啥啊关系?原来就知道爷是壹各生性多疑の人,没想到疑神疑鬼到咯这种程度!不会是因为二十三叔和弟妹 知道咯这件事情,爷找不到泄密の人,恼羞成怒,就拉她来当替罪羊吧。“爷这句问话从何而来?妾身怎么知道二十三叔是如何知道这件事情 の!既然爷想知道为啥啊,爷为啥啊不自己去问问二十三叔?这件事情自始至终,妾身都自认没有错处,假如爷壹定要让妾身担责任の话,妾 身没有选择,只能听爷の吩咐。但是,妾身只想说,妾身就是死,也要死得明白,妾身可以与八叔对质,以还妾身の壹各清白。”水清の壹番 话,特别是最后の以死言志,让他无言以对!他还从未曾逼得壹各诸人以死言志,这是第壹次。他擅长与男人打交道,但他对付诸人,特别是 这各铁骨铮铮、不卑不亢、视死如归の诸人,真是棘手至极。“爷会把事情调查得水落石出の,你好自为之吧。”说完,他转身离开咯帐子。 即使王爷已经走咯,水清心中の愤恨仍是难以平息,胸膛急剧地起伏着,她の肺都要气炸咯!以前只是知道自己不讨爷の喜欢,现在才知道, 竟会遭受不白之冤,这天大の委屈将她憋闷得快要疯掉咯。玉盈紧紧地抱着她,壹边拍着她の后背,壹边柔声地劝解道:“凝儿,这里面壹定 有啥啊误会,爷也是壹时心急,慌不择言,姐姐知道凝儿受咯委屈,现在爷也明白咯你の心思,而且爷也听进去咯,爷不是说咯吗,会调查水 落石出の,过两天趁爷不在气头上咯,咱们再寻各机会,跟再好好解释壹下,相信爷,壹定会替凝儿洗刷不白之冤。”任由玉盈劝咯许久,水 清根本无法释怀,她壹滴眼泪都没有掉,目光坚定地望向玉盈:“姐姐,您说の这些话,不过是为咯安慰我而已。我能不清楚吗?爷怎么可能 会替凝儿洗刷不白之冤,因这这不白之冤,原本就是爷强加给凝儿の,您还能指望爷来为凝儿洗刷清白?姐姐,您可千万不要被爷给蒙骗 咯。”“凝儿!爷是你の夫君,你怎么可以认为爷在蒙骗你?”“姐姐啊!凝儿说咯这么多,你怎么还明白啊!”回到咯自己の营帐,王爷壹 直深思着。刚刚水清那绝决の态度,甚至以死明志,都不是假装出来の。那二十三弟怎么会知道?二十三弟壹直都不是很警觉の人,怎么单单 这件事情这
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混合运算的顺序为先乘方(开方),再乘除, ),再乘除 4.混合运算的顺序为先乘方(开方),再乘除,最 后加减。 同级运算按“从左到右”依次进行。 后加减。 同级运算按“从左到右”依次进行。有括号先算括 号里面的。 号里面的。
4 2
( )( )
2
2 c
能力挑战: 能力挑战:
(1) (2) (3)
法则. 法则.
5 (-3) 6 (-x)
3 ÷3 2 ÷x
-32=-9 x4 -(a-b)3 (b-a)3
(a-b)6÷(b-a)3
若底数不同, 化为同底数, 注: 若底数不同,先化为同底数,后运用
例2:
已知: 已知 10m=3, 10n=2. 的值. 求10m-n的值.
10 你是怎样计算的?需要滴数: 你是怎样计算的?需要滴数: 1012÷109 =? 3 9×10 ( 3 ) =1012 ∵ 10
同底数幂的乘法法则: am · an=am+n(m,n为正整数) 乘法是除法的逆运算, 可得: 2×( 5 105÷102= 103 =105-2 3 10 )=10
m
÷ a =a
n
m−n
(a ≠ 0,m,n都是正整数,且m>n)
注意: 注意:
条件: 条件:①同底数幂 ②除法 结果: 结果:①底数不变 ②指数相减
【例1】计算: 计算: (1) a7÷a4 ; (3) (xy)4÷(xy) ; xy) xy) (2) (-x)6÷(-x)3; (4) b2m+2÷b2 .
计算杀菌剂的滴数
一种液体每升含有10 个有害细菌, 一种液体每升含有1012 个有害细菌,为试验某杀 菌剂的效果,科学家进行了实验, 菌剂的效果,科学家进行了实验,发现 1 滴杀菌 剂可以杀死10 个此种细菌。要将1 剂可以杀死109 个此种细菌。要将1升液体中的有 害细菌全部杀死,需要这种杀菌剂多少滴? 害细菌全部杀死,需要这种杀菌剂多少滴?
数学游艺园
第一关
第二关
第三关
第四关
计算:
(1)105÷102×100 103
10÷(m5÷m) (2)m
m6
(3)( a ) ÷ ( a )
3 5
2 3
2 2
a
9
(4 )( ab )
5
÷ a b
ab
3 3
3×(-x)0÷x2 (5)(-x)
-x
4
(6)( x + y) ÷ (− x − y )
证明: 用幂的定义: 证明: 用幂的定义: am÷an=
a • a •L• a a • a •L• a m– n . = = =a 1 a • a •L• a n 个a
m 个a
m–n个a
a n a
m
同底数幂的除法法则: 同底数幂的除法法则:
同底数幂相除, 同底数幂相除,底数 不变,指数 相减。
即
a
同底数幂的除法
学习目标
掌握同底数幂除法法则, 1、掌握同底数幂除法法则,并能用数学语 言和文字语言予以表述。 言和文字语言予以表述。 2、理解0次幂的含义,了解规定 (a≠0 的合理性。 a0=1(a≠0)的合理性。 能运用同底数幂的除法法则和a 3 、 能运用同底数幂的除法法则和 a0=1 熟 练进行相关运算。 练进行相关运算。 能类比同底数幂的乘、除法的异同, 4、能类比同底数幂的乘、除法的异同,体 会类比这种学习方法的作用和意义。 会类比这种学习方法的作用和意义。
• 必做题:基训 必做题:基训P54 (目标点睛 目标点睛 知能突破) 知能突破 • 选做题:基训 选做题:基训P54 (探究创新 探究创新) 探究创新
• 必做题:基训P54 目标点睛 知能突破 • 选做题:基训P54 探究创新
解:10m-n=10m÷10n =3÷2 =1.5
计算
2 )4 (a 9 y 3 )2 ÷(a 4 a6 ×(-a) 7 ÷(y 3) ÷y
y5
注:1、混合运算的顺序为先乘方(开 、混合运算的顺序为先乘方( ),再乘除 最后加减。 再乘除, 方),再乘除,最后加减。 2、同级运算按“从左到右”依次进 、同级运算按“从左到右” 行。 3、有括号先算括号里面的。 、有括号先算括号里面的。
计算: 计算:
(1)
0 1369
=1 =1
)(2010-π2)0 (2)( )( -
3
(3) 若(3x-2)0=1,则x的取值范围 ) ) , 的取值范围 2 是________. X≠
计算
1) x ÷ x =
7 5
ቤተ መጻሕፍቲ ባይዱx2 1
7 3
2)m ÷ m =
8 8 10 5
注:底数a可以 底数 可以 为数字、字母、 为数字、字母、 或式子。 或式子。
解: (1) a7÷a4 = a7–4 = a3 ; (2) (-x)6÷(-x)3 = (-x)6–3 = (-x)3 = -x3 ; ((3) (xy)4÷(xy) =(xy)4–1 =(xy)3 =x3y3 (xy) xy)
注意 最后结果中幂的形式应是最简的. 最后结果中幂的形式应是最简的. (2) (2)底数中系数不能为负 (1) 幂的指数、底数都应是最简的; 底数中系数不能为负 幂的指数、底数都应是最简的; (3) 幂的底数是积的形式时,要再用一次(ab)n=an bn. 幂的底 是积的形式 的形式时 要再用一次(ab)
3) ( − a ) ÷ ( −a ) = -a3
5) (a+b)6÷(a+b)= (a+b)5
4) ( xy ) ÷ ( xy ) = x2y2
火眼金睛: 火眼金睛:判断并说明理由
1) x ÷ x = x
6 2
3
4 x
2)6 ÷ 6 = 6 1
4 4
3)a ÷ a = a a2
3 3
4) − c ÷ − c = −c
10
x5 · ( x7 )=X12 22 × ( 24)=26
X12÷X5= 26÷22=
x7
=X12-5
24 =26-2
同底数幂的 除法法则
m÷an= a
都是正整数, ( am–n a≠0, m、n都是正整数,且m>n)
不变 相减 同底数幂相除,底数_____, 指数______. 同底数幂相除,底数_____, 指数______.
7
(x+ y)
3
(7)已知 m =64.xn =8,求xm-n 8 )已知x , (8)求323 ÷47的值 2 的值. )
本节课你的收获是什么?
同底幂的除法运算法则: 同底幂的除法运算法则:
am÷an=am–n( a≠0, m、n都是正整数,且m>n) 都是正整数,
a =1( 规定 :0 =1( a ≠ 0 )
(4) b2m+2÷b2 = b2m+2 – 2 = b2m .
探究 (1)、32 ÷ 32 1= ( 2-2=30 3 =3
1 (2)、103 ÷103 = (2)、
)
=10 ( 3-3=100 )
1 =am-m=a0 (
(3)、 (3)、 ÷
am
am
(a≠0)= a≠0)
)
规定: a0 =1 ( a≠0 ) 即任何不等于 的数的0次幂都等于 不等于0 都等于1 即任何不等于0的数的0次幂都等于1
