江苏省盐城市2013届高三年级第二次模拟考试
2014届一轮复习数学试题选编34不等式选讲(教师版)

一、解答题
.(江苏省徐州市2013届高三考前模拟数学试题)D.[选修4-5:不等式选讲]已知 为正数,且满足 ,求证: .
【答案】D.由柯西不等式,得
.(江苏省2013届高三高考模拟卷(二)(数学))选修4—5:不等式选讲
已知a,b都是正实数,且a+b=2,求证:+≥1.
证明:∵
又∵ >0,∴ >0, ,
∴
∴
∴
.(镇江市2013届高三上学期期末考试数学试题)(选修4—5:不等式选讲)
设函数 .
(1)当 时,求函数 的定义域;
(2)若函数 的定义域为R,试求 的取值范围.
【答案】解:(1)由题设知: ,
如图,在同一坐标系中作出函数
和 的图象(如图所示),
知定义域为
(2)由题设知,当 时,恒有 ,
于是
,
当且仅当 时,等号成立.………………………………………8分
即 ,故 的最小值为1.………10分
.(2011年高考(江苏卷))解不等式:
【答案】【命题立意】本小题主要考查解绝对值不等式的基础知识,考查分类谈论、运算求解能力.
【解析】原不等式可化为 ;或 ,
解得 .所以原不等式的解集是 .
.(江苏省南京市2013届高三9月学情调研试题(数学)WORD版)D.选修4—5:不等式选讲
【答案】选修4—5:不等式选讲
证明:由
=
= .
.(苏州市第一中学2013届高三“三模”数学试卷及解答)[选修4 - 5:不等式选讲]设 ,实数 满足 ,求证: .
【答案】D证: ,
,
又
.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)(选修4-5:不等式选讲)
3 盐城中学2013届高三第一次模拟考试英语试题

命题人:陈巍苏远源审核人:郭乃华高洪洋第一部分:听力(共两节, 满分20分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the man doing ?A. Making a suggestion.B. Making an apology.C. Making a request.2. How does the man feel about the interview?A. Confident.B. Angry.C. Terrible.3. Where is Dr. Smith now?A. In Mexico.B. In California.C. In New York.4. What mistake did the man make?A. He forgot to take the package.B. He gave the wrong package to Mr. Wells.C. He gave the package to Mr. Smith.5. Who is probably the man?A. Helen‟s father.B. Helen‟s boss.C. Helen‟s classmate.第二节(共15小题;每小题1分,满分15分)听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6至7题。
6. How did the woman find the part-time job?A. She got it through a notice.B. Her teacher recommended her to do it.C. Her friend introduced the job to her.7. What do we know about the man?A. He teaches English.B. He wants to find a job.C. He is too busy.听第7段材料,回答第8至10题。
13大市2013年高三历次考试数学试题分类汇编1:集合

【推荐】江苏省13大市2013年高三历次考试数学试题分类汇编1:集合一、填空题1 .(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)若集合{}1,0,1A =-,{}|cos(),B y y x x A ==π∈,则A B = ____.【答案】{1,1}-;2 .(扬州市2012-2013学年度第一学期期末检测高三数学试题)若集合}11|{≤≤-=x x M ,2{|20}N x x x =-≤,则M∩N=____.【答案】[0,1]3 .(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)已知全集},3,2,1,0{=U 集合},3,2,1{},1,0{==B A 则=B A C U )(_____.【答案】{2,3}4 .(苏州市2012-2013学年度第一学期高三期末考试数学试卷)已知集合{}1,1,2,4A =-,{}1,0,2B =-,则A B = _____________.【答案】{}1,2-5 .(连云港市2012-2013学年度第一学期高三期末考试数学试卷)集合A ={1,2,3},B ={2,4,6},则A B =_________.【答案】{2};6 .(常州市2013届高三教学期末调研测试数学试题)设集合{}1,A a =,{}B a =,若B A ⊆,则实数a 的值为______.【答案】07 .(江苏省无锡市2013届高三上学期期末考试数学试卷)设全集U=R,集合A={}{}2|20,|1x x x B x x -<=>,则集U A B = ð___________. 【答案】{}|01x x <≤8 .(南通市2013届高三第一次调研测试数学试卷)已知全集U =R,集合{}10A x x =+>,则U A =ð________.【答案】 答案:(,1]-∞-.考查集合运算.注意集合的规范表示法,重视集合的交并补的运算.9 .(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)已知集合{}1,2,3A =,{}1,2,5B =,则A B ⋂=___________【答案】{}2,110.(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)已知集合(]2 1A =-,,[)1 2B =-,,则A B =U ______.【答案】(2 2)-,11.(南京市、盐城市2013届高三第三次模拟考试数学试卷)记函数f (x )=3-x 的定义域为A ,函数g (x )=lg(x -1)的定义域为B ,则A ∩B =________.【答案】(1,3]12.(南京市、淮安市2013届高三第二次模拟考试数学试卷)已知集合A={2a,3},B={2,3}.若A B={1,2,3},则实数a 的值为____.【答案】013.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)已知全集{}1,2,3,4,5,6U =,{}1,3,5A =,{}1,2,3,5B =,则()U A B = ð______.【答案】{}2,4,614.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)设全集U R =,集合{}|13A x x =-≤≤,{}|1B x x =>,则U A B = ð______.【答案】[1,1]-15.(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)设集合{}{}2223050A x x x B x x x =--=-≤,≥,则()A B =R I ð____.【答案】(]03,16.(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)若集合}2,1{-=m A ,且}2{=B A ,则实数m 的值为________.【答案】417.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)已知集合{}2,1,0,1-=U ,{}1,1-=A , 则U A ð= .【答案】{}0,218.(镇江市2013届高三上学期期末考试数学试题)已知集合M ={1 ,2,3, 4,5},N ={2,4,6,8,10},则M ∩N =______.【答案】{}4,2;。
盐城市2013届高三第二次模拟考试语文试题

一、语言文字运用(15分)1.(13届江苏盐城高三二模)下列各组词语中,没有错误字的一项是(3分) A.简练紧箍咒波光粼粼温良恭俭让B.朝廷恶作剧浆声灯影冰炭不同炉C.彗星姣姣者催人泪下兄弟阋于墙D.悔约闭门羹变幻莫测疾风知劲草2.(13届江苏盐城高三二模)在下面一段话空缺处依次填入成语,最恰当的一组是(3分)季羡林先生在《八十述怀》中说:“我从来没有想到,我能活到八十岁,如今竟然活到了八十岁,然而又一点也没有八十岁的感觉。
岂非▲!我服从任何人的调遣与指挥。
只敢规规矩矩,不敢乱说乱动。
然而我的脑筋还在,我的思想还在,我的感情还在,我的理智还在。
我不甘心成为▲,我必须干点事情。
二百多万字的印度大史诗《罗摩衍那》,就是在这时候译完的。
”季老的话让读者感觉到他文章的语言没有八十岁的▲,反而多了一些活泼与生动。
A.出人意料行尸走肉老气横秋B.咄咄怪事酒囊饭袋老态龙钟C.咄咄怪事行尸走肉老气横秋D.出人意料酒囊饭袋老态龙钟3.(13届江苏盐城高三二模)下面是描写春天的一段文字,请在横线上补写恰当的话,形象地表现“人”的神态和感受。
要求运用一种不超过40个字。
(4分)春天,大地从冬寒里苏醒复活过来,被人们砍割过陈旧了的草木茬上,又野性茁壮地抽出了嫩芽。
不用人工修培,它们就在风吹雨浇和阳光的抚照下,生长起来。
这时,遍野是望不到边的绿海,衬托着红的、白的、黄的、紫的……种种野花卉,一阵潮润的微风吹来,那浓郁的花粉青草气息,直向人心里钻。
无论谁,▲。
(选自冯德英《苦菜花》)4.(13届江苏盐城高三二模)顾炎武是清代著名思想家,爱国学者。
他在著作《日知录》中提出的“天下兴亡,匹夫有责”,是其一生思想的高度概括和写照。
2013年7月15日是顾炎武诞辰400周年纪念日,其家乡昆山将发起网上纪念活动。
请你在网上留言,表达颂扬和纪念之意。
要求:仿照对联,写成两句,上下句字数相同,不要求严格对仗。
不超过40个字。
(5分)二、文言文阅读(19分)(13届江苏盐城高三二模)阅读下面的文言文,完成后面题目。
江苏省南京市、盐城市2023届高三下学期3月第二次模拟考试 化学含答案
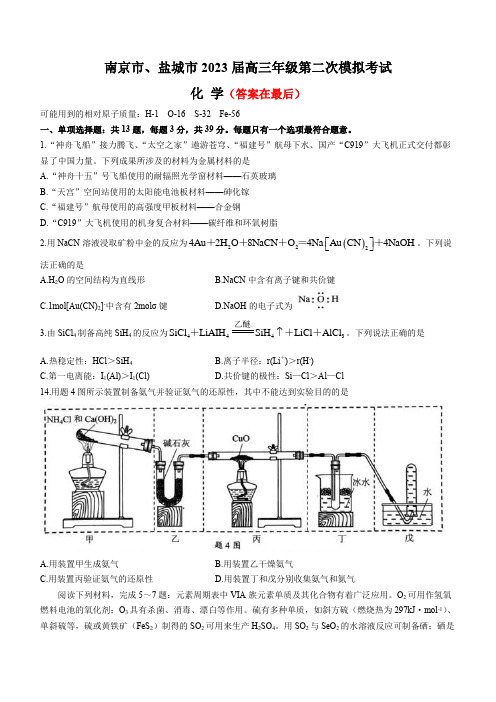
南京市、盐城市2023届高三年级第二次模拟考试化 学(答案在最后)可能用到的相对原子质量:H-1 O-16 S-32 Fe-56一、单项选择题:共13题,每题3分,共39分。
每题只有一个选项最符合题意。
1.“神舟飞船”接力腾飞、“太空之家”遨游苍穹、“福建号”航母下水、国产“C919”大飞机正式交付都彰显了中国力量。
下列成果所涉及的材料为金属材料的是 A.“神舟十五”号飞船使用的耐辐照光学窗材料——石英玻璃 B.“天宫”空间站使用的太阳能电池板材料——砷化镓 C.“福建号”航母使用的高强度甲板材料——合金钢D.“C919”大飞机使用的机身复合材料——碳纤维和环氧树脂2.用NaCN 溶液浸取矿粉中金的反应为()2224Au 2H O 8NaCN O 4Na Au CN 4NaOH ⎡⎤⎣⎦+++=+。
下列说法正确的是A.H 2O 的空间结构为直线形B.NaCN 中含有离子键和共价键C.1mol[Au(CN)2]-中含有2molσ键D.NaOH 的电子式为3.由SiCl 4制备高纯SiH 4的反应为4443SiCl LiAIH SiH LiCl AlCl ↑乙醚+++。
下列说法正确的是A.热稳定性:HCl >SiH 4B.离子半径:r(Li +)>r(H -) C.第一电离能:I 1(Al)>I 1(Cl)D.共价键的极性:Si —Cl >Al —Cl14.用题4图所示装置制备氨气并验证氨气的还原性,其中不能达到实验目的的是A.用装置甲生成氨气B.用装置乙干燥氨气C.用装置丙验证氨气的还原性D.用装置丁和戊分别收集氨气和氮气阅读下列材料,完成5~7题:元素周期表中VIA 族元素单质及其化合物有着广泛应用。
O 2可用作氢氧燃料电池的氧化剂;O 3具有杀菌、消毒、漂白等作用。
硫有多种单质,如斜方硫(燃烧热为297kJ ·mol -1)、单斜硫等,硫或黄铁矿(FeS 2)制得的SO 2可用来生产H 2SO 4。
江苏省2014届一轮复习数学试题选编29:算法初步(学生版)
江苏省2014届一轮复习数学试题选编29:算法初步(学生版)填空题1 .(江苏省苏南四校2013届高三12月月考试数学试题)已知某算法的流程图如下图所示,则输出的结果是______________.2 .(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)右图是一个算法流程图,则输出的S的值是____.(第3题图)3 .(2010年高考(江苏))右图是一个算法的流程图,则输出S的值是_____________4 .(江苏省2013届高三高考压轴数学试题)阅读右侧程序框图,输出的结果i的值为_______.5 .(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)右图是一个算法流程图,则输出的S 的值是______.6 .(2011年高考(江苏卷))根据如图所示的伪代码,当输入b a ,分别为2,3时,最后输出的m 的值是________7 .(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)根据如图所示的伪代码,最后输出的S 的值为____.8 .(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)根据右图所示的流程图,输出的结(第6题)(第3题),Pr int Read a b If a b Then m a Else m b End Ifm>←←(第4题)果T为_____.9 .(南京市、淮安市2013届高三第二次模拟考试数学试卷)右图是一个算法流程图,其输出的n的值是_____.10.(江苏省南京市四区县2013届高三12月联考数学试题)程序框图(即算法流程图)如图(右)所示,其输出结果是________.Y结束输出T4n≤开始1T←2n←1n n←+1(1)nT Tn←--N11.(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)右图是一个算法流程图,则输出p=____________12.(江苏省淮安市2013届高三上学期第一次调研测试数学试题)如图,是一个算法的伪代码,则输出的结果是__________.13.(连云港市2012-2013学年度第一学期高三期末考试数学试卷)右图是一个算法流程图,若输入x 的值为-4,则输出y 的值为__.14.(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)运行如图语句,则输出的结果T=______.15.(江苏省无锡市2013届高三上学期期末考试数学试卷)右边的程序语句运行后,输出的S 为____________.16.(江苏省南京市2013届高三9月学情调研试题(数学)WORD 版)右图是一个算法的流程图,最后输出的k =_______.T ←1I ←3While I<50 T ←T +I I ←I +2 End While Print T(第6题图)(第8题)17.(苏州市第一中学2013届高三“三模”数学试卷及解答)阅读右边的程序框图,运行相应的程序,输出的结果为______.(第9题图)18.(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)如图是一个算法的流程图,若输入n的值是10,则输出S的值是_____.19.(2013江苏高考数学)下图是一个算法的流程图,则输出的n 的值是________.20.(2012年江苏理)下图是一个算法流程图,则输出的k 的值是____.21.(南京市、盐城市2013届高三第三次模拟考试数学试卷)某算法的伪代码如图所示,若输出y 的值为3,则输入x 的值为________.开始 输入n0←S2<n(第4题图结束n S S +←1-←n n输出S22.(扬州市2012-2013学年度第一学期期末检测高三数学试题)如图所示的流程图,若输出的结果是15,则判断框中的横线上可以填入的最大整数为____.23.(江苏省无锡市2013届高三上学期期中考试数学试题)右图是一个算法流程图,则执行该算法后输出的=s __________.(第6题图)24.(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)如图,该程序运行后输出的结果为________.开始i ←1,s ←1i ≥5s ←s ⋅3i ←i +1输出s结束否 是Read xIf x ≤0 Then y ←x +2 Elsey ←log 2x End If Print y (第3题)25.(江苏省盐城市2013届高三10月摸底考试数学试题)执行如图所示的算法流程图,则输出的结果是S=________.26.(2009高考(江苏))右图是一个算法的流程图,最后输出的W __★__.27.(江苏省徐州市2013届高三上学期模底考试数学试题)已知某算法的流程图如图所示,则程序运行结束时输出的结果为________.(第5题图)28.(南通市2013届高三第一次调研测试数学试卷)已知实数x∈[1,9],执行如右图所示的流程图,则输出的x不小于55的概率为________.29.(江苏省徐州市2013届高三期中模拟数学试题)阅读下列程序:Read S←1For I from 1 to 5 step 2S←S+IPrint SEnd forEnd输出的结果是______ .30.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)根据右图的伪代码,输出的结果T 为______.31.(江苏省2013届高三高考模拟卷(二)(数学) )根据如图所示的算法流程图,输出的结果T 为__________.32.(江苏省徐州市2013届高三考前模拟数学试题)已知某算法的伪代码如右,根据伪代码,若函数()()g x f x m =-在R 上有且只有两个零点,则实数m 的取值范围是________.Read xIf x ≤1- Then f (x )←x +2 ElseIf 1-<x ≤1 Then f (x )←x 2 Elsef (x )←x -+2 End If End If Print f (x )(第6题图)33.(常州市2013届高三教学期末调研测试数学试题)根据右图所示的算法,可知输出的结果为______.34.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)如图所示是一算法的伪代码, 执行此算法时, 输出的结果是.35.(苏州市2012-2013学年度第一学期高三期末考试数学试卷)右边一段伪代码中,()Int x 表示不超过x 的最大整数,若输入6,4m n ==,则最终输出的结果n 为______.36.(苏北老四所县中2013届高三新学期调研考试)阅读下列程序:Read S ←1For I from 1 to 5 step 2 S ←S+I End for Print S End0102321Pr int n S n While S S S n n End While n++ ≤ ←←0←←4(第题)Read m ,n While()m mInt n n≠ ()mc m n Int n←-⨯m n ← n c ←End While Print n输出的结果是▲江苏省2014届一轮复习数学试题选编29:算法初步(学生版)参考答案填空题 1. 52. 58;3. 634. 75. 24006. 【命题立意】本题主要考查算法的基本概念,选择结构对应分段函数.3.【解析】本小题算法的功能是输入两个数,输出其中较大的一个. 7. 1458.7129. 5 10. 283 11.6512. 5 13. 2; 14. 625 15. 17 16. 1117.13818. 5419.解析:本题主要考察准确读算法及流程图,注意执行过程,∴3=n20.根据流程图所示的顺序,程序的运行过程中变量值变化如下表:是否继续循环k 2k 5k 4-+循环前 0 0 第一圈 是 1 0 第二圈 是 2 -2 第三圈 是 3 -2 第四圈 是 4 0 第五圈 是 5 4 第六圈否输出5∴最终输出结果k=5.21. 8 22. 49; 23. 8124. 16 25. 15 26. 【答案】22【解析】略27. (27,-5) 28.答案:38.本题主要考查算法及几何概型等知识.法一 当输入x =1时,可输出x =15;当输入x =9时,可输出y =79.于是当输入x 的取值范围为[1,9]时,输出x 的取值范围为[15,79],所求概率为7955379158-=-.法二 输出值为87x +.由题意:8755x +≥,故69x ≤≤. 29. 2,5,10 30. 10031. 832. (,0){1}-∞U33. 11 34. 3 35. 2 36. 10。
【市级联考】江苏省南京市、盐城市2023届高三第二次模拟考试全真演练物理试题

【市级联考】江苏省南京市、盐城市2023届高三第二次模拟考试全真演练物理试题一、单选题 (共7题)第(1)题如图所示,质量分别为m、2m的小球P、Q,通过完全相同的甲、乙两弹簧竖直悬挂在天花板上。
已知弹簧的劲度系数为k,重力加速度大小为g,弹簧质量可忽略不计且始终在弹性限度内,不计一切阻力。
用水平挡板竖直向上缓慢托起小球Q,直至将甲弹簧压缩到弹力大小为mg,之后在某时刻突然撤去挡板,下列说法正确的是( )A.在撤去挡板的瞬间,小球P的加速度大小为gB.在撤去挡板的瞬间,小球Q的加速度大小为gC.在撤去挡板的瞬间,甲、乙两弹簧的弹力之比为1:2D.在撤去挡板的瞬间,甲、乙两弹簧的长度之比一定为2:1第(2)题AB、CD两块正对的平行金属板与水平面成30°角固定,竖直截面如图所示。
两板间距10cm,电荷量为、质量为的小球用长为5cm的绝缘细线悬挂于A点。
闭合开关S,小球静止时,细线与AB板夹角为30°;剪断细线,小球运动到CD板上的M点(未标出),则()A.MC距离为B.电势能增加了C.电场强度大小为D.减小R的阻值,MC的距离将变大第(3)题中国科研团队利用中国天眼FAST发现迄今轨道周期最短的脉冲星双星系统,并命名为M71E。
设此双星都是质量均匀分布的球体,它们的质量分别为m1、m2,两者绕其中心连线上某点做匀速圆周运动,其中一颗星的速度大小为v1,不计其它天体对它们的作用。
则另一颗星的速度大小为()A.B.C.D.第(4)题嫦娥五号是中国探月工程第六次任务,标志着探月工程“绕、落,回”三步走的圆满完成。
如图所示为“嫦娥五号”着陆月球前部分轨道的简化示意图:Ⅰ是地月转移轨道.Ⅱ、Ⅲ是绕月球运行的椭圆轨道,Ⅳ是绕月球运行的圆形轨道。
P,Q分别为椭圆轨道Ⅱ的远月点和近月点,椭圆轨道Ⅲ的半长轴为a,嫦娥五号在椭圆轨道Ⅲ运行周期为T.圆轨道Ⅳ到月球表面的距离为h,月球半径为R,月球表面的重力加速度为g,万有引力常量为G,不考虑月球的自转,则()A.嫦娥五号在Ⅱ轨道上稳定运行时经过P点的加速度大于经过Q点的加速度B.嫦娥五号由Ⅰ轨道进入Ⅱ轨道,需要在P处向后喷气加速C.由题中已知条件,可以推知月球的密度D.嫦娥五号在Ⅳ轨道上绕月运行的速度大小为第(5)题网课期间,小飞同学向爸爸学习刀削面。
6 历史-盐城市2013届高三第二次模拟考试历史试题

江苏省盐城市2013届高三年级第二次模拟考试历史试题本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分。
考试用时100分钟。
第I卷(选择题共60分)一、选择题:本大题共20小题,每小题3分,共计60分。
在每小题列出的四个选项中,只有一项最符合题目要求。
1.西周在延续前代制度的基础上进行了一系列的完善与创新,以便达到“天下归周”、“天下归宗”和“天下归心”的目的。
下列与“天下归周”相对应的是A.禅让制B.分封制C.察举制D.郡县制2.下列古代生产工具中,功用明显不同于其它三项的是A.B.C.D.3.某位先秦思想家曾有如下评论:齐桓公致力连击诸侯,设法合作维持传统封建秩序,是个执行正道而不行诈谋的国君;晋文公虽协助周王定乱,却僭越礼制,想仿形天子礼仪,是个内行诈谋却装作遵循正道的国君。
该思想家应属于A.儒家B.法家C.道家D.墨家4.下为汉至唐前期东南地区行政区划设置分布简表时期郡县数西汉三国西晋隋朝唐前期苏南浙江会稽郡北部31县4郡50县5郡70县7郡43县13州74县江西豫章郡18县4郡51县6郡58县7郡19县7州34县福建会稽郡南部1县1郡9县2郡14县1郡5县5州28县根据表中东南行政区划设置变化过程的分析,不正确的是A.古代行政区划不断向东南拓展B.人口和经济重心有南移趋势C.中央政府对地方管理不断加强D.中央集权削弱地方权力加强.5.“积之而后高,尽之而后圣:故圣人也者,人之所积也”。
与此观点最接近的思想家是A.朱熹B.陆九渊C.李贽D.顾炎武6.下为晚清财政收入结构表(单位:万两),对该表所含信息解读不正确的是项目年代农业税收入工商杂税收入其他收入总收入数额比重数额比重数额比重数额比重1849 3281 77 969 23 4250 100 1885 3071 40 3923 51 714 9 7708 100 1911 4810 16 20441 69 4445 15 29696 100 A.自然经济逐步解体B.洋务经济兴起C.民族资本主义发展D.农民负担减轻7.某学者认为:“它标示的不只是这场战争失败的严峻性,更因为它标示着以商品和资本来改变中国传统社会的轨道,作为中国近代与中世纪的分界线是显而易见的。
2 数学-盐城市2013届高三第二次模拟考试数学试题

江苏省盐城市2013届高三3月第二次模拟考试数学试卷(总分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,计70分。
不需写出解题过程,请把答案写在答题纸的指定位置上。
⒈若集合}2,1{-=m A ,且}2{=B A ,则实数m 的值为 。
⒉若复数z 满足2)1(=-z i (为虚数单位),则=z 。
⒊现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为 。
⒋已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是 。
⒌若1e ,2e 是两个单位向量,212e e a -=,2145e e b +=,且a ⊥b ,则1e ,2e 的夹角为 。
⒍如图,该程序运行后输出的结果为 。
⒎函数⎪⎭⎫⎝⎛-=4sin 2)(πx x f ,[]0,π-∈x 的单调递增区间为 。
⒏若等比数列{}n a 满足43=-m a 且244a a a m m =-(*N m ∈且4>m ),则51a a 的值为 。
⒐过点)3,2(且与直线1l :0=y 和2l :x y 43=都相切的所有圆的半径之和为 。
⒑设函数)(x f y =满足对任意的R x ∈,0)(≥x f 且9)()1(22=++x f x f 。
已知当]1,0[∈x 时,有242)(--=x x f ,则⎪⎭⎫⎝⎛62013f 的值为 。
⒒椭圆12222=+by a x (0>>b a )的左焦点为F ,直线m x =与椭圆相交于A ,B 两点,若FAB ∆的周长最大时,FAB ∆的面积为ab ,则椭圆的离心率为 。
⒓定义运算,则关于非零实数x 的不等式的解集为 。
⒔若点G 为ABC ∆的重心,且AG ⊥BG ,则C sin 的最大值为 。
⒕若实数a 、b 、c 、d 满足143ln 22=-=-dc b a a ,则22)()(d b c a -+-的最小值为 。
2013届高三下学期最新精选试题(27套)分类汇编7:立体几何

江苏省2013届高三下学期最新精选试题(27套)分类汇编7:立体几何姓名____________班级___________学号____________分数______________一、填空题1 .(南京九中2013届高三第二学期二模模拟)圆柱形容器的内壁底半径是10cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为 ▲ 2cm .2 .(江苏省南京学大教育专修学校2013届高三3月月考数学试题)若圆锥的母线长为2cm ,底面圆的周长为2πcm ,则圆锥的体积为 3cm .3 .(江苏省南通市、泰州市、扬州市、宿迁市2013届高三第二次调研(3月)测试数学试题)若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 cm 的半圆,则该圆锥的高为 ▲ cm .4 .(盱眙县新马中学2013届高三下学期期初检测数学试题)正四面体ABCD 中,,E F 分别是棱,BC AD 的中点,则直线DE 与平面BCF 所成角的正弦值为__________5 .(江苏省扬州中学2013届高三下学期开学质量检测数学试卷)若一个圆锥的侧面展开图是面积为π2的半圆面,则该圆锥的体积为________. 6 .(江苏省扬州中学2013届高三3月月考数学试题)正四面体ABCD 中,AO ⊥平面BCD,垂足为O ,设M 是线段AO 上一点,且BMC ∠是直角,则MOAM的值为___________________.7 .(江苏省盐城市2013届高三第二次模拟(3月)考试数学试题)已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是________.8 .(江苏省泰兴市第三高级中学2013届高三下学期期初调研考试数学试题 )已知正六棱锥ABCDEF P -的底面边长为1cm ,侧面积为32cm ,则该棱锥的体积为___________3cm .9 .(江苏省青阳高级中学2013届高三月测试卷(一)(数学))用一个与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为__________.10.(江苏省青阳高级中学2013届高三3月份检测数学试题 )如图,直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,AC =5,AA 1=3,M 为线段BB 1上的一动点,则当AM +MC 1最小时,△AMC 1的面积为____________.11.(江苏省涟水中学2013届高三下学期期初检测数学试题)如图,二面角l αβ--的大小是60°,线段AB α⊂.B l ∈,AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是_________.12.(江苏省涟水中学2013届高三下学期期初检测数学试题)如图是 一正方体的表面展开图,B 、N 、Q 都是所在棱的中点则在原正方体中,①AB 与CD 相交;②MN∥PQ;③AB∥PE;④MN 与CD 异面;⑤MN∥平面PQC.所给关系判断正确的是_____13.(江苏省金湖中学2013届高三下学期期初检测数学试题)右图是某四棱锥的三视图,则该几何体的表面积为________________________.14.(江苏省金湖中学2013届高三下学期期初检测数学试题)某几何体的三视图如图所示,该几何体的体积是______3cm .15.(江苏省淮阴中学2013届高三3月综合测试数学试题)设,αβ为两个不重合的平面,,m n 为两条不重合的直线,给出下列的四个命题:(1)若,m n m α⊥⊥,则//n α;(2)若,,n m αβ⊂⊂α与β相交且不垂直,则n 与m 不垂直 (3)若,,,,m n n m αβαβα⊥⋂=⊂⊥则n β⊥ (4)若//,,//,m n n ααβ⊥则m β⊥ 其中,所有真命题的序号是__________.16.(2012学年第二学期徐汇区高三学业水平考试数学学科试卷 )已知圆锥的母线长为5,侧面积为π15,则此圆锥的体积为__________.二、解答题17.(苏北老四所县中2013届高三新学期调研考试)如图,四边形ABCD 为矩形,AD ⊥平面ABE ,AE =EB =BC =2,F 为CE 上的点,且BF ⊥平面ACE .(1)求证:AE ⊥BE ;(2)求三棱锥D -AEC 的体积;(3)设M 在线段AB 上,且满足AM =2MB ,试在 线段CE 上确定一点N ,使得MN ∥平面DAE .18.(南通市2013届高三第二次调研测试数学试题)如图,在三棱柱111ABC A B C -中,1A B ABC ⊥平面,AB AC ⊥,且12AB AC A B ===.(1)求棱1AA 与BC 所成的角的大小;(2)在棱11B C 上确定一点P ,使二面角1P AB A --的平面角的余弦值为255.19.(南京九中2013届高三第二学期二模模拟)在直三棱柱111C B A ABC -中,AC=4,CB=2,AA 1=2,60=∠ACB ,E 、F 分别是BC C A ,11的中点.(1)证明:平面⊥AEB 平面C C BB 11; (2)证明://1F C 平面ABE ;(3)设P 是BE 的中点,求三棱锥F C B P 11-的体积.20.(江苏省南京学大教育专修学校2013届高三3月月考数学试题)如图,平行四边形ABCD中,CD BD ⊥,正方形ADEF 所在的平面和平面ABCD 垂直,H 是BE 的中点,G 是,AE DF 的交点.⑴求证: //GH 平面CDE ;⑵求证: BD ⊥平面CDE .ABCEF P1A 1B 1C (第22题)BACA 1B 1C 121.(江苏省南通市、泰州市、扬州市、宿迁市2013届高三第二次调研(3月)测试数学试题)如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,BC //平面P AD ,PBC ∠90= , 90PBA ∠≠ .求证:(1)//AD 平面PBC ; (2)平面PBC ⊥平面PAB .22.(盱眙县新马中学2013届高三下学期期初检测数学试题)如图,在三棱柱ABC —A 1B 1C 1中,AA 1⊥平面A 1B 1C 1,∠B 1A 1C 1=90°,D、E 分别为CC 1和A 1B 1的中点,且A 1A=AC=2AB=2.(I)求证:C 1E∥平面A 1BD;(Ⅱ)求点C 1到平面A 1BD 的距离.23.(南京市四星级高级中学2013届高三联考调研考试(详细解答)2013年3月 )如图,在四棱柱1111D C B A ABCD -中,已知平面⊥C C AA 11平面,ABCD 且3===CA BC AB ,AB CP(第16题)D1==CD AD .(1) 求证:;1AA BD ⊥(2) 若E 为棱BC 的中点,求证://AE 平面11D DCC .24.(江苏省扬州中学2013届高三下学期开学质量检测数学试卷)在直三棱柱111ABC A B C -中,1BC CC AB ===2 ,BC AB ⊥.点N M ,分别是1CC ,C B 1的中点,G 是棱AB 上的动点.(I)求证:⊥C B 1平面BNG ;(II)若CG //平面M AB 1,试确定G 点的位置,并给出证明;25.(江苏省扬州中学2013届高三3月月考数学试题)如图,在四棱锥P ABCD-1AE CD BA1D1B1C第16题中,AB ∥DC ,2DC AB =,AP AD =,PB ⊥AC ,BD ⊥AC ,E 为PD 的中点. 求证:(1)AE ∥平面PBC ; (2)PD ⊥平面ACE .26.(江苏省盐城市2013届高三第二次模拟(3月)考试数学试题)正三棱柱111C B A ABC -的所有棱长都为4,D 为的1CC 中点.(1)求证:1AB ⊥平面BD A 1; (2)求二面角B D A A --1的余弦值.27.(江苏省盐城市2013届高三第二次模拟(3月)考试数学试题)如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E 为的PC 中点.⑴求证:PA∥平面BDE;⑵求证:平面PBC⊥平面PDC.DCBAE P(第16题图)28.(江苏省泰兴市第三高级中学2013届高三下学期期初调研考试数学试题 )如图,已知直四棱柱1111D C B A ABCD -,底面ABCD 为菱形,︒=∠120DAB ,E为线段1CC 的中点,F 为线段1BD 的中点. (Ⅰ)求证:EF ∥平面ABCD ; (Ⅱ)当1D DAD的比值为多少时,⊥DF 平面EB D 1,并说明理由.29.(江苏省青阳高级中学2013届高三月测试卷(一)(数学))如图,已知ABCRt ∆中,2==AC AB ,AD 斜边BC 上的高,以AD 为折痕,将ABD ∆折起,使BDC ∠为直角.(1)求证:平面⊥ABD 平面BDC ;D1B F1A 1D E1C ABC(2)求证:;60 =∠BAC (3)求点D 到平面ABC 的距离.30.(江苏省青阳高级中学2013届高三月测试卷(三)(数学))如图,长方体1111ABCD A B C D -中,12,AA AB =1,2,AD E ==为BC 的中点 (1)求点A 到面1A DE 的距离;(2)设1A DE ∆的重心为G ,问是否存在实数λ,使 得,AM AD λ=且1MG A ED ⊥平面同时成立?若存在,求出λ的值;若不存在,说明理由.31.(江苏省青阳高级中学2013届高三月测试卷(二)(数学))如图,在直三棱柱111C B A ABC -中,BC BA ⊥.(1)若1BB BA =,求证:⊥1AB 平面BC A 1;(2)若21===BB BC BA ,M 是棱BC 上的一动点.试确定点M 的位置,使点M 到平面C B A 11的距离等于22.32.(江苏省青阳高级中学2013届高三3月份检测数学试题 )如图, ABCD 是边长为3的正方形,DE ⊥平面ABCD ,DE AF //,AF DE 3=,BE 与平面ABCD 所成角为060. (1)求证:AC ⊥平面BDE ;(2)设点M 是线段BD 上一个动点,试确定点M 的 位置,使得//AM 平面BEF ,并证明你的结论.33.(江苏省南师附中等五校2013届高三下学期期初教学质量调研数学试卷)【必做题】 如图,在直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =2,AA 1=6,点E 、F 分别在棱BB 1、CC 1上,且BE =13BB 1,C 1F =13CC 1.(1)求异面直线AE 与A 1 F 所成角的大小; (2)求平面AEF 与平面ABC 所成角的余弦值.CAA 1C 1B 1BEFA BCDF E34.(江苏省南师附中等五校2013届高三下学期期初教学质量调研数学试卷)如图,在四棱锥P -ABCD 中,PD ⊥面ABCD ,AD ∥BC ,CD =13,AB=12,BC =10,AD =12BC . 点E 、F 分别是棱PB 、边CD 的中点.(1)求证:AB ⊥面PAD ; (2)求证:EF ∥面PAD .FEPDCAB35.(江苏省南菁高级中学2013届高三第二学期开学质量检测数学试卷)如图,已知三棱柱ABC —A 1B 1C 1的侧棱与底面垂直,AA 1=AB =AC =1,AB ⊥AC ,M 、N 分别是CC 1、BC 的中点,点P 在直线A 1B 1上,且满足()111A P A B R λλ=∈.(1)证明:PN ⊥AM ;(2)若平面PMN 与平面ABC 所成的角为45°,试确定点P 的位置.36.(江苏省南菁高级中学2013届高三第二学期开学质量检测数学试卷)在三棱柱111ABC A B C -中,已知底面ABC 是边长为a 的正三角形,侧棱162AA a =,点,,,D E F O 分别为边11,,,AB AC AA BC 的中点,1AO⊥底面ABC . (Ⅰ)求证:线段DE ∥平面11BB C C ; (Ⅱ)求证:FO ⊥平面11BB C C .CABC 1A 1B 1EODF37.(江苏省涟水县金城外国语学校2013届高三下学期期初检测数学试题)如图,菱形ABCD 的边长为6,60BAD ∠= ,AC BD O = .将菱形ABCD 沿对角线AC 折起,得到三棱锥B ACD -,点M 是棱BC 的中点,32DM =. (Ⅰ)求证://OM 平面ABD ;(Ⅱ)求证:平面ABC ⊥平面M D O ; (III)求三棱锥M A B D -的体积.38.(江苏省姜堰市蒋垛中学2012-2013学年度第二学期期初测试高三数学试题)如图,在棱长为3的正方体1111ABCD A BCD -中,11AE CF ==.⑴求两条异面直线1AC 与1D E 所成角的余弦值;⑵求直线1AC 与平面1BED F 所成角的正弦值.39.(江苏省姜堰市蒋垛中学2012-2013学年度第二学期期初测试高三数学试题)如图,在四棱柱1111D C B A ABCD -中,已知平面⊥C C AA 11平面,A B C D 且3===CA BC AB ,1==CD AD .(1) 求证:;1AA BD ⊥(2) 若E 为棱BC 上的一点,且//AE 平面11D DCC ,求线段BE 的长度1AE CD BA1D1B1C第16题40.(江苏省淮阴中学2013届高三下学期期初检测数学试题)已知四棱锥P ABCD-中,PA ABCD ⊥平面,底面ABCD 是边长为a 的菱形,120BAD ∠=︒,PA b =. (I)求证:PBD PAC ⊥平面平面;(II)设AC 与BD 交于点O ,M 为OC 中点,若二面角O PM D --的正切值为26,求:a b 的值.MO DACBP41.(江苏省淮阴中学2013届高三3月综合测试数学试题)在四棱柱ABCD -A 1B 1C 1D 1中,AA 1⊥平面ABCD ,底面ABCD为菱形,∠BAD =60°,P 为AB 的中点,Q 为CD 1的中点. (1)求证:DP ⊥平面A 1ABB 1; (2)求证:PQ ∥平面ADD 1A 1.42.(江苏省洪泽中学2013届高三下学期期初考试数学试题)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,且AB //CD ,AB ⊥AD ,AD =CD =2AB =2.B 1 A BCD QPA 1C 1D 1侧面PAD ∆为正三角形,且平面PA D ⊥平面ABCD .(1)若M 为PC 上一动点,则M 在何位置时,PC ⊥平面MDB ?并加已证明;(2)若G 为PBC ∆的重心,求二面角G -BD -C 大小.43.(2012学年第二学期徐汇区高三学业水平考试数学学科试卷 )如图所示:1111ABCD A B C D -是底面为正方形的长方体,1160AD A ∠=o ,14AD =,点P 是1AD 的中点,求异面直线1AA 与1B P 所成角的大小.(结果用反三角函数值表示)C.A 1BB 1C 1D 1DAPA BCDP江苏省2013届高三下学期最新精选试题(27套)分类汇编7:立体几何参考答案一、填空题1. 100π.2. 3 3π3. 【答案】34.3 35. π336. 17. 1838.439. 82 3π10. 311.3 412. ①②④⑤13. 3465+14. 4 315. (3)(4)16. 12π二、解答题17.解(1)∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,则AE⊥BC.又∵BF⊥平面ACE,∴AE⊥BF,∴AE⊥平面BCE.又∵BE⊂平面BCE,∴AE⊥BE.(2)111422222233 DAEC EADC EABCDV V V---===⨯⨯⨯⨯=.(3)在三角形ABE中,过M点作MG∥AE交BE于G点,在三角形BEC中,过G点作GN ∥BC 交EC 于N 点,连MN ,则由比例关系易得CN =CE31.MG ∥AE ,MG ⊄平面ADE, AE ⊂平面ADE , ∴MG ∥平面ADE ,同理,GN ∥平面ADE , ∴平面MGN ∥平面ADE . 又∵MN ⊂平面MGN ,∴MN ∥平面ADE , ∴N 点为线段CE 上靠近C 点的一个三等分点.18. 【解】(1)如图,以A 为原点建立空间直角坐标系,则 ()()()()11200020022042C B A B ,,,,,,,,,,,,()1022AA =,, ,()11220BC B C ==-,,.11141cos 288AA BC AA BC AA BC⋅-〈〉===-⋅⋅,, 故1AA 与棱BC 所成的角是π3. ………………………4分(2)P 为棱11B C 中点,设()111220B P B C λλλ==-,,,则()2422P λλ-,,. 设平面PAB 的法向量为n 1(),,x y z =,()=2422AP λλ-,,,则1103202000AP x y z z x y y AB λ⎧⋅=++==-⎧⎧⎪⇒⇒⎨⎨⎨==⋅=⎩⎩⎪⎩,,,.n n 故n 1()10λ=-,,……………………………………………8分 而平面1ABA 的法向量是n 2=(1,0,0),则1212212125cos ,51λ⋅〈〉===⋅+n n n n n n ,解得12λ=,即P 为棱11B C 中点,其坐标为()132P ,,.………………………………………………10分 19. (1)证明:在中ABC ∆,∵AC =2BC =4,060=∠ACB∴32=AB ,∴222AC BC AB =+,∴BC AB ⊥由已知1BB AB ⊥, ∴C C BB AB 11面⊥又∵C C BB ABE ABE AB 11面,故面⊥⊂ …………5分 (2)证明:取AC 的中点M ,连结FM M C ,1在AB FM ABC //中,∆, 而FM ABE ⊄平面,∴直线FM //平面ABE在矩形11A ACC 中,E 、M 都是中点,∴AE M C //1BACA 1B 1C 1zxyP而1C M ABE ⊄平面,∴直线ABE M C 面//1 又∵M FM M C =⋂1 ∴1//FMC ABE 面面故AEB F C 面//1 …………………………10分(或解:取AB 的中点G ,连结FG ,EG ,证明1//C F EG ,从而得证)(3)取11B C 的中点H ,连结EH ,则//EH AB 且132EH AB ==,由(1)C C BB AB 11面⊥,∴11EH BB C C ⊥面, ∵P 是BE 的中点,∴1111111113223P B C F E B C F B C F V V S EH --∆==⨯⋅=…………………………………14分20.证明:⑴G 是,AE DF 的交点,∴G 是AE 中点,又H 是BE 的中点,∴EAB ∆中,AB GH //, ------------------------3分CD AB //,∴//GH CD ,又∵,CD CDE GH CDE ⊂⊄平面平面∴//GH 平面CDE -----------------------6分 ⑵平面ADEF ⊥平面ABCD ,交线为AD , ∵AD ED ⊥,ED ADEF ⊂平面∴ED ⊥平面ABCD , --------------------10分 ∴BD ED ⊥,又∵CD BD ⊥,CD ED D ⋂=∴CDE BD 平面⊥ ----------------------12分21. 【证】(1)因为BC //平面P AD ,而BC ⊂平面ABCD ,平面ABCD I 平面P AD = AD , 所以BC //AD . …………………………………3分 因为AD ⊄平面PBC ,BC ⊂平面PBC , 所以//AD 平面PBC . (6)分HGBA BCPDH (2)自P 作PH ⊥AB 于H ,因为平面PAB ⊥平面ABCD ,且平面PAB I 平面ABCD =AB ,所以PH ⊥平面ABCD .………………………………………9分 因为BC ⊂平面ABCD ,所以BC ⊥PH . 因为PBC ∠90=,所以BC ⊥PB ,而90PBA ∠≠,于是点H 与B 不重合,即PB I PH = H . 因为PB ,PH ⊂平面P AB ,所以BC ⊥平面P AB .…………12分 因为BC⊂平面PBC ,故平面PBC⊥平面P AB .……………………………………………………… 14分22. (Ⅰ)证明:取1A B 中点F,连结EF,FD.∵11,2EF B B,又11B B C C ,1112C D C C =, ∴EF 平行且等于11,2C D所以1C EFD 为平行四边形, ∴1//C E DF ,又DF ⊂平面1ADB , ∴1//C E 平面1A DB(Ⅱ)15A B AD ==,6BD =, 所以11316521222A BD S ∆=⋅-=,11111211323B A C D V -=⋅⋅⨯⨯=1111B A C D C A BD V V --=,及11121323d ⋅⋅=,22121d =. 所以点1C 到平面1A BD 的距离为2212123. ⑴在四边形ABCD 中,因为BA BC =,DA DC =,所以BD AC ⊥,又平面11AAC C ⊥平面ABCD ,且平面11AA C C 平面ABCD AC =,BD ⊂平面ABCD ,所以BD ⊥平面11AA C C ,又因为1AA ⊂平面11AA C C ,所以1BD AA ⊥⑵在三角形ABC 中,因为AB AC =,且E 为BC 中点,所以BC AE ⊥, 又因为在四边形ABCD 中,3AB BC CA ===,1DA DC ==, 所以60ACB ∠=︒,30ACD ∠=︒,所以BC DC ⊥,所以AE DC , 因为DC ⊂平面11D DCC ,AE ⊄平面11D DCC ,所以AE 平面11D DCC24. (I) 证明:∵在直三棱柱111ABC A B C -中,1CC BC =,点N 是C B 1的中点, ∴C B BN 1⊥BC AB ⊥,1BB AB ⊥,B BC BB = 1∴AB ⊥平面11BCC B⊂C B 1平面11BCC B∴AB C B ⊥1,即GB C B ⊥1 又B BG BN = ∴⊥C B 1平面BNG(II)当G 是棱AB 的中点时,CG //平面M AB 1 证明如下:连结1AB ,取1AB 的中点H,连接GC HM HG ,,, 则HG 为B AB 1∆的中位线∴GH ∥1BB ,121BB GH =∵由已知条件,11BCC B 为正方形 ∴1CC ∥1BB ,11BB CC = ∵M 为1CC 的中点,∴121CC CM =∴MC ∥GH ,且GH MC =∴四边形HGCM 为平行四边形∴GC ∥HM又 ∵M AB HM M AB GC 11,平面平面⊄⊂∴CG //平面M AB 1 1425.证明:(1)取PC 中点F ,连结EF ,BF ,∵E 为PD 中点,∴EF ∥DC 且EF =12DC .∵AB ∥DC且12AB DC =,∴EF ∥AB 且EF =AB .∴四边形ABFE 为平行四边形. ∴AE ∥BF . ∵AE ⊄平面PBC ,BF ⊂平面PBC , ∴AE ∥平面PBC .(2)∵PB ⊥AC ,BD ⊥AC ,PB BD B = ,∴AC ⊥平面PBD .∵PD ⊂平面PBD ,∴AC ⊥PD . ∵AP AD =,E 为PD 的中点,∴PD AE ⊥.∵AE AC A = ,∴PD ⊥平面ACE .26.解:取BC 中点O,连AO,∵ABC ∆为正三角形,∴BC AO ⊥,∵在正三棱柱111C B A ABC -中,平面ABC ⊥平面11B BCC ,∴⊥AD 平面11B BCC , 取11C B 中点为1O ,以O 为原点,OB ,1OO ,OA 的方向为,x y ,z 轴的正方向,建立空间直角坐标系,则FP E A BCD(第16题图))0,4,2(),32,0,0(),32,4,0(),0.2,2(),0,0,2(11B A A D B -.∴)32,4,2(),0,2,4(),32,4,2(11-=-=-=BA BD AB ,∵00881=++-=⋅BD AB ,01216411=-+-=⋅BA AB . ∴BD AB ⊥1,11BA AB ⊥,∴⊥1AB 面BD A 1(2)设平面AD A 1的法向量为),,(z y x n =,)0,4,0(),32,2,2(1=--=AA AD .1,AA n AD n ⊥⊥,∴⎪⎩⎪⎨⎧=⋅=⋅01AA n AD n ,∴⎩⎨⎧==-+-0403222y z y x ,⇒⎩⎨⎧-==zx y 30,令1=z ,得)1,0,3(-=n 为平面AD A 1的一个法向量,由(1)知⊥1AB 面BD A 1,∴1AB 为平面AD A 1的法向量,462423232,cos 111-=⨯--=⋅>=<AB n AB n AB n , ∴二面角B D A A --1的余弦值为46-27.证明(1)连接AC 交BD 于O ,连接PO EO ,∵四边形ABCD 是菱形, ∴O 是AC 中点,又E 为PC 中点.∴PA ∥EO又BDE EO 面⊂,BDE PA 面⊄∴PA ∥平面BDE (2)在△PAC 中,易得3===PO CO AO ∴ 90=∠APC ,∴22=PC∴在△PDC 中可求得2=DE ,同理在△PBC 中可求得2=BE∴在△BDE 中可得 90=∠BED ,即BE ⊥DE又BC PB =,E 为PC 中点, ∴BE ⊥PCBE ⊥面PDC ,又⊂BE 面PBC ∴平面⊥PBC 平面PDC28. (Ⅰ)证明:连接1,A C ,由题意可知点F 为1AC 的中点. 因为点E 为1CC 的中点.∴在1ACC ∆中,EF AC又 EF ⊄面ABCD ,AC ABCD ⊆面,∴EF ABCD 面 (Ⅱ)当13D DAD=时,1DF D EB ⊥平面 四边形ABCD 为菱形,且120DAB ∠=︒,∴3BD AD =. 四棱柱1111ABCD A BC D -为直四棱柱,∴四边形11DBB D 为矩形.又13DD AD =,∴1BD DD =,∴四边形11DBB D 为正方形,∴1DF D B ⊥在直四棱柱1A B C D-中,1DD ABCD ⊥底面,AC ABCD ⊆面,∴1AC DD ⊥四边形ABCD 为菱形,AC BD ⊥.111DD DBB D ⊆面,11,BD DBB D ⊆面,1BD DD D = ,∴11AC DBB D ⊥面. 11DF DBB D ⊆面,∴AC DF ⊥,又EF AC ,∴EF DF ⊥1111,,EF D EB D B D EB EF D B F ⊆⊆= 面面,∴1DF D EB ⊥平面29. (1)证明: ,,,D DC BD DC AD BD AD =⊥⊥ BDC AD 平面⊥∴又 ABD AD 平面⊂.BDC ABD 平面平面⊥∴BDC ∆∴为等腰∆Rt .60,,2 =∠∴==∴=∴BAC AC BC AB BC(3)⊥∴⊥⊥∴BC BC AE BC DE ,, 平面ADE,过D 点作,AE DM ⊥则⊥DM 平面ABC∴D 点到平面ABC 的距离为33. 30.解:(1) 222222AE DE AD AE ED AD ===+=AE DE ∴⊥111DE AA AA AE A AA ⊥=⊂ 面1A AE AE ⊂面1A AEDE ∴⊥面1A AE 12A A AE ==取1A E 的中点H 1AH A E ⊥ AH DE ⊥1A E ED E = 1A E ⊂面1A DE ED ⊂面1A DEAH ∴⊥面1A DEAH 为点A 到面1A DE 的距离AH=1 ∴点A 到面1A DE 的距离为1(2) 1AH A ED ⊥ 面,过点G 作//,GM AH AD M 交于1MG A ED ⊥则,且AD AM 31=故存在实数31=λ,使得AD AM λ=,且ED A MG 1平面⊥同时成立. 31. (1)证明:当1BB BA =,可知,B A AB 11⊥ .又 BA BC ⊥,1BB BC ⊥,且B BB BA =⋂1,∴⊥BC 平面1ABB . 而⊂1AB 平面1ABB ,∴BC AB ⊥1.∴由⎪⎩⎪⎨⎧=⋂⊥⊥B BC B A BCA B A A 1111B B ⊥⇒1B A 平面BC A 1. (2)设B到平面CB A 11的距离等于H,则BA CDBCADM E1111B A B C C A B B V V --=,11111133B A BC C A B B s H S CB --=,2H =.所以,当点M 为棱BC 的中点时,点M 到平面C B A 11的距离等于22. 32. (1)证明:因为DE ⊥平面ABCD ,所以AC DE ⊥因为ABCD 是正方形,所以BD AC ⊥,因为DE BD D ⋂= 从而AC ⊥平面BDE(2)当M 是BD 的一个三等分点,即3BM =BD 时,AM ∥平面BEF 取BE 上的三等分点N ,使3BN =BE ,连结MN ,NF ,则DE ∥MN ,且DE =3MN ,因为AF ∥DE ,且DE =3AF ,所以AF ∥MN ,且AF =MN , 故四边形AMNF 是平行四边形 所以AM ∥FN ,因为AM ⊄平面BEF ,FN ⊂平面BEF , 所以AM ∥平面BEF33.解:(1)建立直角坐标系,则)0,0,0(A ,)2,0,2(E ,)6,0,0(1A ,)4,2,0(F ,从而(2,0,2)AE =,1(0,2,2)A F =-记AE 与F A 1的夹角为θ,则有1141cos 2||||88AE A F AE A F θ⋅-===-⋅⋅.又由异面直线AE 与F A 1所成角的范围为),0(π,可得异面直线AE 与F A 1所成的角为60º(2)记平面AEF 和平面ABC 的法向量分别为n 和m ,则由题设可令(1,,)y z =n ,且有平面ABC 的法向量为1(0,0,6)AA ==m , )4,2,0(=AF ,)2,0,2(=AE . 由0AF ⋅= n ,得042=+z y ;由0AE ⋅=n ,得022=+z .所以2,1=-=y z ,即(1,2,1)=-n记平面AEF 与平面ABC 所成的角为β,有66cos ||||666β⋅-===-⋅⋅n m n m .由题意可知β为锐角,所以6cos 6β=34.证明:(1)因为PD ⊥面ABCD , 所以PD ⊥AB 在平面ABCD 中,D 作DM //AB ,则由AB =12得A BCDF EDM =12. 又BC =10,AD =12BC ,则AD =5,从而CM =5. 于是在△CDM 中,CD =13,DM =12,CM=5,则由22251213+=及勾股定理逆定理得DM ⊥BC .又DM //AB ,BC //AD ,所以AD ⊥AB . 又PD ∩AD =D ,所以AB ⊥面PAD(2)[证法一] 取AB 的中点N ,连结EN 、FN . 因为点E 是棱PB 的中点,所以在△ABP 中,EN //12PA .又PA ⊂面PAD ,所以EN //面PAD因为点F 分别是边CD 的中点,所以在梯形ABCD 中,FN //AD . 又AD ⊂面PAD ,所以FN //面PAD又EN ∩FN =N ,PA ∩DA =A ,所以面EFN //面PAD 又EF ⊂面EFN ,则EF //面PAD[证法二] 延长CD ,BA 交于点G . 连接PG ,EG ,EG 与PA 交于点Q. 由题设AD ∥BC ,且AD =12BC ,所以CD =DG ,BA=AG ,即点A 为BG 的中点.又因为点E 为棱PB 的中点,所以EA 为△BPG 的中位线,即EA ∥PG ,且EA :PG =1:2,故有EA :PG =EQ :QG =1:2又F 是边CD 的中点,并由CD =DG ,则有FD :DG=1:2在△GFE 中,由于EQ :QG =1:2,FD :DG =1:2,所以EF ∥DQ . 又EF ⊄面PAD ,而DQ ⊂面PAD ,所以EF ∥面PAD35.解:(1)证明:如图,以AB ,AC ,AA 1分别为x ,y ,z 轴,建立空间直角坐标系A -xyz .则P (λ,0,1),N (12,12,0),M (0,1,12),从而PN =(12-λ,12,-1),AM =(0,1,12),PN AM ⋅ =(12-λ)×0+12×1-1×12=0,所以PN ⊥AM(2)平面ABC 的一个法向量为n =1AA=(0, 0, 1).设平面PMN 的一个法向量为m =(x ,y ,z ),由(1)得MP =(λ,-1,12).由⎪⎪⎩⎪⎪⎨⎧=+-=+--⎪⎩⎪⎨⎧=⋅=⋅.021,021)21(,0,0z y x z y x MP m NP m λλ得QGFEPD C ABNMFEPDCAB解得))1(2,12,3(,3.3)1(2,312λλλλ-+==⎪⎪⎩⎪⎪⎨⎧-=+=m x x z x y 得令 ∵平面PMN 与平面ABC 所成的二面角为45°,∴|cos<m ,n >|=|m ·n |m |·|n ||=|2(1-λ)|9+(2λ+1)2+4(1-λ)2=22, 解得λ=-12故点P 在B 1A 1的延长线上,且|A 1P |=1236. (Ⅰ)因为平面11ACC A 为平行四边行,1E AC 为的中点, 所以1,,A E C 共线, 11 D AB DE BC E AC ⎫⇒⎬⎭为的中点为的中点,又11111111DE BC BC BCC B DE BCC B DE BCC B ⎫⎪⊆⇒⎬⎪⊄⎭平面平面平面 (Ⅱ)因为ABC ∆是边长这a 的正三角形,所以32AO a =. 又1AO ⊥底面ABC ,所以1AO AO ⊥, 又162AA a =,所以132AO a =. 又F 为1AA 的中点,所以1111OF AA OF BB BB AA ⊥⎫⇒⊥⎬⎭又1BC AO BC BC A O ⊥⎫⇒⊥⎬⊥⎭平面1AOA BC OF ⇒⊥, 所以OF ⊥平面11BB C C37.证明:(Ⅰ)因为点O 是菱形ABCD 的对角线的交点,所以O 是AC 的中点.又点M 是棱BC 的中点,所以OM 是ABC ∆的中位线,//OM AB因为OM ⊄平面ABD ,AB ⊂平面ABD ,所以//OM 平面ABD (Ⅱ)由题意,3OM OD ==,因为32DM =,所以90DOM ∠=,OD OM ⊥.又因为菱形ABCD ,所以OD AC ⊥. 因为OM AC O = ,所以OD ⊥平面ABC ,ABCMO因为OD ⊂平面MDO ,所以平面ABC ⊥平面MDO .(Ⅲ)三棱锥M ABD -的体积等于三棱锥D ABM -的体积.由(Ⅱ)知,OD ⊥平面ABC ,所以OD 为三棱锥D ABM -的高,且3OD =.ABM ∆的面积为11393sin120632222BA BM ⨯⨯=⨯⨯⨯=. 所求体积等于19332ABM S OD ∆⨯⨯=38.解:(1)以D 点为原点,建立空间直角坐标系xyz D -如图所示:则)3,3,3(),,3,3,0(),0,0,3(11-=AC C A∴15302103339,cos 11-=⨯-->=<E D AC则两条异面直线1AC 与E D 1所成角的余弦值为15302 (2))1,0,3(),2,3,0(),0,3,3(1-=-=E D E B B vv易知平面F BED 1的一个法向量为)3,2,1(=n 设直线1AC 与平面F BED 1所成角为α, 则21422|1433963|sin =⨯++-=α 39. (1)(2)23 40. 解:(I)因为PA⊥平面ABCD,所以PA⊥BD又ABCD 为菱形,所以AC⊥BD,所以BD⊥平面PAC从而平面PBD⊥平面PAC(II)过O 作OH⊥PM 交PM 于H,连HD因为DO⊥平面PAC,可以推出yz MO DAPDH⊥PM,所以∠OHD 为A-PM-D 的平面角 又33,,244a aOD a OM AM ===,且OH AP OM PM = 从而2222·4191669a bOH b a a abb ==++ 223(169)tan 262b a ODOHD OH b+∠===所以22916a b =,即43a b =.MO DACBPH法二:如图,以A 为原点,,AD AP 所在直线为y 轴,z 轴建立空间直角坐标系,则(0,0,),(0,,0)P b D a ,333(,,0)88M a a ,31(,,0)44O a a从而333(0,,),(,,)88PD a b PM a a b =-=- 33(,,0)44OD a a =-因为BD⊥平面PAC,所以平面PMO 的一个法向量为33(,,0)44OD a a =- .设平面PMD 的法向量为(,,)n x y z = ,由,PD n PM n ⊥⊥得 3330,088PD n ay bz PM n ax ay bz ⋅=-=⋅=+-=取5,,33x b y b z a ===,即5(,,)33n b b a = 设OD 与n的夹角为θ,则二面角O PM D --大小与θ相等从而tan 26θ=,得cos 15θ=22531124cos 5||||5212427ab abOD n OD n a b a θ-+⋅===⋅+从而43b a =,即:4:3a b =.41. 解:略42. (1)当M 为PC 的中点时,PC⊥平面MDB.事实上,连BM,DM,取AD 的中点N,连NB,NP.因为PN AD ⊥,且平面PAD ⊥平面ABCD,所以PN⊥平面ABCD.在Rt PNB ∆中,3,2PN NB ==,所以5PB =,又5BC =所以BN PC ⊥,又MD BM M = ,,MD BM ⊂平面MDB,而PD=DC=2,所以DM PC ⊥,所以PC ⊥平面MDB- (2)易知G 在中线BM 上,过M 作MF BD ⊥于F,连CF, 因为PC ⊥平面MDB,所以CF BD ⊥,故MFC ∠是二面角G —BD —C 的平面角B 1 ABCD QPA 1C 1D 131 在Rt BDC ∆中,5,2,5BD DC BC ===,所以455CF =,又2CM = 所以10sin 4MFC ∠=,故二面角G —BD —C 的大小为10arcsin 4 43.解:过点P 作11PE A D ⊥,垂足为E ,连结1B E (如图),则1PE AA ∥,1B PE ∴∠是异面直线1AA 与1B P 所成的角.在11Rt AA D △中 ∵1160AD A ∠= ∴1130A AD ∠=11111122A B A D AD ===,111112A E A D ==, 2211115B E B A A E ∴=+=.又1132PE AA ==. ∴在1Rt B PE △中,11515tan 33B E B PE PE ∠=== ∴异面直线1AA 与1B P 所成的角为15arctan3.。
江苏省一轮复习数学试题选编:概率学生 含答案

江苏省2014届一轮复习数学试题选编27:概率(学生版)填空题1 .(南京市、盐城市2013届高三年级第一次模拟考试数学试题)袋中装有2个红球, 2个白球, 除颜色外其余均相同, 现从中任意摸出2个小球, 则摸出的两球颜色不同的概率为 .2 .(江苏省徐州市2013届高三考前模拟数学试题)在集合{|,1,2,,10}6n M x x n π===中任取一个元素,所取元素恰好满足方程1cos 2x =的概率是________. 3 .(南京市、淮安市2013届高三第二次模拟考试数学试卷)盒子中有大小相同的3只白球、2只黑球,若从中随机地摸出两只球,则两只球颜色相同的概率是______.4 .(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为________.5 .(2011年高考(江苏卷))从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______6 .(常州市2013届高三教学期末调研测试数学试题)已知某拍卖行组织拍卖的10幅名画中,有2幅是膺品.某人在这次拍卖中随机买入了一幅画,则此人买入的这幅画是膺品的事件的概率为______.7 .(2012年江苏理)现有10个数,它们能构成一个以1为首项,3-为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是____.8 .(苏州市2012-2013学年度第一学期高三期末考试数学试卷)有5个数成公差不为零的等差数列,这5个数的和为15,若从这5个数中随机抽取一个数,则它小于3的概率是_______.9 .(江苏省连云港市2013届高三上学期摸底考试(数学)(选修物理))在4次独立重复试验中,随机事件A 恰好发生l 次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率p 的取值范围是___________________.10.(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)已知数字发生器每次等可能地输出数字1或2中的一个数字,则连续输出的4个数字之和能被3整除的概率是___.11.(2009高考(江苏))现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为___★___.12.(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)如图,ABCD 是4⨯5的方格纸,向此四边形ABCD 内抛撒一粒豆子,则豆子恰好落在阴影部分内的概率为_______________13.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,则露在外面的6个数字恰好是2,0,1,3,0,3的概率为________.14.(江苏省徐州市2013届高三上学期模底考试数学试题)在大小相同的4个小球中,2个是红球,2个是白球,若从中随机抽取2个球,则所抽取的球中至少有一个红球的概率是________.15.(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为______.16.(江苏省连云港市2013届高三上学期摸底考试(数学)(选修物理))已知一组抛物线2y ax bx c =++,其中a 为1、3、5、7中任取的一个数,b 为2、4、6、8中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线12x =交点处的切线相互平行的概率是_________________.17.(江苏省苏南四校2013届高三12月月考试数学试题)一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)骰子四个面上分别标有1,2,3,4这四个数字,抛掷这颗正四面体骰子,观察抛掷后能看到的数字.若连续抛掷两次,两次朝下面上的数字之积大于6的概率是______.18.(2013江苏高考数学)现在某类病毒记作n m Y X ,其中正整数m ,n (7≤m ,9≤n )可以任意选取,则n m ,都取到奇数的概率为____________.19.(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)从0,1,2,3这四个数字中一次随机取两个数字,若用这两个数字组成无重复数字的两位数,则所得两位数为偶数的概率是_____.20.(江苏省2013届高三高考压轴数学试题)从集合{-1,1,2,3}中随机选取一个数记为m,从集合{-1,1,2}中随机选取一个数记为n,则方程22x ym n+=1表示双曲线的概率为________.21.(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)已知某一组数据8,9,11,12,x,若这组数据的平均数为10,则其方差为______.若以连续掷两次骰子得到的点数nm,分别作为点P的横、纵坐标,则点P在直线4x y+=上的概率为______.22.(连云港市2012-2013学年度第一学期高三期末考试数学试卷)在数字1、2、3、4四个数中,任取两个不同的数,其和大于积的概率是___.23.(江苏省淮安市2013届高三上学期第一次调研测试数学试题)连续抛掷一个骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具)两次,则出现向上点数之和大于9的概率是___________.24.(江苏省南京市四区县2013届高三12月联考数学试题)若将一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),先后抛掷两次,则出现向上的点数之和为6的概率是____25.(江苏省盐城市2013届高三10月摸底考试数学试题)已知甲、乙、丙三人在3天节日中值班,每人值班1天,那么甲排在乙前面值班的概率是________.26.(江苏省徐州市2013届高三期中模拟数学试题)在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是_______________.27.(江苏省南京市2013届高三9月学情调研试题(数学)WORD版)有3个兴趣小组,甲、乙两位同学各参加其中一个小组,且他们参加各个兴趣小组是等可能的,则甲、乙两位同学参加同一个兴趣小组的概率为_______.28.(苏州市第一中学2013届高三“三模”数学试卷及解答)有一个容量为66的样本,数据的分组[1.5,3.5)[3.5,5.5)[5.5,7.5)[7.5,9.5)[9.5,11.5)频数 6 14 16 20 10 根据样本的频率分布估计,数据落在[5.5,9.5)的概率约是________.29.(扬州市2012-2013学年度第一学期期末检测高三数学试题)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,则x y 2=的概率为_____.30.(2013江苏高考数学)抽样统计甲、乙两位设计运动员的5此训练成绩(单位:环),结果如下:31.(江苏省2013届高三高考模拟卷(二)(数学) )在一个袋子中装有分别标注数字1,2,3,4的四个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为5的概率是_______.32.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)在不等式组031y x x y x ⎧⎪≤⎪<≤⎨⎪⎪>⎩所表示的平面区域内所有的格点(横、纵坐标均为整数的点称为格点)中任取3个点,则该3点恰能成为一个三角形的三个顶点的概率为______.33.(江苏省南通市、泰州市、扬州市、宿迁市2013届高三第二次调研(3月)测试数学试题)设数列{a n }满足:()()*3118220()n n n n a a a a a n ++=---=∈N ,,则a 1的值大于20的概率为 ▲ .34.(2010年高考(江苏))盒子中有大小相同的3只小球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是____35.(南京市、盐城市2013届高三第三次模拟考试数学试卷)在一个盒子中有分别标有数字1,2,3,4,5的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之积为偶数的概率是________.36.(苏北老四所县中2013届高三新学期调研考试)当A ,B ∈{1,2,3}时,在构成的不同直线Ax -By =0中,任取一条,其倾斜角小于45︒的概率是___________37.(江苏省无锡市2013届高三上学期期中考试数学试题)某学校有两个食堂,甲,乙,丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为___________.解答题38.(2010年高考(江苏))某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%.生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元.设生产各种产品相互独立(1)记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x 的分布列 (2)求生产4件甲产品所获得的利润不少于10万元的概率39.(2012年江苏理)设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,0ξ=;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,1ξ=. (1)求概率(0)P ξ=;(2)求ξ的分布列,并求其数学期望()E ξ.40.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)(1)山水城市镇江有“三山”——金山、焦山、北固山,一位游客游览这三个景点的概率都是0.5,且该游客是否游览这三个景点相互独立,用ξ表示这位游客游览的景点数和没有游览的景点数差的绝对值,求ξ的分布列和数学期望;(2)某城市有n (n 为奇数,3n ≥)个景点,一位游客游览每个景点的概率都是0.5,且该游客是否游览这n 个景点相互独立,用ξ表示这位游客游览的景点数和没有游览的景点数差的绝对值,求ξ的分布列和数学期望.41.(苏北老四所县中2013届高三新学期调研考试)如图,已知面积为1的正三角形ABC 三边的中点分别为D 、E 、F ,从A ,B,C,D ,E ,F 六个点中任取三个不同的点,所构成的三角形的面积为X (三点共线时,规定X=0)(1)求1()2P X ≥;(2)求E (X )42.(苏州市2012-2013学年度第一学期高三期末考试数学试卷)设10件同类型的零件中有2CB件不合格品,从所有零件中依次不放回地取出3件,以X表示取出的3件中不合格品的件数.(1)求“第一次取得正品且第二次取得次品”的概率;E X.(2)求X的概率分布和数学期望()43.(江苏省南京市2013届高三9月学情调研试题(数学)WORD版)在一个盒子中有大小一样的7个球,球上分别标有数字1,1,2,2,2,3,3.现从盒子中同时摸出3个球,设随机变量X为摸出的3个球上的数字和.(1)求概率P(X≥7);(2)求X的概率分布列,并求其数学期望E(X).2013届高三学情调研卷44.(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成.(1)求出甲考生正确完成题数的概率分布列,并计算数学期望; (2)若考生乙每题正确完成的概率都是23,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.45.(江苏省无锡市2013届高三上学期期末考试数学试卷)某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且都是整数分钟,经统计以往100位顾客办理业务所需的时间(t),结果如下:注:银行工作人员在办理两项业务时的间隔时间忽略不计,并将频率视为概率. (Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;(Ⅱ)用X 表示至第4分钟末已办理完业务的顾客人数,求X 的分布列及数学期望.46.(2009高考(江苏))对于正整数n ≥2,用n T 表示关于x 的一元二次方程220xax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈(a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈(a 和b 可以相等),记n P 为关于x 的一元二次方程220x ax b ++=有实数根的概率。
2023届江苏省南京市、盐城市高三第二次模拟考试物理试卷

2023届江苏省南京市、盐城市高三第二次模拟考试物理试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题蹦极是一项非常刺激的户外运动。
一质量为m的体验者(可视为质点),绑着一根原长为L、劲度系数为k的弹性绳从高台上坠下。
已知弹性绳的弹性势能和形变量x的关系为。
若不计空气阻力、体验者的初速度和绳的质量,则下列说法正确的是( )A.下落过程中该体验者的机械能守恒B.当弹性绳伸长量等于时,弹性绳的势能达到最大值C.体验者的最大速度为D.体验者下落的最大距离为第(2)题地球赤道上有一个观察者a,赤道平面内有一颗自西向东做匀速圆周运动的近地卫星b,a观测发现,每隔时间t卫星b就会从其正上方飞过。
已知地球质量为M、半径为R,引力常量为G,下列说法正确的是( )A.a的加速度等于b的加速度B.a的线速度大于b的线速度C.近地卫星b的周期为D.地球自转的周期为第(3)题如图所示,轻质弹簧一端固定在足够长的光滑斜面的顶端,另一端与物块A连接,物块B叠放在A上,两物块质量均为m,斜面倾角为θ,O点为弹簧原长位置。
将两物块从O点上方x0处由静止释放,下滑过程中A、B始终相对静止,则在下滑至最低点过程中( )A.物块A在O点的速度最大B.最低点到O点的距离为x0C.物块B在最低点时加速度大小为D.物块B在最高点与最低点所受摩擦力大小相等第(4)题如图所示,是边长为L的等边三棱镜,一束单色光照射在边上的D点,入射角为45°,折射光线在面的反射光照射到面的E点(图中未标出)。
不考虑光在面的反射,已知三棱镜对该光的折射率为,光在真空中的传播速度为c,则下列说法正确的是( )A.光有可能在面上发生全反射B.光从D点传播到E点所用时间为C.保持入射方向不变,入射点从D点向下移,光从D点传播到面所用时间一定不变D.保持入射点不变,将入射角略增大一些,光从D点传播到面所用时间可能变短第(5)题如图所示为一透明的正方体物块,下列说法正确的是( )A.由于该物块有规则形状,所以它一定为晶体B.由于该物块透明,所以它一定为晶体C.若该物块为绝缘体,则它一定为非晶体D.若将该物块加热到某一温度才开始熔化,且熔化的过程中温度保持不变,则它一定为晶体第(6)题疫情期间,同学们用手机等电子产品学习,但研究发现在低头用手机时,会让颈椎承受很大的压力。
【解析版】江苏省盐城市2013届高三第二次模拟(3月)考试数学试题

名师远程辅导互动平台 网址:
1
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解题过程,请把答案写在答题纸的指定
位置上. 1.(5分)(2013•盐城二模)若集合A={1,m ﹣2},且A ∩B={2},则实数m 的值为 4 .
2.(5分)(2013•盐城二模)若复数z 满足(1﹣i )z=2(i 为虚数单位),则|z|= .
故答案为.3.(5分)(2013•盐城二模)现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为
.
有另一件不合格的抽法有
P=故答案为.4.(5分)(2013•盐城二模)已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是 .
名师远程辅导互动平台
网址:
2 ××故棱锥的高为=4
V=
=
故答案为:5.(5分)(2013•盐城二模)若,
是两个单位向量,
,
,且⊥,则
,
的夹角为
.
<
,﹣,)﹣,
>﹣,
>.再由<,
,可得<,
,.6.(5分)(2013•盐城二模)如图,该程序运行后输出的结果为 16 .
名师远程辅导互动平台 网址:
3
7.(5分)(2013•盐城二模)函数
,x ∈[﹣π,0]的单调递增区间为 .
∈,﹣
,﹣﹣﹣
,﹣
,则,﹣
﹣,﹣
∴由﹣≤≤得:≤)在﹣
,8.(5分)(2013•盐城二模)若等比数列{a n }满足a m ﹣3=4且
(m ∈N *
且m >4),则a 1a 5的值
为 16 .。
【市级联考】江苏省南京市、盐城市2023届高三第二次模拟考试全真演练物理试题

【市级联考】江苏省南京市、盐城市2023届高三第二次模拟考试全真演练物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图所示,空间中分布着磁感应强度大小为B的匀强有界磁场,EF是其左边界,一面积为S的n匝圆形金属线框垂直于磁场放置,圆形线圈的圆心O在EF上,线圈电阻为R,若线框以角速度ω绕EF匀速转动,并从图示位置开始计时,则()A.时,线框中的感应电流最大B.0到时间内,通过线框的电量为C.线框中产生的交变电动势的最大值为nBsωD.线框中产生的交变电动势的有效值为第(2)题如图所示,绷紧的水平传送带始终以恒定速率运行。
初速度大小为的小物块从与传送带等高的光滑水平地面上的A处滑上传送带。
若从小物块滑上传送带开始计时,小物块在传送带上运动的图像(以地面为参考系)如图乙所示。
已知>,则( )A.时刻,小物块离A处的距离达到最大B.时刻,小物块相对传送带滑动的距离达到最大C.0~时间内,小物块受到的摩擦力方向先向右后向左D.0~时间内,小物块始终受到大小不变的摩擦力作用第(3)题如图为某质点的振动图像,下列判断正确的是( )A.质点的振幅为10cmB.质点的周期为4sC.t=4s时质点的速度为0D.t=7s时质点的加速度为0第(4)题如图所示,竖直平面内的光滑金属细圆环半径为R,质量为m的带孔小球穿于环上,同时有一长为R的细绳一端系于球上,另一端系于圆环最低点,绳上的最大拉力为2mg。
当圆环以角速度绕竖直直径转动时,发现小球受到3个力的作用。
则可能为( )A.B.C.D.第(5)题在烹调美食的过程中,所包含的物理知识正确的是( )A.炖排骨时,在汤沸腾后把炖汤的火调小,是为了降低汤的温度B.抽油烟机能将油烟吸走,是因为空气流速越大的位置,压强越大C.汤的温度越高,香味越浓,说明温度越高,分子的无规则运动越剧烈D.锅一般都是用铁制造的,主要是利用了铁的比热容较大的性质第(6)题水电是清洁能源,发展水电对我国实现碳达峰和碳中和有着重要的意义。
高三【解析版】盐城市2013届高三第二次模拟考试化学试题

盐城市2013届高三年级第二次模拟考试化学试题可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 Si 28 K 39 Fe 56选择题单项选择题:本题包括10小题,每小题2分,共计20分。
每小题只有一个选项符合题意。
1.化学在资源合理开发利用和生态环境保护方面正发挥着积极作用,下列行为与可持续发展理念相违背的是A.提高车用燃气、燃油品质,减少大气污染物的排放B.调整能源结构,推广核电、水电、天然气等清洁能源的应用比例C.将造纸废水通过高压水井压到地下,节约生产成本D.探寻新的反应途径、不断提高化学反应过程的选择性,提高合成反应的原子利用率2.下列有关化学用语表示正确的是A.羧基电子式B. O2-的结构示意图C.质子数35,中子数44的溴原子D. Al(OH)3在水溶液中的电离方程式H++H2O+AlO2-\leftrightharpoons AI(OH)3\leftrightharpoonsAl3+++3OH-3.常温下,下列各组离子在指定溶液中一定能大量共存的是A.0.1mo1/L NaI溶液:K+, Na+ , MnO4- , OH-B.能溶解CaCO3的溶液:K+, NH4+, Cl -, NO3-C.0.1mo1/LNaHSO3溶液:Na +, Mg2+, SO42- , ClO-D. c(H+)/c(OH-}=1013,的溶液:K+, Fe2+, Cl-, NO3-4.以0.1000 mol·L-1 NaOH溶液滴定c mol·L-1,某弱酸HA溶液,其滴定曲线如图I所示,下列说法正确的是A.可用甲基橙作滴定指示剂B.指示剂指示的滴定终点就是反应终点C.突变范围的大小与酸的强弱及酸的浓度有关D.滴定时氢氧化钠溶液盛放在带活塞的滴定管中5.下列有关物质的性质与其应用不相对应的是A. NH3分解生成N2和H2吸热热量,液氨可用作致冷剂B.浓硫酸具有吸水性,可用作Cl2的干燥剂C: CaO2能与水缓慢释放O2,可用作供氧剂D.聚合硫酸铁[Fe x(OH)Y(SO4)z·nH2O]能水解得到Fe(OH)3胶体,可用作净水剂6:下列使用漏斗的几个实验装置中,设计正确且能达到实验目的的是A.用图2所示装置进行过滤,过滤时不断搅拌B.用图3所示装置吸收NH3制氨水C.用图4所示装置用苯萃取碘水中的碘,并把碘的苯溶液从漏斗下口放出D.用图5所示装置用石灰石与稀盐酸制取CO2气体7.下列是部分矿物资源的利用及产品流程(如图6),有关说法不平确的是A.粗铜电解精炼时,粗铜作阳极B.生产铝、铜、高纯硅及玻璃过程中都涉及氧化还原反应C.黄铜矿冶铜时,副产物SO2可用于生产硫酸,FeO可用作冶铁的原料D.粗硅制高纯硅时,提纯四氯化硅可用多次分馏的方法8.设N A表示阿伏加德罗常数的值。
2013年江苏高考数学模拟试卷及参考答案【最后一卷】

2013年江苏高考数学最后一卷2013.06.01数学(必试部分)注意事项:1.本试卷总分160分,考试用时120分钟。
2.答题前,考生务必将班级、姓名、学号写在答卷纸的密封线内。
选择题答案填涂在答.........题卡对应的题号下,主观题答案写在答卷纸上对应的题号下空格内的横线上.................................。
考试结束后,上交答题卡和答卷纸。
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上...... 1.设复数z 满足()(1)1i i i z ++=-(i 是虚数单位),则复数z 的模z =___▲____.2.已知tan 2α=,则sin()cos()sin()cos()παπααα++-=-+-___▲_____.3.抛物线y 2 = 8x的焦点到双曲线x 212 – y 24 = 1的渐近线的距离为___▲___.4.阅读下列算法语句: Read S ←1For I from 1 to 5 step 2 S ←S+I End for Print S End输出的结果是 ▲ .5.设集合11{33},{0}3x x A x B x x-=<<=<,则A B =____▲_______.6.设等比数列{a n }的公比q = 12,前n 项和为S n ,则 S 4a 4= ____▲_______.7.在区间[5,5]-内随机地取出一个数a ,则恰好使1是关于x 的不等式2220x ax a +-<的一个解的概率大小为__▲_____.8.已知向量()3,1-b =,2=a ,则2-a b 的最大值为 ▲ .9.已知A (2,4),B (–1,2),C (1,0),点P (x ,y )在△ABC 内部及边界上运动,则z = x – y 的最大值与最小值的和为___▲___10.设,b c 表示两条直线,,αβ表示两个平面,现给出下列命题: ① 若,//b c αα⊂,则//b c ; ② 若,//b b c α⊂,则//c α; ③ 若//,c ααβ⊥,则c β⊥; ④ 若//,c c αβ⊥,则αβ⊥. 其中正确的命题是___▲______.(写出所有正确命题的序号)11.设函数22,0,()log ,0x x f x x x ⎧≤=⎨>⎩,若关于x 的方程2()()0f x af x -=恰有三个不同的实数解,则实数a 的取值范围为___▲_____.12.函数()()g x y f x =在求导数时,可以运用对数法:在函数解析式两边求对数得()()ln ln y g x f x =,两边求导数()()()()()ln f x y g x f x g x y f x '''=+,于是()()g x y f x '= ()()()()()ln f x g x f x g x f x '⎡⎤'+⎢⎥⎢⎥⎣⎦.运用此方法可以探求得知()10x y x x =>的一个单调增区间为____▲_____.13.已知椭圆22134x y +=的上焦点为F ,直线10x y ++=和10x y +-=与椭圆相交于点A ,B ,C ,D ,则AF BF CF DF +++= ▲ .14.已知定义在R 上的函数()f x 满足()12f =,()1f x '<,则不等式()221f x x <+的解集为_▲__.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明或演算步骤.15.(本小题满分14分)如图,点B 在以PA 为直径的圆周上,点C 在线段AB 上,已知1525,3,PA PB PC ===设,APB APC αβ∠=∠=,,αβ均为锐角. (1)求β;(2)求两条向量,AC PC 的数量积AC PC ⋅的值.PCB16. (本小题满分14分)如图,已知AB ⊥平面ACD ,DE //AB ,△ACD 是正三角形,AD = DE = 2AB ,且F 是CD 的中点. ⑴求证:AF //平面BCE ;⑵求证:平面BCE ⊥平面CDE .17.(本大题满分14分)2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数(以百人..为计数单位)作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计数人数的时间,即1n =;9点20分作为第二个计数人数的时间,即2n =;依此类推 ,把一天内从上午9点到晚上24点分成了90个计数单位.第n 个时刻进入园区的人数()f n 和时间n (n *∈N )满足以下关系: ()()()()()24123612436325363216377207390n n n f n n n n -≤≤⎧⎪⎪⎪⋅≤≤=⎨⎪-+≤≤⎪≤≤⎪⎩,n *∈N第n 个时刻离开园区的人数()g n 和时间()n n *∈N 满足以下关系:()()()()012451202572,507390n g n n n n n *≤≤⎧⎪=-≤≤∈⎨⎪≤≤⎩N . (1)试计算在当天下午3点整(即15点整)时,世博园区内共有游客多少百人?(提示:123 1.1取,结果仅保留整数)(2)问:当天什么时刻世博园区内游客总人数最多?A BC D EF18.(本小题满分16分)设圆221:106320C x y x y +--+=,动圆222:22(8)4120 C x y ax a y a +---++=, (1)求证:圆1C 、圆2C 相交于两个定点;(2)设点P 是椭圆2214x y +=上的点,过点P 作圆1C 的一条切线,切点为1T ,过点P 作圆2C 的一条切线,切点为2T ,问:是否存在点P ,使无穷多个圆2C ,满足12PT PT =?如果存在,求出所有这样的点P ;如果不存在,说明理由.19. (本小题满分16分)已知数列{a n }的通项公式为a n = 2⨯3n + 23n – 1(n ∈N *). ⑴求数列{a n }的最大项;⑵设b n = a n + pa n– 2,试确定实常数p ,使得{b n }为等比数列;⑶设*,,,N m n p m n p ∈<<,问:数列{a n }中是否存在三项m a ,n a ,p a ,使数列m a ,n a ,p a 是等差数列?如果存在,求出这三项;如果不存在,说明理由.20.(本大题满分16分)已知函数()()||20,1x x f x a a a a=+>≠,(1)若1a >,且关于x 的方程()f x m =有两个不同的正数解,求实数m 的取值范围; (2)设函数()()[),2,g x f x x =-∈-+∞,()g x 满足如下性质:若存在最大(小)值,则最大(小)值与a 无关.试求a 的取值范围.2013年江苏高考数学最后一卷2013.06.01数学(加试部分)21.【选做题】在A 、B 、C 、D 四小题中只能选做两题....,每小题l0分,共计20分.请在答题..卡指定区域.....内作答,解答时应写出文字说明、证明过程或演算步骤. A.选修4 – 1几何证明选讲如图,△ABC 的外接圆的切线AE 与BC 的延长线相交于点E , ∠BAC 的平分线与BC 交于点D . 求证:ED 2= EB ·EC .B .矩阵与变换 已知矩阵2143-⎡⎤=⎢⎥-⎣⎦A ,4131-⎡⎤=⎢⎥-⎣⎦B ,求满足=AX B 的二阶矩阵X .C.选修4 – 4 参数方程与极坐标若两条曲线的极坐标方程分别为ρ = 1与ρ = 2cos(θ + π3),它们相交于A ,B 两点,求线段AB 的长.D.选修4 – 5 不等式证明选讲设a ,b ,c 为正实数,求证:a 3 + b 3 + c 3 + 1abc ≥2 3.【必做题】第22题、第23题,每题10分,共20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22. (本小题满分10分)如图,在四棱锥P – ABCD 中,底面ABCD 是边长为1的正方形,PA ⊥底面ABCD ,点M 是棱PCB C ED A的中点,AM ⊥平面PBD . ⑴求PA 的长;⑵求棱PC 与平面AMD 所成角的正弦值.23.(本小题满分10分)用,,,a b c d 四个不同字母组成一个含1+n *)(N n ∈个字母的字符串,要求由a 开始,相邻两个字母不同. 例如1=n 时,排出的字符串是,,ab ac ad ;2=n 时排出的字符串是,,,,,,,,aba abc abd aca acb acd ada adb adc ,……, 如图所示.记这含1+n 个字母的所有字符串中,排在最后一个的字母仍是a 的字符串的种数为n a .(1)试用数学归纳法证明:*33(1)(,1)4N n nn a n n +-=∈≥; (2)现从,,,a b c d 四个字母组成的含*1(,2)N n n n +∈≥个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是a 的概率为P ,求证:2193P ≤≤.P B CDA M ab c d n=1abcd n=2ad a b d a b c2010届江苏省海安高级中学、南京外国语学校、南京市金陵中学高三调研测试 数学参考答案及评分标准题号 1 2 3 4 5答案 2 3 1 10 {}11x x -<<题号 6 7 8 9 10 答案 15 0.7 6 –2 ④题号 111213 14答案{}01a a <≤()0,e 8()(),11,-∞-+∞15.解(1):因为点B 在以PA 为直径的圆周上,所以90ABP ∠=,所以34cos ,sin 55PB PA αα===.所以4tan 3α=,………………………………………2分 72cos cos()101527PB CPB PC αβ∠=-===,2sin()10αβ-=, 所以1tan()7αβ-=,………………………………………………………………4分 tan tan()tan tan[()]11tan tan()ααββααβααβ--=--==+-,…………………………6分又(0,)2πβ∈,所以4πβ=.………………………………………………………8分(2)2()AC PC PC PA PC PC PA PC ⋅=-⋅=-⋅…………………………11分2152152275()577249=-⨯⨯=-……………………………………………14分16. ⑴解:取CE 中点P ,连结FP ,BP ,因为F 为CD 的中点,所以FP //DE ,且FP = 12DE , …2分 又AB //DE ,且AB =12DE ,所以AB //FP ,且AB = FP ,所以四边形ABPF 为平行四边形,所以AF //BP . ……………4分 又因为AF ⊂/平面BCE ,BP ⊂平面BCE , 所以AF //平面BCE . …7分 (该逻辑段缺1个条件扣1分)⑵因为△ACD 为正三角形,所以AF ⊥CD .因为AB ⊥平面ACD ,DE //AB ,所以DE ⊥平面ACD ,ABEP又AF ⊂平面ACD ,所以DE ⊥AF . …………………9分 又AF ⊥CD ,CD ∩DE = D ,所以AF ⊥平面CDE .又BP //AF ,所以BP ⊥平面CDE . ……………………………12分 又因为BP ⊂平面BCE ,所以平面BCE ⊥平面CDE . ………………………………………14分17. 解:(1)当024n ≤≤且n *∈N 时,()36f n =,当3625≤≤n 且n *∈N 时,2412()363n f n -=⋅所以[]36(1)(2)(3)(24)S f f f f =+++++…[])36()26()25(f f f ++++=36×24+36×(1212121233131⎡⎤-⎢⎢⎥-⎢⎥⎣⎦=864+792=1656;…………………………2分另一方面,已经离开的游客总人数是:12(25)(26)(36)T g g g =+++12=×5121152⨯+⨯390=;………………………4分 所以361216563901266S S T =-=-=(百人)故当天下午3点整(即15点整)时,世博园区内共有游客1266百人. ……………6分 (2)当0)()(≥-n g n f 时园内游客人数递增;当0)()(<-n g n f 时园内游客人数递减. (i)当241≤≤n 时,园区人数越来越多,人数不是最多的时间;………………………8分 (ii)当3625≤≤n 时,令512036n -≤,得出31≤n ,即当3125≤≤n 时,进入园区人数多于离开人数,总人数越来越多;……………10分 (iii)当3632≤≤n 时,24123635120n n -⋅>-,进入园区人数多于离开人数,总人数越来越多;……………………………………………………………………………12分 (Ⅳ)当7237≤≤n 时, 令32165120n n -+=-时,42n =, 即在下午4点整时,园区人数达到最多.此后离开人数越来越多,故园区内人数最多的时间是下午4点整. ……………………14分 答:(1)当天下午3点整(即15点整)时,世博园区内共有游客1266百人;(2)在下午4点整时,园区人数达到最多.18.解(1)将方程2222(8)4120 x y ax a y a +---++=化为221612(224)0x y y x y a +-++-++=,令22161202240x y y x y ⎧+-+=⎨-++=⎩得42x y =⎧⎨=⎩或64x y =⎧⎨=⎩,所以圆2C 过定点(4,2)和(6,4),……………4分 将42x y =⎧⎨=⎩代入22106320x y x y +--+=,左边=1644012320+--+==右边,故点(4,2)在圆1C 上,同理可得点(6,4)也在圆1C 上,所以圆1C 、圆2C 相交于两个定点(4,2)和(6,4);……………6分(2)设00(,)P x y ,则221000010632PT x y x y =+--+,…………………………8分222000022(8)412 PT x y ax a y a =+---++, …………………………………10分12PT PT =即00001063222(8)412x y ax a y a --+=---++,整理得00(2)(5)0x y a ---=(*)………………………………………………12分存在无穷多个圆2C ,满足12PT PT =的充要条件为0022002014x y x y --=⎧⎪⎨+=⎪⎩有解,解此方程组得0020x y =⎧⎨=⎩或006545x y ⎧=⎪⎪⎨⎪=-⎪⎩,………………………………………………………………………………14分故存在点P ,使无穷多个圆2C ,满足12PT PT =,点P 的坐标为64(2,0)(,)55或-.………………16分19. 解 ⑴由题意a n = 2 + 43n – 1,随着n 的增大而减小,所以{a n }中的最大项为a 1 = 4.…4分 ⑵b n = 2 + 43n – 1 + p 43n – 1= (2 + p )(3n – 1) + 44 = (2 + p )3n + (2 – p )4,若{b n }为等比数列, 则b 2n +1 – b n b n +2= 0(n ∈N * )所以 [(2 + p )3n +1 + ( 2 – p )]2 – [{2 + p )3n + (2 – p )][(2 + p )3n +2 + (2 – p )] = 0(n ∈N *),化简得(4 – p 2)(2·3n +1 – 3n +2 – 3n ) = 0即– (4 – p 2)·3n ·4 = 0,解得p = ±2. ………………………7分 反之,当p = 2时,b n = 3n ,{b n }是等比数列;当p = – 2时,b n = 1,{b n }也是等比数列.所以,当且仅当p = ±2时{b n }为等比数列. ………………………………………………………………10分 ⑶因为4231m m a =+-,4231n n a =+-,4231p pa =+-,若存在三项m a ,n a ,p a ,使数列ma ,n a ,p a 是等差数列,则2n m p a a a =+,所以42(2)31n +-=4231m +-4231p++-,……………12分 化简得3(2331)1323n p n p m p m n m ----⨯--=+-⨯(*),因为*,,,N m n p m n p ∈<<,所以1p m p n -≥-+,1p m n m -≥-+,所以13333p mp n p n --+-≥=⨯,13333p m n m n m --+-≥=⨯,(*)的 左边3(23331)3(31)0np np n n p n ---≤⨯-⨯-=--<,右边13323130n mn m n m ---≥+⨯-⨯=+>,所以(*)式不可能成立,故数列{a n }中不存在三项m a ,n a ,p a ,使数列m a ,n a ,p a 是等差数列. ……………16分20.解:(1)令xa t =,0x >,因为1a >,所以1t >,所以关于x 的方程()f x m =有两个不同的正数解等价于关于t 的方程2t m t+=有相异的且均大于1的两根,即 关于t 的方程220t mt -+=有相异的且均大于1的两根, (2)分所以2280,1,2120m m m ⎧∆=->⎪⎪>⎨⎪⎪-+>⎩,…………………………………………………………………4分解得223m <<,故实数m 的取值范围为区间(22,3).……………………………6分 (2)||()2,[2,)x x g x a a x =+∈-+∞ ①当1a >时,a )0x ≥时,1x a ≥,()3x g x a =,所以 ()[3,)g x ∈+∞,b )20x -≤<时,211x a a≤<()2x x g x a a -=+,所以 ()221'()ln 2ln ln x x x xa g x a a a a a a --=-+=……8分ⅰ当2112a >即412a <<时,对(2,0)x ∀∈-,'()0g x >,所以 ()g x 在[2,0)-上递增, 所以 222()[,3)g x a a ∈+,综合a ) b )()g x 有最小值为222a a +与a 有关,不符合……10分 ⅱ当2112a ≤即42a ≥时,由'()0g x =得1log 22a x =-,且当12log 22a x -<<-时,'()0g x <,当1log 202a x -<<时,'()0g x >,所以 ()g x 在1[2,log 2]2a --上递减,在1[log 2,0]2a -上递增,所以min 1()log 22a g x g ⎛⎫=-= ⎪⎝⎭22a ) b ) ()g x 有最小值为22a 无关,符合要求.………12分②当01a <<时,a ) 0x ≥时,01x a <≤,()3x g x a =,所以 ()(0,3]g x ∈b ) 20x -≤<时,211x a a<≤,()2x x g x a a -=+,所以 ()221'()ln 2ln ln x x x xa g x a a a a a a --=-+= 0<,()g x 在[2,0)-上递减,所以 222()(3,]g x a a ∈+,综合a ) b ) ()g x 有最大值为222a a+与a 有关,不符合………14分 综上所述,实数a 的取值范围是42a ≥.………………………………………………16分数学Ⅱ(附加题)21.【选做题】在A 、B 、C 、D 四小题中只能选做两题....,每小题l0分,共计20分.请在答题..卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤. A.选修4 – 1几何证明选讲证明: 因为EA 是圆的切线,AC 为过切点A 的弦,所以 ∠CAE = ∠CBA . 又因为AD 是∠BAC 的平分线,所以∠BAD = ∠CAD 所以∠DAE = ∠DAC + ∠EAC = ∠BAD + ∠CBA = ∠ADE所以,△EAD 是等腰三角形,所以EA = ED . ……………………………………………………6分 又EA 2 = EC ·EB ,所以ED 2 = EB ·EC . ……………………………………………………………………………4分B .矩阵与变换: 解:由题意得1312221-⎡⎤⎢⎥=⎢⎥⎣⎦A,…………………………………………………5分 =AX B ,1319411222312151-⎡⎤⎡⎤--⎡⎤⎢⎥⎢⎥∴===⎢⎥⎢⎥⎢⎥-⎣⎦-⎣⎦⎣⎦X A B ………………………………………10分 C.选修4 – 4 参数方程与极坐标若两条曲线的极坐标方程分别为ρ = 1与ρ = 2cos(θ + π3),它们相交于A ,B 两点,求线段AB 的长. 解 首先将两曲线的极坐标方程化为直角坐标方程,得 x 2 + y 2 = 1与x 2 + y 2 – x +3y = 0……………………………………………………6分解方程组⎩⎪⎨⎪⎧x 2 + y 2 = 1x 2 + y 2 – x + 3y = 0 得两交点坐标(1,0),(–12, – 32)所以,线段AB 的长为(1 + 12)2 + (0 + 32)2=3即AB = 3.………………………………………………………………………………10分 D.选修4 – 5 不等式证明选讲设a ,b ,c 为正实数,求证:a 3 + b 3 + c 3 + 1abc ≥2 3.证明 因为a ,b ,c 为正实数,所以a 3 + b 3 + c 3≥33a 3b 3c 3 = 3abc >0…………………………5分B C ED A又3abc + 1abc ≥23abc ·1abc = 2 3.所以a 3 + b 3 + c 3 + 1abc ≥2 3.…………………………………………………………………10分【必做题】第22题、第23题,每题10分,共20分.请在答题..卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤.22.解 如图,以A 为坐标原点,AB ,AD ,AP 分别为x ,y ,z 轴建立空间直角坐标系,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),P (0,0,a ).因为M 是PC 中点,所以M 点的坐标为(12,12,a 2),所以AM →= (12,12,a 2),BD → = (–1,1,0),BP →= ( – 1,0,a ).⑴因为AM →⊥平面PBD ,所以AM →·BD → = AM →·BP →= 0.即– 12 + a 22 = 0,所以a = 1,即PA = 1. ………………………………………4分 ⑵由AD → = (0,1,0),M →= (12,12,12),可求得平面AMD 的一个法向量n = ( – 1,0,1).又CP → = ( – 1,–1,1).所以cos<n , CP →> =n ·CP→|n |·|CP →|= 22·3= 63. 所以,PC 与平面AMD 所成角的正弦值为63.……………………………10分 23.解(1):证明:(ⅰ)当1n =时,因为10a =,33(1)04+-=,所以等式正确. (ⅱ)假设n k =时,等式正确,即*33(1)(,1)4N k kk a k k +-=∈≥, 那么,1n k =+时,因为11133(1)4333(1)33(1)33444k k k k k k k kkk k a a ++++-⋅---+-=-=-==, 这说明1n k =+时等式仍正确.据(ⅰ),(ⅱ)可知,*33(1)(,1)4N n nn a n n +-=∈≥正确. ……………………………5分 (2)易知133(1)13(1)[1]4343n n nn nP +--=⋅=+, PB CDAMxyz①当n 为奇数(3n ≥)时,13(1)43n P =-,因为327n ≥,所以132(1)4279P ≥-=,又131(1)434n P =-<,所以2194P ≤<;②当n 为偶数(2n ≥)时,13(1)43n P =+,因为39n≥,所以131(1)493P ≤+=,又131(1)434n P =+>,所以1143P <≤.综上所述,2193P ≤≤.……………………………10分。
2014届一轮复习数学试题选编35几何证明(教师版)

【答案】A.选修4—1:几何证明选讲
证明:连结OC.设PAC=.
因为PC=AC,所以CPA=,COP= 2.
又因为PC与⊙O相切于点C,所以OCPC.
所以3= 90.所以= 30.
又设圆的半径为r,在Rt△POC中,
所以∠CFD=∠CEO=∠DEF,所以DF=DE.
因为DF是⊙O的切线,所以DF2=DB·DA.
所以DE2=DB·DA.
.(2009高考(江苏))如图,在四边形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
【答案】[解析]本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力。满分10分。
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
(1)求证: ;
(2)若 的半径为 , ,求 长.
【答案】A.(1)连结ON.因为PN切⊙O于N,所以 ,
所以 .
因为 ,所以 .
因为 于O,所以 ,
所以 ,所以 .
所以
(2) , , .
因为 ,
所以
.(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)选修4-1:几何证明选讲
如图,已知圆 ,圆 都经过点 , 是圆 的切线,圆 交 于点 ,连结 并延长交圆 于点 ,连结 .求证 .
2014届一轮复习数学试题选编27概率(学生版)

(2)若考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.试从至少正确完成2题的概 率分析比较两位考生的实验操作能力.
.(江苏省无锡市2013届高三上学期期末考试数学试卷)某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且都是整数分钟,经统计以往100位顾客办理业务所需的时间(t),结果如下:
.(江苏省连云港市2013届高三上学期摸底考试(数学)(选修物理))在4次独立重复试验中,随机事件A恰好发生l次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率p的取值范围是___________________.
.(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)已知数字发生器每次等可能地输出数字 或 中的一个数字,则连续输出的 个数字之和能被3整除的概率是___.
.(2009高考(江苏))现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为___★___.
.(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)如图,ABCD是4 5的方格纸,向此四边形ABCD内抛撒一粒豆子,则豆子恰好落在阴影部分内的概率为_______________
.(江苏省盐城市2013届高三10月摸底考试数学试题)已知甲、乙、丙三人在3天节日中值班,每人值班1天,那么甲排在乙前面值班的概率是________.
.(江苏省徐州市2013届高三期中模拟数学试题)在闭区间[-1,1]上任取两个实数,则它们的和不大于1的概率是_______________.
.(江苏省南京市2013届高三9月学情调研试题(数学)WORD版)有3个兴趣小组,甲、乙两位同学各参加其中一个小组,且他们参加各个兴趣小组是等可能的,则甲、乙两位同学参加同一个兴趣小组的概率为_______.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省盐城市2013届高三年级第二次模拟考试历史试题本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分。
考试用时100分钟。
第I卷(选择题共60分)一、选择题:本大题共20小题,每小题3分,共计60分。
在每小题列出的四个选项中,只有一项最符合题目要求。
1.西周在延续前代制度的基础上进行了一系列的完善与创新,以便达到“天下归周”、“天下归宗”和“天下归心”的目的。
下列与“天下归周”相对应的是A.禅让制B.分封制C.察举制D.郡县制2.下列古代生产工具中,功用明显不同于其它三项的是A.B.C.D.3.某位先秦思想家曾有如下评论:齐桓公致力连击诸侯,设法合作维持传统封建秩序,是个执行正道而不行诈谋的国君;晋文公虽协助周王定乱,却僭越礼制,想仿形天子礼仪,是个内行诈谋却装作遵循正道的国君。
该思想家应属于A.儒家B.法家C.道家D.墨家4根据表中东南行政区划设置变化过程的分析,不正确的是A.古代行政区划不断向东南拓展B.人口和经济重心有南移趋势C.中央政府对地方管理不断加强D.中央集权削弱地方权力加强.5.“积之而后高,尽之而后圣:故圣人也者,人之所积也”。
与此观点最接近的思想家是A.朱熹B.陆九渊C.李贽D.顾炎武A.自然经济逐步解体B.洋务经济兴起C.民族资本主义发展D.农民负担减轻7.某学者认为:“它标示的不只是这场战争失败的严峻性,更因为它标示着以商品和资本来改变中国传统社会的轨道,作为中国近代与中世纪的分界线是显而易见的。
”材料中的“它”指A.鸦片战争B.第二次鸦片战争C.甲午战争D.八国联军侵华战争8.辜鸿铭曾在北京大学任教,他梳着辫子走进课堂,学生们觉得很怪异,都在发笑。
辜平静地说:“你们笑我,无非是因为我的辫子。
我的辫子是有形的,可以剪掉,然而诸位同学脑袋里的辫子就不是那么好剪呀!”闻听此言,学生一片默然。
后来促成“同学脑袋里的辫子”逐步被“剪掉”的是①戊戌变法②辛亥革命③新文化运动④五四运动A.①②③B.①②④C.②③④D.③④9.1929年,蒋介石称赞太平天国之历史“为十九世纪东方第一光荣之历史”。
随后中华民国政府通过了《禁止污蔑太平天国案》。
但1930年后国民政府对太平天国运动则进行了全面否定和批判。
与此转变相关的主要因素是A.北伐战争胜利进军B.国共关系开始破裂C.农村革命根据地发展D.国内民主运动高涨10.右图为解放战争时期某一阶段战争形势示意图,与图中战役表述相关的是A.全面内战爆发B.实施战略反攻C.战略决战打响D.渡江战役开始11.建国以来,我国农村生产关系经历了从“一大二公”的人民公社到“保证国家的,留足集体的,剩下部是自己的”生产承包责任制的变化历程。
这从根本上反映了A.土地所有制变更B.分配方式调整C.生产关系变革D.生产规模缩小12.右图为2012年感动中国十大人物之一的台湾老兵高秉涵,他曾把上百位老兵的骨灰带回祖国大陆,使他们魂归故里。
高秉涵老人当选的主要因素是A.发展了“九二共识”B.推动了“一国两制”C.消除了两岸隔阂D.彰显了民族亲情13.菲律宾前外长卡洛斯·罗慕洛在谈到一次国际会议时说:“周恩来是我去时候的敌人,回来时候的朋友。
”这一认识是基于周恩来A.号召亚非国家实行不结盟政策B.首倡和平共处五项原则C.提出求同存异方针D.促成印度支那问题的和平解决14.在雅典民主政治发展过程中,“经济困境从此不再把人们排斥在政事管理之外”。
实现这一局面应归功于A.苏格拉底B.梭伦C.克里斯提尼D.伯利克里15.1832年、1867年和1884的三次议会改革是英国19世纪民主政治发展进程中的重要事件。
其中1832年改革扩大了工业资产阶级权利,1867年改革使小资产阶级和工人上层获得选举权,1884年改革赋予农业工人选举权利。
上述现象反映了19世纪的英国A.改革是推动民主政治发展的唯一方式B.全体人民的普选权得以实现C.工业革命的深入开展D.民主进程滞后于经济发展16.“不合宜者,渐渐澌灭,其合宜者,得以永存,此为天道自然之理。
但其说与耶稣之旨相反,故各国儒士,均不服其言。
初始辩驳蜂起,今佩服者渐多,而格致之学从此大为改变。
”文中“其说”是指A .牛顿运动三定律B .达尔文的进化论C .普朗克的量子论D 17.右图为一学术讲座的海报。
下列各项中与讲座主题内容不相符的是A .英国的国有化政策B .“福利国家”的出现C .凯恩斯主义的失灵D .自由主义的兴起 18.勃列日涅夫执政之初苏共中央文件指出:“近年来农业增长的速度减慢了,这给国家经济的发展造成了一定的困难。
破坏社会主义生产发展的经济规律,……,这些是农业落后的基本原因。
”这表明苏共中央A .正确揭示了农业发展缓慢的原因B .决定改变优先发展重工业的方针C .强化高度集中的计划经济管理体制D .在宏观调控的基础上扩大市场的作用19.据日本贸易振兴会统计,1996年全世界区域性经济合作和一体化组织共101个。
其中1979年以前12个、1980年—1989年20个、1990年后69个。
从区域分布来看,欧洲39个,南北美洲40个,亚洲6个,非洲8个,大洋洲1个,跨地区7个。
由此不能看出世界区域性合作和一体化组织A .地区分布不平衡B .跨地区现象出现C .90年代后增速加快D .阻碍经济全球化 20.他的作品是“动荡时局的最明确的表达”、“迎合了无神时代的猎奇和逃避心态”,他的艺术是“孩子式的病态”的“无理的表现,免费的游戏”。
下列绘画作品体现了上述说法的是A .B .C .D .第Ⅱ卷(非选择题共60分)二、非选择题:本大题共5小题,其中第21题15分,第22题12分,第23题13分,第24~25题各10分,共计60分。
要求分析材料,结合所学知识回答问题。
21.(15分)钱穆先生认为,元代社会经济、文化水准高出春秋时代百倍,但政治上却是倒退的。
阅读下列材料:材料一这座城(杭州)方圆约有一百英里,它的街道和运河都十分宽阔,还有许多广场或集市……。
这些广场的位置十分利于交易,每个市场在一星期的三天中,都有四五万人来赶集。
所有你能想到的商品,在市场上都有销售,……每一方形市场的对面有两个大公署,署内驻有大汗任命的官吏,负责解决外商与本地居民间所发生的各种争执,并且监视附近各桥梁的守卫是否尽忠职守,如有失职,则严惩不怠。
——《马可·波罗游记》材料二至(元)中叶以后,杂剧家悉为杭州人.……盖杂剧之根本地,已移而至南方,岂非以南宋旧都,文化颇盛之故欤。
……盖自唐宋以来,士之竞于科目者,已非一朝一夕之事,一旦废之,彼其才力无所用,而一于词曲发之。
——王国维《宋元戏曲考》材料三(元行省)军国重事,无不领之。
此由中央政府常派重臣镇压地方之上,实为一种变相之封建,而汉、唐州郡地方政府之地位,渺不再得,此制大体上为明、清所承袭,于地方政事之推进,有莫大损害。
自此遂只有中央临制地方,而中央、地方共同推行国政之意义遂失。
——钱穆《国史大纲》请回答:(1)据材料一,指出元代杭州商业发展的特点。
(4分)(2)依据材料一、二,分析杭州成为元杂剧中心的原因。
此外,你认为元杂剧繁荣还有哪些因素?(6分)(3)据材料三,你是否认同钱穆对行省制度的看法?并说明理由。
(3分)(4)综合上述材料,概括指出在人类历史发展过程中,政治与经济文化之间的相互关系。
(2分)22.(12分)阅读下列材料:材料一1912年3月5日临时大总统孙中山通令:“满虏窃国,易于冠裳,强行编发之制,悉以腥之俗,当其初,高士仁人或不屈被执,从容就义;或遁入流,以终余年……今者满廷已覆,民国成功,凡我同胞,允宜涤旧染之污,作新国之民。
”“以除虏俗,而壮观瞻。
”材料二(建国初期)受当时强劲的革命思潮的影响,中国人的服饰也在悄悄地发生变化,呈现出学习借鉴苏联服饰的趋势。
在当时,服装除了最基本的功能外,更承载者表达政治倾向和社会主义国际阵营之间牢不可破的友谊的政治使命。
苏联服装成为思想进步、追求革命的象征,主导着当时人们的服饰取向与选择。
列宁装、依照苏联坦克兵服装设计的“坦克服”、根据苏联款式仿制的各种“布拉吉(连衣裙)”是新中国成立初期闪耀在民众服装中的亮丽风景。
——彭国亮《印象中国民生记忆六十年》材料三20世纪60年代中期以后“文化大革命”兴起,在“破四旧”运动中,谁的穿戴如果被认为不符合无产阶级式样,或带有“封、资、修”的影响,就会在大街上被勒令停下来,强制剪掉头发,撕烂衣服,红卫兵拿着剪刀专干此事,小脚裤管是他们最为仇视的对象,见了就剪。
——彭国亮《印象中国民生记忆六十年》请回答:(1)依据上述材料,结合所学知识,分析近代以来社会服饰变革的主要因素有哪些?(3分)(2)著名历史学家冯尔康先生曾说:“冠服、发型的形成同人们的政治意识紧密联系。
”因此,在特定历史时期,相对应的服饰就成为特定的政治符号。
(9分)请依据上述材料,结合所学知识,加以论证。
(史论结合,逻辑严密,表述清楚,150字左右。
)23.(13分)当前对英国声称退出欧盟、希腊退出欧元区的讨论成为热点话题。
阅读下列材料:材料一近代史上,欧洲各国有众多的思想者一直在为实现欧洲统一进行理论上的探索。
然而,直至经历了两次世界大战血流成河的惨剧之后,欧洲人才痛定思痛,开始脚踏实地,向欧洲统一迈进。
——2002年1月《人民日报》海外版材料二政策设计人员认识到,共产党人正在利用欧洲危机,如果他们进一步得逞,美国安全将会面临严重威胁。
不过他们认为,美国援助欧洲的目的不在于应付共产主义的威胁,而在于恢复欧洲社会的生气和健全经济。
换句话说,其目的不是同共产主义作斗争,而是同经济失调作斗争,因为经济失调很容易使一切极权主义运动在欧洲社会混水摸鱼……——美国国务院政策设计委员会《关于美国援助西欧的政策》材料三60年代,法国不顾美国反对,成功地试验了第一颗原子弹并与中国建交。
70年代,联邦德国展开了旨在改善与苏联等东欧社会主义国家关系的“新东方政策”。
经过10年的不懈努力,英国终于在1973年成为欧洲共同体的成员国,结束了荚美特殊关系。
一一整理自2004年4月人教网材料四第二次世界大战以后,美国与欧共体国民生产总值占世界国民生产总值的比重如下:(注:以1974年时的欧洲共同体九国作为一个整体)——整理自2004年4月人教网请回答:(1)依据材料一指出欧洲开始迈向统一的条件。
(2分)(2)依据材料二分析美国设计对外援助计划的意图。
(3分)(3)依据材料三指出美欧关系发生了怎样的变化?结合材料四和所学知识分析其变化的原因和影响。
(6分)(4)综合上述材料谈谈你对当前欧洲局势的认识。
(2分)24.(10分)【历史上重大改革回眸】阅读下列材料:材料一王安石对变法前后社会景象的描述:(一)河北民,生近二边长辛苦,家家养子学耕织,输与官家事夷狄.今年大旱千里赤,州县仍催给河役。
