江苏省南京市2020届高三9月学情调研数学试题(教师版)

合集下载

2019-2020学年江苏省南京市高三上学期学情调研(9月) 数学

2019-2020学年江苏省南京市高三上学期学情调研（9月）数学（考试时间：120分钟满分：160分）一、填空题（满分每小题5分，共70分）1. 若a ＋i1－i(i 是虚数单位)是实数，则实数a 的值是____________． 2. 已知集合A ＝{x |x ＞1}，B ＝{x |x 2－2x ＜0}，则A ∪B ＝____________.3. 命题“若实数a 满足a ≤2，则a 2＜4”的否命题是______ (填“真”或“假”)命题．4.在如图所示的算法流程图中，若输入m ＝4，n ＝3，则输出的a ＝__________.(第4题)5.把一个体积为27 cm 3的正方体木块表面涂上红漆，然后锯成体积为1 cm 3的27个小正方体，现从中任取一块，则这一块至少有一面涂有红漆的概率为____________．6. 在约束条件⎩⎨⎧0≤x ≤1，0≤y ≤2，2y －x ≥1下，则x －12＋y 2的最小值为__________．7.设α、β是空间两个不同的平面，m 、n 是平面α及β外的两条不同直线．从“① m ⊥n ；② α⊥β；③ n ⊥β；④ m ⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：____________.(填序号)．8.在平面直角坐标系xOy 中，已知A 、B 分别是双曲线x 2－y 23＝1的左、右焦点，△ABC 的顶点C 在双曲线的右支上，则sin A －sin Bsin C的值是____________．9. 已知点A (0,2)，抛物线y 2＝2px (p ＞0)的焦点为F ，准线为l ，线段FA 交抛物线于点B ，过B 作l 的垂线，垂足为M ，若AM ⊥MF ，则p ＝__________.10. 若函数f (x )＝⎩⎨⎧2x，x ＜0，－2－x，x ＞0，则函数y ＝f (f (x ))的值域是____________． 11. 如图所示，在直三棱柱A 1B 1C 1—ABC 中，AC ⊥BC ，AC ＝4，BC ＝CC 1＝2.若用平行于三棱柱A 1B 1C 1—ABC 的某一侧面的平面去截此三棱柱，使得到的两个几何体能够拼接成长方体，则长方体表面积的最小值为________．(第11题)12. 已知椭圆x24＋y22＝1，A、B是其左、右顶点，动点M满足MB⊥AB，连结AM交椭圆于点P，在x轴上有异于点A、B的定点Q，以MP为直径的圆经过直线BP、MQ的交点，则点Q 的坐标为____________．13. 在△ABC中，过中线AD中点E任作一直线分别交边AB、AC于M、N两点，设AM→＝xAB→，AN→＝yAC→(x、y≠0)，则4x＋y的最小值是______________．14.设m∈N，若函数f(x)＝2x－m10－x－m＋10存在整数零点，则m的取值集合为______________．二、解答题（共六大题，满分90分）15．（本小题满分14分）已知函数的定义域为集合A，B={x|x＜a或x＞a+1}（1）求集合A；（2）若A⊆B，求实数a的取值范围．16、（本题满分14分）设p：实数x满足x2－5ax＋4a2<0(其中a>0)，q：实数x满足2<x≤5.(1)若a＝1，且p∧q为真，求实数x的取值范围；(2)若q是p的必要不充分条件，求实数a的取值范围．17、（本题满分15分）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且．(1)确定角的大小：（2）若c＝,且△ABC的面积为,求a＋b的值．18、（本题满分15分）某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度)．设该蓄水池的底面半径为r米，高为h 米，体积为V立方米．假设建造成本仅与表面积有关，侧面的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12 000π元(π为圆周率)．(1)将V表示成r的函数V(r)，并求该函数的定义域；(2)讨论函数V(r)的单调性，并确定r和h为何值时该蓄水池的体积最大．19．（本题满分16分）已知定义在R上的函数f（x）满足为常数（1）求函数f（x）的表达式；（2）如果f（x）为偶函数，求a的值；（3）当f（x）为偶函数时，若方程f（x）=m有两个实数根x1，x2；其中x1＜0，0＜x2＜1；求实数m的范围．20．（本题满分16分）设函数f（x）=ax3+bx2+cx+d（a、b、c、d∈R）满足：∀x∈R都有f （x）+f（﹣x）=0，且x=1时，f（x）取极小值．（1）f（x）的解析式；（2）当x∈[﹣1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直：（3）设F（x）=|xf（x）|，证明：时，．2019-2020学年江苏省南京市高三上学期学情调研（9月）数学参考答案一、填空题：（每题满分5分共70分）1. －12. {x|x＞0}3. 真4. 125. 26276.2557. ①③④⇒②(或②③④⇒①)8. －129. 210.⎝⎛⎭⎪⎫－1，－12∪⎝⎛⎭⎪⎫12，111. 2412. (0,0)13.9414.{0,3,14,30}二、解答题：（共六道题）15、（本题满分14分）解：（1）由，得：，解得：x≤﹣1或x＞2，所以A=（﹣∞，﹣1]∪（2，+∞）-----------------------7分．（2）A=（﹣∞，﹣1]∪（2，+∞），B={x|x＜a或x＞a+1}因为A⊆B，所以，解得：﹣1＜a≤1，所以实数a的取值范围是（﹣1，1]-------------------14分．16、（本题满分14分）解(1)当a＝1时，x2－5ax＋4a2<0即为x2－5x＋4<0，解得1<x<4，当p为真时，实数x的取值范围是1<x<4.若p∧q为真，则p真且q真，所以实数x的取值范围是(2,4)-----------7分．(2)綈q是綈p的必要不充分条件，即p是q的必要不充分条件．设A＝{x|p(x)}，B＝{x|q(x)}，则B A.由x2－5ax＋4a2<0得(x－4a)(x－a)<0，∵a>0，∴A＝{x|a<x<4a}，又B＝{x|2<x≤5}，则a≤2且4a>5，解得54<a≤2.∴实数a的取值范围是⎝⎛⎦⎥⎤54，2.----14分17、（本题满分15分）17．（本小题满分15分）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且．(1)确定角的大小：（2）若c＝,且△ABC的面积为,求a＋b的值．解（1）由及正弦定理得，， ·························· 2分,············································································ 4分是锐角三角形，，．················································ 7分（2）解法1：由面积公式得，由余弦定理得····················11分由②变形得·································································15分解法2：前同解法1，联立①、②得， ········································11分消去b并整理得，解得，所以故． ···································15分18、（本题满分15分）解(1)因为蓄水池侧面的总成本为100·2πrh＝200πrh元，底面的总成本为160πr2元．所以蓄水池的总成本为(200πrh＋160πr2)元．又根据题意得200πrh＋160πr2＝12 000π，所以h＝15r(300－4r2)，从而V(r)＝πr2h＝π5(300r－4r3)．因r>0，又由h>0可得0＜r<53，故函数V(r)的定义域为(0,53)---------7分．(2)因V(r)＝π5(300r－4r3)(0＜r＜53)，故V′(r)＝π5(300－12r2)，令V′(r)＝0，解得r＝5或－5(因r＝－5不在定义域内，舍去)．当r∈(0,5)时，V′(r)>0，故V(r)在(0,5)上为增函数；当r∈(5,53)时，V′(r)<0，故V(r)在(5,53)上为减函数．由此可知，V(r)在r＝5处取得最大值，此时h＝8.即当r＝5，h＝8时，该蓄水池的体积最大．------------------------13分答：----------------， ----------------------------------15分（答，单位各一分）19．（本题满分16分）解：（1）∵为常数令t=则x=∴f（t）==2﹣t+a•2t 从而有f（x）=2﹣x+a•2x；------------------4分（2）∵f（x）为偶函数，∴f（﹣x）=f（x）∴2x+a•2﹣x=2﹣x+a•2x整理可得，（a﹣1）•2x=（a﹣1）•2﹣x∴a=1------------------------------------------------------------------------------------8分（3）由（2）可得f（x）为偶函数，a=1，f（x）=2x+2﹣x令n=2x，n＞0，f（n）=n+，n＞0的图象如图，结合图象可得方程f（x）=m有两个实数根x1，x2，其中x1＜0，0＜x2＜1⇔f（n）=m有两个实数根n1，n2其中0＜n1＜1，1＜n2＜2而函数f（n）=n+在（0，1）上单调递减，在（1，2）单调递增结合图象可得，函数有两个交点-------------------------------------------------16分20．（16分）解：（1）因为，∀x∈R，f（﹣x）=﹣f（x）成立，所以：b=d=0，由：f'（1）=0，得3a+c=0，由：，得解之得：，c=﹣1从而，函数解析式为：----------------------------------5分（2）由于，f'（x）=x2﹣1，设：任意两数x1，x2∈[﹣1，1]是函数f（x）图象上两点的横坐标，则这两点的切线的斜率分别是：k1=f'（x1）=x12﹣1，k2=f'（x2）=x22﹣1又因为：﹣1≤x1≤1，﹣1≤x2≤1，所以，k1≤0，k2≤0，得：k1k2≥0知：k1k2≠﹣1故，当x∈[﹣1，1]是函数f（x）图象上任意两点的切线不可能垂直（10分）（3）当：时，x2∈（0，3）且3﹣x2＞0此时F（x）=|xf（x）|===当且仅当：x2=3﹣x2，即，取等号，故；（16分）。

【数学】南京2020届高三年级学情调研卷及解析

159
1800,
t
2
,
4t 9t
9, 15,
其中
t
N
（1）若平均每趟地铁的载客人数不超过 1500 人，试求发车时间间隔 t 的值；
（2）若平均每趟地铁每分钟的净收益为 Q 6 p t 7920 100（单位：元），问当发车时间
t 间隔 t 为多少时，平均每趟地铁每分钟的净收益最大？并求出最大净收益.
3
tan
1 ，则 tan 2 的值为
.
10. 已知函数 f x x ，则不等式 f x 3 f 2x 0 的解集为
.
1 x
11. 等差数列an 的前 n 项和记为 Sn ，已知 a1 a4 a7 =99，a2 a5 a8 93 ，若存在正整
数 k ，使得对任意 n N* ，都有 Sn Sk 恒成立，则 k 的值为__________
3a4 99 ，∴ a4 33 ， 3a5 93，∴ a5 31，∴ d 2 ， a1 39 ，
Sn n2 40n ， Sn 最大值为 S20 ，所以 k 20 .
【点评】此题考查的是对等差数列求 n 项和的表达式配方求最值的题型，该题属于基础题
南京市 2020 届高三年级学情调研数学
2019.09 注意事项：
1．本试卷共 4 页，包括填空题（第 1 题~第 14 题）、解答题（第 15 题~第 20 题）两部分．本试卷满分为 160 分，考试时间为 120 分钟．
2．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡上对应题目的答案空格内．考试结束后，交回答题卡．参考公式：柱体的体积公式：V Sh ，其中 S 为柱体的底面积， h 为柱体的高. 球的体积公式：V 4 R3 ，其中 R 为球体的半径.

南京市2020届高三年级学情调研卷(定稿)

南京市2020届高三年级学情调研数学 2019.09注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡．参考公式：柱体的体积公式：V ＝Sh ，其中S 为柱体的底面积，h 为柱体的高．球的体积公式：V ＝43πR 3，其中R 为球体的半径．一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答．题卡．．相应位置．．．．上． 1．函数f (x )＝x －1的定义域为 ▲ ．2．已知复数z 满足(z －2)i ＝1＋i ，其中i 是虚数单位，则复数z 的模为 ▲ ． 3．某算法的流程图如图所示，则输出的n 的值为 ▲ ．4．某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，则图中x 的值为 ▲ ．（第3题图）（第4题图）5．有3个兴趣小组，甲、乙两位同学各自选择其中一个参加，且每位同学参加各个兴趣小组的可能性相同，则这两位同学参加了不同的兴趣小组的概率为 ▲ ．6．把一个底面半径为3 cm ，高为4 cm 的钢质实心圆柱熔化，然后铸成一个实心钢球（不计损耗），则该钢球的半径为 ▲ cm ．7．在平面直角坐标系xOy 中，若双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一条准线与两条渐近线恰能围成一个等边三角形，则该双曲线的离心率为 ▲ ．8．若函数f (x )＝2sin(ωx －π6)(ω＞0)的最小正周期为π，则当x ∈[0，π2]时，f (x )的值域为 ▲ ．9．若锐角α满足tan(α＋π4)＝3tan α＋1，则tan2α的值为 ▲ ．10．已知函数f (x )＝x1＋|x |，则不等式f (x －3)＋f (2x )＞0的解集为 ▲ ．11．等差数列{a n }的前n 项和记为S n ．已知a 1＋a 4＋a 7＝99，a 2＋a 5＋a 8＝93，若存在正整数k ，使得对任意n ∈N *，都有S n ≤S k 恒成立，则k 的值为 ▲ ．12．在△ABC 中，P 是边AB 的中点，已知CA ＝4，CP ＝3，∠ACB ＝2π3，则CP →·CA →的值为 ▲ ．13．在平面直角坐标系xOy 中，已知圆M ：(x －a )2＋(y －2a )2＝4，圆N ：(x －2)2＋(y ＋1)2＝4．若圆M 上存在一点P ，使得以点P 为圆心，1为半径的圆与圆N 有公共点，则实数a 的取值范围为 ▲ ．14. 已知函数f (x )＝x 3－3x 2＋1，g (x )＝⎩⎪⎨⎪⎧|2x －1|＋1， x ＞0，－14x 2－x ， x ≤0．若函数y ＝g [f (x )]－a 有6个零点（互不相同），则实数a 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答．题卡．．指定区域内．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a sin2B ＝2b sin A ．（1）求B 的大小；（2）若cos C ＝55，求sin(A －C )的值．16．（本小题满分14分）如图，在三棱柱ABC －A 1B 1C 1中，AC ＝BC ，E ，F 分别为AB ，A 1B 1的中点．（1）求证：AF ∥平面B 1CE ；（2）若A 1B 1⊥B 1C ，求证：平面B 1CE ⊥平面ABC ．17．（本小题满分14分）随着城市地铁建设的持续推进，市民的出行也越来越便利．根据大数据统计，某条地铁线路运行时，发车时间间隔t （单位：分钟）满足：4≤t ≤15，t ∈N ，平均每趟地铁的载客人数p (t )（单位：人）与发车时间间隔t 近似地满足下列函数关系：p (t )＝⎩⎨⎧1800－15(9－t )2， 4≤t ＜9，1800， 9≤t ≤15，其中t ∈N ．（1）若平均每趟地铁的载客人数不超过1500人，试求发车时间间隔t 的值；（2）若平均每趟地铁每分钟的净收益为Q ＝6p (t )－7920t －100（单位：元），问当发车时间间隔t 为多少时，平均每趟地铁每分钟的净收益最大？并求出最大净收益．1（第16题图）18．（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右顶点分别为A ，B ，点(a2，3e )和(b ，3e )都在椭圆上，其中e 为椭圆的离心率．（1）求椭圆的标准方程；（2）若点C 是椭圆上异于左、右顶点的任一点，线段BC 的垂直平分线与直线BC ，AC 分别交于点P ，Q ，求证：→OB ·→PQ 为定值．19．（本小题满分16分）已知函数f (x )＝2ln x ＋ax 2－bx ，a ，b ∈R ．（1）若曲线y ＝f (x )在x ＝1处的切线为y ＝2x －3，求实数a ，b 的值；（2）若a ＝0，且f (x )≤－2对一切正实数x 恒成立，求实数b 的取值范围；（3）若b ＝4，求函数f (x )的单调区间．20．（本小题满分16分）已知数列{a n }的首项a 1＝2，前n 项和为S n ，且数列{S n n }是以12为公差的等差数列.（1）求数列{a n }的通项公式；（2）设b n ＝2n a n ，n ∈N *，数列{b n }的前n 项和为T n ， ①求证：数列{T nn}为等比数列；②若存在整数m ，n (m ＞n ＞1)，使得T m T n ＝m (S m ＋λ)n (S n ＋λ)，其中λ为常数，且λ≥－2，求λ的所有可能值.（第18题图）。

江苏省南京市2020届高三9月学情调研数学试题(学生版)

南京市2020届高三年级学情调研卷数学2019.09参考公式：柱体的体积公式：V=Sh ，其中S 为为柱体的底面积，h 为柱体的高. 球的体积公式：343V R π=，其中R 为球体的半径. 一、填空题：(请将答案写在答题卡相应位置．)1.函数()f x =的定义域是2.已经复数z 满足(2)1z i i -=+（i 是虚数单位），则复数z 的模是________．3.某算法的流程图如图所示，则物出的n 的值为_______．4.某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），［50，60)，［60，70)，［70，80），［80，90），［90，100〕，则图中x 的值为_______5.有3个兴趣小组，甲、乙两位同学各自选择其中一个参加，且每位同学参加各个兴趣小组的可能性相同，则这两位同学参加了不同的兴趣小组的概率为______6.把一个底面半径为3cm ，高为4 cm 的钢质实心圆柱熔化，然后铸成一个实心钢球(不计损耗），则该钢球的半径为_______cm7.在平面直角坐标系xoy 中，若双曲线22221(0,0)x y a b a b-=>>的一条准线与两条渐近线恰能围成一个等边三角形，则该双曲线的离心率为______．8.若函数()2sin()(0)6f x x πωω=->的最小正周期为π，则当[0,]2x π∈时，()f x 的值域为_______． 9.若锐角α满足tan （α＋4π）＝3tanα＋1，则tan 2α的值为_____． 10.已知函数()1||x f x x =+，则不等式(3)(2)0f x f x -+>的解集为____． 11.等差数列｛n a ｝的前n 项和记为n S ，已知147a a a ++＝99，258a a a ++＝93，若存在正整数k ，使得对任意n *N ∈，都有n k S S ≤恒成立，则k 的值为_______．12.在△ABC 中，点P 是边AB 的中点，已知CA ＝4，CP ACB ＝23π，则CP CA 的值为______． 13.在平面直角坐标系xoy 中，已知圆M:22()(2)4x a y a -+-=，圆N ：22(2)(1)4x y -++=，若圆M上存在一点P ，使得以点P 为圆心，1为半径的圆与圆N 有公共点，则实数a 的取值范围为________．14.已知函数32()31f x x x =-+，2211,0()1,04x x g x x x x ⎧-+⎪=⎨--≤⎪⎩＞.若函数[]()y g f x a =-有6个零点（互不相同），则实数a 的取值范围为______．二、解答题。

江苏省南京市届三9月学情调研数学试题x

江苏省南京市届三9月学情调研数学试题x南京市 20xx 届高三年级学情调研卷数学20xx.09．．．．．．．一、填空题：本大题共14 小题，每小题5 分，共70 分．请把答案填写在答题卡相应位置上．22▲．1．函数 f(x)＝ cos x－ sin x 的最小正周期为1，其中 i 是虚数单位，则 |z|＝▲．2．已知复数 z＝ 1＋i3．某学校高一、高二、高三年级的学生人数之比为4：3： 3，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80 的样本，则应从高一年级抽取▲名学生．4．从甲、乙、丙、丁 4 位同学中随机选出 2 名代表参加学校会议，则甲被选中的概率是▲．5．已知向量a＝ (2， 1)， b＝ (0，－ 1)．若 (a＋λb) ⊥ a，则实数λ＝▲．6．右图是一个算法流程图，则输出S 的值是▲．开始S←0k← 1k←k＋2 S←S＋ k2 Nk＞5Y输出 S7．已知双曲线x2y2结束2－ 2＝ 1(a＞ 0， b＞0)的渐近线方程ab（第 6为 y＝±3x，则该双曲线的离心率为▲．题图）8．已知圆锥的侧面展开图是一个半径为2 的半圆，则这个圆锥的高是▲．9．设 f(x)＝ x2－ 3x＋ a．若函数 f(x)在区间 (1，3) 内有零点，则实数 a 的取值范围为▲．10．在△ ABC 中，角 A，B， C 所对边的长分别为a， b，c．已知 a＋2c＝ 2b， sinB＝ 2sinC，则 cosA＝▲．a，x 1，11．若 f(x)＝ xa 的取值范围为是 R 上的单调函数，则实数▲．x＋ 3a， x＜112．记数列 { an} 的前 n 项和为 Sn．若 a1＝ 1，Sn ＝2(a1 ＋an )(n≥2，n∈ N*) ，则 Sn ＝▲．13．在平面直角坐标系 xOy 中，已知圆 C：x2＋ y2－ 6x＋ 5＝ 0，点 A，B 在圆 C 上，且 AB＝ 23，则→→| OA ＋ OB |的最大值是▲．14．已知函数f(x)＝ x－ 1－ (e－ 1)ln x，其中e 为自然对数的底，则满足f(ex)＜ 0的x 的取值范围为▲．二、解答题：本大题共 6 小题，共计．．．．．．．． 90 分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14 分）π已知函数f(x)＝ 2sin(2x＋φ)(0 ＜φ＜2π)的图象过点 (2 ，－2)．（ 1）求φ的值；α 6，－πα－π（ 2）若 f()＝＜α＜ 0，求 sin(2) 的值．252616．（本小题满分14 分）如图，三棱柱 ABC－A1B1C1 中， M， N 分别为 AB， B1C1 的中点．1）求证：MN ∥平面 AA1C1C；2）若 CC1＝ CB1， CA＝CB ，平面CC1B1B⊥平面 ABC，求证： AB 平面 CMN ．C1NB1 A1CB M A（第 16 题图）17．（本小题满分14 分）已知 { an} 是等差数列，其前n 项的和为Sn， { bn} 是等比数列，且a1＝ b1＝ 2， a4＋ b4＝ 21，S4＋ b4＝ 30．1）求数列 { an} 和 { bn} 的通项公式；2）记 cn＝ an bn，n∈ N* ，求数列 { cn} 的前 n 项和．18．（本小题满分16 分）x2y22222给定椭圆 C：a2＋b2＝ 1(a＞ b＞ 0)，称圆 C1： x＋ y＝a ＋ b为椭圆 C 的“伴随圆”．已知椭圆3C 的离心率为 2 ，且经过点 (0， 1)．（ 1）求实数 a， b 的值；（ 2）若过点 P(0， m)(m＞ 0)的直线 l 与椭圆 C 有且只有一个公共点，且 l 被椭圆 C 的伴随圆 C1所截得的弦长为 2 2，求实数m 的值．19．（本小题满分16 分）如图（示意），公路AM、 AN 围成的是一块顶角为α的角形耕地，其中tanα＝－ 2．在该块土地中 P 处有一小型建筑，经测量，它到公路AM ，AN 的距离分别为3km，5km ．现要过点P 修建一条直线公路 BC，将三条公路围成的区域ABC 建成一个工业园．为尽量减少耕地占用，问如何确定 B 点的位置，使得该工业园区的面积最小？并求最小面积．NC·PαMA B（第 19 题图）20．（本小题满分16 分）已知函数f(x)＝ ax3＋ |x－ a|，a∈ R ．1）若 a＝－ 1，求函数 y＝f(x) (x∈ [0，＋∞ ))的图象在 x＝ 1 处的切线方程；2）若 g(x)＝ x4，试讨论方程 f(x)＝ g(x)的实数解的个数；（ 3）当 a＞ 0 时，若对于任意的x1∈ [a，a＋ 2]，都存在x2∈[a ＋2，＋∞ )，使得 f(x1)f(x2)＝ 1024，求满足条件的正整数 a 的取值的集合．南京市 20xx 届高三年级学情调研卷数学附加题20xx.09．．．．21．【选做题】在 A、 B、C、 D 四小题中只能选做 2 题，每小题10 分，共计 20 分．请在答卷卡指．．．．定区域内作答．解答应写出文字说明、证明过程或演算步骤．A．选修 4— 1：几何证明选讲如图， PA 是圆 O 的切线， A 为切点， PO 与圆 O 交于点 B、C，AQ OP，垂足为 Q．若 PA＝ 4，PC＝ 2，求 AQ 的长．AP C Q O BB．选修 4— 2：矩阵与变换（第 21 题 A 图）已知矩阵 A＝2b113属于特征值的一个特征向量为α＝－ 1．（ 1）求实数 b，的值；（ 2）若曲线 C 在矩阵 A 对应的变换作用下，得到的曲线为 C ： x2＋2y2＝ 2，求曲线 C 的方程．C．选修 4— 4：坐标系与参数方程3在平面直角坐标系xOy 中，已知直线x＝3＋2 t，)，圆 C 的参数l 的参数方程为1(t 为参数y＝ 2＋2t方程为 x＝ 3＋cosθ，(θ为参数 ) ．若点 P 是圆 C 上的动点，求点P 到直线 l 的距离的最小值．y＝sinθD．选修 4— 5：不等式选讲已知 a， b 是正数，且a＋ b＝ 1，求证： (ax＋ by)( bx＋ay)≥xy．．．．．．．．．【必做题】第 22 题、第 23 题，每题10 分，共计20 分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．22．如图，已知长方体ABCD － A1B1C1D1 中， AB＝ 3，BC ＝2，CC1＝ 5，E 是棱 CC1 上不同于端→→点的点，且CE ＝λCC1．（ 1）当∠ BEA1 为钝角时，求实数λ的取值范围；2（ 2）若λ＝ 5，记二面角 B1－ A1B－ E 的的大小为θ，求|cosθ|．D 1 C1B1A1EDCA B（第 22 题图）23．某商店为了吸引顾客，设计了一个摸球小游戏，顾客从装有 1 个红球， 1 个白球， 3 个黑球的袋中一次随机的摸2 个球，设计奖励方式如下表：结果奖励1 红 1 白10 元1 红 1 黑5 元2 黑2 元1 白 1 黑不获奖1）某顾客在一次摸球中获得奖励X 元，求 X 的概率分布表与数学期望； 2）某顾客参与两次摸球，求他能中奖的概率．20xx 届高三年级学情调研卷数学参考答案及评分标准20xx.09一、填空题：本大题共14小题，每小题5 分，共 70分．1．π2．24． 15． 522926． 357． 28． 39． (0， 4]10． 411． [1，＋∞ )12． 2－ 2n－ 113． 814．(0， 1)2二、解答题：本大题共6 小题，共计90 分．15．（本小题满分14 分）π解：（ 1）因为函数 f(x)＝2sin(2 x＋φ)(0 ＜φ＜2π)的图象过点( ，－ 2)，2π所以 f(2)＝2sin(π＋φ)＝－ 2，即sinφ＝ 1．,,,,,,,,,,,,,,,,,π因为 0＜φ＜2π，所以φ＝2．,,,,,,,,,,,,,,,,,6 分（ 2）由（ 1）得， f( x)＝ 2cos2x．,,,,,,,,,,,,,,,,8 分α63因为 f()＝5，所以cosα＝．25又因为－π4．,,,,,,,,,,,,,,10 分＜α＜ 0，所以sinα＝－252427所以sin2α＝2sinαcosα＝－ 25，cos2α＝2cos α－ 1＝－25．,,,,,,,,12 分从而sin(2α－πππ7－ 24 3,,,,,,,,14 分6)＝sin2αcos －cos2αsin ＝．665016．（本小题满分 14 分）证明：（ 1）取 A1C1 的中点 P，连接 AP， NP．C1NP1因为 C1 N＝ NB1， C1P＝ PA1 ，所以NP∥ A1B1， NP＝B12 分A1B1 ． ,,,,,,,,A12在三棱柱 ABC－ A1B1C1 中，A1B1∥ AB， A1B1＝ AB． C故NP∥ AB，且1NP＝AB ．2BMA（第 16 题图）因为 M 为 AB 的中点，所以1AM ＝ AB．2所以 NP＝ AM，且NP∥ AM．所以四边形 AMNP 为平行四边形．所以MN ∥ AP．,,,,,,,,,,,,,,,4 分因为 AP平面 AA1C1C，MN平面 AA1C1C，所以MN ∥平面 AA1C1C．,,,,,,,,,,,,,,,,,,6 分（ 2）因为 CA＝ CB， M 为 AB 的中点，所以CM ⊥ AB． ,,,,,,,,,,,8 分因为 CC1＝ CB1， N 为 B1C1 的中点，所以CN⊥B1C1．在三棱柱 ABC－ A1B1C1 中，BC∥B1C1，所以 CN BC．因为平面CC 1B1B⊥平面 ABC ，平面CC1B1B∩平面 ABC＝ BC． CN平面 CC1B1B，所以CN⊥平面 ABC．,,,,,,,,,,,,,,10 分因为 AB平面 ABC ，所以CN⊥ AB．,,,,,,,,,,,,,,12 分因为 CM平面 CMN ， CN 平面 CMN ，CM ∩ CN＝ C，所以AB⊥平面 CMN ．,,,,,,,,,,,,,,14 分17．（本小题满分 14 分）解：（1）设等差数列 { an } 的公差为 d，等比数列 { bn} 的公比为q．由 a1＝ b1＝ 2，得 a4＝ 2＋ 3d， b4＝ 2q3， S4＝ 8＋ 6d．,,,,,,,,,,,, 3 分由条件 a4＋ b4＝21， S4＋ b4＝ 30，得方程组2＋ 3d＋ 2q3＝ 21，解得d＝ 1，3q＝ 2．8＋ 6d＋ 2q ＝ 30，所以 an＝ n＋1， bn＝ 2n，n∈ N* ．,,,,,,,,,,,,7 分（ 2）由题意知， cn＝ (n＋1)× 2n．Tn＝ c1＋ c2＋ c3＋, ＋ cn．Tn＝ c1＋ c2＋ c3＋, ＋ cn＝2× 2＋3× 22＋4× 23＋, ＋n× 2n－ 1＋(n＋1)× 2n，2 Tn＝2× 22＋3× 23 ＋, ＋ (n－1)× 2n－ 1＋n× 2n＋(n＋ 1)2n＋ 1，232n)－ (n＋n＋1， ,,,,,,,,,,,11 分所以－ Tn ＝2× 2＋ (2 ＋ 2 ＋, ＋1)× 2即 Tn＝n· 2n＋ 1，n∈ N* ．,,,,,,,,,,,,14 分18．（本小题满分16 分）解：（1）记椭圆C 的半焦距为 c．由题意，得b＝ 1， ac＝ 23， c2＝ a2＋ b2，解得 a＝ 2， b＝ 1．,,,,,,,,,,,,,,,,,, 4 分22）由（ 1）知，椭圆 C 的方程为 x ＋ y2＝ 1，圆 C1 的方程为 x2＋ y2＝ 5． 4显然直线l 的斜率存在．设直线 l的方程为 y＝ kx＋m，即 kx－ y＋ m＝ 0． ,,,,,,,,,,,,,, 6 分因为直线l 与椭圆 C 有且只有一个公共点，y＝ kx＋ m，2故方程组x ＋ y2＝ 1 （ * ）有且只有一组解．由（ * ）得 (1＋ 4k2)x2＋ 8kmx＋ 4m2－ 4＝0．从而△＝ (8km)2－ 4(1＋ 4k2)( 4m2－ 4)＝ 0．化简，得 m2＝ 1＋4k2．①,,,,,,,,,,,,,,,,10 分因为直线 l 被圆 x2＋ y2＝ 5所截得的弦长为 22，所以圆心到直线l 的距离 d＝5－ 2＝ 3．即|m|＝ 3．②,,,,,,,,,,,,,,,14 分k2＋ 1由①②，解得 k2＝ 2， m2＝ 9．因为 m＞ 0，所以 m＝ 3．,,,,,,,,,,,,,,,16 分19．（本小题满分 16 分）解：（方法一）如图 1，以 A 为原点， AB 为 x 轴，建立平面直角坐标系． Ny因为tanα＝－ 2，故直线 AN 的方程是 y＝－ 2x．C设点 P(x0， y0)．P·因为点 P 到 AM 的距离为 3，故 y0＝ 3．由 P 到直线 AN 的距离为5，(A) OBx（第 19 题图 1）得∣ 2x0＋y0∣ ＝5，解得 x ＝ 1 或 x ＝－ 4(舍去 )，5所以点 P(1， 3)．,,,,,,,,,,,,4 分显然直线 BC 的斜率存在．设直线BC 的方程为y－ 3＝ k(x－ 1)，k∈ (－ 2， 0)．令 y＝ 0得 x ＝ 1－ 3．,,,,,,,,,,,,6 分Bk由 y－ 3＝k(x－1)，解得 y＝6－ 2k．,,,,,,,,,,,,8 分y＝－ 2xCk＋ 21－ k2＋ 6k－ 98k－ 9设△ ABC 的面积为 S，则S＝ 2 xB yC＝k2＋ 2k＝－ 1＋k2＋ 2k．,,,,,10 分－ 2(4k＋ 3)(k－ 3)＝ 0 得 k＝－ 3或 k＝3．由 S ＝2＋ 2k)24当－ 2＜ k＜－ 3时， S ＜ 0， S 单调递减；当－ 3＜k＜ 0 时， S ＞0， S 单调递增．,13 分443所以当 k＝－4时，即 AB＝5 时， S 取极小值，也为最小值15．答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分（方法二）如图 1，以 A 为原点， AB 为 x 轴，建立平面直角坐标系．因为tanα＝－ 2，故直线AN 的方程是 y＝－ 2x．设点 P(x0， y0)．因为点 P 到 AM 的距离为 3，故 y0＝ 3．由 P 到直线 AN 的距离为5，得∣ 2x0＋y0∣5，解得 x0＝ 1 或 x0＝－ 4(舍去 )，＝5所以点 P(1， 3)．显然直线BC 的斜率存在．设直线BC 的方程为令 y＝ 0 得 xB＝ 1－ k．y－ 3＝k(x－1)，解得 yC＝6－ 2k． y＝－ 2x＋ 2k,,,,,,,,,,,,y－ 3＝ k(x－ 1)，k∈ (－ 2， 0)． ,,,,,,,,,,,,,,,,,,,,,,,,分分分设△ ABC 的面积为 S，则 S＝ 1xB yC＝－ k2＋ 6k－ 98k2－ 9 ． ,,,,,2＝－ 1＋2k＋ 2kk ＋ 2kt＋ 9令 8k－ 9＝ t，则t∈ (－25，－ 9)，从而 k＝8 ．因此 S＝－ 1＋t＝－ 1＋ 264t＝－ 1＋64．,,,,t＋9 2t＋ 9＋ 34t＋225(＋2×t34＋ t＋2258)8t因为当t∈ (－ 25，－ 9)时， t＋225∈ (－ 34，－ 30] ， t分分当且仅当t＝－ 15 时，此时 AB＝ 5， 34＋ t＋225的最大值为4．从而 S 有最小值为 15．t答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分（方法三）如图 2，过点 P 作PE⊥AM ， PF ⊥ AN，垂足为E、 F ，连接 PA．设 AB ＝ x，AC ＝ y．因为 P 到 AM ， AN 的距离分别为3，5，NCP·FA EMPE＝ 3， PF ＝ 5．S△ABC ＝S△ ABP＋S△ APC ＝1112 x 3＋ 2 y5 ＝2(3x＋ 5y)．① ,,4 分因为 tan ＝－ 2，所以 sin＝ 2 ．5所以S△ABC ＝ 1 x y2 ．②,,,,,,,,,,,,,,,8 分25由①②可得1x y212＝ (3x＋ 5y)．52即 3 5x＋ 5y＝ 2xy．③,,,,,,,,,,,,,,,10 分因为 3 5x＋5y≥ 2155xy，所以2xy≥ 2 155xy．解得xy≥ 15 5．,,,,,,,,,,,,,,,13 分当且仅当 35x＝5y 取“＝”，结合③解得x＝5， y＝ 35．所以S△ABC ＝ 1 x y2 有最小值 15．25答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分20．（本小题满分16 分）解：（1）当 a＝－ 1，x∈[0 ，＋∞ )时， f(x) ＝－ x3＋ x＋ 1，从而 f ′(x)＝－ 3x2＋ 1．x＝ 1 时， f(1)＝ 1，f ′(1)＝－ 2，所以函数y＝f(x) (x∈ [0，＋∞ )) 的图象在 x＝ 1 处的切线方程为y－1＝－ 2(x－ 1)，即 2x＋ y－ 3＝ 0． ,,,,,,,,,,,,,,,,,,,3 分2） f(x)＝ g(x)即为 ax3＋ |x－ a|＝ x4．所以 x4－ ax3＝ |x－ a|，从而 x3(x－ a)＝ |x－ a|．此方程等价于x＝ a 或 x＞ a，或 x＜ a，,,,,,,,,,,,,,,,,6 分x＝ 1x＝－ 1．所以当a≥1 时，方程 f(x)＝g(x)有两个不同的解 a，－ 1；当－ 1＜ a＜1时，方程 f( x)＝ g(x)有三个不同的解 a，－ 1， 1；当a≤－ 1 时，方程 f(x)＝ g(x)有两个不同的解a， 1．,,,,,,,,,,,9 分3）当 a＞ 0，x∈ (a，＋∞ )时， f(x)＝ ax3＋ x－ a，f ′(x)＝ 3ax2＋ 1＞ 0，所以函数 f(x)在 (a，＋∞ )上是增函数，且 f(x) ＞f(a)＝ a4＞ 0．所以当x∈[a，a＋ 2]时，f(x)∈ [f(a)， f( a＋ 2)] ，1024∈ [1024， 1024f( x)f(a＋ 2)f(a) ] ，当x∈ [a＋ 2，＋∞ )时，f(x)∈ [ f(a＋ 2)，＋∞ )． ,,,,,,,,,,,,,, 11 分因为对任意的x1∈ [a， a＋ 2]，都存在x2∈ [a＋ 2，＋∞ )，使得 f(x1)f(x2)＝1024，所以 [1024，1024[ f(a＋2) ，＋∞ )．,,,,,,,,,,,,,,,,13 分f( a＋ 2)f(a) ]?从而1024 ≥ f(a＋ 2)．f(a＋ 2)所以 f 2(a＋2)≤ 1024 ，即 f(a＋2) ≤32，也即 a(a＋ 2)3＋2≤ 32．因为 a＞ 0，显然 a＝1 满足，而a≥ 2 时，均不满足．所以满足条件的正整数a 的取值的集合为 {1}．,,,,,,,,,,,,,,16 分20xx 届高三年级学情调研卷数学附加题参考答案及评分标准20xx.09说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 21．【选做题】在A 、 B、 C、 D 四小题中只能选做2 题，每小题 10 分，共计20 分．A．选修 4— 1：几何证明选讲证明：连接 AO．设圆 O 的半径为 r．A因为 PA 是圆 O 的切线， PBC 是圆 O 的割线，所以 PA2＝PC· PB．,,,,,,,,,,,,PCQOB3 分因为 PA＝ 4，PC＝ 2，所以 42＝2×(2＋ 2r)，解得 r ＝ 3．,,,,,,5 分（第 21 题 A 图）所以 PO＝PC＋ CO＝ 2＋ 3＝ 5， AO＝ r ＝ 3．由 PA 是圆 O 的切线得PA⊥ AO，故在Rt△ APO 中，因为AQ⊥PO，由面积法可知，1× AQ× PO＝1×AP ×AO ，22AP× AO 4× 312即 AQ＝PO5＝5 ．,,,,,,,,10 分B．选修 4— 2：矩阵与变换解：（1）因为矩阵 A＝2b113 属于特征值的一个特征向量为α＝－ 1，2b12－ b． ,,,,,,,,,3 分所以＝1 ，即＝13－ 1－ 1－2－ b＝，从而－ 2＝－．解得 b＝ 0，＝ 2．,,,,,,,,,,5 分（ 2）由（ 1）知， A＝20 ．13设曲线 C 上任一点 M(x， y)在矩阵 A 对应的变换作用后变为曲线 C 上一点 P(x0， y0 )，则x02x＝2x，＝3yx＋ 3y从而x0＝2x，,,,,,,,,,,,7 分y0＝ x＋ 3y．因为点 P 在曲线 C 上，所以 x02＋ 2y02＝ 2，即 (2x)2＋ 2(x＋3y)2＝ 2，从而 3x2＋ 6xy＋ 9y2＝ 1．所以曲线 C 的方程为3x2＋6xy＋ 9y2＝ 1．,,,,,,,,,,,,10 分C．选修 4— 4：坐标系与参数方程解：（方法一）直线 l 的普通方程为 x－3y＋3＝ 0．,,,,,,,,,,,,,,3 分因为点 P 在圆 C 上，故设 P(3＋cosθ，sinθ)，从而点 P 到直线 l 的距离π|2 3－2sin(θ－)|d＝| 3＋cosθ－3sinθ＋ 3|＝．,,,,,,,,7 分1222＋ (－ 3)所以 dmin＝ 3－ 1．即点 P 到直线 l 的距离的最小值为3－ 1．,,,,,,,,,,,,10 分( 方法二 )直线 l 的普通方程为x－ 3y＋3＝ 0．,,,,,,,,,,,,3 分圆 C 的圆心坐标为 (3，0) ，半径为 1．从而圆心 C 到直线 l 的距离为 d＝ | 3－ 0＋ 3| ＝ 3．,,,,,,,,,,6 分12＋( － 3)2所以点 P 到直线 l 的距离的最小值为 3－ 1．,,,,,,,,,,10 分D．选修 4— 5：不等式选讲证明：因为 a，b 是正数，且 a＋ b＝1，所以 (ax＋ by)(bx＋ ay)＝ abx2＋ ( a2 ＋ b2 )xy＋ aby2＝ ab(x2＋ y2)＋ (a2＋ b2)xy,,,,,,,,,,,3 分≥ ab 2xy＋ (a2＋ b2)xy,,,,,,,,,,,,8 分＝ (a＋ b)2xy＝ xy即 (ax＋ by)(bx＋ay)≥ xy 成立．,,,,,,,,,,,,10 分【必做题】第 22 题、第 23 题，每题10 分，共计20 分．22．解：（ 1）以 D 为原点， DA 为 x 轴， DC 为 y 轴， DD 1 为 z 轴，建立如图所示的空间直角坐标系．由题设，知 B(2， 3， 0)， A1(2， 0， 5)，C(0， 3，0) ，C1(0， 3，5)．z→→D 1C1因为 CE＝λCC1，所以 E(0， 3，5λ)．→A1B12 分从而 EB＝ (2， 0，－5λ)， EA1＝(2，－ 3， 5－5λ)．,, 当∠ BEA1 为钝角时，cos∠ BEA 1＜ 0，E→→DC y2× 2－5λ(5－5λ＜)0，所以EB · EA1＜0，即AB1＜λ＜ 4．x（第 22 题图）解得 5514,,,,,,,,,,,,,,5 分即实数λ的取值范围是 ( ， )．55→→（ 2）当λ＝时， EB ＝(2， 0，－ 2)， EA1＝ (2，－ 3， 3)． 5设平面 BEA1 的一个法向量为n1＝ (x，y， z)，→2x－ 2z＝ 0，由n1· EB ＝0，→得2x－ 3y＋ 3z＝ 0，n1· EA1＝ 05取 x＝ 1，得 y＝ 3， z＝ 1，所以平面 BEA1 的一个法向量为n1＝ (1，5， 1)．,,,,,,,,,,,,,7 分3易知，平面 BA1B1 的一个法向量为n2＝ (1， 0， 0)．因为 cos＝n1· n2 ＝143，| n1|· |n2|43439343,,,,,,,,,,,,,,10 分从而|cosθ|＝ 43 ．123．解：（ 1）因为 P(X＝ 10)＝ 12＝1C3＝ 3 ，， P(X＝ 5)＝ 2C510C51021C3＝ 3 ， P(X＝ 0)＝C3＝ 3 ，P(X＝ 2)＝ 2210C5C5所以 X 的概率分布表为： X1052P133310101010,,,,,,,,,,,4 分1333从而 E(X)＝10 10＋5 10＋210＋ 010＝ 3.1 元．,,,,,,,,,,,6 分（ 2）记该顾客一次摸球中奖为事件A，由（ 1）知， P(A)＝ 7 ，10291从而他两次摸球中至少有一次中奖的概率 P＝1－[1－ P(A)] ＝100．答：他两次摸球中至少有一次中奖的概率为 91 ．,,,,,,,,,,,10 分．100。

江苏省南京市2020高三数学9月学情调研试题(含解析)

江苏省南京市2020届高三数学9月学情调研试题（含解析）一、填空题： (本大题共14小题，每小题5分，共70分．请将答案写在答题卡相应位置． ) 1、函数()1f x x =-的定义域为 ▲【答案】[1,+∞)【解析】被开方式大于等于 0【点评】考查函数定义域的求解，该题属于基础题型.2、已知复数z 满足(2)1z i i -=+，其中i 是虚数单位，则复数z 的模为 ▲ ．【答案】10【解析】z a bi =+，(2)13z i i a -=+⇒=，110b z =-⇒=，【点评】考查复数的运算，属于基础题型.3、某算法的流程图如图所示，则物出的n 的值为 ▲ ．【答案】4【解析】n ＝2，p ＝4；n ＝3，p ＝9；n ＝4，p ＝16．【点评】考查流程图，属于基础题型.4、某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是： [40，50），［50，60)，［60，70)，［70，80），［80，90），［90，100〕，则图中x 的值为 ▲【答案】0.018【解析】0.1(0.0060.0060.010.0540.006)0.018x =-++++=【点评】考查统计知识的基本运用，属于基础题型.5、有3个兴趣小组，甲、乙两位同学各自选择其中一个参加，且每位同学参加各个兴趣小组的可能性相同，则这两位同学参加了不同的兴趣小组的概率为 ▲ 【答案】23【解析】322333P ⨯==⨯ 【点评】考查组合，属于基础题型.6、把一个底面半径为3 cm ，高为4 cm 的钢质实心圆柱熔化，然后铸成一个实心钢球(不计损耗），则该钢球的半径为 ▲ cm. 【答案】 3【解析】由圆柱和球的体积相等得：2343433R R ππ⨯⨯=⇒= 【点评】考查圆柱和球的体积计算，属于基础题型.7、在平面直角坐标系xoy 中，若双曲线22221(0,0)x y a b a b-=>>的一条准线与两条渐近线恰能围成一个等边三角形，则该双曲线的离心率为 ▲ ．【答案】3【解析】由渐近线与准线的交点构成等边三角形，可得22tan 303b a b a c a a c⨯︒===，得e ==【点评】考查双曲线的离心率计算，属于基础题型. 8、若函数()2sin()(0)6f x x πωω=->的最小正周期为π，则当[0,]2x π∈时，()f x 的值域为▲ ．【答案】[﹣1，2]【解析】由周期为π，得2ω=，则()2sin(2)6f x x π=-，x ∈[0，2π]时，()f x ∈[﹣1，2]【点评】考查三角函数的图像和性质，属于基础题型. 9、若锐角α满足tan （α＋4π）＝3tan α＋1，则tan2α的值为 ▲ ．【答案】34【解析】由题意化简得：tan (3tan 1)0αα-=，解得tan 0α=或1tan 3α= ∵α为锐角，∴1tan 3α=，∴tan2α＝34【点评】考查三角函数的图像和性质，属于基础题型. 10、已知函数()1||xf x x =+，则不等式(3)(2)0f x f x -+>的解集为 ▲ ．【答案】x ＞1【解析】由题意得()f x 为奇函数，通过分离常数法得()f x 是R 上的增函数转换可得(3)(2)f x f x ->-，即32x x ->-，x ＞1【点评】考查通过函数的奇偶性和单调性解决不等式的问题11、等差数列｛n a ｝的前n 项和记为Sn ，已知147a a a ++＝99，258a a a ++＝93，若存在正整数k ，使得对任意n *N ∈，都有n k S S ≤恒成立，则k 的值为 ▲ ．【答案】20【解析】由等差数列，可得4399a =，∴433a =；5393a =，∴531a =；∴2d =-，139a = 240n S n n =-+，n S 最大值为20S ，所以k ＝20．【点评】此题考查的是对等差数列求n 项和的表达式配方求最值的题型，该题属于基础题型.12、在△ABC 中，点P 是边AB 的中点，已知CA ＝4，CP ＝3，∠ACB ＝23π，则CP CA u u u r u u u r g的值为 ▲ ．【答案】6【解析】∵1()2CP CA CB =+u u u r u u u r u u u r∴222111cos 442CP CA CB CA CB ACB =++∠u u u r u u u r u u u r u u u r u u u r∴21344CB CB =+-u u ur u u u r ，解得CB u u u r ＝2∴21111111()1642()62222222CP CA CA CB CA CA CA CB ⋅=+⋅=+⋅=⨯+⨯⨯⨯-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r【点评】向量的数量积，考察向量的中点公式和模长；另外还可通过建系去做. 难度适中.13、在平面直角坐标系xoy 中，已知圆若圆M 上存在一点P ，使得以点P 为圆心，1为半径的圆与圆N 有公共点，则实数a 的取值范围为 ▲ ．【答案】[﹣2，2]【解析】设P(x ，y )，因为以P 为圆心，半径为1的圆与圆N 有公共点所以1≤22(2)(1)x y -++≤3，又P 在圆M ，可得22(2)(21)a a -++≤5 可得：实数a 的取值范围为﹣2≤a ≤2．【点评】圆的存在性问题，考察圆与圆的位置关系. 难度适中，14、已知函数若函数有6个零点（互不相同），则实数a 的取值范围为 ▲ ．【答案】(34，2) 【解析】作出()f x 与()g x 的图像由题知，(())g f x a =有6个解，令()f x t =当a ＜0时，()g t a =只有一个解，且t ＜﹣4，对应()f x t =只有一个解，舍去；当0≤a ≤34时，()g t a =有两个解，且143t -≤≤-，210t -≤≤，结合图像可知()f x t = 没有6个解，舍去；当34＜a ＜2时，()g t a =有两个解，且1t ，2t ∈(﹣3，1)，结合图像可知()f x t =有6个解；当a ≥2时，()g t a =只有一个解，且t ＞1，对应()f x t =只有一个解，舍去．综上得 a 的取值范围是34＜a ＜2．【点评】本题主要考查根的个数，利用换元法转化为两个函数的焦点问题个数问题，利用分类讨论和数形结合时解决本题的关键，综合性较大.二、解答题：本大题共5小题，共计90分。

2019-2020学年江苏省南京市高三上学期9月学情调研测试数学试题

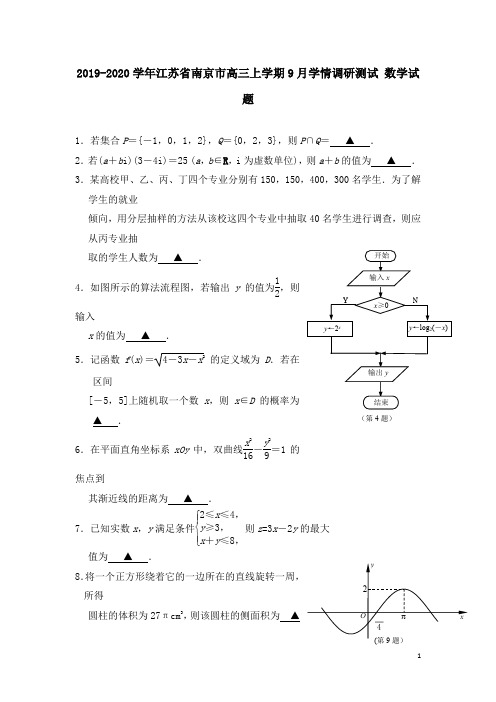
2019-2020学年江苏省南京市高三上学期9月学情调研测试数学试题1．若集合P ＝{－1，0，1，2}，Q ＝{0，2，3}，则P ∩Q ＝ ▲ ．2．若(a ＋b i)(3－4i)＝25 (a ，b ∈R ，i 为虚数单位)，则a ＋b 的值为 ▲ ． 3．某高校甲、乙、丙、丁四个专业分别有150，150，400，300名学生．为了解学生的就业倾向，用分层抽样的方法从该校这四个专业中抽取40名学生进行调查，则应从丙专业抽取的学生人数为 ▲ ．4．如图所示的算法流程图，若输出y 的值为12，则输入x 的值为 ▲ ．5．记函数f (x )＝4－3x －x 2 的定义域为D ．若在区间[－5，5]上随机取一个数x ，则x ∈D 的概率为▲ ．6．在平面直角坐标系xOy 中，双曲线x 216－y 29＝1的焦点到其渐近线的距离为 ▲ ．7．已知实数x ，y 满足条件⎩⎪⎨⎪⎧2≤x ≤4，y ≥3，x ＋y ≤8，则z =3x －2y 的最大值为 ▲ ．8所得圆柱的体积为27πcm 3，则该圆柱的侧面积为 ▲（第4题）4cm 2.9．若函数f (x )＝A sin(x ＋)(A ＞0，＞0，||)的部分图象如图所示，则f ()的值为 ▲ ．10．记等差数列{a n }前n 项和为S n ．若a m ＝10，S 2m －1＝110，则m 的值为 ▲ ． 11．已知函数f (x )是定义在R 上的奇函数，且在(－∞，0]上为单调增函数．若f (－1)＝－2，则满足f (2x －3)≤2的x 的取值范围是 ▲ ． 12．在△ABC 中，AB ＝3，AC ＝2，∠BAC ＝120→BM ＝λ→BC ．若→AM ·→BC ＝－173，则实数λ 的值为 ▲ ．13．在平面直角坐标系xOy 中，若圆(x －2)2＋(y －2)2＝1上存在点M ，使得点M关于x 轴的对称点N 在直线kx ＋y ＋3＝0上，则实数k 的最小值为 ▲ ． 14．已知函数f (x )＝⎩⎪⎨⎪⎧2x 2，x ≤0，－3|x －1|＋3，x ＞0．若存在唯一的整数x ，使得f (x )－ax＞0成立，则实数a 的取值范围为 ▲ ．15．如图,在平面直角坐标系xOy 中,点,,A B C 均在单位圆上,已知点A 在第一象限的横坐标是3,5点B 在第二象限,点()1,0.C（1）设,COA θ∠=求sin 2θ的值；（2）若AOB ∆为正三角形,求点B 的坐标16．如图,在四面体ABCD 中,,AB AC DB DC ===点E 是BC 的中点,点F 在AC 上，且.AFACλ=（1）若//EF 平面,ABD 求实数λ的值；（2）求证：平面BCD ⊥平面AED17．如图,有两条相交直线成060角的直路,,X X Y Y ''交点是,O 甲、乙两人分别在,OX OY 上，甲的起始位置距离O 点3,km 乙的起始位置距离O 点1,km 后来甲沿XX '的方向,乙沿Y Y '的方向,两人同时以4/km h 的速度步行（1）求甲乙在起始位置时两人之间的距离；（2）设th 后甲乙两人的距离为(),d t 写出()d t 的表达式；当t 为何值时,甲乙两人的距离最短,并求出此时两人的最短距离18．如图,,A B 是椭圆()2222:10x y C a b a b+=>>的左右顶点,M 是椭圆上异于,A B的任意一点,直线l 是椭圆的右准线（1）若椭圆C 的离心率为1,2直线:4,l x =求椭圆C 的方程；（2）设直线AM 交l 于点,P 以MP 为直径的圆交MB 于,Q 若直线PQ 恰好过原点,求椭圆C 的离心率19．已知数列{}n a 共有2k 项()*2,k N ≤∈数列{}n a 的前n 项的和为,n S 满足12,a =()()1121,2,3,,21,n n a p S n n +=-+=-其中常数1p >（1）求证：数列{}n a 是等比数列；（2）若2212,k p -=数列{}n b 满足()()2121log 1,2,,2,n n b a a a n n n==求数列{}n b 的通项公式（3）对于（2）中的数列{},n b 记3,2n n c b =-求数列{}n c 的前2k 项的 20．设函数()()x f x ax e a R =+∈（1）若函数()f x 有且只有两个零点()1212,,x x x x <求实数a 的取值范围；（2）当1a =时,若曲线()f x 上存在横坐标成等差数列的三个点,,A B C ①证明：ABC ∆为钝角三角形；②试判断ABC ∆能否为等腰三角形,并说明理由2019-2020学年江苏省南京市高三上学期9月学情调研测试数学试题1．{0，2} 2．7 3．16 4．－ 2 5．126．3 7． 6 8．189．－1 10．611．(－∞，2] 12．13 13．－43 14．[0，2]∪[3，8]15．如图,在平面直角坐标系xOy 中,点,,A B C 均在单位圆上,已知点A 在第一象限的横坐标是3,5点B 在第二象限,点()1,0.C（1）设,COA θ∠=求sin 2θ的值；（2）若AOB ∆为正三角形,求点B 的坐标【答案】()24125()342,1010B ⎛-+ ⎝⎭ 【解析】试题分析：（1）因为点A 在单位圆上,点A 在第一象限，点A 的横坐标是3,5所以点A 的坐标为34,.55⎛⎫⎪⎝⎭根据三角函数定义有34cos ,sin 55x y r r θθ====，从而24sin 22sin cos .25θθθ==（2）因为点B 在单位圆上,,3COB πθ∠=+根据三角函数定义有11cos()cos sin()sin 3232x r y r ππθθθθθθ=+===+=+=因此点B 的坐标为34.1010⎛-+ ⎝⎭试题解析：（1）因为点A 在单位圆上,点A 在第一象限，点A 的横坐标是3,5所以点A 的坐标为34,.55⎛⎫⎪⎝⎭根据三角函数定义有34cos ,sin 55x y r r θθ====，从而24sin 22sin cos .25θθθ==（2）因为点B 在单位圆上,,3COB πθ∠=+根据三角函数定义有1314cos()cos sin()cos sin ,3221032210x r y r ππθθθθθθ-=+=-==+=+=因此点B 的坐标为.⎝⎭考点：三角函数定义，二倍角公式16．如图,在四面体ABCD 中,,AB AC DB DC ===点E 是BC 的中点,点F 在AC 上，且.AFACλ=（1）若//EF 平面,ABD 求实数λ的值；（2）求证：平面BCD ⊥平面AED【答案】()112λ=()2详见解析【解析】试题分析：（1）因为//EF 平面,ABD EF ⊂平面,ABC 平面ABD 平面ABC AB =,所以根据线面平行性质定理得：//.EF AB 因此1.2AF BE AC BC λ=== （2）,AB AC =点E 是BC 的中点,.AE BC ∴⊥同理由,DB DC =点E 是BC 的中点,.DE BC ∴⊥又AE ⊂平面,AED DE ⊂平面,AED AE DE E =,因此BC ⊥平面,AED 而BC ⊂平面,BCD 所以平面BCD ⊥平面AED .试题解析：（1）因为//EF 平面,ABD EF ⊂平面,ABC 平面ABD 平面ABC AB =,所以根据线面平行性质定理得：//.EF AB 因此1.2AF BE AC BC λ=== （2）,AB AC =点E 是BC 的中点,.AE BC ∴⊥同理由,DB DC =点E 是BC 的中点,.DE BC ∴⊥又AE ⊂平面,AED DE ⊂平面,AED AE DE E =,因此BC ⊥平面,AED 而BC ⊂平面,BCD 所以平面BCD ⊥平面AED . 考点：线面平行性质定理，面面垂直判定定理17．如图,有两条相交直线成060角的直路,,X X Y Y ''交点是,O 甲、乙两人分别在,OX OY 上，甲的起始位置距离O 点3,km 乙的起始位置距离O 点1,km 后来甲沿XX '的方向,乙沿Y Y '的方向,两人同时以4/km h 的速度步行（1）求甲乙在起始位置时两人之间的距离；（2）设th 后甲乙两人的距离为(),d t 写出()d t 的表达式；当t 为何值时,甲乙两人的距离最短,并求出此时两人的最短距离【答案】(1 ()124t km =当时,最短距离为2【解析】试题分析：（1）由余弦定理得：7AB ==，所以甲乙在起始位置时两人之间的距离为.（2）当3[0,)4t ∈时，4048247A B t ⨯-+，因此当1=4t 时，两人的最短距离为2km. 当3[,+4t ∈∞）时，))c o s 120A B t t =-=-+，因此当3=4t 时，两人的最短距离为4km. 综上，当1=4t 时，两人的最短距离为2km.试题解析：（1）由余弦定理得：7AB ==，所以甲乙在起始位置时两人之间的距离为.（2）当3[0,)4t ∈时，4048247A B t ⨯-+，因此当1=4t 时，两人的最短距离为2km. 当3[,+4t ∈∞）时，))c o s 120A B t t =-=-+，因此当3=4t 时，两人的最短距离为4km. 综上，当1=4t 时，两人的最短距离为2km. 考点：余弦定理18．如图,,A B 是椭圆()2222:10x y C a b a b+=>>的左右顶点,M 是椭圆上异于,A B的任意一点,直线l 是椭圆的右准线（1）若椭圆C 的离心率为1,2直线:4,l x =求椭圆C 的方程；（2）设直线AM 交l 于点,P 以MP 为直径的圆交MB 于,Q 若直线PQ 恰好过原点,求椭圆C 的离心率【答案】()221143x y += ()2e =【解析】试题分析：（1）由题意得：2c 1,42a a c ==，解得：22,1,3,a c b ===因此椭圆C 的方程为221.43x y += （2）设(,)M x y ，则直线:()y AM y x a x a =++，因此22(,()).y a a P a c x a c++因为MB OP ⊥，所以22()1y a a x a c y a x a c++⋅=--，222c(1)1y x a a +=--，又2222222221,x y y b a b x a a+==--，因此222c (1)1,(1)(1)1b e e a a -+=--+=，210e e +-=，又01e <<，所以1.2e =试题解析：（1）由题意得：2c 1,42a a c ==，解得：22,1,3,a c b ===因此椭圆C 的方程为221.43x y += （2）设(,)M x y ，则直线:()y AM y x a x a =++，因此22(,()).y a a P a c x a c++因为MB OP ⊥，所以22()1y a a x a c y a x a c++⋅=--，222c(1)1y x a a +=--，又2222222221,x y y b a b x a a+==--，因此222c (1)1,(1)(1)1b e e a a -+=--+=，210e e +-=，又01e <<，所以1.2e =考点：椭圆标准方程，直线与椭圆位置关系19．已知数列{}n a 共有2k 项()*2,k N ≤∈数列{}n a 的前n 项的和为,n S 满足12,a =()()1121,2,3,,21,n n a p S n n +=-+=-其中常数1p >（1）求证：数列{}n a 是等比数列；（2）若2212,k p -=数列{}n b 满足()()2121log 1,2,,2,n n b a a a n n n==求数列{}n b 的通项公式（3）对于（2）中的数列{},n b 记3,2n n c b =-求数列{}n c 的前2k 项的和【答案】（1）详见解析（2）()12121n n b k -=+-()22321k k T k =- 【解析】试题分析：（1）证明：因为()112,n n a p S +=-+当2n ≥时，()112n n a p S -=-+。

2024届南京高三上学期9月学情调研数学试题及答案

南京市2024届高三年级学情调研数学 2023.09（第13题~第16题）、解答题（第17题~第22题）四部分．本试卷满分为150分，考试时间为120分钟．2．答卷前，考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置．3．作答选择题时，选出每小题的答案后，用2B 注意事项：1．本试卷包括单项选择题（第1题~第8题）、多项选择题（第9题~第12题）、填空题铅笔在答题卡上将对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上．4．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内，在其他位置作答一律无效．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上． 1．已知集合A ＝{x |x 2－4x ＋3≤0}，B ＝{x |2＜x ＜4}，则A ∩B ＝A ．{x |3≤x ＜4}B ．{x |1≤x ≤3}C ．{x |2＜x ≤3}D ．{x |1≤x ＜4}2．若z ＝3－i1＋i，则z 的虚部为 A ．2B ．－2C ．2iD ．－2i3．(x －2x)4的展开式中常数项为A ．－24B ．－4C ．4D ．244．在△ABC 中，点D 为边AB 的中点．记CA →＝m ，CD →＝n ，则CB →＝A ．2m ＋nB ．m 2C ．2m －nD ．－m ＋2n 5．设O 为坐标原点，A 为圆C ：x 2＋y 2－4x ＋2＝0上一个动点，则∠AOC 的最大值为A ．π12B ．π6C ． π4D ．π36．在正方体ABCD －A 1B 1C 1D 1中，过点B 的平面α与直线A 1C 垂直，则α截该正方体所得截面的形状为 A ．三角形B ．四边形C ．五边形D ．六边形7．新风机的工作原理是，从室外吸入空气，净化后输入室内，同时将等体积的室内空气排向室外．假设某房间的体积为v 0，初始时刻室内空气中含有颗粒物的质量为m ．已知某款新风机工作时，单位时间内从室外吸入的空气体积为v (v ＞1)，室内空气中颗粒物的浓度与时刻t 的函数关系为ρ(t )＝(1－λ)m v 0＋λm v 0e －vt ，其中常数λ为过滤效率．若该款新风机的过滤效率为45，且t ＝1时室内空气中颗粒物的浓度是t ＝2时的32倍，则v 的值约为(参考数据：ln2≈0.6931，ln3≈1.0986) A ．1.3862B ．1.7917C ．2.1972D ．3.58348．若函数f (x )＝sin(ωcos x )－1(ω＞0)在区间(0，2π)恰有2个零点，则ω的取值范围是A ．(0，π2)B ．(π2，3π2)C ．(π2，5π2)D ．(π2，＋∞)二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．若a ＜0＜b ，且a ＋b ＞0，则A ．ab＞－1B ．|a |＜|b |C ．1a ＋1bD ．(a －1)(b －1)＜110．有一组样本数据x 1，x 2，x 3，x 4，x 5，已知∑5i ＝1x i ＝10，∑5i ＝1x i 2＝30，则该组数据的A ．平均数为2B ．中位数为2C ．方差为2D ．标准差为211．在△ABC 中，∠ACB ＝90º，AC ＝BC ＝22，D 是AB 的中点．将△ACD 沿CD 翻折，得到三棱锥A'－BCD ，则 A ．CD ⊥A'BB ．当A'D ⊥BD 时，三棱锥A'－BCD 的体积为83C ．当A'B ＝23时，二面角A'－CD －B 的大小为2π3D ．当∠A'DB ＝2π3时，三棱锥A'－BCD 的外接球的表面积为20π12．函数f (x )及其导函数f '(x )的定义域均为R ，且f (x )－f (－x )＝2x ，f '(1＋x )＋f '(1－x )＝0，则A ．y ＝f (x )＋x 为偶函数B ．f (x )的图象关于直线x ＝1对称C ．f '(0)＝1D ．f '(x ＋2)＝f '(x )＋2三、填空题：本题共4小题，每小题5分，共20分．13．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边经过点 P (3，4)，则sin(π＋α)＝▲________． 14．某批麦种中，一等麦种占90%，二等麦种占10%，一、二等麦种种植后所结麦穗含有50粒以上麦粒的概率分别为0.6，0.2，则这批麦种种植后所结麦穗含有50粒以上麦粒的概率为▲________．15．记S n 为数列{a n }的前n 项和，已知a n ＝ 2n (n ＋2)，n 为奇数，a n －1， n 为偶数，则S 8＝▲________． 16．已知双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点分别为F 1，F 2，P 是C 右支上一点，线段PF 1与C 的左支交于点M ．若∠F 1PF 2＝π3，且|PM |＝|PF 2|，则C 的离心率为▲________．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．(10分)已知公比大于1的等比数列{a n }满足：a 1＋a 4＝18，a 2a 3＝32． (1)求{a n }的通项公式；(2)记数列{b n }的前n 项和为S n ，若S n ＝2b n －a n ，n ∈N *，证明：b n a n 是等差数列．(2)若a ＝3，sin B sin C ＝14，求△ABC 的面积．19．(12分)某地区对某次考试成绩进行分析，随机抽取100名学生的A ，B 两门学科成绩作为样本．将他们的A 学科成绩整理得到如下频率分布直方图，且规定成绩达到70分为良好．已知他们中B 学科良好的有50人，两门学科均良好的有40人．（1）根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为这次考试学生的A 学科良好与B 学科良好有关；（23人中A ，B 学科均良好的人数为随机变量X ，求X 的分布列与数学期望．附：K2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )，其中n ＝a ＋b ＋c ＋d ．P (K 2≥k 0)0.150.100.050.025 0.010 0.0050.001k 02.072 2.7063.841 5.024 6.635 7.879 10.828O0.005 (第19题图)点G 是线段BF 的中点． (1)证明：EG ∥平面DAF ；(2)求直线EF 与平面DAF 所成角的正弦值．21．(12分)已知O 为坐标原点，F (1，0)是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点，过F 且不与坐标轴垂直的直线l 交椭圆C 于A ，B 两点．当A 为短轴顶点时，△OAF 的周长为3＋3． (1)求C 的方程；(2)若线段AB 的垂直平分线分别交x 轴、y 轴于点P ，Q ，M 为线段AB 的中点，求|PM |·|PQ |的取值范围．22．(12分)已知函数f (x )＝a e x －x －a ，其中a ＞0． (1)若a ＝1，证明：f (x )≥0；(2)设函数g (x )＝xf (x )，若x ＝0为g (x)的极大值点，求a 的取值范围．EO FG (第20题图)数学参考答案2023.09一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上．1．C 2．B 3．D 4．D 5．C 6．A 7．B 8．B二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上．全部选对得5分，部分选对得2分，不选或有错选的得0分． 9．ABD 10．AC 11．ACD 12．BC三、填空题：本大题共4小题，每小题5分，共20分．请把答案填写在答题卡相应位置上． 13．－4514．0.56 15．169 16．7四、解答题：本大题共6小题，共70分．请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤． 17．（10分）解：（1）方法1：因为{a n }是等比数列，所以a 2a 3＝a 1a 4＝32，又a 1＋a 4＝18，所以 a 1＝2，a 4＝16或 a 1＝16，a 4＝2． ···················································· 2分又q ＞1，所以a 1＝2，a 4＝16，所以q 3＝8，q ＝2． ················································ 4分因此a n ＝a 1q n －1＝2n ．分方法2：由基本量得出 a 1＝2，q ＝2或a 1＝16，q ＝12． ························································ 2分又q ＞1，所以a 1＝2，q ＝2．··········································································· 4分因此a n ＝a 1q n －1＝2n ． ··············································································· 5分（2）由（1）得S n ＝2b n －2n ，所以S n ＋1＝2b n ＋1－2n ＋1，两式作差可得b n ＋1－2b n ＝2n ，n ∈N *． ·························································· 7分所以b n ＋12n ＋1－b n 2n ＝12，即b n ＋1a n ＋1－b n a n ＝12(n ∈N *)． ··················································· 9分所以数列 b n a n 是公差为12的等差数列． ························································· 10分因为A ∈(0，π)，所以A ＝2π3．···································································· 6分(2)解法1：由正弦定理a sin A ＝b sin B ＝c sin C ，所以b sin B ＝c sin C ＝332＝23，因此b ＝23sin B ，c ＝23sin C ． ································································· 9分所以bc ＝(23)2×sin B sin C ＝3．································································ 10分所以，△ABC 的面积为S ＝12bc sin A ＝12×3×23＝334． ································· 12分解法2：因为sin B sin C ＝14，B ＝π－A －C ＝π3－C ，所以sin(π3－C )sin C ＝14．化简得cos(2C －π3)＝1，因为C ∈(0，π3)，所以2C －π3∈(－π3，π3)，故C ＝π6． ········ 9分因此B ＝π3－C ＝π6，进而可解得b ＝c ＝3． ················································· 10分所以△ABC 的面积为S ＝12×3×3×sin 2π3＝334． ····································· 12分19．（12分）解：（1）由直方图可得A 学科良好的人数为100×(0.040＋0.025＋0.005)×10＝70，所以2×2列联表如下：B 学科良好 B 学科不够良好合计A 学科良好 40 30 70 A 学科不够良好10 20 30 合计5050100············································································································ 2分假设H 0：A 学科良好与B 学科良好无关， ····················································· 3分 K2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )＝100×(30×10－40×20)270×30×50×50＝10021≈4.8＞3.841， ········ 5分所以有95%把握认为A B 学科良好有关． ······································ 6分（2）AB 学科均良好的概率P ＝40100＝25，X 的可能取值为0，1，2，3，且X ~B (3，25)．所以P (X ＝0)＝C 03·(25)0·(35)3＝27125，P (X ＝1)＝C 13·(25)1·(35)2＝54125， P (X ＝2)＝C 23·(25)2·(35)1＝36125，P (X ＝3)＝C 33·(25)3·(35)0＝8125． ······························· 10分所以X 的分布列为因为X ~B (3，25)，所以E (X )＝3×25＝65． ······················································· 12分20．（12分）（1）证法一：连接OE ，OG ．在圆柱OE 中，四边形ABCD 是圆柱OE 的轴截面，所以OE ∥DA ．又OE ⊄平面DAF ，DA ⊂平面DAF ，所以OE ∥平面DAF ． ············· 2分在△ABF 中，点O ，G 分别是AB 和BF 的中点，所以OG ∥AF ．又OG ⊄平面DAF ，AF ⊂平面DAF ，所以OG ∥平面DAF ．又OE ∩OG ＝O ，OE ，OG ⊂平面OEG ，所以平面OEG ∥平面DAF ． 4分又EG ⊂平面OEG ，所以EG ∥平面DAF ．··································· 6分证法二：取AF 的中点M ，连接MD ，MG ．因为点M ，G 分别是F A 和FB 的中点，所以MG _∥AO ． ················ 2分在圆柱OE 的轴截面四边形ABCD 中，AO _∥DE ．所以MG _∥DE ，因此四边形DEGM 是平行四边形． ······················ 4分因此EG ∥DM ．又EG ⊄平面DAF ，DM ⊂平面DAF ，所以EG ∥平面DAF ． ············ 6分证法三：以O 为坐标原点，AB 的中垂线为x 轴，OB 为y 轴，OE 为z 轴，建立如图所示的空间直角坐标系．则B (0，3，0)，E (0，0，3)．因为AB 为底面圆O 的直径，点F 在圆O 上，所以BF ⊥AF ．又OA ＝OB ＝BF ＝3，所以∠BOF ＝60º，因此F (32，32，0)．因为点G 是线段BF 的中点，所以G (34，3340)，因此GE →＝(－34，－334，3)． ·················································· 2分因为AD ⊥平面ABF ，BF ⊂平面ABF ，所以BF ⊥AD ．又BF ⊥AF ，AF ∩AD ＝A ，AF ，AD ⊂平面DAF ，所以BF ⊥平面DAF ，因此→FB ＝(－32，32，0)是平面DAF 的一个法向量． ···················· 4分因为BF →·EG →＝－32×34＋32×0×3＝0，又EG ⊄平面DAF ，所以EG ∥平面DAF ． ··································· 6分（2）解：法一：以O 为坐标原点，AB 的中垂线为x 轴，OB 为y 轴，OE 为z 轴，建立如图所示的空间直角坐标系．则B (0，3，0)，E (0，0，3)． ···· 7分因为AB 为底面圆O 的直径，点F 在圆O 上，所以BF ⊥AF ．又OA ＝OB ＝BF ＝3，所以∠BOF ＝60º，因此F (32，32，0)．因此F (32，32，0)，→EF ＝(32，32，－3)． ··································· 8分因为AD ⊥平面ABF ，BF ⊂平面ABF ，所以BF ⊥AD ．又BF ⊥AF ，AF ∩AD ＝A ，AF ，AD ⊂平面DAF ，所以BF ⊥平面DAF ．因此→FB ＝(－32，32，0)是平面DAF 的一个法向量． ··················· 10分设EF 与平面DAF 所成角为θ，则sin θ＝|cos ＜→EF ，→FB ＞|＝|→EF ·→FB ||→EF |·|→FB |＝3223×3＝14，DEOFGMDECBOF GyxDECBOFGyx所以EF 与平面DAF 所成角的正弦值为14． ································ 12分法二：由(1)得EG ∥平面DAF ，所以点E 到平面DAF 的距离等于点G 到平面DAF 的距离．因为AD ⊥平面ABF ，BF ⊂平面ABF ，所以BF ⊥AD ．因为AB 为底面圆O 的直径，点F 在圆O 上，所以BF ⊥AF ．又AF ∩AD ＝A ，AF ，AD ⊂平面DAF ，所以BF ⊥平面DAF ．所以点E 到平面DAF 的距离d ＝GF ＝12BF ＝32． ························· 9分连结OE ，OF ，易得OF ＝3，所以EF ＝OF 2＋OE 2＝23． ······· 10分设EF 与平面DAF 所成角为θ，则sin θ＝dEF ＝3223＝14，所以EF 与平面DAF 所成角的正弦值为14． ······························· 12分法三：过F 作AD 的平行线交上底面于点H ，连结DH ，平面ADF 即为平面AFH D ．过E 作EK ⊥DH ，K 为垂足，又因为AD ⊥EK ，AD ∩DH ＝D ，则EK ⊥平面AFHD ，则∠EFK 为EF 与平面ADF 所成的角． 8分得EK ＝32，EF ＝OF 2＋OE 2＝23． ····································· 10分设EF 与平面DAF 所成角为θ，则sin θ＝EKEF ＝3223＝14，所以EF 与平面DAF 所成角的正弦值为14． ······························· 12分21．（12分）解：（1）设椭圆C 的焦距为2c ，由题得c ＝1．当A 为短轴顶点时，△OAF 的周长a ＋b ＋1＝3＋3． ·················· 1分又a 2＝b 2＋1，所以a 2＝(2＋3－a )2＋1，解得a ＝2，b ＝3． ········ 3分所以，椭圆C 的标准方程为x 24＋y 23＝1． ······································ 4分（2）法一：易得F (1，0)，设直线AB ：y ＝k (x －1)．联立 y ＝k (x －1)，x 24＋y 23＝1，消去y 并整理得(4k 2＋3)x 2－8k 2x ＋4k 2－12＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝8k 24k 2＋3，y 1＋y 2＝k (x 1＋x 2)－2k ＝－6k 4k 2＋3，则M (4k 24k 2＋3，－3k 4k 2＋3)． ············································································· 6分于是线段AB 的垂直平分线的方程为y ＝－1k(x －4k 24k 2＋3)－3k 4k 2＋3．BM yP xO AFQ ADECB OFGADE CB OFGKH令y ＝0，得x P ＝k 24k 2＋3． ··········································································· 8分处理法1：因为k ≠0，所以x P ＝k 24k 2＋3＝14－34(4k 2＋3)∈(0，14)． ······························ 9分因为∠POQ ＝∠PMF ＝90º，所以Q ，O ，M ，F 四点共圆，由相交弦定理可得|PM |·|PQ |＝|PO |·|PF |＝x P (1－x P )＝x P －x P 2． ···················· 11分因为x P ∈(0，14)，且函数y ＝x P －x P 2在(0，14)上递增，所以|PM |·|PQ |＝x P －x P 2∈(0，316)． ·························································· 12分处理法2：易得△OPQ ∽△MPF ，所以PO PM ＝PQPF ，所以PM ·PQ ＝PO ·PF ．处理法3：|PM |·|PQ |＝1＋1k2|x M －x P |·1＋1k2|x P | ＝(1＋1k 2)|4k 24k 2＋3－k 24k 2＋3|·|k 24k 2＋3|＝3k 2(k 2＋1)(4k 2＋3)2． ················· 10分令t ＝4k2＋3＞3，则|PM |·|PQ |＝3k 2(k 2＋1)(4k 2＋3)2＝3(t 2－2t －3)16t2＝316[－3(1t )2－21t ＋1]，因为t ＞3，所以1t ∈(0，13)，因此－3(1t )2－21t ＋1∈(0，1)，因此|PM |·|PQ |＝316[－3(1t )2－21t ＋1]∈(0，316)． ·········································· 12分法二：易得F (1，0)，设直线AB ：x ＝my ＋1．联立 x ＝my ＋1，x 24＋y 23＝1，消去x 并整理得(3m 2＋4)y 2＋6my －9＝0，设A (x 1，y 1)，B (x 2，y 2)，则y ＋y 2＝－6m 3m 2＋4，x 1＋x 2＝m (y 1＋y 2)＋2＝83m 2＋4，则M (43m 2＋4，－3m 3m 2＋4)． ··········································································· 6分于是线段AB 的垂直平分线的方程为y ＝－m (x －43m 2＋4)－3m3m 2＋4．令y ＝0，得x P ＝13m 2＋4． ·········································································· 8分处理法1：因为m ≠0，所以x P ＝13m 2＋4∈(0，14)． ··············································· 9分因为∠POQ ＝∠PMF ＝90º，所以Q ，O ，M ，F 四点共圆，由相交弦定理可得|PM |·|PQ |＝|PO |·|PF |＝x P (1－x P )＝x P －x P 2． ···················· 11分因为x P ∈(0，14)，且函数y ＝x P －x P 2在(0，14)上递增，所以|PM |·|PQ |＝x P －x P 2∈(0，316)． ·························································· 12分处理法2：易得△OPQ ∽△MPF ，所以PO PM ＝PQPF ，所以PM ·PQ ＝PO ·PF ．处理法3：|PM |·|PQ |＝1＋m 2|x M －x P |·1＋m 2|x P |＝(1＋m 2)|43m 2＋4－13m 2＋4|·|13m 2＋4|＝3(m 2＋1)(3m 2＋4)2． ·············· 10分令t ＝3m 2＋4＞4，则|PM |·|PQ |＝3(m 2＋1)(3m 2＋4)2＝t －1t2＝－1t 2＋1t ∈(0，316)． ············ 12分处理法4：|PM |·|PQ |＝3(m 2＋1)(3m 2＋4)2．令t ＝3(m 2＋1)＞3，则|PM |·|PQ |＝3(m 2＋1)(3m 2＋4)2＝t (t ＋1)2＝1t ＋1t＋2∈(0，316)． ······· 12分 22．（12分）(1)证明：若a ＝1，则f (x )＝e x －x －1，f '(x )＝e x －1， ············································· 1分令f '(x )＝0，得x ＝0．在(－∞，0)上，f '(x )＜0，f (x )单调递减；在(0，＋∞)上，f '(x )＞0，f (x )单调递增； ······················································ 3分故f (x )≥f (0)＝0． ····················································································· 4分 (2)解：g (x )＝ax e x －x 2－ax ，g'(x )＝a (x ＋1)e x －2x －a ＝a [(x ＋1)e x －1]－2x ．当x ＞0时，易得(x ＋1)e x －1＞0，所以由(1)可得，若a ≥1，则g'(x )＝a [(x ＋1)e x －1]－2x ≥(x ＋1)e x －2x －1＞(x ＋1)2－2x －1＝x 2＞0，所以g (x )在(0，＋∞)上单调递增，这与x ＝0为函数g (x )的极大值点相矛盾． ····················································· 7分若0＜a ＜1，g''(x )＝a (x ＋2)e x －2，因为g'''(x )＝a (x ＋3)e x ＞0对x ＞－3恒成立，所以g''(x )在(－3，＋∞)上单调递增． ·························································· 8分又g''(0)＝2a －2＜0，g''(2a －2)＞a (2a －2＋2)－2＝0，因为0＜a ＜1，所以2a －2＞0，因此存在唯一x 0∈(0，2a －2)g''(x 0)＝0．··············································· 9分所以，在(－3，x 0)上，g''(x )＜0，g'(x )单调递减． ··········································· 10分又g'(0)＝0，所以在(－3，0)上，g'(x )＞0，故g (x )单调递增；在(0，x 0)上，g'(x )＜0，故g (x )单调递减． ···················································· 11分所以x ＝0为函数f (x )的极大值点，满足题意．综上，a 的取值范围为(0，1)． ·································································· 12分。

江苏省南京市2020届高三数学9月学情调研考试试题(含解析)

江苏省南京市2020届高三数学9月学情调研考试试题（含解析）参考公式：柱体的体积公式：V=Sh ，其中S 为为柱体的底面积，h 为柱体的高. 球的体积公式：343V R π=，其中R 为球体的半径. 一、填空题：(请将答案写在答题卡相应位置．)1.函数()f x =的定义域是【答案】[1,)+∞【解析】试题分析：要使函数有意义，需满足101x x -≥∴≥，因此定义域为[1,)+∞考点：函数定义域2.已经复数z 满足(2)1z i i -=+（i 是虚数单位），则复数z 的模是________．【解析】【详解】(2)1z i i -=+，11323,i i z i i i++∴=+==-z =.3.某算法的流程图如图所示，则物出的n 的值为_______．【答案】4【解析】【分析】循环代入n p 、的值，直到10p >时输出p 的值.【详解】第一次循环：2,5n p ==；第二次循环：3,10n p ==；第三次循环，4,17n p ==，此时满足10p >可退出循环得：4n =.【点睛】本题考查程序框图循环结构中的判断问题，难度较易.程序框图问题主要是两种处理方法：（1）逐步列举，将退出循环前的情况依次列举；（2）根据循环结构中的特殊形式简化运算.4.某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），［50，60)，［60，70)，［70，80），［80，90），［90，100〕，则图中x 的值为_______【答案】0.018【解析】【分析】根据频率和为1来计算x 的值.【详解】因为(0.00630.010.054)101x ⨯+++⨯=，所以0.018x =.【点睛】本题考查频率分布直方图中频率总和为1这一知识点，难度较易.5.有3个兴趣小组，甲、乙两位同学各自选择其中一个参加，且每位同学参加各个兴趣小组的可能性相同，则这两位同学参加了不同的兴趣小组的概率为______ 【答案】23【解析】【分析】甲、乙参加了不同的兴趣小组的可能数与可能的情况总数的比值即为对应概率.【详解】甲、乙参加了不同的兴趣小组的情况有23A =6种，总的可能情况有339⨯=种，则概率62=93P =. 【点睛】本题考查古典概型的概率计算，难度较易.古典概型的概率计算公式为：P =待求事件包含的基本事件个数可能出现的事件总数. 6.把一个底面半径为3cm ，高为4 cm 的钢质实心圆柱熔化，然后铸成一个实心钢球(不计损耗），则该钢球的半径为_______cm【答案】3【解析】【分析】根据熔化前后的体积不变求解钢球的半径即可.【详解】圆柱体积：=94=36V ππ⨯⨯圆柱，球的体积：34=3V r π球，所以34363r ππ=，解得3r =.【点睛】圆柱的体积公式：2V r h π=；球的体积公式：343V r π=. 7.在平面直角坐标系xoy 中，若双曲线22221(0,0)x y a b a b-=>>的一条准线与两条渐近线恰能围成一个等边三角形，则该双曲线的离心率为______．【答案】3【解析】【分析】根据准线与两条渐近线恰能围成一个等边三角形得到渐近线的斜率，然后再计算离心率的值.【详解】由题意可知其中一条渐近线倾斜角为：30︒，所以tan 30b a =︒=，则3c e a ===. 【点睛】本题考查双曲线的离心率计算，难度较易.求解离心率的时候如果涉及到几何图形，可借助几何图形的特点去分析问题.8.若函数()2sin()(0)6f x x πωω=->的最小正周期为π，则当[0,]2x π∈时，()f x 的值域为_______．【答案】［－1，2］【解析】【分析】先根据最小正周期求出ω的值，再利用给定区间分析函数()f x 的最值. 【详解】因为2||T ππω==，所以2ω=，则()2sin(2)6f x x π=-；又[0,]2x π∈ ，所以5(2)[,]666x πππ-∈-，则max ()2sin 22f x π==，min ()2sin()16f x π=-=-. 所以()f x 的值域为：[1,2]-.【点睛】本题考查三角函数的周期以及值域，难度较易.对于求解()sin()f x A x ωϕ=+在给定区间D 上的值域：先分析x D ∈时，x ωϕ+的范围，再根据sin y x =的单调性求解()f x 的值域.9.若锐角α满足tan （α＋4π）＝3tanα＋1，则tan 2α的值为_____．【答案】34【解析】【分析】先计算tan α的值，再利用二倍角公式计算2tan α的值. 【详解】由题意可知：1tan 3tan 11tan ααα+=+-，则1tan 3α=或tan 0α=（舍，α为锐角），则22122tan 33tan 211tan 41()3ααα⨯===--. 【点睛】常用的二倍角公式：2222cos 2cos sin 2cos 112sin ααααα=-=-=-，sin 22sin cos ααα=，22tan tan21tan ααα=-. 10.已知函数()1||x f x x =+，则不等式(3)(2)0f x f x -+>的解集为____．【答案】（1，＋∞）【解析】【分析】先分析()f x 奇偶性，再分析()f x 单调性，然后将不等式转化为自变量间的关系，计算出解集.【详解】()f x 的定义域为R ，关于原点对称且()()1||x f x f x x -=-=-+，所以()f x 是奇函数；又因为0x >时1()111x f x x x ==-++是增函数，所以()f x 在R 上是增函数；因为(3)(2)0f x f x -+>，所以(3)(2)f x f x ->-且(2)(2)f x f x -=-，则有32x x ->-，故1x >，即(1,)x ∈+∞.【点睛】解关于函数值的不等式，一般可先考虑函数的奇偶性（注意定义域）和单调性，将函数值的大小关系转化为自变量之间的大小关系，然后求解出对应解集.11.等差数列｛n a ｝的前n 项和记为n S ，已知147a a a ++＝99，258a a a ++＝93，若存在正整数k ，使得对任意n *N ∈，都有n k S S ≤恒成立，则k 的值为_______．【答案】20【解析】【分析】先根据条件求解出n S 的表达式，然后分析n S 取最大值时对应n 的值即为k 的值.【详解】因为1474399a a a a ++==，所以433a =；因为2585393a a a a ++==，所以531a =；则5431332d a a =-=-=-，14339a a d =-=，所以221(1)40(20)4002n n n S a n d n n n -=+=-+=--+，则20n =时，n S 有最大值，即20k =.【点睛】（1）等差数列性质：若2m n p q c +=+=，则2m n p q c a a a a a +=+=；（2）等差数列{}n a 中，若10,0a d ><，则n S 有最大值；若10,0a d <>，则n S 有最小值.12.在△ABC 中，点P 是边AB 的中点，已知CA ＝4，CP ACB ＝23π，则CP CA 的值为______．【答案】6【解析】【分析】现根据中点对应向量关系求解出CB 的长度，然后再将CP CA 化简到可利用||||CA CB 、直接进行计算即可.【详解】如图所示，1()2CP CA CB =+，则22211()||||4344CP CA CB CB CB =+=-+=，所以||2CB =；又2111()||8(2)6222CP CA CA CB CA CA CB CA =+=+=+-=. 【点睛】几何图形中的向量问题，一定要先分析图形找到其中的数量关系；其次就是对待求式子的分析，将其变为可以用已知量直接进行计算的形式.解决这类问题，这里还有另一种常用的方法：坐标法，已坐标的方式去考虑各个量之间关系.13.在平面直角坐标系xoy 中，已知圆M:22()(2)4x a y a -+-=，圆N ：22(2)(1)4x y -++=，若圆M 上存在一点P ，使得以点P 为圆心，1为半径的圆与圆N 有公共点，则实数a 的取值范围为________．【答案】［－2，2］【解析】【分析】可将问题转化为圆M 的半径增加1后与圆N 有交点，然后利用圆心距计算即可.【详解】根据题意可知：圆22()(2)9x a y a -+-=与圆22(2)(1)4x y -++=有交点，则22(2)(21)5a a -++≤，得24a ≤，即[2,2]a ∈-.【点睛】解答有关圆的问题的时候，要学会将所给的条件转化成更容易处理的条件，比如针对一些“存在”“恒成立”问题，一般只需要根据已知条件找到临界条件即可进行计算求解.14.已知函数32()31f x x x =-+，2211,0()1,04x x g x x x x ⎧-+⎪=⎨--≤⎪⎩＞.若函数[]()y g f x a =-有6个零点（互不相同），则实数a 的取值范围为______．【答案】（34，2）【解析】【分析】分别画出()f x 、()g x 的图象，采用换元法令()f x t =，考虑()g t a =中t 的取值可使()f x t =有6个解时对应的a 的取值范围.【详解】作出()f x 、()g x 图象如下：因为()g x a =至多有两解，()f x t =至多有三解，则()g x a =有两解时()f x t =有6解；且(0)1f =，(2)3f =-，所以()f x t =有三解时(3,1)t ∈-；当3t =-时，3(3)4a g =-=，当1t =时，(1)2a g ==，故3(,2)4a ∈时，[]()y g f x a =-有6个零点.【点睛】涉及到分段函数的零点问题时，一定记得使用数形结合思想；函数零点或者方成根问题中，出现了复合函数，换元法也是很常规的手段，此时就需要结合多个函数图象来分析问题.二、解答题。

2020年9月江苏省南京市普通高中2021届高三毕业班学情调研考试数学试题(解析版)

绝密★启用前江苏省南京市普通高中2021届高三毕业班上学期学情调研考试数学试题(解析版)2020年9月注意事项：1．本试卷共6页,包括单项选择题（第1题~第8题）、多项选择题（第9题~第12题）、填空题（第13题~第16题）、解答题（第17题~第22题）四部分．本试卷满分为150分,考试时间为120分钟．2．答卷前,考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置．3．作答选择题时,选出每小题的答案后,用2B铅笔在答题卡上将对应题目选项的答案信息点涂黑；如需改动,用橡皮擦干净后,再选涂其他答案．答案不能答在试卷上．4．非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内,在其他位置作答一律无效．一、单项选择题：本大题共8小题,每小题5分,共40分．在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上．1．已知集合A＝{x|x2－x－2＜0},B＝{x|1＜x＜3 },则A∩B＝A．{x|－1＜x＜3} B．{x|－1＜x＜1}C．{x|1＜x＜2} D．{x|2＜x＜3}解析：集合A＝{x|x2－x－2＜0}={x|-1<x<2},A∩B＝{x|1＜x＜2} ,答案选C. 2．已知(3－4i)z＝1＋i,其中i为虚数单位,则在复平面内z对应的点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限解析：z=()()()()25714343431431iiiiiii+-=+-++=-+,z对应的点位于第二象限,答案选B.3．已知向量a ,b 满足|a |＝1,|b |＝2,且|a ＋b |＝ 3,则a 与b 的夹角为A ．π6B ．π3C ．5π6D ．2π3解析：|a ＋b |2=|a |2+2a ·b +|b |2＝5+4cos θ=3,解得[]πθθ，，021cos ∈-=,所以32πθ=,答案选D. 4．在平面直角坐标系xOy 中,若点P (43,0)到双曲线C ：x 2a 2－y 29＝1的一条渐近线的距离为6,则双曲线C 的离心率为A ．2B ．4C ． 2D ． 3解析：双曲线C ：x 2a 2－y 29＝1的一条渐进线方程为3x ±ay=0,则点P 到该渐进线方程的距离为6333422=+⋅=a d ,解得a 2=3,所以椭圆的离心率为2393=+==a c e ,故答案选A.5．在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ．若2b cos C ≤2a －c ,则角B 的取值范围是A ．(0,π3]B ．(0,2π3]C ．[π3,π) D．[2π3,π) 解析：因为2b cos C ≤2a －c ,所以由余弦定理可得abc b a b 22222-+⋅≤2a －c ,化简得ac ≤a 2+c 2－b 2,即21cos ≥B ,因为()π，0∈B ,则⎥⎦⎤ ⎝⎛∈30π，B ,答案选A. 6．设a ＝log 4 9,b ＝2－1.2,c ＝(827)－13,则 A ．a ＞b ＞c B ．b ＞a ＞c C ．a ＞c ＞b D ．c ＞a ＞b 解析：由题意b ＝2－1.2<02=1,a ＝log 4 9=log 2 3=log 2 9＞23log 222=,c ＝(827)－13＝。

南京市2020届高三化学零模试卷(答案版)

塔，下列措施中，能提高烟气中 SO2 去除率的有
（填字母）
A.适当减缓通入烟气的速率
B.采用气-液逆流的方式吸收烟气
C.加水使 Mg(OH)2 完全溶解 ②Mg(OH)2 浆液循环吸收烟气中 SO2 的主要反应为：
Mg(OH)2(s)+SO2(g)+5H2O(l)==MgSO3·6H2O(s)
5
MgSO3·6H2O(s)+ SO2(g)==Mg(HSO3)2(s)+5H2O(l)
选项
实验操作和现象
结论
向 Na2SO3 溶液中加入硝酸酸化的 Ba(NO3)2 溶液，有白色
A
Na2SO3 溶液已经变质
沉淀出现
向蛋白质溶液中滴加 CuSO4 溶液，有沉淀析出，加水，
B 沉淀不溶解
蛋白质发生盐析
C
向苯酚钠溶液中通入足量 CO2，溶液变浑浊
酸性：苯酚<碳酸
向 2 mL NaI、NaCl 的混合稀溶液中滴加 2 滴 AgNO3 稀溶
1
D. Kw/c(OH-)=0.1 mol・L-1 的溶液中:Na+、NH4+、AlO2-、SO42【答案】B 5. 下列实验装置或操作能达到实验目的的是
A. 用装置甲分离乙醇和水 B. 用装置乙干燥氨气
C. 用装置丙制备氯气
D. 用装置丁制备乙酸乙酯
【答案】C
6. 下列有关化学反应叙述正确的是
A. Na 与水反应生成 O2
示，下列叙述不正确的是 A. 放电时，a 电极反应为 I2Br-+2e- ═2I-+BrB. 放电时，溶液中离子的数目增大 C. 充电时，a 电极接外电源负极 D. 充电时，b 电极每增重 0.65 g，溶液中有 0.02 mol I-被氧化

苏教版江苏省南京市玄武区高三(上)9月调研数学试卷押题卷解析版

2019-2020学年苏教版江苏省南京市玄武区高三（上）9月调研数学试卷一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上．1．（5分）复数，则复数z的实部是．2．（5分）设集合A＝{3，6}，B＝{2≤x＜4}，则A∩B＝．3．（5分）函数y＝ln（x2﹣4）+的定义域为．4．（5分）已知向量的夹角为，＝．5．（5分）函数y＝f（x）是奇函数，当x＜0时，f（x）＝x2﹣ax（a∈R），且f（2）＝6，则a＝．6．（5分）曲线y＝x2+在点（1，2）处的切线方程为．7．（5分）已知实数x，y满足条件，则z=3x﹣2y的最大值为．8．（5分）将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27πcm3，则该圆柱的侧面积为cm2．9．（5分）若函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则f（﹣π）的值为．10．（5分）记等差数列{a n}前n项和为S n．若a m=10，S2m﹣1=110，则m的值为．11．（5分）已知函数f（x）是定义在R上的奇函数，且在（﹣∞，0]上为单调增函数．若f（﹣1）=﹣2，则满足f（2x﹣3）≤2的x的取值范围是．12．（5分）在△ABC中，AB=3，AC=2，∠BAC=120°，=λ．若•=﹣，则实数λ的值为．13．（5分）在平面直角坐标系xOy中，若圆（x﹣2）2+（y﹣2）2=1上存在点M，使得点M关于x轴的对称点N在直线kx+y+3=0上，则实数k的最小值为．14．（5分）已知函数f（x）=若存在唯一的整数x，使得＞0成立，则实数a的取值范围为．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）在直三棱柱ABC﹣A1B1C1中，AB=AC，E是BC的中点，求证：（Ⅰ）平面AB1E⊥平面B1BCC1；（Ⅱ）A1C∥平面AB1E．16．（14分）在△ABC中，内角A，B，C所对的边分别为a，b，c，cosB=．（Ⅰ）若c=2a，求的值；（Ⅱ）若C﹣B=，求sinA的值．17．（14分）某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为t1小时，其余工人加工完乙型装置所需时间为t2小时．设f（x）=t1+t2．（Ⅰ）求f（x）的解析式，并写出其定义域；（Ⅱ）当x等于多少时，f（x）取得最小值？18．（16分）如图，在平面直角坐标系xOy中，椭圆C：+=1（a＞b＞0）的离心率为，且过点（1，）．过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x=m（m＞a）于点M．已知点B（1，0），直线PB交l于点N．（Ⅰ）求椭圆C的方程；（Ⅱ）若MB是线段PN的垂直平分线，求实数m的值．19．（16分）已知函数f（x）=2x3﹣3（a+1）x2+6ax，a∈R．（Ⅰ）曲线y=f（x）在x=0处的切线的斜率为3，求a的值；（Ⅱ）若对于任意x∈（0，+∞），f（x）+f（﹣x）≥12lnx恒成立，求a的取值范围；（Ⅲ）若a＞1，设函数f（x）在区间[1，2]上的最大值、最小值分别为M（a）、m（a），记h（a）=M（a）﹣m（a），求h（a）的最小值．20．（16分）已知数列{a n}的各项均为正数，记数列{a n}的前n项和为S n，数列{a n2}的前n项和为T n，且3T n=S n2+2S n，n∈N*．（Ⅰ）求a1的值；（Ⅱ）求数列{a n}的通项公式；（Ⅲ）若k，t∈N*，且S1，S k﹣S1，S t﹣S k成等比数列，求k和t的值．【选做题】在21,22,23,24四小题中只能选做2题，每小题0分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．[选修4-1：几何证明选讲]21．如图，CD是圆O的切线，切点为D，CA是过圆心O的割线且交圆O于点B，DA=DC．求证：CA=3CB．[选修4-2：矩阵与变换]22．设二阶矩阵A=．（Ⅰ）求A﹣1；（Ⅱ）若曲线C在矩阵A对应的变换作用下得到曲线C′：6x2﹣y2=1，求曲线C 的方程．[选修4-4：坐标系与参数方程]23．在平面直角坐标系xOy中，直线l的参数方程为（t为参数），圆C 的参数方程为（θ为参数）．若直线l与圆C相切，求实数a的值．[选修4-5：不等式选讲]24．解不等式：|x﹣2|+|x+1|≥5．【必做题】第25题、第26题，每题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．25．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP=AB=AD=1．（Ⅰ）若直线PB与CD所成角的大小为，求BC的长；（Ⅱ）求二面角B﹣PD﹣A的余弦值．26．袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有4个，分别编号为1，2，3，4．现从袋中随机取两个球．（Ⅰ）若两个球颜色不同，求不同取法的种数；（Ⅱ）在（1）的条件下，记两球编号的差的绝对值为随机变量X，求随机变量X 的概率分布与数学期望．2019-2020学年江苏省南京市高三（上）9月调研数学试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上．7．（5分）已知实数x，y满足条件，则z=3x﹣2y的最大值为6．【解答】解：作出实数x，y满足条件，对应的平面区域如图：由z=3x﹣2y得y=x﹣，平移直线y=x﹣，经过点A时，直线y=x﹣的截距最小，此时z最大．由，解得A（4，3），此时z max=3×4﹣2×3=6，故答案为：6．8．（5分）将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27πcm3，则该圆柱的侧面积为18πcm2．【解答】解：将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27πcm3，设正方形的边长为acm，则V=πa2•a=27π，解得a=3cm，∴该圆柱的侧面积为S=2π×3×3=18πcm2．故答案为：18π．9．（5分）若函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则f（﹣π）的值为﹣1．【解答】解：有函数的图象可得A=2，再根据T=•=π﹣，求得ω=．由于点（π，2）在函数图象上，可得：2=2sin（×π+φ），可得：×π+φ=2kπ+，k∈Z，求得φ=2kπ﹣，k∈Z，又由于|φ|＜π，可得：φ=﹣，故函数的解析式为f（x）=2sin（x﹣），可得：f（﹣π）=2sin（﹣π﹣）=﹣2sin=﹣1．故答案为：﹣1．10．（5分）记等差数列{a n}前n项和为S n．若a m=10，S2m﹣1=110，则m的值为6．【解答】解：由a m=10，∴2a m=a1+a2m﹣1=20，==10（2m﹣1）=110，∴S2m﹣1解的m=6，故答案为：611．（5分）已知函数f（x）是定义在R上的奇函数，且在（﹣∞，0]上为单调增函数．若f（﹣1）=﹣2，则满足f（2x﹣3）≤2的x的取值范围是（﹣∞，2] ．【解答】解：根据题意，函数f（x）是定义在R上的奇函数，且在（﹣∞，0]上为单调增函数，则在f（x）在[0，+∞）上也是增函数，故函数f（x）R上也是增函数；又由f（﹣1）=﹣2，则f（1）=﹣f（﹣1）=2，则f（2x﹣3）≤2⇒2x﹣3≤1，解可得x≤2，即不等式的解集为（﹣∞，2]；故答案为：（﹣∞，2]．12．（5分）在△ABC中，AB=3，AC=2，∠BAC=120°，=λ．若•=﹣，则实数λ的值为．【解答】解：如图所示，△ABC中，AB=3，AC=2，∠BAC=120°，=λ=λ（﹣），∴•=（+）•=（+λ（﹣））•（﹣）=[（1﹣λ）+λ]•（﹣）=（1﹣2λ）•﹣（1﹣λ）+λ=（1﹣2λ）×3×2×cos120°﹣（1﹣λ）×32+λ•22=19λ﹣12=﹣，解得λ=．故答案为：．13．（5分）在平面直角坐标系xOy中，若圆（x﹣2）2+（y﹣2）2=1上存在点M，使得点M关于x轴的对称点N在直线kx+y+3=0上，则实数k的最小值为﹣．【解答】解：根据题意，圆C：（x﹣2）2+（y﹣2）2=1关于x轴的对称图形是：圆D：（x﹣2）2+（y+2）2=1，则圆D上存在点N在直线kx+y+3=0上，又直线kx+y+3=0过定点P（0，﹣3），∴直线与圆D相切时，有d=r，即=1，解得k=﹣或k=0，∴实数k的最小值为﹣．故答案为：﹣．14．（5分）已知函数f（x）=若存在唯一的整数x，使得＞0成立，则实数a的取值范围为[0，2]∪[3，8] ．【解答】解：作出f（x）的函数图象如图所示：（1）当x＞0时，f（x）≤f（1）=3，∵存在唯一的整数x，使得＞0成立，∴a＜f（x）只有1个整数解，又f（2）=0，∴0≤a＜3．（2）若x＜0，则f（x）≥f（0）=0，∵存在唯一的整数x，使得＞0成立，∴a＞f（x）只有1个整数解，又f（﹣1）=2，f（﹣2）=8，∴2＜a≤8．∴当0≤a≤2或3≤a≤8时，＞0只有1个整数解．故答案为：[0，2]∪[3，8]．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）在直三棱柱ABC﹣A1B1C1中，AB=AC，E是BC的中点，求证：（Ⅰ）平面AB1E⊥平面B1BCC1；（Ⅱ）A1C∥平面AB1E．【解答】（本小题满分14分）证明：（Ⅰ）在直三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC．∵AE⊂平面ABC，∴CC1⊥AE．∵AB=AC，E为BC的中点，∴AE⊥BC．∵BC⊂平面B1BCC1，CC1⊂平面B1BCC1，且BC∩CC1=C，∴AE⊥平面B1BCC1．∵AE⊂平面AB1E，∴平面AB1E⊥平面B1BCC1．（Ⅱ）连接A1B，设A1B∩AB1=F，连接EF．在直三棱柱ABC﹣A1B1C1中，四边形AA1B1B为平行四边形，∴F为A1B的中点．∵E是BC的中点，所以EF∥A1C．∵EF⊂平面AB1E，A1C⊄平面AB1E，∴A1C∥平面AB1E．16．（14分）在△ABC中，内角A，B，C所对的边分别为a，b，c，cosB=．（Ⅰ）若c=2a，求的值；（Ⅱ）若C﹣B=，求sinA的值．【解答】（本小题满分14分）解：（Ⅰ）在△ABC中，因为cosB=，所以：．因为：c=2a，所以：=，即=，所以：=，由正弦定理得，所以：．（Ⅱ）因为cosB=，所以cos2B=2cos2B﹣1=．又0＜B＜π，所以sinB==，所以sin2B=2sinBcosB=2×=．因为C﹣B=，即C=B+，所以A=π﹣（B+C）=﹣2B，所以sinA=sin（﹣2B）=sin cos2B﹣cos sin2B=﹣（﹣）×=．17．（14分）某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为t1小时，其余工人加工完乙型装置所需时间为t2小时．设f（x）=t1+t2．（Ⅰ）求f（x）的解析式，并写出其定义域；（Ⅱ）当x等于多少时，f（x）取得最小值？【解答】解：（I）∵t1=，t2==．∴f（x）=t1+t2=+，定义域为{x|1≤x≤99，x∈N*}．（II）f（x）=1000=10[x+（100﹣x）]=10（10+）≥10×（10+2）=10×（10+6）=160．当且仅当x=75人时，函数f（x）取得最小值160小时．18．（16分）如图，在平面直角坐标系xOy中，椭圆C：+=1（a＞b＞0）的离心率为，且过点（1，）．过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x=m（m＞a）于点M．已知点B（1，0），直线PB交l于点N．（Ⅰ）求椭圆C的方程；（Ⅱ）若MB是线段PN的垂直平分线，求实数m的值．【解答】（本小题满分16分）解：（Ⅰ）因为椭圆C的离心率为，所以a2=4b2．又因为椭圆C过点（1，），所以，解得a2=4，b2=1．所以椭圆C的方程为．（Ⅱ）设P（x0，y0），﹣2＜x0＜2，x0≠1，则．因为MB是PN的垂直平分线，所以P关于B的对称点N（2﹣x0，﹣y0），所以2﹣x0=m．由A（﹣2，0），P（x0，y0），可得直线AP的方程为y=（x+2），令x=m，得y=（m+2），即M（m，（m+2））．因为PB⊥MB，所以k PB•k MB=﹣1，所以k PB•k MB=•=﹣1，即=﹣1．因为．所以=1．因为x0=2﹣m，化简得3m2﹣10m+4=0，解得m=．因为m＞2，所以m=19．（16分）已知函数f（x）=2x3﹣3（a+1）x2+6ax，a∈R．（Ⅰ）曲线y=f（x）在x=0处的切线的斜率为3，求a的值；（Ⅱ）若对于任意x∈（0，+∞），f（x）+f（﹣x）≥12lnx恒成立，求a的取值范围；（Ⅲ）若a＞1，设函数f（x）在区间[1，2]上的最大值、最小值分别为M（a）、m（a），记h（a）=M（a）﹣m（a），求h（a）的最小值．【解答】解：（Ⅰ）f′（x）=6x2﹣6（a+1）x+6a，故k=f′（0）=6a，由6a=3，解得：a=；（Ⅱ）f（x）+f（﹣x）=﹣6（a+1）x2≥12lnx对任意x∈（0，+∞）恒成立，故﹣（a+1）≥，g（x）=，x＞0，则g′（x，令g′（x）=0，解得：x=，故g（x）在（0，）递增，在（，+∞）递减，故g（x）max=g（）=，故﹣（a+1）≥，故a≤﹣1﹣，故a的范围是（﹣∞，﹣1﹣]；（Ⅲ）f′（x）=6x2﹣6（a+1）x+6a=6（x﹣1）（x﹣a），f（1）=3a﹣1，f（2）=4，令f′（x）=0，解得：x=1或x=a，①当1＜a≤时，x∈（1，a）时，f′（x）＜0，f（x）在（1，a）递减，x∈（a，2）时，f′（x）＞0，f（x）在（a，2）递增，∵f（1）≤f（2），故M（a）=f（2）=4，m（a）=f（a）=﹣a3+3a2，故h（a）=M（a）﹣m（a）=a3﹣3a2+4，∵h′（a）=3a（a﹣2）＜0，∴h（a）在（1，]递减，故a∈（1，]时，h（a）=h（）=；最小值②当＜a＜2时，x∈（1，a）时，f′（x）＜0，f（x）在（1，a）递减，x∈（a，2）时，f′（x）＞0，f（x）在（a，2）递增，∵f（1）＞f（2），∴M（a）=f（1）=3a﹣1，m（a）=f（a）=﹣a3+3a2，故h（a）=M（a）﹣m（a）=a3﹣3a2+3a﹣1，∵h′（a）=3（a﹣1）2≥0，故h（a）在（，2）递增，故a∈（，2）时，h（a）＞h（）=；③当a≥2时，x∈（1，2）时，f′（x）＜0，f（x）在（1，2）递减，故M（a）=f（1）=3a﹣1，m（a）=f（2）=4，故h（a）=M（a）﹣m（a）=3a﹣5，故h（a）在[2，+∞）上的最小值是h（2）=1，=．综上，h（a）最小值20．（16分）已知数列{a n}的各项均为正数，记数列{a n}的前n项和为S n，数列{a n2}的前n项和为T n，且3T n=S n2+2S n，n∈N*．（Ⅰ）求a1的值；（Ⅱ）求数列{a n}的通项公式；（Ⅲ）若k，t∈N*，且S1，S k﹣S1，S t﹣S k成等比数列，求k和t的值．【解答】解：（I）由3T n=S n2+2S n，n∈N*．n=1时，3T1=+2S1，可得≠0，解得a1=1．（II）由3T n=S n2+2S n，n∈N*．n≥2时，+2S n﹣1，相减可得：=S n2﹣+2a n，∴3a n=S n+S n﹣1+2．∴3a n+1=S n+1+S n+2，可得：3a n+1﹣3a n=a n+1+a n，化为：a n+1=2a n．n=1时，，可得+2（1+a2），a2＞0，解得a2=2，满足上式．∴数列{a n}是等比数列，首项为1，公比为2．∴a n=2n﹣1．（III）由（II）可得：S n==2n﹣1．由S1，S k﹣S1，S t﹣S k成等比数列，∴，可得（2k﹣2）2=2t ﹣2k．化为：2t=（2k）2﹣3•2k+4，可得：2t﹣2=（2k﹣1）2﹣3•2k﹣1+1．（*）k=1时不满足题意，∴k≥2．k=2时，2t=8，解得t=3．k≥3时，t=2时，化为2k=3，不成立舍去．t≥3时，（*）左边为偶数，右边为奇数，不成立．综上可得：t=3，k=2．【选做题】在21,22,23,24四小题中只能选做2题，每小题0分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．[选修4-1：几何证明选讲]21．如图，CD是圆O的切线，切点为D，CA是过圆心O的割线且交圆O于点B，DA=DC．求证：CA=3CB．【解答】证明：连接OD，因为DA=DC，所以∠DAO=∠C．在圆O中，AO=DO，所以∠DAO=∠ADO，所以∠DOC=2∠DAO=2∠C．因为CD为圆O的切线，所以∠ODC=90°，从而∠DOC+∠C=90°，即2∠C+∠C=90°，故∠C=30°，所以OC=2OD=2OB，所以CB=OB，所以CA=3CB．[选修4-2：矩阵与变换]22．设二阶矩阵A=．（Ⅰ）求A﹣1；（Ⅱ）若曲线C在矩阵A对应的变换作用下得到曲线C′：6x2﹣y2=1，求曲线C 的方程．【解答】解：（Ⅰ）∵A=，∴detA==﹣2，A*=，∴=．（Ⅱ）设曲线C上任意一点P（x，y），在矩阵A对应的变换作用下得到点P （x′，y′），则==，∴∵（x′，y′）在曲线C′上，∴6x′2﹣y′2=1，代入6（x+2y）2﹣（3x+4y）2=1，化简得8y2﹣3x2=1，∴曲线C的方程为8y2﹣3x2=1．[选修4-4：坐标系与参数方程]23．在平面直角坐标系xOy中，直线l的参数方程为（t为参数），圆C 的参数方程为（θ为参数）．若直线l与圆C相切，求实数a的值．【解答】解：由直线l的参数方程为，得直线l的普通方程为x﹣y+1=0．由圆C的参数方程为，得圆C的普通方程为（x﹣a）2+（y﹣2a）2=1．因为直线l与圆C相切，所以=1，解得a=1±．所以实数a的值为1±．[选修4-5：不等式选讲]24．解不等式：|x﹣2|+|x+1|≥5．【解答】解：（1）当x＜﹣1时，不等式可化为﹣x+2﹣x﹣1≥5，解得x≤﹣2；（2）当﹣1≤x≤2时，不等式可化为﹣x+2+x+1≥5，此时不等式无解；（3）当x＞2时，不等式可化为x﹣2+x+1≥5，解得x≥3；所以原不等式的解集为（﹣∞，﹣2]∪[3，+∞）．【必做题】第25题、第26题，每题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．25．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP=AB=AD=1．（Ⅰ）若直线PB与CD所成角的大小为，求BC的长；（Ⅱ）求二面角B﹣PD﹣A的余弦值．【解答】解：（Ⅰ）分别以AB、AD、AP所在直线为x、y、z轴建立如图所示的空间直角坐标系A﹣xyz．∵AP=AB=AD=1，∴A（0，0，0），B（1，0，0），D（0，1，0），P（0，0，1）．设C（1，y，0），则=（1，0，﹣1），=（﹣1，1﹣y，0）．∵直线PB与CD所成角大小为，∴|cos＜＞|=||=，即=，解得y=2或y=0（舍），∴C（1，2，0），则BC的长为2；（Ⅱ）设平面PBD的一个法向量为=（x，y，z）．∵=（1，0，﹣1），=（0，1，﹣1），∴，令x=1，则y=1，z=1，=（1，1，1）．∵平面PAD的一个法向量为=（1，0，0），∴cos＜＞==，∴二面角B﹣PD﹣A的余弦值为．26．袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有4个，分别编号为1，2，3，4．现从袋中随机取两个球．（Ⅰ）若两个球颜色不同，求不同取法的种数；（Ⅱ）在（1）的条件下，记两球编号的差的绝对值为随机变量X，求随机变量X 的概率分布与数学期望．【解答】解：（1）两个球颜色不同的情况共有⋅42=96（种）．（2）随机变量X所有可能的值为0，1，2，3．P（X=0）==，P（X=1）==，P（X=2）==，第21页（共21页）P （X=3）==．所以随机变量X 的概率分布列为：X0 1 2 3 P所以E （X ）=0×+1×+2×+3×=．。

南京市2020届高三年级学情调研数学附加卷(定稿)

南京市2020届高三年级学情调研数学附加题 2019.09 注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡．21．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共计20分．请在答卷卡指定区．．．．．．域内．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—2：矩阵与变换已知二阶矩阵A ＝⎣⎢⎡⎦⎥⎤2 321．（1）求A －1；（2）若曲线C 在矩阵A 对应的变换作用下得到曲线C ′：x 2－3y 2＝1，求曲线C 的方程．B ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l ：⎩⎨⎧x ＝4t ，y ＝1＋at (t 为参数，a 为常数)，曲线C ：⎩⎨⎧x ＝2＋cos θ，y ＝sin θ(θ为参数)．若曲线C 上的点P 到直线l 的距离的最大值为3，求a 的值．C ．选修4—5：不等式选讲解不等式x 2＋2|x －1|＜6．（第22题图） A C DPE F 【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内．．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）如图，四棱锥P －ABCD 的底面ABCD 是矩形，P A ⊥平面ABCD ，P A ＝AD ＝2，E ，F 分别为P A ，AB 的中点，且DF ⊥CE ．（1）求AB 的长；（2）求直线CF 与平面DEF 所成角的正弦值．23．（本小题满分10分）已知集合A ＝{1，2，3，4}和集合B ＝{1，2，3，…，n }，其中n ≥5，n ∈N *．从集合A 中任取三个不同的元素，其中最小的元素用S 表示；从集合B 中任取三个不同的元素，其中最大的元素用T 表示．记X ＝T －S ．（1）当n ＝5时，求随机变量X 的概率分布和数学期望E (X )；（2）求P (X ＝n －3)．。

南京市2020届高三年级学情调研卷参考答案和评分标准(定稿)

南京市2020届高三年级学情调研数学参考答案及评分标准 2019.09一、填空题：本大题共14小题，每小题5分，计70分．1．[1，＋∞） 2．10 3．4 4．0.018 5．236．3 7．23 3 8．[－1，2] 9．3410．(1，＋∞)11．20 12．6 13．[－2，2] 14．(34，2)二、解答题：本大题共6小题，共90分． 15．解：（1）因为a sin2B ＝2b sin A ，由正弦定理a sin A ＝bsin B得 2sin A sin B cos B ＝2sin B sin A ． ………………… 3分因为A ，B 为△ABC 的内角，所以sin A ≠0，sin B ≠0，所以cos B ＝22． …………………………… 5分又因为B 为△ABC 的内角，所以0＜B ＜π，所以B ＝π4． …………………………… 7分（2）因为cos C ＝55，C ∈(0，π)，所以sin C ＝1－cos 2C ＝1－(55)2＝255， …………………………… 9分所以sin2C ＝2sin C cos C ＝2×255×55＝45， cos2C ＝2cos 2C －1＝2×(55)2－1＝－35． ………………………… 11分因为B ＝π4，所以A ＋C ＝3π4，从而A －C ＝(3π4－C )－C ＝3π4－2C ，因此 sin(A －C )＝sin(3π4－2C )＝sin 3π4cos2C －cos 3π4sin2C＝22×(－35)－(－22)×45＝210．…………………………… 14分16．证明：（1）在三棱柱ABC －A 1B 1C 1中，AB ∥A 1B 1，AB ＝A 1B 1．因为E ，F 分别为AB 和A 1B 1的中点，所以AE ∥FB 1，AE ＝FB 1，所以四边形AEB 1F 是平行四边形，所以AF ∥EB 1． ………………………… 4分因为AF ⊄平面B 1CE ，B 1E ⊂平面B 1CE ，所以AF ∥平面B 1CE ．……………………… 7分（2）因为AB ∥A 1B 1，A 1B 1⊥B 1C ，所以AB ⊥B 1C ．在△ABC 中，因为AC ＝BC ，E 为AB 的中点，所以AB ⊥CE ． …………………………… 10分因为AB ⊥B 1C ，AB ⊥CE ，B 1C ∩CE ＝C ，B 1C ⊂平面B 1CE ，CE ⊂平面B 1CE ，所以AB ⊥平面B 1CE ． …………………………… 12分因为AB ⊂平面ABC ，所以平面B 1CE ⊥平面ABC ． …………………………… 14分17．解：（1）因为p (t )＝⎩⎨⎧1800－15(9－t )2， 4≤t ＜9，1800， 9≤t ≤15，其中t ∈N ．所以当载客人数不超过1500人时，4≤t ＜9，此时p (t )＝1800－15(9－t )2随着t 的增大而增大．当t ＝4时，p (4)＝1800－15(9－4)2＝1425＜1500，符合题意；当5≤t ＜9时，p (t )≥p (5)＝1800－15(9－5)2＝1560＞1500，不符合题意．因此，发车时间间隔t 的值为4． …………………………… 5分（2）因为Q ＝6p (t )－7920t－100，所以当9≤t ≤15时，Q ＝6×1800－7920t －100＝2880t －100．由于Q 的值随着t 的增大而减少，故t ＝9时Q 取得最大值，此时Q max ＝220． …………………………… 7分1（第16题图）当4≤t ＜9时，Q ＝6p (t )－7920t－100＝6[1800－15(9－t )2]－7920t －100＝－90t 2＋1620t －4410t－100＝1520－90(t ＋49t ) …………………………… 9分≤1520－90×2t ×49t＝260，当且仅当t ＝49t ，即t ＝7时取得最大值． …………………………… 11分由于260＞220，故t ＝7时Q 取得最大值．答：当发车时间间隔为7分钟时，平均每趟地铁每分钟的净收益最大，最大净收益为260元． …………………………… 14分18．解：（1）因为(a 2，3e )和(b ，3e )都在椭圆x 2a 2＋y 2b2＝1上，所以 ⎩⎨⎧14＋9e 2b 2＝1， ①b 2a 2＋3e 2b 2＝1． ② …………………………… 2分由①整理得，e 2b 2＝112．代入②得，b 2a 2＝1－3×112＝34． …………………………… 4分因为e ＝ca，其中c 2＝a 2－b 2，可得b 2＝3c ，a 2＝4c ，从而c 2＝a 2－b 2＝c ，解得c ＝1，即a 2＝4，b 2＝3，故椭圆的标准方程为x 24＋y 23＝1． …………………………… 6分（2）由（1）可知A (－2，0)，B (2，0)．解法一：因为C 是椭圆上异于A ，B 的任意一点，所以直线BC 的斜率存在且不为0．设直线BC 的方程为y ＝k (x －2)，k ≠0．联立⎩⎪⎨⎪⎧x 24＋y 23＝1y ＝k (x －2)，消去y ，得 (3＋4k 2)x 2－16k 2x ＋16k 2－12＝0．解得x ＝2或x ＝8k 2－63＋4k 2，从而C (8k 2－63＋4k 2，－12k 3＋4k 2)． …………………… 9分因为P 是BC 的中点，所以P (8k 23＋4k 2，－6k 3＋4k 2)．因为PQ ⊥BC ，所以直线PQ 的方程为y －(－6k 3＋4k 2)＝－1k (x －8k 23＋4k 2)，化简得y ＝－x k ＋2k3＋4k 2． ③由A (－2，0)，C (8k 2－63＋4k 2，－12k 3＋4k 2)，可得直线AC 的斜率为－12k 3＋4k 28k 2－63＋4k 2＋2＝－34k ，从而直线AC 的方程为y ＝－34k(x ＋2)． ④联立直线PQ ，AC 的方程③④，消去y 得－x k ＋2k 3＋4k 2＝－34k (x ＋2)，解得x ＝32k 2＋183＋4k 2，即点Q 的横坐标为32k 2＋183＋4k 2． …………………… 14分因为→OB ＝(2，0)，所以→OB ·→PQ ＝2(32k 2＋183＋4k 2－8k 23＋4k 2)＝12，即→OB ·→PQ 为定值12． …………………………… 16分解法二：设C (x 0，y 0)，其中x 0≠±2，y 0≠0，则由P 是BC 的中点，得P (x 0＋22，y 02)．直线AC ，BC 的斜率均存在且不为0，直线BC 的斜率为y 0x 0－2．因为PQ ⊥BC ，所以直线PQ 的方程为y －y 02＝－x 0－2y 0(x －x 0＋22)，即y ＝－x 0－2y 0x ＋x 02－42y 0＋y 02．③ …………………………… 9分又直线AC 的斜率为y 0x 0＋2，从而直线AC 的方程为y ＝y 0x 0＋2(x ＋2)．④联立直线PQ ，AC 的方程③④，消去y ，得－x 0－2y 0x ＋x 02－42y 0＋y 02＝y 0x 0＋2(x ＋2)，两边同乘以y 0，得 (2－x 0)x ＋x 02－42＋y 022＝y 02x 0＋2(x ＋2)．由x 024＋y 023＝1，得y 02＝3－3x 024，代入化简得(2－x 0)x ＋x 02－48＝34(2－x 0)(x ＋2)．因为x 0≠2，解得x ＝x 0＋142，即点Q 的横坐标为x 0＋142． …………… 14分因为→OB ＝(2，0)，所以→OB ·→PQ ＝2(x 0＋142－x 0＋22)＝12，即→OB ·→PQ 为定值． …………………………… 16分19．解：（1）由f (x )＝2ln x ＋ax 2－bx ，得f ′(x )＝2ax 2－bx ＋2x，因为曲线y ＝f (x )在x ＝1处的切线为y ＝2x －3，所以f (1)＝a －b ＝－1， f ′(1)＝2a －b ＋2＝2，解得a ＝1，b ＝2． …………………………… 3分（2）因为a ＝0，所以f (x )＝2ln x －bx ，x ∈(0，＋∞)；由f (x )≤－2得2ln x －bx ≤－2，即b ≥2＋2ln xx ． …………………………… 5分设g (x )＝2＋2ln x x ，x ＞0，则g ′(x )＝－2ln xx 2，由g ′(x )＝0得x ＝1．当0＜x ＜1时，g ′(x )＞0，当x ＞1时，g ′(x )＜0，则g (x )在(0，1)单调递增，在(1，＋∞)单调递减，所以当x ＝1时，g (x )有最大值g (1)＝2．于是b ≥2，即实数b 的取值范围为[2，＋∞) ． ……………………… 8分（3）函数f (x )的定义域为(0，＋∞)，当b ＝4时f ′(x )＝2ax 2－4x ＋2x．①当a ＝0时，f ′(x )＝x，由f ′(x )＞0得0＜x ＜12；由f ′(x )＜0得x ＞12，所以f (x )的增区间为(0，12)，减区间为(12，＋∞)； ……………………… 9分②当a ＜0时，由f ′(x )＞0得0＜x ＜1－1－a a ；由f ′(x )＜0得x ＞1－1－aa ，所以f (x )的增区间为(0，1－1－a a )，减区间为(1－1－aa，＋∞)；……………………………11分③当0＜a ＜1时，由f ′(x )＞0，得0＜x ＜1－1－a a 或x ＞1＋1－aa ；由f ′(x )＜0，得1－1－a a ＜x ＜1＋1－aa，所以f (x )的增区间为(0，1－1－a a )和(1＋1－aa，＋∞)，减区间为(1－1－a a ，1＋1－aa)； ……………………… 13分④当a ≥1时，f ′(x )≥0恒成立，于是f (x )的增区间为(0，＋∞)，无减区间；综上，当a ＜0时，f (x )的增区间为(0，1－1－a a )，减区间为(1－1－aa，＋∞)；当a ＝0时，f (x )的增区间为(0，12)，减区间为(12，＋∞)；当0＜a ＜1时，f (x )的增区间为(0，1－1－a a )和(1＋1－aa，＋∞)，减区间为(1－1－a a ，1＋1－aa)；当a ≥1时，f (x )的增区间为(0，＋∞)，无减区间．…………………………… 16分20．解：（1）因为数列{n n }是以2为公差的等差数列，所以S n n ＝S 11＋12(n －1)＝a 1＋12(n －1)＝n ＋32，即S n ＝n (n ＋3)2．…………… 2分所以当n ≥2时，a n ＝S n －S n －1＝n (n ＋3)2－(n －1)(n ＋2)2＝n ＋1，又a 1＝2＝1＋1，所以a n ＝n ＋1，n ∈N *. …………………………… 4分（2）①因为b n ＝2n a n ＝(n ＋1)2n ，所以T n ＝2×21＋3×22＋…＋(n ＋1)2n ，因此2T n ＝2×22＋3×23＋…＋(n ＋1)2n ＋1，两式相减，得－T n ＝2×21＋22＋23＋…＋2n －(n ＋1)2n ＋1＝2＋2×1－2n 1－2－(n ＋1)2n ＋1＝－n·2n ＋1， …………………… 6分所以T n ＝n·2n ＋1，因此T n n ＝2n ＋1，从而T n ＋1n ＋1T nn＝2，故数列{T nn }是以4为首项，2为公比的等比数列. …………………… 8分② 因为T m T n ＝m (S m ＋λ)n (S n ＋λ)，所以m·2m ＋1n·2n ＋1＝m [m (m ＋3)2＋λ]n [n (n ＋3)2＋λ]，即m 2＋3m ＋2λ2m ＝n 2＋3n ＋2λ2n ，…………… 10分设f (n )＝n 2＋3n ＋2λ2n，n ∈N *，则f (n ＋1)－f (n )＝n 2＋5n ＋4＋2λ2n ＋1－n 2＋3n ＋2λ2n ＝－n 2－n ＋4－2λ2n ＋1，当n ≥3时，－n 2－n ＋4－2λ≤－32－3＋4－2λ＝－8－2λ≤－8－2(－2)＝－4＜0，所以当n ≥3时，f (n ＋1)＜f (n )，因此当m ＞n ≥3时，f (n )＞f (m )，与f (n )＝f (m )相矛盾，又n ＞1，于是n ＝2，所以m 2＋3m ＋2λ2m ＝5＋λ2． ………………… 12分当m ≥5时，m 2＋3m ＋2λ2m ≤52＋3×5＋2λ25＝20＋λ16，又20＋λ16－5＋λ2＝－20－7λ16≤－20－7×(－2)16＝－38＜0，即20＋λ16＜5＋λ2，所以当m ≥5时，m 2＋3m ＋2λ2m ＜5＋λ2，与m 2＋3m ＋2λ2m ＝5＋λ2相矛盾．又m ＞n ＝2，所以m ＝3或4． ………………… 14分当m ＝3时，32＋3×3＋2λ23＝5＋λ2，解得λ＝－1；当m ＝4时，42＋3×4＋2λ24＝5＋λ2，解得λ＝－2；因此λ的所有可能值为－1和－2. …………………………… 16分南京市2020届高三学情调研考试数学附加题参考答案及评分标准 2019．0921．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共20分． A ．选修4—2：矩阵与变换解：（1）解法一：因为A ＝⎣⎢⎡⎦⎥⎤2 321，设A －1＝⎣⎢⎡⎦⎥⎤a b c d ，则由A －1A ＝E ，得⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤2 32 1＝⎣⎢⎡⎦⎥⎤1001，所以⎩⎨⎧2a ＋2b ＝1，3a ＋b ＝0，2c ＋2d ＝0，3c ＋d ＝1． …………………………… 2分解得a ＝－14，b ＝34，c ＝12，d ＝－12，从而A－1＝⎣⎢⎡⎦⎥⎤－14 34 12 －12． …………………………… 4分解法二：因为矩阵⎣⎢⎡⎦⎥⎤a b c d (ad －bc ≠0)的逆矩阵为⎣⎢⎡⎦⎥⎤dad －bc －bad －bc －c ad －bc a ad －bc ， ………………………… 2分又A ＝⎣⎢⎡⎦⎥⎤2 321，所以A－1＝⎣⎢⎡⎦⎥⎤－14 3412 －12． …………………………… 4分（2）设曲线C 上任意一点P (x ，y )在矩阵A 对应的变换作用下得到点P ′(x ′，y ′)，则⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤2 321 ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤2x ＋3y 2x ＋y ，所以⎩⎪⎨⎪⎧x ′＝2x ＋3y ，y ′＝2x ＋y ． ……………………7分因为(x ′，y ′)在曲线C ′上，所以x ′2－3y ′2＝1，代入得(2x ＋3y )2－3(2x ＋y )2＝1，化简得6y 2－8x 2＝1，即曲线C 的方程为6y 2－8x 2＝1． ………………… 10分B ．选修4—4：坐标系与参数方程解：将直线l 的参数方程化为普通方程，得ax －4y ＝－4，即ax －4y ＋4＝0．…………………………… 2分将曲线C 的参数方程化为普通方程得(x －2)2＋y 2＝1， …………………… 4分所以曲线C 是以(2，0)为圆心，1为半径的圆，所以曲线C 上的点P 到直线l 的距离的最大值为|2a ＋4|a 2＋16＋1．…………… 6分又因为曲线C 上的点P 到直线l 的距离的最大值为3，所以|2a ＋4|a 2＋16＋1＝3，即(a ＋2)2＝a 2＋16， ………………………… 8分所以4a ＋4＝16，解得a ＝3． ………………………… 10分 C ．选修4—5：不等式选讲解：当x ≥1时，原不等式化为x 2＋2(x －1)＜6，即x 2＋2x －8＜0，解得－4＜x ＜2，所以1≤x ＜2； …………………………… 4分当x ＜1时，原不等式化为x 2－2(x －1)＜6，即x 2－2x －4＜0，解得1－5＜x ＜1＋5，所以1－5＜x ＜1． ………………………… 8分综上1－5＜x ＜2．所以不等式的解集为(1－5，2)． …………………………… 10分【必做题】第22题、第23题，每题10分，共20分． 22．解：（1）因为底面ABCD 是矩形，且P A ⊥平面ABCD ，故以{→AB ，→AD ，→AP }为正交基底建立空间直角坐标系A －xyz ．设AB ＝a ．因为P A ＝AD ＝2，E ，F 分别为P A ，AB 的中点，所以C (a ，2，0)，D (0，2，0)，F (a2，0，0)，E (0，0，1)，所以DF →＝(a 2，－2，0)，CE →＝(－a ，－2，1)， ………………………… 2分因为DF ⊥CE ，所以DF →·CE →＝0，即 a2×(－a )＋(－2)×(－2)＋0×1＝0，解得a ＝22，所以AB 的长为22．………………… 4分（2）因为a ＝22，所以DF →＝(2，－2，0)， EF →＝(2，0，－1)．设平面DEF 的一个法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·EF →＝0，n ·DF →＝0，即⎩⎪⎨⎪⎧2x －z ＝0，2x －2y ＝0，取n ＝(2，1，2)． …………………………… 6分又CF →＝(－2，－2，0)，所以cos ＜CF →，n ＞＝CF →·n |CF →||n |＝－2×2－2×1＋0×26×7＝－24221．………………………… 8分记直线CF 与平面DEF 所成角为α，则sin α＝| cos ＜CF →，n ＞|＝24221，即直线CF 与平面DEF 所成角的正弦值为24221． ……………………… 10分23．解：（1）当n ＝5时，B ＝{1，2，3，4，5}．随机变量X 的所有可能取值为1，2，3，4． P (X ＝1)＝1C 34C 35＝140； P (X ＝2)＝3＋3C 34C 35＝320；P (X ＝3)＝9＋6C 34C 35＝38； P (X ＝4)＝18C 34C 35＝920．…………………………… 4分因此随机变量X 的概率分布如下表：随机变量X E (X )＝1×140＋2×320＋3×38＋4×920＝134． …………………………… 6分（2）由题意知，当S ＝1时，T ＝n －2，此时，符合要求的取法共有C 23C 2n －3种；当S ＝2时，T ＝n －1，此时，符合要求的取法共有C 22C 2n －2种．………… 8分故P (X ＝n －3)＝ C 23C 2n －3＋C 22C 2n －2 C 34C 3n＝3(n －3)(2n －7)2n (n －1)(n －2)． …………… 10分。

江苏省南京市2020届高三英语9月学情调研测试试题

江苏省南京市2020届高三英语9月学情调研测试试题注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第I卷（选择题）一、单项选择1．_______a striking look with a sea of lavender flowers, Guli has become a famous attraction in Nanjing.A．Wearing B．To wearC．To be wearing D．Having won2．---What’s up, Kim? You look very excited!---Sorry, just a moment ago I ran into Tayor Swift so I was a bit .A．Given up B．have their hands upC．carried away D．driven away3．The Spanish National Football Team is such a superb one that they can .A．get their hands dirty B．have their hands fullC．lay their hands on us D．beat us hands down4．What a lucky dog! He’s just a starring role in Spielberg’s next movie.A．landed B．lostC．arranged D．accepted5．Some animal protectors are seen as being two-faced about animal welfare the way they treat domestic animals.A．in need of B．in view ofC．in search of D．in favour of6．The company needs to develop a culture people see that’s OK to take time off.A．that B．whenC．which D．where7．If we just focus on how we want the future to be, we may be to opportunities along the way.A．equal B．closeC．blind D．open8．You say you are innocent, but we have good reasons to think .A．twice B．overC．aloud D．otherwise9．The site in Beijing is an outstanding of the creative art of Chinese garden design.A．distinction B．expressionC．inspiration D．evaluation10．HMV’s rise started with the pop music revolution of the 1960s, when the company began its album sales in London.A．expanding B．exploringC．exporting D．expecting11．It is very encouraging to see Beijing 2022 is using its potential to maximize the use of existing stadiums.A．how B．whyC．when D．whether12．Mr. Wills, who was being helped up onto the platform to take the prize, looked as if he by lightning.A．was just struck B．were just struckC．would just be struck D．had just been struck13．After 40 years of reform and opening-up, China still has a long way to go it becomes a “developed economy”.A．until B．beforeC．after D．unless14．The founding of Shanghai Cooperation Organization, which widely recognized and praised, aims to build friendly international relations.A． .was B．wereC．has been D．had been15．---What a waste of time to watch such a boring match！--- . Why not switch the channel?A．It’s no big deal B．With your permissionC．My feelings exactly D．You’ve got to be kidding 二、完形填空Wildflowers in a mountain meadow are a gift of nature. But what about those wildflowers blooming along busy___16___? Well, nature had a____17___.Claudia Alta “Lady Bird” Johnson, the wife of our thirty-sixth President, Lyndon B．Johnson wanted ___18___to be a national priority.As a little girl growing up in “deep east T exas,” wildflowers helpedher get through___19___times. Her mother had died when she was five, and her father___20_____most of his time at the general store he owned. Her older brothers were away at school, ___21___ Lady Bird turned to nature for ___22___. “Nature was my friend and my teacher,” she says. “It was a joy to me, and it’s never____23____ me.”After high school, Lady Bird left home for the University of Texas in Austin. ____24___ she found joy in nature—in the vast quantities of Texas bluebonnets（德克萨斯州羽扇豆）. It was there that Lady Bird met and fell in love with Lyndon B．Johnson. He proposed to her on their first ____25____.“The whole country ___26___ the President,” Lady Bird said, “but only one man selects the First Lady—and it is highly____27___ that he was thinking of her as First Lady when he proposed!”When she got to know the ___28____ disappearance of “America the Beautiful” due to land development and p ollution, Lady Bird ____29____ the President to propose a Highway Beautification Act that allocated money to ____30___roadsides. The act was passed in 1965.Lady Bird ___31____ that many wildflowers, like people, were immigrants. “They ____32____ the natio n on the wheels of covered wagons, perhaps ___33___ in the pockets of children.”Lady Bird is certainly our First Lady of___34___. She has made us see that highways can be beautiful.She is the reason why wildflowers now____35____our travels through almost every state.16．A．streets B．highways C．roads D．lanes17．A．helper B．discoverer C．creator D．protector18．A．liberty B．traffic C．justice D．beauty19．A．lonely B．exciting C．happy D．disappointed20．A．wasted B．spent C．found D．killed 21．A．so B．but C．or D．for 22．A．aid B．company C．rescue D．happiness23．A．ignored B．scared C．troubled D．failed 24．A．Absolutely B．Naturally C．Again D．Often25．A．date B．try C．vote D．appearance26．A．shapes B．serves C．selects D．supports27．A．unlikely B．unnecessary C．unusual D．uncertain28．A．sudden B．complete C．gradual D．final29．A．warned B．persuade C．forced D．ordered30．A．lengthen B．widen C．monitor D．landscape31．A．let out B．found out C．pointed out D．figured out32．A．visited B．left C．passed D．crossed33．A．then B．even C．yetD．still34．A．wildflowers B．wagons C．roadsides D．travels35．A．decide B．guide C．brighten D．shorten三、阅读理解A36．According to the passage, which of the following is TERE?A．Those Ame ricans who live above the poverty line won’t go hungry.B．13 million American children are food insecure for lack of transportation.C．Among all the states in the USA, food insecurity in Mississippi is severest.D．Neighborhood banks have no additional requirements for food packaging.37．What is the author’s purpose in writing the passage?A．To warn readers against dangers of insecure food.B．To urge readers to help the poor out of poverty.C．To inform readers of the severe food shortage in America.D．To advocate readers contributing to food relief in America.BSo called “sin taxes” on sugary drinks, alcohol and tobacco not only work, but will help rather than improperly punish the poor, according to a major new international analysis.Just a day before the UK brings in a levy on sugary drinks, experts are urging every country in the world to use taxes to keep people from theeating, drinking and smoking habits that will damage their health. The experts analyzed the effects of taxes on sugary drinks, tabacco and alcohol in countries that have introduced them and found that the criticism that they are punishing the poorest in unfounded.Experts did a survey. They looked at 13 countries: Chile, Guatemala, Panama, Nicaragua, Albania, Poland, Turkey, Tajikistan, Tanzania, Niger, Nigeria, India and Timor-Leste. They found that wealthier families generally spend more on alcohol, soft drinks and snacks. In India, for instance, wealthier households spent seven times more on alcohol and three times more on soft drinks and snacks compared to poorer households. So those households end up paying a larger proportion of any tax.On the other hand, taxes have a greater impact on the smaller household budgets of poorer families. They respond by buying less, with greater benefits for their health. In the UK, say the authors, the response to the possible introduction of a minimum price for alcohol was estimated to be 7.6 times larger in the poorest households, compared with the wealthiest.In Mexico, the introduction of a sugary drinks tax resulted in an average of 4.2 litres less of soft drinks purchased per person, with a 17%decrease in purchases among lower income groups and almost no change in higher income groups. In Lebanon, they say, a 50% increase in the price of cigarettes would lead to twice as many people quitting smoking in poorer households as wealthy families.“The evidence suggests that concerns about higher taxes on tobacco, alcohol, and soft drinks harming the poor are overstated,” said Dr. Rachel Nugent from RTI International in Seattle, USA, and chair of the Lancet Taskforce on NCDs and economics.“Some degree of taxation on tobacco is common in many countries, and while we are starting to see progress on alcohol taxes, there is much more governments should be doing –in both high and low income countries –to consider the careful introduction of taxes on other unhealthy products like soft drinks and snacks. Price policies such as taxes will be a key part of the response to rising rates of non-communicablediseases(慢性非传染病).”The UK sugar tax is a levy on the manufacturers of 18p per litre for drinks containing 5g of sugar per 100ml and 24p on those with 8g per 100ml.Many companies have reformulated their products, often swapping artificial sweeteners for sugar. Some –like Coca-Cola –havedecided to stick to the original recipe and the price will rise, although the bottles and cans will shrink to reduce the impact.38．What do we know about the “sin taxes”?A．They receive warm welcome in developing countries.B．They help people get rid of unhealthy lifestyles.C．They have the same effects on the poor and rich.D．They have a deeper influence on groups with high income.39．Which of the following is TRUE about the responses to “sin taxes”?A．The public have turned a deaf ear to it.B．The government has introduced taxes on snacks.C．Many companies have raised the price of their products.D．Coca-Cola will use smaller packages to counter the impacts.40．The author support his ideas in the passage by .A．giving examplesB．telling storiesC．analyzing causes and effectsD．reasoning and concludingCI’d be lying if I said a dog-like robot opening a door for anotherdog-like robot doesn’t creep me out. A full discussion of robot dogs is for another day, but for now, researchers studying the cognition（认知）and welfare of real dogs have a less threatening view of dogs and technology, particularly when touchscreens are involved.Like you, animals can learn to interact with the content displayed on touchscreens, and their touch reveals something about their choice, which in turn reveals something about their mind. Animals both on and off land can be trained to use touchscreens — from chimpanzees to dogs, cats, and even dolphins, among others. Touchscreen studies have explored how and what dogs categorize, their ability to learn by exclusion（排除）, and how they discriminate between different images. An added bonus is that, once a dog has mastered the touchscreen, humans can remove themselves from the study and can’t unconsciously give signals to the dog.Researchers are now posing a new set of questions: are touchscreens beneficial to the user? Can touchscreens exercise the dog’s mind, in addition to serving as a window into it?No better place to start than with older pet dogs, a group facing a unique set of challenges. Aging dogs can have reduced physical activity compared to their younger counterparts. Less attention is often given totheir learning, training and other mental activities; after all, who hasn’t heard the wrong proverb, “You can’t teach an old dog new tricks.” But dog minds are n ot meant to be inactive. Instead, “studies point to the fact that aging seems to be slowed by mental and physical stimulation, and thus stopping these activities might actually lead to faster aging in dogs.”Lisa Wallis and colleagues at the Senior Family Dog Project at ELTE University in Budapest are exploring the effects of touchscreens on dog physiological, behavioral, and cognitive well-being.Their recent conference paper gives us a look at how dogs learn to use the touchscreen and the direction of future research. Over the course of a number of sessions, dogs learned that when they nose-touch a particular image on the screen, a food treat pops out. At first, only a single image appears on the screen. Once the dogs reliably learn to nose-touch the image, they move on to discrimination training where two images appear together and only one image is “correct.” Only two out of one hundred thirty dogs were unable to grasp the task, and three displayed frustration suggesting touchscreens are within the capacity of the majority of senior dogs.Wallis and colleagues will continue investigating long-term effects oftouchscreen use, but it seems promising. “The positive association to the touchscreen is so strong that on several occasions when the dog was alone (the trainer had stepped out to answer the phone), and the feeder failed, dogs continued to work on the touchscreen with no reward until the end of the session.” Owners, even those initially skeptical, were impressed by the strategies their dogs used. They also observed that dogs slept soundly upon returning home from touchscreen sessions, highlighting that mental activity can have some of the same effects as physical exercise.Further studies will explore the effects of long-term touchscreen use on dog personality, activity levels, measures of well-being, and influence on the dog-human bond. Stay tuned.41．What can we learn from the first two paragraphs?A．Animals can decide the content shown on touchscreens.B．Animals naturally have the ability to use touchscreens.C．People can discriminate between dogs’ abilities by exclusion.D．People can tell dogs’ needs through their touch on the screen.42．By using the proverb in paragraph 4, the author intends to stress .A．aging dogs are too old to learn new skillB．aging dogs experience a decline in energyC．training younger dogs is more productiveD．training aging dogs is possible and beneficial43．What is revealed by the research conducted by Lisa Wallis?A．The dogs master the touchscreen use step by step.B．Rewards are a must for dogs to finish the sessionC．The dogs regard nose-touch as a form of physical exercise.D．It remains to be seen whether it has a positive effect on dogs.44．What does the passage mainly talk about?A．How robot dogs have threatened the world.B．How people establish better dog-human bonds.C．How touchscreens can be employed to train dogs.D．How long-held myths about dogs mislead people.D①One by one, prejudices are disappearing in the West. People may harbour private suspicions that other people’s race or sex makes them inferior—but to say so openly is totally taboo. One old prejudice remains respectable, though. Just ask a childless person.②They are not charged to special taxes, as they were in Soviet Russia; nor are they driven from their homes, as they still are in some poorcountries. The childless nonetheless come in for a lot of criticism. Some point out that non-parents are failing to produce the future workers who will pay for their pensions. Childless politicians are charged with not having a proper stake（利害关系）in society. “He talks to us about the future, but he do esn’t have children!” complained Jean-Marie Le Pen, co-founder of the National Front party, of Emmanuel Macron, who went on to win the French presidency. Similar attacks on Theresa May and Angela Merkel also failed—but researchers find that many voters quietly agree.③The charges against the childless should be thrown out, along with other social prejudice. In many rich countries, between 15% and 20% of women, and a slightly higher proportion of men, will not have children. The share is rising. Some have medical problems; others do not meet the right person in time; still others decide they do not want them. Whatever the cause, the attacks on the childless are baseless.④If non-breeders are selfish, they have a strange way of showing it. They are more likely to set up charitable foundations than people with children, and much more likely to donate money to good causes. According to one American estimate, the mere fact of not having children raises the amount a person leaves to charity by a little over $10,000. Thechildl ess are thus a small but useful counterweight to the world’s parents, who stop social immobility by passing on their social and economic advantages to their children.⑤The fact that so many senior politicians lack offspring（子孙）ought to put to rest the idea that they do not care for society. Five of the G7 countries are led by childless men and women. Mr. Macron, Mrs. May, Mrs. Merkel, Shinzo Abe and Paolo Gentiloni have their faults, but they are not notably less able than Justin Trudeau (who has three children) let alone Donald Trump (who has five). Their opportunities for nepotism（裙带关系）are limited. And they spare their countries dynastic politics.⑥The charge that chil dless people fail to pull their weight in population is correct, but is less serious than it appears. Those who do not have children do put pressure on public pension systems. Governments have to do unpopular things like making pensions less generous, as Japan has done, or accepting more immigrants, as some Western countries have done. But to sustain （维持）public pensions in the long term, countries do not actually need more parents. What they need instead is more babies. It is possible to combine a high rate of childlessness with a high birth rate, provided people who become parents have more than one or two children. That was the pattern in manyWestern countries a century ago. Ireland, yet another country with a childless leader, still manages it today.⑦The childless also do everyone else a favour by creating wonderful works of art. British novelists have been especially likely to have no offspring: think of Hilary Mantel, P.G. Wodehouse and the Brontë sisters. In September last year Britain put Jane Austen on its ten-pound note. That decision has was controversial, though it was hard to see why. Few people have written as shrewdly（出神入化）about money or about families—even though Austen did not marry, and had no children.45．What is the main idea of Paragraph 2?A．The childless often get punished in society.B．The childless often come under sharp criticism.C．Most successful politicians have no childrenD．Childlessness affects the result of an election.46．The childless are prejudiced because people think the childless .A．have a strange way to show selfishnessB．set a bad example for young peopleC．are not as able as those with childrenD．are the government’s financial burden47．What does the underlined word “it” in Paragraph 6 refer to?A．Accepting more immigrants.B．Reducing the pensions for the aged.C．Encouraging parents to have more children.D．Supporting the political leaders with no children.48．What is the author’s attitude towards the childless?A．Understanding B．SkepticalC．Disappointed D．Reserved49．Which of the following shows the structure of the passage? (①to⑦ represent Paragraphs 1 to 7)A．B．C．D．50．What is the best title for the passage?A．In defence of the childlessB．In hope of having a child or notC．Reasons for not having childrenD．Measures to address aging problems第II卷（非选择题）四、任务型阅读请认真阅读下列短文，并根据所读内容在文章后表格中的空格里填入一个最恰当的单词。

江苏省南京市高三数学9月学情调研考试试题理新人教A版

第Ⅰ卷（共70分）一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上． 1.已知集合{}2,A x x x R =<∈，集合{}13,B x x x R =<<∈，则AB = .2.命题“2,220x R x x ∀∈-+>”的否定是 .3.已知复数z 满足1iz i =+（i 为虚数单位），则z = .4.下图是某算法的流程图，其输出值a 是 .5.口袋中有形状和大小完全相同的四个球，球的编号分别为1,2,3,4，若从袋中随机抽取两个球，则取出的两个球的编号之和大于5的概率为 .所以事件“取出的两个球的编号大于5”发生的概率2163 P==.考点：古典概型6.若一个圆柱的侧面展开图是边长为2的正方形，则此圆柱的体积为.7.已知点(),P x y 在不等式0024x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的平面区域上运动，则z x y =+的最大值是 .考点：线性规划8.曲线sin y x x =+在点()0,0处的切线方程是 .9.在等差数列{}n a 中，487,15a a ==，则数列{}n a 的前n 项和n S = .10.如图，在ABC ∆中，D 、E 分别为边BC 、AC 的中点. F 为边AB 上的点，且3AB AF =，若AD x AF y AE =+，,x y R ∈，则x y +的值为 .【答案】52. 【解析】11.设函数()f x 是定义在R 上的偶函数，当0x ≥时，()21x f x =+.若()3f a =，则实数a 的值为 .12.已知四边形ABCD 是矩形，2AB =，3AD =，E 是线段BC 上的动点，F 是CD 的中点．若 AEF ∠为钝角，则线段BE 长度的取值范围是 .22223110AF AD DF =+=+，由于AEF ∠为钝角，则cos 0AEF ∠<，则有222AE EF AF +- 0<，即()()2224610102640x x x x x ++-+-=-+<，即2320x x -+<，解得12x <<；13.如图，已知过椭圆()222210x y a b a b+=>>的左顶点(),0A a -作直线l 交y 轴于点P ，交椭圆于点Q ，若AOP ∆是等腰三角形，且2PQ QA =，则椭圆的离心率为 .14.已知函数()32log,031108,3 33x xf xx x x⎧<<⎪=⎨-+≥⎪⎩，若存在实数a、b、c、d，满足()()()f a f b f c== ()f d=，其中0d c b a>>>>，则abcd的取值范围是 .【答案】()21,24.【解析】试题分析：如下图所示，由图形易知01a<<，13b<<，则()33log logf a a a==-，()3logf b b= 3log b=，()()f a f b=，33log loga b∴-=，1ab∴=，令21108033x x-+=，即210240x x-+=，。

南京市2020届高三年级学情调研数学附加卷(定稿)

南京市2020届高三年级学情调研数学附加题 2019.09 注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡．21．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共计20分．请在答卷卡指定区．．．．．．域内．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—2：矩阵与变换已知二阶矩阵A ＝⎣⎢⎡⎦⎥⎤2 321．（1）求A －1；（2）若曲线C 在矩阵A 对应的变换作用下得到曲线C ′：x 2－3y 2＝1，求曲线C 的方程．B ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l ：⎩⎨⎧x ＝4t ，y ＝1＋at (t 为参数，a 为常数)，曲线C ：⎩⎨⎧x ＝2＋cos θ，y ＝sin θ(θ为参数)．若曲线C 上的点P 到直线l 的距离的最大值为3，求a 的值．C ．选修4—5：不等式选讲解不等式x 2＋2|x －1|＜6．（第22题图） A C D PE F 【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内．．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）如图，四棱锥P －ABCD 的底面ABCD 是矩形，P A ⊥平面ABCD ，P A ＝AD ＝2，E ，F 分别为P A ，AB 的中点，且DF ⊥CE ．（1）求AB 的长；（2）求直线CF 与平面DEF 所成角的正弦值．23．（本小题满分10分）已知集合A ＝{1，2，3，4}和集合B ＝{1，2，3，…，n }，其中n ≥5，n ∈N *．从集合A 中任取三个不同的元素，其中最小的元素用S 表示；从集合B 中任取三个不同的元素，其中最大的元素用T 表示．记X ＝T －S ．（1）当n ＝5时，求随机变量X 的概率分布和数学期望E (X )；（2）求P (X ＝n －3)．。

南京市2020届高三年级学情调研卷参考答案和评分标准(答案)

南京市2020届高三年级学情调研数学参考答案及评分标准2019.09一、填空题：本大题共14小题，每小题5分，计70分． 1．[1，＋∞） 2． 3．4 4．0.018 5．10236．3 7．8．[－1，2] 9． 10．(1，＋∞)2333411．2012．613．[－2，2]14．(，2)34二、解答题：本大题共6小题，共90分． 15．解：（1）因为a sin2B ＝b sin A ，2由正弦定理＝得 2sin A sin B cos B ＝sin B sin A ． ………………… 3分a sin Ab sin B2因为A ，B 为△ABC 的内角，所以sin A ≠0，sin B ≠0，所以cos B ＝．…………………………… 5分2又因为B 为△ABC 的内角，所以0＜B ＜π，所以B ＝．…………………………… 7分 π4（2）因为cos C ＝，C ∈(0，π)，55所以sin C ＝＝＝， …………………………… 9分 1－cos 2C 1－()2255所以sin2C ＝2sin C cos C ＝2××＝，2555545 cos2C ＝2cos 2C －1＝2×()2－1＝－． ………………………… 11分5535因为B ＝，所以A ＋C ＝，从而A －C ＝(－C )－C ＝－2C ，π43π43π43π4因此 sin(A －C )＝sin(－2C )＝sin cos2C －cos sin2C3π43π43π4＝×(－)－(－)×＝．…………………………… 14分2352451016．证明：（1）在三棱柱ABC －A 1B 1C 1中，AB ∥A 1B 1，AB ＝A 1B 1．因为E ，F 分别为AB 和A 1B 1的中点，所以AE ∥FB 1，AE ＝FB 1，所以四边形AEB 1F 是平行四边形，所以AF ∥EB 1．………………………… 4分因为AF ⊄平面B 1CE ，B 1E ⊂平面B 1CE ，所以AF ∥平面B 1CE ．……………………… 7分（2）因为AB ∥A 1B 1，A 1B 1⊥B 1C ，所以AB ⊥B 1C ．在△ABC 中，因为AC ＝BC ，E 为AB 的中点，所以AB ⊥CE ．…………………………… 10分因为AB ⊥B 1C ，AB ⊥CE ，B 1C ∩CE ＝C ，B 1C ⊂平面B 1CE ，CE ⊂平面B 1CE ，所以AB ⊥平面B 1CE ． …………………………… 12分因为AB ⊂平面ABC ，所以平面B 1CE ⊥平面ABC ． …………………………… 14分17．解：（1）因为p (t )＝其中t ∈N ．{1800－15(9－t )2， 4≤t ＜9，1800， 9≤t ≤15，)所以当载客人数不超过1500人时，4≤t ＜9，此时p (t )＝1800－15(9－t )2随着t 的增大而增大．当t ＝4时，p (4)＝1800－15(9－4)2＝1425＜1500，符合题意；当5≤t ＜9时，p (t )≥p (5)＝1800－15(9－5)2＝1560＞1500，不符合题意．因此，发车时间间隔t 的值为4． …………………………… 5分（2）因为Q ＝－100，6p (t )－7920t所以当9≤t ≤15时，Q ＝－100＝－100．6×1800－7920t2880t1A （第16题图）由于Q 的值随着t 的增大而减少，故t ＝9时Q 取得最大值，此时Q max ＝220． …………………………… 7分当4≤t ＜9时，Q ＝－1006p (t )－7920t＝－1006[1800－15(9－t )2]－7920t＝－100－90t 2＋1620t －4410t＝1520－90(t ＋) …………………………… 9分49t ≤1520－90×2＝260，t ×当且仅当t ＝，即t ＝7时取得最大值． …………………………… 11分49t 由于260＞220，故t ＝7时Q 取得最大值．答：当发车时间间隔为7分钟时，平均每趟地铁每分钟的净收益最大，最大净收益为260元． …………………………… 14分18．解：（1）因为(，3e )和(b ，e )都在椭圆＋＝1上，a23x 2a 2y 2b2所以…………………………… 2分{＋＝1， ①＋＝1． ②)由①整理得，＝．e 2b 2112代入②得，＝1－3×＝．…………………………… 4分b 2a211234因为e ＝，其中c 2＝a 2－b 2，ca可得b 2＝3c ，a 2＝4c ，从而c 2＝a 2－b 2＝c ，解得c ＝1，即a 2＝4，b 2＝3，故椭圆的标准方程为＋＝1．…………………………… 6分x 24y 23（2）由（1）可知A (－2，0)，B (2，0)．解法一：因为C 是椭圆上异于A ，B 的任意一点，所以直线BC 的斜率存在且不为0．设直线BC 的方程为y ＝k (x －2)，k ≠0．联立，消去y ，得 (3＋4k 2)x 2－16k 2x ＋16k 2－12＝0．{＋＝1y ＝k (x －2))解得x ＝2或x ＝，从而C (，－)． …………………… 9分8k 2－63＋4k 28k 2－63＋4k 212k3＋4k 2因为P 是BC 的中点，所以P (，－)．8k 23＋4k 26k3＋4k 2因为PQ ⊥BC ，所以直线PQ 的方程为y －(－)＝－(x －)，6k 3＋4k 21k 8k 23＋4k 2化简得y ＝－＋． ③x k 2k3＋4k 2由A (－2，0)，C (，－)，可得直线AC 的斜率为＝－，8k 2－63＋4k 212k 3＋4k 2－＋234k 从而直线AC 的方程为y ＝－(x ＋2)． ④34k 联立直线PQ ，AC 的方程③④，消去y 得－＋＝－(x ＋2)，x k 2k 3＋4k 234k解得x ＝，即点Q 的横坐标为． …………………… 14分32k 2＋183＋4k 232k 2＋183＋4k 2因为＝(2，0)，所以·＝2(－)＝12，→ OB → OB →PQ 32k 2＋183＋4k 28k 23＋4k 2即·为定值12． …………………………… 16分→ OB →PQ解法二：设C (x 0，y 0)，其中x 0≠±2，y 0≠0，则由P 是BC 的中点，得P (，)．x 0＋22y 02直线AC ，BC 的斜率均存在且不为0，直线BC 的斜率为．y 0x 0－2因为PQ ⊥BC ，所以直线PQ 的方程为y －＝－(x －)，y 02x 0－2y 0x 0＋22即y ＝－x ＋＋．③ …………………………… 9分x 0－2y 0x 02－42y 0y 02。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

可退出循环得： n 4 .
【点睛】本题考查程序框图循环结构中的判断问题，难度较易
. 程序框图问题主要是两种处理方法：（ 1）逐
步列举，将退出循环前的情况依次列举；（ 2）根据循环结构中的特殊形式简化运算 . 4. 某班 50 位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是： 60) ，［ 60，70) ，［ 70， 80），［ 80， 90），［ 90， 100〕，则图中 x 的值为 _______
则这两位同学参加了不同的兴趣小组的概率为
【答案】 2 3
【解析】
______
【分析】
甲、乙参加了不同的兴趣小组的可能数与可能的情况总数的比值即为对应概率
.
【详解】甲、乙参加了不同的兴趣小组的情况有
A
2 3
=6
种，
总的可能情况有
33
9 种，则概率 P
62 =.
93
【点睛】本题考查古典概型的概率计算，难度较易. 古典概型的概率计算公式为：
南京市 2020 届高三年级学情调研卷
数学 2019.09
参考公式：柱体的体积公式： V=Sh，其中 S 为为柱体的底面积， h 为柱体的高 . 球的体积公式： V 4 R3 ，其中 R 为球体的半径 .
3 一、填空题： ( 请将答案写在答题卡相应位置． )
1. 函数 f x
x 1 的定义域是
【答案】 [1, )
.
【详解】 f ( x) 的定义域为 R ，关于原点对称且 f ( x)
x 1 |x|
f (x) ，所以 f (x) 是奇函数；
又因为 x 0 时 f ( x)
x 1 1 是增函数，所以 f ( x) 在 R 上是增函数；
1x
x1
因为 f ( x 3) f (2 x) 0 ，所以 f ( x 3) f (2 x) 且 f ( 2x) f (2 x) ，则有 x 3
【答案】 2 3 3
【解析】
【分析】
根据准线与两条渐近线恰能围成一个等边三角形得到渐近线的斜率，然后再计算离心率的值
.
【详解】由题意可知其中一条渐近线倾斜角为：
30 ，所以 b tan 30 a
3 ，则 e c
3
a
1
b2 a2
2 3. 3
【点睛】本题考查双曲线的离心率计算，难度较易
. 求解离心率的时候如果涉及到几何图形，可借助几何图
z 10 ，故答案为 10 .
3. 某算法的流程图如图所示，则物出的
n 的值为 _______．
【答案】 4
【解析】
【分析】
循环代入 n、 p 的值，直到 p 10 时输出 p 的值 .
【详解】第一次循环： n 2, p 5 ；第二次循环： n 3, p 10 ；第三次循环， n 4, p 17 ，此时满足 p 10
. 对于求解 f ( x) A sin( x ) 在给定区间 D 上的
值域：先分析 x D 时， x 的范围，再根据 y sin x 的单调性求解 f ( x) 的值域 .
9. 若锐角 α 满足 tan （ α＋）＝ 3tan α＋ 1，则 tan 2α 的值为 _____．
4 【答案】 3
4
【解析】
tan2
2tan 1 tan2 .
为锐角），则
2sin cos ，
10. 已知函数 f ( x)
x ，则不等式 f (x 3) f (2 x) 0 的解集为 ____．
1 |x|
【答案】（1，＋∞）
【解析】
【分析】
先分析 f (x) 奇偶性，再分析 f ( x) 单调性，然后将不等式转化为自变量间的关系，计算出解集
形的特点去分析问题 .
8. 若函数 f ( x) 2sin( x )( 6
【答案】［－ 1， 2］
0) 的最小正周期为
，则当 x [0, ] 时， f ( x) 的值域为 _______． 2
【解析】
【分析】
先根据最小正周期求出
的值，再利用给定区间分析函数 f ( x) 的最值 .
2 【详解】因为 T
[40 ，50），［ 50，
【答案】 0.018 【解析】【分析】
根据频率和为 1来计算 x 的值 .
【详解】因为 (0.006 3 0.01 0.054 x) 10 1 ，所以 x 0.018 .
【点睛】本题考查频率分布直方图中频率总和为
1这一知识点，难度较易 .
5. 有 3 个兴趣小组，甲、乙两位同学各自选择其中一个参加，且每位同学参加各个兴趣小组的可能性相同，
2x ，故 x 1，
【解析】
试题分析：要使函数有意义，需满足 x 1 0 x 1，因此定义域为 [1, )
考点：函数定义域
2. 已经复数 z 满足 ( z 2)i 1 i （ i 是虚数单位），则复数 z 的模是 ________．
【答案】 10
【解析】
【详解】 ( z 2)i 1 i ，
1i
1 3i
z
2
3 i,
i
i
待求事件包含的基本事件个数
P
.
可能出现的事件总数
6. 把一个底面半径为 3cm，高为 4 cm的钢质实心圆柱熔化，然后铸成一个实心钢球的半径为 _______cm 【答案】 3 【解析】
( 不计损耗），则该钢球
【分析】
根据熔化前后的体积不变求解钢球的半径即可
.
【详解】圆柱体积： V圆柱 =
9 4=36
，球的体积：
4 V球 = 3
r 3 ，所以 4 3
r3
36 ，解得 r
3.
【点睛】圆柱的体积公式： V
r 2h ；球的体积公式： V 4 r 3 . 3
7. 在平面直角坐标系
xoy 中，若双曲线
x2 a2
y2 b2
1(a 0,b 0) 的一条准线与两条渐近线恰能围成一个等边
三角形，则该双曲线的离心率为 ______．
||
，所以2Βιβλιοθήκη ，则 f ( x) 2sin(2 x ) ； 6
又 x [0, ] ，所以 (2 x
)[
5 , ]，
2
6
66
则 f (x)max 2sin
2 ， f ( x) min 2sin( ) 1 .
2
6
所以 f (x) 的值域为： [ 1,2] .
【点睛】本题考查三角函数的周期以及值域，难度较易
【分析】
先计算 tan 的值，再利用二倍角公式计算 tan2 的值 .
1 tan
【详解】由题意可知：
1 tan
3tan
tan2
2 tan 1 tan2
1
2 3
3
.
1 (1)2 4
3
【点睛】常用的二倍角公式： cos 2 cos2
1 ，则 tan
sin 2
2cos 2
1 或 tan
3
0（舍，
1 1 2sin 2 ，sin 2

江苏省南京市2020届高三9月学情调研数学试题(教师版)

2019-2020学年江苏省南京市高三上学期学情调研(9月) 数学

【数学】南京2020届高三年级学情调研卷 及解析

南京市2020届高三年级学情调研卷(定稿)

江苏省南京市2020届高三9月学情调研数学试题(学生版)

江苏省南京市届三9月学情调研数学试题x

江苏省南京市2020高三数学9月学情调研试题(含解析)

2019-2020学年江苏省南京市高三上学期9月学情调研测试 数学试题

2024届南京高三上学期9月学情调研数学试题及答案

江苏省南京市2020届高三数学9月学情调研考试试题(含解析)

2020年9月江苏省南京市普通高中2021届高三毕业班学情调研考试数学试题(解析版)

南京市2020届高三化学零模试卷(答案版)

苏教版江苏省南京市玄武区高三(上)9月调研数学试卷押题卷解析版

南京市2020届高三年级学情调研数学附加卷(定稿)

南京市2020届高三年级学情调研卷参考答案和评分标准(定稿)

江苏省南京市2020届高三英语9月学情调研测试试题

江苏省南京市高三数学9月学情调研考试试题 理 新人教A版

南京市2020届高三年级学情调研数学附加卷(定稿)

南京市2020届高三年级学情调研卷参考答案和评分标准(答案)

【数学】南京2020届高三年级学情调研卷及解析

2019-2020学年江苏省南京市高三上学期9月学情调研测试数学试题

江苏省南京市高三数学9月学情调研考试试题理新人教A版