2019-2020年高三调研考试数学试题含答案
2019-2020年高三9月调研考试数学试题含答案

2019-2020年高三9月调研考试数学试题含答案注意事项:1 .本试卷共3页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本 试卷满分为160分,考试时间为120分钟.2 •答题前,请务必将自己的姓名、学校写在答题卡上•试题的答案写在答 .题卡上对应题目的答案空格内.考试结束后,交回答题卡.一、填空题:本大题共 14小题,每小题5分,共70分•请把答案填写在答 题卡相应位置上. 1 .函数f(x)= cos 2x — sin 2x 的最小正周期为▲12. 已知复数z = 1 + i ,其中i 是虚数单位,则|z|=▲3.某学校高一、高二、高三年级的学生人数之比为 4: 3: 3,现用分层抽样的方法从该校高 4. 从甲、乙、丙、丁 4位同学中随机选出 2名代表参加学校会议,则甲被选中的概率是▲5. 已知向量 a = (2 , 1), b = (0, — 1).若(a + ?b)丄 a , 则实数X=▲.2 27. 已知双曲线 为一y 2= 1(a >0, b > 0)的渐近线方程为y =± 3x ,则该双曲线的离心率为 ▲&已知圆锥的侧面展开图是一个半径为2的半圆,则这个圆锥的高是 _______ ▲. 9.设f(x)=x 2— 3x + a .若函数f(x)在区间(1, 3)内有零点,贝U 实数a 的取值范围为▲10. 在△ ABC 中,角A , B , C 所对边的长分别为 a , b , c .已知a + 2c = 2b , sinB = 2sinC ,则 cosA =▲中三个年级的学生中抽取容量为 80的样本,则应从高一年级抽取11.若 f(x) = x.—x + 3a , x > 1,X V 1 是R 上的单调函数,则实数a 的取值范围为▲ 名学生.(第6题图)6. 右图是一个算法流程图,则输出S的值是▲12. 记数列{a n}的前n 项和为S n•若a i= 1, S n = 2佝 + a n)(n》2, n€ N*),则S n = ▲- 13. 在平面直角坐标系xOy中,已知圆C: x2+ y2—6x+ 5 = 0,点A, B在圆C上,且AB= 2 3, 则I"O A + 75B I的最大值是▲.x14. 已知函数f(x)= x—1 —(e—1)1 nx,其中e为自然对数的底,则满足f(e )< 0的x的取值范围为▲二、解答题:本大题共6小题,共计90分.请在答.题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)n已知函数f(x) = 2sin(2x+妨(0 <X 2力的图象过点(;,一2).(1)求$的值;(2)若◎=5, -n< a< 0,求sin(2 a— j的值.16. (本小题满分14分)如图,三棱柱ABC —A1B1C1中,M , N分别为AB, B1C1的中点.(1)求证:MN //平面AA1C1C ;(2)若CC1= CB1, CA = CB,平面CC1B1B丄平面ABC,求证:AB_平面CMN .(第16题图)17. (本小题满分14分)已知{a n}是等差数列,其前n项的和为S n, {b n}是等比数列,且a i = b i= 2, a4+ b4= 21, S4+ b4= 30.(1) 求数列{a n}和{b n}的通项公式;(2) 记C n= a n b n, n € N* ,求数列g}的前n项和.18. (本小题满分16分)2 2给定椭圆C: X2+ y z = 1(a>b>0),称圆C1:x2+ y2= a2+ b2为椭圆C的“伴随圆”.已知a b椭圆C的离心率为j,且经过点(0, 1).(1)求实数a, b的值;(2)若过点P(0, m)(m>0)的直线I与椭圆C有且只有一个公共点,且I被椭圆C的伴随圆C1所截得的弦长为2 2,求实数m的值.19. (本小题满分16分)如图(示意),公路AM、AN围成的是一块顶角为a的角形耕地,其中tan a=—2 .在该块土地中P 处有一小型建筑,经测量,它到公路AM , AN的距离分别为3km , 5km .现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.(第19题图)20. (本小题满分16分)已知函数f(x)= ax3+ |x—a|, a€ R.(1)若 a =—1,求函数y= f(x)(x€,都存在10.厶211. [;, )12. 2 —2n—113. 8 14. (0, 1)二、解答题:本大题共6小题,共计90分.15. (本小题满分14分)解:(1)因为函数f(x)= 2sin(2x+枷0v X 2"的图象过点(才,—2),所以f(;)= 2sin( n+ 閒=—2,即sin ©= 1. ........................................................... 4 分因为0v(V 2 n所以0= n ........................................................... 6分(2)由(1)得,f(x)= 2cos2x. ...................................................... 8 分因为f(;)= 5 所以cos a= 5 .由条件a 4+ b 4= 21, S 4+ b 4= 30,得方程组{8:3d : 2q 3=31,解得<d =1,& = 2.n4又因为-2V a 0,所以sin — 5.所以 sin2a 2sin 处。
2019-2020年高三上学期期末调研测试数学试题含解析.doc

2013.1【试卷总评】本试卷作为高三一轮复习结束后的一次测试,能紧扣2013年江苏《考试说明》,试题难度适中,没有偏题,怪题,注重对基础知识和数学思想方法的考查。
填空题前13题主要体现了基础知识与数学思想方法的考查;第14题体现了字母处理能力以及知识的综合运用能力;第15、16、17、18、19、20题分别从三角向量、立体几何、实际应用、直线与椭圆、数列、函数不等式的综合运用等重点知识进行了基础知识、数学思想方法及基本能力的考查。
试卷整体体现了注重基础知识,全面考查了理解能力、推理能力、分析解决问题的能力。
参考公式:样本数据1x ,2x ,… ,n x 的方差2211()n i i s x x n ==-∑,其中x =11n i i x n =∑.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1.设集合{A =,{}B a =,若B A ⊆,则实数a 的值为 ▲ .【考点定位】本题考查集合的关系和运算,集合中元素的互异性是本题的易错点。
2. 已知复数1i z =-+(i 为虚数单位),计算:z zz z⋅-= ▲ .3.已知双曲线22221(0,0)x ya ba b-=>>的一条渐近线经过点(1,2),则该双曲线的离心率的值为▲.4.根据右图所示的算法,可知输出的结果为▲.【答案】11【解析】5.已知某拍卖行组织拍卖的10幅名画中,有2幅是膺品.某人在这次拍卖中随机买入了一幅画,则此人买入的这幅画是膺品的事件的概率为▲.6. 函数(1)()coscos22x x f x -=p p 的最小正周期为 ▲ .7. 函数22()log (4)f x x =-的值域为 ▲ .【考点定位】此题考查的是复合函数的值域问题,正确的理解定义域是本题的关键。
8. 已知点(1,1)A 和点(1,3)B --在曲线C :32(,,y ax bx d a b d =++为常数)上,若曲线在点A 和点B 处的切线互相平行,则32a b d ++= ▲ .【考点定位】此题考查的是曲线的切线问题和导数的运算,紧扣切点是本题的关键。
2019—2020学年度第一学期高三调研测试文科数学答案

∴ f (x) 在 x ln 2a 时取到极小值,∵ f (x) 的极值为 0
∴ f (ln 2a) 0
…………12 分 …………1 分
…………2 分 …………3 分
…………4 分 …………5 分
∴ eln2a 2a ln 2a 0 即 2a(1 ln 2a) 0
∴a e 2
19. 解:(1) 因为 AD EF ,所以 AD AP, AD AB ,
又 AP AB A, AP, AB 平面ABP
所以 AD 平面ABP
因为 BM 平面ABP ,所以 AD BM ;
由已知得, AB AP BP 2 ,所以 ABP 是等边三角形, 又因为点 M 是 AP 的中点,所以 BM AP ; 因为 AD BM , AP BM , AD AP A, AD, AP 平面ADP
①当 a 0 时, f '(x) 0 恒成立
∴ f (x) 在 (,+) 上单调递增,没有极值.
②当 a 0 时,由 f '(x)=0 ,得 x ln 2a
当 x (, ln 2a) 时, f '(x) 0 , f (x) 在 (, ln 2a) 上单调递减
当 x (ln 2a, ) 时, f '(x) 0 , f (x) 在 (ln 2a, ) 上单调递增
4
min
…………9 分
此时点 P 的坐标为 (0,1) ,
所以 PQ 2 2 ,此时点 P 的坐标为 (0,1) . min
法二:曲线 C 是以 C(2, 3) 为圆心,半径为 2 2 的圆,
…………10 分 …………6 分
2+3+3
2019-2020学年度高三数学12月调研测试2套+参考答案

2019-2020学年度高三12月调研测试数 学 Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上........ 1.已知集合{|02}A x x =<<,{|1}B x x =>,则A B = ▲ .2.已知i 为虚数单位,若复数()()11ai i ++是纯虚数,则实数a= ▲ .3.已知,:(1)(2)0q x x --≥,若是的充分不必要条件,则实数的取值范围是 ▲ .4.运行如图所示的伪代码,其结果为 ▲ .5.圆柱形容器内部盛有高度为4cm 的水,若放入1个铁球(球的半径与圆柱的底面半径相同)沉到水底后,水恰好将球淹没,则球的半径是 ▲ cm .6.角α的终边经过点(3,4)P -,则cos()2πα-= ▲ .7.设直线:340l x y a ++=,与圆()()22:2125C x y -+-=交于,A B ,且6AB =,则a 的值是 ▲ .8.平均数为1010的一组数构成等差数列,其末项为2019,则该数列的首项为 ▲ . 9.我们可以运用以下原理解决一些面积问题:如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比恒为k ,那么甲的面积是乙的面积的k 倍.你可以从图形①、②中体会这个原理.现在图③中的曲线分别是22221(0)x y a b a b+=>>与222x y a +=,运用以上的原理,可知图③中椭圆的面积为 ▲ .10.若曲线()(1)x f x ax e =-在点(0,(0))A f 处的切线与y 轴垂直,则a= ▲ . 21▲ .12.在△ABC 中, 2AB BC =,1,2DB AD CE EA ==,则BE 与CD 的夹角为 ▲ . 13.在平面直角坐标系中,:C ,若直线上存在点P ,使得以点P 为圆心,1为半径的圆与C 有公共点,则的最大值是 ▲ .14.若对任意的0,x ≥都有21x e ax x ≥++恒成立,则a 的取值范围为 ▲ . 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤 15.(本小题满分14分) 已知向量与互相垂直,其中(1)求和的值(2)若,,求的值16.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,,D E 分别为,BC AC 的中点,AB BC =.求证:(1)11A B ∥平面1DEC ;(2) 1BE C E ⊥.某公园为监控“旋转木马”游乐项目,要求在木马一边的护栏上安装监控摄像头,使整个木马始终在摄像头的监控范围内.如图为木马和护栏的水平示意图,分别记作圆C 和直线l,入口为A ,AC 与l 垂直,,,A B C 高度一致.已知木马轮盘的半径为5米,AC 的距离为6米,B 处的摄像头摄像视角的一边固定为直线l.(注:摄像视角指镜头中心点观察物体边缘的光线的夹角)(1)若AB 的长为8米,求最小摄像视角的正切值;(2)若摄像视角最大为60︒,求B 距离A 至少有多远?18.(本小题满分16分)设椭圆 2222:1(0)x y E a b a b+=>>过M N 两点,O 为坐标原点,(1)求椭圆E 的方程;(2)已知椭圆E 上有两点,A B 且OA OB ⊥,证明2211OA OB +是定值,并求出AB 的最小值.已知数列{}n a 的各项均为非零实数,且对于任意的正整数n 都有23331212().n n a a a a a a +++=++……(1)若数列{}n a 共三项,且为等比数列,求数列{}n a 的公比.(2)是否存在满足条件的无穷数列{}n a ,使得20202019?a =-若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由.20.(本小题满分16分)若函数()x f 满足()00f x x =成立,则称函数()x f 有不动点0x (1)判断函数 1()xf x x+=在区间(0,1)内是否有不动点,说明理由; (2)证明:函数2()(01)xxg x a ax a a x-=++->≠且在区间(0,1)内有不动点;(3)若函数()2ln h x ax x =-有两个不动点,求实数m 的取值范围.2019-2020学年度高三12月调研测试数学Ⅱ(附加题)已知可逆矩阵273aA ⎡⎤=⎢⎥⎣⎦的逆矩阵为127b a --⎡⎤=⎢⎥-⎣⎦A ,求1A -的特征值.21C.(本小题满分10分)在直角坐标系xOy 中,圆C 的参数方程为1cos ()sin x y ϕϕϕ=+⎧⎨=⎩为参数. 以O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求圆C 的极坐标方程.(2)直线l 的极坐标方程是(sin )ρθθ=,射线:(0)3OM πθρ=>与圆C 的交点为,O P ,与直线l 的交点为Q ,求线段PQ 的长.22.(本小题满分10分)如图,三棱柱中,平面,,为棱上的动点,.(1)当为的中点,求直线与平面所成角的正弦值;(2)当的值为多少时,二面角的大小是450.23.(本小题满分10分)某空间中存在2n 个基本粒子,每个基本粒子在每个时间均等可能的处于,A B 两种状态之一,若处于A 状态的粒子数和处于B 状态的粒子数相等,则称该空间处于基态.(1)=2n 时,求该空间处于A 状态的粒子数的数学期望.(2)记该空间处于处于基态的概率为()P n ,研究()P n 的单调性,并证明2n ≥时1()()2n P n >恒成立.2019-2020学年度高三12月调研测试数学Ⅰ答案1.{}|0x x >2.13.2a ≥4.50505.66.457.10或8.1. 9.ab π 10.1 11.1(,1)312. 13.14.1(,]2-∞15.解:(1),,即.……2分又∵, ∴,即,∴.……4分又 ,.……7分(2) ∵.……9分, ,即.……11分又, ∴.……14分16.证明:(1)连接DE 因为D ,E 分别为BC ,AC 的中点, 所以ED ∥AB .……2分在直三棱柱ABC-A 1B 1C 1中,AB ∥A 1B 1,所以A 1B 1∥ED . ……4分因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1,所以A 1B 1∥平面DEC 1…6分 (2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC因为三棱柱ABC-A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC .……8分 又因为BE ⊂平面ABC ,所以CC 1⊥BE .……10分因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C ,所以BE ⊥平面A 1ACC 1…12分17、解:(1)如图,过B 作圆C 的切线BE ,切点为E ,连接CE ,BC ,则CE ⊥BE ,3(2)以B 为坐标原点建立如图所示的平面直角坐标系当∠ABE 的最大值为60°时,若直线BE 与圆∴直线BE 的方程为y =3x , ∴CE =5263=-a ,.……11分得a =316 (负值舍去)..……13分 18.解:(1)因为椭圆2222:1(0)x y E a b a b+=>>过两点,所以2222611421a b a b ⎧+=⎪⎪⎨⎪+=⎪⎩解得2284a b ⎧=⎪⎨=⎪⎩椭圆的方程为22184x y += ……4分(2)因为,若,OA OB 斜率不存在或为0,则2211113=+=848OA OB +, ……6分若斜率存在且不为,设OA 斜率为k ,222222222222811121288818412y kx x k k x y OA x y k k y k ⎧==⎧⎪+⎪⎪+⇒⇒==⎨⎨+++=⎪⎪=⎩⎪+⎩……8分 用1k -换,k 2221+288k OB k =+,所以222211333==8+88k OA OB k ++综上,总有22113=8OA OB +成立 .……12分 考虑到2222222811()()3AB OA OB OA OB OA OB =+=++所以222228832(2)(2333OB OA AB OA OB =++≥+=,当且仅当=OA OB 即1k =±时取等号.所以min AB = .……16分19.解:(1)当1n =时,2311a a =,由10,a ≠得1=1.a当2n =时,2322(1)1,a a +=+由20,a ≠得2=2 1.a 或-当3n =时,2332323(1)1,a a a a ++=++若2=2,a 得3=3 2.a 或-若2=1,a -得3=1.a 又数列{}n a 为等比数列,所以122=1,=1,=1,a a a -所以数列{}n a 的公比为1- ……4分(2)令12n n S a a a =++…,则233312n n S a a a =++…,所以23331121()n n n S a a a a +++=++…,相减并考虑到2+11102.n n n n a S a a ++≠=-,得 …8分当1n =时,由(1)得1=1.a 当2n ≥时,2211122()()().n n n n n n n a S S a a a a -++=-=--- 整理得:111()(1)0.+1.n n n n n n n a a a a a a a ++++--==-所以,或 (12)分又12020=1,=2019,a a -则{}n a 的一个通项公式是1,12019;=2019(1),2020.n n n n a n +≤≤⎧⎨⨯-≥⎩ …16分20.解:(1)令1=x x x + ,解得x =均不在区间(0,1)内, 所以 1()xf x x+=在区间(0,1)内没有不动点 ……2分(2)要证()g x 在区间(0,1)内有不动点,即证方程02=-+-xa a xx 在(0,1)上有解即证方程02)(2=+-x a a x x x 在(0,1)上有解记x a a x x h x x +-=2)()(2,因为)(x h 图像在]1,0[上不间断,,02)0(<-=h 0)1(12)1(22>-=+-=a a a h ,所以)(x h 上有零点在)1,0(,所以方程02)(2=+-x a a x x x 在),0(+∞上有解,从而原命题得证 ……6分 (3)记2()ln ,H x ax x x =--则 ()H x 有两个零点.2121()21=,0,ax x H x ax x x x--'=-->所以当 a ≤ 0 时,()0H x '< ,函数()H x 减,最多一个零点,所以 a > 0 .……8分 考虑2ln x xa x+=, 下面证明:ln 1x x ≤-,设()ln 1t x x x =--所以11()1(0)x t x x x x-'=-=> (0,1)x ∈时()0t x '<,()t x 减;1x >时()0t x '>,()t x 增.()(1)0t x t ≥=,ln 1x x ≤-2222ln 21211=(1)11x x x a x x x x x+-=≤-=--+≤,1a =时x 只能取1,(0,1)a ∈…12分 下面证明(0,1)a ∈时()H x 有两个零点(0,1)a ∈时,(1)=10,H a -<22211()=10,a e e a H e e e e-++-=> 1()=ln 0,H a a <()H x 图像不间断,所以()H x 在1(,1)e ,1(1,)a上各有一个零点符合题意.综上,(0,1)a ∈……16分2019-2020学年度高三12月调研测试数学Ⅱ(附加题)答案1.解:∵可逆矩阵273a A ⎡⎤=⎢⎥⎣⎦的逆矩阵为127b a --⎡⎤=⎢⎥-⎣⎦A , ∴12210 73701a b A A a --⎡⎤⎡⎤⎡⎤⋅==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,∴141 72101431ab b a -=⎧⎪-=⎨⎪-+=⎩,解得5a =,3b =, ∴13275A --⎡⎤=⎢⎥-⎣⎦, .……5分 ∴()2328175λf λλλλ-⎡⎤==-+⎢⎥-⎣⎦, 由()0f λ=,得14λ=+,24λ=-. .……10分2.解:(1)圆的普通方程是22(1)1x y -+=,又cos ,sin x y ρθρθ==;所以圆的极坐标方程是2cos ρθ= ..……5分(2)设11(,)ρθ为点P 的极坐标,则有1112cos 3ρθπθ=⎧⎪⎨=⎪⎩解得1113ρπθ=⎧⎪⎨=⎪⎩,设22(,)ρθ为点Q 的极坐标,则有2222(sin )3ρθθπθ⎧+=⎪⎨=⎪⎩解得2233ρπθ=⎧⎪⎨=⎪⎩,由于12θθ=,所以122PQ ρρ=-=,所以线段PQ 的长为2 ..……10分3.解:以1{,,}AB AC AA 为正交基底,建立如图所示的空间直角坐标系A xyz -,依题意得:,(1)因为为中点,则,设是平面的一个法向量, 则,得 取,则, 设直线与平面的法向量的夹角为, 则,..……4分 所以直线与平面所成角的正弦值为; ..……5分(2)设, 设是平面的一个法向量, 则,取,则..……7分 是平面的一个法向量,,得,即, 所以当时,二面角的大小是. ..……10分 4.解:(1)记=2n 时,求该空间处于A 状态的粒子数为ξ, 则ξ的取值集合为{0,1,2,3,4}04411(0)()216P C ξ=== 144141(1)()2164P C ξ====, 244163(2)()2168P C ξ====, 344141(3)()2164P C ξ====, 44411(4)()216P C ξ=== 所以1311()1234248416E ξ=⨯+⨯+⨯+⨯=..……4分 (2)221()()2n n n P n C =,1222222221111(1)()()()()()022222n n n n n n n n n P n P n C C C n +++-+-=-=<+ 所以()P n 单调递减...……7分=2n 时244131(2)()282P C ==> 假设n k =时1()()2k P k >成立 则1n k =+时1211111(1)()()()()()()222222k k k P k P k P k k +++=>>⋅=+成立 综上,2n ≥时1()()2n P n >恒成立. ...……10分。
2019-2020年高三第一次调研考试数学(有答案详解).doc
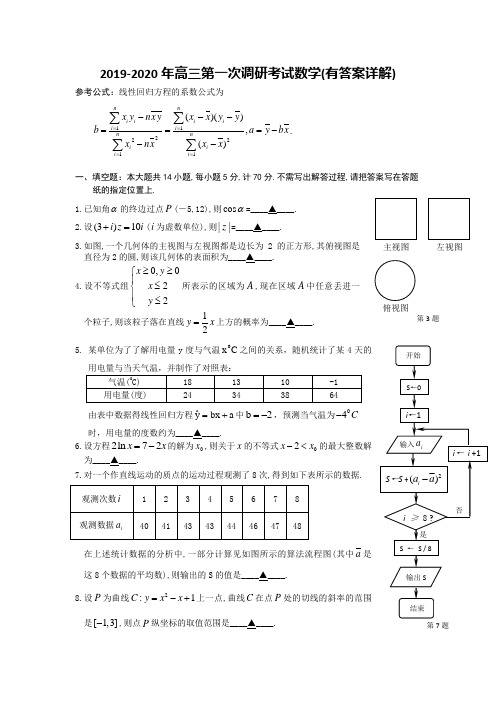
2019-2020年高三第一次调研考试数学(有答案详解)参考公式:线性回归方程的系数公式为1122211()(),()n ni iiii i nniii i x y nx y x x y y b a y bx xnxx x ====---===---∑∑∑∑.一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1.已知角α的终边过点P (-5,12),则cos α=____▲____. 2.设(3)10i z i +=(i 为虚数单位),则||z =____▲____.3.如图,一个几何体的主视图与左视图都是边长为2的正方形,其俯视图是直径为2的圆,则该几何体的表面积为____▲____.4.设不等式组0,022x y x y ≥≥⎧⎪≤⎨⎪≤⎩所表示的区域为A ,现在区域A 中任意丢进一个粒子,则该粒子落在直线12y x =上方的概率为____▲____.5. 某单位为了了解用电量y 度与气温C x 0之间的关系,随机统计了某4天的由表中数据得线性回归方程a bx yˆ+=中2b -=,预测当气温为04C - 时,用电量的度数约为____▲____.6.设方程2ln 72x x =-的解为0x ,则关于x 的不等式02x x -<的最大整数解为____▲____.7.对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.在上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中a 是这8个数据的平均数),则输出的S 的值是____▲____.8.设P 为曲线2:1C y x x =-+上一点,曲线C 在点P 处的切线的斜率的范围是[1,3]-,则点P 纵坐标的取值范围是____▲____.俯视图左视图主视图第3题第7题9.已知{}n a 是等比数列,242,8a a ==,则1223341n n a a a a a a a a ++++⋅⋅⋅+=____▲____. 10.在平面直角坐标平面内,不难得到“对于双曲线xy k =(0k >)上任意一点P ,若点P 在x 轴、y 轴上的射影分别为M 、N ,则PM PN ⋅必为定值k ”.类比于此,对于双曲线22221x y a b-=(0a >,0b >)上任意一点P ,类似的命题为:____▲____.11.现有下列命题:①命题“2,10x R x x ∃∈++=”的否定是“2,10x R x x ∃∈++≠”;② 若{}|0A x x =>,{}|1B x x =≤-,则()A B R ð=A ;③函数()sin()(0)f x x ωφω=+>是偶函数的充要条件是()2k k Z πφπ=+∈;④若非零向量,a b 满足||||||a b a b ==-,则()b a b -与的夹角为 60º.其中正确命题的序号有____▲____.(写出所有你认为真命题的序号)12.设,A F 分别是椭圆22221(0)x y a b a b +=>>的左顶点与右焦点,若在其右准线上存在点P ,使得线段PA 的垂直平分线恰好经过点F ,则椭圆的离心率的取值范围是____▲____.13.如图,在三棱锥P ABC -中, PA 、PB 、PC 两两垂直,且3,2,1PA PB PC ===.设M 是底面ABC 内一点,定义()(,,)f M m n p =,其中m 、n 、p 分别是三棱锥M PAB -、 三棱锥M PBC -、三棱锥M PCA -的体积.若1()(,,)2f M x y =,且18ax y+≥恒成立,则正实数a 的最小值为____▲____.14.若关于x 的不等式22x x t <--至少有一个负数解,则实数t 的取值范围是____▲____.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15. (本小题满分14分) 已知在ABC ∆中,cos A =,,,a b c 分别是角,,A B C 所对的边. (Ⅰ)求tan 2A ; (Ⅱ)若sin()2B π+=,c =求ABC ∆的面积.16. (本小题满分14分)如图,在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,侧棱PA PD ⊥,底面A B C 是直角梯形,其中//BC AD ,090BAD ∠=,3AD BC =,O 是AD 上一点. (Ⅰ)若//CD PBO 平面,试指出点O 的位置; (Ⅱ)求证:PAB PCD ⊥平面平面.OPDBA第16题第13题MCBAP17. (本小题满分15分)如图,某小区准备在一直角围墙ABC 内的空地上植造一块“绿地ABD ∆”,其中AB 长为定值a ,BD 长可根据需要进行调节(BC 足够长).现规划在ABD ∆的内接正方形BEFG 内种花,其余地方种草,且把种草的面积1S 与种花的面积2S 的比值12S S 称为“草花比y ”. (Ⅰ)设DAB θ∠=,将y 表示成θ的函数关系式; (Ⅱ)当BE 为多长时,y 有最小值?最小值是多少?18. (本小题满分15分) 已知C 过点)1,1(P ,且与M :222(2)(2)(0)x y r r +++=>关于直线20x y ++=对称.(Ⅰ)求C 的方程; (Ⅱ)设Q 为C 上的一个动点,求PQ MQ ⋅的最小值;(Ⅲ)过点P作两条相异直线分别与C 相交于B A ,,且直线PA 和直线PB 的倾斜角互补,O 为坐标原点,试判断直线OP 和AB 是否平行?请说明理由.19. (本小题满分16分)已知函数2()(33)xf x x x e =-+⋅定义域为[]t ,2-(2t >-),设n t f m f ==-)(,)2(.(Ⅰ)试确定t 的取值范围,使得函数)(x f 在[]t ,2-上为单调函数; (Ⅱ)求证:n m >;(Ⅲ)求证:对于任意的2->t ,总存在),2(0t x -∈,满足0'20()2(1)3x f x t e =-,并确定这样的0x 的个数.20. (本小题满分16分) 在正项数列{}n a 中,令1nn i S ==.(Ⅰ)若{}n a 是首项为25,公差为2的等差数列,求100S ;第17题GFEDC BA(Ⅱ)若n S =p 为正常数)对正整数n 恒成立,求证{}n a 为等差数列;(Ⅲ)给定正整数k ,正实数M ,对于满足2211k a a M++≤的所有等差数列{}n a , 求1221k k k T a a a +++=++⋅⋅⋅+的最大值.江苏省江都中学2011—2012高三第一次调研考试数学附加题(总分40分,考试时间30分钟)21.[选做题] 在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4—1:几何证明选讲)如图,是ABC ∆⊙O 的内接三角形,是PA ⊙O 的切线,PB 交AC 于点E ,交⊙O 于点D ,若PE PA =, 6018ABC PD BD BC ∠===,,,求的长.B.(选修4—2:矩阵与变换)二阶矩阵M 对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2). (Ⅰ)求矩阵M 的逆矩阵1M -;(Ⅱ)设直线l 在变换M 作用下得到了直线m :2x -y=4,求l 的方程.C.(选修4—4:坐标系与参数方程)在极坐标系中,设圆3ρ=上的点到直线()cos 2ρθθ=的距离为d ,求d 的最大值.D.(选修4—5:不等式选讲)设,,a b c 为正数且1a b c ++=,求证:222111100()()()3a b c a b c +++++≥.[必做题] 第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内. 22.(本小题满分10分)如图,ABCD 是菱形,PA ⊥平面ABCD ,PA=AD =2,∠BAD=60°. (Ⅰ)求点A 到平面PBD 的距离; (Ⅱ)求二面角A —PB —D 的余弦值.第21题(A)第22题O23. (本小题满分10分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为27.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用ξ表示取球终止时所需要的取球次数.(Ⅰ)求袋中原有白球的个数;(Ⅱ)求随机变量ξ的概率分布及数学期望E ξ; (Ⅲ)求甲取到白球的概率.江苏省江都中学2011—2012高三第一次调研考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1. 513-6π 4. 345.686. 47. 78. 3[,3]49.2(14)3n±- 10. 若点P 在两渐近线上的射影分别为M 、N ,则PM PN ⋅必为定值2222a b a b+ 11.②③ 12.1,12⎡⎫⎪⎢⎣⎭ 13.1 14.9,24⎛⎫- ⎪⎝⎭二、解答题:本大题共6小题,计90分.15.解:(Ⅰ)因为co A =,∴sin A =,则tan 2A =…………………………………………(4分) ∴22tan tan 21tan AA A==-………(7分)(Ⅱ)由sin()2B π+=,得cos B =,∴1sin 3B =…………………………………………(9分) 则sin sin()sin cos cos sin C A B A B A B =+=+=…………………………………………(11分)由正弦定理,得sin2sinc AaC==,∴ABC∆的面积为12s i n23S ac B==(14分)16. (Ⅰ)解:因为//CD PBO平面,CD ABCD⊂平面,且ABCD PBO BO=平面平面,所以//BO CD……………………………………………………………………………………………(4分)又//BC AD,所以四边形BCDO为平行四边形,则BC DO=……………………………………(6分)而3AD BC=,故点O的位置满足2AO OD=………………………………………………………(7分)(Ⅱ)证: 因为侧面PAD⊥底面ABCD,AB ABCD⊂底面,且AB AD⊥交线, 所以AB PAD⊥平面,则AB PD⊥…………………………………………………………………(10分)又PA PD⊥,且,,PA PAB AB PAB AB PA A⊂⊂=面面,所以PD PAB⊥平面…………(13分)而PD PCD⊂平面,所以PAB PCD⊥平面平面…………………………………………………(14分)17. 解:(Ⅰ)因为t nB D aθ=,所以ABD∆的面积为21tan2aθ((0,)2πθ∈)………………………(2分)设正方形BEFG的边长为t,则由FG DGAB DB=,得tantant a ta aθθ-=,解得t a n1t a natθθ=+,则2222tan(1tan)aSθθ=+…………………………………………………………………(6分)所以222212211tantan tan22(1tan)aS a S aθθθθ=-=-+,则212(1tan)12tanSySθθ+==-………………(9分)(Ⅱ)因为t a nθ∈+∞,所以1111(t a n2)1(t a n 2t a n2t a nyθθθθ=++-=+1≥……………(13分)当且仅当tan1θ=时取等号,此时2aBE=.所以当BE长为2a时,y有最小值1…………………(15分)18. 解:(Ⅰ)设圆心C(,)a b,则222022212a bba--⎧++=⎪⎪⎨+⎪=⎪+⎩,解得a b =⎧⎨=⎩…………………………………(3分) 则圆C 的方程为222x y r +=,将点P 的坐标代入得22r =,故圆C 的方程为222x y +=………(5分)(Ⅱ)设(,)Q x y ,则222x y +=,且(1,1)(2,2)PQ MQ x y x y ⋅=--⋅++…………………………(7分)=224x y x y +++-=2x y +-,所以PQ MQ ⋅的最小值为4-(可由线性规划或三角代换求得)…(10分)(Ⅲ)由题意知, 直线PA 和直线PB 的斜率存在,且互为相反数,故可设:1(1)PA y k x -=-,:1(1)PB y k x -=--,由221(1)2y k x x y -=-⎧⎨+=⎩,得222(1)2(1)(1)20k x k k x k ++-+--= ………(11分)因为点P 的横坐标1x =一定是该方程的解,故可得22211A k k x k--=+………………………………(13分) 同理,22211B k k x k +-=+,所以(1)(1)21B A B A BAAB B A B A B Ay y k x k x k k x x k x x x x x x ------+====---=OPk 所以,直线AB 和OP 一定平行…………………………………………………………………………(15分)19. (Ⅰ)解:因为2()(33)(23)(1)x x x f x x x e x e x x e '=-+⋅+-⋅=-⋅…………………………………(2分)由()010f x x x '>⇒><或;由()001f x x '<⇒<<,所以()f x 在(,0),(1,)-∞+∞上递增,在(0,1)上递减 …………………………………………………………………………………………(4分)欲)(x f 在[]t ,2-上为单调函数,则20t -<≤………………………………………………………(5分)(Ⅱ)证:因为()f x 在(,0),(1,)-∞+∞上递增,在(0,1)上递减,所以()f x 在1x =处取得极小值e (7分) 又213(2)f e e-=<,所以()f x 在[)2,-+∞上的最小值为(2)f - …………………………………(9分) 从而当2t >-时,(2)()f f t -<,即m n <…………………………………………………………(10分)(Ⅲ)证:因为0'2000()x f x x x e =-,所以0'20()2(1)3x f x t e =-即为22002(1)3x x t -=-, 令222()(1)3g x x x t =---,从而问题转化为证明方程222()(1)3g x x x t =---=0在(2,)t -上有解,并讨论解的个数……………………………………………………………………(12分)因为222(2)6(1)(2)(4)33g t t t -=--=-+-,221()(1)(1)(2)(1)33g t t t t t t =---=+-,所以①当421t t >-<<或时,(2)()0g g t -⋅<,所以()0g x =在(2,)t -上有解,且只有一解 ……(13分) ②当14t <<时,(2)0()0g g t ->>且,但由于22(0)(1)03g t =--<, 所以()0g x =在(2,)t -上有解,且有两解 …………………………………………………………(14分)③当1t =时,2()001g x x x x x =-=⇒==或,所以()0g x =在(2,)t -上有且只有一解;当4t =时,2()6023g x x x x x =--=⇒=-=或, 所以()0g x =在(2,4)-上也有且只有一解…………………………………………………………(15分)综上所述, 对于任意的2->t ,总存在),2(0t x -∈,满足0'20()2(1)3x f x t e =-, 且当421t t ≥-<≤或时,有唯一的0x 适合题意;当14t <<时,有两个0x 适合题意…………(16分)(说明:第(Ⅱ)题也可以令2()x x x ϕ=-,(2,)x t ∈-,然后分情况证明22(1)3t -在其值域内,并讨论直线22(1)3y t =-与函数()x ϕ的图象的交点个数即可得到相应的0x 的个数)20.(Ⅰ)解:由题意得,=,所以100S5=……………………(4分)(Ⅱ)证:令1n =,=,则p =1………………………………………………(5分)所以1nn i S ===(1),111n n i S ++===(2),(2)—(1),化简得1(1)n n n a na a n +++-=≥(3)……………………………………………………………(7分)231(2)(1)(1)n n n a n a a n +++-+=≥(4),(4)—(3)得1322(1)n n n a a a n ++++=≥ …………(9分) 在(3)中令1n =,得1322a a a +=,从而{}n a 为等差数列 …………………………………………(10分)(Ⅲ)记1k t a +=,公差为d ,则1221k k k T a a a +++=++⋅⋅⋅+=(1)(1)2k k k t d +++…………………(12分) 则12T kd t k =++,222211()k M a a t t kd +≥+=+- 222414()(43)()10210102kd kd t t kd t =++-≥+22()51T k =+…………………………………………(14分)则T ≤,当且仅当2432()52t kd kd M t =⎧⎪⎨=+⎪⎩,即1k a t d +⎧==⎪⎪⎨⎪=⎪⎩时等号成立……………(16分)数学附加题部分21.A .(几何证明选讲选做题)解:因为PB=PD+BD=1+8=9,2PA =PD ·BD=9,PA=3,AE=PA=3,连结AD,在ADE ∆中,得AD =(5分) 又AED BEC ∆∆,所以BC =…………………………………………………………………(10分)B .(矩阵与变换选做题)解: (Ⅰ)设b d a c ⎡⎤⎢⎥⎣⎦,则有b d ac ⎡⎤⎢⎥⎣⎦11⎡⎤⎢⎥-⎣⎦=11-⎡⎤⎢⎥-⎣⎦,b d ac ⎡⎤⎢⎥⎣⎦21-⎡⎤⎢⎥⎣⎦=02⎡⎤⎢⎥-⎣⎦, 所以12,122a b a b c d cd-=--+=⎧⎧⎨⎨-=--+=-⎩⎩且,解得1234a b c d =⎧⎪=⎪⎨=⎪⎪=⎩ …………………………………………………………(4分) 所以M=12 34⎡⎤⎢⎥⎣⎦,从而1M -=21 31-22-⎡⎤⎢⎥⎢⎥⎣⎦………………………………………………………………(7分) (Ⅱ)因为122 3434x x x y y y x y '+⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'+⎣⎦⎣⎦⎣⎦⎣⎦且m :24x y ''-=, 所以2(x+2y)-(3x+4y)=4,即x+4 =0,这就是直线l 的方程 ………………………………………(10分) C .(坐标系与参数方程选做题)解:将极坐标方程3ρ=转化为普通方程:229x y +=……………………………………………(2分)()cos 2ρθθ+=可化为2x =…………………………………………………………(5分) 在229x y +=上任取一点A ()3cos ,3sin αα,则点A 到直线的距离为06sin(30)22d α+-==,它的最大值为4 ……………………………(10分)D .(不等式选讲选做题) 证:左=2222221111(111)[()()()]3a b c a b c +++++++21111[1()1()1()]3a b c a b c≥⨯++⨯++⨯+…(5分)2211111111[1()][1()()]33a b c a b c a b c =+++=+++++21100(19)33≥+=……………………(10分)22.解:以OA 、OB 所在直线分别x 轴,y 轴,以过O 且垂直平面ABCD 的直线为z 轴,建立空间直角坐标系,则)2,0,3(),0,1,0(),0,0,3(),0,1,0(),0,0,3(P D C B A --,(0,2,0),(0,0,2)DB AP ==…(2分)(Ⅰ)设平面PDB 的法向量为),,(1111z y x n =,,)0,2,0(),2,1,3(==由1111111102021,(200n DP y z z n y n DB ⎧⋅=++=⎪==-⎨=⋅=⎪⎪⎩⎩,得.令得,(3,1,0),DA =所以11||||n DA A PDB d n ⋅=点到平面的距离=7212…………………………………………………(5分)(Ⅱ)设平面ABP 的法向量),,(2222z y x=,)0,1,3(),2,0,0(-==,2222222222001,1000x x AP n y y y AB n z ⎧=⎪⎪=⎧⎧⋅=⎪⎪⎪==⎨⎨⎨+=⋅=⎪⎪⎪⎩⎩=⎪⎪⎩由,得.令得,)0,1,33(2=∴n , 121212cos ,||||n n n n n n ⋅∴<>==-,而所求的二面角与12,n n <>互补, 所以二面角A —PB —D 的余弦值为77…………………………………………………………………(10分) 23.解:(Ⅰ)设袋中原有n 个白球,由题意知:227(1)2(1)2767762n n n C n n C --===⨯⨯,所以(1)n n -=12,解得n=4(舍去3n =-),即袋中原有4个白球……………………………………………………………(3分)(Ⅱ)由题意,ξ的可能取值为1,2,3,4………………………………………………………………(4分) 4342324432141(1);(2);(3);(4)776776535765435P P P P ξξξξ⨯⨯⨯⨯⨯⨯===========⨯⨯⨯⨯⨯⨯,所以,取球次数ξ的分布列为:………(6分)85E ξ=…………………………………………………………………………………………………(8分)(Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A ,则()("1"P A P ξ==或 “ξ=3”),所以24()(1)(3)35P A P P ξξ==+==………………………(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年高三调研考试数学试题含答案注意事项:考生在答题前请认真阅读本注意事项及答题要求1.本试卷共4页,均为非选择题(第1题~第20题,共20题).本卷满分为160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的相应位置.3.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上指定位置作答,在其它位置作答一律无效.4.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.参考公式:样本数据12,,,n x x x 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑.一、填空题:(每题5分,共计70分) 1、已知{}{}1,0,2,1,1,A B =-=-则A B = ▲ .2、已知复数21iz i=+,(i 为虚数单位)则复数z 的实部为 ▲ . 3、写出命题:“若x =3,则x 2-2x -3=0”的否命题: ▲ .4、一位篮球运动员在最近的5场比赛中得分的“茎叶图”如图,则他在这5场比赛中得分的方差为 ▲ .08910125、如图所示的流程图,输出的n = ▲ .6、已知抛物线28y x =的焦点是双曲线2221(0)3x y a a -=>的右焦点,则双曲线的渐近线方程为 ▲ .7、若实数,x y 满足不等式组0220x y x x y ≥⎧⎪≥⎨⎪-+≥⎩,则2z x y =+的最大值为 ▲ .8、已知圆柱的轴截面是边长为2的正方形,则圆柱的表面积为 ▲ . 9、在等差数列{}n a 中,n S 为其前n 项的和,若338,20,a S ==则5S = ▲ . 10、将x y 2sin =的图像向右平移ϕ单位(0>ϕ),使得平移后的图像过点),23,3(π则ϕ的最小值为 ▲ .11、若直线l : y x a =+被圆()2221x y -+=截得的弦长为2,则a= ▲.12、已知函数f(x)= 22,0,3,0x ax x bx x x ⎧+≥⎪⎨-<⎪⎩为奇函数,则不等式f(x)<4的解集为 ▲13、在三角形ABC 中,已知AB=3,A=0120,ABC ∆的面积为4,则B C B A 的值= ▲ .14、设点P,M,N 分别在函数22,3y x y y x =+==+的图象上,且2MN PN =,则点P 横坐标的取值范围为 ▲ . 二、解答题:(满分90分,作答请写出必要的解答过程) 15、(本小题满分14分)已知()sin cos f x x a x =+,(1)若a =()f x 的最大值及对应的x 的值. (2)若04f π⎛⎫=⎪⎝⎭, ()1(0)5f x x π=<<,求tanx 的值.16、(本小题满分14分)已知三棱锥P ABC -中,PA ⊥平面ABC, AB BC ⊥, D 为PB 中点,E 为PC 的中点, (1)求证:BC 平面ADE ;(2)求证:平面AED ⊥平面AB P .17、(本小题满分14分)小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x 年年底出售,其销售收入为25-x 万元(国家规定大货车的报废年限为10年). (1)大货车运输到第几年年底,该车运输累计收入超过总支出? (2)在第几年年底将大货车出售,能使小张获得的年平均利润.....最大?(利润=累计收入+销售收入-总支出)18、(本小题满分16分)已知椭圆()2222:10x y C a b a b +=>>的离心率为12,且过点31,2A ⎛⎫ ⎪⎝⎭.(1)求椭圆C 的方程;(2)若点B 在椭圆上,点D 在y 轴上,且2BD DA =,求直线AB 方程.19、已知数列{}n a 满足121,0a a a ==>,数列{}n b 满足1n n n b a a += (1)若{}n a 为等比数列,求{}n b 的前n 项的和n s ; (2)若3n n b =,求数列{}n a 的通项公式; (3)若2n b n =+,求证:121113na a a +++>20、已知函数(),()ln x f x e g x x ==, (1)求证:()1f x x ≥+ ;(2)设01x >,求证:存在唯一的0x 使得g(x)图象在点A(00,()x g x )处的切线l 与y=f(x)图象也相切;(3)求证:对任意给定的正数a,总存在正数x,使得()1|1|f x a x--<成立.江苏省淮阴中学2015届高三调研数学试卷参考答案一、填空、(每题5分,满分70分)1、{-1,0,1,2},2、1,3、“若3x ≠则2230x x --≠”, 4、2, 5、4,6、y =,7、6,8、6π,9、40, 10、6π, 11、-2, 12、-4∞(,),13、332, 14、53[,]22-。
二、解答题:(满分90分)15、解:(1)()sin 2sin()3f x x x x π==+………………………………(2分)当sin()12()332x x k k z ππππ+=⇒+=+∈2()6x k k z ππ⇒=+∈时f(x)有最大值2; ……………………………………………(6分)(2) 014f a π⎛⎫=⇒=- ⎪⎝⎭………………………………………………………………(8分)1sin cos 5x x -=21(in cos )25s x x ∴-=12sin cos 25x x ∴= 2112(cos )cos 25cos 5cos 120525x x x x ∴+=⇒+-=3cos 54sin 5x x ⎧=⎪⎪∴⎨⎪=⎪⎩或4cos 53sin 5x x ⎧=-⎪⎪⎨⎪=-⎪⎩(0,)x π∈3cos 54sin 5x x ⎧=⎪⎪∴⎨⎪=⎪⎩∴tanx=43…………………………………………………(14分)16、(1)证明:////PE EC DE BC PD DB DE ADE BC ADE BC ADE=⎫⎫⇒⎬⎪=⎭⎪⎪⊂⇒⎬⎪⊄⎪⎪⎭平面平面平面………………………(7分)(2)PA ABC PA BC BC ABC BC ABPA AB A BC PA ⎫⊥⎫⇒⊥⎬⎪⊂⎭⎪⎪⊥⎪⎪=⇒⊥⎬⎪⊂⎪⎪⊂⎪⎪⎭平面平面平面PAB 平面PABAB 平面PAB………………………(12分)//DE BC DE ∴⊥平面PAB ,又DE ADE ⊂平面ADE ∴⊥平面平面PAB (14分)17、解:(1)设大货车到第x 年年底的运输累计收入与总支出的差为y 万元, 则25[6(1)]50,(0<10)y x x x x x x =-+--∈≤,N ,18、解:(1)122c e a c a ==∴=…………………………………………………(2分)22223b a c c ∴=-=设椭圆方程为:2222143x y c c+=,22131144c c c ∴+=∴=设椭圆方程为:22143x y +=…………………………………………………………(7分)(2)设B(00,x y ),D(0,m),则00(,)BD x m y =--,3(1,)2DA m =- 00-2,32x m y m ∴=-=-即002,33x y m =-=-代入椭圆方程得m=1(0,1)D ∴…(14分)1:12AB l y x ∴=+………………………………………………………………………(16分) 19、(1)1121,n n n n n n a a b a a a ---=∴==……………………….……….…………(2分)当a=1时1n b =,则n s n =……………………………………………………………(3分)当1a ≠时,22(1)1n n a a s a -=-………………………………………………………….…(5分)(2)13n n n a a +=113(2,)n n n a a n n N --∴=≥∈113(2,)n n a n n N a +-∴=≥∈………………………………………………………………(7分) 当*21,()n k k N =+∈时,*11222223()3=a3k k k k ka k N a a a --+∴=∈∴= 当*2,()n k k N =∈时,*121212-13()3k k k k a k N a a -+-∴=∈∴= 12223(=21)3(2)n n n n k a a n k --⎧-⎪∴=⎨⎪=⎩………………………………………………………………(11分)(3)12,n n a a n +=+①,121,3a a =∴=11n n a a n -∴=+(2)n ≥②①-②得11111)1(2)n n n n n na a a a a n a +-+--=∴-=≥( 23111na a a ∴+++314211()()()n n a a a a a a +-=-+-++-=112n n a a a a ++--1231111n a a a a ∴++++=112111+3n n n n a a a a a a a +++--=+- 11222n n n n a a a a n +++>=+1231111na a a a ∴++++>3.…….(16分) 20、(1)令()1,xF x e x =--x R ∈,()'10x F x e =-=得0x =, ∴当0x >时()()'0,;F x F x >当0x <时()()'0,;F x F x <()()min 00F x F ∴==,由最小值定义得()()min 0F x F x ≥=即1xe x ≥+…………………………………(4分) (2)()g x 在0x x =处切线方程为001ln 1y x x x =+- ① 设直线l 与xy e =图像相切于点()11,xx e ,则:l ()1111x x y e x e x =+- ②……(6分)③ 由①②得④()110011ln 1x x ex x e x ⎧=⎪⎨⎪=-⎩0001ln 01x x x +∴-=- ⑤ 下证0x 在()1,+∞上存在且唯一.令()()1ln 11x G x x x x +=->-,()()221'01x G x x x +=>- ()G x ∴在()1,+∞上.又()()222230,0,11e G e G e e e --=<=>--()G x 图像连续,∴存在唯一0x ∈ ()1,+∞使⑤式成立,从而由③④可确立1x .故得证……………………………………………………(10分)(1) 由(1)知()110f x x-->即证当0a >时不等式1x e x ax --<即10x e ax x ---<在()0,+∞上有解.令()1xH x e ax x =---,即证()min 0H x <………………………………………(12分) 由()'10x H x e a =--=得()ln 10x a =+>. 当()0ln 1x a <<+时,()()'0,H x H x <, 当()ln 1x a >+时,()()'0,H x H x >.()()()min ln 1H x H a ∴=+()()1ln 1ln 11a a a a =+-+-+-. 令()ln 1V x x x x =--,其中11x a =+>则()()'11ln ln 0V x x x =-+=-<,()V x ∴()()10V x V ∴<=.综上得证…………………………………………………………………………………(16分)。
