数值计算方法实验1非线性迭代法求方程
数值计算方法

Inline function: fun(x) = x^3-sin(x)-12*x+1 >> fplot(fun,[-6,6]);grid on;
取x初值为0,-4,3 1、牛顿法 源程序代码
function [x_star,k] = Newton1(fname,dfname,x0,ep,Nmax) %用牛顿法解线性方程组f(x)=0 %x=Newton(fname,dfname,x0,ep,Nmax),fname,和 dfname分别表示f(x)及其导数 %x0为迭代初值,ep为精度(默认值1e-5),x返回解,Nmax为迭代 次数上限以防发散(默认值是500) if nargin<5 Nmax=500;end if nargin<4 ep=1e-5;end x=x0; x0=x+2*ep; k=0; while abs(x0-x)>ep&k<Nmax k=k+1;x0=x;x=x0-
k= 3
②取初值为-4:
在Matlab命令窗口输入:
>> fname=inline('x^3-sin(x)-12*x+1') fname = Inline function: fname(x) = x^3-sin(x)-12*x+1 >> dfname=inline('3*x^2-cos(x)-12') dfname = Inline function: dfname(x) = 3*x^2-cos(x)-12 >> [x_star,k]=Newton1(fname,dfname,-4) x_star = -3.4912
数值分析实验报告之迭代法求非线性方程的根
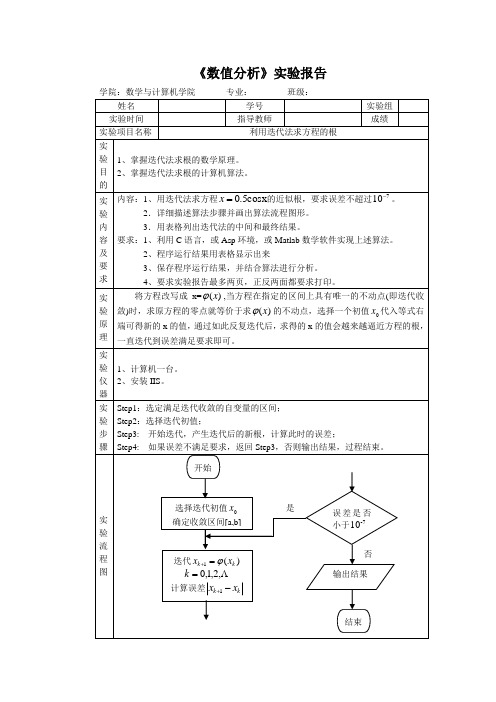
《数值分析》实验报告学院:数学与计算机学院专业:班级:姓名学号实验组实验时间指导教师成绩实验项目名称利用迭代法求方程的根实验目的1、掌握迭代法求根的数学原理。
2、掌握迭代法求根的计算机算法。
实验内容及要求内容:1、用迭代法求方程cosx5.0=x的近似根,要求误差不超过710-。
2.详细描述算法步骤并画出算法流程图形。
3.用表格列出迭代法的中间和最终结果。
要求:1、利用C语言,或Asp环境,或Matlab数学软件实现上述算法。
2、程序运行结果用表格显示出来3、保存程序运行结果,并结合算法进行分析。
4、要求实验报告最多两页,正反两面都要求打印。
实验原理将方程改写成x=)(xϕ,当方程在指定的区间上具有唯一的不动点(即迭代收敛)时,求原方程的零点就等价于求)(xϕ的不动点,选择一个初值x代入等式右端可得新的x的值,通过如此反复迭代后,求得的x的值会越来越逼近方程的根,一直迭代到误差满足要求即可。
实验仪器1、计算机一台。
2、安装IIS。
实验步骤Step1:选定满足迭代收敛的自变量的区间;Step2:选择迭代初值;Step3: 开始迭代,产生迭代后的新根,计算此时的误差;Step4: 如果误差不满足要求,返回Step3,否则输出结果,过程结束。
实验流程图开始选择迭代初值x确定收敛区间[a,b]迭代)(1kkxxϕ=+,2,1,0=k计算误差kkxx-+1结束误差是否小于7-10输出结果是否实验结果实验总结通过本次实验,我对迭代法求方程的根有了更深的认识,对其所用到的数学原理通过编程理解的更加清晰。
我是用Asp完成本次实验的,因为这样可以将结果很方便的用表格显示出来,让结果看起来比较清楚、明白和友好。
同时,我也用C语言编程实现过,结果是一样的,这也说明实验结果的正确性。
因为所给迭代方程是收敛的,不需要收敛性的验证,只要迭代达到误差的要求即可。
实验中遇到的一个问题是如何将结果中的小数点前的0补上去,让显示的更完整,通过网上查询,了解到可以根据对结果的判断将0加上去已达到完整显示,最终解决了这个问题。
数值分析--非线性方程的迭代解法

非线性方程的迭代解法1.迭代函数对收敛性的影响实验目的:初步认识非线性问题的迭代法及其收敛性,认识迭代函数对收敛性的影响,知道当迭代函数满足什麽条件时,迭代法收敛。
实验内容:用迭代法求方程 012)(3=--=x x x f 的根。
方案一: 化012)(3=--=x x x f 为等价方程 )(213x x x φ=+= 方案二: 化012)(3=--=x x x f 为等价方程 )(123x x x φ=-= 实验要求:分别对方案一、方案二取初值00=x ,迭代10次,观察其计算值,并加以分析。
实验程序:实验结果:2. 初值的选取对迭代法的影响实验目的:通过具体的数值实验,体会选取不同的初值对同一迭代法的影响。
实验内容:用牛顿迭代法求方程 013=--x x 在x =1.5附近的根。
实验要求:对牛顿迭代公式 131231----=+k k k k k x x x x x ,分别取00=x ,5.10=x 迭代10次,观察比较其计算值,并分析原因。
实验程序:实验结果:3.收敛性与收敛速度的比较实验目的:通过用不同迭代法解同一非线性方程,比较各种方法的收敛性与收敛速度。
实验内容:求解非线性方程 0232=-+-x e x x 的根,准确到106-。
实验要求:(1) 用你自己设计的一种线性收敛的迭代法求方程的根,然后用斯蒂芬森加速迭代计算。
输出迭代初值、各次迭代值及迭代次数。
(2) 用牛顿迭代法求方程的根,输出迭代初值、各次迭代值及迭代次数,并与(1)的结果比较。
实验程序:1.普通迭代,选用初值0.52. 斯蒂芬森加速迭代3.牛顿迭代法实验结果:。
数值分析非线性方程的数值解法

数值分析非线性方程的数值解法数值分析是一种应用数学方法来分析和解决数学问题的领域。
非线性方程是数值分析中一类重要的问题,其解法包括了迭代法、牛顿法、割线法等。
本文将详细介绍这些数值解法及其原理和应用。
一、迭代法迭代法是解非线性方程的一种常用数值方法。
该方法的基本思想是通过不断迭代逼近方程的根,直到达到所需精度或满足停止准则为止。
迭代法的求根过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = g(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
常用的迭代法有简单迭代法、弦截法和牛顿法。
简单迭代法的迭代公式为xn+1 = f(xn),其中f(x)为原方程的一个改写形式。
该方法的收敛性要求函数f(x)在解附近有收敛性且导数在一个区间内收敛。
弦截法的迭代公式为xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
牛顿法的迭代公式为xn+1 = xn - f(xn) / f'(xn),其中f'(x)为f(x)的导数。
该方法通过用切线来逼近方程的根。
二、牛顿法牛顿法是解非线性方程的一种常用迭代法。
该方法通过使用方程的导数来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = xn - f(xn) / f'(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
牛顿法的收敛速度较快,但要求方程的导数存在且不为0。
三、割线法割线法是解非线性方程的另一种常用迭代法。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0和x12. 计算下一个近似根xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
3.重复步骤2,直到满足停止准则为止。
割线法的收敛速度介于简单迭代法和牛顿法之间。
数值计算(二分法、简单迭代法、Newton迭代法、弦截法(割线法、双点弦法)).

本科生实验报告实验课程数值计算方法学院名称信息科学与技术学院专业名称计算机科学与技术学生姓名学生学号指导教师实验地址实验成绩二〇一六年五月二〇一六年五月1实验一 非线性方程求根1.1问题描绘实验目的:掌握非线性方程求根的基本步骤及方法, 。
实验内容:试分别用二分法、简单迭代法、Newton 迭代法、弦截法(割线法、双点弦法),求x 5-3x 3+x-1=0在区间[-8,8]上的所有实根,偏差限为10-6。
要求:议论求解的全过程,对所用算法的局部收敛性,优弊端等作剖析及比 较,第2章算法思想2.1二分法思想:在函数的单一有根区间内,将有根区间不停的二分,找寻方程的解。
步骤:1.取中点mid=(x0+x1)/2 2.若f(mid)=0,则mid 为方程的根,不然比较与两头的符号,若与f(x0) 异号,则根在[x0,mid]之间,不然在[mid,x1]之间。
3并重复上述步骤,直抵达到精度要求,则 mid 为方程的近似解。
开始读入a,b,emid=(a+b)/2 F(a)*f(b)<0是 a=mid b=mid no |a-b|<e? yes 输出mid结束22.2简单迭代法思想:迭代法是一种逐次迫近的方法,它是固定公式频频校订跟的近似值,使之逐渐精准,最后获得精度要求的结果。
步骤:1.结构迭代公式f(x),迭代公式一定是收敛的。
2.计算x1,x1=f(x0).3.判断|x1-x0|能否知足精度要求,如不知足则重复上述步骤。
4.输出x1,即为方程的近似解。
开始输入x0,eX1=f(x0)f为迭代函数X1=x0;No|x1-x0|<eyes输出x1结束32.3Newton迭代法思想:设r是的根,选用作为r的初始近似值,过点做曲线的切线L,L的方程为,求出L与x轴交点的横坐标,称x1为r的一次近似值。
过点做曲线的切线,并求该切线与x轴交点的横坐标,称为r的二次近似值。
重复以上过程,得r的近似值序列,此中,称为r的次近似值步骤:1.计算原函数的导数f’(x);结构牛顿迭代公式2.计算,若f’(x0)=0,退出计算,不然持续向下迭代。
非线性方程数值求解法总结

(一)非线性方程的迭代解法1.非线性方程的一般形式:f(x)=02.非线性方程的分类:⎩⎨⎧=为其他函数。
超越方程,次代数多项式;为代数方程,)()(0)(x f n x f x f 3.方程的根:若存在常数s 使f(s)=0,则称s 是方程(4.1)的根,又称s 是函数f(x)的零点。
4.重根:若f(x)能分解为)()()(x s x x f m ϕ-= 则称s 是方程(4.1)的m 重根和f(x)的m 重零点。
当m=1时,s 称为方程(4.1)的单根和f(x)的单零点。
5.结论:(1)零点存在定理:设函数f(x)在闭区间[a,b]上连续,且f(a)•f(b)<0,那么在开区间(a,b )内至少有一点ξ,使f(ξ)=0.(2)根的唯一性判别:一阶导数不变号且不为零(3)n 次代数方程在复数域上恰有n 个根(4)高于4次的代数方程没有求根公式6.方法:(1)搜索根方法:①作图法:②逐步搜索法:确定方程根的范围的步骤:步骤1 取含f(x)=0根的区间[a,b],即f(a)•f(b)<0;步骤2 从a 开始,按某个预定的步长h ,不断地向右跨一步进行一次搜索, 即检查kh a x k +=上的函数)(k x f 值的符号。
若0)()(1<•-k k x f x f ,则可以确定一个有根区间],[1k k x x -.步骤3 继续向右搜索,直到找出[a,b]上的全部有根区间],[1k k x x -(k=1,2,…,n).(2)二分法①基本思想:含根区间逐次分半缩小,得到一个区间长度以1/2的比例减小的含根区间序列 {}k I ,在给定根的误差界时,利用长度趋于零的特点,可得到在某个区间中满足要求的近似根。
②迭代终止的条件ε<)(k x fε2<-k k a b或者ε<-≤-2k k k a b s x(3)简单迭代法及其收敛性)(0)(x x x f ϕ=⇔=,2,1,0),(1==+k x x k k ϕ迭代法是一种逐次逼近法,用某个固定公式反复校正根的近似值,使之逐 步精确化,最后得到满足精度要求的解。
《数值分析实验》实验

数值分析实验实验1 方程求根一、实验目的:1.掌握常用的求非线性方程近似根的数值方法,用所学方法求非线性方程满足指定精度要求的数值解,比较各种方法的异同点并进行收敛性分析。
2.通过对二分法与牛顿迭代法作编程练习与上机运算,进一步体会二分法与牛顿迭代法的不同特点。
3.编写割线迭代法的程序,求非线性方程的解,并与牛顿迭代法作比较。
二、实验内容:1.用二分法求方程0104)(23=-+=x x x f 在1.5附近的根。
2.用牛顿迭代法求方程033)(23=--+=x x x x f 在1.5附近的根。
3.用简单迭代法求解非线性方程3sin )1(2=-+x x 的根。
取迭代函数)1sin 3(*5.0)(2x x x --+=ϕ,精度取2101-⨯4.(选做)用牛顿法求下列方程的根: (1)02=-x e x ; (2)01=-x xe ; (3)02lg =-+x x 。
5.(选做)编写一个弦截法程序,求解题目4中的方程。
6.(选做)Matlab 函数fzero 可用于求解非线性方程的根。
例如,fzero(@(x) x^3+4*x^2-10, 1.5)可以求解题目1。
尝试用此方法求解实验中的其他题三、实验要求:1.程序要添加适当的注释,程序的书写要采用缩进格式。
2.程序要具在一定的健壮性,即当输入数据非法时,程序也能适当地做出反应,如插入删除时指定的位置不对等等。
3.程序要做到界面友好,在程序运行时用户可以根据相应的提示信息进行操作。
四、实验步骤1.按照实验内容和实验要求编写代码 2.编译并运行代码 3.检查是否发生错误五、实验源代码与实验结果实验1源代码:运行结果:实验2源代码:运行结果:实验3源代码:运行结果:4(1)的源代码:运行结果:4(2)的源代码:运行结果:4(3)的源代码:运行结果:5(3)的源代码:运行结果:六、实验心得体会通过本次实验我加深了对二分法、简单迭代法、牛顿迭代法和弦截法算法思想的了解,并对各个不同方法的优劣有了更深的理解。
数值分析非线性方程求根实验

实验报告一、实验目的1.迭代函数对收敛性的影响。
2.初值的选择对收敛性的影响。
二、实验题目1.用简单迭代法求方程01)(3=--=x x x f 的根。
分别化方程为如下等价方程: 31+=x x ;13-=x x ;x x 11+=;213-+=x x x 取初值5.10=x ,精度为410-,最大迭代次数为500,观察其计算结果并加以分析。
2.①用牛顿法求方程01)(3=-+=x x x f 在0.5附近的根,分别取初值1000,100,2,1,5.0,5.0,1,2,100,10000-----=x观察并比较计算结果,并加以分析。
②用牛顿法求方程0)(3=-=x x x f 所有根。
三、实验原理简单迭代法程序,牛顿迭代法程序。
四、实验内容及结果fun=inline('x^3-x-1');dfun=inline('3*x^2-1');-1000,x1=manewton(fun,dfun,-1000,1e-4) -100,x2=manewton(fun,dfun,-100,1e-4)-2,x3=manewton(fun,dfun,-2,1e-4)-1,x4=manewton(fun,dfun,-1,1e-4)-0.5,x5=manewton(fun,dfun,-0.5,1e-4) 0.5,x6=manewton(fun,dfun,0.5,1e-4)1,x7=manewton(fun,dfun,1,1e-4)2,x8=manewton(fun,dfun,2,1e-4)100,x9=manewton(fun,dfun,100,1e-4) 1000,x10=manewton(fun,dfun,1000,1e-4)3)在MA TLAB的主程序窗口输出以下结果:ans =-1000k=21x1 =0.682327804075895ans =-100k=16x2 =0.682327803903413ans =-2k=6x3 =0.682327803828020ans =-1k=5x4 =0.682327803828020ans =-0.500000000000000k=4x5 =0.682327803903932ans =0.500000000000000k=3x6 =0.682327803828347五、实验结果分析(1)实验1中用简单迭代法求方程01)(3=--=x x x f 的根:取初始值5.10=x 的时候,等价方程2和4是不收敛的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1实验名称实验1非线性方程的迭代法2实验题目设方程f(x)=x^3-3x-1=0有3个实根x1*=1.8793,x2*=-0.34727,x3*= -1.53209,现采用下面6种不同计算格式,求f(x)=0的根x*,x*.(a)x=(3x+1)/x^2(b)x=(x^3-1)/3(c)x=(x^3-1)^1/3(d)x=1/(x^2-3)(e)x=(3+1/x)^1/2(f)x=x-(x^3-3*x-1)/(3*(x^2-1))3流程图源代码:#include<stdio.h>#include<math.h>int N;double x0,x,y,z,T;void out1(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=(3*x0+1)/(pow(x0,2));z=(3*y+1)/(pow(y,2));x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void out2(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=(pow(x0,3)-1)/3;z=(pow(y,3)-1)/3;x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void out3(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=pow((3*x0+1),1.0/3);z=pow((3*y+1),1.0/3);x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void out4(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=1/(pow(x0,2)-3);z=1/(pow(y,2)-3);x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void out5(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=pow((3+1/x0),1.0/2);z=pow((3+1/y),1.0/2);x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void out6(){int n=1;printf("请输入初值x0:");scanf("%lf",&x0);printf("请输入精度T:");scanf("%lf",&T);printf("请输入迭代次数N:");scanf("%d",&N);printf("\n");printf("迭代结果如下:\n");while(n<=N){y=x0-(1.0/3)*(pow(x0,3)-3*x0-1)/(pow(x0,2)-1);z=y-(1.0/3)*(pow(y,3)-3*y-1)/(pow(y,2)-1);x=x0-(y-x0)*(y-x0)/(z-2*y+x0);printf("%d %lf\n",n,x);if(fabs(x-x0)<T){printf("该方程的值为%lf\n",x);break;}else{n=n+1;x0=x;}}}void main(){int select;printf("方程:f(x)=x^3-3*x-1\t\t");printf("结束请选0\n");printf("1. x=(3*x+1)/x^2\t\t");printf("2. x=(x^3-1)/3\t\t");printf("\n");printf("3. x=(3*x+1)^(1/3)\t\t");printf("4. x=1/(x^2-3)\t\t");printf("\n");printf("5. x=(3+1/x)^(1//2)\t\t");printf("6. x=x-(x^3-3*x-1)/(3*(x^2-1))\t\t");printf("\n");printf("请选择计算格式或结束:");scanf("%d",&select);printf("\n");while(select!=0){switch(select){case 1:out1();break;case 2:out2();break;case 3:out3();break;case 4:out4();break;case 5:out5();break;case 6:out6();break;};printf("\n");printf("请选择计算格式或结束:");scanf("%d",&select);printf("\n");}printf("\n");}。
