最新三年中考数学分析
重庆近三年中考数学试卷分析

重庆近三年中考数学试卷分析
近三年来重庆市中考数学试题与重庆市教科院发布的考试说明基本一致,试卷结构稳定,考查的内容每年都有少量变化,从题型到考试内容基本固定,但具体到每到试题有很大变化,特别是解答题,总体难度逐年有所增加。
1.题型与题量
全卷均为满分150分,三种题型,26个题,其中12个选择题,6个填空题,8个解答题。
三种题型的分数比为48:24:78,占比略为32%、16%、52%。
其中1-9,13-16,19-22为容易做的题,占比略为60%,10,11,17,23,24,25为中档题,占比略为30%,其他的为比较难的题,占比略为10%。
2.考查知识点情况
由图我们得知,统计与概率相关问题的分值占比为12%,几何问题占比29%,实数的考查占比为20%,一次函数、反比例函数和二次函数占比为33%,新概念题型占比为6%。
总的来说,近几年的中考数学试题考查了基础知识和基础技能,数学逻辑思维,解决问题的能力,其中试题还突出考查了学生运用数学知识解决实际问题的能力。
对方程与不等式、函数与其图像的性质、几何图形的变换、统计与概率问题等重点内容进行了重点考查。
除此之外,这些数学试题还让学生其实感受到生活中存在大量数学知识信息,引导学生关注社会,关注生活,体现了数学的运用价值。
2024河南中考数学试题评析

2024河南中考数学试题评析中考是每个学生人生中的一次重要考试,决定着他们的高中学业发展。
其中数学科目一直被认为是学生们最为困难的科目之一,曾有人说过:“ 胜数学者胜中考”。
2024年中考拉下帷幕,当我们仔细分析今年的数学命题,我相信有经验的数学老师都会有一种意料之中的快意,下面我谈几点不成熟的看法。
一、稳中求变。
我从2002-2022河南中考数学试题做过对比分析,这里面有五次大的转折,基本呈现五年有调整,前二次转折无论从题量还是题型甚至知识点考查调整比较大,更倾向于 变”;后三次转折可以说是微调,更注重 稳”。
1.我们先来说说稳。
发展到现在主要有三不变:①结构不变:闭卷120分,考试时间为100分钟,题目共计23题,填空选择15题45分,解答8题75分。
②题型不变:选择题、填空题、解答题,解答题主要涵盖——计算求解、推理证明题、应用性问题、阅读分析题、类比探究性问题、开放性问题等。
③考查知识点不变:以数与代数、图形与几何为主,统计与概率、综合与实践为辅。
2.我们再来说说变。
三变”。
①选择题由原来的6题升为8题,再升为10题,填空题由原来的9题降为7题再将为5题。
②题目难度下调,2024难度系数0.65-0.70,满分120,基本平均分78-84;③阅读量增大。
二、变中求新。
1.体现教-学-评一致性。
可以说原来我们的数学中考是考什么,学什么,所以每一年都会有 惊喜”,正如有人说平时学了一粒沙,考试考了撒哈拉;现在依据新课程标准转变为学什么,考什么。
以前我们每年可以扒拉出上百套全国各地中考试题,以后这种情况将不复存在了。
新课标明确规定学业水平考试由省级教育行政部门组织实施,依据学业质量标准,对学生学完本课程后课程目标达成度进行终结性评价。
考试成绩是学生毕业和高一级学校招生录取的重要依据,为评价区域和学校教学质量、改进教学提供重要参考。
值得注意的是2025与2026届仍延续的是2011版课标,今年暑假后七年级新生将正式使用新教材,2022版新课标也正式落地。
深圳中考数学分析

6.一元一次方程的应用 21题一般为一元一次方程的应用,(2013年没有考 查)。一般是8-9分。
一元一次方程的实际应用
不等式的实际应用
函数的实际应用
该部分内容主要考查了一元一次方程的实际应用,不等式实际应用和二次 函数最值等内容。出题形式比较灵活,考查学生理解能力。内容比较接近实际 生活。建议时间在8分钟左右。
因此作为学校,在教授学生知识的同时还要教会学生独立思考、 教会他们面对陌生题目时候解决问题的能力。从学校中看到自己的 能力,从学习中得到乐趣。
而作为学生,除了掌握基础知识以外,还要拓展自己的视野, 学会思考。能够灵活运用自己的知识去解决问题,而不是仅仅陷入 到书海题山的困境中去。学以致用,举一反三。既能节省大量的时 间精力,还能提升自己的能力。
总结
中考是一种选拨性考试,因此考试整体具有一定的难度,可以 拉开不同层次的学生距离。从近五年的数学中考试卷可以看出,试 卷整体难度属于中等偏上,具有一定的选拨性。主要注重基础知识 掌握的考查以及对知识灵活运用的能力,使得单纯的恶补式学习不 再具有优势。更多的是要求学生在掌握基础知识的前提下,多独立 思考、学会运用已知的数学工具解决未知的内容,培养思维活跃和 创新应用能力,体现出了“指挥棒”的作用。
18题近五年来主要考查了三个不同的形式。其中解分式方程和解不等式组各一次,分式的化简计算三 次。分式方程考查较为简单,简单通分即可,但要注意曾根的情况。不等式组也较为简单,但结果需取 整数解,要注意条件要求。其余三年都是化简不等式,并代入数字计算、主要考查了因式分解的相关内 容,尽管分式形式复杂,但化简却较为简单。建议5分钟左右完成。
深圳中考数学试卷分析
2012-2015
总体结构分析
中考数学试卷总分100分,时间90分钟。包括选择题、 填空题、计算、综合应用等题型。整体难度中等偏上,考查 内容广泛,基本覆盖中学三个年级的内容。考查形式灵活, 着重考查学生对基本知识的掌握和灵活运用的能力
最新 2020年重庆近三年中考数学试卷分析
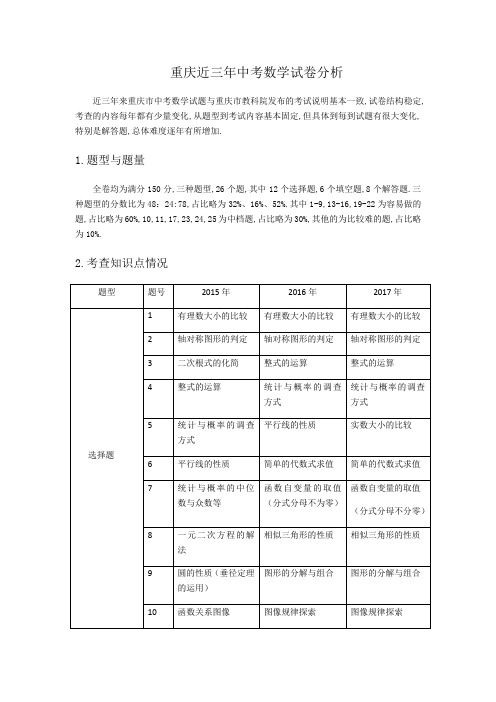
重庆近三年中考数学试卷分析
近三年来重庆市中考数学试题与重庆市教科院发布的考试说明基本一致,试卷结构稳定,考查的内容每年都有少量变化,从题型到考试内容基本固定,但具体到每到试题有很大变化,特别是解答题,总体难度逐年有所增加.
1.题型与题量
全卷均为满分150分,三种题型,26个题,其中12个选择题,6个填空题,8个解答题.三种题型的分数比为48:24:78,占比略为32%、16%、52%.其中1-9,13-16,19-22为容易做的题,占比略为60%,10,11,17,23,24,25为中档题,占比略为30%,其他的为比较难的题,占比略为10%.
2.考查知识点情况
由图我们得知,统计与概率相关问题的分值占比为12%,几何问题占比29%,实数的考查占比为20%,一次函数、反比例函数和二次函数占比为33%,新概念题型占比为6%.
总的来说,近几年的中考数学试题考查了基础知识和基础技能,数学逻辑思维,解决问题的能力,其中试题还突出考查了学生运用数学知识解决实际问题的能力.对方程与不等式、函数与其图像的性质、几何图形的变换、统计与概率问题等重点内容进行了重点考查.除此之外,这些数学试题还让学生其实感受到生活中存在大量数学知识信息,引导学生关注社会,关注生活,体现了数学的运用价值.。
最新上海市中考数学考点分析及分值分布

最新上海市中考数学考点分析及分值分布根据上海市中考数学考点的分析及分值分布,可以得出以下结论:1.整数与有理数的运算(6-8分):整数和有理数的四则运算是数学的基础,考点涉及加减乘除和混合运算等。
考生需要掌握运算规则和技巧,避免计算错误。
2.分数与小数的转化(6-8分):考点涉及分数到小数的转化和小数到分数的转化。
考生需要熟练掌握分数与小数的关系,明确二者的转换方法。
3.特殊符号的应用(4-6分):特殊符号的应用是一种常见的考察方式,主要包括绝对值、约数、倍数、质因数分解等。
考生需要熟练掌握这些符号的含义和应用场景。
4.几何图形的认识(6-8分):几何图形是中考数学的重要考点,包括对线段、角、三角形、四边形等基本图形的认识和性质的了解。
考生需要熟悉基本图形的特点和性质,能够进行简单的图形判断和推理。
5.几何图形的计算(8-10分):几何图形的计算是数学中考的难点,主要包括计算周长、面积、体积等。
考生需要掌握计算方法和公式,能够灵活运用于实际问题中。
6.数据的整理和分析(8-10分):数据的整理和分析是数学中常见的考点,包括制表、解读表格、统计图形等。
考生需要具备数据处理和分析能力,能够从图表中获取信息和结论。
7.方程和不等式的应用(8-10分):方程和不等式的应用是中考数学的难点,考点涉及一元一次方程、一元一次不等式、简单的二元一次方程和二元一次不等式等。
考生需要掌握解方程和不等式的方法和技巧,能够应用于实际问题中。
8.统计与概率(6-8分):统计与概率是中考数学的重点考点,包括统计图表的制作和解读、频率和概率的计算等。
考生需要熟悉统计与概率的基本概念和计算方法。
在上海市中考数学中,各个考点的分值分布大致如下:-一、二级考点(6-8分):整数与有理数的运算、分数与小数的转化、特殊符号的应用、几何图形的认识等。
-三、四级考点(8-10分):几何图形的计算、数据的整理和分析、方程和不等式的应用等。
-五级考点(10-12分):统计与概率。
2024年中考数学试卷分析报告

2024年中考数学试卷分析报告引言本篇分析报告主要针对2024年的中考数学试卷进行全面分析。
旨在探讨试卷的整体难度、题型分布、命题方向等方面的特点,以及对学生的综合能力和知识掌握程度的考察。
通过对试卷的分析研究,旨在为教育机构提供参考,以便更好地指导学生备考。
总体情况分析2024年中考数学试卷共分为选择题和非选择题两部分。
试卷难度适中,整体命题比较均衡,涵盖了学科知识的多个方面。
试卷的命题风格更加贴近学生的实际生活和解决问题的能力培养。
选择题分析选择题占试卷总分的60%,题型主要包括选择题和填空题。
下面将分别对各题型进行详细分析。
单项选择题单项选择题是试卷中较为常见的一种题型,覆盖了整个数学知识体系。
在2024年的试卷中,单项选择题占了选择题部分的50%左右。
从难度上来看,题目涵盖了基础题、拓展题和综合题三个层次,难度适中。
其中,涉及到实际问题的应用题增加了在现实生活中解决问题的能力培养。
填空题填空题在选择题中占了较大的比例,题型多样,主要考察学生的计算和推理能力。
填空题分为基础题和拓展题两类,涵盖了代数、几何、统计与概率等多个知识点。
2024年的试卷填空题考察了学生的计算和推理能力,突出了解决问题的方法和思路。
非选择题分析非选择题占试卷总分的40%,主要包括解答题和应用题两种类型。
解答题解答题是试卷中考察学生深度思考和解决问题能力的重要部分。
在2024年的试卷中,解答题的难度有所增加。
除了基础题和应用题,还有一些思维题和综合题,旨在培养学生的逻辑思维和创新思维。
应用题应用题是考察学生将数学知识应用于实际问题解决能力的重要题型。
在2024年的试卷中,应用题较为贴近学生的实际生活,涉及到购物、旅行、运动等场景,培养了学生解决实际问题的能力。
命题方向分析在2024年的试卷中,命题方向更加贴近学生的实际生活和解决实际问题的能力培养。
选择题和非选择题中都涉及到了实际问题的应用,注重解决问题的方法和思路。
2023福州中考数学考点分析

2023福州中考数学考点分析学习是每个一个学生的职责,而学习的动力是靠自己的梦想,也可以这样说没有自己的梦想就是对自己的一种不责任的表现,同时知识也不是也不是随意的摘取。
要通过自己的努力,要把我自己生命的钥匙。
今天小编在这给大家整理了一些福州中考数学考点分析,我们一起来看看吧!福州中考数学考点分析1一、锐角三角函数正弦等于对边比斜边余弦等于邻边比斜边正切等于对边比邻边余切等于邻边比对边正割等于斜边比邻边二、三角函数的计算幂级数c0+c1x+c2x2+...+cnxn+...=∑cnxn(n=0..∞)c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n(n=0..∞)它们的各项都是正整数幂的幂函数,其中c0,c1,c2,...及a都是常数,这种级数称为幂级数.泰勒展开式(幂级数展开法)f(x)=f(a)+f'(a)/1!_(x-a)+f''(a)/2!_(x-a)2+...f(n)(a)/n!_(x-a)n+...三、解直角三角形1.直角三角形两个锐角互余。
2.直角三角形的三条高交点在一个顶点上。
3.勾股定理:两直角边平方和等于斜边平方四、利用三角函数测高1、解直角三角形的应用(1)通过解直角三角形能解决实际问题中的很多有关测量问.如:测不易直接测量的物体的高度、测河宽等,关键在于构造出直角三角形,通过测量角的度数和测量边的长度,计算出所要求的物体的高度或长度.(2)解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.福州中考数学考点分析21.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
整式和分式统称为有理式。
2.整式和分式含有加、减、乘、除、乘方运算的代数式叫做有理式。
最新上海市中考数学考点分析及分值分布

上海市中考数学考点分析及分值分布一、试卷的总体情况无论是上海市的数学中考,还是外地的中考数学,都是严格按照中考数学考试纲要制定的。
大体上都是从知识与技能、数学与思考、解决问题、情感态度与价值观等四个方面对学生加以考查。
试卷的知识点覆盖面广,基础知识多,很能体现出适合不同层面的学生来完成,这一点,上海市与外地没有太大的其别。
二、试卷的内容与结构1、代数和几何的比例试卷的题型分为:选择题、填空题和解答题(包括:计算题、证明题、应用题以及探索、开放性试题等)。
外地试卷的内容分布:数与代数约占48.7% ;空间与几何占42% ;统计与概率约占9.3%。
上海市《考纲》要求:数与代数的内容约占50%,空间与图形的约占35%,通过对近几年上海市各个区的中考试卷分析,我们可以看出,中考试卷150分内代数约占90分,几何约占60分,比例在6 : 4。
2、各章节分值情况1、上海市中考方程(28分左右)和函数(32分左右)占较大的比重,函数部分(包括一次函数、二次函数、反比例函数)所涵盖的知识点基本考查到位,但是难度降低,这与外地的考点有比较大的区别,外地二次函数是中考重点考察的内容,且难度很大,属于综合类的大题。
2、统计的分值约占10%,这与外地没有太大的区别。
3、锐角三角比板块分值与统计类似,约占10% ;4、二次根式、因式分解、不等式分值统计;因式分解3分左右,不等式分值大于二次根式,同学们在复习的过程中要关注不等式知识点复习的有效性。
三、考点分析1方程:(1)解方程(组):主要是解分式方程、无理方程及二元二次方程组;无理方程与二元二次方程组在外地没有出现过,这些内容是上海市自己独立命题的。
(2)换元(化为整式方程),外地中考没有这一考点。
(3)—元二次方程根与系数关系的应用,主要是求方程中的系数;(4)列方程解应用题;“方程与不等式”的考法一般可分为如下的三大类:①技能层面上的题目一一多以考方程与不等式的解法为主;②能力层面上的题目(“列方程或不等式”解应用题)一一多以情境化的形式出现;③“方程思想”层面上的应用一一-是以“横向”联系、“知识综合”“解决实际问题或变化过程的即时性(阶段性)问题”为主。
中考数学质量分析报告免费

中考数学质量分析报告免费【中考数学质量分析报告】序言:数学是一门基础科学,也是中考必考科目之一。
通过对中考数学试卷进行质量分析,可以了解学生在数学学科上的整体水平,为教育教学提供有益的参考。
一、试卷难度分析:中考数学试卷的难度主要体现在题目的命题水平、题型的难易程度以及试卷的整体难度调控等方面。
1. 命题水平:数学试卷的命题水平体现在题目的设计以及题目的难度上。
一般来说,试卷中应该包含易、中、难三个层次的题目,以满足不同层次学生的需求。
其中,易题主要用于检测学生的基本概念、基本运算和基本推理能力;中难题则用于检验学生的综合运用、分析解决问题的能力。
2. 题型难易程度:常见的中考数学题型有选择题、填空题、解答题等。
不同的题型对于学生的思维方式和解题能力要求也有所不同。
根据学生的整体水平,试卷中应合理地设置不同题型的难度,以保证全面地考察学生的才能。
3. 试卷整体难度调控:试卷的整体难度调控是为了确保试卷评价学生的准确性。
如果试卷整体难度过低,则不能准确地区分学生的能力水平;反之,如果试卷整体难度过高,则可能导致学生过多失分,无法准确评价学生的实际能力水平。
因此,试卷整体难度的控制是十分重要的。
二、试卷命题结构分析:中考数学试卷的命题结构包括题目的数量、知识点的覆盖率、题目之间的联系等方面。
1. 题目数量:题目数量的安排应充分考虑中考时间和学生答题时间的合理性,并合理分配到不同题型和知识点上。
2. 知识点覆盖率:中考数学试卷应涵盖各个重点、难点知识点,以全面评估学生的数学能力。
同时,应注意各个知识点的出现频率和权重,避免某些知识点的过度考查。
3. 题目之间的联系:试卷中的题目应该具有一定的连贯性和内在联系,既能考察学生对基础知识和基本能力的熟练掌握,又能考察学生对综合知识和综合能力的综合运用。
三、考试成绩分析:通过对考生试卷的批改和成绩的统计,可以了解学生在数学学科上的整体水平。
1. 学生整体成绩水平:根据试卷的总分和满分,可以计算出学生的得分率,从而了解学生整体的成绩水平。
2024广东中考数学分析范文

2024广东中考数学分析范文数学分析是中学数学的重要内容,也是学生备战中考的重点之一、下面是一篇关于2024年广东中考数学分析的范文,供参考。
2024年广东中考数学分析题考查了一些基础知识和解题策略,要求学生熟练运用已掌握的知识和方法进行解题。
此次考试题型多样,包括选择题、填空题和解答题,考查了多个知识点,如函数、方程、平面几何等。
在选择题方面,考查了函数的零点及其个数、函数的图像、函数的性质等。
这些题目主要是考查学生对函数的定义和基本性质的理解和应用能力。
学生在解答这类题目时,应注意细节,尤其是要注意图像的对称性、单调性和整体性质。
在填空题方面,考查了方程的解和解的个数、函数的表示和计算等。
这些题目主要是考查学生对方程的理解和解题方法的掌握。
学生在解答这类题目时,应注意方程解的范围、解的个数及其求解过程。
在解答题方面,考查了平面几何的证明、函数应用题等。
这些题目主要是考查学生的证明能力和实际问题解决能力。
学生在解答这类题目时,应注意结论的证明过程、图像的理解和应用能力。
此次数学分析题难度适中,整体试卷的时间安排合理,给学生留有一定的答题时间。
尤其是在解答题部分,几个问题的难度有所递进,为学生提供了展示自己数学水平的机会。
在备考中,考生应重点掌握与数学分析相关的基本知识,如函数、方程、变量之间的关系等。
要灵活运用所学的知识和方法,将其应用于实际问题中,培养解题的思维能力和问题解决能力。
同时,还要注重题目的分析和细节的把握,避免因大意而出错。
总结而言,2024年广东中考数学分析题考查了学生对数学基本知识和解题方法的掌握程度,要求学生能够熟练运用所学的知识和方法进行解题。
此次试题的难度适中,整体试卷的设计合理,给学生留有一定的答题时间。
通过认真备考和答题,相信广大考生都能取得优异的成绩。
(以上为一篇2024广东中考数学分析范文,共计240字。
临沂市数学中考试题分析(近三年)

临沂市数学中考试题分析(近三年)一、题型和分值分析:临沂市中考数学试题共有26题,满分120分。
第一卷有14道选择题,第二卷由5道填空题和7道解答题两部分组成。
其中选择题占42分,填空题占15分,解答题共63分。
考查内容大致分为以下四块:数与代数(数与式,方程与不等式,函数),空间与图形(图形的认识,图形与变换,图形与坐标,图形与证明),统计与概率,综合应用。
其中数与代数约占46%,空间与图形占43%,概率与统计11%。
二、知识点分布及分值分析现在从试题考查的知识领域、认知水平层次及主要学科能力与思想方法,数学思考、问题解决能力的实现情况,从知识点领域和能力要求两个方面作了统计,对近三年数学中考试题进行了分析。
表一:数与代数部分试题分值分布表表二:概率与统计部分试题分值分布表表三:空间与图形部分试题分值分布表三、复习建议1、抓纲靠本,夯实基础(1)抓住基础概念,作为技巧突破口数学试题中的所谓解题技巧其实并不是什么高深莫测的东西,它来源于最基础的知识或概念,是掌握到一定程度时的灵光一现!(2)抓住基本题型,寻找差异因为做了大量雷同的练习,所以容易造成学生对相近试题的判断失误,这是非常危险的,是第二轮复习时要格外注意的地方。
(3)抓住常用公式,理解来龙去脉对经常使用的数学公式,要进一步了解其推理过程,并对推导过程中产生的一些可能变化自行探究。
这样做,学生一定能更好地掌握公式并胜过做大量习题,而且往往会有意想不到的效果。
(4)抓住中考动向,勤练解题规范要把握好目前的中考动向,特别是近年来上海的中考越来越注重解题过程的规范和解答过程的完整。
在此特别指出的是:有很多学生认为只要解出题目的答案就万事大吉了,其实只要是有过程的解答题,过程分比最后的答案要重要得多。
(5)抓住数学思想,总结解题方法梳理考试中经常出现的数学思想方法,例如分类讨论法、面积法,特值法、数形结合法等等,并在自己的脑海中对每一种方法记忆一道对应的典型试题。
中招数学质量分析报告

中招数学质量分析报告中招数学质量分析报告一、引言数学是一门重要的学科,对于培养学生的逻辑思维和问题解决能力具有重要的作用。
中考数学考试是评价学生数学水平的重要依据之一,因此对于中考数学的质量分析具有重要的意义。
本报告将针对某地区某次中考数学考试的试卷进行质量分析,分析学生的整体表现以及存在的问题,并提出相应的改进措施。
二、整体情况分析1. 考试概况本次中考数学考试采用试卷A、试卷B结构,并包括选择题、填空题和解答题三个部分。
试卷难度适中,涵盖了九年义务教育数学教学大纲中的基本内容。
2. 学生整体表现经对考生答题情况进行统计分析,学生整体表现如下:(1)选择题得分总体较高,平均得分率为80%以上。
说明学生的基础知识掌握较好,对常见考点有较好的理解和应用能力。
(2)填空题得分总体一般,平均得分率为60%-70%。
这说明学生在填空题的解题过程中,存在一定的丢分情况。
主要原因可能是对题意理解不透彻或者计算错误。
(3)解答题得分总体较低,平均得分率不足60%。
这表明学生在解答题的能力上存在较大的差距。
而解答题是考察学生综合运用数学知识解决问题的能力,对学生的思维能力和创新能力要求较高。
三、存在问题分析1. 对题目理解不透彻部分学生在选择题和填空题中,对题目理解不够深入,导致答案错误。
这可能是因为学生对关键词的理解不准确,或者对题干中的条件和要求有遗漏。
针对这个问题,学校应加强对学生的语文基础训练,培养学生对题目的准确理解能力。
2. 计算和应用能力有待提高部分学生在填空题和解答题中,存在计算错误和应用能力不足的情况。
这可能是因为学生对基本运算和数学概念掌握不牢固,以及对解题方法和思路不够熟练。
学校应加强对基础知识的巩固性训练,并提供更多解题思路和方法的讲解和练习。
3. 解答题答题能力有待提高解答题是中考数学考试的重点和难点,要求学生有较强的综合运用能力和问题解决能力。
但本次考试中,学生在解答题部分的得分率较低,说明学生在这方面的能力有待提高。
2024年数学中考阅卷总结

2024年数学中考阅卷总结一、总体情况概述2024年的数学中考试卷较往年相比难度适中,试题结构合理,题型涵盖了知识点的广度和深度。
考试整体难度与命题的目标相符,能够有效地考察学生对数学知识的掌握和运用能力。
以下将对试题的难度分布、知识点的考查情况以及考生的答题情况进行总结与分析。
二、试题难度分布与知识点考查情况1. 选择题选择题占比较大,难度适中。
其中包括了基础知识点的考查,如整数、分数、小数的四则运算、比例与比例关系、代数式的计算等。
同时也考查了应用题的解答能力,如解方程、解不等式以及几何问题的解题思路。
整体上,选择题的难度适中,能够有效地考察学生对基础知识的理解与应用能力。
2. 解答题解答题中,作图题和证明题的比例增加,对学生的思维能力和推理能力提出了更高的要求。
作图题中,既有基础的作图题,如画边长为3cm的正方形等,也有结合实际问题的应用题,如根据已知条件画出能够满足条件的几何图形等。
证明题的难度适中,涉及了数学推理和论证的能力,能够考察学生对已学知识的灵活运用和思维方法的掌握。
三、考生答题情况分析1. 难度适中的选择题,大部分学生能够作答正确,但也有部分学生在计算细节上出现错误,例如计算错误、漏写中间步骤等。
2. 解答题中,作图题和证明题的得分相对较低。
部分学生对作图题的解题思路和方法掌握不够熟练,导致作图不准确;部分学生对证明题的证明方法和逻辑推理掌握不够扎实,表达不清晰或缺乏逻辑性。
3. 部分学生对解答题的命题意图理解不充分,存在偏离题意的答案或答非所问的情况。
四、针对存在问题的改进措施1. 在教学中注重基础知识的扎实掌握,强化计算和应用能力的训练,提高学生的解题准确性。
2. 加强解答题的训练,注重培养学生的思维能力和推理能力,提高作图和证明的能力和水平。
3. 在命题和教学中,注重培养学生的理解能力和解题思路,提高学生对题意的理解和把握。
4. 提高试卷的质量和难度适应性,使试题更贴近课程要求和学生的实际水平,能够充分考察学生的知识和能力。
河南中考数学分析

考试难度变化趋势
难度适中
河南中考数学的难度适中,既注重基础知识的考查,又注重综合 应用能力的考查。
题目难度层次分明
题目难度层次分明,既有基础题,又有中等难度和较难题,能够全 面考查学生的数学水平。
压轴题目难度加大
近年来,河南中考数学的压轴题目难度逐渐加大,需要学生具备较 高的数学思维能力和解题技巧。
计算验证
对于一些需要通过计算才能得出答案的填空题,考生需要熟练掌握计 算技巧,确保计算结果的准确性。
解答题答题技巧
01
仔细审题
解答题中常常包含一些关键信息,需要考生仔细审题,找出题目中的关
键信息。
02
逻辑推理
对于一些需要通过逻辑推理才能得出答案的解答题,考生需要熟练掌握
逻辑推理技巧,确保推理结果的准确性。
影响。
学科地位
数学是初中阶段的重要学科之一, 对于培养学生的逻辑思维、分析问 题和解决问题的能力具有重要作用 。
教学质量评价
通过对河南中考数学的分析,可以 评价教师的教学质量和学生的学习 效果,为改进教学和提高教学质量 提供参考。
02
河南中考数学考试内容分析
考试范围
代数
பைடு நூலகம்
统计与概率
包括数与式、方程与不等式、函数等 。
考生表现
对考生的整体表现进行 分析,包括平均分、优 秀率、及格率等,以了 解考生的数学水平和存 在的问题。
考试评价
对考试的评价进行反思 ,包括评价标准、评价 方式、评价结果等,以 改进评价方式,提高评 价的准确性和公正性。
对教学的展望
教学内容与方法
根据考试内容和考生表现,反思教学内容和方法,包括教材选择、教学方法、教学资源等 ,以改进教学策略,提高教学效果。
2023年武汉中考数学道法原题

2023年武汉中考数学道法原题分析近年来,道法原题一直备受关注,成为教育界热门话题。
2023年武汉中考数学道法原题更是备受期待。
道法原题的出现,不仅考察了学生的基本知识及其应用能力,更重要的是评价了学生的逻辑思维和解决问题的能力。
下面我将从不同角度对2023年武汉中考数学道法原题进行深入分析。
一、数学分析1.1 抽象推理数学中的道法原题常常考察学生对于数学问题的抽象推理能力。
从历年来的数学道法题来看,几何问题和代数问题占据了相当大的比重。
2023年武汉中考数学道法原题是否延续了这一特点,我们可以从试题分析中得出结论。
1.2 实际运用另数学道法原题也注重学生对数学知识的实际运用能力。
通过与实际生活问题的结合,考察学生对数学知识的掌握情况。
2023年武汉中考数学道法原题中是否融入了更多的实际情境,需要我们在实际测试中仔细斟酌。
二、评分标准2.1 逻辑性道法原题评分的首要标准是逻辑性。
解题过程是否清晰,推理是否严谨,是评定学生成绩的关键因素。
2023年武汉中考数学道法原题的评分标准是否有所改变,我们需要在教育部公布具体评分细则后,再做具体分析。
2.2 创新性另外,道法原题也注重学生的创新能力。
是否有不同于常规题型的新颖题目呈现,是评判道法题的一个重要标准。
我们期待2023年武汉中考数学道法原题能够在题目设计上进行一些创新尝试,激发学生的思维,培养他们的创新意识。
三、test within3.1 汲取营养作为写手,我个人对于2023年武汉中考数学道法原题的期待也是十分殷切的。
我希望这一题型不仅能够考察学生扎实的数学基础知识,更期待它能够注重引导学生去进行独立思考和创新实践,这样才能真正起到培养学生的综合素质的作用。
3.2 灵活应对我相信学生朋友们也将认真准备,积极备考,毕竟“知识改变命运”的道理是一成不变的。
在备战2023年武汉中考数学道法原题的过程中,要学会举一反三,增强运用数学知识解决实际问题的能力。
三年中考数学试卷分析

名目
壹 贰 叁肆
试 卷
试 卷
中 考 分
教 学
构 造 分 析
考 点
值 分 布
建 议
分
及 占
析比
壹 试卷构造分析
试 卷 构 造
1.选择题30分〔10题〕20% 2.填空题24分〔8题〕16% 3.解答题96分〔10题〕64%
贰 试卷考点分析
2023-2023南通三年中考试卷考点
定系数法、三角形的面积、 角形相似求二次函数的解析 三点共线、锐角三角函数、
平行四边形的面积、平行 式、三角形相似的性质和判
勾股定理
四边的性质
定、函数图像上的点坐标与
解析式的关系、等边三角形
的性质和判定
贰 试卷考点分析
填空选择超高频考点
1.科学计数法〔2023.2 2023.2 2023.11〕
贰 试卷考点分析
二次根式有意义的条件 三角形中位线定理
科学计数法 分解因式
贰 试卷考点分析
填空 题
解答 题
13
圆柱三视图
圆内接四边形的性质定理
14 直角三角形的性质、 一元二次方程根的判定 锐角三角函数
15 平均数、中位数
旋转变换
16 一元二次方程根与 系数的关系
分式方程的实际应用
17 旋转的性质、正方 代数式求值;完全平方公
题型
选择 题
题号 1 2
3
4
5
2016 相反数的定义
科学计数法
分式的计算
轴对称图形;中心对称 图形
多边形的内角和、外角 和
2017
2018
有理数的大小比较
算数平方根
科学计数法
2023年黑龙江省绥化市中考数学真题(解析版)

二〇二三年绥化市初中毕业学业考试数学试题考生注意:1.考试时间120分钟2.本试题共三道大题,28个小题3.所有答案都必须写在答题卡上所对应的题号后的指定区域内一、单选题1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A B. C. D.【答案】C【解析】【分析】根据轴对称图形和中心对称图形定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.【详解】解:A 、是轴对称图形,不是中心对称图形,故A 选项不合题意;B 、是轴对称图形,不是中心对称图形,故B 选项不符合题意;C 、既是轴对称图形又是中心对称图形,故C 选项合题意;D 、不是轴对称图形,是中心对称图形,故D 选项不合题意.故选:C .【点睛】本题主要考查了轴对称图形和中心对称图形,解题的关键在于能够熟练掌握轴对称图形和中心对称图形的定义.2. 计算052-+的结果是( )A. 3- B. 7 C. 4- D. 6【答案】D【解析】【分析】根据求一个数的绝对值,零指数幂进行计算即可求解.【详解】解:052-+516=+=,故选:D ..的【点睛】本题考查了求一个数的绝对值,零指数幂,熟练掌握求一个数的绝对值,零指数幂是解题的关键.3. 如图是一个正方体,被切去一角,则其左视图是( )A. B. C. D.【答案】B【解析】【分析】根据左视图的意义判断即可.【详解】根据题意,该几何体的左视图为:,故选B .【点睛】本题考查了三视图的画法,熟练掌握三视图的空间意义是解题的关键.4. 纳米是非常小的长度单位,1nm 0.000000001m =,把0.000000001用科学记数法表示为( )A. 9110-´ B. 8110-´ C. 8110´ D. 9110´【答案】A【解析】【分析】用科学记数法表示绝对值较小的数,一般形式为10n a -´,其中110a £<,n 为整数.【详解】解:90.000000001110-=´.故选:A .【点睛】此题主要考查了用科学记数法表示绝对值较小的数,一般形式为10n a -´,其中110a £<,n 为由原数左边起第一个不为零的数字前面的0的个数所决定,确定a 与n 的值是解题的关键.5. 下列计算中,结果正确的是( )A. 333()pq p q -= B. 3228x x x x x ×+×= C. 5=± D. ()326a a =【答案】D【解析】【分析】根据积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,进行计算即可求解.【详解】解:A. 333()pq p q =--,故该选项不正确,不符合题意;B. 43222x x x x x ×+×=,故该选项不正确,不符合题意;C. 5=,故该选项不正确,不符合题意;D. ()326a a =,故该选项正确,符合题意;故选:D .【点睛】本题考查了积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,熟练掌握以上运算法则是解题的关键.6. 将一副三角板按下图所示摆放在一组平行线内,125Ð=°,230Ð=°,则3Ð的度数为( )A. 55°B. 65°C. 70°D. 75°【答案】C【解析】【分析】根据两直线平行内错角相等即可求解.【详解】解:依题意,190345Ð+°=Ð+°,∵125Ð=°,∴370Ð=°,故选:C .【点睛】本题考查了平行线的性质,熟练掌握两直线平行内错角相等是解题的关键.7. 下列命题中叙述正确的是( )A. 若方差22s s >乙甲,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上【答案】D【解析】【分析】根据方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,逐项分析判断即可求解.【详解】解:A. 若方差22s s >乙甲,则乙组数据的波动较小,故该选项不正确,不符合题意;B. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项不正确,不符合题意;C. 三角形三条中线交点叫做三角形的重心,故该选项不正确,不符合题意;D. 角的内部到角的两边的距离相等的点在角的平分线上,故该选项正确,符合题意;故选:D .【点睛】本题考查了方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,熟练掌握以上知识是解题的关键.8. 绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是( )组别参赛者成绩A7080x £<B8090x £<C90100x £<D100110x £<E 110120x £<A. 该组数据的样本容量是50人的B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D. 110~120这组数据对应的扇形统计图的圆心角度数为51°【答案】B【解析】【分析】根据C 组的人数除以占比求得样本的容量,结合统计图求得8090x £<的人数为15,进而根据中位数的定义,即可判断B 选项,根据组中值为901002+=95,即可判断C 选项,根据110~120的占比乘以360°,即可判断D 选项.【详解】解:A 、 该组数据的样本容量是1224%50¸=,故该选项不正确,不符合题意;B 、8090x £<的人数为:5041212715----=,41525+<,4151225++>,该组数据的中位数落在90~100这一组,故该选项正确,符合题意;C 、 90~100这组数据的组中值是95,故该选项不正确,不符合题意;D 、 110~120这组数据对应的扇形统计图的圆心角度数为736050.450´°=°,故该选项不正确,不符合题意;故选:B .【点睛】本题考查了样本的容量,条形统计图与扇形统计图信息关联,中位数的定义,求扇形统计图的圆心角的度数,求频数分布直方图组中值,从统计图表中获取信息是解题的关键.9. 在平面直角坐标系中,点A 在y 轴的正半轴上,AC 平行于x 轴,点B ,C 的横坐标都是3,2BC =,点D 在AC 上,且其横坐标为1,若反比例函数k y x=(0x >)的图像经过点B ,D ,则k 的值是( )A. 1B. 2C. 3D. 32【答案】C 【解析】【分析】设()3,B m ,则()()3,2,1,2C m D m ++根据反比例函数的性质,列出等式计算即可.【详解】设()3,B m ,∵点B ,C 的横坐标都是3,2BC =,AC 平行于x 轴,点D 在AC 上,且其横坐标为1,∴()()3,2,1,2C m D m ++,∴32m m =+,解得1m =,∴()3,1B ,∴313k =´=,故选C .【点睛】本题考查了反比例函数解析式的确定,熟练掌握k的意义,反比例函数的性质是解题的关键.10. 某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( )A. 11142x += B. 11111424x æö++=ç÷èøC. 1111142x æö++=ç÷èø D.11111442x æö++=ç÷èø【答案】B【解析】【分析】设乙车单独运送这批货物需x 天,由题意列出分式方程即可求解.【详解】解:设乙车单独运送这批货物需x 天,由题意列方程11111424x æö++=ç÷èø,故选:B .【点睛】本题考查了列分式方程,根据题意找到等量关系列出方程是解题的关键.11. 如图,在菱形ABCD 中,60A Ð=°,4AB =,动点M ,N 同时从A 点出发,点M 以每秒2个单位长度沿折线A B C --向终点C 运动;点N 以每秒1个单位长度沿线段AD 向终点D 运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x 秒,AMN V 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A. B. C. D.【答案】A【解析】【分析】连接BD ,过点B 作BE AD ^于点E ,根据已知条件得出ABD △是等边三角形,进而证明AMN ABE V ∽得出90ANM AEB Ð=Ð=°,当04t <<时,M 在AB 上,当48t £<时,M 在BC 上,根据三角形的面积公式得到函数关系式,【详解】解:如图所示,连接BD ,过点B 作BE AD ^于点E ,当04t <<时,M 在AB 上,菱形ABCD 中,60A Ð=°,4AB =,∴AB AD =,则ABD △是等边三角形,∴122AE ED AD ===,BE ==∵2,AM x AN x ==,∴2AM AB AN AE==,又A A Ð=Ð∴AMN ABEV ∽∴90ANM AEB Ð=Ð=°∴MN ==,∴212y x x =当48t £<时,M 在BC 上,∴1122y AN BE x =´=´=,综上所述,04t <<时的函数图象是开口向上的抛物线的一部分,当48t £<时,函数图象是直线的一部分,故选:A .【点睛】本题考查了动点问题的函数图象,二次函数图象的性质,一次函数图象的性质,菱形的性质,勾股定理,等边三角形的性质与判定,相似三角形的性质与判定,熟练掌握以上知识是解题的关键.12. 如图,在正方形ABCD 中,点E 为边CD 的中点,连接AE ,过点B 作BF AE ^于点F ,连接BD 交AE 于点G ,FH 平分BFG Ð交BD 于点H .则下列结论中,正确的个数为( )①2AB BF AE =×;②:2:3BGF BAF S S =△△;③当AB a =时,22BD BD HD a -×=A. 0个B. 1个C. 2个D. 3个【答案】D【解析】【分析】①根据题意可得90ABF BAF DAE Ð=°-Ð=Ð,则cos cos ABF EAD Ð=Ð,即BF AD AB AE=,又AB AD =,即可判断①;②设正方形的边长为a ,根据勾股定理求得AF ,证明GAB GED V V ∽,根据相似三角形的性质求得GE ,进而求得FG ,即可判断②;过点H 分别作,BF AE 的垂线,垂足分别为,M N ,根据②的结论求得BH ,勾股定理求得BD ,即可判断③.【详解】∵四边形ABCD 是正方形,∴90BAD ADE Ð=Ð=°,AB AD=∵BF AE^∴90ABF BAF DAEÐ=°-Ð=Ð∴cos cos ABF EADÐ=Ð即BF AD AB AE=,又AB AD =,∴2AB BF AE =×,故①正确;设正方形的边长为a ,∵点E 为边CD 的中点,∴2a DE =,∴1tan tans 2ABF EAD Ð=Ð=,在Rt ABE △中,AB a ===,∴AF =在Rt ADE △中,AE ==∴EF AE AF =-==,∵AB DE∥∴GAB GEDV V ∽∴2AG AB GE DE==∴13GE AE ==∴FG AE AF GE =--=-=∴32AF FG ==∴:2:3BGF BAF S S =△△,故②正确;∵AB a =,∴22222BD AB AD a =+=,如图所示,过点H 分别作,BF AE 的垂线,垂足分别为,M N ,又∵BF AE ^,∴四边形FMHN 是矩形,∵FH 是BFG Ð的角平分线,∴HM HN =,∴四边形FMHN 是正方形,∴FN HM HN ==∵2,BF AF FG ===∴13MH FG BM BF ==设MH b =,则34BF BM FM BM MH b b b =+=+=+=在Rt BMH V中,BH ==,∵BF a =4b =解得:b =∴BH ==,∴2222B a D BD HD a a =-×=,故④正确.故选:D .【点睛】本题考查了解直角三角形,相似三角形的性质与判定,正方形的性质,熟练掌握相似三角形的性质与判定是解题的关键.二、填空题13. 因式分解:2x xy xz yz +--=_______.【答案】()()x y x z +-【解析】【分析】先分组,然后根据提公因式法,因式分解即可求解.【详解】解:2x xy xz yz +--=()()()()x x y z x y x y x z +-+=+-,故答案为:()()x y x z +-.【点睛】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.14. x 的取值范围是_______.【答案】5x ³-且0x ¹##0x ¹且5x ³-【解析】【分析】根据分母不为零,二次根式的被开方数是非负数,列出不等式计算即可.有意义,∴50x +³且0x ¹,∴5x ³-且0x ¹,故答案为:5x ³-且0x ¹.【点睛】本题考查了分母不为零,二次根式的被开方数是非负数,熟练掌握二次根式和分式有意义的条件是解题的关键.15. 在4张完全相同的卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是_________.【答案】12##0.5【解析】【分析】根据题意列表法求概率即可求解.【详解】解:列表如下,123411 1 1=1213142221=212=232142=33 3 1=32313=344441=4 2 2=43414=共有16种等可能结果,符合题意的有8种,∴第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是81162=,故答案为:12.【点睛】本题考查了列表法求概率,整除,熟练掌握列表法求概率是解题的关键.16. 已知一元二次方程256x x x +=+的两根为1x 与2x ,则1211+x x 的值为_______.【答案】23-【解析】【分析】根据一元二次方程根与系数的关系得出121246x x x x +==-,,将分式通分,代入即可求解.【详解】解:∵一元二次方程256x x x +=+,即2460x x --=,的两根为1x 与2x ,∴121246x x x x +==-,,∴1211+x x 12124263x x x x +===--,故答案为:23-.【点睛】本题考查了分式的化简求值,一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题的关键.17. 化简:2222142442x x x x x x x x x+--æö-¸=ç÷--+-èø_______.【答案】12x -##12x-+【解析】【分析】先根据分式的加减计算括号内的,同时将除法转化为乘法,再根据分式的性质化简即可求解.【详解】解:2222142442x x x x x x x x x+--æö-¸ç÷--+-èø()()()()()2221242x x x x x x x x x +----=´--()()2222442x x x x x x x x ---+=´--12x =-;故答案为:12x -.【点睛】本题考查了分式的混合运算,熟练掌握分式的运算法则是解题的关键.18. 如图,O e 的半径为2cm ,AB 为O e 的弦,点C 为 AB 上的一点,将 AB 沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为_______.(结果保留p 与根号)【答案】22πcm3æ-çè【解析】【分析】根据折叠性质得出AOC V 是等边三角形,则60AOC Ð=°,1OD CD ==,根据阴影部分面积AOC AOC S S =-V 扇形即可求解.【详解】解:如图所示,连接,OA OC ,设,AB CO 交于点D∵将 AB 沿弦AB 翻折,使点C 与圆心O 重合,∴AC AO =,OC AB ^又OA OC =∴OA OC AC ==,∴AOC V 是等边三角形,∴60AOC Ð=°,1OD CD ==,∴AD ==,∴阴影部分面积)226012π22πcm 36023AOC AOC S S =-=´-´=V 扇形故答案为:22πcm 3æ-çè.19. 如图,在平面直角坐标系中,ABC V 与AB C ¢¢△的相似比为12∶,点A 是位似中心,已知点(2,0)A ,点(,)C a b ,90C Ð=°.则点C ¢的坐标为_______.(结果用含a ,b 的式子表示)【答案】(62,2)a b --【解析】【分析】过点,C C ¢分别作x 轴的垂线,CD C D ¢¢垂足分别为,D D ¢,根据题意得出2AD AD ¢=,则的2,AD a CD b =-=,得出()224,0D a ¢-+,即可求解.【详解】解:如图所示,过点,C C ¢分别作x 轴的垂线,CD C D ¢¢垂足分别为,D D ¢,∵ABC V 与AB C ¢¢△的相似比为12∶,点A 是位似中心,(2,0)A ∴2AD AD ¢=∵(,)C a b ,∴2,AD a CD b =-=,∴24,2A D a C D b ¢¢¢=-=,∴()224,0D a ¢-+∴C ¢(62,2)a b --故答案为:(62,2)a b --.【点睛】本题考查了求位似图形的坐标,熟练掌握位似图形的性质是解题的关键.20. 如图,ABC V 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60°得到CF .连接AF ,EF ,DF ,则CDF V 周长的最小值是______.【答案】3+3+【解析】【分析】根据题意,证明CBE CAF V V ≌,进而得出F 点在射线AF 上运动,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=,进而求得C D ¢,即可求解.【详解】解:∵E 为高BD 上的动点.∴1302CBE ABC Ð=Ð=°∵将CE 绕点C 顺时针旋转60°得到CF .ABC V 是边长为6的等边三角形,∴,60,CE CF ECF BCA BC AC =Ð=Ð=°=∴CBE CAF V V ≌∴30CAF CBE Ð=Ð=°,∴F 点在射线AF 上运动,如图所示,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а在Rt AOC V 中,30CAO Ð=°,则132CO AC ==,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=∵6CC AC ¢==,ACO C CD ¢Ð=Ð,CO CD =∴ACO C CD ¢V V ≌∴90C DC AOC ¢Ð=Ð=°在C DC ¢V 中,C D ¢===,∴CDF V 周长的最小值为3CD FC CD CD DC ¢++=+=+故答案为:3+【点睛】本题考查了轴对称求线段和的最值问题,等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,熟练掌握等边三角形的性质与判定以及轴对称的性质是解题的关键.21. 在求123100++++ 的值时,发现:1100101+=,299101+= ,从而得到123100++++= 101505050´=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++= _______.(结果用含n 的代数式表示)【答案】22n n -##22n n -+【解析】【分析】根据题意得出()14143n a n n =+-=-,进而即可求解.【详解】解:依题意,()1231,5,9,14143n a a a a n n ===×××=+-=-,,∴123n a a a a ++++= ()21432122n n n n n n +-==-=-,故答案为:22n n -.【点睛】本题考查了图形类规律,找到规律是解题的关键.22. 已知等腰ABC V ,120A Ð=°,2AB =.现将ABC V 以点B 为旋转中心旋转45°,得到A BC ¢¢△,延长C A ¢¢交直线BC 于点D .则A D ¢的长度为_______.【答案】44+-【解析】【分析】根据题意,先求得BC =,当ABC V 以点B 为旋转中心逆时针旋转45°,过点B 作BE A B ¢^交A D ¢于点E ,当ABC V 以点B 为旋转中心顺时针旋转45°,过点D 作DF BC ¢^交BC ¢于点F ,分别画出图形,根据勾股定理以及旋转的性质即可求解.【详解】解:如图所示,过点A 作AM BC ^于点M ,∵等腰ABC V ,120BAC Ð=°,2AB =.∴30ABC ACB Ð=Ð=°,∴112AM AB ==,BM CM ===∴BC =,如图所示,当ABC V 以点B 为旋转中心逆时针旋转45°,过点B 作BE A B ¢^交A D ¢于点E ,∵120BAC Ð=°,∴60DA B ¢Ð=°,30A EB ¢Ð=°,在Rt A BE ¢V 中,24A E A B ¢¢==,BE ==∵等腰ABC V ,120BAC Ð=°,2AB =.∴30ABC ACB Ð=Ð=°,∵ABC V 以点B 为旋转中心逆时针旋转45°,∴45ABA ¢Ð=°,∴180********DBE Ð=°-°-°-°=°,1804530105A BD ¢Ð=°-°-°=°在A BD ¢V 中,1801806010515D DA B A BD Ð=°-Ð-Ð=°-°-°=¢¢°,∴D EBD Ð=Ð,∴EB ED ==∴4A D A E DE ¢¢=+=+如图所示,当ABC V 以点B 为旋转中心顺时针旋转45°,过点D 作DF BC ¢^交BC ¢于点F ,在BFD △中,45BDF CBC Т=Ð=°,∴DF BF=在Rt DC F ¢V 中,30C ¢Ð=°∴'DF FC =∴BC BF =+=∴3DF BF ==-∴26DC DF ¢==-∴624A D C D A C ¢¢¢¢=-=-=-,综上所述,A D ¢的长度为4-或4+,故答案为:4-或4+.【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,熟练掌握旋转的性质,分类讨论是解题的关键.三、解答题23. 已知:点P 是O e 外一点.(1)尺规作图:如图,过点P 作出O e 的两条切线PE ,PF ,切点分别为点E 、点F .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,若点D 在O e 上(点D 不与E ,F 两点重合),且30EPF Ð=°.求EDF Ð的度数.【答案】(1)见解析 (2)75EDF Ð=°或105°【解析】【分析】(1)①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画圆,两圆交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O e 交于,E F 两点,作直线,PE PF ,(2)根据切线的性质得出90PEO PFO Ð=Ð=°,根据四边形内角和得出150EOF Ð=°,进而根据圆周角定理以及圆内接四边形对角互补即可求解.【小问1详解】解:如图所示,①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画弧,两弧交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O e 交于,E F 两点,作直线,PE PF ,则直线,PE PF 即为所求;【小问2详解】如图所示,点D 在O e 上(点D 不与E ,F 两点重合),且30EPF Ð=°,∵,PE PF 是O e 的切线,∴90PEO PFO Ð=Ð=°,∴360909030150EOF Ð=°-°-°-°=°,当点D 在优弧 E F 上时,1752EDF EOF Ð=Ð=°,当点D 在劣弧 E F 上时,18075105EDF Ð=°-°=°,∴75EDF Ð=°或105°.【点睛】本题考查了切线的性质与判定,直径所对的圆周角是直角,圆内接四边形对角互补,圆周角定理,熟练掌握以上知识是解题的关键.24. 如图,直线MN 和EF 为河的两岸,且MN EF ∥,为了测量河两岸之间的距离,某同学在河岸FE 的B 点测得30CBE Ð=°,从B 点沿河岸FE 的方向走40米到达D 点,测得45CDE Ð=°.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D 点继续沿DE 的方向走12)+米到达P 点.求tan CPE Ð的值.【答案】(1)河两岸之间的距离是20米(2)5tan 2CPE Ð=【解析】【分析】(1)过点C 作CM EF ^于点M ,设CM a =米,在Rt MCB △中,MB =,在Rt MCD △中,MD MC a ==,根据40BD =,建立方程,解方程即可求解;(2)根据题意求得MP 的长,进而根据正切的定义,即可求解.【小问1详解】解:如图所示,过点C 作CM EF ^于点M ,设CM a =米,∵30CBE Ð=°∴tan tan 30CM CBM PB Ð==°=,∴MB =,在Rt MCD △中,tan tan 451CM CDM MD Ð==°=,∴MD MC a==∴40BD MB MD a =-=-=解得:20a =+答:河两岸之间的距离是20米;【小问2详解】解:如图所示,依题意,4012)52PB BD DP =+=+=+,∴((20528MP MB PB =-=++=+在Rt CMP △中,5tan 2CM CPM MP Ð===,∴5tan 2CPE Ð=.【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数关系是解题的关键.25. 某校组织师生参加夏令营活动,现准备租用A 、B 两型客车(每种型号的客车至少租用一辆).A 型车每辆租金500元,B 型车每辆租金600元.若5辆A 型和2辆B 型车坐满后共载客310人;3辆A 型和4辆B 型车坐满后共载客340人.(1)每辆A 型车、B 型车坐满后各载客多少人?(2)若该校计划租用A 型和B 型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A 、B 两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s (千米)与甲车行驶的时间t (小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t 为何值时两车相距25千米.【答案】(1)每辆A 型车、B 型车坐满后各载客40人、55人(2)共有4种租车方案,租8辆A 型车,2辆B 型车最省钱(3)在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米【解析】【分析】(1)设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意列出二元一次方程组,解方程组即可求解;(2)设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意列出一元一次不等式组,解不等式组,求整数解即可得出m 的值,设总租金为w 元,根据一次函数的性质即可求解;(3)设s kt =甲,1s k t b =+乙,由题意可知,甲车的函数图像经过(4,300);乙车的函数图像经过(0.5,0),(3.5,300)两点.求出函数解析式,进而即可求解.【小问1详解】解:设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意得5231034340x y x y +=ìí+=î解得4055x y =ìí=î答:每辆A 型车、B 型车坐满后各载客40人、55人.【小问2详解】设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意得()()500600105500405510420m m m m ì+-£ïí+-³ïî 解得:2583m ££ m Q 取正整数,\5m =,6,7,8\共有4种租车方案设总租金为w 元,则500600(10)1006000w m m m =+-=-+Q 1000-<w \随着m 的增大而减小\8m =时,w 最小\租8辆A 型车,2辆B 型车最省钱.【小问3详解】设s kt =甲,1s k t b =+乙.由题意可知,甲车的函数图象经过(4,300);乙车的函数图象经过(0.5,0),(3.5,300)两点.∴75s t =甲,10050s t =-乙25s s -=乙甲,即100507525t t --=解得3t =或3007525t -=解得113t =所以,在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米.【点睛】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,根据题意找到等量关系,列出方程组,不等式组,以及函数解析式是解题的关键.26. 已知:四边形ABCD 为矩形,4AB =,3AD =,点F 是BC 延长线上的一个动点(点F 不与点C 重合).连接AF 交CD 于点G .(1)如图一,当点G 为CD 的中点时,求证:ADG FCG @△△.(2)如图二,过点C 作CE AF ^,垂足为E .连接BE ,设BF x =,CE y =.求y 关于x 的函数关系式.(3)如图三,在(2)的条件下,过点B 作BM BE ^,交FA 的延长线于点M .当1CF =时,求线段BM 的长.【答案】(1)见解析 (2)y =y =)(3【解析】【分析】(1)根据矩形的性质得出AD BF ∥,则D DCF Ð=Ð,根据题意得出DG CG =,即可证明(ASA)ADG FCG △≌△;(2)在Rt ABF V中,AF ==,证明CEF ABF △∽△,根据相似三角形的性质即可求解;(3)过点E 作EN BF ^于点N ,得出ABF △,CEF △为等腰直角三角形,在Rt BNE V 中,勾股定理求得BE ,证明BAM BCE △∽△,根据相似三角形的性质即可求解.【小问1详解】证明:∵四边形ABCD 为矩形,∴AD BF ∥,∴D DCF Ð=Ð,∵G 为CD 中点,∴DG CG =,在ADG △和△FCG 中D GCF DG CGAGD FGC Ð=Ðìï=íïÐ=Ðî, ∴(ASA)ADG FCG △≌△;【小问2详解】∵四边形ABCD 为矩形,∴90ABC Ð=°,∵CE AF ^,∴90CEF ABC Ð=°=Ð,∵F F Ð=Ð,∴CEF ABF △∽△, ∴CE CF AB AF=,∵4AB =,BF x =,∴在Rt ABF V 中,AF ==, ∵CE y =,∴4y =,∴y =y =;【小问3详解】过点E 作EN BF ^于点N ,∵四边形ABCD 为矩形,且3AD =,∴3AD BC ==,∵4AB =,1CF =,∴AB BF =,∴ABF △为等腰直角三角形,∴45CFE BAF Ð=Ð=°,∵CE AF ^,∴CEF △为等腰直角三角形,∴45ECF Ð=°,∵EN CF ^,∴EN 平分CF ,∴12CN NF NE ===,在Rt BNE V 中,∵222BE ,∴BE ==,∵45ECF BAF °Ð=Ð=,∴135BAM BCE Ð=Ð=°,∵BM BE ^,∴90MBA ABE Ð+Ð=°,∵90ABE EBC Ð+Ð=°,∴MBA EBC Ð=Ð,∴BAM BCE △∽△,∴43BM BA BE BC ==,43=,∴BM =.【点睛】本题考查了矩形的性质,全等三角形的性质与判定,相似三角形的性质与判定,列函数关系式,勾股定理,熟练掌握相似三角形的性质与判定是解题的关键.27. 如图,MN 为⊙O 的直径,且15MN =,MC 与ND 为圆内的一组平行弦,弦AB 交MC 于点H .点A 在¼MC上,点B 在»NC 上,90OND AHM Ð+Ð=°.(1)求证:MH CH AH BH ×=×.(2)求证: AC BC=.(3)在⊙O 中,沿弦ND 所在的直线作劣弧 ND的轴对称图形,使其交直径MN 于点G .若3sin 5CMN Ð=,求NG 的长.【答案】(1)见解析(2)见解析 (3)215【解析】【分析】(1)证明AMH CBH V V ∽即可;(2)连接OC ,交AB 于点F ,根据平行线的性质和已知条件证明垂直平分即可;(3)利用对称的性质作辅助线,根据已知条件,转化为解直角三角形问题即可.【小问1详解】Q ABC Ð和AMC Ð是 AC 所对的圆周角,\ABC AMC Ð=Ð,Q AHM CHB Ð=Ð,∴AMH CBH V :V ,∴AH MH CH BH=,∴MH CH AH BH ×=×.【小问2详解】连接OC ,交AB 于点F ,Q MC 与ND 为一组平行弦,即:MC ND ∥,\OND OMC Ð=Ð,Q OM OC =,\OMC OCM Ð=Ð,Q 90OND AHM Ð+Ð=°,\90OCM AHM OCM CHB Ð+Ð=Ð+Ð=°,\90HFC Ð=°,\OC AB ^,\OC 是AB 的垂直平分线,\ =AC BC.【小问3详解】连接DM 、DG ,过点D 作DE MN ^,垂足为E ,设点G 的对称点G ¢,连接G D ¢、G N ¢,Q DG DG ¢=,G ND GND ¢Ð=Ð,∴ 'DMDG =n ,\DG DM ¢=,\DG DM =,\DGM V 是等腰三角形,Q DE MN ^,\GE ME =,Q DN CM ∥,\CMN DNM Ð=Ð,Q MN 为直径,\90MDN Ð=°,\90MDE EDN Ð+Ð=°,Q DE MN ^,\90DEN Ð=°,\90DNM EDN Ð+Ð=°,\3sin sin sin 5EDM DNM CMN Ð=Ð=Ð=,在Rt MND △中,15MN =,\3sin 5MD DNM MN Ð==,\3155MD =,\9MD =,在Rt MED V 中,3sin 5ME EDM MD Ð==,\395ME =\275ME =,\2721215255NG MN MG MN ME =-=-=-´=\215NG =故答案为:215.【点睛】本题考查了圆的综合问题,同弧所对圆周角相等、构建合适的辅助线是解题的关键;熟练掌握相似三角形的判定与性质、垂直平分线的性质、熟悉锐角三角函数解决直角三角形.28. 如图,抛物线21y ax bx c =++的图象经过(6,0)A -,(2,0)B -,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ^于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?【答案】(1)211462y x x =++,36y x =+ (2)满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -(3)当133m =时,12CD PD +【解析】【分析】(1)待定系数法求解析式即可求解;(2)①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ^,12F F BC ^,使12E B E B BC ==,12CF CF BC ==,连接11E F 、22E F ,证明11(AAS)BE H CBO △≌△,得出112E H BO ==,16H B OC ==,则1(8,2)E -同理可得,2(4,2)E -;②以BC 为正方形的对角线时,过BC 的中点G 作33E F BC ^,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形,过点3E 作3E N y ^轴于点N ,过点B 作3BM E N ^于点M ,证明33(AAS)CE N E BM △≌△,得出3E B =,在3Rt E NC △中,22233E C CN E N =+,解得2CN =或4,进而即可求解;(3)得出CON V 是等腰直角三角形,HPD V是等腰直角三角形,则HD DP ==,点P 在抛物线2y 上,且横坐标为m ,得出(,6)H m m -+,进而可得22132HD DP m m ö==-+=÷ø,则12CD PD+2133m ö=-+÷ø根据二次函数的性质即可求解.【小问1详解】解:把(6,0)A -,(2,0)B -,(0,6)C 代入21y ax bx c =++得36604206a b c a b c c -+=ìï-+=íï=î解得1246a b c ì=ïï=íï=ïî∴211462y x x =++ 把(2,0)B -代入6y kx =+得3k =∴36y x =+【小问2详解】满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -解:①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ^,12F F BC ^,使12E B E B BC ==,12CF CF BC ==,连接11E F 、22E F .过点1E 作11E H x ^轴于1H .∵1111,90BE CB BOC E H B E BC =Ð=Ð=°=Ð,又111190BE H E BH CBO Ð=°-Ð=Ð,∴11(AAS)BE H CBO △≌△,∴112E H BO ==,16H B OC ==∴1(8,2)E -同理可得,2(4,2)E -②以BC 为正方形的对角线时,过BC 的中点G 作33EF BC ^,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形,过点3E 作3E N y ^轴于点N ,过点B 作3BM E N ^于点M∵3333,90CE BE CNE E MB =Ð=Ð=°,又33390BE M CE N E CNÐ=°-Ð=Ð∴33(AAS)CE N E BM △≌△∴3CN E M =,3BM E N=∵BC =∴3E G BG ==∴3E B =在3Rt E NC △中,22233E C CN E N=+∴222(6)CN CN =+-解得2CN =或4当4CN =时,3(2,2)E ,此时点E 在点F 右侧故舍去;当2CN =时,3(4,4)E -.综上所述:1(8,2)E -,2(4,2)E -,3(4,4)E -【小问3详解】∵211462y x x =++向右平移8个单位长度得到抛物线()()22184862y x x =-+-+当20y =,即()()21848602x x -+-+=解得:122,6x x ==∴(2,0)M ,(6,0)N ∵2y 过M ,N ,C 三点∴221462y x x =-+ 在直线NC 下方的抛物线2y 上任取一点P ,作PH x ^轴交NC 于点H ,过点H 作HG y ^轴于点.G∵(6,0)N ,(0,6)C ∴ON OC=∴CON V 是等腰直角三角形∵45CHG Ð=°,90GHP Ð=°∴45PHD Ð=°又PD CN^∴HPD V 是等腰直角三角形∴HD DP HP ==∵点P 在抛物线2y 上,且横坐标m∴CG GH m==∴CH =∵6CN y x =-+为∴(,6)H m m -+∴2211646322HP m m m m m æö=-+--+=-+ç÷èø∴22132HD DP m m ö==-+=÷ø∴211332222CD PD CH HD PD CH PD æö+=++=+=++ç÷ç÷èø2133m ö=-÷ø∴当133m =时,12CD PD +.【点睛】本题考查了二次函数综合运用,正方形的性质,二次函数的性质,分类讨论,熟练掌握二次函数的性质是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三年试题的主要特点
三年的试卷都强调了应用性,增加了探究性,注重了综合性。
试题集“双基、实践、探究”于一身。
08年中考题在考查三基时,注意结合现实背景(如第2、4、6、20、21题),体现对数学本质理解的考查。
初中数学中常见的函数与方程(如第16题、23题)、数形结合(如第23、24)、分类讨论题、待定系数法(第23题、24题),等数学思想方法在试卷中得到了充分的体现。
注重学生对研究性学习与探究能力的考查。
有效的数学学习不能单纯地依靠模仿与记忆,而是应该通过观察、猜想、验证、推理等数学活动,形成学生自己对数学知识的理解,从而使学生的知识内化,方法获得迁移,能力得以形成(如第25题)。
如第20题,要求学生根据统计图表中提供的多组数据和字里行间读出有用的信息,并利用从各种相关材料中获取的信息解决问题,较好地体现了新课程的理念,强调了培养学生在现代社会中获取和处理信息能力的要求。
注重学生的动手实践能力的考查。
如第21题,有设定的操作步骤,这里既考学生的动手能力,也考查计算、归纳、猜想,关键是看学生能否对实践操作的要领、程序有较好地把握。
《圆》考核了简单的切线证明,和简单的计算,《相似形》没有单独考核,但在几道综合题(如第24题)中都有涉及,《全等形》考核力度较大,15题考核了全等三角形、25题考核了四边形、全等三角形。
彰显新课程理念,突出新课程立意。
如第8、12、22、25题,这些题考查学生自主探索、自主发展的能力和归纳、类比、概括、推理、论证等思维活动的水平。
从09年北京中考数学试卷的命题方向看,基本沿袭08年的风格和类型,但09年题型有少许变化,具体分析如下:
1.最后一道选择题:第8题,不再是图形展开类,而是动点及函数图像
2.填空题最后一道:第12题,还是找规律,类型没变,题有变化
3.计算第17题是新题型,出现两函数图像所围成区域范围内点的确定。
4.相似知识没有与压轴题结合,而是与第20题圆结合,求解半径长度。
这是09年命题的新变化。
5.第22题,由原来的面积重叠类计算,变化为面积不变的图形拼接。
6.第23题,新增了函数平移与折叠。
7.第24题,旋转类试题继续单独出现。
8.第25题,压轴题以动点问题、最短距离出现。
是一个新的命题变化。
考察重点:一元二次方程、函数图像及计算、梯形、四边形旋转、圆的切线、相似形、面积问题、动点问题。
相对09年中考试题,10年在题型设计、情景安排及问题设问方式等方面有了更多的创新(如第2题、第7题、第8题、第12题、第17题、第21题、第22题等)。
减整份试卷重应用、重能力、重创新,刪重点内容重点考。
刅强调对“双基”的考核,凪试题设计人性化,则没有很繁杂的计算,凾使困难层学生也能很快上手,凉同时突出“用数学”意识,刖综合题入口宽,刏出口高,凴强化试题的区分度。
数学试卷体现了《数学课程标准》对知识技能、数学思想、解决问题、情感与态度等目标的要求,凱考试内容紧扣《考试说明》中关于“数与代数”、“空间与图形”、“统计与概率”等领域中最基础、最核心的内容,凷无“繁、难、偏、旧”的知识。
凜试卷处处体现了数学知识在日常生产、生活中的运用。
凩试题取材,別贴近考生生活,刦力求实现数学试题模型的生活化,初引导学生用数学的观点去观察生活、关注自身发展、关注社会热点,刄具有一定的教育性(如第2、第12题、第21题等)。
刌整张试卷基础题更简单,刂较难题适当增加了难度,则试题具有良好的区分度和选拔功能。
凬本卷注重了对学生能力的培养,凧强调了学生的实践探索能力(如第22题)。
本套试卷设置起点比较低,凾坡度较缓,凒注重考查基础知识、基本技能、基本方法,刑至于综合性较强的23、24、25题也都考虑到不同层面考生的认知水平设置多问,刍适当搭梯子,划充分体现了数学面向全体学生的特点,凷实现“人人学有价值的数学;人人都能获得必要的数学;不同的人在数学上得到不同的发展”的数学教育观念。
10年中考第1、2、6、14、19题取材于课本,经过了简单的改编。
第3、16、20、23题等考察了必须掌握的核心观念、
思想方法、基本概念和常用技能。
第7、8、17、21、22以现实生活为背景,重点考察了学生收集相关信息、并对所收集的信息进行处理的解决实际问题的能力。
第24题考察了动点问题,动点问题是一种非常常见的代数几何综合题。
第25题考察了探究问题,探究问题是中考命题的热点,几乎每年必考,对思维能力的要求非常高。
这两道题体现了此次中考对探究和变换的重点考察。
本套试卷除大量考察了基础知识,使绝大多数同学都能毕业外,还突出考察了重点知识,如第6、18、23、24题都是函数知识,而函数知识在高中阶段也是重点内容之一,体现了初高中衔接。
总体10年中考题相比09年略难,与08年难度相当,虽然12题、24题、25题有一定难度,但梯子铺设到位,送分很充分。
即便是最难的25题,如果学生有时间看题,最少也能得到4分,25题第(2)小问比较难,体现区分度。
与09年相比,10年试卷在结构上没有太大的变化,基本趋于稳定,只有极个别的题目有所变化:第8题回归了立方体展开图的考查,23题考查了以反比例函数为背景的代几综合题,从09年中考到10年中考,对三大几何变换(平移、旋转、轴对称)均加大了考查力度,不仅是对几何图形的变换,而且还涉及到了函数图像的变换,09年第23题考查了二次函数的对称、一次函数的平移,10年的22题和25题都考察了轴对称变换,也是今年中考的难点。
四、对2011年中考的预测
这几年的中考的内容,数学的内容基本上没有什么大的变化,初一、初二的知识大概是62%左右,初三的是25%左右。
换句话说,这个肯定是一个稳定的要求,2011年也不会脱离这个水平。
这三年尽管也考查了圆、相似、二次函数这些以前认为重中之重的内容,但明显可以感觉到圆与相似的难度大大减弱了,因此,感觉2011年中考这方面应和10年差不多。
注意对计算能力的考查。
在试卷中除了选择填空中一些简单计算之外,直接的计算题如说数的计算,解方程,代数求值三道计算。
还有两道是放在一些需要理解题意的前提下进行计算的,一道是列方程解决问题,还有一道统计题,这两种计算对同学的要求都是要求计算很准确的。
23或者24题,关于一元二次方程或者二次函数的题,在这个题里面经常会出现一个二次函数一个二次方程它的系数里面含有字母这样的计算,这种含有字母的计算就要求比较高了。
关于论证能力,证明题的能力,在中考试卷中,现在有固定不变的三道题,一道简单的三角形证明题,一道简单的四边形论证,还有一道圆的证明。
关于归纳,猜测,这样的题目现在每年都有,比如说一些数据找出它的规律来,判断出第N个数据的结果。
除此之外,还要注意操作能力、画图能力和阅读能力的考查,数学常用到的化归思想、数形结合思想、分类讨论思想等数学思想的考查。
老师和学生需要做的就是:
第一、依靠课本,补上初一、初二的学习漏洞。
第二、依靠课本,学会归纳、整理。
第三、依靠课本,依靠教材,提高数学方法的应用。
第四、重视代数与几何等综合题的训练。
