湖南省长郡中学2015届高三月考试卷(二)数学(文)试题及答案
2015年湖南省高考数学试卷(文科)

2015 年湖南省高考数学试卷(文科)一、选择题(每题 5 分,共 50 分)1.(5 分)已知=1+i(i 为虚数单位),则复数 z=()A.1+i B.1﹣i C.﹣ 1+i D.﹣ 1﹣ i2.( 5 分)在一次马拉松竞赛中, 35 名运动员的成绩(单位:分钟)的茎叶图以下图.若将运动员按成绩由好到差编为 1﹣ 35 号,再用系统抽样方法从中抽取7 人,则此中成绩在区间 [ 139,151] 上的运动员人数是()A.3B.4C.5D.633.(5 分)设 x∈R,则“x>1“是“x>1”的()A.充足不用要条件B.必需不充足条件C.充要条件D.既不充足也不用要条件4.(5 分)若变量 x, y 知足拘束条件,则z=2x﹣y的最小值为()A.﹣ 1 B.0C.1D.25.(5 分)履行以下图的程序框图,假如输入n=3,则输出的 S=()A.B.C.D.6.(5 分)若双曲线﹣=1 的一条渐近线经过点( 3,﹣ 4),则此双曲线的离心率为()A.B.C.D.7.(5 分)若实数 a,b 知足 + =,则 ab 的最小值为()A.B.2 C.2 D.48.(5 分)设函数 f( x)=ln(1+x)﹣ ln(1﹣x),则 f(x)是()A.奇函数,且在( 0, 1)上是增函数B.奇函数,且在( 0,1)上是减函数C.偶函数,且在( 0,1)上是增函数D.偶函数,且在( 0, 1)上是减函数.(分)已知,,在圆x 2+y2=1上运动,且⊥ ,若点P的坐标为(,9 5 A B C AB BC2 0),则 || 的最大值为()A.6 B.7 C.8 D.910.( 5 分)某工件的三视图以下图,现将该工件经过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件资料的利用率为(资料利用率=)()A .B .C .D .二、填空题(本大题共 5 小题,每题 5 分,共 25 分)11.(5 分)已知会合 U={ 1,2,3,4} ,A={ 1,3} ,B={ 1,3,4} ,则 A ∪(?U B )= .12.(5 分)在直角坐标系 xOy 中,以坐标原点为极点, x 轴的正半轴为极轴成立 极坐标系,若曲线 C 的极坐标方程为 ρ=2sin ,θ则曲线 C 的直角坐标方程为.22 213.(5 分)若直线 3x ﹣4y+5=0与圆 x+y(r >0)订交于 A ,B 两点,且∠ AOB=120°,=r( O 为坐标原点),则 r= .14(.5 分)已知函数 (fx )=| 2x﹣2| ﹣b 有两个零点,则实数 b 的取值范围是 .15.( 5 分)已知 ω>0,在函数 y=2sin ωx 与 y=2cos ωx 的图象的交点中,距离最短的两个交点的距离为 2,则 ω=.三、解答题16.( 12 分)某商场举行有奖促销活动,顾客购置必定金额的商品后即可抽奖,抽奖方法是:从装有 2 个红球 A 1,A 2 和 1 个白球 B 的甲箱与装有 2 个红球 a 1, a 2 和 2 个白球 b 1,b 2 的乙箱中,各随机摸出 1 个球,若摸出的 2 个球都是红球则中奖,不然不中奖.(Ⅰ)用球的标号列出全部可能的摸出结果;(Ⅱ)有人以为:两个箱子中的红球比白球多, 因此中奖的概率大于不中奖的概率,你以为正确吗?请说明原因.17.( 12 分)设△ ABC的内角 A,B,C 的对边分别为 a, b,c,a=btanA.(Ⅰ)证明: sinB=cosA;(Ⅱ)若 sinC﹣sinAcosB= ,且 B 为钝角,求 A, B, C.18.( 12 分)如图,直三棱柱 ABC﹣A1B1C1的底面是边长为 2 的正三角形, E,F 分别是 BC,CC 的中点,1(Ⅰ)证明:平面AEF⊥平面 B1BCC1;(Ⅱ)若直线 A1 C 与平面 A1ABB1所成的角为 45°,求三棱锥 F﹣ AEC的体积.19.( 13 分)设数列 { a n} 的前 n 项和为 S n,已知 a1=1,a2=2,a n+2=3S n﹣ S n+1+3,n∈N*,(Ⅰ)证明 a n+2=3a n;(Ⅱ)求 S n.20.(13 分)已知抛物线 C1:x2=4y 的焦点 F 也是椭圆 C2: +=1( a> b> 0)的一个焦点, C1与 C2的公共弦的长为2,过点F的直线l与C1订交于A,B两点,与 C2订交于 C,D 两点,且与同向.(Ⅰ)求 C2的方程;(Ⅱ)若 | AC| =| BD| ,求直线 l 的斜率.21.( 13 分)已知 a> 0,函数 f(x)=ae x cosx(x∈[ 0, +∞ ] ),记 x n为 f(x)的从小到大的第 n( n∈N*)个极值点.(Ⅰ)证明:数列 { f(x n)} 是等比数列;(Ⅱ)若对全部n∈N*,x n≤ | f (x n)| 恒成立,求 a 的取值范围.2015 年湖南省高考数学试卷(文科)参照答案与试题分析一、选择题(每题 5 分,共 50 分)1.(5 分)已知=1+i(i 为虚数单位),则复数 z=()A.1+i B.1﹣i C.﹣ 1+i D.﹣ 1﹣ i【剖析】由条件利用两个复数代数形式的乘除法法例,求得z 的值.【解答】解:∵已知=1+i(i 为虚数单位),∴z===﹣1﹣i,应选: D.【评论】此题主要考察两个复数代数形式的乘除法法例的应用,属于基础题.2.( 5 分)在一次马拉松竞赛中, 35 名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编为1﹣ 35 号,再用系统抽样方法从中抽取7 人,则此中成绩在区间 [ 139,151] 上的运动员人数是()A.3B.4C.5D.6【剖析】对各数据分层为三个区间,而后依据系统抽样方法从中抽取7 人,获得抽取比率为,而后各层依据此比率抽取.【解答】解:由已知,将个数据分为三个层次是[ 130,138] ,[ 139,151] ,[ 152,153] ,依据系统抽样方法从中抽取7 人,获得抽取比率为,因此成绩在区间 [ 139,151] 中共有 20 名运动员,抽取人数为20×=4;应选: B.【评论】此题考察了茎叶图的认识以及利用系统抽样抽取个体的方法;重点是正确分层,明确抽取比率.33.(5 分)设 x∈R,则“x>1“是“x>1”的()A.充足不用要条件B.必需不充足条件C.充要条件D.既不充足也不用要条件【剖析】利用充要条件的判断方法判断选项即可.3【解答】解:因为 x∈R,“x>1“? “x>1”,3因此“x>1“是“x> 1”的充要条件.应选: C.【评论】此题考察充要条件的判断,基本知识的考察.4.(5 分)若变量 x, y 知足拘束条件,则z=2x﹣y的最小值为()A.﹣ 1 B.0C.1D.2【剖析】由拘束条件作出可行域,由图获得最优解,求出最优解的坐标,数形联合得答案.【解答】解:由拘束条件作出可行域如图,由图可知,最优解为A,联立,解得 A( 0,1).∴z=2x﹣y 的最小值为 2×0﹣1=﹣ 1.应选: A.【评论】此题考察了简单的线性规划,考察了数形联合的解题思想方法,是中档题.5.(5 分)履行以下图的程序框图,假如输入n=3,则输出的 S=()A.B.C.D.【剖析】列出循环过程中 S 与 i 的数值,知足判断框的条件即可结束循环.【解答】解:判断前 i=1,n=3, s=0,第 1 次循环, S=,i=2,第 2 次循环, S=,i=3,第 3 次循环, S=,i=4,此时, i>n,知足判断框的条件,结束循环,输出结果:S===应选: B.【评论】此题考察循环框图的应用,注意判断框的条件的应用,考察计算能力6.(5 分)若双曲线﹣=1 的一条渐近线经过点( 3,﹣ 4),则此双曲线的离心率为()A.B.C.D.【剖析】利用双曲线的渐近线方程经过的点,获得a、b 关系式,而后求出双曲线的离心率即可.【解答】解:双曲线﹣=1 的一条渐近线经过点( 3,﹣ 4),可得 3b=4a,即 9(c2﹣a2) =16a2,解得=.应选: D.【评论】此题考察双曲线的简单性质的应用,基本知识的考察.7.(5 分)若实数 a,b 知足+ =,则ab的最小值为()A.B.2C.2D.4【剖析】由+ =,可判断a>0,b>0,而后利用基础不等式即可求解 ab 的最小值【解答】解:∵+ =,∴a> 0,b> 0,∵(当且仅当 b=2a 时取等号),∴,解可得, ab,即ab的最小值为2,应选: C.【评论】此题主要考察了基本不等式在求解最值中的简单应用,属于基础试题8.(5 分)设函数 f( x)=ln(1+x)﹣ ln(1﹣x),则 f(x)是()A.奇函数,且在( 0, 1)上是增函数B.奇函数,且在( 0,1)上是减函数C.偶函数,且在( 0,1)上是增函数D.偶函数,且在( 0, 1)上是减函数【剖析】求出好的定义域,判断函数的奇偶性,以及函数的单一性推出结果即可.【解答】解:函数 f (x) =ln( 1+x)﹣ ln(1﹣x),函数的定义域为(﹣ 1, 1),函数 f (﹣ x)=ln(1﹣x)﹣ ln( 1+x)=﹣[ ln (1+x)﹣ ln( 1﹣ x)] =﹣f (x),所以函数是奇函数.清除 C,D,正确结果在 A,B,只要判断特别值的大小,即可推出选项, x=0 时,f(0)=0;x=时,f()=ln(1+)﹣ln(1﹣)=ln3>1,明显f(0)<f(),函数是增函数,因此 B 错误, A 正确.应选: A.【评论】此题考察函数的奇偶性以及函数的单一性的判断与应用,考察计算能力.,,在圆x 2+y2=1上运动,且⊥ ,若点P的坐标为(,9.(5 分)已知 A B C AB BC2 0),则 || 的最大值为()A.6 B.7 C.8 D.9【剖析】由题意, AC为直径,因此 ||=|2+| .B 为(﹣ 1,0)时,| 2+| ≤7,即可得出结论.【解答】解:由题意, AC为直径,因此 ||=|2+|因此 B 为(﹣ 1,0)时, | 2+| ≤7.因此 || 的最大值为 7.另解:设 B(cosα, sin α),| 2+| =| 2 (﹣ 2 , 0 ) + ( cosα﹣ 2 , sin α) | =| ( cosα﹣ 6 , sin α) | ==,当 cosα=﹣1 时, B 为(﹣ 1,0),获得最大值7.应选: B.【评论】此题考察向量知识的运用,考察学生剖析解决问题的能力,比较基础.10.( 5 分)某工件的三视图以下图,现将该工件经过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件资料的利用率为(资料利用率=)()A.B.C.D.【剖析】由题意,原资料对应的几何体是圆锥,其内接正方体是加工的新工件,求出它们的体积,正方体的体积与圆锥的体积比为所求.【解答】解:由题意,由工件的三视图获得原资料是圆锥,底面是直径为2的圆,母线长为 3,因此圆锥的高为2,圆锥是体积为;其内接正方体的棱长为x,则,解得x=,因此正方体的体积为,因此原工件资料的利用率为:=;应选: A.【评论】此题考察了由几何体的三视图获得几何体的体积以及几何体的内接正方体棱长的求法;正确复原几何体以及计算内接正方体的体积是重点,属于中档题.二、填空题(本大题共 5 小题,每题 5 分,共 25 分)11.(5 分)已知会合 U={ 1,2,3,4} ,A={ 1,3} ,B={ 1,3,4} ,则 A∪(?U B)= { 1,2,3}.【剖析】第一求出会合 B 的补集,而后再与会合 A 取并集.【解答】解:会合 U={ 1,2,3,4} , A={ 1,3} , B={ 1, 3,4} ,因此 ?U B={ 2} ,因此 A∪( ?U B)={ 1,2,3} .故答案为: { 1, 2,3} .【评论】此题考察了会合的交集、补集、并集的运算;依据定义解答,属于基础题.12.(5 分)在直角坐标系 xOy 中,以坐标原点为极点, x 轴的正半轴为极轴成立极坐标系,若曲线 C 的极坐标方程为ρ=2sin,θ则曲线 C 的直角坐标方程为 x2+(y﹣ 1)2=1 .【剖析】直接利用极坐标与直角坐标互化,求解即可.2【解答】解:曲线 C 的极坐标方程为ρ=2sn,θ即ρ=2ρ sn,θ它的直角坐标方程为: x2+y2 =2y,即 x2+(y﹣1)2=1.故答案为: x2+( y﹣ 1)2=1.【评论】此题考察极坐标与直角坐标方程的互化,基本知识的考察.2 2 213.(5 分)若直线 3x﹣4y+5=0与圆 x +y =r(r>0)订交于 A,B两点,且∠AOB=120°,( O 为坐标原点),则 r= 2 .【剖析】若直线 3x﹣4y+5=0 与圆 x2+y2=r2( r>0)交于 A、B 两点,∠AOB=120°,则△ AOB为顶角为 120°的等腰三角形,极点(圆心)到直线 3x﹣4y+5=0 的距离d= r,代入点到直线距离公式,可结构对于r 的方程,解方程可得答案.【解答】解:若直线 3x﹣4y+5=0 与圆 x2+y2=r2(r> 0)交于 A、 B 两点, O 为坐标原点,且∠ AOB=120°,则圆心( 0, 0)到直线 3x﹣4y+5=0 的距离 d=rcos= r,即= r,解得 r=2,故答案为: 2.【评论】此题考察的知识点是直线与圆订交的性质,此中剖析出圆心(0,0)到直线 3x﹣ 4y+5=0 的距离 d=r 是解答的重点.14.(5 分)已知函数 f(x)=| 2x﹣2| ﹣b 有两个零点,则实数 b 的取值范围是0<b< 2 .【剖析】由函数 f( x) =| 2x﹣2| ﹣b 有两个零点,可得 | 2x﹣ 2| =b 有两个零点,进而可得函数 y=| 2x﹣ 2| 函数 y=b 的图象有两个交点,联合函数的图象可求 b 的范围【解答】解:由函数 f(x)=| 2x﹣2| ﹣ b 有两个零点,可得 | 2x﹣2| =b 有两个零点,进而可得函数 y=| 2x﹣ 2| 函数 y=b 的图象有两个交点,联合函数的图象可得,0<b<2 时切合条件,故答案为:0<b<2【评论】此题主要考察函数的零点以及数形联合方法,数形联合是数学解题中常用的思想方法,可以变抽象思想为形象思想,有助于掌握数学识题的实质.15.( 5 分)已知ω>0,在函数 y=2sin ωx与 y=2cos ωx的图象的交点中,距离最短的两个交点的距离为2,则ω=.【剖析】依据正弦线,余弦线得出交点((k1,),((k2,), k1,k2都为整数,两个交点在同一个周期内,距离近来,即可得出方程求解即可.【解答】解:∵函数 y=2sin ωx与 y=2cosωx的图象的交点,∴依据三角函数线可得出交点((k1,),((k2,),k1, k2都为整数,∵距离最短的两个交点的距离为2,∴这两个交点在同一个周期内,∴ 12=()2+()2,ω=故答案为:【评论】此题考察了三角函数的图象和性质,三角函数线的运用,属于中档题,计算较麻烦.三、解答题16.( 12 分)某商场举行有奖促销活动,顾客购置必定金额的商品后即可抽奖,抽奖方法是:从装有 2 个红球 A1,A2和 1 个白球 B 的甲箱与装有 2 个红球 a1, a2和 2 个白球 b1,b2的乙箱中,各随机摸出 1 个球,若摸出的 2 个球都是红球则中奖,不然不中奖.(Ⅰ)用球的标号列出全部可能的摸出结果;(Ⅱ)有人以为:两个箱子中的红球比白球多,因此中奖的概率大于不中奖的概率,你以为正确吗?请说明原因.【剖析】(Ⅰ)中奖利用列举法列出全部可能的摸出结果;(Ⅱ)在(Ⅰ)中求出摸出的 2 个球都是红球的结果数,而后利用古典概型概率计算公式求得概率,并说明中奖的概率大于不中奖的概率是错误的.【解答】解:(Ⅰ)全部可能的摸出的结果是:{ A1,a1} , { A1, a2} , { A1,b1} ,{ A1,b2} ,{ A2,a1} ,{ A2, a2} ,{ A2,b1} , { A2, b2} ,{ B,a1} , { B,a2} ,{ B,b1} ,{ B, b2 } ;(Ⅱ)不正确.原因以下:由(Ⅰ)知,全部可能的摸出结果共 12 种,此中摸出的 2 个球都是红球的结果为:{ A1,a1} , { A1, a2} , { A2,a1} ,{ A2,a2} ,共 4 种,∴中奖的概率为.不中奖的概率为: 1﹣.故这类说法不正确.【评论】此题考察了古典概型及其概率计算公式,训练了列举法求基本领件个数,是基础题.17.( 12 分)设△ ABC的内角 A,B,C 的对边分别为 a, b,c,a=btanA.(Ⅰ)证明: sinB=cosA;(Ⅱ)若 sinC﹣sinAcosB= ,且 B 为钝角,求 A, B, C.【剖析】(Ⅰ)由正弦定理及已知可得=,由sinA≠0,即可证明sinB=cosA.(Ⅱ)由两角和的正弦函数公式化简已知可得sinC﹣ sinAcosB=cosAsinB= ,由(1)sinB=cosA,可得 sin2B= ,联合范围可求 B,由 sinB=cosA及 A 的范围可求 A,由三角形内角和定理可求 C.【解答】解:(Ⅰ)证明:∵ a=btanA.∴=tanA,∵由正弦定理:,又 tanA=,∴=,∵sinA≠0,∴sinB=cosA.得证.(Ⅱ)∵ sinC=sin[ π﹣( A+B)] =sin(A+B)=sinAcosB+cosAsinB,∴sinC﹣sinAcosB=cosAsinB= ,由( 1)sinB=cosA,∴sin2B= ,∵0< B<π,∴ sinB= ,∵B 为钝角,∴B= ,又∵ cosA=sinB=,∴A= ,∴C=π﹣A﹣B= ,综上, A=C=,B=.【评论】此题主要考察了正弦定理,三角形内角和定理,两角和的正弦函数公式的应用,属于基础题.18.( 12 分)如图,直三棱柱 ABC﹣A1B1C1的底面是边长为2 的正三角形, E,F 分别是 BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面 B1BCC1;(Ⅱ)若直线 A1 C 与平面 A1ABB1所成的角为 45°,求三棱锥 F﹣ AEC的体积.【剖析】(Ⅰ)证明 AE⊥ BB1, AE⊥BC,BC∩ BB1=B,推出 AE⊥平面 B1 BCC1,利用平面余平米垂直的判断定理证明平面AEF⊥平面 B1BCC1;(Ⅱ)取 AB 的中点 G,说明直线 A1C与平面 A1ABB1所成的角为 45°,就是∠ CA1G,求出棱锥的高与底面面积即可求解几何体的体积.【解答】(Ⅰ)证明:∵几何体是直棱柱,∴BB1⊥底面 ABC,AE? 底面 ABC,∴AE⊥BB1,∵直三棱柱 ABC﹣ A1B1C1的底面是边长为 2 的正三角形, E 分别是 BC的中点,∴AE⊥BC,BC∩BB1=B,∴AE⊥平面B1BCC1,∵ AE? 平面 AEF,∴平面 AEF⊥平面 B1BCC1;(Ⅱ)解:取 AB 的中点 G,连接 A1G,CG,由(Ⅰ)可知 CG⊥平面 A1ABB1,直线 A1C 与平面 A1ABB1所成的角为 45°,就是∠ CA1G,则 A1G=CG= ,∴AA1== ,CF=.三棱锥 F﹣AEC的体积:×== .【评论】此题考察几何体的体积的求法,平面与平面垂直的判断定理的应用,考察空间想象能力以及计算能力.19.( 13 分)设数列 { a n} 的前 n 项和为 S n,已知 a1=1,a2=2,a n+2=3S n﹣ S n+1+3,n∈N*,(Ⅰ)明 a n+2=3a n;(Ⅱ)求 S n.【剖析】(Ⅰ)当 n≥2 ,通 a n+2=3S n S n+1+3 与 a n+1=3S n﹣1 S n+3 作差,而后当 n=1 命也成立刻可;(Ⅱ)通( I)写出奇数、偶数的通公式,分奇数的和、偶数的和算即可.【解答】(Ⅰ)明:当 n≥2 ,由 a n+2=3S n S n+1+3,可得 a n+1=3S n﹣1S n+3,两式相减,得 a n+2a n+1=3a n a n+1,∴a n+2=3a n,当 n=1 ,有 a3 =3S1 S2+3=3×1( 1+2)+3=3,∴ a3=3a1,命也成立,上所述: a n+2=3a n;(Ⅱ)解:由( I)可得,此中k是随意正整数,∴S2k﹣1=(a1+a2)+(a3+a4)+⋯+(a2k﹣3+a2k﹣2)+a2k﹣1=3+32+⋯+3k﹣1+3k﹣1=+3k﹣ 1=×3k﹣1,k﹣ 1k﹣ 1S2k=S2k﹣1+a2k= ×3+2×3=,上所述, S n=.【点】本考求数列的通及乞降,考分的思想,注意解方法的累,属于中档.20.(13 分)已知抛物线 C1:x2=4y 的焦点 F 也是椭圆 C2: +=1( a> b> 0)的一个焦点, C1与 C2的公共弦的长为2,过点F的直线l与C1订交于A,B两点,与 C2订交于 C,D 两点,且与同向.(Ⅰ)求 C2的方程;(Ⅱ)若 | AC| =| BD| ,求直线 l 的斜率.【剖析】(Ⅰ)经过 C1方程可知 a2﹣b2=1,经过 C1与 C2的公共弦的长为2且C1与 C2的图象都对于 y 轴对称可得,计算即得结论;(Ⅱ)设 A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),经过=可得(x1+x2)2﹣4x1x2 =( x3+x4)2﹣4x3x4,设直线l方程为 y=kx+1,分别联立直线与抛物线、直线与椭圆方程,利用韦达定理计算即可.【解答】解:(Ⅰ)由 C1方程可知 F(0,1),∵ F 也是椭圆 C2的一个焦点,∴ a2﹣b2=1,又∵ C1与 C2的公共弦的长为2,C1与C2的图象都对于y轴对称,∴易得 C1与 C2的公共点的坐标为(±,),∴,又∵ a2﹣b2=1,∴a2=9,b2=8,∴C2的方程为+ =1;(Ⅱ)如图,设A( x1,y1),B(x2, y2),C( x3,y3),D(x4,y4),∵与同向,且| AC| =| BD|,∴= ,∴ x1﹣x2=x3﹣x4,∴( x1+x2)2﹣ 4x1x2=(x3+x4)2﹣4x3x4,设直线 l 的斜率为 k,则 l 方程: y=kx+1,由,可得 x2﹣4kx﹣4=0,由韦达定理可得x1+x2=4k, x1x2=﹣ 4,由,得( 9+8k2)x2+16kx﹣64=0,由韦达定理可得x3+x4=﹣,x3x4=﹣,又∵( x1+x2)2﹣4x1x2=( x3+x4)2﹣4x3x4,∴ 16(k2+1)=+,化简得 16(k2+1)=,∴( 9+8k2)2=16×9,解得 k=±,即直线 l 的斜率为±.【评论】此题是一道直线与圆锥曲线的综合题,考察求椭圆方程以及直线的斜率,波及到达定理等知,考算能力,注意解方法的累,属于中档.21.( 13 分)已知 a> 0,函数 f(x)=ae x cosx(x∈[ 0, +∞ ] ), x n f(x)的从小到大的第 n( n∈N*)个极点.(Ⅰ)明:数列 { f(x n)} 是等比数列;(Ⅱ)若全部n∈N*,x n≤ | f (x n)| 恒成立,求 a 的取范.【剖析】(Ⅰ)求出函数的数,令数 0,求得极点,再由等比数列的定,即可得;(Ⅱ)由 n=1 可得 a 的范,运用数学法8n>4n+3,当 a≥π,得 | f( x n+1) | > x n+1,即可获得 a 的范.【解答】(Ⅰ)明:函数f(x)=ae x cosx的数 f (′x) =ae x(cosx sinx),a>0,x≥0, e x≥1,由 f ′(x) =0,可得 cosx=sinx,即 tanx=1,解得 x=kπ+,k=0, 1, 2,⋯,当 k 奇数, f ′(x)在 kπ+邻近左右正,当 k 偶数, f ′(x)在 kπ+邻近左正右.故 x=kπ+,k=0,1,2,⋯,均极点,x n=(n 1)π+ =nπ ,f(x n)=a cos( nπ ),f(x n+1)=a cos( nπ+),π当 n 偶数, f(x n+1)= e f(x n),π当 n 奇数, f(x n+1)= e f(x n),即有数列 { f(x n)} 是等比数列;(Ⅱ)解:因为x1≤| f( x1) | ,≤a,解得 a≥π,下边明 8n>4n+3.2015年湖南省高考数学试卷(文科)当 n=1 时, 8>7 明显成立,假定 n=k 时, 8k> 4k+3,当 n=k+1 时, 8k+1=8?8k>8(4k+3)=32k+24=4(k+1)+28k+20>4(k+1)+3,即有 n=k+1 时,不等式成立.综上可得 8n>4n+3(n∈N+),π由 e >8,当 a≥ π时,πn由(Ⅰ)可得 | f( x n+1) | =| (﹣ e ) || f(x1)|>8n| f (x1)| =8n f( x1)>( 4n+3)x1>x n+1,n∈N+,综上可得 a≥π成立.【评论】此题考察导数的运用:求极值,主要考察不等式的恒成立问题,同时考查等比数列的通项公式和数学概括法证明不等式的方法,以及不等式的性质,属于难题.第 21 页(共 21 页)。
【精品解析】湖南省长郡中学2015届高三第五次月考数学文

湖南省长郡中学2015届高三第五次月考数学(文)试题【试卷综析】本试卷是高三文科试卷,以基础知识和基本技能为载体,以能力测试为主导,在注重考查学科核心知识的同时,突出考查考纲要求的基本能力,重视学生科学素养的考查.知识考查注重基础、注重常规、注重主干知识,兼顾覆盖面.试题重点考查:集合、不等式、向量、三视图、导数、简单的线性规划、直线与圆、圆锥曲线、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、充要条件等;考查学生解决实际问题的综合能力,是份较好的试卷.本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。
满分150分。
【题文】一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 【题文】1.设全集U={1,2,3,4,5},集合A={1,3,5},集合B={3,4},则()U A ðB=A .{3}B .{4}C .{3,4}D .{2,3,4}【知识点】集合的补集以及交集 A1【答案】B 【解析】解析:因为{}2,4U C A =,所以(){}4U C A B ⋂=故选择B.【思路点拨】由补集定义以及交集定义可求得.【题文】2.在复平面内,复数3 -4i ,i (2+i )对应的点分别为A 、B ,则线段AB 的中点C 对应的复数为 A .- 2+21 B .2- 21 C .-l 十i D .l-i 【知识点】复数的坐标 L4【答案】D 【解析】解析:因为()()3,4,1,2A B --,所以中点为()1,1-,即对应的复数为1i -,故选择D.【思路点拨】根据复数a bi +,对应的点为(),a b ,以及中点坐标公式可求得. 【题文】3.“m<14”是“方程x 2+x+m=0有实数解”的 A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【知识点】充分必要条件 A2【答案】A 【解析】解析:因为方程x2+x+m=0有实数解,所以11404m m =-≥⇒≤,所以“m<14”是“方程x2+x+m=0有实数解”的充分而不必要条件.故选择A. 【思路点拨】根据方程x2+x+m=0有实数解解得14m ≤,再结合“小能推大,大推不出小”可得结论. 【题文】4.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是 A .108 cm B .100 cm 3 C .92 cm 3 D .84 cm 3【知识点】三视图 G2【答案】B 【解析】解析:如图所示,原几何体为:一个长宽高分别为636,,的长方体砍去一个三棱锥,底面为直角边分别为3,4直角三角形,高为4.因此该几何体的体积11366344108810032=⨯⨯-⨯⨯⨯⨯=-= .故选择B.【思路点拨】如图所示,原几何体为:一个长宽高分别为6,3,6的长方体砍去一个三棱锥,底面为直角边分别为3,4直角三角形,高为4.利用长方体与三棱锥的体积计算公式就看得出.【题文】5.定义在R 上的函数()f x 满足(4)1f =.'()f x 为()f x 的导函数,已知函数y='()f x 的图象如图所示.若两正数a ,6满足(2)1f a b +<,则22b a ++的取值范围是 A .(11,32) B .1,(3,)2⎛⎫-∞⋃+∞ ⎪⎝⎭C .(12,3) D .(,3)-∞-【知识点】线性规划的应用 E5【答案】A 【解析】解析:由图可知,当0x >时,导函数'0f x ()>,原函数单调递增,∵两正数a b ,满足21f a b +()<,又由41f =(),即24f a b +()<,即24a b +<,又由0,0a b >>;点a b (,)的区域为图中阴影部分,不包括边界,而22b a ++的几何意义是区域的点22A --(,)与连线的斜率,直线AB ,AC 的斜率分别是1,32,所以22b a ++得分范围为1,32⎛⎫⎪⎝⎭,故选择A. 【思路点拨】先根据导函数的图象判断原函数的单调性,从而确定a b ,的范围,最后利用不等式的性质得到答案.【题文】6.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数cos (6)(1,2,3,,12)6y a A x x π⎡⎤=+-=⎢⎥⎣⎦来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为A .20℃B .20.5℃C .21℃D .21.5℃【知识点】三角函数的图像与性质 C3【答案】B 【解析】解析:令()()cos 66f x a A x π⎡⎤=+-⎢⎥⎣⎦,由题意可得,()()()()06cos 6628612cos 12618623,5f a A a A f a A ππ⎡⎤=+-=⎢⎥⎣⎦⎡⎤=+-=⎢⎥⎣⎧⎪⎪⇒==⎨⎪⎪⎩⎦,所以()()1023510620.56f π⎡⎤=+-=⎢⎥⎣⎦故选择B.【思路点拨】令()()cos 66f x a A x π⎡⎤=+-⎢⎥⎣⎦,由()()06281218f f ⎧=⎪⎨=⎪⎩解得,a A 的值,即可得到()10f 的值. 【题文】7.过双曲线22221(0,0)x y a b a b-=>>的左焦点F (一c ,0)作圆222x y a +='的切线,切点为E ,延长FE 交抛物线y 2 =4cx 于点P ,若E 为线段FP 的中点,则双曲线的离心率为A .5B .52C .5+1D .512+【知识点】双曲线的几何 H6【答案】D 【解析】解析:设双曲线的右焦点为'F ,则'F 的坐标为0c (,),因为抛物线为24y cx =,所以'F 为抛物线的焦点 O 为'FF 的中点,E 为FP 的中点所以OE 为的'PFF 中位线,那么'OE PF ,因为OE a =,那么'2PF a =,又''2PF PF FF c ⊥=,所以2PF b =,设(),2 2P x y x c a x a c +==-,,过点F 作x 轴的垂线,点P 到该垂线的距离为2a 由勾股定理22244y a b +=得:2224244c a c a c a -+=-()(),解得512e +=,故选择D 【思路点拨】设双曲线的右焦点为'F ,则'F 的坐标为0c (,),因为抛物线为24y cx =,所以'F 为抛物线的焦点 O 为'FF 的中点,E 为FP 的中点所以OE 为的'PFF 中位线,得到2PF b =,再设P (x ,y ) 过点F 作x 轴的垂线,由勾股定理得出a c ,关于的关系式,最后即可求得离心率【题文】8.设函数22221234()(8)(8)(8)(8)f x x x c x x c x x c x x c =-+-+-+-+,集合*127{|()0}{,,,}M x f x x x x N ===⊆,设c 1≥c 2≥c 3≥c 4,则c 1—c 4=A .11B .13C .7D .9【知识点】函数与方程 B9【答案】D 【解析】解析:由根与系数的关系知8.i i i i i x y x y c +==,,这里i i x y ,为方程280i x x c -+=之根,14i =⋯,,. 又*127{|}{}0M x f x x x x N ===⋯⊆(),,,,由集合()i i x y ,性质可得取17263444(,),(,),(,),(,),又1234c c c c ≥≥≥, 故14167c c ==,,149c c ∴-=故选择D.【思路点拨】由已知中集合*127{|}{}0M x f x x x x N ===⋯⊆(),,,,结合函数()f x 的解析式,及韦达定理,我们易求出1c 及4c 的值,进而得到答案.【题文】9.在△ABC 中,已知.9,sin cos .sin ,AB AC B A C ==S △ABC =6,P 为线段AB 上的一点,且..||||CA CBCP x y CA CB =+则11x y+的最小值为 A .76 B .712C .73123+ D .76+33【知识点】解三角形 向量的数量积 C8 F3 【答案】C 【解析】解析:ABC 中•AB c BC a AC b sinB cosA sinC sin A C sinCcosA ====∴+=,,,(),设即000 90sinAcosC sinCcosA sinCcosA sinAcosC sinA cosC C +=∴=≠∴==︒,,,,14•969623ABCAB AC SbccosA bcsinA tanA =∴=∴=,,==,根据直角三角形可得431553455sinA cosA bc c b a ===∴===,,,,,以AC 所在的直线为x 轴,以BC 所在的直线为y轴建立直角坐标系可得()()()0,03,00,4C A B ,P 为AB 线段上的一点,则存在实数λ使得()()()134401CP CA CB λλλλλ+-=-≤≤=,,设()()121122110 |||||0|1CACB e e e e e e CA CB =,=则==,=,,=,,所以..|||0|0CA CBCP x y CA CB x y x y +==+=(,)(,)(,),344x y λλ∴==-,,则4312x y +=,()11111143734371212123x y x y x y x y y x ⎛⎫⎛⎫+=++=++≥+ ⎪ ⎪⎝⎭⎝⎭,故选择C. 【思路点拨】根据ABC 中•sinB cosA sinC sin A C sinCcosA =∴+=,(),设即000 s i n A c o s C s i n C c o s A s i n C c o s A s i n A c o s CC +=∴=≠∴==︒,,,,再由•96ABC AB AC S ==,可得43tanA =,,以AC 所在的直线为x 轴,以BC 所在的直线为y 轴建立直角坐标系可得()()()0,03,00,4C A B ,P 为AB 线段上的一点,则存在实数λ使得()()()134401C P C A C B λλλλλ+-=-≤≤=,,找到4312x y +=,进而利用不等式求得11x y+最小值.【题文】10.已知m R +∈,函数221,1,()1(1),1,x x f x og x x ⎧+<⎪=⎨->⎪⎩,若函数2()221,(())g x x x m y f g x m =-+-=-有6个零点,则实数m 的取值范围是A .30,5⎛⎫ ⎪⎝⎭B .33,54⎛⎫⎪⎝⎭C .3,14⎛⎫⎪⎝⎭D .(1,3)【知识点】函数的零点以及函数图像 B8 B9【答案】A 【解析】解析:∵函数221,1,()1(1),1,x x f x og x x ⎧+<⎪=⎨->⎪⎩,2()221g x x x m =-+-∴当21221g x x m =-+-()()<,即2132x m --()<时, 则2212||143y f g x g x x m ==+=-+-(())()().当21221g x x m =-+-()()>,即2132x m --()<时, 则()2212[]3y f g x log x m ==-+-(()).①当32m ≥时,y m =与()2212[]3y f g x log x m ==-+-(())的图象有两个交点,不满足题意,应该舍去.②当32m <时,y m =与()2212[]3y f g x log x m ==-+-(())的图象有两个交点,需要直线y m =与函数2212||143y f g x g x x m ==+=-+-(())()()的图象有四个交点时才满足题意.∴034m m <-<,又32m <,解得305m <<. 综上可得:m 的取值范围是305m <<.故选择A.【思路点拨】由于函数221,1,()1(1),1,x x f x og x x ⎧+<⎪=⎨->⎪⎩,2()221g x x x m =-+-.可得当21221g x x m =-+-()()<,即2132x m --()<时,则2212||143y f g x g x x m ==+=-+-(())()().当21221g x x m =-+-()()>,即2132x m --()<时, 则()2212[]3y f g x log x m ==-+-(()).再对m 分类讨论,利用直线y m =与函数y f g x =(())图象的交点必须是6个即可得出. 【题文】二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡中对应题号后的横线上.【题文】11.已知实数z ∈[0,10],执行如图所示的程序框图,则输出的x 不小于47概率为 。
【名师解析】湖南省长沙市长郡中学2015届高三上学期第一次月考数学文试题 Word版含解析

炎德英才大联考长郡中学2015届高三月考试卷(-)数学(文科)【试卷综析】试卷注重对基础知识和基本方法全面考查的同时,又突出了对数学思想、数学核心能力的综合考查, 试卷以考查考生对“双基”的掌握情况为原则,重视基础,紧扣教材,回归课本,整套试卷中有不少题目可以在教材上找到原型.对中学数学教学和复习回归课本,重视对基础知识的掌握起到好的导向作用.本试题卷包括选择题、填空题和解答题三部分,共8页,时量120分钟,满分150分.一、选择题本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. 【题文】1.已知A 、B 均为集合{}1,3,5,7,9U =的子集,且{}(){}3,9u A B C B A ⋂=⋂=则A =A. {}1,3B. {}3,7,9C. {}3,5,9D. {}3,9 【知识点】集合.A1【答案解析】D 解析:解:根据韦恩图可知只有A 集合为{}3,9时,才满足已知条件. 【思路点拨】由题意作出韦恩图即可得到正确结果.【题文】2.定义在R 上的偶函数()()1f x f x +=-,且在[]1,0-上单调递增,设()()3,,2a f b fc f ===,则a,b,c 的大小关系是A. a b c >>B. a c b >>C. b c a >>D. c b a >> 【知识点】函数的奇偶性;B4【答案解析】D 解析:解:由题意可得函数为偶函数,所以函数在()0,1上为减函数,再由()()()()12f x f x f x f x +=-∴+=所以函数的周期为2,所可知函数在()1,2上递增 在[]2,3上为递减,所以c>b>a ,所以D 正确 【思路点拨】由题意求出函数的周期,再比较大小.【题文】3.已知()sin ,ααβαβ=-=均为锐角,则β等于 A.512π B. 3π C. 4π D. 6π【知识点】两角和与差的展开式;组合角.C5 【答案解析】C 解析:解:0,0022222πππππαββαβ<<<<∴-<-<∴-<-<又()()sin cos 1010αβαβ-=--=,sin cos 55αα==()()()()sin sin sin cos cos sin βααββααβααβααβ=--∴=--=---⎡⎤⎣⎦24πβ== 【思路点拨】根据角的取值范围求出三角函数值,再利用组合角的形式表示出β角,利用公式进行计算.【题文】4.在等差数列{}n a 中,241,5a a ==,则{}n a 的前5项和5S = A.7 B.15 C. 20 D. 25 【知识点】等差数列的性质;求和公式.D2【答案解析】B 解析:解:()()152415245551522a a a a a a a a S +++=+∴===所以B 正确.【思路点拨】由等差的性质与求和公式直接代入求值即可. 【题文】5.已知函数()()()()22ln ,1f x x f x x f ''=+-=则A.1B.2C. 3D. 4【知识点】导数.B11【答案解析】B 解析:解:由函数的导数可知()()()122112102f x x f f x ⎛⎫'''=+-∴=⨯+= ⎪⎝⎭,所以B 正确.【思路点拨】根据导数求出导数的值.【题文】6.已知函数()()()sin 0,0,f x A x A ϖϕϖπϕπ=+>>-<<的部分图像如图所示,则函数()f x 的解析式为A.()12sin 24f x x π⎛⎫=+ ⎪⎝⎭ B.()132sin 24f x x π⎛⎫=+ ⎪⎝⎭ C.()12sin 24f x x π⎛⎫=- ⎪⎝⎭ D. ()132sin 24f x x π⎛⎫=-⎪⎝⎭【知识点】三角函数的图像与性质;C3【答案解析】B 解析:解:由图像可知A=2,31242222T T ππππϖ=+=∴=∴=又()31302sin 2424f f x x πππϕ⎛⎫⎛⎫=∴=∴=+⎪ ⎪⎝⎭⎝⎭【思路点拨】根据图像求出三角函数的各种参数.【题文】7.某企业为节能减排,用9万元购进一台新设备用于生产,第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该设备每年生产的收入均为11万元,设该设备使用了n(*n N ∈)年后,盈利总额达到最大值(盈利额等于收入减去成本),则n 等于A.4B.5C.6D.7 【知识点】数列的应用.D2设第n 年的盈利总额为S n ,则S n =11n-(n 2+n )-9=-n 2+10n-9=-(n-5)2+16,∴当n=5时,S n 取得最大值16,故选:B .【思路点拨】根据题意建立等差数列模型,利用等差数列的性质以及求和公式即可得到结论. 【题文】8.若,a b R ∈,且0ab >,则下列不等式中,恒成立的是A. a b +≥B. 11a b +> C. 2b a a b +≥ D. 222a b ab +>【知识点】不等式.E6【答案解析】C 解析:解:根据不等式的性质可知当两项均为正值时有不等式a b +≥,所以满足条件的不等关系只有C 正确.【思路点拨】由重要的基本不等式可直接判定出结果.【题文】9.已知三个正数a,b,c 满足2,2b a c b a b c a <+≤<+≤,则ab的取值范围是 A. 23.,32A ⎛⎫ ⎪⎝⎭ B. 12,33⎛⎫⎪⎝⎭ C. 30,2⎛⎫⎪⎝⎭ D. 2,23⎛⎫ ⎪⎝⎭【知识点】其他不等式的解法;简单线性规划.E1,E5 【答案解析】D 解析:解:三个正数a,b,c 满足2,2b a c b a b c a<+≤<+≤,2212,1,1b c b c b b c ba a a a a a a a∴<+≤<+≤≤--<-即-不等式的两边同时相加得212b b b a a a <-<-1-2112b b a a b b a a ⎧<-⎪⎪∴⎨⎪-<-⎪⎩1-即22333322b b a b a a ⎧>⎪⎪∴<<⎨⎪<⎪⎩即2332a b ∴<<所以A 正确【题文】10.函数()3222132f x ax ax ax a =+-++的图像经过四个象限,则实数a 的取值范围是 A. 316a >-B. 63516a -<<-C. 65a >-D. 63516a -≤≤- 【知识点】导数与函数的单调性.B3,B11【思路点拨】根据导数与函数的单调性可知函数的变化情况. 二、填空题:本大题5小题,每小题5分,共25分.【题文】11.在等比数列{}n a 中,已知4848,60S S ==,则12S = 【知识点】等差数列的前n 项和的性质.D2 【答案解析】63 解析:解:由等比数列的性质可知8412812812484363S S S S S S S S S S --=⇒-=∴=- 【思路点拨】根据等比数列的前n 项和的性质.【题文】12.设1m >,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数5z x y =+的最大值为4,则m的值为【知识点】线性规划.E5【答案解析】3 解析:解:由题意可知目标函数在1y x y mx +==与的交点处取得最大值,因为交点为1,11m m m ⎛⎫⎪++⎝⎭,代入目标函数可得3m =.【思路点拨】根据题意可求出最大值点,再代入目标函数即可求出m 的值. 【题文】13.已知命题:,21000,n p n N ∃∈>则p ⌝为 【知识点】命题.A2【答案解析】,21000n n N ∀∈≤ 解析:解:根据命题与否命题的关系我们可知:,21000n p n N ⌝∀∈≤【思路点拨】根据命题的关系可直接写出否命题.【题文】14.已知a,b,c 分别为ABC 内角A ,B ,C 的对边,在ABC中,b =,且sin cos 0B B +=,则角A 的大小为 .【知识点】正弦定理;解三角形.C8【答案解析】6π解析:解:解:∵sinB+cosB=0,∴tanB=-1,∵B ∈(0,π),()()310,sin 0,4sin sin 26a b B B A A A A B ππππ∴∈∴==∴=∈∴=【思路点拨】根据三角形性质与正弦定理可求出角的大小. 【题文】15.给出定义:若1122m x m -<≤+(其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x m =,在此基础上给出下列关于函数(){}f x x x =-的四个命题: ①函数()y f x =的定义域为R ,值域10,2⎡⎤⎢⎥⎣⎦②函数()y f x =的图像关于直线()2kx k Z =∈对称 ③函数()y f x =是周期函数,最小正周期为1④函数()y f x =在11,22⎡⎤-⎢⎥⎣⎦上是增函数. 【知识点】函数的性质.B1,B3,B4【答案解析】3 解析:解:①中,令x=m+a ,11(,]22a ∈- ∴f (x )=|x-{x}|=|a|∈10,2⎡⎤⎢⎥⎣⎦所以①正确;④中,12x =-时,m=-1,1122f ⎛⎫-= ⎪⎝⎭x =1122f ⎛⎫= ⎪⎝⎭ 所以1122f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭所以④错误. 故选C【思路点拨】根据让函数解析式有意义的原则确定函数的定义域,然后根据解析式易用分析法求出函数的值域;根据f (k-x )与f (-x )的关系,可以判断函数y=f (x )的图象是否关于直线对称;再判断f (x+1)=f (x )是否成立,可以判断③的正误;而由①的结论,易判断函数y=f (x )11,22⎡⎤-⎢⎥⎣⎦上的单调性,但要说明④不成立,我们可以举出一个反例.三、解答题:本大题6小题,共75分,解答应写出文字说明,证明过程或演算步骤.【题文】16.(本小题满分12分)已知集合{}{}2|22,|540A x a x a B x x x =-≤≤+=-+≥(1)当3a =时,求A B ⋂;(2)若0a >,且A B φ⋂=,求实数a 的取值范围. 【知识点】集合与二次不等式.A1,E3【答案解析】(1){}|114x 5A B x x ⋂=-≤≤≤≤或 (2) 01a << 解析:解:(1)当3a =时,{}{}{}15,141145A x B x x A B x x =-≤≤=≤≥∴⋂=-≤≤≤≤或或(2){}(){},|220,14A B A x a x a a B x x φ⋂==-≤≤+>=≤≥或21100124a a a a a ->⎧∴∴<>∴<<⎨+<⎩【思路点拨】根据条件直接解出不等式,再按集合的关系求出集合. 【题文】17. (本小题满分12分)设向量()8cos 21,cos ,1,5m A A n ⎛⎫=+=- ⎪⎝⎭(1)若//m n ,求cos A 的值; (2)若m n ⊥,求tan 4A π⎛⎫+⎪⎝⎭的值. 【知识点】向量的运算.F3 【答案解析】(1) 516-(2) tan 74A π⎛⎫+= ⎪⎝⎭解析:解:(1) ()288//cos 21cos ,2cos cos 55m n A A A A ∴-+=-⋅=即5cos 0cos 16A A ≠∴=-(2)2880,cos 21cos 02cos cos 055m n m n A A A A ⊥∴⋅=+-=∴-=即224cos 0,cos ,sin cos 1,sin 05A A A A A ≠∴=+=>331tan sin ,tan ,tan 75441tan A A A A A π+⎛⎫==+== ⎪-⎝⎭则【思路点拨】根据已知条件利用向量的运算公式进行运算.【题文】18. (本小题满分12分)已知圆内接四边形ABCD 的边1,3, 2.AB BC CD DA ==== (1)求角C 的大小和BD 的长;(2)求四边形ABCD 的面积及外接圆的半径. 【知识点】解三角形.C8【答案解析】(1)60,C BD =︒= (2)S =2sin 603BD R ==︒解析:解:(I)连结BD ,由题设及余弦定理得2222cos 1312cos BD BC CD BC CD C C =+-⋅=-①2222cosA54cosBD AB DA AB DA C=+-⋅=+②由①②得1 cos2C=故60,C BD=︒(2)四边形ABCD的面积11sin sin22S AB DA A BC CD C=⋅+⋅=四边形ABCD的外接圆半径2sin603BDR==︒【思路点拨】利用余弦定理求出边长及角,分割法出求面积,再利用正弦定理求出半径. 【题文】19. (本小题满分12分)某公司是专做产品A的国内外销售企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的国内外市场销售情况进行了跟踪调查,调查结果如图所示,其中图①中的拆线表示的是国外市场的日销售量与上市时间的关系,图②中的抛物线表示是国内市场的日销售量与上市时间的关系:图③中折线表示的是每件产品A的销售利润与上市时间的关系(国内外市场相同)(1)分别写出国外市场的日销售量()f t,国内市场的日销售量()g t与第一批产品A上市时间t的关系式:(2)第一批产品A上市后的哪几天,这家公司的日销售利润超过6300万元?【知识点】函数的应用,导数.B10,B11【答案解析】(1)()()22,03036,0406240,304020t tf tg t t t tt t≤≤⎧==-+≤≤⎨-+<≤⎩(2)第24,25,26,27,28,29天解析:解(I)()()22,03036,0406240,304020t tf tg t t t tt t≤≤⎧==-+≤≤⎨-+<≤⎩(2)每件产品A的销售利润()h t与上市时间t的关系为()3,02060,2040t th tt≤≤⎧=⎨<≤⎩设这家公司的日销售利润为()F t,则()()()()2223362,0202036062,20302036066240,304020t t t t tF t f t g t h t t t t tt t t t⎧⎛⎫-++≤≤⎪⎪⎝⎭⎪⎪⎛⎫=+=-++<≤⎡⎤⎨ ⎪⎣⎦⎝⎭⎪⎪⎛⎫-+-+<≤⎪ ⎪⎝⎭⎩222338,020203608,203020360240,304020t t t t t t t t t ⎧⎛⎫-+≤≤ ⎪⎪⎝⎭⎪⎪⎛⎫=-+<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-+<≤⎪ ⎪⎝⎭⎩当020t ≤≤时,()22727484802020F t t t t t ⎛⎫'=-+=-≥ ⎪⎝⎭,故()F t 在[]0,20上单调递增,此时()F t 的最大值是()2060006300F =<当2030t <≤时,令23608630020t t ⎛⎫-+> ⎪⎝⎭解得70303t <<,当3040t <≤时,()223360240603024063002020F t t ⎛⎫⎛⎫=-+<-⨯+= ⎪ ⎪⎝⎭⎝⎭答:第一批产品A 上市后,在第24,25,26,27,28,29天,这家公司的日销售利润超过6300万元.【思路点拨】根据题意列出函数关系式,再利用导数求出值的大小.【题文】20.等比数列{}n a 的各项均为正数,且212326231,9a a a a a +==,(1)求数列{}n a 的通项公式; (2)设31323log log log n n b a a a =+++,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和. 【知识点】数列的通项公式;裂项求和法.D1.D4【答案解析】(1) 13n n a = (2) 21nn -+解析:解:(1)设数列{}n a 的公比为q ,由23269a aa =得22349a a =,所以219q =,由条件可知各项均为正数,故13q =,由1211112312313a a a a q a +=+=∴=得,故数列{}a n 的通项公式为13n n a =(2) ()()313231log log +log 122n n n n b a a a n +=++=-++=-故()1211211n b n n n n ⎛⎫=-=-- ⎪++⎝⎭则12111111112122311n n b b b n n n ⎡⎤⎛⎫⎛⎫⎛⎫+++=--+-++-=-⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦所以数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和为21n n -+ 【思路点拨】根据数列的性质求出数列的通项,再根据通项的特点求出数列的和. 【题文】21.已知函数()1xf x e ax =--(e 为自然对数的底数).(1)求函数()f x 的单调区间:(2)当0a >时,若()0f x ≥对任意的x R ∈恒成立,求实数a 的值:(3)求证:()()()22222232323ln 1ln 1ln 12313131n n ⎡⎤⎡⎤⎡⎤⨯⨯⨯⎢⎥⎢⎥++++++<⎢⎥⎢⎥⎢⎥-⎢⎥--⎣⎦⎣⎦⎣⎦【知识点】导数;函数的单调性.B3,B11.【答案解析】略 解析:解:(1) ()()()00,xf x e a a x f x ''=-∴≤>时,f 在R 上高、单调递增. ()()()0,ln 0,a x a f x f x '>∈-∞<时,时,单调递减.()()()ln ,0,x a f x f x '∈+∞>时,单调递增.(2)由(1),()()()min 0ln ,ln 0,a alna 10a f x f a f a >=∴≥--≥时,即记()()()()g a alna 101ln 1ln a a g a a a '=-->=-+=-()g a '∴在()0,1上递增,在()1,+∞上递减,()()10g a g ∴≤=,故()0g a ∴=得1a =(3)证明:()()()()2212332323111,,22313131333131nn n n n n n n n n n -⨯⨯⨯==≥<=-------时时,()212331122223131kn n kk n =⨯≥<+-<--∑时, 【思路点拨】根据函数的导数判定单调性,再利用导数与函数值求出参数的值,最后证明不等式.。
湖南省长沙市长郡中学2023-2024学年高三上学期月考(二)语文试题

英才大联考长郡中学2024届高三月考试卷(二)语文本试卷共四道大题,23道小题。
时量150分钟,满分150分。
一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:文学的自觉是一个相当漫长的过程,它贯穿于整个魏晋南北朝,经过大约三百年才实现。
所谓文学的自觉有三个标志:首先,文学从广义的学术中分化出来,成为独立的一个门类。
汉朝人所谓的文学是指学术,特别是儒学,《史记》中“赵绾、王臧等以文学为公卿”,所说的文学显然是指学术。
到了南朝,文学有了新的独立于学术的地位,宋文帝立四学,文学与儒学、玄学、史学并立。
同时又有文笔之分,刘勰《文心雕龙》言:“今之常言,有文有笔,以为无韵者笔也,有韵者文也。
”梁元帝萧绎对文笔之分有进一步说明:“至如不便为诗如阎纂,善为章奏如伯松,若此之流,谓之笔。
吟咏风谣,流连哀思者,谓之文。
”萧绎所说的文笔之别已不限于有韵无韵,而强调了文之抒发感情以情动人的特点,并且更广泛地注重语言的形式美,他所说的“文”已接近我们今天所说的文学了。
其次,对文学的各种体裁有了比较细致的区分,更重要的是对各种体裁的体制和风格特点有了比较明确的认识。
文体辨析可以上溯至《汉书·艺文志》,更为明晰而自觉的文体辨析则始自曹丕的《典论·论文》,他将文体分为四科,并指出它们各自的特点:奏议宜雅,书论宜理,铭诛尚实,诗赋欲丽。
《文赋》进一步将文体分为十类,对每一类的特点也有所论述。
特别值得注意的是将诗和赋分成两类,并指出“诗缘情而绮靡,赋体物而浏亮”的特点。
到了南朝,文体辨析更加深入、系统。
《文心雕龙》和《文选》对文体的区分更系统,讨论更深入。
《文心雕龙》上篇的主要篇幅讨论文体,分33大类。
其《序志》说:“原始以表末,释名以章义,选文以定篇,敷理以举统。
”对每种文体都追溯其起源,叙述其演变,说明其名称的意义,并举例加以评论。
《文选》是按文体编成的一部文学总集,当然对文体有详细的辨析。
湖南省长沙市长郡中学2022-2023学年高三上学期月考(二)数学试题(含解析)

长郡中学2022-2023届高三月考试卷(二)数学2022.10一、选择题1.已知全集U =R ,集合{}2,3,4A =,集合{}0,2,4,5B =,则图中的阴影部分表示的集合为()A.{}2,4 B.{}0 C.{}5 D.{}0,52.若i1ia z +=-(i 为虚数单位)是纯虚数,则=a ()A.-1B.0C.1D.23.已知函数()y f x =的图像在点()()33P f ,处的切线方程是27y x =-+,则()()33f f '-=()A.2- B.2C.3- D.34.命题p :“2R,240x ax ax ∃∈+-≥”为假命题,则a 的取值范围是()A.40a -<£B.40a -≤< C.30a -≤≤ D.40a -≤≤5.当102x <≤时,4log xa x <,则a 的取值范围是()A.0,2⎛⎫ ⎪ ⎪⎝⎭B.,12⎛⎫ ⎪ ⎪⎝⎭C.D.2)6.已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点,则ω的取值范围是()A.81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B.111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C.111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D.141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭7.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为()(注:()()22221211236n n n n ++++++=)A.1624B.1198C.1024D.15608.已知函数()3f x x ax b =++,a 、b R ∈.1x 、()2,x m n ∈且满足()()1f x f n =,()()2f x f m =,对任意的[],x m n ∈恒有()()()f m f x f n ≤≤,则当a 、b 取不同的值时,()A.12n x +与22m x -均为定值B.12n x -与22m x +均为定值C.12n x -与22m x -均为定值D.12n x +与22m x +均为定值二、选择题9.已知奇函数())cos()(0,0π)f x x x ωϕωϕωϕ=+-+><<的最小正周期为π,将函数()f x 的图象向右平移π6个单位长度,可得到函数()y g x =的图象,则下列结论正确的是()A.函数π()2sin(2)3g x x =- B.函数()g x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称C.函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增 D.当π0,2x ⎡⎤∈⎢⎥⎣⎦时,函数()g x10.正四棱锥P ABCD -的所有棱长为2,用垂直于侧棱PC 的平面α截该四棱锥,则()A.PC BD⊥ B.四棱锥外接球的表面积为8πC.PA 与底面ABCD 所成的角为60︒D.当平面α经过侧棱PC 中点时,截面分四棱锥得到的上、下两部分几何体体积之比为3:111.已知数列{}n a 满足18a =,21a =,2,2,n n na n a a n +-⎧=⎨-⎩为偶数为奇数,n T 为数列{}n a 的前n 项和,则下列说法正确的有()A.n 为偶数时,()221n n a -=- B.229n T n n =-+C.992049T =- D.n T 的最大值为2012.设定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x ',若()()212f x g x +--=,()()1f x g x ''=+,且()1g x +为奇函数,则下列说法中一定正确的是()A.()10g = B.函数()g x '的图象关于2x =对称C.()20221k g k ==∑ D.()()20211k f k g k ==∑三、填空题13.若22log log 6a b +=,则a b +的最小值为________.14.已知边长为2的菱形ABCD 中,点F 为BD 上一动点,点E 满足22,3BE EC AE BD =⋅=- ,则AF EF ⋅的最小值为______.15.已知等差数列{}n a 和正项等比数列{}n b 满足117332,2a b a b a ====,则数列{}2(2)n n a b -的前n 项和为______.16.已知函数()ln xf x x =,()x xg x e=,若存在1>0x ,2x R ∈,使得()()120f x g x =<成立,则12x x 的最小值为______.四、解答题17.已知数列{}n a 中,n S 为{}n a 的前n 项和,13n n a S n +=-+,*n N ∈,12a =.(1)求{}n a 的通项公式;(2)设()*2n n n b n N S n =∈-+,数列{}n b 的前n 项和为n T ,求证:()*1433n T n N <∈.18.如图,在梯形ABCD 中,//AB CD ,2AB =,5CD =,23ABC π∠=.(1)若AC =,求梯形ABCD 的面积;(2)若AC BD ⊥,求tan ABD ∠.19.如图,在三棱柱111ABCA B C ﹣中点,E 在棱1BB 上,点F 在棱CC 1上,且点,E F 均不是棱的端点,1,AB AC BB ⊥=平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.(1)求证:四边形BEFC 是矩形;(2)若2,3AE EF BE ==,求平面ABC 与平面AEF 所成角的正弦值.20.统计与概率主要研究现实生活中的数据和客观世界中的随机现象,通过对数据的收集、整理、分析、描述及对事件发生的可能性刻画,来帮助人们作出合理的决策.(1)现有池塘甲,已知池塘甲里有50条鱼,其中A 种鱼7条,若从池塘甲中捉了2条鱼.用ξ表示其中A 种鱼的条数,请写出ξ的分布列,并求ξ的数学期望()E ξ;(2)另有池塘乙,为估计池塘乙中的鱼数,某同学先从中捉了50条鱼,做好记号后放回池塘,再从中捉了20条鱼,发现有记号的有5条.(ⅰ)请从分层抽样的角度估计池塘乙中的鱼数.(ⅱ)统计学中有一种重要而普遍的求估计量的方法─最大似然估计,其原理是使用概率模型寻找能够以较高概率产生观察数据的系统发生树,即在什么情况下最有可能发生已知的事件.请从条件概率的角度,采用最大似然估计法估计池塘乙中的鱼数.21.已知椭圆C :22221(0)x y a b a b+=>>的四个顶点构成的四边形的面积为312⎛⎫ ⎪⎝⎭,在椭圆C 上.(1)求椭圆C 的方程;(2)若矩形MNPQ 满足各边均与椭圆C 相切.求证:矩形MNPQ 对角线长为定值.22.已知函数2()e ,2xmx f x m =-∈R .(1)讨论()f x 极值点的个数;(2)若()f x 有两个极值点12,x x ,且12x x <,证明:()()122e f x f x m +<-.长郡中学2023届高三月考试卷(二)数学一、选择题1.已知全集U=R ,集合{}2,3,4A =,集合{}0,2,4,5B =,则图中的阴影部分表示的集合为()A.{}2,4 B.{}0 C.{}5 D.{}0,5【答案】D 【解析】【分析】根据给定条件,利用韦恩图表达的集合运算直接计算作答.【详解】依题意,图中的阴影部分表示的集合是()U A B ð,而全集U =R ,{}2,3,4A =,{}0,2,4,5B =,所以(){0,5}UA B ⋂=ð.故选:D2.若i1ia z +=-(i 为虚数单位)是纯虚数,则=a ()A.-1B.0C.1D.2【答案】C 【解析】【分析】根据复数的除法运算化简复数,进而根据纯虚数实部为0,虚部不为0即可求解.【详解】()()()i 1i 11i i ==1i 22a a a a z ++-+++=-,由于z 为纯虚数,因此10a -=且10a +,故1a =,故选:C3.已知函数()y f x =的图像在点()()33P f ,处的切线方程是27y x =-+,则()()33f f '-=()A.2- B.2C.3- D.3【答案】D 【解析】【分析】利用导数的几何意义求出()3f 和()3f ',即可求得.【详解】函数()f x 的图像在点()()33P f ,处的切线的斜率就是在该点处的导数,即()3f '就是切线27y x =-+的斜率,所以()32f '=-.又()32371f =-⨯+=,所以()()()33123f f -=--='.故选:D4.命题p :“2R,240x ax ax ∃∈+-≥”为假命题,则a 的取值范围是()A.40a -<£ B.40a -≤< C.30a -≤≤ D.40a -≤≤【答案】A 【解析】分析】存在命题为假命题,则其否定是全称命题且为真命题,写出命题的否定,由不等式的性质可得结论.【详解】命题2:R,240p x ax ax ∃∈+-≥为假命题,即命题2:R,240p x ax ax ⌝∀∈+-<为真命题.首先,0a=时,40-<恒成立,符合题意;其次0a ≠时,则0a <且2(2)160a a ∆=+<,即40a -<<,综上可知,-4<0a ≤故选:A 5.当102x <≤时,4log xax <,则a 的取值范围是()A.0,2⎛⎫ ⎪ ⎪⎝⎭B.,12⎛⎫⎪ ⎪⎝⎭C.D.2)【答案】B 【解析】【分析】利用指数函数以及对数函数的单调性,结合已知条件可得关于a 的不等式,即可求得答案.【详解】由题意得,当1a>时,log a y x =是增函数,102x <≤时,log 0a x <,不合题意;当01a <<时,log a y x =在102x <≤时单调递减,4xy =递增,要使得4log xa x <成立,需满足1214log 2a<,即21log 2log 2a a a >=,则212a>,解得12a <<,故选:B6.已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点,则ω的取值范围是()A.81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭ B.111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C.111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭ D.141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】C 【解析】【分析】先由零点个数求出36ω≤<,再用整体法得到不等式组,求出ω的取值范围.【详解】π,π3x ⎡⎤∈⎢⎥⎣⎦,ππππ,π3333x ωωω⎡⎤+∈++⎢⎥⎣⎦,其中2ππ4ππ3ωω≤-<,解得:36ω≤<,则ππ4π333ω+≥,要想保证函数在π,π3⎡⎤⎢⎥⎣⎦恰有三个零点,满足①1111πππ+2π2π+2π33π4π+2π<π5π+2π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩,1k Z ∈,令10k =,解得:1114,33ω⎡⎫∈⎪⎢⎣⎭;或要满足②2222ππ2ππ+2π33π2π+3π<π2π+4π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩,2k Z ∈,令21k =,解得:175,3ω⎛⎫∈ ⎪⎝⎭;经检验,满足题意,其他情况均不满足36ω≤<条件,综上:ω的取值范围是111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭.故选:C 【点睛】三角函数相关的零点问题,需要利用整体思想,数形结合等进行解决,通常要考虑最小正周期,确定ω的范围,本题中就要根据零点个数,先得到ππ23TT ≤-<,从而求出36ω≤<,再进行求解.7.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为()(注:()()22221211236n n n n ++++++=)A.1624B.1198C.1024D.1560【答案】C 【解析】【分析】设该数列为{}n a ,令1n n n b a a +=-,设{}n b 的前n 项和为n B ,又令1+=-n n n c b b ,则n c n =,依次用累加法,可求解.【详解】设该数列为{}n a ,令1n n n b a a +=-,设{}n b 的前n 项和为n B ,又令1+=-n n n c b b ,设{}n c 的前n 项和为n C ,易得n c n =,()()()111121n n n n n n n C c c c b b b b b b +----=+++=++++- 所以11nn b b C +=-,1213b a a -==22n n n C +=,进而得21332n n n n b C ++=+=+,所以()21133222nn n n bn -=+=-+,()()()()2221111121233226n n n n B n n n n+-=+++-++++= 同理:()()()111112n n n n n n n B b b b a a a a a a +---=+++=+++-- 11n n a a B +-=所以11n n a B +=+,所以191024a =.故选:C【点睛】本题考查构造数列,用累加法求数列的通项公式,属于中档题.8.已知函数()3f x x ax b =++,a 、b R ∈.1x 、()2,x m n ∈且满足()()1f x f n =,()()2f x f m =,对任意的[],x m n ∈恒有()()()f m f x f n ≤≤,则当a 、b 取不同的值时,()A.12n x +与22m x -均为定值 B.12n x -与22m x +均为定值C.12n x -与22m x -均为定值D.12n x +与22m x +均为定值【答案】D 【解析】【分析】分析得出0a<,利用导数分析函数()f x 的单调性,可得知1x 为函数()f x 的极大值点,2x 为函数()f x 的极小值点,再由()()1f x f n =、()()2f x f m =结合因式分解可得出结论.【详解】当0a≥时,()230f x x a '=+≥,此时,函数()f x 在R 上为增函数,当1x 、()2,x m n ∈时,()()1f x f n <,()()2f x f m >,不合乎题意,所以,0a <.由()0f x '=可得x =,当x <x >()0f x '>;当x <<()0f x '<.所以,函数()f x 的单调递增区间为,⎛-∞ ⎝,⎫+∞⎪⎪⎭,单调递减区间为⎛ ⎝.对任意的[],x m n ∈恒有()()()f m f x f n ≤≤,()()min f x f m =,()()max f x f n =,又当1x 、()2,x m n ∈且满足()()1f x f n =,()()2f x f m =,所以,1x 为函数()f x 的极大值点,2x 为函数()f x 的极小值点,则1x =,2x =,由()()1f x f n =可得3311x ax b n an b ++=++,可得()()33110x n a x n -+-=,即()()221110x n x nx n a -+++=,因为1x n ≠,则22110x nx n a +++=,1x = ,可得213ax =-,所以,221120n nx x +-=,即()()1120n x n x -+=,所以,120n x +=,同理可得220m x +=,故选:D.【点睛】关键点点睛:解本题的关键在于以下两点:(1)利用已知条件分析出1x 、2x 为函数()f x 的极值点;(2)利用等式()()1f x f n =,()()2f x f m =结合因式化简得出结果.二、选择题9.已知奇函数())cos()(0,0π)f x x x ωϕωϕωϕ=+-+><<的最小正周期为π,将函数()f x 的图象向右平移π6个单位长度,可得到函数()y g x =的图象,则下列结论正确的是()A.函数π()2sin(2)3g x x =- B.函数()g x 的图象关于点π,03⎛⎫-⎪⎝⎭对称C.函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增 D.当π0,2x ⎡⎤∈⎢⎥⎣⎦时,函数()g x 【答案】AB 【解析】【分析】利用两角差的正弦公式将()f x 化为π()2sin()6f x x ωϕ=+-,根据函数的最小正周期确定ω,根据奇偶性确定π6ϕ=,可得其解析式,根据三角函数的平移变换可得函数()g x 的解析式,判断A;代入验证可判断B ;根据x 的范围,确定π23x -的范围,结合正弦函数性质,可判断C,D.【详解】由题意可得π())cos()2sin(6f x x x x ωϕωϕωϕ=+-+=+-,因为()f x 的最小正周期为π,所以2π2πω==,又因为()f x 为奇函数,所以πππ,π,Z 66k k k ϕϕ-=∴=+∈,而0πϕ<<,故π6ϕ=,所以()2sin 2f x x =,则将函数()f x 的图象向右平移π6个单位长度,可得到函数()y g x =的图象,故ππ()2sin[2()]2sin(2)63g x x x =-=-,A 正确;将π3x =-代入π()2sin(2)3g x x =-中,有ππ2sin[2()]033---=,即函数()g x 的图象关于点π,03⎛⎫-⎪⎝⎭对称,B 正确;当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时,π2π2[,]333x -∈-,由于正弦函数sin y x =在2ππ[,]33-上不单调,故()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上不是单调递增函数,故C 错误;当π0,2x ⎡⎤∈⎢⎣⎦时,ππ2π2[,333x -∈-,π()2sin(2)[2]3g x x =-∈,函数最大值为2,D 错误,故选:AB 10.正四棱锥P ABCD -的所有棱长为2,用垂直于侧棱PC 的平面α截该四棱锥,则()A.PC BD⊥ B.四棱锥外接球的表面积为8πC.PA 与底面ABCD 所成的角为60︒D.当平面α经过侧棱PC 中点时,截面分四棱锥得到的上、下两部分几何体体积之比为3:1【答案】ABD 【解析】【分析】根据BD ⊥平面PAC 即可判断A,由PO ⊥底面ABCD ,即可判断外接球的球心在PO 上,利用勾股定理即可求半径,进而可判断B,PAO ∠即为PA 与底面ABCD 所成角,根据几何法即可判断C,取PC 的中点E ,连接BE ,DE ,BD ,能证明PC ⊥面BDE ,分别求出截面分四棱锥得到的上下两部分几何体体积,能判断D .【详解】过P 作PO ⊥底面ABCD 于O ,则O 为AC 中点,由于BD ⊂底面ABCD ,所以PO BD ⊥,又,,,AC BD AC PO O AC PO ⊥⋂=⊂平面PAC ,故BD ⊥平面PAC ,PC ⊂平面PAC ,故BD PC ⊥,故A 正确,由正四棱锥的特征可知,其外接球的球心在PO 上,设半径为R ,则()222OCOP R R +-=,又PO ==,解得R =,故外接球的表面积为24π8πR =,故B 正确,过P 作PO ⊥底面ABCD 于O ,则O 为AC 中点,则PAO ∠即为PA 与底面ABCD 所成角,正四棱锥P ABCD -所有棱长为2,2AP ∴=,12AO AC ==cos AO PAO AP ∴∠==,45PAO ∴∠=︒,故C 错误,取PC 的中点E ,连接BE ,DE ,BD ,正四棱锥P ABCD -的所有棱长为2,PBC ∴ 为正三角形,PC DE ∴⊥,PC BE ⊥,又DE BE E ⋂=,,DE BE ⊂平面BDE所以PC ⊥面BDE ,故当平面α经过侧棱PC 中点时,平面α即为平面BDE ,此时111112232322E BCDBCD VS OP -=⋅=⨯⨯⨯⨯⨯,1122333P ABCD ABCD V S OP -=⋅=⨯⨯⨯,P ABCD E BCD V V V --∴=-=上,∴3E BCDV V -=上,故D 正确.故选:ABD11.已知数列{}n a 满足18a =,21a =,2,2,n n na n a a n +-⎧=⎨-⎩为偶数为奇数,n T 为数列{}n a 的前n 项和,则下列说法正确的有()A.n 为偶数时,()221n n a -=- B.229n T n n =-+ C.992049T =- D.n T 的最大值为20【答案】AC 【解析】【分析】对选项A ,偶数项构成等比数列,即可求得通项;对选项B ,检验当1n =时,所给表达式不满足;对选项C ,按照n为奇数和偶数分别讨论,根据10099100T T a -=,可直接求得;对选项D ,n T 的最大值为71021T T ==【详解】根据递推关系可知,n 为奇数时,()18292nn a n-⎛⎫=+⨯-=- ⎪⎝⎭n 为偶数时,()221n n a -=-,故A 对;()()212342121321242n n n n n T a a a a a a a a a a a a --=++++⋅⋅⋅++=++⋅⋅⋅++++⋅⋅+根据奇数项构成等差数列可得:()21321862109n a a a n n n -++⋅⋅⋅+=++⋅⋅⋅+-+=-+而又:2421,0,n n a a a n ⎧++⋅⋅+=⎨⎩当为奇数当为偶数则有:2229,91,n n n n T n n n ⎧-+=⎨-++⎩为偶数为奇数,故B 错误;()100222991010005095012049a T T -=-=-+⨯--=-,故C 对;根据n T 中的奇数项构成等差数列,而偶数项之和不是1就是0,因此根据n T 特点可知:n T 的最大值在奇数项之和取得最大值的附近,26393119T =-+⨯+=,76719221T T a =+=+=,2849420T =-+⨯=,98920020T T a =+=+=,210595121T =-+⨯+=,11101119T T a =+=,n T 的最大值为71021T T ==,故D 错故选:AC12.设定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x ',若()()212f x g x +--=,()()1f x g x ''=+,且()1g x +为奇函数,则下列说法中一定正确的是()A.()10g = B.函数()g x '的图象关于2x =对称C.()20221k g k ==∑ D.()()20211k f k g k ==∑【答案】AD 【解析】【分析】由()1g x +为奇函数可得()10g =,由()()212f x g x +--=取导数可得()()30f x g x ''+-=,结合条件()()1f x g x ''=+,判断B ,再由条件判断函数()f x ,()g x 的周期,由此计算()20221k g k =∑,()()20211k f k g k =∑,判断C ,D.【详解】因为()1g x +为奇函数,所以()()11g x g x +=--+,取0x =可得()10g =,A 对,因为()()212f x g x +--=,所以()()210f x g x ''++-=所以()()30f x g x ''+-=,又()()1f x g x ''=+()()130g x g x ''++-=,故()()220g x g x ''++-=,所以函数()g x '的图象关于点(2,0)对称,B 错,因为()()1f x g x ''=+,所以()()10f xg x '-+=⎡⎤⎣⎦所以()()1f x g x c -+=,c 为常数,因为()()212f x g x +--=,所以()()32f x g x --=,所以()()132g x g x c +--=-,取1x =可得2c =,所以()()13g x g x +=-,又()()11g x g x +=--+,所以()()31g x g x -=--+,所以()()2g x g x =--,所以()()42()g x g x g x +=-+=,故函数()g x 为周期为4的函数,因为()()2g x g x +=-,所以()()310g g =-=,()()42g g =-,所以(1)(2)(3)(4)0g g g g +++=,所以()[][]20221(1)(2)(3)(4)(5)(6)(7)(8)k g k g g g g g g g g ==++++++++⋅⋅⋅∑[](2017)(2018)(2019)(2020)(2021)(2022)g g g g g g ++++++,所以()202215050(2021)(2022)(1)(2)(2)k g k g g g g g ==⨯++=+=∑,由已知无法确定(2)g 的值,故()20221k g k =∑的值不一定为0,C 错;因为()()212f x g x +--=,所以()()221f x g x +=-+,()()625f x g x +=-+,所以()2(6)f x f x +=+,故函数()f x 为周期为4的函数,(4)(4)()()f xg x f x g x ++=所以函数()()f x g x 为周期为4的函数,又(1)2(0)f g =-,(2)2(1)2f g =-=,(3)2(2)2(0)f g g =-=+,(4)2(3)2f g =-=,所以(1)(1)(2)(2)(3)(3)(4)(4)02(2)2(4)0f g f g f g f g g g +++=++=,所以()()[]20211505(1)(1)(2)(2)(3)(3)(4)(4)(2021)(2021)k f k g k f g f g f g f g f g ==++++∑()()20211(1)(1)0k f k g k f g ===∑,D 对,故选:AD.【点睛】本题解决的关键在于根据条件判断函数的周期性,对称性,并结合函数性质求函数值得和.三、填空题13.若22log log 6a b +=,则a b +的最小值为________.【答案】16【解析】【分析】由题得62ab =,再利用基本不等式求解.【详解】因为22log log 6a b +=,所以2log 6ab =.所以62ab=所以622216a b ab +≥≥=.当且仅当8ab ==时取等.故答案为:1614.已知边长为2的菱形ABCD 中,点F 为BD 上一动点,点E 满足22,3BE EC AE BD =⋅=- ,则AF EF ⋅ 的最小值为______.【答案】7336-【解析】【分析】由22,3BE EC AE BD =⋅=- ,根据向量的线性运算以及数量积的运算律,可求得∠DAB =π3;以菱形对角线交点为原点,对角线所在直线为坐标轴建立平面直角坐标系,利用坐标表示出AF EF ⋅,得到关于t 的二次函数,求得二次函数最小值即为所求.【详解】由题意知:2=3BE BC,设=DAB θ∠,所以()()22222333AE BD AB BE AD AB AB AD AB BC BC AB ⋅=+⋅-=⋅-+-⋅=-故()22214cos 444cos cos 3332θθθ-+⨯-⨯=-⇒=由于()0,πθ∈,所以π=3θ,以AC 与BD 交点为原点,AC 为x 轴,BD 为y 轴建立如图所示的直角坐标系,所以A (﹣3,0),C (3,0),D (0,1),B (0,﹣1),E (231,33-),设F (0,t ),则AF =(3,t ),EF =23133,t ⎛⎫-+ ⎪ ⎪⎝⎭,所以2117323636AF EF t t t ⎛⎫⎛⎫⋅=-++=+- ⎪ ⎪⎝⎭⎝⎭ 当t =16-时,AF EF ⋅ 取最小值7336-,故答案为:7336-15.已知等差数列{}n a 和正项等比数列{}n b 满足117332,2a b a b a ====,则数列{}2(2)n n a b -的前n 项和为______.【答案】212n n +⋅【解析】【分析】根据等差等比数列基本量的计算可得公比和公差,进而得1,2nn na nb =+=,因此可得()22(2)=212n n n a b n n -+-,根据裂项求和即可求解.【详解】设公差和公比分别为(),0d q q >,由117332,2a b a b a ====得()2262222d q d +==+,解得1,2d q ==,因此1,2n nn an b =+=,所以()22(2)=212nnn a b n n -+-()()()()22222221212=2122212212n n n n n nnn n n n n n n +⎡⎤+---=⋅--⋅=⋅--⋅⎣⎦,设{}2(2)nn a b -的前n 项和为n S ,因此()2222123222112022212212n n nS n n +⎡⎤⎡⎤⎡⎤⋅-⋅+⋅-⋅++⋅--⋅⎣⎦⎦=⎣⎦⎣ 212=n n +⋅故答案为:212n n +⋅16.已知函数()ln xf x x =,()xx g x e =,若存在1>0x ,2x R ∈,使得()()120f x g x =<成立,则12x x 的最小值为______.【答案】1e-【解析】【分析】利用导数研究函数()f x 可得函数()f x 的单调性情况,且(0,1)x ∈时,()0f x <,(1,)x ∈+∞时,()0f x >,同时注意()()x x xx x lne g x f e e e===,则21xx e =,所以2122x x x x e =,构造函数()x h x xe =,0x <,利用导数求其最小值即可.【详解】函数()f x 的定义域为(0,)+∞,21()lnxf x x -'=,∴当(0,)x e ∈时,()0f x '>,()f x 单调递增,当(,)x e ∈+∞时,()0f x '<,()f x 单调递减,又(1)f 0=,所以(0,1)x ∈时,()0f x <;(1,)x e ∈时,()0f x >;(,)x e ∈+∞时,()0f x >,同时注意到()()xx xx x lne g x f e e e===,所以若存在1(0,)x ∈+∞,2x R ∈,使得12()()0f x g x =<成立,则101x <<且212()()()x f x g x f e ==,所以21x x e =2(0)x <,所以2122xx x x e =,所以构造函数()x h x xe =(0)x <,而()(1)x h x e x '=+,当(1,0)x ∈-时,()0h x '>,()h x 单调递增;当(,1)x ∈-∞-时,()0h x '<,()h x 单调递减,所以1()(1)h x h e=-=-最小值,即12)1(x x e =-最小值.故答案为:1e-.【点睛】关键点睛:利用同构的方式将12x x ,联系起来,这样就构造了新函数,然后利用导数研究函数的单调性及最值.四、解答题17.已知数列{}n a 中,n S 为{}n a 的前n 项和,13n n a S n +=-+,*n N ∈,12a =.(1)求{}n a 的通项公式;(2)设()*2nn nb n N S n =∈-+,数列{}n b 的前n 项和为n T ,求证:()*1433n T n N <∈.【答案】(1)22,13·21,1nn n a n -=⎧=⎨+>⎩.(2)证明见解析.【解析】【分析】(1)由已知得13n n a S n +=-+,即有14n n a S n -=-+,两式相减得()1121n n a a +-=-,根据等比数列的定义得数列{}1n a -为第二项起为等比数列,由等比数列的通项公式可得答案;(2)由(1)得123·2nn n n nb S n -==-+,运用错位相减法和数列的单调性可得证.【小问1详解】解:当1n =时,2111324a S a =-+=+=,13n n a S n +=-+,得()142n n a S n n -=-+≥,两式相减得,11n n n a a a +-=-,即有()1121n n a a +-=-,即为数列{}1n a -为第二项起为等比数列,则213·2n na--=,1n >,n N ∈,即有22,13·21,1n n n a n -=⎧=⎨+>⎩;【小问2详解】解:13n n a S n +=-+,得13·22n n S n -=-+,则123·2n n n n nb S n -==-+,即有前n 项和为2112333·23·23·2n n nT -=+++⋯+,23112323·23·23·23·2n n n T =+++⋯+,两式相减可得,2111111233·23·23·23·2nn nnT -=+++⋯+-1112·133·212nn n ⎛⎫- ⎪⎝⎭=--,化简得4412·3323·2nn nn T ⎛⎫=-- ⎪⎝⎭,由于{}n b 各项大于0,得113nT T =,由不等式的性质可得43nT <.故()*1433n T n N <∈.18.如图,在梯形ABCD 中,//AB CD ,2AB =,5CD =,23ABC π∠=.(1)若AC =ABCD 的面积;(2)若AC BD ⊥,求tan ABD ∠.【答案】(1)(2)tan 3ABD ∠=.【解析】【分析】(1)ABC 中,利用含ABC ∠的余弦定理表达式建立BC 的方程,求出BC 而得ABC 面积,再利用面积关系求ADC 的面积得解;(2)由题设中角的信息用ABD ∠表示出ABC 与BDC 中的相关角,再在这两个三角形中利用正弦定理建立两个方程,联立整理得tan ABD ∠的方程,解之即得.【详解】(1)设BC x =,在ABC 中,由余弦定理2222cos AC AB BC AB BC ABC =+-⋅∠得:22228222cos3x x π=+-⋅⋅⋅,即22240x x +-=,而x>0,解得4x =,所以4BC =,则ABC的面积11sin 24222ABC S AB BC ABC =⋅⋅∠=⋅⋅⋅=△,梯形ABCD 中,//AB CD ,ABC 与ADC 等高,且52ABCD =,所以ADC的面积52ABCADCS S ==△△,则梯形ABCD的面积ABC ADC S S S =+=△△;(2)在梯形ABCD 中,设ABD α∠=,而AC BD ⊥,则BDC α∠=,2BAC πα∠=-,23DBC a π∠=-,6BCA πα∠=-,在ABC 中,由正弦定理sin sin AB BC BCA BAC=∠∠得:2sin()sin()62BCππαα=--,在BDC 中,由正弦定理sin sin CD BC DBC BDC=∠∠得:52sin sin()3BCπαα=-,两式相除得:212sin()2cos sin )sin sin 3cos 5sin()sin()6222παααααππααα-⋅+=⇒--,整理得227sin cos 0αααα--=,即27tan 0αα--=解得tan 3α=或tan 5α=-,因为(,62ππα∈,则tan 3α=,即tan 3ABD ∠=.【点睛】(1)三角形中已知两边及一边对角求第三边,利用余弦定理建立关于第三边的一元二次方程求解;(2)涉及平面多边形问题,把图形拆分成若干个三角形,再在各个三角形内利用正弦、余弦定理求解.19.如图,在三棱柱111ABC A B C ﹣中点,E 在棱1BB 上,点F 在棱CC 1上,且点,E F 均不是棱的端点,1,AB AC BB ⊥=平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.(1)求证:四边形BEFC 是矩形;(2)若2,3AE EF BE ==,求平面ABC 与平面AEF 所成角的正弦值.【答案】(1)证明见解析;(2)10【解析】【分析】(1)由1BB ⊥平面AEF ,知1CC ⊥平面AEF ,求得2AEB AFC π∠=∠=,由四边形11AA B B 与四边形11AAC C 面积相等知,AE AF =,则AEB AFC ≅△△,故BE CF =,结合1BB EF⊥,从而有四边形BEFC 为矩形.(2)证得AG ⊥平面11BB C C ,取BC 的中点H ,以G 点为坐标原点,,,GF GA GH→→→的方向分别为x ,y ,z 轴建立空间直角坐标系,求得平面AEF 和平面ABC 的一个法向量,利用向量夹角求得二面角的正弦值.【详解】(1)在三棱柱中,11//BB CC ,则由1BB ⊥平面AEF ,知1CC ⊥平面AEF ,故1BB AE ^,1BB EF ⊥,1CC AF ⊥,从而2AEB AFC π∠=∠=,由四边形11AA B B 与四边形11AAC C 面积相等知,AE AF=又AB AC =,则AEB AFC ≅△△,故BE CF =结合//BE CF ,知四边形BEFC 为平行四边形,又1BB EF ⊥,故四边形BEFC 为矩形.(2)取EF 的中点G ,联结AG ,由(1)知AE AF =,且1BB ⊂平面11BB C C ,则平面AEF ⊥平面11BB C C ,又平面AEF 平面11BB C C EF=,则AG ⊥平面11BB C C ,取BC 的中点H ,以G 点为坐标原点,,,GF GA GH→→→的方向分别为x ,y ,z 轴建立如图所示空间直角坐标系,由2AE AF EF ===知,AEF 为正三角形,故AG =故A,(1,0,)3B -,(1,0,3C,(1,3AB →=-,(1,3AC →=-,设平面ABC 的一个法向量为(,,)a x y z →=则00a AB a AC ⎧⋅=⎪⎨⋅=⎪⎩,故0303x z x z ⎧--+=⎪⎪⎨⎪+=⎪⎩,取1y =,则0,3x z ==,(0,1,3)a →=因为平面AEF 的一个法向量为(0,0,1)b →=则cos ,10a ba b a b→→→→→→⋅<>===则二面角的余弦值为10,故二面角的正弦值为1020.统计与概率主要研究现实生活中的数据和客观世界中的随机现象,通过对数据的收集、整理、分析、描述及对事件发生的可能性刻画,来帮助人们作出合理的决策.(1)现有池塘甲,已知池塘甲里有50条鱼,其中A 种鱼7条,若从池塘甲中捉了2条鱼.用ξ表示其中A 种鱼的条数,请写出ξ的分布列,并求ξ的数学期望()E ξ;(2)另有池塘乙,为估计池塘乙中的鱼数,某同学先从中捉了50条鱼,做好记号后放回池塘,再从中捉了20条鱼,发现有记号的有5条.(ⅰ)请从分层抽样的角度估计池塘乙中的鱼数.(ⅱ)统计学中有一种重要而普遍的求估计量的方法─最大似然估计,其原理是使用概率模型寻找能够以较高概率产生观察数据的系统发生树,即在什么情况下最有可能发生已知的事件.请从条件概率的角度,采用最大似然估计法估计池塘乙中的鱼数.【答案】(1)分布列见解析,()725E =ξ(2)(i )200;(ii )199或200【解析】【分析】(1)根据超几何概率公式即可求解概率,进而得分布列和期望,(2)根据抽样比即可求解总数,根据最大似然思想结合概率的单调性即可求解最大值.【小问1详解】0,1,2ξ=,2112434377222505050C C C C 129433(0),(1),(2),C 175C 175C 175P P P ξξξ⋅=========故分布列为:ξ012P129175431753175()129433701217517517525E =⨯+⨯+⨯=ξ.【小问2详解】(i )设池塘乙中鱼数为m ,则50520m =,解得200m =,故池塘乙中的鱼数为200.(ii )设池塘乙中鱼数为n ,令事件B =“再捉20条鱼,5条有记号”,事件C =“池塘乙中鱼数为n ”则515505020C C ()C n n np P B C -⋅==∣,由最大似然估计法,即求n p 最大时n 的值,其中65n ,1(49)(19)(64)(1)n n p n n p n n +--∴=-+当65,......198n =时11n n p p +>,当199n =时11n n pp +=,当200,201,...n =时11n np p +<所以池塘乙中的鱼数为199或200.21.已知椭圆C :22221(0)x y a b a b+=>>的四个顶点构成的四边形的面积为,点312⎛⎫ ⎪⎝⎭,在椭圆C 上.(1)求椭圆C 的方程;(2)若矩形MNPQ 满足各边均与椭圆C 相切.求证:矩形MNPQ 对角线长为定值.【答案】(1)22143x y +=(2)证明见解析【解析】【分析】(1)利用待定系数法求解;(2)对当MN 的斜率的情况进行分类讨论,当MN 的斜率存在且不为0时,设直线MN :ykx t =+,与椭圆方程联立,根据0∆=,求得,k t的关系,利用两平行线之间的距离公式分别求得矩形边长,从而可求得对角线,即可得证.【小问1详解】解:由已知2212221914a b a b ⎧⋅⋅=⎪⎪⎨⎪+=⎪⎩,解得2a b =⎧⎪⎨=⎪⎩所以椭圆方程C :22143x y +=;【小问2详解】证明:当MN 的斜率为0或不存在时,对角线MP NQ ===,当MN 的斜率存在且不为0时,设直线MN :y kx t =+,联立223412y kx t x y =+⎧⎨+=⎩消去y 得()2223484120k x ktx t +++-=,()()222264163430k t t k ∆=--+=,化简得2243k t +=,所以两平行线MN 和PQ的距离1dNP ===,以1k -代替k ,两平行线MQ 和NP的距离2d MN ===,所以矩形MNPQ的对角线MP NQ ==综上所述,矩形MNPQ对角线长为定值22.已知函数2()e ,2xmx f x m =-∈R .(1)讨论()f x 极值点的个数;(2)若()f x 有两个极值点12,x x ,且12x x <,证明:()()122e f x f x m +<-.【答案】(1)见解析(2)见解析【解析】【分析】(1)分类讨论导函数e ()xf x x m x ⎛⎫'=- ⎪⎝⎭的实数根即可求解极值点,(2)构造函数()()(2),(0,1)F x g x g x x =--∈和2e ()(3)e e,(0,1)xxxG x x x x-=-+-∈,通过判断函数的单调性,求解最值,当导数正负不好确定的时候,需要构造新的函数,不断的通过求导判断单调性.【小问1详解】2()e 2xmx f x =-,则()e x f x mx '=-,0x = 显然不是()'f x 的零点,e (),x f x x m x '⎛⎫∴=- ⎪⎝⎭令e ()=xg x x,则2e (1)()-'=x x g x x ,()g x ∴在(,0)-∞单调递减,在(0,1)单调递减,在(1,)+∞单调递增.当0x <时,()0g x <,当0x >时,()0>g x ,且()(1)eg x g ==极小值(,0)m ∴∈-∞时,e=x m x只有一个实数根,所以此时()f x 有1个极值点,[)0,e m ∈时,e=x m x没有实数根,故()f x 有0个极值点,当e m =时,e =x m x ,有一个实数根1x =,但1x =不是极值点,故此时()f x 没有极值点,(e,)m ∈+∞时,e =x m x有两个不相等的实数根,故()f x 有2个极值点.【小问2详解】由(1)知,(e,)m ∈+∞,且()()121201,,()x x g x g x m g x <<<==在(0,1)单调递减,在(1,)+∞单调递增,先证:122x x +>,即证:212x x >-,1201x x <<< 121x ∴->即证:()()212g x g x >-.即证:()()112g x g x >-.令()()(2),(0,1)F x g x g x x =--∈,即证:(0,1),()0x F x ∀∈>,2'22e e ()(1)()(2)x xF x x x x -=---令2(1,2)t x =-∈则x t<令2e ()h =λλλ,则4)(e (2)h'⋅⋅-=λλλλλ,则()h λ在(0,2)λ∈单调递减()()(2)h x h t h x ∴>=-,()0F x '∴<,即()F x 在(0,1)x ∈单调递减,()(1)0F x F ∴>=,证毕.再证:()()122e f x f x m +<-,1201x x <<< ,且122x x +>1122x x x ∴<-<.()f x 在()10,x 单调递增,在()12,x x 单调递减,在()2,x +∞单调递增,()()122f x f x ∴->.即证:()()1122e f x f x m +-<-,又11e x m x =,即证:()()()11121111e 23e e2e x x x f x f x m x x -+-+=-+-<.令2e ()(3)e e,(0,1)xx xG x x x x-=-+-∈,()23222222e 21e e (1)()(2)e e exx x xxxx x x x G x x x x '--+-+--∴=---=.令()23222()e 21e x p x x x x x =-+-+-,()2322()e 2212e x p x x x x x '∴=-+++-,令()()q x p x '=()2322()2e 22322e x x q x x x ∴=-+--'-,令()()r x q x '=()232()2e 41027x x x x r x ∴=-'+--令32()41027,(0,1)m x x x x x =+--∈,2()12202m x x x '∴=+-,11(0,1),()x m x ∴∃∈在()110,x 单调递减,在()11,1x 单调递增.(0)7,(1)5m m =-= ,12(0,1)x ∴∃∈,当()120,x x ∈时,()()0,r x q x >''单调递增;当()12,1x x ∈时,()()0,r x q x <''单调递减.()()2042e 0,10q q '<'=-= ,13(0,1),()x p x '∴∃∈在()130,x 单调递减,在()13,1x 单调递增.(0)10,(1)0p p ''=>= ,14(0,1),()x p x ∴∃∈在()140,x 单调递增,在()14,1x 单调递减.(0)1,(1)0p p == ,()0p x ∴>,()0G x '∴>,()G x ∴在(0,)x x ∈单调递增,()(1)2e G x G ∴<=,所以原命题得证.【点睛】本题考查了导数的综合运用,利用导数求单调性时,如果求导后的正负不容易辨别,往往可以将导函数的一部分抽离出来,构造新的函数,利用导数研究其单调性,进而可判断原函数的单调性.在证明不等式时,常采用两种思路:求直接求最值和等价转化.无论是那种方式,都要敢于构造函数,构造有效的函数往往是解题的关键.。
2024-2025学年湖南省长沙市长郡中学高三上学期月考语文试题及答案

大联考长郡中学2025届高三月考试卷(一)语文本试卷共四道大题,23道小题。
时量150分钟,满分150分。
得分:一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
不管是要找出第二次世界大战的原因,还是查明天花板上水印的来由,我们通常都要考察可能的解释。
比如说天花板上的水印,是屋顶漏水了?还是管子漏水了?我们可能会这样推理:“这个水印在厨房天花板上,正好是在浴室的下面,所以很可能是管子漏水。
”现在到楼上去检查一下,如果发现了漏水的管子,那么就可以合理地得出结论,对于水印的最佳解释是管子漏水,当然,也可能屋顶和管子同时漏水。
这个简单而实际的例子展示了科学研究的推理过程:提出各种假说,一个一个地排除,直到得出最佳解释。
地质学的历史为科学研究如何运用这样的推理过程提供了一个清楚的例子。
地球已经有上亿年的历史、大陆在漂移,这些都是非常惊人的发现。
它们被接受的过程是漫长而复杂的,要求仔细的观察、改良的技术、大量的集体努力以及在很多学科中共享知识。
地质学最近的发展历史就展现了这样的过程。
1912年,德国科学家阿尔弗雷德·魏格纳提出了板块漂移理论来解释这个明显的事实——非洲大陆和南美洲大陆看上去好像很吻合。
但是在他之前的理论家,通过观察过去的地图,也推测这些太陆原本是连在一起的。
魏格纳对这一理论的补充是,在两个大陆相对应的边缘,岩石的形成和动植物化石都非常相似。
因为他不能提出一个解释或者模型来说明像板块这样巨大的东西是如何“漂移”的,他的理论遭到了普遍的拒绝,甚至被嘲笑。
虽然他的理论解释了一些观察到的现象,但是并没有被采信,因为它与当时人们所相信的关于大洋和大陆的物理结构方面的观点不一致。
拥有可接受的解释模型是科学断言能被接受的重要标准。
魏格纳的理论在20世纪60年代被美国地质学家哈雷·赫斯复兴。
赫斯提出,最近发现洋中脊在延伸,而大陆居于板块之上,因此板块应是由底层的地慢缓慢运动的“环流”所推动的。
【名师解析】湖南省长郡中学2015届高三月考试卷(二)地理试题 Word版含答案

长郡中学2015届高三月考试卷(二)地理本试题卷分选择题和非选择题两部分,共8页。
时量90分钟,满分100分。
第Ⅰ卷选择题(共60分)一、选择题(本大题共25个小题,每小题2分,共50分。
在每小题给出的四个选项中,只有一项最符合题目要求。
)地理研究性学习小组野外考查绘制了某地地貌景观图及地形剖面图,读图回答1-2题。
1.形成图中成都附近地区地貌景观的主导因素是()A.流水搬运B. 地壳运动C. 流水侵蚀D. 流水沉积2.在野外,研究小组利用目视估算法估测地形高度。
下列结论正确的是()A.在①地估测出山的相对高度B.在②地估测出山的相对高度C.在③地估测出山谷的海拔高度D.在④地估测出谷底的相对深度中高纬度地区东西走向山脉的南北两侧,由于光照时间长短不同,出现了明显的温度差异,即阳坡温度高于阴坡。
读中纬度某内陆地区等值线图,回答3~4题。
3.若a为12°C等温线,则乙地气温的数值可能是A.16℃B.14℃C.10 ℃ D.8℃4.下列关于甲、乙、丙、丁四地所在位置的叙述正确的是A.甲、乙位于北半球的阳坡 B.甲、乙位于南半球的阳坡C.丙、丁位于北半球的阳坡 D.丙、丁位于南半球的阳坡下图示意某小区域地形,图中等高距为50米,瀑布的落差为22米,据此完成5-6题.5.Q地的海拔可能为A.550米B.320米C.520米D.420米6.图中河流最低处与山峰的高差最接近A.140米B.160米C.360米D.260米下图为某区域的海上航线示意图。
在一艘驶往印度洋的轮船上,悉尼时间6:00船员在图中②处看到了海上日出景观。
读图回答7-8题。
7、该日②处海上日出时刻,下列说法可信的是A.④地也可能正好日出 B.此刻全球新的一天比重小C.我国长城站可能出现极昼D.长沙长郡学生在在校早读8、下图中的四幅图,与②处当日轮船桅杆日影在地面上移动方向一致的是下图示意某地锋面过境时等温面分布状况。
读图回答9——10题。
湖南省长郡中学2015届高三第二次月考试卷(语文)

湖南省长郡中学2015届高三第二次月考试卷(语文)高三2011-11-28 11:31湖南省长郡中学2015届高三第二次月考试卷(语文)word版长郡中学高三语文备课组组稿本试题卷共7道大题,21道小题,共10页。
时量150分钟,满分150分。
一、语言文字运用(12分,每小题3分)1.下列词语中加点的字,注音全都正确的一组是A.青睐(lài)名嫒(yuán)涮羊肉(shuàn)引咎辞职(jiù)B.曝光(bào)蕴藉(jiâ)回头率(lǜ)重蹈覆辙(zhã)C.游弋(yâ)挨宰(ái)捂一捂(wǔ)面面相觑(qù)D.数落(shǔ)深邃(suì)翻砂工(shā)四处走穴(xuâ)2.下列各句中,加点的成语使用不恰当的一句是A.上海取得自主招生选拔录取资格的考生,有一些因考分低于协议所规定的分数而未被录取,招生部门借此表示,自主招生绝不是对人才降格以求。
B.在过去的30多年风云激荡的改革历程中,中国青年释放出无限活力和创造力,一次又一次以敢为人先的勇气,书写了青春的壮美和祖国的辉煌。
C.中国小说史上的很多“续书”,质量有好有坏,评论有褒有贬,但几乎没有一部续书的艺术质量可以与原书相媲美,这是不容置喙的。
D.“敬鬼神而远之’的理解和翻译各家基本一致,解说或结论更是众口一词,均认为孔子对鬼神的态度是存而不论,这是对孔子思想的误解。
3.下列各句中,没有语病的一句是A.电信业内人士报料,“高额吸费电话”之所以能大行其道,是因为电信运营商参与了不法垃圾短信公司和声讯服务台的收益分成的结果。
B.后金融危机时代,欧洲一些国家如希腊,由于债务危机已经导致债务负担出现不断加剧的趋势,使国家主权风险迅速提高。
C.在华盛顿核安全峰会上,与会的国家首脑以防止“核恐怖”为中心话题,进行了积极的讨论和磋商,提出了一些基本共识。
湖南省长郡中学2015届高三月考试卷(二)数学(文)试题 Word版含答案

长郡中学2015届高三月考试卷(二)数 学(文科)长郡中学高三数学命题组组稿得分:____________ 本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。
满分150分。
一、选择题:本大题共10小题,没小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、若x B ∈成立的一个充分不必要条件是x A ∈,则实数m 的取值范围是A.2m ≥B.2m ≤C.2m >D.22m -<<2、若直线1ax by +=与不等式组1210210y x y x y ≤⎧⎪--≤⎨⎪++≥⎩表示的平面区域无公共点,则23a b +的取值范围是A.()7,1--B.()3,5-C.()7,3-D.R3、如图,在一个正方体内放入两个半径不相等的球12,O O ,这两个球相外切,且球1O 与正方体共顶点A 的三个面相切,球2O 与正方体共顶点1B的三个面相切,则两球在正方体的面11AAC C 上的正投影是A.B.C. D.4A.C.5,定义域为D ,任意,m n D ∈,点(),()P m f n 组成的图形为正方形,则实数a 的值为A. 1-B. 2-C. 3-D.4-6、已知M 是ABC ∆内的一点,且23,30AB AC ⋅=,若,MBC MCA ∆∆和MAB ∆的面A.20B. 18C. 16D. 97、一束光线从点()1,1A -出发,经x 轴反射到圆()()22:231C xy -+-=上的最短路程是C.4D.58、已知直线()()20y k x k =+>与抛物线2:8C y x =相交于,A B 两点,F 为C 的焦点,若则k =B.C.9、函数()f x 的导函数是'()f x ,若对任意的x R ∈,都有()2'()0f x f x +<成立,则B. C. D.无法比较 10、在平面直角坐标系xOy 中,点()5,0A ,对于某个正实数k ,存在函数()2()0f x ax a =>,使得OA OQ OP OA OQ λ⎛⎫ ⎪=+ ⎪(λ),这里点,P Q 的坐标分别为()()1(,1),()P f Q k f k ,,,则k 的取值范围为A.()2,+∞B. ()3,+∞C. [)4,+∞D.[)8,+∞选择题答题卡二、填空题:本大题共5小题,每小题5分,共25分。
2024-2025学年湖南省长沙市长郡中学大联考高三(上)月考数学试卷(二)(含答案)

2024-2025学年湖南省长沙市长郡中学大联考高三(上)月考数学试卷(二)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={x||x|⩽2},B ={t|1⩽2t ⩽8(t ∈Z)},则A ∩B =( )A. [−1,3]B. {0,1}C. [0,2]D. {0,1,2}2.已知复数z 满足|z−i|=1,则|z|的取值范围是( )A. [0,1]B. [0,1)C. [0,2)D. [0,2]3.已知p :f(x)=ln(21−x +a)(−1<x <1)是奇函数,q :a =−1,则p 是q 成立的( )A. 充要条件 B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4.若锐角α满足sinα−cosα=55,则sin (2α+π2)=( )A. 45B. −35 C. −35或35D. −45或455.某大学在校学生中,理科生多于文科生,女生多于男生,则下述关于该大学在校学生的结论中,一定成立的是( )A. 理科男生多于文科女生B. 文科女生多于文科男生C. 理科女生多于文科男生D. 理科女生多于理科男生6.如图,某车间生产一种圆台形零件,其下底面的直径为4cm ,上底面的直径为8cm ,高为4cm ,已知点P 是上底面圆周上不与直径AB 端点重合的一点,且AP =BP ,O 为上底面圆的圆心,则OP 与平面ABC 所成的角的正切值为( )A. 2B. 12C.5D.557.在平面直角坐标系xOy 中,已知直线l :y =kx +12与圆C :x 2+y 2=1交于A ,B 两点,则△AOB 的面积的最大值为( )A. 1B. 12C.32D.348.设函数f(x)=(x 2+ax +b)lnx ,若f(x)≥0,则a 的最小值为( )A. −2B. −1C. 2D. 1二、多选题:本题共3小题,共18分。
湖南省长郡中学2015届高三第五次月考试题(语文)

湖南省长郡中学2015届高三第五次月考试题(语文)高三2012-02-28 15:26长郡中学2015届高三月考试卷(五)语文试题本试题卷共7道大题,21道小题。
时量150分,满分150分。
一、语言文字运用(12分,每小题3分)1.下列各句注音和字形无误的一项是()A.如果是一块石头,我是选择在山野中沉埋一生,还是在市井间喧器蒙诟.(gîu)?是坚守仁静的心,还是随缘于风尘的侵陵?B.看似.(sì)两件风马牛不相及的事情,但却被奇妙地交织在一起,观石的喜悦与思乡的愁怅密密揉和,真有悲欣交集之感。
C.常常碰到一些愤世嫉.(jí)俗的文学青年,骂编辑有眼无珠,是势力眼,只会用名家的稿子,而看轻自己才华横溢的作品。
D.舟首之人峨冠博带,茕.(qiïng)然而立,他并不觉茫然,若非那场“乌台诗案”,自己又岂能从云谲波诡的党争中全身而退?2.下列句子中,加点的词语使用不恰当的一项是()A.近日,地产分析人士孙田告诉记者,在房地产调控下,今年以来各地土地市场成交持续低迷,地方政府的土地财政收入也明显锐减..。
B.经主办方介绍,此次的“好书评选”经过了严格而公平的程序,同时融合了凤凰媒体一以贯之....的全球视野、媒体责任与人文情怀。
C.位于2011西安世园会主轴线上的自然馆,建筑体形独特,器宇轩昂....,是2011年西安世界园艺博览会的标志性建筑,格外引人注目。
D.2011年底,《收获》杂志新推史铁生绝笔,作品显示,尽管当时史铁生身体已每况愈下....,但丝毫没有影响其娴熟的技巧和厚重的功力。
3.下列选项中,没有语病的一项是()A.省委、省政府高度重视文化建设和文化改革发展,今年以来已多次专题研究文化工作,研究制定了一系列文化改革发展的重要文件,全省文化建设取得显著成绩,文化改革发展进展顺利。
B.今天(25日)是西方传统的圣诞节,不少人都盼望能够下一场雪,浪漫一下,不过湖南的天气并不应景。
湖南省长郡中学2015届高三第五次月考生物试题(PDF高清扫描版)

题答 要 不 内 线 封密号 学名 姓级 班 校 学炎德 英才大联考长郡中学#$"%届高三月考试卷五 生 物长郡中学高三生物命题组组稿时量 &$分钟 满分 &$分得分本试题卷分选择题和非选择题两部分共'页 时量&$分钟 满分&$分 第 卷 选择题 共($分一 选择题 每小题给出的四个选项中 只有一个符合题目要求的 将选出的正确答案填在答题卡上 " )$每小题"分 )")%每小题#分 共($分 "*对火星进行探测表明 火星过去曾有丰富的水资源 由此推测火星上可能存在过生命 这一推测的理由是+*水是细胞中含量最多的化合物,*结合水是细胞和生物体的成分-*一切生命活动都离不开水.*代谢旺盛的细胞中水的含量高#*有关细胞中的有机物下列说法正确的是+*含有元素- / 0 1的物质是核酸酶 果糖 脂肪,*花生种子中没有蛋白质 只有脂肪 故用来作为检测脂肪的材料-*淀粉 蛋白质 脂肪在氧化分解时都能释放出能量.*蛋白质的检测可用斐林试剂 且要现配现用)*下列有关细胞器的说法正确的是+*核糖体是噬菌体 细菌 酵母菌唯一共有的细胞器,*线粒体是有氧呼吸的主要场所 在其中生成的产物有丙酮酸 -0#和/#0-*叶绿体是所有生物进行光合作用的场所 含有.1+ 21+ 蛋白质和磷脂等成分.*在植物细胞有丝分裂的末期 细胞中的高尔基体活动加强(*用洋葱鳞片叶表皮制备 观察细胞质壁分离实验 的临时装片 观察细胞的变化 下列有关实验操作和结果的叙述 正确的是+*将装片在酒精灯上加热后 再观察细胞质壁分离现象,*在盖玻片一侧滴入清水 细胞吸水膨胀但不会破裂-*用不同浓度的硝酸钾溶液处理细胞后 均能观察到质壁分离复原现象.*当质壁分离不能复原时细胞仍具有正常的生理功能%*右图表示不同3/及温度对某反应产物生成量的影响 下列相关叙述正确的是+*随着3/的升高 酶的活性先降低后增大,*该酶的最适温度是)%4-*酶的最适3/是一定的 不随着温度的升高而升高.*随着温度的升高 酶的活性逐渐降低5*细胞呼吸对生命活动意义重大 下面关于细胞呼吸的叙述正确的是+*线粒体是有氧呼吸的主要场所 没有线粒体的细胞只能进行无氧呼吸,*有叶绿体的细胞不需要细胞呼吸提供能量就可合成所有的+67-*动物停止细胞呼吸就不能合成+67 作为生命基本特征的新陈代谢就此终结.*细胞呼吸中有机物的分解必须有水和氧气的参与才能释放储存的能量8*下列各项措施中 能提高农作物的光合作用效率的是延长作物的光合作用时间 增加作物的光合作用面积 对不同的作物给予适宜的光照强度 确保通风以保证二氧化碳的供给量+* ,* -* .*'*依据细胞生理特点 鉴别一个正在进行有丝分裂的细胞是植物细胞还是动物细胞 最可靠的方法是检查它的+*.1+自我复制的方式,*是否出现星射线-*细胞质分成两部分的方式.*自身的蛋白质合成的方式&*下列有关叙述中 正确的是+*兔的白毛与黑毛 狗的长毛与卷毛都是相对性状,*隐性性状是指生物体不能表现出来的性状-*纯合子的自交后代中不会发生性状分离 杂合子的自交后代中不会出现纯合子.*表现型相同的生物 基因型不一定相同"$*下列关于基因和染色体关系的叙述 错误的是+*染色体是基因的主要载体,*基因在染色体上呈线性排列-*一条染色体上有多个等位基因.*体细胞 细胞核 中基因成对存在 染色体也成对存在""*已知玉米的某两对基因按照自由组合定律遗传 子代的基因型及比值如右图所示 则双亲的基因型是+*..99:..9;,*.<9;:.<9;-*.<9;:..9;.*.<99:..9;"#*右图表示基因在染色体上的分布情况 其中不遵循基因自由组合定律的相关基因是+*+=与.<,*,,与+=-*+=与->.*->与.<")*小鼠中有一种毛皮颜色的性状 其杂交实验如下: 子代性状及比例实验一黄鼠:黑鼠黄鼠 #)8'只 ?黑鼠 #)&'只 "?"实验二黄鼠:黄鼠黄鼠 #)&5只 ?黑鼠 "#)%只 #?"有关叙述正确的是+*小鼠毛皮颜色的遗传不遵循分离定律,*小鼠毛皮的黑色对黄色为显性-*小鼠中不存在黄色纯种个体.*小鼠中不存在黑色纯种个体"(*南瓜果实的颜色是由一对等位基因 +和= 控制的 用一株黄色果实南瓜和一株白色果实南瓜杂交 子代 @" 既有黄色果实南瓜也有白色果实南瓜 让@"自交产生的@#表现型如图甲所示 为研究豌豆的高茎与矮茎和花的顶生与腋生性状的遗传规律 设计了两组纯种豌豆杂交实验 如图乙所示 根据图示分析 说法错误的是+*由图甲 可知黄果是隐性性状 白果是显性性状,*图甲7中黄果的基因型是== @#中黄果与白果的理论比例是%?)-*由图乙可知花的着生位置和茎的高度各由一个基因控制 都遵循基因分离定律.*图乙中@"所有个体的基因型相同 该实验中亲代的腋生花都需做去雄处理"%*以下 为动物生殖细胞形成过程中某些时期的示意图按分裂时期的先后排序 正确的是+* ,* -* .*"5*犬色盲性状的遗传基因控制机制尚不清楚 右图为某一品种犬的系谱图 涂黑表示色盲 请据图判断 下列叙述不可能的是+*此系谱的犬色盲性状遗传符合伴A染色体隐性遗传,*此系谱的犬色盲性状遗传符合伴A染色体显性遗传-*此系谱的犬色盲性状遗传符合常染色体隐性遗传.*此系谱的犬色盲性状遗传符合常染色体显性遗传"8*菜豆是自花传粉的植物 其花色中有色花对无色花为显性 一株杂合有色花菜豆 -> 生活在海岛上 如果海岛上没有其他菜豆植株存在 且菜豆为一年生植物 那么三年之后 海岛上开有色花菜豆植株和开无色花菜豆植株的比例是+*)?",*"%?8-*&?8.*"%?&"'*下列有关人类对遗传物质探索历程的叙述正确的是+*格里菲思的体内转化实验证明了.1+是遗传物质,*艾弗里的体外转化实验采用了物质提纯 鉴定与细菌体外培养等技术-*赫尔希和蔡斯的实验证明了.1+是生物界中主要的遗传物质.*烟草花叶病毒侵染烟草的实验证明了蛋白质和21+是遗传物质"&*在豌豆杂交实验中 高茎与矮茎杂交得@" @"自交所得@#中高茎和矮茎的比例为8'8?#88 上述实验结果的实质是+*高茎基因对矮茎基因有显性作用,*@"自交 后代出现性状分离-*控制高#矮茎的基因不在一对同源染色体上.*等位基因随同源染色体的分离而分离#$*细胞分裂过程实质上是细胞内染色体的行为变化过程"下列配子的产生与减数第一次分裂后期染色体的异常行为密切相关的是+*基因型为+=,B的个体产生+,#+B#=,#=B四种配子,*基因型为..的个体产生.#<的配子-*基因型为A=C的雄性个体产生A=C的异常精子.*基因型为A,A B的雌性个体产生A,A,的异常卵细胞#"*豌豆是一年生植物!高茎对矮茎为显性!绿色豆荚对黄色豆荚为显性"用纯合矮茎绿色豆荚豌豆和纯合高茎黄色豆荚豌豆培育出矮茎黄色豆荚豌豆植株!用杂交育种和单倍体育种!分别需要的时间是+*)##,*###-*)#).*##"##*一次性过量饮水会造成人体细胞肿胀!功能受损!可静脉滴注高浓度的生理盐水&质量分数为"*'D的1=-E溶液'对患者进行治疗"其原理是+*升高细胞外液的离子浓度,*促进抗利尿激素的分泌-*降低细胞内液的离子浓度.*减少细胞外液液体总量#)*甘氨酸是脊髓中主要的抑制性神经递质!能使突触后膜的-E!通道开放!使-E!内流"下列叙述正确的是+*某种毒素可阻止神经末梢释放甘氨酸!从而引起肌肉痉挛,*甘氨酸以主动运输的方式经突触前膜释放到突触间隙-*甘氨酸与突触后膜上受体结合后引起膜外电位由正变负.*脊髓神经元静息状态时膜内外没有离子进出#(*右图表示人体在某种环境条件发生改变时!内环境中某种激素的含量变化"下列各项所示条件变化和激素对应正确的是+*食物缺碘***生长激素,*食物过咸***抗利尿激素-*过度饥饿***胰岛素.*温度过高***甲状腺激素#%*斯坦曼因发现能够激活并调节适应性免疫的树突状细胞而分享了诺贝尔奖"树突状细胞是一种免疫细胞!是目前人体内功能最强的专职抗原呈递细胞!能有效激发6细胞应答&如右图'"下列相关叙述不正确的是+*树突状细胞激发6细胞应答体现了细胞间的信息交流,*树突状细胞激发6细胞分化形成各种淋巴细胞-*树突状细胞既参与细胞免疫也参与体液免疫.*树突状细胞能够摄取和处理侵入机体的抗原#5*科萨奇病毒-+F"5常引起儿童手足口病和其他并发症"下列关于人体对该病毒免疫过程的叙述!正确的是+*-+F"5侵入后!刺激6细胞分泌淋巴因子与该病毒结合,*,细胞经-+F"5刺激后分裂#分化为浆细胞!与抗原结合-*患儿痊愈后!若再次感染该病毒!记忆细胞会迅速产生抗体消灭病毒.*-+F"5侵入后!体内的吞噬细胞#,细胞和效应6细胞都具有识别功能#8*右图为突触结构示意图!有关叙述不正确的是+*神经递质存在于 中!它的释放需要 和高尔基体等参与,*由图中 构成一个突触!其中 为突触后膜-*突触后膜上完成的是$电信号 化学信号%的转变.*兴奋在突触处的传递是单向的#'*果实的生长发育和成熟受多种激素调节"下列叙述正确的是+*细胞分裂素在果实生长中起促进作用,*生长素对果实的发育和成熟没有影响-*乙烯在果实生长和成熟中起抑制作用.*脱落酸在果实成熟中促进细胞分裂和果实脱落#&*下列不属于植物体内从产生部位运输到作用部位的物质是+*#!(G .,*赤霉素-*细胞分裂素.*脱落酸)$*右图是麻风树林中两个营养级的能量流动图解!已知麻风树同化的总能量为1!方框中字母代表能量"下列叙述不正确的是+*从麻风树输入下一营养级的能量传递效率为,+1,*.是指呼吸作用消耗的能量-*,是第二营养级用于生长#发育和繁殖的能量.*该图解中不包含非生物的物质和能量)"*在家鼠遗传实验中!一黑色家鼠与白色家鼠杂交&白色与黑色由两对等位基因控制且独立遗传'!@"均为黑色"@"个体间随机交配得@#!@#中出现黑色?浅黄色?白色H "#?)?"!则@#黑色个体和浅黄色个体中杂合子比例分别为+*"+5##+),*"+'#"+)-*%+5##+).*%+'##+))#*下图所示为四个遗传系谱图!则有关的叙述中正确的是+*肯定不是红绿色盲遗传家系的是甲#丙#丁,*家系乙中患病男孩的父亲一定是该病基因携带者-*四图都可能表示白化病遗传的家系.*家系丁中这对夫妇若再生一个女儿!正常的几率是)+())*如下图曲线 表示黄豆在适宜温度#-0#浓度为$*$)D 的环境中光合速率与光照强度的关系"在I 点时改变某条件!结果发生了如曲线 的变化"下列分析合理的是+*与I点相比较 J点时叶绿体中-)含量低,*在I点时 适当升高温度可导致曲线由 变为-*制约J点的光合速率的因素主要是叶绿体中色素的含量.*制约K点的光合速率的因素可能是-0#浓度)(*小鼠中有一对控制灰砂色的基因 6 和正常灰色的基因 L 位于A染色体上 正常灰色但性染色体组成为A0的雌鼠与灰砂色雄鼠交配 预期后代表现型之比为 胚胎的存活至少要有一条A染色体+*灰砂 ?灰色 H#?",*灰砂 ?灰色 H"?#-*灰砂 ?灰色 H"?".*灰砂 ?灰色 H)?")%*图中+所示细胞通讯方式为人体内常见的一种信号分子及其信号传导方式 图,表示这种信号分子对靶细胞作用的方式 据图分析正确的是+*图中的信号分子 是神经递质 它通过 血液的运输 与 受体结合 作用于靶细胞,*若 是胰岛素 则靶细胞有可能是肝细胞 激酶激活细胞的功能是肝糖原分解-*若靶细胞是垂体细胞 则 可能是促甲状腺激素释放激素.*若靶细胞是甲状腺细胞 则 是甲状腺激素第 卷答题卡题号"#)(%58'&"$"""#答案题号")"("%"5"8"'"&#$#"###)#(答案题号#%#5#8#'#&)$)")#)))()%得分答案第 卷 非选择题 共%$分二 填空题 共%个小题 每空#分 共"$分)5*为了对细胞中的各种结构进行分析 我们通常用 法将它们相互分离 )8*孟德尔认为 控制不同性状的 的分离和组合是互不干扰的)'*多基因遗传病是指受 基因控制的人类遗传病)&*激素调节的特点是 微量和高效 作用于靶器官和靶细胞 ($*能量流动是指生态系统中能量的 的过程三 简答题 共四道大题 共($分("* '分 为研究棉花去棉铃 果实 后对叶片光合作用的影响 研究者选取至少具有"$个棉铃的植株 去除不同比例棉铃 )天后测定叶片的-0#固定速率以及蔗糖和淀粉含量 结果如图" 由图"可知 随着去除棉铃百分率的提高 叶片光合速率 本固定速率相对值是 实验中对照组 空白对照组 植株-0## 由图#可知 去除棉铃后 植株叶片中 增加 已知叶片光合产物会被运到棉铃等器官并被利用 因此去除棉铃后 叶片光合产物利用量减少 降低 进而在叶片中积累(#* "#分 图甲曲线表示三类遗传病在人体不同发育阶段的发病风险 表乙是某一小组同学对一个乳光牙女性患者家庭成员的情况进行调查后的记录 空格中 代表乳光牙患者 代表牙齿正常祖父祖母外祖父外祖母父亲母亲姐姐弟弟女性患者乙分析回答下列问题" 图甲中多基因遗传病的显著特点是 # 图甲中 染色体异常遗传病的发病风险在出生后明显低于胎儿期 这是因为 克莱费尔特征患者的性染色体组成为A A C 父亲色觉正常 A,C 母亲患红绿色盲 A B A B 生了一个色觉正常的克莱费尔特征患者 原因是 ) 请根据表乙统计的情况绘制遗传性乳光牙遗传系谱图 利用下边提供的图例绘制 从遗传方式上看 该病属于 遗传病 致病基因位于染色体上()* '分 生物兴趣小组为研究某植物生长发育过程中植物激素间的共同作用 进行了相关实验" 上图为去掉其顶芽前后 侧芽部位生长素和细胞分裂素的浓度变化及侧芽长度变化坐标曲线图 据图分析激素甲代表的是高浓度的生长素和细胞分裂素对侧芽萌动分别起的作用是# 为研究根的向地生长与生长素和乙烯的关系 该兴趣小组又做了这样的实验 将该植物的根尖放在含不同浓度生长素的培养液中 并加入少量蔗糖作为能源物质 发现在这些培养液中出现了乙烯 且生长素浓度越高 乙烯的浓度也越高 根尖生长所受的抑制也越强该实验的因变量是为使实验严谨 还需要另设对照组 对照组的处理是 ((* "#分 调查草原老鼠数量变化对畜牧业有一定的指导意义 假如某时期有一批田鼠迁入内蒙古草原 该田鼠以优质牧草的根为食 某科研小组对该草原的这一批田鼠进行了长期追踪调查 并绘制了如右图所示的曲线图回答以下问题" 图中虚线表示在 条件下田鼠种群的增长方式 该增长方式中 选填 增长率 或 增长速率 保持不变# 图中实线表示该田鼠种群在该草原上实际增长情况 图中+,时间段内实线和虚线重合的原因是 而,点以后同一时刻虚线与实线的差值表示 用自然选择理论描述) 图中.点时刻 该田鼠的年龄组成的具体特点是 牧民为了减少田鼠的数量 在图中 点 选填 , - . 或 M 投放鼠药效果最好炎德 英才大联考生物参考答案 长郡版 !"炎德 英才大联考长郡中学#$"%届高三月考试卷五 生物参考答案一 选择题 本大题共&$分 " '$每小题"分 '"'%每小题#分 每小题四个选项中只有一个符合题意 题号"#'&%()*+"$"""#答案,,-.,,-,-,,/题号"'"&"%"(")"*"+#$#"###'#&答案,,..,.-,///.题号#%#(#)#*#+'$'"'#'''&'%答案.-,//,,/-/,二 填空题 每空#分 "$分 '(0差速离心')0遗传因子'*0两对以上等位'+0通过体液运输&$0输入 传递 转化和散失三 简答题 共四道大题 共&$分 &"0 共*分 每空#分 " 逐渐下降 #*#淀粉和蔗糖的含量 输出量� 共"#分 每空#分 "成年人发病风险显著增加 #大多数染色体异常遗传病是致死的 患病胎儿在出生前就死亡了 母亲减数分裂形成12型卵细胞 父亲减数第一次分裂时 1 3染色体未正常分离 形成1.3型精子 二者结合形成1.123型的受精卵'显性 常&'0 共*分 每空#分 " 生长素生长素起抑制作用细胞分裂素起促进作用 # 乙烯浓度和根的生长情况取等量的根尖放在含等量蔗糖但不含生长素的培养液中&&0 共"#分 每空#分 " 营养 空间充足 没有天敌等 增长率 #迁入之初 草原的食物和空间充足 并且没有天敌 近似理想条件 生存斗争中被淘汰的个体数 '各年龄阶段的田鼠所占比例适中 .。
2015年全国统一高考数学试卷(完整版+答案解析)(新课标ⅱ)

2015年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本大题共12小题,每小题5分1.(5分)(2015•新课标Ⅱ)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)2.(5分)(2015•新课标Ⅱ)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.43.(5分)(2015•新课标Ⅱ)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关4.(5分)(2015•新课标Ⅱ)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.25.(5分)(2015•新课标Ⅱ)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.116.(5分)(2015•新课标Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.7.(5分)(2015•新课标Ⅱ)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.8.(5分)(2015•新课标Ⅱ)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.149.(5分)(2015•新课标Ⅱ)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.10.(5分)(2015•新课标Ⅱ)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π11.(5分)(2015•新课标Ⅱ)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.12.(5分)(2015•新课标Ⅱ)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x ﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)二、填空题13.(3分)(2015•新课标Ⅱ)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=.14.(3分)(2015•新课标Ⅱ)若x,y满足约束条件,则z=2x+y的最大值为.15.(3分)(2015•新课标Ⅱ)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是.16.(3分)(2015•新课标Ⅱ)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=.三.解答题17.(2015•新课标Ⅱ)△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC (Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.18.(2015•新课标Ⅱ)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.19.(12分)(2015•新课标Ⅱ)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.20.(2015•新课标Ⅱ)椭圆C:=1,(a>b>0)的离心率,点(2,)在C 上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.21.(2015•新课标Ⅱ)设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.四、选修4-1:几何证明选讲22.(10分)(2015•新课标Ⅱ)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.五、选修4-4:坐标系与参数方程23.(10分)(2015•新课标Ⅱ)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.六、选修4-5不等式选讲24.(10分)(2015•新课标Ⅱ)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.2015年全国统一高考数学试卷(文科)(新课标Ⅱ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分1.(5分)(2015•新课标Ⅱ)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)【分析】根据集合的基本运算进行求解即可.【解答】解:∵A={x|﹣1<x<2},B={x|0<x<3},∴A∪B={x|﹣1<x<3},故选:A.【点评】本题主要考查集合的基本运算,比较基础.2.(5分)(2015•新课标Ⅱ)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.4【分析】根据复数相等的条件进行求解即可.【解答】解:由,得2+ai=(1+i)(3+i)=2+4i,则a=4,故选:D.【点评】本题主要考查复数相等的应用,比较基础.3.(5分)(2015•新课标Ⅱ)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关【分析】A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多,故A正确;B从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,与年份负相关,故D错误.【解答】解:A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少,且减少的最多,故A正确;B2004﹣2006年二氧化硫排放量越来越多,从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,而不是与年份正相关,故D错误.故选:D.【点评】本题考查了学生识图的能力,能够从图中提取出所需要的信息,属于基础题.4.(5分)(2015•新课标Ⅱ)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.2【分析】利用向量的加法和数量积的坐标运算解答本题.【解答】解:因为=(1,﹣1),=(﹣1,2)则(2+)=(1,0)•(1,﹣1)=1;故选:C.【点评】本题考查了向量的加法和数量积的坐标运算;属于基础题目.5.(5分)(2015•新课标Ⅱ)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.11【分析】由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3.再利用等差数列的前n项和公式即可得出.【解答】解:由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3=1.则S5==5a3=5.故选:A.【点评】本题考查了等差数列的通项公式及其性质、前n项和公式,考查了推理能力与计算能力,属于中档题.6.(5分)(2015•新课标Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.【分析】由三视图判断,正方体被切掉的部分为三棱锥,把相关数据代入棱锥的体积公式计算即可.【解答】解:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,∴正方体切掉部分的体积为×1×1×1=,∴剩余部分体积为1﹣=,∴截去部分体积与剩余部分体积的比值为.故选:D.【点评】本题考查了由三视图判断几何体的形状,求几何体的体积.7.(5分)(2015•新课标Ⅱ)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.【分析】利用外接圆的性质,求出圆心坐标,再根据圆心到原点的距离公式即可求出结论.【解答】解:因为△ABC外接圆的圆心在直线BC垂直平分线上,即直线x=1上,可设圆心P(1,p),由PA=PB得|p|=,得p=圆心坐标为P(1,),所以圆心到原点的距离|OP|===,故选:B.【点评】本题主要考查圆性质及△ABC外接圆的性质,了解性质并灵运用是解决本题的关键.8.(5分)(2015•新课标Ⅱ)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.14【分析】模拟执行程序框图,依次写出每次循环得到的a,b的值,当a=b=2时不满足条件a≠b,输出a的值为2.【解答】解:模拟执行程序框图,可得a=14,b=18满足条件a≠b,不满足条件a>b,b=4满足条件a≠b,满足条件a>b,a=10满足条件a≠b,满足条件a>b,a=6满足条件a≠b,满足条件a>b,a=2满足条件a≠b,不满足条件a>b,b=2不满足条件a≠b,输出a的值为2.故选:B.【点评】本题主要考查了循环结构程序框图,属于基础题.9.(5分)(2015•新课标Ⅱ)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.【分析】利用等比数列的通项公式即可得出.【解答】解:设等比数列{a n}的公比为q,∵,a3a5=4(a4﹣1),∴=4,化为q3=8,解得q=2则a2==.故选:C.【点评】本题考查了等比数列的通项公式,属于基础题.10.(5分)(2015•新课标Ⅱ)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【分析】当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,利用三棱锥O﹣ABC体积的最大值为36,求出半径,即可求出球O的表面积.【解答】解:如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体=V C﹣AOB===36,故积最大,设球O的半径为R,此时V O﹣ABCR=6,则球O的表面积为4πR2=144π,故选:C.【点评】本题考查球的半径与表面积,考查体积的计算,确定点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大是关键.11.(5分)(2015•新课标Ⅱ)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.【分析】根据函数图象关系,利用排除法进行求解即可.【解答】解:当0≤x≤时,BP=tan x,AP==,此时f(x)=+tan x,0≤x≤,此时单调递增,当P在CD边上运动时,≤x≤且x≠时,如图所示,tan∠POB=tan(π﹣∠POQ)=tan x=﹣tan∠POQ=﹣=﹣,∴OQ=﹣,∴PD=AO﹣OQ=1+,PC=BO+OQ=1﹣,∴PA+PB=,当x=时,PA+PB=2,当P在AD边上运动时,≤x≤π,PA+PB=﹣tan x,由对称性可知函数f(x)关于x=对称,且f()>f(),且轨迹为非线型,排除A,C,D,故选:B.【点评】本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤时的解析式是解决本题的关键.12.(5分)(2015•新课标Ⅱ)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x ﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)【分析】根据函数的奇偶性和单调性之间的关系,将不等式进行转化即可得到结论.【解答】解:∵函数f(x)=ln(1+|x|)﹣为偶函数,且在x≥0时,f(x)=ln(1+x)﹣,导数为f′(x)=+>0,即有函数f(x)在[0,+∞)单调递增,∴f(x)>f(2x﹣1)等价为f(|x|)>f(|2x﹣1|),即|x|>|2x﹣1|,平方得3x2﹣4x+1<0,解得:<x<1,所求x的取值范围是(,1).故选:B.【点评】本题主要考查函数奇偶性和单调性的应用,综合考查函数性质的综合应用,运用偶函数的性质是解题的关键.二、填空题13.(3分)(2015•新课标Ⅱ)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=﹣2.【分析】f(x)是图象过点(﹣1,4),从而该点坐标满足函数f(x)解析式,从而将点(﹣1,4)带入函数f(x)解析式即可求出a.【解答】解:根据条件得:4=﹣a+2;∴a=﹣2.故答案为:﹣2.【点评】考查函数图象上的点的坐标和函数解析式的关系,考查学生的计算能力,比较基础.14.(3分)(2015•新课标Ⅱ)若x,y满足约束条件,则z=2x+y的最大值为8.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z 的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线y=﹣2x+z的截距最大,此时z最大.由,解得,即A(3,2)将A(3,2)的坐标代入目标函数z=2x+y,得z=2×3+2=8.即z=2x+y的最大值为8.故答案为:8.【点评】本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.15.(3分)(2015•新课标Ⅱ)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是x2﹣y2=1.【分析】设双曲线方程为y2﹣x2=λ,代入点,求出λ,即可求出双曲线的标准方程.【解答】解:设双曲线方程为y2﹣x2=λ,代入点,可得3﹣=λ,∴λ=﹣1,∴双曲线的标准方程是x2﹣y2=1.故答案为:x2﹣y2=1.【点评】本题考查双曲线的标准方程,考查学生的计算能力,正确设出双曲线的方程是关键.16.(3分)(2015•新课标Ⅱ)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=8.【分析】求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y =ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.【解答】解:y=x+lnx的导数为y′=1+,曲线y=x+lnx在x=1处的切线斜率为k=2,则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2,即y=2x﹣1.由于切线与曲线y=ax2+(a+2)x+1相切,故y=ax2+(a+2)x+1可联立y=2x﹣1,得ax2+ax+2=0,又a≠0,两线相切有一切点,所以有△=a2﹣8a=0,解得a=8.故答案为:8.【点评】本题考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处的导数,设出切线方程运用两线相切的性质是解题的关键.三.解答题17.(2015•新课标Ⅱ)△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC (Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.【分析】(Ⅰ)由题意画出图形,再由正弦定理结合内角平分线定理得答案;(Ⅱ)由∠C=180°﹣(∠BAC+∠B),两边取正弦后展开两角和的正弦,再结合(Ⅰ)中的结论得答案.【解答】解:(Ⅰ)如图,由正弦定理得:,∵AD平分∠BAC,BD=2DC,∴;(Ⅱ)∵∠C=180°﹣(∠BAC+∠B),∠BAC=60°,∴,由(Ⅰ)知2sin∠B=sin∠C,∴tan∠B=,即∠B=30°.【点评】本题考查了内角平分线的性质,考查了正弦定理的应用,是中档题.18.(2015•新课标Ⅱ)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.【分析】(I)根据分布表的数据,画出频率直方图,求解即可.(II)计算得出∁A表示事件:“A地区用户的满意度等级为不满意”,∁B表示事件:“B地区用户的满意度等级为不满意”,P(∁A),P(∁B),即可判断不满意的情况.【解答】解:(Ⅰ)通过两个地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B地区的用户满意度评分的比较集中,而A地区的用户满意度评分的比较分散.(Ⅱ)A地区用户的满意度等级为不满意的概率大.记∁A表示事件:“A地区用户的满意度等级为不满意”,∁B表示事件:“B地区用户的满意度等级为不满意”,由直方图得P(∁A)=(0.01+0.02+0.03)×10=0.6得P(∁B)=(0.005+0.02)×10=0.25∴A地区用户的满意度等级为不满意的概率大.【点评】本题考查了频率直方图,频率表达运用,考查了阅读能力,属于中档题.19.(12分)(2015•新课标Ⅱ)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.【分析】(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.【解答】解:(Ⅰ)交线围成的正方形EFGH如图所示;(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EFGH为正方形,所以EH=EF=BC=10,于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.【点评】本题考查平面与平面平行的性质,考查学生的计算能力,比较基础.20.(2015•新课标Ⅱ)椭圆C:=1,(a>b>0)的离心率,点(2,)在C 上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.【分析】(1)利用椭圆的离心率,以及椭圆经过的点,求解椭圆的几何量,然后得到椭圆的方程.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),联立直线方程与椭圆方程,通过韦达定理求解K OM,然后推出直线OM的斜率与l的斜率的乘积为定值.【解答】解:(1)椭圆C:=1,(a>b>0)的离心率,点(2,)在C上,可得,,解得a2=8,b2=4,所求椭圆C方程为:.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),把直线y=kx+b代入可得(2k2+1)x2+4kbx+2b2﹣8=0,故x M==,y M=kx M+b=,于是在OM的斜率为:K OM==,即K OM•k=.∴直线OM的斜率与l的斜率的乘积为定值.【点评】本题考查椭圆方程的综合应用,椭圆的方程的求法,考查分析问题解决问题的能力.21.(2015•新课标Ⅱ)设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.【分析】(Ⅰ)先求导,再分类讨论,根据导数即可判断函数的单调性;(2)先求出函数的最大值,再构造函数(a)=lna+a﹣1,根据函数的单调性即可求出a 的范围.【解答】解:(Ⅰ)f(x)=lnx+a(1﹣x)的定义域为(0,+∞),∴f′(x)=﹣a=,若a≤0,则f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,若a>0,则当x∈(0,)时,f′(x)>0,当x∈(,+∞)时,f′(x)<0,所以f(x)在(0,)上单调递增,在(,+∞)上单调递减,(Ⅱ),由(Ⅰ)知,当a≤0时,f(x)在(0,+∞)上无最大值;当a>0时,f(x)在x=取得最大值,最大值为f()=﹣lna+a﹣1,∵f()>2a﹣2,∴lna+a﹣1<0,令g(a)=lna+a﹣1,∵g(a)在(0,+∞)单调递增,g(1)=0,∴当0<a<1时,g(a)<0,当a>1时,g(a)>0,∴a的取值范围为(0,1).【点评】本题考查了导数与函数的单调性最值的关系,以及参数的取值范围,属于中档题.四、选修4-1:几何证明选讲22.(10分)(2015•新课标Ⅱ)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【分析】(1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;﹣S (2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC计算即可.△AEF【解答】(1)证明:∵△ABC为等腰三角形,AD⊥BC,∴AD是∠CAB的角平分线,又∵圆O分别与AB、AC相切于点E、F,∴AE=AF,∴AD⊥EF,∴EF∥BC;(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,又∵EF为圆O的弦,∴O在AD上,连结OE、OM,则OE⊥AE,由AG等于圆O的半径可得AO=2OE,∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,∵AE=2,∴AO=4,OE=2,∵OM=OE=2,DM=MN=,∴OD=1,∴AD=5,AB=,∴四边形EBCF的面积为×﹣××=.【点评】本题考查空间中线与线之间的位置关系,考查四边形面积的计算,注意解题方法的积累,属于中档题.五、选修4-4:坐标系与参数方程23.(10分)(2015•新课标Ⅱ)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.【分析】(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,把代入可得直角坐标方程.同理由C3:ρ=2cosθ.可得直角坐标方程,联立解出可得C2与C3交点的直角坐标.(2)由曲线C1的参数方程,消去参数t,化为普通方程:y=x tanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),利用|AB|=即可得出.【解答】解:(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,∴x2+y2=2y.同理由C3:ρ=2cosθ.可得直角坐标方程:,联立,解得,,∴C2与C3交点的直角坐标为(0,0),.(2)曲线C1:(t为参数,t≠0),化为普通方程:y=x tanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),∵A,B都在C1上,∴A(2sinα,α),B.∴|AB|==4,当时,|AB|取得最大值4.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.六、选修4-5不等式选讲24.(10分)(2015•新课标Ⅱ)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.【分析】(1)运用不等式的性质,结合条件a,b,c,d均为正数,且a+b=c+d,ab>cd,即可得证;(2)从两方面证,①若+>+,证得|a﹣b|<|c﹣d|,②若|a﹣b|<|c﹣d|,证得+>+,注意运用不等式的性质,即可得证.【解答】证明:(1)由于(+)2=a+b+2,(+)2=c+d+2,由a,b,c,d均为正数,且a+b=c+d,ab>cd,则>,即有(+)2>(+)2,则+>+;(2)①若+>+,则(+)2>(+)2,即为a+b+2>c+d+2,由a+b=c+d,则ab>cd,于是(a﹣b)2=(a+b)2﹣4ab,(c﹣d)2=(c+d)2﹣4cd,即有(a﹣b)2<(c﹣d)2,即为|a﹣b|<|c﹣d|;②若|a﹣b|<|c﹣d|,则(a﹣b)2<(c﹣d)2,即有(a+b)2﹣4ab<(c+d)2﹣4cd,由a+b=c+d,则ab>cd,则有(+)2>(+)2.综上可得,+>+是|a﹣b|<|c﹣d|的充要条件.【点评】本题考查不等式的证明,主要考查不等式的性质的运用,同时考查充要条件的判断,属于基础题.。
2015年高考全国2卷文科数学试题(含解析)

绝密★启用前 2015年高考全国2卷文科数学试题(含解析)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释)1.已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =( )A .()1,3- B .()1,0- C .()0,2 D .()2,32.若为a 实数,且2i3i 1ia +=++,则a =( ) A .4- B .3- C .3 D .43.根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化碳排放量的效果最显著B .2007年我国治理二氧化碳排放显现成效C .2006年以来我国二氧化碳年排放量呈减少趋势D .2006年以来我国二氧化碳年排放量与年份正相关4.已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a ( )A .1-B .0C .1D .25.设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( ) A .5 B .7 C .9 D .116.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为()1A.81B.71C.61D.57.已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为( )5A.334D.38.下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为( )A.0B.2C.4D.149.已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( )A.2B.11C.21D.810.已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为( ) A.36π B. 64π C.144π D. 256π11.如图,长方形的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC,CD 与DA 运动,记BOP x ∠= ,将动点P 到A,B 两点距离之和表示为x 的函数()f x ,则的图像大致为( )12.设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫-⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)13.已知函数()32f x ax x=-的图像过点(-1,4),则a=.14.若x,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z=2x+y 的最大值为.15.已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为. 16.已知曲线lny xx =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a=.三、解答题(题型注释)17.(本小题满分12分)△ABC 中D 是BC 上的点,AD 平分∠BAC,BD=2DC. (Ⅰ)求sin sin BC∠∠ ;(Ⅱ)若60BAC ∠=,求B ∠.18.(本小题满分12分)某公司为了了解用户对其产品的满意度,从A,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频率分布表 满意度评分分组[50,60)[50,60)[50,60)[50,60)[50,60)频数 2814106(Ⅰ)在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)B 地区用户满意度评分的频率分布直方图(Ⅱ)根据用户满意度评分,将用户的满意度评分分为三个等级: 满意度评分 低于70分 70分到89分 不低于90分 满意度等级 不满意满意非常满意估计那个地区的用户的满意度等级为不满意的概率大,说明理由.19.(本小题满分12分)如图,长方体1111ABCD A B C D -中AB=16,BC=10,18AA =,点E,F 分别在1111,A B DC上,11 4.A E D F ==过点E,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法与理由); (Ⅱ)求平面α把该长方体分成的两部分体积的比值.20.(本小题满分12分)已知椭圆()2222:10x y C a b a b+=>>,点(在C 上.(Ⅰ)求C 的方程;(Ⅱ)直线l 不经过原点O,且不平行于坐标轴,l 与C 有两个交点A,B,线段AB 中点为M,证明:直线OM 的斜率与直线l 的斜率乘积为定值.21.(本小题满分12分)已知()()ln 1f x x a x =+-.(Ⅰ)讨论()f x 的单调性;(Ⅱ)当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.22.(本小题满分10分)选修4-1:几何证明选讲如图O 是等腰三角形ABC 内一点,圆O 与△ABC 的底边BC 交于M,N 两点,与底边上的高交于点G,且与AB,AC 分别相切于E,F 两点.(Ⅰ)证明EFBC ;(Ⅱ)若AG 等于圆O 半径,且AE MN ==求四边形EBCF 的面积. 23.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ==(Ⅰ)求2C 与3C 交点的直角坐标;(Ⅱ)若1C 与2C 相交于点A,1C 与3C 相交于点B,求AB最大值.24.(本小题满分10分)选修4-5:不等式证明选讲 设,,,a b c d 均为正数,且a b c d +=+.证明:(Ⅰ)若ab cd > ,>>a b c d-<-的充要条件.参考答案1.A 【解析】因为{}|12A x x =-<<,{}|03B x x =<<,所以{}|13.A B x x =-<<故选A.考点:本题主要考查不等式基础知识及集合的交集运算. 2.D【解析】由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D.考点:本题主要考查复数的乘除运算,及复数相等的概念. 3. D【解析】由柱形图可知2006年以来,我国二氧化碳排放量基本成递减趋势,所以二氧化碳排放量与年份负相关,故选D.考点:本题主要考查统计知识及对学生柱形图的理解 4.C 【解析】试题分析:由题意可得2112=+=a ,123,⋅=--=-a b 所以()222431+⋅=+⋅=-=a ba a ab .故选C.考点:本题主要考查向量数量积的坐标运算. 5.A 【解析】试题解析:由13533331a a a a a ++==⇒=,所有()15535552a a S a +===.故选A. 考点:本题主要考查等差数列的性质及前n 项和公式的应用. 6.D 【解析】试题分析:如图所示,截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为15,故选D. 考点:本题主要考查三视图及几何体体积的计算. 7.B 【解析】试题分析:△ABC 外接圆圆心在直线BC 垂直平分线上即直线1x =上,设圆心D ()1,b ,由DA=DB得3b b =⇒=,所以圆心到原点的距离3d ==. 故选B. 考点:本题主要考查圆的方程的求法,及点到直线距离公式. 8.B 【解析】试题分析:由题意可知输出的a 是18,14的最大公约数2,故选B. 考点:本题主要考查程序框图及更相减损术. 9.C【解析】试题分析:由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C. 考点:本题主要考查等比数列性质及基本运算.【解析】试题分析:设球的半径为R,则△AOB 面积为212R ,三棱锥O ABC - 体积最大时,C 到平面AOB 距离最大且为R,此时313666V R R ==⇒= ,所以球O 的表面积24π144πS R ==.故选C.考点:本题主要考查球与几何体的切接问题及空间想象能力. 11.B 【解析】试题分析:由题意可得ππππ12424f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==⇒< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,由此可排除C,D ;当π04x <<时点P 在边BC 上,tan PB x =,PA =,所以()tan f x x =可知π0,4x ⎛⎫∈ ⎪⎝⎭时图像不是线段,可排除A,故选B. 考点:本题主要考查函数的识图问题及分析问题解决问题的能力. 12.A 【解析】试题分析:由21()ln(1||)1f x x x =+-+可知()f x 是偶函数,且在[)0,+∞是增函数,所以()()()()()2212121212113f x f x f x f x x x x x x >-⇔>-⇔>-⇔>-⇔<< .故选A.考点:本题主要考查函数的奇偶性、单调性及不等式的解法. 13.-2 【解析】试题分析:由()32f x ax x=-可得()1242f a a -=-+=⇒=- .考点:本题主要考查利用函数解析式求值.【解析】试题分析:不等式组50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩表示的可行域是以()()()1,1,2,3,3,2为顶点的三角形区域,2z x y =+的最大值必在顶点处取得,经验算,3,2x y ==时max 8z =. 考点:本题主要考查线性规划知识及计算能力.15.2214x y -= 【解析】试题分析:根据双曲线渐近线方程为12y x =±,可设双曲线的方程为224x y m -= ,把(代入224x y m -=得1m =.所以双曲线的方程为2214x y -=.考点:本题主要考查双曲线几何性质及计算能力. 16.8 【解析】试题分析:由11y x'=+可得曲线ln y x x =+在点()1,1处的切线斜率为2,故切线方程为21y x =-,与()221y ax a x =+++ 联立得220ax ax ++=,显然0a ≠,所以由2808a a a ∆=-=⇒=.考点:本题主要考查导数的几何意义及直线与抛物线相切问题. 17.(Ⅰ)12;(Ⅱ)30. 【解析】试题分析:(Ⅰ)利用正弦定理转化得:sin 1.sin 2B DC C BD ∠==∠(Ⅱ)由诱导公式可得()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由(Ⅰ)知2sin sin B C ∠=∠,所以tan 30.B B ∠=∠= 试题解析:(Ⅰ)由正弦定理得,,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠ 因为AD 平分∠BAC,BD=2DC,所以sin 1.sin 2B DC C BD ∠==∠.(Ⅱ)因为()180,60,C BAC B BAC ∠=-∠+∠∠=所以()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由(I )知2s i n s i n B C ∠=∠,所以tan 30.B B ∠=∠= 考点:本题主要考查正弦定理及诱导公式的应用,意在考查考生的三角变换能力及运算能力. 18.(Ⅰ)见试题解析(Ⅱ)A 地区的用户的满意度等级为不满意的概率大. 【解析】试题分析:(Ⅰ)通过两地区用户满意度评分的频率分布直方图可以看出,B 地区用户满意度评分的平均值高于A 地区用户满意度评分的平均值,B 地区用户满意度评分比较集中,而A 地区用户满意度评分比较分散.(II )由直方图得()A P C 的估计值为0.6,()B PC 的估计值为0.25.,所以A 地区的用户的满意度等级为不满意的概率大. 试题解析:(Ⅰ)通过两地区用户满意度评分的频率分布直方图可以看出,B 地区用户满意度评分的平均值高于A 地区用户满意度评分的平均值,B 地区用户满意度评分比较集中,而A 地区用户满意度评分比较分散.(Ⅱ)A 地区的用户的满意度等级为不满意的概率大.记A C 表示事件“A 地区的用户的满意度等级为不满意”;B C 表示事件“B 地区的用户的满意度等级为不满意”.由直方图得()A P C 的估计值为()0.010.020.03100.6++⨯=,()B PC 的估计值为()0.0050.02100.25.+⨯=,所以A 地区的用户的满意度等级为不满意的概率大. 考点:本题主要考查频率分布直方图及概率估计. 19.(Ⅰ)见试题解析(Ⅱ)97 或79【解析】试题分析:(Ⅰ)分别在,AB CD 上取H,G,使10AH DG ==;长方体被平面α 分成两个高为10的直棱柱,可求得其体积比值为97 或79试题解析:解:(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作,EM AB ⊥ 垂足为M,则14AM A E ==,112EB =,18EM AA ==,因为EHGF 是正方形,所以10EH EF BC ===,于是6,10, 6.MH AH HB ====因为长方体被平面α 分成两个高为10的直棱柱,所以其体积比值为97 (79也正确). 考点:本题主要考查几何体中的截面问题及几何体的体积的计算.20.(Ⅰ)2222184x y +=(Ⅱ)见试题解析【解析】试题分析:(Ⅰ)由2242,1,2a a b=+=求得228,4a b ==,由此可得C 的方程.(II )把直线方程与椭圆方程联立得()222214280.k x kbx b +++-=,所以12222,,22121M M M x x kb bx y kx b k k +-===+=++于是1,2M OM M y k x k==-12OM k k ⇒⋅=-.试题解析:解:(Ⅰ)由题意有2242,1,2a a b =+= 解得228,4a b ==,所以椭圆C 的方程为2222184x y +=. (Ⅱ)设直线():0,0l y kx b k b =+≠≠,()()()1122,,,,,M M A x y B x y M x y ,把y kx b=+代入2222184x y +=得()222214280.k x kbx b +++-=故12222,,22121M M M x x kb bx y kx b k k +-===+=++ 于是直线OM 的斜率1,2M OM M y k x k ==- 即12OM k k ⋅=-,所以直线OM 的斜率与直线l 的斜率乘积为定值. 考点:本题主要考查椭圆方程、直线与椭圆及计算能力、逻辑推理能力.21.(Ⅰ)0a ≤,()f x 在()0,+∞是单调递增;0a >,()f x 在10,a ⎛⎫ ⎪⎝⎭单调递增,在1,a⎛⎫+∞⎪⎝⎭单调递减;(Ⅱ)()0,1.【解析】试题分析:(Ⅰ)由()1f x a x'=-,可分0a ≤,0a >两种情况来讨论;(II )由(I )知当0a ≤时()f x 在()0,+∞无最大值,当0a >时()f x 最大值为1ln 1.f a a a ⎛⎫=-+- ⎪⎝⎭因此122ln 10f a a a a ⎛⎫>-⇔+-< ⎪⎝⎭.令()ln 1g a a a =+-,则()g a 在()0,+∞是增函数,当01a <<时,()0g a <,当1a >时()0g a >,因此a 的取值范围是()0,1.试题解析:(Ⅰ)()f x 的定义域为()0,+∞,()1f x a x'=-,若0a ≤,则()0f x '>,()f x 在()0,+∞是单调递增;若0a >,则当10,x a ⎛⎫∈ ⎪⎝⎭时()0f x '>,当1,x a ⎛⎫∈+∞ ⎪⎝⎭时()0f x '<,所以()f x 在10,a ⎛⎫ ⎪⎝⎭单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭单调递减.(Ⅱ)由(Ⅰ)知当0a ≤时()f x 在()0,+∞无最大值,当0a >时()f x 在1x a=取得最大值,最大值为111l n1l n 1.f a a a a a a ⎛⎫⎛⎫⎛⎫=+-=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因此122l n 10f a a aa ⎛⎫>-⇔+-< ⎪⎝⎭.令()ln 1g a a a =+-,则()g a 在()0,+∞是增函数,()10g =,于是,当01a <<时,()0g a <,当1a >时()0g a >,因此a 的取值范围是()0,1.考点:本题主要考查导数在研究函数性质方面的应用及分类讨论思想.22. 【解析】试题分析:(Ⅰ)要证明EFBC ,可证明,AD BC ⊥AD EF ⊥;(Ⅱ)先求出有关线段的长度,然后把四边形EBCF 的面积转化为△ABC 和△AEF 面积之差来求. 试题解析:(Ⅰ)由于△ABC 是等腰三角形,,AD BC ⊥ 所以AD 是CAB ∠的平分线,又因为圆O 与AB,AC 分别相切于E,F,所以AE AF =,故AD EF ⊥,所以EFBC .(Ⅱ)由(Ⅰ)知AE AF =,AD EF ⊥,故AD 是EF 的垂直平分线,又EF 为圆O 的弦,所以O 在AD 上,连接OE,OF,则OE AE ⊥,由AG 等于圆O 的半径得AO=2OE,所以30OAE ∠=,因此,△ABC 和△AEF 都是等边三角形,,因为AE =,所以4,2,AO OE == 因为2,OM OE ==12DM MN == 所以OD=1,于是AD=5,AB = 所以四边形DBCF的面积为(221122⨯-⨯=⎝⎭考点:本题主要考查几何证明、四边形面积的计算及逻辑推理能力.23.(Ⅰ)()30,0,22⎛⎫⎪ ⎪⎝⎭;(Ⅱ)4.试题分析:(Ⅰ)把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,220x y +-=,联立解方程组可得交点坐标;(Ⅱ)先确定曲线1C 极坐标方程为(),0,θαρρ=∈≠R 进一步求出点A 的极坐标为()2si n ,αα,点B 的极坐标为(),αα,,由此可得2sin 4sin 43AB πααα⎛⎫=-=-≤ ⎪⎝⎭.试题解析:解:(Ⅰ)曲线2C 的直角坐标方程为2220x y y +-=,曲线3C 的直角坐标方程为220x y +-=,联立两方程解得00x y =⎧⎨=⎩或32x y ⎧=⎪⎪⎨⎪=⎪⎩,所以2C 与3C 交点的直角坐标()30,0,22⎛⎫⎪ ⎪⎝⎭.(Ⅱ)曲线1C 极坐标方程为(),0,θαρρ=∈≠R 其中0απ≤< ,因此点A 的极坐标为()2sin ,αα,点B的极坐标为(),αα,所以2sin cos 4sin 3AB πααα⎛⎫=-=- ⎪⎝⎭,当56πα=时AB 取得最大值,最大值为4.考点:本题主要考查参数方程、直角坐标及极坐标方程的互化.圆的方程及三角函数的最值. 24. 【解析】试题分析:(Ⅰ)由a b c d +=+及ab cd >,可证明22>,开方即得>(Ⅱ)本小题可借助第一问的结论来证明,但要分必要性与充分性来证明.解:(Ⅰ)因为22a b c d =++=++由题设a b c d +=+,ab cd >,得22>,>(Ⅱ)(ⅰ)若a b c d-<-,则()()22a b c d -<-,即()()2244,a b ab c d cd +-<+- 因为a b c d +=+,所以ab cd >,>(ⅱ)若>,则22>,即a b c d ++>++因为a b c d +=+,所以ab cd >,于是()()()()222244,a b a b a b c d c dc d-=+-<+-=-因此a b c d-<-,综上a b c d-<-的充要条件.考点:本题主要考查不等式证明及充分条件与必要条件.。
湖南省长郡中学2015届高三月考试卷(三)数学(文)试卷
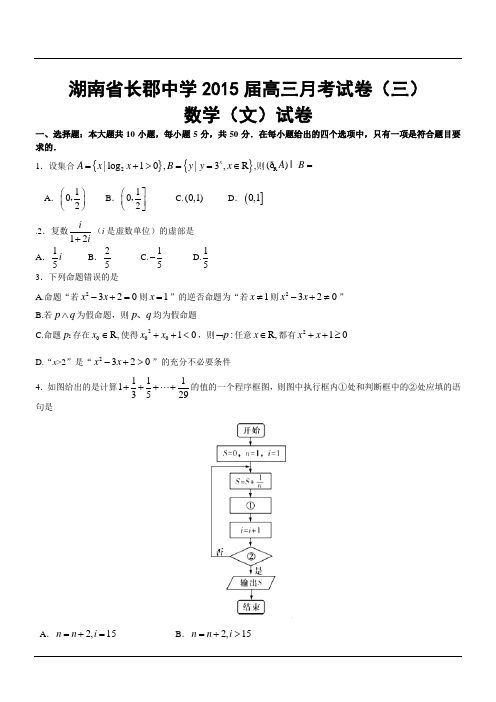
湖南省长郡中学2015届高三月考试卷(三)数学(文)试卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}{}2|log 10,|3,R xA x xB y y x =+>==∈,则R ()A B =ðA .102⎛⎫ ⎪⎝⎭, B .102⎛⎤ ⎥⎝⎦,C.(0,1)D .(]0,1.2.复数12ii +(i 是虚数单位)的虚部是 A .15i B .25 C.15- D.153.下列命题错误的是A.命题“若2320x x -+=则1x =”的逆否命题为“若1x ≠则2320x x -+≠” B.若p q ∧为假命题,则p q 、均为假命题C.命题p :存在0R,x ∈使得20010x x ++<,则:p ⌝任意R,x ∈都有210x x ++≥ D.“x >2”是“2320x x -+>”的充分不必要条件 4.如图给出的是计算11113529+++⋅⋅⋅+的值的一个程序框图,则图中执行框内①处和判断框中的②处应填的语句是A .2,15n n i =+=B .2,15n n i =+>C .1,15n n i =+=D .1,15n n i =+>5.则两变量的回归直线方程为A.0.56997.4y x =+B.0.63231.2y x =-C.50.2501.4y x =+D.60.4400.7y x =+6.已知函数21,(0),()(1)1,(0),x x f x f x x ⎧-≤=⎨-+>⎩把方程()0f x x -=的根按从小到大的顺序排成一个数列,则该数列的前n 项和为A.21(N )n n S n +=-∈B.(1)(N )2n n n S n +-=∈ C.1(N )n S n n +=-∈D.12(N )n n S n -+=∈7.一个几何体的三视图如图所示,则这个几何体的体积等于8.已知点F 1、F 2分别是椭圆22221x y a b+=的左、右焦点,过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点,若△ABF 2为正三角形,则该椭圆的离心率e 是A.12 B. 2 C. 13 D 9.已知函数()xf x e ax b =--,若()0f x ≥恒成立,则ab 的最大值为B.2eC.eD.2e 10.A ,B ,C 是平面内不共线的三点,点P 在该平面内且有23PA PB PC ++=0,现将一粒芝麻随机撒在△ABC 内,则这粒芝麻落在△PBC 内的概率为A.13B.14C.15D.16二、填空题:本大题共5小题,每小题5分,共25分。
湖南省长沙长郡中学2015届高三上学期第四次月考英语试题(word版)

湖南省长沙长郡中学2015届高三上学期第四次月考英语试题(word版)本试卷分为四个部分,包括听力、语言知识运用、阅读和书面表达。
时量1 20分钟。
满分1 50Part I Listening Comprehension (30 marks)Section A (22.5 marks)Directions In this section ,you will hear six conversations between two speakers.For each conversation , there are.several questions and each question is followed by three choices markedA ,B and C.Listen carefully and then choose the best answer for each question.You will hear each conversation TWICE.Conversation 11.Who used the car this morning?A.The son.B.The aunt.C.The mother.2.Where are the keys found?A.In the purse.B.In the pocket. C.In the drawer.Conversation 23.Which of the following is TRUE about the man?A.He borrowed some money.B.He is caught in the traffic.C.He will meet his teacher.4.How is the man going home?A.By train.B.By bus.C.By taxi.Conversation 35.When was the party held?A.In the morning.B.In the afternoon. C.In the evening.6.Why didn't the woman go to the party?A.She didn't feel well.B.She didn't have the time.C.She didn't get an invitation.Conversation 47.What does the man want to buy?A.A camera.B.A mobile phone.C.A music player.8.Which of the following does the man choose?A.The PE310.B.The RT230.C.The FG160.9.How much does the man pay?A.$300.B.$270.C.$100.Conversation 510.What is the woman?A.A dress designer.B.A basketball player. C.A headmaster.11.What do we know about the man s travel plan?A.He's going by air.B.He's leaving for Paris.C.He's arriving this afternoon.12.Who is going to pick up the man?A.The woman's son.B.The woman's brother.C.The woman herself.Conversation 613.What is the man doing now?A.Looking for a job.B.Studying in a university.C.Teaching at a high school.14.What kind of movie does the man like best?A.Adventure.B.Comedy.C.Drama.15.Where are the speakers going first?A.The supermarket.B.The cinema. C.The cafe.Section B (7.5 marks)Directions In this section @ you will hear a short passage.Listen carefully and then fill in thenumbered blanks with the information you've got.Fill in each blank with NO MORE TH.AN THREE WORDS.You will hear the short passage.TWICE.Essav competition introductionPart ⅡLanguage Knowledge (45 marks)Section A (15 marks)Directions Beneath each of the following sentences there, are four choices marked A,B,C and.D.Choose the one that best completes the sentence.21.It was never clear _____ the man hadn't reported the accident sooner.A.that B.what C.when D.why 22.After the fierce competition, the students were taken to their camp, _____ they would rest for next round.A.where B.who C.which D.what23.To learn English well, we should find opportunities to hear English as much as we can.A.speak B.speaking C.spoken D.to speak24.—Why.Jack, you look so tired!—Well.I the house and I must finish the work tomorrow.A.was painting B.will be paintingC.have painted D.have been painting25.So sudden_____ that the enemy had no time to escape.A.did the attack B.the attack didC.was the attack D.the attack was26.It's not the score you've got, but the attitude you choose ______ determines our evaluation of your work.A.which B.that C.what D.who27.All we are required to do ______ record a "weike" where we explain what we think students are puzzled about.A.are B.is C.was D.were 28.Our school called on us to donate our pocket money to the school damaged by the flood, _____ the students to return to their classrooms.A.enabling B.having enabled C.enable D.to have enabled 29.—I prefer shutting myself in and listening to music all day on Sundays.—That's_____I don't agree.You should have a more active life.A.where B.how C.when D.what 30.John thinks it won't be long _____ he is ready for his new job.A.when B.after C.before D.since31._____ an important decision more on emotion than on reason, you will regret it sooner or later.A.Based B.Basing C.Base D.To base 32.The manager is said to have arrived back from Paris where he ______ some European partners.A.would meet B.is meeting C.meets D.had met 33._____ something to drink, as the movie will last three hours.A.Grab B.To grab C.Grabbing D.Grabbed 34.The president hopes that the people will be better off when he quits than when he _____.A.has started B.starts C.started D.will start 35.—I left my handbag on the train, but luckily someone gave it to a railway official.—How unbelievable to get it back! I mean.someone _____ it.A.will have stolen B.might have stolenC.should have stolen D.must have stolenSection B (18 marks)Directions For each blank in the following passage there, are.four words or phrases marked A, B, C and D.Fill in each blank with the word or phrase that best fits the context.Michael Greenberg is a very popular New Yorker.He is not famous in sports or the arts.But people in the streets know about him, especially those who are 36For those people, he is "Gloves" Greenberg.How did he get that name? He looks like anyother businessman, wearing a suit and carrying a briefcase (公文箱).But he's 37 His briefcase always has some gloves.In winter, Mr.Greenberg does not 38 like other New Yorkers.who look at the sidewalk and 39 the street.He looks around at people.He stops when he sees someone with no gloves.He gives them a pair and then he 40 , looking for more people with cold hands.On winter days.Mr.Greenberg gives away gloves.During the rest of the year, he 41 gloves.People who have heard about him 42 him gloves, and he has many in his apartment.Mr.Greenberg began doing this 21 years ago.Now.many poor New Yorkers know him and 43 his behavior.But people who don't know him are sometimes 44 him.They don't realize that he just wants to make them 45 .It runs in the 46 Michael's father always helped the poor as he believed it made everyone happier.Michael Greenberg feels the same.A pair of gloves may be a 47 thing.but it can make a big difference in winter.36.A.old B.busy C.kind D.poor 37.A.calm B.different C.crazy D.curious 38.A.act B.Sound C.feel D.dress 39.A.cross over B.drive along C.hurry down D.keep off 40.A.holds up B.hangs out C.moves on D.turns around 41.A.borrows B.sells C.returns D.buys 42.A.call B.send C.lend D.show 43.A.understand B.dislike C.study D.excuse 44.A.sorry for B.satisfied with C.proud of D.surprised by 45.A.smart B.rich C.special D.happy 46.A.city B.family C.neighborhood D.company 47.A.small B.useful C.delightful D.comforting Section C (12 marks)Directions Complete the following passage by filling in each blank with one word.that best fits the context.One day the employees of a large company returned from their lunch and were greeted with a sign on the front door.48 sign said "Yesterday the person who has been limiting your growth in this company passed 49 .We invite you to join the funeral in the room that has been prepared in the gym."At first everyone was sad to hear 50 one of their colleagues had died.but after a while they started getting curious 51 who this person might be.The excitement grew 52 the employees arrived at the gym to pay their last respect.Everyone wondered "Who is this person that was limiting my progress? Well.at least he is no longer here."One by one the employees got closer to the coffin(棺材)53 when they look inside it they suddenly became speechless.There was a mirror inside the coffin everyone 54 looked inside it could see himself.There was also a sign next to the mirror that said "There is only one person who is capable to set limits to your growth it is 55 "Part m Reading Comprehension (30 marks)Directions Read the following three passages.Each passage is followed by several questions or unfinished statements.For each of them there, are four choices marked A,B,C and D.Choosethe.one that fits best according to the information given in the.passage.AJerry was a unique manager because he had several waiters who had followed him around from restaurant to restaurant.The reason the waiters followed Jerry was because of his attitude.He was a natural motivator.It an employee was having a bad day.Jerry was there telling the employee how to look on the positive side of the situation.Seeing this style really made me curious, so one day I went up to Jerry and asked him, "I don't get it! You can't be a positive person all of the time.How do you do it?" Jerry replied, "Each morning I wake up and say to myself, "Jerry, you have two choices today.You can choose to be in a good mood or you can choose to be in a bad mood.' I choose to be in a good mood.Each time something bad happens, I can choose to be a victim or I can choose to learn from it.I choose to learn from it.Every time someone comes to me complaining.I can choose to accept their complaining or I can point out the positive side of life.I choose the positive side of life.The bottom line It's your choice how you live life." I reflected on what Jerry said.Later.I left the restaurant industry to start my own business.We lost touch, but I often thought about him when I made a choice about life.Several years later.I heard that Jerry did something you are never supposed to do in a restaurant business he left the back door open one morning and was held up at gun point by three armed robbers.While trying to open the safe, he forgot the password, nervous.The robbers panicked and shot him.Luckily, Jerry was found relatively quickly and rushed to the local hospital.After 18 hours of surgery and weeks of intensive care.Jerry was released from the hospital with fragments(碎片)of the bullets still in his body.I saw Jerry about six months after the accident.When I asked him how he was.he replied."The first thing that went through my mind was that I should have locked the back door," Jerry replied."Then, as I lay on the floor.I remembered that I had two choices I could choose to live.or I could choose to die.I chose to live." " Weren ' t you scared? Did you lose consciousness?" I asked.Jerry continued, "The doctors and nurses were great.They kept telling me I was going to be fine.But when they wheeled me into the emergency room and I saw the expressions on the faces of the doctors and nurses, I got really scared.I knew I needed to take action.""What did you do?" I asked."Well, there was a big.strong nurse shouting questions at me." said Jerry."She asked if I was allergic (过敏的)to anything."Yes.' I replied.The doctors and nurses stopped working as they waited for my reply.I took a deep breath and yelled, "Bullets!' Over their laughter, I told them."I am choosing to live.Operate on me as if I am alive, not dead.'"Jerry lived thanks to the skill of his doctors, but also because of his amazing attitude.I learned from him that every day we have the choice to live fully.56.The author left Jerry's restaurant because he_____.A.wanted to start business on his ownB.was afraid of another robbery laterC.was not equal to the job any longerD.didn't get along well with others57.Why was Jerry shot?A.Because he left the back door open.B.Because he opened the safe too slowly.C.Because he pretended to forget the password.D.Because he didn't open the safe in time.58.What was Jerry really afraid in the emergency room?A.The doctors and nurses refused to save him.B.He decided to take action to live again.C.The doctors and nurses came with expressions of regret at his being shotD.He might not be saved by doctors and nurses.59.From the passage we can learn that Jerry _____.A.was no longer positive to his life after the operationB.was optimistic even when things were at their worstC.influenced all his colleagues in many waysD.was badly injured and stayed in hospital for six months60.Which of the following is conveyed in this article?A.Where there is life.there is hope.B.Everything comes to him who waits.C.Humor is the best medicine that creates miracle.D.Attitude determines everything.BAn old problem is getting new attention in the United State s—bullying.Recent cases included the tragic case of a fifteen-year-old girl whose family moved from Ireland.She hanged herself in Massachusetts in January following months of bullying.Her parents criticized her school for failing to protect her.Officials have brought criminal charges against several teenagers.Judy Kaczynski is president of an anti-bullying group called Bully Police USA.Her daughter Tina was the victim of severe bullying starting in middle school in the state of Minnesota.She said, "Our daughter was a very outgoing child.She was a bubbly personality, very involved in all kinds of things, had lots of friends.And over a period of time her grades fell completely.She started having health issues.She couldn't sleep.She wasn't eating.She had terrible stomach pains.She started clenching(紧握,紧咬)her jaw and grinding her teeth at night.She didn't want to go to school."Bullying is defined as negative behavior repeated over time against the same person.It can involve physical violence.Or it can be verba l—for example, insults or threats.Spreading lies about someone or excluding a person from a group is known as social or relational bullying.And now there is cyberbullying, which uses the Internet, e-mail or text messages.It has easy appeal for the bully because it does not involve face-to-face contact and it can be done at any time.The first serious research studies into bullying were done in Norway in the late 1970s.The latest government study in the United States was released last year.It found that about one-third of students aged twelve to eighteen were bullied at school.Susan Sweater is a psychologist at the University of Nebraska-Lincoln and co-director of the Bullying Research Network.She says schools should treat bullying as a mental health problem to get bullies and victims the help they need.She says bullying is connected to depression, anxiety and anti-social behavior, and bullies are often victims themselves.61.From the case of Tina, we can know that _____.A.bullying is rare B.victims suffered a lotC.schools are to blame D.personalities are related 62.Which of the following is NOT bullying?A.To beat someone repeatedly.B.To call someone names.C.To isolate someone from friends.D.To refuse to help someone in need.63.Why is cyberbullying appealing to the bully?A.Because it can involve more people.B.Because it can create worse effects.C.Because it is more convenient.D.Because it can avoid cheating.64.According to Susan Sweater._____.A.bullies are anti-socialB.bullies should give victims helpC.students are not equally treatedD.bullies themselves also need help65.Which of the following can be the best title of the text?A.Bullyin g—An Irish Girl Committed SuicideB.15-year-old Irish Girl Committed SuicideC.Cyberbullyin g—Taking Off in SchoolsD.How to Find Bullying among TeensC"The days when the management in Western companies presented gold watches to long-serving employees to thank them for loyal service is now just a memory." says the Educational and Training Support Agency.This new development in the shape and movement of the workforce throughout Western businesses is partly a result of the way that layers of middle management are being removed, leaving more workers responsible for their own development."Having workers take responsibility for their own development might be dramatic, but it is now the rule," says the Educational and Training Support Agency."Today, not only are workers more mobile, they have to run to keep up with changes." says the Government-founded agency."It is no longer enough for a worker to gain a set of skills.Workers need the ability to react and get used to changes." This new system is also being pushed along by the way that industry is looking to its workers to renew their own skills.In the United States, some companies have contracts (合同)which repair their employees to show regularly how they have their skills up to date.Contrary to this traditions of the past, employers in the West are now looking for autonomous learners as recruits, people who can develop their own continuing education beyond the school and university system.At the same time.businesses are developing the capacity for workers to take up autonomous learning on site in workplace, so that the skills and abilities of all workers in a business continue to improve and increase."This.of course," says business theory."will also improve the productivity (生产率)of the workers and therefore the profits of the company."66.The management in western companies no longer presents gold watches to their employees because _____.A.they are not loyal to companiesB.other rewards replace gold watchesC.the way prove to be a failureD.serving a company for life is rare now67.The western workforce frequently changes their jobs partly because _____.A.hopping from job to job has become a new trendB.employees are expecting to have more experiences in their lifeC.workers have to take more responsibility for themselvesD.it is easy to complete themselves by doing so68.The passage seems to suggest that the present situation in society requires that workers shouldA.show more loyalty to their companiesB.try to develop their skills to fit in with changesC.go to college to have their skills up to dateD.be quick in changing their careers if there is the possibility69.The phrase "autonomous learner" in the last paragraph means _____.A.people who have received higher educationB.people who study hard themselvesC.people who learn things very quicklyD.people who continue their study beyond regular education70.Companies require their employee's development mainly because _____.A.it will finally help to bring more profits to the companyB.it can attract more workers who pay special attention to self-developmentC.it is good for the employees to develop their skillsD.it will make workers more responsible and loyal to the companyPart Iv Writing (45 marks)Section A (10 marks)Directions Read.the following passage.Fill.in the numbered, blanks by using the information from the passage.Write NO MORE THAN THREE WORDS for each answer.Learning to improve your focus throughout the day can be a little difficult, only because we are talking about 18 to 24 hours, depending on the number of hours you sleep.However, if we break down your day into manageable time frames, it would make it much easier to learn to improve your focus.Focus, or concentration, is a skill that can be taught, so there are some exercises you can do to improve your focus.Start with easy exercises like staring at a picture on the wall for a few minutes without moving or talking to anyone.Once you learn how to block out your surroundings, your focus will improve.Other mind exercises you can do are internalizing.This is when you picture yourself in a desired situation, and then you work around your picture.Actors do this a lot to block out laughter, noise, or other distractions.An example of this would be to imagine you in a potentially stressful situation, like a singer in a concert.Try to play out the scene in your mind what you would do if different scenarios were to happen.This can actually be a lot of fun.and you learn how to improve your focus by concentrating on one thing only.If this sounds a little strange to you, you could try another strategy.Why not make lists? Make a list for the things you need to accomplish for the morning, another for the afternoon.and finally, another list for the evening.Study your lists carefully and see where you can move thingsaround.For instance, if you have a dinner to arrange that evening, don't bunch up everything in the afternoon, right before the guests arrive.Divide your chores and errands between morning and afternoon, and give yourself an hour or two to relax before the guests arrive.Planning helps you focus.It will also not stress you out.Another way to improve your focus is to take breaks.If children have rest and lunch as their breaks, adults should also allow themselves the privilege of stopping for a drink or a 30 minute sitcom on TV.Of course, if you are working in an office, you are allowed coffee breaks.Use this time wisely.Don't spend it with your co-workers beside the coffee machine talking about problems in the office.Doing this would actually stress you and get you to lose focus on the things that need to be done.Your breaks should be as quiet as possible.Read a book.take a walk.or visit a daycare.Go and do anything that will give your brain a rest.The reason why we lose focus so easily is because we have too much on our minds.Of course, it could also be because you are bored with nothing to do all day.A good balance between a too relaxed brain and an overly active brain is a desirable situation to be in.Find your capacity to work, and try not to veer away too far from it on a daily basis.Improving your focus also means knowing what you can do and being confident about doing it well.Focus is important but difficult to improve1.71 to improve your focusI .Staring at picture.◆Staring at a wall picture 72 to learn to block out surroundingsⅡ.73 .◆Concentrating on imagining a potentially stressful work place to block out 74Ⅲ.75 .◆Dividing a day into 76 for chores and errands to be done.as well as arranging time for relaxationIV.Taking breaks.◆Wisely using time to have a drink, watch TV quietly instead of 77 ; just resting your brain2.78 for easily losing focus◆Having too much on minds◆79 all dayConclusion Keeping 80 between extremely relaxed brain and too active brain.Section B (10 marks)Directions Read.the following passage.Answer the questions according to the information given in the passage and the required words limit.Write your answers on your answer sheet.When I was 10 years old, my friend Sydney was diagnosed with a brain tumor.Sydney fought against it, but the tumor did not respond to treatment, and could not be surgically removed.The mass wrapped around her brain stem, the area of the brain that controls the vital functions of life such as breathing and blood pressure.Sydney died at the age of 11.After her death, I felt immense sadness and frustration about pediatric cancer.I decided to turn these negative emotions into positive actions.When I was 11 years old.I founded the Pink Polka Dots Guild(PPD)with two friends.The guild is named after Sydney s favorite color and pattern, which represents both the memory of my friend and the guild's positive approach.Mygoal has been to raise enough money to find a cure for brain cancer, which is the second most common cancer in children.Over the years, PPD has held fundraisers from lemonade stands to art expositions to golf tournaments.I have played a leading role in planning and organizing each PPD event.The very first Pink Polka Dots event, a garage sale.raised $ 9.000, and our most recent fundraiser, the fifth annual golf tournament, brought in over $ 73.000.The guild progressed faster than I ever anticipated.In five years, we have become 40 members strong, and raised almost half of a million dollars.I've been shocked by the public recognition that the guild has earned.PPD received an award from a U.S.Senator, spoke at a TED Conference, was featured in Teen Vogue, and appeared on The Note Berkus Show.Each of these honors has raised awareness and money for our cause.The initiative that I have taken has truly impacted the world of cancer research.PPD has provided start-up funding for scientific discoveries, such as "Tumor Paint", which illuminates cancerous cells so that surgeons can remove them with unprecedented accuracy.The discovery appeared in Time Magazine., and will be reviewed by the Food & Drug Administration starting in early 2012.1 am extremely proud to have helped fund the research of this life-saving technology.Pink Polka Dots has inspired me to be an activist.My experience has taught me that with passion and dedication, it is possible to make a difference to the world.The determination that Pink Polka Dots sparked in me has carried over to all aspects of my life, making me a driven academic, a competitive debater and a dedicated volunteer.81.Why did the author feel sad and frustrated? (No more than 8 words)82.What was the author s purpose of founding PPD? (No more than 15 words)83.What achievement has PPD made in helping cancer research? (No more than 13 words)84.What did the author learn trom his own experience of founding PPD? (No more than 15 words)Section C (25 marks)Directions Write, an English composition according to the instructions given below.现今,中学生由于学业繁重几乎都没有在家承担任何家务责任。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长郡中学2015届高三月考试卷(二)
数 学(文科)
长郡中学高三数学命题组组稿
本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。
满分150分。
一、选择题:本大题共10小题,没小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、 ,若x B ∈成立的一个充分不必要条件是x A ∈,则实数m 的取值范围是
A.2m ≥
B.2m ≤
C.2m >
D.22m -<<
2、若直线1ax by +=与不等式组1210210y x y x y ≤⎧⎪--≤⎨⎪++≥⎩
表示的平面区域无公共点,则23a b +的取值范围
是
A.()7,1--
B.()3,5-
C.()7,3-
D.R
3、如图,在一个正方体内放入两个半径不相等的球12,O O ,这两个球相外切,且球1O 与正方体共顶点A 的三个面相切,球2O 与正方体共顶点1B 的三个面相切,则两球在正方体的面11AAC C 上的正投影是
A.
B.
C. D.
4
A.
C.
5,定义域为D ,任意,m n D ∈,点(),()P m f n 组成的图形为正方形,则实数a 的值为
A. 1-
B. 2-
C. 3-
D.4-
6、已知M 是ABC ∆内的一点,且23,30AB AC ⋅=,若
,MBC MCA ∆∆和MAB ∆的面
A.20
B. 18
C. 16
D. 9
7、一束光线从点()1,1A -出发,经x 轴反射到圆()()22
:231C x y
-+-=上的最短路程是
C.4
D.5
8、已知直线()()20y k x k =+>与抛物线2:8C y x =相交于,A B 两点,F 为C 的焦点,若
则k =
B.
C.
9、函数()f x 的导函数是'()f x ,若对任意的x R ∈,都有()2'()0f x f x +<成立,则
B. C. D.无法比较 10、在平面直角坐标系xOy 中,点()5,0A ,对于某个正实数k ,存在函数()2()0f x ax a =>,使
得OA OQ OP OA OQ λ⎛⎫ ⎪=+ ⎪(λ),这里点,P Q 的坐标分别为()()1(,1),()P f Q k f k ,,,则k 的取值范围为
A.()2,+∞
B. ()3,+∞
C. [)4,+∞
D.[)8,+∞
选择题答题卡
二、填空题:本大题共5小题,每小题5分,共25分。
把答案填在答题卡中对应题号后的横线上。
11、已知数列{}n a 的前n 项和29n S n n =-,则其通项公式n a =____________..
12、给出下列关于互不相同的直线,,m n l 和平面,αβ的四个命题:
①,,,m l A A m l m αα⊂=∉点则与不共面; ②//,//,,,l m l m n l n m n ααα⊥⊥⊥、是异面直线,且则; ③,,,//,//.//l m l m A l m ααββαβ⊂⊂=若点则;
④//,//,//,//.l m l m αβαβ若则
其中真命题是_____________(填序号)
13、已知线段AB 两个端点()()2,3,3,2A ---,直线l 过点()1,2P 且与线段AB 相交,则l 的斜率k 的取值范围为________________.
14、已知圆C 过双曲线中心的距离是__________.
15、定义在区间[],a b 上的函数()y f x =,'()f x 是函数()f x 的导数,如果[],a b ξ∃∈,使得()()()'()f b f a f b a ξ-=-,则称ξ为[],a b 上的“中值点”。
下列函数:
①()21,f x x =+②2()1f x x x =-+,③()()ln 3f x x =+,其中在区间[]2,2-上的“中值点”多于一个的函数是___________(请写出你认为正确的所有结论的序号)
三、解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
16、(本小题满分12分)
(1) 求函数()f x 的解析式;
(2) 求函数()(2)y f x f x =++的最小正周期和最值。
17、(本小题满分12分) 如图,AB 为圆O 的直径,点E F 、在圆O 上,//AB EF ,矩形ABCD 所在的平面和圆O 所在的平面互相垂直,且2,1AB AD EF ===.
(1)求证:AF CBF ⊥平面;
(2)设FC 的中点为M ,求证://OM DAF 平面;
(3)设平面CBF 将几何体EFABCD 分成的两个椎体的体积分别为,,:F ABCD F CBE F ABCD F CBE V V V V ----求。
18、(本小题满分12分)
已知:为圆心的圆与x 轴交于点,O A ,与y 轴交于点,O B ,其中O
为原点。
(1)求证:OAB ∆的面积为定值;
(2)设直线24y x =-+与圆C 交于点,M N ,若OM ON =,求圆C 的方程。
19、(本小题满分13分) 已知{}n a 为等差数列,且5714,20a a ==,数列{}n b 的前n 项和为n S ,且22n n b S =-。
(1)求数列{}{},n n a b 的通项公式;
(2)若n n n c a b =⋅,n T 为数列{}n c 的前n 项和,求证:
20、(本小题满分13分)
椭圆上的点P 满足1290PF F ∠=,且12PF F ∆的面积为(1)求椭圆C 的方程; (2)设椭圆C 的左、右顶点分别为A B 、,过点Q (1,0)
的动直线l 与椭圆C 相交于M N 、两点,直线AN 与直线4x =的交点为R ,证明:点R 总在直线BM 上。
21、(本小题满分13分)
已知函数()ln 3()f x a x ax a R =--∈。
(1) 求函数()f x 的单调区间;
(2) 若函数()y f x =的图像在点()2,(2)f 处的切线的倾斜角为45,对于任意的[]1,2t ∈,
在区间(),3t上总不是单调函数,求m的取值范围;
(3)
ln n
n
⨯⨯<。
