专题五力学之杠杆
中考物理压轴题大揭秘专题专题05杠杆型综合计算含解析

专题05杠杆型综合计算考点01:杠杆平衡类力学综合计算:此考点重点是对杠杆的平衡条件即F1×L1=F2×L2的考查,同时能正确分析物体受力情况,并在确定动力与及阻力的前题下正确确定动、阻力对应的力臂,然后运用杠杆平衡条件及平衡力的知识,即可求解相应的未知量。
例1:(·潍坊)疫情期间,大壮同学自制了如图所示的健身器材,坚持锻炼身体。
用细绳系在轻杆的O点将轻杆悬挂起来,在杆的A端悬挂质量m1=10kg的重物,在B端竖直向下缓慢拉动轻杆至水平位置。
已知AO长1.5m,OB长0.5m,大壮质量m2=56kg,g取10N/kg,求此时:(1)大壮对杆的拉力大小;(2)地面对大壮的支持力大小。
【答案】(1)300N,260N。
【解析】(1)缓慢拉动轻杆至水平位置,根据杠杆平衡条件可得:F A·OA=F B·OB,F A的大小等于G A,即F A=G A= m1g=10kg ×10N/kg=100N,则F B=F A×OA/OB=100N×1.5m/0.5m=300N.即大壮对杆的拉力为300N。
(2)大壮受三个力,重力G、杆对大壮的拉力F、地面对大壮的支持力F支,三个力平衡,杆对大壮的拉力与大壮对杆的拉力为相互作用力,大小相等,则地面对大壮的支持力F支=G-F=m2g-F=56kg 10N/kg-300N=260N,地面对大壮的支持力为260N。
【变式1-1】(杭州中考)杆秤是一种用来测量物体质量的工具,小金尝试做了如图所示的杆秤。
在秤盘上不放重物时,将秤砣移到O点提纽处时,杆秤恰好水平平衡,于是小金将此处标为O刻度。
当秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡,测得OA=5cm,OB=10cm,(1)计算秤砣的质量。
(2)小金在B处标的刻度应为kg.若图中OC=2OB,则C处的刻度应为kg..(3)当秤盘上放一质量为2kg的物体时,若换用一个质量更大的秤砣,移动秤砣使杆秤再次水平平衡时,其读数(填“>”“<”)kg,由此可知一杆秤不能随意更换秤砣。
杠杆的原理应用条件

杠杆的原理应用条件1. 引言杠杆是一种简单机械装置,利用杠杆原理可以实现力的放大或方向的改变。
在物理学和工程学中,杠杆被广泛应用于各种领域,包括机械工程、结构力学、力学设计等。
本文将介绍杠杆的原理以及其应用条件。
2. 杠杆的原理杠杆原理是基于力的平衡条件和力矩的平衡条件,通过调整力的作用点和力臂的长度来实现力的放大或方向的改变。
2.1 力的平衡条件力的平衡条件是指在一个平衡状态下,合力为零。
对于杠杆,当一个力向下作用于杠杆的一端,并且另一个力向上作用于杠杆的另一端时,如果这两个力的大小和方向适当,杠杆就可以平衡并保持在静止状态。
2.2 力矩的平衡条件力矩的平衡条件是指在一个平衡状态下,合力矩为零。
对于杠杆,力的力矩等于力乘以其到转轴的距离。
通过合理调整力的作用点和力臂的长度,可以使力矩平衡,从而实现杠杆的稳定。
3. 杠杆的应用条件3.1 支点的选取杠杆的应用条件之一是正确选择支点的位置。
支点是杠杆的旋转中心,它决定了杠杆的力矩平衡条件。
应选择一个合适的支点位置,使得杠杆在应用力下保持平衡。
支点的选择应基于具体的应用需求,包括所需的力放大倍数、杠杆的长度以及杠杆的材料等。
3.2 力的作用点及方向另一个杠杆的应用条件是正确选择力的作用点及方向。
根据杠杆原理,力的作用点和方向必须能够实现力的平衡和力矩的平衡。
要实现力的平衡,杠杆上的作用力必须具有相等的大小和反向的方向。
此外,力的作用点还需要满足力矩平衡的条件,即力矩乘以力臂的长度在平衡状态下为零。
3.3 杠杆的长度和强度杠杆的长度和强度是杠杆应用条件的重要考虑因素。
杠杆的长度决定了力矩的大小,因此在选择杠杆长度时需要根据所需的力放大倍数进行考虑。
此外,杠杆的强度也需要满足所需的力的大小,以避免杠杆在应用过程中发生变形或破裂。
4. 杠杆的应用示例4.1 力的放大杠杆的常见应用之一是力的放大。
通过合理选择支点的位置和力的作用点及方向,可以实现力的放大。
例如,门锁的杠杆原理,使得我们可以轻松地用手推开重门。
杠杆知识点总结初二物理

杠杆知识点总结初二物理初中物理学中把一根在力的作用下可绕固定点转动的硬棒叫做杠杆。
杠杆可以是任意形状的硬棒。
今天小编为大家精心整理了一篇有关初二物理杠杆重要知识点总结的相关内容,以供大家阅读!知识点总结杠杆是中学学习的一种简单机械,在学习中要了解杠杆的定义,理解杠杆的五要素(支点、动力、阻力、动力臂、阻力臂),并能够在图中表示出他们,可以画出实际的杠杆简图。
运用杠杆的平衡条件(动力×动力臂=阻力×阻力臂,即:F1L1=F2L2)解决实际问题,可以分析天平、杆秤等工具来理解。
知道杠杆的几种类别,并能列举实例说明。
省力杠杆:撬杠;费力杠杆:门把手;等臂杠杆:托盘天平。
常见考法本知识点的考查形式多变,常见的有选择题、填空题、画图题等,考查的知识点多在:杠杆的要素、杠杆平衡的条件以及杠杆的分类。
误区提醒1、杠杆的平衡条件:动力×动力臂=阻力×阻力臂,即:F1L1=F2L2。
2、杠杆的分类:(1)省力杠杆:L1>L2,F12。
动力臂越长越省力(费距离)。
(2)费力杠杆:L12,F1>F2。
动力臂越短越费力(省距离)。
(3)等臂杠杆:L1=L2,F1=F2。
不省力也不费力。
【典型例题】例析:如图所示,杠杆OA在重物G和F1力的作用下,处于水平位置且保持平衡。
如果用力F2代替F1,使杠杆仍然在图中所示位置保持平衡,下面各力关系正确的是(B为OA的中点)()A.F1>F2=G/2B.F1=F2>GC.F12=2GD.F1>F2>G解析:当杠杆OA受两个作用力F1(或F2)和右端绳子拉力F而处于平衡状态时,只要比较F1、F2二力关于对支点的力臂的长短,即可找到二力的大小关系。
答案:正确选项为D。
《杠杆》ppt课件

contents
目录
• 杠杆原理基本概念 • 杠杆平衡条件分析 • 杠杆应用:省力、费力和等臂杠杆 • 杠杆在物理学中重要意义 • 实验探究:测量滑轮组机械效率 • 生活中应用拓展与创新思维培养
01
杠杆原理基本概念
杠杆定义及作用
杠杆定义
一根在力的作用下可绕固定点转动 的硬棒就叫杠杆。
减小误差的方法:使用更精确的测量工具、规范操作、 多次测量取平均值等
06
生活中应用拓展与创新思维培 养
生活中创意应用案例分享
杠杆原理在建筑中的应用
杠杆原理在生物中的应用
如古代建筑中的斗拱结构,利用杠杆 原理实现力的平衡和支撑。
如人体骨骼和肌肉系统,通过杠杆作 用实现运动。
杠杆原理在机械中的应用
如自行车刹车系统、汽车悬挂系统等, 通过杠杆放大或减小力量,实现精确 控制。
生活中常见杠杆实例
筷子
费力杠杆,动力臂小于阻力臂, 虽然费力但是省了距离。
起瓶器
省力杠杆,动力臂大于阻力臂, 省力但费了距离。
剪刀
根据用途不同可以是省力杠杆或 费力杠杆,如理发剪是费力杠杆, 而裁衣剪则是省力杠杆。
镊子
费力杠杆,动力臂小于阻力臂, 用于夹取细小物品。
02
杠杆平衡条件分析
平衡状态与条件概述
等臂杠杆原理及应用举例
等臂杠杆原理
等臂杠杆的动力臂等于阻力臂,平衡时动力和阻力大小相等。 既不省力也不费力,既不省距离也不费距离。
天平
天平是一种测量物体质量的仪器,使用等臂杠杆原理。在天 平两端放置质量相等的物体,天平就会保持平衡。
定滑轮
定滑轮是一种固定不动的滑轮,使用等臂杠杆原理。通过定 滑轮可以改变力的方向,但是不改变力的大小。
杠杆ppt课件

杠杆的基本原理
杠杆平衡条件
支点、施力点、阻力点在同一直线上,且支点到施力点的 距离与支点到阻力点的距离之比等于施力点到支点的距离 与阻力点到支点的距离之比。
费力杠杆
施力点与支点之间的距离小于阻力点与支点之间的距离, 费力但省距离。
省力杠杆
施力点与支点之间的距离大于阻力点与支点之间的距离, 可以省力但费距离。
02 剪刀
剪刀是利用省力杠杆的原理,通过缩短距离来省 力,因此在剪切厚重或坚韧的物体时特别方便。
03 指甲刀
指甲刀也是利用省力杠杆的原理,可以让人们轻 松修剪指甲。
费力杠杆的应用
01 镊子
镊子虽然可以夹起小物体,但是使用时需要用较 大的力气,因此是费力杠杆的应用。
02 筷子
筷子虽然可以轻松夹起食物,但是在使用过程中 需要用较大的力气来移动,因此也属于费力杠杆 的应用。
省力杠杆
总结词
能够省力的杠杆
详细描述
省力杠杆的特点是动力臂较长,阻力臂较短,可以节省施加的力,但会使得作用距离减小。例 如,开瓶器、老虎钳、剪刀等都属于省力杠杆。
费力杠杆
总结词
费力的杠杆
详细描述
费力杠杆的特点是动力臂较短,阻力臂较长,需 要施加较大的力,但作用距离会增加。例如,船 桨、钓鱼竿、镊子等都属于费力杠杆。
展望
未来发展方向
随着科学技术的不断发展和人们的需 求不断变化,杠杆原理的应用也在不 断发展和变化。未来,人们将继续探 索杠杆原理的新应用,并开发出更加 高效和实用的设备和技术。
未来挑战
尽管杠杆原理的应用已经非常广泛, 但是在实际应用中仍然存在一些挑战 和问题。例如,杠杆的设计和制造需 要精确的计算和材料选择,否则可能 会导致失败或损坏。此外,对于一些 复杂的杠杆系统,需要进行详细的分 析和模拟才能得到正确的结果。
杠杆的平衡条件

杠杆的平衡条件在力学中,杠杆是一种利用力的乘法原理来增加力量的器械。
它由两个主要部分组成:杠杆臂和支点。
杠杆原理的应用范围广泛,从简单的剪刀到复杂的机械工具都可以看到杠杆的身影。
然而,要使杠杆保持平衡,有一些条件需要满足。
本文将详细介绍杠杆的平衡条件及其应用。
一、要使杠杆保持平衡,需要满足以下两个条件:1. 力矩平衡条件力矩是力对于旋转轴的转动效果的量度。
在杠杆上,力矩是由施加在杠杆上的力对于支点的距离产生的。
平衡的条件是,所有作用在杠杆上的力矩之和等于零。
数学上,力矩可以用以下公式表示:力矩 = 力 ×距离当所有力矩之和等于零时,杠杆处于平衡状态。
这意味着,如果一个力矩的大小增加,那么另一个力矩必须减小,以保持平衡。
2. 力的平衡条件除了力矩平衡条件外,杠杆也必须满足力的平衡条件。
即,所有作用在杠杆上的力之和等于零。
在杠杆上,力可以分为两种类型:作用在支点上的支持力和作用在其他位置的载荷力。
支持力是使杠杆保持平衡的关键,它提供了一个抵消载荷力的作用。
二、杠杆的应用1. 增加力的作用杠杆的一个主要应用是增加力的作用。
通过改变施力点和支点之间的距离,可以以较小的力产生更大的力矩。
这使得人们能够更轻松地承受大量的重量或施加更大的力。
举个例子,开启一个僵硬的门。
如果你在门的边缘施加力,门可能很难打开。
但如果你将施力点移至靠近门铰链的位置,就能轻松打开门。
这是因为靠近门铰链的位置距离支点更远,从而生成更大的力矩,以克服门上的摩擦力。
2. 制造平衡另一个常见的杠杆应用是制造平衡。
杠杆可以用于平衡不平衡的物体或系统。
通过调整质量分布或改变支点的位置,可以使整个系统达到平衡状态。
举个例子,平衡秤就是一个使用杠杆原理的应用。
当你在一侧放置一定质量的物体时,平衡秤的另一侧会上下移动,直到两侧的力矩平衡。
这样就可以精确地测量物体的质量。
3. 调节速度和力的传递最后,杠杆还可以用于调节速度和力的传递。
通过改变施加力的位置和支点的位置,可以改变输出力的大小和方向。
初中物理力学之杠杆的解析

初中物理力学之杠杆的解析杠杆是一种简单的机械装置,常用于增加或改变力的方向。
它由一个杠杆臂和一个支点组成。
在物理力学中,杠杆被广泛用于解析力的大小和方向。
一、杠杆的定义与分类杠杆是指由两个部分组成的刚性物体,一个是有固定支点的杠杆臂,另一个是施加力的力臂。
根据支点与力的相对位置,杠杆可分为三类:第一类杠杆、第二类杠杆和第三类杠杆。
三类杠杆的定义分别如下:1. 第一类杠杆:支点位于杠杆的两端,力臂和杠杆臂都在支点的同一侧。
2. 第二类杠杆:支点位于杠杆的一端,力臂在支点的另一侧,杠杆臂在支点的同一侧。
3. 第三类杠杆:支点位于杠杆的一端,力臂和杠杆臂都在支点的另一侧。
二、杠杆平衡条件的解析根据力的平衡条件,杠杆平衡时满足以下公式:力1 ×力臂1 = 力2 ×力臂2其中,力1和力2分别是杠杆两侧施加的力,力臂1和力臂2分别是支点到力的垂直距离。
根据杠杆的分类,我们可以分别解析三类杠杆的平衡条件。
1. 第一类杠杆的平衡条件:在第一类杠杆中,支点位于杠杆两端,力臂和杠杆臂都在支点的同一侧。
根据平衡条件公式,可以得出:力1 ×力臂1 = 力2 ×力臂2其中,力1和力2分别是杠杆两侧施加的力,力臂1和力臂2分别是支点到力的垂直距离。
在第一类杠杆中,力1和力2的大小和方向不同,但力臂却具有相同的大小和方向。
2. 第二类杠杆的平衡条件:在第二类杠杆中,支点位于杠杆的一端,力臂在支点的另一侧,杠杆臂在支点的同一侧。
根据平衡条件公式,可以得出:力1 ×力臂1 = 力2 ×力臂2在第二类杠杆中,力1和力2的大小和方向不同,力臂1和力臂2的大小和方向也不同。
然而,根据公式,当力臂1较大时,力1可以比力2小,从而达到杠杆平衡。
3. 第三类杠杆的平衡条件:在第三类杠杆中,支点位于杠杆的一端,力臂和杠杆臂都在支点的另一侧。
根据平衡条件公式,可以得出:力1 ×力臂1 = 力2 ×力臂2在第三类杠杆中,力1和力2的大小和方向不同,力臂1和力臂2的大小和方向也不同。
杠杆ppt课件

利用杠杆和滑轮组,验证物体在液体 中所受浮力等于排开液体的重力。
杠杆在力学计算中的技巧
力的合成与分解
利用平行四边形法则或 三角形法则进行力的合 成与分解,简化计算过
程。
相似三角形法
通过构造相似三角形, 利用相似比例关系求析 图或示意图,直观展示 物理过程,便于分析和
杠杆在生活中的应用技巧
选择合适的支点位置
在使用杠杆时,选择合适的支点位置可以使得力臂更长,从而减小所需的作用力。例如, 在使用撬棍时,将支点靠近重物可以更容易地撬起重物。
调整力臂长度
通过调整力臂的长度可以改变杠杆的机械效益。例如,在使用剪刀时,可以通过移动手柄 来改变力臂的长度,从而适应不同剪切需求。
如何创新应用杠杆原理解决实际问题
深入分析问题本质
在应用杠杆原理解决问题时, 首先需要深入分析问题本质, 明确问题的关键点和影响因素 ,以便找到合适的杠杆点。
创新思维和跨界融 合
通过创新思维和跨界融合,可 以将杠杆原理与其他领域的知 识和方法相结合,创造出新的 解决方案和商业模式。
量化分析和风险管 理
保持杠杆平衡
在使用杠杆时,需要保持杠杆的平衡状态,否则会导致力的浪费或者对物体造成损坏。例 如,在使用天平称重时,需要调整两边的砝码使得天平保持平衡状态。
如何利用杠杆原理解决生活问题
省力
利用杠杆原理可以实现省力的目 的。例如,使用撬棍可以轻松地 撬起重物;使用瓶起子可以轻松 地打开瓶盖。
改变力的方向
杠杆ppt课件
目录
• 杠杆基本概念与原理 • 杠杆在力学中的应用 • 杠杆在经济学中的应用 • 杠杆在工程学中的应用 • 杠杆在生活中的应用 • 杠杆原理的拓展与应用前景
01
杠杆ppt课件

THANKS 感谢观看
在机械制造中,杠杆原理的应用可以实现力的放大和缩小,从而实现对加工过程的 精确控制。
杠杆原理在机械制造中还可以实现力的平衡和调节,提高机器的稳定性和可靠性。
建筑行业中的杠杆应用
在建筑行业中,杠杆原理的应用 主要体现在建筑设备和工具上,
如吊车、升降机等。
这些设备和工具利用杠杆原理实 现重物的升降、移动和搬运,提
。
改变力的方向
通过使用杠杆,可以改变力的方向 ,使得工作更加方便。
改变运动状态
通过使用杠杆,可以改变物体的运 动状态,例如加速或减速。
02 杠杆的工作原理
杠杆平衡条件
杠杆平衡条件是指杠杆在动力 和阻力作用下保持静止或匀速 转动的状态。
杠杆平衡时,动力矩等于阻力 矩,即动力乘以动力臂等于阻 力乘以阻力臂。
高了建筑工地的作业效率。
建筑行业中杠杆原理的应用还体 现在建筑结构的稳定性设计上, 如桥梁、高层建筑的支撑结构等
。
交通运输中的杠杆应用
01
02
03
04
在交通运输领域,杠杆原理的 应用主要体现在车辆的悬挂系
统和转向系统上。
车辆的悬挂系统利用杠杆原理 来吸收和缓冲路面不平引起的
振动,提高乘坐舒适性。
转向系统则利用杠杆原理实现 车轮的转向,使车辆能够按照
驾驶员的意图进行行驶。
交通运输中的杠杆应用还体现 在车辆的制动系统上,通过杠 杆原理实现车辆的减速和停车
。
05 杠杆的拓展知识
滑轮与滑轮组
滑轮
滑轮是一个可以绕着轴心转动的机械 零件,通常由金属或塑料制成。滑轮 可以分为定滑轮和动滑轮两种类型。
滑轮组
滑轮与滑轮组的应用
在建筑、起重、运输、纺织等行业中 ,滑轮与滑轮组被广泛应用于各种机 械设备中,以提高工作效率和安全性 。
初中物理杠杆原理

初中物理杠杆原理杠杆原理是物理学中的基础概念,广泛应用于日常生活和工程领域。
本文将详细介绍初中物理中的杠杆原理,包括杠杆的定义、工作原理以及实际应用。
一、杠杆的定义杠杆是由一个支点和两个或多个力臂组成的物体。
支点通常称为杠杆的轴,力臂指的是量度支点到力的距离。
杠杆分为三类:一类杠杆、二类杠杆和三类杠杆。
一类杠杆是指支点位于力的一侧,二类杠杆是指支点位于力和负载之间,三类杠杆是指支点位于力的一侧但离负载更近。
二、杠杆的工作原理杠杆的工作原理基于力矩的平衡。
力矩是指力在杠杆上产生的转动效应。
杠杆平衡的条件是力矩的总和为零。
根据杠杆原理,可以得出以下公式:力1 ×力臂1 = 力2 ×力臂2其中,力1和力2分别是作用在杠杆上的两个力,力臂1和力臂2分别是力1和力2的距离。
三、杠杆原理的应用1. 杠杆在平衡天平中的应用平衡天平是一个常见的应用杠杆原理的实例。
平衡天平由一个杠杆支撑两个相互连通但不平衡的物体。
通过移动物体的位置,可以达到平衡。
利用杠杆原理,我们可以确定两个物体的质量比例。
2. 杠杆在门上的应用门是我们日常生活中常见的使用杠杆原理的物体。
门的支点位于一侧,使得推开门变得轻松。
门的杠杆原理也体现在门把手和锁上。
我们可以通过调整把手或锁的位置,改变门的力矩和平衡点。
3. 杠杆在钳子和剪刀中的应用钳子和剪刀也是杠杆原理的典型应用。
它们都由两个杠杆组成,使得施加的力能够通过支点聚焦在工作部位,从而增加力的效果。
4. 杠杆在刷子和拨片中的应用刷子和拨片也利用杠杆原理来提供力的效果。
例如,我们用牙刷刷牙时,通过在刷柄上施加力,可以使刷毛产生旋转,从而更好地清洁牙齿表面。
5. 杠杆在推车中的应用推车也是常见的杠杆原理的应用。
通过调整物品放置在车上的位置,可以改变车的平衡点,使其更容易推动。
结论杠杆原理是物理学中的基础概念,广泛应用于日常生活和工程领域。
了解和掌握杠杆原理对于理解和解决现实问题具有重要意义。
杠杆的原理分类及应用

杠杆的原理分类及应用1. 杠杆的定义杠杆是一种力的应用工具,它由一个支点和施力点组成。
通过施加力在支点上,可以产生一个较大的输出力。
2. 杠杆的原理杠杆原理是基于物理学中的力矩原理的。
力矩是一种旋转力,是由施力点到支点的垂直距离乘以施力点施加的力的大小所决定的。
根据力矩的定义,可以得出以下公式:力矩 = 施力点与支点的距离 × 施力点施加的力杠杆的原理则是基于这个公式,通过改变力的大小和力臂的长度,可以改变输出力的大小。
3. 杠杆的分类根据杠杆的结构和应用场景,杠杆可以分为以下几种分类:3.1. 一级杠杆一级杠杆是最简单的杠杆,由一个支点和施力点组成。
当施加的力和力臂的长度相等时,输出力与输入力相等,这是一种平衡状态。
一级杠杆常见的应用包括剪刀、门铃等。
3.2. 二级杠杆二级杠杆由两个支点和施力点组成。
施力点与支点1之间的力臂称为一级力臂,支点1与支点2之间的力臂称为二级力臂。
当一级力臂和二级力臂的长度不相等时,输出力与输入力不相等。
二级杠杆常见的应用包括推拉门、刨子等。
3.3. 多级杠杆多级杠杆由多个支点和施力点组成。
每个支点和施力点之间可以形成不同长度的力臂。
通过改变不同力臂的长度,可以调整输出力的大小。
多级杠杆常见的应用包括手动液压千斤顶、工程起重机等。
3.4. 固定杠杆固定杠杆是指支点固定,不可移动的杠杆。
固定杠杆常被用于平衡物体的重力,实现力的平衡。
常见的固定杠杆应用包括天平、秋千等。
3.5. 移动杠杆移动杠杆是指支点可以移动的杠杆。
通过移动支点的位置,可以改变杠杆的作用效果。
常见的移动杠杆应用包括滑竿传动装置、手动起重机等。
4. 杠杆的应用杠杆的原理被广泛应用于各个领域。
以下是一些常见的杠杆应用:•建筑领域:起重机、千斤顶•机械领域:刨子、剪刀、钳子•交通运输领域:汽车离合器、刹车系统•物理实验:杠杆平衡实验、天平实验•工程学:平衡桥梁设计、推土机设计杠杆的应用不仅能够增加力的效果,还可以提高工作效率。
八年级物理杠杆物理杠杆知识点

八年级物理杠杆物理杠杆知识点
八年级物理杠杆主要涉及以下知识点:
1. 杠杆的定义和组成:杠杆由一个固定支点(也称为轴)和两个力臂(力臂是指力作
用点与支点之间的距离)组成。
2. 力矩的概念:力矩是指力对物体的旋转效果,其大小等于力的大小乘以力臂的长度。
3. 杠杆的平衡条件:当杠杆处于平衡状态时,对于一个给定的支点,左边的力乘以左
边的力臂的力矩等于右边的力乘以右边的力臂的力矩。
4. 杠杆的原理和分类:根据支点的位置和作用力的位置,杠杆可分为一级杠杆、二级
杠杆和三级杠杆。
一级杠杆是指支点在力的中间,二级杠杆是指支点在力的一边,三
级杠杆是指支点在力的另一边。
5. 杠杆的机械优势和力学等式:机械优势是指杠杆所能提供的力矩比上施加在杠杆上
的力的大小。
力学等式是指施加在杠杆上的力乘以施加在力臂上的力的长度等于承受
在另一边力臂上的力乘以承受的力臂长度。
6. 杠杆的应用:杠杆常用于实际生活中的工具和机械装置中,如平衡秤、钳子、螺丝
刀等。
这些是八年级物理杠杆的基本知识点,通过理解和掌握这些知识点,可以帮助解决与
杠杆相关的问题和应用。
八年级物理杠杆知识点

八年级物理杠杆知识点在物理学中,杠杆是一种基本的机械装置,广泛应用于各个领域。
而杠杆的运用也是我们生活中不可缺少的,比如看起来非常轻松自如的扳手,其实就是运用了杠杆的原理。
下面我们来详细探究一下关于杠杆的知识点。
一、杠杆的定义杠杆是一种基本的物理机械,由坚硬、笔直、不变形的杠条、固定在杠条上的固定点和施力点组成。
二、受力分析杠杆分为三种:一级杠杆、二级杠杆、三级杠杆。
⑴一级杠杆一级杠杆是固定点在杠条的两端,施力点在固定点的一侧,力臂和负载臂等长。
在一级杠杆中,F1和F2相等,力臂和负载臂的长度也相等。
⑵二级杠杆二级杠杆是固定点在杠条的中央,施力点在固定点的一侧,力臂较长,负载臂较短。
在二级杠杆中,力臂较长,负载臂较短,F1和F2的大小和方向不同。
⑶三级杠杆三级杠杆是固定点在杠条末端,施力点在固定点的一侧,力臂和负载臂的长度都较短。
在三级杠杆中,力臂和负载臂的长度都较短,F1和F2的大小和方向不同。
三、力臂和力矩在杠杆中,力臂是沿垂直于力的方向测量的距离。
力臂的长度越长,所需的力就越小。
力矩是力在力臂上产生的翻转力,是杠杆能够发挥机械功的关键。
四、杠杆原理杠杆的运用是基于杠杆原理的。
杠杆原理是指,在一个杠杆中,负载臂和力臂的长度成反比例关系,所以当负载臂的长度增加时,所需要的施力就会减小。
五、杠杆的应用⑴利用杠杆进行升降和固定物体升降机、自行车、体重秤等都是利用杠杆的原理进行升降和固定。
⑵利用杠杆进行平衡和调整厨房里常用的调制勺、扳手以及机器人等都是利用杠杆进行平衡和调整。
六、总结以上是关于八年级物理杠杆知识点的详细介绍。
希望通过对杠杆的分析和应用,大家能够更加深入地了解到物理机械方面的知识。
同时,我们也应用到生活中合理地运用杠杆,从而让我们的生活更加方便和舒适。
杠杆课件ppt

轮轴的应用
轮轴是一种特殊的杠杆,由轮和轴组成。轮轴的原理是当轮转动时,轴也会随之转动。这种原理被广 泛应用于各种机器和工具中,如车轮、齿轮、滑轮等。
轮轴的优点在于可以放大力量和移动距离。例如,当人们使用滑轮组时,可以通过滑轮组放大力量或 移动距离。此外,轮轴还可以改变力的方向,使得人们可以更加方便地完成各种工作。
动力臂
施加在杠杆上的动力作用线到 支点的距离。
杠杆的基本原理
杠杆平衡
杠杆在动力和阻力作用下平衡, 即动力×动力臂=阻力×阻力臂。
杠杆移动
当动力和阻力同时增加或减少相 同的值时,杠杆会沿阻力方向移 动。
杠杆的应用范围
01
02
03
04
简单机械
如镊子、剪刀、撬棒等,利用 杠杆原理实现省力或方便操作 的目的。
通过学习杠杆课件,学生可以深入理解杠杆原理, 掌握杠杆的应用方法,提高解决实际问题的能力。
展望
未来,杠杆原理的应用将会更加广泛 ,特别是在人工智能、机器人、航空 航天等领域,杠杆原理将会有更加深 入的应用。
随着科学技术的不断发展,杠杆原理 的应用将会更加智能化、精细化,未 来我们需要更加深入地研究杠杆原理 ,探索更加广泛的应用前景。
工程结构
如桥梁、起重机等,利用杠杆 原理设计合理的结构,实现稳 定性和承载能力要求。
工业制造
如车床、铣床等,利用杠杆原 理进行精密加工和测量。
日常生活
如火钳、钓鱼竿等,利用杠杆 原理方便日常生活。
02
杠杆的分类及特点
省力杠杆
撬棒
撬棒是典型的省力杠杆,通过较长的棒和较小的力 臂来撬动重物。
拔钉锤
拔钉锤的手柄较长,使得施加较小的力量就可以产 生较大的拔出力。
杠杆的公式原理及应用

杠杆的公式原理及应用1. 杠杆的定义杠杆是物理学中常用的工具,用于实现力的放大或方向的改变。
杠杆由杠杆臂和支点组成,通过施加力于杠杆臂上的一点来产生力矩。
力矩的大小取决于施加力的大小和距离支点的距离。
在金融领域,杠杆也是一种常用的工具,用于放大投资收益或债务。
2. 杠杆原理杠杆的原理基于力的平衡定律和力矩的平衡定律。
根据力矩的平衡定律,如果一个杠杆在支点处平衡,则施加在杠杆上的两个力的力矩相等。
力的平衡定律可以表示为力的合力等于零。
根据这两个定律,可以推导出杠杆的公式。
3. 杠杆公式在物理学中,杠杆公式可以表示为:$$ F_1 \\cdot d_1 = F_2 \\cdot d_2 $$其中,F1和F2是施加在杠杆上的两个力,d1和d2分别是这两个力距离支点的距离。
这个公式可以用来计算杠杆的力矩。
在金融领域,杠杆公式指的是杠杆比例(Leverage Ratio)。
4. 杠杆比例的计算在金融领域,杠杆比例用于衡量融资的比例。
杠杆比例可以通过以下公式计算:$$ 杠杆比例 = \\frac{总债务}{股东权益} $$总债务指的是公司的债务总额,股东权益指的是股东对公司的投资。
通过计算杠杆比例,可以了解公司的资本结构和融资风险。
5. 杠杆的应用杠杆在金融领域有广泛的应用。
以下是几个常见的杠杆应用场景:5.1 融资杠杆可以用于融资,通过借债来扩大投资。
借助杠杆,投资者可以用较少的自有资金进行较大的投资,从而放大投资收益。
但是,杠杆也带来了风险,如果投资失败,债务仍然需要偿还。
5.2 金融衍生品交易杠杆也常用于金融衍生品交易,如期货和期权。
交易者可以用较少的资金交易较大价值的金融工具。
杠杆使得交易者可以放大盈利,但同时也增加了交易风险。
5.3 投资组合管理在投资组合管理中,杠杆可以用于调整投资组合的风险和回报。
通过加入具有杠杆效应的资产,投资者可以提高投资组合的收益率。
但是,杠杆也会增加投资组合的波动性和风险。
杠杆(物理课件)(52)
实验结论
杠杆平衡的条件是: 动力×动力臂=阻力×阻力臂 ;
它的公式是___F_1_L_1_=_F__2_L_2__;
或是___FF_2_1__=__L_L_12______;
也称作__杠__杆__原__理________。
早晨给自己一个微笑,种下一天旳阳光。 当你对自己诚实的时候,世界上没有人能够欺骗得了你。 一个常常看别人缺点的人,自己本身就不够好,因为他没有时间检讨他自己。 对人恭敬,就是在庄严你自己。 当你手中抓住一件东西不放时,你只能拥有这件东西,如果你肯放手,你就有机会选择别的。人的心若死执自己的观念,不肯放下,那么他的 智慧也只能达到某种程度而已。 士不可以不弘毅,任重而道远。——《论语·泰伯》 勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳 成熟的人不问过去;聪明的人不问现在;豁达的人不问未来。
身体健康, 最常见的勇气就是在日常生活中做到诚实和正直,能够抵制诱惑,敢于讲真话,表现自己真实的一面,而不要虚伪造作。
你的丑和你的脸没有关系。
学习进步!
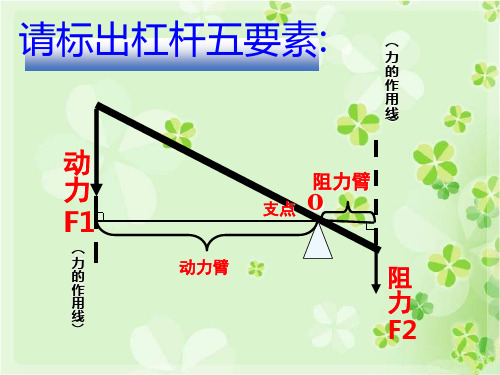
请标出杠杆五要素: ( 力 的 作 用 线
)
动
力
动力臂
的
阻
作 用
力
线 )
F2
杠杆:在力的作用下能够绕固定点转动
的硬棒
支 点(o):杠杆绕着转动的点
动 力(F1):促使杠杆转动的力 阻 力(F2):阻碍杠杆转动的力 动力臂(L1):从支点到动力作用线的垂直距离 阻力臂(L2):从支点到阻力作用线的垂直距离
初中物理-杠杆定理【精品】

初中物理-杠杆定理【精品】杠杆定义:在力的作用下绕着固定点转动的硬棒叫杠杆。
说明:①杠杆可直可曲,形状任意。
②有些情况下,可将杠杆实际转一下,来帮助确定支点。
如:鱼杆、铁锹。
杠杆分类:省力杠杆、费力杠杆和等臂杠杆。
杠杆五要素——组成杠杆示意图杠杆五要素图如上图所示,杠杆五要素主要有以下几个方面:①支点:杠杆绕着转动的点。
用字母O表示。
②动力:使杠杆转动的力。
用字母F1表示。
③阻力:阻碍杠杆转动的力。
用字母F2表示。
(说明:动力、阻力都是杠杆的受力,所以作用点在杠杆上。
动力、阻力的方向不一定相反,但它们使杠杆的转动的方向相反。
)④动力臂:从支点到动力作用线的距离。
用字母l1表示。
⑤阻力臂:从支点到阻力作用线的距离。
用字母l2表示。
杠杆原理中画力臂方法:⑴找支点O;⑵画力的作用线(虚线);⑶画力臂(虚线,过支点垂直力的作用线作垂线);⑷标力臂(大括号)。
杠杆平衡知识点杠杆平衡原理:亦称“杠杆平衡条件”。
要使杠杆平衡,作用在杠杆上的两个力(动力点、支点和阻力点)的大小跟它们的力臂成反比。
杠杆平衡公式:动力×动力臂=阻力×阻力臂,用代数式表示为F1×L1=F2×L2。
式中,F1表示动力,L1表示动力臂,F2表示阻力,L2表示阻力臂。
从上式可看出,欲使杠杆达到平衡,动力臂是阻力臂的几倍,动力就是阻力的几分之一。
杠杆平衡的应用:1.在使用杠杆时,为了省力,就应该用动力臂比阻力臂长的杠杆;2.如果想要省距离,就应该用动力臂比阻力臂短的杠杆。
因此使用杠杆可以省力,也可以省距离。
3.但是,要想省力,就必须多移动距离;要想少移动距离,就必须多费些力。
要想又省力而又少移动距离,是不可能实现的。
正是从这些公理出发,在“重心”理论的基础上,阿基米德发现了杠杆原理,即“二重物平衡时,它们离支点的距离与重量成反比。
杠杆(物理课件)(15)

为你制造一些困难和障碍的人未必是你的敌人,把你从困境里拉出来的人未必是你的朋友。不要用眼前的利益得失看人,因为拥有的多而是计较的少。
道德教育成功的“秘诀”在于,当一个人还在少年时代的时候,就应该在宏伟的社会生活背景上给他展示整个世界个人生活的前景。——苏霍姆 林斯 生活若剥去了理想、梦想、幻想,那生命便只是一堆空架子。
画虚线、标垂足、注符号
人体中的杠杆: 杠杆:由骨构成 动力: 肌肉收缩产生力
(肌腱附着在骨上)
支点:关节
中国古代对杠杆也有广泛的使用
观察、找出自行车上的杠杆。
人,其实不需要太多的东西,只要健康地活着,真诚地爱着,也不失为一种富有。 勤奋,是步入成功之门的通行证。 读书给人以快乐、给人以光彩、给人以才干。 你的成就将永远不会比你的自信的高度高出一厘米。 善良的人永远是受苦的,那忧苦的重担似乎是与生俱来的,因此只有忍耐。 多讲点笑话,以幽默的态度处事,这样子日子会好过一点。
第三节 认识简单机械 ——杠杆
杠杆的定义
一根硬棒,如果在力的作用下能绕 固定点转动,这根硬棒就叫杠杆。
【或直或弯】
杠 杆
支点O
的 五
动力F1 动力臂l1
要 素
阻力F2 阻力臂l2
O
FF21
FF21
F1
O F2
O
F1
F2
F2
F1 O
O
F1
F2
画力臂的步骤
1、找支点 2、画动力阻力的作用线
3、画支点到动力和阻力作用线的垂线
杠杆原理公式及图解

杠杆原理公式及图解
杠杆原理:(1)在无重量的杆的两端离支点相等的距离处挂上相等的重量,它们将平衡。
(2)在无重量的杆的两端离支点相等的距离处挂上不相等的重量,重的一端将下倾。
(3)在无重量的杆的两端离支点不相等距离处挂上相等重量,距离远的一端将下倾。
(4)一个重物的作用可以用几个均匀分布的重物的作用来代替,只要重心的位置保持不变。
相反,几个均匀分布的重物可以用一个悬挂在它们的重心处的重物来代替。
(5)相似图形的重心以相似的方式分布。
公式:F₁·L₁=F₂·L₂
扩展资料:
杠杆可分为省力杠杆、费力杠杆和等臂杠杆,没有任何一种杠杆既省距离又省力。
省力杠杆:
L₁>L₂,F₁<F₂,省力、费距离。
如拔钉子用的羊角锤、铡刀,开瓶器,轧刀,动滑轮,手推车剪铁皮的剪刀及剪钢筋用的剪刀等。
费力杠杆:
L₁<L₂,F₁>F₂,费力、省距离。
如钓鱼竿、镊子,筷子,船桨裁缝用的剪刀理发师用的剪刀等。
等臂杠杆:
L₁=L₂,F₁=F₂,既不省力也不费力,又不多移动距离。
如天平、定滑轮等。
杠杆课件ppt

动力臂:从支点到动力
作用线的距离。(L1)
阻力臂:从支点到阻力作用
线的距离。(L2)
动力和阻力使杠杆转动的 方向(转动效果)相反
o
F1
l2
l1
F2
A
F1
L1
O
L2
B
F2
2、画出下列图中的力臂
二、杠杆的平衡条件实验
1.把杠杆安装在支架上,调节两端的螺母,使 杠杆在水平位置平衡。(便于直接在杠杆上测力臂)
F2
L1
上式表明:动力臂L1是阻力臂L2的几倍,动力 F1就是阻力F2的几分之一。
省力杠杆(动力臂大于 阻力臂)
O
L2
L1
F1
F2
费力杠杆(动力臂小于 阻力臂)
O
L2 L1 F1
F2
等臂杠杆(动力臂等于 阻力臂)
O
L2
Hale Waihona Puke L1F2F1
四、杠杆的种类
省力杠杆:L1>L2
实例:羊角锤、起子、剪刀、铡刀
费力杠杆:L1<L2
实例:鱼竿、镊子、火钳、船桨
等臂杠杆:L1=L2
实例:天平
杠杆的分类
请对下列器具应用的杠杆进行分类:
等臂杠杆
费力杠杆
费力杠杆
费力杠杆
费力杠杆
请对下列器具应用的杠杆进行分类:
费力杠杆
省力杠杆
省力杠杆
省力杠杆
1.如图所示为使杠杆平衡,F1、F2、F3
三次分别作用在A点,其中__F_2 ___最小。
2. 在杠杆两边挂钩码,把支点右边的钩码对 杠杆的作用力当作动力,支点左边的钩码对 杠杆的作用力当作阻力。改变钩码的位置, 使杠杆在水平位置平衡,记下动力F1、阻力 F2、动力臂L1、阻力臂L2的数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图8-5
专题五 力学之杠杆
1、如图甲所示,杠杆OA 处于平衡状态,在图中分别画出力F 1和F 2对支点0的力臂L 1和L 2。
2、如下图甲所示,杠杆OA 在力F 1、F 2的作用下处于静止状态,L 2是力F 2的力臂.在图中画出力F 1的力臂L 1和力F 2.
3、如图8-5所示,O 为杠杆AC 的支点,在O 处挂一小球,AO=OB=BC ,为使杠杆在水平位置平衡,画出施加在杠杆上最小动力F 1的力臂L 1:,并标出F 1的方向。
4.杠杆在我国古代就有了许多巧妙的应用。
护城河上安装使用的吊桥就是一个杠杆,由图8-21可知它的支点是 点(填“A ”、B ”或“C ”),在匀速拉起时,它属于一个______杠杆(填“省力”或“费力”),并在图中画出动力臂L 1。
5.如图8-13所示的杠杆中,动力的力臂用L 表示,图中所画力臂正确的是( )
6.在“研究杠杆平衡条件”的实验中
(1)把杠杆挂在支架上,实验前没有挂钩码时,发现杠杆右端下倾,可将右端螺母向_____边旋转,使杠杆在水平位置平衡(填“左”或“右”)。
(2)实验中共有6个钩码,杠杆上每格距离相等,调节好杠杆后,在杠杆左边离支点2格的A 处挂了3个钩码,如图8-32所示,为使杠杆在水平位置平衡,请你在杠杆右边挂上钩码(用一种方法).你的方法是_________。
(3)实验中改变支点两侧的钩码位置和个数,用同样的方法一般要做三次,得到三组数据并进行分析.这样做的目的是________。
7.下列工具中,属于省力杠杆的是 ( )
A .夹邮票用的镊子
B .理发师修剪头发用的剪刀
C .剪铁丝用的钢丝钳
D .钓鱼用的鱼竿
甲
甲
图
8-32
8、如图8-7所示是一个指甲刀的示意图,它由三个杠杆ABC、OBD和OED组成,用指甲刀剪指甲时,下面说法正确的是( )
A .三个杠杆都是省力杠杆
B .三个杠杆都是费力杠杆
C .ABC是省力杠杆,OBD、OED是费力杠杆
D .ABC是费力杠杆,OBD、OED是省力杠杆
9、如图8-8是自卸车的示意图,车厢部分视为杠杆,则下列分析正确的是( )
A .
B 点是支点,液压杆施的力是动力,货物重是阻力
B .B 点是支点,物体A 放在车厢前部可省力
C .C 点是支点,物体A 放在车厢后部可省力
D .C 点是支点,物体A 放在车厢前部可省力 10、如图所示,AOB 为一轻质杠杆(杠杆自重忽略不计),O 为支点,OA =OB ,在杠杆的B 端挂一重20N 的重物,要
使杠杆平衡,则在A 端施加的力F 至少为 N 。
(
11、人体内也存在三种类型的杠杆,即省力杠杆、费力杠杆和等臂杠杆.跺脚时要靠腓肠肌收缩,骨骼和腓肠
肌状况如图所示.踮着的脚可以看作是 杠杆(填类型).
12、如图所示,用始终与杠杆垂直的力F ,将杠杆缓慢地由位置A 拉至位置B ,阻力G 的力臂 ,动力F 。
(填“变大”或“变小”“不变”)
13、如图8-4所示,一根重木棒在水平动力(拉力)F的作用下以 O点为轴,由竖直位置逆时针匀速转到水平位置的过程中,若动力臂为l ,动力与动力臂的乘积为 M,则( )
A .F增大,l增大,M增大
B .F增大,l减小,M减小
C .F增大,l减小,M增大
D .F减小,l增大,M增大 14、一根杠杆两端挂有等重的实心铜块和铁块,当它们都浸没在水中时,杠杆恰好平衡,现将铜块和铁块同时从水中取出,则杠杆将( )
A .铜块端向下运动
B .铁块端向下运动
C .杠杆仍然平衡
D .条件不足,无法判断
图
8-4
图
8-7
图
8-8
15、图11是油压千斤顶的示意图,大活塞的直径是小活塞直径的5倍,大活塞上的重物G=5×103牛,O为支点,AB∶OB=3∶1。
要将重物G举起来,至少在A端加多大的力?不计摩擦。
