品保手法箱线图使用说明
《品保七大手法》课件

详细描述
PDPC法的优点在于其前瞻性和预防性,能 够预测可能出现的问题并提前制定对策。它 有助于减少问题发生的可能性并降低损失。 然而,PDPC法也有其局限性,例如对于某 些不确定因素较多的问题,可能难以准确预
测并制定有效的对策。
05
如何选择合适的品保七大手法
根据问题性质选择合适的手法
针对具体问题选择
详细描述
在制定城市交通规划时,采用系统图法对城市交通系统 进行全面分析。通过绘制系统图,将城市交通的各个方 面如公共交通、自行车、步行等展示出来,有助于规划 者全面了解城市交通状况并制定合理的规划方案。
PDPC法的应用案例
总结词
PDPC法是一种风险预测和对策制定的方法,通过对 未来可能发生的情况进行全面考虑并制定应对措施。
对于规模较小、复杂度较低的项 目,可以选择简单的手法,如检 查表、层别法等。
针对大型项目
对于规模较大、复杂度较高的项 目,需要选择更为系统、全面的 手法,如因果图、流程图等。
根据团队特点和资源状况选择合适的手法
团队特点
根据团队成员的技能和经验,选择适合团队的手法。例如,如果团队成员对统 计分析比较熟悉,可以选择柏拉图、直方图等手法。
详细描述
鱼骨图法的优点在于其直观性和系统性,能够全面展示问题的各个方面,有助于系统性地分析问题。此外,鱼骨 图法有助于团队成员共同参与问题的分析和解决。然而,鱼骨图法也有其局限性,例如对于某些复杂问题,可能 难以通过鱼骨图法找到根本原因,需要结合其他方法进行分析。
流程图法的优缺点分析
总结词
流程图法是一种直观展示流程和步骤的方法,有助于理解和优化流程。
。
其他领域
品保七大手法还可应用于政府机 构、教育机构等非营利组织,帮 助其提高工作效率和品质水平。
箱线图

箱线图
样本分布的图形化汇总,显示其形状、中心趋势和变异性。
默认箱线图显示包括以下内容:
箱线图可帮助您了解分布情况。
例如,上面的箱线图表示客户支持电话的等待时间。
上部端点处的异常值、较长的 whisker 上限以及框的上半部分表明数据呈正偏斜,这是符合实际的,因为在分布的下部端点处,等待时间不可能低于零。
箱线图还可用于比较多个分布。
例如,质量工程师可以比较三周内每周生产的塑料管件的直径。
下面的箱线图表示了结果。
箱线图默认显示四分位间距框,但是对于某些箱线图,可以选择显示不同的框类型:
·中位数置信区间框 - 为中位数显示 95% 置信区间(默认设置)。
·极差框 - 从最小值延伸至最大值。
箱线图(BoxPlot)
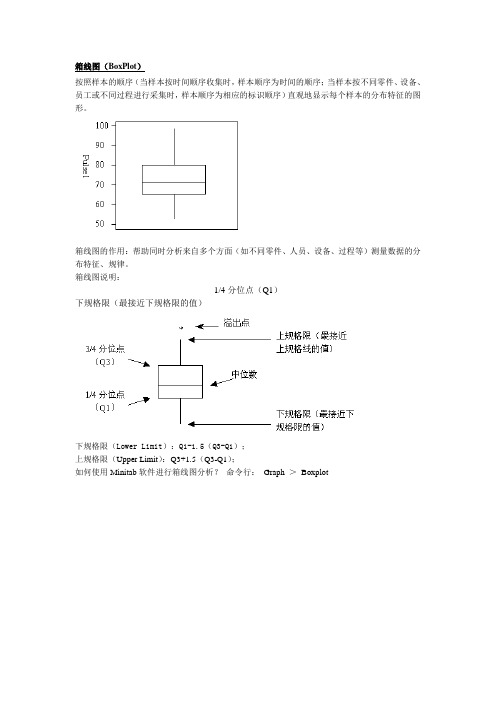
箱线图(BoxPlot)
按照样本的顺序(当样本按时间顺序收集时,样本顺序为时间的顺序;当样本按不同零件、设备、员工或不同过程进行采集时,样本顺序为相应的标识顺序)直观地显示每个样本的分布特征的图形。
箱线图的作用:帮助同时分析来自多个方面(如不同零件、人员、设备、过程等)测量数据的分布特征、规律。
箱线图说明:
1/4分位点(Q1)
下规格限(最接近下规格限的值)
下规格限(Lower Limit):Q1-1.5(Q3-Q1);
上规格限(Upper Limit):Q3+1.5(Q3-Q1);
如何使用Minitab软件进行箱线图分析?命令行:Graph >Boxplot
将需要分析的数据列分别输入Graph-Y和Grpah-X栏中,如需要,可对其他设置进行调整。
案例分析:
某研究机构想要对国民的身体素质进行调查,共对92人进行了抽查,调查了体重、性别、身高、脉搏(运动前后)、吸烟与否等信息。
其中按性别的不同对国民的脉搏进行了箱线图分析,如下图所示:
从该箱线图中可以得到如下信息:
男性(1)的平均脉搏约为70,女性(2)的平均脉搏约为78左右,高于男性;
男性脉搏的分布(箱体的高度)较为紧密,女性脉搏的分布比较分散;
最大值出现在女性中,最小值出现在男性中;
两组数据中都没有出现溢出值,表明分布比较正常。
解读箱线如何读懂和分析箱线上的数据

解读箱线如何读懂和分析箱线上的数据箱线图(Box-Plot),也被称为盒须图或箱须图,是一种用于展示一组数据分布的统计图表。
它由五个关键统计量组成:最小值、第一四分位数(Q1)、中位数(Q2)、第三四分位数(Q3)和最大值。
箱体表示数据的离散程度,而上下两个“须”则表示数据的范围和异常值。
本文将解读如何读懂和分析箱线图上的数据,并通过实例进行说明。
首先,我们来看一个典型的箱线图:[插入示例箱线图]从上述图中,我们可以观察到以下几个关键点:1. 箱体部分:箱体由横向的矩形表示,矩形的两端分别代表第一四分位数(Q1)和第三四分位数(Q3),而矩形的中线则表示中位数(Q2)。
通过观察箱体的长度和密度,可以初步判断数据的分布情况。
2. 上须和下须:箱体上下分别延伸出两条线,称为须。
须的延伸长度并非固定,而是根据数据的分布情况确定的。
一般情况下,须的长度相当于1.5倍的四分位距(IQR = Q3 - Q1),即(Q3 + 1.5 * IQR)和(Q1 - 1.5 * IQR)。
超出这个范围的数据点被认为是异常值(Outlier)。
3. 离群点:在须的范围之外,也就是超出1.5倍四分位距的数据点被认定为离群点。
离群点的存在可能是由于数据测量误差、实验异常或其他异常情况所导致。
通过观察箱线图,我们可以获得以下几类信息:1. 中位数:箱体中的一条线(也就是箱体的中线)表示数据的中位数,即将数据按照从小到大的顺序排列,处在中间位置的数值。
中位数可以反映数据的中心位置。
2. 上下四分位数:箱体的上边缘和下边缘分别代表第三四分位数(Q3)和第一四分位数(Q1),它们将整个数据分布划分为四等分。
四分位数可以用来描述数据的离散程度。
3. 箱体长度和密度:箱体长度反映了数据在中位数两侧的离散程度,箱体越长表示数据的离散程度越大,反之则离散程度较小。
同时,箱体较密集也代表数据较为集中。
4. 异常值:箱体上下的须以外的数据点被认为是异常值。
品检数据分析中的异常检测方法探讨

品检数据分析中的异常检测方法探讨在品检过程中,异常检测是至关重要的一环。
通过及时发现和处理异常数据,可以提高产品质量,避免损失和风险。
本文将聚焦于品检数据分析中的异常检测方法,探讨几种常见的技术和方法,并讨论其适用性和优缺点。
一、控制图法控制图是品检数据分析中最常用的异常检测方法之一。
它通过绘制统计图表,检测数据中的异常点。
常见的控制图包括平均数图、范围图和方差图等。
控制图法适用于连续型数据,并且对数据的分布情况不做过多假设。
其优势在于易于理解和实施,可以实时检测异常情况,帮助快速调整生产工艺。
然而,控制图方法较为简单,无法识别复杂的异常模式,对于非连续型和分布不均匀的数据效果较差。
二、箱线图法箱线图是一种常用的异常检测方法,它通过绘制数据的分位数来判断是否存在异常值。
箱线图利用数据的四分位数、中位数和离群值范围,判断数据是否落在正常范围之内。
箱线图相比控制图更适合处理非连续型和分布不均匀的数据。
其优势在于能较好地捕捉不同数据类型的异常情况,同时也易于理解和解释。
然而,箱线图方法对于小样本和离群值处理较为敏感,不能很好地应对复杂的异常模式。
三、聚类分析法聚类分析是一种无监督学习方法,通过将数据集划分为不同的组别,检测异常值所在的群组。
聚类分析方法适用于大规模数据集和多维数据的异常检测。
其优势在于可以自动发现异常群组,帮助准确定位异常值,发现潜在问题。
然而,聚类分析方法对于噪声、离群值和数据集特征的选择较为敏感,对初始参数和聚类算法的选择要求较高。
四、机器学习方法随着机器学习技术的发展,各种监督学习和无监督学习模型也被应用于异常检测。
例如,基于分类的方法可以通过训练模型来判定给定样本是否为异常值;基于聚类的方法可以将数据集划分为多个群组,检测异常群组。
机器学习方法具有较强的灵活性和自适应性,可以适应复杂的异常模式和多维数据。
然而,机器学习方法对于大规模数据集和计算资源要求较高,同时模型的建立和参数调整也需要较多的专业知识和经验。
指标 上箱体 下箱体 中线 长线

指标是衡量某一对象或事物特定特征或性质的标准或尺度。
在箱线图中,上箱体、下箱体、中线和长线是常用的统计指标,用于描述数据的分布情况和变异程度。
下面将对这四个指标进行详细讨论:一、上箱体上箱体是箱线图中的一个重要指标,它代表了数据中位数以上的部分。
在箱线图中,上箱体通常用一条水平线来表示。
上箱体的长度越长,表示数据上四分位数之间的差异越大,数据的分布越分散。
通过上箱体的长度,可以直观地了解数据的波动情况,从而判断数据的集中程度和变异程度。
二、下箱体下箱体是箱线图中的另一个重要指标,它代表了数据中位数以下的部分。
和上箱体一样,下箱体也可以用一条水平线来表示。
下箱体的长度越长,表示数据下四分位数之间的差异越大,数据的分布越分散。
通过下箱体的长度,可以进一步了解数据的波动情况,从而更全面地判断数据的集中程度和变异程度。
三、中线中线是箱线图中的一条垂直线,它代表了数据的中位数。
中线的位置和长度都可以直观地展现数据的集中程度和离散程度。
如果中线位于箱体的中间位置,表明数据的分布相对均匀,波动较小;如果中线偏离箱体的中间位置,表明数据的分布不均匀,波动较大。
中线可以作为数据分布的中心点,帮助我们了解数据的整体特征。
四、长线长线是箱线图中的一条水平线,它通常用来表示异常值或离裙点。
如果一个数据点偏离长线较远,就被认为是离裙点,可能是由于测量误差、数据异常或实际情况的特殊性所致。
长线的位置和长度能够直观地展现数据中异常值的数量和程度。
通过长线,我们可以对数据中的离裙点进行快速的识别和分析。
上箱体、下箱体、中线和长线是箱线图中常用的统计指标,它们可以帮助我们直观地了解数据的分布情况和变异程度。
在实际应用中,通过对这些指标的分析,我们可以更准确地把握数据的特征,从而为进一步的数据处理和决策提供有力支持。
上文讲述了在箱线图中常用的四个统计指标:上箱体、下箱体、中线和长线。
这些指标可以帮助我们更好地理解数据的分布情况和变异程度。
盒形图(boxplot)[宝典]
![盒形图(boxplot)[宝典]](https://img.taocdn.com/s3/m/f8c7161b854769eae009581b6bd97f192279bf7d.png)
盒形图(box plot)又名:盒形-虚线图( box-and-whisker plot)概述盒形图实际上是以图形来概括频数分布的最重要的统计特征,以便更容易地理解和对比数据。
从图中可以看到数据下降的位置及分布情况。
盒形图是一个非常有用的工具,因为其绘制简便且提供大量的信息。
适用场合·当分析或交流数据的总体特征而不是数据细节时;·当对比两组或更多数据时;·当没有足够的数据做直方图时;·概括另一张图代表的数据时,例如控制图或趋势图。
实施步骤1按从小到大的顺序列出所有的数值,把所有数值的个数记为n。
按顺序这样排号:X1是最小的数,X2是次小的数,直到最大的数X n。
2中位数:把数据分成两半,找到中位数——一半数值大于它、一半数值小于它的那个点。
·如果整个数值的个数(n)是奇数:中位数就是中间的那个。
从一端数到第(n+1)/2个数。
中位数=X(n+1)/2·如果整个数值的个数(n)是偶数:中位数是中间两个数的均值。
从一端数到第n/2和n/2+1个数,求这两个数的均值:中位数=[X n/2+X n/2+1]/23四分位数( Hinges):把数据分为四个部分。
找到四分位数——一半数据的中位数。
·如果整个数值的个数是偶数,中位数即是X n/2和X n/2+1的均值。
按照步骤2再找出从1到X n/2的这些数值的中位数,这就是第1四分位数。
·如果整个数值的个数是奇数,中位数是X(n+1)/2。
按照步骤2再找出从1到中位数这些数值的中位数。
这就是第1四分位数。
按照相同的方法在较大的数值部分找到第3四分位数。
4四分位距(H-spread):计算两个分位数之间的距离,又叫四分位距:四分位距=第3四分位数-第1四分位数5内部范围(Inner fences):区分属于特定分布和分布之外的数值。
内部范围的上限处在高于第3四分位数1.5倍四分位距的位置,下限则处在低于第1四分位数1.5倍四分位距的位置。
教学节段PPT1 - 箱线图的应用30页PPT

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
教学节段PPT1 - 箱线图的应 用
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
某公司品保部图表的使用与说明

排列圖示例
废品统计表 废品统计表
第20頁
第21頁
第五章 特性要因圖
一、何謂特性要因圖?
一個問題的特性受到一些要因的 影響時,我們將這些要因加以整理,成為 有相互關系而且有條理的圖形,這個圖 形稱為特性要因圖.由於形狀就像魚的 骨頭,所以又叫做魚骨圖.首先提出了这 个概念的是日本品管权威石川馨博士, 所以特性要因图又称[石川图]。
數據之前應該考慮數據的條件背景以后,先把它層別化,再
開始收集數據.(在做查檢時,考慮適當分類)
2.QC手法的運用應該特別注意層別法的使用.
QC七大手法中的柏拉圖.查檢表.散佈圖.直方圖和管制圖
都必須以發現的問題或原因來作層別法.
例如製作柏拉圖時,如果設定太多項目或設定項目中其他
欄所估的比例過高,就不知道問題的重心,這就是層別不良的
第19頁
二、柏拉圖的製作方法 1.決定不良的分類項目. 2.決定數據收集期間,並且按照分類項目收集數據. 3.記入圖表紙並且依數據大小排列畫出柱狀圖. 4.點上累計值並用線連結. 5.記入柏拉圖的主題及相關資料. 三、柏拉圖的使用 1.掌握問題點 2.發現原因 3.效果確認(改善前後效果對比) 四、製作應注意以下三項 1.柏拉圖收集數據的期間和對象必須一樣 2.柏拉圖的橫軸是按項目別,依大小順序由高到低排列,
原因.另外直方圖的雙峰型或高原型都有層別的問題.
對收集的數據資料使用推移圖進行層別分析效果會更好。
四、管理工作上也應該活用層別法
第16頁
分層法示例
某空調維修部,幫助客戶安裝後經常發生製冷液泄漏。通過
現場調查,得知泄漏的原因有兩個:一是管子裝接時,操作
教学节段PPT1 - 箱线图的应用

95
91 88 86 82 77 74 68 62 55
95
90 88 86 81 76 74 68 61 54
95
90 88 85 81 76 74 65 60 50
94
89 88 85 81 76 72 64 59 48
94
89 88 84 80 76 71 64 59 44
93
89 87 83 80 75 70 63 57 43
Application of Box Plot
箱线图的应用
自然科学基础学科组 统计学
LOGO
安徽省第二届普通本科院校青年教师教学竞赛
3.3.2 箱线图的应用
案例导入 箱线图的概念
箱线图的作用
多批箱线图的分析
生活中的多批箱线图
案例导入
99
91 88 87 83 78 75 69 62 56
99
91 88 86 82 78 74 69 62 55
方法1
考虑直方图
直方图
能看出
呈左偏分布, 80~90分人数最多, 考试成绩看似较好。
看不出
平均水平 差异水平
案例分析
• 评价班级的考试成绩,应该从集中趋
势、离散程度、分布形状来综合度量。
方法2
考虑箱线图
可用SPSS 软件绘制
3.3.2 箱线图的应用
案例导入 箱线图的概念
箱线图的作用
多批箱线图的分析
94
89 88 85 81 76 72 64 59 48
94
89 88 84 80 76 71 64 59 44
93
89 87 83 80 75 70 63 57 43
93
89 87 83 79 75 70 63 57 41
箱线图(Box Plot)的技术细节及应用

对经常做质量数据分析的人而言,箱线图(Box Plot)可以说是再常见不过的了。
从应用而非理论的角度出发,虽然我们不一定需要了解其背后的每一个技术细节,但在本文中讨论的几个关键点无疑是需要我们注意的。
箱线图的构成及相关计算箱线图又称为盒形图、箱形图等,其图形如下:其中,IQR为四分位距,IQR=Q3-Q1;由此可见,箱线图上下两端的引线长度是相同的。
箱线图常见应用1. 观察数据的总体状态这也是箱线图最常用的作用,从中我们可以观察到数据的分位数、中位数及平均值等统计信息,并可以根据中位数和平均值的相对位置大致判断数据的分布形态。
2.识别数据中的异常值在箱线图中,上图中的下边界和上边界也成为内限,此外箱线图还有外限(Q1-3IQR和Q3+3IQR),箱线图上,超过内限的数据都被认为是异常值,其中在内限和外限之间的数据被称作温和异常值(mild outliers),在外限之外的数据被称为极端异常值(extreme outliers)。
用箱线图识别异常值的好处:一批数据中的异常值是值得关注的,我们通过分析异常值产生的原因,往往能够发现解决问题的机会。
虽然箱线图判断异常值的方法看起来有一定的任意性,但经验表明其在实际工作中具有较大的实用价值,其在处理需要特别注意的数据方面表现不错。
事实上,箱线图识别异常值的方法与其他经典方法有所不同,这使其具备一定的优越性:一方面,基于3倍西格玛法则或z分数方法都是以假定数据服从正态分布为前提的,但实际数据往往并不严格服从正态分布。
而且,它们判断异常值时都需要计算数据的均值和标准差,并以此作为判断异常值的标准,而均值和标准差的稳定性很小,而且异常值本身会对它们产生较大影响(这样产生的异常值个数不会多于总数0.7%)。
因此,如果用这两种方法来识别非正态分布数据中的异常值,其作用是比较有限的。
而箱形图基于实际数据,不需要事先假定数据服从特定的分布,而只是真实地表现数据的本来状态;另一方面,箱形图基于四分位数和四分位距来判断异常值,而四分位数具有一定的稳定性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,可见,箱形图识别异常值的结果相对比较客观。
箱线图的制作和使用 经典 易懂

从本组数据看,最上端应画到21,最下端画到8。 绘图完毕后,本例中的数值“48”判为异常值。
中位数:将一组数据从小到大按顺序排列后,将该组数据从中间分开使两边数 量相等的那个数。若本组数据有奇数个数,则按顺序排列后最中间的那个数就 是中位数,若本组数据有偶数个数,在按顺序排列后中间两个数的平均值是中 位数。
四分位数:一组数据按从小到大顺序排列后,把该组数据四等分的数,程为四 分位数。
3
宇宙无敌大元帅King穷银
1
2
3
4
5
6
7
8
9
8
9
10 12 13 19 19 21 48
8
宇宙无敌大元帅King穷银
箱线图的判读
1.最大值和最小值,中位数,平均值。 2.50%的数据在[9.5,20]之间,25%的数据大于20,25%的数 据小于9.5; 3.数据分布较广,中间50%的极差在20-9.5=10.5,跨度大; 4.本组数据有一个异常值; 5.多个箱线图在同一个窗口制作时,便于对比。
11
宇宙无敌大元帅King穷银
Thank You
12
宇宙无敌大元帅King穷银
9
宇宙无敌大元帅King穷银
Maximum Power
现场练习
250.0 247.5 245.0 242.5 240.0 237.5 235.0
3M背板与常规DNP背板组件功率对比
3M
DNP
背板类型
箱形图简介

箱形图箱形图(Box-plot)又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。
因型状如箱子而得名。
在各种领域也经常被使用,常见于品质管理。
1.定义"盒式图"或叫"盒须图""箱形图"boxplot须图又称为箱形图,其绘制须使用常用的统计量,最适宜提供有关数据的位置和分散的参考,尤其在不同的母体数据时更可表现其差异。
如右图所示,标示了图中每条线表示的含义,其中应用到了分位值(数)的概念。
主要包含六个数据节点,将一组数据从大到小排列,分别计算出他的上边缘,上四分位数,中位数,下四分位数,下边缘,还有一个异常值。
2.箱形图的绘制箱形图提供了一种只用5个点对数据集做简单的总结的方式。
这5个点包括中点、Q1、Q3、分部状态的高位和低位。
箱形图很形象的分为中心、延伸以及分部状态的全部范围箱形图中最重要的是对相关统计点的计算,相关统计点都可以通过百分位计算方法进行实现。
箱形图的绘制步骤:1、画数轴,度量单位大小和数据批的单位一致,起点比最小值稍小,长度比该数据批的全距稍长。
2、画一个矩形盒,两端边的位置分别对应数据批的上下四分位数(Q1和Q3)。
在矩形盒内部中位数(Xm)位置画一条线段为中位线。
3、在Q3+1.5IQR(四分位间距)和Q1-1.5IQR处画两条与中位线一样的线段,这两条线段为异常值截断点,称其为内限;在Q3+3IQR和Q1-3IQR处画两条线段,称其为外限。
处于内限以外位置的点表示的数据都是异常值,其中在内限与外限之间的异常值为温和的异常值(mild outliers),在外限以外的为极端的异常值(extreme outliers)。
四分位间距=Q3-Q1。
.4、从矩形盒两端边向外各画一条线段直到不是异常值的最远点,表示该批数据正常值的分布区间。
5、用“〇”标出温和的异常值,用“*”标出极端的异常值。
相同值的数据点并列标出在同一数据线位置上,不同值的数据点标在不同数据线位置上。
异常点判断-箱线图

统计小知识分享异常点判断(箱线图法)---felixsong为什么需要检测异常值�数据清洗需要异常值会影响我们的统计,均值、方差等受异常值影响大,例如平均工资。
�发现问题的契机异常值往往意味着某些问题,分析其产生的原因,是分析问题的重要入口。
�运营监控和质量控制DAU等指标异常监控、数据质控等用什么方法检测异常值箱线图(Boxplot、Box-whisker Plot)利用数据中的五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息,特别可以用于对几个样本的比较。
为啥是1.5?箱线图示例为啥不对称?箱线图的作用�直观明了地识别数据批中的异常值箱线图为我们提供了识别异常值的一个标准(经验值):异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值。
�利用箱线图判断数据批的偏态和尾重�利用箱线图比较几批数据的形状为什么用箱线图?�方法相对简单,用R语言、Excel等工具可以轻松实现。
�常用的基于正态分布的3σ法则或z分数方法需要数据服从正态分布�箱线图对数据作任何限制性要求,它只是真实直观地表现数据形状的本来面貌。
�箱线图稳健性较好,识别异常值的结果比较客观。
对称分布数据的箱线图非对称分布数据的箱线图箱线图分析DAU附录:为什么是1.5倍?1.5倍是进过大量分析和经验积累起来的标准,有一点的参考意义。
统计学中离群点微超出平均数 ±N 个标准差的范围的数值。
这个数据并非随意而定,其中运用的是统计学知识。
当一组数据为对称分布时:�约有68%的数据在平均数±1个标准差的范围之内。
�约有95%的数据在平均数±2个标准差的范围之内。
�约有99%的数据在平均数±3个标准差的范围之内。
当一组数据为不对称分布时:�至少有75%的数据落在平均数±2个标准差范围内。
�至少有89%的数据落在平均数±3个标准差范围内。
medcouple boxplot法

medcouple boxplot法
中位数偏差比(Median Absolute Deviation Ratio, MADR)是一种测量数据分散程度的方法,也被称为中位数偏差中位数比(Median Absolute Deviation Median Ratio, MADMR)或中位数系数(Median Coefficient, MC)。
MADR可以用来替代标准差,特别是在数据中存在异常值或极值的情况下。
Box Plot(箱线图)是一种可视化数据分布情况的图表,其中箱子表示数据的四分位数范围,中位数用一条线表示,而箱子外的触须表示数据的整体分布情况。
MedCouple(MC)是用来刻画数据偏态程度的统计量,它是基于中位数的偏度系数的一种改进,可用于区分数据分布的左偏、右偏或对称情况。
MedCouple Box Plot(MCBP)将MedCouple与Box Plot结合使用,可以更准确地分析数据分布情况。
MCBP的箱子宽度表示数据的中位数偏差,箱子高度表示数据的四分位数范围,而箱子顶部和底部的触须则表示数据的整体分布情况。
MCBP能够有效地检测到数据中的异常值和极值,并且能够更准确地描述数据分布的偏态情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
箱线图(Boxplot)也称箱须图(Box-whisker Plot),它是用一组数据中的最小值、第一四分位数、中位数、第三四分位数和最大值来反映数据分布的中心位置和散布范围,可以粗略地看出数据是否具有对称性。
通过将多组数据的箱线图画在同一坐标上,则可以清晰地显示各组数据的分布差异,为发现问题、改进流程提供线索。
1.什么是四分位数
箱线图需要用到统计学的四分位数(Quartile)的概念,所谓四分位数,就是把组中所有数据由小到大排列并分成四等份,处于三个分割点位置的数字就是四分位数。
第一四分位数(Q1),又称“较小四分位数”或“下四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
第二四分位数(Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
第三四分位数(Q3),又称“较大四分位数”或“上四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
第三四分位数与第一四分位数的差距又称四分位间距(InterQuartile Range,IQR)。
计算四分位数首先要确定Q1、Q2、Q3的位置(n表示数字的总个数):
Q1的位置=(n+1)/4
Q2的位置=(n+1)/2
Q3的位置=3(n+1)/4
对于数字个数为奇数的,其四分位数比较容易确定。
例如,数字“5、47、48、15、42、41、7、39、45、40、35”共有11项,由小到大排列的结果为“5、7、15、35、39、40、41、42、45、47、48”,计算结果如下:
Q1的位置=(11+1)/4=3,该位置的数字是15。
Q2的位置=(11+1)/2=6,该位置的数字是40。
Q3的位置=3(11+1)/4=9,该位置的数字是45。
而对于数字个数为偶数的,其四分位数确定起来稍微繁琐一点。
例如,数字“8、17、38、39、42、44”共有6项,位置计算结果如下:
Q1的位置=(6+1)/4=1.75
Q2的位置=(6+1)/2=3.5
Q3的位置=3(6+1)/4=5.25
这时的数字以数据连续为前提,由所确定位置的前后两个数字共同确定。
例如,Q2的位置为3.5,则由第3个数字38和第4个数字39共同确定,计算方法是:38+(39-38)×3.5的小数部分,即38+1×0.5=38.5。
该结果实际上是38和39的平均数。
同理,Q1、Q3的计算结果如下:
Q1 = 8+(17-8)×0.75=14.75
Q3 = 42+(44-42)×0.25=42.5
Excel为计算四分位数提供了QUARTILE(array,quart)函数,其中array参数用于指定要计算四分位数值的数组或数值型单元格区域,quart指定返回哪一个四分位值,可用值如下:
0,返回最小值;
1,返回第一个四分位数;
2,返回第二个四分位数,即中位数;
3,返回第三个四分位数;
4,返回最大值。
2.箱线图的结构
箱线图包括一个矩形箱体和上下两条竖线,箱体表示数据的集中范围,上下两条竖线分别表示数据向上和向下的延伸范围,结构如图9-51所示。
图9-51箱线图的结构
四分位间距框的顶部线条是第三四分位数的位置,即Q3,表示有75%的数据小于等于此值。
底部线
条是第一四分位数的位置,即Q1,表示有25%的数据小于此值。
则整个四分位间距框所代表的是数据集中50%(即75%-25%)的数据,四分位间距框的高度就是这些数据涉及的范围,能够表现出数据的集中程度。
Q2是数据中位数的位置。
Whisker上限是延伸至距框顶部1.5倍框高范围内的最大数据点,Whisker下限是延伸至距框底部1.5倍框高范围内的最小数据点,超出Whisker上限或下限的数值将使用星号“*”表示。
但是,在Excel中绘制箱线图需要借助股价图来实现,因此无法展现异常值,Whisker上限将延伸至数据最大值的位
置,Whisker下限将延伸至数据最小值的位置。
3.绘制箱线图
图9-52中的A2:F8区域和H2:M8区域分别是华北和华南是某段时间客户订单收货天数的统计结果,
C11:C15和J11:J15是利用QUARTILE函数计算的华北、华南收货天数的四分位数结果。
图9-52收货天数的四分位数计算结果
在Excel中绘制箱线图需要借助股价图的“开盘-盘高-盘底-收盘”图来实现。
根据Excel绘图时放置数据系列的位置,开盘、盘高、盘底、收盘应分别对应Q1、Q0、Q2、Q4。
下面是绘图步骤:
准备图表数据。
根据对应关系,在表格的B18:E18区域分别输入华北客户的Q1、Q0、Q2、Q4统计数字,将Q3输入到最后的F18单元格中,在A18中输入一个日期型数据(注意,必须为日期型),如“2013/1/1”。
然后在第19行中输入华南客户的数据,A19中的日期递增1天,最终结果如图9-53所示。
图9-53准备图表数据
插入图表。
选定A18:E19区域,在“插入”功能区的“图表”模块中单击“其他图表”,选择股价图部分的“开盘-盘高-盘底-收盘图”按钮,即可看到绘制的股价图,如图9-54所示。
图9-54插入股价图
添加Q3数据系列。
由图9-54可以看出,四分位间距框的顶部线条使用的是Q4(最大值)位置,而是不是箱线图要求的Q3位置。
右击绘图区,在弹出的快捷菜单中选择“选择数据”命令,打开“选择数据源”对话框。
单击“添加”按钮打开“编辑数据系列”对话框,在“系列名称”折叠框中输入“Q3”,在系列值折叠框中选择F18:F19区域,单击“确定”按钮即可看到股价图变成了箱线图,如图9-55所示。
四分位间距框的高度小了很多,单击顶部线条与Whisker上限交汇处,可以看到使用
图9-55 添加Q3数据系列
显示中位数线。
至此,四分位间距框虽然已经绘制正确了,但是还缺少中位数线,即Q2。
选择图例中的“系列3”标签,然后单击鼠标右键,在弹出的快捷菜单中选择“设置数据系列格式”命令,打开“设置数据系列格式”对话框。
在“数据标记选项”中将标记类型设置为内置的“-”形状,单击
图9-56显示中位数线
美化图表。
首先要修改分类轴(横轴)标签,由于插入股价图时的限制在A18和A19单元格中输入了日期型数据,但是在图表插入后,可以将其修改为其他数据类型的值,因此在A18和A19单元格分别输入“华北”、“华南”。
其次是删除图例栏,对于箱线图而言这并不需要。
最后,可以为图表添加一个标题。
最终美化后结果如图9-57所示。
图9-57美化后的图表
由图9-57可以看出,华北和华南客户的中位数位置、四分位间距框的位置与高度基本相同,说明两区域的客户收货天数基本相同。
但是,从Whisker上限和Whisker下限看,华南客户的收货天数范围小于华北客户,说明流程更加稳定。
