第1章 计算机中数的表示
合集下载
第1讲 计算机中数据的表示
要完整地表示一个机器数，应考虑机器数的 符号表示、有效值范围、小数点表示三个重要因 素。 （1）机器数的符号表示 用二进制数的最高有效位约定为符号位（符号 位只占1位），其它位表示数值。符号位为0表示 正数，为1表示负数。小数点不占数位（隐含）。 例如： 真值：N1=+0.1001B， N2=-0.1001B, N3=+1001B， N4=-1001B
（10） （2）
3 .数制的转换 (1)二进制数和十进制数间的转换 1)二进制数转换成十进制数 只要把要转换的数按权展开后相加即可。例如： ll0l0．0lB＝l×2^4十l×2^3十l×2^1十l×2^-2 ＝26.25D
2)十进制数转换成二进制数 其转换过程为上述转换过程的逆过程，但十进 制整数和小数转换成二进制的整数和小数的方 法是不相同的。 ①十进制整数转换成二进制整数的方法有很 多，最常用的是“除2取余法”，即除2取余， 后余先排。 例: 将十进制数129转换成二进制数。 解：把129连续除以2，直到商数为0，余数 小于2，其过程如下：
计算机中浮点表示是要把机器数分为两部分，一 部分表示阶码（指数，用有符号整数表示），另一 部分表示尾数（数值的有效数字部分，一般用定点 小数表示），阶码和尾数均有各自的符号位。即任 意一个二进制数N可以写成下面的形式： N＝±d· 2^±P d是尾数，一般用定点二进制纯小数表示，是数 值的有效数字部分。d前面的“±”表示数的符号， 用尾数的最高位表示，此符号常常称为数符或尾符； P称为阶码（或阶数），它前面的符号称为阶符，表 示阶码的符号，用阶码的最高位表示。阶码和阶符 指明小数点的位置，小数点随着P的符号和大小而浮 动。
例如： 将十进制数3938转换成十六进制数。 解： 把3938连续除以l6，直到商数为0，余数小 于16，其过程如下：
1-2 计算机中数和字符的表示
1.2
概述
计算机中数和字符的表示
一、计算机中数和字符的存放
数据存放于存储器或寄存器中。 数据按字长一般分为：
8位（字节BYTE）
16位（字WORD） 32位（双字DWORD） 64位、128位、256位
数据在微机(INTEL)中存放的原则是
数 据 在 内 存 的 存 储 方 式
低地址放低字节，高地址放高字节
三、二进制数的运算
1、二进制数的算术运算
特点：按一定字长进行，运算结果超过字长则产生 进位、借位或自动丢失。
加法运算：11010011 + 10001100 1 01011111 进位 减法运算 ：01110011 -11010010 1 10100001 借位
2、二进制数的逻辑运算 特点：按位进行，无进位或借位
• 1、次高位有进位，而最高位没有进位，这种情况对 应：正数+正数＝负数 • 如：72+98＝ • 01001000 • +01100010 • 10101010 • 2、次高位没进位，而最高位有进位，这种情况对应 ：负数+负数＝正数 • 如：-83+（-80）＝ • 10101101 • + 10110000 • 1 01011101 • 丢失
[+33]补 = 0010 0001B
[+15]补 = 0000 1111B 0 0 1 0 0 0 0 1B [+33]补 ＋ 0 0 0 0 1 1 1 1B [+15]补
符号位和数值位 一起进行运算
0 0 1 1 0 0 0 0 B [+48]补
[(＋33)＋(－15)]补= [＋33]补+ [－15]补
例1.3
概述
计算机中数和字符的表示
一、计算机中数和字符的存放
数据存放于存储器或寄存器中。 数据按字长一般分为：
8位（字节BYTE）
16位（字WORD） 32位（双字DWORD） 64位、128位、256位
数据在微机(INTEL)中存放的原则是
数 据 在 内 存 的 存 储 方 式
低地址放低字节，高地址放高字节
三、二进制数的运算
1、二进制数的算术运算
特点：按一定字长进行，运算结果超过字长则产生 进位、借位或自动丢失。
加法运算：11010011 + 10001100 1 01011111 进位 减法运算 ：01110011 -11010010 1 10100001 借位
2、二进制数的逻辑运算 特点：按位进行，无进位或借位
• 1、次高位有进位，而最高位没有进位，这种情况对 应：正数+正数＝负数 • 如：72+98＝ • 01001000 • +01100010 • 10101010 • 2、次高位没进位，而最高位有进位，这种情况对应 ：负数+负数＝正数 • 如：-83+（-80）＝ • 10101101 • + 10110000 • 1 01011101 • 丢失
[+33]补 = 0010 0001B
[+15]补 = 0000 1111B 0 0 1 0 0 0 0 1B [+33]补 ＋ 0 0 0 0 1 1 1 1B [+15]补
符号位和数值位 一起进行运算
0 0 1 1 0 0 0 0 B [+48]补
[(＋33)＋(－15)]补= [＋33]补+ [－15]补
例1.3
微机原理第1章-数制
无符号二进制数的除法运算有可能产生溢出，当除数较小时，运算
结果可能超出微处理器为除法运算结果准备的存储空间，从而溢出 。除法溢出时微处理器会产生溢出中断，提醒程序员程序出错。
33
知识点1.3.3
带符号整数的表示方法：
原码、反码、补码
34
带符号数的表示方法
【例1-17】 十进制 +1 -1 ＋79 －79 0 0 二进制 +1 -1 + 1001111 - 1001111 0 0000000 1 0000000 符号数值化 0 0000001 1 0000001 0 1001111 1 1001111
15
2. 十进制数到非十进制数的转换
转换为二进制， 对整数：除2取余； 对小数：乘2取整。
转换为十六进制， 对整数：除16取余； 对小数：乘16取整。
整数部分 小数部分
余数
低位
高位
2 115 2 57 2 28 2 14 2 7 2 3 2 1 0
1 1 0 0 1 1 1
高位
0.75 2 × 1.5 0.5 2 × 1.0
例如：(3FC.6)H =3×162+F×161+C×160+6×16-1 =(1020.375)D
知识点1.2.2
数制转换
14
1. 非十进制转换为十进制
按权表达式展开，再按十进制运算规则求和，即可得到对应的十进制数。
例： (1101.101)2=23+22+2-1+2-3=(13.625)10 (3FC.6)H=3×162+15×161+12×160+6×16-1=(1020.375)D
678.34=6×102+7×101+8×100 +3×10-1+4×10-2
第1章数据在计算机中的表示形式讲义.
第1章
数据在计算机中的表示形式
本章主要内容
(1) 机器数与真值的概念 (2) 常见的机器数表示形式 (3) 数的定点表示与浮点表示
1.1 机器数与真值
电子计算机实质上是一个二进制的数字系统，在机器
内部，二进制数总是存放在由具有两种相反状态的存储 元件构成的寄存器或存储单元中，即二进制数码0和1是 由存储元件的两种相反状态来表示的。
① 若定点小数原码序列为x0. x1x2… xn ,则 [x]原= x 0≤x＜1 1-x -1＜x≤0 式中x代表真值，[x]原为原码表示的机器数。 例如：
x＝＋0.1011，则[x]原 =0.1011 x＝－0.1011，则[x]原 =1-(-0.1011)=1+0.1011=1.1011 ② 若定点整数原码序列为x0 x1 x2… xn ，则 [x]原= x 0≤x＜2n 2n - x -2n＜x≤0
例如： x＝＋1011，则[x]原=01011 x＝－1011，则[x]原=24 –(–1011)=10000+1011=11011 对于原码表示，具有如下特点： ① 原码表示中，真值0有两种表示形式。 以定点小数的原码表示为例： [+0]原=0.00…0 [-0]原=1-(-0.00…0)=1+0.00…0=1.00…0 ② 在原码表示中，符号位不是数值的一部分，它们仅是 人为约定（“ 0 为正， 1 为负”），所以符号位在运算 过程中需要单独处理，不能当作数值的一部分直接参 与运算。
移码特点：
1）移码是把真值映射到一个正数域，因此移码的大小 可以直观地反映真值的大小。无论是正数还是负数， 用移码表示后，可以按无符号数比较大小。 2）移码的数值部分与相应的补码各位相同，而符号位 与补码相反。在移码中符号位为0表示真值为负数，符 号位为1表示真值为正数。 3）移码为全0时，它对应的真值最小。 4）真值0在移码中的表示是唯一的，即：
数据在计算机中的表示形式
本章主要内容
(1) 机器数与真值的概念 (2) 常见的机器数表示形式 (3) 数的定点表示与浮点表示
1.1 机器数与真值
电子计算机实质上是一个二进制的数字系统，在机器
内部，二进制数总是存放在由具有两种相反状态的存储 元件构成的寄存器或存储单元中，即二进制数码0和1是 由存储元件的两种相反状态来表示的。
① 若定点小数原码序列为x0. x1x2… xn ,则 [x]原= x 0≤x＜1 1-x -1＜x≤0 式中x代表真值，[x]原为原码表示的机器数。 例如：
x＝＋0.1011，则[x]原 =0.1011 x＝－0.1011，则[x]原 =1-(-0.1011)=1+0.1011=1.1011 ② 若定点整数原码序列为x0 x1 x2… xn ，则 [x]原= x 0≤x＜2n 2n - x -2n＜x≤0
例如： x＝＋1011，则[x]原=01011 x＝－1011，则[x]原=24 –(–1011)=10000+1011=11011 对于原码表示，具有如下特点： ① 原码表示中，真值0有两种表示形式。 以定点小数的原码表示为例： [+0]原=0.00…0 [-0]原=1-(-0.00…0)=1+0.00…0=1.00…0 ② 在原码表示中，符号位不是数值的一部分，它们仅是 人为约定（“ 0 为正， 1 为负”），所以符号位在运算 过程中需要单独处理，不能当作数值的一部分直接参 与运算。
移码特点：
1）移码是把真值映射到一个正数域，因此移码的大小 可以直观地反映真值的大小。无论是正数还是负数， 用移码表示后，可以按无符号数比较大小。 2）移码的数值部分与相应的补码各位相同，而符号位 与补码相反。在移码中符号位为0表示真值为负数，符 号位为1表示真值为正数。 3）移码为全0时，它对应的真值最小。 4）真值0在移码中的表示是唯一的，即：
第一章计算机基础知识
(2)应用软件 在计算机软硬件基础上为某一专门应用目的而设计开发的软件称为应 用软件.应用软件大致可以分为三大类:通用应用软件,用于专门行业的应 用软件和定制软件. 1.2.4 微型计算机系统的硬件组成 1.CPU(Central Processing Unit) CPU即中央处理单元,又称微处 CPU即中央处理单元,又称微处 理器.是一块集成了运 算器和控制器的半导体芯片,是整个计算机系统的 "大脑". 大脑" 2.系统主板(Main board)系统主板又称为母板是微型计算机中最大的一块集 .系统主板(Main board)系统主板又称为母板是微型计算机中最大的一块集 成电路板.
1.2 计算机系统的基本组成及工作原理
1.2.1 计算机系统的组成 一个完整的计算机系统有硬件系统和软件系统两部分组成.
运算器 CPU 控制器 主 机 内存(主存) 硬件系统 计 算 机 系 统 输入设备:键盘,鼠标,扫描仪 输出设备:显示器,打印机,绘图仪
系统软件:操作体统,语言处理程序
软件系统
CMOS ISA 插槽 主板电池 控制芯片 PCI 插槽 串 行/并 口 插 槽 Socket7 插槽 键盘插座 CACHE 内存插槽
3.内存储器 (1)随机存取存储器(Random Access Memory,简称RAM) )随机存取存储器(Random Memory,简称RAM)
(2)只读存储器(Read Only Memory,简称ROM) )只读存储器(Read Memory,简称ROM) 只读存储器简称ROM.CPU从它们中读取信息,而不能写入信息. 只读存储器简称ROM.CPU从它们中读取信息,而不能写入信息. (3)高速缓冲存储器(Cache) )高速缓冲存储器(Cache)
1.1计算机中数的表示及运算
考点1.1 计算机中数据的表示及运算一. 机器数和码制原码、反码、补码具体概念我就不重复了，只重申下相关结论：a.正数的原码、反码、补码都相同。
b.负数的反码为原码的按位取反（保持符号位不变），补码为反码加1。
二．存储单元中的数据（存储单元包括存储器中的存储单元和寄存器）在计算机的存储器的存储单元中的数据均以补码形式存放的，于是在计算机中的数据表示有下面结论：a不使用原码与反码。
但原码与反码可以作为计算真值的中间媒介。
b存储单元中的数据以补码形式存在。
c 数据的存取与运算都以补码形式进行。
d补码就是机器数，机器数就是补码三．定点数与浮点数1. 数的定点表示方法定点数是小数点固定的数。
在计算机中没有专门表示小数点的位，小数点的位置是约定默认的。
一般固定在机器数的最低位之后，或是固定在符号位之后。
前者称为定点纯整数，后者称为定点纯小数。
(1). 定点整数——小数点位置固定在数的最低位之后如：Dn-1 Dn-2 • • • • • • D1 D0.范围：2n-1 -1~ -2n-1 (采用字长n=16位补码时其值为32767 ~ -32768)(2). 定点小数——小数点位置固定在数的符号位之后、数值最高位之前。
如：D0. D-1 • • • • • • D-(n-2) D-(n-1)范围：1 - 2-(n-1) ~ -1(采用字长n=16位时其值为32767/32768 ~ -1)其中n表示字长多少位例1：2. 数的浮点表示方法浮点数：浮点数是指小数点位置不固定的数，它既有整数部分又有小数部分，如123.55、33.789等。
(1). 浮点数的表示：是把字长分成阶码和尾数两部分。
其根据就是:与科学计数法相似，任意一个J进制数N，总可以写成N = J E× M式中M称为数N的尾数(mantissa)，是一个纯小数；E为数N的阶码(e x ponent)，是一个整数，J称为比例因子J E的底数。
1no 计算机中的数据和编码
十六进制
之
进位计数制
表1.1 计算机中的数制对照表 0 1 2 3 4 5 6 7 十进制 二进制 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111
十六进制
8 9 A B C D E F
1.1 计算机中的数制
之
进位计数制
在进位计数制中，一个数码处在数的不同位置时， 它所代表的数值是不同的。每一个数位赋予的数值称为 位权，简称权。 权的大小是以基数为底，数位的序号为指数的整数 次幂，用I 表示数位的序号，用R 表示数位的权。 例:342.54各数位的权分别为102, 101, 100, 10−1和 10−2； 1011.01B各数位的权分别为23,
X1 X2
…
【例1.11】 写出真值X1 = ＋1001110，X2 = −1001110的补码。 [X1]补= 01001110 [X2]补= 10110010 【例1.12】 写出8位补码表示的最大和最小整数。 Max[X]补= [01111111]补 =＋1111111B =＋127 Min[X]补 = [10000000]补 = −10000000B = −128 8位补码表示整数的范围是＋127～−128。 用补码表示法能使减法运算转化为加法运算，并且在进行加减运算时， 能使符号位和数值位一起运算，从而简化运算规则。
Xn
＋1）。
计算机中数的表示 1.2 计算机中数的
之
机器数的表示方法
4．移码表示法 ． 移码也称作增码，就是在补码的基础上增加一个偏移量。根据多数高 级程序语言软件包的实数标准格式，字长为8位的移码，其偏移量为 127（7FH）；字长为11位的移码，其偏移量为1023（3FFH）。 【例1.14】 写出X1 =＋0000011B，X2 = −0000011B的移码。 [X1]移 = [X1]补＋偏移量 = [00000011B]补＋01111111B = [10000010B]移； [X2]移 = [X2]补＋偏移量= [11111101B]补＋01111111B = [01111100B]移。
之
进位计数制
表1.1 计算机中的数制对照表 0 1 2 3 4 5 6 7 十进制 二进制 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111
十六进制
8 9 A B C D E F
1.1 计算机中的数制
之
进位计数制
在进位计数制中，一个数码处在数的不同位置时， 它所代表的数值是不同的。每一个数位赋予的数值称为 位权，简称权。 权的大小是以基数为底，数位的序号为指数的整数 次幂，用I 表示数位的序号，用R 表示数位的权。 例:342.54各数位的权分别为102, 101, 100, 10−1和 10−2； 1011.01B各数位的权分别为23,
X1 X2
…
【例1.11】 写出真值X1 = ＋1001110，X2 = −1001110的补码。 [X1]补= 01001110 [X2]补= 10110010 【例1.12】 写出8位补码表示的最大和最小整数。 Max[X]补= [01111111]补 =＋1111111B =＋127 Min[X]补 = [10000000]补 = −10000000B = −128 8位补码表示整数的范围是＋127～−128。 用补码表示法能使减法运算转化为加法运算，并且在进行加减运算时， 能使符号位和数值位一起运算，从而简化运算规则。
Xn
＋1）。
计算机中数的表示 1.2 计算机中数的
之
机器数的表示方法
4．移码表示法 ． 移码也称作增码，就是在补码的基础上增加一个偏移量。根据多数高 级程序语言软件包的实数标准格式，字长为8位的移码，其偏移量为 127（7FH）；字长为11位的移码，其偏移量为1023（3FFH）。 【例1.14】 写出X1 =＋0000011B，X2 = −0000011B的移码。 [X1]移 = [X1]补＋偏移量 = [00000011B]补＋01111111B = [10000010B]移； [X2]移 = [X2]补＋偏移量= [11111101B]补＋01111111B = [01111100B]移。
微机原理及应用 第一章 计算机基础知识
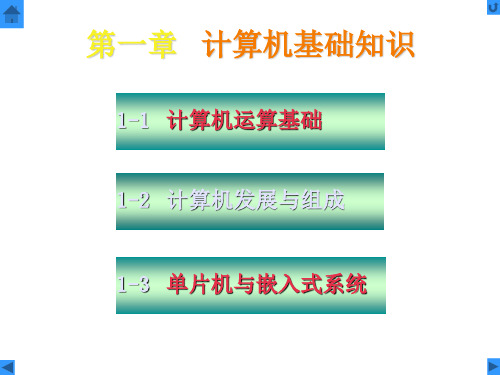
× 0.6225
×
1.250 2
1 (b-1)
×
0.5 0 2
0 (b-2)
1.0
1 (b-3)
• 0.625 = 0.101B
2. 0.625转换成十六进制数 0.625 × 16 = 10.0 0.625 = 0.AH
3. 208.625 转换成十六进制数 208.625 = D0.AH
（三）二进制与十六进制数之间的转换
第一章 计算机基础知识
1-1 计算机运算基础 1-2 计算机发展与组成 1-3 单片机与嵌入式系统
1-1 计算机运算基础
1-1-1 数制及其转换 1-1-2 计算机中数的表示法 1-1-3 计算机中数的运算方法 1-1-4 计算机中的编码系统
1-1-1 数制及其转换
数制（即计数制）是计数的规则、计数的方式。 进制（即进位计数制）是按不同的进位规则(方式) 计数的 数制。
+0 +0 +0
1
+1 +1 +1
… … ……
127 +127 +127 +127
128 - 0 - 127 -128
… … ……
254 -126 - 1 - 2
255 -127 - 0 - 1
0~255 -127 -127 -128
~+127 ~+127 ~+127
1-1-3 计算机中数的运算方法
• 24=16 ，四位二进制数对应一位十六进制数。 • 举例：
• 3AF.2H = 0011 1010 1111.0010 = 1110101111.001B 3 A F2
• 1111101.11B = 0111 1101.1100 = 7D.CH 7DC
《大学计算机基础》第1章-计算机基础知识
17
1.1.5 计算机的类型
按速度等指标分类
巨型机 大型通用机 微型计算机
工作站 服务器
按用途及使用范围分类
专用计算机 通用计算机
18
1.1.6 计算机的新技术
嵌入式技术
将计算机作为信息处理的部件， 嵌入到应用系统中的一种技术。
网格计算
充分利用成千上万个网络中 的闲置计算机共同参与计算。
中间件技术
9
第三代计算机
采用中、小 规模集成电 路代替了独 立元件晶体 管。
10
将电脑浓缩在一颗芯片上
750,000,000 晶
体
管
数
0.18微米芯片
目
2,300
10微米芯片 4004
奔腾4
11
计算机第一定律——摩尔定律
晶 体 管 数
计算机的CPU性能 每18个月，集成度将翻一番，速度
将提高一倍，而其价格将降低一半。
信息技术 ➢ 联合国教科文组织对信息技术的定义
应用在信息加工和处理中的科学、技术与工 程的训练方法和管理技巧；上述方面的技巧 和应用；计算机及其与人、机的相互作用； 与之相应的社会、经济和文化等诸种事物。
24
现代信息技术的内容和特点
现代信息技术的内容 ➢ 信息基础技术
新材料、新能源、新器件的开发和制造技术
单
位
时
间百
执
万 条
/
行每
的秒
指
令
数
12
1.1.2 计算机发展的几个阶段
根据计算机所采用的物理器件，将计算机的发展 分为四个阶段
第一代
(1946~1958) 电子管
5千~几万（次/秒）
第二代
微机原理 1-4数的表示
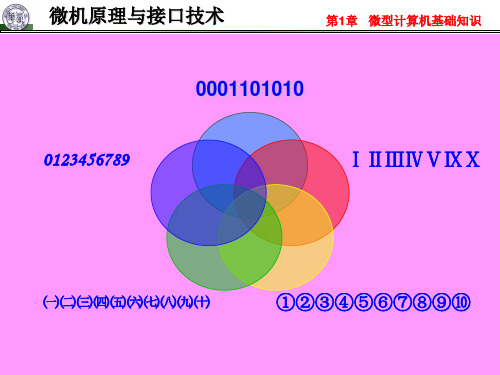
0000B-1001B来表示十进制数0-9。
例如：十进制数4256的压缩BCD码表示为：
0100 0010 0101 0110 B
微机原理与接口技术
第1章 微型计算机基础知识
2、非压缩BCD码格式（Unpacked BCD Format）
也叫未组合BCD码
用8个二进制位表示一个十进制位 其高四位无意义，用xxxx表示，低四位和压缩 BCD码相同。 例：十进制数4256的非压缩BCD码表示为： xxxx0100 xxxx0010 xxxx0101 xxxx0110 B
Hexdecim al
16
注解：16进制中字母对应数值：
A 10
B 11
C 12
D 13
E 14
F 15
微机原理与接口技术
第1章 微型计算机基础知识
n 1 i S rR i i m
i 表示这些符号排列的位号，从 -m (m小数后位数)到 n1(n小数前的位数)
ri
是位号为 i 的位上的一个数码
i
i
R
是这个数制位号为 i 的位上的权 表示-m到n-1位的值求累加和 代表一个数值
ri R 是第 i 位的所代表的实际值
S
微机原理与接口技术
各种数制对照表
第1章 微型计算机基础知识
读作”壹零”,不读为”十”
二 进制 0000 0001 0010 0011 0100 0101 0110 0111
微机原理与接口技术
第1章 微型计算机基础知识
（1）二、八 、十六进制数和十进制数之间的转换
①、 二进制数转换为十进制数：按权展开相加 例: 11101.101 =1×24+1×23+1×22+0×21+1×20+
计算机中数据的表示
2、字节(Byte) 人们规定8位二进制数为一个字节（简称B，1B＝8bit) 计算机中信息存储以字节作为基本单位。 常见信息存储的单位有千字节（KB）、兆字节（MB）、吉 字节（GB) 它们的换算关系： 1KB=1024(210)B 1MB=1024(210)KB=1024×1024(220)B 1GB=1024(210)MB=1024×1024(220)KB=1024×1024×102 4(230)B
例：把（10110.1001）2 转成八进制 （010 110 . 100 100） （26.44） 8 2 =
二进制转八进制
②八进制转二进制
方法： （一分为三） 将每位八进制码展开为3位二 进制码，再去掉首位的‚0”
八进制转二进制
例：把（10.2） 8 转成二进制
（001 000.010） （10.2） = 2 8 = （1 000.01） 2
2016/11/29
（4）位权的计算：
对于N进制数，整数部分第i位的位权为N -j 部分第j位的位权为N 。
i-1
，而小数
如：十进制第2位的位权为101，第3位的位权为102； 而：二进制第2位的位权为21，第3位的位权为22
（5）按位权展开的形式
十进制数512可以写成：
（512）10=5×102+1×101+2×100
将（3AB.11）16按位权展开
十进制转非十进制
三、十进制转非十进制
1、十进制数转换成二进制数
一个十进制数转换为二进制数，只需将该数反复除以2，所得的余数(先
从最后一个余数读起)就是二进制的表示形式。
2 57 2 28 2 14 2 7 2 3 2 1 0
……余1 ……余0 ……余0 ……余1 ……余1 ……余1
第一章微型计算机基础知识
CPU
内容
读写控制
…
1023 10100111
（3）存储器的分类 ROM：只读存储器。 工作时从ROM中读出信息，不能随意改写。 断电后信息不会丢失。ROM常用作程序存储器， 存放已调试好的固定程序和常数。 RAM：随机读写存储器。 能方便读出和改写信息，但失电后信息将不 复存在。 RAM 常用作数据存储器，暂存各种现 场数据、运算结果和正在调试的程序。
指令代码3
… 指令代码n
2、存储器
位 b (bit)：一个二进制位，信息最小单位 字节 B (Byte)：8位为一个字节
字长 W (Word Length)：一个字包含的二 进制位数
（1）存储器结构
存储器功能：存放程序和数据等信息 存储内容：程序或数据的二进制代码 存储地址：存储器每个单元的位置编 号 存储器容量：指存储单元的多少，如 存储器容量为1KB = 1024×8位 1KB存储器 地址 存储内容 0 1 10011010 01101011
微处理器
微处理器是用一片或少数几片大规模集成电路组 成的中央处理器（CPU，Central Processing Unit）。 这些电路执行控制部件和算术逻辑部件的功能。微处 理器的基本组成部分有：寄存器堆、运算器、时序控 制电路以及数据和地址总线。微处理器能完成取指令、 执行指令以及与外界存储器和逻辑部件交换信息等操 作，是微型计算机的运算控制部分，它可与存储器和 外围电路芯片组成微型计算机。
第1章 微型计算机基础知识
1.1计算机中的数和数制
一、计算机中的数制 表示:最简单,可靠；运算规则最简单。 （一）二进制数 特点：1．具有两个不同的数字符号，即0和1。 2．逢二进位。 例如： 111．11 （二）十六进制数 特点： 1．具有16个数字符号，采用0～9和A～F。 2．逢16进位 小数点左边的权是16的正次幂 小数点右边的权是16的负次幂
1-2_计算机中数和字符的表示解析
符号位相反 数值位相同
[－0-2n-1+1≤X≤＋2n-1-1
原码特点： 简单、直观，与真值的转换简单 原码缺点： 进行减法运算麻烦
解决办法： 引入补码表示法
可使减法运算简化为加法运算
3．补码表示法 正数的补码和原码相同 负数的补码可由其原码除符号位保持不变外，其余 各位按位取反，再在最末位加1而形成。 例1.3 假设机器字长为8位，则 则 [＋97]补= 01100001B [+97]原=01100001B [-97]原=11100001B
2、数制之间的转换
二－十进制转换
二－八进制转换
二－十六进制转换
1.2.1 无符号数表示 机器字长的所有位都参与表示数值。
若计算机的字长为n位，则n位无符号数可表示的 数X的范围是
0≤X≤2n－1
当n=8时，可表示的无符号数的范围为0～255， 当n=16时，可表示的无符号数的范围为 0～65535。
该式表明，求[X-Y]补可以用［X］补与 [-Y]补相加来实现
[－Y]补是对减数进行求负操作。 一般称已知 [Y]补求得 [－Y]补的过程叫变补或求负。
变补（求负）运算（NEG）: 已知[+X]补 ，求[-X]补
规则： 全部位（含符号位）按位取反后再加1
例如：已知[+15]补=0 0 0 0 1 1 1 1B
1.2.2 有符号数的表示方法
1．机器数与真值 计算机中的数是用二进制表示的，数的符号也是用 二进制表示的。 0：表示正数 符号位：通常为一个数的最高位 1：表示负数 若计算机的字长为8位，则D7为符号位，D6～D0为数值位
D7
D6
D5
D4
D3
D2
D1
数字在计算机中的表示
数字在计算机中的表⽰ 现实⽣活中，我们通常使⽤10进制来表⽰我们的数字，⽽在计算机中使⽤的是“0”和“1”表⽰数字的⼆进制。
如果我们⽤⼀个字节来存储⼀个数字，那么这个数字在计算机中的存储形式可能是这样的：00010011。
最左边的0位在带符号数字中⽤来表⽰正负号，0代表正号，1代表负号，所以它也就叫做符号位；其他位数⽤来表⽰具体数字，因此叫做数值位。
00010011如果⽤来表⽰带符号整数，那么它代表的数字是+19。
+19叫做真值，00010011⽤于在计算机中表⽰，所以叫做机器数。
机器数在计算机中的表⽰形式有三种，原码，反码和补码。
原码的表⽰： 左边是符号位，正数为0，负数为1。
其他位表⽰数值 【+10】原码 = 00001010 【-10】原码 = 10001010 【+0】原码 = 00000000 【-0】原码 = 10000000 反码的表⽰： 正数的反码和原码相同，负数的反码由原码除了符号位的其余位取反（即0表1,1表0） 【+10】反码 = 00001010 【-10】反码 = 11110101 【+0】反码 = 00000000 【-0】反码 = 11111111 补码的表⽰： 正数的补码与原码相同，负数的补码由原码的反码加1得到 【+10】补码 = 00001010 【-10】补码 = 【-10】反码 + 1 = 11110101 + 1 = 11110110 【+0】补码 = 00000000 【-0】补码 = 【-0】反码 + 1 = 11111111 + 1 = 【1】00000000（mod（256）） 补码的意义：补码实际上是⼀种模运算，以时钟为例，时钟⼀圈是12个⼩时，即时钟的模为12。
如果当前时刻是3点钟，在12个⼩时之后时刻变为15点，15在模12之后，依然是3点。
再如，将3点的时针调慢⼀个⼩时，即调成2点，和将时针向前调整11个⼩时的效果是⼀样的。
因此⽤3-1和（3+11）mod（12）的结果⼀样。
计算机中如何表示数字(1-6讲)
计算机中如何表示数字-01机器数与真值机器数就是数值在计算机中的表示形式，真值则是它在现实中的实际数值。
可以这样简单的理解。
因为计算机只能直接识别和处理用0、1两种状态的二进制形式的数据，所以在计算机中无法按人们的日常书写习惯用正、负符号加绝对值来表示数值，而与数字一样采用二进制代码0和1来表示正、负号。
这样在计算机中表示带符号的数值数据时，符号和数均采用了0、1进行了代码化。
这种采用二进制表示形式，连同正负符号一起代码化的数据，称为机器数或者机器码（即，数值在计算机中的二进制表示形式）。
与机器数对应,用正、负符号加绝对值来表示的实际数值称为真值。
根据约定机器数是否存在符号位，机器数可以分为无符号数和带符号数。
无符号数是指计算机字长的所有二进制位均表示数值。
带符号数是指机器数分为符号位和数值两部分，且均采用二进制表示。
一般约定最高位表示符号。
例1-1: 10011001作为无符号定点整数时，真值是153；作为带符号定点整数时，第一位是符号位，1代表负号，二进制数10011001的真值是-0011001，转化成十进制是-25。
对于带符号数，根据小数点位置固定与否，又可以分为定点数和浮点数。
在介绍浮点数之前我们要将注意力完全放在定点数上面，要有点耐心，对定点数的理解程度决定了我们对浮点数的理解程度，因为可以将浮点数看成是对定点数的一种应用，以后就会明白了。
好了，先看一看什么是定点数。
定点数约定所有数据的小数点位置均是相同且固定不变的。
计算机中通常使用的定点数有定点小数和定点整数两类。
定点小数：对于一个长度为n位的机器数，定点小数约定小数点在符号位和最高数值位之间，如下数符（最高位，占用1位）. 尾数（剩余n-1位）小数点只是一个约定，是隐含的，不占用空间。
定点整数：对于一个长度为n位的机器数，定点整数约定小数点在最低数值位之后，如下数符（最高位，占用1位）尾数（剩余n-1位）.小数点也是隐含的。
例1-2:下的八位二进制数，我们看看它们所代表的值是多少定点小数：1.1011001 真值=-0.1011001=-0.6953125定点整数：11011001 真值=-1011001=-89真值：127=+1111111 定点整数：01111111真值：-0.125=-0.001 定点小数：1.0010000总结上面的内容，机器数的特点是：1. 符号数值化，0代表正、1代表负。
第1章 基础知识2机器中符号数的表示法
例如n=16： -32767～+32767 反码表示范围： -(2n-1-1) ~ +(2n-1-1)
例如n=16: -32767~+32767 补码表示范围： -(2n-1) ~ +(2n-1-1)
例如n=16: -32768~+32767
2013-08
17
6. 二进制数的扩展
是指：数据从位数少扩展到位数较多——增加二进制位数。 例如从八位变为十六位 一个二进制数扩展后，应该保持这个数的大小和符号不变。 （1）源码表示的二进制数： 将符号位左移到最高位，其他全部扩展为补0 例如： 1100 0110B → 1000 0000 0100 0110B 0010 1101B → 0000 0000 0010 1101B
真值
- 1101001B (-105)
+1101110B (+110)
2013-08
4
（3）带符号数与无符号数 用一位二进制位表示数的符号：0表示正数，1表示负数， 这种表示数的方法，称为带符号数的表示方法。所表示的数， 叫做带符号的数。 带符号的数其最高位为符号位。
如果将全部有效位都用来表示数的大小，这种数的表示方
0000 0000 0000 0001 0000 0010
0111 0111 1000 1000 1110 1111 0000 0001
1111 1101 1111 1110 2013-08 1111 1111
253 254 255
-125 -126 -127
-2 -1 -0
-3 -2 -1 15
对于8位二进制数 00000000B～11111111B 源码表示范围： 11111111B ~ 01111111B: -(27-1) ~ +(27-1)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
汇编语言程序设计
思考: 把字数据3A50H存入20002H地址单元，如何存放? …
20000H 20001H 20002H 20003H 20004H
50 3A …
字数据的存取原则: 高— 高 低 — 低 即:高字节数据存放在高地址单元，低字节数据存放在低地址单元 低字节对应的存储单元的地址就是字数据的地址
…
return 15
汇编语言程序设计
本章小结
数制转换 原码、反码、补码 ASCⅡ码 BCD码 计算机内数据的存取
(1) 十进制、二进制、十六进 (1) 字长、无符号数、有符号 制数据的表示 数、机器数真值、机器数 (2)(1) 数据的存取单位 相互转换（重点: 整数） (1) 常用字符的ASCⅡ码 (2) 求补码；由补码求真值； (2) 数据的地址与存放 补码的运算；补码的扩展 (1) BCD码的表示
-8的真值: -0001000 -8的机器数:10001000 -8的原码: 10001000 -8的反码: 11110111 -8的补码: 11111000
next
例2: 设字长为16，根据补码求真值，计算对应的十进制数 (1) 00000000 00001000 (2) 11111111 11111000 (1) (2) 00001000 11111000 ← 8的补码（字长为16位） ← -8的补码（字长为16位） ← 8的补码（字长为8位） ← -8的补码（字长为8位）
0 0 1 0 0 1 1
0 1 0 1 1
next
例2: 1101101110.110101 (B) = ? (H)
00 1101101110.110101 00 (B) = 36E.D4 3 6 E D 4
(H)
return
汇编语言程序设计
2. 原码、反码、补码
术语
字长、无符号数、有符号数
next part
结论: 补码的符号位向左扩展n位后，仍是该数的补码。
next
例3: 设字长为8，计算[8]补+[-8]补，计算结果对应的十进制数 值。
00001000 + 11111000 1000]补 [0]
补码的运算规则: [x+y]补 = [x]补 + [y]补 [x- y]补 = [x]补 + [-y]补
汇编语言程序设计
第1章 计算机中数的表示
1
汇编语言程序设计
本章学习内容
数制及相互转换 原码、反码、补码 ASCⅡ码 BCD码 数据的存取
2
汇编语言程序设计
本章学习目标
掌握十进制、二进制、十六进制之间的相互转换 掌握补码的计算与应用 了解常见字符的ASCⅡ码 掌握数据的BCD码表示 掌握计算机内数据的存取方式
4. BCD码
压缩BCD码
每位十进制数用4个bit位的二进制数据表示
next part
非压缩BCD码
每位十进制数用8个bit位的二进制数据表示 例: 18 (1) 压缩BCD码表示: (2) 非压缩BCD码表示: 0001 1000 00000001 00001000
12
汇编语言程序设计
5. 计算机内数据的存取
16
汇编语言程序设计
本章课后任务
复习本章内容，理清基本概念和术语 自行完成书后习题，以检验对本章知识点的掌握情 况
17
术语: 地址 计算机内数据的存取单位
字节: 字: 双字: 四字: 8bit 16bit 32bit 64bit
20000H 20001H 20002H 20003H 20004H
next part
0011 0000 0011 0001 0011 0010 0011 0011 0011 0100
…
13
3
汇编语言程序设计
1. 数制及相互转换
基本概念
数制、基数、位权
next part
十进制、二进制、十六进制数据
表示 运算（算术运算、逻辑运算）
十六进制
相互转换
二进制 十进制
4
example
? 例1: 100.345(D) = 1100100.01011 (B) 2 2 2 2 2 2 2 100 50 25 12 6 3 1 0 0.345 2 0.69 2 1.38 2 0.76 2 1.52 2 1.04
return
汇编语言程序设计
3. ASCⅡ码
ASCII码字符集采用一个字节表示字符 常见字符的ASCII码
数字’0’~’9’ : 30H~39H 字母’A’~’Z’ : 41H~5AH 字母’a’~’z’ : 61H~7AH 回车CR：0DH 换行LF：0AH 空字符：0
next part
11
汇编语言程序设计
无符号数在计算机内的表示: 二进制形式 有符号数在计算机内的表示: 补码
机器数、机器数的真值 补码的求取及运算
example
7
例1: 设字长为8， 则: 十进制数8、-8的机器数真值、机器数、原码、反码、 补码是?
8的真值: +0001000 8的机器数:00001000 8的原码: 00001000 8的反码: 00001000 8的补码: 00001000
14
汇编语言程序设计
练习: 设内存单元输出存储如下,根据要求取出数据 从地址单元20001H取出一个: (1) 字节数据 (2) 字数据 (3) 双字数据 34H 4134H 43424134H
20000H 20001H 20002H 20003H 20004H
5AH 34H ‘A’ ‘B’ ‘C’