三角函数高考题型解析(含作业)
高三数学三角函数试题答案及解析

高三数学三角函数试题答案及解析1.设角的终边在第一象限,函数的定义域为,且,当时,有,则使等式成立的的集合为.【答案】【解析】令得:,令得:,由得:,又角的终边在第一象限,所以因而的集合为.【考点】抽象函数赋值法2.“θ≠”是“cos θ≠”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】因为“cos θ=”是“θ=”的必要不充分条件,所以“θ≠”是“cos θ≠”的必要不充分条件,选B.3.已知函数,则一定在函数图象上的点是()A.B.C.D.【答案】C.【解析】根据的解析式,求出,判断函数的奇偶性,由函数的奇偶性去判断四个选项是否在图象上..为奇函数,在图象上.故选C.【考点】函数的奇偶性.4.函数y=的定义域是.【答案】{x|kπ-<x≤kπ+,k∈Z}【解析】由1-tanx≥0,即tanx≤1,结合正切函数图象可得,kπ-<x≤kπ+,k∈Z,故函数的定义域是{x|kπ-<x≤kπ+,k∈Z}.5.若方程有实根,则实数的取值范围为【答案】【解析】由方程得,,即,因为,所以,若方程有实根,则,解得.【考点】方程的根.6.已知的三个内角所对的边分别为,且,则角的大小为 .【答案】【解析】根据正弦定理:,,即:,,【考点】1、正弦定理;2、两角和与差的三角函数公式.7.已知函数上有两个零点,则的值为()A.B.C.D.【答案】D【解析】,由于,故,由于函数在区间上有两个零点,所以,所以,所以,故选D.【考点】1.三角函数的图象;2.三角函数的对称性8.已知函数d的最大值为2,是集合中的任意两个元素,且的最小值为.(1)求函数的解析式及其对称轴;(2)若,求的值.【答案】(1),;(2).【解析】本题主要考查两角和与差的正弦公式、二倍角的余弦公式、诱导公式、三角函数的最小正周期、单调性等基础知识,考查运算能力.第一问,利用倍角公式化简表达式,先利用周期求出,再求最值,通过解方程求出,确定了解析式后求正弦函数的对称轴;第二问,通过角之间的关系转化角,考查诱导公式和倍角公式.试题解析:(1),由题意知:的周期为,由,知 2分由最大值为2,故,又, 4分∴ 5分令,解得的对称轴为 7分(2)由知,即, 8分∴ 10分12分【考点】1.倍角公式;2.两角和与差的三角函数;3.函数的周期;4.函数的对称轴.9.已知函数时有极大值,且为奇函数,则的一组可能值依次为( )A.B.C.D.【答案】D【解析】,因为当时有极大值,所以=0,解得当k=0时,;因为=为奇函数,所以,当k=0时,,故选D.【考点】1.求函数的导数及其导数的性质;2.三角函数的性质.10.已知函数的最大值为4,最小值为0,最小正周期为,直线是其图像的一条对称轴,则下列各式中符合条件的解析式是()A.B.C.D.【答案】D【解析】由题意可得,则据此可知答案选D.【考点】函数的图像与性质.11.中,角所对的边分别为且.(Ⅰ)求角的大小;(Ⅱ)若向量,向量,,,求的值.【答案】(Ⅰ);(Ⅱ);【解析】(Ⅰ)主要利用三角形中内角和定理、三角恒等变换来求;(Ⅱ)通过余弦定理、解方程组可求;试题解析:(Ⅰ)∵∴,∴,∴或∴(II)∵∴,即①又,∴,即②由①②可得,∴又∴,∴【考点】解三角形中内角和定理以及余弦定理的使用、三角恒等变换等知识点,考查学生的计算能力.12.在中,角的对边分别为向量,,且.(1)求的值;(2)若,,求角的大小及向量在方向上的投影.【答案】(1);(2),向量在方向上的投影.【解析】(1)由向量数量积坐标形式列式,可求得的值,再利用平方关系可求得的值;(2)先利用正弦定理可求得的值,再利用大边对大角可求得角的大小.由投影的定义可求得向量在方向上的投影.试题解析:(1)由,得, 1分, 2分.. 3分.4分(2)由正弦定理,有, 5分.6分,, 7分. 8分由余弦定理,有, 9分或(舍去). 10分故向量在方向上的投影为 11分. 12分【考点】1、向量数量积、投影;2、三角恒等变换;3、解三角形.13.已知函数若方程有三个不同的实根,且从小到大依次成等比数列,则m的值为 .【答案】【解析】设三个根由小到大依次为,结合余弦函数图像可知关于直线对称,关于直线对称,代入计算得【考点】三角函数图像及性质点评:题目中主要结合三角函数图像的轴对称性找到三根之间的联系14.函数的最小正周期为.【答案】【解析】根据题意,由于即为其周期,故答案为【考点】三角函数的性质点评:主要是考查了三角函数的性质的运用,属于基础题。
三角函数典型例题(高考题)及详细解答

1.已知ΔABC_三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c ,0). (1)若0AB AC ⋅=,求c 的值; (2)若c=5,求sin ∠A 的值.2 已知函数()sin()(0,0),f x A x A x R ϕϕπ=+><<∈的最大值是1,其图像经过点1(,)32M π。
(1)求()f x 的解析式;(2)已知,(0,)2παβ∈,且312(),(),513f f αβ==求()f αβ-的值 3.已知向量)2,(sin -=θa 与)cos ,1(θ=b 互相垂直,其中)2,0(πθ∈(1)求θsin 和θcos 的值;(2)若ϕϕθcos 53)cos(5=-,<<ϕ02π,求ϕcos 的值 4.设函数()3sin 6f x x πω⎛⎫=+⎪⎝⎭,0ω>,(),x ∈-∞+∞,且以2π为最小正周期. (1)求()0f ;(2)求()f x 的解析式;(3)已知94125f απ⎛⎫+= ⎪⎝⎭,求sin α的值. 5.已知函数1()2sin(),36f x x x π=-∈R .(1)求(0)f 的值;(2)设10,0,,(3)2213f ππαβα⎡⎤∈+=⎢⎥⎣⎦,6(32)5f βπ+=,求sin()αβ+的值. 一.选择填空题1.在ABC 中,若15,,sin 43b B A π=∠==,则a = . 2..在ABC ∆中,角,,A B C 所对的边分,,a b c .若cos sin a A b B =,则2sin cos cos A A B +=(A)-12 (B) 12(C) -1 (D) 1 3.设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于(A )13(B )3 (C )6 (D )94.设函数(A )y=在单调递增,其图像关于直线对称(B )y=在单调递增,其图像关于直线对称(C )y= f (x) 在(0,2π)单调递减,其图像关于直线x = 4π对称(D )y= f (x) 在(0,2π)单调递减,其图像关于直线x = 2π对称5.)已知角θ的顶点为坐标原点,始边为x 轴的正半轴,若()4,p y 是角θ终边上一点,且25sin 5θ=-,则y=_______.6.已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈恒成立,且()()2f f ππ>,则()f x 的单调递增区间是(A ),()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ (B ),()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦ (C )2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(D ),()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦ 7.在△ABC 中,222sin sin sin sin sin A B C B C ≤+-,则A 的取值范围是(A )(0,]6π(B )[,)6ππ(C )(0,]3π(D )[,)3ππ二:解答题1.已知函数()4cos sin() 1.6f x x x π=+-(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值。
高中三角函数习题解析精选(含详细解答)

三角函数题解1.(2003上海春,15)把曲线y cos x +2y -1=0先沿x 轴向右平移2π个单位,再沿y 轴向下平移1个单位,得到的曲线方程是( )A.(1-y )sin x +2y -3=0B.(y -1)sin x +2y -3=0C.(y +1)sin x +2y +1=0D.-(y +1)sin x +2y +1=0 2.(2002春北京、安徽,5)若角α满足条件sin2α<0,cos α-sin α<0,则α在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.(2002上海春,14)在△ABC 中,若2cos B sin A =sinC ,则△ABC 的形状一定是( ) A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形4.(2002京皖春文,9)函数y =2sin x 的单调增区间是( ) A.[2k π-2π,2k π+2π](k ∈Z )B.[2k π+2π,2k π+23π](k ∈Z )C.[2k π-π,2k π](k ∈Z )D.[2k π,2k π+π](k ∈Z )5.(2002全国文5,理4)在(0,2π)内,使sin x >cos x 成立的x 取值范围为( ) A.(4π,2π)∪(π,45π)B.(4π,π)C.(4π,45π)D.(4π,π)∪(45π,23π)6.(2002北京,11)已知f (x )是定义在(0,3)上的函数,f (x )的图象如图4—1所示,那么不等式f (x )cos x <0的解集是( )A.(0,1)∪(2,3)B.(1,2π)∪(2π,3)图4—1C.(0,1)∪(2π,3)D.(0,1)∪(1,3)7.(2002北京理,3)下列四个函数中,以π为最小正周期,且在区间(2π,π)上为减函数的是( )A.y =cos 2xB.y =2|sin x |C.y =(31)cos xD.y =-cot x8.(2002上海,15)函数y =x +sin|x |,x ∈[-π,π]的大致图象是( )9.(2001春季北京、安徽,8)若A 、B 是锐角△ABC 的两个内角,则点P (cos B -sin A ,sin B -cos A )在( )A.第一象限B.第二象限C.第三象限D.第四象限10.(2001全国文,1)tan300°+cot405°的值是( ) A.1+3B.1-3C.-1-3D.-1+311.(2000全国,4)已知sin α>sin β,那么下列命题成立的是( ) A.若α、β是第一象限角,则cos α>cos β B.若α、β是第二象限角,则tan α>tan β C.若α、β是第三象限角,则cos α>cos β D.若α、β是第四象限角,则tan α>tan β12.(2000全国,5)函数y =-x cos x 的部分图象是( )13.(1999全国,4)函数f (x )=M sin (ωx +ϕ)(ω>0),在区间[a ,b ]上是增函数,且f (a )=-M ,f (b )=M ,则函数g (x )=M cos (ωx +ϕ)在[a ,b ]上( )A.是增函数B.是减函数C.可以取得最大值-D.可以取得最小值-m14.(1999全国,11)若sin α>tan α>cot α(-2π<α<2π),则α∈( ) A.(-2π,-4π) B.(-4π,0)C.(0,4π) D.(4π,2π)15.(1999全国文、理,5)若f (x )sin x 是周期为π的奇函数,则f (x )可以是( ) A.sin x B.cos x C.sin2x D.cos2x16.(1998全国,6)已知点P (sin α-cos α,tan α)在第一象限,则在[0,2π]内α的取值范围是( )A.(2π,43π)∪(π,45π) B.(4π,2π)∪(π,45π) C.(2π,43π)∪(45π,23π) D.(4π,2π)∪(43π,π) 17.(1997全国,3)函数y =tan (3121-x π)在一个周期内的图象是( )18.(1996全国)若sin 2x >cos 2x ,则x 的取值范围是( ) A.{x |2k π-43π<x <2k π+4π,k ∈Z }B.{x |2k π+4π<x <2k π+45π,k ∈Z }C.{x |k π-4π<x <k π+4π,k ∈Z }D.{x |k π+4π<x <k π+43π,k ∈Z }19.(1995全国文,7)使sin x ≤cos x 成立的x 的一个变化区间是( ) A.[-43π,4π] B.[-2π,2π]C.[-4π,43π] D.[0,π]20.(1995全国,3)函数y =4sin (3x +4π)+3cos (3x +4π)的最小正周期是( )A.6πB.2πC.32πD.3π21.(1995全国,9)已知θ是第三象限角,若sin 4θ+cos 4θ=95,那么sin2θ等于( ) A.322 B.-322 C.32D.-32 22.(1994全国文,14)如果函数y =sin2x +a cos2x 的图象关于直线x =-8π对称,那么a等于( )A.2B.-2C.1D.-123.(1994全国,4)设θ是第二象限角,则必有( ) A.tan2θ>cot 2θ B.tan2θ<cot 2θC.sin2θ>cos 2θD.sin2θ-cos 2θ 24.(2002上海春,9)若f (x )=2sin ωx (0<ω<1)在区间[0,3π]上的最大值是2,则ω= .25.(2002北京文,13)sin 52π,cos 56π,tan 57π从小到大的顺序是 .26.(1997全国,18)︒︒-︒︒︒+︒8sin 15sin 7cos 8sin 15cos 7sin 的值为_____.27.(1996全国,18)tan20°+tan40°+3tan20°·tan40°的值是_____.28.(1995全国理,18)函数y =sin (x -6π)cos x 的最小值是 .29.(1995上海,17)函数y =sin 2x +cos 2x在(-2π,2π)内的递增区间是 .30.(1994全国,18)已知sin θ+cos θ=51,θ∈(0,π),则cot θ的值是 .31.(2000全国理,17)已知函数y =21cos 2x +23sin x cos x +1,x ∈R .(1)当函数y 取得最大值时,求自变量x 的集合;(2)该函数的图象可由y =sin x (x ∈R )的图象经过怎样的平移和伸缩变换得到?32.(2000全国文,17)已知函数y =3sin x +cos x ,x ∈R .(1)当函数y 取得最大值时,求自变量x 的集合;(2)该函数的图象可由y =sin x (x ∈R )的图象经过怎样的平移和伸缩变换得到?33.(1995全国理,22)求sin 220°+cos 250°+sin20°cos50°的值.34.(1994上海,21)已知sin α=53,α∈(2π,π),tan (π-β)=21,求tan (α-2β)的值.35.(1994全国理,22)已知函数f (x )=tan x ,x ∈(0,2π),若x 1、x 2∈(0,2π),且x 1≠x 2,证明21[f (x 1)+f (x 2)]>f (221x x +).36.已知函数12()log (sin cos )f x x x =-⑴求它的定义域和值域; ⑵求它的单调区间; ⑶判断它的奇偶性; ⑷判断它的周期性.37. 求函数f (x )=121log cos()34x π+的单调递增区间38. 已知f (x )=5sin x cos x -35cos 2x +325(x ∈R ) ⑴求f (x )的最小正周期; ⑵求f (x )单调区间;⑶求f (x )图象的对称轴,对称中心。
(完整版)高考三角函数经典解答题及答案

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值. 解:(1) 由余弦定理:conB=14sin22A B ++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号)故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,,0sin .cos sin 3sin ,cos sin 3)sin(,cos sin 3cos sin cos sin ,cos sin cos sin 3cos sin ,cos sin 2cos sin 6cos sin 2≠==+=+-=-=A B A A B A C B B A B C C B B C B A C B B C R B A R C B R 又可得即可得故则因此.31cos =B(II )解:由2cos ,2==⋅B a 可得,,,0)(,12,cos 2,6,31cos 222222c a c a c a B ac c a b ac B ==-=+-+===即所以可得由故又 所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3,其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
高考三角函数专题(含答案)

高考专题复习三角函数专题模块一——选择题一、选择题: (将正确答案的代号填在题后的括号内. )π5π1.(2021天·津)以下图是函数 y =Asin(ωx+φ)(x∈R)在区间 -6,6上的图象,为了得到这个函数的图象,只要将 y =sinx(x∈R)的图象上所有的点 ( )π1A .向左平移3个单位长度,再把所得各点的横坐标缩短到原来的2,纵坐标不变π2倍,纵坐标不变B .向左平移个单位长度,再把所得各点的横坐标伸长到原来的3π1C .向左平移6个单位长度,再把所得各点的横坐标缩短2,纵坐标不变到原来的π2倍,纵坐标不变D .向左平移个单位长度,再把所得各点的横坐标伸长到原来的6y =Asin(ωx+φ)中A =1,2ππ π解析:观察图象可知,函数 ω=π,故ω=2,ω×-6+φ=0,得φ= 3,所以函数y =sin 2x + ,故只要把y =sinx 的图象向左平移π1即个单位,再把各点的横坐标缩短到原来的2可.答案:A2.(2021全·国Ⅱ)为了得到函数 y =sin2x -π的图象,只需把函数y =sin2x +π的图象()36πB .向右平移A .向左平移个长度单位个长度单位44πD .向右平移C .向左平移2个长度单位2个长度单位解析:由y=sin2x+πx→x+φ=sin2x-πππ――→y=sin2(x+φ),即2x+2φ+=2x-,解得φ=-6634π即向右平移4个长度单位.应选B. 答案:B3.(2021重·庆)函数y=sin(ωx +φ)ω>0,|φ|<π的局部图象如下图,那么()2πB.ω=1,φ=-πππA.ω=1,φ=66C.ω=2,φ=6D.ω=2,φ=-6解析:依题意得T=2π7ππππ2πππω=412-3=π,ω=2,sin2×3+φ=1.又|φ|<2,所以3+φ=2,φ=-6,选D.答案:D4.函数 y=2sin(ωx+φ)(ω>0)在区间[0,2π]上的图象如下图,那么ω=( )11A.1B.2 C.2D.32π解析:由函数的图象可知该函数的周期为π,所以 ω=π,解得ω=2.答案:Bπ()5.函数y =sinx -12cosx -12,那么以下判断正确的选项是A .此函数的最小正周期为2π,其图象的一个对称中心是π,012B .此函数的最小正周期为 π,其图象的一个对称中心是π,012C .此函数的最小正周期为 2π,其图象的一个对称中心是π,6D .此函数的最小正周期为 π,其图象的一个对称中心是π,6ππ1π解析:∵y=sinx -12·cosx-12=2sin2x -6,∴T=2ππ2=π,且当x =12时,y=0.答案:Bπa 的值为()6.如果函数y =sin2x +acos2x 的图象关于直线对称,那么实数 x =-8A.2B .-2C.1D.-1π分析:函数f(x)在x =- 时取得最值;或考虑有8ππf-+x=f--x对一切x∈R恒成立.88解析:解法一:设f(x)=sin2x+acos2x,因为函数的图象关于直线x=-πππ8对称,所以f-8+x=f-8-x对一切实数x都成立,即sin2ππ-+x+acos2-+x=sin2ππ--x+acos2--xππsin-4+2x+sin4+2xππ=acos4+2x-cos-4+2x,ππ∴2sin2x·cos4=-2asin2x·sin4,即(a+1)sin2x·=0对一切实数x恒成立,而sin2x不能恒为,∴a+1=0,即a=-1,应选D.π解法二:∵f(x)=sin2x+acos2x关于直线x=-8对称.ππ∴有f-+x=f--x对一切x∈R恒成立.88π特别,对于x=8应该成立.π将x=8代入上式,得f(0)=f-,ππ∴sin0+acos0=sin-2+acos-2∴0+a=-1+a×0.∴a=-1.应选D.解法三:y=sin2x+acos2x=1+a2sin(2x+φ),其中角φ的终边经过点(1,a).其图象的对称轴方程π2x+φ=kπ+2(k∈Z),kππφx=2+4-2(k∈Z).kππφπ令2+4-2=-8(k∈Z).3π得φ=kπ+4(k∈Z).π但角φ的终边经过点(1,a),故k为奇数,角φ的终边与-2角的终边相同,∴a=-1.解法四:y=sin2x+acos2x=21+asin(2x+φ),其中角φ满足tanφ=a.因为f(x)的对称轴为πy=-8,π∴当x=-8时函数y=f(x)有最大值或最小值,所以1+a2=fπ-8或-1+a2=fπ-8,即1+a2=sinπ-4+acosπ-4,或-1+a2=sinπ-4+acosπ-4.解之得a=-1.应选D.答案:D评析:此题给出了四种不同的解法,充分利用函数图象的对称性的特征来解题.解法一是运用了方程思想或恒等式思想求解.解法二是利用了数形结合的思想求解,抓住f(m+x)=f(m-x)的图象关于直线=m对称的性质,取特殊值来求出待定系数a的值.解法三利用函数y=Asin(ωx+φ)的对称轴是方程xωxππkπ+2-φπ+φ=kπ+2(k∈Z)的解x=ω(k∈Z),然后将x=-8代入求出相的φ,再求a的.解法四利ππ用称的特殊性,在此函数f(x)取最大或最小.于是有f-8=[f(x)]max或f-8=[f(x)]min.从而化解方程,体了方程思想.由此可,本体了丰富的数学思想方法,要从多种解法中悟出其西.模块二——填空题二、填空:(把正确答案填在后的横上.)π7.(2021福·建)函数f(x)=3sinωx-6(ω>0)和g(x)=2cos(2x+φ)+1的象的称完全相同.假设π,f(x)的取范是________.x∈0,2解析:∵f(x)与g(x)的象的称完全相同,∴f(x)与g(x)的最小正周期相等,∵ω>0,∴ω=2,∴f(x)ππππ5π13≤3,即f(x)=3sin2x-6,∵≤2x-≤≤sin2x-61,∴-≤3sin2x-6 0≤x≤2,∴-666,∴-22的取范,3.答案:-3,318.函数y=cos2πx的象位于y 右所有的称中心从左依次A1,A2,⋯,An,⋯.A50的坐是________.解析:称中心横坐x=2k+1,k≥0且k∈N,令k=49即可得.答案:(99,0)9.把函数y=cosx+π的象向左平移m个位(m>0),所得象关于y称,m的最小是3________.解析:由y=cos(x+πππ3+m)的象关于y称,所以3+m=kπ,k∈Z,m=kπ-3,当k=1,m最2小3π.答案:2π310.定义集合A,B的积A×B={(x,y)|x∈A,y∈B}.集合M={x|0≤x≤2π},N={y|cosx≤y≤1},那么M×N所对应的图形的面积为________.解析:如下图阴影面积可分割补形为ABCD的面积即BC×CD=π·2=2π.答案:2π模块三——解答题三、解答题:(写出证明过程或推演步骤.) 11.假设方程3sinx+cosx=a在[0,2π]上有两个不同的实数解x1、x2,求a的取值范围,并求x1+x2的值.分析:设函数y1=3sinx+cosx,y2=a,在同一平面直角坐标系中作出这两个函数的图象,应用数形结合解答即可.解:设f(x)=π3 sinx +cosx =2sin x+6,x∈[0,2.π]π令x+6=t,那么f(t)=2sint,且t∈π6,13π6 .在同一平面直角坐标系中作出y=2sint及y=a的图象,从图中可以看出当1<a<2和-2<a<1时,两图象有两个交点,即方程3sinx+cosx=a在[0,2上π]有两个不同的实数解.当1<a<2时,t1+t2=π,ππ即x1+6+x2+6=π,2π∴x1+x2=3;当-2<a<1时,t1+t2=3π,ππ即x1+6+x2+6=3π,8πx1+x2=3.综上可得,a的取值范围是(1,2)∪(-2,1).2π当a∈(1,2)时,x1+x2=3;8πa∈(-2,1)时,x1+x2=3.评析:此题从方程的角度考查了三角函数的图象和对称性,运用的主要思想方法有:函数与方程的思想、数形结合的思想及换元法.解答此题常见的错误是在换元时忽略新变量t的取值范围,仍把t当成在[0,2 π]中处理,从而出错.11πφ<π),其图象过点π1+φ(0<,12.(2021山·东)函数f(x)=2sin2xsinφ+cosxcosφ-2sin262.(1)求φ的值;(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的1,纵坐标不变,得到函数y=g(x)的图象,求函2π数g(x)在0,4上的最大值和最小值.11π解:(1)因为f(x)=sin2xsinφ+cos2xcosφ-sin+φ(0<φ<π),2211+cos2x1所以f(x)=2sin2xsinφ+2cosφ-2cosφ1 12sin2xsinφ+2cos2xcosφ12(sin2xsinφ+cos2xcosφ)1π2cos(2x-φ),π1又函数图象过点6,2,11ππ所以2=2cos2×6-φ,即cos3-φ=1,π又0<φ<π,所以φ=3.1π1(2)由(1)知f(x)=2cos2x-3,将函数y=f(x)的图象上各点的横坐标缩短到原来的2,纵坐标不变,得1 2 3 4 56π到函数y =g(x)的象,可知g(x)=f(2x)=2cos4x -3,π4x∈[0,π],因x∈0,4 ,所以ππ2π1因此4x - 3∈-3,3 ,故- 2≤cos4x -3≤1. 所以y =g(x)在0,π114上的最大和最小分 2和-4.13.〔2021天津卷理〕在⊿ ABC 中,BC=5,AC=3,sinC=2sinA求AB 的: (II) 求sin 2A 的4本小主要考正弦定理、余弦定理、同角三角函数的根本关系、二倍角的正弦与余弦、两角差的正弦等基知,考根本运算能力。
三角函数高三计算题解析

三角函数高三计算题解析一、单选题1.(2024·湖北·二模)若ππcos ,,tan 223sin αααα⎛⎫∈-= ⎪-⎝⎭,则πsin 23α⎛⎫-= ⎪⎝⎭()A .718-B .718-C .18-D .182.(23-24高三下·重庆·阶段练习)若,π2α⎛⎫∈ ⎪⎝⎭,且cos 13αα=,则sin 212α⎛⎫- ⎪⎝⎭的值为()A B .338C .D .3.(2024·全国·模拟预测)已知角θ的顶点为坐标原点,始边与x轴的正半轴重合,点2023π2023πsin,cos46P⎛⎫⎪⎝⎭在角θ的终边上,则sin21cos2θθ=+()AB.C D.4.(2024·陕西咸阳·二模)当函数3sin4cosy x x=+取得最小值时,sin6x⎛⎫+=⎪⎝⎭()A.4+-B.310+-C.310+D.410+5.(2024·安徽·模拟预测)已知()tan 4αβ-=,()()sin 3cos αβαβ-=+,则tan tan αβ-=()A .12B .35C .65D .536.(2024·山东泰安·一模)若2πcos 24sin 22αα⎛⎫+-=- ⎪⎝⎭,则tan2α=()A .2-B .12-C .2D .127.(2024·贵州毕节·模拟预测)已知sin 125α⎛⎫+= ⎪⎝⎭,0,2α⎛⎫∈ ⎪⎝⎭,则cos 3α⎛⎫+= ⎪⎝⎭()A .10-B .5-C .4D .34-8.(2024·福建泉州·模拟预测)若0,2α⎛⎫∈ ⎪⎝⎭,3sin 2cos 2sin cos 20αααα+=,则tan α=()A .4B .2C .12D .149.(2024·河北·模拟预测)已知1tan 22θ=-,则3cos sin cos θθθ=+()A .925-B .925C .2725-D .272510.(2024·江苏盐城·模拟预测)在ABC 中,已知tan tan tan tan 1A B A B ++=,则cos 2sin C C +的值为()A .2B .2C D .11.(2024·辽宁·一模)已知,αβ满足πππ2π,44αβ≤≤-≤≤,且553π32cos 5,962sin252ααββ⎛⎫-+=+=- ⎪⎝⎭,则24πsin 994αβ⎛⎫+-=⎪⎝⎭()A B C D12.(23-24高三下·内蒙古锡林郭勒盟·开学考试)若cos 20501)a -=,则=a ()A .12B .1C .32D .213.(23-24高三下·江苏扬州·阶段练习)已知()cos(),cos 35αβαβ+=-=,则2log (tan tan )αβ-=()A .12B .12-C .2D .2-【答案】D根据余弦的和差角公式求得tan tan αβ,再求结果即可.【详解】因为()11cos(),cos35αβαβ+=-=,14.(2024高三·全国·专题练习)已知sin 1523α︒⎛⎫-= ⎪⎝⎭,则()cos 30α︒-=()A .13B .13-C .23D .23-【答案】A 【详解】因为sin (15°-)=,所以cos (30°-α)=cos 2(15°-)=1-2sin2(15°-)=1-2×=.15.(2024·吉林白山·二模)若πcos 43πcos 4αα⎛⎫+ ⎪⎝⎭=⎛⎫- ⎪⎝⎭,则πtan 24α⎛⎫-= ⎪⎝⎭()A .7-B .7C .17-D .17【详解】因为πcos cos sin 1tan 43πcos sin 1tan cos 4αααααααα⎛⎫+ ⎪--⎝⎭===++⎛⎫- ⎪⎝⎭,故1tan 2α=-,则22122tan 42tan21tan 3112ααα⎛⎫⨯- ⎪⎝⎭===--⎛⎫-- ⎪⎝⎭,故4π1tan2tanπ34tan 27π441tan2tan 143ααα---⎛⎫-== ⎪⎝⎭+⋅-.故选:B.16.(23-24高三下·江西·开学考试)已知α为锐角,且πtan tan 14αα⎛⎫++= ⎪⎝⎭,则sin 21cos 2αα+=()A .12B .3-C .2-D .13【答案】C 【分析】根据已知条件结合两角和的正切公式可得出关于tan α的方程,由已知可得出tan 0α>,可得出关于tan α的方程,求出tan α的值,利用二倍角的正弦和余弦公式可求得所求代数式的值.【详解】因为α为锐角,则tan 0α>,则πtantan π4tan tan tan π41tan tan 4ααααα+⎛⎫++=+⎪⎝⎭-1tan tan 11tan ααα+=+=-,整理可得2tan 3tan 0αα-=,解得tan 3α=,所以,()()()22222cos sin sin 21cos 2sin cos sin cos 2cos sin cos sin cos sin αααααααααααααα++++==--+cos sin 1tan 132cos sin 1tan 13αααααα+++====----.故选:C.17.(2023·全国·高考真题)已知()11sin ,cos sin 36αβαβ-==,则()cos 22αβ+=().A .79B .19C .19-D .79-18.(2021·全国·高考真题)若tan 2θ=-,则sin 1sin 2sin cos θθ+=+()A .65-B .25-C .25D .6519.(2021·全国·高考真题)若0,,tan 222sin παααα⎛⎫∈= ⎪-⎝⎭,则tan α=()A .15B C D20.(1995·全国·高考真题)已知θ是第三象限的角,且44sin cos 9+=θθ,那么sin 2θ的值为A B .C .23D .23-。
高考三角函数大题及解析

高考三角函数大题一.解答题(共14小题)2.(2018•新课标Ⅰ)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求cos∠ADB;(2)若DC=2,求BC.3.(2018•北京)在△ABC中,a=7,b=8,cosB=﹣.(Ⅰ)求∠A;(Ⅱ)求AC边上的高.4.(2018•北京)已知函数f(x)=sin2x+sinxcosx.(Ⅰ)求f(x)的最小正周期;(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,求m的最小值.5.(2018•上海)设常数a∈R,函数f(x)=asin2x+2cos2x.(1)若f(x)为偶函数,求a的值;(2)若f()=+1,求方程f(x)=1﹣在区间[﹣π,π]上的解.6.(2018•天津)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.7.(2017•新课标Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为.(1)求sinBsinC;(2)若6cosBcosC=1,a=3,求△ABC的周长.8.(2017•新课标Ⅱ)△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.(1)求cosB;(2)若a+c=6,△ABC的面积为2,求b.9.(2017•新课标Ⅲ)△ABC的内角A,B,C的对边分别为a,b,c,已知sinA+cosA=0,a=2,b=2.(1)求c;(2)设D为BC边上一点,且AD⊥AC,求△ABD的面积.10.(2017•天津)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=.(Ⅰ)求b和sinA的值;(Ⅱ)求sin(2A+)的值.11.(2017•北京)在△ABC中,∠A=60°,c=a.(1)求sinC的值;(2)若a=7,求△ABC的面积.12.(2017•江苏)已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].(1)若,求x的值;(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.14.(2017•上海)已知函数f(x)=cos2x﹣sin2x+,x∈(0,π).(1)求f(x)的单调递增区间;(2)设△ABC为锐角三角形,角A所对边a=,角B所对边b=5,若f(A)=0,求△ABC的面积.2017-2018高考三角函数大题参考答案与试题解析一.解答题(共14小题)2.【解答】解:(1)∵∠ADC=90°,∠A=45°,AB=2,BD=5.∴由正弦定理得:=,即=,∴sin∠ADB==,∵AB<BD,∴∠ADB<∠A,∴cos∠ADB==.(2)∵∠ADC=90°,∴cos∠BDC=sin∠ADB=,∵DC=2,∴BC===5.3.【解答】解:(Ⅰ)∵a<b,∴A<B,即A是锐角,∵cosB=﹣,∴sinB===,由正弦定理得=得sinA===,则A=.(Ⅱ)由余弦定理得b2=a2+c2﹣2accosB,即64=49+c2+2×7×c×,即c2+2c﹣15=0,得(c﹣3)(c+5)=0,得c=3或c=﹣5(舍),则AC边上的高h=csinA=3×=.4.【解答】解:(I)函数f(x)=sin2x+sinxcosx=+sin2x=sin(2x﹣)+,f(x)的最小正周期为T==π;(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,可得2x﹣∈[﹣,2m﹣],即有2m﹣≥,解得m≥,则m的最小值为.5.【解答】解:(1)∵f(x)=asin2x+2cos2x,∴f(﹣x)=﹣asin2x+2cos2x,∵f(x)为偶函数,∴f(﹣x)=f(x),∴﹣asin2x+2cos2x=asin2x+2cos2x,∴2asin2x=0,∴a=0;(2)∵f()=+1,∴asin+2cos2()=a+1=+1,∴a=,∴f(x)=sin2x+2cos2x=sin2x+cos2x+1=2sin(2x+)+1,∵f(x)=1﹣,∴2sin(2x+)+1=1﹣,∴sin(2x+)=﹣,∴2x+=﹣+2kπ,或2x+=π+2kπ,k∈Z,∴x=﹣π+kπ,或x=π+kπ,k∈Z,∵x∈[﹣π,π],∴x=或x=或x=﹣或x=﹣6.【解答】解:(Ⅰ)在△ABC中,由正弦定理得,得bsinA=asinB,又bsinA=acos(B﹣).∴asinB=acos(B﹣),即sinB=cos(B﹣)=cosBcos+sinBsin=cosB+,∴tanB=,又B∈(0,π),∴B=.(Ⅱ)在△ABC中,a=2,c=3,B=,由余弦定理得b==,由bsinA=acos(B﹣),得sinA=,∵a<c,∴cosA=,∴sin2A=2sinAcosA=,cos2A=2cos2A﹣1=,∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB==.7.【解答】解:(1)由三角形的面积公式可得S△ABC=acsinB=,∴3csinBsinA=2a,由正弦定理可得3sinCsinBsinA=2sinA,∵sinA≠0,∴sinBsinC=;(2)∵6cosBcosC=1,∴cosBcosC=,∴cosBcosC﹣sinBsinC=﹣=﹣,∴cos(B+C)=﹣,∴cosA=,∵0<A<π,∴A=,∵===2R==2,∴sinBsinC=•===,∴bc=8,∵a2=b2+c2﹣2bccosA,∴b2+c2﹣bc=9,∴(b+c)2=9+3cb=9+24=33,∴b+c=∴周长a+b+c=3+.8.【解答】解:(1)sin(A+C)=8sin2,∴sinB=4(1﹣cosB),∵sin2B+cos2B=1,∴16(1﹣cosB)2+cos2B=1,∴16(1﹣cosB)2+cos2B﹣1=0,∴16(cosB﹣1)2+(cosB﹣1)(cosB+1)=0,∴(17cosB﹣15)(cosB﹣1)=0,∴cosB=;=ac•sinB=2,∴ac=,(2)由(1)可知sinB=,∵S△ABC∴b2=a2+c2﹣2accosB=a2+c2﹣2××=a2+c2﹣15=(a+c)2﹣2ac﹣15=36﹣17﹣15=4,∴b=2.9.【解答】解:(1)∵sinA+cosA=0,∴tanA=,∵0<A<π,∴A=,由余弦定理可得a2=b2+c2﹣2bccosA,即28=4+c2﹣2×2c×(﹣),即c2+2c﹣24=0,解得c=﹣6(舍去)或c=4,故c=4.(2)∵c2=b2+a2﹣2abcosC,∴16=28+4﹣2×2×2×cosC,∴cosC=,=AB•AC•sin∠BAC=×4×2×=2,∴CD===∴CD=BC∵S△ABC=S△ABC=∴S△ABD10.【解答】解:(Ⅰ)在△ABC中,∵a>b,故由sinB=,可得cosB=.由已知及余弦定理,有=13,∴b=.由正弦定理,得sinA=.∴b=,sinA=;(Ⅱ)由(Ⅰ)及a<c,得cosA=,∴sin2A=2sinAcosA=,cos2A=1﹣2sin2A=﹣.故sin(2A+)==.11.【解答】解:(1)∠A=60°,c=a,由正弦定理可得sinC=sinA=×=,(2)a=7,则c=3,∴C<A,由(1)可得cosC=,∴sinB=sin(A+C)=sinAcosC+cosAsinC=×+×=,=acsinB=×7×3×=6.∴S△ABC12.【解答】解:(1)∵=(cosx,sinx),=(3,﹣),∥,∴﹣cosx=3sinx,∴tanx=﹣,∵x∈[0,π],∴x=,(2)f(x)==3cosx﹣sinx=2(cosx﹣sinx)=2cos(x+),∵x∈[0,π],∴x+∈[,],∴﹣1≤cos(x+)≤,当x=0时,f(x)有最大值,最大值3,当x=时,f(x)有最小值,最小值﹣2.14.【解答】解:(1)函数f(x)=cos2x﹣sin2x+=cos2x+,x∈(0,π),由2kπ﹣π≤2x≤2kπ,解得kπ﹣π≤x≤kπ,k∈Z,k=1时,π≤x≤π,可得f(x)的增区间为[,π);(2)设△ABC为锐角三角形,角A所对边a=,角B所对边b=5,若f(A)=0,即有cos2A+=0,解得2A=π,即A=π,由余弦定理可得a2=b2+c2﹣2bccosA,化为c2﹣5c+6=0,解得c=2或3,若c=2,则cosB=<0,即有B为钝角,c=2不成立,则c=3,△ABC的面积为S=bcsinA=×5×3×=.第11页(共11页)。
高考数学解答题(新高考)三角函数的图象与性质(五点法作图)(典型例题+题型归类练)(解析版)
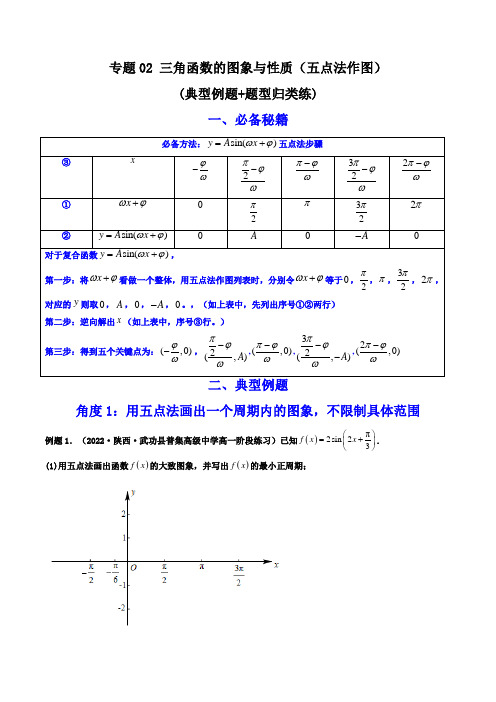
专题02 三角函数的图象与性质(五点法作图)(典型例题+题型归类练)一、必备秘籍角度1:用五点法画出一个周期内的图象,不限制具体范围例题1.(2022·陕西·武功县普集高级中学高一阶段练习)已知()π2sin23f x x⎛⎫=+⎪⎝⎭.(1)用五点法画出函数()f x的大致图象,并写出()f x的最小正周期;【答案】(1)图象见解析,T=π令ππ3π2=0π2π322x +,,,,,得到对应的,()x f x 值如下表所示: π23x +π2π3π2 2πxπ6-π12 π37π125π6 ()f x22-所以()f x 过πππ7π5π(,0),(,2),(,0),(,2),(,0)6123126--,图象如图所示思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3) (1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象周期为T=π例题2.(2022·宁夏吴忠区青铜峡市教育局高一开学考试)已知函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭.请用“五点法”列表并画出函数()f x 在一个周期上的图象;思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3)(1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象【答案】(1)答案见解析列表如下:函数f x在一个周期上的图象如下:角度2:用五点法画出具体某个范围内的图象例题1.(2022·全国·高一课时练习)用五点法画出π2sin23y x⎛⎫=+⎪⎝⎭在π5π,66⎡⎤-⎢⎥⎣⎦内的图象时,应取的五个点为 ______;【答案】π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭由题意可知,令π23X x =+,则123x X π⎛⎫=- ⎪⎝⎭,π5π,66x ⎡⎤∈-⎢⎥⎣⎦,列表,描点.xπ6-π12π3 7π12 5π6X0 π2π3π22π思路点拨:由题意知,目标要求写出五点法画在内的图象时对应的五个关键点解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到由列表可得,应取的五个点为 π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭,故答案为:π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭.例题2.(2022·黑龙江·大庆外国语学校高一期末)已知函数()()3sin 2f x x πϕϕ=+∈-,(,2π)函数关于4x π=对称.(1)求()f x ϕ的值及的解析式;(2)用五点法在下列直角坐标系中画出()f x 在744ππ⎡⎤-⎢⎥⎣⎦,上的图象;【答案】(1)4πϕ=,()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)详见解析(1)因为函数关于直线4x π=对称,所以,42k k Z ππϕπ+=+∈,,4k k Z πϕπ=+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以4πϕ=, 所以()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)首先根据“五点法”,列表如下:第一问略;第(2)问思路点拨:由题意知,目标要求用五点法画在内的图象解答过程: 先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到三、题型归类练1.(2021·全国·高一专题练习)用“五点法”作y =2sin2x 的图象,首先描出的五个点的横坐标是( ) A .30,,,,222ππππ B . 30,,,,424ππππ C . 0,,2,3,4ππππ D .20,,,,6323ππππ【答案】B由“五点法”作图知:令2x =0,2π,π,32π,2π,解得x =0,4π,2π,34π,π,即为五个关键点的横坐标, 故选:B.2.(2022·北京东城·高一期末)某同学用“五点法”画函数()sin()(0,0)f x A x A ωϕω=+>>在一个周期内的简图时,列表如下:则()f x 的解析式为( )A .()2sin 12f x x π⎛⎫=- ⎪⎝⎭ B .()2sin 312⎛⎫=+ ⎪⎝⎭f x x πC .()sin 212f x x π⎛⎫=- ⎪⎝⎭D .n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭【答案】D由表中数据知:2A =且721243T πππ=-=,则23T π=, ∴223ππω=,即3ω=,又342ππϕ⨯+=,可得4πϕ=-. ∴n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭.故选:D.3.(2021·广东揭阳·高一期末)某同学用“五点法”画函数()()πsin 0,2f x A x ωϕωϕ⎛⎫=+>< ⎪⎝⎭在某一个周期内的图象时,列表并填入了部分数据,如下表:根据表格中的数据,函数f x 的解析式可以是( ) A .()π5sin 26f x x ⎛⎫=- ⎪⎝⎭B .()π5sin 26f x x ⎛⎫=+ ⎪⎝⎭C .()π5sin 23f x x ⎛⎫=- ⎪⎝⎭D .()π5sin 23f x x ⎛⎫=+ ⎪⎝⎭【答案】A由题意得最大值为5,最小值为-5,所以A =5,52632T πππ=-=,解得2T ππω==,解得2ω=,又232ππϕ⨯+=,解得6πϕ=-,所以()f x 的解析式可以是()π5sin 26f x x ⎛⎫=- ⎪⎝⎭故选:A4.(2022·北京·高一阶段练习)某同学用“五点法”画函数sin()(0,)2y A x ϖϕϖϕπ=+><在某一个周期内的图像时,列表并填入了部分数据,如下表.【答案】3sin(2)3y x π=+由表格知:3A =且12231227πϕπϕϖπϖπ⎧+=⎪⎪⎨⎪+=⎪⎩,可得23ϖπϕ=⎧⎪⎨=⎪⎩,所以3sin(2)3y xπ=+.故答案为:3sin(2)3y x π=+.5.(2022·河南省嵩县第一高级中学高一阶段练习)已知函数π()2sin 23f x x ⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面的表格,并画出()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象;【答案】(1)答案见解析 完成表格如下:()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象如图所示:6.(2022·辽宁省康平县高级中学高一阶段练习)已知函数()sin 23πf x x ⎛⎫=- ⎪⎝⎭.(1)请用“五点法”画出函数()f x 在一个周期7,66ππ⎡⎤⎢⎥⎣⎦上的简图;【答案】(1)答案见解析 因为()sin 23πf x x ⎛⎫=- ⎪⎝⎭取值列表:7.(2022·广西·钦州一中高一期中)已知函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.(1)请用“五点法”画出函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭在一个周期上的图象;【答案】(1)作图见解析由图横坐标的范围,函数()f x 的周期为π,画出函数()f x 在11,1212ππ⎡⎤-⎢⎥⎣⎦上的图象.列表如下,8.(2022·江西·上饶中学高一阶段练习)已知函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面表格,并画出函数()f x 在区间9,88ππ⎡⎤⎢⎥⎣⎦上的图象.由正弦函数的性质,9,88ππ⎡⎤⎢⎥⎣⎦上的五点如下表:9.(2022·云南玉溪·高一期末)已知函数21()sin cos cos 22f x x x x x =+-.(2)填上面表格并用“五点法”画出()f x 在一个周期内的图象.【答案】(1)T π=,它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈(2)答案见解析.(1)21()sin cos cos 22f x x x x x =+-12cos 2sin 226x x x π⎛⎫+=+ ⎪⎝⎭ ∴函数()f x 的最小正周期22T ππ==;令26x k ππ+=,k Z ∈,解得212k x ππ=-,k Z ∈,可得它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈.。
2024年高考数学真题分类汇编(三角函数篇,解析版)

专题三角函数1(新课标全国Ⅰ卷)已知cos (α+β)=m ,tan αtan β=2,则cos (α-β)=()A.-3mB.-m3C.m 3D.3m【答案】A【分析】根据两角和的余弦可求cos αcos β,sin αsin β的关系,结合tan αtan β的值可求前者,故可求cos α-β 的值.【详解】因为cos α+β =m ,所以cos αcos β-sin αsin β=m ,而tan αtan β=2,所以=12×2b ×kb ×sin A 2+12×kb ×b ×sin A2,故cos αcos β-2cos αcos β=m 即cos αcos β=-m ,从而sin αsin β=-2m ,故cos α-β =-3m ,故选:A .2(新课标全国Ⅰ卷)当x ∈[0,2π]时,曲线y =sin x 与y =2sin 3x -π6 的交点个数为()A.3B.4C.6D.8【答案】C【分析】画出两函数在0,2π 上的图象,根据图象即可求解【详解】因为函数y =sin x 的的最小正周期为T =2π,函数y =2sin 3x -π6 的最小正周期为T =2π3,所以在x ∈0,2π 上函数y =2sin 3x -π6有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C3(新课标全国Ⅱ卷)设函数f (x )=a (x +1)2-1,g (x )=cos x +2ax ,当x ∈(-1,1)时,曲线y =f (x )与y =g (x )恰有一个交点,则a =()A.-1B.12C.1D.22024年高考数学真题分类汇编——三角函数篇【分析】解法一:令F x =ax 2+a -1,G x =cos x ,分析可知曲线y =F (x )与y =G (x )恰有一个交点,结合偶函数的对称性可知该交点只能在y 轴上,即可得a =2,并代入检验即可;解法二:令h x =f (x )-g x ,x ∈-1,1 ,可知h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即可得a =2,并代入检验即可.【详解】解法一:令f (x )=g x ,即a (x +1)2-1=cos x +2ax ,可得ax 2+a -1=cos x ,令F x =ax 2+a -1,G x =cos x ,原题意等价于当x ∈(-1,1)时,曲线y =F (x )与y =G (x )恰有一个交点,注意到F x ,G x 均为偶函数,可知该交点只能在y 轴上,可得F 0 =G 0 ,即a -1=1,解得a =2,若a =2,令F x =G x ,可得2x 2+1-cos x =0因为x ∈-1,1 ,则2x 2≥0,1-cos x ≥0,当且仅当x =0时,等号成立,可得2x 2+1-cos x ≥0,当且仅当x =0时,等号成立,则方程2x 2+1-cos x =0有且仅有一个实根0,即曲线y =F (x )与y =G (x )恰有一个交点,所以a =2符合题意;综上所述:a =2.解法二:令h x =f (x )-g x =ax 2+a -1-cos x ,x ∈-1,1 ,原题意等价于h x 有且仅有一个零点,因为h -x =a -x 2+a -1-cos -x =ax 2+a -1-cos x =h x ,则h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即h 0 =a -2=0,解得a =2,若a =2,则h x =2x 2+1-cos x ,x ∈-1,1 ,又因为2x 2≥0,1-cos x ≥0当且仅当x =0时,等号成立,可得h x ≥0,当且仅当x =0时,等号成立,即h x 有且仅有一个零点0,所以a =2符合题意;故选:D .4(全国甲卷数学(理)(文))已知cos αcos α-sin α=3,则tan α+π4=()A.23+1 B.23-1C.32D.1-3【答案】B【分析】先将cos αcos α-sin α弦化切求得tan α,再根据两角和的正切公式即可求解.【详解】因为cos αcos α-sin α=3,所以11-tan α=3,⇒tan α=1-33,所以tan α+π4 =tan α+11-tan α=23-1,故选:B .5(新高考北京卷)已知f x =sin ωx ω>0 ,f x 1 =-1,f x 2 =1,|x 1-x 2|min =π2,则ω=()A.1B.2C.3D.4【分析】根据三角函数最值分析周期性,结合三角函数最小正周期公式运算求解.【详解】由题意可知:x 1为f x 的最小值点,x 2为f x 的最大值点,则x 1-x 2 min =T 2=π2,即T =π,且ω>0,所以ω=2πT=2.故选:B .6(新高考天津卷)已知函数f x =sin3ωx +π3ω>0 的最小正周期为π.则函数在-π12,π6 的最小值是()A.-32B.-32C.0D.32【答案】A【分析】先由诱导公式化简,结合周期公式求出ω,得f x =-sin2x ,再整体求出x ∈-π12,π6时,2x 的范围,结合正弦三角函数图象特征即可求解.【详解】f x =sin3ωx +π3 =sin 3ωx +π =-sin3ωx ,由T =2π3ω=π得ω=23,即f x =-sin2x ,当x ∈-π12,π6 时,2x ∈-π6,π3,画出f x =-sin2x 图象,如下图,由图可知,f x =-sin2x 在-π12,π6上递减,所以,当x =π6时,f x min =-sin π3=-32故选:A7(新高考上海卷)下列函数f x 的最小正周期是2π的是()A.sin x +cos xB.sin x cos xC.sin 2x +cos 2xD.sin 2x -cos 2x【答案】A【分析】根据辅助角公式、二倍角公式以及同角三角函数关系并结合三角函数的性质一一判断即可 .【详解】对A ,sin x +cos x =2sin x +π4,周期T =2π,故A 正确;对B ,sin x cos x =12sin2x ,周期T =2π2=π,故B 错误;对于选项C ,sin 2x +cos 2x =1,是常值函数,不存在最小正周期,故C 错误;对于选项D ,sin 2x -cos 2x =-cos2x ,周期T =2π2=π,故D 错误,故选:A .8(新课标全国Ⅱ卷)对于函数f(x)=sin2x和g(x)=sin2x-π4,下列说法正确的有() A.f(x)与g(x)有相同的零点 B.f(x)与g(x)有相同的最大值C.f(x)与g(x)有相同的最小正周期D.f(x)与g(x)的图像有相同的对称轴【答案】BC【分析】根据正弦函数的零点,最值,周期公式,对称轴方程逐一分析每个选项即可.【详解】A选项,令f(x)=sin2x=0,解得x=kπ2,k∈Z,即为f(x)零点,令g(x)=sin2x-π4=0,解得x=kπ2+π8,k∈Z,即为g(x)零点,显然f(x),g(x)零点不同,A选项错误;B选项,显然f(x)max=g(x)max=1,B选项正确;C选项,根据周期公式,f(x),g(x)的周期均为2π2=π,C选项正确;D选项,根据正弦函数的性质f(x)的对称轴满足2x=kπ+π2⇔x=kπ2+π4,k∈Z,g(x)的对称轴满足2x-π4=kπ+π2⇔x=kπ2+3π8,k∈Z,显然f(x),g(x)图像的对称轴不同,D选项错误.故选:BC9(新课标全国Ⅱ卷)已知α为第一象限角,β为第三象限角,tanα+tanβ=4,tanαtanβ=2+1,则sin(α+β)=.【答案】-22 3【分析】法一:根据两角和与差的正切公式得tanα+β=-22,再缩小α+β的范围,最后结合同角的平方和关系即可得到答案;法二:利用弦化切的方法即可得到答案.【详解】法一:由题意得tanα+β=tanα+tanβ1-tanαtanβ=41-2+1=-22,因为α∈2kπ,2kπ+π2,β∈2mπ+π,2mπ+3π2,k,m∈Z,则α+β∈2m+2kπ+π,2m+2kπ+2π,k,m∈Z,又因为tanα+β=-22<0,则α+β∈2m+2kπ+3π2,2m+2kπ+2π,k,m∈Z,则sinα+β<0,则sinα+βcosα+β=-22,联立sin2α+β+cos2α+β=1,解得sinα+β=-223.法二:因为α为第一象限角,β为第三象限角,则cosα>0,cosβ<0,cosα=cosαsin2α+cos2α=11+tan2α,cosβ=cosβsin2β+cos2β=-11+tan2β,则sin(α+β)=sinαcosβ+cosαsinβ=cosαcosβ(tanα+tanβ)=4cosαcosβ=-41+tan2α1+tan2β=-4(tanα+tanβ)2+(tanαtanβ-1)2=-442+2=-223故答案为:-22 3.10(全国甲卷数学(文))函数f x =sin x-3cos x在0,π上的最大值是.【答案】2【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【详解】f x =sin x -3cos x =2sin x -π3 ,当x ∈0,π 时,x -π3∈-π3,2π3,当x -π3=π2时,即x =5π6时,f x max =2.故答案为:2一、单选题1(2024·宁夏石嘴山·三模)在平面直角坐标系中,角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点P 1,2 ,则7cos 2θ-2sin2θ=()A.-15B.15C.-2D.2【答案】A【分析】由题意可知:tan θ=2,根据倍角公式结合齐次化问题分析求解.【详解】由题意可知:tan θ=2,所以7cos 2θ-2sin2θ=7cos 2θ-4sin θcos θsin 2θ+cos 2θ=7-4tan θtan 2θ+1=7-4×222+1=-15.故选:A .2(2024·广东茂名·一模)已知cos α+π =-2sin α,则sin 2α-3cos α+π2cos αcos2α+1=()A.-1B.-25C.45D.78【答案】D【分析】根据给定条件,求出tan α,再结合诱导公式及二倍角的余弦公式,利用正余弦齐次式法计算得解.【详解】由cos α+π =-2sin α,得cos α=2sin α,则tan α=12,所以sin 2α-3cos α+π2 cos αcos2α+1=sin 2α+3sin αcos α2cos 2α=12tan 2α+32tan α=18+34=78.故选:D3(2024·河北保定·二模)函数f (x )=1-e x1+e xcos2x 的部分图象大致为()A. B.C. D.【答案】A【分析】根据函数的奇偶性判断即可.【详解】设g x =1-e x1+e x,则g-x=1-e-x1+e-x=e x-11+e x=-g x ,所以g x 为奇函数,设h x =cos2x,可知h x 为偶函数,所以f x =1-e x1+e xcos2x为奇函数,则B,C错误,易知f0 =0,所以A正确,D错误.故选:A.4(2024·山东济宁·三模)已知函数f(x)=(3sin x+cos x)cos x-12,若f(x)在区间-π4,m上的值域为-3 2,1,则实数m的取值范围是()A.π6,π2B.π6,π2C.π6,7π12D.π6,7π12【答案】D【分析】利用二倍角公式、辅助角公式化简函数f(x),再借助正弦函数的图象与性质求解即得.【详解】依题意,函数f(x)=3sin x cos x+cos2x-12=32sin2x+12cos2x=sin2x+π6,当x∈-π4,m时,2x+π6∈-π3,2m+π6,显然sin-π3=sin4π3=-32,sinπ2=1,且正弦函数y=sin x在π2,4π3上单调递减,由f(x)在区间-π4,m上的值域为-32,1,得π2≤2m+π6≤4π3,解得π6≤m≤7π12,所以实数m的取值范围是π6,7π12.故选:D5(2024·江西景德镇·三模)函数f x =cosωx x∈R在0,π内恰有两个对称中心,fπ=1,将函数f x 的图象向右平移π3个单位得到函数g x 的图象.若fα +gα =35,则cos4α+π3=()A.725B.1625C.-925D.-1925【答案】A【分析】根据y轴右边第二个对称中心在0,π内,第三个对称中心不在0,π内可求得32≤ω<52,结合fπ=1可得ω=2,再利用平移变换求出g x ,根据三角变换化简fα +gα =35可得sin2α+π6=35,然后由二倍角公式可解.【详解】由x∈0,π得ωx∈0,ωπ,因为函数f x 在0,π内恰有两个对称中心,所以3π2≤ωπ5π2>ωπ,解得32≤ω<52,又fπ=cosωπ=1,所以ωπ=kπ,k∈Z,即ω=k,k∈Z,所以ω=2,将函数f x 的图象向右平移π3个单位得到函数y=cos2x-π3=cos2x-2π3,即g x =cos2x-2π3,因为fα +gα =cos2α+cos2α-2π3=32sin2α+12cos2α=sin2α+π6=35,所以cos4α+π3=1-2sin22α+π6=1-2×35 2=725.故选:A6(2024·安徽马鞍山·三模)已知函数f(x)=sin2ωx+cos2ωx(ω>1)的一个零点是π2,且f(x)在-π6,π16上单调,则ω=()A.54B.74C.94D.114【答案】B【分析】整理可得f(x)=2sin2ωx+π4,以2ωx+π4为整体,根据单调性分析可得1<ω≤2,再结合零点分析求解.【详解】因为f(x)=sin2ωx+cos2ωx=2sin2ωx+π4,x∈-π6,π16,且ω>1时,可得2ωx+π4∈-π3ω+π4,π8ω+π4,且-π3ω+π4<0<π8ω+π4,若f(x)在-π6,π16上单调,则-π3ω+π4≥-π2π8ω+π4≤π2,解得1<ω≤2,又因为f(x)的一个零点是π2,则πω+π4=kπ,k∈Z,解得ω=k-14,k∈Z,所以k=2,ω=7 4 .故选:B.7(2024·山东临沂·二模)已知函数f x =sin2x+φϕ <π2图象的一个对称中心为π6,0,则()A.f x 在区间-π8,π3上单调递增B.x=5π6是f x 图象的一条对称轴C.f x 在-π6,π4上的值域为-1,32D.将f x 图象上的所有点向左平移5π12个长度单位后,得到的函数图象关于y轴对称【答案】D【分析】借助整体代入法结合正弦函数的性质可得A、B;结合正弦函数最值可得C;得到平移后的函数解析式后借助诱导公式即可得D.【详解】由题意可得2×π6+φ=kπk∈Z,解得φ=-π3+kπk∈Z,又ϕ <π2,故φ=-π3,即f x =sin2x-π3;对A :当x ∈-π8,π3 时,2x -π3∈-7π12,π3,由函数y =sin x 在-7π12,π3上不为单调递增,故f x 在区间-π8,π3上不为单调递增,故A 错误;对B :当x =5π6时,2x -π3=4π3,由x =4π3不是函数y =sin x 的对称轴,故x =5π6不是f x 图象的对称轴,故B 错误;对C :当x ∈-π6,π4 时,2x -π3∈-2π3,π6,则f x ∈-1,12,故C 错误;对D :将f x 图象上的所有点向左平移5π12个长度单位后,可得y =sin 2x +2×5π12-π3 =sin 2x +π2=cos2x ,该函数关于y 轴对称,故D 正确.故选:D .8(2024·广东广州·二模)已知函数f (x )=2sin (ωx +φ)ω>0,|φ|<π2的部分图象如图所示,若将函数f (x )的图象向右平移θ(θ>0)个单位后所得曲线关于y 轴对称,则θ的最小值为()A.π8B.π4C.3π8D.π2【答案】A【分析】根据给定的图象特征,结合五点法作图列式求出ω和φ,再根据图象的平移变换,以及图象的对称性即可得解.【详解】由f π4=1,得sin π4ω+φ =22,又点π4,1 及附近点从左到右是上升的,则π4ω+φ=π4+2k π,k ∈Z ,由f 5π8 =0,点5π8,0 及附近点从左到右是下降的,且上升、下降的两段图象相邻,得5π8ω+φ=π+2k π,k ∈Z ,联立解得ω=2,φ=-π4+2k π,k ∈Z ,而|φ|<π2,于是φ=-π4,f (x )=2sin 2x -π4,若将函数f (x )的图像向右平移θ(θ>0)个单位后,得到y =sin 2x -2θ-π4,则-2θ-π4=π2-k π,k ∈Z ,而θ>0,因此θ=-3π8+k π2,k ∈N ,所以当k =1时,θ取得最小值为π8.故选:A9(2024·四川雅安·三模)已知函数f x =sin ωx +3cos ωx (ω>0),则下列说法中正确的个数是()①当ω=2时,函数y =f x -2log πx 有且只有一个零点;②当ω=2时,函数y =f x +φ 为奇函数,则正数φ的最小值为π3;③若函数y =f x 在0,π3 上单调递增,则ω的最小值为12;④若函数y =f x 在0,π 上恰有两个极值点,则ω的取值范围为136,256.A.1 B.2C.3D.4【答案】B【分析】利用辅助角公式化简函数,由图象分析判断①;由正弦函数的性质判断②③;由极大值的意义结合正弦函数的性质判断④.【详解】依题意,ω>0,函数f (x )=212sin ωx +32cos ωx =2sin ωx +π3,对于①:f (x )=2sin 2x +π3,令y =f x -2log πx =0,即f x =2log πx ,作出函数y =f (x )和函数y =2log πx 的图象,如图,观察图象知,两个函数在0,7π12 上只有一个零点,f 13π12 =2sin 5π2=2,当x =13π12时,y =2log π13π12=2log π1312+2log ππ=2+2log π1312>2,当x >13π12时,2log πx >2≥f (x ),因此函数y =f x 与函数y =2log πx 的图象有且只有一个交点,①正确;对于②:f (x +φ)=2sin 2x +2φ+π3 为奇函数,则2φ+π3=k π,k ∈Z ,φ=-π6+k π2,k ∈Z ,即正数φ的最小值为π3,②正确;对于③:当x ∈0,π3 时,ωx +π3∈π3,π(ω+1)3,由y =f x 在0,π3 上单调递增,得π(ω+1)3≤π2ω>0,解得0<ω≤12,正数ω有最大值12,③错误;对于④:当x ∈(0,π)时,ωx +π3∈π3,ωπ+π3,而y =f x 在(0,π)上恰有两个极值点,由正弦函数的性质得3π2<ωπ+π3≤5π2,解得76<ω≤136,因此ω的取值范围是76,136,④错误.综上,共2个正确,故选:B .10(2024·河北保定·二模)已知tan α=3cos αsin α+11,则cos2α=()A.-78B.78C.79D.-79【答案】B【分析】利用切化弦和同角三角函数的关系,解出sin α,再结合二倍角公式即可求解.【详解】因为sin αcos α=3cos αsin α+11,所以4sin 2α+11sin α-3=0,解得sin α=14或sin α=-3(舍去),所以cos2α=1-2sin 2α=78.故选:B .11(2024·河北衡水·三模)已知sin (3α-β)=m sin (α-β),tan (2α-β)=n tan α,则m ,n 的关系为()A.m =2nB.n =m +1mC.n =m m -1D.n =m +1m -1【答案】D【分析】利用和差角的正弦公式化简,结合已知列出方程即可求解.【详解】依题意,sin (3α-β)=sin [(2α-β)+α]=sin (2α-β)cos α+cos (2α-β)sin α,sin (α-β)=sin [(2α-β)-α]=sin (2α-β)cos α-cos (2α-β)sin α,则sin (2α-β)cos α+cos (2α-β)sin α=m sin (2α-β)cos α-m cos (2α-β)sin α,即sin (2α-β)cos αcos (2α-β)sin α=m +1m -1,即tan (2α-β)tan α=m +1m -1=n .故选:D12(2024·辽宁沈阳·三模)已知tan α2=2,则sin 2α2+sin α的值是()A.25B.45C.65D.85【答案】D【分析】利用二倍角公式和同角之间的转化,进行求解判断选项【详解】当tan α2=2,则sin 2α2+sin α=sin 2α2+2sin α2cos α2sin 2α2+cos 2α2=tan 2α2+2tan α2tan 2α2+1=22+2×222+1=85故选:D13(2024·贵州黔东南·二模)已知0<α<β<π,且sin α+β =2cos α+β ,sin αsin β-3cos αcos β=0,则tan α-β =()A.-1 B.-32C.-12D.12【答案】C【分析】找出tan α和tan β的关系,求出tan α和tan β即可求解.【详解】∵sin αsin β-3cos αcos β=0,∴sin αsin β=3cos αcos β,∴tan αtan β=3①,∵sin α+β =2cos α+β ,∴tan α+β =2⇒tan α+tan β1-tan αtan β=2⇒tan α+tan β1-3=2,∴tan α+tan β=-4②,由①②解得tan α=-1tan β=-3或tan α=-3tan β=-1 ,∵0<α<β<π,∴tan α<tan β,∴tan α=-3tan β=-1 ,∴tan α-β =tan α-tan β1+tan αtan β=-12.故选:C .二、多选题14(2024·河北张家口·三模)已知函数f (x )=23cos 2x +2sin x cos x ,则下列说法正确的是()A.函数f (x )的一个周期为2πB.函数f (x )的图象关于点π3,0 对称C.将函数f (x )的图象向右平移φ(φ>0)个单位长度,得到函数g (x )的图象,若函数g (x )为偶函数,则φ的最小值为5π12D.若f 12α-5π24 -3=12,其中α为锐角,则sin α-cos α的值为6-308【答案】ACD【分析】利用三角恒等变换公式化简,由周期公式可判断A ;代入验证可判断B ;根据平移变化求g (x ),由奇偶性可求出φ,可判断C ;根据已知化简可得sin α-π12 =14,将目标式化为2sin α-π12 -π6 ,由和差角公式求解可判断D .【详解】对于A ,因为f (x )=31+cos2x +sin2x =2sin 2x +π3+3,所以f (x )的最小值周期T =2π2=π,所以2π是函数f (x )的一个周期,A 正确;对于B ,因为f π3 =2sin 2×π3+π3 +3=3,所以,点π3,0 不是函数f (x )的对称中心,B 错误;对于C ,由题知,g x =f (x -φ)=2sin 2(x -φ)+π3 +3=2sin 2x +π3-2φ +3,若函数g (x )为偶函数,则π3-2φ=π2+k π,k ∈Z ,得φ=-π12-k π2,k ∈Z ,因为φ>0,所以φ的最小值为5π12,C 正确;对于D ,若f 12α-5π24-3=2sin 212α-5π24 +π3 =2sin α-π12 =12,则sin α-π12 =14,因为α为锐角,-π12<α-π12<5π12,所以cos α-π12 =154,所以sin α-cos α=2sin α-π4 =2sin α-π12 -π6=232sin α-π12 -12cos α-π12=232×14-12×154=6-308,D 正确.故选:ACD 15(2024·辽宁鞍山·模拟预测)已知函数f x =sin x ⋅cos x ,则()A.f x 是奇函数B.f x 的最小正周期为2πC.f x 的最小值为-12D.f x 在0,π2上单调递增【答案】AC【分析】首先化简函数f x =12sin2x ,再根据函数的性质判断各选项.【详解】f x =sin x ⋅cos x =12sin2x ,函数的定义域为R ,对A ,f -x =-12sin2x =-f x ,所以函数f x 是奇函数,故A 正确;对B ,函数f x 的最小正周期为2π2=π,故B 错误;对C ,函数f x 的最小值为-12,故C 正确;对D ,x ∈0,π2 ,2x ∈0,π ,函数f x 不单调,f x 在0,π4 上单调递增,在π4,π2上单调递减,故D 错误.故选:AC16(2024·安徽·三模)已知函数f x =sin x -3cos x ,则()A.f x 是偶函数B.f x 的最小正周期是πC.f x 的值域为-3,2D.f x 在-π,-π2上单调递增【答案】AC【分析】对于A ,直接用偶函数的定义即可验证;对于B ,直接说明f 0 ≠f π 即可否定;对于C ,先证明-3≤f x ≤2,再说明对-3≤u ≤2总有f x =u 有解即可验证;对于D ,直接说明f -5π6>f -2π3 即可否定.【详解】对于A ,由于f x 的定义域为R ,且f -x =sin -x -3cos -x =-sin x -3cos x =sin x -3cos x =f x ,故f x 是偶函数,A 正确;对于B ,由于f 0 =sin0 -3cos0=-3,f π =sinπ -3cosπ=3,故f 0 ≠f π ,这说明π不是f x 的周期,B 错误;对于C ,由于f x =sin x -3cos x ≤sin x +3cos x =sin x +3cos x 2≤sin x +3cos x 2+3sin x -cos x 2=sin 2x +3cos 2x +23sin x cos x +3sin 2x +cos 2x -23sin x cos x =4sin 2x +4cos 2x =4=2,且f x =sin x -3cos x ≥-3cos x ≥-3,故-3≤f x ≤2.而对-3≤u ≤2,有f 0 =-3≤u ,f 5π6 =2≥u ,故由零点存在定理知一定存在x ∈0,5π6使得f x =u .所以f x 的值域为-3,2 ,C 正确;对于D ,由于-π<-5π6<-2π3<-π2,f -5π6 =2>3=f -2π3 ,故f x 在-π,-π2上并不是单调递增的,D 错误.故选:AC .17(2024·山西太原·模拟预测)已知函数f x =sin 2x +φ 0<φ<π2 的图象关于直线x =π12对称,且h x =sin2x -f x ,则()A.φ=π12B.h x 的图象关于点π6,0中心对称C.f x 与h x 的图象关于直线x =π4对称 D.h x 在区间π6,5π12内单调递增【答案】BCD【分析】根据正弦函数的对称性求解φ判断A ,先求出h x =sin 2x -π3,然后利用正弦函数的对称性求解判断B ,根据对称函数的性质判断C ,结合正弦函数的单调性代入验证判断D .【详解】由题意得2×π12+φ=π2+k π,k ∈Z ,解得φ=π3+k π,k ∈Z ,又因为0<φ<π2,所以φ=π3,A 错误;由φ=π3可知f x =sin 2x +π3,则h x =sin2x -sin 2x +π3 =12sin2x -32cos2x =sin 2x -π3,令2x -π3=k π,k ∈Z ,解得x =π6+k π2,k ∈Z ,令k =0,得x =π6,所以点π6,0 是曲线y =h x 的对称中心,B 正确;因为f π2-x =sin 2π2-x +π3 =sin 4π3-2x =sin 2x -π3=h x ,所以f x 与h x 的图象关于直线x =π4对称,C 正确;当x ∈π6,5π12 时,2x -π3∈0,π2 ,故h x 在区间π6,5π12内单调递增,D 正确.故选:BCD 18(2024·浙江金华·三模)已知函数f x =sin2ωx cos φ+cos2ωx sin φω>0,0<φ<π2的部分图象如图所示,则()A.φ=π6B.ω=2C.f x +π6为偶函数 D.f x 在区间0,π2的最小值为-12【答案】ACD【分析】先由正弦展开式,五点法结合图象求出f x =sin 2x +π6,可得A 正确,B 错误;由诱导公式可得C 正确;整体代入由正弦函数的值域可得D 正确.【详解】由题意得f x =sin 2ω+φ ,由图象可得f 0 =12⇒sin φ=12,又0<φ<π2,所以φ=π6,由五点法可得ω×4π3+π6=3π2⇒ω=1,所以f x =sin 2x +π6 .A :由以上解析可得φ=π6,故A 正确;B :由以上解析可得ω=1,故B 错误;C :f x +π6 =sin 2x +π6 +π6=cos2x ,故C 正确;D :当x ∈0,π2 ⇒2x +π6∈π6,7π6 时,sin 2x +π6 ∈-12,1,所以最小值为-12,故D 正确;故选:ACD .19(2024·浙江温州·二模)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,P -3,4 为其终边上一点,若角β的终边与角2α的终边关于直线y =-x 对称,则()A.cos π+α =35B.β=2k π+π2+2αk ∈Z C.tan β=724D.角β的终边在第一象限【答案】ACD【分析】根据三角函数的定义,可求角α的三角函数,结合诱导公式判断A 的真假;利用二倍角公式,求出2α的三角函数值,结合三角函数的概念指出角2α的终边与单位圆的交点,由对称性确定角β终边与单位圆交点,从而判断BCD 的真假.【详解】因为角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边经过点P -3,4 ,所以:OP =5,所以sin α=45,cos α=-35,所以cos π+α =-cos α=35,故A 对;又sin2α=2sin α⋅cos α=2×45×-35 =-2425,cos2α=cos 2α-sin 2α=-35 2-45 2=-725,所以2α的终边与单位圆的交点坐标为:-725,-2425 ,因为角β的终边与角2α的终边关于直线y =-x 对称,所以角β的终边与单位圆的交点为2425,725,所以tan β=724,且β的终边在第一象限,故CD 正确;又因为终边在直线y =-x 的角为:k π-π4,k ∈Z ,角2α的终边与角β的终边关于y =-x 对称,所以2α+β2=k π-π4⇒β=2k π-π2-2αk ∈Z ,故B 错误.故选:ACD20(2024·广东佛山·二模)已知函数f x =sin x +cos2x 与g x =sin2x +cos x ,记h x =λf x +μg x ,其中λ,μ∈R 且λ2+μ2≠0.下列说法正确的是()A.h x 一定为周期函数B.若λ⋅μ>0,则h x 在0,π2上总有零点C.h x 可能为偶函数 D.h x 在区间0,2π 上的图象过3个定点【答案】ABD【分析】对于A :计算h x +2π ,化简即可;对于B :求出h x ,然后计算h 0 h π2的正负即可;对于C :计算h x ,h -x 是否恒相等即可;对于D :令f x =0g x =0,求解x 即可.【详解】对于A ,∀x ∈R ,h x +2π =λf x +2π +μg x +2π =λf x +μg x =h x ,A 正确;对于B ,h x =λcos x -2sin2x +μ2cos2x -sin x ,则h 0 =λ+2μ,h π2=-3μ,因为λμ>0,即λ,μ同号,所以h 0 h π2<0,由零点存在定理知h x 在0,π2上总有零点,故B 正确;对于C ,h x =λsin x +λcos2x +μsin2x +μcos x ,h -x =-λsin x +λcos2x -μsin2x +μcos x ,由h x =h -x 得2λsin x +2μsin2x =2λsin x +2μ⋅2sin x cos x =2sin x λ+2μcos x =0对x ∈R 恒成立,则λ=μ=0与题意不符,故C 错误;对于D ,令f x =0g x =0 ,则sin x +cos2x =1-2sin 2x +sin x =-sin x -1 2sin x +1 =0sin2x +cos x =cos x 2sin x +1 =0 ⇒sin x =1或sin x =-12cos x =0或sin x =-12,即x ∈-π6+2k π,π2+2k π,7π6+2k π ,k ∈Z ,故所有定点坐标为-π6+2k π,0 ,π2+2k π,0 ,7π6+2k π,0 ,k ∈Z ,又因为x ∈0,2π ,所以函数h x 的图象过定点π2,0 ,7π6,0 ,11π6,0 ,故D 正确;故选:ABD .21(2024·湖南·二模)已知函数f x =12cos 2x -π3 ,把y =f x 的图象向右平移π3个单位长度,得到函数y =g x 的图象,以下说法正确的是()A.x =π6是y =f x 图象的一条对称轴B.f x 的单调递减区间为k π+π6,k π+2π3k ∈Z C.y =g x 的图象关于原点对称D.f x +g x 的最大值为12【答案】ABD【分析】根据题意,求得g x =-12cos2x 的图象,结合三角函数的图象与性质,以及两角差的正弦公式,逐项判定,即可求解.【详解】将函数f x =12cos 2x -π3 的图象向右平移π3个单位长度,得到函数y =g x =12cos 2x -π =-12cos2x 的图象,对于A 中,令x =π6,求得f x =12,即为函数y =f x 最大值,所以直线x =π6是函数f x 图象的一条对称轴,所以A 正确;对于B 中,令2k π≤2x -π3≤2k π+π,k ∈Z ,解得k π+π6≤x ≤k π+2π3,k ∈Z ,可得f x 的单调减区间为k π+π6,k π+2π3,k ∈Z ,所以B 正确.对于C 中,由于g x =-12cos2x 是偶函数,可得函数g x 的图象关于y 轴对称,所以C 错误.对于D 中,由f x +g x =12cos 2x -π3 +-12cos2x =1212cos2x +32sin2x -12cos2x =34sin2x -14cos2x =12sin 2x -π6 ≤12,即f x +g x 的最大值为12,所以D 正确.故选:ABD .22(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0),则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2,则ω=2B.当ω=1,x ∈0,π2时,f x 的值域为-3,2 C.当ω=1时,f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点,则5≤ω<8【答案】BCD【分析】根据三角恒等变换化简f x =2sin 2ωx +π3,进而根据周期可判断A ,根据整体法求解函数的值域判断B ,根据函数图象的平移可判断C ,根据零点个数确定不等式满足的条件可判断D .【详解】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3,对于A ,若f x 相邻两条对称轴的距离为π2,则T =2×π2=π=2π2ω,故ω=1,A 错误,对于B ,当ω=1,f x =2sin 2x +π3 ,当x ∈0,π2 时,2x +π3∈π3,4π3,则f x 的值域为-3,2 ,B 正确,对于C ,当ω=1,f x =2sin 2x +π3,f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6,C 正确,对于D ,当x ∈0,π6 时,2ωx +π3∈π3,2ωπ6+π3,若f x 在区间0,π6 上有且仅有两个零点,则2π≤2ωπ6+π3<3π,解得5≤ω<8,故D 正确,故选:BCD 三、填空题23(2024·北京·三模)已知函数f (x )=sin x cos ωx ,x ∈R .①若ω=1,则f (x )的最小正周期是;,②若ω=2,则f (x )的值域是.【答案】π[-1,1]【分析】把ω=1代入,t 明智二倍角的正弦,结合正弦函数的周期求出f (x )的最小正周期;把ω=2代入,利用二倍角的余弦公式,借助换元法,利用导数求出f (x )的值域.【详解】当ω=1时,f (x )=sin x cos x =12sin2x ,函数f (x )的最小正周期为2π2=π;当ω=2时,f (x )=sin x cos2x =sin x (1-2sin 2x ),令sin x =t ∈[-1,1],g (t )=t (1-2t 2)=-2t 3+t ,求导得g (t )=-6t 2+1,当-1≤t <-66或66<t ≤1时,g (t )<0,当-66<t <66时,g (t )>0,函数g (t )在-1,-66 ,66,1 上单调递减,在-66,66上单调递增,g (-1)=1,g 66 =69,g (1)=-1,g -66 =-69,所以g (t )min =-1,g (t )max =1,f (x )的值域是[-1,1].故答案为:π;[-1,1]24(2024·北京·模拟预测)已知函数f (x )=sin ωx -2cos ωx (ω>0),且f α+x =f α-x .若两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,则sin4α=.【答案】-45/-0.8【分析】利用辅助角公式化简f (x )的解析式,再由题意可得函数关于x =α对称,且最小正周期T =π,即可求出ω的值,从而得到2α=φ+π2+k π,k ∈Z ,再由二倍角公式及同角三角函数的基本关系计算可得.【详解】因为f (x )=sin ωx -2cos ωx =5sin ωx -φ ,其中tan φ=2,由f α+x =f α-x ,可得f x 关于x =α对称,又两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,所以f x 的最小正周期T =π,又ω>0,所以2πω=π,解得ω=2,所以f x =5sin 2x -φ ,所以2α-φ=π2+k π,k ∈Z ,则2α=φ+π2+k π,k ∈Z ,所以sin4α=sin2φ+π2+k π =sin 2φ+π+2k π =-sin2φ=-2sin φcos φsin 2φ+cos 2φ=-2tan φtan 2φ+1=-2×222+1=-45.故答案为:-4525(2024·湖北荆州·三模)设0<α<β<π2,tan α=m tan β,cos α-β =35,若满足条件的α与β存在且唯一,则m =,tan αtan β=.【答案】191【分析】由tan α=m tan β得到sin αcos β=m cos αsin β,再结合cos α-β =35,利用sin α-β =-45,得到cos αsin β=-45m -1 ,sin αcos β=-4m5m -1 ,从而sin α+β =-4m +1 5m -1,再由满足条件的α与β存在且唯一,得到α+β唯一,从而sin α+β =-4m +15m -1=1,求得m 即可.【详解】解:由tan α=m tan β,得sin αcos α=m sin βcos β,即sin αcos β=m cos αsin β,因为0<α<β<π2,tan α=m tan β,所以-π2<α-β<0,0<m <1,又cos α-β =35,所以sin α-β <0,从而sin α-β =sin αcos β-cos αsin β=m -1 cos αsin β=-45,所以cos αsin β=-45m -1,所以sin αcos β=m cos αsin β=-4m5m -1,所以sin α+β =sin αcos β+cos αsin β=-4m +15m -1,因为α,β∈0,π2,所以α+β∈0,π ,因为满足条件的α与β存在且唯一,所以α+β唯一,所以sin α+β =-4m +1 5m -1=1,所以m =19,经检验符合题意,所以tan α=19tan β,则tan α-β =-43=tan α-tan β1+tan αtan β=tan α-9tan α1+9tan 2α,解得tan α=13,所以tan αtan β=9tan 2α=1.故答案为:19,1【点睛】关键点点睛:关键是结合已知得出sin α+β =-4m +15m -1 =1,求出m ,由此即可顺利得解.。
高考三角函数重点题型解析及常见试题

高考三角函数重点题型解析及常见试题三角函数的主要考点是:三角函数的概念和性质(单调性,周期性,奇偶性,最值),三角函数的图象,三角恒等变换(主要是求值),三角函数模型的应用,正余弦定理及其应用,平面向量的基本问题及其应用.题型1 三角函数的最值:最值是三角函数最为重要的内容之一,其主要方法是利用正余弦函数的有界性,通过三角换元或者是其它的三角恒等变换转化问题.例1 若x 是三角形的最小内角,则函数sin cos sin cos y x x x x =++的最大值是( ) A .1-BC.12-D.12+例2.已知函数2()2sin cos 2cos f x a x x b x =+.,且(0)8,()126f f π==.(1)求实数a ,b 的值;(2)求函数)(x f 的最大值及取得最大值时x 的值.题型2 三角函数的图象:三角函数图象从“形”上反应了三角函数的性质,一直是高考所重点考查的问题之一. 例3.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图象,只需将函数sin 2y x =的图象 A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位例4,函数tan sin tan sin y x x x x =+--在区间3(,)22ππ内的图象是 .题型3 用三角恒等变换求值:其主要方法是通过和与差的,二倍角的三角变换公式解决. 例5已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭7πsin 6α⎛⎫+ ⎪⎝⎭的值是 A. BC .45-D .45例6若cos 2sin αα+=则tan α= A .21B .2C .21-D .2-例7,已知函数()sin()(00π)f x A x A ϕϕ=+><<,,x ∈R 的最大值是1,其图像经过点π132M ⎛⎫ ⎪⎝⎭,.(1)求()f x 的解析式;(2)已知π02αβ⎛⎫∈ ⎪⎝⎭,,,且3()5f α=,12()13f β=,求()f αβ-的值.ABCD-例8:已知函数()2sin()cos f x x x π=-.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.题型4 正余弦定理的实际应用:这类问题通常是有实际背景的应用问题,主要表现在航海和测量上,解决的主要方法是利用正余弦定理建立数学模型.例9,在ABC ∆中,角,,A B C 所对的边分别为,,a b c,且满足cos2A =, 3AB AC ⋅=.(I )求ABC ∆的面积; (II )若6b c +=,求a 的值. ,例10,已知锐角△ABC 中,三个内角为A 、B 、C ,两向量)sin cos ,sin 22(A A A p +-=,)sin 1,cos (sin A A A q +-=,若p ,q 是共线向量.(I )求∠A 的大小;(II )求函数y =232sin cos()2C BB -+取最大值时,∠B 的大小.例11.在一个特定时段内,以点E 为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A .某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45且与点A 相距402B ,经过40分钟又测得该船已行驶到点A 北偏东45θ+ (其中26sin 26θ=,090θ<<)且与点A 相距1013C . (1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.题型5 三角函数与平面向量的结合:三角函数与平面向量的关系最为密切,这二者的结合有的是利用平面向量去解决三角函数问题,有的是利用三角函数去解决平面向量问题,更多的时候是平面向量只起衬托作用,三角函数的基本问题才是考查的重点.例12,已知向量)1,(sin ),2cos ,cos 2(x b x x a ωωω==,(0>ω),令b a x f ⋅=)(,且)(x f 的周期为π.(1) 求4f π⎛⎫⎪⎝⎭的值;(2)写出()f x 在]2,2[ππ-上的单调递增区间. ,例13,已知向量()3sin ,cos a αα=,()2sin ,5sin 4cos b ααα=-,3,22παπ⎛⎫∈ ⎪⎝⎭,且a b ⊥.(1)求tan α的值; (2)求cos 23απ⎛⎫+⎪⎝⎭的值.题型6 三角形中的三角恒等变换:这是一类重要的恒等变换,其中心点是三角形的内角和是π,有的时候还可以和正余弦定理相结合,利用这两个定理实现边与角的互化,然后在利用三角变换的公式进行恒等变换,是近年来高考的一个热点题型.例14,三角形的三内角A ,B ,C 所对边的长分别为a ,b ,c ,设向量(,),(,)m c a b a n a b c =--=+,若//m n ,(1)求角B 的大小;(2)求sin sin A C +的取值范围. ,题型7 用平面向量解决平面图形中的问题:由于平面向量既有数的特征(能进行类似数的运算)又具有形的特征,因此利用平面向量去解决平面图形中的问题就是必然的了,这在近年的高考中经常出现.考试大纲明确指出用会用平面向量解决平面几何问题. 例15. 如图,已知点G 是ABO ∆的重心,点P 在OA 上,点Q 在OB 上,且PQ 过ABO ∆ 的重心G ,OP mOA =,OQ nOB =,试证明11m n+为常数,并求出这个常数.题型8 用导数研究三角函数问题:导数是我们在中学里引进的一个研究函数的重要工具,利用导数探讨三角函数问题有它极大的优越性,特别是单调性和最值. 例12. 已知函数22()cos 2sin cos sin f x x t x x x =+-,若函数()f x 在区间(,]126ππ上是增函数,求实数t 的取值范围.题型9 三角函数性质的综合应用:将三角函数和其它的知识点相结合而产生一些综合性的试题,解决这类问题往往要综合运用我们的数学知识和数学思想,全方位的多方向进行思考.例13. 设二次函数2()(,)f x x bx c b c R =++∈,已知不论α,β为何实数,恒有(sin )0f α≥和(2cos )0f β+≤.(1)求证:1b c +=- ; (2)求证:3c ≥;(3)若函数(sin )f α的最大值为8,求b ,c 的值. .【专题训练与高考预测】 一、选择题1.若[0,2)απ∈,sin cos αα+=-,则α的取值范围是( )A .[0,]2πB .[,]2ππ C .3[,]2ππ D .3[,2)2ππ 2.设α是锐角,且lg(1cos )m α-=,1lg 1cos n α=+,则lgsin α=( ) A .m n - B .11()2m n - C .2m n - D .11()2n m-3.若00||2sin15,||4cos15a b ==,a 与b 的夹角为30。
(完整版)高考三角函数经典解答题及答案

(完整版)高考三角函数经典解答题及答案1. 在△ABC 中,角 A、B、C 所对的边分别是 a、b、c,且 a²+c²-b²=(1) 求 sin²(2A+C)+cos²B 的值;(2) 若 b=2,求△ABC 面积的最大值。
解:(1) 由余弦定理:cosB=(a²+ c²- b²)/(2ac)=4/√115,得sinB=√(1-cos²B)=3√(23)/23。
由正弦定理sin²(2A+C)+cos²B=4sin²B+cos²B=13/23。
2. 在△ABC 中,角 A、B、C 的对边分别为 a、b、c,且bcosC=3acosB-ccosB。
(I) 求 cosB 的值;(II) 若 BA·BC=2,且b=√2,求 a 和 c·b 的值。
解:(I) 由正弦定理得 a=2RsinA,b=2RsinB,c=2RsinC,则 2RsinBcosC=6RsinAcosB-2RsinCcosB,故sinBcosC=3sinAcosB-sinCcosB,可得sinBcosC+sinCcosB=3sinAcosB,即 sin(B+C)=3sinAcosB,可得 sinA=3sinAcosB/sinB。
又sinA≠0,因此 cosB=1/3。
3. 已知向量 m=(sinB,1-cosB),向量 n=(2,k),且 m 与 n 所成角为π/3,其中 A、B、C 是△ABC 的内角。
(1) 求角 B 的大小;(2) 求 sinA+sinC 的取值范围。
解:(1) ∠m与∠n所成角为π/3,且 m·n=2sinB+ k(1-cosB)=2√3/2cosB+k√(1-cos²B),又 m·n=2cosB+k(1-cosB),解得 k=4/3。
高考数学最新真题专题解析—三角函数(全国通用)

高考数学最新真题专题解析—三角函数(全国通用)考向一 三角函数的图像【母题来源】2022年高考全国I 卷【母题题文】 设函数π()sin 3f x x ω⎛⎫=+ ⎪⎝⎭在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是( )A. 513,36⎫⎡⎪⎢⎣⎭B. 519,36⎡⎫⎪⎢⎣⎭C. 138,63⎛⎤ ⎥⎝⎦D.1319,66⎛⎤ ⎥⎝⎦【答案】C【试题解析】解:依题意可得0>ω,因为()0,x π∈,所以,333x πππωωπ⎛⎫+∈+ ⎪⎝⎭, 要使函数在区间()0,π恰有三个极值点、两个零点,又sin y x =,,33x ππ⎛⎫∈ ⎪⎝⎭的图象如下所示:则5323ππωππ<+≤,解得13863ω<≤,即138,63ω⎛⎤∈ ⎥⎝⎦. 故选:C .【命题意图】本题主要考查正弦型函数的图象的变换,考查学生的数学运算能力,逻辑分析那能力,是一道中档题.【命题方向】这类试题在考查题型上主要以选择形式出现.多为低档题,本类题型主要考查三角函数的图像和性质以及三角函数的平移变换问题. 常见题型:平移变换、辅助角公式、诱导公式. 【得分要点】(1)利用降幂公式、辅助角公式对三角函数进行化简; (2)利用三角函数的一些性质解题. 考向二 三角函数的性质 【母题来源】2022年高考北京卷【母题题文】 已知函数22()cos sin f x x x =-,则( ) A.()f x 在,26ππ⎛⎫-- ⎪⎝⎭上单调递减 B.()f x 在,412ππ⎛⎫-⎪⎝⎭上单调递增 C. ()f x 在0,3π⎛⎫⎪⎝⎭上单调递减 D.()f x 在7,412ππ⎛⎫⎪⎝⎭上单调递增 【答案】C【试题解析】因为()22cos sin cos2f x x x x =-=.对于A 选项,当26x ππ-<<-时,23x ππ-<<-,则()f x 在,26ππ⎛⎫-- ⎪⎝⎭上单调递增,A 错; 对于B 选项,当412x ππ-<<时,226x ππ-<<,则()f x 在,412ππ⎛⎫- ⎪⎝⎭上不单调,B 错;对于C 选项,当03x π<<时,2023x π<<,则()f x 在0,3π⎛⎫⎪⎝⎭上单调递减,C 对;对于D 选项,当7412x ππ<<时,7226x ππ<<,则()f x 在7,412ππ⎛⎫⎪⎝⎭上不单调,D 错. 故选:C.【命题意图】本题考查倍角公式及三角函数的单调性.【命题方向】这类试题在考查题型选择、填空、解答题都有可能出现,多为中档题,是历年高考的热点. 常见的命题角度有:(1)三角函数的图像;(2)三角函数的性质:定义域、值域、奇偶性、单调性、对称性等; 【得分要点】(3)利用倍角公式、降幂公式及辅助角公式对三角函数进行化简; (4)利用三角函数的一些性质解题. 真题汇总及解析 一、单选题1.(2022·天津市求真高级中学高二期末)函数()()sin 0f x x ωω=>的最小正周期为2π,则ω的值为( ) A .4 B .2 C .1D .12【答案】A 【解析】 【分析】根据正弦型函数的周期计算公式2T πω=即可求解.【详解】由2T πω=,∴2242Tππωπ===.故选:A. 2.(2022·上海·华师大二附中模拟预测)已知,x y ∈R ,则表达式22cos cos cos x yxy( )A .既有最大值,也有最小值B .有最大值,无最小值C .无最大值,有最小值D .既无最大值,也无最小值【答案】D 【解析】 【分析】结合余弦函数,可分别得到2cos x ,2cos y ,()cos xy 的范围,再确定端点值是否可以同时取等,即可判断. 【详解】由[]22cos ,cos 0,1x y ∈,()[]cos 1,1xy ∈-,易知22cos cos cos 1,3x yxy.同时,由于π是无理数,因此当cos cos 0xy时,cos 1xy ;当22cos cos 1xy时,cos 0xy,故两端均不能取得等号.补充证明:二元表达式22cos cos cos x yxy(,x y R )可以取到任意接近1-和3的值,从而该式无最值.①取x π=,y n (*n ∈N ),则222cos cos cos 2cos x y xy n .对任意0ε>,由抽屉原理,存在*N N ,使得22N N .再考虑*k ∈N ,使得1k k(由π的无理性,两头都不取等).则nkN 时,212122NN kkN k,从而2cos 1,coskN,22cos cos cos 2cos ,3x y xy ,即证.②取2x π=,2yn(*n ∈N ),则22221cos cos cos cos4n x y xy .对任意0ε>,由抽屉原理,存在*N N ,使得224N N .再考虑k ∈Z ,使得4k k(不取等的理由同上).则nkN 时,2244244N kN N kk,从而221cos cos ,14kN ,22cos cos cos 1,cosxy xy,即证.故选:D 【点睛】易错点点睛:2cos x ,2cos y ,()cos xy 均有最值,但三者加和后,需确定能否同时取得最值.3.(2022·河南安阳·模拟预测(文))已知函数()sin cos f x a x b x c ωω=++(a ,b ,0>ω)的部分图象如图所示,则=a ( )A .1B 2C 3D .2【答案】B 【解析】 【分析】整理()()22f x a b x c ωϕ=+++,且tan b aϕ=222a b +,利用相邻对称轴的距离求得ω,根据对称轴求得ϕ,进而可得tan 1ϕ=,即a b =,即可求解. 【详解】由题,()()22sin cos f x a x b x c a b x c ωωωϕ=+++++,tan b aϕ=,223a b c +=,221a b c -+=-,所以1c =222a b +,又51882T ππ-=,所以T π=,则22T πω==,因为对称轴为8x π=,所以2282k ππϕπ⨯+=+,k ∈Z ,则24k ϕπ=+π,k ∈Z 所以tan 1ϕ=,即a b =, 所以2a = 故选:B4.(2023·广西柳州·模拟预测(文))若()4sin π5α-=,则cos2α=( ) A .-2425B .725C .-725D .2425【答案】C 【解析】 【分析】根据给定条件,利用诱导公式、二倍角的余弦公式化简计算作答. 【详解】依题意,4sin 5α=,所以2247cos 212sin 12525αα⎛⎫=-=-⨯=- ⎪⎝⎭.故选:C5.(2022·四川成都·模拟预测(理))函数2cos 34cos f x x x 的最小正周期为( ) A .23πB .43π C .π D .2π【答案】A 【解析】 【分析】利用三角恒等变换化简函数()f x 的解析式,利用余弦型函数的周期公式可求得函数()f x 的最小正周期. 【详解】222cos 22cos 2cos 1cos 2sin cos2sin sin 2cos2cos f xx x x x x xx x x xcos3x =-,所以,函数()f x 的最小正周期为23T π=. 故选:A.6.(2022·上海闵行·二模)“角,αβ的终边关于y 轴对称”是“cos cos 0αβ+="的( ) A .充要条件 B .充分不必要条件 C .必要不充分条许 D .既不充分也不必要各件【答案】B 【解析】 【分析】先证明充分性,再举出反例说明必要性不成立,得到答案. 【详解】由角,αβ的终边关于y 轴对称,则π2π,k k αβ+=+∈Z ,可知cos cos αβ=-,即cos cos 0αβ+=成立,充分性成立;当cos cos 0αβ+=时,角,αβ的终边关于y 轴对称或(21),k k Z αβπ=++∈, 所以“角,αβ的终边关于y 轴对称”是“cos cos 0αβ+=”的充分不必要条件, 故选:B.7.(2022·甘肃·武威第六中学模拟预测(理))已知函数()12sin 32f x x πϕϕ⎛⎫⎛⎫=+< ⎪⎪⎝⎭⎝⎭,直线x π=-为()f x 图象的一条对称轴,则下列说法正确的是( ) A .6π=ϕB .()f x 在区间,2ππ⎡⎤--⎢⎥⎣⎦单调递减C .()f x 在区间[],ππ-上的最大值为2D .()f x θ+为偶函数,则()23k k Z θππ=+∈【答案】D 【解析】 【分析】由已知得()2sin 23f ππϕ⎛⎫-=-+=± ⎪⎝⎭,由2πϕ<可求得ϕ,可判断A 选项,由此有()12sin 36x f x π⎛⎫=- ⎪⎝⎭;对于B ,由,2x ππ⎡⎤∈--⎢⎥⎣⎦得12363x πππ-≤-≤-,由正弦函数的单调性可判断;对于C ,由[],x ππ∈-得12366x πππ-≤-≤,由此得()f x 在区间[],ππ-上的最大值为2sin16π=;对于D ,()11+2sin +336f x x πθθ⎛⎫=- ⎪⎝⎭,由()1+362k k Z ππθπ-=∈,解得()23k k Z θππ=+∈. 【详解】解:因为函数()12sin 32f x x πϕϕ⎛⎫⎛⎫=+< ⎪⎪⎝⎭⎝⎭,直线x π=-为()f x 图象的一条对称轴,所以()2sin 23f ππϕ⎛⎫-=-+=± ⎪⎝⎭,所以+,32k k Z ππϕπ-+=∈,又2πϕ<,所以6πϕ=-,故A 不正确;所以()12sin 36x f x π⎛⎫=- ⎪⎝⎭,对于B ,当,2x ππ⎡⎤∈--⎢⎥⎣⎦时,12363x πππ-≤-≤-,所以()f x 在区间,2单调递增,故B 不正确;对于C ,当[],x ππ∈-时,12366x πππ-≤-≤,()f x 在区间[],ππ-上的最大值为2sin16π=,故C 不正确;对于D ,若()f x θ+为偶函数,且()()111+2sin +2sin +36336f x x x ππθθθ⎡⎤⎛⎫=-=- ⎪⎢⎥⎣⎦⎝⎭,所以()1+362k k Z ππθπ-=∈,解得()23k k Z θππ=+∈,故D 正确,故选:D.8.(2022·青海·海东市第一中学模拟预测(理))已知函数()()23sin cos cos 0f x x x x ωωωω+>,若函数f (x )在,2ππ⎛⎫⎪⎝⎭上单调递减,则实数ω的取值范围是( )A .13,32⎡⎤⎢⎥⎣⎦B .12,33⎡⎤⎢⎥⎣⎦C .10,3⎛⎤⎥⎝⎦D .20,3⎛⎤⎥⎝⎦【答案】B 【解析】 【分析】利用二倍角和辅助角公式化简解析式,然后利用正弦函数的单调性解决即可. 【详解】 函数()()()2313sin cos cos 0sin 21cos222f x x x x x x ωωωωωω=+>=++311sin 2cos2222x x ωω=++1sin 262x πω⎛⎫=++ ⎪⎝⎭,由函数f (x )在,2ππ⎛⎫ ⎪⎝⎭上单调递减,且2,2666x πππωωπωπ⎛⎫+∈++ ⎪⎝⎭,得26232262k k ππωππππωππ⎧+≥+⎪⎪⎨⎪+≤+⎪⎩,k ∈Z ,解12233k k ω+≤≤+,k ∈Z .又因为ω>0,12222πππω⨯≥-,所以k =0,所以实数ω的取值范围是12,33⎡⎤⎢⎥⎣⎦.故选:B9.(2022·浙江·模拟预测)如图所示的是函数()y f x =的图像,则函数()f x 可能是( )A .sin y x x =B .cos y x x =C .sin cos y x x x x =+D .sin cos y x x x x =-【答案】C 【解析】 【分析】由图象确定函数的性质,验证各选项是否符合要求即可. 【详解】由图可知:()f x 是非奇非偶函数,且在y 轴右侧,先正后负.若()sin f x x x =,则()()()sin sin f x x x x x -=--=,所以函数sin y x x =为偶函数, 与条件矛盾,A 错,若()cos f x x x =,则()()()cos cos f x x x x x -=--=-,所以函数cos y x x =为奇函数,与条件矛盾,B 错,若()sin cos f x x x x x =-,则()2sin 4f x x x π⎛⎫=- ⎪⎝⎭,当04x π⎛⎫∈ ⎪⎝⎭,时,()2sin 04f x x x π⎛⎫=-< ⎪⎝⎭,与所给函数图象不一致,D 错,若()sin cos f x x x x x =+,则()2sin 4f x x x π⎛⎫=+ ⎪⎝⎭,当304x π⎛⎫∈ ⎪⎝⎭,时,()0f x >,又2()4f π=, ()04f π-=,所以函数sin cos y x x x x =+为非奇非偶函数,与所给函数图象基本一致, 故选:C .10.(2022·北京·北大附中三模)如图矩形,6ABCD AB =,沿PQ 对折使得点B 与AD 边上的点1B 重合,则PQ 的长度可以用含α的式子表示,那么PQ 长度的最小值为( )A .4B .8C .2D 93【答案】D 【解析】 【分析】设PQ y =,由三角比的定义可得sin PB y α=,sin cos2PA y αα=⋅,继而求得()262sin 1sin y αα=-,令()()221g t t t =-和2sin t α⎛=∈ ⎝⎭,求导可得()g t 的最大值为:343g =⎝⎭PQ 长度的最小值. 【详解】设PQ y =,1PB PB =,11180APB B PB ∠+∠=,12180B PB α+∠=,则12APB α∠=,则有sin PB y α=和11cos cos2PA PB APB PB ∠α==,代入6AB PA PB =+=,解得:()()266sin 1cos22sin 1sin y αααα==+-,令()()221g t t t =-和2sin t α⎛=∈ ⎝⎭, 导函数()226g t t '=-,即可得()g t 的最大值在3t =此时343g =⎝⎭min 93y =, 故选:D .二、填空题11.(2022·辽宁实验中学模拟预测)已知tan 2α=,则222222cos 2sin 2cos 3sin sin 1cos 2αααααα--+=++_________.【答案】16799-##68199-【解析】 【分析】利用同角间的三角函数关系,把待求式化为关于tan α的式子,然后代入已知计算. 【详解】2222222222222222cos 2sin 2cos 3sin cos 2sin 2cos 3sin sin 1cos 2sin sin cos cos 2(sin cos )αααααααααααααααα----+=+++++++22222222cos 2sin 2cos 3sin 2sin cos 2sin 3cos αααααααα--++=+222212tan 23tan 2tan 12tan 3αααα--+=++ 182128183--=+++16799=-. 故答案为:16799-. 12.(2022·内蒙古·乌兰浩特一中模拟预测(文))将最小正周期为π的函数()2sin(2)1(0)6f x x πωω=-+>的图像向左平移4π个单位长度,得到()g x 的图像,则函数()g x 的一个对称中心为___________【答案】,13π⎛⎫⎪⎝⎭,不唯一【解析】 【分析】根据最小正周期求出ω ,再根据函数平移规则即可求出()g x 的解析式. 【详解】由题意,T π= ,2,12ππωω∴== ,即()2sin 216f x x π⎛⎫=-+ ⎪⎝⎭ ,()f x 向左平移4π得()g x , ()2sin 212sin 21463g x x x πππ⎡⎤⎛⎫⎛⎫∴=+-+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ ,令2,33x x πππ+== ,∴()g x 的一个对称中心为,13π⎛⎫ ⎪⎝⎭;故答案为: ,13π⎛⎫⎪⎝⎭.13.(2022·福建·三明一中模拟预测)已知函数2()322cos 1f x x x =-+,且方程()0f x a -=在,36ππ⎡⎤-⎢⎥⎣⎦内有实数根,则实数a 的取值范围是___________.【答案】[2,1]- 【解析】 【分析】由题意可得()a f x =在,36ππ⎡⎤-⎢⎥⎣⎦内有实数根,a 的取值范围即为函数()f x 的值域.【详解】2()322cos 132cos 22sin(2)6f x x x x x x π-+=-=-,方程()0f x a -=在,36ππ⎡⎤-⎢⎥⎣⎦内有实数根,即()a f x =在,36ππ⎡⎤-⎢⎥⎣⎦内有实数根, ,36x ππ⎡⎤∈-⎢⎥⎣⎦,52,666x πππ⎡⎤-∈-⎢⎥⎣⎦,得2()1f x -≤≤,即a 的取值范围是[2,1]-,故答案为:[2,1]-14.(2022·北京工业大学附属中学三模)已知函数ππ()sin()sin()44f x x x =+-给出下列四个结论: ①f (x )的值域是[1,1]-; ②f (x )在π[0,]2上单调递减: ③f (x )是周期为π的周期函数④将f (x )的图象向左平移π2个单位长度后,可得一个奇函数的图象 其中所有正确结论的序号是___________. 【答案】②③ 【解析】 【分析】先将()f x 化简,然后根据余弦函数的性质逐一判断即可 【详解】ππ()sin()sin()44f x x x =+-2222()()x x x x =+ 2211cos sin 22x x =- 1cos22x =所以()f x 的值域为11[,]22- ,故①错误; 令2π2π2π,k x k k Z ≤≤+∈ ,πππ,2k x k k Z ∴≤≤+∈当0k =时,()f x 的一个单调递减区间为π[0,]2,故②正确;()f x 的周期2ππT ω== ,故③正确()f x 的图像向左平移π2个单位长度后得到的函数图像对应的解析式为π1π1()()cos[2()]cos 22222g x f x x x =+=+=- ,是偶函数,故④错误故答案为:②③ 三、解答题15.(2022·浙江绍兴·模拟预测)函数()sin(π),R f x A x x ϕ=+∈(其中π0,02A ϕ>≤≤)部分图象如图所示,1(,)3P A 是该图象的最高点,M ,N 是图象与x 轴的交点.(1)求()f x 的最小正周期及ϕ的值; (2)若π4PMN PNM ∠+∠=,求A 的值. 【答案】(1)2;π6ϕ=;(2)71A =. 【解析】 【分析】(1)利用()f x 的解析式求出周期,再由给定的最高点P 求出ϕ作答.(2)由(1)求出点M ,N 的坐标,结合图形求出PMN ∠和PNM ∠的正切,再利用和角公式计算作答.(1)函数()sin(π)f x A xϕ=+的最小正周期2π2πT==,因1(,)3P A是函数()f x图象的最高点,则1ππ2π,Z32k kϕ+=+∈,而02πϕ≤≤,有0k=,π6ϕ=,所以函数()f x的最小正周期为2,π6ϕ=.(2)由(1)知,π()sin(π)6f x A x=+,由ππ06x+=得16x=-,即点1(,0)6M-,由ππ2π6x+=得116x,即点11(,0)6N,于是得tan211()36APMN A∠==--,2tan111363APNM A∠==-,而π4PMN PNM∠+∠=,则22tan tan3tan()121tan tan123A APMN PNMPMN PNMPMN PNM A A+∠+∠∠+∠===-∠⋅∠-⋅,又0A>,解得712A=-,所以712A=-.16.(2022·上海奉贤·二模)如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处.20AB=km,10BC=km.为了处理这三家工厂的污水,现要在该矩形区域内(含边界)且与A、B等距的一点O处,建造一个污水处理厂,并铺设三条排污管道AO,BO,PO.记铺设管道的总长度为y km.(1)设BAOθ∠=(弧度),将y表示成θ的函数并求函数的定义域;(2)假设铺设的污水管道总长度是(10103+km ,请确定污水处理厂的位置. 【答案】(1)2010sin π10,0cos 4y θθθ-=+≤≤(2)位置是在线段AB 的中垂线上且离AB 103km 【解析】 【分析】(1)依据题给条件,先分别求得OA OB OP 、、的表达式,进而得到管道总长度y 的表达式,再去求其定义域即可解决; (2)先解方程2010sin 1010103cos θθ-+=+π6θ=,再去确定污水处理厂的位置. (1)矩形ABCD 中,20AB =km ,10BC =km ,DP PC =,DC PO ⊥,BAO ABO θ∠=∠=则()10km,1010tan km cos OA OB OP θθ===-, 201010tan cos y OA OB OP θθ∴=++=+- 则2010sin π10,0cos 4y θθθ-=+≤≤(2)令2010sin 1010103cos θθ-+=+π10sin 10320,20sin 20,3θθθ⎛⎫∴+=∴+= ⎪⎝⎭则πsin 1,3θ⎛⎫+= ⎪⎝⎭又π04θ≤≤,即ππ7π3312θ≤+≤,则ππ32θ+=,则π6θ=此时π101010tan 103(km)63OP =-=所以确定污水处理厂的位置是在线段AB的中垂线上且离AB103km。
三角函数的图象与性质6大题型(解析版)--2024高考数学常考题型精华版

三角函数的图象与性质6大题型【题型目录】题型一:三角函数的周期性题型二:三角函数对称性题型三:三角函数的奇偶性题型四:三角函数的单调性题型五:三角函数的值域题型六:三角函数的图像【典例例题】题型一:三角函数的周期性【例1】(2022·全国·兴国中学高三阶段练习(文))下列函数中,最小正周期为π的奇函数是().A .tan y x =B .sin 2y x =C .sin cos y x x =D .sin y x=【例2】(2022江西景德镇一中高一期中(文))下列函数中①sin y x =;②sin y x =;③tan y x =;④12cos y x =+,其中是偶函数,且最小正周期为π的函数的个数为()A .1B .2C .3D .4【答案】B【解析】①的图象如下,根据图象可知,图象关于y 轴对称,sin y x =是偶函数,但不是周期函数,∴排除①;②的图象如下,根据图象可知,图象关于y 轴对称,sin y x =是偶函数,最小正周期是π,∴②正确;③的图象如下,根据图象可知,图象关于y 轴对称,tan y x =是偶函数,最小正周期为π,∴③正确;④的图象如下,根据图象可知,图象关于y 轴对称,12cos y x =+是偶函数,最小正周期为2π,∴排除④.故选:B.【例3】(2022·全国·高三专题练习)函数ππ()sin 2cos 233f x x x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期是()A .π4B .π2C .πD .2π【例4】设函数()c x b x x f ++=sin 2cos ,则()x f 的最小正周期()A .与b 有关,且与c 有关B .与b 有关,但与c 无关C .与b 无关,且与c 无关D .与b 无关,但与c 有关【答案】B【解析】因x y 2cos =的最小正周期为ππ==22T ,x y sin =的最小正周期为ππ212==T 所以当0≠b 时,()x f 的最小正周期为π2;当0=b 时,()x f 的最小正周期为π;【例5】(2022·全国·高一课时练习)函数22cos 14y x π⎛⎫=+- ⎪⎝⎭的最小正周期为()A .4πB .2πC .πD .2π【例6】(2022·广西桂林·模拟预测(文))函数()2sin6cos6f x x x =+的最小正周期是()A .2πB .3πC .32πD .6π【例7】(2022·全国·高一专题练习)()|sin ||cos |f x x x =+的最小正周期是()A .2πB .πC .2πD .3π【题型专练】1.(2023全国高三题型专练)在函数①cos |2|y x =,②|cos |y x =,③πcos 26y x ⎛⎫=+ ⎪⎝⎭,④πtan 24y x ⎛⎫=- ⎪⎝⎭中,最小正周期为π的所有函数为()A .②④B .①③④C .①②③D .②③④【答案】C【解析】∵cos |2|y x ==cos2x ,∴T =22π=π;|cos |y x =图象是将y =cos x 在x 轴下方的图象对称翻折到x 轴上方得到,所以周期为π,由周期公式知,cos(2)6y x π=+为π,tan(2)4y x π=-为2π,故选:C .2.(2022·河北深州市中学高三阶段练习)下列函数中,最小正周期为π的奇函数是()A .sin 4y x π⎛⎫=+ ⎪⎝⎭B .()()sin cos y x x ππ=+-C .22cos cos 2y x x π⎛⎫=-+ ⎪D .sin 2y x=3.(2022·北京昌平·高一期末)下列函数中,最小正周期为π的奇函数是()A .sin 4y x π⎛⎫=+ ⎪⎝⎭B .sin 2y x =C .sin cos y x x =D .22cos sin y x x=-4.(2022·陕西渭南·高二期末(理))函数()2sin cos f x x x x =+的最小正周期是________.5.(2022·全国·高一专题练习)已知函数()cos f x x x ωω=-(0)ω>的最小正周期为π,则ω=___.6.(2022·浙江·杭十四中高一期末)函数2cos cos cos 2y x x x π⎛⎫=+- ⎪的最小正周期为__________.题型二:三角函数对称性【例1】(江西省“红色十校”2023届高三上学期第一联考数学(文)试题)已知函数π()sin()0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的两个相邻的零点为12,33-,则()f x 的一条对称轴是()A .16x =-B .56x =-C .13x =D .23x =,【例2】(2022全国高一课时练习)函数cos 23y x ⎛⎫=+ ⎪⎝⎭的图象()A .关于点,03π⎛⎫⎪⎝⎭对称B .关于点,06π⎛⎫⎪⎝⎭对称C .关于直线6x π=对称D .关于直线3x π=对称【答案】D【解析】由题设,由余弦函数的对称中心为,2)0(k ππ+,令232x k πππ+=+,得212k x ππ=+,k Z ∈,易知A 、B 错误;由余弦函数的对称轴为x k π=,令23x k ππ+=,得26k x ππ=-,k Z ∈,当1k =时,3x π=,易知C 错误,D 正确;故选:D 【例3】(2022·江西省万载中学高一阶段练习)把函数4πsin 23y x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0ϕϕ>个单位长度,所得图像关于y 轴对称,则ϕ的最小值是()A .5π6B .2π3C .5π12D .π6【例4】(2023福建省福州屏东中学高三开学考试多选题)已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称,则()A .函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B .函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C .函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称,则a 的最小值是3πD .若方程()f x a =在2,63ππ⎡⎤⎢⎥上有2个不同实根12,x x ,则12x x -的最大值为2π故结合正弦函数的性质可知,若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ,不妨设12x x <,则12x x -取得最大值时满足1266x ππ-=且25266x ππ-=,所以,12x x -的最大值为3π,故错误.故选:AC【例5】(2023江西省高三月考)若函数y cos 6x πω⎛⎫=+ ⎪⎝⎭(ω∈N +)图象的一个对称中心是,06π⎛⎫⎪⎝⎭,则ω的最小值为()A .1B .2C .4D .8【答案】B 【解析】当6x π=时,0y =,即cos 066πωπ⎛⎫+=⎪⎝⎭,()662k k Z πωπππ∴+=+∈,解得62k ω=+,N ω*∈ ,故当0k =时,ω取最小值2.【例6】【2016高考新课标2理数】若将函数2sin 2y x =的图像向左平移12π个单位长度,则平移后图象的对称轴为()(A )()26k x k Z ππ=-∈(B )()26k x k Z ππ=+∈(C )()212k x k Z ππ=-∈(D )()212k x k Z ππ=+∈【答案】B【解析】由题意,将函数2sin 2y x =的图像向左平移12π个单位得2sin 2()2sin(2)126y x x ππ=+=+,则平移后函数的对称轴为2,62x k k Z πππ+=+∈,即,62k x k Z ππ=+∈,故选B.【题型专练】1.(2020·四川省泸县第四中学高三开学考试)已知函数()sin 22f x x π⎛⎫=+ ⎪⎝⎭,则函数()f x 的图象的对称轴方程为()A .,4x k k Z ππ=-∈B .+,4x k k Z ππ=∈C .1,2x k k Z π=∈D .1+,24x k k Zππ=∈【答案】C【解析】由已知,()cos 2f x x =,令2,π=∈x k k Z ,得1,2x k k Z π=∈.故选:C.2.【2017·天津卷】设函数()2sin()f x x ωϕ=+,x ∈R ,其中0ω>,||ϕ<π.若5(28f π=,(08f 11π=,且()f x 的最小正周期大于2π,则A .23ω=,12ϕπ=B .23ω=,12ϕ11π=-C .13ω=,24ϕ11π=-D .13ω=,24ϕ7π=【答案】A【解析】由题意得125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩,其中12,k k ∈Z ,所以2142(2)33k k ω=--,又22T ωπ=>π,所以01ω<<,所以23ω=,11212k ϕ=π+π,由ϕ<π得12ϕπ=,故选A .3.(2023·全国·高三专题练习)将函数sin 22y x x =的图象沿x 轴向右平移a 个单位(a >0)所得图象关于y 轴对称,则a 的最小值是()A .712πB .4πC .12πD .6π4.【2018·江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称,则ϕ的值是________.【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ,所以2πππππ()326k k k +=+=-+∈Z ,ϕϕ,因为ππ22-<<ϕ,所以π0,.6k ==-ϕ5.(2022·广西南宁·高二开学考试多选题)把函数()sin f x x =的图像向左平移π3个单位长度,再把横坐标变为原来的12倍(纵坐标不变)得到函数()g x 的图像,下列关于函数()g x 的说法正确的是()A .最小正周期为πB .单调递增区间5πππ,π()1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z C .图像的一个对移中心为π,03⎛⎫- ⎪⎝⎭D .图像的一条对称轴为直线π12x =题型三:三角函数的奇偶性【例1】(2022·全国·清华附中朝阳学校模拟预测)已知函数()sin 2sin 23f x x x π⎛⎫=++ ⎪⎝⎭向左平移θ个单位后为偶函数,其中0,2π⎡⎤θ∈⎢⎥⎣⎦.则θ的值为()A .2πB .3πC .4πD .6π【例2】(2022·广东·执信中学高一期中)对于四个函数sin y x =,cos y x =,sin y x =,tan y x =,下列说法错误的是()A .sin y x =不是奇函数,最小正周期是π,没有对称中心B .cos y x =是偶函数,最小正周期是π,有无数多条对称轴C .sin y x =不是奇函数,没有周期,只有一条对称轴D .tan y x =是偶函数,最小正周期是π,没有对称中心由图可知,函数sin y x =不是奇函数,最小正周期是π,没有对称中心,A 对;对于B 选项,如下图所示:由图可知,cos y x =是偶函数,最小正周期是π,有无数多条对称轴,B 对;对于C 选项,如下图所示:由图可知,sin y x =不是奇函数,没有周期,只有一条对称轴,C 对;对于D 选项,如下图所示:由图可知,函数tan y x =是偶函数,不是周期函数,没有对称中心,D 错.故选:D.【例3】(2022·陕西师大附中高一期中)已知函数2π()sin ()24f x x =++,若(lg5)a f =,1(lg 5b f =,则()A .0a b +=B .0a b -=C .5a b +=D .5a b -=【例4】(2022·江西省铜鼓中学高二开学考试)将函数()sin 22f x x x =+的图象向左平移()0ϕϕ>个单位长度得到一个偶函数,则ϕ的最小值为()A .12πB .6πC .3πD .56π【例5】(2022·四川成都·模拟预测(理))函数2()ln(2)sin(1)211f x x x x x x -=+--+++在[0,2]上的最大值与最小值的和为()A .-2B .2C .4D .6【例6】(2022·贵州贵阳·高三开学考试(理))已知函数()2cos(2)02f x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象向右平移3π个单位长度后,得到函数()g x 的图象,若()g x 的图象关于原点对称,则ϕ=()A .3πB .4πC .6πD .12π【例7】(2022·陕西·定边县第四中学高三阶段练习(理))已知函数()sin cos f x a x b x =-在4x π=处取到最大值,则4f x π⎛⎫+ ⎪⎝⎭()A .奇函数B .偶函数C .关于点(),0π中心对称D .关于2x π=轴对称【例8】(2023·全国·高三专题练习)写出一个最小正周期为3的偶函数()f x =___________.【题型专练】1.(2022·全国·高一课时练习)下列函数中,既为偶函数又在,02π⎛⎫- ⎪⎝⎭上单调递增的是()A .cos y x =B .cos y x=C .sin 2y x π⎛⎫=- ⎪D .tan cos y x x=-2.(2022·陕西·武功县普集高级中学高三阶段练习(文))已知函数()e e sin x xf x x a -=-++,若()1ln 1,ln 3f m f m ⎛⎫== ⎪⎝⎭,则=a ()A .1B .2C .1-D .2-3.(2022·湖南·周南中学高二期末)函数为()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭偶函数的一个充分条件是()A .6π=ϕB .3πϕ=C .2ϕπ=D .()3k k πϕπ=+∈Z故选:A4.(2022·贵州黔东南·高二期末(理))已知函数()πcos 2(0)3f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期为π,将其图象向右平移(0)ϕϕ>个单位长度,得到函数()g x 的图象,若函数()g x 为偶函数,则ϕ的最小值为()A .6πB .π4C .π3D .π25.(2023·全国·高三专题练习)已知函数2()(2)sin(1)1f x x x x x =--+-在[1,1)-(1,3]⋃上的最大值为M ,最小值为N ,则M N +=()A .1B .2C .3D .4可得()h t 的最大值与最小值之和为0,那么()g t 的最大值与最小值之和为2.故选:B .6.(2022辽宁丹东·高一期末)写出一个最小正周期为1的偶函数()f x =______.【答案】cos2πx【解析】因为函数cos y x ω=的周期为2π||ω,所以函数cos 2πy x =的周期为1.故答案为:cos2πx .(答案不唯一)7.(2022·全国·高三专题练习)已知()2sin()cos f x x x α=++是奇函数,则sin α的值为______.8.(2022·河南·高二开学考试)将函数()()cos 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像向左平移4π个单位长度后得到偶函数()g x 的图像,则ω的最小值是______.【答案】1039.(2022·全国·高一单元测试)写出一个同时具有性质①()02f =;②()()πf x f x +=的函数()f x =______(注:()f x 不是常数函数).题型四:三角函数的单调性【例1】(湖南省永州市2023届高三上学期第一次高考适应性考试数学试题)将函数2()cos cos 1f x x x x =+-的图象向右平移6π个单位长度,然后将所得函数图象上所有点的横坐标变为原来的12(纵坐标不变),得到函数()y g x =的图象,则()g x 的单调递增区间是()A .ππππ,(Z)12262k k k ⎡⎤-++∈⎢⎥⎣⎦B .ππ5ππ,(Z)242242k k k ⎡⎤-++∈⎢⎥⎣⎦C .π2π2π,2π(Z)33k k k ⎡⎤-++∈⎢⎥D .π5π2π,2π(Z)66k k k ⎡⎤-++∈⎢⎥故选:A【例2】(2022·陕西师大附中高一期中)sin1,sin 2,sin 3按从小到大排列的顺序为()A .sin3sin2sin1<<B .sin3sin1sin2<<C .sin1sin2sin3<<D .sin2sin1sin3<<【例3】(2022·全国·高一单元测试)下列四个函数中,以π为周期且在π0,2⎛⎫ ⎪⎝⎭上单调递增的偶函数有()A .cos 2y x =B .sin 2y x =C .tan y x =D .lg sin y x=也是以【例4】(2023·全国·高三专题练习)已知函数()()cos 02f x x πωϕωϕ⎛⎫=+≤ ⎪⎝⎭>,,4x π=-为f (x )的零点,4x π=为y =f (x )图象的对称轴,且f (x )在186ππ⎛⎫⎪⎝⎭,上单调,则ω的最大值为()A .3B .4C .5D .6当ππ,π2u k k ⎡⎤=+⎢⎥⎣⎦,k Z ∈时,函数sin y u =递增.即πππ,π42x k k ⎡⎤+∈+⎢⎥⎣⎦,解得:πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈,所以函数sin()4πy x =+的单调递增区间是πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈.故答案为:πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈.【例6】(2023·全国·高三专题练习)函数πsin(2)3y x =-+的单调递减区间是()A .π5π[π,π],Z 1212k k k -+∈B .π5π[2π,2π],Z 1212k k k -+∈C .π5π[π,πZ66k k k -+∈D .π5π[2π,2πZ66k k k -+∈【题型专练】1.(2022·辽宁·新民市第一高级中学高一阶段练习)已知函数2sin()y x ωθ=+为偶函数(0)θπ<<,其图像与直线2y =的两个交点的横坐标分别为12x x 、,若21||x x -的最小值为π,则该函数的一个单调递增区间为()A .ππ,24⎛⎫-- ⎪B .ππ,44⎛⎫- ⎪C .π0,2⎛⎫ ⎪⎝⎭D .π3π,44⎛⎫⎪⎝⎭2.(2022·四川省成都市新都一中高二开学考试(理))已知函数()sin(),022f x x ππωϕϕω⎛⎫=+-<<> ⎪⎝⎭,若()00166f x f x ππ⎛⎫⎛⎫==≠ ⎪ ⎪⎝⎭⎝⎭,0min6x ππ-=,则函数()f x 的单调递减区间为()A .2,()63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z B .22,2()63Z k k k ππππ⎛⎫++∈ ⎪⎝⎭C .,()36Z k k k ππππ⎛⎫-++∈ ⎪D .2,2()36Z k k k ππππ⎛⎫-++∈ ⎪3.(2022六盘山高级中学)函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为()A .5,()212212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B .5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭C .5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D .5,()1212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭【答案】B【解析】因为函数tan y x =的单调递增区间为,()22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,所以2()223,k k k x Z πππππ-<-<+∈,解得5,()212212k k x k Z ππππ-<<+∈,所以函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭.故选:B 4.(2023·全国·高三专题练习)已知函数()()sin 2f x x ϕ=+,其中()0,2πϕ∈,若()6f x f π⎛⎫≤ ⎪⎝⎭对于一切R x ∈恒成立,则()f x 的单调递增区间是()A .,2k k πππ⎡⎤+⎢⎥⎣⎦()k ∈Z B .,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z C .2,63k k ππππ⎡⎤++⎢⎥()k ∈Z D .,2k k πππ⎡⎤-⎢⎥()k ∈Z 5.(2022·全国·高二单元测试)已知函数()cos f x x x =,()()g x f x '=,则().A .()g x 的图像关于点π,06⎛⎫⎪⎝⎭对称B .()g x 图像的一条对称轴是π6x =C .()g x 在5π5π,66⎛⎫- ⎪上递减D .()g x 在ππ,33⎛⎫- ⎪的值域为(0,1)6.(2022天津市静海区大邱庄中学高三月考)设函数()cos 26f x x π⎛⎫=- ⎪⎝⎭,给出下列结论:①()f x 的一个周期为π②()y f x =的图象关于直线12x π=对称③()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称④()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减其中所有正确结论的编号是()A .①④B .②③C .①②③D .②③④【答案】C【解析】对于①,2T ππω==,故①正确;对于②,12x π=时,(112f π=,函数取得最大值,故②正确;对于③,6x π=-时,()06f π-=,故③正确;对于④,2,63x ππ⎡⎤∈⎢⎥⎣⎦ ,当712x π=时,7112f π⎛⎫=- ⎪⎝⎭,函数取得最小值,()f x ∴在2,63ππ⎡⎤⎢⎥⎣⎦有增有减,故④不正确.故选:C .7.(2022·全国·高一课时练习)关于函数1()sin sin f x x x=+,下列说法正确的是()A .()f x 的一个周期是πB .()f x 的最小值为2C .()f x 在π(0,2上单调递增D .()f x 的图象关于直线π2x =对称上单调递减,而8.(2022·内蒙古包头·高三开学考试(文))若()sin cos f x x x =+在[]0,a 是增函数,则a 的最大值是()A .4πB .2πC .34πD .π9.(2022·全国·高一专题练习)若函数()sin 23f x x ⎛⎫=- ⎪⎝⎭与()cos 4g x x ⎛⎫=+ ⎪⎝⎭都在区间()(),0πa b a b <<<上单调递减,则b a -的最大值为()A .π3B .π2C .6πD .π10.(2022·全国·高三专题练习)将函数()2sin()(0)3f x x ωω=->的图象向左平移3ωπ个单位得到函数()y g x =的图象,若()y g x =在[,64ππ-上为增函数,则ω最大值为()A .32B .2C .3D .11.(2022·全国·高一课时练习多选题)已知直线8x =是函数()sin(2)(0π)f x x ϕϕ=+<<图象的一条对称轴,则()A .π8f x ⎛⎫+ ⎪⎝⎭是偶函数B .3π8x =是()f x 图象的一条对称轴C .()f x 在ππ,82⎡⎤⎢⎥⎣⎦上单调递减D .当π2x =时,函数()f x 取得最小值题型五:三角函数的值域【例1】(2022·陕西·安康市教学研究室高三阶段练习(文))下列函数中,最大值是1的函数是()A .|sin ||cos |=+y x xB .2cos 4sin 4y x x =+-C .cos tan y x x =⋅D .y =【例2】(2022·全国·高三专题练习)函数1ππ()sin()cos()363f x x x =++-的最大值是()A .43B .23C .1D .13【答案】8【解析】【分析】由题意可得()22sin sin 1f x x x =-++,令[]sin 0,1x t ∈=,可得[]221,0,1y t t t =-++∈,利用二次函数的性质可求f (x )的最大值.【详解】解:()22cos 2sin 2sin sin 12sin sin 1f x x x x x x x =+=-++=-++,令[]sin 0,1x t ∈=,可得[]2219212,0,148y t t t t ⎛⎫=-++=--+∈ ⎪⎝⎭,当14t =时,y 取得最大值为98,故答案为:98.【例4】(2022·江西·高三开学考试(文))已知函数()()2πsin sin 022f x x x x ωωωω⎛⎫+--> ⎪⎝⎭的最小正周期为π,则()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域为()A .11,22⎡⎤-⎢⎥⎣⎦B .22⎡-⎢⎥⎣⎦C .⎡⎤⎢⎥⎣⎦D .⎡-⎢⎣⎦【例5】(2022·湖北·襄阳五中模拟预测)已知函数()sin()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在区间,33ππ⎛⎫⎪⎝⎭上单调,且对任意实数x 均有4()33f f x f ππ⎛⎫⎛⎫≤≤⎪ ⎪⎝⎭⎝⎭成立,则ϕ=()A .12πB .6πC .4πD .3π【例6】(2023·全国·高三专题练习)已知函数()22sin s ()3in f x x x π+=+,则()f x 的最小值为()A .12B .14C .D .2【例7】(2022·全国·高三专题练习)函数2()cos 2f x x x =+-0,2x π⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是__________.【答案】14-##-0.25【解析】【详解】22()1sin 2sin 1f x x x x x =--=--=21sin24x ⎛⎫-- ⎪ ⎪⎝⎭,所以当sin x =时,有最大值14-.故答案为14-.【例8】(2022·全国·高三专题练习)已知函数()sin cos 2sin cos 2f x x x x x =+++,则()A .()f x 的最大值为3,最小值为1B .()f x 的最大值为3,最小值为-1C .()f x的最大值为3,最小值为34D .()f x的最大值为33【例9】(2022·全国·高一课时练习)已知关于x 的方程2cos sin 20x x a -+=在02π⎛⎤⎥⎝⎦,内有解,那么实数a 的取值范围()A .58a -≤B .102a -≤≤C .1122a -<≤D .12a -<≤0【题型专练】1.(2022·江西九江·高一期末)函数()193sin cos 2R 24y x x x =+-∈的最小值是()A .14B .12C .234-D .414-2.(2022·河南焦作·高一期末)函数2cos22cos y x x =+的最小值为()A .3-B .2-C .1-D .0【答案】C【分析】利用二倍角的降幂公式化简函数解析式,利用余弦型函数的有界性可求得结果.【详解】2cos 22cos cos 2cos 212cos 21y x x x x x =+=++=+ ,min 211y ∴=-+=-.故选:C.3.【2018·北京卷】设函数f (x )=πcos(0)6x ωω->,若π()()4f x f ≤对任意的实数x 都成立,则ω的最小值为__________.【答案】23【解析】因为()π4f x f ⎛⎫≤ ⎪⎝⎭对任意的实数x 都成立,所以π4f ⎛⎫⎪⎝⎭取最大值,所以()()ππ22π 8463k k k k -=∈∴=+∈Z Z ,ωω,因为0>ω,所以当0k =时,ω取最小值为23.4.(2022·广西南宁·高二开学考试)已知函数ππ()sin ,0,36f x x x ⎛⎫⎡⎤=+∈ ⎪⎢,则函数()f x 的最大值为__________.5.(2022·全国·高一课时练习)函数()1sin cos =++f x x x的值域为_____________.6.(2022·全国·高一专题练习)若奇函数()f x 在其定义域R 上是单调减函数,且对任意的R x ∈,不等式2(cos 3sin )(sin )0f x x f x a -+-≤恒成立,则a 取值范围是_________.【答案】(,2]-∞-【分析】根据给定条件,脱去法则“f ”,再利用含sin x 的二次函数求解作答.【详解】因奇函数()f x 在R 上单调递减,则R x ∀∈,2(cos 3sin )(sin )0f x x f x a -+-≤2(cos 3sin )(sin )f x x f a x ⇔-≤-22cos 3sin sin cos 2sin x x a x a x x ⇔-≥-⇔≤-,令222cos 2sin sin 2sin 1(sin 1)2y x x x x x =-=--+=-++,而1sin 1x -≤≤,因此当sin 1x =时,min 2y =-,即有2a ≤-,所以a 取值范围是(,2]-∞-.故答案为:(,2]-∞-【点睛】思路点睛:涉及求含正(余)的二次式的最值问题,可以换元或整体思想转化为二次函数在区间[-1,1]或其子区间上的最值求解.7.【2018·全国Ⅲ】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π,的零点个数为________.【答案】3【解析】0πx ≤≤ ,ππ19π3666x ∴≤+≤,由题可知πππ3π336262x x +=+=,或π5π362x +=,解得π4π,99x =,或7π9,故有3个零点.8.(2022·上海市第十中学高一期末)已知函数()2cos 2cos 1f x x x x =+-(R x ∈).求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥上的最大值和最小值.9.(2022·湖南·雅礼中学高一期末)已知函数()2cos sin 4f x x a x a =-++-,[]0,x π∈.(1)求()f x 的最小值()g a ;(2)若()f x 在[]0,π上有零点,求a 的取值范围,并求所有零点之和.题型六:三角函数的图像【例1】(2022·陕西师大附中高三开学考试(理))函数()sin()(0,0,0)f x A x A ωϕωπϕ=+>>-<<的部分图象如图所示,为了得到()sin g x A x ω=的图象,只需将函数()y f x =的图象()A .向左平移6π个单位长度B .向左平移12π个单位长度C .向右平移6π个单位长度D .向右平移12π个单位长度【例2】(2022·陕西·延安市第一中学高一期中)函数()()sin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,则()2f π的值为()A .B .C .D .1-的部分图象知,【例3】(2022·湖南·宁乡市教育研究中心模拟预测)如图表示电流强度I 与时间t 的关系()()()sin 0,0I A x A ωϕω=+>>在一个周期内的图像,则下列说法正确得是()A .50πω=B .π6ϕ=C .0=t 时,I =D .1300100t I ==时,【例4】(2022·江苏·沭阳如东中学高三阶段练习多选题)已知函数()()sin f x A x ωϕ=+(其中0A >,0>ω,2πϕ<)的部分图象如图所示,则()A .2ω=B .()f x 的图象关于直线23x π=对称C .()2cos 26f x x π⎛⎫=- ⎪⎝⎭D .()f x 在5[,63ππ--上的值域为[2,1]-【例5】(2022·河北·沧县风化店中学高二开学考试多选题)函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,且满足223f π⎛⎫=- ⎪⎝⎭,现将()f x 图象沿x 轴向左平移4π个单位,得到函数()y g x =的图象.下列说法正确的是()A .()g x 在,126ππ⎡⎤-⎢⎥⎣⎦上是增函数B .()g x 的图象关于56x π=对称C .()g x 是奇函数D .()g x 的最小正周期为23π【例6】(2022·福建·高三阶段练习多选题)函数()sin()(0,0,02π)f x A x A ωϕωϕ=+>><<的部分图像如图所示,则()A .3π2ωϕ+=B .(2)2f -=-C .()f x 在区间()0,2022上存在506个零点D .将()f x 的图像向右平移3个单位长度后,得到函数π()cos 4g x x ⎛⎫=- ⎪的图像【例7】(2022·江苏南通·高三开学考试多选题)已知函数()()sin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示,则下列结论正确的是()A .()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B .()f x 的图象向右平移π12个单位后得到sin2y x =的图象C .()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递増D .π6f x ⎛⎫+ ⎪为偶函数【例8】(2022·全国·高一单元测试多选题)已知函数()()sin f x A x =+ωϕ(0A >,0>ω,2πϕ<)的部分图象如图所示,下列说法错误的是()A .()f x 的图象关于直线23x π=-对称B .()f x 的图象关于点5,012π⎛⎫-⎪⎝⎭对称C .将函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象向左平移2π个单位长度得到函数()f x 的图象D .若方程()f x m =在,02π⎡⎤-⎢⎥上有两个不相等的实数根,则m 的取值范围是(2,-【题型专练】1.(2022·广东·仲元中学高三阶段练习多选题)已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()f x 的图象向右平移316π个单位长度,再将图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数()y g x =的图象,则()A .()2sin 24x f x π⎛⎫=+ ⎪⎝⎭B .()g x 的图象关于直线8x π=-对称C .()g x 的图象关于点,08π⎛⎫⎪⎝⎭对称D .函数()()f x g x +的最小值为4-2.(2022·湖北·襄阳市襄州区第一高级中学高二阶段练习多选题)函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图像如图所示,则下列结论正确的是()A .()12sin 33f x x π⎛⎫=- ⎪⎝⎭B .若把()f x 图像上的所有点的横坐标变为原来的23倍,纵坐标不变,得到函数()g x 的图像,则函数()g x 在[],ππ-上是增函数C .若把函数()f x 的图像向左平移2π个单位长度,得到函数()h x 的图像,则函数()h x 是奇函数D .,33x ππ⎡⎤∀∈-⎢⎥,若()332f x a f π⎛⎫+≥ ⎪恒成立,则a 的取值范围为)2,+∞3.(2022·安徽·高三开学考试)已知函数π()2sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,其中ππ,2,,0123A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则下列说法错误的是()A .()f x 的最小正周期为πB .将()f x 的图象向右平移6π个单位长度后关于原点对称C .()f x 在2ππ,3⎡⎤--⎢⎣⎦上单调递减D .直线7π12x =为()f x 图象的一条对称轴4.(2022·天津·南开中学高三阶段练习)已知函数π()sin()(R,0,0,)2f x A x x A ωϕωϕ=+∈>><的部分图象如图所示,则下列说法正确的是()A .直线πx =是()f x 图象的一条对称轴B .()f x 图象的对称中心为π(π,0)12k -+,Z k ∈C .()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增D .将()f x 的图象向左平移π12个单位长度后,可得到一个奇函数的图象5.(2022·江苏省如皋中学高三开学考试多选题)函数()()sin 0,0,0πy A x A ωϕωϕ=+>><<在一个周期内的图象如图所示,则().A .该函数的解析式为2π2sin 33y x ⎛⎫=+ ⎪⎝⎭B .该函数图象的对称中心为ππ,03k ⎛⎫- ⎪⎝⎭,Zk ∈C .该函数的单调递增区间是5ππ3π,3π44k k ⎛⎫-+ ⎪⎝⎭,Zk ∈D .把函数π2sin 3y x ⎛⎫=+ ⎪的图象上所有点的横坐标伸长为原来的32倍,纵坐标不变,可得到该函数图象6.(2021·福建·福州十八中高三开学考试多选题)已知函数()sin()(010f x x ωϕω=+<<,0π)ϕ<<的部分图象。
高中三角函数习题解析含详细解答

三角函数题解1.2003上海春;15把曲线y cos x +2y -1=0先沿x 轴向右平移2π个单位;再沿y 轴向下平移1个单位;得到的曲线方程是A.1-y sin x +2y -3=0B.y -1sin x +2y -3=0C.y +1sin x +2y +1=0D.-y +1sin x +2y +1=02.2002春北京、安徽;5若角α满足条件sin2α<0;cos α-sin α<0;则α在 A.第一象限 B.第二象限 C.第三象限 D.第四象限3.2002上海春;14在△ABC 中;若2cos B sin A =sinC;则△ABC 的形状一定是 A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形4.2002京皖春文;9函数y =2sin x 的单调增区间是 A.2k π-2π;2k π+2πk ∈ZB.2k π+2π;2k π+23πk ∈Z C.2k π-π;2k πk ∈Z D.2k π;2k π+πk ∈Z5.2002全国文5;理4在0;2π内;使sin x >cos x 成立的x 取值范围为 A.4π;2π∪π;45πB.4π;π C.4π;45πD.4π;π∪45π;23π6.2002北京;11已知fx 是定义在0;3上的函数;fx 的图象如图4—1所示;那么不等式fx cos x <0的解集是A.0;1∪2;3B.1;2π∪2π;3图4—1C.0;1∪2π;3D.0;1∪1;37.2002北京理;3下列四个函数中;以π为最小正周期;且在区间2π;π上为减函数的是 A.y =cos 2xB.y =2|sin x |C.y =31cos xD.y =-cot x8.2002上海;15函数y =x +sin|x |;x ∈-π;π的大致图象是9.2001春季北京、安徽;8若A 、B 是锐角△ABC 的两个内角;则点P cos B -sin A ;sin B -cos A 在A.第一象限B.第二象限C.第三象限D.第四象限10.2001全国文;1tan300°+cot405°的值是 A.1+3B.1-3C.-1-3D.-1+311.2000全国;4已知sin α>sin β;那么下列命题成立的是 A.若α、β是第一象限角;则cos α>cos β B.若α、β是第二象限角;则tan α>tan β C.若α、β是第三象限角;则cos α>cos β D.若α、β是第四象限角;则tan α>tan β12.2000全国;5函数y =-x cos x 的部分图象是13.1999全国;4函数fx =M sin ωx +ϕω>0;在区间a ;b 上是增函数;且fa =-M ;fb =M ;则函数gx =M cos ωx +ϕ在a ;b 上A.是增函数B.是减函数C.可以取得最大值-D.可以取得最小值-m14.1999全国;11若sin α>tan α>cot α-2π<α<2π);则α∈A.-2π;-4π B.-4π;0C.0;4πD.4π;2π15.1999全国文、理;5若fx sin x 是周期为π的奇函数;则fx 可以是 A.sin x B.cos x C.sin2x D.cos2x16.1998全国;6已知点P sin α-cos α;tan α在第一象限;则在0;2π内α的取值范围是 A.2π;43π∪π;45πB.4π;2π∪π;45π C.2π;43π∪45π;23πD.4π;2π∪43π;π 17.1997全国;3函数y =tan 3121-x π在一个周期内的图象是18.1996全国若sin 2x >cos 2x ;则x 的取值范围是 A.{x |2k π-43π<x <2k π+4π;k ∈Z } B.{x |2k π+4π<x <2k π+45π;k ∈Z }C.{x |k π-4π<x <k π+4π;k ∈Z }D.{x |k π+4π<x <k π+43π;k ∈Z }19.1995全国文;7使sin x ≤cos x 成立的x 的一个变化区间是A.-43π;4πB.-2π;2πC.-4π;43πD.0;π20.1995全国;3函数y =4sin3x +4π+3cos3x +4π的最小正周期是A.6πB.2πC.32πD.3π21.1995全国;9已知θ是第三象限角;若sin 4θ+cos 4θ=95;那么sin2θ等于 A.322 B.-322 C.32D.-32 22.1994全国文;14如果函数y =sin2x +a cos2x 的图象关于直线x =-8π对称;那么a 等于A.2B.-2C.1D.-123.1994全国;4设θ是第二象限角;则必有 A.tan2θ>cot 2θ B.tan2θ<cot 2θC.sin2θ>cos 2θ D.sin2θ-cos 2θ 24.2002上海春;9若fx =2sin ωx 0<ω<1)在区间0;3π上的最大值是2;则ω= .25.2002北京文;13sin 52π;cos 56π;tan 57π从小到大的顺序是 .26.1997全国;18︒︒-︒︒︒+︒8sin 15sin 7cos 8sin 15cos 7sin 的值为_____.27.1996全国;18tan20°+tan40°+3tan20°·tan40°的值是_____.28.1995全国理;18函数y =sin x -6πcos x 的最小值是 .29.1995上海;17函数y =sin 2x +cos 2x在-2π;2π内的递增区间是 .30.1994全国;18已知sin θ+cos θ=51;θ∈0;π;则cot θ的值是 .31.2000全国理;17已知函数y =21cos 2x +23sin x cos x +1;x ∈R .1当函数y 取得最大值时;求自变量x 的集合;2该函数的图象可由y =sin xx ∈R 的图象经过怎样的平移和伸缩变换得到32.2000全国文;17已知函数y =3sin x +cos x ;x ∈R .1当函数y 取得最大值时;求自变量x 的集合;2该函数的图象可由y =sin xx ∈R 的图象经过怎样的平移和伸缩变换得到33.1995全国理;22求sin 220°+cos 250°+sin20°cos50°的值. 34.1994上海;21已知sin α=53;α∈2π;π;tan π-β=21; 求tan α-2β的值.35.1994全国理;22已知函数fx =tan x ;x ∈0;2π;若x 1、x 2∈0;2π;且x 1≠x 2;证明21fx 1+fx 2>f 221x x +.36.已知函数12()log (sin cos )f x x x =-⑴求它的定义域和值域; ⑵求它的单调区间; ⑶判断它的奇偶性; ⑷判断它的周期性.37. 求函数f x =121log cos()34x π+的单调递增区间38. 已知fx =5sin x cos x -35cos 2x +325x ∈R ⑴求fx 的最小正周期; ⑵求fx 单调区间;⑶求fx 图象的对称轴;对称中心..39若关于x 的方程2cos 2π + x - sin x + a = 0 有实根;求实数a 的取值范围..参考答案1.答案:C解析:将原方程整理为:y =x cos 21+;因为要将原曲线向右、向下分别移动2π个单位和1个单位;因此可得y =)2cos(21π-+x -1为所求方程.整理得y +1sin x +2y +1=0.评述:本题考查了曲线平移的基本方法及三角函数中的诱导公式.如果对平移有深刻理解;可直接化为:y +1cos x -2π+2y +1-1=0;即得C 选项.2.答案:B解析:sin2α=2sin αcos α<0 ∴sin αcos α<0 即sin α与cos α异号;∴α在二、四象限; 又cos α-sin α<0 ∴cos α<sin α由图4—5;满足题意的角α应在第二象限3.答案:C解析:2sin A cos B =sin A +B +sin A -B 又∵2sin A cos B =sin C ; ∴sin A -B =0;∴A =B 4.答案:A解析:函数y =2x 为增函数;因此求函数y =2sin x 的单调增区间即求函数y =sin x 的单调增区间.5.答案:C解法一:作出在0;2π区间上正弦和余弦函数的图象;解出两交点的横坐标4π和45π;由图4—6可得C 答案.图4—6 图4—7解法二:在单位圆上作出一、三象限的对角线;由正弦线、余弦线知应选C.如图4—7 6.答案:C图4—5解析:解不等式fx cos x <0⎪⎩⎪⎨⎧<<><⎪⎩⎪⎨⎧<<<>⇒300cos 0)(300cos 0)(x x x f x x x f 或∴⎩⎨⎧<<<<⎪⎩⎪⎨⎧<<<<1010231x x x x 或ππ ∴0<x <1或2π<x <3 7.答案:B解析:A 项:y =cos 2x =22cos 1x+;x =π;但在区间2π;π上为增函数.B 项:作其图象4—8;由图象可得T =π且在区间2π;π上为减函数.C 项:函数y =cos x 在2π;π区间上为减函数;数y =31x 为减函数.因此y =31cos x 在2π;π区间上为增函数.D 项:函数y =-cot x 在区间2π;π上为增函数. 8.答案:C解析:由奇偶性定义可知函数y =x +sin|x |;x ∈-π;π为非奇非偶函数. 选项A 、D 为奇函数;B 为偶函数;C 为非奇非偶函数. 9.答案:B解析:∵A 、B 是锐角三角形的两个内角;∴A +B >90°; ∴B >90°-A ;∴cos B <sin A ;sin B >cos A ;故选B. 10.答案:B 解析:tan300°+cot405°=tan360°-60°+cot360°+45°=-tan60°+cot45°=1-3.11.答案:D解析:因为在第一、三象限内正弦函数与余弦函数的增减性相反;所以可排除A 、C;在第二象限内正弦函数与正切函数的增减性也相反;所以排除B.只有在第四象限内;正弦函数与正切函数的增减性相同.12.答案:D解析:因为函数y =-x cos x 是奇函数;它的图象关于原点对称;所以排除A 、C;当 x ∈0;2π时;y =-x cos x <0.13.答案:C图4—8解法一:由已知得M >0;-2π+2k π≤ωx +ϕ≤2π+2k πk ∈Z ;故有gx 在a ;b 上不是增函数;也不是减函数;且当ωx +ϕ=2k π时gx 可取到最大值M ;答案为C.解法二:由题意知;可令ω=1;ϕ=0;区间a ;b 为-2π;2π;M =1;则gx 为cos x ;由基本余弦函数的性质得答案为C.评述:本题主要考查函数y =A sin ωx +ϕ的性质;兼考分析思维能力.要求对基本函数的性质能熟练运用正用逆用;解法二取特殊值可降低难度;简化命题. 14.答案:B解法一:取α=±3π;±6π代入求出sin α、tan α、cot α之值;易知α=-6π适合;又只有-6π∈-4π;0;故答案为B.解法二:先由sin α>tan α得:α∈-2π;0;再由tan α>cot α得:α∈-4π;0评述:本题主要考查基本的三角函数的性质及相互关系;1995年、1997年曾出现此类题型;运用特殊值法求解较好.15.答案:B解析:取fx =cos x ;则fx ·sin x =21sin2x 为奇函数;且T =π. 评述:本题主要考查三角函数的奇偶与倍角公式. 16.答案:B解法一:P sin α-cos α;tan α在第一象限;有tan α>0; A 、C 、D 中都存在使tan α<0的α;故答案为B.解法二:取α=3π∈2,4ππ;验证知P 在第一象限;排除A 、C;取α=65π∈43π;π;则P 点不在第一象限;排除D;选B.解法三:画出单位圆如图4—10使sin α-cos α>0是图中阴影部分;又tan α>0可得24παπ<<或π<α<45π;故选B. 评述:本题主要考查三角函数基础知识的灵活运用;突出考查了转化思想和转化方法的选择;采用排除法不失为一个好办法.17.答案:A解析:y =tan 3121-x π=tan 21x -32π;显然函数周期为T =2π;且x =32π时;y =0;故选A.评述:本题主要考查正切函数性质及图象变换;抓住周期和特值点是快速解题的关键.18.答案:D解析一:由已知可得cos2x =cos 2x -sin 2x <0;所以2k π+2π<2x <2k π+23π;k ∈Z .解得k π+4π<x <k π+43π;k ∈Z 注:此题也可用降幂公式转化为cos2x <0. 解析二:由sin 2x >cos 2x 得sin 2x >1-sin 2x ;sin 2x >21.因此有sin x >22或sin x <-22.由正弦函数的图象或单位圆得2k π+4π<x <2k π+43π或2k π+45π<x <2k π+47πk ∈Z ;2k π+45π<x <2k π+47π可写作2k +1π+4π<x <2k +1π+43π;2k 为偶数;2k +1为奇数;不等式的解可以写作n π+4π<x <n π+43π;n ∈Z . 评述:本题考查三角函数的图象和基本性质;应注意三角公式的逆向使用. 19.答案:A 解法一:由已知得:2 sin x -4π≤0;所以2k π+π≤x -4π≤2k π+2π;2k π+45π≤x ≤2k π+49π;令k =-1得-43π≤x ≤4π;选A. 解法二:取x =32π;有sin 2132cos ,2332-==ππ;排除C 、D;取x =3π;有sin3π=213cos ,23=π;排除B;故选A. 解法三:设y =sin x ;y =cos x .在同一坐标系中作出两函数图象如图4—11;观察知答案为A.解法四:画出单位圆;如图4—12;若sin x ≤cos x ;显然应是图中阴影部分;故应选A.评述:本题主要考查正弦函数、余弦函数的性质和图象;属基本求范围题;入手容易;方法较灵活;排除、数形结合皆可运用.20.答案:C图4—12图4—11解析:y =4sin3x +4π+3cos3x +4π=554sin3x +4π+53cos3x +4π=5sin3x +4π+ϕ其中tan ϕ=43所以函数y =sin3x +4π+3cos3x +4π的最小正周期是T =32π. 故应选C.评述:本题考查了a sin α+b cos α=22b a +sin α+ϕ;其中sinϕ=22ba b +;cos ϕ=22ba a +;及正弦函数的周期性.21.答案:A解法一:将原式配方得sin 2θ+cos 2θ2-2sin 2θcos 2θ=95 于是1-21sin 22θ=95;sin 22θ=98;由已知;θ在第三象限; 故2k π+π<θ<2k π+23π从而4k π+2π<2θ<4k π+3π 故2θ在第一、二象限;所以sin2θ=322;故应选A. 解法二:由2k π+π<θ<2k π+23π;有4k π+2π<4k π+3πk ∈Z ;知sin2θ>0;应排除B 、D;验证A 、C;由sin2θ=322;得2sin 2θcos 2θ=94;并与sin 4θ+cos 4θ=95相加得sin 2θ+cos 2θ2=1成立;故选A.评述:本题考查了学生应用正余弦的平方关系配方的能力及正弦函数值在各象限的符号的判别.22.答案:D解析:函数y =sin2x +a cos2x 的图象关于直线x =-8π对称;表明:当x =-8π时;函数取得最大值12+a ;或取得最小值-12+a ;所以有sin -4π+a ·cos -4π2=a 2+1;解得a =-1.评述:本题主要考查函数y =a sin x +b cos x 的图象的对称性及其最值公式.23.答案:A解法一:因为θ为第二象限角;则2k π+2π<θ<2k π+πk ∈Z ;即2θ为第一象限角或第三象限角;从单位圆看是靠近轴的部分如图4—13;所以tan2θ>cot 2θ. 解法二:由已知得:2k π+2π<θ<2k π+π;k π+4π<2θ< k π+2π;k 为奇数时;2n π+45π<2θ<2n π+23πn ∈Z ; k为偶数时;2n π+4π<2θ<2n π+2πn ∈Z ;都有tan 2θ>cot 2θ;选A.评述:本题主要考查象限角的概念和三角函数概念;高于课本.24.答案:43 解析:∵0<ω<1 ∴T =ωπ2>2π ∴fx 在0;3π区间上为单调递增函数∴fx max =f3π即2sin23=ωπ又∵0<ω<1 ∴解得ω=4325.答案:cos56π<sin 52π<tan 57π 解析:cos56π<0;tan 57π=tan 52π ∵0<x <2π时;tan x >x >sin x >0 ∴tan 52π>sin 52π>0 ∴tan 57π>sin 52π>cos 56π26.答案:2-3解析:︒︒︒︒=︒︒-︒-︒︒︒+︒-︒=︒︒-︒︒︒+︒8cos 15cos 8cos 15sin 8sin 15sin )815cos(8sin 15cos )815sin(8sin 15sin 7cos 8sin 15cos 7sin图4—133230sin 30cos 115tan -=︒︒-=︒=.评述:本题重点考查两角差的三角公式、积化和差公式、半角公式等多个知识点.27.答案:3解析:tan60°=︒︒-︒+︒40tan 20tan 140tan 20tan ;∴tan20°+tan40°=3-3tan20°tan40°;∴tan20°+tan40°+3tan20°tan40°=3.28.答案:-43 解析:y =sin x -6πcos x =21sin2x -6π-sin 6π=21sin2x -6π-21当sin2x -6π=-1时;函数有最小值;y 最小=21-1-21=-43. 评述:本题考查了积化和差公式和正弦函数有界性或值域.29.答案:2,23ππ-解析:y =sin2x +cos 2x =2sin 42π+x ;当2k π-2π≤2x +4π≤2k π+2πk ∈Z 时;函数递增;此时4k π-23π≤x ≤4k π+2πk ∈Z ;只有k =0时;-23π;2π-2π;2π. 30.答案:-43 解法一:设法求出sin θ和cos θ;cot θ便可求了;为此先求出sin θ-cos θ的值. 将已知等式两边平方得1+2sin θcos θ=251 变形得1-2sin θcos θ=2-251;即sin θ-cos θ2=2549 又sin θ+cos θ=51;θ∈0;π 则2π<θ<43π;如图4—14 所以sin θ-cos θ=57;于是 sin θ=54;cos θ=-53;cot θ=-43. 解法二:将已知等式平方变形得sin θ·cos θ=-2512;又θ∈0;π;有cos θ<0<sin θ;且cos θ、sin θ是二次方程x 2-51x -2512=0的两个根;故有cos θ=-53; sin θ=54;得cot θ=-43. 评述:本题通过考查三角函数的求值考查思维能力和运算能力;方法较灵活. 31.解:1y =21cos 2x +23sin x cos x +1=412cos 2x -1+41+432sin x cos x +1 =41cos2x +43sin2x +45=21cos2x ·sin 6π+sin2x ·cos 6π+45=21sin2x +6π+45y 取得最大值必须且只需2x +6π=2π+2k π;k ∈Z ;图4—14即x =6π+k π;k ∈Z .所以当函数y 取得最大值时;自变量x 的集合为{x |x =6π+k π;k ∈Z }.2将函数y =sin x 依次进行如下变换: ①把函数y =sin x 的图象向左平移6π;得到函数y =sin x +6π的图象;②把得到的图象上各点横坐标缩短到原来的21倍纵坐标不变;得到函数 y =sin2x +6π的图象;③把得到的图象上各点纵坐标缩短到原来的21倍横坐标不变;得到函数 y =21sin2x +6π的图象;④把得到的图象向上平移45个单位长度;得到函数y =21sin2x +6π+45的图象;综上得到函数y =21cos 2x +23sin x cos x +1的图象.评述:本题主要考查三角函数的图象和性质;考查利用三角公式进行恒等变形的技能以及运算能力.32.解:1y =3sin x +cos x =2sin x cos6π+cos x sin6π=2sin x +6π;x ∈Ry 取得最大值必须且只需x +6π=2π+2k π;k ∈Z ;即x =3π+2k π;k ∈Z .所以;当函数y 取得最大值时;自变量x 的集合为{x |x =3π+2k π;k ∈Z }2变换的步骤是:①把函数y =sin x 的图象向左平移6π;得到函数y =sin x +6π的图象;②令所得到的图象上各点横坐标不变;把纵坐标伸长到原来的2倍;得到函数 y =2sin x +6π的图象;经过这样的变换就得到函数y =3sin x +cos x 的图象.评述:本题主要考查三角函数的图象和性质;利用三角公式进行恒等变形的技能及运算能力.33.解:原式=211-cos40°+211+cos100°+21sin70°-sin30° =1+21cos100°-cos40°+21sin70°-41=43-sin70°sin30°+21sin70° =43-21sin70°+21sin70°=43. 评述:本题考查三角恒等式和运算能力.34.解:由题设sin α=53;α∈2π;π; 可知cos α=-54;tan α=-43又因tan π-β=21;tan β=-21;所以tan2β=34tan 1tan 22-=-ββtan α-2β=2471134432tan tan 12tan tan =++-=+-βαβα 35.证明:tan x 1+tan x 2=2121212211cos cos sin cos cos sin cos sin cos sin x x x x x x x x x x +=+ 2121cos cos )sin(x x x x +=)cos()cos()sin(2212121x x x x x x -+++=因为x 1;x 2∈0;2π;x 1≠x 2;所以2sin x 1+x 2>0;cos x 1cos x 2>0;且0<cos x 1-x 2<1; 从而有0<cos x 1+x 2+cos x 1-x 2<1+cos x 1+x 2; 由此得tan x 1+tan x 2>)cos(1)sin(22121x x x x +++;所以21tan x 1+tan x 2>tan 221x x +即21fx 1+fx 2>f 221x x +.36.解1x 必须满足sin x -cos x >0;利用单位圆中的三角函数线及52244k x k ππππ+<<+;k ∈Z ∴函数定义域为)45k 2,4k 2(π+ππ+π;k ∈Z ∵sin cos )4x x x π--∴当x ∈5(2,2)44k k ππππ++时;0sin()14x π<-≤∴0sin cos x x <-∴121log 2y -≥∴ 函数值域为+∞-,213∵()f x 定义域在数轴上对应的点关于原点不对称;∴()f x 不具备奇偶性4∵ fx+2π=fx ∴ 函数fx 最小正周期为2π 注;利用单位圆中的三角函数线可知;以Ⅰ、Ⅱ象限角平分线为标准;可区分sin x -cos x 的符号;以Ⅱ、Ⅲ象限角平分线为标准;可区分sin x +cos x 的符号37.解:∵f x =121log cos()34x π+令431π+=x t ;∴y=t cos log 21;t 是x 的增函数;又∵0<21<1;∴当y=t cos log 21为单调递增时;cost 为单调递减 且cost>0;∴2k π≤t<2k π+2πk ∈Z;∴2k π≤431π+x <2k π+2π k ∈Z ;6k π-43π≤x<6k π+43π k ∈Z;∴f x =)431cos(log 21π+x 的单调递减区间是6k π-43π;6k π+43πk ∈Z38.解: 1T=π 2增区间k π-12π;k π+125π;减区间k π+]1211k ,125π+ππ 3对称中心62k π+π;0;对称轴π+π=1252k x ;k ∈Z39.解:原方程变形为:2cos 2x - sin x + a = 0 即 2 - 2sin 2x - sin x + a = 0;∴817)41(sin 22sin sin 222-+=-+=x x x a ;∵- 1≤sin x ≤1 ;∴81741sin m in -=-=a x 时,当; 11sin m ax ==a x 时,当; ∴a 的取值范围是1,817-。
三角函数高考试题精选(含详细答案解析)

三角函数高考试题精选一.选择题(共18小题)1.(2017•山东)函数y=sin2x+cos2x的最小正周期为()A.B.C.πD.2π2.(2017•天津)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f()=2,f()=0,且f(x)的最小正周期大于2π,则()A.ω=,φ=B.ω=,φ=﹣C.ω=,φ=﹣D.ω=,φ=3.(2017•新课标Ⅱ)函数f(x)=sin(2x+)的最小正周期为()A.4πB.2πC.πD.4.(2017•新课标Ⅲ)设函数f(x)=cos(x+),则下列结论错误的是()A.f(x)的一个周期为﹣2πB.y=f(x)的图象关于直线x=对称C.f(x+π)的一个零点为x=D.f(x)在(,π)单调递减5.(2017•新课标Ⅰ)已知曲线C1:y=cosx,C2:y=sin(2x+),则下面结论正确的是()A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C26.(2017•新课标Ⅲ)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.B.1 C.D.7.(2016•上海)设a∈R,b∈[0,2π),若对任意实数x都有sin(3x﹣)=sin(ax+b),则满足条件的有序实数对(a,b)的对数为()A.1 B.2 C.3 D.48.(2016•新课标Ⅲ)若tanα=,则cos2α+2sin2α=()A.B.C.1 D.9.(2016•新课标Ⅲ)若tanθ=﹣,则cos2θ=()A.﹣B.﹣C.D.10.(2016•浙江)设函数f(x)=sin2x+bsinx+c,则f(x)的最小正周期()A.与b有关,且与c有关 B.与b有关,但与c无关C.与b无关,且与c无关D.与b无关,但与c有关11.(2016•新课标Ⅱ)若将函数y=2sin2x的图象向左平移个单位长度,则平移后的图象的对称轴为()A.x=﹣(k∈Z)B.x=+(k∈Z)C.x=﹣(k∈Z)D.x=+(k∈Z)12.(2016•新课标Ⅰ)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.513.(2016•四川)为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x 的图象上所有的点()A.向左平行移动个单位长度B.向右平行移动个单位长度C.向左平行移动个单位长度D.向右平行移动个单位长度14.(2016•新课标Ⅰ)将函数y=2sin(2x+)的图象向右平移个周期后,所得图象对应的函数为()A.y=2sin(2x+)B.y=2sin(2x+)C.y=2sin(2x﹣)D.y=2sin(2x﹣)15.(2016•北京)将函数y=sin(2x﹣)图象上的点P(,t)向左平移s(s>0)个单位长度得到点P′,若P′位于函数y=sin2x的图象上,则()A.t=,s的最小值为B.t=,s的最小值为C.t=,s的最小值为D.t=,s的最小值为16.(2016•四川)为了得到函数y=sin(x+)的图象,只需把函数y=sinx 的图象上所有的点()A.向左平行移动个单位长度B.向右平行移动个单位长度C.向上平行移动个单位长度D.向下平行移动个单位长度17.(2016•新课标Ⅱ)函数y=Asin(ωx+φ)的部分图象如图所示,则()A.y=2sin(2x﹣)B.y=2sin(2x﹣) C.y=2sin(x+)D.y=2sin(x+)18.(2016•新课标Ⅱ)函数f(x)=cos2x+6cos(﹣x)的最大值为()A.4 B.5 C.6 D.7二.填空题(共9小题)19.(2017•北京)在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,若sinα=,则sinβ= .20.(2017•上海)设a1、a2∈R,且+=2,则|10π﹣α1﹣α2|的最小值为.21.(2017•新课标Ⅱ)函数f(x)=sin 2x+cosx﹣(x∈[0,])的最大值是.22.(2017•新课标Ⅱ)函数f(x)=2cosx+sinx的最大值为.23.(2016•上海)设a,b∈R,c∈[0,2π),若对于任意实数x都有2sin(3x ﹣)=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为.24.(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.25.(2016•新课标Ⅲ)函数y=sinx﹣cosx的图象可由函数y=2sinx的图象至少向右平移个单位长度得到.26.(2016•新课标Ⅲ)函数y=sinx﹣cosx的图象可由函数y=sinx+cosx 的图象至少向右平移个单位长度得到.27.(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC 的最小值是.三.解答题(共3小题)28.(2017•北京)已知函数f(x)=cos(2x﹣)﹣2sinxcosx.(I)求f(x)的最小正周期;(II)求证:当x∈[﹣,]时,f(x)≥﹣.29.(2016•山东)设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.30.(2016•北京)已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)的单调递增区间.三角函数2017高考试题精选(一)参考答案与试题解析一.选择题(共18小题)1.(2017•山东)函数y=sin2x+cos2x的最小正周期为()A.B.C.πD.2π【解答】解:∵函数y=sin2x+cos2x=2sin(2x+),∵ω=2,∴T=π,故选:C2.(2017•天津)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f()=2,f()=0,且f(x)的最小正周期大于2π,则()A.ω=,φ=B.ω=,φ=﹣C.ω=,φ=﹣D.ω=,φ=【解答】解:由f(x)的最小正周期大于2π,得,又f()=2,f()=0,得,∴T=3π,则,即.∴f(x)=2sin(ωx+φ)=2sin(x+φ),由f()=,得sin(φ+)=1.∴φ+=,k∈Z.取k=0,得φ=<π.∴,φ=.故选:A.3.(2017•新课标Ⅱ)函数f(x)=sin(2x+)的最小正周期为()A.4πB.2πC.πD.【解答】解:函数f(x)=sin(2x+)的最小正周期为:=π.故选:C.4.(2017•新课标Ⅲ)设函数f(x)=cos(x+),则下列结论错误的是()A.f(x)的一个周期为﹣2πB.y=f(x)的图象关于直线x=对称C.f(x+π)的一个零点为x=D.f(x)在(,π)单调递减【解答】解:A.函数的周期为2kπ,当k=﹣1时,周期T=﹣2π,故A正确,B.当x=时,cos(x+)=cos(+)=cos=cos3π=﹣1为最小值,此时y=f(x)的图象关于直线x=对称,故B正确,C当x=时,f(+π)=cos(+π+)=cos=0,则f(x+π)的一个零点为x=,故C正确,D.当<x<π时,<x+<,此时函数f(x)不是单调函数,故D 错误,故选:D5.(2017•新课标Ⅰ)已知曲线C1:y=cosx,C2:y=sin(2x+),则下面结论正确的是()A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2【解答】解:把C1上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=cos2x图象,再把得到的曲线向左平移个单位长度,得到函数y=cos2(x+)=cos(2x+)=sin(2x+)的图象,即曲线C2,故选:D.6.(2017•新课标Ⅲ)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.B.1 C.D.【解答】解:函数f(x)=sin(x+)+cos(x﹣)=sin(x+)+cos (﹣x+)=sin(x+)+sin(x+)=sin(x+).故选:A.7.(2016•上海)设a∈R,b∈[0,2π),若对任意实数x都有sin(3x﹣)=sin(ax+b),则满足条件的有序实数对(a,b)的对数为()A.1 B.2 C.3 D.4【解答】解:∵对于任意实数x都有sin(3x﹣)=sin(ax+b),则函数的周期相同,若a=3,此时sin(3x﹣)=sin(3x+b),此时b=﹣+2π=,若a=﹣3,则方程等价为sin(3x﹣)=sin(﹣3x+b)=﹣sin(3x﹣b)=sin (3x﹣b+π),则﹣=﹣b+π,则b=,综上满足条件的有序实数组(a,b)为(3,),(﹣3,),共有2组,故选:B.8.(2016•新课标Ⅲ)若tanα=,则cos2α+2sin2α=()A.B.C.1 D.【解答】解:∵tanα=,∴cos2α+2sin2α====.故选:A.9.(2016•新课标Ⅲ)若tanθ=﹣,则cos2θ=()A.﹣B.﹣C.D.【解答】解:由tanθ=﹣,得cos2θ=cos2θ﹣sin2θ==.故选:D.10.(2016•浙江)设函数f(x)=sin2x+bsinx+c,则f(x)的最小正周期()A.与b有关,且与c有关 B.与b有关,但与c无关C.与b无关,且与c无关D.与b无关,但与c有关【解答】解:∵设函数f(x)=sin2x+bsinx+c,∴f(x)图象的纵坐标增加了c,横坐标不变,故周期与c无关,当b=0时,f(x)=sin2x+bsinx+c=﹣cos2x++c的最小正周期为T==π,当b≠0时,f(x)=﹣cos2x+bsinx++c,∵y=cos2x的最小正周期为π,y=bsinx的最小正周期为2π,∴f(x)的最小正周期为2π,故f(x)的最小正周期与b有关,故选:B11.(2016•新课标Ⅱ)若将函数y=2sin2x的图象向左平移个单位长度,则平移后的图象的对称轴为()A.x=﹣(k∈Z)B.x=+(k∈Z)C.x=﹣(k∈Z)D.x=+(k∈Z)【解答】解:将函数y=2sin2x的图象向左平移个单位长度,得到y=2sin2(x+)=2sin(2x+),由2x+=kπ+(k∈Z)得:x=+(k∈Z),即平移后的图象的对称轴方程为x=+(k∈Z),故选:B.12.(2016•新课标Ⅰ)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.5【解答】解:∵x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,∴,即,(n∈N)即ω=2n+1,(n∈N)即ω为正奇数,∵f(x)在(,)上单调,则﹣=≤,即T=≥,解得:ω≤12,当ω=11时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=﹣,此时f(x)在(,)不单调,不满足题意;当ω=9时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=,此时f(x)在(,)单调,满足题意;故ω的最大值为9,故选:B13.(2016•四川)为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x 的图象上所有的点()A.向左平行移动个单位长度B.向右平行移动个单位长度C.向左平行移动个单位长度D.向右平行移动个单位长度【解答】解:把函数y=sin2x的图象向右平移个单位长度,可得函数y=sin2(x﹣)=sin(2x﹣)的图象,故选:D.14.(2016•新课标Ⅰ)将函数y=2sin(2x+)的图象向右平移个周期后,所得图象对应的函数为()A.y=2sin(2x+)B.y=2sin(2x+)C.y=2sin(2x﹣)D.y=2sin(2x﹣)【解答】解:函数y=2sin(2x+)的周期为T==π,由题意即为函数y=2sin(2x+)的图象向右平移个单位,可得图象对应的函数为y=2sin[2(x﹣)+],即有y=2sin(2x﹣).故选:D.15.(2016•北京)将函数y=sin(2x﹣)图象上的点P(,t)向左平移s(s>0)个单位长度得到点P′,若P′位于函数y=sin2x的图象上,则()A.t=,s的最小值为B.t=,s的最小值为C.t=,s的最小值为D.t=,s的最小值为【解答】解:将x=代入得:t=sin=,将函数y=sin(2x﹣)图象上的点P向左平移s个单位,得到P′(+s,)点,若P′位于函数y=sin2x的图象上,则sin(+2s)=cos2s=,则2s=+2kπ,k∈Z,则s=+kπ,k∈Z,由s>0得:当k=0时,s的最小值为,故选:A.16.(2016•四川)为了得到函数y=sin(x+)的图象,只需把函数y=sinx 的图象上所有的点()A.向左平行移动个单位长度B.向右平行移动个单位长度C.向上平行移动个单位长度D.向下平行移动个单位长度【解答】解:由已知中平移前函数解析式为y=sinx,平移后函数解析式为:y=sin(x+),可得平移量为向左平行移动个单位长度,故选:A17.(2016•新课标Ⅱ)函数y=Asin(ωx+φ)的部分图象如图所示,则()A.y=2sin(2x﹣)B.y=2sin(2x﹣) C.y=2sin(x+)D.y=2sin(x+)【解答】解:由图可得:函数的最大值为2,最小值为﹣2,故A=2,=,故T=π,ω=2,故y=2sin(2x+φ),将(,2)代入可得:2sin(+φ)=2,则φ=﹣满足要求,故y=2sin(2x﹣),故选:A.18.(2016•新课标Ⅱ)函数f(x)=cos2x+6cos(﹣x)的最大值为()A.4 B.5 C.6 D.7【解答】解:函数f(x)=cos2x+6cos(﹣x)=1﹣2sin2x+6sinx,令t=sinx(﹣1≤t≤1),可得函数y=﹣2t2+6t+1=﹣2(t﹣)2+,由∉[﹣1,1],可得函数在[﹣1,1]递增,即有t=1即x=2kπ+,k∈Z时,函数取得最大值5.故选:B.二.填空题(共9小题)19.(2017•北京)在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,若sinα=,则sinβ= .【解答】解:∵在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,∴α+β=π+2kπ,k∈Z,∵sinα=,∴sinβ=sin(π+2kπ﹣α)=sinα=.故答案为:.20.(2017•上海)设a1、a2∈R,且+=2,则|10π﹣α1﹣α2|的最小值为.【解答】解:根据三角函数的性质,可知sinα1,sin2α2的范围在[﹣1,1],要使+=2,∴sinα1=﹣1,sin2α2=﹣1.则:,k1∈Z.,即,k2∈Z.那么:α1+α2=(2k1+k2)π,k1、k2∈Z.∴|10π﹣α1﹣α2|=|10π﹣(2k1+k2)π|的最小值为.故答案为:.21.(2017•新课标Ⅱ)函数f(x)=sin2x+cosx﹣(x∈[0,])的最大值是 1 .【解答】解:f(x)=sin 2x+cosx﹣=1﹣cos2x+cosx﹣,令cosx=t且t∈[0,1],则y=﹣t 2+t+=﹣(t﹣)2+1,当t=时,f(t)max=1,即f(x)的最大值为1,故答案为:122.(2017•新课标Ⅱ)函数f(x)=2cosx+sinx的最大值为.【解答】解:函数f(x)=2cosx+sinx=(cosx+sinx)=sin(x+θ),其中tanθ=2,可知函数的最大值为:.故答案为:.23.(2016•上海)设a,b∈R,c∈[0,2π),若对于任意实数x都有2sin(3x ﹣)=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 4 .【解答】解:∵对于任意实数x都有2sin(3x﹣)=asin(bx+c),∴必有|a|=2,若a=2,则方程等价为sin(3x﹣)=sin(bx+c),则函数的周期相同,若b=3,此时C=,若b=﹣3,则C=,若a=﹣2,则方程等价为sin(3x﹣)=﹣sin(bx+c)=sin(﹣bx﹣c),若b=﹣3,则C=,若b=3,则C=,综上满足条件的有序实数组(a,b,c)为(2,3,),(2,﹣3,),(﹣2,﹣3,),(﹣2,3,),共有4组,故答案为:4.24.(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是7 .【解答】解:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:由图可知,共7个交点.故答案为:7.25.(2016•新课标Ⅲ)函数y=sinx﹣cosx的图象可由函数y=2sinx的图象至少向右平移个单位长度得到.【解答】解:∵y=sinx﹣cosx=2sin(x﹣),令f(x)=2sinx,则f(x﹣φ)=2in(x﹣φ)(φ>0),依题意可得2sin(x﹣φ)=2sin(x﹣),故﹣φ=2kπ﹣(k∈Z),即φ=﹣2kπ+(k∈Z),当k=0时,正数φmin=,故答案为:.26.(2016•新课标Ⅲ)函数y=sinx﹣cosx的图象可由函数y=sinx+cosx 的图象至少向右平移个单位长度得到.【解答】解:∵y=f(x)=sinx+cosx=2sin(x+),y=sinx﹣cosx=2sin(x﹣),∴f(x﹣φ)=2sin(x+﹣φ)(φ>0),令2sin(x+﹣φ)=2sin(x﹣),则﹣φ=2kπ﹣(k∈Z),即φ=﹣2kπ(k∈Z),当k=0时,正数φmin=,故答案为:.27.(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC 的最小值是8 .【解答】解:由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,可得sinBcosC+cosBsinC=2sinBsinC,①由三角形ABC为锐角三角形,则cosB>0,cosC>0,在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,又tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣②,则tanAtanBtanC=﹣•tanBtanC,由tanB+tanC=2tanBtanC可得tanAtanBtanC=﹣,令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,由②式得1﹣tanBtanC<0,解得t>1,tanAtanBtanC=﹣=﹣,=()2﹣,由t>1得,﹣≤<0,因此tanAtanBtanC的最小值为8,另解:由已知条件sinA=2sinBsinc,sin(B十C)=2sinBsinC,sinBcosC十cosBsinC=2sinBcosC,两边同除以cosBcosC,tanB十tanC=2tanBtanC,∵﹣tanA=tan(B十C)=,∴tanAtanBtanC=tanA十tanB十tanC,∴tanAtanBtanC=tanA十2tanBtanC≥2,令tanAtanBtanC=x>0,即x≥2,即x≥8,或x≤0(舍去),所以x的最小值为8.当且仅当t=2时取到等号,此时tanB+tanC=4,tanBtanC=2,解得tanB=2+,tanC=2﹣,tanA=4,(或tanB,tanC互换),此时A,B,C均为锐角.三.解答题(共3小题)28.(2017•北京)已知函数f(x)=cos(2x﹣)﹣2sinxcosx.(I)求f(x)的最小正周期;(II)求证:当x∈[﹣,]时,f(x)≥﹣.【解答】解:(Ⅰ)f(x)=cos(2x﹣)﹣2sinxcosx,=(co2x+sin2x)﹣sin2x,=cos2x+sin2x,=sin(2x+),∴T==π,∴f(x)的最小正周期为π,(Ⅱ)∵x∈[﹣,],∴2x+∈[﹣,],∴﹣≤sin(2x+)≤1,∴f(x)≥﹣29.(2016•山东)设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.【解答】解:(Ⅰ)∵f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2 =2sin2x ﹣1+sin2x=2•﹣1+sin2x=sin2x﹣cos2x+﹣1=2sin(2x﹣)+﹣1,令2kπ﹣≤2x﹣≤2kπ+,求得kπ﹣≤x≤kπ+,可得函数的增区间为[kπ﹣,kπ+],k∈Z.(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),可得y=2sin(x﹣)+﹣1的图象;再把得到的图象向左平移个单位,得到函数y=g(x)=2sinx+﹣1的图象,∴g()=2sin+﹣1=.30.(2016•北京)已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)的单调递增区间.【解答】解:(1)f(x)=2sinωxcosωx+cos2ωx=sin2ωx+cos2ωx==.由T=,得ω=1;(2)由(1)得,f(x)=.再由,得.∴f(x)的单调递增区间为[](k∈Z).。
高考数学解答题(新高考)三角函数的图象与性质(零点或根的问题)(典型例题+题型归类练)(解析版)

专题03 三角函数的图象与性质(零点或根的问题)(典型例题+题型归类练)一、必备秘籍()()sin f x A x k ωϕ=+=实根问题,换元法令t x ωϕ=+将函数()f x 化简为sin y A t =,在利用正弦函数sin t 的图象来解决交点(根,零点)的问题.二、典型例题例题1.(2022·河南驻马店·高一期中(文))已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭在一个周期内的图像如图所示. (1)求函数()f x 的解析式; (2)设02x π<<,且方程()f x m =有两个不同的实数根,求实数m 的取值范围.第(2)问思路点拨:本小题要求时,方程有两个根,求的取值范围,可采用换元法解答过程:由(1)知,令,由,则,作出函数的图象,根据图象讨论的的个数.图象可知:与的图象在内有两个不同的交点时,,故实数的取值范围为.【答案】(1)()2sin 26f x x π⎛⎫=+ ⎪⎝⎭(2)()1,2(1)显然2A =,又1121212T ππππω⎛⎫=--== ⎪⎝⎭,所以2ω=, 所以()()2sin 2f x x ϕ=+,又函数过点,012π⎛⎫- ⎪⎝⎭,所以2sin 06πϕ⎛⎫-+= ⎪⎝⎭,所以()Z 6k k πϕπ-+=∈,又2πϕ<,所以6π=ϕ, 所以所求的函数的解析式为()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.(2)02x π<<,且方程()f x m =有两个不同的实数根,即()y f x =与y m =的图像在02x π<<内有两个不同的交点,令26t x π=+,则7,66t ππ⎛⎫∈ ⎪⎝⎭,作出函数2sin y t =的图像如下:由图像可知:2sin y t =与y m =的图像在7,66t ππ⎛⎫∈ ⎪⎝⎭内有两个不同的交点时,12m <<,故实数m 的取值范围为()1,2.例题2.(2022·山东德州·高一期中)已知()3sin ,sin cos a x x x ωωω=+,()1cos ,cos sin 2b x x x ωωω⎛⎫=- ⎪⎝⎭()01ω<≤,函数()1f x a b =⋅+,直线6x π=是函数()f x 图像的一条对称轴.(1)求函数()f x 的解析式;(2)当[]0,x π∈时,讨论方程()0f x m -=的根的情况.【答案】(1)()sin 216f x x π⎛⎫=++ ⎪⎝⎭(2)答案见解析(1)已知()3sin ,sin cos a x x x ωωω=+,()()1cos ,cos sin 012b x x x ωωωω⎛⎫=-<≤ ⎪⎝⎭,第(2)问思路点拨:本小题要求时,讨论方程的根的情况,可采用换元法解答过程:由(1)知,令,由,则,则讨论方程的根的情况,转化为的根的情况.作出的图象.1.当或,即或时,有0个根; 2.当或,即或时,有1个根;3.当或,即或时,有2个根;4.当,即时,有3个根由图象可知则()12cos 21sin 2126f x x x x πωωω⎛⎫++=++ ⎪⎝⎭, 由于直线6x π=是函数()f x 图像的一条对称轴.所以26f π⎛⎫= ⎪⎝⎭或0,所以2662k πππωπ⋅⋅+=+,()k ∈Z ,所以31k ω=+. 由于01ω<≤,所以,当0k =时,1ω=,所以()sin 216f x x π⎛⎫=++ ⎪⎝⎭(2)由题意得sin 216x m π⎛⎫+=- ⎪⎝⎭,因为[]0,x π∈,所以132,666x πππ⎡⎤+∈⎢⎥⎣⎦, 令26u x π=+,13,66u ππ⎡⎤∈⎢⎥⎣⎦, 则sin 1u m =-,如图.1.当11m ->或11m -<-,即0m <或2m >时,()f x 有0个根; 2.当11m -=或11m -=-,即0m =或2m =时,()f x 有1个根; 3.当1112m <-<或1112m -<-<,即322m <<或302m <<时,()f x 有2个根;4.当112m -=,即32m =时,()f x 有3个根 综上,当0m <或2m >时,()f x 有0个根; 当0m =或2m =时,()f x 有1个根; 当322m <<或302m <<时,()f x 有2个根;32m =时,()f x 有3个根.例题3.(2022·山东·日照青山学校高一期中)已知函数()2sin f x x =,将()f x的图象向右平移3π个单位长度,再把所有点的横坐标缩小为原来的12(纵坐标不变),得到函数()y g x =的图象. (1)求函数()g x 的解析式及单调递增区间; (2)方程()25g x =在17,612ππ⎛⎫ ⎪⎝⎭上的根从小到大依次为123,,x x x ,求1232x x x ++的值.第(2)问思路点拨:方程在上的根从小到大依次为,求的值.可采用换元法解答过程:由(1)知,令,由,则其中,;即,, ,,.根据图象作答转化为:方程在有个解,作出图象和问题转化作图象,找交点【答案】(1)()2sin 23g x x π⎛⎫=- ⎪⎝⎭,单调递增区间为()5,1212k k k ππππ-++⎡⎤∈⎢⎥⎣⎦Z (2)123823x x x π++= (1)2sin 33f x x ππ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭,()2sin 23g x x π⎛⎫∴=- ⎪⎝⎭;令()222232k x k k πππππ-+≤-≤+∈Z ,解得:()51212k x k k ππππ-+≤≤+∈Z , ()f x ∴的单调递增区间为()5,1212k k k ππππ-++⎡⎤∈⎢⎥⎣⎦Z(2)令()22sin 235g x x π⎛⎫=-= ⎪⎝⎭,即1sin 235x π⎛⎫-= ⎪⎝⎭;17,612x ππ⎛⎫∈ ⎪⎝⎭,520,32x ππ⎡⎤∴-∈⎢⎥⎣⎦,设23x πθ=-,其中50,2πθ⎡⎤∈⎢⎥⎣⎦,即1sin 5θ=, 结合正弦函数5sin 02y x x π⎛⎫=≤≤⎪⎝⎭的图象可知:方程1sin 5θ=在50,2πθ⎡⎤∈⎢⎥⎣⎦有3个解123,,θθθ,其中12θθπ+=,233θθπ+=; 即122233x x πππ-+-=,2322333x x πππ-+-=,1256x x π∴+=,23116x x π+=,123823x x x π∴++=. 三、题型归类练1.(2022·河南驻马店·高一期中(理))已知点()()11,A x f x ,()()22,B x f x 是函数()()2sin 0,02f x x πωϕωϕ⎛⎫=+>-<< ⎪⎝⎭图象上的任意两点,且角ϕ的终边经过点(1,P ,()()124f x f x -=时,12x x -的最小值为3π. (1)求函数()f x 的解析式;(2)()y f x m =-在0,3x π⎛⎫∈ ⎪⎝⎭内有两个不同的零点,求实数m 的取值范围.【答案】(1)()2sin 33f x x π⎛⎫=- ⎪⎝⎭;2m <.(1)角ϕ的终边经过点(1,P ,∴tan ϕ=∵02πϕ-<<,∴3πϕ=-,由()()124f x f x -=时,12x x -的最小值为3π, 得23T π=,即223ππω=,∴3ω=,∴()2sin 33f x x π⎛⎫=- ⎪⎝⎭;(2)∵()y f x m =-在0,3x π⎛⎫∈ ⎪⎝⎭内有两个不同的零点,即()y f x =与y m =的图象在0,3x π⎛⎫∈ ⎪⎝⎭内有两个不同的交点,令33t x π=-,由0,3x π⎛⎫∈ ⎪⎝⎭,则2,33t ππ⎛⎫∈- ⎪⎝⎭, 即2sin y t =与y m =在2,33t ππ⎛⎫∈- ⎪⎝⎭上有两个交点,2m <.2.(2022·辽宁·大连市第一中学高一期中)已知函数()4cos cos 1(0)3f x x x πωωω⎛⎫=⋅-- ⎪>⎝⎭的部分图像如图所示,若288AB BC π⋅=-,B ,C 分别为最高点与最低点.(1)求函数()f x 的解析式;(2)若函数()y f x m =-在130,12π⎡⎤⎢⎥⎣⎦,上有且仅有三个不同的零点1x ,2x ,3x ,(123x x x <<),求实数m 的取值范围,并求出123 cos (2)x x x ++的值.【答案】(1)()2sin 26f x x π⎛⎫=+ ⎪⎝⎭(2)m ⎡∈⎣,12(1)解:)()2cos cos 1f x xx x ωωω=+-,2cos 2cos 1x x x ωωω=⋅+-,2cos 2x x ωω=+,2sin 26x πω⎛⎫=+ ⎪⎝⎭,设函数()f x 的周期为T ,则,24T AB ⎛⎫= ⎪⎝⎭,,42T BC ⎛⎫=- ⎪⎝⎭,则228888T AB BC π⋅=-=-,所以T π=.故22T ππω==,故1ω=, 所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.(2)由题意,函数()y f x m =-在130,12π⎡⎤⎢⎥⎣⎦上有且仅有三个不同的零点,1x ,2x ,3x ,即曲线()y f x =与y m =在130,12π⎡⎤⎢⎥⎣⎦上有且仅有三个不同的交点.设26t x π=+,当130,12x π⎡⎤∈⎢⎥⎣⎦时,7,63t ππ⎡⎤∈⎢⎥⎣⎦.则2sin y t =,7,63t ππ⎡⎤∈⎢⎥⎣⎦,则m ⎡∈⎣,12t t π+=,233t t π+=,所以12324t t t π++=,即12322224666x x x ππππ⎛⎫⎛⎫⎛⎫+++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即123523x x x π++=, 所以12351cos(2)cos32π++==x x x .3.(2022·四川省内江市第六中学高一期中(文))已知函数()()2sin cos 23f x x x x π=+. (1)求函数f (x )的最小正周期T 及()1003f π的值;(2)若关于x 的方程()12f x a π+=在20,3π⎡⎤⎢⎥⎣⎦上有2个解,求实数a 的取值范围.【答案】(1)最小正周期π,(2)1142a ⎡⎫∈⎪⎢⎣⎭,.(1)解:()2sin cos 3f x x x x π⎛⎫=+ ⎪⎝⎭12sin cos 2x x x x ⎛⎫= ⎪ ⎪⎝⎭2sin cos x x x x =1sin22x x =1sin22x =T π=,100133sin 233323f f f πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+==⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(2)解:sin 22126f x a x a ππ⎛⎫⎛⎫+=⇒+= ⎪ ⎪⎝⎭⎝⎭. 23023662x x ππππ⎡⎤⎡⎤∈⇒+∈⎢⎥⎢⎥⎣⎦⎣⎦,,,设32,[,]662t x t πππ=+∈,所以sin 2t a =有两个解, 结合图像可知1212a ≤< 故1142a ⎡⎫∈⎪⎢⎣⎭,.4.(2022·山东潍坊·高一期中)已知函数()33sin 26sin sin 644f x x x x πππ⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)求函数()f x 的最小正周期和单调递增区间;(2)若函数()y f x k =-在区间130,12π⎡⎤⎢⎥⎣⎦上有且仅有两个零点12,x x ,求k 的取值范围,并求12x x +的值.【答案】(1)最小正周期π,单调递增区间为(),63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ;(2)k 的范围为()33,0,32⎛⎫--⋃ ⎪⎝⎭,12x x +为53π或23π.(1)因为()33sin 26sin sin 644f x x x x πππ⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()3cos 223sin cos sin cos 2x x x x x x =++-()22cos 223sin c 3s 2o x x x x =+-cos 223cos 223x x x =- 63sin 2x π⎛⎫=- ⎪⎝⎭,所以()f x 的最小正周期22T ππ==, 令222262k x k πππππ-≤-≤+,k ∈Z ,则()63k x k k ππππ-≤≤+∈Z ,所以()f x 的单调递增区间为(),63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z .(2)由题意,()0f x k -=在130,12π⎡⎤⎢⎥⎣⎦上有且仅有两个解12,x x ,即()y f x =与y k =在130,12π⎡⎤⎢⎥⎣⎦上有且仅有两个交点,由130,12x π⎡⎤∈⎢⎥⎣⎦,则2,266x πππ⎡⎤-∈-⎢⎥⎣⎦,设26t x π=-,则3sin ,,26y t t ππ⎡⎤=∈-⎢⎥⎣⎦, 3sin ,,26y t t ππ⎡⎤=∈-⎢⎥⎣⎦的图象如下,由图知:k 的取值范围为()33,0,32⎛⎫--⋃ ⎪⎝⎭, 设3sin y t =与y k =在,26ππ⎡⎤-⎢⎥⎣⎦上的两个交点的横坐标分别为12,t t , 当33,2k ⎛⎫∈-- ⎪⎝⎭时12,t t 关于32t π=对称,即12,x x 关于56x π=对称,则1253x x π+=; 当()0,3k ∈时12,t t 关于2t π=对称,即12,x x 关于3x π=对称,则1223x x π+=; 综上,12x x +的值是53π或23π. 5.(2022·辽宁·鞍山一中高一期中)已知函数()()sin 22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图像向左平移6π个单位,得到函数()g x 的图像,且()g x 为偶函数.(1)求函数()f x 和()g x 的解析式;(2)若对a ∀,[]0,b m ∈.当a b <时,都有()()()()f b f a g a g b ->-成立,求m 的取值范围;(3)若关于x 的方程()()f x g x k +=在130,6π⎡⎤⎢⎥⎣⎦上恰有四个不等实根1x ,2x ,3x ,()41234x x x x x <<<,求k 的取值范围和123422x x x x +++的值.【答案】(1)()sin 26f x x π⎛⎫+ ⎝=⎪⎭,()cos2g x x =(2)012m π<≤.(3)32<k ,132π (1)由题意()sin 263g x f x x ππϕ⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭, 因为()g x 为偶函数,所以()()g x g x -=,即sin 2sin 233x x ππϕϕ⎛⎫⎛⎫-++=++ ⎪ ⎪⎝⎭⎝⎭,所以32k ππϕπ+=+,k Z ∈, 而2πϕ<,故0k =,6π=ϕ,()sin 26f x x π⎛⎫+ ⎝=⎪⎭,()sin 2cos 22π⎛⎫=+= ⎪⎝⎭g x x x . (2)对a ∀,[]0,b m ∈,a b <,都有()()()()f b f a g a g b ->-,()()()()f b g b f a g a +>+,设()()()h x f x g x =+,则()h x 在[]0,m 单调递增.又()()()3sin 2cos 22cos 22623h x f x g x x x x x x ππ⎛⎫⎛⎫=+=++=+=+ ⎪ ⎪⎝⎭⎝⎭,令23u x π=+,则,233u m ππ⎡⎤∈+⎢⎥⎣⎦,y u =在,233u m ππ⎡⎤∈+⎢⎥⎣⎦递增, 故232m ππ+≤,012m π<≤.(3)()()()23h x f x g x x π⎛⎫=+=+ ⎪⎝⎭,令23t x π=+,则14,33t ππ⎡⎤∈⎢⎥⎣⎦, 则sint =恰有4个不等实根1t ,2t ,3t ,4t ,则32<k ,不妨设1234t t t t <<<, 函数()sin t t ϕ=,14,33t ππ⎡⎤∈⎢⎥⎣⎦与函数y =4个交点,如图所示(略),()sin t t ϕ=在,32ππ⎡⎤⎢⎥⎣⎦,35,22ππ⎡⎤⎢⎥⎣⎦,79,22ππ⎡⎤⎢⎥⎣⎦递增,在3,22ππ⎡⎤⎢⎥⎣⎦,57,22ππ⎡⎤⎢⎥⎣⎦,914,22ππ⎡⎤⎢⎥⎣⎦递减,1433ππϕϕ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭591222πππϕϕϕ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,37122ππϕϕ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭, 12322t t π+=,23522t t π+=,34722t t π+=,12342215t t t t π+++=, ()1234222215x x x x ππ++++=,123413222x x x x π+++=. 6.(2022·陕西·西安建筑科技大学附属中学高一阶段练习)已知函数()()cos f x A x ωϕ=+(0A >,0>ω,2πϕ≤)的部分图象大致如图.(1)求()f x 的单调递增区间.(2)将函数()f x 的图象向右平移4π个单位长度得到曲线C ,把C 上各点的横坐标保持不变,纵坐标变为原来的2倍得到函数()g x 的图象.若关于x 的方程()0g x m -=在0,2π⎡⎤⎢⎥⎣⎦上有两个不同的实数解,求实数m 的取值范围.【答案】(1)5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦,Z k ∈(2)[)1,2 (1)根据图象,可得1A =,由124312πππω⋅=-,得2ω=. 所以()()cos 2f x x φ=+,由2012πϕ⨯+=,得6πϕ=-, 所以()cos 26f x x π⎛⎫=- ⎪⎝⎭. 令2226k x k ππππ-≤-≤,Z k ∈,得51212k x k ππππ-+≤≤+,Z k ∈, 所以()f x 的单调递增区间为5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦,Z k ∈. (2)将函数()y f x =的图象向右平移4π个单位长度得到曲线C :cos 2sin 2466y x x πππ⎡⎤⎛⎫⎛⎫=--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再把C 上各点的横坐标保持不变,纵坐标变为原来的2倍得到()2sin 26g x x π⎛⎫=- ⎪⎝⎭的图象. 由()0g x m -=在0,2π⎡⎤⎢⎥⎣⎦上有两个不同的实数解,即2sin 26m x π⎛⎫=- ⎪⎝⎭在0,2π⎡⎤⎢⎥⎣⎦上有两个不同的实数解, 因为0,2x π⎡⎤∈⎢⎥⎣⎦,设26t x π=-,则5,66t ππ⎡⎤∈-⎢⎥⎣⎦,则需直线y m =与2sin y t =的图象在5,66t ππ⎡⎤∈-⎢⎥⎣⎦两个不同的公共点.画出2sin y t =在5,66t ππ⎡⎤∈-⎢⎥⎣⎦时的简图如下:1,2.所以实数m的取值范围为[)。
三角函数部分高考题(带答案)

22.设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且3cos cos 5a Bb Ac -=. 〔Ⅰ〕求tan cot A B 的值; 〔Ⅱ〕求tan()A B -的最大值.解析:〔Ⅰ〕在ABC △中,由正弦定理及3cos cos 5a Bb Ac -= 可得3333sin cos sin cos sin sin()sin cos cos sin 5555A B B A C A B A B A B -==+=+ 即sin cos 4cos sin A B A B =,那么tan cot 4A B =; 〔Ⅱ〕由tan cot 4A B =得tan 4tan 0A B =>2tan tan 3tan 3tan()1tan tan 14tan cot 4tan A B B A B A B B B B --===+++≤34当且仅当14tan cot ,tan ,tan 22B B B A ===时,等号成立,故当1tan 2,tan 2A B ==时,tan()A B -的最大值为34.23.在ABC △中,5cos 13B =-,4cos 5C =.〔Ⅰ〕求sin A 的值;〔Ⅱ〕设ABC △的面积332ABC S =△,求BC 的长.解:〔Ⅰ〕由5cos 13B =-,得12sin 13B =,由4cos 5C =,得3sin 5C =.所以33sin sin()sin cos cos sin 65A B C B C B C =+=+=. ··········· 5分 〔Ⅱ〕由332ABC S =△得133sin 22AB AC A ⨯⨯⨯=, 由〔Ⅰ〕知33sin 65A =,故65AB AC ⨯=, ···························· 8分又sin 20sin 13AB B AC AB C ⨯==, 故2206513AB =,132AB =. 所以sin 11sin 2AB A BC C ⨯==. ························ 10分24.函数2π()sinsin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭〔0ω>〕的最小正周期为π.〔Ⅰ〕求ω的值;〔Ⅱ〕求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦,上的取值范围.解:〔Ⅰ〕1cos 2()22x f x x ωω-=+112cos 222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭.因为函数()f x 的最小正周期为π,且0ω>, 所以2ππ2ω=,解得1ω=. 〔Ⅱ〕由〔Ⅰ〕得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭. 因为2π03x ≤≤, 所以ππ7π2666x --≤≤,所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤, 因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤,即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦,. 25.求函数2474sin cos 4cos 4cos y x x x x =-+-的最大值与最小值。
高考数学三角函数解三角形题型分析(含答案)

高考数学三角函数解三角形题型分析(含答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN三角函数小题:5年8考.题目难度较小,主要考察公式熟练运用,平移,由图像性质、化简求值、解三角形等问题(含应用题),基本属于“送分题”.考三角小题时,一般是一个考查三角恒等变形或三角函数的图象性质,另一个考查解三角形. 年份 题目 答案2017年 14. 函数()23sin 3cos 4f x x x =+-(0,2x π⎡⎤∈⎢⎥⎣⎦)的最大值是 .1 2016年(7)若将函数y =2sin 2x 的图像向左平移12π个单位长度,则平移后图象的对称轴为 (A )x =62k ππ- (k ∈Z ) (B )x=62ππ+k (k ∈Z ) (C )x=122k ππ- (k ∈Z ) (D )x =122k ππ+ (k ∈Z ) B2016年(9)若cos(4π–α)= 53,则sin 2α= (A )257(B )51(C )51- (D )257-D2016年(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若cos A =,cosC =,a =1,则b = .2014年 4. 钝角三角形ABC 的面积是12,AB=1,BC=2 ,则AC=( )A. 5B. 5C. 2D. 1B2014年 12. 设函数()3sin x f x mπ=.若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦,则m 的取值范围是( )A. ()(),66,-∞-⋃∞B. ()(),44,-∞-⋃∞C. ()(),22,-∞-⋃∞D.()(),14,-∞-⋃∞C2014年 14. 函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________. 12013年15.设θ为第二象限角,若π1tan 42θ⎛⎫+= ⎪⎝⎭,则sin θ+cos θ=__________.105-三角函数解答题在全国2卷中每年只考一个类型,交错考法不分奇偶数年.不考的那一个一般用两道小题代替.三角函数大题侧重于考解三角形,重点考查正、余弦定理,小题中侧重于考查三角函数的图象和性质.数列一般考求通项、求和.数列应用题已经多年不考了,总体来说数列的地位已经降低,题目难度小.1sin 2ADCAD CAD =∠因为ABDS由正弦定理可得1B AC ∠ABD 和ADC 中,由余弦定理知222AD BD =+222AC AD DC =+-222232AB AC AD BD DC +=+,所以1AC =的内角A ,B ,C又a 2+c 2≥2ac ,故422ac ≤-,当且仅当a =c 时,等号成立.因此△ABC 面积的最大值为2+1.其他三角函数典型难题1、(2014年1卷)如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为 B2、设函数()cos()3f x x π=+,则下列结论错误的是() DA .()f x 的一个周期为2π-B .()y f x =的图像关于直线83x π=对称 C .()f x π+的一个零点为6x π=D .()f x 在(,)2ππ单调递减3、已知函数()()sin cos 0,,f x x x x ωωω=+>∈R 若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为 .π4、A.512π B.3π C.4π D.6π 【答案】D. 【解析】试题分析:向右平移ϕ个单位后,得到)22sin()(ϕ-=x x g ,又∵2|)()(|21=-x g x f ,∴不妨ππk x 2221+=,ππϕm x 22222+-=-,∴πϕπ)(221m k x x -+-=-,又∵12min 3x x π-=,∴632πϕπϕπ=⇒=-,故选D.考点:三角函数的图象和性质.5、(2016全国1卷12)已知函数()sin()(0),24f x x+x ππωϕωϕ=>≤=-,为()f x 的零点,4x π=为()y f x =图像的对称轴,且()f x 在5()1836ππ,单调,则ω的最大值为 B (A )11 (B )9 (C )7 (D )56、已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是( )A()A 15[,]24 ()B 13[,]24 ()C 1(0,]2()D (0,2]7、.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则 BA .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=8、函数的图像可由函数的图像至少向右平移_____________个单位长度得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的主要考点是:三角函数的概念和性质(单调性,周期性,奇偶性,最值),三角函数的图象,三角恒等变换(主要是求值),三角函数模型的应用,正余弦定理及其应用,平面向量的基本问题及其应用.题型1 三角函数的最值:最值是三角函数最为重要的内容之一,其主要方法是利用正余弦函数的有界性,通过三角换元或者是其它的三角恒等变换转化问题.例1 若x 是三角形的最小内角,则函数sin cos sin cos y x x x x =++的最大值是( ) A .1-BC.12-+D.12+分析:三角形的最小内角是不大于3π的,而()2sin cos 12sin cos x x x x +=+,换元解决.点评:涉及到sin cos x x ±与sin cos x x 的问题时,通常用换元解决.例2.已知函数2()2sin cos 2cos f x a x x b x =+.,且(0)8,()126f f π==.(1)求实数a ,b 的值;(2)求函数)(x f 的最大值及取得最大值时x 的值.分析:待定系数求a ,b ;然后用倍角公式和降幂公式转化问题. 点评:结论()sin cos a b θθθϕ+=+是三角函数中的一个重要公式,它在解决三角函数的图象、单调性、最值、周期以及化简求值恒等式的证明中有着广泛应用,是实现转化的工具,是联系三角函数问题间的一条纽带,是三角函数部分高考命题的重点内容.题型2 三角函数的图象:三角函数图象从“形”上反应了三角函数的性质,一直是高考所重点考查的问题之一.例3.(2009年福建省理科数学高考样卷第8题)为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin 2y x =的图象A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位分析:先统一函数名称,在根据平移的法则解决.例4 (2008高考江西文10)函数tan sin tan sin y x x x x =+--在区间3(,)22ππ内的图象是分析:分段去绝对值后,结合选择支分析判断.点评:本题综合考察三角函数的图象和性质,当不注意正切函数的定义域或是函数分段不准确时,就会解错这个题目.题型3 用三角恒等变换求值:其主要方法是通过和与差的,二倍角的三角变换公式解决.例5 (2008高考山东卷理5)已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭7πsin 6α⎛⎫+ ⎪⎝⎭的值是A. BC .45-D .45分析:所求的7πsin sin()66παα⎛⎫+=+ ⎪⎝⎭,将已知条件分拆整合后解决. 点评:本题考查两角和与差的正余弦、诱导公式等三角函数的知识,考查分拆与整合的数学思想和运算能力.解题的关键是对πcos sin 6αα⎛⎫-+= ⎪⎝⎭ 例6(2008高考浙江理8)若cos 2sin αα+=则tan α= A .21B .2C .21-D .2- 分析:可以结合已知和求解多方位地寻找解题的思路.点评:本题考查利用三角恒等变换求值的能力,试题的根源是考生所常见的“已知()1sin cos ,0,5βββπ+=∈,求tan β的值(人教A 版必修4第三章复习题B 组最后AB-CD-一题第一问)”之类的题目 ,背景是熟悉的,但要解决这个问题还需要考生具有相当的知识迁移能力.题型4 正余弦定理的实际应用:这类问题通常是有实际背景的应用问题,主要表现在航海和测量上,解决的主要方法是利用正余弦定理建立数学模型. 例7.(2008高考湖南理19)在一个特定时段内,以点E 为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A .某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45且与点A相距B ,经过40分钟又测得该船已行驶到点A 北偏东45θ+ (其中sin 26θ=,090θ<<)且与点A相距C .(1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由. 分析:根据方位角画出图形,如图.第一问实际上就是求BC 的长,在ABC ∆中用余弦定理即可解决;第二问本质上求是求点E 到直线BC 的距离,即可以用平面解析几何的方法,也可以通过解三角形解决.点评:本题以教材上所常用的航海问题为背景,考查利用正余弦定理解决实际问题的能力,解决问题的关键是根据坐标方位画出正确的解题图. 本题容易出现两个方面的错误,一是对方位角的认识模糊,画图错误;二是由于运算相对繁琐,在运算上出错. 题型5 三角函数与平面向量的结合:三角函数与平面向量的关系最为密切,这二者的结合有的是利用平面向量去解决三角函数问题,有的是利用三角函数去解决平面向量问题,更多的时候是平面向量只起衬托作用,三角函数的基本问题才是考查的重点. 例8(2009年杭州市第一次高考科目教学质量检测理科第18题)已知向量)1,(sin ),2cos ,cos 2(x x x ωωω==,(0>ω),令x f ⋅=)(,且)(x f 的周期为π. (1) 求4f π⎛⎫⎪⎝⎭的值;(2)写出()f x 在]2,2[ππ-上的单调递增区间. 分析:根据平面向量数量积的计算公式将函数()f x 的解析式求出来,再根据)(x f 的周期为π就可以具体确定这个函数的解析式,下面只要根据三角函数的有关知识解决即可.点评:本题以平面向量的数量积的坐标运算为入口,但本质上是考查的三角函数的性质,这是近年来高考命题的一个热点. 例9 (2009江苏泰州期末15题)已知向量()3sin ,cos a αα=,()2sin ,5sin 4cos b ααα=-,3,22παπ⎛⎫∈⎪⎝⎭,且a b ⊥. (1)求tan α的值;(2)求cos 23απ⎛⎫+ ⎪⎝⎭的值.分析:根据两个平面向量垂直的条件将问题转化为一个三角函数的等式,通过这个等式探究第一问的答案,第一问解决后,借助于这个结果解决第二问.点评:本题以向量的垂直为依托,实质上考查的是三角恒等变换.在解题要注意角的范围对解题结果的影响.题型6 三角形中的三角恒等变换:这是一类重要的恒等变换,其中心点是三角形的内角和是π,有的时候还可以和正余弦定理相结合,利用这两个定理实现边与角的互化,然后在利用三角变换的公式进行恒等变换,是近年来高考的一个热点题型. 例10.(安徽省皖南八校2009届高三第二次联考理科数学17题)三角形的三内角A ,B ,C 所对边的长分别为a ,b ,c ,设向量(,),(,)m c a b a n a b c =--=+,若//m n ,(1)求角B 的大小;(2)求sin sin A C +的取值范围.分析:根据两个平面向量平行的条件将向量的平行关系转化为三角形边的关系,结合余弦定理解决第一问,第一问解决后,第二问中的角,A C 就不是独立关系了,可以用其中的一个表达另一个,就把所要解决的问题归结为一个角的三角函数问题.点评:本题从平面向量的平行关系入手,实质考查的是余弦定理和三角形中的三角恒等变换,解决三角形中的三角恒等变换要注意三角形内角和定理和角的范围对结果的影响. 题型7 用平面向量解决平面图形中的问题:由于平面向量既有数的特征(能进行类似数的运算)又具有形的特征,因此利用平面向量去解决平面图形中的问题就是必然的了,这在近年的高考中经常出现.考试大纲明确指出用会用平面向量解决平面几何问题. 例11. 如图,已知点G 是ABO ∆的重心,点P 在OA 上,点Q 在OB 上,且PQ 过ABO ∆ 的重心G ,OP mOA =,OQ nOB =,试证明11m n+为常数,并求出这个常数.分析:根据两向量共线的充要条件和平面向量基本定理,把题目中需要的向量用基向量表达出来,本题的本质是点,,P G Q 共线,利用这个关系寻找,m n 所满足的方程.【点评】平面向量是高中数学的重要工具,它有着广泛的应用,用它解决平面几何问题是一个重要方面,其基本思路是根据采用基向量或坐标把所要解决的有关的问题表达出来,再根据平面向量的有关知识加以处理.课标区已把几何证明选讲列入选考范围,应引起同学们的注意.题型8 用导数研究三角函数问题:导数是我们在中学里引进的一个研究函数的重要工具,利用导数探讨三角函数问题有它极大的优越性,特别是单调性和最值. 例12. 已知函数22()cos 2sin cos sin f x x t x x x =+-,若函数()f x 在区间(,]126ππ上是增函数,求实数t 的取值范围. 分析:函数的()f x 导数在(,]126ππ大于等于零恒成立. 点评:用导数研究函数问题是导数的重要应用之一,是解决高中数学问题的一种重要的思想意识.本题如将()f x 化为()sin 2cos 2)f x t x x x ϕ=+=+的形式,则ϕ与t 有关,讨论起来极不方便,而借助于导数问题就很容易解决.题型9 三角函数性质的综合应用:将三角函数和其它的知识点相结合而产生一些综合性的试题,解决这类问题往往要综合运用我们的数学知识和数学思想,全方位的多方向进行思考.例13. 设二次函数2()(,)f x x bx c b c R =++∈,已知不论α,β为何实数,恒有(sin )0f α≥和(2cos )0f β+≤.(1)求证:1b c +=- ; (2)求证:3c ≥;(3)若函数(sin )f α的最大值为8,求b ,c 的值.分析:由三角函数的有界性可以得出()10f =,再结合有界性探求.点评:本题的关键是1b c +=-,由(sin )0(2cos )0f f αβ≥⎧⎨+≤⎩利用正余弦函数的有界性得出()()1010f f ≥⎧⎪⎨≤⎪⎩,从而(1)0f =,使问题解决,这里正余弦函数的有界性在起了重要作用.【专题训练】 一、选择题1.若[0,2)απ∈,sin cos αα=-,则α的取值范围是( )A .[0,]2πB .[,]2ππ C .3[,]2ππ D .3[,2)2ππ 2.设α是锐角,且lg(1cos )m α-=,1lg 1cos n α=+,则lgsin α= ( )A .m n -B .11()2m n -C .2m n -D .11()2n m-3.若00||2sin15,||4cos15a b ==,a 与b 的夹角为30。
,则a b ⋅= ( )ABC.D .124.若O 为ABC ∆的内心,且满足()(2)0OB OC OB OC OA -⋅+-=,则ABC ∆的形状为( )A .等腰三角形B .正三角形C .直角三角形D .钝角三角形 5.在ABC ∆中,若CcB b A a cos cos cos ==,则ABC ∆是( )A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形6.已知向量)02(,=→-OB 、)22(,=→-OC 、)sin 2cos 2(αα,=→-CA ,则直线OA 与直线OB 的夹角的取值范围是( )A .]12512[ππ,B .]1254[ππ,C .]2125[ππ, D .]40[π,二、填空题7.6622sin cos 3sin cos x x x x ++的化简结果是__________.8.若向量a 与b 的夹角为θ,则称a b ⨯为它们的向量积,其长度为||||||sin a b a b θ⨯=⋅,已知||1a =,||5b =,且4a b ⋅=-,则||a b ⨯=_______________.9. 一货轮航行到某处,测得灯塔S 在货轮的北偏东15︒,与灯塔S 相距20海里,随后货轮按北偏西30︒的方向航行30分钟后,又得灯塔在货轮的东北方向,则货轮的速度为每小时 海里.三、解答题10. 已知:1tan()3πα+=-,22sin 2()4cos 2tan()10cos sin 2παααβαα-++=-.(1)求tan()αβ+的值; (2)求tan β的值. 11. 已知函数()222sin ()612f x x x ππ⎛⎫=-+- ⎪⎝⎭ ()x R ∈. (1)求函数()f x 的最小正周期;(2)求使函数()f x 取得最大值的x 的集合. 12.已知向量(cos ,sin )a αα=, (cos ,sin )b ββ=, 25a b -=. (1)求c o s ()αβ-的值; (2)若02πα<<, 02πβ-<<, 且5sin 13β=-, 求sin α. 13.(2008北京理13分)已知函数2π()sin sin 2f x x x x ωωω⎛⎫=++ ⎪⎝⎭(0ω>)的最小正周期为π.(Ⅰ)求ω的值;Ⅱ)求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦,上的取值范围.7已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如题(6)图所示,则A . ω=1 ϕ=6πB .ω=1 ϕ=- 6πC .ω=2 ϕ=6πD .ω=2 ϕ= -6π8已知函数2()22sin f x x x =-.(Ⅰ)求函数()f x 的最大值; (II )求函数)(x f 的零点集合。
