第一章线性规划及单纯形法
第一章 线性规划及单纯形法

线性规划问题的标准形式: 线性规划问题的标准形式:
max f = ∑ c j x
j =1 j n
n ∑ aij x j = bi , i = 1,2,L , m j =1 x j ≥ 0, j = 1,2,L , n
日产量( 日产量(吨) 9 5 7 21
11
)(模型 例2(运输问题)(模型) (运输问题)(模型)
minf = 2 x11 + 9 x12 + 10 x13 + 7 x14 + x21 + 3 x22 + 4 x23 + 2 x24 + 8 x31 + 4 x32 + 2 x33 + 5 x34 x11 + x12 + x13 + x14 = 9 x +x +x +x =5 23 24 21 22 x31 + x32 + x33 + x34 = 7 x11 + x21 + x31 = 3 s.t. x12 + x22 + x32 = 8 x13 + x23 + x33 = 4 x14 + x24 + x34 = 6 xij ≥ 0(i = 1,2,3; j = 1,2,3,4)
18
3、(线性规划)数学模型的三要素 、(线性规划) 、(线性规划 变量/决策变量 决策变量; ①变量 决策变量; 目标函数( ②目标函数(max/min); ); 约束条件。 ③约束条件。
19
决策变量: ①变量/决策变量:指决策者为实现规划目标采 变量 决策变量 取的方案、措施,是问题中要确定的未知量; 取的方案、措施,是问题中要确定的未知量;
第1章-线性规划及单纯形法-课件(1)

✓ x1、 x2 0
IБайду номын сангаас
设备
1
原材料 A 4
原材料 B 0
利润
2
II 资源限量
2 8 台时
0
16kg
4
12kg
3
第一章 线性规划及单纯形法 运筹学
该计划的数学模型
✓ 目标函数 ✓ 约束条件
Max Z = 2x1 + 3x2
x1 + 2x2 8 4x1 16 4x2 12 x1、 x2 0
x1
✓ 美国航空公司关于哪架飞机用于哪一航班和哪些 机组人员被安排于哪架飞机的决策。
✓ 美国国防部关于如何从现有的一些基地向海湾运 送海湾战争所需要的人员和物资的决策。
✓ ……
第一章 线性规划及单纯形法 运筹学
二、线性规划问题的数学模型
✓ 1、一般形式 ✓ 2、简写形式 ✓ 3、表格形式 ✓ 4、向量形式 ✓ 5、矩阵形式
1、唯一最优解
max Z 2 x 1 3 x 2
2 x 1 2 x 2 12 ⑴
x1 4 x1
2 x2
8 16
⑵ ⑶
4 x 2 12 ⑷
x 1 0 , x 2 0
1 234 56
x2
⑶ ⑷
(4,2)
0 1 234 5678
x1
⑵
⑴
✓最优解:x1 = 4,x2 = 2,有唯一最优解Z=14。
第一章 线性规划及单纯形法 运筹学
三、线性规划模型的标准形式
✓ 1、标准形式 ✓ 2、转换方式
第一章 线性规划及单纯形法 运筹学
1、标准形式
maZx cjxj
xj
aijxj 0
bi
运筹学第1章:线性规划问题及单纯型解法

原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8
运筹学第一章

30
1.1.3解的概念
概念: 1、可行解:满足所有约束条件的解。 2、可行域:即可行解的集合。所有约束条件的交 集,也就是各半平面的公共部分。满足所有约 束条件的解的集合,称为可行域。 3、凸集:集合内任意两点的连线上的点均属于这 个集合。如:实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
(无界解)
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
(无解)
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士?
5
例题2建模
目标函数:min Z=x1+x2+x3+x4+x5+x6 约束条件: x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束:xj ≥0,j=1,2,…6
OR1
6
例题3:运输问题
三个加工棉花的加工厂,并且有三个仓库供应棉花,各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示:问如何运输才能使总的运费最小?
OR1
14
总
结
从以上 5 个例子可以看出,它们都属于优化问题,它们 的共同特征: 1 、每个问题都用一组决策变量表示某一方案;这组决 策变量的值就代表一个具体方案,一般这些变量取值是 非负的。 2 、存在一定的约束条件,这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标,它可用决策变量的线性 函数(称为目标函数)来表示。按问题的不同,要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。
第01次课--第一章 线性规划

(如果取≥0)
x1 , x2 , , xn (, )0
约束条件 (1-3)
决策变量
30
非负约束条件
国防科技大学
第一节 线性规划的问题及其数学模型
标准形式
max Z c1 x1 c2 x2
cn xn
顶点同时得到最优解,则它们连线上的任意一点都是最
优解,即有无穷最优解。
28
国防科技大学
第一节 线性规划的问题及其数学模型
图解法的优缺点分析
• 直观、简便 • 变量数多于三个以上时,无能为力
通用普遍的 求解方法 (代数方法)
?
单纯形法
模型的标准形式
?
29
国防科技大学
第一节 线性规划的问题及其数学模型 线性规划的数学模型的一般形式:
2
国防科技大学
第一章 线性规划与单纯形法
在军事活动,以及生产、管理、经营等社 会活动中经常提出一类问题,即如何合理地利用 有限的人力、物力、财力等资源,以得到最好的 效果。
3
国防科技大学
第一节 线性规划的问题及其数学模型
例 兵力运送问题 设有A、B两种型号的直升机,每次A能运 载35人,需驾驶员2人,B能运载20人,需驾
目标函数取 最大值
j 1 a11 x1 a12 x2 a1n xn b1 n a21 x1 a22 x2 a2 n xn b2 简记做 aij x j bi (i 1, 2, , m) j 1 x 0 ( j 1, 2, , m) a x a x a x b j mn n m m1 1 m 2 2 约束条件为等式, x , x , , x 0 且右端项为非负 1 2 n 值
第一章线性规划及单纯形法

第一章线性规划及单纯形法6.6单纯形法小结Drawingontheexampl,thetwoaxisinterceptsareplotted.2、求初始基可行解并进行最优性检验Cj比值CBXBb 检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000令非基变量x1=0,x2=0,找到一个初始基可行解:x1=0,x2=0,x3=8,x4=12,x5=36,σj>0,此解不是最优(因为z=3x1+5x2+0x3+0x4+0x5)即X0=(0,0,8,12,36)T,此时利润Z=03、寻找另一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9主元首先确定入基变量再确定出基变量检验数?j81010060101/2012300-21x3x2x5050-30300-5/20Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9令x1=0,x4=0,得x2=6,x3=8,x5=12,即得基可行解X1=(0,6,8,0,12)T此时Z=30σ1=3>0,此解不是最优迭代4、寻找下一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010060101/2012300-21x3x2x5050-30300-5/208-4检验数?j40012/3-1/360101/204100-2/31/3x3x2x1053-42000-1/2-1令x4=0,x5=0,得x1=4,x2=6,x3=4,即X0=(4,6,4,0,0)T?j<0最优解:X=(4,6,4,0,0)T最优值:Z=42小结:单纯形表格法的计算步骤①将线性规划问题化成标准型。
②找出或构造一个m阶单位矩阵作为初始可行基,建立初始单纯形表。
第1章线性规划与单纯形法

一、选择填空1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 二、判断正误1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 三、将下列问题化为标准型1.123412341231324237..2358,0,0,Max Z x x x x x x x x s t x x x x x x x =++++++≤⎧⎪-+=-⎨⎪≥≤⎩符号不限[解] 令'22x x =-,'445x x x =-,在约束1中引入非负的松弛变量6x ,约束2两边同乘以-1。
整理得:''12345''123456'123''12345623()()7..23()58,,,,,0Max Z x x x x x x x x x x x s t x x x x x x x x x =-++-⎧-++-+=⎪-+--=⎨⎪≥⎩即:12345123456123123456237..2358,,,,,0Max Z x x x x x x x x x x x s t x x x x x x x x x =-++--++-+=⎧⎪---=⎨⎪≥⎩2. Min Z=-x 1+5x 2-2x 3x 1 +x 2- x 3 ≤ 61 - x2 +3x3 ≥ 5x 1 + x 2 = 10x1 ≥0, x2 ≤0, x3符号不限[解] 首先,令对变量x3进行处理,令x3 = x’3- x4;再令x’2 = - x2。
然后对目标函数和约束条件进行标准化。
Max Z=x1+5x2+2x3-2x4x1 - x2 - x3+x4+x5 = 61 + x2 +3x3 - 3x4 -x6 = 5x1 - x2 = 10x1, x2, x3, x4, x5, x6≥0四、用图解法求解下列线性规1. min Z= - x1+2x2x1 - x2 ≥-2x1 +2x2 ≤6x1, x2 ≥0[解]根据上图,最优解为X*=(x1, x2)T =(6, 0)T,最优值为-6。
第一章 线性规划及单纯形法1图解2006
简写为:
n
ma或 x(minz) cjxj
j1
jn1aijxj (,)bi (i 1,,m)
xj 0 (j 1,,n)
向量表达形式:
ma或 xm ( izn)CX
n
j 1
Pj
x
j
(, )b
X 0
C(c1,c2,,cn)
x 1
X
x2 xn
a 1 j
Pj
a2j
目标函数 mzi n 28(x1 0 1x 0 2 1x3 1x4)145(x1 02 0 x22 x3)260(x1 0 3x 0 2)373x10 4 0
约束条件
x11 x12 x13 x14 15
xx1132
x13 x14
x14 x22
x21 x23
x22 x31
x23 x32
第一章 线性规划及单纯形法
第一节 线性规划问题及其数学模型
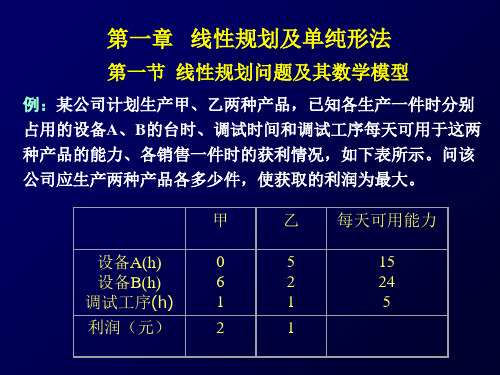
例:某公司计划生产甲、乙两种产品,已知各生产一件时分别 占用的设备A、B的台时、调试时间和调试工序每天可用于这两 种产品的能力、各销售一件时的获利情况,如下表所示。问该 公司应生产两种产品各多少件,使获取的利润为最大。
甲
乙 每天可用能力
设备A(h)
可行域中使目标函数值达到最优的可行解称为最优解。
图解法的步骤:
(1)在平面上建立直角坐标系 (2)图示约束条件,找出可行域 (3)图示目标函数,寻求最优解
线性规划的图解
max z = x1+3x2 s.t. x1+ x2≤6
-x1+2x2≤8 x1 ≥0, x2≥0
x2 6
4
最优解 可行域
-8
0
目标函数等ห้องสมุดไป่ตู้线
运筹学第一章
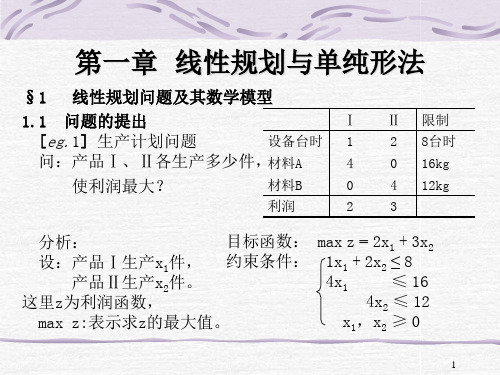
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
x1,x2 ≥ 0
1
[eg.2]污水处理问题
环保要求河水含污低于2‰,河水可自身净化20%。 问:化工厂1、2每天各处理多少污水,使总费用最少?
分析:
500万m3
化工厂1
2万m3 1000元/万m3 化工厂2
(2)不等式(≤,≥) 对于“≤”情况:在“≤”左边加上一个松弛变量(非
负),变为等式; 对于“≥”情况:在“≥”左边减去一个剩余变量(非
负),变为等式。 注意:松弛变量、剩余变量在目标函数中的价值系数为0。
(3)无约束变量 令xk = xk’ - xk”,xk’,xk” ≥ 0,代入即可。
13
[eg.7]将下述问题化为标准型
22
3、人工基
[eg.10]max z = x1 + 2x2 + 3x3
x1 + 3x2 + 2x3 = 3 2x1 + x2 + x3 = 4 x1,x2,x3 ≥ 0 分析: A= 1 3 2 211 ∵ 找不到单位矩阵基 ∴ 引入人工变量为初始基变量(2个)
23
3.2 最优性的检验与解的判别
min z = -x1+2x2-3x3 x1+ x2+ x3 ≤ 7 ① x1- x2+ x3 ≥ 2 ②
-3x1+ x2+2x3 = 5 ③ x1,x2 ≥ 0,x3无约束
解:令x3 = x3’-x3”,x3’,x3” ≥ 0;
①式加上一个松弛变量x4;②式减去一个剩余变量x5; 令z’ = -z
运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习
![运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/83512a81ba0d4a7303763a31.png)
第一章线性规划与单纯形法1.线性规划问题的数学模型(1)一般形式(2)标准型式]2.数学模型化为标准型(1)若目标函数实现最小化,则min z=-max z'(令z'=-z)(2)若约束方程为不等式,则若约束方程为“≤”不等式左端+松驰变量(≥0)=右端若约束方程为“≥”不等式左端-剩余变量(≥0)=右端(3)若存在取值无约束的变量x k(1≤k≤咒),则在标准型中x k=x'k-x"k(其中x k=x',x"k≥0)3.线性规划的解线性规划问题:(1)可行解:满足约束条件②和③的解X=(x1,x2,…,x n)T。
(2)最优解:使目标函数①达到最大值的可行解。
(3)基:设A为约束方程组②的m×n阶系数矩阵,设n>m,其秩为m,B 为矩阵A中的一个m×m阶的满秩子矩阵,则称B为线性规划问题的一个基。
不失一般性,设B中每一个列向量P j(j=1,2,…,m)称为基向量,与基向量PJ对应的变量x j称为基变量。
除基变量以外的变量为非基变量。
(4)基本解:在约束方程组②中,令所有非基变量x m+1=x m+2=…=x n=0,此时方程组②有唯一解X B=(x1,x2,…,x m)T,将此解加上非基变量取0的值有X=(x1,x2,…,x m,0,0…,0)T,称X为线性规划问题的基本解。
(5)基本可行解:满足非负条件③的基本解。
(6)可行基:对应于基本可行解的基。
4.初始基可行解的确定(1)直接从A中观察到存在一个初始可行基。
(2)对所有约束条件是“≤”形式的不等式,可利用化为标准型的方法,在每个约束条件左端加上一个松弛变量,这m个松弛变量就构成一个基变量,则对应的m个向量组成的单位矩阵B就是线性规划问题的一个可行基。
(3)对所有约束条件是“≥”形式的不等式以及等式约束情况,采用人造基的方法。
即对不等式约束的左端减去一个非负的剩余变量后,再加上一个非负的人工变量;对于等式约束的左端再加上一个非负的人工变量。
运筹学基础及应用第五版胡运权第一章

xi 0
aij
aLj
xL 0
i
∴ P1 , P2,······,PL-1, PL+1,······ Pm, Pj 线性无关。
∴ X1 也为基本可行解。
四、最优性检验和解的判别
令
,其中 随基的改变而改变
X1 = (x1 0- a1j ,x2 0- a2j ,···,xm 0- amj ,0,···,,···,0)T
必要性:X非基本可行解 X非凸集顶点 不失一般性,设X=(x1,x2,······,xm,0,0,······,0)T,为非基本可行解, ∵ X为可行解,
证:等价于 X非基本可行解X非凸集顶点
又 X是非基本可行解, ∴ P1,P2,······,Pm线性相关,即有 1P1+2P2+······+mPm=0, 其中1,2,······,m不全为0,两端同乘≠0,得 1P1+2P2+······+mPm=0,······(2)
∵ >0, 1->0 ,当xj=0, 必有yj=zj=0
∴
pjyj =
j=1
n
pjyj=b ······(1)
j=1
r
pjzj =
j=1
n
pjzj=b ······(2)
运筹学第1章线性规划及单纯形法复习题

max (min)
Z = CX
AX ≤ ( = , ≥ ) b X ≥ 0
3、线性规划的标准形式 、
ma0
4、线性规划问题的解 、 (一)求解方法
一 般 有 两种方法 图 解 法 单纯形法 两个变量、 两个变量、直角坐标 三个变量、 三个变量、立体坐标
适用于任意多个变量、 适用于任意多个变量、但需将 一般形式变成标准形式
(二)线性规划问题的解
1、解的概念 可行解:满足约束条件② 的解为可行解。 ⑴ 可行解:满足约束条件②、③的解为可行解。 所有解的集合为可行解的集或可行域。 所有解的集合为可行解的集或可行域。 最优解: 达到最大值的可行解。 ⑵ 最优解:使目标函数①达到最大值的可行解。 ⑶ 基:B是矩阵A中m×m阶非奇异子矩阵 是矩阵A ≠0), ),则 是一个基。 (∣B∣≠0),则B是一个基。
§2 图 解 法
例一、 例一、 max
Z = 2 x 2 x 2 x 4 x
2 2 1
+ 3 x
2
2 x1 + x + 1 4 x1 x1 ≥
≤ 12 ≤ 8 ≤ 16 ≤ 12
2
⑴ ⑵ ⑶ ⑷
2
0, x
≥ 0
max
Z = 2 x1 + 3 x 2 x 2 x
2 2
当xj=0时, 必有 j=zj=0, 因此 时 必有y
∑P x = ∑P y = ∑P z
j =1
r
r
r
r
j
j
j =1
j
j
j =1
j
j
=b
∑(y
j =1
j
− z j ) Pj = 0
运筹学第一章

第一章、 线性规划和单纯形法1.1 线性规划的概念一、线性规划问题的导出1.(引例) 配比问题——用浓度为45%和92%的硫酸配置100t 浓度为80%的硫酸。
取45%和92%的硫酸分别为x1和x2t,则有: 求解二元一次方程组得解。
目的相同,但有5种不同浓度的硫酸可选(30%,45%,73%,85%,92%)会出现什么情况?设取这5种硫酸分别为 x1、x2、x3、x4、x5 t, 则有: ⎩⎨⎧⨯=++++=++++1008.092.085.073.045.03.01005432154321x x x x x x x x x x 请问有多少种配比方案?为什么?哪一种方案最好?假设5种硫酸价格分别为:400,700,1400,1900,2500元/t ,则有:2.生产计划问题如何制定生产计划,使三种产品总利润最大?考虑问题:⎩⎨⎧⨯=+=+1008.092.045.01002121x x x x ⎪⎩⎪⎨⎧=≥⨯=++++=++++++++=5,,2,1,01008.092.085.073.045.03.0100..250019001400700400543215432154321 j x x x x x x x x x x x t s x x x x x MinZ j(1)何为生产计划?(2)总利润如何描述?(3)还要考虑什么因素?(4)有什么需要注意的地方(技巧)?(5)最终得到的数学模型是什么?二、线性规划的定义和数学描述(模型)1.定义:对于求取一组变量xj (j =1,2,......,n),使之既满足线性约束条件,又使具有线性表达式的目标函数取得极大值或极小值的一类最优化问题称为线性规划问题,简称线性规划。
2.配比问题和生产计划问题的线性规划模型的特点:用一组未知变量表示要求的方案,这组未知变量称为决策变量;存在一定的限制条件,且为线性表达式;有一个目标要求(最大化,当然也可以是最小化),目标表示为未知变量的线性表达式,称之为目标函数; 对决策变量有非负要求。
第1章线性规划与单纯形法

线性规划问题的数学模型
7. 线性规划问题的解
线性规划问题
n
max Z cj xj (1) j 1
s.t
n j 1
aij
xj
bi
(i 1, 2,
, m) (2)
x
j
0,
j
1, 2,
, n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
解: Max z = 3x1–5x2’+5x2”–8x3 +7x4 s.t. 2x1–3x2’+3x2”+5x3+6x4+x5= 28 4x1+2x2’-2x2”+3x3-9x4-x6= 39 -6x2’+6x2”-2x3-3x4-x7 = 58 x1 ,x2’,x2”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0
x1 , x2 0, x3无约束
解:(1)因为x3无符号要求 ,即x3取正值也可取负值,标准 型中要求变量非负,所以
用 x3 x3 替换 x3 ,且 x3 , x3 0
20
线性规划问题的数学模型
(2) 第一个约束条件是“≤”号,在“≤”左端加入松驰变量x4, x4≥0,化为等式;
(3) 第二个约束条件是“≥”号,在“≥”左端减去剩余变量x5, x5≥0;
11
线性规划问题的数学模型
3. 建模条件 (1) 优化条件:问题所要达到的目标能用线型函数描述,且 能够用极值 (max 或 min)来表示;
(2) 限定条件:达到目标受到一定的限制,且这些限制能够 用决策变量的线性等式或线性不等式表示;
(3) 选择条件:有多种可选择的方案供决策者选择,以便找 出最优方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
am1x1+am2x2+……+amnxn ≥ (≤, =)bm x1, x2, ……, xn ≥0 (≤, Free)
2019/9/14
运筹学
——经济学院
1
课堂要求
1.要求同学们上课不迟到,不早退,不得 旷课;
2.上课认真听讲,要求每位同学都做笔记; 3.上课不得讲话,看书,玩手机等与课堂
无关的内容;
4.课后要求独自完成作业,不得抄袭或不 做课后作业。
2019/9/14
2
参考资料
1.胡运权主编,运筹学教程(第三版),清华大 学出版社;
设备能力 (小时)
设备A
1.5
1.0
2.4
1.0
2000
设备B
1.0
5.0
1.0
3.5
8000
设备C
1.5
3.0
3.5
1.0
5000
利润(元/件) 5.24 7.30 8.34 4.18
设四种产品的产量分别为x1,x2,x3,x4,总利润为z,线性规划模型为:
max z=5.24x1+7.30x2+8.34x3+4.18x4
2.周华任主编,运筹学解题指导,清华大学出版 社;
3.运筹学习题集(修订版),清华大学出版社; 4.熊伟编著,运筹学,机械工业出版社; 5.运筹学——数据、模型、决策,科学出版社。
2019/9/14
3
教学计划与方法
• 教学计划
以线性规划和运输问题为讲授重点,其 它部分作为选讲内容。
• 教学方法
以授课为主,案例分析与上机演示为辅。 而讲课中主要培养用最优化方法解决实 际问题的能力。
2019/9/14
13
2. 配料问题(Material Blending)
某工厂要用四种合金T1、T2、T3、T4为原料,经熔炼成 为新的不锈钢G。这四种原料含铬(Cr)、锰(Mn)和 镍(Ni)的含量(%),这四种原料的单价以及新的不 锈钢G所要求的Cr、Mn、Ni的最低含量(%)如下表:
Cr Mn Ni 单价(元/公斤)
=10
x12
+x22
=30
x13
+x23 =20
x , 2019/91/114 x12, x13, x21, x22, x23≥0
供应量 (吨)
35
25
60
供应地A1 供应地A2 需求地B1 需求地B2 需求地B3
21
这个问题的最优解表示如下:
运量(吨)
B1
B2
A1
30
A2
10
需求量(吨) 10
30
max z=17x1+72x2+35x3
s.t. 10x1+41x2+20x3≤50 x1,x2,x3≥0 x1,x2,x3为整数
这是一个整数规划问题(Integer Programming)。这 个问题的最优解为:
x1=1件,x2=0件,x3=2件,最高价值z=87元
2019/9/14
17
4. 运输问题(Transportation)
T4
G
Cr
3.21 4.53 2.19 1.76
3.20
Mn
2.04 1.12 3.57 4.33
2.10
Ni
5.82 3.06 4.27 2.73
4.30
单价(元/公斤) 115
97
82
76
设四种原料分别选取x1,x2,x3,x4公斤,总成本为z。
min z=115x1+97x2+82x3+76x4
B3 供应量(吨)
5
35
15
25
20
60
35吨 25吨
2
A1
3 5
4 7
A2 8
B1 10吨 10吨
30吨 B2 30吨
5吨
15吨 B3 20吨
最小总运费为:z=3×30+5×5+4×10+8×15=275元
2019/9/14
22
5. 指派问题(Assignment Problem)
有n项任务由n个人完成,每项任务交给一个人,每人都有一项 任务。由i个人完成j项任务的成本(或效益)为cij。求使总成本 最小(或总效益最大)的分配方案。
T1
3.21 2.04 5.82 115
T2
4.53 1.12 3.06 97
T3
2.19 3.57 4.27 82
T4
1.76 4.33 2.73 76
G
3.20 2.10 4.30
要求配100公斤不锈钢G,并假定在配制过程中没有损耗。
求使得总成本最低的配料方案。
2019/9/14
14
T1
T2
T3
产品甲
设备A 设备B 设备C 利润(元/件)
1.5 1.0 1.5 5.24
产品乙
1.0 5.0 3.0 7.30
产品丙
2.4 1.0 3.5 8.34
产品丁
1.0 3.5 1.0 4.18
设备能力 (小时)
2000 8000 5000
求使得总利润最大的生产计划。
2019/9/14
12
产品甲 产品乙 产品丙 产品丁
s.t. 3.21x1+4.53x2+2.19x3+1.76x4≥320 Cr的含量下限约束
2.04x1+1.12x2+3.57x3+4.33x4≥210 Mn的含量下限约束
5.82x1+3.06x2+4.27x3+2.73x4≥430 Ni的含量下限约束
x1+x2+x3+x4=100
物料平衡约束
x1, x2, x3, x4≥0
B1
B2
B3
A1
x11
x12
x13
A2
x21
x22
x23
2019/9/14
20
运价
(元/吨)
B1
B2
B3
A1
2
3
5
A2
4
7
8
需求量(吨) 10
30
20
min z=2x11+3x12+5x13+4x21+7x22+8x23
s.t. x11+x12+x13
=35
x21+x22+x23 =25
x11
+x21
某种物资从两个供应地A1,A2运往三个需求地B1,B2, B3。各供应地的供应量、各需求地的需求量、每个供应 地到每个需求地每吨物资的运输价格如下表:
运价(元/吨) B1
B2
B3 供应量(吨)
A1
2
3
5
35
A2
4
7
8
25
需求量(吨) 10
30
20
60
求总运费最低的运输方案。
2019/9/14
18
运价
• 运筹学的内容十分广泛,包括线性规划、 整数规划、动态规划、非线性规划、图论 与网络优化、排队论、决策理论、库存理 论等。在本课程中,结合管理学科的特点, 主要介绍线性规划和运输问题。
2019/9/14
7
运筹学的主要内容
线性规划
数
非线性规划
学
整数规划
规
动态规划
划
多目标规划学双层规划科组最优计数问题
x13+x23+x33+x43=1
(7)
x14+x24+x34+x44=1
(8)
李 x31 x32 x33
xij=0,1
赵 x41 x42 x43
化学 x14 x24 x34 x44
2019/9/14
25
最优解为:x14=1,x23=1,x32=1,x41=1,max z=336
即张老师教化学,王老师教语文,李老师教数学,赵老师 教语文。
合 网络优化
内
优 排序问题 化 统筹图
容
对策论
随 排队论
机
优 库存论
2019/9/14
化 决策分析 可靠性分析
8
目录: 第一章 第二章 第三章 第四章 第五章
线性规划及单纯形法 对偶问题 灵敏度分析 线性规划的建模与应用 运输问题
2019/9/14
9
第一章 线性规划
线性规划问题 线性规划模型 线性规划的图解 可行域的性质 线性规划的基本概念 基础解、基础可行解 单纯形表
(元/吨)
B1
B2
B3
供应量 (吨)
A1
2
3
5
35
A2
4
7
8
25
需求量(吨) 10
30
20
60
35吨 25吨
2
A1
3
5
4 7
A2 8
2019/9/14
B1 10吨
B2 30吨
B3 20吨
19
运价
(元/吨)
B1
B2
B3
供应量 (吨)
A1
2
3
5
35
A2
4
7
8
25
需求量(吨) 10
30
20
60
设从两个供应地到三个需求地的运量(吨)如下表:
设:
0 第i个人不从事第j项任务 xij 1 第i个人被指派完成第j项任务
