大学物理(许瑞珍_贾谊明) 第13章答案

合集下载

《物理学基本教程》课后答案第十三章电磁感应

第十三章电磁感应13-1 地球表面的磁感应强度约为5105-⨯T,若将一个电阻Ω5.0,半径为20cm 的金属圆环翻转︒180,则流过该圆环截面的电荷量的最大值为多少?若将该金属圆环放在中子星的表面作同样的翻转,流过圆环截面的最大电荷量又为多少 (中子星表面的磁感应强度为810T)?分析由（13-4）式可知，金属环在翻转中要获得流穿过环截面的感应电量的最大值，应将翻转前金属环面的法线方向置于地磁场方向，则通过环面的磁通量有最大值，翻转后磁通量为最大负值，这样翻转才有最大的磁通量改变，才能产生最大的感应电量．解在地球表面, 最大感应电荷量为RBSR R q 221)(1121==-=ΦΦΦ 5251051.2C 5.02.014.31052--⨯=⨯⨯⨯⨯= C在中子星表面, 最大感应电荷量为RBS R R q 221)(1121==-=ΦΦΦ81002.5⨯= C 13-2半径分别为R 和r 的金属圆环共轴放置，且R >>r ,在大圆环中有恒定电流,而小圆环则以恒定速度沿轴线方向运动,问当小圆环运动到什么位置时,其内部的感应电流为最大?分析本题中载流大圆环半径远大于小圆环的半径，小圆环所围面积内的磁场可视为均匀，其中各点的磁感应强度均近似等于位于大圆环轴线上的小圆环圆心处的值．在真空中恒定电流的磁场一章（11-10）式给出，载流圆环轴线上某点的磁感应强度B 是该点到圆环圆心距离x 的函数，小圆环沿轴线远离大圆环运动时，所围面积的磁通量减小，小圆环中将产生感生电动势和感应电流．应用极值条件可以求出感应电流为最大时小圆环的位置.解如图13-2所示，小圆环所围面积内的磁感应强度近似等于其圆心处的值，由（11-10）式得2/3222)(2x R IR B +=μ 小圆环以恒定的速度t xd d =v 运动到轴线上x 处，圆环中的感生电动势为 2/5222202/3222202/322220i )(3d d )(2d d )(2d d d d d d x R xI R r tx x R r IR x x R r IR t BS t t +=⋅⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛+=-=-=2v πμπμπμΦE 圆环中感生电动势最大时感应电流也为最大值．令0d d i=xE ，得 02)(25)()(d d 227222/5222522=+-+=+--x x R x R x R x x解得2R x ±=，并取2Rx =．计算可得22i 2d d Rx x =E < 0，故小圆环运动到轴线上2R 处时，环中感应电流最大．13-3 一立方体在坐标系中的位置如图13-3所示，它的一边长为1m ，磁感应强度为0.2T 的均匀磁场沿y 轴方向，导体A 、C 和D 沿图中所示的方向以0.5m/s 的速度运动，试求每一导体内的感应电动势．分析与用法拉第电磁感应定律比较，本题用动生电动势的定义式⎰⋅⨯=Li d )(l B v E 计算较简便．从该定义式可以看出，i E 的计算涉及到三个矢量的矢量积和标量积，因此必须先确定)(B ⨯v 的方向，以及导体棒上线元d l 的方向.解对于导体A ，因)//(B v ，则0=⨯B v ， E i = 0对于导体C ，因v 与B 夹角为 45，且 //)(B ⨯v d l ，则⎰⋅︒=⋅⨯=ll B 0i 45sin d )(v l B v E V 1007.7V 1222.05.02-⨯=⨯⨯⨯= 对于导体D ，因B v ⊥，)(B ⨯v 方向与l d 夹角为︒45，︒⋅=⋅⨯=⎰45cos 2d )(20i l B lv l B v E V 1.0V 22122.05.0=⨯⨯⨯⨯= 13-4 一载流长直导线中电流为I ，一矩形线框置于同一平面中，线框以速度v 垂直于导体运动，如图13-4所示.当线框AB 边与导线的距离为d 时，试用如下两种方法求出此时线框内的感应电动势，并标明其方向.（1）用动生电动势定义式；（2）用法拉第电磁感应定律.分析这是一道很典型的求动生电动势题．注意以下几点：长直导线的磁场具有轴对称性，因而矩形框沿垂直于轴线方向运动时，框内将产生动生电动势；线框内的感应电动势大小与运动中矩形框的位置有关；可以用动生电动势定义式和法拉第定律求解；用法拉第定律需先求穿过闭合回路的磁通量. 在线框平面内凡与长直导线距离相等处B 大小相等方向相同，而在垂直长直导线方向B 大小不等，于是计算穿过矩形框的磁通量时，应该取平行于长直导线的细长条面元，面元内各点磁感强度可视为大小相等方向相同，其磁通量等于磁感强度与面积的乘积，再积分计算整个矩形框的磁通量．解1 用动生电动势的定义式计算对于AD 和BC 边，因)(B ⨯v 方向与l d 方向垂直，电动势为零．取AB 边上线元l d 方向从A 到B ，CD 边上线元l d 方向从C 到D ，动生电动势分别为d Ibl d I ABbAB πμππμ2d cos 2d )(000v v-=⋅=⋅⨯=⎰⎰l B v E )(2d )(2d )(000a d Ibl a d ICDbCD +=+=⋅⨯=⎰⎰πμπμv vl B v E)(2)11(200a d d I d a d b I ABCDA +-=-+=πμπμvab v E 其中负号表明电动势的方向为ADCBA ．解2 用法拉第定律计算如图13-4所示，以长直导线为坐标原点取x 轴向右．t 时刻AB 边距长直导线为x . 在框内取宽为x d 的面元x b S d d =，面元法线垂直纸面向里，穿过矩形框的磁通量为xax Ib x x Ib ax x+==⎰+ln2d 200πμπμΦ )(2d d ln d d 2d d 00i a x x aIb t x x a x x Ib t +=⋅⎪⎭⎫ ⎝⎛+-=-=πμπμΦv E 当d x =时矩形框上的电动势为0)(20i >+=a d d aIb πμv E即矩形框电动势i E 的方向为ADCBA ．也可以用楞次定律判定框内电动势的方向为ADCBA 方向.13-5 一长为L 的导体棒CD ，在与一均匀磁场垂直的平面内，绕位于L 处的轴O 以匀角速度ω沿反时针方向旋转，磁场方向如图13-5所示，磁感强度为B ，求导体棒内的感应电动势，并指出哪一端电势较高.分析导体棒在磁场中转动，导体棒切割磁感线，棒中产生感应电动势．如果转轴位于2L 处，棒两端电势相等，与转轴间有电势差．假如用铜盘代替导体棒，盘心与盘边缘便有一定的电势差，分别用导线从盘心和盘边缘接出，就构成一个直流发电机．解在棒上取线元l d 沿CD 方向，则导体棒内的感应电动势为⎰⎰⋅⨯+⋅⨯=+O CDOOD CO l B l B d )(d )(v v E E⎰⎰+=3320d cos d lll Bl l Bl πωω6)32(2)3(2222L B L B L B ωωω-=-= 即棒内感应电动势大小为62L B ω,方向从D 指向C ．CD 两端间的电势差为261L B V V ODCO C D ω-=+=-E E 表明C 点电势较高.13-6 如图13-6，一半径为R 的半圆形导线，保持与一载流长直导线共面，且直径CD 与长直电流垂直，C 端到直电流的距离为d .当半圆导线以匀速度v 平行于长直电流向上运动时,求半圆导线中的感应电动势大小，那一端电势较高？设cm 0.10=d ；.A 0.2;s m 0.2;m 0.15===I R v分析连接直径CD ,与半圆弧导线构成闭合回路CDOC ，设回路顺时针绕行.由于回路匀速地平行长直导线运动，磁通量没有变化，回路中感应电动势为零，则沿回路绕行方向半圆弧导线与直线上的感应电动势大小相等，方向相反．因直径CD 上的感应电动势计算简单，可由此确定半圆弧导线上的感应电动势．解如图13-6，在直径CD 上距长直导线为x 处取线元x d ，方向从D C →，CD 上的动生电动势为1.04.0ln 2d 2d )(04.01.00πμπμI x x I CD CD v v ==⋅⨯=⎰⎰x B v E 0V 1011.1V 4ln 22210467<⨯-=⨯⨯⨯⨯=--ππ故C 点电势高.半圆弧导线上感应电动势与直径CD 上的大小相等为V 1011.16-⨯.13-7如图13-7(a),在通有电流的无限长直导线附近，有一直角三角形线圈ABC 与其共面，并以速度v 垂直于导线运动，求当线圈的A 点距导线为d 时，线圈中的感应电动势的大小及方向．已知θ=∠=ACB b AB ,．分析本题与13-4题相似.要注意的是AC 边与v 有一夹角，BA 边上l d 方向与)(B v ⨯方向垂直，0=AB E .解1 用动生电动势的定义如图13-7(a),取ACBA 为回路绕行方向．对于AC 段，)(B v ⨯方向竖直向上，平行长直导线，在AC 上与A 相距为l 处取线元l d ，方向C A →，动生电动势为⎰⋅+=CAAC l l d Id cos )sin (20θθπμvE⎰+=θθπθμsin 0sin d 2cos b l d l I v db d I +⋅=ln cot 20θπμv方向C A →.对于CB 段，)(B v ⨯方向竖直向上，得θπμοcot )(2b b d ICB⋅+⋅-=v E方向C B →．对于BA 段，)(B v ⨯方向与l d 垂直，则0=BA E ．所以直角三角形线框上电动势大小为)(ln cot 20i bd bd b d I BA CB AC +-+⋅=++=θπμv E E E E 因b d bd b d +>+ln，则0i >E ，表明感应电动势方向为ACBA ．解2 用法拉第定律如图13-7(b),在距直导线x 处取宽为x d 的面元x t x S d cot )(d θv -=，面元法线方向垂直纸面向里．设t 时刻A 点距离长直导线t v ，面元处磁感强度方向垂直纸面向里 ,大小为xIB x πμ20=穿过直角三角形的磁通量为⎰+-=b t t x x t I v v v d )1(cot 20θπμΦ)ln (cot 20tbt t b I v v v +-=θπμ当d t =v 时，应用法拉第电磁感应定律，直角三角形中的感应电动势为)(ln cot 2d d 0i bd bd b d I tdt +-+=-==θπμΦv v E >0 电动势的方向为ACBA .13-8 如图13-8，在水平放置的光滑平行导轨上，放置质量为m 的金属杆,其长度为l ab =,导轨一端由一电阻相连(其他电阻忽略),导轨又处于竖直向下的均匀磁场B 中,当杆以初速度为0v 运动时,求(1)金属杆能够移动的距离;(2)在此过程中电阻R 所放的焦耳热.分析金属杆以0v 的初速度在磁场中向右运动,金属杆与导轨组成的回路中有感应电流,因而金属杆受到向左的安培力作用.在安培力作用下杆的运动速度渐慢,最后为0.速度的变化使安培力为变力.于是本题不能简单地用匀加速直线运动公式aS 22-=v -计算,而应从牛顿第二定律出发建立运动方程后求解．根据能量守恒定律，在此过程中杆的初动能全部转化电阻所发出的焦耳热．解（1）取向右为x 正向，当杆的速度为v ，金属杆ba 上的感应电动势为⎰=⋅⨯=abBl v l B d )(v E感应电流为 RBl R I v==E 方向沿b 到a .在金属杆ba 上取电流元I l d 方向从b 到a ，I B l ⊥d ，安培力B l F ⨯=d d I ，所以作用于杆的安培力沿x 轴的负方向.Rl B B l I F F ab x v22 d -=⋅-==⎰负号表示F 与v 反向．应用牛顿第二定律，得mRl B m F t v v 22d d -== x mRl B t mR l B d d d 2222-=-=v v 设杆的移动距离为d ，由上式分离变量两边积分，有⎰⎰-=022d d v v dx mRl B得 d mRl B 220-=-v 即杆可移动的最大距离为 220l B mR d v =(2)由焦耳热公式, 电阻R 上释放的焦耳热为⎰⎰==t R Rl B t R I Q d d 22222v (1) 又 v v mRl B t 22d d -= 分离变量两边积分,t 时刻有⎰⎰-=t t mR l B 022d d vv 0vv t mRl B 22e0-=v v (2)(2)式代入(1)式,且当∞→t 时0→v ,得⎰⎰∞-=-==222022222221d ed 22v v v m t R l B t R R l B Q t mRl B 即杆从开始运动到停止,其间电阻所放的焦耳热在量值上等于2021v m ．13-9磁场沿x 方向,磁感强度大小为T )6(y -,在yOz 平面内有一矩形线框,在0=t 时刻的位置如图13-9所示,求在以下几种情况下,线框中的感应电动势与t 的函数关系:(1)线框以速度m 2=v 的速度平行于y 轴匀速运动;(2)线框从静止开始,以2s m 2=a 的加速度平行于y 轴运动;(3)线框在yOz 平面内平行于z 轴重复以上两种运动.分析磁场沿x 轴方向，矩形线框沿y 轴运动，所以DC 、BA 边上的电动势为0. 磁感强度是y 的函数，AD 边上的各点B 相等，BC 边上的各点B 相等.此题可以用动生电动势定义式和法拉第定律两种方法求解．不过，对此类既有感生又有动生电动势的题，一般来说先求磁通量，再用法拉第定律求解较易．解1 （1）)(B v ⨯的方向为z 轴负向，DC 、BA 边的感应电动势为0，设AD 边感应电动势为1E ，BC 边的为2E ，方向分别为从D 到A 、从C 到B ，矩形框的总电动势为)]6()6[()(212121i y y l B B l ---=-=-=v v E E E lb v =2.0V 2.05.02=⨯⨯=V 方向为逆时针方向．（2）矩形框作加速运动时，框上的动生电动势为lb y y l B B l v v v =---=-=-=)]6()6[()(212121i E E E其中 at =v 故 2.0i ==a t l bE t 解2 （1）以下均取逆时针方向为回路绕行方向，若0i >E ，则其沿回路绕行方向，反之亦然．穿过矩形框的磁通量为)2(26)2(26d )6(d b t lblb b y lb lb y l y by y +-=+-=-=⋅=⎰⎰+v s B Φ 其中y=vt ．矩形框中的电动势为2.0d d i ==-=bl tv ΦE V （2）取回路逆时针绕行，矩形框作加速运动时穿过框的磁通量为⎰⎰++-=-=⋅=by yb y lblb y l y )2(26d )6(d s B Φ其中 2202121at at t y =+=v即 22622lb labt lb --=Φ 矩形框上的电动势为 t l a b t t2.0d d i ==-=ΦE (3)线框沿z 轴方向运动时，Φ不变，则i E 均为0.13-10 如图13-10所示,在两无限长载流导线组成的平面内,有一固定不动的矩形导体回路.两电流方向相反,若有电流A t I )12(+=,求线圈中的感应电动势的大小和方向.分析在本题中，应用法拉第电磁感应定律求感应电动势有两条途径：分别求出两个直电流在框上产生的感应电动势，再进行叠加；或者，先求出两直电流的合磁感强度，再求磁通量，应用法拉第定律．载流长直导线磁场是不均匀的，欲求磁通量，应该取平行于长直导线的细长条面元，面元内各点磁感强度可视为大小相等方向相同，其磁通量等于磁感强度与面积的乘积，再积分计算整个矩形框的磁通量．因两直电流方向相反，靠近线框的直电流在框上电动势大一些，它的贡献决定了线框上电动势的方向．解框内任一点磁感应强度为)(22120021d d x Ix I B B B -+-=-=πμπμ取逆时针方向为回路绕行方向,如图13-10,在线框上取面元d S ,且d S =h d x ,穿过框的磁通量为x d d x x Ih S B ld d d )11(2d 12011-+-==⎰⎰+πμΦ其中12+=t I ．矩形框上的电动势为)ln (ln 22d d 11220i d l d d l d ht +-+=-=πμΦE )()(ln 12120l d d d l d h ++=πμ 因(l +d 2)d 1<d 2(l +d 1)，得0i <E ，即i E沿顺时针方向. 13-11 如图13-11所示, 均匀磁场与半径为r 的圆线圈垂直 (图中l d 表示绕行回路的正方向).如果磁感强度随时间的变化的规律为τ-t/0e B B =,其中B 0和τ为常量, 试将线圈中的感应电动势表示为时间的函数,并标明方向.分析本题用法拉第定律可方便求解.解回路绕行方向为逆时针, 穿过圆线圈的磁通量为τππΦt B r B r -==e 022τττπτπΦ/02/02e e )1(d d t t B r B r t ---=-= 圆线圈上的电动势为ττπΦ/02ie d d t B r t -=-=E 方向沿回路正方向即逆时针方向.13-12 如图13-12所示，在与均匀磁场垂直的平面内有一折成α角的V 型导线框，其MN 边可以自由滑动，并保持与其它两边接触.今使ON MN ⊥，当t =0时，MN 由O 点出发，以匀速v 平行于ON 滑动，已知磁场随时间的变化规律为2)(2t t B =，求线框中的感应电动势与时间的关系.分析导线在磁场中运动，磁感强度又随时间变化，因而线框中的电动势由动生电动势和感生电动势两部分组成，可以直接求出面积不断变化的回路MONM 任一时刻的磁通量，再应用法拉第电磁感应定律求解．也可以分别计算由于MN 边滑动产生的动生电动势和由于线框中磁感强度随时间变化引起磁通量变化产生的感生电动势．解1 取顺时针方向为回路绕行方向, t 时刻穿过V 型导线框的磁通量为B xl2=Φ 其中 t x v =，αtan x l =，22t B =，应用法拉第电磁感应定律，导线框上的感应电动势为)2(d d d d B xlt t -=-=ΦE ααt a n )t a n 4(d d 3242t t t v v -=-= 负号表明E 与回路绕行方向相反，即沿逆时针方向．解2 由于MN 边滑动产生的动生电动势为⎰==⋅⨯=MN t Bx ααtan 21tan d )(32v v l B v 动E 沿NM 方向．t 时刻回路面积xl S 21=，取逆时针方向为回路绕行方向，回路法向矢量n e 与B 相反，则())2(d d 2d d d d d d 2t t xl t B S BS t t ==--=-=Φ感E =αtan 2132t v总感应电动势为感动E E E +==αtan 32t v 沿逆时针方向．13-13 一导线弯成如图13-13的形状，在均匀磁场中绕轴O O '转动，角速度为1ω.若电路的总电阻为R ，当0=t 时从图示的位置开始转动.（1）当磁感强度B 为常量时；（2）当t B B 20sin ω=时，求导线中的感应电流和感应电动势.解（1）B 为常量，t 时刻穿过线圈的磁通量为t l Bl 112cos ωΦ=，线圈上的感应电动势为t l Bl t1112i sin d d ωωΦ=-=E 线圈上的感应电流为t R l Bl R I 1112i i sin ωω==E(2)t B B 20sin ω=时,t 时刻穿过线圈的磁通量为t l l t B 11220cos sin ωωΦ⋅=线圈上的电动势为sin (d d 212211120i l l B tωωΦ=-=E线圈上的感应电流为)cos cos sin sin (212211120it t t t Rl l B R I i ωωωωωω-==E 13-14 均匀磁场B 被限制在如图13-14所示的圆柱型空间中, B 从0.5T 以0.1T/s 的速率减小,(1)确定涡旋电场电场线的形状和方向并示于图中；(2)求图中半径为r =10cm 的导体回路上各点的涡旋电场场强和回路中的感生电动势；(3)设回路的电阻为Ω2,求其中感应电流的大小；(4)回路中任意两点b a ,间的电势差为多大?(5)如果在回路某点将其切断,两端稍微分开,问此时两端的电势差为多大?分析例题413-讨论了这种在圆柱形空间中随时间改变的均匀磁场所产生的涡旋电场，可以直接利用其结果计算该涡旋电场中的电场强度的大小和方向．解 (1)由例题413-的讨论知，该圆柱形空间中随时间改变的均匀磁场产生涡旋电场，其电场线是圆心在轴线上的一系列同心圆，又因0d d <t B ，该涡旋电场中的电场强度涡E 为同心圆上沿顺时针绕行的切线方向，如图13-14所示．(2)利用例题413-的结果，r = 10cm 的回路上涡旋电场强度大小为V/m 005.0V/m 1.021.0d d 2=⨯==t B r E 涡内回路上的感生电动势为V 1014.3V 1.01.014.3d d d d 322i -⨯=⨯⨯=-=-=tBr t B SπE 方向为顺时针方向．(3)回路中感应电流为 A 1057.1A 21014.333ii --⨯=⨯==R I E (4)根据一段含源电路的欧姆定律，弧⋂b a 上的电势差等于该段导线上电阻引起的电势差减去该圆弧上的感应电动势⋂abE ，即0)(2)(2 2)2(i ii i=-⋅=-=⋅-⋅=-=-⋂⋂⋂⋂⋂⋂E E E E E R Rr ab IR r ab abrab r R I IR V V ab ab b a ππππ(5)断开一个缺口cd 后回路不再闭合，因此回路中无电流，则cd 两点间电势差为V 1014.303i -⨯-=-=-E d c V V由于d c V V <，表明d 点电势高．13-15 在半径为R 的圆柱形空间中,存在着变化的均匀磁场)(t B ,有一长为l 的导体棒放在磁场中,如图13-15(a)所示,设磁场的变化率为t B d d ,(1)用感生电动势定义⎰⋅=ba l E d i 涡E 求棒中的感生电动势；(2)用法拉第电磁感应定律求棒中的感生电动势；(3)若导体棒在图示位置时有一个方向与棒垂直指向O 点、大小为v 的速度，再求棒上的感应电动势．分析这是与上题特征相同的磁场．利用例题413-的结果，涡旋电场线是一系列同心圆，涡E 在圆的切线方向，所以用感生电动势定义计算时应注意ab 棒上各点的涡E 与l d 有一夹角．如果应用电磁感应法拉第定律计算，将ab 棒连接半径Oa ,Ob 构成闭合回路OabO ,考虑到沿半径方向0d =⋅⎰l E 涡，则回路中的感应电动势就等于导体棒中的感应电动势．当导体棒运动时，闭合回路OabO 中的磁通量随时间变化，求出任一时刻t 回路OabO 所围面积的磁通量，便可求解．解 (1)如图13-15(b)所示，在ab 棒上取线元l d ,方向从b a →.该处涡E 在切线方向，大小为tBr d d 2，涡E 与l d 的夹角为θ，且rlR 22)2(cos -=θ，得ab 棒上感应电动势ab E 的方向从b a →，大小为⎰⎰=⋅=b abaab l tBr d cos d d 2d θl E 涡E 0)2(2d d d d d 2)2(02222>-=-=⎰l l R l t B l t B l R(2)连接Ob Oa ,成闭合回路OabO ,设回路逆时针绕行，穿过回路的磁通量为4222l R Bl --=Φ闭合回路OabO 上的感应电动势为42d d d d 22l R l t B t oabo-=-=ΦE因沿半径方向0d =⋅⎰l E 涡，则回路中的感应电动势就等于导体棒中的感应电动势，即42d d 22l R l t B oabo ab -==E E方向从b a →.(3) 如图13-15(c),经t 时间棒向着O 点移动t v ,连接Oa 、Ob 成闭合回路OabO ,设回路逆时针绕行.穿过回路的磁通量为t l R Bl v ---=4222Φ导体棒中的感应电动势为v v 2Bl t l R l t B t oaboab 21)4(2d d d d 2---=-==ΦE E若0>oabo E ,则ab E 从b a →；若0<oabo E ,则ab E 从a b →.13-16 如图13-16(a),均匀磁场被限制在半径为R 的圆柱形空间，磁感强度对时间的变化率0d d >t B ，在圆柱形空间外与磁场垂直的平面内有一导体AB .（1）计算AB 上的感应电动势；（2）B A 、两点间的电势差有多高？（3）在图中表示出B A 、两点的涡旋电场强度.分析磁场局限在圆柱形空间内部，连接OB OA 、，计算穿过三角形OAB ∆的磁通量时，只需计算该三角形所包围的圆柱形空间内扇形面积的磁通量．解1 (1) 如图13-16(a)，连接OB OA 、，穿过OAB ∆的磁通量与穿过扇形的磁通量相等为tBd b l a b R t dbl a b R B d d )arctan (arctan 21d d )arctan(arctan 212i 2-+-=-=-+⋅=ΦΦE（2） 0d d >tB，应用楞次定律判定电动势从B A →，所以B 点的电势高. tBd b l a b R U BA d d )arctan (arctan 212-+= （3）kB kA E E 、都在该点切线方向，且沿逆时针绕行的切线方向.解2 (1) 如图13-16(b),在AB 上取线元l d 方向从A 到B ，到圆心的距离为r ，据(13-7)式,有⎰⎰=⋅=BA BA l tB r R d cos d d 2d 2i θl E 涡E而θθcos d d r l =，AB 上的感生电动势为 )(21cos cos d d d 221202i 21θθθθθθθ+-=⋅-=⎰+R r t B r R E 其中d bl ab-==arctanarctan21θθ，得 tBd b l a b R d d )arctan (arctan 212i-+-=E 13-17截面为矩形的环形螺线管，平均半径为R ，截面边长为b 和c ，螺线管共有N 匝导线，管内充满磁导率为μ的均匀磁介质，如图13-17（a ）所示，试求其自感系数.分析螺绕环的磁感线是以对称中心为圆心的一系列同心圆，每条磁感线都要穿过矩形截面，于是求自感系数的问题归结为求穿过矩形截面的磁通量．由于沿螺绕环半径方向的磁场分布不均匀，需在矩形截面上取面元S d ，算出ϕd ，再积分得ϕ.解如图13-17(b)，在矩形截面上取面元r c S d d =，与螺绕环中心距离为r .由安培环路定理(11-15)式得S d 处的磁感应强度为rNIB πμ2=穿过螺绕环的磁通链为⎰⋅==sS N N d B ϕΦ22ln 2d 22222b a b a Ic N r r Ic N b a b a -+==⎰+-πμπμ 螺绕环的自感系数为22ln 22b a b a c N I L -+==πμΦ13-18 如图13-18, 两平行长直导线，其中心距离为d ，载有等大反向的电流（可以想象它们在相当远的地方汇成单一回路），每根导线的半径均为R ，如果不计导线内部磁通量的贡献，试求单位长度的自感系数.分析两平行长直导线间的磁感应强度为两长直导线在该处磁感应强度之代数和.沿着以下思路解题：先求出两导线间的B ，再求两导线间的磁通量,再求自感系数.解如图13-18,由磁场叠加原理，在两条导线间距左边一根为r 远（R r <）处磁感应强度为)11(20rd r I B -+=πμ取长为l 的一段导线，通过图中阴影部分的磁通量为⎰--+=R d Rr r d r Il d )11(20πμΦRR d Il -=ln 0πμ 长为l 的一段导线的自感系数为RRd l IL l -==ln 0πμΦ单位长导线的自感系数为RR d l L L l -==ln 0πμ 13-19 如图13-19,两圆形线圈共轴放置在一平面内，它们的半径分别为1R 和2R ，21R R >>，匝数分别为1N 和2N ，试求它们之间的互感系数.（大线圈中有电流时，小线圈所在处的磁场可看作是均匀的.）分析题目给出条件21R R >>，2R 线圈与1R 线圈共轴，所以2R 线圈所在处的磁感应强度可视为均匀，且等于1R 线圈圆心处的磁感应强度. 解因21R R >>,当大线圈中有电流1I 时，小线圈所在处各点的磁感应强度近似相等，且等于圆心处的磁感应强度，即1110212R N I B μ=穿过小线圈的磁通链为1221102212212R R N I N N πμϕΦ==互感系数为1222101212R R N N I M πμΦ==13-20 在如图13-20所示的电路中，线圈I 连线上有一长为l 的导线棒CD 可在垂直于均匀磁场B 的平面内左右滑动并保持与线圈I 连线接触，导体棒的速度与棒垂直.设线圈I 和线圈Ⅱ的互感系数为M ，电阻为1R 和2R .分别就以下两种情况求通过线圈I 和线圈Ⅱ的电流：（1）CD 以匀速v 运动；（2）CD 由静止开始以加速度a 运动.分析 CD 边运动，线圈I 中有感应电流. 由于互感,线圈I 中的电流变化将在线圈Ⅱ中产生感应电流.解（1）CD 匀速运动时,线圈I 中的感应电流是常量，为111R lB R I i v ==E 它在线圈Ⅱ中引起的磁通量的变化率为0 d d 21=tΦ 在线圈Ⅱ中引起的互感电动势021=E ，因此线圈Ⅱ中的感应电流为零．（2）CD 加速运动时, 线圈I 中的感应电流为11R BlatI =在线圈Ⅱ中引起的磁通量为at R BlMMI 1121==Φ在线圈Ⅱ中引起的互感电动势为12121 d d R BlMat -=-=ΦE因此线圈Ⅱ中的感应电流为212212R R BlMa R I -==E13-21 如图13-21所示的两个共轴圆形线圈，它们的间距为d ，半径为R 和r ,且r R >>，大线圈中有电流时，小线圈所在处的磁场可看作是均匀的，试求（1）大线圈中的电流t I I ωsin 0=时小线圈中的感应电动势；（2）两线圈的互感系数M ；（3）当小线圈偏转，使得两线圈平面法线的夹角分别为︒︒︒90 60 30、、时，再求M .解 (1)大线圈在小线圈处产生的磁感强度为2/3222021)(2d R R IB +=μ 大线圈电流产生的磁场穿过小线圈的磁通量为232222022121)(2d R r IR S B +==πμΦ大线圈电流变化, 在小线圈中产生的互感电动势为232222002121)(2cos d d d R t R r I t +-=-=ωωπμΦE (1) （2）两电流的互感电动势又可表示为 t MI tIM ωωcos d d 021-=-=E 将(1)式代入上式，得232222021)(2d d d R r R t I M +=-=πμE（3）两线圈平面法向夹角为 30时穿过小线圈的磁通量为2121212330cos ΦΦΦ==' 互感系数 2322220)(43d R r R M +='πμ 夹角为 60时，得 2121212160cos ΦΦΦ==' 2322220)(4d R r R M +='πμ夹角为 90时，得 021='Φ 0='M13-22 试求题13-10中二长直导线组成的回路与矩形框之间的互感系数. 分析在本题中，显然求出长直导线在矩形框处的磁通量，然后求互感系数较容易.解利用习题13-10的结果，两长直导线在矩形线圈处产生的磁通量为)ln (ln 222110d ld d l d Ih +-+=πμΦ 得互感系数为 )()(ln 2)ln (ln 22112022110l d d l d d h d ld d l d h IM ++=+-+==πμπμΦ13-23 两线圈的自感系数分别为1L 和2L ，它们的互感系数为M ，当两线圈串联时，试证它的等效自感系数为M L L L 221±+=，其中的正负号分别是对应图13-23中的两种连接情况．分析两线圈串联后的等效自感系数，应该等于输入端与输出端间自感电动势与回路电流变化率之比．任一线圈两端的感应电动势应等于各自的自感电动势与另一线圈在其上产生的互感电动势的代数和．根据楞次定律，线路顺接如图13-23(a)时，互感电动势与自感电动势方向相同；反接如图13-23(b)时，互感电动势与自感电动势方向相反.假如再拓展考虑两线圈顺并联和反并联的情况.这时流经两线圈的电流分别为1I 和2I ,但互感系数M 不变，且并联后的总电动势12E E E ==.可解出顺并联时M L L M L L L 221221-+-+=,反并联时ML L M L L L 221221++-+=. 解顺连接如图13-23（a ）,设左边的线圈为(1),右边的线圈为(2).根据楞次定律,线圈(1)上的总电动势1E ,应为其上的自感电动势11E 与线圈(2)在线圈(1)上产生的互感电动势12E 之和,有)d d d d (112111tIM t I L +-=+=E E E 同理 )d d d d (221222tI M t I L +-=+=E E E 输入端与输出端间的电动势为tIM L L d d )2(2121++-=+=E E E 两线圈串联顺接时的等效自感系数为M L L tI L 2d d 21++=-=E反连接如图13-23（b ）,根据楞次定律,线圈(1)上的总电动势E 1 ,应为其上的自感电动势E 11与线圈(2)在线圈(1)上产生的互感电动势E 12之差,有)d d d d (112111tIM t I L --=-=E E E同理 )d d d d (221222tI M t I L --=-=E E E 输入端与输出端间的电动势为tIM L L d d )2(2121-+-=+=E E E 两线圈串联反接时的等效自感系数为M L L tI L 2d d 21-+=-=E13-24 在一细线密绕螺线管内填满了某种磁导率为μ（常量）的均匀介质，若该介质的电阻率为ρ，在介质中存在感应电流的情况，由定义tI L d d E-=求该螺线管的自感系数．设螺线管半径为R 、长为l 、总匝数为N ，且R l >>，忽略边缘效应．分析缠绕螺线管的传导电流I 变化时，传导电流要产生自感电动势1E .现螺线管内充满磁导率为μ的磁介质，变化的传导电流在介质中激发感应电流,变化的感应电流也要产生自感电动势2E .总的自感电动势为21E E E +=.由传导电流激发的螺线管内磁场，方向沿轴线，且分布均匀，所以由变化的传导电流激发的感应电流是以轴线为圆心的圆电流.考虑到介质有电阻，感应电流在介质的径向分布不均匀，因而感应电流产生的磁场方向沿轴线，为非均匀磁场，在计算感应电流产生的磁通量时要注意．。

大学物理第13章习题解答

引言概述:大学物理第13章是力学的一个重要章节，主要介绍了质点系和刚体的运动学和动力学问题。

习题作为巩固章节知识和培养解决问题能力的重要手段，对于学生的学习具有重要的意义。

本文将对大学物理第13章的习题进行解答，以帮助读者更好地理解和掌握力学的相关知识。

正文内容:1.质点系的运动学问题1.1相对位矢和质心位矢的关系1.2质心速度的计算方法1.3质心加速度的计算方法1.4相对位矢和质心位矢之间的关系1.5相对位矢和质心位矢的运动规律2.质点系的动力学问题2.1质点间相互作用力的计算方法2.2质点系受到的合外力和合内力的关系2.3质点系统的动量守恒定律2.4质点系的动量定理2.5质点系的冲量和动量变化的关系3.刚体的运动学问题3.1刚体的转动轴和转动角速度的关系3.2刚体的几何中心和质心的关系3.3刚体的角速度和线速度的关系3.4刚体的力矩和角加速度的关系3.5刚体的运动规律和动能的计算方法4.刚体的动力学问题4.1刚体的力矩和合外力的关系4.2刚体的力矩定理和动力学定理的关系4.3刚体的动量矩定理4.4刚体的角动量守恒定律4.5刚体的角动量定理和动能定理的关系5.刚体的平衡问题5.1刚体的平衡条件5.2刚体的平衡方程的推导和应用5.3刚体的平衡条件和力矩定理的关系5.4刚体的平衡问题和静力学问题的区别和联系5.5刚体的平衡问题和静态平衡问题的应用总结:大学物理第13章习题解答了质点系和刚体的运动学和动力学问题，并深入探讨了质点系和刚体的平衡问题。

通过解答这些习题，我们可以更好地理解和掌握力学的相关知识，提高解决问题的能力和方法。

同时，我们也应该注重理论与实际结合，将所学的知识应用到实际问题中，不断提高自己的应用能力和创新能力。

希望读者通过本文的阐述，能够对大学物理第13章有更深入的理解，并能够在学习和解题中取得更好的成绩。

[工学]大学物理第13章

i i i i ( B, n) 90 ( B, n) 90 ( B, n) 90 ( B, n) 90 Bcos ds 0 0 0 0 d d d d 0 若 | | , 0 若, 0 若||, 0 dt dt dt dt 则 i<0 若, 则 i<0 则 >0 则 i>0 i 反向与假定方向相反同向同向
v
共同因素：穿过导体回路的磁通量M发生变化。
d i dt
法拉第电磁感应定律
其中i为回路中的感应电动势（i为回路中载流子提供能量）
注意:
“–”表示感应电动势的方向， i和都是标量，方向只是相对回路的绕行方向而言。如下所示： n n n n B B
静电场E不能为闭合回路运动的电荷提供能量！麦克斯韦引入感应电场的概念非保守场产生电场磁场 Bt 变化的同时
此电场的电力线是闭合的，称为有旋电场—感应电场Ei。
感应电场 E i 的特点： 1）E i 与 E e 一样，对场中的电荷有电场力的作用。 F F qEi Ei q 2） E i 不依赖空间是否有导体存在，只要有 dB 0 ，则就有Ei的存在。 dt 3） E i 是非保守力场， Ei dl 0 。
为正；成钝角时， i 为负。因此，由上式算出的电动势有正负之分， i为正时，表示电动势方向顺着 d l 的方向； i为负时，则表示电动势的方向逆着 d l 的方向。对于闭合回路
i 由上式可以看出，矢积 v B 与 d l 成锐角时，
L
i v B d l
2
1
磁通计原理
与d/dt无关

《大学物理》第13章电磁感应电磁场练习题及答案

《大学物理》第13章电磁感应电磁场练习题及答案练习1一. 选择题1. 一闭合正方形线圈放在均匀磁场中，绕通过其中心且与一边平行的转轴OO′转动，转轴与磁场方向垂直，转动角速度为ω，如图所示．用下述哪一种办法可以使线圈中感应电流的幅值增加到原来的两倍(导线的电阻不能忽略)：( ) A. 把线圈的匝数增加到原来的两倍；B. 把线圈的面积增加到原来的两倍，而形状不变；C. 把线圈切割磁力线的两条边增长到原来的两倍；D. 把线圈的角速度增大到原来的两倍。

2. 将形状完全相同的铜环和木环静止放置，并使通过两环面的磁通量随时间的变化率相等，则不计自感时： ( ) A. 铜环中有感应电动势，木环中无感应电动势； B. 铜环中感应电动势大，木环中感应电动势小； C. 铜环中感应电动势小，木环中感应电动势大； D. 两环中感应电动势相等。

3. 对于位移电流，下列说法中正确的是 ( ) A. 与电荷的定向运动有关； B. 揭示了变化的电场能激发磁场； C. 产生焦耳热； D. 与传导电流一样。

4. 一圆形线圈在均匀磁场中作下列运动时，会产生感应电流的情况是 ( ) A. 沿垂直磁场方向平移；B. 以直径为轴转动，轴跟磁场垂直；C. 沿平行磁场方向平移；D. 以直径为轴转动，轴跟磁场平行。

OB二. 填空题1.如图所示，在一长直导线L中通有电流I，ABCD为一矩形线圈，它与L皆在纸面内，且AD边与L平行：(1) 矩形线圈在纸面内向右移动时，线圈中感应电动势方向为____________；(2) 矩形线圈绕AD边旋转，当BC边已离开纸面正向外运动时，线圈中感应动势的方向为_________________________。

2.引起动生电动势的非静电力是力；引起感生电动势的非静电力是力。

3.∮H⃗∙dlL=I+I d表明磁场强度沿任一闭合回路的线积分等于通过以该回路为边界的任意曲面的；∮E⃗∙dll =−dΦdt的物理意义是变化的磁场产生。

大学物理第十三章课后答案

习题十三13-1 衍射的本质是什么？衍射和干涉有什么联系和区别？答：波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象• 其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生. 而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成.13-2 在夫琅禾费单缝衍射实验中，如果把单缝沿透镜光轴方向平移时，衍射图样是否会跟着移动？若把单缝沿垂直于光轴方向平移时，衍射图样是否会跟着移动？答：把单缝沿透镜光轴方向平移时，衍射图样不会跟着移动. 单缝沿垂直于光轴方向平移时，衍射图样不会跟着移动.13-3 什么叫半波带？单缝衍射中怎样划分半波带？对应于单缝衍射第 3级明条纹和第4级暗条纹，单缝处波面各可分成几个半波带？λ答：半波带由单缝 A 、B 首尾两点向'方向发出的衍射线的光程差用2来划分•对应于第3级明纹和第4级暗纹，单缝处波面可分成 7个和8个半波带. a Sin =(2k • 1) “ =(2 3 ■ 1) “ =7∙.∙由 22 2a Sin -4 ' - 8—213-4 在单缝衍射中，为什么衍射角，愈大(级数愈大)的那些明条纹的亮度愈小？答：因为衍射角「愈大则asin「值愈大，分成的半波带数愈多，每个半波带透过的光通量就愈小，而明条纹的亮度是由一个半波带的光能量决定的，所以亮度减小.13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化？如果此时用公mλasin =(2k 1) (k =1,2,)式 2来测定光的波长，问测出的波长是光在空气中的还是在水中的波长？k ■解：当全部装置浸入水中时，由于水中波长变短，对应asin 「= k ∙ = n ,而空气中为asi n「= k ∙,∙. Si n 「=n Sin ",即「=n :,水中同级衍射角变小，条纹变密.λ如用asin(2k ■ I)2 (k=1,2,…)来测光的波长，则应是光在水中的波长.(因asin‘ 只代表光在水中的波程差)•13-6 在单缝夫琅禾费衍射中，改变下列条件，衍射条纹有何变化 ?(1)缝宽变窄；(2)入射光波长变长；(3)入射平行光由正入射变为斜入射. 解：(1)缝宽变窄，由asin ' =k'知，衍射角「变大，条纹变稀；(2) ,变大，保持a, k不变，则衍射角「亦变大，条纹变稀； (3) 由正入射变为斜入射时，因正入射时asin即=k ∙；斜入射时，a(Sin「-Sin^)^k-,保持a ,'不变，则应有 ^ k或k二：：k •即原来的k 级条纹现为k级.13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似，两者是否矛盾？怎样说明？λ答：不矛盾•单缝衍射暗纹条件为.asin=k' =2k 2 ,是用半波带法分析(子波叠加问题)•相邻两半波带上对应点向'方向发出的光波在屏上会聚点一一相消，而半波带为偶数，故形成暗纹；而双缝干涉明纹条件为dsin a ,描述的是两路相干波叠加问题，其波程差为波长的整数倍，相干加强为明纹.13-8 光栅衍射与单缝衍射有何区别？为何光栅衍射的明条纹特别明亮而暗区很宽？答：光栅衍射是多光束干涉和单缝衍射的总效果. 其明条纹主要取决于多光束干涉.光强与缝数N 2成正比，所以明纹很亮；又因为在相邻明纹间有 (N -1)个暗纹，而一般很大，故实际上在两相邻明纹间形成一片黑暗背景.13-9 试指出当衍射光栅的光栅常数为下述三种情况时，哪些级次的衍射明条纹缺级 ?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.解：由光栅明纹条件和单缝衍射暗纹条件同时满足时，出现缺级.即"(a +b)si n d =±k ?* (k =0,1,2,…) a sin W = ±k 九 (^ = 1,2∙…)a +b * k = k H可知，当 a 时明纹缺级.(1)a∙b =2a 时，k = 2,4,6,•…偶数级缺级；(2) a b =3a 时，k=3,6,9,•…级次缺级；⑶ a ∙b =4a , k=4,8,12,∙∙级次缺级.13-10 若以白光垂直入射光栅，不同波长的光将会有不同的衍射角.问 (1)零级明条纹能否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大？不同波长的光分开程度与什么因素有关？解：(1)零级明纹不会分开不同波长的光. 因为各种波长的光在零级明纹处均各自相干加强. ⑵可见光中红光的衍射角最大，因为由(a' b) sin :护=k ‘，对同一 k 值，衍射角 -'.ο13-11 一单色平行光垂直照射一单缝，若其第三级明条纹位置正好与 6000 A的单色平行光的第二级明条纹位置重合，求前一种单色光的波长. 解：单缝衍射的明纹公式为a sin = (2 k 1)2o当人=6000 A 时 k = 2，='X 时，k = 3 重合时'角相同，所以有5 ■ X6000 =4286 o7Ao13-12 单缝宽0.10mm,透镜焦距为50Cm 用^ =5000 A 的绿光垂直照射单缝•求：(1) 位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少 ?(2)若把此装置浸入水中(n=1.33),中央明条纹的半角宽度又为多少？AλL X = 2 f解：中央明纹的宽度为na-Sin —半角宽度为 na(1)空气中，n=1,所以A5000 汇 10 “J：x =2 0.5厂=5.0 100.10 汉 10ma sin 即=(22 1)-6000=(2 3 ■ 1)1015000 X 10 一 3V - Sin厂=5.0 10 一0.10x10 一rad(2)浸入水中，n=1.33 ,所以有105000 x10一3：^=2 0.50- 3.76 10 _1.33x0.10x10—mI5000 00」° 3V - Sin 3 : 3.7610 一 1.33 X 0.1 X10 一 rad13-13 用橙黄色的平行光垂直照射一宽为 a=0.60mm 的单缝，缝后凸透镜的焦距 f=40.0cm ,观察屏幕上形成的衍射条纹•若屏上离中央明条纹中心 1.40mm 处的P 点为一明条纹；求：（1）入射光的波长；（2）P 点处条纹的级数；（3）从P 点看，对该光波而言，狭缝处的波面可分成几个半波带？X 1.4 J3.5 10 tan f 4002 0.6 3.5 10 2k 1k = 4 得)-4 = 4700o若-3 = 6000 A ,则P 点是第3级明纹;o若-4 =4700 A ,贝U P 点是第4级明纹.a Sin = （2k 亠 1）-⑶由2可知，当k=3时，单缝处的波面可分成2k 1当k=4时，单缝处的波面可分成2kTo13-14用‘氛=5900A 的钠黄光垂直入射到每毫米有500条刻痕的光栅上，问最多能看到第几级明条纹？ 1 a+b = J二o解：500 mm =2.010 mm = 2.010 A由（a ' b ）sin ' = k '知，最多见到的条纹级数ka +b 2.0 汇104k max ==fc3.39∣Z-Qkmax^3所以有5900,即实际见到的最高级次为o 13-15 波长为5000A 的平行单色光垂直照射到每毫米有200条刻痕的光栅上，光栅后的透解：（1）由于P 点是明纹，故有a sin ' = (2k 1)—2 , k =1,2,3 - ■ 2a sin 2k 1X4.2 X10 °2k 1k =3，得 K =6000 mmoA=7个半波带;=9个半波带.<Pmax 对应的max镜焦距为60cm. 求：（1）屏幕上中央明条纹与第一级明条纹的间距；（2）当光线与光栅法线成30°斜入射时，中央明条纹的位移为多少？1a +b = ------ =5.0x10~6解： 200 mm 5.0 10 - m(1)由光栅衍射明纹公式X Sin Φ = tan W =— (a +b) sin 申=k k ,因k =1 ,又fX 1(a +b)所以有f这就是中央明条纹的位移值•o13-16 波长九=6000A 的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在 Sin=0∙20与Sin =0∙30处，第四级缺级.求：(1)光栅常数；(2)光栅上狭缝的宽度;⑶ 在90°> ’ > -90 °范围内，实际呈现的全部级数.解：(1)由(a b) Sin= k，式对应于Sin ：1=0∙2° 与Sin ；：2=0∙30 处满足：-Lo0.20 (a b) =2 6000 10 I. 100.30 (a b) =3 600010得 a ∙ b =6.0 10 * m(2)因第四级缺级，故此须同时满足(a ■ b) Sin = k ■a sin = k ，= 1.5 10 "βk解得取=1 ,得光栅狭缝的最小宽度为 1.5 10 m⑶由(a b) Sin = k ■k 土(a ■ b) Sin λπW =—当 2,对应 k = k m aXa +b .66.0 10 k10λ6000 10500010 210 恥 60 10 一X l5.0 10 -⑵对应中央明纹, 2= 6.0 10 一k = 0 =6 Cm正入射时, (a -b) Sin 斜入射时, (a -b)(sin=0二Sin所以 Sin=0日)=0 即Sin 申±sin 日=0Sinl : tanXCP二 30=1 60 10 2 2=3010m = 30Cm因_4 , _ 8缺级，所以在-9°：：：「：：： 9°范围内实际呈现的全部级数为k = 0, 一1, _2, _3, _5, _6, 一7, _9 共 15 条明条纹（k= 1° 在 k= 9° 处看不到）.o13-17 一双缝，两缝间距为 0.1mm ,每缝宽为0.02mm ,用波长为4800A 的平行单色光垂直入射双缝，双缝后放一焦距为 50cm 的透镜.试求：（1）透镜焦平面上单缝衍射中央明条纹的宽度；（2）单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹？解：（1）中央明纹宽度为（2）由缺级条件a sin = k '■(a - b) sin = k ■0.1k " = 5k ' 0.02 k =1,2,即k=5,10,15,…缺级V -1.221 .22 5000= 30.5 10 D0.2d4f tan v : f v - 50030 .5 10 一 =1.5.∙.爱里斑半径2mm13-19已知天空中两颗星相对于一望远镜的角距离为 4.84 × 10-6rad ,它们都发出波长为o5500A 的光，试问望远镜的口径至少要多大，才能分辨出这两颗星？解：由最小分辨角公式J -1.22 —D5λ5.5j<10D =1.22 — =1 .22- = 13.864.84 10 Cmo13-20已知入射的X 射线束含有从0.95〜1.30A 范围内的各种波长，晶体的晶格常数为 o2.75 A ,当X 射线以45°角入射到晶体时，问对哪些波长的 X 射线能产生强反射？解：由布喇格公式2d Sin=k'_ 2d Sin 申λ = --------得k时满足干涉相长Qo当 k =1 时，& = m 、s in 45=3.89 A2 2.75 sin 45Λ --1.91 ok =2 时，2AI 。

许瑞珍、贾谊明大学物理课后答案(机械工业出版社)

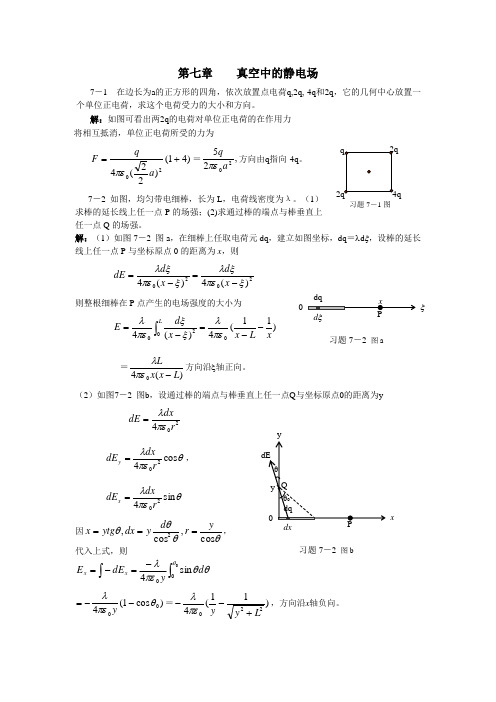
第七章真空中的静电场7－1 在边长为a 的正方形的四角，依次放置点电荷q,2q,-4q 和2q ，它的几何中心放置一个单位正电荷，求这个电荷受力的大小和方向。

解：如图可看出两2q 的电荷对单位正电荷的在作用力将相互抵消，单位正电荷所受的力为)41()22(420+=a q F πε＝,2520aqπε方向由q 指向-4q 。

7－2 如图，均匀带电细棒，长为L ，电荷线密度为λ。

（1）求棒的延长线上任一点P 的场强；(2)求通过棒的端点与棒垂直上任一点Q 的场强。

解：（1）如图7－2 图a ，在细棒上任取电荷元dq ，建立如图坐标，dq ＝λd ξ，设棒的延长线上任一点P 与坐标原点0的距离为x ，则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(4002xL x x d E L--=-=⎰πελξξπελ ＝)(40L x x L-πελ方向沿ξ轴正向。

（2）如图7－2 图b ，设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204r dxdE πελ=θπελcos 420rdxdE y =， θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===，代入上式，则)cos 1(400θπελ--=y＝)11(4220Ly y +--πελ，方向沿x 轴负向。

习题7－1图dq ξd ξ习题7－2 图axθθπελθd y dE E x x ⎰⎰-=-=00sin 4xdx习题7－2 图byθθπελθd y dE E y y ⎰⎰==00cos 400sin 4θπελy =＝2204Ly y L +πελ 7－3 一细棒弯成半径为R 的半圆形，均匀分布有电荷q ，求半圆中心O 处的场强。

解：如图，在半环上任取d l =Rd θ的线元，其上所带的电荷为dq=λRd θ。

《大学物理学》习题解答(第13章稳恒磁场)(1)

第 13 章稳恒磁场
【13.1】如题图所示的几种载流导线，在 O 点的磁感强度各为多少？
(a)
(b) 习题 13－1 图
(c)
【13.1 解】 (a) B 0
I 1 0 I 0 0 ，方向朝里。 4 2R 8R 0 I 。 2R
(b) B
0 I
2R

(c) B
mv eB
2mE k eB
6.71 m 和轨迹可得其向东偏转距离为
x R R 2 y 2 2.98 10 3 m
【13.17 解】利用霍耳元件可以测量磁感强度，设一霍耳元件用金属材料制成，其厚度为 0.15 mm，载流－子数密度为 1024m 3，将霍耳元件放入待测磁场中，测得霍耳电压为 42μV，通过电流为 10 mA。求待测磁场的磁感强度。【13.17 解】由霍耳电压的公式可得 B
B 4
2 0 I 0 I 。 (cos 45 cos135) 4a a
习题 13－2 图
习题 13－3 图
【13.3】以同样的导线联接成如图所示的立方形，在相对的两顶点 A 及 C 上接一电源。试求立方形中心的磁感强度 B 等于多少？【13.3 解】由对称性可知，相对的两条棱在立方体中心产生的磁感强度相等而方向相反，故中心处的磁感强度为零。【13.4】如图所示，半径为 R 的半球上密绕有单层线圈，线圈平面彼此平行。设线圈的总匝数为 N，通过线圈的电流为 I，求球心处 O 的磁感强度。【13.4 解】在半球上距球心 y 处取一个宽度为 Rdθ 的园环，其对球心的张角为 θ，半径为 r＝Rsinθ，包含的电流为 dI
2rB 0, 2rB 0 NI , 2rB 0,

大学物理第二版许瑞珍贾谊明编著课后答案 1-3章汇编

1－7 一人扔石头的最大出手速率为 v＝25m/s，他能击中一个与他的手水平距离 L=50m，
高 h=13m 的目标吗？在此距离上他能击中的最大高度是多少？
解：由运动方程
x
vt
cos
,
y
vt
sin
1 2
gt 2
,消去
t
得轨迹方程
y
xtg
g 2v2
(tg 2
1) x 2
以x＝05.0m ，v＝25ms－1代入后得
l 2 v02t2 (H h)2
dl dt
v02t v02t 2 (H h)2
d 2l dt 2
(H h)2 v02 (H h)2 v02t 2 3/ 2
H v0
h
所以小车移动的速度 v
v02t
(H h)2 v02t 2
图 1-18 习题 1-4 图
小车移动的加速度 a
(H h)2 v02 (H h) 2 v02t 2 3/ 2
z
h 2
t
这是一条空间螺旋线。
在 O xy 平面上的投影为圆心在原点，半径为 R 的圆，螺距为 h
（2） vx
dx dt
R sin t
v
v
2 x
v
2 y
v
2 z
R2
h2 4 2
（3） ax R 2 cost a y R 2 sin t az 0
a
a
2 x
a
2 y
R 2
1－10 飞机以 100m·s-1的速度沿水平直线飞行，在离地面高为 100m时，驾驶员要把物品投到前方某一地面目标处。问：（1）此时目标在飞机下方前多远？（2）投放物品时，驾驶员看目标的视线和水平线成何角度？（3）物品投出 2s后，它的法向加速度和切向加速度各为多少？

《大学物理》第13单元课后答案高等教育出版社

在图面内与界面 P 成某一角度.那么粒子在从磁场中射出前是做半径
8. 一个通有电流 I 的导体,厚度为 D, 横截面积为 S, 放置在磁感应强度为 B 的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示,现测得导体上下面电势差为 V, 则此导体的霍尔系数等于:
(A)
VDS IB
p X X
n=500, 形成有铁芯的螺绕环.当线圈中电流 I 4 A 时,试求: (1) 环内 B 和 H 的大小.[1T, 2000H]
(2) 束缚面电流产生的附加磁感应强度.[0.9975T] 解：根据介质中的安培环路定理：

L
H dl I ， H 2r NI
磁场强度： H
H 2r NI
w.
B
磁场强度： H
0 NI -5 ， B 8 10 T 2r
kh

L
NI ， H 200 A / m ，磁感应强度： 2r
题 12图
da
-5
12. 螺绕环平均周长 l =10cm, 环上线圈 N=200 匝, 线圈中电流 I=100mA,试求:
课
m
NI ， H 2000 A / m 2r
成绩登记号：
学号：
姓名：
单元十三
单元十三：（二）习题课
一、填空、选择: 1. 将同样的n根线焊成立方体,并在其对顶角A, B上接上电源,则立方体框架中的电流在其中心处所产生的磁感应强度等于________0_________.
B I
o. A
S1 a a
( A) 7.96 10 2
(C ) 199 . 10 2
( D) 63.3 10 2

大学物理13章答案

第13章静电场中的导体和电介质13.1一带电量为q ，半径为r A 的金属球A ，与一原先不带电、内外半径分别为r B 和r C 的金属球壳B 同心放置，如图所示，则图中P 点的电场强度如何？若用导线将A 和B 连接起来，则A 球的电势为多少？（设无穷远处电势为零）[解答]过P 点作一个同心球面作为高斯面，尽管金属球壳内侧会感应出异种，但是高斯面内只有电荷q ．根据高斯定理可得 E 4πr 2 = q /ε0，可得P 点的电场强度为204q E r πε=．当金属球壳内侧会感应出异种电荷-q 时，外侧将出现同种电荷q ．用导线将A 和B 连接起来后，正负电荷将中和．A 球是一个等势体，其电势等于球心的电势．A 球的电势是球壳外侧的电荷产生的，这些电荷到球心的距离都是r c ，所以A 球的电势为04c q U r πε=．13.2 同轴电缆是由半径为R 1的导体圆柱和半径为R 2的同轴薄圆筒构成的，其间充满了相对介电常数为εr 的均匀电介质，设沿轴线单位长度上导线的圆筒的带电量分别为+λ和-λ，则通过介质内长为l ，半径为r 的同轴封闭圆柱面的电位移通量为多少？圆柱面上任一点的场强为多少？[解答]介质中的电场强度和电位移是轴对称分布的．在内外半径之间作一个半径为r 、长为l 的圆柱形高斯面，根据介质中的高斯定理，通过圆柱面的电位移通过等于该面包含的自由电荷，即 Φd = q = λl ．设高斯面的侧面为S 0，上下两底面分别为S 1和S 2．通过高斯面的电位移通量为 ⎰⋅=ΦSdD d 012d d d 2S S S rlDπ=⋅+⋅+⋅=⎰⎰⎰D S D S D S ，可得电位移为 D = λ/2πr ，其方向垂直中心轴向外．电场强度为 E = D/ε0εr = λ/2πε0εr r ，方向也垂直中心轴向外．13.3 金属球壳原来带有电量Q ，壳内外半径分别为a 、b ，壳内距球心为r 处有一点电荷q ，求球心o 的电势为多少？ [解答]点电荷q 在内壳上感应出负电荷-q ，不论电荷如何分布，距离球心都为a ．外壳上就有电荷q+Q ，距离图13.3球为b ．球心的电势是所有电荷产生的电势叠加，大小为000111444o q q Q q U r a b πεπεπε-+=++13.4 三块平行金属板A 、B 和C ，面积都是S = 100cm 2，A 、B 相距d 1 = 2mm ，A 、C 相距d 2 = 4mm ，B 、C 接地，A 板带有正电荷q =3×10-8C ，忽略边缘效应．求（1）B 、C 板上的电荷为多少？（2）A 板电势为多少？ [解答](1)设A 的左右两面的电荷面密度分别为σ1和σ2，所带电量分别为σ1S 和q 2 = σ2S ，q 1 = 在B 、C 板上分别感应异号电荷-q 1和-q 2，由电荷守恒得方程q = q 1 + q 2 = σ1S + σ2S ． ① A 、B 间的场强为 E 1 = σ1/ε0， A 、C 间的场强为 E 2 = σ2/ε0．设A 板与B 板的电势差和A 板与C 板的的电势差相等，设为ΔU ，则ΔU = E 1d 1 = E 2d 2， ②即 σ1d 1 = σ2d 2． ③解联立方程①和③得σ1 = qd 2/S (d 1 + d 2)，所以 q 1 = σ1S = qd 2/(d 1+d 2) = 2×10-8(C)；q 2 = q - q 1 = 1×10-8(C)．B 、C 板上的电荷分别为q B = -q 1 = -2×10-8(C)； q C = -q 2 = -1×10-8(C)． (2)两板电势差为ΔU = E 1d 1 = σ1d 1/ε0 = qd 1d 2/ε0S (d 1+d 2)，由于 k = 9×109 = 1/4πε0，所以 ε0 = 10-9/36π，因此 ΔU = 144π = 452.4(V)．由于B 板和C 板的电势为零，所以U A = ΔU = 452.4(V)．13.5 一无限大均匀带电平面A ，带电量为q ，在它的附近放一块与A 平行的金属导体板B ，板B 有一定的厚度，如图所示．则在板B 的两个表面1和2上的感应电荷分别为多少？[解答]由于板B 原来不带电，两边感应出电荷后，由电荷守恒得 0． ①q 1 + q 2 = 虽然两板是无限大的，为了计算的方便，不妨设它们的面积为S ，则面电荷密度分别为σ1 = q 1/S 、σ2 = q 2/S 、σ = q/S ，图13.42 图13.5它们产生的场强大小分别为E 1 = σ1/ε0、E 2 = σ2/ε0、E = σ/ε0．在B 板内部任取一点P ，其场强为零，其中1面产生的场强向右，2面和A 板产生的场强向左，取向右的方向为正，可得E 1 - E 2 – E = 0，即 σ1 - σ2 – σ = 0，或者说 q 1 - q 2 + q = 0． ② 解得电量分别为q 2 = q /2，q 1 = -q 2 = -q /2．13.6 两平行金属板带有等异号电荷，若两板的电势差为120V ，两板间相距为 1.2mm ，忽略边缘效应，求每一个金属板表面的电荷密度各为多少？[解答]由于左板接地，所以σ1 = 0．由于两板之间的电荷相互吸引，右板右面的电荷会全部吸引到右板左面，所以σ4 = 0．由于两板带等量异号的电荷，所以 σ2 = -σ3．两板之间的场强为E = σ3/ε0，而 E = U/d ，所以面电荷密度分别为σ3 = ε0E = ε0U/d = 8.84×10-7(C·m -2)，σ2 = -σ3 = -8.84×10-7(C·m -2)．13.7一球形电容器，内外球壳半径分别为R 1和R 2，球壳与地面及其他物体相距很远．将内球用细导线接地．试证：球面间电容可用公式202214R C R R πε=-表示．（提示：可看作两个球电容器的并联，且地球半径R >>R 2）[一：并联电容法．在外球外面再接一个半径为R 3壳，外壳也接地．内球壳和外球壳之间是容为 104C πε=壳之间也是一个电容器，电容为2023141/1/C R R πε=-．外球壳是一极，由于内球壳和大外球壳都接地，共用一极，所以两个电容并联．当R 3趋于无穷大时，C 2 = 4πε0R 2．并联电容为12120022144R R C C C R R R πεπε=+=+-图13.6202214R R R πε=-．方法二：电容定义法．假设外壳带正电为q ，则内壳将感应电荷q`．内球的电势是两个电荷产生的叠加的结果．由于内球接地，所以其电势为零；由于内球是一个等势体，其球心的电势为0201`044q q R R πεπε+=，因此感应电荷为12`R q q R =-．根据高斯定理可得两球壳之间的场强为122002`44R q q E r R r πεπε==-，负号表示场强方向由外球壳指向内球壳．取外球壳指向内球壳的一条电力线，两球壳之间的电势差为1122d d R R R R U E r=⋅=⎰⎰E l121202()d 4R R R qr R rπε=-⎰1212021202()11()44R q R R q R R R R πεπε-=-=球面间的电容为202214R q C U R R πε==-．13.8球形电容器的内、外半径分别为R 1和R 2，其间一半充满相对介电常量为εr 的均匀电介质，求电容C 为多少？[解答]球形电容器的电容为12012211441/1/R R C R R R R πεπε==--．对于半球来说，由于相对面积减少了一半，所以电容也减少一半：0121212R R C R R πε=-．当电容器中充满介质时，电容为：0122212r R R C R R πεε=-．由于内球是一极，外球是一极，所以两个电容器并联：01212212(1)r R R C C C R R πεε+=+=-．13.9设板面积为S 的平板电容器析板间有两层介质，介电常量分别为ε1和ε2，厚度分别为d 1和d 2，求电容器的电容．[解答]假设在两介质的介面插入一薄导体，可知两个电容器串联，电容分别为 ε1S/d 1和C 2 = ε2S/d 2． C 1 = 总电容的倒数为122112*********d d d d C C C S S S εεεεεε+=+=+=，总电容为122112SC d d εεεε=+．13.10 圆柱形电容器是由半径为R 1的导线和与它同轴的内半径为R 2的导体圆筒构成的，其长为l ，其间充满了介电常量为ε的介质．设沿轴线单位长度导线上的电荷为λ，圆筒的电荷为-λ，略去边缘效应．求：（1）两极的电势差U ；（2）介质中的电场强度E 、电位移D ；（3）电容C ，它是真空时电容的多少倍？ [解答]介质中的电场强度和电位移是轴对称分布的．在内外半径之间作一个半径为r 、长为l 的圆柱形高斯面，侧面为S 0，上下两底面分别为S 1和S 2．通过高斯面的电位移通量为 ⎰⋅=ΦS d S D d12d d d 2S S S rlDπ=⋅+⋅+⋅=⎰⎰⎰D S D S D S ，高斯面包围的自由电荷为 q = λl ，根据介质中的高斯定理 Φd = q ，可得电位为 D = λ/2πr ，方向垂直中心轴向外．电场强度为 E = D/ε = λ/2πεr ，方向也垂直中心轴向外．取一条电力线为积分路径，电势差为21d d d 2R LLRU E r r r λπε=⋅==⎰⎰⎰E l21ln 2R R λπε=．电容为212ln(/)q l C U R R πε==．在真空时的电容为00212ln(/)l q C U R R πε==，所以倍数为C/C 0 = ε/ε0．13.11在半径为R 1的金属球外还有一层半径为R 2的均匀介质，相对介电常量为εr ．设金属球带电Q 0，求：（1）介质层内、外D 、E 、P 的分布；（2）介质层内、外表面的极化电荷面密度．[解答]（1）在介质内，电场强度和电位移以及极化强度是球对称分布的．在内外半径之间作一个半径为r 的球形高斯面，通过高斯面的电位移通量为 Dr S D SSd 24d d π==⋅=Φ⎰⎰S D高斯面包围的自由电荷为q = Q 0，根据介质中的高斯定理 Φd = q ，可得电位为 D = Q 0/4πr 2，方向沿着径向．用矢量表示为D = Q 0r /4πr 3．电场强度为E = D /ε0εr = Q 0r /4πε0εr r 3，方向沿着径向．由于 D = ε0E + P ，所以 P = D - ε0E =031(1)4rQ r επ-r ．在介质之外是真空，真空可当作介电常量εr = 1的介质处理，所以 D = Q 0r /4πr 3，E = Q 0r /4πε0r 3，P = 0．（2）在介质层内靠近金属球处，自由电荷Q 0产生的场为E 0 = Q 0r /4πε0r 3；极化电荷q 1`产生的场强为E` = q 1`r /4πε0r 3；总场强为 E = Q 0r /4πε0εr r 3．由于 E = E 0 + E `，解得极化电荷为`101(1)rq Q ε=-，介质层内表面的极化电荷面密度为``01122111(1)44r Q q R R σπεπ==-．在介质层外表面，极化电荷为``21q q =-，面密度为``02222221(1)44r Q q R R σπεπ==-．13.12 两个电容器电容之比C 1:C 2 = 1:2，把它们串联后接电源上充电，它们的静电能量之比为多少？如果把它们并联后接到电源上充电，它们的静电能之比又是多少？[解答]两个电容器串联后充电，每个电容器带电量是相同的，根据静电能量公式W = Q 2/2C ，得静电能之比为W 1:W 2 = C 2:C 1 = 2:1．两个电容器并联后充电，每个电容器两端的电压是相同的，根据静电能量公式W = CU 2/2，得静电能之比为W 1:W 2 = C 1:C 2 = 1:2．13.13一平行板电容器板面积为S ，板间距离为d ，接在电源上维持其电压为U ．将一块厚度为d 相对介电常量为εr 的均匀介电质板插入电容器的一半空间内，求电容器的静电能为多少？[解答]平行板电容器的电容为C = ε0S/d ，当面积减少一半时，电容为C 1 = ε0S /2d ；另一半插入电介质时，电容为C 2 = ε0εr S /2d ．两个电容器并联，总电容为C = C 1 + C 2 = (1 + εr )ε0S /2d ，静电能为W = CU 2/2 = (1 + εr )ε0SU 2/4d ．13.14 一平行板电容器板面积为S ，板间距离为d ，两板竖直放着．若电容器两板充电到电压为U 时，断开电源，使电容器的一半浸在相对介电常量为εr 的液体中．求：（1）电容器的电容C ；（2）浸入液体后电容器的静电能；（3）极板上的自由电荷面密度．[解答]（1）如前所述，两电容器并联的电容为C = (1 + εr )ε0S /2d ．（2）电容器充电前的电容为C 0 = ε0S/d ，充电后所带电量为 Q = C 0U ．当电容器的一半浸在介质中后，电容虽然改变了，但是电量不变，所以静电能为 W = Q 2/2C = C 02U 2/2C = ε0SU 2/(1 + εr )d ．（3）电容器的一半浸入介质后，真空的一半的电容为 C 1 = ε0S /2d ；介质中的一半的电容为 C 2 = ε0εr S /2d ．设两半的所带自由电荷分别为Q 1和Q 2，则Q 1 + Q 2 = Q ． ①由于C = Q/U ，所以U = Q 1/C 1 = Q 2/C 2． ②解联立方程得01112211/C U C Q Q C C C C ==++，真空中一半电容器的自由电荷面密度为00112122/2(1/)(1)r C U U Q S C C S d εσε===++．同理，介质中一半电容器的自由电荷面密度为0021222(/1)(1)r r C U UC C S d εεσε==++．13.15平行板电容器极板面积为200cm 2，板间距离为 1.0mm ，电容器内有一块1.0mm 厚的玻璃板(εr = 5)．将电容器与300V 的电源相连．求：（1）维持两极板电压不变抽出玻璃板，电容器的能量变化为多少？（2）断开电源维持板上电量不变，抽出玻璃板，电容器能量变化为多少？ [解答]平行板电容器的电容为C 0 = ε0εr S/d ，静电能为 W 0 = C 0U 2/2．玻璃板抽出之后的电容为C = ε0S/d ．（1）保持电压不变抽出玻璃板，静电能为 W = CU 2/2，电能器能量变化为ΔW = W - W 0 = (C - C 0)U 2/2 = (1 - εr )ε0SU 2/2d = -3.18×10-5(J)．（2）充电后所带电量为 Q = C 0U ，保持电量不变抽出玻璃板，静电能为W = Q 2/2C ，电能器能量变化为2000(1)2C C U W W W C ∆=-=-20(1)2r r SU dεεε=-= 1.59×10-4(J)．13.16设圆柱形电容器的内、外圆筒半径分别为a 、b ．试证明电容器能量的一半储存在半径R[解答]设圆柱形电容器电荷线密度为λ，场强为 E = λ/2πε0r ，能量密度为 w = ε0E 2/2，体积元为 d V = 2πrl d r ，能量元为 d W = w d V ．在半径a 到R 的圆柱体储存的能量为20d d 2V V W w V E Vε==⎰⎰2200d ln 44Ral l R r r a λλπεπε==⎰．当R = b 时，能量为210ln4l b W a λπε=；当R =22200ln48l l b W a λλπεπε==，所以W 2 = W 1/2，即电容器能量的一半储存在半径R13.17 两个同轴的圆柱面，长度均为l ，半径分别为a 、b ，柱面之间充满介电常量为ε的电介质（忽略边缘效应）．当这两个导体带有等量异号电荷(±Q )时，求：（1）在半径为r (a < r < b )、厚度为d r 、长度为l 的圆柱薄壳中任一点处，电场能量体密度是多少？整个薄壳层中总能量是多少？（2）电介质中总能量是多少（由积分算出）？（3）由电容器能量公式推算出圆柱形电容器的电容公式？[解答]（1）圆柱形内柱面的电荷线密度为 λ = Q/l ，根据介质是高斯定理，可知电位移为D = λ/2πr = Q /2πrl ，场强为 E = D/ε = Q /2πεrl ，能量密度为w = D ·E /2 = DE /2 = Q 2/8π2εr 2l 2．薄壳的体积为d V = 2πrl d r ，能量为 d W = w d V = Q 2d r /4πεlr ．（2）电介质中总能量为22d d ln44bV aQ Q bW W r lr l a πεπε===⎰⎰．（3）由公式W = Q 2/2C 得电容为222ln(/)Q l C W b a πε==．13.18 两个电容器，分别标明为200PF/500V 和300PF/900V ．把它们串联起来，等效电容多大？如果两端加上1000V 电压，是否会被击穿？[解答]当两个电容串联时，由公式211212111C C C C C C C +=+=，得1212120PFC C C C C ==+．加上U = 1000V 的电压后，带电量为Q = CU ，第一个电容器两端的电压为U 1 = Q/C 1 = CU/C 1 = 600(V)；第二个电容器两端的电压为U 2 = Q/C 2 = CU/C 2 = 400(V)．由此可知：第一个电容器上的电压超过它的耐压值，因此会被击穿；当第一个电容器被击穿后，两极连在一起，全部电压就加在第二个电容器上，因此第二个电容器也接着被击穿．。

大学物理课后题答案13

习题十三13-1 求各图中点P 处磁感应强度的大小和方向。

[解] (a) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB 对于导线1：01=θ，22πθ=，因此aI B πμ401=对于导线2：πθθ==21，因此02=BaIB B B πμ4021p =+= 方向垂直纸面向外。

(b) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB对于导线1：01=θ，22πθ=，因此r I a I B πμπμ44001==，方向垂直纸面向内。

对于导线2：21πθ=，πθ=2，因此rI a I B πμπμ44002==，方向垂直纸面向内。

半圆形导线在P 点产生的磁场方向也是垂直纸面向内，大小为半径相同、电流相同的圆形导线在圆心处产生的磁感应强度的一半，即rIr I B 4221003μμ==，方向垂直纸面向内。

所以，rIr I r I r I r I B B B B 4244400000321p μπμμπμπμ+=++=++=(c) P 点到三角形每条边的距离都是a d 63=o 301=θ，o 1502=θ每条边上的电流在P 点产生的磁感应强度的方向都是垂直纸面向内，大小都是()a I d I B πμπμ23150cos 30cos 400000=-=故P 点总的磁感应强度大小为aIB B πμ29300==方向垂直纸面向内。

13-2 有一螺线管长L ＝20cm ，半径r =2.0cm ，导线中通有强度为I =5.0A 的电流，若在螺线管轴线中点处产生的磁感应强度B ＝310166-⨯.T 的磁场，问该螺线管每单位长度应多少匝?[解] 已知载流螺线管轴线上场强公式为()120cos cos 2θθμ-=nIB由图知： 10410cos 2=θ，10410cos 1-=θ，所以，⎪⎪⎭⎫ ⎝⎛⨯=10410220nI B μ，所以，匝＝1000101040IBn μ=13-3 若输电线在地面上空25m 处，通以电流31081⨯.A 。

大学物理第十三章课后习题答案

第十三章热力学基础13 －1 如图所示，bca 为理想气体绝热过程，b1a 和b2a 是任意过程，则上述两过程中气体作功与吸收热量的情况是( )(A) b1a 过程放热，作负功；b2a 过程放热，作负功(B) b1a 过程吸热，作负功；b2a 过程放热，作负功(C) b1a 过程吸热，作正功；b2a 过程吸热，作负功(D) b1a 过程放热，作正功；b2a 过程吸热，作正功分析与解 bca ，b1a 和b2a 均是外界压缩系统，由⎰=V p W d 知系统经这三个过程均作负功，因而(C)、(D)不对.理想气体的内能是温度的单值函数，因此三个过程初末态内能变化相等，设为ΔE .对绝热过程bca ，由热力学第一定律知ΔE ＝－W bca .另外，由图可知：｜W b2a ｜＞｜W bca ｜＞｜W b1a ｜，则W b2a ＜W bca ＜W b1a .对b1a 过程：Q ＝ΔE ＋W b1a ＞ΔE ＋W bca ＝0 是吸热过程.而对b2a 过程：Q ＝ΔE ＋W b2a ＜ΔE ＋W bca ＝0 是放热过程.可见(A)不对，正确的是(B).13 －2 如图，一定量的理想气体，由平衡态A 变到平衡态B ，且它们的压强相等，即p A ＝p B ,请问在状态A 和状态B 之间，气体无论经过的是什么过程，气体必然( )(A) 对外作正功 (B) 内能增加(C) 从外界吸热 (D) 向外界放热分析与解由p －V 图可知，p A V A ＜p B V B ，即知T A ＜T B ，则对一定量理想气体必有E B ＞E A .即气体由状态A 变化到状态B,内能必增加.而作功、热传递是过程量，将与具体过程有关.所以(A)、(C)、(D)不是必然结果，只有(B)正确.13 －3 两个相同的刚性容器，一个盛有氢气，一个盛氦气(均视为刚性分子理想气体).开始时它们的压强和温度都相同，现将3J 热量传给氦气，使之升高到一定的温度.若使氢气也升高同样的温度，则应向氢气传递热量为( )(A) 6J (B) 3 J (C) 5 J (D) 10 J分析与解当容器体积不变，即为等体过程时系统不作功，根据热力学第一定律Q ＝ΔE ＋W ，有Q ＝ΔE .而由理想气体内能公式T R i M m E Δ2Δ=，可知欲使氢气和氦气升高相同温度，须传递的热量 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=e e e 222e 2H H H H H H H H /:i M m i M m Q Q .再由理想气体物态方程pV ＝mM RT ，初始时，氢气和氦气是具有相同的温度、压强和体积，因而物质的量相同，则3/5/:e 2e 2H H H H ==i i Q Q .因此正确答案为(C).13 －4 有人想像了四个理想气体的循环过程，则在理论上可以实现的为( )分析与解由绝热过程方程pVγ＝常量，以及等温过程方程pV＝常量，可知绝热线比等温线要陡，所以(A)过程不对，(B)、(C)过程中都有两条绝热线相交于一点，这是不可能的.而且(B)过程的循环表明系统从单一热源吸热且不引起外界变化，使之全部变成有用功，违反了热力学第二定律.因此只有(D)正确.13 －5一台工作于温度分别为327 ℃和27 ℃的高温热源与低温源之间的卡诺热机，每经历一个循环吸热2 000 J，则对外作功()(A) 2 000J(B) 1 000J(C) 4 000J(D) 500J分析与解热机循环效率η＝W/Q吸，对卡诺机，其循环效率又可表为：η＝1－T2 /T1，则由W /Q吸＝1 －T2 /T1可求答案.正确答案为(B).13 －6根据热力学第二定律()(A) 自然界中的一切自发过程都是不可逆的(B) 不可逆过程就是不能向相反方向进行的过程(C) 热量可以从高温物体传到低温物体，但不能从低温物体传到高温物体(D) 任何过程总是沿着熵增加的方向进行分析与解对选项(B)：不可逆过程应是指在不引起其他变化的条件下，不能使逆过程重复正过程的每一状态，或者虽然重复但必然会引起其他变化的过程.对选项(C)：应是热量不可能从低温物体自动传到高温物体而不引起外界的变化.对选项(D)：缺少了在孤立系统中这一前提条件.只有选项(A)正确. 13 －7 位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布，它高979m.如果在水下落的过程中，重力对它所作的功中有50％转换为热量使水温升高，求水由瀑布顶部落到底部而产生的温差.( 水的比热容c 为4.18×103 J·kg－1·K －1 ) 分析取质量为m 的水作为研究对象，水从瀑布顶部下落到底部过程中重力作功W ＝mgh ，按题意，被水吸收的热量Q ＝0.5W ，则水吸收热量后升高的温度可由Q ＝mc ΔT 求得.解由上述分析得mc ΔT ＝0.5mgh水下落后升高的温度ΔT ＝0.5gh /c ＝1.15K13 －8 如图所示，一定量的空气，开始在状态A ，其压强为2.0×105Pa ，体积为2.0 ×10－3m 3 ，沿直线AB 变化到状态B 后，压强变为1.0 ×105Pa ，体积变为3.0 ×10－3m 3 ，求此过程中气体所作的功.分析理想气体作功的表达式为()⎰=V V p W d .功的数值就等于p －V 图中过程曲线下所对应的面积.解 S ABCD ＝1/2(BC ＋AD)×CD故 W ＝150 J13 －9 汽缸内储有2.0mol 的空气，温度为27 ℃，若维持压强不变，而使空气的体积膨胀到原体积的3s 倍，求空气膨胀时所作的功.分析本题是等压膨胀过程，气体作功()1221d V V p V p W V V -==⎰，其中压强p 可通过物态方程求得.解根据物态方程11RT pV v =,汽缸内气体的压强11/V RT p v = ，则作功为 ()()J 1097.92/31112112⨯==-=-=RT V V V RT V V p W v v13 －10 一定量的空气，吸收了1.71×103J 的热量，并保持在1.0 ×105Pa 下膨胀，体积从1.0×10－2m 3 增加到1.5×10－2m 3 ，问空气对外作了多少功？它的内能改变了多少？分析由于气体作等压膨胀，气体作功可直接由W ＝p (V 2 －V 1 )求得.取该空气为系统，根据热力学第一定律Q ＝ΔE ＋W 可确定它的内能变化.在计算过程中要注意热量、功、内能的正负取值.解该空气等压膨胀，对外作功为W ＝p (V 2－V 1 )＝5.0 ×102J其内能的改变为Q ＝ΔE ＋W ＝1.21 ×103J13 －11 0.1kg 的水蒸气自120 ℃加热升温到140℃，问(1) 在等体过程中；(2) 在等压过程中，各吸收了多少热量？根据实验测定，已知水蒸气的摩尔定压热容C p,m ＝36.21J·mol -1·K -1，摩尔定容热容C V,m ＝27.82J·mol -1·K -1. 分析由量热学知热量的计算公式为T C Q m Δv =.按热力学第一定律，在等体过程中，T C E Q ΔΔm V,V v ==；在等压过程中， T C E V p Q ΔΔd m p,p v =+=⎰.解 (1) 在等体过程中吸收的热量为J 101.3ΔΔ3m V,V ⨯===T C Mm E Q (2) 在等压过程中吸收的热量为 ()J 100.4Δd 312m p,p ⨯=-=+=⎰T T C M m E V p Q 13 －12 如图所示，在绝热壁的汽缸内盛有1mol 的氮气，活塞外为大气，氮气的压强为1.51 ×105 Pa ，活塞面积为0.02m 2 .从汽缸底部加热，使活塞缓慢上升了0.5m.问(1) 气体经历了什么过程？ (2) 汽缸中的气体吸收了多少热量？ (根据实验测定，已知氮气的摩尔定压热容C p ，m ＝29.12J·mol －1·K －1，摩尔定容热容C V,m ＝20.80J·mol -1·K -1 )分析因活塞可以自由移动，活塞对气体的作用力始终为大气压力和活塞重力之和.容器内气体压强将保持不变.对等压过程，吸热T C Q Δm p,p v =.ΔT 可由理想气体物态方程求出.解 (1) 由分析可知气体经历了等压膨胀过程.(2) 吸热T C Q Δm p,p v =.其中ν ＝1 mol ，C p,m ＝29.12Ｊ·mol －1·Ｋ－1.由理想气体物态方程pV ＝νRT ，得ΔT ＝(p 2V 2 －p 1 V 1 )/R ＝p(V 2 －V 1 )/R ＝p· S· Δl /R则 J 105.293m p,p ⨯==pS ΔSΔl C Q13 －13 一压强为1.0 ×105Pa,体积为1.0×10－3m 3的氧气自0℃加热到100 ℃.问：(1) 当压强不变时，需要多少热量?当体积不变时，需要多少热量?(2) 在等压或等体过程中各作了多少功?分析 (1) 求Q p 和Q V 的方法与题13-11相同.(2) 求过程的作功通常有两个途径.① 利用公式()V V p W d ⎰=；② 利用热力学第一定律去求解.在本题中，热量Q 已求出，而内能变化可由()12m V,V ΔT T C E Q -==v 得到.从而可求得功W .解根据题给初态条件得氧气的物质的量为mol 1041.4/2111-⨯===RT V p Mm v 氧气的摩尔定压热容R C 27m p,=，摩尔定容热容R C 25m V,=. (1) 求Q p 、Q V等压过程氧气(系统)吸热()J 1.128Δd 12m p,p =-=+=⎰T T C E V p Q v等体过程氧气(系统)吸热()J 5.91Δ12m V,V =-==T T C E Q v(2) 按分析中的两种方法求作功值解1 ① 利用公式()V V p W d ⎰=求解.在等压过程中，T R Mm V p W d d d ==，则得 J 6.36d d 21p ===⎰⎰T T T R Mm W W 而在等体过程中，因气体的体积不变，故作功为()0d V ==⎰V V p W② 利用热力学第一定律Q ＝ΔE ＋W 求解.氧气的内能变化为()J 5.91Δ12m V,V =-==T T C Mm E Q 由于在(1) 中已求出Q p 与Q V ，则由热力学第一定律可得在等压过程、等体过程中所作的功分别为J 6.36Δp p =-=E Q W0ΔV V =-=E Q W13 －14 如图所示，系统从状态A 沿ABC 变化到状态C 的过程中，外界有326J 的热量传递给系统，同时系统对外作功126J.当系统从状态C 沿另一曲线CA 返回到状态A 时，外界对系统作功为52J ，则此过程中系统是吸热还是放热？传递热量是多少？分析已知系统从状态C 到状态A ，外界对系统作功为W CA ，如果再能知道此过程中内能的变化ΔE AC ，则由热力学第一定律即可求得该过程中系统传递的热量Q CA .由于理想气体的内能是状态(温度)的函数，利用题中给出的ABC 过程吸热、作功的情况，由热力学第一定律即可求得由A 至C 过程中系统内能的变化ΔE AC ，而ΔE AC ＝－ΔE AC ，故可求得Q CA .解系统经ABC 过程所吸收的热量及对外所作的功分别为Q ABC ＝326J ， W ABC ＝126J则由热力学第一定律可得由A 到C 过程中系统内能的增量ΔE AC ＝Q ABC －W ABC ＝200J由此可得从C 到A ，系统内能的增量为ΔE CA ＝－200J从C 到A ，系统所吸收的热量为Q CA ＝ΔE CA ＋W CA ＝－252J式中负号表示系统向外界放热252 J.这里要说明的是由于CA 是一未知过程，上述求出的放热是过程的总效果，而对其中每一微小过程来讲并不一定都是放热.13 －15 如图所示，一定量的理想气体经历ACB 过程时吸热700J ，则经历ACBDA 过程时吸热又为多少？分析从图中可见ACBDA 过程是一个循环过程.由于理想气体系统经历一个循环的内能变化为零，故根据热力学第一定律，循环系统净吸热即为外界对系统所作的净功.为了求得该循环过程中所作的功，可将ACBDA 循环过程分成ACB 、BD 及DA 三个过程讨论.其中BD 及DA 分别为等体和等压过程，过程中所作的功按定义很容易求得；而ACB 过程中所作的功可根据上题同样的方法利用热力学第一定律去求.解由图中数据有p A V A ＝p B V B ,则A 、B 两状态温度相同，故ACB 过程内能的变化ΔE CAB ＝0，由热力学第一定律可得系统对外界作功W CAB ＝Q CAB －ΔE CAB ＝Q CAB ＝700J在等体过程BD 及等压过程DA 中气体作功分别为()⎰==0d BD V V p W()⎰-=-==J 1200d 12A DA V V P V p W则在循环过程ACBDA 中系统所作的总功为J 500DA BD ACB -=++=W W W W负号表示外界对系统作功.由热力学第一定律可得，系统在循环中吸收的总热量为J 500-==W Q负号表示在此过程中，热量传递的总效果为放热.13 －16 在温度不是很低的情况下，许多物质的摩尔定压热容都可以用下式表示2m p,2--+=cT bT a C式中a 、b 和c 是常量，T 是热力学温度.求：(1) 在恒定压强下，1 mol 物质的温度从T 1升高到T 2时需要的热量；(2) 在温度T 1 和T 2 之间的平均摩尔热容；(3) 对镁这种物质来说，若C p ，m 的单位为J·mol －1·K －1，则a ＝25.7J·mol -1·Ｋ-1 ，b ＝3.13 ×10-3J·mol -1·Ｋ-2，c ＝3.27 ×105J·mol －1·K.计算镁在300Ｋ时的摩尔定压热容C p,m ，以及在200Ｋ和400Ｋ之间C p,m 的平均值. 分析由题目知摩尔定压热容C p,m 随温度变化的函数关系，则根据积分式⎰=21d m p,p T T T C Q 即可求得在恒定压强下，1mol 物质从T 1 升高到T 2所吸收的热量Qp .故温度在T 1 至T 2之间的平均摩尔热容()12p m p,/T T Q C -=. 解 (1) 11 mol 物质从T 1 升高到T 2时吸热为()()()()11122122122m p,p d 2d 21----+-+-=-+==⎰⎰T T c T T b T T a T cT bT a T C Q T T (2) 在T 1 和T 2 间的平均摩尔热容为()()21212p m p,//T T c T T a T T Q C -+=-=(3) 镁在T ＝300 K 时的摩尔定压热容为-1-12m p,K mol J 9.232⋅⋅=-+=-cT bT a C镁在200 K 和400 K 之间C p ，m 的平均值为()-1-12112m p,K mol J 5.23/⋅⋅=-+=T T c T T a C13 －17 空气由压强为1.52×105 Pa ，体积为5.0×10－3m 3 ，等温膨胀到压强为1.01×105 Pa ，然后再经等压压缩到原来的体积.试计算空气所作的功. 解空气在等温膨胀过程中所作的功为()()2111121T /ln /ln p p V p V V RT Mm W == 空气在等压压缩过程中所作的功为()⎰-==12d V V p V p W利用等温过程关系p 1 V 1 ＝p 2 V 2 ，则空气在整个过程中所作的功为()J 7.55/ln 11122111=-+=+=V p V p p p V p W W W T p13 －18 如图所示，使1mol 氧气(1) 由A 等温地变到B ；(2) 由A 等体地变到C ，再由C 等压地变到B.试分别计算氧气所作的功和吸收的热量.分析从p －V 图(也称示功图)上可以看出，氧气在AB 与ACB 两个过程中所作的功是不同的，其大小可通过()V V p W d ⎰=求出.考虑到内能是状态的函数，其变化值与过程无关，所以这两个不同过程的内能变化是相同的，而且因初、末状态温度相同T A ＝T B ，故ΔE ＝0，利用热力学第一定律Q ＝W ＋ΔE ，可求出每一过程所吸收的热量.解 (1) 沿AB 作等温膨胀的过程中，系统作功()()J 1077.2/ln /ln 31⨯===A B B A A B AB V V V p V V RT Mm W 由分析可知在等温过程中，氧气吸收的热量为Q AB ＝W AB ＝2.77 ×103Ｊ (2) 沿A 到C 再到B 的过程中系统作功和吸热分别为W ACB ＝W AC ＋W CB ＝W CB ＝p C (V B －V C )＝2.0×103ＪQ ACB ＝W A CB ＝2.0×103 Ｊ13 －19 将体积为1.0 ×10-4m 3 、压强为1.01×105Pa 的氢气绝热压缩，使其体积变为2.0 ×10-5 m 3 ，求压缩过程中气体所作的功.(氢气的摩尔定压热容与摩尔定容热容比值γ＝1.41)分析可采用题13－13 中气体作功的两种计算方法.(1) 气体作功可由积分V p W d ⎰=求解，其中函数p (V )可通过绝热过程方程pV C γ= 得出.(2)因为过程是绝热的，故Q ＝0，因此，有W ＝－ΔE ；而系统内能的变化可由系统的始末状态求出.解根据上述分析，这里采用方法(1)求解,方法(2)留给读者试解.设p 、V 分别为绝热过程中任一状态的压强和体积，则由γγpV V p =11得 γγV V p p -=11氢气绝热压缩作功为J 0.231d d 121211121-=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-===⎰⎰-V V V V γp V V V p V p W V V γγ 13 －20 试验用的火炮炮筒长为3.66 m ，内膛直径为0.152 m ，炮弹质量为45.4kg ，击发后火药爆燃完全时炮弹已被推行0.98 m ，速度为311 m·s -1 ，这时膛内气体压强为2.43×108Pa.设此后膛内气体做绝热膨胀，直到炮弹出口.求(1) 在这一绝热膨胀过程中气体对炮弹作功多少？设摩尔定压热容与摩尔定容热容比值为 1.2γ=.(2) 炮弹的出口速度(忽略摩擦).分析 (1) 气体绝热膨胀作功可由公式1d 2211--==⎰γV p V p V p W 计算.由题中条件可知绝热膨胀前后气体的体积V 1和V 2，因此只要通过绝热过程方程γγV p V p 2211=求出绝热膨胀后气体的压强就可求出作功值.(2) 在忽略摩擦的情况下，可认为气体所作的功全部用来增加炮弹的动能.由此可得到炮弹速度.解由题设l ＝3.66 m,D ＝0.152 m ，m ＝45.4 kg ，l 1＝0.98 m ，v 1＝311 m·s -1 ，p 1 ＝2.43×108Pa ，γ＝1.2.(1) 炮弹出口时气体压强为()()Pa 1000.5//7112112⨯===γγl l p V V p p 气体作功J 1000.54π11d 6222112211⨯=--=--==⎰D γl p l p γV p V p V p W (2) 根据分析2122121v v m m W -=，则 -121s m 563⋅=+=v 2W/m v13 －21 1mol 氢气在温度为300Ｋ，体积为0.025m 3 的状态下，经过(1)等压膨胀，(2)等温膨胀，(3)绝热膨胀.气体的体积都变为原来的两倍.试分别计算这三种过程中氢气对外作的功以及吸收的热量.分析这三个过程是教材中重点讨论的过程.在p －V 图上，它们的过程曲线如图所示.由图可知过程(1 ) 作功最多，过程( 3 ) 作功最少.温度T B ＞T C ＞T D ，而过程(3) 是绝热过程，因此过程(1)和(2)均吸热，且过程(1)吸热多.具体计算时只需直接代有关公式即可.解 (1) 等压膨胀()()J 1049.23⨯==-=-=A A B AA AB A p RT V V V RT V V p W v()J 1073.8273,,⨯===-=+=A A m p A B m p p p T R T C T T C E ΔW Q v v (2) 等温膨胀 J 1073.12ln /3⨯===A A RT V W C T vRTlnV对等温过程ΔE ＝0，所以J 1073.13⨯==T T W Q(3) 绝热膨胀T D ＝T A (V A ／V D )γ－1＝300 ×(0.5)0.4＝227.4Ｋ对绝热过程a 0Q =，则有 ()()J 1051.125Δ3,⨯=-=-=-=D A D A m V a T T R T T C E W v 13 －22 绝热汽缸被一不导热的隔板均分成体积相等的A 、B 两室，隔板可无摩擦地平移，如图所示.A 、B 中各有1mol 氮气，它们的温度都是T0 ，体积都是V0 .现用A 室中的电热丝对气体加热，平衡后A 室体积为B 室的两倍，试求(1) 此时A 、B 两室气体的温度；(2) A 中气体吸收的热量.分析 (1) B 室中气体经历的是一个绝热压缩过程，遵循绝热方程TVγ－1 ＝常数，由此可求出B 中气体的末态温度TB .又由于A 、B 两室中隔板可无摩擦平移，故A 、B 两室等压.则由物态方程pV A ＝νRT A 和pV B ＝νRT B 可知T A ＝2T B .(2) 欲求A 室中气体吸收的热量，我们可以有两种方法.方法一：视A 、B 为整体，那么系统(汽缸)对外不作功，吸收的热量等于系统内能的增量.即QA ＝ΔE A ＋ΔE B .方法二：A 室吸热一方面提高其内能ΔE A ，另外对“外界”B 室作功WA.而对B 室而言，由于是绝热的，“外界” 对它作的功就全部用于提高系统的内能ΔEB .因而在数值上W A ＝ΔE B .同样得到Q A ＝ΔE A ＋ΔE B . 解设平衡后A 、B 中气体的温度、体积分别为T A ，T B 和V A ，V B .而由分析知压强p A ＝p B ＝p .由题已知⎩⎨⎧=+=022V V V V V B A B A ，得⎩⎨⎧==3/23/400V V V V B A (1) 根据分析，对B 室有B γB γT V T V 1010--=得 ()0010176.1/T T V V T γB B ==-；0353.2T T T B A ==(2) ()()0007.312525ΔΔT T T R T T R E E Q B A A A A =-+-=+= 13－23 0.32 kg 的氧气作如图所示的ABCDA 循环，V 2 ＝2V 1 ,T 1＝300Ｋ，T 2＝200Ｋ,求循环效率.分析该循环是正循环.循环效率可根据定义式η＝W /Q 来求出，其中W 表示一个循环过程系统作的净功，Q 为循环过程系统吸收的总热量.解根据分析，因AB 、CD 为等温过程，循环过程中系统作的净功为()()()J 1076.5/ln /ln 32121211⨯=-==+=V V T T R M m V V RT Mm W W W CD AB由于吸热过程仅在等温膨胀(对应于AB 段)和等体升压(对应于DA 段)中发生,而等温过程中ΔE ＝0,则AB AB W Q =.等体升压过程中W ＝0，则DA DA E Q Δ=,所以，循环过程中系统吸热的总量为()()()()J 1081.325/ln /ln Δ42112121,121⨯=-+=-+=+=+=T T R M m V V RT Mm T T C M m V V RT Mm E W Q Q Q m V DAAB DA AB 由此得到该循环的效率为 %15/==Q W η13 －24 图(ａ)是某单原子理想气体循环过程的V －T 图，图中V C ＝2V A .试问：(1) 图中所示循环是代表制冷机还是热机？ (2) 如是正循环(热机循环)，求出其循环效率.分析以正、逆循环来区分热机和制冷机是针对p －V 图中循环曲线行进方向而言的.因此，对图(ａ)中的循环进行分析时，一般要先将其转换为p －V 图.转换方法主要是通过找每一过程的特殊点，并利用理想气体物态方程来完成.由图(ａ)可以看出，BC 为等体降温过程，CA 为等温压缩过程；而对AB 过程的分析，可以依据图中直线过原点来判别.其直线方程为V ＝CT ，C 为常数.将其与理想气体物态方程pV ＝m/MRT 比较可知该过程为等压膨胀过程(注意：如果直线不过原点，就不是等压过程).这样，就可得出p －V 图中的过程曲线，并可判别是正循环(热机循环)还是逆循环(制冷机循环)，再参考题13－23的方法求出循环效率.解 (1) 根据分析，将V －T 图转换为相应的p －V 图，如图(ｂ)所示.图中曲线行进方向是正循环，即为热机循环.(2) 根据得到的p －V 图可知，AB 为等压膨胀过程，为吸热过程.BC 为等体降压过程，CA 为等温压缩过程，均为放热过程.故系统在循环过程中吸收和放出的热量分别为()A B m p T T C M m Q -=,1 ()()A C A A B m V V V RT Mm T T C M m Q /ln ,2+-= CA 为等温线，有T A ＝T C ；AB 为等压线，且因V C ＝2V A ，则有T A ＝T B /2.对单原子理想气体，其摩尔定压热容C p ，m ＝5R/2，摩尔定容热容C V ，m ＝3R/2.故循环效率为()()3/125/2ln 2312/5/2ln 321/112=+-=⎥⎦⎤⎢⎣⎡+-=-=A A A T T T Q Q η 13 －25 一卡诺热机的低温热源温度为7℃，效率为40％，若要将其效率提高到50％，问高温热源的温度需提高多少？解设高温热源的温度分别为1T '、1T '',则有12/1T T η'-='， 12/1T T η''-=''其中T 2 为低温热源温度.由上述两式可得高温热源需提高的温度为K 3.931111Δ211=⎪⎪⎭⎫ ⎝⎛'--''-='-''=T ηηT T T 13 －26 一定量的理想气体，经历如图所示的循环过程.其中AB 和CD 是等压过程，BC 和DA 是绝热过程.已知B 点温度T B ＝T 1,C 点温度T C ＝T 2.(1) 证明该热机的效率η＝1－T 2/T 1 ，(2) 这个循环是卡诺循环吗？分析首先分析判断循环中各过程的吸热、放热情况.BC 和DA 是绝热过程，故Q BC 、Q DA 均为零；而AB 为等压膨胀过程(吸热)、CD 为等压压缩过程(放热)，这两个过程所吸收和放出的热量均可由相关的温度表示.再利用绝热和等压的过程方程，建立四点温度之间的联系，最终可得到求证的形式. 证 (1) 根据分析可知 ()()⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=---=---=-=B A C D B C A B D CA B m p C D m p AB CD T T T T T T T T T T T T C MT T C M m Q Q η1/11111,, (1) 与求证的结果比较，只需证得BA C D T T T T = .为此，对AB 、CD 、BC 、DA 分别列出过程方程如下V A /T A ＝V B /T B (2)V C /T C ＝V D /T D (3) C γC B γB T V T V 11--= (4)A γA D γD T V T V 11--= (5)联立求解上述各式，可证得η＝1－T C /T B ＝1－T 2/T 1(2) 虽然该循环效率的表达式与卡诺循环相似，但并不是卡诺循环.其原因是：① 卡诺循环是由两条绝热线和两条等温线构成,而这个循环则与卡诺循环不同；② 式中T 1、T 2的含意不同，本题中T 1、T 2只是温度变化中两特定点的温度，不是两等温热源的恒定温度.13 －27 一小型热电厂内，一台利用地热发电的热机工作于温度为227℃的地下热源和温度为27℃的地表之间.假定该热机每小时能从地下热源获取1.8 ×1011Ｊ的热量.试从理论上计算其最大功率为多少？分析热机必须工作在最高的循环效率时，才能获取最大的功率.由卡诺定理可知，在高温热源T 1和低温热源T 2之间工作的可逆卡诺热机的效率最高，其效率为η＝1－T 2/T 1 .由于已知热机在确定的时间内吸取的热量，故由效率与功率的关系式Q pt Q W η//==，可得此条件下的最大功率.解根据分析，热机获得的最大功率为()-1712s J 100.2//1/⋅⨯=-==t Q T T t Q ηp13 －28 有一以理想气体为工作物质的热机，其循环如图所示，试证明热()()1/1/12121---=p p V V γη 分析该热机由三个过程组成，图中AB 是绝热过程，BC 是等压压缩过程，CA 是等体升压过程.其中CA 过程系统吸热，BC 过程系统放热.本题可从效率定义CA BC Q Q Q Q η/1/112-=-=出发,利用热力学第一定律和等体、等压方程以及γ＝C p,m 桙C V,m 的关系来证明.证该热机循环的效率为CA BC Q Q Q Q η/1/112-=-=其中Q BC ＝m /M C p,m (T C －T B )，Q CA ＝m/M C V,m (T A －T C )，则上式可写为1/1/11---=---=C A CB C A B C T T T T γT T T T γη 在等压过程BC 和等体过程CA 中分别有T B /V 1 ＝T C /V 2,T A /P 1 ＝T C /P 2,代入上式得()()1/1/12121---=p p V V γη 13 －29 如图所示为理想的狄赛尔(Diesel)内燃机循环过程,它由两绝热线AB 、CD 和等压线BC 及等体线DA 组成.试证此内燃机的效率为()()()1//1/12312123---=-V V V V γV V ηγγ证求证方法与题13－28相似.由于该循环仅在DA 过程中放热、BC 过程中吸热，则热机效率为 ()()BC AD B C m p A D m V BCDA T T T T γT T C M T T C M m Q Q η---=---=-=111/1,, (1) 在绝热过程AB 中，有1211--=γB γA V T V T ，即()121//-=γA B V V T T (2)在等压过程BC 中，有23//V T V T B C =，即23//V V T T B C = (3)再利用绝热过程CD,得1311--=γC γD V T V T (4)解上述各式，可证得()()()1//1/12312123---=-V V V V γV V ηγγ 13 －30 如图所示，将两部卡诺热机连接起来，使从一个热机输出的热量，输入到另一个热机中去.设第一个热机工作在温度为T 1和T 2的两热源之间，其效率为η1 ，而第二个热机工作在温度为T 2 和T 3 的两热源之间，其效率为η2.如组合热机的总效率以η＝(W 1 ＋W 2 )/Q 1 表示.试证总效率表达式为η＝(1 －η1 )η2 ＋η1 或 η＝1 －T 3/T 1分析按效率定义，两热机单独的效率分别为η1＝W 1 /Q 1和η2＝W 2 /Q 2，其中W 1 ＝Q 1－Q 2 ，W 2 ＝Q 2－Q 3 .第一个等式的证明可采用两种方法：(1) 从等式右侧出发，将η1 、η2 的上述表达式代入，即可得证.读者可以一试.(2) 从等式左侧的组合热机效率η＝(W 1 ＋W 2 )/Q 1出发，利用η1、η2的表达式，即可证明.由于卡诺热机的效率只取决于两热源的温度，故只需分别将两个卡诺热机的效率表达式η1＝1－T 2 /T 1 和η2＝1－T 3 /T 2 代入第一个等式，即可得到第二个等式.证按分析中所述方法(2) 求证.因η1＝W 1 /Q 1 、η2＝W 2 /Q 2 ，则组合热机效率12211211121Q Q ηηQ W Q W Q W W η+=+=+= (1) 以Q 2 ＝Q 1－W 1 代入式(1) ，可证得η＝η1 ＋η2 (1－η1 ) (2) 将η1＝1－T 2 /T 1 和η2＝1－T 3 /T 2代入式(2)，亦可证得η＝1－T 2 /T 1 ＋(1－T 3 /T 2 )T 2 /T 1 ＝1－T 3 /T 113 －31 在夏季，假定室外温度恒定为37℃，启动空调使室内温度始终保持在17 ℃.如果每天有2.51 ×108 J 的热量通过热传导等方式自室外流入室内，则空调一天耗电多少？ (设该空调制冷机的制冷系数为同条件下的卡诺制冷机制冷系数的60％)分析耗电量的单位为kW·h ，1kW·h ＝3.6 ×106J.图示是空调的工作过程示意图.因为卡诺制冷机的制冷系数为212T T T e k -=，其中T 1为高温热源温度(室外环境温度)，T 2为低温热源温度(室内温度).所以，空调的制冷系数为e ＝e k · 60％＝0.6 T 2/( T 1 －T 2 )另一方面，由制冷系数的定义，有e ＝Q 2 /(Q 1 －Q 2 )其中Q 1为空调传递给高温热源的热量，即空调向室外排放的总热量；Q 2是空调从房间内吸取的总热量.若Q ′为室外传进室内的热量，则在热平衡时Q 2＝Q ′.由此，就可以求出空调的耗电作功总值W ＝Q 1－Q 2 .解根据上述分析，空调的制冷系数为7.8%60212=-=T T T e在室内温度恒定时，有Q 2＝Q ′.由e ＝Q 2 /(Q 1－Q 2 )可得空调运行一天所耗电功W ＝Q 1－Q 2＝Q 2/e ＝Q ′/e ＝2.89×107＝8.0 kW·h13 －32 一定量的理想气体进行如图所示的逆向斯特林循环(回热式制冷机中的工作循环)，其中1→2为等温(T 1 )压缩过程，3→4为等温(T 2 )膨胀过程，其他两过程为等体过程.求证此循环的制冷系数和逆向卡诺循环制冷系数相等.(这一循环是回热式制冷机中的工作循环，具有较好的制冷效果.4→1过程从热库吸收的热量在2→3过程中又放回给了热库，故均不计入循环系数计算.)证明 1→2 过程气体放热2111lnV V RT Q v = 3→4 过程气体吸热 2122ln V V RT Q v = 则制冷系数 e ＝Q 2 /(Q 1－Q 2 )= T 2/( T 1－T 2 ).与逆向卡诺循环的制冷系数相同.13 －33 物质的量为ν的理想气体，其摩尔定容热容C V,m ＝3R/2，从状态A(p A ，V A ，T A )分别经如图所示的ADB 过程和ACB 过程，到达状态B(p B ，V B ，T B ).试问在这两个过程中气体的熵变各为多少？图中AD 为等温线.分析熵是热力学的状态函数，状态A 与B 之间的熵变ΔSAB 不会因路径的不同而改变.此外，ADB 与ACB 过程均由两个子过程组成.总的熵变应等于各子过程熵变之和，即DB AD AB S S S ΔΔΔ+=或CB AC AB S S S ΔΔΔ+=.解 (1) ADB 过程的熵变为()()D B p,m A D B D D A T BD P D A T DBAD AB T T C V V T T C T W T Q T Q S S S /ln /ln /d /d /d /d ΔΔΔm p,v vR v +=+=+=+=⎰⎰⎰⎰ (1)在等温过程AD 中，有T D ＝T A ；等压过程DB 中，有V B /T B ＝V D /T D ；而C p ，m ＝C V ，m ＋R ，故式(1)可改写为()()()()A B A B A B p,m A B B D ADB V T V V V T C V T V T S /ln 23/ln /ln /ln ΔvR vR v vR +=+=(2) ACB 过程的熵变为()()C B V,m A C p,m CB AC BA ACB T TC V T C S S Q/T S /ln /ln ΔΔd Δv v +=+==⎰ (2)利用V C ＝V B 、p C ＝p A 、T C /V C ＝T A /V A 及T B /p B ＝T C /p C ，则式(2)可写为()()()()()()()A B A B A A B B V,m A B A B A B V,m ACB V T V V V p V p C V V p p V V R C S /ln 23/ln /ln /ln /ln /ln ΔvR vR v vR v v +=+=++=通过上述计算可看出，虽然ADB 及ACB 两过程不同，但熵变相同.因此，在计算熵变时，可选取比较容易计算的途径进行.13 －34 有一体积为2.0 ×10-2m 3的绝热容器，用一隔板将其分为两部分，如图所示.开始时在左边(体积V 1 ＝5.0 ×10-3m 3)一侧充有1mol 理想气体，右边一侧为真空.现打开隔板让气体自由膨胀而充满整个容器，求熵变.分析在求解本题时，要注意⎰=BA T Q S d Δ 的适用条件.在绝热自由膨胀过程中，d Q ＝0，若仍运用上式计算熵变，必然有ΔS ＝0.显然，这是错误的结果.由于熵是状态的单值函数，当初态与末态不同时，熵变不应为零.出现上述错误的原因就是忽视了公式的适用条件. ⎰=BA T Q S d Δ 只适用于可逆过程，而自由膨胀过程是不可逆的.因此，在求解不可逆过程的熵变时，通常需要在初态与末态之间设计一个可逆过程，然后再按可逆过程熵变的积分式进行计算.在选取可逆过程时，尽量使其积分便于计算.解根据上述分析，在本题中因初末态时气体的体积V 1 、V 2 均已知，且温度相同，故可选一可逆等温过程.在等温过程中，d Q ＝d W ＝p d V ，而VRT M m p =，则熵变为 ()1-12K J 52.11/ln d 1d d Δ12⋅=====⎰⎰⎰V V R M m V V R M m T V p T Q S V V。

大学物理13章习题详细答案

习题1313-3．如习题13-3图所示，把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ，平行放置。

设两板面积都是S ，板间距为d ，忽略边缘效应，求：(1)板B 不接地时，两板间的电势差。

(2)板B 接地时，两板间的电势差。

[解] (1)两带电平板导体相向面上电量大小相等符号相反，而相背面上电量大小相等符号相同，因此当板B 不接地，电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时，在B 板上感应出负电荷，电荷分布为故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε== B A-Q/2Q/2Q/2Q/2A B -QQ13-4 两块靠近的平行金属板间原为真空。

使两板分别带上面电荷密度为σ0的等量异号电荷，这时两板间电压为U 0=300V 。

保持两板上电量不变，将板间空间一半如图习题13-4图所示充以相对电容率为εr =5的电介质，试求（1）金属板间有电介质部分和无电介质部分的E,D 和板上的自由电荷密度σ；（2）金属板间电压变为多少？电介质上下表面束缚电荷面密度多大？13-5．如习题13-5图所示，三个无限长的同轴导体圆柱面A 、B 和C ，半径分别为R A 、R B 、R C 。

圆柱面B 上带电荷，A 和C 都接地。

求B 的内表面上线电荷密度λ1和外表面上线电荷密度λ2之比值λ1/λ2。

[解] 由A 、C 接地 BC BA U U = 由高斯定理知 r E 01I 2πελ-=rE 02II 2πελ= AB 0101I BA ln 2d 2d ABA BR Rr r U R R R R πελπελ=-==⎰⎰r E IIIB C 0202II BC ln 2d 2d CB CBR R r r U R R R R πελπελ===⎰⎰r EBC 02A B 01ln 2ln 2R R R R πελπελ= 因此 AB BC 21ln :ln:R R R R =λλ13-6．如习题13-6图所示，一厚度为d 的无限大均匀带电导体板，单位面积上两表面带电量之和为σ。

普通物理学第13章习题答案

13-14
13-22 13-30 13-38
13-15
13-23 13-31 13-39
13-13
13-24 13-32 13-40
结束
习题总目录
13-1 AB和BC两段导线，其长均为10 cm,在B处相接成300角，若使导线在均匀磁场中以速度v =1.5m/s运动，方向如图，磁场方向垂直纸面向内，磁感应强度为B = 2.5×10-2 T。问A、C 两端之间的电势差为多少？哪一端电势高。
× A ×
× ×
× C ×
× ×
× ×× 1
×
×
×
×
o1
×
× B
×
v× 2
×
×
×
×
×
×
×
×
× D
o2
×
×
B×
×
×
×
8 4 I= = =1(A) R R 4 4 1 R R´= = × 4 =2(W) 2 2
结束目录
(2) UA + eAB I R´ = UB UBA = eAB I R´ =8-2=6(V) UDC = eCD + I R´ =4+2=6(V) (3) Δ UO1O2 =0
0 0 0 0 0
结束目录
13-6 如图所示，导线AB在导线架上以速度 v 向右滑动。已知导线AB 的长为50 cm, v =4.0m/s, R = 0.20 W,磁感应强度B =0.50T，方向垂直回路平面。试求：（1）AB运动时所产生的动生电动势；（2）电阻R上所 × × × × × × × × A 消耗的功率 × × × × × × × × （3）磁场作用在 × × × × × × × × B R AB上的力。 × × × × × × ×v ×

大学物理课后习题及答案第13章

第13章光学一选择题*13-1 在水中的鱼看来，水面上和岸上的所有景物，都出现在一倒立圆锥里，其顶角为（）(A)48.8(B)41.2(C)97.6(D)82.4解：选(C)。

利用折射定律，当入射角为1=90i 时，由折射定律1122sin sin n i n i = ，其中空气折射率11n =，水折射率2 1.33n =，代入数据，得折射角2=48.8i ，因此倒立圆锥顶角为22=97.6i 。

*13-2 一远视眼的近点在1 m 处，要看清楚眼前10 cm 处的物体，应配戴的眼镜是（）(A)焦距为10 cm 的凸透镜 (B)焦距为10 cm 的凹透镜 (C)焦距为11 cm 的凸透镜 (D)焦距为11 cm 的凹透镜解：选(C)。

利用公式111's s f+=，根据教材上约定的正负号法则，'1m s =-，0.1m s =，代入得焦距0.11m =11cm f =，因为0f >，所以为凸透镜。

13-3 在双缝干涉实验中，若单色光源S 到两缝S 1、S 2距离相等，则观察屏上中央明纹位于图中O 处，现将光源S 向下移动到图13-3中的S ′位置，则[ ] (A) 中央明纹向上移动，且条纹间距增大(B) 中央明纹向上移动，且条纹间距不变(C) 中央明纹向下移动，且条纹间距增大 (D) 中央明纹向下移动，且条纹间距不变解：选(B)。

光源S 由两缝S 1、S 2到O 处的光程差为零，对应中央明纹；当习题13-3图向下移动至S ′时，S ′到S 1的光程增加，S ′到S 2的光程减少，为了保持光程差为零，S 1到屏的光程要减少，S 2到屏的光程要增加，即中央明纹对应位置要向上移动；条纹间距dD x λ=∆，由于波长λ、双缝间距d 和双缝所在平面到屏幕的距离D 都不变，所以条纹间距不变。

13-4 用平行单色光垂直照射在单缝上时，可观察夫琅禾费衍射。

若屏上点P 处为第二级暗纹，则相应的单缝波阵面可分成的半波带数目为[ ](A) 3个 (B) 4个 (C) 5个 (D) 6个解：选(B)。

大学物理课后答案第十三章

第十三章几何光学一、基本要求1. 了解光的直线传播定律，光的折射和反射定律及全反射定律。

2. 理解光在平面上的反射和折射成像。

3. 理解光在球面上的反射和折射，掌握在近轴条件下，球面反射成像的物像公式'111s s f +=及球面折射成像的物像公式1221'n n n n s s R-+=，并掌握横向放大率，理解符号法则。

4. 理解薄透镜逐次成像法，掌握薄透镜成像的高斯公式'111s s f+=及磨镜者公式'12111(1)()L f f n R R ==--，掌握透镜的像的横向放大率，会计算一些简单问题。

5. 了解显微镜和放大镜的工作原理及放大倍数。

二、基本内容1. 几何光学的基本定律（1）光的直线传播定律光在均匀介质中沿直线传播。

（2）光的反射和折射定律反射定律 '11i i =折射定律 1122s i n s i n n i n i =（3）光的独立传播定律光在不太强时，传播过程中与其它光束相遇时，各光束相互不受影响，不改变传播方向，各自独立传播。

2. 全反射定律21arcsinc n i n = 其中，c i 为全反射临界角，2n 为折射空间的折射率，1n 为入射空间的折射率。

3. 光在单球面上的反射近轴成像（1）球面反射近轴物像公式 '111s s f +=，其中2Rf =（R 是单球面的曲率半径），s 是物距，'s 是像距。

（2）符号约定法则a 球面的曲率半径R ：若曲率中心C 与出射光在反射面的同侧时，半径R 为正，反之为负。

b 物距s ：当物与入射光在反射面的同侧时，物距s 为正，反之为负。

s 为正时，物为实物，s 为负时，物为虚物。

c 像距's ：当像与出射光在反射面的同侧时，像距's 为正，反之为负。

's 为正时，像是实像，'s 为负时，像是虚像。

（3）横向放大率 's sβ=-注意：当0β>，像是正立的；0β<，像是倒立的。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十三章振动13－1 一质点按如下规律沿x 轴作简谐振动：x = 0.1 cos (8πt +2π/3 ) (SI)，求此振动的周期、振幅、初相、速度最大值和加速度最大值。

解：周期T = 2π/ ω= 0.25 s振幅A = 0.1m初相位φ= 2π/ 3V may = ωA = 0.8πm / s ( = 2.5 m / s )a may = ω2 A = 6.4π2m / s ( = 63 m / s 2)13－2 一质量为0.02kg 的质点作谐振动，其运动方程为：x = 0.60 cos( 5 t -π/2) (SI)。

求：（1）质点的初速度；（2）质点在正向最大位移一半处所受的力。

解：（1） )( )25sin(0.3 SI t dt dx v π--==0.3 20x m ma x ω-== （2） 2x m ma F ω-==5.13.052.0,2/ 2N F A x -=⨯⨯-==时13－3 如本题图所示，有一水平弹簧振子，弹簧的倔强系数k = 24N/m ，重物的质量m = 6kg ，重物静止在平衡位置上，设以一水平恒力F = 10 N 向左作用于物体（不计摩擦），使之由平衡位置向左运动了0.05m ，此时撤去力F ，当重物运动到左方最远位置时开始计时，求物体的运动方程。

解：设物体的运动方程为：x = A c o s (ωt +φ)恒外力所做的功即为弹簧振子的能量：F ⨯ 0.05 = 0.5 J当物体运动到左方最位置时，弹簧的最大弹性势能为0.5J ，即：1 /2 kA 2 = 0.5 J ∴A = 0.204 mA 即振幅ω2 = k / m = 4 ( r a d / s )2ω= 2 r a d / s按题目所述时刻计时，初相为φ= π∴ 物体运动方程为x = 0.204 c o s (2 t +π) ( SI ) 13－4 一水平放置的弹簧系一小球。

已知球经平衡位置向右运动时，v =100cm ⋅s -1，周期T =1.0s ，求再经过1/3秒时间，小球的动能是原来的多少倍？弹簧的质量不计。

解：设小球的速度方程为：v = v m c o s (2π/ Tt +φ)以经平衡位置的时刻为t = 0根据题意t = o 时 v = v 0 = 100 c m s -1 且 v ＞0∴v m = v 0 φ= 0小球的动能 E k0 = 1 / 2 m v 02过1 / 3秒后，速度为 v = v 0 c o s ( 2π/T. 1/ 3) = - V 0 / 2x 习题13－3图动能 E k = 1 / 2 m v 2 = 1 / 2m 1/ 4v 02∴E K / E 0 = 1/ 4 动能是原来的1/ 4倍13－5 设地球是一个半径为R 的均匀球体，密度 ρ = 5.5 ⨯ 103 kg ⋅m －3。

现假定沿直径凿一条隧道。

若有一质量为m 的质点在此隧道内做无摩擦运动。

（1）证明此质点的运动是简谐振动；（2）计算其周期。

解：（l ）取图所示坐标。

当质量为m 的质点位于x 处时，它受地球的引力为2x x mm G F -=式中G 为引力常量，m x 是以x 为半径的球体质量，即3/43x x m πρ=。

令3/4Gm k πρ=，则质点受力kx Gmx F -=-=3/4πρ因此，质点作简谐运动。

（2）质点振动的周期为s 1007.5/3/23⨯===ρππG k m T13－6 在一块平板下装有弹簧，平板上放一质量为1.0kg 的重物。

现使平板沿竖直方向做上下简谐运动，周期为0.50s ，振幅为2.0⨯10－2 m 。

求：（1）平板到最低点时，重物对平板的作用力；（2）若频率不变，则平板以多大的振幅振动时，重物会跳离平板？（3）若振幅不变，则平板以多大的频率振动时，重物会跳离平板？分析：按题意作示意图，如图所示。

物体在平衡位置附近随板作简谐运动，其间受重力P 和板支持力F N 作用，F N 是一个变力。

按牛顿定律，有 22N d d t y m F mg F =-= （l ）由于物体是随板一起作简谐运动，因而有)cos(d d 222ϕωω+-==t A t y a ，则式（l ）可改写为)cos(2N ϕωω++=t mA mg F （2）(1）根据板运动的位置，确定此刻振动的相位ϕω+t ，由式（2）可求板与物体之间的作用力。

（2）由式（2）可知支持力F N 的值与振幅A 、角频率ω和相位ϕω+t 有关。

在振动过程中，当πϕω=+t 时F N 最小。

而重物恰好跳离平板的条件为F N = 0，因此由式（2）可分别求出重物跳离平板所需的频率或振幅。

解：（l ）由分析可知，重物在最低点时，相位0=+ϕωt ，物体受板的支持力为N 96.12)2(22N =+=+=mA mg mA mg F πω重物对木块的作用力'N F 与F N 大小相等，方向相反。

（2）当频率不变时，设振幅变为'A 。

根据分析中所述，将F N = 0及πϕω=+t 代入分析中式（2），可得 m 102.64//2222-⨯==='πωgT m mg A（3）当振幅不变时，设频率变为'ν。

同样将F N =0及πϕω=+t 代入分析中式（2），可得Hz52.3/212=='='mA mg v ππω13－7 一物体沿x 轴做简谐运动，振幅为0.06m ，周期为2.0s ，当t = 0时位移为0.03m ，且向x 轴正方向运动。

求：（1）t = 0.5s 时，物体的位移、速度和加速度；（2）物体从x =－ 0.03m 处向x 轴负向运动开始，到平衡位置，至少需要多少时间？解：（1）由题意知A = 0.06m 、1s /2-==ππωT 由旋转矢量图可确定初相则30πϕ-=，振动方程为)3cos(06.0ππ-=t x当t = 0.5s 时质点的位移、速度、加速度分别为m x 052.0)32cos(06.0=-=ππ m/s 094.0)32sin(06.0　-=-==πππdt dx v 2222/ 513.0)32cos(06.0s m dtx d a -=--==πππ （2）质点从x = -0.03 m 运动到平衡位置的过程中，旋转矢量从图中的位置M 转至位置N ，矢量转过的角度(即相位差)6/5πϕ=∆。

该过程所需时间为 s833.0=∆=∆ωϕt13－8 有一密度均匀的金属T 字形细尺，如本题图所示，它由两根金属米尺组成。

若它可绕通过点O 的垂直纸面的水平轴转动，求其微小振动的周期。

解：T 字形尺的微小振动是复摆振动。

T 字形尺绕轴O 的转动惯量J 。

由两部分组成，其中尺OD 对该轴的转动惯量为2311ml J =尺AB 对轴O 的转动惯量为J 2，根据平行轴定理可得22212131212ml ml ml J =+=故有 21O 12172ml J J J =+= 图中T 字形尺的质心C 至点O 的距离为C l ，由质心定义可得l l 75.0C =。

则T 字形尺的振动周期为s 95.11817222C O ===g l mgl J T ππ13－9 如本题图所示，一劲度系数为k 的轻弹簧，其下挂有一质量为m 1的空盘.现有一质量为m 2的物体从盘上方高为h 处自由落到盘中，并和盘粘在一起振动.问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？分析：原有空盘振动系统由于下落物体的加入，振子质量由m 1变为m 1 +m 2，因此新系统的角频率（或周期）要改变。

由于2020)(ωv x A +=因此，确定初始速度0v 和初始位移0x 是求解振幅A 的关键。

物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度0v ，这也是该振动系统的初始速度。

在确定初始时刻的位移0x 时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置。

因此，本题中初始位移0x ，也就是空盘时的平衡位置相对新系统的平衡位置的位移。

解：（l ）空盘时和物体落入盘中后的振动周期分别为 k m m T km T )(2222211+='='==πωπππ可见T T >'，即振动周期变大了。

（2）如图所示，取新系统的平衡位置为坐标原点O 。

则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即k g m g k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量，k g m m l )(212+=为物体粘在盘上后，静止时弹簧的伸长量。

由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度习题13－8图习题13－9图gh m m m v m m m v 22122120+=+=式中gh v 2=是物体由h 高下落至盘时的速度。

故系统振动的振幅为g m m khk gm v x A )(21)(2120202++='+=ω本题也可用机械能守恒定律求振幅A 。

13－10 一质量M 的物体在光滑水平上作谐振动，振幅是12cm ，在距平衡位置6cm 处速度是24cm / s ，求（1）周期T ；（2）当速度是12cm / s 时的位移。

解：设振动方程为x = A c o s ωt ，则x ∙= A ωsin ωt（1）在x = 6 c m ，x ∙= 24 c m / s 状态下有6 = 12 c o s ωt ， 24 = -12ωsin ωt ，解以上两式得ω = 4 /3, ∴T = 2π/ ω= 3π/ 2 = 2.72 s （2）设对应于x ∙= 12 c m / s 的时刻为l 2，则由x ∙= - A ωsin ωt得12 = - 12×4 /3×sin ωl 2，解得上式得sin 2ωl 2 = 0.1875相应的位移为x = A co s ωt 2 = ±A 110822-=±sin .ωt cm13－11 若在一竖直轻弹簧的下端悬挂一小球，弹簧被拉长l 0 = 1.2cm 而平衡，经推动后，该小球在竖直方向作振幅为A = 2cm 的振动，试证明此振动为谐振动；若选小球在正最大位移处开始计时，写出此振动的数值表达式。

解：设小球的质量为m ，由弹簧的倔强系数k = m g / l 0选平衡位置为原点，向下为正方向，小球在x 处，根据牛顿定律得m g - k ( l 0 + x ) = m d 2 x / d t 2将倔强系数k = m g / l 0代入整理后得d 2 x / d t 2 + g x / l 0 = 0∴此振动为谐振动令 ωπ==g l /.0910解得x = A c o s (ωt + φ) A = 2×10 -2由题意： t = 0时，x 0 = A ，v 0 = 0， ∴φ = 0∴x = 2×10 -2 c o s (9.1πt ) (SI)13－12 一台摆钟的等效摆长l =0.995m ，摆锤可上、下移动以调节其周期，该钟每天快1分27秒，假如将此摆当作质量集中在摆锤中心的一个单摆来考虑，则应将摆锤向下移动多少距离，才能使钟走得准确？解：钟摆周期的相对误差△T / T = 钟的相对误差△t / t ，等效单摆的周期T l g =2π/设重力加速度g 不变，则有2 d T / T = d l / l 令△T = d T ，△t = d l ，并考虑到△T / T = △t / t ，则摆锤向下移动的距离 △l = 2 l △t / t = 2.00 mm摆锤应向下移2.00mm ，才能使钟走得准确。