华东师大初中数学九年级下册弧长和扇形面积、圆锥的侧面展开图—巩固练习(基础)[精品]

合集下载

华东师大初中数学九年级下册《圆》全章复习与巩固—知识讲解(基础)

《圆》全章复习与巩固—知识讲解（基础）【学习目标】1．理解圆及其有关概念，理解弧、弦、圆心角的关系；2.探索并了解点与圆、直线与圆、圆与圆的位置关系，探索并掌握圆周角与圆心角的关系、直径所对的圆周角的特征；3．了解切线的概念，探索并掌握切线与过切点的半径之间的位置关系，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线；4．了解三角形的内心和外心，探索如何过一点、两点和不在同一直线上的三点作圆；5．了解正多边形的概念，掌握用等分圆周画圆的内接正多边形的方法；会计算弧长及扇形的面积、圆锥的侧面积及全面积；6．结合相关图形性质的探索和证明，进一步培养合情推理能力，发展逻辑思维能力和推理论证的表达能力；通过这一章的学习，进一步培养综合运用知识的能力，运用学过的知识解决问题的能力.【知识网络】【要点梳理】要点一、圆的定义、性质及与圆有关的角1．圆的定义(1)线段OA绕着它的一个端点O旋转一周，另一个端点A所形成的封闭曲线，叫做圆.(2)圆是到定点的距离等于定长的点的集合.要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；②圆是一条封闭曲线.2．圆的性质(1)旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心.在同圆或等圆中，两个圆心角，两条弧，两条弦，两条弦心距，这四组量中的任意一组相等，那么它所对应的其他各组分别相等.(2)轴对称：圆是轴对称图形，经过圆心的任一直线都是它的对称轴.(3)垂径定理及推论：①垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.③弦的垂直平分线过圆心，且平分弦对的两条弧.④平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦.⑤平行弦夹的弧相等. 要点诠释：在垂径定理及其推论中：过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧，在这五个条件中，知道任意两个，就能推出其他三个结论.（注意：“过圆心、平分弦”作为题设时，平分的弦不能是直径） 3．两圆的性质(1)两个圆是一个轴对称图形，对称轴是两圆连心线.(2)相交两圆的连心线垂直平分公共弦，相切两圆的连心线经过切点. 4．与圆有关的角(1)圆心角：顶点在圆心的角叫圆心角.圆心角的性质：圆心角的度数等于它所对的弧的度数. (2)圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角. 圆周角的性质：①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等. ③90°的圆周角所对的弦为直径；半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形. ⑤圆内接四边形的对角互补；外角等于它的内对角. 要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交. (2)圆周角定理成立的前提条件是在同圆或等圆中.要点二、与圆有关的位置关系 1．判定一个点P 是否在⊙O 上设⊙O 的半径为，OP=，则有点P 在⊙O 外；点P 在⊙O 上；点P 在⊙O 内. 要点诠释：点和圆的位置关系和点到圆心的距离的数量关系是相对应的，即知道位置关系就可以确定数量关系；知道数量关系也可以确定位置关系.2．判定几个点12nA A A 、、在同一个圆上的方法当时，在⊙O 上.3．直线和圆的位置关系设⊙O 半径为R ，点O 到直线的距离为. (1)直线和⊙O 没有公共点直线和圆相离. (2)直线和⊙O 有唯一公共点直线和⊙O 相切.(3)直线和⊙O 有两个公共点直线和⊙O 相交. 4．切线的判定、性质 (1)切线的判定：①经过半径的外端并且垂直于这条半径的直线是圆的切线. ②到圆心的距离等于圆的半径的直线是圆的切线. (2)切线的性质：①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点. ③经过切点作切线的垂线经过圆心.(3)切线长：从圆外一点作圆的切线，这一点和切点之间的线段的长度叫做切线长.(4)切线长定理：从圆外一点作圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.5．圆和圆的位置关系设的半径为，圆心距.(1)和没有公共点，且每一个圆上的所有点在另一个圆的外部外离.(2)和没有公共点，且的每一个点都在内部内含(3)和有唯一公共点，除这个点外，每个圆上的点都在另一个圆外部外切.(4)和有唯一公共点，除这个点外，的每个点都在内部内切.(5)和有两个公共点相交.两圆的五种位置关系可以概括为三类：要点三、三角形的外接圆与内切圆、圆内接四边形与外切四边形1．三角形的内心、外心、重心、垂心(1)三角形的内心：是三角形三条角平分线的交点，它是三角形内切圆的圆心，在三角形内部，它到三角形三边的距离相等，通常用“I”表示.(2)三角形的外心：是三角形三边中垂线的交点，它是三角形外接圆的圆心，锐角三角形外心在三角形内部，直角三角形的外心是斜边中点，钝角三角形外心在三角形外部，三角形外心到三角形三个顶点的距离相等，通常用O表示.(3)三角形重心：是三角形三边中线的交点，在三角形内部；它到顶点的距离是到对边中点距离的2倍，通常用G表示.(4)垂心：是三角形三边高线的交点.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).2．圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形，圆内接四边形对角互补，外角等于内对角.(2)各边都和圆相切的四边形叫圆外切四边形，圆外切四边形对边之和相等.要点四、圆中有关计算1．圆中有关计算圆的面积公式：，周长.圆心角为、半径为R的弧长.圆心角为，半径为R，弧长为的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形，底面半径为R，母线长为的圆柱的体积为，侧面积为，全面积为.圆锥的侧面展开图为扇形，底面半径为R，母线长为，高为的圆锥的侧面积为，全面积为，母线长、圆锥高、底面圆的半径之间有.要点诠释：(1)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即；(2)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.(3)扇形面积公式，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；(4)扇形两个面积公式之间的联系：.【典型例题】类型一、圆的有关概念及性质【高清ID号： 362179 高清课程名称：《圆》单元复习关联的位置名称（播放点名称）：经典例题1-2】1．如图所示，△ABC的三个顶点的坐标分别为A(－1，3)、B (－2，－2)、C (4，－2)，则△ABC 外接圆半径的长度为．【解析】由已知得BC ∥x 轴，则BC 中垂线为2412x -+== 那么，△ABC 外接圆圆心在直线x=1上，设外接圆圆心P(1,a)，则由PA=PB=r 得到：PA 2=PB 2即(1+1)2+(a-3)2=(1+2)2+(a+2)2化简得 4+a 2-6a+9=9+a 2+4a+4 解得 a=0即△ABC 外接圆圆心为P(1,0) 则 22(11)(03)13r PA ==++-=【总结升华】三角形的外心是三边中垂线的交点，由B 、C 的坐标知：圆心P （设△ABC 的外心为P ）必在直线x=1上；由图知：BC 的垂直平分线正好经过（1，0），由此可得到P （1，0）；连接PA 、PB ，由勾股定理即可求得⊙P 的半径长．类型二、弧、弦、圆心角、圆周角的关系及垂径定理2．如图所示，⊙O 的直径AB 和弦CD 相交于点E ，已知AE ＝1cm ，EB ＝5cm ，∠DEB ＝60°，求CD 的长．【思路点拨】作OF ⊥CD 于F ，构造Rt △OEF ，求半径和OF 的长；连接OD ，构造Rt △OFD ，求CD 的长．【答案与解析】作OF ⊥CD 于F ，连接OD ．∵ AE ＝1，EB ＝5，∴ AB ＝6． ∵ 32ABOA ==，∴ OE ＝OA-AE ＝3-1＝2．在Rt △OEF 中，∵ ∠DEB ＝60°，∴ ∠EOF ＝30°，∴ 112EF OE ==，∴ 223OF OE EF =-=．在Rt △DFO 中，OF ＝3，OD ＝OA ＝3，∴ 22223(3)6DF OD OF =-=-=(cm)． ∵ OF ⊥CD ，∴ DF ＝CF ，∴ CD ＝2DF ＝26cm ．【总结升华】因为垂径定理涉及垂直关系，所以常常可以利用弦心距（圆心到弦的距离）、半径和半弦组成一个直角三角形，用勾股定理来解决问题，因而，在圆中常作弦心距或连接半径作为辅助线，然后用垂弦定理来解题．举一反三：【变式】如图，AB 、AC 都是圆O 的弦，OM⊥AB，ON⊥AC，垂足分别为M 、N ，如果MN ＝3，那么BC ＝．【答案】由OM⊥AB，ON⊥AC，得M 、N 分别为AB 、AC 的中点（垂径定理），则MN 是△ABC 的中位线，BC=2MN=6.3．（2017•曲靖一模）如图，⊙O 的半径为4，△ABC 是⊙O 的内接三角形，连接OB 、OC ，若∠BAC 和∠BOC 互补，则弦BC 的长度为.【思路点拨】首先过点O 作OD ⊥BC 于D ，由垂径定理可得BC=2BD ，又由圆周角定理，可求得∠BOC 的度数，然后根据等腰三角形的性质，求得∠OBC 的度数，利用余弦函数，即可求得答案．【答案】4.【解析】解：过点O 作OD ⊥BC 于D ，则BC=2BD ，∵△ABC 内接于⊙O ，∠BAC 与∠BOC 互补， ∴∠BOC=2∠A ，∠BOC+∠A=180°， ∴∠BOC=120°， ∵OB=OC ，∴∠OBC=∠OCB=（180°﹣∠BOC ）=30°， ∵⊙O 的半径为4， ∴BD=OB•cos∠OBC=4×=2，∴BC=4．故答案为：4．【总结升华】此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识．注意掌握辅助线的作法，注意数形结合思想的应用．举一反三：【变式】如图，⊙O 的半径是2，AB 是⊙O 的弦，点P 是弦AB 上的动点，且1≤OP≤2，则弦AB 所对的圆周角的度数是（）N MO C BAA．60°B．120°C．60°或120°D．30°或150°【答案】C.【解析】作OD⊥AB，如图，∵点P是弦AB上的动点，且1≤OP≤2，∴OD=1，∴∠OAB=30°，∴∠AOB=120°，∴∠AEB=∠AOB=60°，∵∠E+∠F=180°，∴∠F=120°，即弦AB所对的圆周角的度数为60°或120°．故选C．类型三、与圆有关的位置关系【高清ID号： 362179 高清课程名称：《圆》单元复习关联的位置名称（播放点名称）：经典例题6】4．如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F，且∠ACB=∠DCE．请判断直线CE与⊙O的位置关系，并证明你的结论.【答案与解析】直线CE与⊙O相切理由：连接OE∵OE=OA∴∠OEA=∠OAE∵四边形ABCD是矩形∴∠B=∠D=∠BAD=90°，BC∥AD,CD=AB∴∠DCE+∠DEC=90°, ∠ACB=∠DAC又∠DCE=∠ACB∴∠DEC+∠DAC=90°∵OE=OA∴∠OEA=∠DAC∴∠DEC+∠OEA=90°∴∠OEC=90°∴OE⊥EC∴直线CE与⊙O相切.【总结升华】本题考查了切线的判定：经过半径的外端点与半径垂直的直线是圆的切线．举一反三：【变式】如图，P为正比例函数图象上的一个动点，的半径为3，设点P的坐标为(x、y).(1)求与直线相切时点P的坐标.(2)请直接写出与直线相交、相离时x的取值范围.【答案】(1)过作直线的垂线，垂足为.当点在直线右侧时，，得，(5，7.5).当点在直线左侧时，，得，(，).当与直线相切时，点的坐标为(5，7.5)或(，).(2)当时，与直线相交.当或时，与直线相离.类型四、圆中有关的计算5．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．（1）求证：DF⊥AC；（2）若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积．【答案与解析】（1）证明：连接OD，∵OB=OD ，∴∠ABC=∠ODB ， ∵AB=AC ，∴∠ABC=∠ACB ， ∴∠ODB=∠ACB ， ∴OD ∥AC ，∵DF 是⊙O 的切线， ∴DF ⊥OD ， ∴DF ⊥AC ．（2）解：连接OE ，∵DF ⊥AC ，∠CDF=22.5°， ∴∠ABC=∠ACB=67.5°， ∴∠BAC=45°， ∵OA=OE ，∴∠AOE=90°， ∵⊙O 的半径为4，∴S 扇形AOE =4π，S △AOE=8 ， ∴S 阴影=4π﹣8．【总结升华】本题主要考查了切线的性质，扇形的面积与三角形的面积公式，圆周角定理等，作出适当的辅助线，利用切线性质和圆周角定理，数形结合是解答此题的关键．类型五、圆与其他知识的综合运用6．如图(1)是某学校存放学生自行车的车棚示意图(尺寸如图(1))，车棚顶部是圆柱侧面的一部分，其展开图是矩形．图(2)是车棚顶部截面的示意图，AB 所在圆的圆心为O ．车棚顶部用一种帆布覆盖，求覆盖棚顶的帆布的面积(不考虑接缝等因素，计算结果保留π)．【思路点拨】求覆盖棚顶的帆布的面积，就是求以AB 为底面的圆柱的侧面积．根据题意，应先求出AB 所对的圆心角度数以及所在圆的半径，才能求AB 的长．【答案与解析】连接OB ，过点O 作OE ⊥AB ，垂足为E ，交AB 于点F ，如图(2)．由垂径定理，可知E 是AB 中点，F 是AB 的中点，∴ 12AE AB ==EF ＝2．设半径为R 米，则OE ＝(R-2)m ．在Rt △AOE 中，由勾股定理，得222(2)R R =-+．解得R ＝4．∴ OE ＝2，12OE AO =，∴ ∠AOE ＝60°，∴ ∠AOB ＝120°．∴AB的长为120481803ππ⨯=(m)．∴帆布的面积为8601603ππ⨯=(m2)．【总结升华】本题以学生校园生活中的常见车棚为命题背景，使考生在考场上能有一种亲切的感觉，这也体现了中考命题贴近学生生活实际的原则．举一反三：【变式】某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径，如图所示是水平放置的破裂管道有水部分的截面.①请你补全这个输水管道的圆形截面图；②若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径.【答案】①作法略.如图所示.②如图所示，过O作OC⊥AB于D，交于C，∵ OC⊥AB，∴.由题意可知，CD=4cm.设半径为x cm，则.在Rt△BOD中，由勾股定理得：∴.∴.即这个圆形截面的半径为10cm.。

弧长、扇形的面积、圆锥的侧面积压轴题十种模型全攻略(解析版)-初中数学

弧长、扇形的面积、圆锥的侧面积压轴题十种模型全攻略【考点导航】目录【典型例题】【考点一已知圆心角的度数，求弧长】【考点二已知弧长，求圆心角的度数】【考点三求某点的弧形运动路径长度】【考点四已知圆心角的度数或弧长，求扇形的面积】【考点五求图形旋转后扫过的面积】【考点六求弓形的面积】【考点七求其他不规则图形的面积】【考点八求圆锥的侧面积与底面半径】【考点九求圆锥侧面展开图的圆心角】【考点十圆锥侧面上最短路径问题】【过关检测】22【典型例题】【考点一已知圆心角的度数，求弧长】1(2023秋·江苏·九年级专题练习)已知扇形的半径为3cm ，圆心角为150°，则该扇形的弧长为cm ．【答案】52π/2.5π【分析】直接利用弧长公式进行计算即可．【详解】解：∵L =n πr180，扇形的半径为3cm ，圆心角为150°，∴扇形的弧长L =150π×3180=52π，故答案为：52π．【点睛】本题主要考查了弧长公式的应用，熟练掌握弧长公式：L =n πr180是解题的关键．【变式训练】1(2023·浙江湖州·统考一模)一个扇形的半径为4，圆心角为90°，则此扇形的弧长为．【答案】2π【分析】利用弧长公式进行计算即可．【详解】解：弧长为=90180π×4=2π；故答案为：2π【点睛】本题考查求弧长．熟练掌握弧长公式，是解题的关键．2(2023·浙江温州·统考中考真题)若扇形的圆心角为40°，半径为18，则它的弧长为．【答案】4π【分析】根据弧长公式l =n πr180即可求解．【详解】解：扇形的圆心角为40°，半径为18，∴它的弧长为40180×18π=4π，故答案为：4π．【点睛】本题考查了求弧长，熟练掌握弧长公式是解题的关键．【考点二已知弧长，求圆心角的度数】1(2023·黑龙江哈尔滨·统考三模)一个扇形的面积为10π，弧长为10π3，则该扇形的圆心角的度数为．【答案】100°/100度【分析】根据弧长和扇形面积关系可得S =12lR ，求出R ，再根据扇形面积公式求解.【详解】∵一个扇形的弧长是10π3，面积是10π，∴S =12lR ，即10π=12×10π3R ，解得：R =6，∴S =10π=n π×62360，解得：n =100°，故答案为：100°．【点睛】本题考查了扇形面积的计算；弧长的计算．熟记公式，理解公式间的关系是关键.【变式训练】1(2023·江苏镇江·统考二模)扇形的弧长为6π，半径是12，该扇形的圆心角为度．【答案】90【分析】设此扇形的圆心角为x °，代入弧长公式计算，得到答案．【详解】解：设此扇形的圆心角为x °，由题意得，12πx180=6π，解得，x =90，故答案为：90．【点睛】本题考查的是弧长的计算，掌握弧长的公式l =n πr180是解题的关键．2(2023·浙江温州·校考三模)若扇形半径为4，弧长为2π，则该扇形的圆心角为．【答案】90°/90度【分析】设扇形圆心角的度数为n ，根据弧长公式即可得出结论．【详解】解：设扇形圆心角的度数为n ，∵扇形的弧长为2π，∴n π×4180°=2π，∴n =90°．故答案为：90°．【点睛】本题考查的是扇形的面积公式，熟记扇形的面积公式及弧长公式是解答此题的关键．【考点三求某点的弧形运动路径长度】1(2023秋·云南昭通·九年级校联考阶段练习)如图，在平面直角坐标系xOy 中，以原点O 为旋转中心，将△AOB 顺时针旋转90°得到△A OB ，其中点A 与点A 对应，点B 与点B 对应．如果A -4,0 ，B -1,2 ．则点A 经过的路径长度为(含π的式子表示)【答案】2π【分析】A 点坐标为已知，求出OA 长度，再利用弧长公式l =n πr180求解即可．【详解】解：∵A -4,0如图，由题意A 点以原点O 旋转中心旋转了90°∴点A 经过的路径AA的长度=90⋅π×4180=2π故答案为：2π．【点睛】本题考查图形的旋转、弧长等知识点，需要熟练掌握弧长计算公式．【变式训练】1(2023·湖南郴州·统考中考真题)如图，在Rt △ABC 中，∠BAC =90°，AB =3cm ，∠B =60°．将△ABC 绕点A 逆时针旋转，得到△AB C ，若点B 的对应点B 恰好落在线段BC 上，则点C 的运动路径长是cm (结果用含π的式子表示)．【答案】3π【分析】由于AC 旋转到AC ，故C 的运动路径长是CC 的圆弧长度，根据弧长公式求解即可．【详解】以A 为圆心作圆弧CC ，如图所示．在直角△ABC 中，∠B =60°，则∠C =30°，则BC =2AB =2×3=6cm ．∴AC =BC 2-AB 2=62-32=33cm ．由旋转性质可知，AB =AB ，又∠B =60°，∴△ABB 是等边三角形．∴∠BAB =60°．由旋转性质知，∠CAC =60°．故弧CC 的长度为：60360×2×π×AC =π3×33=3πcm ；故答案为：3π【点睛】本题考查了含30°角直角三角形的性质、勾股定理、旋转的性质、弧长公式等知识点，解题的关键是明确C 点的运动轨迹．2(2023·广东东莞·校考一模)如图，△ABC 和△A B ′C ′是两个完全重合的直角三角板，∠B =30°，斜边长为12cm ．三角板A ′B ′C 绕直角顶点C 顺时针旋转，当点A ′落在AB 边上时，则点A ′所转过的路径长为cm ．【答案】2π【分析】根据三角形内角和和含30度的直角三角形三边的关系得到∠A =60°,AC =12AB =6cm ，再根据旋转的性质得CA ′=CA ，于是可判断△CAA ′为等边三角形，所以∠ACA ′=60°，然后根据弧长公式计算弧AA ′的长度即可．【详解】∵∠ACB =90°，∠B =30°，AB =12cm ，∴∠A =60°,AC =12AB =6cm ，∵三角板A ′B ′C 绕直角顶点C 顺时针旋转，当点A ′落在AB 边上，∴CA ′=CA ，∴△CAA ′为等边三角形，∴∠ACA ′=60°，∴弧AA ′的长度=60°π×6180°=2πcm ，即点A ′所转过的路径长为2πcm ．答案为：2π．【点睛】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了弧长公式．【考点四已知圆心角的度数或弧长，求扇形的面积】1(2023·江苏·九年级假期作业)已知扇形的圆心角为80°，半径为3cm ，则这个扇形的面积是cm 2．【答案】2π【详解】根据扇形的面积公式即可求解．【分析】解：扇形的面积=80π×32360=2πcm 2 ．故答案是：2π．【点睛】本题主要考查了扇形的面积公式，熟练掌握扇形面积公式是解题的关键．【变式训练】1(2023·黑龙江哈尔滨·哈尔滨市第十七中学校校考模拟预测)一个扇形的弧长是8πcm ，圆心角是144°，则此扇形的面积是．【答案】40π【分析】设该扇形的半径为rcm ，然后根据弧长公式计算半径，然后根据扇形面积公式计算即可．【详解】解：设该扇形的半径为rcm ，由题意得：144πr180=8π，解得：r =10，S 扇形=12lr =12×8π×10=40π，故答案为：40π．【点睛】本题主要考查弧长计算公式及扇形面积计算公式，熟练掌握弧长计算公式和扇形面积计算公式是解题的关键．2(2023·海南海口·海师附中校考三模)如图，正五边形ABCDE 的边长为4，以顶点A 为圆心，AB 长为半径画圆，则图中阴影部分的面积是．【答案】245π【分析】首先确定扇形的圆心角的度数，然后利用扇形的面积公式计算即可．【详解】解：∵正五边形的外角和为360°，∴每一个外角的度数为360°÷5=72°，∴正五边形的每个内角为180°-72°=108°，∵正五边形的边长为4，∴S 阴影=108⋅π×42360=245π，故答案为：245π．【点睛】本题考查了正多边形和圆及扇形的面积的计算的知识，解题的关键是求得正五边形的内角的度数并牢记扇形的面积计算公式，难度不大．【考点五求图形旋转后扫过的面积】1(2023·河南安阳·统考一模)如图，将半径为1，圆心角为60°的扇形OAB 绕点A 逆时针旋转36°，得到扇形OAB，则AB扫过的区域(即图中阴影部分)的面积为．【答案】π10【分析】结合已知条件及旋转性质，根据面积的和差可得S 阴影=S 扇形BAB，然后利用扇形面积公式计算即可．【详解】∵OA =OB =1，∠AOB =60°，∴△AOB 为等边三角形，∴AB =OA =1，由旋转性质可得，∠OAO =∠BAB =36°，S △AOB =S △AO B，则S 阴影=S 扇形BAB+S △AOB -S 扇形AOB +S 扇形AO B-S △AO B，=S 扇形BAB，=36π×12360，=π10，故答案为：π10．【点睛】此题考查了扇形的面积及旋转性质，结合已知条件将阴影部分面积转化为扇形的面积是解题的关键．【变式训练】1(2022春·四川德阳·九年级校考阶段练习)如图，将△ABC 绕点C 顺时针旋转120°得到△A B C ，已知AC =3，BC =2，则线段AB 扫过的图形(阴影部分)的面积为．【答案】5π3/53π【分析】由于将△ABC 绕点C 旋转120°得到△A B C ，可见，阴影部分面积为扇形ACA ′减扇形BCB ′，分别计算两扇形面积，在计算其差即可．【详解】解：从图中可以看出，线段AB 扫过的图形面积为一个环形，环形中的大圆半径是AC ，小圆半径是BC ，圆心角是120°，所以阴影面积=大扇形面积-小扇形面积=120π×32-22 360=53π【点睛】本题考查了扇形面积的计算和阴影部分的面积，将阴影部分面积转化为两扇形面积的查是解题的关键．2(2022秋·山东烟台·九年级统考期末)如图，在Rt △ABC 中，∠ACB =90°，∠BAC =60°，AB =8，将△ABC 绕点A 按逆时针方向旋转到△A B C 的位置，使C 、A 、B 三点在同一条直线上，则直角边BC 扫过的图形面积为．【答案】16π【分析】根据题意可得：AC =AC =4，BC =B C =43，∠B AC =∠B AC =∠CAB =60°，因此直角边BC 扫过的图形面积为S =S △ABC+S 扇形BAB -S 扇形CAC -S △ABC ，因为S △ABC=S △ABC ，因此S =S 扇形BAB-S 扇形CAC ，代入数值即可求得答案．【详解】解：根据题意可得：AC =AC =4，BC =B C =43，∠B AC =∠B AC =∠CAB =60°，△ABC ≌△AB C ，所以直角边BC 扫过的图形面积为S =S △ABC+S 扇形BAB -S 扇形CAC -S △ABC ，由于S △ABC=S △ABC ，所以S =S 扇形BAB -S 扇形CAC =120°×π×82360°-120°×π×42360°=64π3-16π3=16π，故答案为：16π．【点睛】本题考查了轨迹问题，关键是根据旋转的性质，找出BC 扫过的面积构成，利用扇形的面积公式计算即可．【考点六求弓形的面积】1(2023·云南昆明·昆明八中校考模拟预测)如图，在扇形OAB 中，∠AOB =90°，OA =6，则阴影部分的面积是．【答案】9π-18【分析】利用扇形的面积减去三角形的面积，即可得解．【详解】∵OA =OB =6，∠AOB =90°，∴S 阴=S 扇形OAB -S △AOB =90π×62360-12×6×6=9π-18．故答案为：9π-18．【点睛】本题考查求阴影部分的面积．熟练掌握割补法求面积，是解题的关键．【变式训练】1(2023·山东泰安·统考二模)如图C 、D 在直径AB =4的半圆上，D 为半圆弧的中点，∠BAC =15°，则阴影部分的面积是【答案】23π-3【分析】设AB 的中点为O ，连接OD ,OC ，用扇形COD 的面积减去△COD 的面积即可得出结果．【详解】解：设AB 的中点为O ，连接OD ,OC ，∵C 、D 在直径AB =4的半圆上，D 为半圆弧的中点，∠BAC =15°，∴OD =OC =2，∠DOB =90°,∠COB =2∠BAC =30°，∴∠DOC =∠DOB -∠COB =60°，∴△COD 为等边三角形，∴CD =OD =OC =2，过点O 作OE ⊥CD ，则：CE =12CD =1，∴OE =OC 2-CE 2=3，∴阴影部分的面积=S 扇形COD -S △COD =60π×22360-12×2×3=23π-3；故答案为：23π-3．【点睛】本题考查求弓形的面积，同时考查了圆周角定理，等边三角形的判定和性质．将阴影部分的面积转化为扇形的面积减去三角形的面积，是解题的关键．2(2023·河南周口·校联考三模)如图，在△ABC 中，BC =BA =4，∠C =30°，以AB 中点D 为圆心、AD 长为半径作半圆交线段AC 于点E ，则图中阴影部分的面积为．【答案】4π3-3【分析】连接DE ，BE ，然后根据已知条件求出∠ABE =60°，AE =23，从而得到∠ADE =120°，最后结合扇形的面积计算公式求解即可．【详解】解：如图，连接DE ，BE ．∵AB 为直径，∴∠BEA =90°．∵BC =BA ，∴∠BAC =∠BCA =30°，∴∠ABE =60°，BE =12AB =2，AE =3BE =32AB =23，∵BD =DE ，∴△BDE 是等边三角形，∴∠ADE =120°，∴阴影部分的面积=S 扇形DAE -S △ADE=120π×22360-12S △ABE=120π×22360-12×12×23×2=4π3-3=4π3-3．故答案为：4π3-3．【点睛】本题考查阴影部分面积计算问题，涉及到扇形面积计算，等边三角形的判定与性质，直径所对的圆周为直角等，掌握扇形面积计算公式是解题关键．【考点七求其他不规则图形的面积】1(2023春·河南漯河·九年级校考阶段练习)图1是以AB 为直径的半圆形纸片，AB =8，沿着垂直于AB 的半径OC 剪开，将扇形OAC 沿AB 向右平移至扇形O A C ，如图2，其中O 是OB 的中点，O C 交BC于点F ，则图中阴影部分的面积为．【答案】8π3-23【分析】根据题意和图形，利用勾股定理，可以求得O F 的长，再根据图形，可知阴影部分的面积=扇形COB 的面积∽△OO F 的面积-扇形OFC 的面积，计算即可．【详解】解：连接OF ，由题意可得，OB =4，OO =2，∠OO F =90°，∴∠OFO =30°，∴∠O OF =60°，∴O F =23，∴阴影部分的面积是：90π×42360-2×232-30×π×42360=8π3-23，故答案为：8π3-23．【点睛】本题考查扇形面积的计算、平移的性质，解答本题的关键是明确题意，利用数形结合的思想解答．【变式训练】1(2023·河南信阳·统考一模)如图，正五边形ABCDE 的边长为1，分别以点C ，D 为圆心，CD 长为半径画弧，两弧交于点F ，图中阴影部分的面积为．(结果保留π)【答案】32-π15【分析】连接CF ，DF ，由CF =DF =CD =1，得∠FCD =∠FDC =60°，求出∠FCD =∠FDC =60°，根据公式求出S 扇形BCF ，S 正△CFD ，S 扇形CDF ，即可得到阴影面积．【详解】如图，连接CF ，DF ，由题意，得∠BCD =(5-2)×180°5=108°，∵CF =DF =CD =1，∴∠FCD =∠FDC =60°，∴∠BCF =108°-60°=48°，∴S 扇形BCF =48π×12360=2π15，S 正△CFD =34×12=34，S 扇形CDF =60π×12360=π6，∴S 阴影BCF =2π15+34-π6=34-π30，∴S 阴影=34-π30 ×2=32-π15，故答案为：32-π15．【点睛】此题考查了求不规则图形的面积，扇形面积公式，正多边形的性质，正确理解图形面积的计算方法连接辅助线是解题的关键．2(2023·河南南阳·统考模拟预测)如图，在矩形ABCD 中，AD =2，AB =1，以D 为圆心，以AD 长为半径画弧，以C 为圆心，以CD 长为半径画弧，两弧恰好交于BC 上的点E 处，则阴影部分的面积为．【答案】12【分析】如图，连接DE ，根据勾股定理，得DE =2，根据阴影部分的面积S 1为：扇形AED 的面积减去S 2，根据S 2的等于扇形DCE 的面积减去S 3，即可求解．【详解】解：连接DE ，如图：∵四边形ABCD 是矩形，∴∠ADC =∠BCD =90°，AB =DC =1，∵EC =DC =1，∴∠CDE =45°，∴∠ADE =45°，∴扇形DAE 的面积为：45π×2 2360=π4，∵S 2=S 扇形DCE -S 3=90π×12360-12×1×1=π4-12，∴阴影部分的面积为：S 1=S 扇形ADE -S 2=π4-π4-12 =12．故答案为：12．【点睛】本题考查矩形的性质，扇形的面积，三角形面积，解题的关键是掌握扇形的面积公式，矩形的性质．【考点八求圆锥的侧面积与底面半径】1(2023·全国·九年级专题练习)若圆锥的底面圆半径为2，母线长为5，则该圆锥的侧面积是．(结果保留π)【答案】10π【分析】根据圆锥的底面圆半径为2，母线长为5，直接利用圆锥的侧面积公式求出即可．【详解】解：根据圆锥的侧面积公式：πrl=π×2×5=10π，故答案为：10π．【点睛】本题主要考查了圆锥侧面面积的计算，熟练记忆圆锥的侧面积公式是解决问题的关键．【变式训练】1(2023春·云南昭通·九年级统考期中)若圆雉的侧面积为12π，底面圆半径为3，则该圆雉的母线长是．【答案】4【分析】根据圆锥的侧面积=πrl，列出方程求解即可．【详解】解：∵圆锥的侧面积为12π，底面半径为3，3πl=12π．解得：l=4，故答案为：4．【点睛】本题考查了圆锥的侧面积，解题关键是熟记圆锥的侧面积公式，列出方程进行求解．2(2023·广东梅州·统考一模)若圆锥的底面半径为3cm，母线长为4cm，则圆锥的侧面积为cm2．(结果保留π)【答案】12π【分析】根据圆锥的侧面积公式计算即可．【详解】解：∵圆锥的底面半径为3cm，母线长为4cm，∴圆锥的侧面积为12×2×3π×4=12πcm2．故答案为：12π．【点睛】本题主要考查了圆锥的侧面积，属于简单题，熟练掌握扇形面积公式是解题关键．3(2023·江苏·九年级假期作业)已知圆锥侧面展开图圆心角的度数是120°，母线长为3，则圆锥的底面圆的半径是．【答案】1【分析】设该圆锥的底面半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πr=120×π×3180，然后解关于r的方程即可．【详解】设该圆锥的底面半径为r，根据题意得2πr=120×π×3180，解得r=1．故答案为1．【点睛】本题考查圆锥的计算，解题的关键是知道圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．4(2023·浙江衢州·统考二模)某个圆锥的侧面展开图是一个半径为6cm，圆心角为120°的扇形，则这个圆锥的底面半径为cm．【答案】2【分析】把扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．【详解】解：设此圆锥的底面半径为rcm，根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得，2πr=120π×6180，r=2故答案为2．【点睛】此题考查了圆的周长和圆弧长的计算，熟练掌握它们的计算公式是解题的关键．【考点九求圆锥侧面展开图的圆心角】1(2022秋·广东惠州·九年级校考阶段练习)已知圆锥的底面圆半径是2，母线长是4，则圆锥侧面展开的扇形圆心角是．【答案】180°/180度【分析】根据圆锥的底面周长，就是圆锥的侧面展开图的弧长，利用弧长公式可得圆锥侧面展开图的角度，把相关数值代入即可求解．【详解】解：∵圆锥底面半径是2，∴圆锥的底面周长为4π，设圆锥的侧面展开的扇形圆心角为n°，∴nπ×4180=4π，解得：n=180，∴圆锥侧面展开的扇形圆心角是180°．故答案为：180°．【点睛】本题考查求圆锥侧面展开图的圆心角．掌握圆锥的侧面展开图的弧长等于圆锥的底面周长是解题的关键．【变式训练】1(2023·江苏·九年级假期作业)已知圆锥的母线长5，底面半径为3，则圆锥的侧面积为，圆锥侧面展开图形的圆心角是度．【答案】15π216【分析】根据圆锥的侧面积公式S侧=πrl即可求解该圆锥的侧面积；结合弧长公式求出圆锥侧面展开图形的圆心角即可．【详解】解：圆锥的侧面积S侧=π×3×5=15π，圆锥的底面周长L=2π×3=6π，扇形圆心角=180×6ππ×5=216°．故答案为：15π，216．【点睛】本题主要考查了圆锥的计算，解题的关键是弄清圆锥的侧面积的计算方法，特别是圆锥的底面周长等于圆锥的侧面扇形的弧长．2(2023·江苏·九年级假期作业)若要制作一个母线长为9cm，底面圆的半径为4cm的圆锥，则这个圆锥的侧面展开图的圆心角度数是．【答案】160°/160度【分析】利用圆锥侧面展开图，扇形圆心角与母线和底面圆半径的关系计算，即可求解．【详解】解：设这个圆锥的侧面展开图的圆心角的度数是n，根据题意得：2π×4=n π×9180，解得n =160，即这个圆锥的侧面展开图的圆心角是160°，故答案为：160°．【点睛】本题考查了圆锥侧面展开图，扇形圆心角与母线和底面圆半径的关系，明确圆锥的底面圆的周长=扇形的弧长是解答本题的关键．【考点十圆锥侧面上最短路径问题】1(2023秋·山东东营·九年级东营市胜利第一初级中学校考期末)如图，已知圆锥底面半径为20cm ，母线长为60cm ，一只蚂蚁从A 处出发绕圆锥侧面一周(回到原来的位置A )所爬行的最短路径为cm ．(结果保留根号)【答案】603【分析】把圆锥的侧面展开得到圆心角为120°，半径为60的扇形，求出扇形中120°的圆心角所对的弦长即为最短路径．【详解】解：圆锥的侧面展开如图：过S 作SC ⊥AB ,∴AC =BC设∠ASB =n °，即：2π×20=n π×60180，得：n =120，∴∠ASC =60°∴AC =AS ×sin ∠ASC =60×32=303∴AB =2AC =603，故答案为：603．【点睛】本题考查了圆锥侧面展开图的圆心角，特殊角的锐角三角函数值，将圆锥中的数据对应到展开图中是解题的关键．【变式训练】1(2023春·黑龙江齐齐哈尔·九年级校联考期中)如图，AB 是圆锥底面的直径，AB =6cm ，母线PB=9cm ．点C 为PB 的中点，若一只蚂蚁从A 点处出发，沿圆锥的侧面爬行到C 点处，则蚂蚁爬行的最短路程为．【答案】932/923【分析】先画出圆锥侧面展开图(见解析)，再利用弧长公式求出圆心角∠APA 的度数，然后利用等边三角形的判定与性质、勾股定理可得AC =932，最后根据两点之间线段最短即可得．【详解】画出圆锥侧面展开图如下：如图，连接AB 、AC ，设圆锥侧面展开图的圆心角∠APA 的度数为n °，因为圆锥侧面展开图是一个扇形，扇形的弧长等于底面圆的周长，扇形的半径等于母线长，所以n π×9180=2π×3，解得n =120，则∠APB =12APA =60°，又∵AP =BP =9，∴△ABP 是等边三角形，∵点C 为PB 的中点，∴AC ⊥BP ，CP =12BP =92，在Rt △ACP 中，AC =AP 2-CP 2=932，由两点之间线段最短可知，蚂蚁爬行的最短路程为AC =932，故答案为：932．【点睛】本题考查了圆锥侧面展开图、弧长公式、等边三角形的判定与性质等知识点，熟练掌握圆锥侧面展开图是解题关键．2(2022秋·重庆沙坪坝·八年级重庆八中校考期中)如图1，一只蚂蚁从圆锥底端点A 出发，绕圆锥表面爬行一周后回到点A ，将圆锥沿母线OA 剪开，其侧面展开图如图2所示，若∠AOA =120°，OA =3，则蚂蚁爬行的最短距离是．【答案】3【分析】连接AA ′，作OB ⊥AA ′于点B ，根据题意，结合两点之间线段最短，得出AA ′即为蚂蚁爬行的最短距离，再根据三角形的内角和定理得出∠OAB =30°，再根据直角三角形中30°所对的直角边等于斜边的一半，得出OB =32，再根据勾股定理，得出AB =32，再根据三线合一的性质，得出AB =A ′B ，再根据线段之间的数量关系，得出AA ′=3即可解答．【详解】解：如图，连接AA ′，作OB ⊥AA ′于点B ，∴AA ′即为蚂蚁爬行的最短距离，∵OA =OA ′，∠AOA ′=120°，∴∠OAB =30°，在△OAB 中，OB ⊥AA ′，∠OAB =30°，∴OB =12OA =12×3=32，∴AB =OA 2-OB 2=3 2-32 2=32，在△AOA ′中，OA =OA ′，OB ⊥AA ′，∴AB =A ′B ，∴AA ′=2AB =2×32=3．∴蚂蚁爬行的最短距离为3．故答案为：3【点睛】本题考查了圆锥侧面上最短路径问题、三角形的内角和定理、直角三角形的特征、勾股定理、三线合一的性质等知识点，正确作出辅助线、构造等腰三角形和直角三角形是解题的关键．【过关检测】一、单选题1(2023·黑龙江哈尔滨·哈尔滨市第四十七中学校考模拟预测)一个扇形的半径是4cm ，圆心角是45°，则此扇形的弧长是()A.πcmB.2πcmC.4πcmD.8πcm 【答案】A【分析】根据弧长公式进行计算即可．【详解】解：由题意得，扇形的半径为4cm，圆心角为45°，故此扇形的弧长为45π×4180=πcm，故选：A．【点睛】此题考查了扇形弧长的计算，属于基础题，解答本题的关键是熟练掌握弧长计算公式，难度一般．2(2023·浙江温州·校联考三模)已知圆锥的底面半径为4，母线长为5，则圆锥的侧面积为() A.8π B.10π C.12π D.20π【答案】D【分析】圆锥的侧面积=π×底面半径×母线长，把相关数值代入即可求解．【详解】解：根据题意可得：圆锥的侧面积为：π×4×5=20π，故选：D．【点睛】本题考查了圆锥的侧面积展开图公式，解题的关键是掌握圆锥的侧面积的计算公式：圆锥的侧面积=π×底面半径×母线长．3(2023秋·江苏·九年级专题练习)如图，一块含有30°角的直角三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A B C的位置．若BC的长为7.5cm，那么顶点A从开始到结束所经过的路径长为()A.10πcmB.103πcmC.15πcmD.20πcm【答案】A【分析】顶点A从开始到结束所经过的路径是一段弧长是以点C为圆心，AC为半径的圆弧，旋转的角度是180°-60°=120°，所以根据弧长公式可得．【详解】解：在含有30°角的直角三角板ABC中，∠ACB=60°，BC=7.5cm，∴∠ACA =120°，AC=2BC=15cm，∴120π×15180=10πcm，故选：A．【点睛】本题考查弧长公式，解题的关键是弄准弧长的半径和圆心角的度数．4(2023秋·江苏·九年级专题练习)如图，在扇形AOB中，∠AOB=90°，半径OA=3，将扇形AOB沿过点B的直线折叠，使点O恰好落在AB上的点D处，折痕为BC，则阴影部分的面积为()A.3π-332B.9π4-33 C.π-34D.3π-34【答案】B【分析】连接OD ，由折叠的性质可得CD =CO ，BD =BO ，∠DBC =∠OBC ，从而得到△OBD 为等边三角形，再求出∠CBO =30°，从而得出OC =3，进行得出S △BOC =332，最后由△BOC 与△BDC 面积相等及S 阴影=S 扇形AOB -S △BOC -S △BDC ，进行计算即可得到答案．【详解】解：如图，连接OD ，，根据折叠的性质，CD =CO ，BD =BO ，∠DBC =∠OBC ，∴OB =BD =OD ，∴△OBD 为等边三角形，∴∠DBO =60°，∴∠CBO =12∠DBO =30°，∵∠AOB =90°，∴OC =OB ⋅tan ∠CBO =3×33=3，∴S △BOC =12OB ⋅OC =332，∵△BOC 与△BDC 面积相等，∴S 阴影=S 扇形AOB -S △BOC -S △BDC =14π×32-332-332=94π-33，故选：B ．【点睛】本题主要考查了等边三角形的判定与性质、折叠的性质、扇形面积的计算-求不规则图形的面积，添加适当的辅助线，得到S 阴影=S 扇形AOB -S △BOC -S △BDC 是解题的关键．5(2023·辽宁抚顺·统考一模)如图1是一块弘扬“社会主义核心价值观”的扇面宜传展板，该展板的部分示意图如图2所示，它是以O 为圆心，OA ,OB 长分别为半径，圆心角∠O =120°形成的扇面，若OA =3m ,OB =1.5m ，则阴影部分的面愁为()A.4.25πm 2B.25πm 2C.3πm 2D.2.25πm 2【答案】D【分析】根据S 阴影=S 扇形DOA -S 扇形BOC 计算即可．【详解】S 阴影=S 扇形DOA -S 扇形BOC =120π×9360-120π×94360=2.25πm 2故选：D ．【点睛】本题考查的是扇形面积的计算，掌握扇形的面积公式S =n πR 2360是解题的关键．二、填空题6(2023·福建福州·福建省福州第一中学校考模拟预测)圆锥母线长l =8，底面圆半径r =2，则圆锥侧面展开图的圆心角θ是．【答案】90°/90度【分析】根据弧长公式，弧长与圆锥底面圆的周长相等，建立等式计算即可．【详解】∵圆锥母线长l =8，底面圆半径r =2，圆锥侧面展开图的圆心角θ，∴2πr =θπl180，∴θ=360×2×π8π=90°，故答案为：90°．【点睛】本题考查了圆锥的侧面展开，弧长公式，熟练掌握展开的特点，牢记弧长公式是解题的关键．7(2023秋·河北唐山·九年级统考期末)如图，半圆O 的直径AB =6，弦CD =3，AD的长为34π，则BC的长为．【答案】5π4【分析】由题意可知：△OCD 是等边三角形，从而可求出弧CD 的长度，再求出半圆弧的长度后，即可求出弧BC 的长度．【详解】解：连接OD 、OC ，∵CD =OC =OD =3，∴△CDO 是等边三角形，∴∠COD =60°，∴CD 的长=60⋅π×3180=π，又∵半圆弧的长度为：12×6π=3π，∴BC =3π-π-3π4=5π4．故答案为：5π4【点睛】本题考查圆了弧长的计算，等边三角形的性质等知识，属于中等题型．8(2023·江苏扬州·统考中考真题)用半径为24cm ，面积为120πcm 2的扇形纸片，围成一个圆锥的侧面，则这个圆锥的底面圆的半径为cm ．【答案】5【分析】应为圆锥侧面母线的长就是侧面展开扇形的半径，利用圆锥侧面面积公式：S =π⋅r ⋅l ，就可以求出圆锥的底面圆的半径．【详解】解：设圆锥底面圆的半径为r ，l =24，由扇形的面积：S =π⋅r ⋅l =120π，得：r =5故答案为：5【点睛】本题考查了圆锥侧面面积的相关计算，熟练掌握圆锥侧面面积的计算公式是解题的关键，注意用扇形围成的圆锥，扇形的半径就是圆锥的母线．9(2023·吉林长春·校联考二模)如图，AB 是⊙O 的直径，AB =4，点C 在⊙O 上(点C 不与A 、B 重合)，过点C 作⊙O 的切线交AB 的延长线于点D ，连接AC ．若∠D =45°，则BC的长度是(结果保留π)【答案】π2/12π【分析】连接OC ，根据切线的性质，得出∠OCD =90°，再根据三角形的内角和定理，得出∠DOC =45°，即∠BOC =45°，再根据圆的基本概念，得出OB =2，再根据弧长公式，计算即可．【详解】解：如图，连接OC ，∵CD 是⊙O 的切线，∴CD ⊥OC ，。

九年级数学下册第24章圆24.7弧长与扇形面积(第2课时圆锥的侧面展开图)练习(新版)沪科版

第2课时圆锥的侧面展开图一、课前预习 (5分钟训练)1.圆锥的底面积为25π，母线长为13 cm ，这个圆锥的底面圆的半径为________ cm ，高为________ cm ，侧面积为________ cm2. 2.圆锥的轴截面是一个边长为10 cm 的正三角形，则这个圆锥的侧面积为________ cm 2，锥角为_________，高为________ cm.3.已知Rt△ABC 的两直角边AC=5 cm ，BC=12 cm ，则以BC 为轴旋转所得的圆锥的侧面积为_________ cm 2，这个圆锥的侧面展开图的弧长为_________ cm ，面积为_________ cm 2.4.如图，已知圆锥的底面直径为4，母线长为6，则它的全面积为__________.二、课中强化(10分钟训练)1.粮仓的顶部是圆锥形，这个圆锥的底面直径是4 m ，母线长为3 m ，为防雨需在粮仓的顶部铺上油毡，那么这块油毡的面积至少为( )A.6 m 2B.6π m 2C.12 m 2D.12π m 22.若圆锥的侧面展开图是一个半径为a 的半圆，则圆锥的高为( ) A.a B. 33a C.3a D.23a 3.用一张半径为9 cm 、圆心角为120°的扇形纸片，做成一个圆锥形冰淇淋的侧面(不计接缝)，那么这个圆锥形冰淇淋的底面半径是_________ cm.4.如图，已知圆锥的母线长OA=8，地面圆的半径r=2.若一只小虫从A 点出发，绕圆锥的侧面爬行一周后又回到A 点，则小虫爬行的最短路线的长是______(结果保留根式).5.一个圆锥的高为33 cm ，侧面展开图是半圆，求：(1)圆锥母线与底面半径的比；(2)锥角的大小；(3)圆锥的全面积.三、课后巩固(30分钟训练)1.已知圆锥的母线与高的夹角为30°，母线长为4 cm，则它的侧面积为_________ cm2(结果保留π).2.如图，有一圆锥形粮堆，其主视图是边长为6 m的正三角形ABC，母线AC的中点P处有一老鼠正在偷吃粮食，小猫从B处沿圆锥表面去偷袭老鼠，则小猫经过的最短路程是___________ m.(结果不取近似数)第2题图第5题图3.若圆锥的底面直径为6 cm，母线长为5 cm，则它的侧面积为___________.(结果保留π)4.在Rt△ABC中，已知AB=6，AC=8，∠A=90°.如果把Rt△ABC绕直线AC旋转一周得到一个圆锥，其全面积为S1；把Rt△ABC绕直线AB旋转一周得到另一个圆锥，其全面积为S2.那么S1∶S2等于( )A.2∶3B.3∶4C.4∶9D.5∶125.如图是小芳学习时使用的圆锥形台灯灯罩的示意图，则围成这个灯罩的铁皮的面积为____________ cm2(不考虑接缝等因素，计算结果用π表示).6.制作一个底面直径为30 cm、高为40 cm的圆柱形无盖铁桶,所需铁皮至少为( )A.1 425π cm2B.1 650π cm2C.2 100π cm2D.2 625π cm27.如图所示，在半径为27 m的广场中央，点O的上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角为120°，求光源离地面的垂直高度SO.(精确到0.1 m；2=1.414，3=1.732，5=2.236，以上数据供参考)。

圆锥的侧面积(巩固篇)(专项练习)

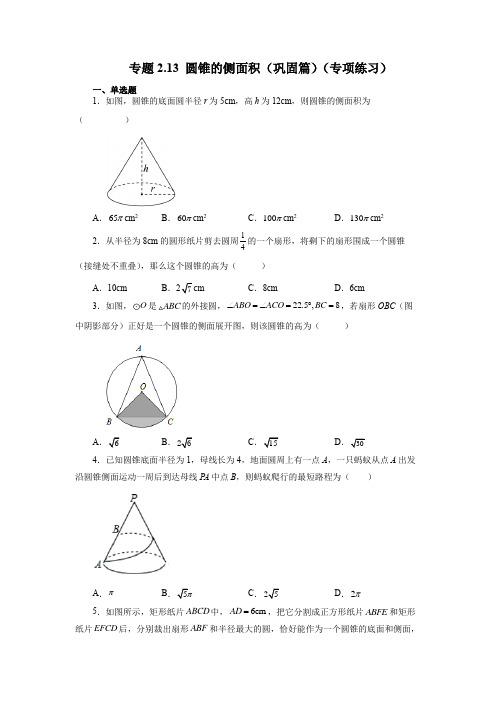
专题2.13 圆锥的侧面积（巩固篇）（专项练习）一、单选题1．如图，圆锥的底面圆半径r 为5cm ，高h 为12cm ，则圆锥的侧面积为（）A ．65πcm 2B ．60πcm 2C ．100πcm 2D ．130πcm 22．从半径为8cm 的圆形纸片剪去圆周14的一个扇形，将剩下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）A ．10cmB ．C ．8cmD ．6cm3．如图，O 是ABC 的外接圆，22.5,8ABO ACO BC ∠=∠=︒=，若扇形OBC （图中阴影部分）正好是一个圆锥的侧面展开图，则该圆锥的高为（）AB ．CD 4．已知圆锥底面半径为1，母线长为4，地面圆周上有一点A ，一只蚂蚁从点A 出发沿圆锥侧面运动一周后到达母线P A 中点B ，则蚂蚁爬行的最短路程为（）A ．πB C ．D ．2π5．如图所示，矩形纸片ABCD 中，6cm AD =，把它分割成正方形纸片ABFE 和矩形纸片EFCD 后，分别裁出扇形ABF 和半径最大的圆，恰好能作为一个圆锥的底面和侧面，则圆锥的表面积为（）A ．24πcmB ．25πcmC ．26πcmD ．28πcm6．已知圆锥的母线长为2，底面圆的半径为1，如果一只蚂蚁从圆锥的点B 出发，沿表面爬到AC 的中点D 处，则最短路线长为（）AB C ．D ．27．如图，圆柱的底面周长为12cm ，AB 是底面圆的直径，在圆柱表面的高BC 上有一点D ，且10cm BC =，2cm DC =．一只蚂蚁从点A 出发，沿着圆柱体的表面爬行到点D 的最短路程是（）cm ．A ．14B ．12C ．10D ．88．如图，从一张腰长为90cm ，顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面圆的半径为（）cm ．A ．15B ．30C ．45D ．30π9．斐波那契螺旋线也称“黄金螺旋线”，是根据斐波那契数列1，1，2，3，5，…画出来的螺旋曲线．如图，在每个边长为1的小正方形组成的网格中，阴影部分是依次在以1，1，2，3，5的一个四分之一圆做圆锥的侧面，则该圆锥的底面半径为（）A．54B．2C．52D．410．如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画圆，用图中阴影部分围成一个圆锥的侧面（接缝忽略不计），则该圆锥的高为（）A．4B．C．D．二、填空题11．如果圆锥底面圆的半径为3cm，它的侧面积为12 cm2，则这个圆锥的母线长为_____cm．12．如图，圆锥的母线长l为10cm，侧面积为50πcm2，则圆锥的底面圆半径r＝___cm．13．如图，菱形ABCD，∠A＝135°，以点C为圆心的弧EF分别与AB、AD相切于点G、H，与BC、CD分别相交于点E、F，用扇形CEF做成圆锥的侧面，则这个圆锥的高是_____．（结果保留根号）14．一个母线长为6cm ，底面半径为3cm 的圆锥展开后得到的侧面展开图扇形的圆心角是___度．15．用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面，则这个圆锥底面圆的周长为_____．16．如图，已知圆锥的母线AB 长为40 cm ，底面半径OB 长为10 cm ，若将绳子一端固定在点B ，绕圆锥侧面一周，另一端与点B 重合，则这根绳子的最短长度是______________．17．如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点B 出发，沿表面爬到AC 的中点D 处，则最短路线长为__________．18．如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC ，如果剪下来的扇形围成一个圆锥，则该圆锥的底面圆的周长为______m ．三、解答题19．一块四边形ABCD 余料如图所示，已知AD BC ∥，2AD =米，AB =点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F，用扇形AFD围成一个圆锥的侧面，求这个圆锥底面圆的半径．20．如图，已知一个圆锥的侧面展开图是一个半径为9cm，圆心角为120°的扇形．求：（1）圆锥的底面半径；（2）圆锥的全面积．21．如图，在单位长度为1的正方形网格中建立直角坐标系，一条圆弧恰好经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）：(1) 利用网格找出该圆弧所在圆的圆心D点的位置，则D点的坐标为_______；(2) 连接AD、CD，若扇形DAC是一个圆锥的侧面展开图，则该圆锥底面半径为_______；(3) 连接AB，将线段AB绕点D旋转一周，求线段AB扫过的面积．22．如图，已知扇形AOB的圆心角为120°，半径OA为9cm．(1) 求扇形AOB的弧长和扇形面积；(2) 若把扇形纸片AOB卷成一个圆锥形无底纸帽，求这个纸帽的高OH．23．如图，已知圆锥的底面半径r为10cm，母线长为40cm．求它的侧面展开扇形的圆心角的度数和它的全面积．24．已知圆锥的底面半径为r＝20cm，高h=,现在有一只蚂蚁从底边上一点A 出发．在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离．参考答案1．A【分析】根据圆锥的侧面积公式：S =πrl ，直接代入数据求出即可．解：由圆锥底面半径r =5cm ，高h =12cm ，根据勾股定理得到母线长l （cm ）， πrl =π×5×13=65π（cm 2），故选：A ．【点拨】此题主要考查了圆锥侧面积公式，熟练地应用圆锥侧面积公式求出是解决问题的关键．2．B【分析】先求得扇形的弧长，即圆锥的底面周长，则底面半径即可求得，然后利用勾股定理即可求得圆锥的高.解：圆心角是：1704360(1)2,︒⨯-=︒则弧长是：270812(cm),180ππ⨯= 设圆锥的底面半径是r ，则212r ππ=，解得：r =6, 则圆锥的高是：=故选：B.【点拨】本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长.3．D【分析】根据圆的性质，勾股定理求出圆的半径OB ，再根据扇形的弧长公式即可求解；解：根据圆的性质，2BOC A ∠=∠180180A ABO OBC ACO OCB OBC BOC OCB ∠+∠+∠+∠+∠=︒∠+∠+∠=︒∵， A ABO ACO BOC ∠+∠+∠=∠∴∵2BOC A ∠=∠，22.5ABO ACO ∠=∠=︒90BOC ∴∠=︒∵8OB OC BC ==，∴OB OC =∴124BC π=⋅⋅=∴圆锥底面圆的半径为：2r π==∴圆锥的高h =故选：D【点拨】本题主要考查圆的性质、勾股定理、弧长公式的应用，掌握相关知识并灵活应用是解题的关键．4．C【分析】要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，连接AB ，根据展开所得扇形的弧长等于圆锥底面圆的周长求得扇形的圆心角，进而解三角形即可求解．解：根据题意，将该圆锥展开如下图所示的扇形，则线段AB 就是蚂蚁爬行的最短距离．∵点B 是母线P A 的中点，4PA =， ∴2PB =，∵圆锥的底面圆的周长=扇形的弧长，又∵圆锥底面半径为1，∴扇形的弧长=圆锥底面周长，即22l r ππ==，扇形的半径=圆锥的母线=P A =4，由弧长公式可得：42180180n R n l πππ⨯=== ∴扇形的圆心角90n =︒，在Rt △APB 中，由勾股定理可得：AB =所以蚂蚁爬行的最短路程为故选：C．【点拨】.本题考查平面展开--最短路径问题、圆的周长计算公式、弧长计算公式，勾股定理等知识，解题的关键是“化曲为直”，将立体图形转化为平面图形．5．B【分析】设圆锥的底面的半径为rcm，则DE＝2rcm，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到()9062180rπ⨯-=2πr，解方程求出r，然后求得直径即可．解：设圆锥的底面的半径为rcm，则AE=BF=6-2r根据题意得()9062180rπ⨯-=2 πr，解得r＝1，侧面积=1·2?442rππ=，底面积=2rππ=所以圆锥的表面积=25πcm，故选：B．【点拨】本题综合考查有关扇形和圆锥的相关计算．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系：（1（2）圆锥的底面周长等于侧面展开图的扇形弧长．正确对这两个关系的记忆是解题的关键．6．A【分析】把圆锥的侧面展开，易得展开图是一个半圆，在平面内求出线段BD的长，则此时便是最短路线长，这只要在直角三角形中应用勾股定理解决即可．解：∵圆锥的底面周长为2π∴圆锥的侧面展开后的扇形的圆心角为21801802nππ⨯︒==︒，如图∴∠BAD=90゜∵D为AC的中点∴112122AD AC==⨯=在Rt△BAD中，由勾股定理得BD故选：A【点拨】本题考查了圆锥的侧面展开图，勾股定理，扇形弧长公式，本题体现了空间问题平面化，这是一种重要的数学思想方法．7．C【分析】首先画出圆柱的侧面展开图，根据底面周长12cm，求出AB的值，由BC=10cm，DC=2cm，求出DB的值，再在Rt△ABD 中，根据勾股定理求出AD 的长，即可得答案．解：圆柱侧面展开图如下图所示，∵圆柱的底面周长为12cm，∴AB =6cm，∵BC=10cm，DC=2cm，∴DB=8，在Rt△ABD 中，10AD=( cm )，即蚂蚁从A点出发沿着圆柱体的表面爬行到点D 的最短距离是10cm，故选：C ．【点拨】此题主要考查了圆柱的平面展开图，以及勾股定理的应用，解题的关键是画出圆柱的侧面展开图．8．A【分析】作出等腰三角形底边上的高线OE，首先根据直角三角形30°所对的直角边等于斜边的一半求出等腰三角形底边上的高线OE的长度，即得到扇形OCD所在的圆的半径R，然后根据弧长公式求出CD的长度，CD的长度即为圆锥底面圆的周长，最后根据周长求出半径即可．解：如图，过点O作OE⊥AB，垂足为E，∵△OAB为顶角为120°的等腰三角形，∴A ∠=30°，1452OE OA ==cm ， ∴12024530360CD ππ=⨯⨯=cm ，设圆锥的底面圆半径为r cm ，根据题意得，230r ππ=，解得15r =，所以该圆锥的底面圆的半径为15cm ，故选A ．【点拨】本题考查了直角三角形30°所对的直角边等于斜边的一半、扇形的弧长公式、圆的周长公式，准确将扇形的弧长转化为底面圆的周长是解决本题的关键． 9．A【分析】根据斐波那契数的规律，求出下一个圆弧的底面半径和弧长，结合圆锥的侧面积性质进行求解即可．解：有根据斐波那契数的规律可知，从第三项起，每一个数都是前面两个数之和，即半径为5的扇形对应的弧长152542l ππ=⨯⨯= 设圆锥底面半径为r ，则522r ππ= 54r ∴= 故选：A ．【点拨】本题考查圆锥侧面积的计算，结合斐波那契数的规律，及扇形的弧长公式进行转化是解题关键．10．C【分析】先计算出扇形的弧长，即圆锥的底面周长，从而得到圆锥的底面半径，然后利用勾股定理求出圆锥的高．解：正六边形的外角和为360︒，∴正六边形的每个外角的度数为360660，∴正六边形的每个内角的度数为18060120︒-︒=︒，设该圆锥的底面半径为r ，则120226360r ππ=⨯⨯，解得2r =，∴=故选：C ．【点拨】本题考查了正多边形与圆及圆锥的相关计算，以及勾股定理的应用，熟练掌握扇形与扇形所围圆锥侧面之间的等量关系是解题的关键．11．4【分析】设圆锥的母线长为l cm ，根据圆锥的侧面展开图为扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式得到123122l ππ⨯⨯⨯=，然后解方程即可．解：由扇形面积公式2360n S r π=⨯和弧长公式2360n l r π=⨯可得12扇形S lr ，设圆锥的母线长为l cm ，根据题意知侧面展开扇形的弧长为23π⨯，从而得到123122l ππ⨯⨯⨯=，解得l ＝4，即圆锥的母线长为4cm ，故答案为：4．【点拨】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．12．5【分析】根据圆锥的侧面积和圆锥的母线长求得圆锥的弧长，利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径即可．解：∵圆锥的母线长是10cm ，侧面积是50πcm 2，∴圆锥的侧面展开扇形的弧长为：l 210010s r π===10π（cm ）， ∵圆锥的侧面展开扇形的弧长等于圆锥的底面周长，∴r 1022l πππ===5（cm ），故答案为：5．【点拨】本题考查了圆锥的计算，解题的关键是正确地进行圆锥与扇形的转化．13 【分析】先连接CG ，设CG R =，由三角函数定义求得扇形的半径即圆锥的母线长，根据弧长公式180n R l π=，再由2180n R r ππ=，求出底面半径r ，最后根据勾股定理即可求得圆锥的高．解：如图：连接CG ，135C ∠=︒，45B ∴∠=︒，AB 与EF 相切，CG AB ∴⊥，在直角CBG ∆中，sin 451CG BC =⋅︒==，即圆锥的母线长是1，设圆锥底面的半径为r ，则：13512180r ππ⨯=， 38r ∴=．则圆锥的高h ==．【点拨】本题考查的是圆锥的计算，先利用直角三角形求出扇形的半径，运用弧长公式计算出弧长，然后根据底面圆的周长等于扇形的弧长求出底面圆的半径．14．180【分析】先计算出展开的扇形的弧长，再计算出以母线为半径的圆的周长，再根据圆心角公式即可得到答案．解：∵母线长为6l =cm ，底面半径为3r =cm ，∴展开的扇形的弧长为26r ππ=，以母线为半径的圆的周长为212l ππ=，∴侧面展开图扇形的圆心角=636018012ππ︒⨯=︒，故答案为：180︒．【点拨】本题考查圆锥的性质，解题的关键是熟练掌握圆锥的相关知识． 15．83π【分析】由圆锥底面的周长=扇形的弧长，利用弧长公式解题．解：圆锥底面的周长=扇形的弧长120481801803n r l πππ⨯=== 故答案为：83π．【点拨】本题考查扇形的弧长等知识，是基础考点，掌握相关知识是解题关键． 16．【分析】根据底面圆的周长等于扇形的弧长求解扇形的圆心角90,BAB '∠=︒ 再利用勾股定理求解即可.解：圆锥的侧面展开图如图所示：设圆锥侧面展开图的圆心角为n °，圆锥底面圆周长为210=20，40=20,180n BB 则n =90， ∵40,AB AB 224040402,BB即这根绳子的最短长度是，故答案为：【点拨】本题考查的是圆锥的侧面展开图，弧长的计算，掌握“圆锥的底面圆的周长等于展开图的弧长求解圆心角”是解本题的关键.17．【分析】将圆锥的侧面展开，设顶点为B'，连接BB'，AE ．线段AC 与BB'的交点为F ，线段BF 是最短路程．解：如图将圆锥侧面展开，得到扇形ABB′，则线段BF 为所求的最短路程．设∠BAB′＝n°．∵6180n π⋅＝4π， ∴n ＝120即∠BAB′＝120°．∵E 为弧BB′中点，∴∠AFB ＝90°，∠BAF ＝60°，∴BF ＝AB•sin ∠BAF ＝∴最短路线长为故答案为：【点拨】本题考查了平面展开−最短路径问题，解题时注意把立体图形转化为平面图形的思维．18．23π 【分析】连接OA ，OB ，OC ，证明AOB 是等边三角形，从而求得AB 的长，然后利用弧长公式计算出BOC 的长度，即是该圆锥底面圆的周长．解：如图，连接OA ，OB ，OC ，∵OB OC =，∴OB OC =， ∴1602BAO CAO BAC ∠=∠=∠=︒， ∴AOB 是等边三角形，∴1AB OA ==，∵120BAC ∠=︒，∴BOC 的长为：12021803AB ππ⋅⋅= ，即该圆锥的底面圆的周长为23π ．故答案为：23π．【点拨】本题主要考查了弧长公式以及扇形弧长与底面圆周长相等的知识点，解题的关键要掌握扇形弧长与底面圆周长相等．19．34r = 【分析】连接AE ，利用勾股定理得AE =BE ，由此即可求出∠ABE 的度数，再先求出扇形的圆心角∠DAB 的度数，再由弧长公式求出弧长，此弧长就是所得圆锥的底面圆的周长，由圆的周长公式即可求得所得圆锥的底面半径．解：如图，连接AE ，∵AD 为半径的圆与BC 相切于点E ，∴AE ⊥BC ，AE =AD =2．在Rt △AEB 中，∵AB =AE =2，∴AE =BE =2，∴∠ABE =45°．∴ABE △是等腰直角三角形，45BAE ∠=︒，设圆锥底面半径为r ，由题意得135222360r ππ⨯⨯=，解得34r =．【点拨】本题考查了切线的性质、平行线的性质、圆锥的计算，解题的关键是掌握所涉及的知识要点，并能够灵活运用．20．（1）圆锥的底面半径为3cm ；（2）圆锥的全面积236cm S π=【分析】（1）扇形的弧长公式l =180n r π，利用展开后扇形的弧长即为展开前圆锥底面圆的周长求出半径；（2）S 圆锥= S 侧+S 底，S 侧面=12lR ，S 底=2r π，（R =扇形半径即圆锥母线长，r =底面圆半径）将已知条件代入即可.解：（1）设圆锥的底面半径为cm r ．扇形的弧长为12096180l ππ⨯==， ∴26r ππ=，解得3r =，∴圆锥的底面半径为3cm ．（2）圆锥的侧面积：S 侧面=12lR =()216927cm 2ππ⨯⨯=．园锥的底面积：S 底=239(cm)ππ⨯=．∴圆锥的全面积S 全=S 侧+S 底=()227936cm πππ+=．【点拨】本题考查圆锥相关的计算，要求掌握圆锥侧面积与底面积的计算公式，侧面展开图扇形相关的面积和弧长的求算，注意求圆锥面积时母线与底面圆半径的区分.21．(1)（2，0）(3)4π 【分析】（1）线段AB 与BC 的垂直平分线的交点为D ；（2）连接AC ，先判断∠ADC =90°，则可求AC 的弧长，该弧长即为圆锥底面圆的周长，由此可求底面圆的半径；（3）设AB 的中点为E ，线段AB 的运动轨迹是以D 为圆心DA 、DE 分别为半径的圆环面积．（1）解：过点（2，0）作x 轴垂线，过点（5，3）作与BC 垂直的线，两线的交点即为D 点坐标，∴D （2，0），故答案为：（2，0）；（2）解：连接AC ，∵A （0，4），B （4，4），C （6，2），∴AD =CD =AC =∵AC 2＝AD 2+CD 2，∴∠ADC ＝90°，∴AC 的长124π=⨯⨯， ∵扇形DAC 是一个圆锥的侧面展开图，2r π=，∴r =，；（3）解：设AB 的中点为E ，∴E （2，4），∴DE ＝4，∴S ＝π×（AD 2﹣DE 2）＝4π，∴线段AB 扫过的面积是4π.,【点拨】本题考查圆锥的展开图，垂径定理，能够由三点确定圆的圆心位置，理解圆锥展开图与圆锥各部位的对应关系是解题的关键．22．(1)6cm π，227cm π(2)【分析】（1）根据弧长公式和扇形面积公式求解即可；（2）先求出底面圆的半径，然后利用勾股定理求解即可．（1）解：由题意得扇形AOB 的弧长12096cm 180ππ⨯⨯==，221209==27cm 360AOB S ππ⨯⨯扇形；（2）解：如图所示，AH 为底面圆的半径，OA 为母线长，由题意可得=9cm OA ，63cm 2AH ππ==，∴OH ==．【点拨】本题主要考查了求扇形面积，求弧长，求圆锥的高，勾股定理等等，解题的关键在于能够熟练掌握弧长公式和扇形面积公式．23．90°，500π【分析】根据由圆锥的底面圆的周长等于侧面展开扇形的弧长可求．解：由圆锥的底面圆的周长等于侧面展开扇形的弧长可知：π402π10180n ⨯⨯⨯=，90n =︒， ∴侧面展开扇形的圆心角的度数是90°．全面积＝底面积＋展开侧面积，全面积为：2290π40π10500π360⨯⨯⨯+=．【点拨】本题考查了圆锥全面积和展开图圆心角的度数，解题关键是明确圆锥的底面圆的周长等于侧面展开扇形的弧长，根据题意列方程求解．24．【分析】蚂蚁爬行的最短距离是圆锥的展开图的扇形中AA′的长度．根据勾股定理求得母线长后，利用弧长等于底面周长求得扇形的圆心角的度数为90度，再由等腰直角三角形的性质求解．解：设扇形的圆心角为n ，圆锥的在Rt △AOS 中，∵r=20cm ，h=，∴由勾股定理可得母线，而圆锥侧面展开后的扇形的弧长为2×20π=18080n π⨯. ∴n=90°即△SAA′是等腰直角三角形，∴由勾股定理得：．∴蚂蚁爬行的最短距离为．【点拨】本题利用了勾股定理，弧长公式，圆的周长公式，等腰直角三角形的性质求解．。

2第1课时弧长、扇形面积公式课件华东师大版数学九年级下册

形
再进行计算.
合作探究
(1)已知扇形的面积为12π cm2，圆心角为120°，则扇
形的弧长为
4π cm.
(2)圆心角为120°的扇形的弧长是6π，则此扇形的面积是
27π .
圆心角的度数是
180° .
(3)一条长度为10π cm的弧所对的圆心角为60°，则这条弧
所在的圆的半径是
30 cm .
合作探究
利用扇形面积公式进行计算
2.(1)在半径为6的☉O中，30°圆心角所对的扇形的面积为
3π .
(2)若扇形的面积为3π，圆心角为60°，则该扇形的半径为
3 .
(3)若扇形的面积为3π，半径是3，则该扇形的圆心角为
圆心角的度数
占周角的比例
所对弧占圆周长的比例
弧长
1°
90°
180°
n°
预习导学
解:
圆心角的度数
1°
90° 180°
占周角的比例
所对弧占圆周长的比例
弧长
πr
n°
预习导学
归纳总结
如果弧长为l，圆心角的度数为n，圆的半径为r，
那么弧长公式为l＝

.
预习导学
·导学建议·
通过回顾圆周长公式，加强新旧知识的联系，类比旧知识，
第27章圆
27.3 圆中的计算问题
第1课时弧长、扇形面积公式
素养目标
1.知道弧长、扇形面积的公式，会推导两者之间的关系.
2.会恰当熟练地运用公式计算弧长及扇形面积，增强数学应
用能力.
◎重点:弧长及扇形面积公式的推导及应用.
◎难点:弧长及扇形面积公式的应用.
预习导学
一块空旷的草地上有一根柱子，柱子上拴着一条长3米的绳

九年级数学下册第3章圆3.4弧长和扇形的面积圆锥的侧面展开图3.4.1弧长和扇形的面积课件湘教版20

1201 2. 180 3
【总结提升】求与弧长相关的计算的两个步骤
知识点 2 扇形的面积公式及应用【例2】如图，点A，B，C在半径为2的 ⊙O上，∠BAC=30°，求阴影部分弓形的面积. 【思路点拨】连结OB，OC，得△OBC为等边三角形，根据阴影部分的面积=扇形的面积-等边三角形的面积去计算.
【解析】∵∠C=90°，AC=8，BC=6，∴AB=10， ∴扇形的半径为5，∴阴影部分的面积= 9052 25．
360 4
答案：2 5
4
4.已知扇形的半径为3，扇形的面积为3π,则该扇形的圆心角
为_______，弧长为________.
【解析】把r=3,S=3π代入S n 中r 2 得,
360 3 n 9 , n 120,
2
2
∴r=5.
2.如图，正方形OABC的边长为2，OA为⊙O
的半径，则扇形OAC的面积为( )
A. B. 2
C. 3 D.2 2
【解析】选B.∵四边形OABC为正方形，边长为2， ∴OA=OC=2，∠AOC=90 °S，扇形OAC9036022 .
3.(2013·凉山州中考)如图，在Rt△ABC 中，∠C=90°，AC=8，BC=6，两等圆⊙A， ⊙B外切，那么图中两个扇形(即阴影部分)的面积之和为______.
其中 CD,DE,EF的圆心依次是A,B,C，如果 AB＝1，那么曲线CDEF的长是_____.
【解析】 CD 的长是 12012,
180 3
DE的长是： 12024,EF的长是： 12032,
180 3
180
则曲线 CDEF的长是： 2424. 33
答案：4π
5.如图所示，在Rt△ABC中，斜边AB= 2 2 ， ∠A=45°，把△ABC绕点B顺时针旋转60°

九年级数学下册第3章圆3.4弧长和扇形的面积,圆锥的侧面展开图3.4.2 圆锥的侧面积和全面积教学

3.4.2 圆锥的侧面积和全面积
1.经历探索圆锥侧(全)面积计算公式的过程，发展学生的实践探索能力. 2.了解圆锥的侧(全)面积计算公式后，能用公式进行计算，训练学生的数学应用能力.
圆锥可以看做是一个直角三角形绕它的一条直角边旋转一周所形成的图形.
C
A
O
B
圆锥知识知多少
O 母线
高 h
B
r
A1
底面半径
A2
侧面
A 底面
根据图形，圆锥的底面半径、母线及其高有什么数量关系？
A
l
O
B
设圆锥的底面半径为r，母线长为l,高为h，则有： l2＝r2+h2 即：OA2+OB2=AB2
【跟踪训练】
填空:根据下列条件求值（其中r，h，l分别是圆锥的底面半径、高线、母线长）
(1)l=2,r=1 则h=____3___ (2)h=3,r=4 则l=____5___ (3)l=10, h=8 则r=__6_____
解:∵l=80，h=38.7 ∴r= l 2 h2 802 38.72 70 cm
∴S侧=πrl≈3.14×70×80≈1.8×104（cm2）答：烟囱帽的面积约为1.8×104cm2.
圆锥的轴截面一个圆锥形的零件, 经过轴的剖面是一个等腰三角形,
这个三角形就叫做圆锥的轴截面；它的腰长等于圆锥的母线长, 底边长等于圆锥底面的直径. A
2
2π
S圆锥侧＝rl
1 2
58
22.03＝638.87(cm2 )
638.87×20=12777.4 (cm2)
所以, 至少要12777.4 cm2的纸.
【跟踪训练】
1.高为４㎝，底面直径为６㎝的圆锥侧面积为＿1＿5π＿cm2. （结果可含π）

华东师大初中数学九年级下册弧长和扇形面积、圆锥的侧面展开图—巩固练习(提高)

弧长和扇形面积、圆锥的侧面展开图—巩固练习（提高）【巩固练习】一、选择题1. 一个直角三角形绕它的一边所在直线旋转一周所得到的几何体一定是( )． A ．圆锥 B ．圆柱 C ．圆锥或圆柱 D ．以上都不对2. （2016•甘孜州）如图，在5×5的正方形网格中，每个小正方形的边长都为1，若将△AOB 绕点O 顺时针旋转90°得到△A′OB′，则A 点运动的路径的长为（）A ．πB ．2πC ．4πD ．8π3．如图所示，已知点A 、B 、C 、D 均在已知圆上，AD ∥BC ，AC 平分∠BCD ，∠ADC ＝120°，四边形ABCD 的周长为10cm ，图中阴影部分的面积为( )．A ．32 B ．233π- C ．23 D ．43第3题图第4题图第5题图4．如图所示，Rt △ABC 中，∠BAC 是直角，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为( )． A ．1 B ．2 C ．14π+D ．24π-5．如图所示，在△ABC 中，BC ＝4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于点E ，交AC于点F ，点P 是⊙A 上一点，且∠EPF ＝40°，则图中阴影部分的面积是( )． A ．49π-B ．849π-C ．489π-D ．889π- 6．在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型，如图所示，它的底面半径OB ＝6cm ，高OC ＝8cm ，则这个圆锥漏斗的侧面积是( )．A ．30cm 2B ．30π cm 2C ．60π cm 2D ．120cm 2二、填空题7. 如图，已知矩形纸片ABCD ，AD=2，3AB =，以A 为圆心，AD 长为半径画弧交BC 于点E ，将扇形AED 剪下围成一个圆锥，则该圆锥的底面半径为．第6题第7题8．（2016•孝感）若一个圆锥的底面圆半径为3cm ，其侧面展开图的圆心角为120°，则圆锥的母线长是___ cm ．9．已知在△ABC 中，AB ＝6，AC ＝8，∠A ＝90°，把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1，把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，则S 1:S 2等于________． 10．如图所示，有一圆心角为120°、半径长为6 cm 的扇形，若将OA 、OB 重合后围成一圆锥侧面，那么圆锥的高是．A BO第10题图第11题图第12题图11．矩形ABCD 的边AB ＝8，AD ＝6，现将矩形ABCD 放在直线l 上且沿着l 向右做无滑动地翻滚，当它翻滚到类似于开始的位置A 1B 1C 1D 1时(如图所示)，则顶点A 所经过的路线长是________． 12．如图，用一张半径为24cm 的扇形纸板制作一顶圆锥形帽子（接缝忽略不计），如果圆锥形帽子的底面半径为10cm ，那么这张扇形纸板的面积是 .三、解答题13. 如图所示，圆锥的母线长为4，底面圆半径为1，若一小虫P 从A 点开始绕着圆锥表面爬行一圈到SA 的中点C ，求小虫爬行的最短距离是多少?14．现有一张边长为20cm 的正方形纸片，你能用这张纸片制成一个表面积尽可能大的有底圆锥吗?说明你的做法并计算圆锥的表面积(结果精确到0.1cm ，2＝1.414)． ABCDE15．如图所示，有一直径是1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC．求：(1)被剪掉阴影部分的面积；(2)用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆半径是多少?(结果用根号表示)16.如图，AB为⊙O的直径，弦AC=2，∠B=30°，∠ACB的平分线交⊙O于点D，求：（1）BC、AD的长；（2）图中两阴影部分面积的和．【答案与解析】一、选择题 1．【答案】D ；【解析】绕直角边所在直线旋转一周所得到的几何体与绕斜边的不同． 2.【答案】B.【解析】∵每个小正方形的边长都为1， ∴OA=4，∵将△AOB 绕点O 顺时针旋转90°得到△A′OB′， ∴∠AOA′=90°， ∴A 点运动的路径的长为：=2π．故选B ． 3．【答案】B ；【解析】如图，因为AD ∥BC ，∠ADC ＝120°，所以∠BCD ＝60°，因为AC 平分∠BCD ，所以∠BCA ＝∠DAC ＝∠DCA ＝30°，所以∠BAC ＝90°，BC 为圆的直径，所以AD ＝DC ＝AB ．设BC 的中点为O ，连接OA 、OD ，由题意可知点A 、D 三等分半圆，则∠AOD ＝60°，且OA ＝OD ＝AB ＝AD ＝CD ，BC ＝2AD ，所以AB+AD+CD+BC ＝10，所以半径为2，则233AOD S S S π∆=-=-扇形扇．第3题答案图第5题答案图4.【答案】A ；【解析】连接AD ，12ABC S S ∆=阴影． 5．【答案】B ；【解析】如图，连接AD ，因为BC 为⊙A 切线、D 为切点，所以AD ⊥BC ．又由∠BAC ＝2∠EPF ＝2×40°＝80°，∴ 280283609EAF S ππ⨯==扇形． ∴ 1884299ABC EAF S S S BC AD ππ∆=-=⨯⨯-=-阴影阴影．6．【答案】C ；【解析】在Rt △COB 中，由CO 2+BO 2＝BC 2，得BC ＝10cm ，所以21261060(cm )2S ππ=⨯⨯⨯=侧．二、填空题7．【答案】13；【解析】在Rt △ABE 中， 2212(3)12BE AE =-==∴∠BAE=30°， ∴∠DAE=60°，∴圆锥的侧面展开图的弧长为：=π，∴圆锥的底面半径为π÷2π=．8.【答案】9.【解析】设母线长为l ，则=2π×3 ,解得：l=9．故答案为：9．9．【答案】2:3；【解析】如图所示，当以AC 为轴旋转时，21S r S π=+侧，AB 为底面圆半径，BC 为母线长10，则S 1＝36π+60π＝96π．当以AB 为轴旋转时，AC 为底面圆半径，BC 为母线长，80S rl ππ==侧，所以2S S S =+侧底6480144πππ=+=，所以S 1:S 2＝96π:144π＝2:3．10．【答案】42cm ；【解析】扇弧长12064cm 180ππ⨯=，而扇形的弧长等于圆锥底面圆的周长，设底面圆半径为r ，∴ 4π＝2πr ，∴ r ＝2cm ．如图所示，AC ＝2cm ，OA ＝6cm ，Rt △OAC 中，OC ＝2242OA AC -=cm ．11．【答案】12π；【解析】分析题意，考虑A 所经过的路线可分为三段孤长，如图所示，第一段是以B 为圆心，AB 长为半径，圆心角∠ABE ＝90°的弧长；第二段是以F 为圆心，EF 长为半径，圆心角∠EFM ＝90°的弧长；第三段是以N 为圆心，NA 1长为半径，圆心角∠A 1NM ＝90°的孤长．EF ＝10，NA 1＝6．则顶点A 所经过的路线长＝145312AE EM MA ππππ++=++=． 12.【答案】240π cm 2.【解析】这张扇形纸板的面积=×2π×10×24=240π（cm 2）．三、解答题 13.【答案与解析】将圆锥的侧面展开如图所示，取SA '的中点C ，连接AC ．则AC 是小虫爬行的最短路线．∵ 421180n ππ⨯⨯=，∴ 90n =°，即90ASA '∠=°．∵ SA ＝4，SC ＝2，∴ 224225AC =+=． ∴ 小虫爬行的最短距离为25．14. 【答案与解析】用一张正方形纸片制成一个有底圆锥，方法有多种，但使其表面积尽可能大的只有一种，确定了扇形、圆、正方形三者之间的关系之后；就可通过计算求出扇形及圆的半径，并制成符合条件的圆锥．具体做法：(1)通过分析、比较确定符合条件的扇形、圆与正方形的位置关系，并画出示意图，如图所示． (2)通过它们的位置关系计算出扇形和圆的半径，并根据计算结果在纸片上画出截剪线． (3)剪下符合条件的扇形与圆，用扇形作侧面，圆作底面粘接成圆锥．其表面积的计算过程是：如上图所示，设扇形的半径为Rcm ，⊙O 的半径为r cm ，M 、N 均为切点，连接OM 、ON ．则有OM ⊥BC ，ON ⊥DC ． ∵ OM ＝ON ＝r ．∴ 四边形OMCN 为正方形． ∴ OC ＝2r ．∵ AC ＝AG+GO+OC ，AC ＝2AB ＝202cm ，∴ 2202R r r ++=． ① ∵ EF 的弧长等于⊙O 的周长， ∴1224R r ππ⨯=，即R ＝4r ． ②由①②得2024.4152r =+≈，∴ 2214S S S R r ππ=+=+侧表底．222255 3.14 4.41cm 305.3cm r π==⨯⨯≈．故所做圆锥的表面积约为305.3cm 2．15. 【答案与解析】（1）连接BC ．∵ ∠BAC ＝90°，∴ BC 是⊙O 的直径，∴ BC ＝1m ． ∵ AB ＝AC ， ∴ 22AB AC ==m ． ∴ OABCS SS =-阴扇形222221121m m m 2428πππ⎛⎫⎛⎫=-= ⎪ ⎪ ⎪⎝⎭⎝⎭．（2）设圆锥底面圆的半径为r ，∴29022180r ππ=．∴2m 8r =．16. 【答案与解析】解：（1）∵AB 是直径，∴∠ACB=∠ADB=90°（直径所对的圆周角是直角），在Rt△ABC 中，∠B=30°，AC=2， ∴AB=4， ∴BC==2，∵∠ACB 的平分线交⊙O 于点D ， ∴∠DCA=∠BCD ∴=，∴AD=BD，（2）连接OC，OD，∵∠B=30°，∴∠AOC=∠2∠B=60°，∵OA=OB，∴S△AOC=S△ABC=××AC×BC=××2×2=，由（1）得∠AOD=90°，∴∠COD=150°，S△AOD=×AO×O D=×22=2，∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=﹣﹣2=π﹣﹣2．。

华师大版初中数学九年级下册总复习《弧长、扇形的面积和圆锥侧面积》学案

华师大版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！华师大初中数学和你一起共同进步学业有成！弧长、扇形的面积和圆锥侧面积一：【课前预习】（一）：【知识梳理】1.弧长公式：(n 为圆心角的度数上为圆半径)180n R l π= 2.扇形的面积公式S=(n 为圆心角的度数,R 为圆的半径）． 213602n R lR π= 3.圆锥的侧面积S=πRl ,(l 为母线长，r 为底面圆的半径),圆锥的侧面积与底面积之和称为圆锥的全面积．（二）：【课前练习】1.在半径为3的⊙O 中，弦AB=3，则AB 的长为2.扇形的周长为16，圆心角为’，则扇形的面积为（）A ．16B ．32C ．64D ．16π3.如图是小芳学习时使用的圆锥形台灯灯罩的示意图，则围成这个灯罩的铁皮的面积为________cm 2 (不考虑接缝等因素，计算结果用π表示）．4.底面半径为人高为h 的圆柱，两底的面积之和与它们的侧面积相等中与r 的关系为__________5.已知扇形的圆心角为120°，弧长为10π㎝，则这个扇形的半径为___cm二：【经典考题剖析】1.制作一个底面直径为30cm ，高40cm 的圆柱形无盖铁桶，所需铁皮至少为（），A ．1425πcm 2B ．1650πcm 2C ．2100πcm 2D ．2625πcm 22.如图，在⊙O 中，AB 是直径，半径为R ，求：AC R.3π=(1)∠AOC 的度数.(2)若D 为劣弧BC 上的一动点，且弦AD 与半径OC 交于E 点.试探求△AEC ≌△DEO 时，D 点的位置.3.如图，把直角三角形 ABC 的斜边AB 放在定直线l 上，按顺时针方向在l 上转动两次，使它转到△A ″B ′C ″的位置，设BC=1，AC=，则顶点A 运动到 A ″的位置时，点A 经3过的路线与直线l 所围成的面积是____________（计算结果不取近似值）4.如图，粮仓顶部是圆锥形，这个圆锥的底面圆的周长为36m ，母线长为8m ．为防雨需在粮食顶部铺上油毡，需要铺油毡的面积是_________好．5.如图，⊙O 的半径为1，圆周角∠ABC=30°，则图中阴影部分的面积是________. 三：【课后训练】1.已知Rt △ABC 的斜边AB=5，一条直角边AC=3，以直线BC 为轴旋转一周得到一个圆锥，则这个圆锥的侧面积为（）A ．8πB ．12πC ．15πD ．20π2.如图，圆锥的母线长为5cm ，高线长为4cm ，则圆锥的底面积是（）A ．3πcm Z ；B ．9πcm Z ；C ．16πcm Z ；D ．25πcm Z3.如果圆锥的高为8cm ，母线长为10cm ，则它的侧面展开图的面积为_____4.正方形ABCD 的边长为2 cm ，以边AB 所在直线为轴旋转一周，所得到的圆柱的侧面积为（）m 2相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

华师大版初中数学九年级下册27.3 第1课时弧长和扇形面积

华师大版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！华师大初中数学和你一起共同进步学业有成！27.3 圆中的计算问题第1课时弧长和扇形面积知识点一弧长2.一个扇形的圆心角为60°，弧长为2π厘米，则这个扇形的半径为（） A ．6厘米 B ．12厘米 C ．厘米4．在半径为的圆中，45°的圆心角所对的弧长等于．4π5.如图，⊙O 过△ABC 的顶点A 、B 、C ，且∠C=30°，AB=3，则弧AB 长为__________.6.如图，将半径为1、圆心角为的扇形纸片，在直线上向右作无滑动的滚动至︒60AOB l 扇形处，则顶点经过的路线总长为_________.B O A '''O7.如图，在△ABC中，AB=4cm，∠B=30°，∠C=45°，以A为圆心，以AC长为半径作弧与AB相交于点E，与BC相交于点F．（1）求弧CE的长；（2）求CF的长．8.如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米（左右对称），请计算该秋千所荡过的圆弧长（精确到0.1米）？9.一段圆弧形公路弯道，圆弧的半径为2km，弯道所对圆心角为10°，一辆汽车从此弯道上驶过，用时20s，弯道有一块限速警示牌，限速为40km/h，问这辆汽车经过弯道时有没有超速？（π取3）知识点二扇形面积1.圆心角为240°的扇形的半径为3cm ，则这个扇形的面积是（）cm 2． A ．π B ．3π C ．9π D ．6π2.若扇形的弧长是16cm ，面积是56cm 2，则它的半径是（） A ．2.8cm B ．3.5cm C ．7cm D ．14cm3.已知圆心角为120°的扇形面积为12π，那么扇形的弧长为（） A ．4 B ．2 C ．4π D ．2π4.一个商标图案如图中阴影部分，在长方形ABCD 中，AB=8cm ，BC=4cm ，以点A 为圆心，AD 为半径作圆与BA 的延长线相交于点F ，则商标图案的面积是（） A ．（4π+8）cm 2 B ．（4π+16）cm 2 C ．（3π+8）cm 2 D ．（3π+16）cm 2′第4题图第7题图第8题图5.已知扇形的弧长为6πcm ，圆心角为60°，则扇形的面积为_________．6.如图，扇形的弧长是20π，面积是240π，则此扇形的圆心角的度数是7.如图，已知点A 、B 、C 、D 均在以BC 为直径的圆上，AD ∥BC ，AC 平分∠BCD ，∠ADC=120°，四边形ABCD 的周长为10，则图中阴影部分的面积为___________.8．如图，将ABC △绕点B 逆时针旋转到A BC ''△使A 、B 、C’在同一直线上，若90BCA ∠=°，304cm BAC AB ∠==°，，则图中阴影部分面积为 cm 2． 9. 如图，已知点A 、B 、C 、D 均在已知圆上，AD ∥BC ，BD 平分∠ABC ，∠BAD=，四边120形ABCD 的周长为15.（1）求此圆的半径；（2）求图中阴影部分的面积。

华师版九年级下册数学第27章圆圆锥的侧面展开图

面积是( )
A．48π B．45π
A
C．36π D．32π
9．丁丁和当当用大小相同的圆形纸片分别剪成扇形(如图)做圆锥形的帽子，
请你判断哪个小朋友做成的帽子更高一些？( )
A．丁丁 B．当当
C．一样高
D．不确定 B
10．【中考·宁波】如图所示，矩形纸片ABCD中，AD＝6cm，把它分割成正方
形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好
∴蚂蚁爬行的最短路线长为 4 2dm.
14. 铁匠王老五要制作一个圆锥模型，操作规则如下：在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他首先设计了如图所示的方案一，发现这种方案不可行，于是他调整了扇形和圆的半径，设计了如图所示的方案二．(两个方案的图中，圆与正方形相邻两边及扇形的弧均相切．方案一中扇形的弧与正方形的两边相切)
能作为一个圆锥的侧面和底面，则AB的长为( )
A．3.5cm
B．4cm
C．4.5cm
D．5cm
B
【点拨】设AB＝x cm，则DE＝(6－x)cm，根据题意，得＝
π(6－x)，解得x＝4.故选B.
90πx 180
11．【中考·金华】如图物体由两个圆锥组成，其主视图中，∠A＝90°， ∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为( )
HS版九年级下
第27章圆
27.3 圆中的计算问题第2课时圆锥的侧面展开图
提示：点击进入习题
新知笔记
1 l；2πr； l2－r2
1C 22
2 πrl；πr2＋πrl
3 见习题
4D

九年级下第24章圆24-7弧长与扇形面积第2课时圆锥的侧面展开图作业新版沪科版

4．如图，蒙古包可近似地看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为 25π m2，圆柱高为 3 m，圆锥高为 2 m 的蒙古包，则需要毛毡的面积是( A )
A．(30＋5 29 )π m2 B．40π m2 B．(30＋5 21 )π m2 D．55π m2
5．(黑龙江中考)已知圆锥的母线长为13 cm，侧面积为65π cm2，则这个圆锥的高是 __1_2__ cm.
(B) A．5
B．3 3
C．3 2
D．6 3
8．在数学实验课上，小莹将含30°角的直角三角尺分别以两个直角边为轴旋转一周，得到甲、乙两个圆锥，并用作图软件画出如下示意图．
小亮观察后说：“甲、乙圆锥的侧面都是由三角尺的斜边AB旋转得到，所以它们的侧面积相等．”小亮的说法正确吗？请说明理由．
解：小亮的说法不正确．设直角三角尺三边长分别为 BC＝a，AC＝ 3 aa2.乙圆锥的侧面积：S 乙＝ π·AC·AB＝π× 3 a×2a＝2 3 πa2，∴S 甲≠S 乙，∴小亮的说法不正确∴S 甲≠S 乙， ∴小亮的说法不正确
24.7 弧长与扇形面积第2课时圆锥的侧面展开图
知识点圆柱、圆锥侧面展开图相关的计算 1．如果圆柱的底面半径为 4 cm，母线长为 5 cm，那么它的侧面积等于( B ) A．20π cm2 B．40π cm2 C．20 cm2 D．40 cm2 2．如图，圆锥底面圆的半径为 4，则这个圆锥的侧面展开图中 AA′的长为( C ) A．4π B．6π C．8π D．16π
3．如果圆锥侧面展开图的面积是15π，母线长是5，则这个圆锥的底面半径是
( A) A．3 B．4 C．5 D．6 【变式】(合肥蜀山区二模)如图，用一个圆心角为θ的扇形纸片围成一个底面

华东师大版九年级数学下册27.3：第2课时圆锥的侧面展开图同步测试题(含答案)

华东师大版九年级数学下册第27章圆27.3第2课时圆锥的侧面展开图同步测试题一、选择题（每小题3分，共33分）1.下列图形中，是圆锥侧面展开图的是(B)2.如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是(D)A.15πB.30πC.45πD.60π3.若圆锥的母线长为6 cm，底面半径为2 cm，则圆锥的高为(C)A. 2 cmB.3 2 cmC.4 2 cmD.4 cm4.若将半径为12 cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径是(D)A.2 cmB.3 cmC.4 cmD.6 cm5.如图是某几何体的三视图及相关数据，则该几何体的侧面积是(B)A.10πB.15πC.20πD.30π6.如图，在Rt△ABC中，AC＝5 cm，BC＝12 cm，∠ACB＝90°，把Rt△ABC沿BC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为(B)A.60π cm2B.65π cm2C.120π cm2D.130π cm27.如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽(接缝忽略不计)，圆锥底面圆的直径是60 cm，则这块扇形铁皮的半径是(A)A.40 cmB.50 cmC.60 cmD.80 cm8.将直径为60 cm的圆形铁皮，做成三个相同的圆锥容器的侧面(不浪费材料，不计接缝处的材料损耗)，那么每个圆锥容器的底面半径为(A)A.10 cmB.30 cmC.45 cmD.300 cm9.如图，蒙古包可近似地看作由圆锥和圆柱组成.若用毛毡搭建一个底面圆面积为25π m2，圆柱高为3 m，圆锥高为2 m的蒙古包，则需要毛毡的面积是(A)A.(30＋529)π m2B.40π m2C.(30＋521)π m2D.55π m210.如图所示，矩形纸片ABCD中，AD＝6 cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为(B)A.3.5 cmB.4 cmC.4.5 cmD.5 cm11.如图，点C 为扇形OAB 的半径OB 上一点，将△OAC 沿AC 折叠，点O 恰好落在AB ︵上的点D 处，且BD l ∶AD l ＝1∶3(BD l 表示BD ︵的长).若将此扇形OAB 围成一个圆锥，则圆锥的底面半径与母线长的比为(D)A.1∶3B.1∶πC.1∶4D.2∶9 二、填空题（每小题3分，共15分）12.若一个圆锥的底面圆的周长是5π cm，母线长是6 cm ，则该圆锥的侧面展开图的圆心角度数是150°.13.一个圆锥的侧面展开图是半径为8 cm ，圆心角为120°的扇形，则此圆锥的底面半径为83cm.14.若一圆锥的轴截面是等边三角形，则其侧面展开图的圆心角是180°. 15.一个底面直径是80 cm ，母线长为90 cm 的圆锥的侧面展开图的圆心角的度数为160°.16.用一个圆心角为120°，半径为6的扇形做一个圆锥的侧面，则这个圆锥的底面圆的面积为4π. 三、解答题（共52分）17.已知圆锥的侧面展开图是一个半径为12 cm ，弧长为12π cm 的扇形，求这个圆锥的侧面积及高.解：这个圆锥的侧面积为12×12×12π＝72π(cm2)，设底面圆的半径为r cm，则2πr＝12π，解得r＝6.故这个圆锥的高为122－62＝63(cm).18.如图，一个圆锥形工艺品，它的高为3 3 cm，侧面展开图是半圆.求：(1)圆锥的母线长与底面半径之比；(2)圆锥的侧面积.解：(1)设圆锥底面半径为r cm，母线长为l cm，由题意，知2πr＝πl.则l∶r＝2∶1.∴圆锥的母线长与底面半径之比为2∶1.(2)由题意，知r2＋(33)2＝l2.把l＝2r代入，解得r1＝－3(舍去)，r2＝3.∴l＝6.∴圆锥的侧面积为πrl＝18π cm 2.19.如图，有一直径是2米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC.(1)求AB 的长度；(2)若用该扇形铁皮围成一个圆锥，则所得圆锥的底面圆的半径为多少米？解：(1)∵∠BAC＝90°， ∴BC 为⊙O 的直径，即BC ＝2米.∴AB＝22BC ＝1米. (2)设所得圆锥的底面圆的半径为r 米，根据题意，得2πr＝90×π×1180，解得r＝14. ∴底面圆的半径为14米.20.如图是一纸杯，它的母线AC 和EF 延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量，纸杯上开口圆的直径为6 cm ，下底面圆的直径为4 cm ，母线长EF ＝8 cm. (1)求扇形OAB 的圆心角；(2)求这个纸杯的表面积(面积计算结果用π表示).解：(1)由题意可知： AB ︵＝6π cm，CD ︵＝4π cm.设∠AOB＝n°，AO ＝R cm ，则CO ＝(R －8)cm ，由弧长公式得：n πR 180＝6π，nπ（R －8）180＝4π.解方程组⎩⎨⎧6×180＝nR ，4×180＝nR －8n ，得⎩⎨⎧n ＝45，R ＝24. ∴扇形OAB 的圆心角是45°. (2)∵R＝24 cm ，R －8＝16 cm ， ∴S 扇形OCD ＝12×4π×16＝32π(cm 2)，S 扇形OAB ＝12×6π×24＝72π(cm 2).∴S纸杯侧面积＝S扇形OAB－S扇形OCD＝72π－32π＝40π(cm2).又∵S纸杯底面积＝π×22＝4π(cm2)，∴S纸杯表面积＝40π＋4π＝44π(cm2).。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

弧长和扇形面积、圆锥的侧面展开图—巩固练习（基础）
【巩固练习】
一、选择题
1.一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（）
A.5π
B. 4π
C.3π
D.2π
2．如图所示，边长为12m的正方形池塘的周围是草地，池塘边A、B、C、D处各有一棵树，且AB＝BC＝CD＝3m．现用长4m的绳子将一头羊拴在其中的一棵树上，为了使羊在草地上活动区域的面积最大，应将绳子拴在( )．
A．A处 B．B处 C．C处 D．D处
3．（2016•台湾）如图，有一圆O通过△ABC的三个顶点．若∠B=75°，∠C=60°，且的长度为4π，则BC的长度为何？（）
A．8 B．8C．16 D．16
4．一圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图所对应的扇形的圆心角是( )．
A．120° B．180° C．240° D．300°
5．底面圆半径为3cm，高为4cm的圆锥侧面积是( )．
A．7.5π cm2 B．12π cm2 C．15πcm2 D．24π cm2
6．如图，半径为1的圆O与正五边形ABCDE相切于点A、C，劣弧AC的长度为（）
A．πB．πC．πD．π
二、填空题
7．已知扇形圆心角是150°，弧长为20πcm，则扇形的面积为________．
8．如图，某传送带的一个转动轮的半径为40cm，转动轮转90°传送带上的物品A被传送厘米.
第8题图第9题图第11题图
9．如图所示，已知扇形的半径为3cm，圆心角为120°，则扇形的面积为________cm2(结果保留π)．10.用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是．
''的位11．如图所示，把一块∠A＝30°的直角三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A B C 置．若BC的长为15cm，求顶点A从开始到结束所经过的路径长．
12．（2016•绥化）如图，在半径AC为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，连接CD，则图中阴影部分的面积是．
三、解答题
13．如图是两个半圆，点O为大半圆的圆心， AB是大半圆的弦关与小半圆相切，且AB=24．问：能求出阴影部分的面积吗？若能，求出此面积；若不能，试说明理由．
14. 圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起，连接AC、BD．
(1)求证：△AOC≌△BOD；
(2)若OA＝3cm，OC＝1cm，求阴影部分的面积．
15．如图所示，线段AB与⊙O相切于点C，连接OA、OB，OB交⊙0于点D，已知OA＝OB＝6cm，AB＝63cm，求：(1)⊙O的半径；(2)图中阴影部分的面积．
16.已知：如图△ABC内接于⊙O，OH⊥AC于H，过A点的切线与OC的延长线交于点D，∠B=30°，．请求出：
（1）∠AOC的度数；
（2）线段AD的长（结果保留根号）；
（3）求图中阴影部分的面积．
【答案与解析】
一、选择题
1.【答案】C .
【解析】圆锥的侧面展开图的弧长为2π，
圆锥的侧面面积为2π，底面半径为1，
圆锥的底面面积为π，则该圆锥的全面积是2π+π=3π.
故选C.
2.【答案】B
【解析】小羊的活动区域是扇形，或是扇形的组合图形，只要算出每个扇形的面积，
即可比较出拴在B处时活动区域的面积最大．
3.【答案】B.
【解析】连接OB，OC，
∵∠B=75°，∠C=60°，
∴∠A=45°，∴∠BOC=90°，
∵的长度为4π，
∴=4π，
∴OB=8，
∴BC===8，
故选B．
4.【答案】B ；
【解析】由2
2rl r ππ=得2l r =， ∴ 22180
n r
r ππ=．∴ n ＝180°． 5.【答案】C ；
【解析】可求圆锥母线长是5cm ． 6.【答案】B ；
【解析】因为正五边形ABCDE 的内角和是（5﹣2）×180=540°，
则正五边形ABCDE 的一个内角=
=108°；
连接OA 、OB 、OC ，
∵圆O 与正五边形ABCDE 相切于点A 、C ， ∴∠OAE=∠OCD=90°，
∴∠OAB=∠OCB=108°﹣90°=18°， ∴∠AOC=144°
所以劣弧AC 的长度为
=π．故选B ．
二、填空题
7.【答案】240πcm 2
；
【解析】先由弧长求出扇形的半径，再计算扇形的面积． 8．【答案】20π（cm ）；【解析】9040
20180180
n r l πππ⨯=
==(cm)． 9．【答案】3π；
【解析】由扇形面积公式得22
12033360360
n R S πππ⨯===扇形(cm 2)． 10．【答案】2 ；【解析】扇形的弧长=
=4π，
∴圆锥的底面半径为4π÷2π=2．
故答案为：2．．
11．【答案】20()cm π；
【解析】顶点A 经过的路径是一段弧，弧所在的扇形的圆心角是120°，半径AC=2BC=30cm,
12030
20()180
l cm ππ⨯=
=.
12.【答案】π﹣1．
【解析】在Rt △ACB 中，AB==2
，
∵BC 是半圆的直径， ∴∠CDB=90°，
在等腰Rt △ACB 中，CD 垂直平分AB ，CD=BD=，
∴D 为半圆的中点，
S 阴影部分=S 扇形ACB ﹣S △ADC =π×22﹣×（）2=π﹣1．
故答案为π﹣1．
三、解答题
13.【答案与解析】
将小圆向右平移，使两圆变成同心圆，如图，连OB ，
过O 作OC ⊥AB 于C 点，则AC=BC=12， ∵AB 是大半圆的弦且与小半圆相切， ∴OC 为小圆的半径， ∴S 阴影部分=S 大半圆-S 小半圆 =π•OB 2
-π•OC
2
=π（OB 2-OC 2） =πAC 2 =72π．故答案为72π．
14.【答案与解析】
(1)证明：同圆中的半径相等，即OA ＝OB ，OC ＝OD ．
再由∠AOB ＝∠COD ＝90°，得∠1＝∠2，所以△AOC ≌△BOD ． (2)解：22211
()(91)2(cm )44
S S S OA OC πππ=-=
-=-=阴影扇形AOB 扇形COD ． 15.【答案与解析】
(1)如图所示，连接OC ，则OC ⊥AB ，
∴ OA ＝OB ，
∴ AC ＝BC ＝
11
63cm 33cm 22
AB =⨯=．在Rt △AOC 中，
22226(33)cm 3cm OC OA AC =-=-=．
∴ ⊙O 的半径为3 cm ．
(2)∵ OC ＝3cm 1
2
=
OB ，∠B ＝30°，∠COD ＝60°． ∴ 扇形OCD 的面积为
226033
(cm )3602
ππ=． ∴ 阴影部分的面积为 213933(cm )222
BOC OCD S S OC CB π
π∆--=-=扇形． 16. 【答案与解析】
解：（1）∵∠B=30°，
∴∠AOC=2∠B=60°；
（2）∵∠AOC=60°，AO=CO ， ∴△AOC 是等边三角形； ∵OH=， ∴AO=4；
∵AD 与⊙O 相切， ∴AD=；
（3）∵S 扇形OAC ==π，S △AOD =×4×4
=8
；
∴．。