图形与证明专题(三)

合集下载

2019版二轮复习数学(理)全国版专题三第二讲大题考法——立体几何

第二讲大题考法——立体几何[典例感悟][典例1] (2018·全国卷Ⅱ)如图，在三棱锥P -ABC 中，AB ＝BC ＝22，P A ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M -P A -C 为30°，求PC 与平面P AM 所成角的正弦值.[解] (1)证明：因为P A ＝PC ＝AC ＝4，O 为AC 的中点，所以PO ⊥AC ，且PO ＝2 3. 连接OB ，因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.所以PO 2＋OB 2＝PB 2，所以PO ⊥OB . 又因为OB ∩AC ＝O ，所以PO ⊥平面ABC .(2)以O 为坐标原点，OB ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系O -xyz .由已知得O (0,0,0)，B (2,0,0)，A (0，－2,0)，C (0,2,0)，P (0,0，23)，AP ―→＝(0,2,23)．取平面P AC 的一个法向量OB ―→＝(2,0,0)．设M (a,2－a,0)(0<a ≤2)，则AM ―→＝(a,4－a,0)．设平面P AM 的法向量为n ＝(x ，y ，z )．由⎩⎪⎨⎪⎧AP ―→·n ＝0，AM ―→·n ＝0，得⎩⎪⎨⎪⎧2y ＋23z ＝0，ax ＋(4－a )y ＝0，令y ＝3a ，得z ＝－a ，x ＝3(a －4)，所以平面P AM 的一个法向量为n ＝(3(a －4)，3a ，－a )，所以cos 〈OB ―→，n 〉＝23(a －4)23(a －4)2＋3a 2＋a2.由已知可得|cos 〈OB ―→，n 〉|＝cos 30°＝32，所以23|a －4|23(a －4)2＋3a 2＋a 2＝32，解得a ＝43或a ＝－4(舍去)．所以n ＝⎝⎛⎭⎫－833，433，－43.又PC ―→＝(0,2，－23)，所以cos 〈PC ―→，n 〉＝833＋8334＋12·643＋163＋169＝34.所以PC 与平面P AM 所成角的正弦值为34.[典例2] (2016·全国卷Ⅲ)如图，四棱锥P -ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点．(1)证明MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值.[解] (1)证明：由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN ，由N 为PC 的中点知TN ∥BC ，TN ＝12BC ＝2.又AD ∥BC ，故TN 綊AM ，所以四边形AMNT 为平行四边形，于是MN ∥AT . 因为MN ⊄平面P AB ，AT ⊂平面P AB ，所以MN ∥平面P AB . (2)取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，且AE ＝AB 2－BE 2＝AB 2－⎝⎛⎭⎫BC 22＝ 5.以A 为坐标原点，AE ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系A -xyz . 由题意知P (0,0,4)，M (0,2,0)，C (5，2,0)，N ⎝⎛⎭⎫52，1，2，PM ―→＝(0,2，－4)，PN ―→＝⎝⎛⎭⎫52，1，－2，AN ―→＝⎝⎛⎭⎫52，1，2.设n ＝(x ，y ，z )为平面PMN 的法向量，则⎩⎪⎨⎪⎧n ·PM ―→＝0，n ·PN ―→＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0,2,1)．于是|cos 〈n ，AN ―→〉|＝|n ·AN ―→||n ||AN ―→|＝8525.所以直线AN 与平面PMN 所成角的正弦值为8525.[类题通法]1．证明空间位置关系要抓两点一是平面图形中的平行与垂直关系，这是证明空间线面平行与垂直关系的起点，特别是三角形、梯形中的平行与垂直关系；二是准确利用空间线、面平行与垂直的判定与性质定理，尤其是定理中的条件要记全、记准，切忌因记漏条件或错用定理等导致出错．2．利用空间向量求线面角的解题模型[对点训练](2018·唐山模拟)如图，在四棱锥P -ABCD 中，PC ⊥底面ABCD ，ABCD 是直角梯形，AB ⊥AD ，AB ∥CD ，AB ＝2AD ＝2CD ，E 是PB 的中点．(1)求证：平面EAC ⊥平面PBC ； (2)若二面角P -AC -E 的余弦值为63，求直线P A 与平面EAC 所成角的正弦值．解：(1)证明：因为PC ⊥平面ABCD ，AC ⊂平面ABCD ，所以AC ⊥PC . 因为AB ＝2AD ＝2CD ，所以AC ＝BC ＝2AD ＝2CD ，所以AC 2＋BC 2＝AB 2，故AC ⊥BC . 又BC ∩PC ＝C ，所以AC ⊥平面PBC . 因为AC ⊂平面EAC ，所以平面EAC ⊥平面PBC .(2)如图，以C 为原点，CB ―→，CA ―→，CP ―→的方向分别为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系，并设CB ＝2，CP ＝2a (a >0)．则C (0,0,0)，A (0,2,0)，B (2,0,0)，P (0,0,2a )，则E (1,0，a )，CA ―→＝(0,2,0)，CP ―→＝(0,0,2a )，CE ―→＝(1,0，a )，易知m ＝(1,0,0)为平面P AC 的一个法向量．设n ＝(x ，y ，z )为平面EAC 的法向量，则n ·CA ―→＝n ·CE ―→＝0，即⎩⎪⎨⎪⎧2y ＝0，x ＋az ＝0，取x ＝a ，则z ＝－1，n ＝(a,0，－1)．依题意，|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝a a 2＋1＝63，则a ＝ 2.于是n ＝(2，0，－1)，P A ―→＝(0,2，－22)．设直线P A 与平面EAC 所成角为θ，则sin θ＝|cos 〈P A ―→，n 〉|＝|P A ―→·n ||P A ―→||n |＝23，即直线P A 与平面EAC 所成角的正弦值为23.[典例1] (2018·全国卷Ⅲ)如图，边长为2的正方形ABCD 所在的平面与半圆弧C D 所在平面垂直，M 是C D 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M -ABC 体积最大时，求平面MAB 与平面MCD 所成二面角的正弦值.[解] (1)证明：由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，所以BC ⊥DM .因为M 为CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM .又BC ∩CM ＝C ，所以DM ⊥平面BMC .因为DM ⊂平面AMD ，所以平面AMD ⊥平面BMC .(2)以D 为坐标原点，DA ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系D -xyz .当三棱锥M -ABC 的体积最大时，M 为CD 的中点．由题设得D (0,0,0)，A (2,0,0)，B (2,2,0)，C (0,2,0)，M (0,1,1)，AM ―→＝(－2，1,1)，AB ―→＝(0,2,0)，DA ―→＝(2,0,0)，设n ＝(x ，y ，z )是平面MAB 的法向量，则⎩⎪⎨⎪⎧n ·AM ―→＝0，n ·AB ―→＝0，即⎩⎪⎨⎪⎧－2x ＋y ＋z ＝0，2y ＝0.可取n ＝(1,0,2)，又DA ―→是平面MCD 的一个法向量，所以cos 〈n ，DA ―→〉＝n ·DA ―→|n ||DA ―→|＝55，sin 〈n ，DA ―→〉＝255.所以平面MAB 与平面MCD 所成二面角的正弦值是255.[典例2] (2017·全国卷Ⅰ)如图，在四棱锥P -ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，求二面角A -PB -C 的余弦值.[解] (1)证明：由已知∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD . 因为AB ∥CD ，所以AB ⊥PD . 又AP ∩PD ＝P ，所以AB ⊥平面P AD . 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AD .(2)在平面P AD 内作PF ⊥AD ，垂足为F .由(1)可知，AB ⊥平面P AD ，故AB ⊥PF ，可得PF ⊥平面ABCD .以F 为坐标原点，F A ―→的方向为x 轴正方向，|AB ―→|为单位长度，建立如图所示的空间直角坐标系F -xyz .由(1)及已知可得A ⎝⎛⎭⎫22，0，0，P ⎝⎛⎭⎫0，0，22，B ⎝⎛⎭⎫22，1，0，C ⎝⎛⎭⎫－22，1，0. 所以PC ―→＝⎝⎛⎭⎫－22，1，－22，CB ―→＝(2，0,0)，P A ―→＝⎝⎛⎭⎫22，0，－22，AB ―→＝(0,1,0)．设n ＝(x 1，y 1，z 1)是平面PCB 的法向量，则⎩⎪⎨⎪⎧ n ·PC ―→＝0，n ·CB ―→＝0，即⎩⎪⎨⎪⎧－22x 1＋y 1－22z 1＝0，2x 1＝0.所以可取n ＝(0，－1，－2)．设m ＝(x 2，y 2，z 2)是平面P AB 的法向量，则⎩⎪⎨⎪⎧ m ·P A ―→＝0，m ·AB ―→＝0，即⎩⎪⎨⎪⎧22x 2－22z 2＝0，y 2＝0.所以可取m ＝(1,0,1)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－23×2＝－33. 由图知二面角A -PB -C 为钝角，所以二面角A -PB -C 的余弦值为－33. [类题通法]利用空间向量求二面角的解题模型[对点训练]如图，四棱锥P-ABCD的底面ABCD为菱形，平面P AD⊥平面ABCD，P A＝PD＝5，AD＝6，∠DAB＝60°，E为AB的中点．(1)证明：AC⊥PE；(2)求二面角D-P A-B的余弦值．解：(1)证明：如图，取AD的中点O，连接OP，OE，BD，∵四边形ABCD为菱形，∴BD⊥AC，∵O，E分别为AD，AB的中点，∴OE∥BD，∴AC⊥OE.∵P A＝PD，O为AD的中点，∴PO⊥AD，又∵平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，∴PO⊥平面ABCD，∴PO⊥AC，∵OE∩OP＝O，∴AC⊥平面POE，∴AC⊥PE.(2)连接OB，∵四边形ABCD为菱形，∴AD＝AB，又∠DAB＝60°，∴△DAB为等边三角形，又O为AD的中点，∴OB⊥AD，∵PO⊥平面ABCD，OA⊂平面ABCD，OB⊂平面ABCD，∴PO⊥OA，PO⊥OB，∴OP，OA，OB两两垂直．以OA ，OB ，OP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系O -xyz ，则A (3,0,0)，B (0,33，0)，P (0，0,4)，OB ―→＝(0,33，0)为平面P AD 的一个法向量．设平面P AB 的法向量为n ＝(x ，y ，z )，又AP ―→＝(－3,0,4)，AB ―→＝(－3,33，0)，∴⎩⎪⎨⎪⎧AP ―→·n ＝0，AB ―→·n ＝0，即⎩⎪⎨⎪⎧－3x ＋4z ＝0，－3x ＋33y ＝0，取x ＝1，则y ＝33，z ＝34，n ＝⎝⎛⎭⎫1，33，34为平面P AB 的一个法向量，∴cos 〈OB ―→，n 〉＝OB ―→·n |OB ―→||n |＝333×1＋13＋916＝49191，结合图形可知二面角D -P A -B 的余弦值为49191.[典例感悟][典例] (2016·北京高考)如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A ＝PD ，AB ⊥AD ，AB ＝1，AD ＝2，AC ＝CD ＝ 5.(1)求证：PD ⊥平面P AB ；(2)求直线PB 与平面PCD 所成角的正弦值；(3)在棱P A 上是否存在点M ，使得BM ∥平面PCD ？若存在，求AMAP 的值；若不存在，说明理由．[解](1)证明：因为平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，AB⊥AD，AB⊂平面ABCD，所以AB⊥平面P AD.所以AB⊥PD.又因为P A⊥PD，P A∩AB＝A，所以PD⊥平面P AB.(2)取AD的中点O，连接PO，CO.因为P A＝PD，所以PO⊥AD.又因为PO⊂平面P AD，平面P AD⊥平面ABCD，所以PO ⊥平面ABCD . 因为CO ⊂平面ABCD ，所以PO ⊥CO .因为AC ＝CD ，所以CO ⊥AD . 如图所示，建立空间直角坐标系O -xyz .由题意得，A (0,1,0)，B (1,1,0)，C (2,0,0)，D (0，－1,0)，P (0,0,1)．则PD ―→＝(0，－1，－1)，PC ―→＝(2,0，－1)，PB ―→＝(1,1，－1)，设平面PCD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·PD ―→＝0，n ·PC ―→＝0，即⎩⎪⎨⎪⎧－y －z ＝0，2x －z ＝0.令z ＝2，则x ＝1，y ＝－2. 所以n ＝(1，－2,2)．又PB ―→＝(1,1，－1)，所以cos 〈n ，PB ―→〉＝n ·PB ―→| n ||PB ―→|＝－33.所以直线PB 与平面PCD 所成角的正弦值为33. (3)设M 是棱P A 上一点，则存在λ∈[0,1]，使得AM ―→＝λAP ―→.因此点M (0,1－λ，λ)，BM ―→＝(－1，－λ，λ)．因为BM ⊄平面PCD ，所以要使BM ∥平面PCD ，当且仅当BM ―→·n ＝0，即(－1，－λ，λ)·(1，－2,2)＝0.解得λ＝14.所以在棱P A 上存在点M 使得BM ∥平面BCD ，此时AM AP ＝14.[类题通法]利用空间向量求解探索性问题的策略(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论．(2)在(1)的前提下进行逻辑推理，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标(或参数)是否有解，是否有规定范围内的解”等．若由此推导出矛盾，则否定假设；否则，给出肯定结论．[对点训练](2018·湖南五市十校联考)如图，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，AD ∥BC ，AD ⊥CD ，且AD ＝CD ＝22，BC ＝42，P A ＝2.(1)求证：AB ⊥PC;(2)在线段PD 上，是否存在一点M ，使得二面角M -AC -D 的大小为45°，如果存在，求BM 与平面MAC 所成角的正弦值，如果不存在，请说明理由．解：(1)证明：由已知得四边形ABCD 是直角梯形，由AD ＝CD ＝22，BC ＝42，可得△ABC 是等腰直角三角形，即AB ⊥AC ，因为P A ⊥平面ABCD ，所以P A ⊥AB ，又P A ∩AC ＝A ，所以AB ⊥平面P AC ，所以AB ⊥PC .(2)建立如图所示的空间直角坐标系，则A (0,0,0)，C (22，22，0)，D (0,22，0)，P (0,0,2)，B (22，－22，0)，PD ―→＝(0,2 2，－2)，AC ―→＝(22，22，0)，AP ―→＝(0,0,2)．设PM ―→＝t PD ―→ (0<t <1)，则PM ―→＝(0,22t ，－2t )，所以AM ―→＝AP ―→＋PM ―→＝(0,22t,2－2t )．设平面MAC 的法向量是n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·AC ―→＝0，n ·AM ―→＝0，即⎩⎪⎨⎪⎧22x ＋22y ＝0，22ty ＋(2－2t )z ＝0，则可取n ＝⎝ ⎛⎭⎪⎫1，－1，2t 1－t .又m ＝(0,0,1)是平面ACD 的一个法向量，所以|cos 〈m ，n 〉|＝|m ·n || m || n |＝⎪⎪⎪⎪⎪⎪2t t －12＋⎝ ⎛⎭⎪⎫2t t －12＝cos 45°＝22，解得t ＝12，即点M 是线段PD 的中点．此时平面MAC 的法向量n ＝(1，－1，2)，M (0，2，1)， BM ―→＝(－22，32，1)．设BM 与平面MAC 所成的角为θ，则sin θ＝|cos 〈n ，BM ―→〉|＝|n ·BM ―→||n ||BM ―→|＝269.所以存在PD 的中点M 使得二面角M -AC -D 的大小为45°，且BM 与平面MAC 所成角的正弦值为269.[解题通法点拨] 立体几何问题重在 “建”——建模、建系[循流程思维——入题快]立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深．解决这类题目的原则是建模、建系．建模——将问题转化为平行模型、垂直模型、平面化模型或角度、距离等的计算模型；建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解．[按流程解题——快又准][典例] (2017·全国卷Ⅱ)如图，四棱锥P -ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面P AB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M -AB -D 的余弦值．[解题示范](1)证明：取P A 的中点F ，连接EF ，BF .因为E 是PD 的中点，所以EF ∥AD ，EF ＝12AD .由∠BAD ＝∠ABC ＝90°，得BC ∥AD ，又BC ＝12AD ，所以EF 綊BC ，所以四边形BCEF 是平行四边形， CE ∥BF ，又BF ⊂平面P AB ，CE ⊄平面P AB ，故CE ∥平面P AB .❶(2)由已知得BA ⊥AD ，以A 为坐标原点，AB ―→的方向为x 轴正方向，|AB ―→|为单位长度，建立如图所示的空间直角坐标系A -xyz ，则A (0,0,0)，B (1，0,0)，C (1,1,0)，P (0，1，3)，PC ―→＝(1,0，－3)，AB ―→＝(1,0,0)．❷❶建模：证明线面平行的模型：⎭⎬⎫a ⊄αb ⊂αa ∥b ⇒a ∥α.❷建系：将线面角、二面角的求解问题转化为空间向量的计算问题．设M (x ，y ，z )(0<x <1)，则BM ―→＝(x －1，y ，z )，PM ―→＝(x ，y －1，z －3)．因为BM 与底面ABCD 所成的角为45°，而n ＝(0,0,1)是底面ABCD 的法向量，所以|cos 〈BM ―→，n 〉|＝sin 45°，|z |(x －1)2＋y 2＋z 2＝22，即(x －1)2＋y 2－z 2＝0.① 又M 在棱PC 上，设PM ―→＝λPC ―→，则x ＝λ，y ＝1，z ＝3－3λ.②由①②解得⎩⎨⎧x ＝1＋22，y ＝1，z ＝－62(舍去)，或⎩⎨⎧x ＝1－22，y ＝1，z ＝62，所以M ⎝⎛⎭⎫1－22，1，62，从而AM ―→＝⎝⎛⎭⎫1－22，1，62. 设m ＝(x 0，y 0，z 0)是平面ABM 的法向量，则⎩⎪⎨⎪⎧m ·AM ―→＝0，m ·AB ―→＝0，即⎩⎨⎧(2－2)x 0＋2y 0＋6z 0＝0，x 0＝0，所以可取m ＝(0，－6，2)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝105.由图知二面角M -AB -D 为锐角，因此二面角M -AB -D 的余弦值为105. [思维升华] 立体几何的内容在高考中的考查情况总体上比较稳定．在平时的学习中，要加强“一题两法(几何法与向量法)”的训练，切勿顾此失彼；要重视识图训练，能正确确定关键点或线的位置，将局部空间问题转化为平面模型；能依托于题中的垂直条件，建立适当的空间直角坐标系，将几何问题化归为代数问题的计算模型．[应用体验](2018·全国卷Ⅰ)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF .(1)证明：平面PEF ⊥平面ABFD ； (2)求DP 与平面ABFD 所成角的正弦值．解：(1)证明：由已知可得BF ⊥PF ，BF ⊥EF ，又PF ∩EF ＝F ，所以BF ⊥平面PEF . 又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD .(2)如图，作PH ⊥EF ，垂足为H . 由(1)得，PH ⊥平面ABFD .以H 为坐标原点，HF ―→的方向为y 轴正方向，|BF ―→|为单位长，建立如图所示的空间直角坐标系H -xyz .由(1)可得，DE ⊥PE .又因为DP ＝2，DE ＝1，所以PE ＝ 3. 又PF ＝1，EF ＝2，所以PE ⊥PF . 所以PH ＝32，EH ＝32. 则H (0,0,0)，P ⎝⎛⎭⎫0，0，32，D ⎝⎛⎭⎫－1，－32，0， DP ―→＝⎝⎛⎭⎫1，32，32，HP ―→＝⎝⎛⎭⎫0，0，32.又HP ―→为平面ABFD 的法向量，设DP 与平面ABFD 所成角为θ，则sin θ＝|HP ―→·DP ―→||HP ―→||DP ―→|＝343＝34.所以DP 与平面ABFD 所成角的正弦值为34.[课时跟踪检测] A 卷——大题保分练1.(2018·洛阳模拟)如图，在四棱锥P -ABCD 中，E ，F 分别是PC ，PD 的中点，底面ABCD 是边长为2的正方形，P A ＝PD ＝2，且平面P AD ⊥平面ABCD .(1)求证：平面AEF ⊥平面PCD ；(2)求平面AEF 与平面ACE 所成锐二面角的余弦值．解：(1)证明：由题意知，P A ＝PD ＝AD ，F 为PD 的中点，可得AF ⊥PD ，∵平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，CD ⊂平面ABCD ，CD ⊥AD ， ∴CD ⊥平面P AD .又AF ⊂平面P AD ，∴CD ⊥AF ，又CD ∩PD ＝D ，∴AF ⊥平面PCD ，又AF ⊂平面AEF ， ∴平面AEF ⊥平面PCD .(2)取AD 的中点O ，BC 的中点G ，连接OP ，OG ，∵P A ＝PD ＝AD ，∴OP ⊥AD .∵平面P AD ⊥平面ABCD ，OP ⊂平面P AD ，∴OP ⊥平面ABCD . 分别以OA ，OG ，OP 所在直线为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，则A (1,0,0)，C (－1,2,0)，E ⎝⎛⎭⎫－12，1，32，F ⎝⎛⎭⎫－12，0，32，AF ―→＝⎝⎛⎭⎫－32，0，32，FE―→＝(0,1,0)．设平面AEF 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ m ·AF ―→＝0，m ·FE ―→＝0，即⎩⎪⎨⎪⎧－32x ＋32z ＝0，y ＝0，可取m ＝(1,0，3)，为平面AEF 的一个法向量．同理，可得平面ACE 的一个法向量为n ＝(3，3，1)． cos 〈m ，n 〉＝m ·n |m |·|n |＝1×3＋3×12×7＝217.∴平面AEF 与平面ACE 所成锐二面角的余弦值为217. 2.(2018·山西八校联考)如图，三棱柱ABC -A1B 1C 1中，∠ACB ＝90°，CC 1⊥底面ABC ，AC ＝BC ＝CC 1＝2，D ，E ，F 分别是棱AB ，BC ，B 1C 1的中点，G 是棱BB 1上的动点．(1)当BGBB 1为何值时，平面CDG ⊥平面A 1DE? (2)求平面A 1BF 与平面A 1DE 所成的锐二面角的余弦值．解：(1)当BG BB 1＝12，即G 为BB 1的中点时，平面CDG ⊥平面A 1DE .证明如下：因为点D ，E 分别是AB ，BC 的中点，所以DE ∥AC 且DE ＝12AC ，又AC ∥A 1C 1，AC ＝A 1C 1，所以DE ∥A 1C 1，DE ＝12A 1C 1，故D ，E ，C 1，A 1四点共面．如图，连接C1E 交GC 于H .在正方形CBB 1C 1中，tan ∠C 1EC ＝2，tan ∠BCG ＝12，故∠CHE ＝90°，即CG ⊥C 1E .因为A 1C 1⊥平面CBB 1C 1，CG ⊂平面CBB 1C 1，所以DE ⊥CG ，又C 1E ∩DE ＝E ，所以CG ⊥平面A 1DE ，故平面CDG ⊥平面A 1DE .(2)由(1)知，当G 为BB 1的中点时，平面A 1DE 的一个法向量为CG ―→.三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，CC 1⊥底面ABC ，所以以C 为原点，CA ，CB ，CC 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示．因为AC ＝BC ＝CC 1＝2，D ，E ，F 分别是棱AB ，BC ，B 1C 1的中点，所以C (0,0,0)，A 1(2,0,2)，D (1,1,0)，E (0,1,0)，B (0,2,0)，F (0,1,2)，G (0,2,1)，A 1B ―→＝(－2,2，－2)，A 1F ―→＝(－2,1,0)，CG ―→＝(0,2,1)．由CD 知CG ―→为平面A 1DE 的一个法向量．设平面A 1BF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·A 1F ―→＝0，n ·A 1B ―→＝0，即⎩⎪⎨⎪⎧－2x ＋y ＝0，－2x ＋2y －2z ＝0，令x ＝1得n ＝(1,2,1)，为平面A 1BF 的一个法向量．设平面A 1BF 与平面A 1DE 所成的锐二面角为θ，则cos θ＝|CG ―→·n ||CG ―→|·|n |＝530＝306，所以平面A 1BF 与平面A 1DE 所成的锐二面角的余弦值为306. 3．如图①，在矩形ABCD 中，AB ＝4，AD ＝2，E 是CD 的中点，将△ADE 沿AE 折起，得到如图②所示的四棱锥D 1-ABCE ，其中平面D 1AE ⊥平面ABCE .(1)设F 为CD 1的中点，试在AB 上找一点M ，使得MF ∥平面D 1AE ；(2)求直线BD 1与平面CD 1E 所成的角的正弦值．解：(1)如图，取D1E 的中点，记为L ，连接AL ，FL ，则FL ∥EC ，又EC ∥AB ，∴FL ∥AB ，且FL ＝14AB ， ∴M ，F ，L ，A 四点共面，且平面D 1AE ∩平面AMFL ＝AL ，若MF ∥平面D 1AE ，则MF ∥AL ，∴四边形AMFL 为平行四边形，∴AM ＝FL ＝14AB .(2)取AE 的中点O ，过点O 作OG ⊥AB 于G ，OH ⊥BC 于H ，连接OD 1.∵AD 1＝D 1E ，∴D 1O ⊥AE ，∴D 1O ⊥平面ABCE ，D 1O ⊥OG ，D 1O⊥OH ，又易得OG ⊥OH ，故OG ，OH ，OD 1两两垂直，以O 为坐标原点，OG ，OH ，OD 1为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示．则B (1,3,0)，C (－1,3,0)，E (－1,1,0)，D 1(0,0，2)．故BD 1―→＝(－1，－3，2)，CD 1―→＝(1，－3，2)，CE ―→＝(0，－2,0)．设平面CD 1E 的一个法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ m ·CD 1―→＝0，m ·CE ―→＝0，即⎩⎪⎨⎪⎧x －3y ＋2z ＝0，－2y ＝0，取x ＝2，得m ＝(2，0，－1)．设直线BD 1与平面CD 1E 所成的角为θ，则sin θ＝|cos 〈m ，BD 1―→〉|＝|m ·BD 1―→||m ||BD 1―→|＝|－22|3×12＝23. 即直线BD 1与平面CD 1E 所成的角的正弦值为23.4.如图，在多面体ABCDEF 中，底面ABCD 是边长为2的菱形，∠BAD ＝60°，四边形BDEF 是矩形，平面BDEF ⊥平面ABCD ，BF ＝3，H是CF 的中点．(1)求证：AC ⊥平面BDEF ；(2)求直线DH 与平面BDEF 所成角的正弦值；(3)求二面角H -BD -C 的大小．解：(1)证明：∵四边形ABCD 是菱形，∴AC ⊥BD .又∵平面BDEF ⊥平面ABCD ，平面BDEF ∩平面ABCD ＝BD ，且AC ⊂平面ABCD ，∴AC ⊥平面BDEF .(2)设AC ∩BD ＝O ，取EF 的中点N ，连接ON ，∵四边形BDEF 是矩形，O ，N 分别为BD ，EF 的中点，∴ON ∥ED .∵ED ⊥平面ABCD ，∴ON ⊥平面ABCD .由AC ⊥BD ，得OB ，OC ，ON 两两垂直．∴以O 为原点，OB ，OC ，ON 所在直线分别为x 轴，y 轴，z 轴，建立如图所示空间直角坐标系．∵底面ABCD 是边长为2的菱形，∠BAD ＝60°，BF ＝3，∴A (0，－3，0)，B (1,0,0)，D (－1，0,0)，E (－1,0,3)，F (1,0,3)，C (0，3，0)，H ⎝⎛⎭⎫12，32，32. ∵AC ⊥平面BDEF ，∴平面BDEF 的法向量AC ―→＝(0,23，0)．设直线DH 与平面BDEF 所成角为α，∵DH ―→＝⎝⎛⎭⎫32，32，32， ∴sin α＝|cos 〈DH ―→，AC ―→〉|＝⎪⎪⎪⎪⎪⎪⎪⎪DH ―→·AC ―→|DH ―→||AC ―→|＝77， ∴直线DH 与平面BDEF 所成角的正弦值为77. (3)由(2)，得BH ―→＝⎝⎛⎭⎫－12，32，32，DB ―→＝(2,0,0)．设平面BDH 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－x ＋3y ＋3z ＝0，2x ＝0，令z ＝1，得n ＝(0，－3，1)．由ED ⊥平面ABCD ，得平面BCD 的法向量为ED ―→＝(0,0，－3)，则cos 〈n ，ED ―→〉＝n ·ED ―→|n ||ED ―→|＝－12，由图可知二面角H -BD -C 为锐角，∴二面角H -BD -C 的大小为60°.B 卷——深化提能练1.(2019届高三·辽宁五校联考)如图，在四棱锥E -ABCD 中，底面ABCD为直角梯形，其中CD ∥AB ，BC ⊥AB ，侧面ABE ⊥平面ABCD ，且AB ＝AE ＝BE ＝2BC ＝2CD ＝2，动点F 在棱AE ，且EF ＝λF A .(1)试探究λ的值，使CE ∥平面BDF ，并给予证明；(2)当λ＝1时，求直线CE 与平面BDF 所成角的正弦值．解：(1)当λ＝12时，CE ∥平面BDF .证明如下：连接AC 交BD 于点G ，连接GF (图略)，∵CD ∥AB ，AB ＝2CD ，∴CG GA ＝CD AB ＝12， ∵EF ＝12F A ，∴EF F A ＝CG GA ＝12，∴GF ∥CE ，又CE ⊄平面BDF ，GF ⊂平面BDF ，∴CE ∥平面BDF .(2)如图，取AB 的中点O ，连接EO ，则EO ⊥AB ，∵平面ABE ⊥平面ABCD ，平面ABE ∩平面ABCD ＝AB ，∴EO ⊥平面ABCD ，连接DO ，∵BO ∥CD ，且BO ＝CD ＝1，∴四边形BODC 为平行四边形，∴BC ∥DO ，又BC ⊥AB ，∴AB ⊥OD ，则OD ，OA ，OE 两两垂直，以OD ，OA ，OE 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O -xyz ，则O (0,0,0)，A (0,1,0)，B (0，－1,0)，D (1,0,0)，C (1，－1，0)，E (0,0，3)．当λ＝1时，有EF ―→＝F A ―→，∴F ⎝⎛⎭⎫0，12，32， ∴BD ―→＝(1,1,0)，CE ―→＝(－1,1，3)，BF ―→＝⎝⎛⎭⎫0，32，32. 设平面BDF 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧ n ·BD ―→＝0，n ·BF ―→＝0，即⎩⎪⎨⎪⎧ x ＋y ＝0，32y ＋32z ＝0，令z ＝3，得y ＝－1，x ＝1，则n ＝(1，－1，3)为平面BDF 的一个法向量，设直线CE 与平面BDF 所成的角为θ，则sin θ＝|cos 〈CE ―→，n 〉|＝15，故直线CE 与平面BDF 所成角的正弦值为15.2.(2018·山东潍坊模拟)如图，在四棱锥P -ABCD 中，底面四边形ABCD内接于圆O ，AC 是圆O 的一条直径，P A ⊥平面ABCD ，P A ＝AC ＝2，E是PC 的中点，∠DAC ＝∠AOB .(1)求证：BE ∥平面P AD ；(2)若二面角P -CD -A 的正切值为2，求直线PB 与平面PCD 所成角的正弦值．解：(1)证明：∵∠DAC ＝∠AOB ，∴AD ∥OB .∵E 为PC 的中点，O 为圆心，连接OE ，∴OE ∥P A ，又OB ∩OE ＝O ，P A ∩AD ＝A ，∴平面P AD ∥平面EOB ，∵BE ⊂平面EOB ，∴BE ∥平面P AD .(2)∵四边形ABCD 内接于圆O 且AC 为直径，∴AD ⊥CD ，又P A ⊥平面ABCD ，∴P A ⊥CD ，又P A ∩AD ＝A ，∴CD ⊥平面P AD ，∴CD ⊥PD ，∴∠PDA 是二面角P -CD -A 的平面角，∵tan ∠PDA ＝2，P A ＝2，∴AD ＝1，如图，以D 为坐标原点，DA所在的直线为x 轴，DC 所在的直线为y 轴，过点D 且垂直于平面ABCD的直线为z 轴建立空间直角坐标系D -xyz .P A ＝AC ＝2，AD ＝1，延长BO 交CD 于点F ，∵BO∥AD ，∴BF ⊥CD ，∴BF ＝BO ＋OF ，∴BF ＝1＋12＝32，又CD ＝3，∴DF ＝32，∴P (1,0,2)，B ⎝⎛⎭⎫32，32，0，C (0，3，0)，CP ―→＝(1，－3，2)，DC ―→＝(0，3，0)，设平面PCD 的法向量n ＝(x ，y ，z )，∵⎩⎪⎨⎪⎧ n ·CP ―→＝0，n ·DC ―→＝0.即⎩⎪⎨⎪⎧x －3y ＋2z ＝0，3y ＝0. 令z ＝1，则x ＝－2，y ＝0.∴n ＝(－2,0,1)是平面PCD 的一个法向量，又PB ―→＝⎝⎛⎭⎫12，32，－2， ∴|cos 〈PB ―→，n 〉|＝⎪⎪⎪⎪⎪⎪⎪⎪PB ―→·n |PB ―→||n |＝⎪⎪⎪⎪⎪⎪－1＋0－25×5＝35， ∴直线PB 与平面PCD 所成角的正弦值为35. 3.(2018·合肥一模)如图，已知平行四边形ABCD 与△EMN 所在的平面都与矩形BDEF 所在的平面垂直，且∠BAD ＝60°，AB ＝MN ＝2AD ＝2，EM ＝EN ，F 为MN 的中点．(1)求证：MN ∥AD ；(2)若直线AE 与平面ABCD 所成的角为60°，求二面角M -AB -C 的余弦值．解：(1)证明：在△ABD 中，∠BAD ＝60°，AB ＝2，AD ＝1，由余弦定理可得BD 2＝AB 2＋AD 2－2AB ·AD ·cos ∠BAD ＝22＋12－2×2×1×cos 60°＝3，所以BD ＝3，AD 2＋BD 2＝AB 2，所以AD ⊥BD .又平面ABCD ⊥平面BDEF ，平面ABCD ∩平面BDEF ＝BD ，所以AD ⊥平面BDEF .在△EMN 中，EM ＝EN ，F 为MN 的中点，所以MN ⊥EF ，又平面EMN ⊥平面BDEF ，平面EMN ∩平面BDEF ＝EF ，所以MN ⊥平面BDEF .所以MN ∥AD .(2)在矩形BDEF 中，ED ⊥BD ，又平面ABCD ⊥平面BDEF ，平面ABCD ∩平面BDEF ＝BD ，所以ED ⊥平面ABCD . 所以∠EAD 为直线AE 与平面ABCD 所成的角，故∠EAD ＝60°.在Rt △EAD 中，ED ＝AD tan ∠EAD ＝1×tan 60°＝ 3.如图，以D 为坐标原点，分别以DA ，DB ，DE 所在直线为x轴，y 轴，z 轴建立空间直角坐标系，则D (0,0,0)，A (1,0,0)，B (0，3，0)，E (0,0，3)，F (0，3，3)，M (1，3，3)，MA ―→＝(0，－3，－3)，AB ―→＝(－1，3，0)．因为DE ⊥平面ABCD ，所以DE ―→＝(0,0，3)为平面ABCD 的一个法向量．设平面MAB 的法向量为n ＝(x ，y ，z )，所以⎩⎪⎨⎪⎧ n ⊥MA ―→，n ⊥AB ―→，即⎩⎪⎨⎪⎧n ·MA ―→＝－3y －3z ＝0，n ·AB ―→＝－x ＋3y ＝0，整理得⎩⎪⎨⎪⎧y ＋z ＝0，x ＝3y ，令y ＝1，则x ＝3，z ＝－1，所以n ＝(3，1，－1)是平面MAB 的一个法向量．所以cos 〈DE ―→ ，n 〉＝DE ―→·n |DE ―→|×|n |＝－3×13×(3)2＋12＋(－1)2＝－55. 设二面角M -AB -C 的大小为θ，由图可知θ为钝角，所以cos θ＝cos 〈DE ―→，n 〉＝－55. 4．已知直角梯形ABCD 中，AB ∥CD ，AB ⊥AD ，CD ＝2，AD ＝2，AB ＝1，如图①所示，将△ABD 沿BD 折起到△PBD 的位置得三棱锥P -BCD ，如图②所示．(1)求证：BD ⊥PC ；(2)当平面PBD ⊥平面PBC 时，求二面角P -DC -B 的大小．解：(1)证明：在图①中，连接AC ，交BD 于点G ，因为∠CDA ＝∠DAB ＝90°，所以tan ∠CAD ＝CD AD ＝2，tan ∠DBA ＝AD AB＝2，所以∠CAD ＝∠DBA ，因为∠CAD ＋∠BAG ＝90°，所以∠DBA ＋∠BAG ＝90°，所以BD ⊥AC .所以将△ABD 沿BD 折起到△PBD 的位置后，仍有BD ⊥PG ，BD ⊥CG ，如图②所示，又PG ∩CG ＝G ，所以BD ⊥平面PCG ，又PC ⊂平面PCG ，所以BD ⊥PC .(2)因为平面PBD ⊥平面PBC ，PB ⊥PD ，平面PBD ∩平面PBC ＝PB ，PD ⊂平面PBD ，所以PD ⊥平面PBC ，因为PC ⊂平面PBC ，所以PD ⊥PC ，又BD ⊥PC ，BD ∩PD ＝D ，所以PC ⊥平面PBD ，所以BP ⊥CP . 以P 为坐标原点，PC ，PB ，PD 所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系如图③所示，则P (0,0,0)，B (0,1,0)，C (2，0,0)，D (0,0，2)，BD ―→＝(0，－1，2)，BC ―→＝(2，－1,0)，易知平面PCD 的一个法向量为m ＝(0,1,0)，设n ＝(x ，y ，z )为平面BCD 的法向量，则⎩⎪⎨⎪⎧ BD ―→·n ＝0，BC ―→·n ＝0，即⎩⎪⎨⎪⎧－y ＋2z ＝0，2x －y ＝0，令x ＝1，则y ＝2，z ＝1，得n ＝(1，2，1)是平面BCD 的一个法向量．则cos 〈m ，n 〉＝m ·n |m |·|n |＝22，易知二面角P -DC -B 为锐角，所以二面角P -DC -B 的大小为45°.。

专题全等三角形(三) 课后练习二及详解

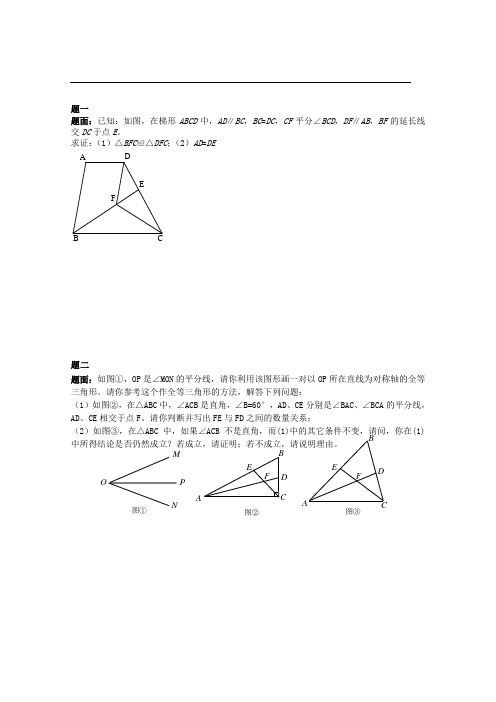
题一题面：已知：如图，在梯形ABCD 中，AD ∥BC ，BC =DC ，CF 平分∠BCD ，DF ∥AB ，BF 的延长线交DC 于点E 。

求证：（1）△BFC ≌△DFC ；（2）AD =DE题二题面：如图①，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。

请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC 中，∠ACB 是直角，∠B=60°，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F 。

请你判断并写出FE 与FD 之间的数量关系；（2）如图③，在△ABC 中，如果∠ACB 不是直角，而(1)中的其它条件不变，请问，你在(1)中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

O P AM N E B C DF A E F BD图① 图② 图③题三题面：我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等。

那么在什么情况下，它们会全等?(1)阅读与证明：对于这两个三角形均为直角三角形，显然它们全等．对于这两个三角形均为钝角三角形，可证它们全等(证明略)．对于这两个三角形均为锐角三角形，它们也全等，可证明如下：已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1C l，∠C=∠C l。

求证：△ABC≌△A1B1C1。

(请你将下列证明过程补充完整。

)证明：分别过点B，B1作BD⊥CA于D，B1 D1⊥C1 A1于D1.则∠BDC=∠B1D1C1=90°，∵BC=B1C1，∠C=∠C1，∴△BCD≌△B1C1D1，∴BD=B1D1．(2)归纳与叙述：由(1)可得到一个正确结论，请你写出这个结论。

题四题面：下列4个判断：（1）有两边及其中一边上的高对应相等的两个三角形全等；（2）有两边及第三边上的高对应相等的两个三角形全等；（3）三角形6个边、角元素中，有5个元素分别相等的两个三角形全等；（4）一边及其他两边上的高对应相等的两个三角形全等。

图像与证明

专题复习训练卷三专题复习训练卷三图形与证明时间:６０分钟㊀㊀满分:１００分题㊀序一二三总㊀分结分人核分人得㊀分一㊁选择题(每题４分,共３２分)１．下列说法中,错误的是(㊀㊀)．A．同角的补角相等B ．同位角相等C ．垂直于同一条直线的两直线平行D．两条直线相交有且只有一个交点２．如图,点B 是әA D C 的边A D 延长线上的一点,D E ʊA C ,若øC ＝５０ʎ,øB D E ＝６０ʎ,则øC D B 的度数等于(㊀㊀)．A．７０ʎB ．１００ʎC ．１１０ʎD．１２０ʎ(第２题)㊀㊀(第３题)㊀㊀(第４题)３．如图,l １ʊl ２,ø１＝１２０ʎ,ø２＝１００ʎ,则ø３等于(㊀㊀)．A．２０ʎB ．４０ʎC ．５０ʎD．６０ʎ４．如图,一根直尺E F 压在三角板３０ʎ的øB A C 上,与两边A C ㊁A B 交于点M ㊁N ,那么øC M E ＋øB N F 等于(㊀㊀)．A．１５０ʎB ．１８０ʎC ．１３５ʎD．不能确定５．下列描述不属于定义的是(㊀㊀)．A．两组对边分别平行的四边形叫做平行四边形B ．等边三角形是特殊的等腰三角形C ．在同一平面内三条线段首尾顺次连接得到的图形叫做三角形D．含有未知数的等式叫做方程６．下列命题是假命题的是(㊀㊀)．A．三角形三条角平分线都在三角形内部B ．三角形三条高都在三角形内部C ．三角形三条中线都在三角形内部D．三角形三条高至少有一条在三角形内部七年级数学(下)７．已知四个命题:①如果一个数的相反数等于它本身,则这个数是０;②一个数的倒数等于它本身,则这个数是１;③一个数的平方等于它本身,则这个数是１或０;④如果一个数的绝对值等于它本身,则这个数是正数．其中真命题有(㊀㊀)．A．１个B ．２个C ．３个D．４个８．某超级市场失窃,大量的商品在夜间被罪犯用汽车运走．三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(１)罪犯不在A ㊁B ㊁C 三人之外;(２)C 作案时总得有A 作从犯;(３)B不会开车．在此案中能肯定的作案对象是(㊀㊀)．A．嫌疑犯AB ．嫌疑犯BC ．嫌疑犯CD．嫌疑犯A 和C二㊁填空题(每题２分,共２０分)９．如图,A D ʊB C ,B D 平分øA B C ,且øA ＝１１０ʎ,则øD ＝㊀㊀㊀㊀．(第９题)㊀㊀(第１０题)㊀㊀(第１１题)１０．如图,A B ʊC D ,A C ʅB C ,øB A C ＝６５ʎ,则øB C D ＝㊀㊀㊀㊀．１１．如图,A B ʊC D ,C E 平分øA C D ,若ø１＝２５ʎ,那么ø２的度数是㊀㊀㊀㊀．１２．命题等腰三角形两腰上的中线相等的题设为㊀㊀㊀㊀,结论为㊀㊀㊀㊀．１３．命题如果一个数能被３整除,那么这个数也能被４整除是㊀㊀㊀㊀命题(填真或假 ),如果是假命题,举一个反例为:㊀㊀㊀㊀㊀㊀㊀㊀．１４．在命题在同一个平面内,两条直线不平行,它们一定相交中,条件是㊀㊀㊀㊀㊀㊀㊀,结论是㊀㊀㊀㊀㊀㊀㊀㊀．将它改为如果那么㊀㊀㊀㊀㊀㊀㊀㊀．１５．命题如果a b ＜０,那么a ＋b ＜０是假命题．反例:㊀㊀㊀㊀㊀㊀㊀㊀．１６．下列命题:①对顶角相等;②等腰三角形的两个底角相等;③两直线平行,同位角相等．其中逆命题为真命题的有:㊀㊀㊀㊀．(请填上所有符合题意的序号)１７．已知三条不同的直线a ,b ,c 在同一平面内,下列四个命题:①如果a ʊb ,a ʅc ,那么b ʅc ;㊀㊀②如果b ʊa ,c ʊa ,那么b ʊc ;③如果b ʅa ,c ʅa ,那么b ʅc ;㊀㊀④如果b ʅa ,c ʅa ,那么b ʊc ．其中真命题的是㊀㊀㊀㊀㊀．(填写所有真命题的序号)１８．将一个正方体的各个面上分别标上字母a ,b ,c ,d ,e ,f ．有甲㊁乙㊁丙三个同学站在不同的角度观察,结果如图所示,则a 的对面为㊀㊀㊀㊀,b 的对面为㊀㊀㊀㊀,c 的对面为㊀㊀㊀㊀．(第１８题)专题复习训练卷三三㊁解答题(第１９,２０题每题９分,其余每题１０分,共４８分)１９．观察下面的变形规律:１１ˑ２＝１－１２;１２ˑ３＝１２－１３;１３ˑ４＝１３－１４;解答下面的问题:(１)若n 为正整数,请你猜想:１n (n ＋１)＝㊀㊀㊀㊀;(２)证明你猜想的结论;(３)求和:１１ˑ２＋１２ˑ３＋１３ˑ４＋＋１２０１２ˑ２０１３．２０．如图,直线a ʊb ,试用两种不同的方法证明:øA C B ＝ø１＋ø２．(第２０题)２１．(１)填写下列命题的证明过程:已知:点D ㊁E ㊁F 分别在A B ㊁A C ㊁B C 上,D E ʊB C ,E F ʊA B ．求证:ø１＝ø２．证明:D E ʊB C ⇒ø１＝ø㊀㊀㊀㊀E F ʊA B ⇒ø２＝ø㊀㊀㊀㊀}⇒ø１＝ø２．(２)你还有不同的方法证明ø１＝ø２吗?写出你的证明过程．(第２１题)七年级数学(下)２２．如图,现有３句话:①a ʅc ,②b ʅc ,③a ʊb ．请以其中２句话为条件,第三句话为结论构造命题．(１)你构造的是哪几个命题?(２)你构造的命题是真命题还是假命题?请加以证明．(第２２题)２３．如图,已知A B ʊC D ,分别探索下列四个图形中øP 与øA ㊁øC 的关系,请你从所得的四个关系中任选一个加以证明．(１)㊀㊀(２)㊀㊀(３)㊀㊀(４)(第２３题)专题复习训练卷三１．B ㊀２．C ㊀３．B ㊀４．A㊀５．B ㊀６．B ㊀７．B ㊀８．A９．３５ʎ㊀１０．２５ʎ㊀１１．５０ʎ１２．等腰三角形㊀两腰上的中线相等１３．假㊀６(答案不唯一)１４．在同一个平面内,两条直线不平行㊀它们一定相交㊀在同一个平面内,如果两条直线不平行,那么它们一定相交．１５．设a ＝４,b ＝－３,a b ＝４ˑ(－３)＝－１２＜０,而a ＋b ＝４＋(－３)＝１＞０．１６．②㊀③㊀１７．①②④㊀１８．e ㊀d ㊀f １９．(１)１n －１n ＋１(２)１n －１n ＋１＝n ＋１n (n ＋１)－n n (n ＋１)＝n ＋１－nn (n ＋１)＝１n (n ＋１)．(３)原式＝１－１２＋１２－１３＋１３－１４＋＋１２０１２－１２０１３＝１－１２０１３＝２０１２２０１３．２０．提示:过点C 作C D ʊa ,利用平行线的性质解决问题;或连接A B ,借助三角形的内角和定理解决问题．２１．略２２．(１)由①②,推出③;由①③,推出②;由②③,推出①;(２)略２３．(１)øP ＝３６０ʎ－øA －øC ,(２)øP ＝øA ＋øC ,(３)øP＝øC －øA ,(４)øP ＝øA －øC ．证明略。

中考数学总复习专题三解答题重难点题型突破题型二几何图形探究题类型与三角形、四边形有关的探究题课件

(2)如图②，过点 F 作 FG⊥AB 于 G，连接 FE.∵AF＝BE，AF∥BE，∴ 四边形 ABEF 是平行四边形，∵AF＋BE＝16，∴AB＝AF＝BE＝8，∵32 3＝ 8×FG，∴FG＝4 3，在 Rt△FAG 中，AF＝8，∴∠FAG＝60°，当点 G 在线段 AB 上时，∠FAB＝60°，当点 G 在线段 BA 延长线时，∠FAB＝120°，
解：(1)原命题不成立，新结论为：∠APB＝90°， AF＋BE＝2AB(或 AF＝BE＝AB)，证明：∵AM∥BN， ∴∠MAB＋∠NBA＝180°，∵AE，BF 分别平分∠MAB，∠NBA，
∴∠EAB＝12∠MAB，∠FBA＝12∠NBA，
∴∠EAB＋∠FBA＝12(∠MAB＋∠NBA)＝90°， ∴∠APB＝90°，∵AE 平分∠MAB，∴∠MAE＝∠BAE， ∵AM∥BN，∴∠MAE＝∠BAE，∴∠BAE＝∠BEA， ∴AB＝BE，同理：AF＝AB，∴AF＋BE＝2AB(或 AF＝BE＝AB)；
辽宁专用
专题三解答题重难点题型突破
题型二几何图形探究题类型1 与三角形、四边形有关的探究题
【例1】 (2016·抚顺)如图，在△ABC中，BC >AC，点E在BC上，CE＝CA，点D在AB上，连接DE，∠ACB＋∠ADE＝180°，作CH⊥AB，垂足为H.
(1)如图①，当∠ACB＝90°时，连接CD，过点C作CF⊥CD交BA的延长线于点F. ①求证：FA＝DE； ②请猜想三条线段DE、AD、CH之间的数量关系，直接写出结论； (2)如图②，当∠ACB＝120°时，三条线段DE、AD、CH之间存在怎样的数量关系？请证明你的结论．
(3)成立．∵四边形 ABCD 是正方形，∴BC＝CD，∠FBC＝∠ECD＝90 °，

2025年四川省聚焦中考数学必备考点透析-第4章三角形微专题三三角形中的基本模型

12
证明：如后图，过点 P 作 PM ⊥ AB 于点 M ， PN ⊥ AC 于点 N .
由折叠可知∠ DPE ＝∠ A ＝90°，
∴∠ ADP ＋∠ AEP ＝180°.
∵∠ PEN ＋∠ AEP ＝180°，
∴∠ ADP ＝∠ PEN .
∵∠ DMP ＝∠ ENP ＝90°，

∴△ DMP ∽△ ENP ，∴ ＝ .
AC 、 BD 交于点 P ，∴ PA ＝ PD ，∠ PAE ＝∠ PDF ＝45°.∵∠ APE ＋
∠ EPD ＝∠ DPF ＋∠ EPD ＝90°，∴∠ APE ＝∠ DPF . 在△ APE 和
∠＝∠，
△ DPF 中，∵ቐ＝，
∴△ APE ≌△ DPF （ ASA ），∴ AE ＝
△ AFE ≌△ AGE .
返回目录
6
证明：如后图，将△ ADF 绕点 A 顺时针旋转90°得到△ ABG ，使
AD 与 AB 重合.
由旋转的性质可知△ ADF ≌△ ABG ，
∴ DF ＝ BG ，∠ D ＝∠ ABG ＝90°， AF ＝ AG ，∠ FAD ＝
∠ GAB ，∴∠ ABG ＋∠ ABE ＝180°，即点 G 、 B 、 E 三点共线.
∵∠ EAF ＝45°，∠ BAD ＝90°，∴∠ BAE ＋∠ FAD ＝45°，
∴∠ BAE ＋∠ GAB ＝45°，即∠ EAG ＝45°，∴∠ EAG ＝∠ EAF ，
∴△ AFE ≌△ AGE （ SAS ），∴ EF ＝ EG .
∵ EG ＝ BE ＋ BG ，∴ EF ＝ BE ＋ DF .

∴ PC ·PD ＝ PB ·PE .
返回目录

专题3-2 解三角形最值范围与图形归类-2023年高考数学二轮复习讲练测(全国通用)(原卷版)

专题3-2解三角形最值、范围与图形归类目录讲高考 ............................................................................................................................................................................... 1 题型全归纳 ...................................................................................................................................................................... 2 【题型一】最值与范围1：角与对边 .................................................................................................................... 2 【题型二】最值与范围2：角与邻边 .................................................................................................................... 2 【题型三】范围与最值3：有角无边型 ............................................................................................................... 3 【题型四】最值与范围4：边非对称型 ............................................................................................................... 4 【题型五】最值：均值型 .......................................................................................................................................... 4 【题型六】图形1：内切圆与外接圆 .................................................................................................................... 4 【题型七】图形2：“补角”三角形 .................................................................................................................... 6 【题型八】图形3：四边形与多边形 .................................................................................................................... 7 【题型九】三大线1：角平分线应用 .................................................................................................................... 8 【题型十】三大线2：中线应用 ............................................................................................................................. 8 【题型十一】三大线3：高的应用 ......................................................................................................................... 9 【题型十二】证明题 ................................................................................................................................................. 10 专题训练 (10)讲高考1．（2022·全国·统考高考真题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，分别以a ，b ，c 为边长的三个正三角形的面积依次为123,,S S S ，已知12313S S S B -+==． (1)求ABC 的面积；(2)若sin sin A C =，求b ．2．（2022·全国·统考高考真题）记ABC 的内角,,A B C 的对边分别为,,a b c ，已知sin sin()sin sin()C A B B C A -=-． (1)证明：2222a b c =+；(2)若255,cos 31a A ==，求ABC 的周长．3．（2022·全国·统考高考真题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos sin 21sin 1cos2A B A B =++．(1)若23C π=，求B ；(2)求222a b c +的最小值．4．（2021·全国·统考高考真题）在ABC 中，角A 、B 、C 所对的边长分别为a 、b 、c ，1b a =+，2c a =+.．（1）若2sin 3sin C A =，求ABC 的面积；（2）是否存在正整数a ，使得ABC 为钝角三角形?若存在，求出a 的值；若不存在，说明理由．5．（2021·北京·统考高考真题）在ABC 中，2cos c b B =，23C π=．（1）求B ∠；（2）再从条件①、条件①、条件①这三个条件中选择一个作为已知，使ABC 存在且唯一确定，求BC 边上中线的长．条件①：c =；条件①：ABC 的周长为4+条件①：ABC题型全归纳【题型一】最值与范围1：角与对边【讲题型】例题1.已知ABC 的内角,,A B C 所对的边分别为()()22,,,sin sin sin sin sin a b c B C A B C -=- （1）求A ；（2）已知a =.例题2.在ABC ∆中，a ，b ，c 分别为角A ，B ，C 的对边，已知22222202b c a ca b c b c+-+=+-+. （1）求角A 的值；1.在锐角三角形ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且2sin 2cos )A ABC +sin 30A -. （1）求A 的大小；（2）若2a =，求ABC ∆的周长L 的取值范围.2.在锐角三角形ABC 中，角A ，B ，C 所对的边分别为a,b,c ，且()222πcos B b a c ac sinAcosA---=（1）求角A ；（2）若a =bc 的取值范围．【题型二】最值与范围2：角与邻边【讲题型】例题1..已知ABC 为锐角三角形，角,,A B C 所对边分别为,,a b c ，ABC 满足：222sin sin sin sin sin A B C B C +-≤.（1）求角A 的取值范围；1.．在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，已知sinsin 2A Ca b A +=．（1）求角B ；（2）若△ABC 为锐角三角形，且2c =，求△ABC 面积的取值范围．2.在ABC 中，设A ，B ，C 所对的边长分别为a ，b ，c ，且()()()sin sin sin c b C a b A B -=-+. （1）求A ；（2）若2b =，且ABC 为锐角三角形，求ABC 的面积S 的取值范围.【题型三】范围与最值3：有角无边型【讲题型】例题1.三角形ABC 中，已知222sin sin +sin sin sin A B A B C +=，其中，角A B C 、、所对的边分别为a b c 、、.（△）求角C 的大小；（△）求a b c+的取值范围.例题2.在锐角三角形ABC,若 (I)求角B(II)求的取值范围【练题型】1.设锐角三角形ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，2sin a b A =．（△）若a =5c =，求b （△）求cos sin A C +的取值范围．ac c b a c b a 3))((=+++-A A cos sin 3+2.在锐角三角形ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，且2sin sin cos sin cos C B a BB b A-=.（1）求A ；（2）求bc的取值范围.【题型四】最值与范围4：边非对称型【讲题型】例题1.在ABC ∆中，,,a b c 分别是角,,A B C 的对边()()3a b c a b c ab +++-=.（1）求角C 的值；（2）若2c =，且ABC ∆为锐角三角形，求2a b -的范围.【练题型】在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，222sin sin sin 2sin sin A C B A C +=+．（△）求角B 的大小；（△）若ABC 为锐角三角形，2b =，求2a c -的取值范围．【题型五】最值：均值型【讲题型】例题1.已知ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，2A π≠，且满足()sin 220cos 0bc A B C ++=.（1）求ABC ∆的面积S ；（2）若24a S =，求c bb c+的最大值.【练题型】1.在△ABC 中，设AD 为BC 边上的高，且AD =BC BC ，b ，c 分别表示角B ，C 所对的边长，则的取值范围是_．【题型六】图形1：内切圆与外接圆【讲题型】例题1.在①ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，已知4b =，2c =，且sin sin sin()C B A B =+-． (1)求角A 和边a 的大小； (2)求①ABC 的内切圆半径．例题2.ABC 中，已知1AB =，7BC =D 为AC 上一点，2AD DC =，AB BD ⊥. (1)求BD 的长度；(2)若点P 为ABD △外接圆上任意一点，求2+PB PD 的最大值.b cc b+【讲技巧】外接圆：1.外接圆的圆心到三角形的三个顶点的距离相等。

中考数学难点突破与经典模型精讲练全等三角形中的一线三垂直模型(解析版)

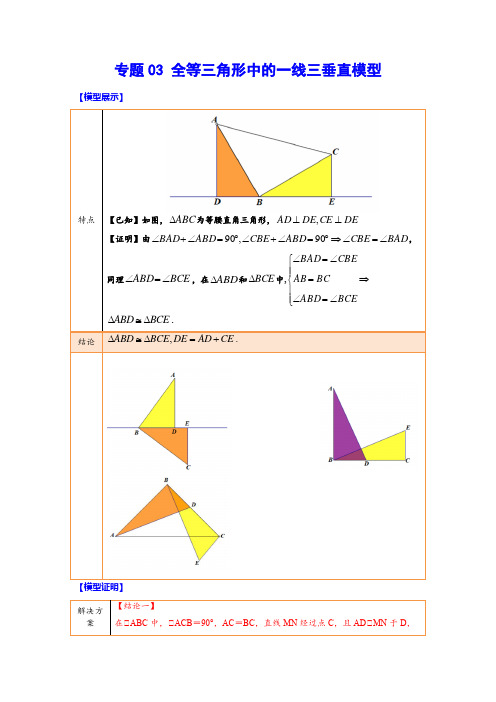
专题03 全等三角形中的一线三垂直模型【模型展示】【已知】如图，ABC ∆为等腰直角三角形，DE CE DE AD ⊥⊥, 【证明】由BAD CBE ABD CBE ABD BAD ∠=∠⇒︒=∠+∠︒=∠+∠90,90，同理BCE ABD ∠=∠，在ABD ∆和BCE ∆中,⇒⎪⎪⎩⎪⎪⎨⎧∠=∠=∠=∠BCEABD BCAB CBE BAD ABD BCE ∆≅∆.,ABD BCE DE AD CE ∆≅∆=+【模型证明】BE△MN于E，则有以下结论成立：△△ADC△△CEB；△DE＝AD+BE【证明】：△证明：△AD△DE，BE△DE，△△ADC＝△BEC＝90°，△△ACB＝90°，△△ACD+△BCE＝90°，△DAC+△ACD＝90°，△△DAC＝△BCE，在△ADC和△CEB中△△ADC△△CEB（AAS）．△证明：由（1）知：△ADC△△CEB，△AD＝CE，CD＝BE，△DC+CE＝DE，△DE＝AD+BE．【结论二】（其他形状一线三垂直）△DE＝AD﹣BE△DE ＝BE ﹣AD【题型演练】一、单选题1．一天课间，顽皮的小明同学拿着老师的等腰直角三角板玩，不小心将三角板掉到两根柱子之间，如图所示，这一幕恰巧被数学老师看见了，于是有了下面这道题：如果每块砖的厚度a ＝8cm ，则DE 的长为（）A ．40cmB ．48cmC ．56cmD ．64cm【答案】C【详解】由等腰直角三角形的性质可得△ACB ＝90°，AC ＝CB ，因此可以考虑证明△ACD 和△CBE 全等，可以证明DE 的长为7块砖的厚度的和．【分析】解：由题意得△ADC ＝△CEB ＝△ACB ＝90°，AC ＝CB ，△△ACD ＝90°﹣△BCE ＝△CBE ，在△ACD 和△CBE 中， ADC CEB ACD CBE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ACD △△CBE （AAS ），△CD ＝BE ＝3a ，AD ＝CE ＝4a ，△DE ＝CD +CE ＝3a +4a ＝7a ，△a ＝8cm ，△7a ＝56cm ，△DE ＝56cm ，故选C ．【点睛】本题主要考查了全等三角形的性质与判定，解题的关键在于能够熟练掌握全等三角形的性质与判定条件．2．如图，点P ，D 分别是△ABC 边BA ，BC 上的点，且4BD =，60ABC ∠=︒．连结PD ，以PD 为边，在PD 的右侧作等边△DPE ，连结BE ，则△BDE 的面积为（）A ．B ．2C ．4D ．【答案】A【分析】要求BDE ∆的面积，想到过点E 作EF BC ⊥，垂足为F ，因为题目已知60ABC ∠=︒，想到把ABC ∠放在直角三角形中，所以过点D 作DG BA ⊥，垂足为G ，利用勾股定理求出DG 的长，最后证明GPD FDE ∆≅∆即可解答．【详解】解：过点E 作EF BC ⊥，垂足为F ，过点D 作DG BA ⊥，垂足为G ，在Rt BGD 中，4BD =，60ABC ∠=︒，30BDG ∴∠=︒，122BG BD ∴==，GD ∴PDE ∆是等边三角形，60PDE ∴∠=︒，PD DE =，180120PDB EDF PDE ∴∠+∠=︒-∠=︒，60ABC ∠=︒，180120PDB BPD ABC ∴∠+∠=︒-∠=︒，BPD EDF ∴∠=∠，90PGD DFE ∠=∠=︒，()GPD FDE AAS ∴∆≅∆，GD EF ∴==BDE ∴∆的面积12BD EF =⋅，142=⨯⨯=，故选：A ．【点睛】本题考查了等边三角形的性质，全等三角形、勾股定理，解题的关键是根据题目的已知条件并结合图形添加适当的辅助线．3．如图，AC ＝CE ，△ACE ＝90°，AB △BD ，ED △BD ，AB ＝6cm ，DE ＝2cm ，则BD 等于（）A ．6cmB ．8cmC ．10cmD ．4cm【答案】B【分析】根据题意证明ABC CDE △≌△即可得出结论．【详解】解：△AB △BD ，ED △BD ，△90ABC CDE ∠=∠=︒，△△ACE ＝90°，△90ACB DCE ∠+∠=︒，△90ACB BAC ∠+∠=︒，△BAC DCE ∠=∠，在ABC 和CDE △中，90ABC CDE BAC DCE AC CE ∠=∠=︒⎧⎪∠=∠⎪⎨⎪⎪⎩＝， △()ABC CDE AAS ≌，△6cm AB CD ==，2cm BC DE ==，△268cm BD BC CD =+=+=，故选：B ．【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理以及性质定理是解本题的关键．二、填空题4．如图，已知ABC 是等腰直角三角形，△ACB ＝90°，AD △DE 于点D ，BE △DE 于点E，且点C 在DE 上，若AD ＝5，BE ＝8，则DE 的长为_____．【答案】13【分析】先根据AD △DE ，BE △DE ，△ADC =△CEB =90°，则△DAC +△DCA =90°，△ABC 是等腰直角三角形，△ACB =90°，可得AC =CB ，推出△DAC =△ECB ，即可证明△DAC △△ECB 得到CE =AD =5，CD =BE =8，由此求解即可．【详解】解：△AD △DE ，BE △DE ，△△ADC =△CEB =90°，△△DAC +△DCA =90°，△△ABC 是等腰直角三角形，△ACB =90°，△△DCA +△BCE =90°，AC =CB△△DAC =△ECB ，△△DAC △△ECB （AAS ），△CE =AD =5，CD =BE =8，△DE =CD +CE =13，故答案为：13．【点睛】本题主要考查了全等三角形的性质与判定，垂线的定义，解题的关键在于能够熟练掌握全等三角形的性质与判定条件．5．如图所示，ABC 中，,90AB AC BAC =∠=︒．直线l 经过点A ，过点B 作BE l ⊥于点E ，过点C 作CF l ⊥于点F ．若2,5==BE CF ，则EF =__________．【答案】7【分析】根据全等三角形来实现相等线段之间的关系，从而进行计算，即可得到答案；【详解】解：△BE △l ，CF △l ，△△AEB =△CF A =90°．△△EAB +△EBA =90°．又△△BAC =90°，△△EAB +△CAF =90°．△△EBA =△CAF ．在△AEB 和△CF A 中△△AEB =△CF A ，△EBA =△CAF ，AB =AC ，△△AEB △△CF A ．△AE =CF ，BE =AF ．△AE +AF =BE +CF ．△EF =BE +CF ．△2,5==BE CF ，△257EF =+=；故答案为：7．【点睛】本题考查了全等三角形的判定和性质，余角的性质，解题的关键是熟练掌握所学的知识，正确的证明三角形全等．三、解答题6．已知：如图，AB △BD ，ED △BD ，C 是BD 上的一点，AC △CE ，AB ＝CD ，求证：BC ＝DE ．【答案】见解析【分析】根据直角三角形全等的判定方法，ASA 即可判定三角形全等．【详解】证明：△AB △BD ，ED △BD ，AC △CE （已知）△△ACE ＝△B ＝△D ＝90°（垂直的意义）△△BCA +△DCE +△ACE ＝180°（平角的意义）△ACE ＝90°（已证）△△BCA +△DCE ＝90°（等式性质）△△BCA +△A +△B ＝180°（三角形内角和等于180°）△B ＝90°（已证）△△BCA +△A ＝90°（等式性质）△△DCE ＝△A （同角的余角相等）A DCE AB CD B D ∠=∠⎧⎪=⎨⎪∠=∠⎩，△△ABC △△CDE （ASA ）△BC ＝DE （全等三角形对应边相等）【点睛】本题考查了全等三角形的判定和性质；熟练掌握三角形全等的判定定理是解题的关键．7．在△ABC 中，△ACB =90°，AC =BC ，直线MN 经过点C ，且AD △MN 于D ，BE △MN 于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：△△ADC △△CEB ；△DE =AD +BE ；(2)当直线MN 绕点C 旋转到图2的位置时，AD =5，BE =2，求线段DE 的长．【答案】(1)△证明见解析；△证明见解析；(2)DE =3【分析】（1）△由已知可知，AD △MN ，BE △MN ，得到90ADC CEB ∠=∠=︒，再根据三角形内角和与平角性质，得到CAD BCE ∠=∠，即可证明ADC CEB △≌△（AAS ）；△根据ADC CEB △≌△，得到AD CE =，DC BE =，即可证明DE =AD +BE ．（2）由已知可知，AD △MN ，BE △MN ，得到90ADC CEB ∠=∠=︒，再根据90CAD ACD ∠+∠=︒、90ACD BCE ∠+∠=︒，得到CAD BCE ∠=∠，可证明ADC CEB △≌△，得到CE AD =，CD BE =，即可求出DE 长．（1）△证明：△AD △MN ，BE △MN ，90ACB ∠=︒△90ADC CEB ACB ∠=∠=∠=︒，△180CAD ADC ACD ∠+∠+∠=︒，180ACD ACB BCE ∠+∠+∠=︒，△CAD BCE ∠=∠，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△ADC CEB △≌△（AAS ）；△证明：△ADC CEB △≌△，△AD CE =，DC BE =，△DE CE DC AD BE =+=+；（2）证明：△AD △MN ，BE △MN ，△90ADC CEB ∠=∠=︒，△90CAD ACD ∠+∠=︒，△90ACB ∠=︒，△90ACD BCE ∠+∠=︒△CAD BCE ∠=∠，在ADC △和CEB △中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，ADC CEB △≌△（AAS ），△5CE AD ==，2CD BE ==，△523DE CE CD =-=-=．【点睛】本题主要考查了三角形全等的判定与性质，根据已知准确找到符合全等的条件是解题关键．8．（1）课本习题回放：“如图△，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别为D ，E ， 2.5cm AD =， 1.7cm DE =．求BE 的长”，请直接写出此题答案：BE 的长为________．（2）探索证明：如图△，点B ，C 在MAN ∠的边AM 、AN 上，AB AC =，点E ，F 在MAN ∠内部的射线AD 上，且BED CFD BAC ∠=∠=∠．求证：ABE CAF ∆∆≌．（3）拓展应用：如图△，在ABC ∆中，AB AC =，AB BC >．点D 在边BC 上，2CD BD =，点E 、F 在线段AD 上，BED CFD BAC ∠=∠=∠．若ABC ∆的面积为15，则ACF ∆与BDE ∆的面积之和为________．（直接填写结果，不需要写解答过程）【答案】（1）0.8cm ；（2）见解析（3）5【分析】（1）利用AAS 定理证明△CEB △△ADC ，根据全等三角形的性质解答即可；（2）由条件可得△BEA ＝△AFC ，△4＝△ABE ，根据AAS 可证明△ABE △△CAF ；（3）先证明△ABE △△CAF ，得到ACF ∆与BDE ∆的面积之和为△ABD 的面积，再根据2CD BD =故可求解．【详解】解：（1）△BE △CE ，AD △CE ，△△E ＝△ADC ＝90°，△△EBC ＋△BCE ＝90°．△△BCE ＋△ACD ＝90°，△△EBC ＝△DCA ．在△CEB 和△ADC 中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CEB △△ADC （AAS ），△BE ＝DC ，CE ＝AD ＝2.5cm ．△DC ＝CE −DE ，DE ＝1.7cm ，△DC ＝2.5−1.7＝0.8cm ，△BE ＝0.8cm故答案为：0.8cm ；（2）证明：△△1＝△2，△△BEA ＝△AFC ．△△1＝△ABE ＋△3，△3＋△4＝△BAC ，△1＝△BAC ，△△BAC ＝△ABE ＋△3，△△4＝△ABE ．△△AEB ＝△AFC ，△ABE ＝△4，AB ＝AC ，△△ABE △△CAF （AAS ）．（3）△BED CFD BAC ∠=∠=∠△△ABE +△BAE =△F AC +△BAE =△F AC +△ACF△△ABE =△CAF ，△BAE =△ACF又AB AC =△△ABE △△CAF ，△ABE CAF S S =△ACF ∆与BDE ∆的面积之和等于ABE ∆与BDE ∆的面积之和，即为△ABD 的面积， △2CD BD =，△ABD 与△ACD 的高相同则13ABD ABC S S =△△=5 故ACF ∆与BDE ∆的面积之和为5故答案为：5．【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理，掌握全等三角形的判定定理和性质定理是解题的关键．9．问题背景：（1）如图△，已知ABC 中，90BAC ∠=︒，AB AC =，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D ，E ，易证：DE =______+______．（2）拓展延伸：如图△，将（1）中的条件改为：在ABC 中，AB AC =，D ，A ，E 三点都在直线m 上，并且有BDA AEC BAC ∠=∠=∠，请求出DE ，BD ，CE 三条线段的数量关系，并证明．（3）实际应用：如图△，在ACB △中，90ACB ∠=︒，AC BC =，点C 的坐标为()2,0-，点A 的坐标为()6,3-，请直接写出B 点的坐标．【答案】（1）BD ；CE ；证明见详解；（2）DE=BD+CE ；证明见详解；（3）点B 的坐标为()1,4B ．【分析】（1）根据全等三角形的判定和性质得到AE BD =，AD CE =，结合图形解答即可；（2）根据三角形内角和定理、平角的定义证明ABD CAE ∠=∠，证明ABD CAE ≌，根据全等三角形的性质得到AE BD =，AD CE =，结合图形解答即可；（3）根据AEC CFB ≌，得到3CF AE ==，4BF CE OE OC ==-=，根据坐标与图形性质解答即可．【详解】（1）证明：△BD m ⊥，CE m ⊥，△90ADB CEA ∠=∠=︒，△90BAC ∠=︒，△90BAD CAE ∠+∠=︒，△90BAD ABD ∠+∠=︒，△ CAE ABD ∠=∠，在ADB 和CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩，△ADB CEA ≌，△AE BD =，AD CE =，△DE AE AD BD CE =+=+，即：DE BD CE =+，故答案为：BD ；CE ；（2）解：数量关系：DE BD CE =+ ，证明：在ABD 中，180ABD ADB BAD ∠=︒-∠-∠，△180CAE BAC BAD ∠=︒-∠-∠，BDA AEC ∠=∠，△ABD CAE ∠=∠，在ABD 和CAE 中，ABD CAE BDA AEC AB CA ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ △ABD CAE ≌，△AE BD =，AD CE =，△DE AD AE BD CE =+=+；（3）解：如图，作AE x ⊥轴于E ，BF x ⊥轴于F ，由（1）可知，AEC CFB ≌，△3CF AE ==，4BF CE OE OC ==-=，△1OF CF OC =-=，△点B 的坐标为()1,4B ．【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质，掌握全等三角形的判定定理和性质定理是解题的关键．10．如图，在ABC 中，AB BC =．（1）如图△所示，直线NM 过点B ，AM MN ⊥于点M ，⊥CN MN 于点N ，且90ABC ∠=︒．求证：MN AM CN =+．（2）如图△所示，直线MN 过点B ，AM 交MN 于点M ，CN 交MN 于点N，且AMB ABC BNC ∠=∠=∠，则MN AM CN =+是否成立？请说明理由．【答案】（1）见解析；（2）MN AM CN =+仍然成立，理由见解析【分析】（1）首先根据同角的余角相等得到BAM CBN ∠=∠，然后证明()AMB BNC AAS ≅△△，然后根据全等三角形对应边相等得到AM BN =，BM CN =，然后通过线段之间的转化即可证明MN AM CN =+；（2）首先根据三角形内角和定理得到MAB CBN ∠=∠，然后证明()AMB BNC AAS ≅△△，根据全等三角形对应边相等得到MN MB BN =+，最后通过线段之间的转化即可证明MN AM CN =+．【详解】证明：（1）△AM MN ⊥，⊥CN MN ，△90AMB BNC ∠=∠=︒，△90ABM BAM ∠+∠=︒，△90ABC ∠=︒，△90ABM CBN ，△BAM CBN ∠=∠，在AMB 和BNC 中，AMB BNC BAM CBN AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△()AMB BNC AAS ≅△△，△AM BN =，BM CN =，△BN MB MN +=，△MN AM CN =+；（2）MN AM CN =+仍然成立，理由如下：△180AMB MAB ABM ABM ABC CBN ∠+∠+∠=∠+∠+∠=︒，△AMB ABC ∠=∠，△MAB CBN ∠=∠，在AMB 和BNC 中，AMB BNC BAM CBN AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△()AMB BNC AAS ≅△△，△AM BN =，NC MB =，△MN MB BN =+，△MN AM CN =+．【点睛】此题考查了全等三角形的性质和判定，同角的与相等，三角形内角和定理等知识，∠=∠．解题的关键是根据同角的余角相等或三角形内角和定理得到BAM CBN11．在直线m上依次取互不重合的三个点D，A，E，在直线m上方有AB＝AC，且满足△BDA ＝△AEC＝△BAC＝α．(1)如图1，当α＝90°时，猜想线段DE，BD，CE之间的数量关系是；(2)如图2，当0＜α＜180时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．【答案】(1)DE＝BD+CE．(2)DE＝BD+CE仍然成立，证明见解析【分析】（1）由△BDA＝△BAC＝△AEC＝90°得到△BAD+△EAC＝△BAD+△DBA＝90°，进而得到△DBA＝△EAC，然后结合AB＝AC得证△DBA△△EAC，最后得到DE＝BD+CE；（2）由△BDA＝△BAC＝△AEC＝α得到△BAD+△EAC＝△BAD+△DBA＝180°﹣α，进而得到△DBA＝△EAC，然后结合AB＝AC得证△DBA△△EAC，最后得到DE＝BD+CE．（1）解：DE＝BD+CE，理由如下，△△BDA＝△BAC＝△AEC＝90°，△△BAD+△EAC＝△BAD+△DBA＝90°，△△DBA＝△EAC，△AB＝AC，△△DBA△△EAC（AAS），△AD＝CE，BD＝AE，△DE＝AD+AE＝BD+CE，故答案为：DE＝BD+CE．（2）DE＝BD+CE仍然成立，理由如下，△△BDA＝△BAC＝△AEC＝α，△△BAD +△EAC ＝△BAD +△DBA ＝180°﹣α，△△DBA ＝△EAC ，△AB ＝AC ，△△DBA △△EAC （AAS ），△BD ＝AE ，AD ＝CE ，△DE ＝AD +AE ＝BD +CE ；【点睛】本题是三角形综合题，考查了全等三角形的判定与性质、直角三角形的性质，解题的关键是熟练掌握全等三角形的判定与性质．12．如图，90,ABC FA AB ∠=⊥于点A ，点D 在直线AB 上，,AD BC AF BD ==．(1)如图1，若点D 在线段AB 上，判断DF 与DC 的数量关系和位置关系，并说明理由；(2)如图2，若点D 在线段AB 的延长线上，其他条件不变，试判断（1）中结论是否成立，并说明理由．【答案】(1)DF =DC ，DF △DC ；理由见解析(2)成立，理由见解析【分析】（1）先证△ADF △△BCD ，得DF =DC ，ADF BCD ∠=∠，再证△FDC =90°即可得垂直；（2）先证△ADF △△BCD ，得DF =DC ，ADF BCD ∠=∠，再证△FDC =90°即可得垂直．（1）解：△90,ABC FA AB ∠=⊥，△90ABC DAF ∠∠==，在△ADF 与△BCD 中AF BD DAF ABC AD BC =⎧⎪∠=∠⎨⎪=⎩，△△ADF △△BCD ，△DF =DC ，ADF BCD ∠=∠，△△BDC +△BCD =90°，△△BDC +△ADF =90°，△△FDC =90°，即DF △DC ．（2）△90,ABC FA AB ∠=⊥，△90DBC DAF ∠∠==，在△ADF 与△BCD 中AF BD DAF DBC AD BC =⎧⎪∠=∠⎨⎪=⎩，△△ADF △△BCD ，△DF =DC ，ADF BCD ∠=∠，△△BDC +△BCD =90°，△△BDC +△ADF =90°，△△FDC =90°，即DF △DC ．【点睛】本题考查全等三角形的判定与性质，解题关键是能判断哪两个三角形全等．13．（1）如图1，已知：在△ABC 中，△BAC =90°，AB =AC ，直线m 经过点A ，BD △直线m ，CE △直线m ，垂足分别为点D 、E ．证明：DE =BD +CE ．（2）如图2，将（1）中的条件改为：在△ABC 中，AB =AC ，D 、A 、E 三点都在直线m 上，并且有△BDA =△AEC =△BAC =α，其中α为任意钝角，请问结论DE =BD +CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．【答案】（1）见解析；（2）成立，见解析【分析】（1）根据AAS 可证明△ADB △△CEA ，可得AE =BD ，AD =CE ，可得DE =BD +CE ．（2）由已知条件可知△BAD +△CAE =180α︒-，△DBA +△BAD =180α︒-，可得△DBA =△CAE ，结合条件可证明△ADB △△CEA ，同（1）可得出结论．【详解】（1）如图1，△ BD △ 直线m ，CE △直线m ，△△BDA =△CEA =90°，△△BAC =90°，△△BAD +△CAE =90°△△BAD +△ABD =90°，△△CAE =△ABD ，在△ADB 和△CEA 中，BDA CEA CAE ABD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADB △△CEA （AAS ），△AE =BD ，AD =CE ，△DE =AE +AD =BD +CE ；（2）如图2，△△BDA =△BAC =α，△△DBA +△BAD =△BAD +△CAE =180α︒-，△△DBA =△CAE ，在△ADB 和△CEA 中，BDA CEA CAE ABD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ADB △△CEA （AAS ），△AE =BD ，AD =CE ，△DE =AE +AD =BD +CE ；【点睛】本题主要考查了全等三角形的判定和性质，由条件证明三角形全等得到BD =AE ，CE =AD 是解题的关键．14．在直线m 上依次取互不重合的三个点,,D A E ，在直线m 上方有AB AC =，且满足BDA AEC BAC α∠=∠=∠=．(1)如图1，当90α=︒时，猜想线段,,DE BD CE 之间的数量关系是____________；(2)如图2，当0180α<<︒时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在ABC 中，BAC ∠是钝角，AB AC =，,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠，直线m 与CB 的延长线交于点F ，若3BC FB =，ABC 的面积是12，求FBD 与ACE 的面积之和．【答案】(1)DE ＝BD +CE(2)DE ＝BD +CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【分析】（1）由△BDA ＝△BAC ＝△AEC ＝90°得到△BAD +△EAC ＝△BAD +△DBA ＝90°，进而得到△DBA ＝△EAC ，然后结合AB ＝AC 得证△DBA △△EAC ，最后得到DE ＝BD +CE ；（2）由△BDA ＝△BAC ＝△AEC ＝α得到△BAD +△EAC ＝△BAD +△DBA ＝180°﹣α，进而得到△DBA ＝△EAC ，然后结合AB ＝AC 得证△DBA △△EAC ，最后得到DE ＝BD +CE ；（3）由△BAD ＞△CAE ，△BDA ＝△AEC ＝△BAC ，得出△CAE ＝△ABD ，由AAS 证得△ADB △△CAE ，得出S △ABD ＝S △CEA ，再由不同底等高的两个三角形的面积之比等于底的比，得出S △ABF 即可得出结果．（1）解：DE ＝BD +CE ，理由如下，△△BDA ＝△BAC ＝△AEC ＝90°，△△BAD +△EAC ＝△BAD +△DBA ＝90°，△△DBA ＝△EAC ，△AB ＝AC ，△△DBA △△EAC （AAS ），△AD ＝CE ，BD ＝AE ，△DE ＝AD +AE ＝BD +CE ，故答案为：DE ＝BD +CE ．（2）DE ＝BD +CE 仍然成立，理由如下，△△BDA ＝△BAC ＝△AEC ＝α，△△BAD +△EAC ＝△BAD +△DBA ＝180°﹣α，△△DBA ＝△EAC ，△AB ＝AC ，△△DBA △△EAC （AAS ），△BD ＝AE ，AD ＝CE ，△DE ＝AD +AE ＝BD +CE ；（3）解：△△BAD ＜△CAE ，△BDA ＝△AEC ＝△BAC ，△△CAE ＝△ABD ，在△ABD 和△CAE 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ABD △△CAE （AAS ），△S △ABD ＝S △CAE ，设△ABC 的底边BC 上的高为h ，则△ABF 的底边BF 上的高为h ，△S △ABC ＝12BC •h ＝12，S △ABF ＝12BF •h ，△BC ＝3BF ，△S △ABF ＝4，△S △ABF ＝S △BDF +S △ABD ＝S △+S △ACE ＝4，△△FBD 与△ACE 的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．15．在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C 且AD MN ⊥于D ，BE MN ⊥于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：△ADC △CEB △；△DE AD BE =+；(2)当直线MN 烧点C 旋转到图2的位置时，求证：DE AD BE =-；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】(1)△证明见解析；△证明见解析(2)证明见解析(3)DE BE AD =-（或者对其恒等变形得到AD BE DE =-，BE AD DE =+），证明见解析【分析】（1）△根据AD MN ⊥，BE MN ⊥，90ACB ∠=︒，得出CAD BCE ∠=∠，再根据AAS即可判定ADC CEB ∆≅∆；△根据全等三角形的对应边相等，即可得出CE AD =，CD BE =，进而得到DE CE CD AD BE =+=+；（2）先根据AD MN ⊥，BE MN ⊥，得到90ADC CEB ACB ∠=∠=∠=︒，进而得出CAD BCE ∠=∠，再根据AAS 即可判定ADC CEB ∆≅∆，进而得到CE AD =，CD BE =，最后得出DE CE CD AD BE =-=-；（3）运用（2）中的方法即可得出DE ，AD ，BE 之间的等量关系是：DE BE AD =-或恒等变形的其他形式．（1）解：△AD MN ⊥，BE MN ⊥，90ADC ACB CEB ∴∠=∠=︒=∠，90CAD ACD ∴∠+∠=︒，90BCE ACD ∠+∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆；△ADC CEB ∆≅∆，CE AD ∴=，CD BE =，DE CE CD AD BE ∴=+=+；（2）证明：AD MN ⊥，BE MN ⊥，90ADC CEB ACB ∴∠=∠=∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆；CE AD ∴=，CD BE =，DE CE CD AD BE ∴=-=-；（3）证明：当MN 旋转到题图（3）的位置时，AD ，DE ，BE 所满足的等量关系是：DE BE AD =-或AD BE DE =+或BE AD DE =+．理由如下：AD MN ⊥，BE MN ⊥，90ADC CEB ACB ∴∠=∠=∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆，CE AD ∴=，CD BE =，DE CD CE BE AD ∴=-=-（或者对其恒等变形得到AD BE DE =+或BE AD DE =+）．【点睛】本题属于三角形综合题，主要考查了全等三角形的判定与性质的综合应用，解题时注意：全等三角形的对应边相等，同角的余角相等，解决问题的关键是根据线段的和差关系进行推导，得出结论．16．（1）如图1，在△ABC 中，△BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD △直线m ，CE △直线m ，垂足分别为点D 、E ．求证：△ABD △△CAE ；（2）如图2，将（1）中的条件改为：在△ABC 中，AB ＝AC ，D 、A 、E 三点都在直线m 上，并且有△BDA ＝△AEC ＝△BAC ＝α，其中α为任意锐角或钝角．请问结论△ABD △△CAE 是否成立？如成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图3，D ，E 是D ，A ，E 三点所在直线m 上的两动点（D ，A ，E 三点互不重合），点F 为△BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD ，CE ，若△BDA ＝△AEC ＝△BAC ，求证：△DEF 是等边三角形．【答案】（1）见详解；（2）成立，理由见详解；（3）见详解【分析】（1）根据BD ⊥直线m ，CE ⊥直线m 得90BDA CEA ∠=∠=︒，而90BAC ∠=︒，根据等角的余角相等得CAE ABD ∠=∠，然后根据“AAS ”可判断ADB CEA ∆∆≌；（2）利用BDA BAC α∠=∠=，则180DBA BAD BAD CAE ∠∠∠∠α+=+=︒-，得出CAE ABD ∠=∠，然后问题可求证；（3）由题意易得,60BF AF AB AC ABF BAF FAC ===∠=∠=∠=︒，由（1）（2）易证ADB CEA ∆∆≌，则有AE BD =，然后可得FBD FAE ∠=∠，进而可证DBF EAF ∆∆≌，最后问题可得证．【详解】（1）证明：BD ⊥直线m ，CE ⊥直线m ，90BDA CEA ∴∠=∠=︒，90BAC ∠=︒，90BAD CAE ∴∠+∠=︒，90BAD ABD ∠+∠=︒，CAE ABD ∴∠=∠，在ADB ∆和CEA ∆中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADB CEA AAS ∴∆∆≌；解：（2）成立，理由如下：α∠=∠=BDA BAC ，180α∴∠+∠=∠+∠=︒-DBA BAD BAD CAE ，CAE ABD ∴∠=∠，在ADB ∆和CEA ∆中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADB CEA AAS ∴∆∆≌；（3）证明：△△ABF 和△ACF 均为等边三角形，△,60BF AF AB AC ABF BAF FAC ===∠=∠=∠=︒，△△BDA ＝△AEC ＝△BAC =120°，△180120DBA BAD BAD CAE ∠+∠=∠+∠=︒-︒，△CAE ABD ∠=∠，△()ADB CEA AAS ∆∆≌，△AE BD =，△,FBD FBA ABD FAE FAC CAE∠=∠+∠∠=∠+∠，△FBD FAE∠=∠，△DBF EAF∆∆≌（SAS），△,FD FE BFD AFE=∠=∠，△60BFA BFD DFA AFE DFA DFE∠=∠+∠=∠+∠=∠=︒，△△DFE是等边三角形．【点睛】本题主要考查全等三角形的判定与性质及等边三角形的性质与判定，熟练掌握全等三角形的判定与性质及等边三角形的性质与判定是解题的关键．17．已知△ABC中，△ACB=90°，AC=BC．BE、AD分别与过点C的直线垂直，且垂足分别为D，E．学习完第十二章后，张老师首先让同学们完成问题1：如图1，若AD=2.5cm，DE=1.7cm，求BE的长；然后，张老师又提出问题2：将图1中的直线CE绕点C旋转到△ABC的外部，BE、AD与直线CE的垂直关系不变，如图2，猜想AD、DE、BE三者的数量关系，并给予证明．【答案】BE的长为0.8cm；DE=AD+BE．【分析】如图1，由“AAS”可证△ACD△△CBE，可得AD=CE=2.5cm，BE=CD，由线段的和差关系可求解；如图2，由“AAS”可证△ACD△△CBE，可得AD=CE，BE=CD，即可求解．【详解】解：如图1，△△ACB=△BEC=△ADC=90°，△△ACD+△BCE=90°=△ACD+△CAD，△△BCE=△CAD，在△ACD和△CBE中，BEC ADCBCE CADBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ACD△△CBE（AAS），△AD=CE=2.5cm，BE=CD，△DE=1.7cm，△BE =CD =CE -DE =2.5-1.7=0.8cm ，△BE 的长为0.8cm ；如图2，DE =AD +BE ，理由如下：△△ACB =△BEC =△ADC =90°，△△ACD +△BCE =90°=△ACD +△CAD ，△△BCE =△CAD ，在△ACD 和△CBE 中，BEC ADC BCE CAD BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ACD △△CBE （AAS ），△AD =CE ，BE =CD ，△DE =AD +BE ．【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形的性质，灵活运用这些性质解决问题是解题的关键．18．在△ABC 中，△ACB ＝90°，AC ＝BC ，且AD △MN 于D ，BE △MN 于E ．(1)直线MN 绕点C 旋转到图（1）的位置时，求证：DE ＝AD +BE ；(2)当直线MN 绕点C 旋转到图（2）的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请直接写出这个等量关系（不写证明过程）；(3)当直线MN 绕点C 旋转到图（3）的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请直接写出这个等量关系（不写证明过程）．【答案】(1)证明见详解(2)DE +BE =AD ．理由见详解(3)DE =BE -AD （或AD =BE -DE ，BE =AD +DE 等）．理由见详解.【分析】（1）根据题意由垂直得△ADC =△BEC =90°，由同角的余角相等得：△DAC =△BCE ，因此根据AAS 可以证明△ADC △△CEB ，结合全等三角形的对应边相等证得结论；（2）由题意根据全等三角形的判定定理AAS 推知△ACD △△CBE ，然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE +BE =AD ；（3）由题意可知DE 、AD 、BE 具有的等量关系为：DE =BE -AD （或AD =BE -DE ，BE =AD +DE等）．证明的方法与（2）相同．(1)证明：如图1，△AD △MN ，BE △MN ，△△ADC =△BEC =90°，△△DAC +△ACD =90°，△△ACB =90°，△△ACD +△BCE =90°，△△DAC =△BCE ，在△ADC 和△CEB 中，△ADC BEC DAC BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ADC △△CEB ；△DC =BE ，AD =EC ，△DE =DC +EC ，△DE =BE +AD ．(2)解：DE +BE =AD ．理由如下：如图2，△△ACB =90°，△△ACD +△BCE =90°．又△AD △MN 于点D ，△△ACD +△CAD =90°，△△CAD =△BCE ．在△ACD 和△CBE 中，90ADC CEB CAD BCEAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， △△ACD △△CBE （AAS ），△CD =BE ，AD =CE ，△DE +BE =DE +CD =EC =AD ，即DE +BE =AD ．(3)解：DE =BE -AD （或AD =BE -DE ，BE =AD +DE 等）．理由如下：如图3，易证得△ADC △△CEB ，△AD =CE ，DC =BE ，△DE=CD-CE=BE-AD，即DE=BE-AD．【点睛】本题属于几何变换综合题，考查等腰直角三角形和全等三角形的性质和判定，熟练掌握全等三角形的四种判定方法是关键：SSS、SAS、AAS、ASA；在证明线段的和与差时，利用全等三角形将线段转化到同一条直线上得出结论．。

七年级初一下学期数学专题03 三角形(知识点串讲)(解析版)

专题03 三角形知识网络重难突破知识点一三角形的有关概念及分类1、三角形的有关概念名称内容图形三角形由3条不在同一条直线上的线段，首尾依次相接组成的图形叫作三角形．边组成三角形的线段叫作三角形的边．组成三角形的三条线段叫做三角形的三条边．三角形的边可以用一个小写字母或两个大写字母表示，如：a，b，c或BC，CA，AB．顶点相邻两边的公共端点叫作三角形的顶点．角相邻两条边所组成的角，叫作三角形的内角，简称三角形的角．三角形的记法三角形用符号“V”来表示，顶点是A，B，C的三角形记作ABCV，读作“三角形ABC”．2、三角形的分类（1）按角分类三个角都是锐角的三角形叫作锐角三角形，有一个角是直角的三角形叫作直角三角形，有一个角是钝角的三角形叫作钝角三角形．（2）按边分类注意：①任何一个三角形最多有三个锐角，最少有两个锐角，最多有一个钝角，最多有一个直角；②等边三角形是特殊的等腰三角形；③顶点是直角的等腰三角形叫做等腰直角三角形.典例1（2019春•东台市校级月考）若一个三角形三个内角度数的比为3:4:11，那么这个三角形是() A．锐角三角形B．直角三角形C．等腰三角形D．钝角三角形【解答】解：设这个三角形三个内角度数依次为3x︒，4x︒，11x︒，则3411180++=，x x x解得：10x=，∴这个三角形三个内角度数依次为30︒，40︒，110︒，则这个三角形是钝角三角形，故选：D ．典例2（2019春•徐州期中）ABC ∆中，若::1:2:3A B C ∠∠∠=，则ABC ∆的形状是( ) A ．直角三角形B ．等腰三角形C ．锐角三角形D ．钝角三角形【解答】解：Q 在ABC ∆中，::1:2:3A B C ∠∠∠=，∴设A x ∠=，则2B x ∠=，3C x ∠=．180A B C ∠+∠+∠=︒Q ，即23180x x x ++=︒，解得30x =︒， 390C x ∴∠==︒， ABC ∴∆是直角三角形．故选：A ．知识点二三角形的三边关系（1）对于任意的ABC V ，如果把其中任意两个顶点看成定点（假设B 、C 为定点），由“两点之间，线段最短”可得：b c a +>．同理可得：a b c +>，a c b +>．即：三角形任意两边之和大于第三边．推论：三角形任意两边之差小于第三边．理论依据：两点之间，线段最短. （2）三角形三边关系的应用①已知三角形的两边长，求第三边的取值范围； ②判断三条线段能否组成三角形.注意：判断三条线段能否组成三角形时，首先找出三条边中的最长边，然后计算另外两边的长度和，若两条短边的长度之和大于最长边的长度，就能组成三角形.典例1（2019春•泰州市泰兴市期中）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是( ) A ．3cm ，4cm ，8cm B ．8cm ，7cm ，15cm C ．5cm ，5cm ，11cmD ．13cm ，12cm ，20cm【解答】解：A 、348+<，故以这三根木棒不可以构成三角形，不符合题意；B 、8715+=，故以这三根木棒不能构成三角形，不符合题意；C 、5511+<，故以这三根木棒不能构成三角形，不符合题意；D 、121320+>，故以这三根木棒能构成三角形，符合题意．故选：D ．典例2（2019春•新吴区期中）有4根小木棒，长度分别为2cm 、3cm 、4cm 、5cm ，任意取3根小木棒首尾相接搭三角形，可搭出不同的三角形的个数为（） A ．1个B ．2个C ．3个D ．4个【解答】解：可搭出不同的三角形为：2cm 、3cm 、4cm ；2cm 、4cm 、5cm ；3cm 、4cm 、5cm 共3个．故选：C ．典例3（2019春•常熟市校级月考）已知三角形的三边长分别为4，5，x ，则x 不可能是( ) A ．3B ．5C ．7D ．9【解答】解：5454x -<<+，即19x <<，则x 的不可能的值是9，故选D ．知识点三三角形的高、中线与角平分线名称图形定义几何语言三角形的高从三角形的一个顶点向它的对边所在的直线画垂线．顶点与垂足之间的线段叫作三角形的高线．简称三角形的高因为AD是ABCV的高（已知），所以AD BC⊥于点D （或90ADC ADB∠∠︒==）三角形的角平分线在三角形中，一个内角的平分线与这个角的对边相交，这个角的顶点与交点之间的线段叫作三角形的角平分线因为AD是ABCV的角平分线（已知），所以1122BAC∠∠∠==三角形的中线在三角形中，连接一个顶点和它的对边中点的线段叫作三角形的中线．三角形的三条中线相交于一点，交点叫作三角形的重心因为AD为ABCV的中线（已知），所以12BD DC BC==（或22BC BD DC==）注意：三角形的中线、角平分线、高都是一条线段；中线、角平分线都在三角形内部，三角形的高有两种特例：直角三角形中其中一条直角边的高就是另一条直角边；钝角三角形中锐角所对的边上的高在三角形的外部．（2019春•相城区期中）在ABC∆中，画出边AC上的高，下面4幅图中画法正确的是（）A．B．C．D．【解答】解：如图，BE为AC边上的高．故选：D．典例2（2019春•盐城市东台市期中）下列说法中错误的是()A．三角形的中线、角平分线、高线都是线段B．任意三角形的内角和都是180︒C．三角形按边分可分为不等边三角形和等腰三角形D．三角形的一个外角大于任何一个内角【解答】解：A、正确，符合线段的定义；B、正确，符合三角形内角和定理；C、正确；D、三角形的一个外角大于任何一个和它不相邻的内角，错误．故选：D．（2019春•徐州期中）如图，在ABC ∆中，AD BC ⊥，AE 平分BAC ∠．（1）若70C ∠=︒，30B ∠=︒求DAE ∠的度数；（2）若20C B ∠-∠=︒，则DAE ∠= ︒．【解答】解：（1）如图，Q 在ABC ∆中70C ∠=︒，30B ∠=︒，180180703080BAC C B ∴∠=︒-∠-∠=︒-︒-︒=︒，AE Q 平分BAC ∠，11804022CAE BAC ∴∠=∠=⨯︒=︒；AD BC ⊥Q ，70C ∠=︒，90907020CAD C ∴∠=︒-∠=︒-︒=︒，40CAE ∠=︒Q ，402020DAE CAE CAD ∴∠=∠-∠=︒-︒=︒；（2）如图，AE Q 平分BAC ∠，1(180)2CAE C B ∴∠=︒-∠-∠，AD BC ⊥Q ，90CAD C ∴∠=︒-∠，11(90)(180)()1022DAE CAD CAE C C B C B ∴∠=∠-∠=︒-∠-︒-∠-∠=∠-∠=︒．故答案为：10．巩固训练一、单选题（共8小题）1．（2019春•靖江市期中）下列长度的三根木棒首尾相接，不能做成三角形框架的是( ) A ．4cm 、7cm 、3cm B ．7cm 、3cm 、8cmC ．5cm 、6cm 、7cmD ．2cm 、4cm 、5cm【解答】解：A 、437+=，不能组成三角形，故本选项正确；B 、738+>，能组成三角形，故本选项错误；C 、567+>，能组成三角形，故本选项错误；D 、425+>，能组成三角形，故本选项错误．故选：A ．2．图中三角形的个数为( )A ．5B ．6C ．7D ．8【解答】解：图中是三角形的有：ABC ∆、ADE ∆、BDF ∆、DEF ∆、CEF ∆共5个．故选：A ．3．（2019春•邗江区校级月考）已知三角形三边分别为2，1a -，4，那么a 的取值范围是( ) A ．15a <<B ．26a <<C ．37a <<D ．46a <<【解答】解：依题意得：42142a -<-<+，即：216a <-<， 37a ∴<<．故选：C ． 4．下列说法：①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形； ②等边三角形是特殊的等腰三角形； ③等腰三角形是特殊的等边三角形； ④有两边相等的三角形一定是等腰三角形；其中，说法正确的个数是( ) A ．1个B ．2个C ．3个D ．4个【解答】解：①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形；错误． ②等边三角形是特殊的等腰三角形；正确． ③等腰三角形是特殊的等边三角形；错误． ④有两边相等的三角形一定是等腰三角形；正确，故选：B ．5．如图，若CD 是ABC ∆的中线，10AB =，则(AD = )A ．5B ．6C ．8D ．4【解答】解：Q 如图，若CD 是ABC ∆的中线，10AB =， 152AD BD AB ∴===．故选：A ．6．如图所示，ABC ∆中AC 边上的高线是( )A ．线段DAB ．线段BAC ．线段BCD ．线段BD【解答】解：由图可得，ABC ∆中AC 边上的高线是BD ，故选：D ．7．（2019春•东台市校级月考）如图，AD 是ABC ∆的角平分线，点O 在AD 上，且OE BC ⊥于点E ，60BAC ∠=︒，80C ∠=︒，则EOD ∠的度数为( )A ．20︒B ．30︒C ．10︒D ．15︒【解答】解：60BAC ∠=︒Q ，80C ∠=︒， 40B ∴∠=︒．又AD Q 是BAC ∠的角平分线， 1302BAD BAC ∴∠=∠=︒，70ADE ∴∠=︒，又OE BC ⊥Q ， 20EOD ∴∠=︒．故选：A ．8．如图，ABC ∆中，12∠=∠，G 为AD 中点，延长BG 交AC 于E ，F 为AB 上一点，且CF AD ⊥于H ，下列判断，其中正确的个数是( ) ①BG 是ABD ∆中边AD 上的中线；②AD 既是ABC ∆中BAC ∠的角平分线，也是ABE ∆中BAE ∠的角平分线； ③CH 既是ACD ∆中AD 边上的高线，也是ACH ∆中AH 边上的高线．A ．0B ．1C ．2D ．3【解答】解：①G 为AD 中点，所以BG 是ABD ∆边AD 上的中线，故正确；②因为12∠=∠，所以AD 是ABC ∆中BAC ∠的角平分线，AG 是ABE ∆中BAE ∠的角平分线，故错误； ③因为CF AD ⊥于H ，所以CH 既是ACD ∆中AD 边上的高线，也是ACH ∆中AH 边上的高线，故正确．故选：C ．二、填空题（共3小题）9．（2019春•东台市校级月考）已知等腰三角形两边的长分别是15和7，则其周长为．【解答】解：①7cm是腰长时，三角形的三边分别为7、7、15，Q，771415+=<∴不能组成三角形，②7cm是底边时，三角形的三边分别为7、15、15，能组成三角形，周长7151537=++=，综上所述，它的周长是37．故答案为：37．10．已知三角形的三边长都是整数，其中两条边长分别是1cm和3cm，则第三条边长_____cm．【解答】解：Q两条边长分别是1cm和3cm，<，∴第三边的取值范围是2<第三边4Q三边均为整数，∴第三边的长为3cm，故答案为：3．11．已知三角形的三边长均为整数，其中两边长分别为1和3，则第三边长为．【解答】解：设第三边长为a，则3131-<<+，a即24<<，aQ是整数，a∴=．a3故答案为：3．三、解答题（共3小题）12．（2019春•大丰区期中）如图，在ABC∆中，点D在BC上，且BAD CAD∠=∠，E是AC的中点，BE 交AD于点F．图中哪条线段是哪个三角形的角平分线？哪条线段是哪个三角形的中线？【解答】解：AD是ABC∆的角平分线；∆的角平分线，AF是ABEBE是ABC∆的中线，DE是ADC∆的中线．13．（2018秋•丹阳市期中）如图，ABC∆中，90∆的高、中线、角ACB∠=︒，CD、CE、CF分别是ABC平分线．求证：12∠=∠．【解答】证明：CFQ是ACB∠的平分线，∴∠=∠．ACF BCF∠=︒，CD ABACBQ，90⊥∴∠=∠（同角的余角相等）．ACD BCEQ是AB边上的中线，∴=，BE CE∴∠=∠（等边对等角），BCE B1ACF ACD ACF B∴∠=∠-∠=∠-∠，∠=∠-∠=∠-∠，2BCF BCE ACF B∴∠=∠．1214．如图，ABC∆中，点D在AC上，点P在BD上，求证：AB AC BP CP+>+．【解答】证明：在ABD+>，∆中，AB AD BD 在PDC+>，∆中，CD PD PCAB AD CD PD BD PC∴+++>+∴+>+．AB AC BP CP。

专题3 空间图形的基本关系与公理(解析版)-2021年高考数学立体几何中必考知识专练

专题3：空间图形的基本关系与公理（解析版）一公理1 公理2 公理3图形语言文字语言如果一条直线上的两点在一个平面内，那么这条直线在此平面内.过不在一条直线上的三点，有且只有一个平面.如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.符号语言,,A lB llA Bααα∈∈⎫⇒⊂⎬∈∈⎭,,,,A B CA B Cα⇒不共线确定平面,lP PP lαβαβ=⎧∈∈⇒⎨∈⎩作用判断线在面内确定一个平面证明多点共线推论1 经过一条直线和这条直线外的一点，有且只有一个平面；推论2 经过两条相交直线，有且只有一个平面；推论3 经过两条平行直线，有且只有一个平面.二．直线与直线的位置关系直线：相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；直线：不同在任何一个平面内，没有公共点。

（既不平行，也不相交）三．直线与平面的位置关系有三种情况：在平面内——有无数个公共点．符号 aα相交——有且只有一个公共点符号 a∩α= A平行——没有公共点符号 a∥α说明：直线与平面相交或平行的情况统称为直线在平面外，可用a α来表示对应练习一、单选题1．如图所示的是平行四边形ABCD所在的平面，有下列表示方法：①平面ABCD；②平面BD；③平面AD；④平面ABC；⑤AC；⑥平面α.其中不正确的是（）A．④⑤B．③④⑤C．②③④⑤D．③⑤【答案】D【分析】根据平面的表示方法判断．【详解】③中AD不为对角线，故错误；⑤中漏掉“平面”两字，故错误.故选：D.2．下列叙述错误的是（）A．若p∈α∩β，且α∩β=l，则p∈l.B．若直线a∩b=A，则直线a与b能确定一个平面.C．三点A，B，C确定一个平面.D．若A∈l，B∈l且A∈α，B∈α则l α.【答案】C【分析】由空间线面位置关系，结合公理即推论，逐个验证即可．【详解】选项A，点P在是两平面的公共点，当然在交线上，故正确；选项B，由公理的推论可知，两相交直线确定一个平面，故正确；选项C，只有不共线的三点才能确定一个平面，故错误；选项D，由公理1，直线上有两点在一个平面内，则整条直线都在平面内．故选：C3．在空间中，下列结论正确的是（）A．三角形确定一个平面B．四边形确定一个平面C．一个点和一条直线确定一个平面D．两条直线确定一个平面【答案】A【分析】根据确定平面的公理及其推论对选项逐个判断即可得出结果.【详解】三角形有且仅有3个不在同一条直线上的顶点，故其可以确定一个平面，即A正确；当四边形为空间四边形时不能确定一个平面，故B错误；当点在直线上时，一个点和一条直线不能确定一个平面，故C错误；当两条直线异面时，不能确定一个平面，即D错误；故选：A.【点睛】本题主要考查平面的基本定理及其推论，解题时要认真审题，仔细解答，属于基础题.4．下列命题中正确的是（）A ．若直线l 上有无数个点不在平面α内，则//l αB ．如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行C ．若两条直线都与第三条直线垂直，则这两条直线互相平行D ．垂直于同一个平面的两条直线互相平行【答案】D 【分析】利用空间中直线与直线、直线与平面的位置关系进行判断. 【详解】解:选项A: 若直线l 上有无数个点不在平面α内，则//l α或相交,故A 错误;选项B: 如果两条平行直线中的一条与一个平面平行，那么另一条可能与这个平面平行,也可包含于这个平面,故B 错误;选项C: 若两条直线都与第三条直线垂直，则这两条直线相交、平行或异面,故C 错误; 选项D: 垂直于同一个平面的两条直线互相平行, 故D 正确, 故选:D 【点睛】本题考查空间中直线与直线、直线与平面的位置关系的判断，解题时要认真审题，注意空间思维能力的培养.5．已知直线l 和不重合的两个平面α，β，且l α⊂，有下面四个命题：①若//l β，则//αβ；②若//αβ，则//l β；③若l β⊥，则αβ⊥；④若αβ⊥，则l β⊥ 其中真命题的序号是（） A ．①② B ．②③ C ．②③④ D ．①④【答案】B 【分析】对于①，由//l β可得α与β可平行，可相交；对于②，若//αβ，则由面面平行的性质定理可判断；对于③，由线面垂直的判定定理可判断；对于④，当αβ⊥时，l 可能在β内，可能与β平行，可能相交【详解】解：对于①，由//l β可得α与β可平行，可相交，故错误；对于②，若//αβ，则由面面平行的性质定理可得//l β，故正确；对于③，若l β⊥，则由线面垂直的判定定理可得αβ⊥，故正确；对于④，当αβ⊥时，l 可能在β内，可能与β平行，可能相交，所以不一定有l β⊥，故错误，故选：B 【点睛】此题考查线线、线面、面面关系的判断，属于基础题6．四个顶点不在同一平面上的四边形ABCD 中，E ，F ，G ，H 分别是边AB ，BC ，CD ，DA 上的点，如果直线EF ，GH 交于点P ，那么（）A ．点P 一定在直线AC 上B ．点P 一定在直线BD 上C ．点P 一定在平面ABC 外D ．点P 一定在平面BCD 内【答案】A 【分析】由两个面的交点在两个面的交线上，知P 在两面的交线上，由AC 是两平面的交线，知点P 必在直线AC 上．【详解】解：∵EF 在面ABC 内，而GH 在面ADC 内，且EF 和GH 能相交于点P ， ∴P 在面ABC 和面ADC 的交线上， ∵AC 是两平面的交线，所以点P 必在直线AC 上．故选：A ．【点睛】本题考查平面的基本性质及其推论，是基础题．解题时要认真审题，仔细解答． 7．平面α平面l β=，点A α∈，点B β∈，且B l ∉，点C α∈，又ACl R =，过A 、B 、C 三点确定的平面为γ，则βγ⋂是（）A ．直线CRB ．直线BRC ．直线ABD ．直线BC【答案】B 【分析】确定平面β、γ的公共点，利用公理可得出平面β与γ的交线. 【详解】如下图所示：由题意可知，AC γ⊂，AC l R =，则R γ∈，又平面α平面l β=，则l α⊂，l β⊂，AC l R =，R β∴∈，B β∈，B γ∈，因此，βγ⋂=直线BR .故选：B. 【点睛】本题考查两平面交线的确定，关键是确定两平面的公共点，属于基础题.8．设l ，m 是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（） A ．若l m ⊥，m α⊂，则l α⊥ B ．若//l α，m α⊂，则//l m C ．若//αβ，m β⊄，//m α，则//m β D ．若//l α，//m α，则//l m【答案】C 【分析】由线面垂直的判定定理可判断A ，由线面平行的性质定理可判断B ，由面面平行的性质定理可判断C ，由线面平行的性质定理可判断D. 【详解】解：对于A ，由线面垂直的判定定理可知当直线l 垂直平面α内的两条相交直线时，l α⊥才成立，所以A 不正确；对于B ，若//l α，m α⊂，则//l m 或l ，m 异面，所以B 不正确；对于C ，由面面平行的性质定理可知是正确的，对于D ，若//l α，//m α，则l ，m 有可能相交、平行或异面，所以D 不正确，故选：C 【点睛】此题考查了线线、线面和面面的位置关系，考查平行和垂直的判定和性质，考查空间想象能力和推理能力，属于基础题.9．下列命题中，正确的是 ( )A ．经过正方体任意两条面对角线，有且只有一个平面B ．经过正方体任意两条体对角线，有且只有一个平面C ．经过正方体任意两条棱，有且只有一个平面D ．经过正方体任意一条体对角线与任意一条面对角线，有且只有一个平面【答案】B 【解析】因为正方体的四条体对角线相交于同一点(正方体的中心)，因此经过正方体任意两条体对角线，有且只有一个平面，故选B ．点睛：确定平面方法: 过不在一条直线上的三点，有且只有一个平面;经过一条直线和这条直线外一点有且只有一个平面；经过两条相交直线有且只有一个平面；经过两条平行直线有且只有一个平面．10．设α，β表示平面，l 表示直线，A ，B ，C 表示三个不同的点，给出下列命题：①若∈A l ，A α∈，B l ∈，B α∈，则l α⊂；②若A α∈，A β∈，B α∈，B β∈，则AB αβ=；③若l α⊄，∈A l ，则A α；④若,,A B C α∈，,,A B C β∈，则α与β重合.其中，正确的有（） A ．1个 B ．2个C ．3个D ．4个【答案】B 【分析】根据平面的基本性质及推论进行判断. 【详解】若∈A l ，A α∈，B l ∈，B α∈，根据公里1，得l α⊂，①正确；若A α∈，A β∈，B α∈，B β∈，则直线AB 既在平面α内，又在平面β内，所以AB αβ=，②正确；若l α⊄，则直线l 可能与平面α相交于点A ，所以∈A l 时， A α∈，③不正确；若,,A B C α∈，,,A B C β∈，当,,A B C 共线时，α与β可能不重合，④不正确；故选：B. 【点睛】本题主要考查平面的性质，明确平面的基本性质及推论是求解的关键，侧重考查直观想象的核心素养.11．平面α的一条斜线AP 交平面α于P 点，过定点A 的直线l 与AP 垂直，且交平面α于M 点，则M 点的轨迹是（）.A ．一条直线B ．一个圆C ．两条平行直线D ．两个同心圆【答案】A 【分析】由过定点A 的直线l 与AP 垂直可知，直线l 绕点A 旋转形成一个平面，由此可知两平面的交线即为所求．【详解】解：如图，设直线l与l'是其中两条任意的直线，⊥，则这两条相交直线确定一个平面β，且斜线APβ由过平面外一点有且只有一个平面与已知直线垂直可知，过定点定点A且与AP垂直的直线都在平面β内，∴M点都在平面α与平面β的交线上，故选：A．【点睛】本题主要考查空间中点、线、面的位置关系，考查空间想象能力，属于基础题．12．和直线l都平行的直线,a b的位置关系是（）A．相交B．异面C．平行D．平行、相交或异面【答案】C【分析】直接利用平行公理，即可得到答案．【详解】由平行公理，可知平行与同一直线的两直线是平行的，所以和直线l都平行的直线,a b的位置关系是平行，故选C．【点睛】本题考查两直线的位置关系的判断，考查空间中线线、线面、面面间的位置关系，考查运算求解能力，考查数形结合思想，是中档题．二、填空题13．如图，已知正方体1111ABCD A B C D -的棱长为a ，则异面直线1BC 与AC 所成的角为_____．【答案】60︒ 【解析】11//BC AD ∴ 异面直线1BC 与AC 所成的角为0160CAD ∠=14．已知l ，m 是两条不同的直线，α，β是两个不同的平面，给出下列四个论断：①//l m ，②//αβ，③m α⊥，④l β⊥.以其中的两个论断作为命题的条件，l α⊥作为命题的结论，写出一个真命题：______.【答案】若//l m ，m α⊥，则l α⊥ 【分析】若//l m ，m α⊥，则l α⊥，运用线面垂直的性质和判定定理，即可得到结论. 【详解】解：l ，m 是两条不同的直线，α，β是两个不同的平面，可得若//l m ，m α⊥，则l α⊥，理由：在α内取两条相交直线a ，b ，由m α⊥可得m a ⊥.m b ⊥，又//l m ，可得l a ⊥.l b ⊥，而a ，b 为α内的两条相交直线，可得l α⊥. 故答案为：若//l m ，m α⊥，则l α⊥ 【点睛】此题考查线面垂直的判定定理和性质定理的应用，考查推理能力，属于基础题15．如图，在正方体1111ABCD A B C D -中，E ，F 依次是11A D 和11B C 的中点，则异面直线AE 与CF 所成角的余弦值为__．【答案】35【分析】连AE 、BF 、EF ，利用平行四边形可得//BF AE ，可得BFC ∠是异面直线AE 与CF 所成角（或所成角的补角），然后用余弦定理可得结果. 【详解】在正方体1111ABCD A B C D -中，连AE 、BF 、EF ，E ，F 依次是11A D 和11B C 的中点，所以11//A E B F 且11A E B F =，所以四边形11A B FE 为平行四边形，所以11//EF A B 且11EF A B =，又11//A B AB 且11A B AB =，所以//EF AB 且EF AB =，所以四边形ABFE 为平行四边形，//BF AE ∴，BFC ∴∠是异面直线AE 与CF 所成角（或所成角的补角），设正方体1111ABCD A B C D -的棱长为2，则415BF CF ==+3cos5BFC∴∠==．∴异面直线AE与CF所成角的余弦值为35．故答案为：35．【点睛】本题考查了求异面直线所成的角，考查了余弦定理，属于基础题.16．在长方体1111ABCD A B C D-中，11AA AD==，2AB=，则直线AC与1A D所成的角的大小等于__________.【答案】arccos10【分析】连接11,B A B C，可得直线AC与1A D所成的角为1B CA∠，利用余弦定理求1cos B CA∠即可.【详解】解：如图，连接11,B A B C，由长方体的结构特点可知11//B C A D，则直线AC与1A D所成的角为1B CA∠（或其补角），因为11B A BC AC======，在1B CA中，2221111cos210BC AC ABB CABC AC+-∠===⋅，1arccos10B CA∴∠=.故答案为：arccos10.【点睛】本题考查异面直线所成的角，关键是要通过平移找到异面直线所成的角的平面角，是基础题.三、解答题17．如图，在正方体1111ABCD A B C D -中，E ，F ，1E ，1F 分别为棱AD ，AB ，11B C ，11C D 的中点.求证：111EA F E CF ∠=∠.【答案】见解析【分析】根据空间中两个角的两边平行时,角的关系可知两个角相等或互补. 结合空间中平行线的传递性及当两个角的方向相同时,即可证明两个角相等. 【详解】证明：如图,在正方体1111ABCD A B C D -中,取11A B 的中点M ,连接名BM ,1F M由题意得112BF A M AB ==又1BF M A ∥∴四边形1A FBM 为平行四边形 ∴1A F BM ∥又1F ,M 分别为11C D ,11A B 的中点,则111F M C B =∥而11C B BC =∥∴1F M BC =∥∴四边形1F MBC 为平行四边形 ∴1BM F C ∥ 又1BM A F ∥ ∴11A F F C ∥ 同理可得11A ECE∴1EA F ∠与11E CF ∠的两边分别平行,且方向都相反 ∴111EA F E CF ∠=∠. 【点睛】本题考查了直线与直线平行的证明,空间中角的两边分别平行时两个角的关系,属于基础题. 18．（不写做法）（1）如图，直角梯形ABCD 中，//AB CD ，AB CD >，S 是直角梯形ABCD 所在平面外一点，画出平面SBD 和平面SAC 的交线．（2）如图所示，在正方体1111ABCD A B C D -中，试画出平面11AB D 与平面11ACC A 的交线．【答案】（1）见解析（2）见解析【分析】（1）延长BD 和AC 交于点O ，再连接SO ，即得到交线；（2）先记11B D 与11A C 的交点为O ，连接AO ，即可得出交线. 【详解】（1）（延长BD 和AC 交于点O ，连接SO ，SO 即为平面SBD 和平面SAC 的交线），如图：（2）（记11B D 与11A C 的交点为O ，连接AO ，则AO 即为平面11AB D 与平面11ACC A 的交线），如图:【点睛】本题主要考查画出平面与平面的交线，考查空间想象能力，属于基础题型. 19．如图，已知正方体ABCD -A ′B ′C ′D .（1）哪些棱所在直线与直线BA′是异面直线？（2）直线BA′和CC′的夹角是多少？（3）哪些棱所在的直线与直线AA′垂直？【答案】（1）棱AD、DC、CC′、DD′、D′C′、B′C′（2）45°（3）AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′【分析】（1）根据异面直线的定义判断即可；（2）∠B′BA′为异面直线BA′与CC′的夹角，进而可得直线BA′和CC′的夹角；（3）根据正方体的性质即可判断．【详解】（1）由异面直线的定义可知，棱AD、DC、CC′、DD′、D′C′、B′C′所在直线分别与直线BA′是异面直线；（2）由BB′∥CC′可知，∠B′BA′为异面直线BA′与CC′的夹角，∠B′BA′＝45°，所以直线BA′和CC′的夹角为45°；（3）直线AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′分别与直线AA′垂直.【点睛】本题考查异面直线的定义，考查线线角的求解，考查线线垂直的判断，是基础题．VB VC的中点，求异20．如图，AB是圆O的直径，点C是弧AB的中点，,D E分别是,面直线DE与AB所成的角.【答案】45︒ 【分析】根据题意，直径所对圆周角是直角，BC AC ∴⊥，又知点C 是弧AB 的中点，则等腰直角三角形，再根据中位线平行，找到异面直线所成角的平面角，即可求解. 【详解】AB 是圆O 的直径，BC AC ∴⊥.∵点C 是弧AB 的中点，,45BC AC ABC ∴=∴∠=︒. 在VBC △中，,D E 分别为,VB VC 的中点，DE BC ∴∥，DE ∴与AB 所成的角为45ABC ∠=︒.故答案为：45︒ 【点睛】本题考查异面直线所成角问题，考查转化与化归思想，属于基础题.21．如图1所示，在梯形ABCD 中，//AB CD ，E ，F 分别为BC ，AD 的中点，将平面CDFE 沿EF 翻折起来，使CD 到达C D ''的位置（如图2），G ，H 分别为AD '，BC '的中点，求证:四边形EFGHEFGH 为平行四边形.图1 图2【答案】证明见详解.【分析】通过证明EF //GH ，且EF =GF ，即可证明. 【详解】在题图1中，∵四边形ABCD 为梯形，//AB CD ，E F ，分别为BC AD ，的中点，∴//EF AB 且()12EF AB CD =+. 在题图2中，易知////C D EF AB ''. ∵,G H 分别为AD '，BC '的中点， ∴//GH AB 且()()1122GH AB C D AB CD ''=+=+， ∴//GH EF ，GH EF =，∴四边形EFGH 为平行四边形.即证. 【点睛】本题考查通过线线平行证明平行四边形，主要借助几何关系进行证明.22．如图所示,已知,E F 分别是正方体1111ABCD A B C D -的棱11,AA CC 的中点,求证:四边形1BED F 是平行四边形.【答案】见解析【分析】取1D D 的中点G ,连接,EG GC ，证明四边形EGCB 是平行四边形，再证四边形1D GCF 为平行四边形，即可证明四边形1BED F 是平行四边形. 【详解】证明取1D D 的中点G ,连接,EG GC .∵E 是1A A 的中点,G 是1D D 的中点,//EG AD ∴. 由正方体的性质知//AD BC ,//EG BC ∴, ∴四边形EGCB 是平行四边形,//EB GC ∴. 又,G F 分别是1D D ,1C C 的中点,1//D G FC ∴,且1D G FC =,∴四边形1D GCF 为平行四边形,1//D F GC ∴, 1//EB D F ∴,∴四边形1BED F 是平行四边形. 【点睛】本题考查了线线平行的判定，利用平行四边形的对边平行且相等证明线线平行，是基础题.。

人教八上：专题三--角平分线的性质与判定(含解析)

专题三角平分线的性质与判定一、单选题1．如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若BC=15，且BD:CD=3:2，则点D到AB的距离为（）2345．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，AB+BC+CA=18，过O作OD⊥BC于点D，且OD=3，则△ABC的面积是．6．如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE7得8910．如图，△ABC中，∠ABC，∠ACB的角平分线交于点O，过O点作MN∥BC分别交AB，AC于M，N 两点，AB=6，ΔAMN的周长是15．则AC的长为．三、解答题11．如图1，△ABC的两条外角平分线AO，BO相交于点O，∠ACB=50°．(1)直接写出∠AOB的大小；(2)如图2，连接OC交AB于K．①求∠BCK的大小；②如图3，作AF⊥OC于F，若∠BAC=105°，求证：AB=2CF．12．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，若∠ABC=60°，FD=10，求DC的长．13．如图，四边形ABCD中，∠B=90°，AB∥CD，M是BC边上的一点，且AM平分∠BAD,DM平分∠ADC,求证：(1)BM=MC；(2)AM⊥MD．14．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．(1)如图1，△ABC中，AB=AC,∠A=36°，求证：△ABC是倍角三角形；(2)如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE=AB，若AB+AC=BD，请你找出图中的倍角三角形，并进行证明．15．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，设∠ABC=α．(1)α=50°时，求∠DFC的度数；(2)证明：BE∥DF．16．在△ABC中，AO、BO分别平分∠BAC、∠ABC．(1)如图1，若∠C=32°，则∠AOB=________；(2)如图2，连结OC，求证：OC平分∠ACB；(3)如图3，若∠ABC=2∠ACB，AB=4，AC=7，求OB的长．17．如图，在△ABC中，D在BC边的延长线上，∠ACD的平分线CE交BA的延长线于点E，已知∠B=30°，∠E=40°，求证：AE=CE．18．如图，在四边形ABCD中，AB∥CD，∠C=90°，点E为BC的中点，DE平分∠CDA.(1)求证：AD=AB+CD；(2)若S△CDE=3，S△ABE=4，则四边形ABCD的面积为______.（直接写出结果）19．如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O与AB，AC分别相交于点M，N，且MN∥BC．(2)已知AB=7，AC=6，求△AMN的周长．参考答案题号12答案B B1．B【分析】本题考查的是角平分线的性质，作DE⊥AB于E，根据角平分线的性质得到CD=DE，根据题意求出CD的长即可．∵∴∵∴2∴3【详解】试题分析：本题需要分两种情况进行讨论：如图1所示：根据∠B=40°，∠C=70°可得：∠BAC=70°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=35°，则∠DAE=35°-20°=15°；如图2所示：根据∠B=40°，∠ACD=70°可得：∠BAC=30°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=15°，则∠DAE=15°+20°=35°.点睛：对于这种在三角形中求角度问题的时候，如果题目中没有给出图形，我们首先一定要根据题意画出图形，然后根据图形求出角的度数.特别要注意分类讨论的思想，在画图时一定要注意锐角三角形和钝角三角形两种情况.在画垂线的时候要注意高线在三角形内部和三角形外部两种情况.4．3：2【分析】过点D作DE⊥AB于点E，由角平分线的性质得到DE=CD，再根据三角形面积公式解答即可．【详解】解：过点D作DE⊥AB于点E，∵AD是Rt△ABC的角平分线，CD⊥AC,DE⊥AB∴DE=CDS△ABD S△ACD =12AB⋅DE12AC⋅CD=ABAC=128=32故答案为：3：2．【点睛】本题考查角平分线的性质、三角形面积公式等知识，是基础考点，掌握相关知识是解题关键．5．27【分析】作OE⊥AB于E,OF⊥AC于F，连接OA，根据角平分线的性质求出OE=OD=3和OF=OD=3，根据三角形面积公式计算即可．【详解】解：作OE⊥AB于E,OF⊥AC于F，连接OA，∵OB是∠ABC的平分线，OD⊥BC,OE⊥AB，∴OE=OD=3，同理OF=OD=3，∵AB+BC+CA=18．∴△ABC的面积=12×AB×3+12×AC×3+12×BC×3=27．故答案为：27．【点睛】本题主要考查角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．4【分析】根据角平分线的性质以及平行线的性质即可得出PM =PE =2，PE =PN =2，即可得出答案．【详解】解：过点P 作MN ⊥AD ，∵AD ∥BC ，∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ，PE ⊥AB 于点E ，∴AP ⊥BP ，PN ⊥BC ，∴PM =PE =2，PE =PN =2，∴MN =2+2=4．故答案为：4．7．2【分析】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，根据三角形的面积公式计算即可．【详解】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，由题意得，PE=PD=PF ， S △APC +S △APB +S △BPC =S △ACB ，∴12AC·PE+12AB·PD+12BC·PF=12AC·BC ，即12×12·PD+12×13•PD+12×5•PD=12×5×12，解得，PD=2，故答案为：2．【点睛】本题考查的是三角形的面积计算，掌握三角形的面积公式是解题的关键．8．60【分析】根据五边形的内角和求出∠BCD和∠CDE的和，再根据角平分线及三角形内角和求出∠CPD．【详解】解：∵五边形的内角和等于540°，∠A+∠B+∠E＝300°，∴∠BCD+∠CDE＝540°﹣300°＝240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，（∠BCD+∠CDE）＝120°，∴∠PDC+∠PCD＝12∴∠CPD＝180°﹣120°＝60°．故答案是：60．【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质．9．5【分析】本题考查角平分线的性质定理，过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，利用角平分线的性质可得PF=PG=PE，然后根据三角形的面积求出PF=PE=PG=2，再利用△OMP的面积+△ONP的面积−△PMN的面积=4，进行计算即可解答．根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【详解】解：过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，∵MP平分∠AMN，NP平分∠MNB，∴PF=PG=PE，∵MN=1，△PMN的面积是1，∴ 12MN ⋅PF =1，∴PF =2，∴PG =PE =2，∵△OMN 的面积是4，∴△OMP 的面积+△ONP 的面积−△PMN 的面积=4，∴ 12OM ⋅PG +12ON ⋅PE−1=4，∴OM +ON =5．故答案为：5．10．9【分析】本题考查了等腰三角形的判定与性质，平行线的性质，根据角平分线的定义和平行线的性质可得△MOB 和△NOC 是等腰三角形，从而可得MO =MB ，NO =NC ，然后利用等量代换可得ΔAMN 的周长=AB +AC ，从而进行计算即可解答．【详解】解：∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABO =∠OBC ，∠ACO =∠OCB ，∵MN ∥BC ，∴∠MON =∠OBC ，∠NOC =∠OCB ，∴∠ABO =∠MON ，∠ACO =∠NOC ，∴MO =MB ，NO =NC ，∵△AMN 的周长是15，∴AM +MN +AN =15，∴AM +MO +ON +AN =15∴AM +MB +NC +AN =15，∴AB +AC =15，∵AB =6，∴AC =15−6=9，故答案为：9．11．(1)65°；(2)①25°；②证明见解析．【分析】（1）根据三角形内角和定理求得∠CBA +∠CAB =130°，则∠EBA +∠BAD =230°，再由角平分线的定义求出∠OBA +∠OAB =115°，根据四边形内角和求出∠AOB 即可；（2）①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，根据角平分线的性质求解即可；②先求出KB=KC，过点A作AH∥BC交CO于点H，再求出KA=KH，则AB=CH，分别求出AH=AC，HF=CF，即可得出结论．【详解】（1）解：∵AO平分∠BAD，∴∠DAO=∠OAB，∵BO平分∠EOA，∴∠EBO=∠OBA，∵∠ACB=50°，∴∠CBA+∠CAB=130°，∴∠EBA+∠BAD=360°−130°=230°，∴∠OBA+∠OAB=115°，∴∠AOB=360°−50°−115°−130°=65°；（2）解：如图2，①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，∵AO、BO分别平分∠DAB、∠EBA，∴OM=OP，OP=ON，∴OM=ON，∴CO平分∠ACB，∵∠ACB=50°，∴∠BCK=∠ACK=25°；②证明：∵∠BAC=105°，∠ACB=50°，∴∠ABC=25°，∵∠KCB=25°，∴∠KBC=∠KCE，∴KB=KC，如图3，过点A作AH∥BC交CO于点H，∴∠AHK=∠KCB，∠HAK=∠KBC，∴∠AHK=∠HAK，∴KA=KH，∴AB=CH，∵∠AHK=∠ACH，∴AH=AC，∵AF⊥CO，∴HF=CF，∴CH=2CF，∴AB=CH=2CF．12∴∵∴∴∵∴∴故DC=5．【点睛】此题主要考查了角平分线的定义，四边形内角和定理，含30°角的直角三角形的性质等知识，解题关键是熟练掌握各性质与定理．13．(1)见详解(2)见详解【分析】（1）作NM⊥AD，根据角平分线的性质得到BM=MN,MN=CM，等量代换得到答案．（2）根据平行线的性质得到∠BAD+∠ADC=180°，根据角平分线的定义得到∠MAD+∠ADM=90°，根据垂直的定义得到答案；【详解】（1）作NM⊥AD交AD于N，∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM；（2）证明：∵AB∥CD，∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM；【点睛】本题考查的是角平分线的性质，掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键．14．(1)见解析(2)△ADC和△ABC是倍角三角形，见解析【分析】（1）利用等边对等角及三角形的内角和求出∠B=∠C=72°，得到2∠A=∠C即可；（2）根据SAS证明△ABD≌△AED，得到∠ADE=∠ADB，BD=DE，证明CE=DE，得出∠C=∠BDE=2∠ADC，可得出∠ABC=2∠C．则结论得证．【详解】（1）证明：∵AB=AC，∴∠B=∠C，∵∠A+∠B+∠C=180°，∠A=36°，∴∠B=∠C=72°，∴2∠A=∠C，即△ABC是倍角三角形；（2）解：△ADC和△ABC是倍角三角形，证明如下：∵AD平分∠BAE，∴∠BAD=∠EAD，∵AB=AE，AD=AD，∴∴又∴∴∴∴∵15(2)∠EBC=∠DFC即可得出结论．【详解】（1）解：在四边形ABCD中，∠A=∠C=90°，∠ABC=α，α=50°，∴∠ADC=360°−∠A−∠C−∠ABC=130°，∵DF平分∠CDA，∠ADC=65°，∴∠FDC=12∴∠DFC =90°−65°=25°；（2）证明：在四边形ABCD 中，∠A =∠C =90°，∠ABC =α，∴∠ADC =360°−∠A−∠C−∠ABC =180°−α，∵DF 平分∠CDA ，∴∠FDC =12∠ADC =12(180°−α)，∴∠DFC =90°−12(180°−α)=12α，∵BE 平分∠ABC ，∴∠EBC =12α，∴∠EBC =∠DFC ，∴BE ∥DF ．16．(1)106°；(2)见解析；(3)3；【分析】（1）本题考查与角平分线有关的三角形内角和关系，根据∠C =32°得到∠CAB +∠CBA ，再结合角平分线求出∠CAO +∠CBO ，即可得到答案；（2）本题考查角平分线判定与性质，过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，根据角平分线性质得到OD =OF =OE ，结合角平分线的判定即可证明；（3）本题主要考查三角形全等的性质与判定，解题的关键是根据截长补短作出辅助线，在AC 上截取一点D ，使AD =AB ，连OD ，证明△ABO≌△ADO ，即可得到答案；【详解】（1）解：∵∠C =32°，∴∠CAB +∠CBA =180°−32°=148°，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴∠CAO +∠CBO =148°2=74°，∴∠AOB =180°−74°=106°；（2）证明：过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴OD =OF ，OD =OE ，∴OC 平分∠ACB ；（3）解：在AC 上截取一点D ，使AD =AB ，连OD ，设∠ACO =∠BCO =α，∵∠ABC =2∠ACB ，∴∠ABC =4α，∵BO 平分∠ABC ，∴∠ABO =∠CBO =2α，∵AO 平分∠BAC ，∴∠BAO =∠DAO ，在△ABO 与△ADO 中，AO =AO ∠BAO =∠DAO AB =AD，∴△ABO≌△ADO(SAS)，∴∠ABO =∠ADO =2α，OB =OD,AB =AD =4，又∵∠ACO =α，∴∠ACO =∠DCO =α，∴OD =OC =AC−AD =7−4=3，∴OB =3．17．证明见解析【分析】本题主要考查了角平分线的定义，三角形外角的性质以及等腰三角形的判定和三角形内角和定理的应用，根据外角的性质求出∠ECD=702，由角平分线的定义得∠ACE=∠ECD=70°，根据三角形内角和定理求出∠CAE=70°，可得∠ACE=∠CAE，从而可得结论．【详解】证明：∠B=30°，∠E=40°，∴∠ECD=∠B+∠E=70°，∵CE平分∠ACD，∴∠ACE=∠ECD=70°，在△ABE中，∠ACE+∠E+∠CAE=180°，∴∠CAE=180°−∠ACE−∠E=180°−70°−40°=70°，∴∠ACE=∠CAE，∴AE=CE．18．(1)见解析(2)14【分析】本题考查角平分线的性质，全等三角形的判定与性质．（1）过点E作EF⊥AD于F，根据角平分线的性质得出CE=EF，再证明△ABE≌△AFE，△CED≌△FED，根据全等三角形的性质得出AB=AF，DC=DF，进而得出结论；（2）由△ABE≌△AFE，△CED≌△FED，推出S△CED=S△FED，S△ABE=S△AFE，据此求解即可．【详解】（1）证明：如图，过点E作EF⊥AD于F，∵∠C=90°，AB∥CD，∴∠B=90°，∵DE平分∠CDA，∴CE=EF，∴Rt△CED≌Rt△FED(HL)，∴DC=DF，∵E是BC的中点，∴BE=CE，∴BE=EF，∵AE=AE，∴Rt△ABE≌Rt△AFE(HL)，∴AD=AF+FD=AB+CD；（2）解：∵△CED≌△FED，△ABE≌△AFE，∴S△CED=S△FED，S△ABE=S△AFE，∵S∴19(2)（（∴∴∴（∴∵∴∴∠BOM=∠ABO，∴BM=OM，同理可得：CN=ON，∴MN=OM+ON=BM+CN，∵AB=7，AC=6，∴△AMN的周长是AM+MN+AN=AM+BM+CN+AN=AB+AC=13．。

初三数学图形与证明试题

初三数学图形与证明试题1.若用半径为9，圆心角为的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（）．A．1.5B．2C．3D．6【答案】C【解析】等弧长计算，半径为9，圆心角为的弧长=即这个圆锥的底面周长=6，即2r=6,故选C2.赵洲桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙。

如图，若桥跨度AB约为40米，主拱高CD约10米，则桥弧AB所在圆的半径R＝米．【答案】25．【解析】根据垂径定理，得AD=AB=20米．设圆的半径是R，根据勾股定理，得R2=202+（R﹣10）2，解得R=25米．【考点】垂径定理的应用；勾股定理．3.如图，AB是⊙O的直径，AB=8，点M在⊙O上，,N是弧MB的中点，P是直径AB上的一动点，若MN=1，则周长的最小值为（）A．4B．5C．6D．7【答案】B.【解析】本题考查的是轴对称﹣最短路径问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．作N关于AB的对称点N′，连接MN′，NN′，ON′，ON，由两点之间线段最短可知MN′与AB的交点P′即为△PMN周长的最小时的点，根据N是弧MB的中点可知∠A=∠NOB=∠MON=20°，故可得出∠MON′=60°，故△MON′为等边三角形，由此可得出结论．作N关于AB的对称点N′，连接MN′，NN′，ON′，ON．∵N关于AB的对称点N′，∴MN′与AB的交点P′即为△PMN周长的最小时的点，∵N是弧MB的中点，∴∠A=∠NOB=∠MON=20°，∴∠MON′=60°，∴△MON′为等边三角形，∴MN′=OM=4，∴△PMN周长的最小值为4+1=5．故选B．【考点】轴对称-最短路线问题；圆周角定理．4.观光塔是潍坊市的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°，已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是 m．【答案】135【解析】根据题意可得：∠BDA=30°,∠DAC =60°,在Rt△ABD中，因为AB=45m，所以AD= m，所以在Rt△ACD中，CD= AD=×=135m．【考点】解直角三角形的应用．5.长、宽分别为a、b的矩形，它的周长为14，面积为10，则a2b+ab2的值为．【答案】70．【解析】应把所给式子进行因式分解，整理为与所给周长和面积相关的式子，代入求值即可．试题解析：∵矩形的长和宽分别为a，b，周长为14，面积为10，∴a+b=7，ab=10，∴a2b+ab2=ab（a+b）=70．【考点】因式分解的应用．6.如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是在14，则DM等于（）A．1B．2C．3D．4【答案】C．【解析】∵BM是∠ABC的平分线，∴∠ABM=∠CBM，∵AB∥CD，∴∠ABM=∠BMC，∴∠BMC=∠CBM，∴BC=MC=2，∵▱ABCD的周长是14，∴BC+CD=7，∴CD=5，则DM=CD﹣MC=3，故选C．【考点】平行四边形的性质．7.在3×3的方格中，A、B、C、D、E、F分别位于如图所示的小正方形的顶点上，从C、D、E、F四点中任意取一点，以所取得一点及点A、B为顶点画三角形，则所画三角形为等腰三角形的概率是．【答案】．【解析】根据从C、D、E、F四个点中任意取一点，一共有4种可能，只有选取C、F点时，所画三角形是等腰三角形，即可得出答案；试题解析：根据从C、D、E、F四个点中任意取一点，一共有4种可能，只有选取C、D，F点时，所画三角形是等腰三角形，=．故P（所画三角形是等腰三角形）【考点】1．概率公式；2．等腰三角形的判定．8.如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm2，y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为．【答案】y=-3x+18．【解析】根据从图②可以看出当Q点到B点时的面积为9，求出正方形的边长，再利用三角形的面积公式得出EF所在的直线对应的函数关系式．试题解析：∵点P沿边DA从点D开始向点A以1cm/s的速度移动；点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．∴当Q到达B点，P在AD的中点时，△PAQ的面积最大是9cm2，设正方形的边长为acm，∴×a×a=9，解得a=6，即正方形的边长为6，当Q点在BC上时，AP=6-x，△APQ的高为AB，∴y=（6-x）×6，即y=-3x+18．【考点】动点问题的函数图象．9.（3分）在底面直径为2cm，高为3cm的圆柱体侧面上，用一条无弹性的丝带从A至C按如图所示的圈数缠绕，则丝带的最短长度为 cm．（结果保留π）【答案】．【解析】如图所示，∵无弹性的丝带从A至C，∴展开后AB=2πcm，BC=3cm，由勾股定理得：AC==cm．故答案为：．【考点】1．平面展开-最短路径问题；2．最值问题．10.（12分）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB 于点E ，交CA 的延长线于点F ．（1）求证：FE ⊥AB ；（2）当EF=6，时，求DE 的长．【答案】（1）证明见试题解析；（2）9．【解析】（1）连接AD 、OD ，由直径所对的圆周角是直角得出∠ADC=90°，由等腰三角形的性质可得到D 是BC 的中点，从而OD 是△ABC 的中位线，根据切线的性质证明结论；（2）由平行线分线段成比例定理，列出比例式计算得到答案．试题解析：（1）连接AD 、OD ，∵AC 为⊙O 的直径，∴∠ADC=90°，又∵AB=AC ，∴CD=DB ，又CO=AO ，∴OD ∥AB ，∵FD 是⊙O 的切线，∴OD ⊥EF ，∴FE ⊥AB ；（2）∵，∴，∵OD ∥AB ，∴，又EF=6，∴DE=9．【考点】1．切线的性质；2．相似三角形的判定与性质；3．综合题．11. （3分）如图，▱ABCD 的对角线AC 、BD 相交于点O ，EF 、GH 过点O ，且点E 、H 在边AB 上，点G 、F 在边CD 上，向▱ABCD 内部投掷飞镖（每次均落在▱ABCD 内，且落在▱ABCD 内任何一点的机会均等）恰好落在阴影区域的概率为（）A ．B ．C ．D ．【答案】C ．【解析】∵四边形ABCD 为平行四边形，∴△OEH 和△OFG 关于点O 中心对称，∴S △OEH =S △OFG ，∴S 阴影部分=S △AOB =S 平行四边形ABCD ，∴飞镖（每次均落在▱ABCD 内，且落在▱ABCD 内任何一点的机会均等）恰好落在阴影区域的概率==．故选C ．【考点】1．几何概率；2．平行四边形的性质．12. 如图，以△ABC 的BC 边上一点O 为圆心的圆，经过A ，B 两点，且与BC 边交于点E ，D 为BE 的下半圆弧的中点，连接AD 交BC 于F ，AC=FC ．（1）求证：AC是⊙O的切线；（2）已知圆的半径R=5，EF=3，求DF的长．【答案】（1）见解析；（2）【解析】连结OA、OD，如图，根据垂径定理的推理，由D为BE的下半圆弧的中点得到OD⊥BE，则∠D+∠DFO=90°，再由AC=FC得到∠CAF=∠CFA，根据对顶角相等得∠CFA=∠DFO，所以∠CAF=∠DFO，加上∠OAD=∠ODF，则∠OAD+∠CAF=90°，于是根据切线的判定定理即可得到AC是⊙O的切线；由于圆的半径R=5，EF=3，则OF=2，然后在Rt△ODF中利用勾股定理计算DF的长．[来试题解析：（1）证明：连结OA、OD，如图，∵D为BE的下半圆弧的中点，∴OD⊥BE，∴∠D+∠DFO=90°，∵AC=FC，∴∠CAF=∠CFA，∵∠CFA=∠DFO，∴∠CAF=∠DFO，而OA=OD，∴∠OAD=∠ODF，∴∠OAD+∠CAF=90°，即∠OAC=90°，∴OA⊥AC，∴AC是⊙O的切线；（2）解：∵圆的半径R=5，EF=3，∴OF=2，在Rt△ODF中，∵OD=5，OF=2，∴DF=．【考点】切线的判定13.（3分）如图，AB∥CD，∠1=58°，FG平分∠EFD，则∠FGB的度数等于（）A．122°B．151°C．116°D．97°【答案】B．【解析】∵AB∥CD，∠1=58°，∴∠EFD=∠1=58°，∵FG平分∠EFD，∴∠GFD=∠EFD=×58°=29°，∵AB∥CD，∴∠FGB=180°﹣∠GFD=151°．故选B．【考点】平行线的性质．14.（3分）如图是一个正方体的平面展开图，折叠成正方体后与“建”字所在面相对的面的字是（）A．创B．教C．强D．市【答案】C．【解析】∵正方体的表面展开图，相对的面之间一定相隔一个正方形，∴“建”与“强”是相对面．故选C．【考点】专题：正方体相对两个面上的文字．15.在面积为60的▱ABCD中，过点A作AE⊥直线BC于点E，作AF⊥直线CD于点F，若AB=10，BC=12，则CE+CF的值为（）A．22+11B．22-11C．22+11或22-11D．22+11或2+【答案】D．【解析】分两种情况：①由平行四边形ABCD的面积求出AE=5，AF=6，再根据勾股定理求出BE、DF，求出CE、CF，即可得出结果；②CE=10-5，CF=6-10，即可得出结果．试题解析：分两种情况：①如图1所示：∠A为锐角时；∵平行四边形ABCD的面积=BC•AE=AB•AF=60，AB=10，BC=12，∴AE=5，AF=6，∵AE⊥直线BC于点E，作AF⊥直线CD于F，∴∠AEB=∠AFD=90°，∴BE=，DF=，∴CE=12+5，CF=10+6∴CE+CF=22+11；②如图2所示：∠A为钝角时；由①得：CE=10-5，CF=6-10，∴CE+CF=2+；故选D．【考点】平行四边形的性质．16.如图，在▱ABCD中，过A、C、D三点的⊙O交AB于点E，连接DE、CE，∠CDE=∠BCE．（1）求证：AD=CE；（2）判断直线BC与⊙O的位置关系，并说明理由；（3）若BC=3，DE=6，求BE的长．【答案】（1）证明见解析；（2）直线BC与⊙O相切，理由见解析；（3）．【解析】（1）由平行四边形的性质得出∠AED=∠EDC，证出，即可得出AD=CE；（2）作直径CF，连接EF，则∠EFC=∠EDC，证出∠EFC=∠BCE，再由CF是⊙O的直径，得出∠FEC=90°，得出∠BCF=90°，即可得出结论；（3）证明△BCE∽△EDC，得出对应边成比例，即可得出结果．试题解析：（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠AED=∠EDC．∴，∴AD=CE；（2）解：直线BC与⊙O相切，理由如下：如图所示：作直径CF，连接EF．则∠EFC=∠EDC，∵∠BCE=∠CDE，∴∠EFC=∠BCE．∵CF是⊙O的直径，∴∠FEC=90°，∴∠EFC+∠FCE=90°，∴∠BCE+∠FCE=90°∴∠BCF=90°．∴OC⊥CB．∴直线BC与⊙O相切；（3）解：∵四边形ABCD是平行四边形，∴AD=BC，AB∥CD，由（1）得：AD=CE，∴BC=CE，∵AB∥CD，∴∠BEC=∠DCE．又∵∠BCE=∠CDE，∴△BCE∽△EDC，∴，∵BC=3∴CE=3，即，解得，BE=．【考点】1．切线的判定；2．平行四边形的性质；3．相似三角形的判定与性质．17.（3分）如图，在五边形ABCDE中，AB=AC=AD=AE，且AB∥ED，∠EAB=120°，则∠DCB=（）A．150°B．160°C．130°D．60°【答案】A．【解析】∵AB∥ED，∴∠E=180°﹣∠EAB=180°﹣120°=60°，∵AD=AE，∴△ADE是等边三角形，∴∠EAD=60°，∴∠BAD=∠EAB﹣∠DAE=120°﹣60°=60°，∵AB=AC=AD，∴∠B=∠ACB，∠ACD=∠ADC，在四边形ABCD中，∠BCD=（360°﹣∠BAD）=（360°﹣60°）=150°．故选A．【考点】1．等腰三角形的性质；2．平行线的性质；3．多边形内角与外角．18.如图，在Rt△ABC中，∠C=90°，现将△ABC进行翻折，点C恰落在边AB上的点D处，折痕为EF，此时恰有∠DEF=∠A，则AD与BD的大小关系是 .【答案】AD=BD【解析】如图，连接CD由题意得：∠EDF=∠ECF，∴∠EDF+∠ECF=180°，∴D、E、C、F四点共圆，∴∠DEF=∠DCF；而∠DEF=∠A，∴∠DCF=∠A（设为α），DA=DC；∵∠B+α=∠BCD+α=90°，∴∠B=∠BCD，∴DB=DC，DA=DB，【考点】翻折变换（折叠问题）．19.如图，PA、PB与⊙O相切，切点分别为A、B，PA=3，∠P=60°，若BC为⊙O的直径，则图中阴影部分的面积为．【答案】π．【解析】如图，连接OP，∵PA、PB与⊙O相切，∴PA=PB，∠PAO=∠PBO=90°∵∠BPA=60°，∴△PAB为等边三角形，∠AOB=120°∴PB=AB=PA=3，∠POB=60°∴OB=．∵OB=OC，∴S△AOB =S△AOC∴S阴影=S扇形OAB==π．【考点】1.切线的性质；2.扇形面积的计算．20.如图，直线a∥b，AB⊥BC，∠1=40°，则∠2的度数为（）A．30°B．40°C．50°D．60°【答案】C【解析】先根据平行线的性质求出∠ACB的度数，再由垂直的定义得出∠ABC的度数，根据三角形内角和定理即可得出结论．∵直线a∥b，∠1=40°，∴∠ACB=∠1=40°．∵AB⊥BC，∴∠ABC=90°，∴∠2=90°﹣∠ACB=90°﹣40°=50°．【考点】平行线的性质21.海中两个灯塔A、B，其中B位于A的正东方向上，渔船跟踪鱼群由西向东航行，在点C处测得灯塔A在西北方向上，灯塔B在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D，这时测得灯塔A在北偏西60°方向上，求灯塔A、B间的距离．（计算结果用根号表示，不取近似值）【答案】【解析】过点A作AF⊥CD，垂足为F，过点D作DE⊥CD，可得出∠FCA=∠ACN=45°，∠NCB=30°，∠ADE=60°，则∠FAD=60°，∠FAC=∠FCA=45°，∠ADF=30°，从而AF=FC=AN=NC，设AF=FC=x，则tan30°=，解得x=，由tan30°=，得到，解得：BN=，由AB=AN+BN，即可得出结论．试题解析：过点A作AF⊥CD，垂足为F，过点D作DE⊥CD，如图所示：由题意可得出：∠FCA=∠ACN=45°，∠NCB=30°，∠ADE=60°，则∠FAD=60°，∠FAC=∠FCA=45°，∠ADF=30°，∴AF=FC=AN=NC，设AF=FC=x，∴tan30°=，解得：x=，∵tan30°=，∴，解得：BN=，∴AB=AN+BN==．答：灯塔A、B间的距离为（）海里．【考点】1．解直角三角形的应用-方向角问题；2．几何图形问题．22.如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形EBF的半径为2，圆心角为60°，则图中阴影部分的面积是．【答案】．【解析】如图，连接BD ．∵四边形ABCD 是菱形，∠A=60°， ∴∠ADC=120°， ∴∠1=∠2=60°， ∴△DAB 是等边三角形， ∵AB=2， ∴△ABD 的高为，∵扇形BEF 的半径为2，圆心角为60°， ∴∠4+∠5=60°，∠3+∠5=60°， ∴∠3=∠4，设AD 、BE 相交于点G ，设BF 、DC 相交于点H ，在△ABG 和△DBH 中，，∴△ABG ≌△DBH （ASA ）， ∴四边形GBHD 的面积等于△ABD 的面积，∴图中阴影部分的面积是：S 扇形EBF -S △ABD =．【考点】1．扇形面积的计算；2．全等三角形的判定与性质；3．菱形的性质．23. 一个矩形被分成不同的4个三角形，其中绿色三角形的面积占矩形面积的15%，黄色的三角形的面积是21cm 2，则该矩形的面积为（）A ．60cm 2B ．70cm 2C ．120cm 2D ．140cm 2【答案】A ．【解析】黄色三角形与绿色三角形面积之和是矩形面积的50%，而绿色三角形面积占矩形面积的15%，所以黄色三角形面积占矩形面积的（50%-15%）=35%，已知黄色三角形面积是21平方厘米，故矩形的面积=21÷（50%-15%）=21÷35%=60（cm 2）．故选A ．【考点】矩形的性质．24. 如图，以Rt △ABC 的边AC 为直径的⊙O 交斜边AB 于点D ，点F 为BC 上一点，AF 交⊙O于点E，且DE∥AC．（1）求证：∠CAF=∠B．（2）若⊙O的半径为4，AE=2AD，求DE的长．【答案】【解析】（1）连接CE，根据圆周角定理可知∠AEC=90°，故∠CAF+∠ACE=90°．再由题意可知∠B+∠DAC=90°，根据DE∥AC，可得，故，由圆周角定理可知∠ACE=∠DAC，故可得出结论；（2）连接DC，由（1）知DE∥AC，故可得出AD=CE，由全等三角形的判定定理得出Rt△ACD≌Rt△CAE，所以CD=AE=2AD，设AD=x，则CD=2x，在Rt△ABD中根据勾股定理可求出AD，CD的长，过D作DM⊥AC，过O作ON⊥ED，由AD•CD=AC•DM可得出DM的长，连OD，在Rt△OND中，由勾股定理可求出DN的长，由ED=2DN即可得出结论．试题解析：（1）证明：连接CE，∵AC是⊙O的直径，∴∠AEC=90°，∴∠CAF+∠ACE=90°．∵∠ACB=90°，∴∠B+∠DAC=90°，∵DE∥AC，∴，∴，∴∠ACE=∠DAC，∴∠CAF=∠B；（2）解：连DC，∵DE∥AB，∴∠CAE=∠AED，∴AD=DE，在Rt△ACD与Rt△CAE中，∵，∴Rt△ACD≌Rt△CAE（HL），∴CD=AE=2AD，设AD=x，则CD=2x，在Rt△ACD中，x2+（2x）2=82，∴AD=，CD=．过D作DM⊥AC，过O作ON⊥ED，∴AD•CD=AC•DM，∴DM====ON，连OD，在Rt△OND中，∵DN===∴ED=2DN=．【考点】圆周角定理；勾股定理25.一个正方体的平面展开图如图所示，将它折成正方体后“设”字对面是（）A．和B．谐C．泰D．州【答案】B．【解析】已知，这是一个正方体的平面展开图，共有六个面，其中面“建”与面“州”相对，面“和”与面“泰”相对，“谐”与面“设”相对．故答案选B．【考点】正方体的侧面展开图.26.如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，3），M是第三象限内上一点，∠BMO=120°，则⊙C的半径长为（）A.6B.5C.3D.3【答案】C.【解析】∵四边形ABMO是圆内接四边形，∠BMO=120°，∴∠BAO=60°，∵AB是⊙C的直径，∴∠AOB=90°，∴∠ABO=90°-∠BAO=90°-60°=30°，∵点A的坐标为（0，3），∴OA=3，∴AB=2OA=6，∴⊙C的半径长==3．故选：C．【考点】1.圆内接四边形的性质；2.坐标与图形性质；3.含30度角的直角三角形．27.如图，四边形OBCD中的三个顶点在⊙O上，点A是优弧BD上的一个动点（不与点B、D 重合）．（1）当圆心O在∠BAD内部，∠ABO+∠ADO=60°时，∠BOD= ；（2）当圆心O在∠BAD内部，四边形OBCD为平行四边形时，求∠A的度数；（3）当圆心O在∠BAD外部，四边形OBCD为平行四边形时，请直接写出∠ABO与∠ADO的数量关系．【答案】（1）120 °；（2）60°；（3）60°．【解析】（1）连接OA，如图1，根据等腰三角形的性质得∠OAB=∠ABO，∠OAD=∠ADO，则∠OAB+∠OAD=∠ABO+∠ADO=60°，然后根据圆周角定理易得∠BOD=2∠BAD=120°；（2）根据平行四边形的性质得∠BOD=∠BCD，再根据圆周角定理得∠BOD=2∠A，则∠BCD=2∠A，然后根据圆内接四边形的性质由∠BCD+∠A=180°，易计算出∠A的度数；（3）讨论：当∠OAB比∠ODA小时，如图2，与（1）一样∠OAB=∠ABO，∠OAD=∠ADO，则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD，由（2）得∠BAD=60°，所以∠ADO﹣∠ABO=60°；当∠OAB比∠ODA大时，用样方法得到∠ABO﹣∠ADO=60°．试题解析：（1）连接OA，如图1，∵OA=OB，OA=OD，∵∠OAB=∠ABO，∠OAD=∠ADO，∴∠OAB+∠OAD=∠ABO+∠ADO=60°，即∠BAD=60°，∴∠BOD=2∠BAD=120°；（2）∵四边形OBCD为平行四边形，∴∠BOD=∠BCD，∵∠BOD=2∠A，∴∠BCD=2∠A，∵∠BCD+∠A=180°，即3∠A=180°，∴∠A=60°；（3）当∠OAB比∠ODA小时，如图2，∵OA=OB，OA=OD，∵∠OAB=∠ABO，∠OAD=∠ADO，∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD，由（2）得∠BAD=60°，∴∠ADO﹣∠ABO=60°；当∠OAB比∠ODA大时，同理可得∠ABO﹣∠ADO=60°，综上所述，|∠ABO﹣∠ADO|=60°．【考点】1．圆周角定理；2．平行四边形的性质；3．圆内接四边形的性质．28.如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于 °．【答案】130【解析】∵四边形ABCD内接与⊙O，∴∠A+∠C=180°，∵∠A=115°，∴∠C=65°，∴∠BOD＝2∠C＝130°；【考点】1．圆内接四边形的性质；2．圆周角定理．29.如图，将半径为8的⊙O沿AB折叠，弧AB恰好经过与AB垂直的半径OC的中点D，则折痕AB长为（）A．B．C．8D．10【答案】B．【解析】延长CO交AB于E点，连接OB，∵CE⊥AB，∴E为AB的中点，由题意可得CD=4，OD=4，OB=8，DE=（8×2﹣4）=×12=6，OE=6﹣4=2，在Rt△OEB中，根据勾股定理可得：OE2+BE2=OB2，代入可求得BE=，∴AB=．故选B．【考点】1．垂径定理；2．翻折变换（折叠问题）．30.有一边长为4的正n边形，它的一个内角为120°，则其外接圆的半径为（）A．B．4C．D．2【答案】B【解析】经过正n边形的中心O作边AB的垂线OC，则∠B=60°，∠O=30°，在直角△OBC中，根据三角函数得到OB=2BC=AB=4．点评：正多边形的计算31.如图，AC是△ABD的高，∠D＝45°，∠B＝60°，AD＝10．求AB的长．【答案】【解析】首先根据Rt△ACD的三角函数求出AC的长度，然后根据Rt△ABC的三角形函数求出AB的长度．试题解析：在Rt△ACD中，AC=10×sin∠D=10×sin45°=5在Rt△ABC中，AB=．【考点】锐角三角函数的应用．32.如图，矩形ABCD中，AB=2，BC=3，分别以A、D为圆心，1为半径画圆，E、F分别是⊙A、⊙D上的一动点，P是BC上的一动点，则PE+PF的最小值是（）A．2 B．3 C．4 D．5【答案】C．【解析】试题解析：∵矩形ABCD中，AB=2，BC=3，圆A的半径为1，∴A′D′=BC=3，DD′=2DC=4，AE′=1，∴A′D=5，∴DE′=5-1=4∴PE+PD=PE′+PD=DE′=4，故选C．【考点】轴对称-最短路线问题．33.如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD为⊙O的直径，AB＝3，则AD的值为（）A．6B．3C．3D．3【答案】D【解析】根据AB=AC以及∠BAC=120°可得：∠D=30°，根据BD为直径可得：∠BAD=90°，则根据Rt△ABD的性质可得：BD=2AB=6，AD=3【考点】圆的基本性质34.已知圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为（）A．2．5B．5C．10D．15【解析】试题解析：设母线长为x，根据题意得2πx÷2=2π×5，解得x=10．故选C．【考点】圆锥的计算．35.如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为60°，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为（）A．160m B．80mC．120（－1）m D．120（+1）m【答案】A【解析】过点A作AD⊥BC，则CD=120m，BD=40m，则BC=CD+BD=160m．【考点】三角形函数的应用．36.如图，晚上小明站在路灯P的底下观察自己的影子时发现，当他站在F点的位置时，在地面上的影子为BF，小明向前走2米到D点时，在地面上的影子为AD，若AB=4米，∠PBF=60°，∠PAB=30°，通过计算，求出小明的身高．（结果保留根号）．【答案】米【解析】设CD=EF=x，根据Rt△CAD，求出AD与x的关系，根据Rt△BEF，求出BF与x的关系，然后根据BD=DF－BF=2－BF，AB=AD+BD=4求出x的值．试题解析：设小明的身高为x米，则CD=EF=x米．在Rt△ACD中，∠ADC=90°，tan∠CAD=，即tan30°=，AD=x在Rt△BEF中，∠BFE=90°，tan∠EBF=EF/BF，即tan60°=，BF=由题意得DF=2，∴BD=DF-BF=2-，∵AB=AD+BD=4，∴x+2-=4 解得：x=．答：小明的身高为米．【考点】锐角三角函数的应用．37.在Rt△ABC中，∠C=90°，a=4，b=3，则sinA的值是（）A．B．C．D．【解析】试题解析：如图所示：∵在Rt△ABC中，∠C=90°，a=4，b=3，∴c=5，∴sinA=．故选B．【考点】1．锐角三角函数的定义；2．勾股定理．38.如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为．【答案】10cm．【解析】圆锥的底面周长=扇形的弧长，据此列等式求出r的值．，解得r=10cm．故答案为：10cm．【考点】圆锥的有关计算．39.计算：2sin60°+tan45°= ．【答案】．【解析】试题解析：原式=2×+1=．【考点】特殊角的三角函数值．40.（2015•盐城校级模拟）已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为．【答案】3π．【解析】根据弧长公式L=求解．解：L===3π．故答案为：3π．【考点】弧长的计算．41.（2015•徐州）如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA= °．【答案】125．【解析】连接OD，构造直角三角形，利用OA=OD，可求得∠ODA=36°，从而根据∠CDA=∠CDO+∠ODA计算求解．解：连接OD，则∠ODC=90°，∠COD=70°；∵OA=OD，∴∠ODA=∠A=∠COD=35°，∴∠CDA=∠CDO+∠ODA=90°+35°=125°，故答案为：125．【考点】切线的性质．42. （2015秋•芜湖期末）若一个圆锥的侧面展开图是半径为18cm ，圆心角为240°的扇形，则这个圆锥的底面半径长是 cm ．【答案】12【解析】设这个圆锥的底面半径为rcm ，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=，然后解方程求出r 即可．解：设这个圆锥的底面半径为rcm ，根据题意得2πr=，解得r=12，所以这个圆锥的底面半径长为12cm ．故答案为12．【考点】圆锥的计算．43. 如图，菱形ABCD 的对角线的长分别为2和5，P 是对角线AC 上任一点（点P 不与点A 、C 重合），且PE ∥BC 交AB 于E ，PF ∥CD 交AD 于F ，则阴影部分的面积是．【答案】2.5【解析】根据题意可得阴影部分的面积等于△ABC 的面积，因为△ABC 的面积是菱形面积的一半，根据已知可求得菱形的面积则不难求得阴影部分的面积．解：设AP 与EF 相交于O 点． ∵四边形ABCD 为菱形， ∴BC ∥AD ，AB ∥CD ． ∵PE ∥BC ，PF ∥CD ， ∴PE ∥AF ，PF ∥AE ．∴四边形AEFP 是平行四边形． ∴S △POF =S △AOE ．即阴影部分的面积等于△ABC 的面积．∵△ABC 的面积等于菱形ABCD 的面积的一半，菱形ABCD 的面积=AC•BD=5， ∴图中阴影部分的面积为5÷2=2.5．故答案为：2.5．【考点】菱形的性质．44. 如图1，是工人将货物搬运上货车常用的方法，把一块木板斜靠在货车车厢的尾部，形成一个斜坡，货物通过斜坡进行搬运．根据经验，木板与地面的夹角为20°（即图2中∠ACB=20°）时最为合适，已知货车车厢底部到地面的距离AB=1.5m ，木板超出车厢部分AD=0.5m ，则木板CD 的长度为．（参考数据：sin20°≈0.3420，cos20°≈0.9397，精确到0.1m）．【答案】4.9m．【解析】根据∠ACB的正弦函数和AB的长度求AC的长，再加上AD即可．解：由题意可知：AB⊥BC．∴在Rt△ABC中，sin∠ACB=，∴AC===≈4.39，∴CD=AC+AD=4.39+0.5=4.89≈4.9（m）．故答案为：4.9m．【考点】解直角三角形的应用-坡度坡角问题．45.如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为_________．【答案】120°【解析】根据中点可得DE∥BC，则∠DEC+∠C=180°，根据∠C=60°，可得∠DEC=120°．【考点】三角形中位线的性质．46.如图，AB为⊙O直径，弦CD⊥AB于E，则下面结论中错误的是（）A．CE＝DE B．＝C．∠BAC＝∠BAD D．OE=BE【答案】D【解析】根据垂径定理分析即可．根据垂径定理和等弧对等弦，得A、B、C正确，只有D错误．故选D．【考点】垂径定理．47.圆内接四边形ABCD的内角∠A：∠B：∠C=2：3：4，则∠D= 度．【答案】90【解析】根据圆内接四边形的性质可求得四个角的比值，再根据四边形的内角和为360°，从而求得∠D的度数．解：∵圆内接四边形的对角互补∴∠A：∠B：∠C：∠D=2：3：4：3设∠A=2x，则∠B=3x，∠C=4x，∠D=3x∴2x+3x+4x+3x=360°∴x=30°∴∠D=90°．【考点】圆内接四边形的性质．48.如图所示，动点C在⊙O的弦AB上运动，AB=，连接OC，CD⊥OC交⊙O于点D．则CD的最大值为．【答案】．【解析】作OH⊥AB，延长DC交⊙O于E，如图，根据垂径定理得到AH=BH=AB=，CD=CE，再利用相交弦定理得CD•CE=BC•AC，易得CD=，当CH最小时，CD最大，C点运动到H点时，CH最小，所以CD的最大值为．解：作OH⊥AB，延长DC交⊙O于E，如图，∴AH=BH=AB=，∵CD⊥OC，∴CD=CE，∵CD•CE=BC•AC，∴CD2=（BH﹣CH）（AH+CH）=（﹣CH）（+CH）=3﹣CH2，∴CD=，∴当CH最小时，CD最大，而C点运动到H点时，CH最小，此时CD=，即CD的最大值为．故答案为．【考点】垂径定理；勾股定理．49.在△ABC中，∠A，∠B都是锐角，且（sinA﹣）2+（tanB﹣1）2=0，则∠C= ．【答案】75°．【解析】根据偶次幂具有非负性可得sinA﹣=0，tanB﹣1=0，再根据特殊角的三角函数值可得：∠A=60°，∠B=45°，然后再利用三角形内角和定理可得答案．解：由题意得：sinA﹣=0，tanB﹣1=0，解得：∠A=60°，∠B=45°，则∠C=180°﹣60°﹣45°=75°，故答案为：75°．【考点】特殊角的三角函数值；非负数的性质：偶次方．50.如图，正六边形ABCDEF的边长为2，两顶点A、B分别在x轴和y轴上运动，则顶点D到原点O 的距离的最大值和最小值的乘积为．【答案】12 【解析】当O 、D 、AB 中点共线时，OD 有最大值和最小值，BD=2，BK=1， ∴DK=，OK=BK=1， ∴OD 的最大值为：1+，同理，把图象沿AB 边翻折180°得最小值为：-1，∴顶点D 到原点O 的距离的最大值和最小值的乘积为：（1+）（-1）=12．【考点】(1)、正多边形和圆；(2)、坐标与图形性质51. 下列四边形中，对角线相等且互相垂直平分的是A ．平行四边形B ．正方形C ．等腰梯形D ．矩形【答案】B ．【解析】试题解析：对角线相等且互相垂直平分的四边形是正方形，故选B ．【考点】1.等腰梯形的性质；2.平行四边形的性质；3.矩形的性质；4.正方形的性质．52. 如图，矩形ABCD 中，AE 平分∠BAD 交BC 于E ，∠CAE=15°，则下列结论：① △ODC 是等边三角形；②BC=2AB ；③∠AOE=135°； ④S △AOE =S △COE ，其中正确的结论的个数有A ．1B ．2C ．3D ．4【答案】C【解析】∵四边形ABCD 是矩形，∴∠BAD=90°，OA=OC ，OD=OB ，AC=BD ，<BR>∴OA=OD=OC=OB ，∵AE 平分∠BAD ，∴∠DAE=45°，∵∠CAE=15°，∴∠DAC=30°，∵OA=OD ，∴∠ODA=∠DAC=30°，∴∠DOC=60°，∵OD=OC ，∴△ODC 是等边三角形，∴①正确；∵四边形ABCD 是矩形，∴AD ∥BC ，∠ABC=90°，∴∠DAC=∠ACB=30°，∴AC=2AB ，∵AC ＞BC ，∴2AB ＞BC ，∴②错误；∵AD ∥BC ，∴∠DBC=∠ADB=30°，∵AE 平分∠DAB ，∠DAB=90°，∴∠DAE=∠BAE=45°，∵AD ∥BC ，∴∠DAE=∠AEB ，∴∠AEB=∠BAE ，∴AB=BE ，∵四边形ABCD 是矩形，∴∠DOC=60°，DC=AB ，∵△DOC 是等边三角形，∴DC=OD ，∴BE=BO ，∴∠BOE=∠BEO=（180°-∠OBE ）=75°，∵∠AOB=∠DOC=60°，∴∠AOE=60°+75°=135°，∴③正确；∵OA=OC ，∴根据等底等高的三角形面积相等得出S △AOE =S △COE ，∴④正确；故选C ．【考点】矩形的性质.53.如图，、是以线段为直径的⊙上两点，若，且，则( ).A．B．C．D．【答案】B.【解析】因为∠ACD=40°,CA=CD,所以∠CAD=∠D=（180°-40°）÷2=70°，所以∠B=∠D=70°，又因为AB为直径，所以∠ACB=90°,所以∠CAB=90°-∠B=90°-70°=20°,故选B.【考点】1.圆周角定理；2.弧，弦圆心角定理；3.三角形内角和定理.54.如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离约为（由科学计算器得到sin68°=0.9272，sin46°=0.7193，sin22°=0.3746，sin44°=0.6947）（）A．22.48B．41.68C．43.16D．55.63【答案】B【解析】过点P作PA⊥MN于点A，则若该船继续向南航行至离灯塔距离最近的位置为PA的长度，利用锐角三角函数关系进行求解即可，如图，过点P作PA⊥MN于点A，MN=30×2=60（海里），∵∠MNC=90°，∠CPN=46°，∴∠MNP=∠MNC+∠CPN=136°，∵∠BMP=68°，∴∠PMN=90°﹣∠BMP=22°，∴∠MPN=180°﹣∠PMN﹣∠PNM=22°，∴∠PMN=∠MPN，∴MN=PN=60（海里），∵∠CNP=46°，∴∠PNA=44°，∴PA=PN·sin∠PNA=60×0.6947≈41.68（海里）【考点】锐角三角函数的应用55.一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（）A．10海里/小时B．30海里/小时C．20海里/小时D．30海里/小时【答案】D.【解析】试题解析：∵∠CAB=10°+20°=30°，∠CBA=80°-20°=60°，∴∠C=90°，∵AB=20海里，∴AC=AB•cos30°=10（海里），∴救援船航行的速度为：10÷=30（海里/小时）．故选D．【考点】解直角三角形的应用-方向角问题．56.如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=42°32′，则∠2的度数（）A．17°28′B．18°28′C．27°28′D．27°32′【答案】A.【解析】试题解析：过点A作AE∥NM，∵NM∥GH，∴AE∥GH，∴∠3=∠1=42°32′，∵∠BAC=60°，∴∠4=60°-42°32′=17°28′，∵NM∥AE，∴∠2=∠4=17°28′，故选A．【考点】平行线的性质．57.下列命题中，正确的是（）A．平分弦的直径垂直于弦B．对角线相等的平行四边形是正方形C．对角线互相垂直的四边形是菱形D．三角形的一条中线能将三角形分成面积相等的两部分【答案】D.【解析】试题解析：A、平分弦（非直径）的直径垂直于弦，所以A选项错误；B、对角线垂直且相等的平行四边形是正方形，所以B选项错误；C、对角线互相垂直平分的四边形是菱形，所以C选项错误；D、三角形的一条中线能将三角形分成面积相等的两部分，所以D选项正确．故选D．【考点】命题与定理.58.如图，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F．（1）判断四边形CEGF的形状，并证明你的结论；（2）若AB=3，BC=9，求线段CE的取值范围．【答案】（1）四边形CEGF为菱形，理由详见解析；（2）3≤CE≤5．【解析】（1）根据折叠的性质，易证△EFG是等腰三角形，根据等腰三角形的性质可得GF=EC，又由GF∥EC，即可得四边形CEGF为平行四边形，根据邻边相等的平行四边形是菱形，即可得四边形BGEF为菱形；（2）如图1，当G与A重合时，CE取最大值，由折叠的性质得CD=DG，∠CDE=∠GDE=45°，推出四边形CEGD是矩形，根据矩形的性质即可得到CE=CD=AB=3；如图2，当F与D重合时，CE取最小值，由折叠的性质得AE=CE，根据勾股定理即可得到结论．试题解析：（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠GFE=∠FEC，∵图形翻折后点G与点C重合，EF为折线，∴∠GEF=∠FEC，∴∠GFE=∠FEG，∴GF=GE，∵图形翻折后BC与GE完全重合，∴BE=EC，∴GF=EC，∴四边形CEGF为平行四边形，∴四边形CEGF为菱形；（2）解：如图1，当F与D重合时，CE取最小值，由折叠的性质得CD=DG，∠CDE=∠GDE=45°，∵∠ECD=90°，∴∠DEC=45°=∠CDE，∴CE=CD=DG，∵DG∥CE，∴四边形CEGD是矩形，∴CE=CD=AB=3；如图2，当G与A重合时，CE取最大值，由折叠的性质得AE=CE，∵∠B=90°，∴AE2=AB2+BE2，即CE2=32+（9﹣CE）2，∴CE=5，。

专题06 几何图形的初步认识(3)原卷版

专题06 几何图形的初步认识（3）考点13：度分秒的换算1．用度、分、秒表示21.24°为（）A．21°14'24″B．21°20'24″C．21°34'D．21°2．计算：2.5°＝（）A．15′B．25′C．150′D．250′3．下面等式成立的是（）A．83.5°＝83°50'B．90°﹣57°23'27″＝32°37'33″C．15°48'36″+37°27'59″＝52°16'35″D．41.25°＝41°15'4．1.5°＝（）A．9′B．15′C．90′D．150′5．35.48°＝________度________分________秒．6．35.15°＝________°________′________″；12°15′36″＝________°．7．计算：65°19′48″+35°17′6″＝________（将计算结果换算成度）．8．计算：（1）48°39′+67°31′（2）3×（﹣）÷（﹣1）．（3）7﹣（﹣6）+（﹣4）×（﹣3）（4）（）×（﹣6）2考点14：角的大小比较1．将两块相同的直角三角板的顶点重合（如图所示），则∠1与∠2的大小关系是（）A．∠1＞∠2B．∠1＜∠2C．∠1＝∠2D．以上答案都有可能2．若∠A＝20°18′，∠B＝20°15″，∠C＝20.25°，则有（）A．∠A＞∠B＞∠C B．∠B＞∠A＞∠C C．∠A＞∠C＞∠B D．∠C＞∠A＞∠B3．已知∠A＝18°20′36″，∠B＝18.35°，∠C＝18°21′，下列比较正确的是（）A．∠A＜∠B B．∠B＜∠A C．∠B＜∠C D．∠C＜∠B4．下列说法正确的个数是（）（1）连接两点之间的线段叫两点间的距离；（2）两点之间，线段最短；（3）若AB＝2CB，则点C是AB的中点；（4）角的大小与角的两边的长短无关．A．1个B．2个C．3个D．4个5．∠α＝10.5°，∠β＝10°20′，则∠α，∠β的大小关系是∠α________∠β（在横线上填“＞”，“＜“或“＝“）．6．如图所示的网格式正方形网格，∠ABC________∠DEF（填“＞”，“＝”或“＜”）7．下列说法：①连接两点间的线段叫这两点的距离；②木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；③若A、B、C三点在同一直线上，且AB＝2CB，则C是线段AB的中点；④若∠A＝20°18′，∠B＝20°28″，∠C＝20.25°，则有∠A＞∠C＞∠B．其中一定正确的是________．（把你认为正确结论的序号都填上）8．∠AOB与∠COD有共同的顶点O，其中∠AOB＝∠COD＝60°．（1）如图①，试判断∠AOC与∠BOD的大小关系，并说明理由；（2）如图①，若∠BOC＝10°，求∠AOD的度数；（3）如图①，猜想∠AOD与∠BOC的数量关系，并说明理由；（4）若改变∠AOB，∠COD的位置，如图②，则（3）的结论还成立吗？若成立，请证明；若不成立，请直接写出你的猜想．考点15：角的计算1．如图所示，将一张长方形纸片斜折过去，使顶点A落在A′处，BC为折痕，然后再把BE折过去，使之与BA′重合，折痕为BD，若∠ABC＝58°，则求∠E′BD的度数（）A．29°B．32°C．58°D．64°2．将一副三角板按如图所示平放在一平面上（点B在AD上），则∠1的度数为（）A．135°B．105°C．95°D．75°3．如图，已知∠AOB：∠BOC＝2：3，∠AOC＝75°，那么∠AOB＝（）A．20°B．30°C．35°D．45°4．α，β都是钝角，有四名同学分别计算（α+β），却得到了四个不同的结果，分别为26°，50°，72°，90°，老师判作业时发现其中有正确的结果，那么计算正确的结果是（）A．26°B．50°C．72°D．90°5．如图，将长方形ABCD纸片按如图所示的方式折叠，EF，EG为折痕，点A落在A'，点B落在B'，点A'，B'，E在同一直线上，则∠FEG＝________度．6．中华人民共和国国旗上的五角星的五个角的和是________度．7．在同一平面内，已知∠AOB＝30°，∠BOC＝50°，则∠AOC＝________．8．已知：∠AOB和∠COD是直角．（1）如图1，当射线OB在∠COD内部时，请探究∠AOD和∠BOC之间的关系；（2）如图2，当射线OA，射线OB都在∠COD外部时，过点O作射线OE，射线OF，满足∠BOE＝∠BOC，∠DOF＝∠AOD，求∠EOF的度数；（3）如图3，在（2）的条件下，在平面内是否存在射线OG，使得∠GOF：∠GOE＝2：3，若不存在，请说明理由，若存在，求出∠GOF的度数．考点16：余角和补角1．如图所示的是正方形网格，则∠AOB___∠COD（）A．＞B．＜C．＝D．≥2．若∠A与∠B互为补角，∠A＝40°，则∠B＝（）A．50°B．40°C．140°D．60°3．一个角的余角是44°，这个角的补角是（）A．134°B．136°C．156°D．146°4．下列叙述正确的是（）A．一个钝角和一个锐角一定互为补角B．每一个锐角都有余角C．两个锐角一定互为余角D．一个钝角的余角是锐角5．若∠A与∠B互为余角，∠A＝30°，则∠B的补角是________度．6．已知，∠A＝46°28'，则∠A的余角＝________．7．一个角的度数为25°24′，这个角的补角度数为________．8．如图，两个直角三角形的直角顶点重合，∠AOC＝40°，求∠BOD的度数．结合图形，完成填空：解：因为∠AOC+∠COB＝________°，∠COB+∠BOD＝90．①所以∠AOC＝________．②因为∠AOC＝40°，所以∠BOD＝________°．在上面①到②的推导过程中，理由依据是：________．考点17：生活中的旋转现象1．将图中可爱的“小鸭子”图片按顺时针方向旋转90°后得到的图片是（）A．B．C．D．2．下列运动属于旋转的是（）A．火箭升空的运动B．足球在草地上滚动C．大风车运动的过程D．传输带运输的东西的运动3．下列现象中：①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头开关的转动；⑤钟摆的运动；⑥荡秋千运动．属于旋转的有（）A．2个B．3个C．4个D．5个4．如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA 连续翻转（小正方形起始位置在AB边上），那么这个小正方形翻转到DA边的终点位置时，它的方向是（）A．B．C．D．5．时钟的时针不停地旋转，从上午6时到上午10时，时针旋转的旋转角是120度．6．如图，某游乐场的摩天轮（圆形转盘）上的点距离地面最大高度为160米，转盘直径为153米，旋转一周约需30分钟．某人从该摩天轮上到地面距离最近的点登舱，逆时针旋转20分钟，此时，他离地面的高度是________米．7．时针从钟面上2点旋转到6点，共旋转了________度．8．如图（1）所示，魔术师把4张扑克牌放在桌子上，然后蒙住眼睛，请一位观众上台，把某一张牌旋转180°．魔术师解除蒙具后，看到4张扑克牌如图（2）所示，他很快确定了哪一张牌被旋转过．你能吗？考点18：旋转的性质1．如图，在△ABC中，∠CAB＝65°，现将△ABC绕着点A逆时针旋转一定角度α（0＜α＜180°）△AB'C′，并且使AC'⊥AB，那么旋转角的度数α为（）A．65°B．25°C．35°D．40°2．如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB＝40°，∠BOC＝25°，则旋转角度是（）A．25°B．15°C．65°D．40°3．如图，若△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合，则∠AB1B＝（）A．50°B．55°C．60°D．65°4．将△ABC绕点B按逆时针方向旋转32°到△EBD的位置，斜边AC和DE相交于点F，则∠DFC的度数等于（）A．28°B．30°C．32°D．30°5．如图所示，在△ABC纸片中，∠BAC＝50°，将△ABC纸片绕点A按逆时针方向旋转50°，得到△ADE，此时AD边经过点C，连接BD，若∠DBC的度数为40°，则∠ACB的度数为________．6．如图，将△OAB绕点O逆时针旋转70°到△OCD的位置，若∠AOB＝40°，则∠AOD的大小为________度．7．如图，将△OAB绕点O逆时针旋转80°，得到△OCD，若∠A＝2∠D＝100°，则∠α的度数________．8．如图，△ABC中，∠B＝15°，∠ACB＝25°，AB＝4cm，△ABC按逆时针方向旋转一定角度后与△ADE重合，且点C恰好成为AD的中点，①指出旋转中心，并求出旋转的度数；②求出∠BAE的度数和AE的长．考点19：旋转对称图形1．如图是一个标准的五角星，若将它绕旋转中心旋转一定角度后能与自身重合，则至少应将它旋转的度数是（）A．144°B．90°C．72°D．60°2．下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是（）A．等边三角形B．平行四边形C．正八边形D．圆及其一条弦3．如图，该图案绕它的中心至少旋转m度能与自身完全重合，则m的值是（）A．45°B．90°C．135°D．180°4．如图，图案由三个叶片组成，且其绕点O旋转120°后可以和自身重合，若三个叶片的总面积为12平方厘米，∠AOB＝120°，则图中阴影部分的面积之和为（）平方厘米．A．2B．4C．6D．85．点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转________°后能与原来的图案互相重合．6．若一个正六边形旋转一定的角度后，与原图形完全重合，则旋转的度数至少是________°．7．把一个正九边形绕它的中心旋转，至少旋转________度，就能与原来的位置重合．8．如图，已知△ABC和△AEF中，∠B＝∠E，AB＝AE，BC＝EF，∠EAB＝25°，∠F＝57°；（1）请说明∠EAB＝∠F AC的理由；（2）△ABC可以经过图形的变换得到△AEF，请你描述这个变换；（3）求∠AMB的度数．考点20：作图-旋转变换1．将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（）A．B．C．D．2．将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（）A．B．C．D．3．如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均在格点上．（1）∠ACB的大小为________（度）（2）在如图所示的网格中，以A为中心，取旋转角等于∠BAC，把△ABC逆时针旋转，请用无刻度的直尺，画出旋转后的△ABC，并简要说明旋转后点C和点B的对应点点C′和点B′的位置是如何而找到的（不要求证明）4．如图，在每个小正方形边长为1的网格中，△OAB的顶点O，A，B均在格点上（1）的值为；（2）是以O为圆心，2为半径的一段圆弧在如图所示的网格中，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A，E′B，当E′A+E′B的值最小时，请用无刻度的直尺画出点E′，并简要说明点E′的位置是如何找到的（不要求证明）________．5．如图，在平面直角坐标系中，若将△ABC绕点C顺时针旋转90°得到△A1B1C1，则点B的对应点B1的坐标为________．6．如图，在每个小正方形的边长为1的网格中，点A，B，C都在格点上．（1）△ABC的面积是________；（2）将△ABC绕点C顺时针旋转得△DEC，点B的对应点E落在AC所在的网格线上．请用无刻度的直尺在网格中画出△DEC，并简要说明点D，E的位置是如何找到的，________________．7．如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均在格点上，（Ⅰ）∠ACB的大小为________（度）；（Ⅰ）在如图所示的网格中，P是BC边上任意一点，以A为中心，取旋转角等于∠BAC，把点P逆时针旋转，点P的对应点为P′，当CP′最短时，请用无刻度的直尺，画出点P′，并简要说明点P′的位置是如何找到的（不要求证明）________________．8．如图，△ABC的顶点坐标分别为A（0，1），B（3，3），C（1，3）．（1）画出△ABC关于点O的中心对称图形△A1B1C1．（2）①画出△ABC绕原点O逆时针旋转90°的△A2B2C2；②直接写出点B2的坐标为________．考点21：几何变换的类型1．如图，平面内某正方形内有一长为10宽为5的矩形，它可以在该正方形的内部及边界通过平移或旋转的方式，自由地从横放变换到竖放，则该正方形边长的最小整数n为（）A．10B．11C．12D．132．将铁丝围成的△ABC铁框平行地面放置，并在灯泡的照射下，在地面上影子是△A1B1C1，那么△ABC与△A1B1C1之间是属于（）A．位似变换B．平移变换C．对称变换D．旋转变换3．视力表的一部分如图，其中开口向上的两个“E”之间的变换是（）A．平移B．旋转C．对称D．都不对4．如图的四个图形中，由基础图形通过平移、旋转或轴对称这三种变换都能得到的是（）A．B．C．D．5．如果，那么________．6．如图，点O，A，B都在正方形网格的格点上，点A，B的旋转后对应点A'，B'也在格点上，请描述变换的过程．________．7．在平面内，________，这种图形的变换叫做平移．8．图中，点A，B，C，P，Q，R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间（单位：h）．（1）用有序数对表示图中点A，B，C，P，Q，R．（2）图中方格纸的对角线的左上方的点有什么共同的特点？它右下方的点呢？（3）三角形ABC的图形经过怎样的变换后得到三角形PQR的图形？其中点A对应点P，点B对应点Q，点C对应点R．。

初三数学图形与证明试题

初三数学图形与证明试题1.若凸n边形的内角和为1260°，则从一个顶点出发引的对角线条数是___________【答案】6【解析】根据凸n边形的内角和为1260°，求出凸n边形的边数，即可得出，从一个顶点出发可引出（n-3）条对角线．解：∵凸n边形的内角和为1260°，∴（n-2）×180°=1260°，得，n=9；∴9-3=6．故答案为：6．本题考查了多边形的内角和定理及多边形的对角线，熟记多边形的内角和计算公式是正确解答本题的基础．2.如图所示几何体的左视图是（）．【答案】A【解析】找到从左面看所得到的图形即可．解答：解：从左面看可得到上下两个相邻的正方形．故选A．3.如图，已知菱形ABCD的两条对角线相交于点O，AC＝6cm，BD＝8cm，则菱形的高AE为 cm．【答案】4.8【解析】由四边形ABCD是菱形，AC=6cm，BD=8cm，即可得AC⊥BD，OC=AC=3cm，OB=BD=4cm，然后由勾股定理求得BC的长，又由S菱形ABCD=1AC•BD=BC•AE，即可求得答案．试题解析：∵四边形ABCD是菱形，AC=6cm，BD=8cm，∴AC⊥BD，OC=AC=3cm，OB=BD=4cm，∴BC= =5（cm），∵S菱形ABCD=AC•BD=BC•AE，∴×6×8=5×AE，∴AE=4.8（cm）．【考点】菱形的性质．4.一个圆锥形零件的高线长为，底面半径为2，则圆锥形的零件的侧面积为（）．A．2B．C．3D．6【答案】D．【解析】∵高线长为，底面半径为2，∴母线长为：，∴圆锥侧面积公式为：S=πrl=π×2×3=6π，故选D．【考点】圆锥的计算．5.如图，AB为⊙0的弦，AB=6，点C是⊙0上的一个动点，且∠ACB=45°，若点M、N分别是AB、BC的中点，则MN长的最大值是______________。

初三数学图形与证明试题答案及解析

初三数学图形与证明试题答案及解析1.顺次连接矩形ABCD各边的中点，所得四边形必定是（）A．邻边不等的平行四边形B．矩形C．正方形D．菱形【答案】D【解析】如图：E，F，G，H为矩形的中点，则AH=HD=BF=CF，AE=BE=CG=DG，在Rt△AEH与Rt△DGH中，AH=HD，AE=DG，所以△AEH≌△DGH，因此根据全等三角形的性质可得EH=HG，同理，△AEH≌△DGH≌△BEF≌△CGF，因此可得EH=HG=GF=EF，所以四边形EFGH为菱形．故选A【考点】菱形的判定2.如图，某仓储中心有一斜坡AB，其坡度为，顶部A处的高AC为4m，B、C在同一水平地面上。

（1）求斜坡AB的水平宽度BC；（2）矩形DEFG为长方形货柜的侧面图，其中DE=2.5m，EF=2m.将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高。

（，结果精确到0.1m）【答案】(1) 8m．(2) 4.5m．【解析】（1）根据坡度定义直接解答即可；（2）作DS⊥BC，垂足为S，且与AB相交于H．证出∠GDH=∠SBH，根据，得到GH=1m，利用勾股定理求出DH的长，然后求出BH=5m，进而求出HS，然后得到DS．试题解析：（1）∵坡度为i=1：2，AC=4m，∴BC=4×2=8m.（2）作DS⊥BC，垂足为S，且与AB相交于H.∵∠DGH=∠BSH，∠DHG=∠BHS，∴∠GDH=∠SBH，∵DG=EF=2m，∴GH=1m，∴DH=m，BH=BF+FH=3.5+（2.5-1）=5m，设HS=xm，则BS=2xm，∴x2+（2x）2=52，∴x=m，∴DS=+=2m≈4.5m．【考点】解直角三角形的应用-坡度坡角问题．3.如图，矩形纸片ABCD中，AB＝4，BC＝8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是（）A．AF＝AE B．△ABE≌△AGF C．EF＝D．AF＝EF【答案】D．【解析】∵AD∥BC，∴∠AFE=∠FEC，∵∠AEF=∠FEC，∴∠AFE=∠AEF，∴AF=AE，∴选项A正确；∵ABCD是矩形，∴AB=CD，∠B=∠C=90°，∵AG=DC，∠G=∠C，∴∠B=∠G=90°，AB=AG，∵AE=AF，∴△ABE≌△AGF，∴选项B正确；设BE=x，则CE=BC﹣BE=8﹣x，∵沿EF翻折后点C与点A重合，∴AE=CE=8﹣x，在Rt△ABE中，，即，解得x=3，∴AE=8﹣3=5，由翻折的性质得，∠AEF=∠CEF，∵矩形ABCD的对边AD∥BC，∴∠AFE=∠CEF，∴∠AEF=∠AFE，∴AE=AF=5，过点E作EH⊥AD于H，则四边形ABEH是矩形，∴EH=AB=4，AH=BE=3，∴FH=AF﹣AH=5﹣3=2，在Rt△EFH中，EF=，∴选项C正确；由已知条件无法确定AF和EF的关系，故选D．【考点】翻折变换（折叠问题）．4.（7分）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE= cm时，四边形CEDF是矩形；②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）【答案】（1）证明见解析；（2）①当AE＝3．5cm时，四边形CEDF是矩形．②当AE＝2cm时，四边形CEDF是菱形．【解析】（1）利用“ASA”即可得证；①当四边形CEDF是矩形时，则有EG=DG=1．5cm，又由已知可得∠ADC＝60°，从而得△EGD为等边三角形，从而得DE=1．5cm，从而得AE=3．5cm；②．当四边形CEDF是菱形时，则有EF⊥CD，由已知可知∠ADC=60°，从而可得∠DEG＝30°，从而得DE＝2DG＝3，从而得AE＝2．试题解析：（1）∵四边形ABCD是平行四边形，∴ CF∥ED，∴∠FCG＝∠EDG，∵ G是CD的中点，∴ CG＝DG，在△FCG和△EDG中，，∴△FCG ≌△EDG（ASA），∴ FG＝EG，∵ CG＝DG，∴四边形CEDF是平行四边形；（2）①当AE＝3．5cm时，四边形CEDF是矩形．②当AE＝2cm时，四边形CEDF是菱形．【考点】1．平行四边形的性质；2．全等三角形的判定与性质；3．矩形的判定；4．菱形的判定．5.如图，点A、B、C、D在⊙O上，O点在∠D的内部，四边形OABC为平行四边形，则∠OAD+∠OCD= 度．【答案】60°．【解析】由四边形OABC为平行四边形，根据平行四边形对角相等，即可得∠B=∠AOC，由圆周角定理，可得∠AOC=2∠ADC，又由内接四边形的性质，可得∠B+∠ADC=180°，即可求得∠B=∠AOC=120°，∠ADC=60°，然后由三角形外角的性质，即可求得∠OAD+∠OCD的度数．试题解析：连接DO并延长，∵四边形OABC为平行四边形，∴∠B="∠AOC，"∵∠AOC="2∠ADC，"∴∠B="2∠ADC，"∵四边形ABCD是⊙O的内接四边形，∴∠B+∠ADC="180°，"∴3∠ADC="180°，"∴∠ADC="60°，"∴∠B="∠AOC=120°，"∵∠1="∠OAD+∠ADO，∠2=∠OCD+∠CDO，"∴∠OAD+∠OCD=（∠1+∠2）-（∠ADO+∠CDO）=∠AOC-∠ADC=120°-60°=60°．【考点】1．圆周角定理；2．平行四边形的性质．6.下列四个命题中真命题是（）A．对角线互相垂直平分的四边形是正方形B．对角线垂直且相等的四边形是菱形C．对角线相等且互相平分的四边形是矩形D．四边都相等的四边形是正方形【答案】C【解析】因为对角线互相垂直平分的四边形是菱形，所以A错误；因为对角线垂直且相等的四边形可能是菱形也可能是等腰梯形，所以B错误；因为对角线相等且互相平分的四边形是矩形，所以C正确；因为四边都相等的四边形是菱形，所以D错误；故选：C．【考点】特殊的平行四边形的判定．7.挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走。

专题03 一线三等角模型证全等(原卷版)

专题03 一线三等角模型证全等模型感知1．【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一，请根据以下问题，把你的感知填写出来：如图1，ABC 是等腰直角三角形，90C ∠=︒，AE =BD ，则AED ≌_______；如图2，ABC 为正三角形，,60BD CF EDF =∠=︒，则BDE ≌________；如图3，正方形ABCD 的顶点B 在直线l 上，分别过点A 、C 作AE l ⊥于E ，CF l ⊥于F ．若1AE =，2CF =，则EF 的长为________．类型一一线三直角证全等2．在△ABC 中，∠ACB ＝90°，AC ＝BC ，且AD ⊥MN 于D ，BE ⊥MN 于E ．(1)直线MN 绕点C 旋转到图（1）的位置时，求证：DE ＝AD +BE ；(2)当直线MN 绕点C 旋转到图（2）的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请直接写出这个等量关系（不写证明过程）；(3)当直线MN 绕点C 旋转到图（3）的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请直接写出这个等量关系（不写证明过程）．3．通过对下面数学模型的研究学习，解决下列问题：(1)如图1，点A 在直线l 上，90,BAD AB AD ∠=︒=，过点B 作BC l ⊥于点C ，过点D 作DE l⊥交于点E ．由12290D ∠+∠=∠+∠=︒，得1D ∠=∠．又90BCA AED ∠=∠=︒，可以推理得到()ABC DAE AAS ≌．进而得到结论：AC =_____，BC =_____．我们把这个数学模型称为“K 字”模型或“一线三直角”模型；(2)如图2，90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ，NG l ⊥于点G ，由（1）易知NG =_______，ND 与直线l 交于点P ，求证：NP DP =．类型二一线非直角证全等4．（1）如图1，直线m 经过等边三角形ABC 的顶点A ，在直线m 上取两点D ，E ，使得∠ADB＝60°，∠AEC ＝60°．求证：BD ＋CE ＝DE ；（2）将（1）中的直线m 绕着点A 逆时针方向旋转一个角度到如图2的位置，并使∠ADB ＝120°，∠AEC ＝120°．若BD ＝3，CE ＝7，求DE 的长．5．已知：CD 是经过BCA ∠的顶点C 的一条直线，CA CB =．E 、F 是直线CD 上两点，BEC CFA α∠=∠=∠．（1）若直线CD 经过BCA ∠的内部，BCD ACD ∠>∠．①如图1，90BCA ∠=︒，90α∠=︒，直接写出BE ，EF ，AF 间的等量关系：__________． ②如图2，α∠与BCA ∠具有怎样的数量关系，能使①中的结论仍然成立？写出α∠与BCA ∠的数量关系，并对结论进行证明；（2）如图3，若直线CD 经过BCA ∠的外部，BCA α∠=∠，①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．类型三综合运用6．（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在ABC中，90BAC∠=︒，AB AC=，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D，E．求证：DE BD CE=+．（2）组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在ABC中，AB AC=，D，A，E三点都在直线l上，并且有BDA AEC BACα∠=∠=∠=，其中α为任意锐角或钝角．请问结论DE BD CE=+是否成立？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过ABC的边AB，AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高．延长HA交EG于点I．若7AEGS=△，则AEIS=△______．7．（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明∶DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m 上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．8．通过对下面数学模型的研究学习，解决下列问题：【模型呈现】（1）如图，90BAD ∠=︒，AB AD =，过点B 作BC AC ⊥于点C ，过点D 作DE AC ⊥于点E ．由12290D ∠+∠=∠+∠=︒，得1D ∠=∠．又90ACB AED ∠=∠=︒，可以推理得到ABC DAE ∆∆≌．进而得到AC =__________，BC AE =．我们把这个数学模型称为“K 字”模型或“一线三等角”模型；【模型应用】（2）如图，90BAD CAE ∠=∠=︒，AB AD =，AC AE =，连接BC ，DE ，且BC AF ⊥于点F ，DE 与直线AF 交于点G ．求证：点G 是DE 的中点；【深入探究】（3）如图，已知四边形ABCD 和DEGF 为正方形，AFD ∆的面积为1S ，DCE ∆的面积为2S ，则有1S __________2S （填“＞、=、＜”）（4）如图，点A 、B 、C 、D 、E 都在同一条直线上，四边形ABAH 、KCMG 、DENM 都是正方形，若该图形总面积是16，正方形KCMG 的面积是4，则HKG 的面积是__________．9．（1）【问题情境】八上《伴你学》第138页有这样一个问题：如图1，把一块三角板（,90AB BC ABC =∠=︒）放入一个“U ”形槽中，使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动，已知90D E ∠=∠=︒，在滑动过程中，你发现线段AD 与BE 有什么关系？试说明你的结论；（2）【变式探究】小明在解决完这个问题后，将其命名为“一线三等角”模型；如图2，在ABC ∆中，点D 、E 、F 分别在边BC 、AC 、AB 上，若B FDE C ∠=∠=∠，则这三个相等的角之间的联系又会使图形中出现其他的一些等角．请你写出其中的一组，并加以说理；（3）【拓展应用】如图3，在ABC ∆中，BA BC =，45B ∠=︒，点D 、F 分别是边BC 、AB 上的动点，且2AF BD =．以DF 为腰向右作等腰DEF ∆，使得DE DF =，45EDF ∠=︒，连接CE ．①试判断线段DC 、BD 、BF 之间的数量关系，并说明理由；②如图4，已知2AC =，点G 是AC 的中点，连接EA 、EG ，直接写出EA EG +的最小值．。

(2021年整理)图形与证明(三条线段之间的数量关系)

（完整）图形与证明(三条线段之间的数量关系)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）图形与证明(三条线段之间的数量关系)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）图形与证明(三条线段之间的数量关系)的全部内容。

图形与证明（2）1（09河北)在图14-1至图14—3中，点B 是线段AC 的中点，点D 是线段CE 的中点．四边形BCGF 和CDHN 都是正方形．AE 的中点是M ．(1)如图14—1，点E 在AC 的延长线上，点N 与点G重合时，点M 与点C 重合，求证:FM = MH ，FM ⊥MH ；(2)将图14—1中的CE 绕点C 顺时针旋转一个锐角，得到图14-2，求证:△FMH 是等腰直角三角形；（3）将图14-2中的CE 缩短到图14—3的情况，△FMH 还是等腰直角三角形吗？（不必说明理由）2. (10沈阳）如图1，在△ABC 中，点P 为BC 边中点，直线a 绕顶点A 旋转，若B 、P 在直线a 的异侧，BM 直线a 于点M ，CN 直线a 于点N ，连接PM 、PN ；（1）延长MP 交CN 于点E (如图2）。

求证：△BPM △CPE ; 求证：PM = PN ； (2) 若直线a 绕点A 旋转到图3的位置时，点B 、P 在直线a 的同侧，其它条件不变。

此时PM =PN 还成立吗？若成立，请给予证明；若不成立，请说明理由;（3）若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变。

请直接判断四边形MBCN的形状及此时PM =PN 还成立吗?不必说明理由。

3．（08北京)请阅读下列材料:图14-1 A HC (M )DE BFG (N )G 图14-2AHC DEB F NMAHCDE 图14-3BFG MN aA BCPMNA BCM N aPA BCPNMa图1 图2 图3问题：如图1，在菱形ABCD 和菱形BEFG 中，点A B E ，，在同一条直线上，P 是线段DF 的中点，连结PG PC ，．若60ABC BEF ∠=∠=，探究PG 与PC 的位置关系及PGPC的值．小聪同学的思路是：延长GP 交DC 于点H ，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题: （1）写出上面问题中线段PG 与PC 的位置关系及PGPC的值; (2)将图1中的菱形BEFG 绕点B 顺时针旋转，使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上，原问题中的其他条件不变（如图2）．你在（1)中得到的两个结论是否发生变化?写出你的猜想并加以证明．（3)若图1中2(090)ABC BEF αα∠=∠=<<，将菱形BEFG 绕点B 顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出PGPC的值（用含α的式子表示）．4。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

∴ S ∆ECD = S ∆EFC + S ∆DCF =
∴ S ∆ABF + S ∆DCF = S ∆EFC + S ∆DCF ∴ S ∆ABF = S ∆EFC
【说明】如上的解法，一是恰当地运用了“平行四边形对边平行”所带来的三角形面积的转换；二是把说明】不易直接沟通的两个三角形的面积同时加上
【说明】这样依变换性质指导下的思考既有秩序又全面。说明】 2、平行四边形的对边平行关系的应用
相信责任的力量！相信责任的力量！
南京易学教育咨询有限公司制
平行四边形的对边平行且相等（即可经过平移后重合），其作用常体现在以下两个方面： Ⅰ、构造相似三角形； Ⅱ、进行等积变换。（1）平行四边形基础上的相似三角形例 3 如图，已知平行四边形 ABCD 中，过点 B 的直线顺次与 AC，AD 以及 CD 的延长线相交于点 E，F，G，若 BE=5，EF=2，则 FG 的长是。
（2）
∵ S 正方形ABCD = AB 2 = 7 2 = 49，而S四边形OEBF = 49 1 25 − × 3× 4 = 4 2 4
∴ S ∆EOF = S四边形OEBF − S ∆EFB =
【说明】对于正方形的“90°旋转对称性”的认识，不仅帮我们顺利地发现了问题的解决思路，并借助说明】 “90°旋转对称性” ，规则地找到了全等三角形的对应元素。另外，在求 ∆EOF 的面积时更是借助正方形的“90°旋转对称性”巧妙而有效地沟通了该面积与正方形 ABCD 的面积及 Rt∆EFB 面积的关系，使问题快速得解。
【观察与思考】由四边形 ABCD 是平行四边形，不难发现观察与思考】
S ∆ABF + S ∆DCF =
1 S 平行四边形ABCD = S ∆EDC = S ∆EFC + S ∆DCF ，得S ∆ABF = S ∆EFC 2
S ∆EFC = S ∆ABF
被证明
这样一来，（1）和（2）的解决途径同时被发现了，其实，点 F 为 BC 上任意一点时了，当然（1）的情况已包含于其中了。解；在情况（1）和情况（2）中，均有设 F 为 BC 上任意一点，则有
例2
如图（1），四边形 ABCD 是正方形，直线
l1 , l 2 , l 3 ，分别经过 A，B，C 三点，且 l1 // l 2 // l 3 ，若 l1 与
。
l 2 的距离为 a, l 2与l 3 的距离为 b, 则正方形 ABCD 的面积等于 l1
A B
l2
A F
l1
B
l2
（1`） D C
l3
2 2 2 2 1 1 − , ,1 − 2 2 2 2 或此时的图形如图（11`）和图（22`）解：（1） 2 ；（2）直角顶点的坐标为
y
相信责任的力量！相信责任的力量！
y
1
G
F 1 G F
南京易学教育咨询有限公司制
（22`）
（11`）【说明】正是对正方形邻的“90°旋转重合性”的深刻认识，使本题的解决顺畅而简捷说明】 3、正方形轴对称性及其应用我们知道，正方形是轴对称图形，它有四条对称轴，正方形的这一性质，也在许多题目中起着很好的作用。例 4 如图，已知 P 是正方形 ABCD 对角线 BD 上一点， PE ⊥ DC , PF ⊥ BC , E，F 分别是垂足。求证： AP = EF 。 A P D E A P D E
S ∆DCF
后，便与原平行四边形的面积巧妙地联系起来了。
七、正方形变换性质从变换的角度来看，正方形的本质特征可以反映在以下三个方面；特征Ⅰ、正方形是以其中心（即对角线的交点）为中心的“90°旋转对称”图形；特征Ⅱ、正方形的邻边以其公共顶点为中心“90°旋转重合” ；特征Ⅲ、正方形是轴对称图形，对边中点连线和两条对角线，都是它的对称轴。与正方形有关的许多问题，正是要以这些特征为解决的依据和思考的线索。正方形的“90°旋转对称性” 1、正方形的“90°旋转对称性”及其应用如图，正方形 ABCD 的对角线交于点 O，若以 O 为中心，按顺时针（或逆时针）旋转 90°，则 A C， B ，B C D， D A。即旋转后的图形与原正方形重合，这就是正方形的“90°旋转对称性” 。这一性质是正方形本质特征的最为典型的表现，因此有着极广的应用。 D A
教学目标
重点难点利用图形的旋转对称性解决图形变化问题教学过程教学内容
第一部分：第一部分：平行四边形的变换性质平行四边形的变换性质从变换的视角来看，平行四边形的基本特征反映在如下的两个方面：特征Ⅰ：平行四边形是“中心对称图形” ，两条对角线的交点就是它的对称中心；特征Ⅱ：平行四边形的两组对边，分别具有“平移重合”的关系。与平行四边形有关的的问题，大都可以沿着如上的两个特征去观察、研究，并获得解决。平行四边的“中心对称性” 1、平行四边的“中心对称性”和其应用绕点 O 逆（顺）时针如图， O 是平行四边形 ABCD 对角线的交点，若那么平行四边形 ABCD 重合于平行四边形 CDAB。旋转 180° 在上述的 180°旋转变换中，不仅有 ,A , , C B , D OA OC OB 还有关于点 O 所有中心对称的元素都是相互重合的。平行四边形的这一特征，有着极为广泛的应用。如图，四边形 ABCD 为平行四边形， AE ⊥ BD 于点 E， B A OD D
D
E O C
l3
【观察与思考】关键是要把正方形的边长和两个距离 a, b 沟通起来。观察与思考】若作 AE ⊥ l 2 点 E，作 CF ⊥ l 2 点 F，则 AE = a, CF = b, （如图（1`），这时容易看到：）绕点 O 顺时针旋转 90° 重合于
Rt∆BAE
Rt∆CBF
2 2 2 2 2
S ∆EFC = S ∆ABF
。证明如下：
S ∆ABF + S ∆DCF = S 平行四边形ABCD − S ∆FAB =
1 S 平行四边形ABCD 2 ，
相信责任的力量！相信责任的力量！
南京易学教育咨询有限公司制
S ∆ECD
1 S 平行四边形ABCD = S ∆ACD （这是因为 AE//CD）= 2 。 1 S 平行四边形ABCD 2
∴ ∆AEO ≅ ∆BFO, 得AE = BF = 4
∴ BC = BF + FC = 4 + 3 = 7 = AB，∴ EB = AB − AE 7 − 4 = 3
在 Rt∆EFB中，EB = 3，BF = 4，得EF =
EB 2 + BF 2 = 3 2 + 4 2 = 5
1 49 S 正方形ABCD = 4 4
绕点 O 逆时针旋转 90°
S四边形OEBF =
1 S 正方形ABCD，进而可求出S ∆EOF 4 。
相信责任的力量！相信责任的力量！
南京易学教育咨询有限公司制
解：（1）在 ∆AEO 和 ∆BFO 中， AO = BO, ∠OAE = ∠OBF = 45°, ∠AOE = ∠BOF （同为 ∠EOB 的余角）
（1`）（1）
B
F
C
B
F
C
【观察与思考】注意到 BD 是正方形 ABCD 的一条对称轴，点 C 和 A 关于该对称轴对称，立刻有如下的解。观察与思考】解：如图（1`）连结 PC。根据已知条件四边形 CEPF 是矩形，得 CP=EF。而在 ∆DAP和∆DCP 中， DA = DC，DP 公用，
S = CB = BF + CF = a + b 可知，在 Rt∆CBF 中，由 CF = b, BF = AE = a, 可推得正方形ABCD
解：填 a + b
2 2
相信责任的力量！相信责任的力量！
南京易学教育咨询有限公司制
【说明】在本题的解法思考中，正方形的“90°旋转对称性”发挥着关键的引导作用。说明】正方形邻边的“90°旋转重合性” 2、正方形邻边的“90°旋转重合性”及其应用如图，正方形 ABCD 中，若以顶点 A 为中心，将边 AB 逆时针旋转 90°，则与边 AD 重合，这一性质可简称为正方形邻边“90°旋转重合性” ，这一性质在一些关于正方形题目有着很好的作用。 A D 例3 在平面直角坐标系 xOy 中，四边形 OEFG 为正方形，点 F 的坐标为（1，1）。 B C
将一个最短边长大于 2 的直角三角形纸片的直角顶点放在对角线 FO 上。
（1）如图（1），当三角形纸片的直角顶点与点 F 重合，一条直线边落在直线 FO 上时，这个三角形纸片与正方形 OEFG 重叠部分（即阴影部分）的面积为。
y
（2）若三角形纸片的直角顶点不与点 O，F 重合，且两条直角边与正方形相邻两边相交，当这个三角形纸片与正方形 OEFG 重叠部分的面积是正方形面积的一半时，试确定三角形纸片直角顶点的坐标（不要求写出求解过程），并画出此时（1）的图形。
∠ADP = 45° = ∠CDP ，
∴ ∆DAP ≅ ∆DCP ，有 AP=CP，进而有 AP=EF
而 FG = EG − EF = 12.5 − 2 = 10.5 解： FG = 10.5 。 E
B
F
C
（2）平行四边形基础上的面积问题例4 已知如图，平行四边形 ABCD 中， AD = a, AB = b, ∠ABC = α ，点 F 为线段 BC 上的一点（端点
B，C 除外），连结 AF，AC，连结 DF，并延长 DF 交 AB 的延长线于点 E，连结 CE。（1）当 F 为 BC 的中点时，求证 ∆EFC 与 ∆ABF 和面积相等；（2）当 F 为 BC 上任意一点时， ∆EFC 与 ∆ABF 的面积还相等吗？说明理由。

图形与证明专题(三)

最新人教版中考数学复习专题17 证明题(3)——代数与规律探究

2019版二轮复习数学(理)全国版专题三 第二讲 大题考法——立体几何

专题 全等三角形(三) 课后练习二及详解

图像与证明

中考数学总复习专题三解答题重难点题型突破题型二几何图形探究题类型与三角形、四边形有关的探究题课件

2025年四川省聚焦中考数学必备考点透析-第4章 三角形微专题三 三角形中的基本模型

专题3-2 解三角形最值范围与图形归类-2023年高考数学二轮复习讲练测(全国通用)(原卷版)

中考数学难点突破与经典模型精讲练全等三角形中的一线三垂直模型(解析版)

七年级初一下学期数学 专题03 三角形(知识点串讲)(解析版)

专题3 空间图形的基本关系与公理(解析版)-2021年高考数学立体几何中必考知识专练

人教八上：专题三--角平分线的性质与判定(含解析)

初三数学图形与证明试题

专题06 几何图形的初步认识(3)原卷版

初三数学图形与证明试题

初三数学图形与证明试题答案及解析

专题03 一线三等角模型证全等(原卷版)

(2021年整理)图形与证明(三条线段之间的数量关系)

2019版二轮复习数学(理)全国版专题三第二讲大题考法——立体几何

专题全等三角形(三) 课后练习二及详解

2025年四川省聚焦中考数学必备考点透析-第4章三角形微专题三三角形中的基本模型

七年级初一下学期数学专题03 三角形(知识点串讲)(解析版)