材料力学答案第6章
合集下载
材料力学第六章 弯曲变形
4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 （rad）
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w （3）校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知：EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
第二版《材料力学》第六章至第九章习题解答-(华中科大版-倪樵主编)
2 z
W
M
2 x
W2
[ ]
7-17 图示直角曲拐，C端受铅垂集中力F作用。已知a=160mm，AB杆直径D=40mm，
l=200mm ，E=200GPa， μ=0.3，实验测得D点沿45º方向的线应变 ε45º=0.265 × 10-3。试求：
（1）力F的大小；（2）若AB杆的[σ]=140MPa，试按最大切应力理论校核其强度。
T Wp
16 M 0
D3
16 125 .6
0.023
79.96MPa
单元体可画成平面单元体如图(从上往下观察)
A
6-5 试用求下列各单元体中ab面上的应力（单位MPa） 。
解：(a)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70 1 2
35
(MPa)
x y sin(2 30 ) 70
2
3 60.62 (MPa) 2
(b)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70
(MPa)
x
y
2
sin(2 30 )
0
6-6 各单元体的受力如图所示，试求：（1）主应力大小及方向并在原单元体图上绘出主 单元体；（2）最大切应力（单位MPa） 。
解： (3) My 、Mz、Mx 和F 同时作用，拉弯扭组合，任一截 面D1点是危险点
应力状态：
D1
FN M F
M
2 y
M
2 z
y
AW A
材料力学习题册答案_第6章_弯曲变形
15
得 x=0.519l
所以
W
m
ax
=0.00652
ql 4 EI
3 用叠加法求如图 7 所示各梁截面 A 的挠度和转角。EI 为已知常数。
解 A 截面的挠度为 P 单独作用与 M 0 单独作用所产生的挠度之和。 查表得：
y AP
Pl 3 24 EI
y = M 0l 2 Pl 3
AM 0
8EI
度 y = Fl 3 。 C 32 EI
4. 如图 4 所示两梁的横截面大小形状均相同，跨度为 l , 则两梁的力 图 相同 ，两梁的变形 不同 。（填“相同”或“不同”）
5. 提高梁的刚度措施有 提高Wz 、 降低 M MAX 等。 四、计算题 1 用积分法求图 5 所示梁 A 截面的挠度和 B 截面的转角。
8EI
y y 则 y A
AP
= Pl 3
AM0 12 EI
同理，A 截面的转角为 P 单独作用与 M 0 单独作用所产生的转角之和。
查表得
AP
Pl 2 8EI
对于 AM0 可求得该转角满足方程 EI =-Plx+C 边界条件 x=0 0 可得 C=0
现 4 个积分常数，这些积分常数需要用梁的 边界 条件和 光滑连
续 条件来确定。
2. 用积分法求图 2 所示梁变形法时，边界条件为：YA 0,A 0,YD 0 ；
连续条件为：
YA
1
YA
2
,
B
1
B
2
,
YC3.
如图
3
所示的外伸梁，已知
B
截面转角
B
=
Fl 2 16 EI
，则 C 截面的挠
于零的截面处。
得 x=0.519l
所以
W
m
ax
=0.00652
ql 4 EI
3 用叠加法求如图 7 所示各梁截面 A 的挠度和转角。EI 为已知常数。
解 A 截面的挠度为 P 单独作用与 M 0 单独作用所产生的挠度之和。 查表得：
y AP
Pl 3 24 EI
y = M 0l 2 Pl 3
AM 0
8EI
度 y = Fl 3 。 C 32 EI
4. 如图 4 所示两梁的横截面大小形状均相同，跨度为 l , 则两梁的力 图 相同 ，两梁的变形 不同 。（填“相同”或“不同”）
5. 提高梁的刚度措施有 提高Wz 、 降低 M MAX 等。 四、计算题 1 用积分法求图 5 所示梁 A 截面的挠度和 B 截面的转角。
8EI
y y 则 y A
AP
= Pl 3
AM0 12 EI
同理，A 截面的转角为 P 单独作用与 M 0 单独作用所产生的转角之和。
查表得
AP
Pl 2 8EI
对于 AM0 可求得该转角满足方程 EI =-Plx+C 边界条件 x=0 0 可得 C=0
现 4 个积分常数，这些积分常数需要用梁的 边界 条件和 光滑连
续 条件来确定。
2. 用积分法求图 2 所示梁变形法时，边界条件为：YA 0,A 0,YD 0 ；
连续条件为：
YA
1
YA
2
,
B
1
B
2
,
YC3.
如图
3
所示的外伸梁，已知
B
截面转角
B
=
Fl 2 16 EI
，则 C 截面的挠
于零的截面处。
材料力学(金忠谋)第六版答案第06章
弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。
解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4，h 1=，h 2=。
刘鸿文版材料力学第六章
F6bl
(l2
b2 ) x1
CB 段： a x2 l
y
F
A A
DC
FAy x1
x2
a
ym ax b
B B x
FBy
EI
Fb 2 2l
2
x2
F 2
(
x2
a)2
Fb (l2 6l
b2 )
EIy2
Fb 6l
x32
F 6
(
x2
a)3
F6lb (l2 b2 ) x2
目录
§6-3 用积分法求弯曲变形
目录
§6-5 简单超静定梁
例7 梁AB 和BC 在B 处铰接，A、C 两端固定，梁的抗弯刚度均为EI，F = 40kN， q = 20kN/m。画梁的剪力图和弯矩图。
解 从B 处拆开，使超静定结构变成两个悬臂 梁。
MA
FA FB
FB FB
yB2
yB1
FB
变形协调方程为： 物理关系
yB1 yB 2
4
EI
ql 4 48EI
ql 4 16 EI
11ql 4 ( ) 384 EI
3
ql 3
B i 1 Bi 24EI
ql 3 16EI
ql 3 3EI
11ql 3 ( ) 48EI
目录
§6-4 用叠加法求弯曲变形
例4 已知：悬臂梁受力如图示，q、l、
yC
EI均为已知。求C截面的挠度yC和转角C
§6-4 用叠加法求弯曲变形
讨论 叠加法求变形有什么优缺点？
目录
§6-5 简单超静定梁
1.基本概念： 超静定梁：支反力数目大于有效平衡方程数目的梁 多余约束：从维持平衡角度而言,多余的约束 超静定次数：多余约束或多余支反力的数目。 相当系统：用多余约束力代替多余约束的静定系统
《材料力学》第6章 简单超静定问题 习题解
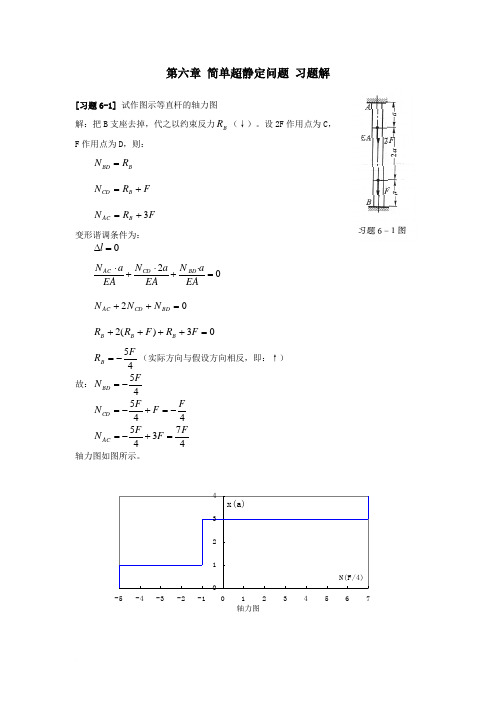
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解：把B 支座去掉，代之以约束反力B R （↓）。
设2F 作用点为C ， F 作用点为D ，则：B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为：0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=（实际方向与假设方向相反，即：↑） 故：45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=，1，2，3各杆由同一种材料制成，其横截面面积分别为21100mm A =，22150mm A =，23200mm A =。
试求各杆的轴力。
解：以节点A 为研究对象，其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件：设A 节点的水平位移为x δ，竖向位移为y δ，则由变形协调图（b ）可知：00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31，则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得：kN N 45.81=；kN N 68.22=；kN N 54.111=（方向如图所示，为压力，故应写作：kN N 54.111-=）。
工程力学c材料力学部分第六章 弯曲变形
q
A l/2
C l
B
解：此梁上的荷载可视为 正对称和反对称荷载的叠加， 正对称和反对称荷载的叠加， 如图所示。 如图所示。 正对称荷载作用下：
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解：将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然，在反对称力( / )作用下， 显然，在反对称力(P/2)作用下，wc=0 对称力作用的简支梁， 对称力作用的简支梁，可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件： 连续条件
P A C θC左 wC左= wC右， =θ C右 B
的悬臂梁， 例1：图示一弯曲刚度为 的悬臂梁，在自由端受一集中力 作 ：图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程，并求最大挠度及最大转角。 用，试求梁的挠曲线方程，并求最大挠度及最大转角。 解：① 建立坐标系并写出弯矩方程 ①
在小变形情况下， 曲线弯曲平缓， 在小变形情况下，挠曲线弯曲平缓，
∴ w′ ≪ 1
2
A l/2
C l
B
解：此梁上的荷载可视为 正对称和反对称荷载的叠加， 正对称和反对称荷载的叠加， 如图所示。 如图所示。 正对称荷载作用下：
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解：将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然，在反对称力( / )作用下， 显然，在反对称力(P/2)作用下，wc=0 对称力作用的简支梁， 对称力作用的简支梁，可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件： 连续条件
P A C θC左 wC左= wC右， =θ C右 B
的悬臂梁， 例1：图示一弯曲刚度为 的悬臂梁，在自由端受一集中力 作 ：图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程，并求最大挠度及最大转角。 用，试求梁的挠曲线方程，并求最大挠度及最大转角。 解：① 建立坐标系并写出弯矩方程 ①
在小变形情况下， 曲线弯曲平缓， 在小变形情况下，挠曲线弯曲平缓，
∴ w′ ≪ 1
2
材料力学-第6章梁的应力分析与强度计算 (B)
dx＝－yd
式中的负号表示 y 坐标为正的线段产生 压缩变形； y 坐标为负的线段产生伸长 变形。
第6章 梁的应力分析与强度计算(B)
平面弯曲时梁横截面上的正应力
应用平面假定确定应变分布
dx＝－yd
将线段的长度改变量除以原长dx，即 为线段的正应变，于是得到
dx d y ＝ ＝－y ＝－ dx dx
第6章 梁的应力分析与强度计算(B)
平面弯曲时梁横截面上的正应力
对称面—— 梁的横截面具有对称轴，所有相同的对 称轴组成的平面，称为梁的对称面(symmetric plane)。
梁的对称面
第6章 梁的应力分析与强度计算(B)
平面弯曲时梁横截面上的正应力
主轴平面 —— 梁的横截面没有对称轴，但是
加载平面与主轴平面一致
q
FP1
M
FP2
平面弯曲 —— 所有外力（包括力偶）都作用于梁的同一主
轴平面内时，梁的轴线弯曲后将弯曲成平面曲线，这一曲线位 于外力作用平面内。这种弯曲称为平面弯曲(plane bending)。
第6章 梁的应力分析与强度计算(B)
平面弯曲时梁横截面上的正应力
M l
FP M
怎样确定横截面上的内力分布规律呢？
第6章 梁的应力分析与强度计算(B)
应力是不可见的，但变形却是可见的，而且二 者之间通过材料的物性关系相联系。因此，为了确 定内力的分布规律，必须分析和研究杆件的变形， 必须研究材料受力与变形之间的关系，即必须涉及 变形协调与物性关系两个重要方面。二者与平衡原 理一起组成分析弹性体内力分布规律的基本方法。
第6章 梁的应力分析与强度计算(B)
平面弯曲时梁横截面上的正应力 斜弯曲的应力计算 弯矩与轴力同时作用时横截面上的正应力 弯曲强度计算 结论与讨论
材料力学第六章 应力状态理论和强度理论
单元体的各个面均为主平面，其上的主应力为： 单元体的各个面均为主平面，其上的主t
9
工程力学
Engineering mechanics
§6-1 应力状态理论的概念 和实例
3、三向应力状态（空间应力状态） 、三向应力状态（空间应力状态） 定义：三个主应力均不为零。 定义：三个主应力均不为零。 例如：导轨与滚轮接触点处，取导轨表面任一点 的单元体 的单元体， 例如：导轨与滚轮接触点处，取导轨表面任一点A的单元体， 它各侧面均受到压力作用，属于三向应力状态。 它各侧面均受到压力作用，属于三向应力状态。
工程力学
Engineering mechanics
第六章 应力状态理论 和强度理论
1
工程力学
Engineering mechanics
引
言
前面的分析结果表明， 前面的分析结果表明，在一般情况下杆件横截面上不同点 的应力是不相同的，过一点不同方向面上的应力也是不相同的。 的应力是不相同的，过一点不同方向面上的应力也是不相同的。 因此，当提及应力时，必须明确“哪一个面上哪一点” 因此，当提及应力时，必须明确“哪一个面上哪一点”的应力或 哪一点哪一个方向面上”的应力。 者“哪一点哪一个方向面上”的应力。 如果危险点既有正应力，又有切应力，应如何建立其强度 如果危险点既有正应力，又有切应力， 条件？ 条件？ 如何解释受力构件的破坏现象？ 如何解释受力构件的破坏现象？ 对组合变形杆应该如何进行强度计算？ 对组合变形杆应该如何进行强度计算？ 要全面了解危险点处各截面的应力情况。 要全面了解危险点处各截面的应力情况。
2
工程力学
Engineering mechanics
§6-1 应力状态理论的概念 和实例
一、一点的应力状态 定义：过受力体内一点所有方向面上应力的集合。 定义：过受力体内一点所有方向面上应力的集合。 一点的应力状态的四要素 四要素： 一点的应力状态的四要素： ）、应力作用点的坐标 （1）、应力作用点的坐标； ）、应力作用点的坐标； ）、过该点所截截面的方位 （2）、过该点所截截面的方位； ）、过该点所截截面的方位； ）、应力的大小 （3）、应力的大小； ）、应力的大小； ）、应力的类型 （4）、应力的类型。 ）、应力的类型。 二、研究应力状态的目的 对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件， 对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件， ）、扭转 其危险点处于单向应力状态或纯剪切应力状态，受力简单， 其危险点处于单向应力状态或纯剪切应力状态，受力简单，可直 接由相应的试验确定材料的极限应力，建立相应的强度条件。 接由相应的试验确定材料的极限应力，建立相应的强度条件。
材料力学简明教程(景荣春)课后答案第六章
( ) wA
= − q0l 4 30EI
↓
，θB
= q0l3 24EI
（顺）
讨论：请读者按右手坐标系求 wA ，θB 并与以上解答比较。
(c)
(c1)
解 图(c1)
( ) ∑ M B = 0 ， FC
= − Me l
↓
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
l 2
≤
x2
≤
l ⎟⎞ ⎠
Ew1′′
=
3 8
qlx1
−
1 2
qx12
EIw1′
=
3 16
qlx12
−
1 6
qx13
+
C1
EIw1
=
1 16
qlx13
−
1 24
qx14
+
C1 x1
+
D1
EIw′2′
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l ⎟⎞ 4⎠
EIw′2
=
3 16
qlx22
−
ql 4
⎜⎛ ⎝
x2
24
EIw′(l) = 0 ，− q l 3 + 3Al 2 + 2Bl = 0
6
解式（a），（b）得
A = ql ， B = − ql 2
12
24
即挠曲线方程为
EIw = − q x4 + ql x3 − ql 2 x2 24 12 24
材料力学第6章 弯曲内力
精品文档
6.1 梁的内力—剪力和弯矩
例题 6-2
（2）计算(jìsuàn)指定截面上的剪力和 弯矩
C截截面面C左（以侧梁的左力半：边为研究对象）：
FAy 2 kN () (+)
FSC Fy FAy 2kN
C截面左侧的力矩：
FAy * 2m (+)
M e 8kN m (-)
M C
M F 2m - M -4kN m O
19
精品文档
6.2 剪力图和弯矩图
例题 6-3
(2) 作剪力图(lìtú)和弯矩图
由剪力、弯矩方程画剪力、弯矩图。
注意： 画图时应将剪力图、弯矩图与计算简图 对齐，并注明图名（FS图、M图）、 峰值点的值及正负号。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内
20
力
精品文档
6.2 剪力图和弯矩图
(plane bending)。当所有外力均作用在纵向对称面内时，梁只发生平面弯曲。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内力
6
精品文档
6.1 梁的内力(nèilì)—剪力和弯 矩
梁在外力作用下，其任一横截面上的内力可用截面法确定。
（1）截：在横截面m-m处假想地将梁分为两段
原来处于平衡状态的梁，被截出的任意段也处于平衡状态。
秦飞A编y 著《材料力学(cái lieào lìxué)》 第6章 弯
16
曲内力
精品文档
6.1 梁的内力(nèilì)—剪力和弯矩 例题 6-2
截面B（以梁右半边为研究对象）：
B左截面
F 2kN (+)
FBy 4kN (-)
FSB左 F FBy -2kN
材料力学习题 应力状态分析答案详解
解析： 与 无关
13、在图示梁的A点测得梁在弹性范围内的纵横方向的线应变 、 后，所能算出的材料常数有（ D ）。
（A）只有E；（B）只有v；（C）只有G；（D）E、v和G均可算出。
解析：中间段为纯弯曲，A点为单向拉伸，
则
14、纯剪应力状态下，各向同性材料单元体的体积改变有四种答案，正确答案是（ C ）。
解答：
确定 ， 确定
6、 物体内某一点，载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图（a）和（b）所示。试求两载荷系统同时作用时（仍处于弹性小变形）的主单元体和主应力。
解答：
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值，并画出三向应力状态的应力圆。
解答：
8、图示单元体，已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答：
确定
确定
2、已知应力状态如图。试求主应力及其方向角，并确定最大切应力值。
解答：
确定
所以 确定
3、图示单元体，求：（1）指定斜截面上的应力：（2）主应力大小，并将主平面标在单元体图上。
解答：
确定
所以 确定
4、用解析法求图示单元体ab面上的应力（ ），并求 及主应力。
解答：
5、试求图示单元体主应力及最大切应力，并将主平面在单元体上标出。
由第三强度理论 安全
10、直径为20mm的圆截面折杆受力情况如图所示，已知：F＝0.2kN，材料的许用应力为 。试用第三强度理论确定折杆的长度a的许用值。
解答：
在危险截面A上危险点在七上下边缘
由第三强度理论
取
11、AB、CD两杆互相垂直，在水平面内，C点的集中力2F及D点的集中力F与刚架平面垂直。已知F＝20kN，l＝1m，各杆直径相同d＝10cm， 。试按最大切应力强度理论校核强度。
13、在图示梁的A点测得梁在弹性范围内的纵横方向的线应变 、 后，所能算出的材料常数有（ D ）。
（A）只有E；（B）只有v；（C）只有G；（D）E、v和G均可算出。
解析：中间段为纯弯曲，A点为单向拉伸，
则
14、纯剪应力状态下，各向同性材料单元体的体积改变有四种答案，正确答案是（ C ）。
解答：
确定 ， 确定
6、 物体内某一点，载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图（a）和（b）所示。试求两载荷系统同时作用时（仍处于弹性小变形）的主单元体和主应力。
解答：
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值，并画出三向应力状态的应力圆。
解答：
8、图示单元体，已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答：
确定
确定
2、已知应力状态如图。试求主应力及其方向角，并确定最大切应力值。
解答：
确定
所以 确定
3、图示单元体，求：（1）指定斜截面上的应力：（2）主应力大小，并将主平面标在单元体图上。
解答：
确定
所以 确定
4、用解析法求图示单元体ab面上的应力（ ），并求 及主应力。
解答：
5、试求图示单元体主应力及最大切应力，并将主平面在单元体上标出。
由第三强度理论 安全
10、直径为20mm的圆截面折杆受力情况如图所示，已知：F＝0.2kN，材料的许用应力为 。试用第三强度理论确定折杆的长度a的许用值。
解答：
在危险截面A上危险点在七上下边缘
由第三强度理论
取
11、AB、CD两杆互相垂直，在水平面内，C点的集中力2F及D点的集中力F与刚架平面垂直。已知F＝20kN，l＝1m，各杆直径相同d＝10cm， 。试按最大切应力强度理论校核强度。
材料力学第6章拉压杆件的应力变形分析与强度设计
解：首先分析钢杆和铝筒的受力：钢杆BC承受拉伸，铝筒承受 压缩。C点的位移等于钢杆的伸长量与铝筒的压缩量之和：
Rigid plate
F´P B
FP AsB Ea
Aa Es
Fixed rigid plate
A
FP
l l
C F´P
第2类习题 变形计算
长为1.2m、横截面面积为1.10×10－3m2的铝制筒放置在固定刚块上，直径 为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上，若二者轴线重合、载荷作 用线与轴线一致，且已知钢和铝的弹性模量分别为Es = 200GPa，Ea = 70GPa， FP = 60kN。试求钢杆上C处位移。
50mm。求铝板与钢板横截面上的最大正应力。
steel aluminum
Rigid plate
FNs
Es As Es As Ea Aa
FP
FNa
Ea Aa Es As Ea Aa
FP
TSINGHUA UNIVERSITY
1．复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式
图示由铝板和钢板组成的复合材料柱，纵向截荷FP通过刚性平板沿着柱的中心线施加 在其上。试：
1．导出复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式； 2．已知FP = 385kN；Ea = 70GPa，Es = 200GPa；b0 = 30mm，b1 = 20mm，h =
50mm。求铝板与钢板横截面上的最大正应力。
铝板
a
FNa EaFP
Aa
b0hsE2b1haE
钢板
s A F s N sE sb 0 h E sE F P a2 b 1 hb 0 hs E E sF 2 P b 1 haE
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-简单的超静定问题(圣才出品)
图 6-2-4 （2）补充方程 作铰 A 的位移图，由几何关系可得变形协调方程： Δl1/sin30°＝2Δl2/tan30°＋Δl3/sin30°③ 其中，由胡克定律可得物理关系：
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1＝FN1l1/EA1＝FN1l/（EA1cos30°） Δl2＝FN2l2/EA2＝FN2l/（EA2） Δl3＝FN3l3/EA3＝FN3l/（EA3cos30°） 代入式③可得补充方程： FN1l/（EA1sin30°·cos30°）＝2FN2l/（EA2tan30°）＋FN3l/（EA3sin30°·cos30°）④ （3）求解 联立式①②④，可得各杆轴力：FN1＝8.45kN，FN2＝2.68kN，FN3＝11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2＝FN4③
（2）补充方程
如刚性板的位移图所示，根据几何关系可得：Δl1＋Δl3＝2Δl2④
由结构对称可知 Δl2＝Δl4，其中，由胡克定律可得各杆伸长量：
Δl1＝FN1l/EA，Δl2＝FN2l/EA，Δl3＝FN3l/EA
代入式④，整理可得补充方程：FN1＋FN3＝2FN2⑤
（3）求解
联立式①②③⑤，解得各杆轴力：
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1＝FN1l1/EA1＝FN1l/（EA1cos30°） Δl2＝FN2l2/EA2＝FN2l/（EA2） Δl3＝FN3l3/EA3＝FN3l/（EA3cos30°） 代入式③可得补充方程： FN1l/（EA1sin30°·cos30°）＝2FN2l/（EA2tan30°）＋FN3l/（EA3sin30°·cos30°）④ （3）求解 联立式①②④，可得各杆轴力：FN1＝8.45kN，FN2＝2.68kN，FN3＝11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2＝FN4③
（2）补充方程
如刚性板的位移图所示，根据几何关系可得：Δl1＋Δl3＝2Δl2④
由结构对称可知 Δl2＝Δl4，其中，由胡克定律可得各杆伸长量：
Δl1＝FN1l/EA，Δl2＝FN2l/EA，Δl3＝FN3l/EA
代入式④，整理可得补充方程：FN1＋FN3＝2FN2⑤
（3）求解
联立式①②③⑤，解得各杆轴力：
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
材料力学性能 习题解答
第6章 热学性能 习题解答名词解释：格波：晶格振动波。
声子：晶格振动波的量子化，严格意义上是晶格简谐振动的量子化。
光子：光波的量子化。
声频支振动：晶格振动波的振动频率在声频范围。
光频支振动：晶格振动波的振动频率在声频范围。
热容: “当一系统由于加给一微小的热量dQ 而温度升高dT 时，dQ/dT 这个量即是该系统的热容。
”（GB3102.4-93）即单位温度升高时所需要的热量。
杜隆—珀替定律：无论晶体属于何种类型，其比热容（单位焦耳／（开尔文·千克））均为3R/MM ，其中R 为普适气体常数（单位焦耳／（开尔文·摩尔））MM 为摩尔质量（单位千克／摩尔）。
热膨胀系数：实际应用中，有两种主要的热膨胀系数，分别是：线性热膨胀系数(CLTE)：体积热膨胀系数：热导率：单位温度梯度下，单位时间内通过单位垂直面积的热量。
热应力：温度改变时，物体由于外在约束以及内部各部分之间的相互约束，使其不能完全自由胀缩而产生的应力。
又称变温应力。
综合题：1． 热容的本质是什么？dT dx Q t S λ∆⨯∆⨯∆=-答案：物体分子对热量的敏感程度和反应强度。
敏感程度决定吸收多少热；反应强度决定升高多少温度。
这些与分子结构,分子间距离有关。
2. 阐述晶态固体的热容随温度的变化规律。
用经典理论解释热容的经验理论。
❖答案：高温下： C V =3N A K B=3R；低温下： C V正比于 T3。
能量均分3．德拜热容理论取得了什么成功?讨论德拜热容理论在实际应用中的优点及不足。
❖答案：高温下： C V =3N A K B=3R；低温下： C V正比于 T3。
理论与实验数据符合得比较好。
计算复杂。
4．影响热容的因素有哪些？答案：过程，等温过程，等压过程。
5．什么是非简谐振动？由于非简谐振动，引起声子发生怎样的变化？答案：非简谐振动，引起声子导热。
6．阐述固体材料的热膨胀机理。
答案：固体材料中原子受力不对称，导致热膨胀。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转
该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6－5 图
解：1． τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2． M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3． τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
16 M x
3 π d1
=
16 M x
3 π D2 (1 − α 4 )
即
d1 = (1 − α 4 ) 3 D2
1
（a）
二者重量之比
W1 A1 d2 = = 2 1 2 W2 A2 D2 (1 − α )
（b）
式（a）代入式（b） ，得
W1 (1 − α 4 ) = W2 1−α2
2 3
所以，正确答案是
16 M x 3 16 × 10.53 × 10 6 = = 96.3 π [τ ] π × 60
（3）按刚度条件求轴的直径
θ=
Mx ≤ [θ ] GI P
[θ ] = 1D / 2m =
π
180 × 2 × 10 3
rad/mm
6
D≥4
32M x 32 × 10.53 × 10 6 =4 = 110.6mm Gπ [θ ] 82 × 10 3 π [θ ]
材料力学习题第六章应力状态分析答案详解
第6章 应力状态分析一、选择题1、对于图示各点应力状态，属于单向应力状态的是（A ）。
（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点 。
2、在平面应力状态下，对于任意两斜截面上的正应力αβσσ=成立的充分必要条件，有下列四种答案，正确答案是（ B ）。
（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ，现关于AC 面上应力有下列四种答案，正确答案是（ C ）。
（A ）AC AC /2,0ττσ==； （B）AC AC /2,/2ττσ==； （C）AC AC /2,/2ττσ==；（D）AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图（a ）所示，横截面上各点的应力状态如图（b ）所示。
关于它们的正确性，现有四种答案，正确答案是（ D ）。
（A ）点1、2的应力状态是正确的；（B ）点2、3的应力状态是正确的； （C ）点3、4的应力状态是正确的；（D ）点1、5的应力状态是正确的。
5、对于图示三种应力状态（a ）、（b ）、（c ）之间的关系，有下列四种答案，正确答案是（ D ）。
（A ）三种应力状态均相同；（B ）三种应力状态均不同； （C ）（b ）和（c ）相同； （D ）（a ）和（c ）相同；6、关于图示主应力单元体的最大切应力作用面有下列四种答案，正确答案是（ B ）。
解答：max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围，有下列四种答案，正确答案是（ C ）。
（A ）脆性材料；（B ）塑性材料；（C ）材料为各向同性，且处于线弹性范围内；（D ）任何材料； 8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适用于（ C ）。
（A ）任何材料在任何变形阶级； （B ）各向同性材料在任何变形阶级； （C ）各向同性材料应力在比例极限范围内；（D ）任何材料在弹性变形范围内。
材料力学课后答案d
(3)、(4) 四种情况的最大剪力和最大弯矩，那么，下列式子中，正确的有 D E 。
-3-
工程力学习题解答
A． M 1 > M 2 > M 3 > M 4 C． M1 > M 2 = M 3 > M 4 E． FS1 = FS2 = FS3 = FS4
F
B． M1 = M 2 > M 3 > M 4 D． M 1 > M 2 > M 3 = M 4 F． FS1 > FS2 > FS3 > FS4
A
B
C
D
分析：这是对称结构承受对称荷载的情况，支反力偶矩必定对称，扭矩图必定反对称。
-2-
第 6 章 杆件的内力
因此只需根据支反力偶矩进一步判断扭矩正负即可。
6-2(4) 在梁的集中力作用处，其左、右两侧无限接近的横截面上的弯矩是 A 的。
A．相同
B．数值相等，符号相反
C．不相同
D．符号一致，数值不相等
−
1 4
q0 L
−
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⎠
−
FS
=
0
，
FS
=
1 4
q0 L
−
q0 x
。
∑m = 0 ，
M
+
q0 L 4
⎜⎛ x ⎝
−
L 2
⋅
2 ⎟⎞ 3⎠
+
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⋅ ⎠
1 ⎜⎛ x 2⎝
−
L 2
⎟⎞ ⎠
=
0，
M = − q0 (12x2 − 6Lx + L2 ) 。 24
-3-
工程力学习题解答
A． M 1 > M 2 > M 3 > M 4 C． M1 > M 2 = M 3 > M 4 E． FS1 = FS2 = FS3 = FS4
F
B． M1 = M 2 > M 3 > M 4 D． M 1 > M 2 > M 3 = M 4 F． FS1 > FS2 > FS3 > FS4
A
B
C
D
分析：这是对称结构承受对称荷载的情况，支反力偶矩必定对称，扭矩图必定反对称。
-2-
第 6 章 杆件的内力
因此只需根据支反力偶矩进一步判断扭矩正负即可。
6-2(4) 在梁的集中力作用处，其左、右两侧无限接近的横截面上的弯矩是 A 的。
A．相同
B．数值相等，符号相反
C．不相同
D．符号一致，数值不相等
−
1 4
q0 L
−
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⎠
−
FS
=
0
，
FS
=
1 4
q0 L
−
q0 x
。
∑m = 0 ，
M
+
q0 L 4
⎜⎛ x ⎝
−
L 2
⋅
2 ⎟⎞ 3⎠
+
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⋅ ⎠
1 ⎜⎛ x 2⎝
−
L 2
⎟⎞ ⎠
=
0，
M = − q0 (12x2 − 6Lx + L2 ) 。 24
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
wC = − 5qa 4 48 EI (↓)
，得截面 B 的转角为 将以上所得 C 值和 x = 2a 代入式（a）
θB =
q q 7qa 3 3qa 3 1 3qa ]= ( 2a ) 2 − ( 2 a ) 3 + ( 2a − a ) 3 − [ EI 8 48EI 16 6 6
和
1 qa 3 q 4 3qa 3 ( x − x − x) EI 8 24 16
5
w2 =
5．计算 wC 和 θB
3qa 3 1 qa 3 q 4 q x + x] [ x − ( x − a) 4 − EI 8 16 24 24
将 x = a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
(也可通过左侧题号书签直接查找题目与解)
6-2
大致形状。
图示各梁，弯曲刚度 EI 均为常数。试根据梁的弯矩图与约束条件画出挠曲轴的
题 6-2 图 解：各梁的弯矩图及挠曲轴的大致形状示如图 6-2。
1
6-4
图示简支梁，左、右端各作用一个力偶矩分别为 M1 与 M2 的力偶。如欲使挠曲
轴的拐点位于离左端 l/3 处，则力偶矩 M1 与 M2 应保持何种关系。
2．建立挠曲轴近似微分方程并积分
3
自 A 向右取坐标 x ，由题图可见，弯矩的通用方程为
M =
挠曲轴的通用近似微分方程为
Me x − M e < x − a >0 2a
EI
将其相继积分两次，得
d2w M e = x − M e < x − a >0 2 2a dx
dw M e 2 = x − M e < x − a > +C dx 4a M M EIw = e x 3 − e < x − a > 2 +Cx + D 12a 2 EI
由此得 AC 段与 CB 段的挠曲轴方程分别为
w1 =
和
1 M e 3 M ea ( x − x) 12 EI 12a
w2 =
M a 1 Me 3 Me [ x − ( x − a) 2 − e x] 2 12 EI 12a
θ 5．计算 wC 和
B
将 x = a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
题 6-4 图 解：解法 1，常规解法 1．建立弯矩方程 左端 A 的支反力为
FAy =
自左端向右取坐标 x ，弯矩方程为
M1 + M 2 l
()
M ( x) =
2．建立挠曲轴近似微分方程
M1 + M 2 x − M1 l
EI
M + M2 d2w = M ( x) = 1 x − M1 2 l dx
3．确定积分常数 该梁的位移边界条件为： 在 x = 0 处， w = 0 在 x = 2a 处， w = 0 将条件(c)代入式(b)，得
(a) (b)
(c) (d)
D=0
将条件(d)代入式(b)，得
C=−
M ea 12
4．建立挠曲轴方程 将所得 C、D 值代入式(b)，得挠曲轴的通用方程为
w=
M a 1 Me 3 Me < x − a > 2 − e x] [ x − 2 12 EI 12a
M 2 : M1 =
直接得到
2l l : 3 3
M 2 = 2M 1
6-6
的挠度。
图示各梁，弯曲刚度 EI 均为常数。试用奇异函数法计算截面 B 的转角与截面 C
题 6-6 图 (a)解：1.求支反力 由梁的平衡方程
∑M
B
= 0 和 ∑ Fy = 0 可得
FAy = Me M (↑)，FBy = e (↓) 2a 2a
2
依题意，在 x = l / 3 处有拐点，即 w′′ = 0 ，于是，
(
由此得
M1 + M 2 l ) − M1 = 0 3 l
M 2 = 2M 1
解法 2，简便解法 分析本题的弯矩图:左端为 − M 1 ，右端为 + M 2 ，将这两个端值点连线，即得到 M 图， 示如图 6-4。 M ( x ) = 0 的点为拐点，依题意，此点应在 x = l / 3 处，由几何上的比例关系
dw 3qa 2 q 3 q = x − x + < x − a > 3 +C dx 8 6 6 qa 3 q 4 q EIw = x − x + < x − a > 4 +Cx + D 8 24 24
EI
(a) (b)
3．确定积分常数 该梁的位移边界条件为： 在 x = 0 处， w = 0 在 x = 2a 处， w = 0 将条件(c)、(d)分别代入式(b)，得
(c) (d)
D = 0，C = −
3qa 3 16
4．建立挠曲轴方程 将所得 C 、 D 值代入式(b),得挠曲轴的通用方程为
w=
1 qa 3 q 4 q 3qa 3 [ x − x + < x − a >4 − x] EI 8 24 24 16
由此得 AC 段与 CB 段的挠曲轴方程分别为
w1 =
FBy =
1 qa (↑) 4
2．建立挠曲轴近似微分方程并积分 自 A 向右取坐标 x ，由题图可见，弯矩的通用方程为
M =
q q 3qa x − x2 + < x − a >2 4 2 2
挠曲轴的通用近似微分方程为
EI
将其相继积分两次，得
d 2 w 3qa q q = x − x2 + < x − a >2 2 4 2 2 dx
wC = 0
4
将以上所得 C 值和 x = 2a 代入式(a)，得截面 B 的转角为
θB =
(b)解：1.求支反力 由梁的平衡方程
1 4 M ea 2 Ma Ma − M ea − e ) = − e (3) ( EI 4a 12 12 EI
∑M
B
= 0 和 ∑ Fy = 0 可得
FAy =
3 qa (↑)， 4
第六章
题号
弯曲变形
页码
6-2 .........................................................................................................................................................1 6-4 .........................................................................................................................................................2 6-6 .........................................................................................................................................................3 6-8 .........................................................................................................................................................8 6-9 .......................................................................................................................................................10 6-12 .....................................................................................................................................................11 6-14 .....................................................................................................................................................11 6-15 .....................................................................................................................................................13 6-16 .....................................................................................................................................................14 6-18 .....................................................................................................................................................16 6-20 .....................................................................................................................................................17 6-22 .....................................................................................................................................................18 6-24 .....................................................................................................................................................19 6-25 .....................................................................................................................................................19 6-26 .....................................................................................................................................................20 6-27 .....................................................................................................................................................22 6-28 .....................................................................................................................................................24 6-29 .....................................................................................................................................................25
，得截面 B 的转角为 将以上所得 C 值和 x = 2a 代入式（a）
θB =
q q 7qa 3 3qa 3 1 3qa ]= ( 2a ) 2 − ( 2 a ) 3 + ( 2a − a ) 3 − [ EI 8 48EI 16 6 6
和
1 qa 3 q 4 3qa 3 ( x − x − x) EI 8 24 16
5
w2 =
5．计算 wC 和 θB
3qa 3 1 qa 3 q 4 q x + x] [ x − ( x − a) 4 − EI 8 16 24 24
将 x = a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
(也可通过左侧题号书签直接查找题目与解)
6-2
大致形状。
图示各梁，弯曲刚度 EI 均为常数。试根据梁的弯矩图与约束条件画出挠曲轴的
题 6-2 图 解：各梁的弯矩图及挠曲轴的大致形状示如图 6-2。
1
6-4
图示简支梁，左、右端各作用一个力偶矩分别为 M1 与 M2 的力偶。如欲使挠曲
轴的拐点位于离左端 l/3 处，则力偶矩 M1 与 M2 应保持何种关系。
2．建立挠曲轴近似微分方程并积分
3
自 A 向右取坐标 x ，由题图可见，弯矩的通用方程为
M =
挠曲轴的通用近似微分方程为
Me x − M e < x − a >0 2a
EI
将其相继积分两次，得
d2w M e = x − M e < x − a >0 2 2a dx
dw M e 2 = x − M e < x − a > +C dx 4a M M EIw = e x 3 − e < x − a > 2 +Cx + D 12a 2 EI
由此得 AC 段与 CB 段的挠曲轴方程分别为
w1 =
和
1 M e 3 M ea ( x − x) 12 EI 12a
w2 =
M a 1 Me 3 Me [ x − ( x − a) 2 − e x] 2 12 EI 12a
θ 5．计算 wC 和
B
将 x = a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
题 6-4 图 解：解法 1，常规解法 1．建立弯矩方程 左端 A 的支反力为
FAy =
自左端向右取坐标 x ，弯矩方程为
M1 + M 2 l
()
M ( x) =
2．建立挠曲轴近似微分方程
M1 + M 2 x − M1 l
EI
M + M2 d2w = M ( x) = 1 x − M1 2 l dx
3．确定积分常数 该梁的位移边界条件为： 在 x = 0 处， w = 0 在 x = 2a 处， w = 0 将条件(c)代入式(b)，得
(a) (b)
(c) (d)
D=0
将条件(d)代入式(b)，得
C=−
M ea 12
4．建立挠曲轴方程 将所得 C、D 值代入式(b)，得挠曲轴的通用方程为
w=
M a 1 Me 3 Me < x − a > 2 − e x] [ x − 2 12 EI 12a
M 2 : M1 =
直接得到
2l l : 3 3
M 2 = 2M 1
6-6
的挠度。
图示各梁，弯曲刚度 EI 均为常数。试用奇异函数法计算截面 B 的转角与截面 C
题 6-6 图 (a)解：1.求支反力 由梁的平衡方程
∑M
B
= 0 和 ∑ Fy = 0 可得
FAy = Me M (↑)，FBy = e (↓) 2a 2a
2
依题意，在 x = l / 3 处有拐点，即 w′′ = 0 ，于是，
(
由此得
M1 + M 2 l ) − M1 = 0 3 l
M 2 = 2M 1
解法 2，简便解法 分析本题的弯矩图:左端为 − M 1 ，右端为 + M 2 ，将这两个端值点连线，即得到 M 图， 示如图 6-4。 M ( x ) = 0 的点为拐点，依题意，此点应在 x = l / 3 处，由几何上的比例关系
dw 3qa 2 q 3 q = x − x + < x − a > 3 +C dx 8 6 6 qa 3 q 4 q EIw = x − x + < x − a > 4 +Cx + D 8 24 24
EI
(a) (b)
3．确定积分常数 该梁的位移边界条件为： 在 x = 0 处， w = 0 在 x = 2a 处， w = 0 将条件(c)、(d)分别代入式(b)，得
(c) (d)
D = 0，C = −
3qa 3 16
4．建立挠曲轴方程 将所得 C 、 D 值代入式(b),得挠曲轴的通用方程为
w=
1 qa 3 q 4 q 3qa 3 [ x − x + < x − a >4 − x] EI 8 24 24 16
由此得 AC 段与 CB 段的挠曲轴方程分别为
w1 =
FBy =
1 qa (↑) 4
2．建立挠曲轴近似微分方程并积分 自 A 向右取坐标 x ，由题图可见，弯矩的通用方程为
M =
q q 3qa x − x2 + < x − a >2 4 2 2
挠曲轴的通用近似微分方程为
EI
将其相继积分两次，得
d 2 w 3qa q q = x − x2 + < x − a >2 2 4 2 2 dx
wC = 0
4
将以上所得 C 值和 x = 2a 代入式(a)，得截面 B 的转角为
θB =
(b)解：1.求支反力 由梁的平衡方程
1 4 M ea 2 Ma Ma − M ea − e ) = − e (3) ( EI 4a 12 12 EI
∑M
B
= 0 和 ∑ Fy = 0 可得
FAy =
3 qa (↑)， 4
第六章
题号
弯曲变形
页码
6-2 .........................................................................................................................................................1 6-4 .........................................................................................................................................................2 6-6 .........................................................................................................................................................3 6-8 .........................................................................................................................................................8 6-9 .......................................................................................................................................................10 6-12 .....................................................................................................................................................11 6-14 .....................................................................................................................................................11 6-15 .....................................................................................................................................................13 6-16 .....................................................................................................................................................14 6-18 .....................................................................................................................................................16 6-20 .....................................................................................................................................................17 6-22 .....................................................................................................................................................18 6-24 .....................................................................................................................................................19 6-25 .....................................................................................................................................................19 6-26 .....................................................................................................................................................20 6-27 .....................................................................................................................................................22 6-28 .....................................................................................................................................................24 6-29 .....................................................................................................................................................25