安徽省滁州市重点中学2019-2020学年高一下学期期末2份数学调研试题
安徽省名校2019-2020学年高一下学期期末联考数学题(原卷版)

3.本试卷主要考试内容:人教A版必修2第一、二章,必修5.
第I卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一个几何体有6个顶点,则这个几何体可能是()
A.三棱柱B.四棱锥C.四棱柱D.五棱台
2.在 中,角 , , 所对 边分别为 , , .已知 , , ,则 ()
16.如图,在正方体 中,点P是 上的任意一点,点M,N分别是AB和BC上的点,且 ,若 ,则三棱锥 体积的最大值是_______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.如图,在正方体 中,M,N分别是 , 的中点.证明:
(1) 平面 ;
(2) 平面 .
如图在三棱柱111abcabc?中1aa?平面abc四边形11bccb为正方形24bcab??abbc?d为11cb的中点则异面直线11ac与ad所成角的余弦值为a
2019~2020高一第二学期期末考试
数学试卷
考生注意:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分.考试时间120分钟.
A.-2B.1C. D.
7.已知l,m,n为不同 直线, , , 为不同的平面,则下列判断错误的是()
A.若 , , .则
B.若 , , ,则
C.若 , , , ,则
D.若 , ,则
8.已知 , ,且 ,则 的最小值是()
A.4B.6C.8D.2
9.如图,在三棱柱 中, 平面 ,四边形 为正方形, , ,D为 的中点,则异面直线 与 所成角的余弦值为()
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上.
安徽省滁州市2020年高一下期末质量跟踪监视数学试题含解析

安徽省滁州市2020年高一下期末质量跟踪监视数学试题一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知,,a b c 分别是ABC ∆的内角,,A B C 的的对边,若cos cA b<,则ABC ∆的形状为( ) A .钝角三角形 B .直角三角形C .锐角三角形D .等边三角形【答案】A 【解析】 【分析】由已知结合正弦定理可得sin sin cos A C B <利用三角形的内角和及诱导公式可得,sin()sin cos A B B A +<整理可得sin cos sin cos sin cos A B B A B A +<从而有sin cos 0A B <结合三角形的性质可求 【详解】 解:A 是ABC ∆的一个内角,0A π<<,sin 0cos A cA b∴>< 由正弦定理可得,sin sin cos C B A <sin()sin cos sin cos sin cos sin cos sin cos 0A B B AA B B A B A A B ∴+<∴+<∴< 又sin 0A >,cos 0B ∴<,即B 为钝角,故选A . 【点睛】本题主要考查了正弦定理,三角形的内角和及诱导公式,两角和的正弦公式,属于基础试题. 2.若函数()gx 的图象可由函数()sin 22f x x x =+ 的图象向右平移6π个单位长度变换得到,则()g x 的解析式是( )A . ()2sin 2g x x =B .()2sin 26g x x π⎛⎫=+⎪⎝⎭ C .()2cos2g x x = D .2g()2sin 23x x π⎛⎫=+⎪⎝⎭【答案】A 【解析】 【分析】先化简函数()f x ,然后再根据图象平移得()g x .【详解】由已知()2sin(2)3f x x π=+,∴()2sin[2()]2sin 263g x x x ππ=-+=.故选A . 【点睛】本题考查两角和的正弦公式,考查三角函数的图象平移变换,属于基础题. 3.如图,设、两点在河的两岸,一测量者在的同侧,在所在河岸边选定一点,测出的距离为,,后,就可以计算、两点的距离为( )A .B .C .D .【答案】A 【解析】 【分析】 计算出三个角的值,然后利用正弦定理可计算出的值.【详解】 在中,,,,即,由正弦定理得,,解得,故选A.【点睛】本题考查正弦定理解三角形,要熟悉正弦定理解三角形对三角形已知元素类型的要求,考查运算求解能力,属于基础题. 4.函数32cos 2y x x =-的图象向右平移02πϕϕ⎛⎫<<⎪⎝⎭个单位后,得到函数()y g x =的图象,若()y g x =为偶函数,则ϕ的值为( )A .12πB .6π C .4π D .3π 【答案】B 【解析】f (x )=3sin2x ﹣cos2x=2sin (2x ﹣6π)的图象向左平移φ(0<φ<2π)个单位,得到 g (x )=2sin (2x-2φ﹣6π).()y g x =为偶函数,故得到()02g =±,故得到2sin (-2φ﹣6π)=-2或2,,32k k z ππφ=--∈. 因为02πϕ<<,故得到,k=-1,ϕ的值为6π. 故答案为B .5.如图为某班35名学生的投篮成绩(每人投一次)的条形统计图,其中上面部分数据破损导致数据不完全。
安徽省滁州市高一下学期数学期末考试试卷

安徽省滁州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)下列向量中不是单位向量的是()A . (﹣1,0)B . (1,1)C . (cosa,sina)D .2. (2分)已知如图所示的程序框图(未完成).设当箭头a指向①时,输出的结果为s=m,当箭头a指向②时,输出的结果为s=n,则m+n=()A . 30B . 20C . 15D . 53. (2分) (2018高三上·昆明期末) 已知,则等于()A .B .C .D .4. (2分)(2017·池州模拟) 某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为a,b,且直线ax+by+8=0与以A(1,﹣1)为圆心的圆交于B,C两点,且∠BAC=120°,则圆C的方程为()A . (x﹣1)2+(y+1)2=1B . (x﹣1)2+(y+1)2=2C . (x﹣1)2+(y+1)2=D . (x﹣1)2+(y+1)2=5. (2分)已知下列命题中:(1)若,且,则k=0或,(2)若,则或(3)若不平行的两个非零向量,,满足,则(4)若与平行,则其中真命题的个数是()A . 0B . 1C . 2D . 36. (2分)(2019·江门模拟) 某地气象局把当地某月(共30天)每一天的最低气温作了统计,并绘制了如下图所示的统计图,假设该月温度的中位数为,众数为,平均数为,则()A .B .C .D .7. (2分) (2017高二下·陕西期末) 函数y= 的部分图象大致为()A .B .C .D .8. (2分) (2017高三上·东莞期末) 已知函数的最小正周期为π,将函数f(x)的图象向右平移个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是()A . g(x)为奇函数B . 关于直线对称C . 关于点(π,0)对称D . 在上递增9. (2分) (2017高二下·杭州期末) 设A,B是函数f(x)=sin|ωx|与y=﹣1的图象的相邻两个交点,若|AB|min=2π,则正实数ω=()A .B . 1C .D . 210. (2分) (2017高一上·武汉期末) 如图,在圆C中,C是圆心,点A,B在圆上,• 的值()A . 只与圆C的半径有关B . 只与弦AB的长度有关C . 既与圆C的半径有关,又与弦AB的长度有关D . 是与圆C的半径和弦AB的长度均无关的定值11. (2分)一条直线的倾斜角的正弦值为,则此直线的斜率为()A .B . ±C .D . ±12. (2分) (2017高三上·珠海期末) 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)图象如图所示,则下列关于函数 f (x)的说法中正确的是()A . 对称轴方程是x= +kπ(k∈Z)B . 对称中心坐标是(+kπ,0)(k∈Z)C . 在区间(﹣,)上单调递增D . 在区间(﹣π,﹣)上单调递减二、填空题 (共4题;共13分)13. (1分)(2020·包头模拟) 若函数在和上均单调递增,则实数m 的取值范围为________.14. (1分)用秦九韶算法求多项式f(x)=3x5﹣2x4+3x3﹣6x2+7x﹣8当x=2时的值的过程中v3=________.15. (1分) (2016高二上·潮阳期中) 已知圆O:x2+y2=1和点A(﹣2,0),若顶点B(b,0)(b≠﹣2)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则λ﹣b=________.16. (10分) (2016高一下·珠海期末) 在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:(1)当a,b均为整数时;(2)当a,b均为实数时.三、解答题 (共6题;共45分)17. (5分)已知=﹣1,求下列各式的值:(1);(2)sin2α+sinαcos α+2.18. (10分) (2020高二下·海丰月考) 2020年年初,新冠肺炎疫情防控工作全面有序展开.某社区对居民疫情防控知识进行了网上调研,调研成绩全部都在40分到100分之间.现从中随机选取200位居民的调研成绩进行统计,绘制了如图所示的频率分布直方图.(1)求a的值,并估计这200位居民调研成绩的中位数;(2)在成绩为,的两组居民中,用分层抽样的方法抽取6位居民,再从6位居民中随机抽取2位进行详谈.记X为2位居民的调研成绩在的人数,求随机变量X的分布列.19. (5分) (2016高一下·卢龙期中) 如图,在平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若 = , = ,试以,为基底表示、、.20. (5分) (2017高三上·山西开学考) 在某大学自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.(Ⅰ)求该考场考生中“阅读与表达”科目中成绩为A的人数;(Ⅱ)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;(Ⅲ)已知参加本考场测试的考生中,恰有两人的两科成绩均为A.在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.21. (10分)已知圆: x2+y2+Dx+Ey+3=0 ,圆关于直线 x+y-1=0对称,圆心在第二象限,半径为.(1)求圆的方程;(2)已知不过原点的直线 l 与圆相切,且在轴、轴上的截距相等,求直线 l 的方程.22. (10分) (2016高三上·台州期末) 已知函数f(x)=2 sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.(1)求B;(2)若• =3,求b的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共13分)13-1、14-1、15-1、16-1、16-2、三、解答题 (共6题;共45分)17-1、18-1、18-2、19-1、20-1、21-1、21-2、22-1、22-2、。
2020学年安徽省滁州市新高考高一数学下学期期末调研试题

2019-2020学年高一下学期期末数学模拟试卷一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在平面直角坐标系xOy 中,直线:0l x y -=的倾斜角为( ) A .0︒ B .45︒C .90︒D .135︒2.已知1tan 2α=,则cos2=α( ) A .35B .25C .35D .25-3.设n S 为等比数列{}n a 的前n 项和,若2580a a +=,则52S S =( ) A .-11B .-8C .5D .114.一组数123,,,,n x x x x 平均数是x ,方差是2s123,3n x)A 2sB2sC2s+D2+5.在集合{6x x ≤且}x N ∈中任取一个元素,所取元素x 恰好满足方程()11x-=的概率是( ) A .37B .47C .12D .256.已知β为锐角,角α的终边过点((),2sin αβ+=cos β=( ) A .12B.4C.4D.47.已知等比数列{a n }中,a 3•a 13=20,a 6=4,则a 10的值是( ) A .16B .14C .6D .58.已知等差数列{a n },若a 2=10,a 5=1,则{a n }的前7项和为 A .112B .51C .28D .189.一个圆柱的侧面展开图是一个正方形,这个圆柱全面积与侧面积的比为( ) A .122ππ+ B .144ππ+ C .12ππ+ D .142ππ+ 10.将函数sin 23y x π⎛⎫=-⎪⎝⎭的图象向右平移6π个的单位长度,再将所得到的函数图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),则所得到的图象的函数解析式为( ) A .2sin 3y x π⎛⎫=-⎪⎝⎭B .2sin 43y x π⎛⎫=-⎪⎝⎭C .sin 2y x π⎛⎫=-⎪⎝⎭D .sin 42y x π⎛⎫=-⎪⎝⎭11.已知数列1,x ,y ,9是等差数列,数列1,a ,b ,c ,9是等比数列,则bx y=+() A .910B .310C .310-D .310±12.已知,x y 都是正数,且211x y+=,则x y +的最小值等于 A .6 B .42 C .322+D .422+二、填空题:本题共4小题 13.函数1()ln f x x=的定义域记作集合D ,随机地投掷一枚质地均匀的正方体骰子(骰子的每个面上分别标有点数1,2,⋅⋅⋅,6),记骰子向上的点数为t ,则事件“t D ∈”的概率为________.14.已知{}n a 是以15-为首项,2为公差的等差数列,n S 是其前n 项和,则数列{}n S 的最小项为第___项15.如图,四棱锥P ABCD -中,所有棱长均为2,O 是底面正方形ABCD 中心,E 为PC 中点,则直线OE 与直线PD 所成角的余弦值为____________.16.等比数列{}n a 前n 项和为n S ,若634S S =,则96S S =______. 三、解答题:解答应写出文字说明、证明过程或演算步骤。
安徽省滁州市天长市某中学2019-2020学年高一下学期期末模考数学试卷

数学试题一、选择题(本题共计12 小题,每题5 分,共计60分,)1. 若角的终边过点,则的值为( )A. B. C. D.2. 已知,则A. B. C. D.3. 在中,若,,,则)A. B. C. D.4. 在中,角,,的对边分别为,,,若,,成等差数列,,,成等比数列,则A. B. C. D.5. 已知等差数列中,=,前项的和等于前项的和,若=,则=A. B. C. D.6. 若实数,满足,则=的最大值为()A. B. C. D.7. 如图是函数=在区间上的图象,为了得到=的图象,只需将函数的图象上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变B.向右平移个单位长度,再把所得各点的横坐标伸长到原来的倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变D.向右平移个单位长度,再把所得各点的横坐标伸长到原来的倍,纵坐标不变8. 若不等式对一切成立,则的最小值为A. B. C. D.9. 设,满足条件若目标函数的最大值为,则的最小值为()A. B. C. D.10. 如图,半圆的直径,为圆心,为半圆上不同于,的任意一点,若为半径上的动点,则的最小值为( )A. B. C. D.11. 若函数在上有两个零点,则的取值范围是A. B. C. D.12. 一辆邮车从地往地运送邮件,沿途共有地,依次记为,,…(为地,为地).从地出发时,装上发往后面地的邮件各件,到达后面各地后卸下前面各地发往该地的邮件,同时装上该地发往后面各地的邮件各件,记该邮车到达,,…各地装卸完毕后剩余的邮件数记为=,…,.则的表达式为()A. B. C. D.二、填空题(本题共计4 小题,每题5 分,共计20分,)13. 点和在直线=的两侧,则实数的取值范围是________.14. 记为数列的前项和,,则_______.15. 已知是单位向量,且满足,则向量在方向上的投影是______.16. 已知函数的周期为,当时,函数恰有两个不同的零点,则实数的取值范围是________.三、解答题(本题共计6 小题,共计70分,)17.(10分) 设等差数列的前项和为,已知,.求数列的通项公式;若数列满足:,求数列的前项和.18.(12分) 在锐角中,角,,所对的边分别是,,,且.(1)求角的大小;(2)求的范围.19.(12分) 在中,内角,,所对的边分别为,,,已知.证明:;若的面积,求角的大小.20.(12分) 已知,且,求:的最小值;的最小值.21.(12分) 设数列中=,=,且数列,,…,,…,是以为公比的等比数列.(1)求数列的通项公式;(2)求数列的前项和.22.(12分) 已知函数.求函数的最小正周期及单调递增区间;在中,角所对的边分别为,且,求面积的最大值.数学答案一、选择题(本题共计12 小题,每题 5 分,共计60分)1.【答案】C【解答】解:∵角的终边过点,∴根据三角函数的定义知,故选.2.【答案】D【解答】解:,.故选.3.【答案】A【解答】解:∵在中,,,∴由正弦定理可得,∴.故选.4.【答案】A【解答】解:由题意可得,,成等差数列,可得,,,成等比数列,,由正弦定理可得,∴,∴,∵,∴.故选.5.【答案】B【解答】设等差数列的公差为,=,前项的和等于前的和,=,则=,=,解得=.6.【答案】D【解答】画出实数,满足可行域,由图可知目标函数=经过点时取得最大值.7.【答案】D【解答】根据函数=在区间上的图象,可得=,,∴=.再根据五点法作图,=,求得,故函数=.故把的图象向右平移个单位长度,可得=的图象;再把所得各点的横坐标伸长到原来的倍,纵坐标不变,可得=的图象,8.【答案】C【解答】解:设,则对称轴为,若,即时,则在,上是减函数,应有,若,即时,则在,上是增函数,应有恒成立,故,若,即,则应有恒成立,故,综上,有.故选.9.【答案】D【解答】解:不等式表示的平面区域如图所示阴影部分,当直线过直线与直线的交点时,目标函数取得最大值,∴,即,∴.当且仅当时,的最小值为.故选D.10.【答案】C【解答】解:∵圆心是直径的中点,∴,所以,∵与共线且方向相反∴当大小相等时点乘积最小,由条件知当时,最小值为.故选.11.【答案】C【解答】解:,则当,,又在上有两个零点,,解得.故选.12.【答案】D【解答】根据题意,该邮车到第站时,一共装上了……件邮件,需要卸下……件邮件,则,二、填空题(本题共计4 小题,每题 5 分,共计20分)13.【答案】【解答】由题意点和在直线=的两侧∴即解得14.【答案】【解答】解:由,得,两式相减得,即,所以,由,得,所以,故答案为:.15.【答案】【解答】解:∵,∴,∴,∴.又∵,∴向量在方向上的投影为:.故答案为:.16.【答案】【解答】解:.因为,所以,所以.因为,所以,所以,由得,即的图象与直线恰有两个交点,结合图象(图略)可知,即.故实数的取值范围是.故答案为:.三、解答题(本题共计6 小题,共计70分)17.【答案】解:设数列的公差为,由,得,又.解得,,因此的通项公式是:.由知,所以.【解答】解:设数列的公差为,由,得,又.解得,,因此的通项公式是:.由知,所以.18.【答案】解:(1)因为,所以,因为,所以,又,所以,可得:,因为是锐角三角形,所以,,,(2)因为,所以,,因为是锐角三角形,所以,的范围.【解答】解:(1)因为,所以,因为,所以,又,所以,可得:,因为是锐角三角形,所以,,,(2)因为,所以,,因为是锐角三角形,所以,的范围.19.【答案】证明:∵,∴由正弦定理得,∴,∴,∴. ∵,是三角形中的角,∴,∴;∵的面积,∴,∴,∴,∴,∴,或,∴或.【解答】证明:∵,∴由正弦定理得,∴,∴,∴. ∵,是三角形中的角,∴,∴;∵的面积,∴,∴,∴,∴,∴,或,∴或.20.【答案】解:∵,且,∴,∴,∴,当且仅当时取等号,故的最小值为;由,得:,又,,∴,当且仅当时取等号,故的最小值为.【解答】解:∵,且,∴,∴,∴,当且仅当时取等号,故的最小值为;由,得:,又,,∴,当且仅当时取等号,故的最小值为.21.【答案】数列,,…,,…,是以为首项,为公比的等比数列,可得=,可得===;由=,可得数列为首项为,为公比的等比数列,可得前项和.【解答】数列,,…,,…,是以为首项,为公比的等比数列,可得=,可得===;由=,可得数列为首项为,为公比的等比数列,可得前项和.22.【答案】解:,所以函数的最小正周期为.令,解得,所以函数的单调递增区间为.由,得,又,所以,解得.由,得,即,亦即,当且仅当时等号成立.从而,所以面积的最大值为.【解答】解:,所以函数的最小正周期为.令,解得,所以函数的单调递增区间为.由,得,又,所以,解得.由,得,即,亦即,当且仅当时等号成立.从而,所以面积的最大值为.。
2019-2020学年安徽省滁州市民办高中高一下学期期末数学试题(解析版)

2019-2020学年安徽省滁州市民办高中高一下学期期末数学试题一、单选题1.若x,y 均大于零,且1x y +=,则14x y+的最小值为( ) A .5 B .4C .9D .10【答案】C【解析】做乘法144()()559y x x y x y x y ++=++≥+= ,则149x y +≥ ,选C2.等差数列{}n a 的前n 项和为n S ,已知32110S a a =+,534a =,则1a =( ) A .2 B .3C .4D .5【答案】A【解析】设等差数列{a n }的公差为d ,∵S 3=a 2+10a 1,a 5=34,∴3a 1+3d =11a 1+d ,a 1+4d =34, 则a 1=2. 本题选择A 选项.3.已知ABC 中,A 、B 、C 的对边分别为a 、b 、c .若a c ==且75A =︒,则b 等于( )A .2B -C .4-D .4+ 【答案】A【解析】由正弦的和角公式可求得sin 4A =180-B AC =-,利用正弦定理即可求得结果. 【详解】()sin sin 75sin 3045A =︒=︒+︒=, 由a c =知,75C =°,30B =︒,1sin 2B =,由正弦定理624sin sin 62b aB A+===+,∴4sin 2b B ==.故选:A. 【点睛】本题考查正弦的和角公式及正弦定理在解三角形中的应用,难度较易.4.从原点O 引圆222()(2)1x m y m -+-=+的切线为y kx =,当m 变化时切点P 的轨迹方程是( ) A .222x y += B .22(1)3x y -+= C .22(1)(1)1x y -+-=D .223x y +=【答案】D 【解析】22224133OP m m x y =+--=∴+= 选D.5.若直线l 经过点()1,2A ,且在x 轴上的截距的取值范围是()3,3-,则其斜率的取值范围是( ) A .115k -<< B .1k >或12k < C .12k >或1k <- D .115k << 【答案】C【解析】因为直线l 过点2(1)A , ,在x 轴上的截距取值范围是(33)-, ,所以直线端点的斜率分别为:20201113132--=-=-+, ,如图:所以12k >或1k <-.故选C . 6.若某空间几何体的三视图如图所示,则该几何体的体积为( )A .2π+3B .4π+3C 23D 23【答案】C【解析】【详解】试题分析:由三视图知几何体是一个简单的组合体,上面是一个四棱锥,四棱锥的底面是一个正方形,对角线长是2,侧棱长22213-=是一个圆柱,圆柱的底面直径是2,高是2,所以组合体的体积是2112322312232ππ⨯⨯⨯⨯⨯=,故选C. 【考点】几何体的三视图及体积的计算. 【方法点晴】本题主要考查了几何体的三视图及其体积的计算,着重考查了推理和运算能力及空间想象能力,属于中档试题,解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则,还原出原几何体的形状,本题的解答中根据三视图得出上面一个四棱锥、下面是一个圆柱组成的组合体,得到几何体的数量关系是解答的关键,属于基础题.7.设1321211a 2b logc log 33-===,,,则( ) A .a b c << B .a c b <<C .b a c <<D .b c a <<【答案】C【解析】构造函数,利用函数单调性,比较大小. 【详解】1302102-<=<,12222211log log 3log 210log 1log 33=>=>=>.所以c a b >>,故选C. 【点睛】本题主要考查数值的比较大小.一般求解思路有:一是利用中间值(0或1)比较大小;二是在函数图像上找到对应的点,比较点的纵坐标的大小.8.设l 是一条直线,α,β,γ是不同的平面,则下列说法不正确的是( ) A .如果αβ⊥,那么α内一定存在直线平行于βB .如果α不垂直于β,那么α内一定不存在直线垂直于βC .如果αγ⊥,βγ⊥,l αβ=,那么l γ⊥D .如果αβ⊥,l 与α,β都相交,那么l 与α,β所成的角互余 【答案】D【解析】根据线面平行、线面垂直、面面垂直、线面角的有关知识对选项逐一分析,由此确定正确选项. 【详解】对于A 选项,若αβ⊥,且l αβ=,则α内与l 平行的直线与β平行,所以A 选项说法正确.对于B 选项,“如果α不垂直于β,那么α内一定不存在直线垂直于β”的逆否命题为“若α内存在一条直线l 垂直于β,则αβ⊥”,这是面面垂直的判定定理.所以B 选项正确.对于C 选项,设,,,,a b l αγαγβγβγαβ⊥⋂=⊥⋂=⋂=,设C 是平面γ内一点,过C 在平面γ内作,CA a CB b ⊥⊥,分别交,a b 于,A B 两点. 根据面面垂直的性质定理可知,CA CB αβ⊥⊥,所以,CA l CB l ⊥⊥,而CA CB C ⋂=,所以l ⊥平面ABC ,也即l γ⊥.所以C 选项正确.对于D选项,设正方体1111ABCD A B C D-的棱长为1,设平面ABCD即平面α,平面11CDD C即平面β,平面ABCD⊥平面11CDD C.设直线1AC即直线l.根据正方体的性质以及线面角的定义可知,直线1AC与平面ABCD所成的角为1C AC∠,则在1Rt C AC中,1113sin3CCC ACAC∠===.根据正方体的性质以及线面角的定义可知,直线1AC与平面11CDD C所成的角为1AC D∠,则在1Rt ADC中,11126cos3C DAC DAC∠===.由于11sin cosC AC AC D∠≠∠.即l与α,β所成的角不互余,所以D选项说法错误.故选:D 【点睛】本小题主要考查空间线面、面面位置关系,属于基础题.9.如图,在空间四边形ABCD 中,AD=BC=2,E ,F 分别为AB ,CD 的中点,EF=2,则AD 与BC 所成的角为( )A .30°B .60°C .90°D .120°【答案】C【解析】取AC 的中点M ,连ME,MF , 因为点E ,F 分别为AB ,CD 的中点, 所以,ME BC MFAD ,且11==1,==122ME BC MF AD所以EMF ∠为异面直线AD 与BC 所成的角(或其补角), 在MEF ∆中, 1,2ME MF EF ===,所以222ME MF EF +=, 所以90EMF ∠=︒.即异面直线AD 与BC 所成的角为90︒.选C .10.如图,为测得河对岸塔AB 的高,先在河岸上选一点C ,使C 在塔底B 的正东方向上,测得点A 的仰角为60°,再由点C 沿北偏东15°方向走10m 到位置D ,测得45BDC ∠=︒,则塔AB 的高是(单位:m )( )A.B.C.D .10【答案】B【解析】设塔高为x 米,根据题意可知在△ABC 中,∠ABC=90°,∠ACB=60°,AB=x ,从而有BC=3x ,在△BCD 中,CD=10,∠BCD=105°,∠BDC=45°,∠CBD=30°,由正弦定理可求 BC ,从而可求x 即塔高. 【详解】设塔高为x 米,根据题意可知在△ABC 中,∠ABC=90°,∠ACB=60°,AB=x , 从而有x ,x , 在△BCD 中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30° 由正弦定理可得,sin sin BC CDBDC CBD=可得,BC=10sin 45sin 30x==.则;所以塔AB 的高是米; 故选B . 【点睛】本题主要考查了正弦定理在实际问题中的应用,解决本题的关键是要把实际问题转化为数学问题,即正确建立数学模型,结合已知把题目中的数据转化为三角形中的数据,进而选择合适的公式进行求解.11.在等比数列{}n a 中,315,a a 是方程2680x x -+=的根,则1179a a a = A . B .2 C .1 D .2-【答案】A 【解析】由题得3153156,8a a a a +=⎧⎨=⎩所以211798a a a ==,再求出9a 即得解.【详解】由题得3153156,8a a a a +=⎧⎨=⎩所以211798a a a ==,因为3153156080a a a a +=>⎧⎨=>⎩,所以315990,0,0,a a a a >>∴>∴=所以1179a a a==故答案为A 【点睛】(1)本题主要考查等比数列的性质,意在考察二次方程的韦达定理,意在考察学生对这些知识的掌握水平和分析推理能力.(2)解答本题容易得到9a =±列的性质,等比数列的奇数项必须同号,偶数项必须同号,所以9a =12.设M 是ABC ∆内一点,且ABC S ∆的面积为2,定义()(,,)f M m n p =,其中,,m n p 分别是MBC ∆,MCA ∆,MAB ∆的面积,若ABC ∆内一动点P 满足()(1,,)f P x y =,则14x y+的最小值是( ) A .1 B .4C .9D .12【答案】C 【解析】由已知得14144121()5ABC x yS x y x y x y x y x y y x ∆⎛⎫=++=⇒+=⇒+=+⋅+=++≥ ⎪⎝⎭59+= ,故选C.二、填空题13.在正方体1111ABCD A B C D -中,,M N 分别是11,AB A B 的中点,P 在AD 上,若平面CMN ⊥平面1A BP ,则ADAP=__________. 【答案】2 【解析】【详解】画出图像如下图所示,由图可知,要两个平面垂直,注意到BP MN ⊥是恒成立的,则只需BP CM ⊥就有BP ⊥平面CMN ,显然,当P 为AD 中点时,ABP BCM ∆≅∆,π2PBA CMB ∠+∠=,即BP CM ⊥,从而BP ⊥平面CMN ,也即有平面CMN ⊥平面1A BP ,所以2ADAP =.点睛:本题主要考查空间点线面的位置关系,考查已知面面垂直探究点的位置.要使两个平面垂直,就需要满足面面垂直的判定定理,也即是要在一个平面上找到另一个平面的垂线,根据图像可以判断出PB 最有可能满足条件,使得,PB CM PB MN ⊥⊥,利用全等三角形易得P 为AD 中点.14.设等差数列{}n a 的前n 项和为n S ,若首项13a =-,公差2d =,5k S =,则正整数k =______. 【答案】5【解析】由等差数列的前n 项和公式可得:()()21131452k k k S ka d k k k k k -=+=-+-=-= ,则:()()2450,150k k k k --=+-= ,据此可得正整数k =5.15.在ABC ∆中,设角,,A B C 所对的边分别为,,a b c ,若3sin cos 2A A +=,3a =,512C π=,则b = . 【答案】【解析】【详解】试题分析:即sin 16A π⎛⎫+= ⎪⎝⎭, 又,3A π∴=,4B π=由正弦定理,得3sinsin46sin sin3a BbAππ===【考点】三角函数两角和公式;正弦定理.16.若实数,x y满足205yx yx y≥⎧⎪-≥⎨⎪+≤⎩,则2x y+的最小值是__________.【答案】0【解析】画出满足条件的可行域,令2z x y=+,根据图象求出目标函数的最小值. 【详解】画出满足205yx yx y≥⎧⎪-≥⎨⎪+≤⎩的可行域,如下图所示,设2z x y=+,由图形可得,目标函数过原点O时,取得最小值,所以2x y+的最小值为0.故答案为:0【点睛】本题考查二元一次不等式组表示平面区域,利用数形结合求线性目标函数的最值,属于基础题.三、解答题17.已知()f x是偶函数,()g x是奇函数,且2()()2f xg x x x+=+-.(1)求()f x和()g x的解析式;(2)设2()33h x mx mx=+-(其中m R∈),解不等式()()h x g x<.【答案】(1)2()2f x x =-,()g x x =;(2)答案见解析.【解析】试题分析:(1)根据函数奇偶性的性质利用方程组法即可求f (x )和g (x )的解析式;(2)()()h x g x < 即()23130mx m x +--<,讨论当0m =时,当0m ≠时,即()()130mx x -+<,对应方程的两个根为11x m =,23x =-,比较1m与-3的大小,进行讨论; 试题解析:(1)由题意()()22f x g x x x -+-=--,即()()22f x g x x x -=--,又()()22f x g x x x +=+-联立得()22f x x =-,()g x x =.(2)由题意不等式即()23130mx m x +--<,当0m =时,即30x --<,解得3x >-;当0m ≠时,即()()130mx x -+<,对应方程的两个根为11x m=,23x =-, 故当0m >时,易知13m >-,不等式的解为13x m -<<; 当0m <时,若13m >-,即13m <-时,不等式的解为3x <-或1x m>;若13m =-,即13m =-时,不等式的解为3x ≠-; 若13m <-,即13m >-时,不等式的解为1x m<或3x >-; 综上所述,当13m <-时,不等式的解为1|3x x x m 或⎧⎫-⎨⎬⎩⎭;当103m -≤<时,不等式的解集为1|3x x x m ⎧⎫-⎨⎬⎩⎭或; 当0m =时,不等式的解集为{}3x x -; 当0m >时,不等式的解集为1|3x x m ⎧⎫-<<⎨⎬⎩⎭. 点睛:本题主要考查根据奇偶性的定义利用方程组法求函数解析式及求含参的一元二次不等式解集;在讨论时从二次项系数等于0,不等于0入手,当不等于0时,往往先对式子进行因式分解得出对应二次方程的根,然后比较根的大小,讨论要不重不漏. 18.若ABC ∆中,角,,A B C 的对边分别是,,a b c ,且cos cos 2cos A B c Ca b ab+=. (1)求C 的值;(2)若2,5a c ==,求b 的大小. 【答案】(1)3C π=;(2)12b =+.【解析】试题分析:(1)由题意结合正弦定理求得1cos 2C =,则C 3π=; (2)由题意结合余弦定理得到关于边长b 的方程,解方程可得12b =+. 试题解析:(1)在ABC ∆中,由已知得cos cos 2cos a B b A c C +=, 利用正弦定理,得sin cos cos sin 2sin cos A B A B C C +=, ∴()sin =2sin cos A B C C +,又()sin sin 0A B C +=>,∴1cos 2C =, ∵0C π<<,∴3C π=;(2)在ABC ∆中,2222cos c a b ab C =+-,2542b b =+-,2210b b --=,∴12b =+.19.已知在三棱锥A BCD -中,ABC ∆是等腰直角三角形,且,2,AC BC BC ⊥=AD ⊥平面, 1.BCD AD =(Ⅰ)求证:平面ABC ⊥平面ACD ;(Ⅱ)若E 为AB 的中点,求二面角A CE D --的余弦值. 【答案】(1)见解析;155. 【解析】试题分析:(1)通过AD BC ⊥,AC BC ⊥可证得BC ⊥平面ACD ,又BC ⊂平面ABC ,利用面面垂直的判定定理可得证.(2) 求出面ACE 的法向量(1,0,3n =-和平面CED 的法向量()0,1,2m =-, 试题解析:(1)证明:因为AD ⊥平面,BCD BC ⊂平面BCD ,所以AD BC ⊥,又因为,AC BC AC AD A ⊥⋂=,所以BC ⊥平面,ACD BC ⊂平面ABC ,所以平面ABC ⊥平面ACD .由已知可得3CD =如图所示建立空间直角坐标系,由已知()0,0,0C ,()0,2,0B ,)3,0,1A,()3,0,0D,312E ⎫⎪⎪⎝⎭.有312CE ⎛⎫= ⎪ ⎪⎝⎭,()3,0,1CA =,()3,0,0CD =,设平面ACE 的法向量(),,n x y z =,有30{310022x z n CA n CE x y z +=⋅=⋅=++=,令1x =,得(1,0,3n =-, 设平面CED 的法向量(),,m x y z =,有30{,{31002x m CD m CE x y z =⋅=⋅=++=,令1y =,得()0,1,2m =-,二面角A CE D --的余弦值2315cos 25n m n mθ⋅===⋅点晴:本题考查的是空间的线面关系和空间角的求解.第一问要考查的是面面垂直,通过先证明线和面内的两条相交直线垂直证得线面垂直,再结合面面垂直的判定定理,可证得;对于第二问空间角的考查是合理建立空间右手系,并求出两个平面的法向量,要注意判断二面角是锐角还是钝角.20.设数列{}n a 满足123(21)2n a a n a n ++⋯+-=. (1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.【答案】(1) 221n a n =-;(2)221n n +. 【解析】(1)利用递推公式,作差后即可求得{}n a 的通项公式.(2)将{}n a 的通项公式代入,可得数列21n a n ⎧⎫⎨⎬+⎩⎭的表达式.利用裂项法即可求得前项和. 【详解】(1)数列{}n a 满足()123212=n a a n a n ++⋯+-2n ≥时,()()12132321n a a n a n ++⋯+--﹣= ∴()212n n a -= ∴221n a n =- 当1n =时,12a =,上式也成立 ∴221n a n =- (2)21121(21)(21)2121n a n n n n n ==-+-+-+ ∴数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和1111113352121n n ⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1212121nn n =-=++ 【点睛】本题考查了利用递推公式求通项公式,裂项法求和的简单应用,属于基础题.21.如图,已知四棱锥P-ABCD ,PD ⊥底面ABCD ,且底面ABCD 是边长为2的正方形,M 、N 分别为PB 、PC 的中点. (Ⅰ)证明:MN//平面PAD ; (Ⅱ)若PA 与平面ABCD 所成的角为,求四棱锥P-ABCD 的体积V .【答案】(1)详见解析(2)83【解析】分析:(1)由三角形中位线定理可得MN //BC ,结合BC//AD ,可得MN //AD ,由线面平行的判定定理得出MN //平面PAD ;(2)PA 与平面ABCD 所成的角为PAD ∠,由PAD 45∠=,得出 PD AD =,由棱锥的体积公式可得四棱锥P ABCD -的体积.详解:(1)证明:M 、N 分别是棱PB 、PC 中点,MN //BC ∴,又 ABCD 是正方形,AD //BC ,MN //AD ∴.MN ⊄平面PAD ,AD ⊂平面PAD , MN //∴平面PAD .(2)PD ⊥平面ABCD ,PA ∴与平面ABCD 所成的角为PAD ∠,PAD 45∠∴=.PD AD 2∴==,故四棱锥P ABCD -的体积2ABCD 118V S PD 22333=⋅=⨯⨯=正方形. 点睛:本题主要考查线面平行的判定定理、直线和平面成的角的定义、三棱锥的体积,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.22.如图,OA 、OB 是两条公路(近似看成两条直线),3AOB π∠=,在AOB ∠内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.(1)求纪念塔P到两条公路交点O处的距离;(2)若纪念塔P为小路MN的中点,求小路MN的长.【答案】(1)P到点O处的距离为421(2)小路MN的长为24千米.【解析】试题分析:(1)建立平面直角坐标系,结合点到直线距离公式可得P到点O处的距离为21(2)利用两点之间的距离公式有小路MN的长为24千米.试题解析:解法一:(1)以O为原点,OA所在直线为x轴,建立直角坐标系,则直线OB的方程为3y x=,又P到直线OA的距离PD=6千米,设(),6P t,3612t-=,解得103t=或63-,所以()221036421OP=+=分(2)因P为小路MN的中点,点M在x轴上,即0My=,所以12Ny=,又点N在OB上,所以3N Ny x=,所以43Nx=由(1)知()103,6P,所以163Mx=()()221634312024MN=-+-=.答:(1)P到点O处的距离为21(2)小路MN的长为24千米.解法二:(1)设POA α∠=,则3POB πα∠=-,因P 到直线OA 、OB 的距离分别为PD 、PE ,PD =6千米,PE =12千米,所以612sin sin 3OP παα==⎛⎫- ⎪⎝⎭, 所以2sin sin 3παα⎛⎫=-⎪⎝⎭,化简得tan α=, 又22sin cos 1αα+=,所以sin α=,6sin OP α==. (2)设PMO θ∠=,则23PMN πθ∠=-, 因P 为小路MN 的中点,即PM PN =,所以6122sin sin 3πθθ=⎛⎫- ⎪⎝⎭,即2sin 2sin 3πθθ⎛⎫-=⎪⎝⎭, 解得6πθ=,所以12224sin6MN PM π===.答:(1)P 到点O处的距离为(2)小路MN 的长为24千米.。
安徽省滁州市天长市某中学2019-2020学年高一下学期第二次大考数学试卷

数 学 试 卷一、选择题(本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在ABC ∆中, ()2,4AB =, ()1,3AC =,则CB =( )A. ()3,7B. ()3,5C. ()1,1D. ()1,1--2.集合2*{|70}A x x x x N =-<∈,,则*6{|}B y N y A y=∈∈,中子集的个数为( ) A. 4个 B . 8个 C. 15个 D. 16个3.函数()f x 在()-∞+∞,上单调递增,且为奇函数,若()23f =,则满足()313f x -≤+≤的x 的取值范围是( )A. []22-,B. []33-,C. []04,D. []31-,4.下列四个函数中,以π为最小正周期,且在区间,2ππ⎛⎫⎪⎝⎭上为减函数的是( ) A. sin2y x = B. 2cos y x = C. cos2x y = D. ()tan y x =-5.已知()2x af x -=是定义在R 上的偶函数,则下列不等关系正确的是( )A. ()()()20.5log 3log 5f f f a <<B. ()()()0.52log 5log 3f f f a <<C. ()()()0.52log 5log 3f a f f <<D. ()()()20.5log 3log 5f a f f <<6.设直线l 的斜率为k ,且1k -<≤l 的倾斜角α的取值范围( )A. 3034πππ⎡⎫⎛⎫⋃⎪⎪⎢⎣⎭⎝⎭,,B. 3064πππ⎡⎫⎛⎫⋃⎪⎪⎢⎣⎭⎝⎭,, C. 364ππ⎛⎫⎪⎝⎭,D. 3034πππ⎡⎤⎛⎫⋃⎪⎢⎥⎣⎦⎝⎭,,7.为了得到函数sin cos y x x =+的图象, 可以将函数)4y x π=-的图象( )A .向左平行移动4π个单位 B .向右平行移动4π个单位C .向左平行移动2π个单位 D .向右平行移动2π个单位 8.函数⎪⎩⎪⎨⎧>+-≤<=10,621100,lg )(x x x x x f ,若()()()f a f b f c ==且a , b , c 互不相等,则abc的取值范围是( ) A. ()110, B. ()56, C. ()1012, D. ()2024,9.已知单位向量1e 与2e 的夹角为23π,则向量1e 在向量2e 方向上的投影为( ) A. 12-B. 12C. 32-D.3210.等差数列{}n a 中, 564,a a +=则=⋅⋅⋅⋅⋅⋅⋅⋅⋅)2222(log 103212a aaa( )A. 40B. 20C. 10D. 2+2log 511.函数()()21616log x x f x x -=-的图像大致为( )A .B .C .D .12.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且BC 边上的高为36a ,则c bb c+的最大值是( ) A. 8B. 62D. 4二、填空题(本大题共 4 小题,每小题 5 分)13.已知()(),4,2,1a m b m ==-,满足222a b a b +=+,则m =__________. 14.若实数,x y 满足2234x y xy ++=,则x y +的最大值是____________. 15.已知数列{}n a 的前n 项之和为n S ,若1112,21n n n a a a -+==++,则10S =_________.16.如图, ,,A B C 是直线l 上的三点, P 是直线l 外一点,已知112AB BC ==,90CPB ∠=, 4tan 3APB ∠=.则PA PC ⋅=________.三、解答题(本大题共 6 小题,共 70 分.其中17题10分,其他12分.解答时应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)设向量→→b a ,满足.7|2-3|1||||===→→→→b a b a 及(1)求向量→→b a ,的夹角的大小; (2)求|3|→→+b a 的值.18. (本小题满分12分)已知()3sin cos a x x =-,, ()cos cos b x x =,, ()f x a b =⋅ (1)求函数()f x 的单调递增区间;(2)若A , B , C 为锐角ABC 的三个内角,且2A B =,求()f A 的取值范围.PCBA19. (本小题满分12分)已知正项等比数列{}n b (*n N ∈)中,公比1q >,且3540b b +=, 35·256b b =, 2log 2n n a b =+. (1)求证:数列{}n a 是等差数列. (2)若11·n n n c a a +=,求数列{}n c 的前n 项和n S .20. (本小题满分12分)在ABC ∆中, ,,a b c 分别为角,,A B C 的对边,若2cos cos c b Ba A-=. (1)求角A 的大小;(2)已知a =ABC ∆面积的最大值.21.(本小题满分12分)南康某服装厂拟在2020年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m 万件与年促销费用x (04x ≤≤)万元满足131m x =-+.已知2020年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2020年该产品的利润y 万元表示为年促销费用x 万元的函数; (2)该服装厂2020年的促销费用投入多少万元时,利润最大?22. (本小题满分12分)已知幂函数()()23122233p p f x p p x--=-+满足()()24f f <.(1)求函数()f x 的解析式;(2)若函数()()()[]2,1,9g x f x mf x x =+∈,是否存在实数m 使得()g x 的最小值为0?若存在,求出m 的值;若不存在,说明理由;(3)若函数()()3h x n f x =-+,是否存在实数(),a b a b <,使函数()h x 在[],a b 上的值域为[],a b ?若存在,求出实数n 的取值范围;若不存在,说明理由.数学答案一、选择题(本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要求的) DDD1.C 【解析】()()()2,41,31,1CB AB AC =-=-=.2.D 【解析】{}2*{|70}1,2,3,4,5,6A x x x x N =-<∈=,,{}*6{|}1,2,3,6B y N y A y=∈∈=,,其子集的个数为4216=,选D. 3.D 【解析】由奇函数的性质可得: ()()223f f -=-=-, 则不等式()313f x -≤+≤即: ()()()212f f x f -≤+≤, 结合函数的单调性脱去f 符号有: 212,31x x -≤+≤∴-≤≤. 本题选择D 选项.4.D 【解析】A 选项,函数在3,24ππ⎛⎫ ⎪⎝⎭上单调递减,在3,4ππ⎛⎫⎪⎝⎭上单调递增,故排除;B 选项,函数在,2ππ⎛⎫⎪⎝⎭上单调递增,故排除;C 选项,函数的周期是4π,故排除;故选D5.D 【解析】因为()=2x af x -是偶函数,则()()11f f -=,所以11a a -=--,所以0a =。
★试卷3套汇总★安徽省滁州市2020年高一数学下学期期末调研试题
2019-2020学年高一下学期期末数学模拟试卷一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.各棱长均为a 的三棱锥的表面积为( ) A .243aB .233aC .23aD .223a2.在计算机BASIC 语言中,函数mod(),a b 表示整数a 被整数b 除所得的余数,如mod 6,(4)2=.用下面的程序框图,如果输入的1365a =,147b =,那么输出的结果是( )A .7B .21C .35D .493.若直线22(0,0)mx ny m n -=->>被圆222410x y x y ++-+=截得弦长为4,则41m n+的最小值是( ) A .9B .4C .12D .144.已知等差数列{}n a 的前n 项和为n S ,且24S =,416S =,则56a a +=( ) A .11 B .16C .20D .285.已知259a =°,sin15cos15b =+°°,2231cos31c =°°,则实数a 、b 、c 的大小关系是()A .a c b <<a c b <<B .a b c <<C .a c b ≥≥D .a b c ≥≥6.已知|1,|2a b ==,a 与b 的夹角=120θ,则a 在b 方向上的投影是( )7.若点()()(),0,0,2,1,3A a B C 共线,则a 的值为( ) A .2- B .1-C .0D .18.函数1lgy x=的大致图像是下列哪个选项( ) A . B .C .D .9.已知圆()()221 221:C x y ++-=,圆 ()()222 2516:C x y -+-= ,则圆1C 与圆2 C 的位置关系是( ) A .相离B .相交C .外切D .内切10.已知单位向量OA ,OB ,满足0OA OB ⋅=.若点C 在AOB ∠内,且60AOC ∠=︒,(,)OC mOA nOB m n =+∈R ,则下列式子一定成立的是( )A .1m n +=B .1mn =C .221+=m nD .33m n =11.已知向量(2,tan )a θ=,(1,1)b =-.且a b ,则tan 4πθ⎛⎫-= ⎪⎝⎭( ) A .2B .3-C .3-D .13-12.若将函数2sin 26y x π⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位后,所得图象对应的函数为( )A .2sin 2y x =B .2sin 26y x π⎛⎫=-⎪⎝⎭C .2cos2y x=D .2sin 23y x π⎛⎫=+⎪⎝⎭二、填空题:本题共4小题13.已知向量()4,2a =,(),1b λ=,若2a b +与a b -的夹角是锐角,则实数λ的取值范围为______. 14.已知α,β均为锐角,()5cos 13αβ+=-,π3sin 35β⎛⎫+= ⎪⎝⎭,则πsin 3α⎛⎫-= ⎪⎝⎭______.15.已知角α的终边经过点()3,4P -,则sin cos αα+的值为__________.16.1232e 2(){log (1)2x x f x x x ,,-<=-≥,则f (f (2))的值为____________. 三、解答题:解答应写出文字说明、证明过程或演算步骤。
安徽省滁州市明光中学2019-2020学年高一下学期第二次月考数学试题(word无答案)

安徽省滁州市明光中学2019-2020学年高一下学期第二次月考数学试题一、单选题(★) 1 . 设a,,若,则A.B.C.D.(★) 2 . 已知向量,,若,则实数 a的值为A.B.2或C.或1D.(★) 3 . 已知集合,,则A.B.C.D.(★) 4 . 在中,,则∠ 等于( )A.30°或150°B.60°C.60°或120°D.30°(★) 5 . 已知数列是公比为的等比数列,且成等差数列,则公比的值为()A.B.1C.D.(★★★★) 6 . 在△ ABC中,内角 A、 B、 C所对的边分别为 a、 b、 c, S为△ ABC的面积,,且 A、 B、 C成等差数列,则 C的大小为()A.B.C.D.(★) 7 . 已知,则向量在方向上的投影为()A.B.C.D.(★★) 8 . 在中,角的对边分别为,若, ,则的面积为A.B.C.D.(★) 9 . 记为等差数列的前项和,若,,则为()A.B.C.D.(★) 10 . 等比数列的前项和为,若,,则()A.510B.255C.127D.6540(★) 11 . 已知向量,且∥ ,若均为正数,则的最小值是A.24B.8C.D.(★★) 12 . 在中,, G为的重心, H为的垂心.则( )A.4B.5C.-4D.-5二、填空题(★) 13 . 的三个内角所对的边分别是,则=__________.(★★) 14 . 在中,角所对的边分别为满足,,且,则的周长为__________.(★) 15 . 已知,则函数的最小值为_______.(★★) 16 . 等比数列的公比为,其前项和的积为,并且满足下面条件,,,.给出下列结论:① ;② ;③ 的值是中最大的;④ 成立最大的自然数等于198.其中正确的结论是__________.三、解答题(★★) 17 . 已知平面内三个向量:(1)若,求实数的值;(2)设,且满足,,求.(★★) 18 . 设的内角的对应边分别为且满足.(1)求角 B的大小;(2)若,求边上高 h的最大值.(★) 19 . 记公差不为0的等差数列的前项和为, S 3=9,成等比数列. (1)求数列的通项公式及;(2)若, n=1,2,3,,问是否存在实数,使得数列为单调递增数列?若存在,请求出的取值范围;不存在,请说明理由.(★★) 20 . 在四边形中,的面积为.(1)求;(2)若,求的长.(★★) 21 . 已知是等差数列的前 n项和,且,是数列的前 n项和,且.(1)求数列和的通项公式;(2)设,求数列的前 n项和.(★★) 22 .投资商到一开发区投资72万元建起一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元,设表示前n年的纯利润总和(前年总收入-前年的总支出 -投资额72万元)(Ⅰ)该厂从第几年开始盈利?(Ⅱ)该厂第几年平均纯利润达到最大?并求出年平均纯利润的最大值.。
2019-2020学年安徽省滁州市高一下学期期末数学试卷

2019-2020学年安徽省滁州市高一下学期期末数学试卷一、单选题(本大题共12小题,共60.0分)1. 已知直线l 经过点(3,−2),且在两坐标轴上的截距相等,直线l 的方程是( )A. x +y −1=0B. 2x +3y =0C. 2x +3y =0或x +y −1=0D. x −y −1=0或x +y −1=0 2. △ABC 的三个内角A ,B ,C 所对的边分别是a ,b ,c ,设p ⃗ =(a +c,b),q ⃗ =(b −a,c −a),若p ⃗ //q ⃗ ,则角C 的大小为( ) A. 2π3 B. π2 C. π6 D. π3 3. “a >b >0”是“a 2>b 2”的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既不充分也不必要条件4. 在空间,下列命题正确的是( ) A. 平行直线的平行投影重合B. 平行于同一直线的两个平面平行C. 垂直于同一平面的两个平面平行D. 垂直于同一平面的两条直线平行 5. 设等差数列{a n }的前n 项和为S n ,若S 5=20,且S 6−a 1=30,则a 5的值是( )A. 8B. 10C. 4D. 4或10 6. 要做一个圆锥形的漏斗,其母线长为20cm ,要使其体积最大,则高为( )A. √33 B. 10√33 C. 16√33 D. 20√337. 设m ∈R ,过定点A 的动直线mx +y −1=0与过定点B 的动直线x −my +m +2=0交于点P(x,y),则|PA⃗⃗⃗⃗⃗ |+|PB ⃗⃗⃗⃗⃗ |的最大值是( ) 最大值为( )A. 2B. √2+1C. 2√2D. √2+2 8. 如图是一个多面体的三视图,则其全面积为( )A. √3B. √32+6 C. √3+6D. √3+49.已知△ABC中,∠A,∠B,∠C的度数成等差数列,则此三角形的形状是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定10.圆x2+y2−4x+6y=0和圆x2+y2−6x=0交于A. B两点,则AB的垂直平分线的方程是()A.x+y+3=0B. 3x−y−9=0C. 2x−y−5=0D. 4x−3y+7=011.已知数列{x n}满足x n+3=x n,x n+2=|x n+1−x n|(n∈N∗),若x1=1,x2=a(a≤1,a≠0)则数列{x n}的前2016项的和S2016为()A. 671B. 670C. 1342D. 134412.已知三棱锥S−ABC中,底面ABC为边长等于2的等边三角形,SA垂直于平面ABC,SA=3,SA与平面SBC所成角的正弦值为()A. √34B. √54C. 12D. √32二、单空题(本大题共4小题,共20.0分)13.在空间直角坐标系中,点A(1,−2,3)关于平面xOz的对称点为B,关于x轴的对称点为C,则B、C间的距离为______ .14.(1)在(1+2x)5的展开式中,x2的系数等于____.(用数字作答)(2)若x,y满足约束条件{x≥0x−y≤02x+y−2≤0,则z=x+2y的最大值为__________.(3)3位男生和 3 位女生共 6 位同学站成一排,若男生甲不站两端, 3 位女生中有且只有两位女生相邻,则不同排法的种数是________.(4)已知a,b满足ab+2=2(a+b),则ab的最小值是________.15. 二次不等式ax2+bx+c<0的解集为R的条件是______ .16. 正整数数列{a n}满足a n+1={12a n,a n是偶3a n+1,a n是奇,已知a7=2,{a n}的前7项和的最大值为S,把a1的所有可能取值按从小到大排成一个新数列{b n},{b n}所有项和为T,则S−T=______.三、解答题(本大题共6小题,共72.0分)17. 设数列{a n}(n∈N+)的前n项和为S n,已知S n=2a n−a1,且a1,a2+2,a3成等差数列,(1)求数列{a n}的通项公式;(2)记数列{1a n }的前n项和为T n,求使得|T n−12|<11000成立的n的最小值;(3)若数列{b n}满足b n=n2+3n+4(n+2)⋅log2a n,求数列{b n}的前n项和R n.18. 二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:x−3−2−101234y60−4−6−6−406求不等式ax2+bx+c>0的解集.19. 在△ABC中,角A,B,C对应的边分别是a,b,c,且2acosBcosC+2ccosAcosB−b=0.(1)求角B的大小;(2)若△ABC的面积S=3√3,a=3,求sin A sin C的值.20. 如图,在四棱锥ABCD−A1B1C1D1中,底面ABCD是等腰梯形,AB//CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.(1)求证:AD1⊥BC;(2)若直线DD1与直线AB所成角为π3,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.21. 在等差数列{a n}和等比数列{b n}中,a1=1,b1=2,b n>0(n∈N∗),且b1,a2,b2成等差数列,a2,b2,a3+2成等比数列(1)求数列{a n},{b n}的通项公式;(2)设c n=a b,数列{c n}的前n项和为S nn①求S n>a n+t对所有正整数n恒成立,求常数t的取值范围.②若S2n+4nS n+2n22. 已知直线L被两平行直线L1:2x−5y=−9与L2:2x−5y−7=0所截线段AB的中点恰在直线x−4y−1=0上,已知圆C:(x+4)2+(y+1)2=25.(Ⅰ)求两平行直线L1与L2的距离;(Ⅱ)证明直线L与圆C恒有两个交点;(Ⅲ)求直线L被圆C截得的弦长最小时的方程.【答案与解析】1.答案:C解析:解:根据题意,分两种情况讨论:当直线l在两坐标轴上的截距都等于0时,直线过点(3,−2),则其斜率k=−23=−23,直线方程为y=−23x,即2x+3y=0;当直线l在两坐标轴上的截距不等于0时,设该直线的方程为xa +ya=1,直线过点(3,−2),将其代入直线方程可得a=3−2=1,则直线方程为x+y−1=0;综上可得:所求的直线方程为2x+3y=0或x+y−1=0.故选:C.分别求出直线l在两坐标轴上的截距都等于0时和直线l在两坐标轴上的截距不等于0时的直线方程即可.本题考查了直线的截距式方程应用问题,注意理解截距的定义,容易忽略截距为0即直线过原点的情况.2.答案:D解析:解:∵p⃗=(a+c,b),q⃗=(b−a,c−a),p⃗//q⃗,∴(a+c)(c−a)=b(b−a),即a2+b2−c2=ab,根据余弦定理,cosC=a2+b2−c22ab =12,∵△ABC的三个内角A,B,C,∴C=π3,故选:D.先根据向量平行得到a2+b2−c2=ab,再根据余弦定理,即可求出角C.本题考查了向量平行的坐标运算和余弦定理,属于基础题.3.答案:A解析:略4.答案:D解析:试题分析:对于A ,由于平行直线的平行投影依然是平行的,因此错误对于B ,平行与同一直线的两个平面可能平行也可能相交,因此错误对于C ,由于垂直于同一平面的两个平面可能平行也可能相交,故错误,对于D ,垂直于同一平面的两条直线平行,显然成立。
2019-2020学年滁州市部分高中高一(下)期末数学试卷(含答案解析)

2019-2020学年滁州市部分高中高一(下)期末数学试卷一、单选题(本大题共12小题,共60.0分)1.已知三角形的三边构成等比数列,它们的公比为q,则q的一个可能的值是()A. B. C. 2 D.2.三棱椎A−BCD的三视图为如图所示的三个直角三角形,则三棱锥A−BCD的表面积为()A. 2+2√5B. 4+4√5C. 4+4√53D. 4+√63.在△ABC中,若a=2√3,A=30°,则b+csinB+sinC的值为()A. 4√3B. 2√3C. 4D. 24.设等差数列{a n}满足:3a8=5a13,且a1>0,S n为其前n项之和,则S n中最大的是()A. S21B. S20C. S11D. S105.在△ABC中,b=2,a=4,C=45°,则△ABC的面积S=()A. 2√3B. 2C. 4D. 2√26.直线x=√3的倾斜角是()A. 0°B. 60°C. 90°D. 120°7.Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若ACAB =34,则BDCD=()A. 34B. 43C. 169D. 9168.如果底面是菱形的直棱柱(侧棱与底面垂直的棱柱)ABCD−A1B1C1D1的所有棱长都相等,∠ABC=60°,E,M,N分别为AB,BC,CC1的中点,现有下列四个结论:①CE⊥平面CC1D1D②A1B//MN③AD1//平面A1MN④异面真线D1C与MN所成的角的余弦值为34,其中正确结论的个数为()A. 1个B. 2个C. 3个D. 4个9.四棱锥P−ABCD的五个顶点都在同一球面上,平面PAB⊥平面ABCD,PA⊥PB,PA=PB=2√2,四边形ABCD为正方形,则该球的表面积为()A. 32πB. 16πC. 8πD. 64π10.已知x,y∈R,且x>y>0,则下列结论正确的是()A. 1x >1yB. x12>y12C. (13)x>(13)y D. log3x<log3y11.若等差数列{a n}和等比数列{b n}满足a1=b1=1,a2=b2=2,则a5b5=()A. 5B. 16C. 80D. 16012.已知不等式组{x+y≤1x−y≥−1y≥0所表示的平面区域为D,直线l:y=3x+m不经过区域D,则实数m的取值范围是()A. [−3,1]B. [−3,3]C. (−∞,−3)∪(1,+∞)D. (−∞,−3)∪(3,+∞)二、单空题(本大题共4小题,共20.0分)13.已知a⃗=(2,3),b⃗ =(−1,5),则a⃗+3b⃗⃗⃗⃗ =______ .14.将一颗骰子投掷两次分别得到点数a,b,则直线ax−by=0与圆(x−2)2+y2=2没有公共点的概率为______ .15.已知平面区域D由以A(2,4)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成,若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最大值,则m=______.16.已知实数x>0,y>0,且4x +1y=2,则xy的最小值为______.三、解答题(本大题共6小题,共70.0分)17.如图所示,已知抛物线C1:x2=2py的焦点在抛物线C2:y=12x2+1上,点P是抛物线C1上的动点.(1)求抛物线C1的方程及其准线方程;(2)过点P作抛物线C2的两条切线,M,N分别为两个切点,设点P到直线MN的距离为d,求d的最小值.18. (12分)设为实数,函数,(1)若,求的取值范围;(1)求的最小值。
安徽省滁州市城南中学2019-2020学年高一数学理下学期期末试卷含解析

安徽省滁州市城南中学2019-2020学年高一数学理下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. △ABC中,已知,,则∠C等于( )A.30° B.45° C.60° D.135°参考答案:D2. 如右图所示,是的边上的中点,记,,则向量A. B. C. D.参考答案:B3. (5分)直线x+y﹣1=0的倾斜角为()A.30°B.60°C.120°D.150°参考答案:D考点:直线的倾斜角.专题:直线与圆.分析:利用直线的倾斜角与斜率的关系即可得出.解答:设直线x+y﹣1=0的倾斜角为α.直线x+y﹣1=0化为.∴tanα=﹣.∵α∈[0°,180°),∴α=150°.故选:D.点评:本题考查了直线的倾斜角与斜率的关系,属于基础题.4. 若函数与函数在区间上都是减函数,则实数的取值范围为()A. B. C. D.参考答案:D略5.参考答案:D6. 已知函数在(-∞,5]上具有单调性,则实数k的取值范围是()A.(-24,40) B.[-24,40] C.(-∞,-24] D.[40,+∞)参考答案:D7. 集合的子集个数是()A.1 B.2 C.3 D.4参考答案:D略8. 在空间中,下列命题正确的是()A.平行于同一平面的两条直线平行B.平行于同一直线的两个平面平行C.垂直于同一直线的两条直线平行D.垂直于同一平面的两条直线平行参考答案:D【考点】平面的基本性质及推论.【分析】对4个命题分别进行判断,即可得出结论.【解答】解:对于A,平行于同一平面的两条直线平行、相交或异面,不正确;对于B,平行于同一直线的两个平面平行或相交,不正确;对于C,垂直于同一直线的两条直线平行、相交或异面,不正确;对于D,垂直于同一平面的两条直线平行,正确.故选D.9. 为了得到函数y=cos(2x+),x∈R的图象,只需把函数y=cos2x的图象()A.向左平行移动个单位长度B.向右平行移动个单位长度C.向左平行移动个单位长度D.向右平行移动个单位长度参考答案:C【考点】函数y=Asin(ωx+φ)的图象变换.【分析】由已知中把函数y=cos2x的图象平移后,得到函数的图象,我们可以设出平移量为a,然后根据平移法则“左加右减,上加下减”构造关于平移量的方程,解方程求出平移量,即可得到答案.【解答】解:设将函数y=cos2x的图象向左平移a个单位后,得到函数的图象则cos2(x+a)=,解得a=∴函数y=cos2x的图象向左平行移动个单位长度,可得到函数的图象,故选C10. 定义在R上的偶函数满足,且在区间上是减函数,若A、B是锐角三角形的两个内角,则A、 B、C、 D、参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 函数的零点的个数是__________参考答案:912. 已知那么= ,= 。
2020年滁州市高一数学下期末模拟试卷含答案
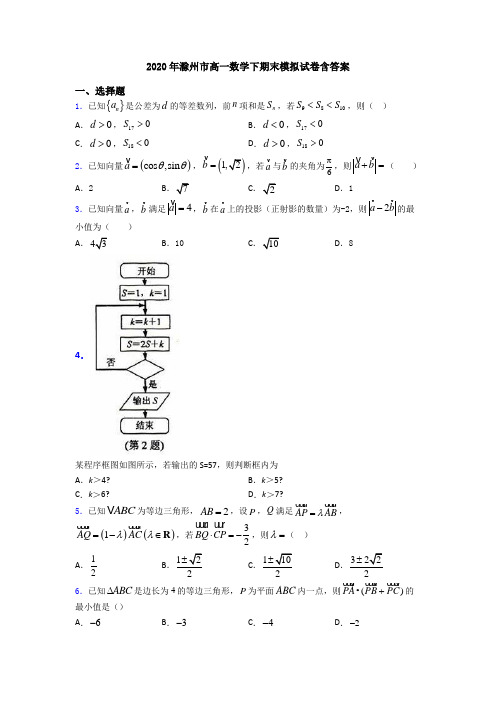
2020年滁州市高一数学下期末模拟试卷含答案一、选择题1.已知{}n a 是公差为d 的等差数列,前n 项和是n S ,若9810S S S <<,则( )A .0d >,170S >B .0d <,170S <C .0d >,180S <D .0d >,180S >2.已知向量()cos ,sin a θθ=v ,()1,2b =v ,若a v 与b v 的夹角为6π,则a b +=v v ( )A .2B .7C .2D .13.已知向量a v ,b v 满足4a =v,b v 在a v 上的投影(正射影的数量)为-2,则2a b -v v 的最小值为( ) A .43B .10C .10D .84.某程序框图如图所示,若输出的S=57,则判断框内为 A .k >4? B .k >5? C .k >6?D .k >7?5.已知ABC V 为等边三角形,2AB =,设P ,Q 满足AP AB λ=uu u r uu u r,()()1AQ AC λλ=-∈R u u u r u u u r ,若32BQ CP ⋅=-uu u r uu r ,则λ=( )A .12B .122± C 110± D .322± 6.已知ABC ∆是边长为4的等边三角形,P 为平面ABC 内一点,则•()PA PB PC +u u u v u u u v u u u v的最小值是() A .6-B .3-C .4-D .2-7.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y 对x 的线性回归方程为 A .y = x-1B .y = x+1C .y =88+12x D .y = 1768.已知0,0a b >>,并且111,,2a b成等差数列,则4a b +的最小值为( ) A .2 B .4 C .5 D .9 9.函数()(1)lg(1)35f x x x x =-+--的零点个数为( )A .3B .2C .1D .010.(2018年天津卷文)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为 A .6B .19C .21D .4511.若tan()24πα+=,则sin cos sin cos αααα-=+( )A .12B.2C .2-D .12-12.设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则5a = A .12-B .10-C .10D .12二、填空题13.在ABC ∆中,若3B π=,AC =2AB BC +的最大值为__________.14.已知函数())ln1f x x =+,()4f a =,则()f a -=________.15.等边ABC ∆的边长为2,则AB u u u v在BC uuu v方向上的投影为________.16.若函数()6,23log ,2a x x f x x x -+≤⎧=⎨+>⎩(0a >且1a ≠)的值域是[)4,+∞,则实数a 的取值范围是__________.17.已知数列{}n a 满足1121,2n n a a a n +==+,则na n的最小值为_______. 18.如图,某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积为________.19.已知函数2()1f x x mx =+-,若对于任意的[],1x m m ∈+都有()0f x <,则实数m的取值范围为 .20.已知()()2,3,4,3A B -,点P 在直线AB 上,且32AP PB =u u u v u u u v,则点P 的坐标为________三、解答题21.已知矩形ABCD 的两条对角线相交于点20M (,),AB 边所在直线的方程为360x y --=,点11T -(,)在AD 边所在直线上. (1)求AD 边所在直线的方程; (2)求矩形ABCD 外接圆的方程.22.已知数列{}n a 的前n 和为n S ,若0n a >,21n n a S =. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若3nn n a b =,求数列{}n b 的前n 项和n T . 23.已知数列{}n a 满足()*112112n n n n na a a n Nb a a +==∈=+,,,. ()1证明数列{}n b 为等差数列;()2求数列{}n a 的通项公式.24.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,已知10cos 10A =-,2b =5c =(1)求a ;(2)求cos()B A -的值.25.已知四点A (-3,1),B (-1,-2),C (2,0),D (23,4m m +) (1)求证:AB BC ⊥u u u v u u u v;(2) //AD BC u u u v u u u v,求实数m 的值.26.在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知sin 4sin a A b B =,222)ac a b c =--.(I )求cos A 的值; (II )求sin(2)B A -的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】利用等差数列的通项公式求和公式可判断出数列{}n a 的单调性,并结合等差数列的求和公式可得出结论. 【详解】9810S S S <<Q ,90a ∴<,9100a a +>,100a ∴>,0d >. 179017S a =<∴,()1891090S a a =+>.故选:D. 【点睛】本题考查利用等差数列的前n 项和判断数列的单调性以及不等式,考查推理能力与计算能力,属于中等题.2.B解析:B 【解析】 【分析】先计算a r 与b r的模,再根据向量数量积的性质22()a b a b +=+r r r r 即可计算求值.【详解】因为()cos ,sin a θθ=r,(b =r ,所以||1a =r ,||b =r又222222()2||2||||cos ||6a b a b a a b b a a b b +=+=+⋅+=+π+r r r r r r r r r r r r1372=++=,所以a b+=r r,故选B.【点睛】本题主要考查了向量的坐标运算,向量的数量积,向量的模的计算,属于中档题.3.D解析:D【解析】【分析】br在ar上的投影(正射影的数量)为2-可知||cos,2b a b<>=-r r r,可求出||2b≥r,求22a b-r r的最小值即可得出结果.【详解】因为br在ar上的投影(正射影的数量)为2-,所以||cos,2b a b<>=-r r r,即2||cos,ba b=-<>rr r,而1cos,0a b-≤<><r r,所以||2b≥r,因为222222 2(2)44||4||||cos,4||a b a b a a b b a a b a b b-=-=-⋅+=-<>+r r r r r r r r r r r r r r22=1644(2)4||484||b b-⨯⨯-+=+r r所以22484464a b-≥+⨯=r r,即28a b-≥r r,故选D.【点睛】本题主要考查了向量在向量上的正射影,向量的数量积,属于难题.4.A解析:A【解析】试题分析:由程序框图知第一次运行112,224k S=+==+=,第二次运行213,8311k S=+==+=,第三次运行314,22426k S=+==+=,第四次运行4154,52557k S=+=>=+=,输出57S=,所以判断框内为4?k>,故选C.考点:程序框图.5.A解析:A【解析】【分析】运用向量的加法和减法运算表示向量BQ BA AQ=+u u u r u u u r u u u r,CP CA AP=+u u u r u u u r u u u r,再根据向量的数量积运算,建立关于λ的方程,可得选项. 【详解】∵BQ BA AQ =+u u u r u u u r u u u r ,CP CA AP =+u u u r u u u r u u u r ,∴()()BQ CP BA AQ CA AP AB AC AB AP AC AQ AQ AP ⋅=+⋅+=⋅-⋅-⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r()()2211AB AC AB AC AB AC λλλλ=⋅---+-⋅u u u r u u u r u u u r u u u r u u u r u u u r()()232441212222λλλλλλ=---+-=-+-=-,∴12λ=.故选:A. 6.A解析:A 【解析】 【分析】建立平面直角坐标系,表示出点的坐标,利用向量坐标运算和平面向量的数量积的运算,求得最小值,即可求解. 【详解】由题意,以BC 中点为坐标原点,建立如图所示的坐标系, 则(0,23),(2,0),(2,0)A B C -,设(,)P x y ,则(,23),(2,),(2,)PA x y PB x y PC x y =--=---=--u u u r u u u r u u u r, 所以22()(2)(23)(2)2432PA PB PC x x y y x y y •+=-⋅-+-⋅-=-+u u u r u u u r u u u r222[(3)3]x y =+--,所以当0,3x y ==时,()PA PB PC •+u u u r u u u r u u u r取得最小值为2(3)6⨯-=-,故选A.【点睛】本题主要考查了平面向量数量积的应用问题,根据条件建立坐标系,利用坐标法是解答的关键,着重考查了推理与运算能力,属于基础题.7.C解析:C 【解析】 【分析】 【详解】试题分析:由已知可得176,176x y ==∴中心点为()176,176, 代入回归方程验证可知,只有方程y =88+12x 成立,故选C 8.D解析:D 【解析】 ∵111,,2a b成等差数列, ()1111441445529a b a b a b a b a b a b b a b a ⎛⎫∴+=∴+=++=+++⋅= ⎪⎝⎭,…, 当且仅当a =2b 即33,2a b ==时“=“成立, 本题选择D 选项.点睛:在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.9.B解析:B 【解析】 【分析】可采用构造函数形式,令()()()35lg 1,1x h x x g x x +=+=-,采用数形结合法即可求解 【详解】由题可知,1x >-,当1x =时,()80f x =-≠, 令358()(1)lg(1)350lg(1)311x f x x x x x x x +=-+--=⇒+==+--, 令()()()35lg 1,1x h x x g x x +=+=-,画出函数图像,如图:则两函数图像有两交点,故函数()(1)lg(1)35f x x x x =-+--的零点个数为2个 故选:B 【点睛】本题考查函数零点个数的求解,数形结合思想,属于中档题10.C解析:C 【解析】分析:首先画出可行域,然后结合目标目标函数的几何意义确定函数取得最大值的点,最后求解最大值即可.详解:绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标函数在点A 处取得最大值,联立直线方程:51x y x y +=⎧⎨-+=⎩,可得点A 的坐标为:()2,3A ,据此可知目标函数的最大值为:max 35325321z x y =+=⨯+⨯=.本题选择C 选项.点睛:求线性目标函数z =ax +by (ab ≠0)的最值,当b >0时,直线过可行域且在y 轴上截距最大时,z 值最大,在y 轴截距最小时,z 值最小;当b <0时,直线过可行域且在y 轴上截距最大时,z 值最小,在y 轴上截距最小时,z 值最大.11.D解析:D 【解析】 由tan()24πα+=有tan 112,tan 1tan 3ααα+==-,所以11sin cos tan 1131sin cos tan 1213αααααα---===-+++,选D.点睛:本题主要考查两角和的正切公式以及同角三角函数的基本关系式,属于中档题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
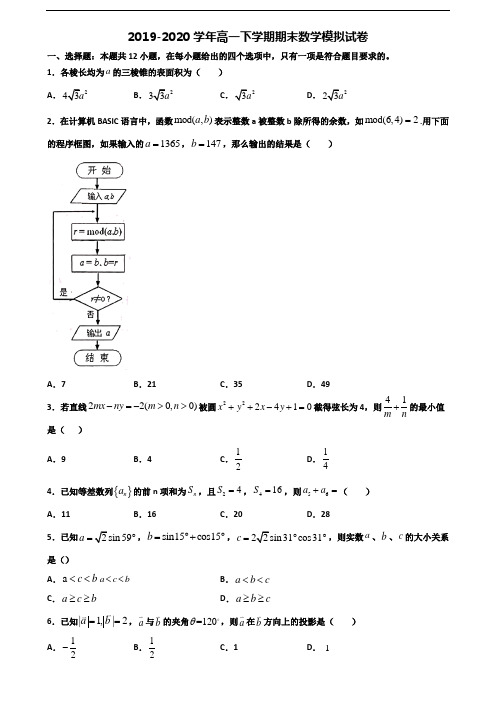
2019-2020学年高一下学期期末数学模拟试卷一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在三棱锥P ABC -中,222ACAB ==,10BC =,90APC ∠=,平面ABC ⊥平面PAC ,则三棱锥P ABC -外接球的表面积为() A .4π B .5πC .8πD .10π2.过点()1,3P-且垂直于直线230x y -+=的直线方程为( )A .250x y --=B .250x y ++=C .210x y ++=D .270x y +-=3.如图,这是某校高一年级一名学生七次月考数学成绩(满分100分)的茎叶图去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别是( )A .87,9.6B .85,9.6C .87,5,6D .85,5.64.在数列{}n a 中,121,64a a ==,且数列1n n a a +⎧⎫⎨⎬⎩⎭是等比数列,其公比12q =-,则数列{}n a 的最大项等于( ) A .7aB .8aC .6a 或9aD .10a5.某工厂对一批新产品的长度(单位:mm )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )A .20,22.5B .22.5,25C .22.5,22.75D .22.75,22.756.在ABC ∆中,角A B 、均为锐角,且cos sin A B >,则ABC ∆的形状是( ) A .直角三角形B .锐角三角形C .钝角三角形D .等腰三角形7.已知a 与b 均为单位向量,它们的夹角为60︒,那么3a b -等于( ) A 7B 10C 13D .48.已知()3sin 5αβ-=,()3cos 5αβ+=-,且,2παβπ⎛⎫-∈ ⎪⎝⎭,,2παβπ⎛⎫+∈ ⎪⎝⎭,则cos 2β的值为( )A .2425B .1C .45-D .1-9.若sinA cosB cosCa b c==,则ABC ∆是( ) A .等边三角形 B .等腰三角形 C .直角或等腰三角形 D .等腰直角三角形10.集合,那么( )A .B .C .D .11.若(0,),(,0)22ππαβ∈∈-,13cos ,cos +4342ππβα⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭ ,则cos 2βα⎛⎫-= ⎪⎝⎭ ( )A .33B .33-C .6-D .53912.如图所示,在直角梯形BCEF 中,∠CBF=∠BCE=90°,A ,D 分别是BF ,CE 上的点,AD ∥BC ,且AB=DE=2BC=2AF (如图1),将四边形ADEF 沿AD 折起,连结BE 、BF 、CE (如图2).在折起的过程中,下列说法中正确的个数( )①AC ∥平面BEF ;②B 、C 、E 、F 四点可能共面;③若EF ⊥CF ,则平面ADEF ⊥平面ABCD ; ④平面BCE 与平面BEF 可能垂直 A .0B .1C .2D .3二、填空题:本题共4小题 13.函数的定义域是_______________.14.若0x ≤,2M x x =+,42N x =-,则M 与N 的大小关系为___________. 15.在ABC ∆中,2a =,3b =,19c =,则ABC ∆的面积等于______.16.在长方体1111ABCD A B C D -中,12AA =,4=AD ,6AB =,如图,建立空间直角坐标系D xyz -,则该长方体的中心M 的坐标为_________.三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.设数列{}n a 的前n 项和n S .已知2*112121,,33nn S a a n n n N n +==---∈. (1)求数列{}n a 的通项公式; (2)是否对一切正整数n ,有121115131n a a a n ++⋯+<-+?说明理由. 18.在ABC 中,角,,A B C 对应的边分别是,,a b c ,且sin (sin sin )sin 0a A b A B c C ++-=. (1)求角C ;(2)若2c =,求+a b 的取值范围.19.(6分)如图,在△ABC 中,AB=8,AC=3,∠BAC=60°,以点A 为圆心,r=2为半径作一个圆,设PQ 为圆A 的一条直径.(1)请用,AP AB 表示BP ,用,AP AC 表示CQ ; (2)记∠BAP=θ,求·BP CQ 的最大值.20.(6分)设n S 为正项数列{}n a 的前n 项和,且满足2243n n n a a S +=+.(1)求{}n a 的通项公式; (2)令11n n n b a a +=,12n n T b b b =+++…,若n T m <恒成立,求m 的取值范围.21.(6分)已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭在一个周期内的图像经过点,412π⎛⎫ ⎪⎝⎭和点5,412π⎛⎫-⎪⎝⎭,且()f x 的图像有一条对称轴为12x π=.(1)求()f x 的解析式及最小正周期; (2)求()f x 的单调递增区间.22.(8分)在等差数列{}n a 中,38a =,724a a a =+. (1)求数列{}n a 的通项公式; (2)设1n nb na =,求数列{}n b 的前n 项和n S . 参考答案一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.D 【解析】 【分析】结合题意,结合直线与平面垂直的判定和性质,得到两个直角三角形,取斜边的一半,即为外接球的半径,结合球表面积计算公式,计算,即可. 【详解】过P 点作PN AC ⊥,结合平面ABC ⊥平面PAC 可知,PN ABC ⊥平面,故PN AB ⊥,结合AB AC ⊥可知,AB PAC ⊥平面,所以AB PC ⊥,结合PC PA ⊥所以PC PAB ⊥平面,所以090CPB ∠=,故该外接球的半径等于102BC =,所以球的表面积为2210=4410S R πππ=⋅=⎝⎭,故选D .【点睛】考查了平面与平面垂直的性质,考查了直线与平面垂直的判定和性质,难度偏难. 2.C 【解析】 【分析】先求出直线230x y -+=的斜率,再求出所求直线的斜率,再利用直线的点斜式方程求解. 【详解】由题得直线230x y -+=的斜率为1122-=-, 所以所求的直线的斜率为2-,所以所求的直线方程为32(1),y x +=--即210x y ++=. 故选:C 【点睛】本题主要考查互相垂直直线的性质,考查直线方程的求法,意在考查学生对这些知识的理解掌握水平,属于基础题. 3.D 【解析】 【分析】去掉一个最高分和一个最低分后,所剩数据为82,84,84,86,89,由此能求出所剩数据的平均数和方差. 【详解】 平均数8284848689855x ++++==,方差()()()()()22222282858485848586858985 5.65s -+-+-+-+-==,选D.【点睛】本题考查所剩数据的平均数和方差的求法,考查茎叶图、平均数、方差的性质等基础知识,考查运算求解能力,是基础题. 4.C 【解析】 【分析】在数列{}n a 中,11a =,264a =,且数列1{}n n a a +是等比数列,其公比12q =-,利用等比数列的通项公式可得:171(1)2n n n n a a --+=-⋅.可得(2)(1)(1)(68)32221121(1)2n n n n nn n aa a a a a a a ---+--=⨯⨯⨯⨯=-,利用二次函数的单调性即可得出. 【详解】在数列{}n a 中,11a =,264a =,且数列1{}n n a a +是等比数列,其公比12q =-, ∴1171641()(1)212n n n n n a a ---+=⨯-=-⋅. ∴01(2)65(8)3211211(1)2n n nn n a a a a a a a a +++-+++--=⨯⨯⨯⨯=⨯-⨯(2)(1)(1)(68)22(1)2n n n n ---+-=-,2(1)(14)115169()2228n n n --=--+.由7n =或8时,(2)(1)2(1)1n n ---=-,6n =或9时,20692a a ==,∴数列{}n a 的最大项等于6a 或9a .故选:C. 【点睛】本题考查等比数列的通项公式、累乘法、二次函数的单调性,考查推理能力与计算能力,属于中档题. 5.C 【解析】 【分析】根据平均数的定义即可求出.根据频率分布直方图中,中位数的左右两边频率相等,列出等式,求出中位数即可. 【详解】:根据频率分布直方图,得平均数为1(12.1×0.02+17.1×0.04+22.1×0.08+27.1×0.03+32.1×0.03)=22.71, ∵0.02×1+0.04×1=0.3<0.1, 0.3+0.08×1=0.7>0.1; ∴中位数应在20~21内, 设中位数为x ,则0.3+(x ﹣20)×0.08=0.1, 解得x =22.1;∴这批产品的中位数是22.1.故选C . 【点睛】本题考查了利用频率分布直方图求数据的中位数平均数的应用问题,是基础题目. 6.C 【解析】cos sin ,sin 2A B sin A B π⎛⎫>∴-> ⎪⎝⎭,又角,A B 均为锐角,则022B A ππ<<-<,02A B π∴<+<,且ABC ∆中,,2A B C C πππ++=∴<<,ABC ∆的形状是钝角三角形,故选C.【方法点睛】本题主要考查利用诱导公式、正弦函数的单调性以及判断三角形形状,属于中档题.判断三角形状的常见方法是:(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断;(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出边与边之间的关系进行判断;(3)根据余弦定理确定一个内角为钝角进而知其为钝角三角形. 7.A 【解析】本题主要考查的是向量的求模公式.由条件可知==,所以应选A .8.A 【解析】 【分析】由已知求出cos()αβ-,sin()αβ+的值,再由cos 2cos[()()]βαβαβ=+--,展开两角差的余弦求解,即可得答案. 【详解】 由3sin()5αβ-=,3cos()5αβ+=-,且(2παβ-∈,)π,(2παβ+∈,)π, ∴2234cos()1()1()55sin αβαβ-=---=-=-, ∴2234sin()1()1()55cos αβαβ+=-+=--=, cos 2cos[()()]cos()cos()sin()sin()βαβαβαβαβαβαβ∴=+--=+-++-434324()()555525=-⨯-+⨯=.故选:A . 【点睛】本题考查两角和与差的余弦、倍角公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意“拆角配角”思想的运用. 9.D 【解析】 【分析】先根据题中条件,结合正弦定理得到sin cos B Bbb =,求出角B ,同理求出角C ,进而可判断出结果. 【详解】因为sin cos cos A B Ca b c==, 由正弦定理可得sin sin sin A B Ca b c==, 所以sin cos B B b b =,即sin cos B B =,因为角B 为三角形内角,所以4B π=; 同理,4Cπ;所以2A π=,因此,ABC ∆是等腰直角三角形. 故选D 【点睛】本题主要考查判定三角形的形状问题,熟记正弦定理即可,属于常考题型. 10.D 【解析】 【分析】根据并集定义计算. 【详解】 由题意.故选D . 【点睛】本题考查集合的并集运算,属于基础题. 11.D 【解析】 【分析】由于02<<πα,02πβ-<<,143cos πα⎛⎫+= ⎪⎝⎭,342cos πβ⎛⎫+=⎪⎝⎭,利用“平方关系”可得4sin πα⎛⎫+ ⎪⎝⎭,42sin πβ⎛⎫+ ⎪⎝⎭,变形2442cos cos βππβαα⎡⎤⎛⎫⎛⎫⎛⎫-=+-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦即可得出.【详解】 ∵02<<πα,1043cos πα⎛⎫+=>⎪⎝⎭, ∴442πππα+<<,∴2221443sin cos ππαα⎛⎫⎛⎫+=-+=⎪ ⎪⎝⎭⎝⎭. ∵02πβ-<<,∴0424πβπ+<<,∵342cos πβ⎛⎫+=⎪⎝⎭, ∴2614242sin cos πβπβ⎛⎫⎛⎫+=-+=⎪ ⎪⎝⎭⎝⎭. ∴2442442442cos cos cos cos sin sin βππβππβππβαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=+-+=+++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 1322633=⨯+⨯53=. 故选D. 【点睛】本题考查了两角和的余弦公式、三角函数同角基本关系式、拆分角等基础知识与基本技能方法,属于中档题. 12.C 【解析】 【分析】根据折叠前后线段、角的变化情况,由线面平行、面面垂直的判定定理和性质定理对各命题进行判断,即可得出答案. 【详解】对①,在图②中,连接,AC BD 交于点O ,取BE 中点,连接MO ,易证AOMF 为平行四边形,即AC//FM ,所以AC//平面BEF ,故①正确;对②,如果B 、C 、E 、F 四点共面,则由BC//平面ADEF ,可得BC//EF ,又AD//BC ,所以AD//EF ,这样四边形ADEF为平行四边形,与已知矛盾,故②不正确;对③,在梯形ADEF中,由平面几何知识易得EF⊥FD,又EF⊥CF,∴EF⊥平面CDF,即有CD⊥EF,∴CD⊥平面ADEF,则平面ADEF⊥平面ABCD,故③正确;对④,在图②中,延长AF至G,使得AF=FG,连接BG,EG,易得平面BCE⊥平面ABF,BCEG四点共面.过F作FN⊥BG于N,则FN⊥平面BCE,若平面BCE⊥平面BEF,则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.故选:C.【点睛】本题主要考查线面平行、线面垂直、面面垂直的判定定理和性质定理的应用,意在考查学生的直观想象能力和逻辑推理能力,属于中档题.二、填空题:本题共4小题13.【解析】【分析】解方程即得函数的定义域.【详解】由题得,解之得故答案为.【点睛】本题主要考查正切型函数的定义域的求法,意在考查学生对该知识的理解掌握水平,属于基础题.>14.M N【解析】【分析】根据自变量的取值范围,利用作差法即可比较大小.【详解】2M x x =+,42N x =-,0x ≤,所以()()242M N x x x -=+-- 232x x =-+()()12x x =--当0x ≤时,()()120x x -->所以0M N ->,即M N >,故答案为:M N >.【点睛】本题考查了作差法比较整式的大小,属于基础题.15.2【解析】【分析】先用余弦定理求得2221cos 22a b c C ab +-==-,从而得到n si C =积公式求解.【详解】因为在ABC ∆中,2a =,3b =,c = 由余弦定理得,2221cos 22a b c C ab +-==-所以sin C ==由正弦定理得1sin 22ABC S ab C ∆==故答案为:2【点睛】 本题主要考查正弦定理和余弦定理的应用,还考查了运算求解的能力,属于中档题.16.(2,3,1)【解析】【分析】先求出点B 的坐标,再求出M 的坐标.【详解】由题得B(4,6,0),1(0,0,2)D ,因为M 点是1BD 中点,所以点M 坐标为(2,3,1).故答案为(2,3,1)【点睛】本题主要考查空间坐标的求法,意在考查学生对该知识的理解掌握水平,属于基础题.三、解答题:解答应写出文字说明、证明过程或演算步骤。
