(同济大学朱慈勉) 结构力学教学视频下载链接

“结构力学I”课程标准

“结构力学I”课程标准课程名称：结构力学I英文名称：Structural Mechanics I课程代码：课程类别：专业教育必修课程（专业核心课程）课程学时：56课程学分：3.5适用专业：土木工程先修课程：高等数学、理论力学、材料力学等授课学院：建筑工程学院教研室：土木工程教研室制定人：赵腾飞、袁立群、孟昭博审定人：张绪涛、孟昭博、崔诗才一、课程性质《结构力学I》是土木工程专业必修的专业核心课程之一，将为后续专业课程学习打下良好的基础。

通过本课程的学习，学生在理论力学和材料力学的基础上可以进一步掌握分析计算杆件体系的基本原理和方法，了解各类结构的受力性能，培养学生结构分析与计算的能力，为学习有关专业课程及进行结构设计和科学研究打下基础，并能够应用结构力学基本理论和方法解决工程实际问题。

二、目标要求（一）总体目标掌握结构在荷载、支座移动等因素作用下结构强度、刚度等的分析、计算方法；掌握结构的合理组成形式及分析方法；熟悉结构力学相关的基本概念，了解近似计算方法、了解计算结构力学的相关分析方法。

在头脑中初步建立结构的力学思维方式，能正确应用力学知识对结构的强度、刚度以及结构合理组成进行分析。

（二）具体目标1.知识目标（1）能理解结构力学的一般概念及结构受力、变形等特点；（2）能正确建立力学相关计算模型并对其进行结构几何组成分析；（3）能正确利用多种方法对结构进行受力分析、绘制相应的内力图；（4）能正确通过虚功法求解结构的位移，并能大致绘制结构的变形图。

2.能力目标（1）能熟练计算、绘制静定结构、超静定结构的内力；（2）能熟练求出指定截面的广义位移；（3）能判别平面杆系结构的几何组成合理性。

3.素质目标（1）能将力学知识应用于实际工程中，着力培养工程实践能力；（2）引入前延、后续课程，做好课程衔接，形成课程体系，为后学专业课学习打好基础；（3）培养学生的受力概念、直观受力感觉和力学意识，勇于担当结构安全和经济两大重任。

第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件

根据对称结构的受力特征，在对称或反对称荷载作用下，可以取半结构计算，另外半结构的内力可通过对称或反对称镜像得到。
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。判别方法有两种：
根据对称轴上的杆件和截面的变形（或位移）特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11

144 EI
,
1 p

1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
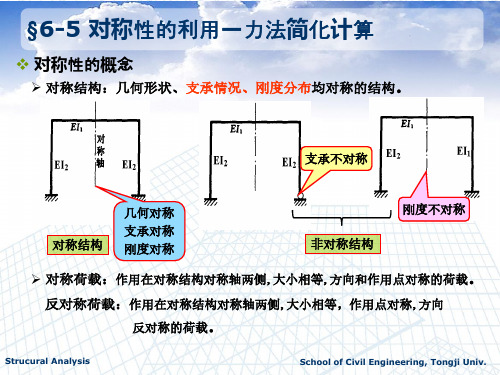
对称性的概念
对称结构：几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称支承对称刚度对称
非对称结构
刚度不对称
对称荷载：作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。反对称荷载：作用在对称结构对称轴两侧,大小相等，作用点对称,方向

13X 3 23X 3

1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0

朱慈勉语录完整版同济史上最受争议

朱慈勉语录完整版同济史上最受争议的老师（转）朱慈勉，同济大学土木工程学院教授，博士学位，博士研究生导师，结构力学研究室主任，国家教育部高等学校力学基础课程教学指导分委员会委员，上海市土木工程学会会员，国家一级注册结构工程师。

1970年毕业于清华大学工程力学数学系固体力学专业，此后几年在国家第一机械工业部第八设计院从事结构设计工作，1978年进入同济大学。

长期从事结构力学等课程的教学和结构工程领域的科学研究与工程实践，曾多次获得国家级和上海市科技进步奖和教学成果奖，发表论文数十篇。

提出了“概念结构力学”与“计算结构力学”并进发展的结构力学学科发展思想，并付诸于教学实践。

1997 年和2003年曾先后获得上海市育才奖和高校名师奖。

曾先后主持和参加数十项大型结构工程的设计和技术咨询，具有深厚的学科造诣，并善于解决实际工程问题。

研究方向：概念结构力学，结构非线性分析，结构与地基的共同工作工号：1981128 姓名：朱慈勉性别：男籍贯：上海民族：汉出生日期：保密政治面貌：中XXXXX员参加时间：保密系/所：建筑工程系部门：结构力学教学管理室职称：教授，博士生导师现任职务：结构力学研究室主任传真:65986345 办公电话:65982927最高学历：博士研究生最高学位：博士第一外语：英语家庭电话：保密博导任职时间：1999年08月享受津贴时间：电子由E件:zcm@抽烟，骂人，捧自己，瞧不起女生…朗诵俄文，抨击时政……上课时幽默到极点，下课时古怪到极点1。

全世界的结构力学书上就我编的有这个内容，不信你去看2。

你平时也算是好学生，怎么每次都出这些低级错误?3。

我上周去中南地区开会，那些人都说是我的"粉丝",叫我出个题目讲解一下, 我看下面全是五六十岁的老教授，都教了一辈子结构力学了，不想为难他们，但是他们就是要我讲，没办法，我就讲了一个，就是我刚才问你们的这个，竟然没有一个人能回答，唉，概念都没掌握，教了一辈子结构力学，连最基本的都做不来，还搞出什么抛物线形4o ――（朱）实际上振型是由第一，第二…第n个振型合成的，就像你的基因里有你爸爸的，你妈妈的。

结构力学I课程标准

“结构力学I”课程标准课程名称：结构力学I英文名称：Structural Mechanics I课程代码：课程类别：专业教育必修课程（专业核心课程）课程学时：56课程学分：3.5适用专业：土木工程先修课程：高等数学、理论力学、材料力学等授课学院：建筑工程学院教研室：土木工程教研室制定人：赵腾飞、袁立群、孟昭博审定人：张绪涛、孟昭博、崔诗才一、课程性质《结构力学I》是土木工程专业必修的专业核心课程之一，将为后续专业课程学习打下良好的基础。

通过本课程的学习，学生在理论力学和材料力学的基础上可以进一步掌握分析计算杆件体系的基本原理和方法，了解各类结构的受力性能，培养学生结构分析与计算的能力，为学习有关专业课程及进行结构设计和科学研究打下基础，并能够应用结构力学基本理论和方法解决工程实际问题。

二、目标要求（一）总体目标掌握结构在荷载、支座移动等因素作用下结构强度、刚度等的分析、计算方法；掌握结构的合理组成形式及分析方法；熟悉结构力学相关的基本概念，了解近似计算方法、了解计算结构力学的相关分析方法。

在头脑中初步建立结构的力学思维方式，能正确应用力学知识对结构的强度、刚度以及结构合理组成进行分析。

（二）具体目标1.知识目标（1）能理解结构力学的一般概念及结构受力、变形等特点；（2）能正确建立力学相关计算模型并对其进行结构几何组成分析；（3）能正确利用多种方法对结构进行受力分析、绘制相应的内力图；（4）能正确通过虚功法求解结构的位移，并能大致绘制结构的变形图。

2.能力目标（1）能熟练计算、绘制静定结构、超静定结构的内力；（2）能熟练求出指定截面的广义位移；（3）能判别平面杆系结构的几何组成合理性。

3.素质目标（1）能将力学知识应用于实际工程中，着力培养工程实践能力；（2）引入前延、后续课程，做好课程衔接，形成课程体系，为后学专业课学习打好基础；（3）培养学生的受力概念、直观受力感觉和力学意识，勇于担当结构安全和经济两大重任。

完整的结构力学答案-同济大学朱慈勉

完整的结构力学答案-同济大学朱慈勉结构力学朱慈勉版本答案朱慈勉结构力学第2章课后答案全解2-2试求出图示体系的计算自由度，并分析体系的几何构造。

(a) (ⅠⅡ)(ⅠⅢ)舜变体系(b)ⅠⅡⅢW=5某3-4某2–6=1>0几何可变(c)结构力学朱慈勉版本答案有一个多余约束的几何不变体系(d)W=3某3-2某2–4=1>0可变体系2-3试分析图示体系的几何构造。

(a)(ⅡⅢ)结构力学朱慈勉版本答案(b)Ⅲ几何不变2-4试分析图示体系的几何构造。

(a)几何不变(b)W=4某3-3某2-5=1>0几何可变体系结构力学朱慈勉版本答案（ⅠⅢ）（ⅡⅢ）几何不变(d)Ⅲ（ⅠⅢ）有一个多余约束的几何不变体结构力学朱慈勉版本答案（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）舜变体系(f)（ⅠⅢ）无多余约束内部几何不变（ⅡⅢ）结构力学朱慈勉版本答案(h)W=3某8-9某2–7=-1,有1个多余约束二元体结构力学朱慈勉版本答案2-5试从两种不同的角度分析图示体系的几何构造。

(a)ⅡⅠ（ⅠⅡ）Ⅲ（ⅠⅢ）舜变体系（ⅡⅢ）（ⅡⅢ）Ⅲ（ⅠⅢ）结构力学朱慈勉版本答案同济大学朱慈勉结构力学第3章习题答案3-2试作图示多跨静定梁的弯矩图和剪力图。

(a) FPaFPa2ＱFPFP23FP4(b)结构力学朱慈勉版本答案2020Q10/31026/3(c)60(d)3m结构力学朱慈勉版本答案M7.54484Q2.5523-3试作图示刚架的内力图。

(a)1kN/mC4kN·mA3m6mM181824Q20616(b)40kN·B10kNm3m结构力学朱慈勉版本答案M303030210(c)m3m36mM(d)mm26mQ10110Q54结构力学朱慈勉版本答案M4444N(e)484(f)Q244/3``结构力学朱慈勉版本答案M22203-4试找出下列各弯矩图形的错误之处，并加以改正。

(a)FP(b)(c)结构力学朱慈勉版本答案(d)(e)(f)F3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件，确定E、F两铰的位置。

(完整版)!完整的结构力学答案-同济大学朱慈勉!

朱慈勉结构力学第2章课后答案全解2-2 试求出图示体系的计算自由度，并分析体系的几何构造。

(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。

(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ（ⅠⅡ）（ⅠⅢ）（ⅡⅢ）几何不变2-4 试分析图示体系的几何构造。

(a)（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）几何不变(d)（ⅠⅡ）ⅢⅠⅡ（ⅡⅢ）（ⅠⅢ）二元杆有一个多余约束的几何不变体ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）舜变体系(f)ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）无多余约束内部几何不变ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体(h)ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。

(a)（ⅠⅢ）ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）舜变体系(b)ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）（ⅠⅢ）几何不变同济大学朱慈勉结构力学第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。

(a)4P F a2P F a 2P F a Ｍ4P F Ｑ34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m４2020M Q10/326/3４10(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。

朱慈勉语录完整版同济史上最受争议

朱慈勉语录完整版同济史上最受争议的老师（转）朱慈勉，同济大学土木工程学院教授，博士学位，博士研究生导师，结构力学研究室主任，国家教育部高等学校力学基础课程教学指导分委员会委员，上海市土木工程学会会员，国家一级注册结构工程师。

1970年毕业于清华大学工程力学数学系固体力学专业，此后几年在国家第一机械工业部第八设计院从事结构设计工作，1978年进入同济大学。

长期从事结构力学等课程的教学和结构工程领域的科学研究与工程实践，曾多次获得国家级和上海市科技进步奖和教学成果奖，发表论文数十篇。

提出了“概念结构力学”与“计算结构力学”并进发展的结构力学学科发展思想，并付诸于教学实践。

1997年和2003年曾先后获得上海市育才奖和高校名师奖。

曾先后主持和参加数十项大型结构工程的设计和技术咨询，具有深厚的学科造诣，并善于解决实际工程问题。

研究方向：概念结构力学，结构非线性分析，结构与地基的共同工作工号: 1981128 姓名: 朱慈勉性别: 男籍贯: 上海民族: 汉出生日期: 保密政治面貌: 中XXXXX员参加时间: 保密系/所: 建筑工程系部门: 结构力学教学管理室职称: 教授，博士生导师现任职务: 结构力学研究室主任传真: 65986345 办公电话: 65982927最高学历: 博士研究生最高学位: 博士第一外语: 英语家庭电话: 保密博导任职时间: 1999年08月享受津贴时间:电子邮件: zcm@抽烟，骂人，捧自己，瞧不起女生......朗诵俄文，抨击时政......上课时幽默到极点，下课时古怪到极点.....1。

全世界的结构力学书上就我编的有这个内容，不信你去看2。

你平时也算是好学生，怎么每次都出这些低级错误？3。

我上周去中南地区开会，那些人都说是我的"粉丝",叫我出个题目讲解一下，我看下面全是五六十岁的老教授，都教了一辈子结构力学了，不想为难他们，但是他们就是要我讲，没办法，我就讲了一个，就是我刚才问你们的这个，竟然没有一个人能回答，唉，概念都没掌握，教了一辈子结构力学，连最基本的都做不来，还搞出什么抛物线形........4。

新版朱慈勉_结构力学_第4章课后习题(全)-新版.pdf

(b)
以 A 为坐标原点，向右为
当0
x
a 时，
分析 F 以右部分，
x/a
F
B
G
E Fp=1
F
B
G
x 轴正方向。弯矩
MF
0
F RA
1
GCD 为附属部分，可不考虑
x ()
a
ME F NE
x x a
当a
x
M E =(2a-x),F
3 a 时，去掉
AF,GCD
NE
1
M 以右侧受拉为正附属部分结构
, 分析中间部分
18. 405.
2 1010
x (0x75).
A=1186
1
x
x
1
(153x).2
(75.
x
44 12)015.x2 27x.
742. 5(75.x
12)
2 52 102 5
1 18x153.x
09x. 1147.5(12x153).
[
] 45.(12x153).
25 5
当75.x1时2d，A03x. 27.0 x9。此A=时29.-7801.15-7.425=4.725 dx
Fy
0
F N2
3x 16 d
x 4d
F N2 5 2
x 2
4d 5x
16 d
F N1
5 4
2
F RB
0
5
2
F RA
5
F N1 F N1
5x 16 d
5x
5
16 d
2
F N1
F N2
35 16
F N3
1
15

北京科技大学宁波大学上海大学结构力学(高等教育出版社朱慈勉)教学讲义

§1-2 §1 2 结构的计算简图
例如：图示木屋架的结点
▲ 刚结点几何特征：各杆不能绕结点作相对转动。受力状况：由于结点能阻止杆件之间发生相对转角因此杆端有弯矩剪力和轴力。角，因此杆端有弯矩、剪力和轴力
§1-2 §1 2 结构的计算简图
表示方法：
例如：图示现浇钢筋混凝土框架的结点
§1-2 §1 2 结构的计算简图
4）结构简化
§1-3 §1 3 荷载的类型
1）按分布分 ▲ 面荷载如：风荷载、雪荷载、雨荷载、人群荷载、水压力等 ▲ 体荷载如：结构自重，温度荷载等 ▲ 集中荷载如：集中力、集中力矩等 2）按作用在结构上的时间分 ▲ 恒荷载如：结构自重和设备重量等 ▲ 活荷载如：人群荷载、雪荷载、雨荷载等 ▲ 移动荷载如：吊车荷载、汽车荷载、火车荷载
§1-1 §1 1 结构力学的主要内容和教学要求
2）主要研究内容
▲
结构由荷载、支座移动、温度变化、制造误差引起的内力计算——称为强度计算；结构由荷载支座移动温度变化制造误差结构由荷载、支座移动、温度变化、制造误差引起的变形及位移计算——称为刚度计算；结构的稳定计算；结构的组成规律及计算简图的选择结构的组成规律及计算简图的选择。
▲
▲ ▲
§1-1 §1 1 结构力学的主要内容和教学要求
3）结构力学与其它课程的关系理论力学和材料力学是结构力学的先修课程，专业课程（钢筋混凝土、钢结构、桥梁结构等）是结构力学的后续课程。结构力学的后续课程
§1-2 §1 2 结构的计算简图
在工程设计中对结构进行力学分析时需要一在工程设计中对结构进行力学分析时，需要一个图形，这个图形与实际结构完全一样，实际上是做不到的，因此必须对实际结构进行抽象和简化，得到一个计算时所用的计算简图抽象和简化必须得到一个计算时所用的计算简图。抽象和简化必须遵循以下原则： 1）正确反映结构的实际受力情况，使计算结果与实际情况比较吻合；实际情况比较吻合 2）略去次要因数，便于分析和计算。

结构力学课后习题答案(朱慈勉)

(a)
(b)
(c)
(d)
4-7试绘制图示结构主梁指定量值的影响线，并加以比较。
(a)
(b)
4-8试绘制图示刚架指定量值的影响线。
(a)
(b)
4-9试绘制图示桁架指定杆的内力影响线，分别考虑荷载为上承和下承两种情况。
(a)
下承荷载情况可同样方法考虑
(b)
下称荷载时，用同样方法分析，得到影响线如下
4-13试求图示简支梁在吊车竖向荷载作用下B支座的最大反力。设一台吊车轮压为FP1=FP2=285kN,另一台轮压为FP3=FP4=250kN，轮距及车挡限位的最小车距如图所示。
7-3试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？
7-5试用位移法计算图示结构，并绘出其内力图。
(a)
解：（1）确定基本未知量和基本结构
有一个角位移未知量，基本结构见图。
（2）位移法典型方程
（3）确定系数并解方程
5-6试用积分法计算图示结构的位移：（a）；（b）；（c）；（d）。
(a)
(b)
(c)
(d)
5-7试用图乘法计算图示梁和刚架的位移：（a）；（b）；（c）；（d）；（e）；（f）。
(a)
(b)
(c)
(e)
5-9图示结构材料的线膨胀系数为α，各杆横截面均为矩形，截面高度为h。试求结构在温度变化作用下的位移：（a）设h＝l/10，求；（b）设h＝0.5m，求（C、D点距离变化）。
6-15试判断下列超静定结构的弯矩图形是否正确，并说明理由。
(a) (b) (c)

结构力学(朱慈勉版)上课件

图乘。 a
MK图
ql 2
8
a
l
c
MP图
d
ql 2
8
l
Δ

1 EI
(
al 2
)

(
2c 3

d) 3
(2 3
l

ql )(c 8
d 2
)
第6章
使用乘法时应注意的问题小结： 1、yo必须取自直线图形； 2、当MK为折线图形时，必须分段计算； 3、当杆件为变截面时亦应分段计算； 4、图乘有正负之分； 5、若两个图形均为直线图形时，则面积、纵标可任意
A
A
p
A B
p
A
AB B
AB A B AB A B
第6章
4、上述各种位移统称为“广义位移”。与广义位移相对应的力称为“广义力”。
二、计算结构位移的目的
1、刚度验算：电动吊车梁跨中挠度 fmax≤l/600。
2、计算超静定结构必须考虑位移条件。
3、施工技术的需要。
190.59 0.03m( ) EA
第6章
例题3 试求图示半径为R的圆弧形曲梁B点的竖向位移BV。梁的抗弯刚度EI为常数。
M P PR sin
M K R sin
第6章
解：（1）在B点加一单位力（右图），写出单位力作用下的弯
矩表达式
（2）写出单位力作用下的弯矩表达式（左图）
第6章
二、图乘法证明
y
MP(x) d
M K M P ds l EI
1 EI
B
A M K M Pdx
1 EI
B
A x tgM Pdx

同济大学朱慈勉版结构力学课后答案(下)

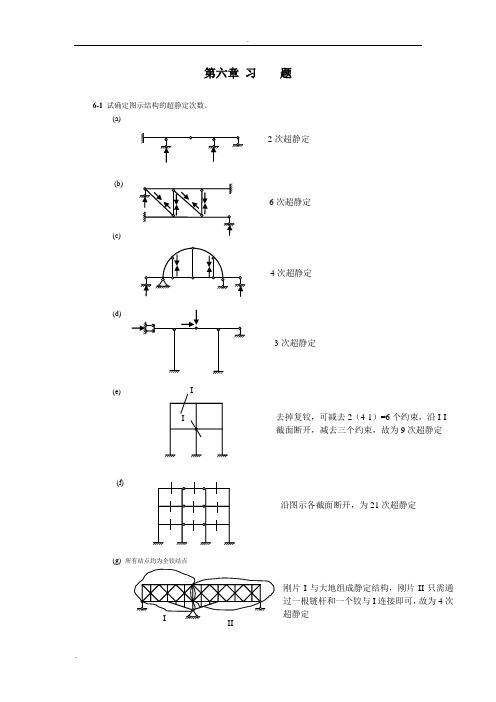
第六章习题6-1 试确定图示结构的超静定次数。

(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰，可减去2（4-1）=6个约束，沿I-I 截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定刚片I 与大地组成静定结构，刚片II 只需通过一根链杆和一个铰与I 连接即可，故为4次超静定(h)6-2 试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？ 6-3 试用力法计算图示超静定梁，并绘出M 、F Q 图。

(a) 解：上图=l1M p M01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误，为可变体系。

+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解：基本结构为：l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构，并绘其内力图。

(a)l2l 2 l2l l 2Q 图12解：基本结构为：1Mp M01111=∆+p X δ p M X M M +=11(b)解：基本结构为：4a 2a4a4a3m6m6m810810计算1M，由对称性知，可考虑半结构。

朱慈勉结构力学力法

M图、FN
2h
M 1 ds
l
h3
EI EA 3EI
X1
k
3EI h3
柱的侧移刚度
t0
1 1 h3 EA l 3EI
X1h
t0
1 EA
1 kl
例6-11 求图示结构因AB段温度均匀
下降 t0 引起的内力。线膨胀系数α。
⑴ 在温度变化作用下, 超静定结构的内力与
平均温度变化值t0以及材料的线膨胀系数 α成正比。内力数值还随受温度变化作用
在原结构的任意一个基本结
2
构上沿拟求位移方向施加虚单位力，并计算由此产生的
内力；
3 将以上所得两种状态内力代入位移计算公式计算。
§6-7 超静定结构的位移计算
C
MMP EI
ds
0
2 EI
2 3
l 2
ql 2 8
l 32
ql 4 384EI
ql 2 12
ql 2
ql 2
12
8
ql 2
M图
ql 12
MM EI
ds F R
c
1)载作用下的位移计算
F N FNP ds EA
k0
F Q FQP GA
ds
M M P ds EI
虚力状态（单位力作用下），仍可由力法基本体系（基本结构在荷载等其他一切外因和多余力共同作用的体系）与原结
构一致的位移条件考虑。
基本体系不仅在多余力方向与原结构的位移一致（力法方程条件），并且显然应满足基本结构在任一截面上的位移都一定与原结构一致。
已知AD和BD杆：EA EI m2 9
解：⑴ 确定超静定次数; 2次超静定 ⑵ 用力法求解, 并作M图和FN图; ⑶ 选取基本结构为铰结体系求位移;

(同济大学 朱慈勉) 结构力学教学视频 下载链接

“结构力学I”课程标准

第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件

朱慈勉语录完整版同济史上最受争议

结构力学I课程标准

完整的结构力学答案-同济大学朱慈勉

(完整版)!完整的结构力学答案-同济大学朱慈勉!

朱慈勉语录完整版同济史上最受争议

新版朱慈勉_结构力学_第4章课后习题(全)-新版.pdf

北京科技大学宁波大学上海大学结构力学(高等教育出版社 朱慈勉)教学讲义

结构力学课后习题答案(朱慈勉)

结构力学(朱慈勉版)上课件

同济大学朱慈勉版结构力学课后答案(下)

朱慈勉结构力学力法

(同济大学朱慈勉) 结构力学教学视频下载链接

北京科技大学宁波大学上海大学结构力学(高等教育出版社朱慈勉)教学讲义