朱慈勉版《结构力学》第2章参考答案
结构力学习题解答(第二章)
W 3 5 (2 7 6) 5
分析:刚片ACD与刚片DEG都固接在地基上,组成一个几 何不变体系且无多余约束,而铰D、链杆BD、BF、DF均是 整个体系的内部联系,并非刚片ACD、刚片DEG与地基构 成几何不变体系的必要约束,对整个体系而言是多余约束, (一个铰相当于2个约束)。 结论:有5个多余约束的几何不变体系,
W 2 8 ( 3) 0 - 13
分析:由于该体系与地基是由三根既不相互平行也不相交于 一点的链杆连接,分析时可先抛开地基。ABF可视为一刚片, 在其基础上依次增加二元体BCF、CGA后形成扩大刚片Ⅰ; DEH可视为一刚片,在其基础上增加二元体DCH后形成扩 大刚片Ⅱ,扩大刚片Ⅰ、Ⅱ由铰C和链杆GE连接,满足两刚 片规则。 结论:无多余约束的几何不变体系
分析:刚片AB、AC与地基由铰A、B、C连接,满足 三钢片规则,形成一个几何不变体系,故链杆DE为多 余约束。 结论:有一个多余约束的几何不变体系
H G F E B A C D M N
W 2 15 (27 3) 0
分析:ABC可视为一刚片,在其基础上依次增加二元体 BFC、FDC、FED、FGE、GHE后形成扩大刚片Ⅰ,同理 HMN可视为刚片Ⅱ,刚片Ⅰ、Ⅱ由铰H和链杆DM连接,由 两刚片规则可知AHN为几何不变体系,视AHN为一大刚片, 它与地基由两刚片规则连接而成。 结论:无多余约束的几何不变体系
W 3 8 (2 10 4) 0
N
W 2 6 (8 4) 0
分析:把地基及其上的固定铰 支座链杆视为刚片Ⅰ,链杆DE 视为刚片Ⅱ,铰接三角形BCE 视为刚片Ⅲ,ⅠⅡ通过链杆1、 AD连接,形成虚铰M,ⅠⅢ通过 链杆2、AB连接,形成虚铰 C,ⅡⅢ通过链杆DB、FE连接, 形成虚铰N,铰C、M、N不共线, 满足三钢片规则。
结构力学课后习题答案(朱慈勉)

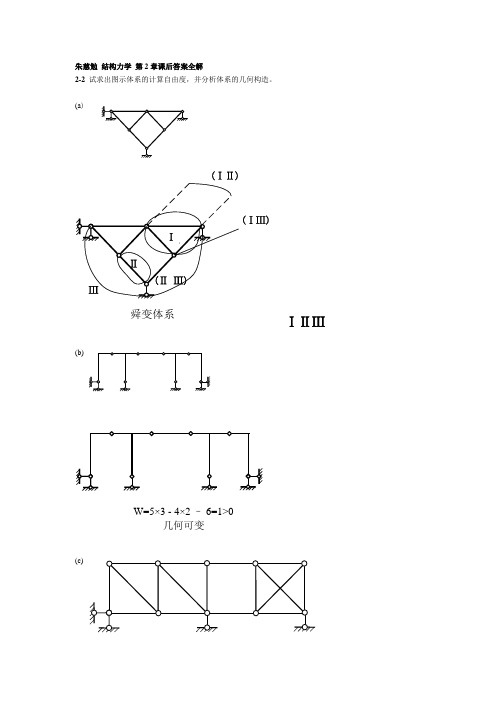
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m 2m2mA2m2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
结构力学答案-同济大学朱慈勉

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ) (b)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)无多余约束内部几何不变(g)(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)aa aaa2P F a 2P F a4P F Q34P F 2P F(b)2020Q10/326/310(c)2m6m2m4m2m3m2m2m3m3m4m18060(d)7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2mA2m 2m2m2m4kN ·m6m1k N /m2kN CB242018616MQ18(b)30303011010QM 210(c)6m10kN3m3m 40kN ·mABC D 3m3m6m45MQ(d)444444/32MQN(e)6m2m 2m4m4m4481``(f)222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)2m3m4mF P (b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学第2章习题及参考答案
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
结构力学朱慈勉版课后答案【重要】

朱慈勉 结构力学 第2章课后答案全解(b)解:基本结构为:1M2Mp M M()EIEI 1086623323326611=⨯⨯+⨯⨯+⨯⨯=δ EI=常数6m6m6mEDACB20kN/m X1 X120kN/mX2 X2363361 11 118090 15030150()03323326612=⨯⨯-⨯⨯=EI δ ()EIEI 1086623323326622=⨯⨯+⨯⨯+⨯⨯=δEI EI p 27003231806212362081632323180621121=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆EI EI p 5403231806212362081632323180621122=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯-⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆ ⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧=+=+5250540108027001082111X X EI X EIEIX EI m KN M CA ⋅=⨯-⨯-=9035253180 m KN M CB ⋅=⨯+⨯-=12035253180 ()m KN M CD ⋅-=-⨯=3056(c)解:基本结构为: ⊕6m 3m5III 10kN ·m10kN ·mEA =∞C ABD 5I12m10kN ·m10kN ·mX110kN ·m 119 339 10kN ·m10kN ·m 10 101N 1M p M()EI I E EI 5558293299233256633263111=⨯⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯=δ ()EI I E p 1442103109109231025661-=⨯⎥⎦⎤⎢⎣⎡⨯+⨯+⨯⨯+⨯⨯⨯-=∆ 01111=∆+p X δ29.11=⇒Xm KN M AC ⋅=-⨯=61.11029.19m KN M DA ⋅-=-⨯=13.61029.13 m KN M DC ⋅=⨯=87.329.13M题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
结构力学第2章习题及参考答案

结构力学第2章习题及参考答案word文档,精心编排整理,均可修改你的满意,我的安心2第2章 习 题字体如需要请自己调整2-1 试判断图示桁架中的零杆。
2-1(a )解 静定结构受局部平衡力作用,平衡力作用区域以外的构件均不受力。
所有零杆如图(a-1)所示。
2-1 (b)解 从A 点开始,可以依次判断AB 杆、BC 杆、CD 杆均为无结点荷载作用的结点单杆,都是零杆。
同理,从H 点开始,也可以依次判断HI 杆、IF 杆、FD 杆为零杆。
最后,DE 杆也变成了无结点荷载作用的结点D 的单杆,也是零杆。
所有零杆如图(b-1)所示。
(a-(a)(b)(b-32-1(c)解 该结构在竖向荷载下,水平反力为零。
因此,本题属对称结构承受对称荷载的情况。
AC 、FG 、EB 和ML 均为无结点荷载作用的结点单杆,都是零杆。
在NCP 三角形中,O 结点为“K ”结点,所以F N OG =-F N OH (a )同理,G 、H 结点也为“K ”结点,故F N OG =-F N GH (b ) F N HG =-F N OH (c )由式(a )、(b )和(c )得(c-1)FN OG=F N GH=F N OH=0同理,可判断在TRE三角形中FN SK=F N KL=F N SL=0D结点也是“K”结点,且处于对称荷载作用下的对称轴上,故ID、JD杆都是零杆。
所有零杆如图(c-1)所示。
2-2试用结点法求图示桁架中的各杆轴力。
2-2(a)(a-33 3(a-33 345解 (1)判断零杆①二杆结点的情况。
N 、V 结点为无结点荷载作用的二杆结点,故NA 、NO 杆件和VI 、VU 杆件都是零杆;接着,O 、U 结点又变成无结点荷载作用的二杆结点,故OP 、OJ 、UT 、UM 杆件也是零杆。
②结点单杆的情况。
BJ 、DK 、QK 、RE 、HM 、SL 、LF 杆件均为无结点荷载作用的结点单杆,都是零杆;接着,JC 、CK 、GM 、LG 杆件又变成了无结点荷载作用的结点单杆,也都是零杆。
同济大学朱慈勉结构力学课后习题答案

更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
结构力学第2章习题及参考答案备课讲稿
题章习第2试判断图示桁架中的零杆。
2-1a)2-1(F P1 F F P1P2 F P2aF F P2P1 F P14a(a-1)(a)静定结构受局部平衡力作用,平衡力作用区域以外的构件均不受解)所示。
力。
所有零杆如图(a-12-1 (b)FF FF PP F C PP FC E E F F FF H H AAIBDIBDF F PP(b)(b-1)杆均为无结点荷CD杆、ABBC杆、从解A点开始,可以依次判断HI点开始,也可以依次判断载作用的结点单杆,都是零杆。
同理,从H的D杆也变成了无结点荷载作用的结点最后,FDIF 杆、杆、杆为零杆。
DE)所示。
b-1单杆,也是零杆。
所有零杆如图(.2-1(c) F2paa FF pp×al=6 (c)F2pQ P O S R N TM F H J LI K G A B E C D FF pp(c-1)该结构在竖向荷载下,水平反力为零。
因此,本题属对称结构承受解均为无结点荷载作用的结点单杆,FGAC、、EB和ML对称荷载的情况。
都是零杆。
NCP三角形中,O结点为“K”结点,所以在)(a F=-F OHOG NN”结点,故结点也为“K同理,G、H)(b =-FF GH NN OG)(c =-FF OHHG NN)得c由式(a)、(b)和(0=F=FF=OHGH N OG NN三角形中同理,可判断在TRE0=FFF==SL NN SKKL N JD故结点,K结点也是D“”且处于对称荷载作用下的对称轴上,ID、)所示。
c-1杆都是零杆。
所有零杆如图(.2-2试用结点法求图示桁架中的各杆轴力。
2-2(a)aaF F F pppal=8×(a) P O N Q R S VU TL KM J A I HD GE FB C F F F ppp(a-1)Q P R S TL MK JA I H D GE BF C F F F ppp (a-2)(解1)判断零杆、结点为无结点荷载作用的二杆结点,故N、VNA①二杆结点的情况。
结构力学章节习题及参考答案
习题7.2填空题
(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角,若选图(b)所示力法基本结构,则力法方程为_____________,代表的位移条件是______________,其中1c=_________;若选图(c)所示力法基本结构时,力法方程为____________,代表的位移条件是______________,其中1c=_________。
(a)
习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。
(a)(b)(c)
(d)(e)(f)
习题3.7图
习题3.8作习题3.8图所示刚架的内力图。
(a)
(b)
习题3.8图
第4章 静定拱习题解答
习题4.1是非判断题
(1) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。( )
(2) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。 ( )
习题3.2(2)图
习题3.3作习题3.3图所示单跨静定梁的M图和 图。
(a) (b)
(c) (d)
(e) (f)
习题3.3图
习题3.4作习题3.4图所示单跨静定梁的内力图。
(c)
习题3.4图
习题3.5作习题3.5图所示斜梁的内力图。
习题3.5图
习题3.6作习题3.6图所示多跨梁的内力图。
(a)
习题3.6图
(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。( )
(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。( )
习题 2.1(5)图
结构力学答案-同济大学朱慈勉

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ) (b)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)无多余约束内部几何不变(g)(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)aa aaa2P F a 2P F a4P F Q34P F 2P F(b)2020Q10/326/310(c)2m6m2m4m2m3m2m2m3m3m4m18060(d)7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2mA2m 2m2m2m4kN ·m6m1k N /m2kN CB242018616MQ18(b)30303011010QM 210(c)6m10kN3m3m 40kN ·mABC D 3m3m6m45MQ(d)444444/32MQN(e)6m2m 2m4m4m4481``(f)222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)2m3m4mF P (b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学第2章习题参考答案_khdaw

C A
E
F
J A B C Fp
K D
(c)
ww
(a) 三杆结点、结点无荷载,单杆为零杆。因此杆件 AB、BC、CD、DE、DF、FG、GH 为 零杆,共计 7 根轴力为零的杆件。 (b) 竖向荷载下水平反力为零,因此属对称结构对称荷载情况。从三杆结点、结点无荷载 单杆为零杆,对称轴结点无荷载非垂直对称轴的两杆为零杆可知,杆件 AC、FG、EB、LM、 ID、JD 为零杆。在 NGCHPON,RKELTSR 两个三角形部分中,可有多种分析判断方法证明 GO、GH、HO、SK、KL、SL 为零杆。其一种方法是,因为 O、H、G 三点都是两杆共线的 四杆结点,从垂直共线杆方向投影应该平衡的角度,可以证明 GO、GH、HO 三杆为零杆, 另三杆同理。故本题共计 12 根轴力为零的杆件。 (c) 利用减二元体、三杆结点、结点无荷载,单杆为零杆,分析可得杆件 AN、NO、OJ、 OP、JB、JC、KC、KQ、KD、ER 为零杆,考虑对称,则另一侧的 SL、LF、LG、GM、MU、 MH、TU、UV、VI 也为零杆。因此,共计 19 根轴力为零的杆件。 (d) 从 B、C、E、G、D 三点是三杆结点、结点无荷载,单杆为零杆,在考虑两杆结点无荷 载,可得杆件 AC、CD、CF、FD、FG、GD、GH、DE、DB 为零杆,共计 9 根轴力为零的 杆件。
2
A
∑Fy = 0
取 I 结点隔离体有:
FA y = 15.33 kN
FNID = −8 kN
再取 D 结点为隔离体有: FN1 = 4 2 NEF
ww
w.
kh
da
课
后
答
w.
案 网
用截面从杆 2、JK、EF 截开,取右侧为隔离体, 列投影方程有: ∑ F y = 0 FN 2 = 5FB y = 28.33 kN
结构力学第2章习题及参考答案

(2)BC部分(图(c-2)):
: ; :
:
(3)可以很方便地画出整个结构的弯矩图。
2-19(d)
解D结点(图(d-1)):
(考虑对称性):
AD杆(图(d-2)):
(考虑对称性):
取整体为隔离体
:
这样,ECF部分为一个顶铰作用集中荷载2FP的三铰刚架。整个结构的弯矩图就可以画了。
2-20试作图示结构的弯矩图。
第2章习题
2-1试判断图示桁架中的零杆。
2-1(a)
解静定结构受局部平衡力作用,平衡力作用区域以外的构件均不受力。所有零杆如图(a-1)所示。
2-1 (b)
解从A点开始,可以依次判断AB杆、BC杆、CD杆均为无结点荷载作用的结点单杆,都是零杆。同理,从H点开始,也可以依次判断HI杆、IF杆、FD杆为零杆。最后,DE杆也变成了无结点荷载作用的结点D的单杆,也是零杆。所有零杆如图(b-1)所示。
,
,
2-12图示圆弧三饺拱,求支座反力及截面D的M、FQ、FN值。
解(1)求支座反力。
, ,
(2)求等代梁D截面内力
(3)求三铰拱D截面内力
,
2-13求图示三铰拱结构的支座反力,链杆轴力,并求指定截面K的弯矩。
解(1)求支座反力
, ,
(2)链杆轴力
取CEB部分为隔离体
(3)求K截面的弯矩
取KAD部分为隔离体
由式(a)、(b)和(c)得
FNOG=FNGH=FNOH=0
同理,可判断在TRE三角形中
FNSK=FNKL=FNSL=0
D结点也是“K”结点,且处于对称荷载作用下的对称轴上,故ID、JD杆都是零杆。所有零杆如图(c-1)所示。
结构力学朱慈勉版课后答案【重要】
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
《结构力学》习题解答(内含解答图)

习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解:将题中的折杆用直杆代替,如图(b)所示。杆CD和链杆1由铰D联结构成二元体可以去掉;同理,去掉二元体杆CE和链杆2,去掉二元体ACB,则只剩下基础,故整个体系为几何不变体系,且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结,组成几何不变体,在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。,
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解:将原图结点进行编号,并将固定铰支座换为单铰,如图(b)。折杆AD上联结杆EF,从几何组成来说是多余约束;同理,折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ,折杆AD为刚片Ⅱ,折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连,刚片Ⅰ与刚片Ⅲ是由链杆C相连,注意,杆BD只能使用一次。由规则二知,体系为几何可变体系。
结构力学 第2章习题参考答案

FN3 FN2
0
1
45o Fp
0
w.
45
o
FN2
FN4 45o FN3
Fp
Fp
K
(a)隔离体图
3.5Fp
da
30 kN 3×2m 2 3 30 kN 30 kN
(b)隔离体图
FN2 +FP × cos 45D = 0
FN2 = −
取隔离体图(b)所示,列方程有:
∑ M K = 0 FN4 × 2d + FN3 cos 45D × 2d + 3.5FP × 2d − FP × d = 0 FN4 = −4 FP
∑F
y
= 0 FN3 sin 45D − FN2 sin 45D − 3.5 FP + 2 FP = 0
FN1 + FN3 sin 45D = 0 , FN1 = − FP
ww
(b)对称情况 (a)反对称情况 根据隔离体图(a) 依次利用结点法可求得 1、2、3 杆轴力:
FN1 = 30 kN
FN 2 = −30 2 kN=42.42 kN
隔离体 (c)
cos β = 5 13 FN1 = −1.802 8 FP
5
本题是对称结构对称荷载情况,只须计算一半杆件即可。由隔离体图(a)列投影方程如下 FN1 cos β + FN2 sin α + FP = 0 FN1 sin β + FN2 cos α = 0 可得
FN2 = 1.118 0 FP
2 FP 2
FN3 = 2 FP
1
m
l
∑M
FN2 × 2 m+FN1 × sin 45D × 2 m = 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
: 424327084
″Ⅳ Ⅵ ∽ ,sh0p36635188.ta0bao.conV
29试 求出图示体系的计箅 自由度 ,并 分析体系的几诃构造 。
⑴
`
/ / / /
(IⅡ )
/厂一 、
舜变体系
l IIIE
∶
馕 黟 耧 ∷
W△ 5× 3o4× 2 - 6=约柬的几何不变体系
可变体系
加3试 分析 图示 体系 的几何构 造 。
。
(IⅡ )
Ⅲ 几何 不变
ˉ
(Ⅱ IⅡ )
考研 吧 工 作 窒 一 同济 大 学考研 资料 专卖店 QQ:424327084
| "M内 讥shoo36s361B8~妇 obao.CoΠ l`
(Ⅱ
Ⅱ D
(IⅡ[)
几 何 不变
卜4试 分析图示体系的几阿构造。
(a)
`
几何不变
W=4× 3ˉ 3x2ˉ 5=l>0
几何可变 体 系
424327084
(IⅡ 【 )
\
几 何不变
tIⅡ
)
Ⅲ
(Ⅱ
Ⅱ)
(
有 一 个 多余 约 束 的几何不变 体
考研 吧工 作 室 一 同济 大 学考研 资料 专 卖店
QQ∶
424327084
Ⅵ 〃sh00366351渴 8~妇 obao.C0ΠV ~∽ 。
(IⅡ 1)
(Ⅱ
Ⅱ I)
.¨
.△ 忄心
(I Ⅱ I)
\
无多余约束 内部几何不变
(Ⅱ Ⅱ F)
(ω
工 考研吧・ 作 窒一 同济 太学考研资料 专卖店
QQ∶
424327084
N∽ 。 η ″shop3663弓 188口 r
I(IⅡ )
W=3× 8ˉ 9x9-7=ˉ 1, 有置 个多余约束
二元体
⒉5试 从两种不同的角度分析图示体系的几何构造 。
〈IⅡ
)
考研 吧 工 作 室
△ 同济 大 学考 研 资料 专 卖店 QQ:~华 4327084
sh0D36bN田⒒
(Ⅱ 皿 冫
几何不变
(IⅢ )
