运筹学结课论文
管理运筹学结业论文11

运筹学论文运筹学(operational research,缩写O.R.)的“运筹”就是运算、筹划的意思。
实际上,现实生活中几乎在每个人的头脑中都自然地存在着一种朴素的“选优”和“求好”的思想。
例如,当准备去完成一项任务或去做一件事情时,人们脑子里自然地会产生一个想法,就是在条件允许的范围内,尽可能地找出一个“最好”的办法,去把需要做的事情做好。
实际上这就是运筹学的基本思想。
运筹学作为一门科学最早出现在第二次世界大战前夕,英国面临如何抵御德国飞机轰炸的问题。
当时英国的鲍德西雷达站负责人A.P.罗威建议马上展开对雷达系统运用方面的研究。
为区分于技术方面的研究,他提出了“operational research”这个术语,原意为“作战研究”。
当时所研究和解决的问题都是短期和战术性的问题,第二次世界大战结束以后,在英美两国的军队中相继成立了正式的运筹学研究组织。
并以RAND公司为首的一些部门开始着重研究战略性问题。
例如,未来的武器系统的设计和其合理运用的方法,各种轰炸机系统的评价,未来的武器系统和未来战争的战略部署,以及苏联的军事能力和未来的发展预测等问题。
进入了20世纪60年代,运筹学的研究转入了战略力量的构成和数量问题的研究,同时除了军事领域的应用研究以外,相继在工业、农业、经济和社会问题等各领域都有了应用。
与此同时,运筹学的研究进入了快速发展阶段,并形成了运筹学的许多新的应用分支。
O.R.传入中国后,曾一度被译为“作业研究”或“运用研究”。
1956年,中国学术界通过钱学森、许国志等科学家的介绍,在了解了这门学科后,有关专家就译名问题达成共识,即译为“运筹学”。
其译意恰当的反映了运筹学既源于军事决策,又军民通用的特点,并且赋予其作为一门学科的含义。
同时,相继有以华罗庚教授为首的一大批数学家加入了运筹学的研究队伍,使中国运筹学研究的很多分支很快跟上国际水平,并结合我国的特点在国内进行了推广应用。
特别是经济领域,关于投入产出表的研究与应用、质量控制(质量管理)等方面的应用很有特色。
大学生运筹学论文

大学生运筹学论文第一篇:大学生运筹学论文论数学与生活内容提要:步入大学,我们的学习已经不再停留于刻板的书本,我们学习的目的也不仅仅是去掌握那些常规的知识,大学学习,我们更多的是去学习一种思想,学习一种态度,然后用我们所学去实践生活。
当我们用心思考,我们也会发现,陪伴我们十几年的恼人的数学也蕴含了丰富的人生哲理。
关键字:生活,思考,哲理一、数学里的奇妙现象有时候我们会思考:无穷的边缘是什么?就像我们弄不懂广袤宇宙的边境是什么,无论多么科学的解释我们也始终想不明白怎么可以存在这样的一个空间去包括宇宙以及宇宙之外的东西。
而代表着这个含义的π=3.1415……..,无穷尽的不规则小数,没有尽头,但是它却确确实实是我们每天都会用到的具有现实意义的数值;二、最美丽的数字——0.618(1)人体上的黄金分割《达芬奇密码》一书中说讲,肩膀到指尖的距离除以肘关节到指尖的距离;臀部到地面的距离除以膝盖到地面的距离。
再看看手指关节、脚趾、脊柱的分节,都会得到PHI(黄金分割比)。
真的会这样吗?我半信半疑地进行了一点近似的计算。
按照一个正常体型的人为例:肩膀到指尖的距离:70㎝肘关节到指尖的距离:43㎝43÷70≈0.614 臀部到地面的距离:80㎝膝盖到地面的距离:49㎝49÷80≈0.613 这些数据的结果都接近于0.618。
(2)生理上的黄金分割再如网上说,人在环境气温22℃-24℃下生活感到最适宜.因为人体的正常体温是36℃-37℃,这个体温与0.618的乘积恰好是22.4℃-22.8℃,而且在这一环境温度中,人体的生理功能、生活节奏等新陈代谢水平均处于最佳状态。
37℃×0.618=22.866℃所以当所有的这些都和黄金分割比联系上时,我们不得不感叹数学的奥秘,真的很不可思议,如果说是巧合,但是当种种现象都联系在一起的时候,就不仅仅是巧合可以解释的了,我们不得不承认这就是数学中蕴含的奥妙。
运筹学论文

吴禹锟一院八队201101044032 运筹学摘要:临近年末,家中生产的冰糖橙到了一个大卖的时候,采摘下来的冰糖橙需要合理的保存,才能够长期保鲜。
而摘下来的冰糖橙需要进行进一步包装,才能卖到一个更好的价格。
最后就是运输问题,怎样用最少的运价运到更多的地方。
这就需要制定一个严密的计划,使自己所用的花费最少。
关键字:生产与存储 动态规划 经济批量订货模型 运输问题 lingo正文:研究背景:家中种有3000余棵冰糖橙树,每年到年底时,也就是冰糖橙成熟的时候。
冰糖橙采摘需分阶段,且采摘需要请员工,这会产生一个费用,存贮需要存储空间,就会产生一个存储费用。
这就涉及到一个生产与存储的问题,可以建立一个数学模型。
采摘下来的冰糖橙,需要装入保鲜袋,然后装进箱子中,箱子需要订购。
这就会涉及到一个经济批量(EOQ )问题,是一个优化问题,且不允许缺货。
最后就是卖往各个地区,这里还可能产生产销不平衡的情况,需要寻求最优解。
研究内容:一、生产与存储问题:这是一个动态规划问题,需要合理的安排生产与库存的问题,达到既要满足需求,又要尽量降低成本费用。
一次,确定不同时期的的的生产量和库存量,以使总的雇佣费与库存费之和最小。
设d k 为第k 阶段对产品的需求量,x k 为第k 阶段该产品的生产数量,sk 为第k 阶段初的产品数量,则有z k =s k -1+x k -1-d k -1。
C k (x k )表示第k 阶段生产xk 数量的产品使的成本费用,它包括生产准备费用k 和产品城北ax k 两项费用。
即C k (x k )={0, xk =0k +axk,0<xk ≤mk其中m k 为第k 阶段生产xk 数量的上限。
用h k (s k )表示在地k 阶段初库存量为s k 时的存储费用。
因此,第k 阶段的成本费用为C k (x k )+h k (s k )所以,上述问题的数学模型为Minz=∑ck (xk )+ℎk(sk )n k=1s.t.{s0=0,sn +1=0sk =∑(xj −dj ), k =1,2,…,n −1k j=10≤xk ≤mk, k =1,2,…,n xk 为正整数用动态规划方法求解,s k 为状态变量,他表示第k 阶段开始时的库存量x k 为决策变量,他表示第k 阶段的生产量;状态转移方程为S k+1=s k +x k -d k , k=1,2,…,n 最优值函数f k (s k )表示从第k 阶段初始库存量为s k 到底n 阶段末的最小总费用。
运筹学结课论文

运筹学与博弈论思想的应用概要:本文从“运筹帷幄”引入运筹学和博弈论,从历史、经济、民生等领域所举例子详细解说了运筹学与博弈论思想在现实中的应用。
关键字:运筹学、博弈论、企业管理、运输问题、影子价格、运筹工作者一、运筹学的的起源与发展普遍认为,运筹学起源于第二次世界大战初期,当时, 英国(随即是美国) 军事部门迫切需要研究如何将非常有限的物资以及人力和物力, 分配与使用到各种军事活动的运行中, 以达到最好的作果。
在第二次世界大战期间, 德国已拥有一支强大的空军, 飞机从德国起飞17 分钟即到达英国本土。
在如此短的时间内, 如何预警和拦截成为一大难题。
1935 年, 为了对付德国空中力量的严重威胁, 英国在东海岸的鲍德西(Birdseye) 成立了关于作战控制技术的研究机构。
1938 年, 鲍德西科学小组负责人( Rowe , A1 P) 把他们从事的工作称为运筹学(Operational research[ 英] ,Operations research[美] ,直译为“作战研究”) 。
因此, 人们把鲍德西作为运筹学的诞生地, 将1935 —1938 年这一时间段作为运筹学产生的酝酿时期。
其实早在古代中国就有“运筹于帷幄之中,决胜于千里之外”之说,后来人们用“运筹帷幄”表示善于策划用兵、指挥战争。
然而“运筹”发展到现代已成为一门重要的学科“运筹学”。
由上述运筹学发展历史可知,运筹学是由军事、经济、生产等各个领域所提出的决策问题的推动而发展起来的一门新兴的学科分支。
所谓运筹学,可以说是一系列用以提高所研究系统的有效性的分析工具。
博弈论属于运筹学的一个分支,是研究博弈行为中竞争各方是否存在着最合理的行动方案,以及如何找到这一合理方案的数学理论和方法。
运筹学包括以下内容:线性规划、非线性规划、动态规划、多目标规划、网络分析、网络规划、排队论、存储论、博弈论、决策论、模型论等。
运筹学作为一门用来解决实际问题的学科,在处理千差万别的各种问题时,一般有以下几个步骤:确定目标、制定方案、建立模型、制定解法。
(2020年整理)运筹学结课论文.pptx

材料的库存量
材料A/10kg
0
5
15
材料B/10kg
6
2
24
材料C/10kg
1
1
5
利润/元
2
1
解: 先用 X1 和 X2 分别表示该公司制造两种面粉的数量。则该公司可获取
的利润为(2X1+X2)元,令 Z=2X1+X2,因问题中要求获得最大利润,即 max z。
目标函数 约束条件
max Z 2x1 x2
Cj
2
1
0
0
0
Cb
基
b
X1
X2
X3
X4
X5
0
X3
15
0
5
1
0
0
2
X1
4
1 2/6
0 1/6
0
0
X5
1
0
4/6
0
-1/6 1
Cj-Zj
0
1/3
0
-1/3 0
由于表中还存在大于零的检验数,故重复上述步骤,可得到下表
Cj
2
1
0
0
0
Cb
基
b
X1
X2
X3
X4
X5
0
X3
15/2
0
0
1 5/4 -15/2
2
X1
7/2
0 0 1 1 4 6 6 3 -3 1 3 3 0
-1
0 6 21 0 5 31 0 0 01 1 3 20 在变换后的系数矩阵中确定独立的零元素。若独立零元素有 n 个,则已 得出最优解;若独立零元素少于 n 个,则做能覆盖所有零元素的最少直 线数目的直线集合。 继续变换系数矩阵。方法是在未被直线覆盖的元素中找出一个最小元 素。对未被直线覆盖的元素所在行(或列)中各元素都减去这一最小元 素。这样,在未被直线覆盖的元素中势必会出现零元素,但同时却又使已
运筹学论文

中国矿业大学运筹学结课论文姓名:魏恒征学院:矿业工程学院班级:采矿工程09-7班学号:01090235教师:付乳燕运筹学的初步学习及认识背景:本学期在付老师的指导下学习了运筹学,初步了解运筹学的发展历史及运筹学在生活实例中的应用。
运筹学是一门和社会生活紧密联系的一门科学,学习运筹学不仅是仅仅的学习知识,运筹学的诸多思想在实际决策中很有指导意义。
关键词:运筹学历史特点学习收获前景一、运筹学简介英语全称为:Operational Research(英国)或者是Operations Resear ch(美国)在中国战国时期,曾经有过一次流传后世的赛马比赛,相信大家都知道,这就是田忌赛马。
田忌赛马的故事说明在已有的条件下,经过筹划、安排,选择一个最好的方案,就会取得最好的效果。
可见,筹划安排是十分重要的。
现在普遍认为,运筹学是近代应用数学的一个分支,主要是将生产、管理等事件中出现的一些带有普遍性的运筹问题加以提炼,然后利用数学方法进行解决。
前者提供模型,后者提供理论和方法。
运筹学的思想在古代就已经产生了。
敌我双方交战,要克敌制胜就要在了解双方情况的基础上,做出最优的对付敌人的方法,这就是“运筹帷幄之中,决胜千里之外”的说法。
但是作为一门数学学科,用纯数学的方法来解决最优方法的选择安排,却是晚多了。
也可以说,运筹学是在二十世纪四十年代才开始兴起的一门分支。
运筹学主要研究经济活动和军事活动中能用数量来表达的有关策划、管理方面的问题。
当然,随着客观实际的发展,运筹学的许多内容不但研究经济和军事活动,有些已经深入到日常生活当中去了。
运筹学可以根据问题的要求,通过数学上的分析、运算,得出各种各样的结果,最后提出综合性的合理安排,已达到最好的效果。
运筹学作为一门用来解决实际问题的学科,在处理千差万别的各种问题时,一般有以下几个步骤:确定目标、制定方案、建立模型、制定解法。
虽然不大可能存在能处理及其广泛对象的运筹学,但是在运筹学的发展过程中还是形成了某些抽象模型,并能应用解决较广泛的实际问题。
地方高校信息管理专业运筹学课程的论文

地方高校信息管理专业运筹学课程的论文•相关推荐地方高校信息管理专业运筹学课程的论文信息管理专业是地方型院校的新专业,主要学习经济、管理、数量分析、信息管理、计算机及信息系统方面的基本理论和基本知识,得到系统分析和设计方面以及信息管理方法的基本训练。
运筹学课程不仅是信息管理专业的必修课,同时也是许多理工科专业的必修、限选或者任选课程。
如何根据不同专业特征来优化课程结构和教学内容,提高运筹学的教学效率,是目前众多高校重点研究的课题之一。
国内外不少高校己经推出了一些积极举措,包括组织编写或者翻译能够反映新需求的高水平教材、丰富教学环节、改革教学内容等。
如清华大学组织出版了美国著名的《introductiontooperationsresearch》、《运筹学:决策方法》等一系列教材,对于国内运筹学教材改革起到了很好的促进作用:山东大学通过国家精品课程建设系统地优化了运筹学课程体系,改革了考核体系,重视实践教学和学生能力培养等,;北京理工大学韩伯棠教授主持了运筹学精品课程网站建设,内容丰富,使用先进的教学方法,注重学以致用,在网上不仅提供相关的参考文献,还为学生和读者提供互动在线答疑的功能,为运筹学课程的教学方法改革提供了有效参考。
1教学现状、存在的问题1.1教学目的不够明确目前,多数运筹学课程的教材存在着重理论、轻应用的倾向,罗列了一大堆定理、公式和算法,很少有运用运筹学解决实际问题的案例。
教学中忽略了运筹学与多学科的横向交叉联系和运用运筹学解决实际问题,使得学生只会按照规定的模式算题,而不善于处理大量的现实生活问题。
1.2教学内容选择不够恰当目前许多高校在运筹学教材和教学内容的选择上存在着一定的随意性,甚至存在着教材因人而定,教学内容因人而选,实验课因人而开的现象。
运筹学具有多个理论分支,每一个分支用于处理不同的问题,各分支之间处理问题的方法差别较大。
对于信息管理类专业,需要将经济、管理、计算机等系列知识充分联系,单纯掌握某一个分支的求解技巧或者概念的符号表述,对于其培养学生运用现有的数学工具建立模型求解实际问题的能力是很不利的。
关于运筹学论文范例整理分享(共5篇)

关于运筹学论文范例整理分享(共5篇)关于运筹学论文范例整理分享(共5篇)运筹学是一门应用性很强的学科,在培养学生分析和解决问题的能力,提高学生应用和创新能力方面发挥着重大的作用.本文针对运筹学教学的特点和现今存在的问题,提出了一系列改革建议及方案,构建了理论与实践相结合的教学体系,该体系能够使学生学以致用,增强学生的实践能力,为培养应用创新型人才创造良好条件.第1篇:新业态下民航类专业运筹学教学模式改革研究从网络售票到微信值机,从单一的“售舱位”到运用大数据“提供综合服务”,互联网在深刻改变整个社会的同时,也在冲击传统的航空运输业,航空公司开始关注乘客的兴趣爱好、企业的运输需求,重新定义飞行。
在移动互联网时代,随着消费者对服务要求的不断提高,从关注服务本身,向客户体验和价值链两端不断延伸,服务提供方需要把标准化的服务产品或项目细化拆分,让客户选择自由结合。
航空运输业要想取得竞争优势,也必须不断创新服务理念,发展新业态。
新业态是指基于不同产业间的组合、企业内部价值链和外部产业链环节的分化、融合、行业跨界整合以及嫁接信息及互联网技术所形成的新型企业、商业乃至产业的组织形态。
信息技术革命、产业升级、消费者需求倒逼不断推动新业态产生和发展,也要求高校教育与人才培养模式必须进行与之相适应的变革。
运筹学是民航类专业的一门专业基础课,它是民航运营活动有关数量方面的理论,运用科学的方法来决定如何最佳地运营和设计各种系统的一门学科,对系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
通常以最优、最佳等作为决策目标,避开最劣的方案[1]。
近年来,郑州航院运筹学课程组秉承“航空为本管工结合”的办学理念,针对民航类专业的特点进行了一系列教育教学改革,达到了预期效果。
本文旨在介绍《运筹学》课程的教学改革过程,研究总结成功经验,并提出未来改革发展的思路。
一、运筹学教育教学现况郑州航院交通运输(航空物流)专业、安全工程(民航方向)及工业工程(航空方向)着重培养能够从事民航运输管理、机场运营管理、航空安全管理、跨境电商等经营与管理应用型人才。
运筹与优化课程论文

运筹与优化——我的认知黄德志(上海大学文学院“运筹与优化”第三组11123850)摘要:运筹学是一门现代科学,作为一门用来解决实际问题的学科,发展至今天已经有诸多的分支。
其中,网络规划是其重要的一支分支,确立目标,制定方案,建立模型,制定解法一般是处理网络规划问题的四部曲,模型、案例、解法是迈进网络规划知识殿堂的三个重要关口。
下面,我将选取运筹学中的重要分支之一——网络规划为例来带领大家进入运筹学的丰富世界,并通过模型、案例和求解三方面展开分析网络规划包含的最短路、最小费用流和最大流等问题,并列举几种相关的求解方法加以分析。
网络规划无论是在市场销售、生产计划、库存管理还是在运输问题、设备维修更新、工程的最佳化设计等方面都有广泛的应用,其在政治、经济、社会、民生等方面发挥的作用越来越大。
关键词:网络规划、模型、案例、求解1引言在展开分析网络规划包含的最短路、最小费用流和最大流等具体问题前,我们先得理解网络规划的一些基本概念和特征。
(1)网络规划含有七个最基本概念,它们分别是:1)图:由点和边组成的集合。
常记为:G=(V,E);其中:V={v1,v2,…,vn}表示点的集合,E={e1,e2,…,em}表示边的集合。
如下图2.1-1为无向图,图2.1-2为有向图。
图2.1—1 无向图图2.1-2 有向图2)网络:带有某种数量指标的图(即:赋权图)称为网络如下图2.1-3为无向网络,图2.1-4为有向网络。
图2.1-3 无向网络图2.1-4 有向网络3) 链:无向图G=(V,E)中与边依次交替出现的序列{vi0,ei1,vi1,ei2,vi2,…,vik-1,eik,vik}, 且eit=(vit-1,vit),t=1,…,k,则称这个点边序列为连接vi0到vik的一条链,链长为k。
4)圈:链{vi0,ei1,vi1,ei2,vi2,…,vik-1,eik,vik}中当vi0=vik时, 该链称为圈。
运筹学论文

纳什均衡的效率及选择摘要: 对策论主要研究策略选择问题, 强调的是个人理性。
纳什均衡在非合作博弈理论中起着核心作用, 但其均衡的多重性限制了纳什均衡的应用。
就纳什均衡的经济含义及多重均衡的效率选择进行简要描述和分析。
纳什均衡既符合人们的理性要求, 又是稳定的博弈结果,所以它作为局中人的一致预测能帮助局中人制定决策。
关键词: 纳什均衡; 效用函数; 博弈; 策略1 博弈问题与纳什均衡从独立决策问题到博弈问题, 决策者面临的困难增加了, 决策者进行决策面临的外部条件是不确定的,而且该决策者的行为还会影响其他局中人的利益, 进而影响他们的行为, 局中人之间形成互动关系。
在独立决策中, 优化理论符合人们追求自身利益的最大化的理性要求, 它的解告诉在什么条件下选择什么策略, 所以它的决策方法能预测人们的某些经济行为。
同样, 研究利益相关和互动关系问题的博弈理论, 局中人也各自追求自身利益的最大化。
从表1中可见, 对两个犯罪嫌疑人整体而言(抵赖, 抵赖)是两个犯罪嫌疑人最佳的策略组合, 但在两犯罪嫌疑人被抓后分别关押且彼此不知道对方会采取什么策略时, 每个犯罪嫌疑人就会在警察所给的策略下选择自己的最优策略/坦白0, 于是/囚徒困境0中的纳什均衡解正好是策略组合(坦白, 坦白)。
警察最终达到了预定的目的。
囚徒困境这个简单的博弈模型之所以经典, 在于它颠覆了新古典经济学中一个重要的结论, 即个人理性的选择会自然而然的达到集体理性这个结论。
从而为主流经济学的建立打下了现实的基础。
求解囚徒困境博弈的困难在于个人激励与群体目标并不一致, 因而, 要求参与人把个人目标放在第二位, 而把集体目标放在第一位[ 1] 。
2 纳什均衡的多重性及其经济含义2.1 纳什均衡的多重性纳什均衡满足所有局中人的个人理性要求是局中人的一致预测, 它似乎解决了这种互动决策问题, 然而相当多的博弈问题存在多个纳什均衡,均衡的多重性限制了纳什均衡的应用, 纳什均衡是一个局部最优而非全局最优的均衡概念, 并不关注均衡的效率。
运筹学结课论文

运筹学结课论文 LELE was finally revised on the morning of December 16, 2020中国矿业大学(北京)研究生课程考试试卷考试科目运筹学考试时间 2015年7月30日学号姓名王长波所属学院管理学院类别(硕士、博士、进修生)硕士评语:任课教师签名:基于排队论的火车站售票系统的优化摘要:售票是火车站重要的服务系统,随着客流量的增多,乘客排队购票现象日益严峻。
基于现实情况的考虑,火车站售票窗口的数量是有限的,而乘客的要求是越多越好。
本文以北京西站为例,通过运筹学中排队论的原理,建立了北京西站售票服务系统多窗口等待制M/M/c/∞/∞排队模型,通过计算得出最优服务窗口数量,最后根据对计算结果的研究分析,给出了北京西站售票服务系统优化的措施。
关键词:火车站;售票系统;排队论;M/M/c/∞/∞模型The Improvement of Railway Station Ticketing System Based onQueuing Theory and OptimizationAbstract: the ticket is an important service station system, along with the increase in traffic, passenger phenomenon growing standing in lineto buy on the consideration of the reality, the number of the train station ticket window is limited, and the requirement of the passengers is the more the on the Beijing west railway station as an example, through the principle of queuing theory in operational research, established the system of Beijing west railway station ticketing service system more window waiting for M/M/n/up/up queuing model, calculated the optimal number of service window, according to the research on the calculation results of analysis, Beijing west railway station ticketing service system optimization measures are given.Keywords: train station; ticketing system; queuing theory; M/M/c/∞/∞model1引言北京西站作为北京市重要的火车站之一,承担着服务市内外旅客的重任。
运筹学论文(合集5篇)

运筹学论文(合集5篇)第一篇:运筹学论文摘要:运筹学就是以数学为主要手段、着重研究最优化问题解法的学科。
运筹学可以用来很好的解决生活中的许多问题。
运筹学有着广泛的应用,对现代化建设有重要作用。
关键词:运筹学;应用;最优方案人们无论从事任何工作,不管采取什么行动,都希望所制订的工作或行动方案,是一切可行方案中的最优方案,以期获得满意的结果诸如此类的问题,通常称为最优化问题。
运筹学就是以数学为主要手段、着重研究最优化问题解法的学科。
求解最优化问题的关键,一是建立粗细适宜的数学模型,把实际问题化为数学问题;二是选择正确而简便的解法,以通过计算确定最优解和最优值。
最优解与最优值相结合,便是最优方案。
人们按照最优方案行事,即可达到预期的目标。
运筹学是现代数学的一个重要分支,属于信息科学和数学的综合科学,是20世纪4O年代发展起来的一门具有较强实践性的综合学科,它使用许多数学工具(包括概率统计、数理分析、线性代数等)和逻辑判断方法,来研究系统中人、财、物等的组织管理、筹划调度问题,以发挥系统的最大效益。
它的特点是:1.运筹学已被广泛应用于工商企业、军事部门、民政事业等研究组织内的统筹协调问题,故其应用不受行业、部门之限制;2.运筹学既对各种经营进行创造性的科学研究,又涉及到组织的实际管理问题,它具有很强的实践性,最终应能向决策者提供建设性意见,并应收到实效;3.它以整体最优为目标,从系统的观点出发,力图以整个系统最佳的方式来解决该系统各部门之间的利害冲突。
对所研究的问题求出最优解,寻求最佳的行动方案,所以它也可看成是一门优化技术,提供的是解决各类问题的优化方法。
通常在遇到这些复杂繁琐的事的时候,人们不会考虑太多,仅是凭着第一直觉去处理,结果也因为处理方式的不同而不同。
有的人第一直觉好,就能把事情处理的很好,而有的人却只能接受糟糕的结果。
生活中,如果我们能理智的去分析问题,找到处理问题的最佳办法,那么我们将会避免很多损失和烦恼,取得更大的成功和收获。
运筹学课程论文

运筹学人力资源分配问题”和“最优投资策略问题”模型摘要: 先是对一个学期的课程学习的总结,然后是分别对“人力资源分配问题”和“最优投资策略问题”的两个案例的分析与建模,并得出其最优方案 ,以及对案例职场规划的方案设计,我们讲解了运筹学的起源、特点、分支、研究方法、涉及重点领域,对运筹学应用案例的数学模型建立于分析,以及解决运筹学问题的方法和对待运筹学问题的大概思维方式等有关运筹学的各方面知识。
总之,在这堂课上我收获许许多多有形或无形的财富,让我受益匪浅。
通过一个学期在老师生动详细的讲解,以及阅读一些有关运筹学的书籍等方式的学习下,我已经掌握了一些对问题进行分析、建模等处理方法。
下面是对三个案例的简单分析及处理。
关键词:运筹学;数学模型;目标函数;人力资源分配;职场规划;最优投资策略 案例1: 人力资源分配问题“好又美”超市是个建在大学城边上的大型百货商场,每周对收银人员的需求,统计如下表为了保证收银人员充分休息,收银人员每周工作5天,休息2天。
问应如何安排收银人员的工作时间,使得所配收银人员的总费用最小?解:为了让员工们休息更愉快、方便,可将每位员工的休息时间安排在连续的两天;则可设ix (i=1,2,3,…,7)表示星期一至日开始休息的人数,依题意我们可建立如下数学模型:目标函数:Min Z = 1234567x x x x x x x ++++++约束条件:1234x x x x x ++++≥623456x x x x x ++++≥5 34567x x x x x ++++≥845671x x x x x ++++≥756712x x x x x ++++≥1067123x x x x x ++++≥1871234x x x x x ++++≥15 (1,2,3,4,5,6,7)i x N i ∈=于以上数学模型,通过计算可得:当:1x = 9;2x = 1;3x = 0;4x = 5;5x = 0;6x = 0;7x =3;时,Z 取最小值18。
运筹学课程论文

运筹学课程论文《运筹学》心得体会摘要:线性规划问题是运筹学的一个重要分支~广泛应用于军事作战、经济分析、经营管理和工程技术等方面。
为合理地利用有限的人力、物力、财力等资源做出的最优决策~提供科学的依据。
如何利用现有的有限资源~最大限度地发挥资源的能力~产生最优的效果~这就是线性规划问题甚至于整个运筹学学科一直在研究的问题关键词:运筹学,线性规划,生产运作管理一、线性规划的发展与运用1832年法国数学家傅里叶首次提出线性规划的思想;1939年苏联数学家坎托罗维奇为解决生产组织中的相关问题,如机器负荷的分配、原材料的合理利用等,发表《生产组织与计划中的数学方法》等论文,这是世界上最早研究线性规划的文章;1947年美国数学家丹齐克首次提出线性规划的概念,并提出了线性规划的一般模型和求解线性规划问题的通用单纯形法,为这门学科奠定了基础;1951年美国经济学家库普曼斯把线性规划应用到经济领域,为此与康托罗维奇一起获得1975年诺贝尔经济学奖;与此同时由于电子计算机的发展,出现了许多线性规划软件,可以很方便地求解几千个变量的线性规划问题,使得线性规划的应用范围更加广阔,从解决技术问题的最优设计到工业、农业、商业、交通运输、军事、经济、管理决策等众多领域都可以发挥作用。
二、线性规划模型的建立建立线性规划模型需要找到问题中的三个要素,找到三个要素的过程也就是建立模型的三个步骤:1.根据影响所要达到目标的因素找到决策变量;2.由决策变量和所要达到目标之间的函数关系确定目标函数;3.找到决策变量的限制条件,即约束条件。
所建立的数学模型具有以下特点:1.每个模型都有若干个影响目标的决策变量(x1,x2,x3…xn),其中n为决策变量个数。
每一组决策变量的值表示一种解决方案,每个问题都有多组决策变量的值,即有多种解决方案,线性规划就是要在多组解决方案中,找到最优的解决方案。
最优的方案可以只有一个,也有可能有多个,多个最优方案达到的效果应是一样的。
运筹学期末论文
运筹管理学论文引言:运筹学是一门寻求由于运筹学研究的广泛性和复杂性,人们至今没有形成一个统一的定义。
以下给出几种定义:运筹学是一种科学决策的方法。
运筹学是依据给定目标和条件从众多方案中选择最优方案的最优化技术。
运筹学是一门寻求在给定资源条件下,在给定资源条件下,如何设计和运行一个系统的科学决策的方法。
运筹学与管理科学(Management Science MS)关系:管理科学涵盖的领域比运筹学更宽一些。
可以说,运筹学是管理科学最重要的组成部分。
运筹学研究的特点:科学性(1)它是在科学方法论的指导下通过一系列规范化步骤进行的;(2)它是广泛利用多种学科的科学技术知识进行的研究。
运筹学研究不仅仅涉及数学,还要涉及经济科学、系统科学、工程物理科学等其他学科。
实践性运筹学以实际问题为分析对象,通过鉴别问题的性质、系统的目标以及系统内主要变量之间的关系,利用数学方法达到对系统进行最优化的目的。
更为重要的是分析获得的结果要能被实践检验,并被用来指导实际系统的运行。
系统性运筹学用系统的观点来分析一个组织(或系统),它着眼于整个系统而不是一个局部,通过协调各组成部分之间的关系和利害冲突,使整个系统达到最优状态。
综合性运筹学研究是一种综合性的研究,它涉及问题的方方面面,应用多学科的知识,因此,要由一个各方面的专家组成的小组来完成。
下面我们通过一个运筹学案例和它的分析过程,来反应运筹学的一些特点和性质。
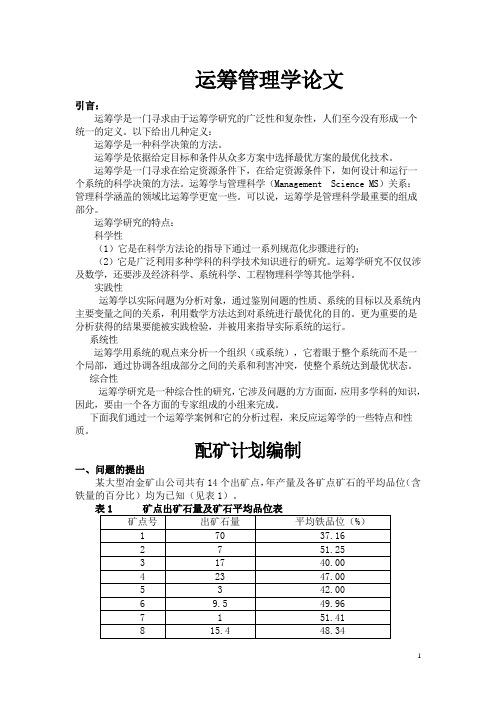
配矿计划编制一、问题的提出某大型冶金矿山公司共有14个出矿点,年产量及各矿点矿石的平均品位(含铁量的百分比)均为已知(见表1)。
定的品位值T Fe进行不同品位矿石的混合配料,然后进入烧结工序,最后,将小球状的烧结球团矿送入高炉进行高温冶炼,生产出生铁。
该企业要求:将这14个矿点的矿石进行混合配矿。
依据现有生产设备及生产工艺的要求,混合矿石的平均品位T Fe规定为45%。
问:如何配矿才能获得最佳的效益?二、分析与建立模型我们可以很快判定此项目属于运筹学中最成熟的分支之一——线性规划的范畴。
运筹学论文

运筹学论文论文摘要:运筹学是一门定量决策科学,它利用定量分析的方法(数学、管理科学、计算机科学)进行科学决策以实现最有效的管理来获得满意的经济效益,是现代管理的重要理论基础。
以下是结合个人所学专业,经济学,对运筹学的一些理解。
一、运筹学的产生人们一般认为运筹学最早出现在第二次世界大战初期,英国军事部门迫切需要研究如何将非常有限的屋子以及人力分配与使用到各种军事活动中,已达到最好的作战效果。
在世界第二次大战期间,德国已经拥有一支强大的空军,飞机从德国起飞17分钟即到达英国本土。
在如此短的时间内,如何预警和拦截成为一大难题。
1935年,为了对付德国空军力量的严重威胁,德国在海岸的鲍德西成立了关于作战控制技术的研究机构。
1938年,鲍德西科学小组负责人把他们从事的工作称为运筹学。
因此,人们把鲍德西作为运筹学的诞生地,将1935—1938年这一段时间作为运筹学产生的酝酿时期。
第二次世界大战期间,运筹学成功地解决了许多重要作战问题,显示了科学的巨大物质威力,这也为运筹学后来的发展铺平了道路。
当战后的工业恢复繁荣时,由于组织内与日俱增的复杂性和专门化所产生的问题,使人们认识到这些问题基本上与战争中所曾面临的问题类似,只是具有不同的现实环境而已,运筹学就这样潜入工商企业和其它部门,在50年代以后得到了广泛的应用。
对于系统配置、聚散、竞争的运用机理深入的研究和应用,形成了比较完备的一套理论,如规划论、排队论、存贮论、决策论等等,由于其理论上的成熟,电子计算机的问世,又大大促进了运筹学的发展,世界上不少国家已成立了致力于该领域及相关活动的专门学会,美国于1952年成立了运筹学会,并出版期刊《运筹学》,世界其它国家也先后创办了运筹学会与期刊,1957年成立了国际运筹学协会。
二、运筹学在当今社会的发展与应用运筹学发展至今,它的应用已经不仅仅局限于军事领域了,运筹学已被广泛应用于工商企业,民政企业等研究组织内的统筹协调问题,既对各种经营进行创造性的科学研究,又涉及到组织的实际管理问题,它具有很强的实践性,最终应能向决策者提供建设性意见,并应收到实效。
运筹学期末论文

运筹学的发展与运用【摘要】运筹学是系统工程学的一门重要专业基础课。
它是20世纪30年代初发展起来的一门新兴学科,其主要目的是在决策时为管理人员提供科学依据,是实现有效管理、正确决策和现代化管理的重要方法之一。
他的产生、发展与具体实施运用均随着其在各个领域的推广而深入人心。
通过对本学科的学习,我深刻认识到运筹学思想的重要性和实用性,并将其运用于以后的学习、生活和工作中。
【Abstract】Systems Engineering Operations Research is important for a basic course. It is the beginning of the 1930s developed a new discipline, its main purpose is to provide decision-making in the scientific basis for the management is to achieve effective management, one of the important methods correct decision and modern management. His emergence, development and application of specific implementation are with their promotion in various fields and popular. . Through the discipline of study, I deeply understand the importance and usefulness of operations research ideas and applied their future learning, life and work.【关键词】运筹学、运用、发展、心得体会【key words】operational research, apply, develop, comments一、运筹学的产生运筹学原意是操作研究、作业研究、运用研究、作战研究,译作运筹学,是借用了《史记》“运筹策于帷幄之中,决胜于千里之外”一语中“运筹”二字,既显示其军事的起源,也表明它在我国已早有萌。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
评分中国矿业大学(北京)研究生课程考试试卷考试科目运筹学考试时间2015年7月30日学号TSP140501074姓名王长波所属学院管理学院类别(硕士、博士、进修生)硕士评语:任课教师签名:基于排队论的火车站售票系统的优化摘要:售票是火车站重要的服务系统,随着客流量的增多,乘客排队购票现象日益严峻。
基于现实情况的考虑,火车站售票窗口的数量是有限的,而乘客的要求是越多越好。
本文以北京西站为例,通过运筹学中排队论的原理,建立了北京西站售票服务系统多窗口等待制M/M/c/∞/∞排队模型,通过计算得出最优服务窗口数量,最后根据对计算结果的研究分析,给出了北京西站售票服务系统优化的措施。
关键词:火车站;售票系统;排队论;M/M/c/∞/∞模型The Improvement of Railway Station Ticketing System Based onQueuing Theory and OptimizationAbstract: the ticket is an important service station system, along with the increase in traffic, passenger phenomenon growing standing in line to buy tickets.Based on the consideration of the reality, the number of the train station ticket window is limited, and the requirement of the passengers is the more the better.Based on the Beijing west railway station as an example, through the principle of queuing theory in operational research, established the system of Beijing west railway station ticketing service system more window waiting for M/M/n/up/up queuing model, calculated the optimal number of service window, according to the research on the calculation results of analysis, Beijing west railway station ticketing service system optimization measures are given.Keywords: train station; ticketing system; queuing theory; M/M/c/∞/∞ model1引言北京西站作为北京市重要的火车站之一,承担着服务市内外旅客的重任。
随着我国国民经济的快速发展,来往首都北京的旅客日益增多,铁路运输作为我国主要交通运输方式,接纳的全国各地的旅客数量呈现上升的趋势,随之而来的就是旅客排长队购票的问题。
这种现象在北京西站的售票厅几乎每天都在发生,有的旅客需要排队二、三十分钟,甚至更长的时间才能够买到火车票,在节假日的时候更是一票难求,这不仅影响了旅客的出行效率,也严重影响了旅客的满意度。
另外,火车站也不可能过多地开放售票窗口,那会增加铁路运营成本,减弱其客运竞争力。
因此,如何合理地开设售票窗口数目,缩短旅客排队等待时间,给旅客创造一个良好的购票环境,显得尤为重要。
本文根据运筹学中的排队论理论,建立相应于火车站售票系统的数学模型,并通过研究分析,已达到优化北京西站售票系统的目的。
2火车站售票窗口排队系统2.1排队系统的组成实际中的排队系统是各种各样的,但从决定排队系统的主要因素来看,它由输入过程、排队规则、服务机构三个部分组成。
(1)输入过程输入过程是描述顾客来源及顾客是按怎样的规律到达排队系统。
在火车站售票排队系统中,由于北京西站的旅客非常多,可以认为顾客来源是无限的。
另外,旅客到达火车站售票窗口是相互独立的,旅客到达的时间间隔也是随机的,从整体上来看单位时间内到达的顾客数服从泊松分布。
(2)排队规则火车站售票窗口的排队规则遵循先到先服务的原则,火车作为主要的交通运输工具,是大多数旅客所必须选择的,故该系统的排队规则可认为是等待制。
对于北京西站的售票厅来说,从为限制过旅客的进出,可以认为该系统的容量是无限的。
(3)服务机构火车站的售票窗口是多台并列存在的,并且是一对一服务。
对于车站售票系统来说,服务时间是随机的,认为服从负指数分布。
综上所述,单位时间内到达的旅客数服从泊松分布,λ表示平均到达旅客数,1/λ表示相继旅客到达的平均间隔时间。
每个窗口对一个顾客的服务时间服从负指数分布,μ表示单位时间内能被服务完成的顾客数,称为平均服务率,1/μ表示一个顾客的平均服务时间,这里的平均就是期望值。
2.2排队问题的求解研究售票排队系统的目的是通过了解系统运行状况,对系统进行调整和控制,使系统的服务质量处于最优状态[1]。
所以必须确定用以判断系统运行优劣的基本数量指标,这些指标包括:(1)队长和排队长(队列长)队长是指系统中旅客的平均数(包括正在接受服务的顾客和排队等待的顾客),其期望值记作L s。
排队长是指系统中排队等待接受服务的旅客平均数,其期望值记作L q。
一般情况下,队长(或排队长)越大,说明服务效率越低,这是旅客最厌烦的。
(2)等待时间和逗留时间从旅客进入系统的时刻起直到开始接受服务止的这段时间称为等待时间,其期望值记作W q。
逗留时间是指从旅客到达时间起到他接受完服务为止这段时间,其期望值记作W s。
这两个都是随机变量,对于火车站售票等待时间是旅客们所关心的。
(3)忙期(busy period)忙期是指从顾客到达空闲服务机构起到拂去机构再次为空闲止这段时间长度,即服务机构连续繁忙的时间长度,它关系到服务员的工作强度[2]。
(4)服务强度服务设施用于服务顾客的时间与总服务时间的比值,通常记作ρ[3-4]。
令ρ=λ/cμ,其中,λ为系统的平均到达率,μ为单个服务台的平均服务率,cμ为整个系统的平均服务率。
3火车站售票系统排队模型的建立及解析3.1北京西站客流现状北京西站是中国最大的人口集散地和交通枢纽,接发旅客列车已达70-90对/天,日均客流量在18万到20万之间,客流高峰期达到40-60万人次,每年覆盖人群近1.8亿人次。
2015年初日均客流量突破20万,至2月中旬已达到23万人次。
北京西站共有四个售票处,北售票大厅:位于西站北广场东侧,分为东、西两个售票厅,为旅客办理普通售票业务。
售票东厅为“036”售票厅,为旅客提供以下特色服务:军人、记者优先购票窗口。
直达特快列车预约订票窗口。
老年人优先购票窗口。
铁路公免签证、提供双语服务窗口。
值班站长窗口,办理旅客投诉、解决旅客疑难问题,各次列车及直达特快列车的改签业务,同时办理上访人员换票业务。
团体旅客预约订票窗口。
无障碍购票窗口,重点为残疾旅客提供售票服务。
有41个人工窗口,13台自助售票机和取票机。
南售票大厅:位于西站南广场西侧,为旅客办理普通售票业务、团体订票业务、代售处取票业务。
设置以下特色窗口:团体订票窗口。
直达特快列车预约订票窗口。
为各代售处提供发票服务。
有20个人工窗口,13台自助售票机和取票机。
出站口售票处:分别位于地下二层北一、北二出站口处,为刚下车的旅客提供购票方便,重点发售北京站、北京南站、北京北站的换乘列车车票,同时发售北京西站各次始发列车的车票。
有10个人工窗口,4台自助售票机和取票机。
北广场二楼的售票厅:有26台自助售票机和取票机。
以上共有71个人工窗口,56台自助售票机和取票机,共127个服务台,春节期间全部开放。
3.2售票系统排队模型根据以上分析,对于北京西站售票厅的旅客排队模型近似地认为为多服务负指数分布排队模型(M/M/c/∞/∞模型),即输入为泊松输入、负指数分布服务、c 个开放的售票服务台、系统容量不受限制、以及顾客源数为无限的等待制排队模型,如图1所示。
图1旅客购票排队模型3.2.1实际数据的收集整理北京西站在春运期间为客流高峰期,临时增加售票窗口120个,通过网络调查,测定春运期间某天十个时间段的旅客进厅和购票情况,如表1和表2所示。
表1游客进厅购票人数 时间段 平均到达率λ(人/h ) 时间间隔1/λ(min/人) 8:00-9:00 10373 0.005784 9:00-10:00 11246 0.005335 10:00-11:00 12247 0.004899 13:00-14:00 11589 0.005177 14:00-15:00 12145 0.004940 15:00-16:00 13077 0.004588 16:00-17:00 12458 0.004816 18:00-19:00 10111 0.005934 19:00-20:00 9897 0.006062 20:00-21:00 90460.006633表2售票服务台人数 时间段 平均服务率μ(人/h ) 平均服务时间1/μ(min/人)8:00-9:00 41 1.4634 9:00-10:00 46 1.3043 10:00-11:00 50 1.2000 13:00-14:00 47 1.2766 14:00-15:00 49 1.2245 15:00-16:00531.1321旅客源 等待服务 12 c 输入 队伍服务系统服务台输出16:00-17:00 51 1.1765 18:00-19:00 41 1.4634 19:00-20:00 40 1.5000 20:00-21:00371.6216由表1可知,北京西站春运期间旅客平均到达率λ=11219人/h ,约为187人/min ;旅客到达的平均时间间隔为0.0054min/人。
由表2可知,每个售票服务台的平均服务率为μ=45.5人/h ,约为0.75人/min ;旅客的平均服务时间为1.34min/人,整个系统的平均服务率ρ=0.9962。
3.2.2模型建立由上述排队系统组成分析结果可知,北京西站售票系统排队模型符合标准的M/M/c 模型。
在M/M/c 模型中,系统处于稳态时,稳态的概率关系表现为:⎪⎪⎩⎪⎪⎨⎧>≤=--c n P n c n P n P n n n ,,11μλμλ(1)以ρ=λ/c μ作为整个系统的服务强度,带入上式可得:⎪⎪⎩⎪⎪⎨⎧>==≤===--c n P c c P c n P n c P n c P c n nn n ,!)(,!)(0101ρρρρ (2) 又由P 0+P 1+…+P n-1+P n =1可得:初始概率为:1100)1(!)(!)(--=⎪⎪⎭⎫ ⎝⎛-+=∑c n cnc c n c P ρρρ (3) 可得系统的运行指标如下: (1)队列长:2)1(!)(P c c L cq ρρρ-= (4)(2)排队时间: λqq L W =(5)3.2.3优化分析火车站售票系统的优化分析就是综合考虑运营商和旅客的利益,既要避免排队过长,浪费旅客的宝贵时间,又要避免售票服务台的闲置造成浪费,使两者利益之和达到最优[5-6]。
