资料的正态性检验汇总
spss判断是否符合正态分布
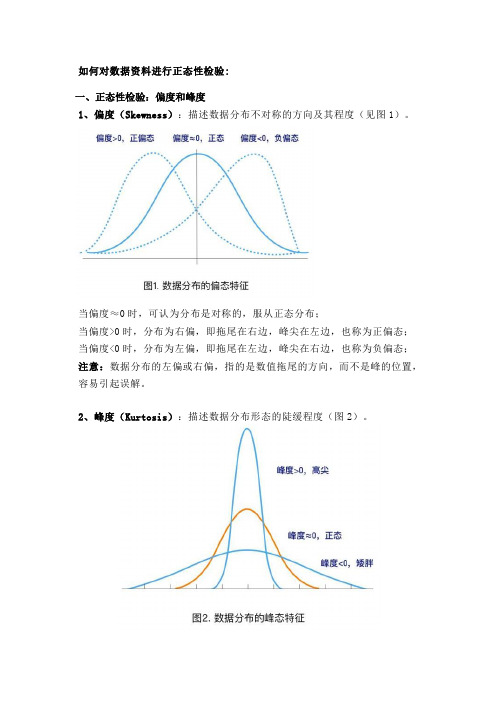
如何对数据资料进行正态性检验:一、正态性检验:偏度和峰度1、偏度(Skewness):描述数据分布不对称的方向及其程度(见图1)。
当偏度≈0时,可认为分布是对称的,服从正态分布;当偏度>0时,分布为右偏,即拖尾在右边,峰尖在左边,也称为正偏态;当偏度<0时,分布为左偏,即拖尾在左边,峰尖在右边,也称为负偏态;注意:数据分布的左偏或右偏,指的是数值拖尾的方向,而不是峰的位置,容易引起误解。
2、峰度(Kurtosis):描述数据分布形态的陡缓程度(图2)。
当峰度≈0时,可认为分布的峰态合适,服从正态分布(不胖不瘦);当峰度>0时,分布的峰态陡峭(高尖);当峰度<0时,分布的峰态平缓(矮胖);利用偏度和峰度进行正态性检验时,可以同时计算其相应的Z评分(Z-score),即:偏度Z-score=偏度值/标准误,峰度Z-score=峰度值/标准误。
在α=0.05的检验水平下,若Z-score在±1.96之间,则可认为资料服从正态分布。
了解偏度和峰度这两个统计量的含义很重要,在对数据进行正态转换时,需要将其作为参考,选择合适的转换方法。
3、SPSS操作方法以分析某人群BMI的分布特征为例。
(1) 方法一选择Analyze → Descriptive Statistics → Frequencies将BMI选入Variable(s)框中→点击Statistics →在Distribution框中勾选Skewness和Kurtosis(2) 方法二选择Analyze → Descriptive Statistics → Descriptives将BMI选入Variable(s)框中→点击Options →在Distribution框中勾选Skewness和Kurtosis4、结果解读在结果输出的Descriptives部分,对变量BMI进行了基本的统计描述,同时给出了其分布的偏度值0.194(标准误0.181),Z-score = 0.194/0.181 = 1.072,峰度值0.373(标准误0.360),Z-score = 0.373/0.360 = 1.036。
spss_数据正态分布检验方法及意义

spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布,可以有两种方法(目前我知道这两种,并且这两种方法只是直观观察,不是定量的正态分布检验):1:在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下:Analyze-----Descriptive S tatistics-----Frequencies,打开频数统计对话框,在Statistics里可以选择获得各种描述性的统计量,如:均值、方差、分位数、峰度、标准差等各种描述性统计量。
在Charts里可以选择显示的图形类型,其中Histograms选项为柱状图也就是我们说的直方图,同时可以选择是否绘制该组数据的正态曲线(With nor ma curve),这样我们可以直观观察该组数据是否大致符合正态分布。
如下图:从上图中可以看出,该组数据基本符合正态分布。
2:正态分布的Q-Q图:在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下:Analyze-----Descriptive Statistics-----Explore打开对话框,选择Plots选项,选择Normality plots with tests选项,可以绘制该组数据的q-q 图。
图的横坐标为改变量的观测值,纵坐标为分位数。
若该组数据服从正态分布,则图中的点应该靠近图中直线。
纵坐标为分位数,是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置,n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图(也就是图中的直线)基本符合。
对于理论的标准正态分布,其q-q图为y=x直线。
非标准正态分布的斜率为样本标准差,截距为样本均值。
如下图:如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签:杂谈一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
SPSS学习笔记-正态性检验

如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。
试验数据的正态性检验、数据的转换及卡方检验
试验数据的正态检验、数据的转换和卡方检验目录一、符合正态分布的例子 (1)二、不符合正态分布的例子 (6)三、不符合正态分布数据的转换及转换后数据的方差分析 (11)四、次数分布资料的卡方检验 (14)在对试验数据进行方差分析前,应对数据的三性(即同质性、独立性和正态性)进行检验。
本文介绍对资料的正态性进行检验的方法,主要介绍3种检验方法:(1)频数检验——作频率分布图、看偏度系数和峰度系数,(2)作Q-Q图检验,(3)非参数检验——单个样本K-S检验。
下面以两个试验数据为例,例1为84头育肥猪的体重数据,通常符合正态分布。
例2为生长育肥猪7个试验处理组的腹泻率(百分数资料)统计结果,这类资料往往不符合正态,而大多数人以为是符合正态分布,进行方差分析的,因而不能得出正确的结论,却可能得出错误结论。
一、符合正态分布的例子【例1】 84头生长育肥猪的“体重”数据如表1-1,检验该数据是否呈正态分布。
表1-1 84头育肥猪的“体重”数据(排序后)检验方法一:频数检验——作频率分布图、看偏度系数和峰度系数步骤1:数据录入SPSS中,如图1-1。
图1-1 体重数据录入SPSS中步骤2:在SPSS里执行“分析—>描述统计—>频率”,然后弹出“频率”对话框(图1-2a),变量选择“体重”;再点右边的“统计量”按钮,弹出图“频率:统计量”对话框(图1-2b),选择“偏度”和“丰度”(图1-2b);再点右边的“图表”按钮,弹出图“频率:图表”对话框(图1-2c),选择“直方图”,并选中“在直方图显示正态曲线”图1-2a “频率”对话框图1-2b “频率:统计量”对话框图1-2c “频率:图表”对话框设置完后点“确定”后,就会出来一系列结果,包括2个表格和一个图,我们先来看看“统计量”表,如下:统计量体重N 有效84缺失0偏度.040偏度的标准误.263峰度-.202峰度的标准误.520偏度系数=0.040,峰度系数-0.202;两个系数都小于1,可认为近似于正态分布。
正态性资料的 t 检验

1.采集数据1.1 首先选择variable view(变量窗)在name下输入“group”在value下输入1治疗组2对照组group下输入“x ”lable 下输入“住院时间”如图1.3打开data view (数据窗)输入你的组别共两组为1和2组1组13个样本2组13个样本X 代表住院时间如图输入数据2.分析正态性2.1 选择analysis(分析)选择descriptive statistics(描述统计量)选择explore在dependent list(自变量在此处也就是x)选择“住院时间”在factor list(分组变量)Display 要展示什么一般选择both 既要统计量又要统计图Statistics (统计量如标准差中位数四分位数等)Plots(统计图)在此图选择statistics 显示下图选择描述均数的95%的可信区间在此图选择Plots 显示下图选择normality plots with tests (检验正态性)选择OK 显示下图Missing (丢失的样本)此处N为0%,因为你的13个1或2后面全都有数值亦显示下图(统计量)Mean 均数median 中位数亦显示下图(分析正态性)其中sig 为显著性的意思即为P值图中Sig =0.591 sig=0.562 两组sig均大于0.1 (只有sig>0.1才是正态性的资料。
)3.进行T检验(两组数据符合正态性要用T检验,两组数据部符合正态性要用致合检验)analysis(分析)选择compare means 选择independent- samples T test (独立样本T检验)显示下图Test variable 即为自变量(观察对象)选中住院时间Group variable 即为组别变量选中group在此图中选择Define group 显示下图进行组别输入(输入组别数字1或2)Group1 输入1Group2 输入2 (注意1带表治疗组2代表对照组)点continue显示下图Std error mean 均数标准误Std deviation 标准差Mean 均数亦显示下图Levene’s test for equality of variances 是方差齐性检验情况1.表中Sig=0.207 数值大于0.1 故数据方差齐。
数据的正态分布

数据的正态性检验汇总2012-11-21 00:01:04| 分类:统计学习|字号订阅如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的"偏度和峰度都接近0……可以认为……近似服从正态分布"并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。
由此可见,部分SPSS教材里面关于"Shapiro – Wilk 适用于样本量3-50之间的数据"的说法实在是理解片面,误人子弟。
正态资料统计方法

正态资料统计方法
正态资料统计方法是统计学中一种常用的方法,用于对正态分布的数据进行分析和描述。
正态分布是一种常见的连续概率分布,它具有均值和标准差两个参数,可以用于描述许多自然现象和社会现象的变量,例如身高、体重、智力、收入等。
在使用正态资料统计方法时,我们通常需要采用以下步骤:
1. 收集数据:首先需要确定研究对象,然后根据研究对象的特
征进行数据采集。
2. 数据处理:对收集到的数据进行整理、分类和清洗,确保数
据的准确性和完整性。
3. 统计分析:使用正态资料统计方法进行数据分析,包括描述
统计和推断统计两个方面。
描述统计主要用于对数据进行概括性描述,包括均值、标准差、中位数、众数等;推断统计主要用于对总体参数进行推断,包括参数估计和假设检验等。
4. 结果解释:对分析结果进行解释和评价,包括结果的意义、
可靠性和适用性等方面。
正态资料统计方法在许多领域都有广泛的应用,例如医学、经济、社会学、心理学等,能够帮助研究人员更好地理解和利用数据。
同时,正态资料统计方法也存在一些限制和局限性,例如对数据分布的要求较高、对异常值的敏感性较强等,因此需要在应用中慎重考虑。
- 1 -。
正态性检验

正态性检验安德森-达令检验、柯尔莫哥洛夫-斯米诺夫检验、雅克-贝拉检验、偏度检验、峰度检验、爱泼斯-普利检验、夏皮洛-威尔克检验。
有些统计方法只适用于正态分布或近似正态分布资料,如用均数和标准差描述资料的集中或离散情况,用正态分布法确定正常值范围及用t检验两均数间相差是否显著等,因此在用这些方法前,需考虑进行正态性检验。
正态分布的特征是对称和正态峰。
分布对称时众数和均数密合,若均数-众数>0,称正偏态。
因为有少数变量值很大,使曲线右侧尾部拖得很长,故又称右偏态;若均数-众数<0称负偏态。
因为有少数变量值很小,使曲线左侧尾部拖得很长,故又称左偏态,见图7.1(a)。
正态曲线的峰度叫正态峰,见图7.1(b)中的虚线,离均数近的或很远的变量值都较正态峰的多的称尖峭峰,离均数近或很远变量值都较正态峰的少的称平阔峰。
图7.1频数分布的偏度和峰度正态性检验的方法有两类。
一类对偏度、峰度只用一个指标综合检验,另一类是对两者各用一个指标检验,前者有W法、D法、正态概率纸法等,后者有动差法亦称矩法。
现仅将W法与动差法分述于下;1.W法此法宜用于小样本资料的正态性检验,尤其是n≤50时,检验步骤如下;(1)将n个变量值Xi从小至大排队编秩。
X1<X2<……<XN< p>见表7.5第(1)栏,表中第(2)、第(3)栏是变量值,第(2)栏由上而下从小至大排列,第(3)栏由下而上从小至大排列。
第(4)栏是第(3)栏与第(2)栏之差。
(2)由附表5按n查出ain系数列入表7.5第(5)栏,由于当n为奇数时,对应于中位数秩次的ain为0,所以中位数只列出,不参加计算。
第(6)栏是第(5)栏与第(4)栏的乘积。
(3)按式(7.8)计算W值(7.8)式中分子的∑,当n是偶数时,为的缩写,当n是奇数时为的缩写,表7.5 第(6)栏的合计平方后即为分子。
分母按原始资料计算。
(4)查附表6得P值,作出推断结论,按n查得W(n,α),α是检验前指定的检验水准,若W>W(n,α)则在α水准上按受H0,资料来自正态分布总体,或服从正态分布;若W≤W(n,α),则在α水准上拒绝H0,接受H1,资料非正态。
正态性检验的一般方法汇总

Lilliefor提出用样本均值和标准差代替总体的期望和标
Kolmogorov-Smirnov正态性检验法,它定义了一个
统计量;
Fn(x)- Fo(x)|参数未知,由计算得
查表得Lilliefor检验的临界值,确定拒绝域,得出结论。
若两者间的差距很小,则推
样本所来自的总体分布服从某特定分布
:样本所来自的总体分布不服从某特定分布
Fo(x)表示分布的分布函数,Fn(x)表示一组随机
D为Fo(x)与Fn(x)差距的最大值,定义如下式:
a,P{Dn>d}=a.
35位健康男性在未进食前的血糖浓度如表所示,试测验这组
μ=80,标准差σ=6的正态分布
2)检验原理
2=0,则=,意味着对于,观测频数与期望频数完全一致,
2值越小。
与不应有较大差异,即2值
2值过大,则怀疑原假设。
R={2d} ,判断统计量是否落入拒绝域,得出结论。
Kolmogorov-Smirnov正态性检验:
检验法是检验单一样本是否来自某一特定
比如检验一组数据是否为正态分布。它的检验方法是以样本数
)/2; 值可查表得出;
2]
1)()
[()]()niniiiniiaXXWXX
α(可通过查表求得),按表上行
α舍弃正态性假设;若W>Wα,接受正态性假
21()niiXX
六、大样本场合(50<n<100)的D检验
检验统计量:
)
2
)
1()2()()niiniiniXDnXX
时,拒绝域为。其中
1101200203
正态性检验的一般方法汇总

正态性检验的一般方法汇总1. 引言正态性检验是统计学中一项重要的方法,用于确定数据是否服从正态分布。
正态分布在许多统计分析和假设检验中起着关键的作用,因此正态性检验对于数据分析的准确性和可靠性至关重要。
本文将综合介绍正态性检验的一般方法,包括直方图和正态概率图的可视化检验方法以及统计量检验方法。
2. 直方图检验直方图是一种用柱状图表示数据分布情况的可视化工具。
在正态性检验中,直方图可以帮助我们初步判断数据是否服从正态分布。
具体操作时,我们将数据划分为若干个区间,并统计每个区间内数据的频数。
如果直方图呈现钟形曲线,则表明数据具有较好的正态性。
反之,如果直方图呈现偏态分布,则可能说明数据不符合正态分布。
3. 正态概率图检验正态概率图是一种常用的正态性检验方法,其基本原理是将数据的分位数与标准正态分布的分位数进行比较。
通过在图上绘制数据的累积分布函数与标准正态分布的理论分布函数之间的关系,我们可以直观地判断数据是否服从正态分布。
在正态概率图中,数据点应当分布在一条直线上,如果数据点在直线上,则说明数据分布接近正态分布。
4. 统计量检验除了可视化方法,我们还可以使用统计量进行正态性检验。
常见的统计量检验方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验和D'Agostino-Pearson检验等。
这些检验方法都基于假设检验的原理,通过计算统计量并与理论分布进行比较,从而判断数据是否服从正态分布。
4.1 Kolmogorov-Smirnov检验Kolmogorov-Smirnov检验是一种常见的非参数检验方法,用于检验数据是否来自特定的分布。
在正态性检验中,Kolmogorov-Smirnov检验可以用来检验数据是否符合正态分布。
该检验基于经验分布函数和理论分布函数之间的最大差异,通过计算统计量并与临界值进行比较,可以判断数据的正态性。
4.2 Shapiro-Wilk检验Shapiro-Wilk检验是一种适用于小样本数据的正态性检验方法,其原理是通过计算统计量来衡量数据与正态分布之间的偏差程度。
假设检验之正态性检验,F 检验,T 检验

案例解析
• • • 如下图是BOSA AOP和ER用三种方法做出来的正态性检验 一般我们认为P>α (通常取0.05 或0.1) 就可以认为其不能拒绝正态的,也就是 大致认为其是正态分布的,而且P值越大,数据正态的信心越大。 下述参数中BOSA AOP是为非正态分布的,而ER是正态分布的。
方差齐性检验
拒绝H0
a/2
1 - a
a/2
临界值
0
样本统计量 临界值
显著性水平和拒绝域
(双侧检验 )
抽样分布
拒绝H0
置信水平 拒绝H0
a/2
1 - a
a/2
0 临界值
临界值
样本统计量
显著性水平和拒绝域
(单侧检验 )
抽样分布
拒绝H0
置信水平
a
1 - a
0 临界值
样本统计量
显著性水平和拒绝域
(左侧检验 )
... 如果这是总体 的假设均值
20
= 50 H0
样本均值
假设检验的过程
提出假设 作出决策
拒绝原假设 别无选择!
我认为人口的平 均年龄是50岁
总体
抽取随机样本
均值 x = 20
原假设与备择假设
假设(hypothesis)
原假设 备择假设 (Null Hypothesis) (Alternative Hypothesis)
检验统计量与拒绝域
检验统计量(test
statistic)
1. 根据样本观测结果计算得到的,并据以对 原假设和备择假设作出决策的某个样本统 计量 2. 对样本估计量的标准化结果
– 原假设H0为真
判断数据正态分布

生成正态概率图并进行假设检验,以检查观测值是否服从正态分布。
对于正态性检验,假设为H0:数据服从正态分布与H1:数据不服从正态分布图形中的垂直尺度类似于正态概率图中的垂直尺度,水平轴为线性尺度,此线形成数据所来自总体的累积分布函数的估计值。
图中会显示总体参数的数字估计(均值和标准差)、正态性检验值以及关联的p 值。
正态性检验的方法很多,但具体原理是不相同的,有些是拟合优度检验,有些是偏峰度检验。
用Minitab作数据的正态性检验的方法:统计>基本统计量>正态性检验 (stat>Basic Statistic>Normality test)最后都是看P值,P>就基本可以认为数据正态有如下三种检验方法:(1 Anderson-Daling,缺省状态即为此检验法,AD法最灵敏。
AD检验是很准确的判断方法,表面上在直线附近, 但很可能被拒绝。
(2 Ryan-Joiner (它实际上与W检验很相似,ISO将它定为标准检验方法,中国国标也采用此法)。
(3 Kolmogorov-Smirnov方法。
Anderson-Darling和Kolmogorov- Smirnov检定方法是基于经验分布函数,Ryan-Joiner (类似Shapiro-Wilk)是基于相关与回归的,一般而言都选Anderson-Darling。
三种检验方法的详细解释如下:Anderson-Darling检验(A-D检验),是一种基于经验累积分布函数(ECDF)的算法,特别适用于小样本(当然也适用于大样本),AD值越小,表明分布对数据拟合度越好,A-D检验只适合特定的连续分布如:normal、lognormal、exponential、Weibull、logistic、extreme-value type 1。
A-D检验是对K-S检验的一种修正,相比K-S检验它加重了对尾部数据的考量,K-S检验具有分布无关性,它的临界值并不依赖被测的特定分布,而A-D检验使用特定分布去计算临界值,这使得A-D检验具有更灵敏的优势。
正态分布和非正态分布使用的检验方法

正态分布和非正态分布使用的检验方法下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!正态分布和非正态分布是统计学中经常涉及的概念,在进行数据分析时需要对数据的分布进行检验。
资料的正态性检验汇总

资料的正态性检验汇总S PSS和SAS常用正态检验方法一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法实在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。
第二节 正态总体参数的检验

2
9
二、两个正态总体参数的假设检验
2 设 有 两 个 相 互 独 立 的 正 态 总 体 X ~ N ( µ1,σ 1 ) ,
Y ~ N ( µ 2,σ ) , 分别抽取独立的样本 ( X1 , X2 ,⋯, Xn1 ) 和
2
µ 第六章证明, X = ( (− , ) 第六章证明,若 χ 2 ~ Nn−1σS 证明 (2) 检验统计量 2
2 2 H 下 O χ1−α / 2(n−1) 2 0 ), 2 则
x
( n − 1) S
~ χ (n −1) ,
(4) 由样本值算得
χ的值; 的值;
2
则拒绝H 否则 不能 若 χ 2 < λ1 或 χ 2 > λ2 ,则拒绝 0 ; 否则, 拒绝H 拒绝 0 .
− tα / 2 ( n − 1) O
tα / 2 (n − 1)
x
~
(4) 由样本值算得 t 的值; 的值; 则拒绝H 如果 | t |> tα 2 (n − 1) ,则拒绝 0 ; 否则, 不能拒绝H 否则 不能拒绝 0 .
5
两家生产同一类产品, 例2 两家生产同一类产品,其质量指标假定都服从正 态分布,标准规格为均值等于120.现从甲厂抽出5 120.现从甲厂抽出 态分布,标准规格为均值等于120.现从甲厂抽出5件 产品,测得其指标值为119,120,119.2,119.7,119.6; 产品,测得其指标值为119,120,119.2,119.7,119.6; 从乙厂也抽出5件产品,测得其指标值为110.5,106.3, 从乙厂也抽出5件产品,测得其指标值为110.5,106.3, 122.2,113.8,117.2。 122.2,113.8,117.2。试判断这两家厂的产品是否符 合标准. 合标准. (α = 0.05 )
2组计量资料正态分布统计学方法

2组计量资料正态分布统计学方法
如果两组计量资料服从正态分布,可以采用以下统计学方法:
1. 成组t检验:适用于大样本资料或服从正态分布的小样本资料。
如果方差齐性,则作成组t检验;如果方差不齐,则作t’检验或用成组的Wilcoxon 秩和检验。
2. 完全随机的方差分析:适用于多组大样本资料或服从正态分布的资料,且方差齐性。
如果统计检验有统计学意义,则进一步作统计分析,选择合适的方法进行两两比较。
3. 配对样本t检验:适用于两组数据配对且服从正态分布的情况。
可以检验某医院30个病人注射某药剂前后血压是否一致。
4. 配对样本Wilcoxon符号秩检验:适用于非正态分布的数据,可以检验两列差值非正态分布、样本数一样的数据之间是否存在差异。
请注意,以上方法仅供参考,在进行统计学分析时,请咨询专业统计学专家,以获取准确和专业的分析结果。
数据正态性检验及正态转化在spss中的实现

2.2
(1)以上文的胫围数据为例,在spss中打开胫围数据资料,依次点击“转换--计算变量”,如下图:
(2)弹出如下对话框。首先,在“目标变量”对话框中填入所要转换成的变量名称,方便理解,本文以胫围为例,将转换成的变量名称设为“胫围(转换)”;然后,在“函数组”对话框中选择“全部”;其次,在“函数和特殊变量”对话框中根据需要选择函数,本文胫围的偏度为2.486,远大于其标准误差0.061,因此本文选用纠偏作用最强的函数,即以10为底数的对数,因此选择“函数和特殊变量”对话框中的函数“Lg10”,点击本对话框左上角向上的箭头,将所选函数选入“数字表达式对话框”;之后,点击“类型与标签”对话框中所要转换的变量,本文选择“胫围”,再点击本对话框右上角的箭头,将该变量选入“数字表达式”中函数的相应部位(即代替标着“?”的部位);最后点击确定。
1.2
采用spss中非参数分析方法对数据资料进行正态性检验,具体步骤如下:
(1)在spss中打开数据资料文件,依次点击“分析—非参数检验—单样本k-s”,如下图:
(2)在弹出的对话框中,选择左边方框中要研究的变量,点击中间的箭头,将其选入右边的对话框,本文选择“胫围”作示例分析,如下图:
(3)之后,点击最右边的“精确”选项卡,在弹出的对话框中有三个选项,1、“仅渐进法”:是基于渐进分布的显著性水平的检验指标,适用于大样本,如果样本过小或者分布不好,就会影响检验的效力;2、“蒙特卡洛法”:适用于精确显著性水平的无偏估计,如果样本过大,数据处理过程太长,就应该使用这个选项;3、“精确”:精确计算概率值,可以设定数据处理的时间,如果数据处理时间超过了所设定时间30分钟,就应该使用“蒙特卡洛法”。本文选择“仅渐进法”进行正态显著性检验,点击继续,如下图:
数据分析方法汇总

数据分析方法汇总一、描述统计描述性统计是指运用制表和分类,图形以及计筠概括性数据来描述数据的集中趋势、离散趋势、偏度、峰度。
1、缺失值填充:常用方法:剔除法、均值法、最小邻居法、比率\回归法、决策树法。
2、正态性检验:很多统计方法都要求数值服从或近似服从正态分布,所以之前需要进行正态性检验。
常用方法:非参数检验的K-量检验、P-P图、Q-Q图、W检验、动差法。
二、假设检验 1、参数检验参数检验是在已知总体分布的条件下(一股要求总体服从正态分布)对一些主要的参数(如均值、百分数、方差、相关系数等)进行的检验。
1)U验使用条件:当样本含量n较大时,样本值符合正态分布 2)T检验使用条件:当样本含量n较小时,样本值符合正态分布A 单样本t检验:推断该样本来自的总体均数μ与已知的某一总体均数μ0 (常为理论值或标准值)有无差别;B 配对样本t检验:当总体均数未知时,且两个样本可以配对,同对中的两者在可能会影响处理效果的各种条件方面扱为相似;C 两独立样本t检验:无法找到在各方面极为相似的两样本作配对比较时使用。
2、非参数检验非参数检验则不考虑总体分布是否已知,常常也不是针对总体参数,而是针对总体的某些一股性假设(如总体分布的位罝是否相同,总体分布是否正态)进行检验。
适用情况:顺序类型的数据资料,这类数据的分布形态一般是未知的。
A 虽然是连续数据,但总体分布形态未知或者非正态;B 体分布虽然正态,数据也是连续类型,但样本容量极小,如10以下;主要方法包括:卡方检验、秩和检验、二项检验、游程检验、K-量检验等。
三、信度分析检査测量的可信度,例如调查问卷的真实性。
分类:1、外在信度:不同时间测量时量表的一致性程度,常用方法重测信度2、内在信度;每个量表是否测量到单一的概念,同时组成两表的内在体项一致性如何,常用方法分半信度。
四、列联表分析用于分析离散变量或定型变量之间是否存在相关。
对于二维表,可进行卡方检验,对于三维表,可作Mentel-Hanszel分层分析。
正态性检验的一般方法汇总资料

正态性检验的一般方法汇总资料
正态性检验是统计学中常用的一种方法,用于检验数据是否符合正态分布。
正态分布在统计学中非常重要,因为很多统计模型都基于该假设。
如果数据不符合正态分布,可能需要使用其他分布或采用非参数方法来处理数据。
常见的正态性检验方法有以下几种:
1. Shapiro-Wilk检验
Shapiro-Wilk检验是最常用的正态性检验方法。
该方法利用样本数据计算统计量W和p值来判断数据是否符合正态分布。
W值越接近1,p值越大,说明数据越符合正态分布。
2. Kolmogorov-Smirnov检验
3. Anderson-Darling检验
4. Lilliefors检验
Lilliefors检验是基于Kolmogorov-Smirnov检验的一种改进方法。
该方法可以在小样本和大样本情况下都得到准确的结果。
正态性检验的一般流程如下:
1. 整理数据并画出直方图来观察数据特征。
2. 利用正态性检验方法来判断数据是否符合正态分布,比如Shapiro-Wilk检验、Kolmogorov-Smirnov检验、Anderson-Darling检验、Lilliefors检验等。
3. 如果数据不符合正态分布,则需要采用其他方法来处理数据,比如变换数据、采用非参数方法等。
4. 如果数据符合正态分布,可以采用基于正态分布假设的统计方法来分析数据。
总之,正态性检验是统计学中必不可少的一个环节。
在进行统计分析前对数据进行正态性检验,有助于选择合适的统计方法,保证分析结果的准确性和可信度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
资料的正态性检验汇总作者:huaxie 来源:【整理】发布时间:2009-4-22 浏览: 567 访问者:58.23.96.242摘要提示:本文汇总了通常在对资料进行正态性检验时遇到的问题,比如Kolmogorov-Smirnov检验(简称K-S检验),还是Shapiro-Wilk检验,SPSS里面用哪个过程,SAS程序等。
SPSS和SAS常用正态检验方法如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U 检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W 检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法实在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。
对于此两种检验,如果P值大于0.05,表明资料服从正态分布。
三、SPSS操作示例SPSS中有很多操作可以进行正态检验,在此只介绍最主要和最全面最方便的操作:1、工具栏--分析—描述性统计—探索性2、选择要分析的变量,选入因变量框内,然后点选图表,设置输出茎叶图和直方图,选择输出正态性检验图表,注意显示(Display)要选择双项(Both)。
3、Output结果(1)Descriptives:描述中有峰度系数和偏度系数,根据上述判断标准,数据不符合正态分布。
S k=0,K u=0时,分布呈正态,Sk>0时,分布呈正偏态,Sk<0时,分布呈负偏态,时,Ku>0曲线比较陡峭,Ku<0时曲线比较平坦。
由此可判断本数据分布为正偏态(朝左偏),较陡峭。
(2)Tests of Normality:D检验和W检验均显示数据不服从正态分布,当然在此,数据样本量为1000,应以W检验为准。
(3)直方图直方图验证了上述检验结果。
(4)此外还有茎叶图、P-P图、Q-Q图、箱式图等输出结果,不再赘述。
结果同样验证数据不符合正态分布。
许多计量资料的分析方法要求数据分布是正态或近似正态,因此对原始独立测定数据进行正态性检验是十分必要的。
通过绘制数据的频数分布直方图来定性地判断数据分布正态性。
这样的图形判断决不是严格的正态性检验,它所提供的信息只是对正态性检验的重要补充。
正态性检验主要有三类方法:一、计算综合统计量如动差法、夏皮罗-威尔克Shapiro-Wilk 法(W 检验) 、达戈斯提诺D′Agostino 法(D 检验) 、Shapiro-Francia法(W′检验) .二、正态分布的拟合优度检验如皮尔逊χ2检验、对数似然比检验、柯尔莫哥洛夫Kolmogorov-Smirov 法检验 .三、图示法(正态概率图Normal Probability plot)如分位数图(Quantile Quantileplot ,简称QQ 图) 、百分位数(Percent Percen t plot ,简称PP 图) 和稳定化概率图(Stablized Probability plot ,简称SP 图)等.下面介绍几种较统计软件中常用的正态性检验方法1、用偏态系数和峰态系数检验数据正态性偏态系数Sk,它用于检验不对称性;峰态系数Ku,它用于检验峰态。
S k= 0, K u = 0 时, 分布呈正态, S k> 0 时, 分布呈正偏态,S k < 0 时, 分布呈负偏态。
适用条件:样本含量应大于2002、用夏皮罗-威尔克(Shapiro-Wilk)法检验数据正态性即W检验,1965 年提出,适用于样本含量n ≤50 时的正态性检验;。
3、用达戈斯提诺(D′Agostino)法检验数据正态性即D检验,1971提出,正态性D检验该方法效率高,是比较精确的正态检验法。
4、Shapiro-Francia 法即W′检验,于1972 年提出,适用于50 < n < 100 时的正态性检验。
5、QQ图或PP图散点聚集在固定直线的周围,可以认为数据资料近似服从正态分布SPSS&SAS规则:SPSS 规定:当样本含量3 ≤n ≤5000 时,结果以Shapiro - Wilk (W 检验) 为难,当样本含量n > 5000 结果以Kolmogorov - Smirnov 为准。
而SAS 规定:当样本含量n ≤2000 时,结果以Shapiro - Wilk (W 检验) 为准,当样本含量n >2000 时,结果以Kolmogorov - Smirnov (D 检验) 为准问:对照组和病例组都是20例,拟对某指标进行正态性检验,是用Kolmogorov-Smirnov检验(简称K-S检验),还是Shapiro-Wilk检验?已用K-S 检验不能认为该指标不是正态分布,但是Shapiro-Wilk检验表明其为非正态分布,我该相信哪个检验结果?答:Kolmogorov-Smirnov检验:检验频数分布的正态性检验,适合大样本。
Shapiro-Wilk检验:小样本数据的正态性检验。
矩法正态性检验: 不限样本。
问:用SPSS中analysze/discriptive statistics/explore 法和用analyze/nonparametric tests/1-sample K-S法评价正态性,结果不完全相同,为什么?答:以第二个为准,第一种方法是参数检验,而第二种是非参数检验,第一种是在知道总体分布的情况下做的,第二种是在不知道总体分布的情况进行的检验,而且大多数的检验,我们都是不知道总体分布到底是什么才做的K-S检验。
因此在做分析的时候一般用第二种,标准的检验单样本分布的方法。
不过一般推荐用上面的,并且和SAS的结果比较吻合。
同时样本量小的时候选S-W的结果,至于结果的不同,应该是不同的方法算出的值不同,这很正常,因为这几个方法的数学表达式就不一样,中间对数据的处理也不一样,会有信息损失等原因的,在正态检验中,尤其是接近α水准时,往往容易出现问题,所以要根据资料的性质判断用什么方法进行检验更合适。
不是把所有的方法都做一遍。
对于到底P取多少才有意义,说法有好多种,常用的是0.1 吧,SPSS自带的是0.2的界值。
其实还是得结合QQ,PP图之类的来观察会好些。
小样本最好不要看Kolmogorov-Smirnov的结果,常常会有问题,Shapiro-Wilk 的结果会好些。
补充:如果根据国标,其偏态和峰态算法,其值为多少时符合正态别有规定呢?K-S 检验记得在资料上见过8<=n<=50时可以利用,小样本就不推荐,W检验在国标中不推荐,具体原因未知,不过,推荐了EPPS-PULLEY法(在SPSS,SAS软件中未见有这种检验,但有针对的软件对该法有独立开发)。
问:那为什么用analysze/discriptive statistics/explore法的结果中,nonparametric tests 图下有一句话:test distribution is normal。
这句话和P值不就矛盾了吗?答:这个是对前面给出均数标准差时候的一个假定,因为如果不服从正态,给出这两个参数是没有实用价值的,或者说是错误的,所以它给了一个假定。
你看a,b标注在什么地方?问:大样本的非正态资料可看作近似正态分布的资料,那么其描述能不能用均数加减标准差来表示呢?一定要用中位数和四分位数间距来表示吗?答:“大样本的非正态资料可看作近似正态分布的资料”这是基于中心极限定理,大样本均数服从正态分布,可用U检验进行两组均数的比较。
并非大样本的非正态资料可看作近似正态分布的资料。
大样本资料的描述可以用均数加减标准差。
数据的描述正态X±S 非正态M(QR) (M代表中位数,QR=Q3-Q1,代表四分位数间距)非正态资料也有用M(P25,P75)来进行描述的,能够更直观的看到数据的分布形状疑问:这儿有个值得考虑的问题,多大属于大样本?如果样本是我们常说的“大样本”那么只能说明样本参数是符合正态分布。
就样本资料来说,如果这个样本的资料偏态严重,那么就不适合采用均数加减标准差来对这个样本资料进行描述。
问:SPSS中只有关于t检验的程序,请问U检验的程序在哪里呢?答:U 检验SAS程序(只有样本量、均数、标准差的情况)data utest;n1=116; x1=0.2189; s1=0.2351;n2=125; x2=0.2280;s2=0.2561;u=(x1-x2)/sqrt(s1**2/n1+s2**2/n2);p=(1-probnorm(abs(u))*2;p roc print;var u p;run;SAS的正态性检验PROC UNIVARIATE DATA=data1 NORMALVAR x;RUN;注:以上问题即回答来自各大论坛,本工作室对其进行整理,和修正,以方便读者。
如有不妥支出,请及时帮我们斧正,谢谢!如有与“GBT4882-2001数据的统计处理和解释-正态性检验”冲突的,请参照国标。
下载地址/netdisk/GetFile.asp提取码:09042123310309MMH两种正态性检验方法差异比较SPSS 2010-06-26 13:20:34 阅读56 评论0 字号:大中小SPSS里面有两处可以检验数据正态性,一个是: Analysis - Descriptive Statistics --Explore,这可能是常用的方法另一处是:Analysis -Nonparametric tests -- One sample K-S test,两个地方虽然都用到了名称相同的Kolmogorov-Smirnov Test,但是经常会出现检验的结果不一致的情况。
