第四讲：正态性检验和方差齐性检验

公卫医师医学统计学辅导正态性检验与两方差的齐性检验.

公卫医师医学统计学辅导：正态性检验与两方差的齐性检验检验两个样本均数相差的显著性时，我们先有假定：第一个样本系从均数为μ1、方差为σ12的正态总体中随机取出，第二个样本取自另一个类似的总体，相应的总体参数为μ2与σ22，两个总体的方差应相等即σ12=σ22，然后才可用上述方法进行显著性检验，如果资料呈显著偏态，或两组方差相差悬殊，就要考虑用第十章非参数统计方法处理，或者通过变量代换，使上述条件得到满足。

那么，怎样知道手头的样本资料是否服从正态分布及两组方差是否相差显著呢？要对手头资料作正态检验及方差齐性检验。

下面分别用实例介绍常用的正态性检验和两方差齐性检验的方法。

一、正态性检验有些统计方法只适用于正态分布或近似正态分布资料，如用均数和标准差描述资料的集中或离散情况，用正态分布法确定正常值范围及用t检验两均数间相差是否显著等，因此在用这些方法前，需考虑进行正态性检验。

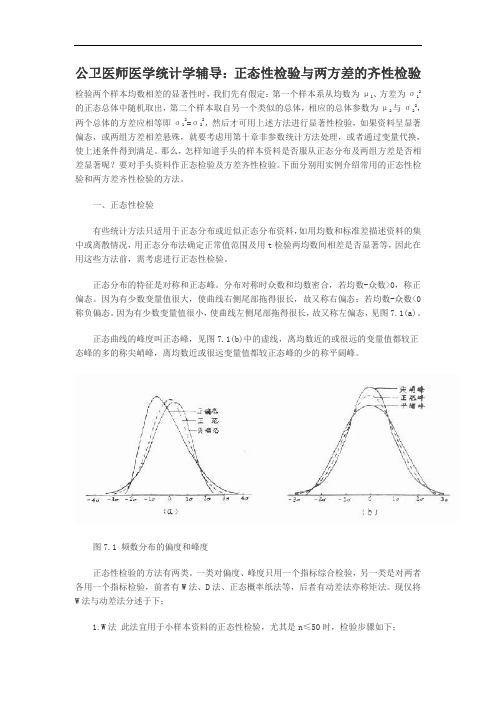
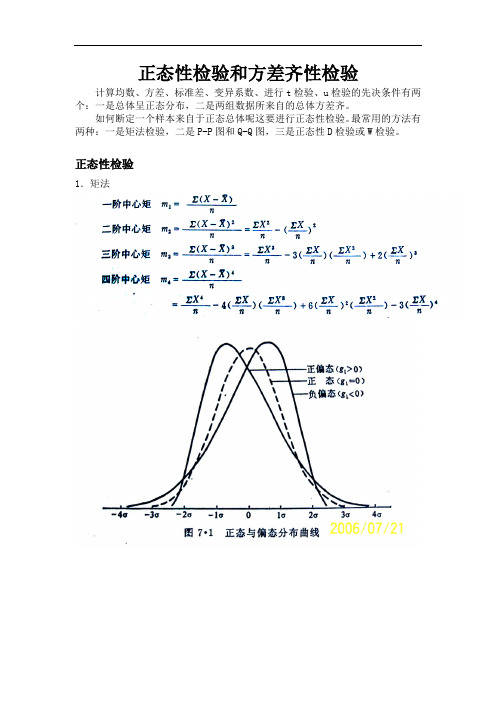
正态分布的特征是对称和正态峰。

分布对称时众数和均数密合，若均数-众数>0，称正偏态。

因为有少数变量值很大，使曲线右侧尾部拖得很长，故又称右偏态；若均数-众数<0称负偏态。

因为有少数变量值很小，使曲线左侧尾部拖得很长，故又称左偏态，见图7.1(a)。

正态曲线的峰度叫正态峰，见图7.1(b)中的虚线，离均数近的或很远的变量值都较正态峰的多的称尖峭峰，离均数近或很远变量值都较正态峰的少的称平阔峰。

图7.1 频数分布的偏度和峰度正态性检验的方法有两类。

一类对偏度、峰度只用一个指标综合检验，另一类是对两者各用一个指标检验，前者有W法、D法、正态概率纸法等，后者有动差法亦称矩法。

现仅将W法与动差法分述于下；1.W法此法宜用于小样本资料的正态性检验，尤其是n≤50时，检验步骤如下；(1)将n个变量值X i从小至大排队编秩。

X1<X2<……<XN< />见表7.5第(1)栏，表中第(2)、第(3)栏是变量值，第(2)栏由上而下从小至大排列，第(3)栏由下而上从小至大排列。

方差分析中的方差齐性检验方法

方差分析中的方差齐性检验方法方差分析是一种常用的统计方法，用于比较两个或多个样本均值之间的差异是否显著。

在进行方差分析之前，我们需要先进行方差齐性检验，以确保所使用的统计方法的有效性和准确性。

本文将介绍方差齐性检验的方法及其在方差分析中的重要性。

方差齐性检验是用来检验不同样本的方差是否相等的一种统计方法。

在方差分析中，我们假设不同样本的方差是相等的，即方差齐性假设。

如果方差不齐，那么方差分析的结果将可能出现偏差，影响我们对不同样本均值的比较。

常用的方差齐性检验方法有Levene检验和Bartlett检验。

Levene检验是一种非参数检验方法，不依赖于数据的分布情况。

它通过比较不同样本的方差差异来判断方差是否齐性。

Bartlett检验则是一种基于正态分布假设的参数检验方法，适用于样本数较大的情况。

在进行方差齐性检验时，我们首先需要将数据按照不同的组别进行分类。

然后，我们计算每个组别的方差，并进行方差齐性检验。

Levene检验的原假设是各组别的方差相等，备择假设是各组别的方差不等。

我们可以通过计算Levene检验的统计量和对应的p值来判断方差是否齐性。

如果p值小于显著性水平（通常为0.05），则拒绝原假设，认为各组别的方差不等。

反之，则接受原假设，认为各组别的方差相等。

Bartlett检验的原假设和备择假设与Levene检验相同。

我们可以通过计算Bartlett检验的统计量和对应的p值来判断方差是否齐性。

如果p值小于显著性水平，则拒绝原假设，认为各组别的方差不等。

反之，则接受原假设，认为各组别的方差相等。

方差齐性检验在方差分析中的重要性不言而喻。

如果我们在进行方差分析之前没有进行方差齐性检验，那么我们得到的结果可能是不准确的。

如果方差不齐，那么方差分析的假设条件将不满足，我们无法得到准确的p值和显著性结论。

因此，在进行方差分析之前，我们必须进行方差齐性检验，以确保统计分析的有效性和准确性。

除了Levene检验和Bartlett检验，还有其他一些方法可以用来检验方差的齐性，如F检验和Brown-Forsythe检验等。

方差齐性检验分析

方差齐性检验分析方差齐性检验是数据分析中常用的一种检验方法，用于检验不同样本组内数据的方差是否相等。

在分析实验数据或调查数据时，我们通常需要进行多个组间的比较，这时就需要进行方差齐性检验，以保证结果的有效性。

为什么需要方差齐性检验在进行数据分析时，我们通常需要比较不同组之间的统计差异，比如比较两个或多个治疗方法的疗效、比较不同性别、不同年龄段等的差异。

这时，我们通常会使用方差分析（ANOVA）进行比较。

在使用ANOVA进行比较时，我们假设不同组的方差是相等的，即方差齐性假设。

如果方差不相等，则ANOVA的结果可能会被影响，导致得到不可靠的结论。

因此，为了避免这种情况发生，我们需要进行方差齐性检验，以确定是否需要对ANOVA结果进行修正。

如何进行方差齐性检验常用的方差齐性检验方法包括Levene检验和Bartlett检验。

这两种检验方法都是基于F分布的。

Levene检验Levene检验是最常用的方差齐性检验方法之一，它适用于等间距数据和非等间距数据。

Levene检验的原假设是各组数据的方差相等，备择假设是各组数据的方差不相等。

Levene检验的统计量为：$$W=\frac{(N-k)\sum_{j=1}^{k}n_j(\bar{z_{j\cdot}}-\bar{z_{\cdot\cdot}})^2}{(k-1)\sum_{j=1}^{k}\sum_{i=1}^{n_j}(z_{ij}-\bar{z_{j\cdot}})^2}$$其中，N为总样本数，k为组数，$n_j$为第j组的样本量，$z_{ij}$为第j组中第i个观测值，$\bar{z_{j\cdot}}$为第j组的均值，$\bar{z_{\cdot\cdot}}$为总体均值。

当样本量较大时，W的分布近似于自由度为k-1的F分布。

如果W的p值小于显著性水平，则拒绝原假设，认为各组数据的方差不相等。

Bartlett检验Bartlett检验也是一种常用的方差齐性检验方法，它假定每个样本都服从正态分布。

多因素方差分析前的正态性和方差齐性考察

多因素方差分析前的正态性和方差齐性考察SPSS中的Univariate过程是被轻视了的一个分析方法，尤其是在较新版本的一些功能增加之后。

在线性回归中遇到多分类变量时，我们是需要将其设置成哑变量的，你可以手动设置，也可以通过创建哑变量过程（转换Transform>>创建虚拟变量Create Dummy Variables），虽非难事，但我还是会奇怪为什么在线性回归的对话框里面不能像logistic回归那样有一个可以把分类变量设置成哑变量的按钮。

我们常常说方差分析是线性回归的一个特殊形式，线性回归可以实现方差分析，但其实线性回归也可以在Univariate过程中实现，只需要将分类变量放入因子框、连续变量放入协变量框就可以了。

放入因子框的变量会自动按哑变量处理。

结果除了可以获得方差分析表，也可以获得线性回归里的参数估计表，只需要在【选项】按钮中选中参数估计[Parameter estimates]就可以了。

另外【选项】里面提供的异方差检验[Heteroskedasticity test]也可以直接实现对线性模型方差齐同性的Breusch-Pagan、White等统计学检验，甚至还可以进行稳健回归，这在线性回归里面反而做不到。

其他像趋势检验、事后（Post Hoc）多重比较，边际均值（EM means）估计与比较也不是线性回归能比拟的，而且还提供了估计值/残差/模型诊断参数的保存。

独立、正态、方差齐同是我们进行方差分析时的前提条件，在进行方差分析前我们需要对这些条件进行考察。

这里面独立性最重要，可根据专业做出判断。

正态性和方差齐性对的考察方法也很多，可参见《正态分布与方差齐性的检验方法》。

需要特别注意的是这里的正态性是指各个单元格的残差都呈正态分布，方差齐同是指各个单元格的残差的方差相等。

什么是单元格？单元格指的是模型中各个因素各个水平的组合。

比如一个三水平的单因素方差分析中，会有三个单元格，而在一个两因素的方差分析中，如果一个因素两水平，另外一个因素三水平，结果会有6个单元格。

方差齐性检验

方差齐性检验
方差齐性检验是方差分析的重要前提，是方差可加性原则应用的一个条件。

方差齐性检验的时候，首先需要知道方差齐性检验的本质：样本以及总体的方差的分布是常数，和自变量或者因变量没有关系。

然后绘制散点图，在方差齐性检验中，因变量被设置为横轴，纵轴是学生化残差。

原因就是，要弄清究竟因变量和残差之间有没有关系。

如果残差随机分布在一条穿过零点的水平直线的两侧，就说明残差独立，也就是证明因变量方差齐性。

第四讲：正态性检验和方差齐性检验Word版

正态性检验和方差齐性检验计算均数、方差、标准差、变异系数、进行t检验、u检验的先决条件有两个：一是总体呈正态分布，二是两组数据所来自的总体方差齐。

如何断定一个样本来自于正态总体呢？这要进行正态性检验。

最常用的方法有两种：一是矩法检验，二是P-P图和Q-Q图，三是正态性D检验或W检验。

正态性检验1．矩法2．P-P图/Q-Q图PP图和QQ图原理一样，都是用图形来大致检测数据是否服从某种分布的。

以PP图为例，横坐标是某检验分布的概率值，纵坐标是观测数据的经验分布的概率值（谁作横坐标谁作纵坐标无所谓）。

如果数据服从检验分布，那么图形画出来应该是一条直线（对角线）；至于QQ图，只不过把概率换成了分位点而已。

红细胞数组中值频数累计频数累计频率概率单位420- 430 2 2 1.4 2.8 440- 450 4 6 4.2 3.27 460- 470 7 13 9.0 3.66 480- 490 16 29 20.1 4.16 500- 510 20 49 34.0 4.59 520- 530 25 74 51.4 5.04 540- 550 24 98 68.1 5.47 560- 570 22 120 83.3 5.97 580- 590 16 136 94.4 6.59 600- 610 2 138 95.8 6.73 620- 630 5 143 99.3 7.46 640-660 650 1 144 100.087654324005006007003．正态性D 检验正态性W 检验Shapiro-Wilk 即正态性W 检验统计量。

Kolmogorov-Smirnov test 的原理是寻找最大距离（Distance ），所以常称为D 法。

当N≤2000时正态性检验用Shapiro-Wilk 统计量，N>2000时用Kolmogorov D 统计量。

∑∑-+-=nx x n x n i D i/)(]2/)1([24W=[∑a in (X a-i+1-X i )]2 /∑(X -X )2方差齐性检验2221S S F =111-=n ν 122-=n ν（注：可编辑下载，若有不当之处，请指正，谢谢!）。

方差齐性检验

方差齐性检验是用于判断多个正态分布的方差是否相等的重要方法。在进行方差分析时，要求各方差相等，即方差齐性，这是方差分析的前提条件。当正态性假定不满足时，F检验对方差齐性的偏离较为敏感，因此方差齐性检验十分必要。检验的基本假设是各方差相等，备择假设是各方差不全相等。常用的检验方法包括Hartley检验、Bartlett检验和修正的Bartlett检验。Hartley检验适用于样本量相等的场合，通过比较各样本方差的最大值与最小值之比来构造检验统计量。该统计量的分布依赖于水平数和样本方差的自由度，可通过随机模拟方法获得分位数。当检防锈能力的实例，具体演示了Hartley检验的步骤，包括计算样本方差、确定检验统计量和拒绝域、作出检验决策等。

为何需要正态分布和方差齐性的检验

为何需要正态分布和方差齐性的检验？很多时候，我们都需要使用从单一样本中获取的样本信息利用统计推断的方法来估计总体的参数信息，这是一种非常有用的统计方法，但在执行相关推断之前，我们需要验证一些假定，任何一条假定若是不能满足，则得到的统计结论就是无效的。

通常数据的分析假设为：随机数据，独立的，正态分布，等方差，稳定，当然，测量系统的精确性和准确性也是要满足测量要求的。

什么是正态分布假定？在再进行统计分析之前，需要识别出数据的分布，否则，错误的统计检验将带来一定的风险，许多统计方法在执行之前嘉定数据服从正态分布，比如，单/双样本-T检验，过程能力分析，Ｉ－ＭＲ和方差分析等。

如果数据不满足正态分布，则需要使用非参数方法，利用中位数进行检验而不是均值，也可以使用BOX－COX转换或ＪＯＨＮＳＯＮ变换的方法把数据转换为正态分布。

但是需要知道许多统计工具虽然假定数据满足正态但实际上当样本量大于15或20的时候就不需要正态分布了，但是如果样本量小于15且数据不满足正态分布，P值得数据就是错误的，相关统计结论就需要特别注意了。

在Minitab中，有许多方法可以判断数据的分布是否满足正态，下面我们来了解两种比较常用的方法：正态检验和图形化汇总Minitab的正态检验将生成概率图和执行单样本假设检验来判断数据的分布是否来自满足正态的分布总体，原假设是数据满足正态分布而备择假设是不满足选择统计—基本统计量—正态检验下面我们先看看数据的正态检验图形中的数据点应该在直线的附近，如果有些数据点在尾巴上远离直线也可以接受，但前提条件是必须在置信区间内才可以。

图形中的数据点应该靠近你和分布直线且通过“粗笔检验”，用一只“粗笔”盖在拟合直线上，如果铅笔能盖住所有数据点，则数据满足正态分布与之相连的Anderson-Darling检验统计量应该很小P值应该大于选择的Alpha风险（通常取或）Anderson-Darling统计量用来衡量数据点远离拟合直线的程度，是每个数据点到直线距离的平方和，对于一组给定的数据分布来说，分布拟合的越好，该值就会越小。

统计推断中方差分析方法在应用中注意事项

统计推断中方差分析方法在应用中注意事项统计推断是一种通过对样本数据的分析和推断来推断总体特征的方法。

在统计推断中，方差分析是一种常用的方法来检验不同总体的均值是否存在差异。

然而，在使用方差分析方法进行统计推断时，我们需要注意以下几个方面的问题，以保证结果的准确性和可靠性。

一、样本的独立性在进行方差分析前，我们要确保样本之间的独立性。

样本的独立性意味着各个样本之间的观测值相互独立，不受其他样本观测值的影响。

如果样本之间存在相互依赖的情况，那么方差分析的结果可能会出现偏差，导致错误的结论。

因此，在采集样本数据时，要避免重复抽样和样本间的相关性，以确保样本的独立性。

二、方差齐性检验方差分析假设不同总体的方差相等，即方差齐性。

方差齐性的检验是方差分析前的重要步骤，用来判断样本数据是否满足方差齐性的假设。

如果样本数据不满足方差齐性的假设，那么方差分析的结果可能会失真。

常用的方差齐性检验方法包括Levene检验和Bartlett检验等，可以根据实际情况选择合适的方法进行检验。

三、正态性检验方差分析假设样本数据符合正态分布。

在进行方差分析前，我们需要对样本数据进行正态性检验，以确定数据是否满足正态分布的假设。

如果样本数据不符合正态分布，那么方差分析的结果可能会失效。

常用的正态性检验方法有Shapiro-Wilk检验和Kolmogorov-Smirnov检验等，可以根据实际情况选择适合的方法进行检验。

四、确定显著性水平在方差分析中，我们需要设定显著性水平来判断不同总体均值之间的差异是否显著。

通常，显著性水平设定为0.05或0.01，可以根据实际需求进行调整。

在进行假设检验时，如果计算得到的p值小于设定的显著性水平，可以拒绝原假设，认为不同总体均值之间存在显著差异。

五、报告分析结果在进行方差分析后，我们需要清晰地报告分析结果。

报告中应包括分析方法、统计值、自由度、p值等关键信息。

通过清晰准确地报告分析结果，可以使读者理解分析过程和结果，并进行进一步的判断和推断。

第四讲：正态性检验和方差齐性检验

正态性检验和方差齐性检验计算均数、方差、标准差、变异系数、进行t检验、u检验的先决条件有两个：一是总体呈正态分布，二是两组数据所来自的总体方差齐。

如何断定一个样本来自于正态总体呢这要进行正态性检验。

最常用的方法有两种：一是矩法检验，二是P-P图和Q-Q图，三是正态性D检验或W检验。

正态性检验1．矩法2．P-P图/Q-Q图PP图和QQ图原理一样，都是用图形来大致检测数据是否服从某种分布的。

以PP图为例，横坐标是某检验分布的概率值，纵坐标是观测数据的经验分布的概率值（谁作横坐标谁作纵坐标无所谓）。

如果数据服从检验分布，那么图形画出来应该是一条直线（对角线）；至于QQ图，只不过把概率换成了分位点而已。

红细胞数组中值频数累计频数累计频率概率单位420- 430 2 2440- 450 4 6460- 470 7 13480- 490 16 29500- 510 20 49520- 530 25 74540- 550 24 98560- 570 22 120580- 590 16 136600- 610 2 138620- 630 5 143640-660 650 1 14487654324005006007003．正态性D 检验正态性W 检验Shapiro-Wilk 即正态性W 检验统计量。

Kolmogorov-Smirnov test 的原理是寻找最大距离（Distance ），所以常称为D 法。

当N≤2000时正态性检验用Shapiro-Wilk 统计量，N>2000时用Kolmogorov D 统计量。

∑∑-+-=nx x n x n i D i/)(]2/)1([24W=[∑a in (X a-i+1-X i )]2 /∑(X -X )2方差齐性检验2221S S F =111-=n ν 122-=n ν。

为何需要正态分布和方差齐性的检验

为何需要正态分布和方差齐性的检验？为何需要正态分布和方差齐性的检验？很多时候，我们都需要使用从单一样本中获取的样本信息利用统计推断的方法来估计总体的参数信息，这是一种非常有用的统计方法，但在执行相关推断之前，我们需要验证一些假定，任何一条假定若是不能满足，则得到的统计结论就是无效的。

通常数据的分析假设为：随机数据，独立的，正态分布，等方差，稳定，当然，测量系统的精确性和准确性也是要满足测量要求的。

什么是正态分布假定？在再进行统计分析之前，需要识别出数据的分布，否则，错误的统计检验将带来一定的风险，许多统计方法在执行之前嘉定数据服从正态分布，比如，单/双样本-T检验，过程能力分析，Ｉ－ＭＲ和方差分析等。

如果数据不满足正态分布，则需要使用非参数方法，利用中位数进行检验而不是均值，也可以使用BOX－COX转换或ＪＯＨＮＳＯＮ变换的方法把数据转换为正态分布。

但是需要知道许多统计工具虽然假定数据满足正态但实际上当样本量大于15或20的时候就不需要正态分布了，但是如果样本量小于15且数据不满足正态分布，P值得数据就是错误的，相关统计结论就需要特别注意了。

在Minitab中，有许多方法可以判断数据的分布是否满足正态，下面我们来了解两种比较常用的方法：正态检验和图形化汇总Minitab的正态检验将生成概率图和执行单样本假设检验来判断数据的分布是否来自满足正态的分布总体，原假设是数据满足正态分布而备择假设是不满足选择统计—基本统计量—正态检验下面我们先看看数据的正态检验∙图形中的数据点应该在直线的附近，如果有些数据点在尾巴上远离直线也可以接受，但前提条件是必须在置信区间内才可以。

∙图形中的数据点应该靠近你和分布直线且通过“粗笔检验”，用一只“粗笔”盖在拟合直线上，如果铅笔能盖住所有数据点，则数据满足正态分布∙与之相连的Anderson-Darling检验统计量应该很小∙P值应该大于选择的Alpha风险（通常取0.05或0.1）Anderson-Darling统计量用来衡量数据点远离拟合直线的程度，是每个数据点到直线距离的平方和，对于一组给定的数据分布来说，分布拟合的越好，该值就会越小。

SPSS应用t检验及方差齐性检验、正态性检验

→paried variables:配对的两个变量
→ok 例3-6：
四.t检验：两样本均数的比较 analyze→compare means →independent-samples t test
→test variable:分析变量 →grouping variable:分组变量
→define groups:分组变量的值
→ok
正态性检验有两种结果：
未转换数据（的方差齐性检验）
Shapiro-Wilk:W检验(小样本)
Kolmogorov-Smirnov:D检验(大样本)
“Paste”按钮的使用
→ok 例3-7：
五.正态性检验和方差齐性检验：
Analyze → descriptive statistics→ Explore(探索性分析)
→ dependent list:分析变量 factor:分组变量
正态性检验
plots:normality test
untransformed →continue
二.t检验：样本均数与总体均数的比较 analyze→compare means →one-sample t test
→test variable:分析变量 →test value:总体均数的值
→ok 例3-5：
三.t检验：配对t检验 analyze→compare means →paried-samples t test
SPSS应用：t检验和正态性、方差齐性检验
一、统计描述：
Analyze → descriptive statistics → descriptives → variables: 分析变量→ok 例2-1：
descriptive statistics： frequencies(频数分布分析) Descriptives (描述性统计分析) Explore(探索性分析) Crosstabs (列联表资料分析) …

研究生统计学讲义第4讲第4章正态性检验和方差齐性检验

方差齐性检验（test for homogeneity of variance）是利用理论上来自正态分布的总体的各样本信息，来推断它们的总体方差是否相等。
研究生统计学讲义第4讲第4章正态性检验和方差齐性检验
方差齐性检验主要用于：①两组或多组间变异度的比较；②两个或多个样本均数间比较时，须先进行方差齐性检验，若方差齐，可用 t 检验或方差分析，否则可用变量变换的方法，使之方差齐后再用 t 检验或方差分析，或用对方差没有特别要求的 t´检验或其他非参数的统计方法。
统计量F的分子大于分母计算 F 值。所以附表4中F界
值都大于1。
从附表6最后一列看的出来，随机变量取值的单侧 P 界值（即单侧α时的界值）与同侧的双侧2P界值（即双侧α时的界值）相等，
F 分布具有倒数性质：
1
F（1－α）, （df2,df1）＝
F (df1 ,df 2 )
研究生统计学讲义第4讲第4章正态
研究生统计学讲义第4讲第4章正态性检验和方差齐性检验
本书附表6 录用了按P（F> Fα（df1，df2））=α编制的F界值表，表中横标目为分母的自由度df2，纵标目为分子的自由度df1，表中数字表示F 的界值Fα（df1，df2）；附表6右上角插图中阴影部分，表示 F 分布曲线下，界值 Fα（df1，df2）右侧面积占总面积的百分数，意义是：从正态总体作随机抽样，得到统计量F值大于界值 Fα（df1， df2）的概率P（F > Fα（df1，df2）） =α。例如：查附表6，界值F0.05（5，10） =3.33，它表示自由度df1=5，df2=10 时，
（2）若从均数为μ，标准差为σ的正态总体中，每次抽取样本含量为 n 的样本，计算样本标准差S，则

SPSS应用：t检验及方差齐性检验、正态性检验

SPSS应用：t检验和正态性、方差齐性检验
一、统计描述:
Analyze → descriptive statistics → descriptives → variables: 分析变量→ok 例2-1:
descriptive statistics: frequencies(频数分布分析) Descriptives (描述性统计分析) Explore(探索性分析) Crosstabs (列联表资料分析) …
→paried variables:配对的两个变量 →ok 例3-6:
四.t检验: 两样本均数的比较 analyze→compare means →independent-samples t test
→test variable:分析变量 →grouping variable:分组变量
→define groups:分组变量的值 →ok Nhomakorabea例3-7:
二.t检验: 样本均数与总体均数的比较 analyze→compare means →one-sample t test
→test variable:分析变量 →test value:总体均数的值 →ok 例3-5:
三.t检验: 配对t检验 analyze→compare means →paried-samples t test
五.正态性检验和方差齐性检验:
Analyze → descriptive statisti正c态s性→检验Explore(探索性分析)
→ dependent list:分析变量
factor:分组变量
plots:normality test
未转换数据（的方差齐性检验）
untransformed →continue

SPSS应用t检验及方差齐性检验、正态性检验

SPSS应用：t检验和正态性、方差齐性检验
一、统计描述：
Analyze → descriptive statistics → descriptives → variables: 分析变量→ok 例2-1：
descriptive statistics： frequencies(频数分布分析) Descriptives (描述性统计分析) Explore(探索性分析) Crosstabs (列联表资料分析) …
二.t检验：样本均数与总体均数的比较 analyze→compare means →one-sample t test
→test variable:分析变量 →test value:总体均数的值
→ok 例3-5：
三.t检验：配对t检验 analyze→compare means →paried-samples t test
→ok
正态性检验有两种结果：
未转换数据（的方差齐性检验）
Shapiro-Wmirnov:D检验(大样本)
“Paste”按钮的使用
→paried variables:配对的两个变量
→ok 例3-6：
四.t检验：两样本均数的比较 analyze→compare means →independent-samples t test
→test variable:分析变量 →grouping variable:分组变量
→define groups:分组变量的值
→ok 例3-7：
五.正态性检验和方差齐性检验：
Analyze → descriptive statistics→ Explore(探索性分析)
→ dependent list:分析变量 factor:分组变量

方差齐性检验

10
进一步，我们可用方差分析方法对四种不同型号的防锈剂比较其防锈能力．由表 8.3.1 的数据可以算出：
T T1 T2 T3 T4 2410 ，
从而求得三个偏差平方和分别为
ST
r i 1
m
Yij2
j 1
T2 n
16174.50 ，
fT 39 ；
S A
1 m
r
Ti 2
i 1
T2 n
6.14
总和 T
16174.50
39
若给定显著性水平 0.05，查表可得
F1 fA, fe F0.95 3, 36 2.87 ，
F比 866.09
由观测值所得的 F 866.09 2.87 ，故拒绝原假设 H0 ，认为四种防锈剂的防锈能力有显著性差异．
12
二、Bartlett检验
168 .42
7.92 6.22 6.12 7.42
168 .42 24
65.27 ，
fT 23 ；
Se 65.27 23.50 41.77 ，
fe 20 ．
25
方差分析见表 8.3.4
表 8.3.4 绿茶的叶酸含量的方差分析表
来源
平方和
方差齐性检验
在单因子试验中， r 个水平的指标可以用 r 个正态分布
N i,
2 i
， i 1,
2,
,
r
表示．在进行方差分析时，要求 r 个方差相等，这时称为方
差齐性．而方差齐性不一定自然具有．理论研究表明，当正
态性假定不满足时，对 F 检验影响较小，即 F 检验对正态性
的偏离具有一定的稳健性，而 F 检验对方差齐性的偏离较为
（8.3.3）