偏微分方程数值解实验报告
偏微分方程数值解第三次上机实验报告
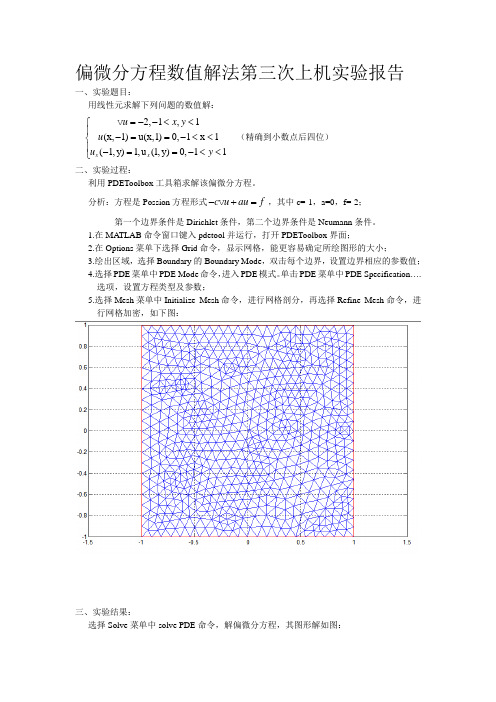
偏微分方程数值解法第三次上机实验报告一、实验题目:用线性元求解下列问题的数值解:2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ (精确到小数点后四位)二、实验过程:利用PDEToolbox 工具箱求解该偏微分方程。
分析:方程是Possion 方程形式c u au f -+=,其中c=-1,a=0,f=-2; 第一个边界条件是Dirichlet 条件,第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行,打开PDEToolbox 界面;2.在Options 菜单下选择Grid 命令,显示网格,能更容易确定所绘图形的大小;3.绘出区域,选择Boundary 的Boundary Mode ,双击每个边界,设置边界相应的参数值;4.选择PDE 菜单中PDE Mode 命令,进入PDE 模式。
单击PDE 菜单中PDE Specification ….选项,设置方程类型及参数;5.选择Mesh 菜单中Initialize Mesh 命令,进行网格剖分,再选择Refine Mesh 命令,进行网格加密,如下图:三、实验结果:选择Solve 菜单中solve PDE 命令,解偏微分方程,其图形解如图:图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh,得到结点xy坐标;选择Solve菜单中的Export Solution…,得到每个节点处的值,输出u,即解的数值。
四、实验总结:通过本次试验,掌握了利用Matlab中的PDE求解工具得到PDE的解的方法,并对偏微分方程的形式有了更多的掌握。
偏微分方程数值算法和matlab实验报告

偏微分方程数值实验报告六实验题目:用Ritz-Galerkin 方法求边值问题2(0)0,(1)1u u x u u ''-+===⎧⎨⎩01x << 的第n 次近似()n u x ,基函数为(),i 1,2,.()..x n i sin i x πφ==并用表格列出0.25,0.5,0.75三点处的真解和1,2,3,4n =时的数值解。
实验算法:将上述边值问题转化为基于虚功方程的变分问题为: 求10()u H I ∈,满足10(,)(,(v H ,))a u v x x I ∀∈=-其中1100(u''v uv)(,)(,)dx (u'v'uv)dx a u v Lu v +=-+==⎰⎰ 记(x)sin()w x π=,引入10()H I 的n 维近似子空间12{,},,n n U φφφ=⋯(),i 1,2,,i sin i x n πφ==⋯利用Ritz-Galerkin 公式:1()(f,),j 1,,,2,n j i jj a n φφφ==⋯=∑,则问题关于n U 下的近似变分问题解1()()n i i n i c u x x φ==∑中的系数12(,,,)T nn c c c c =⋯∈满足12()(,,)n j i j j a x φφφ==∑程序代码:%主函数pde=modeldata();I=[0,1];%积分精度quadorder=10;n=[1,2,3,4];for i=1:length(n)uh{i}=Galerkin(pde,I,n(i),quadorder); endshowsolution(uh{1},'-bo');hold onshowsolution(uh{2},'-rx');hold onshowsolution(uh{3},'-.ko');hold onshowsolution(uh{4},'--k*');hold offtitle('the solution of the un');xlabel('x');ylabel('u');legend('n=1','n=2','n=3','n=4');%计算这三点的数值解x=[1/4,1/2,3/4];un=zeros(length(n),3);for i=1:length(n)[v, ]=basis(x,n(i));un(i,:)=(v'*uh{i})';endformat shortedisp('un');disp(un);%存储数据function pde=modeldata()pde=struct('f',@f);function z=f(x)z=x.*x;endend%Galerkin方法function uh=Galerkin(pde,I,n,quadorder) h=I(2)-I(1);[lambda,weight]=quadpts1d(I,quadorder);nQuad=length(weight);A=zeros(n,n);b=zeros(n,1);for q=1:nQuadgx=lambda(q);w=weight(q);x=[0.25;0.5;0.75];[phi,gradPhi]=basis(gx,n);A=A+(-gradPhi*gradPhi'+phi*phi')*w; b=b+pde.f(gx)*phi*w;endA=h*A;b=h*b;uh=A\b;end%构造基函数function [phi,gradPhi]=basis(x,n)m=length(x);w=sin(pi*x);v=ones(n,m);v(2:end,:)=bsxfun(@times,v(2:end,:),x);v=cumprod(v,1);phi=bsxfun(@times,v,w);gw=pi*cos(pi*x);gv=[zeros(1,m);v(1:end-1,:)];gv(3:end,:)=bsxfun(@times,(2:n-1)',gv(3:end,:)); gradPhi=bsxfun(@times,v,gw)+bsxfun(@times,gv,w); end%数值解的图像function showsolution(u,varargin)x=0:0.01:1;n=length(u);[v, ]=basis(x,n);y=v'*u;plot(x,y,varargin{:});% varargin: an input variable in a functionend%系数矩阵Afunction [lambda,weight] = quadpts1d(I,quadorder)numPts = ceil((quadorder+1)/2);if numPts> 10numPts = 10;endswitch numPtscase 1A = [0 2.0000000000000000000000000];case 2A = [0.57735026918962576450914881.0000000000000000000000000-0.57735026918962576450914881.0000000000000000000000000];case 3A = [ 00.88888888888888888888888890.77459666924148337703585310.5555555555555555555555556-0.7745966692414833770358531 0.5555555555555555555555556];case 4A = [0.33998104358485626480266580.65214515486254614262693610.8611363115940525752239465 0.3478548451374538573730639-0.3399810435848562648026658 0.6521451548625461426269361-0.8611363115940525752239465 0.3478548451374538573730639];case 5A = [ 00.56888888888888888888888890.5384693101056830910363144 0.47862867049936646804129150.9061798459386639927976269 0.2369268850561890875142640-0.5384693101056830910363144 0.4786286704993664680412915-0.9061798459386639927976269 0.2369268850561890875142640];case 6A = [0.23861918608319690863050170.46791393457269104738987030.6612093864662645136613996 0.36076157304813860756983350.9324695142031520278123016 0.1713244923791703450402961-0.2386191860831969086305017 0.4679139345726910473898703-0.6612093864662645136613996 0.3607615730481386075698335-0.9324695142031520278123016 0.1713244923791703450402961];case 7A = [00.41795918367346938775510200.4058451513773971669066064 0.38183005050511894495036980.7415311855993944398638648 0.27970539148927666790146780.9491079123427585245261897 0.1294849661688696932706114-0.4058451513773971669066064 0.3818300505051189449503698-0.7415311855993944398638648 0.2797053914892766679014678-0.9491079123427585245261897 0.1294849661688696932706114];case 8A = [0.18343464249564980493947610.36268378337836198296515040.5255324099163289858177390 0.31370664587788728733796220.7966664774136267395915539 0.22238103445337447054435600.9602898564975362316835609 0.1012285362903762591525314-0.1834346424956498049394761 0.3626837833783619829651504-0.5255324099163289858177390 0.3137066458778872873379622-0.7966664774136267395915539 0.2223810344533744705443560-0.9602898564975362316835609 0.1012285362903762591525314];case 9A = [00.33023935500125976316452510.3242534234038089290385380 0.31234707704000284006863040.6133714327005903973087020 0.26061069640293546231874290.8360311073266357942994298 0.18064816069485740405847200.9681602395076260898355762 0.0812743883615744119718922-0.3242534234038089290385380 0.3123470770400028400686304-0.6133714327005903973087020 0.2606106964029354623187429-0.8360311073266357942994298 0.1806481606948574040584720-0.9681602395076260898355762 0.0812743883615744119718922];case 10A = [0.14887433898163121088482600.29552422471475287017389300.4333953941292471907992659 0.26926671930999635509122690.6794095682990244062343274 0.21908636251598204399553490.8650633666889845107320967 0.14945134915058059314577630.9739065285171717200779640 0.0666713443086881375935688-0.1488743389816312108848260 0.2955242247147528701738930-0.4333953941292471907992659 0.2692667193099963550912269-0.6794095682990244062343274 0.2190863625159820439955349-0.86506336668898451073209670.1494513491505805931457763-0.97390652851717172007796400.0666713443086881375935688];endlambda = (I(2)+I(1)+(I(2)-I(1))*A(:,1))/2; weight = A(:,2)*(I(2)-I(1))/2;数值解:x=x=3/4x=1/21/4u-3.0184e-02 -4.2686e-02 -3.0184e-02 1u-2.1919e-02 -4.2686e-02 -3.8448e-02 2u-2.3232e-02 -4.0652e-02 -3.9761e-02 3u-2.3472e-02 -4.0652e-02 -3.9521e-02 4图像:00.10.20.30.40.50.60.70.80.91the solution of the unx u。
偏微分方程数值求解的算法研究与实现

偏微分方程数值求解的算法研究与实现随着计算机技术的日益发展,偏微分方程数值求解成为了热门的数值计算领域之一。
偏微分方程(PDE)是许多科学和工程领域的数学模型。
它们描述了物理过程,因此在流体动力学、机械工程、材料科学以及生命科学中都有广泛应用。
在本文中,我们将讨论偏微分方程数值求解的算法研究与实现。
一、偏微分方程的数值解法偏微分方程最常见的数值解法是有限差分法(FDM)、有限元法(FEM)和谱方法(SP)。
FDM是将PDE的导数转化为差分方程的方法。
它将解域划分为网格,并在每个网格点上估计解(即差分)。
通过这种方法,PDE可以被重写成一个差分方程组。
FEM通过将解域划分为有限数量的单元,然后估计每个单元内的解。
这个过程包括将PDE转化为一系列局部的差分方程,并将它们组合成一个大的线性方程组。
最后,SP使用特定的基函数表示解,通常是正交多项式。
这个过程产生一个矩阵形式的线性方程。
二、偏微分方程数值求解中的挑战偏微分方程数值求解涉及到许多挑战。
首先,PDE的数值解是无限精度的,但在计算机上是有限精度的,这意味着数值误差会在计算过程中逐渐累积。
其次,由于PDEs具有复杂的非线性行为,因此需要使用高阶算法才能在合理的时间内获得解。
最后,PDEs在解域的不同区域上可能具有不同的特征,这需要使用适当的算法来解决。
三、算法研究与实现针对偏微分方程数值求解中的挑战,研究者们一直在开发新的算法和优化现有算法。
许多研究都集中在如何提高数值解的精度和计算效率上。
在FDM中,高精度的近似解可以通过使用更高阶导数的差分来获得。
例如,中心差分代替前向或后向差分可以更准确地计算二阶导数。
在FEM中,使用高阶元素可以获得更好的精度。
此外,研究者还开发了基于多层网格技术的自适应算法,这些算法可以根据解的特性在解域的不同区域使用不同的网格大小来提高计算效率。
在SP中,使用高阶谱方法可以获得更好的精度和更高的计算效率。
除了以上算法,其他一些更复杂的方法也被广泛研究。
微分方程数值解法实验报告

微分方程数值解法实验报告2篇微分方程数值解法实验报告(一)在实际科学与工程问题中,我们经常会遇到微分方程的求解。
然而,许多微分方程往往没有解析解,这就需要我们利用数值方法来获得近似解。
本篇实验报告将介绍两种常见的微分方程数值解法:欧拉方法和改进的欧拉方法。
一、欧拉方法欧拉方法是最简单的微分方程数值解法之一。
其基本原理为离散化微分方程,将微分方程中的导数用差商代替。
设要求解的微分方程为dy/dx = f(x, y),步长为h,则可用以下公式进行递推计算:y_{n+1} = y_n +hf(x_n, y_n)二、算法实现为了对欧拉方法进行数值实验,我们以一阶线性常微分方程为例:dy/dx = x - y, y(0) = 1步骤如下:(1)选择合适的步长h和求解区间[a, b],这里我们取h=0.1,[a, b] = [0, 1];(2)初始化y_0 = 1;(3)利用欧拉方法递推计算y_{n+1} = y_n + 0.1(x_n - y_n);(4)重复步骤(3),直到x_n = 1。
三、实验结果与讨论我们通过上述步骤得到了在[0, 1]上的近似解y(x)。
下图展示了欧拉方法求解的结果。
从图中可以看出,欧拉方法得到的近似解与精确解有一定的偏差。
这是因为欧拉方法只是通过递推计算得到的近似解,并没有考虑到更高阶的误差。
所以在需要高精度解时,欧拉方法并不理想。
四、改进的欧拉方法针对欧拉方法的不足,我们可以考虑使用改进的欧拉方法(也称为改进的欧拉-柯西方法)。
它是通过利用前后两个步长欧拉方法得到的结果作为差商的中间项,从而提高了求解精度。
一阶线性常微分方程的改进欧拉方法可以表示为:y_{n+1} = y_n + h(f(x_n, y_n) + f(x_{n+1}, y_n + hf(x_n,y_n)))/2五、算法实现与结果展示将改进的欧拉方法应用于前述的一阶线性常微分方程,我们同样选择h=0.1,[a, b] = [0, 1]。
偏微分方程的数值解法研究

偏微分方程的数值解法研究偏微分方程是数学中的一个重要分支,它研究的是包含未知函数及其偏导数的方程。
这类方程在物理、工程、金融等领域中有着广泛的应用。
然而,由于偏微分方程的复杂性,往往难以找到解析解。
因此,数值解法成为解决偏微分方程的重要手段之一。
数值解法是通过离散化空间和时间,将连续的偏微分方程转化为离散的代数方程组,从而求得近似解。
常用的数值解法有有限差分法、有限元法和谱方法等。
有限差分法是最常用的数值解法之一。
它将求解区域划分为有限个网格点,并通过差分近似来逼近偏微分方程中的导数。
例如,对于一维热传导方程,我们可以将求解区域划分为若干个等距的网格点,然后利用中心差分公式来近似一阶导数。
通过迭代计算,可以逐步求得方程的数值解。
有限元法是另一种常用的数值解法。
它将求解区域划分为若干个小区域,称为有限元。
每个有限元内部的解通过插值函数来逼近,然后通过加权残差法将偏微分方程转化为代数方程组。
有限元法在处理复杂的几何形状和边界条件时具有优势,因此在工程领域得到广泛应用。
谱方法是一种基于傅里叶级数展开的数值解法。
它利用傅里叶级数的收敛性和正交性质,将未知函数展开为一系列基函数的线性组合。
通过选取适当的基函数和展开系数,可以将偏微分方程转化为代数方程组。
谱方法在处理高精度问题时具有优势,但对几何形状和边界条件的要求较高。
除了以上三种常见的数值解法,还有很多其他方法可以用于求解偏微分方程。
例如,有限体积法、边界元法等。
每种数值解法都有其适用的范围和优势,选择合适的方法需要根据具体问题的特点和求解要求进行综合考虑。
在实际应用中,数值解法的稳定性和收敛性是非常重要的考虑因素。
稳定性保证了数值解的长期行为是合理的,而收敛性则保证了数值解能够逼近真实解。
为了提高数值解法的稳定性和收敛性,常常需要选择合适的网格划分、时间步长和插值函数等参数,并进行误差估计和收敛性分析。
总之,偏微分方程的数值解法在科学计算和工程实践中发挥着重要作用。
数统学院_偏微分方程数值解实验报告1

1.6905
0.0000
Hale Waihona Puke 0.02501.02531.0253
0.0000
0.5500
1.7333
1.7333
0.0000
0.0500
1.0513
1.0513
0.0000
0.5750
1.7772
1.7771
0.0001
0.0750
1.0779
1.0779
0.0000
0.6000
1.8222
0.0080
0.9500
2.5557
2.5857
0.0300
0.4500
1.5597
1.5683
0.0087
0.9750
2.6196
2.6512
0.0316
0.4750
1.5987
1.6080
0.0094
1.0000
2.6851
2.7183
0.0332
0.5000
1.6386
1.6487
0.0101
0.0001
0.1750
1.1913
1.1912
0.0000
0.7000
2.0138
2.0138
0.0001
0.2000
1.2214
1.2214
0.0000
0.7250
2.0648
2.0647
0.0001
0.2250
1.2523
1.2523
0.0000
0.7500
2.1171
2.1170
0.0001
1.7716
1.8221
0.0506
微分方程数值解实验报告三

Columns 61 through 65
0.4598 0.4598 0.4598 0.4598 0.4598
Columns 66 through 70
0.4598 0.4598 0.4598 0.4598 0.4598
Columns 71 through 75
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 56 through 60
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 61 through 65
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 66 through 70
0.4597
parabolicFD(80,3200)
ans =
Columns 1 through 5
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 6 through 10
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 11 through 15
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 16 through 20
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 21 through 25
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 26 through 30
Columns 21 through 25
0.4598 0.4598 0.4598 0.4598 0.4598
偏微分方程数值及matlab实验报告(8)

偏微分方程数值及m a t l a b实验报告(8)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII偏微分方程数值实验报告八实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x e x u x -=-实现算法:对于两点边值问题,)(,)(,,d 22βα==∈=-b u a u l x f dxu(1)其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为nab h -=.2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈(2)将(2)带入(1)可以得到)()()()(2)(211u R x f h x u x u x u i i i i i +=+---+,其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ,(3)3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0(4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .实验题目:用Lax-Wendroff 格式求解方程:.4sin 1),1(],1,0[,2sin 1)0,(,0),1,0(,02t t u x x x u t x u u x t ππ+=∈+=>∈=- (1) (精确解).2(2sin 1t x u ++=π) 数值边值条件分别为:(a )).(20101n 0nn n u u hu u -+=+τ(b ).1nn u u = (c ).02-12111n 0=++++n n u u u 请将计算结果与精确解进行比较。
偏微分方程解的几道算例(差分、有限元)-含matlab程序(1)

A(i-1,i)=-r; A(i,i-1)=-r; end end u=zeros(N+1,M+1); u(N+1,:)=u1; for k=1:N b=u(N+2-k,2:M)+0.02; u(N+1-k,2:M)=inv(A)*b';%求解迭代方程组 end uT=u(1,:);%0.25时刻的解 %精确解与数值解画图 x1=[0,x,1]; plot(x1,uT,'o') hold u_xt = exp (-pi*pi*T)*sin (pi*x1) + x1.*(1 - x1); plot (x1, u_xt, ' r') e=u_xt-uT; 六点格式 function [e]=six(dx,dt,T) %用六点对称格式求解,dx为x方向步长,dt为t方向步长 % e为误差 M=1/dx; N=T/dt; %得到第一层的值 u1=zeros(1,M+1); x=[1:M-1]*dx; u1([2:M])= sin(pi*x)+x.*(1 - x); %网比 r=dt/dx/dx;r2=2+2*r;r3=2-2*r; %构造三对角矩阵A for i=1:M-1 A(i,i)=r2;
0.0070 0.0027
-0.0097 -0.0037
-0.0013 -0.0005
0.0082 0.0000
-0.0114 0.0000
-0.0015 0.0000
0.0087 -0.0120
-0.0016
注:这里的"误差"=精确解-数值解. 2.精确解与数值解结果图像对比
“向前差分格式”:
微分方程数值解实验报告

微分方程数值解实验报告微分方程数值解实验报告一、引言微分方程是数学中一类重要的方程,广泛应用于各个科学领域。
在实际问题中,往往难以得到微分方程的解析解,因此需要借助数值方法来求解。
本实验旨在通过数值解法,探索微分方程的数值解及其应用。
二、数值解法介绍常用的微分方程数值解法有欧拉法、改进欧拉法、四阶龙格-库塔法等。
在本实验中,我们将采用改进欧拉法进行数值解的求取。
改进欧拉法是一种一阶的显式迭代法,其基本思想是将微分方程的导数用差商来近似表示,并通过迭代逼近真实解。
具体迭代公式如下:\[y_{n+1} = y_n + h \cdot f(x_n + \frac{h}{2}, y_n + \frac{h}{2} \cdot f(x_n, y_n))\]其中,\(y_n\)表示第n步的近似解,\(h\)表示步长,\(f(x_n, y_n)\)表示微分方程的导数。
三、实验步骤1. 确定微分方程及初始条件在本实验中,我们选择经典的一阶常微分方程:\[y' = -2xy\]并给定初始条件\(y(0) = 1\)。
2. 设置步长和迭代次数为了得到较为准确的数值解,我们需要合理选择步长和迭代次数。
在本实验中,我们将步长设置为0.1,迭代次数为10。
3. 迭代计算数值解根据改进欧拉法的迭代公式,我们可以通过编写计算程序来求解微分方程的数值解。
具体计算过程如下:- 初始化:设定初始条件\(y_0 = 1\),并给定步长\(h = 0.1\)。
- 迭代计算:使用改进欧拉法的迭代公式,通过循环计算得到\(y_1, y_2, ...,y_{10}\)。
- 输出结果:将计算得到的数值解输出,并进行可视化展示。
四、实验结果与分析通过以上步骤,我们得到了微分方程的数值解\(y_1, y_2, ..., y_{10}\)。
将这些数值解进行可视化展示,可以更直观地观察到解的变化趋势。
根据实验结果,我们可以发现随着迭代次数的增加,数值解逐渐逼近了真实解。
偏微分方程数值解上机实验报告(matlab做的)

偏微分方程数值解法上机报告(一)一、实验题目:用Ritz-Galerkin 方法求解边值问题2u '',01(0)0,(1)1u x x u u ⎧-+=<<⎨==⎩的第n 次近似()n u x ,基函数()sin(),1,2,...,i x i x i n ϕπ==.二、实验目的:通过本次上机实验,理解求解初值问题的变分问题的最重要的近似解法——Ritz-Galerkin 方法,以便为学习有限元法打好基础。
此外,要熟悉用Matlab 解决数学问题的基本编程方法,提高运用计算机解决问题的能力。
三、实验代码:n=5;syms x;for i=1:np(i)=sin(i*pi*x);q(i)=-i^2*pi^2*sin(i*pi*x);endfor i=1:nb(i)=2*int(p(i),0,1);for j=1:nA(i,j)=int((-q(j)+p(j))*p(i),0,1);endendt=inv(A)*b'四、运行结果:t=2251799813685248/3059521645650671/pi281474976710656/9481460623939047/pi281474976710656/43582901062631895/pi五、总结:通过本次上机,我了解了Ritz-Galerkin 方程 n j j p f cj p i p a n i i ,...,2,1)),(,())(),((1==∑=,明白了用Ritz-Galerkin 方法解决边值问题的变分问题的基本原理,并接近一步提高自己的编程动手能力,受益匪浅。
偏微分方程数值解法上机报告(二)一、 实验题目:用线性元求下列边值问题的数值解2''2sin ,0142(0)0,'(1)0y y x x y y ππ⎧-+=<<⎪⎨⎪==⎩二、 实验目的:通过本次上机,熟悉和掌握用Galerkin 法观点出发导出的求解处置问题数值解的线性有限元法。
偏微分方程数值解实验报告

(2) u
uh H 1 、 u
uh
L2
、
max
0 x1
u - uh
2、用线性元求解下列问题的数值解:
u = -2,-1< x, y < 1, u(x,-1)= u(x,1)= 0,-1< x < 1, ux(-1, y)= 1,ux = 0,-1< y < 1.
精确到小数点后第六位,并画出解曲面。
偏微分方程数值实验报告及算法实现(1)

偏微分方程数值实验报告一实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x ex u x -=-实现算法:对于两点边值问题 ,)(,)(,,d 22βα==∈=-b u a u l x f dxu (1) 其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为na b h -=. 2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα 方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈ (2) 将(2)带入(1)可以得到)()()()(2)(211u R x f hx u x u x u i i i i i +=+---+, 其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i , (3) 3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0 (4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .程序代码:第一步:编写有限差分格式相关函数function [ x,U ]=FDld_bvp(N,f,a,b,u)%******************************************************************** %% FD1d_bvp利用中心差分格式求解两点边值问题%参数:% 输入参数:% 整数N,网格节点数,% 函数f(x),计算右端函数f(x);% a,计算区间左端点% b,计算区间右端点% u,真解函数% 输出参数:% 差分解向量U% 均匀剖分区间[a,b],得到网格x(i)=a+(i-1)*(b-a)/(N-1)h=(b-a)/(N-1);x=(a:h:b)';% 创建线性差分方程组系数矩阵c1=-1/h/h;c2=2/h/h+1;g=[c1*ones(1,N-2),0];c=[0,c1*ones(1,N-2)];d=[1,c2*ones(1,N-2),1];A=diag(g,-1)+diag(d)+diag(c,1);% 创建线性差分方程组右端项rhs=f(x);rhs(1)=u(x(1));rhs(N)=u(x(N));% 求解上述代数系统U=A\rhs;endfunction[e0,e1,emax]=FD1d_error(x,U,u_exact)%% FD1d_ERROR 计算有限差分误差% 参数:% 输入参数:% x,网格节点坐标向量% U,网格节点坐标向量上的有限差分数值解向量Ux% u_exact,真解函数% 输出参数:% e0% e1% emaxN=length(x);h=(x(end)-x(1))/(N-1);ue=u_exact(x);%真解在网格点处的值xee=ue-U;e0=h*sum(ee.^2);e1=sum((ee(2:end)-ee(1:end-1)).^2)/h;e1=e1+e0;e0=sqrt(e0);e1=sqrt(e1);emax=max(abs(ue-U));endfunction FD1d_bvp_test%%测试脚本% 初始化相关数据N=[6,11,21,41,81];L=-1;R=1;emax=zeros(5,1);e0=zeros(5,1);e1=zeros(5,1);%%求解并计算误差for i = 1:5[x,U] =FD1d_bvp(N(i),@f ,L,R,@u);[e0(i),e1(i),emax(i)]=FD1d_error(x,U,@u);X{i}=x;UN{i}=U;endue=u(X{5});%% 显示真阶及不同网格剖分下的数值解plot(X{5},ue,'-k*',X{1},UN{1},'-ro',X{2},...UN{2},'-gs',X{3},UN {3},'-bd ',...X{4},UN{4},'-ch ',X{5} , UN {5},'-mx');title('The solution plot');xlabel('x');ylabel ('u');legend('exact','N=6','N =11','N=21','N =41','N =81'); %% 显示误差format shortedisp ('emax e0 e1 ');disp ([ emax , e0 , e1 ]);end第二步:编写方程的右端函数和真解分别保存为m f .和m u . function f=f(x)f=exp(-x.^2).*(4.*x.^4-15.*x.^2+5);endfunction u=u(x)u=exp(-x.^2).*(1-x.^2);end实验结果:在命令窗口输入>> FD1d_bvp_test回车可得运算结果和图像emax e0 e15.8219e-02 5.3470e-02 1.1724e-011.5919e-02 1.2802e-022.9349e-023.9305e-03 3.1663e-03 7.3357e-039.7959e-04 7.8946e-04 1.8338e-032.4471e-04 1.9723e-04 4.5844e-04。
微分方程数值解法实验报告

微分方程数值解法实验报告实验题目:数值解微分方程的实验研究引言:微分方程是描述自然现象、科学问题和工程问题中变量之间的关系的重要数学工具。
然而,大部分微分方程很难找到解析解,因此需要使用数值方法来近似求解。
本实验旨在研究数值解微分方程的方法和工具,并通过实验验证其有效性和准确性。
实验步骤:1.了解微分方程的基本概念和求解方法,包括欧拉法、改进的欧拉法和龙格-库塔法。
2. 配置实验环境,准备实验所需的工具和软件,如Python编程语言和相关数值计算库。
3.选择一种微分方程进行研究和求解,可以是一阶、二阶或更高阶的微分方程。
4.使用欧拉法、改进的欧拉法和龙格-库塔法分别求解选定的微分方程,并比较其结果的准确性和稳定性。
5.计算数值解与解析解之间的误差,并进行误差分析和讨论。
6.对比不同数值解法的性能,包括计算时间和计算精度。
7.结果展示和总结,根据实验结果对数值解方法进行评价和选取。
实验结果:以一阶线性常微分方程为例,我们选择经典的“衰减振荡”问题进行实验研究。
该问题的微分方程形式为:dy/dt = -λy其中,λ为正实数。
我们首先使用Python编程语言实现了欧拉法、改进的欧拉法和龙格-库塔法。
进一步,我们选择了λ=0.5和初始条件y(0)=1,使用这三种数值解法求解该微分方程,并比较结果的准确性。
通过对比数值解和解析解可以发现,在短时间内,欧拉法、改进的欧拉法和龙格-库塔法的结果与解析解非常接近。
但随着时间的增加,欧拉法的结果开始偏离解析解,而改进的欧拉法和龙格-库塔法仍然能够提供准确的近似解。
这是因为欧拉法采用线性逼近的方式,误差随着步长的增加而累积,而改进的欧拉法和龙格-库塔法采用更高阶的逼近方式,可以减小误差。
为了更直观地比较不同方法的性能,我们还计算了它们的计算时间。
实验结果显示,欧拉法计算时间最短,而龙格-库塔法计算时间最长。
这表明在计算时间要求较高的情况下,可以选择欧拉法作为数值解方法。
偏微分实验报告八-张伟-20122058

重庆大学学生实验报告实验课程名称偏微分方程数值解开课实验室数统学院学院数统年级2012 专业班信计1班学生姓名张伟学号20122058 开课时间2014 至2015 学年第 2 学期数学与统计学院制开课学院、实验室: 数统学院 实验时间 : 2015年 6月17日1,2k i j u u +-+考虑边界条件()(),,0,,u x y t x y =∈∂Ω,差分格式为:,利用二阶差商近似:时刻的点为内点,则满足差分格式(2),代入上式得到:()(),0,sin sin ,,0,1,N N ih jh i j ππ=0,1,,10j =图1 t=0.1、0.5时刻的数值解、精确解 图2 t=1.0、1.4时刻的数值解、精确解 注:上两图为四个时刻的数值解与精确解,()10.12r p p hpτ==<=代表维数,本文,三层显格式达二阶收敛,不难看出,收敛效果很好,符合理论。
下图是四个时刻的绝对误差图像,从图中看出,绝对误差较小,且经过计算得到,收敛阶近似于2,正好符合理论值。
图3 四个时刻的绝对误差3、四个时刻(t=0.1、0.5、1.0、1.4)的绝对误差表t=0.1时刻的绝对误差0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000.0000 0.0001 0.0001 0.0002 0.0002 0.0002 0.0002 0.0002 0.0001 0.0001 0.00000.0000 0.0001 0.0003 0.0004 0.0004 0.0005 0.0004 0.0004 0.0003 0.0001 0.00000.0000 0.0002 0.0004 0.0005 0.0006 0.0006 0.0006 0.0005 0.0004 0.0002 0.00000.0000 0.0002 0.0004 0.0006 0.0007 0.0007 0.0007 0.0006 0.0004 0.0002 0.00000.0000 0.0002 0.0005 0.0006 0.0007 0.0008 0.0007 0.0006 0.0005 0.0002 0.00000.0000 0.0002 0.0004 0.0006 0.0007 0.0007 0.0007 0.0006 0.0004 0.0002 0.0000。
偏微分方程数值解法研究

偏微分方程数值解法研究偏微分方程是数学中的一个分支,它研究的是一些与空间位置、时间以及其它因素有关的物理现象,如热传导、波动现象、电磁场分布、流体运动等。
在现实世界中,很多问题都可以用偏微分方程来描述。
这些方程具有复杂性和多变性,因此需要采用数值解法来求解。
数值解法是将巨大的偏微分方程转变为离散化的点值问题,通过数值计算得出近似解。
为了达到更高的计算精度和效率,研究者们不断地探索各种数值解法,如有限差分方法、有限元方法、谱方法、边界元法等,并在不断地发展和改进。
有限差分是常用的数值解法,它利用差商来离散化微分方程,将连续的问题转化为离散的问题。
通过对偏微分方程进行逐点离散化,使用差商逼近微分方程,从而得到一组有限个代数方程组,即差分方程组。
然后再利用数值计算的方法求解差分方程组,从而得到近似解。
有限差分方法具有简单易操作和精度高的优点,但是它在处理边界问题和非线性问题时会遇到一些困难。
有限元法是数值解法中最常见的一种,主要用于求解复杂的分布参数系统和非线性问题。
与有限差分相比,有限元法可以更精确地模拟物理问题,具有对几何形状更自由、适用性更广、计算量更小的特点。
它的基本思想是采用离散化方法将复杂的问题简化成一些基本单元的组合,然后在每个单元内解微分方程,最后将这些单元的解组合在一起得到整个问题的近似解。
谱方法是基于特殊基函数构造法的一种数值解法,通过选取一些特殊的基函数(例如三角函数,Legendre多项式或Chebyshev多项式等),对偏微分方程进行逐点离散化。
然后通过基函数的线性组合来逼近未知解,从而得到一组代数方程组,利用数值计算方法解出方程组后得到近似解。
谱方法具有高精度、高效率、不受网格形状限制以及基函数可以选取自由、适用范围广等优点,但谱方法也有一些不足之处,需要根据具体问题进行选择。
边界元法是一种确定性的数值分析方法,也是一种离散化的方法。
与有限差分与有限元方法的差异在于,它不需要对求解区域进行离散化处理,而是将偏微分方程从区域的内部转移到区域的边界上进行求解。
偏微分方程报告

2009级数学与应用数学和信息与计算科学专业偏微分方程数值解上机实验实验题目利用有限元方法和有限差分方法求解偏微分方程完成日期 2012年12月17日学生姓名张灵刚所在班级 1102090 任课教师王晓东西北工业大学理学院应用数学系目录一.实验目的 (2)二.实验要求 (2)三.实验题目 (3)四.实验二 (4)1.实验内容 (4)2.实验原理.................................................(4). 3算法流程. (5)4结果分析 (5)5总结讨论 (6)6源程序 (6)五. 实验三1.实验内容 (17)2.实验原理...............................................(17). 3算法流程. (18)4结果分析……………………………………….….(18).5总结讨论 (21)6源程序 (21)偏微分方程数值解上机实验报告实验地点:数学系机房实验时间:第13—15周,周一、四下午5、6节实验分数:占期末考试成绩的30%一、实验目的及意义掌握有限元方法和有限差分方法的程序实现;学会选择合适的有限差分格式求解一维非线性对流占优的非定常对流扩散问题;学会使用三角线性元和四边形线性元的有限元方法求解二维椭圆方程边值问题,并对计算结果进行收敛性分析;尝试采用有限元方法或有限差分方法实现二维初边值抛物型方程的大规模数值求解。
通过实验可以提高学生的动手能力,加深学生对算法的理解。
二、实验要求在下列给出的三个问题中,最少选择两个问题进行编程实现。
要求给出格式的推导过程、算法流程、实现程序、选取的网格参数、以表格或图形的方式给出计算结果、对计算结果进行分析、最后对实验进行总结和讨论。
问题2:用三角线性元和四边形线性元的有限元方法求解方程:28cos(2)sin(2),(,)(0,1)(0,1)(,0)(,1)0;(0,)(1,)sin(2).u x y x y u x u x u y u y y ππππ-∆=∈⨯====取=1/4, 1/8, 1/16, 1/32, 1/64,h 比较两种方法的计算精度,并给出数值收敛率.问题3:选用合适的数值方法求解方程:22122(444),(,)(0,1)(0,1)(0,,)(1,,)(,0,)(,1,)0;(,,0)sin()cos().y y ux y u x y tu y t u y t u x t u x t u x y x y ππππ-∂=-++∆∈⨯∂''=====求0.1,0.5,1.0t =时,点3331(,)6464、1517(,)6464、4749(,)6464、7137(,)128128、4367(,)128128、10989(,)128128、127129(,)256256、6391(,)256256、3133(,)256256处的数值解。
偏微分方程数值解实验报告

偏微分方程数值解上机实验报告(一)实验一一、上机题目:用线性元求解下列边值问题的数值解:-y′′+π24y=π22sinπ2x,0<x<1y(0)=0,y′(1)=0二、实验程序:function S=bzx=fzero(@zfun,1);[t y]=ode45(@odefun,[0 1],[0 x]);S.t=t;S.y=y;plot(t,y)xlabel('x:´从0一直到1')ylabel('y')title('线性元求解边值问题的数值解')function dy=odefun(x,y)dy=[0 0]';dy(1)=y(2);dy(2)=(pi^2)/4*y(1)-((pi^2)/2)*sin(x*pi/2);function z=zfun(x);[t y]=ode45(@odefun,[0 1],[0 x]);z=y(end)-0;三、实验结果:1.以步长h=0.05进行逐步运算,运行上面matlab程序结果如下:2.在0<x<1区间上,随着x 的不断变化,x ,y 之间关系如下图所示:(二)实验二四、 上机题目:求解Helmholtz 方程的边值问题:21u k u -∆-=,于(0,1)*(0,1)Ω=0u =,于1{0,01}{01,1}x y x y Γ==≤≤≤≤= 12{0,01}{01,1}0,{01,0}{1,01}x y x y u x y x y n Γ==≤≤≤≤=∂=Γ=≤≤==≤≤∂于其中k=1,5,10,15,20五、实验程序:(采用有限元方法,这里对[0,1]*[0,1]采用n*n的划分,n为偶数)n=10;a=zeros(n);f=zeros(n);b=zeros(1,n);U=zeros(n,1);u=zeros(n,1);for i=2:na(i-1,i-1)=pi^2/(12*n)+n;a(i-1,i)= pi^2/(24*n)-n;a(i,i-1)= pi^2/(24*n)-n;for j=1:nif j==i-1a(i,j)=a(i,i-1);else if j==ia(i-1,j-1)=2*a(i-1,i-1);else if j==i+1a(i,j)=a(i,i+1);elsea(i,j)=0;endendendendenda(n,n)=pi^2/(12*n)+n;for i=2:nf(i-1,i)=4/pi*cos((i-1)*pi/2/n)-8*n/(pi^2)*sin(i*pi/2/n)+8*n/(pi^2)*s in((i-1)*pi/2/n);endfor i=1:nf(i,i)=-4/pi*cos(i*pi/2/n)+8*n/(pi^2)*sin(i*pi/2/n)-8*n/(pi^2)*sin((i -1)*pi/2/n);end%b(j)=f(i-1,j)+f(i,j)for i=1:(n-1)b(i)=f(i,i)+f(i,i+1);endb(n)=f(n,n);tic;n=20;can=20;s=zeros(n^2,10);h=1/n;st=1/(2*n^2);A=zeros((n+1)^2,(n+1)^2);syms x y;for k=1:1:2*n^2s(k,1)=k;q=fix(k/(2*n));r=mod(k,(2*n));if (r~=0)r=r;else r=2*n;q=q-1;endif (r<=n)s(k,2)=q*(n+1)+r;s(k,3)=q*(n+1)+r+1;s(k,4)=(q+1)*(n+1)+r+1;s(k,5)=(r-1)*h;s(k,6)=q*h;s(k,7)=r*h;s(k,8)=q*h;s(k,9)=r*h;s(k,10)=(q+1)*h;elses(k,2)=q*(n+1)+r-n;s(k,3)=(q+1)*(n+1)+r-n+1;s(k,4)=(q+1)*(n+1)+r-n;s(k,5)=(r-n-1)*h;s(k,6)=q*h;s(k,7)=(r-n)*h;s(k,8)=(q+1)*h;s(k,9)=(r-n-1)*h;s(k,10)=(q+1)*h;endendd=zeros(3,3);B=zeros((n+1)^2,1);b=zeros(3,1);for k=1:1:2*n^2L(1)=(1/(2*st))*((s(k,7)*s(k,10)-s(k,9)*s(k,8))+(s(k,8)-s(k,10))*x+(s(k,9)-s(k,7))*y);L(2)=(1/(2*st))*((s(k,9)*s(k,6)-s(k,5)*s(k,10))+(s(k,10)-s(k,6))*x+(s (k,5)-s(k,9))*y);L(3)=(1/(2*st))*((s(k,5)*s(k,8)-s(k,7)*s(k,6))+(s(k,6)-s(k,8))*x+(s(k ,7)-s(k,5))*y);for i=1:1:3for j=i:3d(i,j)=int(int(((((diff(L(i),x))*(diff(L(j),x)))+((diff(L(i),y))*(dif f(L(j),y))))-((can^2)*L(i)*L(j))),x,0,1),y,0,1);d(j,i)=d(i,j);endendfor i=1:1:3for j=1:1:3A(s(k,(i+1)),s(k,(j+1)))=A(s(k,(i+1)),s(k,(j+1)))+d(i,j);endendfor i=1:1:3b(i)=int(int((L(i)),x,0,1),y,0,1);B(s(k,(i+1)),1)=B(s(k,(i+1)),1)+b(i);endendM=zeros((n+1)^2,n^2);j=n^2;for i=(n^2+n):-1:1if ((mod(i,(n+1)))~=1)M(:,j)=A(:,i);j=j-1;else continueendendpreanswer=M\B;answer=zeros((n+1)^2,1);j=1;for i=1:1:(n^2+n)if ((mod(i,(n+1)))~=1)answer(i)=preanswer(j);j=j+1;else answer(i)=0;endendZ=zeros((n+1),(n+1));for i=1:1:(n+1)^2s=fix(i/(n+1))+1;r=mod(i,(n+1));if(r==0)r=n+1;s=s-1;elseendZ(r,s)=answer(i);end[X,Y]=meshgrid(1:-h:0,0:h:1);surf(X,Y,Z);toc;t=toc;K=a ;B=b';U=inv(K)*Bfor i=1:nu(i,1)=4/(pi^2)*sin(pi*i/n/2);endue=U-u六、实验结果:程序中的变量can为问题中的k,为了方便比较,采用了画图的方式。
微分方程数值方法实验报告

一、实验题目(1)用Ritz-Galerkin 方法求解边值问题)10(0)1()0(''<<⎩⎨⎧==-=+x u u x u u精确解x xu -=1sin sin * (2)用有限元方法求解⎩⎨⎧==+=+-0)1()0()sin()1(2''u u x u u ππ)sin(*x u π= 二、实验目的运用MATLAB 数学软件编写Ritz-Galerkin 方法和有限元方法程序,进一步熟悉MATLAB的应用及掌握偏微分方程数值方法中Ritz-Galerkin 方法和有限元方法,对各个方法求解精度进一步明确。
三、实验原理(1)Ritz-Galerkin 方法Ritz 方法设给出二次泛函),(,21)(v F v v A v J -=)( (1)其中)(v v A ,是Hilbert 空间V 上的双线性泛函,而且满足对称性、有界性、正定性;)(v F 是V 上的有界线性泛函。
考虑一下变分问题:V v ∈求满足).(min )(v J u J Vv ∈= (2)设Hilbert 空间V 是可分的,即V 中有可数多个元素构成一个稠密集。
在V 中取N 个线性无关的元素N ϕϕϕ,...,,21,他们张成一个N 维子空间N S ,即},...,;|{11为实数N Ni i i N c c c v v S ∑===ϕ,或记成},...,,{21N N span S ϕϕϕ=。
(3)上述元素N ϕϕϕ,...,,21称为空间N S 的基.用N S 代替V ,在NS 上求泛函)(u J 的极小,即求NN S u ∈满足).(min )(v J u J NS v N ∈= (4)显然,原先的变分问题(2)与后面的变分问题(4)是不同的,他们的解Nu u 与也是不同的。
如果V 的子空间NS 充分接近V ,那么,用NS 代替V 而得到的解Nu 也就充分接近u ,从而把Nu 作为原变分问题的近似解,亦即把无穷维空间V 中的极值问题近似为有限维空间NS 中的极值问题,这就是Ritz 方法得基本思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
偏微分方程数值解
上
机
实
验
报
告
(一)实验一
一、上机题目:
用线性元求解下列边值问题的数值解:
精品文档
′′22??
??
??,0<x<1
-?? +
??=??sin
422
′
y(0)=0 ,??(
1)=0
二、实验程序:
function S=bz
x=fzero(@zfun,1);
[t y]=ode45(@odefun,[0 1],[0 x]);
S.t=t;
S.y=y;
plot(t,y)
xlabel( 'x:′从0一直到1' )
ylabel( 'y' )
title(' 线性元求解边值问题的数值解' )
function dy=odefun(x,y)
dy=[0 0]';
dy(1)=y(2);
dy(2)=(pi^2)/4*y(1)-((pi^2)/2)*sin(x*pi/2);
function z=zfun(x);
[t y]=ode45(@odefun,[0 1],[0 x]);
z=y(end)-0;
三、实验结果:
1.以步长 h=0.05 进行逐步运算,运行上面matlab 程序结果如下:2.在 0<x<1 区间上,随着 x 的不断变化,x,y 之间关系如下图所示:
精品文档
(二)实验二
四、上机题目:
求解 Helmholtz 方程的边值问题:
u k 2u 1
,于(0,1)*(0,1)
u0,于1{ x0,0y1} U{0x1, y 1} 1{ x0,0y1} U{0x1, y1}
u
0,于2{0x1, y 0} U { x1,0y1}
n
其中 k=1,5,10,15,20
五、实验程序:
(采用有限元方法,这里对[0,1]*[0,1]采用n*n的划分,n为偶数)n=10;
a=zeros(n);f=zeros(n);b=zeros(1,n);U=zeros(n,1);u=zeros(n,1);
for i=2:n
a(i-1,i-1)=pi^2/(12*n)+n;
a(i-1,i)= pi^2/(24*n)-n;
a(i,i-1)= pi^2/(24*n)-n;
for j=1:n
if j==i-1
a(i,j)=a(i,i-1);
else if j==i
a(i-1,j-1)=2*a(i-1,i-1);
else if j==i+1
a(i,j)=a(i,i+1);
else
a(i,j)=0;
end
end
end
end
end
a(n,n)=pi^2/(12*n)+n;
for i=2:n
f(i-1,i)=4/pi*cos((i-1)*pi/2/n)-8*n/(pi^2)*sin(i*pi/2/n)+8*n/(pi^2)*sin((i-1)*pi/2/ n);
end
for i=1:n
f(i,i)=-4/pi*cos(i*pi/2/n)+8*n/(pi^2)*sin(i*pi/2/n)-8*n/(pi^2)*sin((i-1)*pi/2/n);
end
%b(j)=f(i-1,j)+f(i,j)
for i=1:(n-1)
b(i)=f(i,i)+f(i,i+1);
end
b(n)=f(n,n);
tic;
n=20;
can=20;
s=zeros(n^2,10);
h=1/n;
st=1/(2*n^2);
A=zeros((n+1)^2,(n+1)^2);
syms x y ;
for k=1:1:2*n^2
s(k,1)=k;
q=fix(k/(2*n));
r=mod(k,(2*n));
if(r~=0)
r=r;
else r=2*n;q=q-1;
end
if(r<=n)
s(k,2)=q*(n+1)+r;
s(k,3)=q*(n+1)+r+1;
s(k,4)=(q+1)*(n+1)+r+1;
s(k,5)=(r-1)*h;
s(k,6)=q*h;
s(k,7)=r*h;
s(k,8)=q*h;
s(k,9)=r*h;
s(k,10)=(q+1)*h;
else
s(k,2)=q*(n+1)+r-n;
s(k,3)=(q+1)*(n+1)+r-n+1;
s(k,4)=(q+1)*(n+1)+r-n;
s(k,5)=(r-n-1)*h;
s(k,6)=q*h;
s(k,7)=(r-n)*h;
s(k,8)=(q+1)*h;
s(k,9)=(r-n-1)*h;
s(k,10)=(q+1)*h;
end
end
d=zeros(3,3);
B=zeros((n+1)^2,1);
b=zeros(3,1);
for k=1:1:2*n^2
L(1)=(1/(2*st))*((s(k,7)*s(k,10)-s(k,9)*s(k,8))+(s(k,8)-s(k,10))*x+(s(k,9)-
s(k,7))* y);
L(2)=(1/(2*st))*((s(k,9)*s(k,6)-s(k,5)*s(k,10))+(s(k,10)-s(k,6))*x+(s(k,5)-s(k,9))*
y);
L(3)=(1/(2*st))*((s(k,5)*s(k,8)-s(k,7)*s(k,6))+(s(k,6)-s(k,8))*x+(s(k,7)-s(k,5))*y) ;
for i=1:1:3
for j=i:3
d(i,j)=int(int(((((diff(L(i),x))*(diff(L(j),x)))+((diff(L(i),y))*(diff(L(j),y))))-
( (can^2)*L(i)*L(j))),x,0,1),y,0,1);
d(j,i)=d(i,j);
end
end
for i=1:1:3
for j=1:1:3
A(s(k,(i+1)),s(k,(j+1)))=A(s(k,(i+1)),s(k,(j+1)))+d(i,j);
end
end
for i=1:1:3
b(i)=int(int((L(i)),x,0,1),y,0,1);
B(s(k,(i+1)),1)=B(s(k,(i+1)),1)+b(i);
end
end
M=zeros((n+1)^2,n^2);
j=n^2;
for i=(n^2+n):-1:1
if((mod(i,(n+1)))~=1)
M(:,j)=A(:,i);
j=j-1;
else continue
end
end
preanswer=M\B;
answer=zeros((n+1)^2,1);
j=1;
for i=1:1:(n^2+n)
if((mod(i,(n+1)))~=1)
answer(i)=preanswer(j);
j=j+1;
else answer(i)=0;
end
end
Z=zeros((n+1),(n+1));
for i=1:1:(n+1)^2
s=fix(i/(n+1))+1;
r=mod(i,(n+1));
if (r==0)
r=n+1;
s=s-1;
else
end
Z(r,s)=answer(i);
end
[X,Y]=meshgrid(1:-h:0,0:h:1);
surf(X,Y,Z);
toc;
t=toc;
K=a ;
B=b';
U=inv(K)*B
for i=1:n
u(i,1)=4/(pi^2)*sin(pi*i/n/2);
end
u
e=U-u
六、实验结果:
程序中的变量 can 为问题中的 k,为了方便比较,采用了画图的方式。
在 n=10 时,分别考察 can=k=1,5,10,15,20时的情况。
1.can=k=1 时
2.can=k=5 时
3.can=k=10 时
4.can=k=15 时
5.can=k=20 时
六、实验总结
本次实验第二题很难,通过查找资料和请教同学,学到了很多。
通过本次实验,我也进一步了解了线性元求边值问题的数值解的思想和方法,同时了解了matlab 工具包中相关类库对求边值问题数值解的支持,更加熟悉了matlab 的编程语法。
