定螺距螺旋桨攻角算法及其3D图绘制
螺旋桨螺距的测量方法

螺旋桨螺距的测量方法龙叶新造螺旋桨由于铸造误差,其毛坯件的螺距往往与图纸要求有一定误差,因此必须进行螺距测量以检验其是否合格。
误差不大的可经加工后消除,误差较大经加工后虽可消除,但却叶片厚度减薄。
为防止厚度较薄这一不良后果,对某些用铸铜、钢板制造的螺旋桨可以先进行校正,误差太大而有无法校正的则应重铸。
螺距测量的原理是:“沿着叶片压力面半径R处的螺旋线上取一线段PQ,其相应的角度为a,测出P、Q口两点在螺旋桨轴线方向h的高度h,通过换算即可求得该位置上的螺距。
”测量螺距的方法很多,有用螺距测最仪侧量螺距、螺距三角板检验螺距、螺距板测量螺距和量角和量角仪测量螺距等万法,目前通常采用的是用螺距仪测量螺距等方法量螺距,有立式测量和水平测量。
1、用螺距仪测量螺距螺距仪是由三爪卡盘、中心轴、刻度盘、转臂、量杆等所组成。
在刻度盘上刻有一周360°的刻度,每一度又可分成若干角度等分。
转臂绕中心轴转动后,即可由指针在刻板盘上指示出所转过的角度。
在转臂和量杆上都有表示距离的刻度,以毫米为单位。
量杆可在转臂上沿叶面作径向移动,每移动到一定位置即表示叶面上的某一半径,量杆本身还可作上下移动。
测量螺距的操作步骤测量螺距的操作步骤有如下几点:(1)将桨毂锥孔和两端面已加工过的螺旋桨,大端朝下平放在平台上。
如无平台也可放在平整的地面上。
(2)将螺距仪装在螺旋桨上端面上,三爪卡盘装人锥孔内并卡紧,使平面与桨毂上端面贴平。
以保证三爪卡盘中心线与桨毂中心线重合。
(3)在各叶片压力面上刷上白粉,移动量杆的径向距离,分别以0.95R,0.8R,0.6R...(或按图纸规定)为半径,转动转臂,在各叶片的压力面上划出各半径圆线。
(4)以测量半径线AB圆弧上的螺距为例,将量杆放在O点位置上调整到0°位置。
这时由量杆上所测得的读数为L1,,并记录之。
再将转臂转过一个角度到a点位置(此角度为计算方便起见,应取整数如15°、20°、30°等),记录从O点到a点转过的角度α,并同时测得量杆在a点位置上的读数L2。
CAD画一把螺丝刀

AutoCAD三维技巧之三画一把三维螺丝刀提醒:如果你还没有熟练掌握AutoCAD的平面制图技巧,请不要阅读本文。
本文要点:用旋转方法建立三维实体,三维阵列、对齐等编辑技巧。
第一步,按照图1的尺寸画出图形,再将图形转换成面域。
第二步,操作菜单“工具”→“新建UCS”→“原点”,命令行窗口提示“指定新原点<0,0,0>:”,捕捉并点击刚才画的面域的左上角,坐标原点被移动到了该处。
第三步,操作菜单“工具”→“命名UCS”,在“命名UCS”选项卡上右击“未命名”,在快捷菜单上点选“重命名”,将其改名为“my”。
在“正交UCS”选项卡上的“相对于”下拉列表里选择“my”。
点击“确定”按钮,关闭对话框。
第四步,操作菜单“绘图”→“建模”→“旋转”,命令行窗口提示“选择要旋转的对象:”,点击面域的边线接着右击鼠标;命令行窗口接着提示“指定轴起点或根据以下选项之一定义轴[对象(O)/X/Y/Z]<对象>:”,键入“x”并回车;命令行窗口又提示“指定旋转角度或[起点角度(ST)]<360>:”,直接回车,面域围绕x轴旋转成了三维实体,螺丝刀柄基本成形,如图2。
第五步,操作菜单“视图”→“三维视图”→“右视”。
第六步,操作菜单“绘图”→“建模”→“圆柱体”,命令行窗口提示“指定底面的中心点或[三点(3P)/两点(2P)/相切、相切、半径(T)/椭圆(E)]:”,键入“20,0,0”并回车;命令行窗口接着提示“指定底面半径或[直径(D)]:”,键入“10”并回车;命令行窗口又提示“指定高度或[两点(2P)/轴端点(A)]:”,键入“90”并回车,和螺丝刀柄平行的一个圆柱体就画好了。
第七步,操作菜单“修改”→“三维操作”→“三维阵列”,命令行窗口提示“选择对象:”,点选圆柱体接着右击鼠标;接着命令行窗口提示“输入阵列类型[矩形(R)/环形(P)]<矩形>:”,键入“p”并回车;命令行窗口又提示“输入阵列中的项目数目:”,键入“6”并回车;命令行窗口又提示“指定要填充的角度(+=逆时针,-=顺时针)<360>:”,直接回车;命令行窗口又提示“旋转阵列对象?[是(Y)/否(N)]<Y>:”,直接回车;命令行窗口又提示“指定阵列的中心点:”,键入“0,0,0”并回车;命令行窗口又提示“指定旋转轴上的第二点:”,键入“0,0,90”并回车,圆柱体变成6个并且围绕螺丝刀柄排列,如图3。
定螺距螺旋桨攻角算法及其3D图绘制

定螺距螺旋桨攻角算法及其3D图绘制多旋翼无人机一般采用定螺距螺旋桨,而定螺距螺旋桨在其不同半径处的截面的攻角都不相同,随着半径增大,桨叶的攻角会按一定规律逐渐变小,本文将讨论其攻角变化的规律,并介绍其3D图绘制方法。
一.首先要明确螺距和攻角的概念。
螺距指的是在理想状态下,螺旋桨旋转一周后,在轴向移动的距离。
攻角是指将桨叶水平放置,其某个半径处的截面与水平面的夹角。
二.当螺旋桨在旋转时,桨叶上的每一个点的运动轨迹都是一条螺旋线。
桨叶在旋转一周后,桨叶上的每一个点上升的距离都一样,越靠近旋转轴的点,运动轨迹线就越陡峭,攻角也就越大。
反之,离旋转轴越远的点,运动轨迹就越平缓,攻角就越小。
将一条螺旋线所在的圆柱面展平,则会得到一条斜直线,将此圆柱面的周长当做底边,螺距当做高,即可得到一个直角三角形,∠ɑ就是此处的攻角。
螺旋线的半径越大,则攻角越小。
由反正切函数∠ɑ=atan(a/b) [a为对边,b为邻边]代入本例,得出:∠ɑ=atan(p/(2*π*r)) [p为螺距,r为半径]三.在PROE中,我们可以利用上面的公式,来确定螺旋桨在任意半径上的攻角,扫描出一个角度渐变的曲面,并在此曲面的基础上,按照选定的翼形,扫描出最终桨叶。
下面,我们用一个实例来介绍具体操作方法。
1.首先在TOP平面上拉伸一个圆柱体,当做螺旋桨的旋转轴。
并沿着x轴的方向绘制一条直线a,直线长度等于桨叶的半径。
2.在TOP平面绘制两条曲线b和c,即桨叶的俯视轮廓外观线。
3.将作为迎风面的一侧的曲线b做为截面,在TOP平面上拉伸出一个曲面。
4.在此曲面上投影一条曲线d,即桨叶主视角上轮廓线。
5.以曲线a为主轨迹做可变截面扫描曲面,以曲线d为辅助轨迹,参数如图。
6.截面为一条直线,使曲线d的端点位于直线的中点,标注直线与TOP平面的夹角(sd7),如下图,并在关系中加入关系式。
在PROE的关系式中,反正切函数格式为∠ɑ=atan2(a,b) [a为对边,b为邻边]在本例中,可得:∠ɑ=atan2(p,(2*pi*r)) [p为螺距,r为半径]设螺距p为4.5英寸,即为114.3mm;螺旋桨半径为127mm;trajpar为PROE内置函数,其值从0到1匀速变化。
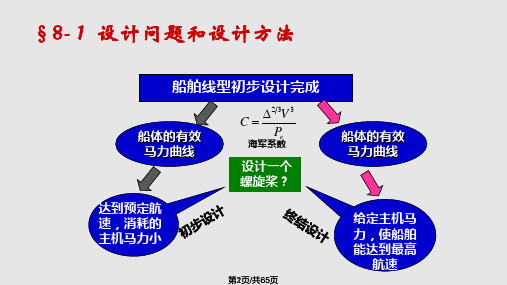
螺旋桨设计与绘制讲解

第1章螺旋桨设计与绘制1.1 螺旋桨设计螺旋桨设计是船舶快速性设计的重要组成分。
在船舶型线初步设计完成后,通过有效马力的估算获船模阻力试验,得出该船的有效马力曲线。
在此基础上,要求我们设计一个效率最佳的螺旋桨,既能达到预定的航速,又能使消耗的主机马力最小;或者当主机已经选定,要求设计一个在给定主机条件下使船舶能达到最高航速的螺旋桨。
螺旋桨的设计问题可分为两类,即初步设计和终结设计。
螺旋桨的初步设计:对于新设计的船舶,根据设计任务书对船速要求设计出最合适的螺旋桨,然后由螺旋桨的转速计效率决定主机的转速及马力。
终结设计:主机马力和转速决定后,求所能达到的航速及螺旋桨的尺度。
在本文中,根据设计航速17.5kn,设计螺旋桨直径6.6m,进行初步设计,获得所需主机的马力和主机转速,然后选定主机;根据选定的主机,计算最佳的螺旋桨要素及所能达到的最大航速等。
1.1.1 螺旋桨参数的选定(1)螺旋桨的数目选择螺旋桨的数目必须综合考虑推进性能、震动、操纵性能及主机能力等各方面因素。
若主机马力相同,则当螺旋桨船的推进效率高于双螺旋浆船,因为单螺旋桨位于船尾中央,且单桨的直径较双桨为大,故效率较高。
本文设计船的设计航速约为17.5kn 的中速船舶,为获得较高的效率,选用单桨螺旋桨。
(2)螺旋桨叶数的选择根据过去大量造成资料的统计获得的桨叶数统计资料,取设计船螺旋桨的叶数为4 叶。
考虑到螺旋桨诱导的表面力是导致强烈尾振的主要原因,在图谱设计中,单桨商船的桨叶数也选为4 叶。
(3)桨叶形状和叶切面形状螺旋桨最常用的叶切面形状有弓形和机翼型两种。
弓形切面的压力分布较均匀,不易产生空泡,但在低载时效率较机翼型约低3%~4%。
若适当选择机翼型切面的中线形状使其压力分均匀,则无论对空泡或效率均有得益,故商用螺旋桨采用机翼型切面根据以上分析,选择MAU4 叶桨系列进行螺旋桨设计。
1.1.2螺旋桨推进因子螺旋桨的伴流分数取螺旋桨以等推力法进行敞水实验获得的实效伴流:0.404推力减额按照汉克歇尔关于单桨螺旋桨标准商船公式进行计算:t 0.50C P 0.12 0.22主机的轴系传递效率:s 0.97相对旋转效率:R 1.00船身效率:H 1 t1.3111.1.3 有效马力曲线有效马力曲线表征的是船体阻力特征。
螺旋桨UG建模

由桨叶截面尺寸表得到三维建模坐标直径D螺距P后倾角θ螺距角φ1、 计算出0.2R 、0.3R ……2、 利用反正切函数计算出螺距角:以0.2R 举例φ-0.2R=ATAN(P/(2*π*0.2R)),弧度表示φ-0.2R/π*180°或用=DEGREES(φ-0.2R)函数,角度表示3、 中心线距导边-最厚点距导边=中心线距最厚点=H X4、 h X =最厚点距导边-X5、 计算0.2R-0坐标注:h X =最厚点距导边-X ;H X =中心线距导边-最厚点距导边=中心线距最厚点6、叶梢坐标7、通过延伸插值得到0.1R处的叶宽、最大叶厚、最大叶厚至导边、中心线至导边,再用第5步计算。
螺旋桨UG中建模1、导入三维坐标2、连接样条曲线,随边点-导边点-随边点;连接螺旋桨轮廓3、将螺旋桨轮廓打断于叶梢点:编辑-曲线-分割曲线,类型选“在结点处”,选择曲线,结点方法选“选择结点”,确定。
或者采用添加点然后重新绘制两条样条曲线的方式,添加点:插入-基准/点,选择几何体中选择要添加点的样条曲线,等弧长定义中点数输入需要的点即可。
4、建立螺旋桨包面:主曲线—叶梢点+桨叶切面;次曲线—随边+导边+随边。
5、将桨叶表面封闭起来:插入-网格曲面-N边曲面-外环选择曲线即可裁去上述封闭曲面多余部分:修剪片体-目标选择片体-边界对象选择边界曲线-选择区域保留!6、桨叶片体缝合:插入-组合-缝合,选择需要缝合的片体即可7、阵列桨叶:阵列特征-选择特征(选桨叶包面)-布局(选圆形)-旋转轴(选桨榖对称轴)-角度方向(间距选数量和节距,数量选叶数,节距角为360/n),确定。
阵列后可能所有桨叶多余的片体都要修剪—此功能好像不成功或者采用旋转功能:编辑-移动对象-运动选角度-角度72°-结果复制原先的-非关联副本数48、建立桨榖。
目测回转的曲线为拍照CAD得到。
回转-选择曲线-指定矢量(选桨榖对称轴)-其他默认即可。
螺旋桨制图

D=4.78 m
P/D=0.6825 MAU Z=4
AE/A0=0.544
ε=8o η=0.545
Vmax =15.48 kn dh/D=0.18
right
ZQAL12-8-3-2 8406.75 kg
97893.4 kg cm s2
精品文档
13、螺旋桨总图(zǒnɡ tú)的绘制 在计算说明书中需给出实际绘图所用的桨叶轮廓尺寸表和叶切面尺寸表。
精品文档
由上表(shànɡ biǎo)计算结果画右 图(可用AUTOCAD或坐标纸 画),从 PTE 曲线 与满载有效马 力曲线PE 的交点,可获得不同盘 面比所对应的设计航速及螺旋桨 最佳要素P/D、D及 如下表所 列。
精品文档
5、空泡校核(xiào hé)
按柏利尔空泡限界线中商船上限线,计算(jìsuàn)不发生空泡之最小展开面积比。
Inertia of whole propeller:
Gh 2874 kgf G 8406.75 kgf Ib 89453.4 kgf cm s2 Ih 8440 kgf cm s2 I 97893.4 kgf cm s2
精品文档
9、敞水性(shuǐxìng)征曲线之确定
10、系柱特性计算(jìsuàn)(不做要求)
t0.4R 153.9 mm, t0.5R 131.0 mm
t0.6R 108.2 mm, t0.7R 185.3 mm
t0.8R 62.4 mm, t0.9R 39.6 mm
精品文档
7、螺距(luójù)修正
由于毂径比和标准桨相同 0.18,故对此项螺距不需修正。 但是实际(shíjì)桨叶厚度大于标准桨叶厚度,故需因厚度差异进行螺距修正。 修正方法可参考第七章第四节。
螺旋桨图谱设计PPT课件
η0 P/D
单 位 kn V1 kn VA1
N
BP1
δ1 D1 D﹡ δ﹡1
η01 (P/D
)
1
数 V2 VA2
N BP2
δ2 D2 D﹡ δ﹡2 η02 (P/D )
第98页/共65页
注意:
N —— 螺旋桨转速(rpm,即r/min),
PD —— 螺旋桨敞水收到马力(hp), VA —— 螺旋桨进速(kn), D —— 螺旋桨直径(m).
ρ --- 为海水密度,取104.51 kgf·s2/m4
BP --- 功率系数 直径系数δ
NPD0.5 VA2.5
BP
33.30
1. 根据造船统计资料选择螺旋桨叶数 2. 螺旋桨叶数对推进性能的影响 3.综合考虑螺旋桨效率与空泡性能 4.螺旋桨叶数的选择与振动的关系
第321页/共65页
三、螺旋桨的直径
直径 , 转速
效率
船舶吃水、尾框间隙
有限船舶直径
设计图谱
螺旋桨直径
船后间隙等因素
修正
第332页/共65页
常处于压载航行的船舶,宜采用直径较小的螺旋 桨,以照顾压载时的效率和避免叶梢露出水面。 从振动方面考虑,螺旋桨与船体间的间隙不宜过 小,否则可能引起严重振动。
第76页/共65页
一、AU型螺旋桨 设计图谱及其应 用
1. B-δ型设计 图谱的建立
AU5-50螺旋 桨敞水性征 曲线组
0.9
AU5-50
0.8
K T = T /ρn D2 4 K Q = Q/ρn2D 5
η0 = KTJ /2πKQ
0.7
J = V A/nD
0.6
K T , 10K Q
螺旋桨设计计算表格

螺旋桨直径 D= 3.023m Pd1746hp螺距比 P/D=0.688N200.000rpm型式 MAU叶数 Z= 4.000盘面比 Ad=0.546纵倾角ε=8.000°螺旋桨效率 η0=0.512毂径比 dn/D=0.180一 绘制伸张轮廓线螺矩P 2.080m螺旋桨半径R 1.511m最大叶片宽度b0.66R0.932m叶片宽度r/R0.2000.3000.4000.5000.600R 1.511 1.511 1.511 1.511 1.511r0.3020.4530.6050.7560.907母线到随边距离占最大宽度的百分比27.96033.45038.76043.54047.960母线到导边距离占最大宽度的百分比38.58044.25048.32050.80051.150最大叶片宽度b0.66R0.9320.9320.9320.9320.932母线到随边距离AH0.2610.3120.3610.4060.447母线到导边距离AJ0.3600.4120.4500.4730.477母线到随边距离占最大宽度的百分比母线到导边距离占最大宽度的百分比最大叶片宽度母线到随边距离母线到导边距离叶片宽度r/R b0.66R AH AJ b0.20027.96038.5800.9320.2610.3600.6200.30033.45044.2500.9320.3120.4120.7240.40038.76048.3200.9320.3610.4500.8120.50043.54050.8000.9320.4060.4730.8790.60047.96051.1500.9320.4470.4770.9240.66049.74050.2600.9320.4640.4680.9320.70051.33048.3100.9320.4780.4500.9290.80052.39040.5300.9320.4880.3780.8660.90048.49025.1300.9320.4520.2340.6860.95042.07013.5500.9320.3920.1260.5181.00017.2900.9320.161二 绘制叶切面0,0.04291645869465520.0124022341882876,0.06357766809479640.0248044683765752,0.07326452591444710.0372067025648628,0.08111210693289840.062011170941438,0.0932513338208151三 绘制正视图直径D 3.023螺距 2.080盘面比Ae/Ao0.546叶数Z 4.000螺距比P/D0.688叶倾角8.000毂径比0.18r/R0.2000.3000.4000.5000.6000.660四绘制侧投影r/R0.2000.3000.4000.5000.6000.660302.263453.394604.526755.657906.788997.467265.543243.214216.328190.009163.506147.570192.446183.854173.528162.854153.309146.0430.1400.1400.1400.1400.1400.140 Xa'223.065179.499131.37483.81636.0757.396 Xb'-234.923-247.569-258.482-269.047-280.740-286.218 Y'302.263453.394604.526755.657906.788997.467 t122.618x'80.141Y'302.263yH252.633385.281523.395666.091811.319902.011 yS210.166336.489480.036634.620798.464900.038 XH-227.949-237.997-247.081-256.460-267.324-272.803 XS236.008195.928148.868100.82551.29821.087 spline236.007912106677,210.165552029477195.927582448472,336.48855566468148.868095253228,480.036395165528100.825250475277,634.62045604166651.2976682513845,798.46403167180821.0873017604667,900.038021778329 -245.719979465939,1503.12523353177-282.773425256055,1385.21939280483-288.161764740243,1289.92834599714-286.148734635905,1118.50113276049-277.929811546305,960.936857348212-272.80309016539,902.01101304639-267.323898280845,811.319113322175侧视图上最大厚度线r/R0.2000.3000.4000.5000.6000.660302.263453.394604.526755.657906.788997.467 t0.1230.1090.0950.0810.0670.05812310995816758 X80.14144.8989.654-25.589-60.832-81.979spline80.1413539479564,302.26282287115944.897897388683,453.3942343067399.65444082940959,604.525645742318-25.5890157298638,755.657057177898-60.8324722891372,906.788468613477-81.9785462247012,997.467315474825五桨毂实取值桨轴直径dt255.907255.907PD1746.000hp456.500lineN200.000rpm684.750line power(PD/N,1/3) 2.059913.000line毂径dh537.405537.4051141.250lined2/dh0.7500.7501369.500lined1/dh 1.050 1.0501506.450lined2403.0541597.750lined1564.2751826.000lineL0639.7682054.250line191.930191.9302168.375line91.96491.9642282.500line99.74799.747r2132.996132.996d3206.694206.694l-319.884,201.527-319.884,0l319.884,282.1375319.884,0l-319.884,103.347319.884,127.9535l-319.884,201.527319.884,282.13750.6600.7000.8000.9000.950 1.0001.511 1.511 1.511 1.511 1.511 1.5110.997 1.058 1.209 1.360 1.436 1.51149.74051.33052.39048.49042.07017.29050.26048.31040.53025.13013.5500.9320.9320.9320.9320.9320.9320.4640.4780.4880.4520.3920.1610.4680.4500.3780.2340.126叶片厚度螺距t R r p122.6180.123 1.5110.3020.416 1.000 2.080 108.6140.109 1.5110.4530.6240.950 1.976 94.6090.095 1.5110.6050.8320.900 1.872 80.6040.081 1.5110.756 1.0400.800 1.664 66.5990.067 1.5110.907 1.2480.700 1.456 58.1960.058 1.5110.997 1.3730.600 1.248 52.5940.053 1.511 1.058 1.4560.500 1.040 38.5890.039 1.511 1.209 1.6640.4000.832 24.5840.025 1.511 1.360 1.8720.3000.624 17.5820.018 1.511 1.436 1.9760.2000.416 10.5790.011 1.511 1.511 2.0800.093016756412157,0.1045322315348390.124022341882876,0.1130542140470630.186033512824314,0.1223732165064740.198435747012602,0.1226184534133010.248044683765752,0.1198595382115010.31005585470719,0.1102952988452640.372067025648628,0.09582632134249450.434078196590066,0.07743355333049930.496089367531504,0.05548485016951850.7000.8000.9000.950 1.0000.7000.8000.9000.950 1.000 1057.9201209.0511360.1831435.7481511.314 134.48299.77055.39528.378142.889128.965106.88888.10834.4850.1400.1400.1400.1400.140 -14.188-70.138-135.752-173.388-291.559-298.874-298.035-289.874-246.871 1057.9201209.0511360.1831435.7481511.31410.579-201.8061511.314960.9371118.5011289.9281385.2191503.125 971.8601154.5821341.1931430.479-277.930-286.149-288.162-282.773-245.720 -2.094-62.483-133.084-172.648-2.09371804135856,971.860298750337-62.4834448170139,1154.58166482182-133.0836********,1341.19312743561-172.647649817075,1430.47887047229-256.459878261195,666.0908********-247.080686450922,523.394843052442-237.99735002755,385.281375555136-227.948749150267,252.633481145430.7000.8000.9000.950 1.000 1057.9201209.0511360.1831435.7481511.3140.0530.0390.0250.0180.0115339251811 -96.076-131.319-166.563-184.185-201.806-96.0759288484105,1057.91988004906-131.319385407684,1209.0512*******-166.562841966957,1360.182********-184.184570246594,1435.74840863801-201.806298526231,1511.3141143558-1000,456.51000,456.5-1000,684.751000,684.75-1000,9131000,913-1000,1141.251000,1141.25-1000,1369.51000,1369.5-1000,1506.451000,1506.45-1000,1597.751000,1597.75-1000,18261000,1826-1000,2054.251000,2054.25-1000,2168.3751000,2168.375-1000,2282.51000,2282.50.558100538472942,0.03102246871356510.589106123943661,0.01839276801199510.62011170941438,0.00551783040359853。
船舶推进_螺旋桨图谱设计

D
=1
.2
1.0
0. 8
1.0
1.0
0.8
1.2
0.8 0.7 0.6 0.4 0.3 0.5
P /D
0.6
=0
.4
P /D
0.4
0.2 0.1
0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0
J
14
η0
=1 .2
0.8
0.6
8.2 B-δ型设计图谱及其应用
Q KQ ρ n 2 D5
D VA / nJ
功率系数BP
(收到马力系数)
NP V
0.5 D 2.5 A
BP 33.30
0.5 KQ
J 2.5
直径系数δ
ND 30.86 δ VA J
16
8.2 B-δ型设计图谱及其应用
ND 30.86 δ VA J
0.5 0.5 KQ NPD BP 33.30 2.5 2.5 VA J
M HP 147k W 200hp
PD 0 M H P S R 2 0 0 0 . 9 6 0 . 9 8 1 8 8 . 1 6 ( h p )
11
第8章 螺旋桨图谱设计
本章主要内容
8.1 螺旋桨的设计问题及设计方法 8.2 B-δ型设计图谱及其应用
8.3 设计螺旋桨时应考虑的若干问题
8.4 船体-螺旋桨-主机的匹配问题 8.5 螺旋桨图谱设计举例
8.6 螺旋桨制图
12
8.2 B-δ型设计图谱及其应用
8.2 B-δ型设计图谱及其应用
在进行螺旋桨设计时,必需针对船舶的特点和要求
4-2螺旋桨的工作原理

121【上一节】【下一节】【返回主页】§4-2 螺旋桨的工作原理动量理论:环流理论:一、动量理论1.理想推进器理论鼓动盘:图4-2-1 流管内水流流动图形伯努里定理:122鼓动盘前:21120)(2121a A A u V p V p ++=+ρρ鼓动盘后:21120)(21)(21a A a A u V p u V p ++'=++ρρ由上两式相减,得:])[(212211A a A V u V p p -+=-'ρ 鼓动盘前后压力差即形成推力:)(110p p A T -'=将式(4-2-3)代入上式,得:002)21(]2[21A u u V A u u V T a a A a a A +=+=ρρ根据动量定理,推力等于动量的变化率,可得:a A a A mu V u V m T =-+=])[(式中:01)(A u V m a A +=ρ将此关系式代入a mu T =后,得:a a A u A u V T 01)(+=ρ123aa u u 211=。
理想推进器的效率:Aaa A A a A A i V u Tu TV TV mu TV TV 211121212+=+=+=η推进器的载荷系数:221/A V T C A T ρ=Ti C ++=112η2. 理想螺旋桨理论124 图4-2-2 尾流扭转现象单位时间内流过此圆环的流体质量:)21(0a A u V dA dm +=ρ图4-2-3 理想螺旋桨运动模型桨盘紧前方的动量矩:0='L桨盘紧后方的动量矩:t u dmr L '=''单位时间内动量矩的增量:t u dmr L L '='-''根据动量矩定理:流体在单位时间内流经流管两截面的动量矩增量等于作用在流管上的力矩。
在我们所讨论的情形下,是指对螺旋桨轴线所取的力矩。
即:125dQ L L ='-''作用在流体上的力矩:rdF dQ = t u dm dF '=t t u u ='根据动能定理可知,质量为dm 的流体在旋转运动时动能的改变应等于旋转力dF 在单位时间内所作的功,即:221tt udmdFu =tt u u 211=能量守恒:222121ta A dmu dmu dTV rdF ++=ω126 22aA tta u V u r u u +-=ω结论:诱导速度n u 垂直于合速R V 。
螺旋桨图谱设计

第九章螺旋桨图谱设计§9-1 设计问题与设计方法螺旋桨设计是整个船舶设计中的一个重要组成部分。
在船舶线型初步设计完成后,通过有效马力的估算或船模阻力试验,得出该船的有效马力曲线。
在此基础上,要求我们设计一个效率最佳的螺旋桨,既能达到预定的航速,又要使消耗的主机马力小;或者当主机已选定,要求设计一个在给定主机条件下使船舶能达到最高航速的螺旋桨。
因此,螺旋桨的设计问题可分为两类。
一、螺旋桨的初步设计对于新设计的船舶,根据设计任务书对船速的要求设计出最合适的螺旋桨,然后由螺旋桨的转速及效率决定主机的转速及马力,并据此订购主机。
具体地讲就是:①已知船速V,有效马力PE,根据选定的螺旋桨直径D,确定螺旋桨的最佳转速n、效率η0、螺距比P/D和主机马力P s;②已知船速V,有效马力PE,根据给定的转速n,确定螺旋桨的最佳直径D、效率η0、螺距比P/D和主机马力Ps。
二、终结设计主机马力和转速决定后(最后选定的主机功率及转速往往与初步设计所决定者不同),求所能达到的航速及螺旋桨的尺度。
具体地讲就是:已知主机马力Ps、转速n和有效马力曲线,确定所能达到的最高航速V,螺旋桨的直径D、螺距比P/D及效率η0。
新船采用现成的标准型号主机或旧船调换螺旋桨等均属此类问题。
在造船实践中,一般采用标准机型,所以在实际设计中,极大多数是这类设计问题。
目前设计船用螺旋桨的方法有两种,即图谱设计法及环流理论设计法。
图谱设计法就是根据螺旋桨模型敞水系列试验绘制成专用的各类图谱来进行设计。
用图谱方法设计螺旋桨不仅计算方便,易于为人们所掌握,而且如选用图谱适宜,其结果也较为满意,是目前应用较广的一种设计方法。
应用图谱设计螺旋桨虽然受到系列组型式的限制,但此类资料日益丰富,已能包括一般常用螺旋桨的类型。
环流理论设计方法是根据环流理论及各种桨叶切面的试验或理论数据进行螺旋桨设计。
用此种方法可以分别选择各半径处最适宜的螺距和切面形状,并能照顾到船后伴流不均匀的影响,因而对于螺旋桨的空泡和振动问题可进行比较正确的考虑。
螺旋桨设计计算公式

螺旋桨设计计算公式桨叶的迎角只会影响升力的大小,不会前进。
直升机前进是靠螺旋桨的旋转面向前倾斜实现的,桨叶的迎角变化,指的只是桨叶本身绕横向的轴旋转。
就是对称的两只桨,成一条直线,以这个直线为轴旋转。
迎角增大,旋转阻力增大,如果转速不变的情况下,升力就会增大,直升机上升。
飞机螺旋桨由两个或者多个桨叶以及一个中轴组成,桨叶安装在中轴上。
飞机螺旋桨的每一个桨叶基本上是一个旋转翼。
由于他们的结构,螺旋桨叶类似机翼产生拉动或者推动飞机的力。
旋转螺旋桨叶的动力来自引擎。
引擎使得螺旋桨叶在空气中高速转动,螺旋桨把引擎的旋转动力转换成前向推力。
空气中飞机的移动产生和它的运动方向相反的阻力。
所以,飞机要飞行的话,就必须由力作用于飞机且等于阻力,而方向向前。
这个力称为推力。
典型螺旋桨叶的横截面如图3-26。
桨叶的横界面可以和机翼的横截面对比。
一种桨叶的表面是拱形的或者弯曲的,类似于飞机机翼的上表面,而其他表面类似机翼的下表面是平的。
弦线是一条划过前缘到后缘的假想线。
类似机翼,前缘是桨叶的厚的一侧,当螺旋桨旋转时前缘面对气流。
桨叶角一般用度来度量单位,是桨叶弦线和旋转平面的夹角,在沿桨叶特定长度的的特定点测量。
因为大多数螺旋桨有一个平的桨叶面,弦线通常从螺旋桨桨叶面开始划。
螺旋角和桨叶角不同,但是螺旋角很大程度上由桨叶角确定,这两个术语长交替使用。
一个角的变大或者减小也让另一个随之增加或者减小。
当为新飞机选定固定节距螺旋桨时,制造商通常会选择一个螺旋距使得能够有效的工作在预期的巡航速度。
然而,不幸运的是,每一个固定距螺旋桨必须妥协,因为他只能在给定的空速和转速组合才高效。
飞行时,飞行员是没这个能力去改变这个组合的。
当飞机在地面静止而引擎工作时,或者在起飞的开始阶段缓慢的移动时,螺旋桨效率是很低的,因为螺旋桨受阻止不能全速前进以达到它的最大效率。
这时,每一个螺旋桨叶以一定的迎角在空气中旋转,相对于旋转它所需要的功率大小来说产生的推力较少。
船舶原理(螺旋桨 螺距)

第一章绪论第二章螺旋桨的几何特征一、主要内容1、本课题的主要研究内容;2、有效马力、机器马力、收到马力和传送效率、推进效率和推进系数的概念;3、螺旋桨的外形和名称及几何特征的有关专业术语。
二、重点内容1、有效马力、机器马力、收到马力和传送效率、推进效率和推进系数的概念;2、桨叶数、桨的直径、螺距比和盘面比等概念。
三、教学方法多媒体授课、结合螺旋桨模型组织教学四、思考题1、什么是有效马力、机器马力、收到马力和传送效率、推进效率和推进系数?2、表征螺旋桨几何特征的主要参数有哪些?三、下讲主要内容理想推进器理论。
第一章绪论一、本课题的研究对象和内容1、船舶快速性船舶在给定主机马力(功率)情况下,在一定装载时于水中航行的快慢问题。
2、推进器将能源(发动机)发出的功率转换为推船前进的功率的专门装置或机构。
常见的推进器为螺旋桨。
3、主要内容1)推进器在水中运动时产生推力的基本原理及其性能好坏;2)螺旋桨的图谱设计方法。
二、马力及效率1、有效马力P E1)公制有效马力(本教材常用)2)英制有效马力式中,Te 为有效推力(kgf ),R 为阻力(kgf ),v 为船速(m/s )E ()7575P v Rv UShp =e=或hp T E ()7676P v Rv UKhp =e =T 思考:在船舶专业中常用的速度单位还有哪些?2、主机马力和传送效率推进船舶所需要的功率由主机供给,主机发出的马力称为主机马力,以PS表示。
主机马力经减速装置、推力轴承及主轴等传送至推进器,在主轴尾端与推进器联接处所量得的马力称为推进器的收到马力,以PD表示。
传送效率ηs =PD/ PS,它反映了推力轴承、轴承地、尾轴填料函及减速装置等的摩擦损耗。
2、推进效率和推进系数推进效率ηD =P E / P D ,它反映了推进器在操作时有一定的能量损耗,及船身与推进器间的相互影响的能量损耗。
推进效率也称为似是推进系数或准推进系数QPC 。
推进系数PC =P E / P S ,它反映了用某种机器及推进器以推进船舶的全面性能。
AutoCAD2004绘制三维螺纹2
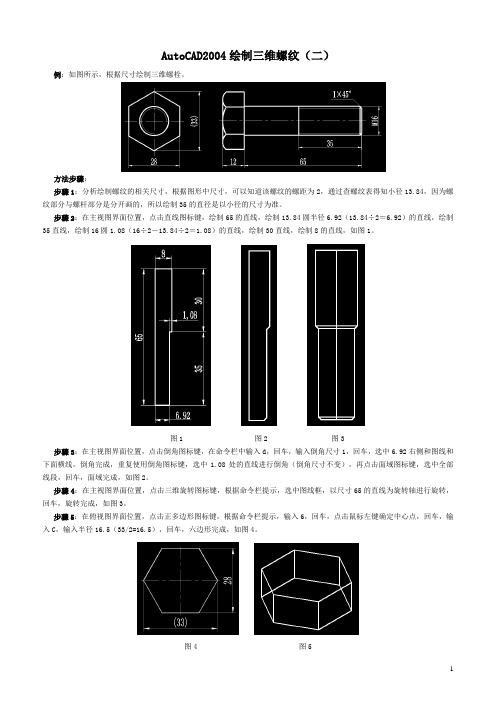
AutoCAD2004绘制三维螺纹(二)例:如图所示,根据尺寸绘制三维螺栓。
方法步骤:步骤1:分析绘制螺纹的相关尺寸,根据图形中尺寸,可以知道该螺纹的螺距为2,通过查螺纹表得知小径13.84,因为螺纹部分与螺杆部分是分开画的,所以绘制35的直径是以小径的尺寸为准。
步骤2:在主视图界面位置,点击直线图标键,绘制65的直线,绘制13.84圆半径6.92(13.84÷2=6.92)的直线,绘制35直线,绘制16圆1.08(16÷2-13.84÷2=1.08)的直线,绘制30直线,绘制8的直线,如图1。
图1 图2 图3步骤3:在主视图界面位置,点击倒角图标键,在命令栏中输入d,回车,输入倒角尺寸1,回车,选中6.92右侧和图线和下面横线,倒角完成,重复使用倒角图标键,选中1.08处的直线进行倒角(倒角尺寸不变),再点击面域图标键,选中全部线段,回车,面域完成,如图2。
步骤4:在主视图界面位置,点击三维旋转图标键,根据命令栏提示,选中图线框,以尺寸65的直线为旋转轴进行旋转,回车,旋转完成,如图3。
步骤5:在俯视图界面位置,点击正多边形图标键,根据命令栏提示,输入6,回车,点击鼠标左键确定中心点,回车,输入C,输入半径16.5(33/2=16.5),回车,六边形完成,如图4。
图4 图5步骤6:在俯视图界面位置,点击拉伸图标键,根据命令栏提示,选中六边形图线框,输入尺寸12,回车,六边形拉伸完成,点击西南等测图标键,查看六边形,如图5。
步骤7:在俯视图界面位置,打开螺杆和六角图形,使两图在俯视图界面位置,点击西南等测图标键,把图形转换到西南等测界面,再点击移动图标键,移动六角与螺杆连接,最后点击并集图标键,使动六角与螺杆成为整体,如图6。
图6步骤8:在主视图界面位置,点击直线图标键绘制图形,如图7,点击面域图标键,选中红线各线段,回车,面域转换完成,点击旋转图标键,选中红线部分,以右侧尺寸2的直线为路径,回车,旋转完成,如图8。
螺旋桨制图讲述

100
1 伸张轮廓图
◆
伸张轮廓
假想线—虚线表示
126.29
上表见《螺旋桨计算书》第14页
204.22 281.79
1 伸张轮廓图
◆桨叶切面
X-叶片横坐标,Yo-叶背纵坐标,Yu-叶面纵坐标
X从导边到随边量取
1 伸张轮廓图
◆桨叶切面
注意事项
1 伸张轮廓图
◆最大厚度线
2 正视图
投影原理
r1=0.033D,r2=0.044D
5 标注尺寸、型值表、主尺度、标题栏
5 标注尺寸、型值表、主尺度、标题栏
欢迎提问!
螺旋桨制图
柯枭各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
径 向 位 置
T1
T1
T'
3 侧视图
◆顶点绘制
◆最大厚度线
5 包毂线—桨叶叶面与桨毂的相交线
5 包毂线—桨叶叶面与桨毂的相交线
d1
dh
d2
5 包毂线—桨叶叶面与桨毂的相交线
5 包毂线—桨叶叶面与桨毂的相交线
5 包毂线—桨叶叶面与桨毂的相交线
5 包毂线—桨叶叶面与桨毂的相交线
5 包毂线—桨叶叶面与桨毂的相交线
◆从船尾向船首看
船
侧投影
正投影
正投影
2 正视图
◆从船后向船首看
2 正视图
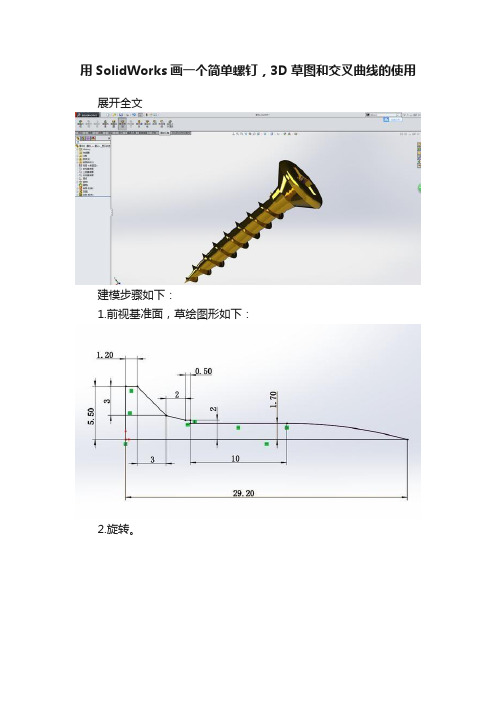
用SolidWorks画一个简单螺钉,3D草图和交叉曲线的使用
用SolidWorks画一个简单螺钉,3D草图和交叉曲线的使用展开全文
建模步骤如下:
1.前视基准面,草绘图形如下:
2.旋转。
3.圆角,半径1.2 。
4.前视基准面,草绘水平直线一条。
(扫描路径)
5.前视基准面,草绘竖直线一条,距离上图的直线0.2 。
(扫描轮廓)
6.曲面扫描,选项:以发向不变沿路径扭转旋转角度8度。
7.前视基准面,草绘图形如下:(轮廓)
8.点3D草图,工具——草图工具——交叉曲线。
点扫描曲面和和螺钉的面。
交叉曲线形成的样条曲线(路径)
9.隐藏扫描曲面。
扫描轮廓为三角形,路径为3D草图(交叉曲线)。
选项:随路径变化,方向向量点三角形的竖直边。
10.在螺钉顶部草绘
镜像
11.拉伸切除,深度2,拔模角度17 。
12.完成。
一种快速制作变螺距螺旋面三维立体图的方法

一种快速制作变螺距螺旋面三维立体图的方法
吴英
【期刊名称】《塔里木大学学报》
【年(卷),期】2005(17)2
【摘要】本文提出一种与AutoCAD相结合绘制所需变螺距螺旋面三维立体图的方法,利用AutoLISP语言编程,在AutoCAD2000环境下,根据给定的参数可自动生成变螺距螺旋线的三维图.然后导入3DS MAX中再进行编辑,即可获得所需的变螺距螺旋面立体图.此方法对其他螺旋面的制作也有一定的借鉴.
【总页数】3页(P82-83,93)
【作者】吴英
【作者单位】塔里木大学农业工程学院,新疆,阿拉尔,843300
【正文语种】中文
【中图分类】TP391.72
【相关文献】
1.一种铣削螺旋面的方法 [J], 雒运强
2.AutoCAD矿山三维立体图制作方法及应用浅议 [J], 何秀珍;孟继红
3.基于AutoCAD的三视图快速转换三维立体图的方法 [J], 张晓
4.基于AutoCAD的三视图快速转换三维立体图的方法 [J], 张晓
5.可变螺距螺旋桨的一种机浆联合优化控制方法 [J], 闫仁武;虞平良
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定螺距螺旋桨攻角算法及其3D图绘制多旋翼无人机一般采用定螺距螺旋桨,而定螺距螺旋桨在其不同半径处的截面的攻角都不相同,随着半径增大,桨叶的攻角会按一定规律逐渐变小,本文将讨论其攻角变化的规律,并介绍其3D图绘制方法。
一.首先要明确螺距和攻角的概念。
螺距指的是在理想状态下,螺旋桨旋转一周后,在轴向移动的距离。
攻角是指将桨叶水平放置,其某个半径处的截面与水平面的夹角。
二.当螺旋桨在旋转时,桨叶上的每一个点的运动轨迹都是一条螺旋线。
桨叶在旋转一周后,桨叶上的每一个点上升的距离都一样,越靠近旋转轴的点,运动轨迹线就越陡峭,攻角也就越大。
反之,离旋转轴越远的点,运动轨迹就越平缓,攻角就越小。
将一条螺旋线所在的圆柱面展平,则会得到一条斜直线,将此圆柱面的周长当做底边,螺距当做高,即可得到一个直角三角形,∠ɑ就是此处的攻角。
螺旋线的半径越大,则攻角越小。
由反正切函数
∠ɑ=atan(a/b) [a为对边,b为邻边]
代入本例,得出:
∠ɑ=atan(p/(2*π*r)) [p为螺距,r为半径]
三.在PROE中,我们可以利用上面的公式,来确定螺旋桨在任意半径上的攻角,扫描出一个角度渐变的曲面,并在此曲面的基础上,按照选定的翼形,扫描出最终桨叶。
下面,我们用一个实例来介绍具体操作方法。
1.首先在TOP平面上拉伸一个圆柱体,当做螺旋桨的旋转轴。
并沿着x轴的方向绘制一条直线a,直线长度等于桨叶的半径。
2.在TOP平面绘制两条曲线b和c,即桨叶的俯视轮廓外观线。
3.将作为迎风面的一侧的曲线b做为截面,在TOP平面上拉伸出一个曲面。
4.在此曲面上投影一条曲线d,即桨叶主视角上轮廓线。
5.以曲线a为主轨迹做可变截面扫描曲面,以曲线d为辅助轨迹,参数如图。
6.截面为一条直线,使曲线d的端点位于直线的中点,标注直线与TOP平面的夹角(sd7),如下图,并在关系中加入关系式。
在PROE的关系式中,反正切函数格式为
∠ɑ=atan2(a,b) [a为对边,b为邻边]
在本例中,可得:
∠ɑ=atan2(p,(2*pi*r)) [p为螺距,r为半径]
设螺距p为4.5英寸,即为114.3mm;螺旋桨半径为127mm;trajpar为PROE内置函数,其值从0到1匀速变化。
在本次扫描过程中,半径从0到127匀速变化,并由此计算出其旋转周长的变化,可表示为(2*pi*127*trajpar)。
将数值代入关系式中:
sd7=atan2(114.3, (2*pi*127*trajpar))
点击确定后,图中sd7的值即变为90︒,表示半径为0时,攻角为90︒。
扫描得出的曲面,即为桨叶攻角随半径变化而变化的曲面。
7,最后在此曲面上投影下轮廓线,以上下轮廓线为轨迹,绘制合适的翼形作为截面,即可扫描出桨叶主体。
桨叶靠近旋转轴的一端约30%左右效率很低,将其切除,与旋转轴接顺即可。
