数学动点问题练习(含答案)

合集下载

(完整版)初一上学期动点问题(含答案)

初一上学期动点问题练习1。

如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0)秒．（1）写出数轴上点B表示的数 ,点P表示的数用含t的代数式表示)；（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化?若变化，请说明理由；若不变，请你画出图形,并求出线段MN的长;解：(1）由题意得点B表示的数为－6；点P表示的数为8－5t;（2）设点P运动x秒时，在点C处追上点Q(如图）则AC=5，BC=3，∵AC－BC=AB∴5－3=”14”解得：=7，∴点P运动7秒时,在点C处追上点Q；(3）没有变化．分两种情况：①当点P在点A、B两点之间运动时：MN=MP+NP=AP+BP=(AP+BP)=AB="7"②当点P运动到点B的左侧时：MN=MP－NP= AP－BP=（AP－BP)=AB="7"∴综上所述,线段MN的长度不发生变化，其值为7；2。

已知数轴上有A、B、C三点,分别表示有理数—26，-10,10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．(1）用含t的代数式表示P到点A和点C的距离:PA=______，PC=______．（2）当点P运动到B点时，点Q从A出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后,请用t的代数式表示P、Q两点间的距离．解:（1）PA=t，PC=36—t；（2）当16≤t≤24时PQ=t-3（t—16）=-2t+48，当24＜t≤28时PQ=3（t-16)—t=2t—48，当28＜t≤30时PQ=72—3（t—16)-t=120-4t，当30＜t≤36时PQ=t—[72—3(t-16)]=4t-120．3。

动点问题练习含答案

动点问丿所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目•解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1,梯形ABCD 中,AD〃BC, ZB=90° , AB= 14cm,AD= 18cm,BC=21 cm,点P 从A开始沿AD边以1cm/秒的速度務动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A, C同时出发，设移动时间为t秒。

当匸______ 时，四边形是平行四边形：6当匸______ 时，四边形是等腰梯形.82、如图2,正方形ABCD的边长为4,点M在边DC上，且DM=1, N为对角线AC ±任意一点，则DN+MN的最小值为 ________ 53、如图，在RtAABC 中，ZACB = 90J, ZB = 60 \ BC = 2 .点。

是AC 的中点，过6点°的直线/从与AC重合的位宜开始，绕点。

作逆时针旋转，交人3边于点过点C作CEH血交直线/于点设直线/的旋转角为°・(1) ________________ ①当 __________________________________________________ 度时，四边形EMC是等腰梯形，此时AQ的长为_______________________________________________②当_____________ 度时，四边形EMC是直角梯形，此时的长为 _______________(2)当« = 90时，判断四边形EQ3C是否为菱形，并说明理由.解:(1)①30, 1：②60, 1.5；(2)当Z « =90°时，四边形EDBC是菱形.V Z <1 =ZACB=90°, :.BCHED••:CEHAB、：•四边形EDBC 是平行四边形在RtAABC中，ZACB=90°, ZB=60°.BC=2, .•- ZA=30°・:.AB=4AC=2^. :.AO=^AC =.在RtZXAOD 中，ZA=30°, :,AD=2.:.BD=2. :.BD=BC.又・••四边形EDBC是平行四边形，.•・四边形EDBC是菱形4、在AABC 中，ZACB=90% AC=BC,直线MN 经过点C,且AD丄MN 于D,(1) 当直线MN 绕点C 旋转到图1的位置时，求证：(DAADC^ACEB ：②DE =AD +BE ； (2) 当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；⑶当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写岀这个等疑关系，并加以证明.解： ⑴① •••ZACD=ZACB=90。

中考数学动点问题(含答案)

中考数学之动点问题一、选择题：1. 如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停顿，设点P运动的路程为*，△ABP的面积为y，如果y关于*的函数图象如图2所示，则△ABC的面积是〔〕A、10B、16C、18D、20二、填空题：1. 如上右图，C为线段AE上一动点〔不与点A，E重合〕，在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.恒成立的结论有_______________________〔把你认为正确的序号都填上〕。

三、解答题：1．〔2008年大连〕如图12，直角梯形ABCD中，AB∥CD，∠A = 90°，CD = 3，AD = 4，tan B = 2，过点C作CH⊥AB，垂足为H．点P为线段AD上一动点，直线PM∥AB，交BC、C H于点M、Q．以PM为斜边向右作等腰Rt△PMN，直线MN交直线AB于点E，直线PN交直线A B于点F．设PD的长为*，EF的长为y．⑴求PM的长(用*表示)；⑵求y与*的函数关系式及自变量*的取值范围(图13为备用图)；⑶当点E在线段AH上时，求*的取值范围(图14为备用图)．2.〔2008年福建宁德〕如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时0＜x＜，△DCQ的8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为*秒()8面积为y1平方厘米，△PCQ的面积为y2平方厘米．⑴求y1与*的函数关系，并在图2中画出y1的图象；⑵如图2，y2的图象是抛物线的一局部，其顶点坐标是〔4，12〕，求点P的速度及AC的长；⑶在图2中，点G是*轴正半轴上一点〔0＜OG＜6＝，过G作EF垂直于*轴，分别交y1、y2于点E、F．①说出线段EF的长在图1中所表示的实际意义；②当0＜*＜６时，求线段EF长的最大值．3.〔2008年白银〕如图，在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为〔4，3〕．平行于对角线AC 的直线m 从原点O 出发，沿*轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边．．分别交于点M 、N ，直线m 运动的时间为t 〔秒〕． (1) 点A 的坐标是__________，点C 的坐标是__________； (2) 当t=秒或秒时，MN=21AC ； (3) 设△OMN 的面积为S ，求S 与t 的函数关系式；(4) 探求(3)中得到的函数S 有没有最大值？假设有，求出最大值；假设没有，要说明理由．参考答案一、选择 A二、填空：〔1〕〔2〕〔3〕〔5〕三、解答： 2、解：⑴∵CD CQ S DCQ ⋅⋅=∆21，CD ＝3，CQ ＝*， ∴x y 231=．图象如下图．⑵方法一：CP CQ S PCQ ⋅⋅=∆21，CP ＝8k －*k ，CQ ＝*， ∴()kx kx x kx k y 42182122+-=⋅-⨯=．∵抛物线顶点坐标是〔4，12〕，∴12444212=⋅+⋅-k k ．解得23=k ．图1C Q → B图2则点P 的速度每秒23厘米，AC ＝12厘米．方法二：观察图象知，当*=4时，△PCQ 面积为12．此时PC ＝AC －AP ＝8k －4k ＝4k ，CQ ＝4．∴由CP CQ S PCQ ⋅⋅=∆21，得 12244=⨯k ．解得23=k ．则点P 的速度每秒23厘米，AC ＝12厘米．方法三：设y 2的图象所在抛物线的解析式是c bx ax y ++=2． ∵图象过〔0，0〕，〔4，12〕，〔8，0〕，∴⎪⎩⎪⎨⎧=++=++=.0864124160c b a c b a c ，，解得 ⎪⎪⎩⎪⎪⎨⎧==-=.0643c b a ，， ∴x x y 64322+-=． ①∵CP CQ S PCQ ⋅⋅=∆21，CP ＝8k －*k ，CQ ＝*，∴kx kx y 42122+-=． ②比拟①②得23=k .则点P 的速度每秒23厘米，AC ＝12厘米．⑶①观察图象，知线段的长EF ＝y 2－y 1，表示△PCQ 与△DCQ 的面积差〔或△PDQ 面积〕． ②由⑵得 x x y 64322+-=.〔方法二，x x x x y 643232382122+-=⋅⎪⎭⎫ ⎝⎛-⨯⨯=〕∵EF ＝y 2－y 1， ∴EF ＝x x x x x 29432364322+-=-+-， ∵二次项系数小于０，∴在60＜x＜范围，当3=x 时，427=EF 最大． 3、解：(1)〔4，0〕，〔0，3〕； 2分 (2) 2，6； 4分 (3) 当0＜t ≤4时，OM =t ．由△OMN ∽△OAC ，得OCONOA OM =， ∴ ON =t 43，S=283t ． 6分当4＜t ＜8时，如图，∵ OD =t ，∴ AD = t-4．方法一：由△DAM ∽△AOC ，可得AM =)4(43-t ，∴ BM =6-t 43． 7分由△BMN ∽△BAC ，可得BN =BM 34=8-t ，∴ CN =t-4． 8分S=矩形OABC 的面积-Rt △OAM 的面积- Rt △MBN 的面积- Rt △NCO 的面积=12-)4(23-t -21〔8-t 〕〔6-t 43〕-)4(23-t =t t 3832+-． ·························· 10分方法二：易知四边形ADNC 是平行四边形，∴ CN =AD =t-4，BN =8-t ．7分由△BMN ∽△BAC ，可得BM =BN 43=6-t 43，∴ AM =)4(43-t ．8分以下同方法一． (4) 有最大值．方法一：当0＜t ≤4时，∵ 抛物线S=283t 的开口向上，在对称轴t=0的右边， S 随t 的增大而增大， ∴ 当t=4时，S 可取到最大值2483⨯=6； 11分当4＜t ＜8时， ∵ 抛物线S=t t 3832+-的开口向下，它的顶点是〔4，6〕，∴ S ＜6．综上，当t=4时，S 有最大值6． 12分方法二：∵ S=22304833488t t t t t ⎧<⎪⎪⎨⎪-+<<⎪⎩，≤，∴ 当0＜t ＜8时，画出S 与t 的函数关系图像，如下图． 11分显然，当t=4时，S有最大值6． 12分说明：只有当第〔3〕问解答正确时，第〔4〕问只答复"有最大值〞无其它步骤，可给1分；否则，不给分．。

初二数学动点问题练习(含答案)

动态问题之袁州冬雪创作所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.处理这类问题的关键是动中求静,矫捷运用有关数学知识处理问题.关键:动中求静.数学思想：分类思想数形连系思想转化思想1、如图1，梯形ABCD 中，AD ∥ BC ，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P 从A 开端沿AD 边以1cm/秒的速度移动，点Q 从C 开端沿CB 向点B 以2 cm/秒的速度移动，如果P ，Q 分别从A ，C 同时出发，设移动时间为t 秒. 当t=时，四边形是平行四边形；6 当t=时，四边形是等腰梯形. 82、如图2，正方形ABCD 的边长为4，点M 在边DC 上，且DM=1，N 为对角线AC 上任意一点，则DN+MN 的最小值为53、如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开端，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α=度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α=度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，断定四边形EDBC 是否为菱形，并O E CDAα lOCA（备用图）说明来由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形在Rt △ABC 中，∠ACB =900，∠B =600,BC =2, ∴∠A =300. ∴AB =4,AC∴AO在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形4、在△ABC 中，∠ACB =90°，AC=BC ，直线MN 颠末点C ，且AD ⊥MN于D ，BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ；(2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.解：（1）①∵∠ACD=∠ACB=90°∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB②∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE 又∵AC=BCCBAE D图1 N MA B CDE M N图2ACB EDNM图3∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等)∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD. 5、数学课上，张教师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BCEF 行线CF 于点F ，求证：AE =EF ．颠末思考，小明展示了一种正确的解题思路：取AB 的中点M ，毗连ME ，则AM=EC在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那末结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明来由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明来由．解：（1）正确．ADF C GE B图1ASA ）．（2）正确．ASA ）．6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的间隔为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t.求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB为直角三角形的t 值7、如图1求：（1间隔；（2ADFC GE B图3ADFGB 图2ADFC G E BN23明来由解（1）如图1，于点∵为的中点，（2不发生改变．图1A DEBFCGA DEBFC图4（备A DEBFC图5（备A DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM（第25题）如图2cos30︒=中，PN的周长=PM在线段DC等边三角形．3当时，如图4548中点．图3A D E BFCPN M图4A D EBF CP MN 图5A D EBF CMN GGRG图2A D E BF CPNMG H(1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等，颠末1②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B P与点Q解：（1∴②∵，∴，又∵，，则/秒.（2）设颠末秒后点与点第一次相遇，由题意，得上相遇，∴颠末803秒点P与点Q第一次在边AB上相遇．9、如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC．CD上滑动，且E、F不与B．C．D重合．（1）证明不管E、F在BC．CD上如何滑动，总有BE=CF；（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF和△CEF 的面积是否发生变更？如果不变，求出这个定值；如果变更，求出最大（或最小）值．【答案】解：（1）证明：如图，毗连AC∵四边形ABCD为菱形，∠BAD=120°，∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，∴∠BAE=∠FAC.∵∠BAD=120°，∴∠ABF=60°.∴△ABC和△ACD为等边三角形.∴∠ACF=60°，AC=AB.∴∠ABE=∠AFC.∴在△ABE和△ACF中，∵∠BAE=∠FAC，AB=AC，∠ABE=∠AFC，∴△ABE≌△ACF（ASA）.∴BE=CF.（2）四边形AECF 的面积不变，△CEF 的面积发生变更.来由如下：由（1）得△ABE ≌△ACF ，则S △ABE =S △ACF .∴S 四边形AECF =S △AEC +S △ACF =S △AEC +S △ABE =S △ABC ，是定值.作AH ⊥BC 于H 点，则BH =2，22AECF ABC 11S S BC AH BC AB BH 4322∆==⋅⋅=⋅-=四形边.由“垂线段最短”可知：当正三角形AEF 的边AE 与BC 垂直时，边AE 最短．故△AEF 的面积会随着AE 的变更而变更，且当AE最短时，正三角形AEF 的面积会最小，又S △CEF =S 四边形AECF ﹣S △AEF ，则此时△CEF 的面积就会最大．∴S △CEF =S四边形AECF ﹣S △AEF()()221432323332=-⋅⋅-=.∴△CEF 的面积的最大值是3.【考点】菱形的性质，等边三角形的断定和性质，全等三角形的断定和性质，勾股定理，垂直线段的性质.【分析】（1）先求证AB =AC ，进而求证△ABC 、△ACD 为等边三角形，得∠ACF =60°，AC =AB ，从而求证△ABE ≌△ACF ，即可求得BE =CF .（2）由△ABE ≌△ACF 可得S △ABE =S △ACF ，故根据S四边形AECF =S △AEC +S △ACF =S △AEC +S △AB E =S △ABC 即可得四边形AECF 的面积是定值.当正三角形AEF 的边AE 与BC 垂直时，边AE 最短．△AEF 的面积会随着AE的变更而变更，且当AE最短时，正三角形AEF的面积会最小，根据S△CEF=S四边形AECF－S△AEF，则△CEF的面积就会最大.10、如图，在△AOB中，∠AOB=90°，OA=OB=6，C为OB上一点，射线CD⊥OB交AB于点D，OC=2．点P从点A出发以每秒个单位长度的速度沿AB方向运动，点Q从点C出发以每秒2个单位长度的速度沿CD方向运动，P、Q两点同时出发，当点P到达到点B时停止运动，点Q也随之停止．过点P作PE⊥OA于点E，PF⊥OB于点F，得到矩形PEOF．以点Q为直角顶点向下作等腰直角三角形QMN，斜边MN∥OB，且MN=QC．设运动时间为t（单位：秒）．（1）求t=1时FC的长度．（2）求MN=PF时t的值．（3）当△QMN和矩形PEOF有重叠部分时，求重叠（阴影）部分图形面积S与t的函数关系式．（4）直接写出△QMN的边与矩形PEOF的边有三个公共点时t的值．考点：相似形综合题．分析：（1）根据等腰直角三角形，可得，OF=EP=t，再将t=1代入求出FC的长度；（2）根据MN=PF，可得关于t的方程6﹣t=2t，解方程即可求解；（3）分三种情况：求出当1≤t≤2时；当2＜t≤时；当＜t≤3时；求出重叠（阴影）部分图形面积S与t的函数关系式；（4）分M在OE上；N在PF上两种情况讨论求得△QMN的边与矩形PEOF的边有三个公共点时t的值．解答：解：（1）根据题意，△AOB、△AEP都是等腰直角三角形．∵，OF=EP=t，∴当t=1时，；（2）∵AP=t，AE=t，PF=OE=6﹣t∴6﹣t=2t解得t=2．故当t=2时，MN=PF；（3）当1≤t≤2时，S=2t2﹣4t+2；当2＜t≤时，S=﹣t2+30t﹣32；当＜t≤3时，S=﹣2t2+6t；（4）△QMN的边与矩形PEOF的边有三个公共点时t=2或．点评：程思想，分类思想的运用，有一定的难度．。

动点问题练习(含标准答案)

动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t=时，四边形是平行四边形；6当t=时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中，∠ACB=900，∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC.在Rt△AOD中，∠A=300，∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形，∴四边形EDBC是菱形4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E. (1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD＋BE；(2)当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.（备用图）CBED图1NMA BCDEMACBEDNM解：（1）①∵∠ACD=∠ACB=90°∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB②∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE ，又∵AC=BC ，∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°．CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°．AME ECF ∴∠=∠． 90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥． DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． AE EF ∴=． 6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t. 求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值AD F GB图1A D FC G B 图3ADFGB 图2AD FC GE B MA D FG B N7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠.求：（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PM N △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由解（1）如图1，过点E 作EG BC ⊥于点G ．∵E 为AB 的中点，∴122BE AB ==．在Rt EBG△中，60B =︒∠，∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC（2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变．∵PM EF EG EF ⊥⊥，，∴PM EG ∥． ∵EF BC ∥，∴EP GM =，PM EG ==同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥，∴6030NMC B PMH ==︒=︒∠∠，∠．∴122PH PM ==∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．图1 A D E BF CGA D E BFCPNMG HA D E BF C图4（备用）AD EBF C 图5（备用）A D E BF C图1 图2A D E BF C PNM图3A D EBFCPNM（第25题）在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==．∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN=时，如图4，这时MC MN MP ==此时，615x EP GM ===-=当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠，∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5-时，PMN △为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘M ，8BC =厘M ，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘M ， ∵10AB =厘M ，点D 为AB 的中点， ∴5BD =厘M ．图3A D E BFCPN M图4A D EBF CP MN 图5A DEBF （P ） CM NGGRG又∵8PC BC BP BC =-=，厘M ， ∴835PC =-=厘M ， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘M/秒。

初一数学动点问题20题及答案

初一数学动点问题20题及答案数轴上动点问题1．已知：如图，数轴上点A表示的数为6，点B表示的数为2，点C表示的数为﹣8，动点P从点A出发，沿数轴向左运动，速度为每秒1个单位长度．点M为线段BC中点，点N为线段BP中点．设运动时间为t秒．（1）线段AC的长为__________个单位长度；点M表示的数为；（2）当t=5时，求线段MN的长度；（3）在整个运动过程中，求线段MN的长度．（用含t的式子表示）．2．已知数轴上点A，B，C所表示的数分别是x，﹣6，4．（1）线段BC的长为_________，线段BC的中点D所表示的数是；（2）若AC=8，求x的值；（3）在数轴上有两个动点P，Q，P的速度为1个单位长度/秒，Q的速度为2个单位/秒，点P，Q分别从点B，C同时出发，在数轴上运动，则经过多少时间后P，Q两点相距4个单位？3．动点A、B同时从数轴上的原点出发向相反的方向运动，且A、B的速度之比是1：4（速度单位：长度单位/秒），3秒后，A、B两点相距15个单位长度．（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置．（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间？4．如图A、B两点在数轴上分别表示﹣10和20，动点P从点A出发以10个单位每秒的速度向右运动，动点Q从点B出发以每秒5个单位的速度出向右运动．设运动时间为t．（1）当点P运动到B点时，求出t的值；（2）当t为何值时，P、Q两点相遇，并求出此时P点对应的数？（3）在此运动过程中，若P、Q相距10个单位，直接写出运动时间t？5．已知a，b满足（a+2）2+|b﹣1|=0，请回答下列问题：（1）a=_______，b=_______；（2）a，b在数轴上对应的点分别为A，B，在所给的数轴上标出点A，点B；（3）若甲、乙两个动点分别从A，B两点同时出发沿x轴正方向运动，已知甲的速度为每秒2个单位长度，乙的速度为每秒1个单位长度，更多好题请进入：437600809，请问经过多少秒甲追上乙？6．在数轴上有A、B两动点，点A起始位置表示数为﹣3，点B起始位置表示数为12，点A的速度为1单位长度/秒，点B的运动速度是点A速度的二倍．（1）若点A、B同时沿数轴向左运动，多少秒后，点B与点A相距6单位长度？（2）若点A、点B同时沿数轴向左运动，是否有一个时刻，表示数﹣3的点是线段AB 的中点？如果有，求出运动时间；如果没有，说明理由．7．如图，已知数轴上点A表示的为8，B是数轴上一点，且AB=14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；（2）动点H从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、H 同时出发，问点P运动多少秒时追上点H？8．如图，数轴上的点A，B对应的数分别为﹣10，5．动点P，Q分别从A，B同时出发，点P以每秒3个单位长度的速度沿数轴向右匀速运动，点Q以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．（1）求线段AB的长；（2）直接用含t的式子分别表示数轴上的点P，Q对应的数；（3）当PQ=AB时，求t的值．9．如图，已知数轴上点A表示的数为6，B是你数轴上一点，且AB=10，动点P从点O 出发，以每秒6个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B所表示的数______；当t=3时，OP=_______．（2）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R 同时出发，问点R运动多少秒时追上点P？10．如图．点A、点C是数轴上的两点，0是原点，0A=6，5AO=3CO．（1）写出数轴上点A、点C表示的数；（2）点P、Q分别从A、C同时出发，点P以每秒1个单位长度的速度沿数轴向右匀速运动，点Q以每4个单位长度的速度沿数轴向左匀速运动，问运动多少秒后，这两个动点到原点O的距离存在2倍关系？11．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）数轴上是否存在点P，使P到点A、点B的之和为5？若存在，请求出x的值；若不存在，说明理由；（2）当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动．问，它们同时出发几分钟时点P到点A、点B的距离相等？12．A、B两个动点在数轴上做匀速运动，它们的运动时间以及位置记录如下．（1）根据题意，填写下列表格；（2）A、B两点能否相遇？如果相遇，求相遇时的时刻及在数轴上的位置；如果不能相遇，请说明理由；（3）A、B两点能否相距18个单位长度？如果能，求相距18个单位长度的时刻；如不能，请说明理由．13．如图1，点A，B是在数轴上对应的数字分别为﹣12和4，动点P和Q分别从A，B 两点同时出发向右运动，点P的速度是5个单位/秒，点Q的速度是2个单位/秒，设运动时间为t秒．（1）AB=．（2）当点P在线段BQ上时（如图2）：①BP=______________（用含t的代数式表示）；②当P点为BQ中点时，求t的值．。

初二数学动点问题练习(含答案)

动态问题之五兆芳芳创作所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关头是动中求静,灵活运用有关数学知识解决问题.关头:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q辨别从A，C同时出发，设移动时间为t秒.当t=时，四边形是平行四边形；6当t=时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时ADOE CDAαlOCA（备用图）的长为；（2解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形在Rt △ABC 中，∠ACB =900，∠B =600,BC =2, ∴∠A =300. ∴AB =4,AC∴AO在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形4、在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ；(2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.解：（1）①∵∠ACD=∠ACB=90°∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEBCBAE D图1 N MA B CDE M N图2ACB EDNM图3②∵△ADC≌△CEB∴CE=AD，CD=BE ∴DE=CE+CD=AD+BE(2) ∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE又∵AC=BC∴△ACD≌△CBE ∴CE=AD，CD=BE∴DE=CE-CD=AD-BE(3) 当MN旋转到图3的位置时，DE=BE-AD(或AD=BE-DE，BE=AD+DE等)∵∠ADC=∠CEB=∠ACB=90°∴∠ACD=∠CBE，又∵AC=BC，∴△ACD≌△CBE，∴AD=CE，CD=BE，∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD是正方EF形，点E是边BC经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC在此根本上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改成“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的不雅点正确吗？如果正确，写出证明进程；如果不正确，请说明理由；（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的不雅点正确吗？如果正确，写出证明进程；如果不正确，请说明理由．解：（1）正确．ASA）．（2）正确．ASA）．6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB标的目的以1个单位/秒的速度移动，设P的运动时间为t.求（1）△PAB为等腰三角形的t值；（2）△PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△PAB为直角三角形的t值7、如图1A DFC GEB图1A DFC GEB图3A DFC GEB图2A DFGBN求：（1距离；（223明理由解（1）如图1，于点∵为的中点，∴（2图1A DEBFCGA DEBFC图4（备A DEBFC图5（备A DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM（第25题）不产生改动．如图2cos30︒=中，PN的周长=PM在线段DC等边三角形．3当时，如图45图3A DEBFCPNM图4A DEBFCPMN图5A DEBFCMNGGRG图2A DEBFCPNMGH48中点．(1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等，经过1②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B点P与点Q解：（1又米，米，∴②∵，∴，又∵，，则/秒.（2）设经过秒后点与点第一次相遇，由题意，得1532104x x =+⨯，解得803x =秒．∴点P 共运动了803803⨯=厘米． ∵8022824=⨯+，∴点P、点Q 在AB 边上相遇，∴经过803秒点P 与点Q 第一次在边AB 上相遇．9、如图所示，在菱形ABCD 中，AB =4，∠BAD =120°，△AEF 为正三角形，点E 、F 辨别在菱形的边BC ．CD 上滑动，且E 、F 不与B ．C ．D 重合．（1）证明不管E 、F 在BC ．CD 上如何滑动，总有BE =CF ；（2）当点E 、F 在BC ．CD 上滑动时，辨别探讨四边形AECF 和△CEF 的面积是否产生变更？如果不变，求出这个定值；如果变更，求出最大（或最小）值．【答案】解：（1）证明：如图，连接AC∵四边形ABCD 为菱形，∠BAD =120°，∠BAE +∠EAC =60°，∠FAC +∠EAC =60°，∴∠BAE =∠FAC .∵∠BAD =120°，∴∠ABF =60°. ∴△ABC 和△ACD 为等边三角形.∴∠ACF =60°，AC =AB .∴∠ABE =∠AFC .∴在△ABE 和△ACF 中，∵∠BAE =∠FAC ，AB =AC ，∠ABE =∠AFC ，∴△ABE ≌△ACF （ASA ）.∴BE =CF .（2）四边形AECF 的面积不变，△CEF 的面积产生变更.理由如下：由（1）得△ABE ≌△ACF ，则S △ABE =S △ACF . ∴S 四边形AECF =S △AEC +S △ACF =S △AEC +S △ABE =S △ABC ，是定值.作AH ⊥BC 于H 点，则BH =2，22AECF ABC 11S S BC AH BC AB BH 4322∆==⋅⋅=⋅-=四形边.由“垂线段最短”可知：当正三角形AEF 的边AE 与BC 垂直时，边AE 最短．故△AEF 的面积会随着AE 的变更而变更，且当AE最短时，正三角形AEF 的面积会最小，又S △CEF =S 四边形AECF ﹣S △AEF ，则此时△CEF 的面积就会最大．∴S △CEF =S 四边形AECF ﹣S △AEF()()221432323332=-⋅⋅-=.∴△CEF 的面积的最大值是3.【考点】菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，垂直线段的性质.【阐发】（1）先求证AB=AC，进而求证△ABC、△ACD为等边三角形，得∠ACF=60°，AC=AB，从而求证△ABE≌△ACF，便可求得BE=CF.（2）由△ABE≌△ACF可得S△ABE=S△ACF，故按照S四边形F=S△AEC+S△ACF=S△AEC+S△AB E=S△ABC便可得四边形AECF的面积AEC是定值.当正三角形AEF的边AE与BC垂直时，边AE最短．△AEF 的面积会随着AE的变更而变更，且当AE最短时，正三角形AEF 的面积会最小，按照S△CEF=S四边形AECF－S△AEF，则△CEF的面积就会最大.10、如图，在△AOB中，∠AOB=90°，OA=OB=6，C为OB上一点，射线CD⊥OB交AB于点D，OC=2．点P从点A出发以每秒个单位长度的速度沿AB标的目的运动，点Q从点C出发以每秒2个单位长度的速度沿CD标的目的运动，P、Q两点同时出发，当点P到达到点B时停止运动，点Q也随之停止．过点P作PE⊥OA 于点E，PF⊥OB于点F，得到矩形PEOF．以点Q为直角顶点向下作等腰直角三角形QMN，斜边MN∥OB，且MN=QC．设运动时间为t（单位：秒）．（1）求t=1时FC的长度．（2）求MN=PF时t的值．（3）当△QMN和矩形PEOF有重叠部分时，求重叠（阴影）部分图形面积S与t的函数关系式．（4）直接写出△QMN的边与矩形PEOF的边有三个公共点时t的值．考点：相似形综合题．阐发：（1）按照等腰直角三角形，可得，OF=EP=t，再将t=1代入求出FC的长度；（2）按照MN=PF，可得关于t的方程6﹣t=2t，解方程便可求解；（3）分三种情况：求出当1≤t≤2时；当2＜t≤时；当＜t≤3时；求出重叠（阴影）部分图形面积S与t的函数关系式；（4）分M在OE上；N在PF上两种情况讨论求得△QMN的边与矩形PEOF的边有三个公共点时t的值．解答：解：（1）按照题意，△AOB、△AEP都是等腰直角三角形．∵，OF=EP=t，∴当t=1时，FC=1；（2）∵AP=t，AE=t，PF=OE=6﹣tMN=QC=2t∴6﹣t=2t解得t=2．故当t=2时，MN=PF；（3）当1≤t≤2时，S=2t2﹣4t+2；当2＜t≤时，S=﹣t2+30t﹣32；当＜t≤3时，S=﹣2t2+6t；（4）△QMN的边与矩形PEOF的边有三个公共点时t=2或．点评：程思想，分类思想的运用，有一定的难度．。

数学动点问题习题及答案

1、（09包头）如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．（1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？2.（09河南））如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，判断四边形EDBC 是否为菱形，并说明理由．3.如图1，已知抛物线的顶点为A （2，1），且经过原点O ，与x 轴的另一个交点为B 。

⑴求抛物线的解析式；（用顶点式求得抛物线的解析式为xx 41y 2+-=）⑵若点C 在抛物线的对称轴上，点D 在抛物线上，且以O 、C 、D 、B 四点为顶点的四边形为平行四边形，求D 点的坐标；⑶连接OA 、AB ，如图2，在x 轴下方的抛物线上是否存在点P ，使得△OBP 与△OAB 相似？若存在，求出P 点的坐标；若不存在，说明理由。

AQCDB POE CBDAαlOCBA（备用图）4. 2008浙江温州)如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．5、如图过Ａ（８,０），Ｂ（０，38）两点的直线与直线x y 3=交于Ｃ点。

数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时，四边形是平行四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为 53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中，∠ACB=900，∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC.在Rt△AOD中，∠A=300，∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形，∴四边形EDBC是菱形4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.（备用图）CEDNM CDMCEM(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE (3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ．BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°． CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°．AME ECF ∴∠=∠．90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥．ADF CGB图1A DFADFC GE B 图2ADFC GB M ADFNDAE BEA∴∠=∠．NAE CEF∴∠=∠．ANE ECF∴△≌△（ASA）．AE EF∴=．6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动，设P的运动时间为t.求（1）△PAB为等腰三角形的t值；（2）△PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△PAB为直角三角形的t值7、如图1，在等腰梯形ABCD中，AD BC∥，E是AB的中点，过点E作EF BC∥交CD于点F．46AB BC==，，60B=︒∠.求：（1）求点E到BC的距离；（2）点P为线段EF上的一个动点，过P作PM EF⊥交BC于点M，过M作MN AB∥交折线ADC 于点N，连结PN，设EP x=.①当点N在线段AD上时（如图2），P M N△的形状是否发生改变？若不变，求出PMN△的周长；若改变，请说明理由；②当点N在线段DC上时（如图3），是否存在点P，使PMN△为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由A DEBFCA DEBFCA DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM（第25题）解（1）如图1，过点E 作EG BC ⊥于点G ． ∵E 为AB 的中点， ∴122BE AB ==．在Rt EBG △中，60B =︒∠， ∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC（2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变． ∵PM EF EG EF ⊥⊥，， ∴PM EG ∥．∵EF BC ∥， ∴EP GM =，PM EG == 同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥，∴6030NMC B PMH ==︒=︒∠∠，∠．∴122PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==． ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．图3A D E BFCPN M图4A D EBF CP MN 图5A D EBF （P ） CMN GGRG图1 A D E BF CG图2A D E BFCPNMG H当MP MN =时，如图4，这时MC MN MP ===此时，615x EP GM ===-= 当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5-时，PMN △为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

初二数学动点问题练习含答案

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,敏捷运用有关数学学问解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD 中，AD ∥ BC ，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P 从A 开场沿AD 边以1cm/秒的速度挪动，点Q 从C 开场沿CB 向点B 以2 cm/秒的速度挪动，假如P ，Q 分别从A ，C 同时动身，设挪动时间为t 秒。

当t= 时，四边形是平行四边形；6 当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD 的边长为4，点M 在边DC 上，且DM=1，N 为对角线AC 上随意一点，则DN+MN 的最小值为 53、如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC的中点，过点O 的直线l 从与AC 重合的位置开场，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为；（2）当90α=°时，推断四边形EDBC 是否为菱形，并说明O ECDα lOC理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形.∵∠α=∠ACB=900，∴BC //ED . ∵CE //AB , ∴四边形EDBC 是平行四边形在Rt △ABC 中，∠ACB =900，∠B =600,BC =2, ∴∠A =300. ∴AB =4,AC. ∴AO =12AC.在Rt △AOD 中，∠A =300，∴AD =2.∴BD =2. ∴BD =BC . 又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形4、在△ABC 中，∠ACB =90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ； (3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90°∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BEC B AE D图1 N M A B CDEM N图2 A C B ED N M 图3(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ， ∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张教师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思索，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此根底上，同学们作了进一步的讨论：（1）小颖提出：如图2，假如把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的随意一点”，其它条件不变，那么结论“AE =EF ”仍旧成立，你认为小颖的观点正确吗？假如正确，写出证明过程；假如不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的随意一点，其他条件不变，结论“AE =EF ”仍旧成立．你认为小华的观点正确吗？假如正确，写出证明过程；假如不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°．90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°，∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．A DFCGE B 图1A DFC GE B图2A DF CGE BM证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥． ANE ECF ∴△≌△（ASA ）． 6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的间隔为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度挪动，设P 的运动时间为t.求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，干脆写出△ PAB 为直角三角形的t 值7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC∥交CD 于点F ．46AB BC ==，，60B =︒∠.求：（1）求点E 到BC 的间隔；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PMN △的形态是否发生变更？若不变，求出PMN △的周长；若变更，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，恳求出全部满意要求的x 的值；若不存在，请说明理由A D FC GE B图3A D FC GE BN解（1）如图1，过点E作EG BC⊥于点G ． ∵E为AB的中点，∴122BE AB ==．在Rt EBG △中，60B =︒∠， ∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC 的间隔（2）①当点N 在线段AD 上运动时，PMN △的形态不发生变更．∵EF BC ∥， ∴EP GM =，PM EG ==同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥， ∴6030NMC B PMH ==︒=︒∠∠，∠．∴122PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形态发生变更，但MNC △恒为等图1A D EB F CG图2A DE BF CPN MG HA D E BFC图4（备AD EBF C图5（备A D E BF C 图图A DE BF C P N M图A DEBFC P N M（第25边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==． ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN=时，如图4，这时MC MN MP ===此时，615x EP GM ===-=-当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5时，PMN △为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点． (1）假如点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，可以使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 动身，点P 以原来的运动速度从点B 同时动身，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第图3A DE B FCPN M图4A D E BFCP M N 图5A D E BF CMN GGR G一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ≠，又∵BPD CQP△≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

初中数学几何的动点问题专题练习-附答案版

动点问题专题练习【1 】1.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点．（1）假如点P 在线段BC 上以3厘米/秒的速度由B 点向C 点活动,同时,点Q 在线段CA 上由C 点向A 点活动．①若点Q 的活动速度与点P 的活动速度相等,经由1秒后,BPD △与CQP △是否全等,请解释来由;②若点Q 的活动速度与点P 的活动速度不相等,当点Q 的活动速度为若干时,可以或许使BPD △与CQP △全等？（2）若点Q 以②中的活动速度从点C 动身,点P 以本来的活动速度从点B 同时动身,都逆时针沿ABC △三边活动,求经由多长时光点P 与点Q 第一次在ABC △的哪条边上相遇？ 1.解：（1）①∵1t =秒, ∴313BP CQ ==⨯=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米, ∴835PC =-=厘米, ∴PC BD =．又∵AB AC =, ∴B C ∠=∠,∴BPD CQP △≌△． ············································································· （4分） ②∵P Q v v ≠, ∴BP CQ ≠,又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====，, ∴点P ,点Q 活动的时光433BP t ==秒, ∴515443Q CQ v t===厘米/秒． ·································································· （7分）（2）设经由x 秒后点P 与点Q 第一次相遇,由题意,得1532104x x =+⨯, 解得803x =秒．∴点P 共活动了803803⨯=厘米．∵8022824=⨯+,∴点P .点Q 在AB 边上相遇,∴经由803秒点P 与点Q 第一次在边AB 上相遇． ········································· （12分） 2.直线364y x =-+与坐标轴分离交于A B 、两点,动点P Q 、同时从O 点动身,同时到达A点,活动停滞．点Q 沿线段OA 活动,速度为每秒1个单位长度,点P 沿路线O →B →A 活动．（1）直接写出A B 、两点的坐标;（2）设点Q 的活动时光为t 秒,OPQ △的面积为S ,求出S 与t 之间的函数关系式; （3）当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为极点的平行四边形的第四个极点M 的坐标． 2.解（1）A （8,0）B （0,6） ················· 1分（2）86OA OB ==，10AB ∴=点Q 由O 到A 的时光是881=（秒） ∴点P 的速度是61028+=（单位/秒） ·1分当P 在线段OB 上活动（或03t ≤≤）时,2OQ t OP t ==，2S t = ·········································································································· 1分当P 在线段BA 上活动（或38t <≤）时,6102162OQ t AP t t ==+-=-，, 如图,作PD OA ⊥于点D ,由PD AP BO AB =,得4865tPD -=, ······································· 1分21324255S OQ PD t t ∴=⨯=-+ ······································································· 1分（自变量取值规模写对给1分,不然不给分．）（3）82455P ⎛⎫ ⎪⎝⎭， ···························································································· 1分12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，，， ···················································· 3分5.在Rt △ABC 中,∠C=90°,AC = 3,AB = 5．点P 从点C 动身沿CA 以每秒1个单位长的速度向点A 匀速活动,到达点A 后连忙以本来的速度沿AC 返回;点Q 从点A 动身沿AB 以每秒1个单位长的速度向点B 匀速活动．陪同着P.Q 的活动,DE 保持垂直等分PQ,且交PQ 于点D,交折线QB-BC-CP 于点E ．点P.Q 同时动身,当点Q 到达点B 时停滞活动,点P 也随之停滞．设点P.Q 活动的时光是t 秒（t ＞0）．（1）当t = 2时,AP =,点Q 到AC 的距离是;（2）在点P 从C 向A 活动的进程中,求△APQ 的面积S与t 的函数关系式;（不必写出t 的取值规模）（3）在点E 从B 向C 活动的进程中,四边形QBED 可否成为直角梯形？若能,求t 的值．若不克不及,请解释来由; （4）当DE 经由点C 时,请直接写出t 的值． 5.解：（1）1,85;（2）作QF ⊥AC 于点F,如图3, AQ = CP= t,∴3AP t =-．由△AQF ∽△ABC,4BC =, 得45QF t =．∴45QF t =． ∴14(3)25S t t =-⋅, 即22655S t t =-+．（3）能．①当DE ∥QB 时,如图4．∵DE ⊥PQ,∴PQ ⊥QB,四边形QBED 是直角梯形．此时∠AQP=90°．P图16P图4由△APQ ∽△ABC,得AQ APAC AB=, 即335t t -=．解得98t =． ②如图5,当PQ ∥BC 时,DE ⊥BC,四边形QBED 是直角梯形．此时∠APQ =90°．由△AQP ∽△ABC,得AQ APAB AC=, 即353t t -=．解得158t =．（4）52t =或4514t =． ①点P 由C 向A 活动,DE 经由点C ．衔接QC,作QG ⊥BC 于点G,如图6．PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--．由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =．②点P 由A 向C 活动,DE 经由点C,如图7． 22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】6如图,在Rt ABC △中,9060ACB B ∠=∠=°，°,2BC =．点O 是AC 的中点,过点O 的直线l 从与AC 重合的地位开端,绕点O 作逆时针扭转,交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ,设直线l 的扭转角为α．（1）①当α=度时,四边形EDBC 是等腰梯形,此时AD 的长为;②当α=度时,四边形EDBC 是直角梯形,此时AD 的长为; （2）当90α=°时,断定四边形EDBC 是否为菱形,并解释来由．6.解（1）①30,1;②60,1.5; ……………………4分（2）当∠α=900时,四边形EDBC 是菱形. ∵∠α=∠ACB=900,∴BC//ED.∵CE//AB, ∴四边形EDBC 是平行四边形. ……………………6分在Rt △ABC 中,∠ACB=900,∠B=600,BC=2,∴∠A=300.OE CDAα lOCA （备用图）ACBPQ E D 图5AC (E ) BPQD图6GA C (E )B PQD图7G∴∴AO=12AC. ……………………8分在Rt △AOD 中,∠A=300,∴AD=2. ∴BD=2. ∴BD=BC.又∵四边形EDBC 是平行四边形,∴四边形EDBC 是菱形 ……………………10分7如图,在梯形ABCD 中,3545AD BC AD DC AB B ====︒∥，，，．动点M 从B 点动身沿线段BC 以每秒2个单位长度的速度向终点C 活动;动点N 同时从C 点动身沿线段CD 以每秒1个单位长度的速度向终点D 活动．设活动的时光为t 秒．（1）求BC 的长．（2）当MN AB ∥时,求t 的值．（3）试探讨：t 为何值时,MNC △为等腰三角形．7.解：（1）如图①,过A .D 分离作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形∴3KH AD ==． ················································································ 1分在Rt ABK △中,sin 4542AK AB =︒==．2cos 454242BK AB =︒== ··························································2分在Rt CDH △中,由勾股定理得,3HC ==∴43310BC BK KH HC =++=++= ················································· 3分（2）如图②,过D 作DG AB ∥交BC 于G 点,则四边形ADGB 是平行四边形 ∵MN AB ∥ ∴MN DG ∥ CM ADCB KHAD CBG MN∴3BG AD ==∴1037GC =-= ············································································· 4分由题意知,当M .N 活动到t 秒时,102CN t CM t ==-，． ∵DG MN ∥ ∴NMC DGC =∠∠ 又C C =∠∠ ∴MNC GDC △∽△∴CN CMCD CG =··················································································· 5分即10257t t -= 解得,5017t = ······················································································ 6分（3）分三种情形评论辩论：①当NC MC =时,如图③,即102t t =- ∴103t =·························································································· 7分②当MN NC =时,如图④,过N 作NE MC ⊥于E解法一：由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cosEC t c NC t-== 又在Rt DHC △中,3cos 5CH c CD ==∴535t t -=解得258t = ······················································································· 8分解法二：∵90C C DHC NEC =∠=∠=︒∠∠， ∴NEC DHC △∽△ ∴NC ECDC HC= ADCB MN（图③）（图④）AD CB M NH E即553t t-=∴258t = ·························································································· 8分③当MN MC =时,如图⑤,过M 作MF CN ⊥于F 点.1122FC NC t ==解法一：（办法同②中解法一）132cos 1025tFC C MC t ===-解得6017t =解法二：∵90C C MFC DHC =∠=∠=︒∠∠， ∴MFC DHC △∽△∴FC MCHC DC =即1102235tt -= ∴6017t =综上所述,当103t =.258t =或6017t =时,MNC △为等腰三角形 ······················ 9分10数学课上,张先生出示了问题：如图1,四边形ABCD 是正方形,点E 是边BC 的中点．90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F,求证：AE=EF ．经由思虑,小明展现了一种准确的解题思绪：取AB 的中点M,衔接ME,则AM=EC,易证AME ECF △≌△,所以AE EF =．在此基本上,同窗们作了进一步的研讨：（1）小颖提出：如图2,假如把“点E 是边BC 的中点”改为“点E 是边BC 上（除B,C 外）的随意率性一点”,其它前提不变,那么结论“AE=EF”仍然成立,你以为小颖的不雅点准确吗？假如准确,写出证实进程;假如不准确,请解释来由;（2）小华提出：如图3,点E 是BC 的延伸线上（除C 点外）的随意率性一点,其他前提不变,结论“AE=EF”仍然成立．你以为小华的不雅点准确吗？假如准确,写出证实进程;假如不（图⑤）A DCBH N MF10.解：（1）准确． ················································· （1分）证实：在AB 上取一点M ,使AM EC =,衔接ME ． ···· （2分）BM BE ∴=．45BME ∴∠=°,135AME ∴∠=°． CF 是外角等分线, 45DCF ∴∠=°, 135ECF ∴∠=°． AME ECF ∴∠=∠．90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠．AME BCF ∴△≌△（ASA ）． ··································································· （5分） AE EF ∴=． ························································································· （6分）（2）准确． ····················································· （7分）证实：在BA 的延伸线上取一点N ．使AN CE =,衔接NE ． ····································· （8分）BN BE ∴=．45N PCE ∴∠=∠=°．四边形ABCD 是正方形,AD BE ∴∥．DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． ································································· （10分） AE EF ∴=．（11分）11已知一个直角三角形纸片OAB ,个中9024AOB OA OB ∠===°，，．如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D ． A DF C GEBM ADFC GE BN则ACD BCD △≌△.设点C 的坐标为()()00m m >，. 则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中,由勾股定理,得222AC OC OA =+, 即()22242m m -=+,解得32m =. ∴点C 的坐标为302⎛⎫⎪⎝⎭，. ··················································································· 4分（Ⅱ）若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并肯定y 的取值规模;（Ⅱ）如图②,折叠后点B 落在OA 边上的点为B ', 则B CD BCD '△≌△. 由题设OB x OC y '==，, 则4B C BC OB OC y '==-=-,在Rt B OC '△中,由勾股定理,得222B C OC OB ''=+.()2224y y x ∴-=+,即2128y x =-+ ···························································································· 6分由点B '在边OA 上,有02x ≤≤,∴解析式2128y x =-+()02x ≤≤为所求.∴当02x ≤≤时,y 随x 的增大而减小,y ∴的取值规模为322y ≤≤. ····································································· 7分（Ⅲ）若折叠后点B 落在边OA 上的点为B ',且使B D OB '∥,求此时点C 的坐标．（Ⅲ）如图③,折叠后点B 落在OA 边上的点为B '',且B D OB ''∥. 则OCB CB D ''''∠=∠.又CBD CB D OCB CBD ''''∠=∠∴∠=∠，,有CB BA ''∥.Rt Rt COB BOA ''∴△∽△.有OB OCOA OB''=,得2OC OB ''=. ····································································· 9分在Rt B OC ''△中,设()00OB x x ''=>,则02OC x =. 由（Ⅱ）的结论,得2001228x x =-+, 解得000808x x x =-±>∴=-+，∴点C 的坐标为()016. ··································································· 10分 12如图（1）,将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E （不与点C ,D 重合）,压平后得到折痕MN ．当CE/CD=1/2时,求AM/BN 的值．类比归纳在图（1）中,若13CE CD =，则AM BN 的值等于;若14CE CD =，则AM BN 的值等于;若1CE CD n =（n 为整数）,则AMBN的值等于．（用含n 的式子暗示）接洽拓广如图（2）,将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E （不与点C D ，重合）,压平后得到折痕MN ，设()111AB CE m BC m CD n =>=，，则AMBN的值等于．（用含m n ，的式子暗示）12解：办法一：如图（1-1）,衔接BM EM BE ，，．由题设,得四边形ABNM 和四边形FENM 关于直线MN 对称．∴MN 垂直等分BE ．∴BM EM BN EN ==，． ··············································· 1分 ∵四边形ABCD 是正方形,∴902A D C AB BC CD DA ∠=∠=∠=====°,． ∵112CE CE DE CD =∴==，．设BN x =，则NE x =，2NC x =-．在Rt CNE △中,222NE CN CE =+．∴()22221x x =-+．解得54x =,即54BN =． ······················································ 3分在Rt ABM △和在Rt DEM △中, 办法指点：为了求得AM BN 的值,可先求BN .AM 的长,无妨设：AB =2 图（2） NAB C D EFM图（1）A B CDEFMNN 图（1-1）A B C EFM222AM AB BM +=,222DM DE EM +=,∴2222AM AB DM DE +=+． ····························································· 5分设AM y =，则2DM y =-，∴()2222221y y +=-+．解得14y =，即14AM =． ····································································· 6分 ∴15AM BN =． ································································································ 7分办法二：同办法一,54BN =． ·································································· 3分如图（1－2）,过点N 做NG CD ∥，交AD 于点G ,衔接BE ．∵AD BC ∥，∴四边形GDCN是平行四边形． ∴NG CD BC ==．同理,四边形ABNG 也是平行四边形．∴54AG BN ==． ∵90MN BE EBC BNM ⊥∴∠+∠=，°． 90NG BC MNG BNM EBC MNG ⊥∴∠+∠=∴∠=∠，°，．在BCE △与NGM △中90EBC MNG BC NG C NGM ∠=∠⎧⎪=⎨⎪∠=∠=⎩，，°．∴BCE NGM EC MG =△≌△，． ·································· ５分 ∵114AM AG MG AM =--=5，=．4 ····················································· 6分 ∴15AM BN =． ··················································································· 7分 12..如图所示,在直角梯形ABCD 中,AD//BC,∠A ＝90°,AB ＝12,BC ＝21,AD=16.动点P 从点B 动身,沿射线BC 的偏向以每秒2个单位长的速度活动,动点Q 同时从点A 动身,在线段AD 上以每秒1个单位长的速度向点D 活动,当个中一个动点到达端点时另一个动点也随之停滞活动.设活动的时光为t （秒）.（1）设△DPQ 的面积为S,求S 与t 之间的函数关系式;（2）当t 为何值时,四边形PCDQ 是平行四边形？（3）分离求出出当t 为何值时,① PD ＝PQ,② DQ ＝PQ ？类比归纳N 图（1-2） A B C D EF M G25（或410）;917;()2211n n -+ ······································································ 10分接洽拓广 2222211n m n n m -++ ······················································································· 12分解1：依题意,得AQ=t,BP=2t,QD=16-t.过点Q 作QF ⊥BP,又∵AQ‖BF,∴∠ABP=90°∴四边形AQFB 是矩形∴AQ=BF=t ∵BP=2t ∴FP=t,∴在Rt △QFP 中,QP=√(12²+t²)又∵QD=QP=PD ∴√(12²+t²)=16-t ∴12²+t²=16²-2*16*t+t²∴解得:t=7/2解2：如图所示,:这P 作PE 垂直AD 于E,垂足为E 点,则ABPE 为矩形.PE=AB=12;AE=BP(1).s=1/2×AB×DQ=1/2×12×(AD-AQ)=6×(16-t)=96-6t;(2).当 BC-2t=21-2t=PC=DQ=AD-t=16-t,即t=5时,四边形PCDQO 为平形四边形.(3).①QE=AE-AQ=BP-AQ=2t-t=t,而ED=AD-AE=16-BP=16-2t;当QE=ED 时,PE 为QD 的垂直等分线时,PQ=PD,而此时t=16-2t; t=16/3;所以当t=16/3时,PD=PQ;.②在Rt △PEQ 中,PE=AB=12; EQ=AE-AQ=PB-AQ=2t-t=t; PQ²=QE²+PE²=t²+12²; QD²=(AD-AQ)²=(16-t)²; 所以当t²+12²=(16-t)²,即:t=3.5时,DQ=PQ;解：因为∠C=90°,∠CBA=30°,BC=20√3所以可求出AB ＝40如图,圆心从A 向B 的偏向活动时,共有三个地位能使此圆与直线AC 或直线BC 相切当圆心在O1点时,设切点为P显然PO1＝6,∠APO1＝90°,∠AO1P＝30°所以AO1＝4√3因为圆O以2个单位长度/秒的速度向右活动所以当t1＝4√3/2＝2√3（秒）时,圆O与直线AC相切当圆心在O2点时,设切点为Q显然QO2＝6,∠BQO2＝90°,∠QBO2＝30°所以BO2＝12,AO2＝40－12＝28因为圆O以2个单位长度/秒的速度向右活动所以当t2＝28/2＝14（秒）时,圆O与直线BC相切当圆心在O3点时,设切点为R显然RO3＝6,∠BRO3＝90°,∠RBO3＝30°所以BO3＝12,AO3＝40＋12＝52因为圆O以2个单位长度/秒的速度向右活动所以当t3＝52/2＝26（秒）时,圆O与直线BC相切综上所述,当圆O活动2√3秒.14秒.26秒时与△ABC的一边地点的直线相切.。

(完整版)初二数学动点问题练习(含答案)

eandr动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥ BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时，四边形是平行四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中，∠ACB=900，∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC.在Rt△AOD中，∠A=300，∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形，∴四边形EDBC是菱形4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD＋BE；(2)当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等AA（备用图）CBAED图1NMA BCDEMN图2ACBEDNM图3量关系，并加以证明.解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等)∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，又∵AC=BC ，∴△ACD ≌△CBE ， ∴AD=CE ，CD=BE ， ∴DE=CD-CE=BE-AD.5、数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠= ，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ．BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°．CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°． AME ECF ∴∠=∠．90AEB BAE ∠+∠= °，90AEB CEF ∠+∠=°，∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形， AD BE ∴∥．DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）．AE EF ∴=．6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t.求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值AD F C GB图1ADFC GEB图3A DFC GB 图2AD FC GE B MADFGE BNAllthisinth7、如图1，在等腰梯形ABCD中，AD BC∥，E是AB的中点，过点E作EF BC∥交CD于点F．46AB BC==，，60B=︒∠.求：（1）求点E到BC的距离；（2）点P为线段EF上的一个动点，过P作PM EF⊥交BC于点M，过M作MN AB∥交折线ADC于点N，连结PN，设EP x=.①当点N在线段AD上时（如图2），PMN△的形状是否发生改变？若不变，求出PMN△的周长；若改变，请说明理由；②当点N在线段DC上时（如图3），是否存在点P，使PMN△为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由解（1）如图1，过点E作EG BC⊥于点G．∵E为AB的中点，∴122BE AB==．在Rt EBG△中，60B=︒∠，∴30BEG=︒∠．∴112BG BE EG====，．即点E到BCA DA DEBFC图4（备用）A DEBFC图5（备用）A DEBFC图1图2A DEBFCPNM图3A DEBFCPNM（第25题）si（2）①当点N在线段AD上运动时，PMN△的形状不发生改变．∵PM EF EG EF⊥⊥，，∴PM EG∥．∵EF BC∥，∴EP GM=，PM EG==同理4MN AB==．如图2，过点P作PH MN⊥于H，∵MN AB∥，∴6030NMC B PMH==︒=︒∠∠，∠．∴12PH PM==∴3cos302MH PM=︒=A．则35422NH MN MH=-=-=．在Rt PNH△中，PN===∴PMN△的周长=4PM PN MN++=++．②当点N在线段DC上运动时，PMN△的形状发生改变，但MNC△恒为等边三角形．当PM PN=时，如图3，作PR MN⊥于R，则MR NR=．类似①，32MR=∴23MN MR==．∵MNC△是等边三角形，∴3MC MN==．此时，6132x EP GM BC BG MC===--=--=．当MP MN=时，如图4，这时MC MN MP===此时，615x EP GM===--=当NP NM=时，如图5，30NPM PMN==︒∠∠．则120PMN=︒∠，又60MNC=︒∠，∴180PNM MNC+=︒∠∠．因此点P与F重合，PMC△为直角三角形．∴tan301MC PM=︒=A．此时，6114x EP GM===--=．综上所述，当2x=或4或(5时，PMN△为等腰三角形．8、如图，已知ABC△中，10AB AC==厘米，8BC=厘米，点D为AB的中点．(1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等，经过1秒后，BPD△与CQP△是否全等，请说明理由；图3A DEBFCPNM图4A DEBFCPMN图5A DEBF（PCMNGGRG图2A DEBFCPNMGH②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米，∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△．②∵P Qv v ≠，∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

数学动点问题练习(含答案)

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1.梯形ABCD中.AD∥ BC.∠B=90°.AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动.点Q从C开始沿CB向点B以2 cm/秒的速度移动.如果P.Q分别从A.C同时出发.设移动时间为t秒。

当t= 时.四边形是平行四边形；6当t= 时.四边形是等腰梯形. 82、如图2.正方形ABCD的边长为4.点M在边DC上.且DM=1.N为对角线AC上任意一点.则DN+MN的最小值为 53、如图.在Rt ABC△中.9060ACB B∠=∠=°，°.2BC=．点O是AC的中点.过点O的直线l从与AC重合的位置开始.绕点O作逆时针旋转.交AB边于点D．过点C作CE AB∥交直线l于点E.设直线l的旋转角为α．（1）①当α=度时.四边形EDBC是等腰梯形.此时AD的长为；②当α=度时.四边形EDBC是直角梯形.此时AD的长为；（2）当90α=°时.判断四边形EDBC是否为菱形.并说明理由．解：（1）①30.1；②60.1.5；（2）当∠α=900时.四边形EDBC是菱形.∵∠α=∠ACB=900.∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形在Rt△ABC中.∠ACB=900.∠B=600,BC=2, ∴∠A=300.∴AB=4,AC∴AO=12AC在Rt△AOD中.∠A=300.∴AD=2.∴BD=2. ∴BD=BC. 又∵四边形EDBC是平行四边形.∴四边形EDBC是菱形4、在△ABC中.∠ACB=90°.AC=BC.直线MN经过点C.且AD⊥MN于D.BE⊥MN于E.（备用图）CEDNM CDMCEM(1)当直线MN 绕点C 旋转到图1的位置时.求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时.求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时.试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系.并加以证明.解：（1）① ∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB② ∵△ADC ≌△CEB ∴CE=AD.CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE 又∵AC=BC ∴△ACD ≌△CBE ∴CE=AD.CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时.DE=BE-AD(或AD=BE-DE.BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE. 又∵AC=BC. ∴△ACD ≌△CBE. ∴AD=CE.CD=BE. ∴DE=CD-CE=BE-AD.5、数学课上.张老师出示了问题：如图1.四边形ABCD 是正方形.点E 是边BC 的中点．90AEF ∠=.且EF 交正方形外角DCG ∠的平行线CF 于点F .求证：AE =EF ．经过思考.小明展示了一种正确的解题思路：取AB 的中点M .连接ME .则AM =EC .易证AME ECF△≌△.所以AE EF =．在此基础上.同学们作了进一步的研究：（1）小颖提出：如图2.如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B .C 外）的任意一点”.其它条件不变.那么结论“AE =EF ”仍然成立.你认为小颖的观点正确吗？如果正确.写出证明过程；如果不正确.请说明理由；（2）小华提出：如图3.点E 是BC 的延长线上（除C 点外）的任意一点.其他条件不变.结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确.写出证明过程；如果不正确.请说明理由．解：（1）正确．证明：在AB 上取一点M .使AM EC =.连接ME ．BM BE ∴=．45BME ∴∠=°.135AME ∴∠=°． CF 是外角平分线.45DCF ∴∠=°.135ECF ∴∠=°．AME ECF ∴∠=∠．90AEB BAE ∠+∠=°.90AEB CEF ∠+∠=°. ∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取一点N ．使AN CE =.连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°．四边形ABCD 是正方形. AD BE ∴∥．ADFCGB图1A DF ADFC GE B 图2ADFC GB M ADFNDAE BEA∴∠=∠．NAE CEF∴∠=∠．ANE ECF∴△≌△（ASA）．AE EF∴=．6、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动.设P的运动时间为t.求（1）△ PAB为等腰三角形的t值；（2）△ PAB为直角三角形的t值；（3）若AB=5且∠ABM=45 °.其他条件不变.直接写出△ PAB为直角三角形的t值7、如图 1.在等腰梯形ABCD中.AD BC∥.E是AB的中点.过点E作EF BC∥交CD于点F．46AB BC==，.60B=︒∠.求：（1）求点E到BC的距离；（2）点P为线段EF上的一个动点.过P作PM EF⊥交BC于点M.过M作MN AB∥交折线ADC 于点N.连结PN.设EP x=.①当点N在线段AD上时（如图2）.PMN△的形状是否发生改变？若不变.求出PMN△的周长；若改变.请说明理由；②当点N在线段DC上时（如图3）.是否存在点P.使PMN△为等腰三角形？若存在.请求出所有满足要求的x的值；若不存在.请说明理由A DEBFCA DEBFCA DEBFC图1 图2A DEBFCPNM图3A DEBFCPNM（第25题）解（1）如图1.过点E 作EG BC ⊥于点G ． ∵E 为AB 的中点. ∴122BE AB ==．在Rt EBG △中.60B =︒∠， ∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC（2）①当点N 在线段AD 上运动时.PMN △的形状不发生改变． ∵PM EF EG EF ⊥⊥，， ∴PM EG ∥．∵EF BC ∥， ∴EP GM =.PM EG == 同理4MN AB ==．如图2.过点P 作PH MN ⊥于H .∵MN AB ∥，∴6030NMC B PMH ==︒=︒∠∠，∠．∴122PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中.PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时.PMN △的形状发生改变.但MNC △恒为等边三角形．当PM PN =时.如图3.作PR MN ⊥于R .则MR NR =．类似①.32MR =．∴23MN MR ==． ∵MNC △是等边三角形.∴3MC MN ==．此时.6132x EP GM BC BG MC ===--=--=．图3A D E BFCPN M图4A D EBF CP MN 图5A D EBF （P ） CMN GGRG图1 A D E BF CG图2A D E BFCPNMG H当MP MN =时.如图4.这时MC MN MP ===此时.615x EP GM ===-=- 当NP NM =时.如图5.30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合.PMC △为直角三角形． ∴tan301MC PM =︒=．此时.6114x EP GM ===--=．综上所述.当2x =或4或(5-时.PMN △为等腰三角形．8、如图.已知ABC △中.10AB AC ==厘米.8BC =厘米.点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动.同时.点Q 在线段CA 上由C 点向A 点运动 ①若点Q 的运动速度与点P 的运动速度相等.经过1秒后.BPD △与CQP △是否全等.请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等.当点Q 的运动速度为多少时.能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发.点P 以原来的运动速度从点B 同时出发.都逆时针沿ABC △三边运动.求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒. ∴313BP CQ ==⨯=厘米. ∵10AB =厘米.点D 为AB 的中点. ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米. ∴835PC =-=厘米. ∴PC BD =．又∵AB AC =. ∴B C ∠=∠. ∴BPD CQP △≌△． ②∵P Qv v ≠. ∴BP CQ ≠. 又∵BPD CQP △≌△.B C ∠=∠.则45BP PC CQ BD ====，.∴点P .点Q 运动的时间433BP t ==秒. ∴515443Q CQ v t===厘米/秒。

初中数学动点问题及练习题附参考答案

例 1.如图，已知在矩形 AB C D 中，A D=8，C D=4，点 E 从点 D 出发，沿线段 DA 以每秒 1 个单位长的速度向点 A 方向移动，同时点 F 从点 C 出发，沿射线 C D 方向以每秒 2 个单位长的速度移动，当B ，E ，F 三点共线时，两点同时停止运动．设点E 移动的时间为 t （秒）．（1）求当 t 为何值时，两点同时停止运动；（2）设四边形 BC FE 的面积为 S ，求 S 与 t 之间的函数关系式，并写出 t 的取值范围；（3）求当 t 为何值时，以 E ，F ，C 三点为顶点的三角形是等腰三角形；（4）求当 t 为何值时，∠BEC=∠BF C ．E AD FOBC例 2. 正方形 AB C D M B C C D、 M 上的两个动点，当点在边长为 4，、 N 分别是 B C A M M N和垂直，上运动时，保持（1）证明：Rt △AB M ∽Rt △M C N；B Mx AB C Ny y x M的面积为，求与之间的函数关系式；当点运动到（2）设，梯形 AB C N 什么位置时，四边形 M 面积最大，并求出最大面积；，求此时的值．x （3）当点运动到什么位置时Rt △AB M ∽Rt △A M NA DNBCM例 3.如图，在梯形 AB C DA D ∥BC ，A D 3，D C 5，AB 4 2，∠B 45．动中， M B B CC C 以每秒 2 个单位长度的速度向终点运动；动点 N 同时从点点从点出发沿线段出发沿线段C D以每秒 1 个单位长度的速度向终点运动．设运动的时间为秒． t D B C （09 年济南中考）（1）求的长。

A DM N ∥ ABt 时，求的值．（2）当 t△M N C 为等腰三角形．（3）试探究：为何值时， N BCM例 1. 解：（1）当 B ，E ，F 三点共线时，两点同时停止运动，如图2 所示．………（1 分）由题意可知：E D =t ，BC=8，F D= 2t -4，FC= 2t ．FFD ED∵E D ∥B C ，∴△FE D ∽△FB C ．∴． EFCBCABD2t 4 t∴．解得 t=4． 2t8 C图 2∴当 t=4 时，两点同时停止运动；……（3 分）1 1（2）∵E D =t ，CF =2t ， ∴S=S + S = ×8×4+ ×2t ×t=16+ t 2．△BCE △BCF 2 2即 S=16+ t 2．（0 ≤t ≤4）；………………………………………………………（6 分）（3）①若 EF =EC 时，则点 F 只能在 C D 的延长线上，(2t 4) t 5t 16t 16 ，∵EF 2= 22 2 4t t 16 5t 16t 16 t 16 = 2 ．∴t=4 或 t=0（舍去）；E C = 2 ，∴ 2 2 2 2 44 t t 16 t 16 =4t 2．∴t，FC 2=4t 2，∴ 23 ； ②若 EC =F C 时，∵EC 2= 22 23 (2t 4) t 5t 16t 16 ③若 EF =F C 时，∵EF 2= ，FC 2=4t 2， 22 2 5t 16t 16 16 83 16 8 3 ．∴ 2 =4t 2．∴t = （舍去），t =1 2 43 16 8 3，时，以 E ，F ，C 三点为顶点的三角形是等腰三∴当 t 的值为 4， 3 角形；………………………………………………………………………………（9 分）B C CFC D E D 2 ，（4）在 Rt △BCF 和 Rt △CE D 中，∵∠BC D=∠C D E =90°，∴Rt △BCF ∽Rt △C E D ．∴∠BF C=∠CE D ．………………………………………（10 分）∵A D ∥B C ，∴∠B CE=∠CE D ．若∠BEC=∠BF C ，则∠BE C=∠BCE ．即 BE=B C ．t16t 80 ∵BE 2= 2t 16t 80，∴ 2=64．16 8 3 16 8 3 ．∴t = （舍去），t = 1 2∴当 t=16 8 3时，∠BEC=∠BFC ．……………………………………………（12 分）AB C D 例 2. 解：（1）在正方形中，AB BC C D 4，B C 90° ， DAA M ⊥M N ， A M N 90° ，C M N AM B 90° ，Rt △AB M 中，MAB A MB 90°在， C M N MAB N，Rt △AB M ∽Rt △M C N ， CBRt △AB M ∽Rt △M C N （2）， MAB B M M C C N 4x ，， 4 x CNx 4x2 CN ，41 x 4x 1 12 y S4·4 x 2x 8 x 2 10 2 2 ， 2 4 2 2 梯形ABC Nx 2 y 当时，取最大值，最大值为 10．（3）B AM N 90°，A M AB要使△AB M ∽△A M N ，必须有，M N B MA M AB由（1）知， M N M CB M MC ，当点 M 运动到 B C 的中点时，△AB M ∽△A M Nx 2，此时．A D A K BC K D HBC A D H K于，于 H ，则四边形例 3.解：（1）如图①，过、分别作是矩形K H AD 3．∴ 在 2Rt △ABK A K AB s in 45 4 2． 4 中， 2 2 B K AB cos 45 4 2 42Rt △C D H H C 5 4 3 在 ∴ 中，由勾股定理得， 22 B C BK K HHC 4 3 3 10ADADNBCBCK HG M（图①）（图②）D D G ∥ AB BC G A D G B是平行四边形（2）如图②，过作交于点，则四边形 M N ∥ ABM N ∥D G B G AD 3∵ ∴ ∴ ∴G C 10 3 7M N C Nt ，C M 10 2t ．由题意知，当、运动到t 秒时， D G ∥M N∵ ∴∠N M C ∠DG C 又∠C ∠C∴△M N C ∽△G D C即 t 10 2t 5 7 50 17解得，t （3）分三种情况讨论：N C M C 时，如图③，即t 10 2t10 ①当 ∴t3AD ADNNBCBCEM H M（图④）（图③）M N NCN N E M C E 时，如图④，过作于 ②当 ∵∠C ∠C ，D H C NEC 90∴△NE C ∽△D H CN C E CD C H C ∴即 t 5t 5 3 25 ∴t81 1M N M C MM F CN 作 F C NC t 于 F 点. ③当时，如图⑤，过 2 2 AD∵∠C∠C ，M F C D H C 90∴△M F C ∽△D H C F C M CN ∴H C D CF1B CtH M10 2t2 即3 5 （图⑤） 60 17∴t103 25 8 60 17 综上所述，当t 、t 或t时，△M N C 为等腰三角形即 t 10 2t 5 7 50 17解得，t （3）分三种情况讨论：N C M C 时，如图③，即t 10 2t10 ①当 ∴t3AD ADNNBCBCEM H M（图④）（图③）M N NCN N E M C E 时，如图④，过作于 ②当 ∵∠C ∠C ，D H C NEC 90∴△NE C ∽△D H CN C E CD C H C ∴即 t 5t 5 3 25 ∴t81 1M N M C MM F CN 作 F C NC t 于 F 点. ③当时，如图⑤，过 2 2 AD∵∠C∠C ，M F C D H C 90∴△M F C ∽△D H C F C M CN ∴H C D CF1B CtH M10 2t2 即3 5 （图⑤） 60 17∴t103 25 8 60 17 综上所述，当t 、t 或t时，△M N C 为等腰三角形即 t 10 2t 5 7 50 17解得，t （3）分三种情况讨论：N C M C 时，如图③，即t 10 2t10 ①当 ∴t3AD ADNNBCBCEM H M（图④）（图③）M N NCN N E M C E 时，如图④，过作于 ②当 ∵∠C ∠C ，D H C NEC 90∴△NE C ∽△D H CN C E CD C H C ∴即 t 5t 5 3 25 ∴t81 1M N M C MM F CN 作 F C NC t 于 F 点. ③当时，如图⑤，过 2 2 AD∵∠C∠C ，M F C D H C 90∴△M F C ∽△D H C F C M CN ∴H C D CF1B CtH M10 2t2 即3 5 （图⑤） 60 17∴t103 25 8 60 17 综上所述，当t 、t 或t时，△M N C 为等腰三角形。

初二数学动点问题练习（含答案）

初⼆数学动点问题练习（含答案）动态问题所谓“动点型问题”是指题设图形中存在⼀个或多个动点,它们在线段、射线或弧线上运动的⼀类开放性题⽬.解决这类问题的关键是动中求静,灵活运⽤有关数学知识解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动，点Q从C开始沿CB向点B以2 cm/秒的速度移动，如果P，Q分别从A，C同时出发，设移动时间为t秒。

当t= 时，四边形是平⾏四边形；6当t= 时，四边形是等腰梯形. 82、如图2，正⽅形ABCD的边长为4，点M在边DC上，且DM=1，N为对⾓线AC上任意⼀点，则DN+MN的最⼩值为 53、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转⾓为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直⾓梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．解：（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC是菱形.∵∠α=∠ACB=900，∴BC//ED. ∵CE//AB, ∴四边形EDBC是平⾏四边形在Rt△ABC中，∠ACB=900，∠B=600,BC=2, ∴∠A=300.∴AB=4,AC=23. ∴AO=12AC=3.在Rt△AOD中，∠A=300，∴AD=2.∴BD=2. ∴BD=BC. ⼜∵四边形EDBC是平⾏四边形，∴四边形EDBC是菱形4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD＋BE；(2)当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明. OE CDAαlOCA（备⽤图）CBAED图1NMA BCDEMACBEDNM解：（1）①∵∠ACD=∠ACB=90° ∴∠CAD+∠ACD=90° ∴∠BCE+∠ACD=90° ∴∠CAD=∠BCE ∵AC=BC ∴△ADC ≌△CEB②∵△ADC ≌△CEB ∴CE=AD ，CD=BE ∴DE=CE+CD=AD+BE (2) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ⼜∵AC=BC ∴△ACD ≌△CBE ∴CE=AD ，CD=BE ∴DE=CE-CD=AD-BE(3) 当MN 旋转到图3的位置时，DE=BE-AD(或AD=BE-DE ，BE=AD+DE 等) ∵∠ADC=∠CEB=∠ACB=90° ∴∠ACD=∠CBE ，⼜∵AC=BC ，∴△ACD ≌△CBE ，∴AD=CE ，CD=BE ，∴DE=CD-CE=BE-AD.5、数学课上，张⽼师出⽰了问题：如图1，四边形ABCD 是正⽅形，点E 是边BC 的中点．90AEF ∠=o，且EF 交正⽅形外⾓DCG ∠的平⾏线CF 于点F ，求证：AE =EF ．经过思考，⼩明展⽰了⼀种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进⼀步的研究：（1）⼩颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意⼀点”，其它条件不变，那么结论“AE =EF ”仍然成⽴，你认为⼩颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）⼩华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意⼀点，其他条件不变，结论“AE =EF ”仍然成⽴．你认为⼩华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取⼀点M ，使AM EC =，连接ME ． BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°． CF Q 是外⾓平分线，45DCF ∴∠=°，135ECF ∴∠=°．AME ECF ∴∠=∠． 90AEB BAE ∠+∠=Q °，90AEB CEF ∠+∠=°，∴BAE CEF ∠=∠． AME BCF ∴△≌△（ASA ）． AE EF ∴=．（2）正确．证明：在BA 的延长线上取⼀点N ．使AN CE =，连接NE ．BN BE ∴=． 45N PCE ∴∠=∠=°． Q 四边形ABCD 是正⽅形， AD BE ∴∥． DAE BEA ∴∠=∠． NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． AE EF ∴=． 6、如图, 射线MB 上,MB=9,A 是射线MB 外⼀点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB ⽅向以1个单位/秒的速度移动，设P 的运动时间为t. 求（1）△ PAB 为等腰三⾓形的t 值；（2）△ PAB 为直⾓三⾓形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直⾓三⾓形的t 值AD FGB 图1 A D FC G B 图3A D FGB 图2A D F C GE B M A D FG B N7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =?∠.求：（1）求点E 到BC 的距离；（2）点P 为线段EF 上的⼀个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PMN △的形状是否发⽣改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三⾓形？若存在，请求出所有满⾜要求的x 的值；若不存在，请说明理由解（1）如图1，过点E 作EG BC ⊥于点G ．∵E 为AB 的中点，∴122BE AB ==．在Rt EBG△中，60B =?∠，∴30BEG =?∠．∴112BG BE EG =即点E 到BC（2）①当点N 在线段AD 上运动时，PMN △的形状不发⽣改变．∵PM EF EG EF ⊥⊥，，∴PM EG ∥．∵EF BC ∥，∴EP GM =，PM EG ==同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥，∴6030NMC B PMH ==?=?∠∠，∠．∴12PH PM == ∴3cos302MH PM =?=g ．则35422NH MN MH =-=-=．图1 A D E BF CGA D E BFCPNMG HA D E BF C图4（备⽤）AD EBF C 图5（备⽤）A D E BF CA D E BF C PNM图3A D EBFCPNM（第25题）在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形状发⽣改变，但MNC △恒为等边三⾓形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==．∵MNC △是等边三⾓形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN=时，如图4，这时MC MN MP ===此时，615x EP GM ===--= 当NP NM =时，如图5，30NPM PMN ==?∠∠．则120PMN =?∠，⼜60MNC =?∠，∴180PNM MNC +=?∠∠．因此点P 与F 重合，PMC △为直⾓三⾓形．∴tan301MC PM =?=g ．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5-时，PMN △为等腰三⾓形．8、如图，已知ABC △中，10AB AC ==厘⽶，8BC =厘⽶，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第⼀次在ABC △的哪条边上相遇？解：（1）①∵1t =秒，∴313BP CQ ==?=厘⽶，∵10AB =厘⽶，点D 为AB 的中点，∴5BD =厘⽶．图3A D E BFCPN M图4A D EBF CP MN 图5A DEBF （P ） CM NGGRG⼜∵8PC BC BP BC =-=，厘⽶，∴835PC =-=厘⽶，∴PC BD =．⼜∵AB AC =，∴B C ∠=∠，∴BPD CQP △≌△．②∵P Qv v ≠，∴BP CQ ≠，⼜∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒，∴515443Q CQ v t===厘⽶/秒。

初二数学动点问题练习(含答案)

当t= 时，四边形是平行四边形；当t= 时，四边形是等腰梯形.2、如图2，正方形ABCD的边长为4，点M在边DC上，且DM=1，N为对角线AC上任意一点，则DN+MN的最小值为3、如图，在Rt ABC△中，9060ACB B∠=∠=°，°，2BC=．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE AB∥交直线l于点E，设直线l的旋转角为α．（1）①当α=度时，四边形EDBC是等腰梯形，此时AD的长为；②当α=度时，四边形EDBC是直角梯形，此时AD的长为；（2）当90α=°时，判断四边形EDBC是否为菱形，并说明理由．4、在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.（备用图）CBED图1NMA BCDEMACBEDNM图3(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE=AD ＋BE ； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD-BE ；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明.6、如图, 射线MB 上,MB=9,A 是射线MB 外一点,AB=5且A 到射线MB 的距离为3,动点P 从M 沿射线MB 方向以1个单位/秒的速度移动，设P 的运动时间为t. 求（1）△ PAB 为等腰三角形的t 值；（2）△ PAB 为直角三角形的t 值；（3）若AB=5且∠ABM=45 °，其他条件不变，直接写出△ PAB 为直角三角形的t 值7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠.求：（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PM N △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由解（1）如图1，过点E 作EG BC ⊥于点G ． ∵E 为AB 的中点， ∴122BE AB ==．在Rt EBG △中，60B =︒∠， ∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC（2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变．∵PM EF EG EF ⊥⊥，， ∴PM EG ∥． ∵EF BC ∥， ∴EP GM =，PM EG == 同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥，∴6030NMC B PMH ==︒=︒∠∠，∠．∴12PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==． ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．图1 A D E BF CG图2A D E BFCPNMG HA D E BFC图4（备用）ADEBF C图5（备用）A D E BF C图1 图2A D E BF C PNM图3A D EBF C PN M （第25题）当MP MN =时，如图4，这时MC MN MP ===此时，615x EP GM ===-= 当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5-时，PMN △为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．(1）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

七年级动点问题20道含答案

七年级动点问题20道含答案一、七年级动点问题20道1. 函数$y=3cos\frac{3\pi x}{4}$的图像称作：(A.余弦曲线)2. 斜率等于负一，斜截式为$y=7x-5$的直线称作：(B.负斜率直线)3. 求函数$f(x)=x^3-7x+2$在$x=2$处取得最大值：(D.8)4. 直线$y=mx+b$中，m 为：(A.斜率)5. 闭合曲线$\frac{x^2}{4}+\frac{y^2}{9}=1$在$x$=4处的坐标是：(C. $(4,\frac{3}{2})$)6. 函数$f(x)=2x^{2}-3$的最小值是：(B. -3)7. 函数$f(x)=\frac{x^2}{2}+1$的图像是：(A.抛物线)8. 函数$f(x)=2x+5$的大致图象是：(B.直线)9. 三维坐标中，z 轴表示的为：(C.高度)10. 绘制抛物线需要：(A.二个点)11. 点$A(-1,2)$绕原点旋转$90^{\circ}$后，其新坐标是：(B. $(2,-1)$)12. 子弹以15米/秒的速度射出，它从出射点到返回出射点所需要的时间为：(B.2秒)13. 平面内的向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为30°，且$|\overrightarrow{a}|=3$，$|\overrightarrow{b}|=4$，则$\overrightarrow{a}\cdot\overrightarrow{b}$ 为：(D.6)14. 直线$y=2/3x-3$的斜率为：(B. 2/3)15. 一个三角形的两个锐角都为$60^{\circ}$，则这个三角形是：(D.等腰三角形)16. 半径为4的圆的面积为：(B.50.27公分平方）17. 在正方形ABCD中，点P到边AB的距离是4，A点到点P的垂直平分线的距离为：(D. 2)18. 圆$x^{2}+y^{2}+8x+2y-13=0$的圆心坐标是：(C. (-4, -1))19. $f(x)=-2x^2+4$的最小值是：(A. 0)20. 角A,B,C构成的夹角是60度，AB=5,BC=7，AC=：(B. 8)二、七年级动点文章今天，我们就来一起练习一下关于七年级动点的知识吧！首先，对于函数问题，函数$y=3cos\frac{3\pi x}{4}$的图像应当称作余弦曲线。

中考数学动点问题专题练习(含答案)

动点专题一、应用勾股定理建立函数解析式例1(2000年·上海)如图1，在半径为6，圆心角为90°的扇形OAB 的弧ＡB 上,有一个动点P,ＰH ⊥O Ａ,垂足为H,△OPH 的重心为G ．（1)当点Ｐ在弧AB 上运动时，线段ＧO 、GP 、GH 中,有无长度保持不变的线段？如果有，请指出这样的线段，并求出相应的长度．(２)设P Ｈx =,GP y =，求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围)．(3）如果△PG Ｈ是等腰三角形,试求出线段PH 的长．二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ＡBC 中,ＡＢ=AC ＝1,点D,Ｅ在直线B Ｃ上运动.设BD=,x ＣＥ=y . (1)如果∠B ＡC=3０°,∠DA Ｅ=105°,试确定y 与x 之间的函数解析式;(２)如果∠B ＡＣ的度数为α,∠DAE 的度数为β,当α，β满足怎样的关系式时,（1)中y 与x 之间的函数解析式还成立?试说明理由.AEDCB 图2H M NG PO A B 图1 x yC三、应用求图形面积的方法建立函数关系式例4(２0０4年·上海）如图,在△A ＢＣ中,∠BAC ＝９0°,AB=AC ＝22,⊙A 的半径为1.若点Ｏ在BC 边上运动(与点B 、C 不重合)，设ＢO=x ,△AOC 的面积为y .（1）求y 关于x 的函数解析式，并写出函数的定义域．(2)以点O 为圆心,BO 长为半径作圆Ｏ，求当⊙O 与⊙Ａ相切时， △AO Ｃ的面积．一、以动态几何为主线的压轴题（一）点动问题．１.(09年徐汇区)如图，ABC ∆中，10==AC AB ,12=BC ，点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ，交射线CA 于点F . (1)当6=AE 时，求AF 的长；（２)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; （3）当以边AC 为直径的⊙O 与线段DE 相切时,求BE的长．AB C O 图8HAB CDEOlA ′(二）线动问题2,在矩形A ＢＣD 中,AB ＝3,点O 在对角线A Ｃ上，直线ｌ过点O ，且与AC 垂直交ＡＤ于点E ．（1)若直线l 过点B,把△ABE 沿直线l 翻折,点A 与矩形A ＢＣＤ的对称中心A ＇重合，求BC 的长; （2)若直线l 与AB 相交于点F,且ＡＯ=41AC,设AD 的长为x ,五边形ＢＣDEF 的面积为S.①求S 关于x 的函数关系式，并指出x 的取值范围;②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在，请求出x 的值;若不存在,请说明理由．(三)面动问题３.如图，在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点（D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG .(１）试求ABC ∆的面积；(２)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =，ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4）当BDG ∆是等腰三角形时,请直接写出AD 的长.解决动态几何问题的常见方法有:C一、特殊探路,一般推证例２:（２00４年广州市中考题第11题)如图,⊙O １和⊙Ｏ2内切于A,⊙O1的半径为３，⊙O2的半径为2，点Ｐ为⊙O1上的任一点（与点A 不重合)，直线ＰA 交⊙O2于点Ｃ,PB 切⊙O2于点B ，则PCBP的值为(A)2 (Ｂ）3 （C)23（Ｄ)26二、动手实践,操作确认例４(２003年广州市中考试题）在⊙Ｏ中，C 为弧AB 的中点,D 为弧A Ｃ上任一点(与A 、C 不重合）,则(A)A Ｃ+CB=AD+ＤB (B) A Ｃ＋C Ｂ<AD+DB（Ｃ） AC+CB ＞A Ｄ＋D Ｂ（D) ＡＣ+C Ｂ与AD+ＤB 的大小关系不确定例５:如图，过两同心圆的小圆上任一点C 分别作小圆的直径CA 和非直径的弦CD ，延长CA 和C Ｄ与大圆分别交于点B 、Ｅ，则下列结论中正确的是( ＊ ) （A)AB DE = (B ）AB DE >(Ｃ）AB DE <(D ）AB DE ,的大小不确定三、建立联系，计算说明例6:如图,正方形ABCD 的边长为4,点Ｍ在边DC 上,且ＤM=１,Ｎ为对角线A Ｃ上任意一点,则ＤN ＋ＭN 的最小值为 .BMND CBA以圆为载体的动点问题中,AC＝５，ＢC=12，∠ＡCＢ＝90°,P是ＡB边上的动点（与点A、B不重例1．在Rt ABC合）,Q是BC边上的动点（与点B、C不重合),当PQ与ＡＣ不平行时，△CPＱ可能为直角三角形吗?若有可能，请求出线段CＱ的长的取值范围；若不可能,请说明理由。

数学动点问题专项训练

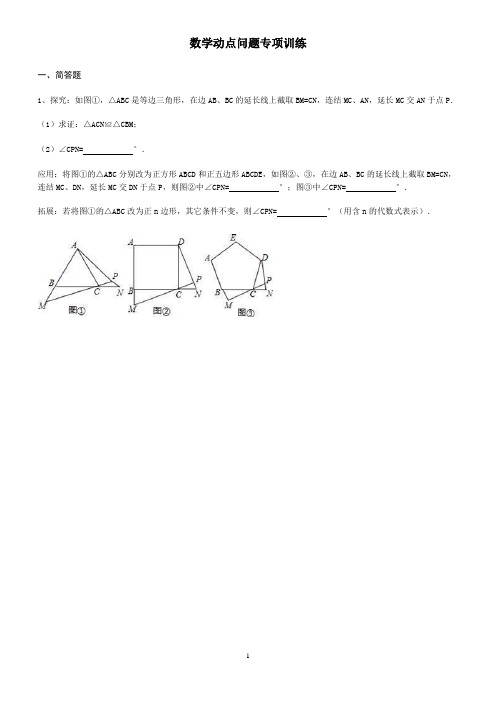
数学动点问题专项训练一、简答题1、探究：如图①，△ABC是等边三角形，在边AB、BC的延长线上截取BM=CN，连结MC、AN，延长MC交AN于点P．（1）求证：△ACN≌△CBM；（2）∠CPN= °．应用：将图①的△ABC分别改为正方形ABCD和正五边形ABCDE，如图②、③，在边AB、BC的延长线上截取BM=CN，连结MC、DN，延长MC交DN于点P，则图②中∠CPN= °；图③中∠CPN= °．拓展：若将图①的△ABC改为正n边形，其它条件不变，则∠CPN= °（用含n的代数式表示）．2、已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点O．点E从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点F从点C出发，沿CD方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接EO并延长，交BC于点G，．设运动时间为t（s）（0＜t＜6），解答下列问题：(1)在运动的过程中，四边形EGCD的面积是否发生变化，请说明理由；如果不变化，并请求出四边形EGCD的面积；（2）当t为何值时，△AOE是等腰三角形？（3）连接EF，在运动过程中，是否存在某一时刻t，使EF与BD垂直？请说明理由．（4）连接OF，在运动过程中，是否存在某一时刻t，使OC平分∠GOF？若存在，直接写出t的值；若不存在，请说明理由．3、如图，E、F分别是□ABCD的边BC、AD上的点，且BE＝DF(1)求证：四边形AECF是平行四边形；(2)若BC＝10，∠BAC＝90°，且四边形AECF是菱形，求BE的长．4、如图，▱ABCD中，点O是AC与BD的交点，过点O的直线与直线BA、DC的延长线分别交于点E、F．（1）求证：△AOE≌△COF；（2）请连接EC、AF，则EF与AC满足什么条件时，四边形AECF是矩形，并说明理由．5、如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/秒的速度向点A 匀速运动，同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒(0<t≤15)．过点D作DF⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，请说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由．6、（1）操作发现：如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．（2）问题解决：保持（1）中的条件不变，若DC=2DF，求的值；（3）类比探求：保持（1）中条件不变，若DC=nDF，求的值．参考答案一、简答题1、【考点】四边形综合题．【分析】探究：（1）利用等边三角形的性质得到BC=AC，∠ACB=∠ABC，从而得到△ACN≌△CBM．（2）利用全等三角形的性质得到∠CAN=∠BCM，再利用三角形的外角等于与它不相邻的两内角之和，即可求解．应用：利用正方形（或正五边形）的性质得到BC=DC，∠ABC=∠BCD，从而判断出△DCN≌△CBM，再利用全等三角形的性质得到∠CDN=∠BCM，再利用三角形的外角等于与它不相邻的两内角之和（或者三角形的内角和），即可．拓展：利用正n五边形的性质得到BC=DC，∠ABC=∠BCD，从而判断出△DCN≌△CBM，再利用全等三角形的性质得到∠CDN=∠BCM，再利用三角形的内角和，即可．【解答】探究：（1）解：∵△ABC是等边三角形，∴BC=AC，∠ACB=∠ABC=60°．∴∠ACN=∠CBM=60°．在△ACN和△CBM中，∴△ACN≌△CBM．（2）解：∵△DCN≌△CBM，∴∠CAN=∠BCM，∵∠ABC=∠BMC+∠BCM，∠BAN=∠BAC+∠CAN，∴∠CPN=∠BMC+∠BAN=∠BMC+∠BAC+∠CAN=∠BMC+∠BAC+∠BCM=∠ABC+∠BAC=60°+60°=120°，故答案为120．应用：将等边三角形换成正方形，解：四边形ABCD是正方形，∴BC=DC，∠ABC=∠BCD=90°．∴∠MBC=∠DCN=120°．在△DCN和△CBM中，∴△DCN≌△CBM．∴∠CDN=∠BCM，∵∠BCM=∠PCN∴∠CDN=∠PCN在Rt△DCN中，∠CDN+∠CND=90°，∴∠PCN+∠CND=90°，∴∠CPN=90，将等边三角形换成正五边形，五边形ABCDE是正五边形，∴BC=DC=108°．∴∠MBC=∠DCN=72°．在△DCN和△CBM中，∴△DCN≌△CBM．∴∠BMC=∠CND，∠BCM=∠CDN，∵∠ABC=∠BMC+∠BCM=108°∴∠CPN=180°﹣（∠CND+∠PCN）=180°﹣（∠CND+∠BCM）=180°﹣（∠BCM+∠BMC）=180°﹣108°=72°．故答案为90，72．拓展解：方法和上面正五边形的方法一样，得到∠CPN=180°﹣（∠CND+∠PCN）=180°﹣（∠CND+∠BCM）=180°﹣（∠BCM+∠BMC）=180°﹣108°=72°故答案为．2、（1）不变化为24；（2）25/8，5；（3）不存在；（4）25/73、4、(1)略；（2）EF=AC5、(1)证明：在△DFC中，∠DFC＝90°，∠C＝30°，DC＝4t，∴DF＝2t. ∵AE＝2t，∴AE＝DF. ……3分(2)能．理由如下：∵AB⊥BC，DF⊥BC，∴AE∥DF.∵AE＝DF，∴四边形AEFD为平行四边形，AE＝AD＝AC－DC＝60－4t＝2t.解得t＝10，∴当t＝10秒时，四边形AEFD为菱形．……6分(3)①当∠DEF＝90°时，由(2)知EF∥AD，∴∠ADE＝∠DEF＝90°.∵∠A＝60°，∴AD＝AE＝t.又AD＝60－4t，即60－4t＝t.解得t＝12. ……7分②当∠EDF＝90°时，四边形EBFD为矩形，在Rt△AED中，∠A＝60°，则∠ADE＝30°，∴AD＝2AE，即60－4t＝4t，解得t＝. ……8分③若∠EFD＝90°，则E与B重合，D与A重合，此种情况不存在．……9分∴当t＝秒或12秒时，△DEF为直角三角形．6、【分析】（1）求简单的线段相等，可证线段所在的三角形全等，即连接EF，证△EGF≌△EDF即可；（2）可设DF=x，BC=y；进而可用x表示出DC、AB的长，根据折叠的性质知AB=BG，即可得到BG的表达式，由（1）证得GF=DF，那么GF=x，由此可求出BF的表达式，进而可在Rt△BFC中，根据勾股定理求出x、y的比例关系，即可得到的值；（3）方法同（2）．【解答】解：（1）同意，连接EF，则根据翻折不变性得，∠EGF=∠D=90°，EG=AE=ED，EF=EF，在Rt△EGF和Rt△EDF中，∴GF=DF；（2）由（1）知，GF=DF，设DF=x，BC=y，则有GF=x，AD=y∵DC=2DF，∴CF=x，DC=AB=BG=2x，∴BF=BG+GF=3x；在Rt△BCF中，BC2+CF2=BF2，即y2+x2=（3x）2∴y=2x，∴；（3）由（1）知，GF=DF，设DF=x，BC=y，则有GF=x，AD=y∵DC=nDF，∴BF=BG+GF=（n+1）x在Rt△BCF中，BC2+CF2=BF2，即y2+[（n﹣1）x]2=[（n+1）x]2∴y=2x，∴或．【点评】此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识，难度适中．。

初二年级数学动点问题练习（含答案）

.. Word 格式格式动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目开放性题目..解决这类问题的关键是动中求静解决这类问题的关键是动中求静,,灵活运用有关数学知识解决问题灵活运用有关数学知识解决问题. .关键关键::动中求静动中求静. .数学思想：分类思想数学思想：分类思想数形结合思想数形结合思想转化思想 1、如图1，梯形ABCD 中，中，AD AD AD∥∥ BC BC，∠，∠，∠B=90B=90B=90°，°，°，AB=14cm,AD=18cm,BC=21cm,AB=14cm,AD=18cm,BC=21cm,AB=14cm,AD=18cm,BC=21cm,点点P 从A 开始沿AD 边以1cm/1cm/秒的速度移动，点秒的速度移动，点Q 从C 开始沿CB 向点B 以2 cm/2 cm/秒的速度移动，如果秒的速度移动，如果P ，Q 分别从A ，C 同时出发，设移动时间为t 秒。

当t= t= 时，四边形是平行四边形；时，四边形是平行四边形；时，四边形是平行四边形；6 6 当t= t= 时，四边形是等腰梯形时，四边形是等腰梯形时，四边形是等腰梯形. 8 . 82、如图2，正方形ABCD 的边长为4，点M 在边DC 上，且DM=1DM=1，，N 为对角线AC 上任意一点，则DN+MN 的最小值为的最小值为 5 53、如图，在Rt ABC △中，9060ACB B Ð=Ð=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为a ．（1）①当a = 度时，四边形度时，四边形EDBC 是等腰梯形，此时AD 的长为的长为；；②当a = 度时，四边形度时，四边形EDBC 是直角梯形，此时AD 的长为的长为；；（2）当90a =°时，判断四边形EDBC 是否为菱形，并说明理由．解：（1）①）①303030，，1；②；②606060，，1.51.5；；（2）当∠α）当∠α=90=900时，四边形EDBC 是菱形是菱形. .∵∠α∵∠α==∠ACB=900，∴BC //ED . . ∵∵CE //AB , , ∴四边形∴四边形EDBC 是平行四边形在Rt Rt△△ABC 中，∠ACB =900，∠B =600,BC =2, =2, ∴∠∴∠A =300.∴AB =4,AC =23. . ∴∴AO =12AC =3 . .在在Rt Rt△△AOD 中，∠A =300，∴AD =2.∴BD =2. =2. ∴∴BD =BC . . 又∵四边形又∵四边形EDBC 是平行四边形， ∴四边形EDBC 是菱形是菱形4、在△、在△ABC ABC 中，∠中，∠ACB ACB ACB=90°，=90°，=90°，AC=BC AC=BC AC=BC，直线，直线MN 经过点C ，且AD AD⊥⊥MN 于D ，BE BE⊥⊥MN 于E.OE CBDA a l OCB A（备用图）（备用图） CBAE D 图1NM ABCDE M N图2AC BEDN M图3(1)(1)当直线当直线MN 绕点C 旋转到图1的位置时，求证：①△的位置时，求证：①△ADC ADC ADC≌△≌△≌△CEB CEB CEB；②；②；②DE=AD DE=AD DE=AD＋＋BE BE；； (2)(2)当直线当直线MN 绕点C 旋转到图2的位置时，求证：的位置时，求证：DE=AD-BE DE=AD-BE DE=AD-BE；； (3)(3)当直线当直线MN 绕点C 旋转到图3的位置时，试问DE DE、、AD AD、、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明系，并加以证明. . 解：（1）①）① ∵∠∵∠∵∠ACD=ACD=ACD=∠ACB=90°∠ACB=90°∠ACB=90° ∴∠∴∠∴∠CAD+CAD+CAD+∠∠ACD=9ACD=90° 0° 0° ∴∠∴∠∴∠BCE+BCE+BCE+∠ACD=90°∠ACD=90°∠ACD=90° ∴∠∴∠CAD=CAD=CAD=∠∠BCE BCE ∵∵AC=BC AC=BC ∴△∴△∴△ADC ADC ADC≌△≌△≌△CEB CEB ② ∵△∵△∵△ADC ADC ADC≌△≌△≌△CEB CEB CEB ∴∴CE=AD CE=AD，，CD=BE CD=BE ∴∴DE=CE+CD=AD+BE (2) (2) ∵∠∵∠∵∠ADC=ADC=ADC=∠∠CEB=CEB=∠ACB=90°∠ACB=90°∠ACB=90° ∴∠∴∠∴∠ACD=ACD=ACD=∠∠CBE CBE 又∵又∵又∵AC=BC AC=BC ∴△∴△∴△ACD ACD ACD≌△≌△≌△CBE CBE CBE ∴∴CE=AD CE=AD，，CD=BE CD=BE ∴∴DE=CE-CD=AD-BE (3) (3) 当当MN 旋转到图3的位置时，的位置时，DE=BE-AD(DE=BE-AD(DE=BE-AD(或或AD=BE-DE AD=BE-DE，，BE=AD+DE 等) ∵∠∵∠ADC=ADC=ADC=∠∠CEB=CEB=∠ACB=90°∠ACB=90°∠ACB=90° ∴∠∴∠∴∠ACD=ACD=ACD=∠∠CBE CBE，，又∵又∵AC=BC AC=BC AC=BC，， ∴△∴△ACD ACD ACD≌△≌△≌△CBE CBE CBE，， ∴∴AD=CE AD=CE，，CD=BE CD=BE，， ∴∴DE=CD-CE=BE-AD.5、数学课上，数学课上，张老师出示了问题：张老师出示了问题：张老师出示了问题：如图如图1，四边形ABCD 是正方形，是正方形，点点E 是边BC 的中点．90AEF Ð=，且EF 交正方形外角DCG Ð的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ． BM BE \=．45BME \Ð=°，135AME \Ð=°． CF 是外角平分线，45DCF \Ð=°，135ECF \Ð=°． AME ECF \Ð=Ð． 90AEB BAE Ð+Ð=°，90AEB CEF Ð+Ð=°， \BAE CEF Ð=Ð． AME BCF \△≌△（ASA ASA））． AE EF \=．（2）正确．）正确．证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ．BN BE \=． 45N PCE \Ð=Ð=°．四边形ABCD 是正方形， AD BE \∥． DAE BEA \Ð=Ð． NAE CEF \Ð=Ð．ANE ECF \△≌△（ASA ASA））． AE EF \=．6、如图如图, , , 射线射线MB 上,MB=9,A 是射线MB 外一点外一点,AB=5,AB=5且A 到射线MB 的距离为3,3,动点动点P 从M 沿射线MB 方向以1个单位个单位//秒的速度移动，设P 的运动时间为t. 求（求（11）△）△ PAB PAB 为等腰三角形的t 值；（2）△）△ PAB PAB 为直角三角形的t 值；（3）若AB=5且∠且∠ABM=45 ABM=45 ABM=45 °，其他条件不变，直接写出△°，其他条件不变，直接写出△°，其他条件不变，直接写出△ PAB PAB 为直角三角形的t 值A D FCGE B图1A D FC GE B 图3ADFC GE B图2A D FCGE B M ADFC G E B N7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =°∠.求：（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ^交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），P M N△的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由解（解（11）如图1，过点E 作EG BC ^于点G ． ∵∵E 为AB 的中点，的中点， ∴∴122BE AB ==．在Rt EBG △中，60B =°∠， ∴∴30BEG =°∠． ∴∴22112132BG BE EG ===-=，．A D E BFC图4（备用）ADEBF C图5（备用）A D EBFC 图1 图2A D EB FC PNM图3A D EBFC PNM （第25题）题）即点E 到BC 的距离为3．（2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变．∵PM EF EG EF ^^，，∴PM EG ∥．∵EF BC ∥， ∴EP GM =，3PM EG ==．同理4MN AB ==．如图2，过点P 作PH MN ^于H ，∵MN AB ∥，∴6030NMC B PMH ==°=°∠∠，∠． ∴1322PH PM ==． ∴3cos302MH PM =°=．则35422NH MN MH =-=-=．在Rt PNH △中，222253722PNNHPHæöæö=+=+=ç÷ç÷ç÷èøèø． ∴PMN △的周长的周长==374PM PN MN ++=++．②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ^于R ，则MR NR =．类似①，32MR =．∴23MN MR ==．∵∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN =时，如图4，这时3MC MN MP ===．此时，61353x EP GM ===--=-．当NP NM =时，如图5，30NPM PMN ==°∠∠．则120PMN =°∠，又60MNC =°∠， ∴180PNM MNC +=°∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =°=．此时，6114x EP GM ===--=．综上所述，当2x =或4或()53-时，PMN △为等腰三角形．为等腰三角形．8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．(1(1）如果点）如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动图 3A D EBFCPN M 图4A D EBF CP MN 图5A DEBF （P ） CM NGGRG图1A D EBFCG 图 2 A D EBFCPNMG H①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==´=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =．又∵AB AC =， ∴B C Ð=Ð， ∴BPD CQP △≌△． ②∵P Qv v ¹， ∴BP CQ ¹，又∵BPD CQP △≌△，B C Ð=Ð，则45BP PC CQ BD ====，，∴点P ，点Q运动的时间433BPt ==秒，∴515443Q CQ v t===厘米厘米//秒。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,敏捷运用有关数学学问解决问题.关键:动中求静.数学思想：分类思想数形结合思想转化思想1、如图1，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm,AD=18cm,BC=21cm,点P从A开场沿AD边以1cm/秒的速度挪动，点Q从C开场沿CB向点B以2 cm/秒的速度挪动，假如P，Q分别从A，C同时动身，设挪动时间为t秒。

（1）求点E 到BC 的间隔；（2）点P 为线段EF 上的一个动点，过PA DF CGE 图A D FC GE B图ADF CGE B 图A DF CGE B MA D FC GEN作PM⊥EF交BC于点M，过M作MN‖AB交折线ADC于点N，连接PN，设EP=x①当点N在线段AD上时，△PMN的形态是否发生变更？若不变，求出△PMN的周长；若变更，请说明理由②当点N在线段DC上时，是否存在点P，使△PMN为等腰三角形？若存在，恳求出全部满意要求的X的值，若不存在，请说明理由。

①②1°①②1°2°3°2° 3°8、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点． (1）假如点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，可以使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 动身，点P 以原来的运动速度从点B 同时动身，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米， ∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴A QD BPPC BD =．又∵AB AC =， ∴B C ∠=∠， ∴BPD CQP △≌△． ②∵P Qv v ≠， ∴BP CQ≠，又∵BPD CQP△≌△，B C ∠=∠，则45BP PC CQ BD ====，，∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒。

（2）设经过x 秒后点P 与点Q 第一次相遇，由题意，得1532104x x =+⨯，解得803x =秒．∴点P 共运动了803803⨯=厘米． ∵8022824=⨯+，∴点P 、点Q 在AB 边上相遇，∴经过803秒点P 与点Q 第一次在边AB 上相遇．7、如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC∥交CD 于点F ．46AB BC ==，，60B =︒∠.求：（1）求点E 到BC 的间隔；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①当点N 在线段AD 上时（如图2），PMN △的形态是否发生变更？若不变，求出PMN △的周长；若变更，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，恳求出全部满意要求的x 的值；若不存在，请说明理由解（1）如图1，过点E 作EG BC⊥于点G ．∵E为AB的中点，∴122BE AB ==．在Rt EBG △中，60B =︒∠， ∴30BEG =︒∠．∴112BG BE EG ====，即点E 到BC 的间隔（2）①当点N 在线段AD 上运动时，PMN △的形态不发生变更．∵EF BC ∥， ∴EP GM =，PM EG ==同理4MN AB ==．如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥， ∴6030NMC B PMH ==︒=︒∠∠，∠． ∴122PH PM ==． ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=．②当点N 在线段DC 上运动时，PMN △的形态发生变更，但MNC △恒为等图A D EB F CG图A DE BF CP N MG HA D E BF C图4（备AD E BFC图5（备A D E BFC 图图A DE BFC PN M图A D EBFC P N M（第25边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =．∴23MN MR ==． ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=．当MP MN =时，如图4，这时MC MN MP ===此时，615x EP GM ===-=-当NP NM =时，如图5，30NPM PMN ==︒∠∠．则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5时，PMN △为等腰三角形．图A D EB FC PN M图4A DEB FC P M N图A DEBFC M N GGR G。