导数的运算专项练习(含答案)

合集下载

导数经典练习题及答案

1．设函数f(x)在0x 处可导，则xx f x x f x ∆-∆-→∆)()(lim000等于A ．)('0x fB ．)('0x f -C ．0'()f x -D ．0'()f x -- 2．若13)()2(lim000=∆-∆+→∆xx f x x f x ，则)('0x f 等于 A ．32 B ．23C ．3D ．23．若函数f(x)的导数为f ′(x)=-sinx ，则函数图像在点（4，f （4））处的切线的倾斜角为A ．90°B ．0°C ．锐角D ．钝角 4．对任意x ，有34)('x x f =，f(1)=-1，则此函数为A ．4)(x x f =B ．2)(4-=x x fC ．1)(4+=x x fD ．2)(4+=x x f 5．设f(x)在0x 处可导，下列式子中与)('0x f 相等的是（1）x x x f x f x ∆∆--→∆2)2()(lim000；（2）x x x f x x f x ∆∆--∆+→∆)()(lim 000；（3）x x x f x x f x ∆∆+-∆+→∆)()2(lim000（4）x x x f x x f x ∆∆--∆+→∆)2()(lim 000.A ．（1）（2）B ．（1）（3）C ．（2）（3）D ．（1）（2）（3）（4） 6．若函数f(x)在点0x 处的导数存在，则它所对应的曲线在点))(,(00x f x 处的切线方程是___. 7．已知曲线xx y 1+=，则==1|'x y _____________.8．设3)('0-=x f ，则=---→hh x f h x f h )3()(lim000_____________.9．在抛物线2x y =上依次取两点，它们的横坐标分别为11=x ，32=x ，若抛物线上过点P 的切线与过这两点的割线平行，则P 点的坐标为_____________. 10．曲线3)(x x f =在点A 处的切线的斜率为3，求该曲线在A 点处的切线方程. 11．在抛物线2x y =上求一点P ，使过点P 的切线和直线3x-y+1=0的夹角为4π. 12．判断函数⎩⎨⎧<-≥=)0()0()(x x x x x f 在x=0处是否可导.13．求经过点（2，0）且与曲线xy 1=相切的直线方程. 同步练习X030131．函数y =f （x ）在x =x 0处可导是它在x =x 0处连续的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．在曲线y =2x 2－1的图象上取一点（1，1）及邻近一点（1+Δx ，1+Δy ），则xy ∆∆ 等于A ．4Δx +2Δx 2B ．4+2ΔxC ．4Δx +Δx 2D ．4+Δx3．若曲线y =f （x ）在点（x 0，f （x 0））处的切线方程为2x +y －1=0，则A ．f ′（x 0）>0B ．f ′（x 0）<0C ．f ′（x 0）=0D ．f ′（x 0）不存在4．已知命题p ：函数y =f （x ）的导函数是常数函数；命题q ：函数y =f （x ）是一次函数，则命题p 是命题q 的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．设函数f （x ）在x 0处可导，则0lim→h hh x f h x )()(00--+等于A ．f ′（x 0）B ．0C ．2f ′（x 0）D ．－2f ′（x 0）6．设f （x ）=x （1+|x |），则f ′（0）等于A ．0B ．1C ．－1D ．不存在7．若曲线上每一点处的切线都平行于x 轴，则此曲线的函数必是___________． 8．曲线y =x 3在点P （2，8）处的切线方程是___________．9．曲线f （x ）=x 2+3x 在点A （2，10）处的切线斜率k =___________． 10．两曲线y =x 2+1与y =3－x 2在交点处的两切线的夹角为___________． 11．设f （x ）在点x 处可导，a 、b 为常数，则lim→∆x xx b x f x a x f ∆∆--∆+)()(=___________．12．已知函数f （x ）=⎩⎨⎧>+≤++0 012x b ax x x x ，试确定a 、b 的值，使f （x ）在x =0处可导． 13．设f （x ）=)()2)(1()()2)(1(n x x x n x x x +⋅⋅⋅++-⋅⋅⋅--，求f ′（1）．14．利用导数的定义求函数y =|x |（x ≠0）的导数．同步练习 X030211．物体运动方程为s =41t 4－3，则t =5时的瞬时速率为A ．5 m/sB ．25 m/sC ．125 m/sD ．625 m/s2．曲线y =x n （n ∈N ）在点P （2，)22n 处切线斜率为20，那么n 为A ．7B ．6C ．5D ．4 3．函数f （x ）=x x x 的导数是A ．81x（x >0） B ．－887x（x >0） C ．8781x（x >0） D ．881x（x >0）4．f （x ）与g （x ）是定义在R 上的两个可导函数，若f （x ），g （x ）满足f ′（x ）=g ′（x ），则f （x ）与g （x ）满足 A ．f （x ）=g （x ）B ．f （x ）－g （x ）为常数函数C ．f （x ）=g （x ）=0D ．f （x ）+g （x ）为常数函数5．两车在十字路口相遇后，又沿不同方向继续前进，已知A 车向北行驶，速率为30 km/h ，B 车向东行驶，速率为40 km/h ，那么A 、B 两车间直线距离的增加速率为 A ．50 km/hB ．60 km/hC ．80 km/hD ．65 km/h6．细杆AB 长为20 cm ，AM 段的质量与A 到M 的距离平方成正比，当AM =2 cm 时，AM 段质量为8 g ，那么，当AM =x 时，M 处的细杆线密度ρ（x ）为A ．2xB ．4xC ．3xD ．5x7．曲线y =x 4的斜率等于4的切线的方程是___________．8．设l 1为曲线y 1=sin x 在点（0，0）处的切线，l 2为曲线y 2=cos x 在点（2π，0）处的切线，则l 1与l 2的夹角为___________． 9．过曲线y =cos x 上的点（21,6π）且与过这点的切线垂直的直线方程为_____________．10．在曲线y =sin x （0<x <π）上取一点M ，使过M 点的切线与直线y =x 23平行，则M 点的坐标为___________．11．质点P 在半径为r 的圆周上逆时针做匀角速率运动，角速率为1 r a d/s ，设A 为起点，那么t 时刻点P 在x 轴上射影点M 的速率为___________．12．求证：双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形面积等于常数．13．路灯距地平面为8 m ，一个身高为1．6 m 的人以84 m/min 的速率在地面上行走，从路灯在地平面上射影点C ，沿某直线离开路灯，求人影长度的变化速率v ．14．已知直线x +2y －4=0与抛物线y 2=4x 相交于A 、B 两点，O 是坐标原点，试在抛物线的弧上求一点P ，使△PAB 面积最大．同步练习 X030311．若f （x ）=sin α－cos x ，则f ′（α）等于A ．sin αB ．cos αC ．sin α+cos αD ．2sin α2．f （x ）=ax 3+3x 2+2，若f ′（－1）=4，则a 的值等于A ．319B ．316 C ．313D ．3103．函数y =x sin x 的导数为A ．y ′=2x sin x +x cos xB ．y ′=xx 2sin +x cos xC ．y ′=xx sin +x cos x D ．y ′=xx sin －x cos x4．函数y =x 2cos x 的导数为A ．y ′=2x cos x －x 2sin xB ．y ′=2x cos x +x 2sin xC ．y ′=x 2cos x －2x sin xD ．y ′=x cos x －x 2sin x5.若y =(2x 2-3)(x 2-4),则y ’= .6. 若y =3cosx -4sinx ,则y ’= .7．与直线2x －6y +1=0垂直，且与曲线y =x 3+3x 2－1相切的直线方程是______． 8．质点运动方程是s =t 2（1+sin t ），则当t =2时，瞬时速度为___________． 9.求曲线y=x3+x2-1在点P （-1，-1）处的切线方程.10．用求导的方法求和：1+2x +3x 2+…+nx n －1（x ≠1）．11．水以20米3/分的速度流入一圆锥形容器，设容器深30米，上底直径12米，试求当水深10米时，水面上升的速度．同步练习 X030321．函数y =22xa x +（a >0）的导数为0，那么x 等于A ．aB ．±aC ．－aD ．a 22．函数y =xxsin 的导数为 A ．y ′=2sin cos xxx x + B ．y ′=2sin cos xxx x - C ．y ′=2cos sin xxx x -D ．y ′=2cos sin xxx x + 3.若21,2xy x +=-则y ’= . 4.若423335,x x y x -+-=则y ’= . 5.若1cos ,1cos xy x+=-则y ’= .6．已知f （x ）=354337xx x x ++，则f ′（x ）=___________．7．已知f （x ）=xx++-1111，则f ′（x ）=___________．8．已知f （x ）=xx2cos 12sin +，则f ′（x ）=___________．9．求过点（2，0）且与曲线y =x 1相切的直线的方程．10.质点的运动方程是23,s t t=+求质点在时刻t=4时的速度.同步练习 X030411．函数y =2)13(1-x 的导数是 A ．3)13(6-x B ．2)13(6-x C ．－3)13(6-x D ．－2)13(6-x2．已知y =21sin2x +sin x ，那么y ′是A ．仅有最小值的奇函数B ．既有最大值，又有最小值的偶函数C ．仅有最大值的偶函数D ．非奇非偶函数 3．函数y =sin 3（3x +4π）的导数为 A ．3sin 2（3x +4π）cos （3x +4π） B ．9sin 2（3x +4π）cos （3x +4π）C ．9sin 2（3x +4π）D ．－9sin 2（3x +4π）cos （3x +4π）4.若y=（sinx-cosx 3)，则y ’= .5. 若y=2cos 1x +，则y ’= .6. 若y=sin 3(4x+3)，则y ’= .7．函数y =（1+sin3x ）3是由___________两个函数复合而成． 8．曲线y =sin3x 在点P （3π，0）处切线的斜率为___________．9.求曲线2211(2,)(3)4y M x x =-在处的切线方程. 10. 求曲线sin 2(,0)y x M π=在处的切线方程.11．已知函数y =（x ）是可导的周期函数，试求证其导函数y =f ′（x ）也为周期函数．同步练习 X030421．函数y =cos （sin x ）的导数为A ．－［sin （sin x ）］cos xB ．－sin （sin x ）C ．［sin （sin x ）］cos xD ．sin （cos x ）2．函数y =cos2x +sin x 的导数为A ．－2sin2x +xx2cos B ．2sin2x +xx 2cosC ．－2sin2x +xx 2sin D ．2sin2x －xx 2cos3．过曲线y =11+x 上点P （1，21）且与过P 点的切线夹角最大的直线的方程为 A ．2y －8x +7=0 B ．2y +8x +7=0 C ．2y +8x －9=0D ．2y －8x +9=04．函数y =x sin （2x －2π）cos （2x +2π）的导数是______________． 5．函数y =)32cos(π-x 的导数为______________．6．函数y =cos 3x1的导数是___________．7.已知曲线y=2400x + +53(100-x) (0100≤≤x ) 在点M 处有水平切线,8．若可导函数f （x ）是奇函数，求证：其导函数f ′（x ）是偶函数．9．用求导方法证明：21C 2C n n ++…+n n n C =n ·2n －1．同步练习 X030511．函数y =ln （3－2x －x 2）的导数为A ．32+x B ．2231x x -- C ．32222-++x x xD ．32222-+-x x x2．函数y =lncos2x 的导数为A ．－tan2xB ．－2tan2xC ．2tan xD ．2tan2x3．函数y =x ln 的导数为A ．2x x lnB ．xx ln 2C ．xx ln 1 D ．xx ln 214．在曲线y =59++x x 的切线中，经过原点的切线为________________． 5．函数y =log 3cos x 的导数为___________． 6.函数y =x 2lnx 的导数为 . 7. 函数y =ln （lnx ）的导数为 . 8. 函数y =lg (1+cosx )的导数为9. 求函数y =ln 22132x x+-的导数．10. 求函数y = 12．求函数y =ln （21x +－x ）的导数．同步练习 X030521．下列求导数运算正确的是A ．（x +x 1）′=1+21xB ．（log 2x ）′=2ln 1xC ．（3x ）′=3x log 3eD ．（x 2cos x ）′=－2x sin x 2．函数y =xxa 22-（a >0且a ≠1），那么y ′为A ．xxa 22-ln aB ．2（ln a ）xx a 22-C ．2（x －1）xxa 22-·ln aD ．（x －1）xxa 22-ln a3．函数y =sin32x 的导数为A ．2（cos32x ）·32x ·ln3B ．（ln3）·32x ·cos32xC ．cos32xD ．32x ·cos32x4．设y =xx ee 2)12(+，则y ′=___________． 5．函数y =x22的导数为y ′=___________．6．曲线y =e x －e ln x 在点（e ，1）处的切线方程为___________．7.求函数y=e 2x lnx 的导数. 8．求函数y =x x （x >0）的导数．9．设函数f （x ）满足：af （x ）+bf （x 1）=xc（其中a 、b 、c 均为常数，且|a |≠|b |），试求f ′（x ）同步练习 x030611．若f （x ）在［a ，b ］上连续，在（a ，b ）内可导，且x ∈（a ，b ）时，f ′（x ）>0，又f （a ）<0，则A ．f （x ）在［a ，b ］上单调递增，且f （b ）>0B ．f （x ）在［a ，b ］上单调递增，且f （b ）<0C ．f （x ）在［a ，b ］上单调递减，且f （b ）<0D ．f （x ）在［a ，b ］上单调递增，但f （b ）的符号无法判断 2．函数y =3x －x 3的单调增区间是A ．（0，+∞）B ．（－∞，－1）C ．（－1，1）D ．（1，+∞） 3．三次函数y =f （x ）=ax 3+x 在x ∈（－∞，+∞）内是增函数，则A ．a >0B ．a <0C ．a =1D ．a =314．f （x ）=x +x2（x >0）的单调减区间是A ．（2，+∞）B ．（0，2）C ．（2，+∞）D ．（0，2）5．函数y =sin x cos 2x 在（0，2）上的减区间为A ．（0，arctan 22） B ．（arctan2,22π） C ．（0，2π）D ．（arctan 2,21π）6．函数y =x ln x 在区间（0，1）上是A ．单调增函数B ．单调减函数C ．在（0，e 1）上是减函数，在（e 1，1）上是增函数D ．在（0，e 1）上是增函数，在（e1，1）上是减函数7．函数f （x ）=cos 2x 的单调减区间是___________． 8．函数y =2x +sin x 的增区间为___________．9．函数y =232+-x x x的增区间是___________． 10．函数y =xxln 的减区间是___________．11．已知0<x <2π，则tan x 与x +33x 的大小关系是tan x _____x +33x ．12．已知函数f （x ）=kx 3－3（k +1）x 2－k 2+1（k >0）．若f （x ）的单调递减区间是（0，4）. （1）求k 的值；（2）当k <x 时，求证：2x >3－x1．13．试证方程sin x =x 只有一个实根．14．三次函数f （x ）=x 3－3bx +3b 在［1，2］内恒为正值，求b 的取值范围．同步练习 X030711．下列说法正确的是A ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极大值B ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极小值C ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极值D ．当f （x 0）为函数f （x ）的极值且f ′（x 0）存在时，则有f ′（x 0）=0 2．下列四个函数，在x =0处取得极值的函数是①y =x 3 ②y =x 2+1 ③y =|x | ④y =2x A ．①②B ．②③C ．③④D ．①③3．函数y =216xx的极大值为 A ．3 B ．4 C ．2 D ．54．函数y =x 3－3x 的极大值为m ，极小值为n ，则m +n 为A ．0B ．1C ．2D ．4 5．y =ln 2x +2ln x +2的极小值为A ．e －1B ．0C ．－1D ．16．y =2x 3－3x 2+a 的极大值为6，那么a 等于A ．6B ．0C ．5D ．17．函数f （x ）=x 3－3x 2+7的极大值为___________．8．曲线y =3x 5－5x 3共有___________个极值．9．函数y =－x 3+48x －3的极大值为___________；极小值为___________．10．函数f （x ）=x －3223x 的极大值是___________，极小值是___________．11．若函数y =x 3+ax 2+bx +27在x =－1时有极大值，在x =3时有极小值，则a =___________，b =___________．12．已知函数f （x ）=x 3+ax 2+bx +c ，当x =－1时，取得极大值7；当x =3时，取得极小值．求这个极小值及a 、b 、c 的值．13．函数f （x ）=x +xa+b 有极小值2，求a 、b 应满足的条件．14．设y =f （x ）为三次函数，且图象关于原点对称，当x =21时，f （x ）的极小值为－1，求函数的解析式．同步练习 X030811．下列结论正确的是A ．在区间[a ，b]上，函数的极大值就是最大值B ．在区间[a ，b]上，函数的极小值就是最小值C ．在区间[a ，b]上，函数的最大值、最小值在x=a 和x=b 时到达D ．在区间[a ，b]上连续的函数f(x)在[a ，b]上必有最大值和最小值 2．函数14)(2+-=x x x f 在[1，5]上的最大值和最小值是A ．f(1)，f(3)B ．f(3)，f(5)C ．f(1)，f(5)D ．f(5)，f(2) 3．函数f(x)=2x-cosx 在(-∞，+∞)上A ．是增函数B ．是减函数C ．有最大值D ．有最小值 4．函数a ax x x f --=3)(3在(0，1)内有最小值，则a 的取值范围是 A ．0<a<1 B ．a<1 C ．a>0 D ．21<a 5．若函数x x a x f 3sin 31sin )(+=在3π=x 处有最值，那么a 等于A ．2B ．1C ．332 D ．0 6．函数5224+-=x x y ，x ∈[-2，2]的最大值和最小值分别为 A ．13，-4 B ．13，4 C ．-13，-4 D ．-13，4 7．函数x xe y =的最小值为________________. 8．函数f(x)=sinx+cosx 在]2,2[ππ-∈x 时函数的最大值，最小值分别是___. 9．体积为V 的正三棱柱，底面边长为___________时，正三棱柱的表面积最小．10．函数21)(x x x f -+=的最大值为__________，最小值为____________。

(完整word)导数的计算练习题及答案

【巩固练习】一、选择题1．设函数310()(12)f x x =-，则'(1)f =（）A ．0B ．―1C ．―60D ．602．(2014 江西校级一模）若2()2ln f x x x =-，则'()0f x >的解集为( ） A.(0,1） B 。

()(),10,1-∞- C 。

()()1,01,-+∞ D.()1,+∞3．（2014春永寿县校级期中）下列式子不正确的是（）A 。

()'23cos 6sin x x x x +=- B. ()'1ln 22ln 2x x x x-=-C 。

()'2sin 22cos 2x x = D 。

'2sin cos sin x x x xx x -⎛⎫= ⎪⎝⎭4．函数4538y x x =+-的导数是（ ) A ．3543x + B ．0 C ．3425(43)(38)x x x ++- D ．3425(43)(38)x x x +-+- 5．（2015 安徽四模）已知函数()f x 的导函数为'()f x ，且满足关系式2'()3(2)ln f x x xf x =++，则'(2)f 的值等于（）A. 2B.-2 C 。

94 D 。

94- 6．设曲线1(1)1x y x x +=≠-在点（3,2）处的切线与直线ax+y+1=0垂直，则a=（） A ．2 B ．12 C ．―12D ．―27．23log cos (cos 0)y x x =≠的导数是（）A ．32log tan e x -⋅B ．32log cot e x ⋅C ．32log cos e x -⋅D ．22log cos ex二、填空题8．曲线y=sin x 在点,12π⎛⎫⎪⎝⎭处的切线方程为________。

9．设y=（2x+a)2，且2'|20x y ==,则a=________.10．31sin x x '⎛⎫-= ⎪⎝⎭____________，()2sin 25x x '+=⎡⎤⎣⎦____________. 11．在平面直角坐标系xOy 中，点P 在曲线C ：y=x 3―10x+3上，且在第二象限内，已知曲线C 在点P 处的切线的斜率为2，则点P 的坐标为________。

导数的计算练习题及答案

导数的计算练习题及答案1. 计算函数f(x) = 3x^2 - 4x + 2的导数f'(x)。

解答：根据函数f(x) = 3x^2 - 4x + 2，使用导数的定义来计算导数f'(x)。

f'(x) = lim(delta x -> 0) (f(x + delta x) - f(x)) / delta x代入函数f(x)的表达式：f'(x) = lim(delta x -> 0) [(3(x + delta x)^2 - 4(x + delta x) + 2) -(3x^2 - 4x + 2)] / delta x化简并展开：f'(x) = lim(delta x -> 0) [3(x^2 + 2x * delta x + (delta x)^2) - 4x - 4 * delta x + 2 - 3x^2 + 4x - 2] / delta xf'(x) = lim(delta x -> 0) [3x^2 + 6x * delta x + 3(delta x)^2 - 4x - 4* delta x + 2 - 3x^2 + 4x - 2] / delta xf'(x) = lim(delta x -> 0) [6x * delta x + 3(delta x)^2 - 4 * delta x] / delta xf'(x) = lim(delta x -> 0) [6x + 3 * delta x - 4]由于求导数时delta x趋近于0，所以delta x也可以看作一个无穷小量，其平方项可以忽略不计，即delta x^2 = 0。

化简结果：f'(x) = 6x - 4所以函数f(x) = 3x^2 - 4x + 2的导数f'(x)为6x - 4。

2. 计算函数g(x) = 2sin(x) + 3cos(x)的导数g'(x)。

求导练习题带答案

求导练习题带答案求导是微积分中的一项基本技能，它可以帮助我们理解函数的变化率以及找到函数的极值点。

以下是一些求导的练习题及其答案，适合初学者练习。

练习题1：求函数 f(x) = x^3 的导数。

解：根据幂函数的求导法则，对于函数 f(x) = x^n，其导数为 f'(x) = n * x^(n-1)。

因此，对于 f(x) = x^3，我们有 f'(x) = 3 *x^(3-1) = 3x^2。

练习题2：求函数 g(x) = sin(x) 的导数。

解：根据三角函数的求导法则，sin(x) 的导数是 cos(x)。

所以，g'(x) = cos(x)。

练习题3：求函数 h(x) = 2x^2 + 3x - 1 的导数。

解：根据多项式的求导法则，我们可以分别对每一项求导，然后将结果相加。

对于 h(x) = 2x^2 + 3x - 1，我们有 h'(x) = 2 * 2x^(2-1) + 3 * 1x^(1-1) - 0 = 4x + 3。

练习题4：求函数 k(x) = (x^2 - 1)^3 的导数。

解：这里我们使用链式法则和幂函数的求导法则。

首先，设 u = x^2- 1，那么 k(x) = u^3。

u 的导数是 u' = 2x，而 u^3 的导数是3u^2。

应用链式法则，我们得到 k'(x) = 3u^2 * u' = 3(x^2 - 1)^2 * 2x = 6x(x^2 - 1)。

练习题5：求函数 m(x) = e^x 的导数。

解：根据指数函数的求导法则，e^x 的导数是它自身。

所以，m'(x) = e^x。

练习题6：求函数 n(x) = ln(x) 的导数。

解：自然对数函数 ln(x) 的导数是 1/x。

因此，n'(x) = 1/x。

练习题7：求函数 p(x) = (3x - 2)^5 的导数。

解：使用链式法则和幂函数的求导法则。

导数练习题含答案完整版

导数练习题含答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】导数练习题班级姓名一、选择题1．当自变量从x0变到x1时函数值的增量与相应自变量的增量之比是函数( )A．在区间[x0，x1]上的平均变化率B．在x0处的变化率C．在x1处的变化量D．在区间[x0，x1]上的导数2．已知函数y＝f(x)＝x2＋1，则在x＝2，Δx＝0.1时，Δy的值为( )A．0.40 B．0.41 C．0.43D．0.443．函数f(x)＝2x2－1在区间(1,1＋Δx)上的平均变化率ΔyΔx等于( )A．4 B．4＋2ΔxC．4＋2(Δx)2D．4x4．如果质点M按照规律s＝3t2运动，则在t＝3时的瞬时速度为( )A． 6 B．18C．54D．815．已知f(x)＝－x2＋10，则f(x)在x＝32处的瞬时变化率是( )A．3 B．－3C． 2D．－26．设f′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0))处的切线( )A．不存在B．与x轴平行或重合C．与x轴垂直D．与x轴相交但不垂直7．曲线y＝－1x在点(1，－1)处的切线方程为( )A．y＝x－2 B．y＝xC．y＝x＋ 2D．y＝－x－28．已知曲线y＝2x2上一点A(2,8)，则A处的切线斜率为( )A．4 B．16 C．8D．29．下列点中，在曲线y＝x2上，且在该点处的切线倾斜角为π4的是( )A．(0,0) B．(2,4)C．(14，116)D．(12，14)10．若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则( )A．a＝1，b＝ 1B．a＝－1，b＝1C．a＝1，b＝－ 1D．a＝－1，b＝－111．已知f(x)＝x2，则f′(3)＝( )A．0 B．2xC． 6D．912．已知函数f(x)＝1x，则f′(－3)＝( )A． 4 B.19C ．－14D ．－1913．函数y ＝x 2x ＋3的导数是( )A.x 2＋6x x ＋3?2B.x 2＋6x x ＋3C.－2xx ＋3?2D.3x 2＋6x x ＋3?2 14．若函数f (x )＝12f ′(－1)x 2－2x ＋3，则f ′(－1)的值为( )A ．0B ．－1C ．1D ．215．命题甲：对任意x ∈(a ，b )，有f ′(x )>0；命题乙：f (x )在(a ，b )内是单调递增的．则甲是乙的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件16．函数f (x )＝(x －3)e x 的单调递增区间是( )A ．(－∞，2)B ．(0,3)C ．(1,4)D ．(2，17．函数y ＝ax 3－x 在R 上是减函数，则( )A ．a ≥13B ．a ＝1C ．a ＝2D ．a ≤18．函数y ＝4x 2＋1x的单调递增区间是( ) A ．(0，＋∞) B ．(－∞，1)C ．(12，＋∞)D ．(1，19．“函数y ＝f (x )在一点的导数值为0”是“函数y ＝f (x )在这点取极值”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 20．设x 0为可导函数f (x )的极值点，则下列说法正确的是( )A ．必有f ′(x 0)＝B ．f ′(x 0)不存在C ．f ′(x 0)＝0或f ′(x 0)不存在D ．f ′(x 0)存在但可能不为022．函数f (x )＝x 3＋ax 2＋3x －9，已知f (x )在x ＝－3时取得极值，则a ＝( ) A ．2 B ．3C ．4D ．523．函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图象如图所示，则函数f (x )在开区间(a ，b )内的极小值点有( )A ．1个B ．2个C ．3个D ．4个24．函数f (x )＝－13x 3＋12x 2＋2x 取极小值时，x 的值是( )A ．2B ．2，－ 1C ．－1D ．－325．函数f (x )＝－x 2＋4x ＋7，在x ∈[3,5]上的最大值和最小值分别是( ) A ．f (2)，f (3) B ．f (3)，f (5)C ．f (2)，f (5)D ．f (5)，f (3)26．f (x )＝x 3－3x 2＋2在区间[－1,1]上的最大值是( )A ．－2B ．0C ．2D ．427．函数f (x )＝x 3－3x 2－9x ＋k 在区间[－4,4]上的最大值为10，则其最小值为( )A ．－10B．－71C ．－15D ．－22 28．(2010年高考山东卷)已知某生产厂家的年利润y (单元：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x－234，则使该生产厂家获取最大年利润的年产量为( )A ．13万件B ．11万件C ．9万件D ．7万件29．一点沿直线运动，如果由始点起经过t 秒运动的距离为s ＝14t 4－53t 3＋2t 2，那么速度为零的时刻是( )A ．1秒末B ．0秒C ．4秒末D ．0,1,4秒末二、填空题1．设函数y ＝f (x )＝ax 2＋2x ，若f ′(1)＝4，则a ＝________.2．若曲线y ＝2x 2－4x ＋a 与直线y ＝1相切，则a ＝________.3．已知函数y ＝ax 2＋b 在点(1,3)处的切线斜率为2，则ba＝________.4．令f (x )＝x 2·e x ，则f ′(x )等于________．5．函数y ＝x 2＋4x 在x ＝x 0处的切线斜率为2，则x 0＝________. 6．若y ＝10x ，则y ′|x ＝1＝________.7．一物体的运动方程是s (t )＝1t，当t ＝3时的瞬时速度为________．8．设f (x )＝ax 2－b sin x ，且f ′(0)＝1，f ′(π3)＝12，则a ＝________，b ＝________.9．y ＝x 3－6x ＋a 的极大值为________．10．函数y ＝x e x 的最小值为________．11．做一个容积为256 dm 3的方底无盖水箱，它的高为______dm 时最省料．12．有一长为16 m 的篱笆，要围成一个矩形场地，则矩形场地的最大面积是________m 2.三、解答题1．求下列函数的导数：(1)y＝3x2＋x cos x； (2)y＝x1＋x；(3)y＝lg x－e x.2．已知抛物线y＝x2＋4与直线y＝x ＋10，求：(1)它们的交点； (2)抛物线在交点处的切线方程．3．求下列函数的单调区间：(1)y＝x－ln x；(2)y＝12x .4．已知函数f(x)＝x3＋ax2＋bx＋c，当x＝－1时，取得极大值7；当x＝3时，取得极小值，求这个极小值及a、b、c的值．5．已知函数f(x)＝13x3－4x＋4.(1)求函数的极值；(2)求函数在区间[－3,4]上的最大值和最小值．导数练习题答案班级姓名一、选择题1．当自变量从x0变到x1时函数值的增量与相应自变量的增量之比是函数( ) A．在区间[x0，x1]上的平均变化率B．在x0处的变化率C．在x1处的变化量D．在区间[x0，x1]上的导数答案：A2．已知函数y＝f(x)＝x2＋1，则在x＝2，Δx＝0.1时，Δy的值为( )A．0.40B．0.41C．0.43D．0.44解析：选 B.Δy＝f(2.1)－f(2)＝2.12－22＝0.41.3．函数f(x)＝2x2－1在区间(1,1＋Δx)上的平均变化率ΔyΔx等于( )A． 4B．4＋2ΔxC．4＋2(Δx)2D．4x解析：选B.因为Δy＝[2(1＋Δx)2－1]－(2×12－1)＝4Δx＋2(Δx)2，所以ΔyΔx＝4＋2Δx，故选B.4．如果质点M按照规律s＝3t2运动，则在t＝3时的瞬时速度为( )A． 6B．18C．54D．81解析：选B.ΔsΔt＝3?3＋Δt2－3×32Δt，s′＝li mΔt→0ΔsΔt＝li mΔt→0(18＋3Δt)＝18，故选B.5．已知f(x)＝－x2＋10，则f(x)在x＝32处的瞬时变化率是( )A． 3B．－3C． 2D．－2解析：选B.6．设f′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0))处的切线( )A．不存在B．与x轴平行或重合C．与x轴垂直D．与x轴相交但不垂直解析：选 B.函数在某点处的导数为零，说明相应曲线在该点处的切线的斜率为零．7．曲线y＝－1x在点(1，－1)处的切线方程为( )A．y＝x－ 2B．y＝xC．y＝x＋ 2D．y＝－x－2解析：选 A.f′(1)＝li mΔx→0－11＋Δx＋11Δx＝li mΔx→011＋Δx＝1，则在(1，－1)处的切线方程为y＋1＝x－1，即y＝x－2.8．已知曲线y＝2x2上一点A(2,8)，则A 处的切线斜率为( )A． 4B．16C．8D．2解析：选C.9．下列点中，在曲线y＝x2上，且在该点处的切线倾斜角为π4的是( )A．(0,0)B．(2,4)C．(14，116)D．(12，14)故选D.10．若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则( )A ．a ＝1，b ＝ 1B ．a ＝－1，b ＝1C ．a＝1，b＝－1D ．a ＝－1，b ＝－1 解析：选A.11．已知f (x )＝x 2，则f ′(3)＝( )A ．0B ．2xC ．6D ．9解析：选 C.∵f ′(x )＝2x ，∴f ′(3)＝6.12．已知函数f (x )＝1x，则f ′(－3)＝( )A ．4B.19C ．－14D ．－19解析：选 D.∵f ′(x )＝－1x 2，∴f ′(－3)＝－19.13．函数y ＝x 2x ＋3的导数是( )A.x 2＋6x x ＋3?2B.x 2＋6x x ＋3C.－2x x ＋3?2D.3x 2＋6x x ＋3?2解析：选A14．若函数f (x )＝12f ′(－1)x 2－2x ＋3，则f ′(－1)的值为( ) A ．0B ．－1C ．1D ．2解析：选 B.∵f (x )＝12f ′(－1)x 2－2x ＋3， ∴f ′(x )＝f ′(－1)x －2.∴f ′(－1)＝f ′(－1)×(－1)－2.∴f ′(－1)＝－1.15．命题甲：对任意x ∈(a ，b )，有f ′(x )>0；命题乙：f (x )在(a ，b )内是单调递增的．则甲是乙的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选A.f (x )＝x 3在(－1,1)内是单调递增的，但f ′(x )＝3x 2≥0(－1<x <1)，故甲是乙的充分不必要条件，选A.16．函数f (x )＝(x －3)e x 的单调递增区间是( )A ．(－∞，2)B ．(0,3)C ．(1,4)D ．(2，＋∞)解析：选 D.f ′(x )＝(x －3)′e x＋(x －3)(e x)′＝(x －2)e x，令f ′(x )>0，解得x >2，故选D.17．函数y ＝ax 3－x 在R 上是减函数，则( )A ．a ≥13B ．a ＝1C ．a ＝2D ．a ≤0解析：选D.因为y ′＝3ax 2－1，函数y ＝ax 3－x 在(－∞，＋∞)上是减函数，所以y ′＝3ax 2－1≤0恒成立，即3ax 2≤1恒成立．当x ＝0时，3ax 2≤1恒成立，此时a ∈R ；当x ≠0时，若a ≤13x2恒成立，则a ≤0.综上可得a ≤0. 18．函数y ＝4x 2＋1x的单调递增区间是( )A ．(0，＋∞)B ．(－∞，C ．(12，＋∞)D ．(1，＋解析：选 C.∵y′＝8x－1x2＝8x3－1 x2>0，∴x>12.即函数的单调递增区间为(12，＋∞)．19．“函数y＝f(x)在一点的导数值为0”是“函数y＝f(x)在这点取极值”的( ) A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选B.对于f(x)＝x3，f′(x)＝3x2，f′(0)＝0，不能推出f(x)在x＝0处取极值，反之成立．故选B.20．设x0为可导函数f(x)的极值点，则下列说法正确的是( )A．必有f′(x0)＝0B．f′(x0)不存在C．f′(x0)＝0或f′(x0)不存在D．f′(x0)存在但可能不为0答案：A22．函数f(x)＝x3＋ax2＋3x－9，已知f(x)在x＝－3时取得极值，则a＝( )A．2 B．3C．4 D．5解析：选D.f′(x)＝3x2＋2ax＋3，∵f(x)在x＝－3处取得极值，∴f′(－3)＝0，即27－6a＋3＝0，∴a＝5.23．函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内的极小值点有( )A．1个B．2个C．3个D．4个解析：选A.函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如题图所示，函数f(x)在开区间(a，b)内有极小值点即函数由减函数变为增函数的点，其导数值为由负到正的点，只有1个．24．函数f(x)＝－13x3＋12x2＋2x取极小值时，x的值是( )A．2 B．2，－1C．－1 D．－3解析：选 C.f′(x)＝－x2＋x＋2＝－(x－2)(x＋1)．∵在x＝－1的附近左侧f′(x)<0，右侧f′(x)>0，如图所示：∴x＝－1时取极小值．25．函数f(x)＝－x2＋4x＋7，在x∈[3,5]上的最大值和最小值分别是( )A．f(2)，f(3)B．f(3)，f(5)C．f(2)，f(5) D．f(5)，f(3)解析：选B.∵f′(x)＝－2x＋4，∴当x∈[3,5]时，f′(x)<0，故f(x)在[3,5]上单调递减，故f(x)的最大值和最小值分别是f(3)，f(5)．26．f(x)＝x3－3x2＋2在区间[－1,1]上的最大值是( )A．－2 B．0C．2 D．4解析：选C.f′(x)＝3x2－6x＝3x(x－2)，令f′(x)＝0可得x＝0或x＝2(舍去)，当－1≤x<0时，f′(x)>0，当0<x≤1时，f′(x)<0.所以当x＝0时，f(x)取得最大值为2. 27．函数f(x)＝x3－3x2－9x＋k在区间[－4,4]上的最大值为10，则其最小值为( )A．－10 B．－71C．－15 D．－22解析：选B.f′(x)＝3x2－6x－9＝3(x －3)(x＋1)．由f′(x)＝0得x＝3，－1.又f(－4)＝k－76，f(3)＝k－27，f(－1)＝k＋5，f(4)＝k－20.由f(x)max＝k＋5＝10，得k＝5，∴f(x)min＝k－76＝－71.28．(2010年高考山东卷)已知某生产厂家的年利润y(单元：万元)与年产量x(单位：万件)的函数关系式为y＝－13x3＋81x－234，则使该生产厂家获取最大年利润的年产量为( )A．13万件B ．11万件C．9万件D ．7万件解析：选C29．一点沿直线运动，如果由始点起经过t秒运动的距离为s＝14t4－53t3＋2t2，那么速度为零的时刻是( )A．1秒末B ．0秒C．4秒末D ．0,1,4秒末解析：选D.∵s′＝t3－5t2＋4t，令s′＝0，得t1＝0，t2＝1，t3＝4，此时的函数值最大，故选D.二、填空题1．设函数y＝f(x)＝ax2＋2x，若f′(1)＝4，则a＝________.答案：12．若曲线y＝2x2－4x＋a与直线y＝1相切，则a＝________.答案：33．已知函数y＝ax2＋b在点(1,3)处的切线斜率为2，则ba＝________.答案：24．令f(x)＝x2·e x，则f′(x)等于________．解析：f′(x)＝(x2)′·e x＋x2·(e x)′＝2x·e x＋x2·e x＝e x(2x＋x2)．答案：e x(2x＋x2)5．函数y＝x2＋4x在x＝x0处的切线斜率为2，则x0＝________.解析：2＝li mΔx→0x＋Δx2＋4?x0＋Δx－x20－4x0Δx＝2x0＋4，∴x0＝－1.答案：－16．若y＝10x，则y′|x＝1＝________.解析：∵y′＝10x ln10，∴y′|x＝1＝10ln10.答案：10ln107．一物体的运动方程是s(t)＝1t，当t＝3时的瞬时速度为________．解析：∵s′(t)＝－1t2，∴s′(3)＝－132＝－19.答案：－198．设f(x)＝ax2－b sin x，且f′(0)＝1，f′(π3)＝12，则a＝________，b＝________.解析：∵f′(x)＝2ax－b cos x，f′(0)＝－b＝1得b＝－1，f ′(π3)＝23πa ＋12＝12，得a ＝0.答案：0 －19．y ＝x 3－6x ＋a 的极大值为________．解析：y ′＝3x 2－6＝0，得x ＝± 2.当x <－2或x >2时，y ′>0；当－2<x <2时，y ′<0.∴函数在x ＝－2时，取得极大值a ＋4 2.答案：a ＋4210．函数y ＝x e x 的最小值为________．解析：令y ′＝(x ＋1)e x ＝0，得x ＝－1.当x <－1时，y ′<0；当x >－1时，y ′>0.∴y min ＝f (－1)＝－1e.答案：－1e11．做一个容积为256 dm 3的方底无盖水箱，它的高为______dm 时最省料．解析：设底面边长为x ，则高为h ＝256x 2，其表面积为S ＝x 2＋4×256x2×x ＝x 2＋256×4x，S ′＝2x －256×4x 2，令S ′＝0，则x ＝8，则高h ＝25664＝4 (dm)．答案：412．有一长为16 m 的篱笆，要围成一个矩形场地，则矩形场地的最大面积是________m 2.解析：设矩形的长为x m ，则宽为16－2x2＝(8－x ) m(0<x <8)， ∴S (x )＝x (8－x )＝－x 2＋8x∴S ′(x )＝－2x ＋8，令S ′(x )＝0，则x ＝4，又在(0,8)上只有一个极值点，且x∈(0,4)时，S(x)单调递增，x∈(4,8)时，S(x)单调递减，故S(x)max＝S(4)＝16.答案：16三、解答题1．求下列函数的导数：(1)y＝3x2＋x cos x；(2)y＝x1＋x；(3)y＝lg x－e x.解：(1)y′＝6x＋cos x－x sin x.(2)y′＝1＋x－x1＋x2＝11＋x2.(3)y′＝(lg x)′－(e x)′＝1x ln10－e x.2．已知抛物线y＝x2＋4与直线y＝x＋10，求：(1)它们的交点；(2)抛物线在交点处的切线方程．解：(1)由⎩⎨⎧y＝x2＋4，y＝x＋10，得x2＋4＝10＋x，即x2－x－6＝0，∴x＝－2或x＝3.代入直线的方程得y＝8或13.∴抛物线与直线的交点坐标为(－2,8)或(3,13)．(2)∵y＝x2＋4，∴y′＝limΔx→0x＋Δx2＋4－x2＋4?Δx＝limΔx→0Δx2＋2x·ΔxΔx＝limΔx→0(Δx＋2x)＝2x.∴y′|x＝－2＝－4，y′|x＝3＝6，即在点(－2,8)处的切线斜率为－4，在点(3,13)处的切线斜率为6.∴在点(－2,8)处的切线方程为4x＋y＝0；在点(3,13)处的切线方程为6x－y－5＝0.3．求下列函数的单调区间：(1)y＝x－ln x；(2)y＝1 2x .解：(1)函数的定义域为(0，＋∞)．其导数为y′＝1－1 x .令1－1x>0，解得x>1；再令1－1x<0，解得0<x<1.因此，函数的单调增区间为(1，＋∞)，函数的单调减区间为(0,1)．4．已知函数f(x)＝x3＋ax2＋bx＋c，当x ＝－1时，取得极大值7；当x＝3时，取得极小值，求这个极小值及a、b、c的值．解：f′(x)＝3x2＋2ax＋b，依题意可知－1,3是方程3x2＋2ax＋b＝0的两个根，则有⎩⎪⎨⎪⎧－1＋3＝－23a，－1×3＝b3，解得⎩⎨⎧a＝－3，b＝－9，∴f(x)＝x3－3x2－9x＋c.由f(－1)＝7，得－1－3＋9＋c＝7，∴c＝2.∴极小值为f(3)＝33－3×32－9×3＋2＝－25.5．已知函数f(x)＝13x3－4x＋4.(1)求函数的极值；(2)求函数在区间[－3,4]上的最大值和最小值．解：(1)f′(x)＝x2－4，解方程x2－4＝0，得x1＝－2，x2＝2.当x变化时，f′(x)，f(x)的变化情况如下表：从上表可看出，当x＝－2时，函数有极大值，且极大值为283；而当x＝2时，函数有极小值，且极小值为－4 3 .(2)f(－3)＝13×(－3)3－4×(－3)＋4＝7，f(4)＝13×43－4×4＋4＝283，与极值比较，得函数在区间[－3,4]上的最大值是283，最小值是－43.。

导数的运算专题含答案

导数的运算专题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 已知函数f(x)=x3−f′(1)x2+2，则f(2)=（）A.−2B.1C.6D.142. 已知函数f(x)=x2+ln x，则f′(1)=（）A.3B.4C.1D.73. 下列求导运算不正确的是（）A.(x2)′=2xB.(e x+ln3)′=e x+13C.(3x)′=3x ln3D.(sin x)′=cos x4. 若函数f(x)=x2+sin x，则f′(0)=（）A.−1B.0C.1D.35. 某运动物体的位移s（单位：米）关于时间t（单位：秒）的函数关系式为s=2t2−1，则该物体在t=1秒时的瞬时速度为()A.1米/秒B.2米/秒C.3米/秒D.4米/秒6. 已知函数f(x)=sin(2x−π6)，则f′(π6)=( )A.1 2B.1C.√3D.√327. 函数f(x)=x3−2x2−3的导数( )A.f′(x)=3x2−4xB.f′(x)=3x2−4x−3C.f′(x)=3x2−2xD.f′(x)=3x2−2x−38. 记函数f(x)的导函数为f′(x)．若f(x)=e x sin x，则f′(0)=( )A.1B.0C.−1D.29. 记函数f(x)的导函数为f′(x)．若f(x)=e x sin2x，则f′(0)=（）A.2B.1C.0D.−110. 已知函数f(x)的导函数为f′(x)，且满足f(x)=2xf′(e)+ln x（其中e为自然对数的底数），则f′(e)=()A.eB.−1C.−e−1D.−e11. 已知f(x)为二次函数，且f(x)=x2+f′(x)−1，则f(x)=( )A.x2−2x+1B.x2+2x+1C.2x2−2x+1D.2x2+2x−112. 若函数f(x)=ax4+bx2+c满足f′(1)=2，则f′(−1)=()A.−1B.−2C.2D.013. 已知函数f(x)的导函数为f′(x)，且满足f(x)=2xf′(1)+ln x，则f′(1)=（）A.−1B.−12C.1D.e14. 已知函数f(x)=ax−bx2+c(a≠0)是定义在R上的奇函数，x=1是f(x)的一个极大值点，且f(1)=1，则f(x)=（）A.2x x2+1B.3xx2+2C.−xx2−2D.2x−1x215. 已知函数f(x)=x2+2x−xe x，则f′(0)=（）A.1B.0C.−1D.216. 设y=e3，则y′=（）A.3e2B.0C.e2D.e317. 已知函数y=f(x)的导函数为f′(x)，且满足f(x)=2xf′(1)+ln x，则曲线在点P(1,f(1))处的切线的斜率等于（）A.−eB.−1C.1D.e18. f(x)=x2+2xf′(1)，则f′(1)=________.19. 设函数f(x)=x3+ax+3，f′(1)=5，则实数a=________.20. 写出导函数是f′(x)=x+1x的一个函数为________.（答案不唯一，写出一个即可）21. 若f(x)=xe x，则f′(1)=________.22. 已知函数f(x)=ln x+x2f′(a)，且f(1)=−1，则实数a等于________．23. 设函数f(x)的导函数为f′(x)，且f(x)=x2+2xf′(2)，则f′(1)=________.24. 设函数f(x)在(0,+∞)内可导，且f(e x)=x+e x，则f′(e)=________.25. 对于三次函数f(x)=ax3+bx2+cx+d(a≠0)，定义：设f′′(x)是函数y=f(x)的导数y=f′(x)的导数，若方程f′′(x)=0有实数解x0，则称点(x0,f(x0))为函数y=f(x)的“拐点”．有同学发现“任何一个三次函数都有拐点，任何一个三次函数都有对称中心，且拐点就是对称中心”根据这一结论，请你写出函数f(x)=x3−32x2+3x−14的对称中心，应是________；并计算f(12021)+f(22021)+f(32021)+⋯+f(20202021)=________.26. 已知函数y=x ln x．(1)求这个函数的导数；(2)求这个函数的图像在点x=e处的切线方程．27. 已知函数f(x)=ln xx．(1)求函数f(x)导数；(2)求函数f(x)的单调区间．28. 求下列函数的导数：(Ⅰ)y＝x4−3x2−5x+6；(Ⅱ)y＝x3e x．29. 求下列函数的导函数．（1）y＝e x cos x；（2）y＝+ln x．30. 求下列函数的导数：(1)y=sin x−x+1；(2)y=−2e x⋅x3；(3)y=ln xx+1−2x.31. 已知函数且，. （1）求，的值；（2）求的值.32. 已知函数f(x)=f′(0)e x+x2−(f(0)−1)x．(1)求函数f(x)的解析式；(2)若函数g(x)=f(x)−mx在[1,2]上单调递增，求m的取值范围．33. 求下列函数的导数：(1)y=x(x−1x2)；(2)y=e x−2x；(3)y=x2(ln x+sin x)．34. 已知函数f(x)=13x3+a2x2+bx，其导函数y=f′(x)的图像经过点(0,0),(2,0).(1)求a，b的值；(2)求函数g(x)=f(x)+1在区间[−3,3]上的最值．35. 已知函数f(x)=x2+bx+ce x（e为自然对数的底数），f′(x)为f(x)的导函数，且f′(1)=0.(1)求实数c的值；(2)若函数f(x)在x=0处的切线经过点(−1,0)，求函数f(x)的极值；(3)若关于x的不等式f(x)≤2对于任意的x∈[0,2]恒成立，求实数b的取值范围．36. 已知函数f(x)=ax3+x2+bx（其中常数a，b∈R)，g(x)=f(x)+f′(x)是奇函数．(1)求a，b的值；(2)求g(x)在区间[1,2]上的最大值与最小值．37. 已知函数f(x)=12x2+cos x，f′(x)为f(x)的导函数．（1）求函数f(x)的极值；（2）设函数g(x)=(x 22−x+sin x+cos x2)e x−a(16x3+sin x−x),a∈R，讨论g(x)的单调性；（3）当x≥0时，f′(x)≤e x+bx−1，求实数b的取值范围．参考答案与试题解析导数的运算专题含答案一、选择题（本题共计 17 小题，每题 3 分，共计51分）1.【答案】C【考点】导数的运算函数的求值【解析】求导，代入x=1，求得f′(0)，然后将x=2代入原函数求得函数值．【解答】解：f′(x)=3x2−2f′(1)x，则f′(1)=3−2f′(1)⇒f′(1)=1，则f(x)=x3−x2+2，f(2)=23−22+2=6．故选C．2.【答案】A【考点】导数的运算【解析】求导，将x=1代入导函数中即可.【解答】解：函数f(x)=x2+ln x，∴f′(x)=2x+1，x则f′(1)=2+1=3.故选A.3.【答案】B【考点】导数的运算【解析】根据基本函数的导函数公式对选项进行逐一求解，注意常数的导数为0，即可判定．【解答】解：(x2)′=2x，(e x+ln3)′=e x，(3x)′=3x ln3，(sin x)′=cos x，故选项B错误，故选B．4.【答案】C【考点】【解析】利用导数的运算求解即可.【解答】解：f(x)=x2+sin x，∴f′(x)=2x2+cos x，∴f′(0)=0+cos0=1.故选C.5.【答案】D【考点】变化的快慢与变化率导数的运算【解析】根据瞬时速度与导数的关系，先对s求导，再把t=1代入s′进行运算即可得解. 【解答】解：∵s=2t2−1，∴s′=4t，当t=1时，s′=4×1=4.故选D.6.【答案】C【考点】导数的运算【解析】先由复合函数的求导公式求出f′(x)，再把x=π6代入计算．【解答】解：∵函数f(x)=sin(2x−π6)，则f′(x)=[sin(2x−π6)]′⋅(2x−π6)′=2cos(2x−π6)，所以f′(π6)=2cos(2×π6−π6)=2cosπ6=√3.故选C.7.【答案】A【考点】导数的运算【解析】利用导数运算法则，直接计算即可.【解答】解：根据题意得f′(x)=(x3−2x2−3)′=3x2−4x.8.【答案】A【考点】导数的运算【解析】先求导，再代入即可.【解答】解：f(x)=e x sin x，所以f′(x)=e x sin x+e x cos x则f′(0)=e0sin0+e0cos0=1 .故选A.9.【答案】A【考点】简单复合函数的导数导数的运算【解析】可求出导函数f(x)，然后将x换上0即可求出f(0)的值．【解答】解：∵f(x)=e x sin2x，∴f′(x)=e x sin2x+2e x cos2x=e x(sin2x+2cos2x)，∴f′(0)=e0(sin0+2cos0)=2．故选A．10.【答案】C【考点】导数的运算【解析】此题暂无解析【解答】，解：求导得：f′(x)=2f′(e)+1x把x=e代入得：f′(e)=e−1+2f′(e)，解得：f′(e)=−e−1．故选C.11.【答案】B【考点】函数解析式的求解及常用方法导数的运算利用待定系数法，即可得出解析式.【解答】解：设f(x)=ax2+bx+c，(a≠0)，则f′(x)=2ax+b，由题意得，ax2+bx+c=x2+2ax+b−1，则有{a=1,b=2a,c=b−1,解得{a=1,b=2,c=1,故f(x)=x2+2x+1.故选B.12.【答案】B【考点】导数的运算【解析】根据导数的运算法则先求导，问题得以解决【解答】解：∵f(x)=ax4+bx2+c，∴f′(x)=4ax3+2bx，∴f′(−x)=−4ax3−2bx=−f′(x)，∴f′(−1)=−f′(1)=−2.故选B.13.【答案】A【考点】导数的运算【解析】此题暂无解析【解答】解：∵f(x)=2xf′(1)+ln x，求导得：f′(x)=2f′(1)+1x，令x=1，得到f′(1)=2f′(1)+1，解得：f′(1)=−1.故选A.14.【答案】A【考点】函数奇偶性的性质函数恒成立问题利用导数研究函数的极值导数的运算【解析】利用奇偶性以及极值关系列出关系式求解参数即可【解答】解：∵ f (1)=1且f (x )为奇函数，∴ f (−1)=−1，代入{a−b 1+c =1，−a−b 1+c =−1，∴ b =0， ∵ f (x )=ax −b x 2+c ⇒f ′(x )=a (c−x 2)(x 2+c )2， ∵ x =1是极大值点，∴ f ′(1)=0⇒⇒a (c−12)(1+c )2=0，∵ a ≠0，∴ c −1=0解得c =1，∴ a−01+1=1⇒a =2，∴ f (x )=2x x 2+1.故选A .15.【答案】A【考点】导数的运算【解析】无【解答】解：∵ f(x)=x 2+2x −xe x ，∴ f ′(x)=2x +2−(e x +xe x )，∴ f ′(0)=2−1=1．故选A ．16.【答案】B【考点】导数的运算【解析】利用常数的导数为零求解即可.【解答】解：y =e 3，则y ′=0.故选B .17.【答案】B【考点】利用导数研究曲线上某点切线方程导数的运算【解析】根据题意，求出函数的导数，进而可得f′(1)=2f′(1)+1，解可得f′(1)的值，由导数的几何意义分析可得答案．【解答】解：根据题意，函数f(x)满足f(x)=2xf′(1)+ln x，，其导函数f′(x)=2f′(1)+1x则有f′(1)=2f′(1)+1，解可得f′(1)=−1，则f(x)图象在点M(1,f(1))处的切线斜率k=−1.故选B．二、填空题（本题共计 8 小题，每题 3 分，共计24分）18.【答案】−2【考点】导数的运算【解析】由f(x)的解析式，利用求导法则求出f(x)的导函数，把x=1代入导函数中求出f′(1)的值，从而确定出f(x)的解析式，然后分别把x等于1和−1代入即可求出f(1)和f(−1)的值，即可比较出大小．【解答】解：由f(x)=x2+2xf′(1)，求导得f′(x)=2x+2f′(1)，把x=1代入得：f′(1)=2+2f′(1)，解得：f′(1)=−2.故答案为：−2.19.【答案】2【考点】导数的运算【解析】由题得到f′(x)=3x2+a，根据f′(1)=3+a=5，即可得解.【解答】解：因为f′(x)=3x2+a，所以f′(1)=3+a=5，所以a=2.故答案为：2.20.【答案】f(x)=12x2+ln x【考点】常用函数的导数导数的运算【解析】答案未提供解析．【解答】解：由题意，导函数f′(x)=x+1x，则函数f(x)可能为f(x)=12x2+ln x.故答案为：f(x)=12x2+ln x.21.【答案】2e【考点】导数的运算【解析】认真审题，首先需要了解基本求导法则(若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导)．【解答】解：∵f(x)=xe x，∴f′(x)=e x+xe x，∴f′(1)=2e．故答案为：2e.22.【答案】1【考点】导数的运算【解析】无【解答】解：因为f(x)=ln x+x2f′(a)，令x=1，则f(1)=0+f′(a)，所以f′(a)=−1．又f′(x)=1x+2xf′(a)，令x=a，得−1=1a+2a×(−1)，故2a2−a−1=0，解得a=1或a=−12，故a=1．故答案为：1．23.【答案】−6【考点】导数的运算【解析】先求导得f′(x)=2x+2f′(2)，令x=2求得f′(2)得到f′(x)=2x−8，即可求解．【解答】解：由题意，得f′(x)=2x+2f′(2)，∴f′(2)=2×2+2f′(2)，解得f′(2)=−4，∴f′(x)=2x−8，∴f′(1)=2×1−8=−6.故答案为：−6.24.【答案】1+1e【考点】导数的运算函数解析式的求解及常用方法【解析】根据题意，求出函数f(x)的解析式，对其求导即可得答案．【解答】解：根据题意，得f(e x)=x+e x，令t=e x，则f(t)=ln t+t，∴f(x)=ln x+x，∴f′(x)=1+1，x∴f′(e)=1+1.e+1.故答案为：1e25.【答案】,1),2020(12【考点】函数的对称性函数的求值函数新定义问题【解析】【解答】解：∵ f (x )=x 3−32x 2+3x −14， ∴ f ′(x )=3x 2−3x +3，则f ″(x )=6x −3.令f ″(x )=0，可得x =12，则f (12)=1，根据题意可得，函数f (x )=x 3−32x 2+3x −14的对称中心为(12,1)，∴ f (1−x )+f (x )=2，∴ f (12021)+f (22021)+f (32021)+⋯+f (20202021)=2×20202=2020.故答案为：(12,1)；2020.三、解答题（本题共计 12 小题，每题 10 分，共计120分）26.【答案】解：(1)y =x ln x ，∴ y ′=1×ln x +x ⋅1x =1+ln x ， ∴ y ′=ln x +1.(2)k =y ′|x=e =ln e +1=2.又当x =e 时，y =e ，所以切点为(e, e)，∴ 切线方程为y −e =2×(x −e)，即2x −y −e =0．【考点】导数的运算利用导数研究曲线上某点切线方程【解析】（1）运用积函数的求导公式计算这个函数的导数即可．（2）欲求在点x =e 处的切线方程，只须求出其斜率的值即可，故先利用导数求出在x =e 处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．【解答】解：(1)y =x ln x ，∴ y ′=1×ln x +x ⋅1x =1+ln x ，∴ y ′=ln x +1.(2)k =y ′|x=e =ln e +1=2.又当x =e 时，y =e ，所以切点为(e, e)，∴ 切线方程为y −e =2×(x −e)，即2x −y −e =0．27.【答案】解：f(x)=ln xx，f′(x)=1x×x−ln x×1x2=1−ln xx2．(2)当f′(x)=0时，x=e，当f′(x)>0时，0<x<e，当f′(x)<0时，x>e，∴f(x)的单调增递增区间为(0,e)，单调递减区间为(e,+∞)．【考点】导数的运算利用导数研究函数的单调性利用导数研究函数的极值【解析】此题暂无解析【解答】解：f(x)=ln xx，f′(x)=1x×x−ln x×1x2=1−ln xx2．(2)当f′(x)=0时，x=e，当f′(x)>0时，0<x<e，当f′(x)<0时，x>e，∴f(x)的单调增递增区间为(0,e)，单调递减区间为(e,+∞)．28.【答案】（1）因为y＝x4−3x2−5x+6，所以y′＝4x3−6x−5；（2）因为y＝x3e x，所以y′＝3x2⋅e x+x3⋅e x＝e x x2(3+x)．【考点】导数的运算【解析】(Ⅰ)利用常见函数的求导公式以及导数的运算法则进行求解即可；(Ⅱ)利用常见函数的求导公式以及导数的运算法则进行求解即可．【解答】（1）因为y＝x4−3x2−5x+6，所以y′＝4x3−6x−5；（2）因为y＝x3e x，所以y′＝3x2⋅e x+x3⋅e x＝e x x2(3+x)．29.【答案】y′＝e x cos x−e x sin x＝e x(cos x−sin x)；．【考点】导数的运算【解析】此题暂无解析【解答】此题暂无解答30.【答案】【考点】利用导数研究函数的单调性导数的运算【解析】此题暂无解析【解答】此题暂无解答31.【答案】（1）f(2)=13g(2)=6；（2）f[g(2)]=17【考点】函数的求值求函数的值导数的运算【解析】（1）根据函数解析式，直接计算，得出f(2)=13g(2)=6（2）由（1）可直接计算出结果．【解答】（1）因为f(x)=11+x ,g(x)=x2+2，所以f(2)=11+2=13g(2)=22+2=6（2）由（1）得f[g(2)]=f(6)=1732.【答案】解：(1)f′(x)=f′(0)e x+2x−f(0)+1，令x=0，解得f(0)=1，则f(x)=f′(0)e x+x2，令x=0，得f(0)=f′(0)=1，所以f(x)=e x+x2．(2)因为g(x)=e x+x2−mx在[1,2]上单调递增，所以g′(x)≥0在[1,2]上恒成立，即g′(x)=e x+2x−m≥0在[1,2]上恒成立，所以m≤e x+2x在[1,2]上恒成立．又因为函数y=e x+2x在[1,2]上单调递增，所以m≤e+2，所以m的取值范围为(−∞,e+2]．【考点】函数解析式的求解及常用方法导数的运算已知函数的单调性求参数问题【解析】左侧图片未给出解析左侧图片未给出解析【解答】解：(1)f′(x)=f′(0)e x+2x−f(0)+1，令x=0，解得f(0)=1，则f(x)=f′(0)e x+x2，令x=0，得f(0)=f′(0)=1，所以f(x)=e x+x2．(2)因为g(x)=e x+x2−mx在[1,2]上单调递增，所以g′(x)≥0在[1,2]上恒成立，即g′(x)=e x+2x−m≥0在[1,2]上恒成立，所以m≤e x+2x在[1,2]上恒成立．又因为函数y=e x+2x在[1,2]上单调递增，所以m≤e+2，所以m的取值范围为(−∞,e+2]．33.【答案】解：(1)∵y=x(x−1x2)=x2−1x，∴y′=2x+1x2.(2)∵y=e x−2x，∴(e x)′=e x，(2x)′=2x ln2，∴y′=e x−2x ln2.(3)∵y=x2(ln x+sin x)=x2ln x+x2⋅sin x，∴y′=2x⋅ln x+x2⋅1x+2x⋅sin x+x2⋅cos x=2x(ln x+sin x+12)+x2⋅cos x.【考点】导数的运算【解析】无无【解答】解：(1)∵y=x(x−1x2)=x2−1x，∴y′=2x+1x2.(2)∵y=e x−2x，∴(e x)′=e x，(2x)′=2x ln2，∴y′=e x−2x ln2.(3)∵y=x2(ln x+sin x)=x2ln x+x2⋅sin x，∴y′=2x⋅ln x+x2⋅1x+2x⋅sin x+x2⋅cos x=2x(ln x+sin x+12)+x2⋅cos x.34.【答案】解：(1)f(x)=13x3+a2x2+bx，所以f′(x)=x2+ax+b，函数y=f′(x)的图像经过点(0,0),(2,0)，所以b=0，a=−2．(2)由(1)g(x)=13x3−x2+1可得，g′(x)=x2−2x，令g′(x)=x2−2x=0，解得x=0,x=2，列出表格如下：所以函数g x在−3,3上的最大值为1，最小值为−17．【考点】导数的运算利用导数研究函数的单调性利用导数研究函数的最值【解析】此题暂无解析【解答】解：(1)f(x)=13x3+a2x2+bx，所以f′(x)=x2+ax+b，函数y=f′(x)的图像经过点(0,0),(2,0)，所以b=0，a=−2．(2)由(1)g(x)=13x3−x2+1可得，g′(x)=x2−2x，令g′(x)=x2−2x=0，解得x=0,x=2，列出表格如下：35.【答案】解：(1)因为f(x)=x 2+bx+ce x，所以f′(x)=−x2+(2−b)x+b−ce x. 又因为f′(1)=0，所以−1+(2−b)+b−ce=0，解得c=1.(2)由(1)知c=1，所以f(x)=x 2+bx+1e x，所以f(0)=1，因为f′(x)=−x2+(2−b)x+b−1e x，所以f′(0)=b−1，因为函数y=f(x)在x=0处的切线方程为y−1=(b−1)x，又切线过点(−1,0)，即−1=−(b−1)，解得b=2.因为f′(x)=−(x−1)(x+1)e x，令f′(x)=0，得x=±1，列表如下：所以当x=−1时，函数y=f x取得极小值f−1=0，当x=1时，函数y=f(x)取得极大值为f(1)=4e.(3)因为f(x)=x2+bx+1e x≤2在x∈[0,2]上恒成立，所以bx≤2e x−(x2+1)在x∈[0,2]上恒成立．当x=0时，0≤1成立；当x∈(0,2]时，b≤2e xx −(x+1x)恒成立，记g(x)=2e xx −(x+1x)，x∈(0,2]，则g′(x)=2e x(x−1)x2−(1−1x2)=(x−1)(2e x−x−1)x2.令ℎ(x)=2e x−x−1，x∈(0,2]，则ℎ′(x)=2e x−1>2e0−1=1>0，所以函数y=ℎ(x)在区间(0,2]上单调递增，所以ℎ(x)>ℎ(0)=2e0−0−1=1>0，即2e x−x−1>0在区间(0,2]上恒成立．当x∈(0,2]，令g′(x)=0，得x=1，所以函数y=g(x)在区间(0,1)上单调递减，在区间(1,2]上单调递增，所以g(x)min=g(1)=2e−2，所以b≤2e−2，因此实数b的取值范围是(−∞,2e−2].【考点】导数的运算利用导数研究曲线上某点切线方程利用导数研究函数的极值利用导数研究不等式恒成立问题【解析】此题暂无解析【解答】解：(1)因为f(x)=x 2+bx+ce x，所以f′(x)=−x2+(2−b)x+b−ce x. 又因为f′(1)=0，所以−1+(2−b)+b−ce=0，解得c=1.(2)由(1)知c=1，所以f(x)=x 2+bx+1e x，所以f(0)=1，因为f′(x)=−x2+(2−b)x+b−1e x，所以f′(0)=b−1，因为函数y=f(x)在x=0处的切线方程为y−1=(b−1)x，又切线过点(−1,0)，即−1=−(b−1)，解得b=2.因为f′(x)=−(x−1)(x+1)e x，令f′(x)=0，得x=±1，列表如下：所以当x =−1时，函数y =f x 取得极小值f −1=0，当x =1时，函数y =f (x )取得极大值为f (1)=4e .(3)因为f (x )=x 2+bx+1e x ≤2在x ∈[0,2]上恒成立，所以bx ≤2e x −(x 2+1)在x ∈[0,2]上恒成立．当x =0时， 0≤1成立；当x ∈(0,2]时， b ≤2e x x −(x +1x )恒成立，记g(x)=2e x x −(x +1x )，x ∈(0,2]，则g ′(x )=2e x (x−1)x 2−(1−1x 2)=(x−1)(2e x −x−1)x 2.令ℎ(x)=2e x −x −1，x ∈(0,2]，则ℎ′(x )=2e x −1>2e 0−1=1>0，所以函数y =ℎ(x )在区间(0,2]上单调递增，所以ℎ(x )>ℎ(0)=2e 0−0−1=1>0，即2e x −x −1>0在区间(0,2]上恒成立．当x ∈(0,2]，令g ′(x )=0，得x =1，所以函数y =g (x )在区间(0,1)上单调递减，在区间(1,2]上单调递增，所以g (x )min =g (1)=2e −2，所以 b ≤2e −2，因此实数b 的取值范围是(−∞,2e −2].36.【答案】解：(1)因为f ′(x )=3ax 2+2x +b ，所以g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b ．因为g (x )是奇函数，所以g (−x )=−g (x )恒成立，从而3a +1=0，b =0，解得a =−13，b =0．(2)由(1)知g (x )=−13x 3+2x ，所以g ′(x )=−x 2+2，令g ′(x )=0．解得x =−√2（舍去）或x =√2，而g (1)=53，g(√2)=4√23，g (2)=43，因此g (x )在区间[1,2]上的最大值为g(√2)=4√23，最小值为g (2)=43．【考点】函数奇偶性的性质导数的运算利用导数研究函数的最值【解析】【解答】解：(1)因为f ′(x )=3ax 2+2x +b ，所以g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b ．因为g (x )是奇函数，所以g (−x )=−g (x )恒成立，从而3a +1=0，b =0，解得a =−13，b =0．(2)由(1)知g (x )=−13x 3+2x ，所以g ′(x )=−x 2+2，令g ′(x )=0．解得x =−√2（舍去）或x =√2，而g (1)=53，g(√2)=4√23，g (2)=43，因此g (x )在区间[1,2]上的最大值为g(√2)=4√23，最小值为g (2)=43．37. 【答案】解：（1）f ′(x )=x −sin x ，因为(x −sin x )′=1−cos x ≥0，所以f ′(x )在(−∞,+∞)单调递增，又f ′(0)=0所以当x ∈(−∞,0)时，f ′(x )<0,f (x )单调递减，当x ∈(0,+∞)时，f ′(x )>0,f (x )单调递增，所以当x =0时， f (x )的极小值f (0)=1 ，无极大值．（2）g ′(x )=(x 22+cos x −1)(e x −a )由（1）知，f (x )≥f (0) ，即x 22+cos x −1≥0，当a ≤0时， e x −a >0,g ′(x )≥0， g (x )在(−∞,+∞)上单调递增，当a >0时，令e x −a =0 ，得x =ln a ，于是当x ∈(−∞,ln a )，e x −a <0，g ′(x )≤0，g (x )单调递减，当x ∈(ln a,+∞),e x −a >0,g ′(x )≥0，g (x )单调递增，综上，当a ≤0时，g (x )在(−∞,+∞)单调递增，当a >0时，g (x )在(−∞,ln a )上单调递减，在(ln a,+∞)单调递增．（3）令ℎ(x)=f′(x)−e x−bx+1则ℎ(x)=−e x+(1−b)x−sin x+1，x∈[0,+∞)ℎ′(x)=−e x−cos x+1−b，ℎ′(x)的导函数ℎ′′(x)=−e x+sin x，因为x∈[0,+∞），所以g′′(x)≤−1+sin x≤0ℎ′(x)=−e x+sin x在[0,+∞）上单调递减，当b≥−1时，对任意x≥0时，ℎ′(x)≤ℎ′(0)=−1−b≤0，所以ℎ(x)在[0,+∞）上单调递减，所以对任意x≥0时，ℎ(x)≤ℎ(0)=0，当b<−1时，因为ℎ′(x)在[0,+∞）上单调递减，ℎ′(0)=−1−b>0当x→+∞时，ℎ′(x)→−∞，故∃x0∈(0,+∞)，使ℎ′(x0)=0，且x∈(0,x0)时，ℎ′(x)>0，ℎ(x)单调递增，所以ℎ(x0)>ℎ(0)=0，与任意x≥0，ℎ(x)≤0矛盾，所以实数b的取值范围为[−1,+∞）．【考点】利用导数研究函数的极值导数的运算【解析】此题暂无解析【解答】解：（1）f′(x)=x−sin x，因为(x−sin x)′=1−cos x≥0，所以f′(x)在(−∞,+∞)单调递增，又f′(0)=0所以当x∈(−∞,0)时，f′(x)<0,f(x)单调递减，当x∈(0,+∞)时，f′(x)>0,f(x)单调递增，所以当x=0时，f(x)的极小值f(0)=1，无极大值．（2）g′(x)=(x22+cos x−1)(e x−a)由（1）知，f(x)≥f(0)，即x 22+cos x−1≥0，当a≤0时，e x−a>0,g′(x)≥0，g(x)在(−∞,+∞)上单调递增，当a>0时，令e x−a=0，得x=ln a，于是当x∈(−∞,ln a)，e x−a<0，g′(x)≤0，g(x)单调递减，当x∈(ln a,+∞),e x−a>0,g′(x)≥0，g(x)单调递增，综上，当a≤0时，g(x)在(−∞,+∞)单调递增，当a>0时，g(x)在(−∞,ln a)上单调递减，在(ln a,+∞)单调递增．（3）令ℎ(x)=f′(x)−e x−bx+1则ℎ(x)=−e x+(1−b)x−sin x+1，x∈[0,+∞)ℎ′(x)=−e x−cos x+1−b，ℎ′(x)的导函数ℎ′′(x)=−e x+sin x，因为x∈[0,+∞），所以g′′(x)≤−1+sin x≤0ℎ′(x)=−e x+sin x在[0,+∞）上单调递减，当b≥−1时，对任意x≥0时，ℎ′(x)≤ℎ′(0)=−1−b≤0，所以ℎ(x)在[0,+∞）上单调递减，所以对任意x≥0时，ℎ(x)≤ℎ(0)=0，当b<−1时，因为ℎ′(x)在[0,+∞）上单调递减，ℎ′(0)=−1−b>0当x→+∞时，ℎ′(x)→−∞，故∃x0∈(0,+∞)，使ℎ′(x0)=0，且x∈(0,x0)时，ℎ′(x)>0，ℎ(x)单调递增，所以ℎ(x0)>ℎ(0)=0，与任意x≥0，ℎ(x)≤0矛盾，所以实数b的取值范围为[−1,+∞）．。

导数高中试题及解析答案

导数高中试题及解析答案1. 计算函数 $ f(x) = x^3 - 3x^2 + 2x $ 在 $ x = 1 $ 处的导数。

解析：首先，我们需要找到函数 $ f(x) $ 的导数。

根据导数的定义，我们有：\[ f'(x) = \frac{d}{dx}(x^3 - 3x^2 + 2x) \]对每一项分别求导，我们得到：\[ f'(x) = 3x^2 - 6x + 2 \]现在，将 $ x = 1 $ 代入 $ f'(x) $ 得到：\[ f'(1) = 3(1)^2 - 6(1) + 2 = 3 - 6 + 2 = -1 \]答案：函数 $ f(x) $ 在 $ x = 1 $ 处的导数为 $ -1 $。

2. 已知函数 $ g(x) = \sin(x) $，求 $ g'(x) $。

解析：根据三角函数的导数规则，我们知道 $ \sin(x) $ 的导数是$ \cos(x) $。

因此，我们可以直接写出 $ g(x) $ 的导数：\[ g'(x) = \cos(x) \]答案：函数 $ g(x) $ 的导数是 $ \cos(x) $。

3. 计算复合函数 $ h(x) = (x^2 - 1)^4 $ 的导数。

解析：这是一个复合函数，我们可以使用链式法则来求导。

首先，设$ u = x^2 - 1 $，那么 $ h(x) = u^4 $。

对 $ u $ 求导得到：\[ u' = \frac{d}{dx}(x^2 - 1) = 2x \]然后，对 $ h(x) $ 求导：\[ h'(x) = \frac{d}{dx}(u^4) = 4u^3 \cdot u' = 4(x^2 - 1)^3\cdot 2x \]答案：复合函数 $ h(x) $ 的导数是 $ 8x(x^2 - 1)^3 $。

导数考试题型及答案详解

导数考试题型及答案详解一、选择题1. 函数f(x) = x^2 + 3x + 2的导数是：A. 2x + 3B. x^2 + 2C. 2x + 6D. 3x + 2答案：A2. 若f(x) = sin(x)，则f'(π/4)的值是：A. 1B. √2/2C. -1D. -√2/2答案：B二、填空题1. 求函数g(x) = x^3 - 2x^2 + x的导数，g'(x) = __________。

答案：3x^2 - 4x + 12. 若h(x) = cos(x)，求h'(x) = __________。

答案：-sin(x)三、解答题1. 求函数f(x) = x^3 - 6x^2 + 9x + 2的导数，并求f'(2)的值。

解：首先求导数f'(x) = 3x^2 - 12x + 9。

然后将x = 2代入得到f'(2) = 3 * 2^2 - 12 * 2 + 9 = 12 - 24 + 9 = -3。

2. 已知函数y = ln(x)，求y'。

解：根据对数函数的导数公式，y' = 1/x。

四、证明题1. 证明：若函数f(x) = x^n，其中n为常数，则f'(x) = nx^(n-1)。

证明：根据幂函数的导数公式，对于任意实数n，有f'(x) = n * x^(n-1)。

五、应用题1. 某物体的位移函数为s(t) = t^3 - 6t^2 + 9t + 5，求该物体在t = 3时的瞬时速度。

解：首先求位移函数的导数s'(t) = 3t^2 - 12t + 9。

然后将t = 3代入得到s'(3) = 3 * 3^2 - 12 * 3 + 9 = 27 - 36 + 9 = 0。

因此，该物体在t = 3时的瞬时速度为0。

六、综合题1. 已知函数f(x) = x^4 - 4x^3 + 6x^2 - 4x + 5，求f'(x)，并求曲线y = f(x)在点(1, f(1))处的切线斜率。

完整版)导数大题练习带答案

完整版)导数大题练习带答案1.已知 $f(x)=x\ln x-ax$，$g(x)=-x^2-2$，要求实数 $a$ 的取值范围。

Ⅰ）对于所有 $x\in(0,+\infty)$，都有 $f(x)\geq g(x)$，即$x\ln x-ax\geq -x^2-2$，整理得 $a\leq \ln x +\frac{x}{2}$，对于 $x\in(0,+\infty)$，$a$ 的取值范围为 $(-\infty。

+\infty)$。

Ⅱ）当 $a=-1$ 时，$f(x)=x\ln x+x$，求 $f(x)$ 在 $[m。

m+3]$ 上的最值。

$f'(x)=\ln x+2$，令 $f'(x)=0$，解得 $x=e^{-2}$，在 $[m。

m+3]$ 上，$f(x)$ 单调递增，所以最小值为$f(m)=me^{m}$。

Ⅲ）证明：对于所有 $x\in(0,+\infty)$，都有 $\lnx+1>\frac{1}{x}$。

证明：$f(x)=\ln x+1-\frac{1}{x}$，$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{1}{x^2}(x-1)>0$，所以$f(x)$ 在 $(0,+\infty)$ 上单调递增，即对于所有$x\in(0,+\infty)$，都有 $\ln x+1>\frac{1}{x}$。

2.已知函数 $f(x)=\frac{2}{x}+a\ln x-2(a>0)$。

Ⅰ）若曲线 $y=f(x)$ 在点 $P(1,f(1))$ 处的切线与直线$y=x+2$ 垂直，求函数 $y=f(x)$ 的单调区间。

$f'(x)=-\frac{2}{x^2}+a$，在点 $P(1,f(1))$ 处的切线斜率为 $f'(1)=a-2$，由于切线垂直于直线 $y=x+2$，所以 $a-2=-\frac{1}{1}=-1$，解得 $a=1$。

导数应用精选50题(含有答案)

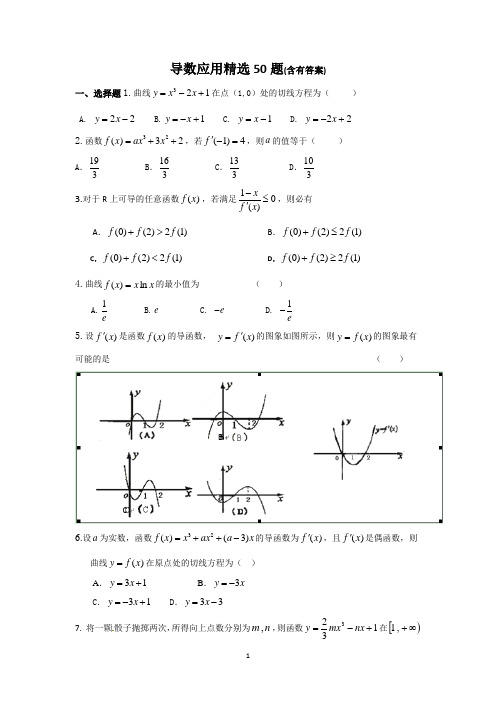
C.2
D. 3
2
13.对于三次函数 f (x) ax3 bx2 cx d （ a 0 ），定义：设 f (x) 是函数 y f (x) 的
导数，若方程 f (x) 0 有实数解 x0，则称点（x0，（f x0））为函数 y f (x) 的“拐点”．有
同学发现:“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’
)
99
A. a b c
B. c > b > a
C. c > a > b
D. a > c > b
10. f (x)是函数f (x)的导函数, 将y f (x)和y f (x) 的图象画在同一直角坐标系中，不
可能正确的是
()
11.已知函数 y xf (x) 的图象如图 3 所示（其中 f (x) 是函数 f (x) 的导函数）．下面四个图象中， y f (x) 的图象大致是（）
常数为方程 f (x) = x 的实数根。 (1) 求证：当 x > 时，总有 x > f (x) 成立； (2) 对任意 x1、x2 若满足| x1－ | < 1,| x2－ | < 1,求证：| f (x1)－f (x2)| < 2.
25.（本小题满分 12 分）
已知函数 f (x) ax3 bx2 ，当 x 1 时，有极大值 3 ；
f
( ) ， f 3
(x ) 为 f(x)的导函数，令 a＝
12，b＝log32，则下列关系
正确的是( )
A．f(a)>f(b) B．f(a)<f(b)
C．f(a)＝f(b)
D．f(|a|)<f(b)
16.设在函数 y x sin x cos x 的图象上的点 x0, y0 处的切线斜率为 k，若 k g x0 ，则

高中导数试题题型及答案

高中导数试题题型及答案一、选择题1. 函数 $ y = 3x^2 - 2x + 1 $ 在 $ x = 1 $ 处的导数是：A. 6B. 4C. 5D. 72. 已知 $ f(x) = x^3 + ax^2 + bx + c $，其中 $ a = 1 $，$ b = -1 $，$ c = 1 $，求 $ f'(x) $：A. $ 3x^2 + 2x - 1 $B. $ 3x^2 + 2x + 1 $C. $ 3x^2 + 2x $D. $ 3x^2 + 1 $二、填空题3. 函数 $ y = x^3 $ 的导数是 ______ 。

答案：$ 3x^2 $4. 如果 $ f(x) = \sin(x) $，那么 $ f'(x) $ 是 ______ 。

答案：$ \cos(x) $三、计算题5. 求函数 $ y = x^4 - 5x^3 + 6x^2 $ 的导数。

答案：$ y' = 4x^3 - 15x^2 + 12x $6. 已知 $ f(x) = \ln(x) + 2x^2 - 3x $，求 $ f'(x) $。

答案：$ f'(x) = \frac{1}{x} + 4x - 3 $四、应用题7. 某物体的位移函数是 $ s(t) = 2t^3 - 3t^2 + 4t $，求物体在$ t = 2 $ 秒时的瞬时速度。

答案：首先求导数 $ s'(t) = 6t^2 - 6t + 4 $，然后将 $ t= 2 $ 代入，得到 $ s'(2) = 6 \times 2^2 - 6 \times 2 + 4 =24 - 12 + 4 = 16 $ 米/秒。

8. 某工厂的产量函数是 $ P(x) = 100x - x^2 $，求工厂在 $ x= 10 $ 时的边际产量。

导数的练习题及答案

导数的练习题及答案导数是微积分中的一个重要概念，它描述了函数在某一点上的变化率。

掌握导数的概念对于解决各种数学和物理问题至关重要。

在这篇文章中，我们将给出一些关于导数的练习题及其答案，帮助读者更好地理解和应用导数。

练习题一：求函数 $f(x) = 2x^3 - 5x^2 + 3x - 1$ 在 $x = 2$ 处的导数。

解答一：根据导数的定义，我们知道导数可以通过函数的极限来求解。

在这个例子中，我们可以使用直接求导的方法来计算导数。

首先，我们对每一项使用求导法则。

对于 $2x^3$，它的导数是$6x^2$；对于 $-5x^2$，它的导数是 $-10x$；对于 $3x$，它的导数是$3$；对于常数项 $-1$，它的导数是 $0$。

然后，将这些导数相加，得到函数 $f(x)$ 的导数 $f'(x)$。

所以，$f'(x) = 6x^2 - 10x + 3$。

接下来，我们求函数 $f(x)$ 在 $x = 2$ 处的导数。

将 $x$ 替换为 $2$，得到 $f'(2) = 6(2)^2 - 10(2) + 3 = 28$。

所以，函数 $f(x) = 2x^3 - 5x^2 + 3x - 1$ 在 $x = 2$ 处的导数为 $f'(2) = 28$。

练习题二：求函数 $y = e^x \sin(x)$ 的导数。

解答二：这个问题涉及到两个函数的乘积，所以我们需要使用乘积规则来求解。

首先，我们将函数 $y = e^x \sin(x)$ 分解为两个函数的乘积：$y =u(x) v(x)$，其中 $u(x) = e^x$，$v(x) = \sin(x)$。

然后，我们求出每个函数的导数。

对于 $u(x) = e^x$，它的导数仍然是 $e^x$；对于 $v(x) = \sin(x)$，它的导数是 $\cos(x)$。

根据乘积规则，函数 $y$ 的导数为 $y' = u'v + uv'$。