机械原理课程设计--基于矢量图解法的平面六杆机构运动分析
平面六杆机构课程设计

平面六杆机构课程设计一、课程目标知识目标:1. 让学生掌握平面六杆机构的基本构成和特点,理解其运动规律和动力学特性。
2. 使学生了解平面六杆机构在实际工程中的应用,并能结合具体案例进行分析。
3. 帮助学生理解平面六杆机构与其他类型机构之间的区别与联系。
技能目标:1. 培养学生运用平面六杆机构进行简单机构设计的能力,能够根据实际需求进行参数优化。
2. 提高学生运用计算机软件(如CAD等)进行平面六杆机构运动仿真和分析的能力。
3. 培养学生运用数学工具对平面六杆机构进行运动学和动力学计算的能力。
情感态度价值观目标:1. 培养学生对机械设计学科的兴趣和热情,激发其创新意识和探索精神。
2. 培养学生具备良好的团队合作精神和沟通能力,使其在项目实践中能够相互协作、共同进步。
3. 引导学生关注我国机械工程技术的发展,培养其爱国情怀和社会责任感。
本课程针对高年级学生,结合学科特点和教学要求,将目标分解为具体的学习成果,以使学生能够在实际操作中掌握平面六杆机构的相关知识,提高综合运用能力。
在教学过程中,注重理论联系实际,充分调动学生的主观能动性,培养其创新意识和实践能力。
通过本课程的学习,使学生能够为今后的机械设计工作打下坚实基础。
二、教学内容1. 平面六杆机构基本概念:介绍平面六杆机构的定义、分类及其应用场景,对应教材第二章第一节。
- 六杆机构的构成与特点- 六杆机构的运动副类型及功能2. 平面六杆机构运动分析:- 分析平面六杆机构的运动规律,对应教材第二章第二节;- 掌握平面六杆机构的自由度和速度、加速度的计算方法。
3. 平面六杆机构动力学分析:- 动力学基本方程及其应用,对应教材第二章第三节;- 力、力矩和功率的计算方法。
4. 平面六杆机构设计方法:- 介绍平面六杆机构设计的基本原则和步骤,对应教材第二章第四节;- 结合实际案例,进行参数设计和优化。
5. 计算机辅助设计与分析:- 利用CAD软件进行平面六杆机构建模和运动仿真,对应教材第二章第五节;- 学会对仿真结果进行分析和优化。
六杆机构
平面六杆机构的运动分析
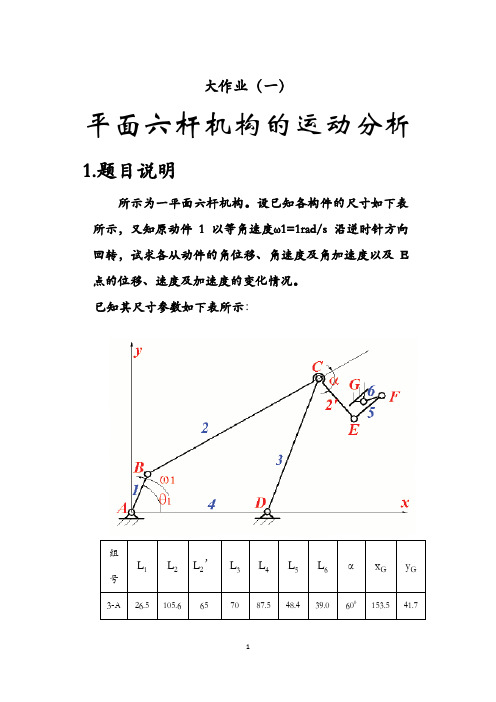
1.题目说明
所示为一平面六杆机构。设已知各构件的尺寸如下表 所示,又知原动件 1 以等角速度ω1=1rad/s 沿逆时针方向 回转,试求各从动件的角位移、角速度及角加速度以及 E 点的位移、速度及加速度的变化情况。 已知其尺寸参数如下表所示:
组 号 3-A
L1
26.5
Asin 3 Bcos 3 C 0
2
A 2l 1l3 sin 1 B 2l3 (l 1cos 1 l4 ) 式中: 2 2 2 2 C l2 l1 l3 l4 2l1 l4 cos 1
有:
x l4 l3c o s l o s2 ( 3 2 ' c e l s i n 3 l s i n ( ) 2 2 ye 3
y ye tan g xe x g ( x e x g ) 2 ( y y ) 2 l5 2 l6 2 e g cos 2 2l5 ( x e x g ) ( y y ) 2 e g 5 ' 5 5 ' y e l5 sin 5 ' y g tan 6 x e l5 cos 5 ' x g
322.59 299.43 285.25 276.08 269.39 263.77 258.21 251.4 239.86 216.63 187.66 166.33 153.4 145.85 141.4 138.64 136.71 135.07 133.37 131.38 128.95 126.01 122.52 118.5 113.99 109.04 103.67 97.868 91.565 84.606 76.759 67.689 56.881 43.29 24.225 355.19
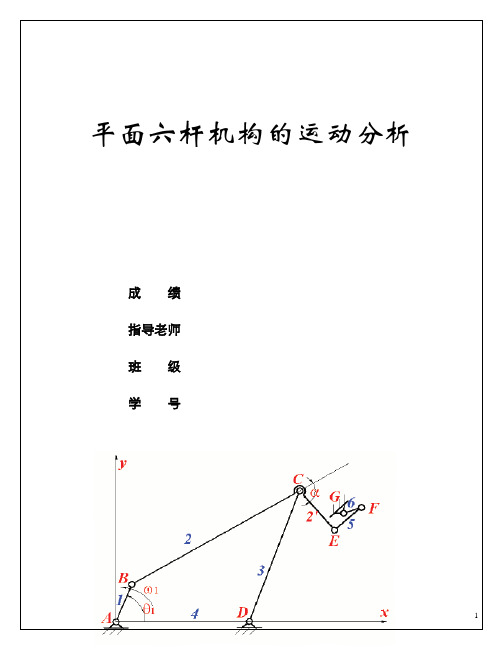
机械原理课程设计大作业平面六杆机构
evy=0:360;
ev=0:360;
fori=1:1:361
evx(i)=-l6*w6(i)*sind(thed6(i))-l5*w5(i)*sind(thed5(i));
evy(i)=l6*w6(i)*cosd(thed6(i))+l5*w5(i)*cosd(thed5(i));
%angularvelocity.m%
%-------------------------角速度-------------------------%
w2=0:360;
w3=0:360;
w5=0:360;
w6=0:360;
fori=1:1:361
V1=[-105.6*sind(thed2(i)) 67.5*sind(thed3(i)) 0 0;
ev(i)=(evx(i)^2+evy(i)^2)^0.5;
end
figure(4);
x=0:360;
y1=[evx;evy;ev];
plot(x,y1);
xlabel('\theta1');
ylabel('Evx,Evy,Ev');
gridminor;
legend('Evx','Evy','Ev');
L4
L5
L6
α
xG
yG
1-A
26.5
105.6
65.0
67.5
87.5
34.4
25.0
600
153.5
41.7
题目要求:
两人一组计算出原动件从0到360时(计算点数361)所要求的各运动变量的
机械原理大作业平面连杆机构报告

平面连杆机构的运动分析(题号:平面六杆机构)一、题目说明图示为一平面六杆机构。
设已知各构件的尺寸如表1所示,又知原动件1以等角速度ω1=1 rad/s沿逆时针方向回转,试求各从动件的角位移、角速度及角加速度以及E点的位移、速度及加速度的变化情况。
已知其尺寸参数如下表所示:二、题目分析1、建立封闭图形:L 1 + L 2= L 3+ L 4组号1ll2l 3 l 4 l 5 l 6 α A B C2-A2-B 2-C26.5 67.5 87.5 52.4 43.0 60l 2=116.6 l 2=111.6l 2=126.6L 1 + L 2= L 5+ L 6+AG2、机构运动分析:a 、角位移分析由图形封闭性得:⎪⎪⎩⎪⎪⎨⎧⋅-⋅+=+-⋅-⋅+⋅⋅-⋅+=+-⋅-⋅+⋅⋅=⋅+⋅+⋅=⋅+⋅55662'2221155662'222113322114332211sin sin )sin(sin sin cos cos )cos(cos cos sin sin sin cos cos cos θθθαπθθθθθαπθθθθθθθθL L y L L L L L x L L L L L L L L L L G G 将上式化简可得:⎪⎪⎩⎪⎪⎨⎧=⋅-⋅+-⋅+⋅-=⋅-⋅+-⋅+⋅⋅-=⋅-⋅⋅-=⋅-⋅G G y L L L L L x L L L L L L L L L L L 66552'233466552'2331133221143322sin sin )sin(sin cos cos )cos(cos sin sin sin cos cos cos θθαθθθθαθθθθθθθθb 、角速度分析上式对时间求一阶导数,可得速度方程:化为矩阵形式为:⎪⎪⎩⎪⎪⎨⎧=⋅⋅-⋅⋅+⋅-⋅+⋅⋅=⋅⋅+⋅⋅-⋅-⋅-⋅⋅-⋅⋅-=⋅⋅-⋅⋅⋅⋅=⋅⋅+⋅⋅-0cos cos )cos(cos 0sin sin )sin(sin cos cos cos sin sin sin 66655522'233366655522'2333111333222111333222ωθωθωαθωθωθωθωαθωθωθωθωθωθωθωθL L L L L L L L L L L L L L⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅-⋅⋅⋅-⋅--⋅-⋅-⋅⋅⋅-00cos sin cos cos cos )cos(sin sin sin )sin(00cos cos 00sin sin 1111165326655332'26655332'233223322θθωωωωωθθθαθθθθαθθθθθL L L L L L L L L L L L L Lc 、角加速度分析:矩阵对时间求一阶导数,可得加速度矩阵2233222333'223355665'22335566622332233'22sin sin 0cos cos 00sin()sin sin sin cos()cos cos cos cos cos 00sin sin 00cos(L L L L L L L L L L L L L L L L L θθεθθεθαθθθεθαθθθεθθθθθα-⋅⋅⎡⎤⎡⎤⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅=⎢⎥⎢⎥-⋅--⋅-⋅⋅⎢⎥⎢⎥⋅-⋅⋅-⋅⎣⎦⎣⎦-⋅⋅-⋅⋅⋅-211221123123355665'2223355666cos sin )cos cos cos 0sin()sin sin sin 0L L L L L L L L L θωθωωθθθωθαθθθω⎡⎤⋅⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⋅+⋅⎢⎥⎢⎥⎢⎥⋅⋅-⋅⎢⎥⎢⎥⎢⎥⋅-⋅⋅-⋅⎢⎥⎣⎦⎣⎦⎣⎦d 、E 点的运动状态位移:⎩⎨⎧⋅-⋅+=⋅-⋅+=55665566sin sin cos cos θθθθL L y y L L x x G EG E速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅=⋅⋅+⋅⋅-=555666555666cos cos sin sin ωθωθωθωθL L v L L v yx E E 加速度:⎪⎩⎪⎨⎧⋅⋅-⋅⋅+⋅⋅+⋅⋅-=⋅⋅+⋅⋅+⋅⋅-⋅⋅-=5552555666266655525556662666cos sin cos sin sin cos sin cos εθωθεθωθεθωθεθωθL L L L a L L L L a yx E E三、流程图四、源程序#include<stdio.h>#include<stdlib.h>#include<math.h>#define PI 3.1415926#define N 4void Solutionangle(double [18],double ); /*矢量法求角位移*/void Solutionspeed(double [N][N],double [N],double [18],double ); /*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [18]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [18],double [N][N]); //创建系数矩阵Avoid FoundmatrixB(double [18],double ,double [N]);//创建系数矩阵Bvoid FoundmatrixDA(double [18],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [18],double ,double [N]);//创建矩阵DB//定义全局变量double l1=26.5,l2=111.6,l3=67.5,l4=87.5,l5=52.4,l6=43.0;double l2g=65.0,xg=153.5,yg=41.7,inang=60*PI/180,as1=1.0;//主函数void main(){int i,j;FILE *fp;double shuju[36][18];double psvalue[18],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件,并制表头if((fp=fopen("filel","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n The Kinematic Parameters of Point 5\n"); fprintf(fp," ang2 ang3 ang5 ang6"); fprintf(fp," as2 as3 as5 as6"); fprintf(fp," aas2 aas3 aas5 aas6");fprintf(fp," xe ye vex vey aex aey\n");//计算数据并写入文件for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=0;j<4;j++){shuju[i][j]=psvalue[j]*180/PI;}for(j=4;j<18;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<18;j++)fprintf(fp,"%12.3f",shuju[i][j]);}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration E:\n"); for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=12;j<18;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[18],double ang1){double xe,ye,A,B,C,phi,alpha,csn,ang5g,d2,d,ang2,ang3,ang5,ang6; A=2*l1*l3*sin(ang1);B=2*l3*(l1*cos(ang1)-l4);C=l2*l2-l1*l1-l3*l3-l4*l4+2*l1*l4*cos(ang1);ang3=2*atan((A+sqrt(A*A+B*B-C*C))/(B-C));if(ang3<0)//限定ang3大小{ang3=2*atan((A-sqrt(A*A+B*B-C*C))/(B-C));}ang2=asin((l3*sin(ang3)-l1*sin(ang1))/l2);xe=l4+l3*cos(ang3)+l2g*cos(ang2-inang);ye=l3*sin(ang3)+l2g*sin(ang2-inang);phi=atan2((yg-ye),(xg-xe));d2=(yg-ye)*(yg-ye)+(xg-xe)*(xg-xe);d=sqrt(d2);csn=(l5*l5+d2-l6*l6)/(2.0*l5*d);alpha=atan2(sqrt(1.0-csn*csn),csn);ang5g=phi-alpha;ang5=ang5g-PI;ang6=atan2(ye+l5*sin(ang5g)-yg,xe+l5*cos(ang5g)-xg);value[0]=ang2;value[1]=ang3;value[2]=ang5;value[3]=ang6;value[12]=xe;value[13]=ye;//限定角度大小for(int i=0;i<4;i++){while(value[i]>2*PI)value[i]-=2*PI;while(value[i]<0)value[i]+=2*PI;}}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[18],double ang1) {double ang2,ang3;ang2=value[0];ang3=value[1];double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];value[14]=-l3*value[5]*sin(ang3)-l2g*value[4]*sin(ang2-inang);value[15]=l3*value[5]*cos(ang3)+l2g*value[4]*cos(ang2-inang);}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N],double db3[N],double value[18]){int i,j;double ang2,ang3;ang2=value[0];ang3=value[1];double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];value[16]=-l3*value[9]*sin(ang3)-l3*value[5]*value[5]*cos(ang3)-l2g*value[8]*si n(ang2-inang)-l2g*value[4]*value[4]*cos(ang2-inang);value[17]=l3*value[9]*cos(ang3)-l3*value[5]*value[5]*sin(ang3)+l2g*value[8]*cos (ang2-inang)-l2g*value[4]*value[4]*sin(ang2-inang);}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]){int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//使主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;}t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;}t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];} b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[18],double a5[N][N]){double ang2,ang3,ang5,ang6;ang2=value5[0];ang3=value5[1];ang5=value5[2];ang6=value5[3]; a5[0][0]=-l2*sin(ang2);a5[0][1]=l3*sin(ang3);a5[1][0]=l2*cos(ang2);a5[1][1]=-l3*cos(ang3);a5[2][0]=-l2*sin(ang2)-l2g*sin(ang2-inang);a5[2][2]=l5*sin(ang5);a5[2][3]=l6*sin(ang6);a5[3][0]=l2*cos(ang2)+l2g*cos(ang2-inang);a5[3][2]=-l5*cos(ang5);a5[3][3]=-l6*cos(ang6);a5[0][2]=a5[0][3]=a5[1][2]=a5[1][3]=a5[2][1]=a5[3][1]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[18],double ang1,double b6[N]){b6[0]=b6[2]=l1*sin(ang1)*as1;b6[1]=b6[3]=-l1*cos(ang1)*as1;}//创建矩阵DAvoid FoundmatrixDA(double value7[18],double da7[N][N]){double ang2,ang3,ang5,ang6,as2,as3,as5,as6;ang2=value7[0];ang3=value7[1];ang5=value7[2];ang6=value7[3]; as2=value7[4];as3=value7[5];as5=value7[6];as6=value7[7];da7[0][0]=-l2*as2*cos(ang2);da7[0][1]=l3*as3*cos(ang3);da7[1][0]=-l2*as2*sin(ang2);da7[1][1]=l3*as3*sin(ang3);da7[2][0]=as2*(-l2*cos(ang2)-l2g*cos(ang2-inang));da7[2][2]=as5*l5*cos(ang5);da7[2][3]=as6*l6*cos(ang6);da7[3][0]=as2*(-l2*sin(ang2)-l2g*sin(ang2-inang));da7[3][2]=as5*l5*sin(ang5);da7[3][3]=as6*l6*sin(ang6);da7[0][2]=da7[0][3]=da7[1][2]=da7[1][3]=da7[2][1]=da7[3][1]=0; }//创建矩阵DBvoid FoundmatrixDB(double value8[18],double ang1,double db8[N]){db8[0]=db8[2]=l1*as1*cos(ang1);db8[1]=db8[3]=l1*as1*sin(ang1);}五、计算结果及相关曲线图:A组:数据图像角位移角速度角加速度E点的位移、速度及加速度六、体会及建议:这次的作业给了我们一次锻炼机会,让我们基本掌握了平面六杆机构解析算法的基本原理,从理论到程序实践,每一步都环环相扣,每一个结果都息息相关,最终在我们共同的努力下完成了本次作业。
机械原理课程设计六杆机构运动与动力分析

机械原理课程设计六杆机构运动与动⼒分析⽬录第⼀部分:六杆机构运动与动⼒分析⼀.机构分析分析类题⽬ 3 1分析题⽬ 32.分析内容 3 ⼆.分析过程 4 1机构的结构分析 42.平⾯连杆机构运动分析和动态静⼒分析 53机构的运动分析8 4机构的动态静⼒分析18 三.参考⽂献21第⼆部分:齿轮传动设计⼀、设计题⽬22⼆、全部原始数据22三、设计⽅法及原理221传动的类型及选择22 2变位因数的选择22四、设计及计算过程241.选取两轮齿数242传动⽐要求24 3变位因数选择244.计算⼏何尺⼨25 五.齿轮参数列表26 六.计算结果分析说明28 七.参考⽂献28第三部分:体会⼼得29⼀.机构分析类题⽬3(⽅案三)1.分析题⽬对如图1所⽰六杆机构进⾏运动与动⼒分析。
各构件长度、构件3、4绕质⼼的转动惯量如表1所⽰,构件1的转动惯量忽略不计。
构件1、3、4、5的质量G1、G3、G4、G5,作⽤在构件5上的阻⼒P⼯作、P空程,不均匀系数δ的已知数值如表2所⽰。
构件3、4的质⼼位置在杆长中点处。
2.分析内容(1)对机构进⾏结构分析;(2)绘制滑块F的运动线图(即位移、速度和加速度线图);(3)绘制构件3⾓速度和⾓加速度线图(即⾓位移、⾓速度和⾓加速度线图);(4)各运动副中的反⼒;(5)加在原动件1上的平衡⼒矩;(6)确定安装在轴A上的飞轮转动惯量。
图1 六杆机构⼆.分析过程:通过CAD制图软件制作的六杆机构运动简图:图2 六杆机构CAD所做的图是严格按照题所给数据进⾏绘制的。
并机构运动简图中活动构件的序号从1开始标注,机架的构件序号为0。
每个运动副处标注⼀个字母,该字母既表⽰运动副,也表⽰运动副所在位置的点,在同⼀点处有多个运动副,如复合铰链处或某点处既有转动副⼜有移动副时,仍只⽤⼀个字母标注。
见附图2所⽰。
1.机构的结构分析如附图1所⽰,建⽴直⾓坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
机械原理课程设计六杆机构运动分析

机械原理课程设计说明书题目六杆机构运动分析学院工程机械学院专业机械设计制造及其自动化班级机制三班设计者秦湖指导老师陈世斌2014年1月15日目录一、题目说明∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 21、题目要求∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 32、原理图∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 33、原始数据∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 3二、结构分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 4三、运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 51、D点运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ 82、构件3运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙93、构件4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙94、点S4运动分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10四、结论∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10五、心得体会∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10六、参考文献∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11一、题目说明1、题目要求此次机械原理课程设计是连杆机构综合,通过对其分析,选择合适的机构的尺寸大小,并进行下列操作:⑴对机构进行结构分析;⑵绘制滑块D的运动线图(即位移、速度和加速度线图);⑶绘制构件3和4的运动线图(即角位移、角速度和角加速度线图);⑷绘制S4点的运动轨迹。
基于UGCAE的平面六杆机构的运动分析

基于UG/CAE的平面六杆机构的运动分析1、题目说明如上图所示平面六杆机构,试用计算机完成其运动分析。
已知其尺寸参数如下表所示:题目要求:两人一组计算出原动件从0到360时(计算点数37)所要求的各运动变量的大小,并绘出运动曲线图及轨迹曲线。
注:为了使计算的结果更好的拟合运动的实际情况,同时考虑到UG在运动仿真分析计算方面的快速性,我们决定在绘制曲线时将计算点由37点增加到600点。
数据输出到Excel表格时计算点取100点。
建模及其分析方法附后!2、建模及其运动分析软件介绍:UG NX是集CAD\CAE\CAM于一体的三维参数化软件,也是当今世界最先进的设计软件,它广泛应用于航空航天、汽车制造、机械电子等工程领域。
还有在系统创新、工业设计造型、无约束设计、装配设计、钣金设计、工程图设计等方面的功能。
运动仿真是UG/CAE(Computer Aided Engineering)模块中的主要部分,它能对任何二维或三维机构进行复杂的运动学分析、动力分析和设计仿真。
通过UG/Modeling的功能建立一个三维实体模型,利用UG/Motion的功能给三维实体模型的各个部件赋予一定的运动学特性,再在各个部件之间设立一定的连接关系既可建立一个运动仿真模型。
UG/Motion的功能可以对运动机构进行大量的装配分析工作、运动合理性分析工作,诸如干涉检查、轨迹包络等,得到大量运动机构的运动参数。
通过对这个运动仿真模型进行运动学或动力学运动分析就可以验证该运动机构设计的合理性,并且可以利用图形输出各个部件的位移、坐标、加速度、速度和力的变化情况,对运动机构进行优化。
我们通过学习UG,通过建立平面六杆机构模型,通过UG/CAE模块对平面连杆的运动进行分析。
3.六连杆机构的三维造型连杆L1连杆L2连杆L3连杆L5连杆L6六杆机构装配示意图机构装配后运动演示见附件—平面六杆运动演示.avi (本报告相同目录下)3. 运动分析数据计算结果在附件的Excel表格中。
【机械原理课程设计】向量法运动分析

单位
数据
mm
70
mm
200
mm
315
度
60
度
120
mm
70
mm
320
mm
225
mm
150
mm
60
转/分
100
• 偏置直动滚子从动件盘形凸轮中升程h=28mm, 偏距e=12mm,基圆半径r=30mm,滚子半径 r=10mm,[α]=30°,从动件运动规律:凸 轮转过60°时,从动件以余弦加速度运动规律 上升,其后转过30°从动件保持不动,再转过 60°时,从动件以余弦加速度运动规律返回原 处,其后又转过230°从动件保持不动。凸轮 与曲柄共轴以逆时针回转。
平面机构运动分析
(矢量方程图解法)
•矢量方程的图解法
•同一构件上各点间的运动关系
•两构件瞬时重合点间的运动关系
§3
用矢量方程图解法分析平面机构的运动 b
A
一、矢量方程的图解法
矢量:大小、方向
矢量方程
AB C
a
B
x
一个矢量方程可以解两个未知量。
AB C
大小 √ √ 方向 √ √
? √ √ √
2
无ak 1 2 B 3
3
无ak
1
2 3
有ak B 有ak
2 B 3 1
1 B
3有ak 2
2
B 有a k 3
2 1 B 3 有ak
1
B
1
例 求图3-5所示机构的运动关系(P52) B 解:1)以长度比例尺L作机构位置图 2)速度分析 求Vc、 2 (第一类问题) VB2 4 D 2 3 C
D
//EF VD5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理课程设计设计题目:基于矢量图解法的平面六杆机构运动分析姓名:专业班级:学号:指导老师:目录目录 (1)一、设计说明 (2)二、设计内容及数据 (2)1.构件位置的确定及相应尺寸 (3)2.速度分析 (3)3.加速度分析 (5)三、数据汇总 (9)四、参考文献 (10)一、设计说明机构的运动分析,是指原动件的运动规律已知时,求解其余构件的运动规律,确定指定构件上点的位移、轨迹、速度与加速度。
对机构作运动分析的方法很多,本课程设计采用矢量方程图解法。
对机构作运动分析的目的是确定机构的运动空间、检验相关构件的运动规律是否符合设计要求以及为构件的强度设计、运动副的尺寸设计提供计算惯性力与惯性力矩的参数。
矢量方程图解法,也称相对运动图解法,其依据的原理是将动点的运动划分为伴随参考构件的运动以及相对于参考构件的运动。
二、设计内容及数据=AB=0.122m, 图(a)为一平面六杆机构,主动件1的杆长r1ϕ==40°,角速度ωL=10rad/s,机架6上的h1=AC=0.280m,=0.164m,比例尺μl=实际尺寸/图上尺寸=2。
试用相对运动图解h2法求移动从动件5的速度V5与加速度a5。
图(a )AUTOCAD 绘制图 2L μ=1.构件位置的确定及相应尺寸由图(a )得导杆3上B 、C 两点之间的实际长度BC L = 381.6mm ,C 、D 两点之间的实际长度 CD L =167.45mm; B 、C 两点之间的图上长度BC=190.8mm , C 、D 两点之间的图上长度CD=83.7mm 。
2.速度分析列出方程,进行分析,对两个位置点的分析。
(1)根据两构件上重合点之间的速度合成原理,得导杆3上的B 3点与滑块2上的B 2点之间的速度方程为:B3V = B2V + B3B2V1BA : //: ? ?BC BA CBωl ⊥⊥方向大小 (1)式(2)根据两构件上重合点之间的速度合成原理及已知条件,速度分析应由B 点开始,滑块2上的B 2点的速度为:2B V =1B V =1ω1r =10⨯0.122=1.22 m/s其方向垂直于AB ,指向与1ω的转向一致。
(3)取速度比例尺,v μ=实际速度(m/s )/图上尺寸(m )=10。
取任意一点p 作为作图的起点,作2pb AB ⊥,由2v pb μ•=1ω1r (2)式可得:2pb =1ω1r /v μ=10⨯0.122/10=0.122m=122mm ,作3pb ⊥BC ,作23b b //CD ,得交点3b ,如图(b )所示。
图(b )AUTOCAD 绘制图从图(b )中量取3pb =107.57mm ,23b b = 57.54mm 。
由3pb •v μ=3ω•BC L (3)式可得:3ω=3pb •v μ/BC L =107.57⨯10 / 381.6=2.82rad/s,方向为顺时针;再由:23b b •v μ=B3B2V (4)式可得:相对速度B3B2V =23b b •v μ=57.54mm ⨯10 =575.4mm/s 。
由构件2、3之间无相对转动,所以,2ω=3ω。
导杆3上3D 点的速度:3D V =3ωCD L = 2.82⨯ 167.45mm=472.2mm/s(4)对D 5点进行速度分析:从动件5上的5D 点与导杆3的3D 点之间的速度方程为 :D5V = D3V + D5D3V3CD : //5//: ? ?CD CDωl ⊥方向构件大小 (5)式从动件5上的5D 点与导杆3的3D 点之间的速度方程为D5V = D3V + D5D3V 。
(6)式由:3D V =3v pd μ (7)式可得:3pd =3D V /v μ=472.2/10mm=47.22mm ,3D 点的速度矢量为3pd ,过3d 点作35d d //CD ,过p 点5pd 平行于从动件5的运动方向,得交点5d 。
于是,得从动件5的速度5V =5pd •v μ=48.04⨯10 =480 mm/s53D D V =5d 3d •v μ= 9.89⨯10=99mm/s 。
3.加速度分析根据两构件重合点之间的加速度合成原理,得重合点2B 、3B 之间的加速度方程为:B3a = nB3a + tB3a = nB2a + tB2a + k B3B2a + rB3B2aB3B22223BC1AB2B3B2: ? {90} //: ? ? 0 2 ?B C BC B A BA BC l l V ωωωω→⊥→⊥方向沿转大小V (8)式根据两构件重合点之间的加速度合成原理,得重合点2B 、3B 之间的加速度, 方程为B3a = nB3a +tB3a = nB2a +tB2a + k B3B2a + rB3B2a 。
其中n B2a 、n B3a 与k B3B2a 分别为: n B2a =211r ω=2100.122⨯=12.2m/2s n B3a =23ωBC L =2.822×0.3816 m/2s =3000mm/2sk B3B2a =22ωB3B2V =2×2.82×575.4 m/2s =3249mm/2sB3B2V 方向为沿2ω转90°。
取加速度比例尺a μ=实际加速度(m/2s )/图上尺寸(m )=100,取任意一点'p 作为作图的起点,如图(c )所示。
图(C )AUTOCAD 绘制图作''2//p b AB ,''2p b =nB2a /a μ= 12200/100 =122mm ;作''2b b k BC ⊥,''2b b k =kB3B2a /a μ= 3249/100 =32.49mm ; 过'b k 作''3//b k b BC ;过'p 点作'''3p b //BC ,'''3p b =nB3a /a μ=30mm ;过''3b 作'''33b b ⊥'''3p b ,与''3b k b 的交点为'3b 。
连''3p b ,''3p b 表示3B a 。
为此,相对加速度rB3B2a = ''3a k b μ•= 77.58×100mm/2s =7758mm/2s ;导杆3上3B 点的切向加速度:t B3a = '''33b b a μ•=25.05×100mm/2s=2505mm/2s ;导杆3上3B 点的加速度3B a = ''3p b a μ•=39.08×100mm/2s =3908mm/2s ;导杆3上3D 点的加速度3D a = ''3p d a μ•= 17.15×100mm/2s =1715mm/2s 。
图(d )AUTOCAD 绘制图5D 点的加速度分析重合点5D 、3D 之间的加速度方程为:D5a = n D3a + t D3a + k D5D3a + rD5D3a''03D5D3323DC3DC 3D5D3: // 5 {90} //: ? 2 ?ak b D C DC DC l l V ωωαωμ→⊥•方向构件沿转大小V(9)式注:先求t B33BC=a l α,再求tD3a重合点5D 、3D 之间的加速度方程为D5a =n D3a +t D3a +k D5D3a + rD5D3a 。
其中kD5D3a 与3D a 分别为:kD5D3a =23ωD5D3V =2×2.82×99mm/2s = 558.36mm/2s , 方向为D5D3V 沿3ω转90°,如图(d )所示。
由3B a /3D a =''3pb /''3p d =BC L /CD L 得3D a =3(/)B CD BC a L L =3908×(167.45/381.6) mm/2s =1714.87mm/2s ,为此,3D 点的加速度''3p d =3D a /a μ= 17.15mm ;过'3d 点作''3d d k 表示kD5D3a ,''3d d k =kD5D3a /a μ= 558.36/100mm=5.6mm ;过'd k 点作''5d k d ,过'p 作''5p d ,得交点'5d 。
于是,得相对加速度r D5D3a =''5d k d a μ•= 12.03×100mm/2s =1203mm/2s ;从动件5的加速度5a =D5a =''5p d a μ•=5.51×100mm/2s =551mm/2s 。
从动件5的在一个周期内的位移5S 、速度5V 与加速度5a 如图(e )所示。
三、数据汇总可修改可编辑四、参考文献[1]王洪欣冯雪君主编《机械原理》东南大学出版社 2011年6月 . .精选文档。
