2018年上海市春考数学试卷(含答案)
2018年上海高考春考卷(精确回忆版)

2018年上海高考春考卷(精确回忆版)(考试时间:90分钟,满分:100分)一、选择题(共7题,每题4分,满分28分)1. ()(4分)2. ()(4分)3. ()(4分)4. ()(4分)5. ()(4分)6. ()(4分)7. ()(4分)二、填空题(共7题,每题4分,满分28分)1. ()(4分)2. ()(4分)3. ()(4分)4. ()(4分)5. ()(4分)6. ()(4分)7. ()(4分)三、解答题(共3题,每题10分,满分30分)1. (10分)2. (10分)3. (10分)四、分析题(共2题,每题10分,满分20分)1. (10分)2. (10分)五、论述题(共1题,满分14分)1. (14分)一、选择题A. 力是改变物体运动状态的原因B. 物体在没有外力作用下,总保持静止或匀速直线运动状态C. 两个物体之间的作用力和反作用力大小相等,方向相反D. 物体受到的合外力等于其质量与加速度的乘积A. 氧B. 氢C. 钠D. 硫A. 温故知新B. 不耻下问C. 三思而行D. 一日千里A. 美国B. 德国C. 日本D. 中国A. 北京B. 上海C. 广州D. 深圳A. 秦朝B. 汉朝C. 唐朝D. 宋朝A. 牛顿B. 爱因斯坦C. 波尔D. 海森堡二、填空题1. 一元二次方程 ax^2 + bx + c = 0(a≠0)的解为 x1 = ______,x2 = ______。
2. 我国第一部纪传体通史是《______》。
3. 在化学反应中,______是指物质在反应过程中失去电子。
4. 地球自转的方向是______。
5. “民为贵,社稷次之,君为轻”出自______。
6. 人体内最大的消化腺是______。
7. 我国四大发明包括:______、______、______、______。
三、解答题2. 请简述三国演义中赤壁之战的主要过程。
3. 请解释光合作用的过程及其意义。
四、分析题1. 请分析我国近年来经济发展迅速的原因。
2018年上海市普通高等学校春季招生统一文化考试数学试卷

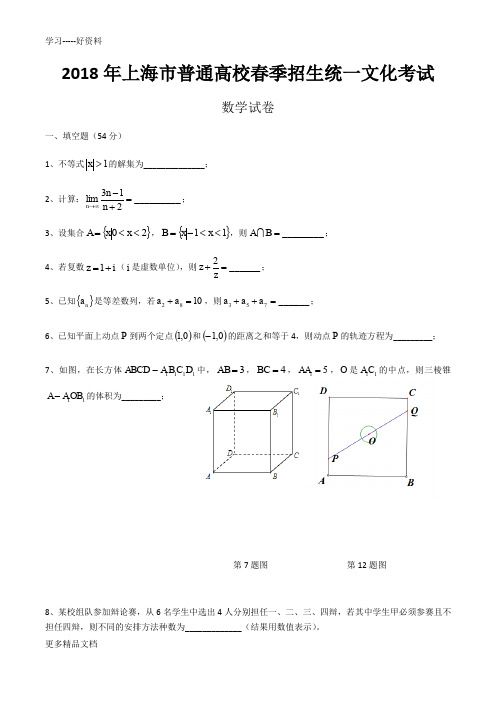
2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.不等式||1x >的解集为__________.2.计算:31lim 2n n n →∞-=+__________. 3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B =__________.4.若复数z i i =+(i 是虚数单位),则2z z+=__________. 5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=__________.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹为 __________.7.如图,在长方形1111B ABC A C D D -中,3AB =,4BC =,15AA =, O 是11A C 的 中点,则三棱锥11A AOB -的体积为__________.第7题图 第12题图8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、 四辩.若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为__________.9.设a R ∈,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =__________. 10.设m R ∈,若z 是关于x 的方程2210x mx m -+=+的一个虚根,则||z 的取值范围是__________.11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x = 的图象有且仅有两个不同的公共点,则a 的取值范围是__________. 12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲 区”中.已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度 从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为__________秒(精确到0.1)二、选择题(本大题共有4题,满分20分,每题5分)13.下列函数中,为偶函数的是( )(A )2y x -= (B )13y x =(C )12y x -= (D )3y x = 14.如图,在直三棱柱111AB A B C C -的棱虽在的直线中,与直线1BC异面的直线条数为( )(A )1 (B )2(C )3 (D )415.记n S 为数列{}n a 的前n 项和.“{}n a 是递增数列”是“n S 为递增数列”的( )(A )充分非必要条件 (B )必要非充分条件 (C )充要条件 (D )既非充分也非必要条件16.已知A 、B 为平面上的两个定点,且|2|AB =.该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AB AP ⋅=,2AQ AP =-,则动线段PQ 所形成图形的面积为( )(A )36 (B )60 (C )81 (D )108三、解答题(本大题共有5题,满分76分,第17~19题每题14分,20题16分,21题18分)17.(本题满分14分,第1小题满分6分,第2小题满分8分)已知cos y x =.(1)若3(1)f α=,且[0,]απ∈,求()3f πα-的值; (2)求函数(2)2()y f x f x =-的最小值.18. (本题满分14分,第1小题满分6分,第2小题满分8分)已知a R ∈,双曲线222:1x y aΓ-=.(1)若点(2,1)在Γ上,求Γ的焦点坐标; (2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分7分,第2小题满分7分)利用“平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离; (2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).图1 图2图320.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分) 设0a >,函数1()12x f x a =+⋅. (1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x ⋅-=的最大值(用a 表示);(3)设()()(1)g x f x f x =--.若对任意(,0]x ∈-∞,)(()0g x g ≥恒成立,求a 的取值范围.21.(本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分) 若{}n c 是递增数列,数列{}n a 满足:对任意*n N ∈,存在*m N ∈,使得10m n m n a c a c +-≤-,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的“分隔数列”;(2)设4n c n =-,n S 是{}n c 的前n 项和,31n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T {}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.。
2018年上海卷春季高考真题数学试卷-学生用卷

2018年上海卷春季高考真题数学试卷-学生用卷一、填空题(1~6每小题4分,7~12每小题5分,共54分)1、【来源】 2018~2019学年10月上海闵行区上海市七宝中学高一上学期月考第1题2018年1月高考真题上海卷第1题4分不等式|x|>1的解集为.2、【来源】 2018年1月高考真题上海卷第2题4分计算:limn→∞3n−1n+2=.3、【来源】 2018年1月高考真题上海卷第3题4分设集合A={x|0<x<2},B={x|−1<x<1},则A∩B=.4、【来源】 2018年1月高考真题上海卷第4题4分若复数z=1+i(i是虚数单位),则z+2z=.5、【来源】 2018年1月高考真题上海卷第5题4分已知{a n}是等差数列,若a2+a8=10,则a3+a5+a7=.6、【来源】 2018年1月高考真题上海卷第6题4分已知平面上动点P到两个定点(1,0)和(−1,0)的距离之和等于4,则动点P的轨迹方程为.7、【来源】 2018年1月高考真题上海卷第7题5分如图,在长方体ABCD−A1B1C1D1中,AB=3,BC=4,AA1=5,O是A1C1的中点,则三棱锥A−A1OB1的体积为.8、【来源】 2018年1月高考真题上海卷第8题5分某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩.若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为.9、【来源】 2018年1月高考真题上海卷第9题5分设a∈R,若(x2+2x )9与(x+ax2)9的二项展开式中的常数项相等,则a=.10、【来源】 2020~2021学年上海徐汇区高一下学期期末第9题2018年1月高考真题上海卷第10题5分设m∈R,若z是关于x的方程x2+mx+m2−1=0的一个虚根,则|z|的取值范围是.11、【来源】 2018年1月高考真题上海卷第11题5分设a>0,函数f(x)=x+2(1−x)sin(ax),x∈(0,1),若函数y=2x−1与y=f(x)的图象有且仅有两个不同的公共点,则a的取值范围是.12、【来源】 2018年1月高考真题上海卷第12题5分2019~2020学年12月上海闵行区上海市七宝中学高二上学期月考第12题5分如图,正方形ABCD的边长为20米,圆O的半径为1米,圆心是正方形的中心,点P、Q分别在线段AD、CB上,若线段PQ与圆O有公共点,则称点Q在点P的“盲区”中.已知点P以1.5米/秒的速度从A出发向D移动,同时,点Q以1米/秒的速度从C出发向B移动,则在点P从A移动到D的过程中,点Q在点P的盲区中的时长约为秒.(精确到0.1)二、选择题(每小题5分,共20分)13、【来源】 2018年1月高考真题上海卷第13题5分下列函数中,为偶函数的是().A. y=x−2B. y=x13C. y=x−12D. y=x314、【来源】 2018年1月高考真题上海卷第14题5分2019~2020学年广东深圳罗湖区深圳市美术学校高一下学期开学考试第7题5分如图,在直三棱柱ABC−A1B1C1的棱所在的直线中,与直线BC1异面的直线条数为().A. 1B. 2C. 3D. 415、【来源】 2018~2019学年10月上海宝山区上海市吴淞中学高三上学期月考第15题5分 2018年1月高考真题上海卷第15题5分记S n 为数列{a n }的前n 项和.“{a n }是递增数列”是“{S n }为递增数列”的( ).A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件16、【来源】 2018年1月高考真题上海卷第16题5分已知A 、B 为平面上的两个定点,且|AB →|=2.该平面上的动线段PQ 的端点P 、Q ,满足|AP →|⩽5,AP →⋅AB →=6,AQ →=−2AP →,则动线段PQ 所形成图形的面积为( ).A. 36B. 60C. 81D. 108三、解答题(第17题14分,第18题14分,第19题14分,第20题16分,第21题18分)17、【来源】 2018年1月高考真题上海卷第17题14分2017~2018学年上海嘉定区高一下学期期末第18题8分已知y =cosx .(1) 若f(α)=13,且α∈[0,π],求f(α−π3)的值. (2) 求函数y =f(2x)−2f(x)的最小值.18、【来源】 2018年1月高考真题上海卷第18题14分已知a ∈R ,双曲线Γ:x 2a 2−y 2=1.(1) 若点(2,1)在Γ上,求Γ的焦点坐标.(2) 若a=1,直线y=kx+1与Γ相交于A、B两点,且线段AB中点的横坐标为1,求实数k的值.19、【来源】 2018年1月高考真题上海卷第19题14分利用“平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O、A、B在抛物线上,OC是抛物线的对称轴,OC⊥AB于C,AB=3米,OC=4.5米.(1) 求抛物线的焦点到准线的距离.(2) 在图3中,已知OC平行于圆锥的母线SD,AB、DE是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).20、【来源】 2020~2021学年上海杨浦区上海复旦大学附属中学高一上学期期末第20题16分2018年1月高考真题上海卷第20题16分设a>0,函数f(x)=11+a⋅2x.(1) 若a=1,求f(x)的反函数f−1(x).(2) 求函数y=f(x)⋅f(−x)的最大值(用a表示).(3) 设g(x)=f(x)−f(x−1).若对任意x∈(−∞,0],g(x)⩾g(0)恒成立,求a的取值范围.21、【来源】 2018年1月高考真题上海卷第21题18分若{c n}是递增数列,数列{a n}满足:对任意n∈N∗,存在m∈N∗,使得a m−c na m−c n+1⩽0,则称{an}是{c n}的“分隔数列”.(1) 设c n=2n,a n=n+1,证明:数列{a n}是{c n}的“分隔数列”.(2) 设c n=n−4,S n是{c n}的前n项和,d n=c3n−2,判断数列{S n}是否是数列{d n}的分隔数列,并说明理由.(3) 设c n=aq n−1,T n是{c n}的前n项和,若数列{T n}是{c n}的分隔数列,求实数a、q的取值范围.1 、【答案】(−∞,−1)∪(1,+∞);2 、【答案】3;3 、【答案】(0,1);4 、【答案】2;5 、【答案】15;6 、【答案】x24+y23=1;7 、【答案】5;8 、【答案】180;9 、【答案】4;10 、【答案】(√33,+∞) ;11 、【答案】(11π6,19π6];12 、【答案】4.4;13 、【答案】 A;14 、【答案】 C;15 、【答案】 D;16 、【答案】 B;17 、【答案】 (1) 1+2√66.;(2) −32.;18 、【答案】 (1) (±√3,0).;(2) √5−1.2;19 、【答案】 (1) 1米.4;(2) 9.59°.;(0<x<1).20 、【答案】 (1) f−1(x)=log21−xx;(2) 1.1+2a+a2;(3) (0,√2].;21 、【答案】 (1) 证明见解析.;(2) 不是,理由见解析.;(3) a>0且q⩾2.;。
2018年上海春季招生统一文化考试数学(含答案)

C9k x9k
a2k x2k
C9k ak x93k ,k
3,
常数项为C93a3 a 4
10.设 m R ,若 z 是关于 x 的方程 x2 mx m2 1 0 的一个虚根,则 | z | 的取值范围
是__________.
答案:( 3 ,+) 3
解析:
法一:设z a bi,(b 0)代入方程得:(a bi)2 +m(a bi) m2 1 0,即 a2 b2 ma m2 1 0, 2ab mb 0
(B)60
(C)81
(D)108
本题考查向量的投影,因为 AP 5,所以P点在以A为圆心半径为5的圆面上, 又AP AB 6= AB AP cos ,所以 AP cos =3,根据题意作图如下:
三、解答题(本大题共有 5 题,满分 76 分,第 17~19 题每题 14 分,20 题 16 分, 21 题 18 分)
3/7
仅供学习交流、勿做商用!
答案:A
14.如图,在直三棱柱 ABC A1B1C1 的棱虽在的直线中,与直线 BC1
异面的直线条数为( )
(A)1
(B)2
(C)3
(D)4
答案:C
15.记 Sn 为数列{an}的前 n 项和.“{an}是递增数列”是“ Sn 为递增数列”的( )
(A)充分非必要条件
答案: C31C53P33 180
9.设 a R
,若
x2
2 x
9
与
x
a x2
9
的二项展开式中的常数项相等,则 a
2018年上海春考数学试卷

2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每 题5分)1.不等式 lxl>1的解集为3n -1 2.计算: lim -------- =.n—厂 n 23.设集合 A={xl0cx£2},B={xl —1cxc1},则 AC B = .4.若复数2Z =1 • i ( i 是虚数单位),则z ■z5•已知{a .}是等差数列,若a 2 a^ 10,则a 3 a s a 7 =6 .已知平面上动点P 到两个定点(1,0)和(-1,0)的距离之和等于 4,则动点P 的轨迹为7•如图,在长方形 ABCD —ABQU 中,AB=3,BC =4,AA =5, O 是 A 1C 1 的中点,则三棱锥A-AOB 1的体积为 ______________10.设m • R ,若z 是关于x 的方程x 2 mx m 20的一个虚根, 是 __________ .11.设 a 0,函数 f (x) =x 2(1 -x)sin( ax),x (0,1),若函数 y =2x T 与 y = f (x)四辩.若其中学生{ 229.设 a R ,若 I x< x与X •刍 的二项展开式中的常数项相等, x 2则|z|的取值范围第12题图的图象有且仅有两个不同的公共点,则a 的取值范围是 ___________ .12•如图,正方形 ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段 AD 、CB 上,若线段PQ 与圆0有公共点,则称点Q 在点P 的盲区”中•已知点P 以1. 5米/秒的速度从 A 出发向D 移动,同时,点 Q 以1米/秒的速 度 从C 出发向B 移动,则在点 P 从A 移动到D 的过程中,点 Q 在点P 的盲区中的时长约为 _____________ 秒(精确到0. 1)15.记S n 为数列{a n }的前n 项和.{a n }是递增数列"是 S 为递增数列"的()(A )充分非必要条件 (B )必要非充分条件 (C )充要条件(D )既非充分也非必要条件T16.已知A 、B 为平面上的两个定点, 且| AB | =2 .该平面上的动线段 PQ 的端点P 、Q ,满足| AP F 5, AP A^ 6, AQ = -2AP ,则动线段PQ 所形成图形的面积为()(A) 36 (B) 60 (C) 81三、解答题(本大题共有5题,满分76分,第17~佃题每题14分,20题16分,21题18分)17. (本题满分14分,第1小题满分6分,第2小题满分8分)二、选择题(本大题共有 4题,满分20分,母题5分)13•下列函数中,为偶函数的是()2(A ) y =x1(B ) y = x 3 1(C ) y=x^3(D ) y =x14•如图,在直三棱柱 ABC-ABG 的棱所在的直线中,与直线 BG异面的直线条数为( )(A ) 1(B ) 2 (C ) 3(D ) 4(D) 108已知y =cosx .⑴若f(»3,且一[°C,求(巧)的值;(2)求函数y二f (2x)-2f(x)的最小值.18.(本题满分14分,第1小题满分6分,第2小题满分8分)2X 2已知a • R,双曲线-I, -讨=1.a(1)若点(2,1)在丨上,求-的焦点坐标;(2)若a =1,直线y =kx • 1与丨相交于A、B两点,且线段AB中点的横坐标为1, 求实数k 的值.19.(本题满分14分,第1小题满分7分,第2小题满分7分)利用平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥) 在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O、A、B在抛物线上,OC是抛物线的对称轴,OC_AB于C , AB=3米,0C =4.5米.(1)求抛物线的焦点到准线的距离;圆锥的母线与轴的夹角的大小(精确到0. 01°.(2)在图3中,已知0C平行于圆锥的母线SD , AB、DE是圆锥底面的直径,求图3设a -0,函数f(x)二20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)(1) 若a =1,求f (x)的反函数f J (x);(2) 求函数y 二f(x) ・f(-x)的最大值(用a 表示);(3) 设 g(x) =f (x) -f (x -1).若对任意 x (-::,0] , g(x)_g(O)恒成立,求 a 的 取值范围.21. (本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分)若{C n }是递增数列,数列{a n }满足:对任意n • N *,存在m • N *,使得 為一 C n< 0 ,am -C n 卅则称{a n }是{q }的分隔数列”(1) 设C n =2n , a n = n ,1,证明:数列 佝}是G }的分隔数列”(2) 设c n = n- 4 , S n 是{c n }的前n 项和,d n =务」,判断数列{S n }是否是数列{d n } 的分隔数列,并说明理由;n_ ________________________________________(3)设C n =aq , T n 是{C n }的前n 项和,若数列{人}是{q }的分隔数列,求实数a 、 q 的取值范围.、填空题;0 :: ax :: a 11 二12. 4.4提示:以A 为原点建立坐标系,设时刻为t ,则P(0,1.5t),Q(20, 20-t),0岂t 乞403,化简得(8—t)x —8y+12t=020-020—t —1.5t、选择题16. BP(x, y)的轨迹为线段 x =3,-4乞y 空4 , AP 扫过的三角形面积为12,则利用相似三角形可知AQ 扫过的面积为48,因此和为60参考答案1. (」:,-1)U(1,2. 33.(0,1)4. 25. 156.2 2x y ‘ 1437. 5 8. 180 9. 411.11二 19二提示:2x -1—X = 2(1-x)sin( ax)—1 x -1 二 2(1 -x)sin( ax) = sin(ax)二 27 二 11二 7二11■:11 ■:ax , , 2-, 2二,4二,4 二,||( 6 6 6 6 6 6 x -0y —1.5t 则 I PQ :点0(10,10)到直线PQ 的距离|(8-t)10-80 创胡,化简得 3t 2 愀-128_0 .(8 -1)2 83即于『3,则0十邑旦1=心二J:4.413. A 14. C15. D提示:建系 A(0,0), B(2,0),则三、解答题32a —,(t =2X (0,1]) 22 a t 3at因为-a<0,所以当X=0,t=1时,分母取到最小值从而分式值取到最小值,(3)a 0q _2【a A 0 ②当q .1时,G18.(1) (_ .3,0) ; (2)19.(1) 1 1 ; (2) 9.59 420.(1) 1 1 f —(x)Jog ? —.x(0 ::: X ::: 1) ;( 2)y1 2 ( x = 0时取最值);1 2a a 2提示:g(X )=1 y 2X「1 a 2X」-a=__X__2a 2 2X X . 3a2X21. (1)证明:存在m = 2n ,此时一 n N ,c n = 2n :: a m = 2n 1 :: c n2n 2 证毕(2)不是•反例:n =4时,m 无解;提示:因为{aq n4}为递增数列,因此a 0或者…q 10 ::①当a 0时,0 cq v1~n N *,c n <0,因此 IH ::: T2 :::可=q ::: 9C 3111因此不存在C 2 ^T m ::.C3,不合题意。
高考最新-2018年上海市普通高等学校春季招生考试数学(附答案)001 精品

2018年上海市普通高等学校春季招生考试数学试卷考生注意:1.答卷前,考生务必将姓名、高考座位号、校验码等填写清楚.2.本试卷共有22道试题,满分150分.考试时间120分钟.. 填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每题填对得4分,否则一律得零分.1. 方程2lg lg(2)0x x-+=的解集是.2. =++++∞→nnn212lim.3. 若3cos5α=,且⎪⎭⎫⎝⎛∈2,0πα,则=2tgα.4. 函数2()f x x=-)]2,((-∞-∈x的反函数=-)(1xf.5. 在△ABC中,若90C∠=,4AC BC==,则BA BC⋅=.6. 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,则这对双胞胎的作业同时被抽中的概率是(结果用最简分数表示).7. 双曲线116922=-yx的焦距是.8. 若()()3,2223≥∈+++++=+nnxcxbxaxx nnn且N,且2:3:=ba,则=n.9. 设数列{}n a的前n项和为n S(N∈n). 关于数列{}n a有下列三个命题:(1)若{}n a既是等差数列又是等比数列,则)(1N∈=+naann;(2)若()R∈+=banbnaSn、2,则{}na是等差数列;(3)若()nnS11--=,则{}n a是等比数列.这些命题中,真命题的序号是.10. 若集合{}R∈==xxxA x,32cos3π,{}R∈==yyyB,12,则BA = .11. 函数xxy arcsinsin+=的值域是.12. 已知函数2()2log x f x x =+,数列{}n a 的通项公式是n a n 1.0=(N ∈n ),当 |()2005n f a -取得最小值时,n = . 二.选择题(本大题满分16分)本大题共有4题,每题都给出 四个结论,其中有且只有一个结论是正确的,必须把正确结论的 代号写在题后的圆括号内,选对得 4分,否则一律得零分.13. 已知直线n m l 、、及平面α,下列命题中的假命题是 (A )若//l m ,//m n ,则//l n . (B )若l α⊥,//n α,则l n ⊥. (C )若l m ⊥,//m n ,则l n ⊥. (D )若//l α,//n α,则//l n .[答] ( ) 14. 在△ABC 中,若CcB b A a cos cos cos ==,则△ABC 是 (A )直角三角形. (B )等边三角形. (C )钝角三角形. (D )等腰直角三角形.[答] ( ) 15. 若c b a 、、是常数,则“0402<->c a b a 且”是“对任意R ∈x ,有02>++c x b x a ” 的(A )充分不必要条件. (B )必要不充分条件. (C )充要条件. (D )既不充分也不必要条件.[答] ( ) 16. 设函数()f x 的定义域为R ,有下列三个命题:(1)若存在常数M ,使得对任意R ∈x ,有()f x M ≤,则M 是函数()f x 的最大值; (2)若存在R ∈0x ,使得对任意R ∈x ,且0x x ≠,有)()(0x f x f <,则)(0x f 是函数()f x 的最大值;(3)若存在R ∈0x ,使得对任意R ∈x ,有)()(0x f x f ≤,则)(0x f 是函数()f x 的最大值. 这些命题中,真命题的个数是(A )0个. (B )1个. (C )2个. (D )3个.[答] ( )三.解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.已知z 是复数,izi z -+22、均为实数(i 为虚数单位),且复数2)(i a z +在复平面上对应的点在第一象限,求实数a 的取值范围.[解] 18. (本题满分12分) 已知αtg 是方程01sec 22=++αx x 的两个根中较小的根,求α的值. [解]19. (本题满分14分) 本题共有2个小题,第1小题满分6分, 第2小题满分8分.已知正三棱锥ABC P -的体积为372,侧面与底面所成的二面角的大小为 60. (1)证明:BC PA ⊥;(2)求底面中心O 到侧面的距离. [证明](1)[解](2)某市2018年底有住房面积1200万平方米,计划从2018年起,每年拆除20万平方米的旧住房. 假定该市每年新建住房面积是上年年底住房面积的5%. (1)分别求2018年底和2018年底的住房面积 ;(2)求2184年底的住房面积.(计算结果以万平方米为单位,且精确到0.01) [解](1)(2)21. (本题满分16分)本题共有3个小题,第1小题满分3分, 第2小题满分6分,第3小题满分7分. 已知函数xax x f +=)(的定义域为),0(∞+,且222)2(+=f . 设点P 是函数图象上的任意一点,过点P 分别作直线x y =和y 轴的垂线,垂足分别为N M 、. (1)求a 的值;(2)问:||||PN PM ⋅是否为定值?若是,则求出该定值,若不是,则说明理由; (3)设O 为坐标原点,求四边形OMPN 面积的最小值. [解](1) (2) (3)(1)求右焦点坐标是)0,2(,且经过点)2,2(--的椭圆的标准方程;(2)已知椭圆C 的方程是12222=+b y a x )0(>>b a . 设斜率为k 的直线l ,交椭圆C 于A B 、两点,AB 的中点为M . 证明:当直线l 平行移动时,动点M 在一条过原点的定直线上;(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心. [解](1)[证明](2)[解](3)2018年上海市普通高等学校春季招生考试数 学 试 卷参考答案及评分标准说明1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.3.第17题至第22题中右端所注的分数,表示考生正确做到这一步应得的该题的累加分数.4.给分或扣分均以1分为单位.答案及评分标准一.(第1至12题)每一题正确的给4分,否则一律得零分.1. }2,1{-.2. 0.3.21. 4. ]4,(,--∞∈--x x . 5. 16. 6.2601. 7. 65. 8. 11. 9. (1)、(2)、(3). 10. {}1.11. ⎥⎦⎤⎢⎣⎡+--21sin ,21sin ππ. 12. 110二.(第13至16题)每一题正确的给4分,否则一律得零分.三.(第17至22题)17. [解] 设R)∈+=y x yi x z 、(,i y x i z )2(2++=+ ,由题意得 2-=y . …… 2分i x x i i x i i x i z )4(51)22(51)2)(2(51222-++=+-=--=-由题意得 4=x . …… 6分 ∴ i z 24-=.∵ 2)(ai z +i a a a )2(8)412(2-+-+=, …… 9分根据条件,可知⎩⎨⎧>->-+0)2(804122a a a ,解得 62<<a ,∴ 实数a 的取值范围是)6,2(. …… 12分 18. [解] ∵ αtg 是方程01sec 22=++αx x 的较小根, ∴ 方程的较大根是αctg . ∵ αtg +αctg =αsec 2-,即αααcos 2cos sin 1-= ∴ 21sin -=α. …… 5分 解得 672ππα+=k ,或Z ∈-=k k ,62ππα. …… 8分 当)(672Z ∈+=k k ππα时,αtg 33=,αctg 3=; 当)(62Z ∈-=k k ππα时,αtg 33-=,αctg 3-=,不合题意. ∴ Z ∈+=k k ,672ππα. …… 12分19. [证明](1)取BC 边的中点D ,连接AD 、PD ,则BC AD ⊥,BC PD ⊥,故⊥BC 平面APD . …… 4分 ∴ BC PA ⊥. …… 6分 [解](2)如图, 由(1)可知平面⊥PBC 平面APD ,则PDA ∠是侧面与底面所成二面角的平面角.过点O 作E PD OE ,⊥为垂足,则OE 就是点O 到侧面的距离. …… 9分设OE 为h ,由题意可知点O 在AD 上, ∴ 60=∠PDO ,h OP 2=.h BC h OD 4,32=∴=, …… 11分∴ 2234)4(43h h S ABC ==∆, ∵ 3233823431372h h h =⋅⋅=,∴ 3=h . 即底面中心O 到侧面的距离为3. …… 14分 20. [解](1)2018年底的住房面积为124020%)51(1200=-+(万平方米), 2018年底的住房面积为128220%)51(20%)51(12002=-+-+(万平方米)∴ 2018年底的住房面积为1240万平方米,2018年底的住房面积约为1282万平方米. …… 6分 (2)2184年底的住房面积为20%)51(20%)51(20%)51(20%)51(1200181920-+--+-+-+ …… 10分 64.252205.0105.120%)51(12002020≈-⨯-+=(万平方米)∴ 2184年底的住房面积约为2522.64万平方米. …… 14分 21. [解](1)∵ 22222)2(+=+=a f ,∴ 2=a . …… 3分 (2)设点P 的坐标为),(00y x ,则有0002x x y +=,00>x ,由点到直线的距离公式可知:0000||,12||||x PN x y x PM ==-=, 故有1||||=⋅PN PM ,即||||PN PM ⋅为定值,这个值为1. …… 9分 (3)由题意可设),(t t M ,可知),0(0y N .∵ PM 与直线x y =垂直,∴ 11-=⋅PM k ,即100-=--tx ty ,解得 )(2100y x t +=,又0002x x y +=,∴ 0022x x t +=. ∴22212+=∆x S OPM ,222120+=∆x S OPN , ∴ 212)1(212020+≥++=+=∆∆x x S S S OPN OPM OMPN , 当且仅当10=x 时,等号成立.∴ 此时四边形OMPN 面积有最小值21+. …… 16分22. [解](1)设椭圆的标准方程为12222=+b y a x ,0>>b a ,∴ 422+=b a ,即椭圆的方程为142222=++b y b x , ∵ 点(2,2--)在椭圆上,∴ 124422=++b b , 解得 42=b 或22-=b (舍),由此得82=a ,即椭圆的标准方程为14822=+y x . …… 5分(2)设直线l 的方程为m kx y +=, …… 6分 与椭圆C 的交点A (11,y x )、B (22,y x ),则有⎪⎩⎪⎨⎧=++=12222b y a x m kx y , 解得 02)(222222222=-+++b a m a kmx a x k a b ,∵ 0>∆,∴ 2222k a b m +<,即 222222k a b m k a b +<<+-.则 222221212222212,2ka b mb m kx m kx y y k a b kma x x +=+++=++-=+, ∴ AB 中点M 的坐标为⎪⎪⎭⎫⎝⎛++-22222222,k a b m b k a b km a . …… 11分∴ 线段AB 的中点M 在过原点的直线 022=+y k a x b 上. …… 13分 (3)如图,作两条平行直线分别交椭圆于A 、B 和D C 、,并分别取AB 、CD 的中点N M 、,连接直线MN ;又作两条平行直线(与前两条直线不平行)分别交椭圆于1A 、1B 和11D C 、,并分别取11B A 、11D C 的中点11N M 、,连接直线11N M ,那么直线MN 和11N M 的交点O 即为椭圆中心. …… 18分。
2018年上海市春考数学试卷

上海市教育考试院保留版权2018年春考数学第1页(共4页)2018年上海市普通高校春季招生统一文化考试数学试卷考生注意:1.本场考试时间120分钟.试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名.将核对后的条形码贴在指定位置.3.所有作答必须涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.1.不等式||1x >的解集为.2.计算:31lim 2n n n →∞-=+.3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B = .4.若复数1i z =+(i 是虚数单位),则2z z +=.5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹方程为.7.如图,在长方体1111ABCD A B C D -中,3AB =,4BC =,15AA =,O 是11A C 的中点,则三棱锥11A A OB -的体积为.8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为.(结果用数值表示)9.设a ∈R ,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =.10.设m ∈R ,若z 是关于x 的方程2210x mx m ++-=的一个虚根,则||z 的取值范围是.2018年春考数学第2页(共4页)11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图像有且仅有两个不同的公共点,则a 的取值范围是.12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为.二、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.13.下列函数中,为偶函数的是().(A)2y x -=(B)13y x =(C)12y x -=(D)3y x =14.如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为().(A)1(B)2(C)3(D)415.设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}n S 是递增数列”的().(A)充分非必要条件(B)必要非充分条件(C)充要条件(D)既非充分又非必要条件16.已知A 、B 为平面上的两个定点,且||2AB = ,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AP AB ⋅= ,2AQ AP =- ,则动线段PQ 所形成图形的面积为().(A)36(B)60(C)72(D)108三、解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸的相应位置写出必要的步骤.17.(本题满分14分,第1小题满分6分,第2小题满分8分)已知函数()cos f x x =.(1)若1()3f α=,且[0,π]α∈,求π3f α⎛⎫- ⎪⎝⎭的值;(2)求函数(2)2()y f x f x =-的最小值.2018年春考数学第3页(共4页)18.(本题满分14分,第1小题满分6分,第2小题满分8分)已知a ∈R ,双曲线222:1x y aΓ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分6分,第2小题满分8分)利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)设0a >,函数1()12x f x a =+⋅.(1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 的取值范围.图1图3图22018年春考数学第4页(共4页)21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)若{}n c 是递增数列,数列{}n a 满足:对任意*n ∈N ,存在*m ∈N ,使得10m n m n a c a c +--≤,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的分隔数列;(2)设4n c n =-,n S 是{}n c 的前n 项和,32n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T 是{}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.。
2018上海春考

2018上海春考D的半径为1米,圆心是正方形的中心,点P、Q分别在线段AD、CB上,若线段PQ与圆O有公共点,则称点Q在点P的“盲区”中,已知点P以1.5米/秒的速度从A出发向D移动,同时,点Q以1米/秒的速度从C出发向B 移动,则在点P从A移动到D的过程中,点Q在点P的盲区中的时长约为秒(精确到0.1)二. 选择题(本大题共4题,每题5分,共20分)13. 下列函数中,为偶函数的是( )A.2y x -= B. 13y x = C. 12y x -= D. 3y x =14. 如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为( )A. 1B. 2C. 3D. 415. 设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}nS 是递增数列”的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件16. 已知A 、B 为平面上的两个定点,且||2AB =,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AP AB ⋅=,2AQ AP =-,则动线段PQ 所形成图形的面积为( )A. 36B. 60C. 72D. 108三. 解答题(本大题共5题,共14+14+14+16+18=76分)17. 已知cos y x =.(1)若1()3f α=,且[0,]απ∈,求()3f πα-的值; (2)求函数(2)2()y f x f x =-的最小值.18. 已知a R ∈,双曲线222:1x y a Γ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a=,直线1y kx=+与Γ相交于A、B两点,且线段AB中点的横坐标为1,求实数k的值.19. 利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).(图1) (图2) (图3)20. 设0a >,函数1()12xf x a =+⋅. (1)若1a =,求()f x 的反函数1()fx -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 取值范围.21. 若{}n c是递增数列,数列{}n a满足:对任意*∈,m N∈,存在*n N使得1m nmn a ca c +-≤-,则称{}na 是{}nc 的“分隔数列”.(1)设2ncn=,1nan =+,证明:数列{}na 是{}nc 的分隔数列;(2)设4ncn =-,nS 是{}nc 的前n 项和,32nn dc -=,判断数列{}nS 是否是数列{}nd 的分隔数列,并说明理由; (3)设1n ncaq -=,nT 是{}nc 的前n 项和,若数列{}nT 是{}nc 的分隔数列,求实数a 、q 的取值范围.参考答案一. 填空题1. (,1)(1,)-∞-+∞ 2. 3 3.(0,1)4. 25. 156.22143x y += 7. 5 8. 180 9. 410. )+∞11. 1119(,]66ππ 12. 4.4二. 选择题13. A 14. C 15. D 16. B三. 解答题17.(1)16+;(2)32-. 18.(1),(;(219.(1)14;(2)9.59°. 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x;(2)()()xxxxx a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x,则()111222+++=+++=ata at a t a at t y ,因为0>a ,所以a ta at 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a at a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ;(3)()223222221122+⋅+⋅-=⋅+-⋅+=x xxx a t a a a a x g ,设tx=2,因为()0,∞-∈x ,所以()1,0∈t ,则()att a a t g 322++-=,若at tt a 222=⇒=,1°当12≥a时,即20≤<a ,a tt a y 322++=单调递减,所以()+∞++∈,232a a y ,则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意;2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=,则()()0,322-∈a g ,因为()()02log 2ming a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去;综上:(]2,0∈a 。
最新上海市春考数学试卷(含答案)
2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim=+-∞→n n n ;3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A ;4、若复数i z +=1(i 是虚数单位),则______2=+zz ; 5、已知{}n a 是等差数列,若1082=+a a ,则______753=++a a a ;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O 是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1). 二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=xy D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( ) A 1 B 2 C 3 D 415. 若数列}{n a 的前n 项和,“}{n a 是递增数列”是“}{n S 是递增数列”的( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(=(1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到01.0).20.设0>a ,函数xa x f 211)(⋅+=(1).若1=a ,求)(x f 的反函数)(1x f -(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示)(3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a 的取值范围?21.若}{n c 是递增数列,数列}{n a 满足:对任意*,N m R n ∈∃∈,使得01≤--+n m nm c a a a ,则称}{n a 是}{n c 的“分隔数列”(1)设1,2+==n a n c n n ,证明:数列}{n a 是}{n c 的分隔数列;(2)设n n S n c ,4-=是}{n c 的前n 项和,23-=n n c d ,判断数列}{n S 是否是数列}{n d 的分隔数列,并说明理由;(3)设n n n T aq c ,1-=是}{n c 的前n 项和,若数列}{n T 是}{n C 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11, ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180; 9、4;10、⎪⎪⎭⎫⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ; 三、解答题:17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-; 19、(1)41;(2)59.9; 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x ; (2)()()xx x x x a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x, 则()111222+++=+++=a taat at a at ty ,因为0>a ,所以a taat 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ; (3)()223222221122+⋅+⋅-=⋅+-⋅+=xx x x a t a a a a x g ,设t x=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a a t g 322++-=,若a t t t a 222=⇒=,1°当12≥a 时,即20≤<a ,a t t a y 322++=单调递减,所以()+∞++∈,232a a y , 则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意;2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=, 则()()0,322-∈a g ,因为()()02log 2ming a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去; 综上:(]2,0∈a 。
高考最新-2018年上海市普通高等学校春季招生考试数学(

2018年上海市普通高等学校春季招生考试数 学 试 卷考生注意:1.答卷前,考生务必将姓名、高考座位号、校验码等填写清楚. 2.本试卷共有22道试题,满分150分.考试时间120分钟. 一、填空题(本大题满分48分,本大题共有12题,只要求直接填写结果,每题填对得4分,否则一律得零分) 1. 计算:∞→n lim3423+-n n = .2. 方程log 3(2x-1)=1的解x= .3. 函数f(x)=3x+5,x∈[0,1] 的反函数f 1-(x)= .4. 不等式121+-x x>0的解集是 . 5. 已知圆C :(x+5)2+y 2=r 2(r >0)和直线l :3x+y+5=0.若圆C 与直线l 没有公共点,则r的取值范围是 .6. 己知函数f(x)是定义在(-∞,+∞)上的偶函数,当x∈(-∞,0)时,f(x)=x-x 4,则当x∈(0,+∞)时,f(x)= . 7. 电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有 种不同的播放方式(结果用数值表示). 8. 正四棱锥底面边长为4,侧棱长为3,则其体积为 .9. 在⊿ABC 中,已知BC=8,AC=5,三角形面积为12,则cos2C= .10. 若向量、的夹角为150°,││=3,││=4,则│2+│= . 11. 己知直线l 过点P (2,1),且与x 轴、y 轴的正半轴分别交于A 、B 两点,O 为坐标原点,则三角形OAB 面积的最小值为 .12. 同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;反之,如果按顺序去掉一些低分,那么班级的平均分将提高,这两个事实可以用数学语言描述为:若有限数列a 1,a 2…,a n 满足a 1≤a 2≤…≤a n ,则 (结论用数学式于表示).二、选择题(本大题满分16分,共有4题,每题都给出四个结论,其中有且只有一个结沦是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分。
2018年上海市春考数学试卷(含答案)

2018年上海市春考数学试卷(含答案)2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim =+-∞→n n n ; 3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A I;4、若复数i z +=1(i 是虚数单位),则______2=+z z ;5、已知{}na 是等差数列,若1082=+a a,则______753=++a a a;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1).二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=x y D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( )A 1B 2C 3D 415. 若数列}{na 的前n 项和,“}{na 是递增数列”是“}{nS 是递增数列”的( )A 充分不必要条件B 必要不充分条件C 充要条件D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72 D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(=(1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米. (1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到ο01.0).20.20.设0>a ,函数xa x f 211)(⋅+= (1).若1=a ,求)(x f 的反函数)(1x f-(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示) (3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a的取值范围?21.若}{nc 是递增数列,数列}{na 满足:对任意*,N m R n ∈∃∈,使得01≤--+n mnm c a aa ,则称}{na 是}{nc 的“分隔数列”(1)设1,2+==n a n cn n,证明:数列}{na 是}{nc 的分隔数列;(2)设nnS n c,4-=是}{nc 的前n 项和,23-=n nc d,判断数列}{nS 是否是数列}{nd 的分隔数列,并说明理由; (3)设nn nT aq c,1-=是}{nc 的前n 项和,若数列}{nT 是}{nC 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11,Y ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180;9、4;10、⎪⎪⎭⎫⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ; 三、解答题:17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-;19、(1)41;(2)ο59.9; 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x;(2)()()xxxxx a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x,则()111222+++=+++=ata at a t a at t y ,因为0>a ,所以a ta at 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ;(3)()223222221122+⋅+⋅-=⋅+-⋅+=x xxx a t a a a a x g ,设tx=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a at g 322++-=,若at tt a 222=⇒=,1°当12≥a时,即20≤<a ,a tt a y 322++=单调递减,所以()+∞++∈,232a a y ,则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意; 2°当120<<a 时,即2>a ,则a a a aa tt a y 322322322+=+⋅≥++=,则()()0,322-∈a g ,因为()()02log 2ming a g x g ≠⎪⎪⎭⎫ ⎝⎛=,故不符合题意,舍去;综上:(]2,0∈a 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim=+-∞→n n n ;3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A I ; 4、若复数i z +=1(i 是虚数单位),则______2=+zz ; 5、已知{}n a 是等差数列,若1082=+a a ,则______753=++a a a ;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O 是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________; 11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1). 二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=xy D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( ) A 1 B 2 C 3 D 415. 若数列}{n a 的前n 项和,“}{n a 是递增数列”是“}{n S 是递增数列”的( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(= (1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到ο01.0).20.设0>a ,函数xa x f 211)(⋅+=(1).若1=a ,求)(x f 的反函数)(1x f -(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示)(3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a 的取值范围?21.若}{n c 是递增数列,数列}{n a 满足:对任意*,N m R n ∈∃∈,使得01≤--+n m nm c a a a ,则称}{n a 是}{n c 的“分隔数列”(1)设1,2+==n a n c n n ,证明:数列}{n a 是}{n c 的分隔数列;(2)设n n S n c ,4-=是}{n c 的前n 项和,23-=n n c d ,判断数列}{n S 是否是数列}{n d 的分隔数列,并说明理由;(3)设n n n T aq c ,1-=是}{n c 的前n 项和,若数列}{n T 是}{n C 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11,Y ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180; 9、4;10、⎪⎪⎭⎫⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ; 三、解答题: 17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-; 19、(1)41;(2)ο59.9; 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x ; (2)()()xx x x x a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x, 则()111222+++=+++=a taat at a at ty ,因为0>a ,所以a taat 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ; (3)()223222221122+⋅+⋅-=⋅+-⋅+=xx x x a t a a a a x g ,设t x=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a a t g 322++-=,若a t t t a 222=⇒=,1°当12≥a 时,即20≤<a ,a tt a y 322++=单调递减,所以()+∞++∈,232a a y ,则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意; 2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=, 则()()0,322-∈a g ,因为()()02log 2min g a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去; 综上:(]2,0∈a 。
21、解析(1)依题意得,()[][]12120)12(0)12(120)22(1211+<≤-⇔⎩⎨⎧≠+-≤+---⇔≤+-+-+=--+n m n n m n m n m n m nm c a c a n m n m因为*∈N m ,于是,可得,n m 2=,故存在这样的m ,使得01≤--+n m nm c a c a ,所以数列{}m a 是{}n c 的分隔数列,得证;(2)6323-==-n c d n n ,又因为n S 是{}n c 的前n 项和,所以()n n n n S n2722432-=-+-=,假设数列{}n S 是否是数列{}n d 的分隔数列,则必定存在*∈N m ,使得01≤--+n m nm d S d S ,代入不并化简得:()()()[]()[]()⎪⎩⎪⎨⎧≠+--≤+--+--⇔≤+--+--0667066712670667126722222n m m n m mn m m n m m n m m所以,6671262-<-≤-n m m n ,又因为()()Z k k m m ∈=-27,所以{}86,106,126)7(---=-n n n m m ,对于任意的*∈N n ,三个方程⎪⎩⎪⎨⎧-=--=--=-③②①ΛΛΛΛΛΛ86710671267222n m m n m m n m m 都不能确保m 一直偶整数解,故不符合定义,所以数列{}n S 不是数列{}n d 的分隔数列; 另解:举出反例即可! 1°当1=n 时,()6076=⇒⎩⎨⎧∈<-≤-*m Nm m m ,存在;2°当2=n 时,()7670=⇒⎩⎨⎧∈<-≤*m Nm m m ,存在;3°当3=n 时,()81276=⇒⎩⎨⎧∈<-≤*m N m m m ,存在; 4°当4=n 时,()∅=⇒⎩⎨⎧∈<-≤*m N m m m 18712,不存在; 综上,数列{}n S 不是数列{}n d 的分隔数列; (3)因为{}n c 是递增数列,所以⎩⎨⎧>>01a q ,或⎩⎨⎧<<<100q a ; ①当1=q 时,na T a c n n =⇒=,则011>=--=--+ama ama c T c T n m n m ,不符合数列{}n T 是{}n c 的分隔数列,故舍去。
②当1>q 时,()q q a T n n --=11,因为01≤--+n m nmc T c T ,代入并化简得: 1111+-<≤+-+-n n m n n q q q q q ,令n m =,则()01211≥+-⇒>+-+q q q q q n n n n ,对任意的*∈N n 恒成立,则2≥q ,而1111≥⇒≤+---n n n nq q qq (恒成立),故数列{}n T 是{}n c 的分隔数列,且此时0>a ;③当10<<q 时,因为01≤--+n m nm c T c T ,代入并化简得:1111+-<≤+-+-n n m n n q q q q q ,因为mq 单调递减,而111−−→−+-∞→-n n nq q ,111−−→−+-∞→+n n n q q ,此时m 不存在,故这种情况,舍去; 综上,0>a 或2≥q 。
