高考中常见的立体几何题型和解题方法
高考复习立体几何考点常见题型

咼考复习立体几何考点常见题型立体几何常见题型考点1点到平面的距离求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用•典型例题例1如图,正三棱柱的所有棱长都为,为中点(2DABCABC,CC1111A (?)求证:平面;AAB?ABD111(?)求二面角的大小;AADB,,1C C1D (?)求点到平面的距离(CABD1B考查目的:本小题主要考查直线与平面的位置关系,二面角的B1大小,点到平面的距离等知识,考查空间想象能力、逻辑思维能力和运算能力(A解答过程:取中点,连结(BCOAOA1■ •■为正三角形,(?ABC? AOBC? F正三棱柱中,平面平面,ABC?BCCBABCABC,11111C CD平面( ?AO?BCCB11 B B连结,在正方形中,分别为BOOD BBCC111■I ■的中点,,(?BOBD? ABBD?BCCC111在正方形中,,平面(ABAB??AB?ABBAABD111111(?)设与交于点,在平面中,作于F,连结,由(?)得AFGABGFAD?ABABDAB?1 平面(ABD1, 为二面角的平面角(??AFGAADB? AFAD?1145在中,由等面积法可求得,?AADAF,15• •1AG210又,(AGAB,,21 ? ,,,sin?AFG2AF445510所以二面角的大小为(AADB,,arcsin14(?)中,,(S,1?ABDBDADABS,,,? ,5226,,?BCD111?ABD1在正三棱柱中,到平面的距离为(3ABCCB111设点到平面的距离为(dCABD1P □|11 由,得,VV,SSd,3ABCDCABD,,??BCDABD111333S2?BCD(?,,dS2?ABD12点到平面的距离为(?CABD12例2.( 2006年湖南卷)如图,已知两个正四棱锥P-ABCD与Q-ABCD勺高分别为1 和2,AB=4.(?)证明PQ平面ABCD;(?)求异面直线AQ与PB所成的角;(?)求点P到平面QAM距离.命题目的:本题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离基本知识,考查空间想象能力、逻辑思维能力和运算能力•过程指引:方法一关键是用恰当的方法找到所求的空间距离和角;方法二关键是掌握利用空间向量求空间距离和角的一P般方法•解答过程:D C 方法一(?)取AD的中点,连结PM QM. O M B因为P,ABCD与Q,ABCD都是正四棱锥,A 所以AD?PM AD?QM.从而AD?平面PQM. 又平面PQM所以PQ?AD. PQ,同理PQ?AB所以PQ平面ABCD. Q (?)连结AC BD设,由PQ平面ABCDAC:BD,O及正四棱锥的性质可知0在PQ上,从而P、A Q C四点共面.取0C的中点N,连接PN.P01N0N01P0N0,,,因为,所以,OQ2OAOC2OQOA从而AQ?PN ?BPN或其补角)是异面直线AQ与PB所成的角.2222222PB0B0P,,, ,,(22)13PN0N0P,,, ,,(2)13. 因为,2222 BN,0B0N,(22),(2),1022293103PB,PN,BN,,cos 所以. ,BPN,,,29PB,PN233,,3arccos从而异面直线AQ与PB所成的角是.911(?)连结0M 贝U OMABOQ,,,2.22所以?MQP,45?.由⑺知AD?平面PMQ所以平面PMQ平面QAD.过P作PH?QMF H, PH?平面QAD从而PH的长是点P到平面QAD勺距离.320PQPOQOPHP,Q,,?,,3,sin45. 又. 232即点P到平面QAD勺距离是.2考点 2 异面直线的距离此类题目主要考查异面直线的距离的概念及其求法,考纲只要求掌握已给出公垂线段的异面直线的距离典型例题42例3已知三棱锥,底面是边长为的正三角形,棱的长为2,且垂直于底S,ABCS(面.分别为的中点,求CD与SE间的距离.E、DBC ABC曲思路启迪:由于异面直线CD与SE的公垂线不易寻找,所以设法将所求异面直线的距离,转化成求直线与平面的距离,再进一步转化成求点到平面的距离•解答过程:如图所示,取BD的中点F,连结EF,SF, CF,?EF?EF为的中位线,??面,CD, ?CD,BCDSEF到平面的距离即为两异面直线间的距离.?CDSEF又线面之间的距离可转化为线上一点C到平面?CDSEF的距离,设其为h,由题意知,,D、E、F分别是BC,42AB BC BD的中点,1 ?CD,26,EF,CD,6,DF,2,SC,22111123?,,,,,,,,6,2,2,VEFDFSC S,CEF3232322在Rt 中, SE,SC,CE,23,SCE22在Rt 中,SF,SC, CF,4, 24, 2,30,SCF又?EF,6, ?S,3,SEF112323,3,h,h,由于,即,解得V,V,,S,hC,SEFS,CEF,SEF333323故CD与SE间的距离为.3小结: 通过本例我们可以看到求空间距离的过程,就是一个不断转化的过程.考点 3 直线到平面的距离此类题目再加上平行平面间的距离,主要考查点面、线面、面面距离间的转化典型例题ACAAGB例4(如图,在棱长为2的正方体中,G是的中点,求BD到平面的距离. 1111 思路启迪: 把线面距离转化为点面距离,再用点到平面距离的方法求解.D1 C1O1解答过程:A 1B1 ? BDGB解析一?平面,11HG ?BDGB上任意一点到平面的距离皆为所求,以下求11D CO GBD点0平面的距离,11A B?BD,ACBD,A?ABD,AACC,,平面, 11111111111?BD,GBD又平面1111AACC,GBDO平面,两个平面的交线是,? 11111OH,OGGBDG作于H,则有平面,即0H是0点到平面的距离.0H,1111111,00G中,.在S,,OO,AO,,2,2,21,OOG1122112632,S,,OH,OG,,,OH, ?OH又.,OOG1122326GBD!卩BD到平面的距离等于.113?BDGB解析二?平面,11?BDGBDGBD任意一点到平面的距离皆为所求,以下求点B平面的距离.1111 GBDB,GB设点B到平面的距离为h,将它视为三棱锥的高,则11111 V,V, 由于S,,22,3,6,B,GBDD,GBB,GBD1111112114426222, ?h,,,V, ,,,,,D,GBB1132336 26GBDI卩BD到平面的距离等于.113小结:当直线与平面平行时,直线上的每一点到平面的距离都相等,都是线面距离.所以求线面距离关键是选准恰当的点,转化为点面距离•本例解析一是根据选出的点直接作出距离;解析二是等体积法求出点面距离•考点4异面直线所成的角此类题目一般是按定义作出异面直线所成的角,然后通过解三角形来求角•异面直线所成的角是高考考查的重点•典型例题例5(2007年北京卷文)n AB,4如图,在中,,斜边(可以通过Rt?AOBRt?AO,C,OAB6A以直线为轴旋转得到,且二面角的直二面AOBAOC,,Rt?AOBDAB角(是的中点((I)求证:平面平面;DCOD,AOB(II)求异面直线与所成角的大小(AOCD思路启迪:(II)的关键是通过平移把异面直线转化到一个三角形内•解答过程:解法1:(I)由题意,,,COAO,BOAO,EB是二面角是直二面角,?,BOCBAOC,,C,又,AOBOO? ,COBO平面,?,COAOB平面(又CO,COD平面平面(?COD,AOB AE(II)作,垂足为,连结(如图),贝U, DEOB,CEDEAO?是异面直线与所成的角(AOCD?, CDE1 在中,,,DRt?COECOBO,,2OEBO,,1222(? ,,,CECOOE51 又(DEAO,,3yO2BxC CE515在中,(?Rt?CDEtanCDE,,, DE3315异面直线与所成角的大小为(?AOCDarctan3例6((2006年广东卷)如图所示,AF、DE分别是?O ?O的直径.AD与两圆所在的平1面均垂直,AD,8,BC是?O的直径,AB,AC,6, OE//AD. (?)求二面角B— AD-F的大小;(?)求直线BD与EF所成的角.命题目的:本题主要考查二面角以及异面直线所成的角等基本知识,考查空间想象能力、逻辑思维能力和运算能力•过程指引:关键是用恰当的方法找到所求的空间距离和角并掌握利用空间向量求空间距离和角的一般方法.解答过程:⑺?AD与两圆所在的平面均垂直,?AD?AB, AD?AF,故?BAF是二面角B—AD—F的平面角.,? AF、BC是圆O的直径,?ABFC是矩形又? AB,AC,6,? ABFC是正方形0由于ABFC是正方形,所以?BAF,45.0即二面角B—AD- F的大小为45;(?)以O为原点,BC AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0, 0, 0),A(0,,32,0),B(32,0, 0),D(0,,32,8),E(0,0,8),F(0,32, 0)所以,BD,(,32,,32,8),FE,(0,,32,8)设异面直线BD与EF所成角为,则82,,,,,coscos,.BDFE. 1082arccos故直线BD与EF所成的角为.10考点5直线和平面所成的角例7.(2007年全国卷?理)° ——四棱锥中,底面为平行四边形,侧面底面(已知,SABCD,?ABC,45ABCDSBC,ABCD AB,2,, ( SASB,,3BC,22S(?)证明;SABC,C(?)求直线与平面所成角的大小(SDSABB考查目的:本小题主要考查直线与直线,直线与平面的位置关系,DA二面角的大小,点到平面的距离等知识,考查空间想象能力、逻辑思维能力和运算能力(解答过程:解法一:(?)作,垂足为,连结,由侧面底面,SOBC?AOSBC?ABCDO 得底面(SO?ABCD因为,所以,SASB,AOBO,°又,故为等腰直角三角形,,?ABC,45?AOBAOBO?由三垂线定理,得(SABC?(?)由⑺知,依题设,SABC?ADBC?SSA,3故,由,,,得ADBC,,22AO,2SAAD?,(SD,11SO,1O C B 211,,2 的面积(?SABSABSAAB,,,21,,D 22A ,,1DB连结,得的面积?DABSABAD,,sin135222DVV设到平面的距离为,由于,得SABhDSABSABD,, 卩□ |11,解得(h,2hSSOS,1233h222设与平面所成角为,则(,SDSAB,,,,sinSD111122所以,直线与平面所成的我为(SDSBCarcsi nil考点6二面角此类题主要是如何确定二面角的平面角,并将二面角的平面角转化为线线角放到一个合适的三角形中进行求解•二面角是高考的热点,应重视•典型例题例8((2007年湖南卷文)b —如图,已知直二面角,,,,,,,,,,PQAPQ,C,, , ,BAP45B,,CACB直线和平面,所成的角为(30CAC ,A P QB,;(I)证明BCPQ?(II)求二面角的大小(BACP,,命题目的:本题主要考查直线与平面垂直、二面角等基本知识,考查空间想象能力、逻辑思维能力和运算能力过程指引:⑴在平面内过点作COPC于点,连结(,COOBn |因为,,所以,,,?,,,PQCO?,C ,又因为,所以(CACB,OAOB,H卜o |A P 而,所以,,,,BAO45 ,ABO45 ,AOB9OQ O B,从而,又,BOPQ?COPC所以平面(因为平面,故(PQBC?PQ?OBCBC,OBC n - I(II)解法一:由(I)知,,又,,BOPQ?,,?,,,PQ,所以(BO?,BO,,BHH过点作于点,连结,由三垂线定理知,(OOHAC?BHA故是二面角的平面角(,BHOBACP,,°由(I)知,,所以是和平面所成的角,贝, , ,CAO3OCO?” CAOCA3AO,3OHAO,,si n30 不妨设,贝U,( AC,22BOAO,,3在中,,所以,,,,,ABOBAO45Rt?OABBO3tan2, ,,,BHO 于是在中,(Rt?BOHOH32故二面角的大小为(BACP,,arctan2,,例9(( 2006年重庆卷)如图,在四棱锥P,ABCD中, PA底面ABCDQA为直CD AD=CD=2AB, E F分别为PC CD的中点.,(?)试证:CD平面BEF;(?)设PA,k?AB,且二面角E-BD-C的平面角大于,30:,解法一:(?)证:由已知DFAB且DAD为直角,〃,,故ABFD是矩形,从而CDBF.,,又PA底面ABCD,CDAD故由三垂线定理知,CDPD在?PDC中, E、F 分别,,PC、CD的中点,故EF?PD从而CDEF由此得CD面BEF.(?)连结AC交BF于G.易知G为AC的中点.连接EG则在?PAC中易知EG?PA又,,PA 底面ABCD故EG底面ABCD在底面ABCD中,过G作GHBD垂足为H,连接EH.由三垂线定理知,,EHBD从而EHG为二面角E-BD-C的平面角.设AB=a则在?PAC中,有11EG=PA=ka.22 以下计算GH考察底面的平面图•连结GD.11 因S=BD?GH=GB?DF. ?GBD22求k的取值范围.解答过程:GB,DF故GH=. BD5 在?ABD中,因为AB,a,AD=2a,得BD=a.11 而GB=FB=AD=aDF=AB从而得22GB,ABa,a5a.GH== , 5BD5a1kaEG52因此tan?EHG== ,k.2GH5a5由k,0 知是锐角,故要使, ,必须,EHG,EHG30:53k,,tan= 30:32 215.解之得,k的取值范围为k, 15。
立体几何题型及解题方法

立体几何题型及解题方法
立体几何是数学中研究三维空间几何图形的学科。
以下是一些常见的立体几何题型及其解题方法:
1. 计算体积和表面积:这类题目通常涉及到三维空间中的几何形状,如长方体、圆柱体、圆锥体等。
解题方法包括使用体积和表面积的公式,以及根据题目描述建立数学模型。
2. 证明定理和性质:这类题目通常涉及到几何图形的性质和定理,如平行线性质、勾股定理等。
解题方法包括使用已知定理和性质进行推导,以及通过构造辅助线或辅助图形来证明。
3. 求解最值问题:这类题目通常涉及到求几何图形中的最值,如最短路径、最大面积等。
解题方法包括使用不等式、极值定理和优化方法等。
4. 判定和性质应用:这类题目通常涉及到判定几何图形是否满足某个性质,或应用某个性质到实际场景中。
解题方法包括根据性质进行推导和判断,以及根据实际场景建立数学模型。
以上是一些常见的立体几何题型及其解题方法,当然还有其他的题型和解题方法。
在解决立体几何问题时,需要灵活运用几何知识和方法,多做练习,提高自己的解题能力。
高考中常见的立体几何题型和解题方法

高考中常见的立体几何题型和解题方法黔江中学高三数学教师:付 超高考立体几何试题一般共有2——3道(选择、填空题1——2道, 解答题1道),共计总分18——23分左右,考查的知识点在20个以内. 选择填空题考核立几中的逻辑推理型问题, 而解答题着重考查立几中的计算型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的方向发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题.一、知识整合1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力.2. 判定两个平面平行的方法:(1)根据定义——证明两平面没有公共点;(2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面;(3)证明两平面同垂直于一条直线。
3.两个平面平行的主要性质:⑴由定义知:“两平行平面没有公共点”。
⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那么它们的交线平行”。
⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⑸夹在两个平行平面间的平行线段相等。
⑹经过平面外一点只有一个平面和已知平面平行。
以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过程中均可直接作为性质定理引用。
4.空间角和距离是空间图形中最基本的数量关系,空间角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决.空间角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线所成的角θ∈(0,2π],直线与平面所成的角θ∈0,2π⎡⎤⎢⎥⎣⎦,二面角的大小,可用它们的平面角来度量,其平面角θ∈[0,π].对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把 它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力.如求异面直线所成的角常用平移法(转化为相交直线)与向量法;求直线与平面所成的角常利用射影转化为相交直线所成的角;而求二面角α-l-β的平面角(记作)通常有以下几种方法:(1) 根据定义;(2) 过棱l上任一点O作棱l的垂面,设∩α=OA,∩β=OB,则∠AOB =;(3) 利用三垂线定理或逆定理,过一个半平面α内一点A,分别作另一个平面β的垂线AB(垂足为B),或棱l的垂线AC(垂足为C),连结AC,则∠ACB=或∠ACB=π-;(4) 设A为平面α外任一点,AB⊥α,垂足为B,AC⊥β,垂足为C,则∠BAC =或∠BAC=π-;(5) 利用面积射影定理,设平面α内的平面图形F的面积为S,F在平面β内的S'.射影图形的面积为S',则cos=S5.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.求距离的一般方法和步骤是:一作——作出表示距离的线段;二证——证明它就是所要求的距离;三算——计算其值.此外,我们还常用体积法求点到平面的距离.6.棱柱的概念和性质⑴理解并掌握棱柱的定义及相关概念是学好这部分知识的关键,要明确“棱柱直棱柱正棱柱”这一系列中各类几何体的内在联系和区别。
高考数学立体几何多种解法

高考数学立体几何多种解法高考数学立体几何题目通常有多种解法,这取决于问题的具体形式和你所掌握的工具。
以下是一些常见的立体几何问题和它们的多种解法:问题1:求多面体的体积解法1:直接计算如果题目给出了多面体的底面积和高,可以直接使用体积公式 V=底面积×高来计算。
解法2:分割法如果多面体可以被分割成几个简单的几何体(如长方体、三棱锥等),可以先计算每个简单几何体的体积,然后求和。
解法3:向量法如果题目中涉及到了向量的知识,可以通过计算底面的法向量和顶点到底面的距离(即高),然后使用向量体积公式V=1/3 A⋅(B×C)来计算体积。
问题2:求多面体的表面积解法1:直接计算如果题目给出了多面体的各个面的面积,可以直接求和得到总表面积。
解法2:分割法如果多面体可以被分割成几个简单的几何体,可以先计算每个简单几何体的表面积,然后求和。
解法3:向量法对于某些复杂的多面体,可以通过计算各个面的法向量和对应的面积向量,然后使用向量点积来计算每个面的面积,最后求和得到总表面积。
问题3:证明线面平行或垂直解法1:定义法直接使用线面平行或垂直的定义来证明。
解法2:判定定理使用线面平行或垂直的判定定理来证明。
解法3:向量法通过计算向量之间的点积或叉积来证明线面平行或垂直。
问题4:求点到平面的距离解法1:公式法如果知道点到平面的垂线段的长度和垂足在平面上的坐标,可以使用距离公式 d=(x2−x1)2+(y2−y1)2+(z2−z1)2 来计算。
解法2:向量法通过计算点到平面上任意一点的向量和平面的法向量,然后使用向量点积和模长来计算距离。
问题5:求二面角的平面角解法1:定义法直接在图形中找出二面角的平面角,然后计算。
解法2:向量法通过计算两个平面的法向量,然后计算这两个法向量的夹角,即为二面角的平面角。
问题6:判断几何体的形状解法1:直接观察通过观察几何体的形状和尺寸来判断。
解法2:计算法通过计算几何体的各个面的面积、边长、角度等来判断。
高中数学高考专题(5)立体几何的高考解答题型及求解策略

高中数学高考专题(5)立体几何的高考解答题型及求解策略立体几何的解答题型主要采用“论证与计算”相结合的模式,即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再计算几何体的体积.试题背景有折叠问题、探索性问题等,考查空间想象能力、逻辑思维能力及转化与化归思想的应用能力.题型一线面位置关系的证明题型概览:空间中线面的平行与垂直的证明有两种思路:一是利用相应的判定定理和性质定理去解决;二是利用空间向量法来论证,应用向量证明线、面的位置关系的关键是把空间线面位置关系的判定定理和性质定理与空间向量建立对应关系,把空间位置关系的证明转化为空间向量的运算,通过运算解决证明问题.这里以传统方法为例建立审题程序与答题模板,向量方法参照本专题题型二.如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN⊥平面ABCD,E、F分别为MA、DC的中点,求证:(1)EF∥平面MNCB;(2)平面MAC⊥平面BND.[审题程序]第一步:利用中位线、平行四边形的性质在四边形MNCB内确定与EF平行的直线;第二步:在平面MAC和平面BND中寻找与另一平面垂直的直线;第三步:应用面面垂直、菱形的性质,由线线垂直解决.[规范解答](1)如图,取NC的中点G,连接FG,MG.因为ME∥ND且ME=12ND,F、G分别为DC、NC的中点,FG∥ND且FG=12ND,所以FG与ME平行且相等,所以四边形MEFG是平行四边形,所以EF∥MG,又MG⊂平面MNCB,EF⊄平面MNCB,所以EF∥平面MNCB.(2)如图,连接BD、MC.因为四边形MADN是矩形,所以ND⊥AD.因为平面MADN⊥平面ABCD,平面ABCD∩平面MADN=AD,DN⊂平面MADN,所以ND⊥平面ABCD,所以ND⊥AC.因为四边形ABCD是菱形,所以AC⊥BD.因为BD∩ND=D,所以AC⊥平面BDN.又AC⊂平面MAC,所以平面MAC⊥平面BDN.[答题模板]解决这类问题的答题模板如下:1.(2016·北京西城区高三期末)如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE,CF的中点.(1)求证:AC⊥平面BDEF;(2)求证:平面BDGH∥平面AEF;(3)求多面体ABCDEF的体积.[解](1)证明:因为四边形ABCD是正方形,所以AC⊥BD.又平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,且AC⊂平面ABCD,所以AC⊥平面BDEF.(2)证明:在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF.又GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC∩BD=O,连接OH.在△ACF中,因为OA=OC,CH=HF,所以OH∥AF.因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.因为OH∩GH=H,OH,GH⊂平面BDGH,所以平面BDGH∥平面AEF.(3)由(1)得AC⊥平面BDEF.因为AO=2,四边形BDEF的面积S▱BDEF=3×22=62,=4.所以四棱锥A-BDEF的体积V1=13×AO×S▱BDEF同理,四棱锥C-BDEF的体积V2=4.所以多面体ABCDEF的体积V=V1+V2=8.题型二求空间几何体的体积题型概览:计算几何体的体积,关键是根据条件找出相应的底面和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题.(1)直接法:对于规则几何体,直接利用公式计算即可.(2)割补法:当一个几何体的形状不规则时,常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.经常考虑将三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体.(3)等体积法:一般利用三棱锥的“等积性”求三棱锥体积,可以把任何一个面作为三棱锥的底面.注意两点:一是求体积时,可选择“容易计算”的方式来计算;二是利用“等积性”可求“点到面的距离”,关键是在面中选取三个点,与已知点构成三棱锥.(2016·全国卷Ⅲ)如图,四棱锥P-ABCD中,P A⊥底面ABCD,AD∥BC,AB=AD=AC=3,P A=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面P AB;(2)求四面体N-BCM的体积.[审题程序]第一步:由线线平行或面面平行证明(1);第二步:由N 为PC 中点,推证四面体N -BCM 的高与P A 的关系; 第三步:利用直接法求四面体的体积.[规范解答] (1)由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形, 于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB , 所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5, 故S △BCM =12×4×5=2 5.所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. [答题模板] 解决这类问题的答题模板如下:2.(2016·深圳一模)如图所示,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧面SBC是正三角形,E是SB的中点,且AE⊥平面SBC.(1)证明:SD∥平面ACE;(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.[解](1)证明:连接BD,交AC于点F,连接EF.∵四边形ABCD是平行四边形,∴F是BD的中点,又∵E是SB的中点,∴EF∥SD.∵SD⊄平面ACE,EF⊂平面ACE,∴SD∥平面ACE.(2)∵AB⊥AS,BC=BS=2,且E是SB的中点,∴AE=1.∵AE⊥平面SBC,BS、CE⊂平面SBC,∴AE⊥BS,AE⊥CE.∴AB=AE2+BE2= 2.又侧面SBC 是正三角形,∴CE =3, ∴AC =AE 2+CE 2=2,∴△ABC 是底边长为2,腰长为2的等腰三角形, ∴S △ABC =12×2×4-12=72.设点S 到平面ABC 的距离为h .由V 三棱锥S -ABC =V 三棱锥A -SBC ,得13h ·S △ABC =13AE ·S △SBC ,∴h =AE ·S △SBC S △ABC =237=2217.题型三 立体几何中的探索性问题题型概览:如果知道的是试题的结论,而要求的却是试题的某一个存在性条件(如存在某个定点、定直线、定值等),这种试题称为存在探索型试题.解题策略一般是先假设结论成立,然后以该结论作为一个已知条件,再结合题目中的其他已知条件,逆推(即从后往前推),一步一步推出所要求的特殊条件,即要求的存在性条件.若能求出,则存在;若不能求出,则不存在.(2016·石家庄调研)如图,在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,AC ⊥BC ,E 在线段B 1C 1上,B 1E =3EC 1,AC =BC =CC 1=4.(1)求证:BC ⊥AC 1;(2)试探究:在AC 上是否存在点F ,满足EF ∥平面A 1ABB 1?若存在,请指出点F 的位置,并给出证明;若不存在,请说明理由.[审题程序]第一步:由B 1E =3EC 1及EF ∥平面A 1ABB 1猜想点F 的位置;第二步:在平面A 1ABB 1内探求与EF 平行的直线或寻找经过EF 与平面A 1ABB 1平行的平面; 第三步:由线线平行或面面平行推理论证.[规范解答] (1)证明:∵AA 1⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥AA 1. 又∵BC ⊥AC ,AA 1∩AC =A ,∴BC ⊥平面AA 1C 1C . 又AC 1⊂平面AA 1C 1C ,∴BC ⊥AC 1.(2)解法一:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图1,在平面A1B1C1内过点E作EG∥A1C1交A1B1于点G,连接AG.∵B1E=3EC1,∴EG=34A1C1.又AF∥A1C1且AF=3,4A1C1∴AF∥EG且AF=EG,∴四边形AFEG为平行四边形,∴EF∥AG.又EF⊄平面A1ABB1,AG⊂平面A1ABB1,∴EF∥平面A1ABB1.解法二:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图2,在平面BCC1B1内过点E作EG∥BB1交BC于点G,连接FG. ∵EG∥BB1,EG⊄平面A1ABB1,BB1⊂平面A1ABB1,∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,∴FG∥AB.又AB⊂平面A1ABB1,FG⊄平面A1ABB1,∴FG∥平面A1ABB1.又EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面A1ABB1.∵EF⊂平面EFG,∴EF∥平面A1ABB1.[答题模板]解决这类问题的答题模板如下:3.如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1⊥底面ABC,M为A1B1的中点.(1)证明:MC⊥AB;(2)若AA1=26,侧棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,求PC的长;若不存在,请说明理由.[解](1)证明:取AB的中点N,连接MN,CN,则MN⊥底面ABC,MN⊥AB.因为△ABC是正三角形,所以NC⊥AB.因为MN∩NC=N,MN⊂平面MNC,NC⊂平面MNC,所以AB⊥平面MNC,所以AB⊥MC.(2)由(1)知MC⊥AB,若存在点P使得MC⊥平面ABP,则必有MC⊥BP.过M作MQ⊥B1C1,垂足为Q,连接QC,则QC是MC在平面BCC1B1内的射影,只需QC⊥BP即可,此时Rt△QC1C与Rt△PCB相似,QC1C1C =PCCB,所以PC=QC1·CBC1C=3×426=6,点P恰好是CC1的中点.。
立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高考数学各题型答题方法技巧总结

高考数学各题型答题方法技巧总结数学选择题目还是比较多的,占的分值也挺大的,因此,对于不同的数学选择题,就需要掌握不同的解题技巧,数学选择题的解题方法也是多种多样的,下面是给大家带来的高考数学各题型答题方法技巧总结(大全),以供大家参考!数学各题型解题方法一、立体几何题1、证明线面位置关系,一般不需要去建系,更简单;2、求异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积、体积等问题时,最好要建系;3、注意向量所成的角的余弦值(范围)与所求角的余弦值(范围)的关系(符号问题、钝角、锐角问题)。
二、导数、极值、最值、不等式恒成立(或逆用求参)问题1、先求函数的定义域,正确求出导数,特别是复合函数的导数,单调区间一般不能并,用“和”或“,”隔开(知函数求单调区间,不带等号;知单调性,求参数范围,带等号);2、注意最后一问有应用前面结论的意识;3、注意分论讨论的思想;4、不等式问题有构造函数的意识;5、恒成立问题(分离常数法、利用函数图像与根的分布法、求函数最值法);6、整体思路上保6分,争10分,想14分。
三、概率问题1、搞清随机试验包含的所有基本事件和所求事件包含的基本事件的个数;2、搞清是什么概率模型,套用哪个公式;3、记准均值、方差、标准差公式;4、求概率时,正难则反(根据p1+p2+。
+pn=1);5、注意计数时利用列举、树图等基本方法;6、注意放回抽样,不放回抽样;7、注意“零散的”的知识点(茎叶图,频率分布直方图、分层抽样等)在大题中的渗透;8、注意条件概率公式;9、注意平均分组、不完全平均分组问题。
四、圆锥曲线问题1、注意求轨迹方程时,从三种曲线(椭圆、双曲线、抛物线)着想,椭圆考得最多,方法上有直接法、定义法、交轨法、参数法、待定系数法;2、注意直线的设法(法1分有斜率,没斜率;法2设x=my+b(斜率不为零时),知道弦中点时,往往用点差法);注意判别式;注意韦达定理;注意弦长公式;注意自变量的取值范围等等;3、战术上整体思路要保7分,争9分,想12分。
高考数学立体几何截面问题的十大热门题型
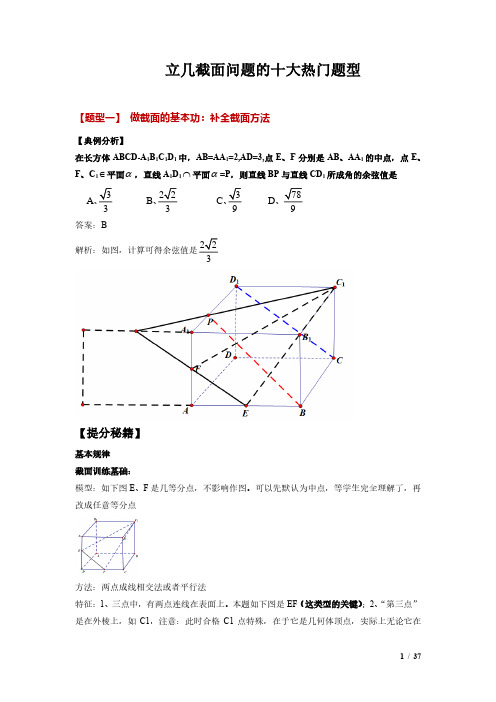
立几截面问题的十大热门题型【题型一】 做截面的基本功:补全截面方法【典例分析】在长方体ABCD -A 1B 1C 1D 1中,AB=AA 1=2,AD=3,点E 、F 分别是AB 、AA 1的中点,点E 、F 、C 1∈平面α,直线A 1D 1⋂平面α=P ,则直线BP 与直线CD 1所成角的余弦值是3378 A 22 C B 3 D 3 99、、、、答案:B解析:如图,计算可得余弦值是223【提分秘籍】基本规律 截面训练基础:模型:如下图E 、F 是几等分点,不影响作图。
可以先默认为中点,等学生完全理解了,再改成任意等分点方法:两点成线相交法或者平行法特征:1、三点中,有两点连线在表面上。
本题如下图是EF (这类型的关键);2、“第三点”是在外棱上,如C1,注意:此时合格C1点特殊,在于它是几何体顶点,实际上无论它在何处,只要在棱上就可以。
方法一:相交法,做法如图方法二:平行线法。
做法如图【变式演练】1.如图,在正方体1111ABCD A B C D −中,M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,则经过M 、N 、P 的平面与正方体1111ABCD A B C D −相交形成的截面是一个( )A .三角形B .平面四边形C .平面五边形D .平面六边形 【答案】D分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,先证明、、、H P M F 四点共面,再证明N ∈平面HPMF ,P ∈平面HPMF 可得答案.【详解】如图,分别取11A D 、AB 、1C C 的中点、、F H E ,连接MF 、FN 、NH 、HP 、PE 、EM 、11A C 、AC 、NE 、1A B ,且M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,所以11//A C FM 、//HP AC ,且11//A C AC ,所以//HP FM , 即、、、H P M F 四点共面,因为11//=,F BP F BP A A ,所以四边形1A FPB 是平行四边形,所以1//A B FP ,又因为1//A B NH ,得//NH FP ,且FP ⊂平面HPMF ,H ∈平面HPMF , 所以NH ⊂平面HPMF ,得N ∈平面HPMF ,因为11//=,M H MC B C BH ,所以四边形1C MHB 是平行四边形,所以1//C B MH , 又因为1//C B EP ,得//MH EP ,又MH ⊂平面HPMF ,P ∈平面HPMF ,所以PE ⊂平面HPMF ,得E ∈平面HPMF ,所以、、、、、H P E M F N 六点共面, 平面六边形HPEMFN 即为经过M 、N 、P 与正方体1111ABCD A B C D −相交形成的截面,故选:D.2.如图,在正方体1111ABCD A B C D −中,E 是棱1CC 的中点,则过三点A 、D1、E 的截面过( )A .AB 中点 B .BC 中点 C .CD 中点 D .BB1中点【分析】根据截面特点结合正方形结构性质求解. 【详解】取BC 的中点F ,连接EF ,AF ,如图,则1EF AD ∥,所以F 在截面上,故选:B3.如图正方体1111ABCD A B C D −,棱长为1,P 为BC 中点,Q 为线段1CC 上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为Ω.若1CQ CC λ→→=,则下列结论错误的是( )A .当102λ∈⎛⎫⎪⎝⎭,时,Ω为四边形B .当12λ=时,Ω为等腰梯形C .当3,14λ⎛⎫∈ ⎪⎝⎭时,Ω为六边形D .当1λ=时,Ω6【答案】C 【分析】根据题意,依次讨论各选项,作出相应的截面,再判断即可. 【详解】 解:当102λ<<时,如下图1,Ω是四边形,故A 正确; 当12λ=时,如下图2,Ω为等腰梯形,B 正确: 当314λ<<时,如下图3,Ω是五边形,C 错误; 当1λ=时,Q 与1C 重合,取11A D 的中点F ,连接AF ,如下图4,由正方体的性质易得1////BM PC AF ,且=1PC AF ,截面Ω为1APC F 为菱形,其面积为1162AC PF ⋅=D 正确.【题型二】截面形状的判断【典例分析】一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是()A.B.C.D.【答案】B【分析】根据题意可知,该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可判断出选项B正确.【详解】如图所示:因为三棱锥的各棱长均相等,所以该三棱锥为正四面体,内切球与各面相切于各个面的中心,即可知过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是.故选:B.【提分秘籍】基本规律一些容易出错误的地方1.截面与几何体表面相交,交线不会超过几何体表面个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考中常见的立体几何题型和解题方法黔江中学高三数学教师:付 超高考立体几何试题一般共有2——3道(选择、填空题1——2道, 解答题1道),共计总分18——23分左右,考查的知识点在20个以内. 选择填空题考核立几中的逻辑推理型问题, 而解答题着重考查立几中的计算型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的方向发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题.一、知识整合1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力.2. 判定两个平面平行的方法:(1)根据定义——证明两平面没有公共点;(2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面;(3)证明两平面同垂直于一条直线。
3.两个平面平行的主要性质:⑴由定义知:“两平行平面没有公共点”。
⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那么它们的交线平行”。
⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⑸夹在两个平行平面间的平行线段相等。
⑹经过平面外一点只有一个平面和已知平面平行。
以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过程中均可直接作为性质定理引用。
4.空间角和距离是空间图形中最基本的数量关系,空间角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决.空间角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线所成的角θ∈(0,2π],直线与平面所成的角θ∈0,2π⎡⎤⎢⎥⎣⎦,二面角的大小,可用它们的平面角来度量,其平面角θ∈[0,π].对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把 它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力.如求异面直线所成的角常用平移法(转化为相交直线)与向量法;求直线与平面所成的角常利用射影转化为相交直线所成的角;而求二面角α-l-β的平面角(记作θ)通常有以下几种方法:(1) 根据定义;(2) 过棱l上任一点O作棱l的垂面γ,设γ∩α=OA,γ∩β=OB,则∠AOB=θ;(3) 利用三垂线定理或逆定理,过一个半平面α内一点A,分别作另一个平面β的垂线AB(垂足为B),或棱l的垂线AC(垂足为C),连结AC,则∠ACB=θ或∠ACB =π-θ;(4) 设A为平面α外任一点,AB⊥α,垂足为B,AC⊥β,垂足为C,则∠BAC =θ或∠BAC=π-θ;(5) 利用面积射影定理,设平面α内的平面图形F的面积为S,F在平面β内的S'.射影图形的面积为S',则cosθ=S5.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.求距离的一般方法和步骤是:一作——作出表示距离的线段;二证——证明它就是所要求的距离;三算——计算其值.此外,我们还常用体积法求点到平面的距离.6.棱柱的概念和性质⑴理解并掌握棱柱的定义及相关概念是学好这部分知识的关键,要明确“棱柱直棱柱正棱柱”这一系列中各类几何体的内在联系和区别。
⑵平行六面体是棱柱中的一类重要的几何体,要理解并掌握“平行六面体直平行六面体长方体正四棱柱正方体”这一系列中各类几何体的内在联系和区别。
⑶须从棱柱的定义出发,根据第一章的相关定理对棱柱的基本性质进行分析推导,以求更好地理解、掌握并能正确地运用这些性质。
⑷关于平行六面体,在掌握其所具有的棱柱的一般性质外,还须掌握由其定义导出的一些其特有的性质,如长方体的对角线长定理是一个重要定理并能很好地掌握和应用。
还须注意,平行六面体具有一些与平面几何中的平行四边形相对应的性质,恰当地运用平行四边形的性质及解题思路去解平行六面体的问题是一常用的解题方法。
⑸多面体与旋转体的问题离不开构成几何体的基本要素点、线、面及其相互关系,因此,很多问题实质上就是在研究点、线、面的位置关系,与《直线、平面、简单几何体》第一部分的问题相比,唯一的差别就是多了一些概念,比如面积与体积的度量等.从这个角度来看,点、线、面及其位置关系仍是我们研究的重点.7.经纬度及球面距离⑴根据经线和纬线的意义可知,某地的经度是一个二面角的度数,某地的纬度是一个线面角的度数,设球O的地轴为NS,圆O是0°纬线,半圆NAS是0°经线,若某地P是在东经120°,北纬40°,我们可以作出过P的经线NPS交赤道于B,过P的纬线圈圆O1交NAS于A,那么则应有:∠AO1P=120°(二面角的平面角) ,∠POB=40°(线面角)。
⑵两点间的球面距离就是连结球面上两点的大圆的劣弧的长,因此,求两点间的球面距离的关键就在于求出过这两点的球半径的夹角。
例如,可以循着如下的程序求A 、P 两点的球面距离。
S 球表=4πR 2 V 球=34πR 3⑴球的体积公式可以这样来考虑:我们把球面分成若干个边是曲线的小“曲边三角形”;以球心为顶点,以这些小曲边三角形的顶点为底面三角形的顶点,得到若干个小三棱锥,所有这些小三棱锥的体积和可以看作是球体积的近似值.当小三棱锥的个数无限增加,且所有这些小三棱锥的底面积无限变小时,小三棱锥的体积和就变成球体积,同时小三棱锥底面面积的和就变成球面面积,小三棱锥高变成球半径.由于第n 个小三棱锥的体积=31S n h n (S n 为该小三棱锥的底面积,h n 为小三棱锥高),所以V 球=31S 球面·R =31·4πR 2·R =34πR 3.⑵球与其它几何体的切接问题,要仔细观察、分析、弄清相关元素的位置关系和数量关系,选择最佳角度作出截面,以使空间问题平面化。
二、注意事项1. 须明确《直线、平面、简单几何体》中所述的两个平面是指两个不重合的平面。
2.三种空间角,即异面直线所成角、直线与平面所成角。
平面与平面所成二面角。
它们的求法一般化归为求两条相交直线的夹角,通常“线线角抓平移,线面角找射影,面面角作平面角”而达到化归目的,有时二面角大小出通过cos θ=原射S S 来求。
3.有七种距离,即点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离,点到平面的距离有时用“体积法”来求。
三、例题分析例1、⑴已知水平平面α内的两条相交直线a, b 所成的角为θ,如果将角θ的平分线l '绕着其顶点,在竖直平面内作上下转动, 转动到离开水平位值的l '处,且与两条直线a,b 都成角α,则α与2θ的大小关系是 ( )A. 2θα≤或2θα≥B. α>2θ或 α<2θ C. α>2θ D. α<2θ ⑵已知异面直线a,b 所成的角为700,则过空间一定点O,与两条异面直线a,b⌒⌒⌒都成600角的直线有( )条.A. 1B. 2C. 3D. 4⑶异面直线a,b 所成的角为θ,空间中有一定点O,过点O 有3条直线与a,b 所成角都是600,则θ的取值可能是 ( ). A. 300 B. 500 C. 600 D. 900分析与解答:⑴ 如图1所示,易知直线l '上点A在平面α上的射影是ι上的点B,过点B 作BC⊥b,则AC ⊥b. 在Rt △OBC 和Rt △OAC 中,tg α=OC AC ,tg 2θ=OCBC .显然,AC>BC, ∴tan α> tan 2θ,又α、2θ∈(0,)2π,∴ α>2θ.故选a ' ιb '(2)D (3)C例2、已知PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点.(1)求证:MN ⊥AB ;(2)设平面PDC 与平面ABCD 所成的二面角为锐角θ,问能否确定θ使直线MN 是异面直线AB 与PC 的公垂线?若能,求出相应θ的值;若不能,说明理由.解:(1)∵PA ⊥矩形ABCD ,BC ⊥AB ,∴PB ⊥BC ,PA ⊥AC ,即△PBC 和△PAC都是以PC 为斜边的直角三角形,BN PC AN ==∴21,又M 为AB 的中点,∴MN ⊥AB.(2)∵AD ⊥CD ,PD ⊥CD.∴∠PDA 为所求二面角的平面角,即∠PDA=θ.设AB=a ,PA=b ,AD=d ,则2241a b PM +=,2241a d CM += 设PM=CM 则由N 为PC 的中点,∴MN ⊥PC 由(1)可知MN ⊥AB ,∴MN 为PC 与AB 的公垂线,这时PA=AD ,∴θ=45°。
例3、如图,直三棱柱ABC-A 1B 1C 1的底面ABC 0,AC=1,C 点到AB 1的距离为CE=23,D 为AB 的中点. (1)求证:AB 1⊥平面CED ;(2)求异面直线AB 1与CD 之间的距离;(3)求二面角B 1—AC —B 的平面角.解:(1)∵D 是AB 中点,△ABC ∠ABC=900,∴CD ⊥AB 又AA 1⊥平面ABC ,∴CD ⊥∴CD ⊥平面A 1B 1BA ∴CD ⊥AB 1,又CE ⊥AB 1,∴AB 1⊥平面CDE ;(2)由CD ⊥平面A 1B 1BA ∴CD ⊥DE∵AB 1⊥平面CDE ∴DE ⊥AB 1,∴DE 是异面直线AB 1与CD 的公垂线段∵CE=23,AC=1 , ∴CD=.22∴21)()(22=-=CD CE DE ; (3)连结B 1C ,易证B 1C ⊥AC ,又BC ⊥AC ,∴∠B 1CB 是二面角B 1—AC —B 的平面角.在Rt △CEA 中,CE=23,BC=AC=1,∴∠B 1AC=600 ∴260cos 121==AB , ∴2)()(2211=-=AB AB BB , ∴ 211==∠BCBB CB B tg , ∴21arctg CB B =∠. 说明:作出公垂线段和二面角的平面角是正确解题的前提, 当然, 准确地作出应当有严格的逻辑推理作为基石.例4、在直角梯形ABCD 中,∠A=∠D=90°,AB <CD ,SD ⊥平面ABCD ,AB=AD=a ,S D=a 2,在线段SA 上取一点E (不含端点)使EC=AC ,截面CDE 与SB于点F 。
