蒲丰投针试验
蒲丰投针――MonteCarlo算法

蒲丰投针 ―― Monte Carlo 算法背景:蒙特卡罗方法(Monte Carlo ),也称统计模拟方法,是在二次世界大战期间随着科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为基础的一类非常重要的数值计算方法。
蒙特卡罗方法在应用物理、原子能、固体物理、化学、生态学、社会学以及经济行为等领域中得到广泛利用。
蒙特卡罗方法的名字来源于世界著名的赌城 —— 摩纳哥的蒙特卡罗。
其历史起源可追溯到1777年法国科学家蒲丰提出的一种计算圆周的方法 —— 随机投针法,即著名的蒲丰投针问题。
问题:设在平面上有一组平行线,间距为d ,把一根长L 的针随机投上去,则这根针和平行线相交的概率是多少?(其中 L < d )分析:由于 L < d ,所以这根针至多只能与一条平行线相交。
设针的中点与最近的平行线之间的距离为 y ,针与平行线的夹角为 θ (0 ≤ θ ≤ π)。
相交情形 不相交情形易知针与平行线相交的充要条件是:sin 2Ly x θ≤=由于1[0,], [0, ]2y d θπ∈∈,且它们的取值均满足平均分布。
建立直角坐标系,则针与平行线的相交条件在坐标系下就是曲线所围成的曲边梯形区域(见右图)。
所以有几何概率可知针与平行线相交的概率是sin d 2212LL p d d πθθππ==⎰Monte Carlo 方法:随机产生满足平均分布的 y 和 θ,其中1[0,], [0, ]2y d θπ∈∈,判断 y 是否在曲边梯形内。
重复上述试验,并统计 y 在曲边梯形内的次数 m ,其与试验次数 n 的比值即为针与平行线相交的概率的近似值。
clear;n = 100000; L = 1; d = 2; m = 0;for k = 1 : ntheta = rand(1)*pi; y = rand(1)*d/2;if y < sin(theta)*L/2m = m + 1; end endfprintf('针与平行线相交的概率大约为 %f\n', m/n)计算π的近似值利用该方法可以计算 π 的近似值:sin d 22 22 1n LL m p d m d L d n πθθπππ⇒≈==≈⎰下面是一些通过蒲丰投针实验计算出来的 π 的近似值:蒲丰投针问题的重要性并非是为了求得比其它方法更精确的π值,而是在于它是第一个用几何形式表达概率问题的例子。
蒲丰投针试验讲解课件

该试验不仅在理论上具有重要意义,对 于理解随机性和几何规律的本质有重要 贡献,而且在实际应用中也有广泛的应
用价值。
蒲丰投针试验可以应用于统计学、物理 学、计算机科学等多个领域,为相关领
域的研究提供了重要的启示和工具。
蒲丰投针试验的局限性
01
02
03
04
蒲丰投针试验虽然是一个经典 的试验,但是它也存在一些局
针方向与平行线垂直。
重复投掷蒲丰投针N次,记录每 次投掷的结果。
测量与计算阶段
测量投掷后蒲丰投针 与平行线之间的距离 ,记录下来。
根据公式π=2*n/N ,计算π的近似值, 其中n为相交次数, N为投掷次数。
根据记录的数据,计 算蒲丰投针与平行线 相交的次数。
CHAPTER 03
试验结果分析
蒲丰投针试验的预期结果
蒲丰投针试验是一种估算π值的方法,其预期结果是通过投掷 一根针到一张白纸上,然后统计针与白纸边缘相交的次数, 来估算π的值。
蒲丰投针试验的预期结果是根据概率论和几何学原理推导出 来的,即当投掷次数足够多时,针与白纸边缘相交的频率接 近于π/4。
实际结果与预期结果的比较
在实际进行蒲丰投针试验时,需要记录针与白纸边缘相交的次数,并计 算出相应的π值。
限性。
首先,该试验的结果受到投针 方式、试验环境等因素的影响 ,可能导致结果存在误差。
其次,蒲丰投针试验的应用范 围相对有限,主要适用于一些 特定的几何形状和随机性问题
。
最后,蒲丰投针试验的结论仅 适用于理想化的模型,与实际
情况可能存在差异。
未来研究方向与展望
随着科学技术的发展和研究的深入, 蒲丰投针试验在未来仍有广阔的研究 前景。
蒲丰投针试验讲解课 件
蒲丰投针问题

蒲丰投针问题1.蒲丰简介蒲丰有的时候翻译成布丰,是18世纪法国著名的博物学家。
他喜欢研究数学和生物学。
主要的贡献有:(1)翻译了牛顿的《流数法》,流数法按现在的说法就叫微积分。
(2)写了一本巨著,这部巨著的名字叫《自然史》,因为他特别喜欢研究生物。
这个自然史一共有44卷,其中他生前写了36卷,后来他学生又完成了。
这本书对后来的世界有很大的影响,尤其影响到一个人叫达尔文,所以蒲丰这个人其实是很厉害的。
2.蒲丰投针1777年,在蒲丰晚年的时候,他有一次举行了一个家庭宴会。
邀请了一大堆他的朋友来帮他做实验。
做什么实验呢,就“投针”。
那朋友来了之后发现,就是桌子上有很多根间距相等的平行线。
然后蒲丰就说了,给你们同样大的针,你把这些针随机扔到这个桌子上。
然后宾客就随便扔吗,有可能这样,有可能这样……,随便扔是吧,这都有可能,什么情况都有可能。
有的针就没有跟平行线相交,比如这个,这个,这个,就没有相交,也有相交的,比如这个,这个,这个,这是相交的,对吧,然后他就数,他说这个针一共投了多少个呢?一共投了n =2212个。
其中与这个平行线相交的针有多少个,数了一下有m =704个。
然后他说,我现在可以计算圆周率了,别人都不信,他说你看我圆周率怎么算,我只要把这两个数相除就行了。
我用n 除以m ,这个数除完了大概是3.142,这个就是圆周率了。
别人说好神奇,这怎么回事儿,蒲丰说我给你解释解释这个原理是什么?其实这个原理并不复杂,我们来看一下它的原理是什么。
3. 蒲丰投针原理(1)首先,它这个平行线是严格平行的,那平行线之间的距离是固定的,是a 。
然后我随意地把一根针投上去,也许相交,也许不相交,这不一定。
比如说这个针投上去了,投上去了之后,针的总长是b ,针有一个中点叫M ,对吧,这个M 到它比较近的平行线之间的距离我们设为x ,大家注意,这个是针的中点到比较近的平行线的距离是x ,所以我们应该知道x 的范围。
x 的最小值就是这个终点正好落在平行线上,那最小值是0,对吧。
蒲丰(Buffon)投针试验

一、利用Matlab计算机语言验证蒲丰(Buffon)投针试验问题给定a=10,b=5时,模拟100万次投针实验的Matlab程序如下:a=10;b=5;n=1000000;p=10; % a为平行线间距,b为针的长度,n为投掷次数,p为有效数字位数x=unifrnd(0,a/2,[n,1]);phi=unifrnd(0,pi,[n,1]); % 产生均匀分布的随机数,分别模拟针的中点与最近平行线的距离和针的倾斜角y=x<0.5*b*sin(phi); m=sum(y); % 计数针与平行线相交的次数PI=vpa(2*b*n/(a*m),p)运行结果PI =3.138919145二、利用C++计算机语言编程通过大量重复实验验证以下结论:三个阄,其中一个阄内写着“有”字,两个阄内不写字,三人依次抓取,各人抓到“有”字阄的概率均为1/3。
程序如下:#include<stdio.h>#include<stdlib.h>#include<time.h>void main(){int n=500000;int i,a[3]={0};srand(time(NULL));for(i=0;i<n;i++)a[rand()%3]++;printf("共测试%d次,其中有字事件有%d次, 占%.2f%%\n""抓到无字事件1有%d次,占%.2f%%\n""抓到无字事件2有%d次,占%.2f%%\n""抓到无字事件共%d次,占%.2f%%",n,a[0],a[0]*100.0/n,a[1],a[1]*100.0/n,a[2],a[2]*100.0/n,a[1]+a[2],(a[1]+a[2])*100.0/n);return 0;}。
蒲丰投针实验模拟

一、蒲丰投针问题在平面上画有等距离的一些平行线,平行线间的距离为a(a>0) ,向平面上随机投一长为l(l<a)的针,针与平行线相交的概率p,结果发现π =2*l/(a*p).二、试验方法能够采纳MATLAB软件进行模拟实验,即用MATLAB编写程序来进行“蒲丰投针实验”。
1、基来源理因为针投到纸上的时候,有各样不一样方向和地点,但是,每一次投针时,其地点和方向都能够由两个量独一确立,那就是针的中点和偏离水平的角度。
以 x 表示针的中点到近来的一条平行线的距离,β表示针与平行线的交角。
明显有0<=x<=a/2 ,0<=β <=Pi 。
用边长为 a/2 及 Pi 的长方形表示样本空间。
为使针与平行线相交,一定x<=l*sinβ * ,知足这个关系的地区面积是从0 到Pi的l*sinβ对β的积分,可计算出这个概率值是(2l)/(Pi*a)。
只需随机生成n 对这样的x 和β,就能够模拟 n 次的投针实验,而后统计知足 x<=l*sin β * 的 x 的个数,就能够以为这是订交的次数。
而后利用公式求得π值。
2、MATLAB编程clear ('n')clear('a')clear('x')clear('f')clear ('y')clear ('m')disp(' 本程序用来进行投针实验的演示, a 代表两线间的宽度,针的长度 l=a/2 ,n 代表实验次数 '); a=input(' 请输入 a:');n=input(' 请输入 n:');x=unifrnd(0,a/2,[n,1]);f=unifrnd(0,pi,[n,1]);y=x<*a*sin(f);m=sum(y);PI=vpa(a*n/(a*m))三、实验数据 ( 部分程序截屏见后 )a n PI第一次310000第二次310000第三次3100000第四次3100000第五次31000000第六次31000000第七次3第八次3第九次3第十次3四、实验结论从上述数据剖析可知,跟着模拟次数的愈来愈多, PI 的值渐渐稳固在π值邻近,即愈来愈趋近于π,故蒲丰投针实验的确能够模拟出π的值。
蒲丰投针问题

蒲丰投针问题
1.有一只小猫,抓到20只老鼠,他准备每次吃掉奇数位置的老鼠,直到最后一只老鼠就把它放生,有一只很聪明的老鼠听到这里,就站到了一个位置上,最后它果然是那只被放生的老鼠,请问它站的是第几个位置?
2.伟大的数学家蒲丰,他邀请了他的很多朋友到他家,他在纸上画了很多间距相同的平行线,他给了他朋友很多长度是平行线间距一半的针,经过几千次的数据收集,针与平行线相交的数量与总数量的比值是
3.14,与π接近,各位知道是什么原因吗?。
浦丰投针问题

怎么办呢?
如果我们将针的每一个位置看作是一个基 本事件,此时,假定每一个位置都“同等可能” 是合理的。这样就可以用几何概率去解决。
模型建立与求解
x 以M 表示针落下后的中点, 表示中点 M 到最近一条平行线的距离, 表示针于平行线
x
a 2
的交角
则基本事件区域为 a 0 x : 2 0
这种方法由于来源于浦丰投针问题,常常被 称为随机投针法。更进一步的,这种方法成为了 现代计算机模拟的基础——蒙特卡洛方法。
结束
L ( A)
a
x
x
a 2
投针简图
0
1 l sin d l 2
o
从而所求概率为 L( A) l 2l p L ( ) 1 a a 2
模型分析
2l 2)由于 p a
l 1)当比值 不变时, 值始终不变 p a
2l a 所以可以利用它来计算 的近似值
o
基本事件简图
它为 ox 平面上的一个矩形,其面积为:
a L() 2M 为使针与平线(这线必定是它与 最近的一条平行线)相交,其充要条件是 l 0 x sin , A 2 (为什么?) 0 显然A 是Ω 中的一个区域(如图) , 而 A 的面积为
对于一些不确定的自然现象和科学实验 结果,我们通常用概率统计学去研究,建立 概率统计模型(随机现象)
问题:平面上画有等距离为a ( a 0) l 的一些平行线,向此平面投一长为 (l a ) 的针,试求此针与任一平行线 相交的概率?
分析: 针投到平面上与平行线的关系有两种可能:
针与这些平行线中的某一根相交,或不相交。 这两种可能性一般来说不一样大,即不具有等 可能性。因此无法用古典概率来求解。
浦丰投针

l
l sin 2
l 针与一平行线相交 0 x sin , 2
设 A=“针与一平行线相交”,则
l A : 0 x sin , 2 m ( A) P ( A) m (Ω)
l x sin 2
x a/2 A
0
0
l sin d 2l 2 . a a 2
1777年,法国科学家蒲丰( Buffon )提出了投针 试验问题.平面上画有等距离a (a>0)的一些平行线, 向平面任意投一长为l (l<a)的针,试求针与平行线 相交的概率. 解 设M表示针落下后,针 的中心,x 表示M与最近 一平行线的距离, 表示 针与这平行线的夹角,则 样本空间: a 0 x , 0 , 2
试验者
Wolf Smith De Morgan
时间
1850 1855 1860
针长 投掷次数
0.8 0.6 1.0 5000 3204 600
相交次 π的近似值 数
2532 1218 382 3.1596 3.1554 3.137
Fox Lazzerini Reina
1884 1901 1925
0.75 0.83 0.5419
1030 3408 2520
489 1808 859
3.1595 3.1415929 3.1795
蒲丰投针试验的应用及意义
2l P ( A) = aπ
根据频率的稳定性,当投针试验次数n很大时, m 算出针与平行直线相交的次数m,则频率值 即可 n 作为P(A)的近似值代入上式,那么
m 2l 2ln π n aπ am
蒲丰投针原理
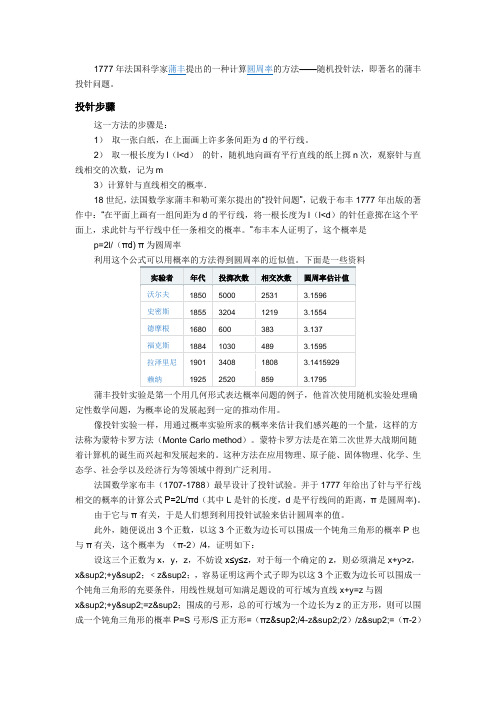
/4.因为对于每一个z,这个概率都为(π-2)/4,因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
为了估算π的值,我们需要通过实验来估计它的概率,这一过程可交由计算机编程来实现,事实上x+y>z,x²+y²;﹤z²;等价于(x+y-z)(x²+y²-z²;)﹤0,因此只需检验这一个式子是否成立即可。
若进行了m 次随机试验,有n次满足该式,当m足够大时,n/m趋近于(π-2)/4,令n/m=(π-2)/4,解得π=4n/m+2,即可估计出π值。
值得注意的是这里采用的方法:设计一个适当的试验,它的概率与我们感兴趣的一个量(如π)有关,然后利用试验结果来估计这个量,随着计算机等现代技术的发展,这一方法已经发展为具有广泛应用性的蒙特卡罗方法。
计算π最稀奇方法之一计算π的最为稀奇的方法之一,要数18世纪法国的博物学家C·布丰和他的投针实验:在一个平面上,用尺画一组相距为d的平行线;一根长度小于d的针,扔到画了线的平面上;如果针与线相交,则该次扔出被认为是有利的,否则则是不利的.布丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于d,那么有利扔出的概率为2/π.扔的次数越多,由此能求出越为精确的π的值.公元1901年,意大利数学家拉兹瑞尼作了3408次投针,给出π的值为3.1415929——准确到小数后6位.不过,不管拉兹瑞尼是否实际上投过针,他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑.通过几何、微积分、概率等广泛的范围和渠道发现π,这是着实令人惊讶的!证明下面就是一个简单而巧妙的证明。
找一根铁丝弯成一个圆圈,使其直径恰恰等于平行线间的距离d。
可以想象得到,对于这样的圆圈来说,不管怎么扔下,都将和平行线有两个交点。
蒲丰投针问题_概率论论文

Buffon投针问题摘要本文讨论了Buffon投针问题的解法及其不同解法之间的内在联系,同时从投针到投平面图形对Buffon投针问题给出了一些推广,并得到一般的结论,指出了其概率在探矿、近似计算中的应用。
关键词蒲丰投针概率随机试验近似计算一、引言蒲丰投针问题是由法国科学家蒲丰(Buffon)在1777年提出的,它是概率中非常有代表性的问题,它是第一个用几何形式表达概率问题的例子,其结论具有很强的理论与实际意义。
蒲丰针问题的解决不仅较典型的反应了集合概率的特征及处理方法,而且还可以由此领略到从“概率土壤”上开出的一朵瑰丽的鲜花——蒙特卡洛(Monte-Carlo)方法。
二、Buffon投针问题及其解法Buffon投针问题:平面上画有等距离的平行线,每两条平行线之间的距离为2a,向平面任意投掷一枚长为2l(l<a)的针,试求针与平行线相交的概率。
解:以x表示针的中点M到最近一条平行线的距离,以φ表示该针与平行线的夹角。
针与平行线的关系见图1.则有:0≤x≤a,0≤φ≤π,由它们所围成的矩形区域记为G1。
针与平行线相交的充要条件是:0≤x≤lsinφ,记满足这个关系的区域为g1(图2中的阴影部分)。
则所求概率为P1=g1的面积G1的面积=∫lsinφdφπaπ=2laπ三、Buffon投针问题不同解法及其内在联系上述解法是常见解法之一(记为解法一),这里讨论一下蒲丰针问题的其他解法及其之间的联系。
1.其他解法解法二:以x表示针的重点M到最近一条平行线的距离,y表示该针在此平行线上投影和长度,如图3所示。
易知x和y的取值范围是0≤x≤a,0≤y≤2l,这两个不等式确定了xOy平面上的矩形区域G2,针与平行线相交的充要条件是(y2)2+x2≤l2,该不等式确定了矩形区域G2(如图4所示)中的区域g2,从而所求概率为P2=g2的面积G2的面积=14·l·2l·π2l·a=lπ4a解法三:作垂直于平行线的直线,在该直线上选定一方向为正向,用z1,z2分别表示针头与针尾关于某平行线的纵坐标(如图5所示),该平行线的选取应使|z1+z2|≤2a。
实验说明一:蒲丰投针

实验说明1:蒲丰投针一、 实验目的1、 运用基本采样技术计算积分;2、 体会用随机模拟方法解决实际问题。
二、 问题描述在历史上人们对π的计算非常感兴趣性,发明了许多求π的近似值的方法。
1777年法国科学家蒲丰(Buffon )提出并解决了如下的投针问题来近似求解π。
蒲丰投针问题如图1所示。
桌面上画有间隔为a (a >0) 的一些平行线,向平面任意投一枚长为l (l <a )的针,可以通过求针与任一平行线相交的概率,进而求得π的近似值。
用X 表示针的中点与最近一条平行线的距离,Y 表示针与此直线间的夹角。
如果sin 2X l Y <,或sin 2l X Y <时,针与一条直线相交。
图1:蒲丰投针示意图由于向桌面投针是随机的,所以可以用二维随机向量(X ,Y )来确定针在桌面上位置。
并且X 在0,2a ⎛⎞⎜⎜⎜⎝上服从均匀分布, Y 在0,2π⎛⎞⎟⎜⎟⎜⎟⎜⎝⎠上服从均匀分布, X 与Y 相互独立。
由此可以写出的联合概率密度函数为: ()40,0,220a x y f x y a ππ⎧⎪⎪<<<<⎪=⎨⎪⎪⎪⎩其他。
用随机事件A 针与平行线相交,则事件A 发生的概率为{}()sin 2200sin 242sin ,2l y l x y l l A X Y f x y dxdy dxdy a aπππ<⎧⎫⎪⎪=<===⎨⎬⎪⎪⎪⎪⎩⎭∫∫∫∫P P 。
如果{}A P 已知,则有该概率得到{}2l a A π=P 。
当蒲丰的实验中,通过投针N 次,其中针与平行线相交n 次,用频率n N 作为{}A P 的估计值,于是得到2Nl anπ≈。
三、 实验内容1、上述概率{}A P 为积分计算,可用Monte Carlo 积分近似。
通过从分布(),f x y 中产生随机数,近似积分{}A P ,从而计算π;2、当样本数N (N =50、100、1000、10000、50000)时,每个N 重复10次实验。
关于用蒲丰投针求∏值的实验报告

关于用蒲丰投针求∏值的实验报告实验目的理解蒲丰投针的模型,逐渐掌握用数学知识解决实际问题的能力掌握运用matlab 进行一般的数学运算培养团队合作精神实验原理在一张纸上画出间距为l 的多条直线,随机在上面投放长度为 a 的针,投放n 次,记与直线相交的次数为m ,当n 相当大之后,则针与线相交的概率n m p =如下图,通过分析,针与线相交的条件简化为 ϕsin 21≤x 而πϕ≤≤≤≤0,20dx这是一个几何特型的概率问题,通过推理可得(*)22s i n 210d l dd G g p ππϕϕπ===⎰的面积的面积所以,实验过程及结果用matlab 模拟投针过程求∏值 的函数:function f=fun(a,l,n)x=pi.*rand(1,n);y=(a/2).*rand(1,n);c=(y<=((l/2).*sin(x)));m=sum(c);f=2*l*n/(m*a);随机一次实验求得的∏值>> a=input('a=');l=input('l=');n=input('n=');a=20l=15n=1000>> fun(a,l,n)ans =3.131524008350731>>以上得到的∏值不是十分精确,这是由于实验次数有限导致的误差,当实验的次数相当大之后,所得结果必定会更加逼近∏的精确值。
缺点和改进上述模拟实验还不是十分精确,而且没有绘图,不够直观,下次会注意模拟的更加精确,更加直观。
布丰投针数学分析与实验设计(原创)

l 由(1)和(2)我们可以得出一些结论: n 根长度为 的小 n 针仍出去后压线的概率之和与一根长为 l 的针扔出去后压线 l 的概率相等;将 n 根长为 的小针连接成任意形状后扔出去 n 压线的概率与长为 l 的针扔出去压线的概率相等;当 n ,线就是曲线,所以结论可以进一步推广:随机投
k
称作这个连分式的第 k 个渐进分数。同时,
k
它也是所有分母不超过
q 的分数中最接近实数 x 的分数,
k
k
是实数 x 的第 k 个最佳渐进分数。
k
求渐进连分式,当然可以用上面分式求出,下面给出第
p k 个渐进连分式 的递推求法: q p a q 1 p a a 1 q a a p p ( k 2) p q a q q ( k 2 )
如上图所示,AB 针的长度为 2l ,CD 针长度为 l 。在 AB 针 或 AB 针的延长线与直线的夹角为 ,AB 针的中点 M 的取
角 相等,所以 M ' , M ' ' 是 m' , m' ' 的两倍,于是 CD 与直线相交的概率是 AB 与直线相交的概率的一半。对于其 余任意夹角都有这个结论。所以:长度为 l 的针与直线相交 的概率是长度为 2l 的针与直线相交概率的一半。
产生误差原因 1:m/n 的精度问题,这个是数学造 成的误差。解决办法:选取合适的 m 值,使 m/n 的有 效数字达到要求的精度。 产生误差原因 2:如果针的端点与直线非常接近, 例如相距万分之一毫米,用肉眼无法判断针是否与直线 相交,造成误差。解决办法:该次事件无效,不予统计, 继续进行下一次实验。 产生误差原因 3:l/d 的精度问题,这是测量问题。 产生误差的原因 1 和 2,我们都可以解决,使之达
投针试验

投针试验投针问题1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法,即著名的布丰投针问题。
投针步骤这一方法的步骤是:1)取一张白纸,在上面画上许多条间距为a的平行线。
2)取一根长度为l(l<a)的针,随机地向画有平行直线的纸上掷n次,观察针与直线相交的次数,记为m3)计算针与直线相交的概率.18世纪,法国数学家布丰和勒可莱尔提出的“投针问题”,记载于布丰1777年出版的著作中:“在平面上画有一组间距为a的平行线,将一根长度为l(l<a)的针任意掷在这个平面上,求此针与平行线中任一条相交的概率。
”布丰本人证明了,这个概率是p=2l/(πd) π为圆周率利用这个公式可以用概率的方法得到圆周率的近似值。
下面是一些资料试验者时间投掷次数相交次数圆周率估计值Wolf1850年5000 2532 3.1596Smith 1855年3204 1218.5 3.1554C.De Morgan 1680年600 382.5 3.137Fox1884年1030 489 3.1595Lazzerini 1901年3408 1808 3.1415929Reina 1925年2520 859 3.1795设这三个正数为x,y,z,不妨设x≤y≤z,对于每一个确定的z,则必须满足x+y>z,x²+y²;﹤z²;,容易证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件,用线性规划可知满足题设的可行域为直线x+y=z与圆x²+y²=z²;围成的弓形,总的可行域为一个边长为z的正方形,则可以围成一个钝角三角形的概率P=S弓形/S正方形=(πz²/4-z²/2)/z²=(π-2)/4.因为对于每一个z,这个概率都为(π-2)/4,因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
蒲丰投针试验---------概率论与数理统计

蒲丰资料
1777年,法国科学家蒲丰(Buffon)提ห้องสมุดไป่ตู้了投针 试验问题.平面上画有等距离为a(a>0)的一些平行直 线,现向此平面任意投掷一根长为b( b<a )的针,试求 针与某一平行直线相交的概率. 解 以 x表示针投到平面上时,
针的中点M到最近的一条平行
a
M x
直线的距离, 表示针与该平行直线的夹角.
1.0
0.75 0.83 0.5419
600
1030 3408 2520
382
489 1808 859
3.137
3.1595 3.1415929 3.1795
利用蒙特卡罗(Monte Carlo)法进行计算机模拟. 单击图形播放/暂停 ESC键退出 取a 1, b 0.85.
利用上式可计算圆周率π 的近似值.
历史上一些学者的计算结果(直线距离a=1)
试验者 Wolf Smith 时间 1850 1855 针长 0.8 0.6 投掷次数 相交次数 π的近似值 5000 3204 2532 1218 3.1596 3.1554
De Morgan 1860
Fox Lazzerini Reina 1884 1901 1925
那么针落在平面上的位置可由( x , )完全确定.
投针试验的所有可能结果与 矩形区域
a S {( x , ) 0 x ,0 π} 2 中的所有点一一对应 . 由投掷的任意性可知 这是一个几何概型问题.
a
M x
所关心的事件
o
A { 针与某一平行直线相交} 发生的充分必要条件为S 中的点满足 b 0 x sin , 0 π . 2
概率论与数理统计 南京大学 1 第一章概率论的基本概念 (1.2.1) 蒲丰投针实验

m( A) m()
A对应区域D的度量 对应区域S的度量
即等可能性
例(蒲丰投针问题)平面上有等距离的平行线,平行线间
的距离为a。向此平面任意投掷一枚长为l (l≤a) 的针,求针
与任一平行线相交的概率。
解:设M为针的中点,M点到最近平行线的距离为x,针与 平行线的夹角为θ。针的位置可由(x, θ)决定,
De Morgan(1860 1.0 600 年) Fox(1884年) 0.75 1030
相交次数 近似值 m
2532
3.1596
1219
3.1541
383
3.1332
489
3.1596
2
2l
m() a / 2 a
蒲丰投针实验的应用
利用随机模拟方法计算
P(A) 2l 2l
a
aP( A)
利用P(A)m/n。其中n为投掷次数,m为相交次数。 就可以近似计算。
实验者
l/a 投掷次数n
Wolf(1850年) 0.8 5000
Smith(1855年) 0.6 3204
概率论与数理统计
蒲丰投针试验
几何概型
定义: 若随机试验的样本空间对应一个度
量有限的几何区域S,每一基本事件与S内的 点一一对应,则任一随机事件A对应S中的某 一子区域D。若事件A的概率只与A对应的区 域D的度量成正比,而与D的形状及D在S中的 位置无关。则称为几何概型。
事件A发生的概率为:
样本空间:
{(x, ) | 0 x a / 2, 0 }
设A:针与任一条平行线相交。其充要条件为:
x l sin
2
l/2
蒲丰(Buffon)投针随机试验的讨论 (修改稿)

(2006-3-7, 2009-9-18再修改)例 ( 蒲丰(Buffon )投针随机试验的讨论 ) 在平面上画有相互距离均为2a 的平行线束,向平面上随机投一枚长为2l 的针,为了避免针与两平行线同时相交的复杂情况,假定0>>l a , 设M 为针的中点,y 为M 与最近平行线的距离,φ为针与平行线的交角(如图1)a y ≤≤0, πϕ≤≤0. 于是,很明显,针与平行线相交的充要条件是ϕsin l y ≤(如图2),故相交的概率为ald l a dy d a p l πϕϕπϕπϕππ2 sin 1 1sin 000===⎰⎰⎰ (1) 我们用n 表示投针次数, n S 表示针与平行线相交次数,由大数定理知,当n 充分大时,频率接近于概率,即aln S n π2≈ 于是有naS nl2≈π (2)这就是上面所说的用随机试验求π值的基本公式。
根据公式(2),19—20世纪,曾有不少学者做了随机投针试验,并得到了π的估计值 . 其中最详细的有如下两个 :其中π的估计值就是利用π的近似公式(8)得到的,即1596.363320002532455000362≈=⨯⨯⨯≈π (Wolf )1415929.31133551808334085.22≈=⨯⨯⨯≈π (Lazzarini )一般情况下,随机抽样试验的精度是不高的,Wolf 的试验结果是π≈3.1596,只准确两位有效数字 .精度是由方差n p p n S D n )1(-=⎪⎭⎫⎝⎛决定的,为了确定概率p ,不妨取l =a 这一极限情况,这时π2≈p =0.6366,n n S D n 2313.0≈⎪⎭⎫⎝⎛,由积分极限定理, dx n p p p n S P x n n ⎰-∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤--λλπλ221-e21)1(lim即频率n S n /近似地服从正态分布律()n p p p N /)1(,- . 如果要求以大于95%的概率(96.1=λ),保证以频率n S n /作为p 的近似值精确到三位有效数字,001.0≤-=p nS nε 即≈⎪⎪⎭⎫⎝⎛≤-001,0p n S P n 95.021/)1(001.0)1(001.0212≥⎰----np p np p x dx eπ则必须有96.1/)1(001.0=≥-λnp p根据上式,要求试验次数7.88001.0/231.096.122≈⨯≥n 万次 .至于Lazzarini 的试验,为什么实验次数少反而精确度却很高呢?这是由于这一试验结果恰好和祖冲之密率355/113相合,而祖冲之密率为无理数π的连分式,属于π的最佳有理逼近 . 很明显,作为一种具有随机性质的试验,其结果恰好与最佳有理逼近的结果一致是非常偶然的;顾及到上述讨论,故Lazzarini 的试验结果是不大可能的 .注:以上的讨论是第6章“假设检验”方法的一个有实际意义的例子。
蒲丰投针实验原理

蒲丰投针实验原理1.地球是一个球体:在蒲丰时代,人们普遍相信地球是一个球体,而蒲丰的实验就是为了验证这一点。
2.光线传播是直线传播:蒲丰认为光线传播是呈直线传播的,这是基于他对光学的观察和实验中得到的结论。
基于以上前提,蒲丰提出了以下实验步骤来验证地球的球形:1.准备一个平坦的地面:选择一个平坦的地面,比如一块大理石板或者是一个平整的木板。
2.准备一把针:选择一根细长的针,尽量确保它是笔直的。
3.垂直投放针:将针垂直地向地面投放,确保它垂直于地面,并且尽量避免针倾斜或弯曲。
4.观察针在地面上的分布:观察针在地面上的分布情况,看是否存在一定的规律。
理论上,如果地球是一个平坦的平面,那么无论针的位置如何投放,针都应该均匀地分布在地面上。
然而,如果地球是一个球体,那么针的位置投放将会影响其在地面上的分布。
由于地球表面的曲率,针的投放位置不同将导致一些规律的变化。
根据蒲丰的实验,当针被随机分布在地面上时,如果地球是一个球体,那么在一些特定范围内的细长物体的位置分布将会有所偏差。
这是因为在投针的过程中,总有一些针会与地面相交,而一些则不会。
蒲丰实验的原理是基于概率统计的方法。
通过计算和观察一系列接触和不接触地面的针,可以推导出地球的曲率和球形。
如果这些数据和理论上的期望一致,那么可以得出结论地球是球状的。
总结起来,蒲丰投针实验的原理是基于光线的直线传播以及地球的球形假设。
通过观察针在地面上的分布情况,可以验证地球是否是球状的。
这个实验的重要性在于它提供了一种简单直观的方法来验证古代关于地球形状的理论,并且可以通过实验数据来验证理论的正确性。
蒲丰投针问题与无理数π的模拟

5、在C4输入=3*SIN(C4)/2。下托到C1003;在D4输入=IF(D4<=1,"1","0")下托到D1003,在E4输入=COUNTIF(E4:E10003,"1")在下托到E1003,在F4输入=2*10000*3/(F4*4)。
教师评语与成绩:
实验结果总结:计算机上模拟蒲丰投针试验,可以求出π的近似的值.我的到的值为3.225133和3.123367.他与.31415926存在了差别.可能是由于计算机取的1000个随机数的差别.虽然它们存在差别,但是它们已经很接近啦,这比人工或其它方法计远的快和准确于人的计算.
本实验旨在让实验者在计算机上模拟蒲丰投针试验,掌握无理数 的近似计算方法,理解随机模拟法的基本原理,从中体会到新思想、新方法产生的过程。
实验内容:
蒲丰投针问题:平面上画有间隔为 的等距平行线,向平面任意投一枚长为 的针,求针与任一平行线相交的概率,进而求 的近似值。若做了 次投针试验,有 次针与线相交,那么由教材例1.2.9结论知所求概率为 ,而 ,故有 。
2、单击数据/数据分析/随机数发生器,选择变量个数2,随机数1000,均匀分布,介于-1到1,输出区域$A$2,确定;
3、在C2输入=A2^2+B2^2;
4、在D2输入=IF(C6<=1,"1","0"),在E2输入=COUNTIF(D2:D10002,"1");
5、在F2输入=4*E2/10000。
实验二、蒲丰投针问题与无理数π的模拟
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
针长
投掷次数
相交次数
π的近似值
1
0.7
1000
462
3.0303
1
0.9
2000
1146
3.1414
2
1.7
3000
1649
3.0928
2
1.9
4000
2401
3.1653
3
2.7
5000
2932
3.0696
3
2.9
6000
3696
3.1385
4
3.8
7000
4238
3.1383
4
3.6
考核结果
教师签名:年 月 日
模拟法(也称为Monte-Carlo法).
实验的目的与作用
(1)理解频率具有客观稳定性;
(2)理解概率是频率的稳定值;
(3)知道我们常用频率作为计算概率的近似值;
(4)掌握通过设计一个随机实验,使一个事件的概率与某一未知数有关,然后通过重复实验,以频率近似概率,即可求得未知数的方法。
实验方法
运用计算机模拟蒲丰投针实验,通过重复实验,以频率近似概率,并通过公式推导,求的圆周率π的近似值。
实 验 报 告
课程名称:___概率论与数理统计___
学院名称:____数学与统计学院____
班 级:__________
姓 名:
学 号:
2013-2014______学年第 _____2____学期
数 学 与 统 计 学 院 制
实验地点ห้องสมุดไป่ตู้
课程类别
①公共课□ ②专业课□
实验日期
2014.4.28
实验编组
第 组
实验所
用时间
2小时
实验名称
蒲丰投针试验
问题陈述及原理
在一个平面上,用尺画一组相距为n的平行线;一根长度小于l(l<=n)的针,扔到画了线的平面上;如果针与线相交,则该次扔出被认为是有利的,否则则是不利的.
蒲丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于l,那么有利扔出的概率为2/π.扔的次数越多,由此能求出越为精确的π的值.
实验环境
MATLABR2010a
实验内容:
(1)利用计算机模拟蒲丰投针问题;
(2)根据蒲丰投针实验模拟结果估计圆周率π的近似值。
实验的意义
蒲丰投针问题是几何概率早起应用的一个例子。该实验的重要性并非是为了求得比其它方法更精确的π值,而在于这种通过
建立一个概率模型,并设计适当的随机实验,然后利用计算机模拟所设计的随机实验,来解决确定性数学问题方法,称为随机
问题的数学描述
个实验方法的操作很简单:找一根粗细均匀,长度为l的细针,并在一张白纸上画上一组间距为n的平行线(方便起见,常取 l>=n/2),然后一次又一次地将针任意投掷在白纸上。这样反复地投多次,数数针与任意平行线相交的次数。于是就可以得到 π 的近似值。因为蒲丰本人证明了针与任意平行线相交的概率为 p =2l/πl。
8000
4602
3.1291
5
4.85
9000
5538
3.1528
6
5.7
10000
5965
3.1852
实验分析:通过实验可以看到,无论改变平行线间的距离,针的长度或是投掷的次数,得到的π的值都很相近。而且又可以感觉到,针的长度越接近平行线间的距离,在实验中得到的π的值与3.1416越接近,即也说明频率的稳定。因此也得到和学习了有一种计算π的值的计算方法。
实验原理
在平面上画有等距离的平行线,平行线间的距离为 a(a>0),向平面任意投掷一枚长为l(l<a)的针,求针与平行线相交的概率p。以 x表示针的中点到最近一条平行线距离,以Φ表示针与平行线的交角.于是投针试验就相当于向平面区域Ω={(x,φ)|0≤x≤a/2,0≤φ≤π}投点的几何概型。
针与平行线相交的充要条件是(x,Φ)满足:
编程如下:
function buffon(a,l,N)
X=unifrnd(0,a/2,1,N);
phi=unifrnd(0,pi,1,N);
half_sin=l*sin(phi)./2;
M=sum(X<=half_sin);
hat_pi=2*N*l./(a*M);
M
hat_pi
(蒲丰投针实验模拟结果及有关数据)
于是:
投针N次,记录下针与平行线相交的次数M,再用频率M/N代替概率p,从而得到π≈2lN/aM
实验准备
Matlab程序中的命令:
均匀分布 unif
随机数生成 rnd
实验过程
计算机模拟投针N次,针与平行线相交M次,由公式π≈2lN/aM
计算出π。
产生随机数
时生成均匀分布随机数:unifrnd(a,b,1,N)或unifrnd(a,b,N,1)其中,N为重复实验次数.。
