二维导热物体温度场的数值模拟
热处理数值模拟

热处理数值模拟热处理数值模拟是一种通过数值计算方法模拟材料在热处理过程中的温度分布、相变行为和应力变化等物理现象的过程。
下面是一个详细精确的热处理数值模拟的步骤:1. 确定模拟的材料和几何形状:首先需要确定要进行热处理数值模拟的材料和其几何形状。
这包括材料的热物性参数(如热导率、比热容等)和几何形状的尺寸。
2. 建立数值模型:根据材料和几何形状的信息,建立数值模型。
数值模型可以是二维或三维的,可以采用有限元方法或有限差分方法等数值计算方法。
3. 确定边界条件:根据实际热处理过程中的边界条件,如加热温度、冷却速率等,确定数值模型的边界条件。
边界条件可以是恒定的,也可以是随时间变化的。
4. 确定材料的热物性参数:根据实验数据或已有的文献资料,确定材料的热物性参数。
这些参数包括热导率、比热容、相变温度等。
5. 设置数值计算参数:确定数值计算的时间步长、网格尺寸等参数。
这些参数的选择需要保证数值模拟的精度和计算效率之间的平衡。
6. 进行数值计算:根据数值模型、边界条件和材料的热物性参数,进行数值计算。
数值计算可采用显式或隐式的数值方法,如前向差分法、后向差分法等。
7. 分析计算结果:根据数值计算的结果,分析材料在热处理过程中的温度分布、相变行为和应力变化等物理现象。
可以通过可视化技术将计算结果以图形或动画的形式展示出来,以便更直观地理解和分析。
8. 验证和优化模型:根据实验数据或已有的文献资料,对数值模型进行验证和优化。
可以通过与实验结果的对比来评估数值模拟的准确性,并对模型进行调整和改进。
以上是热处理数值模拟的详细精确步骤,通过这些步骤可以对材料在热处理过程中的物理现象进行准确的数值模拟和分析。
简单的二维热传导模拟-c_c++ code

HANDLE_ERROR(cudaMalloc((void**)&data.dev_constSrc,bitmap.image_size()));
float *temp=(float*)malloc(bitmap.image_size());
}
int main(void)
{
DataBlock data;
CPUAnimBitmap bitmap(DIM,DIM,&data);
data.bitmap=&bitmap;
data.totalTime=0;
data.frames=0;
HANDLE_ERROR(cudaEventCreate(&data.start));
//将作为热源的单元温度值复制到网格中相应的单元中,
__global__ void copy_const_kernel(float *iptr,const float *cptr){
//
int x=threadIdx.x+blockIdx.x*blockDim.x;
int y=threadIdx.y+blockIdx.y*blockDim.y;
{
for(int x=400;x<500;x++)
{
temp[x+y*DIM]=MIN_TEMP;
}
}
HANDLE_ERROR(cudaMemcpy(data.dev_constSrc,temp,bitmap.image_size(),cudaMemcpyHostToDevice));
二维导热物体温度场的数值模拟

传热大作业二维导热物体温度场的数值模拟(等温边界条件)姓名:班级:学号:墙角稳态导热数值模拟(等温条件)一、物理问题有一个用砖砌成的长方形截面的冷空气空道,其截面尺寸如下图所示,假设在垂直于纸面方向上冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
外矩形长为,宽为;内矩形长为,宽为。
第一种情况:内外壁分别均匀地维持在0℃及30℃;第二种情况:内外表面均为第三类边界条件,且已知:外壁:30℃ ,h1=10W/m2·℃,内壁:10℃ ,h2= 4 W/m2·℃砖墙的导热系数λ= W/m ·℃由于对称性,仅研究1/4部分即可。
二、数学描写对于二维稳态导热问题,描写物体温度分布的微分方程为拉普拉斯方程 02222=∂∂+∂∂y t x t这是描写实验情景的控制方程。
三、方程离散用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为确定温度值的空间位置,即节点。
每一个节点都可以看成是以它为中心的一个小区域的代表。
由于对称性,仅研究1/4部分即可。
依照实验时得点划分网格:建立节点物理量的代数方程对于内部节点,由∆x=∆y ,有)(411,1,,1,1,-+-++++=n m n m n m n m n m t t t t t由于本实验为恒壁温,不涉及对流,故内角点,边界点代数方程与该式相同。
设立迭代初场,求解代数方程组。
图中,除边界上各节点温度为已知且不变外,其余各节点均需建立类似3中的离散方程,构成一个封闭的代数方程组。
以C t 000=为场的初始温度,代入方程组迭代,直至相邻两次内外传热值之差小于,认为已达到迭代收敛。
四、编程及结果1)源程序#include<>#include<>int main(){int k=0,n=0;double t[16][12]={0},s[16][12]={0};double epsilon=;double lambda=,error=0;double daore_in=0,daore_out=0,daore=0;FILE *fp;fp=fopen("data3","w");for(int i=0;i<=15;i++)for(int j=0;j<=11;j++){if((i==0) || (j==0)) s[i][j]=30;if(i==5)if(j>=5 && j<=11) s[i][j]=0;if(j==5)if(i>=5 && i<=15) s[i][j]=0;}for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)t[i][j]=s[i][j];n=1;while(n>0){n=0;for(int j=1;j<=4;j++)t[15][j]=*(2*t[14][j]+t[15][j-1]+t[15][j+1]);for(int i=1;i<=4;i++)t[i][11]=*(2*t[i][10]+t[i-1][11]+t[i+1][11]);for(int i=1;i<=14;i++)for(int j=1;j<=4;j++)t[i][j]=*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=1;i<=4;i++)for(int j=5;j<=10;j++)t[i][j]=*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)if(fabs(t[i][j]-s[i][j])>epsilon)n++;for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)s[i][j]=t[i][j];k++;实验结果可知:等温边界下,数值解法计算结果与“二维导热物体温度场的电模拟实验“结果相似,虽然存在一定的偏差,但由于点模拟实验存在误差,而且数值解法也不可能得出温度真实值,同样存在偏差,但这并不是说数值解法没有可行性,相反,由于计算结果与电模拟实验结果极为相似,恰恰说明数值解法分析问题的可行性。
热流体课程实验报告-二维导热物体温度场的计算机模拟实验

二维导热物体温度场的计算机模拟实验一、实验目的(1)学习电、热类比的原理及边界条件的处理;(2)通过计算机编程的方式求出墙角导热的离散温度场。
二、实验原理二维稳态过程,导热方程为∂2t ðx2+∂2tðy2=0二维稳态导热内部节点的差分方程为t i+1,j+t i−1,j+t i,j+1+t i,j−1−4t i,j=0于是内部节点的迭代计算式为t i,j=t i+1,j+t i−1,j+t i,j+1+t i,j−14对于恒温边界条件,除了绝热边界时使用对称性外,只使用上面一个迭代计算式即可。
但是对于对流边界,边界上的点,按位置分为内角点、外角点和平直边界,按类型分为对流边界、绝热边界,计算步骤相比恒温边界下更为复杂。
按位置:a)内角点:4个方向均有导热热流,有dx2+dy2面积的对流换热b)外角点:2个方向有导热,有dx2+dy2面积的对流换热c)平直边界:3个方向有导热,有dx或dy面积的对流换热按类型:a)绝热边界:该点的绝热一侧没有热流量,基尔霍夫定律中,此方向的热流量代入0计算b)对流边界:该点该方向的对流换热量由牛顿冷却公式q=hA(t∞−t i,j)计算得出综上所述:对流边界下的差分方程为:Φi−1,j+Φi+1,j+Φi,j−1+Φi,j+1+Φ对流=0其中,Φi−1,j,Φi+1,j,Φi,j−1,Φi,j+1为导热量,q对流为对流边界换热量。
Φi−1,j=λA(t i−1,j−t i,j)dx,Φ对流=ℎA(t∞−t i,j)。
代入所有q的计算式,可解得t i,j=∑λA k t kdxk+ℎ对流A对流t∞∑λA kdxk+ℎ对流A对流注意:a)k为实际参与导热的几个方向,对于内角点有4项,外角点有2项,平直边界有3项,绝热边界还要去掉这一方向的那一项b)A k的值根据实际位置确定,内角点得两个方向为0.5dx两个方向为1dx,外角点的两实验名称个方向均为0.5dx,平直边界有两个0.5dx和一个1dxc)内外测流体的ℎ不相等,对流面积为该网格实际与流体接触的面积角点为0.5dx,平直边界为1dx。
二维导热物体温度场的数值模拟

金属凝固过程计算机模拟题目:二维导热物体温度场的数值模拟Solidworks十字接头的传热分析作者:张杰学号:S2*******学院:北京有色金属研究总院专业:材料科学与工程成绩:2015 年12 月二维导热物体温度场的数值模拟图1 二维均质物体的网格划分用有限差分法模拟二维导热物体的温度场,首先将二维物体划分为如图1所示的网格,x ∆与y ∆可以是不变的常量,即等步长,也可以是变量(即在区域内的不同处是不同的),即变步长。如果区域内各点处的温度梯度相差很大,则在温度变化剧烈处,网格布得密些,在温度变化不剧烈处,网格布得疏些。至于网格多少,步长取多少为宜,要根据计算精度与计算工作量等因素而定。在有限的区域内,将二维不稳定导热方程式应用于节点,)i j (可写成: ,2222 ,i jPPp i j T T T C x y ρλτ⎛⎫∂∂∂=+ ⎪∂∂∂⎝⎭,1 , ,()i jP P Pi j i jT T T οτττ+-∂⎛⎫=+∆ ⎪∂∆⎝⎭ (), 1 , , 1 ,222()i j P P P Pi j i j i j T T T T x x x ο+--+∂⎛⎫=+∆ ⎪∂⎝⎭∆ () , ,1 , ,1222()i jPP P Pi j i j i j T T T T y y y ο+--+⎛⎫∂=+∆ ⎪∂∆⎝⎭τ∆、x ∆、y ∆ 当τ∆、x ∆、y ∆较小时,忽略()οτ∆、2()x ο∆、2()y ο∆项。
当x y ∆=∆时,即x 、y 方向网格划分步长相等。最后得到节点,)i j (的差分方程: ()1 , ,0 1 , 1 , ,1 ,1 ,4P P P P P P Pi j i j i j i j i j i j i j T T F T T T T T ++-+-=++++-式中:()02p F C x λτρ∆=∆。假设边界为对流和辐射边界,对流用以下公式计算:()(),1 , ,0 1 , ,1 ,1 ,24Pc f i j P P P P P P i j i j i j i j i j i j p a T T T T F T T T T C xτρ+-+-∆-=+++-+∆MATLAB 编程模拟clc; clear;format long %% 参数输入moni_canshu=xlsread('模拟参数输入.xlsx',1,'B2:B11'); %读取excel 中的模拟参数 s=moni_canshu(1); %几何尺寸,m t0=moni_canshu(2); %初始温度,℃tf=moni_canshu(3); %辐射(空气)边界,℃ rou=moni_canshu(4); %密度,kg/m3lamda=moni_canshu(5); %导热系数,w/(m ℃) Cp=moni_canshu(6); %比热,J/(kg ℃)n=moni_canshu(7); %工件节点数,个<1000 dt=60*moni_canshu(8); %时间步长,min to s m=moni_canshu(9); %时间步数,个<100 dx=s/(n-1);%计算dxf0=lamda*dt/(rou*Cp*dx*dx);%计算f0 %% 初始参数矩阵,初始温度 for iii=1:n for jjj=1:nTold(iii,jjj)=t0; end endTold(1,:)=tf; Told(n,:)=tf; Told(:,1)=tf;Told(:,n)=tf;%% 写文件表头xlswrite('data.xlsx',{['坐标位置']},'sheet1','A1');asc=97;for ii=1:nbiaotou1={['第' num2str(ii) '点']};asc=asc+1;xlswrite('data.xlsx',biaotou1,'sheet1',[char(asc) '1']);xlswrite('data.xlsx',biaotou1,'sheet1',['A' num2str(ii+1)]);end%% 模拟运算for jj=1:2copyfile('data.xlsx','data1.xlsx')Tnew(1,1:n)=tf;Tnew(n,1:n)=tf;Tnew(1:n,1)=tf;Tnew(1:n,n)=tf;for i=2:n-1for j=2:n-1Tnew(i,j)=Told(i,j)+f0*(Told(i-1,j)-4*Told(i,j)+Told(i+1,j)+Told(i,j-1)+Told(i,j+1)); endendTold=Tnew;pcolor(Told);%绘图shading interpcolormap(jet)pause(0.1)saveas(gcf,['第' num2str(jj*0.1) 's温度图像.jpg']);xlswrite('data1.xlsx',Told,'sheet1','B2');copyfile('data1.xlsx',['第' num2str(jj*0.1) 's数据.xlsx'])delete('data1.xlsx');end图3 模拟物体的温度分布图2 模拟物体的温度等高线图和温度梯度分布图。
西安交通大学传热学大作业---二维温度场热电比拟实验

二维导热物体温度场的数值模拟一、物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图1-1所示,假设在垂直于纸面方向上用冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算: 砖墙横截面上的温度分布;垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:内外壁分别均匀维持在0℃及30℃; 第二种情况:内外壁均为第三类边界条件,且已知:Km K m W h C t Km W h C t ∙=∙=︒=∙=︒=∞∞/35.0/93.3,10/35.10,30222211λ砖墙导热系数二、数学描写由对称的界面必是绝热面,可取左上方的四分之一墙角为研究对象,该问题为二维、稳态、无内热源的导热问题。
控制方程:02222=∂∂+∂∂y tx t边界条件: 第一种情况:由对称性知边界1绝热: 0=w q ; 边界2为等温边界,满足第一类边界条件: C t w ︒=0;1-1图2-1图边界3为等温边界,满足第一类边界条件: C t w ︒=30。
第一种情况:由对称性知边界1绝热: 0=w q ;边界2为对流边界,满足第三类边界条件: )()(2f w w w t t h n tq -=∂∂-=λ; 边界3为对流边界,满足第三类边界条件: )()(2f w w w t t h ntq -=∂∂-=λ。
三、方程离散用一系列与坐标轴平行的间隔0.1m 的二维网格线将温度区域划分为若干子区域,如图1-3所示。
采用热平衡法,利用傅里叶导热定律和能量守恒定律,按照以导入元体(m,n )方向的热流量为正,列写每个节点代表的元体的代数方程,第一种情况: 边界点:边界1(绝热边界):5~2)2(411,11,12,1,m =++=+-m t t t t m m m , 11~8)2(411,161,16,15,16=++=+-n t t t t n n n n,3-1图边界2(等温内边界): 7,16~7;7~1,6,0,=====n m n m t nm边界3(等温外边界): 12,16~2;12~1,1,30,=====n m n m t n m内节点:11~8,15~6;11~2,5~2)(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m第二种情况 边界点:边界1(绝热边界): 5~2)2(411,11,12,1,m =++=+-m t t t t m m m , 11~8)2(411,161,16,15,16=++=+-n t t t t n n n n ,边界2(内对流边界):6~1)2(222111,61,6,5,6=++++=∆∆-+n Bi t Bi t t t t n n n n ,16~7)2(2221117,17,18,7,=++++=∆∆-+m Bi t Bi t t t t m m m m ,边界3(外对流边界):11~1)2(2222221,11,1,2,1=++++=∆∆-+n Bi t Bi t t t t n n n n,16~2)2(22222212,112,111,12,=++++=∆∆-+m Bi t Bi t t t t m m m m ,内角点: )3(22)(21116,67,78,67,57,6+++++=∆∆Bi t Bi t t t t t外角点:)1(222211,112,212,1+++=∆∆Bi t Bi t t t内节点:11~8,15~6;11~2,5~2);(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m(10,22121==∆=∞∆t t xh Bi λ;30,21212==∆=∞∆t t xh Bi λ)四、编程思路及流程图编程思路为设定两个二维数组t(i,j)、ta(i,j)分别表示本次迭代和上次迭代各节点的温度值,iter (实际编程时并未按照此名称来命名迭代步长)表示迭代进行的次数, 1Q 、2Q 分别表示外边界、内边界的散热量。
二维导热物体温度场的数值模拟

二维导热物体温度场的数值模拟班级:建环11姓名:谢庄璞学号:2110701017物理问题:一个长方形截面的冷空气通道的尺寸如图1所示。
假设在垂直于纸面的方向上冷空气及通道墙壁的温度变化很小,可以忽略。
试用数值方法计算下列两种情况下通道壁面中的温度分布及每米长度上通过壁面的冷量损失:(1).内、外壁分别维持在0摄氏度及30摄氏度;(2).内、外壁与流体发生对流传热,且已知:(由于本人实验做的是对流边界条件,专门编写了第三类的程序,第一类边界条件参考的是别人的程序,节点设计有所不同)T1=30,h1=10(实验值是10.34)T2=10,h2=4(实验值是3.93)(图1)(图2)分析问题:因为截面材料均匀,且边界条件对称,故截面上的温度分布也对称,可去1/4的截面如图2,本题采用数值法求解,将截面上的点进行划分,如图3所示,网格的交点为所选取的节点。
图30.53程序内容:(1)PROGRAM MAINIMPLICIT NONEINTEGER::I,J,KREAL::V=0.53,TF1=10,TF2=30REAL::M1=0,M2=0,N1=0,N2=0,Q1=0,Q2=0REAL::T(16,12)=0 !初设节点温度均为0摄氏度!设置内壁温度为10摄氏度DO I=6,16T(I,6)=TF1END DODO J=6,12T(6,J)=TF1END DO!设置外壁温度为30摄氏度T(I,1)=TF2END DODO J=1,12T(1,J)=TF2END DO!设置其他节点DO K=1,1000!设置内部节点DO I=2,5DO J=2,11T(I,J)=(T(I-1,J)+T(I+1,J)+T(I,J-1)+T(I,J+1))/4 END DOEND DODO I=6,15DO J=2,5T(I,J)=(T(I-1,J)+T(I+1,J)+T(I,J-1)+T(I,J+1))/4 END DOEND DO!设置对称线上的节点DO J=2,5T(16,J)=(2*T(15,J)+T(16,J-1)+T(16,J+1))/4END DODO I=2,5T(I,12)=(2*T(I,11)+T(I-1,12)+T(I+1,12))/4END DOEND DODO I=1,16DO J=1,12WRITE(*,*)I,J,T(I,J)OPEN(1,FILE='T01.txt')WRITE(1,*)T(I,J)END DOEND DODO J=6,11M1=M1+V*(T(5,J)-T(6,J))END DOM2=M2+V*(T(I,5)-T(I,6))END DOQ1=0.5*V*(T(5,12)-T(6,12))+0.5*V*(T(16,5)-T(16,6))+M1+M2 !内壁面能放出的热量DO J=2,11N1=N1+V*(T(1,J)-T(2,J))END DODO I=2,15N2=N2+V*(T(I,1)-T(I,2))END DOQ2=0.5*V*(T(1,12)-T(2,12))+0.5*V*(T(16,1)-T(16,2))+N1+N2 !外壁面能吸收的热量WRITE(*,*)"Q1=",Q1,"Q2=",Q2,"冷量损失为:",(Q1+Q2)/2END PROGRAM MAIN(2)program mainimplicit nonereal h1,h2,lenda,tf1,tf2real t(16,12)integer i,j,xh1=10.34h2=3.93lenda=0.53tf1=30tf2=10h1=h1/10 !注:由于下面未算节点长度,在次进行修正h2=h2/10open(01,file='CH.dat')!zhengti fu chuzhido j=1,12,1do i=1,16,1t(i,j)=10end doend dodo x=1,1000000do j=2,11,1!dui yu di 1 lie j cong 2 dao 11------------------------------------------------------1t(1,j)=1./(h1+2*lenda)*(h1*tf1+lenda/2*t(1,j+1)+lenda/2*t(1,j-1)+lenda*t(2,j)) end do!dui yu wai jiao dian t(1,12)---------------------------------------------------------2t(1,12)=1./(h1+lenda)*(h1*tf1+lenda/2*(t(2,12)+t(1,11)))do i=2,15,1!dui yu di 12 hang i cong 2 dao 15----------------------------------------------------3t(i,12)=1./(h1+2*lenda)*(lenda/2*(t(i-1,12)+t(i+1,12))+lenda*t(i,11)+h1*tf1) end dodo i=7,15,1!dui yu di 7 hang i cong 7 dao 15-----------------------------------------------------4t(i,7)=1./(h2+2*lenda)*(lenda*t(i,8)+lenda/2*(t(i-1,7)+t(i+1,7))+h2*tf2)end dodo j=2,6,1!dui yu di 6 lie j cong 2 dao 6-------------------------------------------------------5t(6,j)=1./(h2+2*lenda)*(lenda*t(5,j)+lenda/2*(t(6,j+1)+t(6,j-1))+h2*tf2)end do!dui yu nei jiao dian t(6,7)----------------------------------------------------------6t(6,7)=1./(3*lenda+h2)*(lenda*(t(6,8)+t(5,7))+lenda/2*(t(7,7)+t(6,6))+h2*tf2)do i=2,5,1!dui yu di 1 hang i cong 2 dao 5------------------------------------------------------7t(i,1)=1./4*(t(i-1,1)+t(i,2)+t(i+1,1)+t(i,2))end dodo j=8,11,1!duiyu di 16 lie j cong 8 dao11------------------------------------------------------8t(16,j)=1./4*(t(15,j)+t(15,j)+t(16,j+1)+t(16,j-1))end do!dui yu jiedian t(1,1)----------------------------------------------------------------9t(1,1)=1./(2*lenda+h1)*(lenda*(t(2,1)+t(1,2))+h1*tf1)!duiyu jiedian t(6,1)-----------------------------------------------------------------10t(6,1)=1./(2*lenda+h2)*(lenda*(t(6,2)+t(5,1))+h2*tf2)!duiyu jiedian t(16,7)----------------------------------------------------------------11t(16,7)=1./(2*lenda+h2)*(lenda*(t(16,8)+t(15,7))+h2*tf2)!dui yu jiedian t(16,12)--------------------------------------------------------------12t(16,12)=1./(2*lenda+h1)*(lenda*(t(16,11)+t(15,12))+h1*tf1)do j=2,7,1do i=2,5,1!dui yu niebujiedian------------------------------------------------------------------1 3t(i,j)=1./4*(t(i-1,j)+t(i+1,j)+t(i,j+1)+t(i,j-1))end doend dodo j=8,11,1do i=2,15,1!dui yu niebujiedian------------------------------------------------------------------1 4t(i,j)=1./4*(t(i-1,j)+t(i+1,j)+t(i,j+1)+t(i,j-1))end doend doend doprint*,tdo j=1,12do i=1,16write(01,*) i,j,t(i,j)1 !用于导出数据方便作图end doend doclose(01)do i=2,11q1=q1+10.34*0.1*(30-t(1,i)) end doq1=q1+10.34*0.05*(30-t(1,1)) do i=2,15q1=q1+10.34*0.1*(30-t(i,12)) end doq1=q1+10.34*0.05*(30-t(16,12)) q1=q1+10.34*0.1*(30-t(1,12)) print*,q1do i=2,6q2=q2+3.93*0.1*(t(6,i)-10)end dodo i=7,15q2=q2+3.93*0.1*(t(i,7)-10)end doq2=q2+3.93*0.1*(t(6,7)-10)q2=q2+3.93*0.05*(t(6,1)-10)q2=q2+3.93*0.05*(t(16,7)-10) print*,q2q=(q1+q2)/2print*,qEndprogram由于有4个部分,所以总热量是q=28.24457*4=112.97828 w编程思路:对整个区域进行节点离散化,写出各个节点与周围节点的关系式,然后进行迭代,直到前后两次算出来的结果相差符合误差要求为止(本实验中循环次数足够多后数值基本不变,故没有设计判断的部分)。
二维热传导方程数值解及matlab实现

在热传导学科中,二维热传导方程是一个非常重要的数学模型,用于描述二维热传导过程中温度分布随时间的变化规律。
通过对二维热传导方程的数值解及其在Matlab中的实现,可以更好地理解热传导过程及其在工程学、物理学和地球科学等领域的应用。
让我们来了解一下二维热传导方程的基本形式。
二维热传导方程通常可以表示为:$$\frac{\partial u}{\partial t} = \alpha \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) $$在这里,$u(x, y, t)$代表温度随空间坐标$(x, y)$和时间$t$的变化,$\alpha$代表热扩散系数。
方程右侧的两项分别表示温度在$x$方向和$y$方向的二阶导数。
通过数值方法对这个方程进行离散化处理,可以得到其数值解。
在进行数值解的求解过程中,一个常用的方法是有限差分法。
有限差分法将空间和时间进行离散化,将连续的问题转化为离散的问题。
通过将偏导数用差分的形式进行逼近,可以得到关于温度在不同空间点和时间点的离散方程,进而通过迭代求解得到数值解。
这里要注意,为了保证数值解的准确性和稳定性,需要对离散化步长进行合理的选择,并对边界条件和初始条件进行适当的处理。
那么,在Matlab中,我们如何实现二维热传导方程的数值解呢?我们可以通过定义空间网格和时间步长来进行离散化处理,然后利用循环结构和矩阵运算来进行迭代求解。
Matlab提供了丰富的矩阵运算和可视化工具,可以方便地实现对二维热传导方程数值解的求解和结果的可视化呈现。
我个人认为,二维热传导方程的数值解及其在Matlab中的实现,不仅仅是一个数学问题,更是一个工程问题。
通过对二维热传导方程的数值解,可以更好地理解热传导过程的规律,为工程实践中的热传导问题提供重要的参考依据。
通过Matlab的实现,可以更好地将数学模型与工程实践相结合,实现对热传导问题的仿真分析和优化设计。
材料数值模拟——温度场模拟

材料数值模拟——温度场模拟材料数值模拟是利用计算机技术对材料的性质进行模拟和预测的方法之一、在材料科学领域,温度场模拟是一种非常重要的数值模拟方法,可以通过对材料的热传导过程进行数值计算,来预测材料的温度分布和温度变化情况。
本文将对温度场模拟进行详细介绍。
首先,温度场模拟是基于热传导方程进行计算的。
热传导方程描述了热量在材料中的传递过程,其一般形式可以写作:∂T/∂t=∇(k∇T)+Q,其中T表示温度,t表示时间,∇表示温度梯度,k表示热导率,Q表示体积热源项。
这个方程可以用来计算材料内部不同位置的温度分布,以及随着时间推移的温度变化。
在进行温度场模拟之前,首先需要确定模型的边界条件。
边界条件包括材料的初始温度分布和外部环境对材料的热辐射和对流散热等影响。
通过对边界条件的设定,可以更准确地模拟实际情况下的温度场。
其次,进行温度场模拟时,需要确定材料的热物理参数。
热物理参数包括热导率、比热容和密度等物性参数。
这些参数是计算热传导方程中的关键参数,对于模拟结果的准确性和可靠性有着重要的影响。
进行温度场模拟的关键步骤是将热传导方程离散化,并通过数值解法求解离散化后的方程。
提供了一种常用的数值求解方法,有限差分法。
有限差分法将连续的热传导方程离散化为差分方程,然后通过迭代计算得到温度场的数值解。
有限差分法不仅适用于简单的几何形状和边界条件,还可以通过适当的扩展和修正来处理复杂的几何形状和边界条件。
此外,为了提高温度场模拟的精度和效率,还可以采用一些优化方法和近似技术。
例如,可以使用自适应网格技术来调整网格的密度,使得在温度变化明显的区域网格更加细化,在温度变化缓慢的区域网格更加稀疏。
还可以使用多重网格方法和并行计算技术来加速计算过程,提高模拟效率。
最后,进行温度场模拟后,可以通过可视化技术将模拟结果以图像或动画的形式展示出来。
这样可以直观地观察温度分布和变化情况,揭示材料内部的热传导过程,并对实际系统的性能进行预测和优化。
温度场数值模拟与分析

温度场数值模拟与分析一、引言温度场是工业制造、自然环境等领域中经常涉及到的现象,通过数值模拟和分析可以深入了解温度场的变化规律,并为后续的研究工作提供有效的参考。
本文将介绍温度场的数值模拟方法和分析技术,并结合实际案例进行分析和讨论。
二、数值模拟方法1.有限元方法有限元方法是数值模拟的一种常用方法,其核心思想是将复杂的物理问题抽象为有限个单元,通过单元之间的相对运动以及单元内部的运动来计算物理量的变化。
在温度场的数值模拟中,有限元方法可以通过建立合适的有限元模型、选择适当的数值方法和求解器来计算温度场的分布和变化规律。
2.计算流体力学方法计算流体力学方法是将物理问题建模为一系列守恒方程和运动方程的数学问题,通过求解这些方程来计算物理量的分布和变化。
在温度场的数值模拟中,计算流体力学方法可以通过建立流体系统的数值模型、指定流体系统的初始和边界条件以及选择适当的求解算法来计算温度场。
3.反向传播神经网络方法反向传播神经网络方法是在深度学习技术的支持下,将物理问题转化为神经网络的训练问题,通过优化网络的结构和参数,实现对物理问题的数值模拟。
在温度场的数值模拟中,反向传播神经网络方法可以通过建立网络模型、选择适当的损失函数和优化算法,来计算温度场的分布和变化规律。
三、分析技术1.可视化分析可视化分析是通过图表、图像和动画等可视化方式来展示温度场的分布和变化规律,通过可视化分析可以直观地了解温度场的变化情况,并且可以更好地理解温度场的复杂性。
2.数据挖掘分析数据挖掘分析是通过分析温度场数据中的模式和关联规则,来发现与温度场相关的重要信息和规律。
通过数据挖掘分析可以发现温度场的非线性规律、异常状态和趋势等信息,为后续的研究工作提供有效的参考。
3.时间序列分析时间序列分析是通过分析温度场数据的时间波动和趋势变化,来了解温度场的周期性和逐渐变化趋势。
通过时间序列分析可以发现温度场中的周期性波动规律和变化趋势,为后续的预测和控制工作提供有效的参考。
二维热传导问题

二维热传导问题通常涉及到描述材料内部温度分布随时间的变化,常用热传导方程进行建模。
热传导方程的一般形式如下:
\[ \frac{\partial T}{\partial t} = \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right) \]
其中,\( T \) 是温度场的函数,\( t \) 是时间,\( \alpha \) 是热扩散系数,\( x \) 和\( y \) 是空间坐标。
解决这个方程可以通过使用不同的数值方法,如有限差分法或有限元法,具体取决于问题的边界条件和几何形状。
以下是一个简化的二维热传导问题的示例:
问题描述:一个矩形金属板,初始时刻整个板的温度均匀为\( T_0 \),边界上温度保持不变。
随着时间的推移,研究金属板内部温度的分布。
建模:使用二维热传导方程
\[ \frac{\partial T}{\partial t} = \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right) \]
边界条件:初始条件\( T(x, y, 0) = T_0 \),边界条件\( T(0, y, t) = T(L, y, t) = T(x, 0, t) = T(x, H, t) = T_0 \)。
这个问题的数值解可以通过离散化空间和时间,并应用适当的数值方法来获得。
例如,使用有限差分法将偏微分方程转化为差分方程,并迭代求解。
试验一二维导热物体温度场的电模拟试验

实验一: 二维导热物体温度场的电模拟试验一.实验的目的1.学习电、热类比的原理。
2.通过对电模型的电量测量,求出墙角导热的温度场。
二.实验原理对于稳态过程,二维固体导电及导热系统的数学描述均为拉普拉斯方程。
即:0//2222=∂∂+∂∂y e x e 和 0//2222=∂∂+∂∂y t x t (1) 由于数学描述的一致,现象之间将是类似的。
即可用电势的变化规律描述温势(温差)的变化规律。
电势的测量较温差测量要方便得多。
固体稳定温度场的电模拟法可分为连续式和网络式两类。
连续式使用导电纸作电模型;网络式则用电阻元件构成的电阻网络作模型。
本实验采用网络式。
显然,对网络而言,模拟是建立在差分方程类似的基础上。
当导热系数为常数时,对均匀网络,二维稳态导热差分方程为(图1):图1 内部节点网络单元→t i +1,j +t i-1,j +t i,j +1+t i.j-1-4t i,j =0______________________(2)相应的网络上的电势方程由电学中的可希霍夫定律可得出.为:041=∑=n In___________________(3)即 (e i-1,j -e i,j )/R 1+(e i+1,j -e i,j )/R 3+(e i,j+1-e i,j )/R 4+(e i,j-1-e i,j )/R 2=0________(4) 只要满足 R 1=R 2=R 3=R 4,则e i+1,j +e i-1,j +e i,j+1+e i,j-1-e i,j =0______________________(5)式(2)和(5)完全类似,适用于一切二维稳态无内热源导热与导电问题的网络内部节点。
但是用电阻网络来模拟某一具体的热系统时,还必须使电—热系统之间有类似的边界条件,既当满足了电—热系统之间的边界条件类似后。
在电网络节点上测得的电势分布才能真正模拟热系统中的温度分布。
下面分别讨论二维的等温、绝热和对流边界条件的边界电模拟条件:1.等温边界时最简单的情况。
西安交通大学传热学上机报告材料-墙角导热数值分析报告

实用文档传热大作业二维导热物体温度场的数值模拟:璇班级:能动A02学号:10031096一.物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图所示,假设在垂直于纸面方向上用冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:外壁分别均与地维持在0℃及30℃;第二种情况:外壁均为第三类边界条件,且已知:t ∞1=30℃,ℎ1=10wm2∙℃t ∞2=10℃,ℎ2=4wm2∙℃砖墙的导热系数λ=0.53 Wm∙℃二.数学描写由对称的界面必是绝热面,可取左上方的四分之一墙角为研究对象,该问题为二维、稳态、无热源的导热问题,其控制方程和边界条件如下:ðt2ðx2+ðt2ðy2=0边界条件(情况一) t(x,0)=30 0≤x≤1.5t(0,y)=30 0≤y≤1.1t(0.5,y)=0 0.5≤y≤1.1t(x,0.5)=0 0.5≤x≤1.5ðt(1.5,y)=0 0≤y≤0.5ðy∂t(x,1.1)=0 0≤x≤0.5ℎ(t−t f1) x=0,0≤y≤1.11=ℎ(t−t f2) x=0.5,0.5≤y≤1.12ℎ(t−t f1) y=0,0≤x≤1.51ℎ(t−t f2) y=0,0.5≤x≤21.50 0≤y≤0.5=0 0≤x≤0.5∂x三.网格划分网格划分与传热学实验指导书中“二维导热物体温度场的电模拟实验”一致,如下图所示:四.方程离散对于节点,离散方程t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1])对于边界节点,则应对一、二两种情况分开讨论:情况一:绝热平直边界点:t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1])1≤j≤4t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]) 1≤i≤4外等温边界点:t[i][j]=30等温边界点:t[i][j]=0情况二:(Bi1,Bi2为网格Bi数,Bi1=ℎ1∆xλ Bi2=ℎ2∆xλ)绝热平直边界点:t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1])1≤j≤4t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]) 1≤i≤4外侧对流平直边界:t[i][0]=(2*t[i][1]+t[i+1][0]+t[i-1][0]+2*Bi1*tf1)/(2*Bi1+4) 1≤i≤14t[0][j]=(2*t[1][j]+t[0][j+1]+t[0][j-1]+2*Bi1*tf1)/(2*Bi1+4) 1≤j≤10侧对流平直边界:t[i][5]=(2*t[i][4]+t[i+1][5]+t[i-1][5]+2*Bi2*tf2)/(2*Bi2+4) 6≤i≤14t[5][j]=(2*t[4][j]+t[5][j+1]+t[5][j-1]+2*Bi2*tf2)/(2*Bi2+4) 6≤j≤10特殊点:a点t[15][0]=(t[14][0]+t[15][1]+tf1*Bi1)/(Bi1+2)b点t[15][5]=(t[14][5]+t[15][4]+tf2*Bi2)/(Bi2+2)c点t[5][5]=(2*t[4][5]+2*t[5][4]+t[5][6]+t[6][5]+3*Bi2*tf2)/(2*Bi2+6) d点t[5][11]=(t[5][10]+t[4][11]+tf2*Bi2)/(Bi2+2)e点t[0][11]=(t[0][10]+t[1][11]+tf1*Bi1)/(Bi1+2)f点t[0][0]=(t[0][1]+t[1][0]+tf1*Bi1*2)/(2*Bi1+2)五.编程思路及流程图编程思路为设定两个二维数组t[i][j]、ta[i][j]分别表示本次迭代和上次迭代各节点的温度值,iter表示迭代进行的次数,daore_in、daore_out分别表示外边界的散热量。
材料研究的温度场模拟资料

温度场变化
枝晶生长过程中不同时刻固相形貌
(a)
(b)
(c)
(d)
(e)
(f)
钢卷冷却过程的温度场模拟
热轧钢卷示意图
钢卷的热损失主要 是由钢卷表面的热 辐射与钢卷周围空 气的对流造成的, 而孔内的辐射得到 自持,计算时可以 忽略。
卷取温度控制数学模型
层流冷却设备: 12组主冷、3组精冷 和侧喷组成。
定解问题的方程组。
Ti1, j
2Ti, j Ti1, j (x)2
Ti,
j
1
2Ti, j (y)2
Ti,
j 1
0
Ti1, j
Ti,
j
x
k (Ti, j
Tf )
如果选择步长x=y。则
Ti,
j
1 y
Ti
,
j
qw
Ti, j Ti1, j 0
差分方程变为:
Ti, j
1 4
(Ti
1,
j
T x
k (T
Tf
)
L2
2)热流边界条件
Tf,k
y
0, 0
x
L1,
T y
qw
0
3)绝热边界条件
T x L1, 0 y L2 , x 0 4)给定温度边界条件
y L2 , 0 x L1,T Tw
Tw
绝热
x L1 qw
设x, y为步长,Ti, j表示结点(i, j)处的温度,以差商代替微商, 并舍去截断误差,则差分方程式与边界的差分形式一起组成
第三章
材料科学研究中 温度场的数值模拟
材料科学与工程技术与加热、冷却等传 热过程密切相关。各种材料的加工、成 型过程都会遇到与温度场有关的问题。
数值计算方法解决二维热传导方程问题研究

数值计算方法解决二维热传导方程问题研究概述:热传导方程是描述物体中温度分布随时间演化的常见方程之一。
解决热传导方程的问题在工程、科学及实际应用中具有重要的意义。
然而,解析解往往难以得到,因此我们需要借助数值计算方法来求解这类问题。
本文将研究使用数值计算方法解决二维热传导方程问题,并介绍常用的数值方法及其应用。
引言:热传导方程是描述物体中温度分布的偏微分方程,通常形式为:∂u/∂t =α(∂^2u/∂x^2 + ∂^2u/∂y^2),其中u(x, y, t)表示温度分布,α为热扩散系数。
本文将研究如何使用数值计算方法求解该方程的初始值问题。
数值方法介绍:1. 空间离散化在二维情况下,我们将区域划分为网格点,并对温度进行离散化。
常用的方法有有限差分法和有限元法。
有限差分法将二维空间离散化为矩形网格,根据差分近似导数并代入热传导方程,得到离散的方程组。
有限元法则通过将区域分解为多个小区域,利用试探函数对温度进行表示,在每个小区域内代入试探函数并求解线性方程组来得到温度分布。
2. 时间离散化对时间进行离散化也是求解二维热传导方程的重要步骤。
常用的方法有显式方法和隐式方法。
显式方法使用差分公式来逐步推进时间,从而求解温度在每个时间步长上的值。
隐式方法则利用迭代算法来求解线性方程组,通过反复迭代使得解逼近真实解。
数值方法应用与优缺点分析:1. 有限差分法有限差分法是最常用的数值方法之一,简单易于实现。
它将二维空间划分为网格点,并利用中心差分公式来近似偏导数。
在时间方向上,显式差分方法使用向前差分公式,而隐式差分方法则使用向后差分公式。
有限差分法的优点是计算效率高,在稳定性和精度上具有较好的表现,但对于非线性问题的处理稍显困难。
2. 有限元法有限元法是一种更为复杂的数值计算方法,对于复杂的边界条件和几何形状具有较好的适应性。
它将区域分解为小区域,并在每个小区域内引入试探函数。
通过求解线性方程组,可以得到温度的离散解。
实验一二维墙角导热水电模拟

实验一 二维墙角导热水电模拟一 实验目的1 巩固所学传热学和相似原理方面的知识,熟悉电模拟实验方法,测定出二维墙角导热温度场;2 参考二维墙角导热数值模拟的结果,对比实测与数值模拟之间方法和结果的差别。
二 实验原理大自然中有许多相类似的现象。
所谓类似,就是指事物客观发展过程不同,而描述它们的数学模型形式相同的现象。
固体内无内热源的稳定导热现象和导电体内无感应的稳定导电现象就是属于两种性质、但微分方程形式相同的类似现象。
它们都可以用拉普拉斯方程来描述,即02=ϕ∇ (1)式中,ϕ可以代表电势,又可以代表温度。
因此,人们可以通过研究电学现象去确定导热现象的规律性。
这并不是利用现象本身的相似性,而是用类比的方法,用其它物理现象来重演所要研究的现象。
也可以说,是利用那些具有相同的数学微分方程式所表达的物理现象来互相模拟。
而测量电压、电流和电阻等参数比起测量热量和温度来说,既简便又精确。
这种研究方法称为电模拟,它具有很大的实用价值。
由于它们的数学方程属于同一类型,故两个现象的对应量之间存在一个类比关系。
由导热现象中的付立叶定律写出T R t x t q ∆∆∆==λ (2) 由导电现象中的欧姆定律写出AR uI ∆=(3) 式中 q — 导热量, WΔt —温度差, Cλ — 物体的导热系数, )/(C m W ⋅x ∆— 导热物体的厚度,mT R — 导热体内的热阻, ℃/ WI — 导电量, A Δu — 电位差, VA R — 导电体内的电阻, Ω于是,可以建立用电流来模拟热流、用电势差来模拟温度差、用电阻来模拟热阻的类比关系。
根据相似原理,只要建立二者的几何条件相似和边界条件相似,则方程式的解就具有同一形式。
对于工程上简单的二维或三维导热温度场,如二维墙角的导热温度场,完全可以通过水电模拟方法来确定它的分布规律。
所谓几何条件相似,就是使导热体模型的各方向几何尺寸和导电体模型的各方向几何尺寸比值为同一相似倍数。
传热学上机作业-墙角温度场分布的数值模拟
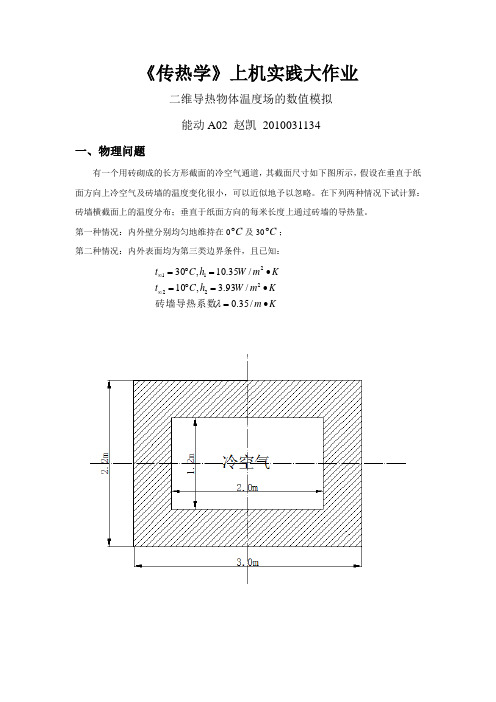
《传热学》上机实践大作业二维导热物体温度场的数值模拟 能动A02 赵凯 2010031134一、物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图所示,假设在垂直于纸面方向上冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:砖墙横截面上的温度分布;垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:内外壁分别均匀地维持在0C ︒及30C ︒; 第二种情况:内外表面均为第三类边界条件,且已知:Km K m W h C t Km W h C t •=•=︒=•=︒=∞∞/35.0/93.3,10/35.10,30222211λ砖墙导热系数二、数学描写1、控制方程该问题为无内热源的二维稳态导热问题,因此控制方程为导热微分方程:02222=∂∂+∂∂y t x t 2、边界条件该问题中,导热物体在x 方向上,y 方向上都是对称的,因此可以只取其中的四分之一部分作为研究对象,其他部分情况完全相同,如下图所示:对于上图所示各边界:边界1:由对称性可知:其为绝热边界,即0=w q 。
边界2:第一种情况:其为等温边界,满足第一类边界条件。
即: C t w ︒=0第二种情况:其为对流边界,满足第三类边界条件。
即:)()(2f w w w t t h ntq -=∂∂-=λ 边界3:第一种情况:其为等温边界,满足第一类边界条件。
即: C t w ︒=30 第二种情况:其为对流边界,满足第三类边界条件。
即:)()(1f w w w t t h ntq -=∂∂-=λ三、方程离散如下图所示,用一系列与坐标轴平行的间隔10cm 的网格线将求解区域划分成子区域。
可将上图所示各节点分成内节点与边界点两类。
分别利用热平衡法列各个节点的代数方程。
第一种情况(等温边界): 边界点:边界1(绝热边界):5~2),2(411,11,12,1,=++=+-m t t t t m m m m 11~8),2(411,161,16,15,16=++=+-n t t t t n n n n 边界2(内等温边界): 7,16~7;7~1,6,0,=====n m n m t n m边界3(外等温边界): 12,16~2;12~1,1,30,=====n m n m t n m内节点:11~8,15~6;11~2,5~2);(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m第二种情况(对流边界): 边界点:边界1(绝热边界):5~2),2(411,11,12,1,=++=+-m t t t t m m m m11~8),2(411,161,16,15,16=++=+-n t t t t n n n n边界2(内对流边界):6~1,)2(222111,61,6,5,6=++++=∆∆-+n Bi t Bi t t t t n n n n16~7,)2(2221117,17,18,7,=++++=∆∆-+m Bi t Bi t t t t m m m m边界3(外对流边界):11~1,)2(2222221,11,1,2,1=++++=∆∆-+n Bi t Bi t t t t n n n n16~2,)2(22222212,112,111,12,=++++=∆∆-+m Bi t Bi t t t t m m m m内角点: )3(22)(21116,67,78,67,57,6+++++=∆∆Bi t Bi t t t t t外角点: )1(222211,112,212,1+++=∆∆Bi t Bi t t t内节点:11~8,15~6;11~2,5~2);(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m(10,22121==∆=∞∆t t xh Bi λ;30,21212==∆=∞∆t t xh Bi λ)四、编程求解第一种情况(等温边界):Fortran程序代码如下所示:Program denwengimplicit noneinteger::t1=0integer::t2=30integer m,nreal::t(16,12),ta(16,12),et(16,12)real::epslona=1realfainei,fainei1,fainei2,fainei3,fainei4,fainei5,fai nei6,fainei7realfaiwai,faiwai1,faiwai2,faiwai3,faiwai4,faiwai5 ,faiwai6,faiwai7real pianchado n=1,7t(6,n)=t1end dodo m=7,16t(m,7)=t1end dodo n=1,12t(1,n)=t2end dodo m=2,16t(m,12)=t2end dodo m=2,5do n=1,11t(m,n)=10end doend dodo m=6,16do n=8,11t(m,n)=10end doend doopen(01,file='dengwen.dat')do while(epslona>0.00000001)do m=2,5ta(m,1)=0.25*(2*t(m,2)+t(m-1,1)+t(m+1,1)) end dodo m=2,5do n=2,11ta(m,n)=0.25*(t(m+1,n)+t(m-1,n)+t(m,n+1)+t( m,n-1))end doend dodo m=6,15do n=8,11ta(m,n)=0.25*(t(m+1,n)+t(m-1,n)+t(m,n+1)+t( m,n-1))end doend dodo n=8,11ta(16,n)=0.25*(2*t(15,n)+t(16,n-1)+t(16,n+1)) end dodo n=1,7ta(6,n)=t1end dodo m=7,16ta(m,7)=t1end dodo n=1,12ta(1,n)=t2end dodo m=2,16ta(m,12)=t2end dodo m=1,16do n=1,12et(m,n)=abs(ta(m,n)-t(m,n))end doend doepslona=maxval(et(1:16,1:12))do m=1,16do n=1,12t(m,n)=ta(m,n)end doend doend dofainei1=0.5*lanbuda*t(5,1)fainei3=lanbuda*t(5,8)fainei5=0.5*lanbuda*t(16,8)fainei2=0do n=2,7fainei6=lanbuda*t(5,n)fainei2=fainei2+fainei6end dofainei4=0do m=6,15fainei7=lanbuda*t(m,8)fainei4=fainei4+fainei7end dofainei=4*(fainei1+fainei2+fainei3+fainei4+fai nei5)faiwai1=0.5*lanbuda*(30-t(2,1))faiwai3=lanbuda*(30-t(2,11))faiwai5=0.5*lanbuda*(30-t(16,11))faiwai2=0do n=2,10faiwai6=lanbuda*(30-t(2,n))faiwai2=faiwai2+faiwai6end dofaiwai4=0do m=3,15faiwai7=lanbuda*(30-t(m,11))faiwai4=faiwai4+faiwai7end dofaiwai=4*(faiwai1+faiwai2+faiwai3+faiwai4+ faiwai5)print*,' m n t 'do m=1,16do n=1,12print*, m,n,t(m,n)write(01,*) m,n, t(m,n)end doend dopiancha=abs(fainei-faiwai)/((fainei+faiwai)/2) print*,'内部热流量=',faineiprint*,'外部热流量=',faiwaiprint*,'热平衡偏差=',pianchaend program denweng运行结果如图所示:第二种情况(对流边界): Fortran程序代码如下所示:program duiliuimplicit noneinteger::t1=10integer::t2=30integer m,nreal::t(16,12),ta(16,12),et(16,12)real::epslona=1real bi1,bi2realfainei,fainei1,fainei2,fainei3,fainei4,fainei5,fai nei6,fainei7realfaiwai,faiwai1,faiwai2,faiwai3,faiwai4,faiwai5 ,faiwai6,faiwai7real pianchabi1=h1*detax/lanbudabi2=h2*detax/lanbudado m=1,16do n=1,12t(m,n)=10end doend doopen(01,file='crs.dat')do while(epslona>0.000000001)do m=2,5ta(m,1)=0.25*(2*t(m,2)+t(m-1,1)+t(m+1,1)) end dodo n=8,11ta(16,n)=0.25*(2*t(15,n)+t(16,n-1)+t(16,n+1)) end dodo n=2,6 ta(6,n)=(2*t(5,n)+t(6,n+1)+t(6,n-1)+2*bi1*t1) /(2*bi1+4)end dodo m=7,15ta(m,7)=(2*t(m,8)+t(m+1,7)+t(m-1,7)+2*bi1* t1)/(2*bi1+4)end dodo n=2,11ta(1,n)=(2*t(2,n)+t(1,n+1)+t(1,n-1)+2*bi2*t2) /(2*bi2+4)end dodo m=2,15ta(m,12)=(2*t(m,11)+t(m+1,12)+t(m-1,12)+2 *bi2*t2)/(2*bi2+4)end dodo m=2,5do n=2,11ta(m,n)=0.25*(t(m+1,n)+t(m-1,n)+t(m,n+1)+t( m,n-1))end doend dodo m=6,15do n=8,11ta(m,n)=0.25*(t(m+1,n)+t(m-1,n)+t(m,n+1)+t( m,n-1))end doend dota(6,7)=(2*t(5,7)+2*t(6,8)+t(7,7)+t(6,6)+2*bi1*t1)/(2*bi1+6)ta(1,12)=(t(2,12)+t(1,11)+2*bi2*t2)/(2*bi2+2) ta(6,1)=(t(5,1)+t(6,2)+bi1*t1)/(bi1+2)ta(16,7)=(t(16,8)+t(15,7)+bi1*t1)/(bi1+2)ta(16,12)=(t(16,11)+t(15,12)+bi2*t2)/(bi2+2) ta(1,1)=( t(2,1)+t(1,2)+bi2*t2)/(bi2+2)do m=1,16do n=1,12et(m,n)=abs(ta(m,n)-t(m,n))end doend doepslona=maxval(et(1:16,1:12))do m=1,16do n=1,12t(m,n)=ta(m,n)end doend doend dofainei1=0.05*h1*(t(6,1)-10)fainei3=0.1*h1*(t(6,7)-10)fainei5=0.05*h1*(t(16,7)-10)fainei2=0do n=2,6fainei6=0.1*h1*(t(6,n)-10)fainei2=fainei2+fainei6end dofainei4=0do m=7,15fainei7=0.05*h1*(t(m,8)-10)fainei4=fainei4+fainei7end dofainei=4*(fainei1+fainei2+fainei3+fainei4+fai nei5)faiwai1=0.05*h2*(30-t(1,1))faiwai3=0.1*h2*(30-t(1,12))faiwai5=0.05*h2*(30-t(16,12))faiwai2=0do n=2,11 faiwai6=0.1*h2*(30-t(1,n))faiwai2=faiwai2+faiwai6end dofaiwai4=0do m=2,15faiwai7=0.1*h2*(30-t(m,12))faiwai4=faiwai4+faiwai7end dofaiwai=4*(faiwai1+faiwai2+faiwai3+faiwai4+ faiwai5)do n=1,12do m=1,16print*, m,n,t(m,n)write(01,*) m,n,t(m,n)end doend dopiancha=abs(fainei-faiwai)/((fainei+faiwai)/2) print*,'内部热流量=',faineiprint*,'外部热流量=',faiwaiprint*,'热平衡偏差=',pianchaclose(01)end program duiliuWORD完整版----可编辑----教育资料分享运行结果如图所示:----完整版学习资料分享----五、结果讨论1,、温度场分布图用以上数值模拟得到的各节点温度绘制温度场分布图。
二维导热微分方程

二维导热微分方程1二维导热微分方程简介在热传导方面,二维导热微分方程是一类非常重要的微分方程。
它可以用来描述物体中温度的变化,并且被广泛应用于静态和动态热传导问题的数学建模和分析。
在本文中,我们将探讨二维导热微分方程的基本定义与性质。
2二维导热微分方程的一般形式考虑一个平板物体在时间t内的温度场u(x,y,t),其中(x,y)是平面上的点。
物体的热传导简化为二维情况,并忽略热源。
那么,二维导热微分方程可以表示为:\[\frac{\partial u}{\partial t}=\alpha(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}) \]其中α是热扩散系数。
3二维导热微分方程的解析解一般来说,二维导热微分方程的解析解很难得到。
但是,在某些特殊情况下,它们可以通过分离变量法得到。
假设u(x,y,t)的解可以表示为u(x,y,t)=X(x)Y(y)T(t),进行变量分离,得到:\frac{1}{\alpha T}\frac{d T}{d t}=\frac{1}{X}\frac{d^2 X}{d x^2}+\frac{1}{Y}\frac{d^2Y}{d y^2}\]由于等式右侧只依赖于x,y变量,它等于一个常数-k²,因此我们得到三个方程:\[\frac{d^2X}{d x^2}+k^2X=0,\frac{d^2Y}{d y^2}+k^2Y=0,\frac{d T}{d t}+\alpha k^2T=0\]这三个方程的解分别是:\[X(x)=A\sin kx+B\cos kx,Y(y)=C\sin ky+D\cos ky,T(t)=Ee^{-\alpha k^2t}\]其中A,B,C,D,E是任意常数,因此,u(x,y,t)的一般解为:u(x,y,t)=\sum_{n=1}^{\infty}\sum_{m=1}^{\infty}(a_{m,n}\sin{k_mx}\sin{k_n y}e^{-\alpha(k_m^2+k_n^2)t})\]4二维导热微分方程的数值解法由于二维导热微分方程的解析解很难得到,数值解法成为了解决实际问题的主要手段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传热大作业二维导热物体温度场的数值模拟(等温边界条件)姓名:班级:学号:墙角稳态导热数值模拟(等温条件)一、物理问题有一个用砖砌成的长方形截面的冷空气空道,其截面尺寸如下图所示,假设在垂直于纸面方向上冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
外矩形长为3.0m ,宽为2.2m ;内矩形长为2.0m ,宽为1.2m 。
第一种情况:内外壁分别均匀地维持在0℃及30℃;第二种情况:内外表面均为第三类边界条件,且已知:外壁:30℃ ,h1=10W/m2·℃,内壁:10℃ ,h2= 4 W/m2·℃砖墙的导热系数λ=0.53 W/m ·℃由于对称性,仅研究1/4部分即可。
二、数学描写对于二维稳态导热问题,描写物体温度分布的微分方程为拉普拉斯方程 02222=∂∂+∂∂y t x t这是描写实验情景的控制方程。
三、方程离散用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为确定温度值的空间位置,即节点。
每一个节点都可以看成是以它为中心的一个小区域的代表。
由于对称性,仅研究1/4部分即可。
依照实验时得点划分网格:建立节点物理量的代数方程对于内部节点,由∆x=∆y ,有 )(411,1,,1,1,-+-++++=n m n m n m n m n m t t t t t由于本实验为恒壁温,不涉及对流,故内角点,边界点代数方程与该式相同。
设立迭代初场,求解代数方程组。
图中,除边界上各节点温度为已知且不变外,其余各节点均需建立类似3中的离散方程,构成一个封闭的代数方程组。
以C t 000=为场的初始温度,代入方程组迭代,直至相邻两次内外传热值之差小于0.01,认为已达到迭代收敛。
四、编程及结果1) 源程序#include <stdio.h>#include <math.h>int main(){int k=0,n=0;double t[16][12]={0},s[16][12]={0}; double epsilon=0.001;double lambda=0.53,error=0; double daore_in=0,daore_out=0,daore=0; FILE *fp;fp=fopen("data3","w");for(int i=0;i<=15;i++)for(int j=0;j<=11;j++){if((i==0) || (j==0)) s[i][j]=30;if(i==5)if(j>=5 && j<=11) s[i][j]=0;if(j==5)if(i>=5 && i<=15) s[i][j]=0;}for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)t[i][j]=s[i][j];n=1;while(n>0){n=0;for(int j=1;j<=4;j++)t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1]);for(int i=1;i<=4;i++)t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]);for(int i=1;i<=14;i++)for(int j=1;j<=4;j++)t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=1;i<=4;i++)for(int j=5;j<=10;j++)t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)if(fabs(t[i][j]-s[i][j])>epsilon)n++;for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)s[i][j]=t[i][j];k++;//printf("%d\n",k);}for(int j=0;j<=5;j++){ for(int i=0;i<=15;i++){ printf("%4.1f ",t[i][j]);fprintf(fp,"%4.1f ",t[i][j]);}printf("\n");fprintf(fp,"\n");}for(int j=6;j<=11;j++){ for(int i=0;i<=5;i++){ printf("%4.1f ",t[i][j]);fprintf(fp,"%4.1f ",t[i][j]);}fprintf(fp,"\n");printf("\n");}for(int i=1;i<=14;i++)daore_out+=(30-t[i][1]);for(int j=1;j<=10;j++)daore_out+=(30-t[1][j]);daore_out=4*(lambda*(daore_out+0.5*(30-t[1][11])+0.5*(30-t[15][1])));for(int i=5;i<=14;i++)daore_in+=t[i][4];for(int j=5;j<=10;j++)daore_in+=t[4][j];daore_in=4*(lambda*(daore_in+0.5*t[4][11]+0.5*t[15][4]));error=abs(daore_out-daore_in)/(0.5*(daore_in+daore_out));daore=(daore_in+daore_out)*0.5;printf("k=%d\n内墙导热=%f\n外墙导热=%f\n平均值=%f\n偏差=%f\n",k,daore_in,daore_out,daore,error);}2)结果截图七.总结与讨论1.由实验结果可知:等温边界下,数值解法计算结果与“二维导热物体温度场的电模拟实验“结果相似,虽然存在一定的偏差,但由于点模拟实验存在误差,而且数值解法也不可能得出温度真实值,同样存在偏差,但这并不是说数值解法没有可行性,相反,由于计算结果与电模拟实验结果极为相似,恰恰说明数值解法分析问题的可行性。
用数值解法仅用计算机模拟就能解决某些复杂的工程问题,为复杂工程问题的求解提供了极大的便利。
2.在实验中,内外边界散热量存在偏差,这在很大程度上是由于用数值计算分析问题时,采用离散平均的思想,用节点中心的温度代替节点的平均温度从而产生误差。
不断提高所划分的网格数目,实验偏差会得到不断改善。
3.通过这次的上机实验,对传热的很多问题和数值算法都有一定的加深理解和掌握,收获很多,同时对于个人的动手动脑及解决问题的能力都有一定的提高。
同样,这也反过来证实了“二维导热物体温度场的电模拟实验”的正确性和可行性。
// mm.cpp : 定¡§义°?控?制?台¬¡§应®|用®?程¨¬序¨°的Ì?入¨?口¨²点Ì?。
¡ê//#include"stdafx.h"#include<stdio.h>#include<math.h>int main(){int k=0,n=0;double t[16][12]={0},s[16][12]={0};double epsilon=0.01;double lambda=0.53,error=0;double daore_in=0,daore_out=0,daore=0;FILE *fp;fp=fopen("data3","w");for(int i=0;i<=15;i++)for(int j=0;j<=11;j++){if((i==0) || (j==0)) s[i][j]=30;if(i==5)if(j>=5 && j<=11) s[i][j]=0;if(j==5)if(i>=5 && i<=15) s[i][j]=0;}for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)t[i][j]=s[i][j];n=1;while(n>0){n=0;for(int j=1;j<=4;j++)t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1]);for(int i=1;i<=4;i++)t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]);for(int i=1;i<=14;i++)for(int j=1;j<=4;j++)t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=1;i<=4;i++)for(int j=5;j<=10;j++)t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1]);for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)if(fabs(t[i][j]-s[i][j])>epsilon)n++;for(int i=0;i<=15;i++)for(int j=0;j<=11;j++)s[i][j]=t[i][j];k++;//printf("%d\n",k);}for(int j=0;j<=5;j++){ for(int i=0;i<=15;i++){ printf("%4.1f ",t[i][j]);fprintf(fp,"%4.1f ",t[i][j]);}printf("\n");fprintf(fp,"\n");}for(int j=6;j<=11;j++){ for(int i=0;i<=5;i++){ printf("%4.1f ",t[i][j]);fprintf(fp,"%4.1f ",t[i][j]);}fprintf(fp,"\n");printf("\n");}for(int i=1;i<=14;i++)daore_out+=(30-t[i][1]);for(int j=1;j<=10;j++)daore_out+=(30-t[1][j]);daore_out=4*(lambda*(daore_out+0.5*(30-t[1][11])+0.5*(30-t[15][1]))); for(int i=5;i<=14;i++)daore_in+=t[i][4];for(int j=5;j<=10;j++)daore_in+=t[4][j];daore_in=4*(lambda*(daore_in+0.5*t[4][11]+0.5*t[15][4]));error=abs(daore_out-daore_in)/(0.5*(daore_in+daore_out));daore=(daore_in+daore_out)*0.5;printf("k=%d\n内¨²墙?导Ì?热¨¨¨q1=%f\n外ªa墙?导Ì?热¨¨¨q2=%f\n平?均¨´值¦Ìq=%f\n偏?差?error=%f\n",k,daore_in,daore_out,daore,error);getchar();}#include<iostream>#include<fstream>#include<iomanip>using namespace std;int main(){cout <<setiosflags(ios::fixed);int i,j;double temp,q_in,q_out,q;double eps=1;double A[16][12];//设¦¨¨置?迭̨¹代䨲初?场?for(i=1;i<16;i++){for(j=1;j<6;j++)A[i][j]=0;}for(i=1;i<6;i++){for(j=6;j<12;j++)A[i][j]=0;}for(i=0;i<16;i++)A[i][0]=30;for(j=0;j<12;j++)A[0][j]=30;//建¡§立¢¡é迭̨¹代䨲方¤?程¨¬组Á¨¦并¡é求¨®解awhile(eps>1.0E-4){for(j=1;j<5;j++)A[15][j]=(A[15][j+1]+A[15][j-1]+2*A[14][j])/4;for(i=5;i<15;i++){for(j=1;j<5;j++){A[i][j]=(A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4;}}for(i=1;i<5;i++){for(j=1;j<11;j++)A[i][j]=(A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4;}for(i=1;i<5;i++){temp=A[i][11];A[i][11]=(A[i+1][11-1]+A[i][11]+2*A[i][10])/4;eps=A[i][11]-temp;}}//计?算?墙?体¬?外ªa表À¨ª面?导Ì?热¨¨¨量¢?q_out=0;for(j=1;j<12;i++)q_out=q_out+A[0][j]-A[1][j];for(i=1;i<16;j++)q_out=q_out+A[i][0]-A[i][1];q_out=q_out+(A[0][11]-A[10][1]+A[15][0]-A[15][1])/2; q_out=q_out*0.53; //计?算?墙?体¬?内¨²表À¨ª面?导Ì?热¨¨¨量¢?q_in=0;for(i=5;i<16;i++)q_in=q_in+A[i][4]-A[i][5];for(j=5;j<12;j++)q_in=q_in+A[4][j]-A[5][j];q_in=q_in+(A[15][4]-A[15][5]+A[4][11]-A[5][11])/2; q_in=q_in*0.53;//计?算?平?均¨´导Ì?热¨¨¨量¢?和¨ª相¨¤对?误¨®差?q=(q_in+q_out)/2;eps=abs(q_in-q_out);//输º?出?结¨¢果?for (j=0;j<6;j++){for(i=0;i<16;i++){cout<<setprecision(2)<<A[i][j]<<" ";}cout<<endl;}for(j=6;j<12;j++){for(i=0;i<6;i++){cout<<setprecision(2)<<A[i][j]<<" ";}cout<<endl;}cout<<"墙?体¬?内¨²表À¨ª面?导Ì?热¨¨¨量¢?="<<q_in<<"\n"; cout<<"墙?体¬?外ªa表À¨ª面?导Ì?热¨¨¨量¢?="<<q_out<<"\n"; cout<<"墙?体¬?平?均¨´导Ì?热¨¨¨量¢?q="<<q<<"\n";return 0;}。
