ewma控制图
EWMA控制图说明
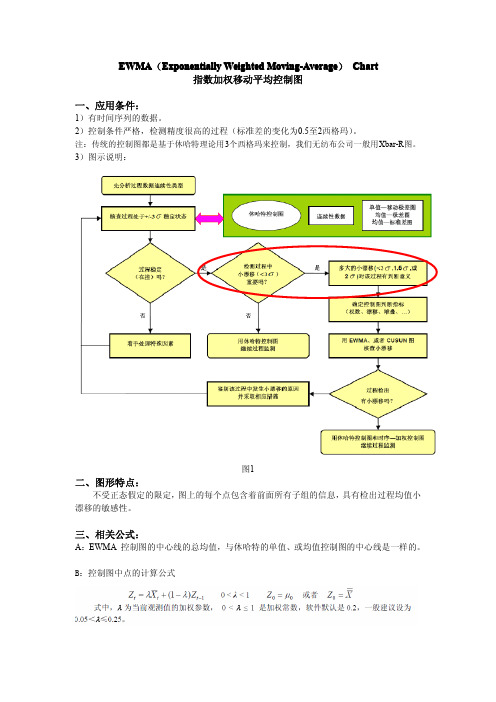
EWMA(Exponentially Weighted Moving-Average)Chart指数加权移动平均控制图一、应用条件:1)有时间序列的数据。
2)控制条件严格,检测精度很高的过程(标准差的变化为0.5至2西格玛)。
注:传统的控制图都是基于休哈特理论用3个西格玛来控制,我们无纺布公司一般用Xbar-R图。
3)图示说明:图1二、图形特点:不受正态假定的限定,图上的每个点包含着前面所有子组的信息,具有检出过程均值小漂移的敏感性。
三、相关公式:A:EWMA控制图的中心线的总均值,与休哈特的单值、或均值控制图的中心线是一样的。
B:控制图中点的计算公式注:从公式中可以看出每个点包含着前面所有子组的信息。
C:控制限的计算公式五:举例说明以某精密标准件的厚度为例,用Xbar-R图控制,没有异常,如图2图2但是用EWMA控制图来控制却有异常:图3可以从上控制线的数据来说明,Xbar-R的UCL值是3.178;而EWMA的UCL值是3.07596。
而他们的中心线都是一致的3.0385。
六:目前我司应用的控制图(以亲水产品的回渗为例):图4七、个人总结:没必要在无纺布领域应用EWMA控制图,因为休哈特理论是从电子和机加工行业延伸出来的,这种行业基本上是标准模具控制,加工条件相对稳定,才用3个西格玛进行控制。
而我们的无纺布这种流程性材料工艺本身决定随机因素影响较大,用0.5-2个西格玛来控制,基本上是不可行,可以说是作茧自缚。
克重还勉强可以控制(取样数据较多的情况下),如强力、伸长率、亲水性能就更难控制。
如果客户问及,我们可以说无纺布领域的物理性能控制用3西格玛就已经足以严格。
如果要用EWMA控制图,我们可以用minitab来做相应的分析用如图5。
图5。
失效模式及后果分析

一、CUSUM(累积和)控制图和EWMA(指数加权滑动平均)控制图随着SPC控制理论中常规控制图的普遍使用,其缺点也逐渐显现出来,其中一条就是对过程的小偏移不灵敏。
而CUSUM和EWMA则可解决类似问题。
控制图的设计思想就是对数据的信息加以积累。
CUSUM控制图分别可用于计量性数据(正态分布),不合格品数(泊松分布变数),不和格品率(二项分布变数)。
CUSUM控制图的理论基础是序贯分析原理中的序贯概率比检验,这是一种基本的序贯检验法。
该控制图通过对信息的累积,将过程的小偏移累加起来,达到放大的效果,提高检测过程小偏移的灵敏度。
2、EWMA控制图中控制统计量同样利用了历史资料,且该控制图可以对不同阶段的数据取不同的权重,距今越近的资料权重越大,距今越远,数据权重越小。
EWMA控制图设计的本质就是寻找最优参数(λ,K)组合的过程,所依据的原则是:对给定的稳态ARL(0),使过程出现设定偏移量的偏移时具有最小失控ARL。
二、稳健设计技术产品/工艺过程的稳健设计方法和技术开发阶段的稳健技术开发方法统称为稳健设计技术。
它是开发高质量低成本产品最有效的方法。
在实际生产中噪声因素(原材料的微小变化、操作人员水平的差异、机器设备的微笑波动等)的存在,由此产生的波动也不可避免?quot;永无止境地减少波动,使产品、工艺过程、技术功能对各种噪声因素不敏感,向着波动为零的目标不断迈进。
(即位质量工程的理论支柱-波动理论)。
而如果采用源头治理的办法,利用稳健技术设计寻找可控因素的一组水平组合,使产品/工艺过程性能或技术功能的输出质量特性围绕设计目标值的波动尽可能减少。
基本功能的性能稳健取决于两点:一是输出质量特性本身的波动小;二是该质量特性应尽可能接近设计目标值。
而S/N该度量指标可以比较准确反映这两个目标。
稳健技术开发的实现过程:1、进行初始设计并确认理想功能2、识别可控因素和噪声因素3、实施一步优化,即优化系统的稳健性4、实施二步优化,确定对灵敏度影响显著的可调因素三、质量机能展开(QFD)(又名品质屋)质量功能展开是一项强有力的综合策划技术,尤其适用于大型产品(如飞机、汽车和大型设备)。
具有可变抽样区间的PoissonEWMA控制图_丛方媛

第37卷第13期2007年7月数学的实践与认识M AT HEMA TICS IN PRACTICE AND T HEORYV o l.37 No.13 July ,2007 具有可变抽样区间的Poisson EWMA 控制图丛方媛, 赵选民, 师义民, 王彩玲(西北工业大学应用数学系,陕西西安 710072)摘要: 传统的EW M A 控制图通常都是针对计量型质量特性值的,而对于计数型质量特征值少有研究.设计了单位缺陷数服从Pois son 分布的EW M A 控制图,并对Pois son EW M A 控制图进行了可变抽样区间设计,利用M arkov chain 方法计算了其平均报警时间,计算结果表明,所设计的动态Pois son EW M A 控制图较Sh ew hart c-图和固定抽样区间的Poiss in EWM A 控制图能更好的监控过程的变化.关键词: Pois son EWM A 控制图;可变抽样区间;M arkov chain ;平均报警时间1 引 言收稿日期:2007-01-22基金项目:国家自然科学基金(79970022);航空科学基金(02J 53079);陕西省自然基金(NSG5002) 由于质量特性值通常有两大类,一类是计量型的,如温度,长度,电阻等;一类是计数型的,如不合格品数,缺陷数等,因此,常规的质量控制图也分计量型控制图和计数型控制图两种[1].自从1924年Shew har t 提出了控制图的概念以来,Shew hart 的x --图,R -图等,以及EWM A(指数加权移动平均)控制图和CU SU M (累积和)控制图已经对计量型控制图有了很好的研究,而对于计数型质量特征值控制图的研究还只停留在Shew har t c-图和u-图上.且由于传统的休哈特控制图的统计变量是由当前观测值得出的,而其他观测值经过了它所在的当前时刻就被弃置不用,因此浪费了大量的历史信息和相关信息,造成了传统的休哈特控制图无法具有较高的精度且对小波动的持续上升、下降不敏感.EWM A 控制图的统计变量是观测值的一个加权线性组合,其对过程均值的微小变化比较敏感,正好弥补了Shew hart 控制图的缺陷[2—5].因此,针对计数型质量特征值,为了能更有效的发现过程均值的微小变化,本文在单位缺陷数服从Poisson 分布的假设下,提出了Poisson EW MA 控制图模型.静态控制图都是假定抽样区间,样本容量以及其控制限是固定不变的,其不利于及时有效的发现过程的变化,尤其是过程的微小变化,于是Rey no lds et al 提出了具有可变抽样区间的Shew hart 均值控制图,从此开启了动态控制图这一新的研究领域[6—7].因此,本文在前人研究的基础上对Poisson EWM A 控制图进行可变抽样区间设计,并且利用Markov chain 方法计算出其平均报警时间,计算结果表明,与Shew hatr 控制图和静态Poisson EWMA 控制图相比,可变抽样区间Poisson EWM A 控制图在过程失控时具有较短的平均报警时间,从而能够更有效的提高生产效率.2 Poisson EWMA 控制图的描述设X 表示生产过程中的单位缺陷数,通常情况下假设X 服从Poisson 分布.从该过程中获得的一列质量特征观测值X1,X2,…独立同分布于期望为L的Poisson分布,当过程处于受控状态时,L=L0.要对这个过程进行控制,定义Poisson EWM A统计量为:Z0=L0Z t=K X t+(1-K)Z t-1(1)根据Z t的定义可以直接得出E(Z t)=L0Var(Z t)=K2-K[1-(1-K)2t]L0(2)当t充分大时,可以得到Z t方差的渐近形式:Var(Z t)≈K2-KL0=Var(Z∞)(3)其中K为平滑参数,且0<K F1.这时Po isso n EWMA控制图的控制限可以基于(2)式得出,也可以基于方差的渐进形式(3)式得出,这样就产生了两种控制效果不同的控制图.为方便计算,在本文中我们将仅考虑基于渐近形式(3)式所生成控制限的控制图.因此,当Z t> h U或者Z t<h L时,过程失控.其中h L=L0-A L Var(Z∞)=L0-A LK L0 2-K,h U=L0+A U Var(Z∞)=L0+A UK L0 2-K,A U和A L可根据特定的受控时的ARL(平均运行长度,Average Run Leng th)的大小来确定,有时取A=A L=A U.但需要注意的是,由于X1,X2,…独立同分布于期望为L的Po isso n分布,则由(1)式定义的Poisson EW MA统计量Z t是一个非负数,那么当控制下限小于或等于零时,对过程均值的向下偏移就不会发出报警信号,即不能检测出过程的向下偏移,所以这时取A L≠A U是很有必要的.3 Poisson EWMA控制图的动态设计3.1 动态控制图的描述动态控制图是指下一个样本的抽样区间或样本容量依赖于现时样本点统计量的控制图.控制图的动态设计一般有可变抽样区间(Variable Sampling Interval,VSI),可变样本容量(Variable Sample Size,VSS)及可变样本容量和抽样区间(V SSI)这三种情况.其主要思想为:在控制图的中心限和控制限之间加上警戒限,将中心限与警戒限之间的区域称为中心域,警戒限与控制限之间的区域称为警戒域.如果现时样本点统计量位于中心域,则表明其后的点子超出控制限的可能性相对较小,这时可等待较长的时间再去抽取下一个样本,且下一个样本的样本容量可以较小;反之,若现时样本点统计量位于警戒域内,这表明其后的点子很有可能超出控制限,为了能尽快地发现过程的偏移,应等待较短的时间就去抽取下一个样本,且其样本容量应该较大,也就是说下一个样本的抽样区间和样本容量的大小取决于现时样本点统计量的大小.一般只取两个抽样区间长度d1和d2,d1>d2和两个样本容量n1和n2,n1<n2.当现时样本点统计量位于中心域时,选取样本容量n1和抽样区间d1;当其位于警戒域时,选用样本容量n2和抽样区间d2;若其超出警戒限,则发出报警信号,过程失控. 80数 学 的 实 践 与 认 识37卷一般情况下,用检测过程偏移的速度来评价一个控制图的有效性.当抽样区间和样本容量固定时,一般采用ARL 的大小来进行比较.即在过程处于受控状态的ARL 一定时,其失控状态的ARL 越小,表明该控制图对过程偏移检测的效果越好,越能及时地发现偏移.但是可变抽样区间控制图的抽样区间长度是变化的,故其无法采用ARL 来进行比较.这时我们将采用另外一种比较法则:平均报警时间(Aver age Time to Signal ,AT S )来比较.平均报警时间(AT S)是指从过程发生偏移到控制图发出报警信号所需要的平均时间.若过程偏移在零时刻发生,那么ATS 就是从过程开始检测到发出报警信号所需要的平均时间.本文将只考虑可变抽样区间Poisson EWM A 控制图.令<i 表示报警前采用抽样区间d i 的样本数(i =1,2),d 0表示从过程开始到第一个样本之间的抽样区间,可取d 0=d 1或d 2.则根据AT S 的定义可知:A T S =d 0+<1d 1+<2d 2计算ATS 的方法很多,本文我们采用M arko r chain 的方法计算Poisson EWM A 控制图的AT S.3.2 Poisson EWMA 控制图ATS 计算本文只考虑偏移L ′>L 0的情况.假设过程失控从零时刻开始,过程均值从L 0偏移到L 0+D L 0,为了能用M arkov chain 方法来计算失控过程的平均报警时间,如图1所示,将控制图的受控区域分成N 个长度相同的小区间,每个区间的长度为h U -h LN,第j 个子区间是(L j ,U j ),其中L j =h L +(j -1)(h U -h L )N ,U j =h L +j (h U -h L )N,第j 个子区间的中点m j =h L +(2j -1)(h U -h L )2N .这样对应于N 个M ar ko v chain 状态,从下到上分别记为E 1,E 2,…,E N ,第N +1个状态是吸收状态,表示超出h U 或小于h L 的失控区域.定义b =(b 1,b 2,…,b N )T ,若状态E i (i =1,2,…,N )的中心点位于中心域,则b i =d 1;若状态E i 的中心点位于警戒域内,则取b i =d 2.那么从状态E i (i =1,2,…,N )到状态E j (j =1,2,…,N )的转移概率记为p i ,j ,p i ,j =P (L j <Z t <U j ûZ t -1=m i )=P (L j <K X t +(1-K )Z t -1<U j ûZ t -1=m i )=P (L j <K X t +(1-K )m i <U j )=h L +(j -1)(h U -h L )N<K X t +(1-K )h L +(2i -1)(h U -h L )2N<h L +j (h U -h L )N =P h L +h U -h L2N K [(2(j -1)-(1-K)(2i -1)]<X t<h L +h U -h L2N K[(2j -(1-K )(2i -1)]令该M ar ko v chain 对于这N 个状态的转移矩阵为P =[p i ,j ]N ×N .令Q =(I -P )-1=(m ij )k ×k .其中I 为N ×N 的单位矩阵.则根据参考文献[2]推广可得到可变抽样区间的8113期丛方媛,等:具有可变抽样区间的P oisson EW M A 控制图图1 把受控区域划分成N 个相等的子区间Po isso n EWMA 控制图的平均报警时间AT S 为:A TS =∑Ni =1mk 0,i b i,(4)其中k 0表示中心限L 0处于状态E k 0.(若控制图的上控制限和下控制限关于中心限对称时,应取N 为奇数,这样可以使得中心限L 0正好处于状态E (N +1)/2的中点处,即k 0=(N +1)/2.因此根据AT S 的计算公式(4)即可求出过程质量特性对于不同偏移量D 的平均报警时间,当过程的质量特性X 的偏移量D =0时,由公式(4)求出的平均报警时间即为过程受控时平均报警时间.4 VSI Poisson EWMA 控制图与Poisson EWMA 控制图及c -图的比较要对不同控制图的控制效果进行比较,应使这些控制图处于同样的条件下进行比较,即使控制图在受控状态时具有相同的平均报警时间AT S .首先我们假设过程的单位缺陷数X 服从均值为4的Poisson 分布,即L 0= 4.则标准c -图的上控制限和下控制限可分别计算得:L CL =L 0-3L 0=4-34=-2UCL =L 0+3L 0=4+34=10此时的LCL 小于0,这时应重新设置LCL 为0.对于c -图,该过程受控时的平均报警时间AT S 为:82数 学 的 实 践 与 认 识37卷A T S =1P (x >10ûL 0=4)≈352即在受控时的AT S 约为352时,来比较这三种控制图的控制效果.具体数据见表1所示:表1 对于L 0=4时的c -图,P oisso n EW M A 和V SI P oisso n EW M A 控制图AT S 的比较,其中V SI 图上下警戒限分别为4.8和3.2,N =11D c -图Pois son EWM A 控制图(K =0.2)VS I Poiss on EW M A 控制图(K =0.2)(d 1,d 2)=(1.05,0.6)(d 1,d 2)=(1.10,0.80)0352348.70339.70358.330.5149.2588.0978.0085.851.071.9929.8126.0529.401.539.5315.2212.7214.632.023.479.657.909.172.514.96 6.95 5.66 6.593.010.155.424.425.14同样我们还可以得出这三种控制图对各种不同均值的控制效果的比较,表2为这三种控制图对L 0=10时的控制效果的比较:表2 对于L 0=10时的c -图,P oisso n EW M A 和V SI P oisso n EW M A 控制图A T S 的比较,其中V SI 图上下警戒限分别为11和9,N =11D c -图Pois son EWM A 控制图(K =0.2)VS I Poiss on EW M A 控制图(K =0.2)(d 1,d 2)=(1.3,0.65)(d 1,d 2)=(1.1,0.8)0284.74276.48275.20283.540.5171.87147.25144.87148.651.0107.4665.6661.9863.471.569.7934.2430.8731.532.046.9820.8218.1518.512.532.6814.2012.1712.393.023.4410.528.979.14从表1和表2中的数据可以看出,静态的Poisson EWM A 控制图的平均报警时间较标准的Shewhart 的c -图要小,而VSI Poisson EWMA 控制图的平均报警时间又较静态的Po isso n EWMA 控制图要小,即在这三种控制图中,VSI Poisson EW MA 控制图对过程均值的偏移最为敏感,能够最快最准确的检测出过程均值的偏移.因此,在实际的应用中,对于单位缺陷数,可以采取VSI Po isso n EWM A 控制图来提高生产的效率,降低生产成本.参考文献:[1] 周纪芗,茆诗松.质量管理统计方法[M ].北京:中国统计出版社,1999.[2] Douglas C M ontgomery.Introduction to Statis tical Quality Control[M ].Fourth Edition J oh n Wiley &Sons Inc,2001.8313期丛方媛,等:具有可变抽样区间的P oisson EW M A 控制图84数 学 的 实 践 与 认 识37卷[3] Gan F F.Joint monitoring of proces s mean an d variance u sing ex ponentially w eig hted moving average controlchart[J].T echnometrics,1995,37:446—453.[4] Connie M B,Charles W C,S teven E R.Poisson EW M A control charts[J].Journ al of Quality Techn ology,1998,30(4):352—361.[5] Gan F F.Designs of one-and tw o-sided expon ential EW M A chart[J].Journ al of Quality Tech nology,1998,30(1):55—69.[6] Antonio F B Costa.X-bar chart w ith varialb e sample s ize and samplin g intervals[J].Journ al of QualityTech nology,1997,29(2):197—204.[7] Baxley R V,Jr.An ap plication of variable sampling inter val control char ts[J].Jour nal of Q uality Technology,1995,27:275—282.[8] 王兆军.关于动态质量控制图的设计理论[J].应用概率统计,2002,18(3):316—333.[9] 赵选民,徐伟等.数理统计[M].北京:科学出版社.Poisson EWMA Control Chart withVariable Sampling Intervals ZHAO Xuan-min, SHI Yi-min, WAN G Cai-lingCONG Fang-yuan, Array (Dept.o f A pplied M athematics,N o rt hw ester n P olyt echnical U niver sity,X i′an710072,China)Abstract: T he measur ing quality character istic has been w idely studied by the t raditionalEWM A contr ol chart,but the counting quality char acter istic ha s been unusual resear ched.APo isson EWM A co nt ro l char t is pr oposed.A nd the Po isson EW M A contr ol char t w ith var iablesampling interv als is constructed also.T he M ar ko v chain method is used t o calculate theaver ag e time to signal.T he computing r esults show that the VSI P oisso n EW M A co nt ro l chartis the most efficient in detecting shift s amo ng the Shew har t c-chart,the fix ed sampling interv alPo isson EWM A co nt ro l char t and the V SI P oisson EW M A co ntr ol char t.Keywords: po isson EW M A co ntr o l chart;var iable sampling inter vals;marko v chain;aver ag etime t o sig nal。
具有可变样本容量的非正态EWMA控制图

具有可变样本容量的非正态EWMA控制图薛丽【摘要】为了提高控制图的监控效率,本文研究非正态分布下,E WMA控制图的可变样本容量设计问题。
首先利用 Burr分布近似各种非正态分布,构造可变样本容量的非正态 EWMA控制图;其次运用马!科夫链法计算可变样本容量非正态E WMA 控制图的平均运行长度;然后与传统的非正态 E WMA 控制图进行比较得出:当过程中出现小波动时,可变样本容量的非正态 E WMA控制图能够更快地发现过程中的异常波动,具有较小的平均运行长度,其监控效率明显优于传统的非正态 E WMA控制图。
%In order to improve the monitoring efficiency of control charts,the EWMA control chart under non-normal distribution with variable sample size (VSS )is constructed in this paper;The Markov chain method is applied to calculate the average run length(ARL)of the VSS EWMA control charts.The computing results show that the VSS EWMA control chart under non-normal distribution is the more efficient in detecting shifts than the traditional EWMA control chart,and has a shorter the average run length to find the abnormal fluctuation.【期刊名称】《运筹与管理》【年(卷),期】2016(025)006【总页数】6页(P224-229)【关键词】可变样本容量;Burr分布;指数加权移动平均(EWMA)图;马!科夫链法【作者】薛丽【作者单位】郑州航空工业管理学院管理工程学院,河南郑州 450000【正文语种】中文【中图分类】TB114.2在产品制造过程中,产品质量特性值总是围绕着设计目标值产生波动,这种制造过程的不稳定性导致了最终产品的质量缺陷。
CUSUM EWMAPPT课件

1
26
第26页/共69页
• 双侧CUSUM控制图可以通过同时使用两个单侧CUSUM控制图来实现,其中:上单侧与下单侧CUSUM的
参考值分别记为K1和K2,它们的ARL记为
和
。
• 单侧CUSUM控制图的ARL与双侧CUSUM控制图的ARL即
之间的关系为
L1 () L2 ()
L()
L1
()
L1 1
()
• 利用CUSUM控制图,过程偏移量可以利用点子倾斜程度的变化进行估计。并且, 通过观察倾斜程度的变化,可找到过程出现变化的起点。
14
第14页/共69页
CUSUM控制方法——V型模板
15
第15页/共69页
V型模板的应用方法: 把V型模板的O点放在 最新得到的点子Si上, 直线OP与x轴平行
每当CUSUM打 点图上出现一个 新的点子,就要 移动V型模板, 把O点移到最新 点子上,OP与x 轴平行,应用V 型模板进行控制。
内容:
• CUSUM控制及其应用 • EWMA控制及其应用 • 自相关过程的质量控制
1
第1页/共69页
2
CUSUM控制及其应用
第2页/共69页
常规控制图的不足
• 常规休哈特控制图存在着对过程小偏移不灵敏的缺陷。 • CUSUM控制图的诞生正是为了解决过程小偏移的质量控制问题。 • CUSUM控制图是1954年佩基(Page)提出的。
SH (i)
SL (i)
SH (i)
SH (i)
0
SL (i) SL (i)
或
为负值,则将其置为0;
30
第30页/共69页
• CUSUM控制图的设计原则 设计CUSUM控制图取决于对参考值K和决策值H的选择。 建议:基于对ARL的设计要求,选取参数。
EWMA控制图的ARL求取方法

本文引用格式:常志远.EWMA 控制图的 ARL 求取方法 [J].新型工业化,2014,4(8):66-70. DIO :10.3969/j.issn.2095-6649.2014.8.10EWMA 控制图的 ARL 求取方法常志远 *(南京理工大学大学自动化学院,南京 210094)摘 要:控制图在统计过程控制中占有很重要的地位,平均运行链长 (Average Run Length, ARL) 是评 价控制图性能的一个重要指标。
E W M A 控制图的 AR L 求取相对复杂,到目前为止,E W M A 控制图的 AR L 求取大致有三种方法:M a r k ov 链法、积分方程法和随机模拟。
本文详细阐述了前两种方法在用于 E W M A 控制图 ARL 计算时的原理及实现,并仿真比较了这两种方法的精度,以及状态划分对其精度的影响。
关键词:ARL ;Markov 链;积分方程;EWMAThe Methods for Calculating the ARL of EWMA Control ChartCHANG Zhiyuan(School of Automation , Nanjing University of Science & Technology , Nanjing 210094, Jiangsu , China )Abstract :The aver age run length is a crucial index of control chart, which is an important tool for st a ti st i ca l co ntro l. The ave ra ge run l eng t h ca l c ul a ti o n a l go ri t hm o f E WM A co ntro l cha rt i s complex . The re are three methods to calculate the ARL of EWMA control so far, which is Markov chain method, initial equation method and stochastic simulation method. In this paper, the principle and implementation of the first two methods are described in detail. And the accuracy of the two methods is analy zed by simulation.Key words :ARL; Markov chain; Initial equation; EWMA0 引言Sh e w h a r t 博士基于假设检验理论提出的控制图思想在统计过程控制中得到了广泛的应用, 对提高产品质量做出了巨大贡献。
具有可变抽样区间的二维EWMA控制图++++

2007年9月系统工程理论与实践第9期 文章编号:100026788(2007)0920142206具有可变抽样区间的二维EW M A 控制图吉明明1,孙 浩2,唐伟广2(11徐州工程学院数学与物理科学学院,徐州221008;21西北工业大学应用数学系,西安710072)摘要: 对二维EW M A 控制图进行了可变抽样区间设计,利用Markov chain 方法计算出了过程的平均报警时间,数据结果显示,所设计的控制图较常规的固定抽样区间控制图能更快更准确地发现过程的变化.关键词: 二维EW M A 控制图;可变抽样区间;平均报警时间;马尔可夫链中图分类号: O21311 文献标志码: A A T w o 2dimensional EW M A C ontrol Chart with Variable Sam pling IntervalsJ I Ming 2ming 1,S UN Hao 2,T ANG Wei 2guang2(11School of Mathematics &Physics Science ,Xuzhou Institute of T echnology ,Xuzhou 221008,China ;21Dept of Applied Mathematics ,N orthwestern P olytechnical University ,X i ’an 710072,China )Abstract : A tw o 2dimensional exponentially weighted m oving average control chart with variable sampling intervals isproposed.The Markov chain method is used to calculate the average time to signal.The datum show that this proposed chart is m ore efficient in detecting shifts than the fixed sampling interval control chart.K ey w ords : tw o 2dimensional EW M A control chart ;variable sampling intervals ;average time to signal ;Markov chain收稿日期:2006205231资助项目:国家自然科学基金(79970022);航空科学基金(02J53079);陕西省自然科学基金(N5CS0002) 作者简介:吉明明(1982-),女,汉族,山西临汾人,硕士,研究方向:应用概率统计.1 引言静态控制图假定抽样区间和样本容量及控制限都固定不变,它不利于及时发现过程的变化,特别是过程较小的变化,于是Reynolds et al [1]提出了具有变化抽样区间的Shewhart 均值控制图,并由此形成了动态控制图这一新的研究领域.之后众多学者研究了动态的累积和(C US UM )控制图[2]、指数加权滑动平均(EW M A )控制图[3,4]等.但上述研究均是针对生产线只有一个可控因素的情形进行的,而实际中影响一个生产线工作是否正常的因素可能不止一个,因此我们很有必要对具有多个影响因素的动态控制图进行相应的研究.本文在前人的基础上对具有两个可控因素的二维EW M A 控制图进行可变抽样区间的设计,利用Markov chain 方法计算出的数据结果表明,与一维可变抽样区间控制图一样,二维可变抽样区间控制图也能够降低过程的平均报警时间,从而更有效地提高生产效率.2 MEWMA 控制图的描述记X t =(X t 1,X t 2,…,X tp )T(t =1,2,…)为从过程中获得的具有p (p ≥2)个质量特性的第t 个测量值,假设X t 独立同分布,当过程处于受控状态时,X t ~N p μ0,∑X,且μ0,∑X均已知.作为单变量EWMA统计量的自然推广,MEWMA 统计量可以定义为[5]:W t =r (X t -μ0)+(1-r )W t -1其中,W 0为p 维零向量,r 为平滑参数,且0<r ≤1.当Q t =W Tt ∑-1WtW t >H 时,过程失控,其中H >0是为达到特定的受控时的平均运行长度AR L (AverageRun Length )而选取的控制限.当r =1时,MEW M A 控制图即为Hotelling ’s χ2控制图.∑Wt是Wt的协方差矩阵,其表达形式为:∑Wt={r [1-(1-r )2t]Π(2-r )}∑X 一般采用其渐近形式,即∑Wt≈[r Π(2-r )]∑X 失控时,设X 的均值从μ0漂移至μ,协方差矩阵∑X未改变,Lowry et al[6]指出,MEW M A 控制图的平均运行长度AR L 仅依赖于非中心参数(μ-μ0)T∑-1X(μ-μ0).对X 进行标准化变换,变换后的随机变量Y =∑-1Π2X(X -μ0),则Y 在受控和失控时的均值分别为零和∑-1Π2X(μ-μ0),且其协方差阵为单位矩阵.因MEWMA控制图的ARL 仅依赖于非中心参数(μ-μ0)T∑-1X(μ-μ0),故不妨假设X 的均值为零,协方差阵为单位矩阵,令u =(2-r )Πr ,则Q t =u ‖W t ‖2.本文对p =2时的二维EW M A 控制图进行可变抽样区间设计.3 具有可变抽样区间的二维EWMA 控制图311 二维EWMA 控制图的描述当p =2时,X t =(X t 1,X t 2)T ,W t =(W t 1,W t 2)T ,Q t =u ‖W t ‖2=u ‖W 2t 1+W 2t 2‖,为了能方便地计算该二维EW M A 控制图的平均运行长度AR L ,定义统计量q t =‖W t ‖=W 2t 1+W 2t 2 因当Q t =u ‖W t ‖2>H 时,控制图发出报警信号,表示过程失控,即‖W t ‖>u-1Π2H1Π2也即,当q t >u-1Π2H 1Π2时,发出报警信号.将统计量q t 描在控制图上,并定义控制限UC L 为UC L =u-1Π2H1/2 当q t >UC L 时,过程失控.从控制图的统计量和控制限可以看出,其受控域为半径为UC L 的一个圆,如图1所示.图1 二维EW M A 控制图的控制域312 可变抽样区间控制图的描述可变抽样区间(Variable Sam pling Intervals ,VSI )控制图是指抽样区间依赖于现时样本点统计量的控制图,其产生思想为:在控制图的中心限和控制限之间加上警戒限,将中心限与警戒限之间的区域称为中心域,警戒限与控制限之间的区域称为警戒域,若现时样本点统计量位于警戒域,则其后的点子可能超出控制限,这时为了较快地发现过程的变化,应提早抽取下一个样本,反之,若现时样本点统计量位于中心域,则等待较长时间抽取下一个样本,抽样区间的长短取决于现时样本点的观测值.众多学者的研究已经证明,可变抽样区间控制图较固定抽样区间(FixedSam pling Interval ,FSI )控制图具有很大的优越性[7].一般选用两个抽样区间长度,d 1和d 2,d 1>d 2,当现时样本点统计341第9期具有可变抽样区间的二维EW M A 控制图量位于中心域时,选用抽样区间d 1;位于警戒域时,选用抽样区间d 2;超出控制限时,发出报警信号,表示过程失控.对于参数固定不变的静态控制图,一般利用AR L 的大小来比较,当过程处于控制状态时,AR L 应尽可能的大使得过程发生第一类错误的概率很小,当过程处于失控状态时,AR L 应尽可能的小使得失控过程能及时被发现.但从AR L 的定义不难看出,对于具有变化抽样区间的动态控制图,无法再利用AR L 进行比较,Reynolds et al [1]针对可变抽样区间控制图提出了如下两个比较法则:・平均报警时间(Average T ime T o Signal ,ATS ):从开始检测到报警所需的平均时间.・报警所需的平均样本数(Average Number of Sam ples T o Signal ,ANSS ):从开始检测到报警所需的平均样本数.对于具有两个抽样区间d 1和d 2的VSI 控制图,用ψi 表示报警前使用抽样区间d i 的样本个数(i =1,2),d 0表示第一个样本之前的抽样区间,一般取d 0=d i (i =1,2).根据ATS ,ANSS ,ψ1,ψ2的定义很容易得到:ANSS =1+ψ1+ψ2ATS =d 0+d 1ψ1+d 2ψ2定义ρ=ψ1+1ANSS,d 0=d 1ψ1ANSS,d 0=d 2则ATS 可以用ANSS 和ρ表示为:ATS =d ・ANSS ,其中d =d 1ρ+d 2(1-ρ),也即d 为过程的平均抽样区间,d 与控制限和警戒限有关.从上述公式可以看出,改变控制图的抽样区间并不改变它的ANSS ,对于VSI 控制图和FSI 控制图,只要其平均抽样区间相同,则ATS 也相同,因此一般采用ATS 法则对控制图的效率进行估计.关于ATS 的计算方法有很多,如Markov chain 方法,积分方程方法以及M onte carlo 模拟方法等,本文采用Markov chain 方法计算二维VSI EW M A 控制图的ATS.313 二维VSI EWMA 控制图的设计及其效率对控制图进行可变抽样区间设计时,在圆心与控制限之间加上警戒限,并定义警戒限为UWL =u -1Π2H ′1Π2(0<H ′<H ),则控制图的受控区域被分成中心域和警戒域两部分,如图2所示.图2 二维VSI EW M A 控制图的中心域与警戒域采用两个抽样区间长度d 1和d 2,且d 1>d 2>0,其检验方案为:若现时样本点统计量q t 落入中心域,则等待较长时间d 1抽取下一个样本;若q t 落入警戒域,则等待较短时间d 2抽取下一个样本,并且每次抽取的样本容量n 不变.下面分别计算二维VSI EW M A 控制图受控和失控时的平均报警时间.31311 受控时的平均报警时间当过程处于控制状态时,将控制图的受控区域分成m +1个宽度为g =UC L Π(m +1)的同心圆壳,如图3所示,每个圆壳表示Markov chain 的一个瞬时状态,从里到外分别记为状态E 0,E 1,…,E m ,状态E m +1为吸收状态,表示过程失控.定义b =(b 0,b 1,b 2,…,b m )T,其中b i (i =0,1,2,…,m )表示现实样本点统计量q t 在状态E i 中时所采用的抽样区间,当E i 的中心线位于中心域时,b i =d 1,位于警戒域时,b i =d 2.Runger et al[8]给出了受控时这m +1个受控状态间的转移概率,记从状态E i 到状态E j 的转移概率为p ij ,则441系统工程理论与实践2007年9月图3 受控时二维VSI EW M A 控制图受控区域的划分p ij =P {(j -015)2g 2Πr 2<χ2(2,c )<(j +015)2g 2Πr 2},j ≠0P {χ2(2,c )<0152g 2Πr 2},j =0其中 c =[(1-r )ig Πr ]2,χ2(2,c )表自由度为2,非中心参数为c 的非中心χ2分布.详细的推导可以参考文献[8].则该Markov chain 在这m +1个瞬时状态中的转移概率矩阵为P =[p ij ](m +1)×(m +1).定义M =(I -P )-1=[m ij ](m +1)×(m +1),其中I 表示m +1维的单位矩阵,对于二维EW M A 控制图,因W 0=(0,0)T,即过程在开始时处于E 0状态,故受控时二维EW M A 控制图的平均报警时间ATS 为ATS =∑mj =0m0j bj31312 失控时的平均报警时间假设失控从零时刻开始发生,过程均值从μ0=(0,0)T 漂移至μ=(δ,0)T,其中δ为Χ1的漂移量,即质量特性X 1的均值发生变化,X 2的均值未发生变化.图4 失控时二维VSI EW M A 控制图受控区域的划分为计算失控过程的平均报警时间,将控制图的受控区域沿w 1方向分成2m 1+1个长度相等的区间,对应于W t 1的2m 1+1个Markov chain 状态,每个区间的长度均为g 1,则g 1=2UC L Π(2m 1+1),分别将这些状态记为h 1,h 2,…,h 2m 1+1.类似地,将受控区域沿w 2方向分成2m 2+1个长度为g 2=2UC L Π(2m 2+1)的区间,对应于W t 2的2m 2+1个Markov chain 状态,分别将其记为v 1,v 2,…,v 2m 2+1.由此,整个受控区域被分成许多小网格,如图4所示,每个小网格对应于此二维Markov chain 的一个瞬时状态,分别将其记为E 1,E 2,…,E k ,显然k <(2m 1+1)×(2m 2+1).若状态E i (i =1,2,…,k )对应的w 1方向的状态为i x (i x ∈(h 1,h 2,…,h 2m 1+1))、w 2方向的状态为i y (i y ∈(v 1,v 2,…,v 2m 2+1)),则状态E i 也可将其记为状态(i x ,i y ).定义b =(b 1,b 2,…,b k )T,若状态E i (i =1,2,…,k )的中心点位于中心域,则b i =d 1,位于警戒域,则b i =d 2.将从状态E i (i =1,2,…,k )到状态E j (j =1,2,…,k )即从状态(i x ,i y )到状态(j x ,j y )的转移概率记为p ij ,则p ij =p (i ,j )=p [(i x ,i y ),(j x ,j y )]=h (i x ,j x )v (i y ,j y ) 下面分别计算h (i ,j )和v (i ,j ).h (i ,j )=P (W t 1位于状态j |W t -1,1位于状态i )=P (-UC L +(j -1)g 1<rX t 1+(1-r )W t -1,1<-UC L +jg 1|W t -1,1=c 1i )=P (-UC L +(j -1)g 1<rX t 1+(1-r )W t -1,1c 1i <-UC L +jg 1)=P [(-UC L +(j -1)g 1-(1-r ))c 1i Πr -δ<X t 1-δ<(-UC L +jg 1-(1-r )c 1i Πr -δ]而X t 1-δ~N (0,1)令a 1=(-UC L +(j -1)g 1-(1-r )c 1i )Πr -δa 2=(-UC L +jg 1-(1-r )c 1i )Πr -δ541第9期具有可变抽样区间的二维EW M A 控制图则h (i ,j )=∫a 2a 112πe -x22dx ,其中c 1i =-UC L +(i -015)g 1同理v (i ,j )=P (W t 2位于状态j |W t -2,1位于状态i )=P (-UC L +(j -1)g 2<rX t 2+(1-r )W t -1,2<-UC L +jg 2|W t -1,2=c 2i )=P (-UC L +(j -1)g 2<rX t 2+(1-r )c 2i <-UC L +jg 2)=P [(-UC L +(j -1)g 2-(1-r )c 2i )Πr <X t 2<(-UC L +jg 2-(1-r )c 2i )Πr ]而X t 2~N (0,1)令b 1=(-UC L +(j -1)g 2-(1-r )c 2i )Πr b 2=(-UC L +jg 2-(1-r )c 2i )Πr则v (i ,j )=∫b 2b112πe -x22dx ,其中c 2i =-UC L +(i -015)g 2 该Markov chain 在这k 个瞬时状态中的转移概率矩阵P =[p ij ]k ×k ,将原点对应的Markov Chain 状态记为E k 0(k 0∈(1,2,…,k )),令M =(1-P )-1=(m ij )k ×k ,故失控时二维EW M A 控制图的平均报警时间ATS为ATS =∑kj =1mk 0j bj 当质量特性X 1的漂移量δ=0时,由上述方法计算出的平均报警时间即为受控时的平均报警时间,因此,上述方法也可用来计算受控时的平均报警时间.4 二维VSI 与FSI EWMA 控制图的比较控制图应在同一条件下进行比较,换言之,当过程处于受控状态时,它们应有相同的平均报警时间ATS.只要VSI 控制图与FSI 控制图的平滑参数r 与控制限UC L 相同,它们就具有相同的ANSS ,也就是说,改变控制图的抽样区间并不改变它的ANSS.当μ=μ0时,固定r 和H ,选取合适的警戒限和可变抽样区间d 1与d 2,使得VSI 控制图和FSI 控制图具有相同的平均抽样区间,此时它们具有相同的平均报警时间.分别计算当μ≠μ0时两个控制图的ATS ,ATS 越小,控制图的效率就越高.表1给出了当H =9,H ′=4时,r 和质量特性X 1的漂移量δ取不同值的情况下二维VSI 与FSI EW M A 两种控制图的ATS ,其中δ>0表示向上漂移,δ<0表示向下漂移.不失一般性,在计算过程中取μ0=0,d =1.从表中数据可以看出,不论r 取何值,在过程处于受控状态(即δ=0时)并且两控制图的平均报警时间ATS 相同的情况下,失控时(即δ≠0时)VSI 控制图较FSI 控制图的平均报警时间要小.例如,当r =012时,选取合适的抽样区间d 1和d 2,使得受控时两控制图的ATS 相等,本文选取d 1=11050,d 2=01586,此时它们的ATS 均为130173,而δ=±015时,它们的ATS 分别为VSI :28105,FSI :29173.这说明,在同一条件下,当过程发生变化时,VSI 控制图较FSI 控制图能更快更及时地发现这种变化.本文只是对一组d 1、d 2数值进行了模拟计算,对于其他的d 1、d 2值,经计算也有同样的结果.因此,同一维可变抽样区间控制图一样,对于二维EW M A 控制图,采用VSI 控制图监控生产过程较采用FSI 控制图也可以缩短过程失控时的平均报警时间,从而减少产品的不合格率,降低生产成本,提高生产效率,在实际生产中具有很好的应用价值.641系统工程理论与实践2007年9月表1 二维VSI EW M A 控制图与FSI EW M A 控制图ATS 的比较δr =011r =012r =013r =014r =015(d 1,d 2)(11050,01600)(d 1,d 2)(11050,01586)(d 1,d 2)(11050,01588)(d 1,d 2)(11050,01592)(d 1,d 2)(11050,01595)VSIFSI VSIFSI VSIFSI VSIFSI VSI FSI 0101701861701871301731301731131041131031031701031699813498134±01526199291122810529173301603119833162341823619538102±11091491017181559164817991829156101551016711167±1155168614141685133414251054146510741655131±2104112416131283170219631372184312321803122±3102176310421142139118821111173119311631181参考文献:[1] Reynolds M R Jr ,Amin R W ,Arnold J C ,et al.X 2bar charts with variable sampling intervals [J ].T echnometrics ,1988,30(2):181-192.[2] Arnolds J C ,Reynolds M R Jr.C US UM control charts with variable sample sizes and sampling intervals [J ].Journal of QualityT echnology ,2001,33(1):66-81.[3] Saccucci M S ,Amin R W ,Lucas J M.Exponentially weighted m oving average control schemes with variable sampling intervals[J ].C ommunications in S tatistics 2S imulation and C omputation ,1992,21(3):627-657.[4] Reynolds M R Jr ,Arnold J C.EW M A control charts with variable sample sizes and variable sampling intervals [J ].IIET ransactions ,2001,32(6):511-530.[5] Prabhu S S ,Runger G C.Designing a multivariate EW M A control chart [J ].Journal of Quality T echnology ,1997,29(1):8-15.[6] Lowry C A ,W oodall W H.A multivariate exponentially weighted m oving average control chart [J ].T echnometrics ,1992,34(1):46-53.[7] 王兆军.关于动态质量控制图的设计理论[J ].应用概率统计,2002,18(3):316-333. Wang Zhaojun.The design theory of adaptive control charts [J ].Chinese Journal of Applied Probability and S tatistics ,2001,18(3),316-333.[8] Runger G C ,Prabhu S S.A markov chain m odel for the multivariate exponentially weighted m oving average control chart [J ].Journal of the American S tatistical Ass ociation ,1996,91(436):1701-1706.[9] 袁志发,周静芋.多元统计分析[M].北京:科学出版社,2002. Y uan Zhifa ,Zhou Jingyu.Multivariate S tatistical Analysis [M].Beijing :Science Press ,2002.[10] S inger S P rge Sample Methods in S tatistics[M].New Y ork :Chapman 2Hall ,1993.741第9期具有可变抽样区间的二维EW M A 控制图。
第三课 CUSUM & EWMA

9
CUSUM控制图包容了观测值序列的全部信 控制图包容了观测值序列的全部信 计算观测值与目标值差值的累积和。 息,计算观测值与目标值差值的累积和。 的样本, 假设采集到样本容量 n ≥ 1 的样本,用 x j 表示第j个样本的均值 个样本的均值。 表示 个样本的均值。如果以 µ0 表示过 程均值的目标值,那么, 统计量为: 程均值的目标值,那么,CUSUM统计量为: 统计量为
j=1
i
其中: 是参考值 是参考值(Reference Value),通常 其中:K是参考值 , 取稳态过程均值µ0 与需要检测出的过程偏 之间差值的一半, 移 之间差值的一半,即
µ1 = µ 0 + ∆
∆ δσ x K= = 2 2
26
假设 µ1 > µ0 小于零, 自动设置为0 如果 Si 小于零,则Si 自动设置为0。 如果 Si 大于决策值 (Decision Value) H, , 那么, 那么,可以判断过程均值已经偏移到µ1
序号 11 12 13 14 15 16 17 18 19 20
CUSUM值 值 -1.20 0.27 0.78 0.18 0.26 -0.37 0.25 0.56 -0.92 -0.08
序号 21 22 23 24 25 26 27 28 29 30
CUSUM值 值 0.32 -0.85 0.94 1.94 2.04 2.62 2.50 3.62 4.43 4.45
——示例 示例CUSUM统计量的结果 示例 统计量的结果
12
——示例 示例CUSUM统计量的打点结果 示例 统计量的打点结果
13
CUSUM控制的设计思想 控制的设计思想
CUSUM控制图的理论基础是序贯分析原理 控制图的理论基础是序贯分析原理 中的序贯概率比检验(Sequential Probability 中的序贯概率比检验 Ratio Test,简称 ,简称SPRT),这是一种基本的 , 序贯检验法。 序贯检验法。 CUSUM控制图的设计思想是对信息加以累 控制图的设计思想是对信息加以累 将过程的小偏移累加起来, 积,将过程的小偏移累加起来,以起到放 大的效果,进而, 大的效果,进而,提高检测过程小偏移的 灵敏度。 灵敏度。
SPC中的EWMA指数加权移动平均控制图

SPC中的EWMA指数加权移动平均控制图========================================================== 本文由QuAInS[注1]根据Douglas Montgomery[注2]相关专注整理而成==========================================================在统计过程控制SPC中,指数加权移动平均(EWMA: Exponentially Weighted Moving Average)控制图常用来侦测流程的微小偏移,作用与累积和控制图(CUSUM:Cumulative Sum)类似,但设置和操作通常要容易一些。
EWMA有时也称为几何移动平均(GMA: Geometric Moving Average),在时间序列建模和预测领域应用十分广泛。
指数加权移动平均控制图由Roberts在1959年提出,后来被广泛使用。
其定义公式为:, 其中常数λ的取值范围为0<λ≤1,z i是EWMA统计量,即所有之前样本均值的加权平均值,。
该公式的初始值z0(当i=1时)取流程的目标值(即在z0=μ0),有时也用初始数据的均值作为初始值,即z0=XBar。
由于EWMA是所有之前和当前样本的加权平均,因此对数据的正态性假设很不敏感,因此,用于单个观测值是十分理想的。
如果观测值x i是独立的随机变量,方差为σ2,那么z i的方差为因此,EWMA控制图的纵轴是z i,横轴是样本序号或时间,中心线和控制限的计算公式为:注意到上述公式中的(1-λ)2i部分,当i逐渐增大时,(1-λ)2i将很快收敛到0,因此当i增大时,UCL和LCL将稳定到下面两个值:,但当i比较小时,强烈建议使用精确公式,这样十分有助于提高此时EWMA控制图的作用以侦测流程的偏移。
以下是一个EWMA控制图的示例:如何决定公式中L和λ的值EWMA控制图对于侦测流程的微小偏移十分有用。
多变量 EWMA 控制图

多变量 EWMA 控制图
EWMA 控制图的多变量形式。
使用多变量 EWMA 控制图可以在指数加权控制图中同时监控两个或多个相关过程特征。
例如,使用多变量 EWMA 控制图可以监控塑料注模过程中的温度和压力。
每个多变量 EWMA 点都结合了来自与用户定义的加权因子组合的所有以前子组或观测值的信息。
多变量 EWMA 控制图可以帮助您较其他多变量控制图(如 T 方控制图)更快地检测出较小的过程偏差。
多变量 EWMA 控制图的另一个优点是,当计算中增加了一个小值或大值时,它们不会受到很大影响。
而且,您还可以将多变量 EWMA 控制图自定义为能检测过程中任意大小的偏差。
因此,它们经常用于监控受控过程,以检测出背离目标的较小偏差。
例如,下面的多变量 EWMA 控制图就是上述塑料注模示例的图示:
多变量 EWMA 控制图
控制上限之上没有点,因此可以认为变异是稳定的。
但是,有几个点比其余的点位置高,可以对这几个点进行分析。
图中的点可以基于子组,也可以基于单个观测值。
当数据在子组中时,计算每个子组中所有观测值的均值。
然后根据这些均值得出指数加权移动平均值。
如果有单个观测值,则根据单个观测值得出指数加权移动平均值。
指数加权移动平均控制图
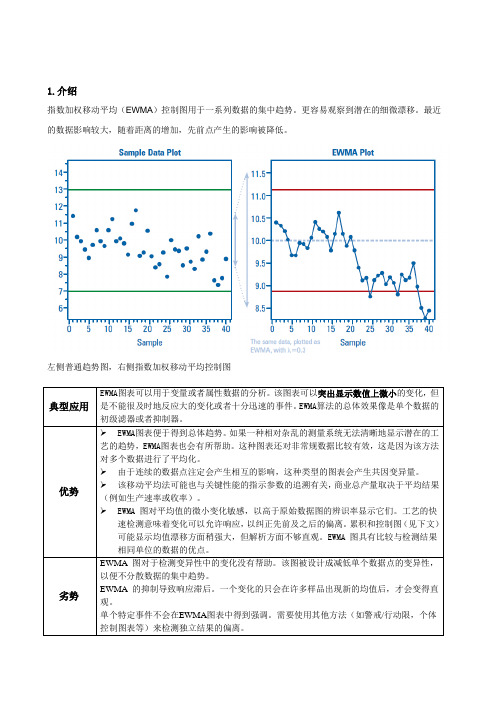
1.介绍指数加权移动平均(EWMA)控制图用于一系列数据的集中趋势。
更容易观察到潜在的细微漂移。
最近的数据影响较大,随着距离的增加,先前点产生的影响被降低。
左侧普通趋势图,右侧指数加权移动平均控制图典型应用EWMA图表可以用于变量或者属性数据的分析。
该图表可以突出显示数值上微小的变化,但是不能很及时地反应大的变化或者十分迅速的事件。
EWMA算法的总体效果像是单个数据的初级滤器或者抑制器。
优势 EWMA图表便于得到总体趋势。
如果一种相对杂乱的测量系统无法清晰地显示潜在的工艺的趋势,EWMA图表也会有所帮助。
这种图表还对非常规数据比较有效,这是因为该方法对多个数据进行了平均化。
由于连续的数据点注定会产生相互的影响,这种类型的图表会产生共因变异量。
该移动平均法可能也与关键性能的指示参数的追溯有关,商业总产量取决于平均结果(例如生产速率或收率)。
EWMA 图对平均值的微小变化敏感,以高于原始数据图的辨识率显示它们。
工艺的快速检测意味着变化可以允许响应,以纠正先前及之后的偏离。
累积和控制图(见下文)可能显示均值漂移方面稍强大,但解析方面不够直观。
EWMA 图具有比较与检测结果相同单位的数据的优点。
劣势EWMA 图对于检测变异性中的变化没有帮助。
该图被设计成减低单个数据点的变异性,以便不分散数据的集中趋势。
EWMA 的抑制导致响应滞后。
一个变化的只会在许多样品出现新的均值后,才会变得直观。
单个特定事件不会在EWMA图表中得到强调。
需要使用其他方法(如警戒/行动限,个体控制图表等)来检测独立结果的偏离。
2.Minitab 17操作统计>控制图>时间加权控制图>EWMA附件:变更/修订记录版本号生效日期修订内容01 按标准化文件要求制定。
EWMA控制图

几何EWMA控制图
传统的c图建立在过程服从泊松分布这个假设的基 础上,但事实上其分布经常服从几何分布:
P X x p 1 p , x 0,1, 2...
x
若取样本容量为n,则在一个样本中的总缺陷数就可 以表示为 Y x x ... x .它服从负二项分布 1 2 n 。
Zt X t 1 Zt 1, 0 1
其中 Z0 0
1 n ,X t X tj n j 1
。 为平滑系数。
2. 监控均值的EWMA控制图
EWMA统计量 Zt 的期望和方差分别为:
E ( Zt ) 1 E ( X t i 1 )
EWMA控制图在实际应用中的计算模型可根据预测模型 给出: ~ ~ ~ Zt 1 Zt t Zt (1 )Zt
~ ~ Z 其中 Z t 为第 t+1点的估计值,t 为第 t点的估计值, t 为第t Z 1 点的实际测量值, t 为第点的观测值和估计值之间的误 差。因而EWMA除了具有控制过程发生偏移的作用以 外,还具有预测的功能,并且被用于处理逐渐漂移的 过程和自相关的数据中。
其中, k 为控制限系数。
2. 监控均值的EWMA控制图
Zt
UCL
CL
LCL
样本编号(或取样时间)
10
3.休哈特图与EWMA图监控效果比较 利用Mintab软件仿真一组正态分布的随机 数据200个,从第101个数据开始漂移 / 3 到第151数据再向上漂移 / 3 。据前100 个数据,取 n 5 建立控制图,用随后20 个样本对过程监控。 下面分两种情形对EWMA图和 X 图的灵 敏性进行比较。
EWMA控制图在ELISA室内质控中的应用

EWMA控制图在ELISA室内质控中的应用目的探讨指数加权移动平均(EWMA)图在ELISA室内质控中的应用价值。
方法对30次HBsAg ELISA室内质控数据分别绘制EWMA控制图和Levey-Jennings质控图,比较两种质控图控制效果。
结果EWMA控制图对系统误差产生的漂移比Levey-Jennings质控图更灵敏,而Levey-Jennings质控图对由随机误差产生的过程突发变化比EWMA控制图敏感。
结论EWMA控制图比Levey-Jennings质控图多规则质控能更早检出微小系统偏移,对于自动化程度较高的检测过程两者可结合使用。
标签:质量控制;指数加权移动平均(EWMA);Levey-Jennings质控图临床实验室室内质控直接影响检测结果的准确性和可靠性,为把检测误差控制在允许范围内,通常采用质控图技术保证检测质量。
目前国内ELISA室内质控多采取与临床定量检测相同,源于休哈特质控图的Levey-Jennings质控图,并按概定的质控规则判定系统误差和随机误差。
指数加权移动平均(EWMA)控制图由Roberts[1]在1959年首次提出,该图采用指数加权累计移动均值设置控制线,因而可以不受正态假定的限定,不同于休哈特控制图只考虑当前数据的统计检验,而将历史数据也考虑进来。
本文旨在通过比较两种质控图在ELISA 室内质控中的差别,探讨EWMA控制图在临床检验室内质控中的应用价值。
1资料与方法1.1仪器与试剂HBsAg ELISA诊断试剂盒(北京万泰公司,批号:BX20100706);HBsAg 1IU 质控血清(康彻斯坦,批号:20110101);TECAN RSP 加样仪,FAME2430自动酶免疫分析系统(瑞士汉密尔顿公司);Minitab 15.0统计控制分析软件。
1.2数据采集收集长沙血液中心检验科2011年1月万泰HBsAg ELISA室内质控数据30个,见表1。
1.3数据分析1.3.1应用Minitab软件分别绘制质控数据的EWMA控制图和Levey-Jennings 质控图。
EWMA控制图的灵敏性分析 .doc

Байду номын сангаас(1)
其中E(X)是X的数学期望, 是X的标准差。
如在生产过程中,仅有偶然因素存在,则产品质量特征X将服从某种典型分布,通常为正态分布;当异常因素出现时,X就会偏离原来的典型分布,可用统计学中的假设检验方法来及时发现这种分布的偏离,从而以此来判断异常因素是否存在。
当过程不存在异常因素时, ,于是就有
Sensitive analysis of ewma control chart
Author:Shi GuodongTutor:Zhang Li
Abstract
Thecontrolchart is a kind of graph which measures, records, assesses and monitors the process quality and makes sure that the process is in control state. The control chart is designed on the theoretical basis of statistical method. Since 1924, the Shewhart control chart came into being and was widely applied in all walks of life; it has brought respectable economic benefits to various industries. However it is only sensitive to large fluctuations but weak in detecting small fluctuations. The EWMA was brought in under this circumstance. As a kind of control chart, EWMA has a good consideration on the historical data, so it has given different weights to different historical data. Based on these conditions, EWMA has good detection ability on the small fluctuations and the process of gradual fluctuations.
EWMA 控制图

EWMA 控制图
一种类型的时间加权控制图,图中标绘了指数加权移动平均值。
每个 EWMA 点都根据用户定义的加权因子结合了来自之前所有子组或观测值的信息。
EWMA 控制图的优点是,当较小值或较大值进入计算时不会严重影响到这些控制图。
通过更改使用的权重以及控制限制的 s 数量,可以构建控制图,该图可以检测过程中几乎任何大小的偏移。
因此,它们经常用于监控受控过程,以检测出背离目标的较小偏差。
例如,一家离心机转子生产商想要跟踪一周内生产的所有转子的直径。
直径与目标值必须非常接近,因为即使很小的偏差都会导致问题的出现。
以下 EWMA 控制图产生的结果如下:
EWMA 控制图
点似乎在中心线附近随机变化,而且在控制限制范围内。
未显示出任何趋势或模式。
转子直径的变异性似乎是稳定的。
图中的点可以基于子组,也可以基于单个观测值。
当数据在子组中时,计算每个子组中所有观测值的均值。
然后根据这些均值得出指数加权移动平均值。
如果有单个观测值,则根据单个观测值得出指数加权移动平均值。
CUSUM和EWMA控制图

• SL = cumulative Sum of Low side…
CuSum Chart and Signals
CUSUM Chart for AtoBDist
EWMA
(EWMA) 模型
• t+1时刻 的EWMA预测值如下: ˆ t 1 yt 1 y ˆt y ˆ t 1 y 其中 y 是 (t+1)时刻的预测值 ˆ t, 是 0 到1之间 y t 的加权因素, 在时刻 t 的当前观测值, 是时 刻 ˆ t 1t的先前的预测值。 yt y ˆt y • 是时刻 t的当前观测值 和 时刻 t 的先前预测 值( )的加权平均值.
EWMA存在ຫໍສະໝຸດ 相关 的,不随机 的倾向于只存 在单值的过 程
h
Example of Chart’s Elements
= sum on high side
k Target k
= X - Target = sum on low side
h
CUSUM
Calculation Elements
• Aim = Target value
教学演示: 正自相关数据的 EWMA图
假警报
• 如果我们不按照数据本身 在电阻系数控制图上描点 ,不对间隔时间中的自相 关影响进行检查,我们就 会看到存在更多的“失控 ”情形。 • 比较以前绘制的电阻系数 的单值控制图和RESI1控制 图。 • 注意失控信号表明实际值 和预测值之间存在非常大 的差异。这在很大程度上 降低了假警报率This (减少 Type I误差), 而且还识别未 被发现的问题 (减少 Type II 误差)。参见数据点 number 60 画圈部分。
MEWMA控制图运行链长分析及实例研究

M EWM A 控制图运行链长分析及实例研究杜福洲1唐晓青1孙 静21.北京航空航天大学,北京,1000832.清华大学,北京,100084摘要:多元指数加权移动平均(M EWMA )控制图常用来监测多元质量过程中存在的小偏移,对其性能评价时多采用平均运行链长。
在马尔可夫链的M EWMA 控制图平均运行链长计算方法的基础上,分析了M EWM A 控制图运行链长的概率分布及累积概率分布。
基于M AT LAB 计算平台,编制了相应的计算程序,给出了M EWM A 控制图运行链长的概率分布曲线及累积概率曲线。
提出了MEWM A 控制图参数优化方法,对电子产品装配中的表面贴片工艺过程的焊点质量控制进行了研究。
关键词:质量控制;统计过程控制;多变量控制系统;马尔可夫过程;优化控制系统中图分类号:T H 165.4;C931.1 文章编号:1004 132X(2007)07 0820 05Run Length Distributions Analysis and C ase Study for MEW MADu Fuzhou 1 T ang Xiaoqing 1 Sun Jing 21.Beihang University,Beijing ,1000832.Tsing hua U niv ersity ,Beijing,100084Abstract :Multivariate ex ponentially weighted mov ing av erag e (MEWM A)control char t w as de signed to detect small shifts in the m ean vecto r of a multiv ar iate quality process;its perform ance w as ev aluated by the average r un length (ARL).Based on the metho d for ARL co mputatio n pr opo sed by Rung er and Prabhu,this paper studied the run leng th distributions of MEWM A control char t,inclu ding the run length probability distributions and cumulative probability distributions.Based on the pro cedure for parametrical optim ization of MEWM A contro l chart,a case study of its applicatio n in surface mount process for the solder joint quality contr ol w as pr esented.Key words :quality control;statistical process control;multivariable contr ol system;M ar ko v pro cess;o ptimal control system收稿日期:2006 02 08基金项目:国家自然科学基金资助项目(50475005,70321001)0 引言多元指数加权移动平均(m ultivariate ex po nentially w eighted mo ving averag e,MEWM A)控制图常用来监控多元质量过程中的小偏移,学术界和实际应用中常用平均运行链长(av er ag e r un leng th,ARL)作为其性能评价指标。
ewma控制图

对比小结
• EWMA 图可以这样理解:通过对所 图可以这样理解: 有过去小波动的累加,使其表现 有过去小波动的累加, 出有较大的波动, 出有较大的波动,从而增加了控 制图对小漂移的敏感性 • 与X 控制图相比,EWMA 图的弊 控制图相比, 端在于不能很好的发现过程中的 突发变化, 突发变化,这种现象同样是对过 去样本数据波动的积累造成的。 去样本数据波动的积累造成的。
LOGO
EWMA控制图 EWMA控制图
组员
杜学敏、王丽静、 杜学敏、王丽静、陈雷 孙晓芳、张越、 孙晓芳、张越、苗凤娜
1
EWMA控制图的提出背景 EWMA控制图的提出背景
2
EWMA控制图的原理 EWMA控制图的原理
EWMA控制图与X EWMA控制图与X图的比较 控制图与
3
EWMA控制图优点 4:EWMA控制图优点 目录
Robert于1959年提出了指数加权滑 Robert于1959年提出了指数加权滑 动平均(Exponentially 动平均(Exponentially Weighted Average,EWMA)控制图 控制图。 Moving Average,EWMA)控制图。
基于EWMA 基于EWMA 控制图采用指数加权累计移动 均值设置控制线, 均值设置控制线,因而可以不受正态假 定的限定、 定的限定、加之图上的每个点包含着前 面所有子组的信息, 面所有子组的信息,具有检出过程均值 小漂移的敏感性。 小漂移的敏档分享能灵敏地检能灵敏地检测出过程的测出过程的变化趋势变化趋势预报的误差较小预报的误差较小方法简单方法简单迅速可靠迅速可靠能使控制参数随机能使控制参数随机的变化得到平滑的变化得到平滑预报误差有预报误差有明确的范围明确; λ ≤1 是加权常数,软件默认是0.2 0.2, 是加权常数,软件默认是0.2,一般建议设 0.05< 0.25。 为0.05<入≤0.25。
STATISTICA JMP与MINITAB软件统计控制图应用(三)3-2-1

2
xij is the jth measurement in the ith subgroup, with j = 1, 2, 3,... ni is the sample size of the ith subgroup k is the number of subgroups Xw is the weighted average of subgroup means 3.EWMA 控制图的标准差估计选项 EWMA 控制图也可以分别适用于单个质控测定数据和分组数据,这两种数据绘制输出 EWMA 控制图 时,要预先选择设置标准差估计方法,可以参考附图 0-1-1 分别选择。 附图 0-1-1
STATISTICA、JMP、MINITAB 软件统计控制图应用简介(三)3-2
1
STATISTICA、JMP 与 MINITAB 软件统计控制图应用(三) 第三篇 移动均值(MA)、指数加权移动均值(EWMA)和累计和(CUSUM)控制图 其二 指数加权移动均值(EWMA)控制图
赵炳华
00 EWMA 控制图统计基础简要描述 ............................................................................................................... 1 01 EWMA 控制图 ............................................................................................................................................... 1 02 两点提示 ......................................................................................................................................................... 2 1 单值数据 EWMA 控制图 ................................................................................................................................ 2 1.2 先看常规单值控制图 .................................................................................................................................... 2 1.3 EWMA 控制图观测与思考 .......................................................................................................................... 3 2 分组数据 EWMA 控制图 ................................................................................................................................ 4 2.1 先看常规均值控制图和 Zone 图 .................................................................................................................. 4 2.2 Zone—图 Zone Score(区域得分)及其含义 ............................................................................................. 4 2.3 EWMA 控制图 .............................................................................................................................................. 6 EWMA 控制图统计基础简要描述 正如上文所述:EWMA 图和 CUSUM 图是用于检测过程含有小漂移(small shifts)的有效方法。本 文先简要讲解 EWMA 图。 01 EWMA 控制图 1.名称 中文全称是指数移动均值控制图, 英文全称是 Exponentially Weighted Moving Averages (EWMA) chart, 缩写为 EWMA 图;也有直接称为指数移动均值图,即:Exponential Moving Average(EMA)chart,或者 称为几何移动均值控制图,即:Geometric Moving Average (GMA) chart。查看文献时,遇有以上的“不同 名称”就会想到这三种叫法的意思都是相同的。 2.EWMA 控制图监测过程均值 (1)统计过程控制在执行的实践中,遇有长期的小漂移时,休哈特计量控制图时时显得不甚敏感, 难以识别这种小波动。基于 EWMA 控制图采用指数加权累计移动均值设置控制线,因而可以不受正态假 定的限定、加之图上的每个点包含着前面所有子组的信息,具有检出过程均值小漂移的敏感性。 (2)用子组均值为例,看看 EWMA 的指数加权移动平均数: 00
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• EWMA 图从第31 点不仅所有的点在中心线 图从第31 以上,从视觉上看几乎是直线上升, 37、 以上,从视觉上看几乎是直线上升,第37、 38、 点失控。由此得出结论: 38、39 和40 点失控。由此得出结论:过 程均值向上漂移了, 程均值向上漂移了,尽管从图上不能精确 地确定漂移了多少,但从第31 地确定漂移了多少,但从第31 点漂移的趋 势非常明显,这就很容易追踪根源。 势非常明显,这就很容易追踪根源。
第一章: EWMA控制图的提出背景 第一章: EWMA控制图的提出背景
在保证和提高产品质量方面, 在保证和提高产品质量方面, 质量技术得到 迅速发展, 迅速发展, 质量工程已经发展成为一门新兴 的学科, 有一整套的理论和方法, 的学科, 有一整套的理论和方法, 其中质量 控制图就是一种行之有效的科学方法. 控制图就是一种行之有效的科学方法.迄今为 止,世界各国用得最广泛的质量控制图是休哈 特图。 特图。 由于休哈特控制图不具有记忆能力, 由于休哈特控制图不具有记忆能力, 即不考虑过 程的历史演变情况缺乏预测能力, 程的历史演变情况缺乏预测能力, 对于一些过 程性的质量控制如化工过程, 就存在着滞后, 程性的质量控制如化工过程, 就存在着滞后, 不能超前预报等问题。 不能超前预报等问题。而且统计过程控制在执 行的实践中,遇有长期的小漂移时, 行的实践中,遇有长期的小漂移时,休哈特计量 控制图时时显得不甚敏感,难以识别这种小波动。 控制图时时显得不甚敏感,难以识别这种小波动。
Robert于1959年提出了指数加权滑 Robert于1959年提出了指数加权滑 动平均(Exponentially 动平均(Exponentially Weighted Average,EWMA)控制图 控制图。 Moving Average,EWMA)控制图。
基于EWMA 基于EWMA 控制图采用指数加权累计移动 均值设置控制线, 均值设置控制线,因而可以不受正态假 定的限定、 定的限定、加之图上的每个点包含着前 面所有子组的信息, 面所有子组的信息,具有检出过程均值 小漂移的敏感性。 小漂移的敏感性。
• 从图可以看出, 对于提供信号来说, 休哈 从图可以看出, 对于提供信号来说, 特图统计值没有记忆功能, 特图统计值没有记忆功能, 它忽略了前面 的历史情况, EWMA具有较深的记忆功能 具有较深的记忆功能, 的历史情况, 而EWMA具有较深的记忆功能, 对于过程中, 不同时间的数据, EWMA 对于过程中, 不同时间的数据, 给予 了不同的注意。 了不同的注意。
t i= 0
• 上式是EWMA控制算法的理论模型和公式推导的标准 上式是EWMA控制算法的理论模型和公式推导的标准 EWMA 模型,这一模型却不利于计算和反映EWMA控制算法 模型,这一模型却不利于计算和反映EWMA控制算法 EWMA 的时域特性,EWMA控制图在实际应用中的计算模型 的时域特性,EWMA控制图在实际应用中的计算模型 可根据预测模型给出:
λ
。 0 < λ ≤1 是加权常数,软件默认是0.2 0.2, 是加权常数,软件默认是0.2,一般建议设 0.05< 0.25。 为0.05<入≤0.25。
λ 为当前观测值的加权参数
• EWMA对历史数据具有“ 记忆能力” , 对 EWMA对历史数据具有“ 记忆能力” 对历史数据具有 不同时期的数据加不同的权, 权系数Wi 不同时期的数据加不同的权, 权系数Wi 随 着时间的增长而变大。离现在愈久的数据, 着时间的增长而变大。离现在愈久的数据, 所加的权愈小;离现在愈近的数据, 所加的权愈小;离现在愈近的数据, 所加的 权愈大。显然,当前的EWMA EWMA值就包括了整个 权愈大。显然,当前的EWMA值就包括了整个 过程的历史信息。EWMA 图上的一点, 就绘 过程的历史信息。 图上的一点, 出了一个较长的记忆, 出了一个较长的记忆, 它能考虑过程历史 信息的影响, 反映过程趋势性变化, 信息的影响, 反映过程趋势性变化, 起到 预报作用。而对于休哈特图, 预报作用。而对于休哈特图, 每一点的信 息是独立的,与过程无关。 息是独立的,与过程无关。这一点的权系 ,而对于所有前面数据的权系数 数Wt = 1 ,而对于所有前面数据的权系数 Wt一 Wt一k = 0 (k≥1) 。对于休哈特图统计值和 的权函数如图1 所示: E WM A 的权函数如图1 所示:
第二章 EWMA控制图的原理 EWMA控制图的原理
• EWMA控制图的统计变量实际上观测值的 EWMA控制图的统计变量实际上观测值的 一个加权线性组合,可由下式表示: 一个加权线性组合,可由下式表示:
EW A = ∑ iyi M ω
i=0
t
• 其中Wi为第i个点的权值,符合相对于i 其中Wi为第i个点的权值,符合相对于i Wi为第 递增的规律, 的限制, 递增的规律,满足 ∑ ω i = 1 的限制, Yi为第 点的观测值。 为第i Yi为第i点的观测值
• 尽管EWMA图比X 图具有更吸引人的特 尽管EWMA EWMA图比 然而,不能用EWMA 性,然而,不能用EWMA 图代替X 图, 两种控制图提供了对过程的不同观察, 两种控制图提供了对过程的不同观察, 由于计算机软件的支持, 由于计算机软件的支持,在实际应用 中同时保持多个控制图是非常方便的。 中同时MA控制图 EWMA控制图
组员
杜学敏、王丽静、 杜学敏、王丽静、陈雷 孙晓芳、张越、 孙晓芳、张越、苗凤娜
1
EWMA控制图的提出背景 EWMA控制图的提出背景
2
EWMA控制图的原理 EWMA控制图的原理
EWMA控制图与X EWMA控制图与X图的比较 控制图与
3
EWMA控制图优点 4:EWMA控制图优点 目录
第四章:EWMA控制图优点 第四章:EWMA控制图优点
能使控制参数随机 的变化得到平滑 预报误差有 明确的范围 能灵敏地检 测出过程的 变化趋势
优 点
方法简单 迅速可靠
预报的误差较小
LOGO
◆
对比小结
• EWMA 图可以这样理解:通过对所 图可以这样理解: 有过去小波动的累加,使其表现 有过去小波动的累加, 出有较大的波动, 出有较大的波动,从而增加了控 制图对小漂移的敏感性 • 与X 控制图相比,EWMA 图的弊 控制图相比, 端在于不能很好的发现过程中的 突发变化, 突发变化,这种现象同样是对过 去样本数据波动的积累造成的。 去样本数据波动的积累造成的。
EWMA 图的控制线
举例说明
确定变异 来源和抽样 方案
1 2 3 4
绘制控制图 描点
5 6
确定 要控制 的关键 质量特 征值
搜集 数据
计算UCL和 计算UCL和 UCL LCL
• 控制图的绘制步骤
• EWMA 控制图的中心线的总均值,与休哈特的单值、或均值控 控制图的中心线的总均值,与休哈特的单值、 制图的中心线是一样的。但是,由于移动宽度、 制图的中心线是一样的。但是,由于移动宽度、或者设定权数大 小不同、各自的计算式不同, 小不同、各自的计算式不同,其控制图上的控制线不仅末端标示 的数值不同,而且上、下控制线的“走势”也不仅相同。即便是 的数值不同,而且上、下控制线的“走势”也不仅相同。 同一幅控制图,由于移动宽度、或者“权数”大小设置不同, 同一幅控制图,由于移动宽度、或者“权数”大小设置不同,其 控制线的上、下宽度和形态也会有改变,并导致检出“小漂移” 控制线的上、下宽度和形态也会有改变,并导致检出“小漂移” 的部位、或者“个数”等等发生改变。 的部位、或者“个数”等等发生改变。
第三章:EWMA控制图与 X 图的比较 第三章:EWMA控制图与 •EWMA EWMA
过程均值小漂移
入=1
权重不同
X图
(1)过程均值小漂移的情形 )
• 如下图所示, 图中所有点都在界内,但从 点 如下图所示, 图中所有点都在界内,但从31 X 后根据判异准则发出警告。 后根据判异准则发出警告。
(2)权重不同
EWMA图与 EWMA图与X 图的不同主要是由于 对观测值权重的不同考虑。 对观测值权重的不同考虑。 图观测值为当前观测值, ◆ X 图观测值为当前观测值,即当前 样本观测值的权重为100%。而EWMA 图 样本观测值的权重为100%。 100% 的观测值不仅包括当前样本观测值, 的观测值不仅包括当前样本观测值, 而且还包括过去的样本。 而且还包括过去的样本。 ◆ EWMA 图在监测小波动持续漂移上 优于X 图。
