自重应力计算表
土中应力计算课件

y
Rz
dzy
dzx dxz
M
dyz dy dyx
dxy
dx
z
3P z3
பைடு நூலகம்
3P
cos3
2 R5 2R 2
R r2 z2
z
3P z3
2 R5
z
3P
2
(r 2
z3 z2 )5/2
3
2
1 [(r / z)2 1]5/ 2
P z2
z
P z2
3.3.3 矩形和圆形荷载下地基附加应力计 算——积分法
3.3 土中附加应力
3.3.1 基本概念
1、定义
附加应力是因为外荷载作用,在地基中产生旳应力增量。
2、基本假定
地基土是各向同性旳、均质旳线性变形体,而且在深度和水平 方向上都是无限延伸旳。
3.3.2 竖向集中力作用时旳地基附加应 力布辛奈斯克解答
P
x
r x2 y2
r
y
x
R r2 z2
dz
z2
arctan
z
lb
]
(l 2 b2 z2 )
z c p0
c
1 2
(m2
mn(m2 2n2 1) n2 )(1 n2 ) m2 n2
1
arctan n
m ]
(m2 n2 1)
c ——均布矩形荷载角点下旳竖向附加应力系数,简称角点 应力系数,可查表得到。
* 对于均布矩形荷载附加应力计算点不位于角点下旳情况:
2z3 p
z b
b
d
0 [(x )2 z 2 ]2
z
p
[n(arctan
n m
arctan
土的自重应力、基底压力和地基附加应力

arctan
lb
2 l2 z2 b2 z2 l2 b2 z2
z l 2 b2 z2
角点下的地基附加应力:
取 m=l/b,n=z/b(注意其中b为荷载面的短边宽 度),令:
Kc
1
2
mn m2 2n2 1 m2 n2 12 n2 m2 n2
12
arctan n
剪应力:
xy
yx
3P
2
xyz
R5
1 2
3
xy(2R z)
R3
(
R
z
)2
yz
zy
3P
2
yz2 R5
3Py
2R3
cos2
xz
zx
3P
2
xz2 R5
3Px
2R3
cos2
x、y、z — 剪应力,其中前一脚标表示与它作用的微
面的法线方向平行的座标轴,后一脚标表示与它作用方 向平行的座标轴;
解:
cz1 1h1 19 2.0 38kPa cz 2 1h1 1'h2
38 (19.4 10) 2.5 61.5kPa
cz3
1h1
1'h2
' 2
h3
61.5 (17.4 10) 4.5 96.6kPa
w 2 (h2 h3 ) 10 7.0 70.0kPa
• 在深基坑开挖中,需 大量抽取地下水,以致 地下水位大幅度下降, 引起土的重度改变,从 而造成地表大面积下沉 的严重后果。 • 若地下水位长期上升, 会引起地基承载力的减 小、湿陷性土的陷塌现 象等,必须引起注意。
【例4-1】
试计算下图所示土层的自重应力及作用在基岩顶面的土自重 应力和静水压力之和,并绘制自重应力分布图。
土中的应力计算

e x
e xL
Ke
L x K=B/2-
L
压力调整 基底压
y
y
e
3K
y
pmin 0
力合力 与总荷
载相等
pmax
pmin
0 pmax
pmin 0
e<B/6: 梯形
pmax
e=B/6: 三角形
e>B/6: 出现拉应力区
2N
2N
pmax 3KL 3(B 2 e)L
12
2.2.3基底附加压力
H 成层
E1 均匀
E2<E1
25
无限均布荷载作用下的附加应力
当条形荷载在宽度方向增加 到无穷时,此时地基中附加应力 分布仍可按均布条形荷载下土中 应力的公式计算,查表2-10。
相当于薄压缩层:h 0.5b
b,z/b 0, αsz=1.0
基础中点处,任意深度处的附加
应力均等于p0,即在大面积荷载
作用下,地基中附加应力分布与 深度无关。
成层 H
均匀 E1
E2>E1
23
2.变薄交互层地基(各向异性地基) • 当Ex/Ez<1 时,应力集中——Ex相对较小,不利于应力扩散 • 当Ex/Ez>1 时,应力扩散——Ex相对较大,有利于应力扩散
24
3.双层地基(非均质地基)
(1)上层软弱,下层坚硬的成层地基 ▪ 中轴线附近σz比均质时明显增大的现象
21
条形荷载与矩形荷载的附加应力对比图
表明荷载作 用面积越大 附加应力传 递的越深。
22
2.3.4 地基附加应力的应用讨论
1.变形模量随深度增大的地基(非均质地基)
B
应力计算

§4.3 地基中附加应力的计算 一. 竖直集中力作用下的附加应力计算-布辛内斯克课题
z
3P 2
z3 R5
zy
3P 2
yz 2 R5
zx
Ph
分解为竖直向和水平向荷 载,水平荷载引起的基底 水平应力视为均匀分布。
根据上述概念,基底平均附加压力p0 可按下式计算
p0 p cd p md (1-19)
式中 p—基底平均压力,kPa;
cd—基底处土中自重应力,kPa; m—基底标高以上天然土层的加权平均重
度,kN/m3; d—从天然地面算起的基础埋深,m。
P A
1
6e B
pmin
P 1 A
6e B
pmax
min
P A
1
6e B
P
矩形面积单向偏心荷载
P
P
土不能承 受拉应力
B
B
e
e
x
Lx
L
y
y
pmax
pmin 0 pmax
pmin 0
e<B/6: 梯形
e=B/6: 三角形
B
压力调整
Ke
基底
x
L
压力
K=B/2-e
合力
与总
3K y pmin 0
荷载 相等
pmax
2P
2P
pmax 3KL 3(B 2 e)L
e>B/6: 出现拉应力区
条形基础竖直偏心荷载
e P
B
p(x) P Mx BI
pmax
min
P 1 B
土力学-地基中的应力计算概述

基础传至地 基的荷载
地基
基础 埋深
(1)集中荷载作用下的解 ( Boussinesq 解,1885 )
P
x
r
y
x
y
R
z
z
• 位移解
ux4PG[R xz3(12)R(Rxz)]
uz
4PG[R z23
(1)1]
R
Valentin Joseph Boussinesq (1842-1929)
法国著名物理家和数学 家,对数学物理、流体力学 和固体力学都有贡献。
a
a
a
b
角点
b
p
b
中心点
1
2
34
任意点
z
z
z
k(a , b
z) b
p
z
z
z
4k(a, b
2z) b
p
z z
k k1 k2 k3 k4
z k p
3)矩形线性荷载 (角点下)
角点
b
角点
p
z
a
z
p
z
k(b , a
z) a
p
查表计算
3. 应力计算小结
(1)自重应力及均匀满布荷载作用下的附加应力,可利用平衡方程 等通过简单方法获得。
(2)线状荷载作用下的应力(Flamant解)
p
1)属平面应变问题,即:
a. 应变 y 0 。
dP pdy
b. 位移、应力等量仅与坐标
x、z有关。
x
2)利用Boussinesq解,通过 沿荷载分布线积分得到应力。
x - dx=2p(x2x2zz2)2
y
xz
2p
《土力学》课后习题答案

1-1 解:
(1)A试样
(1) B试样
1-2解:
已知: =15.3g =10.6g =2.70
饱和 =1
又知: 15.3-10.6=4.7g
(1) 含水量
= =0.443=44.3%
(2) 孔隙比
(3) 孔隙率
(4) 饱和密度及其重度
(5) 浮密度及其重度
(6) 干密度及其重度
1-3 解:
1-4 解:
20.58
(5) 确定压缩层厚度。
由表1可知,在第4计算点处 ,所以,取压缩层厚度为10.5m。
(6) 计算各分层的平均自重应力和平均附加应力(详见表2)。
(7) 由图4-29根据 和 分别查取初始孔隙比e1i和压缩稳定后的孔隙比e2i(结果见表2)。
表2 各分层的平均应力及其孔隙比
层号
层厚
(m)
平均自重应力
e2i
0-1
3.0
85.5
20.31
105.81
0.836
0.812
1-2
3.0
129.0
26.55
155.55
0.776
0.753
2-3
3.0
160.5
30.79
191.29
0.749
0.618
表4 基础侧边2下各分层的平均应力及其孔隙比
层号
层厚
(m)
平均自重应力
(kPa)
平均附加应力
(kPa)
加荷后的总应力
(1)甲基础在O点下2m处引起的竖向附加应力:
由于O点位于基础中心,荷载为梯形荷载,在O点的竖向附加应力和梯形荷载平均得的均布荷载相等,即可取 pn=(100+200)/2=150kPa
土力学清华版第2章 土体中的应力计算
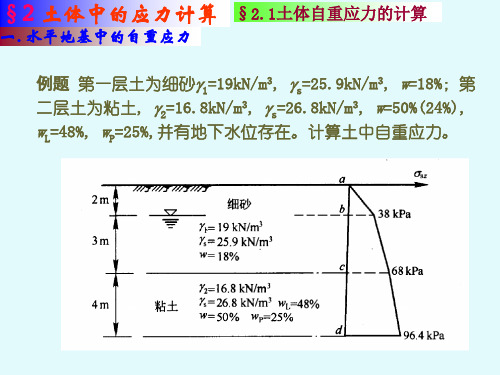
94.0 83.8 57.0 31.6 18.9 12.3
1200 1200 1600 1600 1600
25.6 44.8 60.2 71.7 83.2
88.9 70.4 44.3 25.3 15.6
114.5 115.2 104.5 97.0 98.8
0.970 0.960 0.954 0.948 0.944
a点:z=0,sz= z=0; b点:z=2m,sz=192=38kPa; c点:z=5m,sz=192+103=68kPa; d点:z=9m,sz=192+103+7.14=96.4kPa 分布如图:
§2 土体中的应力计算
§2.3地基中附加应力的计算
例题 土体表面作用一集中力F=200kN,计算地面深度 z=3m处水平面上的竖向法向应力z分布,以及距F作用点 r=1m处竖直面上的竖向法向应力z分布。
§3.3 地基的最终沉降量计算 四、例题分析 5.计算基础中点下地基中附加应力
7.2
6.确定沉降计算深度zn 根据σz = 0.2σc的确定原则,由计算结果,取zn=7.2m 7.最终沉降计算 根据e-σ曲线,计算各层的沉降量
§3土的压缩性与地基沉降计算
z( m ) 0 1.2 2.4 4.0 5.6 7.2 h σc σz σz+ σc e1 ( kPa ) ( mm ) (kPa) (kPa) (kPa) (kPa)
§2.3地基中附加应力的计算
四. 矩形面积三角形分布荷载作用下的附加应力计算
三角形分布荷载AFD作用在aeOh和ebfO上: z2=z2(aeOh)+
z2(ebfO)=p1(t1+t2)
z2=33.3(0.021+0.045)=2.2kPa
土力学与地基基础土的自重应力计算

?z ??
F Z2
α-集中力作用下地基的附加应力系数,查 3.1表
3.2 土的自重应力计算
在荷载作用之前,地基中存在 初始应力场 。初始应力场常与 土体自 重、地基土地质历史 以及地下水位 有关。在工程应用上,计算初始应力 场时常假设天然地基为 水平 、均质、各向同性 的半无限空间 ,土层界面 为水平面。于是在任意竖直面和水平面上均 无剪应力存在。 假设前提: 假设土(岩)体为均匀连续介质,并为半无限空间弹性体。 地面
?
?
3
2?
1
?
5
? ?1 ?
?
? ??
r z
2
? ??
?2 ? ?
一、竖向集中力下的地基附加应力 2、多个竖向集中力下的地基附加应力
?z?
1 z2
? n
? i?1
i Fi
例2:在地基中作用有一集中力 P=100kN,求:(1)在地基中z=2m的水平 面上,水平距离 r=0 ,1,2,3,4m 处各点的附加应力,并绘出分布图;
p min
lb
l
e? M F ?G
三、基底压力的简化计算
2、偏心荷载下的基底压力
(1) e<L/6, 应力呈梯形分布
pmax ? F ? G (1? 6e )
pmin
lb
l
(2) e=L/6, 应力呈三角形分布
pmax
?
2(F ? lb
G)
均质土的自重应力二
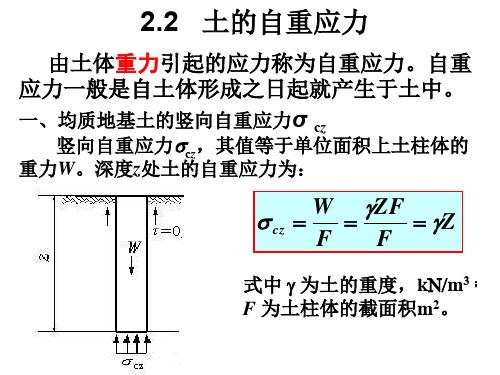
w
h w
例题 2-1
某土层及其物理性质指标如图所示,地下水位 在地表下1.0 m,计算土中自重应力并绘出分布
a 点:s cz h 0
b
s
点:
cz 1h1
18.6 1
18.6kpa
s cz 1h1 2h2
c 点: 18.6 (18.8 10) 1
地下水位以上的土层取天然重度γ,地下水位 以下的土层取有效重度γ`( γ` = γsat- γw) γ w=10kN/m3或9.8kN/m3
二、 成层地基土的自重应力
s cz 1h1 2h2 3h3 i hi
成层土地基中,竖 直向自重应力也是 随深度的增加而增 大,但沿铅垂线的 分布图是一条折线, 转折点在不同土层 的分界面上
应力的变化?如何影响?
第三节 基础底面压力
建筑物荷载通过基础传递给地基的压力称为 基底压力,与此相对应的地基土对基础底面的 反作用力称为地基反力。
F
基础
G
地基
第三节 基础底面压力
建筑物荷载通过基础传递给地基的压力称为
基底压力,与此相对应的地基土对基础底面的
反作用力称为地基反力。
F
基础
基础
基底压 力
2、偏心荷载作用下基底压力:
A
pmax F G M F G ( 1 6e )
pmin
AW
lb
b
Fk—作用在基础顶面形心的竖向力值. Gk-基础自重及台阶回填土总重,
Gk G Ad G 20kN / m 3
式中l,b为基底平面的长边与宽边尺寸。
在b方向偏心.
荷载偏心方向边长为b.
土的自重应力

3dP z 3 3 p z 3 d z dxdy 5 5 2 R 2 R
将它对整个矩形荷载面A进行积分:
3 p0 z 3 z d z 2 A
得:
z Kc p0
1 2 dxdy 2 2 5/2 (x y z ) 0 0
上海市土力学与地基基础精品课程
p0 p c p 0d
基底附加压力
上部荷载F 基础自重G
基底压力
地基中各点附加压力
式中:p —基底平均压力设计值(kPa); c —土中自重应力标准值,基底处: c 0d (kPa) 0 —基础底面标高以上天然土层的加权重度, 0 i hi / hi 其中地下水位下土层的重度取有效重度; d —基础埋深,必须从天然地面算起,对于新填土场地则应 从老天然地面起算,d=h1+h2+...+hn(m)。
均布矩形荷载下任意点的应力计算
利用角点下的应力计算公式和应力叠加原理,推求地基中 任意点的时加应力的方法称为
计算点在荷载面内:
p II I z
III IV
o
III IV
o
II I
z K cⅠ KcⅡ Kc Ⅲ K cⅣ p
上海市土力学与地基基础精品课程
/sub/soil/new/index.php
/sub/soil/new/index.php
分析步骤I:
F=400kN/m 0.1m M=20kN •m
1.5m 2m
0 =18.5kN/m3
荷载偏心距 e=M/(F+G)
基础及上覆 土重G= GAd
1.基底压力计算
条形基础取单 位长度计算
pmax pmin
土力学第二版课后习题答案

∴ 2.70 1.01110.791.51s s w d d G e ρρρρ⨯=-=-=-= ∴ 0.7929.3%2.70sat s e G ω=== 1.60100150.91110.06s m V m g ρωω⨯====+++∴ (29.3%6%)150.935.2w s m m g ω∆=∆=-⨯=1-4 解:w Sm mω=w Sm m m =-sSm m mω=-∴ 1000940110.06s m m g ω===++ 0.16ω∆=∴ 0.16940150w s m m g ω∆=∆=⨯=1-5 解:(1)31.771.61/110.098d g cm w ρρ===++∴ 0 2.7 1.01110.681.61s s w d d G e ρρρρ⨯=-=-=-= (2) 00.6825.2%2.7sat s e G ω=== (3) max 0max min 0.940.680.540.940.46r e e D e e --===-- 1/32/3r D <<∴ 该砂土层处于中密状态。
1-6 解:1. 1S d G eωρρ=+ S r G e S ω=∴0.15 2.750.8250.5A e ⨯== 0.06 2.680.5360.3B e ⨯==32.75 1.50/10.825dA g cm ρ==+ 32.681.74/10.536dB g cm ρ==+ (1)d ρρω=+∴ 3(1) 1.50(10.15) 1.74/A dA A g cm ρρω=+=⨯+= 3(1) 1.74(10.06) 1.84/B dB B g cm ρρω=+=⨯+= A B ρρ<∴ 上述叙述是错误的。
2.32.75 1.50/10.825dA g cm ρ==+ 32.681.74/10.536dB g cm ρ==+dA dB ρρ<∴ 上述叙述是错误的。
土层各层底面处的自重应力

土层各层底面处的自重应力1. 什么是自重应力?自重应力,听上去是不是有点高大上?其实它就是土壤因为自己的重量而产生的压力。
想象一下,咱们站在地上,脚下的土层也在“默默地”承受着咱们的体重。
土层越厚,压力就越大,像是那种你跟朋友一起去吃自助餐,结果他点了满满一盘子,旁边的桌子都快垮掉的感觉。
土壤也有它的承受极限,超过这个极限,那就麻烦了!2. 自重应力的计算2.1 基本概念说到计算自重应力,咱们得用上一个公式,这就像是做数学题,没公式可不行。
自重应力的计算通常是基于土层的厚度和土壤的密度。
密度就像是你喝的饮料,重的喝多了,肚子可受不了。
土壤的密度越大,产生的应力也越大。
可以用公式:σ = γ * h 来表示,其中σ是自重应力,γ是单位重,h是土层厚度。
说白了,就是把土的重量分摊到每一平方厘米上。
2.2 影响因素自重应力受很多因素影响,像土层的种类、湿度、温度等等。
想象一下,夏天和冬天你穿的衣服不一样,土壤也有“季节变化”。
湿土和干土的密度不同,湿土就像你下雨天穿的雨鞋,沉甸甸的。
这样一来,自重应力也随之变化,没准儿有时候都能给你个“意外惊喜”。
3. 自重应力的应用3.1 工程建设自重应力在建筑工程中可是个大角色。
你想啊,咱们要建房子,首先得知道土层能不能承受这房子的重量。
这就好比咱们买房子得看房子的结构一样,不能随便找个地方就盖上去。
要不然,等房子竣工时,底下的土层可能会大喊:“我撑不住了!”那就惨了。
3.2 土层调查在实际应用中,土层调查也是个关键环节。
工程师们就像侦探一样,要去勘探每一层土的情况。
通过钻探、取样等方式,他们能知道每一层土的厚度、密度,甚至是它的“脾气”。
这样一来,咱们就能根据土层的情况,合理规划建筑设计。
这样就不怕土壤在关键时刻掉链子。
4. 结语总之,自重应力虽然听起来复杂,其实生活中随处可见,咱们也能从简单的日常生活中找到它的影子。
就像是那些年咱们在学校学的数学公式,其实都是为了解决生活中的各种问题。
附加应力与自重应力

自重应力:建筑物修建以前,地基中由土体本身的有效重量所产生的应力。
附加应力:建筑物修建以后,(建筑物荷载、交通荷载、地下水的渗流力、地震力等) 外荷载在地基中引起的应力,所谓的“附加”是指在原来自重应力基础上增加的压力。
均质地基土的自重应力: 当地基为成层土体时,设各土层的厚度为hi ,重度为g i ,则在深度z 处土的自重应力计算公式为:计算点在地下水位下时,由于水对土体有浮力作用,则下部分柱体取有效重度,即不透水层层面的自重应力按上覆土层的水土总重计算:● 如果基础砌置在天然地面上,那末全部基底压力就是新增加于地基表面的基底附加压力。
● 埋置在天然地面下一定深度处的的基底压力中应扣除基底标高处原有的土中自重应力后,才是基底平面处新增加于地基的基底附加压力 ,Zcz ⋅=γσzz wcz')(γγγσ=-=G=γ GAd 取室内外平均埋深计算,A=LB=20kN /m 3,但在地下水位以下取10kN /m 3A =lb — 基底面积,条形基础取l =1m 。
当e<l/6时,pmax ,pmin>0,基底压力呈梯形分布当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布Gγp p minp p mine <l /6⎪ ⎭⎫⎝ ⎛ ± + = l e bl G F p p 6 1 min max pmin =0P0:基底附加应力γ0d:自重应力P:基底压力⏹将倾斜偏心荷载的合力分解成竖向分量和水平分量。
⏹竖向分量引起的基底压力按竖直偏心荷载的计算公式计算⏹水平分量引起的基底压力按下式计算⏹当l/b≥10视为平面问题沉降计算深度zn的确定:①一般土层:σz=0.2 σc;②软粘土层:σz=0.1 σc;③至基岩或不可压缩土层。
用e~p曲线法计算地基的沉降量计算步骤(1)首先根据建筑物基础的形状,结合地基土层性状,选择沉降计算点的位置;再按作用在基础上荷载的性质(中心、偏心或倾斜等),求出基底压力的大小和分布。
自重应力确定深度计算公式

自重应力确定深度计算公式在地球科学和土木工程领域中,确定地下深度是非常重要的。
深度的计算可以帮助工程师和科学家们了解地下岩石和土壤的性质,从而为建筑和地质勘探提供重要的信息。
而自重应力是一个重要的参数,它可以帮助我们确定地下深度。
本文将介绍自重应力的概念,以及确定深度的计算公式。
自重应力的概念。
自重应力是指由于地球引力作用于岩石和土壤颗粒之间的相互作用而产生的应力。
在地下深度较大的地方,岩石和土壤受到的自重应力会非常大。
自重应力的大小取决于岩石和土壤的密度和厚度,以及地下深度。
在地球科学和工程领域中,我们通常使用自重应力来确定地下深度。
自重应力的计算公式。
确定地下深度的计算公式通常涉及到自重应力。
下面将介绍一些常用的自重应力确定深度计算公式。
1. 自重应力的基本公式。
自重应力的基本公式可以表示为:σ = ρ g h。
其中,σ表示自重应力,ρ表示岩石或土壤的密度,g表示重力加速度,h表示地下深度。
根据这个公式,我们可以通过已知的岩石或土壤密度和地下深度来计算自重应力。
2. 自重应力的垂直分布公式。
在地下深度较大的地方,自重应力的垂直分布可以用以下公式表示:σ(z) = σ0 + γz。
其中,σ(z)表示深度为z处的自重应力,σ0表示地表处的自重应力,γ表示岩石或土壤的单位重量,z表示地下深度。
根据这个公式,我们可以通过已知的地表自重应力和岩石或土壤的单位重量来计算任意深度处的自重应力。
3. 自重应力的水平分布公式。
在地下深度较大的地方,自重应力的水平分布可以用以下公式表示:σ(x) = K γ H。
其中,σ(x)表示距离地表x处的自重应力,K表示地下应力系数,γ表示岩石或土壤的单位重量,H表示地下深度。
根据这个公式,我们可以通过已知的地下应力系数、岩石或土壤的单位重量和地下深度来计算任意距离地表处的自重应力。
应用举例。
下面通过一个具体的应用举例来说明如何使用自重应力确定深度计算公式。
假设某地区的岩石密度为2.5 g/cm³,重力加速度为9.8 m/s²,地下深度为1000 m。
土层自重应力和深度的关系公式

土层自重应力和深度的关系公式
土层自重应力和深度的关系公式是指在不同深度下土层的自重
应力大小的计算公式。
通常来说,随着深度的增加,土层的自重应力也会逐渐增加。
因此,深度和自重应力之间的关系可以表示为一个函数式,具体公式如下:
σz = γz × z
其中,σz为土层在深度 z 处的自重应力,γz为土层在深度 z 处的体积密度,z为深度。
该公式表明,土层的自重应力正比于深度和体积密度的乘积。
需要注意的是,不同类型的土层在体积密度上有所不同,因此在计算自重应力时需要选择相应的体积密度值。
另外,在实际应用中,还需要考虑土层的压缩性和孔隙水压力等因素对自重应力的影响。
- 1 -。
平均自重应力

平均自重应力平均自重应力是指单位面积上所承受的重力大小,是一个土力学中的重要概念。
本文将从平均自重应力的定义、计算公式、影响因素以及工程中的应用等方面进行探讨。
一、平均自重应力的定义平均自重应力是指土体内单位面积上由于土体自身重力所产生的应力。
在垂直于地表的方向上,土体受到的重力会使土体内部发生应力传递,从而形成平均自重应力。
平均自重应力是土体的基本应力状态之一,对土体的力学性质和稳定性具有重要影响。
平均自重应力的计算公式为:σ = γ * h,其中σ表示平均自重应力,γ表示土体的单位重量,h表示土体的深度。
这个公式表明,平均自重应力与土体的单位重量和深度成正比,单位重量越大、深度越深,则平均自重应力越大。
三、平均自重应力的影响因素1.土体的物理性质:土体的单位重量是影响平均自重应力的重要因素之一。
不同种类的土体具有不同的单位重量,例如黏土的单位重量通常较大,而砂土的单位重量较小。
2.土体的深度:土体的深度也是影响平均自重应力的因素之一。
深度越大,土体受到的重力越大,从而平均自重应力也越大。
3.土体的湿度:土体的湿度也会对平均自重应力产生影响。
湿度较大时,土体的单位重量会增加,从而平均自重应力也会增大。
四、平均自重应力在工程中的应用平均自重应力是土力学中的重要参数,广泛应用于工程实践中。
在土体力学分析和设计中,平均自重应力是计算土体稳定性、承载力和变形等问题的基础。
例如,在地基工程中,计算地基承载力时需要考虑土体的平均自重应力;在挖掘工程中,需要对土体的平均自重应力进行评估,以保证工程的稳定性。
总结起来,平均自重应力是土体内单位面积上由于土体自身重力所产生的应力。
它的计算公式为σ = γ * h,受到土体的物理性质、深度和湿度等因素的影响。
在工程中,平均自重应力是土体力学分析和设计的基础,对于保证工程的稳定性和可靠性起着重要作用。
通过对平均自重应力的研究和应用,可以更好地理解土体力学的基本原理,为工程实践提供科学依据。
