第三章土中应力计算习题及答案解析
第三章 土体中的应力计算(1-3节)

3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时,这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1.三维应力状态(空间应力状态)
局部荷载作用下,地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时,根据弹 性体应力叠加原理求出附加应力的总和
26
(二)水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
(一)矩形面积竖直均布荷载 1.角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为(水表平3向-5应)力,m分布x ,系n 数z和。
BB
55
P
56
57
(三)条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理, 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况:计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点,然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
土力学地基基础章节计算题及答案

章节习题及答案第一章 土的物理性质1 有一块体积为60 cm 3的原状土样,重 N, 烘干后 N 。
已只土粒比重(相对密度)s G =。
求土的天然重度、天然含水量w 、干重度d、饱和重度sat、浮重度’、孔隙比e 及饱和度S r解:分析:由W 和V 可算得,由W s 和V 可算得d,加上G s ,共已知3个指标,故题目可解。
363kN/m 5.1710601005.1=⨯⨯==--V W γ 363s d kN/m 2.1410601085.0=⨯⨯==--V W γ 3w sws kN/m 7.261067.2=⨯===∴γγγγs s G G%5.2385.085.005.1s w =-==W W w 884.015.17)235.01(7.261)1(s =-+=-+=γγw e (1-12) %71884.06.2235.0s =⨯=⋅=e G w S r (1-14) 注意:1.使用国际单位制; 2.w为已知条件,w=10kN/m 3;3.注意求解顺序,条件具备这先做; 4.注意各的取值范围。
2 某工地在填土施工中所用土料的含水量为5%,为便于夯实需在土料中加水,使其含水量增至15%,试问每1000 kg 质量的土料应加多少水 解:分析:加水前后M s 不变。
于是:加水前: 1000%5s s =⨯+M M (1)加水后: w s s 1000%15M M M ∆+=⨯+ (2)由(1)得:kg 952s =M ,代入(2)得: kg 2.95w =∆M 注意:土料中包含了水和土颗粒,共为1000kg ,另外,swM M w =。
3 用某种土筑堤,土的含水量w =15%,土粒比重G s =。
分层夯实,每层先填0.5m ,其重度等=16kN/ m 3,夯实达到饱和度r S =85%后再填下一层,如夯实时水没有流失,求每层夯实后的厚度。
解:分析:压实前后W s 、V s 、w 不变,如设每层填土的土颗粒所占的高度为h s ,则压实前后h s 不变,于是有:2211s 11e he h h +=+=(1) 由题给关系,求出:919.0116)15.01(1067.21)1(s 1=-+⨯⨯=-+=γγw e 471.085.015.067.2s 2=⨯==r S w G e 代入(1)式,得: m 383.05.0919.01471.011)1(1122=⨯++=++=e h e h4 某砂土的重度s γ=17 kN/ m 3,含水量w =%,土粒重度s γ= kN/ m 3。
《土力学》课后习题及详细解答

《土力学》课后习题答案第一章1-1:已知:V=72cm3m=129.1g m s=121.5g G s=2.70则:129.1121.56.3%121.5ssm mwm--===3333 129.1*1017.9/72121.5452.77245271.0*27121.5*1020.6/72sssV ssat w V ssat satmg g KN mvmV cmV V V cmm V mg g g KN mV Vγρρργρ========-=-=++=====3320.61010.6/121.5*1016.9/72sat wsdsat dKN mmg KN mVγγγγγγγγ'=-=-===='>>>则1-2:已知:G s=2.72 设V s=1cm3则33332.72/2.722.72*1016/1.72.720.7*1*1020.1/1.720.11010.1/75%1.0*0.7*75%0.5250.52519.3%2.720.525 2.721.sssd ds V wwrw w V rwsw sg cmm gmg g KN mVm Vg g KN mVKN mm V S gmwmm mg gVργρργργγγργρ======++===='=-=-========++===当S时,3*1019.1/7KN m=1-3:3477777331.70*10*8*1013.6*1013.6*10*20%2.72*1013.6*10 2.72*10850001.92*10s d w s s wm V kg m m w kg m m V m ρρ======++==挖1-4: 甲:33334025151* 2.72.7*30%0.81100%0.812.70.811.94/10.8119.4/2.71.48/1.8114.8/0.81p L P s s s s w r wV ws w s w s d s w d d vsI w w V m V g m g S m V m m g cm V V g KN m m g cm V V g KN m V e V ρρργρργρ=-=-=======∴==++===++=====+====设则又因为乙:3333381 2.682.68*22%0.47960.47962.680.47962.14/10.47962.14*1021.4/2.681.84/1.47961.84*1018.4/0.4796p L p s s s s w s V s w s V s d s w d d VsI w w V m V g m m w g V cm m m g cm V V g KN m m g cm V V g KN m V e V ρργρργρ=-========++===++======+=====设则则γγ∴<乙甲 d d γγ<乙甲 e e >乙甲 p p I I >乙甲则(1)、(4)正确1-5:1s w d G eρρ=+ 则2.7*1110.591.7022%*2.7185%0.59s wds r G e wG S e ρρ=-=-====>所以该料场的土料不适合筑坝,建议翻晒,使其含水率降低。
土力学-第三章-土中应力计算详解

基本假定
地基土是各向同性、均质、半无限空间弹性体 地基土在深度和水平方向都是无限的
地 表 临 空
地基:均质各向同性线性变形半空间体
应用弹性力学关于弹性半空间的理论解答
1.均质土竖向自重应力
若将地基视为均质半无限空间弹性体,土体在自重作用下只能产 生竖向变形,而无侧向位移及剪切变形存在,因此在深度z处平面上, 土体因自身重力产生的竖向应力等于单位面积上土柱体的重力。
3.水平向自重应力
天然地面
地基土在重力作用下,除承受 作用于水平面上的竖向自重应力外, 在竖直面上还作用有水平向自重应 力。由于土柱体在重力作用下无侧 向变形和剪切变形,因此可以证明 侧向自重应力与竖向自重应力成正 比,剪应力均为零。
cz z
cx cy K0 cz
cz
z
cx
cy
侧压力系数或静止 土压力系数
4 地下水位升降对自重应力的影响
自重应力分布曲线的变化规律
土的自重应力分布曲线是一条折线,拐点在土 层交界处和地下水位处。
同一层土的自重应力按直线变化。
自重应力随深度的增加而增大。
【例题3-1 】计算自重应力,并绘分布图。
4. 例题分析 【例】一地基由多层土组成,地质剖面如下图所示,试计算并绘制 自重应力σcz沿深度的分布图。
57.0kPa
80.1kPa
103.1kPa 150.1kPa 194.1kPa
cz 1h1 2 h2 n hn i hi
i 1
n
均质地基
1 (
1
2)
2 2
成层地基
3.2 基底压力与基底附加应力
上部结构
土力学 第三章习题答案
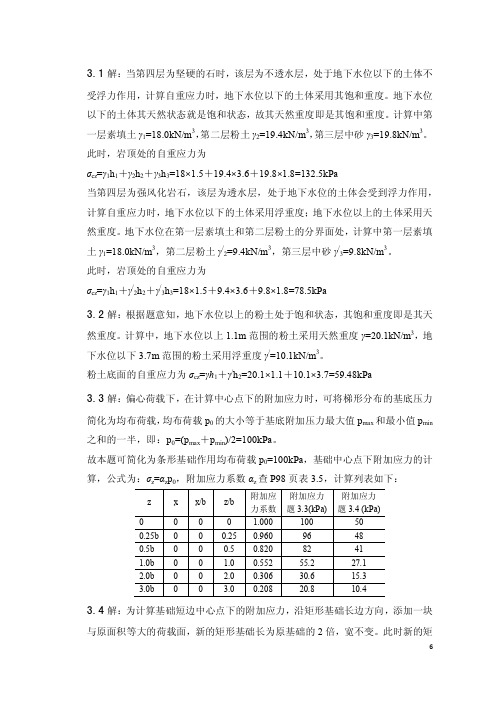
3.1解:当第四层为坚硬的石时,该层为不透水层,处于地下水位以下的土体不受浮力作用,计算自重应力时,地下水位以下的土体采用其饱和重度。
地下水位以下的土体其天然状态就是饱和状态,故其天然重度即是其饱和重度。
计算中第一层素填土γ1=18.0kN/m3,第二层粉土γ2=19.4kN/m3,第三层中砂γ3=19.8kN/m3。
此时,岩顶处的自重应力为σcz=γ1h1+γ2h2+γ3h3=18×1.5+19.4×3.6+19.8×1.8=132.5kPa当第四层为强风化岩石,该层为透水层,处于地下水位的土体会受到浮力作用,计算自重应力时,地下水位以下的土体采用浮重度;地下水位以上的土体采用天然重度。
地下水位在第一层素填土和第二层粉土的分界面处,计算中第一层素填土γ1=18.0kN/m3,第二层粉土γ/2=9.4kN/m3,第三层中砂γ/3=9.8kN/m3。
此时,岩顶处的自重应力为σcz=γ1h1+γ/2h2+γ/3h3=18×1.5+9.4×3.6+9.8×1.8=78.5kPa3.2解:根据题意知,地下水位以上的粉土处于饱和状态,其饱和重度即是其天然重度。
计算中,地下水位以上1.1m范围的粉土采用天然重度γ=20.1kN/m3,地下水位以下3.7m范围的粉土采用浮重度γ/=10.1kN/m3。
粉土底面的自重应力为σcz=γh1+γ/h2=20.1×1.1+10.1×3.7=59.48kPa3.3解:偏心荷载下,在计算中心点下的附加应力时,可将梯形分布的基底压力简化为均布荷载,均布荷载p0的大小等于基底附加压力最大值p max和最小值p min 之和的一半,即:p0=(p max+p min)/2=100kPa。
故本题可简化为条形基础作用均布荷载p0=100kPa,基础中心点下附加应力的计算,公式为:σz=αz p0,附加应力系数αz查P98页表3.5,计算列表如下:3.4解:为计算基础短边中心点下的附加应力,沿矩形基础长边方向,添加一块与原面积等大的荷载面,新的矩形基础长为原基础的2倍,宽不变。
土力学第三章土中应力计算详解

作用于基础底面 形心上的力矩
M=(F+G)∙e
e e b
l
pmax
pmax F G M
pmin
AW
基础底面的抵 抗矩;矩形截 面W=bl2/6
pmin
.
pm ax FG16e pmin bl l
23
讨论
pmax FG16e
pm in
bl
l
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布
土力学
第三章 土中应力计算
.
1
第三章 土中应力计算
3.1 土的自重应力 3.2 基底压力 3.3 地基附加应力 3.4 有效应力原理
.
2
概述
地基变形的原因是由于土体具有可压缩性的内 在因素和地基受到附加压力的作用的外在因素。
为了计算地基沉降以及对地基进行强度与稳定 性分析,必须知道土中应力分布。土中应力包括土的 自重应力和附加应力(新增应力) 。
一. 影响因素
基底压力
•大小 •方向 •分布
荷载条件
基础条件
•刚度 •形状 •大小 •埋深
地基条件
•土类
•密度
•土层结构. 等
17
基底压力分布
弹性地基,完全柔性基础
弹性地基,绝对刚性基础
.
18
基底压力分布
弹塑性地基,有限刚度基础
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
中产生的应力增量。
土力学与地基基础-第三章.土中应力分布及计算解析

从上式可知,自重应力随深度z线性增
加,呈三角形分布图形。
2019/8/25
土中自重应力的计算
8
3.2 土中自重应力的计算
2. 成层土的压力计算
地基土通常为成层土。当地基为成层土体时,设各土层
的厚度为hi,重度为 ,则在i 深度z处土的自重应力计算公式 为:
n
cz ihi i 1
剪应力
xy
yx
3Q xyz
2
R5
1 2 3
xy(2R z)
R3
(
R
z)2
yz
zy
3Q 2
yz 2 R5
ZX
XZ
3Q 2
xz 2 R5
3.4 集中力作用下土中应力计算
X、Y、Z轴方向的位移
分别为:
刚性基础在中心载荷作用下,地基反力呈马鞍形,随着外 力的增大,其形状相应改变。如下图
2019/8/25
基础底面压力的分布和计算
15
3.3 基础底面压力的分布和计算
2019/8/25
基础底面压力的分布和计算
16
3.3 基础底面压力的分布和计算
2. 地基反力的简化计算方法
根据弹性理论的圣维南原理及土中实测结果,当作用在 基础上的总载荷为定值时,地基反力分布的形状对土中 应力分布的影响,只在一定深度范围内,当基底的深度 超过基础宽度的1.5-2.0倍时,它的影响已不显著。因此, 在实用上采用材料力学方法,即将地基反力分布认为是 线性分布的简化计算方法。
因此,基底附加压力p0是上部结构和基础传到基底的地基反力 与基底处原先存在于土中的自重应力之差(新增加的应力)(如图)
土力学-第三章地基中的应力计算2

宽度积分
条形面积竖向均布荷载
圆形面积竖向均布荷载 水平集中力 矩形内积分 矩形面积水平均布荷载
特殊荷载:将荷载和面积进行分 解,利用已知解和叠加原理求解
20
附加应力的分布规律——以带状荷载为例
(1)自重应力及均匀 满布荷载作用下的附 加应力的计算公式利 用对称性获得。 (2)以Boussinesq解 为基础,可得到线状、 带状、局部面积荷载 作用下的附加应力。 (3)线状、带状、局 部面积荷载作用下的 附加应力在水平方向 及深度方向逐渐衰减, 而均匀满布荷载产生 的附加应力不变。
(4)o点位于矩形面积边缘
o
A
B
z (k A kB ) p
(5)o点位于矩形面积外边缘
h
i
d
g
z (kabef kcefd kafgh kdfgi ) p
a
o
f
b
c
e
18
6. 矩形面积三角形分布荷载作用下的附加应力计算
y
z
b
0
a z 0 d z z ( pt , b , b )
8
竖直集中力-布辛涅斯克解
z
3 1 P P K 2 2 [1 ( r / z ) 2 ]5 / 2 z 2 z
P
σz与α无关,呈轴 对称分布 P作用线上
在某一水平面上 在r﹥0的竖直线上 z等值线-应力泡
应力泡
0.1P 0.05P 0.02P 0.01P
9
对于多个竖直集中力作用时可采用叠加原 理求解附加应力
xy xz yz 0
xz yz z x y z
(也可直接建立土柱 的受力平衡关系得到)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章土中应力计算一、填空题1.由土筑成的梯形断面路堤,因自重引起的基底压力分布图形是梯形,桥梁墩台等刚性基础在中心荷载作用下,基底的沉降是相同的。
2.地基中附加应力分布随深度增加呈曲线减小,同一深度处,在基底中心点下,附加应力最大。
3.单向偏心荷载作用下的矩形基础,当偏心距e > l/6时,基底与地基局部脱开,产生应力重分部。
4.在地基中,矩形荷载所引起的附加应力,其影响深度比相同宽度的条形基础浅,比相同宽度的方形基础深。
5.上层坚硬、下层软弱的双层地基,在荷载作用下,将发生应力扩散现象,反之,将发生应力集中现象。
6.土中应力按成因可分为自重应力和附加应力。
7.计算土的自重应力时,地下水位以下的重度应取有效重度(浮重度)。
8.长期抽取地下水位,导致地下水位大幅度下降,从而使原水位以下土的有效自重应力增加,而造成地基沉降的严重后果。
\9.饱和土体所受到的总应力为有效应力与孔隙水压力之和。
二、名词解释1.基底附加应力:基底压应力与基底标高处原土层自重应力之差。
2.自重应力:由土层自身重力引起的土中应力。
3.基底压力:建筑物荷载通过基础传给地基,在基础底面与地基之间的接触应力。
三、选择题1.成层土中竖向自重应力沿深度的增大而发生的变化为:(B )(A)折线减小(B)折线增大(C)斜线减小(D)斜线增大—2.宽度均为b,基底附加应力均为P0的基础,同一深度处,附加应力数值最大的是:(C )(A)方形基础(B)矩形基础(C)条形基础(D)圆形基础(b为直径)3.可按平面问题求解地基中附加应力的基础是:(B )(A)柱下独立基础(B)墙下条形基础(C)片筏基础(D)箱形基础4.基底附加应力P0作用下,地基中附加应力随深度Z增大而减小,Z的起算点为:(A )(A)基础底面(B)天然地面(C)室内设计地面(D)室外设计地面5.土中自重应力起算点位置为:(B )(A)基础底面(B)天然地面(C)室内设计地面(D)室外设计地面6.地下水位下降,土中有效自重应力发生的变化是:(A )(A)原水位以上不变,原水位以下增大(B)原水位以上不变,原水位以下减小》(C)变动后水位以上不变,变动后水位以下减小(D)变动后水位以上不变,变动后水位以下增大7.深度相同时,随着离基础中心点距离的增大,地基中竖向附加应力:(D )(A)斜线增大(B)斜线减小(C)曲线增大(D)曲线减小8.单向偏心的矩形基础,当偏心距e < l/6(l为偏心一侧基底边长)时,基底压应力分布图简化为:( B )(A)矩形(B)梯形(C)三角形(D)抛物线形9.宽度为3m的条形基础,作用在基础底面的竖向荷载N=1000kN/m ,偏心距e=,基底最大压应力为:( C )(A)800 kPa (B)417 kPa (C)833 kPa (D)400 kPa10.矩形面积上作用三角形分布荷载时,地基中竖向附加应力系数K t是l/b、z/b的函数,b 指的是:( D )(A)矩形的长边(B)矩形的短边>(C)矩形的短边与长边的平均值(D)三角形分布荷载方向基础底面的边长11.某砂土地基,天然重度=18 kN/m3,饱和重度sat=20 kN/m3,地下水位距地表2m,地表下深度为4m处的竖向自重应力为:( A )(A)56kPa (B)76kPa (C)72kPa (D)80kPa12.均布矩形荷载角点下的竖向附加应力系数当l/b=1、Z/b=1时,K C=;当l/b=1、Z/b=2时,K C=。
若基底附加应力p0=100kPa,基底边长l=b=2m,基底中心点下Z=2m处的竖向附加应力为:( C )(A)(B)(C)(D)13.某中心受压条形基础,宽2m,埋深1m,室内外高差0.6m,埋深范围内土的重度=17 kN/m3,若上部结构传来荷载F=400kN/m,基底附加应力P0为:(C )(A)(B)(C)209kPa (D)215kPa14.某场地表层为4m厚的粉质黏土,天然重度=18kN/m3,其下为饱和重度sat=19 kN/m3的很厚的黏土层,地下水位在地表下4m处,经计算地表以下2m处土的竖向自重应力为( B )。
(A)72kPa (B)36kPa (C)16kPa (D)38kPa15.同上题,地表以下5m处土的竖向自重应力为(B )。
>(A)91kPa (B)81kPa (C)72kPa (D)41kPa16.某柱作用于基础顶面的荷载为800kN,从室外地面算起的基础深度为1.5m,室内地面比室外地面高0.3m,基础底面积为4m2,地基土的重度为17kN/m3,则基底压力为( C )。
(A)(B)230 kPa (C)233 kPa (D)236 kPa17.由建筑物的荷载在地基内产生的应力称为(B )。
(A)自重应力(B)附加应力(C)有效应力(D)附加压力18.已知地基中某点的竖向自重应力为100 kPa,静水压力为20 kPa,土的静止侧压力系数为,则该点的侧向自重应力为( D )。
(A)60 kPa (B)50 kPa (C)30 kPa (D)25 kPa19.由于建筑物的建造而在基础底面处产生的压力增量称为(C )。
(A)基底压力(B)基底反力(C)基底附加应力(D)基底净反力20.计算基础及上回填土的总重量时,其平均重度一般取(C )。
|(A)17 kN/m3(B)18 kN/m3(C)20 kN/m3(D)22 kN/m321.在单向偏心荷载作用下,若基底反力呈梯形分布,则偏心距与矩形基础长度的关系为( A )。
(A)(B)(C)(D)22.已知两矩形基础,一宽为2m,长为4m,另一宽为4m,长为8m,若两基础的基底附加压力相等,则两基础角点下附加应力之间的关系是( B )。
(A)两基础基底下Z深度处应力竖向应力分布相同(B)小尺寸基础角点下Z深度处应力与大尺寸基础角点下2Z深度处应力相等(C)大尺寸基础角殿下Z深度处应力与小尺寸基础焦点下2Z深度处应力相等23.当地下水位突然从地表下降至基底平面处,对基底附加应力的影响是(A )。
(A)没有影响(B)基底附加压力增大(C)基底附加压力减小24.计算土中自重应力时,地下水位以下的土层应采用(C )。
@(A)湿重度(B)饱和重度(C)浮重度(D)天然重度25.在基底附加压力的计算公式P0=P-m d,d为(D )。
(A)基础平均深度(B)从室内地面算起的深度(C)从室外地面算起的深度(D)从天然地面算起的埋深,对于新填土场地应从老天然地面算起26.只有( B )才能引起地基的附加应力和变形。
(A)基底压力(B)基底附加压力(C)有效应力(D)有效自重应力27.一矩形基础,短边b=3m,长边l=4m,在长边方向作用一偏心荷载F十G=1200 KN。
试问当P min=0时,最大压力应为多少( C )。
(A)120kN/m2(B)150KN/m2(C)200kN/m228.有一基础,宽度4m,长度8m,基底附加压力90 kN/m2,中心线下6m处竖向附加应力为m2,试问另一基础宽度为2m,长度为4m,基底附加压力为100 kN/m2,角点下6m处的附加应力为多少( A )(A)m2(B)m2(C)m229.已知一个宽b=2m,长l=4m和另一个宽b=4m,长l=8m的矩形基础底的附加应力相等,则两基础角点下竖向附加应力之间有何关系( B )*(A)两基础角点下Z深度处竖向应力分布相同(B)小基础角点下Z深度处的应力与大基础角点下2Z深度处的应力相等(C)大基础角点下Z深度处的应力与小基础角点下2Z深度处的应力相等30.当地基中附加应力曲线为矩形时,则地面荷载的形式为:( C )。
(A)条形均布荷载(B)矩形均布荷载(C)无穷均布荷载31.有一个宽度为3m的条形基础,在基底平面上作出用着中心荷载F=240kN/m及力矩M=100kN·m/m。
试问压力较小一侧基础边的底面与地基之间会不会脱开( A )(A)P min>0 (B)P min=0 (C)脱开32.有一独立基础,在允许荷载作用下,基底各点的沉降都相等,则作用在基底的反力分布应该是:( B )。
(A)各点应力相等的矩形分布(B)中间小、边缘大的马鞍形分布(C)中间大、边缘小的钟形分布{33.当地下水自下向上渗流时,土层中骨架应力有何影响( C )(A)不变(B)减小(C)增大34.有一基础埋置深度d=,建筑物荷载及基础和台阶土重传至基底总压力为100kN/m2,若基底以上土的重度为18kN/m2,基底以下土的重度为17kN/m2,地下水位在地表处,则基底竖向附加应力为多少( C )(A )85kN/m 2 (B )73kN/m 2 (C )88kN/m 235.一矩形基础,短边b =3m ,长边l =4m ,在长边方向作用一偏心荷载贯F+G =1200kN 。
偏心距为多少时,基底不会出现拉应力( C ) (A ) (B ) (C )四、判断题1.在均质地基中,竖向自重应力随深度线性增加,而侧向自重应力则呈非线性增加。
( × )2.由于土中自重应力属于有效应力,因而与地下水位的升降无关 ( √ ) ~3.在基底附加压力的计算公式中,对于新填土场地,基底处土的自重应力应从填土面算起 ( × )4.增大柱下独立基础的埋深,可以减小基底的平均附加压力 ( × )5.柱下独立基础埋深的大小对基底附加应力影响不大 ( √ )6.由于土的自重应力属于有效应力,因此在建筑物建造后,自重应力仍会继续使土体产生变形 ( × )7.土的静止侧压力系数K0为土的侧向与竖向自重应力之比 ( × )8.在弱透水土层中,若地下水位短时间下降,则土的自重应力不会明显增大 ( √ )9.基底附加压力在数值上等于上部结构荷载在基底所产生的压力增量 ( × ) 10.竖向附加应力的分布范围相当大,它不仅分布在荷载面积之下,而且还分布到荷载面积以外,这就是所谓的附加应力集中现象 ( × ) 11.矩形均匀荷载作用下基础角点下某深度处的附加应力ZA σ与基础中心点下同一深度处附加压力ZO σ的关系是:ZA σ<1/4ZO σ。
( × )]五、简答题1.地基附加应力分布规律有哪些 答:(1)附加应力不仅发生在荷载面积之下,而且分布在荷载面积以外相当大的范围之下,这就是地基附加应力的扩散分布;(2)在离基底不同深度z 处各个水平面上,以基底中心点下轴线处的σz 值最大,随离中轴线距离增大曲线减小;(3)在荷载分布范围之下任意点沿铅垂线的σz 值,随深度最大曲线减小;(4)条形荷载比相同宽度的方形荷载σz 的影响深度大,在相同深度处,条形荷载在地基中的σz 比相同宽度的方形荷载大得多。
