完全层次结构模型
数学建模——层次分析法

在大石头中的重量比)可用向量
且
n
w ( w1 , w2 ,..., wn
T 表示, )
. 显然, 的各个列向量与 w 1 A i
i 1
w
仅相差一个比例
因子。 一般地,如果一个正互反阵
A
满足 (8.2.4)
aij a jk aik , i, j, k 1, 2,..., n
则
3 计算权向量并做一致性检验
定理1
当
n 阶正互反阵 A的最大特征根 n,
时
当且仅
A为一致阵。 由于 连续的依赖于 aii ,则 比 n 大的越多, 的不 A
n
一致性越严重。用最大特征值对应的特征向量作为被比较因
素对上层某因素影响程度的权向量,其不一致程度越大,引 起的判断误差越大。因而可以用
RI。方法为:
A1 , A2 ,, A500
2.则可得一致性指标 : CI1 , CI 2 ,CI500
CI1 CI 2 CI500 RI 500
n RI
1 2 500 n 500 n 1
1 2 3 4 5 6 7 8 9 10 11 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51
aii 1 ,如用 C1 , C2 ,..., Cn
2 构造成对比较矩阵
2.比较尺度 • 当比较两个可能具有不同性质的因素 Ci 和 C j 对于一个上层 因素 O 的影响时,Saaty提出用1—9尺度(见下表),即aij 的取值范围是1,2,,9 ,及其互反数1,1/ 2,,1/ 9 。其理由 如下:
重,景色次之,居住条件再次。 问题1.怎样由成对比较阵确定诸因素 C , C ,..., C 对上层因 1 2 n 素
层次分析模型(数学建模)

第k层nk个元素对于第k-1层上第j个元素为 准则的单排序向量 uj(k)=(u1j(k),u2j(k),…,un j(k))T j=1,2,…nk-1 其中不受第j个元素支配的元素权重取零,
于是可得到nk×nk-1阶矩阵
u (k ) u21 = ( ) unk1 k
(k ) 11
1 A = ( aij ) n×n , aij > 0, a ji = aij
1/ 2 1 1/ 7 1/ 5 1/ 5 4 7 1 2 3 3 5 1/ 2 1 1
3 成对比较阵 5 A~成对比较阵 1 / 3 是正互反阵 A是正互反阵 1 1
要由A确定 要由 确定C1,… , Cn对O的权向量 确定 的权向量
1. 正互反阵的最大特征根和特征向量的性质 正互反矩阵A 是正单根, 正互反矩阵 的最大特征根λ是正单根, Ak e T 对应正特征向量w, 对应正特征向量 , lim T k = w, e = (1,1, L ,1) k →∞ e A e 定理1 定理1 正互反阵的最大特征根是正数, 正互反阵的最大特征根是正数, 特征向量是正向量。 特征向量是正向量。 定理2 定理2 n阶正互反阵 的最大特征根λ ≥ n , 阶正互反阵A的最大特征根 λ= n是A为一致阵的充要条件。 为一致阵的充要条件。 是 为一致阵的充要条件 一致性指标 CI =
“选择旅游地”思维过程的归 选择旅游地” 选择旅游地 纳 • 将决策问题分为 个层次:目标层 ,准则层 , 将决策问题分为3个层次 目标层O,准则层C, 个层次: 方案层P;每层有若干元素, 方案层 ;每层有若干元素, 各层元素间的关系 用相连的直线表示。 用相连的直线表示。 • 通过相互比较确定各准则对目标的权重,及各方 通过相互比较确定各准则对目标的权重, 案对每一准则的权重。 案对每一准则的权重。 • 将上述两组权重进行综合,确定各方案对目标的 将上述两组权重进行综合, 权重。 权重。 层次分析法将定性分析与定量分析结合起来 完成以上步骤,给出决策问题的定量结果。 完成以上步骤,给出决策问题的定量结果。
层次分析法(AHP)建模

新余高等专科学校 数学建模教练组 2005-
6
Mathematical Contest in Modeling
层次分析法
3
计算权向量并做一致性检验
什么是权重(权系数)? 在决策问题中,通常要把变量Z表成变量x1,x2, … , xn的线性组合:
z w1x1 w2 x2 wn xn
n
其中 wi 0, wi 1 w1, w2 ,...., w则n
1 例: A 1/ 2
2 1
6 4
列向量 归一化
0.6 0.3
0.615 0.308
0.545 0.364
按行求和
1.760 0.972
1/ 6 1/ 4 1
0.1 0.077 0.091
0.268
, 即为
归一化
0.587 0.324 w
0.089
1.769 Aw 0.974
0.268
1 (1.769 0.974 0.268) 3.009
比较因素的权向量,其不一致程度应在容许的范围内.如何确定这个范围?
Mathematical Contest in Modeling 第5讲: 层次分析法(AHP)建模
层次分析法基本简介 层次分析法的基本步骤
1. 建立层次结构模型 2. 构造成对比较阵(判断矩阵) 3. 计算权向量并做一致性检验 4. 计算组合权向量并做组合一致性检验
不完全层次结构模型
新余高等专科学校 数学建模教练组 (设计制作: syllen
权重(权系数)?
a. 将A的每一列向量归一化得 w~ij aij / n aij
w~ b. 对 ij
按行求和得w~i n w~ij
j 1
i 1
完全层次结构模型

层次分析模型一、层次分析法讲解在现实世界中,往往会遇到决策的问题,比如如何选择旅游景点的问题,选择升学志愿的问题等等。
在决策者作出最后的决定以前,他必须考虑很多方面的因素或者判断准则,最终通过这些准则作出选择。
比如下面的问题:例1 选择旅游地国庆节即将来临,张鶇一家准备去旅游,他们想从黄山、桂林、北戴河三个旅游景点选出一个,请帮助他们作出最佳选择。
根据什么作出选择呢?为解决这个问题,我们需要作问题的分析,以便得到选择景点要考虑的因素.问题的分析:景点的选择大体上有两方面要考虑:1、是旅游者自身的情况;2、是对景点的评价。
首先分析旅游者的情况:如果经济条件宽绰、醉心旅游,自然特别看重景色条件,那么景色在他的心目中的比重就大。
如果平素俭朴,则会优先考虑费用,即费用的比重就大.中老年旅游者还会对居住条件,旅游条件,饮食比较关注。
因此,应该考虑景色、费用、居住、饮食、旅途条件等因素在张鶇一家心目中的重要程度.如何衡量这五个因素的重要程度呢?其次,如何评价景点呢?自然应该就上面的五个因素景色、费用、居住、饮食、旅途条件对景点进行评价。
最后,还要把旅游者的情况和对景点的评价进行综合,以便选定最佳的旅游景点.可是如何综合呢?下面我们用层次分析法解决上面提出的问题。
层次分析法的第一步:建立层次分析结构模型深入分析实际问题,将有关因素自上而下分层,上层受下层影响,而层内各因素基本上相对独立,把问题条理化、层次化,构造出一个有层次的结构模型。
大体可以分成三个层次:(1)最高层(目标层):这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果;(2)中间层(准则层):这一层次中包含了为实现目标所涉及的中间环节,它还可以由若干个层次组成,包括所需考虑的准则、子准则;(3)最低层(方案层):这一层次包括了为实现目标可供选择的各种措施、决策方案等。
就本例题而言,通过上面的分析,我们可以建立如下层次模型:层次分析法的第二步:构造成对比较矩阵建立好层次后,就可以进行各因素之间的比较了.首先考虑对于选择旅游地而言,景色、费用、居住、饮食、旅途条件等准则在张鶇一家心目中的影响,即:对于第一层目标来说,第二层各因素的权重。
逻辑数据模型之层次数据模型、网状数据模型和关系数据模型(转)

逻辑数据模型之层次数据模型、⽹状数据模型和关系数据模型(转) 上⼀篇⽂章简单介绍了概念数据模型、逻辑数据模型、物理数据模型的基本概念、特性以及三者所对应的数据库的开发阶段。
现在针对逻辑数据模型中所⽤到的三种数据模型---层次数据模型、⽹状数据模型以及关系数据模型做⼀个相信的介绍与对⽐分析。
⼀、层次数据模型 定义:层次数据模型是⽤树状<层次>结构来表⽰实体类型和实体间联系的数据模型。
(来⾃百度百科) 其实层次数据模型就是的图形表⽰就是⼀个倒⽴⽣长的树,由基本数据结构中的树(或者⼆叉树)的定义可知,每棵树都有且仅有⼀个根节点,其余的节点都是⾮根节点。
每个节点表⽰⼀个记录类型对应与实体的概念,记录类型的各个字段对应实体的各个属性。
各个记录类型及其字段都必须记录。
特征:树的性质决定了树状数据模型的特征 1. 整个模型中有且仅有⼀个节点没有⽗节点,其余的节点必须有且仅有⼀个⽗节点,但是所有的节点都可以不存在⼦节点; 2. 所有的⼦节点不能脱离⽗节点⽽单独存在,也就是说如果要删除⽗节点,那么⽗节点下⾯的所有⼦节点都要同时删除,但是可以单独删除⼀些叶⼦节点; 3. 每个记录类型有且仅有⼀条从⽗节点通向⾃⾝的路径; 实例: 如图1,以学校某个系的组织结构为例,说明层次数据模型的结构。
1. 记录类型系是根节点,其属性为系编号和系名; 2. 记录类型教研室和学⽣分别构成了记录类型系的⼦节点,教研室的属性有教研室编号和教研室姓名,学⽣的属性分别是学号、姓名和成绩;3. 记录类型教师是教研室这⼀实体的⼦节点,其属性由教师的编号,教师的姓名,教师的研究⽅向。
优点: 1. 层次数据模型的结构简单、清晰、明朗,很容易看到各个实体之间的联系; 2. 操作层次数据类型的数据库语句⽐较简单,只需要⼏条语句就可以完成数据库的操作;(百度百科) 3. 查询效率较⾼,在层次数据模型中,节点的有向边表⽰了节点之间的联系,在DBMS中如果有向边借助指针实现,那么依据路径很容易找到待查的记录; 4. 层次数据模型提供了较好的数据完整性⽀持,正如上所说,如果要删除⽗节点,那么其下的所有⼦节点都要同时删除;如图1,如果想要删除教研室,则其下的所有教师都要删除; 缺点: 1. 层次数据模型只能表⽰实体之间的1:n的关系,不能表⽰m:n的复杂关系,因此现实世界中的很多模型不能通过该模型⽅便的表⽰; 2. 查询节点的时候必须知道其双亲节点的,因此限制了对数据库存取路径的控制;图 1. 院系⼈员组成结构图 ⼆、⽹状数据模型 定义:⽤有向图表⽰实体和实体之间的联系的数据结构模型称为⽹状数据模型。
数据模型及组成要素

数据模型及组成要素数据模型是描述数据结构、数据操作、数据约束和数据语义的一种抽象表示。
它定义了如何组织、存储和操作数据,以及数据之间的关系。
在计算机科学领域,常见的数据模型包括层次模型、网络模型、关系模型和对象模型等。
一、层次模型层次模型是最早出现的数据库模型之一,它将数据组织成一个树形结构。
在层次模型中,每个节点都可以有多个子节点,但只能有一个父节点。
这种父子关系反映了实际世界中的“一对多”关系。
1.1 节点在层次模型中,每个节点代表一个实体或记录。
节点可以包含属性,用于存储实体的相关信息。
在一个学生信息管理系统中,每个学生可以被表示为一个节点,包含姓名、年龄、性别等属性。
1.2 关系在层次模型中,父子节点之间通过关系连接起来。
父节点与其子节点之间存在着“一对多”的关系。
在学生信息管理系统中,每个班级可以被表示为一个父节点,而每个学生则是该班级的子节点。
1.3 根节点在层次模型中,根节点是位于最顶层的节点,并且没有父节点。
根节点代表了整个数据结构的起点。
在学生信息管理系统中,根节点可以表示整个学校,而每个班级则是根节点的子节点。
1.4 子节点在层次模型中,子节点是位于父节点下方的节点。
一个父节点可以有多个子节点,但每个子节点只能有一个父节点。
在学生信息管理系统中,每个班级可以有多个学生作为其子节点。
1.5 属性在层次模型中,属性是存储在每个节点中的数据项。
它们用于描述实体或记录的特征和属性。
在学生信息管理系统中,姓名、年龄、性别等都可以作为学生节点的属性。
二、网络模型网络模型是对层次模型的扩展和改进,它引入了更灵活的关系定义和多对多关系。
网络模型通过使用指针来建立不同实体之间的连接。
2.1 实体集在网络模型中,实体集是具有相同结构和属性的一组实体。
每个实体集都有一个唯一标识符,并且可以包含其他实体集作为其成员。
2.2 关系类型在网络模型中,关系类型定义了不同实体集之间的连接方式。
关系类型描述了一个实体与其他实体之间的联系,并定义了该联系所包含的属性。
层次分析模型介绍

层次分析模型介绍
§ 1.2 层次分析法的基本原理和步骤
运用层次分析法解决问题,大体可以分为 四个步骤:
1. 建立问题的递阶层次结构; 2. 构造两两比较判断矩阵; 3. 由判断矩阵计算被比较元素相对权重; 4. 计算各层次元素的组合权重。
层次分析模型介绍
§ 1.2.2 构造两两比较判断矩阵
在建立递阶层次结构以后,上下层次之间元 素的隶属关系就被确定了。假定上一层次的元素 Ck 作为准则,对下一层次的元素 A1, …, An 有支配 关系,我们的目的是在准则 Ck 之下按它们相对重 要性赋予 A1, …, An 相应的权重。
层次分析法
层次分析模型介绍
第一讲 层次分析法
层次分析模型介绍
§ 1.1 引言与引例
层次分析法(Analytic Hierarchy Process, 简称 AHP)是美国运筹学家 T. L. Saaty 教授于 上世纪 70 年代初期提出的一种简便、灵活而又 实用的多准则决策方法。
层次分析模型介绍
人们在进行社会的、经济的以及科学管理 领域问题的系统分析中,面临的常常是一个由 相互关联、相互制约的众多因素构成的复杂而 往往缺少定量数据的系统。
在这样的系统中,人们感兴趣的问题之一 是:就 n 个不同事物所共有的某一性质而言, 应该怎样对任一事物的所给性质表现出来的程 度(排序权重)赋值,使得这些数值能客观地 反映不同事物之间在该性质上的差异?
其中 x1 = 写作水平,x2 = 外语程度, x3 = 公关能力,x4 = 国内外政治经济时事, x5 =计算机操作知识,x6 = 容貌与风度, x7 = 体形高矮与肥瘦,x8 = 音色。
层次分析法

对于不一致(但在允许范围内)的成对比较阵
A, Saaty等人建议用对应于最大特征根
的特征向量作为权向量w ,即
但允许范围是 多大?如何界 定?
Aw w
3. 层次单排序及其一致性检验
对应于判断矩阵最大特征根λmax的特征向量,经 归一化(使向量中各元素之和等于1)后记为W。
层次分析法应用实例
某单位拟从3名干部中选拔一名领导,选拔的标准 有政策水平、工作作风、业务知识、口才、写作能力 和健康状况。下面用AHP方法对3人综合评估、量化 排序。
⑴建立层次结构模型
目标层
选一领导干部
准则层
健业 康务 状知 况识
写口政工
作才 策作
能
水作
力
平风
方案层
P1
P2
P3
⑵构造成对比较矩阵及 层次单排序
层次分析法(AHP法)建模
• 决策是指在面临多种方案时需要依据一定的标准选 择某一种方案。日常生活中有许多决策问题。举例
• 1. 在海尔、新飞、容声和雪花四个牌号的电冰 箱中选购一种。要考虑品牌的信誉、冰箱的功能、 价格和耗电量。
• 2. 在泰山、杭州和承德三处选择一个旅游点。 要考虑景点的景色、居住的环境、饮食的特色、交 通便利和旅游的费用。
心理学家认为成对比较的因素不宜超过9个,即每层 不要超过9个因素。
判断矩阵元素aij的标度方法
标度 1 3 5 7 9
2,4,6,8 倒数
含义 表示两个因素相比,具有同样重要性 表示两个因素相比,一个因素比另一个因素稍微重要 表示两个因素相比,一个因素比另一个因素明显重要 表示两个因素相比,一个因素比另一个因素强烈重要 表示两个因素相比,一个因素比另一个因素极端重要
层次结构模型

层次结构模型
层次结构模型(Hierarchical Model)是一种数据库设计模式,其核心思想是将复杂的数据按照等级分层结构进行存储和管理。
它严格遵循“低层次数据可以构成上层次数据,而上层次数据也可以被细分为低层次数据”的原则,形成一颗层次化的数据结构树,采用树状结构方便了数据的查询、修改、添加和删除操作。
层次结构模型在数据库中主要有三种形式:1. 网状结构(network model)、2. 树型结构(tree model)、3. 层次结构(hierarchical model)。
网状结构是通过建立数据库中的实体之间的关系模型,使数据库中的实体之间能够相互联系;树型结构是把数据库中的实体按照父子关系进行分层,形成一个树形结构;而层次结构是把数据库中的实体按照层次关系进行分层,形成一个层次结构。
层次结构模型的优点有:1.层次结构模型能够以较少的记录容量,容纳大量的数据;2.层次结构模型提供了数据结构之间的强关联性;3.层次结构模型可以实现一对多的关系;4.层次结构模型提供了简化的查询操作;5.层次结构模型可以实现复杂的数据存储和管理。
逻辑数据模型

谢谢观看
(1)层次模型的概念
层次数据结构也称树型结构,树中的每个结点代表一种记录类型。满足以下两个条件的数据模型称为层次模 型:
1)只有一个结点没有双亲结点(双亲结点也称父结点),该结点称为根结点。2)根结点以外的其他结点有 且只有一个双亲结点。层次模型可以很自然地表示家族结构、行政组织结构等。(2)层次模型的三要素1)数据 结构:使用记录类型表示实体,使用结点之间的连线表示一对多的联系。2)数据操作:包括结点的查询和结点的 更新(如插入、删除和修改)操作。3)完整性约束:一个模型只有一个根结点;其他结点只能有一个双亲结点; 结点之间是一对多的联系。(3)层次模型的优缺点层次模型的优点是结构简单、清晰,容易理解,结点之间联系 简单,查询效率高。缺点主要有以下几点:1)不能表示一个结点有多个双亲的情况。2)不能直接表示多对多的 联系,需要将多对多联系分解成多个一对多的联系。常用的分解方法是冗余结点法和虚拟结点法。3)插入、删除 限制多。比如,删除父结点则相应的子结点也被同时删除等。具体内容可参考“数据是通过存取路径实现记录之间的联系,应用程序在访问数据时必须选择适当 的存取路径,用户必须了解系统结构的细节,这样加重了编写应用程序的负担。另外,不支持集合处理,即没有 提供一次处理多个记录的功能。关系模型(Relational Model)在1970年由IBM公司的首次提出。关系模型可以 描述一对一、一对多和多对多的联系,并向用户隐藏存取路径,大大提高了数据的独立性以及程序员的工作效率。 此外,关系模型建立在严格的数学概念和数学理论基础之上,支持集合运算。关系模型由关系数据结构、关系操 作和完整性约束三部分组成。在关系模型中,实体和实体之间的联系均由关系来表示。(1)关系的定义:关系模 型是一种简单的二维表格结构,每个二维表称做一个关系,一个二维表的表头,即所有列的标题称为一个元组, 每一列数据称为一个属性,列标题称属性名。同一个关系中不允许出现重复元组和相同属性名的属性。(2)数据 库体系结构①外模式:或子模式、应用模式、局部模式等,它是对数据库在某个方面局部应用所涉及数据的逻辑 结构和特征的描述,它是终端用户和应用程序员所见到的数据库。②模式:或概念模式、逻辑模式、全局模式等。 它是对整个数据库逻辑结构和特征的描述,用户以DBMS支持的逻辑数据模型为基础。③内模式:或存储模式、物 理模式等。它是对整个数据库的存储结构和特征的描述。(3)DBMS的主要功能①、数据定义和操纵②、数据库 管理控制③、数据库辅助服务④、提供使用数据库工具⑤、建立和维护数据字典(4)关系运算①关系数据结构域: 域是具有相同特性的数据集合。笛卡儿积:笛卡儿积是定义在一组域上的集合,假定一组域用D1、D2、……Dn表 示,则它们的笛卡儿积表示为:D1*D2*……*Dn。关系:关系到笛卡儿积的一个子集,若笛卡儿积具有n个域,则 该笛卡儿积上的关系被称为n元关系。码:码又称为键、关键字等。
层次分析法

~ b. 对 w 按行求和得
ij
n
~ ~ wi wij
j 1
n i 1
n
i 1
T ~ ~ ~ c. 将 wi 归一化 wi wi / wi , w ( w1 , w2 ,..., wn )
, 即为近似权向量
1 ( Aw)i d. 计算 ,作为最大特征根的近似值 n i 1 wi
4
计算权组合向量并做一致性检验
计算组合权向量
在”旅游问题”中已经得到了第2层(准则层)对于第1层(目标层)的权向量,记为
w ( 2 ) ( w1 , w2 ,..., w5 )
( 2) ( 2) ( 2)
即 w (0.263,0.475,0.055,0.099 ,0.110 )
T
用同样的方法构造第3层(方案层)对于第2层的每一个准则的成对比较矩阵,不妨设为:
( 3)
( wk 1 , wk 2 ,..., wkm ) T , k 1,2,..., n
( 3) ( 3) ( 3)
为列向量构成矩阵
W ( 3) [ w1 , w2 ,..., wn ]
( 3) ( 3) ( 3)
则第3层对第1层的组合权向量为:
w
( 3)
W w
( 3)
( 2)
更一般地,若共有s层,则第k层对第1层(设只有一个因素)的组合权向量满足:
2 5 1 B1 1 / 2 1 2 1 / 5 1 / 2 1
1 1 / 3 1 / 8 B2 3 1 1 / 3 8 3 1
1 3 1 B3 1 1 3 1 / 3 1 / 3 1
1 3 4 B3 1 / 3 1 1 1 / 4 1 1
数据结构的数据模型与映射技术

数据结构的数据模型与映射技术数据结构是计算机科学中非常重要的一个概念,它涉及到如何组织和存储数据,以及如何高效地操作和处理数据。
在数据结构中,数据模型和映射技术是两个重要的方面,它们能够帮助我们更好地理解和应用数据结构。
一、数据模型的概念与分类数据模型是对数据、数据关系、数据操作和数据约束的抽象描述,它提供了一种理论框架来描述和处理数据。
常见的数据模型包括层次模型、网状模型、关系模型和对象模型等。
1. 层次模型层次模型将数据组织成层次结构,其中数据之间的关系是通过父子节点的连接来表示的。
这种模型具有良好的组织结构,但对于复杂的关系查询和灵活的数据操作较为不便。
2. 网状模型网状模型是将数据组织成一个网状结构,其中数据之间的关系可以是多对多的。
这种模型在处理复杂的关系和查询时比较方便,但对于数据的维护和更新较为困难。
3. 关系模型关系模型是目前应用最广泛的一种数据模型,它将数据组织成二维表格形式,其中每个表格表示一个关系。
在关系模型中,通过主键和外键来表示数据之间的关系,并使用结构化查询语言(SQL)来操作和查询数据。
4. 对象模型对象模型是一种将数据和操作整合在一起的模型,它将数据组织成对象的形式,并通过对象之间的关联和继承来表示数据之间的关系。
对象模型常用于面向对象的编程语言中,如Java和C++。
二、数据模型的应用不同的数据模型适用于不同的应用场景,我们可以根据具体的需求选择合适的数据模型来组织和管理数据。
1. 层次模型的应用层次模型通常适用于如文件系统等数据结构中,可以很好地表示数据的层次结构和组织关系。
例如,电脑文件系统可以按照目录和文件的层次结构进行组织和管理。
2. 网状模型的应用网状模型适用于复杂的数据关系和查询场景。
例如,在公司的组织结构中,一个员工可能同时上报给多个主管,这种多对多的关系可以通过网状模型来表示和处理。
3. 关系模型的应用关系模型广泛应用于各种企业和组织的数据库管理系统中。
层次分析模型

141层次分析模型T. L. Saaty 等人在20世纪70年代末提出了一种定性和定量相结合的、系统化、层次化的分析方法,称为层次分析法(analytic hicrachy process, 简记成AHP )。
层次分析法是将半定性、半定量的问题转化为定量问题的行之有效的方法,是分析多目标、多准则的复杂大系统的强有力的工具。
它通过逐层比较多种关联因素来为分析、决策、预测或控制事物的发展提供定量的依据。
层次分析法被广泛应用于经济计划和管理、能源分配、军事指挥、交通运输、农业、科学技术、医疗、环境等许多领域中。
层次分析法的基本步骤:1)建立层次结构模型。
在深入分析面临的问题后,将有关因素按照不同属性分成若干层次。
同一层次的因素从属于上一层的因素或对上一层因素有影响,同时又支配下一层因素或对下一层因素有影响。
最上层为目标层,一般只有一个因素;最下层为方案层,可以有多个因素;中间层为准则层,准则层又可以根据实际情况分成若干个子层。
2)构造成对比较矩阵。
对同一层(第一层除外)中的各个因素进行成对比较,利用1-9比较尺度,确定各层中的因素对于上一层中每一因素的影响值,构成若干个成对比较矩阵。
3)单层排序及一致性检验。
求各层次中成对比较矩阵的最大特征值和对应的特征向量,并进行一致性检验。
若检验通过,则可对特征向量归一化求出各层次中的因素对于上一层每一因素的权重向量;否则重新构造成对比较矩阵。
4)层次总排序及一致性检验。
将各层次中因素对于上一层次中各因素的权重向量及上一层次因素对于总目标的权重向量进行组合,确定该层次因素对于总目标的权重向量,并对总排序进行一致性检验,直至方案层。
下面通过实例说明层次分析法的具体实施过程。
例8.1 利润的合理使用。
某工厂有一笔企业留成利润,要由领导决定如何利用,可供选择的方案有三个:(1)以奖金名义发给职工;(2)扩建集体福利设施;(3)引进新技术、新设备等。
在制定方案时,主要考虑的因素有:调动企业员工的积极性;提高企业的技术水平;改善企业员工的生活条件。
(完整版)层次分析法的计算步骤

8.3.2 层次分析法的计算步骤一、建立层次结构模型运用AHP进行系统分析,首先要将所包含的因素分组,每一组作为一个层次,把问题条理化、层次化,构造层次分析的结构模型。
这些层次大体上可分为3类1、最高层:在这一层次中只有一个元素,一般是分析问题的预定目标或理想结果,因此又称目标层;2、中间层:这一层次包括了为实现目标所涉及的中间环节,它可由若干个层次组成,包括所需要考虑的准则,子准则,因此又称为准则层;3、最底层:表示为实现目标可供选择的各种措施、决策、方案等,因此又称为措施层或方案层。
层次分析结构中各项称为此结构模型中的元素,这里要注意,层次之间的支配关系不一定是完全的,即可以有元素(非底层元素)并不支配下一层次的所有元素而只支配其中部分元素。
这种自上而下的支配关系所形成的层次结构,我们称之为递阶层次结构。
递阶层次结构中的层次数与问题的复杂程度及分析的详尽程度有关,一般可不受限制。
为了避免由于支配的元素过多而给两两比较判断带来困难,每层次中各元素所支配的元素一般地不要超过9个,若多于9个时,可将该层次再划分为若干子层。
例如,大学毕业的选择问题,毕业生需要从收入、社会地位及发展机会方面考虑是否留校工作、读研究生、到某公司或当公务员,这些关系可以将其划分为如图8.1所示的层次结构模型。
图8.1再如,国家综合实力比较的层次结构模型如图6 .2:图6 .2图中,最高层表示解决问题的目的,即应用AHP所要达到的目标;中间层表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等;最低层表示解决问题的措施或政策(即方案)。
然后,用连线表明上一层因素与下一层的联系。
如果某个因素与下一层所有因素均有联系,那么称这个因素与下一层存在完全层次关系。
有时存在不完全层次关系,即某个因素只与下一层次的部分因素有联系。
层次之间可以建立子层次。
子层次从属于主层次的某个因素。
它的因素与下一层次的因素有联系,但不形成独立层次,层次结构模型往往有结构模型表示。
层次分析法的计算步骤

层次分析法的计算步骤一、建立层次结构模型运用AHP进行系统分析,首先要将所包含的因素分组,每一组作为一个层次,把问题条理化、层次化,构造层次分析的结构模型。
这些层次大体上可分为3类1、最高层:在这一层次中只有一个元素,一般是分析问题的预定目标或理想结果,因此又称目标层;2、中间层:这一层次包括了为实现目标所涉及的中间环节,它可由若干个层次组成,包括所需要考虑的准则,子准则,因此又称为准则层;3、最底层:表示为实现目标可供选择的各种措施、决策、方案等,因此又称为措施层或方案层。
层次分析结构中各项称为此结构模型中的元素,这里要注意,层次之间的支配关系不一定是完全的,即可以有元素(非底层元素)并不支配下一层次的所有元素而只支配其中部分元素。
这种自上而下的支配关系所形成的层次结构,我们称之为递阶层次结构。
递阶层次结构中的层次数与问题的复杂程度及分析的详尽程度有关,一般可不受限制。
为了避免由于支配的元素过多而给两两比较判断带来困难,每层次中各元素所支配的元素一般地不要超过9个,若多于9个时,可将该层次再划分为若干子层。
例如,大学毕业的选择问题,毕业生需要从收入、社会地位及发展机会方面考虑是否留校工作、读研究生、到某公司或当公务员,这些关系可以将其划分为如图所示的层次结构模型。
图再如,国家综合实力比较的层次结构模型如图6 .2:图6 .2图中,最高层表示解决问题的目的,即应用AHP所要达到的目标;中间层表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等;最低层表示解决问题的措施或政策(即方案)。
然后,用连线表明上一层因素与下一层的联系。
如果某个因素与下一层所有因素均有联系,那么称这个因素与下一层存在完全层次关系。
有时存在不完全层次关系,即某个因素只与下一层次的部分因素有联系。
层次之间可以建立子层次。
子层次从属于主层次的某个因素。
它的因素与下一层次的因素有联系,但不形成独立层次,层次结构模型往往有结构模型表示。
层次分析法模型

例3 科研课题的选择 某研究所现有三个 科研课题,限于人力 及物力,只能研究一 个课题。有三个须考 虑的因素:(1)科研成 果贡献大小(包括实用 价值和科学意义);(2) 人材的培养;(3)课题 的可行性(包括课题的 难易程度、研究周期 及资金)。在这些因素 的影响下,如何选择 课题?
层次分析法的思维过程的归纳
将决策问题分为3个或多个层次: 最高层:目标层。表示解决问题的目的,即层次分析 要达到的总目标。通常只有一个总目标。 中间层:准则层、指标层、…。表示采取某种措施、 政策、方案等实现预定总目标所涉及的中间环节; 一般又分为准则层、指标层、策略层、约束层等。 最低层:方案层。表示将选用的解决问题的各种措施、 政策、方案等。通常有几个方案可选。 每层有若干元素,层间元素的关系用相连直线表示。 层次分析法所要解决的问题是关于最低层对最高层的相 对权重问题,按此相对权重可以对最低层中的各种方案、 措施进行排序,从而在不同的方案中作出选择或形成选择 方案的原则。
三、层次分析法的步骤和方法
运用层次分析法构造系统模型时,大体 可以分为以下四个步骤: 1. 建立层次结构模型 2. 构造判断(成对比较)矩阵 3. 层次单排序及其一致性检验 4. 层次总排序及其一致性检验
1. 建立层次结构模型
• 将决策的目标、考虑的因素(决策准则)和决策 对象按它们之间的相互关系分为最高层、中间层 和最低层,绘出层次结构图。 最高层:决策的目的、要解决的问题。 最低层:决策时的备选方案。 中间层:考虑的因素、决策的准则。 对于相邻的两层,称高层为目标层,低层为因 素层。 下面举例说明。
因素i与j比较的判断aij,则因素j与i比较的判断aji=1/aij
目标层
O(选择旅游地)
准则层
计算机网络体系结构OSI模型课件

信道传输
信号通过物理媒介(如电缆、光纤等 )进行传输。
信号解码
在接收端,信号被解码还原成原始信 息。
差错控制
为了确保数据的完整性和准确性,通 信协议中包含差错控制机制,如校验 和、重传、确认等。
04
OSI模型与TCP/IP模型比较
OSI模型与TCP/IP模型的差异
层次数量
实现方式
OSI模型有7个层次,而TCP/IP模型只 有4个层次。
应用层
总结词
应用程序接口和通信服务
详细描述
应用层为应用程序提供接口,以实现各种网络通信服务。它处理用户请求和响应,并负 责应用程序之间的通信。常见的应用层协议包括HTTP、FTP、SMTP等。
03
OSI模型各层之间的关系与通信原理
各层之间的关系
数据链路层与物理层的关系
数据链路层通过物理层提供的比特流传输数据,对数据进行控制 ,保证数据的正确传输。
层次对应关系
OSI模型中的某些层次与TCP/IP模 型中的层次存在对应关系,例如 OSI模型的应用层与TCP/IP模型的 应用层相对应。
协议独立性
两者都强调协议的独立性,即各层 只关心本层的协议,不受其他层的 影响。
OSI模型与TCP/IP模型的融合与发展
融合
随着网络技术的发展,OSI模型与TCP/IP 模型的界限逐渐模糊,两者在某些方面 开始融合。例如,在实际应用中,某些 设备或系统可能同时实现了OSI模型和 TCP/IP模型的某些层次。
网络层
总结词
数据包的路由和转发
详细描述
网络层负责将数据包从源地址发送到目的地址。它通过路由协议确定最佳路径,并在每个节点上转发数据包。这 一层还处理地址解析和数据包的分段。
电力企业信息化架构元模型视图层次模型示例架构管控编码规则
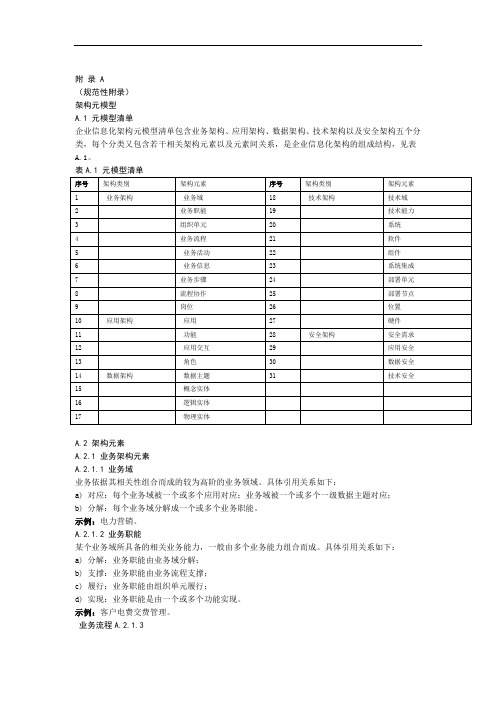
附录 A(规范性附录)架构元模型A.1 元模型清单企业信息化架构元模型清单包含业务架构、应用架构、数据架构、技术架构以及安全架构五个分类,每个分类又包含若干相关架构元素以及元素间关系,是企业信息化架构的组成结构,见表A.1。
表A.1 元模型清单A.2 架构元素A.2.1 业务架构元素A.2.1.1 业务域业务依据其相关性组合而成的较为高阶的业务领域。
具体引用关系如下:a)对应:每个业务域被一个或多个应用对应;业务域被一个或多个一级数据主题对应;b)分解:每个业务域分解成一个或多个业务职能。
示例:电力营销。
A.2.1.2 业务职能某个业务域所具备的相关业务能力,一般由多个业务能力组合而成。
具体引用关系如下:a)分解:业务职能由业务域分解;b)支撑:业务职能由业务流程支撑;c)履行:业务职能由组织单元履行;d)实现:业务职能是由一个或多个功能实现。
示例:客户电费交费管理。
业务流程A.2.1.3在业务领域中为达到业务目标的一类过程和策略,该过程由一组按策略执行的、相互协调的活动步骤组成。
具体引用关系如下:a)支撑:业务流程支撑业务职能;b)分解:业务流程分解为业务活动;c)协作:业务流程关联关系由流程协作完成协作。
示例:电费收费管理。
[业务流程定义源于GB/T 19487-2004]A.2.1.4 业务活动由单一业务目标驱动的、单一岗位完成的业务步骤组合,是业务流程的细化。
具体引用关系如下:a)分解:业务流程分解为业务活动;业务活动分解为业务步骤;b)实现:业务活动由功能实现;c)执行:业务活动由岗位执行;d)输入/输出:业务活动输出业务信息,或业务信息作为业务活动的输入。
示例:电费缴纳。
A.2.1.5 业务步骤岗位或者组织单元为了履行或完成其职责而进行的一系列业务活动中的每项活动。
具体引用关系如下:a)分解:业务步骤由业务活动分解;b)使用:业务步骤使用应用功能。
示例:收取预收电费、受理电费缴纳。
[业务步骤定义源于GB/T 19487-2004,经修改]A.2.1.6 业务信息业务活动所产生、使用和改变的信息内容,作为输入输出在业务活动之间传递交换。
层次分析法(AHP)_百度文库汇总

Mathematical Contest in Modeling 层次分析法三. 不完全层次结构模型完全层次结构:上一层的每个因素都支配着下一层的所有因素, 完全层次结构:上一层的每个因素都支配着下一层的所有因素,或被下一层所有因素影响. 因素影响. 不完全层次结构:准则层中的一个因素,只支配下一准则层的部分因素. 不完全层次结构:准则层中的一个因素,只支配下一准则层的部分因素. 出现在准则层中的情形(准则层与准则层之间出现在准则层中的情形(准则层与准则层之间 MIS综合评价 MIS综合评价A 综合评价A 系统建设B1 系统建设B1 系统性能B2 系统性能B2 目标层A目标层A 系统应用B3 准则层B 系统应用B3 准则层B 科学性 C11 实现程度C12 先进性 C13 经济性 C14 规范性 C15 资源利用率 C16 可靠性 C21 系统效率 C22 可维护性 C23 可扩充性 C24 可移植性 C25 安全性 C26 经济效益C31 社会效益 C32 用户满意度 C33 功能应子准则层 C 用程度 C34 方案层D 方案层D 21 系统D1 系统D1 系统D1 系统D1 …… 系统Dn 系统Dn 20052005-08 新余高等专科学校数学建模教练组Mathematical Contest in Modeling 出现在准则层与方案层之间例:学校要评价教师的贡献,粗略地考只考虑教学学校要评价教师的贡献, 与科研两个指标,P1,P2,P3,P4四位教师中四位教师中P1, 与科研两个指标,若P1,P2,P3,P4四位教师中P1, P2只从事教学,P4只从事科研,P3二者兼顾,层次 P2只从事教学只从事教学,P4只从事科研只从事科研,P3二者兼顾二者兼顾, 结构模型如图. 结构模型如图. 将不支配因素的权向量分量简单置为0.后果如何将不支配因素的权向量分量简单置为0.后果如何? 后果如何? 设C1,C2对第1层的权向量为 w ( 2 = ( w1 , w2 C1,C2对第对第1 C1,C2对第层权向量分别为: 对第3 记C1,C2对第3层权向量分别为: ( 2 ( 2 T 层次分析法教师的贡献Z 教师的贡献Z 教学C1 教学C1 科研C2 科研C2 已确定. 已确定. P1 ( 3 ( 3 P2 P3 P4 w1 ( 3 = ( w11 , w12 , w13 ,0 T w2 ( 3 ( 3 (3 ( 3 = (0,0, w21 , w24 T ( 3 ( 3 于是有: 于是有: w ( 3 = W ( 3 w ( 2 ,W ( 3 = [ w1 , w2 ] ( 2 考察特殊情况:教学与科研两个准则的重要性相同, 考察特殊情况:教学与科研两个准则的重要性相同,即有 w 从事教学或科研,能力都相同, 从事教学或科研,能力都相同,即有代入上述已知数据得到: 代入上述已知数据得到: = (1 / 2,1 / 2 T 4位教师无论 ( 3 w1 ( 3 = (1 / 3,1 / 3,1 / 3,0 T w2 = (0,0,1 / 2,1 / 2 T w ( 3 = (1 / 6,1 / 6,5 / 12,1 / 2 T 公平否? 公平否? 公正的评价为: 被安排只搞教学或科研的P1,P2,P4三位教师公正的评价为: 被安排只搞教学或科研的P1,P2,P4三位教师的贡献相同, P3应为他们的两倍的贡献相同,而P3应为他们的两倍!即为应为他们的两倍! 新余高等专科学校 w ( 3 = (1 / 5,1 / 5,2 / 5,1 / 5 T 20052005-08 22 数学建模教练组Mathematical Contest in Modeling 层次分析法怎样才能得到公平合理的结果呢? 怎样才能得到公平合理的结果呢? ~ 办法: 办法: 用支配因素的数量对权向量 w ( 2 进行加权,做修正为 w ( 2 然后再计算进行加权, 记C1,C2支配因素的数量分别为n1,n2,令: C1,C2支配因素的数量分别为支配因素的数量分别为n1,n2,令归一化的需要 (2 ( 2 ( 2 (2 ~ w ( 2 = (n1 w1 , n2 w2 T /( n1 w1 + n2 w2 w ( 3 ~ w ( 3 = W ( 3 w ( 2 利用前面的数据,代入上面的式子,并且注意到n 利用前面的数据,代入上面的式子,并且注意到n1=3,n2=2,最后得到: =2,最后得到最后得到: w ( 3 = (1 / 5,1 / 5,2 / 5,1 / 5 T 注:上面只考虑了教师从事教学(或科研完全由上级安排的情况,在能力相同的情况下上面只考虑了教师从事教学( 科研完全由上级安排的情况, 承担双份工作的P3的贡献自然要大一倍的贡献自然要大一倍! 承担双份工作的P3的贡献自然要大一倍!若教师从事教学和科研完全靠发挥个人的积极性,且上级希望每位教师都二者兼顾,并鼓励从事人数较少的那份工作,如何决策? 极性,且上级希望每位教师都二者兼顾,并鼓励从事人数较少的那份工作,如何决策? 新余高等专科学校数学建模教练组20052005-08 23Mathematical Contest in Modeling 层次分析法作业: 作业: 干部选拔有三个干部候选人Y1, 有三个干部候选人Y1, Y2, Y3, 选拔的标准有5个:品德,才能, 选拔的标准有5 品德,才能, 资力,年龄,群众关系.如何选择三人之一? 资力,年龄,群众关系.如何选择三人之一? 要求:1. 论文要有摘要; 要求:1. 论文要有摘要; 2. 要有较为完整的建模步骤; 要有较为完整的建模步骤; 3. 要有评注(模型的优缺点; 要有评注(模型的优缺点; 4. 要有参考文献(网络文献也可以; 要有参考文献(网络文献也可以; 5. 尽可能地使用Word排版或做成电子课件(用Powerpoint或其他课尽可能地使用Word排版或做成电子课件 Powerpoint或其他课排版或做成电子课件( 件制作软件形式. 件制作软件形式. 新余高等专科学校数学建模教练组 2005-08 数学建模教练组 2005-08 2005- 24。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
层次分析模型一、层次分析法讲解在现实世界中,往往会遇到决策的问题,比如如何选择旅游景点的问题,选择升学志愿的问题等等。
在决策者作出最后的决定以前,他必须考虑很多方面的因素或者判断准则,最终通过这些准则作出选择。
比如下面的问题:例1 选择旅游地国庆节即将来临,张鶇一家准备去旅游,他们想从黄山、桂林、北戴河三个旅游景点选出一个,请帮助他们作出最佳选择。
根据什么作出选择呢?为解决这个问题,我们需要作问题的分析,以便得到选择景点要考虑的因素.问题的分析:景点的选择大体上有两方面要考虑:1、是旅游者自身的情况;2、是对景点的评价。
首先分析旅游者的情况:如果经济条件宽绰、醉心旅游,自然特别看重景色条件,那么景色在他的心目中的比重就大。
如果平素俭朴,则会优先考虑费用,即费用的比重就大.中老年旅游者还会对居住条件,旅游条件,饮食比较关注。
因此,应该考虑景色、费用、居住、饮食、旅途条件等因素在张鶇一家心目中的重要程度.如何衡量这五个因素的重要程度呢?其次,如何评价景点呢?自然应该就上面的五个因素景色、费用、居住、饮食、旅途条件对景点进行评价。
最后,还要把旅游者的情况和对景点的评价进行综合,以便选定最佳的旅游景点.可是如何综合呢?下面我们用层次分析法解决上面提出的问题。
层次分析法的第一步:建立层次分析结构模型深入分析实际问题,将有关因素自上而下分层,上层受下层影响,而层内各因素基本上相对独立,把问题条理化、层次化,构造出一个有层次的结构模型。
大体可以分成三个层次:(1)最高层(目标层):这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果;(2)中间层(准则层):这一层次中包含了为实现目标所涉及的中间环节,它还可以由若干个层次组成,包括所需考虑的准则、子准则;(3)最低层(方案层):这一层次包括了为实现目标可供选择的各种措施、决策方案等。
就本例题而言,通过上面的分析,我们可以建立如下层次模型:层次分析法的第二步:构造成对比较矩阵建立好层次后,就可以进行各因素之间的比较了.首先考虑对于选择旅游地而言,景色、费用、居住、饮食、旅途条件等准则在张鶇一家心目中的影响,即:对于第一层目标来说,第二层各因素的权重。
由于没有一个绝对的标准来衡量这五个准则的影响,因此层次分析法采用通过相互比较确定各准则对目标的影响(权重)。
具体做法是:通过与张鶇一家交谈,让他们用表一的尺度衡量这五个景色相互之间的重要性:表 一 比较尺度的取值方法i j C C 相等 稍微重要明显重要强烈重要极端重要尺度ij a13579注:如果对i j C C 的判断介于上述相邻判断之间,则ij a 的取值分别为2,4,6,8。
他们在这五个准则之间做了比较:12a =景色的重要性C 1:费用的重要性C 2=1:2 13a =景色的重要性C 1:居住条件的重要性C 3=4:1 14a =景色的重要性C 1 :饮食的重要性C 4=3:115a =景色的重要性C 1 :旅途条件的重要性C 5=3:1 ...其余数据如下:23a =C 2 : C 3=7 : 1 24a =C 2 : C 4=5 : 1 25a =C 2 : C 5=5 : 1 34a =C 3 : C 4=1 : 2 35a =C 3 : C 5=1 : 3 45a =C 4 : C 5=9 : 1 1ij jia a =(i j >) 1ii a =由此可得到矩阵:1143322175511111()4723112153511131355ij A a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭称之为成对比较矩阵(或判断矩阵),是第二层各准则对第一层的比较矩阵。
仿照准则层对目标层构造成对比较矩阵,我们可以构造方案层对准则层的成对比较矩阵:即对准则层的每个因素,将旅游景点进行比较。
方案层对C 1(景色)的成对比较矩阵:1C2C 3C 4C 5C1C 3C 4C5C2C11251/2121/51/21B ⎛⎫ ⎪= ⎪ ⎪⎝⎭方案层对C2(费用)的成对比较矩阵211/31/8311/3831B ⎛⎫ ⎪= ⎪ ⎪⎝⎭方案层对C3(居住)的成对比较矩阵3P 1P2P 3P 1P2P 3P1P 2P 3P 1P 2P3P1P2P 3P1P 2P31131131/31/31B ⎛⎫ ⎪= ⎪ ⎪⎝⎭方案层对C4(饮食)的成对比较矩阵41341/3111/411B ⎛⎫ ⎪= ⎪ ⎪⎝⎭方案层对C5(旅途)的成对比较矩阵3P1P2P 3P1P 2P5111/4111/4441B ⎛⎫ ⎪= ⎪ ⎪⎝⎭这样,我们就得到六个成对比较阵: //////////11243321755141711213131521513153151A ⎛⎫ ⎪⎪⎪= ⎪ ⎪ ⎪⎝⎭11251/2121/51/21B ⎛⎫ ⎪= ⎪ ⎪⎝⎭211/31/8311/3831B ⎛⎫⎪= ⎪⎪⎝⎭31131131/31/31B ⎛⎫ ⎪= ⎪⎪⎝⎭41341/3111/411B ⎛⎫⎪= ⎪ ⎪⎝⎭5111/4111/4441B ⎛⎫ ⎪= ⎪ ⎪⎝⎭层次分析法的第三步:计算这些成对比较矩阵的最大特征值和对应的特征向量(权重),并判断这些矩阵是否能通过一致性检验.层次分析法的第四步:计算组合权向量(并作组合一致性检验) 最后得到的组合权向量就是三个景点在张鶇一家心目中的重要程度,可据此向他们推荐权重最大的景点.将这些矩阵一并输入事先编写好的程序cengcifenxifa.m ,可完成第三步和第四步,然后根据结果进行调整和分析.以上是层次分析法的整个过程,下面讲解如何看程序的运算结果,并对矩阵进行调整。
(1)矩阵的调整在程序的运算结果中,首先是第二层对第一层的运算结果:一致性比率CR>=0.1,表示A 有矛盾, 并且矛盾的程度超过了允许的范围,必须调整.调整的方法可以请张鶇一家重新将景色、费用、居住、饮食、旅途条件进行比较,直至得到一致性比率小于0.1的矩阵,经过调整,张鶇一家将饮食和旅途条件的重要性之比进行了修改,改为4:1,即:3P1P 2P 3P1P 2P//////////11243321755141711213131521413153141A ⎛⎫ ⎪⎪⎪= ⎪ ⎪ ⎪⎝⎭重新运算,可以发现,矩阵A 满足了一致性要求。
同样,如果其它矩阵的一致性比率大于或等于0.1,那么也要进行调整。
顺便讲一下,A 为什么会有矛盾:1143322175511111()4723112153511131355ij A a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,12122323172C C a a C C ====1372C C ⇒= 但从矩阵A 中可以看到,134a =,即122313a a a ⋅≠这就表明,张鶇一家的判断是有矛盾的,此时,称矩阵A 是不一致的.(2)看看结果中的特征向量(归一化后)的含义:第2层对第一层的成对比较矩阵A 的最大特征值对应的特征向量为:(0.2579,0.46239,0.052623,0.14266,0.08564)它依次表示景色、费用、居住、饮食、旅途条件这五个因素在张鶇一家心目中的重要程度。
至于最大特征值,一致性指标,随机一致性指标等等在后面介绍。
在整个程序结果的倒数第二行是: 第 3层(C1,C2,C3)对第一层的组合权重为: 0.32262 0.24408 0.4333它们是对于选择旅游目的地,桂林、黄山、北戴河三个景点的最后权重。
并且在最后一行,总的组合一致性通过的前提下,可据此向他们1C2C 3C 4C 5C1C 3C 4C 5C2C推荐权重最大的旅游景点北戴河。
下面介绍矩阵的特征值和矩阵的一致性: 定义:如果一个矩阵()ijn nA a ⨯=满足如下条件:0ij a >,1ij jia a =则称A 为正互反矩阵。
在此基础上,如果ij jk ik a a a ⨯=则称矩阵A 是一致性矩阵.(3)下面讲解一致性矩阵的特征值的含义:设有一块大石头,重量为W ,被砸成n 个小块,重量分别为12,,...,n w w w ,将这n 个小石头的重量两两比较,令iij jw a w =,那么可以得到成对比较矩阵:111122221212......()...............n n ij n n n n w w w w w w w w w w w w A a w w w w w w ⎛⎫ ⎪⎪ ⎪⎪==⎪ ⎪ ⎪ ⎪ ⎪⎝⎭显然,A 是一致性矩阵。
另一方面,设(,,.)122T w w ww W W W=⋅⋅⋅,它可以表示各个小石头在原先整块大石头里的分量(或权重),作乘积11111222221212........................n n n n n n n w w w w w w w W w w w w w w w A w nw W w w w w W w w w ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪⋅== ⎪ ⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪⎝⎭⎝⎭即:矩阵A 有特征值n,权重向量w 是对应的特征向量。
而对于一致性矩阵,有下面的定理:定理:n 阶正互反矩阵B 的最大特征根n ≥λ,且n =λ时,B 是一致矩阵. 如果B 不是一致矩阵时,它的最大特征根λ必定不等于n ,因此我们完全可以用成对比较一致矩阵A 的最大特征值所对应的特征向量作为各小石块在大石块中的权重.但是如果正互反矩阵A 不是一致矩阵的时候,该怎么办呢?例如下面的矩阵:1143322175511111()4723112153511131355ij A a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪==⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,1223131**72a a a =≠, 如果A 不是一致矩阵时,它的最大特征根λ必定不等于n ,那么用λ对应的特征向量作为权重就存在偏差。
并且λ比n 大的越多,偏差也越大,矩阵A 的不一致程度就越大。
通常定义一致性指标:1nCI n λ-=-,来表示矩阵的不一致程度。
CI 越大,不一致越严重。
由于在实际操作当中,获得一致性矩阵的难度相当大,故在实际操作中,允许成对比较矩阵存在一定的不一致性,为了确定成对比较矩阵A 的不一致程度的容许范围,Saaty 引入了随机一致性指标RI ,其值见下表:表二 随机一致性指标 特征值n 1 2 3 4 5 6 7 8 9 10 11 RI0.580.901.121.241.321.411.451.491.51表中的数据是对固定的n ,随机模拟构造100—500个矩阵,形成A ,计算CI 即得RI 。
定义一致性比率 CR = CI /RI ,当CR <0.1时,认为可以接受A 的不一致性,即A 通过一致性检验(4)下面讲解组合权重和组合一致性那么第三层(桂林、黄山、北戴河)对第一层的权重是多少呢?这个权重就是组合权重。
