简单线性回归分析案例辨析及参考答案
简单线性回归案例

4、显著性检验 显著性检验有两种方法,第一个方法为T检验,第二个方 法为P值法。 (1) T检验 对于b0和b1,t统计量分别为3.608824和52.04354。给 定α=0.5,查t分布表,在自由度为n-2=29下,临界值 tα/2(29)=2.0452。因为, t (b0 ) 3.608824>2.0452 所以、显著不为零。 (2)P值法 看图2.2.20表格中的Prob.列,表示参数估计值T检验对 应的P值,如果P值小于0.05,说明在显著水平为0.05时, t ( b ) 3.608824>2.0452 参数显著不为0。常数项C对应的P值为0.0011<0.05,所 以显著不为零;解释变量X对应P值为0.0000<0.05,所 以显著不为零。图2.2.20最后一行中Prob(F-statistic)是F 检验对应的P值,0.000000<0.05,说明回归方程显著成 立。 这就说明国内生产总值与最终消费支出之间确实具有显 著的线性关系。
2、估计标准误差评价 估计标准误差是根据样本资料计算的,用 来反映被解释变量的实际值与估计值的平 均误差程度的指标,SE越大,则回归直线 的精度越低;反之,则越高,代表性越好。 当SE=0时,表示所有的样本点都落在回归 直线上,解释变量之间的表现为函数关系。 本例中,SE=4322.578,即估计标准误差 为4322.578亿元,它代表我国最终消费支 出估计值与实际值之间的平均误差为 4322.578亿元。
对数似然估计值(Log likelihood):这是 在系数估计值的基础上对对数似然函数的 估计值(假定误差服从正态分布)。可以 通过观察方程的约束式和非约束式的对数 似然估计值的差异来进行似然比检验。 DW统计量(Durbin-Watsonstat):这是对 序列相关性进行检验的统计量,如果它比2 小很多。则证明这个序列正相关。
简单线性回归分析2

)
lXY lXX
a Y bX
03:56
24
b=0.1584,a=-0.1353
Yˆ 0.1353 0.1584X
03:56
25
回归直线的有关性质
(1) 直线通过均点 ( X ,Y )
(2) 各点到该回归线纵向距离平方和较到其它任何直线小。
(Y Yˆ)2 [Yˆ a bX ]2
03:56
残 差 0.0282 22 0.0013
总变异 0.0812 23
R2=SS回归/SS总=0.0530/0.0812=0.6527 说明在空气中NO浓度总变异的65.27%与车流量有关。
03:56
48
二、简单线性回归模型
两变量关系的定量描述 统计推断 统计应用
统计预测
Y 的均值的区间估计:总体回归线的95%置信带(相应X 取值水平下,) ;
回归模型 (regression model):
描述变量之间的依存关系的函数。
简单线性回归(simple linear regression):
模型中只包含两个有“依存关系”的变量,一个变量随 另外一个变量的变化而变化,且呈直线变化趋势,称之 为简单线性回归。
03:56
9
例如,舒张压和血清胆固醇的依存性
统计推断 通过假设检验推断NO平均浓度是否随着车 流量变化而变化;
统计应用 利用模型进行统计预测或控制。
03:56
13
两变量关系的定量描述
散点图 简单线性回归方程 回归系数的计算——回归系数的最小二乘估计 线性回归分析的前提条件
03:56
14
1. 散点图
0.25
0.2
NO浓度/×10-6
正态 (normal)假定是指线性模型的误差项服从正态 分布 。
专题01 线性回归方程(解析版)

【解析】解: x 0 1 2 3 3 , y m 3 5.5 7 m 15.5 ,
4
2
4
4
这组数据的样本中心点是 ( 3 , m 15.5) , 24
关于 y 与 x 的线性回归方程 yˆ 2.1x 0.85 ,
m 15.5 2.1 3 0.85 ,解得 m 0.5 ,
x (次数 / 分
20
30
40
50
60
钟)
y( C)
25
27.5
29
32.5
36
A. 33 C
B. 34 C
C. 35 C
【解析】解:由题意,得 x 20 30 40 50 60 40 , 5
y 25 27.5 29 32.5 36 30 , 5
则 k y 0.25x 30 0.25 40 20 ;
故答案为:10.
例 7.已知一组数据点:
x
x1
x2
x8
y
y1
y2
y8
8
用最小二乘法得到其线性回归方程为 yˆ 2x 4 ,若数据 x1 , x2 , , x8 的平均数为 1,则 yi i 1
16 .
3
原创精品资源学科网独家享有版权,侵权必究!
【解析】解:由题意, x 1 ,设样本点的中心为 (1, y) , 又线性回归方程为 yˆ 2x 4 ,则 y 2 1 4 2 ,
购买一台乙款垃圾处理机器节约政府支持的垃圾处理费用 Y (单位:万元)的分布列为:
Y
30
20
70
120
P
0.3
0.4
0.2
0.1
E(Y ) 30 0.3 20 0.4 70 0.2 120 0.1 25 (万元)
简单线性相关与回归分析

临床科研设计和统计分析错误辨析与释疑简单线性相关与回归分析军事医学科学院生物医学统计咨询中心胡良平一、简单线性相关与回归分析常见错误概述两个变量之间进展简单线性相关与回归分析时,常见的错误有哪些?人们在研究两个变量之间的互相关系或依赖关系时经常运用简单线性相关分析与回归分析,然而,他们经常犯这样或那样的错误,导致结论的可信度低,有时,甚至得出绝对错误的结论来。
这方面常见的错误概括起来有如下几点:其一,脱离专业知识,盲目进展简单线性相关与回归分析;其二,对资料中因“过失误差〞造成的错误视而不见,盲目进展统计计算得出违犯专业知识的结论来;其三,将数据直接录入计算机,调用统计软件快速得出计算结果,作出结论;其四,对于仅在统计学上有意义的计算结果,盲目给出专业上的“肯定结论〞,但结论经不起理论的检验;其五,对于在专业上有联络且成对出现的变量〔X,Y〕,当二者中至少有一个为非随机变量时,也进展相关分析。
二、直线相关与回归分析常见错误案例与释疑脱离专业知识盲目进展统计分析,或者无视因过失误差造成的错误,将可能得出错误的结论。
1、脱离专业知识,盲目进展直线相关与回归分析例1:某人在北京郊区调查居民被狗咬伤的情况,结果显示:各年龄组中被狗咬伤的百分率是不同的,即:年龄由小到大,被狗咬伤的百分率依次为:很小、较小、较大、很大、较大、较小、很小、较大。
原作者的一个惊人的发现是:年龄与百分率之间的相关系数r=0.9956,P<0.0001,因此拟合的直线回归方程也是有统计学意义的。
故原作者认为:在所调查的市郊,被狗咬者的年龄与被狗咬伤的百分率之间有很好的线性关系,可用此直线回归方程来预测该地任何一位居民被狗咬伤的概率,以便提醒人们外出时携带必要的防身器械,要倍加小心,尽可能减少被狗咬的时机。
对过失的辨析与释疑:这是一件多么荒唐可笑的事情啊!不会走的婴儿由大人抱在怀里,其被犬咬伤的发生率肯定很低;刚刚学会走路的小孩,通常都有大人在他们身边,因此,他们被犬咬伤的发生率比前者可能会高一点,但不会太高;只有那些整天到处乱跑,又没有很强抵御才能的3-6岁的孩子,被犬咬伤的时机最大;7-12岁的儿童,通常都有比拟强的抵御才能,因此,他们被犬咬伤的时机较前者会有所减少;依此类推,中青年被犬咬伤的发生率最低,上了年岁的老人,行动不便,他们被犬咬伤的发生率又会有所增大;而更老的体弱多病者整天呆在家中不出门,他们被犬咬伤的发生率几乎为零。
线性回归分析经典例题

1. “团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,下表是2013-2017年全国快递业务量(x 亿件:精确到0.1)及其增长速度(y %)的数据(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,…,2017年记成年的序号t :1,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程a x b yˆˆˆ+=; (Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量附:回归直线的斜率和截距地最小二乘法估计公式分别为:∑∑==--=ni ini ii x n xy x n yx b1221ˆ, x b y aˆˆ-=2.某水果种植户对某种水果进行网上销售,为了合理定价,现将该水果按事先拟定的价格进行试销,得到如下数据:单价元 7 8 9 11 12 13 销量120118112110108104已知销量与单价之间存在线性相关关系求y 关于x 的线性回归方程; 若在表格中的6种单价中任选3种单价作进一步分析,求销量恰在区间内的单价种数的分布列和期望.附:回归直线的斜率和截距的最小二乘法估计公式分别为:, .3. (2018年全国二卷)下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016年的数据(时间变量t 的值依次为1217,,…,)建立模型①:ˆ30.413.5y t =-+;根据2010年至2016年的数据(时间变量t 的值依次为127,,…,)建立模型②:ˆ9917.5y t =+. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由.4.(2014年全国二卷) 某地区2007年至2013年农村居民家庭纯收入y (单位:千元)的数据如下表:年份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y 2.93.33.64.44.85.25.9(Ⅰ)求y 关于t 的线性回归方程;(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.附:回归直线的斜率和截距的最小二乘法估计公式分别为:()()()121niii ni i t t y y b t t ∧==--=-∑∑,ˆˆay bt =-5(2019 2卷)18.11分制乒乓球比赛,每赢一球得1分,当某局打成10∶10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10∶10平后,甲先发球,两人又打了X 个球该局比赛结束.(1)求P(X=2);(2)求事件“X=4且甲获胜”的概率.。
线性回归方程.附答案docx

线性回归方程一、考点、热点回顾一、相关关系:1、⎩⎨⎧<=1||1||r r 不确定关系:相关关系确定关系:函数关系2、相关系数:∑∑∑===-⋅---=ni ini ini iiy y x x y y x x r 12121)()())((,其中:(1)⎩⎨⎧<>负相关正相关00r r ;(2)相关性很弱;相关性很强;3.0||75.0||<>r r3、散点图:初步判断两个变量的相关关系。
二、线性回归方程:1、回归方程:a x b yˆˆˆ+= 其中2121121)())((ˆxn x yx n yx x x y yx x bn i i ni ii n i i ni ii--=---=∑∑∑∑====,x b y aˆˆ-=(代入样本点的中心) 2、残差:(1)残差图:横坐标为样本编号,纵坐标为每个编号样本对应的残差。
(2)残差图呈带状分布在横轴附近,越窄模型拟合精度越高。
(3)残差平方和∑=-ni i iyy12)ˆ(越小,模型拟合精度越高。
3、相关指数:∑∑==---=n i ini i iy yyyR 12122)()ˆ(1(1)其中:∑=-ni i iyy12)ˆ(为残差平方和;∑=-ni i y y 12)(为总偏差平方和。
(2))1,0(2∈R ,越大模型拟合精度越高。
二、典型例题+拓展训练典型例题1:在一组样本数据),,,2)(,(),,(),,(212211不全相等n n n x x x n y x y x y x ≥的散点图中,若所有样本点),2,1)(,(n i y x i i =都在直线121+-=x y 上,则样本相关系数为( ) 21.21.1.1.--D C B A典型例题2:设某大学的女生体重)(kg y 与身高)(cm x 具有线性相关关系,根据一组样本数据)2,1)(,(n i y x i i =,用最小二乘法建立的回归方程为71.8585.0ˆ-=x y ,则不正确的是( )A.y 与x 具有正的线性相关关系;B.回归直线过样本点的中心),(y xC.若该大学某女生身高增加1cm,则其体重约增加0.85kgD.若该大学某女生身高为170cm,则可断定其体重必为58.79kg扩展2.一台机器使用时间较长,但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,下表为抽样试(1)对变量y 与x 进行相关性检验;(2)如果y 与x 有线性相关关系,求回归直线方程;(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?典型例题3.为了对x 、Y 两个变量进行统计分析,现有以下两种线性模型: 6.517.5y x =+,717y x =+,试比较哪一个模型拟合的效果更好.52211521()155110.8451000()i i i ii y y R yy ==-=-=-=-∑∑,221R =-521521()18010.821000()ii i ii yy y y ==-=-=-∑∑,84.5%>82%,所以甲选用的模型拟合效果较好.扩展1.下列说法正确的是( )(1)残差平方和越小,相关指数2R 越小,模型拟合效果越差; (2)残差平方和越大,相关指数2R 越大,模型拟合效果越好; (3)残差平方和越小,相关指数2R 越大,模型拟合效果越好; (4)残差平方和越大,相关指数2R 越小,模型拟合效果越差;A.(1)(2)B.(3)(4)C.(1)(4)D.(2)(3)扩展2.关于某设备的使用年限x (年)和所支出的维修费用y (万元)有下表所示的资料:若由资料知,y 对x 呈线性相关关系,求:(1)线性回归方程a x b yˆˆˆ+=中的回归系数b a ˆ,ˆ; (2)残差平方和与相关指数2R ,作出残差图,并对该回归模型的拟合精度作出适当判断; (3)使用年限为10年时,维修费用大约是多少?三、典型例题4.非线性回归模型:某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费和年销售量(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值。
SPSS操作:简单线性回归(史上最详尽的手把手教程)
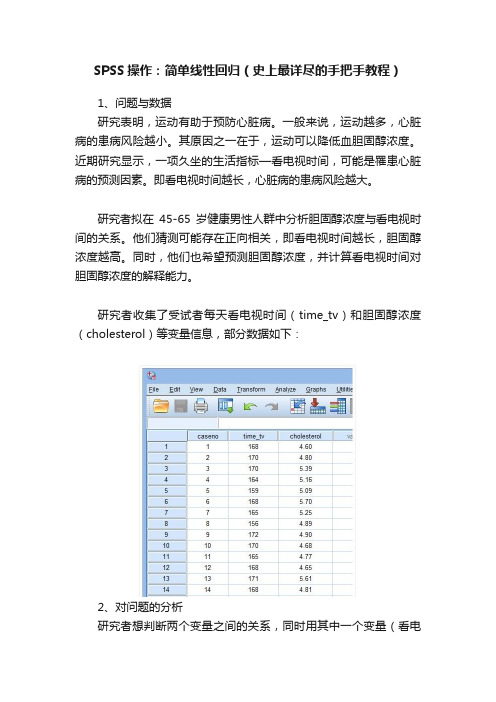
SPSS操作:简单线性回归(史上最详尽的手把手教程)1、问题与数据研究表明,运动有助于预防心脏病。
一般来说,运动越多,心脏病的患病风险越小。
其原因之一在于,运动可以降低血胆固醇浓度。
近期研究显示,一项久坐的生活指标—看电视时间,可能是罹患心脏病的预测因素。
即看电视时间越长,心脏病的患病风险越大。
研究者拟在45-65岁健康男性人群中分析胆固醇浓度与看电视时间的关系。
他们猜测可能存在正向相关,即看电视时间越长,胆固醇浓度越高。
同时,他们也希望预测胆固醇浓度,并计算看电视时间对胆固醇浓度的解释能力。
研究者收集了受试者每天看电视时间(time_tv)和胆固醇浓度(cholesterol)等变量信息,部分数据如下:2、对问题的分析研究者想判断两个变量之间的关系,同时用其中一个变量(看电视时间)预测另一个变量(胆固醇浓度),并计算其中一个变量(看电视时间)对另一个变量(胆固醇浓度)变异的解释程度。
针对这种情况,我们可以使用简单线性回归分析,但需要先满足7项假设:假设1:因变量是连续变量假设2:自变量可以被定义为连续变量假设3:因变量和自变量之间存在线性关系假设4:具有相互独立的观测值假设5:不存在显著的异常值假设6:等方差性假设7:回归残差近似正态分布那么,进行简单线性回归分析时,如何考虑和处理这7项假设呢?3、思维导图(点击图片可查看清晰大图)4、对假设的判断4.1 假设1和假设2因变量是连续变量,自变量可以被定义为连续变量。
举例来说,我们平时测量的反应时间(小时)、智力水平(IQ分数)、考试成绩(0到100分)以及体重(千克)都是连续变量。
在线性回归中,因变量(dependent variable)一般是指研究的成果、目标或者标准值;自变量(independent variable)一般被看作预测、解释或者回归变量。
假设1和假设2与研究设计有关,需要根据实际情况判断。
4.2 假设3简单线性回归要求自变量和因变量之间存在线性关系,如要求看电视时间(time_tv)和胆固醇浓度(cholesterol)存在线性关系。
第一讲线性回归案例分析

第一讲线性回归案例分析参与本讲的嘉宾姓名单位职称、职务罗强江苏省苏州五中特级教师张饴慈首都师范大学数学科学学院教授张思明北大附中特级教师杨彬陕西省户县一中高级教师张红娟江苏省苏州五中高级教师主持人:各位老师大家好,在前面的课里面我们主要结合算法做了一些案例的展示和讨论,从今天的课里开始进入统计概率。
今天主要围绕回归分析,最小二乘法,线性回归方程这些内容展开我们的案例和讨论。
这里我们请来的两位点评嘉宾。
我身边的这位是江苏省苏州市五中的特级教师罗强老师,也是苏州五中的校领导。
一位是首都师范大学的数学系教授(张饴慈)老师,也是我们每次培训都能见到的数学专家。
首先问张老师,在回归分析里面老师会提到很多问题。
一个是必修也有,选修也有,他们两个的差别是什么?还有回归分析的核心思想是我们要教给学生什么是最重要的。
张老师:我想回归分析主要讨论的是相关关系,在统计里面这是一个非常有用的一件事情,可以说在统计之中运用最广的就是回归思想。
在我们必修和选修之间的区别,我们必修是通过孩子们初步认识,通过例子来认识什么是相关关系?它跟函数关系有什么不一样?简单介绍一下线性回归的方程,理解找一个线性回归的直线是有用,只是初步的思想。
在选修阶段就要详细讨论,这个方程是不是有意义?如果用我们的公式来做是不是任何问题都可以套公式来做?怎样判断是不是比较符合一个线性关系?是不是要引入相关系数的概念。
在选修里面还介绍一下非线性的回归,这是从内容定位来讲。
主持人:作为这样的把控,包括在推导过程中,很多老师在我们教材里面或者标准里面对于回归方程的结果,推导要求不要求?张老师:我们在必修里面没有要求推导,在选修里面可能用到配方来推导。
公式能得到这个数,其实是二次函数的极值等问题,它计算比较麻烦,不是在这个公式本身上下工夫,也不要求孩子背这些公式。
只是希望他们会运用这样一个东西来做这个问题。
主持人:张老师对回归分析的定位做了一些分析。
下面一起来看老师们提供的两个教学片段,一个是陕西省户县一中(杨彬)老师提供,最小二乘法的教学设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章简单线性回归分析
案例辨析及参考答案
案例10-1年龄与身高预测研究。
某地调查了4~18岁男孩与女孩身高,数据见教材表10-4,试描述男孩与女孩平均身高与年龄间的关系,并预测10.5岁、16.5岁、19岁与20岁男孩与女孩的身高。
教材表10-4 某地男孩与女孩平均身高与年龄的调查数据
采用SPSS对身高与年龄进行回归分析,结果如表教材10-5和教材表10-6所示。
教材表10-5 男孩身高对年龄的简单线性回归分析结果
估计值标准误P
Constant 83.736 3 1.882 4 44.483 9 0.000 0
AGE 5.274 8 0.167 6 31.479 8 0.000 0
=990.98 =98.5%
教材表10-6 女孩身高对年龄的简单线性回归分析结果
估计值标准误P
Constant 88.432 6 3.280 0 26.961 1 0.000 0
AGE 4.534 0 0.292 0 15.529 0 0.000 0
=241.15 =94.1%
经拟合简单线性回归模型,检验结果提示回归方程具有统计学意义。
结果提示,拟合效果非常好,故可认为:
(1)男孩与女孩的平均身高随年龄线性递增,年龄每增长1岁,男孩与女孩身高分别平均增加5.27 cm与4.53 cm,男孩生长速度快于女孩的生长速度。
(2)依照回归方程预测该地男孩10.5岁、16.5岁、19岁和20岁的平均身高依次为139.1 cm、170.8 cm、184.0 cm和189.2 cm;该地女孩10.5岁、16.5岁、19岁和20岁的平均身高依次为136.0 cm、163.2 cm、174.6 cm和179.1 cm。
针对以上分析结果,请考虑:
(1)分析过程是否符合回归分析的基本规范?
(2)回归模型能反映数据的变化规律吗?
(3)拟合结果和依据回归方程而进行的预测有问题吗?
(4)男孩生长速度快于女孩的生长速度的推断是否有依据?
案例辨析未绘制散点图,盲目进行简单线性回归分析;若实际资料反映两变量之间呈现某种曲线变化趋势,用简单线性回归方程去描述其变化规律就是不妥当的。
正确做法分析策略:作散点图,选择曲线类型,合理选择模型,统计预测。
(1)作散点图(案例图10-1)。
案例图10-1 儿童身高对年龄的散点图
(a)男孩身高;(b)女孩身高
由案例图10-1可见,随着年龄的增加,身高也增加,但呈曲线变化趋势,15~16岁后,增加趋势逐渐趋于平缓。
因此适合于拟合曲线回归方程。
(2)选择曲线类型,进行统计分析,几种曲线方程拟合结果如下。
Model Summary and Parameter Estimates
Dependent Variable: 男孩身高
The independent variable is 年龄。
Dependent Variable: 女孩身高
The independent variable is 年龄。
上述曲线类型依次为线性、二次、三次多项式曲线和生长曲线,由拟合结果可知,曲线拟合效果较好,进一步得到曲线图(案例图10-1):
(3)选择合理的模型,列出回归方程。
以女孩身高二次曲线为例,方程如下:
多项式曲线:
(4)统计预测:预测19岁女孩身高为60.788+10.805×18-0.292×182=160.7,与实际趋势相符。
其他预测方法相同。
案例10-2贫血患者的血清转铁蛋白研究。
第6章例6-1中,为研究某种新药治疗贫血患者的效果,将20名贫血患者随机分成两组,一组用新药,另一组用常规药物治疗,测得血红蛋白增加量(g/L)见表6-1。
问新药与常规药治疗贫血患者后的血红蛋白增加量有无差别?
张医生用检验比较新药与常规药治疗贫血患者后的血红蛋白增加量,计算得:
=27.99,=20.21, =4.137。
王医生认为,可以作线性回归分析。
在该数据中涉及了两个变量,一是观察效应变量(连续性),即血红蛋白增加量,将之作为回归分析中的因变量;另外一个变量为处理因素(二分类变量),即影响因素,将之作为自变量,其中新药组=1,常规药组=0。
数据转换为双变量资料形式(教材表10-7),经分析得回归方程, =4.137。
教材表10-7 两种药物治疗贫血患者结果
请考虑:
(1)王医生的分析方法对不对?
(2)回归分析能代行两样本均数t检验的任务吗?
(3)通过这个案例的实践,你得到哪些启发?
案例辨析王医生的分析方法是对的;回归分析能代行两样本均数t检验的任务。
其理由如下。
正确做法两样本合并后,总例数为=20。
进行直线回归分析,结果如下:
, =0.698。
经检验,贫血患者治疗后的血红蛋白增加量与治疗有关。
正常人均数:=20.21+7.78×0=20.21
患者均数:=20.21+7.78×1=27.99
截距与两样本均数的差值相等。
分别进行回归方程的方差分析与回归系数的t检验,得F=17.112,t=4.137。
回归系数的t检验结果与两样本均数的t检验结果完全一致。
以上结果说明,t检验的结果可以转化为直线回归方程分析。
当分组因素为k个组(样本)时,可以设置为k-1个指示变量,采用第11章的多重线性回归分析,这在多因素分析中是最常采用的办法。
